Hostname: page-component-78c5997874-dh8gc Total loading time: 0 Render date: 2024-11-19T11:50:04.587Z Has data issue: false hasContentIssue false
  • English
  • Français

Existence of solution for quasilinear equations involving local conditions

Part of: Elliptic equations and systems Partial differential equations

Published online by Cambridge University Press:  17 September 2019

Patricio Cerda  and
Leonelo Iturriaga
Patricio Cerda
Affiliation:
Universidad de Santiago de Chile, Casilla 307, Correo 2, Santiago, Chile (patricio.cerda@usach.cl)
Leonelo Iturriaga
Affiliation:
Departamento de Matemática, Universidad Técnica Federico Santa María, Casilla V-110, Avda. España, 1680, Valparaíso, Chile (leonelo.iturriaga@usm.cl)
Get access Rights & Permissions [Opens in a new window]

Abstract

In this paper, we study the existence of weak solutions of the quasilinear equation

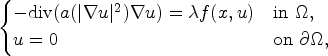\begin{cases} -{\rm div} (a(\vert \nabla u \vert ^2)\nabla u)=\lambda f(x,u) &{\rm in} \ \Omega,\\ u=0 &{\rm on} \ \partial\Omega, \end{cases}
where a : ℝ → [0, ∞) is C1 and a nonincreasing continuous function near the origin, the nonlinear term f : Ω × ℝ → ℝ is a Carathéodory function verifying certain superlinear conditions only at zero, and λ is a positive parameter. The existence of the solution relies on C1-estimates and variational arguments.

Keywords

Existence solutionquasilinear equationsvariational methods

MSC classification

Primary: 35J93: Quasilinear elliptic equations with mean curvature operator
Secondary: 35B09: Positive solutions 35J50: Variational methods for elliptic systems 35J62: Quasilinear elliptic equations
Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 150 , Issue 6 , December 2020 , pp. 3074 - 3086
Check for updates
Copyright
Copyright © 2019 The Royal Society of Edinburgh

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1Ambrosetti, A. and Rabinowitz, P. H.. Dual variational methods in critical point theory and applications. J. Funct. Anal. 14 (1973), 349–381.CrossRefGoogle Scholar
2Bonheure, D., Derlet, A. and Valeriola, S.. On the multiplicity of nodal solutions of a prescribed mean curvature problem. Math. Nach. 286 (2013), 1072–1086.CrossRefGoogle Scholar
3Brézis, H. and Turner, R. E. L.. On a class of superlinear elliptic problems. Commun. Partial Differ. Equ. 2 (1977), 601–614.CrossRefGoogle Scholar
4Coffman, C. V. and Ziemer, W. K.. A prescribed mean curvature problem on domains without radial symmetry. SIAM J. Math. Anal. 22 (1991), 982–990.CrossRefGoogle Scholar
5Furtado, M. and Silva, E. D.. Superlinear elliptic problems under the non-quadraticity condition at infinity. Proc. R. Soc. Edinburgh Sect. A 145 (2015), 779–790.CrossRefGoogle Scholar
6García-Melián, J., Iturriaga, L. and Ramos Quoirin, H.. A priori bounds and existence of solutions for slightly superlinear elliptic problems. Adv. Nonlinear Stud. 15 (2015), 923–938.CrossRefGoogle Scholar
7Habets, P. and Omari, P.. Positive solutions of an indefinite prescribed mean curvature problem on a general domain. Adv. Nonlinear Stud. 4 (2004), 1–13.CrossRefGoogle Scholar
8Iturriaga, L., Lorca, S. and Ubilla, P.. A quasilinear problem without the Ambrosetti–Rabinowitz type condition. Proc. R. Soc. Edinburgh Sect. A 140 (2010), 391–398.CrossRefGoogle Scholar
9Iturriaga, L., Souto, M. A. and Ubilla, P.. Quasilinear problems involving changing-sign nonlinearities without an Ambrosetti Rabinowitz-Type condition. Proc. Edinburgh. Math. Soc. (2) 57 (2014), 755–762.CrossRefGoogle Scholar
10Jabri, M. 2003 The mountain pass theorem. Variants, generalizations and some applications, vol. 95 Encyclopedia of Mathematics and its Applications. Cambridge: Cambridge University Press.CrossRefGoogle Scholar
11Jeanjean, L.. On the existence of bounded Palais–Smale sequences and application to a Landesman–Lazer type problem set on ℝN. Proc. R. Soc. Edinburgh 129A (1999), 787–809.CrossRefGoogle Scholar
12Liu, Z. and Wang, Z. Q.. On the Ambrosetti–Rabinowitz superlinear condition. Adv. Nonlinear Stud. 4 (2004), 563–574.CrossRefGoogle Scholar
13López-Gómez, J., Omari, P. and Rivetti, S.. Bifurcation of positive solutions for a one-dimensional indefinite quasilinear Neumann problem. Nonlinear Anal. 155 (2017), 1–51.CrossRefGoogle Scholar
14López-Gómez, J., Omari, P. and Rivetti, S.. Positive solutions of a one-dimensional indefinite capillarity-type problem: a variational approach. J. Differ. Equ. 262 (2017), 2335– 2392.CrossRefGoogle Scholar
15Lorca, S. and Montenegro, M.. Multiple solutions for the mean curvature equation. Topol. Methods Nonlinear Anal. 35 (2010), 61–68.Google Scholar
16Lorca, S. and Ubilla, P.. Partial differential equations involving subcritical, critical and supercritical nonlinearities. Nonlinear Anal. 56 (2004), 119–131.CrossRefGoogle Scholar
17Miyagaki, O. and Souto, M. A.. Superlinear problems without Ambrosetti and Rabinowitz growth condition. J. Differ. Eqns. 245 (2008), 3628–3638.CrossRefGoogle Scholar
18Moser, J.. A new proof of De Giorgi's theorem concerning the regularity problem for elliptic differential equations. Commun. Pure Appl. Math. 13 (1960), 457–468.CrossRefGoogle Scholar
19Nakao, M.. A bifurcation problem for a quasi-linear elliptic boundary value problem. Nonlinear Anal. 14 (1990), 251–262.CrossRefGoogle Scholar
20Obersnel, F. and Omari, P.. Positive solutions of the Dirichlet problem for the prescribed mean curvature equation. J. Differ. Equ. 249 (2010), 1674–1725.CrossRefGoogle Scholar
21Schechter, M.. A variation of the mountain pass lemma and applications. J. Lond. Math. Soc. (2) 44 (1991), 491–502.CrossRefGoogle Scholar
22Schechter, M. and Zou, W.. Superlinear problems. Pacific J. Math. 214 (2004), 145–160.CrossRefGoogle Scholar
23Serrin, J., Positive solutions of a prescribed mean curvature problem. Calculus of variations and partial differential equations (Trento, 1986), Lecture Notes in Math., vol. 1340 (Springer, Berlin, 1988), 248–255.Google Scholar
24Stampacchia, G.. On some regular multiple integral problems in the calculus of variations. Commun. Pure Appl. Math. 16 (1963), 383–421.CrossRefGoogle Scholar
25Struwe, M. 2008 Variational methods. Applications to nonlinear partial differential equations and Hamiltonian systems. Berlin: Springer-Verlag.Google Scholar
26Szulkin, A. and Zou, W.. Homoclinic orbits for asymptotically linear Hamiltonian systems. J. Funct. Anal. 187 (2001), 25–41.CrossRefGoogle Scholar
27Zhou, H. S.. Positive solution for a semilinear elliptic equations which is almost linear at infinity. Z. Angew. Math. Phys. 49 (1998), 896–906.CrossRefGoogle Scholar