Hostname: page-component-6d856f89d9-4thr5 Total loading time: 0 Render date: 2024-07-16T06:34:08.466Z Has data issue: false hasContentIssue false
  • English
  • Français

Large number of bubble solutions for a fractional elliptic equation with almost critical exponents

Part of: Elliptic equations and systems Miscellaneous topics - Partial differential equations

Published online by Cambridge University Press:  09 November 2020

Chunhua Wang  and
Suting Wei
Chunhua Wang
Affiliation:
School of Mathematics and Statistics & Hubei Key Laboratory of Mathematical Sciences, Central China Normal University, Wuhan, 430079, People's Republic of China (chunhuawang@mail.ccnu.edu.cn)
Suting Wei*
Affiliation:
Department of Mathematics, South China Agricultural University, Guangzhou, 510642, People's Republic of China (stwei@scau.edu.cn)
*
*Corresponding author.
Get access Rights & Permissions [Opens in a new window]

Abstract

This paper deals with the following non-linear equation with a fractional Laplacian operator and almost critical exponents:

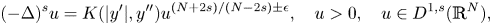\[ (-\Delta)^{s} u=K(|y'|,y'')u^{({N+2s})/(N-2s)\pm\epsilon},\quad u > 0,\quad u\in D^{1,s}(\mathbb{R}^{N}), \]
where N ⩾ 4, 0 < s < 1, (y′, y″) ∈ ℝ2 × ℝN−2, ε > 0 is a small parameter and K(y) is non-negative and bounded. Under some suitable assumptions of the potential function K(r, y″), we will use the finite-dimensional reduction method and some local Pohozaev identities to prove that the above problem has a large number of bubble solutions. The concentration points of the bubble solutions include a saddle point of K(y). 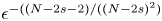Moreover, the functional energies of these solutions are in the order $\epsilon ^{-(({N-2s-2})/({(N-2s)^2})}$.

Keywords

The fractional Laplacian operatorbubble solutionsfinite-dimensional reduction methodalmost critical exponentslocal Pohozaev identities

MSC classification

Primary: 35R11: Fractional partial differential equations
Secondary: 35J60: Nonlinear elliptic equations
Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 151 , Issue 5 , October 2021 , pp. 1642 - 1681
Check for updates
Copyright
Copyright © The Author(s), 2020. Published by Cambridge University Press on behalf of The Royal Society of Edinburgh

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Applebaum, D.. Levy processes and stochastic calculus (Cambridge studies in advanced mathematics, 116), 2nd edn (Cambridge: Cambridge University Press, 2009).Google Scholar
Barrios, B., Colorado, E., de Pablo, A. and Sánchez, U.. On some critical problems for the fractional Laplacian operator. J. Differ. Equ. 252 (2012), 6133–6162.CrossRefGoogle Scholar
Brändle, C., Colorado, E., de Pablo, A. and Sánchez, U.. A concave–convex elliptic problem involving the fractional Laplacian. Proc. R. Soc. Edinburgh Sect. A 143 (2013), 39–71.CrossRefGoogle Scholar
Barrios, B., Colorado, E., Servadei, R. and Soria, F.. A critical fractional equation with concave-convex power nonlinearities. Ann. Inst. Henri Poincaré Anal. Non Linéaire 32 (2015), 875–900.CrossRefGoogle Scholar
Cabré, X. and Tan, J.. Positive solutions of nonlinear problems involving the square root of the Laplacian. Adv. Math. 224 (2010), 2052–2093.CrossRefGoogle Scholar
Caffarelli, L. and Silvestre, L.. An extension problem related to the fractional Laplacian. Commun. Partial Differ. Equ. 32 (2007), 1245–1260.CrossRefGoogle Scholar
Chen, W., Wei, J. and Yan, S.. Infinitely many positive solutions for the Schrödinger equations in ℝN with critical growth. J. Differ. Equ. 252 (2012), 2425–2447.CrossRefGoogle Scholar
Chen, W., Li, Y. and Ma, P.. The fractional Laplacian (Singapore: World Scientific Publishing Co. Pte Ltd, 2019).Google Scholar
del Pino, M., Felmer, P. and Musso, M.. Two-bubble solutions in the super-critcal Bahri–Coron's problem. Calc. Var. Partial Differ. Equ. 16 (2003), 113–145.CrossRefGoogle Scholar
Deng, Y., Lin, C.-S. and Yan, S.. On the prescribed scalar curvature problem in ℝN, local uniqueness and periodicity. J. Math. Pures Appl. 104 (2015), 1013–1044.CrossRefGoogle Scholar
Di Nezzaa, E., Palatuccia, G. and Valdinocia, E.. Hitchhiker's guide to the fractional Sobolev spaces. Bull. Sci. Math. 136 (2012), 521–573.CrossRefGoogle Scholar
Felmer, P., Quaas, A. and Tan, J.. Positive solutions of the nonlinear Schrödinger equation with the fractional Laplacian. Proc. Roy. Soc. Edinburgh Sect. A 142 (2012), 1237–1262.CrossRefGoogle Scholar
Guo, Y., Peng, S. and Yan, S.. Local uniqueness and periodicity induced by concentration. Proc. Lond. Math. Soc. 114 (2017), 1005–1043.CrossRefGoogle Scholar
Guo, Y., Liu, T. and Nie, J.. Construction of solutions for the polyharmonic equation via local Pohozaev identities. Calc. Var. Partial Differ. Equ. 58 (2019), 123.CrossRefGoogle Scholar
Guo, Y. and Nie, J.. Infinitely many non-radial solutions for the prescribed curvature problem of fractional operator. Discrete Contin. Dyn. Syst. 36 (2016), 6873–6898.Google Scholar
Guo, Y., Liu, T. and Nie, J.. Solutions for fractional Schrödinger equation involving critical exponent via local Pohozaev identities. Adv. Nonlinear Stud. 20 (2020), 185–211.CrossRefGoogle Scholar
Jin, J., Li, Y. Y. and Xiong, J.. On a fractional Nirenberg problem, part I: blow up analysis and compactness of solutions. J. Eur. Math. Soc. 16 (2014), 1111–1171.CrossRefGoogle Scholar
Li, Y. Y., Wei, J. and Xu, H.. Multi-bump solutions of ( − Δ)s u = K(x)u (n+2)/(n−2) on lattices in ℝn. J. Reine Angew. Math. 743 (2018), 163–211.CrossRefGoogle Scholar
Lin, F., Ni, W.-M. and Wei, J.. On the number of interior peak solutions for a singularly perturbed Neumann problem. Commun. Pure Appl. Math. 60 (2007), 252–281.CrossRefGoogle Scholar
Liu, Z.. Large number of bubble solutions for the equation Δu + K(y)u (N+2)/(N−2) ± ε = 0 on ℝN. Sci. China Math. 59 (2016), 459–478.CrossRefGoogle Scholar
Niu, M., Tang, Z. and Wang, L.. Solutions for conformally invariant fractional Laplacian equations with multi-bumps centered in lattices. J. Differ. Equ. 266 (2019), 1756–1831.CrossRefGoogle Scholar
Tan, J.. The Brezis–Nirenberg type problem involving the square root of the Laplacian. Calc. Var. Partial Differ. Equ. 42 (2011), 21–41.CrossRefGoogle Scholar
Tan, J. and Xiong, J.. A Harnack inequality for fractional Laplace equations with lower order terms. Discrete Contin. Dyn. Syst. 31 (2011), 975–983.CrossRefGoogle Scholar
Peng, S., Wang, C. and Wei, S.. Constructing solutions for the prescribed scalar curvature problem via local Pohozaev identities. J. Differ. Equ. 267 (2019), 2503–2530.CrossRefGoogle Scholar
Peng, S., Wang, C. and Yan, S.. Construction of solutions via local Pohozaev identities. J. Funct. Anal. 274 (2018), 2606–2633.CrossRefGoogle Scholar
Vátois, J. and Wang, S.. Infinitely many solutions for cubic nonlinear Schrödinger equations in dimension four (English summary). Adv. Nonlinear Anal. 8 (2019), 715–724.CrossRefGoogle Scholar
Wang, X. and Wei, J.. On the equation Δu + K(x)u (N+2)/(N−2) ± ε2 = 0 in ℝN. Rend. Circ. Mat. Palermo 44 (1995), 365–400.CrossRefGoogle Scholar
Wang, C. and Wei, S.. Large number of bubble solutions for a perturbed fractional Laplacian equation, arXiv:1908.03386, 2019.Google Scholar
Wang, L., Wei, J. and Yan, S.. On Lin-Ni's conjecture in convex domains. Proc. Lond. Math. Soc. 102 (2011), 1099–1126.CrossRefGoogle Scholar
Wei, J. and Yan, S.. Infinitely many positive solutions for the nonlinear Schrödinger equations in ℝN. Calc. Var. Partial Differ. Equ. 37 (2010), 423–439.CrossRefGoogle Scholar
Wei, J. and Yan, S.. Infinitely many solutions for the prescribed scalar curvature problem on $\mathbb {S}^N$. J. Funct. Anal. 258 (2010), 3048–3081.CrossRefGoogle Scholar
Wei, J. and Yan, S.. On a stronger Lazer–McKenna conjecture for Ambrosetti–Prodi type problems. Ann. Sci. Norm. Super. Pisa Cl. Sci. 9 (2010), 423–457.Google Scholar
Wei, J. and Yan, S.. Infinitely many positive solutions for an elliptic problem with critical or supercritical growth. J. Math. Pures Appl. 96 (2011), 307–333.CrossRefGoogle Scholar
Yan, S., Yang, J. and Yu, X.. Equations involving fractional Laplacian operator: compactness and application. J. Funct. Anal. 269 (2015), 47–79.CrossRefGoogle Scholar