Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Haraux, Alain
1984.
On a uniqueness theorem of L. Amerio and G. Prouse.
Proceedings of the Royal Society of Edinburgh: Section A Mathematics,
Vol. 96,
Issue. 3-4,
p.
221.
Haraux, Alain
1985.
Non-resonance for a strongly dissipative wave equation in higher dimensions.
Manuscripta Mathematica,
Vol. 53,
Issue. 1-2,
p.
145.
Nakao, Mitsuhiro
1986.
On the decay of solutions of some nonlinear dissipative wave equations in higher dimensions.
Mathematische Zeitschrift,
Vol. 193,
Issue. 2,
p.
227.
Haraux, A.
1988.
Partial Differential Equations.
Vol. 1324,
Issue. ,
p.
118.
Haraux, A.
and
Zuazua, E.
1988.
Decay estimates for some semilinear damped hyperbolic problems.
Archive for Rational Mechanics and Analysis,
Vol. 100,
Issue. 2,
p.
191.
Haraux, Alain
1988.
Attractors of asymptotically compact processes and applications to nonlinear partial differential equations.
Communications in Partial Differential Equations,
Vol. 13,
Issue. 11,
p.
1383.
Haraux, Alain
1989.
Anti-periodic solutions of some nonlinear evolution equations.
Manuscripta Mathematica,
Vol. 63,
Issue. 4,
p.
479.
Borisovich, Yu. G.
Gel'man, B. D.
Myshkis, A. D.
and
Obukhovskii, V. V.
1990.
New results in the theory of multivalued mappings. I. Topological characteristics and solvability of operator relations.
Journal of Soviet Mathematics,
Vol. 49,
Issue. 1,
p.
800.
Chergui, L.
2009.
Convergence of global and bounded solutions of the wave equation with nonlinear dissipation and analytic nonlinearity.
Journal of Evolution Equations,
Vol. 9,
Issue. 2,
p.
405.
Ben Hassen, I.
and
Chergui, L.
2011.
Convergence of Global and Bounded Solutions of Some Nonautonomous Second Order Evolution Equations with Nonlinear Dissipation.
Journal of Dynamics and Differential Equations,
Vol. 23,
Issue. 2,
p.
315.
Cieutat, Philippe
and
Ezzinbi, Khalil
2011.
Almost automorphic solutions for some evolution equations through the minimizing for some subvariant functional, applications to heat and wave equations with nonlinearities.
Journal of Functional Analysis,
Vol. 260,
Issue. 9,
p.
2598.
Yassine, Hassan
2012.
Existence and Asymptotic Behavior of Solutions to Semilinear Wave Equations with Nonlinear Damping and Dynamical Boundary Condition.
Journal of Dynamics and Differential Equations,
Vol. 24,
Issue. 3,
p.
645.
Yassine, Hassan
2013.
Well-posedness and asymptotic behavior of a nonautonomous, semilinear hyperbolic-parabolic equation with dynamical boundary condition of memory type.
Journal of Integral Equations and Applications,
Vol. 25,
Issue. 4,
Jiao, Zhe
and
Xiao, Ti‐Jun
2016.
Convergence and speed estimates for semilinear wave systems with nonautonomous damping.
Mathematical Methods in the Applied Sciences,
Vol. 39,
Issue. 18,
p.
5465.
Benkhalti, Rachid
Es-sebbar, Brahim
and
Ezzinbi, Khalil
2018.
On a Bohr-Neugebauer property for some almost automorphic abstract delay equations.
Journal of Integral Equations and Applications,
Vol. 30,
Issue. 3,
Es-sebbar, Brahim
Ezzinbi, Khalil
Fatajou, Samir
and
Ziat, Mohamed
2020.
Compact almost automorphic weak solutions for some monotone differential inclusions: Applications to parabolic and hyperbolic equations.
Journal of Mathematical Analysis and Applications,
Vol. 486,
Issue. 1,
p.
123805.
Yassine, Hassan
2021.
Well-posedness and asymptotic stability of solutions to the semilinear wave equation with analytic nonlinearity and time varying delay.
Journal of Differential Equations,
Vol. 301,
Issue. ,
p.
169.
Yassine, Hassan
2022.
Compactness Properties and General Stability Result for an Abstract Nonlinear Viscoelastic Equation.
Journal of Dynamics and Differential Equations,
Vol. 34,
Issue. 3,
p.
2229.

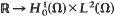 , for any solution of (1) there exists
, for any solution of (1) there exists 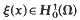 with u(t,.)–ω(t,.)—ξin
with u(t,.)–ω(t,.)—ξin 
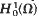 as t → +∞
as t → +∞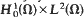 .
.



