Hostname: page-component-848d4c4894-nr4z6 Total loading time: 0 Render date: 2024-05-17T09:03:00.826Z Has data issue: false hasContentIssue false
  • English
  • Français

Classification of simple smooth modules over the Heisenberg–Virasoro algebra

Part of: Lie algebras and Lie superalgebras

Published online by Cambridge University Press:  17 January 2024

Haijun Tan ,
Yufeng Yao  and
Kaiming Zhao
Haijun Tan
Affiliation:
School of Mathematics and Statistics, Northeast Normal University, Changchun, Jilin 130024, P. R. China (tanhj9999@163.com)
Yufeng Yao
Affiliation:
Department of Mathematics, Shanghai Maritime University, Shanghai 201306, China (yfyao@shmtu.edu.cn)
Kaiming Zhao
Affiliation:
Department of Mathematics Wilfrid, Laurier University, Waterloo, ON N2L 3C5, Canada, School of Mathematical Science, Hebei Normal (Teachers) University, Shijiazhuang, Hebei 050024, P. R. China (kzhao@wlu.ca)
Get access Rights & Permissions [Opens in a new window]

Abstract

In this paper, we classify simple smooth modules over the mirror Heisenberg–Virasoro algebra ${\mathfrak {D}}$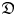, and simple smooth modules over the twisted Heisenberg–Virasoro algebra $\bar {\mathfrak {D}}$ 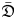with non-zero level. To this end we generalize Sugawara operators to smooth modules over the Heisenberg algebra, and develop new techniques. As applications, we characterize simple Whittaker modules and simple highest weight modules over ${\mathfrak {D}}$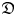. A vertex-algebraic interpretation of our result is the classification of simple weak twisted and untwisted modules over the Heisenberg–Virasoro vertex algebras. We also present a few examples of simple smooth ${\mathfrak {D}}$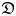-modules and $\bar {\mathfrak {D}}$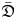-modules induced from simple modules over finite dimensional solvable Lie algebras, that are not tensor product modules of Virasoro modules and Heisenberg modules. This is very different from the case of simple highest weight modules over $\mathfrak {D}$ 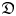and $\bar {\mathfrak {D}}$ 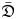which are always tensor products of simple Virasoro modules and simple Heisenberg modules.

Keywords

The Virasoro algebrathe mirror Heisenberg–Virasoro algebrasmooth moduleHeisenberg–Virasoro vertex operator algebratensor product module

MSC classification

Primary: 17B10: Representations, algebraic theory (weights)
Secondary: 17B65: Infinite-dimensional Lie (super)algebras 17B66: Lie algebras of vector fields and related (super) algebras 17B68: Virasoro and related algebras 17B69: Vertex operators; vertex operator algebras and related structures 17B81: Applications to physics
Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , First View , pp. 1 - 45
Check for updates
Copyright
Copyright © The Author(s), 2024. Published by Cambridge University Press on behalf of The Royal Society of Edinburgh

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Adamović, D., Lam, C. H., Pedić, V. and Yu, N.. On irreducibility of modules of Whittaker type for cyclic orbifold vertex algebras. J. Algebra. 539 (2019), 1–23.CrossRefGoogle Scholar
Adamović, D., Lü, R. and Zhao, K.. Whittaker modules for the affine Lie algebra $A^(1)_1$. Adv. Math. 289 (2016), 438–479.CrossRefGoogle Scholar
Adamović, D. and Radobolja, G.. Free field realization of the twisted Heisenberg-Virasoro algebra at level zero and its applications. J. Pure Appl. Algebra. 219 (2015), 4322–4342.CrossRefGoogle Scholar
Arbarello, E., De Concini, C., Kac, V. G. and Procesi, C.. Moduli spaces of curves and representation theory. Comm. Math. Phys. 117 (1988), 1–36.CrossRefGoogle Scholar
Arnal, D. and Pinczon, G.. On algebraically irreducible representations of the Lie algebra $\mathfrak {sl}(2)$. J. Math. Phys. 15 (1974), 350–359.CrossRefGoogle Scholar
Astashkevich, A.. On the structure of Verma modules over Virasoro and Neveu-Schwarz algebras. Comm. Math. Phys. 186 (1997), 531–562.CrossRefGoogle Scholar
Barron, K.. On twisted modules for $N=2$ supersymmetric vertex operator superalgebras, Lie theory and its applications in physics, Springer Proc. Math. Stat., Vol. 36 (Springer, Tokyo, 2013), 411–420.CrossRefGoogle Scholar
Batra, P. and Mazorchuk, V.. Blocks and modules for Whittaker pairs. J. Pure Appl. Algebra 215 (2011), 1552–1568.CrossRefGoogle Scholar
Bekkert, V., Benkart, G., Futorny, V. and Kashuba, I.. New irreducible modules for Heisenberg and affine Lie algebras. J. Algebra 373 (2013), 284–298.CrossRefGoogle Scholar
Benkart, G. and Ondrus, M.. Whittaker modules for generalized Weyl algebras. Represent. Theory. 13 (2009), 141–164.CrossRefGoogle Scholar
Cai, Y., Tan, H. and Zhao, K.. Module structure on $\mathcal {U}(\mathfrak {h})$ for Kac-Moody algebras (in Chinese). Sci. China Math. 47 (2017), 1491–1514.Google Scholar
Chari, V. and Pressley, A.. A new family of irreducible, integrable modules for affine Lie algebras. Math. Ann. 277 (1987), 543–562.CrossRefGoogle Scholar
Chen, H., Han, J., Su, Y. and Yue, X.. Two classes of non-weight modules over the twisted Heisenberg-Virasoro algebra. Manuscripta Math. 160 (2019), 265–284.CrossRefGoogle Scholar
Chen, H. and Guo, X.. New simple modules for the Heisenberg-Virasoro algebra. J. Algebra 390 (2013), 77–86.CrossRefGoogle Scholar
Chen, H. and Guo, X.. Non-weight modules over the Heisenberg-Virasoro algebra and the W algebra W(2,2). J. Algebra Appl. 16 (2017), 1750097.CrossRefGoogle Scholar
Chen, H., Guo, X. and Zhao, K.. Tensor product weight modules over the Virasoro algebra. J. London. Math. Soc. 88 (2013), 829–844.CrossRefGoogle Scholar
Christodoupoulou, K.. Whittaker modules for Heisenberg algebras and imaginary Whittaker modules for affine Lie algebras. J. Algebra. 320 (2008), 2871–2890.CrossRefGoogle Scholar
Di Francesco, P., Mathieu, P. and Sénéchal, D.. Conformal field theory (Springer-Verlag, New York, 1997).CrossRefGoogle Scholar
Dong, C., Mason, G. and Zhu, Y.. Discrete series of the Virasoro algebra and the Moonshine module, Algebraic groups and their generalizations: quantum and infinite-dimensional methods (University Park, PA), Proc. Sympos. Pure Math. (1991), 295–316, Part 2 (Amer. Math. Soc. Providence, RI, 1994).Google Scholar
Feigin, B. and Fuchs, D.. Representations of the Virasoro algebra, representation of Lie groups and related topics, Adv. Stud. Contemp. Math. (Gordon and Breach, New York, 1990), pp. 465–554.Google Scholar
Frenkel, I., Huang, Y. and Lepowsky, J.. On axiomatic approaches to vertex operator algebras and modules, Mem. Am. Math. Soc., Vol. 104 (1993).Google Scholar
Frenkel, I., Lepowsky, J. and Meurman, A.. Vertex operator algebras and the monster, Pure and Appl. Math, Vol. 134 (Academic Press, Massachusetts, 1988),Google Scholar
Frenkel, I. and Zhu, Y.. Vertex operator algebras associated to representations of affine and Virasoro algebras. Duke Math. J. 66 (1992), 123–168.CrossRefGoogle Scholar
Gao, D.. Simple restricted modules for the Heisenberg-Virasoro algebra. J. Algebra 574 (2021), 233–251.CrossRefGoogle Scholar
Gao, D. and Zhao, K.. Tensor product weight modules for the mirror-twisted Heisenberg-Virasoro algebra. J. Pure Appl. Algebra 226 (2022), 106929.CrossRefGoogle Scholar
Goddard, P. and Olive, D.. Kac-Moody and Virasoro algebras in relation to quantum physics. Intemat. J. Modern Phys. A 1 (1986), 303–414.CrossRefGoogle Scholar
Guo, H. and Wang, Q.. Twisted Heisenberg-Virasoro vertex operator algebra. Glas. Mat. 54 (2019), 369–407.CrossRefGoogle Scholar
Guo, X. and Zhao, K.. Irreducible representations of non-twisted affine Kac-Moody algebras, e-print arXiv:1305.4059.Google Scholar
Henkel, M.. Schrödinger invariance and strongly anisotropic critical systems. J. Stat. Phys. 75 (1994), 1023–1029.CrossRefGoogle Scholar
Henkel, M.. Phenomenology of local scale invariance: from conformal invariance to dynamical scaling. Nucl. Phys. B. 641 (2002), 405–410.CrossRefGoogle Scholar
Iohara, K. and Koga, Y.. Representation theory of the Virasoro algebra (Springer-Verlag, London, 2011).CrossRefGoogle Scholar
Kac, V., Raina, A. and Rozhkovskaya, N.. Bombay lectures on highest weight representations of infinite dimensional Lie algebra. 2nd Ed., Adv. Ser. Math. Phys., Vol. 29 (World Scientific Publishing Co. Pte. Ltd., Hackensack, NJ, 2013).CrossRefGoogle Scholar
Kazhdan, D. and Lusztig, G.. Tensor structures arising from affine Lie algebras. III. J. Amer. Math. Soc. 6 (1993), 905–947.CrossRefGoogle Scholar
Kostant, B.. On Whittaker vectors and representation theory. Invent. Math. 48 (1978), 101–184.CrossRefGoogle Scholar
Lepowsk, J. and Li, H.. Introduction to vertex operator algebras and their representations, Progress in Math., Vol. 227 (Birkhäuser, Boston, 2004).Google Scholar
Li, H.. Local systems of vertex operators, vertex superalgebras and modules. J. Pure Appl. Algebra 109 (1996), 143–195.CrossRefGoogle Scholar
Li, J. and Su, Y.. Representations of the Schrödinger-Virasoro algebras. J. Math. Phys. 49 (2008), 053512.CrossRefGoogle Scholar
Liu, D., Pei, Y., Xia, L. and Zhao, K.. Irreducible modules over the mirror Heisenberg-Virasoro algebra. Commun. Contemp. Math. 24 (2022), 2150026.CrossRefGoogle Scholar
Lü, R., Guo, X. and Zhao, K.. Irreducible modules over the Virasoro algebra. Doc. Math. 16 (2011), 709–721.CrossRefGoogle Scholar
Lü, R., Mazorchuk, V. and Zhao, K.. Classification of simple weight modules over the 1-spatial ageing algebra. Algebr. Represent. Theory 18 (2015), 381–395.CrossRefGoogle Scholar
Lü, R. and Zhao, K.. Classification of irreducible weight modules over the twisted Heisenberg-Virasoro algebras. Comm. Contemp. Math. 12 (2010), 183–205.CrossRefGoogle Scholar
Lü, R. and Zhao, K.. Irreducible Virasoro modules from irreducible Weyl modules. J. Algebra 414 (2014), 271–287.CrossRefGoogle Scholar
Lü, R. and Zhao, K.. Generalized oscillator representations of the twisted Heisenberg-Virasoro algebra. Algebr. Represent. Theory 23 (2020), 1417–1442.CrossRefGoogle Scholar
Mathieu, O.. Classification of Harish-Chandra modules over the Virasoro Lie algebra. Invent. Math. 107 (1992), 225–234.CrossRefGoogle Scholar
Mazorchuk, V. and Zhao, K.. Characterization of simple highest weight modules. Canad. Math. Bull. 56 (2013), 606–614.CrossRefGoogle Scholar
Mazorchuk, V. and Zhao, K.. Simple Virasoro modules which are locally finite over a positive part. Selecta Math. (N.S.), 20 (2014), 839–854.CrossRefGoogle Scholar
McDowell, E.. On modules induced from Whittaker modules. J. Algebra 96 (1985), 161–177.CrossRefGoogle Scholar
McDowell, E.. A module induced from a Whittaker module. Proc. Amer. Math. Soc. 118 (1993), 349–354.CrossRefGoogle Scholar
Moody, R. V. and Pianzola, A., Lie algebras with triangular decompositions. Canadian Mathematical Society Series of Monographs and Advanced Texts. A Wiley-Interscience Publication. (John Wiley & Sons, Inc., New York, 1995).Google Scholar
Nilsson, J.. Simple $\mathrm {sl_n+1}$-module structures on $\mathcal {U}(\mathfrak {h}$. J. Algebra 424 (2015), 294–329.CrossRefGoogle Scholar
Rudakov, A. N.. Irreducible representations of infinite-dimensional Lie algebras of Cartan type. Izv. Akad. Nauk SSSR Ser. Mat. 38 (1974), 836–866. English translation in Math USSR-Izv. 8 (1974), 836–866.Google Scholar
Rudakov, A. N.. Irreducible representations of infinite-dimensional Lie algebras of types $S$ and $H$. Izv. Akad. Nauk SSSR Ser. Mat. 39 (1975), 496–511. English translation in Math USSR-Izv. 9 (1975), 465–480.Google Scholar
Tan, H. and Zhao, K.. $W^+_n$ and $W_n$-module structures on $\mathcal {U}(\mathfrak {h_n})$. J. Algebra 424 (2015), 357–375.CrossRefGoogle Scholar