Hostname: page-component-848d4c4894-5nwft Total loading time: 0 Render date: 2024-06-08T05:02:36.647Z Has data issue: false hasContentIssue false
  • English
  • Français

Convergence for the fractional p-Laplacian and its application to the extended Nirenberg problem

Part of: Partial differential equations Miscellaneous topics - Partial differential equations

Published online by Cambridge University Press:  05 April 2023

Zhiwen Zhao Open the ORCID record for Zhiwen Zhao [Opens in a new window]
Zhiwen Zhao*
Affiliation:
Beijing Computational Science Research Center, Beijing 100193, China zwzhao365@163.com
Get access Rights & Permissions [Opens in a new window]

Abstract

The main objective of this paper is to establish the convergence for the fractional $p$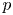-Laplacian of sequences of nonnegative functions with $p>2$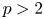. Furthermore, we show the blow-up phenomena for solutions to the extended Nirenberg problem modelled by fractional $p$-Laplacian with the prescribed negative functions.

Keywords

fractional p-Laplacianconvergenceextended Nirenberg problemblow-up

MSC classification

Primary: 35R11: Fractional partial differential equations
Secondary: 35B44: Blow-up 35R09: Integro-partial differential equations
Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 154 , Issue 2 , April 2024 , pp. 660 - 672
Check for updates
Copyright
Copyright © The Author(s), 2023. Published by Cambridge University Press on behalf of The Royal Society of Edinburgh

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Applebaum, D.. Lévy processes—from probability to finance and quantum groups. Not. Am. Math. Soc. 51 (2004), 1336–1347.Google Scholar
Applebaum, D.. Lévy processes and stochastic calculus, 2nd edn. Cambridge Studies in Advanced Mathematics, vol. 116 (Cambridge: Cambridge University Press, 2009).Google Scholar
Bertoin, J.. Lévy processes. Cambridge Tracts in Mathematics, vol. 121 (Cambridge: Cambridge University Press, 1996).Google Scholar
Caffarelli, L. A. and Vasseur, A.. Drift diffusion equations with fractional diffusion and the quasi-geostrophic equation. Ann. Math. 171 (2010), 1903–1930.Google Scholar
Chang, S.-Y. A., Gursky, M. J. and Yang, P. C.. The scalar curvature equation on $2$- and $3$-spheres. Calc. Var. Partial Differ. Equ. 1 (1993), 205–229.Google Scholar
Chen, W. X. and Li, C. M.. A priori estimates for prescribing scalar curvature equations. Ann. Math. 145 (1997), 547–564.Google Scholar
Chen, W. X., Li, Y. and Ma, P.. The fractional Laplacian (Hackensack, NJ: World Scientific Publishing Co. Pte. Ltd., 2020).Google Scholar
Constantin, P.. Euler equations, Navier-Stokes equations and turbulence. Mathematical foundation of turbulent viscous flows. Lecture Notes in Math., vol. 1871, pp. 1–43 (Berlin: Springer, 2006).Google Scholar
Gidas, B. and Spruck, J.. Global and local behavior of positive solutions of nonlinear elliptic equations. Commun. Pure Appl. Math. 34 (1981), 525–598.CrossRefGoogle Scholar
Gidas, B. and Spruck, J.. A priori bounds for positive solutions of nonlinear elliptic equations. Commun. Partial Differ. Equ. 6 (1981), 883–901.CrossRefGoogle Scholar
Du, X. S., Jin, T. L., Xiong, J. G. and Yang, H.. Blow up limits of the fractional Laplacian and their applications to the fractional Nirenberg problem. arXiv:2112.00960.Google Scholar
Jin, T. L., Li, Y. Y. and Xiong, J. G.. On a fractional Nirenberg problem, part I: blow up analysis and compactness of solutions. J. Eur. Math. Soc. 16 (2014), 1111–1171.CrossRefGoogle Scholar
Jin, T. L., Li, Y. Y. and Xiong, J. G.. On a fractional Nirenberg problem, part II: existence of solutions. Int. Math. Res. Not. 2015 (2015), 1555–1589.Google Scholar
Jin, T. L., Li, Y. Y. and Xiong, J. G.. The Nirenberg problem and its generalizations: a unified approach. Math. Ann. 369 (2017), 109–151.Google Scholar
Li, Y. Y.. Prescribing scalar curvature on $\mathbb {S}^n$ and related problem. I. J. Differ. Equ. 120 (1995), 319–410.Google Scholar
Lin, C.-S.. On Liouville theorem and a priori estimates for the scalar curvature equations. Ann. Sc. Norm. Super. Pisa Cl. Sci. 27 (1998), 107–130.Google Scholar
Schoen, R. and Zhang, D.. Prescribed scalar curvature on the $n$-sphere. Calc. Var. Partial Differ. Equ. 4 (1996), 1–25.CrossRefGoogle Scholar
Zhu, M.. Liouville theorems on some indefinite equations. Proc. R. Soc. Edinb. Sect. A 129 (1999), 649–661.Google Scholar