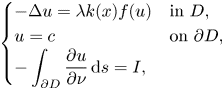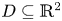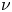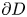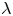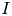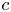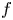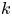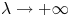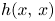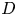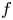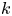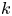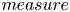1. Introduction and main results
In this paper, we consider the 2D plasma problem

where $D\subseteq \mathbb {R}^2$![]() is a simply-connected bounded domain with smooth boundary, $\nu$
is a simply-connected bounded domain with smooth boundary, $\nu$![]() is the outward unit normal to the boundary $\partial D$
is the outward unit normal to the boundary $\partial D$![]() , $\lambda \in \mathbb {R}^+$
, $\lambda \in \mathbb {R}^+$![]() and $I$
and $I$![]() are given constants and $c$
are given constants and $c$![]() is an unknown constant. The non-autonomous term $k$
is an unknown constant. The non-autonomous term $k$![]() and the nonlinearity $f$
and the nonlinearity $f$![]() are two prescribed functions. In the following, we always assume $f >0$
are two prescribed functions. In the following, we always assume $f >0$![]() on $(0,\,+\infty )$
on $(0,\,+\infty )$![]() and $f \equiv 0$
and $f \equiv 0$![]() on $(-\infty,\,0)$
on $(-\infty,\,0)$![]() .
.
The problem (1.1) arises from a model describing a simplified version of equilibrium of a plasma in a cavity (also called the ‘Tokamak machine’), see [Reference Cao, Peng and Yan13, Reference Temam35, Reference Temam36]. Let $u_+=u$![]() if $u\geq 0$
if $u\geq 0$![]() and $u_+=0$
and $u_+=0$![]() if $u<0$
if $u<0$![]() , $u_-=u_+-u$
, $u_-=u_+-u$![]() . The equilibrium of a plasma confined in a toroidal cavity is governed by the following equations (see the classical paper [Reference Temam35])
. The equilibrium of a plasma confined in a toroidal cavity is governed by the following equations (see the classical paper [Reference Temam35])

where $D\subseteq \mathbf {H}=\{x=(x_1,\,x_2)\mid x_1>0\}$![]() is a bounded domain, $\mathcal {L}=\sum _{i=1}^2({\partial }/{\partial x_i}) (({1}/{x_1})({\partial }/{\partial x_i}))$
is a bounded domain, $\mathcal {L}=\sum _{i=1}^2({\partial }/{\partial x_i}) (({1}/{x_1})({\partial }/{\partial x_i}))$![]() , $\nu$
, $\nu$![]() is the outward unit normal to $\partial D$
is the outward unit normal to $\partial D$![]() at $x$
at $x$![]() , $I$
, $I$![]() is a given positive constant and $\gamma$
is a given positive constant and $\gamma$![]() is an unknown constant. The non-autonomous term $k$
is an unknown constant. The non-autonomous term $k$![]() satisfies
satisfies
The sets $D_p=\{x\in D\mid u(x)<0\}$![]() and $D_v=\{x\in D\mid u(x)>0\}$
and $D_v=\{x\in D\mid u(x)>0\}$![]() are called the plasma set and vacuum set, respectively. $\partial D_p$
are called the plasma set and vacuum set, respectively. $\partial D_p$![]() is called the free boundary. Indeed, from a physical point of view, the nonlinear term $\lambda k u_-$
is called the free boundary. Indeed, from a physical point of view, the nonlinear term $\lambda k u_-$![]() in (1.2) can be replaced by $\lambda k f(u)$
in (1.2) can be replaced by $\lambda k f(u)$![]() for general $f$
for general $f$![]() , which is called the $constitutive~function$
, which is called the $constitutive~function$![]() of the plasma, see Appendix in [Reference Temam35].
of the plasma, see Appendix in [Reference Temam35].
If we simplify the elliptic operator $\mathcal {L}$![]() in (1.2) to $\Delta$
in (1.2) to $\Delta$![]() , one gets a simplified model
, one gets a simplified model

Note that for a solution $u$![]() of (1.3), $v=-u$
of (1.3), $v=-u$![]() satisfies (1.1) with $f(t)=t_+$
satisfies (1.1) with $f(t)=t_+$![]() and $c=-\gamma$
and $c=-\gamma$![]() .
.
Existence of solutions to (1.3) and the general problem (1.1) is studied in many references, see [Reference Bandle and Sperb3, Reference Cao, Peng and Yan13, Reference Flucher and Wei22, Reference Liu28, Reference Schaeffer31, Reference Shibata33, Reference Temam35] and reference therein. In the case $k\equiv 1$![]() , it is well-known in [Reference Temam36] that (1.3) has a solution if and only if $\lambda >0$
, it is well-known in [Reference Temam36] that (1.3) has a solution if and only if $\lambda >0$![]() and
and
where $\lambda _1$![]() is the first eigenvalue of $-\Delta$
is the first eigenvalue of $-\Delta$![]() in $D$
in $D$![]() with Dirichlet boundary condition. Moreover, if $\lambda \in (0,\,\lambda _2)$
with Dirichlet boundary condition. Moreover, if $\lambda \in (0,\,\lambda _2)$![]() , where $\lambda _2$
, where $\lambda _2$![]() is the second eigenvalue of $-\Delta$
is the second eigenvalue of $-\Delta$![]() in $D$
in $D$![]() , the solution of (1.3) is unique, see also [Reference Berestycki and Brezis7, Reference Puel29]. For the asymptotic behaviour of solutions to (1.3) as $\lambda$
, the solution of (1.3) is unique, see also [Reference Berestycki and Brezis7, Reference Puel29]. For the asymptotic behaviour of solutions to (1.3) as $\lambda$![]() tending to infinity, Caffarelli-Friedman [Reference Caffarelli and Friedman10] first proved the non-uniqueness of the solutions to (1.3) and showed that the free boundary $\partial D_p$
tending to infinity, Caffarelli-Friedman [Reference Caffarelli and Friedman10] first proved the non-uniqueness of the solutions to (1.3) and showed that the free boundary $\partial D_p$![]() is approximately a circle as $\lambda \to +\infty.$
is approximately a circle as $\lambda \to +\infty.$![]() Let $G(x,\,y)$
Let $G(x,\,y)$![]() be the Green function of $-\Delta$
be the Green function of $-\Delta$![]() in $D$
in $D$![]() with Dirichlet boundary condition. Then $G(x,\,y)$
with Dirichlet boundary condition. Then $G(x,\,y)$![]() has the decomposition
has the decomposition
where $-({1}/{2\pi })\ln |x-y|$![]() is the fundamental solution of $-\Delta$
is the fundamental solution of $-\Delta$![]() and the regular part $h(x,\,y)\in C^{\infty }(D\times D)$
and the regular part $h(x,\,y)\in C^{\infty }(D\times D)$![]() . It is proved in [Reference Caffarelli and Friedman10] that if there exists $O\subseteq D$
. It is proved in [Reference Caffarelli and Friedman10] that if there exists $O\subseteq D$![]() with $\min _{x\in \partial O}h(x,\, x) > \min _{x\in O}h(x,\, x)$
with $\min _{x\in \partial O}h(x,\, x) > \min _{x\in O}h(x,\, x)$![]() , then (1.3) has a solution $u^\lambda$
, then (1.3) has a solution $u^\lambda$![]() for every $\lambda$
for every $\lambda$![]() sufficiently large, and the corresponding plasma set $D_p$
sufficiently large, and the corresponding plasma set $D_p$![]() shrinks to a point $x^*\in O$
shrinks to a point $x^*\in O$![]() with $h(x^*,\,x^*) = \min _{x\in O}h(x,\, x)$
with $h(x^*,\,x^*) = \min _{x\in O}h(x,\, x)$![]() as $\lambda \to +\infty$
as $\lambda \to +\infty$![]() . This result has been extended to solutions to (1.3) whose plasma set has several components. Under the assumption that the homology of $\Omega$
. This result has been extended to solutions to (1.3) whose plasma set has several components. Under the assumption that the homology of $\Omega$![]() is nontrivial, [Reference Cao, Peng and Yan13] proved that for every $l\geq 1$
is nontrivial, [Reference Cao, Peng and Yan13] proved that for every $l\geq 1$![]() and $\lambda$
and $\lambda$![]() sufficiently large, (1.3) has a solution whose plasma set $D_p$
sufficiently large, (1.3) has a solution whose plasma set $D_p$![]() consists of $l$
consists of $l$![]() components and concentrates near critical points of the Kirchhoff–Routh Hamiltonian as $\lambda \to +\infty$
components and concentrates near critical points of the Kirchhoff–Routh Hamiltonian as $\lambda \to +\infty$![]() by using the Lyapunov–Schmidt reduction method. The Kirchhoff–Routh Hamiltonian $\mathcal {H}_{l}$
by using the Lyapunov–Schmidt reduction method. The Kirchhoff–Routh Hamiltonian $\mathcal {H}_{l}$![]() is defined by (see [Reference Kirchhoff23, Reference Lin27, Reference Routh30])
is defined by (see [Reference Kirchhoff23, Reference Lin27, Reference Routh30])

where $(x_1,\,\ldots,\,x_l)\in D^{(l)}:=\underbrace {D\times D\times \cdots \times D}_{l}$![]() satisfies $x_i\neq x_j$
satisfies $x_i\neq x_j$![]() for $i\neq j$
for $i\neq j$![]() , and $d_1,\,\ldots,\,d_l$
, and $d_1,\,\ldots,\,d_l$![]() are $l$
are $l$![]() prescribed constants. When $D$
prescribed constants. When $D$![]() has non-trivial topology, solutions of (1.1) with $f(t)=t^p_+ (p>1)$
has non-trivial topology, solutions of (1.1) with $f(t)=t^p_+ (p>1)$![]() whose plasma region shrinks down around finitely many different points have been constructed in [Reference Liu28]. See [Reference Bartolucci and Jevnikar4, Reference Bartolucci and Jevnikar5, Reference Berestycki and Brezis8] for more results. Note that the plasma problem (1.1) with $k(x)\equiv 1$
whose plasma region shrinks down around finitely many different points have been constructed in [Reference Liu28]. See [Reference Bartolucci and Jevnikar4, Reference Bartolucci and Jevnikar5, Reference Berestycki and Brezis8] for more results. Note that the plasma problem (1.1) with $k(x)\equiv 1$![]() also corresponds to the vorticity formulation of 2D steady incompressible Euler equations. In [Reference Cao, Liu and Wei12], by using the non-degeneracy of solutions to
also corresponds to the vorticity formulation of 2D steady incompressible Euler equations. In [Reference Cao, Liu and Wei12], by using the non-degeneracy of solutions to
and the Lyapunov–Schmidt finite-dimensional reduction method, [Reference Cao, Liu and Wei12] proved the existence of solutions of (1.1) with $f(t)=t^p_+ (p>1)$![]() concentrating near isolated non-degenerate critical points of $\mathcal {H}_{l}$
concentrating near isolated non-degenerate critical points of $\mathcal {H}_{l}$![]() for $\lambda$
for $\lambda$![]() sufficiently large. [Reference Cao, Peng and Yan14] further proved the existence and asymptotic behaviour of concentrated solutions of (1.1) with $f(t)=t^p_+ (p=0)$
sufficiently large. [Reference Cao, Peng and Yan14] further proved the existence and asymptotic behaviour of concentrated solutions of (1.1) with $f(t)=t^p_+ (p=0)$![]() for $\lambda$
for $\lambda$![]() sufficiently large by using Lyapunov–Schmidt reduction method. Compared to [Reference Cao, Liu and Wei12], results in [Reference Cao, Peng and Yan14] require more delicate estimates since the nonlinearity in [Reference Cao, Peng and Yan14] is not as smooth as it is in [Reference Cao, Liu and Wei12]. For more results, see, e.g., [Reference Cao, Guo, Peng and Yan11, Reference Cao, Wan, Wang and Zhan15–Reference Dávila, del Pino, Musso and Wei18, Reference Smets and Van Schaftingen34, Reference Turkington37].
sufficiently large by using Lyapunov–Schmidt reduction method. Compared to [Reference Cao, Liu and Wei12], results in [Reference Cao, Peng and Yan14] require more delicate estimates since the nonlinearity in [Reference Cao, Peng and Yan14] is not as smooth as it is in [Reference Cao, Liu and Wei12]. For more results, see, e.g., [Reference Cao, Guo, Peng and Yan11, Reference Cao, Wan, Wang and Zhan15–Reference Dávila, del Pino, Musso and Wei18, Reference Smets and Van Schaftingen34, Reference Turkington37].
When $k$![]() is a function rather than a constant, many references also considered the existence and asymptotic behaviour of solutions to (1.1), see [Reference del Pino, Kowalczyk and Musso19, Reference Li and Peng24, Reference Li and Peng25, Reference Shibata32, Reference Wei38] and reference therein. [Reference Temam35] first obtained the existence of solutions of (1.3) by considering minimization of a certain variational problem. For $N\geq 3,$
is a function rather than a constant, many references also considered the existence and asymptotic behaviour of solutions to (1.1), see [Reference del Pino, Kowalczyk and Musso19, Reference Li and Peng24, Reference Li and Peng25, Reference Shibata32, Reference Wei38] and reference therein. [Reference Temam35] first obtained the existence of solutions of (1.3) by considering minimization of a certain variational problem. For $N\geq 3,$![]() Shibata [Reference Shibata32] considered the following equations
Shibata [Reference Shibata32] considered the following equations

where $D\subseteq \mathbb {R}^N$![]() , $\varepsilon >0$
, $\varepsilon >0$![]() is small and $k(x)$
is small and $k(x)$![]() is a positive function in $\overline {D}$
is a positive function in $\overline {D}$![]() . Under the assumption that $f (t) = t_+^p$
. Under the assumption that $f (t) = t_+^p$![]() for $p\in (1,\,({N+2}/{N-2}))$
for $p\in (1,\,({N+2}/{N-2}))$![]() , the author proved that (1.5) has a least energy solution concentrating near global maximum points of $k$
, the author proved that (1.5) has a least energy solution concentrating near global maximum points of $k$![]() as $\varepsilon \to 0^+$
as $\varepsilon \to 0^+$![]() . Here the concentration means that the plasma set $\{x\in D\mid u_\varepsilon (x)>1\}$
. Here the concentration means that the plasma set $\{x\in D\mid u_\varepsilon (x)>1\}$![]() shrinks to some points as $\varepsilon \to 0$
shrinks to some points as $\varepsilon \to 0$![]() . This result has been extended to solutions to (1.5) with general nonlinearities concentrating near several boundary points, see [Reference Li and Peng24]. As for the plasma problem (1.1) for $N\geq 3$
. This result has been extended to solutions to (1.5) with general nonlinearities concentrating near several boundary points, see [Reference Li and Peng24]. As for the plasma problem (1.1) for $N\geq 3$![]() , solutions whose plasma region shrinks down around finitely many distinct points were constructed in [Reference Li and Peng25]. It is worth mentioning that, both in [Reference Shibata32] and in [Reference Li and Peng24, Reference Li and Peng25] the total vorticity vanishes rather than tends to a non-zero constant as $\varepsilon \to 0$
, solutions whose plasma region shrinks down around finitely many distinct points were constructed in [Reference Li and Peng25]. It is worth mentioning that, both in [Reference Shibata32] and in [Reference Li and Peng24, Reference Li and Peng25] the total vorticity vanishes rather than tends to a non-zero constant as $\varepsilon \to 0$![]() , that is,
, that is,
For $N=2,\,$![]() by considering Liouville-type equations
by considering Liouville-type equations

del Pino et al. [Reference del Pino, Kowalczyk and Musso19] proved that solutions of (1.6) have the blow up-concentration phenomenon, i.e., there exist solutions of (1.6) concentrating near small neighbourhoods of critical points $\{x_{1,0},\,\ldots,\, x_{n,0}\}$![]() of the function
of the function

as $\varepsilon \to 0$![]() , and the total vorticity of solutions around each $x_{i,0}$
, and the total vorticity of solutions around each $x_{i,0}$![]() tends to a non-zero constant as $\varepsilon \to 0$
tends to a non-zero constant as $\varepsilon \to 0$![]() . Note that (1.7) is different from the Kirchhoff–Routh Hamiltonian (1.4) since the presence of $K$
. Note that (1.7) is different from the Kirchhoff–Routh Hamiltonian (1.4) since the presence of $K$![]() . Note also that (1.6) coincides with (1.1) by letting $\lambda =\varepsilon ^2$
. Note also that (1.6) coincides with (1.1) by letting $\lambda =\varepsilon ^2$![]() and $f(t)=e^t$
and $f(t)=e^t$![]() . A natural question is, whether there exist solutions $u^\lambda$
. A natural question is, whether there exist solutions $u^\lambda$![]() to (1.1) with general profile function $f$
to (1.1) with general profile function $f$![]() , such that the corresponding ‘plasma set’ $\{x\in D\mid u^\lambda (x)>0\}$
, such that the corresponding ‘plasma set’ $\{x\in D\mid u^\lambda (x)>0\}$![]() concentrates near several points with diameter tending to 0 as $\lambda \to +\infty$
concentrates near several points with diameter tending to 0 as $\lambda \to +\infty$![]() ?
?
In this paper, we will construct solutions to (1.1) concentrating near some prescribed points with a large class of sub-exponential nonlinearities $f$![]() . The nonlinearity $f$
. The nonlinearity $f$![]() can either be continuous (e.g., $f(t)=t^p_+$
can either be continuous (e.g., $f(t)=t^p_+$![]() for some $p\in (0,\,+\infty )$
for some $p\in (0,\,+\infty )$![]() ) or have a jump (e.g., $f$
) or have a jump (e.g., $f$![]() being a Heaviside function), see theorems 1.1 and 1.3. We prove that for any $x_0$
being a Heaviside function), see theorems 1.1 and 1.3. We prove that for any $x_0$![]() being strict local minimizers of $\Gamma (\cdot )$
being strict local minimizers of $\Gamma (\cdot )$![]() defined by (1.8), there exist solutions $u^\lambda$
defined by (1.8), there exist solutions $u^\lambda$![]() of (1.1), whose ‘plasma set’ $\{x\in D\mid u^\lambda (x)>0\}$
of (1.1), whose ‘plasma set’ $\{x\in D\mid u^\lambda (x)>0\}$![]() concentrates near $x_0$
concentrates near $x_0$![]() as $\lambda \to +\infty$
as $\lambda \to +\infty$![]() and total vorticity tends to a non-zero prescribed constant $I$
and total vorticity tends to a non-zero prescribed constant $I$![]() as $\lambda \to +\infty$
as $\lambda \to +\infty$![]() . The idea is to regard the non-autonomous term $k$
. The idea is to regard the non-autonomous term $k$![]() as a $measure$
as a $measure$![]() and to use the Arnold's variational method developed by [Reference Arnol'd1, Reference Arnol'd2, Reference Turkington37]. Note that in [Reference Cao, Liu and Wei12, Reference Cao, Peng and Yan14, Reference Liu28], the constitutive function is $f(t)=t^p_+$
and to use the Arnold's variational method developed by [Reference Arnol'd1, Reference Arnol'd2, Reference Turkington37]. Note that in [Reference Cao, Liu and Wei12, Reference Cao, Peng and Yan14, Reference Liu28], the constitutive function is $f(t)=t^p_+$![]() for $p\geq 0.$
for $p\geq 0.$![]() Thus compared to the classical results, we can construct concentrated solutions to plasma problem (1.1) with very general nonlinearity.
Thus compared to the classical results, we can construct concentrated solutions to plasma problem (1.1) with very general nonlinearity.
Before stating our results, let us first introduce some notations: for every Lebesgue-measurable set $A,\, B\subset D$![]() , $\overline {A}$
, $\overline {A}$![]() denotes the closure of $A$
denotes the closure of $A$![]() and $|A|$
and $|A|$![]() denotes the two-dimensional Lebesque measure of $A$
denotes the two-dimensional Lebesque measure of $A$![]() , except when stated otherwise; $dist(A,\,B)=\inf _{x\in A, y\in B}|x-y|$
, except when stated otherwise; $dist(A,\,B)=\inf _{x\in A, y\in B}|x-y|$![]() denotes the distance between $A$
denotes the distance between $A$![]() and $B$
and $B$![]() ; $B_{r}(y)$
; $B_{r}(y)$![]() denotes the open ball of radius $r$
denotes the open ball of radius $r$![]() centred at $y$
centred at $y$![]() ; $\chi _{A}$
; $\chi _{A}$![]() denotes the characteristic function of $A\in D$
denotes the characteristic function of $A\in D$![]() , namely $\chi _{A}(x)=1$
, namely $\chi _{A}(x)=1$![]() for $x\in A$
for $x\in A$![]() and $\chi _{A}(x)=0$
and $\chi _{A}(x)=0$![]() for $x\notin A$
for $x\notin A$![]() ; $O(1)$
; $O(1)$![]() and $o(1)$
and $o(1)$![]() denote some quantities which remain bounded and go to zero as $\lambda$
denote some quantities which remain bounded and go to zero as $\lambda$![]() tends to infinity, respectively; for any function $h$
tends to infinity, respectively; for any function $h$![]() , $supp(h)$
, $supp(h)$![]() denotes the support set of $h$
denotes the support set of $h$![]() .
.
Let $k(x):D\to \mathbb {R}$![]() be a continuous function satisfying
be a continuous function satisfying
($\mathcal {K}$
 ). There exist two constants $k_0,\, k_1$
). There exist two constants $k_0,\, k_1$ such that
\[ 0< k_0\leq k(x)\leq k_1<{+}\infty, \quad \forall x\in D. \]
such that
\[ 0< k_0\leq k(x)\leq k_1<{+}\infty, \quad \forall x\in D. \]
Let us introduce an auxiliary function which will play a crucial role in the study of the existence of solutions to (1.1). Define
where $h(x,\,y)$![]() is the regular part of the Green's function $G$
is the regular part of the Green's function $G$![]() , and $k$
, and $k$![]() satisfies the assumption ($\mathcal {K}$
satisfies the assumption ($\mathcal {K}$![]() ). Clearly $\Gamma (\cdot )$
). Clearly $\Gamma (\cdot )$![]() is well-defined in $D.$
is well-defined in $D.$![]()
Our first result concerns the existence and asymptotic behaviour of solutions to (1.1) with the nonlinearity being the Heaviside function, i.e., $f(t)=\chi _{\{t>0\}}$![]() .
.
Theorem 1.1 Suppose that $k(\cdot )$![]() satisfies $(\mathcal {K})$
satisfies $(\mathcal {K})$![]() and $f(t)=\chi _{\{t>0\}}$
and $f(t)=\chi _{\{t>0\}}$![]() . Let $x_0$
. Let $x_0$![]() be a strict local minimizer of $\Gamma$
be a strict local minimizer of $\Gamma$![]() . Then there exists $\lambda _0>0$
. Then there exists $\lambda _0>0$![]() , such that for any $\lambda \in (\lambda _0,\,+\infty )$
, such that for any $\lambda \in (\lambda _0,\,+\infty )$![]() , (1.1) has a weak solution pair $(u^\lambda,\, c^\lambda )$
, (1.1) has a weak solution pair $(u^\lambda,\, c^\lambda )$![]() which satisfies the following properties:
which satisfies the following properties:
(1) the diameter of the plasma set $\{x\in D\mid u^\lambda (x)>0\}$
 is of the order $O(\lambda ^{-({1}/{2})})$
is of the order $O(\lambda ^{-({1}/{2})})$ as $\lambda \to +\infty$
as $\lambda \to +\infty$ .
.(2) For any $x\in \{x\in D\mid u^\lambda (x)>0\}$
 , $x$
, $x$ tends to $x_0$
tends to $x_0$ as $\lambda \to +\infty$
as $\lambda \to +\infty$ .
.(3) For $\lambda$
 sufficiently large, $\{x\in D\mid u^\lambda (x)=0\}$
sufficiently large, $\{x\in D\mid u^\lambda (x)=0\}$ is a $C^1$
is a $C^1$ curve and converges to a circle as $\lambda \to +\infty$
curve and converges to a circle as $\lambda \to +\infty$ .
.(4) There holds
(1.9)\begin{align} c^\lambda={-}\frac{I}{4\pi}\ln\lambda- \frac{k(x_0)}{2\pi}\int_{B_{\sqrt{{I}/{\pi k(x_0)}}}(0)}\ln\frac{1}{|x^*-y|}\,{\rm d}y+Ih(x_0,x_0)+o(1), \end{align}where $x^*$
 is any point of $\partial B_{B_{\sqrt {{I}/{\pi k(x_0)}}}(0)}$
is any point of $\partial B_{B_{\sqrt {{I}/{\pi k(x_0)}}}(0)}$ .
.
Remark 1.2 We give an example to show the existence of $x_0$![]() . By (1.8), $\Gamma (x)=({1}/{2})h(x,\,x)-({1}/{8\pi })\ln k(x)$
. By (1.8), $\Gamma (x)=({1}/{2})h(x,\,x)-({1}/{8\pi })\ln k(x)$![]() . Since $\lim _{x\to \partial D}h(x,\,x)=+\infty$
. Since $\lim _{x\to \partial D}h(x,\,x)=+\infty$![]() , by assumption $(\mathcal {K})$
, by assumption $(\mathcal {K})$![]() one can get the existence of minimum points $x_{0,1}\in D$
one can get the existence of minimum points $x_{0,1}\in D$![]() satisfying $\Gamma (x_{0,1})=\min _{x\in D}\Gamma (x)$
satisfying $\Gamma (x_{0,1})=\min _{x\in D}\Gamma (x)$![]() . Thus from theorem 1.1, there exists a family of solutions $u^\lambda$
. Thus from theorem 1.1, there exists a family of solutions $u^\lambda$![]() concentrating near minimizers of $\Gamma$
concentrating near minimizers of $\Gamma$![]() . Note that the limiting location of the plasma set $\{x\in D\mid u^\lambda (x)>0\}$
. Note that the limiting location of the plasma set $\{x\in D\mid u^\lambda (x)>0\}$![]() in theorem 1.1 coincides with that in [Reference del Pino, Kowalczyk and Musso19] since when choosing $n=1$
in theorem 1.1 coincides with that in [Reference del Pino, Kowalczyk and Musso19] since when choosing $n=1$![]() in (1.7), (1.7) is equal to $16\pi$
in (1.7), (1.7) is equal to $16\pi$![]() times $\Gamma$
times $\Gamma$![]() .
.
When $f(t)$![]() is a continuous function satisfying some growth conditions, one can also get solutions to (1.1) concentrating near local minimizers of $\Gamma$
is a continuous function satisfying some growth conditions, one can also get solutions to (1.1) concentrating near local minimizers of $\Gamma$![]() . To this end, let $f:\mathbb {R}\to \mathbb {R}$
. To this end, let $f:\mathbb {R}\to \mathbb {R}$![]() be a continuous function satisfying
be a continuous function satisfying
(f 1). $f$
 is locally Hölder continuous on $\mathbb {R}\backslash \{0\}$
is locally Hölder continuous on $\mathbb {R}\backslash \{0\}$ , $f(s)\equiv 0$
, $f(s)\equiv 0$ for $s\le 0$
for $s\le 0$ , and $f$
, and $f$ is strictly increasing in $(0,\,+\infty )$
is strictly increasing in $(0,\,+\infty )$ ;
;(f 2). there exists some positive number $r_0\in (0,\,1)$
 such that
\[ \int_{0}^{s}f(t)\,{\rm d}t \le r_0 f(s)s, \quad \forall s\ge 0. \]
such that
\[ \int_{0}^{s}f(t)\,{\rm d}t \le r_0 f(s)s, \quad \forall s\ge 0. \]
(f 3). For all $\tau >0$
 ,
\[ \lim_{s\to +\infty}\left(f(s)\,e^{-\tau s}\right)=0. \]
,
\[ \lim_{s\to +\infty}\left(f(s)\,e^{-\tau s}\right)=0. \]
Note that many nonlinearities that frequently appear in nonlinear elliptic equations satisfy ($f_1$![]() )–($f_3$
)–($f_3$![]() ), for instance $f(s)=s_+^p$
), for instance $f(s)=s_+^p$![]() with $p\in (0,\,+\infty )$
with $p\in (0,\,+\infty )$![]() . Our second result is as follows.
. Our second result is as follows.
Theorem 1.3 Suppose that $k(\cdot )$![]() satisfies $(\mathcal {K})$
satisfies $(\mathcal {K})$![]() and $f$
and $f$![]() satisfies $(\text {f}_1)$
satisfies $(\text {f}_1)$![]() –$(\text {f}_3)$
–$(\text {f}_3)$![]() . Let $x_0$
. Let $x_0$![]() be a strict local minimizer of $\Gamma$
be a strict local minimizer of $\Gamma$![]() . Then there exists $\lambda _0>0$
. Then there exists $\lambda _0>0$![]() , such that for any $\lambda \in (\lambda _0,\,+\infty )$
, such that for any $\lambda \in (\lambda _0,\,+\infty )$![]() , (1.1) has a weak solution $(u^\lambda,\, c^\lambda )$
, (1.1) has a weak solution $(u^\lambda,\, c^\lambda )$![]() which satisfies properties as follows$:$
which satisfies properties as follows$:$![]()
(1) the diameter of the plasma set $\{x\in D\mid u^\lambda (x)>0\}$
 is of the order $O(\lambda ^{-({1}/{2})})$
is of the order $O(\lambda ^{-({1}/{2})})$ as $\lambda \to +\infty$
as $\lambda \to +\infty$ .
.(2) For any $x\in \{x\in D\mid u^\lambda (x)>0\}$
 , $x$
, $x$ tends to $x_0$
tends to $x_0$ as $\lambda \to +\infty$
as $\lambda \to +\infty$ .
.(3) For $\lambda$
 sufficiently large, $\{x\in D\mid u^\lambda (x)=0\}$
sufficiently large, $\{x\in D\mid u^\lambda (x)=0\}$ is a $C^1$
is a $C^1$ curve and converges to a circle as $\lambda \to +\infty$
curve and converges to a circle as $\lambda \to +\infty$ .
.(4) There holds
(1.10)\begin{equation} c^\lambda={-}\frac{I}{4\pi}\ln\lambda- \frac{I}{4\pi}\ln k(x_0)+Ih(x_0,x_0)-C_*+o(1). \end{equation}Here $C_*=({1}/{2\pi })\int _{\mathbb {R}^2}\ln ({1}/{|x^*-y'|})f(U)(y')\,{\rm d}y'$
 , where $U$
, where $U$ is the unique radial function satisfying
(1.11)\begin{equation} \begin{cases} -\Delta U(x)= f(U)(x),\quad x\in \mathbb{R}^2,\\ \displaystyle\int_{\mathbb{R}^2}f(U)(x)\,{\rm d}x=I, \end{cases} \end{equation}and $x^*$
is the unique radial function satisfying
(1.11)\begin{equation} \begin{cases} -\Delta U(x)= f(U)(x),\quad x\in \mathbb{R}^2,\\ \displaystyle\int_{\mathbb{R}^2}f(U)(x)\,{\rm d}x=I, \end{cases} \end{equation}and $x^*$
 is any point of $\partial \{x\in \mathbb {R}^2\mid f(U)(x)=0\}$
is any point of $\partial \{x\in \mathbb {R}^2\mid f(U)(x)=0\}$ .
.
Remark 1.4 We give some examples to show the existence of $U$![]() in (1.11). If we choose $f(t)=t_+$
in (1.11). If we choose $f(t)=t_+$![]() , which corresponds to the classical confined plasma problem, then the unique radial $C^1$
, which corresponds to the classical confined plasma problem, then the unique radial $C^1$![]() solution of (1.11) has the explicit profile
solution of (1.11) has the explicit profile

where $s$![]() is a constant such that $1$
is a constant such that $1$![]() is the first eigenvalue of $-\Delta$
is the first eigenvalue of $-\Delta$![]() in $B_s(0)$
in $B_s(0)$![]() with Dirichlet boundary condition, $\varphi _1> 0$
with Dirichlet boundary condition, $\varphi _1> 0$![]() is the first eigenfunction of $-\Delta$
is the first eigenfunction of $-\Delta$![]() in $B_s(0)$
in $B_s(0)$![]() with $\varphi _1(0) = 1$
with $\varphi _1(0) = 1$![]() , $\varphi '_1$
, $\varphi '_1$![]() is the derivative of $\varphi _1$
is the derivative of $\varphi _1$![]() , and $c$
, and $c$![]() is a constant such that $c\int _{B_s(0) }\varphi _1\,{\rm d}x=I.$
is a constant such that $c\int _{B_s(0) }\varphi _1\,{\rm d}x=I.$![]() Note that $U\in C^{2,\alpha }(\mathbb {R}^2)$
Note that $U\in C^{2,\alpha }(\mathbb {R}^2)$![]() for any $\alpha \in (0,\,1).$
for any $\alpha \in (0,\,1).$![]() For more results, see [Reference Berestycki and Lions9, Reference Li and Peng24] for example.
For more results, see [Reference Berestycki and Lions9, Reference Li and Peng24] for example.
The idea of the proof of theorems 1.1 and 1.3 is the Arnold's variational principle, that is, considering maximization of some functional for the vorticity and analysing asymptotic behaviour of solutions. To this end, we introduce the definition of ‘vorticity’ $w=-\Delta u$![]() , which originally comes from the study of the incompressible Euler equation, see [Reference Turkington37]. Then we deduce the vorticity formulation (2.3) of (1.1) and give an equivalent description of main results, i.e., theorems 2.1 and 2.2. Indeed, we can generalize (2.3) to equation (2.5), which corresponds to solutions concentrating near several points. It suffices to prove the existence of solutions to (2.5) concentrating near strict local minimizers of an auxiliary function $\Gamma _l$
, which originally comes from the study of the incompressible Euler equation, see [Reference Turkington37]. Then we deduce the vorticity formulation (2.3) of (1.1) and give an equivalent description of main results, i.e., theorems 2.1 and 2.2. Indeed, we can generalize (2.3) to equation (2.5), which corresponds to solutions concentrating near several points. It suffices to prove the existence of solutions to (2.5) concentrating near strict local minimizers of an auxiliary function $\Gamma _l$![]() , i.e., theorems 2.3 and 2.4, which is a generalized version of theorems 2.1 and 2.2. For the proof of theorem 2.3, the key is to regard the non-autonomous term $k$
, i.e., theorems 2.3 and 2.4, which is a generalized version of theorems 2.1 and 2.2. For the proof of theorem 2.3, the key is to regard the non-autonomous term $k$![]() as a $measure$
as a $measure$![]() . Note that because of the presence of the measure $k(x)\,{\rm d}x$
. Note that because of the presence of the measure $k(x)\,{\rm d}x$![]() in the energy functional and the admissible class, the classical computation of vorticity method fails and we must give new estimates of maximizers, such as the energy $E$
in the energy functional and the admissible class, the classical computation of vorticity method fails and we must give new estimates of maximizers, such as the energy $E$![]() , the Lagrange multiplier $\mu ^\varepsilon$
, the Lagrange multiplier $\mu ^\varepsilon$![]() , the diameter and limiting location of the plasma set of $\omega ^\varepsilon$
, the diameter and limiting location of the plasma set of $\omega ^\varepsilon$![]() . For the proof of theorem 2.4, the differences from theorem 2.3 are as follows. First, to show the existence and profile of maximizers, we introduce another parameter $T$
. For the proof of theorem 2.4, the differences from theorem 2.3 are as follows. First, to show the existence and profile of maximizers, we introduce another parameter $T$![]() . Then we need to compute the upper bound of the stream function $\Psi _i^{\varepsilon,T}$
. Then we need to compute the upper bound of the stream function $\Psi _i^{\varepsilon,T}$![]() to eliminate the patch part and show that maximizers are solutions of (2.5), see lemma 4.5. Second, in order to get asymptotic behaviour of solutions, the limits of $\omega _i^{\varepsilon,T}$
to eliminate the patch part and show that maximizers are solutions of (2.5), see lemma 4.5. Second, in order to get asymptotic behaviour of solutions, the limits of $\omega _i^{\varepsilon,T}$![]() and $\Psi _i^{\varepsilon,T}$
and $\Psi _i^{\varepsilon,T}$![]() need to be estimated accurately.
need to be estimated accurately.
Remark 1.5 We give some comments about the relation between our results and results in [Reference Cao, Liu and Wei12–Reference Cao, Peng and Yan14, Reference del Pino, Kowalczyk and Musso19, Reference Li and Peng24, Reference Li and Peng25, Reference Liu28]. Note that in [Reference Cao, Liu and Wei12–Reference Cao, Peng and Yan14, Reference Liu28], the term $k$![]() has to be a constant and the nonlinearity is $f(t)=t^p_+$
has to be a constant and the nonlinearity is $f(t)=t^p_+$![]() for $p\geq 0$
for $p\geq 0$![]() . The key of proof is the use of the Lyapunov–Schmidt reduction method and the non-degeneracy of solutions to
. The key of proof is the use of the Lyapunov–Schmidt reduction method and the non-degeneracy of solutions to
for $p\geq 0.$![]() Especially in [Reference Cao, Peng and Yan14], the nonlinearity $f$
Especially in [Reference Cao, Peng and Yan14], the nonlinearity $f$![]() is a Heaviside function and not differentiable and thus the proof requires very delicate estimates. Compared to these results, in this paper we can construct solutions of (1.1) with $k$
is a Heaviside function and not differentiable and thus the proof requires very delicate estimates. Compared to these results, in this paper we can construct solutions of (1.1) with $k$![]() not a constant and general nonlinearity $f$
not a constant and general nonlinearity $f$![]() . The key of proof is to use the expansion of Green's function $G(x,\,y)$
. The key of proof is to use the expansion of Green's function $G(x,\,y)$![]() to prove the radius of the plasma set, the concentration location and the order of energy of the solution as $\lambda \to +\infty$
to prove the radius of the plasma set, the concentration location and the order of energy of the solution as $\lambda \to +\infty$![]() . Indeed, the advantage of using Arnold's variational principle is that we do not need the non-degeneracy of solutions to (1.12) with $f(t)=t^p_+$
. Indeed, the advantage of using Arnold's variational principle is that we do not need the non-degeneracy of solutions to (1.12) with $f(t)=t^p_+$![]() replaced by general $f$
replaced by general $f$![]() , which is also not known for general $f$
, which is also not known for general $f$![]() . The argument adopted here is not affected by this issue and all we need is that the nonlinear term $f$
. The argument adopted here is not affected by this issue and all we need is that the nonlinear term $f$![]() satisfies some growth conditions. This is why our result holds for general $f$
satisfies some growth conditions. This is why our result holds for general $f$![]() . When choosing $f(t)=e^t$
. When choosing $f(t)=e^t$![]() , del Pino et al. [Reference del Pino, Kowalczyk and Musso19] constructed concentrated solutions of the equation
, del Pino et al. [Reference del Pino, Kowalczyk and Musso19] constructed concentrated solutions of the equation
such that the energy concentrates near small neighbourhoods of points $x_{1,\varepsilon },\,\ldots,\, x_{n,\varepsilon }$![]() as $\varepsilon \to 0$
as $\varepsilon \to 0$![]() . These points tend to a critical point of the function defined by (1.7). When $n=1$
. These points tend to a critical point of the function defined by (1.7). When $n=1$![]() , the function is $\Gamma$
, the function is $\Gamma$![]() . Thus to some extent, the limiting behaviour of solutions in theorems 1.1 and 1.3 coincides with that in [Reference del Pino, Kowalczyk and Musso19], and the only difference between theorems 1.1, 1.3 and results in [Reference del Pino, Kowalczyk and Musso19] is the choice of the nonlinearity $f$
. Thus to some extent, the limiting behaviour of solutions in theorems 1.1 and 1.3 coincides with that in [Reference del Pino, Kowalczyk and Musso19], and the only difference between theorems 1.1, 1.3 and results in [Reference del Pino, Kowalczyk and Musso19] is the choice of the nonlinearity $f$![]() . Finally, [Reference Li and Peng24, Reference Li and Peng25] considered solutions of equation (1.5) in the case of $N\geq 3$
. Finally, [Reference Li and Peng24, Reference Li and Peng25] considered solutions of equation (1.5) in the case of $N\geq 3$![]() and $k$
and $k$![]() not a constant. As $\varepsilon \to 0$
not a constant. As $\varepsilon \to 0$![]() , the plasma region of solutions to (1.5) will shrink to maximiers of $k$
, the plasma region of solutions to (1.5) will shrink to maximiers of $k$![]() , rather than critical points of $\Gamma$
, rather than critical points of $\Gamma$![]() . Note that the total vorticity vanishes as $\varepsilon \to 0$
. Note that the total vorticity vanishes as $\varepsilon \to 0$![]() , that is, $\int _{\partial D} ({\partial u_\varepsilon }/{\partial \nu })\,{\rm d}s\to 0\ \text {as}\ \varepsilon \to 0.$
, that is, $\int _{\partial D} ({\partial u_\varepsilon }/{\partial \nu })\,{\rm d}s\to 0\ \text {as}\ \varepsilon \to 0.$![]() In contrast to these results, our result holds for $N=2$
In contrast to these results, our result holds for $N=2$![]() , and the total vorticity tends to a non-zero prescribed constant $I$
, and the total vorticity tends to a non-zero prescribed constant $I$![]() as $\varepsilon \to 0$
as $\varepsilon \to 0$![]() . That is one of main differences between our results and results in [Reference Li and Peng24, Reference Li and Peng25]. For more related works, see [Reference Bartolucci and Jevnikar4–Reference Bartsch, Pistoia and Weth6, Reference Berestycki and Brezis8, Reference de Valeriola and Van Schaftingen20, Reference Esposito, Musso and Pistoia21, Reference Wei, Ye and Zhou39] for instance.
. That is one of main differences between our results and results in [Reference Li and Peng24, Reference Li and Peng25]. For more related works, see [Reference Bartolucci and Jevnikar4–Reference Bartsch, Pistoia and Weth6, Reference Berestycki and Brezis8, Reference de Valeriola and Van Schaftingen20, Reference Esposito, Musso and Pistoia21, Reference Wei, Ye and Zhou39] for instance.
This paper is organized as follows. In § 2, we deduce the vorticity formulation of (1.1) and generalize main results to theorems 2.3 and 2.4, respectively. In § 3, we prove theorem 2.3 by solving a maximization problem of an energy functional for vorticity over admissible sets and giving asymptotic estimates of maximizers for $\varepsilon$![]() sufficiently small. The proof of theorem 2.4 will be shown in § 4.
sufficiently small. The proof of theorem 2.4 will be shown in § 4.
2. Equivalent problem of (1.1)
We first reduce (1.1) to a dual problem for the vorticity. Let us define the vorticity $w=-\Delta u$![]() . Since $u$
. Since $u$![]() is a constant on $\partial D$
is a constant on $\partial D$![]() , we have
, we have
for some constant $\mu$![]() , where $G(x,\,y)$
, where $G(x,\,y)$![]() is the Green's function of $-\Delta$
is the Green's function of $-\Delta$![]() in $D$
in $D$![]() with zero Dirichlet condition. Taking this into (1.1) we have
with zero Dirichlet condition. Taking this into (1.1) we have
Using Green's formula, the third equation of (1.1) becomes
Let us define $\varepsilon =\lambda ^{-({1}/{2})}$![]() and $\omega =w/k(x)$
and $\omega =w/k(x)$![]() . Taking $\omega$
. Taking $\omega$![]() into (2.1) and (2.2), we get equations for $\omega$
into (2.1) and (2.2), we get equations for $\omega$![]()

Note that it is equivalent to solve solution pairs $(u^\lambda,\, c^\lambda )$![]() of (1.1) and solution pairs $(\omega ^\varepsilon,\, \mu ^\varepsilon )$
of (1.1) and solution pairs $(\omega ^\varepsilon,\, \mu ^\varepsilon )$![]() of (2.3). Indeed, for a solution pair $(\omega ^\varepsilon,\, \mu ^\varepsilon )$
of (2.3). Indeed, for a solution pair $(\omega ^\varepsilon,\, \mu ^\varepsilon )$![]() of (2.3), one can recover solutions of (1.1) by letting $u^\lambda =G(k(\cdot )\omega ^\varepsilon )-\mu ^\varepsilon$
of (2.3), one can recover solutions of (1.1) by letting $u^\lambda =G(k(\cdot )\omega ^\varepsilon )-\mu ^\varepsilon$![]() and $c^\lambda =-\mu ^\varepsilon$
and $c^\lambda =-\mu ^\varepsilon$![]() .
.
For equation (2.3), we get the following equivalent description of theorems 1.1 and 1.3. Note that $\{x\in D\mid u^\lambda (x)>0\}=supp(\omega ^\varepsilon )$![]() .
.
Theorem 2.1 Suppose that $k(\cdot )$![]() satisfies $(\mathcal {K})$
satisfies $(\mathcal {K})$![]() and $f(t)=\chi _{\{t>0\}}$
and $f(t)=\chi _{\{t>0\}}$![]() . Let $x_0$
. Let $x_0$![]() be a strict local minimizer of $\Gamma$
be a strict local minimizer of $\Gamma$![]() . Then there exists $\varepsilon _0>0$
. Then there exists $\varepsilon _0>0$![]() , such that for any $\varepsilon \in (0,\,\varepsilon _0)$
, such that for any $\varepsilon \in (0,\,\varepsilon _0)$![]() , (2.3) has a weak solution pair $(\omega ^\varepsilon,\, \mu ^\varepsilon )$
, (2.3) has a weak solution pair $(\omega ^\varepsilon,\, \mu ^\varepsilon )$![]() with the following properties:
with the following properties:
(1) $diam(supp(\omega ^\varepsilon ))=O(\varepsilon )$
 .
.(2) For any $x\in supp(\omega ^\varepsilon )$
 , $x$
, $x$ tends to $x_0$
tends to $x_0$ as $\varepsilon \to 0^+$
as $\varepsilon \to 0^+$ .
.(3) For $\varepsilon$
 sufficiently small, $\partial (supp(\omega ^\varepsilon ))$
sufficiently small, $\partial (supp(\omega ^\varepsilon ))$ is a $C^1$
is a $C^1$ curve and converges to a circle as $\varepsilon \to 0^+$
curve and converges to a circle as $\varepsilon \to 0^+$ .
.(4) There holds
\[ \mu^{\varepsilon}= \frac{I}{2\pi}\ln\frac{1}{\varepsilon}+ \frac{k(x_0)}{2\pi}\int_{B_{\sqrt{{I}/{\pi k(x_0)}}}(0)}\ln\frac{1}{|x^*-y|}\,{\rm d}y-Ih(x_0,x_0)+o(1), \]where $x^*$
 is any point of $\partial B_{\sqrt {{I}/{\pi k(x_0)}}}(0)$
is any point of $\partial B_{\sqrt {{I}/{\pi k(x_0)}}}(0)$ .
.
Theorem 2.2 Suppose that $k(\cdot )$![]() satisfies $(\mathcal {K})$
satisfies $(\mathcal {K})$![]() and $f$
and $f$![]() satisfies $(\text {f}_1)$
satisfies $(\text {f}_1)$![]() –$(\text {f}_3)$
–$(\text {f}_3)$![]() . Let $x_0$
. Let $x_0$![]() be a strict local minimizer of $\Gamma$
be a strict local minimizer of $\Gamma$![]() . Then there exists $\varepsilon _0>0$
. Then there exists $\varepsilon _0>0$![]() , such that for any $\varepsilon \in (0,\,\varepsilon _0)$
, such that for any $\varepsilon \in (0,\,\varepsilon _0)$![]() , (2.3) has a weak solution pair $(\omega ^\varepsilon,\, \sigma ^\varepsilon )$
, (2.3) has a weak solution pair $(\omega ^\varepsilon,\, \sigma ^\varepsilon )$![]() with the following properties:
with the following properties:
(1) $diam(supp(\omega ^\varepsilon ))=O(\varepsilon )$
 .
.(2) For any $x\in supp(\omega ^\varepsilon )$
 , $x$
, $x$ tends to $x_0$
tends to $x_0$ as $\varepsilon \to 0^+$
as $\varepsilon \to 0^+$ .
.(3) For $\varepsilon$
 sufficiently small, $\partial (supp(\omega ^\varepsilon ))$
sufficiently small, $\partial (supp(\omega ^\varepsilon ))$ is a $C^1$
is a $C^1$ curve and converges to a circle as $\varepsilon \to 0^+$
curve and converges to a circle as $\varepsilon \to 0^+$ .
.(4) There holds
\[ \sigma^{\varepsilon}= \frac{I}{2\pi}\ln\frac{1}{\varepsilon}+ \frac{I}{4\pi}\ln k(x_0)-Ih(x_0,x_0)+C_*+o(1), \]where $C_*=({1}/{2\pi })\int _{\mathbb {R}^2}\ln ({1}/{|x^*-y'|})f(U)(y')\,{\rm d}y'$
 , $U$
, $U$ is the unique radial function satisfying (1.11) and $x^*$
is the unique radial function satisfying (1.11) and $x^*$ is any point of $\partial \{x\in \mathbb {R}^2\mid f(U)(x)=0\}$
is any point of $\partial \{x\in \mathbb {R}^2\mid f(U)(x)=0\}$ .
.
Indeed, to prove theorems 2.1 and 2.2, one can directly consider solutions of (1.1) concentrating near several distinct points. Let $l$![]() be an integer and $d_i\in \mathbb {R}/\{0\} (i=1,\,\ldots,\,l)$
be an integer and $d_i\in \mathbb {R}/\{0\} (i=1,\,\ldots,\,l)$![]() be $l$
be $l$![]() constants. Let us introduce an auxiliary function $\Gamma _l$
constants. Let us introduce an auxiliary function $\Gamma _l$![]() which generalizes the function $\Gamma$
which generalizes the function $\Gamma$![]() defined by (1.8). Define
defined by (1.8). Define

where $\mathcal {H}_{l}$![]() is defined by (1.4). Notice that if $l=1$
is defined by (1.4). Notice that if $l=1$![]() , then the auxiliary function is $\Gamma (x)$
, then the auxiliary function is $\Gamma (x)$![]() .
.
Let $(x_{0,1},\,\ldots,\,x_{0,l})$![]() be a strict local minimizer of $\Gamma _l$
be a strict local minimizer of $\Gamma _l$![]() , that is, $(x_{0,1},\,\ldots,\,x_{0,l})$
, that is, $(x_{0,1},\,\ldots,\,x_{0,l})$![]() is the unique minimizer of $\Gamma _l$
is the unique minimizer of $\Gamma _l$![]() over $\overline {B_1}\times \cdots \times \overline {B_l}$
over $\overline {B_1}\times \cdots \times \overline {B_l}$![]() . Here $B_i:=B_{\delta }(x_{0,i})$
. Here $B_i:=B_{\delta }(x_{0,i})$![]() for some $\delta >0$
for some $\delta >0$![]() sufficiently small such that $\overline {B_i}\subset D$
sufficiently small such that $\overline {B_i}\subset D$![]() and $\overline {B_i}\cap \overline {B_j}=\varnothing$
and $\overline {B_i}\cap \overline {B_j}=\varnothing$![]() for $i\neq j$
for $i\neq j$![]() . Consider solution pairs $(\omega ^\varepsilon,\, \mu ^\varepsilon _i) (i=1,\,\ldots,\,l)$
. Consider solution pairs $(\omega ^\varepsilon,\, \mu ^\varepsilon _i) (i=1,\,\ldots,\,l)$![]() of the following equations
of the following equations

where $sgn(d_i)=1$![]() if $d_i>0$
if $d_i>0$![]() and $sgn(d_i)=-1$
and $sgn(d_i)=-1$![]() if $d_i<0$
if $d_i<0$![]() . $f_i$
. $f_i$![]() are $l$
are $l$![]() given functions and $\mu _i$
given functions and $\mu _i$![]() are unknown constants. The following result shows that for any strict local minimizer $(x_{0,1},\,\ldots,\,x_{0,l})$
are unknown constants. The following result shows that for any strict local minimizer $(x_{0,1},\,\ldots,\,x_{0,l})$![]() of $\Gamma _l$
of $\Gamma _l$![]() , there exist solutions of (2.5) concentrating near $l$
, there exist solutions of (2.5) concentrating near $l$![]() distinct points $x_{0,i}$
distinct points $x_{0,i}$![]() .
.
Theorem 2.3 Suppose that $k$![]() satisfies $(\mathcal {K})$
satisfies $(\mathcal {K})$![]() and $f_i(t)=\chi _{\{t>0\}}$
and $f_i(t)=\chi _{\{t>0\}}$![]() ($i=1,\,\ldots,\,l$
($i=1,\,\ldots,\,l$![]() ). Then for any strict local minimizer $(x_{0,1},\,\ldots,\,x_{0,l})$
). Then for any strict local minimizer $(x_{0,1},\,\ldots,\,x_{0,l})$![]() of $\Gamma _l$
of $\Gamma _l$![]() , there exists $\varepsilon _0>0$
, there exists $\varepsilon _0>0$![]() , such that for any $\varepsilon \in (0,\,\varepsilon _0)$
, such that for any $\varepsilon \in (0,\,\varepsilon _0)$![]() , (2.5) has a weak solution pair $(\omega ^\varepsilon,\, \mu ^\varepsilon _i)$
, (2.5) has a weak solution pair $(\omega ^\varepsilon,\, \mu ^\varepsilon _i)$![]() with the following properties:
with the following properties:
(1) Define $\omega _i=\omega \chi _{ B_i}$
 . Then $diam(supp(\omega _i^\varepsilon ))=O(\varepsilon )$
. Then $diam(supp(\omega _i^\varepsilon ))=O(\varepsilon )$ .
.(2) The support of $\omega _i^\varepsilon$
 tends to $x_{0,i}$
tends to $x_{0,i}$ as $\varepsilon \to 0^+$
as $\varepsilon \to 0^+$ , that is,
\[ \lim_{\varepsilon \to 0^+}\sup_{x\in supp(\omega_i^\varepsilon)}|x- x_{0,i}|=0. \]
, that is,
\[ \lim_{\varepsilon \to 0^+}\sup_{x\in supp(\omega_i^\varepsilon)}|x- x_{0,i}|=0. \]
(3) For $\varepsilon$
 sufficiently small, $\partial (supp(\omega _i^\varepsilon ))$
sufficiently small, $\partial (supp(\omega _i^\varepsilon ))$ is a $C^1$
is a $C^1$ curve and converges to a circle as $\varepsilon \to 0^+$
curve and converges to a circle as $\varepsilon \to 0^+$ .
.(4) There holds
\begin{align*} \mu_i^{\varepsilon}& = \frac{|d_i|}{2\pi}\ln\frac{1}{\varepsilon}+ \frac{k(x_{0,i})}{2\pi}\int_{B_{\sqrt{{|d_i|}/{\pi k(x_{0,i})}}}(0)}\ln\frac{1}{|x^*-y|}\,{\rm d}y-|d_i|h(x_{0,i},x_{0,i})\\ & \quad+sgn(d_i)\sum_{j=1,j\neq i}^ld_jG(x_{0,i},x_{0,j})+o(1), \end{align*}where $x^*$
 is any point of $\partial B_{B_{\sqrt {{|d_i|}/{\pi k(x_{0,i})}}}(0)}$
is any point of $\partial B_{B_{\sqrt {{|d_i|}/{\pi k(x_{0,i})}}}(0)}$ .
.
Theorem 2.4 Suppose that $k(\cdot )$![]() satisfies $(\mathcal {K})$
satisfies $(\mathcal {K})$![]() and $f_i$
and $f_i$![]() satisfies $(\text {f}_1)-(\text {f}_3)$
satisfies $(\text {f}_1)-(\text {f}_3)$![]() ($i=1,\,\ldots,\,l$
($i=1,\,\ldots,\,l$![]() ). Then for any strict local minimizer $(x_{0,1},\,\ldots,\,x_{0,l})$
). Then for any strict local minimizer $(x_{0,1},\,\ldots,\,x_{0,l})$![]() of $\Gamma _l$
of $\Gamma _l$![]() , there exists $\varepsilon _0>0$
, there exists $\varepsilon _0>0$![]() , such that for any $\varepsilon \in (0,\,\varepsilon _0)$
, such that for any $\varepsilon \in (0,\,\varepsilon _0)$![]() , (2.5) has a weak solution pair $(\omega ^\varepsilon,\, \sigma ^\varepsilon _i)$
, (2.5) has a weak solution pair $(\omega ^\varepsilon,\, \sigma ^\varepsilon _i)$![]() with the same properties as those in theorem 2.3. Moreover, $\sigma ^\varepsilon _i$
with the same properties as those in theorem 2.3. Moreover, $\sigma ^\varepsilon _i$![]() has the following estimates
has the following estimates

Here $C_i=({1}/{2\pi })\int _{\mathbb {R}^2}\ln ({1}/{|x^*-y'|})f_i\circ U_i(y')\,{\rm d}y'$![]() , where $U_i$
, where $U_i$![]() is the unique radial function satisfying
is the unique radial function satisfying

and $x^*$![]() is any point of $\partial \{x\in \mathbb {R}^2\mid f_i\circ U_i(x)=0\}$
is any point of $\partial \{x\in \mathbb {R}^2\mid f_i\circ U_i(x)=0\}$![]() .
.
Note that when $l=1$![]() , results in theorems 2.3 and 2.4 reduce to those in theorems 2.1 and 2.2. We will give the proof of theorems 2.3 and 2.4 directly in the following sections.
, results in theorems 2.3 and 2.4 reduce to those in theorems 2.1 and 2.2. We will give the proof of theorems 2.3 and 2.4 directly in the following sections.
3. Proof of theorem 2.3
3.1. Variational problem
In this section, we give the proof of theorem 2.3. We define the energy functional
where $\,{\rm d}\theta (x)=k(x)\,{\rm d}x$![]() is a $measure$
is a $measure$![]() deduced by the non-autonomous term $k$
deduced by the non-autonomous term $k$![]() . By the assumption $(\mathcal {K})$
. By the assumption $(\mathcal {K})$![]() , we know that $\,{\rm d}\theta (x)$
, we know that $\,{\rm d}\theta (x)$![]() is equivalent to the two-dimensional Lebesgue measure $\,{\rm d}x$
is equivalent to the two-dimensional Lebesgue measure $\,{\rm d}x$![]() .
.
Define a constraint set

The difference between $\mathcal {M}_{\varepsilon }(D)$![]() and the classical results is that we impose the $L^1(B_i,\, \,{\rm d}\theta (x))$
and the classical results is that we impose the $L^1(B_i,\, \,{\rm d}\theta (x))$![]() norm of $\omega _i$
norm of $\omega _i$![]() to be $d_i$
to be $d_i$![]() , rather than the $L^1(B_i,\, \,{\rm d}x)$
, rather than the $L^1(B_i,\, \,{\rm d}x)$![]() norm, which may cause essential difficulty in proving asymptotic behaviour of solutions.
norm, which may cause essential difficulty in proving asymptotic behaviour of solutions.
Consider the maximization problem
To begin with, we show the existence and profile of maximizers of $E$![]() over $\mathcal {M}_{\varepsilon }(D)$
over $\mathcal {M}_{\varepsilon }(D)$![]() .
.
Proposition 3.1 There exists $\omega ^{\varepsilon }\in \mathcal {M}_{\varepsilon }(D)$![]() , such that $E(\omega ^{\varepsilon })=\sup _{\tilde {\omega }\in \mathcal {M}_{\varepsilon }(D)}E(\tilde {\omega })$
, such that $E(\omega ^{\varepsilon })=\sup _{\tilde {\omega }\in \mathcal {M}_{\varepsilon }(D)}E(\tilde {\omega })$![]() .
.
Proof. Since $G(\cdot,\,\cdot )\in L^1(D\times D)$![]() , we know that $E$
, we know that $E$![]() is bounded from above on the set $\mathcal {M}_{\varepsilon }(D)$
is bounded from above on the set $\mathcal {M}_{\varepsilon }(D)$![]() . Now we choose a maximization sequence $\{\omega ^n\}\subset \mathcal {M}_{\varepsilon }(D)$
. Now we choose a maximization sequence $\{\omega ^n\}\subset \mathcal {M}_{\varepsilon }(D)$![]() of $E$
of $E$![]() , that is,
, that is,
By direct computations we can prove that $\mathcal {M}_{\varepsilon }$![]() is a sequentially compact subset of $L^2(D)$
is a sequentially compact subset of $L^2(D)$![]() in the weak topology. So we may assume that, up to a subsequence, $\omega ^n\to \omega ^{\varepsilon }$
in the weak topology. So we may assume that, up to a subsequence, $\omega ^n\to \omega ^{\varepsilon }$![]() weakly in $L^2(D)$
weakly in $L^2(D)$![]() as $n\to +\infty$
as $n\to +\infty$![]() for some $\omega ^{\varepsilon }\in \mathcal {M}_{\varepsilon }$
for some $\omega ^{\varepsilon }\in \mathcal {M}_{\varepsilon }$![]() . So
. So
By elliptic regularity theory,
for any $p>1$![]() , from which we deduce that
, from which we deduce that
So $\omega ^{\varepsilon }$![]() is a maximizer of $E$
is a maximizer of $E$![]() over $\mathcal {M}_{\varepsilon }$
over $\mathcal {M}_{\varepsilon }$![]() .
.
We define $\omega _i^{\varepsilon }=\omega ^{\varepsilon } \chi _{B_i}$![]() to be each piece of the maximizer. Then using classical idea in [Reference Turkington37] we can get that the maximizers has the form of (2.5).
to be each piece of the maximizer. Then using classical idea in [Reference Turkington37] we can get that the maximizers has the form of (2.5).
Proposition 3.2 Let $\omega ^{\varepsilon }$![]() be a maximizer defined as in lemma 3.1. Then
be a maximizer defined as in lemma 3.1. Then

where $\psi _i^\varepsilon :=sgn(d_i)\mathcal {G}(k \omega ^\varepsilon )-\mu ^\varepsilon _i$![]() and $\mu ^\varepsilon _i$
and $\mu ^\varepsilon _i$![]() are constants dependent on $\varepsilon$
are constants dependent on $\varepsilon$![]() for $i=1,\,\ldots,\,l$
for $i=1,\,\ldots,\,l$![]() . Moreover, for $\varepsilon$
. Moreover, for $\varepsilon$![]() sufficiently small there holds
sufficiently small there holds
where $C_0$![]() is a negative constant independent of $\varepsilon$
is a negative constant independent of $\varepsilon$![]() .
.
Proof. Let $\omega ^{\varepsilon }$![]() be a maximizer. For any ${\omega }\in \mathcal {M}_{\varepsilon }$
be a maximizer. For any ${\omega }\in \mathcal {M}_{\varepsilon }$![]() , we set
, we set
Since $\mathcal {M}_{\varepsilon }$![]() is a convex set, $\omega _{(s)}\in \mathcal {M}_{\varepsilon }$
is a convex set, $\omega _{(s)}\in \mathcal {M}_{\varepsilon }$![]() for any $s\in [0,\,1]$
for any $s\in [0,\,1]$![]() . So $E(\omega _{(s)})\leq E(\omega ^\varepsilon )$
. So $E(\omega _{(s)})\leq E(\omega ^\varepsilon )$![]() , which implies that
, which implies that
that is,
for any ${\omega }\in \mathcal {M}_{\varepsilon }(D).$![]() By the definition of $\mathcal {M}_{\varepsilon }(D)$
By the definition of $\mathcal {M}_{\varepsilon }(D)$![]() and the bathtub principle (see [Reference Lieb and Loss26]), we get for any $i=1,\,\ldots,\,l$
and the bathtub principle (see [Reference Lieb and Loss26]), we get for any $i=1,\,\ldots,\,l$![]()

where $\mu _i^{\varepsilon }$![]() is a constant satisfying
is a constant satisfying
Notice that $|\{x\in B_i\mid sgn(d_i) \mathcal {G}(k \omega ^{\varepsilon } ) >s\}|_{\theta }$![]() means that the $\,{\rm d}\theta (x)-$
means that the $\,{\rm d}\theta (x)-$![]() measure of the set $\{x\in B_i\mid sgn(d_i) \mathcal {G}(k \omega ^{\varepsilon } ) >s\}$
measure of the set $\{x\in B_i\mid sgn(d_i) \mathcal {G}(k \omega ^{\varepsilon } ) >s\}$![]() . Thus using (3.5), we get that
. Thus using (3.5), we get that
where $\psi _i^{\varepsilon }=sgn(d_i)\mathcal {G}(k \omega ^{\varepsilon } )-\mu ^{\varepsilon }_i$![]() . So (3.3) is proved.
. So (3.3) is proved.
It remains to prove that $\mu _i^{\varepsilon }\geq C_0$![]() for some $C_0$
for some $C_0$![]() . In fact for any $x\in B_i$
. In fact for any $x\in B_i$![]() ,
,

Combining (3.6) with (3.7), we can get (3.4) by letting $C_0=-\sum _{j\neq i}k_1|d_j| \max _{x\in B_i, y\in B_j}|G(x,\,y)|$![]() .
.
Remark 3.3 Indeed, one can repeat the proof in [Reference Turkington37] to prove proposition 3.2. Without loss of generality, we assume $d_i>0$![]() . For any $z_1,\,z_2 \in L^{\infty }(D)$
. For any $z_1,\,z_2 \in L^{\infty }(D)$![]() satisfying
satisfying

where $a>0$![]() is sufficiently small, we define a family of functions $\omega _s=\omega ^{\varepsilon }+ s(z_1-z_2)$
is sufficiently small, we define a family of functions $\omega _s=\omega ^{\varepsilon }+ s(z_1-z_2)$![]() , $s>0$
, $s>0$![]() . Then one can prove that $\omega _s\in M_{\varepsilon }(D)$
. Then one can prove that $\omega _s\in M_{\varepsilon }(D)$![]() for $s>0$
for $s>0$![]() sufficiently small. So ${{\rm d}E(\omega _s)}/{{\rm d}s}|_{s=0^+}\leq 0$
sufficiently small. So ${{\rm d}E(\omega _s)}/{{\rm d}s}|_{s=0^+}\leq 0$![]() , which implies that
, which implies that
From this we get
Define $\mu _i^{\varepsilon }:=\inf _{\left \{x\in D|\omega ^{\varepsilon }(x)>0\right \}\cap B_i} \mathcal {G}(k \omega ^{\varepsilon })(x),$![]() it is not hard to prove that
it is not hard to prove that

On $\left \{x \in D\mid \mathcal {G}(k \omega ^{\varepsilon })=\mu _i^{\varepsilon }\right \}$![]() , by properties of Sobolev space, we have $k \omega ^{\varepsilon }=0$
, by properties of Sobolev space, we have $k \omega ^{\varepsilon }=0$![]() . So $\omega ^{\varepsilon }=0$
. So $\omega ^{\varepsilon }=0$![]() a.e. in $\left \{x \in D\mid \mathcal {G}(k \omega ^{\varepsilon })=\mu _i^{\varepsilon }\right \}$
a.e. in $\left \{x \in D\mid \mathcal {G}(k \omega ^{\varepsilon })=\mu _i^{\varepsilon }\right \}$![]() . Thus
. Thus
So using this method, we can also get the same results as that in proposition 3.2.
3.2. Asymptotic analysis
In the following, we give asymptotic estimates of $\omega ^\varepsilon _i$![]() . We first give lower bound of the energy $E_i(\omega ^{\varepsilon })$
. We first give lower bound of the energy $E_i(\omega ^{\varepsilon })$![]() and the Lagrange multiplier $\mu _i^\varepsilon$
and the Lagrange multiplier $\mu _i^\varepsilon$![]() . Note that since the measure in (3.1) is $k(x)\,{\rm d}x$
. Note that since the measure in (3.1) is $k(x)\,{\rm d}x$![]() , we need to choose test functions properly. Then using the properties of function $\ln x$
, we need to choose test functions properly. Then using the properties of function $\ln x$![]() and the theory of rearrangement function, we get that the diameter of the plasma set of $\omega ^{\varepsilon }$
and the theory of rearrangement function, we get that the diameter of the plasma set of $\omega ^{\varepsilon }$![]() is the order of $\varepsilon$
is the order of $\varepsilon$![]() and the limiting location is a minimizer of $\Gamma _l$
and the limiting location is a minimizer of $\Gamma _l$![]() .
.
To simplify the proof , we define the energy functional associated with $\omega ^\varepsilon _i$![]()
Direct computation shows that

We first give a rough lower bound of $E_i(\omega ^{\varepsilon })$![]() .
.
Lemma 3.4 Let $\omega ^{\varepsilon }$![]() be a maximizer. Then for $i=1,\,\ldots,\,l$
be a maximizer. Then for $i=1,\,\ldots,\,l$![]()
Proof. We choose

where $t(\varepsilon )\in (({1}/{2})\sqrt {{|d_i|}/{\pi k(x_{0,i})}},\, 2\sqrt {{|d_i|}/{\pi k(x_{0,i})}})$![]() satisfies $\int _{B_i}\tilde {\omega }_i^{\varepsilon }\,{\rm d}\theta (x)=d_i$
satisfies $\int _{B_i}\tilde {\omega }_i^{\varepsilon }\,{\rm d}\theta (x)=d_i$![]() . Direct calculations show that $t(\varepsilon )$
. Direct calculations show that $t(\varepsilon )$![]() exists for $\varepsilon$
exists for $\varepsilon$![]() sufficiently small and $\lim _{\varepsilon \to 0^+}t(\varepsilon )=\sqrt {{|d_i|}/{\pi k(x_{0,i})}}$
sufficiently small and $\lim _{\varepsilon \to 0^+}t(\varepsilon )=\sqrt {{|d_i|}/{\pi k(x_{0,i})}}$![]() . Then $\tilde {\omega }^{\varepsilon }\in \mathcal {M}_{\varepsilon }(D)$
. Then $\tilde {\omega }^{\varepsilon }\in \mathcal {M}_{\varepsilon }(D)$![]() and $E(\omega ^\varepsilon )\geq E(\tilde {\omega }^{\varepsilon })$
and $E(\omega ^\varepsilon )\geq E(\tilde {\omega }^{\varepsilon })$![]() , which implies that
, which implies that

Since the diameter of $supp(\tilde {\omega }_i^\varepsilon )$![]() is $\sqrt {({|d_i|}/{\pi k(x_{0,i})})}\varepsilon +o(\varepsilon )$
is $\sqrt {({|d_i|}/{\pi k(x_{0,i})})}\varepsilon +o(\varepsilon )$![]() , we have
, we have
By the choice of $B_i$![]() we obtain
we obtain
Taking (3.12), (3.13) into (3.11) and using (3.10), we get the desired result.
Then, one can get the lower bound of Lagrange multipliers $\mu _i^\varepsilon$![]() .
.
Lemma 3.5 Let $\omega ^{\varepsilon }$![]() be a maximizer and $\mu _i^\varepsilon$
be a maximizer and $\mu _i^\varepsilon$![]() be the associated Lagrange multiplier. Then there holds
be the associated Lagrange multiplier. Then there holds
Proof. Let us first prove that
Using the definition of $B_i$![]() we get
we get

Define $P^\varepsilon _i=(sgn(d_i)\mathcal {G}(k\omega _i^\varepsilon )-\mu _i^{\varepsilon }+C_0)_+$![]() and $\bar {P}^\varepsilon _i=(sgn(d_i)\mathcal {G}(k\omega ^\varepsilon )-\mu _i^{\varepsilon }+C_0)_+$
and $\bar {P}^\varepsilon _i=(sgn(d_i)\mathcal {G}(k\omega ^\varepsilon )-\mu _i^{\varepsilon }+C_0)_+$![]() . So by (3.4), $P^\varepsilon _i,\,\bar {P}^\varepsilon _i\in H^1_0(D)$
. So by (3.4), $P^\varepsilon _i,\,\bar {P}^\varepsilon _i\in H^1_0(D)$![]() . On the one hand, we get
. On the one hand, we get
On the other hand, by the choice of $C_0$![]() we have $supp(\bar {P}^\varepsilon _i)\cap B_i\subseteq supp(\omega _i^\varepsilon ),\,$
we have $supp(\bar {P}^\varepsilon _i)\cap B_i\subseteq supp(\omega _i^\varepsilon ),\,$![]() which implies that
which implies that

Using the continuous embedding $W^{1,1}(B_i)\subset L^2(B_i)$![]() , we have
, we have

So for $\varepsilon$![]() sufficiently small, we get $\int _{D}P^\varepsilon _i |\omega _i^\varepsilon | \,{\rm d}\theta (x)\leq ({Ck_1 }/{ \varepsilon ^2})|supp(\omega _i^\varepsilon )|^{{1}/{2}} \int _{supp(\omega _i^\varepsilon )} |\nabla P^\varepsilon _i| \,{\rm d}{x}+O(1).$
sufficiently small, we get $\int _{D}P^\varepsilon _i |\omega _i^\varepsilon | \,{\rm d}\theta (x)\leq ({Ck_1 }/{ \varepsilon ^2})|supp(\omega _i^\varepsilon )|^{{1}/{2}} \int _{supp(\omega _i^\varepsilon )} |\nabla P^\varepsilon _i| \,{\rm d}{x}+O(1).$![]() By Hölder's inequality,
By Hölder's inequality,

Combining (3.17), (3.18) and (3.16), we get (3.15).
Notice that
By lemma 3.5, one can prove that the diameter of $\omega _i^{\varepsilon }$![]() is $O(\varepsilon )$
is $O(\varepsilon )$![]() .
.
Lemma 3.6 Let $\omega ^{\varepsilon }$![]() be a maximizer. Then
be a maximizer. Then
where $r_1,\, R_1>0$![]() are constants independent of $\varepsilon$
are constants independent of $\varepsilon$![]() .
.
Proof. By the choice of $\mathcal {M}_\varepsilon (D)$![]() , we know that $k_1|supp(\omega _i^\varepsilon )|\geq |d_i| \varepsilon ^2.$
, we know that $k_1|supp(\omega _i^\varepsilon )|\geq |d_i| \varepsilon ^2.$![]() This implies that
This implies that
for some $r_1> 0$![]() .
.
On the other hand, for any $x\in supp( \omega _i^\varepsilon )$![]() , using (3.3) we have $\psi _i^{\varepsilon }(x)\geq 0$
, using (3.3) we have $\psi _i^{\varepsilon }(x)\geq 0$![]() , which shows that
, which shows that

Thus by (3.14), we have
From the classical estimates in [Reference Turkington37], we get $diam(supp( \omega _i^\varepsilon ))\le R_1\varepsilon$![]() for some $R_1>1$
for some $R_1>1$![]() .
.
We now estimate the limiting location of $\omega _i^{\varepsilon }$![]() as $\varepsilon$
as $\varepsilon$![]() tends to 0. To begin with, we define the $\theta$
tends to 0. To begin with, we define the $\theta$![]() -weighted mass centre of $\omega _i^\varepsilon$
-weighted mass centre of $\omega _i^\varepsilon$![]() as
as
Then $\bar {X}_i^\varepsilon \in \overline {B_i}$![]() . Since $\overline {B_i}$
. Since $\overline {B_i}$![]() is compact, we may choose a subsequence of $\{\bar {X}_i^{\varepsilon _n}\}_{n=1}^{ \infty }$
is compact, we may choose a subsequence of $\{\bar {X}_i^{\varepsilon _n}\}_{n=1}^{ \infty }$![]() (still denoted by $\bar {X}_i^\varepsilon$
(still denoted by $\bar {X}_i^\varepsilon$![]() ) satisfying
) satisfying
Define the scaled function of $\omega _{i}^\varepsilon$![]()
where $D_\varepsilon =\{x\in \mathbb {R}^2\mid \varepsilon x+\bar {X}_i^\varepsilon \in D\}$![]() . Then using the definition of $M_\varepsilon (D)$
. Then using the definition of $M_\varepsilon (D)$![]() , we have $0\leq \zeta ^\varepsilon _i\leq 1.$
, we have $0\leq \zeta ^\varepsilon _i\leq 1.$![]() Moreover, by lemma 3.6 we get that the support set of $\zeta ^\varepsilon _i$
Moreover, by lemma 3.6 we get that the support set of $\zeta ^\varepsilon _i$![]() is contained in $B_{R_1}(0)$
is contained in $B_{R_1}(0)$![]() . Using $\int _{B_i}\omega _i^\varepsilon \,{\rm d}\theta (x)=d_i$
. Using $\int _{B_i}\omega _i^\varepsilon \,{\rm d}\theta (x)=d_i$![]() , we get
, we get
Since $\zeta ^\varepsilon _i$![]() is uniformly bounded in $L^p(B_{R_1}(0))$
is uniformly bounded in $L^p(B_{R_1}(0))$![]() for any $p\in [1,\,+\infty ]$
for any $p\in [1,\,+\infty ]$![]() , then still up to a subsequence, we may assume that $\zeta ^\varepsilon _i\to \zeta ^*_i$
, then still up to a subsequence, we may assume that $\zeta ^\varepsilon _i\to \zeta ^*_i$![]() in $L^p$
in $L^p$![]() weak topology and $L^{\infty }$
weak topology and $L^{\infty }$![]() weak star topology for some $\zeta ^*_i\in L^\infty (B_{R_1}(0))$
weak star topology for some $\zeta ^*_i\in L^\infty (B_{R_1}(0))$![]() as $\varepsilon \to 0.$
as $\varepsilon \to 0.$![]() We now calculate the necessary condition of $\mathbf {x^*_i}$
We now calculate the necessary condition of $\mathbf {x^*_i}$![]() and the profile of $\zeta ^*_i$
and the profile of $\zeta ^*_i$![]() . To this end, we define a real-valued function
. To this end, we define a real-valued function
Direct calculation shows that $Q_i(t)=({d_i^2}/{8\pi })\ln t+C^*$![]() , where $C^*$
, where $C^*$![]() is a universal constant.
is a universal constant.
Proposition 3.7 There holds

As a consequence, $\mathbf {x^*_i}=x_{0,i}$![]() for $i=1,\,\ldots,\,l.$
for $i=1,\,\ldots,\,l.$![]() Moreover,
Moreover,
in $L^p$![]() topology for any $p>1$
topology for any $p>1$![]() as $\varepsilon \to 0.$
as $\varepsilon \to 0.$![]()
Proof. By proposition 3.2, we know that $|\omega ^\varepsilon _i|$![]() is a vortex patch with height ${1}/{\varepsilon ^2}$
is a vortex patch with height ${1}/{\varepsilon ^2}$![]() , so $\zeta ^\varepsilon _i$
, so $\zeta ^\varepsilon _i$![]() is a vortex patch with height 1. So the limiting function $\zeta ^*_i$
is a vortex patch with height 1. So the limiting function $\zeta ^*_i$![]() is also a vortex patch with height 1, that is, $\zeta ^*_i=\chi _{U^*}$
is also a vortex patch with height 1, that is, $\zeta ^*_i=\chi _{U^*}$![]() for some set $U^*\subseteq B_{R_1}(0)$
for some set $U^*\subseteq B_{R_1}(0)$![]() .
.
Since $k$![]() is a $C^0$
is a $C^0$![]() function and $\lim _{\varepsilon \to 0^+}\bar {X}_i^\varepsilon =\mathbf {x^*_i}$
function and $\lim _{\varepsilon \to 0^+}\bar {X}_i^\varepsilon =\mathbf {x^*_i}$![]() , we have
, we have
so by (3.19)
On the one hand, by the definition of $E(\omega ^\varepsilon )$![]() and lemma 3.6, we get
and lemma 3.6, we get

Since $\zeta ^\varepsilon _i\to \zeta ^*_i$![]() in $L^p$
in $L^p$![]() weak topology and $k(\varepsilon x+\bar {X}_i^\varepsilon )\to k(\mathbf {x^*_i})$
weak topology and $k(\varepsilon x+\bar {X}_i^\varepsilon )\to k(\mathbf {x^*_i})$![]() uniformly as $\varepsilon \to 0$
uniformly as $\varepsilon \to 0$![]() , we have
, we have

where we have used the $L^p$![]() theory in elliptic equations and the compact embedding theorem. Thus
theory in elliptic equations and the compact embedding theorem. Thus

where the second inequality we have used (3.23) and the Riesz's rearrangement inequality.
On the other hand, for any $z_i\in B_i (i=1,\,\ldots,\,l)$![]() , we choose a function $\hat {\omega }^\varepsilon =\sum _{i=1}^l\hat {\omega }^\varepsilon _i,\,$
, we choose a function $\hat {\omega }^\varepsilon =\sum _{i=1}^l\hat {\omega }^\varepsilon _i,\,$![]() where $\hat {\omega }^\varepsilon _i$
where $\hat {\omega }^\varepsilon _i$![]() is defined by
is defined by
Here $\tau _i(\varepsilon )\in (({1}/{2})\sqrt { {|d_i|}/{\pi k(z_i)}},\, 2\sqrt {{|d_i|}/{\pi k(z_i)}})$![]() is chosen to satisfy $\int _{B_i}\hat {\omega }^\varepsilon _i(x) {\rm d}\theta (x)=d_i$
is chosen to satisfy $\int _{B_i}\hat {\omega }^\varepsilon _i(x) {\rm d}\theta (x)=d_i$![]() . Then direct calculation shows that such $\tau _i(\varepsilon )$
. Then direct calculation shows that such $\tau _i(\varepsilon )$![]() exists for $\varepsilon$
exists for $\varepsilon$![]() sufficiently small and $\lim _{\varepsilon \to 0^+}\tau _i(\varepsilon )=\sqrt {{|d_i|}/{\pi k(z_i)}}$
sufficiently small and $\lim _{\varepsilon \to 0^+}\tau _i(\varepsilon )=\sqrt {{|d_i|}/{\pi k(z_i)}}$![]() . By the definition of $\hat {\omega }^\varepsilon$
. By the definition of $\hat {\omega }^\varepsilon$![]() , we obtain $\hat {\omega }^\varepsilon \in \mathcal {M}_\varepsilon (D)$
, we obtain $\hat {\omega }^\varepsilon \in \mathcal {M}_\varepsilon (D)$![]() .
.
For $E(\hat {\omega }^\varepsilon )$![]() , similarly as calculations in (3.24), we obtain
, similarly as calculations in (3.24), we obtain

By $E(\omega ^\varepsilon )\geq E(\hat {\omega }^\varepsilon )$![]() , (3.24) and (3.25), we get
, (3.24) and (3.25), we get

Thus we get (3.21). Notice that $\mathcal {H}_l(x_1,\,x_2,\,\ldots,\,x_l)-\sum _{i=1}^lQ_i(k(x_i))=\Gamma _l(x_1,\,x_2, \ldots,\,x_l)+C_0^*$![]() , where $C_0^*$
, where $C_0^*$![]() is a universal constant. Then by the assumption that $(x_{0,1},\,\ldots,\,x_{0,l})$
is a universal constant. Then by the assumption that $(x_{0,1},\,\ldots,\,x_{0,l})$![]() is a strict local minimizer of $\Gamma _l$
is a strict local minimizer of $\Gamma _l$![]() , we get $\mathbf {x^*_i}=x_{0,i}.$
, we get $\mathbf {x^*_i}=x_{0,i}.$![]()
It suffices to prove (3.22). Indeed by (3.24) we have

Using strict Rearrangement inequality (see theorem 3.9, [Reference Lieb and Loss26]), there exists a translation $\bar {\mathcal {T}}$![]() such that $\mathcal {T}(\zeta ^*_i)=\chi _{B_{\sqrt {{|d_i|}/{\pi k(\mathbf {x^*_i})}}}(0)}$
such that $\mathcal {T}(\zeta ^*_i)=\chi _{B_{\sqrt {{|d_i|}/{\pi k(\mathbf {x^*_i})}}}(0)}$![]() . Notice that both the centre of $\zeta ^*_i$
. Notice that both the centre of $\zeta ^*_i$![]() and the centre of $B_{\sqrt {{|d_i|}/{\pi k(\mathbf {x^*_i})}}}(0)$
and the centre of $B_{\sqrt {{|d_i|}/{\pi k(\mathbf {x^*_i})}}}(0)$![]() are the origin, we get $\bar {\mathcal {T}}=id$
are the origin, we get $\bar {\mathcal {T}}=id$![]() , namely, $\zeta ^*_i=\chi _{B_{\sqrt {{|d_i|}/{\pi k(\mathbf {x^*_i})}}}(0)}$
, namely, $\zeta ^*_i=\chi _{B_{\sqrt {{|d_i|}/{\pi k(\mathbf {x^*_i})}}}(0)}$![]() .
.
Finally, by (3.19) we have $\int _{B_{R_1}(0)}k(\varepsilon x+\bar {X}_i^\varepsilon )(\zeta ^\varepsilon _i(x))^p\,{\rm d}x=|d_i|,\,$![]() which implies that
which implies that

Using the strict convexity of $L^p$![]() norm, we finish the proof.
norm, we finish the proof.
Remark 3.8 By proposition 3.7, we know that $E(\omega ^\varepsilon )$![]() has the following expansion
has the following expansion

Direct consequence of lemma 3.6 and proposition 3.7 is that the support set of $\omega _i^\varepsilon$![]() is contained in $B_i$
is contained in $B_i$![]() for $\varepsilon$
for $\varepsilon$![]() sufficiently small.
sufficiently small.
Corollary 3.9 For $\varepsilon$![]() sufficiently small, there holds
sufficiently small, there holds
Moreover, by proposition 3.7, we can repeat the classical result in [Reference Turkington37] to show the boundary of $supp(\zeta _i^{\varepsilon })$![]() is a $C^1$
is a $C^1$![]() curve and converges to the boundary of $supp(\zeta _i^*)$
curve and converges to the boundary of $supp(\zeta _i^*)$![]() (which is a circle) in $C^1$
(which is a circle) in $C^1$![]() sense as $\varepsilon \to 0^+$
sense as $\varepsilon \to 0^+$![]() , see lemma 4.10 for a detailed proof.
, see lemma 4.10 for a detailed proof.
As a corollary of lemmas 3.4, 3.5, 3.6 and proposition 3.7, one can get the order of the functional $E_i(\omega ^\varepsilon )$![]() and constants $\mu _i^\varepsilon.$
and constants $\mu _i^\varepsilon.$![]()
Lemma 3.10 For $\varepsilon$![]() sufficiently small, there holds
sufficiently small, there holds

where $x^*$![]() is any point of $\partial B_{{\sqrt {{|d_i|}/{\pi k(x_{0,i})}}}}(0)$
is any point of $\partial B_{{\sqrt {{|d_i|}/{\pi k(x_{0,i})}}}}(0)$![]() .
.
Proof. Using (3.24), one can immediately get (3.26). For (3.27), notice that for any $x\in \partial supp(\omega _i^\varepsilon )$![]() , $\mu _i^\varepsilon =sgn(d_i)\int _{D}G(x,\,y) \omega ^\varepsilon (y) \,{\rm d}\theta (y)$
, $\mu _i^\varepsilon =sgn(d_i)\int _{D}G(x,\,y) \omega ^\varepsilon (y) \,{\rm d}\theta (y)$![]() . So by lemma 3.6 and proposition 3.7,
. So by lemma 3.6 and proposition 3.7,

Let $x=\varepsilon x'+\bar {X}^\varepsilon _i$![]() , then $x'\in supp(\zeta _i^\varepsilon )$
, then $x'\in supp(\zeta _i^\varepsilon )$![]() . By the definition of $\zeta _i^\varepsilon$
. By the definition of $\zeta _i^\varepsilon$![]() , we get
, we get

By proposition 3.7 and the continuity of $k$![]() , we have
, we have

where $x^*$![]() is any point of $\partial B_{{\sqrt {{|d_i|}/{\pi k(x_{0,i})}}}}(0)$
is any point of $\partial B_{{\sqrt {{|d_i|}/{\pi k(x_{0,i})}}}}(0)$![]() . Taking (3.29), (3.30) into (3.28), we get (3.27).
. Taking (3.29), (3.30) into (3.28), we get (3.27).
3.3. Proof of theorem 2.3
Proof. By proposition 3.2, we know that $\omega ^\varepsilon$![]() has the form
has the form

By lemma 3.6, we have $diam(supp(\omega _i^\varepsilon ))=O(\varepsilon )$![]() . Moreover, by lemmas 3.6, 3.7 and the assumption that $(x_{0,1},\,\ldots,\,x_{0,l})$
. Moreover, by lemmas 3.6, 3.7 and the assumption that $(x_{0,1},\,\ldots,\,x_{0,l})$![]() is the strict local minimizer of $\Gamma _l$
is the strict local minimizer of $\Gamma _l$![]() , the support set of $\omega _i^\varepsilon$
, the support set of $\omega _i^\varepsilon$![]() tends to $x_{0,i}$
tends to $x_{0,i}$![]() as $\varepsilon \to 0^+$
as $\varepsilon \to 0^+$![]() , namely,
, namely,
By proposition 3.7 and lemma 3.10, we get (3)(4) in theorem 2.3. The proof of theorem 2.3 is thus complete.
4. Proof of theorem 2.4
Since proof of theorem 2.4 is similar to that of theorem 2.3 , we only emphasize the differences here, see proposition 4.7, lemmas 4.9, 4.10, 4.12 and 4.13.
By assumption $(f_2)$![]() , we know that $\lim _{s\to +\infty }f(s)=+\infty$
, we know that $\lim _{s\to +\infty }f(s)=+\infty$![]() . Moreover, direct computation shows that $(f_2)$
. Moreover, direct computation shows that $(f_2)$![]() is equivalent to
is equivalent to
$(f_2)'.$![]() there exists $\delta _1\in (0,\,1)$
there exists $\delta _1\in (0,\,1)$![]() such that
such that
for any $s\geq 0$![]() . Here $f^{-1}(s)=0$
. Here $f^{-1}(s)=0$![]() if $t<0$
if $t<0$![]() and $f^{-1}(s)$
and $f^{-1}(s)$![]() be the inverse function of $f$
be the inverse function of $f$![]() if $t\geq 0$
if $t\geq 0$![]() . Let $F(s)=\int _0^s f^{-1}(t)\,{\rm d}t$
. Let $F(s)=\int _0^s f^{-1}(t)\,{\rm d}t$![]() .
.
Notice that $f^{-1}$![]() is nonnegative increasing continuous and $F$
is nonnegative increasing continuous and $F$![]() is a convex $C^1$
is a convex $C^1$![]() function.
function.
Define $F_i(s)=\int _0^sf^{-1}_i(t)\,{\rm d}t$![]() $(i=1,\,\ldots,\,l).$
$(i=1,\,\ldots,\,l).$![]() Our idea is to consider the maximization problem
Our idea is to consider the maximization problem
where

and the set

Here $T>1$![]() is a constant to be determined later. Note that the only difference between $\mathcal {N}_{\varepsilon, T}(D)$
is a constant to be determined later. Note that the only difference between $\mathcal {N}_{\varepsilon, T}(D)$![]() and $\mathcal {M}_{\varepsilon }(D)$
and $\mathcal {M}_{\varepsilon }(D)$![]() defined by (3.2) is the presence of parameter $T$
defined by (3.2) is the presence of parameter $T$![]() . However, we will show that this is a technical trick and it will not affect the final results.
. However, we will show that this is a technical trick and it will not affect the final results.
4.1. Variational problem
Similarly as proof of propositions 3.1 and 3.2, we first get the existence and profile of maximizers of the functional $\mathcal {E}(\omega )$![]() over $\mathcal {N}_{\varepsilon, T}(D)$
over $\mathcal {N}_{\varepsilon, T}(D)$![]() .
.
Lemma 4.1 There exists $\omega ^{\varepsilon,T}\in \mathcal {N}_{\varepsilon, T}(D)$![]() , such that $\mathcal {E}(\omega ^{\varepsilon, T})=\sup _{\tilde {\omega }\in \mathcal {N}_{\varepsilon, T}(D)}\mathcal {E}(\tilde {\omega })$
, such that $\mathcal {E}(\omega ^{\varepsilon, T})=\sup _{\tilde {\omega }\in \mathcal {N}_{\varepsilon, T}(D)}\mathcal {E}(\tilde {\omega })$![]() .
.
Proof. The proof is similar to that of proposition 3.1. So we omit it here.
Then we can get the profile of a maximizer $\omega ^{\varepsilon,T}$![]() as follows.
as follows.
Lemma 4.2 Let $\omega ^{\varepsilon, T}$![]() be a maximizer defined as in lemma 4.1. Then
be a maximizer defined as in lemma 4.1. Then

where $\psi _i^{\varepsilon,T}:=sgn(d_i)\mathcal {G}(k\omega ^{\varepsilon,T})-\sigma ^{\varepsilon,T}_i$![]() , and $\sigma ^{\varepsilon,T}_i$
, and $\sigma ^{\varepsilon,T}_i$![]() are Lagrange multipliers dependent on $\varepsilon$
are Lagrange multipliers dependent on $\varepsilon$![]() for $i=1,\,\ldots,\,l$
for $i=1,\,\ldots,\,l$![]() . Moreover, for $\varepsilon$
. Moreover, for $\varepsilon$![]() sufficiently small there holds
sufficiently small there holds
where $C_0>0$![]() is some constant independent of $\varepsilon,\, T$
is some constant independent of $\varepsilon,\, T$![]() .
.
Proof. For each ${\omega }\in \mathcal {N}_{\varepsilon,T}$![]() , we choose test functions
, we choose test functions
Since $\omega ^{\varepsilon,T}$![]() is a maximizer, we get $\mathcal {E}(\omega _{(s)})\leq \mathcal {E}(\omega _{(0)})$
is a maximizer, we get $\mathcal {E}(\omega _{(s)})\leq \mathcal {E}(\omega _{(0)})$![]() , which implies that $({{\rm d}\mathcal {E}(\omega _{(s)})})/{{\rm d}s}|_{s=0^+}\leq 0$
, which implies that $({{\rm d}\mathcal {E}(\omega _{(s)})})/{{\rm d}s}|_{s=0^+}\leq 0$![]() , that is,
, that is,

for all ${\omega }\in \mathcal {N}_{\varepsilon,T}.$![]() Using the bathtub principle, we obtain
Using the bathtub principle, we obtain

where $\sigma _i^{\varepsilon,T}$![]() is a constant satisfying
is a constant satisfying
Define $\psi _i^{\varepsilon,T}=sgn(d_i)\mathcal {G}(k\omega ^{\varepsilon,T})-\sigma ^{\varepsilon,T}_i$![]() , then by (4.5) one has
, then by (4.5) one has
So we get (4.3).
It remains to prove that $\sigma _i^{\varepsilon, T}\geq -f_i^{-1}(T)-C_0.$![]() For any $x\in B_i$
For any $x\in B_i$![]() ,
,

Choose $C_0=\sum _{j\neq i}|d_j|\max _{x\in B_i, y\in B_j}G(x,\,y)$![]() . Combining (4.6) and (4.8), we get (4.4).
. Combining (4.6) and (4.8), we get (4.4).
4.2. Asymptotic analysis of $\omega ^{\varepsilon,T}$
For simplicity, we define functionals of $\omega \in \mathcal {N}_{\varepsilon,T}$![]()
Direct calculation shows that

for any $\omega \in \mathcal {N}_{\varepsilon,T}$![]() . Here $O(1)$
. Here $O(1)$![]() is uniformly bounded about $\varepsilon$
is uniformly bounded about $\varepsilon$![]() and $T$
and $T$![]() . First we give a rough lower bound of $\mathcal {E}_i(\omega ^{\varepsilon, T})$
. First we give a rough lower bound of $\mathcal {E}_i(\omega ^{\varepsilon, T})$![]() .
.
Lemma 4.3 Let $\omega ^{\varepsilon,T}$![]() be a maximizer. Then for $i=1,\,\ldots,\,l$
be a maximizer. Then for $i=1,\,\ldots,\,l$![]()
Proof. We choose a function $\tilde {\omega }^{\varepsilon, T}=({sgn(d_i)}/{\varepsilon ^2})\chi _{B_{t(\varepsilon )\varepsilon }(x_{0,i})}+ \sum _{j\neq i}\omega _j^{\varepsilon,T}= \sum _{k=1}^l\tilde {\omega }^{\varepsilon, T}_k$ . Here $t(\varepsilon )\in (({1}/{2})\sqrt { {|d_i|}/{\pi k(x_{0,i})}},\, 2\sqrt {{|d_i|}/{\pi k(x_{0,i})}})$
. Here $t(\varepsilon )\in (({1}/{2})\sqrt { {|d_i|}/{\pi k(x_{0,i})}},\, 2\sqrt {{|d_i|}/{\pi k(x_{0,i})}})$![]() satisfies $\int _{B_i}\tilde {\omega }_i^{\varepsilon,T} {\rm d}\theta (x)=d_i$
satisfies $\int _{B_i}\tilde {\omega }_i^{\varepsilon,T} {\rm d}\theta (x)=d_i$![]() . Direct calculations shows that $t(\varepsilon )$
. Direct calculations shows that $t(\varepsilon )$![]() exists for $\varepsilon$
exists for $\varepsilon$![]() sufficiently small and $\lim _{\varepsilon \to 0^+}t(\varepsilon )=\sqrt {{|d_i|}/{\pi k(x_{0,i})}}$
sufficiently small and $\lim _{\varepsilon \to 0^+}t(\varepsilon )=\sqrt {{|d_i|}/{\pi k(x_{0,i})}}$![]() . Then $\tilde {\omega }^{\varepsilon, T}\in \mathcal {N}_{\varepsilon, T}(D)$
. Then $\tilde {\omega }^{\varepsilon, T}\in \mathcal {N}_{\varepsilon, T}(D)$![]() . Notice that
. Notice that

so we get $\mathcal {E}(\tilde {\omega }^{\varepsilon, T})\geq ({d_i^2}/{4\pi })\ln ({1}/{\varepsilon })+\sum _{j\neq i}\mathcal {E}_j(\omega ^{\varepsilon,T})+O(1)$![]() . By $\mathcal {E}(\omega ^{\varepsilon, T})\geq \mathcal {E}(\tilde {\omega }^{\varepsilon, T})$
. By $\mathcal {E}(\omega ^{\varepsilon, T})\geq \mathcal {E}(\tilde {\omega }^{\varepsilon, T})$![]() and (4.9), we get (4.10).
and (4.9), we get (4.10).
Then we give the lower bound of Lagrange multiplier $\sigma _i^{\varepsilon, T}$![]() .
.
Lemma 4.4 Let $\omega ^{\varepsilon,T}$![]() be a maximizer. Then for $\varepsilon$
be a maximizer. Then for $\varepsilon$![]() sufficiently small there holds
sufficiently small there holds
Proof. By the definition of $\mathcal {E}_i$![]() and assumption $(f_2)'$
and assumption $(f_2)'$![]() , we get
, we get

where $\psi _i^{\varepsilon,T}=sgn(d_i)\mathcal {G}(k\omega ^{\varepsilon, T})-\sigma _i^{\varepsilon, T}$![]() .
.
To estimate the first term of the last line of (4.12), we define $W_i^{\varepsilon,T}=(\psi _i^{\varepsilon, T}-f_i^{-1}(T) -C_0 )_+$![]() and $\bar {W}_i^{\varepsilon,T}=(sgn(d_i)\mathcal {G}(k\omega _i^{\varepsilon, T})-\sigma _i^{\varepsilon,T}-f_i^{-1}(T)-C_0 )_+ .$
and $\bar {W}_i^{\varepsilon,T}=(sgn(d_i)\mathcal {G}(k\omega _i^{\varepsilon, T})-\sigma _i^{\varepsilon,T}-f_i^{-1}(T)-C_0 )_+ .$![]() Using (4.4), we have $\bar {W}_i^{\varepsilon,T},\, W_i^{\varepsilon,T}\in H^1_0(D)$
Using (4.4), we have $\bar {W}_i^{\varepsilon,T},\, W_i^{\varepsilon,T}\in H^1_0(D)$![]() .
.
On the one hand,
On the other hand, by (4.3), we get $supp(W_i^{\varepsilon, T})\cap B_i\subseteq \{|\omega _i^{\varepsilon,T}|={T}/{\varepsilon ^2}\}$![]() , which implies that
, which implies that

Using the Sobolev imbedding $W^{1,1}(B_i)\subset L^2(B_i)$![]() , we get
, we get

So by the fact that $|\{|\omega _i^{\varepsilon,T}|={\Lambda }/{\varepsilon ^2}\}|=O(\varepsilon ^2)$![]() and Hölder's inequality, for $\varepsilon$
and Hölder's inequality, for $\varepsilon$![]() sufficiently small we get
sufficiently small we get

Combining (4.13) and (4.14), we get $\int _{D}|\omega _i^{\varepsilon, T}|\bar {W}_i^{\varepsilon,T}\,{\rm d}\theta (x)=O(1),\,$![]() which implies that
which implies that
Taking (4.15) into (4.12) and using lemma 4.3, we get (4.11).
Using assumptions $(f_1)$![]() –$(f_3)$
–$(f_3)$![]() and the rearrangement inequality, one can get the upper bound of $\psi _i^{\varepsilon, T}$
and the rearrangement inequality, one can get the upper bound of $\psi _i^{\varepsilon, T}$![]() . As a result, we show that the vortex patch part of $\omega _i^{\varepsilon,T}$
. As a result, we show that the vortex patch part of $\omega _i^{\varepsilon,T}$![]() indeed vanishes by choosing $T$
indeed vanishes by choosing $T$![]() sufficiently large.
sufficiently large.
Lemma 4.5 Let $\omega ^{\varepsilon,T}$![]() be a maximizer as in lemma 4.1. Then
be a maximizer as in lemma 4.1. Then
As a consequence, one can choose $T=T_0$![]() sufficiently large such that
sufficiently large such that
and so $\omega _i^{\varepsilon, T_0}$![]() has the form
has the form
Proof. For any $x\in B_i$![]() , using the definition of $\psi _i^{\varepsilon, T}$
, using the definition of $\psi _i^{\varepsilon, T}$![]() and the rearrangement inequality
and the rearrangement inequality

Thus using lemma 4.4, we obtain
It follows from assumption $(f_3)$![]() that for each $a_0 > 0$
that for each $a_0 > 0$![]() , $\lim _{s\to +\infty }f_i(s)e^{-a_0 s}=0,\,$
, $\lim _{s\to +\infty }f_i(s)e^{-a_0 s}=0,\,$![]() which implies that $\lim _{s\to +\infty } \tau f^{-1}(s)-\ln s=+\infty.$
which implies that $\lim _{s\to +\infty } \tau f^{-1}(s)-\ln s=+\infty.$![]() Thus we can choose $T=T_0$
Thus we can choose $T=T_0$![]() sufficiently large such that
sufficiently large such that
that is, $|1-2\delta _1|f_i^{-1}(T_0)+({|d_i|}/{4\pi })\ln T_0+O(1)< f_i^{-1}(T_0)$![]() . Thus we have $|\{\psi _i^{\varepsilon,T}\geq f_i^{-1}(T) \}\cap B_i|=0.$
. Thus we have $|\{\psi _i^{\varepsilon,T}\geq f_i^{-1}(T) \}\cap B_i|=0.$![]() Using lemma 4.2, we get (4.17).
Using lemma 4.2, we get (4.17).
In the following, we shall abbreviate $(\mathcal {N}_{\varepsilon, T_0}(D);\omega _i^{\varepsilon, T_0};\sigma _i^{\varepsilon, T_0};\psi _i^{\varepsilon,T_0})$![]() as $(\mathcal {N}_{\varepsilon }(D);\omega _i^{\varepsilon };\sigma _i^{\varepsilon };\psi _i^{\varepsilon })$
as $(\mathcal {N}_{\varepsilon }(D);\omega _i^{\varepsilon };\sigma _i^{\varepsilon };\psi _i^{\varepsilon })$![]() for $i=1,\,\ldots,\,l$
for $i=1,\,\ldots,\,l$![]() . By lemma 4.5, we know that any maximizer $\omega ^{\varepsilon }$
. By lemma 4.5, we know that any maximizer $\omega ^{\varepsilon }$![]() of the maximization problem $(\mathcal {P}^*)$
of the maximization problem $(\mathcal {P}^*)$![]() has the form of (2.5).
has the form of (2.5).
Similarly as lemma 3.6, we can get the diameter of $supp(\omega _i^\varepsilon )$![]() is of the order $O(\varepsilon ).$
is of the order $O(\varepsilon ).$![]()
Lemma 4.6 Let $\omega ^{\varepsilon }$![]() be a maximizer. Then for $\varepsilon$
be a maximizer. Then for $\varepsilon$![]() sufficiently small, there holds
sufficiently small, there holds
for some $0<\bar {r}_1< \bar {R}_1$![]() independent of $\varepsilon$
independent of $\varepsilon$![]() .
.
Proof. Since $|\omega _i^\varepsilon |\leq {T_0}/{\varepsilon ^2}$![]() and $\int _{B_i}\omega _i^\varepsilon \,{\rm d}\theta (x)=d_i$
and $\int _{B_i}\omega _i^\varepsilon \,{\rm d}\theta (x)=d_i$![]() , we get $|supp( \omega _i^\varepsilon )|\geq C\varepsilon ^2$
, we get $|supp( \omega _i^\varepsilon )|\geq C\varepsilon ^2$![]() , which implies that $diam(supp( \omega _i^\varepsilon ))\geq \bar {r}_1\varepsilon$
, which implies that $diam(supp( \omega _i^\varepsilon ))\geq \bar {r}_1\varepsilon$![]() for some $\bar {r}_1>0$
for some $\bar {r}_1>0$![]() .
.
Similarly as the proof of lemma 3.6, one can get the existence of $\bar {R}_1>1$![]() such that
such that
□
Finally, we analyse the limiting location of $\omega _i^\varepsilon$![]() as $\varepsilon \to 0^+$
as $\varepsilon \to 0^+$![]() , which is the most important part in our construction. To this end we define the centre of $\omega _i^\varepsilon$
, which is the most important part in our construction. To this end we define the centre of $\omega _i^\varepsilon$![]() by
by
Since $\overline {B_i}$![]() is compact, we may choose a subsequence $\{\hat {X}_i^{\varepsilon _n}\}_{n=1}^{ \infty }$
is compact, we may choose a subsequence $\{\hat {X}_i^{\varepsilon _n}\}_{n=1}^{ \infty }$![]() (still denoted by $\bar {X}_i^\varepsilon$
(still denoted by $\bar {X}_i^\varepsilon$![]() ) satisfying
) satisfying
Define the scaled functions
Here $D_\varepsilon =\{x\in \mathbb {R}^2 \mid \varepsilon x+\hat {X}_i^\varepsilon \in D\}$![]() .
.
By lemma 4.6, we know that the support set of $\xi ^\varepsilon _i$![]() is contained in $B_{\bar { R}_1}(0)$
is contained in $B_{\bar { R}_1}(0)$![]() . Notice that
. Notice that
which implies that

Since $\|\xi ^\varepsilon _i\|_{L^\infty (B_{\bar { R}_1}(0))}\leq T_0$![]() , $\xi ^\varepsilon _i$
, $\xi ^\varepsilon _i$![]() is uniformly bounded in $L^p(B_{\bar { R}_1}(0))$
is uniformly bounded in $L^p(B_{\bar { R}_1}(0))$![]() for any $p\in [1,\,+\infty ]$
for any $p\in [1,\,+\infty ]$![]() . So up to a subsequence, we may assume that $\xi ^\varepsilon _i\to \xi ^*_i$
. So up to a subsequence, we may assume that $\xi ^\varepsilon _i\to \xi ^*_i$![]() in $L^p$
in $L^p$![]() weak topology as $\varepsilon \to 0.$
weak topology as $\varepsilon \to 0.$![]() By the definition of $\hat {X}_i^\varepsilon$
By the definition of $\hat {X}_i^\varepsilon$![]() and (4.19), one can get
and (4.19), one can get
Since $\omega ^\varepsilon$![]() is a maximizer of $\mathcal {E}$
is a maximizer of $\mathcal {E}$![]() , using lemma 4.6 we can get the necessary condition of $x^*_i$
, using lemma 4.6 we can get the necessary condition of $x^*_i$![]() .
.
Proposition 4.7 There holds

As a consequence, $x^*_i =x_{0,i}$![]() for $i=1,\,\ldots,\,l.$
for $i=1,\,\ldots,\,l.$![]()
Proof. On the one hand, using lemma 4.6 and the definition of $x^*_i$![]() , we get
, we get

By the definition of $\xi _i^\varepsilon$![]() , we have
, we have

Since $supp(\xi _i^\varepsilon )\subseteq B_{\bar { R}_1}(0)$![]() and $||\xi ^\varepsilon _i||_{L^\infty }\leq T_0$
and $||\xi ^\varepsilon _i||_{L^\infty }\leq T_0$![]() , we obtain
, we obtain

For the term involving $F_i$![]() , we have
, we have

Taking those into the definition of $\mathcal {E}$![]() , we get
, we get

On the other hand, for any $z_i\in B_i (i=1,\,\ldots,\,l)$![]() , we choose test functions $\hat {\omega }^\varepsilon =\sum _{i=1}^l\hat {\omega }^\varepsilon _i,\,$
, we choose test functions $\hat {\omega }^\varepsilon =\sum _{i=1}^l\hat {\omega }^\varepsilon _i,\,$![]() where $\hat {\omega }^\varepsilon _i$
where $\hat {\omega }^\varepsilon _i$![]() is defined by
is defined by
$\bar {\tau }_i(\varepsilon )\in (({1}/{2})\sqrt {{k(x_i^*)}/{k(z_i)}} ,\, 2\sqrt {{k(x_i^*)}/{k(z_i)}} )$![]() is chosen to satisfy $\int _{B_i}\hat {\omega }^\varepsilon _i(x)\,{\rm d}\theta (x)=d_i$
is chosen to satisfy $\int _{B_i}\hat {\omega }^\varepsilon _i(x)\,{\rm d}\theta (x)=d_i$![]() . By (4.20) and (4.21), one can prove that such $\bar {\tau }_i(\varepsilon )$
. By (4.20) and (4.21), one can prove that such $\bar {\tau }_i(\varepsilon )$![]() exists for $\varepsilon$
exists for $\varepsilon$![]() sufficiently small and $\bar {\tau }_i(\varepsilon )=\sqrt {({k(x_i^*)}/{k(z_i)})}+o(1)$
sufficiently small and $\bar {\tau }_i(\varepsilon )=\sqrt {({k(x_i^*)}/{k(z_i)})}+o(1)$![]() . Now we calculate the energy expansion of $\hat {\omega }^\varepsilon$
. Now we calculate the energy expansion of $\hat {\omega }^\varepsilon$![]() . It is not hard to prove that
. It is not hard to prove that

Similar as (4.23), we get

Taking $\bar {\tau }_i(\varepsilon )=\sqrt {({k(x_i^*)}/{k(z_i)})}+o(1)$![]() into (4.25) we obtain
into (4.25) we obtain

For the term involving $F_i$![]() , we get
, we get

Taking those into the definition of $\mathcal {E}(\hat {\omega }^\varepsilon )$![]() , we get
, we get

Since $\mathcal {E}(\omega ^\varepsilon )\geq \mathcal {E}(\hat {\omega }^\varepsilon )$![]() , by (4.24) and (4.26) we get
, by (4.24) and (4.26) we get

Thus we get (4.22). By the assumption that $(x_{0,1},\,\ldots,\,x_{0,l})$![]() is a strict local minimizer of $\Gamma _l$
is a strict local minimizer of $\Gamma _l$![]() , we have $x^*_i=x_{0,i}.$
, we have $x^*_i=x_{0,i}.$![]()
Remark 4.8 By lemma 4.6 and proposition 4.7, we get for $\varepsilon$![]() sufficiently small,
sufficiently small,
Using lemma 4.6 and proposition 4.7, we can further get the accurate estimates of $\mathcal {E}$![]() and $\sigma _i^\varepsilon$
and $\sigma _i^\varepsilon$![]() . To this end, we define the scaled functions of $\psi _i$
. To this end, we define the scaled functions of $\psi _i$![]() by
by
Here $( B_i)_\varepsilon =\{x\in \mathbb {R}^2 \mid \varepsilon x+\hat {X}_i^\varepsilon \in B_i\}$![]() . By lemma 4.2 and remark 4.8, we have $supp(\xi ^\varepsilon _i)=supp((\Psi _i^\varepsilon )_+)\subseteq B_{\bar { R}_1}(0)$
. By lemma 4.2 and remark 4.8, we have $supp(\xi ^\varepsilon _i)=supp((\Psi _i^\varepsilon )_+)\subseteq B_{\bar { R}_1}(0)$![]() .
.
It follows from (4.17) that $\Psi _i^\varepsilon$![]() satisfies
satisfies
Thus by the definition of $\Psi _i^\varepsilon$![]() and $\xi ^\varepsilon _i$
and $\xi ^\varepsilon _i$![]() , we get
, we get


Let $\Psi ^*_i$![]() be the unique radial function satisfying
be the unique radial function satisfying

Then $\Psi ^*_i(x)=U_i(k(x^*_i)^{{1}/{2}}x)$![]() , where $U_i$
, where $U_i$![]() is the unique radial function satisfying
is the unique radial function satisfying

We first show that $\xi _i^*$![]() is a radial function. Denote $\tilde {\xi }_i^\varepsilon$
is a radial function. Denote $\tilde {\xi }_i^\varepsilon$![]() the radially symmetric decreasing Lebesque rearrangement function of $\xi _i^\varepsilon$
the radially symmetric decreasing Lebesque rearrangement function of $\xi _i^\varepsilon$![]() . Up to a subsequence we may assume that $\tilde {\xi }_i^\varepsilon \to \tilde {\xi }_i^*$
. Up to a subsequence we may assume that $\tilde {\xi }_i^\varepsilon \to \tilde {\xi }_i^*$![]() weakly in $L^p(B_{\bar { R}_1}(0))$
weakly in $L^p(B_{\bar { R}_1}(0))$![]() as $\varepsilon \to 0^+$
as $\varepsilon \to 0^+$![]() .
.
Lemma 4.9 There holds
So $\xi _i^*$![]() is a radially symmetric function.
is a radially symmetric function.
Proof. On the one hand, by the Riesz's rearrangement inequality, we have

which implies that

On the other hand, let $\tilde {\omega }^\varepsilon =\tilde {\omega }^\varepsilon _i+\sum _{j=1,j\neq i}^l\omega ^\varepsilon _j\in \mathcal {N}_\varepsilon (D)$![]() satisfying
satisfying

where $c(\varepsilon )$![]() is a constant such that $\int _{B_i}\tilde {\omega }^\varepsilon _i\,{\rm d}\theta (x)=d_i$
is a constant such that $\int _{B_i}\tilde {\omega }^\varepsilon _i\,{\rm d}\theta (x)=d_i$![]() . Then $c(\varepsilon )=1+o(1)$
. Then $c(\varepsilon )=1+o(1)$![]() . Similarly as the proof of proposition 4.7, we get
. Similarly as the proof of proposition 4.7, we get

and
Since $\mathcal {E}(\tilde {\omega }^\varepsilon )\le \mathcal {E}({\omega }^\varepsilon )$![]() , we conclude that
, we conclude that

which implies that

Thus the equality holds in (4.32). By the strict Riesz's rearrangement inequality (see theorem 3.9, [Reference Lieb and Loss26]), there exists a translation $\mathcal {T}$![]() such that $\mathcal {T}\xi _i^*=\tilde {\xi }_i^*$
such that $\mathcal {T}\xi _i^*=\tilde {\xi }_i^*$![]() . Since
. Since
we get $\xi _i^*=\tilde {\xi }^*_i$![]() .
.
Lemma 4.10 There holds as $\varepsilon \to 0$![]() ,
,
As a consequence, for $\varepsilon$![]() sufficiently small, $\partial (supp(\xi _i^\varepsilon ))=\{x\in B_{\bar { R}_1}(0)\mid \Psi _i^\varepsilon (x)=0 \}$
sufficiently small, $\partial (supp(\xi _i^\varepsilon ))=\{x\in B_{\bar { R}_1}(0)\mid \Psi _i^\varepsilon (x)=0 \}$![]() is a $C^1$
is a $C^1$![]() curve and converges to the circle $\{x\in B_{\bar { R}_1}(0)\mid \Psi _i^*(x)=0 \}$
curve and converges to the circle $\{x\in B_{\bar { R}_1}(0)\mid \Psi _i^*(x)=0 \}$![]() as $\varepsilon \to 0$
as $\varepsilon \to 0$![]() .
.
Proof. For any $R>\bar { R}_1$![]() , notice that $\xi _i^\varepsilon$
, notice that $\xi _i^\varepsilon$![]() is uniformly bounded in $L^\infty (B_{2R}(0))$
is uniformly bounded in $L^\infty (B_{2R}(0))$![]() . Thus, by (4.28) and classical elliptic estimates, $\Psi ^\varepsilon _i$
. Thus, by (4.28) and classical elliptic estimates, $\Psi ^\varepsilon _i$![]() is uniformly bounded in $W^{2,p}(B_{R}(0))$
is uniformly bounded in $W^{2,p}(B_{R}(0))$![]() for every $1\le p<+\infty$
for every $1\le p<+\infty$![]() . By the Sobolev embedding theorem, we may conclude that $\Psi ^\varepsilon _i$
. By the Sobolev embedding theorem, we may conclude that $\Psi ^\varepsilon _i$![]() is compact in $C^{1,\alpha }(B_{R}(0))$
is compact in $C^{1,\alpha }(B_{R}(0))$![]() for every $0<\alpha <1$
for every $0<\alpha <1$![]() . Then up to a subsequence we may assume $\Psi ^\varepsilon \to \Psi$
. Then up to a subsequence we may assume $\Psi ^\varepsilon \to \Psi$![]() in $C^{1,\alpha }(B_{R}(0))$
in $C^{1,\alpha }(B_{R}(0))$![]() . By (4.28) and (4.29), $\Psi$
. By (4.28) and (4.29), $\Psi$![]() satisfies
satisfies

By lemma 4.9, $\xi _i^*$![]() is a radial function. Using the Green's function representation, $\Psi$
is a radial function. Using the Green's function representation, $\Psi$![]() is also radial. By the uniqueness of radial solutions of (4.30), we have $\Psi =\Psi ^*_i$
is also radial. By the uniqueness of radial solutions of (4.30), we have $\Psi =\Psi ^*_i$![]() .
.
By the strong maximum principle, one can show that for any $x\in \{x\in B_{\bar { R}_1}(0)\mid \Psi _i^*(x)=0 \}$![]() , $|\nabla \Psi _i^*(x)|\neq 0$
, $|\nabla \Psi _i^*(x)|\neq 0$![]() . Thus by the implicit function theorem, we get that for $\varepsilon$
. Thus by the implicit function theorem, we get that for $\varepsilon$![]() sufficiently small, $\{x\in B_{\bar { R}_1}(0)\mid \Psi _i^\varepsilon (x)=0 \}$
sufficiently small, $\{x\in B_{\bar { R}_1}(0)\mid \Psi _i^\varepsilon (x)=0 \}$![]() is a $C^1$
is a $C^1$![]() curve and converges to $\{x\in B_{\bar { R}_1}(0)\mid \Psi _i^*(x)=0 \}$
curve and converges to $\{x\in B_{\bar { R}_1}(0)\mid \Psi _i^*(x)=0 \}$![]() in $C^1$
in $C^1$![]() sense as $\varepsilon \to 0$
sense as $\varepsilon \to 0$![]() .
.
As a corollary, we have $\xi _i^\varepsilon \to \xi _i^*$![]() in $L^p$
in $L^p$![]() topology as $\varepsilon \to 0^+$
topology as $\varepsilon \to 0^+$![]() .
.
Corollary 4.11 For any $p>1$![]() , there holds as $\varepsilon \to 0$
, there holds as $\varepsilon \to 0$![]()
Using lemma 4.10 and corollary 4.11, we can get the asymptotic expansion of the energy $\mathcal {E}(\omega _i^\varepsilon )$![]() as follows
as follows
Lemma 4.12 There holds

where $C_0=({1}/{4\pi })\sum _{i=1}^l\int _{\mathbb {R}^2}\int _{\mathbb {R}^2}\ln ({1}/{|x-y|})f_i\circ U_i(x)f_i\circ U_i(y)\,{\rm d}x\,{\rm d}y-\sum _{i=1}^l\int _{\mathbb {R}^2} F_i\circ f_i\circ U_i(x)\,{\rm d}x$![]() is a constant independent of $\varepsilon$
is a constant independent of $\varepsilon$![]() .
.
Proof. The proof is based on the proof of proposition 4.7. By (4.24), we have

By lemma 4.10 and corollary 4.11, we obtain

Taking those into (4.34), we have

However, by the definition of $\Psi _i^*$![]() and (4.31), we get
and (4.31), we get

where $C_0=({1}/{4\pi })\sum _{i=1}^l\int _{\mathbb {R}^2}\int _{\mathbb {R}^2}\ln ({1}/{|x-y|})f_i\circ U_i(x)f_i\circ U_i(y)\,{\rm d}x\,{\rm d}y-\sum _{i=1}^l\int _{\mathbb {R}^2}F_i\circ f_i\circ U_i(x)\,{\rm d}x$![]() is a constant dependent of $f_i$
is a constant dependent of $f_i$![]() . Taking (4.36) into (4.35), we get the result.
. Taking (4.36) into (4.35), we get the result.
Moreover, one can get the order of the functional $\mathcal {E}_i(\omega ^\varepsilon )$![]() and constants $\sigma _i^\varepsilon$
and constants $\sigma _i^\varepsilon$![]() as follows
as follows
Lemma 4.13 For $\varepsilon$![]() sufficiently small, there holds
sufficiently small, there holds

where $C_1=({1}/{4\pi }) \int _{\mathbb {R}^2}\int _{\mathbb {R}^2}\ln ({1}/{|x-y|})f_i\circ U_i(x)f_i\circ U_i(y)\,{\rm d}x\,{\rm d}y- \int _{\mathbb {R}^2}F_i\circ f_i\circ U_i(x)\,{\rm d}x$![]() , $C_2=({1}/{2\pi })\int _{\mathbb {R}^2}\ln ({1}/{|x^*-y'|})f_i\circ U_i(y')\,{\rm d}y'$
, $C_2=({1}/{2\pi })\int _{\mathbb {R}^2}\ln ({1}/{|x^*-y'|})f_i\circ U_i(y')\,{\rm d}y'$![]() , and $x^*$
, and $x^*$![]() is any point of $\partial \{x\in \mathbb {R}^2\mid f_i\circ U_i(x)=0\}$
is any point of $\partial \{x\in \mathbb {R}^2\mid f_i\circ U_i(x)=0\}$![]() .
.
Proof. Similarly as the proof of lemma 4.12, one can immediately get

For (4.38), notice that for any $x\in \partial (supp(\omega _i^\varepsilon ))$![]() , $\sigma _i^\varepsilon =sgn(d_i)\int _{D}G(x,\,y) \omega ^\varepsilon (y) \,{\rm d}\theta (y)$
, $\sigma _i^\varepsilon =sgn(d_i)\int _{D}G(x,\,y) \omega ^\varepsilon (y) \,{\rm d}\theta (y)$![]() , which implies that
, which implies that

Let $x=\varepsilon x'+\hat {X}^\varepsilon _i$![]() , then $x'\in \partial (supp(\xi _i^\varepsilon ))$
, then $x'\in \partial (supp(\xi _i^\varepsilon ))$![]() . So
. So

By lemma 4.10 and the continuity of $k$![]() , we have
, we have

where $x^*$![]() is any point of $\partial \{x\in \mathbb {R}^2\mid f_i\circ U_i(x)=0\}$
is any point of $\partial \{x\in \mathbb {R}^2\mid f_i\circ U_i(x)=0\}$![]() . Taking (4.40), (4.41) into (4.39), we get (4.38).
. Taking (4.40), (4.41) into (4.39), we get (4.38).
4.3. Proof of theorem 2.4
Proof. The proof is similar to the proof of theorem 2.3. By lemma 4.5, we know that $\omega ^\varepsilon$![]() has the form
has the form

where $\psi _i^{\varepsilon }=sgn(d_i)\mathcal {G}(k\omega ^{\varepsilon })-\sigma ^{\varepsilon }_i$![]() for some $\sigma ^{\varepsilon }_i\in \mathbb {R}.$
for some $\sigma ^{\varepsilon }_i\in \mathbb {R}.$![]() By lemma 4.6, $diam(supp(\omega _i^\varepsilon ))=O(\varepsilon )$
By lemma 4.6, $diam(supp(\omega _i^\varepsilon ))=O(\varepsilon )$![]() .
.
Moreover, by proposition 4.7, the support set of $\omega _i^\varepsilon$![]() tends to $x_{0,i}$
tends to $x_{0,i}$![]() as $\varepsilon \to 0^+$
as $\varepsilon \to 0^+$![]() , namely
, namely
By lemmas 4.10 and 4.13, we get (3)(4) in theorem 2.4. The proof of theorem 2.4 is thus complete.
Acknowledgements
The author would like to thank the anonymous referee for his/her helpful comments and detailed correction of the paper. J. Wan was supported by NNSF of China (No. 1210 1045 and 12271539).
Conflict of interest
On behalf of all authors, the corresponding author states that there is no conflict of interest.
Data
All data generated or analysed during this study are included in this published article and its supplementary information files.