Hostname: page-component-848d4c4894-2pzkn Total loading time: 0 Render date: 2024-05-31T05:29:28.769Z Has data issue: false hasContentIssue false
  • English
  • Français

The monostable cooperative system with nonlocal diffusion and free boundaries

Part of: Miscellaneous topics - Partial differential equations Parabolic equations and systems

Published online by Cambridge University Press:  20 March 2023

Lei Li ,
Xueping Li  and
Mingxin Wang Open the ORCID record for Mingxin Wang [Opens in a new window]
Lei Li
Affiliation:
College of Science, Henan University of Technology, Zhengzhou 450001, PR China
Xueping Li
Affiliation:
School of Mathematics and Information Science, Zhengzhou University of Light Industry, Zhengzhou 450002, PR China
Mingxin Wang
Affiliation:
School of Mathematics and Information Science, Henan Polytechnic University, Jiaozuo 454000, PR China (mxwang@hpu.edu.cn)
Get access Rights & Permissions [Opens in a new window]

Abstract

This paper concerns the monostable cooperative system with nonlocal diffusion and free boundaries, which has recently been discussed by Du and Ni [J. Differential equations 308(2021) 369-420 and arXiv:2010.01244]. We here aim at four aspects: the first is to give more accurate estimates for the longtime behaviours of the solution; the second is to discuss the limits of solution pair of a semi-wave problem; the third is to investigate the asymptotic behaviours of the corresponding Cauchy problem; the last is to study the limiting profiles of the solution as one of the expanding rates of free boundaries converges to $\infty$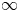. Moreover, some epidemic models are given to illustrate their own rich longtime behaviours, which are quite different from those of the relevant existing works.

Keywords

Monostable cooperative systemNonlocal diffusionFree boundariesAccelerated spreadingSpreading speed

MSC classification

Primary: 35K57: Reaction-diffusion equations
Secondary: 35R09: Integro-partial differential equations 35R20: Partial operator-differential equations (i.e., PDE on finite-dimensional spaces for abstract space valued functions) 35R35: Free boundary problems 92D25: Population dynamics (general)
Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 154 , Issue 2 , April 2024 , pp. 629 - 659
Check for updates
Copyright
Copyright © The Author(s), 2023. Published by Cambridge University Press on behalf of The Royal Society of Edinburgh

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Abdelrazec, A., Lenhart, S. and Zhu, H. P.. Transmission dynamics of West Nile virus in mosquitoes and corvids and non-corvids. J. Math. Biol. 68 (2014), 1553–1582.Google Scholar
Ahn, I., Baek, S. and Lin, Z. G.. The spreading fronts of an infective environment in a man-environment-man epidemic model. Appl. Math. Model. 40 (2016), 7082–7101.CrossRefGoogle Scholar
Alfaro, M. and Coville, J.. Propagation phenomena in monostable integro-differential equations: Acceleration or not?. J. Differ. Equ. 263 (2017), 5727–5758.Google Scholar
Cao, J.-F., Du, Y. H., Li, F. and Li, W.-T.. The dynamics of a Fisher-KPP nonlocal diffusion model with free boundaries. J. Funct. Anal. 277 (2019), 2772–2814.Google Scholar
Cao, J.-F., Li, W.-T., Wang, J. and Zhao, M.. The dynamics of a Lotka-Volterra competition model with nonlocal diffusion and free boundaries. Adv. Differ. Equ. 26 (2021), 163–200.Google Scholar
Capasso, V. and Maddalena, L.. Convergence to equilibrium states for a reaction-diffusion system modelling the spatial spread of a class of bacterial and viral diseases. J. Math. Biol. 13 (1981/82), 173–184.Google Scholar
Cortázar, C., Quirós, F. and Wolanski, N.. A nonlocal diffusion problem with a sharp free boundary. Interfaces Free Bound. 21 (2019), 441–462.Google Scholar
Du, Y. H., Li, F. and Zhou, M. L.. Semi-wave and spreading speed of the nonlocal Fisher-KPP equation with free boundaries. J. Math. Pures Appl. 154 (2021), 30–66.Google Scholar
Du, Y. H. and Lin, Z. G.. Spreading-vanishing dichotomy in the diffusive logistic model with a free boundary. SIAM J. Math. Anal. 42 (2010), 377–405.Google Scholar
Du, Y. H. and Ni, W. J.. Spreading speed for some cooperative systems with nonlocal diffusion and free boundaries, part 1: Semi-wave and a threshold condition. J. Differ. Equ. 308 (2021), 369–420.Google Scholar
Du, Y. H. and Ni, W. J.. Spreading speed for some cooperative systems with nonlocal diffusion and free boundaries, part 2. arXiv:2010.01244.Google Scholar
Du, Y. H. and Ni, W. J.. Analysis of a West Nile virus model with nonlocal diffusion and free boundaries. Nonlinearity 33 (2020), 4407–4448.Google Scholar
Du, Y. H. and Ni, W. J.. The high dimensional Fisher-KPP nonlocal diffusion equation with free boundary and radial symmetry, part 1. SIAM J. Math. Anal. 54 (2022), 3930–3973.Google Scholar
Du, Y. H. and Ni, W. J.. The high dimensional Fisher-KPP nonlocal diffusion equation with free boundary and radial symmetry, part 2, Submitted, (2021), arXiv:2102.05286.Google Scholar
Du, Y. H., Wang, M. X. and Zhao, M.. Two species nonlocal diffusion systems with free boundaries. Discrete Cont. Dyn. Syst. 42 (2022), 1127–1162.Google Scholar
Garnier, J.. Accelerating solutions in integro-differential equations. SIAM J. Math. Anal. 43 (2011), 1955–1974.CrossRefGoogle Scholar
Hsu, C.-H. and Yang, T.-S.. Existence, uniqueness, monotonicity and asymptotic behaviour of travelling waves for epidemic models. Nonlinearity 26 (2013), 121–139.Google Scholar
Lewis, M. A., Renclawowicz, J. and van den Driessche, P.. Traveling waves and spread rates for a West Nile virus model. Bull. Math. Biol. 68 (2006), 3–23.Google Scholar
Li, L., Li, X. P. and Wang, M. X.. A free boundary problem with nonlocal diffusion and unbounded initial range. Z. Angew. Math. Phys. 73 (2022), 192.Google Scholar
Li, L., Li, W.-T. and Wang, M. X.. Dynamics for nonlocal diffusion problems with a free boundary. J. Differ. Equ. 330 (2022), 110–149.Google Scholar
Li, L., Sheng, W. J. and Wang, M. X.. Systems with nonlocal vs. local diffusions and free boundaries. J. Math. Anal. Appl. 483 (2020), 123646.Google Scholar
Li, L., Wang, J. P. and Wang, M. X.. The dynamics of nonlocal diffusion systems with different free boundaries. Comm. Pure Appl. Anal. 19 (2020), 3651–3672.Google Scholar
Li, L. and Wang, M. X.. Free boundary problems of a mutualist model with nonlocal diffusion. J. Dyn. Diff. Equat. (2022), doi:10.1007/s10884-022-10150-5Google Scholar
Li, W.-T., Zhao, M. and Wang, J.. Spreading fronts in a partially degenerate integro-differential reaction-diffusion system. Z. Angew. Math. Phys. 68 (2017), 109.Google Scholar
Lin, Z. G. and Zhu, H. P.. Spatial spreading model and dynamics of West Nile virus in birds and mosquitoes with free boundary. J. Math. Biol. 75 (2017), 1381–1409.Google Scholar
Nguyen, T.-H. and Vo, H.-H.. Dynamics for a two phase free boundaries system in an epidemiological model with nonlocal dispersals. J. Differ. Equ. 335 (2022), 398–463.Google Scholar
Pu, L. Q., Lin, Z. G. and Lou, Y.. A West Nile virus nonlocal model with free boundaries and seasonal succession blue. J. Math. Biol. 86 (2023), 25.Google Scholar
Wang, J. P. and Wang, M. X.. Free boundary problems with nonlocal and local diffusions I: global solution. J. Math. Anal. Appl. 490 (2020), 123974.Google Scholar
Wang, J. P. and Wang, M. X.. Free boundary problems with nonlocal and local diffusions II: Spreading-vanishing and long-time behavior. Discrete Contin. Dyn. Syst. B 25 (2020), 4721–4736.Google Scholar
Wang, R. and Du, Y. H.. Long-time dynamics of a nonlocal epidemic model with free boundaries: spreading-vanishing dichotomy. J. Differ. Equ. 327 (2022), 322–381.Google Scholar
Wang, Z. G., Nie, H. and Du, Y. H.. Spreading speed for a West Nile virus model with free boundary. J. Math. Biol. 79 (2019), 433–466.Google Scholar
Wu, S. L. and Hsu, C.-H.. Existence of entire solutions for delayed monostable epidemic models. Trans. Amer. Math. Soc. 368 (2016), 6033–6062.Google Scholar
Xu, W.-B., Li, W.-T. and Lin, G.. Nonlocal dispersal cooperative systems: Acceleration propagation among species. J. Differ. Equ. 268 (2020), 1081–1105.Google Scholar
Yang, G. Y., Yao, S. W. and Wang, M. X.. An SIR epidemic model with nonlocal diffusion, nonlocal infection and free boundaries. J. Math. Anal. Appl. 518 (2023), 126731.Google Scholar
Yang, G. Y. and Wang, M. X.. An SIR epidemic model with nonlocal diffusion and free boundaries. Discrete Contin. Dyn. Syst. B 28 (2023), 4221–4230. doi:10.3934/dcdsb.2023007Google Scholar
Zhao, M., Li, W.-T and Ni, W. J.. Spreading speed of a degenerate and cooperative epidemic model with free boundaries. Discrete Contin. Dyn. Syst. B 25 (2020), 981–999.Google Scholar
Zhao, M., Li, W.-T. and Du, Y. H.. The effect of nonlocal reaction in an epidemic model with nonlocal diffusion and free boundaries. Comm. Pure Appl. Anal. 19 (2020), 4599–4620.Google Scholar
Zhao, M., Zhang, Y., Li, W.-T. and Du, Y. H.. The dynamics of a degenerate epidemic model with nonlocal diffusion and free boundaries. J. Differ. Equ. 269 (2020), 3347–3386.Google Scholar