Hostname: page-component-848d4c4894-5nwft Total loading time: 0 Render date: 2024-06-07T19:39:21.264Z Has data issue: false hasContentIssue false
  • English
  • Français

Multiple bound states of higher topological type for semi-classical Choquard equations

Part of: Partial differential equations Elliptic equations and systems Equations of mathematical physics and other areas of application

Published online by Cambridge University Press:  04 March 2020

Xiaonan Liu ,
Shiwang Ma  and
Jiankang Xia
Xiaonan Liu
Affiliation:
School of Mathematical Science and LPMC, Nankai University, Tianjin300071, P.R. China (liuxiaonan20131110@163.com; shiwangm@nankai.edu.cn)
Shiwang Ma
Affiliation:
School of Mathematical Science and LPMC, Nankai University, Tianjin300071, P.R. China (liuxiaonan20131110@163.com; shiwangm@nankai.edu.cn)
Jiankang Xia
Affiliation:
Department of Applied Mathematics, Northwestern Polytechnical University, Xi'an 710129, P.R. China (jiankangxia@nwpu.edu.cn)
Get access Rights & Permissions [Opens in a new window]

Abstract

We are concerned with the semi-classical states for the Choquard equation

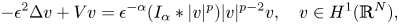$$-{\epsilon }^2\Delta v + Vv = {\epsilon }^{-\alpha }(I_\alpha *|v|^p)|v|^{p-2}v,\quad v\in H^1({\mathbb R}^N),$$
where N ⩾ 2, Iα is the Riesz potential with order α ∈ (0, N − 1) and 2 ⩽ p < (N + α)/(N − 2). When the potential V is assumed to be bounded and bounded away from zero, we construct a family of localized bound states of higher topological type that concentrate around the local minimum points of the potential V as ε → 0. These solutions are obtained by combining the Byeon–Wang's penalization approach and the classical symmetric mountain pass theorem.

Keywords

Choquard equationvariational methodsmultiple semi-classical states

MSC classification

Primary: 35J61: Semilinear elliptic equations
Secondary: 35B25: Singular perturbations 35B40: Asymptotic behavior of solutions 35Q55: NLS-like equations (nonlinear Schrödinger)
Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 151 , Issue 1 , February 2021 , pp. 329 - 355
Check for updates
Copyright
Copyright © The Author(s), 2020. Published by The Royal Society of Edinburgh

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1Ackermann, N.. On a periodic Schrödinger equation with nonlocal superlinear part. Math. Z. 248 (2004), 423–443.CrossRefGoogle Scholar
2Ambrosetti, A., Badiale, M. and Cingolani, S.. Semiclassical states of nonlinear Schrödinger equations. Arch. Ration. Mech. Anal. 140 (1997), 285–300.CrossRefGoogle Scholar
3Ambrosetti, A. and Malchiodi, A., Concentration phenomena for nonlinear Schrödinger equations: Recent results and new perspectives. In Perspectives in nonlinear partial differential equations. Contemporary Mathematics, vol. 446, pp. 19–30 (Providence: American Mathematical Society, 2007).CrossRefGoogle Scholar
4Bartch, T., Clapp, M. and Weth, T.. Configuration spaces, transfer and 2-nodal solutions of semiclassical Schödinger equation. Math. Ann. 338 (2007), 147–185.CrossRefGoogle Scholar
5Battaglia, L. and Van Schaftingen, J.. Existence of groundstates for a class of nonlinear Choquard equations in the plane. Adv. Nonlinear Stud. 17 (2017), 581–594.CrossRefGoogle Scholar
6Byeon, J. and Wang, Z.-Q.. Standing waves with a critical frequency for nonlinear Schrödinger equations II. Calc. Var. Partial Differ. Equ. 18 (2003), 207–219.CrossRefGoogle Scholar
7Chen, S. and Wang, Z.-Q.. Localized nodal solutions of higher topological type for semiclassical nonlinear Schrödinger equations. Calc. Var. Partial Differ. Equ. 56 (2017), 1–26.CrossRefGoogle Scholar
8Cingolani, S. and Lazzo, N.. Multiple semiclassical standing waves for a class of nonlinear Schrödinger equations. Topol. Methods Nonlinear Anal. 10 (1997), 1–13.CrossRefGoogle Scholar
9Cingolani, S. and Tanaka, K.. Semi-classical states for the nonlinear Choquard equations: Existence,multiplicity and concentration at a potential well. Rev. Mat. Iberoam. 35 (2019), 1885–1924.CrossRefGoogle Scholar
10Clapp, M. and Salazar, D.. Positive and sign changing solutions to a nonlinear Choquard equation. J. Math. Anal. Appl. 407 (2013), 1–15.CrossRefGoogle Scholar
11del Pino, M. and Felmer, P.. Semi-classical states for nonlinear Schrödinger equations. J. Funct. Anal. 149 (1997), 245–265.CrossRefGoogle Scholar
12Diósi, L.. Gravitation and quantum-mechanical localization of macro-objects. Phys. Lett. A 105 (1984), 199–202.CrossRefGoogle Scholar
13Floer, A. and Weinstein, A.. Nonspreading wave packets for the cubic Schrödinger equation with a bounded potential. J. Funct. Anal. 69 (1986), 397–408.CrossRefGoogle Scholar
14Ghimenti, M. and Van Schaftingen, J.. Nodal solutions for the Choquard equation. J. Funct. Anal. 271 (2016), 107–135.CrossRefGoogle Scholar
15Giulini, D. and Großardt, A.. The Schrödinger–Newton equation as a non-relativistic limit of self-gravitating Klein–Gordon and Dirac fields. Classical Quantum Gravity 29 (2012), 215010.CrossRefGoogle Scholar
16Hardy, G. H., Littlewood, J. E. and Polya, G.. Inequalities, 2nd edn. (Cambridge: Cambridge University Press, 1952).Google Scholar
17Huang, Z., Yang, J. and Yu, W.. Multiple nodal solutions of nonlinear Choquard equations. Electron. J. Differ. Equ. 2017(268) (2017), 1–18.Google Scholar
18Jones, K. R. W.. Newtonian Quantum Gravity. Aust. J. Phys. 48 (1995), 1055–1082.CrossRefGoogle Scholar
19Kang, X. and Wei, J.. On interacting bumps of semi-classical states of nonlinear Schrödinger equations. Adv. Differ. Equ. 5 (2000), 899–928.Google Scholar
20Lieb, E. H.. Existence and uniqueness of the minimizing solution of Choquard's nonlinear equation. Stud. Appl. Math. 57 (1977), 93–105.CrossRefGoogle Scholar
21Lions, P.-L.. The Choquard equation and related questions. Nonlinear Anal. 4 (1980), 1063–1072.CrossRefGoogle Scholar
22Liu, X., Ma, S. and Zhang, X.. Infinitely many bound state solutions of Choquard equations with potentials. Z. Angew. Math. Phys. 69 (2018), 29. Article No. 118.CrossRefGoogle Scholar
23Ma, L. and Zhao, L.. Classification of positive solitary solutions of the nonlinear Choquard equation. Arch. Ration. Mech. Anal. 195 (2010), 455–467.CrossRefGoogle Scholar
24Moroz, I. M., Penrose, R. and Tod, P.. Spherically-symmetric solutions of the Schrödinger–Newton equations. Classical Quantum Gravity 15 (1998), 2733–2742.CrossRefGoogle Scholar
25Moroz, V. and Van Schaftingen, J.. Groundstates of nonlinear Choquard equations: Existence, qualitative properties and decay asymptotics. J. Funct. Anal. 265 (2013), 153–184.CrossRefGoogle Scholar
26Moroz, V. and Van Schaftingen, J.. Existence of groundstates for a class of nonlinear Choquard equations. Trans. Amer. Math. Soc. 367 (2015), 6557–6579.CrossRefGoogle Scholar
27Moroz, V. and Van Schaftingen, J.. Semi-classical states for the Choquard equation. Calc. Var. Partial Differ. Equ. 52 (2015), 199–235.CrossRefGoogle Scholar
28Moroz, V. and Van Schaftingen, J.. A guide to the Choquard equation. J. Fixed Point Theory Appl. 19 (2017), 773–813.CrossRefGoogle Scholar
29Pekar, S.. Untersuchung über die Elektronentheorie der Kristalle (Berlin: Akademie Verlag, 1954).Google Scholar
30Rabinowitz, P. H., Minimax methods in critical point theory with applications to differential equations. In CBMS regional conference series in mathematics, vol. 65 (Providence: Americian Mathematical Society, 1986).Google Scholar
31Rabinowitz, P. H.. On a class of nonlinear Schrödinger equations. Z. Angew. Math. Phys. 43 (1992), 270–292.CrossRefGoogle Scholar
32Secchi, S.. A note on Schrödinger–Newton systems with decaying electric potential. Nonlinear Anal. 72 (2010), 3842–3856.CrossRefGoogle Scholar
33Van Schaftingen, J. and Xia, J.. Choquard equations under confining external potentials. NoDEA Nonlinear Differ. Equ. Appl. 24 (2017), 1–24.CrossRefGoogle Scholar
34Van Schaftingen, J. and Xia, J.. Standing waves with a critical frequency for nonlinear Choquard equations. Nonlinear Anal. 161 (2017), 87–107.CrossRefGoogle Scholar
35Wang, X.. On concentration of positive bound states of nonlinear Schrödinger equations. Commun. Math. Phys. 153 (1993), 229–244.CrossRefGoogle Scholar
36Wei, J. and Winter, M.. Strongly interacting bumps for the Schrödinger-Newton equations. J. Math. Phys. 50 (2009), 22. Article No. 012905.CrossRefGoogle Scholar
37Willem, M.. Minimax theorems (Boston, Basel, Berlin: Birkhäuser, 1996).CrossRefGoogle Scholar
38Xia, J. and Wang, Z.-Q.. Saddle solutions for the Choquard equation. Calc. Var. Partial Differ. Equ. 58 (2019), 30. Article No. 85.CrossRefGoogle Scholar
39Yang, M. and Ding, Y.. Existence of solutions for singularly perturbed Schrödinger equations with nonlocal part. Commun. Pure Appl. Anal. 12 (2013), 771–783.CrossRefGoogle Scholar
40Yang, M., Zhang, J. and Zhang, Y.. Multi-peak solutions for nonlinear Choquard equation with a general nonlinearity. Commun. Pure Appl. Anal. 16 (2017), 493–512.CrossRefGoogle Scholar
41Zhang, J., Wu, Q. and Qin, D.. Semiclassical solutions for Choquard equations with Berestycki-Lions type conditions. Nonlinear Anal. 188 (2019), 22–49.CrossRefGoogle Scholar