Hostname: page-component-6d856f89d9-4thr5 Total loading time: 0 Render date: 2024-07-16T06:21:03.071Z Has data issue: false hasContentIssue false
  • English
  • Français

Non-monotone waves of a stage-structured SLIRM epidemic model with latent period

Part of: Partial differential equations Representations of solutions Parabolic equations and systems

Published online by Cambridge University Press:  15 September 2020

Wenzhang Huang  and
Chufen Wu
Wenzhang Huang
Affiliation:
Department of Mathematical Sciences, University of Alabama in Huntsville, Huntsville, AL35899, USA (huang@math.uah.edu)
Chufen Wu
Affiliation:
School of Mathematics and Big Data, Foshan University, Foshan528000, China (chufenwu@126.com)
Get access Rights & Permissions [Opens in a new window]

Abstract

We propose and investigate a stage-structured SLIRM epidemic model with latent period in a spatially continuous habitat. We first show the existence of semi-travelling waves that connect the unstable disease-free equilibrium as the wave coordinate goes to − ∞, provided that the basic reproduction number 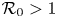$\mathcal {R}_0 > 1$ and $c > c_*$ for some positive number 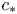$c_*$. We then use a combination of asymptotic estimates, Laplace transform and Cauchy's integral theorem to show the persistence of semi-travelling waves. Based on the persistent property, we construct a Lyapunov functional to prove the convergence of the semi-travelling wave to an endemic (positive) equilibrium as the wave coordinate goes to + ∞. In addition, by the Laplace transform technique, the non-existence of bounded semi-travelling wave is also proved when 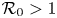$\mathcal {R}_0 > 1$ and 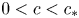$0 < c < c_*$. This indicates that 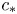$c_*$ is indeed the minimum wave speed. Finally simulations are given to illustrate the evolution of profiles.

Keywords

SLIRM modelnon-local nonlinear infection termnon-monotonetravelling wavespersistence

MSC classification

Primary: 35K57: Reaction-diffusion equations
Secondary: 35C07: Traveling wave solutions 35B40: Asymptotic behavior of solutions 92D30: Epidemiology
Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 151 , Issue 5 , October 2021 , pp. 1407 - 1442
Check for updates
Copyright
Copyright © The Author(s), 2020. Published by Cambridge University Press on behalf of The Royal Society of Edinburgh

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Abta, A., Kaddar, A. and Alaout, H.. Global stability for delay SIR and SEIR epidemic models with saturated incidence rates. Elec. J. Differ. Equ. 23 (2012), 1–13.Google Scholar
Ai, S. and Albashaireh, R.. Traveling waves in spatial SIRS models. J. Dyn. Differ. Equ. 26 (2014), 143–164.CrossRefGoogle ScholarPubMed
Aiello, W. G. and Freedman, H.. A time-delay model of single species growth with stage structure. Math. Biosci. 101 (1990), 139–153.CrossRefGoogle ScholarPubMed
Aiello, W. G., Freedman, H. and Wu, J.. Analysis of a model representing stage-structured population growth with state-dependent time delay. SIAM J. Appl. Math. 52 (1992), 855–869.CrossRefGoogle Scholar
Anderson, R. and May, R.. Infectious diseases in humans: dynamics and control (Oxford: Oxford University Press, 1992).Google Scholar
Capasso, V. and Serio, G.. A generalization of the Kermack–Mckendrick deterministic epidemic model. Math. Biosci. 42 (1978), 41–61.CrossRefGoogle Scholar
Caraco, T., Glavanakov, S., Chen, G., Flaherty, J., Ohsumi, T. and Szymanski, B.. Stage-structured infection transmission and a spatial epidemic: a model for Lyme disease. Am. Nat. 160 (2002), 348–359.CrossRefGoogle Scholar
Carr, J. and Chmaj, A.. Uniqueness of traveling waves for nonlocal monostable equations. Proc. Am. Math. Soc. 132 (2004), 2433–2439.CrossRefGoogle Scholar
Chen, D., Moulin, B. and Wu, J.. Analyzing and modeling spatial and temporal dynamics of infectious diseases (New York: John Wiley & Sons, 2014), pp. 19–42.Google Scholar
Diekmann, O.. Thresholds and traveling waves for the geographical spread of infection. J. Math. Biol. 6 (1978), 109–130.CrossRefGoogle Scholar
Diekmann, O., Gyllenberg, M., Metz, J. and Thieme, H.. On the formulation and analysis of general deterministic structured population models, I. Linear theory. J. Math. Biol. 36 (1998), 349–388.CrossRefGoogle Scholar
Dietz, K.. The evaluation of rubella vaccination strategies. In The mathematical theory of the dynamics of biological populations (eds Hiorns, R.W. and Cooke, K.), vol. II, pp. 81–97 (London: Academic Press, 1981).Google Scholar
Ding, W. and Huang, W.. Traveling wave solutions for some classes of diffusive predator-prey models. J. Dyn. Differ. Equ. 3 (2016), 1–16.Google Scholar
Ducrot, A., Magal, P. and Ruan, S.. Travelling wave solutions in multigroup age structured epidemic models. Arch. Ration. Mech. Anal. 195 (2010), 311–331.CrossRefGoogle Scholar
Ducrot, A. and Magal, P.. Travelling wave solutions for an infection-age structured model with external supplies. Nonlinearity 24 (2011), 2891–2911.CrossRefGoogle Scholar
Fang, J. and Zhao, X.-Q.. Traveling waves for monotone semiflows with weak compactness. SIAM J. Math. Anal. 46 (2014), 3678–3704.CrossRefGoogle Scholar
Fitzgibbon, W., Langlais, M., Parrott, M. and Webb, G.. A diffusive system with age dependency modeling FIV. Nonlinear Anal. 25 (1995), 975–989.CrossRefGoogle Scholar
Fu, S.-C.. Traveling waves for a diffusive SIR model with delay. J. Math. Anal. Appl. 435 (2016), 20–37.CrossRefGoogle Scholar
Gabriela, M., Gomes, M., White, L. and Medley, G.. The reinfection threshold. J. Theor. Biol. 236 (2005), 111–113.Google Scholar
Gourley, S. and Kuang, Y.. Wavefronts and global stability in a time-delayed population model with stage structure. Proc. R. Soc. Lond. Ser. A 459 (2003), 1563– 1579.Google Scholar
Gourley, S. and Kuang, Y.. A delay reaction-diffusion model of the spread of bacteriophage infection. SIAM J. Appl. Math. 65 (2005), 550–566.CrossRefGoogle Scholar
Gourley, S. and So, J. W.-H.. Extinction and wavefront propagation in a reaction-diffusion model of structured population with distributed maturation delay. Proc R. Soc. Edinb. A 133A (2003), 527–548.CrossRefGoogle Scholar
Gourley, S. and Wu, J.. Delayed non-local diffusion systems in biological invasion and disease spread. In Nonlinear dynamics and evolution equations. Fields Inst. Commun. (eds by H. Brunner, X.-Q. Zhao and X. Zou), vol. 48, pp. 137–200 (Providence, RI: American Mathematical Society, 2006).Google Scholar
Greenhalgh, D.. Age-structured models and optimal control in mathematical epidemiology: a survey. In Optimal control of age-structured populations in economy, demography and the environment (eds Boucekkine, R., Hritonenko, N. and Yatsenko, Y.), pp. 174–206 (New York: Routledge, 2010).Google Scholar
Hethcote, H.. The mathematics of infectious diseases. SIAM Rev. 42 (2000), 599–653.CrossRefGoogle Scholar
Huang, W.. A geometric approach in the study of traveling waves for some classes of non-monotone reaction-diffusion systems. J. Differ. Equ. 260 (2016), 2190–2224.CrossRefGoogle Scholar
Kaddar, A., Abta, A. and Alaout, H.. A comparison of delayed SIR and SEIR epidemic models. Nonlinear Anal. Model. Control 16 (2011), 181–190.CrossRefGoogle Scholar
Li, B., Lewis, M. and Weinberger, H.. Existence of traveling waves for integral recursions with nonmonotone growth functions. J. Math. Biol. 58 (2009), 323–338.CrossRefGoogle ScholarPubMed
Li, J. and Zou, X.. Modeling spatial spread of infectious diseases with a fixed latent period in a spatially continuous domain. Bull. Math. Biol. 71 (2009), 2048–2079.CrossRefGoogle Scholar
Liang, X. and Zhao, X.-Q.. Asymptotic speeds of spread and traveling waves for monotone semiflows with applications. Commun. Pure Appl. Math. 60 (2007), 1–40.CrossRefGoogle Scholar
Lin, X.-B., Weng, P. and Wu, C.. Traveling wave solutions for a predator-prey system with sigmoidal response function. J. Dyn. Differ. Equ. 23 (2011), 903–921.CrossRefGoogle Scholar
Lou, Y. and Zhao, X.-Q.. A reaction-diffusion malaria model with incubation period in the vector population. J. Math. Biol. 62 (2011), 543–568.CrossRefGoogle ScholarPubMed
Metz, J. and Diekmann, O. (eds). The dynamics of physiologically structured populations (Berlin: Springer, 1986).CrossRefGoogle Scholar
Murray, J., Stanley, A. and Brown, D.. On the spatial spread of rabies among foxes. Proc. R. Soc. Ser. B 229 (1986), 111–150.Google ScholarPubMed
Neubert, M. and Caswell, H.. Demography and dispersal: calculation and sensitivity analysis of invasion speed for structured populations. Ecology 81 (2000), 1613–1628.CrossRefGoogle Scholar
Ruan, S. and Xiao, D.. Stability of steady states and existence of travelling waves in a vector-disease model. Proc. R. Soc. Edinb. A 134A (2004), 991–1011.CrossRefGoogle Scholar
Wang, Z. and Wu, J.. Traveling waves of a diffusive Kermack–Mckendrick epidemic model with non-local delayed transmission. Proc. R. Soc. Lond. Ser. A 466 (2010), 237–261.Google Scholar
Wu, C. and Xiao, D.. Traveling wave solutions in a nonlocal and time-delayed reaction-diffusion model. IMA J. Appl. Math. 78 (2013), 1290–1317.CrossRefGoogle Scholar
Wu, J. and Zou, X.. Traveling wave fronts of reaction-diffusion systems with delay. J. Dyn. Differ. Equ. 13 (2001), 651–686.CrossRefGoogle Scholar
Xiao, Y., Chen, L. and ven den Bosch, F.. Dynamical behavior for a stage-structured SIR infectious disease model. Nonlinear Anal., Real World Appl. 3 (2002), 175–190.CrossRefGoogle Scholar
Zhang, T. R.. Minimal wave speed for a class of non-cooperative reaction-diffusion systems of three equations. J. Diff. Equ. 262 (2017), 4724–4770.CrossRefGoogle Scholar
Zhao, L., Wang, Z. and Ruan, S.. Traveling wave solutions in a two-group epidemic model with latent period. Nonlinearity 30 (2017), 1287–1325.CrossRefGoogle Scholar