Article contents
On the oscillation of certain second-order linear differential equations
Published online by Cambridge University Press: 09 December 2022
Abstract
This paper consists of three parts: First, letting $b_1(z)$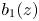 , $b_2(z)$
, $b_2(z)$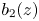 , $p_1(z)$
, $p_1(z)$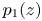 and $p_2(z)$
and $p_2(z)$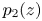 be nonzero polynomials such that $p_1(z)$
be nonzero polynomials such that $p_1(z)$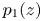 and $p_2(z)$
and $p_2(z)$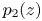 have the same degree $k\geq 1$
have the same degree $k\geq 1$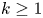 and distinct leading coefficients $1$
and distinct leading coefficients $1$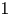 and $\alpha$
and $\alpha$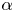 , respectively, we solve entire solutions of the Tumura–Clunie type differential equation $f^{n}+P(z,\,f)=b_1(z)e^{p_1(z)}+b_2(z)e^{p_2(z)}$
, respectively, we solve entire solutions of the Tumura–Clunie type differential equation $f^{n}+P(z,\,f)=b_1(z)e^{p_1(z)}+b_2(z)e^{p_2(z)}$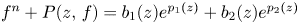 , where $n\geq 2$
, where $n\geq 2$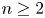 is an integer, $P(z,\,f)$
is an integer, $P(z,\,f)$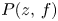 is a differential polynomial in $f$
is a differential polynomial in $f$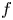 of degree $\leq n-1$
of degree $\leq n-1$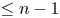 with coefficients having polynomial growth. Second, we study the oscillation of the second-order differential equation $f''-[b_1(z)e^{p_1(z)}+b_2(z)e^{p_2(z)}]f=0$
with coefficients having polynomial growth. Second, we study the oscillation of the second-order differential equation $f''-[b_1(z)e^{p_1(z)}+b_2(z)e^{p_2(z)}]f=0$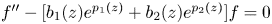 and prove that $\alpha =[2(m+1)-1]/[2(m+1)]$
and prove that $\alpha =[2(m+1)-1]/[2(m+1)]$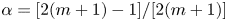 for some integer $m\geq 0$
for some integer $m\geq 0$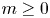 if this equation admits a nontrivial solution such that $\lambda (f)<\infty$
if this equation admits a nontrivial solution such that $\lambda (f)<\infty$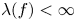 . This partially answers a question of Ishizaki. Finally, letting $b_2\not =0$
. This partially answers a question of Ishizaki. Finally, letting $b_2\not =0$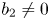 and $b_3$
and $b_3$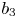 be constants and $l$
be constants and $l$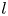 and $s$
and $s$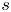 be relatively prime integers such that $l> s\geq 1$
be relatively prime integers such that $l> s\geq 1$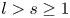 , we prove that $l=2$
, we prove that $l=2$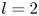 if the equation $f''-(e^{lz}+b_2e^{sz}+b_3)f=0$
if the equation $f''-(e^{lz}+b_2e^{sz}+b_3)f=0$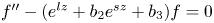 admits two linearly independent solutions $f_1$
admits two linearly independent solutions $f_1$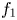 and $f_2$
and $f_2$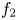 such that $\max \{\lambda (f_1),\,\lambda (f_2)\}<\infty$
such that $\max \{\lambda (f_1),\,\lambda (f_2)\}<\infty$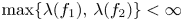 . In particular, we precisely characterize all solutions such that $\lambda (f)<\infty$
. In particular, we precisely characterize all solutions such that $\lambda (f)<\infty$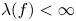 when $l=2$
when $l=2$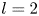 and $l=4$
and $l=4$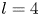 .
.
MSC classification
- Type
- Research Article
- Information
- Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 153 , Issue 6 , December 2023 , pp. 1965 - 1992
- Copyright
- Copyright © The Author(s), 2022. Published by Cambridge University Press on behalf of The Royal Society of Edinburgh
References
- 1
- Cited by



