No CrossRef data available.
Article contents
Semilinear elliptic equations involving power nonlinearities and Hardy potentials with boundary singularities
Published online by Cambridge University Press: 21 December 2023
Abstract
Let $\Omega \subset \mathbb {R}^N$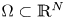 ($N\geq 3$
($N\geq 3$ ) be a $C^2$
) be a $C^2$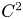 bounded domain and $\Sigma \subset \partial \Omega$
bounded domain and $\Sigma \subset \partial \Omega$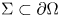 be a $C^2$
be a $C^2$ compact submanifold without boundary, of dimension $k$
compact submanifold without boundary, of dimension $k$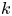 , $0\leq k \leq N-1$
, $0\leq k \leq N-1$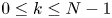 . We assume that $\Sigma = \{0\}$
. We assume that $\Sigma = \{0\}$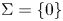 if $k = 0$
if $k = 0$ and $\Sigma =\partial \Omega$
and $\Sigma =\partial \Omega$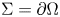 if $k=N-1$
if $k=N-1$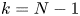 . Let $d_{\Sigma }(x)=\mathrm {dist}\,(x,\Sigma )$
. Let $d_{\Sigma }(x)=\mathrm {dist}\,(x,\Sigma )$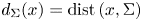 and $L_\mu = \Delta + \mu \,d_{\Sigma }^{-2}$
and $L_\mu = \Delta + \mu \,d_{\Sigma }^{-2}$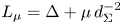 , where $\mu \in {\mathbb {R}}$
, where $\mu \in {\mathbb {R}}$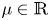 . We study boundary value problems ($P_\pm$
. We study boundary value problems ($P_\pm$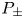 ) $-{L_\mu} u \pm |u|^{p-1}u = 0$
) $-{L_\mu} u \pm |u|^{p-1}u = 0$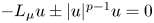 in $\Omega$
in $\Omega$ and $\mathrm {tr}_{\mu,\Sigma}(u)=\nu$
and $\mathrm {tr}_{\mu,\Sigma}(u)=\nu$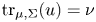 on $\partial \Omega$
on $\partial \Omega$ , where $p>1$
, where $p>1$ , $\nu$
, $\nu$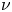 is a given measure on $\partial \Omega$
is a given measure on $\partial \Omega$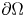 and $\mathrm {tr}_{\mu,\Sigma}(u)$
and $\mathrm {tr}_{\mu,\Sigma}(u)$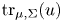 denotes the boundary trace of $u$
denotes the boundary trace of $u$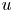 associated to $L_\mu$
associated to $L_\mu$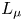 . Different critical exponents for the existence of a solution to ($P_\pm$
. Different critical exponents for the existence of a solution to ($P_\pm$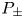 ) appear according to concentration of $\nu$
) appear according to concentration of $\nu$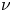 . The solvability for problem ($P_+$
. The solvability for problem ($P_+$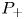 ) was proved in [3, 29] in subcritical ranges for $p$
) was proved in [3, 29] in subcritical ranges for $p$ , namely for $p$
, namely for $p$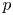 smaller than one of the critical exponents. In this paper, assuming the positivity of the first eigenvalue of $-L_\mu$
smaller than one of the critical exponents. In this paper, assuming the positivity of the first eigenvalue of $-L_\mu$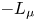 , we provide conditions on $\nu$
, we provide conditions on $\nu$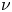 expressed in terms of capacities for the existence of a (unique) solution to ($P_+$
expressed in terms of capacities for the existence of a (unique) solution to ($P_+$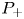 ) in supercritical ranges for $p$
) in supercritical ranges for $p$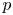 , i.e. for $p$
, i.e. for $p$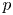 equal or bigger than one of the critical exponents. We also establish various equivalent criteria for the existence of a solution to ($P_-$
equal or bigger than one of the critical exponents. We also establish various equivalent criteria for the existence of a solution to ($P_-$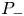 ) under a smallness assumption on $\nu$
) under a smallness assumption on $\nu$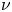 .
.
Keywords
- Type
- Research Article
- Information
- Copyright
- Copyright © The Author(s), 2023. Published by Cambridge University Press on behalf of The Royal Society of Edinburgh





