No CrossRef data available.
Article contents
Singularities of 3-parameter line congruences in $\mathbb {R}^{4}$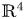
Part of:
Classical differential geometry
Theory of singularities and catastrophe theory
Differential topology
Published online by Cambridge University Press: 21 June 2022
Abstract
In this paper, we give the generic classification of the singularities of 3-parameter line congruences in $\mathbb {R}^{4}$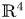
. We also classify the generic singularities of normal and Blaschke (affine) normal congruences.
MSC classification
- Type
- Research Article
- Information
- Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 153 , Issue 3 , June 2023 , pp. 1045 - 1070
- Copyright
- Copyright © The Author(s), 2022. Published by Cambridge University Press on behalf of The Royal Society of Edinburgh
References
Barajas, M., Craizer, M. and Garcia, R.. Lines of affine principal curvatures of surfaces in 3-space. Res. Math. 75 (2020), 1422-6383/20/010001-29–CrossRefGoogle Scholar
Bruce, J. W.. A classification of 1-parameter families of map germs $\mathbb {R}^{3},\, 0 \rightarrow \mathbb {R}^{3},\, 0$
, with applications to condensation problems. J. London Math. Soc. 33 (1986), 375–384.CrossRefGoogle Scholar
, with applications to condensation problems. J. London Math. Soc. 33 (1986), 375–384.CrossRefGoogle ScholarCecil, T.. Focal points and support functions in affine differential geometry. Geom. Dedicata 50 (1994), 291–300.CrossRefGoogle Scholar
Craizer, M., Domitrz, W. and Rios, P. D. M.. Singular improper affine spheres from a given Lagrangian submanifold. Adv. Math. 374 (2020), 107326.CrossRefGoogle Scholar
Craizer, M. and Garcia, R., Curvature lines of an equiaffine vector field transversal to a surface in 3-space, preprint arXiv:2008.04765v3.Google Scholar
Do Carmo, M. P.. Differential Geometry of Curves and Surfaces (Prentice Hall Inc, Upper Saddle River, 1976).Google Scholar
Ghys, E., Gaspar Monge - le mémoire sur les déblais et les remblais. Images des Mathématiques (2012), (www.images.math.cnrs.fr).Google Scholar
Giblin, P. J. and Zakalyukin, V.M.. Singularities of centre symmetry sets. Proc. London Math. Soc. 90 (2005), 132–166.10.1112/S0024611504014923CrossRefGoogle Scholar
Gibson, C. G., Singular Points of Smooth Mappings, Pitman research notes in Mathematics, Vol. 25 (Pitman, Boston, 1979).Google Scholar
Gibson, C. G., Wirthmüller, K., du Plessis, A. A. and Looijenga, E. J. N.. Topological stability of smooth mappings Lecture Notes in Mathematics, Vol. 552 (Springer, Berlin, 1970).Google Scholar
Golubitsky, M. and Guillemin, V., Stable Mappings and Their Singularities. Graduate Texts in Mathematics Vol. 14 (Springer-Verlag, Berlin, 1973).CrossRefGoogle Scholar
Izumiya, S., Romero Fuster, M. C., Ruas, M. A. S. and Tari, F.. Differential Geometry from a Singularity theory viewpoint (World Scientific Publishing Co. Pte. Ltd., Hackensack, NJ, 2016).Google Scholar
Izumiya, S. and Takeuchi, N.. Singularities of ruled surfaces in R3. Math. Proc. Camb. Phil. Soc. 130 (2001), 1–11.CrossRefGoogle Scholar
Izumiya, S., Saji, K. and Takeuchi, N.. Singularities of line congruences. Proc. R. Soc. Edinb. 133A (2003), 1341–1359.CrossRefGoogle Scholar
Leichtweiß, K.. Über eine geometrische Deutung des Affinnormalenvektors einseitig gekümmter Hyperflächen. Arch. Math. 53 (1989), 613–621.CrossRefGoogle Scholar
Li, A.-M, Simon, U., Zhao, G. and Hu, Z., Global affine differential geometry of hypersurfaces, extended ed, 11, De Gruyter Expositions in Mathematics (De Gruyter, Berlin, 2015).CrossRefGoogle Scholar
Marar, W. L. and Tari, F.. On the geometry of simple germs of co-rank 1 maps from $\mathbb {R}^{3}$ to $\mathbb {R}^{3}$. Math. Proc. Cambridge Philos. Soc. 119 (1996), 469–481.CrossRefGoogle Scholar
to $\mathbb {R}^{3}$
. Math. Proc. Cambridge Philos. Soc. 119 (1996), 469–481.CrossRefGoogle ScholarMather, J. N.. Stability of $C^{\infty }$ mappings, II: Infenitesimal stability implies stability. Ann. Math. 89 (1969), 254–291.CrossRefGoogle Scholar
mappings, II: Infenitesimal stability implies stability. Ann. Math. 89 (1969), 254–291.CrossRefGoogle ScholarMond, D. and Nuño Ballesteros, J. J.. Singularities of Mappings: The Local Behaviour of Smooth and Complex Analytic Mappings, Grundlehren der mathematischen Wissenschaften [Fundamental Principles of Mathematical Sciences], 357. (Springer Nature Switzerland, Cham, 2020).10.1007/978-3-030-34440-5CrossRefGoogle Scholar
Monge, G., Mémoire sur la théorie des déblais et des remblais, Histoire de l'Académie royale des sciences avec les mémoires de mathématique et de physique tirés des registres de cette Académie (1781), 666–705.Google Scholar
Montaldi, J. A.. On generic composites of maps. Bull. London Math. Soc. 23 (1991), 81–85.CrossRefGoogle Scholar
Nomizu, K. and Sasaki, T., Affine differential geometry. Geometry of affine immersions. Cambridge Tracts in Mathematics, Vol. 111 (Cambridge University Press, 1994).Google Scholar
Wall, C. T. C.. Finite determinacy of smooth map-germs. Bull. London Math. Soc. 13 (1981), 481–539.CrossRefGoogle Scholar