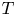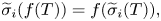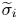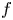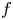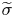1. Introduction
Let $T$![]() be a bounded self-adjoint operator on a Hilbert space $\mathcal {H}$
be a bounded self-adjoint operator on a Hilbert space $\mathcal {H}$![]() . A spectral singularity $\lambda \in \sigma (T)$
. A spectral singularity $\lambda \in \sigma (T)$![]() , where $\sigma (T)$
, where $\sigma (T)$![]() denotes the spectrum of $T$
denotes the spectrum of $T$![]() , is said to be in the essential spectrum of $T$
, is said to be in the essential spectrum of $T$![]() if $\lambda$
if $\lambda$![]() is not an isolated eigenvalue of finite multiplicity, see [Reference Wolf21].
is not an isolated eigenvalue of finite multiplicity, see [Reference Wolf21].
If $T$![]() is not self-adjoint, or if $T$
is not self-adjoint, or if $T$![]() is an operator on a Banach space $X$
is an operator on a Banach space $X$![]() , most modern texts define the essential spectrum $\sigma _{ess}(T)$
, most modern texts define the essential spectrum $\sigma _{ess}(T)$![]() of $T$
of $T$![]() in terms of Fredholm operators, that is, $\lambda \in \sigma _{ess}(T)$
in terms of Fredholm operators, that is, $\lambda \in \sigma _{ess}(T)$![]() iff $\lambda - T$
iff $\lambda - T$![]() is not a Fredholm operator. Recall that a bounded operator $T$
is not a Fredholm operator. Recall that a bounded operator $T$![]() is a Fredholm operator if both its nullity ${\rm nul}(T)$
is a Fredholm operator if both its nullity ${\rm nul}(T)$![]() (dimension of its kernel) and its defect ${\rm def}(T)$
(dimension of its kernel) and its defect ${\rm def}(T)$![]() (codimension of its range) are finite. One of the main useful properties of the essential spectrum (defined this way) is that it is invariant under compact perturbations. As a matter of fact, $\sigma _{ess}(T) = \sigma (p(T))$
(codimension of its range) are finite. One of the main useful properties of the essential spectrum (defined this way) is that it is invariant under compact perturbations. As a matter of fact, $\sigma _{ess}(T) = \sigma (p(T))$![]() , where $p(T)$
, where $p(T)$![]() is the projection of $T$
is the projection of $T$![]() in the Calkin algebra, i.e., the quotient algebra of the bounded operators $\mathcal {L}(X)$
in the Calkin algebra, i.e., the quotient algebra of the bounded operators $\mathcal {L}(X)$![]() on $X$
on $X$![]() modulo the compact operators $\mathcal {K}(X)$
modulo the compact operators $\mathcal {K}(X)$![]() on $X$
on $X$![]() .
.
However, several different definitions for the essential spectrum were introduced in the 1950s and 60 s, especially in the framework of differential operators. For instance, if we denote by $G^l$![]() ($G^r$
($G^r$![]() ) the semigroup of left (right) regular elements in the Calkin algebra $\mathcal {L}(X)/\mathcal {K}(X)$
) the semigroup of left (right) regular elements in the Calkin algebra $\mathcal {L}(X)/\mathcal {K}(X)$![]() , Yood [Reference Yood22] studied the spectral sets of $T\in \mathcal {L}(X)$
, Yood [Reference Yood22] studied the spectral sets of $T\in \mathcal {L}(X)$![]() given by $\sigma _2(T):=\{\lambda \in \mathbb {C} \, : \, \lambda - p(T) \notin G^l\}$
given by $\sigma _2(T):=\{\lambda \in \mathbb {C} \, : \, \lambda - p(T) \notin G^l\}$![]() and $\sigma _3(T) := \{\lambda \in \mathbb {C} \, : \, \lambda - p(T) \notin G^r\}$
and $\sigma _3(T) := \{\lambda \in \mathbb {C} \, : \, \lambda - p(T) \notin G^r\}$![]() . Indeed, he obtained the following characterizations of the semigroups $p^{-1}(G^l), p^{-1}(G^r)$
. Indeed, he obtained the following characterizations of the semigroups $p^{-1}(G^l), p^{-1}(G^r)$![]() :
:

where $\operatorname {ran} T, \, \ker T$![]() denote the range space of $T$
denote the range space of $T$![]() and the kernel of $T$
and the kernel of $T$![]() respectively.
respectively.
Alternatively, spectral sets associated with semi-Fredholm operators have also been referred to as essential spectra. More precisely, let $\Phi ^+$![]() , $\Phi ^-$
, $\Phi ^-$![]() be given by
be given by
Then Gustafson and Weidmann [Reference Gustafson and Weidmann9] used the term essential spectra for the spectral sets $\sigma _4(T) := \{\lambda \in \mathbb {C} \, : \, \lambda - T \notin \Phi ^-\}$![]() , $\sigma _5(T) := \{\lambda \in \mathbb {C} \, : \, \lambda - T \notin \Phi ^+\}$
, $\sigma _5(T) := \{\lambda \in \mathbb {C} \, : \, \lambda - T \notin \Phi ^+\}$![]() , while Kato [Reference Kato13] considered the spectral set $\sigma _6(T):= \sigma _4(T) \cap \sigma _5(T)$
, while Kato [Reference Kato13] considered the spectral set $\sigma _6(T):= \sigma _4(T) \cap \sigma _5(T)$![]() , i.e., $\lambda \in \sigma _6(T)$
, i.e., $\lambda \in \sigma _6(T)$![]() iff $\lambda - T$
iff $\lambda - T$![]() is not in $\Phi ^- \cup \Phi ^+$
is not in $\Phi ^- \cup \Phi ^+$![]() . Note that $\sigma _2(T) = \sigma _4(T)$
. Note that $\sigma _2(T) = \sigma _4(T)$![]() and $\sigma _3(T) = \sigma _5(T)$
and $\sigma _3(T) = \sigma _5(T)$![]() if $T$
if $T$![]() is an operator on a Hilbert space, but these identities do not hold in general in the framework of Banach spaces, see the work of Pietsch [Reference Pietsch18].
is an operator on a Hilbert space, but these identities do not hold in general in the framework of Banach spaces, see the work of Pietsch [Reference Pietsch18].
In another direction, Browder [Reference Browder3] defined the essential spectrum of $T$![]() ($\sigma _8(T)$
($\sigma _8(T)$![]() here) as those spectral values of $T$
here) as those spectral values of $T$![]() which are not isolated eigenvalues of finite multiplicity of $T$
which are not isolated eigenvalues of finite multiplicity of $T$![]() nor isolated eigenvalues of finite multiplicity of the adjoint operator $T^\ast$
nor isolated eigenvalues of finite multiplicity of the adjoint operator $T^\ast$![]() (cf. [Reference Lay14]). It turns out that $\lambda \notin \sigma _8(T)$
(cf. [Reference Lay14]). It turns out that $\lambda \notin \sigma _8(T)$![]() iff $\lambda$
iff $\lambda$![]() is a pole of the resolvent of finite rank [Reference Browder3, Lemma 17]. With this in mind, Gramsch and Lay [Reference Gramsch and Lay8] considered the following additional essential spectrum, which is given by
is a pole of the resolvent of finite rank [Reference Browder3, Lemma 17]. With this in mind, Gramsch and Lay [Reference Gramsch and Lay8] considered the following additional essential spectrum, which is given by
Nevertheless, the essential spectrum of Browder $\sigma _8(T)$![]() fails to be invariant under compact perturbations. In this regard, Schechter [Reference Schechter19] defined the essential spectrum of $T$
fails to be invariant under compact perturbations. In this regard, Schechter [Reference Schechter19] defined the essential spectrum of $T$![]() , $\sigma _7(T)$
, $\sigma _7(T)$![]() here, as the largest subset of $\sigma (T)$
here, as the largest subset of $\sigma (T)$![]() which is invariant under compact perturbations. Equivalently $\lambda \notin \sigma _7(T)$
which is invariant under compact perturbations. Equivalently $\lambda \notin \sigma _7(T)$![]() iff $\lambda - T$
iff $\lambda - T$![]() is Fredholm with index zero, i.e., ${\rm nul}(\lambda - T) = {\rm def}(\lambda - T) < \infty$
is Fredholm with index zero, i.e., ${\rm nul}(\lambda - T) = {\rm def}(\lambda - T) < \infty$![]() . For a more systematic treatment of all these essential spectra, we refer to § 2.
. For a more systematic treatment of all these essential spectra, we refer to § 2.
In this work, we deal with spectral mapping theorems for all the different essential spectra described above, that is, identities of the form
There, $f$![]() is a function in the domain of some functional calculus of a (possibly unbounded) operator $T$
is a function in the domain of some functional calculus of a (possibly unbounded) operator $T$![]() .
.
At this point, the first approach to a Banach space functional calculus of unbounded operators is the so-called Dunford-Taylor calculus. For this calculus, one considers functions $f$![]() which are holomorphic in an open set containing the extended spectrum $\widetilde \sigma (T)$
which are holomorphic in an open set containing the extended spectrum $\widetilde \sigma (T)$![]() of $T$
of $T$![]() , defined by $\widetilde \sigma (T) := \sigma (T) \cup \{\infty \}$
, defined by $\widetilde \sigma (T) := \sigma (T) \cup \{\infty \}$![]() if $T$
if $T$![]() is unbounded and $\widetilde \sigma (T) := \sigma (T)$
is unbounded and $\widetilde \sigma (T) := \sigma (T)$![]() otherwise. Then, for unbounded $T$
otherwise. Then, for unbounded $T$![]() , $f(T)$
, $f(T)$![]() is given by
is given by
where $\Gamma$![]() is a suitable finite cycle that avoids $\widetilde \sigma (T)$
is a suitable finite cycle that avoids $\widetilde \sigma (T)$![]() . Moreover, the Dunford-Taylor formula above (1.2) still works when the curve $\Gamma$
. Moreover, the Dunford-Taylor formula above (1.2) still works when the curve $\Gamma$![]() touches $\widetilde \sigma (T)$
touches $\widetilde \sigma (T)$![]() at some points $a_1, \ldots, a_n$
at some points $a_1, \ldots, a_n$![]() and $f$
and $f$![]() is not holomorphic at $a_1, \ldots, a_n$
is not holomorphic at $a_1, \ldots, a_n$![]() , as long as $f$
, as long as $f$![]() tends to a finite number at each point $a_1, \ldots, a_n$
tends to a finite number at each point $a_1, \ldots, a_n$![]() fast enough to deal with the size of the resolvent at these points. In this case, we say that $f$
fast enough to deal with the size of the resolvent at these points. In this case, we say that $f$![]() has regular limits (at $a_1, \ldots, a_n$
has regular limits (at $a_1, \ldots, a_n$![]() ) and denote it by $\mathcal {E}(T)$
) and denote it by $\mathcal {E}(T)$![]() .
.
Furthermore, in the setting of strip-type operators, Bade [Reference Bade2] introduced a ‘regularization trick’ in order to define $f(T)$![]() for functions which do not grow too fast at $\infty$
for functions which do not grow too fast at $\infty$![]() . This ‘regularization trick’ was further developed, in the framework of sectorial operators, by McIntosh [Reference McIntosh15], Cowling et al [Reference Cowling, Doust, Mcintosh and Yagi4] and Haase [Reference Haase10]. In particular, fractional powers and/or logarithms can be defined for suitable unbounded operators with this ‘regularization trick’.
. This ‘regularization trick’ was further developed, in the framework of sectorial operators, by McIntosh [Reference McIntosh15], Cowling et al [Reference Cowling, Doust, Mcintosh and Yagi4] and Haase [Reference Haase10]. In particular, fractional powers and/or logarithms can be defined for suitable unbounded operators with this ‘regularization trick’.
Here, we consider the ‘regularized’ functional calculus of meromorphic functions developed by Haase [Reference Haase10], which is based on the following idea. A meromorphic function $f$![]() is in the domain of the regularized functional calculus of $T$
is in the domain of the regularized functional calculus of $T$![]() , which we denote by $f \in \mathcal {M}(T)$
, which we denote by $f \in \mathcal {M}(T)$![]() , if there exists a holomorphic function $e \in \mathcal {E}(T)$
, if there exists a holomorphic function $e \in \mathcal {E}(T)$![]() such that $e(T)$
such that $e(T)$![]() is injective and $ef \in \mathcal {E}(T)$
is injective and $ef \in \mathcal {E}(T)$![]() . In this case, one defines
. In this case, one defines
which is a (possibly unbounded) closed operator on $X$![]() .
.
Spectral mapping theorems, i.e., identities of the form (1.1), were proven by Gramsch and Lay [Reference Gramsch and Lay8] in the setting of the Dunford-Taylor calculus, for most (extended) essential spectra described here, see § 2 for their definitions. González and Onieva [Reference González and Onieva7] used a unified approach and gave simpler proofs for these spectral mapping theorems. Their proofs are based on the following observations:
1) a closed operator $T$
 with non-empty resolvent set is essentially invertible iff, for $b \in \mathbb {C}\setminus \sigma (T)$
with non-empty resolvent set is essentially invertible iff, for $b \in \mathbb {C}\setminus \sigma (T)$ , the bounded operator $T(b-T)^{-1}$
, the bounded operator $T(b-T)^{-1}$ is essentially invertible [Reference González and Onieva7, Lemma 1],
is essentially invertible [Reference González and Onieva7, Lemma 1],2) for $f, g$
 in the domain of the Dunford-Taylor calculus of $T$
in the domain of the Dunford-Taylor calculus of $T$ , one has $(fg)(T) =f(T)g(T)=g(T)f(T)$
, one has $(fg)(T) =f(T)g(T)=g(T)f(T)$ . As a consequence, $(fg)(T)$
. As a consequence, $(fg)(T)$ is essentially invertible if/only if (see [Reference González and Onieva7, Lemma 3]) both $f(T), g(T)$
is essentially invertible if/only if (see [Reference González and Onieva7, Lemma 3]) both $f(T), g(T)$ are essentially invertible,
are essentially invertible,
where we say that an operator $A$![]() is essentially invertible (regarding the essential spectrum $\sigma _i$
is essentially invertible (regarding the essential spectrum $\sigma _i$![]() ) if $0 \notin \sigma _i(A)$
) if $0 \notin \sigma _i(A)$![]() ;
;
3) if $f$
 is in the domain of the Dunford-Taylor calculus of $T$
is in the domain of the Dunford-Taylor calculus of $T$ , then one can assume that $f$
, then one can assume that $f$ has a finite number of zeroes of finite multiplicity.
has a finite number of zeroes of finite multiplicity.
It sounds sensible to ask whether these spectral mapping theorems can be extended to cover the functions in the domain of the regularized functional calculus given by (1.3). This is partly motivated by potential applications in Fredholm theory, in particular when considering fractional powers or logarithms of unbounded operators. For instance, we make use, in an ongoing work with L. Abadías, of the results presented here to describe the essential spectrum of fractional Cesàro operators and Hölder operators acting on spaces of holomorphic functions. However, there are two main difficulties for such an extension of the spectral mapping theorem. First, for $f, g \in \mathcal {M}(T)$![]() , it is not true in general that $(fg)(T) = f(T)g(T) =g(T)f(T)$
, it is not true in general that $(fg)(T) = f(T)g(T) =g(T)f(T)$![]() , so item 2) above fails. Indeed, one only has the inclusions $f(T)g(T), g(T)f(T) \subseteq (fg)(T)$
, so item 2) above fails. Indeed, one only has the inclusions $f(T)g(T), g(T)f(T) \subseteq (fg)(T)$![]() , where $S\subseteq T$
, where $S\subseteq T$![]() means that $\operatorname {dom} S \subseteq \operatorname {dom} T$
means that $\operatorname {dom} S \subseteq \operatorname {dom} T$![]() with $Sx = Tx$
with $Sx = Tx$![]() for every $x \in \operatorname {dom} S$
for every $x \in \operatorname {dom} S$![]() . Secondly, since the function $f$
. Secondly, since the function $f$![]() may not be holomorphic at the points $a_1, \ldots, a_n$
may not be holomorphic at the points $a_1, \ldots, a_n$![]() where the integration path touches $\sigma (T)$
where the integration path touches $\sigma (T)$![]() , item 3) above also fails to be true.
, item 3) above also fails to be true.
Nevertheless, in the setting of sectorial operators, Haase [Reference Haase11] overcame these two problems for the usual extended spectrum $\widetilde \sigma$![]() , and obtained the spectral mapping theorem
, and obtained the spectral mapping theorem
for a meromorphic function $f$![]() in the domain of the regularized functional calculus, i.e., $f \in \mathcal {M}(T)$
in the domain of the regularized functional calculus, i.e., $f \in \mathcal {M}(T)$![]() , such that $f$
, such that $f$![]() has almost logarithmic limits at the points $a_1, \ldots, a_n$
has almost logarithmic limits at the points $a_1, \ldots, a_n$![]() where the integration path $\Gamma$
where the integration path $\Gamma$![]() touches $\widetilde \sigma (T)$
touches $\widetilde \sigma (T)$![]() . This ‘almost logarithmic’ condition on the behavior of the limits of $f$
. This ‘almost logarithmic’ condition on the behavior of the limits of $f$![]() is stronger than asking $f$
is stronger than asking $f$![]() to have regular limits at $a_1, \ldots, a_n$
to have regular limits at $a_1, \ldots, a_n$![]() . As a matter of fact, Haase leaves open the question whether the hypothesis of $f$
. As a matter of fact, Haase leaves open the question whether the hypothesis of $f$![]() having regular limits is sufficient to obtain the spectral mapping theorem, see [Reference Haase11, Remark 5.4].
having regular limits is sufficient to obtain the spectral mapping theorem, see [Reference Haase11, Remark 5.4].
Still, it is far from trivial to extend the spectral mapping theorem (1.4) from the usual extended spectrum to the (extended) essential spectra described here. This extension, which is given here, is the main contribution of the paper. Even more, we obtain spectral mapping theorems for the essential spectra described above and for functions $f$![]() with regular limits lying in the domain of the regularized functional calculus of meromorphic functions (1.3), answering in the positive Haase's conjecture on regular limits explained above.
with regular limits lying in the domain of the regularized functional calculus of meromorphic functions (1.3), answering in the positive Haase's conjecture on regular limits explained above.
To obtain these results, on the one hand we provide a slightly simpler proof for the spectral inclusion of the usual extended spectrum, i.e., $f(\widetilde \sigma (A)) \subseteq \widetilde \sigma (f(A))$![]() , than the one given in [Reference Haase11]. As a matter of fact, we no longer make use of the composition rule of the functional calculus. Such a simplification allows us to weaken the condition on the function $f$
, than the one given in [Reference Haase11]. As a matter of fact, we no longer make use of the composition rule of the functional calculus. Such a simplification allows us to weaken the condition on the function $f$![]() from almost logarithmic limits to the (quasi-)regular limits, cf. [Reference Haase11, Remark 5.4]. On the other hand, the core of the paper contained in § 3 and 4, is devoted to address the items 2) and 3) above, so we cover all the essential spectra described here.
from almost logarithmic limits to the (quasi-)regular limits, cf. [Reference Haase11, Remark 5.4]. On the other hand, the core of the paper contained in § 3 and 4, is devoted to address the items 2) and 3) above, so we cover all the essential spectra described here.
In this work, we use the model case of bisectorial-like operators, which is a family of operators that slightly generalizes the one of bisectorial operators, see for instance [Reference Arendt and Duelli1, Reference Mielke16]. This is partly motivated by two reasons. On the one hand, we want our results to cover the case when $T$![]() is the generator of an exponentially bounded group. This is because, in a forthcoming paper, we obtain spectral properties of certain integral operators via subordination of such operators in terms of an exponentially bounded group, namely, a weighted composition group of hyperbolic symbol. On the other hand, the another incentive to do this is the fact that the regularized functional calculus for bisectorial-like operators is easily constructed by mimicking the regularized functional calculus of sectorial operators [Reference Haase10, Reference Haase12]. Finally, bisectorial operators play an important role in the field of abstract inhomogeneous differential equations over the real line, so we are confident that our results have applications of interest in that topic.
is the generator of an exponentially bounded group. This is because, in a forthcoming paper, we obtain spectral properties of certain integral operators via subordination of such operators in terms of an exponentially bounded group, namely, a weighted composition group of hyperbolic symbol. On the other hand, the another incentive to do this is the fact that the regularized functional calculus for bisectorial-like operators is easily constructed by mimicking the regularized functional calculus of sectorial operators [Reference Haase10, Reference Haase12]. Finally, bisectorial operators play an important role in the field of abstract inhomogeneous differential equations over the real line, so we are confident that our results have applications of interest in that topic.
Nevertheless, the proofs presented here are generic and are valid for similar functional calculi to the one presented here. Indeed, the abstract properties collected in lemmas 2.7–2.11 are the key to prove our results. In particular, our method also works for the regularized functional calculus of sectorial operators and the regularized functional calculus of strip-type operators, see Subsection 5.2.
The paper is organized as follows. The regularized functional calculus for bisectorial-like operators is detailed in § 2. In § 3, we give the spectral mapping theorems for a bisectorial-like operator $A$![]() in the case the integration path $\Gamma$
in the case the integration path $\Gamma$![]() does not touch any point of $\widetilde \sigma (T)$
does not touch any point of $\widetilde \sigma (T)$![]() . The general case is dealt with in § 4. We give some final remarks in § 5, such as the answer in the positive to Haase's conjecture [Reference Haase11, Remark 5.4].
. The general case is dealt with in § 4. We give some final remarks in § 5, such as the answer in the positive to Haase's conjecture [Reference Haase11, Remark 5.4].
2. Extended essential spectra and regularized functional calculus for bisectorial-like operators
Let us fix (and recall) the notation through the paper. $X$![]() will denote an infinite dimensional complex Banach space. Let $\mathcal {L}(X)$
will denote an infinite dimensional complex Banach space. Let $\mathcal {L}(X)$![]() , $C(X)$
, $C(X)$![]() denote the sets of bounded operators and closed operators on $X$
denote the sets of bounded operators and closed operators on $X$![]() , respectively. For $T \in C(X)$
, respectively. For $T \in C(X)$![]() , let $\operatorname {dom} T, \, \operatorname {ran} T, \, \ker T$
, let $\operatorname {dom} T, \, \operatorname {ran} T, \, \ker T$![]() denote the domain, range, null space of $T$
denote the domain, range, null space of $T$![]() , respectively. Moreover, we denote the nullity of $T$
, respectively. Moreover, we denote the nullity of $T$![]() by ${\rm nul}(T)$
by ${\rm nul}(T)$![]() , and the defect of $T$
, and the defect of $T$![]() by ${\rm def}(T)$
by ${\rm def}(T)$![]() . The ascent of $T$
. The ascent of $T$![]() , $\alpha (T)$
, $\alpha (T)$![]() , is the smallest integer $n$
, is the smallest integer $n$![]() such that $\ker T^n = \ker T^{n+1}$
such that $\ker T^n = \ker T^{n+1}$![]() , and the descent of $T$
, and the descent of $T$![]() , $\delta (T)$
, $\delta (T)$![]() , is the smallest integer $n$
, is the smallest integer $n$![]() such that $\operatorname {ran} T^n = \operatorname {ran} T^{n+1}$
such that $\operatorname {ran} T^n = \operatorname {ran} T^{n+1}$![]() .
.
Now we recall the definition of the different essential spectra described in the Introduction. Following the notation and terminology of [Reference González and Onieva7, Reference Gramsch and Lay8], set

We observe that these operator families satisfy the following spectral inclusions

Then, the respective spectra $\sigma _i(T)$![]() are defined in terms of the above families by
are defined in terms of the above families by
Note that $\sigma _0(T)$![]() is the usual spectrum $\sigma (T)$
is the usual spectrum $\sigma (T)$![]() and most modern text use the term essential spectrum to denote the set $\sigma _1(T)$
and most modern text use the term essential spectrum to denote the set $\sigma _1(T)$![]() . It is also worth saying that the works [Reference González and Onieva7, Reference Gramsch and Lay8] also considered the essential spectrum $\sigma _{10}(T)$
. It is also worth saying that the works [Reference González and Onieva7, Reference Gramsch and Lay8] also considered the essential spectrum $\sigma _{10}(T)$![]() defined in terms of normally solvable operators, i.e., operators with closed range, see [Reference Dunford and Schwartz5]. However, there exist bounded operators $S, T$
defined in terms of normally solvable operators, i.e., operators with closed range, see [Reference Dunford and Schwartz5]. However, there exist bounded operators $S, T$![]() on Hilbert spaces for which $\sigma _{10}(T^2) \not \subseteq (\sigma _{10}(T))^2$
on Hilbert spaces for which $\sigma _{10}(T^2) \not \subseteq (\sigma _{10}(T))^2$![]() and $\sigma _{10}(S^2) \not \supseteq (\sigma _{10}(S))^2$
and $\sigma _{10}(S^2) \not \supseteq (\sigma _{10}(S))^2$![]() , see [Reference Gramsch and Lay8, Section 5].
, see [Reference Gramsch and Lay8, Section 5].
Next we define the extended essential spectra $\widetilde {\sigma }_i(T)$![]() .
.
Definition 2.1 Let $T \in C(X)$![]() . We define
. We define

Note that $\widetilde {\sigma }_0(T)$![]() is the usual extended spectrum $\widetilde {\sigma }(T)$
is the usual extended spectrum $\widetilde {\sigma }(T)$![]() . If the resolvent set $\rho (T)$
. If the resolvent set $\rho (T)$![]() is not empty, $\widetilde {\sigma }_i(T)$
is not empty, $\widetilde {\sigma }_i(T)$![]() coincides with the extended essential spectrum introduced by González and Onieva [Reference González and Onieva7], which satisfies that $\infty \in \widetilde {\sigma }_i(T)$
coincides with the extended essential spectrum introduced by González and Onieva [Reference González and Onieva7], which satisfies that $\infty \in \widetilde {\sigma }_i(T)$![]() if and only if ${0\in \sigma _i((\mu - T)^{-1})}$
if and only if ${0\in \sigma _i((\mu - T)^{-1})}$![]() for any $\mu \in \rho (T)$
for any $\mu \in \rho (T)$![]() . In particular, if $T$
. In particular, if $T$![]() has non-empty resolvent set, $\widetilde {\sigma }_i(T)$
has non-empty resolvent set, $\widetilde {\sigma }_i(T)$![]() are non-empty compact subsets of $\mathbb {C}_\infty$
are non-empty compact subsets of $\mathbb {C}_\infty$![]() except for $i =9$
except for $i =9$![]() (see [Reference Gramsch and Lay8]), where $\mathbb {C}_\infty$
(see [Reference Gramsch and Lay8]), where $\mathbb {C}_\infty$![]() denotes the Riemann sphere $\mathbb {C} \cup \{\infty \}$
denotes the Riemann sphere $\mathbb {C} \cup \{\infty \}$![]() . If $T$
. If $T$![]() has empty resolvent set, $\sigma _i(T)$
has empty resolvent set, $\sigma _i(T)$![]() is a closed subset of $\mathbb {C}$
is a closed subset of $\mathbb {C}$![]() for $i\in \{0, 1, 2, 4, 5, 6, 7\}$
for $i\in \{0, 1, 2, 4, 5, 6, 7\}$![]() , see [Reference Edmunds and Evans6, Section I.3] and [Reference Yood22]. We do not know if $\widetilde {\sigma}_i(T)$
, see [Reference Edmunds and Evans6, Section I.3] and [Reference Yood22]. We do not know if $\widetilde {\sigma}_i(T)$![]() or $\sigma _i(T)$
or $\sigma _i(T)$![]() are closed in the other cases.
are closed in the other cases.
Now we turn to the definition of the regularized functional calculus of bisectorial-like operators. Its construction is completely analogous to the one of the regularized functional calculus of sectorial operators given by Haase in [Reference Haase10, Reference Haase12], and the adaptation of it from the sectorial operators to the bisectorial-like operators is straightforward.
Given any $\varphi \in (0, \pi )$![]() , we denote the sector $S_{\varphi }:=\left \{z\in \mathbb {C}: \left |\mbox {arg}(z)\right |<\varphi \right \}$
, we denote the sector $S_{\varphi }:=\left \{z\in \mathbb {C}: \left |\mbox {arg}(z)\right |<\varphi \right \}$![]() . For any $\omega \in (0, \pi /2]$
. For any $\omega \in (0, \pi /2]$![]() and $a\geq 0$
and $a\geq 0$![]() , we set the bisector
, we set the bisector

see Fig. 1 for a sketch of such a bisectorial-like set.
Definition 2.2 Let $(\omega, a) \in (0, \pi /2] \times [0, \infty )$![]() and let $A \in C(X)$
and let $A \in C(X)$![]() . We will say that $A$
. We will say that $A$![]() is a $\mathbf{bisectorial}\text{-}\mathbf{like\, operator}$
is a $\mathbf{bisectorial}\text{-}\mathbf{like\, operator}$![]() of angle $\omega$
of angle $\omega$![]() and half-width $a$
and half-width $a$![]() if the following conditions hold:
if the following conditions hold:
• $\sigma (A) \subseteq \overline {BS_{\omega,a}}$
 .
.• For all $\omega ' \in (0, \omega )$
 , $A$
, $A$ satisfies the resolvent bound
\begin{align*} \sup \Big\{ \min\{|\lambda-a|, |\lambda+a|\} \| (\lambda-A)^{{-}1}\| \, : \, \lambda \notin \overline{BS_{\omega',a}} \Big\}< \infty. \end{align*}
satisfies the resolvent bound
\begin{align*} \sup \Big\{ \min\{|\lambda-a|, |\lambda+a|\} \| (\lambda-A)^{{-}1}\| \, : \, \lambda \notin \overline{BS_{\omega',a}} \Big\}< \infty. \end{align*}
We also set $M_A := \widetilde {\sigma }(A) \cap \{-a, a, \infty \}$![]() . For the rest of the paper, $(\omega, a)$
. For the rest of the paper, $(\omega, a)$![]() will denote a pair in $(0, \pi /2] \times [0, \infty )$
will denote a pair in $(0, \pi /2] \times [0, \infty )$![]() .
.
Given a Banach space $X$![]() , we denote the set of all bisectorial-like operators on $X$
, we denote the set of all bisectorial-like operators on $X$![]() of angle $\omega$
of angle $\omega$![]() and half-width $a$
and half-width $a$![]() in $X$
in $X$![]() by ${\rm BSect}(\omega, a)$
by ${\rm BSect}(\omega, a)$![]() . We omit an explicit mention to $X$
. We omit an explicit mention to $X$![]() for the sake of simplicity. Notice that $A \in {\rm BSect}(\omega, a)$
for the sake of simplicity. Notice that $A \in {\rm BSect}(\omega, a)$![]() if and only if both $a+A, a-A$
if and only if both $a+A, a-A$![]() are sectorial of angle $\pi -\omega$
are sectorial of angle $\pi -\omega$![]() in the sense of [Reference Haase12].
in the sense of [Reference Haase12].
We denote by $\mathcal {O}(\Omega ), \mathcal {M}(\Omega )$![]() the sets of holomorphic functions and meromorphic functions defined in an open subset $\Omega \subseteq \mathbb {C}$
the sets of holomorphic functions and meromorphic functions defined in an open subset $\Omega \subseteq \mathbb {C}$![]() , respectively. For $A \in {\rm BSect}(\omega, a)$
, respectively. For $A \in {\rm BSect}(\omega, a)$![]() , let $U_A := \{-a, a, \infty \} \setminus \widetilde \sigma (A)$
, let $U_A := \{-a, a, \infty \} \setminus \widetilde \sigma (A)$![]() . If $\sigma (A) \neq \emptyset$
. If $\sigma (A) \neq \emptyset$![]() , set
, set

where $\mbox {dist}\{\cdot, \cdot \}$![]() denotes the distance between two sets, and $r(A)$
denotes the distance between two sets, and $r(A)$![]() the spectral radius of $A$
the spectral radius of $A$![]() . If $\sigma (A) = \emptyset$
. If $\sigma (A) = \emptyset$![]() (so $\widetilde {\sigma }(A) = \{\infty \}$
(so $\widetilde {\sigma }(A) = \{\infty \}$![]() and $\infty \notin U_A$
and $\infty \notin U_A$![]() ), set $r_a = r_{-a} := \infty$
), set $r_a = r_{-a} := \infty$![]() .
.
For ${\rm d} \in U_A$![]() suppose that $s_d \in (0, r_d)$
suppose that $s_d \in (0, r_d)$![]() . Then, for $\varphi \in (0, \omega )$
. Then, for $\varphi \in (0, \omega )$![]() , set $\Omega (\varphi, (s_d)_{{\rm d}\in U_A})$
, set $\Omega (\varphi, (s_d)_{{\rm d}\in U_A})$![]() as follows. If $U_A = \emptyset$
as follows. If $U_A = \emptyset$![]() (i.e., $M_A = \{-a, a, \infty \}$
(i.e., $M_A = \{-a, a, \infty \}$![]() ), we set $\Omega _\varphi := BS_{\varphi,a}$
), we set $\Omega _\varphi := BS_{\varphi,a}$![]() . Otherwise, for each ${\rm d} \in U_A$
. Otherwise, for each ${\rm d} \in U_A$![]() , let $B_d(s_d)$
, let $B_d(s_d)$![]() be a ball centred at $d$
be a ball centred at $d$![]() of radius $s_d$
of radius $s_d$![]() , where $B_\infty (r_\infty ) = \{z \in \mathbb {C} \, | \, |z|>r_\infty ^{-1}\}$
, where $B_\infty (r_\infty ) = \{z \in \mathbb {C} \, | \, |z|>r_\infty ^{-1}\}$![]() . Then, we set $\Omega (\varphi, (s_d)_{{\rm d}\in U_A}) := BS_{\varphi,a} \setminus (\bigcup _{{\rm d}\in U_A} \overline {B_d (s_d)})$
. Then, we set $\Omega (\varphi, (s_d)_{{\rm d}\in U_A}) := BS_{\varphi,a} \setminus (\bigcup _{{\rm d}\in U_A} \overline {B_d (s_d)})$![]() . Note that, if $\varphi < \varphi ' < \omega$
. Note that, if $\varphi < \varphi ' < \omega$![]() and $s_d < s_d' < r_d$
and $s_d < s_d' < r_d$![]() for each ${\rm d} \in U_A$
for each ${\rm d} \in U_A$![]() , then the inclusion $\Omega (\varphi ', (s_d')_{{\rm d}\in U_A}) \subseteq \Omega (\varphi, (s_d)_{{\rm d}\in U_A})$
, then the inclusion $\Omega (\varphi ', (s_d')_{{\rm d}\in U_A}) \subseteq \Omega (\varphi, (s_d)_{{\rm d}\in U_A})$![]() holds. Thus we can form the inductive limits
holds. Thus we can form the inductive limits

Hence, $\mathcal {O}[\Omega _A], \mathcal {M}[\Omega _A]$![]() are algebras of holomorphic functions and meromorphic functions (respectively) defined on an open set containing $\widetilde {\sigma }(A) \setminus M_A$
are algebras of holomorphic functions and meromorphic functions (respectively) defined on an open set containing $\widetilde {\sigma }(A) \setminus M_A$![]() . Next, we define the following notion of regularity at $M_A$
. Next, we define the following notion of regularity at $M_A$![]() .
.
Definition 2.3 Let $f \in \mathcal {M}[\Omega _A]$![]() . We say that $f$
. We say that $f$![]() is regular at ${\rm d}\in \{-a, a\}\cap M_A$
is regular at ${\rm d}\in \{-a, a\}\cap M_A$![]() if $\lim _{\operatorname {dom} f \ni z \to d} f(z) =: c_d \in \mathbb {C}$
if $\lim _{\operatorname {dom} f \ni z \to d} f(z) =: c_d \in \mathbb {C}$![]() exists and, for some $\varphi \in (0, \omega )$
exists and, for some $\varphi \in (0, \omega )$![]()

where $\partial \Omega$![]() denotes the boundary of a subset $\Omega \subset \mathbb {C}$
denotes the boundary of a subset $\Omega \subset \mathbb {C}$![]() . If $\infty \in M_A$
. If $\infty \in M_A$![]() , we say that $f$
, we say that $f$![]() is regular at $\infty$
is regular at $\infty$![]() if $\lim _{z\to \infty } f(z) =: c_\infty \in \mathbb {C}$
if $\lim _{z\to \infty } f(z) =: c_\infty \in \mathbb {C}$![]() exists and
exists and

We say that $f$![]() is quasi-regular at ${\rm d}\in M_A$
is quasi-regular at ${\rm d}\in M_A$![]() if $f$
if $f$![]() or $1/f$
or $1/f$![]() is regular at $d$
is regular at $d$![]() . Finally, we say that $f$
. Finally, we say that $f$![]() is (quasi-)regular at $M_A$
is (quasi-)regular at $M_A$![]() if $f$
if $f$![]() is (quasi-)regular at each point of $M_A$
is (quasi-)regular at each point of $M_A$![]() .
.
Remark 2.4 Note that if $f$![]() is regular at $M_A$
is regular at $M_A$![]() with every limit being not equal to $0$
with every limit being not equal to $0$![]() , then $1/f$
, then $1/f$![]() is also regular at $M_A$
is also regular at $M_A$![]() . If $f$
. If $f$![]() is quasi-regular at $M_A$
is quasi-regular at $M_A$![]() , then $\mu -f$
, then $\mu -f$![]() and $1/f$
and $1/f$![]() are also quasi-regular at $M_A$
are also quasi-regular at $M_A$![]() for each $\mu \in \mathbb {C}$
for each $\mu \in \mathbb {C}$![]() . A function $f$
. A function $f$![]() which is quasi-regular at $M_A$
which is quasi-regular at $M_A$![]() has well-defined limits in $\mathbb {C}_\infty$
has well-defined limits in $\mathbb {C}_\infty$![]() as $z$
as $z$![]() tends to each point of $M_A$
tends to each point of $M_A$![]() .
.

Figure 1. Spectrum of a bisectorial-like operator and integration path of the functional calculus.
Next, let $\mathcal {E}(A)$![]() be the subset of functions of $\mathcal {O}[\Omega _A]$
be the subset of functions of $\mathcal {O}[\Omega _A]$![]() which are regular at $M_A$
which are regular at $M_A$![]() . Note that $\mathcal {E} (A)$
. Note that $\mathcal {E} (A)$![]() is a subalgebra of $\mathcal {O} [\Omega _A]$
is a subalgebra of $\mathcal {O} [\Omega _A]$![]() . Indeed, it is readily seen that it is a vector space, and the identity $f(z)g(z) - c_f c_g = g(z)(f(z)-c_f) + c_f (g(z)-c_g)$
. Indeed, it is readily seen that it is a vector space, and the identity $f(z)g(z) - c_f c_g = g(z)(f(z)-c_f) + c_f (g(z)-c_g)$![]() yields that $\mathcal {E}(A)$
yields that $\mathcal {E}(A)$![]() is closed under the point-wise product. Then, for any $b \in \mathbb {C} \backslash \overline {BS_{\varphi,a}}$
is closed under the point-wise product. Then, for any $b \in \mathbb {C} \backslash \overline {BS_{\varphi,a}}$![]() , the set identity
, the set identity
holds true, where $\mathbf {1}$![]() is the constant function with value $1$
is the constant function with value $1$![]() , and
, and

Given a bisectorial-like operator $A \in {\rm BSect} (\omega, a)$![]() , we define the mapping $\Phi : \mathcal {E}(A) \to \mathcal {L}(X)$
, we define the mapping $\Phi : \mathcal {E}(A) \to \mathcal {L}(X)$![]() determined by setting $\Phi ({1}/{b+z}) = (b+A)^{-1}$
determined by setting $\Phi ({1}/{b+z}) = (b+A)^{-1}$![]() , $\Phi ({1}/{b-z}) = (b-A)^{-1}$
, $\Phi ({1}/{b-z}) = (b-A)^{-1}$![]() , $\Phi (\mathbf {1}) = I$
, $\Phi (\mathbf {1}) = I$![]() , and
, and
where $\Gamma$![]() is the positively oriented boundary of $\Omega (\varphi ', (s_d')_{{\rm d}\in U_A})$
is the positively oriented boundary of $\Omega (\varphi ', (s_d')_{{\rm d}\in U_A})$![]() with $\varphi < \varphi ' < \omega$
with $\varphi < \varphi ' < \omega$![]() and $s_d < s_d' < r_d$
and $s_d < s_d' < r_d$![]() , where $f \in \mathcal {O}(\Omega (\varphi, (s_d)_{{\rm d}\in U_A}))$
, where $f \in \mathcal {O}(\Omega (\varphi, (s_d)_{{\rm d}\in U_A}))$![]() .
.
Lemma 2.5 Let $a\geq 0, \, 0< \omega \leq {\pi }/{2}$![]() and $A \in {\rm BSect}(\omega, a)$
and $A \in {\rm BSect}(\omega, a)$![]() . The mapping $\Phi : \mathcal {E}(A) \to \mathcal {L}(X)$
. The mapping $\Phi : \mathcal {E}(A) \to \mathcal {L}(X)$![]() is a well-defined algebra homomorphism.
is a well-defined algebra homomorphism.
Proof. The proof is analogous to the case of sectorial operators (see [Reference Haase12, Section 2.3]) with some minor changes. We give below a sketch of such a proof.
First, note that the integral (2.2) is well defined in the Bochner sense since $z \mapsto (z-A)^{-1}$![]() is analytic, so continuous, and $\int _\Gamma |f(z)| \|(z-A)^{-1}\|\, |{\rm d}z| < \infty$
is analytic, so continuous, and $\int _\Gamma |f(z)| \|(z-A)^{-1}\|\, |{\rm d}z| < \infty$![]() for all $f \in \mathcal {E}_0(A)$
for all $f \in \mathcal {E}_0(A)$![]() . Also, such an integral is independent of the choice of $\varphi ', (s_d')_{{\rm d}\in U_A}$
. Also, such an integral is independent of the choice of $\varphi ', (s_d')_{{\rm d}\in U_A}$![]() by Cauchy's theorem. Fix $b \in \mathbb {C} \setminus \overline {BS_{\varphi,a}}$
by Cauchy's theorem. Fix $b \in \mathbb {C} \setminus \overline {BS_{\varphi,a}}$![]() for now. To see that $\Phi$
for now. To see that $\Phi$![]() is well defined one has to prove that $\Phi (g)$
is well defined one has to prove that $\Phi (g)$![]() is independent of the decomposition of $g \in \mathcal {E}(A)$
is independent of the decomposition of $g \in \mathcal {E}(A)$![]() via the set sum (2.1). So take $K, M, N \in \mathbb {C}$
via the set sum (2.1). So take $K, M, N \in \mathbb {C}$![]() such that the function given by
such that the function given by
lies in $\mathcal {E}_0(A)$![]() (note that $K=0$
(note that $K=0$![]() if $\infty \in M_A$
if $\infty \in M_A$![]() ). Let $\Gamma$
). Let $\Gamma$![]() be an integration path as in (2.2). Assume $a \in M_A$
be an integration path as in (2.2). Assume $a \in M_A$![]() (i.e., $a \in \widetilde \sigma (A)$
(i.e., $a \in \widetilde \sigma (A)$![]() ) and $a>0$
) and $a>0$![]() . Since $f \in \mathcal {E}_0(A)$
. Since $f \in \mathcal {E}_0(A)$![]() , an application of Cauchy's theorem shows
, an application of Cauchy's theorem shows
where $\Gamma _\varepsilon$![]() is the (suitable oriented) path given by
is the (suitable oriented) path given by
After applying a similar trick to all the points in $M_A$![]() , one can change $\Gamma$
, one can change $\Gamma$![]() in the integral above by an integration path that does not touch $\widetilde \sigma (A)$
in the integral above by an integration path that does not touch $\widetilde \sigma (A)$![]() (even in the case $a = 0$
(even in the case $a = 0$![]() ). Thus,
). Thus,
where $\widetilde \Phi$![]() denotes the Dunford-Taylor functional calculus of $A$
denotes the Dunford-Taylor functional calculus of $A$![]() , see [Reference Taylor and Lay20, Section V.8] for more details. We conclude that the mapping $\Phi$
, see [Reference Taylor and Lay20, Section V.8] for more details. We conclude that the mapping $\Phi$![]() is well defined, and a similar trick as above shows that $\Phi$
is well defined, and a similar trick as above shows that $\Phi$![]() is independent of the choice of $b \in \mathbb {C} \setminus \overline {BS_{\varphi,a}}$
is independent of the choice of $b \in \mathbb {C} \setminus \overline {BS_{\varphi,a}}$![]() .
.
On the other hand, reasoning as in the case of sectorial operators (see [Reference Haase12, Lemma 2.3.1]), several applications of Cauchy's theorem and the resolvent identity show that $\Phi$![]() is an algebra homomorphism when restricted to $\mathcal {E}_0(A)$
is an algebra homomorphism when restricted to $\mathcal {E}_0(A)$![]() . After that, a few computations with products of the type $(b-z)^{-1} (b+z)^{-1}$
. After that, a few computations with products of the type $(b-z)^{-1} (b+z)^{-1}$![]() , $(b\pm z)^{-1} g(z), \, g \in \mathcal {E}_0(A),$
, $(b\pm z)^{-1} g(z), \, g \in \mathcal {E}_0(A),$![]() show that indeed $\Phi$
show that indeed $\Phi$![]() is an algebra homomorphism from $\mathcal {E}(A)$
is an algebra homomorphism from $\mathcal {E}(A)$![]() to $\mathcal {L}(X)$
to $\mathcal {L}(X)$![]() (see also [Reference Haase12, Theorem 2.3.3]).
(see also [Reference Haase12, Theorem 2.3.3]).
Next, we follow the regularization method given in [Reference Haase10] to extend the functional calculus $\Phi$![]() to a regularized functional calculus (also denoted by $\Phi$
to a regularized functional calculus (also denoted by $\Phi$![]() ), which involves meromorphic functions.
), which involves meromorphic functions.
Definition 2.6 Let $a\geq 0, \, 0< \omega \leq {\pi }/{2}$![]() and $A \in {\rm BSect}(\omega, a)$
and $A \in {\rm BSect}(\omega, a)$![]() . Then, a function $f \in \mathcal {M}[\Omega _A]$
. Then, a function $f \in \mathcal {M}[\Omega _A]$![]() is called regularizable by $\mathcal {E} (A)$
is called regularizable by $\mathcal {E} (A)$![]() if there exists $e \in \mathcal {E}(A)$
if there exists $e \in \mathcal {E}(A)$![]() such that
such that
• $e(A)$
 is injective,
is injective,• $ef \in \mathcal {E}(A)$
 .
.
For any regularizable $f \in \mathcal {M}[\Omega _A]$![]() with regularizer $e \in \mathcal {E}(A)$
with regularizer $e \in \mathcal {E}(A)$![]() , we set
, we set
By [Reference Haase10, Lemma 3.2], this definition is independent of the regularizer $e$![]() , and $f(A)$
, and $f(A)$![]() is a well-defined closed operator. We denote by $\mathcal {M}(A)$
is a well-defined closed operator. We denote by $\mathcal {M}(A)$![]() the subset of functions of $\mathcal {M}[\Omega _A]$
the subset of functions of $\mathcal {M}[\Omega _A]$![]() which are regularizable by $\mathcal {E}(A)$
which are regularizable by $\mathcal {E}(A)$![]() . As in the case for sectorial operators [Reference Haase10, Theorem 3.6], this regularized functional calculus satisfies the properties given in the lemma below. For $A, B \in C(X)$
. As in the case for sectorial operators [Reference Haase10, Theorem 3.6], this regularized functional calculus satisfies the properties given in the lemma below. For $A, B \in C(X)$![]() , we mean by $A \subseteq B$
, we mean by $A \subseteq B$![]() that $\operatorname {dom} A \subseteq \operatorname {dom} B$
that $\operatorname {dom} A \subseteq \operatorname {dom} B$![]() with $Ax = Bx$
with $Ax = Bx$![]() for every $x \in \operatorname {dom} A$
for every $x \in \operatorname {dom} A$![]() .
.
Lemma 2.7 Let $A \in {\rm BSect}(\omega, a)$![]() and $f \in \mathcal {M}(A)$
and $f \in \mathcal {M}(A)$![]() . Then
. Then
1. If $T\in \mathcal {L}(X)$
 commutes with $A$
commutes with $A$ , that is, $TA \subseteq AT$
, that is, $TA \subseteq AT$ , then $T$
, then $T$ also commutes with $f(A)$
also commutes with $f(A)$ , i.e. $T f(A) \subseteq f(A)T$
, i.e. $T f(A) \subseteq f(A)T$ .
.2. $\zeta (A) = A$
 , where $\zeta (z) = z$
, where $\zeta (z) = z$ , $z \in \mathbb {C}$
, $z \in \mathbb {C}$ .
.3. Let $g \in \mathcal {M}(A)$
 . Then
\begin{align*} f(A) + g(A) \subseteq (f+g)(A), \qquad f(A) g(A) \subseteq (f g)(A). \end{align*}Furthermore, $\operatorname {dom}(f(A)g(A)) = \operatorname {dom} (fg)(A) \cap \operatorname {dom} g(A)$
. Then
\begin{align*} f(A) + g(A) \subseteq (f+g)(A), \qquad f(A) g(A) \subseteq (f g)(A). \end{align*}Furthermore, $\operatorname {dom}(f(A)g(A)) = \operatorname {dom} (fg)(A) \cap \operatorname {dom} g(A)$
 , and one has equality in these relations if $g(A) \in \mathcal {L}(X)$
, and one has equality in these relations if $g(A) \in \mathcal {L}(X)$ .
.4. Let $\lambda \in \mathbb {C}$
 . Then
\begin{align*} \frac{1}{\lambda - f(z)} \in \mathcal{M}(A) \iff \lambda - f(A) \text{ is injective}. \end{align*}If this is the case, $(\lambda -f(z))^{-1}(A) = (\lambda -f(A))^{-1}$
. Then
\begin{align*} \frac{1}{\lambda - f(z)} \in \mathcal{M}(A) \iff \lambda - f(A) \text{ is injective}. \end{align*}If this is the case, $(\lambda -f(z))^{-1}(A) = (\lambda -f(A))^{-1}$
 . In particular, $\lambda \in \rho (A)$
. In particular, $\lambda \in \rho (A)$ if and only if $(\lambda - f(z))^{-1} \in \mathcal {M}(A)$
if and only if $(\lambda - f(z))^{-1} \in \mathcal {M}(A)$ with $(\lambda - f(A)^{-1}) \in \mathcal {L}(X)$
with $(\lambda - f(A)^{-1}) \in \mathcal {L}(X)$ .
.
Proof. The statement follows by straightforward applications of the Cauchy's theorem, the resolvent identity, and [Reference Haase10, Section 3].
Let $\sigma _p(T)$![]() denote the point spectrum of a closed linear operator $T$
denote the point spectrum of a closed linear operator $T$![]() .
.
Lemma 2.8 Let $A \in {\rm BSect}(\omega, a)$![]() , $\lambda \in \sigma _{p}(A)$
, $\lambda \in \sigma _{p}(A)$![]() and $f \in \mathcal {M}(A)$
and $f \in \mathcal {M}(A)$![]() . Then $f(\lambda ) \in \mathbb {C}$
. Then $f(\lambda ) \in \mathbb {C}$![]() and $f(A)x = f(\lambda )x$
and $f(A)x = f(\lambda )x$![]() for any $x \in \ker (\lambda - A)$
for any $x \in \ker (\lambda - A)$![]() .
.
Proof. See [Reference Haase11, Proposition 3.1] for the analogous result for sectorial operators.
Lemma 2.9 Let $A \in {\rm BSect}(\omega, a)$![]() , $f \in \mathcal {E}(A)$
, $f \in \mathcal {E}(A)$![]() and $\lambda \in (\operatorname {dom} f) \setminus M_A$
and $\lambda \in (\operatorname {dom} f) \setminus M_A$![]() such that $f(\lambda ) = 0$
such that $f(\lambda ) = 0$![]() . For each $b \in \rho (A)$
. For each $b \in \rho (A)$![]() , the function ${b - (\cdot )}/{\lambda - (\cdot )}f$
, the function ${b - (\cdot )}/{\lambda - (\cdot )}f$![]() lies in $\mathcal {E}(A)$
lies in $\mathcal {E}(A)$![]() .
.
Proof. The claim follows by the definitions of $\mathcal {E}(A)$![]() and regular limits.
and regular limits.
Lemma 2.10 Let $A \in {\rm BSect}(\omega, a)$![]() , $f \in \mathcal {M}(A)$
, $f \in \mathcal {M}(A)$![]() and $\lambda \in \widetilde {\sigma }(A) \setminus M_A$
and $\lambda \in \widetilde {\sigma }(A) \setminus M_A$![]() such that $f(\lambda ) \neq \infty$
such that $f(\lambda ) \neq \infty$![]() . There is a regularizer $e \in \mathcal {E}(A)$
. There is a regularizer $e \in \mathcal {E}(A)$![]() for $f$
for $f$![]() with $e(\lambda ) \neq 0$
with $e(\lambda ) \neq 0$![]() .
.
Proof. The proof is analogous to the case of sectorial operators, see [Reference Haase11,Lemma 4.3].
Lemma 2.11 Let $A\in {\rm BSect}(\omega, a)$![]() and $f \in \mathcal {M}[\Omega _A]$
and $f \in \mathcal {M}[\Omega _A]$![]() . Assume that $f$
. Assume that $f$![]() is regular at $M_A$
is regular at $M_A$![]() and that all the poles of $f$
and that all the poles of $f$![]() are contained in $\mathbb {C} \backslash \sigma _p(A)$
are contained in $\mathbb {C} \backslash \sigma _p(A)$![]() . Then, $f \in \mathcal {M}(A)$
. Then, $f \in \mathcal {M}(A)$![]() . Moreover, if every pole of $f$
. Moreover, if every pole of $f$![]() is contained in $\rho (A)$
is contained in $\rho (A)$![]() , then $f(A)\in \mathcal {L}(X)$
, then $f(A)\in \mathcal {L}(X)$![]() .
.
Proof. The proof is the same as in the case of sectorial operators, see [Reference Haase11, Lemma 6.2]. We include it here since we need it in the proof of Theorem 5.3.
Let $f \in \mathcal {M}[\Omega _A]$![]() be as required. That is, there exists $\varphi \in (0, \omega )$
be as required. That is, there exists $\varphi \in (0, \omega )$![]() and $s_d \in (0, r_d)$
and $s_d \in (0, r_d)$![]() for each ${\rm d} \in U_A$
for each ${\rm d} \in U_A$![]() such that $f \in \mathcal {M}(\Omega (\varphi, (s_d)_{{\rm d}\in U_A}))$
such that $f \in \mathcal {M}(\Omega (\varphi, (s_d)_{{\rm d}\in U_A}))$![]() . Since $f$
. Since $f$![]() has finite limits at $M_A$
has finite limits at $M_A$![]() , we can assume that $f$
, we can assume that $f$![]() has only finitely many poles by making $\varphi, (s_d)_{{\rm d}\in U_A}$
has only finitely many poles by making $\varphi, (s_d)_{{\rm d}\in U_A}$![]() bigger. Thus, let $\lambda _j$
bigger. Thus, let $\lambda _j$![]() for $j\in \{1, \ldots, N\}$
for $j\in \{1, \ldots, N\}$![]() be an enumeration of those poles of $f$
be an enumeration of those poles of $f$![]() and let $n_j \in \mathbb {N}$
and let $n_j \in \mathbb {N}$![]() be the order of pole of $f$
be the order of pole of $f$![]() located at $\lambda _j$
located at $\lambda _j$![]() , for $j \in \{1, \ldots, N\}$
, for $j \in \{1, \ldots, N\}$![]() . Then, the function ${g(z) := f(z) \Pi _{j=1}^{N} {(\lambda _j-z)^{n_j}}/{(b-z)^{n_j}}}$
. Then, the function ${g(z) := f(z) \Pi _{j=1}^{N} {(\lambda _j-z)^{n_j}}/{(b-z)^{n_j}}}$![]() has no poles, i.e. $g\in \mathcal {O}[\Omega _A]$
has no poles, i.e. $g\in \mathcal {O}[\Omega _A]$![]() , and is regular at $M_A$
, and is regular at $M_A$![]() . Hence $g\in \mathcal {E}(A)$
. Hence $g\in \mathcal {E}(A)$![]() . Moreover, setting ${r(z) := \Pi _{j=1}^{N}{(\lambda _j-z)^{n_j}}/{(b-z)^{n_j}}}$
. Moreover, setting ${r(z) := \Pi _{j=1}^{N}{(\lambda _j-z)^{n_j}}/{(b-z)^{n_j}}}$![]() , one has that the operator ${r(A) = \Pi _{j=1}^{N}(\lambda _j-A)^{n_j}(b-A)^{-n_j}}$
, one has that the operator ${r(A) = \Pi _{j=1}^{N}(\lambda _j-A)^{n_j}(b-A)^{-n_j}}$![]() is bounded and injective, since by assumption $\{\lambda _1, \ldots, \lambda _n\} \subseteq \mathbb {C} \setminus \sigma _p(A)$
is bounded and injective, since by assumption $\{\lambda _1, \ldots, \lambda _n\} \subseteq \mathbb {C} \setminus \sigma _p(A)$![]() . In short, $f$
. In short, $f$![]() is regularized by $r$
is regularized by $r$![]() , so $f \in \mathcal {M}(A)$
, so $f \in \mathcal {M}(A)$![]() .
.
Now, assume that the poles of $f$![]() lie inside $\rho (A)$
lie inside $\rho (A)$![]() . Then the operator $r(A)$
. Then the operator $r(A)$![]() is not only bounded and injective, but invertible too, from which follows $f(A) = r(A)^{-1} (rf)(A) \in \mathcal {L}(X)$
is not only bounded and injective, but invertible too, from which follows $f(A) = r(A)^{-1} (rf)(A) \in \mathcal {L}(X)$![]() .
.
3. Spectral mapping theorems for $M_A = \emptyset$
For $A \in {\rm BSect}(\omega, a)$![]() , the spectral mapping theorems (1.1) given in [Reference González and Onieva7, Reference Gramsch and Lay8] are applicable to every $f \in \mathcal {E}(A)$
, the spectral mapping theorems (1.1) given in [Reference González and Onieva7, Reference Gramsch and Lay8] are applicable to every $f \in \mathcal {E}(A)$![]() whenever $M_A = \emptyset$
whenever $M_A = \emptyset$![]() . This section is devoted to extend these spectral mapping theorems to all $f \in \mathcal {M}(A)$
. This section is devoted to extend these spectral mapping theorems to all $f \in \mathcal {M}(A)$![]() when $M_A = \emptyset$
when $M_A = \emptyset$![]() .
.
First, we proceed to state the spectral inclusion of the spectrum $\widetilde {\sigma }$![]() .
.
Proposition 3.1 Let $A \in {\rm BSect}(\omega, a)$![]() , $f \in \mathcal {M}(A)$
, $f \in \mathcal {M}(A)$![]() , and assume that $f$
, and assume that $f$![]() is quasi-regular at $M_A$
is quasi-regular at $M_A$![]() . Then
. Then
Proof. The proof runs along the same lines as in the case of sectorial operators, see [Reference Haase11, Proposition 6.3]. As in lemma 2.11, we include the proof here since it will be needed in the proof of Theorem 5.3.
Take $\mu \in \mathbb {C}$![]() such that $\mu \notin f(\widetilde {\sigma }(A))$
such that $\mu \notin f(\widetilde {\sigma }(A))$![]() . Then $\displaystyle {{1}/{\mu - f} \in \mathcal {M}[\Omega _A]}$
. Then $\displaystyle {{1}/{\mu - f} \in \mathcal {M}[\Omega _A]}$![]() is regular in $M_A$
is regular in $M_A$![]() , and all of its poles are contained in $\rho (A)$
, and all of its poles are contained in $\rho (A)$![]() . By lemma 2.11, we conclude that $(\mu - f)^{-1} \in \mathcal {M}(A)$
. By lemma 2.11, we conclude that $(\mu - f)^{-1} \in \mathcal {M}(A)$![]() and that $(\mu - f)^{-1}(A)$
and that $(\mu - f)^{-1}(A)$![]() is a bounded operator. Thus, it follows that $\mu - f(A)$
is a bounded operator. Thus, it follows that $\mu - f(A)$![]() is invertible, hence $\mu \notin \widetilde {\sigma }(f(A))$
is invertible, hence $\mu \notin \widetilde {\sigma }(f(A))$![]() .
.
Assume now that $\mu = \infty \notin f(\widetilde {\sigma }(A))$![]() . Then $f$
. Then $f$![]() is regular at $M_A$
is regular at $M_A$![]() and its poles are contained in $\rho (A)$
and its poles are contained in $\rho (A)$![]() . Another application of lemma 2.11 yields that $f(A)$
. Another application of lemma 2.11 yields that $f(A)$![]() is a bounded operator, so $\infty \notin \widetilde {\sigma }(f(A))$
is a bounded operator, so $\infty \notin \widetilde {\sigma }(f(A))$![]() .
.
Next, we give some technical lemmas.
Lemma 3.2 Let $A \in {\rm BSect}(\omega, a)$![]() , $e, f, h\in \mathcal {M}(A)$
, $e, f, h\in \mathcal {M}(A)$![]() and $0 \neq c \in \mathbb {C}$
and $0 \neq c \in \mathbb {C}$![]() with $fh = e - c$
with $fh = e - c$![]() . Suppose that $e(A), h(A), f(A) \in \mathcal {L}(X)$
. Suppose that $e(A), h(A), f(A) \in \mathcal {L}(X)$![]() . Then
. Then
Proof. Implication $\implies$![]() follows from $e(A)h(A) = h(A)e(A)$
follows from $e(A)h(A) = h(A)e(A)$![]() ; and $\impliedby$
; and $\impliedby$![]() follows from $I = {1}/{c}(e(A) - h(A)f(A))$
follows from $I = {1}/{c}(e(A) - h(A)f(A))$![]() .
.
The following lemma, which is a refinement of [Reference Haase11, Lemma 4.2], is crucial to deal with regularized functions $f \in \mathcal {M}(A)$![]() which are not in $\mathcal {E}(A)$
which are not in $\mathcal {E}(A)$![]() .
.
Lemma 3.3 Let $f \in \mathcal {M}(A)$![]() and $\lambda \in \sigma (A)\setminus M_A$
and $\lambda \in \sigma (A)\setminus M_A$![]() with $f(\lambda ) = 0$
with $f(\lambda ) = 0$![]() , and let $b \in \rho (A)$
, and let $b \in \rho (A)$![]() . If $\displaystyle {g(z) := f(z) ({b-z})/({\lambda - z})}$
. If $\displaystyle {g(z) := f(z) ({b-z})/({\lambda - z})}$![]() , then $g\in \mathcal {M}(A)$
, then $g\in \mathcal {M}(A)$![]() , $\operatorname {dom} g(A) = \operatorname {dom} f(A)$
, $\operatorname {dom} g(A) = \operatorname {dom} f(A)$![]() and
and
Proof. Let $e$![]() be a regularizer for $f$
be a regularizer for $f$![]() with $c:=e(\lambda ) \neq 0$
with $c:=e(\lambda ) \neq 0$![]() (see lemma 2.10). Then $eg \in \mathcal {E}(A)$
(see lemma 2.10). Then $eg \in \mathcal {E}(A)$![]() by lemma 2.9 and hence $e$
by lemma 2.9 and hence $e$![]() is a regularizer for $g$
is a regularizer for $g$![]() . Define $h:= ({\lambda - (\cdot )})/({b - (\cdot )}) \in \mathcal {E}(A)$
. Define $h:= ({\lambda - (\cdot )})/({b - (\cdot )}) \in \mathcal {E}(A)$![]() . Since $f = hg$
. Since $f = hg$![]() , it follows $\operatorname {dom} g(A) \subseteq \operatorname {dom} f(A)$
, it follows $\operatorname {dom} g(A) \subseteq \operatorname {dom} f(A)$![]() .
.
For the converse, suppose that $x \in \operatorname {dom} f(A)$![]() , so there is $y \in X$
, so there is $y \in X$![]() such that $(ef)(A)x = e(A)y$
such that $(ef)(A)x = e(A)y$![]() , i.e.,
, i.e.,
Observe that $e-c = \widetilde f h$![]() with
with
By lemma 2.9, one has $\widetilde f \in \mathcal {E}(A)$![]() . By lemma 3.2, there exists $v \in X$
. By lemma 3.2, there exists $v \in X$![]() such that $y = h(A)v$
such that $y = h(A)v$![]() . This yields $h(A)(eg)(A) x = e(A)y = e(A)h(A)v = h(A)e(A)v$
. This yields $h(A)(eg)(A) x = e(A)y = e(A)h(A)v = h(A)e(A)v$![]() , that is, $(eg)(A)x - e(A)v \in \ker h(A)$
, that is, $(eg)(A)x - e(A)v \in \ker h(A)$![]() . But $\ker h(A) = \ker (\lambda - A) \subseteq \ker (c - e(A)) \subseteq \operatorname {ran} e(A)$
. But $\ker h(A) = \ker (\lambda - A) \subseteq \ker (c - e(A)) \subseteq \operatorname {ran} e(A)$![]() , see lemma 2.8. Hence $(eg)(A)x \in \operatorname {ran} e(A)$
, see lemma 2.8. Hence $(eg)(A)x \in \operatorname {ran} e(A)$![]() , so $x \in \operatorname {dom} g(A)$
, so $x \in \operatorname {dom} g(A)$![]() as claimed.
as claimed.
Finally, the identity $f(A) = h(A) g(A) = g(A) h(A)$![]() follows by what we have already proven and lemma 2.7(3).
follows by what we have already proven and lemma 2.7(3).
Remark 3.4 Let $T \in C(X)$![]() with non-empty resolvent set, and $\alpha (T), \delta (T) < \infty$
with non-empty resolvent set, and $\alpha (T), \delta (T) < \infty$![]() . Then $\alpha (T) = \delta (T)=:p_T$
. Then $\alpha (T) = \delta (T)=:p_T$![]() and $X = \ker T^{p_T} \oplus \operatorname {ran} T^{p_T}$
and $X = \ker T^{p_T} \oplus \operatorname {ran} T^{p_T}$![]() , see for example [Reference Taylor and Lay20, Theorem V.6.2].
, see for example [Reference Taylor and Lay20, Theorem V.6.2].
Remark 3.5 Let $T \in C(X)$![]() with non-empty resolvent set, and let $b \in \rho (T)$
with non-empty resolvent set, and let $b \in \rho (T)$![]() and $\lambda \in \mathbb {C}$
and $\lambda \in \mathbb {C}$![]() . Then $\lambda - T \in \Phi _i$
. Then $\lambda - T \in \Phi _i$![]() if and only if $\displaystyle {(\lambda - T)(b-T)^{-1}} \in \Phi _i$
if and only if $\displaystyle {(\lambda - T)(b-T)^{-1}} \in \Phi _i$![]() for all $0 \leq i \leq 9$
for all $0 \leq i \leq 9$![]() , see for example [Reference González and Onieva7, Lemma 1].
, see for example [Reference González and Onieva7, Lemma 1].
Lemma 3.6 Let $A\in {\rm BSect}(\omega, a), \, f, g \in \mathcal {M}(A)$![]() with $f, g$
with $f, g$![]() quasi-regular at $M_A$
quasi-regular at $M_A$![]() , $0 \notin g(\widetilde {\sigma }(A))$
, $0 \notin g(\widetilde {\sigma }(A))$![]() and such that
and such that

for some $b \in \rho (A), \, \lambda _j \in \sigma (A)\setminus M_A,$![]() and $n_j \in \mathbb {N}$
and $n_j \in \mathbb {N}$![]() for $j=1, \ldots, N$
for $j=1, \ldots, N$![]() . Then
. Then
(a) if $f(A) \in \Phi _i$
 , then $\lambda _j - A \in \Phi _i$
, then $\lambda _j - A \in \Phi _i$ for all $j=1, \ldots, N$
for all $j=1, \ldots, N$ and for all $i$
and for all $i$ except $i=7$
except $i=7$ ;
;(b) if $\lambda _j - A \in \Phi _i$
 for all $j=1, \ldots, N$
for all $j=1, \ldots, N$ , then $f(A) \in \Phi _i$
, then $f(A) \in \Phi _i$ for all $i$
for all $i$ except $i=6$
except $i=6$ .
.
Proof. Set $r(z):= {\Pi _{j=1}^N ({\lambda _j-z})^{n_j}/({b-z})^{n_j}}$![]() , so $r(A) \in \mathcal {L}(X)$
, so $r(A) \in \mathcal {L}(X)$![]() . Several applications of lemma 3.3 imply $\operatorname {dom} g(A) = \operatorname {dom} f(A)$
. Several applications of lemma 3.3 imply $\operatorname {dom} g(A) = \operatorname {dom} f(A)$![]() and $f(A) = r(A) g(A) = g(A)r(A)$
and $f(A) = r(A) g(A) = g(A)r(A)$![]() . Moreover, proposition 3.1 yields $0 \notin \widetilde {\sigma }(g(A))$
. Moreover, proposition 3.1 yields $0 \notin \widetilde {\sigma }(g(A))$![]() , so $g(A)$
, so $g(A)$![]() is surjective and injective. Therefore $\ker f(A) = \ker r(A)$
is surjective and injective. Therefore $\ker f(A) = \ker r(A)$![]() and $\operatorname {ran} f(A) = \operatorname {ran} r(A)$
and $\operatorname {ran} f(A) = \operatorname {ran} r(A)$![]() , so $f(A) \in \Phi _i$
, so $f(A) \in \Phi _i$![]() iff $r(A) \in \Phi _i$
iff $r(A) \in \Phi _i$![]() for $0\leq i \leq 7$
for $0\leq i \leq 7$![]() . By replacing $f, g, r$
. By replacing $f, g, r$![]() by powers $f^n, g^n, r^n$
by powers $f^n, g^n, r^n$![]() with $n \in \mathbb {N}$
with $n \in \mathbb {N}$![]() , we cover the cases $i=8, 9$
, we cover the cases $i=8, 9$![]() .
.
Since the bounded operators $\displaystyle {(\lambda _j-A)(b-A)^{-1}}$![]() commute with each other, we have:
commute with each other, we have:
1. if $r(A) \in \Phi _i$
 , then $\displaystyle {(\lambda _j - A)(b-A)^{-1} \in \Phi _i}$
, then $\displaystyle {(\lambda _j - A)(b-A)^{-1} \in \Phi _i}$ for all $j=1, \ldots, N$
for all $j=1, \ldots, N$ , and for all $i$
, and for all $i$ except $i = 7$
except $i = 7$ ,
,2. If $\displaystyle {(\lambda _j - A)(b-A)^{-1} \in \Phi _i}$
 for all $j=1, \ldots, N$
for all $j=1, \ldots, N$ , then $r(A) \in \Phi _i$
, then $r(A) \in \Phi _i$ , for all $i$
, for all $i$ except $i=6$
except $i=6$ .
.
see for example [Reference González and Onieva7, Lemma 3] and [Reference Gramsch and Lay8, Lemma 5(c)]. Hence, the claim follows from remark 3.5.
We give now the main result of this section.
Proposition 3.7 Let $A \in {\rm BSect}(\omega, a)$![]() , $f \in \mathcal {M}(A)$
, $f \in \mathcal {M}(A)$![]() , where $f$
, where $f$![]() is quasi-regular at $M_A$
is quasi-regular at $M_A$![]() . Then
. Then
(a) $f(\widetilde {\sigma }_i(A) ) \setminus f(M_A)\subseteq \widetilde {\sigma }_i(f(A))$
 for all $i$
for all $i$ except $i=7$
except $i=7$ .
.(b) $\widetilde {\sigma }_i (f(A)) \subseteq f(\widetilde {\sigma }_i)(A) \cup f(M_A)$
 for all $i$
for all $i$ except $i=6$
except $i=6$ .
.
Proof. Take $i\neq 7$![]() and let $\mu \in \mathbb {C}$
and let $\mu \in \mathbb {C}$![]() be such that $\mu \in f(\widetilde {\sigma }_i(A))\setminus f(M_A)$
be such that $\mu \in f(\widetilde {\sigma }_i(A))\setminus f(M_A)$![]() . By considering the function $f - \mu$
. By considering the function $f - \mu$![]() instead of $f$
instead of $f$![]() , we can assume without loss of generality that $\mu = 0$
, we can assume without loss of generality that $\mu = 0$![]() . As $0\notin f(M_A)$
. As $0\notin f(M_A)$![]() , $f^{-1}\{0\} \cap \widetilde {\sigma }(A)$
, $f^{-1}\{0\} \cap \widetilde {\sigma }(A)$![]() must be finite. Let $\lambda _1, \ldots, \lambda _N$
must be finite. Let $\lambda _1, \ldots, \lambda _N$![]() be all the points in $f^{-1}\{0\} \cap \widetilde {\sigma }(A)$
be all the points in $f^{-1}\{0\} \cap \widetilde {\sigma }(A)$![]() (so $\lambda _j \in \widetilde {\sigma }_i(A)$
(so $\lambda _j \in \widetilde {\sigma }_i(A)$![]() for some $j \in \{1, \ldots, N\}$
for some $j \in \{1, \ldots, N\}$![]() ), and let $n_j$
), and let $n_j$![]() be the order of the zero of $f$
be the order of the zero of $f$![]() at $\lambda _j$
at $\lambda _j$![]() . Let $b \in \rho (A)$
. Let $b \in \rho (A)$![]() and set
and set

Then $0 \notin g(\widetilde {\sigma }(A))$![]() and is $g$
and is $g$![]() quasi-regular at $M_A$
quasi-regular at $M_A$![]() . Several applications of lemma 3.3 imply $g \in \mathcal {M}(A)$
. Several applications of lemma 3.3 imply $g \in \mathcal {M}(A)$![]() , and lemma 3.6(a) yields $f(A) \notin \Phi _i$
, and lemma 3.6(a) yields $f(A) \notin \Phi _i$![]() .
.
Take now $i \neq 6$![]() and let $\mu \in \mathbb {C}$
and let $\mu \in \mathbb {C}$![]() be such that $\mu \notin f(\widetilde {\sigma }_i(A)) \cup f(M_A)$
be such that $\mu \notin f(\widetilde {\sigma }_i(A)) \cup f(M_A)$![]() . We prove that $\mu \notin \widetilde {\sigma }_i(f(A))$
. We prove that $\mu \notin \widetilde {\sigma }_i(f(A))$![]() . We can assume $\mu =0$
. We can assume $\mu =0$![]() . Again, $f^{-1}\{0\} \cap \sigma (A)$
. Again, $f^{-1}\{0\} \cap \sigma (A)$![]() has finite cardinal, so let $g$
has finite cardinal, so let $g$![]() be as given in (3.1). Since $\lambda _j - A \in \Phi _i$
be as given in (3.1). Since $\lambda _j - A \in \Phi _i$![]() for all $j=1, \ldots, n$
for all $j=1, \ldots, n$![]() , applications of lemmas 3.3 and 3.6(b) yield $f(A) \in \Phi _i$
, applications of lemmas 3.3 and 3.6(b) yield $f(A) \in \Phi _i$![]() , as we wanted to show.
, as we wanted to show.
Assume now that $\mu = \infty$![]() . If $\rho (f(A)) \neq \emptyset$
. If $\rho (f(A)) \neq \emptyset$![]() take $b \in \rho (f(A))$
take $b \in \rho (f(A))$![]() . An application of what we have already proven to the function $\displaystyle {{1}/{b-f(z)}}$
. An application of what we have already proven to the function $\displaystyle {{1}/{b-f(z)}}$![]() shows the claim, see the paragraph below definition 2.1. Hence, all that is left to prove is that we can assume without loss of generality that $\rho (f(A)) \neq \emptyset$
shows the claim, see the paragraph below definition 2.1. Hence, all that is left to prove is that we can assume without loss of generality that $\rho (f(A)) \neq \emptyset$![]() . Take $\nu \in \mathbb {C}\setminus f(M_A)$
. Take $\nu \in \mathbb {C}\setminus f(M_A)$![]() , so $f^{-1}\{\nu \} \cap \widetilde {\sigma }(A)$
, so $f^{-1}\{\nu \} \cap \widetilde {\sigma }(A)$![]() has finite cardinality. Let $\nu _1, \ldots, \nu _M$
has finite cardinality. Let $\nu _1, \ldots, \nu _M$![]() be all the points in $f^{-1}\{\nu \} \cap \sigma (A)$
be all the points in $f^{-1}\{\nu \} \cap \sigma (A)$![]() , and let $m_j$
, and let $m_j$![]() be the order of the zero of $f-\nu$
be the order of the zero of $f-\nu$![]() at $\nu _j$
at $\nu _j$![]() . Let $b \in \rho (A)$
. Let $b \in \rho (A)$![]() and set
and set

Lemma 3.3 yields $h \in \mathcal {M}(A)$![]() with $\operatorname {dom} f(A) = \operatorname {dom} h(A)$
with $\operatorname {dom} f(A) = \operatorname {dom} h(A)$![]() , and using (3.2) it is readily seen that $\operatorname {dom} f(A)^n = \operatorname {dom} h(A)^n$
, and using (3.2) it is readily seen that $\operatorname {dom} f(A)^n = \operatorname {dom} h(A)^n$![]() for all $n \in \mathbb {N}$
for all $n \in \mathbb {N}$![]() . In particular, $\infty \in \widetilde {\sigma }_i(f(A))$
. In particular, $\infty \in \widetilde {\sigma }_i(f(A))$![]() if and only if $\infty \in \widetilde {\sigma }_i(h(A))$
if and only if $\infty \in \widetilde {\sigma }_i(h(A))$![]() . Since $0 \notin h(\widetilde {\sigma }(A))$
. Since $0 \notin h(\widetilde {\sigma }(A))$![]() , proposition 3.1 implies $0 \in \rho (h(A))$
, proposition 3.1 implies $0 \in \rho (h(A))$![]() . Therefore, we can assume that $\rho (f(A)) \neq \emptyset$
. Therefore, we can assume that $\rho (f(A)) \neq \emptyset$![]() , and the proof is done.
, and the proof is done.
4. General case
In this section we deal with the case $M_A =\{-a, a, \infty \} \cap \widetilde \sigma (A) \neq \emptyset$![]() . The difficulty of this setting arises from the fact that $f$
. The difficulty of this setting arises from the fact that $f$![]() is not necessarily either holomorphic or meromorphic at $M_A$
is not necessarily either holomorphic or meromorphic at $M_A$![]() , so the factorization techniques used in § 3 do not apply here. Also, note that item 3) in the Introduction is not true if $f$
, so the factorization techniques used in § 3 do not apply here. Also, note that item 3) in the Introduction is not true if $f$![]() has a zero in $M_A$
has a zero in $M_A$![]() . To address this issue, we apply different techniques depending on the topological properties (relative to $\widetilde \sigma (A)$
. To address this issue, we apply different techniques depending on the topological properties (relative to $\widetilde \sigma (A)$![]() ) of $M_A$
) of $M_A$![]() . If these points are isolated points of $\widetilde \sigma (A)$
. If these points are isolated points of $\widetilde \sigma (A)$![]() , we provide useful properties of the spectral projections associated with such points in lemmas 4.4 and 4.5. If otherwise, these points are limit points of $\widetilde \sigma (A)$
, we provide useful properties of the spectral projections associated with such points in lemmas 4.4 and 4.5. If otherwise, these points are limit points of $\widetilde \sigma (A)$![]() , we make use of a mixture of topological properties shared by all the essential spectra considered here, and of the algebraic properties of the regularized functional calculus given in propositions 4.6 and 4.7.
, we make use of a mixture of topological properties shared by all the essential spectra considered here, and of the algebraic properties of the regularized functional calculus given in propositions 4.6 and 4.7.
First, we give some remarks about $M_A$![]() . These are key for the proof of the spectral mapping theorems.
. These are key for the proof of the spectral mapping theorems.
Remark 4.1 Let $T\in C(X)$![]() with non-empty resolvent set, ${\rm d} \in \widetilde {\sigma }(T)$
with non-empty resolvent set, ${\rm d} \in \widetilde {\sigma }(T)$![]() with $d$
with $d$![]() an accumulation point of $\rho (T)$
an accumulation point of $\rho (T)$![]() , and $i \neq 0, 9$
, and $i \neq 0, 9$![]() . The following statements about the essential spectrum are well-known, see for example [Reference Edmunds and Evans6, Sections I.3 & I.4], [Reference Kato13, Chapter 4§5] and [Reference Taylor and Lay20, Section V.6].
. The following statements about the essential spectrum are well-known, see for example [Reference Edmunds and Evans6, Sections I.3 & I.4], [Reference Kato13, Chapter 4§5] and [Reference Taylor and Lay20, Section V.6].
(a) If $d$
 is also an accumulation point of $\widetilde {\sigma }(T)$
is also an accumulation point of $\widetilde {\sigma }(T)$ , then ${\rm d} \in \widetilde {\sigma }_i(T)$
, then ${\rm d} \in \widetilde {\sigma }_i(T)$ .
.(b) If ${\rm d} \in \widetilde {\sigma }_i(T)$
 and $d$
and $d$ is not an accumulation point of $\widetilde {\sigma }_i(T)$
is not an accumulation point of $\widetilde {\sigma }_i(T)$ , then there is a neighborhood $\Omega$
, then there is a neighborhood $\Omega$ of $d$
of $d$ such that $\widetilde \sigma (T) \cap \Omega$
such that $\widetilde \sigma (T) \cap \Omega$ consists of $d$
consists of $d$ and a countable (possibly empty) set of eigenvalues of $T$
and a countable (possibly empty) set of eigenvalues of $T$ with finite dimensional eigenspace, which are isolated between themselves.
with finite dimensional eigenspace, which are isolated between themselves.(c) If ${\rm d} \notin \widetilde {\sigma }_i(T)$
 , then $d$
, then $d$ is an isolated point of $\widetilde {\sigma }(T)$
is an isolated point of $\widetilde {\sigma }(T)$ . Moreover, ${\rm d} \in \sigma _p(T)$
. Moreover, ${\rm d} \in \sigma _p(T)$ with ${\rm nul}(d-T) = {\rm def}(d-T) < \infty$
with ${\rm nul}(d-T) = {\rm def}(d-T) < \infty$ , $\alpha (d-T) = \delta (d-T) < \infty$
, $\alpha (d-T) = \delta (d-T) < \infty$ , and $\dim (\cup _{n\geq 1}\ker (d-T)^n)< \infty$
, and $\dim (\cup _{n\geq 1}\ker (d-T)^n)< \infty$ .
.
Lemma 4.2 Let $A \in {\rm BSect}(\omega, a)$![]() , ${\rm d} \in M_A$
, ${\rm d} \in M_A$![]() and $i, j \neq 0, 9$
and $i, j \neq 0, 9$![]() . Then
. Then
• ${\rm d} \in \widetilde {\sigma }_i(A)$
 if and only if ${\rm d} \in \widetilde {\sigma }_j(A)$
if and only if ${\rm d} \in \widetilde {\sigma }_j(A)$ ,
,• if $\infty \in \widetilde {\sigma }(A)$
 , then $\infty \in \widetilde {\sigma }_i(A)$
, then $\infty \in \widetilde {\sigma }_i(A)$ .
.
Proof. If ${\rm d} \in \widetilde {\sigma }_6(A)$![]() , then ${\rm d} \in \widetilde {\sigma }_i(A)$
, then ${\rm d} \in \widetilde {\sigma }_i(A)$![]() since $\widetilde {\sigma }_6(A) \subseteq \widetilde {\sigma }_i(A)$
since $\widetilde {\sigma }_6(A) \subseteq \widetilde {\sigma }_i(A)$![]() for any $i \neq 0, 9$
for any $i \neq 0, 9$![]() . If ${\rm d} \notin \widetilde {\sigma }_6(A)$
. If ${\rm d} \notin \widetilde {\sigma }_6(A)$![]() , then remark 4.1(c) implies ${\rm d} \notin \widetilde {\sigma }_i(A)$
, then remark 4.1(c) implies ${\rm d} \notin \widetilde {\sigma }_i(A)$![]() for $i \neq 0, 9$
for $i \neq 0, 9$![]() , and the first item follows.
, and the first item follows.
Now, assume $\infty \in \widetilde \sigma (A)$![]() . If $\infty$
. If $\infty$![]() is an accumulation point of $\widetilde \sigma (A)$
is an accumulation point of $\widetilde \sigma (A)$![]() , remark 4.1(a) implies $\infty \in \widetilde \sigma _i(A)$
, remark 4.1(a) implies $\infty \in \widetilde \sigma _i(A)$![]() (note that $\infty$
(note that $\infty$![]() is an accumulation point of the resolvent set of a bisectorial-like operator). Suppose then that $\infty$
is an accumulation point of the resolvent set of a bisectorial-like operator). Suppose then that $\infty$![]() is an isolated point of $\widetilde \sigma (A)$
is an isolated point of $\widetilde \sigma (A)$![]() and take $b \in \rho (A)$
and take $b \in \rho (A)$![]() . Then $0$
. Then $0$![]() is an isolated point of $\widetilde \sigma ((b-A)^{-1})$
is an isolated point of $\widetilde \sigma ((b-A)^{-1})$![]() . Since $(b-A)^{-1}$
. Since $(b-A)^{-1}$![]() is an injective operator, $0 \in \widetilde \sigma _i((b-A)^{-1})$
is an injective operator, $0 \in \widetilde \sigma _i((b-A)^{-1})$![]() by remark 4.1(c), and the claim follows.
by remark 4.1(c), and the claim follows.
Take $T \in C(X)$![]() with non-empty resolvent set, and let $\Lambda$
with non-empty resolvent set, and let $\Lambda$![]() be a subset of $\widetilde \sigma (T)$
be a subset of $\widetilde \sigma (T)$![]() which is open and closed in the relative topology of $\widetilde \sigma (T)$
which is open and closed in the relative topology of $\widetilde \sigma (T)$![]() (i.e. $\Lambda$
(i.e. $\Lambda$![]() is the union of some components of $\widetilde \sigma (T))$
is the union of some components of $\widetilde \sigma (T))$![]() . If $\infty \notin \Lambda$
. If $\infty \notin \Lambda$![]() , the spectral projection $P_\Lambda$
, the spectral projection $P_\Lambda$![]() of $T$
of $T$![]() is given by
is given by
where $\Gamma$![]() is a finite collection of paths contained in $\rho (T)$
is a finite collection of paths contained in $\rho (T)$![]() such that $\Gamma$
such that $\Gamma$![]() has index $1$
has index $1$![]() with respect to every point in $\Lambda$
with respect to every point in $\Lambda$![]() , and has index $0$
, and has index $0$![]() with respect to every point in $\sigma (T) \setminus \Lambda$
with respect to every point in $\sigma (T) \setminus \Lambda$![]() . If $\infty \in \Lambda$
. If $\infty \in \Lambda$![]() , then the spectral projection $P_\Lambda$
, then the spectral projection $P_\Lambda$![]() of $T$
of $T$![]() is given by $P_\Lambda := I - P_{\widetilde \sigma (T) \setminus \Lambda }$
is given by $P_\Lambda := I - P_{\widetilde \sigma (T) \setminus \Lambda }$![]() , where $P_{\widetilde \sigma (T)\setminus \Lambda }$
, where $P_{\widetilde \sigma (T)\setminus \Lambda }$![]() is as in (4.1).
is as in (4.1).
We collect in the form of a lemma some well-known results about spectral projections, see for instance [Reference Dunford and Schwartz5, Section V.9].
Lemma 4.3 Let $T, \Lambda$![]() be as above. Then
be as above. Then
1. $P_\Lambda$
 is a bounded projection commuting with $T$
is a bounded projection commuting with $T$ ;
;2. $\widetilde \sigma (T_\Lambda ) = \Lambda$
 , where $T_\Lambda :\operatorname {ran} P_\Lambda \to \operatorname {ran} P_\Lambda$
, where $T_\Lambda :\operatorname {ran} P_\Lambda \to \operatorname {ran} P_\Lambda$ is the part of $T$
is the part of $T$ in $\operatorname {ran} P_\Lambda$
in $\operatorname {ran} P_\Lambda$ .
.
As a consequence, for $\lambda \in \Lambda \cap \mathbb {C}$![]() , $\ker (\lambda - T) \subseteq \operatorname {ran} P_\Lambda$
, $\ker (\lambda - T) \subseteq \operatorname {ran} P_\Lambda$![]() and $\operatorname {ran}(I - P_\Lambda ) \subseteq {\operatorname {ran}(\lambda - T)}$
and $\operatorname {ran}(I - P_\Lambda ) \subseteq {\operatorname {ran}(\lambda - T)}$![]() . Also, if $\infty \notin \Lambda$
. Also, if $\infty \notin \Lambda$![]() , then $\operatorname {ran} P_\Lambda \subseteq \operatorname {dom} T$
, then $\operatorname {ran} P_\Lambda \subseteq \operatorname {dom} T$![]() .
.
We also need the following two lemmas.
Lemma 4.4 Let $A \in {\rm BSect}(\omega, a)$![]() , and let $\Lambda \subseteq \widetilde \sigma (A)$
, and let $\Lambda \subseteq \widetilde \sigma (A)$![]() be an open and closed subset in the relative topology of $\widetilde \sigma (A)$
be an open and closed subset in the relative topology of $\widetilde \sigma (A)$![]() . Then $A_\Lambda \in {\rm BSect}(\omega, a)$
. Then $A_\Lambda \in {\rm BSect}(\omega, a)$![]() with $\mathcal {M}(A) \subseteq \mathcal {M}(A_\Lambda )$
with $\mathcal {M}(A) \subseteq \mathcal {M}(A_\Lambda )$![]() , and one has
, and one has
for every $f \in \mathcal {M}(A)$![]() and $i \neq 7, 8$
and $i \neq 7, 8$![]() .
.
Proof. It follows by lemma 4.3 that $\widetilde \sigma (A_\Lambda ) = \Lambda \subseteq \overline {BS(\omega, a)} \cup \{\infty \}$![]() . Moreover, it is readily seen that $(z-A_\Lambda )^{-1} = (z-A)^{-1}|_{\operatorname {ran} P_\Lambda }$
. Moreover, it is readily seen that $(z-A_\Lambda )^{-1} = (z-A)^{-1}|_{\operatorname {ran} P_\Lambda }$![]() for every $z \in \rho (A)$
for every $z \in \rho (A)$![]() . As a consequence, one gets that $A_\Lambda$
. As a consequence, one gets that $A_\Lambda$![]() is indeed a bisectorial-like operator on $\operatorname {ran} P_\Lambda$
is indeed a bisectorial-like operator on $\operatorname {ran} P_\Lambda$![]() of angle $\omega$
of angle $\omega$![]() and half-width $a$
and half-width $a$![]() , and that $\mathcal {E}(A) \subseteq \mathcal {E} (A_\Lambda )$
, and that $\mathcal {E}(A) \subseteq \mathcal {E} (A_\Lambda )$![]() with $f(A)|_{\operatorname {ran} P_\Lambda } = f(A_\Lambda )$
with $f(A)|_{\operatorname {ran} P_\Lambda } = f(A_\Lambda )$![]() for all $f \in \mathcal {E}(A)$
for all $f \in \mathcal {E}(A)$![]() . Thus, if $e \in \mathcal {E}(A)$
. Thus, if $e \in \mathcal {E}(A)$![]() is a regularizer for $f \in \mathcal {M}(A)$
is a regularizer for $f \in \mathcal {M}(A)$![]() , then $e$
, then $e$![]() is also a regularizer for $f$
is also a regularizer for $f$![]() with respect to $A_\Lambda$
with respect to $A_\Lambda$![]() , so $\mathcal {M}(A) \subseteq \mathcal {M}(A_\Lambda )$
, so $\mathcal {M}(A) \subseteq \mathcal {M}(A_\Lambda )$![]() .
.
Now, we have $P_\Lambda f(A) \subseteq f(A)P_\Lambda$![]() for every $f \in \mathcal {M}(A)$
for every $f \in \mathcal {M}(A)$![]() by lemma 2.7. From this and the above properties, it is not difficult to get, for every $f \in \mathcal {M}(A)$
by lemma 2.7. From this and the above properties, it is not difficult to get, for every $f \in \mathcal {M}(A)$![]() , $f(A_\Lambda ) = f(A)|_{\operatorname {ran} P_\Lambda }$
, $f(A_\Lambda ) = f(A)|_{\operatorname {ran} P_\Lambda }$![]() , with $\operatorname {dom} f(A_\Lambda ) = \operatorname {dom} f(A)\cap \operatorname {ran} P_\Lambda, \, \ker f(A_\Lambda ) = \ker f(A) \cap \operatorname {ran}(P_\Lambda ), \, \operatorname {ran}(f(A_\Lambda )) = \operatorname {ran} f(A)\cap \operatorname {ran} P_\Lambda$
, with $\operatorname {dom} f(A_\Lambda ) = \operatorname {dom} f(A)\cap \operatorname {ran} P_\Lambda, \, \ker f(A_\Lambda ) = \ker f(A) \cap \operatorname {ran}(P_\Lambda ), \, \operatorname {ran}(f(A_\Lambda )) = \operatorname {ran} f(A)\cap \operatorname {ran} P_\Lambda$![]() . Hence $\widetilde {\sigma }_i(f(A_\Lambda )) \subseteq \widetilde {\sigma }_i(f(A))$
. Hence $\widetilde {\sigma }_i(f(A_\Lambda )) \subseteq \widetilde {\sigma }_i(f(A))$![]() for $i \in \{0, 1, 4, 5, 6\}$
for $i \in \{0, 1, 4, 5, 6\}$![]() .
.
Thus, all that is left to prove are the spectral inclusions for $\widetilde \sigma _2, \widetilde \sigma _3$![]() and $\widetilde \sigma _9$
and $\widetilde \sigma _9$![]() . Regarding the first case, assume $f(A) \in \Phi _2$
. Regarding the first case, assume $f(A) \in \Phi _2$![]() , i.e., $\operatorname {ran} f(A) \oplus W = X$
, i.e., $\operatorname {ran} f(A) \oplus W = X$![]() for some closed linear subspace $W$
for some closed linear subspace $W$![]() . Then $\operatorname {ran} f(A_\Lambda ) \oplus (\operatorname {ran}f(A) \cap \operatorname {ran}(I- P_\Lambda )) \oplus W = X$
. Then $\operatorname {ran} f(A_\Lambda ) \oplus (\operatorname {ran}f(A) \cap \operatorname {ran}(I- P_\Lambda )) \oplus W = X$![]() since $\operatorname {ran} f(A) = \operatorname {ran} f(A_\Lambda ) \oplus (\operatorname {ran} f(A) \cap \operatorname {ran}(I-P_\Lambda ))$
since $\operatorname {ran} f(A) = \operatorname {ran} f(A_\Lambda ) \oplus (\operatorname {ran} f(A) \cap \operatorname {ran}(I-P_\Lambda ))$![]() . Thus, there exists a bounded projection $\tilde {P}$
. Thus, there exists a bounded projection $\tilde {P}$![]() from $X$
from $X$![]() onto $\operatorname {ran} f(A_\Lambda )$
onto $\operatorname {ran} f(A_\Lambda )$![]() . Then, $\tilde P|_{\operatorname {ran} P_\Lambda }$
. Then, $\tilde P|_{\operatorname {ran} P_\Lambda }$![]() is a bounded projection from $\operatorname {ran} P_\Lambda$
is a bounded projection from $\operatorname {ran} P_\Lambda$![]() onto $\operatorname {ran} f(A_\Lambda )$
onto $\operatorname {ran} f(A_\Lambda )$![]() , that is, $\operatorname {ran} f(A_\Lambda )$
, that is, $\operatorname {ran} f(A_\Lambda )$![]() is complemented in $\operatorname {ran} P_\Lambda$
is complemented in $\operatorname {ran} P_\Lambda$![]() , so $f(A_\Lambda ) \in \Phi _2$
, so $f(A_\Lambda ) \in \Phi _2$![]() . An analogous reasoning with $\operatorname {dom} f(A)$
. An analogous reasoning with $\operatorname {dom} f(A)$![]() and $\operatorname {dom} f(A_\Lambda )$
and $\operatorname {dom} f(A_\Lambda )$![]() shows that, if $\infty \in \widetilde {\sigma }_2(f(A_\Lambda ))$
shows that, if $\infty \in \widetilde {\sigma }_2(f(A_\Lambda ))$![]() , then $\infty \in \widetilde {\sigma }_2(f(A))$
, then $\infty \in \widetilde {\sigma }_2(f(A))$![]() . Hence, the inclusion $\widetilde {\sigma }_2(f(B)) \subseteq \widetilde {\sigma }_2(f(A))$
. Hence, the inclusion $\widetilde {\sigma }_2(f(B)) \subseteq \widetilde {\sigma }_2(f(A))$![]() holds for any $f \in \mathcal {M}(A)$
holds for any $f \in \mathcal {M}(A)$![]() .
.
Similar reasoning proves the inclusion for $\widetilde \sigma _3$![]() . For $\widetilde \sigma _9$
. For $\widetilde \sigma _9$![]() , the inclusion follows from $\alpha (f(A)) = \max \{\alpha (f(B)), \alpha (f(A)|_Z)\}$
, the inclusion follows from $\alpha (f(A)) = \max \{\alpha (f(B)), \alpha (f(A)|_Z)\}$![]() and $\delta (f(A)) = \max \{\delta (f(B)), \delta (f(A)|_Z)\}$
and $\delta (f(A)) = \max \{\delta (f(B)), \delta (f(A)|_Z)\}$![]() , see [Reference Taylor and Lay20, Problem V.6].
, see [Reference Taylor and Lay20, Problem V.6].
Let $A \in {\rm BSect}(\omega, a)$![]() . Recall that $M_A \setminus \widetilde {\sigma }_i(A) = M_A \setminus \widetilde {\sigma }_j(A)$
. Recall that $M_A \setminus \widetilde {\sigma }_i(A) = M_A \setminus \widetilde {\sigma }_j(A)$![]() for $i, j \neq 0, 9$
for $i, j \neq 0, 9$![]() , see lemma 4.2. Then, by remark 4.1(c), $M_A \setminus \widetilde {\sigma }_i(A)$
, see lemma 4.2. Then, by remark 4.1(c), $M_A \setminus \widetilde {\sigma }_i(A)$![]() is an open and closed subset of $\widetilde \sigma (A)$
is an open and closed subset of $\widetilde \sigma (A)$![]() (in the relative topology of $\widetilde \sigma (A)$
(in the relative topology of $\widetilde \sigma (A)$![]() ) for $i \neq 0, 9$
) for $i \neq 0, 9$![]() . Also,
. Also,
Lemma 4.5 Let $A \in {\rm BSect}(\omega, a)$![]() , and let $\Lambda = \widetilde \sigma (A) \setminus (M_A \setminus \widetilde {\sigma }_j(A))$
, and let $\Lambda = \widetilde \sigma (A) \setminus (M_A \setminus \widetilde {\sigma }_j(A))$![]() , with $j \neq 0, 9$
, with $j \neq 0, 9$![]() . Then $M_{A_\Lambda } \subseteq \widetilde {\sigma }_i(A_\Lambda )$
. Then $M_{A_\Lambda } \subseteq \widetilde {\sigma }_i(A_\Lambda )$![]() for all $0 \leq i \leq 6$
for all $0 \leq i \leq 6$![]() and
and
Also, ${\rm codim} (\operatorname {ran} P_\Lambda ) < \infty$![]() .
.
Proof. The inclusions $\widetilde {\sigma }_i(f(A_\Lambda )) \subseteq \widetilde {\sigma }_i(f(A))$![]() are given in lemma 4.4. Let us show that the inclusions $\sigma _i(f(A)) \subseteq \sigma _i(f(A_\Lambda ))$
are given in lemma 4.4. Let us show that the inclusions $\sigma _i(f(A)) \subseteq \sigma _i(f(A_\Lambda ))$![]() also hold. To do this, we prove the following claims for all $f \in \mathcal {M}(A)$
also hold. To do this, we prove the following claims for all $f \in \mathcal {M}(A)$![]() ,
,
(1) If ${\rm nul} (f(A_\Lambda )) < \infty$
 , then ${\rm nul} (f(A)) < \infty$
, then ${\rm nul} (f(A)) < \infty$ .
.(2) If ${\rm def} (f(A_\Lambda )) < \infty$
 , then ${\rm def} (f(A)) < \infty$
, then ${\rm def} (f(A)) < \infty$ .
.(3) If $\operatorname {ran} f(A_\Lambda )$
 is closed/complemented in $\operatorname {ran} P_\Lambda$
is closed/complemented in $\operatorname {ran} P_\Lambda$ , then $\operatorname {ran} f(A)$
, then $\operatorname {ran} f(A)$ is closed/complemented in $X$
is closed/complemented in $X$ .
.(4) If $\ker f(A_\Lambda )$
 is complemented in $\operatorname {ran} P_\Lambda$
is complemented in $\operatorname {ran} P_\Lambda$ , then $\ker f(A)$
, then $\ker f(A)$ is complemented in $X$
is complemented in $X$ .
.
Set $\Omega = \widetilde \sigma (A)\setminus \Lambda$![]() , so $\Omega = M_A \setminus \widetilde \sigma _i(A)$
, so $\Omega = M_A \setminus \widetilde \sigma _i(A)$![]() for any $i \in \{1, \ldots, 6\}$
for any $i \in \{1, \ldots, 6\}$![]() . Lemma 4.3 implies $\widetilde {\sigma }_i(A|_\Omega ) = \emptyset$
. Lemma 4.3 implies $\widetilde {\sigma }_i(A|_\Omega ) = \emptyset$![]() for all $1 \leq i \leq 6$
for all $1 \leq i \leq 6$![]() . Note that, given a closed operator $T$
. Note that, given a closed operator $T$![]() with $\rho (T) \neq \emptyset$
with $\rho (T) \neq \emptyset$![]() on a Banach space $Y$
on a Banach space $Y$![]() , the essential spectra $\sigma _i(T)$
, the essential spectra $\sigma _i(T)$![]() , $1\leq i \leq 8$
, $1\leq i \leq 8$![]() , are empty if and only if $Y$
, are empty if and only if $Y$![]() is finite-dimensional. This implies that $\operatorname {ran} P_\Omega$
is finite-dimensional. This implies that $\operatorname {ran} P_\Omega$![]() is finite dimensional (see e.g. [Reference Gramsch and Lay8, Section 5] and remark 3.5), i.e., ${\rm codim}\, \operatorname {ran} P_\Lambda < \infty$
is finite dimensional (see e.g. [Reference Gramsch and Lay8, Section 5] and remark 3.5), i.e., ${\rm codim}\, \operatorname {ran} P_\Lambda < \infty$![]() since $\operatorname {ran} P_\Lambda$
since $\operatorname {ran} P_\Lambda$![]() and $\operatorname {ran} P_\Omega$
and $\operatorname {ran} P_\Omega$![]() are complementary subspaces. Since $\ker f(A_\Lambda ) = \ker f(A) \cap \operatorname {ran} P_\Lambda$
are complementary subspaces. Since $\ker f(A_\Lambda ) = \ker f(A) \cap \operatorname {ran} P_\Lambda$![]() and $\operatorname {ran} f(A_\Lambda ) = \operatorname {ran} f(A) \cap \operatorname {ran} P_\Lambda$
and $\operatorname {ran} f(A_\Lambda ) = \operatorname {ran} f(A) \cap \operatorname {ran} P_\Lambda$![]() (see the proof of lemma 4.4), we conclude that claims (1) and (2) hold true.
(see the proof of lemma 4.4), we conclude that claims (1) and (2) hold true.
For the claim regarding closedness in (3), assume $\operatorname {ran} f(A_\Lambda )$![]() is closed in $\operatorname {ran} P_\Lambda$
is closed in $\operatorname {ran} P_\Lambda$![]() , so $\operatorname {ran} f(A_\Lambda )$
, so $\operatorname {ran} f(A_\Lambda )$![]() is closed in $X$
is closed in $X$![]() too. Since $\operatorname {ran} f(A) = \operatorname {ran} f(A_\Lambda ) \oplus \operatorname {ran} f(A_\Omega )$
too. Since $\operatorname {ran} f(A) = \operatorname {ran} f(A_\Lambda ) \oplus \operatorname {ran} f(A_\Omega )$![]() , we have that $\operatorname {ran} f(A)/\operatorname {ran} f(A_\Lambda )$
, we have that $\operatorname {ran} f(A)/\operatorname {ran} f(A_\Lambda )$![]() is finite-dimensional in $X/\operatorname {ran} f(A_\Lambda )$
is finite-dimensional in $X/\operatorname {ran} f(A_\Lambda )$![]() , hence closed. Thus $\operatorname {ran} f(A)$
, hence closed. Thus $\operatorname {ran} f(A)$![]() is closed in $X$
is closed in $X$![]() . For the claim regarding complementation in (3), assume $\operatorname {ran} f(A_\Lambda ) \oplus U = \operatorname {ran} P_\Lambda$
. For the claim regarding complementation in (3), assume $\operatorname {ran} f(A_\Lambda ) \oplus U = \operatorname {ran} P_\Lambda$![]() for some closed subspace $U$
for some closed subspace $U$![]() . Note that $\operatorname {ran} f(A_\Omega ) \oplus V = \operatorname {ran} P_\Omega$
. Note that $\operatorname {ran} f(A_\Omega ) \oplus V = \operatorname {ran} P_\Omega$![]() for some finite-dimensional closed subspace since $\dim \, \operatorname {ran} P_\Omega < \infty$
for some finite-dimensional closed subspace since $\dim \, \operatorname {ran} P_\Omega < \infty$![]() . Therefore $\operatorname {ran} f(A) \oplus (U \oplus V) = X$
. Therefore $\operatorname {ran} f(A) \oplus (U \oplus V) = X$![]() , and (3) follows. An analogous reasoning proves the claim (4).
, and (3) follows. An analogous reasoning proves the claim (4).
Now, a similar reasoning as above with subspaces $\operatorname {dom} f(A), \operatorname {dom} f(A_\Lambda )$![]() shows that, if $\infty \in \widetilde {\sigma }_i(f(A))$
shows that, if $\infty \in \widetilde {\sigma }_i(f(A))$![]() , then $\infty \in \widetilde {\sigma }_i(f(A_\Lambda ))$
, then $\infty \in \widetilde {\sigma }_i(f(A_\Lambda ))$![]() for all $1 \leq i \leq 6$
for all $1 \leq i \leq 6$![]() . Therefore, $\widetilde {\sigma }_i(f(A)) \subseteq \widetilde {\sigma }_i(f(A_\Lambda ))$
. Therefore, $\widetilde {\sigma }_i(f(A)) \subseteq \widetilde {\sigma }_i(f(A_\Lambda ))$![]() , as we wanted to show.
, as we wanted to show.
Finally, to prove that $M_{A_\Lambda } \subseteq \widetilde {\sigma }_i(A_\Lambda )$![]() (for all $1 \leq i \leq 6$
(for all $1 \leq i \leq 6$![]() ), note that $M_A \setminus \widetilde {\sigma }_i(A) = \widetilde {\sigma }(A)\setminus \Lambda \subseteq \rho (A_\Lambda )$
), note that $M_A \setminus \widetilde {\sigma }_i(A) = \widetilde {\sigma }(A)\setminus \Lambda \subseteq \rho (A_\Lambda )$![]() by lemma 4.3.
by lemma 4.3.
We are now ready to prove the spectral mapping theorems for most of the extended essential spectra considered in the Introduction. For the sake of clarity, we separate the proof of each inclusion into two different propositions.
Proposition 4.6 Let $A \in {\rm BSect}(\omega, a)$![]() and let $f \in \mathcal {M}(A)$
and let $f \in \mathcal {M}(A)$![]() be quasi-regular at $M_A$
be quasi-regular at $M_A$![]() . Then
. Then
Proof. The inclusion for $\widetilde \sigma _0$![]() is already given in Proposition 3.1. For $1 \leq i \leq 5$
is already given in Proposition 3.1. For $1 \leq i \leq 5$![]() , we can assume $M_A \subseteq \widetilde {\sigma }_i(A)$
, we can assume $M_A \subseteq \widetilde {\sigma }_i(A)$![]() without loss of generality by lemma 4.5. Thus $\widetilde {\sigma }_i(f(A)) \subseteq f(\widetilde {\sigma }_i(A))$
without loss of generality by lemma 4.5. Thus $\widetilde {\sigma }_i(f(A)) \subseteq f(\widetilde {\sigma }_i(A))$![]() for $1 \leq i \leq 5$
for $1 \leq i \leq 5$![]() by proposition 3.7(b).
by proposition 3.7(b).
Now, we show the inclusions for $\widetilde \sigma _7, \widetilde \sigma _8$![]() . So take $i \in \{7, 8\}$
. So take $i \in \{7, 8\}$![]() , and let $\mu \in \mathbb {C} \setminus f(\widetilde {\sigma }_i(A))$
, and let $\mu \in \mathbb {C} \setminus f(\widetilde {\sigma }_i(A))$![]() . Note that we can assume $\mu = 0$
. Note that we can assume $\mu = 0$![]() . If $0 \notin f(M_A)$
. If $0 \notin f(M_A)$![]() , proposition 3.7(b) implies $0 \notin \widetilde \sigma _i(f(A))$
, proposition 3.7(b) implies $0 \notin \widetilde \sigma _i(f(A))$![]() . So assume $0 \in f(M_A)$
. So assume $0 \in f(M_A)$![]() . As $0 \notin f(\widetilde {\sigma }_i(A))$
. As $0 \notin f(\widetilde {\sigma }_i(A))$![]() , lemma 4.2 and remark 4.1(c) imply that $f^{-1}\{0\}\cap \widetilde {\sigma }(A)$
, lemma 4.2 and remark 4.1(c) imply that $f^{-1}\{0\}\cap \widetilde {\sigma }(A)$![]() is a finite set. Let $\lambda _1, \ldots, \lambda _N$
is a finite set. Let $\lambda _1, \ldots, \lambda _N$![]() be an enumeration of $(f^{-1}\{0\} \cap \widetilde {\sigma }(a) ) \setminus M_A$
be an enumeration of $(f^{-1}\{0\} \cap \widetilde {\sigma }(a) ) \setminus M_A$![]() , and let $n_1, \ldots, n_N$
, and let $n_1, \ldots, n_N$![]() be the multiplicity of $f$
be the multiplicity of $f$![]() at $\lambda _1, \ldots, \lambda _N$
at $\lambda _1, \ldots, \lambda _N$![]() respectively. Set ${r(z):= \Pi _{j=1}^{N}({\lambda _j - z})^{n_j}/({b-z})^{n_j}}$
respectively. Set ${r(z):= \Pi _{j=1}^{N}({\lambda _j - z})^{n_j}/({b-z})^{n_j}}$![]() for some $b \in \rho (A)$
for some $b \in \rho (A)$![]() , and $g(z): = f(z)/r(z)$
, and $g(z): = f(z)/r(z)$![]() for $z \in \mathbb {D}$
for $z \in \mathbb {D}$![]() . Several applications of lemma 3.6 yield $g \in \mathcal {M}(A)$
. Several applications of lemma 3.6 yield $g \in \mathcal {M}(A)$![]() and $f(A) = r(A)g(A) = g(A)r(A)$
and $f(A) = r(A)g(A) = g(A)r(A)$![]() with $\operatorname {dom} f(A) = \operatorname {dom} g(A)$
with $\operatorname {dom} f(A) = \operatorname {dom} g(A)$![]() . Also, one has $g^{-1}\{0\} \cap \widetilde {\sigma }(A) \subseteq M_A \setminus \widetilde {\sigma }_i(A)$
. Also, one has $g^{-1}\{0\} \cap \widetilde {\sigma }(A) \subseteq M_A \setminus \widetilde {\sigma }_i(A)$![]() . Then, $g^{-1}\{0\} \cap \Lambda = \emptyset$
. Then, $g^{-1}\{0\} \cap \Lambda = \emptyset$![]() where $\Lambda := \widetilde {\sigma }(A) \setminus (M_A \setminus \widetilde {\sigma }_i(A))$
where $\Lambda := \widetilde {\sigma }(A) \setminus (M_A \setminus \widetilde {\sigma }_i(A))$![]() . Thus, $g(A_\Lambda )$
. Thus, $g(A_\Lambda )$![]() is invertible by proposition 3.1 and lemma 4.4. On the other hand, ${\dim \,\operatorname {ran}(I- P_\Lambda ) < \infty}$
is invertible by proposition 3.1 and lemma 4.4. On the other hand, ${\dim \,\operatorname {ran}(I- P_\Lambda ) < \infty}$![]() by lemma 4.5 (see also lemma 4.2), so $g(A_{\widetilde \sigma (A)\setminus \Lambda }), r(A_{\widetilde \sigma (A)\setminus \Lambda }) \in \Phi _i$
by lemma 4.5 (see also lemma 4.2), so $g(A_{\widetilde \sigma (A)\setminus \Lambda }), r(A_{\widetilde \sigma (A)\setminus \Lambda }) \in \Phi _i$![]() . Since $r(A) \in \Phi _i$
. Since $r(A) \in \Phi _i$![]() (see e.g. [Reference González and Onieva7, Lemma 3] and [Reference Gramsch and Lay8, Lemma 5(c)]), we conclude that $r(A_\Lambda ) \in \Phi _i$
(see e.g. [Reference González and Onieva7, Lemma 3] and [Reference Gramsch and Lay8, Lemma 5(c)]), we conclude that $r(A_\Lambda ) \in \Phi _i$![]() . Thus, reasoning with $f, g, r$
. Thus, reasoning with $f, g, r$![]() and $f^n, g^n, r^n$
and $f^n, g^n, r^n$![]() as in the proof of lemma 3.6, we obtain $f(A_\Lambda ) \in \Phi _i$
as in the proof of lemma 3.6, we obtain $f(A_\Lambda ) \in \Phi _i$![]() . Using again that $\dim \,\operatorname {ran}(I- P_\Lambda ) < \infty$
. Using again that $\dim \,\operatorname {ran}(I- P_\Lambda ) < \infty$![]() , one gets $f(A) \in \Phi _i$
, one gets $f(A) \in \Phi _i$![]() as claimed, that is $0 \notin \widetilde {\sigma }_i(f(A))$
as claimed, that is $0 \notin \widetilde {\sigma }_i(f(A))$![]() .
.
Now, for $i=7,8$![]() , assume $\infty \notin f(\widetilde {\sigma }_i(A))$
, assume $\infty \notin f(\widetilde {\sigma }_i(A))$![]() . Reasoning as at the end of the proof of proposition 3.7, we can assume $\rho (f(A)) \neq \emptyset$
. Reasoning as at the end of the proof of proposition 3.7, we can assume $\rho (f(A)) \neq \emptyset$![]() without loss of generality. So let $\nu \in \rho (f(A))$
without loss of generality. So let $\nu \in \rho (f(A))$![]() . An application of what we have already proven to the function $\displaystyle {{1}/({\nu - f}})$
. An application of what we have already proven to the function $\displaystyle {{1}/({\nu - f}})$![]() shows that $\displaystyle {0 \notin \widetilde {\sigma _i}((\nu - f(A))^{-1})}$
shows that $\displaystyle {0 \notin \widetilde {\sigma _i}((\nu - f(A))^{-1})}$![]() , that is $\infty \notin \widetilde {\sigma }_i(f(A))$
, that is $\infty \notin \widetilde {\sigma }_i(f(A))$![]() for $i =7, 8$
for $i =7, 8$![]() , and the proof is finished.
, and the proof is finished.
The proof of the proposition below contains the answer to the question/open problem posed in [Reference Haase11], where the inclusion $f(\widetilde \sigma (A)) \subseteq \widetilde \sigma (f(A))$![]() was established only under additional assumptions on $f$
was established only under additional assumptions on $f$![]() regarding its behaviour at the points in $M_A$
regarding its behaviour at the points in $M_A$![]() . This is done via the following simple observation (missing in [Reference Haase11]), which in the end is very helpful to prove the spectral mapping theorem for the essential spectra: since the inclusion $f(\widetilde \sigma (A) \setminus M_A) \subseteq \widetilde \sigma (f(A))$
. This is done via the following simple observation (missing in [Reference Haase11]), which in the end is very helpful to prove the spectral mapping theorem for the essential spectra: since the inclusion $f(\widetilde \sigma (A) \setminus M_A) \subseteq \widetilde \sigma (f(A))$![]() has already been established in [Reference Haase11, Corollary 4.5] (see also proposition 3.7) and $\widetilde \sigma (f(A))$
has already been established in [Reference Haase11, Corollary 4.5] (see also proposition 3.7) and $\widetilde \sigma (f(A))$![]() is closed, one may suppose without loss of generality that each point in $M_A$
is closed, one may suppose without loss of generality that each point in $M_A$![]() is isolated in $\widetilde \sigma (A)$
is isolated in $\widetilde \sigma (A)$![]() . Passing to a subspace via spectral projections, one may suppose that $\widetilde \sigma (A)$
. Passing to a subspace via spectral projections, one may suppose that $\widetilde \sigma (A)$![]() consists only of a single point of $M_A$
consists only of a single point of $M_A$![]() , say $d$
, say $d$![]() . Now, the inclusion theorem [Reference Haase11, Proposition 6.3] (see also proposition 4.6) tells $\widetilde \sigma (f(A)) \subseteq f(\widetilde \sigma (A)) = \{f(d)\}$
. Now, the inclusion theorem [Reference Haase11, Proposition 6.3] (see also proposition 4.6) tells $\widetilde \sigma (f(A)) \subseteq f(\widetilde \sigma (A)) = \{f(d)\}$![]() . Since the spectral projection is non-trivial, the set $\widetilde \sigma (f(A))$
. Since the spectral projection is non-trivial, the set $\widetilde \sigma (f(A))$![]() must be non-empty, hence equals $\{f(d)\}$
must be non-empty, hence equals $\{f(d)\}$![]() . This tells $f(d) \in \widetilde \sigma (f(A))$
. This tells $f(d) \in \widetilde \sigma (f(A))$![]() , the missing information.
, the missing information.
Proposition 4.7 Let $A \in {\rm BSect}(\omega, a)$![]() and let $f \in \mathcal {M}(A)$
and let $f \in \mathcal {M}(A)$![]() be quasi-regular at $M_A$
be quasi-regular at $M_A$![]() . Then
. Then
Proof. Note that $\widetilde {\sigma }_6(f(A)) \subseteq \widetilde {\sigma }_i(f(A))$![]() for each $i \neq 7, 9$
for each $i \neq 7, 9$![]() . Thus, proposition 3.7 and lemma 4.2 yield that it is enough to prove the claim for $i \in \{0, 6\}$
. Thus, proposition 3.7 and lemma 4.2 yield that it is enough to prove the claim for $i \in \{0, 6\}$![]() . Hence, we assume $i \in \{0, 6\}$
. Hence, we assume $i \in \{0, 6\}$![]() from now on.
from now on.
Let $\mu \in f(\widetilde {\sigma }_i(A))$![]() with $\mu \neq \infty$
with $\mu \neq \infty$![]() , so we can assume $\mu = 0$
, so we can assume $\mu = 0$![]() without loss of generality. If $0 \in f(\widetilde {\sigma }_i(A)) \setminus f(M_A)$
without loss of generality. If $0 \in f(\widetilde {\sigma }_i(A)) \setminus f(M_A)$![]() , then $0 \in \widetilde \sigma _i(f(A))$
, then $0 \in \widetilde \sigma _i(f(A))$![]() by proposition 3.7(a). So assume $0 \in f(\widetilde {\sigma }_i(A))$
by proposition 3.7(a). So assume $0 \in f(\widetilde {\sigma }_i(A))$![]() with $0 \in f(M_A)$
with $0 \in f(M_A)$![]() . If any point in $f^{-1}\{0\} \cap \widetilde {\sigma }_i(A)$
. If any point in $f^{-1}\{0\} \cap \widetilde {\sigma }_i(A)$![]() is an accumulation point of $\widetilde {\sigma }_i(A)$
is an accumulation point of $\widetilde {\sigma }_i(A)$![]() (and we rule out the trivial case where $f$
(and we rule out the trivial case where $f$![]() is constant), then $0$
is constant), then $0$![]() is an accumulation point of $f(\widetilde {\sigma }_i(A))\setminus f(M_A) \subseteq \widetilde {\sigma }_i(f(A))$
is an accumulation point of $f(\widetilde {\sigma }_i(A))\setminus f(M_A) \subseteq \widetilde {\sigma }_i(f(A))$![]() (see proposition 3.7(a)), thus $0 \in \widetilde {\sigma }_i(f(A))$
(see proposition 3.7(a)), thus $0 \in \widetilde {\sigma }_i(f(A))$![]() since $\sigma _i(T)$
since $\sigma _i(T)$![]() is closed for any $T \in C(X)$
is closed for any $T \in C(X)$![]() . So assume that each point in $f^{-1}\{0\} \cap \widetilde {\sigma }_i(A)$
. So assume that each point in $f^{-1}\{0\} \cap \widetilde {\sigma }_i(A)$![]() is an isolated point in $\widetilde {\sigma }_i(A)$
is an isolated point in $\widetilde {\sigma }_i(A)$![]() , and set
, and set
which is a finite set by remark 4.1(c).
Assume first that $V_A$![]() is not empty (thus $i = 6$
is not empty (thus $i = 6$![]() ). One has that, for each ${\rm d} \in V_A$
). One has that, for each ${\rm d} \in V_A$![]() , there is some neighbourhood $\Omega _d$
, there is some neighbourhood $\Omega _d$![]() of $d$
of $d$![]() such that $\Omega _d \cap \widetilde {\sigma }(A) = \{d, \lambda _1^d, \lambda _2^d, \ldots \}$
such that $\Omega _d \cap \widetilde {\sigma }(A) = \{d, \lambda _1^d, \lambda _2^d, \ldots \}$![]() , where $\lambda _j^d \in \sigma _p(A)\setminus \sigma _6(A)$
, where $\lambda _j^d \in \sigma _p(A)\setminus \sigma _6(A)$![]() , each $\lambda _j^d$
, each $\lambda _j^d$![]() is an isolated point of $\sigma (A)$
is an isolated point of $\sigma (A)$![]() , and $\lambda _j^d \xrightarrow [j\to \infty ]{}d$
, and $\lambda _j^d \xrightarrow [j\to \infty ]{}d$![]() . Thus, $(f^{-1}\{0\}\cap \widetilde {\sigma }(A))\setminus (M_A \cup (\cup _{{\rm d} \in V_A} \Omega _d))$
. Thus, $(f^{-1}\{0\}\cap \widetilde {\sigma }(A))\setminus (M_A \cup (\cup _{{\rm d} \in V_A} \Omega _d))$![]() is a finite set. Let $\kappa _1, \ldots, \kappa _N$
is a finite set. Let $\kappa _1, \ldots, \kappa _N$![]() be the elements of this set, let $n_1, \ldots, n_N$
be the elements of this set, let $n_1, \ldots, n_N$![]() be the multiplicity of the zero of $f$
be the multiplicity of the zero of $f$![]() at $\kappa _1, \ldots, \kappa _N$
at $\kappa _1, \ldots, \kappa _N$![]() respectively, and set ${g(z) := f(z) \Pi _{j=1}^N ({b-z})^{n_j}/({\kappa _j-z})^{n_j}}$
respectively, and set ${g(z) := f(z) \Pi _{j=1}^N ({b-z})^{n_j}/({\kappa _j-z})^{n_j}}$![]() . Several applications of lemma 3.3 yield $g\in \mathcal {M}(A)$
. Several applications of lemma 3.3 yield $g\in \mathcal {M}(A)$![]() with $\operatorname {dom} g(A) = \operatorname {dom} f(A)$
with $\operatorname {dom} g(A) = \operatorname {dom} f(A)$![]() , and
, and

where in the last term we regard $(\kappa _j-A)(b-A)^{-1}$![]() as bounded operators on $\operatorname {dom} f(A)$
as bounded operators on $\operatorname {dom} f(A)$![]() . Let us show that $0 \in \widetilde {\sigma }_6(g(A))$
. Let us show that $0 \in \widetilde {\sigma }_6(g(A))$![]() , from which follows $0 \in \widetilde {\sigma }_6(f(A))$
, from which follows $0 \in \widetilde {\sigma }_6(f(A))$![]() , see for example [Reference Edmunds and Evans6, Theorem I.3.20]. Note that $g^{-1}\{0\}\cap \widetilde {\sigma }(A) \subseteq M_A \cup (\cup _{{\rm d}\in V_A} \Omega _d)$
, see for example [Reference Edmunds and Evans6, Theorem I.3.20]. Note that $g^{-1}\{0\}\cap \widetilde {\sigma }(A) \subseteq M_A \cup (\cup _{{\rm d}\in V_A} \Omega _d)$![]() , and that if ${\rm d} \in M_A \setminus \widetilde \sigma _6(A)$
, and that if ${\rm d} \in M_A \setminus \widetilde \sigma _6(A)$![]() then $d$
then $d$![]() is an isolated point of $\widetilde \sigma (A)$
is an isolated point of $\widetilde \sigma (A)$![]() , see remark 4.1(a). As a consequence, $0$
, see remark 4.1(a). As a consequence, $0$![]() is an accumulation point of $\mathbb {C} \setminus g(\widetilde \sigma (A))$
is an accumulation point of $\mathbb {C} \setminus g(\widetilde \sigma (A))$![]() . Thus, proposition 3.1 implies that $0$
. Thus, proposition 3.1 implies that $0$![]() is an accumulation point of $\rho (g(A))$
is an accumulation point of $\rho (g(A))$![]() . If $0$
. If $0$![]() is also an accumulation point of $\widetilde {\sigma }(g(A))$
is also an accumulation point of $\widetilde {\sigma }(g(A))$![]() , then $0 \in \widetilde {\sigma }_6(g(A))$
, then $0 \in \widetilde {\sigma }_6(g(A))$![]() by remark 4.1. So assume that $0$
by remark 4.1. So assume that $0$![]() is not an accumulation point of $\widetilde {\sigma }(g(A))$
is not an accumulation point of $\widetilde {\sigma }(g(A))$![]() . Since $\sigma _p(g(A)) \subseteq g(\sigma _p(A))$
. Since $\sigma _p(g(A)) \subseteq g(\sigma _p(A))$![]() (lemma 2.8), and $\lambda _j^d \in \sigma _p(A)$
(lemma 2.8), and $\lambda _j^d \in \sigma _p(A)$![]() with $\lambda _j^d \xrightarrow [j \to \infty ]{}d$
with $\lambda _j^d \xrightarrow [j \to \infty ]{}d$![]() for each ${\rm d} \in V_A$
for each ${\rm d} \in V_A$![]() , it follows $g(\lambda _j^d)=0$
, it follows $g(\lambda _j^d)=0$![]() for all but finitely many pairs $(j, d) \in \mathbb {N} \times V_A$
for all but finitely many pairs $(j, d) \in \mathbb {N} \times V_A$![]() . Hence, the set $g^{-1}\{0\} \cap \sigma _p(A)$
. Hence, the set $g^{-1}\{0\} \cap \sigma _p(A)$![]() has infinite cardinal, so ${\rm nul}(g(A)) \geq \sum _{\lambda \in g^{-1}\{0\} \cap \sigma _p(A)} {\rm nul}(\lambda - A) = \infty$
has infinite cardinal, so ${\rm nul}(g(A)) \geq \sum _{\lambda \in g^{-1}\{0\} \cap \sigma _p(A)} {\rm nul}(\lambda - A) = \infty$![]() . Then remark 4.1(c) yields $0 \in \widetilde {\sigma }_6(g(A))$
. Then remark 4.1(c) yields $0 \in \widetilde {\sigma }_6(g(A))$![]() , as we wanted to prove.
, as we wanted to prove.
Now, assume $V_A = \emptyset \mbox{ for } i = 0,6$![]() , so each ${\rm d} \in f^{-1}\{0\} \cap \widetilde {\sigma }_i(A)$
, so each ${\rm d} \in f^{-1}\{0\} \cap \widetilde {\sigma }_i(A)$![]() is an isolated point of $\widetilde {\sigma }(A)$
is an isolated point of $\widetilde {\sigma }(A)$![]() . Set $\Lambda := f^{-1}\{0\} \cap M_A \cap \widetilde \sigma _i(A)$
. Set $\Lambda := f^{-1}\{0\} \cap M_A \cap \widetilde \sigma _i(A)$![]() . Note that, in the case $i=6$
. Note that, in the case $i=6$![]() , then $\dim \operatorname {ran} P_\Lambda = \infty$
, then $\dim \operatorname {ran} P_\Lambda = \infty$![]() as a consequence of lemma 4.3. Since $f(\Lambda ) = \{0\}$
as a consequence of lemma 4.3. Since $f(\Lambda ) = \{0\}$![]() , we have $\widetilde \sigma (f(A_\Lambda )) \subseteq \{0\}$
, we have $\widetilde \sigma (f(A_\Lambda )) \subseteq \{0\}$![]() by proposition 3.1. Hence, $\widetilde \sigma _i(f(A_\Lambda )) = \{0\}$
by proposition 3.1. Hence, $\widetilde \sigma _i(f(A_\Lambda )) = \{0\}$![]() since $\widetilde {\sigma }_i(f(A_\Lambda ))$
since $\widetilde {\sigma }_i(f(A_\Lambda ))$![]() cannot be the emptyset (at least for any operator with non-empty resolvent set, see for example [Reference Gramsch and Lay8, Section 5] and remark 3.5). Therefore, $0 \in \widetilde {\sigma }_i(f(A))$
cannot be the emptyset (at least for any operator with non-empty resolvent set, see for example [Reference Gramsch and Lay8, Section 5] and remark 3.5). Therefore, $0 \in \widetilde {\sigma }_i(f(A))$![]() by lemma 4.4, as we wanted to show.
by lemma 4.4, as we wanted to show.
Finally, we deal with the case $\mu = \infty$![]() . Reasoning as at the end of the proof of proposition 3.7, we can assume that $\rho (f(A)) \neq \emptyset$
. Reasoning as at the end of the proof of proposition 3.7, we can assume that $\rho (f(A)) \neq \emptyset$![]() . Take any $\nu \in \rho (f(A))$
. Take any $\nu \in \rho (f(A))$![]() , so $\infty \in \widetilde {\sigma }_i (f(A))$
, so $\infty \in \widetilde {\sigma }_i (f(A))$![]() if and only if $\displaystyle {0 \in \widetilde {\sigma }_i ((\nu - f(A))^{-1})}$
if and only if $\displaystyle {0 \in \widetilde {\sigma }_i ((\nu - f(A))^{-1})}$![]() . But $\displaystyle {0 \in \widetilde {\sigma }_i((\nu - f(A))^{-1})}$
. But $\displaystyle {0 \in \widetilde {\sigma }_i((\nu - f(A))^{-1})}$![]() by applying what we have already proven to the function $\displaystyle {{1}/({\nu - f})}$
by applying what we have already proven to the function $\displaystyle {{1}/({\nu - f})}$![]() , and the proof is finished.
, and the proof is finished.
As a consequence, we have the following
Theorem 4.8 Let $A \in {\rm BSect}(\omega, a)$![]() and $f \in \mathcal {M}(A)$
and $f \in \mathcal {M}(A)$![]() quasi-regular at $M_A$
quasi-regular at $M_A$![]() . Then
. Then

It is known that the spectral mapping theorem does not hold (in general) for $\widetilde {\sigma }_6, \widetilde {\sigma }_7$![]() , see for instance [Reference Edmunds and Evans6, Section 3]. However, we do not know if it holds for $\widetilde {\sigma }_9$
, see for instance [Reference Edmunds and Evans6, Section 3]. However, we do not know if it holds for $\widetilde {\sigma }_9$![]() for the regularized functional calculus considered here. Indeed, it holds if $M_A = \emptyset$
for the regularized functional calculus considered here. Indeed, it holds if $M_A = \emptyset$![]() , see proposition 3.7.
, see proposition 3.7.
5. Final remarks
5.1. Operators with bounded functional calculus
A natural question is whether the condition of quasi-regularity can be relaxed in Theorem 4.8. For instance, one may think of a function $f \in \mathcal {M} (A)$![]() with well-defined limits (through the domain of $f$
with well-defined limits (through the domain of $f$![]() ) at $M_A$
) at $M_A$![]() . The properties of bounded functional calculi (see for instance [Reference Cowling, Doust, Mcintosh and Yagi4, Reference Haase12, Reference Morris17]) are very helpful.
. The properties of bounded functional calculi (see for instance [Reference Cowling, Doust, Mcintosh and Yagi4, Reference Haase12, Reference Morris17]) are very helpful.
Definition 5.1 Let $A \in {\rm BSect}(\omega, a)$![]() . We say that the regularized functional calculus of $A$
. We say that the regularized functional calculus of $A$![]() is bounded if $f(A) \in \mathcal {L}(X)$
is bounded if $f(A) \in \mathcal {L}(X)$![]() for every bounded $f \in \mathcal {M}(A)$
for every bounded $f \in \mathcal {M}(A)$![]() .
.
Lemma 5.2 Let $A \in {\rm BSect}(\omega, a)$![]() and $f \in \mathcal {M}(A)$
and $f \in \mathcal {M}(A)$![]() . Then $f$
. Then $f$![]() is regular at $\sigma _p(A) \cap M_A$
is regular at $\sigma _p(A) \cap M_A$![]() .
.
Proof. The proof is analogous to the case of sectorial operators, see [Reference Haase10, Lemma 4.2].
Theorem 5.3 Let $A \in {\rm BSect}(\omega, a)$![]() such that the regularized functional calculus of $A$
such that the regularized functional calculus of $A$![]() is bounded, and let $f \in \mathcal {M}(A)$
is bounded, and let $f \in \mathcal {M}(A)$![]() with (possibly $\infty$
with (possibly $\infty$![]() -valued) limits at $M_A$
-valued) limits at $M_A$![]() . Then
. Then

Proof. The proof of this claim is completely analogous to the path followed in this paper to prove Theorem 4.8. Indeed, the quasi-regularity notion is only explicitly needed in the proofs of lemma 2.11 and proposition 3.1. This creates a ‘cascade’ effect, and all following results need the quasi-regularity assumption in order to apply proposition 3.1. Therefore, we will prove the claim once we prove the following version of proposition 3.1:
“Let $A \in {\rm BSect}(\omega, a)$![]() such that the regularized functional calculus of $A$
such that the regularized functional calculus of $A$![]() is bounded, and let $f \in \mathcal {M}(A)$
is bounded, and let $f \in \mathcal {M}(A)$![]() with (possibly $\infty$
with (possibly $\infty$![]() -valued) limits at $M_A$
-valued) limits at $M_A$![]() . Then $\widetilde {\sigma }(f(A)) \subseteq f(\widetilde {\sigma }(A))$
. Then $\widetilde {\sigma }(f(A)) \subseteq f(\widetilde {\sigma }(A))$![]() .”
.”
We outline the proof of this claim. Let $\mu \in \mathbb {C}_\infty$![]() with $\mu \notin f(\widetilde {\sigma }(A))$
with $\mu \notin f(\widetilde {\sigma }(A))$![]() , and set $\displaystyle {f_\mu } = {1}/({\mu - f})$
, and set $\displaystyle {f_\mu } = {1}/({\mu - f})$![]() if $\mu \in \mathbb {C}$
if $\mu \in \mathbb {C}$![]() or $f_\mu = f$
or $f_\mu = f$![]() if $\mu = \infty$
if $\mu = \infty$![]() , and we will show that $f_\mu \in \mathcal {M}(A)$
, and we will show that $f_\mu \in \mathcal {M}(A)$![]() with $f_\mu (A) \in \mathcal {L}(X)$
with $f_\mu (A) \in \mathcal {L}(X)$![]() . Note that $f_\mu$
. Note that $f_\mu$![]() has finite limits at $M_A$
has finite limits at $M_A$![]() . Even more, $f_\mu$
. Even more, $f_\mu$![]() is regular at $\sigma _p(A) \cap M_A$
is regular at $\sigma _p(A) \cap M_A$![]() by lemma 5.2. Proceeding as in the proof of lemma 2.11, we can assume that $f_\mu$
by lemma 5.2. Proceeding as in the proof of lemma 2.11, we can assume that $f_\mu$![]() has finitely many poles, all of them contained in $\rho (A)$
has finitely many poles, all of them contained in $\rho (A)$![]() . Let ${r(z) := \Pi _{j=1}^{n}{(\lambda _j-z)^{n_j}}/{(b-z)^{n_j}}}$
. Let ${r(z) := \Pi _{j=1}^{n}{(\lambda _j-z)^{n_j}}/{(b-z)^{n_j}}}$![]() , where $\lambda _j, n_j$
, where $\lambda _j, n_j$![]() are the poles of $f_\mu$
are the poles of $f_\mu$![]() and their order, respectively. Hence, $r f_\mu$
and their order, respectively. Hence, $r f_\mu$![]() has no poles, is regular at $\sigma _p(A) \cap M_A$
has no poles, is regular at $\sigma _p(A) \cap M_A$![]() and has finite limits at $M_A$
and has finite limits at $M_A$![]() , thus $r f_\mu$
, thus $r f_\mu$![]() is bounded. For any $b \in \rho (A)$
is bounded. For any $b \in \rho (A)$![]() , the function ${h(z):={1}/({b-z}) \, \Pi _{{\rm d}\in \{-a, a\}\setminus \sigma _p(A)} ({z-a})/({b-z}})$
, the function ${h(z):={1}/({b-z}) \, \Pi _{{\rm d}\in \{-a, a\}\setminus \sigma _p(A)} ({z-a})/({b-z}})$![]() regularizes $rf_\mu$
regularizes $rf_\mu$![]() , so $rf_\mu \in \mathcal {M}_A$
, so $rf_\mu \in \mathcal {M}_A$![]() . Since the regularized functional calculus of $A$
. Since the regularized functional calculus of $A$![]() is bounded, then $rf_\mu (A) \in \mathcal {L}(X)$
is bounded, then $rf_\mu (A) \in \mathcal {L}(X)$![]() . Moreover, $r(A)$
. Moreover, $r(A)$![]() is bounded and invertible. Therefore, $hr$
is bounded and invertible. Therefore, $hr$![]() regularizes $f_\mu$
regularizes $f_\mu$![]() with $f_\mu (A) = r(A)^{-1} (rf_\mu )(A) \in \mathcal {L}(X)$
with $f_\mu (A) = r(A)^{-1} (rf_\mu )(A) \in \mathcal {L}(X)$![]() , and the claim follows.
, and the claim follows.
5.2. Spectral mapping theorems for sectorial operators and strip-type operators
Lemmas 2.7–2.11 are the key properties of the regularized functional calculus of bisectorial-like operators that we use in the proofs given in § 3 and 4. Therefore, for similar regularized functional calculi satisfying such properties, one may prove spectral mapping theorems for essential spectra analogous to the ones given in Theorem 4.8. In particular, we obtain the following results for the regularized functional calculus of sectorial operators and the regularized functional calculus of strip-type operators considered in [Reference Haase11].
Theorem 5.4 Let $A$![]() be a sectorial operator of angle $\phi \in [0, 2\pi )$
be a sectorial operator of angle $\phi \in [0, 2\pi )$![]() , and let $f$
, and let $f$![]() be a function in the domain of the regularized functional calculus of $A$
be a function in the domain of the regularized functional calculus of $A$![]() that is quasi-regular at $\{0, \infty \}\cap \widetilde {\sigma }(A)$
that is quasi-regular at $\{0, \infty \}\cap \widetilde {\sigma }(A)$![]() . Then
. Then

Theorem 5.5 Let $A$![]() be a strip-type operator of height $h \geq 0$
be a strip-type operator of height $h \geq 0$![]() , and let $f$
, and let $f$![]() be a function in the domain of the regularized functional calculus of $A$
be a function in the domain of the regularized functional calculus of $A$![]() that is quasi-regular at $\{\infty \}\cap \widetilde {\sigma }(A)$
that is quasi-regular at $\{\infty \}\cap \widetilde {\sigma }(A)$![]() . Then
. Then

5.3. A spectral mapping theorem for the point spectrum
To finish this paper, we give a spectral mapping theorem for the point spectrum. To prove it, we need to restrict to functions $f \in \mathcal {M}_A$![]() satisfying the following condition:
(P) For each ${\rm d} \in M_A$
satisfying the following condition:
(P) For each ${\rm d} \in M_A$![]() such that $f(d) \notin f(\sigma _p(A)) \cup \{\infty \}$
such that $f(d) \notin f(\sigma _p(A)) \cup \{\infty \}$![]() , there is some $\beta >0$
, there is some $\beta >0$![]() for which
for which
• if ${\rm d} \in \mathbb {C}$
 , then $|f(z) - c_d| \gtrsim |z-d|^\beta$
, then $|f(z) - c_d| \gtrsim |z-d|^\beta$ as $z\to d$
as $z\to d$ , or
, or• if $d=\infty$
 , then $|f(z) - c_d| \gtrsim |z|^{-\beta }$
, then $|f(z) - c_d| \gtrsim |z|^{-\beta }$ as $z\to d$
as $z\to d$ ,
,
where $c_d$![]() denotes the limit of $f(z)$
denotes the limit of $f(z)$![]() as $z \to d$
as $z \to d$![]() .
.
Proposition 5.6 Let $A \in {\rm BSect}(\omega, a)$![]() and $f \in \mathcal {M}(A)$
and $f \in \mathcal {M}(A)$![]() such that $f$
such that $f$![]() is quasi-regular at $M_A$
is quasi-regular at $M_A$![]() . Then
. Then
If, furthermore, $f$![]() satisfies condition $(\mathbf{P})$
satisfies condition $(\mathbf{P})$![]() above, then $f(\sigma _p(A)) = \sigma _p (f(A))$
above, then $f(\sigma _p(A)) = \sigma _p (f(A))$![]() .
.
Proof. The proof of the inclusions $f(\sigma _p(A)) \subseteq \sigma _p (f(A)) \subseteq f(\sigma _p(A)) \cup f(M_A)$![]() runs the same as for sectorial operators, see [Reference Haase11, Proposition 6.5]. Assume now that $f$
runs the same as for sectorial operators, see [Reference Haase11, Proposition 6.5]. Assume now that $f$![]() satisfies (P). All that is left to prove is that, if $\mu \in f(M_A) \backslash f(\sigma _p(A))$
satisfies (P). All that is left to prove is that, if $\mu \in f(M_A) \backslash f(\sigma _p(A))$![]() , then $\mu \notin \sigma _p(f(A))$
, then $\mu \notin \sigma _p(f(A))$![]() . The statement is trivial if $\mu = \infty$
. The statement is trivial if $\mu = \infty$![]() , so assume $\mu \in \mathbb {C} \backslash f(\sigma _p(A))$
, so assume $\mu \in \mathbb {C} \backslash f(\sigma _p(A))$![]() , and consider the function $g:={1}/({\mu -f})$
, and consider the function $g:={1}/({\mu -f})$![]() , which is quasi-regular at $M_A$
, which is quasi-regular at $M_A$![]() . Note that poles of $g$
. Note that poles of $g$![]() are precisely $f^{-1}\{\mu \} \subseteq \mathbb {C} \backslash \sigma _p(A)$
are precisely $f^{-1}\{\mu \} \subseteq \mathbb {C} \backslash \sigma _p(A)$![]() . Moreover, $g$
. Moreover, $g$![]() is regular at $M_A \cap \sigma _p(A)$
is regular at $M_A \cap \sigma _p(A)$![]() , since by assumption $\mu \notin f(\sigma _p(A))$
, since by assumption $\mu \notin f(\sigma _p(A))$![]() . Let now
. Let now
Then, by the assumptions made on $f$![]() , $h_{l,m,n}g$
, $h_{l,m,n}g$![]() is regular for some $m, n, l$
is regular for some $m, n, l$![]() large enough, and where $l, m, n =0$
large enough, and where $l, m, n =0$![]() if $\infty, a, -a \notin \widetilde {\sigma }(A) \backslash \sigma _p(A)$
if $\infty, a, -a \notin \widetilde {\sigma }(A) \backslash \sigma _p(A)$![]() respectively. Since $h_{l,m,n}(A) = (A-a)^m(A+a)^n (b-A)^{-(m+n+l)}$
respectively. Since $h_{l,m,n}(A) = (A-a)^m(A+a)^n (b-A)^{-(m+n+l)}$![]() is bounded and injective, $h_{l,m,n}$
is bounded and injective, $h_{l,m,n}$![]() regularizes $g$
regularizes $g$![]() . Hence $g \in \mathcal {M}(A)$
. Hence $g \in \mathcal {M}(A)$![]() , which by lemma 2.7(4) implies that $\mu -f$
, which by lemma 2.7(4) implies that $\mu -f$![]() is injective, as we wanted to show.
is injective, as we wanted to show.
The author thanks the anonymous reviewer for several ideas, comments and additional information, which have considerably improved this paper.
Acknowledgements
This research has been partially supported by Project PID2019-105979GB-I00 of the MICINN, and by BES-2017-081552, MINECO, Spain and FSE.