Hostname: page-component-78c5997874-mlc7c Total loading time: 0 Render date: 2024-11-16T15:10:02.826Z Has data issue: false hasContentIssue false
  • English
  • Français

Some problems in automata theory which depend on the models of set theory

Published online by Cambridge University Press:  03 October 2011

Olivier Finkel
Olivier Finkel*
Affiliation:
Équipe de Logique Mathématique, Institut de Mathématiques de Jussieu, CNRS et Université Paris 7, France. finkel@logique.jussieu.fr
Get access

Abstract

We prove that some fairly basic questions on automata reading infinite words depend on the models of the axiomatic system ZFC. It is known that there are only three possibilities for the cardinality of the complement of an ω-language \hbox{$L(\mathcal{A})$}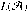L(𝒜) accepted by a Büchi 1-counter automaton \hbox{$\mathcal{A}$}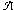𝒜. We prove the following surprising result: there exists a 1-counter Büchi automaton \hbox{$\mathcal{A}$}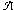𝒜 such that the cardinality of the complement \hbox{$L(\mathcal{A})^-$}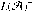L(𝒜) −  of the ω-language \hbox{$L(\mathcal{A})$}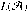L(𝒜) is not determined by ZFC: (1) There is a model V1 of ZFC in which \hbox{$L(\mathcal{A})^-$}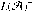L(𝒜) −  is countable. (2) There is a model V2 of ZFC in which \hbox{$L(\mathcal{A})^-$}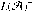L(𝒜) −  has cardinal 2ℵ0. (3) There is a model V3 of ZFC in which \hbox{$L(\mathcal{A})^-$}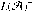L(𝒜) −  has cardinal ℵ1 with ℵ0 < ℵ1 < 2ℵ0.

We prove a very similar result for the complement of an infinitary rational relation accepted by a 2-tape Büchi automaton ℬ. As a corollary, this proves that the continuum hypothesis may be not satisfied for complements of 1-counter ω-languages and for complements of infinitary rational relations accepted by 2-tape Büchi automata. We infer from the proof of the above results that basic decision problems about 1-counter ω-languages or infinitary rational relations are actually located at the third level of the analytical hierarchy. In particular, the problem to determine whether the complement of a 1-counter ω-language (respectively, infinitary rational relation) is countable is in Σ13\(Π12 ∪ Σ12). This is rather surprising if compared to the fact that it is decidable whether an infinitary rational relation is countable (respectively, uncountable).

Keywords

Automata and formal languageslogic in computer sciencecomputational complexityinfinite wordsω-languages1-counter automaton2-tape automatoncardinality problemsdecision problemsanalytical hierarchylargest thin effective coanalytic setmodels of set theoryindependence from the axiomatic system ZFC
Type
Research Article
Information
RAIRO - Theoretical Informatics and Applications , Volume 45 , Issue 4 , November 2011 , pp. 383 - 397
Copyright
© EDP Sciences 2011

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Références

Castro, J. and Cucker, F., Nondeterministic ω-computations and the analytical hierarchy. J. Math. Logik Grundl. Math. 35 (1989) 333–342. Google Scholar
Cohen, R.S. and Gold, A.Y., ω-computations on Turing machines. Theoret. Comput. Sci. 6 (1978) 1–23. Google Scholar
Finkel, O., Borel ranks and Wadge degrees of omega context free languages. Math. Structures Comput. Sci. 16 (2006) 813–840. Google Scholar
Finkel, O., On the accepting power of two-tape Büchi automata, in Proceedings of the 23rd International Symposium on Theoretical Aspects of Computer Science. STACS 2006. Lect. Notes Comput. Sci. 3884 (2006) 301–312. Google Scholar
Finkel, O., The complexity of infinite computations in models of set theory. Log. Meth. Comput. Sci. 5 (2009) 1–19. Google Scholar
Finkel, O., Highly undecidable problems for infinite computations. RAIRO – Theor. Inf. Appl. 43 (2009) 339–364. Google Scholar
Finkel, O., Decision problems for recognizable languages of infinite pictures, in Studies in Weak Arithmetics, Proceedings of the International Conference 28th Weak Arithmetic Days, 2009, Publications of the Center for the Study of Language and Information. Lect. Notes 196 (2010) 127–151. Google Scholar
F. Gire, Relations rationnelles infinitaires. Ph.D. thesis, Université Paris VII (1981).
Gire, F. and Nivat, M., Relations rationnelles infinitaires. Calcolo XXI (1984) 91–125. Google Scholar
E. Grädel, W. Thomas and W. Wilke Eds., Automata, Logics, and Infinite Games : A Guide to Current Research [outcome of a Dagstuhl seminar, February 2001]. Lect. Notes Comput. Sci. 2500 (2002).
Gurevich, Y., Magidor, M. and Shelah, S., The monadic theory of ω 2. J. Symbolic Logic 48 (1983) 387–398. Google Scholar
J.E. Hopcroft, R. Motwani and J.D. Ullman, Introduction to automata theory, languages, and computation. Addison-Wesley Publishing Co., Reading, Mass. Addison-Wesley Series in Computer Science (2001).
T. Jech, Set Theory, 3rd edition. Springer (2002).
A. Kanamori, The Higher Infinite. Springer-Verlag (1997).
Kechris, A.S., The theory of countable analytical sets. Trans. Amer. Math. Soc. 202 (1975) 259–297. Google Scholar
Kuske, D. and Lohrey, M., First-order and counting theories of omega-automatic structures. J. Symbolic Logic 73 (2008) 129–150. Google Scholar
Landweber, L.H., Decision problems for ω-automata. Math. Syst. Theor. 3 (1969) 376–384. Google Scholar
H. Lescow and W. Thomas, Logical specifications of infinite computations, in A Decade of Concurrency, J.W. de Bakker, W.P. de Roever and G. Rozenberg, Eds. Lect. Notes Comput. Sci. 803 (1994) 583–621.
Y.N. Moschovakis, Descriptive set theory. North-Holland Publishing Co., Amsterdam (1980).
Neeman, I., Finite state automata and monadic definability of singular cardinals. J. Symbolic Logic 73 (2008) 412–438. Google Scholar
Niwinski, D., On the cardinality of sets of infinite trees recognizable by finite automata, in Proceedings of the International Conference MFCS. Lect. Notes Comput. Sci. 520 (1991) 367–376. Google Scholar
D. Perrin and J.-E. Pin, Infinite words, automata, semigroups, logic and games. Pure Appl. Math. 141 (2004).
H. Rogers, Theory of Recursive Functions and Effective Computability. McGraw-Hill, New York (1967).
Staiger, L., Hierarchies of recursive ω-languages. Elektronische Informationsverarbeitung und Kybernetik 22 (1986) 219–241. Google Scholar
L. Staiger, ω-languages, in Handbook of formal languages 3. Springer, Berlin (1997) 339–387.
W. Thomas, Automata on infinite objects, in Handbook of Theoretical Computer Science B, Formal models and semantics. J. van Leeuwen, Ed. Elsevier (1990) 135–191.