Hostname: page-component-848d4c4894-nr4z6 Total loading time: 0 Render date: 2024-06-08T09:46:37.426Z Has data issue: false hasContentIssue false
  • English
  • Français

DISJUNCTION AND EXISTENCE PROPERTIES IN MODAL ARITHMETIC

Part of: General logic Proof theory and constructive mathematics

Published online by Cambridge University Press:  23 December 2022

TAISHI KURAHASHI Open the ORCID record for TAISHI KURAHASHI [Opens in a new window]  and
MOTOKI OKUDA
TAISHI KURAHASHI
Affiliation:
GRADUATE SCHOOL OF SYSTEM INFORMATICS KOBE UNIVERSITY 1-1 ROKKODAI, NADA, KOBE 657-8501, JAPAN E-mail: kurahashi@people.kobe-u.ac.jp
MOTOKI OKUDA
Affiliation:
INDEPENDENT SCHOLAR
Get access Rights & Permissions [Opens in a new window]

Abstract

We systematically study several versions of the disjunction and the existence properties in modal arithmetic. First, we newly introduce three classes 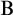$\mathrm {B}$, 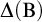$\Delta (\mathrm {B})$, and 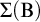$\Sigma (\mathrm {B})$ of formulas of modal arithmetic and study basic properties of them. Then, we prove several implications between the properties. In particular, among other things, we prove that for any consistent recursively enumerable extension T of 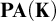$\mathbf {PA}(\mathbf {K})$ with 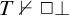$T \nvdash \Box \bot $, the 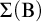$\Sigma (\mathrm {B})$-disjunction property, the 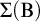$\Sigma (\mathrm {B})$-existence property, and the 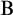$\mathrm {B}$-existence property are pairwise equivalent. Moreover, we introduce the notion of the 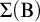$\Sigma (\mathrm {B})$-soundness of theories and prove that for any consistent recursively enumerable extension of $\mathbf {PA}(\mathbf {K4})$, the modal disjunction property is equivalent to the 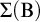$\Sigma (\mathrm {B})$-soundness.

Keywords

modal arithmeticdisjunction propertyexistence property

MSC classification

Primary: 03B45: Modal logic (including the logic of norms) 03F30: First-order arithmetic and fragments 03F40: Gödel numberings and issues of incompleteness
Type
Research Article
Information
The Review of Symbolic Logic , Volume 17 , Issue 1 , March 2024 , pp. 178 - 205
Check for updates
Copyright
© The Author(s), 2022. Published by Cambridge University Press on behalf of The Association for Symbolic Logic

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

BIBLIOGRAPHY

Boolos, G. (1993). The Logic of Provability. Cambridge: Cambridge University Press.Google Scholar
Buchholz, W. (1993). Mathematische Logik II. Available from: http://www.mathematik.uni-muenchen.de/buchholz/articles/LogikII.ps.Google Scholar
Došen, K. (1990). Modal translations of Heyting and Peano arithmetic. Publications de l’Institut Mathématique. Nouvelle Série, 47, 13–23.Google Scholar
Flagg, R. C. & Friedman, H. (1986). Epistemic and intuitionistic formal systems. Annals of Pure and Applied Logic, 32, 53–60.CrossRefGoogle Scholar
Friedman, H. (1975). The disjunction property implies the numerical existence property. Proceedings of the National Academy of Sciences of the United States of America, 72, 2877–2878.CrossRefGoogle ScholarPubMed
Friedman, H. & Sheard, M. (1989). The equivalence of the disjunction and existence properties for modal arithmetic. The Journal of Symbolic Logic, 54(4), 1456–1459.CrossRefGoogle Scholar
Gentzen, G. (1934–1935). Untersuchungen über das logische Schliessen. Mathematische Zeitschrift, 39(2–3), 176–210, 405–431.CrossRefGoogle Scholar
Gödel, K. (1933). An interpretation of the intuitionistic propositional calculus. In Feferman, S., editor. Collected Works, Vol. 1. Oxford: Oxford University Press, pp. 301–303.Google Scholar
Goodman, N. D. (1984). Epistemic arithmetic is a conservative extension of intuitionistic arithmetic. The Journal of Symbolic Logic, 49, 192–203.CrossRefGoogle Scholar
Guaspari, D. (1979). Partially conservative extensions of arithmetic. Transactions of the American Mathematical Society, 254, 47–68.CrossRefGoogle Scholar
Halbach, V. & Horsten, L. (2000). Two proof-theoretic remarks on EA + ECT. Mathematical Logic Quarterly, 46(4), 461–466.3.0.CO;2-I>CrossRefGoogle Scholar
Hughes, G. E. & Cresswell, M. J. (1996). A New Introduction to Modal Logic. London: Routledge.CrossRefGoogle Scholar
Jensen, D. C. & Ehrenfeucht, A. (1976). Some problem in elementary arithmetics. Fundamenta Mathematicae, 92, 223–245.CrossRefGoogle Scholar
Kleene, S. C. (1945). On the interpretation of intuitionistic number theory. The Journal of Symbolic Logic, 10, 109–124.CrossRefGoogle Scholar
Kurahashi, T. (2018). On partial disjunction properties of theories containing Peano arithmetic. Archive for Mathematical Logic 57(7–8), 953–980.CrossRefGoogle Scholar
Kurahashi, T. (2020). A note on derivability conditions. The Journal of Symbolic Logic, 85(3), 1224–1253.CrossRefGoogle Scholar
Makinson, D. (1971). Some embedding theorems for modal logic. Notre Dame Journal of Formal Logic, 12, 252–254.CrossRefGoogle Scholar
Rautenberg, W. (2010). A Concise Introduction to Mathematical Logic (third revised and enlarged edition). London: Springer.CrossRefGoogle Scholar
Reinhardt, W. N. (1985). Absolute versions of incompleteness theorems. Nôus, 19(3), 317–346.Google Scholar
Reinhardt, W. N. (1986). Epistemic theories and the interpretation of Gödel’s incompleteness theorems. Journal of Philosophical Logic, 15, 427–474.CrossRefGoogle Scholar
Shapiro, S. (1985). Epistemic and intuitionistic arithmetic. In Intensional Mathematics (Stewart Shapiro (ed.)). North-Holland: Amsterdam. Studies in Logic and the Foundations of Mathematics, Vol. 113, pp. 11–46.CrossRefGoogle Scholar
Solovay, R. M. (1976). Provability interpretations of modal logic. Israel Journal of Mathematics, 25, 287–304.CrossRefGoogle Scholar