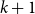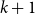1. Introduction
Families of sets are well studied in discrete mathematics and set theory (see e.g. Bollobás Reference Bollobás1986). Sperner families and downward closed families are examples of basic building blocks that can be used to analyze complex families. Considerations on ways how to represent a family as a union of more basic families lead us to several concepts of dimension. Given the finite size of the base set, we use our dimensions to associate families of subsets of the base set with better quantitative measures than their mere size. We show that certain canonical operations on families of sets preserve dimension. This allows us to isolate dimension-bounded collections of families of sets.
By restricting attention to families of subsets of Cartesian powers of finite sets, we obtain finer distinctions between dimensions, as such subsets can be considered relations in the usual way. Such families arise in the context of so-called team semantics. In ordinary Tarski semantics of first-order logic, a formula and a model are associated with the set of assignments satisfying the formula in the model. It is natural to consider such a set as a subset of the Cartesian power of the domain of the model. In team semantics satisfaction is defined with respect to sets (“teams”) of assignments. Accordingly, any formula becomes associated with a family of subsets of such a Cartesian power. We use our dimensions and preservation results for logical operations to prove new non-definability and hierarchy results for logics based on teams semantics. Examples of such logics are dependence logic, independence logic, and inclusion logic.
The background of our work for this paper is the following. Ciardelli defined in his Master’s Thesis Footnote 1 a dimension concept, in the case of downward closed families, namely the cardinality of the set of maximal sets, or equivalently, the smallest number of power sets that cover the family. He proved the preservation properties for basic propositional logic operations, including intuitionistic implication, and referred to them as Groenendijk inequalities. In Hella et al. (Reference Hella, Luosto, Sano and Virtema2014) a similar dimension concept was introduced in modal logic, including preservation of dimension results for logical operations of modal dependence logic. Hella and Stumpf used a form of dimension to prove a succinctness result for the inclusion atom in modal inclusion logic (Hella and Stumpf Reference Hella and Stumpf2015). In Lück and Vilander (Reference Lück and Vilander2019) the notion of dimension was generalized from downward closed families to arbitrary families. They proved preservation of dimension under propositional operations and computed the dimension of dependence and exclusion atoms in the context of propositional logic. An important step in the background of this paper has also been Lück (Reference Lück2020).
There are several other dimension concepts in discrete mathematics. Perhaps the most famous is the matroid rank, which coincides with the usual concept of dimension in the case of vector spaces and with degree of transcendence in the case of algebraically closed fields. However, our families do not necessarily satisfy the Exchange Axiom of matroids and therefore this concept does not work in our context. Another well-known dimension is the Vapnik-Chervonenkis- or VC-dimension. In Section 6.1, we argue that VC-dimension is not preserved by logical operations in the sense that our dimension is. Therefore, it does not serve our purpose well in this paper. Still another dimension is the length of a disjunctive normal form in propositional logic. We show in Section 6.2 that this is equivalent to one of the dimensions (cylindrical dimension) we investigate.
The concepts we introduce in this paper belong to discrete mathematics with no immediate connection to logic. Thus, part of this paper can be read with no knowledge or interest in logic. However, our applications come from logic, more exactly from team semantics. We believe that our results are a potentially interesting new contribution to discrete mathematics of families of sets. At the same time, we suggest that our results lead to a new approach to definability questions in team semantics and, in particular, yield a new strong hierarchy result (Theorem 77).
An outline of the paper
Section 2 presents the basic concepts of our dimension theory. We define three notions of dimension for arbitrary families of sets and give some elementary basic properties of these notions. We define the basic operators on families of sets that we will use in our results. Finally, we introduce some concepts from logic that are relevant for our results. In particular, we introduce the so-called team semantics which gives rise to a wealth of interesting families of subsets of Cartesian products
![]() $M^k$
of finite sets, raising the question what the dimensions of these families are.
$M^k$
of finite sets, raising the question what the dimensions of these families are.
Section 3 introduces some technical tools for explicit dimension computations. Such computations are at the heart of our results.
In Section 4, we introduce the concept of a growth class. These classes are used to measure the rate of growth of dimension of definable sets of subsets of a Cartesian product
![]() $M^k$
when the finite size of M increases. Some important results are proved about preservation of dimension under operators. These preservation results will make it easier to estimate the growth class of a given definable family of sets.
$M^k$
when the finite size of M increases. Some important results are proved about preservation of dimension under operators. These preservation results will make it easier to estimate the growth class of a given definable family of sets.
In Section 5, we put our results together and indicate applications. Our main application is Theorem 77, which gives strong hierarchy results for a number of logics based on team semantics. We also observe that several logical operations that occur in the literature of team semantics are not of the kind that preserve dimension. This allows us to use the quantitative method of dimension to obtain qualitative distinctions between logical operations.
In Section 6, we address the obvious question why not apply the VC-dimension. The answer turns out to be that VC-dimension is not preserved under the logical operations that we are mainly interested in, such as conjunction, disjunction, existential quantifier, and universal quantifier.
In Section 7, we relate one of our dimension concepts to an invariant related to disjunctive normal forms of Boolean polynomials. This allows us to make some conclusions about dimensions of random families of sets.
Finally, in Section 8, we show that it is impossible to obtain on infinite domains the kind of results we are after. The desired hierarchy results are simply false on infinite domains.
2. Basic notions
2.1 Families of sets
In the sequel, our applications will build on heavy use of combinatorial results in the subfield often called set-system combinatorics. We start with commonly used notions.
We use standard set-theoretic notation, including the shorthands
the latter being unambiguous only if
![]() $\mathcal{A}\neq\emptyset$
. In addition, we write
$\mathcal{A}\neq\emptyset$
. In addition, we write
for any sets A and B. Note that if
![]() $A\not\subseteq B$
, then
$A\not\subseteq B$
, then
![]() $[A,B]=\emptyset$
.
$[A,B]=\emptyset$
.
Definition 1. Let
![]() $\mathcal{A}$
be a family of sets. The family
$\mathcal{A}$
be a family of sets. The family
![]() $\mathcal{A}$
is an interval or cylinder, if there exist
$\mathcal{A}$
is an interval or cylinder, if there exist
![]() $A_0$
and
$A_0$
and
![]() $A_1$
such that
$A_1$
such that
![]() $A_0\subseteq A_1$
and
$A_0\subseteq A_1$
and
![]() $\mathcal{A}=[A_0,A_1]$
. The family
$\mathcal{A}=[A_0,A_1]$
. The family
![]() $\mathcal{A}$
is convex if for all
$\mathcal{A}$
is convex if for all
![]() $S,T\in\mathcal{A}$
, we have
$S,T\in\mathcal{A}$
, we have
![]() $[S,T]\subseteq\mathcal{A}$
.
$[S,T]\subseteq\mathcal{A}$
.
![]() $\mathcal{A}$
is downward closed if
$\mathcal{A}$
is downward closed if
![]() $A\in\mathcal{A}$
and
$A\in\mathcal{A}$
and
![]() $S\subseteq A$
imply
$S\subseteq A$
imply
![]() $S\in\mathcal{A}$
. The family
$S\in\mathcal{A}$
. The family
![]() $\mathcal{A}$
is a Sperner family if for all distinct
$\mathcal{A}$
is a Sperner family if for all distinct
![]() $S,T\in\mathcal{A}$
we have
$S,T\in\mathcal{A}$
we have
![]() $S\not\subseteq T$
. Finally,
$S\not\subseteq T$
. Finally,
![]() $\mathcal{A}$
fulfills the Zorn condition if it is closed under nonempty unions of chains, i.e., if
$\mathcal{A}$
fulfills the Zorn condition if it is closed under nonempty unions of chains, i.e., if
![]() $\mathcal{C}$
is a nonempty chain (or a nonempty family linearly ordered by inclusion), then
$\mathcal{C}$
is a nonempty chain (or a nonempty family linearly ordered by inclusion), then
![]() $\bigcup\mathcal{C}\in\mathcal{C}$
. A stricter notion is also useful:
$\bigcup\mathcal{C}\in\mathcal{C}$
. A stricter notion is also useful:
![]() $\mathcal{A}$
is closed under unions if for every subfamily
$\mathcal{A}$
is closed under unions if for every subfamily
![]() $\mathcal{B}\subseteq\mathcal{A}$
, we have
$\mathcal{B}\subseteq\mathcal{A}$
, we have
![]() $\bigcup\mathcal{B}\in\mathcal{A}$
.
$\bigcup\mathcal{B}\in\mathcal{A}$
.
Note that if a family of sets is downward closed or a Sperner family, then it is also convex. The concept of a upward closed family is also useful in set theory but is lacking here, as applications of our methods are very much leaning towards downward closed families.
The concept of Zorn condition is mainly relevant in the context of infinite families. Our emphasis is, however, on finite families of finite sets, for which the Zorn condition, as we have formulated it, trivially holds. We have weakened the standard condition by imposing the requirement only on nonempty chains. The only notable effect is that the empty set is not required to be included in a family fulfilling the Zorn condition, thus allowing all the finite families to meet the condition.
For
![]() $\mathcal{A}$
a family of sets, we denote the family of all maximal (with respect to inclusion) sets in
$\mathcal{A}$
a family of sets, we denote the family of all maximal (with respect to inclusion) sets in
![]() $\mathcal{A}$
by
$\mathcal{A}$
by
![]() $\mathrm{Max}(\mathcal{A})$
. Similarly,
$\mathrm{Max}(\mathcal{A})$
. Similarly,
![]() $\mathrm{Min}(\mathcal{A})$
is the set of all minimal sets in
$\mathrm{Min}(\mathcal{A})$
is the set of all minimal sets in
![]() $\mathcal{A}$
. Observe that
$\mathcal{A}$
. Observe that
![]() $\mathrm{Max}(\mathcal{A})$
and
$\mathrm{Max}(\mathcal{A})$
and
![]() $\mathrm{Min}(\mathcal{A})$
are always Sperner families.
$\mathrm{Min}(\mathcal{A})$
are always Sperner families.
Definition 2. A family of sets
![]() $\mathcal{A}$
is dominated (by
$\mathcal{A}$
is dominated (by
![]() $\bigcup\mathcal{A}$
) if
$\bigcup\mathcal{A}$
) if
![]() $\bigcup\mathcal{A}\in\mathcal{A}$
. The family
$\bigcup\mathcal{A}\in\mathcal{A}$
. The family
![]() $\mathcal{A}$
is supported (by
$\mathcal{A}$
is supported (by
![]() $\bigcap\mathcal{A}$
) if
$\bigcap\mathcal{A}$
) if
![]() $\mathcal{A}$
is nonempty and
$\mathcal{A}$
is nonempty and
![]() $\bigcap\mathcal{A}\in\mathcal{A}$
. Naturally, we say that
$\bigcap\mathcal{A}\in\mathcal{A}$
. Naturally, we say that
![]() $\mathcal{A}$
is dominated convex if it is dominated and convex. Similarly,
$\mathcal{A}$
is dominated convex if it is dominated and convex. Similarly,
![]() $\mathcal{A}$
is supported convex if it is supported and convex.
$\mathcal{A}$
is supported convex if it is supported and convex.
In other words, a family
![]() $\mathcal{A}$
is dominated by a set D if and only if D is the largest element in
$\mathcal{A}$
is dominated by a set D if and only if D is the largest element in
![]() $\mathcal{A}$
with respect to inclusion. Similarly,
$\mathcal{A}$
with respect to inclusion. Similarly,
![]() $\mathcal{A}$
is supported by a set S if and only if S is the smallest element in
$\mathcal{A}$
is supported by a set S if and only if S is the smallest element in
![]() $\mathcal{A}$
with respect to inclusion. We spell out some of the easily seen connections between the basic concepts in the following lemma.
$\mathcal{A}$
with respect to inclusion. We spell out some of the easily seen connections between the basic concepts in the following lemma.
Lemma 3. Let
![]() $\mathcal{A}\subseteq\mathcal{P}(X)$
where X is a set. Denote
$\mathcal{A}\subseteq\mathcal{P}(X)$
where X is a set. Denote
![]() $\mathrm{Co-}\mathcal{A}=\{X\smallsetminus A \mid A\in\mathcal{A} \}$
.
$\mathrm{Co-}\mathcal{A}=\{X\smallsetminus A \mid A\in\mathcal{A} \}$
.
-
(a) The family
 $\mathcal{A}$
is an interval if and only if it is dominated, supported, and convex.
$\mathcal{A}$
is an interval if and only if it is dominated, supported, and convex. -
(b)
 $\mathcal{A}$
is convex if and only if
$\mathcal{A}$
is convex if and only if
 $\mathrm{Co-}\mathcal{A}$
is convex.
$\mathrm{Co-}\mathcal{A}$
is convex. -
(c)
 $\mathcal{A}$
is dominated if and only if
$\mathcal{A}$
is dominated if and only if
 $\mathrm{Co-}\mathcal{A}$
is supported.
$\mathrm{Co-}\mathcal{A}$
is supported.
We proceed to the central dimension concepts which will be studied throughout this paper. The upper dimension was first defined for downwards closed families in Hella et al. (Reference Hella, Luosto, Sano and Virtema2014) and subsequently generalized for arbitrary families in Lück and Vilander (Reference Lück and Vilander2019). The definition presented here is an equivalent reformulation of the latter. We also introduce two new dimension concepts. The idea of the dual upper dimension is that many of the underlying ideas behind the upper dimension work if the inclusion order is reversed, as the previous lemma indicates. The third concept, cylindrical dimension, can be seen as a combination of the two mentioned dimension concepts.
Definition 4. Let
![]() $\mathcal{A}$
be a family of sets. We say that a subfamily
$\mathcal{A}$
be a family of sets. We say that a subfamily
![]() $\mathcal{G}\subseteq\mathcal{A}$
dominates
$\mathcal{G}\subseteq\mathcal{A}$
dominates
![]() $\mathcal{A}$
if there exist dominated convex families
$\mathcal{A}$
if there exist dominated convex families
![]() $\mathcal{D}_G$
,
$\mathcal{D}_G$
,
![]() $G\in\mathcal{G}$
, such that
$G\in\mathcal{G}$
, such that
![]() $\bigcup_{G\in\mathcal{G}}\mathcal{D}_G=\mathcal{A}$
and
$\bigcup_{G\in\mathcal{G}}\mathcal{D}_G=\mathcal{A}$
and
![]() $\bigcup\mathcal{D}_G=G$
, for each
$\bigcup\mathcal{D}_G=G$
, for each
![]() $G\in\mathcal{G}$
. The subfamily
$G\in\mathcal{G}$
. The subfamily
![]() $\mathcal{K}\subseteq\mathcal{A}$
supports
$\mathcal{K}\subseteq\mathcal{A}$
supports
![]() $\mathcal{A}$
if there exist supported convex families
$\mathcal{A}$
if there exist supported convex families
![]() $\mathcal{S}_K$
,
$\mathcal{S}_K$
,
![]() $K\in\mathcal{K}$
, such that
$K\in\mathcal{K}$
, such that
![]() $\bigcup_{K\in\mathcal{K}}\mathcal{S}_K=\mathcal{A}$
and
$\bigcup_{K\in\mathcal{K}}\mathcal{S}_K=\mathcal{A}$
and
![]() $\bigcap\mathcal{S}_K=K$
, for each
$\bigcap\mathcal{S}_K=K$
, for each
![]() $K\in\mathcal{K}$
.
$K\in\mathcal{K}$
.
The upper dimension of the family is
![]() $\mathcal{A}$
$\mathcal{A}$
the dual upper dimension is
and the cylindrical dimension is
Proposition 5. Let
![]() $\mathcal{A}$
be a family of set. Then
$\mathcal{A}$
be a family of set. Then
-
(a) If
 $\mathcal{G}$
dominates
$\mathcal{G}$
dominates
 $\mathcal{A}$
, then
$\mathcal{A}$
, then
 $\mathrm{Max}(\mathcal{A})\subseteq\mathcal{G}$
, and if
$\mathrm{Max}(\mathcal{A})\subseteq\mathcal{G}$
, and if
 $\mathcal{H}$
supports
$\mathcal{H}$
supports
 $\mathcal{A}$
, then
$\mathcal{A}$
, then
 $\mathrm{Min}(\mathcal{A})\subseteq\mathcal{H}$
.
$\mathrm{Min}(\mathcal{A})\subseteq\mathcal{H}$
. -
(b)
 $ \mathrm{D}(\mathcal{A})\le\mathrm{CD}(\mathcal{A}) \text{ and } \mathrm{D}^{\mathrm{d}}(\mathcal{A})\le\mathrm{CD}(\mathcal{A}).$
$ \mathrm{D}(\mathcal{A})\le\mathrm{CD}(\mathcal{A}) \text{ and } \mathrm{D}^{\mathrm{d}}(\mathcal{A})\le\mathrm{CD}(\mathcal{A}).$
-
(c)
 $|\mathrm{Max}(\mathcal{A})|\le \mathrm{D}(\mathcal{A}), |\mathrm{Min}(\mathcal{A})|\le\mathrm{D}^{\mathrm{d}}(\mathcal{A})$
and
$|\mathrm{Max}(\mathcal{A})|\le \mathrm{D}(\mathcal{A}), |\mathrm{Min}(\mathcal{A})|\le\mathrm{D}^{\mathrm{d}}(\mathcal{A})$
and
 $\max\{|\mathrm{Max}(\mathcal{A})|,|\mathrm{Min}(\mathcal{A})|\}\le\mathrm{CD}(\mathcal{A})$
.
$\max\{|\mathrm{Max}(\mathcal{A})|,|\mathrm{Min}(\mathcal{A})|\}\le\mathrm{CD}(\mathcal{A})$
.
If, in addition,
![]() $\mathcal{A}$
is convex, then
$\mathcal{A}$
is convex, then
Proof.
-
(a) Suppose
 $\mathcal{G}$
dominates
$\mathcal{G}$
dominates
 $\mathcal{A}$
and M is maximal in the family
$\mathcal{A}$
and M is maximal in the family
 $\mathcal{A}$
. By definition, there are dominated convex families
$\mathcal{A}$
. By definition, there are dominated convex families
 $\mathcal{D}_G$
,
$\mathcal{D}_G$
,
 $G\in\mathcal{G}$
, such that
$G\in\mathcal{G}$
, such that
 $\bigcup_{G\in\mathcal{G}}\mathcal{D}_G=\mathcal{A}$
and
$\bigcup_{G\in\mathcal{G}}\mathcal{D}_G=\mathcal{A}$
and
 $\bigcup\mathcal{D}_G=G$
, for each
$\bigcup\mathcal{D}_G=G$
, for each
 $G\in\mathcal{G}$
. In particular, there is
$G\in\mathcal{G}$
. In particular, there is
 $G\in\mathcal{G}$
such that
$G\in\mathcal{G}$
such that
 $M\in\mathcal{D}_G$
and
$M\in\mathcal{D}_G$
and
 $M\subseteq G$
. However, by maximality of M and as
$M\subseteq G$
. However, by maximality of M and as
 $G\in\mathcal{G}\subseteq\mathcal{A}$
, this impies
$G\in\mathcal{G}\subseteq\mathcal{A}$
, this impies
 $M=G$
and
$M=G$
and
 $M\in\mathcal{G}$
. Consequently,
$M\in\mathcal{G}$
. Consequently,
 $\mathrm{Max}(\mathcal{A})\subseteq\mathcal{G}$
. The dual statement is proved similarly.
$\mathrm{Max}(\mathcal{A})\subseteq\mathcal{G}$
. The dual statement is proved similarly. -
(b) Let
 $(\mathcal{A}_i)_{i\in I}$
be an indexed family of minimal size of intervals covering
$(\mathcal{A}_i)_{i\in I}$
be an indexed family of minimal size of intervals covering
 $\mathcal{A}$
, i.e.,
$\mathcal{A}$
, i.e.,
 $\bigcup_{i\in I}\mathcal{A}_i=\mathcal{A}$
. Write
$\bigcup_{i\in I}\mathcal{A}_i=\mathcal{A}$
. Write
 $\mathcal{A}_i=[B_i,C_i]$
, for each
$\mathcal{A}_i=[B_i,C_i]$
, for each
 $i\in I$
, and consider the families
$i\in I$
, and consider the families
 $\mathcal{B}=\{B_i \mid i\in I\}$
and
$\mathcal{B}=\{B_i \mid i\in I\}$
and
 $\mathcal{C}=\{C_i\mid i\in I\}$
. Then
$\mathcal{C}=\{C_i\mid i\in I\}$
. Then
 $\mathcal{A}_i$
is a convex set supported by
$\mathcal{A}_i$
is a convex set supported by
 $B_i$
and dominated by
$B_i$
and dominated by
 $C_i$
, for
$C_i$
, for
 $i\in I$
. Consequently,
$i\in I$
. Consequently,
 $\mathcal{B}$
supports
$\mathcal{B}$
supports
 $\mathcal{A}$
and
$\mathcal{A}$
and
 $\mathcal{C}$
dominates
$\mathcal{C}$
dominates
 $\mathcal{A}$
, which implies
$\mathcal{A}$
, which implies  \[ \mathrm{D}^{\mathrm{d}}(\mathcal{A})\le|\mathcal{B}|\le|I|=\mathrm{CD}(\mathcal{A}) \text{ and } \mathrm{D}(\mathcal{A})\le|\mathcal{C}|\le|I|=\mathrm{CD}(\mathcal{A}).\]
\[ \mathrm{D}^{\mathrm{d}}(\mathcal{A})\le|\mathcal{B}|\le|I|=\mathrm{CD}(\mathcal{A}) \text{ and } \mathrm{D}(\mathcal{A})\le|\mathcal{C}|\le|I|=\mathrm{CD}(\mathcal{A}).\]
-
(c) Item a clearly implies
 $|\mathrm{Max}(\mathcal{A})|\le\mathrm{D}(\mathcal{A})$
and
$|\mathrm{Max}(\mathcal{A})|\le\mathrm{D}(\mathcal{A})$
and
 $|\mathrm{Min}(\mathcal{A})|\le\mathrm{D}^{\mathrm{d}}(\mathcal{A})$
. Combining these results with item b gives
$|\mathrm{Min}(\mathcal{A})|\le\mathrm{D}^{\mathrm{d}}(\mathcal{A})$
. Combining these results with item b gives
 $\max\{|\mathrm{Min}(\mathcal{A})|,|\mathrm{Max}(\mathcal{A})|\}\le \mathrm{CD}(\mathcal{A})$
for the cylindrical dimension.
$\max\{|\mathrm{Min}(\mathcal{A})|,|\mathrm{Max}(\mathcal{A})|\}\le \mathrm{CD}(\mathcal{A})$
for the cylindrical dimension.
For the last part of the proposition, assume now that
![]() $\mathcal{A}$
is convex. Let
$\mathcal{A}$
is convex. Let
![]() $\mathcal{G}$
be a family of minimal size that dominates
$\mathcal{G}$
be a family of minimal size that dominates
![]() $\mathcal{A}$
and
$\mathcal{A}$
and
![]() $\mathcal{K}$
be a family of minimal size that supports
$\mathcal{K}$
be a family of minimal size that supports
![]() $\mathcal{A}$
. Then
$\mathcal{A}$
. Then
![]() $\mathrm{D}(\mathcal{A})=|\mathcal{G}|$
and
$\mathrm{D}(\mathcal{A})=|\mathcal{G}|$
and
![]() $\mathrm{D}^{\mathrm{d}}(\mathcal{A})=|\mathcal{K}|$
. Let I be the set of pairs
$\mathrm{D}^{\mathrm{d}}(\mathcal{A})=|\mathcal{K}|$
. Let I be the set of pairs
![]() $(G,K)\in \mathcal{G}\times\mathcal{K}$
with
$(G,K)\in \mathcal{G}\times\mathcal{K}$
with
![]() $K\subseteq G$
. By convexity of
$K\subseteq G$
. By convexity of
![]() $\mathcal{A}$
, we have
$\mathcal{A}$
, we have
![]() $[K,G]\subseteq\mathcal{A}$
, for each
$[K,G]\subseteq\mathcal{A}$
, for each
![]() $(G,K)\in I$
. On the other hand, if
$(G,K)\in I$
. On the other hand, if
![]() $A\in\mathcal{A}$
, then there has to be
$A\in\mathcal{A}$
, then there has to be
![]() $G\in\mathcal{G}$
such that
$G\in\mathcal{G}$
such that
![]() $A\subseteq G$
, as
$A\subseteq G$
, as
![]() $\mathcal{G}$
dominates
$\mathcal{G}$
dominates
![]() $\mathcal{A}$
, and similarly
$\mathcal{A}$
, and similarly
![]() $K\in\mathcal{K}$
such that
$K\in\mathcal{K}$
such that
![]() $K\subseteq A$
. This means that
$K\subseteq A$
. This means that
![]() $A\in[K,G]$
, for some interval [K,G] with
$A\in[K,G]$
, for some interval [K,G] with
![]() $(G,K)\in I$
. Consequently,
$(G,K)\in I$
. Consequently,
which implies
Clearly, if
![]() $\mathcal{A}\subseteq\mathcal{P}(X)$
with
$\mathcal{A}\subseteq\mathcal{P}(X)$
with
![]() $n=|X|\in\mathbb{N}$
, then
$n=|X|\in\mathbb{N}$
, then
![]() $\mathrm{CD}(\mathcal{A})\le 2^n$
. One gets easily a modest improvement to this result, which is the best possible upper bound, as the succeeding example shows.
$\mathrm{CD}(\mathcal{A})\le 2^n$
. One gets easily a modest improvement to this result, which is the best possible upper bound, as the succeeding example shows.
Proposition 6. Let X be a nonempty finite set with
![]() $n=|X|$
, and let
$n=|X|$
, and let
![]() $\mathcal{A}\subseteq\mathcal{P}(X)$
. Then
$\mathcal{A}\subseteq\mathcal{P}(X)$
. Then
Hence also,
![]() $\mathrm{D}(\mathcal{A})\le 2^{n-1}$
and
$\mathrm{D}(\mathcal{A})\le 2^{n-1}$
and
![]() $\mathrm{D}^{\mathrm{d}}(\mathcal{A})\le 2^{n-1}$
.
$\mathrm{D}^{\mathrm{d}}(\mathcal{A})\le 2^{n-1}$
.
Proof. Fix
![]() $b\in X$
and consider the partition of
$b\in X$
and consider the partition of
![]() $\mathcal{P}(X)$
in pairs
$\mathcal{P}(X)$
in pairs
![]() $\{A,A\cup\{b\}\}$
, where
$\{A,A\cup\{b\}\}$
, where
![]() $A\subseteq X\smallsetminus\{b\}$
. For each such pair,
$A\subseteq X\smallsetminus\{b\}$
. For each such pair,
![]() $\mathcal{A}\cap\{A,A\cup\{b\}\}$
is either empty or one of the intervals
$\mathcal{A}\cap\{A,A\cup\{b\}\}$
is either empty or one of the intervals
![]() $[A,A]=\{A\}$
,
$[A,A]=\{A\}$
,
![]() $[A\cup\{b\},A\cup\{b\}]=\{A\cup\{b\}\}$
or
$[A\cup\{b\},A\cup\{b\}]=\{A\cup\{b\}\}$
or
![]() $[A,A\cup\{b\}]=\{A,A\cup\{b\}\}$
. Consequently, there is a family of at most
$[A,A\cup\{b\}]=\{A,A\cup\{b\}\}$
. Consequently, there is a family of at most
![]() $2^{n-1}$
intervals, the union of which is
$2^{n-1}$
intervals, the union of which is
![]() $\mathcal{A}$
. The remaining claims follow from Proposition 5.
$\mathcal{A}$
. The remaining claims follow from Proposition 5.
Example 7. Let X be a nonempty finite set of n elements. Consider the family
Let
![]() $\mathcal{G}$
be a subfamily of
$\mathcal{G}$
be a subfamily of
![]() $\mathcal{E}$
which dominates
$\mathcal{E}$
which dominates
![]() $\mathcal{E}$
. Let
$\mathcal{E}$
. Let
![]() $A\in\mathcal{E}$
and suppose that A is dominated by
$A\in\mathcal{E}$
and suppose that A is dominated by
![]() $G\in\mathcal{G}$
, which means that A belongs to certain dominated convex family
$G\in\mathcal{G}$
, which means that A belongs to certain dominated convex family
![]() $\mathcal{D}_G$
where
$\mathcal{D}_G$
where
![]() $\mathcal{D}_G\subseteq\mathcal{E}$
and
$\mathcal{D}_G\subseteq\mathcal{E}$
and
![]() $\bigcup\mathcal{D}_G=G$
. By convexity,
$\bigcup\mathcal{D}_G=G$
. By convexity,
![]() $[A,G]\subseteq\mathcal{D}_G\subseteq\mathcal{E}$
. Note that
$[A,G]\subseteq\mathcal{D}_G\subseteq\mathcal{E}$
. Note that
![]() $A,G\in\mathcal{E}$
both have even size. However, the interval [A,G] would contain sets of odd size unless
$A,G\in\mathcal{E}$
both have even size. However, the interval [A,G] would contain sets of odd size unless
![]() $A=G$
. As this holds for arbitrary
$A=G$
. As this holds for arbitrary
![]() $A\in\mathcal{E}$
, we conclude that
$A\in\mathcal{E}$
, we conclude that
![]() $\mathcal{G}=\mathcal{E}$
. Hence,
$\mathcal{G}=\mathcal{E}$
. Hence,
![]() $\mathrm{D}(\mathcal{E})=|\mathcal{E}|=2^{n-1}$
. By symmetry, we get
$\mathrm{D}(\mathcal{E})=|\mathcal{E}|=2^{n-1}$
. By symmetry, we get
![]() $\mathrm{D}^{\mathrm{d}}(\mathcal{E})=2^{n-1}$
, too. Combined with the last two propositions, we have that
$\mathrm{D}^{\mathrm{d}}(\mathcal{E})=2^{n-1}$
, too. Combined with the last two propositions, we have that
![]() $\mathrm{CD}(\mathcal{E})=2^{n-1}$
.
$\mathrm{CD}(\mathcal{E})=2^{n-1}$
.
2.2. Operators
In addition to studying the dimensions of fixed families of sets, we are also interested in the behavior of dimensions under various operators. An operator on families of sets on a fixed base set X is a function
![]() $\Delta\colon \mathcal{P}(\mathcal{P}(X))^n\to\mathcal{P}(\mathcal{P}(X))$
for some positive integer n. In some applications to team semantics, it is useful to consider more general operators of the form
$\Delta\colon \mathcal{P}(\mathcal{P}(X))^n\to\mathcal{P}(\mathcal{P}(X))$
for some positive integer n. In some applications to team semantics, it is useful to consider more general operators of the form
![]() $\Delta\colon \mathcal{P}(\mathcal{P}(X))^n\to\mathcal{P}(\mathcal{P}(Y))$
with different base sets X and Y. We list in the next example some natural set-theoretic operators that we will study further in the forthcoming sections. For the related topic of Boolean algebras B with operators
$\Delta\colon \mathcal{P}(\mathcal{P}(X))^n\to\mathcal{P}(\mathcal{P}(Y))$
with different base sets X and Y. We list in the next example some natural set-theoretic operators that we will study further in the forthcoming sections. For the related topic of Boolean algebras B with operators
![]() $B^n\to B$
see e.g. Venema (Reference Venema2007).
$B^n\to B$
see e.g. Venema (Reference Venema2007).
Example 8. Let X be a base set.
-
(a) Union and intersection. The union operator
 $\Delta^X_\cup\colon \mathcal{P}(\mathcal{P}(X))^2\to\mathcal{P}(\mathcal{P}(X))$
on the base set X is defined by
$\Delta^X_\cup\colon \mathcal{P}(\mathcal{P}(X))^2\to\mathcal{P}(\mathcal{P}(X))$
on the base set X is defined by
 $\Delta^X_\cup(\mathcal{A},\mathcal{B})=\mathcal{A}\cup\mathcal{B}$
. Similarly, the intersection operator
$\Delta^X_\cup(\mathcal{A},\mathcal{B})=\mathcal{A}\cup\mathcal{B}$
. Similarly, the intersection operator
 $\Delta^X_\cap\colon \mathcal{P}(\mathcal{P}(X))^2\to\mathcal{P}(\mathcal{P}(X))$
on X is defined by
$\Delta^X_\cap\colon \mathcal{P}(\mathcal{P}(X))^2\to\mathcal{P}(\mathcal{P}(X))$
on X is defined by
 $\Delta^X_\cap(\mathcal{A},\mathcal{B})=\mathcal{A}\cap\mathcal{B}$
.
$\Delta^X_\cap(\mathcal{A},\mathcal{B})=\mathcal{A}\cap\mathcal{B}$
. -
(b) Complementation. Complementation on X is the unary operator
 $\Delta^X_c\colon \mathcal{P}(\mathcal{P}(X))\to\mathcal{P}(\mathcal{P}(X))$
defined by
$\Delta^X_c\colon \mathcal{P}(\mathcal{P}(X))\to\mathcal{P}(\mathcal{P}(X))$
defined by
 $\Delta^X_c(\mathcal{A})=\mathcal{P}(X)\smallsetminus\mathcal{A}$
.
$\Delta^X_c(\mathcal{A})=\mathcal{P}(X)\smallsetminus\mathcal{A}$
. -
(c) Tensor disjunction and conjunction. The idea of tensor disjunction Footnote 2
 $\Delta^X_\lor\colon \mathcal{P}(\mathcal{P}(X))^2\to\mathcal{P}(\mathcal{P}(X))$
and tensor conjunction
$\Delta^X_\lor\colon \mathcal{P}(\mathcal{P}(X))^2\to\mathcal{P}(\mathcal{P}(X))$
and tensor conjunction
 $\Delta^X_\land\colon \mathcal{P}(\mathcal{P}(X))^2\to\mathcal{P}(\mathcal{P}(X))$
is to take unions and intersections inside the families:
$\Delta^X_\land\colon \mathcal{P}(\mathcal{P}(X))^2\to\mathcal{P}(\mathcal{P}(X))$
is to take unions and intersections inside the families:
 $\Delta^X_\lor(\mathcal{A},\mathcal{B})=\{A\cup B\mid A\in\mathcal{A}, B\in\mathcal{B}\}$
and
$\Delta^X_\lor(\mathcal{A},\mathcal{B})=\{A\cup B\mid A\in\mathcal{A}, B\in\mathcal{B}\}$
and
 $\Delta^X_\land(\mathcal{A},\mathcal{B})=\{A\cap B\mid A\in\mathcal{A}, B\in\mathcal{B}\}$
.
$\Delta^X_\land(\mathcal{A},\mathcal{B})=\{A\cap B\mid A\in\mathcal{A}, B\in\mathcal{B}\}$
. -
(d) Tensor negation. Pushing complementation inside a given family, we obtain tensor negation:
 $\Delta^X_\lnot(\mathcal{A})=\{X\smallsetminus A\mid A\in\mathcal{A}\}$
.
$\Delta^X_\lnot(\mathcal{A})=\{X\smallsetminus A\mid A\in\mathcal{A}\}$
. -
(e) Projections. Let
 $f\colon X\to Y$
be a function. The (abstract) projection operator corresponding to f is obtained by lifting f to a function
$f\colon X\to Y$
be a function. The (abstract) projection operator corresponding to f is obtained by lifting f to a function
 $\Delta_f\colon\mathcal{P}(\mathcal{P}(X))\to\mathcal{P}(\mathcal{P}(Y))$
in the usual way:
$\Delta_f\colon\mathcal{P}(\mathcal{P}(X))\to\mathcal{P}(\mathcal{P}(Y))$
in the usual way:
 $\Delta_f(\mathcal{A})=\{f[A]\mid A\in \mathcal{A}\}$
, where f[A] denotes the image
$\Delta_f(\mathcal{A})=\{f[A]\mid A\in \mathcal{A}\}$
, where f[A] denotes the image
 $\{f(a)\mid a\in A\}$
of A under f.
$\{f(a)\mid a\in A\}$
of A under f. -
(f) Inverse projections. Given a function
 $f\colon X\to Y$
, we can also define a useful operator
$f\colon X\to Y$
, we can also define a useful operator
 $\Delta_{f^{-1}}\colon\mathcal{P}(\mathcal{P}(Y))\to\mathcal{P}(\mathcal{P}(X))$
as follows:
$\Delta_{f^{-1}}\colon\mathcal{P}(\mathcal{P}(Y))\to\mathcal{P}(\mathcal{P}(X))$
as follows:
 $\Delta_{f^{-1}}(\mathcal{B})=\{A\in\mathcal{P}(X)\mid f[A]\in\mathcal{B}\}$
.
$\Delta_{f^{-1}}(\mathcal{B})=\{A\in\mathcal{P}(X)\mid f[A]\in\mathcal{B}\}$
. -
(g) Existential and universal quantification. Consider the concrete projection function
 $f\colon X\to Y$
for
$f\colon X\to Y$
for
 $X=X_0\times\cdots\times X_{m-1}$
and
$X=X_0\times\cdots\times X_{m-1}$
and
 $Y=X_0\times\cdots X_{i-1}\times X_{i+1}\times\cdots\times X_{m-1}$
defined by
$Y=X_0\times\cdots X_{i-1}\times X_{i+1}\times\cdots\times X_{m-1}$
defined by
 $f(a_0,\ldots,a_{m-1})=(a_0,\ldots,a_{i-1},a_{i+1},\ldots,a_{m-1})$
(i.e., f is the projection to coordinates
$f(a_0,\ldots,a_{m-1})=(a_0,\ldots,a_{i-1},a_{i+1},\ldots,a_{m-1})$
(i.e., f is the projection to coordinates
 $j\not=i$
). Note that
$j\not=i$
). Note that
 $B\in \Delta_f(\mathcal{A})$
if and only if there is
$B\in \Delta_f(\mathcal{A})$
if and only if there is
 $A\in\mathcal{A}$
such that for each tuple
$A\in\mathcal{A}$
such that for each tuple
 $\vec{a}\in B$
there exists some element
$\vec{a}\in B$
there exists some element
 $a\in X_i$
such that the extension of
$a\in X_i$
such that the extension of
 $\vec{a}$
by a as the ith component is in A. Thus,
$\vec{a}$
by a as the ith component is in A. Thus,
 $\Delta_f$
corresponds to the logical operation of existential quantification, and accordingly we denote it by
$\Delta_f$
corresponds to the logical operation of existential quantification, and accordingly we denote it by
 $\Delta^X_{\exists i}$
.
$\Delta^X_{\exists i}$
.
Similarly, we define an operator
![]() $\Delta^X_{\forall i}\colon\mathcal{P}(\mathcal{P}(X))\to\mathcal{P}(\mathcal{P}(Y))$
that corresponds to universal quantification: Given a set
$\Delta^X_{\forall i}\colon\mathcal{P}(\mathcal{P}(X))\to\mathcal{P}(\mathcal{P}(Y))$
that corresponds to universal quantification: Given a set
![]() $B\in\mathcal{P}(Y)$
, let
$B\in\mathcal{P}(Y)$
, let
![]() $B[X_i/i]=\{(a_0,\ldots,a_{m-1})\in X\mid(a_0,\ldots,a_{i-1},a_{i+1},\ldots,a_{m-1})\in B, a_i\in X_i\}$
. Then we let
$B[X_i/i]=\{(a_0,\ldots,a_{m-1})\in X\mid(a_0,\ldots,a_{i-1},a_{i+1},\ldots,a_{m-1})\in B, a_i\in X_i\}$
. Then we let
![]() $\Delta^X_{\forall i}(\mathcal{A})=\{B\in\mathcal{P}(Y)\mid B[X_i/i]\in \mathcal{A}\}$
.
$\Delta^X_{\forall i}(\mathcal{A})=\{B\in\mathcal{P}(Y)\mid B[X_i/i]\in \mathcal{A}\}$
.
Note that the union and intersection operators
![]() $\Delta^X_\cup$
and
$\Delta^X_\cup$
and
![]() $\Delta^X_\cap$
do not depend on the base set X. Thus, in the sequel we will denote these operators for the sake of simplicity by
$\Delta^X_\cap$
do not depend on the base set X. Thus, in the sequel we will denote these operators for the sake of simplicity by
![]() $\cup$
and
$\cup$
and
![]() $\cap$
, as they actually are what is usually denoted
$\cap$
, as they actually are what is usually denoted
![]() $\cup$
and
$\cup$
and
![]() $\cap$
. The same holds for tensor disjunction and conjunction, whence we will use the notation
$\cap$
. The same holds for tensor disjunction and conjunction, whence we will use the notation
![]() $\mathcal{A}\lor\mathcal{B}:=\Delta^X_\lor(\mathcal{A},\mathcal{B})$
and
$\mathcal{A}\lor\mathcal{B}:=\Delta^X_\lor(\mathcal{A},\mathcal{B})$
and
![]() $\mathcal{A}\land\mathcal{B}:=\Delta^X_\land(\mathcal{A},\mathcal{B})$
. On the other hand, both complementation
$\mathcal{A}\land\mathcal{B}:=\Delta^X_\land(\mathcal{A},\mathcal{B})$
. On the other hand, both complementation
![]() $\Delta^X_c$
and tensor negation
$\Delta^X_c$
and tensor negation
![]() $\Delta^X_\lnot$
depend on X, whence we do not introduce any shorthand notation for them.
$\Delta^X_\lnot$
depend on X, whence we do not introduce any shorthand notation for them.
Note further that the projections
![]() $\Delta^X_{\exists i}$
do not depend on
$\Delta^X_{\exists i}$
do not depend on
![]() $X=X_0\times\cdots\times X_{m-1}$
, since the length and the i-th component of any tuple
$X=X_0\times\cdots\times X_{m-1}$
, since the length and the i-th component of any tuple
![]() $\vec{a}$
is uniquely determined:
$\vec{a}$
is uniquely determined:
![]() $(a_0,\ldots,a_{m-1})=(b_0,\ldots,b_{m'-1})$
if and only if
$(a_0,\ldots,a_{m-1})=(b_0,\ldots,b_{m'-1})$
if and only if
![]() $m=m'$
and
$m=m'$
and
![]() $a_i=b_i$
for all
$a_i=b_i$
for all
![]() $i< m$
. However, the universal projection operator
$i< m$
. However, the universal projection operator
![]() $\Delta^X_{\forall i}$
clearly depends on the base set X. Thus, for the sake of uniformity, we keep using the notation
$\Delta^X_{\forall i}$
clearly depends on the base set X. Thus, for the sake of uniformity, we keep using the notation
![]() $\Delta^X_{\exists i}$
.
$\Delta^X_{\exists i}$
.
2.3 Tensor operators
We have seen in Example 8 that the disjunction and conjunction connectives give rise to tensor disjunction and tensor conjunction operators. This idea can of course be generalized to arbitrary connectives. We introduce here the related concept of tensor operator and show that they preserve intervals but not necessarily dominated convex or supported convex families.
Definition 9. Fix a base set X and let
![]() $\circledast$
be a binary operation on the set
$\circledast$
be a binary operation on the set
![]() $\{0,1\}$
, i.e.,
$\{0,1\}$
, i.e.,
![]() $\circledast$
is a map
$\circledast$
is a map
![]() $\{0,1\}\times\{0,1\}\to\{0,1\}$
. Then the corresponding set-theoretic operation is
$\{0,1\}\times\{0,1\}\to\{0,1\}$
. Then the corresponding set-theoretic operation is
![]() $*\colon\mathcal{P}(X)^2\to\mathcal{P}(X)$
,
$*\colon\mathcal{P}(X)^2\to\mathcal{P}(X)$
,
where
![]() $\chi_C$
is the characteristic function related to a set C. The tensor operator corresponding to
$\chi_C$
is the characteristic function related to a set C. The tensor operator corresponding to
![]() $\circledast$
is
$\circledast$
is
![]() $\Delta^X_{\circledast}\colon \mathcal{P}(\mathcal{P}(X))^2\to\mathcal{P}(\mathcal{P}(X))$
,
$\Delta^X_{\circledast}\colon \mathcal{P}(\mathcal{P}(X))^2\to\mathcal{P}(\mathcal{P}(X))$
,
Remark 10.
-
(a) Naturally, we often identify the binary operation
 $\circledast$
with the corresponding connective, especially on the notational level. We also overload the notation, writing in the sequel simply Note though, that this notation is independent of the set X only if
$\circledast$
with the corresponding connective, especially on the notational level. We also overload the notation, writing in the sequel simply Note though, that this notation is independent of the set X only if \[ \mathcal{A}\circledast\mathcal{B}=\Delta^X_{\circledast}(\mathcal{A},\mathcal{B}).\]
\[ \mathcal{A}\circledast\mathcal{B}=\Delta^X_{\circledast}(\mathcal{A},\mathcal{B}).\]
 $0\circledast 0=0$
.
$0\circledast 0=0$
.
-
(b) We could have considered n-ary operations on
 $\{0,1\}$
in general, which appears to be a non-trivial generalization, but we refrain ourselves from doing that here. Even so, it is worth-while to have notation for the unary operation corresponding to negation.
$\{0,1\}$
in general, which appears to be a non-trivial generalization, but we refrain ourselves from doing that here. Even so, it is worth-while to have notation for the unary operation corresponding to negation. \[ \mathrm{Co-}\mathcal{A} = \Delta^X_{\lnot}(\mathcal{A})=\{X\smallsetminus A \mid A\in\mathcal{A}\}\]
\[ \mathrm{Co-}\mathcal{A} = \Delta^X_{\lnot}(\mathcal{A})=\{X\smallsetminus A \mid A\in\mathcal{A}\}\]
Note that we always have
![]() $\mathcal{A}\circledast\emptyset=\emptyset\circledast\mathcal{B}=\emptyset$
.
$\mathcal{A}\circledast\emptyset=\emptyset\circledast\mathcal{B}=\emptyset$
.
There are
![]() $2^4=16$
binary operations on the set
$2^4=16$
binary operations on the set
![]() $\{0,1\}$
, 4 of which (constant functions and projections) are rather trivial. Among the 8 zero-preserving (i.e.,
$\{0,1\}$
, 4 of which (constant functions and projections) are rather trivial. Among the 8 zero-preserving (i.e.,
![]() $0\circledast 0=0$
) operations, there are 5 non-trivial tensor operations, which are listed below except for the case
$0\circledast 0=0$
) operations, there are 5 non-trivial tensor operations, which are listed below except for the case
![]() $\mathcal{A}\circledast\mathcal{B}=\mathcal{B}-\mathcal{A}$
, which is the set difference with the roles reversed.
$\mathcal{A}\circledast\mathcal{B}=\mathcal{B}-\mathcal{A}$
, which is the set difference with the roles reversed.
 \begin{align*}\begin{array}{l@{\quad}l@{\quad}l}\textit{connective} & \textit{set-theoretic operation} & \textit{tensor operation} \\[5pt]disjunction\,\lor & union\,\cup & \mathcal{A}\lor\mathcal{B} = \{ A\cup B \mid A\in\mathcal{A},\,B\in\mathcal{B} \} \\[5pt]conjunction\,\land & intersection\,\cap & \mathcal{A}\land\mathcal{B} = \{ A\cap B \mid A\in\mathcal{A},\,B\in\mathcal{B} \} \\[5pt]``p\;but\;not\;q'' & set\;difference\,\smallsetminus & \mathcal{A}-\mathcal{B} = \{ A\smallsetminus B \mid A\in\mathcal{A},\,B\in\mathcal{B} \} \\[5pt]exclusive\;disjunction\,\oplus & symmetric\;difference\,\triangle & \mathcal{A}\oplus\mathcal{B} = \{ A\triangle B \mid A\in\mathcal{A},\,B\in\mathcal{B} \}\end{array}\end{align*}
\begin{align*}\begin{array}{l@{\quad}l@{\quad}l}\textit{connective} & \textit{set-theoretic operation} & \textit{tensor operation} \\[5pt]disjunction\,\lor & union\,\cup & \mathcal{A}\lor\mathcal{B} = \{ A\cup B \mid A\in\mathcal{A},\,B\in\mathcal{B} \} \\[5pt]conjunction\,\land & intersection\,\cap & \mathcal{A}\land\mathcal{B} = \{ A\cap B \mid A\in\mathcal{A},\,B\in\mathcal{B} \} \\[5pt]``p\;but\;not\;q'' & set\;difference\,\smallsetminus & \mathcal{A}-\mathcal{B} = \{ A\smallsetminus B \mid A\in\mathcal{A},\,B\in\mathcal{B} \} \\[5pt]exclusive\;disjunction\,\oplus & symmetric\;difference\,\triangle & \mathcal{A}\oplus\mathcal{B} = \{ A\triangle B \mid A\in\mathcal{A},\,B\in\mathcal{B} \}\end{array}\end{align*}
If the connective
![]() $\circledast$
is commutative (resp. associative), then the corresponding tensor operation is commutative (resp. associative), too, but as we shall see in the next example, the same does not apply to idempotence. In general, the well-known logical equivalences do not transfer to equalities about tensor operations. This means that, in contrast to propositional logic where we often reduce problems to some small set of basic connectives, it is better to consider tensor operators separately.
$\circledast$
is commutative (resp. associative), then the corresponding tensor operation is commutative (resp. associative), too, but as we shall see in the next example, the same does not apply to idempotence. In general, the well-known logical equivalences do not transfer to equalities about tensor operations. This means that, in contrast to propositional logic where we often reduce problems to some small set of basic connectives, it is better to consider tensor operators separately.
Example 11. Suppose the base set X is infinite and
![]() $\mathcal{A}=\{\{x\} \mid x\in X\}$
. Consider the families
$\mathcal{A}=\{\{x\} \mid x\in X\}$
. Consider the families
for
![]() $n\in\mathbb{Z}_+$
. An easy induction shows that
$n\in\mathbb{Z}_+$
. An easy induction shows that
![]() $\mathcal{A}_n=\{B\subseteq X \mid B\neq\emptyset,|B|\le n\}$
, so these families are all different. In particular,
$\mathcal{A}_n=\{B\subseteq X \mid B\neq\emptyset,|B|\le n\}$
, so these families are all different. In particular,
![]() $\mathcal{A}\lor\mathcal{A}=\mathcal{A}_2\neq\mathcal{A}$
, so the tensor operation
$\mathcal{A}\lor\mathcal{A}=\mathcal{A}_2\neq\mathcal{A}$
, so the tensor operation
![]() $\lor$
is not idempotent, though the binary operation
$\lor$
is not idempotent, though the binary operation
![]() $\lor$
on
$\lor$
on
![]() $\{0,1\}$
is. A similar example shows that
$\{0,1\}$
is. A similar example shows that
![]() $\land$
(as a tensor operator) is not idempotent either.
$\land$
(as a tensor operator) is not idempotent either.
Elaborating on this example, one sees that distributive law does not hold for
![]() $\lor$
and
$\lor$
and
![]() $\land$
, either. Choose
$\land$
, either. Choose
![]() $\mathcal{B}=\mathcal{C}=\{X\}$
with
$\mathcal{B}=\mathcal{C}=\{X\}$
with
![]() $\mathcal{A}$
as above; then
$\mathcal{A}$
as above; then
We do not aim at a complete analysis on how the tensor operations behave, but we shall show that they preserve intervals. In connection with the following lemma, we will have thus one way to compute the result of tensor operation.
Lemma 12. Let
![]() $\circledast$
be a binary operation on
$\circledast$
be a binary operation on
![]() $\{0,1\}$
, and let
$\{0,1\}$
, and let
![]() $\mathcal{A}_i,\mathcal{B}_j\in\mathcal{P}(\mathcal{P}(X))$
be families of sets, for
$\mathcal{A}_i,\mathcal{B}_j\in\mathcal{P}(\mathcal{P}(X))$
be families of sets, for
![]() $i\in I$
and
$i\in I$
and
![]() $j\in J$
. Then
$j\in J$
. Then
 \[\left(\bigcup_{i\in I}\mathcal{A}_i\right)\circledast\left(\bigcup_{j\in J}\mathcal{B}_j\right)=\bigcup_{\substack{i\in I,\\j\in J}}(\mathcal{A}_i\circledast\mathcal{B}_j).\]
\[\left(\bigcup_{i\in I}\mathcal{A}_i\right)\circledast\left(\bigcup_{j\in J}\mathcal{B}_j\right)=\bigcup_{\substack{i\in I,\\j\in J}}(\mathcal{A}_i\circledast\mathcal{B}_j).\]
Proof. The reader can either prove this as an easy exercise, or wait until Section 4, where it is shown that tensor operators are so-called Kripke operators and that the Union Lemma 52 holds generally for Kripke operators.
We need some auxiliary concepts to handle intervals and tensor operators. We depart for a moment from classical logic (Kleene introduced his logic in Kleene Reference Kleene1952, Section 64) and introduce a new truth value ![]() for “unknown.”
Footnote 3
for “unknown.”
Footnote 3
Definition 13. Let
![]() $\circledast$
be a binary operation on
$\circledast$
be a binary operation on
![]() $\{0,1\}$
. We define Kleene’s extension
$\{0,1\}$
. We define Kleene’s extension
![]() $\widetilde\circledast$
of
$\widetilde\circledast$
of
![]() $\circledast$
as follows. Write
$\circledast$
as follows. Write
![]() $V_0=\{0\}$
,
$V_0=\{0\}$
,
![]() $V_1=\{1\}$
,
$V_1=\{1\}$
, ![]() and
and
![]() $A\circledast B=\{a\circledast b \mid a\in A, b\in B\}$
, for
$A\circledast B=\{a\circledast b \mid a\in A, b\in B\}$
, for
![]() $A,B\subseteq\{0,1\}$
. Then
$A,B\subseteq\{0,1\}$
. Then
![]() $\widetilde\circledast$
is determined by the rule:
$\widetilde\circledast$
is determined by the rule:
for ![]() . Overloading once again the notation, we shall denote also the extension by
. Overloading once again the notation, we shall denote also the extension by
![]() $\circledast$
instead of
$\circledast$
instead of
![]() $\widetilde\circledast$
in the sequel.
$\widetilde\circledast$
in the sequel.
Example 14. In order to calculate ![]() , one observes that
, one observes that ![]() , so
, so![]() , or simply
, or simply ![]() . On the other hand,
. On the other hand, ![]() , which implies
, which implies ![]() .
.
Definition 15.
-
(a) The characteristic function of a family of sets
 $\mathcal{A}\subseteq\mathcal{P}(X)$
is
$\mathcal{A}\subseteq\mathcal{P}(X)$
is  , where
, where
 $E(x)=\{\chi_A(x) \mid A\in\mathcal{A} \}$
.
$E(x)=\{\chi_A(x) \mid A\in\mathcal{A} \}$
.
-
(b) We say that
 $\chi\colon X\to\{0,1\}$
is compatible with the function
$\chi\colon X\to\{0,1\}$
is compatible with the function  if for all
if for all
 $x\in X$
,
$x\in X$
,  implies
implies
 $\chi(x)=\xi(x)$
.
$\chi(x)=\xi(x)$
.
Lemma 16.
Let
![]() $\mathcal{A}\subseteq\mathcal{P}(X)$
.
$\mathcal{A}\subseteq\mathcal{P}(X)$
.
-
(a) For all
 $A\in\mathcal{A}$
, we have that
$A\in\mathcal{A}$
, we have that
 $\chi_A$
is compatible with
$\chi_A$
is compatible with
 $\xi_\mathcal{A}$
.
$\xi_\mathcal{A}$
. -
(b) The family
 $\mathcal{A}$
being an interval is equivalent to the following being true for every
$\mathcal{A}$
being an interval is equivalent to the following being true for every
 $A\subseteq X$
:
$A\subseteq X$
:
 $A\in\mathcal{A}$
if and only if
$A\in\mathcal{A}$
if and only if
 $\chi_A$
is compatible with
$\chi_A$
is compatible with
 $\xi_\mathcal{A}$
. Conversely, if
$\xi_\mathcal{A}$
. Conversely, if
 $\mathcal{A}$
is an interval then the condition holds.
$\mathcal{A}$
is an interval then the condition holds.
Proof.
-
(a) Let
 $A\in\mathcal{A}$
and for every
$A\in\mathcal{A}$
and for every
 $x\in X$
. Using the notation of the previous definition, we note that
$x\in X$
. Using the notation of the previous definition, we note that
 $\chi_A(x)\in E(x)$
. Thus, either
$\chi_A(x)\in E(x)$
. Thus, either
 $\xi_\mathcal{A}(x)=\chi_A(x)$
or
$\xi_\mathcal{A}(x)=\chi_A(x)$
or  , and compatibility follows.
, and compatibility follows. -
(b) Suppose
Put \[ \mathcal{A}=\{ A\subseteq X \mid \chi_A\text{ is compatible with }\xi_\mathcal{A} \}.\]
\[ \mathcal{A}=\{ A\subseteq X \mid \chi_A\text{ is compatible with }\xi_\mathcal{A} \}.\]
 $B=\xi^{-1}_\mathcal{A}[\{1\}]$
and
$B=\xi^{-1}_\mathcal{A}[\{1\}]$
and  . Then for every
. Then for every
 $A\subseteq X$
, compatibility of
$A\subseteq X$
, compatibility of
 $\chi_A$
with
$\chi_A$
with
 $\xi_\mathcal{A}$
is equivalent to the condition
$\xi_\mathcal{A}$
is equivalent to the condition
 $B\subseteq A\subseteq C$
. Hence,
$B\subseteq A\subseteq C$
. Hence,
 $\mathcal{A}=[B,C]$
. The converse direction is easy.
$\mathcal{A}=[B,C]$
. The converse direction is easy.
Lemma 17. Let
![]() $\circledast$
be a binary operation on
$\circledast$
be a binary operation on
![]() $\{0,1\}$
and
$\{0,1\}$
and
![]() $\mathcal{A},\mathcal{B}\subseteq\mathcal{P}(X)$
. Then for every
$\mathcal{A},\mathcal{B}\subseteq\mathcal{P}(X)$
. Then for every
![]() $x\in X$
, it holds that
$x\in X$
, it holds that
Proof. Write
![]() $E_\mathcal{C}(x)=\{\chi_C(x) \mid C\in\mathcal{C}\}$
, for
$E_\mathcal{C}(x)=\{\chi_C(x) \mid C\in\mathcal{C}\}$
, for
![]() $\mathcal{C}\subseteq\mathcal{P}(X)$
and
$\mathcal{C}\subseteq\mathcal{P}(X)$
and
![]() $x\in X$
. Then
$x\in X$
. Then
 \begin{align*}E_{\mathcal{A}\circledast\mathcal{B}}(x) & = \{ \chi_C(x) \mid C\in \mathcal{A}\circledast\mathcal{B} \} \\ & = \{ \chi_{A*B}(x) \mid A\in \mathcal{A},\,B\in\mathcal{B} \} \\ & = \{ \chi_A(x)\circledast \chi_B(x) \mid A\in \mathcal{A},\,B\in\mathcal{B} \} \\ & = \{ \chi_A(x) \mid A\in \mathcal{A}\} \circledast \{\chi_B(x)\mid B\in\mathcal{B} \} \\ & = E_\mathcal{A}(x) \circledast E_\mathcal{B}(x).\end{align*}
\begin{align*}E_{\mathcal{A}\circledast\mathcal{B}}(x) & = \{ \chi_C(x) \mid C\in \mathcal{A}\circledast\mathcal{B} \} \\ & = \{ \chi_{A*B}(x) \mid A\in \mathcal{A},\,B\in\mathcal{B} \} \\ & = \{ \chi_A(x)\circledast \chi_B(x) \mid A\in \mathcal{A},\,B\in\mathcal{B} \} \\ & = \{ \chi_A(x) \mid A\in \mathcal{A}\} \circledast \{\chi_B(x)\mid B\in\mathcal{B} \} \\ & = E_\mathcal{A}(x) \circledast E_\mathcal{B}(x).\end{align*}
Employing the notation that was used to define Kleene’s extension, we may write this equation as
i.e.,
![]() $\xi_{\mathcal{A}\circledast\mathcal{B}}(x) = \xi_\mathcal{A}(x) \circledast \xi_\mathcal{B}(x)$
.
$\xi_{\mathcal{A}\circledast\mathcal{B}}(x) = \xi_\mathcal{A}(x) \circledast \xi_\mathcal{B}(x)$
.
Proposition 18.
Let
![]() $\circledast$
be a tensor operator. Then if
$\circledast$
be a tensor operator. Then if
![]() $\mathcal{A},\mathcal{B}\subseteq\mathcal{P}(X)$
are intervals, then so is
$\mathcal{A},\mathcal{B}\subseteq\mathcal{P}(X)$
are intervals, then so is
![]() $\mathcal{A}\circledast\mathcal{B}$
, too. Indeed, if we write
$\mathcal{A}\circledast\mathcal{B}$
, too. Indeed, if we write
![]() $\xi=\xi_{\mathcal{A}\circledast\mathcal{B}}$
,
$\xi=\xi_{\mathcal{A}\circledast\mathcal{B}}$
,
![]() $C_0=\xi^{-1}[\{1\}]$
and
$C_0=\xi^{-1}[\{1\}]$
and ![]() , then
, then
![]() $\mathcal{A}\circledast\mathcal{B}=[C_0,C_1]$
.
$\mathcal{A}\circledast\mathcal{B}=[C_0,C_1]$
.
Proof. By case (a) of Lemma 16 we have that
![]() $\mathcal{A}\circledast\mathcal{B}\subseteq [C_0,C_1]$
. Let
$\mathcal{A}\circledast\mathcal{B}\subseteq [C_0,C_1]$
. Let
![]() $C\in[C_0,C_1]$
. As
$C\in[C_0,C_1]$
. As
![]() $C\in[C_0,C_1]$
, the characteristic function
$C\in[C_0,C_1]$
, the characteristic function
![]() $\chi_C$
is compatible with
$\chi_C$
is compatible with
![]() $\xi_{\mathcal{A}\circledast\mathcal{B}}$
. By Lemma 17, we know that
$\xi_{\mathcal{A}\circledast\mathcal{B}}$
. By Lemma 17, we know that
![]() $\xi_{\mathcal{A}\circledast\mathcal{B}}=\xi_\mathcal{A}\circledast\xi_\mathcal{B}$
. This enables us to choose (picking the values
$\xi_{\mathcal{A}\circledast\mathcal{B}}=\xi_\mathcal{A}\circledast\xi_\mathcal{B}$
. This enables us to choose (picking the values
![]() $\chi^{(0)}(x)$
and
$\chi^{(0)}(x)$
and
![]() $\chi^{(1)}(x)$
separately for each
$\chi^{(1)}(x)$
separately for each
![]() $x\in X$
) functions
$x\in X$
) functions
![]() $\chi^{(0)},\chi^{(1)}\colon X\to\{0,1\}$
such that
$\chi^{(0)},\chi^{(1)}\colon X\to\{0,1\}$
such that
![]() $\chi_C=\chi^{(0)}\circledast\chi^{(1)}$
,
$\chi_C=\chi^{(0)}\circledast\chi^{(1)}$
,
![]() $\chi^{(0)}$
is compatible with
$\chi^{(0)}$
is compatible with
![]() $\xi_\mathcal{A}$
and
$\xi_\mathcal{A}$
and
![]() $\chi^{(1)}$
is compatible with
$\chi^{(1)}$
is compatible with
![]() $\xi_\mathcal{B}$
. Finally, by case (b) of Lemma 16, we see that there are
$\xi_\mathcal{B}$
. Finally, by case (b) of Lemma 16, we see that there are
![]() $A\in\mathcal{A}$
and
$A\in\mathcal{A}$
and
![]() $B\in\mathcal{B}$
with
$B\in\mathcal{B}$
with
![]() $\chi_A=\chi^{(0)}$
and
$\chi_A=\chi^{(0)}$
and
![]() $\chi_B=\chi^{(1)}$
, which implies
$\chi_B=\chi^{(1)}$
, which implies
![]() $C=A*B\in\mathcal{A}\circledast\mathcal{B}$
.
$C=A*B\in\mathcal{A}\circledast\mathcal{B}$
.
2.4 Families of teams
The abstract concept of a family of sets is so general that it arises naturally in numerous contexts in mathematics. However, in this paper, our focus is on families of sets arising in logic, with applications to logic in mind. These families are collections of sets on the base set of the form of a Cartesian product
![]() $M^m$
. This is because we will consider sets of so-called assignments into a model M. Thus, the elements of our base set are assignments. This particular form of the base set leads to dimension computations which do not arise in the abstract setting. This is simply because finite tuples manifest more complicated combinatorial properties than mere elements. To avoid trivialities, we assume
$M^m$
. This is because we will consider sets of so-called assignments into a model M. Thus, the elements of our base set are assignments. This particular form of the base set leads to dimension computations which do not arise in the abstract setting. This is simply because finite tuples manifest more complicated combinatorial properties than mere elements. To avoid trivialities, we assume
![]() $|M|\ge 2$
.
$|M|\ge 2$
.
Let us see how sets of what we call assignments arise in logic. In classical logic, one associates with a given formula
![]() $\phi(x_0,\ldots,x_{m-1})$
with the free variables
$\phi(x_0,\ldots,x_{m-1})$
with the free variables
![]() $x_0,\ldots,x_{m-1}$
and a given structure M the set of m-tuples satisfying the formula
$x_0,\ldots,x_{m-1}$
and a given structure M the set of m-tuples satisfying the formula
![]() $\phi$
in M:
$\phi$
in M:
Here
![]() $``M\models \phi(a_0,\ldots,a_{m-1})"$
refers to the truth definition (a.k.a. satisfaction relation) of the logic that
$``M\models \phi(a_0,\ldots,a_{m-1})"$
refers to the truth definition (a.k.a. satisfaction relation) of the logic that
![]() $\phi(x_0,\ldots,x_{m-1})$
is considered a formula of. For first-order logic, the truth definition is given in standard textbooks of logic and can be found e.g. in Väänänen (Reference Väänänen2011, Section 6.2). We follow the usual convention and call elements
$\phi(x_0,\ldots,x_{m-1})$
is considered a formula of. For first-order logic, the truth definition is given in standard textbooks of logic and can be found e.g. in Väänänen (Reference Väänänen2011, Section 6.2). We follow the usual convention and call elements
![]() $(a_0,\ldots,a_{m-1})$
of
$(a_0,\ldots,a_{m-1})$
of
![]() $\phi^{{M,\vec x}}$
assignments. Sets
$\phi^{{M,\vec x}}$
assignments. Sets
![]() $\phi^{{M,\vec x}}$
of assignments are aptly called definable subsets of
$\phi^{{M,\vec x}}$
of assignments are aptly called definable subsets of
![]() $M^m$
. The definable subsets of
$M^m$
. The definable subsets of
![]() $M^m$
form a Boolean algebra with Boolean operations corresponding to the logical operations of first-order logic. The study of this algebra is a well-known method in logic.
$M^m$
form a Boolean algebra with Boolean operations corresponding to the logical operations of first-order logic. The study of this algebra is a well-known method in logic.
In the same way as classical logic gives rise to definable sets of assignments, so-called dependence logic (Väänänen Reference Väänänen2007) that we will now recall gives rise to definable families of sets of assignments as follows. If M is a model, a team in M is a set T of assignments s (i.e., functions) which map a fixed set
![]() $\mathrm{dom}(s)=\{x_0,\ldots,x_{m-1}\}$
of variables, called the domain of s (and of T), to M. See Table 1 for an example of a team. The rows of a team are assignments. In principle, a team is simply a table of data. The source of the data can be anything. A good intuition is that the data comes from some experiments concerning the “attributes”
$\mathrm{dom}(s)=\{x_0,\ldots,x_{m-1}\}$
of variables, called the domain of s (and of T), to M. See Table 1 for an example of a team. The rows of a team are assignments. In principle, a team is simply a table of data. The source of the data can be anything. A good intuition is that the data comes from some experiments concerning the “attributes”
![]() $\{x_0,\ldots, x_{m-1}\}$
, each row representing one experiment. Another useful intuition is that the table of data is (a part of) a database. We identify the function s with the tuple
$\{x_0,\ldots, x_{m-1}\}$
, each row representing one experiment. Another useful intuition is that the table of data is (a part of) a database. We identify the function s with the tuple
![]() $(s(x_0),\ldots,s(x_{m-1}))$
and a team with a subset of
$(s(x_0),\ldots,s(x_{m-1}))$
and a team with a subset of
![]() $M^m$
.
$M^m$
.
Table 1. A team

Teams can manifest phenomena that single assignments cannot. For example, the team of Table 1 manifests the circumstance that
![]() $x_0$
does not completely determine
$x_0$
does not completely determine
![]() $x_2$
but
$x_2$
but
![]() $x_1$
does. In dependence logic (Väänänen Reference Väänänen2007), we have so-called dependence atoms (see Definition 20) the semantics of which is defined by means of teams and could not be defined meaningfully in terms of single assignments. Every formula
$x_1$
does. In dependence logic (Väänänen Reference Väänänen2007), we have so-called dependence atoms (see Definition 20) the semantics of which is defined by means of teams and could not be defined meaningfully in terms of single assignments. Every formula
![]() $\phi$
of dependence logic, or any other logic the semantics of which is based on teams, with free variables in
$\phi$
of dependence logic, or any other logic the semantics of which is based on teams, with free variables in
![]() $\vec x=(x_0,\ldots,x_{m-1})$
, gives rise to the set of teams
$\vec x=(x_0,\ldots,x_{m-1})$
, gives rise to the set of teams
where
![]() $M\models_T\phi$
is the satisfaction relation defined in Definitions 19 and 20 below. We consider the families
$M\models_T\phi$
is the satisfaction relation defined in Definitions 19 and 20 below. We consider the families
![]() $\left\Vert \phi \right\Vert^{{M,\vec x}}$
an interesting special case of families of subsets of
$\left\Vert \phi \right\Vert^{{M,\vec x}}$
an interesting special case of families of subsets of
![]() $M^m$
.
$M^m$
.
If
![]() $\ell< m$
, there is a canonical projection
$\ell< m$
, there is a canonical projection
![]() $M^m\to M^\ell$
. We may identify
$M^m\to M^\ell$
. We may identify
![]() $T\subseteq M^\ell$
with
$T\subseteq M^\ell$
with
![]() $T^*=\{s\in M^m : s\restriction \ell\in T\}$
. In this way, it is possible to think of a subset of
$T^*=\{s\in M^m : s\restriction \ell\in T\}$
. In this way, it is possible to think of a subset of
![]() $M^\ell$
at the same time, via
$M^\ell$
at the same time, via
![]() $T^*$
, as a subset of
$T^*$
, as a subset of
![]() $M^m$
, although literally, of course,
$M^m$
, although literally, of course,
![]() $T \ne T^*$
.
$T \ne T^*$
.
Many of the results of this paper hold for arbitrary families of sets but when applied to families of the form
![]() $\left\Vert \phi \right\Vert^{{M,\vec{x}}}$
, results pertaining to dependence and independence logics obtain.
$\left\Vert \phi \right\Vert^{{M,\vec{x}}}$
, results pertaining to dependence and independence logics obtain.
In order to make (1) more exact, we now recall the inductive definition of
![]() $M\models_T\phi$
from Väänänen (Reference Väänänen2007), first for logical operations (Definition 19) and then for new atoms (Definition 20). If
$M\models_T\phi$
from Väänänen (Reference Väänänen2007), first for logical operations (Definition 19) and then for new atoms (Definition 20). If
![]() $a\in M$
, then
$a\in M$
, then
![]() $s(a/x)$
is the unique assignment s’ such that
$s(a/x)$
is the unique assignment s’ such that
![]() $s'(x)=a$
and
$s'(x)=a$
and
![]() $s'(y)=s(y)$
for variables y in the domain of s other than x. If
$s'(y)=s(y)$
for variables y in the domain of s other than x. If
![]() $F:T\to \mathcal{P}(M)\smallsetminus\{\emptyset\}$
, then
$F:T\to \mathcal{P}(M)\smallsetminus\{\emptyset\}$
, then
![]() $T[F/x]=\{s(a/x)\mid s\in T, a\in F(s)\}$
. Finally,
$T[F/x]=\{s(a/x)\mid s\in T, a\in F(s)\}$
. Finally,
![]() $T[M/x]=\{s(a/x) \mid a\in M, s\in T\}$
.
$T[M/x]=\{s(a/x) \mid a\in M, s\in T\}$
.
Definition 19.
-
(a)
 $M\models_T\phi$
, where
$M\models_T\phi$
, where
 $\phi$
is atomic or negated atomic if and only if every assignment s in T satisfies
$\phi$
is atomic or negated atomic if and only if every assignment s in T satisfies
 $\phi$
.
$\phi$
. -
(b)
 $M\models_T\phi\wedge\psi$
if and only if
$M\models_T\phi\wedge\psi$
if and only if
 $M\models_T\phi$
and
$M\models_T\phi$
and
 $M\models_T\psi$
.
$M\models_T\psi$
. -
(c)
 $M\models_T\phi\vee\psi$
if and only if there are U and V such that
$M\models_T\phi\vee\psi$
if and only if there are U and V such that
 $T=U\cup V$
,
$T=U\cup V$
,
 $M\models_U\phi$
and
$M\models_U\phi$
and
 $M\models_V\psi$
. (Tensor disjunction)
$M\models_V\psi$
. (Tensor disjunction) -
(d)
 $M\models_T\phi\,{\wedge}\,\psi$
if and only if there are U and V such that
$M\models_T\phi\,{\wedge}\,\psi$
if and only if there are U and V such that
 $T=U\cap V$
,
$T=U\cap V$
,
 $M\models_U\phi$
and
$M\models_U\phi$
and
 $M\models_V\psi$
. (Tensor conjunction)
$M\models_V\psi$
. (Tensor conjunction) -
(e)
 $M\models_T\phi\ \underline{\vee}\ \psi$
if and only if
$M\models_T\phi\ \underline{\vee}\ \psi$
if and only if
 $M\models_T\phi$
or
$M\models_T\phi$
or
 $M\models_T\psi$
. (Intuitionistic disjunction)
$M\models_T\psi$
. (Intuitionistic disjunction) -
(f)
 $M\models_T\exists x\phi$
if and only if there is
$M\models_T\exists x\phi$
if and only if there is
 $F:T\to \mathcal{P}(M)\smallsetminus\{\emptyset\}$
such that
$F:T\to \mathcal{P}(M)\smallsetminus\{\emptyset\}$
such that
 $M\models_{T[F/x]}\phi$
.
$M\models_{T[F/x]}\phi$
. -
(g)
 $M\models_T\forall x\phi$
if and only if
$M\models_T\forall x\phi$
if and only if
 $M\models_{T[M/x]}\phi$
.
$M\models_{T[M/x]}\phi$
.
This defines
![]() $M\models_T\phi$
for every first-order formula
$M\models_T\phi$
for every first-order formula
![]() $\phi$
in negation normal form (i.e., negation occurs in front of atomic formulas only). Note that Väänänen (Reference Väänänen2007) uses only the first two of the four binary connectives in Definition 19. We have kept here the usual notation
$\phi$
in negation normal form (i.e., negation occurs in front of atomic formulas only). Note that Väänänen (Reference Väänänen2007) uses only the first two of the four binary connectives in Definition 19. We have kept here the usual notation
![]() $\land$
and
$\land$
and
![]() $\lor$
for these connectives. Intuitionistic disjunction was mentioned in Väänänen (Reference Väänänen2007) and elaborated on in Abramsky and Väänänen (Reference Abramsky and Väänänen2009). Tensor conjunction does not seem to have been studied before, and its role is minor here, too.
$\lor$
for these connectives. Intuitionistic disjunction was mentioned in Väänänen (Reference Väänänen2007) and elaborated on in Abramsky and Väänänen (Reference Abramsky and Väänänen2009). Tensor conjunction does not seem to have been studied before, and its role is minor here, too.
It might seem that
![]() $\phi\underline{\vee}\psi$
is a more “natural” disjunction than
$\phi\underline{\vee}\psi$
is a more “natural” disjunction than
![]() $\phi\vee\psi$
. What is natural depends, of course, on one’s intuition about
$\phi\vee\psi$
. What is natural depends, of course, on one’s intuition about
![]() $\models_T$
. In Väänänen (Reference Väänänen2007) an alternative game-theoretic definition of
$\models_T$
. In Väänänen (Reference Väänänen2007) an alternative game-theoretic definition of
![]() $M\models_T\phi$
is given and in that context
$M\models_T\phi$
is given and in that context
![]() $\phi\vee\psi$
is a natural connective corresponding perfectly to the disjunction of classical propositional calculus.
$\phi\vee\psi$
is a natural connective corresponding perfectly to the disjunction of classical propositional calculus.
By Definition 19(a), for every first-order literal (i.e., atomic or negated atomic)
![]() $\phi,$
we have
$\phi,$
we have
![]() $\left\Vert \phi \right\Vert^{{M,\vec x}}=[\emptyset,\phi^{{M,\vec x}}]$
. The same is true if
$\left\Vert \phi \right\Vert^{{M,\vec x}}=[\emptyset,\phi^{{M,\vec x}}]$
. The same is true if
![]() $\phi$
is any formula of first order logic. Thus, for first-order
$\phi$
is any formula of first order logic. Thus, for first-order
![]() $\phi,$
the family
$\phi,$
the family
![]() $\left\Vert \phi \right\Vert^{{M,\vec{x}}}$
is dominated (by
$\left\Vert \phi \right\Vert^{{M,\vec{x}}}$
is dominated (by
![]() $\phi^{{M,\vec x}}$
), downward closed, convex, and supported (by
$\phi^{{M,\vec x}}$
), downward closed, convex, and supported (by
![]() $\emptyset$
).
$\emptyset$
).
Note further that for composite
![]() $\phi$
the family
$\phi$
the family
![]() $\left\Vert \phi \right\Vert^{{M,\vec x}}$
can be obtained from the corresponding families for the components of
$\left\Vert \phi \right\Vert^{{M,\vec x}}$
can be obtained from the corresponding families for the components of
![]() $\phi$
by applying one of the operators introduced in Example 8. For conjunction and (tensor) disjunction, we have
$\phi$
by applying one of the operators introduced in Example 8. For conjunction and (tensor) disjunction, we have
 $$\begin{array}{lcl}\left\Vert \phi\wedge\psi \right\Vert^{{M,\vec x}}&= &\left\Vert \phi \right\Vert^{{M,\vec x}}\cap\left\Vert \psi \right\Vert^{{M,\vec x}} \\\left\Vert \phi\vee\psi \right\Vert^{{M,\vec x}}&= &\left\Vert \phi \right\Vert^{{M,\vec x}}\lor\left\Vert \psi \right\Vert^{{M,\vec x}} \\\end{array} $$
$$\begin{array}{lcl}\left\Vert \phi\wedge\psi \right\Vert^{{M,\vec x}}&= &\left\Vert \phi \right\Vert^{{M,\vec x}}\cap\left\Vert \psi \right\Vert^{{M,\vec x}} \\\left\Vert \phi\vee\psi \right\Vert^{{M,\vec x}}&= &\left\Vert \phi \right\Vert^{{M,\vec x}}\lor\left\Vert \psi \right\Vert^{{M,\vec x}} \\\end{array} $$
Furthermore, for tensor conjunction and intuitionistic disjunction, we have
 $$\begin{array}{lcl}\left\Vert \phi\,{\wedge}\,\psi \right\Vert^{{M,\vec x}}&= &\left\Vert \phi \right\Vert^{{M,\vec x}}\land\left\Vert \psi \right\Vert^{{M,\vec x}} \\\left\Vert \phi\ \underline{\vee}\ \psi \right\Vert^{{M,\vec x}}&= &\left\Vert \phi \right\Vert^{{M,\vec x}}\cup\left\Vert \psi \right\Vert^{{M,\vec x}} \\\end{array} $$
$$\begin{array}{lcl}\left\Vert \phi\,{\wedge}\,\psi \right\Vert^{{M,\vec x}}&= &\left\Vert \phi \right\Vert^{{M,\vec x}}\land\left\Vert \psi \right\Vert^{{M,\vec x}} \\\left\Vert \phi\ \underline{\vee}\ \psi \right\Vert^{{M,\vec x}}&= &\left\Vert \phi \right\Vert^{{M,\vec x}}\cup\left\Vert \psi \right\Vert^{{M,\vec x}} \\\end{array} $$
Note, however, that in the case of existential and universal quantifiers, the quantified variable needs to be dropped from the tuple
![]() $\vec x=(x_0,\ldots,x_{m-1})$
, as it has become a bound variable:
$\vec x=(x_0,\ldots,x_{m-1})$
, as it has become a bound variable:
 $$\begin{array}{lcl}\left\Vert \exists x_i\phi \right\Vert^{{M,{\vec{x}\hspace{0.3 mm}}^-}}&= &\Delta_{\exists i}^{M^m}(\!\left\Vert \phi \right\Vert^{{M,\vec{x}}}) \\\left\Vert \forall x_i\phi \right\Vert^{{M,{\vec{x}\hspace{0.3 mm}}^-}}&= &\Delta_{\forall i}^{M^m}(\!\left\Vert \phi \right\Vert^{{M,\vec{x}}}), \\\end{array} $$
$$\begin{array}{lcl}\left\Vert \exists x_i\phi \right\Vert^{{M,{\vec{x}\hspace{0.3 mm}}^-}}&= &\Delta_{\exists i}^{M^m}(\!\left\Vert \phi \right\Vert^{{M,\vec{x}}}) \\\left\Vert \forall x_i\phi \right\Vert^{{M,{\vec{x}\hspace{0.3 mm}}^-}}&= &\Delta_{\forall i}^{M^m}(\!\left\Vert \phi \right\Vert^{{M,\vec{x}}}), \\\end{array} $$
where
![]() ${\vec{x}\hspace{0.3 mm}}^-$
is the tuple obtained from
${\vec{x}\hspace{0.3 mm}}^-$
is the tuple obtained from
![]() $\vec{x}$
by deleting the component
$\vec{x}$
by deleting the component
![]() $x_i$
.
$x_i$
.
We now recall the extension of
![]() $M\models_T\phi$
from first-order
$M\models_T\phi$
from first-order
![]() $\phi$
to new non first-order atoms. Below, the restriction of a team T to
$\phi$
to new non first-order atoms. Below, the restriction of a team T to
![]() $\vec{x}$
, in symbols
$\vec{x}$
, in symbols
![]() $T\restriction\vec{x}$
, is the set
$T\restriction\vec{x}$
, is the set
![]() $\{s\restriction\vec{x}:s\in T\}$
. We use
$\{s\restriction\vec{x}:s\in T\}$
. We use
![]() $\mathrm{len}(\vec{x})$
to denote the length of the variable (or other) sequence
$\mathrm{len}(\vec{x})$
to denote the length of the variable (or other) sequence
![]() $\vec{x}$
.
$\vec{x}$
.
Definition 20.
-
(a) Dependence atom, introduced in Väänänen (Reference Väänänen2007):
 $M\models_T \,=(\vec{x},y)$
if and only if
$M\models_T \,=(\vec{x},y)$
if and only if
 $s(\vec{x})=s'(\vec{x})$
implies
$s(\vec{x})=s'(\vec{x})$
implies
 $s(y)=s'(y)$
for all
$s(y)=s'(y)$
for all
 $s,s'\in T$
. This atom says that in the relevant data (i.e., T) the values of
$s,s'\in T$
. This atom says that in the relevant data (i.e., T) the values of
 $\vec{x}$
completely determine the value of y. We allow
$\vec{x}$
completely determine the value of y. We allow
 $\mathrm{len}(\vec{x})=0$
and call
$\mathrm{len}(\vec{x})=0$
and call
 $\,=(y)$
the constancy atom. More generally,
$\,=(y)$
the constancy atom. More generally,
 $M\models_T \,=(y)$
if and only if
$M\models_T \,=(y)$
if and only if
 $s(y)=s'(y)$
for all
$s(y)=s'(y)$
for all
 $s,s'\in T,$
that is, y has only one value in the entire team T.
$s,s'\in T,$
that is, y has only one value in the entire team T. -
(b) Exclusion atom, introduced in Galliani (Reference Galliani2012):
 $M\models_T\vec{x}\ |\ \vec{y}$
if and only if for every
$M\models_T\vec{x}\ |\ \vec{y}$
if and only if for every
 $s,s'\in T$
we have
$s,s'\in T$
we have
 $s(\vec{x})\ne s'(\vec{y})$
. We assume
$s(\vec{x})\ne s'(\vec{y})$
. We assume
 $\mathrm{len}(\vec{x})=\mathrm{len}(\vec{y})>0$
. This atom says that in team T the values of
$\mathrm{len}(\vec{x})=\mathrm{len}(\vec{y})>0$
. This atom says that in team T the values of
 $\vec{x}$
cannot occur also as values of
$\vec{x}$
cannot occur also as values of
 $\vec{y}$
.
$\vec{y}$
. -
(c) Inclusion atom, introduced in Galliani (Reference Galliani2012):
 $M\models_T\vec{x}\subseteq \vec{y}$
if and only if for every
$M\models_T\vec{x}\subseteq \vec{y}$
if and only if for every
 $s\in T$
there is
$s\in T$
there is
 $s'\in T$
such that
$s'\in T$
such that
 $s(\vec{x})=s'(\vec{y})$
. We assume
$s(\vec{x})=s'(\vec{y})$
. We assume
 $\mathrm{len}(\vec{x})=\mathrm{len}(\vec{y})>0$
. This is in a sense the opposite of the exclusion atom: all values of
$\mathrm{len}(\vec{x})=\mathrm{len}(\vec{y})>0$
. This is in a sense the opposite of the exclusion atom: all values of
 $\vec{x}$
must occur also as values of
$\vec{x}$
must occur also as values of
 $\vec{y}$
.
$\vec{y}$
. -
(d) Anonymity atom, introduced in Väänänen (Reference Väänänen2023): <texmath>inline472</texmath> if and only if for every
 $s\in T$
there is
$s\in T$
there is
 $s'\in T$
such that
$s'\in T$
such that
 $s(\vec{x})=s'(\vec{x})$
and
$s(\vec{x})=s'(\vec{x})$
and
 $s(y)\ne s'(y)$
. We assume that
$s(y)\ne s'(y)$
. We assume that
 $\vec{x}$
is nonempty. This atom says that values of
$\vec{x}$
is nonempty. This atom says that values of
 $\vec{x}$
do not reveal uniquely the value of y, but leave some freedom for y.
$\vec{x}$
do not reveal uniquely the value of y, but leave some freedom for y. -
(e) Independence atom, introduced in Grädel and Väänänen (Reference Grädel and Väänänen2013):
 $M\models_T \vec{x}\perp_{\vec{z}}\vec{y}$
if and only if for every
$M\models_T \vec{x}\perp_{\vec{z}}\vec{y}$
if and only if for every
 $s,s'\in T$
such that
$s,s'\in T$
such that
 $s(\vec{z})=s'(\vec{z})$
there is
$s(\vec{z})=s'(\vec{z})$
there is
 $s''\in T$
such that
$s''\in T$
such that
 $s''(\vec{z})=s(\vec{z})$
,
$s''(\vec{z})=s(\vec{z})$
,
 $s''(\vec{x})=s(\vec{x})$
and
$s''(\vec{x})=s(\vec{x})$
and
 $s''(\vec{y})=s'(\vec{y})$
. In other words, keeping the values of
$s''(\vec{y})=s'(\vec{y})$
. In other words, keeping the values of
 $\vec{z}$
constant, any two assignments
$\vec{z}$
constant, any two assignments
 $s\in T$
and
$s\in T$
and
 $s'\in T$
can be combined into a (possibly) new assignment
$s'\in T$
can be combined into a (possibly) new assignment
 $s''\in T$
which takes its value at
$s''\in T$
which takes its value at
 $\vec{x}$
from s and its value at
$\vec{x}$
from s and its value at
 $\vec{y}$
from s’. We assume that
$\vec{y}$
from s’. We assume that
 $\vec{x}$
and
$\vec{x}$
and
 $\vec{y}$
are nonempty. The atom
$\vec{y}$
are nonempty. The atom
 $\vec{x}\perp\vec{y}$
, corresponding to the case
$\vec{x}\perp\vec{y}$
, corresponding to the case
 $\vec{z}$
is empty, is called the pure independence atom, while
$\vec{z}$
is empty, is called the pure independence atom, while
 $ \vec{x}\perp_{\vec{z}}\vec{y}$
is otherwise called the conditional independence atom.
$ \vec{x}\perp_{\vec{z}}\vec{y}$
is otherwise called the conditional independence atom. -
(f). The general concept of an atom: Suppose C is a class, closed under isomorphisms, of pairs (A,T) where A is a set and T is a team in A with domain
 $\vec{x}$
. We can associate with C a new atom
$\vec{x}$
. We can associate with C a new atom
 $\alpha_C(\vec{x})$
and define
$\alpha_C(\vec{x})$
and define
 $M\models_T\alpha_C(\vec{x})$
to hold if and only if
$M\models_T\alpha_C(\vec{x})$
to hold if and only if
 $(A,T\restriction\vec{x})\in C$
, where A is the domain of the model M.
$(A,T\restriction\vec{x})\in C$
, where A is the domain of the model M.
By closing the respective atom under the logical operations (b), (c), (f) and (g) of Definition 19 we obtain, respectively, dependence logic, constancy logic, exclusion logic, inclusion logic, anonymity logic, and (pure or conditional) independence logic.
Note that we defined
![]() $\,=(\vec{x},y)$
for single variable y only. This is because
$\,=(\vec{x},y)$
for single variable y only. This is because
![]() $\,=(\vec{x},\vec{y})$
for a vector
$\,=(\vec{x},\vec{y})$
for a vector
![]() $\vec{y}=(y_1\ldots,y_n)$
, which we adopt now as a shorthand, can be defined as
$\vec{y}=(y_1\ldots,y_n)$
, which we adopt now as a shorthand, can be defined as
We use the same convention for
![]() $\,=(\vec{y})$
.
$\,=(\vec{y})$
.
If
![]() $\phi$
is a dependence atom or an exclusion atom, then
$\phi$
is a dependence atom or an exclusion atom, then
![]() $\left\Vert \phi \right\Vert^{{M,\vec{x}}}$
is, as can be easily verified, downward closed and supported by
$\left\Vert \phi \right\Vert^{{M,\vec{x}}}$
is, as can be easily verified, downward closed and supported by
![]() $\emptyset$
but not necessarily closed under unions or dominated. If
$\emptyset$
but not necessarily closed under unions or dominated. If
![]() $\phi$
is an inclusion atom or an anonymity atom, then
$\phi$
is an inclusion atom or an anonymity atom, then
![]() $\left\Vert \phi \right\Vert^{{M,\vec{x}}}$
is, as can be likewise easily verified, closed under unions and dominated by
$\left\Vert \phi \right\Vert^{{M,\vec{x}}}$
is, as can be likewise easily verified, closed under unions and dominated by
![]() $M^{\mathrm{len}(\vec{x})}$
but not necessarily downward closed or supported. For details we refer to Väänänen (Reference Väänänen2007), Galliani (Reference Galliani2012).
$M^{\mathrm{len}(\vec{x})}$
but not necessarily downward closed or supported. For details we refer to Väänänen (Reference Väänänen2007), Galliani (Reference Galliani2012).
Example 21. An example of a sentence combining dependence atoms and logical operations is the following formula which is satisfied by a team T in a model of size n if and only if
![]() $|\hspace{1pt} T\restriction \vec{x} \hspace{1pt}|\le n^k/2$
, where
$|\hspace{1pt} T\restriction \vec{x} \hspace{1pt}|\le n^k/2$
, where
![]() $\mathrm{len}(\vec{x})=k$
:
$\mathrm{len}(\vec{x})=k$
:
Here
![]() $\mathrm{len}(\vec{y})=k$
. An example of a sentence combining a number of different atoms as well as logical operations is the following formula which is satisfied by a team T if and only if
$\mathrm{len}(\vec{y})=k$
. An example of a sentence combining a number of different atoms as well as logical operations is the following formula which is satisfied by a team T if and only if
![]() $|\hspace{1pt} T\restriction \vec{x} \hspace{1pt}|$
is even:
$|\hspace{1pt} T\restriction \vec{x} \hspace{1pt}|$
is even:
 $$\begin{array}{l}\exists u\exists v\exists\vec{y}\exists\vec{z}(\vec{y}\vec{z}\perp \vec{x}\wedge\vec{y}\subseteq\vec{x}\wedge\vec{z}\subseteq\vec{x}\\\qquad\wedge((u=v\wedge\vec{x}\subseteq\vec{y})\vee(u\ne v\wedge \vec{x}\subseteq\vec{z}))\\\qquad\wedge\ \vec{y}\ |\ \vec{z}\ \wedge \,=(\vec{z},\vec{y})\ \wedge \,=(\vec{y},\vec{z})).\end{array}$$
$$\begin{array}{l}\exists u\exists v\exists\vec{y}\exists\vec{z}(\vec{y}\vec{z}\perp \vec{x}\wedge\vec{y}\subseteq\vec{x}\wedge\vec{z}\subseteq\vec{x}\\\qquad\wedge((u=v\wedge\vec{x}\subseteq\vec{y})\vee(u\ne v\wedge \vec{x}\subseteq\vec{z}))\\\qquad\wedge\ \vec{y}\ |\ \vec{z}\ \wedge \,=(\vec{z},\vec{y})\ \wedge \,=(\vec{y},\vec{z})).\end{array}$$
We will also consider the extension of first-order logic with Lindström quantifiers (see Lindström Reference Lindström1966 for definition). For the sake of simplicity, we restrict attention to Lindström quantifiers of type (r) for some positive integer r (i.e., quantifiers binding a single formula). Such a quantifier
![]() $Q_\mathcal{K}$
is associated to any isomorphism closed class
$Q_\mathcal{K}$
is associated to any isomorphism closed class
![]() $\mathcal{K}$
of structures of the form (A,R),
$\mathcal{K}$
of structures of the form (A,R),
![]() $R\subseteq A^r$
. If
$R\subseteq A^r$
. If
![]() $\psi$
is a formula and
$\psi$
is a formula and
![]() $\vec y$
is an r-tuple of variables, then applying the quantifier
$\vec y$
is an r-tuple of variables, then applying the quantifier
![]() $Q_\mathcal{K}$
we obtain a new formula
$Q_\mathcal{K}$
we obtain a new formula
![]() $Q_\mathcal{K}\vec y\,\psi$
in which all occurrences of the variables in
$Q_\mathcal{K}\vec y\,\psi$
in which all occurrences of the variables in
![]() $\vec y$
are bound.
$\vec y$
are bound.
Adding Lindström quantifiers to logics with team semantics was first considered by Engström (Reference Engström2012). We follow here his definition for the semantics of
![]() $Q_\mathcal{K}$
. First, we adapt the notation used for existential quantifier: if
$Q_\mathcal{K}$
. First, we adapt the notation used for existential quantifier: if
![]() $F\colon T\to \mathcal{P}(M^r)$
, then
$F\colon T\to \mathcal{P}(M^r)$
, then
![]() $T[F/\vec y]=\{s(\vec b/\vec y)\mid s\in T, \vec b\in F(s)\}$
.
$T[F/\vec y]=\{s(\vec b/\vec y)\mid s\in T, \vec b\in F(s)\}$
.
Definition 22. (Engström Reference Engström2012).Footnote 4
![]() $M\models_T Q_\mathcal{K}\vec y\,\psi$
if and only if there exists
$M\models_T Q_\mathcal{K}\vec y\,\psi$
if and only if there exists
![]() $F\colon T\to \mathcal{P}(M^r)$
such that
$F\colon T\to \mathcal{P}(M^r)$
such that
![]() $M\models_{T[F/\vec y]}\psi$
and
$M\models_{T[F/\vec y]}\psi$
and
![]() $(M,F(s))\in \mathcal{K}$
for all
$(M,F(s))\in \mathcal{K}$
for all
![]() $s\in T$
.
$s\in T$
.
The semantics of Lindström quantifiers can also be formulated in terms of operators that map sets of the form
![]() $\left\Vert \psi \right\Vert^{{M,\vec{z}}}$
to sets
$\left\Vert \psi \right\Vert^{{M,\vec{z}}}$
to sets
![]() $\left\Vert Q_\mathcal{K}\vec{y}\,\psi \right\Vert^{{M,\vec{x}}}$
, where
$\left\Vert Q_\mathcal{K}\vec{y}\,\psi \right\Vert^{{M,\vec{x}}}$
, where
![]() $\vec{z}$
consists of the variables in the tuples
$\vec{z}$
consists of the variables in the tuples
![]() $\vec{x}$
and
$\vec{x}$
and
![]() $\vec{y}$
. To work out the details of these operators, we fix a quantifier
$\vec{y}$
. To work out the details of these operators, we fix a quantifier
![]() $Q_\mathcal{K}$
of type (r), the length
$Q_\mathcal{K}$
of type (r), the length
![]() $m\ge r$
of
$m\ge r$
of
![]() $\vec{z}$
, the tuple
$\vec{z}$
, the tuple
![]() $\vec\ell=(\ell_0,\ldots,\ell_{r-1})$
for which
$\vec\ell=(\ell_0,\ldots,\ell_{r-1})$
for which
![]() $\vec{y}=(z_{\ell_0},\ldots,z_{\ell_{r-1}})$
, and the universe M of the model. Note that there is no reason to assume that the components of
$\vec{y}=(z_{\ell_0},\ldots,z_{\ell_{r-1}})$
, and the universe M of the model. Note that there is no reason to assume that the components of
![]() $\vec\ell$
are in ascending order; the quantifier
$\vec\ell$
are in ascending order; the quantifier
![]() $Q_\mathcal{K}$
can be applied to any r-tuple of distinct variables in
$Q_\mathcal{K}$
can be applied to any r-tuple of distinct variables in
![]() $\vec{z}$
. On the other hand, we can assume w.l.o.g. that
$\vec{z}$
. On the other hand, we can assume w.l.o.g. that
![]() $\vec{x}$
lists the rest of the variables in
$\vec{x}$
lists the rest of the variables in
![]() $\vec{z}$
in ascending order, i.e., for each
$\vec{z}$
in ascending order, i.e., for each
![]() $i<m-r$
,
$i<m-r$
,
![]() $x_i=z_j$
, where
$x_i=z_j$
, where
![]() $j\not\in\{\ell_0,\ldots,\ell_{r-1}\}$
and
$j\not\in\{\ell_0,\ldots,\ell_{r-1}\}$
and
![]() $i=|\{k<j\mid k\notin\{\ell_0,\ldots,\ell_{r-1}\}\}|$
. Thus,
$i=|\{k<j\mid k\notin\{\ell_0,\ldots,\ell_{r-1}\}\}|$
. Thus,
![]() $\vec{z}$
is obtained from
$\vec{z}$
is obtained from
![]() $\vec{x}$
and
$\vec{x}$
and
![]() $\vec{y}$
by re-ordering the latter and shuffling according to
$\vec{y}$
by re-ordering the latter and shuffling according to
![]() $\vec\ell$
. We use the notation
$\vec\ell$
. We use the notation
![]() $\vec{z}=\vec{x}\otimes_{\vec\ell}\vec{y}$
to denote this shuffling, and similarly
$\vec{z}=\vec{x}\otimes_{\vec\ell}\vec{y}$
to denote this shuffling, and similarly
![]() $\vec{c}=\vec{a}\otimes_{\vec\ell}\vec{b}$
for tuples
$\vec{c}=\vec{a}\otimes_{\vec\ell}\vec{b}$
for tuples
![]() $\vec{c},\vec{a},\vec{b}$
of elements in M.
$\vec{c},\vec{a},\vec{b}$
of elements in M.
Assume then that
![]() $S\subseteq M^m$
is a team with domain
$S\subseteq M^m$
is a team with domain
![]() $\{z_0,\ldots,z_{m-1}\}$
. For each
$\{z_0,\ldots,z_{m-1}\}$
. For each
![]() $\vec{a}\in M^{m-r}$
the
$\vec{a}\in M^{m-r}$
the
![]() $\vec\ell$
-restriction of S on
$\vec\ell$
-restriction of S on
![]() $\vec{a}$
is the set
$\vec{a}$
is the set
![]() $S[\vec{a}]_{\vec\ell}:=\{\vec{b}\in M^r\mid \vec{a}\otimes_{\vec\ell}\vec{b}\in S\}$
. Furthermore, the
$S[\vec{a}]_{\vec\ell}:=\{\vec{b}\in M^r\mid \vec{a}\otimes_{\vec\ell}\vec{b}\in S\}$
. Furthermore, the
![]() $(\mathcal{K},\vec\ell)$
-projection of S is the set
$(\mathcal{K},\vec\ell)$
-projection of S is the set
![]() $\pi_{\mathcal{K},\vec\ell}\,(S):=\{\vec{a}\in M^{m-r}\mid (M,S[\vec{a}]_{\vec\ell})\in\mathcal{K}\}$
. The idea here is that if
$\pi_{\mathcal{K},\vec\ell}\,(S):=\{\vec{a}\in M^{m-r}\mid (M,S[\vec{a}]_{\vec\ell})\in\mathcal{K}\}$
. The idea here is that if
![]() $T=\pi_{\mathcal{K},\vec\ell}\,(S)$
for some team
$T=\pi_{\mathcal{K},\vec\ell}\,(S)$
for some team
![]() $S\in\left\Vert \psi \right\Vert^{{M,\vec{z}}}$
, then defining
$S\in\left\Vert \psi \right\Vert^{{M,\vec{z}}}$
, then defining
![]() $F\colon T\to\mathcal{P}(M^r)$
by
$F\colon T\to\mathcal{P}(M^r)$
by
![]() $F(\vec{a})=S[\vec{a}]_{\vec\ell}$
for each
$F(\vec{a})=S[\vec{a}]_{\vec\ell}$
for each
![]() $\vec{a}\in T$
, we see that the truth condition of Definition 22 holds for the team T, provided that
$\vec{a}\in T$
, we see that the truth condition of Definition 22 holds for the team T, provided that
![]() $S=T[F/\vec{y}]$
. It is clear that
$S=T[F/\vec{y}]$
. It is clear that
![]() $T[F/\vec{y}]\subseteq S$
, and the converse inclusion holds if and only if
$T[F/\vec{y}]\subseteq S$
, and the converse inclusion holds if and only if
![]() $\{\vec{a}\in M^{m-r}\mid S[\vec{a}]_{\vec\ell}\not=\emptyset\}\subseteq T$
. We say that T is the proper
$\{\vec{a}\in M^{m-r}\mid S[\vec{a}]_{\vec\ell}\not=\emptyset\}\subseteq T$
. We say that T is the proper
![]() $(\mathcal{K},\vec\ell)$
-projection of S, in symbols
$(\mathcal{K},\vec\ell)$
-projection of S, in symbols
![]() $T=\pi^p_{\mathcal{K},\vec\ell}\,(S)$
, if this condition holds.
$T=\pi^p_{\mathcal{K},\vec\ell}\,(S)$
, if this condition holds.
The argument above shows that if
![]() $T=\pi^p_{\mathcal{K},\vec\ell}\,(S)$
for some team
$T=\pi^p_{\mathcal{K},\vec\ell}\,(S)$
for some team
![]() $S\in\left\Vert \psi \right\Vert^{{M,\vec{z}}}$
, then
$S\in\left\Vert \psi \right\Vert^{{M,\vec{z}}}$
, then
![]() $T\in\left\Vert Q_\mathcal{K}\vec{y}\,\psi \right\Vert^{{M,\vec{x}}}$
. Assuming that
$T\in\left\Vert Q_\mathcal{K}\vec{y}\,\psi \right\Vert^{{M,\vec{x}}}$
. Assuming that
![]() $(M,\emptyset)\notin\mathcal{K}$
, the converse implication is also true. Indeed, if
$(M,\emptyset)\notin\mathcal{K}$
, the converse implication is also true. Indeed, if
![]() $M\models_T Q_\mathcal{K}\vec y\,\psi$
, then there is a function
$M\models_T Q_\mathcal{K}\vec y\,\psi$
, then there is a function
![]() $F\colon T\to \mathcal{P}(M^r)$
such that
$F\colon T\to \mathcal{P}(M^r)$
such that
![]() $M\models_{T[F/\vec{y}]}\psi$
and
$M\models_{T[F/\vec{y}]}\psi$
and
![]() $(M,F(\vec{a}))\in \mathcal{K}$
for all
$(M,F(\vec{a}))\in \mathcal{K}$
for all
![]() $\vec{a}\in T$
. Since
$\vec{a}\in T$
. Since
![]() $(M,\emptyset)\notin\mathcal{K}$
,
$(M,\emptyset)\notin\mathcal{K}$
,
![]() $F(\vec{a})\not=\emptyset$
for every
$F(\vec{a})\not=\emptyset$
for every
![]() $\vec{a}\in T$
, whence
$\vec{a}\in T$
, whence
![]() $T=\pi_{\mathcal{K},\vec\ell}\,(T[F/\vec{y}])$
. Moreover, the condition
$T=\pi_{\mathcal{K},\vec\ell}\,(T[F/\vec{y}])$
. Moreover, the condition
![]() $\{\vec{a}\in M^{m-r}\mid S[\vec{a}]_{\vec\ell}\not=\emptyset\}\subseteq T$
clearly holds for any team S of the form
$\{\vec{a}\in M^{m-r}\mid S[\vec{a}]_{\vec\ell}\not=\emptyset\}\subseteq T$
clearly holds for any team S of the form
![]() $T[F/\vec{y}]$
. Thus, we see that
$T[F/\vec{y}]$
. Thus, we see that
![]() $T=\pi^p_{\mathcal{K},\vec\ell}\,(T[F/\vec{y}])$
.
$T=\pi^p_{\mathcal{K},\vec\ell}\,(T[F/\vec{y}])$
.
Note, however, that if
![]() $(M,\emptyset)\in\mathcal{K}$
, the argument for
$(M,\emptyset)\in\mathcal{K}$
, the argument for
![]() $T=\pi_{\mathcal{K},\vec\ell}\,(T[F/\vec{y}])$
fails: by the definition we always have
$T=\pi_{\mathcal{K},\vec\ell}\,(T[F/\vec{y}])$
fails: by the definition we always have
![]() $\pi_{\mathcal{K},\vec\ell}\,(T[F/\vec{y}])\subseteq T$
, but if
$\pi_{\mathcal{K},\vec\ell}\,(T[F/\vec{y}])\subseteq T$
, but if
![]() $F(\vec{a})=\emptyset$
for some
$F(\vec{a})=\emptyset$
for some
![]() $\vec{a}\in T$
, then
$\vec{a}\in T$
, then
![]() $\vec{a}\notin \pi_{\mathcal{K},\vec\ell}\,(T[F/\vec{y}])$
. In this case, the correct condition for a team T being in the family
$\vec{a}\notin \pi_{\mathcal{K},\vec\ell}\,(T[F/\vec{y}])$
. In this case, the correct condition for a team T being in the family
![]() $\left\Vert Q_\mathcal{K}\vec{y}\,\psi \right\Vert^{{M,\vec{x}}}$
is that there exist teams
$\left\Vert Q_\mathcal{K}\vec{y}\,\psi \right\Vert^{{M,\vec{x}}}$
is that there exist teams
![]() $S\in\left\Vert \psi \right\Vert^{{M,\vec{z}}}$
and
$S\in\left\Vert \psi \right\Vert^{{M,\vec{z}}}$
and
![]() $T'\subseteq T$
such that
$T'\subseteq T$
such that
![]() $T'=\pi^p_{\mathcal{K},\vec\ell}\,(S)$
.
$T'=\pi^p_{\mathcal{K},\vec\ell}\,(S)$
.
We are now ready to define the operators on families of teams corresponding to Lindström quantifiers.
Definition 23. The
![]() $(\mathcal{K},\vec\ell)$
-projection operator
$(\mathcal{K},\vec\ell)$
-projection operator
![]() $\Delta^{M^m}_{\mathcal{K},\vec\ell}\colon\mathcal{P}(\mathcal{P}(M^m))\to\mathcal{P}(\mathcal{P}(M^{m-r}))$
is defined separately in two cases.
$\Delta^{M^m}_{\mathcal{K},\vec\ell}\colon\mathcal{P}(\mathcal{P}(M^m))\to\mathcal{P}(\mathcal{P}(M^{m-r}))$
is defined separately in two cases.
-
If
 $(M,\emptyset)\notin\mathcal{K}$
, then for each
$(M,\emptyset)\notin\mathcal{K}$
, then for each
 $\mathcal{A}\in\mathcal{P}(\mathcal{P}(M^m))$
,
$\mathcal{A}\in\mathcal{P}(\mathcal{P}(M^m))$
,  $$ \Delta^{M^m}_{\mathcal{K},\vec\ell}(\mathcal{A})=\{B\in\mathcal{P}(\mathcal{P}(M^{m-r}))\mid B=\pi^p_{\mathcal{K},\vec\ell}\,(A)\text{ for some }A\in\mathcal{A}\}.$$
$$ \Delta^{M^m}_{\mathcal{K},\vec\ell}(\mathcal{A})=\{B\in\mathcal{P}(\mathcal{P}(M^{m-r}))\mid B=\pi^p_{\mathcal{K},\vec\ell}\,(A)\text{ for some }A\in\mathcal{A}\}.$$
-
If
 $(M,\emptyset)\in\mathcal{K}$
, then for each
$(M,\emptyset)\in\mathcal{K}$
, then for each
 $\mathcal{A}\in\mathcal{P}(\mathcal{P}(M^m))$
,
$\mathcal{A}\in\mathcal{P}(\mathcal{P}(M^m))$
,  $$ \Delta^{M^m}_{\mathcal{K},\vec\ell}(\mathcal{A})=\{B\in\mathcal{P}(\mathcal{P}(M^{m-r}))\mid \pi^p_{\mathcal{K},\vec\ell}\,(A)\subseteq B\text{ for some }A\in\mathcal{A}\}.$$
$$ \Delta^{M^m}_{\mathcal{K},\vec\ell}(\mathcal{A})=\{B\in\mathcal{P}(\mathcal{P}(M^{m-r}))\mid \pi^p_{\mathcal{K},\vec\ell}\,(A)\subseteq B\text{ for some }A\in\mathcal{A}\}.$$
By the argument given before Definition 23, the operator
![]() $\Delta^{M^m}_{\mathcal{K},\vec\ell}$
captures the semantics of the quantifier
$\Delta^{M^m}_{\mathcal{K},\vec\ell}$
captures the semantics of the quantifier
![]() $Q_\mathcal{K}$
:
$Q_\mathcal{K}$
:
Note further that the standard existential and universal quantifiers are special cases of Lindström quantifiers:
![]() $\exists=Q_{\mathcal{K}_\exists}$
for the class
$\exists=Q_{\mathcal{K}_\exists}$
for the class
![]() $\mathcal{K}_\exists=\{(A,R)\mid R\subseteq A, R\not=\emptyset\}$
, and
$\mathcal{K}_\exists=\{(A,R)\mid R\subseteq A, R\not=\emptyset\}$
, and
![]() $\forall=Q_{\mathcal{K}_\forall}$
for
$\forall=Q_{\mathcal{K}_\forall}$
for
![]() $\mathcal{K}_\forall=\{(A,R)\mid R= A\}$
. Thus, the corresponding operators are also identical: for each
$\mathcal{K}_\forall=\{(A,R)\mid R= A\}$
. Thus, the corresponding operators are also identical: for each
![]() $i<m$
,
$i<m$
,
![]() $\Delta_{\exists i}^{M^m}= \Delta_{{\mathcal{K}_\exists},\vec\ell}^{M^m}$
and
$\Delta_{\exists i}^{M^m}= \Delta_{{\mathcal{K}_\exists},\vec\ell}^{M^m}$
and
![]() $\Delta_{\forall i}^{M^m}= \Delta_{{\mathcal{K}_\forall},\vec\ell}^{M^m}\,$
, where
$\Delta_{\forall i}^{M^m}= \Delta_{{\mathcal{K}_\forall},\vec\ell}^{M^m}\,$
, where
![]() $\vec\ell=i$
(i.e.,
$\vec\ell=i$
(i.e.,
![]() $\ell$
is of length 1, and
$\ell$
is of length 1, and
![]() $\ell_0=i$
). For this reason there is no need to consider the operators
$\ell_0=i$
). For this reason there is no need to consider the operators
![]() $\Delta_{\exists i}^{M^m}$
and
$\Delta_{\exists i}^{M^m}$
and
![]() $\Delta_{\forall i}^{M^m}$
separately in the sequel.
$\Delta_{\forall i}^{M^m}$
separately in the sequel.
Remark 24. Note that if
![]() $(M,\emptyset)\in\mathcal{K}$
and
$(M,\emptyset)\in\mathcal{K}$
and
![]() $M\models_\emptyset\psi$
, then
$M\models_\emptyset\psi$
, then
![]() $M\models_T Q_\mathcal{K}\vec y\,\psi$
for any team T. Indeed, if
$M\models_T Q_\mathcal{K}\vec y\,\psi$
for any team T. Indeed, if
![]() $F\colon T\to \mathcal{P}(M^r)$
is the function with
$F\colon T\to \mathcal{P}(M^r)$
is the function with
![]() $F(s)=\emptyset$
for all
$F(s)=\emptyset$
for all
![]() $s\in T$
, then
$s\in T$
, then
![]() $T[F/\vec y]=\emptyset$
, whence the truth condition in Definition 22 holds. Every formula
$T[F/\vec y]=\emptyset$
, whence the truth condition in Definition 22 holds. Every formula
![]() $\psi$
in the extension of first-order logic by the atoms listed in Definition 20 has the Empty Team Property:
$\psi$
in the extension of first-order logic by the atoms listed in Definition 20 has the Empty Team Property:
![]() $M\models_\emptyset\psi$
holds for all models M (see Väänänen Reference Väänänen2007). It is easy to see that the same holds also if we add arbitrary Lindström quantifiers to the logic. In fact, with the exception of logics with the nonempty atom (see Definition 80), all the logics we consider in this paper have the empty team property. Thus, we see that a quantifier
$M\models_\emptyset\psi$
holds for all models M (see Väänänen Reference Väänänen2007). It is easy to see that the same holds also if we add arbitrary Lindström quantifiers to the logic. In fact, with the exception of logics with the nonempty atom (see Definition 80), all the logics we consider in this paper have the empty team property. Thus, we see that a quantifier
![]() $Q_\mathcal{K}$
becomes trivial (on M) in our setting if
$Q_\mathcal{K}$
becomes trivial (on M) in our setting if
![]() $(M,\emptyset)\in \mathcal{K}$
, as in this case
$(M,\emptyset)\in \mathcal{K}$
, as in this case
![]() $M\models_T Q_\mathcal{K}\vec y\,\psi$
holds for every team T and every formula
$M\models_T Q_\mathcal{K}\vec y\,\psi$
holds for every team T and every formula
![]() $\psi$
.
$\psi$
.
3. Dimension calculations
In this section, we compute exact values, or in some cases just upper and lower bounds, to upper, dual upper, and cylindrical dimensions of some important concrete examples of families of sets. This will be used later to estimate dimensions of definable families of teams in various logics built around the atoms of Definition 20.
3.1 Convex shadows and hulls
In this subsection, we develop some auxiliary tools useful in concrete dimension calculations. In particular, we introduce the notions of convex shadow and the dual notion of dual convex shadow, which facilitate the calculation of upper and dual upper dimension of a given family. The point is that when we need to check if a subfamily dominates the given family, the convex shadows are the canonical dominated convex families we need to relate to the sets in the dominating family.
Definition 25. Let
![]() $\mathcal{A}$
be a family of sets and
$\mathcal{A}$
be a family of sets and
![]() $A\in\mathcal{A}$
. The convex shadow of A in the family
$A\in\mathcal{A}$
. The convex shadow of A in the family
![]() $\mathcal{A}$
is the family
$\mathcal{A}$
is the family
Similarly, the dual convex shadow of A in
![]() $\mathcal{A}$
is
$\mathcal{A}$
is
A set
![]() $A\in\mathcal{A}$
is called critical in
$A\in\mathcal{A}$
is called critical in
![]() $\mathcal{A}$
if its convex shadow is maximal in the family
$\mathcal{A}$
if its convex shadow is maximal in the family
We use the notation
Similarly, we define the notion of dual criticality. We denote the family of dually critical sets in
![]() $\mathcal{A}$
by
$\mathcal{A}$
by
![]() $\mathrm{Crit}^{\mathrm{d}}(\mathcal{A})$
:lla.
$\mathrm{Crit}^{\mathrm{d}}(\mathcal{A})$
:lla.
Lemma 26. Let
![]() $\mathcal{A}$
be a family of sets and
$\mathcal{A}$
be a family of sets and
![]() $A\in\mathcal{A}$
.
$A\in\mathcal{A}$
.
-
(a)
 $\partial_A(\mathcal{A})$
is the largest dominated convex family
$\partial_A(\mathcal{A})$
is the largest dominated convex family
 $\mathcal{C}\subseteq\mathcal{A}$
with
$\mathcal{C}\subseteq\mathcal{A}$
with
 $\bigcup\mathcal{C}=A$
. Similarly,
$\bigcup\mathcal{C}=A$
. Similarly,
 $\partial^A(\mathcal{A})$
is the largest supported convex family
$\partial^A(\mathcal{A})$
is the largest supported convex family
 $\mathcal{C}\subseteq\mathcal{A}$
with
$\mathcal{C}\subseteq\mathcal{A}$
with
 $\bigcap\mathcal{C}=A$
.
$\bigcap\mathcal{C}=A$
. -
(b) A family
 $\mathcal{G}\subseteq\mathcal{A}$
dominates
$\mathcal{G}\subseteq\mathcal{A}$
dominates
 $\mathcal{A}$
if and only if
$\mathcal{A}$
if and only if
 $\bigcup_{G\in\mathcal{G}}\partial_G(\mathcal{A})=\mathcal{A}$
. Dually,
$\bigcup_{G\in\mathcal{G}}\partial_G(\mathcal{A})=\mathcal{A}$
. Dually,
 $\mathcal{H}\subseteq\mathcal{A}$
supports
$\mathcal{H}\subseteq\mathcal{A}$
supports
 $\mathcal{A}$
if and only if
$\mathcal{A}$
if and only if
 $\bigcup_{H\in\mathcal{H}}\partial^H(\mathcal{A})=\mathcal{A}$
.
$\bigcup_{H\in\mathcal{H}}\partial^H(\mathcal{A})=\mathcal{A}$
. -
(c) Suppose that the family
 $\mathcal{A}$
satisfies Zorn condition. Then there is a family
$\mathcal{A}$
satisfies Zorn condition. Then there is a family
 $\mathcal{G}$
dominating
$\mathcal{G}$
dominating
 $\mathcal{A}$
such that
$\mathcal{A}$
such that
 $\mathcal{G}\subseteq\mathrm{Crit}(\mathcal{A})$
and
$\mathcal{G}\subseteq\mathrm{Crit}(\mathcal{A})$
and
 $|\mathcal{G}|= \mathrm{D}(\mathcal{A})$
. The dual result also holds.
$|\mathcal{G}|= \mathrm{D}(\mathcal{A})$
. The dual result also holds.
Proof. The proofs of the dual claims are similar to the primary claims, so we shall skip them.
-
(a) Clearly,
 $\partial_A(\mathcal{A})$
is a dominated convex subfamily of
$\partial_A(\mathcal{A})$
is a dominated convex subfamily of
 $\mathcal{A}$
with
$\mathcal{A}$
with
 $\bigcup\mathcal{A}=A$
. Suppose
$\bigcup\mathcal{A}=A$
. Suppose
 $\mathcal{C}\subseteq\mathcal{A}$
is another dominated convex subfamily with
$\mathcal{C}\subseteq\mathcal{A}$
is another dominated convex subfamily with
 $\bigcup\mathcal{C}=A$
. For
$\bigcup\mathcal{C}=A$
. For
 $C\in\mathcal{C}$
, we have
$C\in\mathcal{C}$
, we have
 $[C,A]\subseteq\mathcal{C}\subseteq\mathcal{A}$
by convexity of
$[C,A]\subseteq\mathcal{C}\subseteq\mathcal{A}$
by convexity of
 $\mathcal{C}$
, so
$\mathcal{C}$
, so
 $\mathcal{C}\subseteq\partial_A(\mathcal{A})$
.
$\mathcal{C}\subseteq\partial_A(\mathcal{A})$
. -
(b) If
 $\bigcup_{G\in\mathcal{G}}\partial_G(\mathcal{A})=\mathcal{A}$
, then the dominated convex families
$\bigcup_{G\in\mathcal{G}}\partial_G(\mathcal{A})=\mathcal{A}$
, then the dominated convex families
 $\partial_G(\mathcal{A})\subseteq\mathcal{A}$
,
$\partial_G(\mathcal{A})\subseteq\mathcal{A}$
,
 $G\in\mathcal{G}$
, witness that
$G\in\mathcal{G}$
, witness that
 $\mathcal{G}$
dominates
$\mathcal{G}$
dominates
 $\mathcal{A}$
.Conversely, suppose that
$\mathcal{A}$
.Conversely, suppose that
 $\mathcal{G}$
dominates
$\mathcal{G}$
dominates
 $\mathcal{A}$
and the families
$\mathcal{A}$
and the families
 $\mathcal{D}_G$
,
$\mathcal{D}_G$
,
 $G\in\mathcal{G}$
, witness that (meaning that
$G\in\mathcal{G}$
, witness that (meaning that
 $\bigcup_{G\in\mathcal{G}}\mathcal{D}_G=\mathcal{A}$
and
$\bigcup_{G\in\mathcal{G}}\mathcal{D}_G=\mathcal{A}$
and
 $\bigcup\mathcal{D}_G=G$
, for each
$\bigcup\mathcal{D}_G=G$
, for each
 $G\in\mathcal{G}$
). Then by the preceding claim, we have that for every
$G\in\mathcal{G}$
). Then by the preceding claim, we have that for every
 $G\in\mathcal{G}$
,
$G\in\mathcal{G}$
,
 $\mathcal{D}_G\subseteq\partial_G(\mathcal{A})$
, implying
$\mathcal{D}_G\subseteq\partial_G(\mathcal{A})$
, implying
 $\bigcup_{G\in\mathcal{G}}\partial_G(\mathcal{A})=\mathcal{A}$
.
$\bigcup_{G\in\mathcal{G}}\partial_G(\mathcal{A})=\mathcal{A}$
. -
(c) Pick a subfamily
 $\mathcal{G}_0\subseteq\mathcal{A}$
dominating
$\mathcal{G}_0\subseteq\mathcal{A}$
dominating
 $\mathcal{A}$
such that
$\mathcal{A}$
such that
 $|\mathcal{G}_0|=\mathrm{D}(\mathcal{A})$
. Let
$|\mathcal{G}_0|=\mathrm{D}(\mathcal{A})$
. Let
 $G\in\mathcal{G}_0$
, and consider the family First we establish that
$G\in\mathcal{G}_0$
, and consider the family First we establish that $$ \mathcal{B}_G = \{ A\in\mathcal{A} \mid \partial_G(\mathcal{A})\subseteq\partial_A(\mathcal{A}) \}.$$
$$ \mathcal{B}_G = \{ A\in\mathcal{A} \mid \partial_G(\mathcal{A})\subseteq\partial_A(\mathcal{A}) \}.$$
 $\mathcal{B}_G$
satisfies the Zorn condition. Indeed, let
$\mathcal{B}_G$
satisfies the Zorn condition. Indeed, let
 $\mathcal{K}\subseteq\mathcal{B}_G$
be a chain. As
$\mathcal{K}\subseteq\mathcal{B}_G$
be a chain. As
 $\mathcal{K}\subseteq\mathcal{A}$
and
$\mathcal{K}\subseteq\mathcal{A}$
and
 $\mathcal{A}$
satisfies the Zorn condition, we have that
$\mathcal{A}$
satisfies the Zorn condition, we have that
 $B=\bigcup\mathcal{K}\in\mathcal{A}$
. We need to show further that
$B=\bigcup\mathcal{K}\in\mathcal{A}$
. We need to show further that
 $\partial_G(\mathcal{A})\subseteq\partial_B(\mathcal{A})$
. Let
$\partial_G(\mathcal{A})\subseteq\partial_B(\mathcal{A})$
. Let
 $A\in\partial_G(\mathcal{A})$
and
$A\in\partial_G(\mathcal{A})$
and
 $C\in[A,B]$
. Studying the chain
$C\in[A,B]$
. Studying the chain
 $\mathcal{K}'=\{C\cap K \mid K\in\mathcal{K} \}$
, we observe that for each
$\mathcal{K}'=\{C\cap K \mid K\in\mathcal{K} \}$
, we observe that for each
 $K\in\mathcal{K}$
, we have that
$K\in\mathcal{K}$
, we have that
 $A=A\cap G\subseteq A\cap K\subseteq C\cap K\subseteq K$
, implying that
$A=A\cap G\subseteq A\cap K\subseteq C\cap K\subseteq K$
, implying that
 $C\cap K\in [A,K]\subseteq\partial_K(\mathcal{A})$
, as
$C\cap K\in [A,K]\subseteq\partial_K(\mathcal{A})$
, as
 $A\in\partial_G(\mathcal{A})\subseteq\partial_K(\mathcal{A})$
. Hence,
$A\in\partial_G(\mathcal{A})\subseteq\partial_K(\mathcal{A})$
. Hence,
 $C\cap K\in\mathcal{A}$
and since this holds for each
$C\cap K\in\mathcal{A}$
and since this holds for each
 $K\in\mathcal{K}$
, we have that
$K\in\mathcal{K}$
, we have that
 $\mathcal{K}'\subseteq\mathcal{A}$
. As
$\mathcal{K}'\subseteq\mathcal{A}$
. As
 $\mathcal{A}$
satisfies the Zorn condition, we have that
$\mathcal{A}$
satisfies the Zorn condition, we have that
 $C=C\cap B=C\bigcup\mathcal{K}=\bigcup\mathcal{K}'\in\mathcal{A}$
. As
$C=C\cap B=C\bigcup\mathcal{K}=\bigcup\mathcal{K}'\in\mathcal{A}$
. As
 $C\in\mathcal{A}$
, for every
$C\in\mathcal{A}$
, for every
 $C\in[A,B]$
, we get
$C\in[A,B]$
, we get
 $[A,B]\subseteq\mathcal{A}$
and consequently
$[A,B]\subseteq\mathcal{A}$
and consequently
 $A\in\partial_B(\mathcal{A})$
. Summarizing, we have that
$A\in\partial_B(\mathcal{A})$
. Summarizing, we have that
 $\partial_G(\mathcal{A})\subseteq\partial_B(\mathcal{A})$
implying
$\partial_G(\mathcal{A})\subseteq\partial_B(\mathcal{A})$
implying
 $B\in\mathcal{B}_G$
, which means that
$B\in\mathcal{B}_G$
, which means that
 $\mathcal{B}_G$
satisfies the Zorn condition.
$\mathcal{B}_G$
satisfies the Zorn condition.
As
![]() $\mathcal{B}_G$
satisfies the Zorn condition, by Zorn’s lemma, there is a maximal element in
$\mathcal{B}_G$
satisfies the Zorn condition, by Zorn’s lemma, there is a maximal element in
![]() $\mathcal{B}_G$
, say,
$\mathcal{B}_G$
, say,
![]() $D_G$
. The maximality of
$D_G$
. The maximality of
![]() $D_G$
clearly impies that
$D_G$
clearly impies that
![]() $D_G$
is critical in
$D_G$
is critical in
![]() $\mathcal{A}$
. Recall that
$\mathcal{A}$
. Recall that
![]() $D_G\in\mathcal{B}_G$
means also that
$D_G\in\mathcal{B}_G$
means also that
![]() $\partial_G(\mathcal{A})\subseteq \partial_{D_G}(\mathcal{A})$
. Collect these set together and put
$\partial_G(\mathcal{A})\subseteq \partial_{D_G}(\mathcal{A})$
. Collect these set together and put
![]() $\mathcal{G}=\{D_G \mid G\in\mathcal{G}_0 \}$
. As
$\mathcal{G}=\{D_G \mid G\in\mathcal{G}_0 \}$
. As
![]() $\mathcal{G}_0$
dominates
$\mathcal{G}_0$
dominates
![]() $\mathcal{A}$
, we have
$\mathcal{A}$
, we have
![]() $\bigcup_{G\in\mathcal{G}_0}\partial_G(\mathcal{A})=\mathcal{A}$
, which now clearly implies
$\bigcup_{G\in\mathcal{G}_0}\partial_G(\mathcal{A})=\mathcal{A}$
, which now clearly implies
Hence,
![]() $\mathcal{G}$
also dominates
$\mathcal{G}$
also dominates
![]() $\mathcal{A}$
, and
$\mathcal{A}$
, and
![]() $|\mathcal{G}|\le|\mathcal{G}_0|=\mathrm{D}(\mathcal{A})$
, so
$|\mathcal{G}|\le|\mathcal{G}_0|=\mathrm{D}(\mathcal{A})$
, so
![]() $|\mathcal{G}|=\mathrm{D}(G)$
.
$|\mathcal{G}|=\mathrm{D}(G)$
.
Convex shadows and dual convex shadows are maximal subfamilies satisfying the appropriate properties. The similar operations that produce superfamilies instead of subfamilies are called hulls. We shall utilize these latter concepts in later sections.
Definition 27. Let
![]() $\mathcal{A}$
be a nonempty family of sets. The convex hull of
$\mathcal{A}$
be a nonempty family of sets. The convex hull of
![]() $\mathcal{A}$
is
$\mathcal{A}$
is
the dominated (convex) hull of
![]() $\mathcal{A}$
is
$\mathcal{A}$
is
and the supported (convex) hull is
We set also
![]() $\mathcal{H}(\emptyset)=\emptyset$
.
$\mathcal{H}(\emptyset)=\emptyset$
.
If the family of sets is finite, we may drop the braces from the notation in the customary manner, writing
![]() $\mathcal{H}_*(A_0,\ldots,A_{k-1})$
instead of
$\mathcal{H}_*(A_0,\ldots,A_{k-1})$
instead of
![]() $\mathcal{H}_*(\{A_0,\ldots,A_{k-1}\})$
, or
$\mathcal{H}_*(\{A_0,\ldots,A_{k-1}\})$
, or
![]() $\mathcal{H}^*(A_0,\ldots,A_{k-1})$
instead of
$\mathcal{H}^*(A_0,\ldots,A_{k-1})$
instead of
![]() $\mathcal{H}_*(\{A_0,\ldots,A_{k-1}\})$
. Note the special cases
$\mathcal{H}_*(\{A_0,\ldots,A_{k-1}\})$
. Note the special cases
![]() $\mathcal{H}_*(A,B)=[A,A\cup B]\cup[B,A\cup B]$
and
$\mathcal{H}_*(A,B)=[A,A\cup B]\cup[B,A\cup B]$
and
![]() $\mathcal{H}^*(A,B)=[A\cap B,A]\cup[A\cap B,B]$
.
$\mathcal{H}^*(A,B)=[A\cap B,A]\cup[A\cap B,B]$
.
We omit the proof of the following lemma, as it is straightforward.
Lemma 28. Let
![]() $\mathcal{A}$
be a nonempty family of sets. Then
$\mathcal{A}$
be a nonempty family of sets. Then
-
(a)
 $\mathcal{H}(\mathcal{A})$
is the least convex family containing
$\mathcal{H}(\mathcal{A})$
is the least convex family containing
 $\mathcal{A}$
,
$\mathcal{A}$
, -
(b)
 $\mathcal{H}_*(\mathcal{A})$
is the least dominated convex family containing
$\mathcal{H}_*(\mathcal{A})$
is the least dominated convex family containing
 $\mathcal{A}$
and
$\mathcal{A}$
and -
(c)
 $\mathcal{H}^*(\mathcal{A})$
is the least supported convex family containing
$\mathcal{H}^*(\mathcal{A})$
is the least supported convex family containing
 $\mathcal{A}$
.
$\mathcal{A}$
.
Note that there is no unique least dominated, or supported, convex family containing the empty family (all the singletons do).
3.2 Dimensions of particular families
In this subsection, we calculate the dimensions of some concrete families of sets that are relevant to team semantics but certainly are familiar from other contexts, too. These calculations will be the basis of our results in the next section.
For nonempty finite base sets X and Y, here is a list of families that we consider:
 \begin{align*}\mathcal{F} &= \{ f\subseteq X\times Y \mid f\text{ is a mapping }\}, \\\mathcal{X} &=\{ R\subseteq X\times X \mid \mathrm{dom}(R)\cap\mathrm{rg}(R)=\emptyset \}\\\mathcal{I}_{\subseteq} &=\{ R\subseteq X\times X \mid \mathrm{dom}(R)\subseteq \mathrm{rg}(R) \}, \\\mathcal{Y} &=\{ R\subseteq X\times Y \mid {\textit{R}} \, \text{is anonymous} \,\\\mathcal{I}_{\perp} &=\{ A\times B \mid A\subseteq X,\,B\subseteq Y \},\end{align*}
\begin{align*}\mathcal{F} &= \{ f\subseteq X\times Y \mid f\text{ is a mapping }\}, \\\mathcal{X} &=\{ R\subseteq X\times X \mid \mathrm{dom}(R)\cap\mathrm{rg}(R)=\emptyset \}\\\mathcal{I}_{\subseteq} &=\{ R\subseteq X\times X \mid \mathrm{dom}(R)\subseteq \mathrm{rg}(R) \}, \\\mathcal{Y} &=\{ R\subseteq X\times Y \mid {\textit{R}} \, \text{is anonymous} \,\\\mathcal{I}_{\perp} &=\{ A\times B \mid A\subseteq X,\,B\subseteq Y \},\end{align*}
where we call a relation
![]() $R\subseteq X\times Y$
anonymous if for all
$R\subseteq X\times Y$
anonymous if for all
![]() $x\in\mathrm{dom}(R)$
there exist distinct
$x\in\mathrm{dom}(R)$
there exist distinct
![]() $y,y'\in Y$
with
$y,y'\in Y$
with
![]() $(x,y),(x,y')\in R$
.
$(x,y),(x,y')\in R$
.
We calculate the dimensions of these families with the aid of shadows and critical sets. The families
![]() $\mathcal{F}$
and
$\mathcal{F}$
and
![]() $\mathcal{X}$
are the easiest cases, as they are downward closed. We handle each of the other families in separate lemmas of their own.
$\mathcal{X}$
are the easiest cases, as they are downward closed. We handle each of the other families in separate lemmas of their own.
Lemma 29.
Assume that
![]() $m=|X|\ge 2$
. Let
$m=|X|\ge 2$
. Let
![]() $R,S\in \mathcal{I}_{\subseteq}$
.
$R,S\in \mathcal{I}_{\subseteq}$
.
-
(a) If
 $S\subseteq R$
, then
$S\subseteq R$
, then  \[ [S,R] \subseteq \mathcal{I}_{\subseteq} \text{ if and only if } \mathrm{dom}(R\smallsetminus\mathrm{id}_X)\subseteq\mathrm{rg}(S).\]
\[ [S,R] \subseteq \mathcal{I}_{\subseteq} \text{ if and only if } \mathrm{dom}(R\smallsetminus\mathrm{id}_X)\subseteq\mathrm{rg}(S).\]
-
(b) We have
where \[ \partial_R(\mathcal{I}_{\subseteq})=\{ T\in\mathcal{I}_{\subseteq} \mid T\subseteq R,\,A\subseteq\mathrm{rg}(T)\}\]
\[ \partial_R(\mathcal{I}_{\subseteq})=\{ T\in\mathcal{I}_{\subseteq} \mid T\subseteq R,\,A\subseteq\mathrm{rg}(T)\}\]
 $A=\mathrm{dom}(R\smallsetminus\mathrm{id}_X)$
.
$A=\mathrm{dom}(R\smallsetminus\mathrm{id}_X)$
.
-
(c) For
 $A\subseteq X$
, put
$A\subseteq X$
, put
 $R_A=(A\times X)\cup\mathrm{id}_X$
. Then we have that
$R_A=(A\times X)\cup\mathrm{id}_X$
. Then we have that
 $R_A\in\mathcal{I}_{\subseteq}$
and
$R_A\in\mathcal{I}_{\subseteq}$
and  \[ \partial_{R_A}(\mathcal{I}_{\subseteq}) = \{ T\in\mathcal{I}_{\subseteq} \mid \mathrm{dom}(T\smallsetminus\mathrm{id}_X)\subseteq A\subseteq\mathrm{rg}(T) \}.\]
\[ \partial_{R_A}(\mathcal{I}_{\subseteq}) = \{ T\in\mathcal{I}_{\subseteq} \mid \mathrm{dom}(T\smallsetminus\mathrm{id}_X)\subseteq A\subseteq\mathrm{rg}(T) \}.\]
-
(d) We have
 $\mathrm{Crit}(\mathcal{I}_{\subseteq})= \{ R_A \mid A\subseteq X\}$
.
$\mathrm{Crit}(\mathcal{I}_{\subseteq})= \{ R_A \mid A\subseteq X\}$
. -
(e)
 $\mathrm{Crit}(\mathcal{I}_{\subseteq})\smallsetminus\{R_{\{a\}} \mid a\in X \}$
is a family of smallest size that dominates
$\mathrm{Crit}(\mathcal{I}_{\subseteq})\smallsetminus\{R_{\{a\}} \mid a\in X \}$
is a family of smallest size that dominates
 $\mathcal{I}_{\subseteq}$
.
$\mathcal{I}_{\subseteq}$
. -
(f) Denote
 $B=\mathrm{rg}(R)$
. Then
$B=\mathrm{rg}(R)$
. Then  \[ \partial^R(\mathcal{I}_{\subseteq}) =\{ T\in\mathcal{I}_{\subseteq} \mid R\subseteq T,\,\mathrm{dom}(T\smallsetminus\mathrm{id}_X)\subseteq B \} =[R,R_B].\]
\[ \partial^R(\mathcal{I}_{\subseteq}) =\{ T\in\mathcal{I}_{\subseteq} \mid R\subseteq T,\,\mathrm{dom}(T\smallsetminus\mathrm{id}_X)\subseteq B \} =[R,R_B].\]
-
(g)
 $\mathrm{Crit}^{\mathrm{d}}(\mathcal{I}_{\subseteq})=\{ R\in\mathcal{I}_{\subseteq} \mid R^{-1}\text{ is a mapping}\}$
.
$\mathrm{Crit}^{\mathrm{d}}(\mathcal{I}_{\subseteq})=\{ R\in\mathcal{I}_{\subseteq} \mid R^{-1}\text{ is a mapping}\}$
. -
(h)
 $\mathrm{Crit}^{\mathrm{d}}(\mathcal{I}_{\subseteq})\smallsetminus\{{\{(a,a)\}} \mid a\in X \}$
is the smallest family that supports
$\mathrm{Crit}^{\mathrm{d}}(\mathcal{I}_{\subseteq})\smallsetminus\{{\{(a,a)\}} \mid a\in X \}$
is the smallest family that supports
 $\mathcal{I}_{\subseteq}$
.
$\mathcal{I}_{\subseteq}$
.
Proof.
-
(a) Suppose
 $\mathrm{dom}(R\smallsetminus\mathrm{id}_X)\subseteq\mathrm{rg}(S)$
and consider
$\mathrm{dom}(R\smallsetminus\mathrm{id}_X)\subseteq\mathrm{rg}(S)$
and consider
 $T\in[S,R]$
, i.e.,
$T\in[S,R]$
, i.e.,
 $S\subseteq T\subseteq R$
. Let
$S\subseteq T\subseteq R$
. Let
 $x\in\mathrm{dom}(T)$
. Pick y such that
$x\in\mathrm{dom}(T)$
. Pick y such that
 $(x,y)\in T$
. If
$(x,y)\in T$
. If
 $x=y$
, then trivially
$x=y$
, then trivially
 $x\in\mathrm{rg}(T)$
. Otherwise
$x\in\mathrm{rg}(T)$
. Otherwise
 $x\neq y$
, so Thus, in both cases, we have
$x\neq y$
, so Thus, in both cases, we have \[ x\in\mathrm{dom}(T\smallsetminus\mathrm{id}_X)\subseteq\mathrm{dom}(R\smallsetminus\mathrm{id}_X)\subseteq\mathrm{rg}(S)\subseteq\mathrm{rg}(T).\]
\[ x\in\mathrm{dom}(T\smallsetminus\mathrm{id}_X)\subseteq\mathrm{dom}(R\smallsetminus\mathrm{id}_X)\subseteq\mathrm{rg}(S)\subseteq\mathrm{rg}(T).\]
 $x\in\mathrm{rg}(T)$
, so
$x\in\mathrm{rg}(T)$
, so
 $\mathrm{dom}(T)\subseteq\mathrm{rg}(T)$
. Hence,
$\mathrm{dom}(T)\subseteq\mathrm{rg}(T)$
. Hence,
 $T\in\mathcal{I}_{\subseteq}$
, and
$T\in\mathcal{I}_{\subseteq}$
, and
 $[S,R]\subseteq\mathcal{I}_{\subseteq}$
.Suppose to the contrary that
$[S,R]\subseteq\mathcal{I}_{\subseteq}$
.Suppose to the contrary that
 $\mathrm{dom}(R\smallsetminus\mathrm{id}_X)\not\subseteq\mathrm{rg}(S)$
. Then we may choose
$\mathrm{dom}(R\smallsetminus\mathrm{id}_X)\not\subseteq\mathrm{rg}(S)$
. Then we may choose
 $x\in\mathrm{dom}(R\smallsetminus\mathrm{id}_X)\smallsetminus\mathrm{rg}(S)$
. Pick
$x\in\mathrm{dom}(R\smallsetminus\mathrm{id}_X)\smallsetminus\mathrm{rg}(S)$
. Pick
 $y\neq x$
with
$y\neq x$
with
 $(x,y)\in R$
, and consider
$(x,y)\in R$
, and consider
 $T=S\cup\{(x,y)\}$
. Clearly,
$T=S\cup\{(x,y)\}$
. Clearly,
 $x\in\mathrm{dom}(T)$
, but
$x\in\mathrm{dom}(T)$
, but
 $x\not\in\mathrm{rg}(T)=\mathrm{rg}(S)\cup\{y\}$
, so
$x\not\in\mathrm{rg}(T)=\mathrm{rg}(S)\cup\{y\}$
, so
 $T\not\in\mathcal{I}_{\subseteq}$
. This proves that
$T\not\in\mathcal{I}_{\subseteq}$
. This proves that
 $[S,R]\not\subseteq\mathcal{I}_{\subseteq}$
.
$[S,R]\not\subseteq\mathcal{I}_{\subseteq}$
.
-
(b) This is a direct application of the previous item.
-
(c) We first note that
 $\mathrm{dom}(R_A)=X=\mathrm{rg}(R_A)$
, as
$\mathrm{dom}(R_A)=X=\mathrm{rg}(R_A)$
, as
 $\mathrm{id}_X\subseteq R_A$
, implying that
$\mathrm{id}_X\subseteq R_A$
, implying that
 $R_A\in\mathcal{I}_{\subseteq}$
. It is easy to see that
$R_A\in\mathcal{I}_{\subseteq}$
. It is easy to see that
 $T\subseteq R_A$
if and only if
$T\subseteq R_A$
if and only if
 $\mathrm{dom}(T\smallsetminus\mathrm{id}_X)\subseteq A$
, so the latter result follows from the preceding item.
$\mathrm{dom}(T\smallsetminus\mathrm{id}_X)\subseteq A$
, so the latter result follows from the preceding item. -
(d) To prove that each critical set in
 $\mathcal{I}_{\subseteq}$
is of the form
$\mathcal{I}_{\subseteq}$
is of the form
 $R_A$
, for some
$R_A$
, for some
 $A\subseteq X$
, let
$A\subseteq X$
, let
 $R\in\mathcal{I}_{\subseteq}$
. Denote
$R\in\mathcal{I}_{\subseteq}$
. Denote
 $A=\mathrm{dom}(R\smallsetminus\mathrm{id}_X)$
. One easily sees that
$A=\mathrm{dom}(R\smallsetminus\mathrm{id}_X)$
. One easily sees that
 $R\subseteq R_A$
, and now the previous items imply that
$R\subseteq R_A$
, and now the previous items imply that
 $\partial_R(\mathcal{I}_{\subseteq})\subseteq\partial_{R_A}(\mathcal{I}_{\subseteq})$
. Consequently, it is enough to show that the shadows of the sets
$\partial_R(\mathcal{I}_{\subseteq})\subseteq\partial_{R_A}(\mathcal{I}_{\subseteq})$
. Consequently, it is enough to show that the shadows of the sets
 $R_A$
,
$R_A$
,
 $A\subseteq X$
, are incomparable. Let
$A\subseteq X$
, are incomparable. Let
 $A,A'\subseteq X$
,
$A,A'\subseteq X$
,
 $A\neq A'$
. Suppose first that
$A\neq A'$
. Suppose first that
 $|A|\ge 2$
. Let f be any permutation of A without fixed points. Then
$|A|\ge 2$
. Let f be any permutation of A without fixed points. Then
 $\mathrm{dom}(f\smallsetminus\mathrm{id}_X)=\mathrm{dom}(f)=A=\mathrm{rg}(f)$
, so the preceding item implies that
$\mathrm{dom}(f\smallsetminus\mathrm{id}_X)=\mathrm{dom}(f)=A=\mathrm{rg}(f)$
, so the preceding item implies that
 $f\in\partial_{R_A}(\mathcal{I}_{\subseteq})$
, but
$f\in\partial_{R_A}(\mathcal{I}_{\subseteq})$
, but
 $f\not\in\partial_{R_{A'}}(\mathcal{I}_{\subseteq})$
. If
$f\not\in\partial_{R_{A'}}(\mathcal{I}_{\subseteq})$
. If
 $A=\emptyset$
, we see similarly that
$A=\emptyset$
, we see similarly that
 $\emptyset\in\partial_{R_A}(\mathcal{I}_{\subseteq})\smallsetminus\partial_{R_{A'}}(\mathcal{I}_{\subseteq})$
. Now suppose
$\emptyset\in\partial_{R_A}(\mathcal{I}_{\subseteq})\smallsetminus\partial_{R_{A'}}(\mathcal{I}_{\subseteq})$
. Now suppose
 $A=\{a\}$
is a singleton. Then there is
$A=\{a\}$
is a singleton. Then there is
 $b\in X$
,
$b\in X$
,
 $b\neq a$
, such that
$b\neq a$
, such that
 $A'\neq\{a,b\}$
. Consider
$A'\neq\{a,b\}$
. Consider
 $T=\{(a,b),(a,a)\}$
. Then
$T=\{(a,b),(a,a)\}$
. Then
 $\mathrm{dom}(T)=\{a\}\subseteq\{a,b\}=\mathrm{rg}(T)$
, whence
$\mathrm{dom}(T)=\{a\}\subseteq\{a,b\}=\mathrm{rg}(T)$
, whence
 $T\in\partial_{R_A}(\mathcal{I}_{\subseteq})$
but
$T\in\partial_{R_A}(\mathcal{I}_{\subseteq})$
but
 $T\not\in\partial_{R_{A'}}(\mathcal{I}_{\subseteq})$
.
$T\not\in\partial_{R_{A'}}(\mathcal{I}_{\subseteq})$
. -
(e) By Lemma 26, we know that
 $\mathrm{Crit}(\mathcal{I}_{\subseteq})$
dominates
$\mathrm{Crit}(\mathcal{I}_{\subseteq})$
dominates
 $\mathcal{I}_{\subseteq}$
, and we can find a dominating family of the smallest size from the collection of its subfamilies. Now the proof of the preceding item actually show that
$\mathcal{I}_{\subseteq}$
, and we can find a dominating family of the smallest size from the collection of its subfamilies. Now the proof of the preceding item actually show that
 $\mathrm{Crit}(\mathcal{I}_{\subseteq})\smallsetminus\{R_A\}$
does not dominate
$\mathrm{Crit}(\mathcal{I}_{\subseteq})\smallsetminus\{R_A\}$
does not dominate
 $\mathcal{I}_{\subseteq}$
, for any
$\mathcal{I}_{\subseteq}$
, for any
 $A\subseteq X$
which is not a singleton. However,
$A\subseteq X$
which is not a singleton. However,
 $\mathrm{Crit}(\mathcal{I}_{\subseteq})\smallsetminus\{R_{\{a\}} \mid a\in X \}$
does, as we see from the following: Let
$\mathrm{Crit}(\mathcal{I}_{\subseteq})\smallsetminus\{R_{\{a\}} \mid a\in X \}$
does, as we see from the following: Let
 $a\in X$
and let
$a\in X$
and let
 $R\in\mathcal{I}_{\subseteq}$
be any set with
$R\in\mathcal{I}_{\subseteq}$
be any set with
 $a\in\mathrm{dom}(R\smallsetminus\mathrm{id}_X)$
. Pick
$a\in\mathrm{dom}(R\smallsetminus\mathrm{id}_X)$
. Pick
 $b\neq a$
with
$b\neq a$
with
 $(a,b)\in R$
. Then
$(a,b)\in R$
. Then
 $a\in\mathrm{dom}(R)\subseteq\mathrm{rg}(R)$
, but also
$a\in\mathrm{dom}(R)\subseteq\mathrm{rg}(R)$
, but also
 $b\in\mathrm{rg}(R)$
, so
$b\in\mathrm{rg}(R)$
, so
 $a,b\in\mathrm{rg}(R)$
. Item c now shows that
$a,b\in\mathrm{rg}(R)$
. Item c now shows that
 $R\subseteq R_A$
where
$R\subseteq R_A$
where
 $A=\mathrm{rg}(R)$
, and
$A=\mathrm{rg}(R)$
, and
 $|A|\ge 2$
.
$|A|\ge 2$
. -
(f) The first equality is a direct consequence of item a. For the second equality, it is enough to observe that
 $R_B$
is, by definition, the largest
$R_B$
is, by definition, the largest
 $T\subseteq X\times X$
such that
$T\subseteq X\times X$
such that
 $\mathrm{dom}(T\smallsetminus\mathrm{id}_X)\subseteq B$
.
$\mathrm{dom}(T\smallsetminus\mathrm{id}_X)\subseteq B$
. -
(g) Assume that
 $R\subseteq S$
and
$R\subseteq S$
and
 $\mathrm{rg}(R)=\mathrm{rg}(S)=B$
hold for
$\mathrm{rg}(R)=\mathrm{rg}(S)=B$
hold for
 $R,S\in\mathcal{I}_{\subseteq}$
. Then by the previous item, we have that
$R,S\in\mathcal{I}_{\subseteq}$
. Then by the previous item, we have that
 $\partial^S(\mathcal{I}_{\subseteq})=[S,R_B]\subseteq[R,R_B]\subseteq\partial^R(\mathcal{I}_{\subseteq})$
. Consequently, R can have a maximal dual shadow only if
$\partial^S(\mathcal{I}_{\subseteq})=[S,R_B]\subseteq[R,R_B]\subseteq\partial^R(\mathcal{I}_{\subseteq})$
. Consequently, R can have a maximal dual shadow only if
 $R\in\mathcal{I}_{\subseteq}$
is minimal among all the relations having the same range, i.e., if
$R\in\mathcal{I}_{\subseteq}$
is minimal among all the relations having the same range, i.e., if
 $R^{-1}$
is a mapping. Let us check that this condition is also sufficient, i.e., if
$R^{-1}$
is a mapping. Let us check that this condition is also sufficient, i.e., if
 $R\in\mathcal{I}_{\subseteq}$
and
$R\in\mathcal{I}_{\subseteq}$
and
 $R^{-1}$
is a mapping, then R has a maximal dual shadow among the dual shadows
$R^{-1}$
is a mapping, then R has a maximal dual shadow among the dual shadows
 $\partial^S(\mathcal{I}_{\subseteq})$
, for
$\partial^S(\mathcal{I}_{\subseteq})$
, for
 $S\in\mathcal{I}_{\subseteq}$
. We need to consider only the case when
$S\in\mathcal{I}_{\subseteq}$
. We need to consider only the case when
 $S\subsetneq R$
and
$S\subsetneq R$
and
 $S^{-1}$
is also a mapping. But then
$S^{-1}$
is also a mapping. But then
 $\mathrm{rg}(S)=\mathrm{dom}(S^{-1})\subsetneq \mathrm{dom}(R^{-1})=\mathrm{rg}(R)=B$
, which implies that
$\mathrm{rg}(S)=\mathrm{dom}(S^{-1})\subsetneq \mathrm{dom}(R^{-1})=\mathrm{rg}(R)=B$
, which implies that
 $\mathrm{dom}(R_B\smallsetminus\mathrm{id}_X)=B\not\subseteq\mathrm{rg}(S)$
. Hence,
$\mathrm{dom}(R_B\smallsetminus\mathrm{id}_X)=B\not\subseteq\mathrm{rg}(S)$
. Hence,
 $R_B\not\in\partial^S(\mathcal{I}_{\subseteq})$
and consequently
$R_B\not\in\partial^S(\mathcal{I}_{\subseteq})$
and consequently
 $\partial^R(\mathcal{I}_{\subseteq})\not\subseteq\partial^S(\mathcal{I}_{\subseteq})$
. This means that R has a maximal dual shadow.
$\partial^R(\mathcal{I}_{\subseteq})\not\subseteq\partial^S(\mathcal{I}_{\subseteq})$
. This means that R has a maximal dual shadow. -
(h) Denote
 $\mathcal{C}=\mathrm{Crit}^{\mathrm{d}}(\mathcal{I}_{\subseteq})\smallsetminus\{{\{(a,a)\}} \mid a\in X \}$
. We first show that
$\mathcal{C}=\mathrm{Crit}^{\mathrm{d}}(\mathcal{I}_{\subseteq})\smallsetminus\{{\{(a,a)\}} \mid a\in X \}$
. We first show that
 $\mathcal{C}$
supports
$\mathcal{C}$
supports
 $\mathcal{I}_{\subseteq}$
. Let
$\mathcal{I}_{\subseteq}$
. Let
 $R\in\mathcal{I}_{\subseteq}$
. If
$R\in\mathcal{I}_{\subseteq}$
. If
 $\mathrm{rg}(R)$
is a singleton, say,
$\mathrm{rg}(R)$
is a singleton, say,
 $\mathrm{rg}(R)=\{a\}$
, then we must have
$\mathrm{rg}(R)=\{a\}$
, then we must have
 $R=\{(a,a)\}$
and
$R=\{(a,a)\}$
and
 $R\in\partial^{\emptyset}(\mathcal{I}_{\subseteq})$
, where
$R\in\partial^{\emptyset}(\mathcal{I}_{\subseteq})$
, where
 $\emptyset\in\mathcal{C}$
. Otherwise, we select any
$\emptyset\in\mathcal{C}$
. Otherwise, we select any
 $R_0\subseteq R$
with
$R_0\subseteq R$
with
 $(R_0)^{-1}$
a mapping and
$(R_0)^{-1}$
a mapping and
 $\mathrm{rg}(R_0)=\mathrm{rg}(R)$
and observe that
$\mathrm{rg}(R_0)=\mathrm{rg}(R)$
and observe that
 $R_0\in\mathcal{C}$
. The rest is proved similarly as above.
$R_0\in\mathcal{C}$
. The rest is proved similarly as above.
Lemma 30.
Assume
![]() $|Y|\ge 2$
.
$|Y|\ge 2$
.
-
(a) Let
 $R\subseteq R'\subseteq X\times Y$
. Then
$R\subseteq R'\subseteq X\times Y$
. Then  \[ [R,R']\subseteq\mathcal{Y} \Leftrightarrow R,R'\in\mathcal{Y}\mbox{ and } \mathrm{dom}(R)=\mathrm{dom}(R').\]
\[ [R,R']\subseteq\mathcal{Y} \Leftrightarrow R,R'\in\mathcal{Y}\mbox{ and } \mathrm{dom}(R)=\mathrm{dom}(R').\]
-
(b)
 $\mathrm{Crit}(\mathcal{Y})=\{ A\times Y \mid A\subseteq X\}$
is the smallest family that dominates
$\mathrm{Crit}(\mathcal{Y})=\{ A\times Y \mid A\subseteq X\}$
is the smallest family that dominates
 $\mathcal{Y}$
.
$\mathcal{Y}$
. -
(c)
 $\mathrm{Crit}^{\mathrm{d}}(\mathcal{Y})=\{ f\cup g \mid A\subseteq X,f,g\colon A\to Y,\forall x\in A: f(x)\neq g(x)\}$
is the smallest family that supports
$\mathrm{Crit}^{\mathrm{d}}(\mathcal{Y})=\{ f\cup g \mid A\subseteq X,f,g\colon A\to Y,\forall x\in A: f(x)\neq g(x)\}$
is the smallest family that supports
 $\mathcal{Y}$
.
$\mathcal{Y}$
.
Proof.
-
(a) This is obvious from the definition of
 $\mathcal{Y}$
.
$\mathcal{Y}$
. -
(b) Consider the following shadowing relation
 $\sqsubseteq$
between elements of
$\sqsubseteq$
between elements of
 $\mathcal{Y}$
:
$\mathcal{Y}$
:
 $R\sqsubseteq S$
if and only if
$R\sqsubseteq S$
if and only if
 $R\in\partial_S(\mathcal{Y})$
. This appeared actually already in the previous item, so for
$R\in\partial_S(\mathcal{Y})$
. This appeared actually already in the previous item, so for
 $R,S\in\mathcal{Y}$
, it holds that
$R,S\in\mathcal{Y}$
, it holds that
 $R\sqsubseteq S$
if and only if
$R\sqsubseteq S$
if and only if
 $R\subseteq S$
and
$R\subseteq S$
and
 $[R,S]\subseteq\mathcal{Y}$
if and only if
$[R,S]\subseteq\mathcal{Y}$
if and only if
 $R\subseteq S$
and
$R\subseteq S$
and
 $\mathrm{dom}(R)=\mathrm{dom}(S)$
. It is immediate that
$\mathrm{dom}(R)=\mathrm{dom}(S)$
. It is immediate that
 $\sqsubseteq$
is a partial ordering on
$\sqsubseteq$
is a partial ordering on
 $\mathcal{Y}$
. Thus, if
$\mathcal{Y}$
. Thus, if
 $R\sqsubseteq S$
, then
$R\sqsubseteq S$
, then
 $\partial_R(\mathcal{Y})\subseteq\partial_S(\mathcal{Y})$
. This implies that, in order for an element of
$\partial_R(\mathcal{Y})\subseteq\partial_S(\mathcal{Y})$
. This implies that, in order for an element of
 $\mathcal{Y}$
be critical, it must be maximal with respect to
$\mathcal{Y}$
be critical, it must be maximal with respect to
 $\sqsubseteq$
. It is easy to see that these maximal elements are of the form
$\sqsubseteq$
. It is easy to see that these maximal elements are of the form
 $A\times Y$
, for some
$A\times Y$
, for some
 $A\subseteq X$
. As each
$A\subseteq X$
. As each
 $R\in\mathcal{Y}$
is also included in the set
$R\in\mathcal{Y}$
is also included in the set
 $\mathrm{dom}(R)\times Y$
for which
$\mathrm{dom}(R)\times Y$
for which
 $R\sqsubseteq \mathrm{dom}(R)\times Y$
, we also see that
$R\sqsubseteq \mathrm{dom}(R)\times Y$
, we also see that
 $\{A\times Y \mid A\subseteq X\}$
dominates
$\{A\times Y \mid A\subseteq X\}$
dominates
 $\mathcal{Y}$
.
$\mathcal{Y}$
.
 $A\times Y$
is certainly critical, as adding any
$A\times Y$
is certainly critical, as adding any
 $(c,d)\not\in A\times Y$
to
$(c,d)\not\in A\times Y$
to
 $A\times Y$
destroys anonymity.
$A\times Y$
destroys anonymity. -
(c) By Lemma 26 item d,
 $\mathrm{Crit}^{\mathrm{d}}(\mathcal{Y})$
supports the family
$\mathrm{Crit}^{\mathrm{d}}(\mathcal{Y})$
supports the family
 $\mathcal{Y}$
. Studying the shadowing relation further, we observe that for
$\mathcal{Y}$
. Studying the shadowing relation further, we observe that for
 $R,S\in\mathcal{Y}$
, we have that
$R,S\in\mathcal{Y}$
, we have that
 $R\sqsubseteq S$
if and only if
$R\sqsubseteq S$
if and only if
 $S\in\partial^R(\mathcal{Y})$
. Consequently, dual critical sets are those which are minimal with respect to the shadowing relation. These are exactly the sets of form
$S\in\partial^R(\mathcal{Y})$
. Consequently, dual critical sets are those which are minimal with respect to the shadowing relation. These are exactly the sets of form
 $f\cup g$
where
$f\cup g$
where
 $f,g\colon A\to Y$
and for all
$f,g\colon A\to Y$
and for all
 $x\in A$
we have
$x\in A$
we have
 $f(x)\neq g(x)$
. Clearly, all such sets have to be included in a supporting family (to support themselves), so
$f(x)\neq g(x)$
. Clearly, all such sets have to be included in a supporting family (to support themselves), so
 $\mathrm{Crit}^{\mathrm{d}}(\mathcal{Y})$
is the smallest family that supports
$\mathrm{Crit}^{\mathrm{d}}(\mathcal{Y})$
is the smallest family that supports
 $\mathcal{Y}$
.
$\mathcal{Y}$
.
Lemma 31.
Suppose
![]() $|X|,|Y|\ge 2$
. Let
$|X|,|Y|\ge 2$
. Let
![]() $A\subseteq X$
and
$A\subseteq X$
and
![]() $B\subseteq Y$
. Then:
$B\subseteq Y$
. Then:
-
(a) If
 $|A|,|B|\ge 2$
, we have
$|A|,|B|\ge 2$
, we have
 $\partial_{A\times B}(\mathcal{I}_{\perp})=\partial^{A\times B}(\mathcal{I}_{\perp})=\{A\times B\}$
.
$\partial_{A\times B}(\mathcal{I}_{\perp})=\partial^{A\times B}(\mathcal{I}_{\perp})=\{A\times B\}$
. -
(b) If
 $|A|\le 1$
or
$|A|\le 1$
or
 $|B|\le 1$
, then
$|B|\le 1$
, then
 $\partial_{A\times B}(\mathcal{I}_{\perp})=\mathcal{P}(A\times B)$
.
$\partial_{A\times B}(\mathcal{I}_{\perp})=\mathcal{P}(A\times B)$
. -
(c) If
 $|A|=1$
and
$|A|=1$
and
 $|B|\ge 2$
, then Similarly,
$|B|\ge 2$
, then Similarly, \[ \partial^{A\times B}(\mathcal{I}_{\perp})=\{ A\times D \mid B\subseteq D\subseteq Y \}.\]
\[ \partial^{A\times B}(\mathcal{I}_{\perp})=\{ A\times D \mid B\subseteq D\subseteq Y \}.\]
 $|A|\ge 2$
and
$|A|\ge 2$
and
 $|B|=1$
implies
$|B|=1$
implies
 $\partial^{A\times B}(\mathcal{I}_{\perp})=\{ C\times B \mid A\subseteq C\subseteq X \}$
.
$\partial^{A\times B}(\mathcal{I}_{\perp})=\{ C\times B \mid A\subseteq C\subseteq X \}$
.
-
(d) If
 $|A|=|B|=1$
, then
$|A|=|B|=1$
, then
 $\partial^{A\times B}(\mathcal{I}_{\perp})$
consists of set of the form
$\partial^{A\times B}(\mathcal{I}_{\perp})$
consists of set of the form
 $A\times D$
and
$A\times D$
and
 $C\times B$
with
$C\times B$
with
 $A\subseteq C\subseteq X$
and
$A\subseteq C\subseteq X$
and
 $B\subseteq D\subseteq Y$
.
$B\subseteq D\subseteq Y$
. -
(e)
 $\partial^\emptyset(\mathcal{I}_{\perp})$
consists of all the sets
$\partial^\emptyset(\mathcal{I}_{\perp})$
consists of all the sets
 $C\times D$
where
$C\times D$
where
 $C\subseteq X$
,
$C\subseteq X$
,
 $D\subseteq Y$
and
$D\subseteq Y$
and
 $|C|\le 1$
or
$|C|\le 1$
or
 $|D|\le 1$
.
$|D|\le 1$
. -
(f) The critical and dual critical families of
 $\mathcal{I}_{\perp}$
are
$\mathcal{I}_{\perp}$
are  \begin{align*} \mathrm{Crit}(\mathcal{I}_{\perp}) =&\{A\times B\subseteq X\times Y \mid |A|\ge 2,|B|\ge 2\} \\ &\cup \{ \{a\}\times Y \mid a\in X \}\\ &\cup \{ X\times \{b\} \mid b\in Y \}. \\ \mathrm{Crit}^{\mathrm{d}}(\mathcal{I}_{\perp})=&\{A\times B\subseteq X\times Y \mid |A|\ge 2,|B|\ge 2\} \cup \{\emptyset\}.\end{align*}
\begin{align*} \mathrm{Crit}(\mathcal{I}_{\perp}) =&\{A\times B\subseteq X\times Y \mid |A|\ge 2,|B|\ge 2\} \\ &\cup \{ \{a\}\times Y \mid a\in X \}\\ &\cup \{ X\times \{b\} \mid b\in Y \}. \\ \mathrm{Crit}^{\mathrm{d}}(\mathcal{I}_{\perp})=&\{A\times B\subseteq X\times Y \mid |A|\ge 2,|B|\ge 2\} \cup \{\emptyset\}.\end{align*}
-
(g) For each
 $R\in\mathcal{I}_{\perp}$
, the shadow
$R\in\mathcal{I}_{\perp}$
, the shadow
 $\partial_R(\mathcal{I}_\perp)$
is an interval.
$\partial_R(\mathcal{I}_\perp)$
is an interval.
Proof.
-
(a) If
 $|A|\ge 2$
and
$|A|\ge 2$
and
 $|B|\ge 2$
, any addition or deletion of a point (x,y) to or from
$|B|\ge 2$
, any addition or deletion of a point (x,y) to or from
 $A\times B$
results in a set that is not a Cartesian product of the form
$A\times B$
results in a set that is not a Cartesian product of the form
 $A'\times B'$
, which implies the result.
$A'\times B'$
, which implies the result. -
(b) The claim is trivial if either of the sets A or B is empty, so assume by symmetry that
 $A=\{a\}$
. Then every subset of
$A=\{a\}$
. Then every subset of
 $A\times B$
can be written as
$A\times B$
can be written as
 $A\times B'$
for some
$A\times B'$
for some
 $B'\subseteq B$
, so
$B'\subseteq B$
, so
 $\partial_{A\times B}(\mathcal{I}_{\perp})=\mathcal{P}(A\times B)$
.
$\partial_{A\times B}(\mathcal{I}_{\perp})=\mathcal{P}(A\times B)$
. -
(c) Suppose
 $A=\{a\}$
and
$A=\{a\}$
and
 $|B|\ge 2$
. Let
$|B|\ge 2$
. Let
 $R\in\mathcal{I}_{\perp}$
with
$R\in\mathcal{I}_{\perp}$
with
 $R\supseteq A\times B$
. Write
$R\supseteq A\times B$
. Write
 $R=C\times D$
where
$R=C\times D$
where
 $C\subseteq X$
and
$C\subseteq X$
and
 $D\subseteq Y$
with
$D\subseteq Y$
with
 $C\supseteq A$
and
$C\supseteq A$
and
 $D\supseteq B$
. If
$D\supseteq B$
. If
 $C\neq A$
, it is easy to see that
$C\neq A$
, it is easy to see that
 $C\times D\not\in\partial^{A\times B}(\mathcal{I}_{\perp})$
as we can pick
$C\times D\not\in\partial^{A\times B}(\mathcal{I}_{\perp})$
as we can pick
 $c\in C\smallsetminus A$
and
$c\in C\smallsetminus A$
and
 $b\in B$
, whence
$b\in B$
, whence
 $A\times B\subseteq (A\times B)\cup\{c,d\}\subseteq C\times D$
, but
$A\times B\subseteq (A\times B)\cup\{c,d\}\subseteq C\times D$
, but
 $(A\times B)\cup\{c,d\}\not\in\mathcal{I}_{\perp}$
. In contrast, for every
$(A\times B)\cup\{c,d\}\not\in\mathcal{I}_{\perp}$
. In contrast, for every
 $D\subseteq Y$
with
$D\subseteq Y$
with
 $D\supseteq B,$
we have
$D\supseteq B,$
we have
 $[A\times B,A\times D]\subseteq\mathcal{I}_{\perp}$
as A is a singleton. For items (d) and (e), the proof is quite similar to the proof of item (c).
$[A\times B,A\times D]\subseteq\mathcal{I}_{\perp}$
as A is a singleton. For items (d) and (e), the proof is quite similar to the proof of item (c). -
(f) Consider first the set
 $A\times B$
where
$A\times B$
where
 $|A|\ge 2$
and
$|A|\ge 2$
and
 $|B|\ge 2$
. Then by items (a)–(e), the only convex shadow or dual convex shadow that covers
$|B|\ge 2$
. Then by items (a)–(e), the only convex shadow or dual convex shadow that covers
 $A\times B$
is the shadow or dual shadow of
$A\times B$
is the shadow or dual shadow of
 $A\times B$
itself. Hence,
$A\times B$
itself. Hence,
 $A\times B$
is both critical and dual critical. Consider then the case
$A\times B$
is both critical and dual critical. Consider then the case
 $A=\{a\}$
(
$A=\{a\}$
(
 $a\in X$
) is a singleton. By item (b), among the sets
$a\in X$
) is a singleton. By item (b), among the sets
 $A\times B$
the set
$A\times B$
the set
 $A\times Y$
has the largest shadow, including the case
$A\times Y$
has the largest shadow, including the case
 $B=\emptyset$
. The symmetric case when B is a singleton and A varies is handled in the same way. For the dual case, items (c)-(e) show that the empty set has the largest dual shadow.
$B=\emptyset$
. The symmetric case when B is a singleton and A varies is handled in the same way. For the dual case, items (c)-(e) show that the empty set has the largest dual shadow. -
(g) This follows from items (a) and (b), as we observe that
 $\{A\times B\}=[A\times B,A\times B]$
and
$\{A\times B\}=[A\times B,A\times B]$
and
 $\mathcal{P}(A\times B)=[\emptyset,A\times B]$
.
$\mathcal{P}(A\times B)=[\emptyset,A\times B]$
.
Theorem 32. Let X and Y be finite base sets with
![]() $\ell=|X|\ge 2$
and
$\ell=|X|\ge 2$
and
![]() $n=|Y|\ge 2$
. Then:
$n=|Y|\ge 2$
. Then:
 \begin{align*}&\mathrm{D}(\mathcal{F})=n^\ell, && \mathrm{D}^{\mathrm{d}}(\mathcal{F})=1,&& \mathrm{CD}(\mathcal{F})=\mathrm{D}(\mathcal{F}), \\&\mathrm{D}(\mathcal{X})=2^\ell-2, && \mathrm{D}^{\mathrm{d}}(\mathcal{X})=1, && \mathrm{CD}(\mathcal{X})=\mathrm{D}(\mathcal{X}), \\&\mathrm{D}(\mathcal{I}_{\subseteq})=2^\ell-\ell, && \mathrm{D}^{\mathrm{d}}(\mathcal{I}_{\subseteq})=1+\sum^\ell_{k=2}\binom{\ell}{k}k^k, && \mathrm{CD}(\mathcal{I}_{\subseteq})=\mathrm{D}^{\mathrm{d}}(\mathcal{I}_{\subseteq}), \\&\mathrm{D}(\mathcal{Y})=2^\ell, &&\mathrm{D}^{\mathrm{d}}(\mathcal{Y})=\sum^\ell_{k=0}\binom{\ell}{k}\binom{n}{2}^k , && \mathrm{CD}(\mathcal{Y})=\mathrm{D}^{\mathrm{d}}(\mathcal{Y}).\\ &\mathrm{D}(\mathcal{I}_{\perp})= \scriptstyle (2^\ell-\ell-1)(2^n-n-1)+\ell+n, && \mathrm{D}^{\mathrm{d}}(\mathcal{I}_{\perp})= \scriptstyle (2^\ell-\ell-1)(2^n-n-1)+1, && \mathrm{CD}(\mathcal{I}_{\perp})=\mathrm{D}(\mathcal{I}_{\perp}),\end{align*}
\begin{align*}&\mathrm{D}(\mathcal{F})=n^\ell, && \mathrm{D}^{\mathrm{d}}(\mathcal{F})=1,&& \mathrm{CD}(\mathcal{F})=\mathrm{D}(\mathcal{F}), \\&\mathrm{D}(\mathcal{X})=2^\ell-2, && \mathrm{D}^{\mathrm{d}}(\mathcal{X})=1, && \mathrm{CD}(\mathcal{X})=\mathrm{D}(\mathcal{X}), \\&\mathrm{D}(\mathcal{I}_{\subseteq})=2^\ell-\ell, && \mathrm{D}^{\mathrm{d}}(\mathcal{I}_{\subseteq})=1+\sum^\ell_{k=2}\binom{\ell}{k}k^k, && \mathrm{CD}(\mathcal{I}_{\subseteq})=\mathrm{D}^{\mathrm{d}}(\mathcal{I}_{\subseteq}), \\&\mathrm{D}(\mathcal{Y})=2^\ell, &&\mathrm{D}^{\mathrm{d}}(\mathcal{Y})=\sum^\ell_{k=0}\binom{\ell}{k}\binom{n}{2}^k , && \mathrm{CD}(\mathcal{Y})=\mathrm{D}^{\mathrm{d}}(\mathcal{Y}).\\ &\mathrm{D}(\mathcal{I}_{\perp})= \scriptstyle (2^\ell-\ell-1)(2^n-n-1)+\ell+n, && \mathrm{D}^{\mathrm{d}}(\mathcal{I}_{\perp})= \scriptstyle (2^\ell-\ell-1)(2^n-n-1)+1, && \mathrm{CD}(\mathcal{I}_{\perp})=\mathrm{D}(\mathcal{I}_{\perp}),\end{align*}
Proof. Observe first that the family
![]() $\mathcal{F}$
is downwards closed, so it is trivially supported by
$\mathcal{F}$
is downwards closed, so it is trivially supported by
![]() $\{\emptyset\}$
, implying
$\{\emptyset\}$
, implying
![]() $\mathrm{D}^{\mathrm{d}}(\mathcal{F})=1$
. Downward closedness and finiteness of
$\mathrm{D}^{\mathrm{d}}(\mathcal{F})=1$
. Downward closedness and finiteness of
![]() $\mathcal{F}$
also implies that
$\mathcal{F}$
also implies that
![]() $\mathrm{D}(\mathcal{F})=|\mathrm{Max}(\mathcal{F})|$
. Clearly, the maximal sets in
$\mathrm{D}(\mathcal{F})=|\mathrm{Max}(\mathcal{F})|$
. Clearly, the maximal sets in
![]() $\mathcal{F}$
are just total functions
$\mathcal{F}$
are just total functions
![]() $f\colon X\to Y$
, so there are
$f\colon X\to Y$
, so there are
![]() $|Y|^{|X|}=n^\ell$
of them and
$|Y|^{|X|}=n^\ell$
of them and
![]() $\mathrm{D}(\mathcal{F})=n^\ell$
. Finally, the downward closedness of
$\mathrm{D}(\mathcal{F})=n^\ell$
. Finally, the downward closedness of
![]() $\mathcal{F}$
implies that for any such maximal f, we have
$\mathcal{F}$
implies that for any such maximal f, we have
![]() $\partial_f(\mathcal{F})=\mathcal{P}(f)=[\emptyset,f]$
, i.e., shadow are intervals. Hence,
$\partial_f(\mathcal{F})=\mathcal{P}(f)=[\emptyset,f]$
, i.e., shadow are intervals. Hence,
![]() $\mathrm{CD}(\mathcal{F})=\mathrm{D}(\mathcal{F})$
.
$\mathrm{CD}(\mathcal{F})=\mathrm{D}(\mathcal{F})$
.
The family
![]() $\mathcal{X}$
is obviously also downward closed, so we have
$\mathcal{X}$
is obviously also downward closed, so we have
![]() $\mathrm{D}^{\mathrm{d}}(\mathcal{X})=1$
and
$\mathrm{D}^{\mathrm{d}}(\mathcal{X})=1$
and
![]() $\mathrm{CD}(\mathcal{X})=\mathrm{D}(\mathcal{X})$
in this case, too. It is easy to see that the maximal set in
$\mathrm{CD}(\mathcal{X})=\mathrm{D}(\mathcal{X})$
in this case, too. It is easy to see that the maximal set in
![]() $\mathcal{X}$
are of form
$\mathcal{X}$
are of form
![]() $A\times B$
where
$A\times B$
where
![]() $\{A,B\}$
is a partition of the set X. (In contrast,
$\{A,B\}$
is a partition of the set X. (In contrast,
![]() $\emptyset=\emptyset\times X=X\times\emptyset\in\mathcal{X}$
is not maximal, as
$\emptyset=\emptyset\times X=X\times\emptyset\in\mathcal{X}$
is not maximal, as
![]() $\{(a,b)\}\in\mathcal{X}$
for any distinct
$\{(a,b)\}\in\mathcal{X}$
for any distinct
![]() $a,b\in X$
.) The number of possible A’s, i.e., nonempty proper subsets of X is indeed
$a,b\in X$
.) The number of possible A’s, i.e., nonempty proper subsets of X is indeed
![]() $2^n-2$
.
$2^n-2$
.
In all the other cases, we have already determined dominating and supporting families of the smallest sizes in the previous lemmas, so the rest is simply combinatorial counting. By Lemma 29, items d and e,
By item f, dual shadows are always intervals, so
![]() $\mathrm{CD}(\mathcal{I}_{\subseteq})=\mathrm{D}^{\mathrm{d}}(\mathcal{I}_{\subseteq})$
. A combinatorial calculation related to items g and h gives the formula for
$\mathrm{CD}(\mathcal{I}_{\subseteq})=\mathrm{D}^{\mathrm{d}}(\mathcal{I}_{\subseteq})$
. A combinatorial calculation related to items g and h gives the formula for
![]() $\mathrm{D}^{\mathrm{d}}(\mathcal{I}_{\subseteq})$
.
$\mathrm{D}^{\mathrm{d}}(\mathcal{I}_{\subseteq})$
.
By Lemma 30 item b,
![]() $\{ A\times Y \mid A\subseteq X\}$
is the unique smallest subfamily dominating
$\{ A\times Y \mid A\subseteq X\}$
is the unique smallest subfamily dominating
![]() $\mathcal{Y}$
, and obviously it is equipotent with
$\mathcal{Y}$
, and obviously it is equipotent with
![]() $\mathcal{P}(X)$
, so
$\mathcal{P}(X)$
, so
![]() $\mathrm{D}(\mathcal{Y})=2^\ell$
. By item c, the set in the smallest family supporting
$\mathrm{D}(\mathcal{Y})=2^\ell$
. By item c, the set in the smallest family supporting
![]() $\mathcal{Y}$
are of the form
$\mathcal{Y}$
are of the form
![]() $f\cup g$
where
$f\cup g$
where
![]() $f,g\colon A\to Y$
with
$f,g\colon A\to Y$
with
![]() $A\subseteq X$
and for everu
$A\subseteq X$
and for everu
![]() $x\in A$
we have
$x\in A$
we have
![]() $f(x)\neq g(x)$
. If the size
$f(x)\neq g(x)$
. If the size
![]() $k=|A|$
is known, there are
$k=|A|$
is known, there are
![]() $\binom{\ell}{k}$
ways to choose A, and given that A and
$\binom{\ell}{k}$
ways to choose A, and given that A and
![]() $x\in A$
, there are
$x\in A$
, there are
![]() $\binom{n}{2}$
ways to choose the pair
$\binom{n}{2}$
ways to choose the pair
![]() $\{f(x),g(x)\}$
(this is all that matters). So for every A with size k, there are
$\{f(x),g(x)\}$
(this is all that matters). So for every A with size k, there are
![]() $\binom{n}{2}^k$
ways to choose
$\binom{n}{2}^k$
ways to choose
![]() $f\cup g$
. Summing this up for different sizes of A, we get the display formula.
$f\cup g$
. Summing this up for different sizes of A, we get the display formula.
![]() $\mathrm{CD}(\mathcal{Y})=\mathrm{D}(\mathcal{Y})$
, as dual shadows are intervals.
$\mathrm{CD}(\mathcal{Y})=\mathrm{D}(\mathcal{Y})$
, as dual shadows are intervals.
By Lemma 31 item g, shadows are intervals, so
![]() $\mathrm{CD}(\mathcal{I}_{\perp})=\mathrm{D}(\mathcal{I}_{\perp})$
. Calculating the sizes of critical and dual critical subfamilies (determined in item f) with get the corresponding formulas for upper dimension and dual upper dimension.
$\mathrm{CD}(\mathcal{I}_{\perp})=\mathrm{D}(\mathcal{I}_{\perp})$
. Calculating the sizes of critical and dual critical subfamilies (determined in item f) with get the corresponding formulas for upper dimension and dual upper dimension.
There remains one interesting team-semantics-related class of families of sets we need to investigate. Let X, Y and Z be nonempty finite sets. We shall consider
This time we will content ourselves on evaluating only lower and upper bounds for this family instead of the exact values. However, this is done within a more general framework which can be applied to other similar cases.
Definition 33. Families of sets
![]() $\mathcal{A}$
and
$\mathcal{A}$
and
![]() $\mathcal{B}$
are called similar if there exists a bijection
$\mathcal{B}$
are called similar if there exists a bijection
![]() $f\colon X\to Y$
such that
$f\colon X\to Y$
such that
![]() $\mathcal{A}\subseteq\mathcal{P}(X)$
and
$\mathcal{A}\subseteq\mathcal{P}(X)$
and
It is then straightforward to show that:
Proposition 34. Let
![]() $\mathcal{A}$
,
$\mathcal{A}$
,
![]() $\mathcal{B,}$
and
$\mathcal{B,}$
and
![]() $\mathcal{C}$
be families of sets. Then:
$\mathcal{C}$
be families of sets. Then:
-
(a) If
 $\mathcal{A}$
and
$\mathcal{A}$
and
 $\mathcal{B}$
are similar, then
$\mathcal{B}$
are similar, then
 $\mathrm{D}(\mathcal{A})=\mathrm{D}(\mathcal{B})$
,
$\mathrm{D}(\mathcal{A})=\mathrm{D}(\mathcal{B})$
,
 $\mathrm{D}^{\mathrm{d}}(\mathcal{A})=\mathrm{D}^{\mathrm{d}}(\mathcal{B})$
and
$\mathrm{D}^{\mathrm{d}}(\mathcal{A})=\mathrm{D}^{\mathrm{d}}(\mathcal{B})$
and
 $\mathrm{CD}(\mathcal{A})=\mathrm{CD}(\mathcal{B})$
.
$\mathrm{CD}(\mathcal{A})=\mathrm{CD}(\mathcal{B})$
. -
(b) If
 $\mathcal{B}=\mathcal{A}\cap \mathcal{P}(B)$
for some B, then
$\mathcal{B}=\mathcal{A}\cap \mathcal{P}(B)$
for some B, then
 $\mathrm{D}(\mathcal{B})\le\mathrm{D}(\mathcal{A})$
,
$\mathrm{D}(\mathcal{B})\le\mathrm{D}(\mathcal{A})$
,
 $\mathrm{D}^{\mathrm{d}}(\mathcal{B})\le\mathrm{D}^{\mathrm{d}}(\mathcal{A})$
and
$\mathrm{D}^{\mathrm{d}}(\mathcal{B})\le\mathrm{D}^{\mathrm{d}}(\mathcal{A})$
and
 $\mathrm{CD}(\mathcal{B})\le\mathrm{CD}(\mathcal{A})$
.
$\mathrm{CD}(\mathcal{B})\le\mathrm{CD}(\mathcal{A})$
.
Definition 35. Let
![]() $(\mathcal{A}_i)_{i\in I}$
be an indexed family of families of sets. Then its general tensor disjunction is the family
$(\mathcal{A}_i)_{i\in I}$
be an indexed family of families of sets. Then its general tensor disjunction is the family
Note that if the base sets of the families
![]() $\mathcal{A}_i\subseteq\mathcal{P}(X_i)$
are all disjoint, i.e., if
$\mathcal{A}_i\subseteq\mathcal{P}(X_i)$
are all disjoint, i.e., if
![]() $(X_i)_{i\in I}$
is a disjoint family, then there is a natural bijection
$(X_i)_{i\in I}$
is a disjoint family, then there is a natural bijection
![]() $A\mapsto (A\cap X_i)_{i\in I}$
between
$A\mapsto (A\cap X_i)_{i\in I}$
between
![]() $\bigvee\limits_{i\in I}\mathcal{A}_i$
and
$\bigvee\limits_{i\in I}\mathcal{A}_i$
and
![]() $\prod_{i\in I}\mathcal{A}_i$
. In the other end of the spectrum, if
$\prod_{i\in I}\mathcal{A}_i$
. In the other end of the spectrum, if
![]() $\mathcal{A}$
is closed under unions, then
$\mathcal{A}$
is closed under unions, then
![]() $\bigvee\limits_{i\in I}\mathcal{A}=\mathcal{A}$
.
$\bigvee\limits_{i\in I}\mathcal{A}=\mathcal{A}$
.
Proposition 36. Let
![]() $(\mathcal{A}_i)_{i\in I}$
be an indexed family of families of sets. Then
$(\mathcal{A}_i)_{i\in I}$
be an indexed family of families of sets. Then
Proof. Pick, for each
![]() $i\in I$
, an index set
$i\in I$
, an index set
![]() $J_i$
and intervals
$J_i$
and intervals
![]() $\mathcal{L}_{i,j}$
,
$\mathcal{L}_{i,j}$
,
![]() $j\in J_i$
with
$j\in J_i$
with
![]() $|J_i|=\mathrm{CD}(\mathcal{A}_i)$
and
$|J_i|=\mathrm{CD}(\mathcal{A}_i)$
and
![]() $\bigcup_{j\in J_i}\mathcal{L}_{i,j}=\mathcal{A}_i$
. Write
$\bigcup_{j\in J_i}\mathcal{L}_{i,j}=\mathcal{A}_i$
. Write
![]() $\mathcal{L}_{i,j}=[B_{i,j},C_{i,j}]$
. For each
$\mathcal{L}_{i,j}=[B_{i,j},C_{i,j}]$
. For each
![]() $f\in J=\prod_{i\in I}J_i$
, consider the interval
$f\in J=\prod_{i\in I}J_i$
, consider the interval
![]() $\mathcal{L}_f=[B_f,C_f]$
where
$\mathcal{L}_f=[B_f,C_f]$
where
Then clearly
![]() $|J|=\prod_{i\in I}|J_i|=\prod_{i\in I}\mathrm{CD}(\mathcal{A}_i)$
and
$|J|=\prod_{i\in I}|J_i|=\prod_{i\in I}\mathrm{CD}(\mathcal{A}_i)$
and
![]() $\bigvee\limits_{i\in I}\mathcal{A}_i=\bigcup_{\in I}\mathcal{L}_f$
.
$\bigvee\limits_{i\in I}\mathcal{A}_i=\bigcup_{\in I}\mathcal{L}_f$
.
As a corollary, we get the desired estimates.
Proposition 37. Let X, Y, and Z be finite base sets with
![]() $\ell=|X|\ge 2$
,
$\ell=|X|\ge 2$
,
![]() $n=|Y|\ge 2$
and
$n=|Y|\ge 2$
and
![]() $s=|Z|\ge 1$
. Then
$s=|Z|\ge 1$
. Then
Proof. For each
![]() $c\in Z$
, put
$c\in Z$
, put
Clearly,
![]() $\mathcal{J}_c$
is similar to
$\mathcal{J}_c$
is similar to
![]() $\mathcal{I}_{\perp}$
, so by Theorem 32 and Proposition 34, case a, we have
$\mathcal{I}_{\perp}$
, so by Theorem 32 and Proposition 34, case a, we have
Since
![]() $\mathcal{J}_c=\mathcal{I}_{\perp,\bullet}\cap\mathcal{P}(X\times Y\times\{c\})$
, Propositions 34 and 5, further imply that
$\mathcal{J}_c=\mathcal{I}_{\perp,\bullet}\cap\mathcal{P}(X\times Y\times\{c\})$
, Propositions 34 and 5, further imply that
It easy to see that
![]() $\bigvee\limits_{c\in Z}\mathcal{J}_c=\mathcal{I}_{\perp,\bullet}$
, so now when we combine the results of Theorem 32 and Proposition 36, we get the inequality
$\bigvee\limits_{c\in Z}\mathcal{J}_c=\mathcal{I}_{\perp,\bullet}$
, so now when we combine the results of Theorem 32 and Proposition 36, we get the inequality
In our logical application, when we apply Theorem 32 and the previous proposition to determine the dimension functions of the corresponding atomic formulas, we shall face a technical complication: The dimension functions of formulas depend on the set of variables that are interpreted in the teams of assignments. The previous result corresponds exactly to the situation where only the variables occurring in the atomic formula are interpreted, but there might be dummy variables to be considered. We shall need the next proposition to overcome this difficulty: the effect of dummy variables is not critical. In this intended application, the surjective function in the proposition will be the restriction of the assignment to the occurring variables.
Proposition 38. Let
![]() $p\colon X\to Y$
be a surjection. Recall that the inverse projection is the operation
$p\colon X\to Y$
be a surjection. Recall that the inverse projection is the operation
![]() $\Delta_{p^{-1}}\colon\mathcal{P}(\mathcal{P}(Y))\to\mathcal{P}(\mathcal{P}(X))$
,
$\Delta_{p^{-1}}\colon\mathcal{P}(\mathcal{P}(Y))\to\mathcal{P}(\mathcal{P}(X))$
,
Let
![]() $\mathcal{B}\subseteq\mathcal{P}(Y)$
and
$\mathcal{B}\subseteq\mathcal{P}(Y)$
and
![]() $\mathcal{A}=\Delta_{p^{-1}}(\mathcal{B})$
. Suppose that
$\mathcal{A}=\Delta_{p^{-1}}(\mathcal{B})$
. Suppose that
![]() $s,r\in\mathbb{N}$
are constants such that for each
$s,r\in\mathbb{N}$
are constants such that for each
![]() $y\in Y$
, we have
$y\in Y$
, we have
![]() $|p^{-1}\{y\}|\le s$
, and for each
$|p^{-1}\{y\}|\le s$
, and for each
![]() $B\in\mathcal{B}$
, we have
$B\in\mathcal{B}$
, we have
![]() $|B|\le r$
.
$|B|\le r$
.
Then
Proof. Choose a subfamily
![]() $\mathcal{G}\subseteq\mathcal{B}$
such that
$\mathcal{G}\subseteq\mathcal{B}$
such that
![]() $\mathcal{G}$
dominates
$\mathcal{G}$
dominates
![]() $\mathcal{B}$
and
$\mathcal{B}$
and
![]() $\mathrm{D}(\mathcal{B})=|\mathcal{G}|$
. Now clearly
$\mathrm{D}(\mathcal{B})=|\mathcal{G}|$
. Now clearly
![]() $\mathcal{G}'=\{p^{-1}[G]\mid G\in\mathcal{G}\}$
dominates
$\mathcal{G}'=\{p^{-1}[G]\mid G\in\mathcal{G}\}$
dominates
![]() $\mathcal{A}$
, so
$\mathcal{A}$
, so
![]() $\mathrm{D}(\mathcal{A})\le\mathrm{D}(\mathcal{B})$
. If there were a family
$\mathrm{D}(\mathcal{A})\le\mathrm{D}(\mathcal{B})$
. If there were a family
![]() $\mathcal{G}''\subseteq\mathcal{A}$
dominating
$\mathcal{G}''\subseteq\mathcal{A}$
dominating
![]() $\mathcal{A}$
such that
$\mathcal{A}$
such that
![]() $|\mathcal{G}''|<\mathrm{D}(\mathcal{B})$
, then
$|\mathcal{G}''|<\mathrm{D}(\mathcal{B})$
, then
![]() $\mathcal{G}^*=p[[\mathcal{G}'']]=\{p[A] \mid A\in\mathcal{G}''\}$
would dominate
$\mathcal{G}^*=p[[\mathcal{G}'']]=\{p[A] \mid A\in\mathcal{G}''\}$
would dominate
![]() $\mathcal{B}$
contrary to the definition of the upper dimension. Hence,
$\mathcal{B}$
contrary to the definition of the upper dimension. Hence,
![]() $\mathrm{D}(\mathcal{A})=\mathrm{D}(\mathcal{B})$
.
$\mathrm{D}(\mathcal{A})=\mathrm{D}(\mathcal{B})$
.
The cases of dual upper dimension and cylindrical dimension are slightly more involved. The point is that even if L were minimal in
![]() $\mathcal{B}$
, the inverse image
$\mathcal{B}$
, the inverse image
![]() $p^{-1}[L]$
is not in general minimal in
$p^{-1}[L]$
is not in general minimal in
![]() $\mathcal{A}$
. Call A a selective inverse image of B, if
$\mathcal{A}$
. Call A a selective inverse image of B, if
![]() $p[A]=B$
and
$p[A]=B$
and
![]() $p\restriction A$
is an injection. Note that A is a selective inverse image of B if and only if A is a minimal set with
$p\restriction A$
is an injection. Note that A is a selective inverse image of B if and only if A is a minimal set with
![]() $p[A]=B$
. Choose now
$p[A]=B$
. Choose now
![]() $\mathcal{K}$
that supports
$\mathcal{K}$
that supports
![]() $\mathcal{B}$
and
$\mathcal{B}$
and
![]() $\mathrm{D}^{\mathrm{d}}(\mathcal{B})=|\mathcal{K}|$
. Consider the family
$\mathrm{D}^{\mathrm{d}}(\mathcal{B})=|\mathcal{K}|$
. Consider the family
![]() $\mathcal{K}'$
of all sets
$\mathcal{K}'$
of all sets
![]() $A\in\mathcal{A}$
such that A is selective inverse image of some
$A\in\mathcal{A}$
such that A is selective inverse image of some
![]() $B\in\mathcal{K}$
. Clearly,
$B\in\mathcal{K}$
. Clearly,
![]() $\mathcal{K}'$
supports
$\mathcal{K}'$
supports
![]() $\mathcal{A}$
. Each
$\mathcal{A}$
. Each
![]() $B\in\mathcal{K}$
has at most
$B\in\mathcal{K}$
has at most
![]() $s^{|B|}\le s^r$
selective inverse images, as for every
$s^{|B|}\le s^r$
selective inverse images, as for every
![]() $b\in B$
, we have
$b\in B$
, we have
![]() $|p^{-1}\{b\}|\le s$
. Hence,
$|p^{-1}\{b\}|\le s$
. Hence,
![]() $\mathrm{D}^{\mathrm{d}}(\mathcal{A})\le |\mathcal{K}'|\le s^r\mathrm{D}(\mathcal{B})$
. In the case of the cylindrical dimension, the proof is similar.
$\mathrm{D}^{\mathrm{d}}(\mathcal{A})\le |\mathcal{K}'|\le s^r\mathrm{D}(\mathcal{B})$
. In the case of the cylindrical dimension, the proof is similar.
3.3 Dimensions of definable families
We have defined three dimension concepts for totally arbitrary families of sets on a finite base set. We now apply these concepts to definable families of subsets of a Cartesian product
![]() $M^m$
. In particular, we are interested in calculating the three dimensions for families of the form
$M^m$
. In particular, we are interested in calculating the three dimensions for families of the form
![]() $\left\Vert \phi \right\Vert^{{M,\vec x}}$
. We rely totally on the computations performed in Section 3.2.
$\left\Vert \phi \right\Vert^{{M,\vec x}}$
. We rely totally on the computations performed in Section 3.2.
Lemma 39. If
![]() $\phi$
is first order, then
$\phi$
is first order, then
![]() $\mathrm{D}(\!\left\Vert \phi \right\Vert^{{M,\vec x}})=\mathrm{D}^{\mathrm{d}}(\!\left\Vert \phi \right\Vert^{{M,\vec x}})=\mathrm{CD}(\!\left\Vert \phi \right\Vert^{{M,\vec x}})=1$
.
$\mathrm{D}(\!\left\Vert \phi \right\Vert^{{M,\vec x}})=\mathrm{D}^{\mathrm{d}}(\!\left\Vert \phi \right\Vert^{{M,\vec x}})=\mathrm{CD}(\!\left\Vert \phi \right\Vert^{{M,\vec x}})=1$
.
Proof. The claim follows from the fact that, as we noted above in Section 2.4, if
![]() $\phi(x_0,\ldots,x_{m-1})$
is first order, then
$\phi(x_0,\ldots,x_{m-1})$
is first order, then
![]() $\left\Vert \phi \right\Vert^{{M,\vec x}}=[\emptyset,\phi^{{M,\vec x}}]$
. This makes the dimension computations trivial.
$\left\Vert \phi \right\Vert^{{M,\vec x}}=[\emptyset,\phi^{{M,\vec x}}]$
. This makes the dimension computations trivial.
As alluded to in Section 2.4, team semantics permits the extension of first order logic by a number of new atoms (see Definition 20) leading to dependence logic (Väänänen Reference Väänänen2007), inclusion logic (Galliani Reference Galliani2012), exclusion logic (Galliani Reference Galliani2012), independence logic (Galliani Reference Galliani2012), and anonymity logic (Väänänen Reference Väänänen2023). In order to estimate the dimensions of families definable in these logics, we first note the following consequence of Theorem 32:
The following theorem, indicating the dimensions of the various atoms, is summarized also in Tables 2 and 3, where
![]() $f(n)\sim g(n)$
means, keeping m and k constant,
$f(n)\sim g(n)$
means, keeping m and k constant,
![]() $\lim_n f(n)/g(n)=1$
and
$\lim_n f(n)/g(n)=1$
and
![]() $f(n)\in{\sim}[g(n),h(n)]$
means, keeping m, k, and s constant, asymptotically
$f(n)\in{\sim}[g(n),h(n)]$
means, keeping m, k, and s constant, asymptotically
![]() $g(n)\le f(n)\le h(n)$
, or more exactly
$g(n)\le f(n)\le h(n)$
, or more exactly
![]() $\liminf_n f(n)/g(n)\ge 1$
and
$\liminf_n f(n)/g(n)\ge 1$
and
![]() $\liminf_n h(n)/f(n)\ge 1$
.
$\liminf_n h(n)/f(n)\ge 1$
.
Table 2. Dimensions of atoms

Table 3. Approximate dimensions of independence atoms

Theorem 40. Suppose
![]() $|M|=n$
.
$|M|=n$
.
-
(a) Let
 $\alpha$
be the dependence atom
$\alpha$
be the dependence atom
 $\,=(\vec{x},y)$
, where
$\,=(\vec{x},y)$
, where
 $\mathrm{len}(\vec{x})=m$
, and let
$\mathrm{len}(\vec{x})=m$
, and let
 $\vec{z}=\vec{x} y$
. Then
$\vec{z}=\vec{x} y$
. Then
 $\mathrm{D}(\!\left\Vert \alpha \right\Vert^{{M,\vec{z}}})=\mathrm{CD}(\!\left\Vert \alpha \right\Vert^{{M,\vec{z}}})=n^{n^m}$
and
$\mathrm{D}(\!\left\Vert \alpha \right\Vert^{{M,\vec{z}}})=\mathrm{CD}(\!\left\Vert \alpha \right\Vert^{{M,\vec{z}}})=n^{n^m}$
and
 $\mathrm{D}^{\mathrm{d}}(\!\left\Vert \alpha \right\Vert^{{M,\vec{z}}})=1$
.
$\mathrm{D}^{\mathrm{d}}(\!\left\Vert \alpha \right\Vert^{{M,\vec{z}}})=1$
. -
(b) Let
 $\alpha$
be the exclusion atom
$\alpha$
be the exclusion atom
 $\vec{x}\mid\vec{y}$
, where
$\vec{x}\mid\vec{y}$
, where
 $\mathrm{len}(\vec{x})=\mathrm{len}(\vec{y})=m$
, and let
$\mathrm{len}(\vec{x})=\mathrm{len}(\vec{y})=m$
, and let
 $\vec{z}=\vec{x} \vec{y}$
. Then
$\vec{z}=\vec{x} \vec{y}$
. Then
 $\mathrm{D}(\!\left\Vert \alpha \right\Vert^{{M,\vec{z}}})=\mathrm{CD}(\!\left\Vert \alpha \right\Vert^{{M,\vec{z}}})=2^{n^m}-2$
and
$\mathrm{D}(\!\left\Vert \alpha \right\Vert^{{M,\vec{z}}})=\mathrm{CD}(\!\left\Vert \alpha \right\Vert^{{M,\vec{z}}})=2^{n^m}-2$
and
 $\mathrm{D}^{\mathrm{d}}(\!\left\Vert \alpha \right\Vert^{{M,\vec{z}}})=1$
.
$\mathrm{D}^{\mathrm{d}}(\!\left\Vert \alpha \right\Vert^{{M,\vec{z}}})=1$
. -
(c) Let
 $\alpha$
be the inclusion atom
$\alpha$
be the inclusion atom
 $\vec{x}\subseteq\vec{y}$
, where
$\vec{x}\subseteq\vec{y}$
, where
 $\mathrm{len}(\vec{x})=\mathrm{len}(\vec{y})=m$
, and let
$\mathrm{len}(\vec{x})=\mathrm{len}(\vec{y})=m$
, and let
 $\vec{z}=\vec{x} \vec{y}$
. Then
$\vec{z}=\vec{x} \vec{y}$
. Then
 $\mathrm{D}(\!\left\Vert \alpha \right\Vert^{{M,\vec{z}}})=2^{n^m}-n^m$
and
$\mathrm{D}(\!\left\Vert \alpha \right\Vert^{{M,\vec{z}}})=2^{n^m}-n^m$
and
 $\mathrm{D}^{\mathrm{d}}(\!\left\Vert \alpha \right\Vert^{{M,\vec{z}}})=\mathrm{CD}(\!\left\Vert \alpha \right\Vert^{{M,\vec{z}}}) =1+\sum^{n^m}_{k=2}\binom{n^m}{k}k^k$
.
$\mathrm{D}^{\mathrm{d}}(\!\left\Vert \alpha \right\Vert^{{M,\vec{z}}})=\mathrm{CD}(\!\left\Vert \alpha \right\Vert^{{M,\vec{z}}}) =1+\sum^{n^m}_{k=2}\binom{n^m}{k}k^k$
. -
(d) Let
 $\alpha$
be the anonymity atom
$\alpha$
be the anonymity atom
 $\vec{x}\mathrel{\Upsilon} y$
, where
$\vec{x}\mathrel{\Upsilon} y$
, where
 $\mathrm{len}(\vec{x})=m$
. Then
$\mathrm{len}(\vec{x})=m$
. Then
 $\mathrm{D}(\!\left\Vert \alpha \right\Vert^{{M,\vec{z}}})=\mathrm{CD}(\!\left\Vert \alpha \right\Vert^{{M,\vec{z}}})=2^{n^m}$
and
$\mathrm{D}(\!\left\Vert \alpha \right\Vert^{{M,\vec{z}}})=\mathrm{CD}(\!\left\Vert \alpha \right\Vert^{{M,\vec{z}}})=2^{n^m}$
and
 $\mathrm{D}^{\mathrm{d}}(\!\left\Vert \alpha \right\Vert^{{M,\vec{z}}}) =\sum^{n^m}_{k=0}\binom{n^m}{k}\binom{n}{2}^k $
.
$\mathrm{D}^{\mathrm{d}}(\!\left\Vert \alpha \right\Vert^{{M,\vec{z}}}) =\sum^{n^m}_{k=0}\binom{n^m}{k}\binom{n}{2}^k $
. -
(e) Let
 $\alpha$
be the pure independence atom
$\alpha$
be the pure independence atom
 $\vec{x}\perp\vec{y}$
, where
$\vec{x}\perp\vec{y}$
, where
 $\mathrm{len}(\vec{x})=m$
and
$\mathrm{len}(\vec{x})=m$
and
 $\mathrm{len}(\vec{y})=k$
, and let
$\mathrm{len}(\vec{y})=k$
, and let
 $\vec{z}=\vec{x} \vec{y}$
. Then
$\vec{z}=\vec{x} \vec{y}$
. Then
 $\mathrm{D}(\!\left\Vert \alpha \right\Vert^{{M,\vec{z}}})=\mathrm{CD}(\!\left\Vert \alpha \right\Vert^{{M,\vec{z}}})= (2^{n^m}-n^m-1)(2^{n^k}-n^k-1)+n^m+n^k$
and
$\mathrm{D}(\!\left\Vert \alpha \right\Vert^{{M,\vec{z}}})=\mathrm{CD}(\!\left\Vert \alpha \right\Vert^{{M,\vec{z}}})= (2^{n^m}-n^m-1)(2^{n^k}-n^k-1)+n^m+n^k$
and
 $\mathrm{D}^{\mathrm{d}}(\!\left\Vert \alpha \right\Vert^{{M,\vec{z}}})=(2^{n^m}-n^m-1)(2^{n^k}-n^k-1)+1$
.
$\mathrm{D}^{\mathrm{d}}(\!\left\Vert \alpha \right\Vert^{{M,\vec{z}}})=(2^{n^m}-n^m-1)(2^{n^k}-n^k-1)+1$
. -
(f) Let
 $\alpha$
be the conditional independence atom
$\alpha$
be the conditional independence atom
 $ \vec{x}\perp_{\vec{u}} \vec{y}$
, where
$ \vec{x}\perp_{\vec{u}} \vec{y}$
, where
 $\mathrm{len}(\vec{x})=m$
,
$\mathrm{len}(\vec{x})=m$
,
 $\mathrm{len}(\vec{y})=k$
,
$\mathrm{len}(\vec{y})=k$
,
 $\mathrm{len}(\vec{u})=s$
, and let
$\mathrm{len}(\vec{u})=s$
, and let
 $\vec{z}=\vec{x} \vec{u}\vec{y}$
. Then
$\vec{z}=\vec{x} \vec{u}\vec{y}$
. Then
 $(2^{n^m}-n^m-1)(2^{n^k}-n^k-1)+n^m+n^k\le\mathrm{D}(\!\left\Vert \alpha \right\Vert^{{M,\vec{z}}})\le\mathrm{CD}(\!\left\Vert \alpha \right\Vert^{{M,\vec{z}}})\le ((2^{n^m}-n^m-1)(2^{n^k}-n^k-1)+n^m+n^k)^{n^s}$
and
$(2^{n^m}-n^m-1)(2^{n^k}-n^k-1)+n^m+n^k\le\mathrm{D}(\!\left\Vert \alpha \right\Vert^{{M,\vec{z}}})\le\mathrm{CD}(\!\left\Vert \alpha \right\Vert^{{M,\vec{z}}})\le ((2^{n^m}-n^m-1)(2^{n^k}-n^k-1)+n^m+n^k)^{n^s}$
and
 $(2^{n^m}-n^m-1)(2^{n^k}-n^k-1)+1\le\mathrm{D}^{\mathrm{d}}(\!\left\Vert \alpha \right\Vert^{{M,\vec{z}}})\le((2^{n^m}-n^m-1)(2^{n^k}-n^k-1)+1)^{n^s}$
.
$(2^{n^m}-n^m-1)(2^{n^k}-n^k-1)+1\le\mathrm{D}^{\mathrm{d}}(\!\left\Vert \alpha \right\Vert^{{M,\vec{z}}})\le((2^{n^m}-n^m-1)(2^{n^k}-n^k-1)+1)^{n^s}$
.
Proof.
-
(a) Letting
 $\mathcal{F} = \{ f\subseteq M^m\times M \mid f\text{ is a mapping }\}$
, Theorem 32 gives
$\mathcal{F} = \{ f\subseteq M^m\times M \mid f\text{ is a mapping }\}$
, Theorem 32 gives
 $\mathrm{D}(\mathcal{F})=\mathrm{CD}(\mathcal{F})=n^{n^m}$
and
$\mathrm{D}(\mathcal{F})=\mathrm{CD}(\mathcal{F})=n^{n^m}$
and
 $\mathrm{D}^{\mathrm{d}}(\mathcal{F})=1$
. By Definition 20 we have
$\mathrm{D}^{\mathrm{d}}(\mathcal{F})=1$
. By Definition 20 we have
 $\mathcal{F}=\left\Vert \alpha \right\Vert^{{M,\vec{z}}}$
and the claim follows. The short argument is the same in each other case (b)-(f). In (f) we use Proposition 37.
$\mathcal{F}=\left\Vert \alpha \right\Vert^{{M,\vec{z}}}$
and the claim follows. The short argument is the same in each other case (b)-(f). In (f) we use Proposition 37.
We may notice that, keeping m and k fixed, the upper and the cylindrical dimension of the dependence atom grows faster than the respective dimensions of the other atoms, except the relativized independence atom. Varying m and k we obtain a host of comparisons between dimensions of the atoms. These will become relevant below when we combine the atoms with logical operations.
Let us now define the important concept of locality:
Definition 41. A formula
![]() $\phi$
of any logic, with the free variables
$\phi$
of any logic, with the free variables
![]() $\vec{x}$
, is said to be local if for all models M and teams T with
$\vec{x}$
, is said to be local if for all models M and teams T with
![]() $\vec{x}\subseteq\mathrm{dom}(T)$
we have
$\vec{x}\subseteq\mathrm{dom}(T)$
we have
All the atoms of Definition 20 are local and the logical operations of Definition 19, as well as all Lindström quantifiers (see Definition 22), preserve locality.
The semantics defined in Definition 58 has a variant called strict semantics (Galliani Reference Galliani2012). In strict semantics, we define the meaning of tensor disjunction by
![]() $M\models_T\phi\vee\psi$
if and only if
$M\models_T\phi\vee\psi$
if and only if
![]() $T=Y\cup Z$
such that
$T=Y\cup Z$
such that
![]() $M\models_Y\phi$
,
$M\models_Y\phi$
,
![]() $M\models_Z\psi$
, and
$M\models_Z\psi$
, and
![]() $Y\cap Z=\emptyset$
. The meaning of existential quantifier in strict semantics is
$Y\cap Z=\emptyset$
. The meaning of existential quantifier in strict semantics is
![]() $M\models_T\exists x\phi$
if and only if there is
$M\models_T\exists x\phi$
if and only if there is
![]() $F:T\to M$
such that
$F:T\to M$
such that
![]() $M\models_{T[F/x]}\phi$
. For dependence logic this change of semantics has no effect because of downward closure. However, inclusion logic with strict semantics is not local. We will not consider strict semantics in detail in this paper.
$M\models_{T[F/x]}\phi$
. For dependence logic this change of semantics has no effect because of downward closure. However, inclusion logic with strict semantics is not local. We will not consider strict semantics in detail in this paper.
It is also important to notice that above we have calculated the dimensions of the families of teams related to certain atomic formulas relative to the variables occurring in the formulas. In general, we need to consider atomic formulas – and, furthermore, also other formulas – as subformulas of larger formulas, so we need to attach also other variables in the context. Usually, the following estimates are good enough for our purposes.
Proposition 42. Let M be a structure and
![]() $\phi$
a local formula with a common vocabulary,
$\phi$
a local formula with a common vocabulary,
![]() $\vec{y}$
the sequence of variables occurring in
$\vec{y}$
the sequence of variables occurring in
![]() $\phi$
and
$\phi$
and
![]() $\vec{x}$
a finite sequence of variables extending
$\vec{x}$
a finite sequence of variables extending
![]() $\vec{y}$
. Suppose M has size n, r is constant such that for every team T in variables
$\vec{y}$
. Suppose M has size n, r is constant such that for every team T in variables
![]() $\vec{y}$
we have that
$\vec{y}$
we have that
![]() $M\models_T\phi$
implies
$M\models_T\phi$
implies
![]() $|T|\le r$
, and
$|T|\le r$
, and
![]() $t=\mathrm{len}(\vec{x})-\mathrm{len}(\vec{y})$
. Then
$t=\mathrm{len}(\vec{x})-\mathrm{len}(\vec{y})$
. Then
Proof. This is a simple application of Proposition 38. Put
![]() $k=\mathrm{len}(\vec{y})$
. Consider the case where
$k=\mathrm{len}(\vec{y})$
. Consider the case where
![]() $T=M^{k+t}$
,
$T=M^{k+t}$
,
![]() $Y=M^k$
,
$Y=M^k$
,
![]() $p\colon T\to Y$
is the natural projection,
$p\colon T\to Y$
is the natural projection,
![]() $\mathcal{A}=\left\Vert \phi \right\Vert^{M,\vec{x}}$
and
$\mathcal{A}=\left\Vert \phi \right\Vert^{M,\vec{x}}$
and
![]() $\mathcal{B}=\left\Vert \phi \right\Vert^{M,\vec{y}}$
. The locality of
$\mathcal{B}=\left\Vert \phi \right\Vert^{M,\vec{y}}$
. The locality of
![]() $\phi$
implies that
$\phi$
implies that
![]() $\mathcal{A}=\Delta_{p^{-1}}(\mathcal{B})$
, and for each
$\mathcal{A}=\Delta_{p^{-1}}(\mathcal{B})$
, and for each
![]() $y\in Y$
,
$y\in Y$
,
![]() $|p^{-1}\{y\}|=n^t$
, and for every
$|p^{-1}\{y\}|=n^t$
, and for every
![]() $T\in\mathcal{B}$
, it holds that
$T\in\mathcal{B}$
, it holds that
![]() $|T|\le r$
. As
$|T|\le r$
. As
![]() $|Y|=n^k$
, the results follow.
$|Y|=n^k$
, the results follow.
4. Growth classes and operators
Although the basic dimension concepts above apply perfectly to any family of sets, we can say more when we focus on families of subsets of Cartesian powers of finite sets, i.e., families of teams. In such a framework, the concept of a growth class arises naturally and is the topic of this section.
4.1 Growth classes
As we apply our dimensional techniques to definability problems on the class of finite structures, we are constantly facing the dilemma that it is usually not sufficient to consider a single structure and families of sets arising from team semantics in that structure, but we rather have to consider the class of all appropriate finite structures. That means that we have to accept the possibility that the size of the base set may change, which calls for a dynamical way to handle matters. To that end, we consider growth classes.
In the definitions that follow, we generalize the arithmetical notation in a pointwise fashion, e.g., for functions
![]() $f,g\colon \mathbb{N}\to\mathbb{N}$
we set
$f,g\colon \mathbb{N}\to\mathbb{N}$
we set
![]() $f+g$
to be the function
$f+g$
to be the function
![]() $\mathbb{N}\to\mathbb{N}$
such that
$\mathbb{N}\to\mathbb{N}$
such that
![]() $(f+g)(n)=f(n)+g(n)$
, for
$(f+g)(n)=f(n)+g(n)$
, for
![]() $n\in\mathbb{N}$
, and
$n\in\mathbb{N}$
, and
![]() $f\le g$
means that
$f\le g$
means that
![]() $f(n)\le g(n)$
holds for every
$f(n)\le g(n)$
holds for every
![]() $n\in\mathbb{N}$
.
$n\in\mathbb{N}$
.
Definition 43.
A set
![]() $\mathbb{O}$
of mappings
$\mathbb{O}$
of mappings
![]() $f\colon\mathbb{N}\to\mathbb{N}$
is a growth class if the following conditions hold for all
$f\colon\mathbb{N}\to\mathbb{N}$
is a growth class if the following conditions hold for all
![]() $f,g\colon\mathbb{N}\to\mathbb{N}$
:
$f,g\colon\mathbb{N}\to\mathbb{N}$
:
-
(a) If
 $g\in\mathbb{O}$
and
$g\in\mathbb{O}$
and
 $f\le g$
, then
$f\le g$
, then
 $f\in\mathbb{O}$
.
$f\in\mathbb{O}$
. -
(b) If
 $f,g\in\mathbb{O}$
, then
$f,g\in\mathbb{O}$
, then
 $f+g\in\mathbb{O}$
and
$f+g\in\mathbb{O}$
and
 $fg\in\mathbb{O}$
.
$fg\in\mathbb{O}$
.
The point of growth classes is that they are closed under natural operators arising from logical operations. As it turns out, if we figure out the growth classes of some atoms, anything definable from those atoms by means of most of the logical operations we deal with will be in the same growth class. Thus, the growth classes represent important dividing lines.
We are interested in the following particular classes:
Definition 44. For
![]() $k\in\mathbb{N}$
, we use
$k\in\mathbb{N}$
, we use
![]() $\mathbb{E}_k$
to denote the class of functions
$\mathbb{E}_k$
to denote the class of functions
![]() $f\colon\mathbb{N}\to\mathbb{N}$
such that there exists a polynomial
$f\colon\mathbb{N}\to\mathbb{N}$
such that there exists a polynomial
![]() $p\colon\mathbb{N}\to\mathbb{N}$
of degree k and with coefficients in
$p\colon\mathbb{N}\to\mathbb{N}$
of degree k and with coefficients in
![]() $\mathbb{N}$
such that for all
$\mathbb{N}$
such that for all
![]() $n\in\mathbb{N}$
$n\in\mathbb{N}$
We use
![]() $\mathbb{F}_k$
to denote the class of functions
$\mathbb{F}_k$
to denote the class of functions
![]() $f\colon\mathbb{N}\to\mathbb{N}$
such that there exists a polynomial
$f\colon\mathbb{N}\to\mathbb{N}$
such that there exists a polynomial
![]() $p\colon\mathbb{N}\to\mathbb{N}$
of degree k and with coefficients in
$p\colon\mathbb{N}\to\mathbb{N}$
of degree k and with coefficients in
![]() $\mathbb{N}$
such that for every
$\mathbb{N}$
such that for every
![]() $n\in\mathbb{N}\smallsetminus\{0,1\}$
we have that
$n\in\mathbb{N}\smallsetminus\{0,1\}$
we have that
Note that
![]() $\mathbb{E}_0$
is the class of bounded functions and
$\mathbb{E}_0$
is the class of bounded functions and
![]() $\mathbb{F}_0$
the class of functions of polynomial growth. The following is immediate:
$\mathbb{F}_0$
the class of functions of polynomial growth. The following is immediate:
Proposition 45. Each
![]() $\mathbb{E}_k$
and
$\mathbb{E}_k$
and
![]() $\mathbb{F}_k$
(for
$\mathbb{F}_k$
(for
![]() $k\in\mathbb{N}$
) is a growth class. Furthermore, we have that
$k\in\mathbb{N}$
) is a growth class. Furthermore, we have that
Definition 46. To each formula
![]() $\phi$
with free variables in
$\phi$
with free variables in
![]() $\vec{x}$
allowing a team-semantical interpretation we relate the following dimension functions:
$\vec{x}$
allowing a team-semantical interpretation we relate the following dimension functions:

The following examples follow from Theorem 40:
Example 47.
-
(a)
 $\mathrm{CDim}_{\phi,\vec x}(n)=1$
, hence
$\mathrm{CDim}_{\phi,\vec x}(n)=1$
, hence
 $\mathrm{CDim}_{\phi,\vec x}$
is in
$\mathrm{CDim}_{\phi,\vec x}$
is in
 $\mathbb{E}_0$
, for every first order
$\mathbb{E}_0$
, for every first order
 $\phi$
. Hence the same holds for
$\phi$
. Hence the same holds for
 $\mathrm{Dim}_{\phi,\vec x}$
and
$\mathrm{Dim}_{\phi,\vec x}$
and
 $\mathrm{Dim}^{\mathrm{d}}_{\phi,\vec x}$
, by Proposition 1.
$\mathrm{Dim}^{\mathrm{d}}_{\phi,\vec x}$
, by Proposition 1. -
(b)
 $\mathrm{Dim}_{=\!(\vec{x},y),\vec{x} y}(n)=n^{n^k}$
, hence
$\mathrm{Dim}_{=\!(\vec{x},y),\vec{x} y}(n)=n^{n^k}$
, hence
 $\mathrm{Dim}_{=\!(\vec{x},y),\vec{x} y}$
is in
$\mathrm{Dim}_{=\!(\vec{x},y),\vec{x} y}$
is in
 $ \mathbb{F}_k$
, where
$ \mathbb{F}_k$
, where
 $\mathrm{len}(\vec{x})=k$
. The same holds for
$\mathrm{len}(\vec{x})=k$
. The same holds for
 $\mathrm{CDim}_{=\!(\vec{x},y),\vec{x} y}$
. However,
$\mathrm{CDim}_{=\!(\vec{x},y),\vec{x} y}$
. However,
 $\mathrm{Dim}^{\mathrm{d}}_{=\!(\vec{x},y),\vec{x} y}(n)=1$
, whence
$\mathrm{Dim}^{\mathrm{d}}_{=\!(\vec{x},y),\vec{x} y}(n)=1$
, whence
 $\mathrm{Dim}^{\mathrm{d}}_{=\!(\vec{x},y),\vec x y}$
is in
$\mathrm{Dim}^{\mathrm{d}}_{=\!(\vec{x},y),\vec x y}$
is in
 $ \mathbb{E}_0$
.
$ \mathbb{E}_0$
. -
(c)
 $\mathrm{Dim}_{\vec{x}|\vec{y},\vec{x}\vec{y}}(n)=2^{n^k}-2$
, hence
$\mathrm{Dim}_{\vec{x}|\vec{y},\vec{x}\vec{y}}(n)=2^{n^k}-2$
, hence
 $\mathrm{Dim}_{\vec{x}|\vec{y},\vec{x}\vec{y}}$
is in
$\mathrm{Dim}_{\vec{x}|\vec{y},\vec{x}\vec{y}}$
is in
 $ \mathbb{E}_k$
, where
$ \mathbb{E}_k$
, where
 $\mathrm{len}(\vec{x})=\mathrm{len}(\vec{y})=k$
. The same holds for
$\mathrm{len}(\vec{x})=\mathrm{len}(\vec{y})=k$
. The same holds for
 $\mathrm{CDim}_{\vec{x}|\vec{y},\vec{x}\vec{y}}$
. However,
$\mathrm{CDim}_{\vec{x}|\vec{y},\vec{x}\vec{y}}$
. However,
 $\mathrm{Dim}^{\mathrm{d}}_{\vec{x}|\vec{y},\vec{x} \vec{y}}(n)=1$
, whence
$\mathrm{Dim}^{\mathrm{d}}_{\vec{x}|\vec{y},\vec{x} \vec{y}}(n)=1$
, whence
 $\mathrm{Dim}^{\mathrm{d}}_{\vec{x}|\vec{y},\vec{x}\vec{y}}$
is in
$\mathrm{Dim}^{\mathrm{d}}_{\vec{x}|\vec{y},\vec{x}\vec{y}}$
is in
 $ \mathbb{E}_0$
.
$ \mathbb{E}_0$
. -
(d)
 $\mathrm{Dim}_{\vec{x}\subseteq\vec{y},\vec{x}\vec{y}}(n)=2^{n^k}-n^k$
, hence
$\mathrm{Dim}_{\vec{x}\subseteq\vec{y},\vec{x}\vec{y}}(n)=2^{n^k}-n^k$
, hence
 $\mathrm{Dim}_{\vec{x}\subseteq\vec{y},\vec{x}\vec{y}}$
is in
$\mathrm{Dim}_{\vec{x}\subseteq\vec{y},\vec{x}\vec{y}}$
is in
 $ \mathbb{E}_k$
, where
$ \mathbb{E}_k$
, where
 $\mathrm{len}(\vec{x})=\mathrm{len}(\vec{y})=k$
.
$\mathrm{len}(\vec{x})=\mathrm{len}(\vec{y})=k$
. -
(e)
 $\mathrm{Dim}_{\vec{x}\Upsilon y,\vec{x} y}(n)=2^{n^k}$
, hence
$\mathrm{Dim}_{\vec{x}\Upsilon y,\vec{x} y}(n)=2^{n^k}$
, hence
 $\mathrm{Dim}_{\vec{x}\Upsilon y,\vec{x} y}\in \mathbb{E}_k$
, where
$\mathrm{Dim}_{\vec{x}\Upsilon y,\vec{x} y}\in \mathbb{E}_k$
, where
 $\mathrm{len}(\vec{x})=k$
.
$\mathrm{len}(\vec{x})=k$
. -
(f)
 $\mathrm{Dim}_{\vec{x}\perp_{\vec{z}}\vec{y},\vec{x}\vec{z}\vec{y}}(n)\in [r,r^{n^s}]$
, where
$\mathrm{Dim}_{\vec{x}\perp_{\vec{z}}\vec{y},\vec{x}\vec{z}\vec{y}}(n)\in [r,r^{n^s}]$
, where
 $r=(2^{n^m}-n^m-1)(2^{n^k}-n^k-1)+n^m+n^k$
, hence
$r=(2^{n^m}-n^m-1)(2^{n^k}-n^k-1)+n^m+n^k$
, hence
 $\mathrm{Dim}_{\vec{x}\perp_{\vec{z}}\vec{y},\vec{x}\vec{z}\vec{y}}$
is in
$\mathrm{Dim}_{\vec{x}\perp_{\vec{z}}\vec{y},\vec{x}\vec{z}\vec{y}}$
is in
 $ \mathbb{E}_{m+k+s}$
, where
$ \mathbb{E}_{m+k+s}$
, where
 $\mathrm{len}(\vec{x})=k$
,
$\mathrm{len}(\vec{x})=k$
,
 $\mathrm{len}(\vec{y})=m$
, and
$\mathrm{len}(\vec{y})=m$
, and
 $\mathrm{len}(\vec{z})=s$
.
$\mathrm{len}(\vec{z})=s$
.
For a summary of the above example, see Table 4. Note that the last row of the table indicates an upper bound only.
Table 4. Growth classes of families arising from atoms

In the example above, the growth classes of the dimension functions of some atoms were determined relative to variables occurring in the formula. In the general case, it is conceivable that the dimension functions are not preserved in the same classes. We need the following concept to show that the situation is, by and large, conserved.
Definition 48. A formula
![]() $\phi$
with free variables
$\phi$
with free variables
![]() $\vec{x}$
is of degree
$\vec{x}$
is of degree
![]() $k\in\mathbb{N}$
if there is a polynomial function
$k\in\mathbb{N}$
if there is a polynomial function
![]() $p\colon\mathbb{N}\to\mathbb{N}$
of degree k, with coefficients in
$p\colon\mathbb{N}\to\mathbb{N}$
of degree k, with coefficients in
![]() $\mathbb{N}$
, such that the following holds: For every structure M of size
$\mathbb{N}$
, such that the following holds: For every structure M of size
![]() $n\in\mathbb{N}$
for the common vocabulary, if
$n\in\mathbb{N}$
for the common vocabulary, if
![]() $M\models_{T}\phi$
holds for a team in variables
$M\models_{T}\phi$
holds for a team in variables
![]() $\vec{x}$
, then
$\vec{x}$
, then
![]() $|T|\le p(n)$
.
$|T|\le p(n)$
.
For a local formula with k free variables the degree is always at most k.
Proposition 49. Let
![]() $l\in\mathbb{N}$
,
$l\in\mathbb{N}$
,
![]() $\mathbb{O}$
be a growth class,
$\mathbb{O}$
be a growth class,
![]() $\phi$
be a local formula of degree k,
$\phi$
be a local formula of degree k,
![]() $\vec{y}$
be the tuple of variables occurring in
$\vec{y}$
be the tuple of variables occurring in
![]() $\phi$
, and
$\phi$
, and
![]() $\vec{x}$
be a finite tuple extending
$\vec{x}$
be a finite tuple extending
![]() $\vec{y}$
.
$\vec{y}$
.
-
(a) If
 $\mathrm{Dim}_{\phi,\vec{y}}$
is in
$\mathrm{Dim}_{\phi,\vec{y}}$
is in
 $\mathbb{O}$
, then
$\mathbb{O}$
, then
 $\mathrm{Dim}_{\phi,\vec{x}}$
is also in
$\mathrm{Dim}_{\phi,\vec{x}}$
is also in
 $\mathbb{O}$
.
$\mathbb{O}$
. -
(b) If
 $\mathbb{F}_k\subseteq\mathbb{O}$
and
$\mathbb{F}_k\subseteq\mathbb{O}$
and
 $\mathrm{Dim}^{\mathrm{d}}_{\phi,\vec{y}}$
is in
$\mathrm{Dim}^{\mathrm{d}}_{\phi,\vec{y}}$
is in
 $\mathbb{O}$
, then
$\mathbb{O}$
, then
 $\mathrm{Dim}^{\mathrm{d}}_{\phi,\vec{x}}$
is also in
$\mathrm{Dim}^{\mathrm{d}}_{\phi,\vec{x}}$
is also in
 $\mathbb{O}$
.
$\mathbb{O}$
. -
(c) If
 $\mathbb{F}_k\subseteq\mathbb{O}$
and
$\mathbb{F}_k\subseteq\mathbb{O}$
and
 $\mathrm{CDim}_{\phi,\vec{y}}$
is in
$\mathrm{CDim}_{\phi,\vec{y}}$
is in
 $\mathbb{O}$
, then
$\mathbb{O}$
, then
 $\mathrm{CDim}_{\phi,\vec{x}}$
is also in
$\mathrm{CDim}_{\phi,\vec{x}}$
is also in
 $\mathbb{O}$
.
$\mathbb{O}$
.
Proof. The proof is a direct application of Proposition 42. Fix the polynomial function p of degree k witnessing that
![]() $\phi$
is of degree k, and put
$\phi$
is of degree k, and put
![]() $t=\mathrm{len}(\vec{x})-\mathrm{len}(\vec{y})$
. Consider an appopriate structure M of size n. By the Proposition (putting
$t=\mathrm{len}(\vec{x})-\mathrm{len}(\vec{y})$
. Consider an appopriate structure M of size n. By the Proposition (putting
![]() $r=p(n)$
), we have
$r=p(n)$
), we have
 \begin{align*} &\mathrm{D}(\!\left\Vert \phi \right\Vert^{M,\vec{x}})=\mathrm{D}(\!\left\Vert \phi \right\Vert^{M,\vec{y}})\\ &\mathrm{D}^{\mathrm{d}}(\!\left\Vert \phi \right\Vert^{M,\vec{x}})\le n^{tp(n)}\mathrm{D}^{\mathrm{d}}(\!\left\Vert \phi \right\Vert^{M,\vec{y}})\text{ and }\\ &\mathrm{CD}(\!\left\Vert \phi \right\Vert^{M,\vec{x}})\le n^{tp(n)}\mathrm{CD}(\!\left\Vert \phi \right\Vert^{M,\vec{y}}).\\\end{align*}
\begin{align*} &\mathrm{D}(\!\left\Vert \phi \right\Vert^{M,\vec{x}})=\mathrm{D}(\!\left\Vert \phi \right\Vert^{M,\vec{y}})\\ &\mathrm{D}^{\mathrm{d}}(\!\left\Vert \phi \right\Vert^{M,\vec{x}})\le n^{tp(n)}\mathrm{D}^{\mathrm{d}}(\!\left\Vert \phi \right\Vert^{M,\vec{y}})\text{ and }\\ &\mathrm{CD}(\!\left\Vert \phi \right\Vert^{M,\vec{x}})\le n^{tp(n)}\mathrm{CD}(\!\left\Vert \phi \right\Vert^{M,\vec{y}}).\\\end{align*}
As tp is a polynomial function of degree k, the function
![]() $n\mapsto n^{tp(n)}$
is in
$n\mapsto n^{tp(n)}$
is in
![]() $\mathbb{F}_k$
, and the results follow.
$\mathbb{F}_k$
, and the results follow.
It is worth noting that dual and cylindrical dimensions of formulas do not behave as well as upper dimension when new variables are added (see Theorem 42). Thus, the dual or cylindrical dimension of a formula may be in
![]() $\mathbb{E}_k$
, but when new variables are taken into account, even if they do not occur in the formula, the (dual or cylindrical) dimension may jump into
$\mathbb{E}_k$
, but when new variables are taken into account, even if they do not occur in the formula, the (dual or cylindrical) dimension may jump into
![]() $\mathbb{F}_k$
as a a new factor
$\mathbb{F}_k$
as a a new factor
![]() $n^{n^k}$
may appear.
$n^{n^k}$
may appear.
4.2 Kripke-operators
Our goal in this section is to find natural criteria for operators to preserve growth classes. We start by defining a class of operators that is inspired by the Kripke semantics of modal logic. Let X and Y be nonempty base sets, and let
![]() $\mathcal{R}\subseteq \mathcal{P}(Y)\times\mathcal{P}(X)^n$
be an
$\mathcal{R}\subseteq \mathcal{P}(Y)\times\mathcal{P}(X)^n$
be an
![]() $(n+1)$
-ary relation. Then we define a corresponding operator
$(n+1)$
-ary relation. Then we define a corresponding operator
![]() $\Delta_\mathcal{R}\colon \mathcal{P}(\mathcal{P}(X))^n\to\mathcal{P}(\mathcal{P}(Y))$
by the condition
$\Delta_\mathcal{R}\colon \mathcal{P}(\mathcal{P}(X))^n\to\mathcal{P}(\mathcal{P}(Y))$
by the condition
Note that
![]() $\Delta_\mathcal{R}$
can be seen as the n-ary second-order version of the function mapping the truth set of a formula
$\Delta_\mathcal{R}$
can be seen as the n-ary second-order version of the function mapping the truth set of a formula
![]() $\varphi$
to the truth set of
$\varphi$
to the truth set of
![]() $\Diamond\varphi$
in a Kripke model.
$\Diamond\varphi$
in a Kripke model.
Definition 50. Let X and Y be nonempty sets. A function
![]() $\Delta\colon \mathcal{P}(\mathcal{P}(X))^n\to\mathcal{P}(\mathcal{P}(Y))$
is a (second-order) Kripke-operator,Footnote
5
if there is a relation
$\Delta\colon \mathcal{P}(\mathcal{P}(X))^n\to\mathcal{P}(\mathcal{P}(Y))$
is a (second-order) Kripke-operator,Footnote
5
if there is a relation
![]() $\mathcal{R}\subseteq \mathcal{P}(Y)\times\mathcal{P}(X)^{n}$
such that
$\mathcal{R}\subseteq \mathcal{P}(Y)\times\mathcal{P}(X)^{n}$
such that
![]() $\Delta=\Delta_\mathcal{R}$
.
$\Delta=\Delta_\mathcal{R}$
.
In the next example, we go through the operators introduced in Example 8, and check which of them are Kripke-operators.
Example 51.
-
(a) Intersection of families is a Kripke-operator on any base set X: If
 $\mathcal{A},\mathcal{B}\subseteq\mathcal{P}(X)$
and
$\mathcal{A},\mathcal{B}\subseteq\mathcal{P}(X)$
and
 $C\in \mathcal{P}(X)$
, then
$C\in \mathcal{P}(X)$
, then
 $C\in\mathcal{A}\cap\mathcal{B}$
if and only if there exist
$C\in\mathcal{A}\cap\mathcal{B}$
if and only if there exist
 $A\in\mathcal{A}$
and
$A\in\mathcal{A}$
and
 $B\in\mathcal{B}$
such that
$B\in\mathcal{B}$
such that
 $(C,A,B)\in\mathcal{R}_\cap$
, where
$(C,A,B)\in\mathcal{R}_\cap$
, where
 $\mathcal{R}_\cap$
is the simple relation
$\mathcal{R}_\cap$
is the simple relation
 $\{(D,D,D)\mid D\in\mathcal{P}(X)\}$
.
$\{(D,D,D)\mid D\in\mathcal{P}(X)\}$
. -
(b) Union of families on X is not a Kripke-operator. This is because for any relation
 $\mathcal{R}\subseteq (\mathcal{P}(X))^3$
and any nonempty family
$\mathcal{R}\subseteq (\mathcal{P}(X))^3$
and any nonempty family
 $\mathcal{A}\subseteq\mathcal{P}(X)$
we have
$\mathcal{A}\subseteq\mathcal{P}(X)$
we have
 $\Delta_\mathcal{R}(\mathcal{A},\emptyset)=\emptyset\not=\mathcal{A}=\mathcal{A}\cup\emptyset$
. However, defining
$\Delta_\mathcal{R}(\mathcal{A},\emptyset)=\emptyset\not=\mathcal{A}=\mathcal{A}\cup\emptyset$
. However, defining
 $\mathcal{R}_{\cup^*}=\{(A,A,\emptyset),(A,\emptyset,A)\mid A\in\mathcal{P}(X)\}$
we obtain a Kripke-operator
$\mathcal{R}_{\cup^*}=\{(A,A,\emptyset),(A,\emptyset,A)\mid A\in\mathcal{P}(X)\}$
we obtain a Kripke-operator
 $\Delta_{\mathcal{R}_{\cup^*}}$
that captures union when restricting to families that contain
$\Delta_{\mathcal{R}_{\cup^*}}$
that captures union when restricting to families that contain
 $\emptyset$
.
$\emptyset$
. -
(c) It is also easy to see that complementation
 $\Delta^X_c$
is not a Kripke-operator:
$\Delta^X_c$
is not a Kripke-operator:
 $\Delta_\mathcal{R}(\emptyset)=\emptyset$
for any relation
$\Delta_\mathcal{R}(\emptyset)=\emptyset$
for any relation
 $\mathcal{R}\subseteq (\mathcal{P}(X))^2$
, but
$\mathcal{R}\subseteq (\mathcal{P}(X))^2$
, but
 $\Delta^X_c(\emptyset)=\mathcal{P}(X)\not=\emptyset$
.
$\Delta^X_c(\emptyset)=\mathcal{P}(X)\not=\emptyset$
. -
(e) Tensor disjunction and tensor negation on X are Kripke-operators: clearly,
 $\mathcal{A}\lor\mathcal{B}=\Delta_{\mathcal{R}_\lor}(\mathcal{A},\mathcal{B})$
and
$\mathcal{A}\lor\mathcal{B}=\Delta_{\mathcal{R}_\lor}(\mathcal{A},\mathcal{B})$
and
 $\Delta^X_\lnot(\mathcal{A})=\Delta_{\mathcal{R}_\lnot}(\mathcal{A})$
where
$\Delta^X_\lnot(\mathcal{A})=\Delta_{\mathcal{R}_\lnot}(\mathcal{A})$
where
 $\mathcal{R}_\lor=\{(A\cup B,A,B)\mid A,B\in\mathcal{P}(X)\}$
and
$\mathcal{R}_\lor=\{(A\cup B,A,B)\mid A,B\in\mathcal{P}(X)\}$
and
 $\mathcal{R}_\lnot=\{(X\smallsetminus A,A)\mid A\in\mathcal{P}(X)\}$
. More generally, for any binary operation
$\mathcal{R}_\lnot=\{(X\smallsetminus A,A)\mid A\in\mathcal{P}(X)\}$
. More generally, for any binary operation
 $\circledast$
on the set
$\circledast$
on the set
 $\{0,1\}$
the corresponding tensor operator is a Kripke-operator:
$\{0,1\}$
the corresponding tensor operator is a Kripke-operator:
 $\Delta^X_{\circledast}=\Delta_{\mathcal{R}_\circledast}$
, where
$\Delta^X_{\circledast}=\Delta_{\mathcal{R}_\circledast}$
, where
 $\mathcal{R}_\circledast=\{(A\ast B,A,B)\mid A,B\in\mathcal{P}(X)\}$
(see Definition 9).
$\mathcal{R}_\circledast=\{(A\ast B,A,B)\mid A,B\in\mathcal{P}(X)\}$
(see Definition 9). -
(f) Projections and inverse projections are Kripke-operators. Indeed, if
 $f\colon X\to Y$
is a function, then clearly
$f\colon X\to Y$
is a function, then clearly
 $\Delta_f=\Delta_{\mathcal{R}_f}$
, where
$\Delta_f=\Delta_{\mathcal{R}_f}$
, where
 $\mathcal{R}_f=\{(f[A],A)\mid A\in\mathcal{P}(X)\}$
. Similarly,
$\mathcal{R}_f=\{(f[A],A)\mid A\in\mathcal{P}(X)\}$
. Similarly,
 $\Delta_{f^{-1}}=\Delta_{\mathcal{R}_{f^{-1}}}$
, where
$\Delta_{f^{-1}}=\Delta_{\mathcal{R}_{f^{-1}}}$
, where
 $\mathcal{R}_{f^{-1}}=\{(A,f[A])\mid A\in\mathcal{P}(X)\}$
.
$\mathcal{R}_{f^{-1}}=\{(A,f[A])\mid A\in\mathcal{P}(X)\}$
. -
(g) Finally, we observe that the
 $(\mathcal{K},\vec\ell)$
-projection operators
$(\mathcal{K},\vec\ell)$
-projection operators
 $\Delta^{M^m}_{\mathcal{K},\vec\ell}$
corresponding to Lindström quantifiers are Kripke-operators: by Definition 23 we have
$\Delta^{M^m}_{\mathcal{K},\vec\ell}$
corresponding to Lindström quantifiers are Kripke-operators: by Definition 23 we have
 $\Delta^{M^m}_{\mathcal{K},\vec\ell}=\Delta_{\mathcal{R}_{\mathcal{K},\vec\ell}}\,$
, where
$\Delta^{M^m}_{\mathcal{K},\vec\ell}=\Delta_{\mathcal{R}_{\mathcal{K},\vec\ell}}\,$
, where
 $\mathcal{R}_{\mathcal{K},\vec\ell}=\{(B,A)\mid B=\pi^p_{\mathcal{K},\vec\ell}\,(A)\}$
if
$\mathcal{R}_{\mathcal{K},\vec\ell}=\{(B,A)\mid B=\pi^p_{\mathcal{K},\vec\ell}\,(A)\}$
if
 $(M,\emptyset)\notin\mathcal{K}$
, and
$(M,\emptyset)\notin\mathcal{K}$
, and
 $\mathcal{R}_{\mathcal{K},\vec\ell}=\{(B,A)\mid \pi^p_{\mathcal{K},\vec\ell}\,(A)\subseteq B\}$
if
$\mathcal{R}_{\mathcal{K},\vec\ell}=\{(B,A)\mid \pi^p_{\mathcal{K},\vec\ell}\,(A)\subseteq B\}$
if
 $(M,\emptyset)\in\mathcal{K}$
.
$(M,\emptyset)\in\mathcal{K}$
.
In particular, the existential quantification operators
![]() $\Delta^{M^m}_{\exists i}$
and the universal quantification operators
$\Delta^{M^m}_{\exists i}$
and the universal quantification operators
![]() $\Delta^{M^m}_{\forall i}$
are Kripke-operators.
$\Delta^{M^m}_{\forall i}$
are Kripke-operators.
An important property of Kripke-operators is that they preserve unions of families:
Lemma 53. (Union Lemma). Let
![]() $\Delta_\mathcal{R}\colon \mathcal{P}(\mathcal{P}(X))^n\to\mathcal{P}(\mathcal{P}(Y))$
be a Kripke-operator, and let
$\Delta_\mathcal{R}\colon \mathcal{P}(\mathcal{P}(X))^n\to\mathcal{P}(\mathcal{P}(Y))$
be a Kripke-operator, and let
![]() $\mathcal{A}_i^k\in\mathcal{P}(\mathcal{P}(X))$
,
$\mathcal{A}_i^k\in\mathcal{P}(\mathcal{P}(X))$
,
![]() $k\in K_i$
, be families of sets for some index sets
$k\in K_i$
, be families of sets for some index sets
![]() $K_i$
,
$K_i$
,
![]() $i<n$
. Then
$i<n$
. Then
where we use the notation
![]() $\vec k=(k_0,\ldots,k_{n-1})$
and
$\vec k=(k_0,\ldots,k_{n-1})$
and
![]() $K=K_0\times\cdots\times K_{n-1}$
.
$K=K_0\times\cdots\times K_{n-1}$
.
Proof. Using the notation
![]() $\mathcal{A}_i=\bigcup_{k\in K_i}\mathcal{A}_i^k$
for
$\mathcal{A}_i=\bigcup_{k\in K_i}\mathcal{A}_i^k$
for
![]() $i<n$
the left hand side of the equation can be written as
$i<n$
the left hand side of the equation can be written as
![]() $\mathcal{A}:=\Delta_\mathcal{R}(\mathcal{A}_0,\ldots,\mathcal{A}_{n-1})$
. The claim follows now from the chain of equivalences below:
$\mathcal{A}:=\Delta_\mathcal{R}(\mathcal{A}_0,\ldots,\mathcal{A}_{n-1})$
. The claim follows now from the chain of equivalences below:
 $$\begin{array}{lcl} A\in\mathcal{A}&\Leftrightarrow &\forall i<n\,\exists A_i\in\mathcal{A}_i: (A,A_0,\ldots,A_{n-1})\in\mathcal{R} \\ &\Leftrightarrow &\forall i<n\,\exists k_i\in K_i\,\exists A_i\in\mathcal{A}_i^{k_i}: (A,A_0,\ldots,A_{n-1})\in\mathcal{R} \\ &\Leftrightarrow &\exists\vec k\in K: A\in\Delta_\mathcal{R}(\mathcal{A}_0^{k_0},\ldots,\mathcal{A}_{n-1}^{k_{n-1}})\\ &\Leftrightarrow &A\in\bigcup_{\vec k\in K}\Delta_\mathcal{R}(\mathcal{A}_0^{k_0},\ldots,\mathcal{A}_{n-1}^{k_{n-1}}). \end{array} $$
$$\begin{array}{lcl} A\in\mathcal{A}&\Leftrightarrow &\forall i<n\,\exists A_i\in\mathcal{A}_i: (A,A_0,\ldots,A_{n-1})\in\mathcal{R} \\ &\Leftrightarrow &\forall i<n\,\exists k_i\in K_i\,\exists A_i\in\mathcal{A}_i^{k_i}: (A,A_0,\ldots,A_{n-1})\in\mathcal{R} \\ &\Leftrightarrow &\exists\vec k\in K: A\in\Delta_\mathcal{R}(\mathcal{A}_0^{k_0},\ldots,\mathcal{A}_{n-1}^{k_{n-1}})\\ &\Leftrightarrow &A\in\bigcup_{\vec k\in K}\Delta_\mathcal{R}(\mathcal{A}_0^{k_0},\ldots,\mathcal{A}_{n-1}^{k_{n-1}}). \end{array} $$
Kripke-operators that preserve the property of being dominated (and/or supported) and convex have a crucial role in our considerations. This is because for such an operator
![]() $\Delta_\mathcal{R}$
the (corresponding) dimension of the image
$\Delta_\mathcal{R}$
the (corresponding) dimension of the image
![]() $\Delta_\mathcal{R}(\mathcal{A}_0,\ldots,\mathcal{A}_{n-1})$
is at most the product of the dimensions of
$\Delta_\mathcal{R}(\mathcal{A}_0,\ldots,\mathcal{A}_{n-1})$
is at most the product of the dimensions of
![]() $\mathcal{A}_i$
,
$\mathcal{A}_i$
,
![]() $i<n$
, and consequently,
$i<n$
, and consequently,
![]() $\Delta_\mathcal{R}$
preserves growth classes.
$\Delta_\mathcal{R}$
preserves growth classes.
Definition 53. Let
![]() $\Delta\colon \mathcal{P}(\mathcal{P}(X))^n\to\mathcal{P}(\mathcal{P}(Y))$
be an operator. We say that
$\Delta\colon \mathcal{P}(\mathcal{P}(X))^n\to\mathcal{P}(\mathcal{P}(Y))$
be an operator. We say that
![]() $\Delta$
weakly preserves dominated (supported, resp.) convexity if
$\Delta$
weakly preserves dominated (supported, resp.) convexity if
![]() $\Delta(\mathcal{A}_0,\ldots,\mathcal{A}_{n-1})$
is dominated (supported, resp.) and convex or
$\Delta(\mathcal{A}_0,\ldots,\mathcal{A}_{n-1})$
is dominated (supported, resp.) and convex or
![]() $\Delta(\mathcal{A}_0,\ldots,\mathcal{A}_{n-1})=\emptyset$
whenever
$\Delta(\mathcal{A}_0,\ldots,\mathcal{A}_{n-1})=\emptyset$
whenever
![]() $\mathcal{A}_i$
is dominated and convex for each
$\mathcal{A}_i$
is dominated and convex for each
![]() $i<n$
. Furthermore, we say that
$i<n$
. Furthermore, we say that
![]() $\Delta$
weakly preserves intervals if
$\Delta$
weakly preserves intervals if
![]() $\Delta(\mathcal{A}_0,\ldots,\mathcal{A}_{n-1})$
is an interval or
$\Delta(\mathcal{A}_0,\ldots,\mathcal{A}_{n-1})$
is an interval or
![]() $\Delta(\mathcal{A}_0,\ldots,\mathcal{A}_{n-1})=\emptyset$
whenever
$\Delta(\mathcal{A}_0,\ldots,\mathcal{A}_{n-1})=\emptyset$
whenever
![]() $\mathcal{A}_i$
is an interval for each
$\mathcal{A}_i$
is an interval for each
![]() $i<n$
.
$i<n$
.
Example 54.
-
(a) Proposition 18 shows that each tensor operator
 $\circledast$
weakly preserves intervals. (In this case, if
$\circledast$
weakly preserves intervals. (In this case, if
 $\mathcal{A}$
and
$\mathcal{A}$
and
 $\mathcal{B}$
are nonempty, then so is
$\mathcal{B}$
are nonempty, then so is
 $\mathcal{A}\circledast\mathcal{B}$
, too, so we could blatantly state that
$\mathcal{A}\circledast\mathcal{B}$
, too, so we could blatantly state that
 $\circledast$
preserves intervals, dropping the specifier “weakly”.)
$\circledast$
preserves intervals, dropping the specifier “weakly”.) -
(b) Suppose now the binary operation
 $\circledast$
on the set
$\circledast$
on the set
 $\{0,1\}$
is not monotone. Recall that monotonicity of
$\{0,1\}$
is not monotone. Recall that monotonicity of
 $\circledast$
means that for all
$\circledast$
means that for all
 $a,a',b,b'\in\{0,1\}$
, whenever
$a,a',b,b'\in\{0,1\}$
, whenever
 $a\le a'$
and
$a\le a'$
and
 $b\le b'$
, then
$b\le b'$
, then
 $a\circledast b\le a'\circledast b'$
where
$a\circledast b\le a'\circledast b'$
where
 $\le$
is the natural ordering of the truth values with
$\le$
is the natural ordering of the truth values with
 $0<1$
. 10 of the 16 operations are not monotone, i.e., all apart from the constant operations, projections, conjunction, and disjunction. As
$0<1$
. 10 of the 16 operations are not monotone, i.e., all apart from the constant operations, projections, conjunction, and disjunction. As
 $\circledast$
is not monotone, there is
$\circledast$
is not monotone, there is
 $c\in\{0,1\}$
with By symmetry, assume the former pair of equations. Consider now any
$c\in\{0,1\}$
with By symmetry, assume the former pair of equations. Consider now any \[\text{either } \begin{cases} c\circledast 0=1\\ c\circledast 1=0\\ \end{cases}\text{ or } \begin{cases} 0\circledast c=1\\ 1\circledast c=0.\\ \end{cases}\]
\[\text{either } \begin{cases} c\circledast 0=1\\ c\circledast 1=0\\ \end{cases}\text{ or } \begin{cases} 0\circledast c=1\\ 1\circledast c=0.\\ \end{cases}\]
 $\mathcal{A}\subseteq\mathcal{P}(X)$
, and choose
$\mathcal{A}\subseteq\mathcal{P}(X)$
, and choose
 $C=\emptyset$
if
$C=\emptyset$
if
 $c=0$
, and
$c=0$
, and
 $C=X$
if
$C=X$
if
 $c=1$
. Note that
$c=1$
. Note that
 $\{C\}=[C,C]\subseteq\mathcal{P}(X)$
is an interval, so it is both dominated convex and supported convex. Now Picking any
$\{C\}=[C,C]\subseteq\mathcal{P}(X)$
is an interval, so it is both dominated convex and supported convex. Now Picking any \[ \{C\}\circledast\mathcal{A} = \{ C*A \mid A\in\mathcal{A} \} = \{ X\smallsetminus A \mid A\in\mathcal{A} \} =\lnot\mathcal{A}.\]
\[ \{C\}\circledast\mathcal{A} = \{ C*A \mid A\in\mathcal{A} \} = \{ X\smallsetminus A \mid A\in\mathcal{A} \} =\lnot\mathcal{A}.\]
 $\mathcal{A}$
that is nonempty, dominated convex, but not supported convex, we see that
$\mathcal{A}$
that is nonempty, dominated convex, but not supported convex, we see that
 $\{C\}\circledast\mathcal{A}=\lnot\mathcal{A}$
is nonempty, but not dominated. Thus,
$\{C\}\circledast\mathcal{A}=\lnot\mathcal{A}$
is nonempty, but not dominated. Thus,
 $\circledast$
does not weakly preserve dominated convexity. Similarly, interchanging the roles of “dominated” and “supported” we get that
$\circledast$
does not weakly preserve dominated convexity. Similarly, interchanging the roles of “dominated” and “supported” we get that
 $\circledast$
does not weakly preserve supported convexity.
$\circledast$
does not weakly preserve supported convexity.
Theorem 55. Let
![]() $\Delta_\mathcal{R}\colon \mathcal{P}(\mathcal{P}(X))^n\to\mathcal{P}(\mathcal{P}(Y))$
be a Kripke-operator, and let
$\Delta_\mathcal{R}\colon \mathcal{P}(\mathcal{P}(X))^n\to\mathcal{P}(\mathcal{P}(Y))$
be a Kripke-operator, and let
![]() $\mathcal{A}=\Delta_\mathcal{R}(\mathcal{A}_0,\ldots,\mathcal{A}_{n-1})$
.
$\mathcal{A}=\Delta_\mathcal{R}(\mathcal{A}_0,\ldots,\mathcal{A}_{n-1})$
.
-
(a) If
 $\Delta_\mathcal{R}$
weakly preserves dominated convexity then
$\Delta_\mathcal{R}$
weakly preserves dominated convexity then
 $\mathrm{D}(\mathcal{A})\le \mathrm{D}(\mathcal{A}_0)\cdot\ldots\cdot \mathrm{D}(\mathcal{A}_{n-1})$
.
$\mathrm{D}(\mathcal{A})\le \mathrm{D}(\mathcal{A}_0)\cdot\ldots\cdot \mathrm{D}(\mathcal{A}_{n-1})$
. -
(b) If
 $\Delta_\mathcal{R}$
weakly preserves supported convexity then
$\Delta_\mathcal{R}$
weakly preserves supported convexity then
 $\mathrm{D}^{\mathrm{d}}(\mathcal{A})\le \mathrm{D}^{\mathrm{d}}(\mathcal{A}_0)\cdot\ldots\cdot \mathrm{D}^{\mathrm{d}}(\mathcal{A}_{n-1})$
.
$\mathrm{D}^{\mathrm{d}}(\mathcal{A})\le \mathrm{D}^{\mathrm{d}}(\mathcal{A}_0)\cdot\ldots\cdot \mathrm{D}^{\mathrm{d}}(\mathcal{A}_{n-1})$
. -
(c) If
 $\Delta_\mathcal{R}$
weakly preserves intervals then
$\Delta_\mathcal{R}$
weakly preserves intervals then
 $\mathrm{CD}(\mathcal{A})\le \mathrm{CD}(\mathcal{A}_0)\cdot\ldots\cdot \mathrm{CD}(\mathcal{A}_{n-1})$
.
$\mathrm{CD}(\mathcal{A})\le \mathrm{CD}(\mathcal{A}_0)\cdot\ldots\cdot \mathrm{CD}(\mathcal{A}_{n-1})$
.
Proof.
-
(a) By Definition 4, for each
 $i<n$
there are dominated and convex subfamilies
$i<n$
there are dominated and convex subfamilies
 $\mathcal{A}_i^{k}\subseteq\mathcal{A}_i$
,
$\mathcal{A}_i^{k}\subseteq\mathcal{A}_i$
,
 $k\in K_i$
, such that
$k\in K_i$
, such that
 $\mathcal{A}_i=\bigcup_{k\in K_i}\mathcal{A}_i^k$
and
$\mathcal{A}_i=\bigcup_{k\in K_i}\mathcal{A}_i^k$
and
 $|K_i|=\mathrm{D}(\mathcal{A}_i)$
. For each tuple
$|K_i|=\mathrm{D}(\mathcal{A}_i)$
. For each tuple
 $\vec k:=(k_0,\ldots,k_{n-1})$
in
$\vec k:=(k_0,\ldots,k_{n-1})$
in
 $K:=K_0\times\cdots\times K_{n-1}$
, let
$K:=K_0\times\cdots\times K_{n-1}$
, let
 $\mathcal{A}_{\vec k}$
denote the family
$\mathcal{A}_{\vec k}$
denote the family
 $\Delta_\mathcal{R}(\mathcal{A}_0^{k_0},\ldots,\mathcal{A}_{n-1}^{k_{n-1}})$
. By our assumption, each
$\Delta_\mathcal{R}(\mathcal{A}_0^{k_0},\ldots,\mathcal{A}_{n-1}^{k_{n-1}})$
. By our assumption, each
 $\mathcal{A}_{\vec k}$
is either dominated and convex, or empty. By Lemma 52,
$\mathcal{A}_{\vec k}$
is either dominated and convex, or empty. By Lemma 52,
 $\mathcal{A}=\bigcup_{\vec k\in K}\mathcal{A}_{\vec k}$
. Thus we see that
$\mathcal{A}=\bigcup_{\vec k\in K}\mathcal{A}_{\vec k}$
. Thus we see that
 $\mathrm{D}(\mathcal{A})\le |K|=|K_0|\cdot\ldots\cdot |K_{n-1}|=\mathrm{D}(\mathcal{A}_0)\cdot\ldots\cdot \mathrm{D}(\mathcal{A}_{n-1})$
.
$\mathrm{D}(\mathcal{A})\le |K|=|K_0|\cdot\ldots\cdot |K_{n-1}|=\mathrm{D}(\mathcal{A}_0)\cdot\ldots\cdot \mathrm{D}(\mathcal{A}_{n-1})$
.
Claim (b) is proved in the same way just by replacing dominated convexity by supported convexity. Finally, to prove (c) it suffices to observe that a nonempty family is an interval if and only if it is dominated, supported, and convex.
As seen above in Example 51, there are well-behaved operators that are not Kripke-operators, but on the other hand, most of the operators arising in our applications are Kripke-operators. Moreover, we can prove relatively simple exact characterizations for weak preservation of dominated convexity and supported convexity for Kripke-operators.
Below we will use the notation
Lemma 56. Let
![]() $\Delta_\mathcal{R}\colon \mathcal{P}(\mathcal{P}(X))^n\to\mathcal{P}(\mathcal{P}(Y))$
be a Kripke-operator for finite X and Y. Then
$\Delta_\mathcal{R}\colon \mathcal{P}(\mathcal{P}(X))^n\to\mathcal{P}(\mathcal{P}(Y))$
be a Kripke-operator for finite X and Y. Then
![]() $\Delta_\mathcal{R}$
weakly preserves dominated convexity if and only if the following condition holds:
$\Delta_\mathcal{R}$
weakly preserves dominated convexity if and only if the following condition holds:
(*#) If
![]() $(A_0,\ldots,A_{n-1})\in \mathcal{R}[A]$
,
$(A_0,\ldots,A_{n-1})\in \mathcal{R}[A]$
,
![]() $(B_0,\ldots,B_{n-1})\in \mathcal{R}[B]$
, and
$(B_0,\ldots,B_{n-1})\in \mathcal{R}[B]$
, and
![]() $C\in \mathcal{H}_*(A,B)$
, then there are
$C\in \mathcal{H}_*(A,B)$
, then there are
![]() $C_0,\ldots,C_{n-1}$
such that
$C_0,\ldots,C_{n-1}$
such that
![]() $(C_0,\ldots,C_{n-1})\in \mathcal{R}[C]$
and
$(C_0,\ldots,C_{n-1})\in \mathcal{R}[C]$
and
![]() $C_i\in \mathcal{H}_*(A_i,B_i)$
for each
$C_i\in \mathcal{H}_*(A_i,B_i)$
for each
![]() $i<n$
.
$i<n$
.
Proof. Assume that (
![]() $*^\sharp$
) holds. Let
$*^\sharp$
) holds. Let
![]() $\mathcal{A}_i$
be dominated convex sets with maximum sets
$\mathcal{A}_i$
be dominated convex sets with maximum sets
![]() $D_i$
for
$D_i$
for
![]() $i<n$
. If
$i<n$
. If
![]() $\Delta_\mathcal{R}(\mathcal{A}_0,\ldots,\mathcal{A}_{n-1})\not=\emptyset$
, it contains maximal sets. We show first that it has a unique maximal set.
$\Delta_\mathcal{R}(\mathcal{A}_0,\ldots,\mathcal{A}_{n-1})\not=\emptyset$
, it contains maximal sets. We show first that it has a unique maximal set.
Thus, assume that A and B are maximal sets in
![]() $\Delta_\mathcal{R}(\mathcal{A}_0,\ldots,\mathcal{A}_{n-1})$
. Then there are
$\Delta_\mathcal{R}(\mathcal{A}_0,\ldots,\mathcal{A}_{n-1})$
. Then there are
![]() $A_i,B_i\in\mathcal{A}_i$
,
$A_i,B_i\in\mathcal{A}_i$
,
![]() $i<n$
, such that
$i<n$
, such that
![]() $(A_0,\ldots,A_{n-1})\in \mathcal{R}[A]$
and
$(A_0,\ldots,A_{n-1})\in \mathcal{R}[A]$
and
![]() $(B_0,\ldots,B_{n-1})\in \mathcal{R}[B]$
. By (
$(B_0,\ldots,B_{n-1})\in \mathcal{R}[B]$
. By (
![]() $*^\sharp$
), there are
$*^\sharp$
), there are
![]() $C_i$
such that
$C_i$
such that
![]() $(C_0,\ldots,C_{n-1})\in \mathcal{R}[A\cup B]$
and
$(C_0,\ldots,C_{n-1})\in \mathcal{R}[A\cup B]$
and
![]() $C_i\in \mathcal{H}_*(A_i,B_i)%\subseteq [A_i,D_i]\cup [B_i,D_i]\subseteq\mathcal{A}_i$
for each
$C_i\in \mathcal{H}_*(A_i,B_i)%\subseteq [A_i,D_i]\cup [B_i,D_i]\subseteq\mathcal{A}_i$
for each
![]() $i<n$
. Hence
$i<n$
. Hence
![]() $A\cup B\in \Delta_\mathcal{R}(\mathcal{A}_0,\ldots,\mathcal{A}_{n-1})$
. Since
$A\cup B\in \Delta_\mathcal{R}(\mathcal{A}_0,\ldots,\mathcal{A}_{n-1})$
. Since
![]() $A,B\subseteq A\cup B$
, this is possible only if
$A,B\subseteq A\cup B$
, this is possible only if
![]() $A=B$
.
$A=B$
.
To prove that
![]() $\Delta_\mathcal{R}(\mathcal{A}_0,\ldots,\mathcal{A}_{n-1})$
is convex, assume that
$\Delta_\mathcal{R}(\mathcal{A}_0,\ldots,\mathcal{A}_{n-1})$
is convex, assume that
![]() $A\subseteq C\subseteq B$
,
$A\subseteq C\subseteq B$
,
![]() $(A_0,\ldots,A_{n-1})\in \mathcal{R}[A]$
and
$(A_0,\ldots,A_{n-1})\in \mathcal{R}[A]$
and
![]() $(B_0,\ldots,B_{n-1})\in \mathcal{R}[B]$
. Then
$(B_0,\ldots,B_{n-1})\in \mathcal{R}[B]$
. Then
![]() $C\in [A,B]=\mathcal{H}_*(A,B)$
, whence by (
$C\in [A,B]=\mathcal{H}_*(A,B)$
, whence by (
![]() $*^\sharp$
), there are
$*^\sharp$
), there are
![]() $C_i$
such that
$C_i$
such that
![]() $C_i\in \mathcal{H}_*(A_i,B_i)\subseteq\mathcal{A}_i$
for each
$C_i\in \mathcal{H}_*(A_i,B_i)\subseteq\mathcal{A}_i$
for each
![]() $i<n$
and
$i<n$
and
![]() $(C_0,\ldots,C_{n-1})\in \mathcal{R}[C]$
. Thus,
$(C_0,\ldots,C_{n-1})\in \mathcal{R}[C]$
. Thus,
![]() $C\in \Delta_\mathcal{R}(\mathcal{A}_0,\ldots,\mathcal{A}_{n-1})$
.
$C\in \Delta_\mathcal{R}(\mathcal{A}_0,\ldots,\mathcal{A}_{n-1})$
.
Assume then that
![]() $\Delta_\mathcal{R}$
weakly preserves dominated convexity. Let
$\Delta_\mathcal{R}$
weakly preserves dominated convexity. Let
![]() $(A_0,\ldots,A_{n-1})\in \mathcal{R}[A]$
,
$(A_0,\ldots,A_{n-1})\in \mathcal{R}[A]$
,
![]() $(B_0,\ldots,B_{n-1})\in \mathcal{R}[B]$
, and
$(B_0,\ldots,B_{n-1})\in \mathcal{R}[B]$
, and
![]() $C\in \mathcal{H}_*(A,B)$
. Since the families
$C\in \mathcal{H}_*(A,B)$
. Since the families
![]() $\mathcal{A}_i:=\mathcal{H}_*(A_i,B_i)$
,
$\mathcal{A}_i:=\mathcal{H}_*(A_i,B_i)$
,
![]() $i<n$
, are convex and dominated, there is a set
$i<n$
, are convex and dominated, there is a set
![]() $D\in\Delta_\mathcal{R}(\mathcal{A}_0,\ldots, \mathcal{A}_{n-1})$
such that
$D\in\Delta_\mathcal{R}(\mathcal{A}_0,\ldots, \mathcal{A}_{n-1})$
such that
![]() $A\cup B\subseteq D$
. Now
$A\cup B\subseteq D$
. Now
![]() $C\in \mathcal{H}_*(A,B,D)$
, and since
$C\in \mathcal{H}_*(A,B,D)$
, and since
![]() $\Delta_\mathcal{R}$
weakly preserves dominated convexity,
$\Delta_\mathcal{R}$
weakly preserves dominated convexity,
![]() $\mathcal{H}_*(A,B,D)\subseteq\Delta_\mathcal{R}(\mathcal{A}_0,\ldots,\mathcal{A}_{n-1})$
. Thus (
$\mathcal{H}_*(A,B,D)\subseteq\Delta_\mathcal{R}(\mathcal{A}_0,\ldots,\mathcal{A}_{n-1})$
. Thus (
![]() $*^\sharp$
) holds.
$*^\sharp$
) holds.
Lemma 57. Let
![]() $\Delta_\mathcal{R}\colon \mathcal{P}(\mathcal{P}(X))^n\to\mathcal{P}(\mathcal{P}(Y))$
be a Kripke-operator for finite X and Y. Then
$\Delta_\mathcal{R}\colon \mathcal{P}(\mathcal{P}(X))^n\to\mathcal{P}(\mathcal{P}(Y))$
be a Kripke-operator for finite X and Y. Then
![]() $\Delta_\mathcal{R}$
weakly preserves supported convexity if and only if the following condition holds:
$\Delta_\mathcal{R}$
weakly preserves supported convexity if and only if the following condition holds:
(
![]() $*^\flat$
) If
$*^\flat$
) If
![]() $(A_0,\ldots,A_{n-1})\in \mathcal{R}[A]$
,
$(A_0,\ldots,A_{n-1})\in \mathcal{R}[A]$
,
![]() $(B_0,\ldots,B_{n-1})\in \mathcal{R}[B]$
, and
$(B_0,\ldots,B_{n-1})\in \mathcal{R}[B]$
, and
![]() $C\in \mathcal{H}^*(A,B)$
, then there are
$C\in \mathcal{H}^*(A,B)$
, then there are
![]() $C_0,\ldots,C_{n-1}$
such that
$C_0,\ldots,C_{n-1}$
such that
![]() $(C_0,\ldots,C_{n-1})\in \mathcal{R}[C]$
and
$(C_0,\ldots,C_{n-1})\in \mathcal{R}[C]$
and
![]() $C_i\in \mathcal{H}^*(A_i,B_i)$
for each
$C_i\in \mathcal{H}^*(A_i,B_i)$
for each
![]() $i<n$
.
$i<n$
.
Proof. The claim is proved in the same way as the previous result.
4.3. Point-wise Kripke-operators
Many natural Kripke-operators
![]() $\Delta_\mathcal{R}$
are point-wise in the sense that the relation
$\Delta_\mathcal{R}$
are point-wise in the sense that the relation
![]() $\mathcal{R}[A]$
is completely determined by its behavior on singletons
$\mathcal{R}[A]$
is completely determined by its behavior on singletons
![]() $\{a\}\subseteq A$
.
$\{a\}\subseteq A$
.
Definition 58. A Kripke-operator
![]() $\Delta_\mathcal{R}\colon \mathcal{P}(\mathcal{P}(X))^n\to\mathcal{P}(\mathcal{P}(Y))$
is point-wiseFootnote
6
if, for any
$\Delta_\mathcal{R}\colon \mathcal{P}(\mathcal{P}(X))^n\to\mathcal{P}(\mathcal{P}(Y))$
is point-wiseFootnote
6
if, for any
![]() $A\in\mathcal{P}(Y)$
,
$A\in\mathcal{P}(Y)$
,
![]() $\mathcal{R}[A]$
is determined by the relations
$\mathcal{R}[A]$
is determined by the relations
![]() $\mathcal{R}[\{a\}]$
,
$\mathcal{R}[\{a\}]$
,
![]() $a\in A$
, as follows:
$a\in A$
, as follows:
![]() $(A_0,\ldots,A_{n-1})\in \mathcal{R}[A]\Leftrightarrow$
for each
$(A_0,\ldots,A_{n-1})\in \mathcal{R}[A]\Leftrightarrow$
for each
![]() $a\in A$
there is
$a\in A$
there is
![]() $(A^a_0,\ldots,A^a_{n-1})\in \mathcal{R}[\{a\}]$
such that
$(A^a_0,\ldots,A^a_{n-1})\in \mathcal{R}[\{a\}]$
such that
![]() $A_i=\bigcup_{a\in A}A_i^a$
for
$A_i=\bigcup_{a\in A}A_i^a$
for
![]() $i<n$
.
$i<n$
.
Lück proved (Lück Reference Lück2020) that all point-wise Kripke-operators
![]() $\Delta$
preserve flatness: if
$\Delta$
preserve flatness: if
![]() $\mathcal{A}_i$
,
$\mathcal{A}_i$
,
![]() $i<n$
, are flat (i.e., dominated and downward closed), then
$i<n$
, are flat (i.e., dominated and downward closed), then
![]() $\Delta(\mathcal{A}_0,\ldots,\mathcal{A}_{n-1})$
is also flat. We generalize this result to dominated convexity.
$\Delta(\mathcal{A}_0,\ldots,\mathcal{A}_{n-1})$
is also flat. We generalize this result to dominated convexity.
Theorem 59. If
![]() $\Delta_\mathcal{R}\colon \mathcal{P}(\mathcal{P}(X))^n\to\mathcal{P}(\mathcal{P}(Y))$
is a point-wise Kripke-operator for finite X and Y, then it weakly preserves dominated convexity.
$\Delta_\mathcal{R}\colon \mathcal{P}(\mathcal{P}(X))^n\to\mathcal{P}(\mathcal{P}(Y))$
is a point-wise Kripke-operator for finite X and Y, then it weakly preserves dominated convexity.
Proof. It suffices to show that
![]() $\mathcal{R}$
satisfies the condition
$\mathcal{R}$
satisfies the condition
![]() $(*^\sharp)$
of Lemma 56. Assume for this that
$(*^\sharp)$
of Lemma 56. Assume for this that
![]() $(A_0,\ldots,A_{n-1})\in \mathcal{R}[A]$
,
$(A_0,\ldots,A_{n-1})\in \mathcal{R}[A]$
,
![]() $(B_0,\ldots,B_{n-1})\in \mathcal{R}[B]$
, and
$(B_0,\ldots,B_{n-1})\in \mathcal{R}[B]$
, and
![]() $C\in\mathcal{H}_*(A,B)=[A,A\cup B]\cup[B,A\cup B]$
. We assume that
$C\in\mathcal{H}_*(A,B)=[A,A\cup B]\cup[B,A\cup B]$
. We assume that
![]() $C\in [A,A\cup B]$
; the case
$C\in [A,A\cup B]$
; the case
![]() $C\in [B,A\cup B]$
is similar.
$C\in [B,A\cup B]$
is similar.
Since
![]() $\Delta_\mathcal{R}$
is point-wise, for each
$\Delta_\mathcal{R}$
is point-wise, for each
![]() $a\in A$
there are sets
$a\in A$
there are sets
![]() $A_i^a$
such that
$A_i^a$
such that
![]() $A_i=\bigcup_{a\in A}A_i^a$
for
$A_i=\bigcup_{a\in A}A_i^a$
for
![]() $i<n$
, and
$i<n$
, and
![]() $(A_0^a,\ldots, A_{n-1}^a)\in \mathcal{R}[\{a\}]$
. Similarly, for each
$(A_0^a,\ldots, A_{n-1}^a)\in \mathcal{R}[\{a\}]$
. Similarly, for each
![]() $b\in B$
there are sets
$b\in B$
there are sets
![]() $B_i^b$
such that
$B_i^b$
such that
![]() $B_i=\bigcup_{b\in B}B_i^b$
for
$B_i=\bigcup_{b\in B}B_i^b$
for
![]() $i<n$
, and
$i<n$
, and
![]() $(B_0^b,\ldots, B_{n-1}^b)\in \mathcal{R}[\{b\}]$
.
$(B_0^b,\ldots, B_{n-1}^b)\in \mathcal{R}[\{b\}]$
.
Now, for each
![]() $i<n$
, we define
$i<n$
, we define
![]() $C_i^c:=A_i^c$
for all
$C_i^c:=A_i^c$
for all
![]() $c\in A$
, and
$c\in A$
, and
![]() $C_i^c:=B_i^c$
for all
$C_i^c:=B_i^c$
for all
![]() $c\in C\smallsetminus A$
(note that
$c\in C\smallsetminus A$
(note that
![]() $A\subseteq C$
and
$A\subseteq C$
and
![]() $C\smallsetminus A\subseteq B$
). Let
$C\smallsetminus A\subseteq B$
). Let
![]() $C_i:=\bigcup_{c\in C}C_i^c$
for
$C_i:=\bigcup_{c\in C}C_i^c$
for
![]() $i<n$
. By Definition 58 we have
$i<n$
. By Definition 58 we have
![]() $(C_0,\ldots,C_{n-1})\in\mathcal{R}[C]$
.
$(C_0,\ldots,C_{n-1})\in\mathcal{R}[C]$
.
We still need to show that
![]() $C_i\in \mathcal{H}_*(A_i,B_i)$
for
$C_i\in \mathcal{H}_*(A_i,B_i)$
for
![]() $i<n$
. Clearly,
$i<n$
. Clearly,
![]() $C_i^c\subseteq A_i\cup B_i$
for each
$C_i^c\subseteq A_i\cup B_i$
for each
![]() $c\in C$
, whence
$c\in C$
, whence
![]() $C_i\subseteq A_i\cup B_i$
for
$C_i\subseteq A_i\cup B_i$
for
![]() $i<n$
. Furthermore,
$i<n$
. Furthermore,
![]() $A_i=\bigcup_{a\in A}A_i^a=\bigcup_{c\in A}C_i^c\subseteq C_i$
, whence we conclude that
$A_i=\bigcup_{a\in A}A_i^a=\bigcup_{c\in A}C_i^c\subseteq C_i$
, whence we conclude that
![]() $C_i\in [A_i,A_i\cup B_i]\subseteq\mathcal{H}_*(A_i,B_i)$
.
$C_i\in [A_i,A_i\cup B_i]\subseteq\mathcal{H}_*(A_i,B_i)$
.
On the other hand, it is not the case that all point-wise Kripke-operators weakly preserve supported convexity. This is seen in the next example.
Example 60.
-
(a) Let
 $X=\{a,b\}$
, and let
$X=\{a,b\}$
, and let
 $\mathcal{R}$
be the relation
$\mathcal{R}$
be the relation
 $\{(Y,X)\mid Y\not=\emptyset\}\subseteq \mathcal{P}(X)^2$
. Then
$\{(Y,X)\mid Y\not=\emptyset\}\subseteq \mathcal{P}(X)^2$
. Then
 $\Delta_\mathcal{R}$
is clearly point-wise, but it does not weakly preserve supported convexity, since the family
$\Delta_\mathcal{R}$
is clearly point-wise, but it does not weakly preserve supported convexity, since the family
 $\mathcal{H}^*(X)=\{X\}$
is convex and supported, but its image
$\mathcal{H}^*(X)=\{X\}$
is convex and supported, but its image
 $\Delta_\mathcal{R}(\{X\})=\{\{a\},\{b\},X\}$
is not supported.
$\Delta_\mathcal{R}(\{X\})=\{\{a\},\{b\},X\}$
is not supported. -
(b) More generally, if
 $\Delta_\mathcal{R}\colon\mathcal{P}(\mathcal{P}(X))^n\to\mathcal{P}(\mathcal{P}(Y))$
is a point-wise Kripke-operator and there are tuples
$\Delta_\mathcal{R}\colon\mathcal{P}(\mathcal{P}(X))^n\to\mathcal{P}(\mathcal{P}(Y))$
is a point-wise Kripke-operator and there are tuples
 $(\{a\},A_0,\ldots,A_{n-1}),(\{b\},B_0,\ldots,B_{n-1})$
in
$(\{a\},A_0,\ldots,A_{n-1}),(\{b\},B_0,\ldots,B_{n-1})$
in
 $\mathcal{R}$
such that
$\mathcal{R}$
such that
 $a\not=b$
and
$a\not=b$
and
 $A_i\cap B_i\not=\emptyset$
for some
$A_i\cap B_i\not=\emptyset$
for some
 $i<n$
, then
$i<n$
, then
 $\Delta_\mathcal{R}$
does not weakly preserve supported convexity. This is because by Definition 58,
$\Delta_\mathcal{R}$
does not weakly preserve supported convexity. This is because by Definition 58,
 $\mathcal{R}[\emptyset]=\{(\emptyset,\ldots,\emptyset)\}$
, whence
$\mathcal{R}[\emptyset]=\{(\emptyset,\ldots,\emptyset)\}$
, whence
 $\emptyset\notin\Delta_\mathcal{R}(\mathcal{H}^*(A_0,B_0),\ldots,\mathcal{H}^*(A_{n-1},B_{n-1}))$
even though
$\emptyset\notin\Delta_\mathcal{R}(\mathcal{H}^*(A_0,B_0),\ldots,\mathcal{H}^*(A_{n-1},B_{n-1}))$
even though
 $\emptyset\in\mathcal{H}^*(\{a\},\{b\})$
.
$\emptyset\in\mathcal{H}^*(\{a\},\{b\})$
.
To avoid the problem exhibited in the example above, we consider the following additional requirement for (point-wise) Kripke-operators:
Definition 61. A Kripke-operator
![]() $\Delta_\mathcal{R}\colon \mathcal{P}(\mathcal{P}(X))^n\to\mathcal{P}(\mathcal{P}(Y))$
is separating if
$\Delta_\mathcal{R}\colon \mathcal{P}(\mathcal{P}(X))^n\to\mathcal{P}(\mathcal{P}(Y))$
is separating if
![]() $A_i\cap B_i=\emptyset$
for all
$A_i\cap B_i=\emptyset$
for all
![]() $i<n$
whenever
$i<n$
whenever
![]() $(A_0,\ldots,A_{n-1})\in\mathcal{R}[\{a\}]$
,
$(A_0,\ldots,A_{n-1})\in\mathcal{R}[\{a\}]$
,
![]() $(B_0,\ldots,B_{n-1})\in\mathcal{R}[\{b\}]$
and
$(B_0,\ldots,B_{n-1})\in\mathcal{R}[\{b\}]$
and
![]() $a\not=b$
.
$a\not=b$
.
Theorem 62. If
![]() $\Delta_\mathcal{R}\colon \mathcal{P}(\mathcal{P}(X))^n\to\mathcal{P}(\mathcal{P}(Y))$
is a point-wise and separating Kripke-operator for finite X and Y, then it weakly preserves supported convexity.
$\Delta_\mathcal{R}\colon \mathcal{P}(\mathcal{P}(X))^n\to\mathcal{P}(\mathcal{P}(Y))$
is a point-wise and separating Kripke-operator for finite X and Y, then it weakly preserves supported convexity.
Proof. We show that
![]() $\mathcal{R}$
satisfies the condition
$\mathcal{R}$
satisfies the condition
![]() $(*^\flat)$
of Lemma 57. Thus, assume that
$(*^\flat)$
of Lemma 57. Thus, assume that
![]() $(A_0,\ldots,A_{n-1})\in \mathcal{R}[A]$
,
$(A_0,\ldots,A_{n-1})\in \mathcal{R}[A]$
,
![]() $(B_0,\ldots,B_{n-1})\in \mathcal{R}[B]$
, and
$(B_0,\ldots,B_{n-1})\in \mathcal{R}[B]$
, and
![]() $C\in\mathcal{H}^*(A,B)=[A\cap B,A]\cup[A\cap B,B]$
. We consider the case
$C\in\mathcal{H}^*(A,B)=[A\cap B,A]\cup[A\cap B,B]$
. We consider the case
![]() $C\in [A\cap B,A]$
; the other case is similar.
$C\in [A\cap B,A]$
; the other case is similar.
By Definition 58, for each
![]() $i<n$
and each
$i<n$
and each
![]() $a\in A$
there are sets
$a\in A$
there are sets
![]() $A_i^a$
such that
$A_i^a$
such that
![]() $(A_0^a,\ldots,A_{n-1}^a)\in \mathcal{R}[\{a\}]$
and
$(A_0^a,\ldots,A_{n-1}^a)\in \mathcal{R}[\{a\}]$
and
![]() $A_i=\bigcup_{a\in A}A^a_i$
. Similarly, for each
$A_i=\bigcup_{a\in A}A^a_i$
. Similarly, for each
![]() $b\in B$
, there are sets
$b\in B$
, there are sets
![]() $B_i^b$
such that
$B_i^b$
such that
![]() $(B_0^a,\ldots,B_{n-1}^a)\in \mathcal{R}[\{b\}]$
and
$(B_0^a,\ldots,B_{n-1}^a)\in \mathcal{R}[\{b\}]$
and
![]() $B_i=\bigcup_{b\in B}B^b_i$
. We define now
$B_i=\bigcup_{b\in B}B^b_i$
. We define now
![]() $C_i=\bigcup_{c\in C} A^c_i$
for
$C_i=\bigcup_{c\in C} A^c_i$
for
![]() $i<n$
. Then by Definition 58 we have
$i<n$
. Then by Definition 58 we have
![]() $(C_0,\ldots,C_{n-1})\in \mathcal{R}[C]$
.
$(C_0,\ldots,C_{n-1})\in \mathcal{R}[C]$
.
It is clear from the definition that
![]() $C_i\subseteq A_i$
. Thus, to complete the proof it suffices to show that
$C_i\subseteq A_i$
. Thus, to complete the proof it suffices to show that
![]() $A_i\cap B_i\subseteq C_i$
for each
$A_i\cap B_i\subseteq C_i$
for each
![]() $i<n$
. To show this, assume that
$i<n$
. To show this, assume that
![]() $d\in A_i\cap B_i$
. Then there are elements
$d\in A_i\cap B_i$
. Then there are elements
![]() $a\in A$
and
$a\in A$
and
![]() $b\in B$
such that
$b\in B$
such that
![]() $d\in A_i^a$
and
$d\in A_i^a$
and
![]() $d\in B_i^b$
. As
$d\in B_i^b$
. As
![]() $\Delta_\mathcal{R}$
is separating this implies that
$\Delta_\mathcal{R}$
is separating this implies that
![]() $a=b\in A\cap B\subseteq C$
, whence
$a=b\in A\cap B\subseteq C$
, whence
![]() $d\in A_i^a=C_i^a\subseteq C_i$
.
$d\in A_i^a=C_i^a\subseteq C_i$
.
Recall from Example 51 the Kripke-relations
![]() $\mathcal{R}_\cap$
,
$\mathcal{R}_\cap$
,
![]() $\mathcal{R}_\lor$
and
$\mathcal{R}_\lor$
and
![]() $\mathcal{R}_{\mathcal{K},\vec\ell}$
that define the Kripke-operators that correspond to conjunction, (tensor) disjunction and quantification with the Lindström quantifier
$\mathcal{R}_{\mathcal{K},\vec\ell}$
that define the Kripke-operators that correspond to conjunction, (tensor) disjunction and quantification with the Lindström quantifier
![]() $Q_\mathcal{K}$
. We prove next that the corresponding Kripke-operators are point-wise and separating.
$Q_\mathcal{K}$
. We prove next that the corresponding Kripke-operators are point-wise and separating.
Proposition 63.
The operators
![]() $\Delta^{M^m}_\cap$
,
$\Delta^{M^m}_\cap$
,
![]() $\Delta^{M^m}_\lor$
and
$\Delta^{M^m}_\lor$
and
![]() $\Delta^{M^m}_{\mathcal{K},\vec\ell}$
are point-wise and separating.
$\Delta^{M^m}_{\mathcal{K},\vec\ell}$
are point-wise and separating.
Proof. Note first that
![]() $\mathcal{R}_\cap[A]=\{(A,A)\}$
for any
$\mathcal{R}_\cap[A]=\{(A,A)\}$
for any
![]() $A\in \mathcal{P}(M^m)$
. Hence, we have
$A\in \mathcal{P}(M^m)$
. Hence, we have
![]() $(A_0,A_1)\in\mathcal{R}_\cap[A]$
if and only if
$(A_0,A_1)\in\mathcal{R}_\cap[A]$
if and only if
![]() $A_0=A_1=A=\bigcup_{\vec{a}\in A}\{\vec{a}\}$
if and only if for each
$A_0=A_1=A=\bigcup_{\vec{a}\in A}\{\vec{a}\}$
if and only if for each
![]() $\vec{a}\in A$
there are sets
$\vec{a}\in A$
there are sets
![]() $A^{\vec{a}}_0,A^{\vec{a}}_1$
such that
$A^{\vec{a}}_0,A^{\vec{a}}_1$
such that
![]() $(A^{\vec{a}}_0,A^{\vec{a}}_1)\in\mathcal{R}_\cap[\{\vec{a}\}]$
and
$(A^{\vec{a}}_0,A^{\vec{a}}_1)\in\mathcal{R}_\cap[\{\vec{a}\}]$
and
![]() $A_i=\bigcup_{\vec{a}\in A}A^{\vec{a}}_i$
for
$A_i=\bigcup_{\vec{a}\in A}A^{\vec{a}}_i$
for
![]() $i<2$
. Thus,
$i<2$
. Thus,
![]() $\Delta^{M^m}_\cap$
is point-wise. Since
$\Delta^{M^m}_\cap$
is point-wise. Since
![]() $\mathcal{R}_\cap[\{\vec{a}\}]=\{(\{\vec{a}\},\{\vec{a}\})\}$
, it is clearly separating, too.
$\mathcal{R}_\cap[\{\vec{a}\}]=\{(\{\vec{a}\},\{\vec{a}\})\}$
, it is clearly separating, too.
Consider then the tensor disjunction operator on
![]() $M^m$
. By the definition of
$M^m$
. By the definition of
![]() $\mathcal{R}_\lor$
we have
$\mathcal{R}_\lor$
we have
![]() $\mathcal{R}_\lor[\{\vec{a}\}]=\{(\{\vec{a}\},\{\vec{a}\}),(\{\vec{a}\},\emptyset),(\emptyset,\{\vec{a}\})\}$
for any
$\mathcal{R}_\lor[\{\vec{a}\}]=\{(\{\vec{a}\},\{\vec{a}\}),(\{\vec{a}\},\emptyset),(\emptyset,\{\vec{a}\})\}$
for any
![]() $\vec{a}\in M^m$
. Using this it is straightforward to verify that
$\vec{a}\in M^m$
. Using this it is straightforward to verify that
![]() $\Delta^{M^m}_\lor$
is point-wise and separating.
$\Delta^{M^m}_\lor$
is point-wise and separating.
Finally, we show that the
![]() $(\mathcal{K},\vec\ell)$
-projection operator
$(\mathcal{K},\vec\ell)$
-projection operator
![]() $\Delta^{M^m}_{\mathcal{K},\vec\ell}$
is separating and point-wise. Assume first that
$\Delta^{M^m}_{\mathcal{K},\vec\ell}$
is separating and point-wise. Assume first that
![]() $(M,\emptyset)\notin\mathcal{K}$
. Then by the definition of
$(M,\emptyset)\notin\mathcal{K}$
. Then by the definition of
![]() $\mathcal{R}_{\mathcal{K},\vec\ell}$
we see that for any tuple
$\mathcal{R}_{\mathcal{K},\vec\ell}$
we see that for any tuple
![]() $\vec a\in M^{m-r}$
,
$\vec a\in M^{m-r}$
,
![]() $\mathcal{R}_{\mathcal{K},\vec\ell}\,[\{\vec a\}]=\{S\in\mathcal{P}(M^m)\mid \pi^p_{\mathcal{K},\vec\ell}\,(S)=\{\vec a\}\}$
. Clearly,
$\mathcal{R}_{\mathcal{K},\vec\ell}\,[\{\vec a\}]=\{S\in\mathcal{P}(M^m)\mid \pi^p_{\mathcal{K},\vec\ell}\,(S)=\{\vec a\}\}$
. Clearly,
![]() $S\cap S'=\emptyset$
if
$S\cap S'=\emptyset$
if
![]() $\pi^p_{\mathcal{K},\vec\ell}\,(S)=\{\vec a\}$
and
$\pi^p_{\mathcal{K},\vec\ell}\,(S)=\{\vec a\}$
and
![]() $\pi^p_{\mathcal{K},\vec\ell}\,(S')=\{\vec b\}$
for
$\pi^p_{\mathcal{K},\vec\ell}\,(S')=\{\vec b\}$
for
![]() $\vec a\not=\vec b$
, whence
$\vec a\not=\vec b$
, whence
![]() $\Delta^{M^m}_{\mathcal{K},\vec\ell}$
is separating.
$\Delta^{M^m}_{\mathcal{K},\vec\ell}$
is separating.
To show that
![]() $\Delta^{M^m}_{\mathcal{K},\vec\ell}$
is point-wise, observe that
$\Delta^{M^m}_{\mathcal{K},\vec\ell}$
is point-wise, observe that
![]() $S\in \mathcal{R}_{\mathcal{K},\vec\ell}\,[T]$
if and only if
$S\in \mathcal{R}_{\mathcal{K},\vec\ell}\,[T]$
if and only if
![]() $T=\pi^p_{\mathcal{K},\vec\ell}\,(S)=\{\vec a\in M^{m-r}\mid S[\vec a]_{\vec\ell}\in \mathcal{K}\}$
. Assume first that this equality holds. Then
$T=\pi^p_{\mathcal{K},\vec\ell}\,(S)=\{\vec a\in M^{m-r}\mid S[\vec a]_{\vec\ell}\in \mathcal{K}\}$
. Assume first that this equality holds. Then
![]() $S=\bigcup_{\vec a\in T}S^{\vec a}$
, where
$S=\bigcup_{\vec a\in T}S^{\vec a}$
, where
![]() $S^{\vec a}:=\{\vec{c}\in S\mid\vec{c}=\vec{a}\otimes_{\vec\ell}\,\vec{b} \text{ for some }\vec{b}\in M^r\}$
. Moreover, the equality implies that
$S^{\vec a}:=\{\vec{c}\in S\mid\vec{c}=\vec{a}\otimes_{\vec\ell}\,\vec{b} \text{ for some }\vec{b}\in M^r\}$
. Moreover, the equality implies that
![]() $S[\vec a]_{\vec\ell}\in \mathcal{K}$
, whence
$S[\vec a]_{\vec\ell}\in \mathcal{K}$
, whence
![]() $S^{\vec a}\in \mathcal{R}_{\mathcal{K},\vec\ell }\,[\{\vec a\}]$
for all
$S^{\vec a}\in \mathcal{R}_{\mathcal{K},\vec\ell }\,[\{\vec a\}]$
for all
![]() $\vec a\in A$
.
$\vec a\in A$
.
Assume then that
![]() $S=\bigcup_{\vec a\in T}S^{\vec a}$
for some sets
$S=\bigcup_{\vec a\in T}S^{\vec a}$
for some sets
![]() $S^{\vec a}\in \mathcal{R}_{\mathcal{K},\vec\ell}\,[\{\vec a\}]$
,
$S^{\vec a}\in \mathcal{R}_{\mathcal{K},\vec\ell}\,[\{\vec a\}]$
,
![]() $\vec a\in A$
. Then by definition
$\vec a\in A$
. Then by definition
![]() $\pi^p_{\mathcal{K},\vec\ell}\,(S^{\vec{a}})=\{\vec{a}\}$
for each
$\pi^p_{\mathcal{K},\vec\ell}\,(S^{\vec{a}})=\{\vec{a}\}$
for each
![]() $\vec a\in A$
, whence
$\vec a\in A$
, whence
![]() $\pi^p_{\mathcal{K},\vec\ell}\,(S)=\bigcup_{\vec{a}\in T}\pi^p_{\mathcal{K},\vec\ell}\,(S^{\vec{a}})=T$
, and consequently
$\pi^p_{\mathcal{K},\vec\ell}\,(S)=\bigcup_{\vec{a}\in T}\pi^p_{\mathcal{K},\vec\ell}\,(S^{\vec{a}})=T$
, and consequently
![]() $S\in\mathcal{R}_{\mathcal{K},\vec\ell}\,[T]$
.
$S\in\mathcal{R}_{\mathcal{K},\vec\ell}\,[T]$
.
In the case
![]() $(M,\emptyset)\in\mathcal{K}$
, we have
$(M,\emptyset)\in\mathcal{K}$
, we have
![]() $\mathcal{R}_{\mathcal{K},\vec\ell}\,[T]=\{S\in\mathcal{P}(M^m)\mid \pi^p_{\mathcal{K},\vec\ell}\,(S)\subseteq T\}$
. This just means that
$\mathcal{R}_{\mathcal{K},\vec\ell}\,[T]=\{S\in\mathcal{P}(M^m)\mid \pi^p_{\mathcal{K},\vec\ell}\,(S)\subseteq T\}$
. This just means that
![]() $\emptyset$
is added to
$\emptyset$
is added to
![]() $\mathcal{R}_{\mathcal{K},\vec\ell}\,[\{\vec a\}]$
for each
$\mathcal{R}_{\mathcal{K},\vec\ell}\,[\{\vec a\}]$
for each
![]() $\vec{a}\in M^{m-r}$
. Clearly, this does not affect the proof that
$\vec{a}\in M^{m-r}$
. Clearly, this does not affect the proof that
![]() $\Delta^{M^m}_{\mathcal{K},\vec\ell}$
is separating. The proof that it is point-wise also goes through by defining
$\Delta^{M^m}_{\mathcal{K},\vec\ell}$
is separating. The proof that it is point-wise also goes through by defining
![]() $S^{\vec{a}}=\emptyset$
for
$S^{\vec{a}}=\emptyset$
for
![]() $\vec{a}\in T\smallsetminus \pi^p_{\mathcal{K},\vec\ell}\,(S)$
.
$\vec{a}\in T\smallsetminus \pi^p_{\mathcal{K},\vec\ell}\,(S)$
.
We end this section by showing that not all of the Kripke-operators of Example 51 are point-wise and separating.
Example 64.
-
(a) Consider the restricted union operator
 $\Delta_{\mathcal{R}_{\cup^*}}$
on a base set X. By the definition of
$\Delta_{\mathcal{R}_{\cup^*}}$
on a base set X. By the definition of
 $\mathcal{R}_{\cup^*}$
we have
$\mathcal{R}_{\cup^*}$
we have
 $\mathcal{R}_{\cup^*}[\{a\}]=\{(\{a\},\emptyset),(\emptyset,\{a\})\}$
for any
$\mathcal{R}_{\cup^*}[\{a\}]=\{(\{a\},\emptyset),(\emptyset,\{a\})\}$
for any
 $a\in X$
. Hence,
$a\in X$
. Hence,
 $\Delta_{\mathcal{R}_{\cup^*}}$
is clearly separating. However, it is not point-wise: if
$\Delta_{\mathcal{R}_{\cup^*}}$
is clearly separating. However, it is not point-wise: if
 $a\not=b$
, then
$a\not=b$
, then
 $(\{a\},\emptyset)\in\mathcal{R}_{\cup^*}[\{a\}]$
and
$(\{a\},\emptyset)\in\mathcal{R}_{\cup^*}[\{a\}]$
and
 $(\emptyset,\{b\})\in\mathcal{R}_{\cup^*}[\{b\}]$
, but
$(\emptyset,\{b\})\in\mathcal{R}_{\cup^*}[\{b\}]$
, but
 $(\{a\},\{b\})=(\{a\}\cup\emptyset,\emptyset\cup\{b\})\notin\mathcal{R}_{\cup^*}[\{a,b\}]$
.
$(\{a\},\{b\})=(\{a\}\cup\emptyset,\emptyset\cup\{b\})\notin\mathcal{R}_{\cup^*}[\{a,b\}]$
. -
(b) Tensor conjunction on a base set X with at least three elements is not point-wise: if
 $a,b,c\in X$
are distinct elements, then
$a,b,c\in X$
are distinct elements, then
 $(\{a,b\},\{a,c\})\in \mathcal{R}_{\land}[\{a\}]$
and
$(\{a,b\},\{a,c\})\in \mathcal{R}_{\land}[\{a\}]$
and
 $(\{b,c\},\{a,b\})\in \mathcal{R}_{\land}[\{b\}]$
, but
$(\{b,c\},\{a,b\})\in \mathcal{R}_{\land}[\{b\}]$
, but
 $(\{a,b\}\cup\{b,c\},\{a,c\}\cup\{b,c\})=(\{a,b,c\},\{a,b,c\})\notin \mathcal{R}_{\land}[\{a,b\}]$
. It is neither separating as the intersection of first components
$(\{a,b\}\cup\{b,c\},\{a,c\}\cup\{b,c\})=(\{a,b,c\},\{a,b,c\})\notin \mathcal{R}_{\land}[\{a,b\}]$
. It is neither separating as the intersection of first components
 $\{a,b\}$
and
$\{a,b\}$
and
 $\{b,c\}$
(as well as that of the second components) is nonempty.
$\{b,c\}$
(as well as that of the second components) is nonempty.
By a similar argument, we see that tensor negation and other non-monotone tensor operators are neither point-wise nor separating.
Note, however, that, as mentioned in Example 54, all tensor operators weakly preserve intervals. Moreover, we will later prove that tensor conjunction weakly preserves both dominated and supported convexity (see Proposition 66).
4.4 Logical operators preserving dimensions
We are now ready to prove that the basic logical operators of first-order logic (except for negation), as well as arbitrary Lindström quantifiers, preserve growth classes.
Corollary 65. Let
![]() $\mathbb{O}$
be a growth class, and let
$\mathbb{O}$
be a growth class, and let
![]() $\mathfrak{Dim}$
be one of the dimension functions Dim,
$\mathfrak{Dim}$
be one of the dimension functions Dim,
![]() $\mathrm{Dim}^{\mathrm{d}}$
and CDim. Furthermore, let
$\mathrm{Dim}^{\mathrm{d}}$
and CDim. Furthermore, let
![]() $\phi=\phi(\vec{x})$
and
$\phi=\phi(\vec{x})$
and
![]() $\psi=\psi(\vec{x})$
be formulas of some logic
$\psi=\psi(\vec{x})$
be formulas of some logic
![]() $\mathcal{L}$
with team semantics.
$\mathcal{L}$
with team semantics.
-
(a) If
 $\mathfrak{Dim}_{\phi,\vec{x}},\mathfrak{Dim}_{\psi,\vec{x}}\in\mathbb{O}$
, then
$\mathfrak{Dim}_{\phi,\vec{x}},\mathfrak{Dim}_{\psi,\vec{x}}\in\mathbb{O}$
, then
 $\mathfrak{Dim}_{\phi\land\psi,\vec{x}}\in\mathbb{O}$
.
$\mathfrak{Dim}_{\phi\land\psi,\vec{x}}\in\mathbb{O}$
. -
(b) If
 $\mathfrak{Dim}_{\phi,\vec{x}},\mathfrak{Dim}_{\psi,\vec{x}}\in\mathbb{O}$
, then
$\mathfrak{Dim}_{\phi,\vec{x}},\mathfrak{Dim}_{\psi,\vec{x}}\in\mathbb{O}$
, then
 $\mathfrak{Dim}_{\phi\lor\psi,\vec{x}}\in\mathbb{O}$
.
$\mathfrak{Dim}_{\phi\lor\psi,\vec{x}}\in\mathbb{O}$
. -
(c) If
 $\mathfrak{Dim}_{\phi,\vec{x}}\in\mathbb{O}$
, then
$\mathfrak{Dim}_{\phi,\vec{x}}\in\mathbb{O}$
, then
 $\mathfrak{Dim}_{\exists x_i\phi,{\vec{x}\hspace{0.3 mm}}^-}\in\mathbb{O}$
and
$\mathfrak{Dim}_{\exists x_i\phi,{\vec{x}\hspace{0.3 mm}}^-}\in\mathbb{O}$
and
 $\mathfrak{Dim}_{\forall x_i\phi,{\vec{x}\hspace{0.3 mm}}^-}\in\mathbb{O}$
, where
$\mathfrak{Dim}_{\forall x_i\phi,{\vec{x}\hspace{0.3 mm}}^-}\in\mathbb{O}$
, where
 ${\vec{x}\hspace{0.3 mm}}^-$
is
${\vec{x}\hspace{0.3 mm}}^-$
is
 $\vec{x}$
without the component
$\vec{x}$
without the component
 $x_i$
.
$x_i$
. -
(d) If
 $Q_\mathcal{K}$
is a Lindström quantifier,
$Q_\mathcal{K}$
is a Lindström quantifier,
 $\vec{x}=\vec{z}\otimes_{\vec\ell}\vec{y}$
and
$\vec{x}=\vec{z}\otimes_{\vec\ell}\vec{y}$
and
 $\mathfrak{Dim}_{\phi,\vec{x}}\in\mathbb{O}$
, then
$\mathfrak{Dim}_{\phi,\vec{x}}\in\mathbb{O}$
, then
 $\mathfrak{Dim}_{Q_\mathcal{K}\vec{y}\,\phi,\vec{z}}\in\mathbb{O}$
.
$\mathfrak{Dim}_{Q_\mathcal{K}\vec{y}\,\phi,\vec{z}}\in\mathbb{O}$
.
Proof.
-
(a) Let M be a finite model, and let
 $\mathrm{len}(\vec{x})=m$
. By Proposition 63, the operator
$\mathrm{len}(\vec{x})=m$
. By Proposition 63, the operator
 $\Delta^{M^m}_\cap$
is point-wise and separating, whence by Theorems 59 and 62 it weakly preserves both dominated and supported convexity. Thus, it follows from Theorem 55 that for each of the dimensions
$\Delta^{M^m}_\cap$
is point-wise and separating, whence by Theorems 59 and 62 it weakly preserves both dominated and supported convexity. Thus, it follows from Theorem 55 that for each of the dimensions $$ D(\!\left\Vert \phi\land\psi \right\Vert^{M,\vec{x}})=D(\!\left\Vert \phi \right\Vert^{M,\vec{x}}\cap\left\Vert \psi \right\Vert^{M,\vec{x}})\le D(\!\left\Vert \phi \right\Vert^{M,\vec{x}})\cdot D(\!\left\Vert \psi \right\Vert^{M,\vec{x}})$$
$$ D(\!\left\Vert \phi\land\psi \right\Vert^{M,\vec{x}})=D(\!\left\Vert \phi \right\Vert^{M,\vec{x}}\cap\left\Vert \psi \right\Vert^{M,\vec{x}})\le D(\!\left\Vert \phi \right\Vert^{M,\vec{x}})\cdot D(\!\left\Vert \psi \right\Vert^{M,\vec{x}})$$
 $D\in\{\mathrm{D},\mathrm{D}^{\mathrm{d}},\mathrm{CD}\}$
. Since this holds for all finite models M, we have
$D\in\{\mathrm{D},\mathrm{D}^{\mathrm{d}},\mathrm{CD}\}$
. Since this holds for all finite models M, we have
 $\mathfrak{Dim}_{\phi\land\psi,\vec{x}}\le \mathfrak{Dim}_{\phi,\vec{x}}\cdot\mathfrak{Dim}_{\psi,\vec{x}}$
, and hence
$\mathfrak{Dim}_{\phi\land\psi,\vec{x}}\le \mathfrak{Dim}_{\phi,\vec{x}}\cdot\mathfrak{Dim}_{\psi,\vec{x}}$
, and hence
 $\mathfrak{Dim}_{\phi\land\psi,\vec{x}}\in\mathbb{O}$
.
$\mathfrak{Dim}_{\phi\land\psi,\vec{x}}\in\mathbb{O}$
.
-
(b) is proved in the same way as (a).
-
(c) follows from (d) as a special case.
-
(d) Let M be a finite model. As in (a), it follows from Proposition 63 and Theorems 59 and 62 that the operator
 $\Delta^{M^m}_{\mathcal{K},\vec\ell}$
weakly preserves both dominated and supported convexity, whence using Theorem 55, we see that for each of the dimensions
$\Delta^{M^m}_{\mathcal{K},\vec\ell}$
weakly preserves both dominated and supported convexity, whence using Theorem 55, we see that for each of the dimensions $$ D(\!\left\Vert Q_\mathcal{K}\vec{y}\,\phi \right\Vert^{M,\vec{z}})=D(\Delta^{M^m}_{\mathcal{K},\vec\ell}(\!\left\Vert \phi \right\Vert^{M,\vec{x}}))\le D(\!\left\Vert \phi \right\Vert^{M,\vec{x}})$$
$$ D(\!\left\Vert Q_\mathcal{K}\vec{y}\,\phi \right\Vert^{M,\vec{z}})=D(\Delta^{M^m}_{\mathcal{K},\vec\ell}(\!\left\Vert \phi \right\Vert^{M,\vec{x}}))\le D(\!\left\Vert \phi \right\Vert^{M,\vec{x}})$$
 $D\in\{\mathrm{D},\mathrm{D}^{\mathrm{d}},\mathrm{CD}\}$
. Hence,
$D\in\{\mathrm{D},\mathrm{D}^{\mathrm{d}},\mathrm{CD}\}$
. Hence,
 $\mathfrak{Dim}_{Q_\mathcal{K}\vec{y}\,\phi,\vec{z}}\le\mathfrak{Dim}_{\phi,\vec{x}}$
, and consequently
$\mathfrak{Dim}_{Q_\mathcal{K}\vec{y}\,\phi,\vec{z}}\le\mathfrak{Dim}_{\phi,\vec{x}}$
, and consequently
 $\mathfrak{Dim}_{Q_\mathcal{K}\vec{y}\,\phi,\vec{z}}\in\mathbb{O}$
.
$\mathfrak{Dim}_{Q_\mathcal{K}\vec{y}\,\phi,\vec{z}}\in\mathbb{O}$
.
The list of logical operators that preserve growth classes of dimensions can be extended by simply appealing to basic definitions. We have already seen in Example 54 that all tensor operators (weakly) preserve intervals. Moreover, in spite of the fact that tensor conjunction is not point-wise (see Example 64(b)), we can prove that it weakly preserves both dominated and supported convexity.
Proposition 66. The operator
![]() $\Delta_\land$
weakly preserves dominated convexity and supported convexity.
$\Delta_\land$
weakly preserves dominated convexity and supported convexity.
Proof. Assume that
![]() $\mathcal{A}_0$
and
$\mathcal{A}_0$
and
![]() $\mathcal{A}_1$
are dominated and convex. We show first that
$\mathcal{A}_1$
are dominated and convex. We show first that
![]() $\Delta_\land(\mathcal{A}_0,\mathcal{A}_1)$
is convex. Thus, assume that
$\Delta_\land(\mathcal{A}_0,\mathcal{A}_1)$
is convex. Thus, assume that
![]() $A\subseteq C\subseteq B$
and
$A\subseteq C\subseteq B$
and
![]() $A,B\in\Delta_\land(\mathcal{A}_0,\mathcal{A}_1)$
. Then there are
$A,B\in\Delta_\land(\mathcal{A}_0,\mathcal{A}_1)$
. Then there are
![]() $A_0,B_0\in\mathcal{A}_0$
and
$A_0,B_0\in\mathcal{A}_0$
and
![]() $A_1,B_1\in\mathcal{A}_1$
such that
$A_1,B_1\in\mathcal{A}_1$
such that
![]() $A=A_0\cap A_1$
and
$A=A_0\cap A_1$
and
![]() $B=B_0\cap B_1$
. Let
$B=B_0\cap B_1$
. Let
![]() $C_0=A_0\cup C$
and
$C_0=A_0\cup C$
and
![]() $C_1=A_1\cup C$
. Then
$C_1=A_1\cup C$
. Then
![]() $A_0\subseteq C_0$
and
$A_0\subseteq C_0$
and
![]() $C_0\subseteq A_0\cup B\subseteq A_0\cup B_0$
, and since
$C_0\subseteq A_0\cup B\subseteq A_0\cup B_0$
, and since
![]() $\mathcal{A}_0$
is dominated and convex,
$\mathcal{A}_0$
is dominated and convex,
![]() $A_0\cup B_0\in\mathcal{A}_0$
. Thus, by convexity of
$A_0\cup B_0\in\mathcal{A}_0$
. Thus, by convexity of
![]() $\mathcal{A}_0$
, we have
$\mathcal{A}_0$
, we have
![]() $C_0\in\mathcal{A}_0$
. In the same way, we see that
$C_0\in\mathcal{A}_0$
. In the same way, we see that
![]() $C_1\in\mathcal{A}_1$
. Observe now that
$C_1\in\mathcal{A}_1$
. Observe now that
![]() $C\subseteq C_0\cap C_1\subseteq (A_0\cap A_1)\cup C= A\cup C=C$
, whence
$C\subseteq C_0\cap C_1\subseteq (A_0\cap A_1)\cup C= A\cup C=C$
, whence
![]() $C\in\Delta_\land(\mathcal{A}_0,\mathcal{A}_1)$
.
$C\in\Delta_\land(\mathcal{A}_0,\mathcal{A}_1)$
.
To prove that
![]() $\Delta_\land(\mathcal{A}_0,\mathcal{A}_1)$
is dominated, it suffices to observe that if
$\Delta_\land(\mathcal{A}_0,\mathcal{A}_1)$
is dominated, it suffices to observe that if
![]() $\mathcal{A}_0$
and
$\mathcal{A}_0$
and
![]() $\mathcal{A}_1$
are dominated by
$\mathcal{A}_1$
are dominated by
![]() $D_0$
and
$D_0$
and
![]() $D_1$
, respectively, then clearly
$D_1$
, respectively, then clearly
![]() $\Delta_\land(\mathcal{A}_0,\mathcal{A}_1)$
is dominated by
$\Delta_\land(\mathcal{A}_0,\mathcal{A}_1)$
is dominated by
![]() $D_0\cap D_1$
.
$D_0\cap D_1$
.
The proof that
![]() $\Delta_\land$
weakly preserves supported convexity is similar.
$\Delta_\land$
weakly preserves supported convexity is similar.
Finally, for the union operator, we obtain the following dimension inequalities:
Proposition 67. Let
![]() $\mathcal{A}_0,\mathcal{A}_1\subseteq \mathcal{P}(X)$
for a base set X, and let
$\mathcal{A}_0,\mathcal{A}_1\subseteq \mathcal{P}(X)$
for a base set X, and let
![]() $\mathcal{A}=\mathcal{A}_0\cup\mathcal{A}_1$
. Then
$\mathcal{A}=\mathcal{A}_0\cup\mathcal{A}_1$
. Then
![]() $\mathrm{D}(\mathcal{A})\le\mathrm{D}(\mathcal{A}_0)+\mathrm{D}(\mathcal{A}_1)$
,
$\mathrm{D}(\mathcal{A})\le\mathrm{D}(\mathcal{A}_0)+\mathrm{D}(\mathcal{A}_1)$
,
![]() $\mathrm{D}^{\mathrm{d}}(\mathcal{A})\le\mathrm{D}^{\mathrm{d}}(\mathcal{A}_0)+\mathrm{D}^{\mathrm{d}}(\mathcal{A}_1)$
and
$\mathrm{D}^{\mathrm{d}}(\mathcal{A})\le\mathrm{D}^{\mathrm{d}}(\mathcal{A}_0)+\mathrm{D}^{\mathrm{d}}(\mathcal{A}_1)$
and
![]() $\mathrm{CD}(\mathcal{A})\le\mathrm{CD}(\mathcal{A}_0)+\mathrm{CD}(\mathcal{A}_1)$
.
$\mathrm{CD}(\mathcal{A})\le\mathrm{CD}(\mathcal{A}_0)+\mathrm{CD}(\mathcal{A}_1)$
.
Proof. Observe that if a subfamily
![]() $\mathcal{G}_0$
dominates
$\mathcal{G}_0$
dominates
![]() $\mathcal{A}_0$
and a subfamily
$\mathcal{A}_0$
and a subfamily
![]() $\mathcal{G}_1$
dominates
$\mathcal{G}_1$
dominates
![]() $\mathcal{A}_1$
, then clearly
$\mathcal{A}_1$
, then clearly
![]() $\mathcal{G}_0\cup\mathcal{G}_1$
dominates
$\mathcal{G}_0\cup\mathcal{G}_1$
dominates
![]() $\mathcal{A}_0\cup\mathcal{A}_1$
. Thus,
$\mathcal{A}_0\cup\mathcal{A}_1$
. Thus,
![]() $\mathrm{D}(\mathcal{A})\le |\mathcal{G}_0\cup\mathcal{G}_1|\le |\mathcal{G}_0|+|\mathcal{G}_1|$
. The first inequality follows from the case where
$\mathrm{D}(\mathcal{A})\le |\mathcal{G}_0\cup\mathcal{G}_1|\le |\mathcal{G}_0|+|\mathcal{G}_1|$
. The first inequality follows from the case where
![]() $\mathcal{G}_0$
and
$\mathcal{G}_0$
and
![]() $\mathcal{G}_1$
are of minimal cardinality. The other two inequalities are proved in the same way.
$\mathcal{G}_1$
are of minimal cardinality. The other two inequalities are proved in the same way.
We can now add the cases of tensor connectives and intuitionistic disjunction to Corollary 65.
Corollary 68. Let
![]() $\mathbb{O}$
be a growth class, and let
$\mathbb{O}$
be a growth class, and let
![]() $\mathfrak{Dim}$
be one of the dimension functions Dim,
$\mathfrak{Dim}$
be one of the dimension functions Dim,
![]() $\mathrm{Dim}^{\mathrm{d}}$
and CDim. Furthermore, let
$\mathrm{Dim}^{\mathrm{d}}$
and CDim. Furthermore, let
![]() $\phi=\phi(\vec{x})$
and
$\phi=\phi(\vec{x})$
and
![]() $\psi=\psi(\vec{x})$
be formulas of some logic
$\psi=\psi(\vec{x})$
be formulas of some logic
![]() $\mathcal{L}$
with team semantics, and let
$\mathcal{L}$
with team semantics, and let
![]() $\circledast$
be a binary tensor connective.
$\circledast$
be a binary tensor connective.
-
(a) If
 $\mathfrak{Dim}_{\phi,\vec{x}},\mathfrak{Dim}_{\psi,\vec{x}}\in\mathbb{O}$
, then
$\mathfrak{Dim}_{\phi,\vec{x}},\mathfrak{Dim}_{\psi,\vec{x}}\in\mathbb{O}$
, then
 $\mathfrak{Dim}_{\phi{\underline{\lor}}\psi,\vec{x}}\in\mathbb{O}$
.
$\mathfrak{Dim}_{\phi{\underline{\lor}}\psi,\vec{x}}\in\mathbb{O}$
. -
(b) If
 $\mathfrak{Dim}_{\phi,\vec{x}},\mathfrak{Dim}_{\psi,\vec{x}}\in\mathbb{O}$
, then
$\mathfrak{Dim}_{\phi,\vec{x}},\mathfrak{Dim}_{\psi,\vec{x}}\in\mathbb{O}$
, then
 $\mathfrak{Dim}_{\phi{\wedge}\psi,\vec{x}}\in\mathbb{O}$
.
$\mathfrak{Dim}_{\phi{\wedge}\psi,\vec{x}}\in\mathbb{O}$
. -
(c) If
 $\mathrm{CDim}_{\phi,\vec{x}},\mathrm{CDim}_{\psi,\vec{x}}\in\mathbb{O}$
, then
$\mathrm{CDim}_{\phi,\vec{x}},\mathrm{CDim}_{\psi,\vec{x}}\in\mathbb{O}$
, then
 $\mathrm{CDim}_{\phi\circledast\psi,\vec{x}}\in\mathbb{O}$
.
$\mathrm{CDim}_{\phi\circledast\psi,\vec{x}}\in\mathbb{O}$
.
Proof.
-
(a) Let M be a finite model. By Proposition 67 we have
for each of the dimensions $$ D(\!\left\Vert \phi{\underline{\lor}}\psi \right\Vert^{M,\vec{x}})=D(\!\left\Vert \phi \right\Vert^{M,\vec{x}}\cup\left\Vert \psi \right\Vert^{M,\vec{x}})\le D(\!\left\Vert \phi \right\Vert^{M,\vec{x}})+ D(\!\left\Vert \psi \right\Vert^{M,\vec{x}})$$
$$ D(\!\left\Vert \phi{\underline{\lor}}\psi \right\Vert^{M,\vec{x}})=D(\!\left\Vert \phi \right\Vert^{M,\vec{x}}\cup\left\Vert \psi \right\Vert^{M,\vec{x}})\le D(\!\left\Vert \phi \right\Vert^{M,\vec{x}})+ D(\!\left\Vert \psi \right\Vert^{M,\vec{x}})$$
 $D\in\{\mathrm{D},\mathrm{D}^{\mathrm{d}},\mathrm{CD}\}$
. Since this holds for all finite models M, we have
$D\in\{\mathrm{D},\mathrm{D}^{\mathrm{d}},\mathrm{CD}\}$
. Since this holds for all finite models M, we have
 $\mathfrak{Dim}_{\phi{\underline{\lor}}\psi,\vec{x}}\le \mathfrak{Dim}_{\phi,\vec{x}}+\mathfrak{Dim}_{\psi,\vec{x}}$
, and hence
$\mathfrak{Dim}_{\phi{\underline{\lor}}\psi,\vec{x}}\le \mathfrak{Dim}_{\phi,\vec{x}}+\mathfrak{Dim}_{\psi,\vec{x}}$
, and hence
 $\mathfrak{Dim}_{\phi{\underline{\lor}}\psi,\vec{x}}\in\mathbb{O}$
.
$\mathfrak{Dim}_{\phi{\underline{\lor}}\psi,\vec{x}}\in\mathbb{O}$
.
-
(b) Using Proposition 66 and Theorem 55 we obtain the inequality
 $\mathfrak{Dim}_{\phi{\wedge}\psi,\vec{x}}\le \mathfrak{Dim}_{\phi,\vec{x}}\cdot\mathfrak{Dim}_{\psi,\vec{x}}$
. Thus we see that
$\mathfrak{Dim}_{\phi{\wedge}\psi,\vec{x}}\le \mathfrak{Dim}_{\phi,\vec{x}}\cdot\mathfrak{Dim}_{\psi,\vec{x}}$
. Thus we see that
 $\mathfrak{Dim}_{\phi{\wedge}\psi,\vec{x}}\in\mathbb{O}$
.
$\mathfrak{Dim}_{\phi{\wedge}\psi,\vec{x}}\in\mathbb{O}$
. -
(c) is proved in the same way as (b) by using Proposition 18 (see Example 54) in place of Proposition 66.
5. Applications
The main application of our dimension theory is to hierarchies of definability in logics based on the atoms of Definition 20 and the logical operations of Definition 19. We obtain also non-expressibility results for some other connectives and quantifiers based on observations that they do not preserve dimension.
5.1 Hierarchy results
We can now apply our results to obtain hierarchy results for extensions of first-order logic by various team-based atoms. We start by defining a family of logics the definition of which is based solely on dimension-theoretic considerations. We use these somewhat artificial logics as yardsticks to compare more traditional logics.
Definition 69.
-
(a) The logic
 $\mathbb{LE}^U_k$
is the closure of literals and all atoms whose upper dimension function is in the growth class
$\mathbb{LE}^U_k$
is the closure of literals and all atoms whose upper dimension function is in the growth class
 $\mathbb{E}_k$
under the connectives
$\mathbb{E}_k$
under the connectives
 $\wedge$
,
$\wedge$
,
 ${\underline{\lor}}$
,
${\underline{\lor}}$
,
 $\vee$
,
$\vee$
,
 ${\wedge}$
, and any Lindström quantifiers. Similarly
${\wedge}$
, and any Lindström quantifiers. Similarly
 $\mathbb{LF}^U_k$
for
$\mathbb{LF}^U_k$
for
 $\mathbb{F}_k$
.
$\mathbb{F}_k$
. -
(b) The logic
 $\mathbb{LF}^D_k$
is the closure of literals and all atoms whose dual dimension function is in the growth class
$\mathbb{LF}^D_k$
is the closure of literals and all atoms whose dual dimension function is in the growth class
 $\mathbb{F}_k$
under the connectives
$\mathbb{F}_k$
under the connectives
 $\wedge$
,
$\wedge$
,
 ${\underline{\lor}}$
,
${\underline{\lor}}$
,
 $\vee$
,
$\vee$
,
 ${\wedge}$
, and any Lindström quantifiers.
${\wedge}$
, and any Lindström quantifiers. -
(c) The logic
 $\mathbb{LF}^C_k$
is the closure of literals and all atoms whose cylindrical dimension function is in the growth class
$\mathbb{LF}^C_k$
is the closure of literals and all atoms whose cylindrical dimension function is in the growth class
 $\mathbb{F}_k$
under the connectives
$\mathbb{F}_k$
under the connectives
 $\wedge$
,
$\wedge$
,
 ${\underline{\lor}}$
,
${\underline{\lor}}$
,
 $\vee$
, any tensor operators, and any Lindström quantifiers.
$\vee$
, any tensor operators, and any Lindström quantifiers.
We did not define what would be denoted
![]() $\mathbb{LE}^D_k$
and
$\mathbb{LE}^D_k$
and
![]() $\mathbb{LE}^{C}_k$
, for the very special reason that the estimates given by Proposition 42 are not good enough for the dual and the cylindric dimensions, rendering logics based on them less natural. See remarks at the end of Subsection 4.1.
$\mathbb{LE}^{C}_k$
, for the very special reason that the estimates given by Proposition 42 are not good enough for the dual and the cylindric dimensions, rendering logics based on them less natural. See remarks at the end of Subsection 4.1.
The logics defined above have some unusual properties. For example, each logic is closed under all Lindström quantifiers which means that every property of finite models, closed under isomorphism, is definable in each of these logics. On the other hand, each of these logics is limited as to what their formulas can express. In classical logic formulas and sentences have more or less the same expressive power because we can always form a sentence from a formula by substituting constant symbols in place of free variables. In team semantics, this does not work because constant symbols do not convey the plural nature of team semantics. The reason for the introduction of these logics is that they help us estimate and delineate dimensions of formulas and thereby expressive power of formulas in a multitude of logics.
Theorem 6.
-
(a) The upper dimension of every formula in
 $\mathbb{LE}^U_k$
is in the growth class
$\mathbb{LE}^U_k$
is in the growth class
 $\mathbb{E}_k$
.
$\mathbb{E}_k$
. -
(b) The upper (dual, cylindrical) dimension of every formula in
 $\mathbb{LF}^U_k$
(
$\mathbb{LF}^U_k$
(
 $\mathbb{LF}^D_k$
,
$\mathbb{LF}^D_k$
,
 $\mathbb{LF}^{CD}_k$
, respectively) is in the growth class
$\mathbb{LF}^{CD}_k$
, respectively) is in the growth class
 $\mathbb{F}_k$
.
$\mathbb{F}_k$
.
Proof.
-
(a) By Definition 69 the atoms of
 $\mathbb{LE}^U_k$
are in
$\mathbb{LE}^U_k$
are in
 $\mathbb{E}_k$
. By an inductive argument based on Corollaries 65 and 68 the upper dimension of every formula from
$\mathbb{E}_k$
. By an inductive argument based on Corollaries 65 and 68 the upper dimension of every formula from
 $\mathbb{LE}^U_k$
is in
$\mathbb{LE}^U_k$
is in
 $\mathbb{E}_k$
, too.
$\mathbb{E}_k$
, too. -
(b) By Definition 69 the atoms of
 $\mathbb{LF}^U_k$
are in
$\mathbb{LF}^U_k$
are in
 $\mathbb{F}_k$
. By an inductive argument based on Corollaries 65 and 68, again, the upper dimension of every formula of
$\mathbb{F}_k$
. By an inductive argument based on Corollaries 65 and 68, again, the upper dimension of every formula of
 $\mathbb{LF}^U_k$
is in
$\mathbb{LF}^U_k$
is in
 $\mathbb{F}_k$
, too. The argument is the same in the case of
$\mathbb{F}_k$
, too. The argument is the same in the case of
 $\mathbb{LF}^D_k$
and
$\mathbb{LF}^D_k$
and
 $\mathbb{LF}^{CD}_k$
.
$\mathbb{LF}^{CD}_k$
.
Note that we have not added the intuitionistic implication
![]() $\to$
(see Definition 78) to the lists of logical operations in the above definition. The reason is that we want to keep dimension under control and intuitionistic implication increases dimension exponentially (Lemma 79). The nonempty atom
$\to$
(see Definition 78) to the lists of logical operations in the above definition. The reason is that we want to keep dimension under control and intuitionistic implication increases dimension exponentially (Lemma 79). The nonempty atom
![]() $\mathsf{N}\hspace{-0.25em}\mathsf{E}$
is in
$\mathsf{N}\hspace{-0.25em}\mathsf{E}$
is in
![]() $\mathbb{LE}^U_0$
. For
$\mathbb{LE}^U_0$
. For
![]() $k>0$
the logics
$k>0$
the logics
![]() $\mathbb{LE}^U_k$
,
$\mathbb{LE}^U_k$
,
![]() $\mathbb{LE}^D_k$
, and
$\mathbb{LE}^D_k$
, and
![]() $\mathbb{LE}^C_k$
,
$\mathbb{LE}^C_k$
,
![]() $\mathbb{LF}^U_k$
,
$\mathbb{LF}^U_k$
,
![]() $\mathbb{LF}^D_k$
, and
$\mathbb{LF}^D_k$
, and
![]() $\mathbb{LF}^C_k$
are closed under
$\mathbb{LF}^C_k$
are closed under
![]() $\exists^1$
, but never under
$\exists^1$
, but never under
![]() $\forall^1$
(see Section 5.2.)
$\forall^1$
(see Section 5.2.)
The trivial properties of the logics of Definition 69 are summarized in the following lemma (see also Fig. 1):

Figure 1. Logics built from growth classes.
Lemma 71.
-
(a)
 $\mathbb{LF}^U_k\subseteq\mathbb{LF}^U_{k+1}$
,
$\mathbb{LF}^U_k\subseteq\mathbb{LF}^U_{k+1}$
,
 $\mathbb{LF}^D_k\subseteq\mathbb{LF}^D_{k+1}$
, and
$\mathbb{LF}^D_k\subseteq\mathbb{LF}^D_{k+1}$
, and
 $\mathbb{LF}^C_k\subseteq\mathbb{LF}^C_{k+1}$
.
$\mathbb{LF}^C_k\subseteq\mathbb{LF}^C_{k+1}$
. -
(b)

-
(c)
 $\mathbb{LF}^C_k\subseteq\mathbb{LF}^U_k$
and
$\mathbb{LF}^C_k\subseteq\mathbb{LF}^U_k$
and
 $\mathbb{LF}^C_k\subseteq\mathbb{LF}^D_k$
.
$\mathbb{LF}^C_k\subseteq\mathbb{LF}^D_k$
.
As it turns out, a crucial factor in the hierarchy results is the length of variable-tuples allowed in the atoms. Let us therefore specify the concept of arity for our atoms:
Definition 72. We say:
-
the atom
 $\,=(\vec{x},y)$
is k-ary, if
$\,=(\vec{x},y)$
is k-ary, if
 $\mathrm{len}(\vec{x})=k$
,
$\mathrm{len}(\vec{x})=k$
, -
the atoms
 $\vec{x}\ |\ \vec{y}$
and
$\vec{x}\ |\ \vec{y}$
and
 $\vec{x}\ \Upsilon\ y$
are k-ary if
$\vec{x}\ \Upsilon\ y$
are k-ary if
 $\mathrm{len}(\vec{x})(=\mathrm{len}(\vec{y}))=k$
,
$\mathrm{len}(\vec{x})(=\mathrm{len}(\vec{y}))=k$
, -
the atom
 $ \vec{t}_2\perp_{\vec{t}_1}\vec{t}_3$
is
$ \vec{t}_2\perp_{\vec{t}_1}\vec{t}_3$
is
 $m+\max(k,l)$
-ary, or alternatively (k,l,m)-ary, if
$m+\max(k,l)$
-ary, or alternatively (k,l,m)-ary, if
 $\mathrm{len}(\vec{t}_1)=m,\mathrm{len}(\vec{t}_2)=k,\mbox{ and }\mathrm{len}(\vec{t}_3)=l$
,
$\mathrm{len}(\vec{t}_1)=m,\mathrm{len}(\vec{t}_2)=k,\mbox{ and }\mathrm{len}(\vec{t}_3)=l$
, -
the atom
 $ \vec{t}_2\perp\vec{t}_3$
is
$ \vec{t}_2\perp\vec{t}_3$
is
 $\max(k,l)$
-ary, or alternatively (k,l)-ary, if
$\max(k,l)$
-ary, or alternatively (k,l)-ary, if
 $\mathrm{len}(\vec{t}_2)=k,\mbox{ and }\mathrm{len}(\vec{t}_3)=l$
,
$\mathrm{len}(\vec{t}_2)=k,\mbox{ and }\mathrm{len}(\vec{t}_3)=l$
, -
a general atom
 $\alpha_C\vec{x}$
(as in Definition 20)
$\alpha_C\vec{x}$
(as in Definition 20)
 $\mathrm{len}(\vec{x})=k$
, is called k-ary,
$\mathrm{len}(\vec{x})=k$
, is called k-ary, -
a logic is k-ary (respectively, (k,l)-ary or (k,l,m)-ary) if its atoms are.
We name logics according to their atoms (Section 3.3). If we allow only at most k-ary dependence atoms in dependence logic, we call the logic k-ary dependence logic. Similarly for anonymity, exclusion etc logics.
Note that the definition of arity for particular atoms, let us call it the effective arity, takes into account the character of the atom and, in consequence, differs from the definition of arity, let us call it the actual arity, for general atoms. In each case effective arity of the atom is lower than the actual arity.
Theorem 73.
-
(a) k-ary inclusion, anonymity, and exclusion logics are all included in
 $\mathbb{LE}^U_k$
.
$\mathbb{LE}^U_k$
. -
(b) The k-ary dependence logic is included in
 $\mathbb{LF}^U_k$
.
$\mathbb{LF}^U_k$
. -
(c) The (k,l,m)-ary independence logic is included in
 $\mathbb{LF}^U_{\max(k,l)+m}$
.
$\mathbb{LF}^U_{\max(k,l)+m}$
.
Proof.
The following theorem is our main application of the dimension analysis of families of sets of n-tuples.
Theorem 74.
-
(a) The
 $k+1$
-ary inclusion, anonymity, and exclusion atoms are not definable in
$k+1$
-ary inclusion, anonymity, and exclusion atoms are not definable in
 $\mathbb{LE}^U_k$
.
$\mathbb{LE}^U_k$
. -
(b) The
 $k+1$
-ary dependence atom is not definable in
$k+1$
-ary dependence atom is not definable in
 $\mathbb{LF}^U_k$
.
$\mathbb{LF}^U_k$
. -
(c) The (k,l,m)-ary independence atom is not definable in
 $\mathbb{LF}^U_{i}$
if
$\mathbb{LF}^U_{i}$
if
 $i<\max(k,l)+m$
.
$i<\max(k,l)+m$
.
Proof. Suppose
![]() $\mathrm{len}(\vec{x})=\mathrm{len}(\vec{y})=k+1$
. By Theorem 40 the upper dimension of
$\mathrm{len}(\vec{x})=\mathrm{len}(\vec{y})=k+1$
. By Theorem 40 the upper dimension of
![]() $\left\Vert \vec{x}\subseteq\vec{y} \right\Vert^{\vec{x}\vec{y}}$
is
$\left\Vert \vec{x}\subseteq\vec{y} \right\Vert^{\vec{x}\vec{y}}$
is
![]() $2^{n^{k+1}}-n^{k+1}$
. Therefore
$2^{n^{k+1}}-n^{k+1}$
. Therefore
![]() $\mathrm{Dim}_{\vec{x}\subseteq\vec{y},\vec{z}}\notin \mathbb{E}_k$
. The argument is the same in the other cases.
$\mathrm{Dim}_{\vec{x}\subseteq\vec{y},\vec{z}}\notin \mathbb{E}_k$
. The argument is the same in the other cases.
Despite the above non-definability results, there are some obvious and also some not so obvious inter-definability results between the atoms. The basic picture is that dependence atoms are definable from the independence atoms but not from the inclusion atoms. The inclusion atoms are definable from the independence atoms but not from the dependence atoms. In both cases the non-definability is a consequence of structural properties of the logics, namely, dependence logic is downward closed and inclusion logic is closed under unions (of teams). The known relationships are as follows:
Proposition 75. (Galliani Reference Galliani2012).
-
(a) The k-ary dependence atom
 $\,=(\vec{x},y)$
is definable from the
$\,=(\vec{x},y)$
is definable from the
 $k+1$
-ary exclusion atom with the formula and also in terms of the
$k+1$
-ary exclusion atom with the formula and also in terms of the $$\forall z(z=y\vee \vec{x} z\ |\ \vec{x} y)$$
$$\forall z(z=y\vee \vec{x} z\ |\ \vec{x} y)$$
 $k+1$
-ary pure independence atom with the formula
Footnote 7
In the other direction, the k-ary exclusion atom
$k+1$
-ary pure independence atom with the formula
Footnote 7
In the other direction, the k-ary exclusion atom $$ \forall\vec{z}\ \exists w((\vec{z}\ne\vec{x}\vee w=y)\wedge\vec{z} y\perp\vec{z} w).$$
$$ \forall\vec{z}\ \exists w((\vec{z}\ne\vec{x}\vee w=y)\wedge\vec{z} y\perp\vec{z} w).$$
 $\vec{t}_1\ |\ \vec{t}_2$
is definable from the k-ary dependence atom with the formula
$\vec{t}_1\ |\ \vec{t}_2$
is definable from the k-ary dependence atom with the formula  $$\forall\vec{z}\exists u_1 u_2(\,=(\vec{z},u_1)\wedge \,=(\vec{z},u_2)\wedge((u_1=u_2\wedge\vec{z}\ne \vec{t}_1)\vee(u_1\ne u_2\wedge\vec{z}\ne\vec{t}_2))).$$
$$\forall\vec{z}\exists u_1 u_2(\,=(\vec{z},u_1)\wedge \,=(\vec{z},u_2)\wedge((u_1=u_2\wedge\vec{z}\ne \vec{t}_1)\vee(u_1\ne u_2\wedge\vec{z}\ne\vec{t}_2))).$$
-
(b) The k-ary exclusion atom
 $\vec{x}\ |\ \vec{y}$
can be defined in terms of the k-ary inclusion and the k-ary pure independence atoms with the formula:
$\vec{x}\ |\ \vec{y}$
can be defined in terms of the k-ary inclusion and the k-ary pure independence atoms with the formula:  $$\exists \vec{z}(\vec{x}\subseteq \vec{z}\wedge \vec{y}\perp\vec{z}\wedge\vec{y}\ne\vec{z}).$$
$$\exists \vec{z}(\vec{x}\subseteq \vec{z}\wedge \vec{y}\perp\vec{z}\wedge\vec{y}\ne\vec{z}).$$
-
(c) The k-ary inclusion atom
 $\vec{t}_1\subseteq\vec{t}_2$
can be defined from the (k,2)-ary pure independence atom with the formula It is also definable from the k-ary anonymity atom with the formula (Rönnholm Reference Rönnholm2018)
$\vec{t}_1\subseteq\vec{t}_2$
can be defined from the (k,2)-ary pure independence atom with the formula It is also definable from the k-ary anonymity atom with the formula (Rönnholm Reference Rönnholm2018) $$\forall v_1v_2\vec{z}((\vec{z}\ne\vec{t}_1\wedge \vec{z}\ne\vec{t}_2)\vee(v_1\ne v_2\wedge\vec{z}\ne \vec{t}_2)\vee ((v_1=v_2\vee\vec{z}=\vec{t}_2)\wedge \vec{z}\perp v_1v_2)).$$
$$\forall v_1v_2\vec{z}((\vec{z}\ne\vec{t}_1\wedge \vec{z}\ne\vec{t}_2)\vee(v_1\ne v_2\wedge\vec{z}\ne \vec{t}_2)\vee ((v_1=v_2\vee\vec{z}=\vec{t}_2)\wedge \vec{z}\perp v_1v_2)).$$
 $$\exists x\forall y(x=y)\vee\forall w_1\forall w_2\exists \vec{y}\exists z(((w_1=w_2\wedge\vec{y}=\vec{t}_1)\vee(\neg w_1=w_2\wedge\vec{y}=\vec{t}_2))\wedge\vec{y}\mathrel{\Upsilon} {z})).$$
$$\exists x\forall y(x=y)\vee\forall w_1\forall w_2\exists \vec{y}\exists z(((w_1=w_2\wedge\vec{y}=\vec{t}_1)\vee(\neg w_1=w_2\wedge\vec{y}=\vec{t}_2))\wedge\vec{y}\mathrel{\Upsilon} {z})).$$
-
(d) The k-ary anonymity atom
 $\vec{x}\mathrel{\Upsilon}{y}$
is definable in terms of the
$\vec{x}\mathrel{\Upsilon}{y}$
is definable in terms of the
 $k+1$
-ary inclusion atom with the formula
$k+1$
-ary inclusion atom with the formula  $$\exists u(\neg u=y\wedge \vec{x} u\subseteq \vec{x} y).$$
$$\exists u(\neg u=y\wedge \vec{x} u\subseteq \vec{x} y).$$
-
(e) The (k,l,m)-ary independence atom
 $\vec{t}_2\perp_{\vec{t}_1}\vec{t}_3$
is definable in terms of the
$\vec{t}_2\perp_{\vec{t}_1}\vec{t}_3$
is definable in terms of the
 $k+l+m$
-ary dependence atom,
$k+l+m$
-ary dependence atom,
 $k+m$
-ary exclusion atoms, and the
$k+m$
-ary exclusion atoms, and the
 $k+l+m$
-ary inclusion atom with the formula
$k+l+m$
-ary inclusion atom with the formula  $$\begin{array}{l} \forall\vec{p}\vec{q}\vec{r}\ \exists u_1 u_2 u_3 u_4((\bigwedge_{i=1}^4\,=(\vec{p}\vec{q}\vec{r},u_i))\wedge((u_1\ne u_2\wedge(\vec{p}\vec{q}\ |\ \vec{t}_1\vec{t}_2))\vee\\(u_1=u_2\wedge u_3\ne u_4\wedge(\vec{p}\vec{r} \ |\ \vec{t}_1\vec{t}_3))\vee\\(u_1=u_2\wedge u_3=u_4\wedge(\vec{p}\vec{q}\vec{r}\subseteq\vec{t}_1\vec{t}_2\vec{t}_3)))). \end{array}$$
$$\begin{array}{l} \forall\vec{p}\vec{q}\vec{r}\ \exists u_1 u_2 u_3 u_4((\bigwedge_{i=1}^4\,=(\vec{p}\vec{q}\vec{r},u_i))\wedge((u_1\ne u_2\wedge(\vec{p}\vec{q}\ |\ \vec{t}_1\vec{t}_2))\vee\\(u_1=u_2\wedge u_3\ne u_4\wedge(\vec{p}\vec{r} \ |\ \vec{t}_1\vec{t}_3))\vee\\(u_1=u_2\wedge u_3=u_4\wedge(\vec{p}\vec{q}\vec{r}\subseteq\vec{t}_1\vec{t}_2\vec{t}_3)))). \end{array}$$
-
(f) The (k,l,m)-ary independence atom
 $\vec{x}\perp_{\vec{z}}\vec{y}$
is definable in terms of the
$\vec{x}\perp_{\vec{z}}\vec{y}$
is definable in terms of the
 $(k+m,l+m)$
-ary pure independence atom with the formula (Wilke Reference Wilke2022)
$(k+m,l+m)$
-ary pure independence atom with the formula (Wilke Reference Wilke2022)  $$\forall\vec{p}\vec{q}\exists\vec{u}\exists\vec{w}((\vec{z}\ne\vec{p}\vee\vec{z}\ne\vec{q}\vee\vec{u}\vec{w}=\vec{x}\vec{y})\wedge(\vec{z}\ne\vec{p}\vee\vec{z}\ne\vec{q}\vee\vec{p}\ne\vec{q}\vee\vec{z}=\vec{p})\wedge\vec{p}\vec{u} \perp\vec{q}\vec{w})).$$
$$\forall\vec{p}\vec{q}\exists\vec{u}\exists\vec{w}((\vec{z}\ne\vec{p}\vee\vec{z}\ne\vec{q}\vee\vec{u}\vec{w}=\vec{x}\vec{y})\wedge(\vec{z}\ne\vec{p}\vee\vec{z}\ne\vec{q}\vee\vec{p}\ne\vec{q}\vee\vec{z}=\vec{p})\wedge\vec{p}\vec{u} \perp\vec{q}\vec{w})).$$
Note that (a) above is in harmony with Theorem 32, as for
![]() $n>2$
$n>2$
Corollary 76. (Hierarchy Theorem). Dependence logic, exclusion logic, inclusion logic, anonymity logic and pure independence logic each has a proper definability hierarchy for formulas based on the arity of their non-first order atoms.
The Corollary holds in fact in a stronger form:
Theorem 77. Suppose k is a positive integer.
-
(a) The k-ary dependence atom is not definable in the extension of first order logic by
 $<k$
-ary dependence (or any other
Footnote 8
$<k$
-ary dependence (or any other
Footnote 8
 $<k$
-ary) atoms,
$<k$
-ary) atoms,
 $\le k$
-ary independence, exclusion, inclusion, anonymity, constancy atoms, and any Lindström quantifiers.
$\le k$
-ary independence, exclusion, inclusion, anonymity, constancy atoms, and any Lindström quantifiers. -
(b) The k-ary exclusion atom is not definable in the extension of first order logic by
 $<k$
-ary exclusion, inclusion, anonymity, dependence, independence, constancy (or any other
$<k$
-ary exclusion, inclusion, anonymity, dependence, independence, constancy (or any other
 $<k$
-ary) atoms, and any Lindström quantifiers.
$<k$
-ary) atoms, and any Lindström quantifiers. -
(c) The k-ary inclusion atom is not definable in the extension of first order logic by
 $<k$
-ary inclusion, exclusion, anonymity, dependence, or constancy (or any other
$<k$
-ary inclusion, exclusion, anonymity, dependence, or constancy (or any other
 $<k$
-ary) atoms, and any Lindström quantifiers.
$<k$
-ary) atoms, and any Lindström quantifiers. -
(d) The k-ary anonymity atom is not definable in the extension of first order logic by
 $<k$
-ary inclusion, anonymity, exclusion, dependence, constancy (or any other
$<k$
-ary inclusion, anonymity, exclusion, dependence, constancy (or any other
 $<k$
-ary) atoms, and any Lindström quantifiers.
$<k$
-ary) atoms, and any Lindström quantifiers. -
(e) The k-ary independence atom (whether pure or not) is not definable in the extension of first order logic by
 $<k$
-ary independence, inclusion, anonymity, exclusion, dependence, constancy (or any other
$<k$
-ary independence, inclusion, anonymity, exclusion, dependence, constancy (or any other
 $<k$
-ary) atoms, and any Lindström quantifiers.
$<k$
-ary) atoms, and any Lindström quantifiers.
There are many open problems arising from comparing the definability results of Lemma 75 and the non-definability results of Theorem 77. We mention a few in Section 7.
Theorem 77 shows that the translations in Lemma 75 necessarily involve increase of arity.
Earlier hierarchy results have been mostly for sentences. In Durand and Kontinen (Reference Durand and Kontinen2012) it is shown that k-ary dependence atom is weaker than
![]() $k+1$
-ary dependence atom for sentences in vocabulary having arity
$k+1$
-ary dependence atom for sentences in vocabulary having arity
![]() $k+1$
. In Galliani et al. (Reference Galliani, Hannula, Kontinen and Rocca2013) it is shown that independence logic with k-ary independence atoms is strictly weaker than independence logic with
$k+1$
. In Galliani et al. (Reference Galliani, Hannula, Kontinen and Rocca2013) it is shown that independence logic with k-ary independence atoms is strictly weaker than independence logic with
![]() $k+1$
-ary independence atoms on the level of sentences. In Hannula (Reference Hannula2018) it is shown (using similar results from Grohe Reference Grohe1996 on transitive closure and fixpoint operator) that inclusion logic with
$k+1$
-ary independence atoms on the level of sentences. In Hannula (Reference Hannula2018) it is shown (using similar results from Grohe Reference Grohe1996 on transitive closure and fixpoint operator) that inclusion logic with
![]() $k-1$
-ary inclusion atoms is strictly weaker than inclusion logic with k-ary inclusion atoms for sentences when
$k-1$
-ary inclusion atoms is strictly weaker than inclusion logic with k-ary inclusion atoms for sentences when
![]() $k\ge2$
. As to earlier results for formulas, in Rönnholm (Reference Rönnholm2018, Theorem 5.17, Corollary 5.18) it is shown that the fullness (the property of containing every assignment of the appropriate kind) of a team with domain
$k\ge2$
. As to earlier results for formulas, in Rönnholm (Reference Rönnholm2018, Theorem 5.17, Corollary 5.18) it is shown that the fullness (the property of containing every assignment of the appropriate kind) of a team with domain
![]() $\{x_1,\ldots,x_{k+1}\}$
, which can be defined by means of the
$\{x_1,\ldots,x_{k+1}\}$
, which can be defined by means of the
![]() $k+1$
-ary inclusion atom, cannot be defined in the extension of first order logic by what are called k-invariant atoms in Rönnholm (Reference Rönnholm2018) and any downward closed atoms.
$k+1$
-ary inclusion atom, cannot be defined in the extension of first order logic by what are called k-invariant atoms in Rönnholm (Reference Rönnholm2018) and any downward closed atoms.
5.2 Other atoms and logical operations
The atoms and logical operations
![]() $\wedge$
,
$\wedge$
,
![]() ${\underline{\lor}}$
,
${\underline{\lor}}$
,
![]() $\vee$
,
$\vee$
,
![]() $\forall$
, and
$\forall$
, and
![]() $\exists$
are by no means the only ones that can be or have been considered. In this section we first introduce two new atoms that have particularly big upper or other dimension. We then show that many other logical operations occurring in the literature actually fail to preserve dimension. We use this to conclude some interesting non-definability results concerning these alternative logical operations.
$\exists$
are by no means the only ones that can be or have been considered. In this section we first introduce two new atoms that have particularly big upper or other dimension. We then show that many other logical operations occurring in the literature actually fail to preserve dimension. We use this to conclude some interesting non-definability results concerning these alternative logical operations.
Intuitionistic implication and disjunction
Definition 78. (Intuitionistic implication) The intuitionistic implication
![]() $\phi\to\psi$
is defined by
$\phi\to\psi$
is defined by
![]() $M\models_T\phi\to\psi$
if and only if every
$M\models_T\phi\to\psi$
if and only if every
![]() $Y\subseteq T$
that satisfies in M the formula
$Y\subseteq T$
that satisfies in M the formula
![]() $\phi$
satisfies also the formula
$\phi$
satisfies also the formula
![]() $\psi$
.
$\psi$
.
As the following lemma demonstrates, the dependence atom can be defined in terms of the constancy atoms and the intuitionistic implication:
Lemma 79. (Abramsky and Väänänen Reference Abramsky and Väänänen2009).
![]() $\models \,=(x_1,\ldots,x_n,y)\leftrightarrow$
$\models \,=(x_1,\ldots,x_n,y)\leftrightarrow$
![]() $\bigl((\,=(x_1)\wedge\ldots\wedge\,=(x_n))\ \to\ \,=(y)\bigr)$
$\bigl((\,=(x_1)\wedge\ldots\wedge\,=(x_n))\ \to\ \,=(y)\bigr)$
ThisFootnote
9
gives an example where the use of
![]() $\phi\to\psi$
leads to something we know is exponential (Example 47). It shows that we cannot hope to prove that the dimension of
$\phi\to\psi$
leads to something we know is exponential (Example 47). It shows that we cannot hope to prove that the dimension of
![]() $\phi\to\psi$
is in general better than exponential in the dimensions of
$\phi\to\psi$
is in general better than exponential in the dimensions of
![]() $\phi$
and
$\phi$
and
![]() $\psi$
.
$\psi$
.
Note, that we can add intuitionistic implication to
![]() $\mathbb{LE}_0$
, because it does not increase upper dimension, when the latter is bounded by a constant.
$\mathbb{LE}_0$
, because it does not increase upper dimension, when the latter is bounded by a constant.
Intuitionistic disjunction can be defined in terms of constancy atoms:
But since it increases upper dimension additively, it cannot be defined in first order logic alone. In fact, the formula
![]() $x=y\ {\underline{\lor}}\ \neg x=y$
has upper dimension 2.
$x=y\ {\underline{\lor}}\ \neg x=y$
has upper dimension 2.
The non-empty atom
 $\mathsf{N}\hspace{-0.25em}\mathsf{E}$
$\mathsf{N}\hspace{-0.25em}\mathsf{E}$
Definition 80. (The non-empty atom). The non-empty atom
![]() $\mathsf{N}\hspace{-0.25em}\mathsf{E}$
is defined by
$\mathsf{N}\hspace{-0.25em}\mathsf{E}$
is defined by
![]() $M\models_T\mathsf{N}\hspace{-0.25em}\mathsf{E}$
if and only if
$M\models_T\mathsf{N}\hspace{-0.25em}\mathsf{E}$
if and only if
![]() $T\ne\emptyset$
.
$T\ne\emptyset$
.
The atom
![]() $\mathsf{N}\hspace{-0.25em}\mathsf{E}$
says that a team is non-empty. Most of the atoms we have considered (dependence, inclusion, independence, etc) satisfy the Empty Team Property, i.e., the empty team satisfies the atom (see the remark in the end of Section 2.4) and our logical operations (conjunction, disjunction, existential quantifier, universal quantifier) preserve the Empty Team Property. Thus we can immediately observe that
$\mathsf{N}\hspace{-0.25em}\mathsf{E}$
says that a team is non-empty. Most of the atoms we have considered (dependence, inclusion, independence, etc) satisfy the Empty Team Property, i.e., the empty team satisfies the atom (see the remark in the end of Section 2.4) and our logical operations (conjunction, disjunction, existential quantifier, universal quantifier) preserve the Empty Team Property. Thus we can immediately observe that
![]() $\mathsf{N}\hspace{-0.25em}\mathsf{E}$
is not definable in them. Still it is sometimes useful. For example, we may want to enhance the disjunction
$\mathsf{N}\hspace{-0.25em}\mathsf{E}$
is not definable in them. Still it is sometimes useful. For example, we may want to enhance the disjunction
![]() $\phi\vee\psi$
to
$\phi\vee\psi$
to
![]() $(\phi\wedge\mathsf{N}\hspace{-0.25em}\mathsf{E})\vee(\psi\wedge\mathsf{N}\hspace{-0.25em}\mathsf{E})$
. The latter would be satisfied by a team which splits into a team satisfying
$(\phi\wedge\mathsf{N}\hspace{-0.25em}\mathsf{E})\vee(\psi\wedge\mathsf{N}\hspace{-0.25em}\mathsf{E})$
. The latter would be satisfied by a team which splits into a team satisfying
![]() $\phi$
and a team satisfying
$\phi$
and a team satisfying
![]() $\psi$
, both non-empty. An example in natural language would be the statement “On Mondays I play tennis or go to swim” with the intention that both cases actually happen.
$\psi$
, both non-empty. An example in natural language would be the statement “On Mondays I play tennis or go to swim” with the intention that both cases actually happen.
Lemma 81. The upper dimension of
![]() $\mathsf{N}\hspace{-0.25em}\mathsf{E}$
is 1. The dual upper dimension
$\mathsf{N}\hspace{-0.25em}\mathsf{E}$
is 1. The dual upper dimension
![]() $\mathrm{D}^{\mathrm{d}}(\!\left\Vert \mathsf{N}\hspace{-0.25em}\mathsf{E} \right\Vert^{{M,\vec{x}}})$
and the cylindric dimension
$\mathrm{D}^{\mathrm{d}}(\!\left\Vert \mathsf{N}\hspace{-0.25em}\mathsf{E} \right\Vert^{{M,\vec{x}}})$
and the cylindric dimension
![]() $\mathrm{CD}(\!\left\Vert \mathsf{N}\hspace{-0.25em}\mathsf{E} \right\Vert^{{M,\vec{x}}})$
in a domain of size n are
$\mathrm{CD}(\!\left\Vert \mathsf{N}\hspace{-0.25em}\mathsf{E} \right\Vert^{{M,\vec{x}}})$
in a domain of size n are
![]() $n^k$
, where
$n^k$
, where
![]() $k=\mathrm{len}(\vec{x})$
.
$k=\mathrm{len}(\vec{x})$
.
Proof. Non-emptyness is a convex property dominated by the maximal team. Hence the upper dimension of
![]() $\mathsf{N}\hspace{-0.25em}\mathsf{E}$
is 1. It is supported by the family of all singleton teams. Hence the dual upper dimension and the cylindrical dimension of
$\mathsf{N}\hspace{-0.25em}\mathsf{E}$
is 1. It is supported by the family of all singleton teams. Hence the dual upper dimension and the cylindrical dimension of
![]() $\left\Vert \mathsf{N}\hspace{-0.25em}\mathsf{E} \right\Vert^{{M,\vec{x}}}$
,
$\left\Vert \mathsf{N}\hspace{-0.25em}\mathsf{E} \right\Vert^{{M,\vec{x}}}$
,
![]() $\mathrm{len}(\vec{x})=k$
, is
$\mathrm{len}(\vec{x})=k$
, is
![]() $n^k$
.
$n^k$
.
Corollary 82.
![]() $\mathrm{Dim}_{\mathsf{N}\hspace{-0.25em}\mathsf{E},{\vec{x}}}$
is in
$\mathrm{Dim}_{\mathsf{N}\hspace{-0.25em}\mathsf{E},{\vec{x}}}$
is in
![]() $\mathbb{E}_0$
while
$\mathbb{E}_0$
while
![]() $\mathrm{Dim}^{\mathrm{d}}_{\mathsf{N}\hspace{-0.25em}\mathsf{E},{\vec{x}}}$
and
$\mathrm{Dim}^{\mathrm{d}}_{\mathsf{N}\hspace{-0.25em}\mathsf{E},{\vec{x}}}$
and
![]() $\mathrm{CDim}_{\mathsf{N}\hspace{-0.25em}\mathsf{E},{\vec{x}}}$
are in
$\mathrm{CDim}_{\mathsf{N}\hspace{-0.25em}\mathsf{E},{\vec{x}}}$
are in
![]() $\mathbb{F}_0$
.
$\mathbb{F}_0$
.
The atom
![]() $\mathsf{N}\hspace{-0.25em}\mathsf{E}$
is an example of an upper dimension 1 operation which still extends the expressive power of first order logic.
$\mathsf{N}\hspace{-0.25em}\mathsf{E}$
is an example of an upper dimension 1 operation which still extends the expressive power of first order logic.
The quantifiers
 $\forall^1$
,
$\forall^1$
,
 $\exists^1$
, and
$\exists^1$
, and
 $\delta^1$
$\delta^1$
We now recall three quantifiers which represent alternative definitions for the semantics of ordinary quantifiers
![]() $\exists$
and
$\exists$
and
![]() $\forall$
. As we shall see, these alternative quantifiers do not preserve dimension in the same strong sense as the received
$\forall$
. As we shall see, these alternative quantifiers do not preserve dimension in the same strong sense as the received
![]() $\exists$
and
$\exists$
and
![]() $\forall$
.
$\forall$
.
Definition 83. If
![]() $a\in M$
, let
$a\in M$
, let
![]() $F_a$
be the constant function
$F_a$
be the constant function
![]() $F_a(s)=\{a\}$
for all
$F_a(s)=\{a\}$
for all
![]() $s\in T$
. The
$s\in T$
. The
![]() $\exists^1$
-quantifier is defined as follows:
$\exists^1$
-quantifier is defined as follows:
![]() $M\models_T\exists^1x\phi$
if for some
$M\models_T\exists^1x\phi$
if for some
![]() $a\in M$
we have
$a\in M$
we have
![]() $M\models_{T[F_a/x]}\phi$
. The
$M\models_{T[F_a/x]}\phi$
. The
![]() $\forall^1$
-quantifier is defined as follows:
$\forall^1$
-quantifier is defined as follows:
![]() $M\models_T\forall^1x\phi$
if for all
$M\models_T\forall^1x\phi$
if for all
![]() $a\in M$
we have
$a\in M$
we have
![]() $M\models_{T[F_a/x]}\phi.$
The public announcement-quantifier
$M\models_{T[F_a/x]}\phi.$
The public announcement-quantifier
![]() $\delta^1x$
is defined as follows:
$\delta^1x$
is defined as follows:
![]() $M\models_T\delta^1x\phi$
if for all
$M\models_T\delta^1x\phi$
if for all
![]() $a\in M$
we have
$a\in M$
we have
![]() $M\models_{T_a}\phi$
, where
$M\models_{T_a}\phi$
, where
![]() $T_a=\{s\in T:s(x)=a\}$
.
$T_a=\{s\in T:s(x)=a\}$
.
We shall now see that the quantifiers
![]() $\forall^1$
,
$\forall^1$
,
![]() $\delta^1$
and
$\delta^1$
and
![]() $\exists^1$
do not preserve upper dimension, whence they are not Lindström quantifiers in the sense of Definition 22.
$\exists^1$
do not preserve upper dimension, whence they are not Lindström quantifiers in the sense of Definition 22.
Lemma 84. (Galliani Reference Galliani2013).
-
(a)
 $\models\forall^1x\phi(x)\leftrightarrow\forall x(\,=(x)\to\phi(x))$
$\models\forall^1x\phi(x)\leftrightarrow\forall x(\,=(x)\to\phi(x))$
-
(b)
 $\models\delta^1x\phi(x)\leftrightarrow\forall^1 y(x\ne y\vee\phi(x))$
$\models\delta^1x\phi(x)\leftrightarrow\forall^1 y(x\ne y\vee\phi(x))$
-
(c)
 $\models\,=(x_1,...,x_n,y)\leftrightarrow\delta^1x_1...\delta^1x_n\,=(y)$
$\models\,=(x_1,...,x_n,y)\leftrightarrow\delta^1x_1...\delta^1x_n\,=(y)$
-
(d)
 $\models\,=(x_1,...,x_n,y)\leftrightarrow\forall^1z_1...\forall^1z_n(z_1\ne x_1\vee\ldots\vee z_n\ne x_k\vee\,=(y))$
.
$\models\,=(x_1,...,x_n,y)\leftrightarrow\forall^1z_1...\forall^1z_n(z_1\ne x_1\vee\ldots\vee z_n\ne x_k\vee\,=(y))$
.
Items (a) and (b) show that
![]() $\forall^1 x\phi$
and
$\forall^1 x\phi$
and
![]() $\delta^1x\phi(x)$
increase upper dimension of
$\delta^1x\phi(x)$
increase upper dimension of
![]() $\phi$
at most exponentially. Items (c) and (d) shows that, as operators,
$\phi$
at most exponentially. Items (c) and (d) shows that, as operators,
![]() $\delta^1x\phi(x,y)$
and
$\delta^1x\phi(x,y)$
and
![]() $\forall^1x\phi(x)$
increase dimension in the worst case exponentially. This shows that we cannot hope to prove that they are in general better than exponential. This also shows that these operators do not arise from a Lindström quantifier.
$\forall^1x\phi(x)$
increase dimension in the worst case exponentially. This shows that we cannot hope to prove that they are in general better than exponential. This also shows that these operators do not arise from a Lindström quantifier.
Note that by iterating
![]() $\forall^1x$
or
$\forall^1x$
or
![]() $\delta^1x$
we can defined dependence atoms of arbitrary arity. This shows that
$\delta^1x$
we can defined dependence atoms of arbitrary arity. This shows that
![]() $\forall^1x$
and
$\forall^1x$
and
![]() $\delta^1x$
increase dimension more than any k-ary atom for a fixed k.
$\delta^1x$
increase dimension more than any k-ary atom for a fixed k.
Lemma 85.
-
(a)
 $\models\exists^1 x\phi\leftrightarrow\exists x(\,=( x)\wedge\phi)$
.
$\models\exists^1 x\phi\leftrightarrow\exists x(\,=( x)\wedge\phi)$
. -
(b)
 $\models \,=(x)\leftrightarrow\exists^1y(x=y)$
.
$\models \,=(x)\leftrightarrow\exists^1y(x=y)$
.
Proof. Easy.
Hence
![]() $\exists^1$
increases upper dimension at most linearly. Also,
$\exists^1$
increases upper dimension at most linearly. Also,
![]() $\exists^1$
does indeed increase dimension, as the dimension of
$\exists^1$
does indeed increase dimension, as the dimension of
![]() $x=y$
is 1 and the dimension of
$x=y$
is 1 and the dimension of
![]() $\,=(x)$
is n. Hence
$\,=(x)$
is n. Hence
![]() $\exists^1$
is not first order definable and not definable even if we add arbitrary Lindström quantifiers to first order logic.
$\exists^1$
is not first order definable and not definable even if we add arbitrary Lindström quantifiers to first order logic.
The point is that
![]() $\exists^1$
preserves dimension in the growth class where constancy logic is, but not in the lower growth class where FO is.
$\exists^1$
preserves dimension in the growth class where constancy logic is, but not in the lower growth class where FO is.
Uniform definability
Uniform definability, introduced by P. Galliani, is a phenomenon which does not exist in classical logic. It seems to be particularly characteristic to team based logics. Roughly speaking, a quantifier
![]() $Qx\phi(x,y)$
is uniformly definable in a logic if there is a single definition which works by substitution. In classical logic all definitions are uniform. In team based logics some quantifiers are definable but the definition is not uniform. In this section we use our dimension theory to prove this fact.
$Qx\phi(x,y)$
is uniformly definable in a logic if there is a single definition which works by substitution. In classical logic all definitions are uniform. In team based logics some quantifiers are definable but the definition is not uniform. In this section we use our dimension theory to prove this fact.
Definition 86. (Galliani Reference Galliani2013).A generalized quantifier (which need not be a Lindström quantifier) Q of a logic
![]() $L_1$
is said to be uniformly definable in another logic
$L_1$
is said to be uniformly definable in another logic
![]() $L_2$
if the logic
$L_2$
if the logic
![]() $L_2$
has a sentence
$L_2$
has a sentence
![]() $\Phi(P)$
, P unary, with only positive occurrences of P, such that for all formulas
$\Phi(P)$
, P unary, with only positive occurrences of P, such that for all formulas
![]() $\phi(x,y)$
of the logic
$\phi(x,y)$
of the logic
![]() $L_1$
we have
$L_1$
we have
Similarly, if there are several formulas, as in
![]() $Qxy\phi(x,z)\psi(y,z)$
.
$Qxy\phi(x,z)\psi(y,z)$
.
Example 87. The equivalence
shows that the quantifier
![]() $\exists^1$
is uniformly definable in dependence logic, with
$\exists^1$
is uniformly definable in dependence logic, with
![]() $\Phi(P)$
the formula
$\Phi(P)$
the formula
![]() $\exists x(\,=(x)\wedge P(x))$
. The equivalence
$\exists x(\,=(x)\wedge P(x))$
. The equivalence
shows that the intuitionistic disjunction is uniformly definable in dependence logic, with
![]() $\Phi(P_0,P_1)$
the formula
$\Phi(P_0,P_1)$
the formula
![]() $\exists x\exists y(\,=(x)\wedge\,=(y)\wedge ((x=y\wedge P_0)\vee(\neg x=y\wedge P_1)$
.
$\exists x\exists y(\,=(x)\wedge\,=(y)\wedge ((x=y\wedge P_0)\vee(\neg x=y\wedge P_1)$
.
Lemma 88. Suppose
where
![]() $\Phi(P)$
is a sentence in dependence logic. Then
$\Phi(P)$
is a sentence in dependence logic. Then
where k is the length of
![]() $\Phi(P)$
and m is the maximum of the lengths of
$\Phi(P)$
and m is the maximum of the lengths of
![]() $\vec{x}$
such that
$\vec{x}$
such that
![]() $\,=(\vec{x},y)$
for some y occurs in
$\,=(\vec{x},y)$
for some y occurs in
![]() $\Phi(P)$
.
$\Phi(P)$
.
Proof. We use induction on
![]() $\Phi$
. The cases of atoms
$\Phi$
. The cases of atoms
![]() $\,=(\vec{x},y)$
, the atom P(z) and other atomic formulas are clear. The induction step for the connectives and the first order quantifiers follow from Corollary 65.
$\,=(\vec{x},y)$
, the atom P(z) and other atomic formulas are clear. The induction step for the connectives and the first order quantifiers follow from Corollary 65.
Corollary 89. (Galliani Reference Galliani2013). The quantifier
![]() $\forall^1$
is not uniformly definable in dependence logic.
$\forall^1$
is not uniformly definable in dependence logic.
Proof. Suppose
![]() $\Phi(P)$
, a sentence of length l, defines
$\Phi(P)$
, a sentence of length l, defines
![]() $\forall^1$
uniformly in dependence logic. Let m be as in Lemma 88. Then there is by Lemma 84 a formula
$\forall^1$
uniformly in dependence logic. Let m be as in Lemma 88. Then there is by Lemma 84 a formula
![]() $\Psi(P)$
of dependence logic, obtained from
$\Psi(P)$
of dependence logic, obtained from
![]() $\Phi(P)$
by k repeated substitutions, which defines
$\Phi(P)$
by k repeated substitutions, which defines
![]() $\,=(x_1,\ldots,x_k,y)$
. By Lemma 88 we obtain an upper bound of
$\,=(x_1,\ldots,x_k,y)$
. By Lemma 88 we obtain an upper bound of
![]() $n^{n^m\cdot l^k}$
for
$n^{n^m\cdot l^k}$
for
![]() $\mathrm{Dim}_{\,=(x_1,\ldots,x_k,y),\vec{x}y}(n)$
. However, we know from Example 47 that
$\mathrm{Dim}_{\,=(x_1,\ldots,x_k,y),\vec{x}y}(n)$
. However, we know from Example 47 that
![]() $\mathrm{Dim}_{\,=(x_1,\ldots,x_k,y),\vec{x}y}(n)=n^{n^k}$
.
$\mathrm{Dim}_{\,=(x_1,\ldots,x_k,y),\vec{x}y}(n)=n^{n^k}$
.
Although Corollary 89 is not new, its proof shows that the concept of upper dimension offers a general method for demonstrating failure of uniform definability.
The “at most half” atom
Definition 90. (The “at most half” atom). Suppose
![]() $\mathrm{len}(\vec{x})=k$
and the model M has size n. We define a new atom as follows:
$\mathrm{len}(\vec{x})=k$
and the model M has size n. We define a new atom as follows:
![]() $M\models_T\ {\tt\bf H}(\vec{x})$
if
$M\models_T\ {\tt\bf H}(\vec{x})$
if
![]() $|\{s(\vec{x}) \mid s\in T\}|\le n^k/2$
.
$|\{s(\vec{x}) \mid s\in T\}|\le n^k/2$
.
Note that
![]() ${\tt\bf H}(\vec{x})$
is clearly definable in dependence logic (see Example 21).
${\tt\bf H}(\vec{x})$
is clearly definable in dependence logic (see Example 21).
Theorem 91. Suppose
![]() $\mathrm{len}(\vec{x})=k$
. The upper dimension of
$\mathrm{len}(\vec{x})=k$
. The upper dimension of
![]() ${\tt\bf H}(\vec{x})$
is
${\tt\bf H}(\vec{x})$
is
![]() $\sim \sqrt{\frac{2}{\pi}}2^{n^k-\frac{k}{2}log(n)}$
.
$\sim \sqrt{\frac{2}{\pi}}2^{n^k-\frac{k}{2}log(n)}$
.
Proof. Bollobás (Reference Bollobás2001, p. 4)
Corollary 92. Suppose
![]() $\mathrm{len}(\vec{x})=k$
. The atom
$\mathrm{len}(\vec{x})=k$
. The atom
![]() ${\tt\bf H}(\vec{x})$
is not definable in the extension of first order logic by
${\tt\bf H}(\vec{x})$
is not definable in the extension of first order logic by
![]() $<k$
-ary dependence (or other) atoms.
$<k$
-ary dependence (or other) atoms.
The parity atom
Definition 93. (The parity atom). Suppose
![]() $\mathrm{len}(\vec{x})=k$
. The k-ary parity atom is defined by
$\mathrm{len}(\vec{x})=k$
. The k-ary parity atom is defined by
![]() $M\models_T\textbf{E}(\vec{x})$
if and only if
$M\models_T\textbf{E}(\vec{x})$
if and only if
![]() $|\{s(\vec{x}) \mid \vec{x}\in T\}|$
is even.
$|\{s(\vec{x}) \mid \vec{x}\in T\}|$
is even.
Note that
![]() $\textbf{E}(\vec{x})$
is definable in independence logic (see Example 21).
$\textbf{E}(\vec{x})$
is definable in independence logic (see Example 21).
Lemma 94.
The upper, dual and cylindrical dimension of the k-ary
![]() $\textbf{E}(\vec{x})$
is
$\textbf{E}(\vec{x})$
is
![]() $2^{n^k-1}$
.
$2^{n^k-1}$
.
Proof. This is a special case of Example 7.
Corollary 95. The k-ary
![]() $\mbox{E}(\vec{x})$
is definable from the independence atoms but not from l-ary independence atoms for
$\mbox{E}(\vec{x})$
is definable from the independence atoms but not from l-ary independence atoms for
![]() $l<k$
.
$l<k$
.
(In)dependence friendly logic
The so-called dependence friendly existential quantifier, as in independence friendly logic (Mann et al. Reference Mann, Sandu and Sevenster2011), can be defined in terms of the dependence atom. Hence we can estimate its effect on the dimension of a formula. We have
Corollary 96. The quantifier
![]() $\exists x/\vec{y}$
,
$\exists x/\vec{y}$
,
![]() $\mathrm{len}(\vec{y})=k$
, is not definable in the extension of first order logic by
$\mathrm{len}(\vec{y})=k$
, is not definable in the extension of first order logic by
![]() $<k$
-ary independence, inclusion, exclusion, dependence and constancy atoms.
$<k$
-ary independence, inclusion, exclusion, dependence and constancy atoms.
A kind of “dependence friendly” disjunction can be defined as follows:
![]() $M\models_T\phi\vee_{\vec{x}}\psi$
if
$M\models_T\phi\vee_{\vec{x}}\psi$
if
![]() $T=Y\cup Z$
such that
$T=Y\cup Z$
such that
![]() $M\models_Y\phi$
,
$M\models_Y\phi$
,
![]() $M\models_Z\psi$
and if
$M\models_Z\psi$
and if
![]() $s,s'\in T$
with
$s,s'\in T$
with
![]() $s(\vec{x})=s'(\vec{x})$
, then
$s(\vec{x})=s'(\vec{x})$
, then
![]() $(s\in Y\Leftrightarrow s'\in Y)$
and
$(s\in Y\Leftrightarrow s'\in Y)$
and
![]() $(s\in Z\Leftrightarrow s'\in Z)$
.
$(s\in Z\Leftrightarrow s'\in Z)$
.
Lemma 97.
![]() $\models\phi\vee_{\vec{x}}\psi\leftrightarrow\exists u\exists v(\,=(\vec{x},u)\wedge\,=(\vec{x},v)\wedge(u=v\to\phi)\wedge(u\ne v\to\psi))$
.
$\models\phi\vee_{\vec{x}}\psi\leftrightarrow\exists u\exists v(\,=(\vec{x},u)\wedge\,=(\vec{x},v)\wedge(u=v\to\phi)\wedge(u\ne v\to\psi))$
.
In the proof of Lemma 97 it is actually enough to use the 2-valued dependence atom
![]() $\,=(\vec{x},y)\wedge(\,=(y)\vee\,=(y))$
. This has dimension
$\,=(\vec{x},y)\wedge(\,=(y)\vee\,=(y))$
. This has dimension
![]() $2^{m^k}$
, when
$2^{m^k}$
, when
![]() $\mathrm{len}(\vec{x})=k$
and the domain has cardinality m. Dimension analysis shows the full dependence atom cannot be defined from the s-valued dependence atom
$\mathrm{len}(\vec{x})=k$
and the domain has cardinality m. Dimension analysis shows the full dependence atom cannot be defined from the s-valued dependence atom
![]() $\,=_s(\vec{x},y)$
, defined by
$\,=_s(\vec{x},y)$
, defined by
for any
![]() $s>0$
. The 2-valued dependence atom
$s>0$
. The 2-valued dependence atom
![]() $=_2\!(\vec{x},y)$
can be defined from
$=_2\!(\vec{x},y)$
can be defined from
![]() $\vee_{\vec{x}}$
and constancy atoms as follows:
$\vee_{\vec{x}}$
and constancy atoms as follows:
This shows that the operation
![]() $\phi\vee_{\vec{x}}\psi$
does not preserve dimension. The situation is similar to the dependence friendly existential quantifier.
$\phi\vee_{\vec{x}}\psi$
does not preserve dimension. The situation is similar to the dependence friendly existential quantifier.
6. Other topics
We mention here some other topics that are not directly related to our main results.
6.1 VC-dimension
An important dimension in finite combinatorics is the Vapnik-Cervonenkis (VC) dimension of a family of sets. It is defined as follows: Let us say that a set A is shattered by a family H of subsets of a finite set if
![]() $\{h\cap A\mid h\in H\}$
contains all the subsets of A. The VC-dimension of H is the largest cardinality of a set shattered by H. This dimension has turned out to be useful e.g. in learning theory (Vapnik Reference Vapnik1995). However, it does not have the same flexibility as our dimension concepts and does not seem to be applicable in the kind of analysis we have at hand in this paper.
$\{h\cap A\mid h\in H\}$
contains all the subsets of A. The VC-dimension of H is the largest cardinality of a set shattered by H. This dimension has turned out to be useful e.g. in learning theory (Vapnik Reference Vapnik1995). However, it does not have the same flexibility as our dimension concepts and does not seem to be applicable in the kind of analysis we have at hand in this paper.
The VC-dimension of the family of teams of an even number of k-tuples in a domain of n elements is
![]() ${n^k}$
. Yet evenness can be expressed in independence logic. As the VC-dimension of the independence atom is 1, this shows that our logical operations do not preserve VC-dimension.
${n^k}$
. Yet evenness can be expressed in independence logic. As the VC-dimension of the independence atom is 1, this shows that our logical operations do not preserve VC-dimension.
6.2 Cylindrical dimension and the DNF
Our cylindircal dimension for a family of sets is actually known in the study of disjunctive normal forms (DNF) of Boolean functions: Suppose
![]() $X=\{a_1,\ldots,a_n\}$
is a finite set. We fix a proposition symbol
$X=\{a_1,\ldots,a_n\}$
is a finite set. We fix a proposition symbol
![]() $p_i$
for each
$p_i$
for each
![]() $i\in [1,n]$
. Now subsets A of X correspond canonically to valuations (truth functions)
$i\in [1,n]$
. Now subsets A of X correspond canonically to valuations (truth functions)
![]() $v_A$
of
$v_A$
of
![]() $\{p_1,\ldots,p_n\}$
. Respectively, families
$\{p_1,\ldots,p_n\}$
. Respectively, families
![]() $\mathcal{A}$
of subsets of X correspond to Boolean functions on
$\mathcal{A}$
of subsets of X correspond to Boolean functions on
![]() $\{p_1,\ldots,p_n\}$
and thereby to propositional formulas
$\{p_1,\ldots,p_n\}$
and thereby to propositional formulas
![]() $\phi_{{\mathcal{A}}}$
in
$\phi_{{\mathcal{A}}}$
in
![]() $\{p_1,\ldots,p_n\}$
. This brings a connection between families of sets and Boolean functions (O’Donnell Reference O’Donnell2014). An interval
$\{p_1,\ldots,p_n\}$
. This brings a connection between families of sets and Boolean functions (O’Donnell Reference O’Donnell2014). An interval
![]() $I=\{Y\subseteq X \mid A\subseteq Y\subseteq B\}$
corresponds to the set
$I=\{Y\subseteq X \mid A\subseteq Y\subseteq B\}$
corresponds to the set
![]() $\bar{I}$
of valuations in which some proposition symbols have a fixed value, namely
$\bar{I}$
of valuations in which some proposition symbols have a fixed value, namely
![]() $p_i$
for
$p_i$
for
![]() $a_i\in A$
must be 1 and
$a_i\in A$
must be 1 and
![]() $p_i$
for
$p_i$
for
![]() $a_i\notin B$
must be 0. The set
$a_i\notin B$
must be 0. The set
![]() $\bar{I}$
can be defined in propositional logic with a conjunction of literals i.e. propositional symbols and their negations. If a family
$\bar{I}$
can be defined in propositional logic with a conjunction of literals i.e. propositional symbols and their negations. If a family
![]() $\mathcal{A}$
of subsets of X can be expressed as the union of d intervals, then the defining formula
$\mathcal{A}$
of subsets of X can be expressed as the union of d intervals, then the defining formula
![]() $\phi_{{\mathcal{A}}}$
can be taken to be a disjunction of d conjunctions of literals. In the theory of Boolean functions our concept of cylindrical dimension corresponds exactly to the concept of length m(f) of the shortest disjunctive normal form for the Boolean function f, meaning the smallest number of disjuncts in the disjunctive normal form of f. The conjunctions in such a “minimal DNF” (where we also stipulate that these consist of as few variables as possible) are the well-known prime implicants of f. The algorithm of Quine (Reference Quine1955) and McCluskey determines these and hence also the number m(f). A classic result about m(f) is the following estimate (Glagolev Reference Glagolev1964) for almost all f of n Boolean variables:
$\phi_{{\mathcal{A}}}$
can be taken to be a disjunction of d conjunctions of literals. In the theory of Boolean functions our concept of cylindrical dimension corresponds exactly to the concept of length m(f) of the shortest disjunctive normal form for the Boolean function f, meaning the smallest number of disjuncts in the disjunctive normal form of f. The conjunctions in such a “minimal DNF” (where we also stipulate that these consist of as few variables as possible) are the well-known prime implicants of f. The algorithm of Quine (Reference Quine1955) and McCluskey determines these and hence also the number m(f). A classic result about m(f) is the following estimate (Glagolev Reference Glagolev1964) for almost all f of n Boolean variables:
Thus this is also an estimate for the cylindrical dimension of almost all families of subsets of a set of n elements. The DNF-dimension has been studied extensively and more estimates have been found, see Koršunov (Reference Koršunov1969), Makarov (Reference Makarov1964), Weber (Reference Weber1982), Kuznetsov (Reference Kuznetsov1983), Aslanyan (Reference Aslanyan1983), Romanov (Reference Romanov1983). For example, in Kuznetsov (Reference Kuznetsov1983) the following better lower bound is proved
where
![]() $\lim \epsilon_n=0$
, for almost all Boolean functions on n variables.
$\lim \epsilon_n=0$
, for almost all Boolean functions on n variables.
In the following application of the estimate (2), we measure probabilities of team properties by using the uniform distribution for teams on
![]() $k+1$
variables in a model of size n. Note that in a non-rigid model a random team property is almost surely not definable in any logic. Therefore the interesting case is the definability of random team properties in rigid models.
$k+1$
variables in a model of size n. Note that in a non-rigid model a random team property is almost surely not definable in any logic. Therefore the interesting case is the definability of random team properties in rigid models.
Corollary 98. In the class of finite rigid models a random
![]() $k+1$
-ary team property
$k+1$
-ary team property
![]() $(k\ge 1)$
is almost surely not definable in the extension of first order logic by k-ary dependence, independence, inclusion, exclusion and anonymity atoms.
$(k\ge 1)$
is almost surely not definable in the extension of first order logic by k-ary dependence, independence, inclusion, exclusion and anonymity atoms.
Proof. If a random
![]() $k+1$
-ary team property is definable in
$k+1$
-ary team property is definable in
![]() $\mathbb{LF}_{k}$
, its cylindrical dimension is asymptotically
$\mathbb{LF}_{k}$
, its cylindrical dimension is asymptotically
![]() $n^{n^{k}}$
. But by (2) the cylindrical dimension is asymptotically almost surely at least of the order
$n^{n^{k}}$
. But by (2) the cylindrical dimension is asymptotically almost surely at least of the order
![]() $2^{n^{k+1}}$
.
$2^{n^{k+1}}$
.
We do not know whether upper dimension and dual upper dimension have been isolated in the study of Boolean functions and whether they have a role there.
6.3 Infinite models
Our dimension analysis can be adapted to the realm of infinite domains but it does not have similar power. The infinite dimensions tend to be all the same and we do not get applications to definability. In fact, the hierarchy results are false in the following sense: Three and higher arity dependence atoms can be expressed in terms of binary dependence atoms. The trick is to use the binary dependence atom to introduce a pairing function:
Theorem 99. In infinite domains all dependence atoms are definable in terms of 2-ary dependence atoms. Respectively, in infinite domains the ternary independence atom
![]() $xyz\perp uvw$
can express all dependence, independence, inclusion, anonymity, and exclusion atoms.
$xyz\perp uvw$
can express all dependence, independence, inclusion, anonymity, and exclusion atoms.
Proof. Suppose
![]() $(x,y)\mapsto\langle x,y\rangle$
is a pairing function (i.e.
$(x,y)\mapsto\langle x,y\rangle$
is a pairing function (i.e.
![]() $\langle x,y\rangle =\langle x',y'\rangle$
if and only if
$\langle x,y\rangle =\langle x',y'\rangle$
if and only if
![]() $x=x'$
and
$x=x'$
and
![]() $y=y'$
) on the (infinite) domain. We prove the following typical case:
$y=y'$
) on the (infinite) domain. We prove the following typical case:
 \begin{equation}\begin{array}{lcl} \models\ \,=(xyz,u)&\leftrightarrow&\forall x_1\forall y_1\exists u_1 (\,=(x_1y_1,u_1)\wedge\\&&\forall x_2\forall y_2\exists u_2(\,=(x_2y_2,u_2)\wedge \\&&((x_1=x_2\wedge y_1=y_2)\leftrightarrow u_1=u_2)\wedge\\&&((x_1=x\wedge y_1=y\wedge x_2=u_1 \wedge y_2=z)\to \,=(u_2,u))))\end{array}\end{equation}
\begin{equation}\begin{array}{lcl} \models\ \,=(xyz,u)&\leftrightarrow&\forall x_1\forall y_1\exists u_1 (\,=(x_1y_1,u_1)\wedge\\&&\forall x_2\forall y_2\exists u_2(\,=(x_2y_2,u_2)\wedge \\&&((x_1=x_2\wedge y_1=y_2)\leftrightarrow u_1=u_2)\wedge\\&&((x_1=x\wedge y_1=y\wedge x_2=u_1 \wedge y_2=z)\to \,=(u_2,u))))\end{array}\end{equation}
Suppose a team T satisfies
![]() $\,=(xyz,u)$
. Let Y be the extension of T by giving all possible values for
$\,=(xyz,u)$
. Let Y be the extension of T by giving all possible values for
![]() $x_1,x_2,y_1$
and
$x_1,x_2,y_1$
and
![]() $y_2$
. We further extend Y to Z by giving values to
$y_2$
. We further extend Y to Z by giving values to
![]() $u_1$
and
$u_1$
and
![]() $u_2$
as follows:
$u_2$
as follows:
Clearly,
![]() $Z\models\ \,=(x_1y_1,u_1)$
and
$Z\models\ \,=(x_1y_1,u_1)$
and
![]() $Z\models\ \,=(x_2y_2,u_2)$
. Also, obviously,
$Z\models\ \,=(x_2y_2,u_2)$
. Also, obviously,
![]() $Z\models (x_1=x_2\wedge y_1=y_2)\Leftrightarrow u_1=u_2$
. Suppose then
$Z\models (x_1=x_2\wedge y_1=y_2)\Leftrightarrow u_1=u_2$
. Suppose then
![]() $\{s,s'\}\subseteq Z$
satisfies
$\{s,s'\}\subseteq Z$
satisfies
![]() $x_1=x\wedge y_1=y\wedge x_2=u_1 \wedge y_2=z$
and, moreover,
$x_1=x\wedge y_1=y\wedge x_2=u_1 \wedge y_2=z$
and, moreover,
![]() $s(u_2)=s'(u_2)$
. A direct calculation yields
$s(u_2)=s'(u_2)$
. A direct calculation yields
![]() $s(u)=s'(u)$
.
$s(u)=s'(u)$
.
Conversely, suppose T satisfies the right hand side of (3). Thus, if T is extended by giving all possible values for
![]() $x_1,x_2,y_1$
and
$x_1,x_2,y_1$
and
![]() $y_2$
, and then further extended to Z by giving suitable values to
$y_2$
, and then further extended to Z by giving suitable values to
![]() $u_1$
and
$u_1$
and
![]() $u_2$
, then Z satisfies the quantifier-free part of the right hand side (3). To prove the left hand side of (3), suppose
$u_2$
, then Z satisfies the quantifier-free part of the right hand side (3). To prove the left hand side of (3), suppose
![]() $s,s'\in T$
agree about xyz. Let f be a function such that if
$s,s'\in T$
agree about xyz. Let f be a function such that if
![]() $s\in Z$
, then
$s\in Z$
, then
![]() $s(u_1)=f(s(x_1),s(y_1))$
. Then, if
$s(u_1)=f(s(x_1),s(y_1))$
. Then, if
![]() $s\in Z$
, then
$s\in Z$
, then
![]() $s(u_2)=f(s(x_2),s(y_2))$
. Clearly, f is one-one. A calculation yields
$s(u_2)=f(s(x_2),s(y_2))$
. Clearly, f is one-one. A calculation yields
![]() $s(u_2)=s'(u_2)$
. Since Z satisfies
$s(u_2)=s'(u_2)$
. Since Z satisfies
![]() $\,=(u_2,u)$
, we obtain
$\,=(u_2,u)$
, we obtain
![]() $s(u)=s'(u)$
.
$s(u)=s'(u)$
.
It remains open, whether the unary dependence atom or the binary independence atom have similar universal power. It remains also open whether the arity hierarchy of the inclusion atom collapses.
7. Conclusion
We have defined three dimension like notions in discrete mathematics and applied them to obtain hierarchy and undefinability results in the area of team semantics. Our results demonstrate that in finite models the arity of atoms puts a definitive bound on what can be expressed. In terms of our approach, the arity of the atoms of a sentence completely determines the dimension of the sentence, and team properties of higher dimension cannot be expressed even if we add all possible Lindström quantifiers. On the other hand, this is only true if certain nicely behaving logical operations are the only ones that are used. If certain strong (from the perspective of our approach) logical operations, such as the intuitionistic implication, are allowed, the dimension analysis fails. Thus our quantitative analysis can be used to show the rationale of choosing some logical operations over some others.
We list below some open questions that remain unanswered by our results:
-
(1) Is the k-ary dependence atom definable in terms of k-ary independence, exclusion, inclusion, anonymity, constancy atoms, and some Lindström quantifiers?
-
(2) Is the k-ary anonymity atom definable in terms of the k-ary inclusion atom?
-
(3) Is the k-ary independence atom definable in terms of the k-ary pure independence atom?
-
(4) Is the (k,l,m)-ary independence atom definable in terms of the
 $\max(k,l)+m$
-ary dependence, anonymity, exclusion and inclusion atoms?
$\max(k,l)+m$
-ary dependence, anonymity, exclusion and inclusion atoms? -
(5) Dependence, exclusion, inclusion, anonymity and independence atoms arise in a natural way from the classes
 $\mathcal{F}$
,
$\mathcal{F}$
,
 $\mathcal{X}$
,
$\mathcal{X}$
,
 $\mathcal{I}_\subseteq$
,
$\mathcal{I}_\subseteq$
,
 $\mathcal{Y}$
and
$\mathcal{Y}$
and
 $\mathcal{I}_\perp$
, and for each of these atoms we have proved an arity hierarchy result. Furthermore, all the classes are first-order definable. Does there exist some other first-order definable families
$\mathcal{I}_\perp$
, and for each of these atoms we have proved an arity hierarchy result. Furthermore, all the classes are first-order definable. Does there exist some other first-order definable families
 $\mathcal{A}\subseteq\{R\mid R\subseteq X_1\times\cdots\times X_n\}$
such that the corresponding atoms satisfy similar hierarchy result, and first-order logic extended with the atoms is strictly contained in dependence/exclusion or inclusion logic?
$\mathcal{A}\subseteq\{R\mid R\subseteq X_1\times\cdots\times X_n\}$
such that the corresponding atoms satisfy similar hierarchy result, and first-order logic extended with the atoms is strictly contained in dependence/exclusion or inclusion logic? -
(6) Our dimension functions are either polynomial or exponential. Is this a general phenomenon for first order definable atoms i.e. is there a Dichotomy Theorem for first order definable atoms? Is it a decidable question to decide whether the dimension function is polynomial?