List of Symbols
1. Introduction
It is customary in theoretical and modeling studies of ice sheets to treat ice as incompressible, and ice-sheet mass balances are often quoted as rates of change of thickness. However, in the accumulation zone of an ice sheet the nearsurface ice consists of firn densifying under its own weight (Reference PatersonPaterson, 1994). When fluctuations in mass accumulation, density and temperature occur at the surface, fluctuations in the density will result throughout the firn layer, and the thickness and mass of an ice sheet will not be simply related.
This is of practical importance if one is to relate observations of changes in ice-sheet thickness over relatively short intervals (e.g. Reference Zwally, Brenner, Major, Bindschadler and MarshZwally and others, 1989; Wingham and others, 1998) to actual or predicted changes in ice-sheet mass. The difficulty is generally appreciated (e.g. Reference Braithwaite, Laternser and PfefferBraithwaite and others, 1994; Warrick and others, 1995), and it is qualitatively understood (Reference Van der VeenVan der Veen, 1993) that the effective density with which mass fluctuations appear in ice-sheet thickness is a function of their duration. Nonetheless, there has been little quantitative investigation of the relation between fluctuations of surface accumulation and surface density and those of ice-sheet thickness. The effect of variations in accumulation rate on the horizontal flow of ice (Reference OerlemansOerlemans, 1981; Reference Van der VeenVan der Veen, 1993) is a separate matter that is ignored here by assuming the fluctuations are short enough to have no effect on the horizontal ice flow.
Any treatment of this problem rests on a densification law for snow. The difficulties in forming a general law are discussed by Reference MellorMellor (1975) and are considerable. On the other hand, Reference BaderBader’s (1960) use of a compactive viscosity (the ratio of the vertical strain rate to the overburden pressure) to characterize the densification of cold firn has been given a theoretical basis in the processes of grain-boundary sliding (Reference Maeno and EbinumaMaeno and Ebinuma, 1983; Reference AlleyAlley, 1987), dislocation creep (Reference Wilkinson and AshbyWilkinson and Ashby, 1975) and boundary and lattice diffusion (Reference CobleCoble, 1970). These mechanisms are expected to dominate dry-firn densification, and their resulting non-linear compactive viscosity describes with reasonable success firn-density profiles in Greenland and Antarctica (Reference AlleyAlley, 1987; Reference Arthern and WinghamArthern and Wingham, 1998). Non-linear creep appears to describe quite well the densification of cold ice sheets. Quite different simplifications of the actual process of densification may be appropriate for warm or seasonal snowpack (e.g. Reference Braithwaite, Laternser and PfefferBraithwaite and others, 1994; Reference Gray and MorlandGray and Morland, 1995).
This paper is an investigation of the variation in thickness of a firn layer whose densification occurs through non-linear viscous creep. By restricting attention to small fluctuations, we are able in section 2 to provide a closed-form expression for the density variation in the firn layer. This is used in section 3 to provide a closed-form expression for the thickness fluctuation. In this expression, the physics of the densification is contained within integration kernels that act on the history of accumulation rate and surface density. The kernels are shift-invariant, allowing a simple description of the effect of densification in terms of the Fourier spectra of the fluctuations of the thickness, accumulation rate and surface density. This allows us in section 4 to discuss with some generality the influence of the observation interval on the effect of densification on estimates of ice-sheet imbalance determined from the rate of change of elevation. Some remarks on the limitations of the treatment are provided in section 5 and some conclusions are drawn in section 6. The numerical treatment of a similar problem, including the effects of temperature fluctuation and finite amplitude fluctuation, has been given by Reference Arthern and WinghamArthern and Wingham (1998).
The theory of the paper is illustrated for sites in Antarctica and Greenland using a non-linear viscous firn-densification model which is described in detail in Reference Arthern and WinghamArthern and Wingham (1998). This allows the practical implication of these results for modern satellite measurements of the Antarctic and Greenland ice sheets to be discussed. One important feature of the results is that they highlight the practical importance of gaining a better understanding of the spatial scale of accumulation fluctuation in connection with satellite measurements of ice-sheet imbalance, as did Reference OerlemansOerlemans (1981) in connection with the contribution of Antarctic ice-sheet mass fluctuation to global sea level.
2. Time-Variant Density of a Firn Column
In this section, we suppose firn may be regarded as a compressible fluid subject to changes which are sufficiently slow that inertial accelerations may be neglected. We consider the firn to be isothermal, and restrict our attention to firn in which the pressure, density and velocity vary only in the vertical. In an inertial reference frame with vertical coordinate z′ the equations of mass and momentum conservation are
where p is the overburden pressure in the firn, p is its density, v′ is the vertical velocity and g is the acceleration due to gravity. We take z′ increasing downwards, so that a positive value of v′ describes a downward motion.
We follow Reference BaderBader (1960) in supposing the densification occurs through a process of creep, at a rate that depends on its density and overburden pressure:
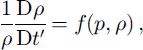
where D/Dt′ = ∂/∂t′ + v′∂/∂z′. From Equation (1), −ρ −1Dρ/Dt′ = ∂v′/∂z′ is the vertical strain rate. With this result, Equation (3) may be written p = − [p/f(p, ρ)]∂v′/∂z′, which identifies the function p/f(p, ρ) as Bader’s “compactive viscosity”. The equality of the densification rate with minus the vertical velocity gradient does not hold in more general flow situations.
At the surface of the firn, lying at z′ = zs, we suppose the surface mass accumulation rate, surface density and surface pressure are known functions. The location of the surface is generally time-variant, with a velocity denoted
, and is not known. Another condition is needed to solve these equations. We suppose that, at a point sufficiently deep in the firn, the density reaches that of ice and the downward velocity is a constant. This point is termed the base of the firn. For reasons which will become apparent, the base will be taken as a fixed point in the inertial system.
These boundary conditions, together with Equations (1–3), determine the pressure, density and velocity uniquely. They do not do so conveniently, however. We therefore introduce the transformation
where z is the depth of firn. With this transformation, Equations (1–3) are unchanged, provided one takes the vertical velocity v in the transformed equations to describe the velocity of the firn observed from a point on the surface. The surface boundary conditions now apply at z = 0. The base of the firn lies at z = z b(t), a function of time in these new coordinates. (A transformation of the form Equation (4) will generally introduce new inertial terms into the momentum conservation equation, Equation (2). However, the inertial acceleration is here negligible by assumption in the inertial frame, and it follows with equality that it remains so in the transformed frame.)
The pressure, density and velocity will vary as a result of fluctuations in the mass-deposition rate and surface density. We shall restrict these to the fluctuations
in the surface mass-accumulation rate and surface density, taking the atmospheric pressure to be
a constant. The fluctuations in the surface conditions will be taken to be small, in the sense that the dimensionless parameter λ in Equations (5) and (6) is assumed to be O(1). (Mathematically, the introduction of the parameter λ makes the solution of the perturbation problem a function of a single parameter. It plays the same role as the single small parameter that would need to appear in a non-dimensional treatment. Practically one may take it as a notational device and regard, for example, O(λ
2) as shorthand for
.)
If the surface conditions are independent of time, the solutions of Equations (1–3) are time-invariant. The density is a function of firn depth only, a result known as “Sorge’s law” in the literature (Reference BaderBader, 1954). Time-invariant solutions may be found on setting ∂/∂t = 0 in Equations (1) and (3) and λ = 0 in Equations (5) and (6). These equations then provide
, an equation that permits the strain rate and compactive viscosity to be determined from observations of density–depth profiles (e.g. Bader, 1953).
When fluctuations in the surface conditions occur, one needs to proceed more generally. Even when restricted to small perturbations, however, Equations (1–3) are equivalent to a second-order equation with variable coefficients, and a closed-form solution cannot be given directly. Therefore a second transformation of the equations is made. The variables {q, q 0} whose definitions are
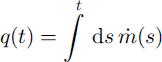
are introduced. q is the mass of firn deposited at the surface up to time t. q 0 may be recognized physically by noting that Equations (2) and (7) show that (p(t, z)/g − p a) is the mass overburden experienced by a firn element at the point (t, z). This must equal the mass deposited at the surface since the element’s own deposition. q 0 is therefore the value of q at the instant it traverses the surface. This implies that q 0 is constant along the material path of a firn element, a result proved directly in Appendix A. The mapping between the {t, z}-plane and the {q, q 0}-plane is shown in Figure 1. The firn occupies the region q ≥ q 0 ≥ q 0(t, z b(t)), with the surface at q 0 = q and the base at q 0 = q(t, z b(t)).
Fig. 1. The mapping between the (a) {t, z}-plane and (b) {q, q0}-plane. In the {t, z}-plane, the surface lies at z = 0 and does not move, and the base of the firn is at a time-variant depth. A material path in this plane is shown as a dashed line. In the {q, q0}-plane, the surface lies along the line {q = q0}, with the firn occupying {q > q0}. In this plane, a material path, shown dashed, is a line of constant q0.
In general, a transformation is invertible if its Jacobian J satisfies 0 < |J| < ∞. In the present case
Using Equation (8), one has
while Equations (9) and (2) provide
The inverse transformation z = z(q, q 0) is given in Appendix B. Equation (11) shows that the transformation is invertible if the mass-deposition rate is strictly positive and the density remains finite. Strictly, this means that our results are not applicable to any circumstance in which surface ablation occasionally equals or exceeds surface accumulation. In applying these results to the practical situation we shall assume it is sufficient for the annual average of accumulation to be positive.
Writing
the transformation of Equation (3) with Equations (8) and (9) provides
while the boundary condition Equation (6) becomes
The advantage of the transformation is now clear. The velocity has been eliminated from the problem, and only a first-order problem with a known surface boundary condition remains.
We now seek solutions to Equations (14) and (15) for small fluctuations. A solution
is assumed. Solving Equation (14) to O(1):
From Equations (17), the solution R 0 is a function of q –q 0. It may be regarded as a function of a single, positive argument whose value is the mass overburden. If f is chosen to be a positive, decreasing function of density that approaches zero as the density approaches that of ice, then R 0(x) → ρ ice for large x.
In O(λ) one has:
In Equation (18), the quantities {·} are O(1) functions whose single argument will be denoted {·}(x), for example. Defining
the function I − may be recognized as the the integrating factor of Equation (18). The solution R 1 may be written
Equation (20) shows a perturbation in the density of firn parcel arising in two ways: because it is deposited at the surface with a perturbed density, and because its density has depended on the fluctuating overburden it has experienced. The form of the argument of the mass-deposition rate m s in the integrand of Equation (20) reflects the fact that the overburden experienced by a parcel of firn depends on the history of the surface deposition rate that followed its own deposition. The density perturbations are acted on by the function I +, which describes the reduction by compression in a density perturbation as it is advected down the column. With f a positive, decreasing function of density, {f + R 0 ∂f/∂R} is a negative function as the density approaches that of ice. We suppose that I +(x) → 0 for large x, so that, with a sufficient mass overburden following burial, the density fluctuations are completely suppressed.
3. Time-Variant Thickness of a Firn Layer
We are concerned with variations in the thickness, or depth h, of the firn. This equals the depth to the base of the firn when viewed from the surface. From Equation (B1), this is given by
The depth h is a function of t only. Its rate of change is given by
We will refer to
as the thickness rate. (The notation d/dt takes its ordinary meaning; it is not an alternative notation for D/Dt.)
In a measurement, it is the change in thickness of an ice sheet that is observed, measured in a frame fixed with respect to the base of the ice sheet. To deal with this situation, we suppose that the firn forms the near surface of an otherwise incompressible ice sheet. We suppose the ice beneath the firn loses mass per unit bed area at a rate of
through mass-flux divergence or basal melting. We suppose the base of the ice sheet is fixed relative to the inertial frame.
is the rate at which the base of the firn appears to move when viewed from the surface. Since the base of the firn is by definition at a fixed location in the inertial system, this must equal the rate at which the surface appears to move when viewed from the bed. Thus
(z
s is positive downwards) and Equation (22) provides a solution for the surface in the inertial, bed-fixed frame.
Equation (22) evidently requires an expression dq 0(t, z b(t))/dt. One has
The second line of the righthand side of Equation (23) uses Equations (4) and (9) and the fact that z
b is a fixed location in the inertial reference frame. The third line uses Equations (2), (11) and (A3),
is simply the firn velocity observed in the inertial frame. Equation (23) identifies dq
0(t, z
b(t))/dt as the mass flux through the base of the firn. Since the base of the firn is by definition at a fixed location in the inertial frame, conservation of mass requires that
It is not necessary to precisely locate the base of the firn. We assume that the firn sensibly achieves the density of ice at its base, that is
and
With these assumptions, no physical boundary exists between the firn and ice. A physical quantity such as
can have no dependence on z
b. In evaluating Equation (22) one may suppose that any dependence on z
b will disappear. Its precise location is then immaterial.
With these preliminaries, Equation (22) may be evaluated using Equations (5), (8), (16), (17), (19), (20), (24) and (25) in Equation (22). The result may be written in the form
Equation (27) is derived in Appendix C. Note that while z b makes an explicit appearance in Equation (27), its value is indeed immaterial, because Equations (25) and (26) cause the integrands to be effectively terminated.
Limiting forms for the thickness rate may be obtained which do not depend on the detailed form of the densification rate f. If the conditions at the surface are time-invariant, one has λ ≡ 0 and
In the static case, the density of the column remains fixed when viewed from the surface. The densification of the firn makes no contribution to the thickness rate, which is proportional to the mass balance of the ice sheet. One may anticipate that this will continue to be the case for fluctuations of sufficiently long duration. Indeed, if one allows the functions
and ρ
s to be slowly varying enough that they may be brought outside the integrals in Equation (27), one has that
and the thickness rate follows the mass balance of the column. Equation (29) is derived in Appendix B.
On the other hand, if the fluctuations are of very short duration, the integrals in Equation (27) become very small, and one then has directly from Equation (27) that the thickness rate may be approximated by
In this limit, the mass fluctuations at the surface appear in the thickness rate at the surface density. Equation (30) may be reached with a simple argument if one accepts that fluctuations of very short duration make negligible contribution to the mass overburden and densification. In the absence of fluctuations, the density is fixed when viewed from the surface, and any change in thickness must result from ice with a density ρ
ice, so that
(which with
is Equation (28)). If the fluctuations do not affect the densification, the velocity at the surface observed in the inertial frame — we write it v
i here — is unaltered when the fluctuations are present. But, in general,
at the surface. Since v
i is fixed by assumption, fluctuations in
at the surface can result only in fluctuations in
. To first order, these are
. Combining these results gives Equation (30).
The two limiting cases, Equations (29) and (30), of very slow and very rapid surface fluctuations, respectively, are memoryless; they depend only on the instantaneous values of the surface fluctuations. At intermediate time-scales, Equation (27) shows that the thickness depends on the history of the surface fluctuations. This more general case may be investigated using Fourier methods by exploiting the fact that the value of q(t, z b) is immaterial, which allows q(t, z b) → −∞ without loss. The quantity
is the Fourier transform of the fluctuations in thickness. If one sets
and
to be the Fourier transforms of the surface mass and density fluctuations, respectively, and allows that q(t, z
b) → −∞, Equation (27) may be Fourier transformed to provide
where the functions H m and Hρ are, respectively, the mass and density fluctuation transfer functions. The form of Equation (32) follows from the fact that the kernels in Equation (27) are convolution kernels when q(t, z b) → −∞ (see, e.g., Reference Porter and StirlingPorter and Stirling, 1992, p. 333). Various particular integral forms may be obtained for the functions H m and Hρ using Equations (27), (31) and (32), but since no use is made of them here, they are not detailed.
Equation (32) provides a simple description of the densification process. The function H m is a reciprocal density. This is the density at which an accumulation-rate fluctuation of a particular frequency appears in the thickness fluctuation. Equations (29) and (30) lead us to suppose the limiting forms
so that fluctuations at very low frequency appear with the density of ice, whereas those of a high frequency appear with the density of snow. High-frequency accumulation-rate fluctuations are amplified in the thickness rate in comparison with low frequencies. The function Hρ plays a similar role for surface density fluctuations. Here one may suppose the limiting forms
Thus, low-frequency fluctuations in density do not appear in the thickness rate.
More generally, the behaviour of the functions H
m and Hρ
will depend on the particular form of the densification function f (Equation (3)), and on the mean surface conditions which determine the O(1) solution. To illustrate their behaviour, I used a model for the strain rate f which accounts for grain-boundary sliding (Reference Maeno and EbinumaMaeno and Ebinuma, 1983; Reference AlleyAlley, 1987), dislocation creep (Reference Wilkinson and AshbyWilkinson and Ashby, 1975) and boundary and lattice diffusion (Reference CobleCoble, 1970). This model provides analytic expressions for the compactive viscosity in terms of the mechanical and thermodynamical constants of firn. A complete tabulation of the model and the values of the constants is given in Reference Arthern and WinghamArthern and Wingham (1998). For now, it is sufficient to note that the densification rate/depends explicitly on the (isothermal) temperature. The functions H
m and Hρ
may be regarded therefore as functions of the mean surface deposition rate
, surface density (ρ
snow) and temperature.
With this model, the kernels of the integrals in Equation (27) are well behaved and smoothly varying. The functions H
m and Hρ
were calculated by Fourier transforming Equations (27) using the Mathematica™ routine NIntegrate, having first used the routine NDSolve to calculate the O(1) solution of Equation (17). Calculations were performed for the cases {
, ρ
snow = 350 kg m−3, T = 245 K}, which describe mean conditions at Byrd station, West Antarctica, and which are close to average values for the Antarctic ice sheet as a whole, and {
, ρ
snow = 350 kg m−3, T = 250 K}, which describe the higher temperature and accumulation-rate conditions at Camp Century, Greenland. Figure 2 shows the function
; Figure 3 the function
. (A value of
equal to 1 means the accumulation-rate fluctuation appears in the thickness rate with the density of ice; a value of
equal to 1 implies the velocity v
i is unperturbed.) It should be noted these illustrations satisfy the relations Equations (33) and (34). (The O(1) solutions in these cases are illustrated in figures 1 and 2 of Reference Arthern and WinghamArthern and Wingham (1998).)
Fig. 2. The normalized elevation-rate mass-transfer function
for Byrd (solid line) and Camp Century (dashed line).
Fig. 3. The normalized elevation-rate density transfer function
for Byrd (solid line) and Camp Century (dashed line).
4. Implication for Remote Geodetic Estimates of Ice-Sheet Mass Imbalance
Satellite observations of thickness change are generally made in ignorance of contemporary or historical fluctuations in accumulation rate and surface density. In consequence, the terms in Equation (27) will introduce uncertainty in relating observed thickness rate to ice mass imbalance. Such is the practical difficulty of obtaining measurements of these quantities, to some degree in time but particularly in space, this situation is likely to continue for the foreseeable future, and the best that may be hoped for at present is a statistical characterization of the magnitude of these terms. In this section, the role of the densification in determining the average properties of the observed thickness rate is described. In section 4.1, point thickness fluctuations arising from uncorrelated surface fluctuations are considered. In section 4.2, the consequence of temporal and spatial covariability of the surface conditions is discussed.
4.1. Thickness fluctuations from random surface conditions
Much of the variability in accumulation rate in Greenland and Antarctica is associated with interannual fluctuations, and interannual fluctuations in density are commonly observed in ice cores. If one assumes annual averages of these fluctuations to have time-independent variances
and
, respectively, and supposes that they are independent year-to-year, their variances when the fluctuations are averaged over a longer interval T are simply
(In Equation (35) the “1” has the dimension of time.) Assuming, in addition, that the fluctuations are independent of each other, the variance of the thickness rate
averaged over the interval T is, from standard methods (see, e. g., Reference PapoulisPapoulis, 1991, ch. 10),
The dimensionless numbers r m and rρ , which are defined by Equation (36), describe the particular contribution made to the thickness-rate variance by the process of densification. The scaling of r m and rρ is chosen so as to make their values consistent with those of H m and H ρ. They are functions of time because the thickness rate responds differently to different frequencies in the surface fluctuations. As the averaging interval increases, fluctuations at higher frequencies are increasingly suppressed. The behaviour of r m with time for the two cases illustrated in Figures 2 and 3 is shown in Figure 4; that of rρ in Figure 5.
Fig. 4. The variation of r m with averaging interval for Byrd (solid line) and Camp Century (dashed line).
Fig. 5. The variation of rρ with averaging interval for Byrd (solid line) and Camp Century (dashed line).
For observations over intervals as short as 5 years, Figures 4 and 5 show that at Byrd and Camp Century, r m is close to the value (ρ ice/ρ snow)2, and rρ is close to 1. At least approximately, accumulation-rate fluctuations at these sites should be treated as if they occurred with the density of snow, i.e. that Equation (30) holds. In this limit, one has the practical advantage that fluctuations in thickness may be algebraically related to the contemporary fluctuations in surface density and accumulation rate. On the other hand, the thickness rate is more sensitive to the fluctuation in accumulation rate than to the longer-term ice imbalance (the O(1) term in Equation (30)) in the ratio ρ ice : ρ snow. This has the important implication that it is possible for the instantaneous thickness rate to have the opposite sign to the instantaneous mass imbalance.
Over longer intervals, Figures 4 and 5 illustrate that the firn column adjusts more rapidly to fluctuations in surface density than in accumulation rate, and that the adjustment is more rapid at a higher-temperature, higher mean accumulation-rate site. The reduction in the values of r m and rρ at these intervals shows that, for accurate estimates at a particular site, one needs to accept the full complexity of Equation (27). This has the practical implication that the fluctuations in thickness rate will not be simply related to the contemporary fluctuations in surface density and accumulation rate.
At sufficiently long intervals, the only contribution to the thickness-rate variance is that due to the ice-mass fluctuation, since from using Equations (33) in Equation (36), one has
For these intervals, the thickness rate follows contemporary fluctuations in accumulation rate, and with the same sensitivity as it has to longer-term ice imbalance. However, Figures 4 and 5 show that in the case of the two examples, this limit has not been reached even with a measurement interval of 50 years, except for the density fluctuation at Camp Century. While r m and rρ are considerably reduced, the assumption that Equation (29) holds will underestimate somewhat the thickness variability.
We now consider the likely magnitude in practice of the thickness fluctuations, for which estimates of
and
are required. Accumulation-rate fluctuation in ice-core records contains a component associated with metre-scale surface processes. For this reason, it is common in considering accumulation-rate variability at a point to distinguish “spatial” and “temporal” variability (see, e.g., Reference Giovinetto and SchwerdtfegerGiovinetto and Schwerdtfeger, 1966). (By variability we mean the square root of the variance.) In practice, the latter means the variability that is common to sites in the (sometimes poorly defined) wider vicinity of the point observation. Since variability at the metre scale will not be observed in satellite observations, and at least at some sites (Reference Petit, Jouzel, Pourchet and MerlivatPetit and others, 1982) the spatial component is largely absent in averages of 4 years or more, we shall take the “point” variability and the “temporal” variability to be equivalent.
In Antarctica, decadal fluctuations have been observed in ice cores (Reference Petit, Jouzel, Pourchet and MerlivatPetit and others, 1982) with a variability of 0.25 of the point mean accumulation rate, or
in our notation. An average figure from ice cores (Wingham and others, 1998) in the Antarctic interior for the 5 year point variability is
, equivalent (according to Equation (35)) to an interannual variability of
. In Greenland, the variability is typically somewhat higher, equivalent to an interannual variability of
(Reference Van der VeenVan der Veen, 1993). A typical figure for the variability of interannual fluctuations in density appears to be 10% of the mean (e.g. Reference GowGow, 1961), which is 0.1 ρ
snow in our notation.
On the basis of these values and the preceding discussion, one has, for Antarctica for example,
It is apparent that, even for short observation intervals for which rρ is largest, the thickness variability is dominated by the accumulation-rate fluctuations. In addition, while there does not seem to have been the same attention given to the distinction between “spatial” and “temporal” fluctuations in respect of density as there has in respect of accumulation rate, contemporary snow-pit records taken within the same vicinity (e.g. Reference Koerner and CraryKoerner, 1971) appear to show a very considerable variation in density. It seems reasonable to assume that the “point” variability in surface density observed in a satellite observation of thickness rate will be smaller than that seen in individual core records. In consequence, in practice, the effect of fluctuations in surface density can probably be ignored.
To illustrate the practical importance of the thickness fluctuation it is useful to express it as a fraction of the mean accumulation rate
. This may be done by multiplying both sides of Equation (38) by
. Taking ρ
snow as 350 kg m−3 and ρ
ice as 917 kg m−3, Equation (38) then shows that, for short observation intervals, the accumulation-rate fluctuation in Antarctica will contribute to the point thickness variability the equivalent of an interannual fluctuation in ice-mass imbalance of
. Although this variability will decrease more rapidly with observation interval T than T
−1/2, it is, practically speaking, a substantial fluctuation. After an observation interval of 10 years, Figure 4 shows that at Byrd the point variability of the thickness rate will be the equivalent of
(r
m = 4), and even after a 50 year interval the thickness-rate variability will be
(r
m = 2.2).
4.2. Effects of covariability
The assumption that accumulation-rate and surface density fluctuations are uncorrelated year-to-year (i.e. in the language of random signal theory they are “white” processes) allows the reduction in fluctuation that occurs through temporal averaging (Equation (35)) to be separated in Equation (36) from the reduction arising from the process of densification. In general, this is an oversimplification. Although accumulation rate appears to be quite close to a white process in some core records (e.g. Reference GowGow, 1961), other records show a distinct absence of fluctuations on scales of > 30 years — a good example is Reference Petit, Jouzel, Pourchet and MerlivatPetit and others (1982) — leading to the view (e.g. Reference Van der VeenVan der Veen, 1993) that accumulation rate is generally a “blue” process. In this case, Equation (38) will overestimate somewhat the fluctuations on time-scales of > 30 years.
However, other core records, particularly at or near ice-sheet margins (e.g. Reference Peel, Bradley and JonesPeel, 1992; Reference Isaksson, Karlen, Gundestrup, Mayewski, Whitlow and TwicklerIsaksson and others, 1996) show a significant degree of variability on 50–100 year time-scales. In the case of a “red” spectrum it is not immediately obvious what, in practice, should be taken to equal the theoretically constant mass-accumulation rate
. However, Figures 4 and 5 show that little amplification (i.e. r
m > 1) of the thickness rate by densification occurs for fluctuations with periods longer than 100 years. Thus, if one sets
to be the accumulation rate averaged on century time-scales, and uses
in place of Equation (5), little difference will result. In such cases, the magnitude of the fluctuation may be larger than Equation (38) implies, since this is based largely on accumulation-rate variability at sites which appear to have “white” or “blue” variability.
The assumption that the accumulation rate and surface density fluctuations are uncorrelated may also be criticized. Sublimation occurs at the surface in summer even in dry firn, and the lowering of surface density that results is directly related to a reduction in accumulation rate. However, it appears this effect may be small in comparison with those due to the mass fluctuations. For example, it has been calculated (personal communication from M. Spencer, 1998) that sublimation may contribute up to 2 cm to the annual cycle of thickness in West Antarctica. In comparison, an interannual fluctuation of thickness
is some 28 cm a−1 ice equivalent in West Antarctica.
Probably more important than the temporal covariability of the accumulation fluctuation is the spatial covariability. The uncertainties in the present imbalances of the grounded Antarctic and Greenland ice sheets are of order 0.25 of their average mean accumulation rate (hereafter, e.g.,
; Reference Warrick, le Provost, Meier, Oerlemans, Woodworth, Houghton, Meira Filho, Callander, Harris, Kattenberg and MaskellWarrick and others, 1996). Uncertainties in the mass imbalances of individual drainage basins are very difficult to determine from the literature (see, e.g., Reference JacobsJacobs, 1992), but perhaps
is a typical figure. These are somewhat smaller than the figure of
that we have argued characterizes the point interannual fluctuation. It is apparent that, if the point variability observed in individual ice cores is characteristic of large areas of the ice sheet, i.e. if the accumulation-rate fluctuations are correlated over large distances, satellite observations of ice-sheet thickness rate must extend over 50 years to significantly reduce present uncertainty in ice-sheet imbalance. If, on the other hand, the correlation scale of accumulation-rate fluctuations is small, point estimates such as Equation (38) may greatly overestimate the importance of accumulation-rate fluctuations in averages of the thickness rate over large areas.
5. Limitations Arising from the Treatment of Densification
A significant limitation of the treatment here is its ignorance of the effect of temperature fluctuations. If the firn temperature approaches or reaches the melting point, refreezing makes a significant contribution to densification (Reference Braithwaite, Laternser and PfefferBraithwaite and others, 1994). Relatively high temperatures may also underlie the strongly non-linear compactive viscosities observed in seasonal snowpack, 4–6 orders of magnitude smaller than those observed in ice-sheet firn (Reference MellorMellor, 1975). Even in cold, dry firn, however, temperature is important in that the processes of densification are thermally activated. Fluctuations in temperature at the surface will be convected and advected into the firn. Numerical calculations by Reference Arthern and WinghamArthern and Wingham (1998) showed that in central Greenland and Antarctica the effects of observed interannual surface temperature fluctuations on the rate of change of thickness will be small in comparison with those of surface density and accumulation rate. Nonetheless, the isothermal treatment used here excludes the present results from practical application to much of southern Greenland and coastal Antarctica. (It should be noted too that, in general, the spatial scale of the thickness fluctuation resulting from temperature variation may be very different from that associated with mass transport by the atmosphere, which predominates in regions of dry firn.)
A second weakness of the treatment is its ignorance of the role of horizontal strain rate. This is avoided by restricting the firn motion, but, even so, a certain sleight of hand has been necessary. In section 3 the quantity
was defined as the rate of mass loss from the ice sheet underlying the firn layer. Theoretically, there is no difficulty with this; it simply restates through Equation (24) the boundary condition at the base of the firn. However,
did service in the discussion of section 4 for practical situations in which the firn and ice lose mass by horizontal flux divergence. Implicitly, I have assumed that the results in so far as they describe the thickness fluctuations hold good if the firn is allowed to diverge horizontally and
is taken as the divergence loss from the firn and ice as a whole. In fact, if the horizontal strain rate is small (which it will be for the most part in the interior of Antarctica and Greenland) this will probably be the case. If the problem were repeated with the horizontal strain rate regarded as a small parameter, the effect of the strain rate on the O(λ) fluctuations would be second-order. The assumption is probably a good one.
6. Conclusions
This paper describes the relationship between the mass imbalance of a dry, isothermal firn layer and its rate of change of thickness. Using a linearized set of equations, the rate of change of thickness may be related to fluctuations of accumulation rate and density occurring at the surface through linear integral operators whose kernels depend on the mean surface conditions. These operators may be regarded as shift-invariant. In consequence, an alternative, spectral description may be used. This description shows that the process of densification may amplify the appearance of the surface accumulation-rate fluctuation in the rate of change of thickness by as much as the ratio of the density of ice to the density of snow. For examples from the Antarctic and Greenland ice sheets, the amplification is most important over short (∼5 year) observation intervals, but remains sensibly large for periods of > 50 years. Variations in surface density also introduce short-duration fluctuations into the thickness rate, although these may be of less practical importance.
Because accumulation rates are generally unknown, their effect on the thickness rate will introduce uncertainty in determining the longer-term imbalance of an ice sheet from short observations by satellite of its elevation rate. At a point, this uncertainty is large in comparison with the present uncertainties in the mass imbalance of the Antarctic and Greenland ice sheets. (It is also large in comparison with the errors associated with modern satellite altimetry (Wingham and others, 1998).) However, whether it remains comparatively large in areal averages of elevation rate depends on the spatial correlation of accumulation-rate fluctuations.
The spatial correlation of accumulation-rate fluctuation has had limited attention in the literature. Reference EnomotoEnomoto (1991) has concluded that decadal fluctuations in accumulation rate at ice-core sites in separate drainage basins in Antarctica have had little common variance in the past century. On the other hand, Reference Morgan, Goodwin, Etheridge and WookeyMorgan and others (1991) have reported strikingly high correlations in recent accumulation rate at sites in Wilkes Land. In general, it appears in Antarctica at least that the accumulation-rate records are too sparse to determine the spatial covariability of accumulation rate. Increased attention to investigating the correlation scale would be timely. In lieu of this, the observed spatial covariance of the thickness rate may itself provide valuable information.
Acknowledgements
This work was supported under Grant F14/6/39 by the U.K. Natural Environment Research Council. M. Spencer and R. Alley of Pennsylvania State University generously computed for me the probable amplitude of the annual cycle of elevation resulting from temperature in East and West Antarctica. An anonymous reviewer provided very useful criticism of the original manuscript.
Appendix A: Mass Conservation of the Firn Layer
In section 2 it was argued that conservation of mass implied that q 0 was constant on a material path. Here the converse is shown, namely, that a necessary consequence of the constancy of q 0 on a material path is the conservation of mass. Consider a parcel of firn that passes through the surface at t = t 0. It will define a material path in the {z, t}-plane that may be described by the function z = z(t, t 0). By definition, the velocity of the parcel equals the gradient of the path with respect to time t :
If q 0 is constant along the material path, dq 0(t, z)/dt = 0 on the path, i.e.
must vanish. The first line of Equation (A2) uses Equation (9), and the second line Equations (2) and (11).
The vanishing of the righthand side of (A2) is a statement of the conservation of mass. Integrating Equation (1) over depth provides
which is the required result. The second line uses Equation (2) to reformulate the first term. The third line uses Equation (5), and the fourth line Equation (7).
Appendix B: The Inverse Transformation z = z(q, q 0)
The conditions for the transformation Equations (8) and (9) to be invertible are given following Equation (12). The inverse transformation t = t(q) cannot be given explicitly. Here we show that the transformation z = z(q, q 0) is
This result is proven by showing that z = z(q, q 0) is the solution of the equations
Integrating Equation (B3) and applying the condition Equation (B2) then provides Equation (B1).
To obtain Equation (B2), note that from Equations (7) and (9), q = q 0 when z = 0, which provides it directly. To obtain Equation (B3), note that by definition the inverse transformations must satisfy
But
The first line of Equation (B6) is the definition of q 0 (t, z) of Equation (9). The second line uses Equation (B4) and Equations (2) and (7). The last line uses the variable substitution u = z(q, w), Equation (B5) and Equation (13). Substituting Equation (B6) into Equation (B5) shows that for Equation (B5) to hold,
Differentiating Equation (B7) with respect to s provides Equation (B3).
Appendix C: Derivation of Equation (27)
In this appendix the central result of the paper, Equation (27), is derived. On substituting from Equation (16) for R in Equation (22) and specializing the argument of R 0 using the result following Equation (17), one has first that
where the third and fourth lines follow by expanding the denominator.
Taking the integral in the third line of Equation (C1), one has directly
Taking each term of the second and third lines of Equation (C2) in turn, one has first that
on using Equations (5), (8) and (17). Second,
on using Equations (24) and (25). Thirdly,
The first two steps follow directly. The final line uses Equations (5), (8), (17) and (25). Substituting Equations (C3), (C4) and (C5) into the third line of Equation (C2) provides
for the integral in the third line of Equation (C1).
Turning now to the second of the two integrals in the second line of Equation (C2), one has on substituting for R 1 from Equation (20)
Taking the first of the two terms on the righthand side of Equation (C7), one has
The first step of Equation (C8) follows directly. The fourth and sixth lines use Equations (5), (8), (17) and (25). The final line then follows directly.
Taking the second of the two terms on the righthand side of Equation (C7) one has
The third and fourth lines reverse the order of the integrations. The fifth to eighth lines follow on performing the differentiation with respect to t. The term containing dq 0(t, z b(t))/dt which is apparently missing from these final lines is zero on account of the upper limit of the integral in the fourth line. The term on the fifth and sixth lines of Equation (C9) may be reformed in the following way:
The second line uses the definition Equation (19) of the functions I + and I −. The third line substitutes for f using Equation (17), the fourth then following directly. The fifth line uses the results of Equation (C5).
The term on the seventh and eighth lines of Equation (C9) may also be simplified:
Substituting from Equations (C10) and (C11) into Equation (C9), and then Equations (C8) and (C9) into (C7), provides an expression for the integral on the fourth line of Equation (C1). Together with the expression of Equation (C6) for the integral on the third line of Equation (C1), one then has:
Substitutions of
for the integration variable in the second line, and
and
in the integration variables of the third line, provide Equation (27). (The symbols used for the integration variable are, of course, immaterial.) This final substitution allows the final line of Equation (27) to be recognized as a convolution integral when q(t, z
b) → −∞.
Appendix D: Derivation of Equation (29)
When ρ s varies sufficiently slowly in Equation (27) that it may be brought outside the integral,
The third line follows directly. The last line uses Equations (17), (19) and (26).
When
varies sufficiently slowly in Equation (27), one has first that
Working with the “inner” integral of Equation (D2) provides
The first two steps follow directly. The final line uses Equation (26). Continuing on the same path,
The second, third, fourth and fifth lines follow directly. The sixth and final lines use Equation (26).
Substituting Equation (D4) into Equation (D3), and substituting the result back into the “outer” integral of Equation (D2) provides:
Reversing the order of integration of the final line of Equation (D5), one has
The third and fourth lines follow directly. The fifth and sixth lines follow on performing the integration directly and using Equation (19). The seventh and final lines make use of the results of Equation (C10) to deal with the integral of f/R 0. Using Equation (D6) in Equation (D5), one has, finally,
Substituting Equations (D1) and (D7) into Equation (27 provides Equation (29).
