Introduction

Recent study of fjords into which large outlet glaciers calve shows that long-period, large-scale surface gravity waves (Reference Amundson, Truffer, Lüthi, Fahnestock, West and MotykaAmundson and others, 2008; Reference NettlesNettles and others, 2008) and seiches (Reference Amundson, Lüthi, Fahnestock, Truffer and MotykaAmundson and others, 2012) are excited by the calving and capsize of large icebergs. This excitation is not surprising because considerable energy is liberated by the calving and capsize process (Reference BurtonBurton and others, 2011; Reference MacAyeal, Abbot and SergienkoMacAyeal and others, 2011). Internal seiches (e.g. Reference CsanadyCsanady, 1973; Reference SchwabSchwab, 1977; Reference Arneborg and LiljebladhArneborg and Liljebladh, 2001) in the stratified waters of fjords are also probable outcomes of large iceberg calving and capsize. These seiches are important for several reasons. First, they cause commotion within the mass of ice melange that typically fills the fjord, thereby causing further break-up and capsize. Second, they determine how the fjord will respond to forcing by the external ocean beyond (e.g. as a harbor seiche that is excited by atmospheric events, tsunami arrivals and arrival of storm waves). Third, they offer a means of quantifying the energy associated with iceberg calving and capsize, when direct local measurements of the event are impractical due to the hazards of deploying instruments on or below ice melange.

Interest in seiches, also called harbor oscillations, free oscillations and normal modes, in the ocean environment is a long-standing object of considerable research because of the many practicalities associated with harbor design (e.g. Reference Miles and MunkMiles and Munk, 1961). (An overview of the literature on seiches and harbor oscillations is provided by Reference Rabinovich and KimRabinovich, 2009.) On a scale much larger than harbors, the normal modes of lakes, bays and even the entire world ocean have been investigated for theoretical and pedagogical reasons. Reference Mortimer and FeeMortimer and Fee (1976) investigated the normal modes of Lakes Michigan and Superior, central North America, because their seiches represent the ‘tides’ of these large inland water bodies. Reference PlatzmanPlatzman (1978) (see also Reference PlatzmanPlatzman, 1984; Reference GotisGotis, 1999) computed the normal modes of the entire global ocean to be used as a means of synthesizing the diurnal and semidiurnal tides. While the application of normal-mode synthesis is not a common method in the numerical simulation of tides, the work of Reference PlatzmanPlatzman (1984) offers insight into why various tidal constituents are amplified in various parts of the world ocean. For example, the relatively large amplitude of the diurnal tide along the circumference of Antarctica was found to be related to a normal mode of the world ocean that expresses highest amplitude around Antarctica that has a frequency close to that of the diurnal tides. Of interest to glaciologists, Reference Schwab and RaoSchwab and Rao (1977) noted the change of frequencies of normal modes in Saginaw Bay, off Lake Huron, central North America, associated with lake ice cover.

In the present study, we examine the frequency spectrum of the normal modes of a large fjord (e.g. resembling Ilulissat Icefjord) associated with a major outlet glacier (e.g. resembling Jakobshavn Isbræ) of the Greenland ice sheet. The purpose of our examination is to conceptualize the influence of ice melange coverage on the wave-propagation characteristics (both surface and internal) of the fjord. The work is not designed to provide an accurate simulation of any specific phenomena, but rather to provide a starting point in the effort to understand what ice melange does to the dynamics that determines how energy is transmitted by waves through a fjord. Our methodology is simple: we construct, using COMSOL^TM, eigensolutions of the surface wave and internal wave equations and examine the variability of the eigenfrequencies under the presence or absence of large icebergs (an array of 20 equally spaced 1 km wide icebergs) within the fjord. Anticipating the results of similar studies of simple systems influenced by regularly spaced imperfections (the icebergs), our objective is to determine if band gaps (e.g. Reference ChouChou, 1998) interrupt spectra of normal modes in the fjord due to the presence of ice. The significance of band gaps, should they prove to exist, is to forbid wave propagation within the frequency band. This means that oscillatory motions of the fjord with frequencies in these gaps will be evanescent, i.e. trapped near the source.

Problem Set-Up

We adopt a simple, idealized one-dimensional channel geometry of constant depth (Fig. 1). This simplification is consistent with the fact that the fjord resembles a narrow channel, 60 km long and ~8 km wide. Although seiches with cross-channel structure would be important components of the fjord’s hydrodynamic response to forcing, we do not consider these modes in the present study. Following observations reported by Reference Holland, Thomas, de Young, Ribergaard and LyberthHolland and others (2008) (see their figs 1d and 3b), we take the channel to be 750m deep and impose a two-layer stratification structure consisting of a 250 m thick upper layer of relatively fresh water and a 500 m thick lower layer of more dense salty water. We assume a density difference, Δρ, of 5 kgm^–3, and an average density, ρ, of 1023 kgm^–3. (Specification of density parameters associated with a two-layer idealization of fjord stratification is highly idealized; see Reference Holland, Thomas, de Young, Ribergaard and LyberthHolland and others, 2008; Reference StraneoStraneo and others, 2011, for an overview of fjord hydrography.)

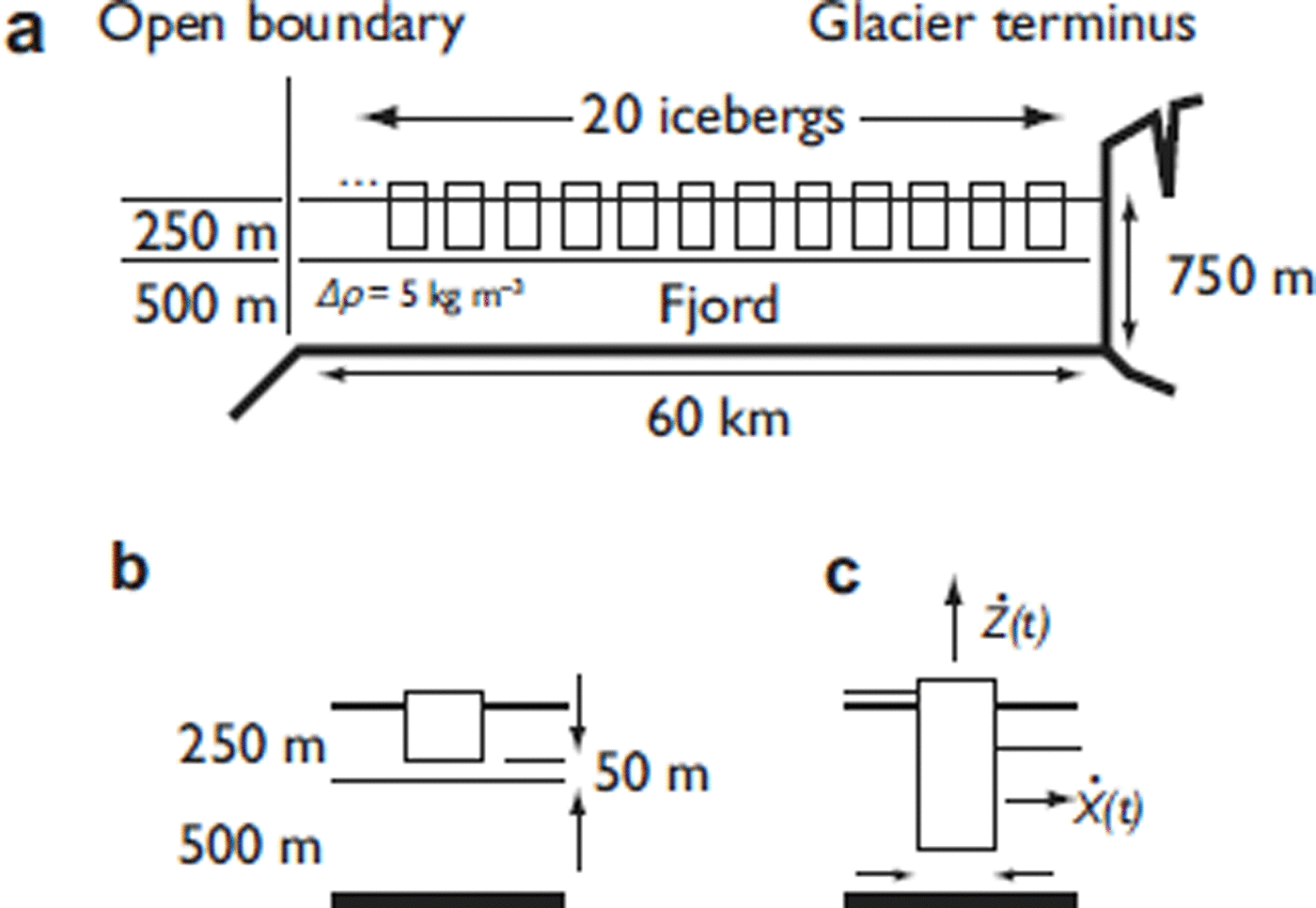
Fig. 1.

Geometry of an idealized fjord containing icebergs for which seich periods are computed. (a) The two-dimensional cross section of the domain on which normal modes are computed. The 60 km long fjord is 750m deep, closed at one end by a vertical glacier terminus, and connected to an open ocean at the other end. Ice melange is represented by filling the fjord with 20 discrete icebergs that are spaced evenly along the length of the fjord. The fjord is assumed to possess a two-layer density structure with a density interface (across which the density varies by 5 kgm^–3) that separates a relatively fresh layer (250m thick) from a relatively salty layer (500m thick). (b) Internal modes are computed by assuming an iceberg draft of 200m, that reduces the upper density layer thickness from 250m to 50m in segments of the fjord in which icebergs float. (c) External, barotropic modes are computed for the free surface (water/air interface) of the fjord, assuming that the combined iceberg/ocean system has two degrees of freedom in the segments of the fjord where icebergs float. The two degrees of freedom are vertical heave, Ż, and horizontal surge, Ẋ.

For the computation of normal modes in circumstances where the fjord is completely free of ice melange, we use the two following wave equations for external and internal modes, respectively:

(1)

and

(2)

where η(x, t) and ῆ(x, t ) are the free-surface and density-interface excursions, respectively, x and t are horizontal coordinate and time, respectively, and c and are the phase velocities for shallow water waves on the free surface and density interface, respectively, given by:

(3)

and

(4)

where g = 9.81ms^–2 is the acceleration of gravity, H = 750 m is the depth of the fjord (Reference Holland, Thomas, de Young, Ribergaard and LyberthHolland and others, 2008), and H _l = 500m and H _u = 250m are the thickness of the lower and upper density layers, respectively. In the treatment of ice melange, we shall assume that is a function of x (depending on whether ice blocks some of the vertical extent of the upper layer) and that c applies to the ice-free case, with simplified low-order dynamics covering the hydrodynamics of ice-covered water.

Idealized treatment of ice melange

We treat ice melange as an array of 20 icebergs of uniform dimensions spaced equally (Fig. 1) along the 60 km channel. The actual ice melange is extremely complex and is composed of thousands of icebergs (Reference Ahn and BoxAhn and Box, 2010; Reference Amundson, Fahnestock, Truffer, Brown, Lüthi and MotykaAmundson and others, 2010). The icebergs are 1000 m wide and occupy 200m of the water column (giving a vertical dimension determined by the density ratio of ice and water). These icebergs are roughly the dimensions that would be obtained from the calving terminus of Jakobshavn Isbræ if the icebergs are assumed to capsize soon after calving, and the aspect ratio (initial width to thickness ratio) is less than 1/2.

External mode

In the case of computing the effect of the icebergs on external modes, we assume that the icebergs constrain the water movement in a manner consistent with having two degrees of freedom: vertical motion (heave) described by Z_j (t ), and horizontal motion (surge) described by X_j (t ), where j = 1,. . . , 20 is an index identifying individual icebergs in the array. For the present, we disregard other degrees of freedom that icebergs may have involving pitch, sway and roll. We further simplify the surge motion of the icebergs by assuming that their horizontal position is held fixed (Ẋ _j = 0), but that water flow is nonzero between the iceberg’s basal surface and the seabed through a vertically restricted water column. The governing equations for Z_j (t) are

(5)

where is the intrinsic frequency of iceberg bobbing motions (Reference SchwerdtfegerSchwerdtfeger, 1980), ρ _i = 900 kgm^–3 is the assumed density of ice, h _i = 200m is the draft of the icebergs (vertical dimension of submerged portion) and η _l and η _r are the free-surface elevation on the left (down-fjord) and right (up-fjord) sides of the iceberg, x_{j l} and x_{j r}, respectively. Equation (5) represents the icebergs as oscillators with an intrinsic frequency that are forced by the average, buoyant force provided by excursions of the free surface on either side (hence the averaging of η on left and right). The volume change of the water column beneath the iceberg as it heaves requires horizontal fluxes, assumed to be equal, on the left- and right-side boundaries of the iceberg:

(6)

where W = 1000m is the width of the iceberg, q _l = (H − h _i)u _l and q _r = (H − h _i)u _r are the fluxes at the left and right side of the iceberg, respectively, and (H − h _i) = 550 m is the space between the bottom of the iceberg and the fjord bottom.

The surge motion of the iceberg, simplified to the utmost by fixing X_j , produces a current that passes below the iceberg whenever there is a pressure gradient across the iceberg. The net flux of ocean water below the iceberg, q = (H − h _i)u, where u is the horizontal velocity, is expressed as follows:

(7)

The above expression is used to determine u on the left and right sides of the iceberg. In the above equation, a positive q represents a flux that is the same (directed in the x direction) at both the left and right sides of the iceberg.

Internal mode

Treatment of the presence of the icebergs in the computation of seiches on the density interface within the fjord is much simpler than the above treatment for external modes. We assume that the icebergs are motionless, providing a constriction that modifies the thickness of the upper layer. (In reality, the icebergs would move in response to flow along their submerged surfaces.) The simplest way to express the presence of the icebergs is to vary the phase velocity, , between ice-free and iceberg-covered portions of the domain. Accordingly, we set

(8)

on the portions of the domain covered by icebergs.

Boundary conditions

Boundary conditions for both the external and internal modes are required at x = 0,L, where L is the length of the fjord. Because the fjord connects to the open ocean, we apply a Dirichlet condition at x = 0 to represent a free, open boundary (this is commonly referred to as the Helmholtz condition (e.g. Reference Rabinovich and KimRabinovich, 2009))

(9)

and

(10)

At the closed end of the fjord, where the calving terminus is located, we apply a no-flow condition for both the external and internal modes:

(11)

and

(12)

For the internal modes, where the icebergs simply change the phase velocity and do not interrupt the continuity of the domain, the above boundary conditions are sufficient to compute the normal modes.

For the external modes, the icebergs are assumed to break up the continuity of the domain into a number of discrete open-water segments separated by ice-covered segments. These segments are stitched together by numerous ‘internal’ boundaries, x_{j l} and x_{j r}, where boundary conditions are applied to account for the simplified, low-order treatment of the hydrodynamics within the ice-covered segments. These boundary conditions are derived from the values of q, q _l and q _r, derived above, and are applied in the usual way, as a nonhomogeneous Neumann condition on the x-derivative of η:

(13)

and

(14)

where the sign changes account for the orientation of the outward-pointing direction at the domain boundaries.

Results

Normal modes were computed for both the external and internal formulations of the fjord with an array of 20 icebergs representing the effects of ice melange. The solutions were obtained using the finite-element package COMSOL^TM, which provides solvers that produce eigenfrequencies and eigenfunctions suited to the problem defined above. The spectra of mode periods, T_n (in minutes), are plotted as a function of mode number, n, in Figures 2 and 3.

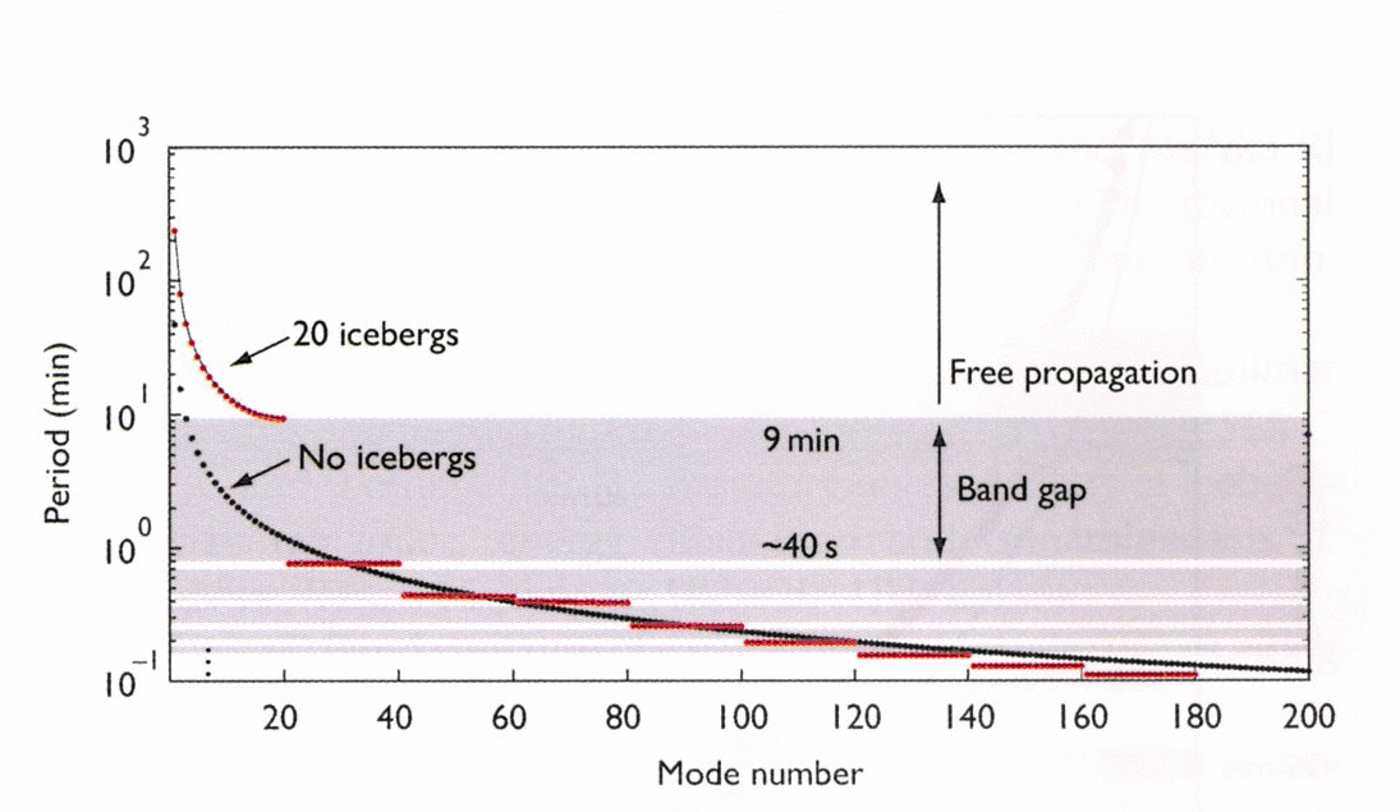
Fig. 2.

Periods of barotropic seiches on the density interface of the fjord. The spectrum in the presence of 20 icebergs is compared with the spectrum in which no icebergs are present. The effects of the icebergs are to substantially lengthen the periodicity of the most fundamental normal modes (seiches with largest length scales) and to introduce band gaps below ~9min. Excitation in the fjord with period <9min will not propagate as a free wave, but will exist as a trapped (evanescent) oscillation near the source of excitation. Below ~40 s period, there are many regions of propagating modes and band gaps. These regions correspond to seiches localized in the fjord segments between individual icebergs. We emphasize that this spectrum was computed to illustrate the possible influence of ice melange, and that other quantitative and qualitative effects are possible if the characterization of the ice melange is changed.

Fig. 3.

Periods of baroclinic (two homogeneous layers of differing density) seiches between 10 and 100min. The spectrum in the presence of 20 icebergs is compared with the spectrum in which no icebergs are present.

As a control, the external and internal modes for the fjord in the absence of icebergs (i.e. no ice melange) were also computed. In both computations, the seiche periods are identical (within numerical accuracy) to the analytic expression provided by Reference Rabinovich and KimRabinovich (2009):

(15)

where n = 0,1,2,. . . is the mode number and c _p is the phase velocity that can be either of its values displayed in Equations (3) or (4), depending on whether the external or internal seiche problem is being solved. The periods of the internal modes are correspondingly longer than those of the external modes because ≪ c. The n = 0 and 1 modes for the internal seiches have periods of 23.6 and 7.9 hours, respectively. For the external modes, the same first two modes have periods of 46.6 and 15.5 min. (We emphasize that the exact values of the mode periods are provided for illustration, and are dependent on the specific geometry of the ice melange, which we simplify to a considerable extent.)

The effects of adding the array of 20 icebergs (i.e. our idealized representation of ice melange) to the fjord in both the external and internal seiche problem are twofold. The first effect is to lengthen the seiche periods by an amount that varies with mode number. This increase in period is caused by the fact that the phase velocity averaged over the length of the fjord is reduced by the icebergs blocking a portion of the water column, yielding a shallower average fjord depth. In the case of the most grave (n = 0) external mode, the period is lengthened by 3.2 hours, a value that is 413% of the period when there is no ice in the fjord. (This large change in mode period reduces with increasing mode number (e.g. it is ~15 min for mode 7).) In the case of the most grave internal mode, the period is lengthened by 8.85 hours, a value that is 37% of the period when there is no ice in the fjord.

The second effect of adding the array of 20 icebergs, and the one which we emphasize as the major outcome of our study, is to introduce gaps in the spacing of mode periods. These ‘band gaps’ are distinctive in two regards. First, they span significant ranges of timescale for which periodic motions may be possible in the fjord due to iceberg capsize. For the external modes, the first (longest period range) band gap extends from 46 to 562 s (~1 to 9.3 min). For the internal modes, the first band gap extends from 38 to 58 min.

A key aspect of the band gaps in both the external and internal mode spectra is that the derivative of mode period, P, with respect to mode number, n, goes to zero as the band gaps are approached from above or below. This implies that the velocity at which energy propagates (group velocity), c _g ≈ Δf /Δn, where f = 2π/P is the frequency, approaches zero in the band gaps (Freed-Brown and Zhang, unpublished information). The implication of this result is that energy cannot propagate through the fjord at the frequencies or periods within the band gaps.

Discussion and Conclusion

The initial reconnaissance presented in this study has shown several specific ways in which seiche behavior, both baroclinic and barotropic (density surface and free-surface, respectively), is modified by the presence of floating ice. Within the context of the idealizations used to simplify this initial study, we show that seiche periods are influenced in two important ways. Most importantly, ice melange (represented by a collection of regularly spaced icebergs) slows down the motions of the fjord and lengthens seiche period. This means that efforts to characterize fjord dynamics and iceberg calving via signals associated with seiches observed by broadband seismometers (e.g. Reference Amundson, Lüthi, Fahnestock, Truffer and MotykaAmundson and others, 2012) must contend with a variable relationship between period and wavelength of the seiches. Most interesting from a fjord dynamics perspective, ice melange can introduce a phenomenon known as ‘band gaps’ into the seiche spectrum of the fjord. Interest in the presence of band gaps is motivated by what band gaps do in other phenomena, such as wave propagation in sea ice (Reference ChouChou, 1998) and other wave transmission media that possess regularly spaced perturbations the wave-propagating properties. In the case of a fjord with regularly spaced icebergs, both internal and external seiches (density interface and free-surface seiches) can have band gaps in the range of periods that are plausibly excited by typical calving and capsize events in the fjord (e.g. as shown in the time-lapse photography of Reference Ahn and BoxAhn and Box, 2010). If it is possible that there are band gaps in an ice-filled fjord, then one can expect that phenomena excited with periods in the gaps will display an evanescent or trapped behavior. The inability of energy to propagate away from excitation sources, such as the calving terminus, may contribute to violent actions of the water motions near the source, that can lead to further fragmentation of the ice melange.

The present study does not delve into the sensitivity of the location and size of band gaps on parameters of the fjord and ice melange, because the intention has been restricted to simply demonstrating that band gaps can exist as a result of ice/ocean interaction. Band gaps are created where two successive eigenmodes of the system have a spatial arrangement of nodes and antinodes such that: (1) the antinodes of the first eigenmode align with the locations where the propagating medium (the fjord) admits a low phase speed and (2) the antinodes of the second eigenmode align with the locations where the medium admits a high phase speed. If the medium of propagation were homogeneous (e.g. there were no icebergs floating in the fjord), the periods of the two modes would be separated by some small time difference. In the case where the antinodes align with either ice-free or iceberg-filled zones, the time difference between the periods of the two modes becomes larger than this separation, and a band gap is created. Following this logic, we can intuitively expect that the mode number where band gaps occur will be determined by the number and spacing of icebergs in the fjord; and that the time difference spanned by the band gap will be determined by the degree to which the icebergs slow the phase speed relative to the phase speed in the ice-free system.

Much remains to be done in the effort to characterize how fjord seiches respond to various physical modifications imparted by the calving of ice into their inland end. (It is also remarkable how long the question of seiche behavior under the influence of geometric changes to a body of water has been studied (e.g. the study of the ‘harbor paradox’ by Reference Miles and MunkMiles and Munk (1961), who examined the dependence of seiche amplitude on various breakwater structures intended to protect harbors from the open ocean).) The present study has achieved the goal of showing how the presence of regularly spaced floating icebergs (an admittedly simplified view of ice melange) can elicit important structural changes in the fjord’s seiche spectrum. One can argue that this demonstration may possibly over-emphasize effects that are unlikely to be possible in fjords that are filled with more realistic patterns of ice melange. Indeed, our intention in this study has been to emphasize and illustrate, as clearly as possible, the strongest possible effects; and we have thus chosen to idealize and simplify our study in ways which achieve this purpose. In a realistic fjord, the size of the floating ice bodies and their spacing will be far more irregular than the manner in which they have been approximated here. Future study will yield a sense of how the more disordered geometry of ice melange will influence wave energy propagation in the fjord. Perhaps the most substantial conclusion of the present study is to serve as motivation for more difficult work to come.