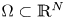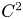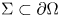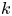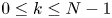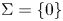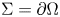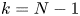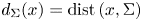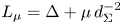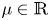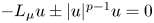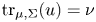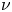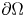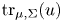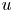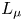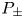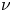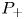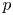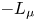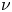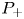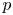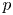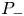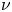1. Introduction
1.1. A survey of the relevant literature
Let $N\geq 3,$![]() $\Omega \subset \mathbb {R}^N$
$\Omega \subset \mathbb {R}^N$![]() be a $C^2$
be a $C^2$![]() bounded domain and $\Sigma \subset \partial \Omega$
bounded domain and $\Sigma \subset \partial \Omega$![]() be a $C^2$
be a $C^2$![]() compact submanifold in $\mathbb {R}^N$
compact submanifold in $\mathbb {R}^N$![]() without boundary, of dimension $0\leq k \leq N-1$
without boundary, of dimension $0\leq k \leq N-1$![]() . We assume that $\Sigma = \{0\}$
. We assume that $\Sigma = \{0\}$![]() if $k = 0$
if $k = 0$![]() and $\Sigma =\partial \Omega$
and $\Sigma =\partial \Omega$![]() if $k=N-1.$
if $k=N-1.$![]() Let $d_{\partial \Omega }(x)=\mathrm {dist}\,(x,\partial \Omega )$
Let $d_{\partial \Omega }(x)=\mathrm {dist}\,(x,\partial \Omega )$![]() and $d_\Sigma (x)=\mathrm {dist}\,(x,\Sigma )$
and $d_\Sigma (x)=\mathrm {dist}\,(x,\Sigma )$![]() . Two typical semilinear elliptic equations involving power nonlinearities and Hardy-type potentials are of the form
. Two typical semilinear elliptic equations involving power nonlinearities and Hardy-type potentials are of the form
where $p>1$![]() , $\mu \in {\mathbb {R}}$
, $\mu \in {\mathbb {R}}$![]() is a parameter and
is a parameter and
The nonlinearity $|u|^{p-1}u$![]() in (E ±) is referred to as an absorption or a source depending whether the plus sign or minus sign appears in (E ±).
in (E ±) is referred to as an absorption or a source depending whether the plus sign or minus sign appears in (E ±).
Boundary value problems for (E ±) with $\mu =0$![]() became a central research subject in the area of partial differential equations with abundant literature. A rich theory has been developed for a boundary value problem with a power absorption in the case $\mu =0$
became a central research subject in the area of partial differential equations with abundant literature. A rich theory has been developed for a boundary value problem with a power absorption in the case $\mu =0$![]() , namely for the problem
, namely for the problem
where $\nu$![]() is a measure on $\partial \Omega$
is a measure on $\partial \Omega$![]() . Throughout this paper, we denote by $\mathfrak M(\partial \Omega )$
. Throughout this paper, we denote by $\mathfrak M(\partial \Omega )$![]() and $\mathfrak M^+(\partial \Omega )$
and $\mathfrak M^+(\partial \Omega )$![]() the space of finite measures on $\partial \Omega$
the space of finite measures on $\partial \Omega$![]() and its positive cone respectively. The first study of (1.1) was carried out by Gmira and Véron in [Reference Gmira and Véron22] where the existence of a solution is obtained for any $\nu \in \mathfrak {M}(\partial \Omega )$
and its positive cone respectively. The first study of (1.1) was carried out by Gmira and Véron in [Reference Gmira and Véron22] where the existence of a solution is obtained for any $\nu \in \mathfrak {M}(\partial \Omega )$![]() in the subcritical case $1< p<\frac {N+1}{N-1}$
in the subcritical case $1< p<\frac {N+1}{N-1}$![]() . In the supercritical case $p \geq \frac {N+1}{N-1}$
. In the supercritical case $p \geq \frac {N+1}{N-1}$![]() , a breakthrough was achieved by Marcus and Véron [Reference Marcus and Véron32], asserting that problem (1.1) possesses a solution if and only if $\nu$
, a breakthrough was achieved by Marcus and Véron [Reference Marcus and Véron32], asserting that problem (1.1) possesses a solution if and only if $\nu$![]() is absolutely continuous with respect to the capacity $\mathrm {Cap}_{\frac {2}{p},p'}^{\partial \Omega }$
is absolutely continuous with respect to the capacity $\mathrm {Cap}_{\frac {2}{p},p'}^{\partial \Omega }$![]() , namely $\nu (E)=0$
, namely $\nu (E)=0$![]() for any Borel set $E\subset \partial \Omega$
for any Borel set $E\subset \partial \Omega$![]() such that $\mathrm {Cap}_{\frac {2}{p},p'}^{\partial \Omega }(E)=0$
such that $\mathrm {Cap}_{\frac {2}{p},p'}^{\partial \Omega }(E)=0$![]() [see (2.9) for the definition of the above capacities and see (2.10) for the meaning of the absolute continuity].
[see (2.9) for the definition of the above capacities and see (2.10) for the meaning of the absolute continuity].
When $\mu \neq 0$![]() , let $C_{\Omega,\Sigma }$
, let $C_{\Omega,\Sigma }$![]() be the optimal Hardy constant defined by
be the optimal Hardy constant defined by

and put
It is known that $C_{\Omega,\Sigma } \in (0,H^2]$![]() (see e.g. [Reference Brezis and Marcus7, Reference Marcus, Mizel and Pinchover26] for $k=N-1$
(see e.g. [Reference Brezis and Marcus7, Reference Marcus, Mizel and Pinchover26] for $k=N-1$![]() and [Reference Fall and Mahmoudi14] for $0 \leq k \leq N-2$
and [Reference Fall and Mahmoudi14] for $0 \leq k \leq N-2$![]() ).
).
Consider the eigen problem

Note that $\lambda _{\mu,\Sigma }>-\infty$![]() if $\mu \leq H^2$
if $\mu \leq H^2$![]() , and $\lambda _{\mu,\Sigma }>0$
, and $\lambda _{\mu,\Sigma }>0$![]() if $\mu < C_{\Omega,\Sigma }$
if $\mu < C_{\Omega,\Sigma }$![]() . Moreover, when $\mu < H^2$
. Moreover, when $\mu < H^2$![]() , problem (1.3) admits a minimizer $\phi _{\mu,\Sigma }\in H_0^1(\Omega )$
, problem (1.3) admits a minimizer $\phi _{\mu,\Sigma }\in H_0^1(\Omega )$![]() which satisfies $L_\mu \phi _{\mu,\Sigma } = \lambda _{\mu,\Sigma } \phi _{\mu,\Sigma }$
which satisfies $L_\mu \phi _{\mu,\Sigma } = \lambda _{\mu,\Sigma } \phi _{\mu,\Sigma }$![]() in $\Omega$
in $\Omega$![]() (see [Reference Fall and Mahmoudi14, corollary 1.3]). When $\mu = H^2$
(see [Reference Fall and Mahmoudi14, corollary 1.3]). When $\mu = H^2$![]() , there is no minimizer of problem (1.3) in $H_0^1(\Omega )$
, there is no minimizer of problem (1.3) in $H_0^1(\Omega )$![]() , but there exists a function $\phi _{\mu,\Sigma } \in H_{\mathrm {loc}}^1(\Omega )$
, but there exists a function $\phi _{\mu,\Sigma } \in H_{\mathrm {loc}}^1(\Omega )$![]() such that $L_\mu \phi _{\mu,\Sigma } = \lambda _{\mu,\Sigma } \phi _{\mu,\Sigma }$
such that $L_\mu \phi _{\mu,\Sigma } = \lambda _{\mu,\Sigma } \phi _{\mu,\Sigma }$![]() in $\Omega$
in $\Omega$![]() in the sense of distributions. In addition, by [Reference Barbatis, Gkikas and Tertikas3, proposition A.2] (see also [Reference Marcus and Nguyen29, lemma 2.2]), for any $\mu \leq H^2$
in the sense of distributions. In addition, by [Reference Barbatis, Gkikas and Tertikas3, proposition A.2] (see also [Reference Marcus and Nguyen29, lemma 2.2]), for any $\mu \leq H^2$![]() , there holds
, there holds
where
It is known that, when $\mu < C_{\Omega,\Sigma }$![]() , there exists a Green function associated with $-L_\mu$
, there exists a Green function associated with $-L_\mu$![]() , denoted by $G_\mu$
, denoted by $G_\mu$![]() (see e.g. [Reference Ancona2, Reference Marcus24] for more general potentials, and [Reference Filippas, Moschini and Tertikas17] for $\Sigma =\partial \Omega$
(see e.g. [Reference Ancona2, Reference Marcus24] for more general potentials, and [Reference Filippas, Moschini and Tertikas17] for $\Sigma =\partial \Omega$![]() and $\mu \leq \frac {1}{4}$
and $\mu \leq \frac {1}{4}$![]() ). In addition, by Ancona [Reference Ancona2], there exists a Martin kernel associated with $-L_\mu$
). In addition, by Ancona [Reference Ancona2], there exists a Martin kernel associated with $-L_\mu$![]() , denoted by $K_\mu$
, denoted by $K_\mu$![]() , which is unique up to a normalization. Marcus and Nguyen [Reference Marcus and Nguyen28] applied results for a class of more general Schrödinger operators in [Reference Marcus24] to the model case $L_\mu$
, which is unique up to a normalization. Marcus and Nguyen [Reference Marcus and Nguyen28] applied results for a class of more general Schrödinger operators in [Reference Marcus24] to the model case $L_\mu$![]() and showed two-sided estimates of $G_\mu$
and showed two-sided estimates of $G_\mu$![]() and $K_\mu$
and $K_\mu$![]() . Recently, Barbatis et al. [Reference Barbatis, Gkikas and Tertikas3] followed a different approach to obtain the existence and sharp two-sided estimates of $G_\mu$
. Recently, Barbatis et al. [Reference Barbatis, Gkikas and Tertikas3] followed a different approach to obtain the existence and sharp two-sided estimates of $G_\mu$![]() and $K_\mu$
and $K_\mu$![]() for the whole range $\mu \leq H^2$
for the whole range $\mu \leq H^2$![]() provided $\lambda _{H^2}>0$
provided $\lambda _{H^2}>0$![]() . These estimates will be quoted in § 3.1.
. These estimates will be quoted in § 3.1.
We denote by $\mathfrak M(\Omega ;\phi _{\mu,\Sigma })$![]() the space of measures $\tau$
the space of measures $\tau$![]() such that $\int _{\Omega }\phi _{\mu,\Sigma } \,\mathrm {d}|\tau |<+\infty$
such that $\int _{\Omega }\phi _{\mu,\Sigma } \,\mathrm {d}|\tau |<+\infty$![]() and by $\mathfrak M^+(\Omega ;\phi _{\mu,\Sigma })$
and by $\mathfrak M^+(\Omega ;\phi _{\mu,\Sigma })$![]() the positive cone of $\mathfrak M(\Omega ;\phi _{\mu,\Sigma })$
the positive cone of $\mathfrak M(\Omega ;\phi _{\mu,\Sigma })$![]() . The Green operator and the Martin operator are respectively defined by
. The Green operator and the Martin operator are respectively defined by

These operators are an important tool in the study of nonhomogenous linear equations involving $-L_\mu$![]() . Main properties of the above operators were established in [Reference Barbatis, Gkikas and Tertikas3] and will be presented in subsections 3.2.
. Main properties of the above operators were established in [Reference Barbatis, Gkikas and Tertikas3] and will be presented in subsections 3.2.
There is a vast literature on boundary value problems for (E ±). We list below some relevant works.
The extreme case $\Sigma =\{0\} \subset \partial \Omega$![]() was considered by Chen and Véron in [Reference Chen and Véron8] in which necessary and sufficient conditions in terms of suitable capacities for the existence of a solution to (E +) with a prescribed boundary measure were established under the condition $\mu \leq H^2$
was considered by Chen and Véron in [Reference Chen and Véron8] in which necessary and sufficient conditions in terms of suitable capacities for the existence of a solution to (E +) with a prescribed boundary measure were established under the condition $\mu \leq H^2$![]() .
.
In the other extreme case $\Sigma =\partial \Omega$![]() , Marcus and Nguyen [Reference Marcus and Nguyen28] introduced a notion of normalized boundary trace to study a boundary value problem for equation (E +) with $0<\mu < C_{\Omega,\partial \Omega }$
, Marcus and Nguyen [Reference Marcus and Nguyen28] introduced a notion of normalized boundary trace to study a boundary value problem for equation (E +) with $0<\mu < C_{\Omega,\partial \Omega }$![]() . In this range of $\mu$
. In this range of $\mu$![]() , they showed that if $1< p<\frac {N-{\alpha _{-}}+1}{N-{\alpha _{-}}-1}$
, they showed that if $1< p<\frac {N-{\alpha _{-}}+1}{N-{\alpha _{-}}-1}$![]() then the problem admits a unique solution for any $\nu \in \mathfrak {M}^+(\partial \Omega )$
then the problem admits a unique solution for any $\nu \in \mathfrak {M}^+(\partial \Omega )$![]() . Marcus and Moroz [Reference Marcus and Moroz27] extended the notion of normalized boundary trace and the results in [Reference Marcus and Nguyen28] to the range $-\infty <\mu <1/4$
. Marcus and Moroz [Reference Marcus and Moroz27] extended the notion of normalized boundary trace and the results in [Reference Marcus and Nguyen28] to the range $-\infty <\mu <1/4$![]() . Independently, under the assumption $\lambda _{\mu,\partial \Omega }>0$
. Independently, under the assumption $\lambda _{\mu,\partial \Omega }>0$![]() , Gkikas and Véron [Reference Gkikas and Véron21] investigated a boundary value problem for (E +) with a prescribed boundary trace defined in a dynamic way and obtained various existence results. Then it was shown in [Reference Gkikas and Nguyen18] that the two notions of boundary trace in [Reference Marcus and Nguyen28] and in [Reference Gkikas and Véron21] coincide.
, Gkikas and Véron [Reference Gkikas and Véron21] investigated a boundary value problem for (E +) with a prescribed boundary trace defined in a dynamic way and obtained various existence results. Then it was shown in [Reference Gkikas and Nguyen18] that the two notions of boundary trace in [Reference Marcus and Nguyen28] and in [Reference Gkikas and Véron21] coincide.
Afterwards, Marcus and Nguyen [Reference Marcus and Nguyen29] generalized the notion of normalized boundary trace in [Reference Marcus and Nguyen28] to the case $\Sigma \subsetneq \partial \Omega$![]() with dimension $0 \leq k\leq N-2$
with dimension $0 \leq k\leq N-2$![]() , under the restriction $\mu <\min \left \{C_{\Omega,\Sigma },H-1/4\right \}$
, under the restriction $\mu <\min \left \{C_{\Omega,\Sigma },H-1/4\right \}$![]() . They proved the solvability for the boundary value problem for (E +) with any prescribed normalized boundary trace $\nu \in \mathfrak {M}^+(\partial \Omega )$
. They proved the solvability for the boundary value problem for (E +) with any prescribed normalized boundary trace $\nu \in \mathfrak {M}^+(\partial \Omega )$![]() in subcritical ranges for $p$
in subcritical ranges for $p$![]() , namely for $1< p<\frac {N+1}{N-1}$
, namely for $1< p<\frac {N+1}{N-1}$![]() if $\nu$
if $\nu$![]() has compact support in $\partial \Omega \setminus \Sigma$
has compact support in $\partial \Omega \setminus \Sigma$![]() or for $1< p<\frac {N-{\alpha _{-}}+1}{N-{\alpha _{-}}-1}$
or for $1< p<\frac {N-{\alpha _{-}}+1}{N-{\alpha _{-}}-1}$![]() if $\nu$
if $\nu$![]() has compact support in $\Sigma$
has compact support in $\Sigma$![]() . They also showed that the problem has no solution either if $\nu =\delta _y$
. They also showed that the problem has no solution either if $\nu =\delta _y$![]() (the Dirac measure concentrated at $y$
(the Dirac measure concentrated at $y$![]() ) in supercritical ranges for $p$
) in supercritical ranges for $p$![]() , namely $p\geq \frac {N+1}{N-1}$
, namely $p\geq \frac {N+1}{N-1}$![]() if $y\in \partial \Omega \setminus \Sigma$
if $y\in \partial \Omega \setminus \Sigma$![]() or $p\geq \frac {N-{\alpha _{-}}+1}{N-{\alpha _{-}}+1}$
or $p\geq \frac {N-{\alpha _{-}}+1}{N-{\alpha _{-}}+1}$![]() if $y\in \Sigma$
if $y\in \Sigma$![]() . Very recently, under the condition $\lambda _{\mu,\Sigma }>0$
. Very recently, under the condition $\lambda _{\mu,\Sigma }>0$![]() , Barbatis et al. [Reference Barbatis, Gkikas and Tertikas3] obtained similar existence results in subcritical ranges for $p$
, Barbatis et al. [Reference Barbatis, Gkikas and Tertikas3] obtained similar existence results in subcritical ranges for $p$![]() and for the whole range $\mu \leq H^2$
and for the whole range $\mu \leq H^2$![]() .
.
For boundary value problems with more general potentials singular on $\partial \Omega$![]() , we refer to Marcus [Reference Marcus25] and Bhakta et al. [Reference Bhakta, Marcus and Nguyen4].
, we refer to Marcus [Reference Marcus25] and Bhakta et al. [Reference Bhakta, Marcus and Nguyen4].
The case of source nonlinearity is sharply different from the case of absorption nonlinearity in the sense that existence results hold under a smallness condition of boundary data, while nonexistence results hold if boundary data are large enough, even in subcritical ranges of $p$![]() . When $\mu =0$
. When $\mu =0$![]() , this phenomenon can be seen in [Reference Bidaut-Véron and Vivier6]. When $\Sigma =\partial \Omega$
, this phenomenon can be seen in [Reference Bidaut-Véron and Vivier6]. When $\Sigma =\partial \Omega$![]() , Bidaut-Véron et al. [Reference Bidaut-Véron, Hoang, Nguyen and Véron5] established existence results for a boundary value problem with measure for ($E_-$
, Bidaut-Véron et al. [Reference Bidaut-Véron, Hoang, Nguyen and Véron5] established existence results for a boundary value problem with measure for ($E_-$![]() ) in a capacity framework under a smallness condition on boundary data. Afterwards, various necessary and sufficient conditions for the existence of a solution to ($E_-$
) in a capacity framework under a smallness condition on boundary data. Afterwards, various necessary and sufficient conditions for the existence of a solution to ($E_-$![]() ) were obtained by Nguyen [Reference Nguyen33], Gkikas and Nguyen [Reference Gkikas and Nguyen18].
) were obtained by Nguyen [Reference Nguyen33], Gkikas and Nguyen [Reference Gkikas and Nguyen18].
When $\Sigma \subset \Omega$![]() , the corresponding boundary problems involving operator $L_\mu$
, the corresponding boundary problems involving operator $L_\mu$![]() with an absorption and with a source were extensively studied by Gkikas and Nguyen in [Reference Gkikas and Nguyen19, Reference Gkikas and Nguyen20] respectively. See also the papers by Dávila and Dupaigne [Reference Dávila and Dupaigne11, Reference Dávila and Dupaigne12], Dupaigne and Nedev [Reference Dupaigne and Nedev13], Fall [Reference Fall15] and Chen and Zhou [Reference Chen and Zhou9] for related results on semilinear equations with a source term.
with an absorption and with a source were extensively studied by Gkikas and Nguyen in [Reference Gkikas and Nguyen19, Reference Gkikas and Nguyen20] respectively. See also the papers by Dávila and Dupaigne [Reference Dávila and Dupaigne11, Reference Dávila and Dupaigne12], Dupaigne and Nedev [Reference Dupaigne and Nedev13], Fall [Reference Fall15] and Chen and Zhou [Reference Chen and Zhou9] for related results on semilinear equations with a source term.
1.2. Aim of the paper
Motivated by the above mentioned works, in the present paper, we aim to study boundary value problems for (E ±), where $\Sigma \subset \partial \Omega$![]() of dimension $0 \leq k \leq N-2$
of dimension $0 \leq k \leq N-2$![]() , for $\mu \leq H^2$
, for $\mu \leq H^2$![]() .
.
• First, we will establish removability results for equation (E +) when $p \geq \frac {N-{\alpha _{-}}+1}{N-{\alpha _{-}}-1}$
 or $p \geq \frac {N+1}{N-1}$
or $p \geq \frac {N+1}{N-1}$ . We will also provide conditions in terms of suitable capacities for the existence of a solution to boundary value problems for (E +).
. We will also provide conditions in terms of suitable capacities for the existence of a solution to boundary value problems for (E +).• Then we will give various criteria for the existence of a solution to boundary value problems for ($E_-$
 ).
).
The precise statement of these results will be presented in § 2.
2. Main results
2.1. Boundary trace, capacitary setting and main results
Throughout this paper, we assume that
Under assumption (2.1), a theory for linear equations involving $L_\mu$![]() was established in [Reference Barbatis, Gkikas and Tertikas3, Reference Marcus and Nguyen29], which forms a basis for the study of equation (E ±). We also note that the first and second inequalities in (2.1) imply that ${\alpha _{+}} \geq H \geq 1$
was established in [Reference Barbatis, Gkikas and Tertikas3, Reference Marcus and Nguyen29], which forms a basis for the study of equation (E ±). We also note that the first and second inequalities in (2.1) imply that ${\alpha _{+}} \geq H \geq 1$![]() . Moreover ${\alpha _{+}}=1$
. Moreover ${\alpha _{+}}=1$![]() if and only if $k=N-2$
if and only if $k=N-2$![]() and $\mu =1$
and $\mu =1$![]() ; in this case, we have ${\alpha _{-}}=1$
; in this case, we have ${\alpha _{-}}=1$![]() .
.
First we focus on the equation with an absorption power nonlinearity
Before stating the main results for equation (E +), we introduce some notations. For any $\beta >0,$![]() we set
we set
It is well known that (see appendix A.1) there is a small enough number $\beta _0>0$![]() such that for any $x\in \Omega _{\beta _0}$
such that for any $x\in \Omega _{\beta _0}$![]() there exists a unique $\xi _x\in \partial \Omega$
there exists a unique $\xi _x\in \partial \Omega$![]() satisfying $d_{\partial \Omega }(x)=|x-\xi _x|$
satisfying $d_{\partial \Omega }(x)=|x-\xi _x|$![]() . Now set
. Now set
where $\mathrm {dist}\,^{\partial \Omega }$![]() denotes the geodesic distance on $\partial \Omega$
denotes the geodesic distance on $\partial \Omega$![]() .
.
Let $\beta _3>0$![]() be the constant in proposition A.1. (One may choose $\beta _3<\beta _0$
be the constant in proposition A.1. (One may choose $\beta _3<\beta _0$![]() .) Let $\eta _{\beta _3}$
.) Let $\eta _{\beta _3}$![]() be a smooth cut-off function such that $0\leq \eta _{\beta _3}\leq 1$
be a smooth cut-off function such that $0\leq \eta _{\beta _3}\leq 1$![]() such that $\eta _{\beta _3}=1$
such that $\eta _{\beta _3}=1$![]() in $\overline {{\Sigma }_{\frac {\beta _3}{4}}}$
in $\overline {{\Sigma }_{\frac {\beta _3}{4}}}$![]() with compact support in $\Sigma _{\frac {\beta _3}{2}}$
with compact support in $\Sigma _{\frac {\beta _3}{2}}$![]() . We define
. We define

where ${\alpha _{+}}$![]() is defined in (1.5), and define
is defined in (1.5), and define
In the particular case $\mu =0$![]() and $\Sigma =\partial \Omega$
and $\Sigma =\partial \Omega$![]() , we have ${\alpha _{+}}=1$
, we have ${\alpha _{+}}=1$![]() , whence $\tilde W(x)\approx 1$
, whence $\tilde W(x)\approx 1$![]() . We note that $\tilde W$
. We note that $\tilde W$![]() is an appropriate function to describe the boundary behaviour in a normalization sense of solutions to ($E_{\pm }$
is an appropriate function to describe the boundary behaviour in a normalization sense of solutions to ($E_{\pm }$![]() ). For more detail, see (4.1) and (4.2) (see also [Reference Barbatis, Gkikas and Tertikas3, lemma 6.8]).
). For more detail, see (4.1) and (4.2) (see also [Reference Barbatis, Gkikas and Tertikas3, lemma 6.8]).
Our first theorem provides a removability result when $p\geq \frac {{\alpha _{+}}+1}{{\alpha _{+}}-1}$![]() in the sense that if a nonnegative solution ‘vanishes’ on $\partial \Omega \setminus \Sigma$
in the sense that if a nonnegative solution ‘vanishes’ on $\partial \Omega \setminus \Sigma$![]() as in (2.5), then it must be identically zero.
as in (2.5), then it must be identically zero.
Theorem 2.1 Assume $\mu \leq H^2$![]() if $k< N-2$
if $k< N-2$![]() or $\mu < H^2$
or $\mu < H^2$![]() if $k=N-2$
if $k=N-2$![]() , and $p\geq \frac {{\alpha _{+}}+1}{{\alpha _{+}}-1}$
, and $p\geq \frac {{\alpha _{+}}+1}{{\alpha _{+}}-1}$![]() . We additionally assume that $\Omega$
. We additionally assume that $\Omega$![]() is a $C^3$
is a $C^3$![]() open bounded domain. If $u \in C^2(\Omega )$
open bounded domain. If $u \in C^2(\Omega )$![]() is a nonnegative solution of (E +) such that
is a nonnegative solution of (E +) such that
locally uniformly in $\partial \Omega \setminus \Sigma$![]() , then $u\equiv 0$
, then $u\equiv 0$![]() in $\Omega$
in $\Omega$![]() .
.
We remark that if $k=0$![]() the result in the theorem 2.1 coincides with the result in [Reference Chen and Véron8, theorem J with $h=0$
the result in the theorem 2.1 coincides with the result in [Reference Chen and Véron8, theorem J with $h=0$![]() ]. In addition, when $p\geq \frac {{\alpha _{+}}+1}{{\alpha _{+}}-1}$
]. In addition, when $p\geq \frac {{\alpha _{+}}+1}{{\alpha _{+}}-1}$![]() , boundary behaviour of solutions on $\Sigma$
, boundary behaviour of solutions on $\Sigma$![]() is not imposed. However, when $\frac {N-{\alpha _{-}}+1}{N-{\alpha _{-}}-1}\leq p< \frac {{\alpha _{+}}+1}{{\alpha _{+}}-1}$
is not imposed. However, when $\frac {N-{\alpha _{-}}+1}{N-{\alpha _{-}}-1}\leq p< \frac {{\alpha _{+}}+1}{{\alpha _{+}}-1}$![]() , zero boundary condition on $\Sigma$
, zero boundary condition on $\Sigma$![]() is additionally required for the removability of isolated singularities, as stated in the following theorem.
is additionally required for the removability of isolated singularities, as stated in the following theorem.
Theorem 2.2 Assume $k \geq 1$![]() , $\mu \leq H^2$
, $\mu \leq H^2$![]() , $z\in \Sigma$
, $z\in \Sigma$![]() and $\frac {N-{\alpha _{-}}+1}{N-{\alpha _{-}}-1}\leq p< \frac {{\alpha _{+}}+1}{{\alpha _{+}}-1}$
and $\frac {N-{\alpha _{-}}+1}{N-{\alpha _{-}}-1}\leq p< \frac {{\alpha _{+}}+1}{{\alpha _{+}}-1}$![]() if ${\alpha _{+}}>1$
if ${\alpha _{+}}>1$![]() or $\frac {N}{N-2} \leq p$
or $\frac {N}{N-2} \leq p$![]() if ${\alpha _{+}}=1$
if ${\alpha _{+}}=1$![]() . We additionally assume that $\Omega$
. We additionally assume that $\Omega$![]() is a $C^3$
is a $C^3$![]() bounded domain. If $u\in C^2(\Omega )$
bounded domain. If $u\in C^2(\Omega )$![]() is a nonnegative solution of (E +) such that
is a nonnegative solution of (E +) such that
locally uniformly in $\partial \Omega \setminus \{z\}$![]() , then $u\equiv 0$
, then $u\equiv 0$![]() .
.
Next, we discuss existence results for a boundary value problem for (E +). In order to formulate the boundary value problem for (E +), we use a notion of boundary trace, introduced in [Reference Barbatis, Gkikas and Tertikas3], the definition of which is recalled below.
A family $\{\Omega _n\}$![]() is called a $C^2$
is called a $C^2$![]() exhaustion of $\Omega$
exhaustion of $\Omega$![]() if $\Omega _n$
if $\Omega _n$![]() is a $C^2$
is a $C^2$![]() bounded domain, $\Omega _n \Subset \Omega _{n+1} \Subset \Omega$
bounded domain, $\Omega _n \Subset \Omega _{n+1} \Subset \Omega$![]() for any $n \in {\mathbb {N}}$
for any $n \in {\mathbb {N}}$![]() and $\cup _{n \in {\mathbb {N}}}\Omega _n = \Omega$
and $\cup _{n \in {\mathbb {N}}}\Omega _n = \Omega$![]() .
.
Let $x_0 \in \Omega$![]() be a fixed reference point.
be a fixed reference point.
Definition 2.3 Boundary trace
We say that a function $u\in W^{1,\kappa }_{\mathrm {loc}}(\Omega )$![]() ($\kappa >1$
($\kappa >1$![]() ) possesses a boundary trace if there exists a measure $\nu \in \mathfrak M(\partial \Omega )$
) possesses a boundary trace if there exists a measure $\nu \in \mathfrak M(\partial \Omega )$![]() such that for any $C^2$
such that for any $C^2$![]() exhaustion $\{ \Omega _n \}$
exhaustion $\{ \Omega _n \}$![]() of $\Omega$
of $\Omega$![]() containing $x_0$
containing $x_0$![]() , there holds
, there holds
The boundary trace of $u$![]() is denoted by $\mathrm {tr}_{\mu,\Sigma}(u)$
is denoted by $\mathrm {tr}_{\mu,\Sigma}(u)$![]() . Here $\omega _{\Omega _n}^{x_0}$
. Here $\omega _{\Omega _n}^{x_0}$![]() is the $L_\mu$
is the $L_\mu$![]() -harmonic measure on $\partial \Omega _n$
-harmonic measure on $\partial \Omega _n$![]() relative to $x_0$
relative to $x_0$![]() (see § 4.1).
(see § 4.1).
It is known by [Reference Barbatis, Gkikas and Tertikas3, lemmas 8.1 and 8.2] that
For $q \in [1,+\infty )$![]() , denote by $L^q(\Omega ;\phi _{\mu,\Sigma })$
, denote by $L^q(\Omega ;\phi _{\mu,\Sigma })$![]() the weighted Lebesgue space
the weighted Lebesgue space

Let $H^1(\Omega ;\phi _{\mu,\Sigma }^2)$![]() be the weighted Sobolev space
be the weighted Sobolev space

We also denote by $H^1_0(\Omega ;\phi _{\mu,\Sigma }^2)$![]() the closure of $C_0^\infty (\Omega )$
the closure of $C_0^\infty (\Omega )$![]() with respect to the norm $\left \|\cdot \right \|_{H^1(\Omega ;\phi _{\mu,\Sigma }^2)}.$
with respect to the norm $\left \|\cdot \right \|_{H^1(\Omega ;\phi _{\mu,\Sigma }^2)}.$![]() It is worth mentioning here that $H^1_0(\Omega ;\phi _{\mu,\Sigma }^2)=H^1(\Omega ;\phi _{\mu,\Sigma }^2)$
It is worth mentioning here that $H^1_0(\Omega ;\phi _{\mu,\Sigma }^2)=H^1(\Omega ;\phi _{\mu,\Sigma }^2)$![]() (see [Reference Barbatis, Gkikas and Tertikas3, theorem 4.5]).
(see [Reference Barbatis, Gkikas and Tertikas3, theorem 4.5]).
Weak solutions of the boundary value problem for (E +) with prescribed boundary trace are defined below.
Definition 2.4 Let $p>1.$![]() We say that $u$
We say that $u$![]() is a weak solution of
is a weak solution of
if $u\in L^1(\Omega ;\phi _{\mu,\Sigma })$![]() , $|u|^p \in L^1(\Omega ;\phi _{\mu,\Sigma })$
, $|u|^p \in L^1(\Omega ;\phi _{\mu,\Sigma })$![]() and
and
where
We remark that in light of [Reference Barbatis, Gkikas and Tertikas3, theorem 2.12], a function $u$![]() is a weak solution to problem (P+) if and only if
is a weak solution to problem (P+) if and only if
It was known by [Reference Barbatis, Gkikas and Tertikas3, theorem B.4 (b)] (see also [Reference Marcus and Nguyen29, theorem 1.18]) that, in the subcritical case $1< p<$![]() $\frac {N-{\alpha _{-}}+1}{N-{\alpha _{-}}-1}$
$\frac {N-{\alpha _{-}}+1}{N-{\alpha _{-}}-1}$![]() , problem (P+) admits a unique weak solution for any $\nu \in \mathfrak {M}(\partial \Omega )$
, problem (P+) admits a unique weak solution for any $\nu \in \mathfrak {M}(\partial \Omega )$![]() with support in $\Sigma$
with support in $\Sigma$![]() . The supercritical case $p \geq$
. The supercritical case $p \geq$![]() $\frac {N-{\alpha _{-}}+1}{N-{\alpha _{-}}-1}$
$\frac {N-{\alpha _{-}}+1}{N-{\alpha _{-}}-1}$![]() is more challenging. In order to treat this case, we will make use of appropriate capacities.
is more challenging. In order to treat this case, we will make use of appropriate capacities.
For $\theta \in {\mathbb {R}}$![]() , we define the Bessel kernel of order $\alpha$
, we define the Bessel kernel of order $\alpha$![]() in ${\mathbb {R}}^d$
in ${\mathbb {R}}^d$![]() by ${\mathcal {B}}_{d,\theta }(\xi ):={\mathcal {F}}^{-1}((1+|.|^2)^{-\frac {\theta }{2}})(\xi )$
by ${\mathcal {B}}_{d,\theta }(\xi ):={\mathcal {F}}^{-1}((1+|.|^2)^{-\frac {\theta }{2}})(\xi )$![]() , where ${\mathcal {F}}$
, where ${\mathcal {F}}$![]() is the Fourier transform in the space ${\mathcal {S}}'({\mathbb {R}}^d)$
is the Fourier transform in the space ${\mathcal {S}}'({\mathbb {R}}^d)$![]() of moderate distributions in $\mathbb {R}^d$
of moderate distributions in $\mathbb {R}^d$![]() . For $\kappa >1$
. For $\kappa >1$![]() , the Bessel space $L_{\theta,\kappa }(\mathbb {R}^d)$
, the Bessel space $L_{\theta,\kappa }(\mathbb {R}^d)$![]() is defined by
is defined by
with norm
The Bessel capacity is defined for compact set $A \subset \mathbb {R}^d$![]() by
by
and is extended to open sets and arbitrary sets in ${\mathbb {R}}^d$![]() in the standard way. Here ${\mathbb 1}_A$
in the standard way. Here ${\mathbb 1}_A$![]() denotes the indicator function of $A$
denotes the indicator function of $A$![]() .
.
We denote by $B^d(x,r)$![]() the open ball of centre $x \in {\mathbb {R}}^d$
the open ball of centre $x \in {\mathbb {R}}^d$![]() and radius $r>0$
and radius $r>0$![]() in ${\mathbb {R}}^d$
in ${\mathbb {R}}^d$![]() .
.
Using the Bessel capacities, we are able to define capacities for subsets of $\partial \Omega$![]() as follows. If $\Gamma \subset \partial \Omega$
as follows. If $\Gamma \subset \partial \Omega$![]() is a $C^2$
is a $C^2$![]() submanifold without boundary, of dimension $d$
submanifold without boundary, of dimension $d$![]() with $1 \leq d \leq N-1$
with $1 \leq d \leq N-1$![]() then there exist open sets $O_1,\ldots,O_m$
then there exist open sets $O_1,\ldots,O_m$![]() in $\mathbb {R}^N$
in $\mathbb {R}^N$![]() , diffeomorphisms $T_i: O_i \to B^{d}(0,1)\times B^{N-d-1}(0,1)\times (-1,1)$
, diffeomorphisms $T_i: O_i \to B^{d}(0,1)\times B^{N-d-1}(0,1)\times (-1,1)$![]() , $i=1,\ldots,m$
, $i=1,\ldots,m$![]() , and compact sets $K_1,...,K_m$
, and compact sets $K_1,...,K_m$![]() in $\Gamma$
in $\Gamma$![]() such that
such that
(i) $K_i \subset O_i$
 , $1 \leq i \leq m$
, $1 \leq i \leq m$ and $\Gamma = \cup _{i=1}^m K_i$
and $\Gamma = \cup _{i=1}^m K_i$ ;
;(ii) $T_i(O_i \cap \Gamma )=B^d(0,1) \times \{ (x_{d+1},\ldots,x_{N-1}) = 0_{\mathbb {R}^{N-d-1}} \}\times \{x_N=0\}$
 , $T_i(O_i \cap \Omega )={B^{d}(0,1)}\times B^{N-d-1}(0,1)\times (0,1)$
, $T_i(O_i \cap \Omega )={B^{d}(0,1)}\times B^{N-d-1}(0,1)\times (0,1)$ ;
;(iii) For any $x \in O_i \cap \Omega$
 , there exists $y \in O_i \cap \Gamma$
, there exists $y \in O_i \cap \Gamma$ such that $d_\Gamma (x)=|x-y|$
such that $d_\Gamma (x)=|x-y|$ (here $d_\Gamma (x)$
(here $d_\Gamma (x)$ denotes the distance from $x$
denotes the distance from $x$ to $\Gamma$
to $\Gamma$ ).
).
We then define the $\mathrm {Cap}_{\theta,\kappa }^{\Gamma }-$![]() capacity of a compact set $E \subset \Gamma$
capacity of a compact set $E \subset \Gamma$![]() by
by

where $T_i(E \cap K_i)=\tilde T_i(E \cap K_i) \times \{ (x_{d+1},\ldots,x_{N-1}) = 0_{\mathbb {R}^{N-d-1}} \}\times \{x_N=0\}$![]() .
.
We remark that the definition of the capacities does not depend on $O_i$![]() , $i=1,\ldots,m$
, $i=1,\ldots,m$![]() .
.
In the sequel, we will say that $\nu \in \mathfrak M^+(\partial \Omega )$![]() is absolutely continuous with respect to a capacity $\mathscr {C}$
is absolutely continuous with respect to a capacity $\mathscr {C}$![]() if
if
Our next main result gives a sufficient condition in terms of appropriate capacities for the solvability of problem (P+) in the range $\frac {N-{\alpha _{-}}+1}{N-{\alpha _{-}}-1}\leq p<\frac {{\alpha _{+}}+1}{{\alpha _{+}}-1}$![]() when the boundary trace is supported in $\Sigma$
when the boundary trace is supported in $\Sigma$![]() .
.
Theorem 2.5 Assume $k \geq 1$![]() , $\mu \leq H^2$
, $\mu \leq H^2$![]() , $\frac {N-{\alpha _{-}}+1}{N-{\alpha _{-}}-1}\leq p<\frac {{\alpha _{+}}+1}{{\alpha _{+}}-1}$
, $\frac {N-{\alpha _{-}}+1}{N-{\alpha _{-}}-1}\leq p<\frac {{\alpha _{+}}+1}{{\alpha _{+}}-1}$![]() if ${\alpha _{+}}>1$
if ${\alpha _{+}}>1$![]() or $\frac {N}{N-2}\leq p$
or $\frac {N}{N-2}\leq p$![]() if ${\alpha _{+}}=1$
if ${\alpha _{+}}=1$![]() . Let $\nu \in \mathfrak M^+(\partial \Omega )$
. Let $\nu \in \mathfrak M^+(\partial \Omega )$![]() with compact support in $\Sigma$
with compact support in $\Sigma$![]() . If $\nu$
. If $\nu$![]() is absolutely continuous with respect to $\mathrm {Cap}^{\Sigma }_{\vartheta,p'}$
is absolutely continuous with respect to $\mathrm {Cap}^{\Sigma }_{\vartheta,p'}$![]() , where $p'=\frac {p}{p-1}$
, where $p'=\frac {p}{p-1}$![]() , then problem (P+) admits a unique weak solution.
, then problem (P+) admits a unique weak solution.
When $\nu$![]() has support in $\partial \Omega \setminus \Sigma$
has support in $\partial \Omega \setminus \Sigma$![]() , we provide a necessary and sufficient condition on the boundary trace for the existence of a solution to problem (P+) in the supercritical range $p \geq \frac {N+1}{N-1}$
, we provide a necessary and sufficient condition on the boundary trace for the existence of a solution to problem (P+) in the supercritical range $p \geq \frac {N+1}{N-1}$![]() .
.
Theorem 2.6 Assume $\mu \leq H^2$![]() , $p \geq \frac {N+1}{N-1}$
, $p \geq \frac {N+1}{N-1}$![]() and $\nu \in \mathfrak M^+(\partial \Omega )$
and $\nu \in \mathfrak M^+(\partial \Omega )$![]() with compact support in $\partial \Omega \setminus \Sigma$
with compact support in $\partial \Omega \setminus \Sigma$![]() . Then problem (P+) admits a unique weak solution if and only if ${\mathbb 1}_{F}\nu$
. Then problem (P+) admits a unique weak solution if and only if ${\mathbb 1}_{F}\nu$![]() is absolutely continuous with respect to $\mathrm {Cap}^{\partial \Omega }_{\frac {2}{p},p'}$
is absolutely continuous with respect to $\mathrm {Cap}^{\partial \Omega }_{\frac {2}{p},p'}$![]() for any compact set $F\subset \partial \Omega \setminus \Sigma.$
for any compact set $F\subset \partial \Omega \setminus \Sigma.$![]()
Next we investigate boundary value problem for ($E_-$![]() ) of the form
) of the form
where $\sigma >0$![]() is a parameter and $\nu \in \mathfrak M^+(\partial \Omega )$
is a parameter and $\nu \in \mathfrak M^+(\partial \Omega )$![]() .
.
Weak solutions to problem ($\mathrm{P}_-^{\sigma}$![]() ) are defined similarly as in definition 2.4 with obvious modifications.
) are defined similarly as in definition 2.4 with obvious modifications.
In the following theorems, for any $\nu \in \mathfrak {M}^+(\partial \Omega )$![]() , we extend it to be a measure defined on $\overline {\Omega }$
, we extend it to be a measure defined on $\overline {\Omega }$![]() by setting $\nu (\Omega )=0$
by setting $\nu (\Omega )=0$![]() and use the same notation $\nu$
and use the same notation $\nu$![]() for the extension.
for the extension.
When $\nu$![]() is concentrated on $\Sigma$
is concentrated on $\Sigma$![]() , various equivalent criteria for the existence of a weak solution to problem ($\mathrm{P}_-^{\sigma}$
, various equivalent criteria for the existence of a weak solution to problem ($\mathrm{P}_-^{\sigma}$![]() ) are described in the following result.
) are described in the following result.
Theorem 2.7 Assume that $\mu < \frac {N^2}{4}$![]() and
and
Let $\nu \in \mathfrak M^+(\partial \Omega )$![]() with compact support in $\Sigma$
with compact support in $\Sigma$![]() . Then the following statements are equivalent.
. Then the following statements are equivalent.
1. Problem ($\mathrm{P}_-^{\sigma}$
 ) has a positive weak solution for $\sigma >0$
) has a positive weak solution for $\sigma >0$ small.
small.2. For any Borel set $E \subset \overline {\Omega }$
 , there holds
(2.12)\begin{equation} \int_E \mathbb{K}_\mu[{\mathbb 1}_E\nu]^p \phi_{\mu,\Sigma} \,\mathrm{d} x \leq C\,\nu(E). \end{equation}
, there holds
(2.12)\begin{equation} \int_E \mathbb{K}_\mu[{\mathbb 1}_E\nu]^p \phi_{\mu,\Sigma} \,\mathrm{d} x \leq C\,\nu(E). \end{equation}
3. The following inequality holds
(2.13)\begin{equation} \mathbb{G}_\mu[\mathbb{K}_\mu[\nu]^p]\leq C\,\mathbb{K}_\mu[\nu]<{+}\infty\quad \text{a.e. in } \Omega. \end{equation}
Assume, in addition, that $k\geq 1$
 and
(2.14)\begin{equation} \left\{ \begin{array}{@{}ll} \max\left\{1,\dfrac{N-k-{\alpha_{-}}+1}{N-1-{\alpha_{-}}} \right\}< p<\dfrac{{\alpha_{+}}+1}{{\alpha_{+}}-1} & \text{if } {\alpha_{+}}>1 \\ \text{or}\quad\max\left\{1,\dfrac{N-k}{N-2} \right\}< p & \text{if}\ {\alpha_{+}}=1 . \end{array} \right. \end{equation}Put
and
(2.14)\begin{equation} \left\{ \begin{array}{@{}ll} \max\left\{1,\dfrac{N-k-{\alpha_{-}}+1}{N-1-{\alpha_{-}}} \right\}< p<\dfrac{{\alpha_{+}}+1}{{\alpha_{+}}-1} & \text{if } {\alpha_{+}}>1 \\ \text{or}\quad\max\left\{1,\dfrac{N-k}{N-2} \right\}< p & \text{if}\ {\alpha_{+}}=1 . \end{array} \right. \end{equation}Put (2.15)\begin{equation} \vartheta: = \frac{{\alpha_{+}}+1-p({\alpha_{+}}-1)}{p}. \end{equation}Then any of the above statements is equivalent to the following statement
(2.15)\begin{equation} \vartheta: = \frac{{\alpha_{+}}+1-p({\alpha_{+}}-1)}{p}. \end{equation}Then any of the above statements is equivalent to the following statement
4. For any Borel set $E \subset \Sigma$
 , there holds
\[ \nu(E)\leq C\, \mathrm{Cap}_{\vartheta,p'}^{\Sigma}(E). \]
, there holds
\[ \nu(E)\leq C\, \mathrm{Cap}_{\vartheta,p'}^{\Sigma}(E). \]
We remark that the case $\Sigma =\{0\}$![]() and $\mu =\frac {N^2}{4}$
and $\mu =\frac {N^2}{4}$![]() is treated in § 6.3 with slightly modified capacities; see in particular remark 6.15.
is treated in § 6.3 with slightly modified capacities; see in particular remark 6.15.
When $\nu$![]() is concentrated on $\partial \Omega \setminus \Sigma$
is concentrated on $\partial \Omega \setminus \Sigma$![]() , we obtain necessary and sufficient conditions for the existence of a weak solution of ($\mathrm{P}_-^{\sigma}$
, we obtain necessary and sufficient conditions for the existence of a weak solution of ($\mathrm{P}_-^{\sigma}$![]() ) for the whole range $\mu \leq \frac {N^2}{4}$
) for the whole range $\mu \leq \frac {N^2}{4}$![]() .
.
Theorem 2.8 Assume that $\mu \leq \frac {N^2}{4}$![]() , $p$
, $p$![]() satisfies ($\mathrm{P}_-^{\sigma}$
satisfies ($\mathrm{P}_-^{\sigma}$![]() ) and $\nu \in \mathfrak M^+(\partial \Omega )$
) and $\nu \in \mathfrak M^+(\partial \Omega )$![]() with compact support in $\partial \Omega \setminus \Sigma$
with compact support in $\partial \Omega \setminus \Sigma$![]() . Then the following statements are equivalent.
. Then the following statements are equivalent.
1. Equation ($\mathrm{P}_-^{\sigma}$
 ) has a positive solution for $\sigma >0$
) has a positive solution for $\sigma >0$ small.
small.2. For any Borel set $E \subset \overline {\Omega }$
 , (2.12) holds.
, (2.12) holds.3. Estimate (2.13) holds.
4. For any Borel set $E \subset \partial \Omega$
 , there holds $\nu (E)\leq C\, \mathrm {Cap}_{\frac {2}{p},p'}^{\partial \Omega }(E)$
, there holds $\nu (E)\leq C\, \mathrm {Cap}_{\frac {2}{p},p'}^{\partial \Omega }(E)$ .
.
We note that the case $p \geq \frac {{\alpha _{-}}+1}{{\alpha _{-}}-1}$![]() (if ${\alpha _{-}}>1$
(if ${\alpha _{-}}>1$![]() ) is still open and requires a different method.
) is still open and requires a different method.
2.2. Proof strategies and comparison with relevant works in the literature
The distinctive feature of the problems (P+) and ($\mathrm{P}_-^{\sigma}$![]() ) is characterized by the interplay between the concentration of $\Sigma$
) is characterized by the interplay between the concentration of $\Sigma$![]() , the type of nonlinearity, the exponent $p$
, the type of nonlinearity, the exponent $p$![]() and the parameter $\mu$
and the parameter $\mu$![]() . By employing a fine analysis in capacitary setting, we are able to obtain existence and nonexistence results in the supercritical ranges for $p$
. By employing a fine analysis in capacitary setting, we are able to obtain existence and nonexistence results in the supercritical ranges for $p$![]() and the critical case for the parameter $\mu$
and the critical case for the parameter $\mu$![]() , which justifies the novelty of our paper in comparison with related works in the literature. This is discussed in more detail below.
, which justifies the novelty of our paper in comparison with related works in the literature. This is discussed in more detail below.
To establish the removability results (theorems 2.1 and 2.2), we treat the cases $p \geq \frac {{\alpha _{-}}+1}{{\alpha _{-}}-1}$![]() and $p \geq \frac {N-{\alpha _{-}}+1}{N-{\alpha _{-}}-1}$
and $p \geq \frac {N-{\alpha _{-}}+1}{N-{\alpha _{-}}-1}$![]() separately. When $p \geq \frac {{\alpha _{-}}+1}{{\alpha _{-}}-1}$
separately. When $p \geq \frac {{\alpha _{-}}+1}{{\alpha _{-}}-1}$![]() , we provide a proof the heart of which is the assertion that all nonnegative solutions $u$
, we provide a proof the heart of which is the assertion that all nonnegative solutions $u$![]() of problem (E +)–(2.5) are dominated by $\tilde W$
of problem (E +)–(2.5) are dominated by $\tilde W$![]() in light of Keller–Osserman type estimates (see proposition 5.2), hence are uniformly bounded in $L^p(\Omega ;\phi _{\mu,\Sigma })$
in light of Keller–Osserman type estimates (see proposition 5.2), hence are uniformly bounded in $L^p(\Omega ;\phi _{\mu,\Sigma })$![]() . Consequently, thanks to the representation theorem (see theorem 3.3), these solutions admit boundary traces concentrated on $\Sigma$
. Consequently, thanks to the representation theorem (see theorem 3.3), these solutions admit boundary traces concentrated on $\Sigma$![]() with uniformly bounded total mass. Therefore, by contradiction, if there is a nontrivial nonnegative solution with positive boundary trace then there is a sequence of solutions whose total mass are unbounded, which clearly contradicts the above assertion. In the larger range $p \geq \frac {N-{\alpha _{-}}+1}{N-{\alpha _{-}}-1}$
with uniformly bounded total mass. Therefore, by contradiction, if there is a nontrivial nonnegative solution with positive boundary trace then there is a sequence of solutions whose total mass are unbounded, which clearly contradicts the above assertion. In the larger range $p \geq \frac {N-{\alpha _{-}}+1}{N-{\alpha _{-}}-1}$![]() , the above assertion is no longer valid and we focus on solutions with possible isolated boundary singularities concentrated at a point on $\Sigma$
, the above assertion is no longer valid and we focus on solutions with possible isolated boundary singularities concentrated at a point on $\Sigma$![]() depicted by (2.6). We offer a proof, which relies on a combination of localization techniques, Keller–Osserman type estimates and weak formulation for nonhomogneous linear equations, to show the removability of isolated singularities. Our results are new and cover [Reference Marcus and Nguyen29, theorem 1.17].
depicted by (2.6). We offer a proof, which relies on a combination of localization techniques, Keller–Osserman type estimates and weak formulation for nonhomogneous linear equations, to show the removability of isolated singularities. Our results are new and cover [Reference Marcus and Nguyen29, theorem 1.17].
We prove the solvability for problem (P+) (theorems 2.5 and 2.6) by extending the method in [Reference Marcus and Véron31]. When the boundary trace $\nu$![]() has support in $\Sigma$
has support in $\Sigma$![]() , a crucial ingredient in the proof of theorem 2.5 is the equivalence between the quantities $\|\mathbb {K}_{\mu }[\nu ]\|_{L^p(\Omega ;\phi _{\mu,\Sigma })}$
, a crucial ingredient in the proof of theorem 2.5 is the equivalence between the quantities $\|\mathbb {K}_{\mu }[\nu ]\|_{L^p(\Omega ;\phi _{\mu,\Sigma })}$![]() and $\| \nu \|_{B^{-\vartheta,p}(\Sigma )}$
and $\| \nu \|_{B^{-\vartheta,p}(\Sigma )}$![]() , where $B^{-\vartheta,p}(\Sigma )$
, where $B^{-\vartheta,p}(\Sigma )$![]() is the dual of an appropriate Besov space (see theorem 5.4). This allows us to utilize an approximation argument to prove the existence of a (unique) weak solution to problem (P+). When $\nu$
is the dual of an appropriate Besov space (see theorem 5.4). This allows us to utilize an approximation argument to prove the existence of a (unique) weak solution to problem (P+). When $\nu$![]() has support in $\partial \Omega \setminus \Sigma$
has support in $\partial \Omega \setminus \Sigma$![]() , we construct the Poisson kernel associated to $-L_\mu$
, we construct the Poisson kernel associated to $-L_\mu$![]() and adapt the idea in [Reference Marcus and Véron32] to prove theorem 2.6. In this case, the effect of the potential $d_{\Sigma }^{-2}$
and adapt the idea in [Reference Marcus and Véron32] to prove theorem 2.6. In this case, the effect of the potential $d_{\Sigma }^{-2}$![]() is not pivotal as it can be seen that the critical exponent and the involved capacities are the same as in the free potential case. To our knowledge, theorems 2.5 and 2.6 are the first existence results for problem (P+) expressed in terms of capacities in case $1 \leq k \leq N-2$
is not pivotal as it can be seen that the critical exponent and the involved capacities are the same as in the free potential case. To our knowledge, theorems 2.5 and 2.6 are the first existence results for problem (P+) expressed in terms of capacities in case $1 \leq k \leq N-2$![]() , which complements or extends the results in [Reference Gkikas and Véron21, Reference Marcus and Nguyen29, Reference Marcus and Véron32].
, which complements or extends the results in [Reference Gkikas and Véron21, Reference Marcus and Nguyen29, Reference Marcus and Véron32].
The source case is sharply different from the absorption case in several aspects due to the distinct effect of the source nonlinearity and hence require a completely different approach. Theorems 2.7 and 2.8 provide various necessary and sufficient conditions for the existence of a weak solution to problems with source nonlinearity ($\mathrm{P}_-^{\sigma}$![]() ) for $\mathrm {supp}\,\nu \subset \Sigma$
) for $\mathrm {supp}\,\nu \subset \Sigma$![]() and $\mathrm {supp}\,\nu \subset \partial \Omega \setminus \Sigma$
and $\mathrm {supp}\,\nu \subset \partial \Omega \setminus \Sigma$![]() respectively. The proofs are in the spirit of [Reference Bidaut-Véron, Hoang, Nguyen and Véron5], requiring several sharp estimates to adapt nontrivially an abstract result in [Reference Kalton and Verbitsky23] to our setting. Our theorems extend the existence results in [Reference Bidaut-Véron, Hoang, Nguyen and Véron5, Reference Bidaut-Véron and Vivier6, Reference Gkikas and Nguyen18, Reference Nguyen33] and can be regarded as a counterpart of the results in [Reference Gkikas and Nguyen20].
respectively. The proofs are in the spirit of [Reference Bidaut-Véron, Hoang, Nguyen and Véron5], requiring several sharp estimates to adapt nontrivially an abstract result in [Reference Kalton and Verbitsky23] to our setting. Our theorems extend the existence results in [Reference Bidaut-Véron, Hoang, Nguyen and Véron5, Reference Bidaut-Véron and Vivier6, Reference Gkikas and Nguyen18, Reference Nguyen33] and can be regarded as a counterpart of the results in [Reference Gkikas and Nguyen20].
It is worth pointing out that the optimal Hardy constant $C_{\Omega,\Sigma }$![]() defined in (1.2), as well as the asymptotic behaviour of the first eigenfunction $\phi _{\mu,\Sigma }$
defined in (1.2), as well as the asymptotic behaviour of the first eigenfunction $\phi _{\mu,\Sigma }$![]() in (1.4), the Green function and the Martin kernel, are different from those in the case where the potentials blow up on subsets of $\Omega$
in (1.4), the Green function and the Martin kernel, are different from those in the case where the potentials blow up on subsets of $\Omega$![]() . As a result, the critical exponents for the existence of a solution to (P+) and ($\mathrm{P}_-^{\sigma}$
. As a result, the critical exponents for the existence of a solution to (P+) and ($\mathrm{P}_-^{\sigma}$![]() ) and the employed capacities are different from those in the [Reference Gkikas and Nguyen19, Reference Gkikas and Nguyen20].
) and the employed capacities are different from those in the [Reference Gkikas and Nguyen19, Reference Gkikas and Nguyen20].
Organization of the paper. In § 3, we quote two-sided estimates of the Green function and the Martin kernel from [Reference Barbatis, Gkikas and Tertikas3], recall the representation theorem and results for linear and semilinear equations with an absorption established in [Reference Barbatis, Gkikas and Tertikas3]. In § 4, we give the definition of the $L_\mu$![]() -harmonic measures and show identities regarding the Poisson kernel and Martin kernel. Section 5 is devoted to the derivation of various results for equation (E +) such as a prior estimate, removable singularities (theorems 2.1 and 2.2) and existence results (theorems 2.5 and 2.6). In § 6, we demonstrate necessary and sufficient conditions for the existence of a weak solution to ($\mathrm{P}_-^{\sigma}$
-harmonic measures and show identities regarding the Poisson kernel and Martin kernel. Section 5 is devoted to the derivation of various results for equation (E +) such as a prior estimate, removable singularities (theorems 2.1 and 2.2) and existence results (theorems 2.5 and 2.6). In § 6, we demonstrate necessary and sufficient conditions for the existence of a weak solution to ($\mathrm{P}_-^{\sigma}$![]() ) (theorems 2.7 and 2.8). Finally, in appendix A, we provide the local representation of $\Sigma$
) (theorems 2.7 and 2.8). Finally, in appendix A, we provide the local representation of $\Sigma$![]() and $\Omega$
and $\Omega$![]() and construct a barrier function for solutions under assumption that $\Omega$
and construct a barrier function for solutions under assumption that $\Omega$![]() is a $C^3$
is a $C^3$![]() bounded domain.
bounded domain.
Notations. We denote by $c,c_1,C...$![]() the constants which depend on initial parameters and may change from one appearance to another. The notation $A \gtrsim B$
the constants which depend on initial parameters and may change from one appearance to another. The notation $A \gtrsim B$![]() (resp. $A \lesssim B$
(resp. $A \lesssim B$![]() ) means $A \geq c\,B$
) means $A \geq c\,B$![]() (resp. $A \leq c\,B$
(resp. $A \leq c\,B$![]() ) where $c$
) where $c$![]() is a positive constant depending on some initial parameters. If $A \gtrsim B$
is a positive constant depending on some initial parameters. If $A \gtrsim B$![]() and $A \lesssim B$
and $A \lesssim B$![]() , we write $A \approx B$
, we write $A \approx B$![]() . Throughout the paper, most of the implicit constants depend on some (or all) of the initial parameters such as $N,\Omega,\Sigma,k,\mu$
. Throughout the paper, most of the implicit constants depend on some (or all) of the initial parameters such as $N,\Omega,\Sigma,k,\mu$![]() and we will omit these dependencies in the notations (except when it is necessary). For a set $D \subset {\mathbb {R}}^N$
and we will omit these dependencies in the notations (except when it is necessary). For a set $D \subset {\mathbb {R}}^N$![]() , ${\mathbb 1}_D$
, ${\mathbb 1}_D$![]() denotes the indicator function of $D$
denotes the indicator function of $D$![]() .
.
3. Preliminaries
3.1. Two-sided estimates on Green function and Martin kernel
In this subsection, we recall sharp two-sided estimates on the Green function $G_\mu$![]() and the Martin kernel $K_\mu$
and the Martin kernel $K_\mu$![]() associated to $-L_\mu$
associated to $-L_\mu$![]() in $\Omega$
in $\Omega$![]() , as well as the representation formula for nonnegative $L_\mu$
, as well as the representation formula for nonnegative $L_\mu$![]() -harmonic functions.
-harmonic functions.
Proposition 3.1 [Reference Barbatis, Gkikas and Tertikas3, proposition 5.3]
Assume that $\mu \leq H^2$![]() and $\lambda _{\mu,\Sigma }>0$
and $\lambda _{\mu,\Sigma }>0$![]() .
.
(i) If $\mu < H^2$
 or $\mu =H^2$
or $\mu =H^2$ and $k> 0$
and $k> 0$ then for any $x,y\in \Omega$
then for any $x,y\in \Omega$ and $x\neq y,$
and $x\neq y,$ there holds
(3.1)$$\begin{align} G_{\mu}(x,y)& \approx\min\left\{\frac{1}{|x-y|^{N-2}},\frac{d_{\partial \Omega}(x)\,d_{\partial \Omega}(y)}{|x-y|^N}\right\} \nonumber\\ & \quad\times\left(\frac{\left(d_\Sigma(x)+|x-y|\right)\left(d_\Sigma(y)+|x-y|\right)}{d_\Sigma(x)\,d_\Sigma(y)}\right)^{{\alpha_{-}}}. \end{align}$$
there holds
(3.1)$$\begin{align} G_{\mu}(x,y)& \approx\min\left\{\frac{1}{|x-y|^{N-2}},\frac{d_{\partial \Omega}(x)\,d_{\partial \Omega}(y)}{|x-y|^N}\right\} \nonumber\\ & \quad\times\left(\frac{\left(d_\Sigma(x)+|x-y|\right)\left(d_\Sigma(y)+|x-y|\right)}{d_\Sigma(x)\,d_\Sigma(y)}\right)^{{\alpha_{-}}}. \end{align}$$
(ii) If $k=0$
 and $\mu =H^2$
and $\mu =H^2$ then for any $x,y\in \Omega$
then for any $x,y\in \Omega$ and $x\neq y,$
and $x\neq y,$ there holds
(3.2)$$\begin{align} G_{\mu}(x,y)& \approx\min\left\{\frac{1}{|x-y|^{N-2}},\frac{d_{\partial \Omega}(x)\,d_{\partial \Omega}(y)}{|x-y|^N}\right\}\nonumber\\& \quad\times\left(\frac{\left(|x|+|x-y|\right)\left(|y|+|x-y|\right)}{|x||y|}\right)^{-\frac{N}{2}}\nonumber\\ & \quad +\frac{d_{\partial \Omega}(x)\,d_{\partial \Omega}(y)}{(|x||y|)^{\frac{N}{2}}}\left|\ln\left(\min\left\{|x-y|^{{-}2},(d_{\partial \Omega}(x)\,d_{\partial \Omega}(y))^{{-}1}\right\}\right)\right|. \end{align}$$
there holds
(3.2)$$\begin{align} G_{\mu}(x,y)& \approx\min\left\{\frac{1}{|x-y|^{N-2}},\frac{d_{\partial \Omega}(x)\,d_{\partial \Omega}(y)}{|x-y|^N}\right\}\nonumber\\& \quad\times\left(\frac{\left(|x|+|x-y|\right)\left(|y|+|x-y|\right)}{|x||y|}\right)^{-\frac{N}{2}}\nonumber\\ & \quad +\frac{d_{\partial \Omega}(x)\,d_{\partial \Omega}(y)}{(|x||y|)^{\frac{N}{2}}}\left|\ln\left(\min\left\{|x-y|^{{-}2},(d_{\partial \Omega}(x)\,d_{\partial \Omega}(y))^{{-}1}\right\}\right)\right|. \end{align}$$
Proposition 3.2 [Reference Barbatis, Gkikas and Tertikas3, theorem 2.8]
Assume that $\mu \leq H^2$![]() and $\lambda _{\mu,\Sigma }>0$
and $\lambda _{\mu,\Sigma }>0$![]() .
.
(i) If $\mu < H^2$
 or $\mu =H^2$
or $\mu =H^2$ and $k>0$
and $k>0$ then
(3.3)\begin{equation} K_{\mu}(x,\xi) \approx\frac{d_{\partial \Omega}(x)}{|x-\xi|^N}\left(\frac{\left(d_\Sigma(x)+|x-\xi|\right)^2}{d_\Sigma(x)}\right)^{{\alpha_{-}}} \quad \text{for all } x \in \Omega, \, \xi \in \partial\Omega. \end{equation}
then
(3.3)\begin{equation} K_{\mu}(x,\xi) \approx\frac{d_{\partial \Omega}(x)}{|x-\xi|^N}\left(\frac{\left(d_\Sigma(x)+|x-\xi|\right)^2}{d_\Sigma(x)}\right)^{{\alpha_{-}}} \quad \text{for all } x \in \Omega, \, \xi \in \partial\Omega. \end{equation}
(ii) If $k=0$
 and $\mu =H^2$
and $\mu =H^2$ and then
(3.4)$$\begin{align} K_{\mu}(x,\xi) & \approx \frac{d_{\partial \Omega}(x)}{|x-\xi|^N}\left(\frac{\left(|x|+|x-\xi|\right)^2}{|x|}\right)^{\frac{N}{2}} \nonumber\\ & \quad +\frac{d_{\partial \Omega}(x)}{|x|^{\frac{N}{2}}}\left|\ln\left(|x-\xi|\right)\right|,\quad \text{ for all } x \in \Omega, \, \xi \in \partial\Omega. \end{align}$$
and then
(3.4)$$\begin{align} K_{\mu}(x,\xi) & \approx \frac{d_{\partial \Omega}(x)}{|x-\xi|^N}\left(\frac{\left(|x|+|x-\xi|\right)^2}{|x|}\right)^{\frac{N}{2}} \nonumber\\ & \quad +\frac{d_{\partial \Omega}(x)}{|x|^{\frac{N}{2}}}\left|\ln\left(|x-\xi|\right)\right|,\quad \text{ for all } x \in \Omega, \, \xi \in \partial\Omega. \end{align}$$
Recall that the Green operator and Martin operator are respectively defined by

A function $u \in L_{\mathrm {loc}}^1(\Omega )$![]() is called an $L_\mu$
is called an $L_\mu$![]() -harmonic function in $\Omega$
-harmonic function in $\Omega$![]() if $L_\mu u = 0$
if $L_\mu u = 0$![]() in the sense of distributions in $\Omega$
in the sense of distributions in $\Omega$![]() .
.
Next we state the representation theorem which provides a bijection between the class of positive $L_\mu$![]() -harmonic functions in $\Omega$
-harmonic functions in $\Omega$![]() and the measure space $\mathfrak M^+(\partial \Omega )$
and the measure space $\mathfrak M^+(\partial \Omega )$![]() .
.
Theorem 3.3 [Reference Barbatis, Gkikas and Tertikas3, theorem 2.9]
For any $\nu \in \mathfrak M^+(\partial \Omega )$![]() , the function $\mathbb {K}_{\mu }[\nu ]$
, the function $\mathbb {K}_{\mu }[\nu ]$![]() is a positive $L_\mu$
is a positive $L_\mu$![]() -harmonic function in $\Omega$
-harmonic function in $\Omega$![]() . Conversely, for any positive $L_\mu$
. Conversely, for any positive $L_\mu$![]() -harmonic function $u$
-harmonic function $u$![]() in $\Omega$
in $\Omega$![]() , there exists a unique measure $\nu \in \mathfrak M^+(\partial \Omega )$
, there exists a unique measure $\nu \in \mathfrak M^+(\partial \Omega )$![]() such that $u=\mathbb {K}_{\mu }[\nu ]$
such that $u=\mathbb {K}_{\mu }[\nu ]$![]() a.e. in $\Omega$
a.e. in $\Omega$![]() .
.
3.2. Boundary value problems for linear equations and semilinear equations
We recall the existence, uniqueness and Kato-type inequalities for solutions to boundary value problems for linear equations.
Theorem 3.4 [Reference Barbatis, Gkikas and Tertikas3, theorem 2.12]
Let $\tau \in \mathfrak {M}(\Omega ;\phi _{\mu,\Sigma })$![]() and $\nu \in \mathfrak {M}(\partial \Omega )$
and $\nu \in \mathfrak {M}(\partial \Omega )$![]() . Then there exists a unique weak solution $u\in L^1(\Omega ;\phi _{\mu,\Sigma })$
. Then there exists a unique weak solution $u\in L^1(\Omega ;\phi _{\mu,\Sigma })$![]() of
of
in the sense
where ${\bf X}_\mu (\Omega )$![]() has been defined in (2.8). Furthermore
has been defined in (2.8). Furthermore
and for any $\zeta \in \mathbf {X}_\mu (\Omega ),$![]() there holds
there holds
where $C=C(N,\Omega,\Sigma,\mu )$![]() . In addition, if $\mathrm {d} \tau =f\mathrm {d} x+\mathrm {d}\rho$
. In addition, if $\mathrm {d} \tau =f\mathrm {d} x+\mathrm {d}\rho$![]() with $\rho \in \mathfrak {M}(\Omega ;\phi _{\mu,\Sigma })$
with $\rho \in \mathfrak {M}(\Omega ;\phi _{\mu,\Sigma })$![]() and $f\in L^1(\Omega ;\phi _{\mu,\Sigma })$
and $f\in L^1(\Omega ;\phi _{\mu,\Sigma })$![]() , then, for any $0 \leq \zeta \in \mathbf {X}_\mu (\Omega )$
, then, for any $0 \leq \zeta \in \mathbf {X}_\mu (\Omega )$![]() , the following Kato-type inequalities are valid
, the following Kato-type inequalities are valid

Here $u^+=\max \{u,0\}$![]() .
.
Proposition 3.5 [Reference Barbatis, Gkikas and Tertikas3, theorem 9.7]
Let $\nu \in \mathfrak {M}(\partial \Omega )$![]() and $g\in C(\mathbb {R})$
and $g\in C(\mathbb {R})$![]() be a nondecreasing function such that $g(0)=0$
be a nondecreasing function such that $g(0)=0$![]() and $g(\mathbb {K}_{\mu }[\nu _+]),g(\mathbb {K}_{\mu }[\nu _-])\in L^1(\Omega ;\phi _{\mu,\Sigma }).$
and $g(\mathbb {K}_{\mu }[\nu _+]),g(\mathbb {K}_{\mu }[\nu _-])\in L^1(\Omega ;\phi _{\mu,\Sigma }).$![]() Then there exists a unique weak solution $u\in L^1(\Omega ;\phi _{\mu,\Sigma })$
Then there exists a unique weak solution $u\in L^1(\Omega ;\phi _{\mu,\Sigma })$![]() of
of
in the sense that $g(u) \in L^1(\Omega ;\phi _{\mu,\Sigma })$![]() and
and
4. $L_\mu$ -harmonic measures and Poisson kernel
-harmonic measures and Poisson kernel
4.1. $L_\mu$ -harmonic measures
-harmonic measures
Let $h\in C(\partial \Omega )$![]() . Then by [Reference Barbatis, Gkikas and Tertikas3, lemma 6.8], there exists a unique solution $v_h$
. Then by [Reference Barbatis, Gkikas and Tertikas3, lemma 6.8], there exists a unique solution $v_h$![]() of the Dirichlet problem
of the Dirichlet problem
Let $\tilde W$![]() be as in (2.4). The boundary value condition in (4.1) is understood as
be as in (2.4). The boundary value condition in (4.1) is understood as
Let $z \in \Omega$![]() and set ${\mathcal {L}}_{\mu,z}(h):=u_h(z),$
and set ${\mathcal {L}}_{\mu,z}(h):=u_h(z),$![]() then the mapping $h\mapsto {\mathcal {L}}_{\mu,z}(h)$
then the mapping $h\mapsto {\mathcal {L}}_{\mu,z}(h)$![]() is a linear positive functional on $C(\partial \Omega )$
is a linear positive functional on $C(\partial \Omega )$![]() . Thus, there exists a unique Borel measure on $\partial \Omega$
. Thus, there exists a unique Borel measure on $\partial \Omega$![]() , called $L_{\mu }$
, called $L_{\mu }$![]() -harmonic measure on $\partial \Omega$
-harmonic measure on $\partial \Omega$![]() relative to $z$
relative to $z$![]() and denoted by $\omega _{\Omega }^{z}$
and denoted by $\omega _{\Omega }^{z}$![]() , such that
, such that
Let $x_0 \in \Omega$![]() be a fixed reference point. Let $\{\Omega _n\}$
be a fixed reference point. Let $\{\Omega _n\}$![]() be a $C^2$
be a $C^2$![]() exhaustion of $\Omega$
exhaustion of $\Omega$![]() , i.e. $\{\Omega _n\}$
, i.e. $\{\Omega _n\}$![]() is an increasing sequence of bounded $C^2$
is an increasing sequence of bounded $C^2$![]() domains such that
domains such that
where $\mathcal {H}^{N-1}$![]() denotes the $(N-1)$
denotes the $(N-1)$![]() -dimensional Hausdorff measure in ${\mathbb {R}}^N$
-dimensional Hausdorff measure in ${\mathbb {R}}^N$![]() .
.
Then $-L_\mu$![]() is uniformly elliptic and coercive in $H^1_0(\Omega _n)$
is uniformly elliptic and coercive in $H^1_0(\Omega _n)$![]() and its first eigenvalue $\lambda _{\mu,\Sigma }^{\Omega _n}$
and its first eigenvalue $\lambda _{\mu,\Sigma }^{\Omega _n}$![]() in $\Omega _n$
in $\Omega _n$![]() is larger than its first eigenvalue $\lambda _{\mu,\Sigma }$
is larger than its first eigenvalue $\lambda _{\mu,\Sigma }$![]() in $\Omega$
in $\Omega$![]() .
.
For $h\in C(\partial \Omega _n)$![]() , the following problem
, the following problem
admits a unique solution which allows to define the $L_{\mu }$![]() -harmonic measure $\omega _{\Omega _n}^{x_0}$
-harmonic measure $\omega _{\Omega _n}^{x_0}$![]() on $\partial \Omega _n$
on $\partial \Omega _n$![]() by
by
Let $G^{\Omega _n}_\mu (x,y)$![]() be the Green kernel of $-L_\mu$
be the Green kernel of $-L_\mu$![]() on $\Omega _n$
on $\Omega _n$![]() . Then $G^{\Omega _n}_\mu (x,y)\uparrow G_\mu (x,y)$
. Then $G^{\Omega _n}_\mu (x,y)\uparrow G_\mu (x,y)$![]() for $x,y\in \Omega, x \neq y$
for $x,y\in \Omega, x \neq y$![]() .
.
Proposition 4.1 [Reference Barbatis, Gkikas and Tertikas3, proposition 7.7]
Assume $x_0\in \Omega _1$![]() . Then for every $Z\in C(\overline {\Omega })$
. Then for every $Z\in C(\overline {\Omega })$![]() ,
,
4.2. Poisson kernel
By the standard elliptic theory, we can easily show that for any $x \in \Omega$![]() , $G_{\mu }(x,\cdot ) \in C^{1,\gamma }(\overline {\Omega } \setminus (\Sigma \cup \{x\})) \cap C^2(\Omega \setminus \{x\})$
, $G_{\mu }(x,\cdot ) \in C^{1,\gamma }(\overline {\Omega } \setminus (\Sigma \cup \{x\})) \cap C^2(\Omega \setminus \{x\})$![]() for all $\gamma \in (0,1)$
for all $\gamma \in (0,1)$![]() . Therefore, we may define the Poisson kernel associated to $-L_\mu$
. Therefore, we may define the Poisson kernel associated to $-L_\mu$![]() in $\Omega \times (\partial \Omega \setminus \Sigma )$
in $\Omega \times (\partial \Omega \setminus \Sigma )$![]() as
as
where ${\bf n}$![]() is the unit outer normal vector of $\partial \Omega$
is the unit outer normal vector of $\partial \Omega$![]() . This kernel satisfies the following properties.
. This kernel satisfies the following properties.
Proposition 4.2 Let $x_0 \in \Omega$![]() be a fixed reference point.
be a fixed reference point.
(i) Then there holds
(4.4)\begin{equation} P_\mu(x,y)=P_\mu(x_0,y)K_\mu(x,y), \quad x \in \Omega, \; y \in \partial \Omega\setminus\Sigma. \end{equation}
(ii) For any $h \in L^1(\partial \Omega ; \mathrm {d} \omega ^{x_0}_{\Omega })$
 with compact support in $\partial \Omega \setminus \Sigma$
with compact support in $\partial \Omega \setminus \Sigma$ , there holds
(4.5)\begin{equation} \int_{\partial\Omega} h(y) \, \mathrm{d} \omega^{x_0}_{\Omega}(y) = \mathbb{P}_\mu[h\tilde W](x_0). \end{equation}Here
, there holds
(4.5)\begin{equation} \int_{\partial\Omega} h(y) \, \mathrm{d} \omega^{x_0}_{\Omega}(y) = \mathbb{P}_\mu[h\tilde W](x_0). \end{equation}Here \[ \mathbb{P}_{\mu}[h\tilde W](x):=\int_{\partial\Omega}P_\mu(x,y)h(y) \tilde W(y)\, \mathrm{d} S_{\partial \Omega}(y), \quad x \in \Omega, \]where $S_{\partial \Omega }$
\[ \mathbb{P}_{\mu}[h\tilde W](x):=\int_{\partial\Omega}P_\mu(x,y)h(y) \tilde W(y)\, \mathrm{d} S_{\partial \Omega}(y), \quad x \in \Omega, \]where $S_{\partial \Omega }$
 is the $(N-1)$
is the $(N-1)$ -dimensional surface measure on $\partial \Omega$
-dimensional surface measure on $\partial \Omega$ .
.
Proof.
(i) We note that $P_\mu (\cdot,y)$
 is $L_\mu$
is $L_\mu$ -harmonic in $\Omega$
-harmonic in $\Omega$ and
\[ \lim_{x\in\Omega,\;x\rightarrow\xi}\frac{P_\mu(x,y)}{\tilde W(x)}=0\quad\text{for all } \xi\in \partial\Omega\setminus \{y\}\quad\text{and}\quad y\in\partial\Omega\setminus\Sigma. \]Hence, $\frac {P_\mu (x,y)}{P_\mu (x_0,y)}$
and
\[ \lim_{x\in\Omega,\;x\rightarrow\xi}\frac{P_\mu(x,y)}{\tilde W(x)}=0\quad\text{for all } \xi\in \partial\Omega\setminus \{y\}\quad\text{and}\quad y\in\partial\Omega\setminus\Sigma. \]Hence, $\frac {P_\mu (x,y)}{P_\mu (x_0,y)}$
 is a kernel function with pole at $y$
is a kernel function with pole at $y$ and basis at $x_0$
and basis at $x_0$ in the sense of [Reference Barbatis, Gkikas and Tertikas3, definition 2.7]. This, together with the fact that any kernel function with pole at $y$
in the sense of [Reference Barbatis, Gkikas and Tertikas3, definition 2.7]. This, together with the fact that any kernel function with pole at $y$ and basis at $x_0$
and basis at $x_0$ is unique (see [Reference Barbatis, Gkikas and Tertikas3, proposition 7.3]), implies (4.4).
is unique (see [Reference Barbatis, Gkikas and Tertikas3, proposition 7.3]), implies (4.4).(ii) Let $\zeta \in C(\partial \Omega )$
 with compact support in $\partial \Omega \setminus \Sigma$
with compact support in $\partial \Omega \setminus \Sigma$ such that $\mathrm {dist}\,(\mathrm {supp}\, \zeta,\Sigma )=r>0$
such that $\mathrm {dist}\,(\mathrm {supp}\, \zeta,\Sigma )=r>0$ . Let $Z\in C(\overline {\Omega })$
. Let $Z\in C(\overline {\Omega })$ be such that $Z(y)=\zeta (y)$
be such that $Z(y)=\zeta (y)$ for any $y\in \partial \Omega$
for any $y\in \partial \Omega$ and $Z(y)=0$
and $Z(y)=0$ in $\Sigma _{\frac {r}{2}}.$
in $\Sigma _{\frac {r}{2}}.$ Set $r_0=\frac {1}{4}\min \{\beta _2,r\}$
Set $r_0=\frac {1}{4}\min \{\beta _2,r\}$ where $\beta _2$
where $\beta _2$ is the constant in (A.7). We consider a decreasing sequence of bounded $C^2$
is the constant in (A.7). We consider a decreasing sequence of bounded $C^2$ domains $\{\Sigma _n\}$
domains $\{\Sigma _n\}$ such that
(4.6)\begin{equation} \Sigma \subset \Sigma_{n+1}\subset\overline{\Sigma}_{n+1}\subset \Sigma_{n}\subset\overline{\Sigma}_{n} \subset\Sigma_{\frac{r_0}{4}}, \quad \cap_n \Sigma_n=\Sigma. \end{equation}
such that
(4.6)\begin{equation} \Sigma \subset \Sigma_{n+1}\subset\overline{\Sigma}_{n+1}\subset \Sigma_{n}\subset\overline{\Sigma}_{n} \subset\Sigma_{\frac{r_0}{4}}, \quad \cap_n \Sigma_n=\Sigma. \end{equation}
Let $\phi _*$
 be the unique solution of
(4.7)\begin{equation} \left\{ \begin{array}{@{}ll} -L_{\mu }\phi_*=0 & \text{in } \Omega\\ \phi_* =1 & \text{on } \partial\Omega, \end{array} \right. \end{equation}where the boundary condition in (4.7) is understood as
be the unique solution of
(4.7)\begin{equation} \left\{ \begin{array}{@{}ll} -L_{\mu }\phi_*=0 & \text{in } \Omega\\ \phi_* =1 & \text{on } \partial\Omega, \end{array} \right. \end{equation}where the boundary condition in (4.7) is understood as \[ \lim_{\mathrm{dist}\,(x,F)\to 0}\frac{\phi_*(x)}{\tilde W(x)}=1 \quad \text{for every compact set } \; F\subset \partial \Omega. \]Then, by [Reference Barbatis, Gkikas and Tertikas3, lemma 6.8 and estimate (6.21)], there exist constants $c_1=c_1(\Omega,\Sigma,\Sigma _n,\mu )$
\[ \lim_{\mathrm{dist}\,(x,F)\to 0}\frac{\phi_*(x)}{\tilde W(x)}=1 \quad \text{for every compact set } \; F\subset \partial \Omega. \]Then, by [Reference Barbatis, Gkikas and Tertikas3, lemma 6.8 and estimate (6.21)], there exist constants $c_1=c_1(\Omega,\Sigma,\Sigma _n,\mu )$
 and $c_2=c_2(\Omega,\Sigma,N,\mu )$
and $c_2=c_2(\Omega,\Sigma,N,\mu )$ such that $0< c_1 \leq \phi _*(x)\leq c_2 d_\Sigma (x)^{-{\alpha _{+}}}$
such that $0< c_1 \leq \phi _*(x)\leq c_2 d_\Sigma (x)^{-{\alpha _{+}}}$ for all $x \in \Omega \setminus \Sigma _n$
for all $x \in \Omega \setminus \Sigma _n$ . By the standard elliptic theory, $\phi _*\in C^2(\Omega ) \cap C^{1,\gamma }(\overline {\Omega }\setminus \Sigma )$
. By the standard elliptic theory, $\phi _*\in C^2(\Omega ) \cap C^{1,\gamma }(\overline {\Omega }\setminus \Sigma )$ for any $0<\gamma <1$
for any $0<\gamma <1$ .
.
Now, for any $\eta \in C(\partial \Omega ),$![]() we can easily show that $u_\eta$
we can easily show that $u_\eta$![]() is a solution of
is a solution of
if and only if $w_\eta =\frac {u_\eta }{\phi _*}$![]() is a solution of
is a solution of

Since the operator $L_{\phi _*}w:=-\text {div}(\phi _*^2\nabla w)$![]() is uniformly elliptic and has smooth coefficients, we may deduce the existence of $L_\mu$
is uniformly elliptic and has smooth coefficients, we may deduce the existence of $L_\mu$![]() -harmonic measure $\omega _n^{x}$
-harmonic measure $\omega _n^{x}$![]() on $\partial ( \Omega \setminus \Sigma _n)$
on $\partial ( \Omega \setminus \Sigma _n)$![]() and the Green kernel $G^n_{\mu }$
and the Green kernel $G^n_{\mu }$![]() of $-L_\mu$
of $-L_\mu$![]() in $\Omega \setminus \Sigma _n$
in $\Omega \setminus \Sigma _n$![]() .
.
Let $v_n$![]() be the unique solution of
be the unique solution of
Then by the representation formula we have
Proceeding as in the proof of [Reference Barbatis, Gkikas and Tertikas3, proposition 7.7], we may show that
On the other hand, the Poisson kernel $P_\mu ^n$![]() of $-L_\mu$
of $-L_\mu$![]() in $\Omega \setminus \Sigma _n$
in $\Omega \setminus \Sigma _n$![]() is well defined and given by
is well defined and given by
where ${\bf n}^n$![]() is the unit outer normal vector to $\partial (\Omega \setminus \Sigma _n)$
is the unit outer normal vector to $\partial (\Omega \setminus \Sigma _n)$![]() . Hence,
. Hence,

where $S_{\partial \Omega }$![]() is the $(N-1)$
is the $(N-1)$![]() -dimensional surface measure on $\partial (\Omega \setminus \Sigma _n)$
-dimensional surface measure on $\partial (\Omega \setminus \Sigma _n)$![]() . Combining all above, we obtain
. Combining all above, we obtain
Put $\beta =\frac {1}{2}\min \{d_{\partial \Omega }(x), r_0\}$![]() . Since $G^n_{\mu }(x,y)\nearrow G_{\mu }(x,y)$
. Since $G^n_{\mu }(x,y)\nearrow G_{\mu }(x,y)$![]() for any $x\neq y$
for any $x\neq y$![]() and $x,y\in \Omega,$
and $x,y\in \Omega,$![]() $\{G_{\mu }^n(x,\cdot )\}_n$
$\{G_{\mu }^n(x,\cdot )\}_n$![]() is uniformly bounded in $W^{2,\kappa }(\Omega _\beta \setminus \Sigma _{r_0})$
is uniformly bounded in $W^{2,\kappa }(\Omega _\beta \setminus \Sigma _{r_0})$![]() for any $\kappa >1$
for any $\kappa >1$![]() . Thus, by the standard compact Sobolev embedding, there exists a subsequence, still denoted by index $n$
. Thus, by the standard compact Sobolev embedding, there exists a subsequence, still denoted by index $n$![]() , which converges to $G_{\mu }(x,\cdot )$
, which converges to $G_{\mu }(x,\cdot )$![]() in $C^1(\overline {\Omega _\beta \setminus \Sigma _{r_0}})$
in $C^1(\overline {\Omega _\beta \setminus \Sigma _{r_0}})$![]() as $n \to \infty$
as $n \to \infty$![]() . This implies that $P_\mu ^n(x,\cdot ) \to P_\mu (x,\cdot )$
. This implies that $P_\mu ^n(x,\cdot ) \to P_\mu (x,\cdot )$![]() uniformly on $\partial \Omega \setminus \Sigma _{r_0}$
uniformly on $\partial \Omega \setminus \Sigma _{r_0}$![]() as $n \to \infty$
as $n \to \infty$![]() .
.
Therefore, by letting $n \to \infty$![]() in (4.9), we obtain
in (4.9), we obtain

By (4.10) and the fact that $\inf _{y \in \partial \Omega \setminus \Sigma _{r}}P_\mu (x_0,y)>0\quad \forall \;r>0,$![]() we deduce that
we deduce that
for any Borel set $E\subset \overline {E}\subset \partial \Omega \setminus \Sigma$![]() . This implies in particular that $\omega _{\Omega }^{x_0}$
. This implies in particular that $\omega _{\Omega }^{x_0}$![]() and $S_{\partial \Omega }$
and $S_{\partial \Omega }$![]() are mutually absolutely continuous with respect to compact subsets of $\partial \Omega \setminus \Sigma$
are mutually absolutely continuous with respect to compact subsets of $\partial \Omega \setminus \Sigma$![]() .
.
Now, assume $0 \leq h \in L^1(\partial \Omega ; \mathrm {d}\omega _{\Omega }^{x_0})$![]() has compact support in $\partial \Omega \setminus \Sigma$
has compact support in $\partial \Omega \setminus \Sigma$![]() and $\mathrm {dist}\,(\mathrm {supp}\, h, \Sigma )=4r>0$
and $\mathrm {dist}\,(\mathrm {supp}\, h, \Sigma )=4r>0$![]() . Then there exists a sequence of nonnegative functions $\{ h_n \} \subset C(\partial \Omega )$
. Then there exists a sequence of nonnegative functions $\{ h_n \} \subset C(\partial \Omega )$![]() with compact support in $\partial \Omega \setminus \Sigma$
with compact support in $\partial \Omega \setminus \Sigma$![]() such that $\mathrm {dist}\,(\mathrm {supp}\, h_n,\Sigma )=2r>0$
such that $\mathrm {dist}\,(\mathrm {supp}\, h_n,\Sigma )=2r>0$![]() for any $n \in {\mathbb {N}}$
for any $n \in {\mathbb {N}}$![]() and $h_n \to h$
and $h_n \to h$![]() in $L^1(\partial \Omega ; \mathrm {d}\omega _{\Omega }^{x_0})$
in $L^1(\partial \Omega ; \mathrm {d}\omega _{\Omega }^{x_0})$![]() as $n \to \infty$
as $n \to \infty$![]() .
.
Applying (4.10) with $\zeta$![]() replaced by $|h_n-h_m|$
replaced by $|h_n-h_m|$![]() for $m, n \in {\mathbb {N}}$
for $m, n \in {\mathbb {N}}$![]() and using the fact that $\inf _{y \in \Sigma _r \cap \partial \Omega }(P_\mu (x_0,y) \tilde W(y))>0$
and using the fact that $\inf _{y \in \Sigma _r \cap \partial \Omega }(P_\mu (x_0,y) \tilde W(y))>0$![]() , we have
, we have

This implies that $\{h_n\}$![]() is a Cauchy sequence in $L^1(\partial \Omega )$
is a Cauchy sequence in $L^1(\partial \Omega )$![]() . Therefore, there exists $\tilde h \in L^1(\partial \Omega )$
. Therefore, there exists $\tilde h \in L^1(\partial \Omega )$![]() such that $h_n \to \tilde h$
such that $h_n \to \tilde h$![]() in $L^1(\partial \Omega )$
in $L^1(\partial \Omega )$![]() . Since $\omega _{\Omega }^{x_0}$
. Since $\omega _{\Omega }^{x_0}$![]() and $S_{\partial \Omega }$
and $S_{\partial \Omega }$![]() are mutually absolutely continuous with respect to compact subsets of $\partial \Omega \setminus \Sigma$
are mutually absolutely continuous with respect to compact subsets of $\partial \Omega \setminus \Sigma$![]() and $h$
and $h$![]() and $\tilde h$
and $\tilde h$![]() have compact support in $\partial \Omega \setminus \Sigma$
have compact support in $\partial \Omega \setminus \Sigma$![]() , we deduce that $h=\tilde h$
, we deduce that $h=\tilde h$![]() $\omega _{\Omega }^{x_0}$
$\omega _{\Omega }^{x_0}$![]() -a.e. and $S_{\partial \Omega }$
-a.e. and $S_{\partial \Omega }$![]() -a.e. in $\partial \Omega$
-a.e. in $\partial \Omega$![]() . In particular, $h \in L^1(\partial \Omega )$
. In particular, $h \in L^1(\partial \Omega )$![]() .
.
Applying (4.10) with $\zeta$![]() replaced by $h_n$
replaced by $h_n$![]() , for any $n \in {\mathbb {N}}$
, for any $n \in {\mathbb {N}}$![]() , we have
, we have
By letting $n \to \infty$![]() in (4.11), we obtain (4.5).
in (4.11), we obtain (4.5).
Next, we assume $h \in L^1(\partial \Omega ; \mathrm {d}\omega _{\Omega }^{x_0})$![]() and drop the assumption that $h \geq 0$
and drop the assumption that $h \geq 0$![]() , then we write $h=h_+ - h_-$
, then we write $h=h_+ - h_-$![]() where $h_\pm \in L^1(\partial \Omega ; \mathrm {d}\omega _{\Omega }^{x_0})$
where $h_\pm \in L^1(\partial \Omega ; \mathrm {d}\omega _{\Omega }^{x_0})$![]() . By applying (4.5) for $h_\pm$
. By applying (4.5) for $h_\pm$![]() , we deduce that (4.5) holds true for $h \in L^1(\partial \Omega ; \mathrm {d}\omega _{\Omega }^{x_0})$
, we deduce that (4.5) holds true for $h \in L^1(\partial \Omega ; \mathrm {d}\omega _{\Omega }^{x_0})$![]() . Moreover, we can show that $h_\pm \in L^1(\partial \Omega )$
. Moreover, we can show that $h_\pm \in L^1(\partial \Omega )$![]() , which implies $h \in L^1(\partial \Omega )$
, which implies $h \in L^1(\partial \Omega )$![]() .
.
Proposition 4.3
(i) For any $h \in L^1(\partial \Omega ; \mathrm {d} \omega ^{x_0}_{\Omega })$
 with compact support in $\partial \Omega \setminus \Sigma$
with compact support in $\partial \Omega \setminus \Sigma$ , there holds
(4.12)\begin{equation} -\int_\Omega \mathbb{K}_\mu[h\mathrm{d} \omega^{x_0}_{\Omega}] L_\mu\eta\,\mathrm{d} x={-}\int_{\partial\Omega}\frac{\partial \eta}{\partial{\bf n}}(y)h(y)\tilde W(y)\, \mathrm{d} S_{\partial \Omega}(y),\quad \forall \eta \in \mathbf{X}_\mu(\Omega). \end{equation}
, there holds
(4.12)\begin{equation} -\int_\Omega \mathbb{K}_\mu[h\mathrm{d} \omega^{x_0}_{\Omega}] L_\mu\eta\,\mathrm{d} x={-}\int_{\partial\Omega}\frac{\partial \eta}{\partial{\bf n}}(y)h(y)\tilde W(y)\, \mathrm{d} S_{\partial \Omega}(y),\quad \forall \eta \in \mathbf{X}_\mu(\Omega). \end{equation}
(ii) For any $\nu \in \mathfrak {M}(\partial \Omega )$
 with compact support in $\partial \Omega \setminus \Sigma$
with compact support in $\partial \Omega \setminus \Sigma$ , there holds
(4.13)\begin{equation} -\int_\Omega \mathbb{K}_\mu[\nu] L_\mu\eta\,\mathrm{d} x={-}\int_{\partial\Omega}\frac{\partial \eta}{\partial{\bf n}}(y)\frac{1}{P_\mu(x_0,y)}\, \mathrm{d} \nu(y),\quad \forall \eta \in \mathbf{X}_\mu(\Omega), \end{equation}where $P_\mu (x_0,y)$
, there holds
(4.13)\begin{equation} -\int_\Omega \mathbb{K}_\mu[\nu] L_\mu\eta\,\mathrm{d} x={-}\int_{\partial\Omega}\frac{\partial \eta}{\partial{\bf n}}(y)\frac{1}{P_\mu(x_0,y)}\, \mathrm{d} \nu(y),\quad \forall \eta \in \mathbf{X}_\mu(\Omega), \end{equation}where $P_\mu (x_0,y)$
 is defined in (4.3) and ${\bf X}_\mu (\Omega )$
is defined in (4.3) and ${\bf X}_\mu (\Omega )$ is defined by (2.8).
is defined by (2.8).
Proof.
(i) Let $\zeta \in C(\partial \Omega )$
 with compact support in $\partial \Omega \setminus \Sigma$
with compact support in $\partial \Omega \setminus \Sigma$ such that $\mathrm {dist}\,(\mathrm {supp}\, \zeta,\Sigma )=r>0$
such that $\mathrm {dist}\,(\mathrm {supp}\, \zeta,\Sigma )=r>0$ . We consider a function $Z\in C(\overline {\Omega })$
. We consider a function $Z\in C(\overline {\Omega })$ such that $Z(y)=\zeta (y)$
such that $Z(y)=\zeta (y)$ for any $y\in C(\partial \Omega )$
for any $y\in C(\partial \Omega )$ and $Z(y)=0$
and $Z(y)=0$ in $\Sigma _{\frac {r}{2}}$
in $\Sigma _{\frac {r}{2}}$ . Set $r_0=\frac {1}{4}\min \{\beta _2,r\}$
. Set $r_0=\frac {1}{4}\min \{\beta _2,r\}$ where $\beta _2$
where $\beta _2$ is the constant in (A.7). Let $\{\Sigma _n\}$
is the constant in (A.7). Let $\{\Sigma _n\}$ be as in (4.6), $\eta \in \mathbf {X}_\mu (\Omega )$
be as in (4.6), $\eta \in \mathbf {X}_\mu (\Omega )$ and $v_n$
and $v_n$ be the solution of (4.8).
be the solution of (4.8).In view of the proof of proposition 4.2, $v_n\in C(\overline {\Omega \setminus \Sigma _n})$
 and
\[ v_n(x)=\int_{\partial\Omega} \zeta(y) \tilde W(y)\,\mathrm{d}\omega^{x}_n(y) =\int_{\partial\Omega} P_{\mu}^n(x,y)\tilde W(y)\zeta(y) \,\mathrm{d} S_{\partial \Omega}(y). \]Put
and
\[ v_n(x)=\int_{\partial\Omega} \zeta(y) \tilde W(y)\,\mathrm{d}\omega^{x}_n(y) =\int_{\partial\Omega} P_{\mu}^n(x,y)\tilde W(y)\zeta(y) \,\mathrm{d} S_{\partial \Omega}(y). \]Put \[ v(x)=\int_{\partial\Omega} \zeta(y) \, \mathrm{d}\omega_{\Omega}^{x}(y) \quad \text{and} \quad w(x)=\int_{\partial\Omega} |\zeta(y)| \, \mathrm{d}\omega_{\Omega}^{x}(y). \]Then $v_n(x)\rightarrow v(x)$
\[ v(x)=\int_{\partial\Omega} \zeta(y) \, \mathrm{d}\omega_{\Omega}^{x}(y) \quad \text{and} \quad w(x)=\int_{\partial\Omega} |\zeta(y)| \, \mathrm{d}\omega_{\Omega}^{x}(y). \]Then $v_n(x)\rightarrow v(x)$
 for any $x\in \Omega$
for any $x\in \Omega$ and $|v_n(x)|\leq w(x)$
and $|v_n(x)|\leq w(x)$ in $\Omega \setminus \Sigma _n$
in $\Omega \setminus \Sigma _n$ . By [Reference Marcus and Véron30, proposition 1.3.7],
(4.14)\begin{equation} -\int_{\Omega\setminus\Sigma_n}v_n L_\mu \tilde Z \, \mathrm{d} x={-}\int_{\partial\Omega}\tilde W\zeta\frac{\partial \tilde Z}{\partial{\bf n}}\,\mathrm{d} S_{\partial \Omega},\quad \forall \tilde Z \in C^2_0(\Omega \setminus \Sigma_n). \end{equation}By approximation, the above equality is valid for any $\tilde Z \in C^{1,\gamma }(\overline {\Omega \setminus \Sigma _n}),$
. By [Reference Marcus and Véron30, proposition 1.3.7],
(4.14)\begin{equation} -\int_{\Omega\setminus\Sigma_n}v_n L_\mu \tilde Z \, \mathrm{d} x={-}\int_{\partial\Omega}\tilde W\zeta\frac{\partial \tilde Z}{\partial{\bf n}}\,\mathrm{d} S_{\partial \Omega},\quad \forall \tilde Z \in C^2_0(\Omega \setminus \Sigma_n). \end{equation}By approximation, the above equality is valid for any $\tilde Z \in C^{1,\gamma }(\overline {\Omega \setminus \Sigma _n}),$
 for some $\gamma \in (0,1)$
for some $\gamma \in (0,1)$ and $\Delta \tilde Z\in L^\infty (\Omega \setminus \Sigma _n)$
and $\Delta \tilde Z\in L^\infty (\Omega \setminus \Sigma _n)$ . Hence, we may choose $\tilde Z=\eta _n$
. Hence, we may choose $\tilde Z=\eta _n$ in (4.14), where $\eta _n$
in (4.14), where $\eta _n$ satisfies
\[ \left\{\begin{array}{ll} -L_{\mu }\eta_n={-}L_\mu\eta & \text{in } \Omega\setminus\Sigma_n\\ \eta_n =0 & \text{on } \partial( \Omega\setminus\Sigma_n) \end{array} \right. \]to obtain
satisfies
\[ \left\{\begin{array}{ll} -L_{\mu }\eta_n={-}L_\mu\eta & \text{in } \Omega\setminus\Sigma_n\\ \eta_n =0 & \text{on } \partial( \Omega\setminus\Sigma_n) \end{array} \right. \]to obtain (4.15)\begin{equation} -\int_{\Omega\setminus\Sigma_n} v_n L_\mu \eta \,\mathrm{d} x={-}\int_{\partial\Omega}\tilde W\zeta\frac{\partial \eta_n}{\partial{\bf n}} \, \mathrm{d} S_{\partial \Omega}. \end{equation}We note that $\eta _n\rightarrow \eta$
(4.15)\begin{equation} -\int_{\Omega\setminus\Sigma_n} v_n L_\mu \eta \,\mathrm{d} x={-}\int_{\partial\Omega}\tilde W\zeta\frac{\partial \eta_n}{\partial{\bf n}} \, \mathrm{d} S_{\partial \Omega}. \end{equation}We note that $\eta _n\rightarrow \eta$
 locally uniformly in $\Omega$
locally uniformly in $\Omega$ and in $C^1(\overline {\Omega \setminus \Sigma _1})$
and in $C^1(\overline {\Omega \setminus \Sigma _1})$ . Therefore, by the dominated convergence theorem, letting $n \to \infty$
. Therefore, by the dominated convergence theorem, letting $n \to \infty$ in (4.15), we obtain
(4.16)\begin{equation} -\int_{\Omega} v L_\mu \eta\,\mathrm{d} x={-}\int_{\partial\Omega}\tilde W \zeta \frac{\partial \eta}{\partial{\bf n}}\, \mathrm{d} S_{\partial \Omega}.\end{equation}
in (4.15), we obtain
(4.16)\begin{equation} -\int_{\Omega} v L_\mu \eta\,\mathrm{d} x={-}\int_{\partial\Omega}\tilde W \zeta \frac{\partial \eta}{\partial{\bf n}}\, \mathrm{d} S_{\partial \Omega}.\end{equation}
Now, let $h \in L^1(\partial \Omega ;\mathrm {d} \omega ^{x}_{\Omega })$
 with compact support in $\partial \Omega \setminus \Sigma$
with compact support in $\partial \Omega \setminus \Sigma$ such that $\mathrm {dist}\,(\mathrm {supp}\, h,\Sigma )=4r>0$
such that $\mathrm {dist}\,(\mathrm {supp}\, h,\Sigma )=4r>0$ . By (4.5) we may construct a sequence $\{h_n\}\subset C(\partial \Omega )$
. By (4.5) we may construct a sequence $\{h_n\}\subset C(\partial \Omega )$ such that $h_n$
such that $h_n$ has compact support in $\partial \Omega \setminus \Sigma$
has compact support in $\partial \Omega \setminus \Sigma$ with $\mathrm {dist}\,(\mathrm {supp}\, h_n,\Sigma )>r$
with $\mathrm {dist}\,(\mathrm {supp}\, h_n,\Sigma )>r$ for any $n\in \mathbb {N}.$
for any $n\in \mathbb {N}.$ In addition, the same sequence can be constructed such that $h_n\rightarrow h$
In addition, the same sequence can be constructed such that $h_n\rightarrow h$ in $L^1(\partial \Omega ;\mathrm {d} \omega ^{x_0}_{\Omega })$
in $L^1(\partial \Omega ;\mathrm {d} \omega ^{x_0}_{\Omega })$ and in $L^1(\partial \Omega )$
and in $L^1(\partial \Omega )$ .
.Set
\[ u_n(x)=\int_{\partial \Omega} K_\mu(x,y)h_n(y)\,\mathrm{d} \omega^{x_0}_{\Omega}(y)= \mathbb{K}_\mu[h_n\, \mathrm{d} \omega_{\Omega}^{x_0}](x), \quad x \in \Omega. \]Since $K_\mu (\cdot,y)\in C^2(\Omega )$
 for any $y \in \partial \Omega$
for any $y \in \partial \Omega$ , by the above equality, we deduce that $u_n \to u$
, by the above equality, we deduce that $u_n \to u$ locally uniformly in $\Omega,$
locally uniformly in $\Omega,$ where
\[ u(x)=\int_{\partial\Omega}K_{\mu}(x,y)h(y) \,\mathrm{d}\omega_{\Omega }^{x_0}(y)= \mathbb{K}_\mu[h\, \mathrm{d} \omega_{\Omega}^{x_0}](x), \quad x \in \Omega. \]By (4.16) with $v=u_n$
where
\[ u(x)=\int_{\partial\Omega}K_{\mu}(x,y)h(y) \,\mathrm{d}\omega_{\Omega }^{x_0}(y)= \mathbb{K}_\mu[h\, \mathrm{d} \omega_{\Omega}^{x_0}](x), \quad x \in \Omega. \]By (4.16) with $v=u_n$
 and $\zeta =h_n$
and $\zeta =h_n$ , there holds
(4.17)\begin{equation} -\int_{\Omega} u_n L_\mu \eta\,\mathrm{d} x={-}\int_{\partial\Omega}\tilde W h_n\frac{\partial \eta}{\partial{\bf n}}\,\mathrm{d} S_{\partial \Omega}.\end{equation}
, there holds
(4.17)\begin{equation} -\int_{\Omega} u_n L_\mu \eta\,\mathrm{d} x={-}\int_{\partial\Omega}\tilde W h_n\frac{\partial \eta}{\partial{\bf n}}\,\mathrm{d} S_{\partial \Omega}.\end{equation}
Now, by [Reference Barbatis, Gkikas and Tertikas3, theorem 9.2], there exists a positive constant $C=C(N,\Omega,\Sigma,\mu, \kappa )$
 such that $\| u_n \|_{L^\kappa (\Omega ;\phi _{\mu,\Sigma })} \leq C\int _\Omega |h_n|\,\mathrm {d}\omega _{\Omega }^{x_0}(y)$
such that $\| u_n \|_{L^\kappa (\Omega ;\phi _{\mu,\Sigma })} \leq C\int _\Omega |h_n|\,\mathrm {d}\omega _{\Omega }^{x_0}(y)$ for all $n \in {\mathbb {N}}$
for all $n \in {\mathbb {N}}$ and for any $1<\kappa <\min \left \{\frac {N+1}{N-1},\frac {N+{\alpha _{-}}+1}{N+{\alpha _{-}}-1}\right \}$
and for any $1<\kappa <\min \left \{\frac {N+1}{N-1},\frac {N+{\alpha _{-}}+1}{N+{\alpha _{-}}-1}\right \}$ . This in turn implies that $\{u_n\}$
. This in turn implies that $\{u_n\}$ is equi-integrable in $L^1(\Omega ;\phi _{\mu,\Sigma })$
is equi-integrable in $L^1(\Omega ;\phi _{\mu,\Sigma })$ . Therefore, by Vitali's convergence theorem, $u_n \to u$
. Therefore, by Vitali's convergence theorem, $u_n \to u$ in $L^1(\Omega ;\phi _{\mu,\Sigma })$
in $L^1(\Omega ;\phi _{\mu,\Sigma })$ . Letting $n\to \infty$
. Letting $n\to \infty$ in (4.17), we obtain (4.12).
in (4.17), we obtain (4.12).(ii) Assume $\mathrm {dist}\,(\mathrm {supp}\, \nu,\Sigma )=4r>0$
 and let $\{h_n\}$
and let $\{h_n\}$ be a sequence of functions in $C(\partial \Omega )$
be a sequence of functions in $C(\partial \Omega )$ with compact support in $\partial \Omega \setminus \Sigma$
with compact support in $\partial \Omega \setminus \Sigma$ such that $\mathrm {dist}\,(\mathrm {supp}\, h_n,\Sigma )\geq r$
such that $\mathrm {dist}\,(\mathrm {supp}\, h_n,\Sigma )\geq r$ and $h_n\rightharpoonup \nu$
and $h_n\rightharpoonup \nu$ , i.e.
(4.18)\begin{equation} \int_{\partial\Omega}\zeta h_n \, \mathrm{d} S_{\partial \Omega}\rightarrow \int_{\partial\Omega}\zeta \mathrm{d} \nu \quad \forall \zeta \in C(\partial\Omega). \end{equation}In addition, we assume that $\|h_n\|_{L^1(\partial \Omega )} \leq C\|\nu \|_{\mathfrak {M}(\partial \Omega )}$
, i.e.
(4.18)\begin{equation} \int_{\partial\Omega}\zeta h_n \, \mathrm{d} S_{\partial \Omega}\rightarrow \int_{\partial\Omega}\zeta \mathrm{d} \nu \quad \forall \zeta \in C(\partial\Omega). \end{equation}In addition, we assume that $\|h_n\|_{L^1(\partial \Omega )} \leq C\|\nu \|_{\mathfrak {M}(\partial \Omega )}$
 for every $n \geq 1$
for every $n \geq 1$ , for some positive constant $C$
, for some positive constant $C$ independent of $n$
independent of $n$ .
.
Set
\[ u_n(x)=\int_{\partial\Omega}K_{\mu}(x,y)\frac{h_n(y)}{\tilde W(y) P_\mu(x_0,y)} \,\mathrm{d}\omega_{\Omega }^{x_0}(y). \]By (4.5) and (4.18), we have \[ u_n(x)=\int_{\partial \Omega}K_{\mu}(x,y)h_n(y)\,\mathrm{d} S_{\partial \Omega}(y) \rightarrow\int_{\partial\Omega}K_{\mu}(x,y)\,\mathrm{d} \nu(y)=:u(x). \]It means $u_n \to u$
\[ u_n(x)=\int_{\partial \Omega}K_{\mu}(x,y)h_n(y)\,\mathrm{d} S_{\partial \Omega}(y) \rightarrow\int_{\partial\Omega}K_{\mu}(x,y)\,\mathrm{d} \nu(y)=:u(x). \]It means $u_n \to u$
 a.e. in $\Omega$
a.e. in $\Omega$ .
.
Finally, equality (4.13) can be obtained by proceeding as in the proof of (i) and hence we omit its proof.
5. Semilinear equations with a power absorption nonlinearity
5.1. Keller–Osserman estimates
In this section, we prove Keller–Osserman type estimates for nonnegative solutions of equation (E +).
Lemma 5.1 Assume $p>1$![]() . Let $u\in C^2(\Omega )$
. Let $u\in C^2(\Omega )$![]() be a nonnegative solution of equation (E +). Then there exists a positive constant $C=C(\Omega,\Sigma,\mu,p)$
be a nonnegative solution of equation (E +). Then there exists a positive constant $C=C(\Omega,\Sigma,\mu,p)$![]() such that
such that
Proof. Let $\beta _0$![]() be as in § A.1 and $\eta _{\beta _0} \in C_c^\infty ({\mathbb {R}}^N)$
be as in § A.1 and $\eta _{\beta _0} \in C_c^\infty ({\mathbb {R}}^N)$![]() such that
such that
where $\Omega _{\epsilon }$![]() is defined in (2.2). For $\varepsilon \in \left (0,\frac {\beta _0}{16}\right )$
is defined in (2.2). For $\varepsilon \in \left (0,\frac {\beta _0}{16}\right )$![]() , we define
, we define
Then $V_\varepsilon \geq 0$![]() in $\Omega \setminus \overline {\Omega }_\epsilon$
in $\Omega \setminus \overline {\Omega }_\epsilon$![]() . It can be checked that there exists $C=C(\Omega,\beta _0,\mu,p)>1$
. It can be checked that there exists $C=C(\Omega,\beta _0,\mu,p)>1$![]() such that the function $W_\varepsilon :=CV_\varepsilon$
such that the function $W_\varepsilon :=CV_\varepsilon$![]() satisfies
satisfies
Combining (E +) and (5.2) yields
We see that $(u-W_\varepsilon )^+\in H_0^1(\Omega \setminus \overline {\Omega }_\varepsilon )$![]() and $(u-W_\varepsilon )^+$
and $(u-W_\varepsilon )^+$![]() has compact support in $\Omega \setminus \overline {\Omega }_\varepsilon$
has compact support in $\Omega \setminus \overline {\Omega }_\varepsilon$![]() . By using $(u-W_\varepsilon )^+$
. By using $(u-W_\varepsilon )^+$![]() as a test function for (5.3), we deduce that
as a test function for (5.3), we deduce that

This and the assumption $\lambda _{\mu,\Sigma } >0$![]() imply $(u-W_\varepsilon )^+ = 0$
imply $(u-W_\varepsilon )^+ = 0$![]() , whence $u\leq W_\varepsilon$
, whence $u\leq W_\varepsilon$![]() in $\Omega \setminus \overline {\Omega }_\varepsilon$
in $\Omega \setminus \overline {\Omega }_\varepsilon$![]() . Letting $\varepsilon \to 0$
. Letting $\varepsilon \to 0$![]() , we obtain the desired result.
, we obtain the desired result.
The following theorem is the main tool in the study of the boundary removable singularities for nonnegative solutions of equation (E +). We assume additionally that $\Omega$![]() is a $C^3$
is a $C^3$![]() domain which is needed to apply proposition A.2.
domain which is needed to apply proposition A.2.
Theorem 5.2 Let $p>1,$![]() $F\subset \Sigma$
$F\subset \Sigma$![]() be a compact subset of $\Sigma$
be a compact subset of $\Sigma$![]() and $d_F(x)=\mathrm {dist}\,(x,F)$
and $d_F(x)=\mathrm {dist}\,(x,F)$![]() . We additionally assume that $\Omega$
. We additionally assume that $\Omega$![]() is a $C^3$
is a $C^3$![]() bounded domain. If $u\in C^2(\Omega )$
bounded domain. If $u\in C^2(\Omega )$![]() is a nonnegative solution of (E +) satisfying
is a nonnegative solution of (E +) satisfying
then there exists a positive constant $C=C(N,\Omega,\Sigma,\mu,p)$![]() such that
such that
Proof. The proof is in the spirit of [Reference Marcus and Véron30, proposition 3.4.3]. Let $\beta _5$![]() be the positive constant defined in proposition A.2. Let $\xi \in (\Sigma _{\beta _5}\cap \partial \Omega )\setminus F$
be the positive constant defined in proposition A.2. Let $\xi \in (\Sigma _{\beta _5}\cap \partial \Omega )\setminus F$![]() and put $d_{F,\xi } = \frac {1}{16} d_F(\xi )<1$
and put $d_{F,\xi } = \frac {1}{16} d_F(\xi )<1$![]() . Denote
. Denote
If $u$![]() is a nonnegative solution of (E +) in $\Omega$
is a nonnegative solution of (E +) in $\Omega$![]() then the function
then the function
is a nonnegative solution of
in $\Omega ^\xi.$![]()
Now we note that $u^\xi$![]() is a nonnegative $L_\mu$
is a nonnegative $L_\mu$![]() subharmonic function and satisfies [by (5.4)]
subharmonic function and satisfies [by (5.4)]
where
$\eta _{\frac {\beta _3}{d_{F, \xi }}}$![]() is the scaled version of the function $\eta _{\beta _3}$
is the scaled version of the function $\eta _{\beta _3}$![]() defined before (2.4), and
defined before (2.4), and

Set $R_0=\min \{\beta _5,1\}$![]() . In view of the proof of [Reference Barbatis, Gkikas and Tertikas3, lemma 6.2 and estimate (6.7)], there exists a positive constant $c$
. In view of the proof of [Reference Barbatis, Gkikas and Tertikas3, lemma 6.2 and estimate (6.7)], there exists a positive constant $c$![]() depending on $\Omega,\Sigma,\mu$
depending on $\Omega,\Sigma,\mu$![]() and
and

such that
Let $r_0=\frac {R_0}{16}$![]() and let $w_{r_0,\xi }$
and let $w_{r_0,\xi }$![]() be the supersolution of (5.7) in $\mathscr {B}(\frac {1}{d_{F,\xi }}\xi,r_0)\cap \Omega ^\xi$
be the supersolution of (5.7) in $\mathscr {B}(\frac {1}{d_{F,\xi }}\xi,r_0)\cap \Omega ^\xi$![]() constructed in proposition A.2 with $R=r_0$
constructed in proposition A.2 with $R=r_0$![]() and $z=\frac {1}{d_{F,\xi }}\xi$
and $z=\frac {1}{d_{F,\xi }}\xi$![]() .
.
Taking into account of (5.9) and using a similar argument as in the proof of lemma 5.1, we can show that
By (5.8), (5.9) and the above inequality, we may deduce that
where $c$![]() depends only on $\Omega,\Sigma,\mu,p,$
depends only on $\Omega,\Sigma,\mu,p,$![]() the $C^3$
the $C^3$![]() characteristic of $\Omega ^\xi$
characteristic of $\Omega ^\xi$![]() and the $C^2$
and the $C^2$![]() characteristic of $\Sigma ^\xi$
characteristic of $\Sigma ^\xi$![]() . As $d_{F, \xi } \leq 1$
. As $d_{F, \xi } \leq 1$![]() the $C^3$
the $C^3$![]() characteristic of $\Omega$
characteristic of $\Omega$![]() (respectively the $C^2$
(respectively the $C^2$![]() characteristic of $\Sigma$
characteristic of $\Sigma$![]() ) is also a $C^3$
) is also a $C^3$![]() characteristic of $\Omega ^\xi$
characteristic of $\Omega ^\xi$![]() (respectively a $C^2$
(respectively a $C^2$![]() characteristic of $\Sigma ^\xi$
characteristic of $\Sigma ^\xi$![]() ), therefore this constant $c$
), therefore this constant $c$![]() can be taken to be independent of $\xi$
can be taken to be independent of $\xi$![]() . Thus, for any $\xi \in (\Sigma _{\beta _5}\cap \partial \Omega )\setminus F$
. Thus, for any $\xi \in (\Sigma _{\beta _5}\cap \partial \Omega )\setminus F$![]() such that $d_{F}(x)\leq 16$
such that $d_{F}(x)\leq 16$![]() , there holds
, there holds
where $r_1=\frac {r_0}{16^2}.$![]()
Now, we consider three cases.
Case 1: $x\in \Sigma _{\frac {r_1}{32}}\cap \Omega$![]() and $d_F(x) < 1$
and $d_F(x) < 1$![]() . If $d_{\partial \Omega }(x)\leq \frac {r_1}{8+r_1}d_F(x)$
. If $d_{\partial \Omega }(x)\leq \frac {r_1}{8+r_1}d_F(x)$![]() then there exits a unique point in $\xi \in \partial \Omega \setminus F$
then there exits a unique point in $\xi \in \partial \Omega \setminus F$![]() such that $|x-\xi |=d_{\partial \Omega }(x)$
such that $|x-\xi |=d_{\partial \Omega }(x)$![]() . Hence,
. Hence,
$d_F(x)\leq \frac {8+r_1}{8}d_{F}(\xi )$![]() and $d_{\partial \Omega }(x)\leq \frac {r_1}{8}d_{F}(\xi )$
and $d_{\partial \Omega }(x)\leq \frac {r_1}{8}d_{F}(\xi )$![]() . This, combined with (5.11), (5.12) and the fact that $d_F(x)\approx d_{F}(\xi )$
. This, combined with (5.11), (5.12) and the fact that $d_F(x)\approx d_{F}(\xi )$![]() , yields
, yields
If $d_{\partial \Omega }(x)> \frac {r_1}{8+r_1}d_F(x)\geq \frac {r_1}{8+r_1}\,d_\Sigma (x)$![]() then by (5.1) and the fact that $d_{\partial \Omega }(x)\approx d_F(x)\approx d_\Sigma (x)$
then by (5.1) and the fact that $d_{\partial \Omega }(x)\approx d_F(x)\approx d_\Sigma (x)$![]() , we obtain
, we obtain
Thus, (5.5) holds for every $x\in \Sigma _{\frac {r_1}{4}}$![]() such that $d_F(x) <1$
such that $d_F(x) <1$![]() .
.
Case 2: $x\in \Sigma _{\frac {r_1}{32}}\cap \Omega$![]() and $d_F(x) \geq 1$
and $d_F(x) \geq 1$![]() . Let $\xi$
. Let $\xi$![]() be the unique point in $\partial \Omega \setminus F$
be the unique point in $\partial \Omega \setminus F$![]() such that $|x-\xi |=d_{\partial \Omega }(x)$
such that $|x-\xi |=d_{\partial \Omega }(x)$![]() . Since $u$
. Since $u$![]() is an $L_\mu$
is an $L_\mu$![]() -subharmonic function in $B(\xi,r_1) \cap \Omega$
-subharmonic function in $B(\xi,r_1) \cap \Omega$![]() , in view of the proof of (5.10), we obtain
, in view of the proof of (5.10), we obtain

where $C$![]() depend only on $\Omega,\Sigma,\mu,p.$
depend only on $\Omega,\Sigma,\mu,p.$![]()
Case 3: $x \in \Omega \setminus \Sigma _{\frac {r_1}{32}}$![]() . The proof is similar to the one of [Reference Gkikas and Véron21, proposition A.3] and we omit it. (ii) Let $x_0\in \Omega$
. The proof is similar to the one of [Reference Gkikas and Véron21, proposition A.3] and we omit it. (ii) Let $x_0\in \Omega$![]() . Put $\ell =d_{\partial \Omega }(x_0)$
. Put $\ell =d_{\partial \Omega }(x_0)$![]() and
and
If $x\in B\left (x_0,\frac {\ell }{2}\right )$![]() then $y=\ell ^{-1}x$
then $y=\ell ^{-1}x$![]() belongs to $B\left (y_0,\frac {1}{2}\right ),$
belongs to $B\left (y_0,\frac {1}{2}\right ),$![]() where $y_0=\ell ^{-1}x_0$
where $y_0=\ell ^{-1}x_0$![]() . Also we have that $\frac {1}{2}\leq d_{\Omega ^\ell }(y)\leq \frac {3}{2}$
. Also we have that $\frac {1}{2}\leq d_{\Omega ^\ell }(y)\leq \frac {3}{2}$![]() and $\frac {1}{2}\leq d_{\Sigma ^\ell }(y)$
and $\frac {1}{2}\leq d_{\Sigma ^\ell }(y)$![]() for each $y\in B\left (y_0,\frac {1}{2}\right )$
for each $y\in B\left (y_0,\frac {1}{2}\right )$![]() . Set $v(y)=u(\ell y)$
. Set $v(y)=u(\ell y)$![]() for $y\in B(y_0,\frac {1}{2})$
for $y\in B(y_0,\frac {1}{2})$![]() then $v$
then $v$![]() satisfies
satisfies
By the standard elliptic estimates and (5.1) we have
This, together with the equality $\nabla v(y)=\ell \nabla u(x)$![]() , estimate (5.5) implies
, estimate (5.5) implies

Therefore, estimate (5.6) follows since $x_0$![]() is an arbitrary point. The proof is complete.
is an arbitrary point. The proof is complete.
5.2. Removable boundary singularities
This subsection is devoted to the study of removable boundary singularities for nonnegative solutions of equation (E +) in the supercritical range. More precisely we will prove theorems 2.1 and 2.2.
Proof of theorem 2.1 We will only consider the case $\mu < H^2$![]() and $p=\frac {{\alpha _{+}}+1}{{\alpha _{+}}-1}$
and $p=\frac {{\alpha _{+}}+1}{{\alpha _{+}}-1}$![]() , since the proof in the other cases is very similar. Let $u$
, since the proof in the other cases is very similar. Let $u$![]() be a nonnegative solution of (E +) satisfying (2.5). By (5.5) with $F=\Sigma$
be a nonnegative solution of (E +) satisfying (2.5). By (5.5) with $F=\Sigma$![]() , there holds
, there holds
for some constant $C$![]() independent of $u$
independent of $u$![]() .
.
Let $\{\Omega _n\}$![]() be a $C^2$
be a $C^2$![]() exhaustion of $\Omega$
exhaustion of $\Omega$![]() and we write
and we write
By the representation formula in $\Omega _n,$![]() we have that
we have that
By (5.13), the definition of $\tilde W$![]() in (2.4), estimate (A.9) and proposition 4.1, we deduce
in (2.4), estimate (A.9) and proposition 4.1, we deduce
Since $G^{\Omega _n}_\mu (x,y)\uparrow G_\mu (x,y)$![]() for $x,y\in \Omega, x \neq y,$
for $x,y\in \Omega, x \neq y,$![]() (5.14) and (5.15) yield
(5.14) and (5.15) yield
Hence, there exists another positive constant $C$![]() independent of $u$
independent of $u$![]() such that
such that
Consequently, the function $v=u+\mathbb {G}_\mu [u^\frac {{\alpha _{+}}+1}{{\alpha _{+}}-1}]$![]() is a nonnegative $L_\mu$
is a nonnegative $L_\mu$![]() -harmonic in $\Omega$
-harmonic in $\Omega$![]() . This, together with theorem 3.3, implies the existence of a measure $\nu \in \mathfrak M^+(\partial \Omega )$
. This, together with theorem 3.3, implies the existence of a measure $\nu \in \mathfrak M^+(\partial \Omega )$![]() such that
such that
By proposition 4.1 and (5.13), we may deduce that $\nu$![]() has compact support in $\Sigma.$
has compact support in $\Sigma.$![]()
Next we will show that $\nu \equiv 0$![]() . Suppose by contradiction that $\nu \not \equiv 0$
. Suppose by contradiction that $\nu \not \equiv 0$![]() . Let $1< M\in \mathbb {N}$
. Let $1< M\in \mathbb {N}$![]() and $v_{M,n}$
and $v_{M,n}$![]() be the positive solution of
be the positive solution of

Since $M u$![]() is a supersolution of the above problem, we have that $0\leq v_{M,n}\leq Mu$
is a supersolution of the above problem, we have that $0\leq v_{M,n}\leq Mu$![]() in $\Omega _n$
in $\Omega _n$![]() for any $n\in \mathbb {N}.$
for any $n\in \mathbb {N}.$![]() As a result, there exists $v_M\in C^2(\Omega )$
As a result, there exists $v_M\in C^2(\Omega )$![]() such that $v_{M,n}\to v_M$
such that $v_{M,n}\to v_M$![]() locally uniformly in $\Omega$
locally uniformly in $\Omega$![]() and $L_\mu v_M+ v_{M}^\frac {{\alpha _{+}}+1}{{\alpha _{+}}-1}=0$
and $L_\mu v_M+ v_{M}^\frac {{\alpha _{+}}+1}{{\alpha _{+}}-1}=0$![]() in $\Omega$
in $\Omega$![]() . As $v_M\leq Mu$
. As $v_M\leq Mu$![]() , it follows that $v_M$
, it follows that $v_M$![]() satisfies (2.5) and hence thanks to theorem 5.2, estimate (5.5) holds for $v_M$
satisfies (2.5) and hence thanks to theorem 5.2, estimate (5.5) holds for $v_M$![]() with $F=\Sigma$
with $F=\Sigma$![]() , namely
, namely
for some constant $C$![]() independent of $v_M$
independent of $v_M$![]() . By using an argument similar to the one leading to (5.16), we derive
. By using an argument similar to the one leading to (5.16), we derive
for some constant $C_0$![]() independent of $v_M$
independent of $v_M$![]() . Also, by the representation formula we have
. Also, by the representation formula we have

From (5.17), we have

By proposition 2.7 (ii), we find
Hence, letting $n\to \infty$![]() in (5.20), we obtain
in (5.20), we obtain

We see that the above display contradicts with (5.18) and (5.19). The proof is complete.
Next we turn to
Proof of theorem 2.2 Without loss of generality, we may assume that $z=0.$![]() Let $\zeta :\mathbb {R}\to [0,\infty )$
Let $\zeta :\mathbb {R}\to [0,\infty )$![]() be a smooth function such that $0\leq \zeta \leq 1,$
be a smooth function such that $0\leq \zeta \leq 1,$![]() $\zeta (t)=0$
$\zeta (t)=0$![]() for $|t|\leq 1$
for $|t|\leq 1$![]() and $\zeta (t)=1$
and $\zeta (t)=1$![]() for $|t|>2$
for $|t|>2$![]() . For $\varepsilon >0$
. For $\varepsilon >0$![]() , we set $\zeta _\varepsilon (x)=\zeta (\frac {|x|}{\varepsilon })$
, we set $\zeta _\varepsilon (x)=\zeta (\frac {|x|}{\varepsilon })$![]() . Since $u\in C^2(\Omega ),$
. Since $u\in C^2(\Omega ),$![]() there holds
there holds
By (5.5) and (5.6) with $F=\{0\} \subset \Sigma$![]() , (1.4) and the estimate $\int _{\Sigma _{\beta }}d_{\Sigma }(x)^{-\alpha }\,\mathrm {d} x \lesssim \beta ^{N-\alpha }$
, (1.4) and the estimate $\int _{\Sigma _{\beta }}d_{\Sigma }(x)^{-\alpha }\,\mathrm {d} x \lesssim \beta ^{N-\alpha }$![]() for $\alpha < N-k$
for $\alpha < N-k$![]() , we have
, we have


The estimates in (5.21) hold because of the assumption $p>1$![]() if ${\alpha _{+}} = 1$
if ${\alpha _{+}} = 1$![]() or $p<\frac {{\alpha _{+}}+1}{{\alpha _{+}}-1}$
or $p<\frac {{\alpha _{+}}+1}{{\alpha _{+}}-1}$![]() if ${\alpha _{+}}>1$
if ${\alpha _{+}}>1$![]() . For the last estimate in (5.22) and (5.23), we have used the assumption $p \geq \frac {N-{\alpha _{-}}+1}{N-{\alpha _{-}}-1}$
. For the last estimate in (5.22) and (5.23), we have used the assumption $p \geq \frac {N-{\alpha _{-}}+1}{N-{\alpha _{-}}-1}$![]() .
.
Estimates (5.21)–(5.23) imply that $L_\mu (\zeta _{\varepsilon }u) \in L^1(\Omega ;\phi _{\mu,\Sigma })$![]() . By [Reference Barbatis, Gkikas and Tertikas3, lemma 8.5], we have
. By [Reference Barbatis, Gkikas and Tertikas3, lemma 8.5], we have
Taking $\eta =\phi _{\mu,\Sigma },$![]() we obtain
we obtain
By letting $\varepsilon \to 0$![]() and Fatou's lemma, we deduce that
and Fatou's lemma, we deduce that

This implies that $u\equiv 0$![]() if $p>\frac {N-{\alpha _{-}}+1}{N-{\alpha _{-}}-1}$
if $p>\frac {N-{\alpha _{-}}+1}{N-{\alpha _{-}}-1}$![]() or $u\in L^p(\Omega ;\phi _{\mu,\Sigma })$
or $u\in L^p(\Omega ;\phi _{\mu,\Sigma })$![]() if $p=\frac {N-{\alpha _{-}}+1}{N-{\alpha _{-}}-1}.$
if $p=\frac {N-{\alpha _{-}}+1}{N-{\alpha _{-}}-1}.$![]()
The rest of the proof can proceed as in the proof of theorem 2.1 and we omit it.
5.3. Existence of solutions in the supercritical range
In this subsection, we discuss the existence of solutions for the following problem

where $p>1$![]() and $\nu \in \mathfrak M(\partial \Omega )$
and $\nu \in \mathfrak M(\partial \Omega )$![]() . We will focus on the supercritical case $p\geq \min \{\frac {N+1}{N-1},\frac {N-{\alpha _{-}}+1}{N-{\alpha _{-}}-1}\}$
. We will focus on the supercritical case $p\geq \min \{\frac {N+1}{N-1},\frac {N-{\alpha _{-}}+1}{N-{\alpha _{-}}-1}\}$![]() . In particular, we will give various sufficient conditions for the existence of solutions to (5.24).
. In particular, we will give various sufficient conditions for the existence of solutions to (5.24).
To this purpose, we use Besov space (see e.g. [Reference Adams and Hedberg1, Reference Stein35]). For $\sigma >0$![]() , $1\leq \kappa <\infty$
, $1\leq \kappa <\infty$![]() , we denote by $W^{\sigma,\kappa }(\mathbb {R}^d)$
, we denote by $W^{\sigma,\kappa }(\mathbb {R}^d)$![]() the Sobolev space over $\mathbb {R}^d$
the Sobolev space over $\mathbb {R}^d$![]() . If $\sigma$
. If $\sigma$![]() is not an integer the Besov space $B^{\sigma,\kappa }(\mathbb {R}^d)$
is not an integer the Besov space $B^{\sigma,\kappa }(\mathbb {R}^d)$![]() coincides with $W^{\sigma,\kappa }(\mathbb {R}^d)$
coincides with $W^{\sigma,\kappa }(\mathbb {R}^d)$![]() . When $\sigma$
. When $\sigma$![]() is an integer we denote $\Delta _{x,y}f:=f(x+y)+f(x-y)-2f(x)$
is an integer we denote $\Delta _{x,y}f:=f(x+y)+f(x-y)-2f(x)$![]() and
and

with norm

Then
with norm

These spaces are fundamental because they are stable under the real interpolation method developed by Lions and Petree.
It is well known that if $1<\kappa <\infty$![]() and $\alpha >0$
and $\alpha >0$![]() , $L_{\alpha,\kappa }(\mathbb {R}^d)=W^{\alpha,\kappa }(\mathbb {R}^d)$
, $L_{\alpha,\kappa }(\mathbb {R}^d)=W^{\alpha,\kappa }(\mathbb {R}^d)$![]() if $\alpha \in \mathbb {N}.$
if $\alpha \in \mathbb {N}.$![]() If $\alpha \notin \mathbb {N}$
If $\alpha \notin \mathbb {N}$![]() then the positive cone of their dual coincide, i.e. $(L_{-\alpha,\kappa '}(\mathbb {R}^d))^+=(B^{-\alpha,\kappa '}(\mathbb {R}^d))^+$
then the positive cone of their dual coincide, i.e. $(L_{-\alpha,\kappa '}(\mathbb {R}^d))^+=(B^{-\alpha,\kappa '}(\mathbb {R}^d))^+$![]() , always with equivalent norms.
, always with equivalent norms.
Lemma 5.3 Let $k\geq 1$![]() , $p$
, $p$![]() be as in (2.14), and $\nu \in \mathfrak {M}^+(\mathbb {R}^k)$
be as in (2.14), and $\nu \in \mathfrak {M}^+(\mathbb {R}^k)$![]() with compact support in $B^k\left (0,\frac {R}{2}\right )$
with compact support in $B^k\left (0,\frac {R}{2}\right )$![]() for some $R>0$
for some $R>0$![]() . Set
. Set
For $x \in \mathbb {R}^{k+1}$![]() , we write $x=(x_1,x') \in \mathbb {R}\times \mathbb {R}^{k}$
, we write $x=(x_1,x') \in \mathbb {R}\times \mathbb {R}^{k}$![]() . Then there exists a constant $C=C(R,N,k,\mu,p)>1$
. Then there exists a constant $C=C(R,N,k,\mu,p)>1$![]() such that
such that

Proof. The proof is very similar to that of [Reference Gkikas and Nguyen19, lemma 8.1], and hence we omit it.
Theorem 5.4 Let $k\geq 1$![]() , $p$
, $p$![]() be as in (2.14), and $\nu \in \mathfrak {M}^+(\partial \Omega )$
be as in (2.14), and $\nu \in \mathfrak {M}^+(\partial \Omega )$![]() with compact support in $\Sigma$
with compact support in $\Sigma$![]() . Then there exists a constant $C=C(\Omega,\Sigma,\mu )>1$
. Then there exists a constant $C=C(\Omega,\Sigma,\mu )>1$![]() such that
such that
where $\vartheta$![]() is given in (5.25).
is given in (5.25).
Proof. By (A.7), there exists $\xi ^j \in \Sigma$![]() , $j=1,2,\ldots,m_2$
, $j=1,2,\ldots,m_2$![]() (where $m_2 \in {\mathbb {N}}$
(where $m_2 \in {\mathbb {N}}$![]() depends on $N,\Sigma$
depends on $N,\Sigma$![]() ), and $\beta _2 \in (0,\frac {\beta _0}{4})$
), and $\beta _2 \in (0,\frac {\beta _0}{4})$![]() such that $\Omega \cap \Sigma _{\beta _2} \subset \cup _{j=1}^{m_2} \mathcal {V}_{\Sigma }(\xi ^j,\frac {\beta _0}{4})\cap \Omega$
such that $\Omega \cap \Sigma _{\beta _2} \subset \cup _{j=1}^{m_2} \mathcal {V}_{\Sigma }(\xi ^j,\frac {\beta _0}{4})\cap \Omega$![]() .
.
Assume $\nu \in \mathfrak {M}^+(\partial \Omega )$![]() with compact support in $\Sigma \cap \mathcal {V}_{\Sigma }(\xi ^j,\frac {\beta _0}{4})$
with compact support in $\Sigma \cap \mathcal {V}_{\Sigma }(\xi ^j,\frac {\beta _0}{4})$![]() for some $j\in \{1,\ldots,m_2\}$
for some $j\in \{1,\ldots,m_2\}$![]() .
.
On one hand, from (1.4), (3.3) and since $p< \frac {{\alpha _{+}}+1}{{\alpha _{+}}-1}$![]() and ${\alpha _{+}}\geq {\alpha _{-}}$
and ${\alpha _{+}}\geq {\alpha _{-}}$![]() , we have
, we have

On the other hand,

Combining the above estimates, we obtain

For any $x \in {\mathbb {R}}^N$![]() , we write $x=(x',x''',x_N)$
, we write $x=(x',x''',x_N)$![]() where $x'=(x_1,\ldots,x_k),$
where $x'=(x_1,\ldots,x_k),$![]() $x'''=(x_{k+1},\ldots,x_{N-1})$
$x'''=(x_{k+1},\ldots,x_{N-1})$![]() and define the $C^2$
and define the $C^2$![]() function
function
Taking into account the local representation of $\Sigma$![]() and $\partial \Omega$
and $\partial \Omega$![]() in § A.1, we may deduce that $\Phi :\mathcal {V}_\Sigma (\xi ^j,\beta _0)\to B^k(0,\beta _0)\times B^{N-1-k}(0,\beta _0)\times (-\beta _0,\beta _0)$
in § A.1, we may deduce that $\Phi :\mathcal {V}_\Sigma (\xi ^j,\beta _0)\to B^k(0,\beta _0)\times B^{N-1-k}(0,\beta _0)\times (-\beta _0,\beta _0)$![]() is $C^2$
is $C^2$![]() diffeomorphism and $\Phi (x)=(x',0_{{\mathbb {R}}^{N-k}})$
diffeomorphism and $\Phi (x)=(x',0_{{\mathbb {R}}^{N-k}})$![]() for $x=(x',x''',x_N) \in \Sigma$
for $x=(x',x''',x_N) \in \Sigma$![]() . In view of the proof of [Reference Adams and Hedberg1, lemma 5.2.2], there exists a measure $\overline {\nu }\in \mathfrak M^+(\mathbb {R}^k)$
. In view of the proof of [Reference Adams and Hedberg1, lemma 5.2.2], there exists a measure $\overline {\nu }\in \mathfrak M^+(\mathbb {R}^k)$![]() with compact support in $B^k\left (0,\frac {\beta _0}{4}\right )$
with compact support in $B^k\left (0,\frac {\beta _0}{4}\right )$![]() such that for any Borel $E\subset B^k\left (0,\frac {\beta _0}{4}\right ),$
such that for any Borel $E\subset B^k\left (0,\frac {\beta _0}{4}\right ),$![]() there holds $\overline {\nu }(E)=\nu (\Phi ^{-1}(E\times \{0_{{\mathbb {R}}^{N-k}}\}))$
there holds $\overline {\nu }(E)=\nu (\Phi ^{-1}(E\times \{0_{{\mathbb {R}}^{N-k}}\}))$![]() .
.
Set $\psi =(\psi ',\psi ''',\psi _N)=\Phi (x)$![]() then
then

By (1.4), (A.6) and (3.3), we have

Therefore,

Since $\nu \mapsto \nu \circ \Phi ^{-1}$![]() is a $C^2$
is a $C^2$![]() diffeomorphism between $\mathfrak M^+(\Sigma \cap \mathcal {V}_\Sigma (\xi ^j,\beta _0))\cap B^{-\vartheta,p}(\Sigma \cap \mathcal {V}_\Sigma (\xi ^j,\beta _0))$
diffeomorphism between $\mathfrak M^+(\Sigma \cap \mathcal {V}_\Sigma (\xi ^j,\beta _0))\cap B^{-\vartheta,p}(\Sigma \cap \mathcal {V}_\Sigma (\xi ^j,\beta _0))$![]() and $\mathfrak M^+(B^k(0,\beta _0))\cap B^{-\vartheta,p}(B^k(0,\beta _0))$
and $\mathfrak M^+(B^k(0,\beta _0))\cap B^{-\vartheta,p}(B^k(0,\beta _0))$![]() , using (5.26), (5.27) and lemma 5.3, we derive that
, using (5.26), (5.27) and lemma 5.3, we derive that
If $\nu \in \mathfrak {M}^+(\partial \Omega )$![]() has compact support in $\Sigma,$
has compact support in $\Sigma,$![]() we may write $\nu =\sum _{j=1}^{m_2}\nu _j$
we may write $\nu =\sum _{j=1}^{m_2}\nu _j$![]() , where $\nu _j\in \mathfrak {M}^+(\partial \Omega )$
, where $\nu _j\in \mathfrak {M}^+(\partial \Omega )$![]() with compact support in $\mathcal {V}(\xi ^j,\frac {\beta _0}{4})\cap \Sigma$
with compact support in $\mathcal {V}(\xi ^j,\frac {\beta _0}{4})\cap \Sigma$![]() . By (5.26), we can show that
. By (5.26), we can show that

The proof is complete.
Using theorem 5.4 and proposition 3.5, we are ready to prove theorem 2.5.
Proof of theorem 2.5 If $\nu$![]() is a positive measure which vanishes on Borel sets $E\subset \Sigma$
is a positive measure which vanishes on Borel sets $E\subset \Sigma$![]() with $\mathrm {Cap}^{\mathbb {R}^{k}}_{\vartheta,p'}$
with $\mathrm {Cap}^{\mathbb {R}^{k}}_{\vartheta,p'}$![]() -capacity zero then there exists an increasing sequence $\{\nu _n\}$
-capacity zero then there exists an increasing sequence $\{\nu _n\}$![]() of positive measures in $B^{-\vartheta,p}(\Sigma )$
of positive measures in $B^{-\vartheta,p}(\Sigma )$![]() which converges weakly to $\nu$
which converges weakly to $\nu$![]() (see [Reference Dal Maso10, Reference Feyel and de la Pradelle16]). By theorem 5.4, we have $\mathbb {K}_{\mu }[\nu _n]\in L^p(\Omega ;\phi _{\mu,\Sigma })$
(see [Reference Dal Maso10, Reference Feyel and de la Pradelle16]). By theorem 5.4, we have $\mathbb {K}_{\mu }[\nu _n]\in L^p(\Omega ;\phi _{\mu,\Sigma })$![]() , hence we may apply proposition 3.5 with $g(t)=|t|^{p-1}t$
, hence we may apply proposition 3.5 with $g(t)=|t|^{p-1}t$![]() to deduce that there exists a unique nonnegative weak solution $u_n$
to deduce that there exists a unique nonnegative weak solution $u_n$![]() of (5.24) with $\mathrm {tr}_{\mu,\Sigma}(u_n)=\nu _n.$
of (5.24) with $\mathrm {tr}_{\mu,\Sigma}(u_n)=\nu _n.$![]()
Since $\{ \nu _n \}$![]() is an increasing sequence of positive measures, by theorem 3.4, $\{u_n\}$
is an increasing sequence of positive measures, by theorem 3.4, $\{u_n\}$![]() is increasing and its limit is denoted by $u$
is increasing and its limit is denoted by $u$![]() . Moreover,
. Moreover,
By taking $\zeta =\phi _{\mu,\Sigma }$![]() in (5.28), we obtain
in (5.28), we obtain
which implies that $\{u_n\}$![]() and $\{u_n^p\}$
and $\{u_n^p\}$![]() are uniformly bounded in $L^1(\Omega ;\phi _{\mu,\Sigma })$
are uniformly bounded in $L^1(\Omega ;\phi _{\mu,\Sigma })$![]() . Therefore, $u_n \to u$
. Therefore, $u_n \to u$![]() in $L^1(\Omega ;\phi _{\mu,\Sigma })$
in $L^1(\Omega ;\phi _{\mu,\Sigma })$![]() and in $L^p(\Omega ;\phi _{\mu,\Sigma })$
and in $L^p(\Omega ;\phi _{\mu,\Sigma })$![]() . By letting $n \to \infty$
. By letting $n \to \infty$![]() in (5.28), we deduce
in (5.28), we deduce
This means $u$![]() is the unique weak solution of (5.24) with $\mathrm {tr}_{\mu,\Sigma}(u)=\nu$
is the unique weak solution of (5.24) with $\mathrm {tr}_{\mu,\Sigma}(u)=\nu$![]() .
.
Proof of theorem 2.6
1. Suppose $u$
 is a weak solution of (5.24) with $\mathrm {tr}_{\mu,\Sigma}(u)=\nu$
is a weak solution of (5.24) with $\mathrm {tr}_{\mu,\Sigma}(u)=\nu$ . Let $\beta >0$
. Let $\beta >0$ . Since
(5.29)$$\begin{align} \phi_{\mu,\Sigma}(x)& \approx C(\beta)\,d_{\partial \Omega}(x) \text{ and } K_{\mu}(x,y)\approx C(\beta)\,d_{\partial \Omega}(x)|x-y|^{{-}N},\nonumber\\& \quad\quad\forall (x,y)\in (\Omega\setminus \Sigma_\beta)\times \partial \Omega, \end{align}$$proceeding as in the proof of [Reference Marcus and Véron32, theorem 3.1], we may prove that $\nu$
. Since
(5.29)$$\begin{align} \phi_{\mu,\Sigma}(x)& \approx C(\beta)\,d_{\partial \Omega}(x) \text{ and } K_{\mu}(x,y)\approx C(\beta)\,d_{\partial \Omega}(x)|x-y|^{{-}N},\nonumber\\& \quad\quad\forall (x,y)\in (\Omega\setminus \Sigma_\beta)\times \partial \Omega, \end{align}$$proceeding as in the proof of [Reference Marcus and Véron32, theorem 3.1], we may prove that $\nu$
 is absolutely continuous with respect to the Bessel capacity $\mathrm {Cap}^{\mathbb {R}^{N-1}}_{\frac {2}{p},p'}$
is absolutely continuous with respect to the Bessel capacity $\mathrm {Cap}^{\mathbb {R}^{N-1}}_{\frac {2}{p},p'}$ .
.2. We assume that $\nu \in \mathfrak M^+(\partial \Omega ) \cap B^{-\frac {2}{p},p}(\partial \Omega )$
 has compact support $F \in \partial \Omega \setminus \Sigma.$
has compact support $F \in \partial \Omega \setminus \Sigma.$ Then by (5.29), we may apply [Reference Marcus and Véron32, Theorem A] to deduce that $\mathbb {K}_{\mu }[\nu ]\in L^p(\Omega \setminus \Sigma _\beta ;\phi _{\mu,\Sigma })$
Then by (5.29), we may apply [Reference Marcus and Véron32, Theorem A] to deduce that $\mathbb {K}_{\mu }[\nu ]\in L^p(\Omega \setminus \Sigma _\beta ;\phi _{\mu,\Sigma })$ for any $\beta >0$
for any $\beta >0$ . Denote $g_n(t)=\max \{ \min \{|t|^{p-1}t,n\},-n\}$
. Denote $g_n(t)=\max \{ \min \{|t|^{p-1}t,n\},-n\}$ . By applying proposition 3.5 with $g=g_n$
. By applying proposition 3.5 with $g=g_n$ , we deduce that there exists a unique weak solution $v_n \in L^1(\Omega ;\phi _{\mu,\Sigma })$
, we deduce that there exists a unique weak solution $v_n \in L^1(\Omega ;\phi _{\mu,\Sigma })$ of
(5.30)\begin{equation} \left\{ \begin{array}{@{}ll} - L_\mu v_n+g_n(v_n)=0 & \text{in }\ \Omega,\\ \mathrm {tr}_{\mu,\Sigma}(v_n)=\nu, \end{array} \right. \end{equation}such that $0 \leq v_n \leq \mathbb {K}_\mu [\nu ]$
of
(5.30)\begin{equation} \left\{ \begin{array}{@{}ll} - L_\mu v_n+g_n(v_n)=0 & \text{in }\ \Omega,\\ \mathrm {tr}_{\mu,\Sigma}(v_n)=\nu, \end{array} \right. \end{equation}such that $0 \leq v_n \leq \mathbb {K}_\mu [\nu ]$
 in $\Omega$
in $\Omega$ . Furthermore, by (3.5), $\{v_n\}$
. Furthermore, by (3.5), $\{v_n\}$ is non-increasing. Set $v=\lim _{n \to \infty }v_n,$
is non-increasing. Set $v=\lim _{n \to \infty }v_n,$ then $0 \leq v \leq \mathbb {K}_\mu [\nu ]$
then $0 \leq v \leq \mathbb {K}_\mu [\nu ]$ in $\Omega$
in $\Omega$ .
.
Since $v_n$
 is a weak solution of (5.30), we have
\[ - \int_{\Omega}v_n L_{\mu }\zeta \, \mathrm{d} x + \int_{\Omega} g_n(v_n) \zeta\,\mathrm{d} x ={-} \int_{\Omega} \mathbb{K}_{\mu}[\nu_n]L_{\mu }\zeta \,\mathrm{d} x\quad\forall \zeta \in\mathbf{X}_\mu(\Omega). \]By taking $\phi _{\mu,\Sigma }$
is a weak solution of (5.30), we have
\[ - \int_{\Omega}v_n L_{\mu }\zeta \, \mathrm{d} x + \int_{\Omega} g_n(v_n) \zeta\,\mathrm{d} x ={-} \int_{\Omega} \mathbb{K}_{\mu}[\nu_n]L_{\mu }\zeta \,\mathrm{d} x\quad\forall \zeta \in\mathbf{X}_\mu(\Omega). \]By taking $\phi _{\mu,\Sigma }$
 as a test function, we obtain
(5.31)\begin{equation} \int_{\Omega}\left(\lambda_{\mu,\Sigma} v_n + g_n(v_n)\right)\phi_{\mu,\Sigma} \,\mathrm{d} x=\lambda_{\mu,\Sigma} \int_{\Omega} \mathbb{K}_{\mu}[\nu]\phi_{\mu,\Sigma} \,\mathrm{d} x, \end{equation}which, together with by Fatou's lemma, implies that $v, v^p\in L^1(\Omega ;\phi _{\mu,\Sigma })$
as a test function, we obtain
(5.31)\begin{equation} \int_{\Omega}\left(\lambda_{\mu,\Sigma} v_n + g_n(v_n)\right)\phi_{\mu,\Sigma} \,\mathrm{d} x=\lambda_{\mu,\Sigma} \int_{\Omega} \mathbb{K}_{\mu}[\nu]\phi_{\mu,\Sigma} \,\mathrm{d} x, \end{equation}which, together with by Fatou's lemma, implies that $v, v^p\in L^1(\Omega ;\phi _{\mu,\Sigma })$
 and
\[ \int_{\Omega}\left(\lambda_{\mu,\Sigma} v + v^p \right)\phi_{\mu,\Sigma} \,\mathrm{d} x\leq \lambda_{\mu,\Sigma} \int_{\Omega} \mathbb{K}_{\mu}[\nu]\phi_{\mu,\Sigma} \,\mathrm{d} x. \]Hence, $v+\mathbb {G}_\mu [v^p]$
and
\[ \int_{\Omega}\left(\lambda_{\mu,\Sigma} v + v^p \right)\phi_{\mu,\Sigma} \,\mathrm{d} x\leq \lambda_{\mu,\Sigma} \int_{\Omega} \mathbb{K}_{\mu}[\nu]\phi_{\mu,\Sigma} \,\mathrm{d} x. \]Hence, $v+\mathbb {G}_\mu [v^p]$
 is a nonnegative $L_\mu$
is a nonnegative $L_\mu$ -harmonic function. By the representation theorem 3.3, there exists a unique $\overline {\nu }\in \mathfrak {M}^+(\partial \Omega )$
-harmonic function. By the representation theorem 3.3, there exists a unique $\overline {\nu }\in \mathfrak {M}^+(\partial \Omega )$ such that $v +\mathbb {G}_\mu [v^p]=\mathbb {K}_\mu [\overline {\nu }]$
such that $v +\mathbb {G}_\mu [v^p]=\mathbb {K}_\mu [\overline {\nu }]$ . Since $v \leq \mathbb {K}_\mu [\nu ]$
. Since $v \leq \mathbb {K}_\mu [\nu ]$ , by proposition 2.7 (i), $\overline \nu = \mathrm {tr}_{\mu,\Sigma}(v) \leq \mathrm {tr}_{\mu,\Sigma}(\mathbb {K}_\mu [\nu ]) = \nu$
, by proposition 2.7 (i), $\overline \nu = \mathrm {tr}_{\mu,\Sigma}(v) \leq \mathrm {tr}_{\mu,\Sigma}(\mathbb {K}_\mu [\nu ]) = \nu$ and hence $\overline {\nu }$
and hence $\overline {\nu }$ has compact support in $F$
has compact support in $F$ .
.
Let $\beta >0$
 be small enough such that $F\cap \overline {\Sigma }_{4\beta }=\emptyset$
be small enough such that $F\cap \overline {\Sigma }_{4\beta }=\emptyset$ . We consider a cut-off function $\psi _{\beta } \in C^\infty ({\mathbb {R}}^N)$
. We consider a cut-off function $\psi _{\beta } \in C^\infty ({\mathbb {R}}^N)$ such that $0\leq \psi _{\beta }\leq 1$
such that $0\leq \psi _{\beta }\leq 1$ in ${\mathbb {R}}^N$
in ${\mathbb {R}}^N$ , $\psi _\beta =1$
, $\psi _\beta =1$ in $\Omega \setminus \Sigma _{\frac {\beta }{2}}$
in $\Omega \setminus \Sigma _{\frac {\beta }{2}}$ and $\psi _{\beta }=0$
and $\psi _{\beta }=0$ in $\overline {\Sigma }_\frac {\beta }{4}$
in $\overline {\Sigma }_\frac {\beta }{4}$ . Let $\phi _0$
. Let $\phi _0$ be the eigenfunction associated to $-\Delta$
be the eigenfunction associated to $-\Delta$ in $\Omega$
in $\Omega$ such that $\sup _{x\in \Omega }\phi _0=1.$
such that $\sup _{x\in \Omega }\phi _0=1.$ Let $\eta \in C^\infty (\partial \Omega )$
Let $\eta \in C^\infty (\partial \Omega )$ such that $\eta =0$
such that $\eta =0$ on $\partial \Omega \cap \Sigma _{2\beta }$
on $\partial \Omega \cap \Sigma _{2\beta }$ . We consider the lifting $R[\eta ]$
. We consider the lifting $R[\eta ]$ in [Reference Marcus and Véron32, (1.11)]. Then $R\in C^2(\overline {\Omega })$
in [Reference Marcus and Véron32, (1.11)]. Then $R\in C^2(\overline {\Omega })$ has compact support in $\overline {\Omega }_{\beta _0}$
has compact support in $\overline {\Omega }_{\beta _0}$ for some $\beta _0>0$
for some $\beta _0>0$ small enough. In addition, $|\nabla R[\eta ] \cdot \nabla \phi _0|\lesssim \phi _0$
small enough. In addition, $|\nabla R[\eta ] \cdot \nabla \phi _0|\lesssim \phi _0$ in $\Omega$
in $\Omega$ , and $R[\eta ]=\eta$
, and $R[\eta ]=\eta$ for any $x\in \partial \Omega$
for any $x\in \partial \Omega$ .
.Then the function $\psi _{\beta,\eta }=\psi _{\beta }R[\eta ]\phi _0 \in C^{1,\gamma }(\overline {\Omega })\cap \mathbf {X}_\mu (\Omega )$
 for any $\gamma \in (0,1),$
for any $\gamma \in (0,1),$ $\psi _{\beta,\eta }=0$
$\psi _{\beta,\eta }=0$ on $\partial \Omega$
on $\partial \Omega$ and has compact support in $\overline {\Omega }\setminus \Sigma _\frac {\beta }{4}$
and has compact support in $\overline {\Omega }\setminus \Sigma _\frac {\beta }{4}$ . Hence, by (4.13) and the fact that $\frac {\partial \psi _{\beta,\zeta }}{\partial {\bf n}}= \frac {\partial \phi _0}{\partial {\bf n}}\eta$
. Hence, by (4.13) and the fact that $\frac {\partial \psi _{\beta,\zeta }}{\partial {\bf n}}= \frac {\partial \phi _0}{\partial {\bf n}}\eta$ on $\partial \Omega$
on $\partial \Omega$ , we obtain
(5.32)\begin{equation} \int_{\Omega}({-}v L_\mu\psi_{\beta,\eta} + v^p\psi_{\beta,\eta})\,\mathrm{d} x={-}\int_{\partial\Omega}\frac{\partial \phi_0}{\partial {\bf n}} \frac{\eta}{P_\mu(x_0,y)}\,\mathrm{d} \overline{\nu}(y). \end{equation}Also,
, we obtain
(5.32)\begin{equation} \int_{\Omega}({-}v L_\mu\psi_{\beta,\eta} + v^p\psi_{\beta,\eta})\,\mathrm{d} x={-}\int_{\partial\Omega}\frac{\partial \phi_0}{\partial {\bf n}} \frac{\eta}{P_\mu(x_0,y)}\,\mathrm{d} \overline{\nu}(y). \end{equation}Also, (5.33)\begin{equation} \int_{\Omega}(- v_nL_\mu\psi_{\beta,\zeta}+g_n(v_n)\psi_{\beta,\zeta})\,\mathrm{d} x={-}\int_{\partial\Omega}\frac{\partial \phi_0}{\partial {\bf n}} \frac{\eta}{P_\mu(x_0,y)}\,\mathrm{d} \nu(y). \end{equation}
(5.33)\begin{equation} \int_{\Omega}(- v_nL_\mu\psi_{\beta,\zeta}+g_n(v_n)\psi_{\beta,\zeta})\,\mathrm{d} x={-}\int_{\partial\Omega}\frac{\partial \phi_0}{\partial {\bf n}} \frac{\eta}{P_\mu(x_0,y)}\,\mathrm{d} \nu(y). \end{equation}
Since $v \leq v_n\leq \mathbb {K}_{\mu }[\nu ]$
 and $\mathbb {K}_{\mu }[\nu ]\in L^p(\Omega \setminus \Sigma _{\frac {\beta }{16}};\phi _{\mu,\Sigma })$
and $\mathbb {K}_{\mu }[\nu ]\in L^p(\Omega \setminus \Sigma _{\frac {\beta }{16}};\phi _{\mu,\Sigma })$ , by letting $n\to \infty$
, by letting $n\to \infty$ in (5.33), we obtain by the dominated convergence theorem that
(5.34)\begin{equation} \int_{\Omega}({-}v L_\mu\psi_{\beta,\zeta} + v^p\psi_{\beta,\zeta})\,\mathrm{d} x={-}\int_{\partial\Omega}\frac{\partial \phi_0}{\partial {\bf n}} \frac{\eta}{P_\mu(x_0,y)}\,\mathrm{d} \nu(y). \end{equation}From (5.32) and (5.34), we deduce that
in (5.33), we obtain by the dominated convergence theorem that
(5.34)\begin{equation} \int_{\Omega}({-}v L_\mu\psi_{\beta,\zeta} + v^p\psi_{\beta,\zeta})\,\mathrm{d} x={-}\int_{\partial\Omega}\frac{\partial \phi_0}{\partial {\bf n}} \frac{\eta}{P_\mu(x_0,y)}\,\mathrm{d} \nu(y). \end{equation}From (5.32) and (5.34), we deduce that \[ -\int_{\partial\Omega}\frac{\partial \phi_0}{\partial {\bf n}} \frac{\eta}{P_\mu(x_0,y)}\,\mathrm{d} \nu(y)={-}\int_{\partial\Omega}\frac{\partial \phi_0}{\partial {\bf n}} \frac{\eta}{P_\mu(x_0,y)}\,\mathrm{d} \overline{\nu}(y), \]which implies that $\nu =\overline {\nu },$
\[ -\int_{\partial\Omega}\frac{\partial \phi_0}{\partial {\bf n}} \frac{\eta}{P_\mu(x_0,y)}\,\mathrm{d} \nu(y)={-}\int_{\partial\Omega}\frac{\partial \phi_0}{\partial {\bf n}} \frac{\eta}{P_\mu(x_0,y)}\,\mathrm{d} \overline{\nu}(y), \]which implies that $\nu =\overline {\nu },$
 since $-\frac {\partial \phi _0}{\partial {\bf n}}\approx 1$
since $-\frac {\partial \phi _0}{\partial {\bf n}}\approx 1$ in $\partial \Omega,$
in $\partial \Omega,$ $P_\mu (x_0,y)\approx 1$
$P_\mu (x_0,y)\approx 1$ in $\partial \Omega \setminus \Sigma _{\frac {\beta }{4}}$
in $\partial \Omega \setminus \Sigma _{\frac {\beta }{4}}$ and $\nu,\;\overline {\nu }$
and $\nu,\;\overline {\nu }$ have compact support in $\partial \Omega \setminus \overline {\Sigma }_{4\beta }$
have compact support in $\partial \Omega \setminus \overline {\Sigma }_{4\beta }$ .
.3. If $\nu \in \mathfrak M^+(\partial \Omega )$
 vanishes on Borel sets $E\subset \partial \Omega$
vanishes on Borel sets $E\subset \partial \Omega$ with zero $\mathrm {Cap}^{\mathbb {R}^{N-1}}_{\frac {2}{p},p'}$
with zero $\mathrm {Cap}^{\mathbb {R}^{N-1}}_{\frac {2}{p},p'}$ -capacity and has compact support in $\partial \Omega \setminus \Sigma$
-capacity and has compact support in $\partial \Omega \setminus \Sigma$ then there exists a nondecreasing sequence $\{\nu _n\}$
then there exists a nondecreasing sequence $\{\nu _n\}$ of positive measures in $B^{-\frac {2}{p},p}(\partial \Omega )$
of positive measures in $B^{-\frac {2}{p},p}(\partial \Omega )$ which converges to $\nu$
which converges to $\nu$ (see [Reference Dal Maso10, Reference Feyel and de la Pradelle16]). Let $u_n$
(see [Reference Dal Maso10, Reference Feyel and de la Pradelle16]). Let $u_n$ be the unique weak solution of (5.24) with $\mathrm {tr}_{\mu,\Sigma}(u_n)=\nu _n$
be the unique weak solution of (5.24) with $\mathrm {tr}_{\mu,\Sigma}(u_n)=\nu _n$ . Since $\{ \nu _n \}$
. Since $\{ \nu _n \}$ is nondecreasing, by (3.5), $\{u_n\}$
is nondecreasing, by (3.5), $\{u_n\}$ is nondecreasing. Moreover, $0 \leq u_n \leq \mathbb {K}_\mu [\nu _n] \leq \mathbb {K}_\mu [\nu ]$
is nondecreasing. Moreover, $0 \leq u_n \leq \mathbb {K}_\mu [\nu _n] \leq \mathbb {K}_\mu [\nu ]$ . Denote $u=\lim _{n \to \infty }u_n$
. Denote $u=\lim _{n \to \infty }u_n$ . By an argument similar to the one leading to (5.31), we obtain
\[ \int_{\Omega}\left(\lambda_{\mu,\Sigma} u_{n} + u_n^p\right)\phi_{\mu,\Sigma} \,\mathrm{d} x=\lambda_{\mu,\Sigma}\int_{\Omega} \mathbb{K}_{\mu}[\nu_n]\phi_{\mu,\Sigma} \,\mathrm{d} x, \]which yields that $u, u^p\in L^1(\Omega ;\phi _{\mu,\Sigma })$
. By an argument similar to the one leading to (5.31), we obtain
\[ \int_{\Omega}\left(\lambda_{\mu,\Sigma} u_{n} + u_n^p\right)\phi_{\mu,\Sigma} \,\mathrm{d} x=\lambda_{\mu,\Sigma}\int_{\Omega} \mathbb{K}_{\mu}[\nu_n]\phi_{\mu,\Sigma} \,\mathrm{d} x, \]which yields that $u, u^p\in L^1(\Omega ;\phi _{\mu,\Sigma })$
 . By the dominated convergence theorem, we derive
\[ \int_{\Omega} \left({-}u L_\mu\zeta + u^p\zeta\right)\,\mathrm{d} x={-}\int_{\Omega}\mathbb{K}_{\mu}[\nu]L_\mu\zeta \, \mathrm{d} x\quad\forall \zeta\in {\bf X}_\mu(\Omega), \]and thus $u$
. By the dominated convergence theorem, we derive
\[ \int_{\Omega} \left({-}u L_\mu\zeta + u^p\zeta\right)\,\mathrm{d} x={-}\int_{\Omega}\mathbb{K}_{\mu}[\nu]L_\mu\zeta \, \mathrm{d} x\quad\forall \zeta\in {\bf X}_\mu(\Omega), \]and thus $u$
 is the unique weak solution of (5.24).
is the unique weak solution of (5.24).4. If ${\mathbb 1}_{F}\nu$
 is absolutely continuous with respect to $\mathrm {Cap}^{\mathbb {R}^{N-1}}_{\frac {2}{p},p'}$
is absolutely continuous with respect to $\mathrm {Cap}^{\mathbb {R}^{N-1}}_{\frac {2}{p},p'}$ for any compact set $F\subset \partial \Omega \setminus \Sigma,$
for any compact set $F\subset \partial \Omega \setminus \Sigma,$ we set $\nu _n={\mathbb 1}_{\partial \Omega \setminus \Sigma _{\frac {1}{n}}}\nu$
we set $\nu _n={\mathbb 1}_{\partial \Omega \setminus \Sigma _{\frac {1}{n}}}\nu$ and $u_n$
and $u_n$ the weak solution of (5.24) with $\mathrm {tr}_{\mu,\Sigma}(u_n)=\nu _n$
the weak solution of (5.24) with $\mathrm {tr}_{\mu,\Sigma}(u_n)=\nu _n$ . By using an argument similar to that in case 3, we obtain the desired result.
. By using an argument similar to that in case 3, we obtain the desired result.
6. Semilinear equations with a power source nonlinearity
In this section, we study the following problem
where $p>1$![]() , $\sigma$
, $\sigma$![]() is a positive parameter and $\nu \in \mathfrak {M}^+(\partial \Omega )$
is a positive parameter and $\nu \in \mathfrak {M}^+(\partial \Omega )$![]() .
.
We remark that a positive function $u$![]() is a weak solution of ($\text{BVP}_-^{\sigma}$
is a weak solution of ($\text{BVP}_-^{\sigma}$![]() ) if and only if
) if and only if
In the following proposition, we give a necessary and sufficient condition for the existence of solutions to problem ($\text{BVP}_-^{\sigma}$![]() ).
).
Proposition 6.1 Assume $\mu \leq H^2$![]() , $p>1$
, $p>1$![]() and $\nu \in \mathfrak {M}^+(\partial \Omega )$
and $\nu \in \mathfrak {M}^+(\partial \Omega )$![]() . Then problem ($\text{BVP}_-^{\sigma}$
. Then problem ($\text{BVP}_-^{\sigma}$![]() ) admits a weak solution if and only if there exists a positive constant $C>0$
) admits a weak solution if and only if there exists a positive constant $C>0$![]() such that
such that
Proof. The proof is similar to that of [Reference Gkikas and Nguyen20, proposition 6.2] with some minor modifications, and hence we omit it.
6.1. Preparative results
For $\alpha \leq N$![]() , set
, set
Let $\alpha < N$![]() , $b>0$
, $b>0$![]() , $\theta >-N+k$
, $\theta >-N+k$![]() and $s>1$
and $s>1$![]() . We define the capacity $\text {Cap}_{\mathbb {N}_{\alpha },s}^{b,\theta }$
. We define the capacity $\text {Cap}_{\mathbb {N}_{\alpha },s}^{b,\theta }$![]() by
by

Here ${\mathbb 1}_E$![]() denotes the indicator function of $E$
denotes the indicator function of $E$![]() . By [Reference Adams and Hedberg1, theorem 2.5.1], we have
. By [Reference Adams and Hedberg1, theorem 2.5.1], we have
If $\mu <\frac {N^2}{4}$![]() and $\nu \in \mathfrak {M}^+(\partial \Omega )$
and $\nu \in \mathfrak {M}^+(\partial \Omega )$![]() , then, by (3.1) and (3.3), we can show that
, then, by (3.1) and (3.3), we can show that
and
Therefore, if the integral equation
has a solution $v$![]() for some $\ell >0$
for some $\ell >0$![]() then $\tilde v=d_{\partial \Omega }d_{\Sigma }^{-{\alpha _{-}}}v$
then $\tilde v=d_{\partial \Omega }d_{\Sigma }^{-{\alpha _{-}}}v$![]() satisfies
satisfies
This, together with [Reference Bidaut-Véron, Hoang, Nguyen and Véron5, proposition 2.7], implies that equation (6.1) has a positive solution $u$![]() for some $\sigma >0$
for some $\sigma >0$![]() , whence problem ($\text{BVP}_-^{\sigma}$
, whence problem ($\text{BVP}_-^{\sigma}$![]() ) has a weak positive solution $u$
) has a weak positive solution $u$![]() for some $\sigma >0$
for some $\sigma >0$![]() .
.
In order to show that (6.5) possesses a solution, we will apply the results in [Reference Kalton and Verbitsky23] which we recall here for the sake of completeness.
Let $\mathbf {Z}$![]() be a metric space and $\omega \in \mathfrak M^+(\mathbf {Z})$
be a metric space and $\omega \in \mathfrak M^+(\mathbf {Z})$![]() . Let $J : \mathbf {Z} \times \mathbf {Z} \to (0,\infty ]$
. Let $J : \mathbf {Z} \times \mathbf {Z} \to (0,\infty ]$![]() be a Borel positive kernel such that $J$
be a Borel positive kernel such that $J$![]() is symmetric and $1/J$
is symmetric and $1/J$![]() satisfies a quasi-metric inequality, i.e. there is a constant $C>1$
satisfies a quasi-metric inequality, i.e. there is a constant $C>1$![]() such that for all $x, y, z \in \mathbf {Z}$
such that for all $x, y, z \in \mathbf {Z}$![]() ,
,
Under these conditions, one can define the quasi-metric $\mathbf {d}$![]() by
by
and denote by $\mathfrak B(x,r):=\{y\in \mathbf {Z}:\; \mathbf {d}(x,y)< r\}$![]() the open $\mathbf {d}$
the open $\mathbf {d}$![]() -ball of radius $r > 0$
-ball of radius $r > 0$![]() and centre $x$
and centre $x$![]() . Note that this set can be empty.
. Note that this set can be empty.
For $\omega \in \mathfrak M^+(\mathbf {Z})$![]() and a positive function $\phi$
and a positive function $\phi$![]() , we define the potentials $\mathbb {J}[\omega ]$
, we define the potentials $\mathbb {J}[\omega ]$![]() and $\mathbb {J}[\phi,\omega ]$
and $\mathbb {J}[\phi,\omega ]$![]() by
by
For $t>1$![]() the capacity $\text {Cap}_{\mathbb {J},t}^\omega$
the capacity $\text {Cap}_{\mathbb {J},t}^\omega$![]() in $\mathbf {Z}$
in $\mathbf {Z}$![]() is defined for any Borel set $E\subset \mathbf {Z}$
is defined for any Borel set $E\subset \mathbf {Z}$![]() by
by
Proposition 6.2 ([Reference Kalton and Verbitsky23]) Let $p>1$![]() and $\lambda,\omega \in \mathfrak M^+(\mathbf {Z})$
and $\lambda,\omega \in \mathfrak M^+(\mathbf {Z})$![]() such that
such that
for any $r > 0,$![]() $x \in \mathbf {Z}$
$x \in \mathbf {Z}$![]() , where $C > 0$
, where $C > 0$![]() is a constant. Then the following statements are equivalent.
is a constant. Then the following statements are equivalent.
1. The equation $v=\mathbb {J}[|v|^p,\omega ]+\ell \mathbb {J}[\lambda ]$
 has a positive solution for $\ell >0$
has a positive solution for $\ell >0$ small.
small.2. For any Borel set $E \subset \mathbf {Z}$
 , there holds $\int _E \mathbb {J}[{\mathbb 1}_E\lambda ]^p \mathrm {d} \omega \leq C\, \lambda (E)$
, there holds $\int _E \mathbb {J}[{\mathbb 1}_E\lambda ]^p \mathrm {d} \omega \leq C\, \lambda (E)$ .
.3. The following inequality holds $\mathbb {J}[\mathbb {J}[\lambda ]^p,\omega ]\leq C\mathbb {J}[\lambda ]<\infty \ \omega -a.e.$

4. For any Borel set $E \subset \mathbf {Z}$
 there holds $\lambda (E)\leq C\, {\rm Cap}_{\mathbb {J},p'}^\omega (E)$
there holds $\lambda (E)\leq C\, {\rm Cap}_{\mathbb {J},p'}^\omega (E)$ .
.
We will point out below that $\mathbb {N}_\alpha$![]() defined in (6.2) with $\mathrm {d} \omega =d_{\partial \Omega }(x)^b\,d_\Sigma (x)^\theta {\mathbb 1}_{\Omega }(x) \mathrm {d}x$
defined in (6.2) with $\mathrm {d} \omega =d_{\partial \Omega }(x)^b\,d_\Sigma (x)^\theta {\mathbb 1}_{\Omega }(x) \mathrm {d}x$![]() satisfies all assumptions of $\mathbb {J}$
satisfies all assumptions of $\mathbb {J}$![]() in proposition 6.2, for some appropriate $b,\theta \in \mathbb {R}$
in proposition 6.2, for some appropriate $b,\theta \in \mathbb {R}$![]() . Let us first prove the quasi-metric inequality.
. Let us first prove the quasi-metric inequality.
Lemma 6.3 Let $\alpha \leq N$![]() . There exists a positive constant $C=C(\Omega,\Sigma,\alpha )$
. There exists a positive constant $C=C(\Omega,\Sigma,\alpha )$![]() such that
such that
Proof. Case 1: $0<\alpha \leq N$![]() . We first assume that $|x-y|<2|x-z|$
. We first assume that $|x-y|<2|x-z|$![]() . Then by the triangle inequality, we have $d_\Sigma (z)\leq |x-z|+d_\Sigma (x)\leq 2\max \{|x-z|,d_\Sigma (x)\}$
. Then by the triangle inequality, we have $d_\Sigma (z)\leq |x-z|+d_\Sigma (x)\leq 2\max \{|x-z|,d_\Sigma (x)\}$![]() hence
hence
If $|x-z|\geq d_\Sigma (x)$![]() then $|x-z|\geq d_{\partial \Omega }(x)$
then $|x-z|\geq d_{\partial \Omega }(x)$![]() which implies that $|x-z|\geq \frac {d_{\partial \Omega }(x)+|x-y|}{4}$
which implies that $|x-z|\geq \frac {d_{\partial \Omega }(x)+|x-y|}{4}$![]() . Now,
. Now,

since $d_{\partial \Omega }(x)\leq d_\Sigma (x).$![]()
If $|x-z|\leq d_\Sigma (x)$![]() then
then

since $d_{\partial \Omega }(y)\leq |x-y|+d_{\partial \Omega }(x)\leq 2\max \{|x-y|,d_\Sigma (x)\}.$![]() Combining (6.11)–(6.12), we obtain (6.10).
Combining (6.11)–(6.12), we obtain (6.10).
Next we consider the case $2|x-z|\leq |x-y|$![]() . Then $\frac {1}{2} |x-y|\leq |y-z|,$
. Then $\frac {1}{2} |x-y|\leq |y-z|,$![]() thus by symmetry we obtain (6.10).
thus by symmetry we obtain (6.10).
Case 2: $\alpha \leq 0$![]() . Let $b\in [0,2],$
. Let $b\in [0,2],$![]() since $d_\Sigma (x)\leq |x-y|+d_\Sigma (y)$
since $d_\Sigma (x)\leq |x-y|+d_\Sigma (y)$![]() , it follows that
, it follows that
Using the above estimate, we obtain

Since $d_{\partial \Omega }(x)\leq |x-y|+d_{\partial \Omega }(y),$![]() we can easily show that $\max \{|x-y|,d_{\partial \Omega }(x), d_{\partial \Omega }(y)\}\leq |x-y|+\min \{d_{\partial \Omega }(x),d_{\partial \Omega }(y)\}$
we can easily show that $\max \{|x-y|,d_{\partial \Omega }(x), d_{\partial \Omega }(y)\}\leq |x-y|+\min \{d_{\partial \Omega }(x),d_{\partial \Omega }(y)\}$![]() . Hence,
. Hence,

The desired result follows by the above inequality and (6.13).
Next we give sufficient conditions for (6.8) and (6.9) to hold.
Lemma 6.4 Let $b>0$![]() , $\theta +b>k-N$
, $\theta +b>k-N$![]() and $\mathrm {d} \omega =d_{\partial \Omega }(x)^b\,d_\Sigma (x)^\theta {\mathbb 1}_{\Omega }(x)\,\mathrm {d}x$
and $\mathrm {d} \omega =d_{\partial \Omega }(x)^b\,d_\Sigma (x)^\theta {\mathbb 1}_{\Omega }(x)\,\mathrm {d}x$![]() . Then
. Then

Proof. Let $\beta _0,\beta _1,\beta _2$![]() be as in § A.1 and $s<\frac {\beta _2}{32}$
be as in § A.1 and $s<\frac {\beta _2}{32}$![]() . We first assume that $x\in \Sigma _{\frac {\beta _2}{4}}$
. We first assume that $x\in \Sigma _{\frac {\beta _2}{4}}$![]() .
.
Case 1: $d_{\partial \Omega }(x)\geq 2s$![]() . Let $\Gamma =\partial \Omega$
. Let $\Gamma =\partial \Omega$![]() or $\Sigma.$
or $\Sigma.$![]() Then $\frac {1}{2}d_{\Gamma }(x)\leq d_\Gamma (y)\leq \frac {3}{2} d_\Gamma (x)$
Then $\frac {1}{2}d_{\Gamma }(x)\leq d_\Gamma (y)\leq \frac {3}{2} d_\Gamma (x)$![]() for any $y\in B(x,s)$
for any $y\in B(x,s)$![]() , therefore (6.14) follows easily in this case.
, therefore (6.14) follows easily in this case.
Case 2: $d_{\partial \Omega }(x)\leq 2s$![]() and $d_\Sigma (x)\geq 2s$
and $d_\Sigma (x)\geq 2s$![]() . By estimate (2.9) in [Reference Bidaut-Véron, Hoang, Nguyen and Véron5, Lemma 2.3], we have that
. By estimate (2.9) in [Reference Bidaut-Véron, Hoang, Nguyen and Véron5, Lemma 2.3], we have that
Therefore,

Case 3: $d_{\partial \Omega }(x)\leq 2s$![]() and $d_\Sigma (x)\leq 2s$
and $d_\Sigma (x)\leq 2s$![]() . By (A.2), there exists $\xi \in \Sigma$
. By (A.2), there exists $\xi \in \Sigma$![]() such that $B(x,s)\cap \Omega \subset V_\Sigma (\xi,\beta _0)$
such that $B(x,s)\cap \Omega \subset V_\Sigma (\xi,\beta _0)$![]() . If $y\in B(x,s),$
. If $y\in B(x,s),$![]() then $|y'-x'|< s$
then $|y'-x'|< s$![]() and $d_\Sigma (y)\leq d_\Sigma (x)+|x-y|\leq 3s$
and $d_\Sigma (y)\leq d_\Sigma (x)+|x-y|\leq 3s$![]() . Thus, by (A.3), $\delta _\Sigma ^\xi (y)\leq C_1s$
. Thus, by (A.3), $\delta _\Sigma ^\xi (y)\leq C_1s$![]() for any $y\in B(x,s)\cap \Omega$
for any $y\in B(x,s)\cap \Omega$![]() , where $C_1$
, where $C_1$![]() depends on $\| \Sigma \|_{C^2},N$
depends on $\| \Sigma \|_{C^2},N$![]() and $k$
and $k$![]() . Therefore,
. Therefore,

Here the similar constants depend on $N,k,\| \Sigma \|_{C^2}$![]() and $\beta _0$
and $\beta _0$![]() .
.
Case 4: $d_{\partial \Omega }(x)\leq 2s$![]() and $d_\Sigma (x)\leq 2s$
and $d_\Sigma (x)\leq 2s$![]() and $\theta <0$
and $\theta <0$![]() . We have that $d_\Sigma (y)^\theta \geq 3^\theta s^{\theta }$
. We have that $d_\Sigma (y)^\theta \geq 3^\theta s^{\theta }$![]() for any $y\in B(x,s).$
for any $y\in B(x,s).$![]() Hence,
Hence,

Case 5: $d_{\partial \Omega }(x)\leq 2s$![]() and $d_\Sigma (x)\leq 2s$
and $d_\Sigma (x)\leq 2s$![]() and $\theta \geq 0$
and $\theta \geq 0$![]() . By (A.7), there exists $\xi \in \Sigma$
. By (A.7), there exists $\xi \in \Sigma$![]() such that $B(x,s)\cap \Omega \subset \mathcal {V}_{\Sigma }(\xi,\beta _0).$
such that $B(x,s)\cap \Omega \subset \mathcal {V}_{\Sigma }(\xi,\beta _0).$![]() Let $C_\Sigma,$
Let $C_\Sigma,$![]() $C_{\partial \Omega }$
$C_{\partial \Omega }$![]() be as in (A.3), $A$
be as in (A.3), $A$![]() be as in (A.5) and $C_2=\max \{C_\Sigma \| \Sigma \|_{C^2},C_{\partial \Omega }\| \partial \Omega \|_{C^2}\}(A+1)$
be as in (A.5) and $C_2=\max \{C_\Sigma \| \Sigma \|_{C^2},C_{\partial \Omega }\| \partial \Omega \|_{C^2}\}(A+1)$![]() .
.
We first assume that $d_{\partial \Omega }(x)\leq \frac {s}{12NC_2}$![]() $d_\Sigma (x) \leq \frac {s}{12NC_2}.$
$d_\Sigma (x) \leq \frac {s}{12NC_2}.$![]() Set
Set
where $r_0=\frac {s}{12N(A+1)}$![]() . By (A.3), we have $\delta _\Sigma ^\xi (x)\leq \frac {s}{12N(A+1)}$
. By (A.3), we have $\delta _\Sigma ^\xi (x)\leq \frac {s}{12N(A+1)}$![]() and $\delta _{\partial \Omega }^\xi (x)\leq \frac {s}{12N(A+1)}$
and $\delta _{\partial \Omega }^\xi (x)\leq \frac {s}{12N(A+1)}$![]() . In addition for any $y\in {\mathcal {A}},$
. In addition for any $y\in {\mathcal {A}},$![]() we have
we have

where in the last inequality we used (A.5). This implies that ${\mathcal {A}}\subset B(x,s)$![]() . Consequently,
. Consequently,

If $d_{\partial \Omega }(x)\leq \frac {s}{12NC_2}$![]() and $d_\Sigma (x)\geq \frac {s}{12NC_2}$
and $d_\Sigma (x)\geq \frac {s}{12NC_2}$![]() then
then

and hence (6.16) follows by case 2.
If $d_{\partial \Omega }(x)\geq \frac {s}{12NC_2}$![]() then
then

and hence (6.16) follows by case 1.
Next we consider $x\in \Omega \setminus \Sigma _{\frac {\beta _2}{4}}$![]() and $s<\frac {\beta _2}{32}$
and $s<\frac {\beta _2}{32}$![]() . Then $d_\Sigma (y)\approx 1$
. Then $d_\Sigma (y)\approx 1$![]() for any $y\in \Omega \cap B(x,s)$
for any $y\in \Omega \cap B(x,s)$![]() . This, together with (6.15), implies the desired result.
. This, together with (6.15), implies the desired result.
If $\frac {\beta _2}{16}\leq s\leq 4 \text {diam}(\Omega )$![]() then $\omega (B(x,s))\approx 1$
then $\omega (B(x,s))\approx 1$![]() , hence estimate (6.14) follows straightforward. The proof is complete.
, hence estimate (6.14) follows straightforward. The proof is complete.
Lemma 6.5 Let $\alpha < N$![]() , $b> 0$
, $b> 0$![]() , $\theta >\max \{k-N-b,-b-\alpha \}$
, $\theta >\max \{k-N-b,-b-\alpha \}$![]() and $\mathrm {d} \omega =d_{\partial \Omega }(x)^b d_\Sigma (x)^\theta$
and $\mathrm {d} \omega =d_{\partial \Omega }(x)^b d_\Sigma (x)^\theta$![]() ${\mathbb 1}_{\Omega }(x)\,\mathrm {d}x$
${\mathbb 1}_{\Omega }(x)\,\mathrm {d}x$![]() . Then (6.8) holds.
. Then (6.8) holds.
Proof. We note that if $s\geq (4\mathrm {diam}\,(\Omega ))^{N-\alpha }$![]() then $\omega (\mathfrak B(x,s))=\omega (\overline {\Omega })<\infty$
then $\omega (\mathfrak B(x,s))=\omega (\overline {\Omega })<\infty$![]() , where $\mathfrak B(x,s)$
, where $\mathfrak B(x,s)$![]() is defined after (6.7), namely $\mathfrak B(x,s)=\{y \in \Omega \setminus \Sigma : \mathbf {d}(x,y)< s\}$
is defined after (6.7), namely $\mathfrak B(x,s)=\{y \in \Omega \setminus \Sigma : \mathbf {d}(x,y)< s\}$![]() and $\mathbf {d}(x,y)= \frac {1}{{\mathcal {N}}_\alpha (x,y)}$
and $\mathbf {d}(x,y)= \frac {1}{{\mathcal {N}}_\alpha (x,y)}$![]() . Let $M=(4\mathrm {diam}\,\Omega )^{N-\alpha }.$
. Let $M=(4\mathrm {diam}\,\Omega )^{N-\alpha }.$![]() We first note that it is enough to show that
We first note that it is enough to show that

Indeed, by the above display, we can easily deduce that

since $b>0$![]() and $b+\theta +\alpha >0.$
and $b+\theta +\alpha >0.$![]() This in turn implies (6.8).
This in turn implies (6.8).
In order to show (6.17), we will consider three cases.
Case 1: $s\leq d_{\partial \Omega }(x)^N\,d_\Sigma (x)^{-\alpha }$![]() .
.
(a) Let $y\in \mathfrak B(x,s)$
 be such that $d_{\partial \Omega }(x)\leq |x-y|$
be such that $d_{\partial \Omega }(x)\leq |x-y|$ and $d_\Sigma (x)\leq |x-y|.$
and $d_\Sigma (x)\leq |x-y|.$ Then
Then
thus if $|x-y|^{N-\alpha }\leq s\leq d_{\partial \Omega }(x)^N\,d_\Sigma (x)^{-\alpha }\leq d_{\partial \Omega }(x)^{N-\alpha }$![]() then $d_{\partial \Omega }(x)\approx d_\Sigma (x)\approx |x-y|$
then $d_{\partial \Omega }(x)\approx d_\Sigma (x)\approx |x-y|$![]() . Hence, there exist constants $C_1,C_2$
. Hence, there exist constants $C_1,C_2$![]() depending only on $\alpha,N$
depending only on $\alpha,N$![]() such that
such that

(b) Let $y\in \mathfrak B(x,s)$![]() be such that $d_{\partial \Omega }(x)\leq |x-y|$
be such that $d_{\partial \Omega }(x)\leq |x-y|$![]() and $d_\Sigma (x)> |x-y|.$
and $d_\Sigma (x)> |x-y|.$![]() Then
Then
thus if $|x-y|^{N}d_\Sigma (x)^{-\alpha } \leq s$![]() , then $|x-y|^{N}\leq s d_\Sigma (x)^{\alpha }\leq d_{\partial \Omega }(x)^N$
, then $|x-y|^{N}\leq s d_\Sigma (x)^{\alpha }\leq d_{\partial \Omega }(x)^N$![]() . Thus, $d_{\partial \Omega }(x)\approx |x-y|$
. Thus, $d_{\partial \Omega }(x)\approx |x-y|$![]() . Hence, there exist constants $C_1,C_2$
. Hence, there exist constants $C_1,C_2$![]() depending only on $\alpha,N$
depending only on $\alpha,N$![]() such that
such that

(c) Let $y\in \mathfrak B(x,s)$![]() be such that $d_{\partial \Omega }(x)>|x-y|$
be such that $d_{\partial \Omega }(x)>|x-y|$![]() . Then, $d_\Sigma (x)\geq d_{\partial \Omega }(x)>|x-y|$
. Then, $d_\Sigma (x)\geq d_{\partial \Omega }(x)>|x-y|$![]() and
and
Hence, there exist constants $C_1,C_2$![]() depending only on $\alpha,N$
depending only on $\alpha,N$![]() such that
such that

Combining (6.19)–(6.20) and lemma 6.4, we deduce
where $s_1=(d_\Sigma (x)^\alpha d_{\partial \Omega }(x)^{-2}s)^\frac {1}{N-2}$![]() .
.
Case 2: $d_{\partial \Omega }(x)^N\,d_\Sigma (x)^{-\alpha }< s\leq d_\Sigma (x)^{N-\alpha }$![]() .
.
(a) Let $y\in \mathfrak B(x,s)$
 be such that $d_{\partial \Omega }(x)\leq |x-y|$
be such that $d_{\partial \Omega }(x)\leq |x-y|$ and $d_\Sigma (x)\leq |x-y|.$
and $d_\Sigma (x)\leq |x-y|.$ Then
Then
Thus, if $|x-y|^{N-\alpha }\leq s\leq d_\Sigma (x)^{N-\alpha }$![]() then $d_\Sigma (x)\approx |x-y|$
then $d_\Sigma (x)\approx |x-y|$![]() . Hence, there exist constants $C_1,C_2$
. Hence, there exist constants $C_1,C_2$![]() which depending only on $\alpha,N$
which depending only on $\alpha,N$![]() such that
such that

(b) Let $y\in \mathfrak B(x,s)$![]() be such that $d_{\partial \Omega }(x)\leq |x-y|$
be such that $d_{\partial \Omega }(x)\leq |x-y|$![]() and $d_\Sigma (x)> |x-y|.$
and $d_\Sigma (x)> |x-y|.$![]() Then
Then
Hence, there exist constants $C_1,C_2$![]() depending only on $\alpha,N$
depending only on $\alpha,N$![]() such that
such that

(c) Let $y\in \mathfrak B(x,s)$![]() be such that $d_{\partial \Omega }(x)>|x-y|$
be such that $d_{\partial \Omega }(x)>|x-y|$![]() . Then $d_\Sigma (x)> |x-y|.$
. Then $d_\Sigma (x)> |x-y|.$![]() In addition,
In addition,
and
since $d_{\partial \Omega }(x)^N\,d_\Sigma (x)^{-\alpha }< s$![]() . Hence, there exist constants $C_1,C_2$
. Hence, there exist constants $C_1,C_2$![]() depending only on $\alpha,N$
depending only on $\alpha,N$![]() such that
such that

Combining (6.21)–(6.22) and lemma 6.4, we derive
where $s_2=(d_\Sigma (x)^{\alpha }s)^\frac {1}{N}.$![]()
Case 3: $d_\Sigma (x)^{N-\alpha }< s\leq (4\mathrm {diam}\,(\Omega ))^{N-\alpha }$![]() .
.
(a) Let $y\in \mathfrak B(x,s)$
 be such that $d_{\partial \Omega }(x)\leq |x-y|$
be such that $d_{\partial \Omega }(x)\leq |x-y|$ and $d_\Sigma (x)\leq |x-y|$
and $d_\Sigma (x)\leq |x-y|$ . Then
. Then
Hence, there exist constants $C_1,C_2$![]() which depend only on $\alpha,N$
which depend only on $\alpha,N$![]() such that
such that

(b) Let $y\in \mathfrak B(x,s)$![]() be such that $d_{\partial \Omega }(x)\leq |x-y|$
be such that $d_{\partial \Omega }(x)\leq |x-y|$![]() and $d_\Sigma (x)> |x-y|.$
and $d_\Sigma (x)> |x-y|.$![]() Then
Then
On one hand, if $\alpha >0,$![]() we have
we have
and since $d_\Sigma (x)^{N-\alpha }< s$![]() , we have
, we have
On the other hand, if $\alpha \leq 0$![]() then
then
and since $d_\Sigma (x)^{N-\alpha }< s$![]() , we obtain
, we obtain
Hence, there exist constants $C_1,C_2$![]() which depend only on $\alpha,N$
which depend only on $\alpha,N$![]() such that
such that

(c) Let $y\in \mathfrak B(x,s)$![]() be such that $d_{\partial \Omega }(x)>|x-y|$
be such that $d_{\partial \Omega }(x)>|x-y|$![]() . Then $d_\Sigma (x)> |x-y|$
. Then $d_\Sigma (x)> |x-y|$![]() and
and
In view of the proof of (6.22), we may deduce the existence of positive constants $C_1,C_2$![]() depending only on $\alpha,N$
depending only on $\alpha,N$![]() such that
such that

This and (6.24) imply the existence of two positive constants $\tilde C_1,\tilde C_2$![]() depending only on $\alpha,N$
depending only on $\alpha,N$![]() such that
such that

Combining (6.23)–(6.25) and lemma 6.4, we obtain
where $s_3=s^\frac {1}{N-\alpha }.$![]()
The proof is complete.
Lemma 6.6 Let $\alpha < N$![]() , $b> 0$
, $b> 0$![]() , $\theta >\max \{k-N-b,-b-\alpha \}$
, $\theta >\max \{k-N-b,-b-\alpha \}$![]() and $\mathrm {d} \omega =d_{\partial \Omega }(x)^b d_\Sigma (x)^\theta$
and $\mathrm {d} \omega =d_{\partial \Omega }(x)^b d_\Sigma (x)^\theta$![]() ${\mathbb 1}_{\Omega }(x)\,\mathrm {d}x$
${\mathbb 1}_{\Omega }(x)\,\mathrm {d}x$![]() . Then (6.9) holds.
. Then (6.9) holds.
Proof. Let $y\in \mathfrak B(x,s).$![]() We will consider three cases.
We will consider three cases.
Case 1: $d_{\partial \Omega }(x)\leq 2|x-y|$![]() and $d_\Sigma (x)\leq 2|x-y|$
and $d_\Sigma (x)\leq 2|x-y|$![]() . We can easily show that $d_{\partial \Omega }(y)\leq 3 |x-y|,$
. We can easily show that $d_{\partial \Omega }(y)\leq 3 |x-y|,$![]() $d_\Sigma (y)\leq 3|x-y|$
$d_\Sigma (y)\leq 3|x-y|$![]() and
and
Therefore, $|x-y|\lesssim s^{\frac {1}{N-\alpha }}$![]() , which implies that $d_\Sigma (x)+d_\Sigma (y)\lesssim s^{\frac {1}{N-\alpha }}$
, which implies that $d_\Sigma (x)+d_\Sigma (y)\lesssim s^{\frac {1}{N-\alpha }}$![]() . By (6.18), we can easily show that
. By (6.18), we can easily show that
Case 2: $d_{\partial \Omega }(x)\leq 2|x-y|$![]() and $d_\Sigma (x)\geq 2|x-y|$
and $d_\Sigma (x)\geq 2|x-y|$![]() . In this case, we have that $d_{\partial \Omega }(y)\leq 3 |x-y|,$
. In this case, we have that $d_{\partial \Omega }(y)\leq 3 |x-y|,$![]() $\frac {1}{2}\,d_\Sigma (x)\leq d_\Sigma (y)\leq \frac {3}{2}\,d_\Sigma (x)$
$\frac {1}{2}\,d_\Sigma (x)\leq d_\Sigma (y)\leq \frac {3}{2}\,d_\Sigma (x)$![]() and
and
This implies
By (6.18), we obtain

Case 3: $d_{\partial \Omega }(x)\geq 2|x-y|$![]() . We first note that $d_\Sigma (x)\geq 2|x-y|$
. We first note that $d_\Sigma (x)\geq 2|x-y|$![]() ,
,
From (6.18), we infer that
Combining cases 1–3, we derive (6.9).
By applying proposition 6.2 with $J(x,y)={\mathcal {N}}_{2{\alpha _{-}}}(x,y)$![]() , $\mathrm {d} \omega = (d_{\partial \Omega }(x)\,d_{\Sigma } (x)^{-{\alpha _{-}}})^{p+1}\mathrm {d}x$
, $\mathrm {d} \omega = (d_{\partial \Omega }(x)\,d_{\Sigma } (x)^{-{\alpha _{-}}})^{p+1}\mathrm {d}x$![]() and $\mathrm {d} \lambda = \mathrm {d} \nu$
and $\mathrm {d} \lambda = \mathrm {d} \nu$![]() , we obtain the following result for any $\nu \in \mathfrak {M}^+(\partial \Omega )$
, we obtain the following result for any $\nu \in \mathfrak {M}^+(\partial \Omega )$![]() .
.
Theorem 6.7 Let $p$![]() satisfy (2.11). Then the following statements are equivalent.
satisfy (2.11). Then the following statements are equivalent.
1. The equation
\[ v=\mathbb{N}_{2{\alpha_{-}}}[|v|^p\left(d_{\partial \Omega}d_{\Sigma}^{-{\alpha_{-}}}\right)^{p+1}]+\ell \mathbb{N}_{2{\alpha_{-}}}[\nu] \]has a positive solution for $\ell >0$
 small.
small.2. For any Borel set $E \subset \overline {\Omega }$
 , there holds
\[ \int_E \mathbb{N}_{2{\alpha_{-}}}[{\mathbb 1}_E\nu]^p \left(d_{\partial \Omega}(x)\,d_{\Sigma}(x)^{-{\alpha_{-}}}\right)^{p+1}\,\mathrm{d}x \leq C\, \nu(E). \]
, there holds
\[ \int_E \mathbb{N}_{2{\alpha_{-}}}[{\mathbb 1}_E\nu]^p \left(d_{\partial \Omega}(x)\,d_{\Sigma}(x)^{-{\alpha_{-}}}\right)^{p+1}\,\mathrm{d}x \leq C\, \nu(E). \]
3. The following inequality holds
\[ \mathbb{N}_{2{\alpha_{-}}}[\mathbb{N}_{2{\alpha_{-}}}[\nu]^p\left(d_{\partial \Omega}d_{\Sigma}^{-{\alpha_{-}}}\right)^{p+1}]\leq C\mathbb{N}_{2{\alpha_{-}}}[\nu]<\infty\quad a.e. \]
4. For any Borel set $E \subset \overline {\Omega }$
 there holds
\[ \nu(E)\leq C\, \mathrm{Cap}_{\mathbb{N}_{2{\alpha_{-}}},p'}^{p+1,-{\alpha_{-}}(p+1)}(E). \]
there holds
\[ \nu(E)\leq C\, \mathrm{Cap}_{\mathbb{N}_{2{\alpha_{-}}},p'}^{p+1,-{\alpha_{-}}(p+1)}(E). \]
Here we implicitly extend $\nu$
 to whole $\overline {\Omega }$
to whole $\overline {\Omega }$ by setting $\nu (\Omega )=0$
by setting $\nu (\Omega )=0$ .
.
6.2. Existence and nonexistence results in the case $\mu <\frac {N^2}{4}$
We first show that theorem 2.7 is a direct consequence of theorem 6.7.
Proof of theorem 2.7 We will use theorem 6.7 and show that statements 1–4 of the present theorem are equivalent to statements 1–4 of theorem 6.7 respectively. By (6.3)–(6.6) and [Reference Bidaut-Véron, Hoang, Nguyen and Véron5, proposition 2.7], we can easily show that equation (6.5) has a solution $v$![]() for some $\ell >0$
for some $\ell >0$![]() if and only if equation
if and only if equation
has a positive solution $u$![]() for some $\sigma >0$
for some $\sigma >0$![]() . This and the fact that $u$
. This and the fact that $u$![]() is a weak solution of ($\mathrm{P}_-^{\sigma}$
is a weak solution of ($\mathrm{P}_-^{\sigma}$![]() ) if and only if $u$
) if and only if $u$![]() is represented by (6.26) imply that statement 1 of theorem 6.7 is equivalent to statement 1 of the present theorem. In addition, in light of (6.3) and (6.4), we can deduce that statements 2–3 of theorem 6.7 are equivalent to statements 2–3 of the present theorem respectively.
is represented by (6.26) imply that statement 1 of theorem 6.7 is equivalent to statement 1 of the present theorem. In addition, in light of (6.3) and (6.4), we can deduce that statements 2–3 of theorem 6.7 are equivalent to statements 2–3 of the present theorem respectively.
Therefore, it remains to prove that, under condition (2.14), statement 4 of this theorem is equivalent to statement 4 of theorem 6.7. It is enough to show that for any compact subset $E \subset \Sigma$![]() , there holds
, there holds
where $\vartheta$![]() is defined in (2.15). Under condition (2.14), in view of (5.26)–(5.27), we may employ a similar argument as in the proof of [Reference Gkikas and Nguyen20, Estimate (6.36)] to reach the desired result.
is defined in (2.15). Under condition (2.14), in view of (5.26)–(5.27), we may employ a similar argument as in the proof of [Reference Gkikas and Nguyen20, Estimate (6.36)] to reach the desired result.
Remark 6.8 By [Reference Barbatis, Gkikas and Tertikas3, theorems B.1 and B.2], the following statements are valid.
(i) If $1< p<\min \{\frac {N+1}{N-1},\frac {N-{\alpha _{-}}+1}{N-{\alpha _{-}}-1}\}$
 then
(6.27)\begin{equation} \int_\Omega \mathbb{K}_\mu[|\nu|]^p \phi_{\mu,\Sigma}\,\mathrm{d}x \leq C(\Omega,\Sigma,\mu,p)\,|\nu|(\Omega)^p, \quad \forall \nu\in\mathfrak{M}(\partial\Omega). \end{equation}
then
(6.27)\begin{equation} \int_\Omega \mathbb{K}_\mu[|\nu|]^p \phi_{\mu,\Sigma}\,\mathrm{d}x \leq C(\Omega,\Sigma,\mu,p)\,|\nu|(\Omega)^p, \quad \forall \nu\in\mathfrak{M}(\partial\Omega). \end{equation}
(ii) If $1< p<\frac {N+1}{N-1}$
 and $\nu \in \mathfrak {M}(\partial \Omega )$
and $\nu \in \mathfrak {M}(\partial \Omega )$ has compact support in $\partial \Omega \setminus \Sigma$
has compact support in $\partial \Omega \setminus \Sigma$ then (6.27) holds true.
then (6.27) holds true.(iii) If $1< p<\frac {N-{\alpha _{-}}+1}{N-{\alpha _{-}}-1}$
 and $\nu \in \mathfrak {M}(\partial \Omega )$
and $\nu \in \mathfrak {M}(\partial \Omega )$ has compact support in $\Sigma$
has compact support in $\Sigma$ then (6.27) holds true.
then (6.27) holds true.
Hence, if one of the above cases occurs, we see that statement 2 of theorem 6.7 holds true, which implies the existence of solution of ($\text{BVP}_-^{\sigma}$![]() ) for some $\sigma >0$
) for some $\sigma >0$![]() .
.
Remark 6.9 Assume $\mu < \frac {N^2}{4}$![]() and $p \geq \frac {N-{\alpha _{-}}+1}{N-{\alpha _{-}}-1}$
and $p \geq \frac {N-{\alpha _{-}}+1}{N-{\alpha _{-}}-1}$![]() . Then for any $z \in \Sigma$
. Then for any $z \in \Sigma$![]() and any $\sigma >0$
and any $\sigma >0$![]() , problem (6.26) with $\nu =\delta _z$
, problem (6.26) with $\nu =\delta _z$![]() does not admit any positive weak solution. Indeed, suppose by contradiction that for some $z \in \Sigma$
does not admit any positive weak solution. Indeed, suppose by contradiction that for some $z \in \Sigma$![]() and $\sigma >0$
and $\sigma >0$![]() , there exists a positive solution $u \in L^p(\Omega ;\phi _{\mu,\Sigma })$
, there exists a positive solution $u \in L^p(\Omega ;\phi _{\mu,\Sigma })$![]() of equation (6.26). Without loss of generality, we can assume that $z =0 \in \Sigma$
of equation (6.26). Without loss of generality, we can assume that $z =0 \in \Sigma$![]() and $\sigma =1$
and $\sigma =1$![]() . From (6.26), $u(x) \geq \mathbb {K}_{\mu }[\delta _0] (x)= K_\mu (x,0)$
. From (6.26), $u(x) \geq \mathbb {K}_{\mu }[\delta _0] (x)= K_\mu (x,0)$![]() for a.e. $x \in \Omega$
for a.e. $x \in \Omega$![]() . Let ${\mathcal {C}}$
. Let ${\mathcal {C}}$![]() be a cone of vertex $0$
be a cone of vertex $0$![]() such that ${\mathcal {C}} \subset \Omega$
such that ${\mathcal {C}} \subset \Omega$![]() and there exist $r>0$
and there exist $r>0$![]() , $0<\ell <1$
, $0<\ell <1$![]() satisfying for any $x \in {\mathcal {C}}$
satisfying for any $x \in {\mathcal {C}}$![]() , $|x|< r$
, $|x|< r$![]() and $d_\Sigma (x)\geq d_{\partial \Omega }(x)> \ell |x|$
and $d_\Sigma (x)\geq d_{\partial \Omega }(x)> \ell |x|$![]() . Then, by (3.3) and (1.4),
. Then, by (3.3) and (1.4),

Since $p \geq \frac {N-{\alpha _{-}}+1}{N-{\alpha _{-}}-1}$![]() , the last integral is divergent, hence $u \not \in L^p(\Omega ;\phi _{\mu,\Sigma })$
, the last integral is divergent, hence $u \not \in L^p(\Omega ;\phi _{\mu,\Sigma })$![]() , which leads to a contradiction.
, which leads to a contradiction.
Remark 6.10 Assume $\mu < \frac {N^2}{4}$![]() and $p \geq \frac {N+1}{N-1}$
and $p \geq \frac {N+1}{N-1}$![]() . Proceeding as in remark 6.10, we may show that any $z \in \partial \Omega \setminus \Sigma$
. Proceeding as in remark 6.10, we may show that any $z \in \partial \Omega \setminus \Sigma$![]() and any $\sigma >0$
and any $\sigma >0$![]() , problem (6.26) with $\nu =\delta _z$
, problem (6.26) with $\nu =\delta _z$![]() does not admit any positive weak solution.
does not admit any positive weak solution.
By using the above capacities and theorem 6.7, we are able to prove theorem 2.8.
Proof Proof of theorem 2.8 when $\mu <\frac {N^2}{4}$
The fact that statements 1–3 are equivalent follows by using a similar argument as in the proof of theorem 2.7. Hence, it remains to show that statement 4 is equivalent to statements 1–3. Since
we may proceed as in the proof of [Reference Gkikas and Nguyen20, estimate (6.40)] to obtain the desired result.
When $p \geq \frac {{\alpha _{+}}+1}{{\alpha _{+}}-1}$![]() , the nonexistence occurs, as shown in the following remark.
, the nonexistence occurs, as shown in the following remark.
Remark 6.11 We additionally assume that $\Omega$![]() is $C^3$
is $C^3$![]() . If $p\geq \frac {{\alpha _{+}}+1}{{\alpha _{+}}-1}$
. If $p\geq \frac {{\alpha _{+}}+1}{{\alpha _{+}}-1}$![]() then, for any measure $\nu \in \mathfrak M^+(\partial \Omega )$
then, for any measure $\nu \in \mathfrak M^+(\partial \Omega )$![]() with compact support in $\Sigma$
with compact support in $\Sigma$![]() and any $\sigma >0$
and any $\sigma >0$![]() , there is no solution of problem (6.26). Indeed, it can be proved by contradiction. Suppose that we can find $\sigma >0$
, there is no solution of problem (6.26). Indeed, it can be proved by contradiction. Suppose that we can find $\sigma >0$![]() and a measure $\nu \in \mathfrak M^+(\partial \Omega )$
and a measure $\nu \in \mathfrak M^+(\partial \Omega )$![]() with compact support in $\Sigma$
with compact support in $\Sigma$![]() such that there exists a solution $0\leq u \in L^p(\Omega ;\phi _{\mu,\Sigma })$
such that there exists a solution $0\leq u \in L^p(\Omega ;\phi _{\mu,\Sigma })$![]() of (6.26). It follows that $\mathbb {K}_\mu [\nu ]\in L^p(\Omega ;\phi _{\mu,\Sigma })$
of (6.26). It follows that $\mathbb {K}_\mu [\nu ]\in L^p(\Omega ;\phi _{\mu,\Sigma })$![]() . Therefore, by proposition 3.5, there is a unique nontrivial nonnegative solution $v$
. Therefore, by proposition 3.5, there is a unique nontrivial nonnegative solution $v$![]() of
of
Moreover, $v \leq \mathbb {K}_{\mu }[\nu ]$![]() in $\Omega$
in $\Omega$![]() . This, together with proposition 3.2 and the fact that $\nu$
. This, together with proposition 3.2 and the fact that $\nu$![]() has compact support in $\Sigma$
has compact support in $\Sigma$![]() , implies $v(x) \leq \mathbb {K}_{\mu }[\nu ](x) \lesssim d_{\partial \Omega }(x)\nu (\Sigma )$
, implies $v(x) \leq \mathbb {K}_{\mu }[\nu ](x) \lesssim d_{\partial \Omega }(x)\nu (\Sigma )$![]() for $x$
for $x$![]() near $\partial \Omega \setminus \Sigma$
near $\partial \Omega \setminus \Sigma$![]() . Therefore, by theorem 2.1, we have that $v \equiv 0$
. Therefore, by theorem 2.1, we have that $v \equiv 0$![]() , which leads to a contradiction.
, which leads to a contradiction.
Remark 6.12 If ${\alpha _{-}}>1$![]() and $p\geq \frac {{\alpha _{-}}+1}{{\alpha _{-}}-1}$
and $p\geq \frac {{\alpha _{-}}+1}{{\alpha _{-}}-1}$![]() then for any measure $\nu \in \mathfrak M^+(\partial \Omega )$
then for any measure $\nu \in \mathfrak M^+(\partial \Omega )$![]() with compact support in $\partial \Omega$
with compact support in $\partial \Omega$![]() and any $\sigma >0$
and any $\sigma >0$![]() , there is no solution of (6.26). Indeed, it can be proved by contradiction. Suppose that we can find a measure $\nu \in \mathfrak M^+(\partial \Omega )$
, there is no solution of (6.26). Indeed, it can be proved by contradiction. Suppose that we can find a measure $\nu \in \mathfrak M^+(\partial \Omega )$![]() with compact support in $\partial \Omega \setminus \Sigma$
with compact support in $\partial \Omega \setminus \Sigma$![]() and $\sigma >0$
and $\sigma >0$![]() such that there exists a solution $0\leq u \in L^p(\Omega ;\phi _{\mu,\Sigma })$
such that there exists a solution $0\leq u \in L^p(\Omega ;\phi _{\mu,\Sigma })$![]() of (6.26). Then by theorem 2.8, estimate (2.13) holds for some constant $C>0$
of (6.26). Then by theorem 2.8, estimate (2.13) holds for some constant $C>0$![]() .
.
For simplicity, we assume that $0\in \Sigma$![]() . Let $\{x_n\} \subset \Omega$
. Let $\{x_n\} \subset \Omega$![]() be such that $\mathrm {dist}\,(x_n,\mathrm {supp}\, \nu )>\varepsilon >0$
be such that $\mathrm {dist}\,(x_n,\mathrm {supp}\, \nu )>\varepsilon >0$![]() for any $n\in \mathbb {N}$
for any $n\in \mathbb {N}$![]() and $x_n\to 0$
and $x_n\to 0$![]() as $n \to \infty$
as $n \to \infty$![]() . Then there exists a positive constant $C_1=C_1(\varepsilon,\Omega,\Sigma,\mu )$
. Then there exists a positive constant $C_1=C_1(\varepsilon,\Omega,\Sigma,\mu )$![]() such that
such that

Set
Then
Let ${\mathcal {C}}$![]() be a cone of vertex $0$
be a cone of vertex $0$![]() such that ${\mathcal {C}} \subset \Omega$
such that ${\mathcal {C}} \subset \Omega$![]() and there exist $r>0$
and there exist $r>0$![]() , $0<\ell <1$
, $0<\ell <1$![]() satisfying for any $x \in {\mathcal {C}}$
satisfying for any $x \in {\mathcal {C}}$![]() , $|x|< r$
, $|x|< r$![]() and $d_\Sigma (x)\geq d_{\partial \Omega }(x)> \ell |x|$
and $d_\Sigma (x)\geq d_{\partial \Omega }(x)> \ell |x|$![]() . Combining all above we have that
. Combining all above we have that

since $p\geq \frac {{\alpha _{-}}+1}{{\alpha _{-}}-1}$![]() . This is clearly a contradiction.
. This is clearly a contradiction.
6.3. Existence results in the case $\Sigma =\{0\}$ and $\mu = \frac {N^2}{4}$
and $\mu = \frac {N^2}{4}$
Let $0<\varepsilon < N$![]() . For any $(x,y)\in \overline {\Omega }\times \overline {\Omega }$
. For any $(x,y)\in \overline {\Omega }\times \overline {\Omega }$![]() such that $x \neq y,$
such that $x \neq y,$![]() we set
we set

and
Put

and
Note that
which, together with (3.2), implies
Next, from the estimates
we obtain
Set

Proceeding as in the proof of theorem 6.7, we obtain the following result
Theorem 6.13 Let $0<\varepsilon <2,$![]() $1< p<\frac {N+2-2\varepsilon }{N-2}$
$1< p<\frac {N+2-2\varepsilon }{N-2}$![]() and $\nu \in \mathfrak M^+(\partial \Omega )$
and $\nu \in \mathfrak M^+(\partial \Omega )$![]() . Then the following statements are equivalent.
. Then the following statements are equivalent.
1. The equation
(6.31)\begin{equation} u=\tilde{\mathbb{G}}_{H^2,\varepsilon}[u^p]+\sigma d_{\partial \Omega}|\cdot|^{-\frac{N}{2}}\mathbb{N}_{N-\varepsilon}[\nu] \end{equation}has a positive solution for $\sigma >0$
 small.
small.2. For any Borel set $E \subset \overline {\Omega }$
 , there holds
\[ \int_E \mathbb{N}_{N-\varepsilon}[{\mathbb 1}_E\nu]^p(x) \phi_{H^2,\Sigma}(x)^{p+1}\, \mathrm{d}x \leq C\nu(E). \]
, there holds
\[ \int_E \mathbb{N}_{N-\varepsilon}[{\mathbb 1}_E\nu]^p(x) \phi_{H^2,\Sigma}(x)^{p+1}\, \mathrm{d}x \leq C\nu(E). \]
3. The following inequality holds
\[ \mathbb{N}_{N-\varepsilon}[\mathbb{N}_{N-\varepsilon}[\nu]^p\left(d_{\partial \Omega}d_{\Sigma}^{-\frac{N}{2}}\right)^{p+1}]\leq C\,\mathbb{N}_{N-\varepsilon}[\nu]<\infty\quad a.e. \]
4. For any Borel set $E \subset \overline {\Omega }$
 there holds
\[ \nu(E)\leq C\, \mathrm{Cap}_{\mathbb{N}_{N-\varepsilon},p'}^{p+1,-\frac{N}{2}(p+1)}(E). \]
there holds
\[ \nu(E)\leq C\, \mathrm{Cap}_{\mathbb{N}_{N-\varepsilon},p'}^{p+1,-\frac{N}{2}(p+1)}(E). \]
Theorem 6.14 We assume that at least one of the statements 1–4 of theorem 6.13 is valid. Then problem ($\mathrm{P}_-^{\sigma}$![]() ) with $\mu =H^2$
) with $\mu =H^2$![]() admits a positive weak solution for $\sigma >0$
admits a positive weak solution for $\sigma >0$![]() small.
small.
Proof. By theorem 6.13, there exists a solution $u$![]() to equation (6.31) for $\sigma >0$
to equation (6.31) for $\sigma >0$![]() small. By (6.29) and (6.30), we have $u\gtrsim \mathbb {G}_{H^2}[u^p]+\sigma \mathbb {K}_{H^2}[\nu ]$
small. By (6.29) and (6.30), we have $u\gtrsim \mathbb {G}_{H^2}[u^p]+\sigma \mathbb {K}_{H^2}[\nu ]$![]() . By [Reference Bidaut-Véron, Hoang, Nguyen and Véron5, proposition 2.7], we deduce that equation
. By [Reference Bidaut-Véron, Hoang, Nguyen and Véron5, proposition 2.7], we deduce that equation
has a solution for $\sigma >0$![]() small. This means that it admits a positive weak solution for $\sigma >0$
small. This means that it admits a positive weak solution for $\sigma >0$![]() .
.
Remark 6.15 Let $\Sigma =\{0\}\subset \partial \Omega,$![]() $\mu =\frac {N^2}{4},$
$\mu =\frac {N^2}{4},$![]() $\nu =\delta _0$
$\nu =\delta _0$![]() and $1< p<\frac {N+2}{N-2}$
and $1< p<\frac {N+2}{N-2}$![]() . Then there exists $\varepsilon >0$
. Then there exists $\varepsilon >0$![]() small enough such that $1< p<\frac {N+2}{N-2+2\varepsilon }\leq \frac {N+2-2\varepsilon }{N-2}$
small enough such that $1< p<\frac {N+2}{N-2+2\varepsilon }\leq \frac {N+2-2\varepsilon }{N-2}$![]() . In addition, we have
. In addition, we have
Hence, statement 2 of theorem 6.13 is satisfied. This and theorem 6.14 imply that equation (6.32) has a solution for $\sigma >0$![]() small.
small.
Proof Proof of theorem 2.8 when $\Sigma =\{0\}$ and $\mu =\frac {N^2}{4}$
and $\mu =\frac {N^2}{4}$
Let $\varepsilon >0$![]() be small enough such that $1< p<\frac {N+2-2\varepsilon }{N-2}.$
be small enough such that $1< p<\frac {N+2-2\varepsilon }{N-2}.$![]() Let $K=\mathrm {supp}\,(\nu )\Subset \partial \Omega \setminus \{0\}$
Let $K=\mathrm {supp}\,(\nu )\Subset \partial \Omega \setminus \{0\}$![]() and $\tilde \beta =\frac {1}{2}\mathrm {dist}\,(K,\{0\})>0$
and $\tilde \beta =\frac {1}{2}\mathrm {dist}\,(K,\{0\})>0$![]() . By (3.4), we can easily show that
. By (3.4), we can easily show that
Hence, by proposition 6.1, (6.33), theorems 6.13 and 6.14, it is enough to show that
By (6.29) and (6.30), it is sufficient to show that
Indeed, on one hand, since $1< p<\frac {N+2-2\varepsilon }{N-2}$![]() , for any $x\in \Omega$
, for any $x\in \Omega$![]() there holds
there holds

The implicit constants in the above inequalities depend only on $\Omega,K,\tilde \beta,p,\varepsilon$![]() .
.
On the other hand, we have

where the implicit constants in the above inequalities depend only on $\Omega,K,\tilde \beta,p$![]() .
.
Hence, by (6.35) and (6.36), we have that
Next, by (3.2) and (6.28), for any $x \in \Omega$![]() and $y \in \Omega \setminus B(0,\frac {\tilde \beta }{4})$
and $y \in \Omega \setminus B(0,\frac {\tilde \beta }{4})$![]() , we have
, we have
This and (6.33) yield
Combining (6.37) and (6.38), we deduce (6.34). The proof is complete.
Acknowledgements
K. T. Gkikas acknowledges support by the Hellenic Foundation for Research and Innovation (H.F.R.I.) under the ‘2nd Call for H.F.R.I. Research Projects to support Post-Doctoral Researchers’ (Project Number: 59). P.-T. Nguyen was supported by Czech Science Foundation, Project GA22-17403S.
Appendix A. Barriers
Appendix A.1 Local representation of $\Sigma$ and $\partial \Omega$
and $\partial \Omega$
In this subsection, we present the local representation of $\Sigma$![]() and $\partial \Omega$
and $\partial \Omega$![]() .
.
If $k=0$![]() we always assume that $\Sigma =\{0\}$
we always assume that $\Sigma =\{0\}$![]() . If $k \in {\mathbb {N}}$
. If $k \in {\mathbb {N}}$![]() such that $1 \leq k \leq N-1$
such that $1 \leq k \leq N-1$![]() , we set $x=(x_1,\ldots,x_k,x_{k+1},\ldots,x_N) \in {\mathbb {R}}^N$
, we set $x=(x_1,\ldots,x_k,x_{k+1},\ldots,x_N) \in {\mathbb {R}}^N$![]() and $x=(x',x'')$
and $x=(x',x'')$![]() where $x'=(x_1,..,x_k) \in {\mathbb {R}}^k$
where $x'=(x_1,..,x_k) \in {\mathbb {R}}^k$![]() and $x''=(x_{k+1},\ldots,x_N) \in {\mathbb {R}}^{N-k}$
and $x''=(x_{k+1},\ldots,x_N) \in {\mathbb {R}}^{N-k}$![]() . For $\beta >0$
. For $\beta >0$![]() , we denote by $B(x,\beta )$
, we denote by $B(x,\beta )$![]() the ball in ${\mathbb {R}}^N$
the ball in ${\mathbb {R}}^N$![]() with centre $x \in {\mathbb {R}}^N$
with centre $x \in {\mathbb {R}}^N$![]() and radius $\beta$
and radius $\beta$![]() , and by $B^k(x',\beta )$
, and by $B^k(x',\beta )$![]() the ball in ${\mathbb {R}}^k$
the ball in ${\mathbb {R}}^k$![]() with centre at $x' \in {\mathbb {R}}^k$
with centre at $x' \in {\mathbb {R}}^k$![]() and radius $\beta$
and radius $\beta$![]() . For any $\xi \in \Sigma$
. For any $\xi \in \Sigma$![]() , we set
, we set
for some functions $\Gamma _i^\xi : {\mathbb {R}}^k \to {\mathbb {R}}$![]() , $i=k+1,\ldots,N$
, $i=k+1,\ldots,N$![]() .
.
Since $\Sigma$![]() is a $C^2$
is a $C^2$![]() compact submanifold in $\mathbb {R}^N$
compact submanifold in $\mathbb {R}^N$![]() without boundary, there exists $\beta _0>0$
without boundary, there exists $\beta _0>0$![]() such that the followings hold.
such that the followings hold.
(i) For any $x\in \Sigma _{6\beta _0}$
 , there is a unique $\xi \in \Sigma$
, there is a unique $\xi \in \Sigma$ satisfying $|x-\xi |=d_\Sigma (x)$
satisfying $|x-\xi |=d_\Sigma (x)$ .
.(ii) $d_\Sigma \in C^2(\Sigma _{4\beta _0})$
 , $|\nabla d_\Sigma |=1$
, $|\nabla d_\Sigma |=1$ in $\Sigma _{4\beta _0}$
in $\Sigma _{4\beta _0}$ and there exists $\eta \in L^\infty (\Sigma _{4\beta _0})$
and there exists $\eta \in L^\infty (\Sigma _{4\beta _0})$ such that
\[ \Delta d_\Sigma(x)=\frac{N-k-1}{d_\Sigma(x)}+ \eta(x) \quad \text{in } \Sigma_{4\beta_0} . \](See [Reference Véron34, lemma 2.2] and [Reference Dupaigne and Nedev13, lemma 6.2].)
such that
\[ \Delta d_\Sigma(x)=\frac{N-k-1}{d_\Sigma(x)}+ \eta(x) \quad \text{in } \Sigma_{4\beta_0} . \](See [Reference Véron34, lemma 2.2] and [Reference Dupaigne and Nedev13, lemma 6.2].)
(iii) For any $\xi \in \Sigma$
 , there exist $C^2$
, there exist $C^2$ functions $\Gamma _{i,\Sigma }^\xi \in C^2({\mathbb {R}}^k;{\mathbb {R}})$
functions $\Gamma _{i,\Sigma }^\xi \in C^2({\mathbb {R}}^k;{\mathbb {R}})$ , $i=k+1,\ldots,N$
, $i=k+1,\ldots,N$ , such that for any $\beta \in (0,6\beta _0)$
, such that for any $\beta \in (0,6\beta _0)$ and $V_\Sigma (\xi,\beta ) \subset \Omega$
and $V_\Sigma (\xi,\beta ) \subset \Omega$ (upon relabelling and reorienting the coordinate axes if necessary), there holds
(A.1)\begin{equation} V_\Sigma(\xi,\beta) \cap \Sigma\!=\!\{x=(x',x''): |x'-\xi'|<\beta,\; x_i\!=\!\Gamma_{i,\Sigma}^\xi (x'), \; \forall i=k+1,\ldots,N\}. \end{equation}
(upon relabelling and reorienting the coordinate axes if necessary), there holds
(A.1)\begin{equation} V_\Sigma(\xi,\beta) \cap \Sigma\!=\!\{x=(x',x''): |x'-\xi'|<\beta,\; x_i\!=\!\Gamma_{i,\Sigma}^\xi (x'), \; \forall i=k+1,\ldots,N\}. \end{equation}
(iv) There exist $m_1 \in {\mathbb {N}}$
 and points $\xi ^{j} \in \Sigma$
and points $\xi ^{j} \in \Sigma$ , $j=1,\ldots,m_1$
, $j=1,\ldots,m_1$ , and $\beta _1 \in (0, \beta _0)$
, and $\beta _1 \in (0, \beta _0)$ such that
(A.2)\begin{equation} \Sigma_{2\beta_1}\subset \cup_{j=1}^{m_1} V_{\Sigma}(\xi^j,\beta_0). \end{equation}
such that
(A.2)\begin{equation} \Sigma_{2\beta_1}\subset \cup_{j=1}^{m_1} V_{\Sigma}(\xi^j,\beta_0). \end{equation}
Now for $\xi \in \Sigma$![]() , set
, set

Then we see that there exists a constant $C_\Sigma$![]() depending only on $N,\Sigma$
depending only on $N,\Sigma$![]() such that
such that
where
with $\xi ^j=((\xi ^j)', (\xi ^j)'') \in \Sigma$![]() , $j=1,\ldots,m_1$
, $j=1,\ldots,m_1$![]() , being the points in (A.2).
, being the points in (A.2).
Moreover, $\beta _1$![]() can be chosen small enough such that for any $x \in \Sigma _{\beta _1}$
can be chosen small enough such that for any $x \in \Sigma _{\beta _1}$![]() ,
,
where $\xi \in \Sigma$![]() satisfies $|x-\xi |=d_\Sigma (x)$
satisfies $|x-\xi |=d_\Sigma (x)$![]() .
.
In the following, when $\Sigma =\partial \Omega$![]() or $\Sigma \subset \partial \Omega$
or $\Sigma \subset \partial \Omega$![]() is a $C^2$
is a $C^2$![]() submanifold, we will keep the same notations $\beta _0$
submanifold, we will keep the same notations $\beta _0$![]() and $\beta _1$
and $\beta _1$![]() for which (i)–(iv) hold.
for which (i)–(iv) hold.
When $\Sigma =\partial \Omega$![]() , we assume that
, we assume that

We also find that (A.1) with $\Sigma =\partial \Omega$![]() becomes
becomes

Thus, when $\Sigma \subset \partial \Omega$![]() is a $C^2$
is a $C^2$![]() compact submanifold in $\mathbb {R}^N$
compact submanifold in $\mathbb {R}^N$![]() without boundary, of dimension $0 \leq k \leq N-1$
without boundary, of dimension $0 \leq k \leq N-1$![]() , for any $x \in \Sigma$
, for any $x \in \Sigma$![]() , we have that
, we have that
Let $\xi \in \Sigma$![]() . For any $x\in V_\Sigma (\xi,\beta _0)\cap \Omega,$
. For any $x\in V_\Sigma (\xi,\beta _0)\cap \Omega,$![]() we define
we define
and

Then by (A.4), there exists a constant $A>1$![]() which depends only on $N$
which depends only on $N$![]() , $k$
, $k$![]() , $\|\Sigma \|_{C^2}$
, $\|\Sigma \|_{C^2}$![]() , $\|\partial \Omega \|_{C^2}$
, $\|\partial \Omega \|_{C^2}$![]() and $\beta _0$
and $\beta _0$![]() such that
such that
Thus, by (A.3) and (A.5), for any $\gamma \in \mathbb {R},$![]() we can show that there exists a constant $C>1$
we can show that there exists a constant $C>1$![]() which depends on $N,k,\|\Sigma \|_{C^2}, \|\partial \Omega \|_{C^2},\beta _0,\gamma$
which depends on $N,k,\|\Sigma \|_{C^2}, \|\partial \Omega \|_{C^2},\beta _0,\gamma$![]() such that
such that
We set
We may assume that

We also assume that there exist $m_2 \in {\mathbb {N}}$![]() and points $\xi ^{j} \in \Sigma$
and points $\xi ^{j} \in \Sigma$![]() , $j=1,\ldots,m_2$
, $j=1,\ldots,m_2$![]() , and $\beta _2 \in (0, \beta _1)$
, and $\beta _2 \in (0, \beta _1)$![]() such that
such that
We recall that the distance $\tilde d_{\Sigma }$![]() is defined in (2.3) as
is defined in (2.3) as
where $\mathrm {dist}\,^{\partial \Omega }$![]() denotes the geodesic distance on $\partial \Omega$
denotes the geodesic distance on $\partial \Omega$![]() .
.
Proposition A.1 [Reference Fall and Mahmoudi14, lemma 2.1]
There exists $\beta _3=\beta _3(\Sigma,\Omega )$![]() small enough such that, for any $x\in \Omega \cap \Sigma _{\beta _3}$
small enough such that, for any $x\in \Omega \cap \Sigma _{\beta _3}$![]() the following expansions hold
the following expansions hold

where $f_i$![]() , $i=1,2,3$
, $i=1,2,3$![]() , satisfy
, satisfy

We may choose $\beta _3$![]() small enough such that
small enough such that
Appendix A.2 Barriers
In this subsection, we assume that $\Omega$![]() is a $C^3$
is a $C^3$![]() open bounded domain. Then there exists $\beta _4>0$
open bounded domain. Then there exists $\beta _4>0$![]() depending on $C^3$
depending on $C^3$![]() characteristic of $\Omega$
characteristic of $\Omega$![]() such that for any $x\in \Omega _{\beta _4}$
such that for any $x\in \Omega _{\beta _4}$![]() the followings hold.
the followings hold.
(i) There exists a unique $\sigma (x)\in \partial \Omega$
 such that
$$\begin{align*} d_{\partial \Omega}(x)& =|x-\sigma(x)|, \quad \sigma(x)=x-d_{\partial \Omega}(x)\nabla d_{\partial \Omega}(x) \\& \quad \quad \text{and} \quad\nabla d_{\partial \Omega}(x)=\frac{x-\sigma(x)}{|x-\sigma(x)|}. \end{align*}$$
such that
$$\begin{align*} d_{\partial \Omega}(x)& =|x-\sigma(x)|, \quad \sigma(x)=x-d_{\partial \Omega}(x)\nabla d_{\partial \Omega}(x) \\& \quad \quad \text{and} \quad\nabla d_{\partial \Omega}(x)=\frac{x-\sigma(x)}{|x-\sigma(x)|}. \end{align*}$$
(ii) $\sigma (x)\in C^2(\overline {\Omega }_{\beta _4})$
 and $d_{\partial \Omega }\in C^3(\overline {\Omega }_{\beta _4}).$
and $d_{\partial \Omega }\in C^3(\overline {\Omega }_{\beta _4}).$
(iii) For any $i={1,\ldots,N}$
 there holds
there holds
For any $(x,z)\in \overline {\Omega }_{\beta _4}\times \partial \Omega$![]() , set
, set
Then
Finally, for any $0< R\leq \beta _4$![]() , we set
, we set
Proposition A.2 Let $\beta _5=\frac {1}{16}\min \{\beta _3,\beta _4\},$![]() $R_0\in (0,\beta _5]$
$R_0\in (0,\beta _5]$![]() and $0< R\leq R_0.$
and $0< R\leq R_0.$![]() For any $z\in \overline {\Sigma }_{R_0}\cap \partial \Omega,$
For any $z\in \overline {\Sigma }_{R_0}\cap \partial \Omega,$![]() there is a supersolution $w:=w_{R,z}$
there is a supersolution $w:=w_{R,z}$![]() of (E +) in $\mathscr {B}(z,R)$
of (E +) in $\mathscr {B}(z,R)$![]() such that
such that

More precisely, for $\gamma \in ({\alpha _{-}},{\alpha _{+}})$![]() , $w$
, $w$![]() can be constructed as
can be constructed as

with $M<0$![]() depending only on the $C^2$
depending only on the $C^2$![]() characteristic of $\partial \Omega,$
characteristic of $\partial \Omega,$![]() $b> \frac {2(p+1)-2(p-1)\min \{\gamma,0\}}{p-1}$
$b> \frac {2(p+1)-2(p-1)\min \{\gamma,0\}}{p-1}$![]() and $\Lambda >0$
and $\Lambda >0$![]() large enough depending only on $\gamma,N,b,p,M,R_0,$
large enough depending only on $\gamma,N,b,p,M,R_0,$![]() the $C^2$
the $C^2$![]() characteristic of $\Sigma$
characteristic of $\Sigma$![]() and the $C^3$
and the $C^3$![]() characteristic of $\partial \Omega.$
characteristic of $\partial \Omega.$![]()
Proof. Without loss of generality, we assume $z=0\in \overline {\Sigma }_{R_0}\cap \partial \Omega$![]() .
.
Case 1: $\mu < H^2$![]() . Set
. Set
where $\gamma >0, b$![]() and $\Lambda >0$
and $\Lambda >0$![]() will be determined later on.
will be determined later on.
Then, by straightforward computation and using proposition A.1, we obtain
where

By (i)–(iii), we have
Also,
Next we choose $\gamma \in ({\alpha _{-}},{\alpha _{+}}),$![]() then $\gamma ^2-\gamma (N-k)+\mu <0$
then $\gamma ^2-\gamma (N-k)+\mu <0$![]() . In addition, there exist $0<\ge _0<1,$
. In addition, there exist $0<\ge _0<1,$![]() $\delta _0>0$
$\delta _0>0$![]() and $M<0$
and $M<0$![]() such that if $\tilde d_\Sigma \leq \delta _0$
such that if $\tilde d_\Sigma \leq \delta _0$![]() then
then
and by (A.8),
It follows that if $\tilde d_\Sigma \leq \delta _0$![]() then
then
We set

In ${\mathcal {A}}_1 \cap {\mathcal {A}}_2$![]() , by (A.10), (A.11) and (A.12), we have
, by (A.10), (A.11) and (A.12), we have
In ${\mathcal {A}}_1^c\cap {\mathcal {A}}_2$![]() , we have $\tilde d_\Sigma \geq c_1(R^2-d_0^2)$
, we have $\tilde d_\Sigma \geq c_1(R^2-d_0^2)$![]() . If $d_{\partial \Omega }(x)\leq c_2(R^2-d_0(x)^2)^2,$
. If $d_{\partial \Omega }(x)\leq c_2(R^2-d_0(x)^2)^2,$![]() where
where
then we can show that
This, together with (A.10) and (A.11), implies (A.13). If $d_{\partial \Omega }(x)\geq c_2(R^2-d_0(x)^2)^2,$![]() then by proposition A.1, $\tilde d_\Sigma (x)\geq c_2c_3(\beta _3,\Sigma )(R^2-d_0(x)^2)^2.$
then by proposition A.1, $\tilde d_\Sigma (x)\geq c_2c_3(\beta _3,\Sigma )(R^2-d_0(x)^2)^2.$![]() Therefore,
Therefore,
If we choose $b>\frac {2(p+1)-2(p-1)\min \{\gamma,0\}}{p-1}=:b_0$![]() , then there exists $\Lambda$
, then there exists $\Lambda$![]() large enough depending on $c_4,R_0,b,p,\gamma$
large enough depending on $c_4,R_0,b,p,\gamma$![]() such that
such that
This and (A.14) yield
Similarly we may show that (A.15) is valid in ${\mathcal {A}}_3$![]() for some positive constant $\Lambda$
for some positive constant $\Lambda$![]() depending on $M,R_0,b,p,\gamma,\Omega,\Sigma.$
depending on $M,R_0,b,p,\gamma,\Omega,\Sigma.$![]()
Combining the above estimates, we deduce that for $\gamma \in ({\alpha _{-}},{\alpha _{+}})$![]() , $b>b_0$
, $b>b_0$![]() and $\Lambda >0$
and $\Lambda >0$![]() large enough, there holds
large enough, there holds
Case 2: $\mu =H^2$![]() . First we note that $\frac {\tilde d_\Sigma }{16R_0}\leq \frac {1}{2}$
. First we note that $\frac {\tilde d_\Sigma }{16R_0}\leq \frac {1}{2}$![]() in $\Omega \cap \mathscr {B}(0,R).$
in $\Omega \cap \mathscr {B}(0,R).$![]() Set
Set

where $\gamma >0, b$![]() and $\Lambda >0$
and $\Lambda >0$![]() will be determined later on. Then, by straightforward calculations we have
will be determined later on. Then, by straightforward calculations we have

where

By (i)–(iii) and the fact that $-\ln \frac {\tilde d_\Sigma }{16R_0}\geq \ln 2$![]() , we have
, we have

Also,

Next we choose $\delta _0>0$![]() and $M<0$
and $M<0$![]() such that if $\tilde d_\Sigma \leq \delta _0$
such that if $\tilde d_\Sigma \leq \delta _0$![]() then
then

and
We set

In $\tilde {\mathcal {A}}_1 \cap \tilde {\mathcal {A}}_2$![]() , by (A.16), (A.17) and (A.18), we have
, by (A.16), (A.17) and (A.18), we have
In $\tilde {\mathcal {A}}_1^c\cap \tilde {\mathcal {A}}_2$![]() , we have $\tilde d_\Sigma \geq \tilde c_1\frac {(R^2-d_0^2)}{|\ln \frac {\tilde d_\Sigma }{16R_0}|}$
, we have $\tilde d_\Sigma \geq \tilde c_1\frac {(R^2-d_0^2)}{|\ln \frac {\tilde d_\Sigma }{16R_0}|}$![]() . If $d_{\partial \Omega }(x)\leq \tilde c_2(R^2-d_0(x)^2)^2,$
. If $d_{\partial \Omega }(x)\leq \tilde c_2(R^2-d_0(x)^2)^2,$![]() where
where
Then, we can easily show that (A.19) is valid. The rest of the proof is the same as in case 1 with obvious modifications so we omit it. The proof is complete.