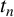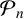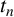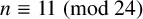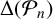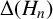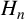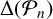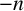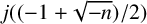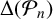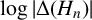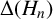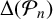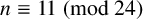1 Introduction and main results
Let E be an elliptic curve over
![]() ${\mathbb {C}}$
that has complex multiplication (CM) by an imaginary quadratic order
${\mathbb {C}}$
that has complex multiplication (CM) by an imaginary quadratic order
![]() $\mathcal {O}$
, by which we mean that the endomorphism ring
$\mathcal {O}$
, by which we mean that the endomorphism ring
![]() $\operatorname {\mathrm {End}}(E)$
is isomorphic to
$\operatorname {\mathrm {End}}(E)$
is isomorphic to
![]() $\mathcal {O}$
. Let K denote the fraction field of
$\mathcal {O}$
. Let K denote the fraction field of
![]() $\mathcal {O}$
. The j-invariant of E is an algebraic integer whose minimal polynomial over K is the ring class polynomial
$\mathcal {O}$
. The j-invariant of E is an algebraic integer whose minimal polynomial over K is the ring class polynomial
![]() $H_n$
, where
$H_n$
, where
![]() $-n$
is the discriminant of
$-n$
is the discriminant of
![]() $\mathcal {O}$
. (When
$\mathcal {O}$
. (When
![]() $\mathcal {O}$
is a maximal order,
$\mathcal {O}$
is a maximal order,
![]() $H_n$
is often called the Hilbert class polynomial.) The ring class polynomial
$H_n$
is often called the Hilbert class polynomial.) The ring class polynomial
![]() $H_n$
is defined by
$H_n$
is defined by
 $$ \begin{align*}H_n(x) := \prod_{j(E)\in\operatorname{\mathrm{Ell}}_{\mathcal{O}}({\mathbb{C}})}(x-j(E)),\end{align*} $$
$$ \begin{align*}H_n(x) := \prod_{j(E)\in\operatorname{\mathrm{Ell}}_{\mathcal{O}}({\mathbb{C}})}(x-j(E)),\end{align*} $$
where
![]() $\operatorname {\mathrm {Ell}}_{\mathcal {O}}({\mathbb {C}}) := \{j(E):\operatorname {\mathrm {End}}(E)\cong \mathcal {O}\}$
is the set of j-invariants of elliptic curves E over
$\operatorname {\mathrm {Ell}}_{\mathcal {O}}({\mathbb {C}}) := \{j(E):\operatorname {\mathrm {End}}(E)\cong \mathcal {O}\}$
is the set of j-invariants of elliptic curves E over
![]() ${\mathbb {C}}$
with CM by the imaginary quadratic order
${\mathbb {C}}$
with CM by the imaginary quadratic order
![]() $\mathcal {O}$
with discriminant
$\mathcal {O}$
with discriminant
![]() $\operatorname {\mathrm {disc}}(\mathcal {O})=-n$
.
$\operatorname {\mathrm {disc}}(\mathcal {O})=-n$
.
Moreover,
![]() $H_n \in {\mathbb {Z}}[x]$
and its splitting field over the imaginary quadratic field K is the ring class field
$H_n \in {\mathbb {Z}}[x]$
and its splitting field over the imaginary quadratic field K is the ring class field
![]() $K_{\mathcal {O}}$
, which is an abelian extension of K whose Galois group
$K_{\mathcal {O}}$
, which is an abelian extension of K whose Galois group
![]() $\operatorname {\mathrm {Gal}}(K_{\mathcal {O}}/K)$
is isomorphic to the class group
$\operatorname {\mathrm {Gal}}(K_{\mathcal {O}}/K)$
is isomorphic to the class group
![]() $\operatorname {\mathrm {Cl}}(\mathcal {O})$
, via the Artin map. This is indeed a remarkable result as it implies that of uncountably many isomorphism classes of elliptic curves over
$\operatorname {\mathrm {Cl}}(\mathcal {O})$
, via the Artin map. This is indeed a remarkable result as it implies that of uncountably many isomorphism classes of elliptic curves over
![]() ${\mathbb {C}}$
, only countably many have CM.
${\mathbb {C}}$
, only countably many have CM.
In his third notebook [Reference Ramanujan11, pages 392–393], Ramanujan defined the values
 $$ \begin{align*} t_n := \dfrac{f(\sqrt[3]{q_n})f(q_n^3)}{f^2(q_n)}\sqrt{3}q_n^{1/18}, \end{align*} $$
$$ \begin{align*} t_n := \dfrac{f(\sqrt[3]{q_n})f(q_n^3)}{f^2(q_n)}\sqrt{3}q_n^{1/18}, \end{align*} $$
where
![]() $q_n=\exp (-\pi \sqrt {n})$
and
$q_n=\exp (-\pi \sqrt {n})$
and
![]() $ f(-q)=\prod _{n\geqslant 1}(1-q^n).$
For all positive
$ f(-q)=\prod _{n\geqslant 1}(1-q^n).$
For all positive
![]() $n\equiv 11\pmod {24}$
, let
$n\equiv 11\pmod {24}$
, let
![]() $\mathcal {P}_n$
be the minimal polynomial of
$\mathcal {P}_n$
be the minimal polynomial of
![]() $t_n$
over
$t_n$
over
![]() ${\mathbb {Q}}$
. Without any further explanation on how he found them, Ramanujan gave the polynomials
${\mathbb {Q}}$
. Without any further explanation on how he found them, Ramanujan gave the polynomials
![]() $\mathcal {P}_n$
based on
$\mathcal {P}_n$
based on
![]() $t_n$
for the first five values of
$t_n$
for the first five values of
![]() $n \equiv 11\pmod {24}$
(see Table 1).
$n \equiv 11\pmod {24}$
(see Table 1).
Table 1 Ramanujan’s table of
![]() $\mathcal {P}_n$
for
$\mathcal {P}_n$
for
![]() $n=11,35,59,83,107$
.
$n=11,35,59,83,107$
.

Berndt and Chan [Reference Berndt and Chan2, Theorem 1.2] later verified these claims, using laborious computations involving Greenhill polynomials and Weber class invariants, and proved that each
![]() $\mathcal {P}_n$
has
$\mathcal {P}_n$
has
![]() $t_n$
as a root. Because of its computational complexity, their method could not be applied for higher values of n. However, they proved the following result.
$t_n$
as a root. Because of its computational complexity, their method could not be applied for higher values of n. However, they proved the following result.
Theorem 1.1 [Reference Berndt and Chan2, Theorem 4.1].
Let
![]() $n \equiv 11 \pmod {24}$
be a squarefree positive integer, and suppose that the class number of the associated imaginary quadratic field
$n \equiv 11 \pmod {24}$
be a squarefree positive integer, and suppose that the class number of the associated imaginary quadratic field
![]() ${\mathbb {Q}}(\sqrt {-n})$
is odd. Then,
${\mathbb {Q}}(\sqrt {-n})$
is odd. Then,
![]() $t_n$
is a real unit generating the ring class field over
$t_n$
is a real unit generating the ring class field over
![]() ${\mathbb {Q}}(\sqrt {-n})$
with respect to the order of discriminant
${\mathbb {Q}}(\sqrt {-n})$
with respect to the order of discriminant
![]() $-n$
.
$-n$
.
Ten years later, Konstantinou and Kontogeorgis [Reference Konstantinou and Kontogeorgis7] generalised this result by removing the constraint that the class number be odd and also provided an efficient method for constructing the minimal polynomials
![]() $\mathcal {P}_n$
of
$\mathcal {P}_n$
of
![]() $t_n$
over
$t_n$
over
![]() $\mathbb {Q}$
from the Ramanujan values
$\mathbb {Q}$
from the Ramanujan values
![]() $t_n$
for
$t_n$
for
![]() $n \equiv 11 \pmod {24}$
, using the Shimura reciprocity law. They also proved that the Ramanujan value
$n \equiv 11 \pmod {24}$
, using the Shimura reciprocity law. They also proved that the Ramanujan value
![]() $t_n$
is a class invariant for
$t_n$
is a class invariant for
![]() $n \equiv 11 \pmod {24}$
[Reference Konstantinou and Kontogeorgis7, Theorem 3.4]. It follows that the degree of
$n \equiv 11 \pmod {24}$
[Reference Konstantinou and Kontogeorgis7, Theorem 3.4]. It follows that the degree of
![]() $\mathcal {P}_n$
equals the class number of the order of discriminant
$\mathcal {P}_n$
equals the class number of the order of discriminant
![]() $-n$
for all positive integers
$-n$
for all positive integers
![]() $n \equiv 11 \pmod {24}$
.
$n \equiv 11 \pmod {24}$
.
Let
![]() $\mathfrak {j}_n=j(({-1+\sqrt {-n})}/{2})$
, for all
$\mathfrak {j}_n=j(({-1+\sqrt {-n})}/{2})$
, for all
![]() $n\in {\mathbb {N}}$
, where j denotes the j-invariant as defined in Section 2.1. In a follow-up paper in 2010, Konstantinou and Kontogeorgis proved the following important result.
$n\in {\mathbb {N}}$
, where j denotes the j-invariant as defined in Section 2.1. In a follow-up paper in 2010, Konstantinou and Kontogeorgis proved the following important result.
Proposition 1.2 [Reference Konstantinou and Kontogeorgis8, Lemma 3].
Suppose
![]() $R_{\mathcal {P}}$
is a real root of a Ramanujan polynomial
$R_{\mathcal {P}}$
is a real root of a Ramanujan polynomial
![]() $\mathcal {P}_n$
. Then, the real number
$\mathcal {P}_n$
. Then, the real number
![]() $R_H=(R_{\mathcal {P}}^6 - 27R_{\mathcal {P}}^{-6}-6)^3$
is a real root of the corresponding ring class polynomial
$R_H=(R_{\mathcal {P}}^6 - 27R_{\mathcal {P}}^{-6}-6)^3$
is a real root of the corresponding ring class polynomial
![]() $H_n$
.
$H_n$
.
In their proof, they show that, letting
![]() $R_{\mathcal {P}}=t_n$
gives
$R_{\mathcal {P}}=t_n$
gives
![]() $ \mathfrak {j}_n=(t_n^6-27t_n^{-6}-6)^3$
[Reference Konstantinou and Kontogeorgis8, page 12]. Moreover, notice that
$ \mathfrak {j}_n=(t_n^6-27t_n^{-6}-6)^3$
[Reference Konstantinou and Kontogeorgis8, page 12]. Moreover, notice that
![]() ${\mathbb {Z}}[\mathfrak {j}_n] \subseteq {\mathbb {Z}}[t_n]$
, which also follows from Section 3.1.
${\mathbb {Z}}[\mathfrak {j}_n] \subseteq {\mathbb {Z}}[t_n]$
, which also follows from Section 3.1.
The coefficients of the polynomial
![]() $\mathcal {P}_n$
have remarkably smaller size compared to the coefficients of the corresponding ring class polynomial
$\mathcal {P}_n$
have remarkably smaller size compared to the coefficients of the corresponding ring class polynomial
![]() $H_n$
, suggesting that they may be useful for generating elliptic curves over prime fields by the CM method. Proposition 1.2 supports this because it shows that the roots of the polynomials
$H_n$
, suggesting that they may be useful for generating elliptic curves over prime fields by the CM method. Proposition 1.2 supports this because it shows that the roots of the polynomials
![]() $\mathcal {P}_n$
can be transformed to the roots of
$\mathcal {P}_n$
can be transformed to the roots of
![]() $H_n$
. For more details on constructing elliptic curves with the CM method, see [Reference Atkin and Morain1, Reference Berndt and Chan4].
$H_n$
. For more details on constructing elliptic curves with the CM method, see [Reference Atkin and Morain1, Reference Berndt and Chan4].
We study the discriminant of
![]() $\mathcal {P}_n$
. The historical precedent for doing so comes from [Reference Gross and Zagier6] in which the prime factorisations of certain resultants of ring class polynomials are computed. In [Reference Gross and Zagier6], Gross and Zagier computed the prime factorisation of the discriminant of the ring class polynomial associated to the fundamental discriminant
$\mathcal {P}_n$
. The historical precedent for doing so comes from [Reference Gross and Zagier6] in which the prime factorisations of certain resultants of ring class polynomials are computed. In [Reference Gross and Zagier6], Gross and Zagier computed the prime factorisation of the discriminant of the ring class polynomial associated to the fundamental discriminant
![]() $-p$
, where
$-p$
, where
![]() $p\equiv 3\pmod {4}$
is a prime. This result was later generalised by Dorman [Reference Dorman5] to ring class polynomials associated to arbitrary fundamental discriminants and by Ye [Reference Ye14] to ring class polynomials associated to certain nonfundamental discriminants.
$p\equiv 3\pmod {4}$
is a prime. This result was later generalised by Dorman [Reference Dorman5] to ring class polynomials associated to arbitrary fundamental discriminants and by Ye [Reference Ye14] to ring class polynomials associated to certain nonfundamental discriminants.
1.1 Notation
Fix a positive integer
![]() $n\equiv 11\pmod {24}$
and let
$n\equiv 11\pmod {24}$
and let
![]() $K={\mathbb {Q}}(\sqrt {-n})$
denote the associated imaginary quadratic field. Let
$K={\mathbb {Q}}(\sqrt {-n})$
denote the associated imaginary quadratic field. Let
![]() $h_n$
and
$h_n$
and
![]() $\operatorname {\mathrm {Cl}}(n)$
denote the class number and ideal class group of the order of discriminant
$\operatorname {\mathrm {Cl}}(n)$
denote the class number and ideal class group of the order of discriminant
![]() $-n$
, respectively, and let
$-n$
, respectively, and let
![]() $\operatorname {\mathrm {Cl}}(n)[2]$
be the subgroup of
$\operatorname {\mathrm {Cl}}(n)[2]$
be the subgroup of
![]() $\operatorname {\mathrm {Cl}}(n)$
consisting of elements of order at most
$\operatorname {\mathrm {Cl}}(n)$
consisting of elements of order at most
![]() $2$
.
$2$
.
1.2 Main results
Our first main result relates
![]() $\Delta (H_n)$
to
$\Delta (H_n)$
to
![]() $\Delta (\mathcal {P}_n)$
.
$\Delta (\mathcal {P}_n)$
.
Theorem 1.3. For all positive
![]() $n\equiv 11\pmod {24}$
,
$n\equiv 11\pmod {24}$
,
where
![]() $[{\mathbb {Z}}[t_n]:{\mathbb {Z}}[\mathfrak {j}_n]]$
is the index of
$[{\mathbb {Z}}[t_n]:{\mathbb {Z}}[\mathfrak {j}_n]]$
is the index of
![]() ${\mathbb {Z}}[\mathfrak {j}_n]$
in
${\mathbb {Z}}[\mathfrak {j}_n]$
in
![]() ${\mathbb {Z}}[t_n]$
.
${\mathbb {Z}}[t_n]$
.
Remark 1.4. Since the quotient
![]() $[{\mathbb {Z}}[t_n]:{\mathbb {Z}}[\mathfrak {j}_n]]^2$
is a perfect square, we deduce that
$[{\mathbb {Z}}[t_n]:{\mathbb {Z}}[\mathfrak {j}_n]]^2$
is a perfect square, we deduce that
![]() $ \Delta (H_n)$
and
$ \Delta (H_n)$
and
![]() $\Delta (\mathcal {P}_n)$
have the same sign for all positive integers
$\Delta (\mathcal {P}_n)$
have the same sign for all positive integers
![]() $n\equiv 11\pmod {24}$
.
$n\equiv 11\pmod {24}$
.
Let
![]() $\mathcal {D}(\mathfrak {F})$
denote the discriminant of an algebraic number field
$\mathcal {D}(\mathfrak {F})$
denote the discriminant of an algebraic number field
![]() $\mathfrak {F}$
. Our next main result is the following result.
$\mathfrak {F}$
. Our next main result is the following result.
Theorem 1.5. For all positive integers
![]() $n\equiv 11\pmod {24}$
,
$n\equiv 11\pmod {24}$
,
where
![]() $[\mathcal {O}_{{\mathbb {Q}}(\mathfrak {j}_n)} : {\mathbb {Z}}[t_n]]$
is the index of
$[\mathcal {O}_{{\mathbb {Q}}(\mathfrak {j}_n)} : {\mathbb {Z}}[t_n]]$
is the index of
![]() ${\mathbb {Z}}[t_n]$
inside
${\mathbb {Z}}[t_n]$
inside
![]() $\mathcal {O}_{{\mathbb {Q}}(\mathfrak {j}_n)}$
.
$\mathcal {O}_{{\mathbb {Q}}(\mathfrak {j}_n)}$
.
Remark 1.6. Dorman explicitly computed
![]() $\mathcal {D}({\mathbb {Q}}(\mathfrak {j}_n))$
in [Reference Dorman5]. More precisely, he proved in [Reference Dorman5, Proposition 5.1] that, for a squarefree positive integer
$\mathcal {D}({\mathbb {Q}}(\mathfrak {j}_n))$
in [Reference Dorman5]. More precisely, he proved in [Reference Dorman5, Proposition 5.1] that, for a squarefree positive integer
![]() $n\equiv 11\pmod {24}$
,
$n\equiv 11\pmod {24}$
,
where
![]() $\mathfrak {t}$
is the number of distinct prime factors of n and
$\mathfrak {t}$
is the number of distinct prime factors of n and
![]() $n=\mathfrak {D}_0 \mathfrak {D}_1$
with
$n=\mathfrak {D}_0 \mathfrak {D}_1$
with
 $$ \begin{align*}\mathfrak{D}_1=\begin{cases} 1 & \textrm{if at least } 2 \textrm{ primes congruent to } 3 \textrm{ mod } 4 \textrm{ divide } n, \\ p & \textrm{if } p \textrm{ is the unique prime congruent to } 3 \textrm{ mod } 4 \textrm{ dividing } n. \end{cases}\end{align*} $$
$$ \begin{align*}\mathfrak{D}_1=\begin{cases} 1 & \textrm{if at least } 2 \textrm{ primes congruent to } 3 \textrm{ mod } 4 \textrm{ divide } n, \\ p & \textrm{if } p \textrm{ is the unique prime congruent to } 3 \textrm{ mod } 4 \textrm{ dividing } n. \end{cases}\end{align*} $$
Note that there is a factor of
![]() $\pm 1$
in (1.1), although this factor does not appear in [Reference Dorman5, Proposition 5.1], because Dorman computes the absolute value of
$\pm 1$
in (1.1), although this factor does not appear in [Reference Dorman5, Proposition 5.1], because Dorman computes the absolute value of
![]() $\mathcal {D}({\mathbb {Q}}(\mathfrak {j}_n))$
.
$\mathcal {D}({\mathbb {Q}}(\mathfrak {j}_n))$
.
Next, we explicitly determine the sign of
![]() $\Delta (\mathcal {P}_n)$
.
$\Delta (\mathcal {P}_n)$
.
Theorem 1.7. For all positive
![]() $n\equiv 11\pmod {24}$
,
$n\equiv 11\pmod {24}$
,
![]() $\Delta (\mathcal {P}_n)>0$
if and only if
$\Delta (\mathcal {P}_n)>0$
if and only if
where
![]() $\operatorname {\mathrm {Cl}}(n)[2]$
is the subgroup of
$\operatorname {\mathrm {Cl}}(n)[2]$
is the subgroup of
![]() $\operatorname {\mathrm {Cl}}(n)$
consisting of elements of order at most
$\operatorname {\mathrm {Cl}}(n)$
consisting of elements of order at most
![]() $2$
.
$2$
.
Using the ambiguous class number formula from genus theory, we find that for all positive squarefree integers
![]() $n\equiv 11\pmod {24}$
,
$n\equiv 11\pmod {24}$
,
where
![]() $\mathfrak {t}$
is the number of distinct prime factors of n. Therefore, we have the following corollary.
$\mathfrak {t}$
is the number of distinct prime factors of n. Therefore, we have the following corollary.
Corollary 1.8. For all positive squarefree
![]() $n\equiv 11\pmod {24}$
,
$n\equiv 11\pmod {24}$
,
![]() $\Delta (\mathcal {P}_n)>0$
if and only if
$\Delta (\mathcal {P}_n)>0$
if and only if
where, as usual,
![]() $\mathfrak {t}$
denotes the number of distinct prime factors of n.
$\mathfrak {t}$
denotes the number of distinct prime factors of n.
Moreover, when the ideal class group is a cyclic group, that is
![]() $\operatorname {\mathrm {Cl}}(n)\cong ({\mathbb {Z}}/h_n{\mathbb {Z}})$
, which is true for all
$\operatorname {\mathrm {Cl}}(n)\cong ({\mathbb {Z}}/h_n{\mathbb {Z}})$
, which is true for all
![]() $n\equiv 11\pmod {24}$
, with
$n\equiv 11\pmod {24}$
, with
![]() $11\leqslant n \leqslant 995$
as illustrated in Table 2, it is easy to see that
$11\leqslant n \leqslant 995$
as illustrated in Table 2, it is easy to see that
 $$ \begin{align*}|\!\operatorname{\mathrm{Cl}}(n)[2]| =\begin{cases} 1 & \textrm{if } h_n \textrm{ is odd},\\ 2 & \textrm{if } h_n \textrm{ is even.} \end{cases}\end{align*} $$
$$ \begin{align*}|\!\operatorname{\mathrm{Cl}}(n)[2]| =\begin{cases} 1 & \textrm{if } h_n \textrm{ is odd},\\ 2 & \textrm{if } h_n \textrm{ is even.} \end{cases}\end{align*} $$
Thus, we have the following corollary.
Table 2 Computation of the class number
![]() $h_n$
, the sign
$h_n$
, the sign
![]() $\operatorname {\mathrm {sgn}}(\Delta )$
of
$\operatorname {\mathrm {sgn}}(\Delta )$
of
![]() $\Delta (\mathcal {P}_n)$
, the structure of the ideal class group
$\Delta (\mathcal {P}_n)$
, the structure of the ideal class group
![]() $\operatorname {\mathrm {Cl}}(n)$
and the prime factorisation of
$\operatorname {\mathrm {Cl}}(n)$
and the prime factorisation of
![]() $|\Delta (\mathcal {P}_n)|$
for all
$|\Delta (\mathcal {P}_n)|$
for all
![]() $n\equiv 11\pmod {24}$
with
$n\equiv 11\pmod {24}$
with
![]() $11\leqslant n \leqslant 995$
.
$11\leqslant n \leqslant 995$
.

Corollary 1.9. For all positive
![]() $n\equiv 11\pmod {24}$
, if
$n\equiv 11\pmod {24}$
, if
![]() $\operatorname {\mathrm {Cl}}(n) \cong ({\mathbb {Z}}/h_n{\mathbb {Z}})$
, then
$\operatorname {\mathrm {Cl}}(n) \cong ({\mathbb {Z}}/h_n{\mathbb {Z}})$
, then
![]() $\Delta (\mathcal {P}_n)>0$
if and only if
$\Delta (\mathcal {P}_n)>0$
if and only if
Remark 1.10. For example, two positive values of
![]() $n \equiv 11 \pmod {24}$
for which the ideal class group
$n \equiv 11 \pmod {24}$
for which the ideal class group
![]() $\operatorname {\mathrm {Cl}}(n) \not \cong {\mathbb {Z}}/h_n{\mathbb {Z}}$
are 1235 and 2555. In particular, we find that
$\operatorname {\mathrm {Cl}}(n) \not \cong {\mathbb {Z}}/h_n{\mathbb {Z}}$
are 1235 and 2555. In particular, we find that
![]() $\operatorname {\mathrm {Cl}}(1235)\cong \operatorname {\mathrm {Cl}}(2555)\cong ({\mathbb {Z}}/6{\mathbb {Z}}) \times ({\mathbb {Z}}/2{\mathbb {Z}})$
. The structure of the ideal class group
$\operatorname {\mathrm {Cl}}(1235)\cong \operatorname {\mathrm {Cl}}(2555)\cong ({\mathbb {Z}}/6{\mathbb {Z}}) \times ({\mathbb {Z}}/2{\mathbb {Z}})$
. The structure of the ideal class group
![]() $\operatorname {\mathrm {Cl}}(n)$
for positive
$\operatorname {\mathrm {Cl}}(n)$
for positive
![]() $n \equiv 11 \pmod {24}$
was computed using Sage [Reference Stein13].
$n \equiv 11 \pmod {24}$
was computed using Sage [Reference Stein13].
In Table 2, it can be observed that 3 seems to be the only prime that never appears in the prime factorisation of
![]() $\Delta (\mathcal {P}_n)$
for positive
$\Delta (\mathcal {P}_n)$
for positive
![]() $n \equiv 11 \pmod {24}$
. To prove this, we show that 3 never divides
$n \equiv 11 \pmod {24}$
. To prove this, we show that 3 never divides
![]() $\Delta (H_n)$
, and thus
$\Delta (H_n)$
, and thus
![]() $\Delta (\mathcal {P}_n)$
, using Ye’s explicit computation of
$\Delta (\mathcal {P}_n)$
, using Ye’s explicit computation of
![]() $\Delta (H_n)$
[Reference Ye14, Corollary 1.2] for squarefree positive integers
$\Delta (H_n)$
[Reference Ye14, Corollary 1.2] for squarefree positive integers
![]() $n \equiv 11 \pmod {24}$
. For more details, see Section 3.4. Therefore, we have the following important theorem.
$n \equiv 11 \pmod {24}$
. For more details, see Section 3.4. Therefore, we have the following important theorem.
Theorem 1.11. For all positive squarefree
![]() $n\equiv 11\pmod {24}$
, we have
$n\equiv 11\pmod {24}$
, we have
![]() ${3 \nmid \Delta (\mathcal {P}_n)}$
.
${3 \nmid \Delta (\mathcal {P}_n)}$
.
1.3 Organisation of the manuscript
We start with a section on the necessary preliminaries and prove some important results that will later play a crucial role in the proofs of our main results. Proofs of Theorems 1.3, 1.5, 1.7 and 1.11 are provided in Sections 3.1, 3.2, 3.3 and 3.4, respectively. In Table 2, we have computed the class number and the ideal class group structure of
![]() ${\mathbb {Q}}(\sqrt {-n})$
, the prime factorisation and sign of
${\mathbb {Q}}(\sqrt {-n})$
, the prime factorisation and sign of
![]() $\Delta (\mathcal {P}_n)$
for all positive integers
$\Delta (\mathcal {P}_n)$
for all positive integers
![]() $n\equiv 11\pmod {24}$
,
$n\equiv 11\pmod {24}$
,
![]() $11\leqslant n \leqslant 995$
, as an illustration of our main results. Finally, in Section 4, we show that all our main results hold for
$11\leqslant n \leqslant 995$
, as an illustration of our main results. Finally, in Section 4, we show that all our main results hold for
![]() $n=227$
, as an example. The computations were performed using Sage [Reference Stein13].
$n=227$
, as an example. The computations were performed using Sage [Reference Stein13].
2 Preliminaries: nuts and bolts
2.1 The j-invariant of a lattice
A lattice is an additive subgroup L of
![]() ${\mathbb {C}}$
which is generated by two complex numbers
${\mathbb {C}}$
which is generated by two complex numbers
![]() $\omega _1$
and
$\omega _1$
and
![]() $\omega _2$
that are linearly independent over
$\omega _2$
that are linearly independent over
![]() ${\mathbb {R}}$
. We express this by writing
${\mathbb {R}}$
. We express this by writing
![]() $L=[\omega _1,\omega _2].$
The j-invariant
$L=[\omega _1,\omega _2].$
The j-invariant
![]() $j(L)$
of a lattice L is the complex number
$j(L)$
of a lattice L is the complex number
 $$ \begin{align*} j(L)=1728\dfrac{g_2(L)^3}{g_2(L)^3-27g_3(L)^2}, \end{align*} $$
$$ \begin{align*} j(L)=1728\dfrac{g_2(L)^3}{g_2(L)^3-27g_3(L)^2}, \end{align*} $$
where
 $$ \begin{align*} g_2(L)=60\sum_{\omega\in L\backslash\{0\} }^{}\dfrac{1}{\omega^4}=60\sum_{\substack{m,n=-\infty\\(m,n)\neq(0,0)}}^{\infty}\dfrac{1}{(m\tau+n)^{4}} \end{align*} $$
$$ \begin{align*} g_2(L)=60\sum_{\omega\in L\backslash\{0\} }^{}\dfrac{1}{\omega^4}=60\sum_{\substack{m,n=-\infty\\(m,n)\neq(0,0)}}^{\infty}\dfrac{1}{(m\tau+n)^{4}} \end{align*} $$
and
 $$ \begin{align*} g_3(L)=140\sum_{\omega\in L\backslash\{0\} }^{}\dfrac{1}{\omega^6}=140\sum_{\substack{m,n=-\infty\\(m,n)\neq(0,0)}}^{\infty}\dfrac{1}{(m\tau+n)^{6}}, \end{align*} $$
$$ \begin{align*} g_3(L)=140\sum_{\omega\in L\backslash\{0\} }^{}\dfrac{1}{\omega^6}=140\sum_{\substack{m,n=-\infty\\(m,n)\neq(0,0)}}^{\infty}\dfrac{1}{(m\tau+n)^{6}}, \end{align*} $$
where
![]() $L=[1,\tau ]$
with
$L=[1,\tau ]$
with
![]() $\tau \in {\mathbb {H}}$
, the upper-half plane.
$\tau \in {\mathbb {H}}$
, the upper-half plane.
Proposition 2.1. Let L be a lattice, and let
![]() $\overline {L}$
denote the lattice obtained by complex conjugation. Then
$\overline {L}$
denote the lattice obtained by complex conjugation. Then
![]() $g_2(\overline {L}) = \overline {g_2(L)}, g_3(\overline {L}) = \overline {g_3(L)}$
and
$g_2(\overline {L}) = \overline {g_2(L)}, g_3(\overline {L}) = \overline {g_3(L)}$
and
![]() $j(\overline {L}) = \overline {j(L)}$
.
$j(\overline {L}) = \overline {j(L)}$
.
Proof. From the definition of
![]() $g_2(L)$
,
$g_2(L)$
,
 $$ \begin{align*} g_2(\overline{L})&=60\sum_{\omega\in\overline{L}\backslash\{0\}}^{}\dfrac{1}{\omega^4} =60\sum_{\omega\in L\backslash\{0\}}^{}\dfrac{1}{\overline{\omega^{4}}} =\overline{60\sum_{\omega\in L\backslash\{0\}}^{}\dfrac{1}{\omega^{4}}} =\overline{g_2(L)}. \end{align*} $$
$$ \begin{align*} g_2(\overline{L})&=60\sum_{\omega\in\overline{L}\backslash\{0\}}^{}\dfrac{1}{\omega^4} =60\sum_{\omega\in L\backslash\{0\}}^{}\dfrac{1}{\overline{\omega^{4}}} =\overline{60\sum_{\omega\in L\backslash\{0\}}^{}\dfrac{1}{\omega^{4}}} =\overline{g_2(L)}. \end{align*} $$
A similar argument shows that
![]() $g_3(\overline {L}) = \overline {g_3(L)}$
and then the result for j follows from its definition.
$g_3(\overline {L}) = \overline {g_3(L)}$
and then the result for j follows from its definition.
We say that two lattices L and
![]() $L'$
are homothetic if there is a nonzero complex number
$L'$
are homothetic if there is a nonzero complex number
![]() $\lambda $
such that
$\lambda $
such that
![]() $L' = \lambda L$
. Note that homothetic lattices have the same j-invariant.
$L' = \lambda L$
. Note that homothetic lattices have the same j-invariant.
Lemma 2.2 [Reference Cox4, Theorem 10.9].
If L and
![]() $L'$
are lattices in
$L'$
are lattices in
![]() ${\mathbb {C}}$
, then
${\mathbb {C}}$
, then
![]() $j(L) = j(L')$
if and only if the lattices L and
$j(L) = j(L')$
if and only if the lattices L and
![]() $L'$
are homothetic.
$L'$
are homothetic.
Next, we prove an important result that will later play a crucial role in the proof of Theorem 1.7.
Proposition 2.3. Let
![]() $\mathfrak {a}$
be a proper fractional
$\mathfrak {a}$
be a proper fractional
![]() $\mathcal {O}$
-ideal, where
$\mathcal {O}$
-ideal, where
![]() $\mathcal {O}$
is an order in an imaginary quadratic number field. Then
$\mathcal {O}$
is an order in an imaginary quadratic number field. Then
![]() $j(\mathfrak {a})$
is a real number if and only if the class of
$j(\mathfrak {a})$
is a real number if and only if the class of
![]() $\mathfrak {a}$
has order at most
$\mathfrak {a}$
has order at most
![]() $2$
in the ideal class group
$2$
in the ideal class group
![]() $\operatorname {\mathrm {Cl}}(\mathcal {O})$
.
$\operatorname {\mathrm {Cl}}(\mathcal {O})$
.
Proof. Let
![]() $\mathfrak {b}$
be the complex conjugate of the ideal
$\mathfrak {b}$
be the complex conjugate of the ideal
![]() $\mathfrak {a}$
. From Proposition 2.1,
$\mathfrak {a}$
. From Proposition 2.1,
![]() $j(\mathfrak {a})$
is a real number if and only if
$j(\mathfrak {a})$
is a real number if and only if
![]() $j(\mathfrak {a})=j(\mathfrak {b})$
. Now Lemma 2.2 tells us that this is only possible when
$j(\mathfrak {a})=j(\mathfrak {b})$
. Now Lemma 2.2 tells us that this is only possible when
![]() $\mathfrak {a}$
and
$\mathfrak {a}$
and
![]() $\mathfrak {b}$
are homothetic or, equivalently, when they represent the same ideal classes in the ideal class group
$\mathfrak {b}$
are homothetic or, equivalently, when they represent the same ideal classes in the ideal class group
![]() $\operatorname {\mathrm {Cl}}(\mathcal {O})$
. Let
$\operatorname {\mathrm {Cl}}(\mathcal {O})$
. Let
![]() $[\mathfrak {c}] \in \operatorname {\mathrm {Cl}}(\mathcal {O})$
denote the ideal class of a proper fractional
$[\mathfrak {c}] \in \operatorname {\mathrm {Cl}}(\mathcal {O})$
denote the ideal class of a proper fractional
![]() $\mathcal {O}$
-ideal
$\mathcal {O}$
-ideal
![]() $\mathfrak {c}$
. Now using [Reference Cox4, Lemma 7.14(iii)],
$\mathfrak {c}$
. Now using [Reference Cox4, Lemma 7.14(iii)],
![]() $[\mathfrak {b}]=[\mathfrak {a}]^{-1}$
for all
$[\mathfrak {b}]=[\mathfrak {a}]^{-1}$
for all
![]() $\mathfrak {a}$
. Therefore,
$\mathfrak {a}$
. Therefore,
Note that this is not true as a statement about ideals; here we are explicitly referring to ideal classes, that is, elements of
![]() $\operatorname {\mathrm {Cl}}(\mathcal {O})$
.
$\operatorname {\mathrm {Cl}}(\mathcal {O})$
.
The proposition has the following important corollary.
Corollary 2.4. The j-invariant
![]() $j(\mathcal {O})$
is a real number for any order
$j(\mathcal {O})$
is a real number for any order
![]() $\mathcal {O}$
.
$\mathcal {O}$
.
2.2 Discriminant of an algebraic number field
Let
![]() $\mathcal {D}(K)$
denote the discriminant of an algebraic number field K. The discriminant of a nonzero finitely generated
$\mathcal {D}(K)$
denote the discriminant of an algebraic number field K. The discriminant of a nonzero finitely generated
![]() ${\mathbb {Z}}$
-submodule
${\mathbb {Z}}$
-submodule
![]() $\mathfrak {M}$
of a number field K is defined as
$\mathfrak {M}$
of a number field K is defined as
where
![]() $\mathfrak {M}={\mathbb {Z}}\alpha _1+{\mathbb {Z}}\alpha _2+\cdots +{\mathbb {Z}}\alpha _n$
and spans K as a
$\mathfrak {M}={\mathbb {Z}}\alpha _1+{\mathbb {Z}}\alpha _2+\cdots +{\mathbb {Z}}\alpha _n$
and spans K as a
![]() ${\mathbb {Q}}$
-vector space.
${\mathbb {Q}}$
-vector space.
Proposition 2.5 [Reference Neukirch10, Proposition 2.12].
If
![]() $\mathfrak {M} \subset \mathfrak {M}'$
are two nonzero finitely generated
$\mathfrak {M} \subset \mathfrak {M}'$
are two nonzero finitely generated
![]() ${\mathbb {Z}}$
-submodules of a number field K that span K as a
${\mathbb {Z}}$
-submodules of a number field K that span K as a
![]() ${\mathbb {Q}}$
-vector space, then the index
${\mathbb {Q}}$
-vector space, then the index
![]() $[\mathfrak {M}' : \mathfrak {M}]$
is finite and
$[\mathfrak {M}' : \mathfrak {M}]$
is finite and
Remark 2.6. Although Neukirch [Reference Neukirch10, Proposition 2.12] only states Proposition 2.5 for finitely generated
![]() $\mathcal {O}_K$
-submodules, the same result and proof also hold more generally for finitely generated
$\mathcal {O}_K$
-submodules, the same result and proof also hold more generally for finitely generated
![]() ${\mathbb {Z}}$
-submodules.
${\mathbb {Z}}$
-submodules.
2.3 Number fields
 ${\mathbb {Q}}(\mathfrak {j}_n)$
and
${\mathbb {Q}}(\mathfrak {j}_n)$
and
 ${\mathbb {Q}}(t_n)$
${\mathbb {Q}}(t_n)$
The main goal of this section is to show that the fields
![]() ${\mathbb {Q}}(\mathfrak {j}_n)$
and
${\mathbb {Q}}(\mathfrak {j}_n)$
and
![]() ${\mathbb {Q}}(t_n)$
are the same. This important result enables us to prove our main theorem, Theorem 1.5, in a very efficient way, as explained in Section 3.2.
${\mathbb {Q}}(t_n)$
are the same. This important result enables us to prove our main theorem, Theorem 1.5, in a very efficient way, as explained in Section 3.2.
Proposition 2.7. For all positive integers
![]() $n\equiv 11\pmod {24}$
, we have
$n\equiv 11\pmod {24}$
, we have
![]() ${\mathbb {Q}}(\mathfrak {j}_n)={\mathbb {Q}}(t_n)$
.
${\mathbb {Q}}(\mathfrak {j}_n)={\mathbb {Q}}(t_n)$
.
Proof. To start with, consider the field diagram in Figure 1. We freely use some standard facts about the ring class fields of K throughout the proof. From class field theory, recall that if H is the ring class field associated to the discriminant of order
![]() $-n$
, then H is a finite Galois extension of K and
$-n$
, then H is a finite Galois extension of K and
![]() ${[H : K] = h_n}$
, where
${[H : K] = h_n}$
, where
![]() $h_n$
denotes the class number of the order of discriminant
$h_n$
denotes the class number of the order of discriminant
![]() $-n$
. Therefore, we have
$-n$
. Therefore, we have
![]() $[H:K]=[H:{\mathbb {Q}}(\sqrt {-n})]=h_n$
. Next, it is easy to see that
$[H:K]=[H:{\mathbb {Q}}(\sqrt {-n})]=h_n$
. Next, it is easy to see that
![]() $[K:{\mathbb {Q}}]=2$
since
$[K:{\mathbb {Q}}]=2$
since
![]() $\{1, i \sqrt {n}\}$
forms a basis. Moreover, since
$\{1, i \sqrt {n}\}$
forms a basis. Moreover, since
![]() $H=({\mathbb {Q}}(\mathfrak {j}_n))(\sqrt {-n}),$
we have
$H=({\mathbb {Q}}(\mathfrak {j}_n))(\sqrt {-n}),$
we have
![]() $[H : {\mathbb {Q}}(\mathfrak {j}_n)] \leqslant 2$
. Therefore, using the tower law, either
$[H : {\mathbb {Q}}(\mathfrak {j}_n)] \leqslant 2$
. Therefore, using the tower law, either
![]() $[{\mathbb {Q}}(\mathfrak {j}_n):{\mathbb {Q}}]=h_n$
or
$[{\mathbb {Q}}(\mathfrak {j}_n):{\mathbb {Q}}]=h_n$
or
![]() $[{\mathbb {Q}}(\mathfrak {j}_n):{\mathbb {Q}}]=2h_n$
. Now let
$[{\mathbb {Q}}(\mathfrak {j}_n):{\mathbb {Q}}]=2h_n$
. Now let
![]() $\mathfrak {f}$
be the minimal polynomial of
$\mathfrak {f}$
be the minimal polynomial of
![]() $\mathfrak {j}_n \in H$
over K. Note that
$\mathfrak {j}_n \in H$
over K. Note that
![]() $\mathfrak {f}\in K[x]$
has degree
$\mathfrak {f}\in K[x]$
has degree
![]() $h_n$
. From Corollary 2.4,
$h_n$
. From Corollary 2.4,
![]() $\mathfrak {j}_n \in {\mathbb {R}}$
, that is,
$\mathfrak {j}_n \in {\mathbb {R}}$
, that is,
![]() $\overline {\mathfrak {j}_n}=\mathfrak {j}_n$
. Thus,
$\overline {\mathfrak {j}_n}=\mathfrak {j}_n$
. Thus,
![]() $\overline {\mathfrak {f}}=\mathfrak {f}$
, which implies
$\overline {\mathfrak {f}}=\mathfrak {f}$
, which implies
![]() $\mathfrak {f}\in {\mathbb {Q}}[x]$
, and we deduce that
$\mathfrak {f}\in {\mathbb {Q}}[x]$
, and we deduce that
![]() $[{\mathbb {Q}}(\mathfrak {j}_n):{\mathbb {Q}}]\leqslant h_n$
.
$[{\mathbb {Q}}(\mathfrak {j}_n):{\mathbb {Q}}]\leqslant h_n$
.

Figure 1 Field diagram 1.
Putting all this together finally produces
![]() $[{\mathbb {Q}}(\mathfrak {j}_n):{\mathbb {Q}}]=h_n$
and
$[{\mathbb {Q}}(\mathfrak {j}_n):{\mathbb {Q}}]=h_n$
and
![]() $[H:{\mathbb {Q}}(\mathfrak {j}_n)]=2.$
Since
$[H:{\mathbb {Q}}(\mathfrak {j}_n)]=2.$
Since
![]() $t_n \in {\mathbb {R}}$
, which easily follows from Ramanujan’s definition of
$t_n \in {\mathbb {R}}$
, which easily follows from Ramanujan’s definition of
![]() $t_n$
, a similar argument can be applied to show that
$t_n$
, a similar argument can be applied to show that
![]() $[{\mathbb {Q}}(t_n):{\mathbb {Q}}]=h_n$
and
$[{\mathbb {Q}}(t_n):{\mathbb {Q}}]=h_n$
and
![]() $[H:{\mathbb {Q}}(t_n)]=2.$
$[H:{\mathbb {Q}}(t_n)]=2.$
The above discussion can be summarised by Figure 2.

Figure 2 Field diagram 2.
Now observe that we have the tower of fields
![]() ${\mathbb {Q}}\subseteq {\mathbb {Q}}(\mathfrak {j}_n)\subseteq {\mathbb {Q}}(t_n)\subseteq H$
, where
${\mathbb {Q}}\subseteq {\mathbb {Q}}(\mathfrak {j}_n)\subseteq {\mathbb {Q}}(t_n)\subseteq H$
, where
![]() ${{\mathbb {Q}}(\mathfrak {j}_n)\subseteq {\mathbb {Q}}(t_n)}$
follows from Proposition 1.2. Therefore, by the tower law,
${{\mathbb {Q}}(\mathfrak {j}_n)\subseteq {\mathbb {Q}}(t_n)}$
follows from Proposition 1.2. Therefore, by the tower law,
which is only possible when
![]() ${\mathbb {Q}}(\mathfrak {j}_n) ={\mathbb {Q}}(t_n)$
. This completes the proof.
${\mathbb {Q}}(\mathfrak {j}_n) ={\mathbb {Q}}(t_n)$
. This completes the proof.
3 Proofs of the main results
3.1 Proof of Theorem 1.3
Since
![]() $t_n \in {\mathbb {Z}}[t_n]$
and the constant term of
$t_n \in {\mathbb {Z}}[t_n]$
and the constant term of
![]() $\mathcal {P}_n$
is always
$\mathcal {P}_n$
is always
![]() $\pm 1$
(see [Reference Konstantinou and Kontogeorgis8, Section 3], where it is shown that
$\pm 1$
(see [Reference Konstantinou and Kontogeorgis8, Section 3], where it is shown that
![]() $t_n$
is a unit), it follows that
$t_n$
is a unit), it follows that
![]() $t_n^{-1}\in {\mathbb {Z}}[t_n]$
. From Proposition 1.2,
$t_n^{-1}\in {\mathbb {Z}}[t_n]$
. From Proposition 1.2,
Therefore,
![]() $\mathfrak {j}_n\in {\mathbb {Z}}[t_n]$
and thus
$\mathfrak {j}_n\in {\mathbb {Z}}[t_n]$
and thus
![]() $ {\mathbb {Z}}[\mathfrak {j}_n] \subseteq {\mathbb {Z}}[t_n]$
. Substituting
$ {\mathbb {Z}}[\mathfrak {j}_n] \subseteq {\mathbb {Z}}[t_n]$
. Substituting
![]() $\mathfrak {M}={\mathbb {Z}}[\mathfrak {j}_n]$
and
$\mathfrak {M}={\mathbb {Z}}[\mathfrak {j}_n]$
and
![]() $\mathfrak {M}'={\mathbb {Z}}[t_n]$
in Proposition 2.5 produces
$\mathfrak {M}'={\mathbb {Z}}[t_n]$
in Proposition 2.5 produces
or, equivalently,
which is the desired result.
3.2 Proof of Theorem 1.5
First, simply notice that
where
![]() $\mathcal {O}_{{\mathbb {Q}}(t_n)}=\mathcal {O}_{{\mathbb {Q}}(\mathfrak {j}_n)}$
follows from the fact that
$\mathcal {O}_{{\mathbb {Q}}(t_n)}=\mathcal {O}_{{\mathbb {Q}}(\mathfrak {j}_n)}$
follows from the fact that
![]() ${\mathbb {Q}}(\mathfrak {j}_n)={\mathbb {Q}}(t_n)$
, as shown in Proposition 2.7. As in the previous proof, substituting
${\mathbb {Q}}(\mathfrak {j}_n)={\mathbb {Q}}(t_n)$
, as shown in Proposition 2.7. As in the previous proof, substituting
![]() $\mathfrak {M}={\mathbb {Z}}[t_n]$
and
$\mathfrak {M}={\mathbb {Z}}[t_n]$
and
![]() $\mathfrak {M}'=\mathcal {O}_{{\mathbb {Q}}(\mathfrak {j}_n)}$
in Proposition 2.5 gives the desired result.
$\mathfrak {M}'=\mathcal {O}_{{\mathbb {Q}}(\mathfrak {j}_n)}$
in Proposition 2.5 gives the desired result.
3.3 Proof of Theorem 1.7
From the definition of the ring class polynomial, its roots are
From Proposition 2.3, we deduce that the real roots of the ring class polynomial
![]() $H_n$
are given by
$H_n$
are given by
which is in bijection with
![]() $\operatorname {\mathrm {Cl}}(n)[2]$
.
$\operatorname {\mathrm {Cl}}(n)[2]$
.
Therefore, the number of nonreal roots of
![]() $H_n$
is given by
$H_n$
is given by
![]() $|\!\operatorname {\mathrm {Cl}}(n)|-|\!\operatorname {\mathrm {Cl}}(n)[2]|= h_n-|\!\operatorname {\mathrm {Cl}}(n)[2]|$
. The discriminant of a polynomial in
$|\!\operatorname {\mathrm {Cl}}(n)|-|\!\operatorname {\mathrm {Cl}}(n)[2]|= h_n-|\!\operatorname {\mathrm {Cl}}(n)[2]|$
. The discriminant of a polynomial in
![]() ${\mathbb {Q}}$
is positive if and only if the number of nonreal roots of the polynomial is divisible by 4. Putting all this together completes the proof.
${\mathbb {Q}}$
is positive if and only if the number of nonreal roots of the polynomial is divisible by 4. Putting all this together completes the proof.
3.4 Proof of Theorem 1.11
Assume that n is a positive squarefree integer. Ye [Reference Ye14, Corollary 1.2] computed the discriminant of the ring class polynomials
![]() $H_n$
as
$H_n$
as
 $$ \begin{align*} &\log|\Delta(H_n)| = \\ &-\dfrac{h_K}{4}\sum_{\substack{[\mathfrak{a}]\in\operatorname{\mathrm{Cl}}_K\\ [\mathfrak{a}]\neq[\mathcal{O}_K]}}\sum_{\ell=0}^{n-1}\sum_{X,Y=-\infty}^{\infty} \kappa\bigg(1-\dfrac{n(2AX+BY)^2+(nY-2A\ell)^2}{4An},\dfrac{B\ell}{n}f_1^{(\mathfrak{a})}-\dfrac{2A\ell}{n}f_{2}^{(\mathfrak{a})}+L_{-}^{(\mathfrak{a})}\bigg), \end{align*} $$
$$ \begin{align*} &\log|\Delta(H_n)| = \\ &-\dfrac{h_K}{4}\sum_{\substack{[\mathfrak{a}]\in\operatorname{\mathrm{Cl}}_K\\ [\mathfrak{a}]\neq[\mathcal{O}_K]}}\sum_{\ell=0}^{n-1}\sum_{X,Y=-\infty}^{\infty} \kappa\bigg(1-\dfrac{n(2AX+BY)^2+(nY-2A\ell)^2}{4An},\dfrac{B\ell}{n}f_1^{(\mathfrak{a})}-\dfrac{2A\ell}{n}f_{2}^{(\mathfrak{a})}+L_{-}^{(\mathfrak{a})}\bigg), \end{align*} $$
where
![]() $h_K$
denotes the class number of
$h_K$
denotes the class number of
![]() $K={\mathbb {Q}}(\sqrt {-n})$
,
$K={\mathbb {Q}}(\sqrt {-n})$
,
![]() $L_{-}^{(\mathfrak {a})}$
denotes the lattice
$L_{-}^{(\mathfrak {a})}$
denotes the lattice
![]() ${\mathbb {Z}} f_1^{(\mathfrak {a})}+{\mathbb {Z}} f_2^{(\mathfrak {a})}$
,
${\mathbb {Z}} f_1^{(\mathfrak {a})}+{\mathbb {Z}} f_2^{(\mathfrak {a})}$
,
 $$ \begin{align*}\mathfrak{a}=\bigg[A,\dfrac{B+\sqrt{-n}}{2}\bigg], \quad f_1^{(\mathfrak{a})}=\begin{pmatrix} -1 & B \\ 0 & A \end{pmatrix}, \quad f_2^{(\mathfrak{a})}=\begin{pmatrix} 0 & C \\ 1 & 0 \end{pmatrix},\end{align*} $$
$$ \begin{align*}\mathfrak{a}=\bigg[A,\dfrac{B+\sqrt{-n}}{2}\bigg], \quad f_1^{(\mathfrak{a})}=\begin{pmatrix} -1 & B \\ 0 & A \end{pmatrix}, \quad f_2^{(\mathfrak{a})}=\begin{pmatrix} 0 & C \\ 1 & 0 \end{pmatrix},\end{align*} $$
 $$ \begin{align} \kappa(m,\mu)\nonumber=&-\dfrac{1}{h_K}\sum_{q \, \textrm{inert} }^{}\xi_q(m,\mu)(\operatorname{\mathrm{ord}}_q(m)+1)\rho_K\bigg(\dfrac{mn}{q}\bigg)\log q \\ & - \dfrac{\rho_K(mn)}{h_K}\sum_{q \mid n}^{}\xi_q(m,\mu)\operatorname{\mathrm{ord}}_q(mn)\log q, \end{align} $$
$$ \begin{align} \kappa(m,\mu)\nonumber=&-\dfrac{1}{h_K}\sum_{q \, \textrm{inert} }^{}\xi_q(m,\mu)(\operatorname{\mathrm{ord}}_q(m)+1)\rho_K\bigg(\dfrac{mn}{q}\bigg)\log q \\ & - \dfrac{\rho_K(mn)}{h_K}\sum_{q \mid n}^{}\xi_q(m,\mu)\operatorname{\mathrm{ord}}_q(mn)\log q, \end{align} $$
and
![]() $\xi _q$
and
$\xi _q$
and
![]() $\rho _K$
are the functions defined in [Reference Ye14, Corollary 1.2].
$\rho _K$
are the functions defined in [Reference Ye14, Corollary 1.2].
To prove Theorem 1.11, we will show that
![]() $\log 3$
never appears in
$\log 3$
never appears in
![]() $\kappa (m,\mu )$
for any choice of parameters m and
$\kappa (m,\mu )$
for any choice of parameters m and
![]() $\mu $
. From the definition of
$\mu $
. From the definition of
![]() $\kappa (m,\mu )$
, it suffices to prove that 3 always splits in
$\kappa (m,\mu )$
, it suffices to prove that 3 always splits in
![]() ${\mathbb {Q}}(\sqrt {-n})$
and does not divide n for all positive squarefree
${\mathbb {Q}}(\sqrt {-n})$
and does not divide n for all positive squarefree
![]() $n\equiv 11\pmod {24}$
.
$n\equiv 11\pmod {24}$
.
Recall that a prime number
![]() $\mathfrak {p}$
splits in the imaginary quadratic field
$\mathfrak {p}$
splits in the imaginary quadratic field
![]() ${\mathbb {Q}}(\sqrt {-n})$
if and only if
${\mathbb {Q}}(\sqrt {-n})$
if and only if
![]() $-n$
is a nonzero quadratic residue mod
$-n$
is a nonzero quadratic residue mod
![]() $\mathfrak {p}$
. The quadratic residues mod 3 are 0 and 1, and it is easy to see that when
$\mathfrak {p}$
. The quadratic residues mod 3 are 0 and 1, and it is easy to see that when
![]() $n\equiv 11\pmod {24}$
, we have
$n\equiv 11\pmod {24}$
, we have
![]() $-n\equiv 1\pmod {3}$
. Thus
$-n\equiv 1\pmod {3}$
. Thus
![]() $-n$
is a nonzero quadratic residue mod 3 for all positive squarefree integers
$-n$
is a nonzero quadratic residue mod 3 for all positive squarefree integers
![]() $n\equiv 11\pmod {24}$
. This completes the proof.
$n\equiv 11\pmod {24}$
. This completes the proof.
4 An illustration of the main results
Example 4.1. Take
![]() $n=227$
. From [Reference Konstantinou and Kontogeorgis7, Table 1],
$n=227$
. From [Reference Konstantinou and Kontogeorgis7, Table 1],
Since 227 is squarefree, the degree of
![]() $\mathcal {P}_{227}$
is equal to the class number of
$\mathcal {P}_{227}$
is equal to the class number of
![]() ${\mathbb {Q}}(\sqrt {-227})$
; thus,
${\mathbb {Q}}(\sqrt {-227})$
; thus,
![]() $h_{227}=5$
. The class group structure of
$h_{227}=5$
. The class group structure of
![]() ${\mathbb {Q}}(\sqrt {-227})$
, computed using Sage, is
${\mathbb {Q}}(\sqrt {-227})$
, computed using Sage, is
![]() ${\mathbb {Z}}/5{\mathbb {Z}}$
(see Table 2). By Corollary 1.9,
${\mathbb {Z}}/5{\mathbb {Z}}$
(see Table 2). By Corollary 1.9,
![]() $\Delta (\mathcal {P}_{227})>0$
, since
$\Delta (\mathcal {P}_{227})>0$
, since
![]() $h_{227}=5\equiv 1\pmod {4}.$
From Table 2,
$h_{227}=5\equiv 1\pmod {4}.$
From Table 2,
![]() $\Delta (\mathcal {P}_{227})=2^4\cdot 227^2$
. Moreover, using the Sage database for ring class polynomials and their discriminants [Reference Stein13], it can be found that
$\Delta (\mathcal {P}_{227})=2^4\cdot 227^2$
. Moreover, using the Sage database for ring class polynomials and their discriminants [Reference Stein13], it can be found that
 $$ \begin{align*}H_{227}(z)=& \,z^5 + 360082897644683264000z^4 \\&- 2562327002832961536000000000z^3 \\&+ 18227340807938993794580480000000000z^2 \\&- 2111118203460821622718464000000000000z \\&+ 5085472193216544027705344000000000000000, \end{align*} $$
$$ \begin{align*}H_{227}(z)=& \,z^5 + 360082897644683264000z^4 \\&- 2562327002832961536000000000z^3 \\&+ 18227340807938993794580480000000000z^2 \\&- 2111118203460821622718464000000000000z \\&+ 5085472193216544027705344000000000000000, \end{align*} $$
and
Therefore,
which is in accord with Theorem 1.3, since the quotient is a perfect square.
By Theorem 1.5,
![]() $\mathcal {D}({\mathbb {Q}}(\mathfrak {j}_{227}))> 0$
since
$\mathcal {D}({\mathbb {Q}}(\mathfrak {j}_{227}))> 0$
since
![]() $\Delta (\mathcal {P}_{227})> 0$
, as already seen above and in Table 2. From Remark 1.6,
$\Delta (\mathcal {P}_{227})> 0$
, as already seen above and in Table 2. From Remark 1.6,
![]() $\mathfrak {D}_0=1$
,
$\mathfrak {D}_0=1$
,
![]() $\mathfrak {D}_1=227$
,
$\mathfrak {D}_1=227$
,
![]() $\mathfrak {t}=1$
, and thus
$\mathfrak {t}=1$
, and thus
Notice that 3 does not appear in the prime factorisation of
![]() $\Delta (\mathcal {P}_{227})$
and
$\Delta (\mathcal {P}_{227})$
and
![]() $\Delta (H_{227})$
.
$\Delta (H_{227})$
.
5 Concluding remarks and further research
We can now replace the ring class polynomials
![]() $H_n$
and their discriminants
$H_n$
and their discriminants
![]() $\Delta (H_n)$
with the Ramanujan polynomials
$\Delta (H_n)$
with the Ramanujan polynomials
![]() $\mathcal {P}_n$
and their discriminants
$\mathcal {P}_n$
and their discriminants
![]() $\Delta (\mathcal {P}_n)$
to simplify computations wherever needed. Ramanujan polynomials
$\Delta (\mathcal {P}_n)$
to simplify computations wherever needed. Ramanujan polynomials
![]() $\mathcal {P}_n$
can be used in the generation of special curves, such as MNT curves [Reference Miyaji, Nakabayashi and Takano9, Reference Scott and Barreto12], and in the generation of elliptic curves that do not necessarily have prime order [Reference Atkin and Morain1].
$\mathcal {P}_n$
can be used in the generation of special curves, such as MNT curves [Reference Miyaji, Nakabayashi and Takano9, Reference Scott and Barreto12], and in the generation of elliptic curves that do not necessarily have prime order [Reference Atkin and Morain1].
Problems such as primality testing and proving [Reference Atkin and Morain1], the generation of elliptic curve parameters [Reference Konstantinou and Kontogeorgis8] and the representability of primes by quadratic forms [Reference Cox4] could be considerably advanced once we know more about Ramanujan polynomials
![]() $\mathcal {P}_n$
and their discriminants and traces.
$\mathcal {P}_n$
and their discriminants and traces.
Acknowledgements
The majority of this research was done during the Research Science Institute (RSI) at MIT in the summer of 2022. First, I would like to thank my research mentor Alan Peng for his invaluable mentorship, constant encouragement, guidance and support. Next, I would like to thank Andrew Sutherland for suggesting this problem and the MIT Math Department for making this research project possible. I am grateful and indebted to the RSI, CEE and MIT for their hospitality and support during the preparation of this work. Finally, I would like to thank the referee for helpful comments, and for pointing out several mistakes in the earlier version of the paper.