Hostname: page-component-5c6d5d7d68-thh2z Total loading time: 0 Render date: 2024-08-16T21:54:32.087Z Has data issue: false hasContentIssue false
  • English
  • Français

Computing theta functions in quasi-linear time in genus two and above

Part of: Abelian varieties and schemes Curves Deformations of analytic structures

Published online by Cambridge University Press:  26 August 2016

Hugo Labrande  and
Emmanuel Thomé
Hugo Labrande
Affiliation:
Université de Lorraine, LORIA (UMR CNRS 7503), INRIA Nancy, 615 rue du jardin botanique, 54602 Villers-lès-Nancy Cedex, France University of Calgary, Department of Computer Science, 2500 University Dr NW, Calgary, Alberta, Canada T2N 1N4 email hugo.labrande@inria.fr
Emmanuel Thomé
Affiliation:
Université de Lorraine, LORIA (UMR CNRS 7503), INRIA Nancy, 615 rue du jardin botanique, 54602 Villers-lès-Nancy Cedex, France email emmanuel.thome@inria.fr

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We outline an algorithm to compute 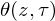$\unicode[STIX]{x1D703}(z,\unicode[STIX]{x1D70F})$ in genus two in quasi-linear time, borrowing ideas from the algorithm for theta constants and the one for 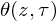$\unicode[STIX]{x1D703}(z,\unicode[STIX]{x1D70F})$ in genus one. Our implementation shows a large speed-up for precisions as low as a few thousand decimal digits. We also lay out a strategy to generalize this algorithm to genus 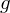$g$.

MSC classification

Primary: 14K25: Theta functions
Secondary: 14H42: Theta functions; Schottky problem 32G81: Applications to physics
Type
Research Article
Information
LMS Journal of Computation and Mathematics , Volume 19 , Special Issue A: Algorithmic Number Theory Symposium XII , 2016 , pp. 163 - 177
Copyright
© The Author(s) 2016 

References

Cosset, R., ‘Applications des fonctions thêta à la cryptographie sur courbes hyperelliptiques’, PhD Thesis, Université Henri Poincaré-Nancy I, 2011.Google Scholar
Cox, D. A., ‘The arithmetic-geometric mean of Gauss’, Enseign. Math. 30 (1984) no. 2, 275–330.Google Scholar
Deconinck, B., Heil, M., Bobenko, A., Van Hoeij, M. and Schmies, M., ‘Computing Riemann theta functions’, Math. Comp. 73 (2004) no. 247, 1417–1442.CrossRefGoogle Scholar
Dupont, R., ‘Moyenne arithmético-géométrique, suites de Borchardt et applications’, PhD Thesis, École polytechnique, Palaiseau, 2006, http://www.lix.polytechnique.fr/Labo/Regis.Dupont/these_soutenance.pdf.Google Scholar
Dupont, R., ‘Fast evaluation of modular functions using Newton iterations and the AGM’, Math. Comp. 80 (2011) no. 275, 1823–1847.Google Scholar
Enge, A., ‘The complexity of class polynomial computation via floating point approximations’, Math. Comp. 78 (2009) no. 266, 1089–1107.Google Scholar
Enge, A., Gastineau, M., Théveny, P. and Zimmerman, P., ‘GNU MPC. INRIA, September 2012. Release 1.0.1’, http://mpc.multiprecision.org/.Google Scholar
Enge, A. and Thomé, E., ‘CMH — Computation of Igusa Class Polynomials, Version 1.0’, 2014, http://cmh.gforge.inria.fr/.Google Scholar
Enge, A. and Thomé, E., ‘Computing class polynomials for abelian surfaces’, Exp. Math. 23 (2014) no. 2, 129–145.Google Scholar
Gaudry, P., ‘Fast genus 2 arithmetic based on theta functions’, J. Math. Cryptol. 1 (2007) no. 3, 243–265.Google Scholar
Gottschling, E., ‘Explizite bestimmung der randflächen des fundamentalbereiches der modulgruppe zweiten grades’, Math. Ann. 138 (1959) no. 2, 103–124.CrossRefGoogle Scholar
Helfrich, B., ‘Algorithms to construct Minkowski reduced and Hermite reduced lattice bases’, Theoret. Comput. Sci. 41 (1985) 125–139.Google Scholar
Igusa, J.-I., Theta functions (Springer, Berlin, Heidelberg, 1972).CrossRefGoogle Scholar
Klingen, H., Introductory lectures on Siegel modular forms (Cambridge University Press, Cambridge, 1990).Google Scholar
Labrande, H., ‘Computing Jacobi’s $\unicode[STIX]{x1D703}$ in quasi-linear time’, Preprint, 2015, arXiv:1511.04248 [math.NT].Google Scholar
Mumford, D., Tata lectures on theta , vol. I (Birkhäuser, Boston, 1983).Google Scholar
Streng, M., ‘Computing Igusa class polynomials’, Math. Comp. 83 (2014) no. 285.Google Scholar
Van Wamelen, P., ‘Equations for the Jacobian of a hyperelliptic curve’, Trans. Amer. Math. Soc. 350 (1998) no. 8, 3083–3106.Google Scholar