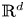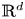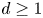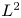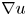1. Introduction
In this article, we investigate the initial value problem (IVP) for the $d$![]() -dimensional isentropic compressible Euler system with source term
-dimensional isentropic compressible Euler system with source term

which governs the motion of a compressible inviscid fluid through a porous medium and describes the compressible gas flow passes a porous medium and the medium induces a friction force, where the functions $\rho (t,\,x)$![]() , $u(t,\,x)=(u_1,\,u_2,\,\cdots,\,u_d)$
, $u(t,\,x)=(u_1,\,u_2,\,\cdots,\,u_d)$![]() and $p(t,\,x)$
and $p(t,\,x)$![]() denote the density, velocity vector fluid and pressure, respectively. The symbol $u\otimes u$
denote the density, velocity vector fluid and pressure, respectively. The symbol $u\otimes u$![]() denotes a matrix whose $ij^{th}$
denotes a matrix whose $ij^{th}$![]() entry is $u_iu_j$
entry is $u_iu_j$![]() , the constant $\mu >0$
, the constant $\mu >0$![]() . The first equation in system (1.1) is just the usual conservation of mass. The second equation in system (1.1) represents the Newton's law (or momentum conservation): the LHS denotes the acceleration of the fluid in Eulerian frame, whereas the RHS describes the force (where $\rho u$
. The first equation in system (1.1) is just the usual conservation of mass. The second equation in system (1.1) represents the Newton's law (or momentum conservation): the LHS denotes the acceleration of the fluid in Eulerian frame, whereas the RHS describes the force (where $\rho u$![]() denotes external forcing field).
denotes external forcing field).
In order to simplify the system (1.1), substitute $(1.1)_1$![]() into $(1.1)_2$
into $(1.1)_2$![]() and $(1.1)_2$
and $(1.1)_2$![]() into $(1.1)_3$
into $(1.1)_3$![]() , one has that
, one has that

where $u\cdot \nabla u=\sum _{i=1}^du_i\partial _{x_i}u$![]() , $\text {div}u=\sum _{i=1}^d\partial _{x_i}u_i$
, $\text {div}u=\sum _{i=1}^d\partial _{x_i}u_i$![]() .
.
The system (1.1) or (1.2) has (d+1) equations, (d+2) unknowns $(\rho,\, u_1,\,\cdots,\,u_d,\, p)$![]() and thus is not formally self-consistent, however, when we introduce the equality of pressure and density, which is given by
and thus is not formally self-consistent, however, when we introduce the equality of pressure and density, which is given by
with the adiabatic exponent $\gamma >1$![]() and constant $A>0$
and constant $A>0$![]() . Now the (d+2) unknowns of system (1.1) become (d+1) unknowns $(\rho,\, u_1,\,\cdots,\,u_d)$
. Now the (d+2) unknowns of system (1.1) become (d+1) unknowns $(\rho,\, u_1,\,\cdots,\,u_d)$![]() , thus system (1.1) or (1.2) is formally self-consistent.
, thus system (1.1) or (1.2) is formally self-consistent.
As is well known, the formation of singularities is a fundamental physical phenomenon manifested in solutions [Reference John17, Reference Lin19, Reference Majda22, Reference Sideris27, Reference Wu34] for the compressible Euler equations (i.e., system (1.1) with $\mu =0$![]() ), which are a prototypical example of hyperbolic systems of conservation laws. This phenomenon can be explained by mathematical analysis by showing the finite time formation of singularities in the solutions. Therefore, the blow-up phenomena for the multi-dimensional compressible Euler flows has attracted lots of interests and attentions because of its physical importance. However, it is a difficult problem to understand the blow-up behaviour of the general solutions of the compressible Euler equations. The earliest work of system (1.1) with $\mu =0$
), which are a prototypical example of hyperbolic systems of conservation laws. This phenomenon can be explained by mathematical analysis by showing the finite time formation of singularities in the solutions. Therefore, the blow-up phenomena for the multi-dimensional compressible Euler flows has attracted lots of interests and attentions because of its physical importance. However, it is a difficult problem to understand the blow-up behaviour of the general solutions of the compressible Euler equations. The earliest work of system (1.1) with $\mu =0$![]() began with Taylor [Reference Taylor30, Reference Taylor31] finding the wave motion produced by an expanding sphere and preceded by a shock front. It is similar to the one-dimensional gas flow produced by a piston with constant speed. The progressing waves were also succeeded in finding some other types of spherical waves like detonation, deflagration, combustion and reflected shocks. In [Reference Chen2, Reference Chen and Glimm4, Reference Makino, Mizohata and Ukai23, Reference Makino, Mizohata and Ukai24, Reference Tsuge32], the authors studied the global weak solution of the isentropic compressible Euler equations with spherical symmetry. Recently, Li and Wang [Reference Li and Wang18] derived some special global and blow-up solutions of system (1.1) as $\mu =0$
began with Taylor [Reference Taylor30, Reference Taylor31] finding the wave motion produced by an expanding sphere and preceded by a shock front. It is similar to the one-dimensional gas flow produced by a piston with constant speed. The progressing waves were also succeeded in finding some other types of spherical waves like detonation, deflagration, combustion and reflected shocks. In [Reference Chen2, Reference Chen and Glimm4, Reference Makino, Mizohata and Ukai23, Reference Makino, Mizohata and Ukai24, Reference Tsuge32], the authors studied the global weak solution of the isentropic compressible Euler equations with spherical symmetry. Recently, Li and Wang [Reference Li and Wang18] derived some special global and blow-up solutions of system (1.1) as $\mu =0$![]() with spherical symmetry. Some other results of system (1.1) with $\mu =0$
with spherical symmetry. Some other results of system (1.1) with $\mu =0$![]() can be found in [Reference Chen and LeFloch3, Reference Chen and Wang5, Reference DiPerna8, Reference Lions, Perthame and Souganidis20, Reference Lions, Perthame and Tadmor21, Reference Smoller29], as well as the references cited therein.
can be found in [Reference Chen and LeFloch3, Reference Chen and Wang5, Reference DiPerna8, Reference Lions, Perthame and Souganidis20, Reference Lions, Perthame and Tadmor21, Reference Smoller29], as well as the references cited therein.
To our best knowledge, there are many mathematical works about system (1.1). For one dimensional case, assuming that the initial data are smooth enough and that the derivatives of the initial data are sufficiently small, the global existence and the large time behaviour of the smooth solutions of system (1.1) were studied by Hsiao, Liu and Luo in [Reference Hsiao and Liu10, Reference Hsiao and Luo11]. If this assumption is violated, the solutions eventually will develop singularities in general, hence it is necessary to consider the weak solutions. If the initial data belong to $L^\infty$![]() and satisfy some conditions, then the equation admits a global entropy weak solution [Reference Ding, Chen and Luo7, Reference Huang and Pan14, Reference Pan and Zhao25] and the solution converges to Barenblatt's profiles of the porous medium equation [Reference Huang, Marcati and Pan13–Reference Huang, Pan and Wang16]. In [Reference Dafermos and Pan6, Reference Hsiao, Luo and Yang12], the global existence of BV solutions for the Cauchy problem of system (1.1) was investigated by using a fractional step version of the Glimm's scheme. For multi-dimensional case, if the initial data are sufficiently small, by analysing the Green function of the linearized system, Wang and Yang [Reference Wang and Yang33] obtained the global existence and pointwise estimates of the solutions by the energy estimates. When the initial data are near its equilibrium, Pan and Zhao [Reference Pan and Zhao26] showed global existence and uniqueness of classical solutions to the initial boundary value problem for the 3D damped compressible Euler equations on bounded domain with slip boundary condition and showed that the classical solutions converge to steady state exponentially fast in time. In 2003, for 3 dimensional case, Sideris, Thomases and Wang [Reference Sideris, Thomases and Wang28] showed that if the initial data are sufficiently small in an appropriate norm, then damping term can prevent the development of singularities and the Cauchy problem of system (1.1) has a unique global smooth solution $u(t,\,x)\in \mathcal {C}(\mathbb {R}^+;H^3)$
and satisfy some conditions, then the equation admits a global entropy weak solution [Reference Ding, Chen and Luo7, Reference Huang and Pan14, Reference Pan and Zhao25] and the solution converges to Barenblatt's profiles of the porous medium equation [Reference Huang, Marcati and Pan13–Reference Huang, Pan and Wang16]. In [Reference Dafermos and Pan6, Reference Hsiao, Luo and Yang12], the global existence of BV solutions for the Cauchy problem of system (1.1) was investigated by using a fractional step version of the Glimm's scheme. For multi-dimensional case, if the initial data are sufficiently small, by analysing the Green function of the linearized system, Wang and Yang [Reference Wang and Yang33] obtained the global existence and pointwise estimates of the solutions by the energy estimates. When the initial data are near its equilibrium, Pan and Zhao [Reference Pan and Zhao26] showed global existence and uniqueness of classical solutions to the initial boundary value problem for the 3D damped compressible Euler equations on bounded domain with slip boundary condition and showed that the classical solutions converge to steady state exponentially fast in time. In 2003, for 3 dimensional case, Sideris, Thomases and Wang [Reference Sideris, Thomases and Wang28] showed that if the initial data are sufficiently small in an appropriate norm, then damping term can prevent the development of singularities and the Cauchy problem of system (1.1) has a unique global smooth solution $u(t,\,x)\in \mathcal {C}(\mathbb {R}^+;H^3)$![]() . Moreover, as the time $t$
. Moreover, as the time $t$![]() becomes large, they studied the long time behaviour of solutions to obtain the following algebra decay of solution $U(t,\,x)$
becomes large, they studied the long time behaviour of solutions to obtain the following algebra decay of solution $U(t,\,x)$![]() and exponential decay of vorticity $\omega (t,\,x)$
and exponential decay of vorticity $\omega (t,\,x)$![]()

Motivated by the article [Reference Sideris, Thomases and Wang28], in this paper, we investigate global existence and the large time behaviour of solution of the Cauchy problem for system (1.1) in $\mathbb {R}^d$![]() . This tells us that if the initial data are sufficiently small in an appropriate norm, then source term can prevent the development of singularities. Compared with the results in [Reference Sideris, Thomases and Wang28], we consider the d-dimensional Euler equations with damping terms and obtain the unique global smooth solution $u(t,\,x)\in \mathcal {C}(\mathbb {R}^+;H^s)\cap \mathcal {C}^1(\mathbb {R}^+;H^{s-1}),\,\; s>1+\frac {d}{2}$
. This tells us that if the initial data are sufficiently small in an appropriate norm, then source term can prevent the development of singularities. Compared with the results in [Reference Sideris, Thomases and Wang28], we consider the d-dimensional Euler equations with damping terms and obtain the unique global smooth solution $u(t,\,x)\in \mathcal {C}(\mathbb {R}^+;H^s)\cap \mathcal {C}^1(\mathbb {R}^+;H^{s-1}),\,\; s>1+\frac {d}{2}$![]() . By a detailed analysis of the semigroup $S(t)$
. By a detailed analysis of the semigroup $S(t)$![]() of the linearized system, we show an important lemma 4.1. As the time $t$
of the linearized system, we show an important lemma 4.1. As the time $t$![]() becomes large, we also have the following algebra decay of solution $v(t,\,x)$
becomes large, we also have the following algebra decay of solution $v(t,\,x)$![]() and exponential decay of vorticity $\Omega (t,\,x)$
and exponential decay of vorticity $\Omega (t,\,x)$![]()

which is the same as the results in 3D derived in [Reference Sideris, Thomases and Wang28]. By introducing a new weight function $J_\infty ^h(t)$![]() (see page 16 in § 4) and the Gagliardo–Nirenberg inequality, one has that the estimate of high order derivative about solutions
(see page 16 in § 4) and the Gagliardo–Nirenberg inequality, one has that the estimate of high order derivative about solutions

where $d$![]() denotes the dimension of space, $0\leq k\leq 1+\frac {d}{2}$
denotes the dimension of space, $0\leq k\leq 1+\frac {d}{2}$![]() , which is optimal in the linearized sense. These extend and improve the result obtained by Sideris et al. in [Reference Sideris, Thomases and Wang28].
, which is optimal in the linearized sense. These extend and improve the result obtained by Sideris et al. in [Reference Sideris, Thomases and Wang28].
The rest of the paper is organized as follows. In § 2, we rewrite the system (1.1) into a quasilinear symmetric system and state the local well-posedness which will be used in this article. In § 3, by virtue of a priori estimates, we establish the global smooth solution of the IVP for system (2.1) with small initial data. Finally, in § 4, we investigate the large time behaviour of solution to the isentropic compressible Euler system with source terms in $\mathbb {R}^d$![]() , one only obtain the algebra decay of solution, besides the $L^2$
, one only obtain the algebra decay of solution, besides the $L^2$![]() -norm of $\nabla u$
-norm of $\nabla u$![]() is exponential decay.
is exponential decay.
2. Preliminaries
In this subsection, for the convenience of the readers, we first introduce some notations. Let $\|\cdot \|_X$![]() denote the norm of the Banach space $X$
denote the norm of the Banach space $X$![]() , such as, $\|\cdot \|_{H^s}$
, such as, $\|\cdot \|_{H^s}$![]() and $(\cdot,\, \cdot )_s$
and $(\cdot,\, \cdot )_s$![]() denote the norm and the inner product of $H^s (\mathbb {R}^d)$
denote the norm and the inner product of $H^s (\mathbb {R}^d)$![]() , $s\in \mathbb {R}$
, $s\in \mathbb {R}$![]() , respectively, where $L^r ,\,\; H^s$
, respectively, where $L^r ,\,\; H^s$![]() denotes $L^r (\mathbb {R}^d),\,\; H^s(\mathbb {R}^d)$
denotes $L^r (\mathbb {R}^d),\,\; H^s(\mathbb {R}^d)$![]() spaces, $r\geq 1,\, s\in \mathbb {R}$
spaces, $r\geq 1,\, s\in \mathbb {R}$![]() . Throughout the article, we will let $c$
. Throughout the article, we will let $c$![]() or $C$
or $C$![]() be a generic constant, which may assume different values in different formulas.
be a generic constant, which may assume different values in different formulas.
In order to achieve the aim, introduce the function
If the Cauchy problem of system (1.2) with the solution $(\rho,\,u)$![]() satisfies
satisfies
let $\omega =\pi -\tilde {\pi },$![]() where $\tilde {\pi }=C_1\tilde {p}^{(\gamma -1)/2\gamma }$
where $\tilde {\pi }=C_1\tilde {p}^{(\gamma -1)/2\gamma }$![]() , $\tilde {p}=A\tilde {\rho }^{\gamma }$
, $\tilde {p}=A\tilde {\rho }^{\gamma }$![]() and $\bar {\pi }=\tilde {\pi }\frac {\gamma -1}{2}$
and $\bar {\pi }=\tilde {\pi }\frac {\gamma -1}{2}$![]() , then system (1.2) is equivalent to the following quasilinear symmetric system
, then system (1.2) is equivalent to the following quasilinear symmetric system

Let $v=(\omega,\,u_1,\,\cdots,\,u_d)^\top$![]() , $\top$
, $\top$![]() denotes transposition of matrix, the well-posedness of system (2.1) in Sobolev space is corollary of theorem 3.2 and 3.7 in [Reference Guo and Wu9].
denotes transposition of matrix, the well-posedness of system (2.1) in Sobolev space is corollary of theorem 3.2 and 3.7 in [Reference Guo and Wu9].
Theorem 2.1 For any initial data $v_0=(\omega _0,\,u_0)\in H^s(\mathbb {R}^d),\,s>1+\frac {d}{2},$![]() there exists a time $T>0$
there exists a time $T>0$![]() such that the initial value problem (2.1) has a unique solution $v=(\omega,\,u),$
such that the initial value problem (2.1) has a unique solution $v=(\omega,\,u),$![]() which belongs to
which belongs to
Moreover, if the $v_0\in H^{s}(\mathbb {R}^d),$![]() then the solution map
then the solution map
is continuous in the sense of Hadmard, and we have the following inequality
where sequence $\{v^n\}_{n\in N}$![]() is approximation solutions to system (2.1). In particular, let $T_{v_0}$
is approximation solutions to system (2.1). In particular, let $T_{v_0}$![]() be the lifespan of the solution $v$
be the lifespan of the solution $v$![]() to system (2.1) with initial datum $v_0$
to system (2.1) with initial datum $v_0$![]() , the lifespan $T_{v_0}$
, the lifespan $T_{v_0}$![]() satisfies
satisfies
If $T_{v_0}<\infty$![]() , then for all $t\leq T_{v_0}$
, then for all $t\leq T_{v_0}$![]() we have
we have
Remark 2.2 The smoothness of solution $(\rho,\,u)$![]() of system (1.1) is equivalent to the smoothness of solution $(\omega,\,u)$
of system (1.1) is equivalent to the smoothness of solution $(\omega,\,u)$![]() of system (2.1) by the definition of $w$
of system (2.1) by the definition of $w$![]() . The positivity of the density $\rho$
. The positivity of the density $\rho$![]() is guaranteed by the positivity of the initial density $\rho _0$
is guaranteed by the positivity of the initial density $\rho _0$![]() , in fact, by the first equation in system (1.1), we have
, in fact, by the first equation in system (1.1), we have

where we have applied the ordinary differential equation of the flow

For all time $t\in [0,\,T]$![]() , by solving the equation (2.3) yields that
, by solving the equation (2.3) yields that
In view of $\|u(t,\,\varphi )\|_{L^\infty }=\|u(t,\,x)\|_{L^\infty }$![]() one has that
one has that
for any $(t,\,x)\in \mathbb {R}^+\times \mathbb {R}^d$![]() , provided the initial density $\rho _0(x)>0$
, provided the initial density $\rho _0(x)>0$![]() .
.
3. The global existence of solution with small initial data
In this subsection, by showing a priori estimates of the IVP of system (2.1) by some lemmas, we shall establish the global smooth solution of system (2.1) with small initial data.
In order to distinguish time and space derivatives, let $\nabla =(\partial _{x_1},\,\cdots,\, \partial _{x_d})$![]() denote the space derivatives, $\partial =(\partial _t,\,\nabla )$
denote the space derivatives, $\partial =(\partial _t,\,\nabla )$![]() is all first time and space derivatives. For $s>1+\frac {d}{2}$
is all first time and space derivatives. For $s>1+\frac {d}{2}$![]() , introduce the energy functions
, introduce the energy functions


where for all $\sigma \in \mathbb {R}$![]() , by the Fourier transformation yields that
, by the Fourier transformation yields that
Next, we state the following lemma of energy estimates.
Lemma 3.1 Assume the function $(\omega,\,u)\in \mathcal {C}([0,\,T[,\,H^s(\mathbb {R}^d))$![]() be a solution of system (2.1) , for some $T>0$
be a solution of system (2.1) , for some $T>0$![]() . Then the following energy inequalities hold:
. Then the following energy inequalities hold:
Proof. Taking inner product of system $(2.1)_1$![]() with $\omega$
with $\omega$![]() , and system $(2.1)_2$
, and system $(2.1)_2$![]() with $u$
with $u$![]() , after integration by parts, adding them together, it yields that
, after integration by parts, adding them together, it yields that

where we have used
in the first equality, the Hölder inequality in the last inequality, and $\|(\omega,\,u)\|_{X}=\|\omega \|_{X}+\|u\|_{X}$![]() .
.
Next, we will show inequality (3.4). Applying the operator $\partial \nabla ^\delta$![]() on both sides of system (2.1), it follows that
on both sides of system (2.1), it follows that
Multiplying equation (3.6) and equation (3.7) by $\partial \nabla ^\delta \omega$![]() and $\partial \nabla ^\delta u$
and $\partial \nabla ^\delta u$![]() respectively, $|\delta |\leq s-1$
respectively, $|\delta |\leq s-1$![]() . Adding them together and integration by parts, one has that
. Adding them together and integration by parts, one has that

where the first equality is guaranteed by
For $|\delta |\geq 0$![]() , we first deal with the term $I_1$
, we first deal with the term $I_1$![]() as follows
as follows

When $\delta =0$![]() , thanks to the Hölder inequality, we have
, thanks to the Hölder inequality, we have

As $\delta >0$![]() , by virtue of the Gagliardo–Nirenberg inequality yields that
, by virtue of the Gagliardo–Nirenberg inequality yields that

where $\frac {1}{p}+\frac {1}{q}=\frac {1}{2}$![]() for $p,\,q\in [2,\,\infty ]$
for $p,\,q\in [2,\,\infty ]$![]() , and $\theta \in (0,\,1)$
, and $\theta \in (0,\,1)$![]() , we also have used Young's inequality in the last inequality. In view of (3.10), (3.11) and the Hölder inequality, $I_1^{(1)}$
, we also have used Young's inequality in the last inequality. In view of (3.10), (3.11) and the Hölder inequality, $I_1^{(1)}$![]() can be dealt with as
can be dealt with as
On the other hand, in order to deal with $I_1^{(2)}$![]() , in view of the Gagliardo–Nirenberg inequality, for $\alpha,\,\beta \leq \delta -1,\,\;\alpha +\beta =\delta$
, in view of the Gagliardo–Nirenberg inequality, for $\alpha,\,\beta \leq \delta -1,\,\;\alpha +\beta =\delta$![]() , one has that
, one has that

where $\frac {1}{p}+\frac {1}{q}=\frac {1}{2}$![]() for $p,\,q\in [2,\,\infty ]$
for $p,\,q\in [2,\,\infty ]$![]() , and $\vartheta \in (0,\,1)$
, and $\vartheta \in (0,\,1)$![]() , we also have used Young's inequality in the last inequality. Similarly, we can show that
, we also have used Young's inequality in the last inequality. Similarly, we can show that

Combining (3.13) with (3.14), it yields that
In view of (3.9), (3.12) and (3.15), it gives that
Similar to the process of proving (3.16), we can estimate $I_2,\,\;I_3$![]() and $I_4$
and $I_4$![]() to derive
to derive
Substituting (3.16) and (3.17) into (3.8), by virtue of (3.1) and (3.2), thus we consequently obtain (3.4).
Lemma 3.2 Let $\bar {\pi }>0$![]() and $s>1+\frac {d}{2}$
and $s>1+\frac {d}{2}$![]() . Assume the function $(\omega,\,u)\in \mathcal {C}([0,\,T[,\,H^s (\mathbb {R}^d))$
. Assume the function $(\omega,\,u)\in \mathcal {C}([0,\,T[,\,H^s (\mathbb {R}^d))$![]() be a solution of system (2.1) , for some $T>0$
be a solution of system (2.1) , for some $T>0$![]() . Then the following inequality holds:
. Then the following inequality holds:
Moreover, if the solution $(\omega,\,u)$![]() satisfies $I(\omega )(t)\ll 1$
satisfies $I(\omega )(t)\ll 1$![]() for any time $t>0,$
for any time $t>0,$![]() then $Q(\omega )(t)$
then $Q(\omega )(t)$![]() can be controlled by $I(u)(t)$
can be controlled by $I(u)(t)$![]() and we have
and we have
Proof. Multiplying the operator $\nabla ^\delta$![]() on both sides of system (2.1), one has that
on both sides of system (2.1), one has that
Taking $L^2$![]() norm of the equation (3.20) and (3.21) for $|\delta |\leq s-1$
norm of the equation (3.20) and (3.21) for $|\delta |\leq s-1$![]() , adding them together yields that
, adding them together yields that

Similar to the method of dealing with (3.9), one can easily check that




where we have used for $s>1+\frac {d}{2}$![]() that
that

Combining (3.22)–(3.25) and (3.26), it yields that
If the solution $\omega$![]() satisfies $I(\omega )(t)\ll 1$
satisfies $I(\omega )(t)\ll 1$![]() for any time $t>0$
for any time $t>0$![]() , choosing $CI(\omega )(t)\leq \frac {1}{3}$
, choosing $CI(\omega )(t)\leq \frac {1}{3}$![]() then we have
then we have
which derives the inequality (3.19).
Next, we will show the existence of global smooth solution for system (2.1).
Theorem 3.3 Assume the initial data $(\omega _0,\,u_0)\in H^s(\mathbb {R}^d),\,\;s>1+\frac {d}{2}$![]() . If the $(\omega _0,\,u_0)$
. If the $(\omega _0,\,u_0)$![]() satisfies $I(\omega _0,\,u_0)=\epsilon _0\ll 1$
satisfies $I(\omega _0,\,u_0)=\epsilon _0\ll 1$![]() , then system (2.1) has a unique global solution $(\omega,\,u)\in \mathcal {C}(\mathbb {R}^+,\,H^s(\mathbb {R}^d))$
, then system (2.1) has a unique global solution $(\omega,\,u)\in \mathcal {C}(\mathbb {R}^+,\,H^s(\mathbb {R}^d))$![]() . Moreover, there exists some $\mu _0>0$
. Moreover, there exists some $\mu _0>0$![]() , for all $t\in \mathbb {R}^+$
, for all $t\in \mathbb {R}^+$![]() , we have the energy inequality
, we have the energy inequality
Proof. Combining (3.3) and (3.4) in lemma 3.1 yields that

Note that


where we have used $s>1+\frac {d}{2}$![]() , which guarantees
, which guarantees
Inserting (3.28) and (3.29) into (3.27), one has that

Suppose the solution $(\omega,\,u)$![]() satisfies $I(\omega,\,u)(t)=\epsilon _0\ll 1$
satisfies $I(\omega,\,u)(t)=\epsilon _0\ll 1$![]() for any $t\in \mathbb {R}^+$
for any $t\in \mathbb {R}^+$![]() , choosing $CI(\omega,\,u)(t)\leq \frac {1}{3}$
, choosing $CI(\omega,\,u)(t)\leq \frac {1}{3}$![]() , then it follows from lemma 3.2 that the solution satisfies (3.19), in view of (3.30) we have
, then it follows from lemma 3.2 that the solution satisfies (3.19), in view of (3.30) we have

Since $\epsilon _0$![]() is sufficiently small, we can choose $\epsilon _0$
is sufficiently small, we can choose $\epsilon _0$![]() such that
such that
Consequently, we have
Integrating the inequality (3.31) with respect to the time variable on interval $[0,\,t]$![]() , it follows that
, it follows that
Thus if the initial data $I(\omega _0,\,u_0)=\epsilon _0$![]() is small enough, then the inequality (3.32) guarantees for all $t>0$
is small enough, then the inequality (3.32) guarantees for all $t>0$![]() that
that
which completes the proof of theorem 3.3.
4. The decay rates of solutions in large time
Base on the global existence of solutions of system (2.1) in § 3, in this subsection, as the time is sufficiently large, we shall derive the decay rates of the solution. In order to obtain the decay estimates, we first study the following linear system

Lemma 4.1 Let the initial data $v_0(x)=(\omega _0,\,u_0)^\top \in L^1(\mathbb {R}^d)\cap H^s(\mathbb {R}^d),\, s>1+\frac {d}{2}$![]() . Then there exists a semigroup $S(t)$
. Then there exists a semigroup $S(t)$![]() such that the solution of system (4.1) is given by
such that the solution of system (4.1) is given by
Moreover, the following estimates hold:

where $d$![]() denotes the dimension of space, $l\geq 0,\,\beta >0,$
denotes the dimension of space, $l\geq 0,\,\beta >0,$![]() ${(2l+d)/2<((2l+d)/2)^+\leq s}$
${(2l+d)/2<((2l+d)/2)^+\leq s}$![]() , and $0\leq k\leq s$
, and $0\leq k\leq s$![]() .
.
Proof. Note that the linear system (4.1) is equivalent to

with initial data $v_0(x)\in L^1(\mathbb {R}^d)\cap H^s(\mathbb {R}^d)$![]() , where $\top$
, where $\top$![]() denotes the transposition of vector, $\bar {\pi }$
denotes the transposition of vector, $\bar {\pi }$![]() and $\mu$
and $\mu$![]() are positive constants, and $\mathbb {I}_d$
are positive constants, and $\mathbb {I}_d$![]() is $d\times d$
is $d\times d$![]() unit matrix. In view of the Fourier transformation and $v=(\omega,\,u)^\top$
unit matrix. In view of the Fourier transformation and $v=(\omega,\,u)^\top$![]() we have
we have
with the $(d+1)\times (d+1)$![]() matrix
matrix
By computing the determinant $|\lambda I-\mathcal {A}(\xi )|=0$![]() , we derive that the eigenvalues of the matrix $\mathcal {A}(\xi )$
, we derive that the eigenvalues of the matrix $\mathcal {A}(\xi )$![]() are $\lambda _1=\cdots =\lambda _{d-1}=-\mu$
are $\lambda _1=\cdots =\lambda _{d-1}=-\mu$![]() , and
, and

By virtue of the eigenvalue $\lambda _i=-\mu$![]() of matrix $\mathcal {A}(\xi )$
of matrix $\mathcal {A}(\xi )$![]() , $i=1,\,\cdots,\,d-1$
, $i=1,\,\cdots,\,d-1$![]() , one has that the unit orthonormal eigenvectors $b_i=(0,\,y_i)^\top =(0,\,y_{i1},\,y_{i2},\,\cdots,\,y_{id})^\top$
, one has that the unit orthonormal eigenvectors $b_i=(0,\,y_i)^\top =(0,\,y_{i1},\,y_{i2},\,\cdots,\,y_{id})^\top$![]() , such that for every $i=1,\,\cdots,\,d-1$
, such that for every $i=1,\,\cdots,\,d-1$![]()
Similarly, it is easy to obtain the unit eigenvectors $b_j$![]() of the eigenvalue $\lambda _j$
of the eigenvalue $\lambda _j$![]() , ${j=d,\,\;d+1}$
, ${j=d,\,\;d+1}$![]() satisfying
satisfying

Thus we can choose the unitary matrix $\mathcal {B}(\xi )=(b_1,\,\cdots,\,b_d,\, \widetilde {b}_{d+1})$![]() such that
such that

where $b_1,\,\cdots,\,b_d$![]() and $\widetilde {b}_{d+1}$
and $\widetilde {b}_{d+1}$![]() are unit orthonormal eigenvectors in $\mathbb {R}^{d+1}$
are unit orthonormal eigenvectors in $\mathbb {R}^{d+1}$![]() , the function $\eta$
, the function $\eta$![]() satisfies
satisfies

Consequently, the solutions of system (4.1) are given by $v(t,\,x)=S(t)v_0(x)$![]() , where
, where

with the function
Next, in order to show (4.2), we first estimate every element of the matrix $\mathcal {D}(t,\,\xi )$![]() .
.
Case 1: if $\mu ^2-4\bar {\pi }^2|\xi |^2<0$![]() , then we have
, then we have

Case 2: if $\mu ^2-4\bar {\pi }^2|\xi |^2\geq 0$![]() , then we have
, then we have

As $0\leq \sqrt {\mu ^2-4\bar {\pi }^2|\xi |^2}\ll 1$![]() , one has that
, one has that
Otherwise, if $\sqrt {\mu ^2-4\bar {\pi }^2|\xi |^2}\in (\delta _0,\,\frac {\mu }{2})$![]() , for some $\delta _0>0$
, for some $\delta _0>0$![]() , then it is easy to check that
, then it is easy to check that
thus we have
On the other hand, if $\sqrt {\mu ^2-4\bar {\pi }^2|\xi |^2}\in [\frac {\mu }{2},\,\mu ]$![]() , then one can easily check that
, then one can easily check that
this implies that
Note that
Thus it follows that

In fact, in a similar way, the bound of all diagonal elements of the matrix $\mathcal {D}(t,\,\xi )$![]() satisfies (4.7).
satisfies (4.7).
Now, we prove the inequality (4.2). Let $(2l+d)/2<((2l+d)/2)^+\leq (2l+d)/ 2+\varepsilon$![]() for any $\varepsilon >0$
for any $\varepsilon >0$![]() . In view of the Fourier transformation and (4.7), for ${((2l+d)/2)^+\leq s}$
. In view of the Fourier transformation and (4.7), for ${((2l+d)/2)^+\leq s}$![]() , it follows that
, it follows that

where the last inequality is guaranteed by

On the other hand, by virtue of the Fourier transformation and (4.7), for $0\leq k\leq s$![]() , one has that
, one has that

which concludes the proof of lemma 4.1.
Theorem 4.2 Assume the initial data $v_0(x)=(\omega _0,\,u_0)^\top \in L^1(\mathbb {R}^d)\cap H^s(\mathbb {R}^d),\,\; s>1+\frac {d}{2},$![]() and $\|v_0\|_{L^1}+I(v_0)=\epsilon _0\ll 1,$
and $\|v_0\|_{L^1}+I(v_0)=\epsilon _0\ll 1,$![]() then system (2.1) has a unique global solution $v=(\omega,\,u)^\top \in \mathcal {C}(\mathbb {R}^+,\,H^s(\mathbb {R}^d)),$
then system (2.1) has a unique global solution $v=(\omega,\,u)^\top \in \mathcal {C}(\mathbb {R}^+,\,H^s(\mathbb {R}^d)),$![]() which is guaranteed by theorem 3.3. In particular, for all time $t>0$
which is guaranteed by theorem 3.3. In particular, for all time $t>0$![]() the solution $v(t,\,x)$
the solution $v(t,\,x)$![]() of system (2.1) satisfies
of system (2.1) satisfies

Furthermore, we have
where $d$![]() denotes the dimension of space, $0\leq k\leq 1+\frac {d}{2}$
denotes the dimension of space, $0\leq k\leq 1+\frac {d}{2}$![]() .
.
Proof. In view of the linear system (4.1) and $v=(\omega,\,u)^\top$![]() , the system (2.1) can be transformed into
, the system (2.1) can be transformed into

with initial data $v_0(x)\in L^1(\mathbb {R}^d)\cap H^s(\mathbb {R}^d)$![]() . By the Duhamel principle, the solutions of system (4.12) are given by
. By the Duhamel principle, the solutions of system (4.12) are given by
By virtue of the assumption in theorem 4.2, inequality (4.2) and equation (4.13), for $(l+\frac {d}{2})^+\leq s$![]() we have
we have

In order to derive the results, introducing the following four functions

Then for all $\tau \in [0,\,t]$![]() and $(l+1+\frac {d}{2})^+\leq s$
and $(l+1+\frac {d}{2})^+\leq s$![]() , the nonlinear term $F(v,\,\nabla v)$
, the nonlinear term $F(v,\,\nabla v)$![]() in (4.14) can be dealt with
in (4.14) can be dealt with



Plugging (4.15) and (4.17) into (4.14) yields that

where we have used for $t\gg 1$![]()
On the other hand, thanks to (4.2), one can easily check that

where the last inequality comes from for $d\geq 2$![]() and $t\gg 1$
and $t\gg 1$![]()
which is guaranteed by

Similarly, we have

Combining (4.18), (4.19) with (4.20), by the definition of $J_i(t),\,\;i=0,\,1,\,\infty$![]() , we end up with
, we end up with
If the initial data satisfy $\|v_0\|_{L^1}+I(v_0)=\epsilon _0\ll 1$![]() , thanks to theorem 3.3, then it implies that
, thanks to theorem 3.3, then it implies that
Define $f(t)=J_0(t)+J_1(t)+J_\infty ^0(t)$![]() , in view of inequality (4.21), one has for all $t\in \mathbb {R}^+$
, in view of inequality (4.21), one has for all $t\in \mathbb {R}^+$![]() that
that
If we choose $\epsilon _0\ll 1$![]() such that $4C^2\epsilon _0<1$
such that $4C^2\epsilon _0<1$![]() , then the equation
, then the equation
has two differential roots
Thanks to
in order to ensure inequality (4.22) hold for all $t\geq 0$![]() , thus we deduce that $f(t)< y_1$
, thus we deduce that $f(t)< y_1$![]() is bound, this implies that
is bound, this implies that

In view of the above inequality (4.23), we can consequently estimate

where we have used
and for $0\leq k\leq 1+\frac {d}{2}$![]()
On the other hand, thanks to (4.2) and (4.23), similar to estimate (4.18) it follows that

This completes the proof of theorem 4.2.
Remark 4.3 In fact, we can show the following estimates of high order derivative of solution

Because the result of (4.24) and (4.25) is not optimal in the sense of linearization, if the solution is sufficiently smooth, we can improve the result of theorem 4.2 and have the following result.
Corollary 4.4 Under the assumptions of theorem 4.2, the system (2.1) has a unique global solution $v=(\omega,\,u)^\top \in \mathcal {C}(\mathbb {R}^+,\,H^s(\mathbb {R}^d))$![]() . Moreover, for all time $t>0$
. Moreover, for all time $t>0$![]() and $s>\frac {d}{2}+2+\frac {1}{d},$
and $s>\frac {d}{2}+2+\frac {1}{d},$![]() the decay rate of solution $v(t,\,x)$
the decay rate of solution $v(t,\,x)$![]() of system (2.1) satisfies
of system (2.1) satisfies
and for $0< k\leq 1+\frac {d}{2}$![]() we have
we have
where $d$![]() denotes the dimension of space.
denotes the dimension of space.
Proof. Taking advantage of the Gagliardo–Nirenberg inequality, it follows that

where the last inequality is guaranteed by $\frac {d}{2}+2+\frac {1}{d}< s$![]() , the constant
, the constant
Using inequality (4.26), we can estimate

Note that $J_0(t),\,\;J_1(t)$![]() and $J_\infty ^0(t)$
and $J_\infty ^0(t)$![]() are bounded, in view of Young's inequality yields that
are bounded, in view of Young's inequality yields that
which implies for $s>\frac {d}{2}+2+\frac {1}{d}$![]() that
that
Finally, thanks to theorem 4.2, we only need to show the last inequality holds for $\frac {d}{2}< k\leq 1+\frac {d}{2}$![]() . Similar to estimate (4.26), one has that
. Similar to estimate (4.26), one has that

where the last inequality is guaranteed by $k\leq [(\frac {3d}{2}+1)(s-1)-\frac {d^2}{4}]/(s+\frac {d}{2})$![]() , the constant
, the constant
By virtue of $J_\infty ^1(t)\leq C$![]() and (4.28), it follows that
and (4.28), it follows that

where we have applied $0< k\leq 1+\frac {d}{2}$![]() and $\frac {d}{2}+2+\frac {1}{d}< s$
and $\frac {d}{2}+2+\frac {1}{d}< s$![]() , which is equivalent to
, which is equivalent to
This completes the proof of corollary 4.4.
Remark 4.5 In view of lemma 4.1, for sufficiently large time $t>0$![]() , the algebra decay rate of solution $v(t,\,x)$
, the algebra decay rate of solution $v(t,\,x)$![]() for linear equation (4.1) satisfies
for linear equation (4.1) satisfies

where $d$![]() denotes the dimension of space, $l\geq 0$
denotes the dimension of space, $l\geq 0$![]() , $d<2(s-l)$
, $d<2(s-l)$![]() and $0\leq k\leq s$
and $0\leq k\leq s$![]() . However, by virtue of theorem 4.2 and corollary 4.1, we only show that the algebra decay rate of $L^\infty$
. However, by virtue of theorem 4.2 and corollary 4.1, we only show that the algebra decay rate of $L^\infty$![]() -norm of $v,\,\nabla v$
-norm of $v,\,\nabla v$![]() and $L^2$
and $L^2$![]() -norm of $\nabla ^\sigma v$
-norm of $\nabla ^\sigma v$![]() satisfies
satisfies
and
which is optimal in the linearized sense (4.30), where $0\leq \sigma \leq 1+\frac {d}{2}$![]() . How to estimate the high order derivative of the solution $v(t,\,x)$
. How to estimate the high order derivative of the solution $v(t,\,x)$![]() in $L^2$
in $L^2$![]() and $L^\infty$
and $L^\infty$![]() norm is an open problem.
norm is an open problem.
Remark 4.6 For the smooth initial data $(\rho _0,\,u_0)\in H^s(\mathbb {R}^d),\,s\geq 1+\frac {d}{2}$![]() with small amplitude, there exists a unique global smooth solution of the Cauchy problem for system (1.1). As the time $t$
with small amplitude, there exists a unique global smooth solution of the Cauchy problem for system (1.1). As the time $t$![]() becomes large, theorem 4.2 tells us that the smooth solution $v(t,\,x)$
becomes large, theorem 4.2 tells us that the smooth solution $v(t,\,x)$![]() is algebra decay which extends and improves the following result
is algebra decay which extends and improves the following result

derived by Sideris, Thomases and Wang in [Reference Sideris, Thomases and Wang28].
In addition, if the initial data belong to $L^1(\mathbb {R}^d)\cap H^s(\mathbb {R}^d)$![]() , then one shows that the following algebra decay rate of smooth solution in $L^p$
, then one shows that the following algebra decay rate of smooth solution in $L^p$![]() norm.
norm.
Corollary 4.7 Under the assumptions of theorem 4.2, the system (2.1) has a unique global solution $v=(\omega,\,u)^\top \in \mathcal {C}(\mathbb {R}^+,\,H^s(\mathbb {R}^d))$![]() . Moreover, for all time $t>0$
. Moreover, for all time $t>0$![]() and $2\leq p\leq \infty,$
and $2\leq p\leq \infty,$![]() the decay rate of solution $v(t,\,x)$
the decay rate of solution $v(t,\,x)$![]() of system (2.1) satisfies
of system (2.1) satisfies

where $d$![]() denotes the dimension of space, $0\leq \alpha <1+\frac {d}{2}$
denotes the dimension of space, $0\leq \alpha <1+\frac {d}{2}$![]() . In particular, we have
. In particular, we have
Proof. In view of interpolation inequality and theorem 4.2 yields that

By the Gagliardo–Nirenberg inequality and corollary 4.1, for $0\leq \alpha <1+\frac {d}{2}$![]() one shows that
one shows that

where $1-\theta =\alpha -\frac {d}{p}$![]() and $\theta \in (0,\,1)$
and $\theta \in (0,\,1)$![]() . Note that
. Note that

which includes the proof of corollary 4.7.
Corollary 4.8 Under the additional assumptions of theorem 4.2, the derivative of velocity decays exponentially in Sobolev space $L^2(\mathbb {R}^d),$![]() i.e.,
i.e.,
Proof. If we define the vorticity $\Omega =Du-\nabla u$![]() , where $Du$
, where $Du$![]() stands for the Jacobian matrix of velocity $u$
stands for the Jacobian matrix of velocity $u$![]() , and $\nabla u$
, and $\nabla u$![]() stands for its transposed matrix, then the vorticity plays a fundamental role in the compressible fluid mechanics. Indeed, by system (2.1), $\Omega$
stands for its transposed matrix, then the vorticity plays a fundamental role in the compressible fluid mechanics. Indeed, by system (2.1), $\Omega$![]() takes the form of a quasi-linear evolution equation of hyperbolic type
takes the form of a quasi-linear evolution equation of hyperbolic type
Multiplying $\Omega$![]() on both sides of equation (4.31), integration by parts, it follows that
on both sides of equation (4.31), integration by parts, it follows that

where we have applied $I(v_0)\ll 1$![]() , which guarantees that
, which guarantees that
In view of Gronwall's inequality to (4.32) one has that
Thanks to $\|\Omega \|_{L^2}\leq C\|\nabla u\|_{L^2}$![]() , and $\|\nabla u\|_{L^2}\leq C\|\Omega \|_{L^2}$
, and $\|\nabla u\|_{L^2}\leq C\|\Omega \|_{L^2}$![]() (see proposition 7.5 on page 294 in [Reference Bahouri, Chemin and Danchin1]), therefore, we have
(see proposition 7.5 on page 294 in [Reference Bahouri, Chemin and Danchin1]), therefore, we have
Acknowledgments
This work is partially supported by NSFC (Grant No.: 11771442) and the Fundamental Research Funds for the Central University (WUT: 2021III056JC). The author thanks the professor Boling Guo and Zhen Wang for their helpful discussions and constructive suggestions.