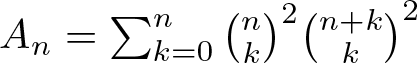1. Introduction
It is well known that the Riemann zeta function was defined by  $\zeta(s)=\sum_{n=1}^\infty\frac1{n^s}$, where s is a complex number with real part larger than 1. In 1979, Apéry [Reference Apéry1] introduced the Apéry numbers
$\zeta(s)=\sum_{n=1}^\infty\frac1{n^s}$, where s is a complex number with real part larger than 1. In 1979, Apéry [Reference Apéry1] introduced the Apéry numbers ![]() ${A_n}$ and
${A_n}$ and ![]() ${A^{'}_n}$ to prove that
${A^{'}_n}$ to prove that ![]() $\zeta(2)$ and
$\zeta(2)$ and ![]() $\zeta(3)$ are irrational, and these numbers are defined by:
$\zeta(3)$ are irrational, and these numbers are defined by:
 \begin{equation*}
A_n=\sum_{k=0}^n\binom{n}k^2\binom{n+k}k^2\ \ \ \mbox{and}\ \ \ A^{'}_n=\sum_{k=0}^n\binom{n}k^2\binom{n+k}k.
\end{equation*}
\begin{equation*}
A_n=\sum_{k=0}^n\binom{n}k^2\binom{n+k}k^2\ \ \ \mbox{and}\ \ \ A^{'}_n=\sum_{k=0}^n\binom{n}k^2\binom{n+k}k.
\end{equation*}It is well known (see [Reference Beukers2]) that:
 \begin{align*}
&(n+1)^3A_{n+1}=(2n+1)(17n(n+1)+5)A_n-n^3A_{n-1}\ \ (n\geq1),\\
&(n+1)^2A^{'}_{n+1}=(11n(n+1)+3)A^{'}_n+n^2A^{'}_{n-1}\ \ (n\geq1).
\end{align*}
\begin{align*}
&(n+1)^3A_{n+1}=(2n+1)(17n(n+1)+5)A_n-n^3A_{n-1}\ \ (n\geq1),\\
&(n+1)^2A^{'}_{n+1}=(11n(n+1)+3)A^{'}_n+n^2A^{'}_{n-1}\ \ (n\geq1).
\end{align*} The Apéry-like numbers ![]() $\{u_n\}$ of the first kind satisfy:
$\{u_n\}$ of the first kind satisfy:
where ![]() $a,b,c$ are integers and c ≠ 0. The well-known Domb numbers
$a,b,c$ are integers and c ≠ 0. The well-known Domb numbers  $D_n=\sum_{k=0}^n\binom{n}k^2\binom{2k}k\binom{2n-2k}{n-k}$ are Apéry-like numbers of this kind, and the following numbers are also Apéry-like numbers of the first kind,
$D_n=\sum_{k=0}^n\binom{n}k^2\binom{2k}k\binom{2n-2k}{n-k}$ are Apéry-like numbers of this kind, and the following numbers are also Apéry-like numbers of the first kind,
 \begin{equation*}
T_n=\sum_{k=0}^n\binom{n}k^2\binom{2k}n^2.
\end{equation*}
\begin{equation*}
T_n=\sum_{k=0}^n\binom{n}k^2\binom{2k}n^2.
\end{equation*} In 2009, Zagier [Reference Zagier, Harnad and Winternitz20] studied the Apéry-like numbers ![]() $\{u_n\}$ of the second kind given by:
$\{u_n\}$ of the second kind given by:
where ![]() $a,b,c$ are integers and c ≠ 0. And the famous Franel numbers
$a,b,c$ are integers and c ≠ 0. And the famous Franel numbers  $f_n=\sum_{k=0}^n\binom{n}k^3$ and
$f_n=\sum_{k=0}^n\binom{n}k^3$ and  $a_n=\sum_{k=0}^n\binom{n}k^2\binom{2k}k$ are Apéry-like sequences of the second kind. For more congruences involving Apéry-like numbers, we refer the readers to [Reference Liu6–Reference Liu and Wang8, Reference Mao and Li11, Reference Mao, Li and Ma12].
$a_n=\sum_{k=0}^n\binom{n}k^2\binom{2k}k$ are Apéry-like sequences of the second kind. For more congruences involving Apéry-like numbers, we refer the readers to [Reference Liu6–Reference Liu and Wang8, Reference Mao and Li11, Reference Mao, Li and Ma12].
In [Reference Sun16], Sun proposed many congruence conjectures involving these numbers, for example:
Conjecture 1.1. ([Reference Sun16, Conjectures 5.1 and 5.3]) Let p be a prime with p > 3. Then
 \begin{align*}
&A_p\equiv A_1-\frac{14}3p^3B_{p-3}\ ({\rm{mod}}\ p^4),\ A^{'}_{p}\equiv A^{'}_1-\frac{5}3p^3B_{p-3}\ ({\rm{mod}}\ p^4),\\
&T_p\equiv T_1-p^3B_{p-3}\ ({\rm{mod}}\ p^4),\ D_p\equiv D_1+\frac{16}3p^3B_{p-3}\ ({\rm{mod}}\ p^4),\\
&f_p\equiv f_1+\frac12p^3B_{p-3}\ ({\rm{mod}}\ p^4),\ a_p\equiv a_1+\frac{p^2}2\left(\frac{p}3\right)B_{p-2}\left(\frac13\right)\ ({\rm{mod}}\ p^3).
\end{align*}
\begin{align*}
&A_p\equiv A_1-\frac{14}3p^3B_{p-3}\ ({\rm{mod}}\ p^4),\ A^{'}_{p}\equiv A^{'}_1-\frac{5}3p^3B_{p-3}\ ({\rm{mod}}\ p^4),\\
&T_p\equiv T_1-p^3B_{p-3}\ ({\rm{mod}}\ p^4),\ D_p\equiv D_1+\frac{16}3p^3B_{p-3}\ ({\rm{mod}}\ p^4),\\
&f_p\equiv f_1+\frac12p^3B_{p-3}\ ({\rm{mod}}\ p^4),\ a_p\equiv a_1+\frac{p^2}2\left(\frac{p}3\right)B_{p-2}\left(\frac13\right)\ ({\rm{mod}}\ p^3).
\end{align*}Remark 1.1. Actually,
 \begin{equation*}a_p\equiv a_1+\frac12p^2\left(\frac{p}3\right)B_{p-2}\left(\frac13\right)\ ({\rm{mod}}\ p^3),\end{equation*}
\begin{equation*}a_p\equiv a_1+\frac12p^2\left(\frac{p}3\right)B_{p-2}\left(\frac13\right)\ ({\rm{mod}}\ p^3),\end{equation*}has been proved by the first author [Reference Mao9] in 2017, which is earlier than the above conjecture. The congruences of Ap and Dp were proved by Zhang [Reference Zhang21].
The above ![]() $\{B_n\}$ and
$\{B_n\}$ and ![]() $\{B_n(x)\}$ are Bernoulli numbers and Bernoulli polynomials given by:
$\{B_n(x)\}$ are Bernoulli numbers and Bernoulli polynomials given by:
 \begin{gather*}
B_0=1,\ \ \ \sum_{k=0}^{n-1}\binom{n}{k}B_{k}=0\ \ (n\geq2),\\ B_n(x)=\sum_{k=0}^n\binom nkB_kx^{n-k}\ \ (n=0,1,2,\ldots).
\end{gather*}
\begin{gather*}
B_0=1,\ \ \ \sum_{k=0}^{n-1}\binom{n}{k}B_{k}=0\ \ (n\geq2),\\ B_n(x)=\sum_{k=0}^n\binom nkB_kx^{n-k}\ \ (n=0,1,2,\ldots).
\end{gather*} For ![]() $n,m\in\{1,2,3,\ldots\}$, define:
$n,m\in\{1,2,3,\ldots\}$, define:
 \begin{equation*}
H_n^{(m)}=\sum_{1\leq k\leq n}\frac1{k^m},
\end{equation*}
\begin{equation*}
H_n^{(m)}=\sum_{1\leq k\leq n}\frac1{k^m},
\end{equation*}these numbers with m = 1 are often called the classic harmonic numbers.
Let p > 3 be a prime. Wolstenholme [Reference Wolstenholme19] proved that:
 \begin{align}
\binom{2p-1}{p-1}\equiv1\ ({\rm{mod}}\ p^3).
\end{align}
\begin{align}
\binom{2p-1}{p-1}\equiv1\ ({\rm{mod}}\ p^3).
\end{align}In 1990, Glaisher [Reference Glaisher3, Reference Glaisher4] showed further that:
 \begin{equation}
\binom{2p-1}{p-1}\equiv1-\frac23p^3B_{p-3}\ ({\rm{mod}}\ p^4).
\end{equation}
\begin{equation}
\binom{2p-1}{p-1}\equiv1-\frac23p^3B_{p-3}\ ({\rm{mod}}\ p^4).
\end{equation}In this paper, our first goal is to prove the rest unsolved congruences in Conjecture 1.1.
Theorem 1.1. Let p be a prime with p > 3. Then
 \begin{align*}
&A^{'}_{p}\equiv A^{'}_1-\frac{5}3p^3B_{p-3}\ ({\rm{mod}}\ p^4),\ \ T_p\equiv T_1-p^3B_{p-3}\ ({\rm{mod}}\ p^4),\\
&f_p\equiv f_1+\frac12p^3B_{p-3}\ ({\rm{mod}}\ p^4).
\end{align*}
\begin{align*}
&A^{'}_{p}\equiv A^{'}_1-\frac{5}3p^3B_{p-3}\ ({\rm{mod}}\ p^4),\ \ T_p\equiv T_1-p^3B_{p-3}\ ({\rm{mod}}\ p^4),\\
&f_p\equiv f_1+\frac12p^3B_{p-3}\ ({\rm{mod}}\ p^4).
\end{align*} And, we also confirm some conjectures of Sun [Reference Sun16, Conjectures 5.1 and 5.3] involving ![]() $()_{2p}$:
$()_{2p}$:
Theorem 1.2. For any prime p > 3, we have:
 \begin{gather*}
A_{2p}\equiv A_2-\frac{1648}3p^3B_{p-3}\ ({\rm{mod}}\ p^4),\ A^{'}_{2p}\equiv A^{'}_2-\frac{280}3p^3B_{p-3}\ ({\rm{mod}}\ p^4),\\
T_{2p}\equiv T_2-136p^3B_{p-3}\ ({\rm{mod}}\ p^4),\ D_{2p}\equiv D_2+\frac{448}3p^3B_{p-3}\ ({\rm{mod}}\ p^4),\\
f_{2p}\equiv f_2-8p^3B_{p-3}\ ({\rm{mod}}\ p^4),\\
a_{2p}\equiv a_2+6p^2\left(\frac{p}3\right)B_{p-2}\left(\frac13\right)\ ({\rm{mod}}\ p^3).
\end{gather*}
\begin{gather*}
A_{2p}\equiv A_2-\frac{1648}3p^3B_{p-3}\ ({\rm{mod}}\ p^4),\ A^{'}_{2p}\equiv A^{'}_2-\frac{280}3p^3B_{p-3}\ ({\rm{mod}}\ p^4),\\
T_{2p}\equiv T_2-136p^3B_{p-3}\ ({\rm{mod}}\ p^4),\ D_{2p}\equiv D_2+\frac{448}3p^3B_{p-3}\ ({\rm{mod}}\ p^4),\\
f_{2p}\equiv f_2-8p^3B_{p-3}\ ({\rm{mod}}\ p^4),\\
a_{2p}\equiv a_2+6p^2\left(\frac{p}3\right)B_{p-2}\left(\frac13\right)\ ({\rm{mod}}\ p^3).
\end{gather*} We also proved some conjecture of Sun [Reference Sun16, Conjecture 5.2] involving ![]() $()_{2p-1}$:
$()_{2p-1}$:
Theorem 1.3. Let p > 3 be a prime. Then,
 \begin{align*}
&A_{2p-1}\equiv A_1+\frac{16}3p^3B_{p-3}\ ({\rm{mod}}\ p^4),\\
&T_{2p-1}\equiv16^{2(p-1)}T_1-6p^3B_{p-3}\ ({\rm{mod}}\ p^4).
\end{align*}
\begin{align*}
&A_{2p-1}\equiv A_1+\frac{16}3p^3B_{p-3}\ ({\rm{mod}}\ p^4),\\
&T_{2p-1}\equiv16^{2(p-1)}T_1-6p^3B_{p-3}\ ({\rm{mod}}\ p^4).
\end{align*} At last, we prove some conjectures of Sun [Reference Sun16, Conjecture 5.1] involving ![]() $()_{3p}$:
$()_{3p}$:
Theorem 1.4. Let p > 3 be a prime. Then,
 \begin{gather*}
A_{3p}\equiv A_3-36738p^3B_{p-3}\ ({\rm{mod}}\ p^4), A^{'}_{3p}\equiv A^{'}_{3}-2475p^3B_{p-3}\ ({\rm{mod}}\ p^4),\\
T_{3p}\equiv T_3-6696p^3B_{p-3}\ ({\rm{mod}}\ p^4),\ D_{3p}\equiv D_3+3168p^3B_{p-3}\ ({\rm{mod}}\ p^4)\\
f_{3p}\equiv f_3-189p^3B_{p-3}\ ({\rm{mod}}\ p^4), \\
a_{3p}\equiv a_3+\frac{135p^2}2\left(\frac{p}3\right)B_{p-2}\left(\frac13\right)\ ({\rm{mod}}\ p^3).
\end{gather*}
\begin{gather*}
A_{3p}\equiv A_3-36738p^3B_{p-3}\ ({\rm{mod}}\ p^4), A^{'}_{3p}\equiv A^{'}_{3}-2475p^3B_{p-3}\ ({\rm{mod}}\ p^4),\\
T_{3p}\equiv T_3-6696p^3B_{p-3}\ ({\rm{mod}}\ p^4),\ D_{3p}\equiv D_3+3168p^3B_{p-3}\ ({\rm{mod}}\ p^4)\\
f_{3p}\equiv f_3-189p^3B_{p-3}\ ({\rm{mod}}\ p^4), \\
a_{3p}\equiv a_3+\frac{135p^2}2\left(\frac{p}3\right)B_{p-2}\left(\frac13\right)\ ({\rm{mod}}\ p^3).
\end{gather*}We are going to prove Theorem 1.1 in the next section. Sections 3–5 are devoted to proving Theorems 1.2–1.4.
2. Proof of Theorem 1.1
Lemma 2.1. (Lemma [Reference Sun15]). Let p > 5 be a prime. Then,
 \begin{gather*}
H_{(p-1)/2}\equiv-2q_p(2)+pq^2_p(2)\ ({\rm{mod}}\ p^2),\ \ H_{\frac{p-1}2}^{(2)}\equiv\frac73pB_{p-3}\ ({\rm{mod}}\ p^2),\\
H_{\frac{p-1}2}^{(3)}\equiv-2B_{p-3}\ ({\rm{mod}}\ p),\ \ H_{p-1}\equiv-\frac13p^2B_{p-3}\ ({\rm{mod}}\ p^3),\\
H_{p-1}^{(2)}\equiv\frac23pB_{p-3}\ ({\rm{mod}}\ p^2),\ \ H_{p-1}^{(3)}\equiv0\ ({\rm{mod}}\ p).
\end{gather*}
\begin{gather*}
H_{(p-1)/2}\equiv-2q_p(2)+pq^2_p(2)\ ({\rm{mod}}\ p^2),\ \ H_{\frac{p-1}2}^{(2)}\equiv\frac73pB_{p-3}\ ({\rm{mod}}\ p^2),\\
H_{\frac{p-1}2}^{(3)}\equiv-2B_{p-3}\ ({\rm{mod}}\ p),\ \ H_{p-1}\equiv-\frac13p^2B_{p-3}\ ({\rm{mod}}\ p^3),\\
H_{p-1}^{(2)}\equiv\frac23pB_{p-3}\ ({\rm{mod}}\ p^2),\ \ H_{p-1}^{(3)}\equiv0\ ({\rm{mod}}\ p).
\end{gather*}Proof of Theorem 1.1
p = 5 can be checked directly. We will assume p > 5 from now on. It is easy to check that:
 \begin{equation}
\binom{p+k}k^2=\frac{(p+k)^2\cdots(p+1)^2}{k!^2}\equiv1+2pH_k\ ({\rm{mod}}\ p^2),
\end{equation}
\begin{equation}
\binom{p+k}k^2=\frac{(p+k)^2\cdots(p+1)^2}{k!^2}\equiv1+2pH_k\ ({\rm{mod}}\ p^2),
\end{equation}and
 \begin{equation}
\binom{p-1}{k-1}^2=\frac{(p-1)^2\cdots(p-k+1)^2}{(k-1)!^2}\equiv1-2pH_{k-1}\ ({\rm{mod}}\ p^2).
\end{equation}
\begin{equation}
\binom{p-1}{k-1}^2=\frac{(p-1)^2\cdots(p-k+1)^2}{(k-1)!^2}\equiv1-2pH_{k-1}\ ({\rm{mod}}\ p^2).
\end{equation}These yield that:
 \begin{align*}
A^{'}_p&=\sum_{k=0}^p\binom{p}k^2\binom{p+k}k=1+\binom{2p}p+\sum_{k=1}^{p-1}\binom{p}k^2\binom{p+k}k\\
&\equiv1+\binom{2p}p+p^2\sum_{k=1}^{p-1}\frac1{k^2}\left(1-pH_k+\frac{2p}k\right)\\
&\equiv1+\binom{2p}p+p^2H_{p-1}^{(2)}+2p^3H_{p-1}^{(3)}-p^3\sum_{k=1}^{p-1}\frac{H_k}{k^2}\ ({\rm{mod}}\ p^4).
\end{align*}
\begin{align*}
A^{'}_p&=\sum_{k=0}^p\binom{p}k^2\binom{p+k}k=1+\binom{2p}p+\sum_{k=1}^{p-1}\binom{p}k^2\binom{p+k}k\\
&\equiv1+\binom{2p}p+p^2\sum_{k=1}^{p-1}\frac1{k^2}\left(1-pH_k+\frac{2p}k\right)\\
&\equiv1+\binom{2p}p+p^2H_{p-1}^{(2)}+2p^3H_{p-1}^{(3)}-p^3\sum_{k=1}^{p-1}\frac{H_k}{k^2}\ ({\rm{mod}}\ p^4).
\end{align*}In view of [Reference Sun18, (3.17)], we have
 \begin{align}
\sum_{k=1}^{p-1}\frac{H_k}{k^2}\equiv B_{p-3}\ ({\rm{mod}}\ p).
\end{align}
\begin{align}
\sum_{k=1}^{p-1}\frac{H_k}{k^2}\equiv B_{p-3}\ ({\rm{mod}}\ p).
\end{align}This, with (1.2), Lemma 2.1 yields that:
 \begin{equation*}
A^{'}_p\equiv3-\frac53p^3B_{p-3}=A^{'}_1-\frac53p^3B_{p-3}\ ({\rm{mod}}\ p^4).
\end{equation*}
\begin{equation*}
A^{'}_p\equiv3-\frac53p^3B_{p-3}=A^{'}_1-\frac53p^3B_{p-3}\ ({\rm{mod}}\ p^4).
\end{equation*} Now, we are ready to evaluate Tp modulo p 4. In the same way of proving (2.1), we have the following congruence for each ![]() $1\leq k\leq (p-1)/2$,
$1\leq k\leq (p-1)/2$,
 \begin{equation*}
\binom{2p-2k}{p-2k}^2\equiv1+2pH_{p-2k}\equiv1+2pH_{2k-1}\ ({\rm{mod}}\ p^2).
\end{equation*}
\begin{equation*}
\binom{2p-2k}{p-2k}^2\equiv1+2pH_{p-2k}\equiv1+2pH_{2k-1}\ ({\rm{mod}}\ p^2).
\end{equation*}This with (2.2) yields that:
 \begin{align*}
T_p&=\sum_{k=0}^p\binom{p}k^2\binom{2k}p^2=\binom{2p}p^2+\sum_{k=\frac{p+1}2}^{p-1}\binom{p}k^2\binom{2k}p^2\\
&=\binom{2p}p^2+\sum_{k=1}^{\frac{p-1}2}\binom{p}k^2\binom{2p-2k}{p-2k}^2\\
&\equiv\binom{2p}p^2+p^2\sum_{k=1}^{\frac{p-1}2}\frac{1}{k^2}(1+2pH_{2k-1}-2pH_{k-1})\\
&\equiv\binom{2p}p^2+p^2H_{\frac{p-1}2}^{(2)}+2p^3\sum_{k=1}^{\frac{p-1}2}\frac{H_{2k}-H_{k}}{k^2}+p^3H_{\frac{p-1}2}^{(3)}\ ({\rm{mod}}\ p^3).
\end{align*}
\begin{align*}
T_p&=\sum_{k=0}^p\binom{p}k^2\binom{2k}p^2=\binom{2p}p^2+\sum_{k=\frac{p+1}2}^{p-1}\binom{p}k^2\binom{2k}p^2\\
&=\binom{2p}p^2+\sum_{k=1}^{\frac{p-1}2}\binom{p}k^2\binom{2p-2k}{p-2k}^2\\
&\equiv\binom{2p}p^2+p^2\sum_{k=1}^{\frac{p-1}2}\frac{1}{k^2}(1+2pH_{2k-1}-2pH_{k-1})\\
&\equiv\binom{2p}p^2+p^2H_{\frac{p-1}2}^{(2)}+2p^3\sum_{k=1}^{\frac{p-1}2}\frac{H_{2k}-H_{k}}{k^2}+p^3H_{\frac{p-1}2}^{(3)}\ ({\rm{mod}}\ p^3).
\end{align*}In view of [Reference Mao9, Reference Mao and Wang13], we have
 \begin{equation}
\sum_{k=1}^{\frac{p-1}2}\frac{H_{2k}}{k^2}\equiv\frac32B_{p-3}\ ({\rm{mod}}\ p)\ \ \mbox{and}\ \ \sum_{k=1}^{\frac{p-1}2}\frac{H_k}{k^2}\equiv-\frac12B_{p-3}\ ({\rm{mod}}\ p).
\end{equation}
\begin{equation}
\sum_{k=1}^{\frac{p-1}2}\frac{H_{2k}}{k^2}\equiv\frac32B_{p-3}\ ({\rm{mod}}\ p)\ \ \mbox{and}\ \ \sum_{k=1}^{\frac{p-1}2}\frac{H_k}{k^2}\equiv-\frac12B_{p-3}\ ({\rm{mod}}\ p).
\end{equation}So with (1.2) and Lemma 2.1, we immediately obtain the desired result:
 \begin{equation*}
T_p\equiv4-p^3B_{p-3}=T_1-p^3B_{p-3}\ ({\rm{mod}}\ p^4).
\end{equation*}
\begin{equation*}
T_p\equiv4-p^3B_{p-3}=T_1-p^3B_{p-3}\ ({\rm{mod}}\ p^4).
\end{equation*}At last, we evaluate fp modulo p 4. This is much easier. By (2.2),
 \begin{align*}
f_p&=\sum_{k=0}^p\binom{p}k^3=2+\sum_{k=1}^{p-1}\binom{p}k^3\equiv2-p^3\sum_{k=1}^{p-1}\frac{(-1)^{k}}{k^3}\\
&=2-p^3\sum_{k=1}^{p-1}\frac{1+(-1)^{k}}{k^3}+p^3H_{p-1}^{(3)}\\
&=2-\frac14p^3H_{\frac{p-1}2}^{(3)}+p^3H_{p-1}^{(3)}\ ({\rm{mod}}\ p^4).
\end{align*}
\begin{align*}
f_p&=\sum_{k=0}^p\binom{p}k^3=2+\sum_{k=1}^{p-1}\binom{p}k^3\equiv2-p^3\sum_{k=1}^{p-1}\frac{(-1)^{k}}{k^3}\\
&=2-p^3\sum_{k=1}^{p-1}\frac{1+(-1)^{k}}{k^3}+p^3H_{p-1}^{(3)}\\
&=2-\frac14p^3H_{\frac{p-1}2}^{(3)}+p^3H_{p-1}^{(3)}\ ({\rm{mod}}\ p^4).
\end{align*}So we immediately get the desired result:
 \begin{equation*}
f_p\equiv 2+\frac12p^3B_{p-3}=f_1+\frac12p^3B_{p-3}\ ({\rm{mod}}\ p^4),
\end{equation*}
\begin{equation*}
f_p\equiv 2+\frac12p^3B_{p-3}=f_1+\frac12p^3B_{p-3}\ ({\rm{mod}}\ p^4),
\end{equation*}with the help of Lemma 2.1.
Now the proof of Theorem 1.1 is complete.
3. Proof of Theorem 1.2
Lemma 3.1. Let p > 3 be a prime. If ![]() $1\leq k\leq (p-1)/2$, then
$1\leq k\leq (p-1)/2$, then
 \begin{equation}
\binom{2k}k\binom{4p-2k}{2p-k}\equiv-\frac{12p}k(1+4pH_{2k-1}-4pH_{k-1})\ ({\rm{mod}}\ p^3).
\end{equation}
\begin{equation}
\binom{2k}k\binom{4p-2k}{2p-k}\equiv-\frac{12p}k(1+4pH_{2k-1}-4pH_{k-1})\ ({\rm{mod}}\ p^3).
\end{equation} If ![]() $(p+1)/2\leq k\leq p-1$, then
$(p+1)/2\leq k\leq p-1$, then
 \begin{equation}
\binom{4p-2k}{2p-k}\equiv2\binom{2p-2k}{p-k}(1+2pH_{2p-2k}-2pH_{k-1})\ ({\rm{mod}}\ p^2).
\end{equation}
\begin{equation}
\binom{4p-2k}{2p-k}\equiv2\binom{2p-2k}{p-k}(1+2pH_{2p-2k}-2pH_{k-1})\ ({\rm{mod}}\ p^2).
\end{equation}Proof. If ![]() $1\leq k\leq (p-1)/2$. Since
$1\leq k\leq (p-1)/2$. Since ![]() $H_{p-1}\equiv0\ ({\rm{mod}}\ p^2)$ and
$H_{p-1}\equiv0\ ({\rm{mod}}\ p^2)$ and ![]() $H_{p-1-k}\equiv H_k\ ({\rm{mod}}\ p)$ for each
$H_{p-1-k}\equiv H_k\ ({\rm{mod}}\ p)$ for each ![]() $0\leq k\leq p-1$, we have
$0\leq k\leq p-1$, we have
 \begin{align*}
&\binom{4p-2k}{2p-k}\\ &=\frac{6p(4p-2k)\cdots(3p+1)(3p-1)\cdots(2p+1)(2p-1)\cdots(2p-k+1)}{(2p-k)\cdots(p+1)(p-1)!}\\
&\equiv\frac{6p(p-2k)!(1+3pH_{p-2k})(-1)^{k-1}(k-1)!(1-2pH_{k-1})}{(p-k)!(1+pH_{p-k})}\\
&\equiv\frac{6p}{k}\frac{(-1)^{k-1}(1+3pH_{2k-1}-2pH_{k-1})}{\binom{p-k}k(1+pH_{k-1})}\ ({\rm{mod}}\ p^3),
\end{align*}
\begin{align*}
&\binom{4p-2k}{2p-k}\\ &=\frac{6p(4p-2k)\cdots(3p+1)(3p-1)\cdots(2p+1)(2p-1)\cdots(2p-k+1)}{(2p-k)\cdots(p+1)(p-1)!}\\
&\equiv\frac{6p(p-2k)!(1+3pH_{p-2k})(-1)^{k-1}(k-1)!(1-2pH_{k-1})}{(p-k)!(1+pH_{p-k})}\\
&\equiv\frac{6p}{k}\frac{(-1)^{k-1}(1+3pH_{2k-1}-2pH_{k-1})}{\binom{p-k}k(1+pH_{k-1})}\ ({\rm{mod}}\ p^3),
\end{align*}and
 \begin{align}
\binom{p-k}k&=\frac{(p-k)\cdots(p-2k+1)}{k!}\notag\\
&\equiv\frac{(-1)^kk\cdots(2k-1)(1-pH_{2k-1}+pH_{k-1})}{k!}\notag\\
&\equiv\frac{(-1)^k}2\binom{2k}k(1-pH_{2k-1}+pH_{k-1})\ ({\rm{mod}}\ p^2).
\end{align}
\begin{align}
\binom{p-k}k&=\frac{(p-k)\cdots(p-2k+1)}{k!}\notag\\
&\equiv\frac{(-1)^kk\cdots(2k-1)(1-pH_{2k-1}+pH_{k-1})}{k!}\notag\\
&\equiv\frac{(-1)^k}2\binom{2k}k(1-pH_{2k-1}+pH_{k-1})\ ({\rm{mod}}\ p^2).
\end{align}Hence
 \begin{align*}
&\binom{2k}k\binom{4p-2k}{2p-k}\equiv\frac{-12p}{k}\frac{1+3pH_{2k-1}-3pH_{k-1}}{1-pH_{2k-1}+pH_{k-1}}\\
&\equiv\frac{-12p}k(1+4pH_{2k-1}-4pH_{k-1})\ ({\rm{mod}}\ p^3).
\end{align*}
\begin{align*}
&\binom{2k}k\binom{4p-2k}{2p-k}\equiv\frac{-12p}{k}\frac{1+3pH_{2k-1}-3pH_{k-1}}{1-pH_{2k-1}+pH_{k-1}}\\
&\equiv\frac{-12p}k(1+4pH_{2k-1}-4pH_{k-1})\ ({\rm{mod}}\ p^3).
\end{align*} If ![]() $(p+1)/2\leq k\leq p-1$. It is easy to see that:
$(p+1)/2\leq k\leq p-1$. It is easy to see that:
 \begin{align*}
&\binom{4p-2k}{2p-k}\\ &=\frac{2(4p-2k)\cdots(2p+1)(2p-1)\cdots(2p-k+1)}{(2p-k)\cdots(p+1)(p-1)!}\\
&\equiv\frac{2(2p-2k)!(1+2pH_{2p-2k})(-1)^{k-1}(k-1)!(1-2pH_{k-1})}{(p-k)!(1+pH_{p-k})}\\
&\equiv2\binom{2p-2k}{p-k}\frac{(-1)^{k-1}(1+2pH_{2p-2k}-2pH_{k-1})}{\binom{p-1}{k-1}(1+pH_{k-1})}\\
&\equiv2\binom{2p-2k}{p-k}(1+2pH_{2p-2k}-2pH_{k-1})\ ({\rm{mod}}\ p^2).
\end{align*}
\begin{align*}
&\binom{4p-2k}{2p-k}\\ &=\frac{2(4p-2k)\cdots(2p+1)(2p-1)\cdots(2p-k+1)}{(2p-k)\cdots(p+1)(p-1)!}\\
&\equiv\frac{2(2p-2k)!(1+2pH_{2p-2k})(-1)^{k-1}(k-1)!(1-2pH_{k-1})}{(p-k)!(1+pH_{p-k})}\\
&\equiv2\binom{2p-2k}{p-k}\frac{(-1)^{k-1}(1+2pH_{2p-2k}-2pH_{k-1})}{\binom{p-1}{k-1}(1+pH_{k-1})}\\
&\equiv2\binom{2p-2k}{p-k}(1+2pH_{2p-2k}-2pH_{k-1})\ ({\rm{mod}}\ p^2).
\end{align*}Now the proof of Lemma 3.1 is complete.
Proof of Theorem 1.2
We can check case p = 5 directly. So we will assume that p > 5 in the following process. As the same way of proving (2.1) and (2.2), we have
 \begin{align}
\binom{2p-1}{k-1}^2\equiv1-4pH_{k-1}\ ({\rm{mod}}\ p^2),
\end{align}
\begin{align}
\binom{2p-1}{k-1}^2\equiv1-4pH_{k-1}\ ({\rm{mod}}\ p^2),
\end{align} \begin{align}
\binom{2p+k}{k}^2\equiv1+4pH_k\ ({\rm{mod}}\ p^2),
\end{align}
\begin{align}
\binom{2p+k}{k}^2\equiv1+4pH_k\ ({\rm{mod}}\ p^2),
\end{align} \begin{align}
\binom{4p-k}{2p-k}^2\equiv9(1+4pH_{k-1})\ ({\rm{mod}}\ p^2).
\end{align}
\begin{align}
\binom{4p-k}{2p-k}^2\equiv9(1+4pH_{k-1})\ ({\rm{mod}}\ p^2).
\end{align}So we have
 \begin{align*}
&A_{2p}-1-\binom{4p}{2p}^2-\binom{3p}p^2\binom{2p}p^2\\
&=\sum_{k=1}^{p-1}\binom{2p}k^2\binom{2p+k}k^2+\sum_{k=p+1}^{2p-1}\binom{2p}k^2\binom{2p+k}k^2\\
&=\sum_{k=1}^{p-1}\binom{2p}k^2\binom{2p+k}k^2+\sum_{k=1}^{p-1}\binom{2p}k^2\binom{4p-k}{2p-k}^2.
\end{align*}
\begin{align*}
&A_{2p}-1-\binom{4p}{2p}^2-\binom{3p}p^2\binom{2p}p^2\\
&=\sum_{k=1}^{p-1}\binom{2p}k^2\binom{2p+k}k^2+\sum_{k=p+1}^{2p-1}\binom{2p}k^2\binom{2p+k}k^2\\
&=\sum_{k=1}^{p-1}\binom{2p}k^2\binom{2p+k}k^2+\sum_{k=1}^{p-1}\binom{2p}k^2\binom{4p-k}{2p-k}^2.
\end{align*}Thus, in view of (3.4), (3.5) and (3.6), we have
 \begin{align*}
&A_{2p}-1-\binom{4p}{2p}^2-\binom{2p}p^2\binom{3p}p^2\equiv4p^2\sum_{k=1}^{p-1}\frac1{k^2}\left(1+\frac{4p}k\right)+4p^2\sum_{k=1}^{p-1}\frac{9}{k^2}\\
&=4p^2H_{p-1}^{(2)}+16p^3H_{p-1}^{(3)}+36p^2H_{p-1}^{(2)}=40p^2H_{p-1}^{(2)}+16p^3H_{p-1}^{(3)}\ ({\rm{mod}}\ p^4).
\end{align*}
\begin{align*}
&A_{2p}-1-\binom{4p}{2p}^2-\binom{2p}p^2\binom{3p}p^2\equiv4p^2\sum_{k=1}^{p-1}\frac1{k^2}\left(1+\frac{4p}k\right)+4p^2\sum_{k=1}^{p-1}\frac{9}{k^2}\\
&=4p^2H_{p-1}^{(2)}+16p^3H_{p-1}^{(3)}+36p^2H_{p-1}^{(2)}=40p^2H_{p-1}^{(2)}+16p^3H_{p-1}^{(3)}\ ({\rm{mod}}\ p^4).
\end{align*}Mao [Reference Mao10, Lemma 4.1] proved that:
 \begin{equation}
\binom{4p}{2p}\equiv6-32p^3B_{p-3}\ ({\rm{mod}}\ p^4).
\end{equation}
\begin{equation}
\binom{4p}{2p}\equiv6-32p^3B_{p-3}\ ({\rm{mod}}\ p^4).
\end{equation}Similarly, with (1.2), Lemma 2.1 and (2.3) we can get that:
 \begin{align}
&\binom{3p}p=\sum_{k=0}^p\binom{2p}k\binom{p}k=1+\binom{2p}p+\sum_{k=1}^{p-1}\binom{2p}k\binom{p}k\notag\\
&=1+\binom{2p}p+\sum_{k=1}^{p-1}\frac{2p^2}{k^2}\binom{2p-1}{k-1}\binom{p-1}{k-1}\notag\\
&\equiv1+\binom{2p}p+\sum_{k=1}^{p-1}\frac{2p^2}{k^2}(1-3pH_{k-1})\equiv3-6p^3B_{p-3}\ ({\rm{mod}}\ p^4).
\end{align}
\begin{align}
&\binom{3p}p=\sum_{k=0}^p\binom{2p}k\binom{p}k=1+\binom{2p}p+\sum_{k=1}^{p-1}\binom{2p}k\binom{p}k\notag\\
&=1+\binom{2p}p+\sum_{k=1}^{p-1}\frac{2p^2}{k^2}\binom{2p-1}{k-1}\binom{p-1}{k-1}\notag\\
&\equiv1+\binom{2p}p+\sum_{k=1}^{p-1}\frac{2p^2}{k^2}(1-3pH_{k-1})\equiv3-6p^3B_{p-3}\ ({\rm{mod}}\ p^4).
\end{align}This, with (1.2), (3.7) and Lemma 2.1 yields that:
 \begin{equation*}
A_{2p}\equiv73-\frac{1648}3p^3B_{p-3}=A_2-\frac{1648}3p^3B_{p-3}\ ({\rm{mod}}\ p^4).
\end{equation*}
\begin{equation*}
A_{2p}\equiv73-\frac{1648}3p^3B_{p-3}=A_2-\frac{1648}3p^3B_{p-3}\ ({\rm{mod}}\ p^4).
\end{equation*} Now, we consider  $A^{'}_{2p}$ modulo p 4. Similarly, we have
$A^{'}_{2p}$ modulo p 4. Similarly, we have
 \begin{align*}
&A^{'}_{2p}-1-\binom{4p}{2p}-\binom{2p}p^2\binom{3p}p\\
&=\sum_{k=1}^{p-1}\binom{2p}k^2\binom{2p+k}k+\sum_{k=1}^{p-1}\binom{2p}k^2\binom{4p-k}{2p-k}.
\end{align*}
\begin{align*}
&A^{'}_{2p}-1-\binom{4p}{2p}-\binom{2p}p^2\binom{3p}p\\
&=\sum_{k=1}^{p-1}\binom{2p}k^2\binom{2p+k}k+\sum_{k=1}^{p-1}\binom{2p}k^2\binom{4p-k}{2p-k}.
\end{align*}In view of (3.4), (3.5) and (3.6), we have
 \begin{align*}
&A^{'}_{2p}-1-\binom{4p}{2p}-\binom{2p}p^2\binom{3p}p\\
&\equiv4p^2\sum_{k=1}^{p-1}\frac1{k^2}(1+2pH_k-4pH_{k-1})+12p^2\sum_{k=1}^{p-1}\frac1{k^2}(1-2pH_{k-1})\\
&=16p^2H_{p-1}^{(2)}-32p^3\sum_{k=1}^{p-1}\frac{H_k}{k^2}+40p^3H_{p-1}^{(3)}\ ({\rm{mod}}\ p^4).
\end{align*}
\begin{align*}
&A^{'}_{2p}-1-\binom{4p}{2p}-\binom{2p}p^2\binom{3p}p\\
&\equiv4p^2\sum_{k=1}^{p-1}\frac1{k^2}(1+2pH_k-4pH_{k-1})+12p^2\sum_{k=1}^{p-1}\frac1{k^2}(1-2pH_{k-1})\\
&=16p^2H_{p-1}^{(2)}-32p^3\sum_{k=1}^{p-1}\frac{H_k}{k^2}+40p^3H_{p-1}^{(3)}\ ({\rm{mod}}\ p^4).
\end{align*}Therefore, with (1.2), (3.7), (3.8), Lemma 2.1 and (2.3), we can deduce that:
 \begin{align*}
A^{'}_{2p}\equiv19-\frac{280}3p^3B_{p-3}=A^{'}_2-\frac{280}3p^3B_{p-3}\ ({\rm{mod}}\ p^4).
\end{align*}
\begin{align*}
A^{'}_{2p}\equiv19-\frac{280}3p^3B_{p-3}=A^{'}_2-\frac{280}3p^3B_{p-3}\ ({\rm{mod}}\ p^4).
\end{align*} Now we evaluate ![]() $T_{2p}$ modulo p 4. In the same way of proving Lemma 3.1, we have, if
$T_{2p}$ modulo p 4. In the same way of proving Lemma 3.1, we have, if ![]() $1\leq k\leq(p-1)/2$,
$1\leq k\leq(p-1)/2$,
 \begin{equation*}
\binom{4p-2k}{2p-2k}^2\equiv9(1+4pH_{2k-1})\ ({\rm{mod}}\ p^2),
\end{equation*}
\begin{equation*}
\binom{4p-2k}{2p-2k}^2\equiv9(1+4pH_{2k-1})\ ({\rm{mod}}\ p^2),
\end{equation*} and if ![]() $(p+1)/2\leq k\leq p-1$,
$(p+1)/2\leq k\leq p-1$,
 \begin{equation*}
\binom{4p-2k}{2p-2k}^2\equiv9(1+4pH_{2p-2k})\ ({\rm{mod}}\ p^2).
\end{equation*}
\begin{equation*}
\binom{4p-2k}{2p-2k}^2\equiv9(1+4pH_{2p-2k})\ ({\rm{mod}}\ p^2).
\end{equation*}So with (3.4) we can deduce that:
 \begin{align*}
&T_{2p}-\binom{2p}p^2-\binom{4p}{2p}^2=\sum_{k=p+1}^{2p-1}\binom{2p}k^2\binom{2k}{2p}^2=\sum_{k=1}^{p-1}\binom{2p}k^2\binom{4p-2k}{2p-2k}^2\\
\equiv&36p^2\sum_{k=1}^{\frac{p-1}2}\frac{1+4pH_{2k-1}-4pH_{k-1}}{k^2}+4p^2\sum_{k=\frac{p+1}2}^{p-1}\frac{1+4pH_{2p-2k}-4pH_{k-1}}{k^2}\\
\equiv&36p^2\sum_{k=1}^{\frac{p-1}2}\frac{1+4pH_{2k-1}-4pH_{k-1}}{k^2}+\sum_{k=\frac{p+1}2}^{p-1}\frac{4p^2}{k^2}+16p^3\sum_{k=1}^{\frac{p-1}2}\frac{H_{2k}-H_{p-k-1}}{k^2}\\
\equiv&32p^2H_{\frac{p-1}2}^{(2)}+4p^2H_{p-1}^{(2)}+72p^3H_{\frac{p-1}2}^{(3)}+160p^3\sum_{k=1}^{\frac{p-1}2}\frac{H_{2k}-H_k}{k^2}\ ({\rm{mod}}\ p^4).
\end{align*}
\begin{align*}
&T_{2p}-\binom{2p}p^2-\binom{4p}{2p}^2=\sum_{k=p+1}^{2p-1}\binom{2p}k^2\binom{2k}{2p}^2=\sum_{k=1}^{p-1}\binom{2p}k^2\binom{4p-2k}{2p-2k}^2\\
\equiv&36p^2\sum_{k=1}^{\frac{p-1}2}\frac{1+4pH_{2k-1}-4pH_{k-1}}{k^2}+4p^2\sum_{k=\frac{p+1}2}^{p-1}\frac{1+4pH_{2p-2k}-4pH_{k-1}}{k^2}\\
\equiv&36p^2\sum_{k=1}^{\frac{p-1}2}\frac{1+4pH_{2k-1}-4pH_{k-1}}{k^2}+\sum_{k=\frac{p+1}2}^{p-1}\frac{4p^2}{k^2}+16p^3\sum_{k=1}^{\frac{p-1}2}\frac{H_{2k}-H_{p-k-1}}{k^2}\\
\equiv&32p^2H_{\frac{p-1}2}^{(2)}+4p^2H_{p-1}^{(2)}+72p^3H_{\frac{p-1}2}^{(3)}+160p^3\sum_{k=1}^{\frac{p-1}2}\frac{H_{2k}-H_k}{k^2}\ ({\rm{mod}}\ p^4).
\end{align*}This, with (1.2), (3.7), Lemma 2.1 and (2.4) yields that:
 \begin{equation*}
T_{2p}\equiv40-136p^3B_{p-3}=T_2-136p^3B_{p-3}\ ({\rm{mod}}\ p^4).
\end{equation*}
\begin{equation*}
T_{2p}\equiv40-136p^3B_{p-3}=T_2-136p^3B_{p-3}\ ({\rm{mod}}\ p^4).
\end{equation*} Next, we consider ![]() $D_{2p}$ modulo p 4. It is easy to see that:
$D_{2p}$ modulo p 4. It is easy to see that:
 \begin{align*}
&D_{2p}-2\binom{4p}{2p}-\binom{2p}p^4\\
&=\sum_{k=1}^{p-1}\binom{2p}k^2\binom{2k}k\binom{4p-2k}{2p-k}+\sum_{k=p+1}^{2p-1}\binom{2p}k^2\binom{2k}k\binom{4p-2k}{2p-k}\\
&=2\sum_{k=1}^{p-1}\binom{2p}k^2\binom{2k}k\binom{4p-2k}{2p-k}.
\end{align*}
\begin{align*}
&D_{2p}-2\binom{4p}{2p}-\binom{2p}p^4\\
&=\sum_{k=1}^{p-1}\binom{2p}k^2\binom{2k}k\binom{4p-2k}{2p-k}+\sum_{k=p+1}^{2p-1}\binom{2p}k^2\binom{2k}k\binom{4p-2k}{2p-k}\\
&=2\sum_{k=1}^{p-1}\binom{2p}k^2\binom{2k}k\binom{4p-2k}{2p-k}.
\end{align*}So by Lemma 3.1 and (3.4), we obtain that:
 \begin{align*}
&D_{2p}-2\binom{4p}{2p}-\binom{2p}p^4\equiv-96p^3H_{\frac{p-1}2}^{(3)}+16p^2\sum_{k=\frac{p+1}2}^{p-1}\frac1{k^2}\binom{2k}k\binom{2p-2k}{p-k}\\
&\equiv-96p^3H_{\frac{p-1}2}^{(3)}+16p^2\sum_{k=\frac{p+1}2}^{p-1}\frac{2p}{k^3}=-128p^3H_{\frac{p-1}2}^{(3)}+32p^3H_{p-1}^{(3)}\ ({\rm{mod}}\ p^4).
\end{align*}
\begin{align*}
&D_{2p}-2\binom{4p}{2p}-\binom{2p}p^4\equiv-96p^3H_{\frac{p-1}2}^{(3)}+16p^2\sum_{k=\frac{p+1}2}^{p-1}\frac1{k^2}\binom{2k}k\binom{2p-2k}{p-k}\\
&\equiv-96p^3H_{\frac{p-1}2}^{(3)}+16p^2\sum_{k=\frac{p+1}2}^{p-1}\frac{2p}{k^3}=-128p^3H_{\frac{p-1}2}^{(3)}+32p^3H_{p-1}^{(3)}\ ({\rm{mod}}\ p^4).
\end{align*}Then, we can obtain the desired result:
 \begin{equation*}
D_{2p}\equiv28+\frac{448}3p^3B_{p-3}=D_2+\frac{448}3p^3B_{p-3}\ ({\rm{mod}}\ p^4),
\end{equation*}
\begin{equation*}
D_{2p}\equiv28+\frac{448}3p^3B_{p-3}=D_2+\frac{448}3p^3B_{p-3}\ ({\rm{mod}}\ p^4),
\end{equation*}with the help of (1.2), (3.7) and Lemma 2.1.
Similarly, ![]() $f_{2p}$ modulo p 4 is also easier. It is easy to check that by (3.4),
$f_{2p}$ modulo p 4 is also easier. It is easy to check that by (3.4),
 \begin{align*}
&f_{2p}-2-\binom{2p}p^3=\sum_{k=1}^{p-1}\binom{2p}k^3+\sum_{k=p+1}^{2p-1}\binom{2p}k^3=2\sum_{k=1}^{p-1}\binom{2p}k^3\\
&\equiv-16p^3\sum_{k=1}^{p-1}\frac{(-1)^k}{k^3}=-16p^3\sum_{k=1}^{p-1}\frac{1+(-1)^k}{k^3}+16p^3H_{p-1}^{(3)}\\
&=-4p^3H_{\frac{p-1}2}^{(3)}+16p^3H_{p-1}^{(3)}\ ({\rm{mod}}\ p^4).
\end{align*}
\begin{align*}
&f_{2p}-2-\binom{2p}p^3=\sum_{k=1}^{p-1}\binom{2p}k^3+\sum_{k=p+1}^{2p-1}\binom{2p}k^3=2\sum_{k=1}^{p-1}\binom{2p}k^3\\
&\equiv-16p^3\sum_{k=1}^{p-1}\frac{(-1)^k}{k^3}=-16p^3\sum_{k=1}^{p-1}\frac{1+(-1)^k}{k^3}+16p^3H_{p-1}^{(3)}\\
&=-4p^3H_{\frac{p-1}2}^{(3)}+16p^3H_{p-1}^{(3)}\ ({\rm{mod}}\ p^4).
\end{align*}In view of (1.2) and Lemma 2.1, we immediately get the desired result:
 \begin{equation*}
f_{2p}\equiv10-8p^3B_{p-3}=f_2-8p^3B_{p-3}\ ({\rm{mod}}\ p^4).
\end{equation*}
\begin{equation*}
f_{2p}\equiv10-8p^3B_{p-3}=f_2-8p^3B_{p-3}\ ({\rm{mod}}\ p^4).
\end{equation*} At last, we evaluate ![]() $a_{2p}$ modulo p 3. By (1.1), (3.4) and (3.7), we have:
$a_{2p}$ modulo p 3. By (1.1), (3.4) and (3.7), we have:
 \begin{align*}
&a_{2p}=1+\binom{4p}{2p}+\binom{2p}p^3+\sum_{k=1}^{p-1}\binom{2p}k^2\binom{2k}k+\sum_{k=p+1}^{2p-1}\binom{2p}k^2\binom{2k}k\\
&\equiv15+\sum_{k=1}^{p-1}\binom{2p}k^2\binom{2k}k+\sum_{k=1}^{p-1}\binom{2p}k^2\binom{4p-2k}{2p-k}\\
&\equiv15+4p^2\sum_{k=1}^{p-1}\frac{\binom{2k}k}{k^2}+4p^2\sum_{k=1}^{p-1}\frac1{k^2}\binom{4p-2k}{2p-k}\ ({\rm{mod}}\ p^3).
\end{align*}
\begin{align*}
&a_{2p}=1+\binom{4p}{2p}+\binom{2p}p^3+\sum_{k=1}^{p-1}\binom{2p}k^2\binom{2k}k+\sum_{k=p+1}^{2p-1}\binom{2p}k^2\binom{2k}k\\
&\equiv15+\sum_{k=1}^{p-1}\binom{2p}k^2\binom{2k}k+\sum_{k=1}^{p-1}\binom{2p}k^2\binom{4p-2k}{2p-k}\\
&\equiv15+4p^2\sum_{k=1}^{p-1}\frac{\binom{2k}k}{k^2}+4p^2\sum_{k=1}^{p-1}\frac1{k^2}\binom{4p-2k}{2p-k}\ ({\rm{mod}}\ p^3).
\end{align*}And then in view of Lemma 3.1, we have
 \begin{align*}
a_{2p}&\equiv15+4p^2\sum_{k=1}^{p-1}\frac{\binom{2k}k}{k^2}+8p^2\sum_{k=\frac{p+1}2}^{p-1}\frac1{k^2}\binom{2p-2k}{p-k}\\
&\equiv15+4p^2\sum_{k=1}^{p-1}\frac{\binom{2k}k}{k^2}+8p^2\sum_{k=1}^{\frac{p-1}2}\frac1{k^2}\binom{2k}{k}\\
&\equiv15+12p^2\sum_{k=1}^{p-1}\frac{\binom{2k}k}{k^2}\ ({\rm{mod}}\ p^3).
\end{align*}
\begin{align*}
a_{2p}&\equiv15+4p^2\sum_{k=1}^{p-1}\frac{\binom{2k}k}{k^2}+8p^2\sum_{k=\frac{p+1}2}^{p-1}\frac1{k^2}\binom{2p-2k}{p-k}\\
&\equiv15+4p^2\sum_{k=1}^{p-1}\frac{\binom{2k}k}{k^2}+8p^2\sum_{k=1}^{\frac{p-1}2}\frac1{k^2}\binom{2k}{k}\\
&\equiv15+12p^2\sum_{k=1}^{p-1}\frac{\binom{2k}k}{k^2}\ ({\rm{mod}}\ p^3).
\end{align*}In view of [Reference Mattarei and Tauraso14], we have
 \begin{equation}
\sum_{k=1}^{p-1}\frac{\binom{2k}k}{k^2}\equiv\frac12\left(\frac{p}3\right)B_{p-2}\left(\frac13\right)\ ({\rm{mod}}\ p).
\end{equation}
\begin{equation}
\sum_{k=1}^{p-1}\frac{\binom{2k}k}{k^2}\equiv\frac12\left(\frac{p}3\right)B_{p-2}\left(\frac13\right)\ ({\rm{mod}}\ p).
\end{equation}Therefore, we immediately get the desired result:
 \begin{equation*}
a_{2p}\equiv15+6p^2\left(\frac{p}3\right)B_{p-2}\left(\frac13\right)=a_2+6p^2\left(\frac{p}3\right)B_{p-2}\left(\frac13\right)\ ({\rm{mod}}\ p^3).
\end{equation*}
\begin{equation*}
a_{2p}\equiv15+6p^2\left(\frac{p}3\right)B_{p-2}\left(\frac13\right)=a_2+6p^2\left(\frac{p}3\right)B_{p-2}\left(\frac13\right)\ ({\rm{mod}}\ p^3).
\end{equation*}Now the proof of Theorem 1.2 is complete.
4. Proof of Theorem 1.3
In the same way of proving Lemma 3.1, we have, for ![]() $1\leq k\leq p-1$
$1\leq k\leq p-1$
 \begin{align}
\binom{2p-1}k^2\binom{2p-1+k}{k}^2\equiv\frac{4p^2}{k^2}\left(1-\frac{4p}k\right)\ ({\rm{mod}}\ p^4),
\end{align}
\begin{align}
\binom{2p-1}k^2\binom{2p-1+k}{k}^2\equiv\frac{4p^2}{k^2}\left(1-\frac{4p}k\right)\ ({\rm{mod}}\ p^4),
\end{align} and for ![]() $0\leq k\leq p-2$:
$0\leq k\leq p-2$:
 \begin{equation}
\binom{2p-1}k^2\binom{4p-2-k}{2p-1-k}^2\equiv\frac{36p^2}{(p-1-k)^2}\left(1+\frac{6p}{k+1}\right)\ ({\rm{mod}}\ p^4).
\end{equation}
\begin{equation}
\binom{2p-1}k^2\binom{4p-2-k}{2p-1-k}^2\equiv\frac{36p^2}{(p-1-k)^2}\left(1+\frac{6p}{k+1}\right)\ ({\rm{mod}}\ p^4).
\end{equation}So we have
 \begin{align*}
&A_{2p-1}-1-\binom{2p-1}{p-1}^2\binom{3p-1}{2p-1}^2\\
&=\sum_{k=1}^{p-1}\binom{2p-1}k^2\binom{2p-1+k}k^2+\sum_{k=p+1}^{2p-1}\binom{2p-1}k^2\binom{2p-1+k}k^2\\
&=\sum_{k=1}^{p-1}\binom{2p-1}k^2\binom{2p-1+k}k^2+\sum_{k=0}^{p-2}\binom{2p-1}k^2\binom{4p-2-k}{2p-1-k}^2\\
&\equiv4p^2\sum_{k=1}^{p-1}\frac{1-\frac{4p}k}{k^2}+\sum_{k=0}^{p-2}\frac{36p^2}{(p-1-k)^2}\left(1+\frac{6p}{k+1}\right)\\
&\equiv4p^2\sum_{k=1}^{p-1}\frac{1-\frac{4p}k}{k^2}+36p^2\sum_{k=1}^{p-1}\frac{k+2p}{k^3}\left(1+\frac{6p}{k}\right)\\
&\equiv40p^2H_{p-1}^{(2)}+272p^3H_{p-1}^{(2)}\ ({\rm{mod}}\ p^4).
\end{align*}
\begin{align*}
&A_{2p-1}-1-\binom{2p-1}{p-1}^2\binom{3p-1}{2p-1}^2\\
&=\sum_{k=1}^{p-1}\binom{2p-1}k^2\binom{2p-1+k}k^2+\sum_{k=p+1}^{2p-1}\binom{2p-1}k^2\binom{2p-1+k}k^2\\
&=\sum_{k=1}^{p-1}\binom{2p-1}k^2\binom{2p-1+k}k^2+\sum_{k=0}^{p-2}\binom{2p-1}k^2\binom{4p-2-k}{2p-1-k}^2\\
&\equiv4p^2\sum_{k=1}^{p-1}\frac{1-\frac{4p}k}{k^2}+\sum_{k=0}^{p-2}\frac{36p^2}{(p-1-k)^2}\left(1+\frac{6p}{k+1}\right)\\
&\equiv4p^2\sum_{k=1}^{p-1}\frac{1-\frac{4p}k}{k^2}+36p^2\sum_{k=1}^{p-1}\frac{k+2p}{k^3}\left(1+\frac{6p}{k}\right)\\
&\equiv40p^2H_{p-1}^{(2)}+272p^3H_{p-1}^{(2)}\ ({\rm{mod}}\ p^4).
\end{align*}In view of (1.2), (3.8) and Lemma 2.1, we immediately get the desired result:
 \begin{equation*}
A_{2p-1}\equiv5+\frac{16}3p^3B_{p-3}=A_1+\frac{16}3p^3B_{p-3}\ ({\rm{mod}}\ p^4).
\end{equation*}
\begin{equation*}
A_{2p-1}\equiv5+\frac{16}3p^3B_{p-3}=A_1+\frac{16}3p^3B_{p-3}\ ({\rm{mod}}\ p^4).
\end{equation*} Now we consider ![]() $T_{2p-1}$ modulo p 4. It is easy to see that:
$T_{2p-1}$ modulo p 4. It is easy to see that:
 \begin{equation*}
T_{2p-1}=\sum_{k=p}^{2p-1}\binom{2p-1}k^2\binom{2k}{2p-1}^2=\sum_{k=0}^{p-1}\binom{2p-1}k^2\binom{4p-2-2k}{2p-1-2k}^2.
\end{equation*}
\begin{equation*}
T_{2p-1}=\sum_{k=p}^{2p-1}\binom{2p-1}k^2\binom{2k}{2p-1}^2=\sum_{k=0}^{p-1}\binom{2p-1}k^2\binom{4p-2-2k}{2p-1-2k}^2.
\end{equation*}So
 \begin{align*}
&T_{2p-1}-\binom{2p-1}{\frac{p-1}2}^2\binom{3p-1}{2p-1}^2\\
=&\sum_{k=0}^{\frac{p-3}2}\binom{2p-1}k^2\binom{4p-2-2k}{2p-1-k}^2+\sum_{k=\frac{p+1}2}^{p-1}\binom{2p-1}k^2\binom{4p-2-2k}{2p-1-2k}^2.
\end{align*}
\begin{align*}
&T_{2p-1}-\binom{2p-1}{\frac{p-1}2}^2\binom{3p-1}{2p-1}^2\\
=&\sum_{k=0}^{\frac{p-3}2}\binom{2p-1}k^2\binom{4p-2-2k}{2p-1-k}^2+\sum_{k=\frac{p+1}2}^{p-1}\binom{2p-1}k^2\binom{4p-2-2k}{2p-1-2k}^2.
\end{align*} In the same way of proving Lemma 3.1, we have, for ![]() $0\leq k\leq (p-3)/2$:
$0\leq k\leq (p-3)/2$:
 \begin{align*}
&\binom{2p-1}k^2\binom{4p-2-2k}{2p-1-2k}^2\\ &\equiv\frac{36p^2}{(p-1-2k)^2}\left(1-4pH_k+4pH_{2k}+\frac{6p}{2k+1}\right)\ ({\rm{mod}}\ p^4),
\end{align*}
\begin{align*}
&\binom{2p-1}k^2\binom{4p-2-2k}{2p-1-2k}^2\\ &\equiv\frac{36p^2}{(p-1-2k)^2}\left(1-4pH_k+4pH_{2k}+\frac{6p}{2k+1}\right)\ ({\rm{mod}}\ p^4),
\end{align*} and for ![]() $(p+1)/2\leq k\leq p-1$,
$(p+1)/2\leq k\leq p-1$,
 \begin{align*}
&\binom{2p-1}k^2\binom{4p-2-2k}{2p-1-2k}^2\\ &\equiv\frac{4p^2}{(2p-1-2k)^2}(1+4pH_{2p-2-2k}-4pH_k)\ ({\rm{mod}}\ p^4).
\end{align*}
\begin{align*}
&\binom{2p-1}k^2\binom{4p-2-2k}{2p-1-2k}^2\\ &\equiv\frac{4p^2}{(2p-1-2k)^2}(1+4pH_{2p-2-2k}-4pH_k)\ ({\rm{mod}}\ p^4).
\end{align*}So we have
 \begin{align*}
&T_{2p-1}-\binom{2p-1}{\frac{p-1}2}^2\binom{3p-1}{2p-1}^2\\
\equiv& 36p^2\sum_{k=0}^{\frac{p-3}2}\frac{2k+1+8p}{(2k+1)^3}+4p^2\sum_{k=0}^{\frac{p-3}2}\frac{1-4pH_k+4pH_{2k}}{(2k+1)^2}\\
\equiv&40p^2\sum_{k=0}^{\frac{p-3}2}\frac{1}{(2k+1)^2}+160p^3\sum_{k=0}^{\frac{p-3}2}\frac{H_{2k}-H_k}{(2k+1)^2}+288p^3\sum_{k=0}^{\frac{p-3}2}\frac{1}{(2k+1)^3}\\
\equiv&10p^2H_{\frac{p-1}2}^{(2)}-26p^3H_{\frac{p-1}2}^{(3)}+160p^3\sum_{k=0}^{\frac{p-3}2}\frac{H_{2k}-H_k}{(2k+1)^2}\ ({\rm{mod}}\ p^4).
\end{align*}
\begin{align*}
&T_{2p-1}-\binom{2p-1}{\frac{p-1}2}^2\binom{3p-1}{2p-1}^2\\
\equiv& 36p^2\sum_{k=0}^{\frac{p-3}2}\frac{2k+1+8p}{(2k+1)^3}+4p^2\sum_{k=0}^{\frac{p-3}2}\frac{1-4pH_k+4pH_{2k}}{(2k+1)^2}\\
\equiv&40p^2\sum_{k=0}^{\frac{p-3}2}\frac{1}{(2k+1)^2}+160p^3\sum_{k=0}^{\frac{p-3}2}\frac{H_{2k}-H_k}{(2k+1)^2}+288p^3\sum_{k=0}^{\frac{p-3}2}\frac{1}{(2k+1)^3}\\
\equiv&10p^2H_{\frac{p-1}2}^{(2)}-26p^3H_{\frac{p-1}2}^{(3)}+160p^3\sum_{k=0}^{\frac{p-3}2}\frac{H_{2k}-H_k}{(2k+1)^2}\ ({\rm{mod}}\ p^4).
\end{align*}In view of [Reference Mao10, (5.1)], we have
 \begin{align*}
\binom{2p-1}{\frac{p-1}2}^2&=\frac{(2p-1)^2\cdots(2p-\frac{p-1}2)^2}{(\frac{p-1}2)!^2}\equiv(16^{p-1}+\frac{11}6p^3B_{p-3})^2\\
&\equiv16^{2(p-1)}+\frac{11}3p^3B_{p-3}\ ({\rm{mod}}\ p^4).
\end{align*}
\begin{align*}
\binom{2p-1}{\frac{p-1}2}^2&=\frac{(2p-1)^2\cdots(2p-\frac{p-1}2)^2}{(\frac{p-1}2)!^2}\equiv(16^{p-1}+\frac{11}6p^3B_{p-3})^2\\
&\equiv16^{2(p-1)}+\frac{11}3p^3B_{p-3}\ ({\rm{mod}}\ p^4).
\end{align*}This, with (3.8), [Reference Mao10, Lemma 2.3] and Lemma 2.1 yields that:
 \begin{equation*}
T_{2p-1}\equiv4\cdot16^{2(p-1)}-6p^3B_{p-3}=16^{2(p-1)}V_1-6p^3B_{p-3}\ ({\rm{mod}}\ p^4).
\end{equation*}
\begin{equation*}
T_{2p-1}\equiv4\cdot16^{2(p-1)}-6p^3B_{p-3}=16^{2(p-1)}V_1-6p^3B_{p-3}\ ({\rm{mod}}\ p^4).
\end{equation*}Now the proof of Theorem 1.3 is complete.□
5. Proof of Theorem 1.4
For any ![]() $n\geq m$, we define the alternating multiple harmonic sum as:
$n\geq m$, we define the alternating multiple harmonic sum as:
 \begin{equation*}
H(a_1,a_2,\ldots,a_m;n)=\sum_{\substack{1\leq k_1 \lt k_2 \lt \ldots \lt k_m\leq n}}\prod_{i=1}^m\frac{\mbox{sign}(a_i)^{k_i}}{k_i^{|a_i|}}.
\end{equation*}
\begin{equation*}
H(a_1,a_2,\ldots,a_m;n)=\sum_{\substack{1\leq k_1 \lt k_2 \lt \ldots \lt k_m\leq n}}\prod_{i=1}^m\frac{\mbox{sign}(a_i)^{k_i}}{k_i^{|a_i|}}.
\end{equation*} The integers m and ![]() $\sum_{i=1}^m|a_i|$ are respectively the depth and the weight of the harmonic sum. As a matter of convenience, we remember
$\sum_{i=1}^m|a_i|$ are respectively the depth and the weight of the harmonic sum. As a matter of convenience, we remember ![]() $H(1;n)$ as Hn. In view of [Reference Hoffman5], we have
$H(1;n)$ as Hn. In view of [Reference Hoffman5], we have
 \begin{align}
H(\{a\}^r;p-1)\equiv\begin{cases}(-1)^r\frac{a(ar+1)}{2(ar+2)}p^2B_{p-ar-2}&\ ({\rm{mod}}\ p^3)\quad \text{if}\ ar\ \text{is odd},\\
(-1)^{r-1}\frac{a}{ar+1}p B_{p-ar-1}&\ ({\rm{mod}}\ p^2)\quad \text{if}\ ar\ \text{is even}.\end{cases}
\end{align}
\begin{align}
H(\{a\}^r;p-1)\equiv\begin{cases}(-1)^r\frac{a(ar+1)}{2(ar+2)}p^2B_{p-ar-2}&\ ({\rm{mod}}\ p^3)\quad \text{if}\ ar\ \text{is odd},\\
(-1)^{r-1}\frac{a}{ar+1}p B_{p-ar-1}&\ ({\rm{mod}}\ p^2)\quad \text{if}\ ar\ \text{is even}.\end{cases}
\end{align}Lemma 5.1. For any prime p > 3, we have
 \begin{gather*}
\binom{4p}p\equiv4-16p^3B_{p-3}\ ({\rm{mod}}\ p^4),\ \ \binom{5p}{2p}\equiv10-100p^3B_{p-3}\ ({\rm{mod}}\ p^4),\\
\binom{6p}{3p}\equiv20-360p^3B_{p-3}\ ({\rm{mod}}\ p^4).
\end{gather*}
\begin{gather*}
\binom{4p}p\equiv4-16p^3B_{p-3}\ ({\rm{mod}}\ p^4),\ \ \binom{5p}{2p}\equiv10-100p^3B_{p-3}\ ({\rm{mod}}\ p^4),\\
\binom{6p}{3p}\equiv20-360p^3B_{p-3}\ ({\rm{mod}}\ p^4).
\end{gather*}Proof. It is easy to see that
 \begin{align*}
&\binom{4p}p=4\binom{4p-1}{p-1}=\frac{(4p-1)\cdots(3p+1)}{(p-1)!}\\
\equiv&1+3pH_{p-1}+\frac{9p^2}2(H_{p-1}^2-H_{p-1}^{(2)})+27p^3H(1,1,1,p-1)\ ({\rm{mod}}\ p^4).
\end{align*}
\begin{align*}
&\binom{4p}p=4\binom{4p-1}{p-1}=\frac{(4p-1)\cdots(3p+1)}{(p-1)!}\\
\equiv&1+3pH_{p-1}+\frac{9p^2}2(H_{p-1}^2-H_{p-1}^{(2)})+27p^3H(1,1,1,p-1)\ ({\rm{mod}}\ p^4).
\end{align*}This, with (5.1) and Lemma 2.1 yields that:
 \begin{equation*}
\binom{4p}p\equiv4-16p^3B_{p-3}\ ({\rm{mod}}\ p^4).
\end{equation*}
\begin{equation*}
\binom{4p}p\equiv4-16p^3B_{p-3}\ ({\rm{mod}}\ p^4).
\end{equation*}Then with this, Lemma 2.1 and (5.1) we have
 \begin{align*}
&\binom{5p}{2p}=\frac52\binom{5p-1}{2p-1}=\frac52\frac{(5p-1)\cdots(4p+1)}{(2p-1)\cdots(p+1)}\binom{4p}{p}\\
&\equiv\frac52\binom{4p}{p}\frac{1+4pH_{p-1}+8p^2(H_{p-1}^2-H_{p-1}^{(2)})+64p^3H(1,1,1,p-1)}{1+pH_{p-1}+\frac{p^2}2(H_{p-1}^2-H_{p-1}^{(2)})+p^3H(1,1,1,p-1)}\\
&\equiv10-100p^3B_{p-3}\ ({\rm{mod}}\ p^4).
\end{align*}
\begin{align*}
&\binom{5p}{2p}=\frac52\binom{5p-1}{2p-1}=\frac52\frac{(5p-1)\cdots(4p+1)}{(2p-1)\cdots(p+1)}\binom{4p}{p}\\
&\equiv\frac52\binom{4p}{p}\frac{1+4pH_{p-1}+8p^2(H_{p-1}^2-H_{p-1}^{(2)})+64p^3H(1,1,1,p-1)}{1+pH_{p-1}+\frac{p^2}2(H_{p-1}^2-H_{p-1}^{(2)})+p^3H(1,1,1,p-1)}\\
&\equiv10-100p^3B_{p-3}\ ({\rm{mod}}\ p^4).
\end{align*}Similarly, with this and (5.1) and Lemma 2.1, we have
 \begin{align*}
&\binom{6p}{3p}\equiv2\binom{5p}{2p}\frac{(6p-1)\cdots(5p+1)}{(3p-1)\cdots(2p+1)}\\
&\equiv2\binom{5p}{2p}\frac{1+5pH_{p-1}+\frac{25}2p^2(H_{p-1}^2-H_{p-1}^{(2)})+125p^3H(1,1,1,p-1)}{1+2pH_{p-1}+2p^2(H_{p-1}^2-H_{p-1}^{(2)})+8p^3H(1,1,1,p-1)}\\
&\equiv20-360p^3B_{p-3}\ ({\rm{mod}}\ p^4).
\end{align*}
\begin{align*}
&\binom{6p}{3p}\equiv2\binom{5p}{2p}\frac{(6p-1)\cdots(5p+1)}{(3p-1)\cdots(2p+1)}\\
&\equiv2\binom{5p}{2p}\frac{1+5pH_{p-1}+\frac{25}2p^2(H_{p-1}^2-H_{p-1}^{(2)})+125p^3H(1,1,1,p-1)}{1+2pH_{p-1}+2p^2(H_{p-1}^2-H_{p-1}^{(2)})+8p^3H(1,1,1,p-1)}\\
&\equiv20-360p^3B_{p-3}\ ({\rm{mod}}\ p^4).
\end{align*}Now the proof of Lemma 5.1 is complete.
In the same way of proving (2.1) and (2.2), we have
 \begin{align}
\binom{3p-1}{k-1}^2\equiv1-6pH_{k-1}\ ({\rm{mod}}\ p^2),
\end{align}
\begin{align}
\binom{3p-1}{k-1}^2\equiv1-6pH_{k-1}\ ({\rm{mod}}\ p^2),
\end{align} \begin{align}
\binom{3p-1}{p+k-1}^2\equiv4(1-6pH_{k-1})\ ({\rm{mod}}\ p^2),
\end{align}
\begin{align}
\binom{3p-1}{p+k-1}^2\equiv4(1-6pH_{k-1})\ ({\rm{mod}}\ p^2),
\end{align} \begin{align}
\binom{3p+k}{k}^2\equiv1+6pH_{k}\ ({\rm{mod}}\ p^2),
\end{align}
\begin{align}
\binom{3p+k}{k}^2\equiv1+6pH_{k}\ ({\rm{mod}}\ p^2),
\end{align} \begin{align}
\binom{4p+k}{p+k}^2\equiv16(1+6pH_{k})\ ({\rm{mod}}\ p^2),
\end{align}
\begin{align}
\binom{4p+k}{p+k}^2\equiv16(1+6pH_{k})\ ({\rm{mod}}\ p^2),
\end{align} \begin{align}
\binom{6p-k}{3p-k}^2\equiv100(1+6pH_{k-1})\ ({\rm{mod}}\ p^2).
\end{align}
\begin{align}
\binom{6p-k}{3p-k}^2\equiv100(1+6pH_{k-1})\ ({\rm{mod}}\ p^2).
\end{align}So, we have
 \begin{align*}
&A_{3p}-1-\binom{3p}p^2\binom{4p}{2p}^2-\binom{3p}{2p}^2\binom{5p}{2p}^2-\binom{6p}{3p}^2\\
=&\sum_{k=1}^{p-1}\binom{3p}k^2\binom{3p+k}k^2+\sum_{k=1}^{p-1}\binom{3p}{p+k}^2\binom{4p+k}{p+k}^2\\
&\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ +\sum_{k=1}^{p-1}\binom{3p}{k}^2\binom{6p-k}{3p-k}^2\\
\equiv&9p^2\sum_{k=1}^{p-1}\frac{1+\frac{6p}k}{k^2}+576p^2\sum_{k=1}^{p-1}\left(\frac1{k^2}+\frac{4p}{k^3}\right)+900p^2H_{p-1}^{(2)}\\
\equiv&1485p^2H_{p-1}^{(2)}+(54+36\cdot64)p^3H_{p-1}^{(3)}\ ({\rm{mod}}\ p^4).
\end{align*}
\begin{align*}
&A_{3p}-1-\binom{3p}p^2\binom{4p}{2p}^2-\binom{3p}{2p}^2\binom{5p}{2p}^2-\binom{6p}{3p}^2\\
=&\sum_{k=1}^{p-1}\binom{3p}k^2\binom{3p+k}k^2+\sum_{k=1}^{p-1}\binom{3p}{p+k}^2\binom{4p+k}{p+k}^2\\
&\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ +\sum_{k=1}^{p-1}\binom{3p}{k}^2\binom{6p-k}{3p-k}^2\\
\equiv&9p^2\sum_{k=1}^{p-1}\frac{1+\frac{6p}k}{k^2}+576p^2\sum_{k=1}^{p-1}\left(\frac1{k^2}+\frac{4p}{k^3}\right)+900p^2H_{p-1}^{(2)}\\
\equiv&1485p^2H_{p-1}^{(2)}+(54+36\cdot64)p^3H_{p-1}^{(3)}\ ({\rm{mod}}\ p^4).
\end{align*}Then with Lemma 2.1, (3.7), (3.8) and Lemma 5.1, we immediately obtain the desired result:
 \begin{equation*}
A_{3p}\equiv1445-36738p^3B_{p-3}= A_3-36738p^3B_{p-3}\ ({\rm{mod}}\ p^4).
\end{equation*}
\begin{equation*}
A_{3p}\equiv1445-36738p^3B_{p-3}= A_3-36738p^3B_{p-3}\ ({\rm{mod}}\ p^4).
\end{equation*} Next we consider  $A^{'}_{3p}$ modulo p 4. Similarly,
$A^{'}_{3p}$ modulo p 4. Similarly,
 \begin{align*}
&A^{'}_{3p}-1-\binom{3p}p^2\binom{4p}{2p}-\binom{3p}{2p}^2\binom{5p}{2p}-\binom{6p}{3p}\\
=&\sum_{k=1}^{p-1}\binom{3p}k^2\binom{3p+k}k+\sum_{k=1}^{p-1}\binom{3p}{p+k}^2\binom{4p+k}{p+k}\\
&+\sum_{k=1}^{p-1}\binom{3p}{k}^2\binom{6p-k}{3p-k}\equiv9p^2\sum_{k=1}^{p-1}\frac{1-3pH_k+\frac{6p}k}{k^2}\\
&+144p^2\sum_{k=1}^{p-1}\left(\frac1{k^2}+\frac{4p}{k^3}-\frac{3pH_k}{k^2}\right)+90p^2\sum_{k=1}^{p-1}\frac{1-3pH_k+\frac{3p}k}{k^2}\\
\equiv&243p^2H_{p-1}^{(2)}+900p^3H_{p-1}^{(3)}-729p^3\sum_{k=1}^{p-1}\frac{H_k}{k^2}\ ({\rm{mod}}\ p^4).
\end{align*}
\begin{align*}
&A^{'}_{3p}-1-\binom{3p}p^2\binom{4p}{2p}-\binom{3p}{2p}^2\binom{5p}{2p}-\binom{6p}{3p}\\
=&\sum_{k=1}^{p-1}\binom{3p}k^2\binom{3p+k}k+\sum_{k=1}^{p-1}\binom{3p}{p+k}^2\binom{4p+k}{p+k}\\
&+\sum_{k=1}^{p-1}\binom{3p}{k}^2\binom{6p-k}{3p-k}\equiv9p^2\sum_{k=1}^{p-1}\frac{1-3pH_k+\frac{6p}k}{k^2}\\
&+144p^2\sum_{k=1}^{p-1}\left(\frac1{k^2}+\frac{4p}{k^3}-\frac{3pH_k}{k^2}\right)+90p^2\sum_{k=1}^{p-1}\frac{1-3pH_k+\frac{3p}k}{k^2}\\
\equiv&243p^2H_{p-1}^{(2)}+900p^3H_{p-1}^{(3)}-729p^3\sum_{k=1}^{p-1}\frac{H_k}{k^2}\ ({\rm{mod}}\ p^4).
\end{align*}This, with (2.3), (3.7), (3.8), Lemma 2.1 and Lemma 5.1 yields that:
 \begin{equation*}
A^{'}_{3p}\equiv147-2475p^3B_{p-3}= A^{'}_{3}-2475p^3B_{p-3}\ ({\rm{mod}}\ p^4).
\end{equation*}
\begin{equation*}
A^{'}_{3p}\equiv147-2475p^3B_{p-3}= A^{'}_{3}-2475p^3B_{p-3}\ ({\rm{mod}}\ p^4).
\end{equation*} Now we evaluate ![]() $T_{3p}$ modulo p 4. It is easy to see that modulo p 4,
$T_{3p}$ modulo p 4. It is easy to see that modulo p 4,
 \begin{align*}
&T_{3p}-\binom{6p}{3p}^2-\binom{3p}{p}^2\binom{4p}p^2\\
=&\sum_{k=1}^{p-1}\binom{3p}k^2\binom{6p-2k}{3p-2k}^2+\sum_{k=1}^{\frac{p-1}2}\binom{3p}{p+k}^2\binom{4p-2k}{p-2k}^2\\
\equiv&\sum_{k=1}^{p-1}\frac{9p^2}{k^2}\binom{3p-1}{k-1}^2\binom{6p-2k}{3p-2k}^2+\sum_{k=1}^{\frac{p-1}2}\frac{9p^2}{(p+k)^2}\binom{3p}{p+k}^2\binom{4p-2k}{p-2k}^2.
\end{align*}
\begin{align*}
&T_{3p}-\binom{6p}{3p}^2-\binom{3p}{p}^2\binom{4p}p^2\\
=&\sum_{k=1}^{p-1}\binom{3p}k^2\binom{6p-2k}{3p-2k}^2+\sum_{k=1}^{\frac{p-1}2}\binom{3p}{p+k}^2\binom{4p-2k}{p-2k}^2\\
\equiv&\sum_{k=1}^{p-1}\frac{9p^2}{k^2}\binom{3p-1}{k-1}^2\binom{6p-2k}{3p-2k}^2+\sum_{k=1}^{\frac{p-1}2}\frac{9p^2}{(p+k)^2}\binom{3p}{p+k}^2\binom{4p-2k}{p-2k}^2.
\end{align*} Similar to prove (2.1) and (2.2), we have, for any ![]() $1\leq k\leq(p-1)/2$,
$1\leq k\leq(p-1)/2$,
 \begin{equation*}
\binom{4p-2k}{p-2k}^2\equiv1+6pH_{2k-1}\ ({\rm{mod}}\ p^2),
\end{equation*}
\begin{equation*}
\binom{4p-2k}{p-2k}^2\equiv1+6pH_{2k-1}\ ({\rm{mod}}\ p^2),
\end{equation*} \begin{equation*}
\binom{6p-2k}{3p-2k}^2\equiv100(1+6pH_{2k-1})\ ({\rm{mod}}\ p^2),
\end{equation*}
\begin{equation*}
\binom{6p-2k}{3p-2k}^2\equiv100(1+6pH_{2k-1})\ ({\rm{mod}}\ p^2),
\end{equation*} and for each ![]() $(p+1)/2\leq k\leq p-1$,
$(p+1)/2\leq k\leq p-1$,
 \begin{equation*}
\binom{6p-2k}{3p-2k}^2\equiv16(1+6pH_{2p-2k})\ ({\rm{mod}}\ p^2).
\end{equation*}
\begin{equation*}
\binom{6p-2k}{3p-2k}^2\equiv16(1+6pH_{2p-2k})\ ({\rm{mod}}\ p^2).
\end{equation*}So we have
 \begin{align*}
&T_{3p}-\binom{6p}{3p}^2-\binom{3p}{p}^2\binom{4p}p^2\\
\equiv&900p^2\sum_{k=1}^{\frac{p-1}2}\frac{1+6pH_{2k-1}-6pH_{k-1}}{k^2}\\
&\ \ \ \ \ \ \ \ \ \ \ \ \ +144p^2\sum_{k=\frac{p+1}2}^{p-1}\frac{1+6pH_{2p-2k}-6pH_{k-1}}{k^2}\\
&\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ +36p^2\sum_{k=1}^{\frac{p-1}2}\left(\frac1{k^2}+\frac{p}{k^3}+\frac{6pH_{2k}-6pH_k}{k^2}\right)\\
\equiv&1080p^2H_{\frac{p-1}2}^{(2)}+3024p^3H_{\frac{p-1}2}^{(3)}+6480p^3\sum_{k=1}^{\frac{p-1}2}\frac{H_{2k}-H_k}{k^2}\ ({\rm{mod}}\ p^4).
\end{align*}
\begin{align*}
&T_{3p}-\binom{6p}{3p}^2-\binom{3p}{p}^2\binom{4p}p^2\\
\equiv&900p^2\sum_{k=1}^{\frac{p-1}2}\frac{1+6pH_{2k-1}-6pH_{k-1}}{k^2}\\
&\ \ \ \ \ \ \ \ \ \ \ \ \ +144p^2\sum_{k=\frac{p+1}2}^{p-1}\frac{1+6pH_{2p-2k}-6pH_{k-1}}{k^2}\\
&\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ +36p^2\sum_{k=1}^{\frac{p-1}2}\left(\frac1{k^2}+\frac{p}{k^3}+\frac{6pH_{2k}-6pH_k}{k^2}\right)\\
\equiv&1080p^2H_{\frac{p-1}2}^{(2)}+3024p^3H_{\frac{p-1}2}^{(3)}+6480p^3\sum_{k=1}^{\frac{p-1}2}\frac{H_{2k}-H_k}{k^2}\ ({\rm{mod}}\ p^4).
\end{align*}Therefore, we immediately obtain the desired result:
 \begin{equation*}
T_{3p}\equiv544-6696p^3B_{p-3}= T_3-6696p^3B_{p-3}\ ({\rm{mod}}\ p^4),
\end{equation*}
\begin{equation*}
T_{3p}\equiv544-6696p^3B_{p-3}= T_3-6696p^3B_{p-3}\ ({\rm{mod}}\ p^4),
\end{equation*}with the help of (3.8), Lemma 5.1, (2.4) and Lemma 2.1.
Then, we consider ![]() $f_{3p}$ modulo p 4. This is easier; it is easy to check that:
$f_{3p}$ modulo p 4. This is easier; it is easy to check that:
 \begin{equation*}
\binom{3p-1}{p+k-1}=\binom{2p+p-1}{p+k-1}\equiv\binom{2p}p\binom{p-1}{k-1}\equiv2(-1)^{k-1}\ ({\rm{mod}}\ p).
\end{equation*}
\begin{equation*}
\binom{3p-1}{p+k-1}=\binom{2p+p-1}{p+k-1}\equiv\binom{2p}p\binom{p-1}{k-1}\equiv2(-1)^{k-1}\ ({\rm{mod}}\ p).
\end{equation*}So
 \begin{align*}
f_{3p}-2-2\binom{3p}p^2&=2\sum_{k=1}^{p-1}\binom{3p}k^3+\sum_{k=1}^{p-1}\binom{3p}{p+k}^3\\
&\equiv54p^3\sum_{k=1}^{p-1}\frac{(-1)^{k-1}}{k^3}+216p^3\sum_{k=1}^{p-1}\frac{(-1)^{k-1}}{k^3}\\
&=-270p^3\sum_{k=1}^{p-1}\frac{1+(-1)^k}{k^3}+270p^3H_{p-1}^{(3)}\\
&=-\frac{135}2p^3H_{\frac{p-1}2}^{(3)}+270p^3H_{p-1}^{(3)}\ ({\rm{mod}}\ p^4).
\end{align*}
\begin{align*}
f_{3p}-2-2\binom{3p}p^2&=2\sum_{k=1}^{p-1}\binom{3p}k^3+\sum_{k=1}^{p-1}\binom{3p}{p+k}^3\\
&\equiv54p^3\sum_{k=1}^{p-1}\frac{(-1)^{k-1}}{k^3}+216p^3\sum_{k=1}^{p-1}\frac{(-1)^{k-1}}{k^3}\\
&=-270p^3\sum_{k=1}^{p-1}\frac{1+(-1)^k}{k^3}+270p^3H_{p-1}^{(3)}\\
&=-\frac{135}2p^3H_{\frac{p-1}2}^{(3)}+270p^3H_{p-1}^{(3)}\ ({\rm{mod}}\ p^4).
\end{align*}This, with (3.8) and Lemma 2.1 yields that:
 \begin{equation*}
f_{3p}\equiv56-189p^3B_{p-3}=f_3-189p^3B_{p-3}\ ({\rm{mod}}\ p^4).
\end{equation*}
\begin{equation*}
f_{3p}\equiv56-189p^3B_{p-3}=f_3-189p^3B_{p-3}\ ({\rm{mod}}\ p^4).
\end{equation*} Now we consider ![]() $D_{3p}$ modulo p 4. In the same way of proving Lemma 3.1, modulo p 2 we have, for
$D_{3p}$ modulo p 4. In the same way of proving Lemma 3.1, modulo p 2 we have, for ![]() $1\leq k\leq (p-1)/2$,
$1\leq k\leq (p-1)/2$,
 \begin{equation*}
\binom{2k}k\binom{6p-2k}{3p-k}\equiv\frac{-60p}k, \ \ \ \binom{4p-2k}{2p-k}\binom{2p+2k}{p+k}\equiv\frac{-24p}k,
\end{equation*}
\begin{equation*}
\binom{2k}k\binom{6p-2k}{3p-k}\equiv\frac{-60p}k, \ \ \ \binom{4p-2k}{2p-k}\binom{2p+2k}{p+k}\equiv\frac{-24p}k,
\end{equation*} and for ![]() $(p+1)/2\leq k\leq p-1$,
$(p+1)/2\leq k\leq p-1$,
 \begin{equation*}
\binom{2k}k\binom{6p-2k}{3p-k}\equiv\frac{12p}k, \ \ \ \binom{4p-2k}{2p-k}\binom{2p+2k}{p+k}\equiv\frac{24p}k.
\end{equation*}
\begin{equation*}
\binom{2k}k\binom{6p-2k}{3p-k}\equiv\frac{12p}k, \ \ \ \binom{4p-2k}{2p-k}\binom{2p+2k}{p+k}\equiv\frac{24p}k.
\end{equation*}In view of [Reference Sun17, Lemma 2.1], we have
 \begin{equation}
j\binom{2j}j\binom{2(p-j)}{p-j}\equiv2p(-1)^{\lfloor 2k/p\rfloor-1}\ ({\rm{mod}}\ p^2).
\end{equation}
\begin{equation}
j\binom{2j}j\binom{2(p-j)}{p-j}\equiv2p(-1)^{\lfloor 2k/p\rfloor-1}\ ({\rm{mod}}\ p^2).
\end{equation}These, with (5.2), (5.3) yield that:
 \begin{align*}
&D_{3p}-2\binom{6p}{3p}-2\binom{3p}p^2\binom{2p}p\binom{4p}{2p}\\
=&2\sum_{k=1}^{p-1}\binom{3p}k^2\binom{2k}k\binom{6p-2k}{3p-k}+\sum_{k=1}^{p-1}\binom{3p}{p+k}^2\binom{2p+2k}{p+k}\binom{4p-2k}{2p-k}\\
\equiv&18p^2\sum_{k=1}^{p-1}\binom{3p-1}{k-1}^2\binom{2k}k\binom{6p-2k}{3p-k}\\
&\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ +9p^2\sum_{k=1}^{p-1}\binom{3p-1}{p+k-1}^2\binom{2p+2k}{p+k}\binom{4p-2k}{2p-k}\\
\equiv&18p^2\sum_{k=1}^{\frac{p-1}2}\frac{-60p}{k^3}+18p^2\sum_{k=\frac{p+1}2}^{p-1}\frac{6}{k^2}\binom{2k}k\binom{2p-2k}{p-2}\\
&\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ +9p^2\sum_{k=1}^{\frac{p-1}2}\frac{-96p}{k^3}+9p^2\sum_{k=\frac{p+1}2}^{p-1}\frac{96p}{k^3}\\
\equiv&-3024p^3H_{\frac{p-1}2}^{(3)}+864p^3B_{p-3}\ ({\rm{mod}}\ p^4).
\end{align*}
\begin{align*}
&D_{3p}-2\binom{6p}{3p}-2\binom{3p}p^2\binom{2p}p\binom{4p}{2p}\\
=&2\sum_{k=1}^{p-1}\binom{3p}k^2\binom{2k}k\binom{6p-2k}{3p-k}+\sum_{k=1}^{p-1}\binom{3p}{p+k}^2\binom{2p+2k}{p+k}\binom{4p-2k}{2p-k}\\
\equiv&18p^2\sum_{k=1}^{p-1}\binom{3p-1}{k-1}^2\binom{2k}k\binom{6p-2k}{3p-k}\\
&\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ +9p^2\sum_{k=1}^{p-1}\binom{3p-1}{p+k-1}^2\binom{2p+2k}{p+k}\binom{4p-2k}{2p-k}\\
\equiv&18p^2\sum_{k=1}^{\frac{p-1}2}\frac{-60p}{k^3}+18p^2\sum_{k=\frac{p+1}2}^{p-1}\frac{6}{k^2}\binom{2k}k\binom{2p-2k}{p-2}\\
&\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ +9p^2\sum_{k=1}^{\frac{p-1}2}\frac{-96p}{k^3}+9p^2\sum_{k=\frac{p+1}2}^{p-1}\frac{96p}{k^3}\\
\equiv&-3024p^3H_{\frac{p-1}2}^{(3)}+864p^3B_{p-3}\ ({\rm{mod}}\ p^4).
\end{align*}Finally, with the help of Lemma 5.1, Lemma 2.1, (1.2), (3.7) and (3.8), we immediately get the desired result:
 \begin{equation*}
D_{3p}\equiv 256+3168p^3B_{p-3}=D_3+3168p^3B_{p-3}\ ({\rm{mod}}\ p^4).
\end{equation*}
\begin{equation*}
D_{3p}\equiv 256+3168p^3B_{p-3}=D_3+3168p^3B_{p-3}\ ({\rm{mod}}\ p^4).
\end{equation*} At last, we evaluate ![]() $a_{3p}$ modulo p 3. It is easy to verify that, for each
$a_{3p}$ modulo p 3. It is easy to verify that, for each ![]() $1\leq k\leq(p-1)/2$,
$1\leq k\leq(p-1)/2$,
 \begin{equation*}
\binom{2p+2p}{p+k}\equiv2\binom{2k}k\ ({\rm{mod}}\ p), \ \ \binom{6p-2k}{3p-k}\equiv0\ ({\rm{mod}}\ p),
\end{equation*}
\begin{equation*}
\binom{2p+2p}{p+k}\equiv2\binom{2k}k\ ({\rm{mod}}\ p), \ \ \binom{6p-2k}{3p-k}\equiv0\ ({\rm{mod}}\ p),
\end{equation*} and for ![]() $(p+1)/2\leq k\leq p-1$,
$(p+1)/2\leq k\leq p-1$,
 \begin{equation*}
\binom{2p+2p}{p+k}\equiv0\ ({\rm{mod}}\ p), \ \ \binom{6p-2k}{3p-k}\equiv6\binom{2p-2k}{p-k}\ ({\rm{mod}}\ p).
\end{equation*}
\begin{equation*}
\binom{2p+2p}{p+k}\equiv0\ ({\rm{mod}}\ p), \ \ \binom{6p-2k}{3p-k}\equiv6\binom{2p-2k}{p-k}\ ({\rm{mod}}\ p).
\end{equation*}These, with (5.2), (5.3) yield that:
 \begin{align*}
&a_{3p}-1-\binom{3p}p^2\binom{2p}p-\binom{3p}p^2\binom{4p}{2p}-\binom{6p}{3p}\\
=&\sum_{k=1}^{p-1}\binom{3p}k^2\binom{2k}k+\sum_{k=1}^{p-1}\binom{3p}{p+k}^2\binom{2p+2k}{p+k}+\sum_{k=1}^{p-1}\binom{3p}k^2\binom{6p-2k}{3p-k}\\
\equiv&9p^2\sum_{k=1}^{p-1}\frac{\binom{2k}k}{k^2}+36p^2\sum_{k=1}^{p-1}\frac{\binom{2p+2k}{p+k}}{k^2}+9p^2\sum_{k=1}^{p-1}\frac{\binom{6p-2k}{3p-k}}{k^2}\\
\equiv&9p^2\sum_{k=1}^{p-1}\frac{\binom{2k}k}{k^2}+36p^2\sum_{k=1}^{\frac{p-1}2}\frac{2\binom{2k}{k}}{k^2}+9p^2\sum_{k=\frac{p+1}2}^{p-1}\frac{6\binom{2p-2k}{p-k}}{k^2}\\
\equiv&135p^2\sum_{k=1}^{p-1}\frac{\binom{2k}k}{k^2}\ ({\rm{mod}}\ p^3).
\end{align*}
\begin{align*}
&a_{3p}-1-\binom{3p}p^2\binom{2p}p-\binom{3p}p^2\binom{4p}{2p}-\binom{6p}{3p}\\
=&\sum_{k=1}^{p-1}\binom{3p}k^2\binom{2k}k+\sum_{k=1}^{p-1}\binom{3p}{p+k}^2\binom{2p+2k}{p+k}+\sum_{k=1}^{p-1}\binom{3p}k^2\binom{6p-2k}{3p-k}\\
\equiv&9p^2\sum_{k=1}^{p-1}\frac{\binom{2k}k}{k^2}+36p^2\sum_{k=1}^{p-1}\frac{\binom{2p+2k}{p+k}}{k^2}+9p^2\sum_{k=1}^{p-1}\frac{\binom{6p-2k}{3p-k}}{k^2}\\
\equiv&9p^2\sum_{k=1}^{p-1}\frac{\binom{2k}k}{k^2}+36p^2\sum_{k=1}^{\frac{p-1}2}\frac{2\binom{2k}{k}}{k^2}+9p^2\sum_{k=\frac{p+1}2}^{p-1}\frac{6\binom{2p-2k}{p-k}}{k^2}\\
\equiv&135p^2\sum_{k=1}^{p-1}\frac{\binom{2k}k}{k^2}\ ({\rm{mod}}\ p^3).
\end{align*}Hence with (1.1), (3.7), (3.8), (3.9) and Lemma 5.1, we immediately obtain the desired result:
 \begin{align*}
a_{3p}&\equiv93+\frac{135}2p^2\left(\frac{p}3\right)p^2B_{p-2}\left(\frac13\right)\\
&=a_3+\frac{135}2p^2\left(\frac{p}3\right)p^2B_{p-2}\left(\frac13\right)\ ({\rm{mod}}\ p^3).
\end{align*}
\begin{align*}
a_{3p}&\equiv93+\frac{135}2p^2\left(\frac{p}3\right)p^2B_{p-2}\left(\frac13\right)\\
&=a_3+\frac{135}2p^2\left(\frac{p}3\right)p^2B_{p-2}\left(\frac13\right)\ ({\rm{mod}}\ p^3).
\end{align*}Therefore the proof of Theorem 1.4 is complete.□
Funding Statement
This research was supported by the National Natural Science Foundation of China (grant no. 12001288).