Previous studies: regional averaging of monthly spherical harmonic fields

To investigate surface mass variations, the GRACE project provides monthly global spherical harmonic gravity fields estimated from the processing of the mission level-1 data (Reference Tapley, Bettadpur, Ries, Thompson and WatkinsTapley and others, 2004). This processing involves the reduction of the inter-satellite KBRR data with precise positioning, attitude and accelerometer data to isolate gravity forces from non-conservative surface forces (Reference Tapley, Bettadpur, Ries, Thompson and WatkinsTapley and others, 2004; Reference Luthcke, Rowlands, Lemoine, Klosko, Chinn and McCarthyLuthcke and others 2006a). The monthly global spherical harmonic gravity fields, in the form of Stokes coefficients, are formally estimated in a weighted least-squares minimization of the KBRR residuals (difference between the observations and a computed observation based on the initial estimates of the gravity fields and forward models) (Reference Luthcke, Rowlands, Lemoine, Klosko, Chinn and McCarthyLuthcke and others, 2006a). The error in surface mass estimates derived from these monthly spherical harmonic fields greatly increases as the spatial wavelength of interest gets smaller, requiring spatial smoothing and regional averaging of mass variation (Reference Swenson and WahrSwenson and Wahr, 2002; Reference Horwath and DietrichHowarth and Dietrich, 2006). In addition, the monthly spherical harmonic Stokes coefficients have significant errors at the orbit resonant orders 15 and 16 causing spatial ‘striping’ error (Reference Luthcke, Rowlands, Lemoine, Klosko, Chinn and McCarthyLuthcke and others, 2006a), further requiring spatial smoothing and averaging.

Smoothing and regional averaging techniques have recently been used to estimate overall glacier mass balance for the GoA region from the GRACE monthly spherical harmonic fields (Reference Tamisiea, Leuliette, Davis and MitrovicaTamisiea and others, 2005; Reference Chen, Tapley and WilsonChen and others, 2006). While these studies represent an important advance in using space-borne gravity measurements to assess glacier mass balance, they are limited in their temporal (monthly) and spatial (800–1000 km) resolution. These studies employ long-wavelength smoothing and averaging compared to the glacier signal source dimension; therefore, they must account for signal attenuation and leakage of signal out of the region, as well as leakage into the region from outside sources such as TWS and GIA. Reference Tamisiea, Leuliette, Davis and MitrovicaTamisiea and others (2005) used a scaling relationship of increasing annual mass variation as a function of decreasing smoothing radii to extrapolate the annual variation and rate for the GoA region’s ice variation. Reference Chen, Tapley and WilsonChen and others (2006) minimized spatial noise by applying a two-step smoothing technique, and attempted to account for attenuation and leakage by matching numerically simulated mass change to that obtained from the smoothed GRACE monthly fields. Rangelova and Sideris (in press) have modeled North American geoid rates using a more advanced spherical harmonic analysis approach that may better avoid leakage using the method of principal component/empirical orthogonal functions. Still, these methods do not formally minimize the discrepancies between the GRACE inter-satellite ranging observations and the computed observation signals derived from the estimates of surface mass variation. In addition to the limited spatial and temporal resolution of the results, these studies employed smoothing, numerical simulations and leakage investigations that do not use the GRACE KBRR observations; the fundamental observations of the GRACE mission are not being used as the objective criteria of performance.

Mascon solutions

Examination of the GRACE KBRR observations reveals coherent mass-variation signals at better than 400 km full wavelength spatial and 10 day temporal resolution at the mid-latitudes, and still better resolution at high latitudes (Reference RowlandsRowlands and others, 2005). In this study we use the GRACE KBRR observations to estimate mass flux directly. This is accomplished by employing unique methods of processing the GRACE inter-satellite KBRR observations, along with the parameterization of local mass variations as surface mascons. The details of our GRACE data processing are discussed by Reference Rowlands, Ray, Chinn and LemoineRowlands and others (2002) for the short-arc analysis and Reference Luthcke, Rowlands, Lemoine, Klosko, Chinn and McCarthyLuthcke and others (2006a) for the GRACE level-1 data processing (including accelerometer calibration). These processing techniques, combined with the mascon parameterization, have been used to estimate mass variation in the Amazon river basin (Reference RowlandsRowlands and others, 2005) and Greenland ice-sheet drainage systems (Reference LuthckeLuthcke and others, 2006b). In this study, we further refine these techniques to formally estimate the mass variation of the GoA glacier regions through a direct reduction of the GRACE inter-satellite KBRR data.

The mean (over a specified period) gravitational potential of the Earth at any point on or above the surface of the Earth can be expressed in standard form as a spherical harmonic expansion (Reference Hofmann-Wellenhof and MoritzHoffmann-Wellenhof and Moritz, 2005):

where r, ϑ, λ are the spherical geocentric radius, latitude and longitude coordinates of the point where the geopotential is evaluated, GM is the product of the universal gravitational constant and the Earth’s mass, R is the Earth’s mean semi-major axis, l, m are the spherical harmonic degree and order, are the fully normalized associated Legendre functions and , are the fully normalized Stokes coefficients.

The formulation for mascon parameters is derived from the fact that a change in the gravitational potential caused by adding a small uniform layer of mass over a region at an epoch t can be represented as a set of (differential) potential coefficients which can be added to the mean field. The delta coefficients can be computed (Reference Chao, O’Connor, Chang, Hall and FosterChao and others, 1987):

where is the loading Love number of degree l, to account for the Earth’s elastic yielding which in general counteracts the additional surface density, σ(t) is the mass of the layer over a unit of surface area at the epoch t, and Ω is the solid-angle surface area of the mascon region where σ(t) is applied, dΩ = cosϑ dϑ dλ.

For each mascon region, the above equation is used to generate a set of differential Stokes coefficients (complete to degree and order 60) that correspond to 1 cm of water over the region of interest. The estimated mascon parameter for each mascon region is a scale factor on the set of differential Stokes coefficients for that mascon region, giving a surface mass delta in equivalent centimeters of water. The solution is relative to the mean field and forward models of other geophysical processes of mass redistribution (e.g. atmosphere and ocean tides). The mascon parameters are estimated using least-squares differential correction, and therefore the change in KBRR observations per change in mascon parameters is needed for the estimation. The partial derivatives of the GRACE KBRR data with respect to the mascon parameters are computed as a dot product of the partials of the KBRR data with respect to standard Stokes coefficients and the differential Stokes coefficients computed from the equation above for the mascon region of interest:

where is the partial derivative of the KBRR observation i with respect to the j mascon parameter P^j at time t, and , are the partial derivatives of the KBRR observations with respect to the geopotential Stokes coefficients. These partial derivatives are computed as part of the KBRR reduction and level-1 data processing. , are the delta Stokes coefficients for mascon region j.

High-resolution mascons

The mascon parameterization has been successfully applied to estimate mass variation of the Greenland ice sheet (GIS) at drainage-system spatial sampling and 10 day temporal sampling (Reference LuthckeLuthcke and others, 2006b). In this study we further advance this technique to estimate mass variation over 2 × 2 arc-degrees equal-area mascon regions (∼49 000 km²), which are significantly smaller than the GIS drainage-system mascons previously used (Reference LuthckeLuthcke and others, 2006b). We term these high-resolution mascons (hi-res mascons) because the spatial resolution of these new mascons is significantly better than those in previous GRACE mascon studies (Reference RowlandsRowlands and others, 2005; Reference LuthckeLuthcke and others 2006b). We define a series of mascons where the GoA glacier mascons (1–12), land mascons (13–103) and ocean mascons (104–262) are separately distinguished (Fig. 1). The mascons are directly estimated from short arc minimization of the GRACE KBRR data residuals exclusively within the local region of interest (Fig. 1a) (Reference Rowlands, Ray, Chinn and LemoineRowlands and others, 2002, Reference Rowlands2005; Reference Luthcke, Rowlands, Lemoine, Klosko, Chinn and McCarthyLuthcke and others, 2006a).

Fig. 1.

(a) Alaska mascon definitions (approx. equal area ∼49 000 km²). Mascons 1–12 (magenta) represent the GoA glacier regions. (b) Detail of glacier region mascons 1–12.

The GRACE KBRR and level-1 attitude and accelerometer data (including accelerometer calibration) are processed in daily arcs as outlined by Reference Luthcke, Rowlands, Lemoine, Klosko, Chinn and McCarthyLuthcke and others (2006a). In order to isolate ice-change signal, our mascon estimates are relative to models of both static and time-varying gravity. These time-varying gravity effects are forward-modeled in the daily arc reductions of the KBRR data (level-1 data processing). Static mean gravity is modeled using the complete GGM02C GRACE gravity model through degree and order 150 (Reference Tapley, Bettadpur, Ries, Thompson and WatkinsTapley and others, 2004). We perform sensitivity analysis to assess the effects of differences in the forward modeling on our mascon solutions. Here we present the results using two very different forward models: v01 which is our simplest and least complete model; and v03 which represents our best forward modeling of the time-varying gravity. Our v01 forward modeling includes:

1. 1. The ocean tides modeled according to GOT00 (Reference RayRay 1999; Reference Ray and PonteRay and Ponte, 2003), and

2. 2. The atmospheric gravity modeled following Reference Chao and AuChao and Au (1991) using potential coefficients to degree and order 50 at 6 hour intervals derived from US National Centers for Environmental Prediction (NCEP) pressure grids (Reference Petrov and BoyPetrov and Boy, 2004) assuming inverted barometer for the ocean response.

Our v03 forward modeling includes:

1. 1. An updated ocean tide model, GOT4.7, with improvements in shallow waters and polar seas.

2. 2. Atmospheric gravity modeled to degree and order 90 at 3 hour intervals derived from European Centre for Medium-Range Weather Forecasts (ECMWF) operational pressure grids.

3. 3. Ocean mass gravity modeled using MOG2D, a barotropic ocean model forced by 6 hourly ECMWF pressure and winds (Reference Carrre and LyardCarrre and Lyard, 2003), represented as potential coefficients to degree and order 90.

4. 4. TWS modeled using the Global Land Data Assimilation System (GLDAS)/Noah 0.25°, 3 hour data represented as potential coefficients to degree and order 90 (Reference EkEk and others, 2003; Reference RodellRodell and others, 2004). We have set the TWS contribution to zero for the major mountain glacier areas of the globe using a 0.25° mask (Reference Raup, Kieffer, Hare and KargelRaup and others, 2000) and have also zeroed the contribution for the Greenland and Antarctic ice sheets.

5. 5. GIA is modeled using the ICE-5G (VM2) model and represented as potential coefficients to degree and order 90 (Reference PeltierPeltier, 2004).

In addition to the forward models just discussed, we further correct our mascon solutions for the viscous component of post-Little Ice Age (LIA) GIA following the collapse of the Glacier Bay Icefield (Reference Larsen, Motyka, Freymueller, Echelmeyer and IvinsLarsen and others, 2005). The regional post-LIA GIA model is rigidly constrained by approximately 100 precise GPS and relative sea-level (RSL) observations of uplift (Reference Larsen, Motyka, Freymueller, Echelmeyer and IvinsLarsen and others, 2005). The magnitude of the post-LIA GIA signal in the mascon glacier regions is 7 Gt a⁻¹ with a ±30% error estimated from the model comparisons to GPS vertical motions, raised shoreline records of RSL and tide-gauge rates of RSL. Nearly all of the GIA forward-modeled signal in our GoA region of interest is attributed to the post-LIA GIA model. Still, the global ICE-5G (VM2) model is included for completeness to investigate the impact on our GoA glacier mascon solutions from signals outside our region of interest.

Figure 1b shows the relationship between the GoA glacier mascons and the glacier-covered areas. In addition to the GoA glacier mascons, we estimate all surrounding local land and ocean mascons defined in Figure 1a, as well as daily GRACE satellite baseline state orbital parameters to account for mass variations occurring outside our GoA glacier mascons of interest. The local solution exploits the fact that the signal from a mascon observed in GRACE KBRR data is centered over the mascon and is spatially limited in extent. The local solution technique minimizes contamination from the global propagation of errors outside the region of interest and takes advantage of the convergence of orbital tracks at high latitudes to improve spatial and temporal resolution over that of global solutions (Reference RowlandsRowlands and others, 2005; Reference LuthckeLuthcke and others, 2006b).

Unlike global spherical harmonic solutions, local mascon solutions lend themselves to the application of both spatial and temporal constraint equations, which enable high spatial and temporal resolution. The spatial and temporal constraints are discussed in detail by Reference RowlandsRowlands and others (2005) and summarized as applied to GIS mass estimates by Reference LuthckeLuthcke and others (2006b). The constraint equation is a simple exponential function of correlation time and distance, and induces pairs of estimated parameters located closely in time and or space to remain close in value. The correlation time and distance and the weight applied to scale the constraint relative to the data define the ‘strength’ which forces the pairs of parameters towards the same value. The use of these neighbor constraints in our mascon solutions provides a flexible trade-off between high resolution (more estimated parameters) and solution stability. These types of constraints have been used in many geophysical inverse problems, as well as, for example, in precise orbit determination (Reference Luthcke, Zelensky, Rowlands, Lemoine and WilliamsLuthcke and others, 2003).

For the solutions presented in this study, we group the ocean, land and GoA glacier mascons separately. Constraint equations are applied only between pairs of mascon parameters belonging to the same group, in order to isolate ice change from land and ocean. We use a correlation time of 10 days and a correlation distance of 200 km, which is approximately one parameter sample in time and distance. We implement the scale of the constraint equations by weighting the data relative to the constraints. The optimal data weight is determined such that the mascon parameters that are one sample away from each other in both space and time have minor influence on each other. We have investigated the impact of the data weight (equivalent to the constraint scale) by performing solutions using data weights that are as much as five times smaller and larger than the optimal data weight, spanning more than an order of magnitude. We find that the impact on the estimated GoA mascon mass balance and annual amplitude is less than 5%, while the 1σ error estimates of the 10 day mascon solutions can change by as much as 50%. Therefore, the constraints as applied here are important in reducing the error of the individual 10 day solutions, but have little impact on the underlying estimated ice-mass variation signal.

Sensitivity to forward models

The total GoA glacier region mass-variation time series computed from the sum of GoA glacier mascons 1–12 is shown in Figure 2. The time series is given for the period April 2003–September 2007 computed from the v01 forward modeling. The mascon solutions using the v03 forward modeling were computed from April 2003 through April 2007. The difference between the total glacier mascon solutions computed using the v01 and v03 forward modeling is shown as the red line in Figure 2. The comparison illustrates the negligible response of the glacier mascon solutions to differences in the forward modeling. Therefore, the systematic errors due to atmospheric and ocean tide mass-variation modeling are shown to be negligible inasmuch as our model difference represents the errors in these models. Leakage errors due to surrounding signals from ocean mass variation, GIA outside our region of interest (ICE-5G; Reference PeltierPeltier, 2004) and hydrology are also shown to be negligible. This is in contrast to the study by Reference Chen, Tapley and WilsonChen and others (2006) that found significant leakage effects from TWS and GIA using monthly spherical harmonic solutions and a regional averaging technique. Our results illustrate how the mascon technique can isolate the surface mass variations from a direct reduction of the GRACE KBRR observations, while regional averaging of the monthly spherical harmonic fields can spread and attenuate the mass signals, thus complicating the analysis of regional mass variation. Furthermore, we find the models comprising the v03 forward modeling represent a 12% reduction in the global KBRR residual variance (before estimation of time-variable gravity) and therefore are an improvement over the v01 models.

The spatial pattern of the hi-res mascon solution rates for the entire local solution area is displayed in Figure 4a. The largest mass losses are observed in the Yakutat and Glacier Bay region. The figure illustrates the significantly improved spatial resolution over that found in previous GRACE studies which exhibited substantial attenuation and spreading of signal throughout the land region and well into the GoA (Reference Tamisiea, Leuliette, Davis and MitrovicaTamisiea and others, 2005; Reference Chen, Tapley and WilsonChen and others, 2006). Figure 4b presents the spatial distribution of the rates estimated from the v03 forward models. The signal is dominated by the TWS model (based on GLDAS/Noah) and accounts for much of the positive signal found in the hi-res mascon solution rates as seen in Figure 4a. The results indicate the rates in the TWS forward model are inconsistent with the GRACE KBRR observations. The mascon solutions (determined directly from the GRACE KBRR observations) for the regions outside the GoA glacier mascons are approximately equal and opposite in sign to the TWS rates, and therefore are compensating for the mis-modeling in order to reduce the KBRR residuals. Much of the positive signal is near zero when performing solutions using the v01 forward modeling that does not include the TWS model. Fortunately, we have shown that the change in forward modeling has little impact on the GoA glacier mascon solutions (Figs 2 and 3). Therefore, the hi-res mascon solutions in this application appear not to suffer from signal leakage problems. While not a significant source of uncertainty for our hi-res mascon estimates of glacier mass balance, the potential error in the TWS rate may have significant ramifications for studies that rely on regional averaging of the harmonic fields and large corrections for TWS leakage.

Mascon glacier mass-balance trends

We interpret the mass trends in the GoA mascon solution time series (Figs 2 and 3; Table 1) as the regional glacier mass balance even though these regions contain both glaciated and non-glaciated areas. This assumes that all non-glacier sources of mass variation have been accounted for in our forward modeling, and that any snow falling on land surfaces outside the glacier regions melts completely in a given balance year (balance years begin in the fall of the previous calendar year).

The total GoA glacier region had a strongly negative mass balance that decreases in magnitude in the later part of the time series (Fig. 2), particularly for the fourth balance year, April 2006–March 2007. The mass balance averaged over the period April 2003–March 2007 is −84.215.0 Gt a⁻¹ (Table 1), contributing 0.23 mm a⁻¹ to GSLR. The sum of 2006 B _s and 2007 B _w is near zero (Table 2), corresponding with the unusually large snowfalls observed in the GoA region during the later part of 2006 and beginning of 2007 (Fig. 5). Excluding the fourth balance year with anomalously large snowfalls, the mass balance averaged over April 2003–March 2006 is −102.1 ± 5.2 Gt a⁻¹.This compares favorably with the −96 ± 3 5 Gt a⁻¹ mass balance obtained from laser altimetry for the period from the mid-1990s to 2000/01 (Reference Arendt, Echelmeyer, Harrison, Lingle and ValentineArendt and others, 2002). However, as we have seen in the mascon time series, there is significant interannual variability, so caution is necessary when comparing results from different periods.

Fig. 5.

Snowfall at three GoA sites during the GRACE mascon solution period. Data from http://climate.gi.alaska.edu/Climate/Location/TimeSeries/index.html

Table 2.

Winter (B _W), summer (B _S) and net balances (B), for the total GoA glacier mascon region between 2003 and 2007, determined as the difference between yearly maximum and minimum in the mascon time series (Fig. 2). Balance years begin in the fall of the previous calendar year

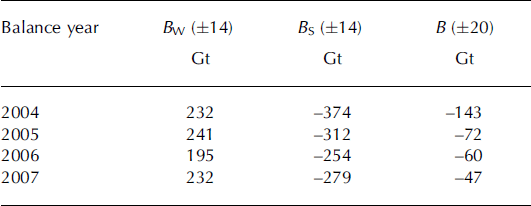
Our mascon solution 3 year mass balance is in agreement with previous GRACE studies: −110 ± 30 Gt a⁻¹ for the period June 2002–July 2004 (Reference Tamisiea, Leuliette, Davis and MitrovicaTamisiea and others, 2005) and −101 ± 22 Gt a⁻¹ for the period April 2002–November 2005 (Reference Chen, Tapley and WilsonChen and others, 2006). However, from our analysis above, an underlying inference is that the rate in the GLDAS/Noah hydrology forward model is inconsistent with the GRACE KBRR observations. This would indicate that the mass-balance estimates of Reference Chen, Tapley and WilsonChen and others (2006) are actually not in agreement with our mascon 3 year mass balance, because the hydrology model accounted for a significant signal leakage correction (−79 Gt a⁻¹) in the Reference Chen, Tapley and WilsonChen and others (2006) analysis.

Large mass losses are observed in the southeast coastal glacier mascons 7, 10 and 11, representing the St Elias, Yakutat, Glacier Bay and Juneau Icefield regions (Fig. 3; Table 1). This is consistent with airborne laser-altimetry measurements that found the largest losses occurred in maritime regions containing numerous tidewater glaciers (Reference Arendt, Echelmeyer, Harrison, Lingle and ValentineArendt and others, 2002). The Yakutat and Glacier Bay mascons 10 and 11 exhibit the largest mass loss, agreeing with Shuttle Radar Topography Mission (SRTM)-based measurements that found substantial ice-mass losses in this region from tidewater and lake-calving glaciers (Reference Larsen, Motyka, Arendt, Echelmeyer and GeisslerLarsen and others, 2007). This region (in particular, Brady and Yakutat Glaciers) is susceptible to climate change because of the generally low elevation of the glaciers relative to their equilibrium-line altitudes (Reference Larsen, Motyka, Arendt, Echelmeyer and GeisslerLarsen and others, 2007). The study found a Yakutat lake-calving glacier to have one of the largest volume losses of any glacier in the region (Reference Larsen, Motyka, Arendt, Echelmeyer and GeisslerLarsen and others, 2007). It is important to note that the SRTM-based study compared SRTM data from 2000, covering 60° N and southward, with digital elevation model data from 1948, 1961 and 1984. The smallest rates of mass loss are found in the interior Alaska Range mascons 1–4 and mascon 8 in the far west of the GoA region containing little glaciated area.

A companion study has used concurrent aircraft laser-altimeter observations to validate the hi-res mascon solution estimates of glacier mass balance in the St Elias Mountains region (Reference Arendt, Luthcke, Larsen, Abdalati, Krabill and BeedleArendt and others, 2008). The study used aircraft laser-altimeter center-line elevation measurements from 17 glaciers in the St Elias Mountains of Alaska and northwestern Canada. The glaciers sampled have a total area of 32 900 km², about 40% of the area of all the glaciers in the GoA study region. The mass balance for the period September 2003–August 2007 was estimated from the altimetry using regional extrapolation methods along with seasonal corrections and error analysis. The balance for the concurrent period was computed from the hi-res mascon solutions containing St Elias glacier area, namely mascons 6, 7 and 10. Each of these mascons contains glacier area other than that from the St Elias region; therefore, the mascon solutions were scaled by the ratio of St Elias glacier area to the area of all other ice contained within each mascon. A mass balance of −21.2 ± 3.7 Gt a⁻¹ is obtained from the laser altimetry while a mass balance of −20.6 ± 3.0 Gt a⁻¹ is determined from our GRACE hi-res mascon solutions. The results are in good agreement within their noted errors and demonstrate the validity of the hi-res mascon solutions to accurately determine the mass balance of regional glacier systems having large mass-change signals. The differences are likely from mascon subsampling uncertainties and the uncertainty in the near-surface density used in the altimetry analysis.

Mascon glacier mass-balance amplitudes

Temporal variations in the GoA mascon solutions result primarily from seasonal variations in snow accumulation and snow/ice wastage (including calving). We interpret the mascon amplitudes as glacier mass-balance amplitudes (Reference MeierMeier, 1984), but we note that there are several factors complicating this interpretation. The first is that the flow of glacier ice redistributes mass throughout the solution domain, potentially resulting in a transfer of ice between adjacent mascons. The second is that some glacier meltwater may reside in subglacial or terrestrial systems and not be measured by GRACE as a mass loss signal. We also note that, although our forward model of terrestrial water storage accounts for snow depth on non-glacier terrain, it likely does not capture all the variability in actual snow accumulation because of the scarcity of climate stations in these regions. Therefore, some of the amplitudes likely contain information on the accumulation and ablation of snow on non-glacier terrain.

The hi-res mascon time series (Fig. 3) illustrate the effects of continentality on mass-balance amplitudes. The largest annual amplitudes are found in the southeast coastal glacier mascons 7, 10, 11 and 12, representing the St Elias, Yakutat and the Glacier Bay, Juneau and Stikine Icefield regions. This is consistent with the high rates of accumulation and large annual ablation found in these maritime glacier regions (Reference Larsen, Motyka, Arendt, Echelmeyer and GeisslerLarsen and others, 2007). These regions show the largest reduction in mass loss during the period April 2006–March 2007, in part likely due to the anomalously large mass input from snowfall in these regions during that period (Fig. 5). The lowest amplitudes were observed in the Alaska Range (mascons 1–3). Our results support the assumption that maritime glaciers have larger rates of mass turnover and a larger sensitivity to climate (Reference MeierMeier, 1984; Reference Oerlemans and FortuinOerlemans and Fortuin, 1992).

Annual amplitudes in mascon 12 were about double those in mascon 7. However, over our study period, the average annual snowfall at Yakutat weather station in mascon 7 (340 cm) is greater than the average annual snowfall at Juneau weather station in mascon 12 (235 cm) (see also Fig. 5). This suggests that factors other than snow accumulation control the magnitude of GRACE amplitudes. We speculate that because mascon 7 has about four times more ice cover than mascon 12, there is a substantial component of winter runoff that offsets the mass gains occurring through snow accumulation. The runoff is continually released from englacial or subglacial storage, and progresses in the winter even in the absence of surface melting. During the summer season, the vast accumulation areas in mascon 7 likely collect summer snowfall and offset mass losses due to ablation. Both of these factors probably combine to dampen the mascon 7 amplitudes relative to what they would be in the absence of glacier ice. Further investigations will be necessary to verify these preliminary explanations.

Summer melt-season mass losses start between 31 March and 20 May, while winter accumulation-season mass gains start between 10 September and 20 October. Table 2 contains mass-balance estimates derived from the total glacier mascon time series in Figure 2. The largest summer and annual negative mass balance observed in the total glacier mascon solution occurred during the balance year 2004. The 2004 summer and annual net balance is 123% and 178% more negative than the 4 year average (balance years 2004–07). This corresponds well with the 2004 record summer heatwave in Alaska, which was reflected in record negative balances of Gulkana and Black Rapids Glaciers as observed from in situ mass-balance records (Reference Truffer, Harrison and MarchTruffer and others, 2005). Mascon solutions 7, 10 and 11, representing the St Elias, Yakutat and the Glacier Bay and Juneau Icefield regions, exhibit the largest negative summer net balance in response to the summer heatwave of 2004.

A mass-balance modeling study has shown that temporal variations in the hi-res mascon solution from the St Elias Mountains can be reproduced from time variations in temperature and precipitation at nearby weather stations (Arendt and others, in press). Two different models were tuned to the mascon time series using correction factors for temperature and precipitation lapse rates, and accounted for 52–60% of the variance in the mascon solution. The ability of both models to reproduce the timing of melt- and accumulation-season events, in the absence of phase adjustments in the model optimization routine, suggests climate variations directly (through surface mass balance) or indirectly (through ice-dynamic cycles linked to seasonal climate events) drive the mass-balance variations in this region.