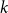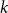1. Introduction
Real business cycle models [Kydland and Prescott, (Reference Kydland and Prescott1982)] state that economic fluctuations or business cycles mainly result from stochastic exogenous shocks. This argument needs to be empirically tested, which is done in this paper.
The National Bureau of Economic Research (NBER) dates the US recessions and expansions, which is regarded as the most authoritative data on the business cycles of the USA in the world. The data consist of two two-valued data recession-expansion time series. One is monthly over from 1854m12 on, while the other is quarterly over from 1854q4 on. A series takes value 1 (0) if the USA is in a recession (an expansion) in a month or a quarter. The Center for Economic and Policy Research (CEPR) dates the Euro Area recessions and expansions from 1970q1 on, generating a similar quarterly two-valued data recession-expansion series. The real business cycle models predict the null hypothesis that these three time series are randomly generated. Applying the runs test developed by Wald and Wolfowitz (Reference Wald and Wolfowitz1940) to them yields that the null hypothesis is rejected even at the 1% significance level, which is surprising.
However, the Wald–Wolfowitz runs test should be extended in order to be applied to these series of recessions and expansions. The reason is that not all the two-valued data series can be considered as a recession-expansion series. According to the definitions of recession adopted by the NBER and the CEPR, a recession lasts several months or at least two quarters. Thus, the runs of a recession-expansion series, consisting of expansions and recessions, are constrained. In contrast, under the Wald–Wolfowitz runs test, the runs are not constrained. Thus, applying the Wald–Wolfowitz runs test may yield a large error.
This paper extends the Wald–Wolfowitz runs test under the assumption that a recession lasts at least two periods (months or quarters) and an expansion lasts at least
![]() $k$
periods with
$k$
periods with
![]() $k\geq 2$
. The test result depends on
$k\geq 2$
. The test result depends on
![]() $k$
. If
$k$
. If
![]() $k$
is sufficiently large, the null hypothesis cannot be rejected. This assumption results from the definitions of recession adopted by the NBER and the CEPR and the features of the three recession-expansion series. For the three series, the shortest recession lasts two months for the US monthly series and two quarters for the US and the Euro Area quarterly series, respectively. Thus, I assume that a recession lasts at least two periods. Because there are more expansion periods than recession periods, I assume that
$k$
is sufficiently large, the null hypothesis cannot be rejected. This assumption results from the definitions of recession adopted by the NBER and the CEPR and the features of the three recession-expansion series. For the three series, the shortest recession lasts two months for the US monthly series and two quarters for the US and the Euro Area quarterly series, respectively. Thus, I assume that a recession lasts at least two periods. Because there are more expansion periods than recession periods, I assume that
![]() $k\geq 2$
. Moreover, the shortest expansion lasts 10 months for the US monthly series, four quarters for the US quarterly series, and nine quarters for the Euro Area series, respectively. Thus, for the three series,
$k\geq 2$
. Moreover, the shortest expansion lasts 10 months for the US monthly series, four quarters for the US quarterly series, and nine quarters for the Euro Area series, respectively. Thus, for the three series,
![]() $k\leq 10$
,
$k\leq 10$
,
![]() $k\leq 4$
, and
$k\leq 4$
, and
![]() $k\leq 9$
, respectively. I show that applying the extended runs test to these three series still leads to reject the null hypothesis at the 1% significance level for any
$k\leq 9$
, respectively. I show that applying the extended runs test to these three series still leads to reject the null hypothesis at the 1% significance level for any
![]() $k$
subject to the constraints.
$k$
subject to the constraints.
My test results are not in favor of the real business cycle theory. The empirical evidence for supporting the theory is that most macro series contain a unit root [e.g., Nelson and Plosser (Reference Nelson and Plosser1982)]. However, randomness test is the premise of unit root test. That is to say, only when a series is randomly generated can one test whether the series contains a unit root. For example, let
![]() $T_{0}$
be an integer. The series which takes value
$T_{0}$
be an integer. The series which takes value
![]() $a+bt$
if
$a+bt$
if
![]() $t\lt T_{0}$
and
$t\lt T_{0}$
and
![]() $c+bt$
if
$c+bt$
if
![]() $t\geq T_{0}$
with
$t\geq T_{0}$
with
![]() $a\neq c$
and
$a\neq c$
and
![]() $b\neq 0$
at period
$b\neq 0$
at period
![]() $t$
is generated in a deterministic way. If the Augmented Dickey–Fuller, Philips–Perron [Phillips and Perron (Reference Phillips and Perron1988)], the Elliott-Rothenberg-Stock [Elliott et al. (Reference Elliott, Rothenberg and Stock1996)] unit root tests are applied, then this series contains a unit root. Moreover, randomness should be tested because randomness is the most fundamental assumption of real business theory. I also apply the Wald–Wolfowitz runs test to the growth rates of real GDP and many other macro indicators with the median being the threshold. The test results also reject their randomness, which are not reported in this paper.
$t$
is generated in a deterministic way. If the Augmented Dickey–Fuller, Philips–Perron [Phillips and Perron (Reference Phillips and Perron1988)], the Elliott-Rothenberg-Stock [Elliott et al. (Reference Elliott, Rothenberg and Stock1996)] unit root tests are applied, then this series contains a unit root. Moreover, randomness should be tested because randomness is the most fundamental assumption of real business theory. I also apply the Wald–Wolfowitz runs test to the growth rates of real GDP and many other macro indicators with the median being the threshold. The test results also reject their randomness, which are not reported in this paper.
This paper is organized as follows. Section 2 presents the null hypothesis. Section 3 proposes the extended runs test. Section 4 tests these three series. And Section 5 concludes. I leave the proofs of all the Lemmas in the Appendix.
2. The null hypothesis
According to the real business cycle theory, economic fluctuations or business cycles result from random exogenous shocks, which predicts that the recessions and expansions occur randomly. The NBER has published two two-valued data series of the US recessions and expansions, one being monthly over from 1854m12 on, while the other being quarterly over from 1854q4 on.Footnote
1
The CEPR has published a quarterly two-valued data series of the Euro Area recessions and expansions from 1970q1 on.Footnote
2
The series takes value 1 at quarter
![]() $t$
if quarter
$t$
if quarter
![]() $t$
is in a recession and 0 otherwise. The real business cycle theory indicates the following hypothesis:
$t$
is in a recession and 0 otherwise. The real business cycle theory indicates the following hypothesis:
H 0 : These three recession-and-expansion series are randomly generated.
H 1 : These series are not randomly generated.
The Wald–Wolfowitz runs test is used to test the null hypothesis and the alternative. I apply it to these three series of the recessions and expansions, and the null hypothesis is rejected even at the 1% significance level.
I argue that applying the Wald–Wolfowitz runs test to these series may yield a large error due to the definitions of recession adopted by the NBER and the CEPR. The NBER stresses that a recession lasts “more than a few months”.Footnote 3 The CEPR stresses that a recession lasts “two or more consecutive quarters”.Footnote 4 In the three recession-expansion series to be tested in this paper, if a “1” follows a “0”, then there must be another “1” which follows the “1”. In other words, the series must not take the values “…0, 1, 0…” but may take the values “…0, 1, 1, 0…”. However, for a series applicable for the Wald–Wolfowitz runs test, the series may take the values “…0, 1, 0…” and “…0, 1, 1, 0…”. In other words, all the series of recessions and expansions are only a part of all the series that are applicable for the Wald–Wolfowitz runs test. Thus, a modification of the Wald–Wolfowitz runs test is required to test the null hypothesis.
The definitions of recession indicate that for a series of recessions and expansions, there is a threshold recession length (TRL) and a threshold expansion length (TEL). The TRL is the minimal length a recession may last and the TEL is the minimal length an expansion may last. The definitions also indicate that the TRL is greater than or equal to 2. Moreover, for each of these three recession-expansion series, there is a recession which just lasts 2 quarters or 2 months. Thus,
![]() $\text{TRL}=2$
. However, neither the NBER nor the CEPR defines expansion. Considering that the USA and the Euro Area stay in expansion longer than in recession, I assume that
$\text{TRL}=2$
. However, neither the NBER nor the CEPR defines expansion. Considering that the USA and the Euro Area stay in expansion longer than in recession, I assume that
![]() $\text{TEL}\geq 2$
and TEL is a parameter.
$\text{TEL}\geq 2$
and TEL is a parameter.
Assumption 1:
![]() $\mathrm{TRL}=2$
and
$\mathrm{TRL}=2$
and
![]() $\mathrm{TEL}=k$
with
$\mathrm{TEL}=k$
with
![]() $k\geq 2$
.
$k\geq 2$
.
However, the TEL must have an upper bound. If the TEL is too large, these three series may not satisfy Assumption 1. Thus, the least upper bound is equal to the length of the shortest expansion of a series. For the quarterly series of the Euro Area recessions and expansions,
![]() $\mathrm{TEL}\leq 9$
; for the quarterly series of the US recessions and expansions,
$\mathrm{TEL}\leq 9$
; for the quarterly series of the US recessions and expansions,
![]() $\mathrm{TEL}\leq 4$
, and for the monthly series of the US recessions and expansions,
$\mathrm{TEL}\leq 4$
, and for the monthly series of the US recessions and expansions,
![]() $\mathrm{TEL}\leq 10$
.
$\mathrm{TEL}\leq 10$
.
3. The extended runs test
Under Assumption 1, for an observed recession-and-expansion series, the recession with which the series begins or ends may last one period or more because the recession may be just a part of a complete recession. Similarly, the expansion with which the series begins or ends may last one or more periods.
For an observed series, denote by
![]() $n_{0}$
and
$n_{0}$
and
![]() $n_{1}$
the number of expansion periods (quarters or months) and that of recession periods, respectively, with
$n_{1}$
the number of expansion periods (quarters or months) and that of recession periods, respectively, with
![]() $n_{0}\gt k$
and
$n_{0}\gt k$
and
![]() $n_{1}\gt 2$
. Just as in the Wald–Wolfowitz runs test, a run is defined as a recession or an expansion. Denote the number of runs (i.e., the total number of expansions and recessions) by
$n_{1}\gt 2$
. Just as in the Wald–Wolfowitz runs test, a run is defined as a recession or an expansion. Denote the number of runs (i.e., the total number of expansions and recessions) by
![]() $r$
. Then
$r$
. Then
![]() $r\geq 2$
. Under the null hypothesis,
$r\geq 2$
. Under the null hypothesis,
![]() $r$
is a random variable. Denote by
$r$
is a random variable. Denote by
![]() $M$
the maximum that
$M$
the maximum that
![]() $r$
may take. Then
$r$
may take. Then
![]() $2\leq r\leq M$
.
$2\leq r\leq M$
.
For convenience, define
![]() $[x]$
as the maximal integer less than or equal to
$[x]$
as the maximal integer less than or equal to
![]() $x$
.
$x$
.
Lemma 1: Under Assumption 1,
 \begin{equation}M=\begin{cases} n_{1}+1\quad\text{if}\quad n_{0}\geq k\left[\frac{n_{1}-1}{2}\right]+2-n_{0}\mathrm{mod}2\\[5pt] \mathrm{Max}\left\{2\left[\frac{n_{0}-2}{k}\right]+3,2\left[\frac{n_{0}-1}{k}\right]+2\right\}\quad\text{otherwise} \end{cases}\end{equation}
\begin{equation}M=\begin{cases} n_{1}+1\quad\text{if}\quad n_{0}\geq k\left[\frac{n_{1}-1}{2}\right]+2-n_{0}\mathrm{mod}2\\[5pt] \mathrm{Max}\left\{2\left[\frac{n_{0}-2}{k}\right]+3,2\left[\frac{n_{0}-1}{k}\right]+2\right\}\quad\text{otherwise} \end{cases}\end{equation}
Here
![]() $n_{0}\mathrm{mod2}$
is equal to 1 if
$n_{0}\mathrm{mod2}$
is equal to 1 if
![]() $n_{0}$
is odd and 0 if
$n_{0}$
is odd and 0 if
![]() $n_{0}$
is even.
$n_{0}$
is even.
I consider two cases that
![]() $n_{1}$
is even and that
$n_{1}$
is even and that
![]() $n_{1}$
is odd, respectively. In each case, expansions and recessions alternate in a series and the maximal difference between the number of recessions and that of expansions is equal to 1. I consider three subcases: (1) the series begins with a recession and ends with a recession; (2) the series “begins with a recession and ends with an expansion” or “begins with an expansion and ends with a recession”; and (3) the series begins with an expansion and ends with an expansion. Intuitively, given
$n_{1}$
is odd, respectively. In each case, expansions and recessions alternate in a series and the maximal difference between the number of recessions and that of expansions is equal to 1. I consider three subcases: (1) the series begins with a recession and ends with a recession; (2) the series “begins with a recession and ends with an expansion” or “begins with an expansion and ends with a recession”; and (3) the series begins with an expansion and ends with an expansion. Intuitively, given
![]() $n_{1}$
, if
$n_{1}$
, if
![]() $n_{0}$
is sufficiently large,
$n_{0}$
is sufficiently large,
![]() $M$
is determined by
$M$
is determined by
![]() $n_{1}$
; if
$n_{1}$
; if
![]() $n_{0}$
is small,
$n_{0}$
is small,
![]() $M$
is determined by
$M$
is determined by
![]() $n_{0}$
. Thus, Lemma 1 holds.
$n_{0}$
. Thus, Lemma 1 holds.
Lemma 2:
Under Assumption 1, let
![]() $R=[\frac{r}{2}]\geq 1$
. Then the number of the series of recessions and expansions with
$R=[\frac{r}{2}]\geq 1$
. Then the number of the series of recessions and expansions with
![]() $r$
runs is equal to
$r$
runs is equal to
 \begin{equation*} N\left(r\right)=\begin{cases} 2C_{n_{1}-R}^{R-1}C_{n_{0}-\left(R-1\right)\left(k-1\right)-1}^{R-1}\\[5pt] C_{n_{1}-R}^{R}C_{n_{0}-R\left(k-1\right)-1}^{R-1}+C_{n_{1}-R-1}^{R-1}C_{n_{0}-\left(R-1\right)\left(k-1\right)-1}^{R} \end{cases}\, \mathrm{if}\, \begin{array}{c} r=2R\\[5pt] r=2R+1 \end{array} \end{equation*}
\begin{equation*} N\left(r\right)=\begin{cases} 2C_{n_{1}-R}^{R-1}C_{n_{0}-\left(R-1\right)\left(k-1\right)-1}^{R-1}\\[5pt] C_{n_{1}-R}^{R}C_{n_{0}-R\left(k-1\right)-1}^{R-1}+C_{n_{1}-R-1}^{R-1}C_{n_{0}-\left(R-1\right)\left(k-1\right)-1}^{R} \end{cases}\, \mathrm{if}\, \begin{array}{c} r=2R\\[5pt] r=2R+1 \end{array} \end{equation*}
If
![]() $r=2R$
, the number of recessions and that of expansions are the same and equal to
$r=2R$
, the number of recessions and that of expansions are the same and equal to
![]() $R$
and the series “begins with a recession and ends with an expansion” or “begins with an expansion and ends with a recession.” The numbers of the qualified series in the two cases are the same. Moreover, in each case, one recession (expansion) may last any periods and each of the other
$R$
and the series “begins with a recession and ends with an expansion” or “begins with an expansion and ends with a recession.” The numbers of the qualified series in the two cases are the same. Moreover, in each case, one recession (expansion) may last any periods and each of the other
![]() $R-1$
recessions (expansions) lasts two (
$R-1$
recessions (expansions) lasts two (
![]() $k$
) periods at least, which yields
$k$
) periods at least, which yields
![]() $C_{n_{1}-R}^{R-1}$
(
$C_{n_{1}-R}^{R-1}$
(
![]() $C_{n_{0}-(R-1)(k-1)-1}^{R-1}$
) combinations of recessions (expansions).
$C_{n_{0}-(R-1)(k-1)-1}^{R-1}$
) combinations of recessions (expansions).
If
![]() $r=2R+1$
, there are two cases. (1) The series begins and ends with recessions, which indicates that there are
$r=2R+1$
, there are two cases. (1) The series begins and ends with recessions, which indicates that there are
![]() $R+1$
recessions and
$R+1$
recessions and
![]() $R$
expansions. Thus, there are
$R$
expansions. Thus, there are
![]() $C_{n_{1}-R}^{R}$
combinations of recessions and
$C_{n_{1}-R}^{R}$
combinations of recessions and
![]() $C_{n_{0}-R(k-1)-1}^{R-1}$
combinations of expansions. (2) The series begins and ends with expansions, which indicates that there are
$C_{n_{0}-R(k-1)-1}^{R-1}$
combinations of expansions. (2) The series begins and ends with expansions, which indicates that there are
![]() $R$
recessions and
$R$
recessions and
![]() $R+1$
expansions. Thus, there are
$R+1$
expansions. Thus, there are
![]() $C_{n_{1}-R-1}^{R-1}$
combinations of recessions and
$C_{n_{1}-R-1}^{R-1}$
combinations of recessions and
![]() $C_{n_{0}-(R-1)(k-1)-1}^{R}$
combinations of expansions.
$C_{n_{0}-(R-1)(k-1)-1}^{R}$
combinations of expansions.
My runs test is similar to the Wald–Wolfowitz runs test. The difference is in that the qualified series under my runs test consist of a subset of the series under the Wald–Wolfowitz runs test. All the qualified series share the same number of recession periods and the same number of expansion periods but differ in their orders. Thus, the following Proposition 3 can be directly derived from Lemmas 1 and 2 and we omit its proof.
Proposition 3:
Under Assumption 1, if all the qualified recession-and-expansion series occur at the same probability, the probability at which the number of runs is equal to
![]() $r$
equals
$r$
equals
![]() $P\left(r\right)=\frac{N(r)}{\sum _{i=2}^{M}N(i)}$
with
$P\left(r\right)=\frac{N(r)}{\sum _{i=2}^{M}N(i)}$
with
![]() $2\leq r\leq M$
.
$2\leq r\leq M$
.
Define
![]() $E(r)=\sum _{r=2}^{M}r*P(r)$
and
$E(r)=\sum _{r=2}^{M}r*P(r)$
and
![]() $D(r)=\sqrt{\sum _{i=2}^{M}(i-E(r))^{2}*P(i)}$
. That is to say,
$D(r)=\sqrt{\sum _{i=2}^{M}(i-E(r))^{2}*P(i)}$
. That is to say,
![]() $E(r)$
is the mean of the number of runs and
$E(r)$
is the mean of the number of runs and
![]() $D(r)$
is the standard deviation of the number of runs.
$D(r)$
is the standard deviation of the number of runs.
For the large sample, the Wald–Wolfowitz runs statistic approximately obeys a normal distribution. The numerical simulation in following three figures reveals that my runs statistic seems to obey a normal distribution, too. This approximation helps to report the test results. However, for the Euro Area quarterly recession-expansion series, the following Figure 3 indicates that the sample size is small so that using the approximation may lead to a large error. Moreover, it is difficult to prove whether my runs statistic approximately obeys a normal distribution. Thus, I do not intend to prove the result.
Let
![]() $\overline{r}$
be the observed number of runs. Define
$\overline{r}$
be the observed number of runs. Define
![]() $F(\overline{r})=\sum _{i=2}^{\overline{r}}P(i)$
. That is to say,
$F(\overline{r})=\sum _{i=2}^{\overline{r}}P(i)$
. That is to say,
![]() $F(\overline{r})$
is the probability at which the number of runs is less than or equal to the observed number of runs. If
$F(\overline{r})$
is the probability at which the number of runs is less than or equal to the observed number of runs. If
![]() $F(\overline{r})$
is less than the significance level, the null hypothesis should be rejected.
$F(\overline{r})$
is less than the significance level, the null hypothesis should be rejected.
4. Test results
In this section, I state that applying my runs test to these three series yields that the null hypothesis is rejected for any TEL even at the 1% significance level. I also divide each of the two US series into two subseries, one before World War II and the other after it, and apply the runs test to them. The null hypothesis is still rejected at the 1% significance level.
Table 1. Descriptive statistics

Table 2. Test results

Probability: the probability which the number of runs is less than or equal to the observed number of runs.
Maximum: the maximum that the number of runs may take.
Mean: the means of the number of runs.
Deviation: the standard deviation of the number of runs.
Table 1 reports the descriptive statistics of the three series, including the number of recession periods, the number of recessions, the number of expansion periods, the number of expansions, the observed number of runs, the longest and the shortest expansions, and the longest and the shortest recessions. For the USA, the range of the lengths of expansion is from 10 months to 120 months or from 4 quarters to 40 quarters, while the range of the lengths of recessions is from 2 months to 65 months or from 2 quarters to 22 quarters. For the Euro Area, the range of the lengths of expansion is from 9 quarters to 58 quarters, while the range of the lengths of recessions is from 2 quarter to 10 quarters. These wide ranges of variances, large numbers of expansion periods, and large numbers of recession periods may lead to a large average number of runs.
I apply the extended runs test to these three series. Table 2 reports the test results, including the value of
![]() $M$
, the probability
$M$
, the probability
![]() $F(\overline{r})$
, the mean
$F(\overline{r})$
, the mean
![]() $E(r)$
, and the standard deviations
$E(r)$
, and the standard deviations
![]() $D(r)$
, in the case that the TEL is greater than 1 and less than or equal to the length of the shortest expansion. It indicates that
$D(r)$
, in the case that the TEL is greater than 1 and less than or equal to the length of the shortest expansion. It indicates that
![]() $F(\overline{r})$
is very small for any TEL and that as the TEL increases, both the mean and the standard deviation decrease.
$F(\overline{r})$
is very small for any TEL and that as the TEL increases, both the mean and the standard deviation decrease.
For the monthly series of the USA over 1854m12–2022m7, Figure 1 illustrates the density distributions
![]() $P(r)$
and their normal-distribution counterparts, defined as
$P(r)$
and their normal-distribution counterparts, defined as
![]() $N(r,E(r), D(r)^{2})$
over the intervals
$N(r,E(r), D(r)^{2})$
over the intervals
![]() $[E(r)-4D(r),E(r)+4D(r)]$
in the case that
$[E(r)-4D(r),E(r)+4D(r)]$
in the case that
![]() $2\leq \text{TEL}\leq 10$
. The values of both
$2\leq \text{TEL}\leq 10$
. The values of both
![]() $P(r)$
and
$P(r)$
and
![]() $N(r,E(r), D(r)^{2})$
over the periods out of the intervals are close to 0. Figure 1 indicates that for large samples, the density distributions are well approximated by their normal-distribution counterparts. If the null hypothesis is true, the observed number of the runs
$N(r,E(r), D(r)^{2})$
over the periods out of the intervals are close to 0. Figure 1 indicates that for large samples, the density distributions are well approximated by their normal-distribution counterparts. If the null hypothesis is true, the observed number of the runs
![]() $\overline{r}$
, which is equal to 70, should be close to the mean
$\overline{r}$
, which is equal to 70, should be close to the mean
![]() $E(r)$
. However,
$E(r)$
. However,
![]() $E(r)$
is far larger than
$E(r)$
is far larger than
![]() $\overline{r}$
for any TEL. As a result, the probability
$\overline{r}$
for any TEL. As a result, the probability
![]() $F(\overline{r})$
is so small that the null hypothesis is rejected at the 1% significance level.
$F(\overline{r})$
is so small that the null hypothesis is rejected at the 1% significance level.
For the US quarterly series over 1854q4–2022q2, Figure 2 illustrates the density distributions
![]() $P(r)$
and their normal-distribution counterparts
$P(r)$
and their normal-distribution counterparts
![]() $N(r,E(r), D(r)^{2})$
over the intervals
$N(r,E(r), D(r)^{2})$
over the intervals
![]() $[E(r)-4D(r),E(r)+4D(r)]$
in the case that
$[E(r)-4D(r),E(r)+4D(r)]$
in the case that
![]() $2\leq \text{TEL}\leq 4$
. Their values over the periods out of the intervals are close to 0. It also indicates that for large samples, the density distributions are well approximated by their normal-distribution counterparts. Similarly, the null hypothesis is rejected at the 1% significance level.
$2\leq \text{TEL}\leq 4$
. Their values over the periods out of the intervals are close to 0. It also indicates that for large samples, the density distributions are well approximated by their normal-distribution counterparts. Similarly, the null hypothesis is rejected at the 1% significance level.
For the Euro Area quarterly series over 1970q1–2022q2, the maximal possible number of runs is identical to 32. Figure 3 illustrates the density distributions
![]() $P(r)$
and their normal-distribution counterparts
$P(r)$
and their normal-distribution counterparts
![]() $N(r,E(r), D(r)^{2})$
over the intervals
$N(r,E(r), D(r)^{2})$
over the intervals
![]() $[E(r)-4D(r),32]$
in the case that
$[E(r)-4D(r),32]$
in the case that
![]() $2\leq \text{TEL}\leq 9$
. Their values over the period out of the intervals are close to 0. Because there are only 210 samples, the maximal difference between
$2\leq \text{TEL}\leq 9$
. Their values over the period out of the intervals are close to 0. Because there are only 210 samples, the maximal difference between
![]() $P(r)$
and
$P(r)$
and
![]() $N(r,E(r), D(r)^{2})$
is large. Despite this, if the null hypothesis is true, the observed number of the runs should still be close to the mean
$N(r,E(r), D(r)^{2})$
is large. Despite this, if the null hypothesis is true, the observed number of the runs should still be close to the mean
![]() $E(r)$
. The probability
$E(r)$
. The probability
![]() $F(\overline{r})$
is so small that the null hypothesis is rejected at the 1% significance level. For comparison, I also apply the test to the US quarterly series over 1970q1–2022q2 and the null hypothesis is rejected at the 1% significance level. I omit reporting the test result.
$F(\overline{r})$
is so small that the null hypothesis is rejected at the 1% significance level. For comparison, I also apply the test to the US quarterly series over 1970q1–2022q2 and the null hypothesis is rejected at the 1% significance level. I omit reporting the test result.

Figure 1. The distribution based on the US monthly series over 1854m12–2012m7 (line) and its normal-distribution counterpart (point).

Figure 2. The distribution based on the US quarterly series over 1854q4–2012q2 (line) and its normal-distribution counterpart (point).

Figure 3. The distribution based on the Euro area quarterly series over 1970q1–2012q2 (line) and its normal-distribution counterpart (point).
The Great Depression is a watershed. Before that, the US government had basically adopted a laissez faire policy when facing business cycles. And since then, various macroeconomic policies have been used to stabilize the economy. One question arises whether macro policies have changed the randomness of the business cycles. I divide the US monthly data and quarterly data into two parts, respectively. No matter how the series are divided with the cutoff point in 1929–1947, the null hypothesis is rejected at the 1% significance level for any TEL. Thus, whether macro policies are adopted does not change the non-randomness of the series.
5. Conclusion
In this paper, I extend the Wald–Wolfowitz runs test under the assumption that a recession lasts for two periods at least and an expansion lasts for
![]() $k$
periods at least with
$k$
periods at least with
![]() $k\geq 2$
. I apply the extended runs test to the three recession-expansion series generated by the NBER and the CEPR. The test results reject the null hypothesis that the series are randomly generated at the 1% significance level for any TEL. The test results are not in favor of the argument made by the real business cycle theory that business cycles mainly result from random exogenous shocks.
$k\geq 2$
. I apply the extended runs test to the three recession-expansion series generated by the NBER and the CEPR. The test results reject the null hypothesis that the series are randomly generated at the 1% significance level for any TEL. The test results are not in favor of the argument made by the real business cycle theory that business cycles mainly result from random exogenous shocks.
Appendix
Proof of Lemma 1: Let
![]() $m=[\frac{n_{1}}{2}]$
. Note that recessions and expansions alternate. The maximal difference between the number of recessions and that of the expansions is equal to 1. I consider two cases.
$m=[\frac{n_{1}}{2}]$
. Note that recessions and expansions alternate. The maximal difference between the number of recessions and that of the expansions is equal to 1. I consider two cases.
Case 1:
![]() $n_{1}$
is even. Then
$n_{1}$
is even. Then
![]() $k\left[\frac{n_{1}-1}{2}\right]+2-n_{1}\text{mod2}=k\left(m-1\right)+2$
.
$k\left[\frac{n_{1}-1}{2}\right]+2-n_{1}\text{mod2}=k\left(m-1\right)+2$
.
(i) I affirm that if and only if
![]() $n_{0}\geq k(m-1)+2$
,
$n_{0}\geq k(m-1)+2$
,
![]() $M=n_{1}+1=2m+1$
.
$M=n_{1}+1=2m+1$
.
If
![]() $M=2\mathrm{m}+1$
, then the series either “begins and ends with recessions” or “begins and ends with expansions.” If the series begins and ends with recessions, there are at most
$M=2\mathrm{m}+1$
, then the series either “begins and ends with recessions” or “begins and ends with expansions.” If the series begins and ends with recessions, there are at most
![]() $m+1$
recessions (i.e., the first and the last recessions last one period, respectively, and each of the other
$m+1$
recessions (i.e., the first and the last recessions last one period, respectively, and each of the other
![]() $m-1$
recessions last two periods) and
$m-1$
recessions last two periods) and
![]() $m$
expansions, which need at least
$m$
expansions, which need at least
![]() $km$
expansion periods. If the series begins and ends with expansions, there are at most
$km$
expansion periods. If the series begins and ends with expansions, there are at most
![]() $m$
recessions (i.e., each recession lasts two periods) and
$m$
recessions (i.e., each recession lasts two periods) and
![]() $m+1$
expansions, which need at least
$m+1$
expansions, which need at least
![]() $k(m-1)+2$
expansion periods (i.e., the first and the last expansions last one period, respectively, and each of the other
$k(m-1)+2$
expansion periods (i.e., the first and the last expansions last one period, respectively, and each of the other
![]() $m-1$
expansions lasts
$m-1$
expansions lasts
![]() $k$
periods at least). Note that
$k$
periods at least). Note that
![]() $km\geq k(m-1)+2$
. Thus,
$km\geq k(m-1)+2$
. Thus,
![]() $n_{0}\geq k(m-1)+2$
.
$n_{0}\geq k(m-1)+2$
.
If
![]() $n_{0}\geq k(m-1)+2$
, these expansion periods and recession periods can form the following series, which has
$n_{0}\geq k(m-1)+2$
, these expansion periods and recession periods can form the following series, which has
![]() $n_{1}+1$
runs. The series begins and ends with a one-period expansion, the other expansion periods form its
$n_{1}+1$
runs. The series begins and ends with a one-period expansion, the other expansion periods form its
![]() $m-1$
expansions with each lasting at least
$m-1$
expansions with each lasting at least
![]() $k$
expansion periods, and
$k$
expansion periods, and
![]() $2m$
recession periods form its
$2m$
recession periods form its
![]() $m$
recessions. Thus,
$m$
recessions. Thus,
![]() $M\geq n_{1}+1$
. We argue that
$M\geq n_{1}+1$
. We argue that
![]() $M=n_{1}+1$
. Otherwise
$M=n_{1}+1$
. Otherwise
![]() $M\geq n_{1}+2=2m+2$
. Thus, there are at least
$M\geq n_{1}+2=2m+2$
. Thus, there are at least
![]() $m+1$
recessions and
$m+1$
recessions and
![]() $m+1$
expansions. However, that
$m+1$
expansions. However, that
![]() $2m$
recession periods form
$2m$
recession periods form
![]() $m+1$
recessions indicates that the series must begin and end with recessions and it is impossible that there are
$m+1$
recessions indicates that the series must begin and end with recessions and it is impossible that there are
![]() $m+1$
expansions. This is a contradiction. Thus,
$m+1$
expansions. This is a contradiction. Thus,
![]() $M=n_{1}+1$
.
$M=n_{1}+1$
.
(ii) I affirm that if
![]() $n_{0}\leq k(m-1)+1$
,
$n_{0}\leq k(m-1)+1$
,
![]() $M=\text{Max}\{2\left[\frac{n_{0}-2}{k}\right]+3,2\left[\frac{n_{0}-1}{k}\right]+2\}$
. In such a case,
$M=\text{Max}\{2\left[\frac{n_{0}-2}{k}\right]+3,2\left[\frac{n_{0}-1}{k}\right]+2\}$
. In such a case,
![]() $2\left[\frac{n_{0}-2}{k}\right]+3\leq 2\left[\frac{k\left(m-1\right)+1-2}{k}\right]+3=2m-1=n_{1}-1$
and
$2\left[\frac{n_{0}-2}{k}\right]+3\leq 2\left[\frac{k\left(m-1\right)+1-2}{k}\right]+3=2m-1=n_{1}-1$
and
![]() $2\left[\frac{n_{0}-1}{k}\right]+2\leq 2\left[\frac{k\left(m-1\right)+1-1}{k}\right]+2=2m=n_{1}$
.
$2\left[\frac{n_{0}-1}{k}\right]+2\leq 2\left[\frac{k\left(m-1\right)+1-1}{k}\right]+2=2m=n_{1}$
.
If the series begins and ends with expansions, then there are at most
![]() $\left[\frac{n_{0}-2}{k}\right]+2$
expansions and
$\left[\frac{n_{0}-2}{k}\right]+2$
expansions and
![]() $\left[\frac{n_{0}-2}{k}\right]+1$
recessions. Note that
$\left[\frac{n_{0}-2}{k}\right]+1$
recessions. Note that
![]() $\left[\frac{n_{1}-2}{k}\right]+1\leq \left[\frac{k\left(m-1\right)-1}{k}\right]+1\leq m-1$
and
$\left[\frac{n_{1}-2}{k}\right]+1\leq \left[\frac{k\left(m-1\right)-1}{k}\right]+1\leq m-1$
and
![]() $2m$
recession periods can form
$2m$
recession periods can form
![]() $\left[\frac{n_{1}-2}{k}\right]+1$
recessions. Moreover, if both the first expansion and the last expansion last one period, then
$\left[\frac{n_{1}-2}{k}\right]+1$
recessions. Moreover, if both the first expansion and the last expansion last one period, then
![]() $n_{0}$
expansion periods can form
$n_{0}$
expansion periods can form
![]() $\left[\frac{n_{0}-2}{k}\right]+2$
expansions. Thus, there are at most
$\left[\frac{n_{0}-2}{k}\right]+2$
expansions. Thus, there are at most
![]() $2\left[\frac{n_{0}-2}{k}\right]+3$
runs and
$2\left[\frac{n_{0}-2}{k}\right]+3$
runs and
![]() $M$
may be equal to
$M$
may be equal to
![]() $2\left[\frac{n_{0}-2}{k}\right]+3$
.
$2\left[\frac{n_{0}-2}{k}\right]+3$
.
If the series begins and ends with recessions, then there are at most
![]() $\left[\frac{n_{0}}{k}\right]$
expansions and
$\left[\frac{n_{0}}{k}\right]$
expansions and
![]() $\left[\frac{n_{0}}{k}\right]+1$
recessions. Note that
$\left[\frac{n_{0}}{k}\right]+1$
recessions. Note that
![]() $\left[\frac{n_{0}}{k}\right]+1\leq \left[\frac{k\left(m-1\right)+1}{k}\right]+1=m$
and
$\left[\frac{n_{0}}{k}\right]+1\leq \left[\frac{k\left(m-1\right)+1}{k}\right]+1=m$
and
![]() $2m$
recession periods can form
$2m$
recession periods can form
![]() $\left[\frac{n_{0}}{k}\right]+1$
recessions. Thus, there are at most
$\left[\frac{n_{0}}{k}\right]+1$
recessions. Thus, there are at most
![]() $2\left[\frac{n_{0}}{k}\right]+1$
runs. However,
$2\left[\frac{n_{0}}{k}\right]+1$
runs. However,
![]() $2\left[\frac{n_{0}-2}{k}\right]+3-\left(2\left[\frac{n_{0}}{k}\right]+1\right)=2(\left[\frac{n_{0}+k-2}{k}\right]-\left[\frac{n_{0}}{k}\right])\geq 0$
. Thus,
$2\left[\frac{n_{0}-2}{k}\right]+3-\left(2\left[\frac{n_{0}}{k}\right]+1\right)=2(\left[\frac{n_{0}+k-2}{k}\right]-\left[\frac{n_{0}}{k}\right])\geq 0$
. Thus,
![]() $M$
does not necessarily take value
$M$
does not necessarily take value
![]() $2\left[\frac{n_{0}}{k}\right]+1$
.
$2\left[\frac{n_{0}}{k}\right]+1$
.
If the series “begins with a recession and ends with an expansion” or “begins with an expansion and ends with a recession,” then the number of runs is even and there are at most
![]() $\left[\frac{n_{0}-1}{k}\right]+1$
expansions and
$\left[\frac{n_{0}-1}{k}\right]+1$
expansions and
![]() $\left[\frac{n_{0}-1}{k}\right]+1$
recessions. Note that
$\left[\frac{n_{0}-1}{k}\right]+1$
recessions. Note that
![]() $\left[\frac{n_{0}-1}{k}\right]+1\leq \left[\frac{k\left(m-1\right)}{k}\right]+1\leq m$
and
$\left[\frac{n_{0}-1}{k}\right]+1\leq \left[\frac{k\left(m-1\right)}{k}\right]+1\leq m$
and
![]() $2m$
recession periods can form
$2m$
recession periods can form
![]() $\left[\frac{n_{0}-1}{k}\right]+1$
recessions. Moreover, if the expansion with which the series begins or ends lasts one period, then
$\left[\frac{n_{0}-1}{k}\right]+1$
recessions. Moreover, if the expansion with which the series begins or ends lasts one period, then
![]() $n_{0}$
expansion periods can form
$n_{0}$
expansion periods can form
![]() $\left[\frac{n_{0}-1}{k}\right]+1$
expansions. Thus, there are
$\left[\frac{n_{0}-1}{k}\right]+1$
expansions. Thus, there are
![]() $2\left[\frac{n_{1}-1}{k}\right]+2$
and
$2\left[\frac{n_{1}-1}{k}\right]+2$
and
![]() $M$
may be equal to
$M$
may be equal to
![]() $2\left[\frac{n_{1}-1}{k}\right]+2$
.
$2\left[\frac{n_{1}-1}{k}\right]+2$
.
Note that
![]() $2\left[\frac{n_{1}-2}{k}\right]+3$
is odd,
$2\left[\frac{n_{1}-2}{k}\right]+3$
is odd,
![]() $2\left[\frac{n_{1}-1}{k}\right]+2$
is even, and one number is not always greater than the other. Thus,
$2\left[\frac{n_{1}-1}{k}\right]+2$
is even, and one number is not always greater than the other. Thus,
![]() $M=\text{Max}\{2\left[\frac{n_{1}-2}{k}\right]+3,2\left[\frac{n_{1}-1}{k}\right]+2\}$
and my affirmation holds.
$M=\text{Max}\{2\left[\frac{n_{1}-2}{k}\right]+3,2\left[\frac{n_{1}-1}{k}\right]+2\}$
and my affirmation holds.
Case 2:
![]() $n_{1}$
is odd. Then
$n_{1}$
is odd. Then
![]() $k\left[\frac{n_{1}-1}{2}\right]+2-n_{1}\text{mod2}=km+1$
.
$k\left[\frac{n_{1}-1}{2}\right]+2-n_{1}\text{mod2}=km+1$
.
(iii) I affirm that if and only if
![]() $n_{0}\geq km+1$
,
$n_{0}\geq km+1$
,
![]() $M=n_{1}+1=2m+2$
.
$M=n_{1}+1=2m+2$
.
If
![]() $M=n_{0}+1=2m+2$
, then there are
$M=n_{0}+1=2m+2$
, then there are
![]() $m+1$
recessions and
$m+1$
recessions and
![]() $m+1$
expansions and the series “begins with a recession and ends with an expansion” or “begins with an expansion and ends with a recession.” Note that
$m+1$
expansions and the series “begins with a recession and ends with an expansion” or “begins with an expansion and ends with a recession.” Note that
![]() $2m+1$
recession periods can form
$2m+1$
recession periods can form
![]() $m+1$
recessions with one recession lasting one period.
$m+1$
recessions with one recession lasting one period.
![]() $m+1$
expansions need at least
$m+1$
expansions need at least
![]() $km+1$
expansion periods. Thus,
$km+1$
expansion periods. Thus,
![]() $n_{0}\geq km+1$
.
$n_{0}\geq km+1$
.
If
![]() $n_{0}\geq km+1$
, the series
$n_{0}\geq km+1$
, the series
![]() $1,\overset{{k}}{\overbrace{0,\ldots 0}},1,1,\overset{{k}}{\overbrace{0,..0,}}1,1,0,\ldots,1,\overset{{k}}{\overbrace{0,..0,}}1,1,\overset{n_{0}-km}{\overbrace{0,..,0}}$
contains
$1,\overset{{k}}{\overbrace{0,\ldots 0}},1,1,\overset{{k}}{\overbrace{0,..0,}}1,1,0,\ldots,1,\overset{{k}}{\overbrace{0,..0,}}1,1,\overset{n_{0}-km}{\overbrace{0,..,0}}$
contains
![]() $n_{1}+1$
runs. Thus,
$n_{1}+1$
runs. Thus,
![]() $M\geq n_{1}+1$
. We argue that
$M\geq n_{1}+1$
. We argue that
![]() $M=n_{1}+1$
. Otherwise,
$M=n_{1}+1$
. Otherwise,
![]() $M\geq n_{1}+2=2m+3$
.
$M\geq n_{1}+2=2m+3$
.
![]() $2m+1$
recession periods form at most
$2m+1$
recession periods form at most
![]() $m+1$
recessions. Thus, at least
$m+1$
recessions. Thus, at least
![]() $m+2$
expansions are required, which indicates that each of the
$m+2$
expansions are required, which indicates that each of the
![]() $m+1$
recessions lasts 2 periods or more or
$m+1$
recessions lasts 2 periods or more or
![]() $2m+2$
recession periods are required. This is a contradiction. Therefore,
$2m+2$
recession periods are required. This is a contradiction. Therefore,
![]() $M=n_{1}+1$
.
$M=n_{1}+1$
.
(iv) I affirm that if
![]() $n_{1}\leq km$
,
$n_{1}\leq km$
,
![]() $M=\text{Max}\{2\left[\frac{n_{0}-2}{k}\right]+3,2\left[\frac{n_{0}-1}{k}\right]+2\}$
. The proof of this affirmation is similar to that of affirmation (ii) and I omit its proof. In the proof, one needs to use the following inequalities:
$M=\text{Max}\{2\left[\frac{n_{0}-2}{k}\right]+3,2\left[\frac{n_{0}-1}{k}\right]+2\}$
. The proof of this affirmation is similar to that of affirmation (ii) and I omit its proof. In the proof, one needs to use the following inequalities:
![]() $\left[\frac{n_{0}-2}{k}\right]+1\leq \left[\frac{km-2}{k}\right]+1\leq m$
,
$\left[\frac{n_{0}-2}{k}\right]+1\leq \left[\frac{km-2}{k}\right]+1\leq m$
,
![]() $\left[\frac{n_{0}}{k}\right]+1\leq \left[\frac{km}{k}\right]+1\leq m+1$
, and
$\left[\frac{n_{0}}{k}\right]+1\leq \left[\frac{km}{k}\right]+1\leq m+1$
, and
![]() $\left[\frac{n_{0}-1}{k}\right]+1\leq \left[\frac{km-1}{k}\right]+1\leq m$
.
$\left[\frac{n_{0}-1}{k}\right]+1\leq \left[\frac{km-1}{k}\right]+1\leq m$
.
Proof of Lemma 2: I consider two cases.
Case 1:
![]() $r$
is even. Then there are
$r$
is even. Then there are
![]() $R$
recessions and
$R$
recessions and
![]() $R$
expansions. Moreover, the series either “begins with a recession and ends with an expansion” or “begins with an expansion and ends with a recession.”
$R$
expansions. Moreover, the series either “begins with a recession and ends with an expansion” or “begins with an expansion and ends with a recession.”
(i) The series begins with a recession and ends with an expansion. For any qualified combination of recessions, the first recession may last any periods, while each of the other
![]() $R-1$
recessions lasts at least 2 periods. I first take out
$R-1$
recessions lasts at least 2 periods. I first take out
![]() $R-1$
recession periods and then divide the left
$R-1$
recession periods and then divide the left
![]() $n_{1}-R+1$
recession periods into
$n_{1}-R+1$
recession periods into
![]() $R$
groups, yielding
$R$
groups, yielding
![]() $C_{n_{1}-R}^{R-1}$
divisions in total. I affirm that there exists a one-to-one correspondence between the divisions and the qualified combinations of recessions, which indicates that there are
$C_{n_{1}-R}^{R-1}$
divisions in total. I affirm that there exists a one-to-one correspondence between the divisions and the qualified combinations of recessions, which indicates that there are
![]() $C_{n_{1}-R}^{R-1}$
qualified combinations of recessions. Given a division, the first group acts as a recession, and adding a recession period to each of the last
$C_{n_{1}-R}^{R-1}$
qualified combinations of recessions. Given a division, the first group acts as a recession, and adding a recession period to each of the last
![]() $R-1$
group leads to
$R-1$
group leads to
![]() $R-1$
recessions, each of which lasts 2 periods at least. These recessions form a qualified combination of recessions. Conversely, for any qualified combination of recessions, taking out a recession period from each of the last
$R-1$
recessions, each of which lasts 2 periods at least. These recessions form a qualified combination of recessions. Conversely, for any qualified combination of recessions, taking out a recession period from each of the last
![]() $R-1$
recessions yields such a division. Thus, my affirmation holds. For any qualified combination of expansions, each of the first
$R-1$
recessions yields such a division. Thus, my affirmation holds. For any qualified combination of expansions, each of the first
![]() $R-1$
expansions lasts at least
$R-1$
expansions lasts at least
![]() $k$
periods, while the last expansion may last any periods. I first take out
$k$
periods, while the last expansion may last any periods. I first take out
![]() $(R-1)(k-1)$
expansion periods and then divide the left
$(R-1)(k-1)$
expansion periods and then divide the left
![]() $n_{0}-(R-1)(k-1)$
expansion periods into
$n_{0}-(R-1)(k-1)$
expansion periods into
![]() $R$
groups, yielding
$R$
groups, yielding
![]() $C_{n_{0}-(R-1)(k-1)-1}^{R-1}$
divisions in total. Similarly, there is also a one-to-one correspondence between the divisions and the qualified combinations of expansions. In fact, for a qualified combination, taking out
$C_{n_{0}-(R-1)(k-1)-1}^{R-1}$
divisions in total. Similarly, there is also a one-to-one correspondence between the divisions and the qualified combinations of expansions. In fact, for a qualified combination, taking out
![]() $k-1$
expansion periods from each of the first
$k-1$
expansion periods from each of the first
![]() $R-1$
expansions yields a division, which builds the correspondence. Thus, in total, there are
$R-1$
expansions yields a division, which builds the correspondence. Thus, in total, there are
![]() $C_{n_{1}-R}^{R-1}C_{n_{0}-(R-1)(k-1)-1}^{R-1}$
combinations of series in such a subcase.
$C_{n_{1}-R}^{R-1}C_{n_{0}-(R-1)(k-1)-1}^{R-1}$
combinations of series in such a subcase.
(ii) The series begins with an expansion and ends with a recession. It is easy to show that there are also
![]() $C_{n_{1}-R}^{R-1}C_{n_{0}-(R-1)(k-1)-1}^{R-1}$
combinations of series in such a subcase.
$C_{n_{1}-R}^{R-1}C_{n_{0}-(R-1)(k-1)-1}^{R-1}$
combinations of series in such a subcase.
Therefore, if
![]() $r=2R$
, Lemma 2 holds.
$r=2R$
, Lemma 2 holds.
Case 2:
![]() $r$
is odd. Then the series either “begins and ends with recessions” or “begins and ends with expansions.” Consider two subcases.
$r$
is odd. Then the series either “begins and ends with recessions” or “begins and ends with expansions.” Consider two subcases.
(iii) The series begins and ends with recessions. In such a subcase, there are
![]() $R+1$
recessions and
$R+1$
recessions and
![]() $R$
expansions; the first recession and the last recession may last any periods; each of the middle
$R$
expansions; the first recession and the last recession may last any periods; each of the middle
![]() $R-1$
recessions lasts at least 2 periods; and each expansion lasts at least
$R-1$
recessions lasts at least 2 periods; and each expansion lasts at least
![]() $k$
periods. Consider the qualified combinations of recessions. Take out
$k$
periods. Consider the qualified combinations of recessions. Take out
![]() $R-1$
recession periods and the left
$R-1$
recession periods and the left
![]() $n_{1}-R+1$
recession periods are divided into
$n_{1}-R+1$
recession periods are divided into
![]() $R+1$
groups, yielding
$R+1$
groups, yielding
![]() $C_{n_{1}-R}^{R}$
divisions. Similarly, there is a one-to-one correspondence between the divisions and the qualified combinations of recessions and there are
$C_{n_{1}-R}^{R}$
divisions. Similarly, there is a one-to-one correspondence between the divisions and the qualified combinations of recessions and there are
![]() $C_{n_{1}-R}^{R}$
qualified combinations of recessions. In fact, taking out a recession period from each of the middle
$C_{n_{1}-R}^{R}$
qualified combinations of recessions. In fact, taking out a recession period from each of the middle
![]() $R-1$
recessions yields a division, which builds the correspondence. For the
$R-1$
recessions yields a division, which builds the correspondence. For the
![]() $n_{0}$
expansion periods, take out
$n_{0}$
expansion periods, take out
![]() $R(k-1)$
expansion periods and divide the left
$R(k-1)$
expansion periods and divide the left
![]() $n_{0}-R(k-1)$
expansion periods into
$n_{0}-R(k-1)$
expansion periods into
![]() $R$
groups, yielding
$R$
groups, yielding
![]() $C_{n_{0}-R(k-1)-1}^{R-1}$
divisions. Note that each expansion lasts at least
$C_{n_{0}-R(k-1)-1}^{R-1}$
divisions. Note that each expansion lasts at least
![]() $k$
expansion periods and there are
$k$
expansion periods and there are
![]() $R$
expansions. There is a one-to-one correspondence between the divisions and the qualified combinations of expansions. Thus, there are
$R$
expansions. There is a one-to-one correspondence between the divisions and the qualified combinations of expansions. Thus, there are
![]() $C_{n_{0}-R(k-1)-1}^{R-1}$
qualified expansion combinations. In total, there are
$C_{n_{0}-R(k-1)-1}^{R-1}$
qualified expansion combinations. In total, there are
![]() $C_{n_{1}-R}^{R}C_{n_{0}-R(k-1)-1}^{R-1}$
combinations of series in such a subcase.
$C_{n_{1}-R}^{R}C_{n_{0}-R(k-1)-1}^{R-1}$
combinations of series in such a subcase.
(iv) The series begins and ends with expansions. There are
![]() $R$
recessions and
$R$
recessions and
![]() $R+1$
expansions; each recession lasts 2 periods at least; the first and the last expansions may last any periods; and each of the middle
$R+1$
expansions; each recession lasts 2 periods at least; the first and the last expansions may last any periods; and each of the middle
![]() $R-1$
expansions lasts at least
$R-1$
expansions lasts at least
![]() $k$
periods. For the
$k$
periods. For the
![]() $n_{1}$
recession periods, take out
$n_{1}$
recession periods, take out
![]() $R$
recession periods and divide the left
$R$
recession periods and divide the left
![]() $n_{1}-R$
recession periods into
$n_{1}-R$
recession periods into
![]() $R$
groups, yielding
$R$
groups, yielding
![]() $C_{n_{1}-R-1}^{R-1}$
divisions. There is a one-to-one correspondence between the divisions and the qualified combinations of recessions and there are
$C_{n_{1}-R-1}^{R-1}$
divisions. There is a one-to-one correspondence between the divisions and the qualified combinations of recessions and there are
![]() $C_{n_{1}-R-1}^{R-1}$
qualified combinations of recessions. For the
$C_{n_{1}-R-1}^{R-1}$
qualified combinations of recessions. For the
![]() $n_{0}$
expansion periods, take out
$n_{0}$
expansion periods, take out
![]() $(R-1)(k-1)$
expansion periods and divide the left
$(R-1)(k-1)$
expansion periods and divide the left
![]() $n_{0}-(R-1)(k-1)$
expansion periods into
$n_{0}-(R-1)(k-1)$
expansion periods into
![]() $R+1$
groups, yielding
$R+1$
groups, yielding
![]() $C_{n_{0}-(R-1)(k-1)-1}^{R}$
divisions. Similarly, there is a one-to-one correspondence between the divisions and the qualified combinations of expansions and there are
$C_{n_{0}-(R-1)(k-1)-1}^{R}$
divisions. Similarly, there is a one-to-one correspondence between the divisions and the qualified combinations of expansions and there are
![]() $C_{n_{0}-(R-1)(k-1)-1}^{R}$
qualified combinations of expansions. In total, there are
$C_{n_{0}-(R-1)(k-1)-1}^{R}$
qualified combinations of expansions. In total, there are
![]() $C_{n_{1}-R-1}^{R-1}C_{n_{0}-(R-1)(k-1)-1}^{R}$
combinations of series in such a subcase.
$C_{n_{1}-R-1}^{R-1}C_{n_{0}-(R-1)(k-1)-1}^{R}$
combinations of series in such a subcase.
Summarizing case (iii) and (iv) yields that if
![]() $r=2R+1$
, Lemma 2 is true.
$r=2R+1$
, Lemma 2 is true.