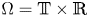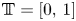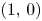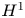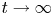1. Introduction
Let $\Omega = \mathbb {T}\times \mathbb {R}$![]() with $\mathbb {T}=[0,\,1]$
with $\mathbb {T}=[0,\,1]$![]() being a one-dimensional (1D) periodic domain and $\mathbb {R}$
being a one-dimensional (1D) periodic domain and $\mathbb {R}$![]() being the real line. Consider the 2D incompressible magnetohydrodynamic (MHD) equations with horizontal dissipation
being the real line. Consider the 2D incompressible magnetohydrodynamic (MHD) equations with horizontal dissipation

where $u$![]() denotes the velocity field, $B$
denotes the velocity field, $B$![]() the magnetic field and $P$
the magnetic field and $P$![]() the pressure, and $\nu >0$
the pressure, and $\nu >0$![]() and $\eta$
and $\eta$![]() are the viscosity and the damping coefficients, respectively. Here the velocity $u$
are the viscosity and the damping coefficients, respectively. Here the velocity $u$![]() obeys a degenerate Navier–Stokes equation with only horizontal dissipation $\nu \partial _{11}u$
obeys a degenerate Navier–Stokes equation with only horizontal dissipation $\nu \partial _{11}u$![]() and with a Lorentz forcing term. The magnetic field $B$
and with a Lorentz forcing term. The magnetic field $B$![]() satisfies the induction equation with a damping term. The goal of this paper is to understand the stability and the large-time behaviour of perturbations near a background magnetic field.
satisfies the induction equation with a damping term. The goal of this paper is to understand the stability and the large-time behaviour of perturbations near a background magnetic field.
This study is partially motivated by the stabilizing phenomenon of a background magnetic field on electrically conducting fluids that has been observed in physical experiments and numerical simulations (see, e.g., [Reference Alexakis1, Reference Alfvén2, Reference Burattini, Zikanov and Knaepen6, Reference Davidson12–Reference Davidson14, Reference Gallet, Berhanu and Mordant24, Reference Gallet and Doering25]). Since the dynamics of electrically conducting fluids is governed by the MHD equations (see, e.g., [Reference Biskamp4, Reference Priest and Forbes39]), the aim here is to establish this remarkable observation as a mathematically rigorous fact on the MHD equations.
We take the background magnetic field to be the unit vector in the $x_1$![]() -direction, $B^{(0)}=(1,\,0)$
-direction, $B^{(0)}=(1,\,0)$![]() . The corresponding steady-state solution of (1.1) is given by
. The corresponding steady-state solution of (1.1) is given by
We write $(u,\, b)$![]() with $b= B- B^{(0)}$
with $b= B- B^{(0)}$![]() for the perturbation near $(u^{(0)},\, B^{(0)})$
for the perturbation near $(u^{(0)},\, B^{(0)})$![]() . Our attention will be focussed on the following new system
. Our attention will be focussed on the following new system

In comparison with the original system in (1.1), there are two extra terms $\partial _1b$![]() and $\partial _1 u$
and $\partial _1 u$![]() in (1.2). We aim to achieve a complete understanding on the stability of solutions to (1.2) in the Sobolev setting. In addition, we also attempt to obtain the precise large-time behaviour of $(u,\, b)$
in (1.2). We aim to achieve a complete understanding on the stability of solutions to (1.2) in the Sobolev setting. In addition, we also attempt to obtain the precise large-time behaviour of $(u,\, b)$![]() and establish the eventual dynamics of (1.2).
and establish the eventual dynamics of (1.2).
Due to the lack of vertical dissipation in (1.2), the resolution of the stability problem is not direct. If we follow the standard energy method approach, the difficulty is immediate. The divergence-free conditions $\nabla \cdot u=\nabla \cdot b=0$![]() allow us to obtain a suitable upper bound on the $H^{1}$
allow us to obtain a suitable upper bound on the $H^{1}$![]() -norm of $(u,\, b)$
-norm of $(u,\, b)$![]() , but it does not appear to be possible to control the $H^{2}$
, but it does not appear to be possible to control the $H^{2}$![]() -norm directly. Even if we completely ignore the terms related to the magnetic field and simply consider the 2D anisotropic Navier–Stokes equations
-norm directly. Even if we completely ignore the terms related to the magnetic field and simply consider the 2D anisotropic Navier–Stokes equations
direct energy estimates fail to generate a suitable $H^{2}$![]() -bound. In fact, when we resort to the corresponding vorticity formulation
-bound. In fact, when we resort to the corresponding vorticity formulation
the one-directional dissipation is insufficient to bound the nonlinearity directly. In the estimate of $\nabla \omega$![]() ,
,
the right-hand side does not admit a suitable upper bound. In fact,

and the two terms in (1.3) can not be controlled suitably.
One novel idea to overcome this difficulty is to explore the stabilizing effect of the magnetic field on the fluids as hinted by the aforementioned experimental results. Mathematically we make full use of the coupling and interaction in the MHD system in (1.2) to unearth the hidden smoothing and stabilizing properties. To do so, we first apply the Leray projection $\mathbb {P} = I -\nabla \Delta ^{-1}\nabla \cdot$![]() to the velocity equation to eliminate the pressure,
to the velocity equation to eliminate the pressure,
By differentiating the linearized system in time

and making several substitutions, we can convert (1.4) into a system of wave equations

(1.5) allows us to decouple $u$![]() and $b$
and $b$![]() and exhibits more smoothing and stabilizing properties than (1.4). In particular, both $u$
and exhibits more smoothing and stabilizing properties than (1.4). In particular, both $u$![]() and $b$
and $b$![]() gain weak horizontal dissipation as can be seen from the pieces $(1+ \nu \eta ) \partial _{11} u$
gain weak horizontal dissipation as can be seen from the pieces $(1+ \nu \eta ) \partial _{11} u$![]() and $(1+ \nu \eta ) \partial _{11} b$
and $(1+ \nu \eta ) \partial _{11} b$![]() . Unfortunately, this extra regularization does not appear to help with the deficiency of vertical dissipation in the velocity equation. As a consequence, this approach fails.
. Unfortunately, this extra regularization does not appear to help with the deficiency of vertical dissipation in the velocity equation. As a consequence, this approach fails.
We remark that a previous work of Feng, Hafeez and Wu [Reference F. Hafeez and Wu23] explored the extra stabilizing and smoothing of the wave structure, and successfully resolved the stability problem on the same MHD system near the background magnetic field $B^{(0)} =(0,\,1)$![]() . When the background magnetic field is $(0,\,1)$
. When the background magnetic field is $(0,\,1)$![]() , the extra regularity is in the vertical direction and complements with the horizontal dissipation in the velocity equation. Therefore, the direction of the background magnetic field plays a crucial role in the stabilizing phenomenon on electrically conduction fluids.
, the extra regularity is in the vertical direction and complements with the horizontal dissipation in the velocity equation. Therefore, the direction of the background magnetic field plays a crucial role in the stabilizing phenomenon on electrically conduction fluids.
This paper seeks a different approach to resolve the stability problem concerned here. The spatial domain here is $\Omega = \mathbb {T}\times \mathbb {R}$![]() and we take full advantage of the geometry of this domain. The horizontal direction is periodic and we can separate the zeroth Fourier mode from the non-zero ones. The zeroth Fourier mode corresponds to the horizontal average. This hints the decomposition of the physical quantities into the horizontal averages and the corresponding oscillation parts. More precisely, for a function $f$
and we take full advantage of the geometry of this domain. The horizontal direction is periodic and we can separate the zeroth Fourier mode from the non-zero ones. The zeroth Fourier mode corresponds to the horizontal average. This hints the decomposition of the physical quantities into the horizontal averages and the corresponding oscillation parts. More precisely, for a function $f$![]() that is integrable in $x\in \mathbb {T}$
that is integrable in $x\in \mathbb {T}$![]() , we define
, we define
This decomposition is orthogonal in the Sobolev space $H^{k}(\Omega )$![]() for any integer $k\ge 0$
for any integer $k\ge 0$![]() (see lemma 2.2 in § 2). More crucially, the oscillation part $\widetilde f$
(see lemma 2.2 in § 2). More crucially, the oscillation part $\widetilde f$![]() obeys a strong version of the Poincaré type inequality
obeys a strong version of the Poincaré type inequality
This inequality allows us to control some of the nonlinear parts in terms of the horizontal dissipation. By invoking the decompositions
and applying the aforementioned Poincaré inequality together with various anisotropic inequalities, we are able to successfully bound the nonlinearity and establish the following stability result.
Theorem 1.1 Let $\eta >0$![]() and $\nu >0$
and $\nu >0$![]() . Consider (1.2) with the initial data $(u_0,\, b_0) \in H^{3}(\Omega ),$
. Consider (1.2) with the initial data $(u_0,\, b_0) \in H^{3}(\Omega ),$![]() and $\nabla \cdot u_0= \nabla \cdot b_0=0$
and $\nabla \cdot u_0= \nabla \cdot b_0=0$![]() . Then there exists a constant $\varepsilon =\varepsilon (\nu,\, \eta )>0$
. Then there exists a constant $\varepsilon =\varepsilon (\nu,\, \eta )>0$![]() such that, if
such that, if
then (1.2) has a unique global classical solution $(u,\, b)$![]() satisfying, for any $t>0,$
satisfying, for any $t>0,$![]()
where $C>0$![]() is independent of $\varepsilon$
is independent of $\varepsilon$![]() and $t$
and $t$![]() .
.
Theorem 1.1 successfully resolves the stability problem on a partially dissipated MHD system near a background magnetic field even when the smoothing effect of the magnetic field is not sufficient to deal with the dissipation deficiency.
Efforts are also devoted to understanding the precise large-time behaviour of the perturbation. We expect the horizontal average $(\bar u,\, \bar b)$![]() to behave differently from the oscillation part $(\widetilde u,\, \widetilde b)$
to behave differently from the oscillation part $(\widetilde u,\, \widetilde b)$![]() . Intuitively $(\bar u,\, \bar b)$
. Intuitively $(\bar u,\, \bar b)$![]() corresponds to the zeroth horizontal Fourier mode and the associated dissipation term vanishes. Thus $(\bar u,\, \bar b)$
corresponds to the zeroth horizontal Fourier mode and the associated dissipation term vanishes. Thus $(\bar u,\, \bar b)$![]() may not decay in time. In contrast, $(\widetilde u,\, \widetilde b)$
may not decay in time. In contrast, $(\widetilde u,\, \widetilde b)$![]() consists of non-zero horizontal Fourier modes and the horizontal dissipation effectively plays the role of damping. As a consequence, $(\widetilde u,\, \widetilde b)$
consists of non-zero horizontal Fourier modes and the horizontal dissipation effectively plays the role of damping. As a consequence, $(\widetilde u,\, \widetilde b)$![]() could decay exponentially in time. Our second theorem rigorously confirms this intuition.
could decay exponentially in time. Our second theorem rigorously confirms this intuition.
Theorem 1.2 Let $u_0,\, b_0\in H^{3}(\Omega )$![]() with $\nabla \cdot u_0=0$
with $\nabla \cdot u_0=0$![]() and $\nabla \cdot b_0=0$
and $\nabla \cdot b_0=0$![]() . Assume that $\|u_0\|_{H^{3}}+ \|b_0\|_{H^{3}} \leq \varepsilon$
. Assume that $\|u_0\|_{H^{3}}+ \|b_0\|_{H^{3}} \leq \varepsilon$![]() for sufficiently small $\varepsilon >0$
for sufficiently small $\varepsilon >0$![]() . Let $(u,\, b)$
. Let $(u,\, b)$![]() be the corresponding solution of (1.2). Then the $H^{1}$
be the corresponding solution of (1.2). Then the $H^{1}$![]() norm of the oscillation part $(\widetilde u,\, \widetilde b)$
norm of the oscillation part $(\widetilde u,\, \widetilde b)$![]() decays exponentially in time,
decays exponentially in time,
for some constant $C_1>0$![]() and for all $t>0$
and for all $t>0$![]() .
.
We explain the main lines in the proof of theorem 1.1. The local well-posedness of (1.2) in the Sobolev space $H^{3}(\Omega )$![]() can be shown via standard procedures such as the approach in the book of Majda and Bertozzi [Reference Majda and Bertozzi37]. Our attention is focussed on the global bound of $(u,\, b)$
can be shown via standard procedures such as the approach in the book of Majda and Bertozzi [Reference Majda and Bertozzi37]. Our attention is focussed on the global bound of $(u,\, b)$![]() in $H^{3}(\Omega )$
in $H^{3}(\Omega )$![]() . One of the most suitable tools for this purpose is the bootstrapping argument [Reference Tao45]. To set up the argument, we first construct the energy functional. For the MHD system in (1.2), the energy functional $E(t)$
. One of the most suitable tools for this purpose is the bootstrapping argument [Reference Tao45]. To set up the argument, we first construct the energy functional. For the MHD system in (1.2), the energy functional $E(t)$![]() is naturally given by the $H^{3}$
is naturally given by the $H^{3}$![]() -norm of $(u,\,b)$
-norm of $(u,\,b)$![]() together with the time integrals from dissipative and damping terms, namely
together with the time integrals from dissipative and damping terms, namely
The main effort is then devoted to proving the energy inequality
Once (1.7) is at our disposal, the bootstrapping argument then implies that, if $E(0) :=\|(u_0,\, b_0)\|_{H^{3}}^{2}$![]() is sufficiently small, say
is sufficiently small, say
for some suitable $\varepsilon >0$![]() , then $E(t)$
, then $E(t)$![]() remains uniformly bounded for any $t>0$
remains uniformly bounded for any $t>0$![]() ,
,
which gives us the desired global bound on $\|(u(t),\, b(t))\|_{H^{3}}$![]() . To prove (1.7), we invoke the orthogonal decompositions $u = \bar u+ \widetilde u$
. To prove (1.7), we invoke the orthogonal decompositions $u = \bar u+ \widetilde u$![]() and $b = \bar b + \widetilde b$
and $b = \bar b + \widetilde b$![]() , apply the Poincaré type inequalities and anisotropic upper bounds for triple products. More technical details are provided in § 3.
, apply the Poincaré type inequalities and anisotropic upper bounds for triple products. More technical details are provided in § 3.
To prove theorem 1.2, we first take the horizontal average of (1.2) to obtain the equations of $(\bar u,\, \bar b)$![]() ,
,

We then write the equations of $(\widetilde u,\, \widetilde b)$![]() by taking the difference of (1.2) and (1.8),
by taking the difference of (1.2) and (1.8),

The proof of (1.6) is divided into the estimates of $\|(\widetilde u,\, \widetilde b)\|_{L^{2}}$![]() and $\|(\nabla \widetilde u,\, \nabla \widetilde b)\|_{L^{2}}$
and $\|(\nabla \widetilde u,\, \nabla \widetilde b)\|_{L^{2}}$![]() . The efforts are devoted to bounding the nonlinearity in terms of the horizontal derivatives of $\widetilde u$
. The efforts are devoted to bounding the nonlinearity in terms of the horizontal derivatives of $\widetilde u$![]() . Poincaré's inequality and anisotropic upper bounds for the triple products are used extensively. After a tedious process of evaluating many terms, we obtain
. Poincaré's inequality and anisotropic upper bounds for the triple products are used extensively. After a tedious process of evaluating many terms, we obtain

which yields the decay rate in (1.6). A detailed proof is provided in § 4.
Finally we briefly summarize some of related results to provide a broader view on the studies of the MHD equations. Fundamental issues on the MHD equations such as well-posedness and stability problems have attracted a lot of attention. Substantial progress has recently been made on the well-posedness problem concerning the MHD equations with various partial or fractional dissipation (see, e.g., [Reference Cao, Regmi and Wu8–Reference Cao, Wu and Yuan10, Reference Dong, Jia, Li and Wu16, Reference Dong, Li and Wu17, Reference Du and Zhou19–Reference Fefferman, McCormick, Robinson and Rodrigo22, Reference Jiu, Niu, Wu, Xu and Yu30, Reference Li, Tan and Yin32, Reference Lin and Du35, Reference Schonbek, Schonbek and Süli42, Reference Sermange and Temam43, Reference Wan46, Reference Wu49, Reference Xiao, Xin and Wu53, Reference Yamazaki55–Reference Yuan and Zhao61]). Since the pioneering work of Alfvén [Reference Alfvén2], the stability problem on various MHD systems has recently gained renewed interests and there are substantial developments. By taking advantage of the Elsässer variables, several papers have successfully solved the stability problem on the ideal MHD equations or the fully dissipated MHD equations with identical (or almost identical) viscosity and magnetic diffusivity (see [Reference Bardos, Sulem and Sulem3, Reference Cai and Lei7, Reference He, Xu and Yu26, Reference Wei and Zhang47]). The stability problem on the MHD equations with only kinematic dissipation in $\mathbb {R}^{2}$![]() or $\mathbb {R}^{3}$
or $\mathbb {R}^{3}$![]() have been solved via different approaches [Reference Deng and Zhang15, Reference Hu27, Reference Hu and Lin28, Reference Lin, Xu and Zhang33, Reference Lin and Zhang34, Reference Ren, Wu, Xiang and Zhang40, Reference Ren, Xiang and Zhang41, Reference Tan and Wang44, Reference Wu and Wu50, Reference Wu, Wu and Xu51, Reference Zhang62, Reference Zhang63]. The same problem in the periodic setting $\mathbb {T}^{3}$
have been solved via different approaches [Reference Deng and Zhang15, Reference Hu27, Reference Hu and Lin28, Reference Lin, Xu and Zhang33, Reference Lin and Zhang34, Reference Ren, Wu, Xiang and Zhang40, Reference Ren, Xiang and Zhang41, Reference Tan and Wang44, Reference Wu and Wu50, Reference Wu, Wu and Xu51, Reference Zhang62, Reference Zhang63]. The same problem in the periodic setting $\mathbb {T}^{3}$![]() has been investigated by [Reference Pan, Zhou and Zhu38]. The MHD equations with only magnetic diffusivity have recently been studied for the small data global well-posedness near the trivial solution or a background magnetic field [Reference Chen, Zhang and Zhou11, Reference Ji and Wu29, Reference Wei and Zhang48, Reference Xu and Zhang54, Reference Zhou and Zhu64], although a complete solution on the stability problem near a background magnetic field is currently lacking. When the velocity equation involves only horizontal or vertical dissipation, the velocity equation itself alone may not be stable and the stability problem relies on the enhanced dissipation resulting from the coupling and interaction. Several such MHD systems with degenerate velocity dissipation have been shown to be stable near suitable background magnetic fields [Reference Boardman, Lin and Wu5, Reference F. Hafeez and Wu23, Reference Li, Wu and Xu31, Reference Lin, Ji, Wu and Yan36, Reference Wu and Zhu52].
has been investigated by [Reference Pan, Zhou and Zhu38]. The MHD equations with only magnetic diffusivity have recently been studied for the small data global well-posedness near the trivial solution or a background magnetic field [Reference Chen, Zhang and Zhou11, Reference Ji and Wu29, Reference Wei and Zhang48, Reference Xu and Zhang54, Reference Zhou and Zhu64], although a complete solution on the stability problem near a background magnetic field is currently lacking. When the velocity equation involves only horizontal or vertical dissipation, the velocity equation itself alone may not be stable and the stability problem relies on the enhanced dissipation resulting from the coupling and interaction. Several such MHD systems with degenerate velocity dissipation have been shown to be stable near suitable background magnetic fields [Reference Boardman, Lin and Wu5, Reference F. Hafeez and Wu23, Reference Li, Wu and Xu31, Reference Lin, Ji, Wu and Yan36, Reference Wu and Zhu52].
The rest of this paper is divided into three sections. Section 2 states several properties on the aforementioned decomposition and provides several anisotropic inequalities. Section 3 proves theorem 1.1 while § 4 presents the proof of theorem 1.2.
2. Preliminaries
This section states several properties on the decomposition defined in the introduction and provides several anisotropic inequalities to be used in the proofs of theorems 1.1 and 1.2. Some of the materials presented here can be found in [Reference Cao and Wu9, Reference Dong, Wu, Xu and Zhu18].
We start by recalling the definition of the horizontal average and the oscillation part. Let $\Omega = \mathbb {T}\times \mathbb {R}$![]() and let $f=f(x_1,\, x_2)$
and let $f=f(x_1,\, x_2)$![]() with $(x_1,\, x_2) \in \Omega$
with $(x_1,\, x_2) \in \Omega$![]() be sufficiently smooth, say integrable in $x_1\in \mathbb {T}$
be sufficiently smooth, say integrable in $x_1\in \mathbb {T}$![]() . The horizontal average $\overline {f}$
. The horizontal average $\overline {f}$![]() is given by
is given by
We decompose $f$![]() into $\overline {f}$
into $\overline {f}$![]() and the oscillation portion $\widetilde {f}$
and the oscillation portion $\widetilde {f}$![]() ,
,
The following lemma is a direct consequence of (2.1) and (2.2).
Lemma 2.1 The average operator and the oscillation operator commute with the partial derivatives, for $i=1,\,2,$![]()
As a special consequence, if $\nabla \cdot f=0,$![]() then
then
The second lemma states that the decomposition in (2.2) is orthogonal in any Sobolev space $\dot H^{k}(\Omega )$![]() .
.
Lemma 2.2 Let $\Omega = \mathbb {T}\times \mathbb {R}$![]() . Let $k\ge 0$
. Let $k\ge 0$![]() be an integer. Let $f\in \dot H^{k}(\Omega )$
be an integer. Let $f\in \dot H^{k}(\Omega )$![]() . Then $\overline {f}$
. Then $\overline {f}$![]() and $\widetilde {f}$
and $\widetilde {f}$![]() are orthogonal in $\dot H^{k}(\Omega ),$
are orthogonal in $\dot H^{k}(\Omega ),$![]() namely
namely
In particular, $\|\overline {f}\|_{\dot H^{k}}\leq \|f\|_{\dot H^{k}}$![]() and $\|\widetilde {f}\|_{\dot H^{k}}\leq \|f\|_{\dot H^{k}}$
and $\|\widetilde {f}\|_{\dot H^{k}}\leq \|f\|_{\dot H^{k}}$![]() .
.
The oscillation part obeys the following Poincaré type inequalities.
Lemma 2.3 If $\|\partial _1 \widetilde {f}\|_{L^{2}(\Omega )}<\infty,$![]() then
then
In addition, if $\|\partial _1 \widetilde {f}\|_{H^{1}(\Omega )} < \infty,$![]() then
then
Proof of lemma 2.3. Since the horizontal average of $\widetilde f$![]() is zero, for any fixed $x_2\in \mathbb {R}$
is zero, for any fixed $x_2\in \mathbb {R}$![]() , there is $a\in \mathbb {T}$
, there is $a\in \mathbb {T}$![]() such that
such that
Then, for any $(x_1,\, x_2)\in \Omega$![]() ,
,
Squaring each side of (2.3) and integrating over $\Omega$![]() yields the first inequality. The second inequality is obtained by taking the $L^{\infty }(\Omega )$
yields the first inequality. The second inequality is obtained by taking the $L^{\infty }(\Omega )$![]() in (2.3) and using the simple fact that $\|f\|_{L^{\infty }(\mathbb {R})} \le C\, \|f\|_{H^{1}(\mathbb {R})}$
in (2.3) and using the simple fact that $\|f\|_{L^{\infty }(\mathbb {R})} \le C\, \|f\|_{H^{1}(\mathbb {R})}$![]() for any 1D function $f \in H^{1}(\mathbb {R})$
for any 1D function $f \in H^{1}(\mathbb {R})$![]() .
.
Next we present several anisotropic inequalities. Anisotropic upper bounds for triple products are frequently used to bound the nonlinear terms when only partial dissipation is present. In the case when the spatial domain is the whole space $\mathbb {R}^{2}$![]() , Cao and Wu [Reference Cao and Wu9] showed and applied the following inequality
, Cao and Wu [Reference Cao and Wu9] showed and applied the following inequality
(2.4) is a consequence of the elementary 1D inequality
Another consequence of (2.5) is the following inequality
When the 1D spatial domain is a bounded domain, say $\mathbb {T}$![]() ,
,
Since the oscillation part $\widetilde {f}$![]() has mean zero, for $\widetilde {f} \in H^{1}(\mathbb {T})$
has mean zero, for $\widetilde {f} \in H^{1}(\mathbb {T})$![]() ,
,
As a consequence of these elementary inequalities, the following two lemmas hold.
Lemma 2.4 Let $\Omega =\mathbb {T}\times \mathbb {R}$![]() . For any $f,\, g,\, h \in L^{2}(\Omega )$
. For any $f,\, g,\, h \in L^{2}(\Omega )$![]() with $\partial _1f \in L^{2}(\Omega )$
with $\partial _1f \in L^{2}(\Omega )$![]() and $\partial _2g\in L^{2}(\Omega ),$
and $\partial _2g\in L^{2}(\Omega ),$![]() then
then
For any $f\in H^{2}(\Omega ),$![]() we have
we have

After replacing $f$![]() by the oscillation part, we have the following inequalities.
by the oscillation part, we have the following inequalities.
Lemma 2.5 Let $\Omega =\mathbb {T}\times \mathbb {R}$![]() . For any $f,\, g,\, h \in L^{2}(\Omega )$
. For any $f,\, g,\, h \in L^{2}(\Omega )$![]() with $\partial _1f \in L^{2}(\Omega )$
with $\partial _1f \in L^{2}(\Omega )$![]() and $\partial _2g\in L^{2}(\Omega ),$
and $\partial _2g\in L^{2}(\Omega ),$![]() then
then
For any $f\in H^{2}(\Omega ),$![]() we have
we have
3. Stability
This section is devoted to the proof of theorem 1.1 on the stability of (1.2).
Proof of theorem 1.1. The local well-posedness of (1.2) in the Sobolev space $H^{3}(\Omega )$![]() can be shown via standard procedures such as the approach in the book of Majda and Bertozzi [Reference Majda and Bertozzi37]. Our attention is focussed on the global bound of $(u,\, b)$
can be shown via standard procedures such as the approach in the book of Majda and Bertozzi [Reference Majda and Bertozzi37]. Our attention is focussed on the global bound of $(u,\, b)$![]() in $H^{3}(\Omega )$
in $H^{3}(\Omega )$![]() .
.
The framework of the proof is the bootstrapping argument. To proceed, we define the energy functional as
Our main efforts are devoted to proving the following energy inequality
As we explain later, a direct application of the bootstrapping argument to (3.2) implies the desired global uniform bound on $\|(u,\, b)\|_{H^{3}}$![]() .
.
Attention is first focussed on proving (3.1). Due to the equivalence of the inhomogeneous norm $\|(u,\, b)\|_{H^{3}}$![]() with the sum of the $L^{2}$
with the sum of the $L^{2}$![]() -norm and the homogeneous norm $\|(u,\, b)\|_{\mathring H^{3}}$
-norm and the homogeneous norm $\|(u,\, b)\|_{\mathring H^{3}}$![]() , it suffices to bound the homogeneous norm $\|(u,\, b)\|_{\mathring H^{3}}$
, it suffices to bound the homogeneous norm $\|(u,\, b)\|_{\mathring H^{3}}$![]() . The uniform $L^{2}$
. The uniform $L^{2}$![]() -bound is an easy consequence of the system in (1.2) itself. Taking the inner product of (1.2) with $(u,\, b)$
-bound is an easy consequence of the system in (1.2) itself. Taking the inner product of (1.2) with $(u,\, b)$![]() , we obtain, after integrating by parts and using $\nabla \cdot u=\nabla \cdot b=0$
, we obtain, after integrating by parts and using $\nabla \cdot u=\nabla \cdot b=0$![]() ,
,
To estimate the homogeneous norm $\|(u,\, b)\|_{\mathring H^{3}}$![]() , we apply $\partial _i^{3} (i=1,\, 2)$
, we apply $\partial _i^{3} (i=1,\, 2)$![]() to (1.2) and then dot with $(\partial _i^{3}u,\, \partial _i^{3}b)$
to (1.2) and then dot with $(\partial _i^{3}u,\, \partial _i^{3}b)$![]() to obtain
to obtain

where

By integration by parts, $J=0$![]() . The estimate of $K$
. The estimate of $K$![]() is long and tedious, and is provided in the later part of the proof. To bound L, we decompose it into two parts,
is long and tedious, and is provided in the later part of the proof. To bound L, we decompose it into two parts,

where $C_3^{k} = \frac {3!}{k! (3-k)!}$![]() is the binomial coefficient. By lemma 2.1 and lemma 2.5,
is the binomial coefficient. By lemma 2.1 and lemma 2.5,

We further decompose $L_2$![]() into three terms,
into three terms,

By Hölder's inequality and lemma 2.4,

Similarly,

By lemma 2.1, $\partial _2 \overline {b_2}=-\partial _{1}\overline {b_1}=0$![]() and lemma 2.5,
and lemma 2.5,

Combining the estimates of $L_1$![]() and $L_2$
and $L_2$![]() , we obtain
, we obtain
Now we estimate $M$![]() ,
,

By lemma 2.1,

By lemma 2.5, Hölder's inequality, and lemma 2.3,

By integration by parts and $\nabla \cdot \widetilde u=0$![]() ,
,
To estimate $M_2$![]() , we split it into four terms,
, we split it into four terms,

$M_{2,4}=0$![]() due to $\nabla \cdot u=0$
due to $\nabla \cdot u=0$![]() . By Hölder's inequality and lemma 2.4,
. By Hölder's inequality and lemma 2.4,

Similarly,

By lemma 2.1, $\partial _2 \overline {u_2}=-\partial _{1}\overline {u_1}$![]() and lemma 2.5,
and lemma 2.5,

Combining the estimates for $M_1$![]() and $M_2$
and $M_2$![]() , we obtain
, we obtain
Now we estimate the term N,

By lemma 2.1, lemma 2.5, Hölder's inequality, and lemma 2.3,

To bound $N_2$![]() we further decompose it into three terms as
we further decompose it into three terms as

By Hölder's inequality and lemma 2.4,

Similarly,

By lemma 2.1, $\partial _2 \overline {b_2}=-\partial _{1}\overline {b_1}=0$![]() and lemma 2.5,
and lemma 2.5,

Combining estimates of $N_1$![]() and $N_2$
and $N_2$![]() , we have
, we have
We now turn to the term $K$![]() . We split K into two terms,
. We split K into two terms,

By integration by parts, lemma 2.1, lemma 2.5 and lemma 2.3,

Therefore,
To bound $K_2$![]() , we further decompose it into four terms,
, we further decompose it into four terms,

By integration by parts and $\nabla \cdot u=0$![]() ,
,
Next we bound $K_{2,2}$![]() . By lemma 2.1 and $\nabla \cdot u=0$
. By lemma 2.1 and $\nabla \cdot u=0$![]() ,
,

By integration by parts and lemma 2.1,

Similarly, $K_{2,2,5}=0$![]() . By lemma 2.5 and lemma 2.3,
. By lemma 2.5 and lemma 2.3,

$K_{2,2,4}$![]() and $K_{2,2,8}$
and $K_{2,2,8}$![]() can be bounded similarly as $K_{2,2,2}$
can be bounded similarly as $K_{2,2,2}$![]() . By lemma 2.5 and lemma 2.3,
. By lemma 2.5 and lemma 2.3,


Therefore,
Now we bound $K_{2,3}$![]() . By lemma 2.1 and the divergence-free condition,
. By lemma 2.1 and the divergence-free condition,

Clearly $K_{2,3,1}=0$![]() and $K_{2,3,5}=0$
and $K_{2,3,5}=0$![]() . To bound the remaining terms of $K_{2,3}$
. To bound the remaining terms of $K_{2,3}$![]() we use lemma 2.5 and lemma 2.3,
we use lemma 2.5 and lemma 2.3,

$K_{2,3,4}$![]() and $K_{2,3,7}$
and $K_{2,3,7}$![]() can be bounded similarly,
can be bounded similarly,

$K_{2,3,8}$![]() can also be bounded similarly. Hence,
can also be bounded similarly. Hence,
Now we bound the last term $K_{2,4}$![]() in (3.9). By lemma 2.1 and $\nabla \cdot u=0$
in (3.9). By lemma 2.1 and $\nabla \cdot u=0$![]() ,
,

Again $K_{2,4,1}=0$![]() and $K_{2,4,5}=0$
and $K_{2,4,5}=0$![]() . To bound the remaining terms of $K_{2,4}$
. To bound the remaining terms of $K_{2,4}$![]() we use lemma 2.5 and lemma 2.3,
we use lemma 2.5 and lemma 2.3,

$K_{2,4,4}$![]() and $K_{2,4,7}$
and $K_{2,4,7}$![]() can be bounded similarly.
can be bounded similarly.

$K_{2,4,8}$![]() can be bounded similarly. Hence,
can be bounded similarly. Hence,
Putting together the upper bounds for $K_{2,1}$![]() through $K_{2,4}$
through $K_{2,4}$![]() , we find
, we find
Collecting the upper bounds in (3.8) and (3.10) yields
Integrating (3.4) in time and then adding to (3.3), we have, after recalling the definition of $E$![]() in (3.1),
in (3.1),
Collecting the upper bounds in (3.5), (3.6), (3.7)and (3.11) leads to the desired inequality in (3.2),

We apply the bootstrapping argument to (3.12). The initial data is taken to be sufficiently small, say
with $\varepsilon$![]() satisfying
satisfying
We make the ansatz that, for $0 \le t \le T$![]()
Then (3.12) implies

or
The bootstrapping argument then implies that $T=\infty$![]() and $E(t) \le \delta _0$
and $E(t) \le \delta _0$![]() . As a consequence, for any $0\le t \le \infty$
. As a consequence, for any $0\le t \le \infty$![]() ,
,
This completes the proof for theorem 1.1.
4. Proof of theorem 1.2
This section proves theorem 1.2, which assesses that the oscillation part $(\widetilde u,\, \widetilde b)$![]() decays exponentially to zero in the $H^{1}$
decays exponentially to zero in the $H^{1}$![]() -norm as $t\to \infty$
-norm as $t\to \infty$![]() . We consider the equations of $(\widetilde {u},\, \widetilde {b})$
. We consider the equations of $(\widetilde {u},\, \widetilde {b})$![]() and apply the properties of the orthogonal decomposition and several anisotropic inequalities.
and apply the properties of the orthogonal decomposition and several anisotropic inequalities.
Proof of theorem 1.2. We first write the equation of $(\bar {u},\, \bar {b})$![]() . By taking the average of (1.2), we have
. By taking the average of (1.2), we have

Taking the difference of (1.2) and (4.1), we obtain

Taking the inner product of (4.2) with $(\widetilde {u},\, \widetilde {b})$![]() , after integration by parts and divergence-free conditions, we find
, after integration by parts and divergence-free conditions, we find

By lemma 2.1,
Similarly, $A_3=0$![]() . By lemma 2.5, lemma 2.3 and the divergence-free conditions,
. By lemma 2.5, lemma 2.3 and the divergence-free conditions,

By lemma 2.1 and the divergence-free conditions,


Similarly, by lemma 2.5, lemma 2.3 and the divergence-free conditions,

By lemma 2.4 and Hölder's inequality,

Collecting the estimates for $A_1$![]() through $A_8$
through $A_8$![]() in (4.3), we obtain
in (4.3), we obtain

According to theorem 1.1, if $\varepsilon >0$![]() is sufficiently small and $\|u_0\|_{H^{3}}+ \|b_0\|_{H^{3}} \leq \varepsilon$
is sufficiently small and $\|u_0\|_{H^{3}}+ \|b_0\|_{H^{3}} \leq \varepsilon$![]() , then $\|u\|_{H^{3}}+ \|b\|_{H^{3}} \leq C\varepsilon$
, then $\|u\|_{H^{3}}+ \|b\|_{H^{3}} \leq C\varepsilon$![]() and
and
By lemma 2.3,
where $C_1=C_1(\nu,\, \eta )>0$![]() .
.
Next we consider the exponential decay for $\|(\nabla \widetilde {u}(t),\, \nabla \widetilde {b}(t))\|_{L^{2}}$![]() . Taking the gradient of (4.2) yields
. Taking the gradient of (4.2) yields

Dotting (4.6) with $(\nabla \widetilde {u},\, \nabla \widetilde {b})$![]() , we have
, we have

By lemma 2.1, $B_1$![]() can be written as
can be written as

By lemma 2.5 and lemma 2.3, $B_{1,1}$![]() can be bounded by
can be bounded by

$B_{1,2}$![]() and $B_{1,3}$
and $B_{1,3}$![]() can be bounded similarly and
can be bounded similarly and
For $B_{1,4}$![]() , using the divergence-free condition of $u$
, using the divergence-free condition of $u$![]() and by lemma 2.5, lemma 2.1 and lemma 2.3, we obtain
and by lemma 2.5, lemma 2.1 and lemma 2.3, we obtain

Hence, $B_1$![]() is bounded by
is bounded by
Similarly, we can bound $B_3$![]() by lemma 2.4 and Hölder's inequality,
by lemma 2.4 and Hölder's inequality,

In order to bound $B_2$![]() , we rewrite it as
, we rewrite it as

According to the definition of $\bar {u}$![]() ,
,
Using lemma 2.3, Hölder's inequality and proceeding as in (4.4) for $\|\partial _2\bar {u}\|_{L^{\infty }}$![]() , we find
, we find

Similarly, $B_{2,3}$![]() has the same bound as $B_{2,1}$
has the same bound as $B_{2,1}$![]() . By lemma 2.5 and lemma 2.3,
. By lemma 2.5 and lemma 2.3,

Hence, the bound for $B_2$![]() is
is
Similarly,

By the definition of $\bar {b}$![]() , $B_{5,2}=0$
, $B_{5,2}=0$![]() . By lemma 2.1, lemma 2.4, lemma 2.3, Hölder's inequality and Young's inequality,
. By lemma 2.1, lemma 2.4, lemma 2.3, Hölder's inequality and Young's inequality,

Similarly, $B_{5,3}$![]() obeys the same bound. By lemma 2.5, lemma 2.3 and Young's inequality,
obeys the same bound. By lemma 2.5, lemma 2.3 and Young's inequality,

Collecting the bounds for $B_{5,1}$![]() , $B_{5,2}$
, $B_{5,2}$![]() , $B_{5,3}$
, $B_{5,3}$![]() and $B_{5,4}$
and $B_{5,4}$![]() ,
,
Similarly, $B_6$![]() and $B_8$
and $B_8$![]() are bounded by
are bounded by
By lemma 2.1 and the divergence-free condition $\nabla \cdot b=0$![]() ,
,

We can rewrite $B_{4,1}$![]() as
as

By lemma 2.4, lemma 2.3, Hölder's inequality and Young's inequality,

$B_{4,1,2},\, B_{4,1,3}$![]() and $B_{4,1,4}$
and $B_{4,1,4}$![]() can be bounded similarly as $B_{4,1,1}$
can be bounded similarly as $B_{4,1,1}$![]() and
and
Therefore, $B_{4,1}$![]() is bounded by
is bounded by
Similarly, $B_{4,2}$![]() obeys the same bound as $B_{4,1}$
obeys the same bound as $B_{4,1}$![]() . Hence,
. Hence,
Inserting the estimates for $B_1$![]() through $B_8$
through $B_8$![]() in (4.7),
in (4.7),

Choosing $\varepsilon >0$![]() sufficiently small and by theorem 1.1, if $\|u_0\|_{H^{3}}+ \|b_0\|_{H^{3}} \leq \varepsilon$
sufficiently small and by theorem 1.1, if $\|u_0\|_{H^{3}}+ \|b_0\|_{H^{3}} \leq \varepsilon$![]() , then $\|u\|_{H^{3}}+ \|b\|_{H^{3}} \leq C\varepsilon$
, then $\|u\|_{H^{3}}+ \|b\|_{H^{3}} \leq C\varepsilon$![]() and
and
By lemma 2.3, we obtain the exponential decay result for $\|(\nabla \widetilde {u}(t),\, \nabla \widetilde {b}(t))\|_{L^{2}}$![]() ,
,
where $C_1=C_1(\nu,\, \eta )>0$![]() . Combining the estimates in (4.5) and (4.10), we obtain the desired decay result in theorem 1.2.
. Combining the estimates in (4.5) and (4.10), we obtain the desired decay result in theorem 1.2.
Acknowledgments
Feng was partially supported by the National Science Foundation under Grant No. DMS-1928930 while participating in the Mathematical Problems in Fluid Dynamics program hosted by the Mathematical Sciences Research Institute in Berkeley, California, during the Spring 2021 semester. Wu was partially supported by the National Science Foundation under grant DMS 2104682 and the AT&T Foundation at Oklahoma State University.