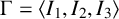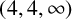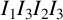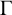1 Introduction
The purpose of this paper is to study the limit set of a discrete complex hyperbolic triangle group.
Recall that a complex hyperbolic
$(p, q, r)$
triangle group is a representation
$\rho $
of the abstract
$(p, q, r)$
reflection triangle group
$$ \begin{align*} \langle \sigma_1,\sigma_2,\sigma_3\ |\ \sigma_1^2=\sigma_2^2=\sigma_3^2=(\sigma_1\sigma_2)^p=(\sigma_2\sigma_3)^q=(\sigma_3\sigma_1)^r =\text{Id}\rangle \end{align*} $$
into
${\mathrm {PU}}(2,1)$
such that
$I_j=\rho (\sigma _j)$
are complex involutions, where
$2\leq p\leq q\leq r\leq \infty $
and
$1/p+1/q+1/r<1$
.
For a given triple
$(p,q,r)$
with
$p,q,r\geq 3$
, it is a classical fact that there is a
$1$
-parameter family
$\{\rho _t: t\in [0,\infty )\}$
of nonconjugate complex hyperbolic
$(p, q, r)$
triangle groups (see for example [Reference Pratoussevitch8]). Here
$\rho _0$
is the embedding of the hyperbolic reflection triangle group, that is, an
$\mathbb {R}$
-Fuchsian representation (preserving a Lagrangian plane of
${\mathbf {H}^{2}_{\mathbb {C}}}$
) and so the limit set is an
$\mathbb {R}$
-circle. In [Reference Schwartz and Li9], Schwartz conjectured that
$\rho _t$
is discrete and faithful if and only if neither
$w_A=I_1I_3I_2I_3$
nor
$w_B=I_1I_2I_3$
is elliptic. Moreover,
$\rho _t$
is discrete and faithful if and only if
$w_A$
is nonelliptic when
$p<10$
, or
$w_B$
is nonelliptic when
$p>13$
. For a discrete complex hyperbolic triangle group, it would be interesting to know its limit set.
In [Reference Schwartz10], Schwartz studied the limit set of the complex hyperbolic
$(4,4,4)$
triangle group with
$(I_1I_2I_1I_3)^7$
= Id.
Theorem 1.1 [Reference Schwartz10].
Let
$\langle I_1, I_2, I_3 \rangle $
be the complex hyperbolic
$(4,4,4)$
triangle group with
$I_1I_2I_1I_3$
being elliptic of order
$7$
. Let
$\Lambda $
be its limit set and
$\Omega $
its complement. Then
$\Lambda $
is connected and the closure of a countable union of
$\mathbb {R}$
-circles in
$\partial {\mathbf {H}^{2}_{\mathbb {C}}}$
. The quotient
$\Omega /\langle I_1I_2, I_2I_3 \rangle $
is a closed hyperbolic
$3$
-manifold.
Recently, in [Reference Acosta1], Acosta studied the limit set of the complex hyperbolic
$(3,3,6)$
triangle group with
$I_1I_3I_2I_3$
being unipotent.
Theorem 1.2 [Reference Acosta1].
Let
$\langle I_1, I_2, I_3 \rangle $
be the complex hyperbolic
$(3,3,6)$
triangle group with
$I_1I_3I_2I_3$
being unipotent. Let
$\Lambda $
be its limit set and
$\Omega $
its complement. Then
$\Lambda $
is connected and the closure of a countable union of
$\mathbb {R}$
-circles in
$\partial {\mathbf {H}^{2}_{\mathbb {C}}}$
, and contains a Hopf link with three components. The quotient
$\Omega /\langle I_1I_2, I_2I_3 \rangle $
is the one-cusped hyperbolic
$3$
-manifold m
$023$
in the SnapPy census.
In this paper, we are interested in describing the limit set of the complex hyperbolic
$(4,4,\infty )$
triangle group with
$I_1I_3I_2I_3$
being unipotent. The main result is the following theorem.
Theorem 1.3. Let
$\Lambda $
be the limit set of the complex hyperbolic
$(4,4,\infty )$
triangle group
$\langle I_1, I_2, I_3 \rangle $
with
$I_1I_3I_2I_3$
being unipotent. Then:
-
(1)
$\Lambda $
contains two linked
$\mathbb {R}$
-circles; -
(2)
$\Lambda $
is the closure of a countable union of
$\mathbb {R}$
-circles; -
(3)
$\Lambda $
is connected.
However, the quotient of the complement of the limit set has been described as follows.
Theorem 1.4 [Reference Jiang, Wang and Xie6].
Let
$\Omega $
be the discontinuity set of the complex hyperbolic
$(4,4,\infty )$
triangle group with
$I_1I_3I_2I_3$
being unipotent. Then the quotient
$\Omega /\langle I_1I_2, I_2I_3 \rangle $
is the two-cusped hyperbolic
$3$
-manifold s
$782$
in the SnapPy census.
2 Preliminaries
In this section, we briefly recall some basic facts and notation about the complex hyperbolic plane
${\mathbf {H}^{2}_{\mathbb {C}}}$
. We refer to Goldman’s book [Reference Goldman5] and Parker’s notes [Reference Parker7] for more details.
2.1 The space
${\mathbf {H}^{2}_{\mathbb {C}}}$
and its isometries
Let
$\mathbb {C}^{2,1}$
denote the three-dimensional complex vector space endowed with a Hermitian form H of signature
$(2,1)$
. We take H to be the matrix
$$ \begin{align*}H=\begin{bmatrix} 0 & 0 & 1\\ 0 & 1 & 0\\1 & 0 & 0 \end{bmatrix}.\end{align*} $$
The corresponding Hermitian form is given by
$$ \begin{align*} {\langle {\mathbf{z},\mathbf{w}}\rangle }=z_1\bar{w}_3+z_2\bar{w}_2+z_3\bar{w}_1.\end{align*} $$
Here
$\mathbf {z}=[ z_1,z_2,z_3]^t$
and
$\mathbf {w}=[w_1,w_2,w_3 ]^t$
are column vectors in
$\mathbb {C}^{2,1}\setminus \{0\}$
. Let
$\mathbb {P}:\mathbb {C}^{2,1}\setminus \{0\}\rightarrow \mathbb {CP}^2$
be the natural projection map onto complex projective space. Define
$$ \begin{align*} V_0 &=\{\mathbf{z}\in \mathbb{C}^{2,1}\setminus\{0\}:\langle\mathbf{z},\mathbf{z}\rangle=0\},\\ V_- &=\{\mathbf{z}\in \mathbb{C}^{2,1}: \langle\mathbf{z},\mathbf{z}\rangle<0\},\\ V_+ &=\{\mathbf{z}\in \mathbb{C}^{2,1}: \langle\mathbf{z},\mathbf{z}\rangle>0\}. \end{align*} $$
The complex hyperbolic plane
${\mathbf {H}^{2}_{\mathbb {C}}}$
is defined as
$\mathbb {P}V_-$
and its boundary
$\partial {\mathbf {H}^{2}_{\mathbb {C}}}$
is defined as
$\mathbb {P}V_0$
. We will denote the point at infinity by
$q_{\infty }$
. Note that a standard lift of
$q_{\infty }$
is
$[1,0,0]^t$
.
Topologically, the complex hyperbolic plane
${\mathbf {H}^{2}_{\mathbb {C}}}$
is homeomorphic to the unit ball of
$\mathbb {C}^2$
and its boundary
$\partial {\mathbf {H}^{2}_{\mathbb {C}}}$
is homeomorphic to the unit
$3$
-sphere
$S^3$
. Note that any point
$q\neq q_{\infty }$
of
${\mathbf {H}^{2}_{\mathbb {C}}}$
admits a standard lift
$\mathbf {q}$
given by
$$ \begin{align*}\mathbf{q}=\begin{bmatrix} (-{\lvert{z}\rvert}^2-u+it)/2 \\z \\1 \end{bmatrix},\end{align*} $$
where
$z\in \mathbb {C},t\in \mathbb {R}$
and
$u>0$
. Let
$\mathbb {R}_{\geq 0}=\{x\in \mathbb {R}:x\geq 0\}$
. Then the triple
$(z,t,u)\in \mathbb {C}\times \mathbb {R}\times \mathbb {R}_{\geq 0}$
is called the horospherical coordinates of q. Let
$\mathcal {N}=\mathbb {C}\times \mathbb {R}$
be the Heisenberg group with group law given by
$$ \begin{align*} [z_1,t_1]\cdot[z_2,t_2]=[z_1+z_2,t_1+t_2-2\,\text{Im}(\overline{z_1}z_2)]. \end{align*} $$
Then
$\partial {\mathbf {H}^{2}_{\mathbb {C}}}=\mathcal {N}\cup \{q_{\infty }\}$
.
Let
$\mathrm {U}(2,1)$
be the subgroup of
${\mathrm {GL}}(3,\mathbb {C})$
preserving the Hermitian form H. Let
${\mathrm {SU}}(2,1)$
be the subgroup of
$\mathrm {U}(2,1)$
consisting of unimodular matrices. The full group of holomorphic isometries of
${\mathbf {H}^{2}_{\mathbb {C}}}$
is
${\mathrm {PU}}(2,1)={\mathrm {SU}}(2,1)/\{\omega I: \omega ^3=1\}$
, which acts transitively on points of
${\mathbf {H}^{2}_{\mathbb {C}}}$
and pairs of distinct points of
$\partial {\mathbf {H}^{2}_{\mathbb {C}}}$
.
An element of
${\mathrm {PU}}(2,1)$
is called elliptic if it has a fixed point in
${\mathbf {H}^{2}_{\mathbb {C}}}$
. If an element is not elliptic, then it is called parabolic or loxodromic if it has exactly one fixed point in
$\partial {\mathbf {H}^{2}_{\mathbb {C}}}$
or exactly two fixed points in
$\partial {\mathbf {H}^{2}_{\mathbb {C}}}$
, respectively. A parabolic element of
${\mathrm {PU}}(2,1)$
is called unipotent if it admits a lift to
${\mathrm {SU}}(2,1)$
that is unipotent. These terms will also be used for elements of
${\mathrm {SU}}(2,1)$
.
2.2 Totally geodesic subspaces and related isometries
There is no totally geodesic subspace of real dimension three of
${\mathbf {H}^{2}_{\mathbb {C}}}$
. Except for the points, geodesics and
${\mathbf {H}^{2}_{\mathbb {C}}}$
(they are obviously totally geodesic), there are two kinds of totally geodesic subspaces of real dimension two: complex lines and Lagrangian planes. A complex line is the intersection of a projective line in
$\mathbb {C}\mathbb {P}^2$
with
${\mathbf {H}^{2}_{\mathbb {C}}}$
. The boundary of a complex line is called a
$\mathbb {C}$
-circle. A Lagrangian plane is the intersection of a totally real subspace in
$\mathbb {C}\mathbb {P}^2$
with
${\mathbf {H}^{2}_{\mathbb {C}}}$
. The boundary of a Lagrangian plane is called an
$\mathbb {R}$
-circle. In particular, if an
$\mathbb {R}$
-circle contains
$q_{\infty }=[1,0,0]^t$
, it is called an infinite
$\mathbb {R}$
-circle.
An elliptic isometry whose fixed point set is a complex line is called a complex reflection. The complex reflections we will use in this paper have order
$2$
and we call them complex involutions.
Similarly, every Lagrangian plane is the set of fixed points of an antiholomorphic isometry of order
$2$
, which is called a real reflection on the Lagrangian plane.
We will need the following lemma, which is [Reference Falbel and Zocca4, Proposition 3.1].
Proposition 2.1 [Reference Falbel and Zocca4].
If
$I_1$
and
$I_2$
are reflections on the
$\mathbb {R}$
-circles
$\mathcal {R}_1$
and
$\mathcal {R}_2$
:
-
(i)
$I_1\circ I_2$
is parabolic if and only if
$\mathcal {R}_1$
and
$\mathcal {R}_2$
intersect at one point; -
(ii)
$I_1\circ I_2$
is loxodromic if and only if
$\mathcal {R}_1$
and
$\mathcal {R}_2$
do not intersect and are not linked; -
(iii)
$I_1\circ I_2$
is elliptic if and only if
$\mathcal {R}_1$
and
$\mathcal {R}_2$
are linked or intersect at two points.
2.3 Limit set
Let
$\Gamma $
be a discrete subgroup of
$PU(2,1)$
. The limit set of
$\Gamma $
is defined as the set of accumulation points of any orbit in
${\mathbf {H}^{2}_{\mathbb {C}}}$
under the action of
$\Gamma $
. It is the smallest closed nonempty
$\Gamma $
-invariant subset of
$\partial {\mathbf {H}^{2}_{\mathbb {C}}}$
. The complement of the limit set of
$\Gamma $
in
$\partial {\mathbf {H}^{2}_{\mathbb {C}}}$
is called the discontinuity set of
$\Gamma $
.
3 The group
Let
$\omega =-1/2+i\sqrt {3}/2$
be the primitive cube root of unity. The complex involutions
$I_1$
,
$I_2$
and
$I_3$
are given by
$$ \begin{align*} I_1=\left[ \begin{array}{@{}ccc@{}} -1 & 2(1+\omega) & 2 \\ 0 & 1 & -2\omega \\ 0 & 0 & -1 \\ \end{array} \right], \quad I_2=\left[ \begin{array}{@{}ccc@{}} -1 & 2\omega & 2 \\ 0 & 1 & -2(1+\omega) \\ 0 & 0 & -1 \\ \end{array} \right], \quad I_3=\left[ \begin{array}{@{}ccc@{}} 0 & 0 & 1 \\ 0 & -1 & 0 \\ 1 & 0 & 0 \\ \end{array} \right]. \end{align*} $$
The products
$I_2I_3$
and
$I_3I_1$
are elliptic elements of order 4 and
$I_2I_1$
is unipotent. In fact,
$\langle I_1, I_2, I_3 \rangle $
is a discrete complex hyperbolic
$(4,4,\infty )$
triangle group. Moreover, the element
$I_1I_3I_2I_3$
is unipotent.
From Theorem 1.4, one can see that the group
$\langle I_1,I_2, I_3 \rangle $
is a subgroup of the Eisenstein–Picard modular group
$\mathrm {PU}(2,1;\mathbb {Z}[\omega ])$
of infinite index and has no fixed point. In [Reference Falbel and Parker3], Falbel and Parker studied the geometry of the Eisenstein–Picard modular group
$\mathrm {PU}(2,1;\mathbb {Z}[\omega ])$
. Moreover, they obtained a presentation of
$\mathrm {PU}(2,1;\mathbb {Z}[\omega ])$
.
Theorem 3.1 [Reference Falbel and Parker3].
The Eisenstein–Picard modular group
$\mathrm {PU}(2,1;\mathbb {Z}[\omega ])$
has a presentation
$$ \begin{align*} \langle P,Q,R \mid R^2=(QP^{-1})^6=PQ^{-1}RQP^{-1}R=P^3Q^{-2}=(RP)^3=1 \rangle, \end{align*} $$
where
$$ \begin{align*} P=\left[ \begin{array}{@{}ccc@{}} 1 & 1 & \omega \\ 0 & \omega & -\omega \\ 0 & 0 & 1 \\ \end{array} \right],\quad Q=\left[ \begin{array}{@{}ccc@{}} 1 & 1 & \omega \\ 0 & -1 & 1 \\ 0 & 0 & 1 \\ \end{array} \right], \quad R=\left[ \begin{array}{@{}ccc@{}} 0 & 0 & 1 \\ 0 & -1 & 0 \\ 1 & 0 & 0 \\ \end{array} \right]. \end{align*} $$
By using this presentation, the complex involutions
$I_1$
,
$I_2$
and
$I_3$
can be expressed as follows.
Proposition 3.2. Let
$M=PQ^{-1}$
and
$T=QM^3$
, then:
-
•
$I_2=-TQ^4T(PM^2)^{-2}M^3$
; -
•
$I_1=I_2T^2Q^2$
; -
•
$I_3=R$
.
4 The limit set
Lemma 4.1. Let
$G_0=\langle I_1,I_2,I_3I_2I_3 \rangle $
, as a subgroup of
$\langle I_1,I_2, I_3 \rangle $
. Let
$\mathcal {L}_0$
be the Lagrangian plane, whose boundary at infinity is the infinite
$\mathbb {R}$
-circle given by
$\mathcal {R}_0=\{[x+i\sqrt {3}/2,\sqrt {3}x-\sqrt {3}/2]\in \mathcal {N}: x\in \mathbb {R}\}\cup \{q_\infty \}$
. Then
$G_0$
preserves
$\mathcal {L}_0$
.
Proof. Using horospherical coordinates,
$$ \begin{align*}\mathcal{L}_0=\{(x+i\sqrt{3}/2,\sqrt{3}x-\sqrt{3}/2,u)\in{\mathbf{H}^{2}_{\mathbb{C}}}: x\in \mathbb{R},u>0\},\end{align*} $$
and one can compute
$$ \begin{align*}I_1(x+i\sqrt{3}/2,\sqrt{3}x-\sqrt{3}/2,u)&=(-x-1+i\sqrt{3}/2,\sqrt{3}(-x-1)-\sqrt{3}/2,u),\\I_2(x+i\sqrt{3}/2,\sqrt{3}x-\sqrt{3}/2,u)&=(-x+1+i\sqrt{3}/2,\sqrt{3}(-x+1)-\sqrt{3}/2,u), \end{align*} $$
$$ \begin{align*} &I_3I_2I_3(x+i\sqrt{3}/2,\sqrt{3}x-\sqrt{3}/2,u)\\ &\quad =\bigg( \frac{(x+1/2)^2-1+u}{2(x-1/2)^2+2u}+i\frac{\sqrt{3}}{2},\sqrt{3} \frac{(x+1/2)^2-1+u}{2(x-1/2)^2+2u} -\frac{\sqrt{3}}{2},\frac{u}{((x-1/2)^2+u)^2}\bigg). \end{align*} $$
Thus,
$I_1\mathcal {L}_0=I_2\mathcal {L}_0=I_3I_2I_3\mathcal {L}_0=\mathcal {L}_0$
. Therefore, the group
$G_0$
preserves the Lagrangian plane
$\mathcal {L}_0$
with boundary
$\mathcal {R}_0$
at infinity.
In the same way, we can prove the following result.
Lemma 4.2. Let
$G_1=\langle I_1, I_2, I_3I_1I_3 \rangle $
, as a subgroup of
$\langle I_1,I_2, I_3 \rangle $
. Let
$\mathcal {L}_1$
be the Lagrangian plane, whose boundary at infinity is the infinite
$\mathbb {R}$
-circle given by
$\mathcal {R}_1=\{[x+i\sqrt {3}/2,\sqrt {3}x+\sqrt {3}/2]\in \mathcal {N}: x\in \mathbb {R}\}\cup \{q_\infty \}$
. Then
$G_1$
preserves
$\mathcal {L}_1$
.
Proposition 4.3. The limit set of
$\langle I_1,I_2, I_3 \rangle $
contains an
$\mathbb {R}$
-circle.
Proof. By Lemma 4.1, the subgroup
$G_0=\langle I_1,I_2,I_3I_2I_3 \rangle $
is an
$\mathbb {R}$
-Fuchsian subgroup of
$\langle I_1,I_2, I_3 \rangle $
. Since
$I_1I_2$
and
$I_1I_3I_2I_3$
are unipotent and
$I_2I_3I_2I_3$
is elliptic of order 2, the restriction
$G_0|_{\mathcal {L}_0}$
is a
$(2,\infty ,\infty )$
-reflection triangle group. Thus, the limit set of
$G_0$
is
$\partial \mathcal {L}_0=\mathcal {R}_0$
. Therefore, the limit set of
$\langle I_1,I_2, I_3 \rangle $
contains the
$\mathbb {R}$
-circle
$\mathcal {R}_0$
.
Remark 4.4. The
$(2,\infty ,\infty )$
-reflection triangle group is a noncompact arithmetic triangle group [Reference Takeuchi11].
Now, let us consider the images of
$\mathcal {R}_0$
and
$\mathcal {R}_1$
by the group
$\langle I_1, I_2, I_3 \rangle $
. Since
$\mathcal {R}_0$
is the limit set of
$G_0$
, the image
$I_j \mathcal {R}_0$
, with
$j=1,2$
, is the limit set of the group
$I_j G_0 I_j$
. One can see that
$I_j G_0 I_j=G_0$
. Thus,
$\mathcal {R}_0$
is stabilised by both
$I_1$
and
$I_2$
. Similarly,
$\mathcal {R}_1$
is stabilised by both
$I_1$
and
$I_2$
.
Lemma 4.5. The limit sets
$I_3 \mathcal {R}_0$
and
$\mathcal {R}_0$
are linked and the limit sets
$I_3 \mathcal {R}_0$
and
$\mathcal {R}_1$
intersect at one point.
Proof. Since
$I_3 \mathcal {R}_0$
is the limit set of
$I_3G_0I_3=\langle I_3I_1I_3, I_3I_2I_3, I_2 \rangle $
, it contains the parabolic fixed point
$P_{I_2I_3I_1I_3}$
. Therefore,
$I_3\mathcal {R}_0\cap \mathcal {R}_1=\{P_{I_2I_3I_1I_3}\}$
.
Since both
$I_3 \mathcal {L}_0$
and
$\mathcal {L}_0$
contain the elliptic fixed point
$P_{I_2I_3I_2I_3}\in I_3\mathcal {L}_0\cap \mathcal {L}_0$
, the product of reflections on the Lagrangian planes
$I_3\mathcal {L}_0$
and
$\mathcal {L}_0$
is elliptic. Therefore, by Proposition 2.1, the two
$\mathbb {R}$
-circles
$I_3 \mathcal {R}_0$
and
$\mathcal {R}_0$
must be linked or intersect at two points.
We claim that
$I_3 \mathcal {R}_0$
and
$\mathcal {R}_0$
do not intersect. One can compute that the points of
$I_3 \mathcal {R}_0$
are given by
$$ \begin{align*}\bigg[ \frac{8(4x^3-3x+3)}{16x^4+72x^2-48x+21}+i\frac{4\sqrt{3}(12x^2-4x+3)}{16x^4+72x^2-48x+21},\frac{-32\sqrt{3}(2x-1)}{16x^4+72x^2-48x+21}\bigg].\end{align*} $$
Suppose that
$I_3 \mathcal {R}_0\cap \mathcal {R}_0\neq \emptyset $
, then
$$ \begin{align*} \frac{8(4x^3-3x+3)}{16x^4+72x^2-48x+21}+i\frac{4\sqrt{3}(12x^2-4x+3)}{16x^4+72x^2-48x+21}=x+i\sqrt{3}/2 \end{align*} $$
should have solutions for x. However, this is impossible by a simple computation. Thus,
$I_3 \mathcal {R}_0\cap \mathcal {R}_0=\emptyset $
. Therefore,
$I_3 \mathcal {R}_0$
and
$\mathcal {R}_0$
are linked.
Similarly, we have the following result.
Lemma 4.6. The limit sets
$I_3 \mathcal {R}_1$
and
$\mathcal {R}_1$
are linked and the limit sets
$I_3 \mathcal {R}_1$
and
$\mathcal {R}_0$
intersect at one point.
Corollary 4.7. The union of
$\mathcal {R}_i$
and
$I_3\mathcal {R}_i$
(
$i=0,1$
) is connected.
Proof. Since
$\mathcal {R}_0$
and
$\mathcal {R}_1$
are infinite
$\mathbb {R}$
-circles, we obtain
$\mathcal {R}_0\cap \mathcal {R}_1=\{q_{\infty }\}$
. From Lemmas 4.5 and 4.6,
$I_3\mathcal {R}_0\cap \mathcal {R}_1=\{P_{I_2I_3I_1I_3}\}$
and
$I_3 \mathcal {R}_1 \cap \mathcal {R}_0=\{P_{I_1I_3I_2I_3}\}$
. It is obvious that
$I_3\mathcal {R}_0\cap I_3\mathcal {R}_1=\{I_3q_{\infty }\}=[0,0]\in \mathcal {N}$
. Now, there is a path in
$\mathcal {R}_0\cup \mathcal {R}_1\cup I_3\mathcal {R}_0\cup I_3\mathcal {R}_1$
between any two points in it. Thus, the union is connected. See Figure 1.
Figure 1 A schematic view of the four
$\mathbb {R}$
-circles. Here
$\mathcal {R}_0$
and
$\mathcal {R}_1$
are two lines intersecting at infinity.
Proof of Theorem 1.3.
(1) This is a consequence of Lemmas 4.5 or 4.6.
(2) From Proposition 4.3, the limit set
$\Lambda $
contains an
$\mathbb {R}$
-circle. Then the
$\Gamma $
-orbit of the
$\mathbb {R}$
-circle is contained in
$\Lambda $
. Since
$\Lambda $
is the smallest closed nonempty invariant subset of
$\partial {\mathbf {H}^{2}_{\mathbb {C}}}$
under the action of
$\Gamma $
, it is the closure of the
$\Gamma $
-orbit of the
$\mathbb {R}$
-circle. Thus,
$\Lambda $
is the closure of a countable union of
$\mathbb {R}$
-circles.
(3) Let n be a positive integer and
$\gamma =\gamma _1\gamma _2\cdots \gamma _n\in \Gamma $
, where
$\gamma _i\in \{I_1,I_2,I_3\}$
for
$i=1,\ldots ,n$
. Let
$\mathcal {U}_0=\mathcal {R}_0\cup \mathcal {R}_1$
and
$\mathcal {U}_i=\gamma _1\cdots \gamma _i\mathcal {U}_0$
. Since
$\mathcal {R}_0\cap \mathcal {R}_1=\{q_{\infty }\}$
, the subset
$\mathcal {U}_i$
of
$\Lambda $
is connected for
$i=0,1,\ldots ,n$
. For
$i\in \{0,1,\ldots ,n-1\}$
, we see that
$$ \begin{align*}\mathcal{U}_i\cap\mathcal{U}_{i+1}=\gamma_1\cdots\gamma_i\mathcal{U}_0\cap\gamma_1\cdots\gamma_{i+1}\mathcal{U}_0=\gamma_1\cdots\gamma_i(\mathcal{U}_0\cap\gamma_{i+1}\mathcal{U}_0).\end{align*} $$
By Lemmas 4.5 and 4.6,
$\mathcal {U}_0\cap \gamma _{i+1}\mathcal {U}_0\neq \emptyset $
, so
$\mathcal {U}_i\cap \mathcal {U}_{i+1}\neq \emptyset $
. Thus, there is a path in
$\Lambda $
from
$q_{\infty }$
to
$\gamma q_{\infty }$
. From item
$(2)$
,
$\Lambda $
is the closure of the
$\Gamma $
-orbit of an
$\mathbb {R}$
-circle. Hence,
$\Lambda $
is connected.
Remark 4.8. We note that
$\Lambda $
is not slim (see [Reference Falbel, Guilloux and Will2] for the definition). In other words, there are three distinct points of
$\Lambda $
lying in the same
$\mathbb {C}$
-circle.
Acknowledgement
We would like to thank the referee for comments which improved a previous version of this paper.
