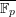1 Introduction
Although the theory of (mixed) motives has in recent years made significant progress, especially in regards to motivic sheaves (i.e. motives over general schemes), our understanding of motives over a field is still limited. It is therefore natural to restrict one’s attention to certain subclasses of motives in order to gain some intuition. One subclass, which has proven particularly fruitful for that purpose, is the class of (mixed) Tate motives. These are the motives that can be constructed from the simple building blocks
![]() $\mathbb{Z}(n)$
(the ‘Tate twists’,
$\mathbb{Z}(n)$
(the ‘Tate twists’,
![]() $n\in \mathbb{Z}$
) by extensions, (de)suspensions, and direct summands. Another view is that they encode the motivic cohomology of the base field. As should be clear from these two descriptions, Tate motives are at the same time relatively simple (compared to the class of all motives), and yet contain complex and interesting information. A striking illustration of the latter fact is their role in the theory of periods, particularly their relation to multiple zeta values, as explained in [Reference Deligne and GoncharovDG05, Reference TerasomaTer02, Reference BrownBro12].
$n\in \mathbb{Z}$
) by extensions, (de)suspensions, and direct summands. Another view is that they encode the motivic cohomology of the base field. As should be clear from these two descriptions, Tate motives are at the same time relatively simple (compared to the class of all motives), and yet contain complex and interesting information. A striking illustration of the latter fact is their role in the theory of periods, particularly their relation to multiple zeta values, as explained in [Reference Deligne and GoncharovDG05, Reference TerasomaTer02, Reference BrownBro12].
One long strand of research into Tate motives has been concerned with uncovering the structural properties of the category of Tate motives, with some success (e.g. [Reference BlochBlo91, Reference Bloch and KřížBK94, Reference Levine and GoerssLev92, Reference Kříž and MayKM95, Reference PositselskiPos11, Reference WildeshausWil09, Reference IwanariIwa14]). The motivation for the present paper is to advance in this direction, by focusing on the particular properties visible to tensor triangular geometry. Indeed, Tate motives form a triangulated category with a compatible tensor structure (a tt-category for short), and one may try to classify its tt-ideals, i.e. its thick subcategories closed under tensor products with arbitrary Tate motives. The classification of tt-ideals gives insights into the composition and complexity of the tt-category; if two objects generate different tt-ideals, this means that they cannot be constructed out of each other using extensions, (de)suspensions, tensor products, and direct summands: they are quite far from being ‘the same’.
The main device in tt-geometry is Balmer’s tt-spectrum [Reference BalmerBal05], a spectral space associated to the tt-category which encodes the (radical) tt-ideals through its topology. For a number of classical mathematical domains, the tt-spectrum has been studied; we refer to [Reference BalmerBal10b] for an overview of the basic theory, its early successes and applications. In relation to the present article, there has been earlier work on the tt-spectrum of certain motives (including Tate motives) [Reference PeterPet13, Reference KellyKel16]. However, the arguments were restricted to rational coefficients (and certain base fields) so that the tt-spectrum turned out to be a singleton space. In other words, in these categories every object can be constructed from every other (non-zero) object.
In contrast, here we work with integral coefficients and find non-trivial tt-spectra. In particular, we determine completely the tt-spectrum of Tate motives over the algebraic numbers (for more general base fields see Theorem 8.6 and Corollary 9.3).
Theorem 1. The tt-spectrum of
![]() $\text{DTM}_{\text{gm}}(\overline{\mathbb{Q}},\mathbb{Z})$
consists of the following points, with specialization relations, depicted by the lines, going upward.
$\text{DTM}_{\text{gm}}(\overline{\mathbb{Q}},\mathbb{Z})$
consists of the following points, with specialization relations, depicted by the lines, going upward.

Here,
![]() $\ell$
runs through all prime numbers, and the points are defined by the vanishing of the cohomology theories as indicated on the right. Moreover, the proper closed subsets are precisely the finite subsets stable under specialization.
$\ell$
runs through all prime numbers, and the points are defined by the vanishing of the cohomology theories as indicated on the right. Moreover, the proper closed subsets are precisely the finite subsets stable under specialization.
From this result we easily deduce a classification of the tt-ideals in
![]() $\text{DTM}_{\text{gm}}(\overline{\mathbb{Q}},\mathbb{Z})$
(see Theorem 9.5).
$\text{DTM}_{\text{gm}}(\overline{\mathbb{Q}},\mathbb{Z})$
(see Theorem 9.5).
Given that motives are supposed to encode the cohomological aspects of algebraic varieties, it is of course not surprising that the tt-spectrum above contains points coming from the different cohomology theories available. But it is reassuring to find that all points are of this form, lending some support to the belief that motives are the universal cohomology theory. (Having said that, it would be very interesting to find non-expected points as these could hint at cohomology theories not yet discovered, or other more mysterious phenomena.)
In order to generalize from rational to integral coefficients we need to understand, in particular, the case of finite coefficients. The following is our result in that direction (cf. Corollary 8.3).
Theorem 2. Let
![]() $\mathbb{F}$
be an algebraically closed field, and
$\mathbb{F}$
be an algebraically closed field, and
![]() $\ell$
a prime number invertible in
$\ell$
a prime number invertible in
![]() $\mathbb{F}$
. The tt-spectrum of
$\mathbb{F}$
. The tt-spectrum of
![]() $\text{DTM}_{\text{gm}}(\mathbb{F},\mathbb{Z}/\ell )$
is canonically isomorphic to the homogeneous spectrum of the polynomial ring in one variable
$\text{DTM}_{\text{gm}}(\mathbb{F},\mathbb{Z}/\ell )$
is canonically isomorphic to the homogeneous spectrum of the polynomial ring in one variable
![]() $\mathbb{Z}/\ell [\unicode[STIX]{x1D6FD}]$
.
$\mathbb{Z}/\ell [\unicode[STIX]{x1D6FD}]$
.
In the proof of this theorem we use on the one hand Positselski’s description of Tate motives in terms of filtered Galois representations [Reference PositselskiPos11], and on the other hand our study of the tt-geometry of filtered modules in [Reference GallauerGal18]. Some of Balmer’s new results in tt-geometry [Reference BalmerBal18] allow us then to patch our findings together with the findings for rational coefficients by Peter [Reference PeterPet13], to determine the underlying set of the tt-spectrum in Theorem 1.
Some interesting properties of Tate motives turn out to be encoded in the tt-spectrum in a slightly subtle way. Indeed, the topology of the tt-spectrum reflects the conservativity of the
![]() $\ell$
-adic realization as well as the fact that the motivic cohomology of (Tate) motives behaves like a finitely generated abelian group (see Remark 5.7).
$\ell$
-adic realization as well as the fact that the motivic cohomology of (Tate) motives behaves like a finitely generated abelian group (see Remark 5.7).
The theory of étale motives is closely related to the theory of motives. For example, the two theories coincide with rational coefficients. We study étale motives both for their own interest, and because we will use the comparison of the two theories to bear on our understanding of Tate motives. This works because with finite coefficients the étale theory is much simpler: the rigidity theorem of Suslin and Voevodsky identifies étale motives with Galois representations. We will use this result together with Rost, Voevodsky, and others’ resolution of the Bloch–Kato conjecture to confirm this simplicity in tt-geometric terms (cf. Theorem 6.2).
Theorem 3. Let
![]() $\mathbb{F}$
be a field, and
$\mathbb{F}$
be a field, and
![]() $\ell$
a prime number invertible in
$\ell$
a prime number invertible in
![]() $\mathbb{F}$
. Assume that
$\mathbb{F}$
. Assume that
![]() $\mathbb{F}$
contains a primitive
$\mathbb{F}$
contains a primitive
![]() $\ell$
th root of unity (respectively, primitive
$\ell$
th root of unity (respectively, primitive
![]() $4$
th root of unity if
$4$
th root of unity if
![]() $\ell =2$
). Then the tt-spectrum of
$\ell =2$
). Then the tt-spectrum of
![]() $\text{DM}_{\text{gm}}^{\acute{\text{e}}\text{t}}(\mathbb{F},\mathbb{Z}/\ell )$
has a single point.
$\text{DM}_{\text{gm}}^{\acute{\text{e}}\text{t}}(\mathbb{F},\mathbb{Z}/\ell )$
has a single point.
When the tt-category is rigid, i.e. every object has a strong tensor dual, then the tt-spectrum can be endowed with a natural structure sheaf turning it into a locally ringed space. This has been used by Balmer to, for example, recover a topologically noetherian scheme from its category of perfect complexes [Reference BalmerBal05, 6.3]. Over fields such as the algebraic numbers, where we know the underlying topological space of the tt-spectrum of Tate motives completely by Theorem 1, we will describe this sheaf explicitly (cf. Proposition 10.2). To do so we need to understand the category one obtains from Tate motives by inverting the image of the Bott elements
![]() $\unicode[STIX]{x1D6FD}:\mathbb{Z}/\ell (0)\rightarrow \mathbb{Z}/\ell (1)$
appearing in Theorem 2 (it amounts to the choice of a primitive
$\unicode[STIX]{x1D6FD}:\mathbb{Z}/\ell (0)\rightarrow \mathbb{Z}/\ell (1)$
appearing in Theorem 2 (it amounts to the choice of a primitive
![]() $\ell$
th root of unity). It has been shown by Haesemeyer and Hornbostel in [Reference Hasemeyer and HornbostelHH05] that (under some assumptions on the base field), by inverting motives with finite coefficients with respect to the Bott element one obtains étale motives. We will upgrade this result to integral coefficients (cf. Theorem C.4).
$\ell$
th root of unity). It has been shown by Haesemeyer and Hornbostel in [Reference Hasemeyer and HornbostelHH05] that (under some assumptions on the base field), by inverting motives with finite coefficients with respect to the Bott element one obtains étale motives. We will upgrade this result to integral coefficients (cf. Theorem C.4).
Theorem 4. Let
![]() $\mathbb{F}$
be a field of exponential characteristic
$\mathbb{F}$
be a field of exponential characteristic
![]() $p$
, containing all roots of unity of order coprime to
$p$
, containing all roots of unity of order coprime to
![]() $p$
, and of finite
$p$
, and of finite
![]() $\ell$
-cohomological dimension for all primes
$\ell$
-cohomological dimension for all primes
![]() $\ell \neq p$
. Then there are canonical equivalences of tt-categories
$\ell \neq p$
. Then there are canonical equivalences of tt-categories
The same result holds for the effective versions.
2 Conventions
Our conventions regarding tensor triangular geometry mostly follow those of [Reference BalmerBal05, Reference BalmerBal10a]. A tensor triangulated category (or tt-category for short) is a triangulated category with a compatible (symmetric, unital) tensor structure. If not specified otherwise, the tensor product is denoted by
![]() $\otimes$
and the unit by
$\otimes$
and the unit by
![]() $\unicode[STIX]{x1D7D9}$
. A tt-functor is an exact tensor functor between tt-categories.
$\unicode[STIX]{x1D7D9}$
. A tt-functor is an exact tensor functor between tt-categories.
A tt-ideal in a tt-category
![]() ${\mathcal{T}}$
is a thick subcategory
${\mathcal{T}}$
is a thick subcategory
![]() ${\mathcal{I}}\subset {\mathcal{T}}$
such that
${\mathcal{I}}\subset {\mathcal{T}}$
such that
![]() ${\mathcal{T}}\otimes {\mathcal{I}}\subset {\mathcal{I}}$
. If
${\mathcal{T}}\otimes {\mathcal{I}}\subset {\mathcal{I}}$
. If
![]() $S$
is a set of objects in
$S$
is a set of objects in
![]() ${\mathcal{T}}$
we denote by
${\mathcal{T}}$
we denote by
![]() $\langle S\rangle$
the tt-ideal generated by
$\langle S\rangle$
the tt-ideal generated by
![]() $S$
. To a small tt-category
$S$
. To a small tt-category
![]() ${\mathcal{T}}$
one associates a ringed space
${\mathcal{T}}$
one associates a ringed space
![]() $\operatorname{Spec}({\mathcal{T}})$
, called the tt-spectrum of
$\operatorname{Spec}({\mathcal{T}})$
, called the tt-spectrum of
![]() ${\mathcal{T}}$
, whose underlying topological space is denoted by
${\mathcal{T}}$
, whose underlying topological space is denoted by
![]() $\operatorname{Spc}({\mathcal{T}})$
. It is a spectral space and consists of prime ideals in
$\operatorname{Spc}({\mathcal{T}})$
. It is a spectral space and consists of prime ideals in
![]() ${\mathcal{T}}$
, i.e. proper tt-ideals
${\mathcal{T}}$
, i.e. proper tt-ideals
![]() ${\mathcal{I}}$
such that
${\mathcal{I}}$
such that
![]() $a\otimes b\in {\mathcal{I}}$
implies
$a\otimes b\in {\mathcal{I}}$
implies
![]() $a\in {\mathcal{I}}$
or
$a\in {\mathcal{I}}$
or
![]() $b\in {\mathcal{I}}$
. A base for the closed subsets of the topology is given by the supports
$b\in {\mathcal{I}}$
. A base for the closed subsets of the topology is given by the supports
![]() $\operatorname{supp}(a)$
of objects
$\operatorname{supp}(a)$
of objects
![]() $a\in {\mathcal{T}}$
; here,
$a\in {\mathcal{T}}$
; here,
![]() $\operatorname{supp}(a)=\{\mathfrak{P}\mid a\notin \mathfrak{P}\}$
. The complement of
$\operatorname{supp}(a)=\{\mathfrak{P}\mid a\notin \mathfrak{P}\}$
. The complement of
![]() $\operatorname{supp}(a)$
is denoted by
$\operatorname{supp}(a)$
is denoted by
![]() $U(a)$
. If
$U(a)$
. If
![]() ${\mathcal{T}}$
is rigid then
${\mathcal{T}}$
is rigid then
![]() $\operatorname{Spec}({\mathcal{T}})$
is a locally ringed space.Footnote
1
$\operatorname{Spec}({\mathcal{T}})$
is a locally ringed space.Footnote
1
All rings are commutative with unit, and morphisms of rings are unital. For
![]() $R$
a ring, we denote by
$R$
a ring, we denote by
![]() $\operatorname{Spec}(R)$
the Zariski spectrum of
$\operatorname{Spec}(R)$
the Zariski spectrum of
![]() $R$
(considered as a locally ringed space) whereas
$R$
(considered as a locally ringed space) whereas
![]() $\operatorname{Spc}(R)$
denotes its underlying topological space (as for the tt-spectrum). We adopt similar conventions regarding graded rings
$\operatorname{Spc}(R)$
denotes its underlying topological space (as for the tt-spectrum). We adopt similar conventions regarding graded rings
![]() $R$
: they are commutative in a general graded sense [Reference BalmerBal10a, 3.4], and possess a unit.
$R$
: they are commutative in a general graded sense [Reference BalmerBal10a, 3.4], and possess a unit.
![]() $\operatorname{Spec}^{\text{h}}(R)$
denotes the homogeneous (Zariski) spectrum with underlying topological space
$\operatorname{Spec}^{\text{h}}(R)$
denotes the homogeneous (Zariski) spectrum with underlying topological space
![]() $\operatorname{Spc}^{\text{h}}(R)$
. This differs from
$\operatorname{Spc}^{\text{h}}(R)$
. This differs from
![]() $\text{Proj}(R)$
in that the prime ideals making up the underlying space may contain the irrelevant ideal in
$\text{Proj}(R)$
in that the prime ideals making up the underlying space may contain the irrelevant ideal in
![]() $R$
. It is still a spectral space though.
$R$
. It is still a spectral space though.
Recall also that Balmer constructs [Reference BalmerBal10a] comparison maps between the tt-spectrum and certain Zariski spectra. Explicitly, there is a canonical spectral morphism
![]() $\unicode[STIX]{x1D70C}:\operatorname{Spec}({\mathcal{T}})\rightarrow \operatorname{Spec}({\mathcal{R}}_{{\mathcal{T}}})$
, where
$\unicode[STIX]{x1D70C}:\operatorname{Spec}({\mathcal{T}})\rightarrow \operatorname{Spec}({\mathcal{R}}_{{\mathcal{T}}})$
, where
![]() ${\mathcal{R}}_{{\mathcal{T}}}=\operatorname{End}_{{\mathcal{T}}}(\unicode[STIX]{x1D7D9})$
denotes the endomorphism ring of the unit in
${\mathcal{R}}_{{\mathcal{T}}}=\operatorname{End}_{{\mathcal{T}}}(\unicode[STIX]{x1D7D9})$
denotes the endomorphism ring of the unit in
![]() ${\mathcal{T}}$
, called the central ring. More generally, fixing an invertible object
${\mathcal{T}}$
, called the central ring. More generally, fixing an invertible object
![]() $u\in {\mathcal{T}}$
, he considers the graded central ring
$u\in {\mathcal{T}}$
, he considers the graded central ring
![]() ${\mathcal{R}}_{{\mathcal{T}}}^{\bullet }=\hom _{{\mathcal{T}}}(\unicode[STIX]{x1D7D9},u^{\otimes \bullet })$
. There is then a canonical spectral morphism
${\mathcal{R}}_{{\mathcal{T}}}^{\bullet }=\hom _{{\mathcal{T}}}(\unicode[STIX]{x1D7D9},u^{\otimes \bullet })$
. There is then a canonical spectral morphism
![]() $\unicode[STIX]{x1D70C}^{\bullet }:\operatorname{Spec}({\mathcal{T}})\rightarrow \operatorname{Spec}^{\text{h}}({\mathcal{R}}_{{\mathcal{T}}}^{\bullet })$
, given by
$\unicode[STIX]{x1D70C}^{\bullet }:\operatorname{Spec}({\mathcal{T}})\rightarrow \operatorname{Spec}^{\text{h}}({\mathcal{R}}_{{\mathcal{T}}}^{\bullet })$
, given by
The map
![]() $\unicode[STIX]{x1D70C}$
is just the restriction of
$\unicode[STIX]{x1D70C}$
is just the restriction of
![]() $\unicode[STIX]{x1D70C}^{\bullet }$
to the degree 0 part. We will repeatedly use the fact that
$\unicode[STIX]{x1D70C}^{\bullet }$
to the degree 0 part. We will repeatedly use the fact that
![]() $\unicode[STIX]{x1D70C}$
(respectively,
$\unicode[STIX]{x1D70C}$
(respectively,
![]() $\unicode[STIX]{x1D70C}^{\bullet }$
) is a homeomorphism if and only if it is an isomorphism of locally ringed spaces [Reference BalmerBal10a, 6.11].
$\unicode[STIX]{x1D70C}^{\bullet }$
) is a homeomorphism if and only if it is an isomorphism of locally ringed spaces [Reference BalmerBal10a, 6.11].
3 Triangulated category of (Tate) motives
Fix a ring
![]() $R$
and a field
$R$
and a field
![]() $\mathbb{F}$
. In these two preliminary sections (§§ 3 and 4) we are going to recall some generalities on categories of motives over
$\mathbb{F}$
. In these two preliminary sections (§§ 3 and 4) we are going to recall some generalities on categories of motives over
![]() $\mathbb{F}$
with coefficients in
$\mathbb{F}$
with coefficients in
![]() $R$
. Many of the constructions and proofs go back to work of Voevodsky, Suslin, Bloch, Levine, and many others. Our discussion will be too brief for some: we recommend [Reference VoevodskyVoe00, Reference Mazza, Voevodsky and WeibelMVW06] as introductions instead. As the main reference for this section we will use [Reference Cisinski and DégliseCD12].
$R$
. Many of the constructions and proofs go back to work of Voevodsky, Suslin, Bloch, Levine, and many others. Our discussion will be too brief for some: we recommend [Reference VoevodskyVoe00, Reference Mazza, Voevodsky and WeibelMVW06] as introductions instead. As the main reference for this section we will use [Reference Cisinski and DégliseCD12].
There is a (large) tt-category of ‘big’ motives
![]() $\text{DM}(\mathbb{F},R)$
[Reference Cisinski and DégliseCD12, 11.1.1, 11.1.2] constructed from the derived category of Nisnevich sheaves with transfers of
$\text{DM}(\mathbb{F},R)$
[Reference Cisinski and DégliseCD12, 11.1.1, 11.1.2] constructed from the derived category of Nisnevich sheaves with transfers of
![]() $R$
-modules on the category
$R$
-modules on the category
![]() $\text{Sm}/\mathbb{F}$
of smooth (finite type, separated)
$\text{Sm}/\mathbb{F}$
of smooth (finite type, separated)
![]() $\mathbb{F}$
-schemes. In particular, it comes with an ‘associated motive’ functor
$\mathbb{F}$
-schemes. In particular, it comes with an ‘associated motive’ functor
The tensor structure on
![]() $\text{DM}(\mathbb{F},R)$
is determined by two facts.
$\text{DM}(\mathbb{F},R)$
is determined by two facts.
∙ The functor
 $R(-)$
is symmetric unital monoidal (also with respect to transfers), for example,
$R(-)$
is symmetric unital monoidal (also with respect to transfers), for example,
 $R(X\times _{\operatorname{Spec}\mathbb{F}}Y)=R(X)\otimes R(Y)$
, and
$R(X\times _{\operatorname{Spec}\mathbb{F}}Y)=R(X)\otimes R(Y)$
, and
 $R(\operatorname{Spec}(\mathbb{F}))=:R(0)$
is the unit. (If the context allows we will write simply
$R(\operatorname{Spec}(\mathbb{F}))=:R(0)$
is the unit. (If the context allows we will write simply
 $R$
for
$R$
for
 $R(0)$
.)
$R(0)$
.)∙ The reduced motive of
 $\mathbb{P}_{\mathbb{F}}^{1}$
, denoted by
$\mathbb{P}_{\mathbb{F}}^{1}$
, denoted by
 $R(1)[2]$
, is (
$R(1)[2]$
, is (
 $\otimes$
-)invertible. One then gets for any integer
$\otimes$
-)invertible. One then gets for any integer
 $n$
an invertible
$n$
an invertible
 $R(n)$
, called the Tate twist of weight
$R(n)$
, called the Tate twist of weight
 $n$
. Clearly,
$n$
. Clearly,
 $R(i)\otimes R(j)=R(i+j)$
, and the dual of
$R(i)\otimes R(j)=R(i+j)$
, and the dual of
 $R(i)$
is
$R(i)$
is
 $R(-i)$
.
$R(-i)$
.
The triangulated category
![]() $\text{DM}(\mathbb{F},R)$
is compactly generated, and a set of compact generators is given by the motives of smooth
$\text{DM}(\mathbb{F},R)$
is compactly generated, and a set of compact generators is given by the motives of smooth
![]() $\mathbb{F}$
-schemes [Reference Cisinski and DégliseCD12, 11.1.6]. In fact, in a sense one can make precise,
$\mathbb{F}$
-schemes [Reference Cisinski and DégliseCD12, 11.1.6]. In fact, in a sense one can make precise,
![]() $\text{DM}(\mathbb{F},R)$
is generated by
$\text{DM}(\mathbb{F},R)$
is generated by
![]() $R(X)$
(
$R(X)$
(
![]() $X$
runs through smooth
$X$
runs through smooth
![]() $\mathbb{F}$
-schemes) and
$\mathbb{F}$
-schemes) and
![]() $R(-1)$
, subject to Nisnevich descent and the relations
$R(-1)$
, subject to Nisnevich descent and the relations
![]() $R(1)\otimes R(-1)=R(0)$
,
$R(1)\otimes R(-1)=R(0)$
,
![]() $R(\mathbb{A}_{\mathbb{F}}^{1})=R(0)$
. We denote the subcategory of compact objects by
$R(\mathbb{A}_{\mathbb{F}}^{1})=R(0)$
. We denote the subcategory of compact objects by
![]() $\text{DM}_{\text{gm}}(\mathbb{F},R)$
. Its objects are often called geometric motives, or just motives if no confusion with big motives is possible (or if the distinction in the given context is immaterial). By what was said above,
$\text{DM}_{\text{gm}}(\mathbb{F},R)$
. Its objects are often called geometric motives, or just motives if no confusion with big motives is possible (or if the distinction in the given context is immaterial). By what was said above,
![]() $\text{DM}_{\text{gm}}(\mathbb{F},R)$
is the thick subcategory generated by
$\text{DM}_{\text{gm}}(\mathbb{F},R)$
is the thick subcategory generated by
![]() $R(X)(n):=R(X)\otimes R(n)$
, where
$R(X)(n):=R(X)\otimes R(n)$
, where
![]() $X$
is a smooth
$X$
is a smooth
![]() $\mathbb{F}$
-scheme and
$\mathbb{F}$
-scheme and
![]() $n\in \mathbb{Z}$
. It is a (small) idempotent complete tt-category. Moreover, it is rigid if the exponential characteristicFootnote
2
of
$n\in \mathbb{Z}$
. It is a (small) idempotent complete tt-category. Moreover, it is rigid if the exponential characteristicFootnote
2
of
![]() $\mathbb{F}$
is invertible in
$\mathbb{F}$
is invertible in
![]() $R$
[Reference KellyKel17, 5.3.18], [Reference Cisinski and DégliseCD15, 8.1]. (Conjecturally, rigidity also holds without inverting the exponential characteristic as shown in [Reference VoevodskyVoe00].)
$R$
[Reference KellyKel17, 5.3.18], [Reference Cisinski and DégliseCD15, 8.1]. (Conjecturally, rigidity also holds without inverting the exponential characteristic as shown in [Reference VoevodskyVoe00].)
The triangulated category of Tate motives is the thick subcategory generated by the Tate twists
![]() $R(n)$
,
$R(n)$
,
![]() $n\in \mathbb{Z}$
. It is denoted by
$n\in \mathbb{Z}$
. It is denoted by
![]() $\text{DTM}_{\text{gm}}(\mathbb{F},R)$
. It is a (small) rigid, idempotent complete tt-category. There is also a ‘big’ version:
$\text{DTM}_{\text{gm}}(\mathbb{F},R)$
. It is a (small) rigid, idempotent complete tt-category. There is also a ‘big’ version:
![]() $\text{DTM}(\mathbb{F},R)$
denotes the localizing subcategory of
$\text{DTM}(\mathbb{F},R)$
denotes the localizing subcategory of
![]() $\text{DM}(\mathbb{F},R)$
generated by Tate twists. It is a (large) tt-category.
$\text{DM}(\mathbb{F},R)$
generated by Tate twists. It is a (large) tt-category.
Given a ring morphism
![]() $R\rightarrow R^{\prime }$
, one can associate to a Nisnevich sheaf with transfers of
$R\rightarrow R^{\prime }$
, one can associate to a Nisnevich sheaf with transfers of
![]() $R$
-modules
$R$
-modules
![]() $F$
the sheafification of
$F$
the sheafification of
![]() $X\mapsto F(X)\otimes _{R}R^{\prime }$
, a Nisnevich sheaf with transfers of
$X\mapsto F(X)\otimes _{R}R^{\prime }$
, a Nisnevich sheaf with transfers of
![]() $R^{\prime }$
-modules. This induces an adjunction
$R^{\prime }$
-modules. This induces an adjunction
the right adjoint being induced by forgetting the
![]() $R^{\prime }$
-structure. The functor
$R^{\prime }$
-structure. The functor
![]() $\unicode[STIX]{x1D6FE}_{\ast }$
is conservative (see the proof of [Reference AyoubAyo14b, A.6] or [Reference Cisinski and DégliseCD16, 5.4.2]), and for any motive
$\unicode[STIX]{x1D6FE}_{\ast }$
is conservative (see the proof of [Reference AyoubAyo14b, A.6] or [Reference Cisinski and DégliseCD16, 5.4.2]), and for any motive
![]() $M\in \text{DM}(\mathbb{F},R)$
, we have
$M\in \text{DM}(\mathbb{F},R)$
, we have
![]() $\unicode[STIX]{x1D6FE}_{\ast }\unicode[STIX]{x1D6FE}^{\ast }(M)=M\otimes R^{\prime }$
, where
$\unicode[STIX]{x1D6FE}_{\ast }\unicode[STIX]{x1D6FE}^{\ast }(M)=M\otimes R^{\prime }$
, where
![]() $R^{\prime }$
is the constant sheaf associated to
$R^{\prime }$
is the constant sheaf associated to
![]() $R^{\prime }$
, considered as an object in
$R^{\prime }$
, considered as an object in
![]() $\text{DM}(\mathbb{F},R)$
. The tt-functor
$\text{DM}(\mathbb{F},R)$
. The tt-functor
![]() $\unicode[STIX]{x1D6FE}^{\ast }$
sends
$\unicode[STIX]{x1D6FE}^{\ast }$
sends
![]() $R(X)(n)$
to
$R(X)(n)$
to
![]() $R^{\prime }(X)(n)$
and therefore restricts to tt-functors
$R^{\prime }(X)(n)$
and therefore restricts to tt-functors
If
![]() $R^{\prime }$
is a perfect
$R^{\prime }$
is a perfect
![]() $R$
-module (i.e.
$R$
-module (i.e.
![]() $R^{\prime }\in \text{D}^{\text{perf}}(R)$
) then the right adjoint
$R^{\prime }\in \text{D}^{\text{perf}}(R)$
) then the right adjoint
![]() $\unicode[STIX]{x1D6FE}_{\ast }$
also preserves compact objects.
$\unicode[STIX]{x1D6FE}_{\ast }$
also preserves compact objects.
The hom sets in the triangulated category of motives are closely related to important algebraic geometric invariants. Specifically, for a smooth
![]() $\mathbb{F}$
-scheme
$\mathbb{F}$
-scheme
![]() $X$
and integers
$X$
and integers
![]() $m,n$
, the groups
$m,n$
, the groups
are the motivic cohomology groups of
![]() $X$
with coefficients in
$X$
with coefficients in
![]() $R$
. There is a canonical identification [Reference VoevodskyVoe02],
$R$
. There is a canonical identification [Reference VoevodskyVoe02],
with a direct generalization of Chow groups, called Bloch’s higher Chow groups, thereby linking motivic cohomology to algebraic cycles. In particular, the motivic cohomology groups of
![]() $\operatorname{Spec}(\mathbb{F})$
on the ‘diagonal’ are canonically isomorphic to Milnor
$\operatorname{Spec}(\mathbb{F})$
on the ‘diagonal’ are canonically isomorphic to Milnor
![]() $K$
-theory [Reference TotaroTot92, Reference Nesterenko and SuslinNS89]:
$K$
-theory [Reference TotaroTot92, Reference Nesterenko and SuslinNS89]:
More generally, we define for any motive
![]() $M\in \text{DM}(\mathbb{F},R)$
and any ring
$M\in \text{DM}(\mathbb{F},R)$
and any ring
![]() $R^{\prime }$
over
$R^{\prime }$
over
![]() $R$
,
$R$
,
the motivic cohomology groups of
![]() $M$
with coefficients in
$M$
with coefficients in
![]() $R^{\prime }$
.
$R^{\prime }$
.
4 Triangulated category of étale (Tate) motives
We want to discuss étale versions of the constructions in the previous section. Thus instead of Nisnevich sheaves with transfers we consider étale sheaves with transfers. Our main references for this section are [Reference Ayoub, Jang, Kim, Lee and YieAyo14a, Reference AyoubAyo14b, Reference Cisinski and DégliseCD16].
There is a (large) tt-category of ‘big’ étale motives
![]() $\text{DM}^{\acute{\text{e}}\text{t}}(\mathbb{F},R)$
[Reference Ayoub, Jang, Kim, Lee and YieAyo14a, §4.1.1], [Reference Cisinski and DégliseCD16, 2.2.4] constructed from the derived category of étale sheaves with transfers of
$\text{DM}^{\acute{\text{e}}\text{t}}(\mathbb{F},R)$
[Reference Ayoub, Jang, Kim, Lee and YieAyo14a, §4.1.1], [Reference Cisinski and DégliseCD16, 2.2.4] constructed from the derived category of étale sheaves with transfers of
![]() $R$
-modules on the category
$R$
-modules on the category
![]() $\text{Sm}/\mathbb{F}$
of smooth (finite type, separated)
$\text{Sm}/\mathbb{F}$
of smooth (finite type, separated)
![]() $\mathbb{F}$
-schemes. In particular, it comes again with a symmetric unital monoidal ‘associated étale motive’ functor
$\mathbb{F}$
-schemes. In particular, it comes again with a symmetric unital monoidal ‘associated étale motive’ functor
In contrast to the situation of the previous section, the image is, in general, not compact, and
![]() $\text{DM}^{\acute{\text{e}}\text{t}}(\mathbb{F},R)$
is, in general, not compactly generated (the reason being that the étale cohomological dimension of
$\text{DM}^{\acute{\text{e}}\text{t}}(\mathbb{F},R)$
is, in general, not compactly generated (the reason being that the étale cohomological dimension of
![]() $\mathbb{F}$
can be infinite). We denote the thick subcategory generated by
$\mathbb{F}$
can be infinite). We denote the thick subcategory generated by
![]() $R^{\acute{\text{e}}\text{t}}(X)(n)$
for
$R^{\acute{\text{e}}\text{t}}(X)(n)$
for
![]() $X$
smooth and
$X$
smooth and
![]() $n$
an integer by
$n$
an integer by
![]() $\text{DM}_{\text{gm}}^{\acute{\text{e}}\text{t}}(\mathbb{F},R)$
. It is called the triangulated category of geometric étale motives [Reference Ayoub, Jang, Kim, Lee and YieAyo14a, 4.3]. It is a (small) idempotent complete tt-category. Moreover, for many coefficient rings
$\text{DM}_{\text{gm}}^{\acute{\text{e}}\text{t}}(\mathbb{F},R)$
. It is called the triangulated category of geometric étale motives [Reference Ayoub, Jang, Kim, Lee and YieAyo14a, 4.3]. It is a (small) idempotent complete tt-category. Moreover, for many coefficient rings
![]() $R$
(including any localization or quotient of
$R$
(including any localization or quotient of
![]() $\mathbb{Z}$
) it is rigid, by [Reference Cisinski and DégliseCD16, 6.3.26] and Remark 4.1 below. The triangulated category of étale Tate motives
$\mathbb{Z}$
) it is rigid, by [Reference Cisinski and DégliseCD16, 6.3.26] and Remark 4.1 below. The triangulated category of étale Tate motives
![]() $\text{DTM}_{\text{gm}}^{\acute{\text{e}}\text{t}}(\mathbb{F},R)$
is the thick subcategory generated by the Tate twists
$\text{DTM}_{\text{gm}}^{\acute{\text{e}}\text{t}}(\mathbb{F},R)$
is the thick subcategory generated by the Tate twists
![]() $R^{\acute{\text{e}}\text{t}}(n)$
,
$R^{\acute{\text{e}}\text{t}}(n)$
,
![]() $n\in \mathbb{Z}$
. It is a (small) rigid, idempotent complete tt-category.
$n\in \mathbb{Z}$
. It is a (small) rigid, idempotent complete tt-category.
Remark 4.1. There are at least two other models for the categories just introduced. One uses étale sheaves without transfers [Reference Ayoub, Jang, Kim, Lee and YieAyo14a, Reference AyoubAyo14b], the other uses
![]() $\text{h}$
-sheaves on the category of finite type
$\text{h}$
-sheaves on the category of finite type
![]() $\mathbb{F}$
-schemes [Reference Cisinski and DégliseCD16, 5.1.3]. That they indeed coincide up to canonical equivalence follows, for example, from [Reference AyoubAyo14b, B.1] and [Reference Cisinski and DégliseCD16, 5.5.5]. When citing results from the literature about étale motives we will therefore freely use any of the three models.
$\mathbb{F}$
-schemes [Reference Cisinski and DégliseCD16, 5.1.3]. That they indeed coincide up to canonical equivalence follows, for example, from [Reference AyoubAyo14b, B.1] and [Reference Cisinski and DégliseCD16, 5.5.5]. When citing results from the literature about étale motives we will therefore freely use any of the three models.
One can define analogous étale motivic cohomology groups, and these again are closely related to algebraic cycles (see [Reference Ayoub, Jang, Kim, Lee and YieAyo14a, 4.12] and [Reference Cisinski and DégliseCD16, 7.1.2]), except that one loses all
![]() $p$
-torsion information if
$p$
-torsion information if
![]() $\operatorname{char}(\mathbb{F})=p>0$
. Indeed, the categories of étale motives just introduced are all
$\operatorname{char}(\mathbb{F})=p>0$
. Indeed, the categories of étale motives just introduced are all
![]() $\mathbb{Z}[1/p]$
-linear. This follows from the existence of the Artin-Schreier sequence of étale sheaves
$\mathbb{Z}[1/p]$
-linear. This follows from the existence of the Artin-Schreier sequence of étale sheaves
where
![]() $F_{p}$
denotes the Frobenius. It induces a triangle in
$F_{p}$
denotes the Frobenius. It induces a triangle in
![]() $\text{DTM}_{\text{gm}}^{\acute{\text{e}}\text{t}}(\mathbb{F},R)$
, and since
$\text{DTM}_{\text{gm}}^{\acute{\text{e}}\text{t}}(\mathbb{F},R)$
, and since
![]() $F_{p}-1$
induces an isomorphism on
$F_{p}-1$
induces an isomorphism on
![]() $R^{\acute{\text{e}}\text{t}}=R^{\acute{\text{e}}\text{t}}(\mathbb{G}_{a})$
in
$R^{\acute{\text{e}}\text{t}}=R^{\acute{\text{e}}\text{t}}(\mathbb{G}_{a})$
in
![]() $\text{DM}_{\text{gm}}^{\acute{\text{e}}\text{t}}(\mathbb{F},R)$
, multiplication by
$\text{DM}_{\text{gm}}^{\acute{\text{e}}\text{t}}(\mathbb{F},R)$
, multiplication by
![]() $p$
is an automorphism.
$p$
is an automorphism.
As before, a ring morphism
![]() $R\rightarrow R^{\prime }$
induces tt-functors (see [Reference AyoubAyo14b, A.2] and [Reference Cisinski and DégliseCD16, 5.4.1])
$R\rightarrow R^{\prime }$
induces tt-functors (see [Reference AyoubAyo14b, A.2] and [Reference Cisinski and DégliseCD16, 5.4.1])
and again, if
![]() $R^{\prime }$
is perfect over
$R^{\prime }$
is perfect over
![]() $R$
then they admit a right adjoint
$R$
then they admit a right adjoint
![]() $\unicode[STIX]{x1D6FE}_{\ast }$
, in which case one has
$\unicode[STIX]{x1D6FE}_{\ast }$
, in which case one has
![]() $\unicode[STIX]{x1D6FE}_{\ast }\unicode[STIX]{x1D6FE}^{\ast }(M)=M\otimes R^{\prime }$
.
$\unicode[STIX]{x1D6FE}_{\ast }\unicode[STIX]{x1D6FE}^{\ast }(M)=M\otimes R^{\prime }$
.
Fix a prime number
![]() $\ell$
, which is invertible in
$\ell$
, which is invertible in
![]() $\mathbb{F}$
, and consider the category
$\mathbb{F}$
, and consider the category
![]() $\operatorname{Mod}(G_{\mathbb{F}},\mathbb{Z}/\ell )$
of discrete
$\operatorname{Mod}(G_{\mathbb{F}},\mathbb{Z}/\ell )$
of discrete
![]() $G_{\mathbb{F}}$
-modules over
$G_{\mathbb{F}}$
-modules over
![]() $\mathbb{Z}/\ell$
, where
$\mathbb{Z}/\ell$
, where
![]() $G_{\mathbb{F}}$
denotes the absolute Galois group of
$G_{\mathbb{F}}$
denotes the absolute Galois group of
![]() $\mathbb{F}$
. Its derived category is denoted by
$\mathbb{F}$
. Its derived category is denoted by
![]() $\text{D}(G_{\mathbb{F}},\mathbb{Z}/\ell )$
. There is an étale realization functor (see [Reference IvorraIvo07], [Reference AyoubAyo14b, 5.2] and [Reference Cisinski and DégliseCD16, 7.2])
$\text{D}(G_{\mathbb{F}},\mathbb{Z}/\ell )$
. There is an étale realization functor (see [Reference IvorraIvo07], [Reference AyoubAyo14b, 5.2] and [Reference Cisinski and DégliseCD16, 7.2])
to the subcategory of
![]() $\text{D}(G_{\mathbb{F}},\mathbb{Z}/\ell )$
spanned by complexes with bounded, finite-dimensional cohomology. This is a tt-functor that, moreover, factors through a fully faithful tt-functor [Reference Cisinski and DégliseCD16, 5.5.4], abusively denoted by the same symbol,
$\text{D}(G_{\mathbb{F}},\mathbb{Z}/\ell )$
spanned by complexes with bounded, finite-dimensional cohomology. This is a tt-functor that, moreover, factors through a fully faithful tt-functor [Reference Cisinski and DégliseCD16, 5.5.4], abusively denoted by the same symbol,
This is a form of the rigidity theorem of Suslin and Voevodsky. Equation (4.2) is an equivalence if
![]() $\mathbb{F}$
is of finite
$\mathbb{F}$
is of finite
![]() $\ell$
-cohomological dimension.
$\ell$
-cohomological dimension.
Finally, there is a canonical étale sheafification tt-functor
which takes
![]() $R(X)(n)$
to
$R(X)(n)$
to
![]() $R^{\acute{\text{e}}\text{t}}(X)(n)$
, restricts to a corresponding tt-functor on Tate (respectively, étale Tate) motives, and is compatible with change of coefficients. We continue to denote by
$R^{\acute{\text{e}}\text{t}}(X)(n)$
, restricts to a corresponding tt-functor on Tate (respectively, étale Tate) motives, and is compatible with change of coefficients. We continue to denote by
![]() $\text{Re}_{\ell }$
the composition
$\text{Re}_{\ell }$
the composition
![]() $\text{Re}_{\ell }\circ a_{\acute{\text{e}}\text{t}}$
whenever this makes sense. Essentially because higher Galois cohomology is torsion, the étale sheafification induces an equivalence
$\text{Re}_{\ell }\circ a_{\acute{\text{e}}\text{t}}$
whenever this makes sense. Essentially because higher Galois cohomology is torsion, the étale sheafification induces an equivalence
whenever
![]() $\mathbb{Q}\subset R$
[Reference Cisinski and DégliseCD12, 16.1.2].
$\mathbb{Q}\subset R$
[Reference Cisinski and DégliseCD12, 16.1.2].
5 Torsion and finite generation in motivic cohomology
In this section we collect some basic properties concerning rational and mod-
![]() $\ell$
motivic cohomology for (Tate) motives. The discussion will culminate in the proof that the motivic cohomology groups of Tate motives behave ‘as if they were finitely generated’. We refer to Remark 5.7 for elaboration.
$\ell$
motivic cohomology for (Tate) motives. The discussion will culminate in the proof that the motivic cohomology groups of Tate motives behave ‘as if they were finitely generated’. We refer to Remark 5.7 for elaboration.
For the reader unfamiliar with the objects introduced in the previous two sections, this is a good opportunity to get better acquainted with the formalism. Throughout the section,
![]() $\mathbb{F}$
is an arbitrary field.
$\mathbb{F}$
is an arbitrary field.
We start with a result characteristic of Tate motives.
Lemma 5.1. Let
![]() $M\in \text{DTM}_{\text{gm}}(\mathbb{F},R)$
be a Tate motive. The following are equivalent:
$M\in \text{DTM}_{\text{gm}}(\mathbb{F},R)$
be a Tate motive. The following are equivalent:
(1)
 $M=0$
;
$M=0$
;(2)
 $\text{H}_{\text{M}}^{\bullet ,\bullet }(M,R)=0$
.
$\text{H}_{\text{M}}^{\bullet ,\bullet }(M,R)=0$
.
Proof. If
![]() $M$
has trivial motivic cohomology groups
$M$
has trivial motivic cohomology groups
![]() $\text{H}_{\text{M}}^{m,n}(M,R)$
for all integers
$\text{H}_{\text{M}}^{m,n}(M,R)$
for all integers
![]() $m,n$
, this means that for the dual
$m,n$
, this means that for the dual
![]() $M^{\vee }$
of
$M^{\vee }$
of
![]() $M$
, we have
$M$
, we have
for all integers
![]() $m,n$
. Since the set of Tate twists generates
$m,n$
. Since the set of Tate twists generates
![]() $\text{DTM}_{\text{gm}}(\mathbb{F},R)$
we see that
$\text{DTM}_{\text{gm}}(\mathbb{F},R)$
we see that
![]() $M^{\vee }=0$
and this implies
$M^{\vee }=0$
and this implies
![]() $M=0$
.◻
$M=0$
.◻
Convention 5.2. From now on and until the end of the section we assume that
![]() $R$
is a localization of
$R$
is a localization of
![]() $\mathbb{Z}$
such that
$\mathbb{Z}$
such that
![]() $\mathbb{Z}\subset R\subset \mathbb{Q}$
.
$\mathbb{Z}\subset R\subset \mathbb{Q}$
.
Let
![]() $F:\text{DTM}_{\text{gm}}(\mathbb{F},R)\rightarrow {\mathcal{T}}$
be a tt-functor, and
$F:\text{DTM}_{\text{gm}}(\mathbb{F},R)\rightarrow {\mathcal{T}}$
be a tt-functor, and
![]() $M\in \text{DTM}_{\text{gm}}(\mathbb{F},R)$
a Tate motive. We say that
$M\in \text{DTM}_{\text{gm}}(\mathbb{F},R)$
a Tate motive. We say that
![]() $M$
is
$M$
is
![]() $F$
-acyclic if
$F$
-acyclic if
![]() $F(M)=0$
. The
$F(M)=0$
. The
![]() $F$
-acyclic objects clearly define a tt-ideal in
$F$
-acyclic objects clearly define a tt-ideal in
![]() $\text{DTM}_{\text{gm}}(\mathbb{F},R)$
.
$\text{DTM}_{\text{gm}}(\mathbb{F},R)$
.
Example 5.3. Suppose
![]() $\ell$
is a prime number invertible in
$\ell$
is a prime number invertible in
![]() $\mathbb{F}$
. Consider the tt-functor
$\mathbb{F}$
. Consider the tt-functor
![]() $\text{Re}_{\ell }:\text{DTM}_{\text{gm}}(\mathbb{F},\mathbb{Z})\rightarrow \text{D}_{c}^{b}(G_{\mathbb{F}},\mathbb{Z}/\ell )$
. The
$\text{Re}_{\ell }:\text{DTM}_{\text{gm}}(\mathbb{F},\mathbb{Z})\rightarrow \text{D}_{c}^{b}(G_{\mathbb{F}},\mathbb{Z}/\ell )$
. The
![]() $\text{Re}_{\ell }$
-acyclic objects are those whose mod-
$\text{Re}_{\ell }$
-acyclic objects are those whose mod-
![]() $\ell$
étale cohomology vanishes.
$\ell$
étale cohomology vanishes.
If
![]() $A\in \text{DM}(\mathbb{F},R)$
is any motive, we say that
$A\in \text{DM}(\mathbb{F},R)$
is any motive, we say that
![]() $M$
is
$M$
is
![]() $A$
-acyclic if it is acyclic with respect to the functor
$A$
-acyclic if it is acyclic with respect to the functor
![]() $-\otimes A:\text{DTM}_{\text{gm}}(\mathbb{F},R)\rightarrow \text{DM}(\mathbb{F},R)$
. We will be most interested in
$-\otimes A:\text{DTM}_{\text{gm}}(\mathbb{F},R)\rightarrow \text{DM}(\mathbb{F},R)$
. We will be most interested in
![]() $A=\mathbb{Z}/\ell$
(
$A=\mathbb{Z}/\ell$
(
![]() $\ell$
a prime) or
$\ell$
a prime) or
![]() $A=\mathbb{Q}$
.
$A=\mathbb{Q}$
.
Lemma 5.4. Let
![]() $S$
be the multiplicative subset
$S$
be the multiplicative subset
![]() $\mathbb{Z}\backslash 0$
. In each case of motives, Tate motives, étale motives, or étale Tate motives, we have canonical equivalences of tt-categories
$\mathbb{Z}\backslash 0$
. In each case of motives, Tate motives, étale motives, or étale Tate motives, we have canonical equivalences of tt-categories
where
![]() $(-)^{\natural }$
denotes the idempotent completion.
$(-)^{\natural }$
denotes the idempotent completion.
Proof. The categorical (or Verdier) localization at
![]() $S$
is the naive localization (i.e. the category obtained by localizing each hom set), by [Reference AyoubAyo14b, 9.1] and [Reference BalmerBal10a, 3.6]. This gives the first equivalence. For the second equivalence, the étale version is [Reference Cisinski and DégliseCD16, 5.4.9]; the non-étale version is simpler, and can be found in [Reference Cisinski and DégliseCD12, 11.1.5]. ◻
$S$
is the naive localization (i.e. the category obtained by localizing each hom set), by [Reference AyoubAyo14b, 9.1] and [Reference BalmerBal10a, 3.6]. This gives the first equivalence. For the second equivalence, the étale version is [Reference Cisinski and DégliseCD16, 5.4.9]; the non-étale version is simpler, and can be found in [Reference Cisinski and DégliseCD12, 11.1.5]. ◻
Corollary 5.5. Let
![]() $M\in \text{DTM}_{\text{gm}}(\mathbb{F},R)$
be a Tate motive. The following are equivalent:
$M\in \text{DTM}_{\text{gm}}(\mathbb{F},R)$
be a Tate motive. The following are equivalent:
(1)
 $\text{H}_{\text{M}}^{\bullet ,\bullet }(M,\mathbb{Q})=0$
;
$\text{H}_{\text{M}}^{\bullet ,\bullet }(M,\mathbb{Q})=0$
;(2)
 $M$
is
$M$
is
 $\mathbb{Q}$
-acyclic;
$\mathbb{Q}$
-acyclic;(3)
 $M$
is
$M$
is
 $n$
-torsion for some positive integer
$n$
-torsion for some positive integer
 $n$
, i.e.
$n$
, i.e.
 $n\cdot \operatorname{id}_{M}=0$
.
$n\cdot \operatorname{id}_{M}=0$
.
Proof. By the change of coefficients adjunction for
![]() $R\rightarrow \mathbb{Q}$
, we have
$R\rightarrow \mathbb{Q}$
, we have
and by Lemma 5.1 these groups all vanish if and only if
![]() $\unicode[STIX]{x1D6FE}^{\ast }M=0$
. But
$\unicode[STIX]{x1D6FE}^{\ast }M=0$
. But
![]() $\unicode[STIX]{x1D6FE}_{\ast }$
is conservative (§ 3) so this is equivalent to
$\unicode[STIX]{x1D6FE}_{\ast }$
is conservative (§ 3) so this is equivalent to
i.e. it is equivalent to
![]() $M$
being
$M$
being
![]() $\mathbb{Q}$
-acyclic. Lemma 5.4 shows that the second and third condition are equivalent as well.◻
$\mathbb{Q}$
-acyclic. Lemma 5.4 shows that the second and third condition are equivalent as well.◻
The first part of the proof also gives the following result.
Lemma 5.6. Let
![]() $M\in \text{DTM}_{\text{gm}}(\mathbb{F},R)$
be a Tate motive, and
$M\in \text{DTM}_{\text{gm}}(\mathbb{F},R)$
be a Tate motive, and
![]() $\ell$
a prime number. The following are equivalent:
$\ell$
a prime number. The following are equivalent:
(1)
 $\text{H}_{\text{M}}^{\bullet ,\bullet }(M,R/\ell )=0$
;
$\text{H}_{\text{M}}^{\bullet ,\bullet }(M,R/\ell )=0$
;(2)
 $M$
is
$M$
is
 $R/\ell$
-acyclic.
$R/\ell$
-acyclic.
Remark 5.7. Among finitely generated abelian groups there is a stark divide between finite and infinite ones. This simple observation is used in many arguments in algebraic topology, which involve the universal coefficient theorem. More explicitly, if
![]() $X$
is a topological space with finitely generated cohomology groups
$X$
is a topological space with finitely generated cohomology groups
![]() $\text{H}^{\bullet }(X,\mathbb{Z})$
then there is the following dichotomy:
$\text{H}^{\bullet }(X,\mathbb{Z})$
then there is the following dichotomy:
∙ if
 $\text{H}^{m}(X,\mathbb{Q})=0$
then for almost all primes
$\text{H}^{m}(X,\mathbb{Q})=0$
then for almost all primes
 $\ell$
,
$\ell$
,
 $\text{H}^{m}(X,\mathbb{Z}/\ell )=0$
;
$\text{H}^{m}(X,\mathbb{Z}/\ell )=0$
;∙ if
 $\text{H}^{m}(X,\mathbb{Q})\neq 0$
then for all primes
$\text{H}^{m}(X,\mathbb{Q})\neq 0$
then for all primes
 $\ell$
,
$\ell$
,
 $\text{H}^{m}(X,\mathbb{Z}/\ell )\neq 0$
.
$\text{H}^{m}(X,\mathbb{Z}/\ell )\neq 0$
.
Now, it is of course not true that the motivic cohomology groups of Tate motives are finitely generated in general. (For example, (3.4) shows that
![]() $\text{H}_{\text{M}}^{1,1}(\mathbb{F},\mathbb{Z})=\mathbb{F}^{\times }$
.) However, we would like to establish that they still exhibit a similar behavior. We can prove the first part of the dichotomy here, as a consequence of the preceding results in this section. The second part of the dichotomy will not be stated here, but is also true (for
$\text{H}_{\text{M}}^{1,1}(\mathbb{F},\mathbb{Z})=\mathbb{F}^{\times }$
.) However, we would like to establish that they still exhibit a similar behavior. We can prove the first part of the dichotomy here, as a consequence of the preceding results in this section. The second part of the dichotomy will not be stated here, but is also true (for
![]() $\ell \in \mathbb{F}^{\times }$
). It will be seen to follow from the conservativity of the
$\ell \in \mathbb{F}^{\times }$
). It will be seen to follow from the conservativity of the
![]() $\ell$
-adic realization for Tate motives (cf. the proof of Theorem 6.10).
$\ell$
-adic realization for Tate motives (cf. the proof of Theorem 6.10).
This observation will have important ramifications for the topology of the tt-spectrum of Tate motives.
Proposition 5.8. Let
![]() $M\in \text{DTM}_{\text{gm}}(\mathbb{F},R)$
be a Tate motive and assume
$M\in \text{DTM}_{\text{gm}}(\mathbb{F},R)$
be a Tate motive and assume
![]() $\text{H}_{\text{M}}^{\bullet ,\bullet }(M,\mathbb{Q})=0$
. Then for almost all primes
$\text{H}_{\text{M}}^{\bullet ,\bullet }(M,\mathbb{Q})=0$
. Then for almost all primes
![]() $\ell$
we have
$\ell$
we have
![]() $\text{H}_{\text{M}}^{\bullet ,\bullet }(M,R/\ell )=0$
.
$\text{H}_{\text{M}}^{\bullet ,\bullet }(M,R/\ell )=0$
.
Proof. Assume that
![]() $M\in \text{DTM}_{\text{gm}}(\mathbb{F},R)$
has trivial rational motivic cohomology, i.e.
$M\in \text{DTM}_{\text{gm}}(\mathbb{F},R)$
has trivial rational motivic cohomology, i.e.
![]() $M$
is
$M$
is
![]() $n$
-torsion for some positive integer
$n$
-torsion for some positive integer
![]() $n$
, by Corollary 5.5. Let
$n$
, by Corollary 5.5. Let
![]() $\ell$
be any prime not dividing
$\ell$
be any prime not dividing
![]() $n$
. Consider the object
$n$
. Consider the object
![]() $\unicode[STIX]{x1D6FE}^{\ast }M\in \text{DTM}_{\text{gm}}(\mathbb{F},R/\ell )$
, where
$\unicode[STIX]{x1D6FE}^{\ast }M\in \text{DTM}_{\text{gm}}(\mathbb{F},R/\ell )$
, where
![]() $\unicode[STIX]{x1D6FE}^{\ast }$
is the change of coefficients functor associated to
$\unicode[STIX]{x1D6FE}^{\ast }$
is the change of coefficients functor associated to
![]() $R\rightarrow R/\ell$
. Multiplication by
$R\rightarrow R/\ell$
. Multiplication by
![]() $n$
on
$n$
on
![]() $\unicode[STIX]{x1D6FE}^{\ast }M$
is at the same time zero (since it is so on
$\unicode[STIX]{x1D6FE}^{\ast }M$
is at the same time zero (since it is so on
![]() $M$
), and an isomorphism (since the category
$M$
), and an isomorphism (since the category
![]() $\text{DTM}_{\text{gm}}(\mathbb{F},R/\ell )$
is
$\text{DTM}_{\text{gm}}(\mathbb{F},R/\ell )$
is
![]() $R/\ell$
-linear). We conclude that
$R/\ell$
-linear). We conclude that
![]() $\unicode[STIX]{x1D6FE}^{\ast }M=0$
as claimed, cf. Lemma 5.6.◻
$\unicode[STIX]{x1D6FE}^{\ast }M=0$
as claimed, cf. Lemma 5.6.◻
Remark 5.9. We have phrased most of the results in this section so far for Tate motives but it should be remarked that they equally hold for étale Tate motives with the same proofs, taking into account the following observations.
∙ Rational étale motivic cohomology is the same thing as rational motivic cohomology as discussed above (4.4).
∙ By rigidity (4.2), mod-
 $\ell$
étale motivic cohomology is the same thing as mod-
$\ell$
étale motivic cohomology is the same thing as mod-
 $\ell$
étale cohomology.
$\ell$
étale cohomology.∙ One sometimes has to modify the statements and arguments to take into account that the category of étale motives is
 $\mathbb{Z}[1/p]$
-linear, where
$\mathbb{Z}[1/p]$
-linear, where
 $p$
is the exponential characteristic of
$p$
is the exponential characteristic of
 $\mathbb{F}$
.
$\mathbb{F}$
.
Moreover, although we are mainly interested in Tate motives in this article, it should be said that some of the arguments in this section apply to motives in general. In particular, we have just shown that an implication similar to the one in Proposition 5.8 holds in
![]() $\text{DM}_{\text{gm}}(\mathbb{F},R)$
or
$\text{DM}_{\text{gm}}(\mathbb{F},R)$
or
![]() $\text{DM}_{\text{gm}}^{\acute{\text{e}}\text{t}}(\mathbb{F},R)$
.
$\text{DM}_{\text{gm}}^{\acute{\text{e}}\text{t}}(\mathbb{F},R)$
.
Proposition 5.10. Let
![]() $M\in \text{DM}_{\text{gm}}(\mathbb{F},R)$
(or
$M\in \text{DM}_{\text{gm}}(\mathbb{F},R)$
(or
![]() $\text{DM}_{\text{gm}}^{\acute{\text{e}}\text{t}}(\mathbb{F},R)$
) be a motive, and assume
$\text{DM}_{\text{gm}}^{\acute{\text{e}}\text{t}}(\mathbb{F},R)$
) be a motive, and assume
![]() $M\otimes \mathbb{Q}=0$
. Then for almost all primes
$M\otimes \mathbb{Q}=0$
. Then for almost all primes
![]() $\ell$
we have
$\ell$
we have
![]() $M\otimes R/\ell =0$
.
$M\otimes R/\ell =0$
.
6 tt-geometry of étale (Tate) motives
The tt-geometry of étale Tate motives is easier to describe than the one of Tate motives, mostly due to our good understanding of étale motives with finite coefficients (the rigidity theorem, see (4.2)). In fact, with finite coefficients it is not more difficult to describe the tt-geometry of étale motives (not necessarily Tate) at the same time, which is what we are going to start with. The integral versions considered subsequently require the (rational) motivic cohomology of the base field to satisfy certain vanishing conditions, and are proved for Tate motives only.
Fix a field
![]() $\mathbb{F}$
and a prime number
$\mathbb{F}$
and a prime number
![]() $\ell$
invertible in
$\ell$
invertible in
![]() $\mathbb{F}$
. We want to recall the Bloch–Kato conjecture (now a theorem). The short exact sequence of étale sheaves
$\mathbb{F}$
. We want to recall the Bloch–Kato conjecture (now a theorem). The short exact sequence of étale sheaves
induces a canonical map
![]() $\mathbb{F}^{\times }\rightarrow \text{H}_{\acute{\text{e}}\text{t}}^{1}(\mathbb{F},\unicode[STIX]{x1D707}_{\ell })$
in étale cohomology. Using the cup product this extends to a morphism of graded rings
$\mathbb{F}^{\times }\rightarrow \text{H}_{\acute{\text{e}}\text{t}}^{1}(\mathbb{F},\unicode[STIX]{x1D707}_{\ell })$
in étale cohomology. Using the cup product this extends to a morphism of graded rings
![]() $K_{\bullet }^{\text{M}}(\mathbb{F})\rightarrow \text{H}_{\acute{\text{e}}\text{t}}^{\bullet }(\mathbb{F},\unicode[STIX]{x1D707}_{\ell }^{\otimes \bullet })$
, which clearly annihilates
$K_{\bullet }^{\text{M}}(\mathbb{F})\rightarrow \text{H}_{\acute{\text{e}}\text{t}}^{\bullet }(\mathbb{F},\unicode[STIX]{x1D707}_{\ell }^{\otimes \bullet })$
, which clearly annihilates
![]() $\ell$
. Voevodsky, Rost, and others, show that the induced map is an isomorphism (as Bloch and Kato conjectured):
$\ell$
. Voevodsky, Rost, and others, show that the induced map is an isomorphism (as Bloch and Kato conjectured):
In order to apply this result we need to know the homogeneous spectrum of the graded rings involved.
Lemma 6.1. Let
![]() $\mathbb{F}$
be a field, and
$\mathbb{F}$
be a field, and
![]() $\ell$
a prime. If
$\ell$
a prime. If
![]() $\ell =2$
we assume that
$\ell =2$
we assume that
![]() $-1$
is a sum of squares in
$-1$
is a sum of squares in
![]() $\mathbb{F}$
. Then the graded ring
$\mathbb{F}$
. Then the graded ring
![]() $K_{\bullet }^{\text{M}}(\mathbb{F})/\ell$
has a unique homogeneous prime ideal (namely,
$K_{\bullet }^{\text{M}}(\mathbb{F})/\ell$
has a unique homogeneous prime ideal (namely,
![]() $K_{{>}0}^{\text{M}}(\mathbb{F})/\ell$
).
$K_{{>}0}^{\text{M}}(\mathbb{F})/\ell$
).
Proof. We distinguish two cases.
-
 $\ell =2$
:
$\ell =2$
: We are assuming that
 $-1$
is a sum of squares in
$-1$
is a sum of squares in
 $\mathbb{F}$
. This is equivalent, by [Reference MilnorMil69/70, 1.4], to every element in
$\mathbb{F}$
. This is equivalent, by [Reference MilnorMil69/70, 1.4], to every element in
 $K_{\bullet }^{\text{M}}(\mathbb{F})$
of positive degree being nilpotent. In particular, the only homogeneous prime ideal containing
$K_{\bullet }^{\text{M}}(\mathbb{F})$
of positive degree being nilpotent. In particular, the only homogeneous prime ideal containing
 $2$
is
$2$
is
 $\langle K_{1}^{\text{M}}(\mathbb{F}),2\rangle$
.
$\langle K_{1}^{\text{M}}(\mathbb{F}),2\rangle$
.-
 $\ell \neq 2$
:
$\ell \neq 2$
: For the reader’s convenience we reproduce the argument in [Reference ThorntonTho16, 3.9]. Let
 $\mathfrak{p}$
be a homogeneous prime in
$\mathfrak{p}$
be a homogeneous prime in
 $K_{\bullet }^{\text{M}}(\mathbb{F})$
, which does not contain
$K_{\bullet }^{\text{M}}(\mathbb{F})$
, which does not contain
 $2$
. Let us write
$2$
. Let us write
 $[a]$
for the symbol in
$[a]$
for the symbol in
 $K_{1}^{\text{M}}(\mathbb{F})$
associated to
$K_{1}^{\text{M}}(\mathbb{F})$
associated to
 $a\in \mathbb{F}^{\times }$
. Since
$a\in \mathbb{F}^{\times }$
. Since
 $2[-1]=[(-1)^{2}]=[1]=0$
we have
$2[-1]=[(-1)^{2}]=[1]=0$
we have
 $[-1]\in \mathfrak{p}$
. But then for every
$[-1]\in \mathfrak{p}$
. But then for every
 $a\in \mathbb{F}^{\times }$
,
$a\in \mathbb{F}^{\times }$
,
 $[a]^{2}=[a][-1]\in \mathfrak{p}$
[Reference MilnorMil69/70, 1.2], and so, again, we find
$[a]^{2}=[a][-1]\in \mathfrak{p}$
[Reference MilnorMil69/70, 1.2], and so, again, we find
 $K_{1}^{\text{M}}(\mathbb{F})\subset \mathfrak{p}$
. ◻
$K_{1}^{\text{M}}(\mathbb{F})\subset \mathfrak{p}$
. ◻
Theorem 6.2. Let
![]() $\mathbb{F}$
be a field, and let
$\mathbb{F}$
be a field, and let
![]() $\ell$
be a prime invertible in
$\ell$
be a prime invertible in
![]() $\mathbb{F}$
. Assume that
$\mathbb{F}$
. Assume that
![]() $\mathbb{F}$
contains a primitive
$\mathbb{F}$
contains a primitive
![]() $\ell$
th root of unity (respectively, primitive
$\ell$
th root of unity (respectively, primitive
![]() $4$
th root if
$4$
th root if
![]() $\ell =2$
). Then both canonical morphisms in the following composition are isomorphisms of locally ringed spaces:
$\ell =2$
). Then both canonical morphisms in the following composition are isomorphisms of locally ringed spaces:
Proof. The proof will proceed in several steps.
(1) Note that it suffices to prove that
 $\operatorname{Spec}(\text{DM}_{\text{gm}}^{\acute{\text{e}}\text{t}}(\mathbb{F},\mathbb{Z}/\ell ))$
has at most one point. Since
$\operatorname{Spec}(\text{DM}_{\text{gm}}^{\acute{\text{e}}\text{t}}(\mathbb{F},\mathbb{Z}/\ell ))$
has at most one point. Since
 $\text{DM}_{\text{gm}}^{\acute{\text{e}}\text{t}}(\mathbb{F},\mathbb{Z}/\ell )$
is not the trivial category, its spectrum then has exactly one point, and therefore the composition
$\text{DM}_{\text{gm}}^{\acute{\text{e}}\text{t}}(\mathbb{F},\mathbb{Z}/\ell )$
is not the trivial category, its spectrum then has exactly one point, and therefore the composition
 $\unicode[STIX]{x1D70C}:\operatorname{Spec}(\text{DM}_{\text{gm}}^{\acute{\text{e}}\text{t}}(\mathbb{F},\mathbb{Z}/\ell ))\rightarrow \operatorname{Spec}(\mathbb{Z}/\ell )$
is a homeomorphism. Since the inclusion
$\unicode[STIX]{x1D70C}:\operatorname{Spec}(\text{DM}_{\text{gm}}^{\acute{\text{e}}\text{t}}(\mathbb{F},\mathbb{Z}/\ell ))\rightarrow \operatorname{Spec}(\mathbb{Z}/\ell )$
is a homeomorphism. Since the inclusion
 $\text{DTM}_{\text{gm}}^{\acute{\text{e}}\text{t}}(\mathbb{F},\mathbb{Z}/\ell )\rightarrow \text{DM}_{\text{gm}}^{\acute{\text{e}}\text{t}}(\mathbb{F},\mathbb{Z}/\ell )$
is (fully) faithful, the induced morphism on tt-spectra is surjective [Reference BalmerBal18, 1.8]. It follows that if the composition is a homeomorphism then so are both maps in the statement. But
$\text{DTM}_{\text{gm}}^{\acute{\text{e}}\text{t}}(\mathbb{F},\mathbb{Z}/\ell )\rightarrow \text{DM}_{\text{gm}}^{\acute{\text{e}}\text{t}}(\mathbb{F},\mathbb{Z}/\ell )$
is (fully) faithful, the induced morphism on tt-spectra is surjective [Reference BalmerBal18, 1.8]. It follows that if the composition is a homeomorphism then so are both maps in the statement. But
 $\unicode[STIX]{x1D70C}$
being a homeomorphism already implies that it is an isomorphism of locally ringed spaces.
$\unicode[STIX]{x1D70C}$
being a homeomorphism already implies that it is an isomorphism of locally ringed spaces.(2) By rigidity,
 $\text{DM}_{\text{gm}}^{\acute{\text{e}}\text{t}}(\mathbb{F},\mathbb{Z}/\ell )$
embeds fully faithfully into
$\text{DM}_{\text{gm}}^{\acute{\text{e}}\text{t}}(\mathbb{F},\mathbb{Z}/\ell )$
embeds fully faithfully into
 $\text{D}_{c}^{b}(G_{\mathbb{F}},\mathbb{Z}/\ell )$
thus again a surjective map on tt-spectra and we reduce to prove that the former is a singleton set.
$\text{D}_{c}^{b}(G_{\mathbb{F}},\mathbb{Z}/\ell )$
thus again a surjective map on tt-spectra and we reduce to prove that the former is a singleton set. $$\begin{eqnarray}\operatorname{Spc}(\text{D}_{c}^{b}(G_{\mathbb{ F}},\mathbb{Z}/\ell ))\rightarrow \operatorname{Spc}(\text{DM}_{\text{gm}}^{\acute{\text{e}}\text{t}}(\mathbb{F},\mathbb{Z}/\ell )),\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{Spc}(\text{D}_{c}^{b}(G_{\mathbb{ F}},\mathbb{Z}/\ell ))\rightarrow \operatorname{Spc}(\text{DM}_{\text{gm}}^{\acute{\text{e}}\text{t}}(\mathbb{F},\mathbb{Z}/\ell )),\end{eqnarray}$$
(3) By the combination of Lemma 6.4 and Proposition 6.5 below, the morphism
is an injection. Since we are assuming that $$\begin{eqnarray}\unicode[STIX]{x1D70C}^{\bullet }:\operatorname{Spc}(\text{D}_{c}^{b}(G_{\mathbb{ F}},\mathbb{Z}/\ell ))\rightarrow \operatorname{Spc}^{\text{h}}(\text{H}^{\bullet }(G_{\mathbb{ F}},\mathbb{Z}/\ell ))\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D70C}^{\bullet }:\operatorname{Spc}(\text{D}_{c}^{b}(G_{\mathbb{ F}},\mathbb{Z}/\ell ))\rightarrow \operatorname{Spc}^{\text{h}}(\text{H}^{\bullet }(G_{\mathbb{ F}},\mathbb{Z}/\ell ))\end{eqnarray}$$
 $\mathbb{Z}/\ell \cong \unicode[STIX]{x1D707}_{\ell }$
, and by Bloch–Kato, the target of this map is the homogeneous spectrum of Milnor
$\mathbb{Z}/\ell \cong \unicode[STIX]{x1D707}_{\ell }$
, and by Bloch–Kato, the target of this map is the homogeneous spectrum of Milnor
 $K$
-theory
$K$
-theory
 $K_{\bullet }^{\text{M}}(\mathbb{F})/\ell$
. But we found in Lemma 6.1 that the latter has indeed just a single point. ◻
$K_{\bullet }^{\text{M}}(\mathbb{F})/\ell$
. But we found in Lemma 6.1 that the latter has indeed just a single point. ◻
To complete the proof we need to compare the tt-spectrum of
![]() $\text{D}_{c}^{b}(G,k)$
, for a (discrete) field
$\text{D}_{c}^{b}(G,k)$
, for a (discrete) field
![]() $k$
and a profinite group
$k$
and a profinite group
![]() $G$
, to the homogeneous spectrum of the cohomology ring of
$G$
, to the homogeneous spectrum of the cohomology ring of
![]() $G$
. This will be done in two steps. Consider the category
$G$
. This will be done in two steps. Consider the category
![]() $\operatorname{mod}(G,k)$
of finite-dimensional discrete
$\operatorname{mod}(G,k)$
of finite-dimensional discrete
![]() $G$
-modules over
$G$
-modules over
![]() $k$
, and its bounded derived category
$k$
, and its bounded derived category
![]() $\text{D}^{b}(\operatorname{mod}(G,k))$
. There is a canonical tt-functor
$\text{D}^{b}(\operatorname{mod}(G,k))$
. There is a canonical tt-functor
Lemma 6.4. The functor
![]() $\unicode[STIX]{x1D704}$
of (6.3) is an equivalence and therefore induces a homeomorphism of tt-spectra:
$\unicode[STIX]{x1D704}$
of (6.3) is an equivalence and therefore induces a homeomorphism of tt-spectra:
Proof. Let
![]() $M$
be a finite-dimensional discrete
$M$
be a finite-dimensional discrete
![]() $G$
-module over
$G$
-module over
![]() $k$
, let
$k$
, let
![]() $N$
be an arbitrary one, and let
$N$
be an arbitrary one, and let
![]() $f:N\rightarrow M$
be an epimorphism. By the definition of discrete modules there exists a finite quotient
$f:N\rightarrow M$
be an epimorphism. By the definition of discrete modules there exists a finite quotient
![]() $G/H$
through which
$G/H$
through which
![]() $G$
acts on
$G$
acts on
![]() $N$
. Choose representatives
$N$
. Choose representatives
![]() $g_{1},\ldots ,g_{r}\in G$
for this quotient, and choose lifts
$g_{1},\ldots ,g_{r}\in G$
for this quotient, and choose lifts
![]() $n_{1},\ldots ,n_{s}\in N$
of a
$n_{1},\ldots ,n_{s}\in N$
of a
![]() $k$
-basis of
$k$
-basis of
![]() $M$
. It is then clear that the
$M$
. It is then clear that the
![]() $k$
-linear hull of
$k$
-linear hull of
is a
![]() $G$
-submodule of
$G$
-submodule of
![]() $N$
, which is in addition finite-dimensional and still surjects onto
$N$
, which is in addition finite-dimensional and still surjects onto
![]() $M$
. This is enough to deduce that the functor
$M$
. This is enough to deduce that the functor
![]() $\text{D}^{b}(\operatorname{mod}(G,k))\rightarrow \text{D}^{b}(G,k)$
is fully faithful [Reference KellerKel96, 12.1]. The image of this functor consists of those complexes with finite-dimensional cohomology. Indeed, the latter subcategory is generated, as a triangulated subcategory, by complexes with finite-dimensional cohomology concentrated in a single degree; and these are clearly in the image of the functor. ◻
$\text{D}^{b}(\operatorname{mod}(G,k))\rightarrow \text{D}^{b}(G,k)$
is fully faithful [Reference KellerKel96, 12.1]. The image of this functor consists of those complexes with finite-dimensional cohomology. Indeed, the latter subcategory is generated, as a triangulated subcategory, by complexes with finite-dimensional cohomology concentrated in a single degree; and these are clearly in the image of the functor. ◻
Let us now consider the graded central ring
![]() ${\mathcal{R}}_{G}^{\bullet }$
in
${\mathcal{R}}_{G}^{\bullet }$
in
![]() $\text{D}^{b}(\operatorname{mod}(G,k))$
with respect to
$\text{D}^{b}(\operatorname{mod}(G,k))$
with respect to
![]() $k[1]$
. The following statement generalizes the analogous result for finite groups, which was proved in [Reference BalmerBal10a, 8.5], completing the work of many others. Our proof will consist in reducing to the finite case and is therefore not independent.
$k[1]$
. The following statement generalizes the analogous result for finite groups, which was proved in [Reference BalmerBal10a, 8.5], completing the work of many others. Our proof will consist in reducing to the finite case and is therefore not independent.
Proposition 6.5. Let
![]() $G$
be a profinite group, and
$G$
be a profinite group, and
![]() $k$
a field. Then:
$k$
a field. Then:
(1)
 ${\mathcal{R}}_{G}^{\bullet }$
is canonically isomorphic to
${\mathcal{R}}_{G}^{\bullet }$
is canonically isomorphic to
 $\text{H}^{\bullet }(G,k)$
;
$\text{H}^{\bullet }(G,k)$
;(2) the comparison morphism
is an isomorphism of locally ringed spaces. $$\begin{eqnarray}\unicode[STIX]{x1D70C}^{\bullet }:\operatorname{Spec}(\text{D}^{b}(\operatorname{mod}(G,k)))\rightarrow \operatorname{Spec}^{\text{h}}(\text{H}^{\bullet }(G,k))\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D70C}^{\bullet }:\operatorname{Spec}(\text{D}^{b}(\operatorname{mod}(G,k)))\rightarrow \operatorname{Spec}^{\text{h}}(\text{H}^{\bullet }(G,k))\end{eqnarray}$$
Proof. The group
![]() $G$
is the inverse limit
$G$
is the inverse limit
![]() $\mathop{\varprojlim }\nolimits_{i}G_{i}$
of a cofiltered diagram
$\mathop{\varprojlim }\nolimits_{i}G_{i}$
of a cofiltered diagram
![]() $I\ni i\mapsto G_{i}$
of finite groups (with the discrete topology). For every transition map
$I\ni i\mapsto G_{i}$
of finite groups (with the discrete topology). For every transition map
![]() $G_{i}\rightarrow G_{j}$
we obtain a functor
$G_{i}\rightarrow G_{j}$
we obtain a functor
![]() $\operatorname{mod}(G_{j},k)\rightarrow \operatorname{mod}(G_{i},k)$
by restricting the action. Notice that a finite-dimensional
$\operatorname{mod}(G_{j},k)\rightarrow \operatorname{mod}(G_{i},k)$
by restricting the action. Notice that a finite-dimensional
![]() $G$
-module is discrete (i.e. the action of
$G$
-module is discrete (i.e. the action of
![]() $G$
is continuous) if and only if the action factors through
$G$
is continuous) if and only if the action factors through
![]() $G_{i}$
, for some
$G_{i}$
, for some
![]() $i$
. It follows easily that
$i$
. It follows easily that
![]() $\mathop{\varinjlim }\nolimits_{i}\operatorname{mod}(G_{i},k)=\operatorname{mod}(G,k)$
and this equivalence passes first to the level of bounded cochain complexes, and then to the bounded derived category so that we have
$\mathop{\varinjlim }\nolimits_{i}\operatorname{mod}(G_{i},k)=\operatorname{mod}(G,k)$
and this equivalence passes first to the level of bounded cochain complexes, and then to the bounded derived category so that we have
![]() $\mathop{\varinjlim }\nolimits_{i}\text{D}^{b}(\operatorname{mod}(G_{i},k))=\text{D}^{b}(\operatorname{mod}(G,k))$
.
$\mathop{\varinjlim }\nolimits_{i}\text{D}^{b}(\operatorname{mod}(G_{i},k))=\text{D}^{b}(\operatorname{mod}(G,k))$
.
We now obtain the first part of the statement since
![]() ${\mathcal{R}}_{G_{i}}^{\bullet }=\text{H}^{\bullet }(G_{i},k)$
and therefore
${\mathcal{R}}_{G_{i}}^{\bullet }=\text{H}^{\bullet }(G_{i},k)$
and therefore
For the second statement, consider the following square, which is commutative by naturality of
![]() $\unicode[STIX]{x1D70C}^{\bullet }$
([Reference BalmerBal10a, 5.6]; recalled in Appendix A).
$\unicode[STIX]{x1D70C}^{\bullet }$
([Reference BalmerBal10a, 5.6]; recalled in Appendix A).

By [Reference GallauerGal18, 8.2], the top horizontal arrow is a homeomorphism. By [Reference BalmerBal10a, 8.5], so is the right vertical map. And, again by
![]() $\varinjlim \text{H}^{\bullet }(G_{i},k)=\text{H}^{\bullet }(G,k)$
, the bottom horizontal map is a homeomorphism. Necessarily then, the left vertical map is a homeomorphism as well. We now conclude since
$\varinjlim \text{H}^{\bullet }(G_{i},k)=\text{H}^{\bullet }(G,k)$
, the bottom horizontal map is a homeomorphism. Necessarily then, the left vertical map is a homeomorphism as well. We now conclude since
![]() $\unicode[STIX]{x1D70C}^{\bullet }$
is then automatically an isomorphism of locally ringed spaces.◻
$\unicode[STIX]{x1D70C}^{\bullet }$
is then automatically an isomorphism of locally ringed spaces.◻
Having described the tt-geometry for finite coefficients, we next consider rational coefficients. Here, we restrict to Tate motives in order to invoke the results of [Reference PeterPet13]. Recall also (4.4) that we have an equivalence of tt-categories
![]() $\text{DTM}_{\text{gm}}(\mathbb{F},\mathbb{Q})\simeq \text{DTM}_{\text{gm}}^{\acute{\text{e}}\text{t}}(\mathbb{F},\mathbb{Q})$
and the discussion therefore applies to both topologies; we will phrase them for
$\text{DTM}_{\text{gm}}(\mathbb{F},\mathbb{Q})\simeq \text{DTM}_{\text{gm}}^{\acute{\text{e}}\text{t}}(\mathbb{F},\mathbb{Q})$
and the discussion therefore applies to both topologies; we will phrase them for
![]() $\text{DTM}_{\text{gm}}(\mathbb{F},\mathbb{Q})$
.
$\text{DTM}_{\text{gm}}(\mathbb{F},\mathbb{Q})$
.

Figure 1. Vanishing in
![]() $\text{H}_{\text{M}}^{m,n}(\operatorname{Spec}(\mathbb{F}),\mathbb{Q})$
.
$\text{H}_{\text{M}}^{m,n}(\operatorname{Spec}(\mathbb{F}),\mathbb{Q})$
.
Consider
![]() $\text{H}_{\text{M}}^{m,n}(\operatorname{Spec}(\mathbb{F}),\mathbb{Q})$
, the rational motivic cohomology ring of the field (see (3.2). There is the following relation between Bloch’s higher Chow groups and algebraic
$\text{H}_{\text{M}}^{m,n}(\operatorname{Spec}(\mathbb{F}),\mathbb{Q})$
, the rational motivic cohomology ring of the field (see (3.2). There is the following relation between Bloch’s higher Chow groups and algebraic
![]() $K$
-theory (cf. (3.3):
$K$
-theory (cf. (3.3):
where the latter denotes the weight
![]() $n$
eigenspace of the Adams operations
$n$
eigenspace of the Adams operations
![]() $(\unicode[STIX]{x1D713}^{k})_{k}$
[Reference BlochBlo94, Reference LevineLev94]. It might be helpful to visualize this bigraded ring as in Figure 1, regarding which we offer a few comments.
$(\unicode[STIX]{x1D713}^{k})_{k}$
[Reference BlochBlo94, Reference LevineLev94]. It might be helpful to visualize this bigraded ring as in Figure 1, regarding which we offer a few comments.
∙ The Milnor
 $K$
-theory is displayed on the diagonal for visual aid.
$K$
-theory is displayed on the diagonal for visual aid.∙ The darker area always vanishes: for
 $n<0$
or
$n<0$
or
 $n<m$
this is for dimension reasons; for
$n<m$
this is for dimension reasons; for
 $n=0$
and
$n=0$
and
 $m<0$
this follows from a simple computation with higher Chow groups.
$m<0$
this follows from a simple computation with higher Chow groups.∙ The lightly shaded area is what we are now interested in: the Beilinson–Soulé vanishing conjecture predicts that the left patch vanishes. It is known in a few cases, for example, if
 $\mathbb{F}$
is any of the following: a finite field, a global field (in any characteristic), a function field of a genus 0 curve over a number field. We now introduce an even stronger hypothesis.
$\mathbb{F}$
is any of the following: a finite field, a global field (in any characteristic), a function field of a genus 0 curve over a number field. We now introduce an even stronger hypothesis.
Hypothesis 6.6 (Vanishing hypothesis on
 $\mathbb{F}$
).
$\mathbb{F}$
).
The rational motivic cohomology groups
![]() $\text{H}_{\text{M}}^{m,n}(\operatorname{Spec}(\mathbb{F}),\mathbb{Q})$
vanish whenever:
$\text{H}_{\text{M}}^{m,n}(\operatorname{Spec}(\mathbb{F}),\mathbb{Q})$
vanish whenever:
∙
 $m\leqslant 0<n$
; or
$m\leqslant 0<n$
; or∙
 $n\geqslant m\geqslant 2$
.
$n\geqslant m\geqslant 2$
.
Remark 6.7. If
![]() $\mathbb{F}$
is the union of subfields all of which satisfy Hypothesis 6.6 then so does
$\mathbb{F}$
is the union of subfields all of which satisfy Hypothesis 6.6 then so does
![]() $\mathbb{F}$
. This can be seen as a very special case of the ‘continuity’ of the assignment
$\mathbb{F}$
. This can be seen as a very special case of the ‘continuity’ of the assignment
![]() $\text{DM}_{\text{gm}}(-,\mathbb{Q})$
discussed in [Reference Cisinski and DégliseCD12, 4.3.3].
$\text{DM}_{\text{gm}}(-,\mathbb{Q})$
discussed in [Reference Cisinski and DégliseCD12, 4.3.3].
Remark 6.8. Using Remark 6.7, classical computations in algebraic K-theory imply that Hypothesis 6.6 is notably satisfied in the following cases:
(1) if
 $\mathbb{F}$
is an algebraic extension of
$\mathbb{F}$
is an algebraic extension of
 $\mathbb{Q}$
this follows from Borel’s computation of the algebraic
$\mathbb{Q}$
this follows from Borel’s computation of the algebraic
 $K$
-theory of number fields;
$K$
-theory of number fields;(2) if
 $\mathbb{F}$
is an algebraic extension of a finite field this follows from Quillen’s computation of the algebraic
$\mathbb{F}$
is an algebraic extension of a finite field this follows from Quillen’s computation of the algebraic
 $K$
-theory of finite fields;
$K$
-theory of finite fields;(3) if
 $\mathbb{F}$
is an algebraic extension of a global field of positive characteristic this follows from Harder’s theorem [Reference HarderHar77].
$\mathbb{F}$
is an algebraic extension of a global field of positive characteristic this follows from Harder’s theorem [Reference HarderHar77].
We recall the following result on Tate motives with rational coefficients.
Proposition 6.9 [Reference PeterPet13, 4.17].
Let
![]() $\mathbb{F}$
be a field satisfying Hypothesis 6.6. Then both morphisms in the following composition are isomorphisms of locally ringed spaces:
$\mathbb{F}$
be a field satisfying Hypothesis 6.6. Then both morphisms in the following composition are isomorphisms of locally ringed spaces:
The Beilinson–Soulé part of Hypothesis 6.6 is used to invoke [Reference Levine and GoerssLev92] and obtain a bounded t-structure on
![]() $\text{DTM}_{\text{gm}}(\mathbb{F},\mathbb{Q})$
. The second part of Hypothesis 6.6 then implies that the tt-spectrum is identified with the ‘coherent spectrum’ of the heart [Reference PeterPet13, 4.2], which is easily seen to be a singleton.
$\text{DTM}_{\text{gm}}(\mathbb{F},\mathbb{Q})$
. The second part of Hypothesis 6.6 then implies that the tt-spectrum is identified with the ‘coherent spectrum’ of the heart [Reference PeterPet13, 4.2], which is easily seen to be a singleton.
Now we can put the results on finite and rational coefficients together to arrive at an integral statement (for more general statements see Remarks 6.11 and 6.13).
Theorem 6.10. Let
![]() $\mathbb{F}$
be a field of exponential characteristic
$\mathbb{F}$
be a field of exponential characteristic
![]() $p$
, and assume that for every
$p$
, and assume that for every
![]() $\ell \neq p$
prime,
$\ell \neq p$
prime,
![]() $\mathbb{F}$
contains a primitive
$\mathbb{F}$
contains a primitive
![]() $\ell$
th root of unity (respectively,
$\ell$
th root of unity (respectively,
![]() $4$
th root of unity if
$4$
th root of unity if
![]() $\ell =2$
). Assume also that
$\ell =2$
). Assume also that
![]() $\mathbb{F}$
satisfies Hypothesis 6.6. Then:
$\mathbb{F}$
satisfies Hypothesis 6.6. Then:
(1) the central ring
 ${\mathcal{R}}_{\text{DTM}_{\text{gm}}^{\acute{\text{e}}\text{t}}(\mathbb{F},\mathbb{Z})}$
is
${\mathcal{R}}_{\text{DTM}_{\text{gm}}^{\acute{\text{e}}\text{t}}(\mathbb{F},\mathbb{Z})}$
is
 $\mathbb{Z}[1/p]$
;
$\mathbb{Z}[1/p]$
;(2) the comparison morphism
is an isomorphism of locally ringed spaces. $$\begin{eqnarray}\unicode[STIX]{x1D70C}:\operatorname{Spec}(\text{DTM}_{\text{gm}}^{\acute{\text{e}}\text{t}}(\mathbb{F},\mathbb{Z}))\rightarrow \operatorname{Spec}(\mathbb{Z}[1/p])\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D70C}:\operatorname{Spec}(\text{DTM}_{\text{gm}}^{\acute{\text{e}}\text{t}}(\mathbb{F},\mathbb{Z}))\rightarrow \operatorname{Spec}(\mathbb{Z}[1/p])\end{eqnarray}$$
Proof. We discussed in § 4 why
![]() $p$
is a unit in the central ring. A more precise statement is [Reference Cisinski and DégliseCD16, 7.1.2] from which the first part of the theorem follows immediately.
$p$
is a unit in the central ring. A more precise statement is [Reference Cisinski and DégliseCD16, 7.1.2] from which the first part of the theorem follows immediately.
For the second part, it suffices to show that
![]() $\unicode[STIX]{x1D70C}$
is a homeomorphism. First we show it is a bijection. For
$\unicode[STIX]{x1D70C}$
is a homeomorphism. First we show it is a bijection. For
![]() $\ell \neq p$
, the fiber of
$\ell \neq p$
, the fiber of
![]() $\unicode[STIX]{x1D70C}$
over
$\unicode[STIX]{x1D70C}$
over
![]() $\langle \ell \rangle$
is by definition
$\langle \ell \rangle$
is by definition
![]() $\operatorname{supp}(\mathbb{Z}/\ell )$
. Since
$\operatorname{supp}(\mathbb{Z}/\ell )$
. Since
![]() $\mathbb{Z}/\ell$
is the image of the unit under
$\mathbb{Z}/\ell$
is the image of the unit under
![]() $\unicode[STIX]{x1D6FE}_{\ast }$
, the right adjoint in the adjunction
$\unicode[STIX]{x1D6FE}_{\ast }$
, the right adjoint in the adjunction
we deduce from [Reference BalmerBal18, 1.7] that the fiber of
![]() $\unicode[STIX]{x1D70C}$
over
$\unicode[STIX]{x1D70C}$
over
![]() $\langle \ell \rangle$
is precisely the image of
$\langle \ell \rangle$
is precisely the image of
![]() $\operatorname{Spc}(\unicode[STIX]{x1D6FE}^{\ast })$
. And by Theorem 6.2 this consists of a single point.
$\operatorname{Spc}(\unicode[STIX]{x1D6FE}^{\ast })$
. And by Theorem 6.2 this consists of a single point.
For the generic fiber of
![]() $\unicode[STIX]{x1D70C}$
we note that the central localization at
$\unicode[STIX]{x1D70C}$
we note that the central localization at
![]() $\mathbb{Z}\backslash 0$
gives, up to idempotent completion, exactly
$\mathbb{Z}\backslash 0$
gives, up to idempotent completion, exactly
![]() $\text{DTM}_{\text{gm}}^{\acute{\text{e}}\text{t}}(\mathbb{F},\mathbb{Q})$
(Lemma 5.4). By [Reference BalmerBal10a, 5.6] (recalled in Corollary A.4), it suffices to show that the latter has a one-point spectrum. This is Proposition 6.9.
$\text{DTM}_{\text{gm}}^{\acute{\text{e}}\text{t}}(\mathbb{F},\mathbb{Q})$
(Lemma 5.4). By [Reference BalmerBal10a, 5.6] (recalled in Corollary A.4), it suffices to show that the latter has a one-point spectrum. This is Proposition 6.9.
Finally, we need to show that the topologies of the two spaces are the same. We use that a bijective spectral map between spectral spaces is a homeomorphism if specializations lift along the map, which allows us to work in
![]() $\text{DTM}_{\text{gm}}^{\acute{\text{e}}\text{t}}(\mathbb{F},\mathbb{Z}_{\langle \ell \rangle })$
(for every
$\text{DTM}_{\text{gm}}^{\acute{\text{e}}\text{t}}(\mathbb{F},\mathbb{Z}_{\langle \ell \rangle })$
(for every
![]() $\ell$
different from
$\ell$
different from
![]() $p$
). In other words, we need to show the inclusion of prime ideals
$p$
). In other words, we need to show the inclusion of prime ideals
in
![]() $\text{DTM}_{\text{gm}}^{\acute{\text{e}}\text{t}}(\mathbb{F},\mathbb{Z}_{\langle \ell \rangle })$
. But suppose
$\text{DTM}_{\text{gm}}^{\acute{\text{e}}\text{t}}(\mathbb{F},\mathbb{Z}_{\langle \ell \rangle })$
. But suppose
![]() $M\otimes \mathbb{Z}/\ell =0$
for some
$M\otimes \mathbb{Z}/\ell =0$
for some
![]() $M\in \text{DTM}_{\text{gm}}^{\acute{\text{e}}\text{t}}(\mathbb{F},\mathbb{Z}_{\langle \ell \rangle })$
. This implies that the
$M\in \text{DTM}_{\text{gm}}^{\acute{\text{e}}\text{t}}(\mathbb{F},\mathbb{Z}_{\langle \ell \rangle })$
. This implies that the
![]() $\ell$
-adic realization of
$\ell$
-adic realization of
![]() $M$
is zero, as is plain from the identification of this realization with
$M$
is zero, as is plain from the identification of this realization with
![]() $\ell$
-adic completion in [Reference Cisinski and DégliseCD16, 7.2.24]. By conservativity of the
$\ell$
-adic completion in [Reference Cisinski and DégliseCD16, 7.2.24]. By conservativity of the
![]() $\ell$
-adic realization (see Proposition 6.9) we deduce that
$\ell$
-adic realization (see Proposition 6.9) we deduce that
![]() $M\otimes \mathbb{Q}=0$
as well, and this concludes the proof.◻
$M\otimes \mathbb{Q}=0$
as well, and this concludes the proof.◻
Remark 6.11. Of course, if
![]() $S\subset \mathbb{Z}\backslash \{0\}$
is a saturated multiplicative subset containing the exponential characteristic of
$S\subset \mathbb{Z}\backslash \{0\}$
is a saturated multiplicative subset containing the exponential characteristic of
![]() $\mathbb{F}$
and such that for each prime
$\mathbb{F}$
and such that for each prime
![]() $\ell \notin S$
,
$\ell \notin S$
,
![]() $\mathbb{F}$
contains a primitive
$\mathbb{F}$
contains a primitive
![]() $\ell$
th root of unity (respectively,
$\ell$
th root of unity (respectively,
![]() $4$
th root of unity if
$4$
th root of unity if
![]() $\ell =2$
) then the same arguments show (still assuming
$\ell =2$
) then the same arguments show (still assuming
![]() $\mathbb{F}$
satisfies Hypothesis 6.6):
$\mathbb{F}$
satisfies Hypothesis 6.6):
(1) the central ring
 ${\mathcal{R}}_{\text{DTM}_{\text{gm}}^{\acute{\text{e}}\text{t}}(\mathbb{F},\mathbb{Z}[S^{-1}])}$
is
${\mathcal{R}}_{\text{DTM}_{\text{gm}}^{\acute{\text{e}}\text{t}}(\mathbb{F},\mathbb{Z}[S^{-1}])}$
is
 $\mathbb{Z}[S^{-1}]$
;
$\mathbb{Z}[S^{-1}]$
;(2) the comparison morphism
is an isomorphism of locally ringed spaces. $$\begin{eqnarray}\unicode[STIX]{x1D70C}:\operatorname{Spec}(\text{DTM}_{\text{gm}}^{\acute{\text{e}}\text{t}}(\mathbb{F},\mathbb{Z}[S^{-1}]))\rightarrow \operatorname{Spec}(\mathbb{Z}[S^{-1}])\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D70C}:\operatorname{Spec}(\text{DTM}_{\text{gm}}^{\acute{\text{e}}\text{t}}(\mathbb{F},\mathbb{Z}[S^{-1}]))\rightarrow \operatorname{Spec}(\mathbb{Z}[S^{-1}])\end{eqnarray}$$
Example 6.12. Let
![]() $\mathbb{F}=\mathbb{Q}(\unicode[STIX]{x1D701}_{\ell })$
be the
$\mathbb{F}=\mathbb{Q}(\unicode[STIX]{x1D701}_{\ell })$
be the
![]() $\ell$
th cyclotomic field, where
$\ell$
th cyclotomic field, where
![]() $\ell$
is an odd prime number. Then, canonically,
$\ell$
is an odd prime number. Then, canonically,
![]() $\operatorname{Spec}(\text{DTM}_{\text{gm}}^{\acute{\text{e}}\text{t}}(\mathbb{Q}(\unicode[STIX]{x1D701}_{\ell }),\mathbb{Z}_{\langle \ell \rangle }))=\operatorname{Spec}(\mathbb{Z}_{\langle \ell \rangle })$
. It follows [Reference BalmerBal05, 4.10] that the thick tensor ideals of
$\operatorname{Spec}(\text{DTM}_{\text{gm}}^{\acute{\text{e}}\text{t}}(\mathbb{Q}(\unicode[STIX]{x1D701}_{\ell }),\mathbb{Z}_{\langle \ell \rangle }))=\operatorname{Spec}(\mathbb{Z}_{\langle \ell \rangle })$
. It follows [Reference BalmerBal05, 4.10] that the thick tensor ideals of
![]() $\text{DTM}_{\text{gm}}^{\acute{\text{e}}\text{t}}(\mathbb{Q}(\unicode[STIX]{x1D701}_{\ell }),\mathbb{Z}_{\langle \ell \rangle })$
are exactly
$\text{DTM}_{\text{gm}}^{\acute{\text{e}}\text{t}}(\mathbb{Q}(\unicode[STIX]{x1D701}_{\ell }),\mathbb{Z}_{\langle \ell \rangle })$
are exactly
Notice, in particular, that étale cohomology
![]() $\text{DTM}_{\text{gm}}^{\acute{\text{e}}\text{t}}(\mathbb{Q}(\unicode[STIX]{x1D701}_{\ell }),\mathbb{Z}_{\langle \ell \rangle })\rightarrow \text{D}^{b}(\mathbb{Z}/\ell )$
is conservative (as its kernel is a tt-ideal).
$\text{DTM}_{\text{gm}}^{\acute{\text{e}}\text{t}}(\mathbb{Q}(\unicode[STIX]{x1D701}_{\ell }),\mathbb{Z}_{\langle \ell \rangle })\rightarrow \text{D}^{b}(\mathbb{Z}/\ell )$
is conservative (as its kernel is a tt-ideal).
Remark 6.13. A statement analogous to Theorem 6.10 (or Remark 6.11) holds for étale Artin–Tate motives if, in addition, Hypothesis 6.6 is satisfied for every finite extension
![]() $\mathbb{F}^{\prime }/\mathbb{F}$
. Indeed, Theorem 6.2 clearly applies for finite coefficients; and for rational coefficients, [Reference PeterPet13, 4.17] gives the required result.
$\mathbb{F}^{\prime }/\mathbb{F}$
. Indeed, Theorem 6.2 clearly applies for finite coefficients; and for rational coefficients, [Reference PeterPet13, 4.17] gives the required result.
7 Filtered Galois representations
In this section we recall Positselski’s approach to describing Tate motives with finite coefficients in [Reference PositselskiPos11]. The upshot is Proposition 7.7, which tells us that the tt-geometry of Tate motives over certain fields and with finite coefficients is the same as the tt-geometry of Galois representations with a ‘unipotent filtration’, the latter being seemingly more tractable. Although in this article we will eventually deal with algebraically closed fields only, it does not cause any difficulties to treat the general case here.
Convention 7.1. Throughout this section we fix a field
![]() $\mathbb{F}$
and a prime
$\mathbb{F}$
and a prime
![]() $\ell$
invertible in
$\ell$
invertible in
![]() $\mathbb{F}$
. The absolute Galois group of
$\mathbb{F}$
. The absolute Galois group of
![]() $\mathbb{F}$
is denoted by
$\mathbb{F}$
is denoted by
![]() $G_{\mathbb{F}}$
as before. We also assume that
$G_{\mathbb{F}}$
as before. We also assume that
![]() $\mathbb{F}$
contains a primitive
$\mathbb{F}$
contains a primitive
![]() $\ell$
th root of unity
$\ell$
th root of unity
![]() $\unicode[STIX]{x1D701}\in \unicode[STIX]{x1D707}_{\ell }(\mathbb{F})$
, which we interpret as a morphism
$\unicode[STIX]{x1D701}\in \unicode[STIX]{x1D707}_{\ell }(\mathbb{F})$
, which we interpret as a morphism
![]() $\unicode[STIX]{x1D6FD}:\mathbb{Z}/\ell (0)\rightarrow \mathbb{Z}/\ell (1)$
in
$\unicode[STIX]{x1D6FD}:\mathbb{Z}/\ell (0)\rightarrow \mathbb{Z}/\ell (1)$
in
![]() $\text{DTM}_{\text{gm}}(\mathbb{F},\mathbb{Z}/\ell )$
, in view of
$\text{DTM}_{\text{gm}}(\mathbb{F},\mathbb{Z}/\ell )$
, in view of
To see this identification, notice that by the change of coefficients adjunctions (3.1) we are supposed to identify
![]() $\hom _{\text{DTM}_{\text{gm}}(\mathbb{F},\mathbb{Z})}(\mathbb{Z},\mathbb{Z}/\ell (1))$
with the
$\hom _{\text{DTM}_{\text{gm}}(\mathbb{F},\mathbb{Z})}(\mathbb{Z},\mathbb{Z}/\ell (1))$
with the
![]() $\ell$
th roots of unity. This follows readily from identifying
$\ell$
th roots of unity. This follows readily from identifying
![]() $\mathbb{Z}(1)$
with the complex
$\mathbb{Z}(1)$
with the complex
![]() ${\mathcal{O}}^{\times }[-1]$
of sheaves with transfers [Reference Mazza, Voevodsky and WeibelMVW06, 4.9].
${\mathcal{O}}^{\times }[-1]$
of sheaves with transfers [Reference Mazza, Voevodsky and WeibelMVW06, 4.9].
For any integer
![]() $n$
, define the replete triangulated subcategories
$n$
, define the replete triangulated subcategories
![]() $\text{DTM}_{\text{gm}}(\mathbb{F},\mathbb{Z}/\ell )^{{\geqslant}n}$
(respectively,
$\text{DTM}_{\text{gm}}(\mathbb{F},\mathbb{Z}/\ell )^{{\geqslant}n}$
(respectively,
![]() $\text{DTM}_{\text{gm}}(\mathbb{F},\mathbb{Z}/\ell )^{{<}n}$
) generated by
$\text{DTM}_{\text{gm}}(\mathbb{F},\mathbb{Z}/\ell )^{{<}n}$
) generated by
![]() $(\mathbb{Z}/\ell )(n^{\prime })$
for
$(\mathbb{Z}/\ell )(n^{\prime })$
for
![]() $n^{\prime }\geqslant n$
(respectively,
$n^{\prime }\geqslant n$
(respectively,
![]() $n^{\prime }<n$
). The vanishing of motivic cohomology
$n^{\prime }<n$
). The vanishing of motivic cohomology
![]() $\text{H}^{p,q}(\mathbb{F},\mathbb{Z}/\ell )$
when
$\text{H}^{p,q}(\mathbb{F},\mathbb{Z}/\ell )$
when
![]() $q<0$
(cf. our remarks regarding Figure 1), implies that the pair
$q<0$
(cf. our remarks regarding Figure 1), implies that the pair
defines a t-structure on
![]() $\text{DTM}_{\text{gm}}(\mathbb{F},\mathbb{Z}/\ell )$
. Indeed, the arguments of [Reference Levine and GoerssLev92, 1.2] go through word for word. In particular, this gives rise to adjoints
$\text{DTM}_{\text{gm}}(\mathbb{F},\mathbb{Z}/\ell )$
. Indeed, the arguments of [Reference Levine and GoerssLev92, 1.2] go through word for word. In particular, this gives rise to adjoints
![]() $W^{{\geqslant}n},W^{{<}n}$
to the inclusions of these subcategories, and one deduces that every object
$W^{{\geqslant}n},W^{{<}n}$
to the inclusions of these subcategories, and one deduces that every object
![]() $M\in \text{DTM}_{\text{gm}}(\mathbb{F},\mathbb{Z}/\ell )$
admits a functorial descending filtration, called the weight filtration,
$M\in \text{DTM}_{\text{gm}}(\mathbb{F},\mathbb{Z}/\ell )$
admits a functorial descending filtration, called the weight filtration,
such that the associated graded piece
![]() $\text{gr}^{n}M:=W^{{\geqslant}n}W^{{<}n+1}M$
is a finite direct sum of copies of shifts of
$\text{gr}^{n}M:=W^{{\geqslant}n}W^{{<}n+1}M$
is a finite direct sum of copies of shifts of
![]() $\mathbb{Z}/\ell (n)$
(as
$\mathbb{Z}/\ell (n)$
(as
![]() $\text{H}_{\text{M}}^{p,q}(\mathbb{F},\mathbb{Z}/\ell )$
vanishes when
$\text{H}_{\text{M}}^{p,q}(\mathbb{F},\mathbb{Z}/\ell )$
vanishes when
![]() $q=0$
and
$q=0$
and
![]() $p\neq 0$
).
$p\neq 0$
).
Define the subcategory
![]() ${\mathcal{F}}(\mathbb{F},\mathbb{Z}/\ell )\subset \text{DTM}_{\text{gm}}(\mathbb{F},\mathbb{Z}/\ell )$
as the smallest full subcategory containing
${\mathcal{F}}(\mathbb{F},\mathbb{Z}/\ell )\subset \text{DTM}_{\text{gm}}(\mathbb{F},\mathbb{Z}/\ell )$
as the smallest full subcategory containing
![]() $\mathbb{Z}/\ell (n)$
for all integers
$\mathbb{Z}/\ell (n)$
for all integers
![]() $n$
, and closed under extensions. (The latter condition means that for any triangle in which the outer two terms lie in the subcategory, the middle one does as well.) The Bloch–Kato conjecture (recalled in § 6) implies the Beilinson–Lichtenbaum conjecture [Reference Suslin and VoevodskySV00, Reference Geisser and LevineGL01], i.e. the étale realization functor induces identifications:
$n$
, and closed under extensions. (The latter condition means that for any triangle in which the outer two terms lie in the subcategory, the middle one does as well.) The Bloch–Kato conjecture (recalled in § 6) implies the Beilinson–Lichtenbaum conjecture [Reference Suslin and VoevodskySV00, Reference Geisser and LevineGL01], i.e. the étale realization functor induces identifications:
For one, this implies that there are no negative Ext groups between the Tate objects
![]() $\mathbb{Z}/\ell (n)$
, and from this one deduces that
$\mathbb{Z}/\ell (n)$
, and from this one deduces that
![]() ${\mathcal{F}}(\mathbb{F},\mathbb{Z}/\ell )$
is in fact an exact subcategory of
${\mathcal{F}}(\mathbb{F},\mathbb{Z}/\ell )$
is in fact an exact subcategory of
![]() $\text{DTM}_{\text{gm}}(\mathbb{F},\mathbb{Z}/\ell )$
(i.e. the triangles of
$\text{DTM}_{\text{gm}}(\mathbb{F},\mathbb{Z}/\ell )$
(i.e. the triangles of
![]() $\text{DTM}_{\text{gm}}(\mathbb{F},\mathbb{Z}/\ell )$
lying in
$\text{DTM}_{\text{gm}}(\mathbb{F},\mathbb{Z}/\ell )$
lying in
![]() ${\mathcal{F}}(\mathbb{F},\mathbb{Z}/\ell )$
define an exact structure, see [Reference DyerDye05]). And secondly, the Beilinson–Lichtenbaum conjecture essentially implies the following result.
${\mathcal{F}}(\mathbb{F},\mathbb{Z}/\ell )$
define an exact structure, see [Reference DyerDye05]). And secondly, the Beilinson–Lichtenbaum conjecture essentially implies the following result.
Proposition 7.3 (Cf. [Reference PositselskiPos11, 3.1]).
The étale realization induces an equivalence of exact tensor categories
where the latter denotes the category of (discrete) Galois modules over
![]() $\mathbb{Z}/\ell$
equipped with a unipotent filtration, i.e. a finite decreasing filtration whose graded pieces are finite direct sums of copies of the trivial Galois module
$\mathbb{Z}/\ell$
equipped with a unipotent filtration, i.e. a finite decreasing filtration whose graded pieces are finite direct sums of copies of the trivial Galois module
![]() $\mathbb{Z}/\ell$
.
$\mathbb{Z}/\ell$
.
A few words about the latter category. The tensor product
![]() $a\,\otimes \,b$
of two filtered Galois modules
$a\,\otimes \,b$
of two filtered Galois modules
![]() $a$
and
$a$
and
![]() $b$
has an induced filtration given by
$b$
has an induced filtration given by
these tensor products being over
![]() $\mathbb{Z}/\ell$
. And the exact structure on
$\mathbb{Z}/\ell$
. And the exact structure on
![]() $\operatorname{mod}_{\text{fil}\text{-}\text{un}}(G_{\mathbb{F}},\mathbb{Z}/\ell )$
is defined as follows: a conflation is a short sequence
$\operatorname{mod}_{\text{fil}\text{-}\text{un}}(G_{\mathbb{F}},\mathbb{Z}/\ell )$
is defined as follows: a conflation is a short sequence
![]() $a\rightarrowtail b{\twoheadrightarrow}c$
with zero composition such that the associated graded sequences
$a\rightarrowtail b{\twoheadrightarrow}c$
with zero composition such that the associated graded sequences
![]() $0\rightarrow \text{gr}^{n}a\rightarrow \text{gr}^{n}b\rightarrow \text{gr}^{n}c\rightarrow 0$
are all split short exact in
$0\rightarrow \text{gr}^{n}a\rightarrow \text{gr}^{n}b\rightarrow \text{gr}^{n}c\rightarrow 0$
are all split short exact in
![]() $\operatorname{mod}(G_{\mathbb{F}},\mathbb{Z}/\ell )$
.
$\operatorname{mod}(G_{\mathbb{F}},\mathbb{Z}/\ell )$
.
The étale realization
![]() $\text{Re}_{\ell }$
sends
$\text{Re}_{\ell }$
sends
![]() $\mathbb{Z}/\ell (n)$
to
$\mathbb{Z}/\ell (n)$
to
![]() $\unicode[STIX]{x1D707}_{\ell }(\overline{\mathbb{F}})^{\otimes n}\cong \mathbb{Z}/\ell$
, using the primitive
$\unicode[STIX]{x1D707}_{\ell }(\overline{\mathbb{F}})^{\otimes n}\cong \mathbb{Z}/\ell$
, using the primitive
![]() $\ell$
th root of unity
$\ell$
th root of unity
![]() $\unicode[STIX]{x1D701}$
. Since the heart of
$\unicode[STIX]{x1D701}$
. Since the heart of
![]() $\text{D}_{c}^{b}(G_{\mathbb{F}},\mathbb{Z}/\ell )$
with respect to the standard t-structure is closed under extensions, we see that the image of
$\text{D}_{c}^{b}(G_{\mathbb{F}},\mathbb{Z}/\ell )$
with respect to the standard t-structure is closed under extensions, we see that the image of
![]() ${\mathcal{F}}(\mathbb{F},\mathbb{Z}/\ell )$
under the étale realization is contained in the heart. Applying the realization to the weight filtration (7.2) of an object
${\mathcal{F}}(\mathbb{F},\mathbb{Z}/\ell )$
under the étale realization is contained in the heart. Applying the realization to the weight filtration (7.2) of an object
![]() $M\in {\mathcal{F}}(\mathbb{F},\mathbb{Z}/\ell )$
therefore yields a discrete Galois module together with a unipotent filtration. This describes the functor in the statement of Proposition 7.3. Note, in particular, that under this identification, the étale realization corresponds to forgetting the (unipotent) filtration of the discrete Galois module.
$M\in {\mathcal{F}}(\mathbb{F},\mathbb{Z}/\ell )$
therefore yields a discrete Galois module together with a unipotent filtration. This describes the functor in the statement of Proposition 7.3. Note, in particular, that under this identification, the étale realization corresponds to forgetting the (unipotent) filtration of the discrete Galois module.
Proof of Proposition 7.3.
The fact that this is an equivalence of exact categories is [Reference PositselskiPos11, 3.1]. (This obviously relies crucially on the truth of the Beilinson–Lichtenbaum conjecture.) We only want to explain why it is compatible with the tensor structure.
Let
![]() ${\mathcal{T}}$
stand for the category
${\mathcal{T}}$
stand for the category
![]() $\text{DTM}_{\text{gm}}(\mathbb{F},\mathbb{Z}/\ell )$
, and correspondingly
$\text{DTM}_{\text{gm}}(\mathbb{F},\mathbb{Z}/\ell )$
, and correspondingly
![]() ${\mathcal{T}}^{{\geqslant}n}$
and
${\mathcal{T}}^{{\geqslant}n}$
and
![]() ${\mathcal{T}}^{{<}n}$
for the subcategories considered above. We first note that the tensor product sends
${\mathcal{T}}^{{<}n}$
for the subcategories considered above. We first note that the tensor product sends
![]() ${\mathcal{T}}^{{\geqslant}p}\times {\mathcal{T}}^{{\geqslant}q}$
into
${\mathcal{T}}^{{\geqslant}p}\times {\mathcal{T}}^{{\geqslant}q}$
into
![]() ${\mathcal{T}}^{{\geqslant}p+q}$
, as follows immediately from
${\mathcal{T}}^{{\geqslant}p+q}$
, as follows immediately from
![]() $\mathbb{Z}/\ell (m)\otimes \mathbb{Z}/\ell (m^{\prime })=\mathbb{Z}/\ell (m+m^{\prime })$
. Also, note that every object
$\mathbb{Z}/\ell (m)\otimes \mathbb{Z}/\ell (m^{\prime })=\mathbb{Z}/\ell (m+m^{\prime })$
. Also, note that every object
![]() $M\in {\mathcal{T}}$
sits in a functorial triangle
$M\in {\mathcal{T}}$
sits in a functorial triangle
Now fix integers
![]() $p,q$
, and objects
$p,q$
, and objects
![]() $M,N\in {\mathcal{T}}$
. The two facts just mentioned imply that the canonical morphism
$M,N\in {\mathcal{T}}$
. The two facts just mentioned imply that the canonical morphism
![]() $W^{{\geqslant}p}M\otimes W^{{\geqslant}q}N\rightarrow M\otimes N$
factors through
$W^{{\geqslant}p}M\otimes W^{{\geqslant}q}N\rightarrow M\otimes N$
factors through
![]() $W^{{\geqslant}p+q}(M\otimes N)$
, and this defines a natural transformation
$W^{{\geqslant}p+q}(M\otimes N)$
, and this defines a natural transformation
![]() $W^{{\geqslant}p}\otimes W^{{\geqslant}q}\rightarrow W^{{\geqslant}p+q}\circ \otimes$
. For
$W^{{\geqslant}p}\otimes W^{{\geqslant}q}\rightarrow W^{{\geqslant}p+q}\circ \otimes$
. For
![]() $M$
and
$M$
and
![]() $N$
in
$N$
in
![]() ${\mathcal{F}}(\mathbb{F},\mathbb{Z}/\ell )$
, there is then an induced morphism
${\mathcal{F}}(\mathbb{F},\mathbb{Z}/\ell )$
, there is then an induced morphism
of filtered modules, using the fact that
![]() $\text{Re}_{\ell }$
is a tensor functor. By functoriality of this construction, it is obvious that (7.5) endows
$\text{Re}_{\ell }$
is a tensor functor. By functoriality of this construction, it is obvious that (7.5) endows
![]() $\text{}\underline{\text{Re}}_{\ell ,\unicode[STIX]{x1D701}}$
with a lax symmetric unital monoidal structure.
$\text{}\underline{\text{Re}}_{\ell ,\unicode[STIX]{x1D701}}$
with a lax symmetric unital monoidal structure.
It remains to check that (7.5) is in fact invertible for all
![]() $M,N\in {\mathcal{F}}(\mathbb{F},\mathbb{Z}/\ell )$
. It is certainly invertible if
$M,N\in {\mathcal{F}}(\mathbb{F},\mathbb{Z}/\ell )$
. It is certainly invertible if
![]() $M=\mathbb{Z}/\ell (m)$
and
$M=\mathbb{Z}/\ell (m)$
and
![]() $N=\mathbb{Z}/\ell (n)$
. Moreover, since the tensor product in
$N=\mathbb{Z}/\ell (n)$
. Moreover, since the tensor product in
![]() $\text{DTM}_{\text{gm}}(\mathbb{F},\mathbb{Z}/\ell )$
is exact in both variables, and the étale realization an exact functor, it follows that, in both variables, the set of objects for which (7.5) is invertible is closed under extensions. Thus the claim is proven.◻
$\text{DTM}_{\text{gm}}(\mathbb{F},\mathbb{Z}/\ell )$
is exact in both variables, and the étale realization an exact functor, it follows that, in both variables, the set of objects for which (7.5) is invertible is closed under extensions. Thus the claim is proven.◻
Let us take stock: we have found an exact tensor category
![]() ${\mathcal{F}}(\mathbb{F},\mathbb{Z}/\ell )$
inside the tt-category
${\mathcal{F}}(\mathbb{F},\mathbb{Z}/\ell )$
inside the tt-category
![]() $\text{DTM}_{\text{gm}}(\mathbb{F},\mathbb{Z}/\ell )$
, which we understand reasonably well, by Proposition 7.3. The question arises whether
$\text{DTM}_{\text{gm}}(\mathbb{F},\mathbb{Z}/\ell )$
, which we understand reasonably well, by Proposition 7.3. The question arises whether
![]() $\text{DTM}_{\text{gm}}(\mathbb{F},\mathbb{Z}/\ell )$
is simply the (bounded) derived category of
$\text{DTM}_{\text{gm}}(\mathbb{F},\mathbb{Z}/\ell )$
is simply the (bounded) derived category of
![]() ${\mathcal{F}}(\mathbb{F},\mathbb{Z}/\ell )$
. This kind of question is, in general, very hard to answer, not least because there is no canonical functor in either direction. Typically, this problem can be solved if the triangulated category has a model. In our case we do not know whether
${\mathcal{F}}(\mathbb{F},\mathbb{Z}/\ell )$
. This kind of question is, in general, very hard to answer, not least because there is no canonical functor in either direction. Typically, this problem can be solved if the triangulated category has a model. In our case we do not know whether
![]() $\text{DTM}_{\text{gm}}(\mathbb{F},\mathbb{Z}/\ell )$
does, but it is a triangulated subcategory of
$\text{DTM}_{\text{gm}}(\mathbb{F},\mathbb{Z}/\ell )$
does, but it is a triangulated subcategory of
![]() $\text{DM}_{\text{gm}}(\mathbb{F},\mathbb{Z}/\ell )$
, which does. This is enough for Positselski to construct an exact functor
$\text{DM}_{\text{gm}}(\mathbb{F},\mathbb{Z}/\ell )$
, which does. This is enough for Positselski to construct an exact functor
Instead of invoking Koszulity of the graded Galois cohomology algebra
![]() $\text{H}^{\bullet }(G_{\mathbb{F}},\mathbb{Z}/\ell )$
as in [Reference PositselskiPos11, 9.1], we will show directly that
$\text{H}^{\bullet }(G_{\mathbb{F}},\mathbb{Z}/\ell )$
as in [Reference PositselskiPos11, 9.1], we will show directly that
![]() $\text{pos}$
is an equivalence if
$\text{pos}$
is an equivalence if
![]() $\mathbb{F}$
is algebraically closed (Proposition 7.9).
$\mathbb{F}$
is algebraically closed (Proposition 7.9).
Unfortunately, it is not clear whether (7.6) is compatible with the tensor structures, and although it should be possible to construct a tensor equivalence using an extension of the methods employed in [Reference PositselskiPos11, Appendix D], we leave it as an open problem for now. Instead, we will establish the following weaker result, which is enough for our purposes.
Proposition 7.7. Assume that (7.6) is an equivalence. Then it induces, together with the equivalence
![]() $\text{}\underline{\text{Re}}_{\ell ,\unicode[STIX]{x1D701}}$
of Proposition 7.3, a bijection
$\text{}\underline{\text{Re}}_{\ell ,\unicode[STIX]{x1D701}}$
of Proposition 7.3, a bijection
Proof. In order to construct the exact functor of (7.6), a weaker version of filtered triangulated categories is used in [Reference PositselskiPos11]. One can easily phrase the proof to be given here in this language but we prefer to work with derivators that we feel yield a conceptually more satisfying argument. The reason is that in the context of derivators, the bounded derived category of an exact category has the expected universal property [Reference PortaPor15, 2.17].
We place ourselves in the following abstract situation:
![]() $\unicode[STIX]{x1D704}:{\mathcal{A}}{\hookrightarrow}{\mathcal{T}}$
is an exact tensor subcategory of a (possibly large) tt-category
$\unicode[STIX]{x1D704}:{\mathcal{A}}{\hookrightarrow}{\mathcal{T}}$
is an exact tensor subcategory of a (possibly large) tt-category
![]() ${\mathcal{T}}$
, which is the base of a stable monoidal derivator
${\mathcal{T}}$
, which is the base of a stable monoidal derivator
![]() $\mathbb{T}$
(defined on finite categories). We also assume that
$\mathbb{T}$
(defined on finite categories). We also assume that
![]() $\hom _{{\mathcal{T}}}(X,Y[-1])=0$
for all
$\hom _{{\mathcal{T}}}(X,Y[-1])=0$
for all
![]() $X,Y\in {\mathcal{A}}$
.
$X,Y\in {\mathcal{A}}$
.
The universal property mentioned above yields an exact morphism of derivators
![]() $\mathbb{F}:\mathbb{A}\rightarrow \mathbb{T}$
, where
$\mathbb{F}:\mathbb{A}\rightarrow \mathbb{T}$
, where
![]() $\mathbb{A}$
denotes the derivator with base
$\mathbb{A}$
denotes the derivator with base
![]() $\text{D}^{b}({\mathcal{A}})$
. It induces an exact functor
$\text{D}^{b}({\mathcal{A}})$
. It induces an exact functor
![]() ${\mathcal{F}}:\text{D}^{b}({\mathcal{A}})\rightarrow {\mathcal{T}}$
, which is the identity on
${\mathcal{F}}:\text{D}^{b}({\mathcal{A}})\rightarrow {\mathcal{T}}$
, which is the identity on
![]() ${\mathcal{A}}$
, and is unique up to unique isomorphism for these properties. Now fix an object
${\mathcal{A}}$
, and is unique up to unique isomorphism for these properties. Now fix an object
![]() $M\in {\mathcal{A}}$
and consider the two functors
$M\in {\mathcal{A}}$
and consider the two functors
They coincide on
![]() ${\mathcal{A}}$
, and satisfy the ‘Toda conditions’ [Reference PortaPor15, 2.17]
${\mathcal{A}}$
, and satisfy the ‘Toda conditions’ [Reference PortaPor15, 2.17]
because
![]() $M\in {\mathcal{A}}$
and
$M\in {\mathcal{A}}$
and
![]() ${\mathcal{A}}$
is closed under tensor products. It follows again from the universal property that the associated functors
${\mathcal{A}}$
is closed under tensor products. It follows again from the universal property that the associated functors
![]() $\mathbb{F}_{1},\mathbb{F}_{2}:\mathbb{A}\rightarrow \mathbb{T}$
are canonically isomorphic. We deduce, in particular, that the following square commutes on the level of objects.
$\mathbb{F}_{1},\mathbb{F}_{2}:\mathbb{A}\rightarrow \mathbb{T}$
are canonically isomorphic. We deduce, in particular, that the following square commutes on the level of objects.

We apply this to
![]() ${\mathcal{A}}={\mathcal{F}}(\mathbb{F},\mathbb{Z}/\ell )$
, and
${\mathcal{A}}={\mathcal{F}}(\mathbb{F},\mathbb{Z}/\ell )$
, and
![]() $\mathbb{T}$
the derivator associated to the stable monoidal model category modeling
$\mathbb{T}$
the derivator associated to the stable monoidal model category modeling
![]() $\text{DM}(\mathbb{F},\mathbb{Z}/\ell )$
. It follows from the uniqueness statement of [Reference PositselskiPos11, A.17] that
$\text{DM}(\mathbb{F},\mathbb{Z}/\ell )$
. It follows from the uniqueness statement of [Reference PositselskiPos11, A.17] that
![]() $\mathbb{F}:\mathbb{A}\rightarrow \mathbb{T}$
in this case induces an exact equivalence
$\mathbb{F}:\mathbb{A}\rightarrow \mathbb{T}$
in this case induces an exact equivalence
In particular, it induces a bijection of thick subcategories. The proof will be complete once we check that:
∙ tt-ideals in
 $\text{D}^{b}(\operatorname{mod}_{\text{fil}\text{-}\text{un}}(G_{\mathbb{F}},\mathbb{Z}/\ell ))$
are exactly the thick subcategories closed under tensoring with
$\text{D}^{b}(\operatorname{mod}_{\text{fil}\text{-}\text{un}}(G_{\mathbb{F}},\mathbb{Z}/\ell ))$
are exactly the thick subcategories closed under tensoring with
 $\mathbb{Z}/\ell (n)$
(i.e.
$\mathbb{Z}/\ell (n)$
(i.e.
 $\mathbb{Z}/\ell$
placed in filtration degree
$\mathbb{Z}/\ell$
placed in filtration degree
 $n$
),
$n$
),
 $n\in \mathbb{Z}$
;
$n\in \mathbb{Z}$
;∙ tt-ideals in
 $\text{DTM}_{\text{gm}}(\mathbb{F},\mathbb{Z}/\ell )$
are exactly the thick subcategories closed under tensoring with
$\text{DTM}_{\text{gm}}(\mathbb{F},\mathbb{Z}/\ell )$
are exactly the thick subcategories closed under tensoring with
 $\mathbb{Z}/\ell (n)$
,
$\mathbb{Z}/\ell (n)$
,
 $n\in \mathbb{Z}$
.
$n\in \mathbb{Z}$
.
Indeed,
![]() $\mathbb{Z}/\ell (n)\in {\mathcal{A}}$
; now apply commutativity of the diagram in (7.8).
$\mathbb{Z}/\ell (n)\in {\mathcal{A}}$
; now apply commutativity of the diagram in (7.8).
The two bullet points are an immediate consequence of the fact that in both cases the objects
![]() $\mathbb{Z}/\ell (n)$
generate the category as a thick subcategory [see Reference GallauerGal18, 3.6].◻
$\mathbb{Z}/\ell (n)$
generate the category as a thick subcategory [see Reference GallauerGal18, 3.6].◻
Proposition 7.9. Assume
![]() $\mathbb{F}$
is algebraically closed. Then the exact functor of (7.6) provides an equivalence
$\mathbb{F}$
is algebraically closed. Then the exact functor of (7.6) provides an equivalence
between the (bounded) filtered derived category of
![]() $\mathbb{Z}/\ell$
-vector spaces and the triangulated category of Tate motives over
$\mathbb{Z}/\ell$
-vector spaces and the triangulated category of Tate motives over
![]() $\mathbb{F}$
with coefficients in
$\mathbb{F}$
with coefficients in
![]() $\mathbb{Z}/\ell$
.
$\mathbb{Z}/\ell$
.
Proof. Since
![]() $\mathbb{F}$
is algebraically closed, the exact category
$\mathbb{F}$
is algebraically closed, the exact category
![]() $\operatorname{mod}_{\text{fil}\text{-}\text{un}}(G_{\mathbb{F}},\mathbb{Z}/\ell )$
identifies with
$\operatorname{mod}_{\text{fil}\text{-}\text{un}}(G_{\mathbb{F}},\mathbb{Z}/\ell )$
identifies with
![]() $\operatorname{mod}_{\text{fil}}(\mathbb{Z}/\ell )$
, the category of filtered (finite-dimensional) vector spaces over
$\operatorname{mod}_{\text{fil}}(\mathbb{Z}/\ell )$
, the category of filtered (finite-dimensional) vector spaces over
![]() $\mathbb{Z}/\ell$
. Its (bounded) derived category is the classical filtered derived category
$\mathbb{Z}/\ell$
. Its (bounded) derived category is the classical filtered derived category
![]() $\text{D}_{\text{fil}}^{b}(\mathbb{Z}/\ell )$
. The category
$\text{D}_{\text{fil}}^{b}(\mathbb{Z}/\ell )$
. The category
![]() $\text{DTM}_{\text{gm}}(\mathbb{F},\mathbb{Z}/\ell )$
is generated, as a thick subcategory, by objects of the form
$\text{DTM}_{\text{gm}}(\mathbb{F},\mathbb{Z}/\ell )$
is generated, as a thick subcategory, by objects of the form
![]() $\mathbb{Z}/\ell (n)$
. These lie in
$\mathbb{Z}/\ell (n)$
. These lie in
![]() $\operatorname{mod}_{\text{fil}}(\mathbb{Z}/\ell )$
, and
$\operatorname{mod}_{\text{fil}}(\mathbb{Z}/\ell )$
, and
![]() $\text{D}_{\text{fil}}^{b}(\mathbb{Z}/\ell )$
is idempotent complete, therefore it suffices to prove fully faithfulness of the functor.
$\text{D}_{\text{fil}}^{b}(\mathbb{Z}/\ell )$
is idempotent complete, therefore it suffices to prove fully faithfulness of the functor.
Let
![]() $M,N$
be two complexes in
$M,N$
be two complexes in
![]() $\operatorname{mod}_{\text{fil}}(\mathbb{Z}/\ell )$
and let us prove that
$\operatorname{mod}_{\text{fil}}(\mathbb{Z}/\ell )$
and let us prove that
is bijective. By induction on the length of these complexes and the five-lemma we reduce to
![]() $M,N$
shifts of objects in
$M,N$
shifts of objects in
![]() $\operatorname{mod}_{\text{fil}}(\mathbb{Z}/\ell )$
. Similarly, by induction on the length of the filtration we reduce to
$\operatorname{mod}_{\text{fil}}(\mathbb{Z}/\ell )$
. Similarly, by induction on the length of the filtration we reduce to
![]() $M=\mathbb{Z}/\ell$
and
$M=\mathbb{Z}/\ell$
and
![]() $N=\mathbb{Z}/\ell (n)[m]$
, some
$N=\mathbb{Z}/\ell (n)[m]$
, some
![]() $n,m\in \mathbb{Z}$
. In other words, we need to show that
$n,m\in \mathbb{Z}$
. In other words, we need to show that
is bijective. Both sides vanish whenever
![]() $m<0$
. It is automatically bijective for
$m<0$
. It is automatically bijective for
![]() $m=0$
since
$m=0$
since
![]() $\operatorname{mod}_{\text{fil}}(\mathbb{Z}/\ell )$
is a full subcategory of
$\operatorname{mod}_{\text{fil}}(\mathbb{Z}/\ell )$
is a full subcategory of
![]() $\text{DTM}_{\text{gm}}(\mathbb{F},\mathbb{Z}/\ell )$
, and the same holds for
$\text{DTM}_{\text{gm}}(\mathbb{F},\mathbb{Z}/\ell )$
, and the same holds for
![]() $m=1$
since the subcategory is closed under extensions, cf. [Reference DyerDye05]. By the Beilinson–Lichtenbaum conjecture recalled above, the right-hand side vanishes when
$m=1$
since the subcategory is closed under extensions, cf. [Reference DyerDye05]. By the Beilinson–Lichtenbaum conjecture recalled above, the right-hand side vanishes when
![]() $m\geqslant 2$
(in fact, when
$m\geqslant 2$
(in fact, when
![]() $m\geqslant 1$
) and the same is true for the left-hand side since the t-structure on
$m\geqslant 1$
) and the same is true for the left-hand side since the t-structure on
![]() $\text{D}_{\text{fil}}^{b}(\mathbb{Z}/\ell )$
is strongly hereditary, see [Reference GallauerGal18, 7.6]. This completes the proof.◻
$\text{D}_{\text{fil}}^{b}(\mathbb{Z}/\ell )$
is strongly hereditary, see [Reference GallauerGal18, 7.6]. This completes the proof.◻
8 tt-primes
In this section we are going to determine the prime ideals in the triangulated category of Tate motives over certain algebraically closed fields. This will use the results in the previous section, as well as the results in [Reference GallauerGal18] where we determined the tt-geometry of filtered modules. As in the étale case (§ 6) we will first treat the case of finite coefficients; the case of rational coefficients is the same as in the étale case due to the equivalence
![]() $\text{DTM}_{\text{gm}}(\mathbb{F},\mathbb{Q})\simeq \text{DTM}_{\text{gm}}^{\acute{\text{e}}\text{t}}(\mathbb{F},\mathbb{Q})$
.
$\text{DTM}_{\text{gm}}(\mathbb{F},\mathbb{Q})\simeq \text{DTM}_{\text{gm}}^{\acute{\text{e}}\text{t}}(\mathbb{F},\mathbb{Q})$
.
Convention 8.1. If not mentioned explicitly otherwise we assume that
![]() $\mathbb{F}$
is algebraically closed throughout this section. (The only exception is Lemma 8.5.)
$\mathbb{F}$
is algebraically closed throughout this section. (The only exception is Lemma 8.5.)
Let
![]() $\ell$
be a prime invertible in
$\ell$
be a prime invertible in
![]() $\mathbb{F}$
, and fix a primitive
$\mathbb{F}$
, and fix a primitive
![]() $\ell$
th root of unity
$\ell$
th root of unity
![]() $\unicode[STIX]{x1D701}\in \unicode[STIX]{x1D707}_{\ell }(\mathbb{F})$
, which we interpret as a morphism
$\unicode[STIX]{x1D701}\in \unicode[STIX]{x1D707}_{\ell }(\mathbb{F})$
, which we interpret as a morphism
![]() $\unicode[STIX]{x1D6FD}:\mathbb{Z}/\ell (0)\rightarrow \mathbb{Z}/\ell (1)$
as in § 7. From the results of the previous section and [Reference GallauerGal18, 7.8] we deduce the following result.
$\unicode[STIX]{x1D6FD}:\mathbb{Z}/\ell (0)\rightarrow \mathbb{Z}/\ell (1)$
as in § 7. From the results of the previous section and [Reference GallauerGal18, 7.8] we deduce the following result.
Proposition 8.2. The tt-category
![]() $\text{DTM}_{\text{gm}}(\mathbb{F},\mathbb{Z}/\ell )$
has a unique non-trivial tt-ideal given by
$\text{DTM}_{\text{gm}}(\mathbb{F},\mathbb{Z}/\ell )$
has a unique non-trivial tt-ideal given by
Proof. We may apply Propositions 7.7 and 7.9 to replace
![]() $\text{DTM}_{\text{gm}}(\mathbb{F},\mathbb{Z}/\ell )$
by
$\text{DTM}_{\text{gm}}(\mathbb{F},\mathbb{Z}/\ell )$
by
![]() $\text{D}_{\text{fil}}^{b}(\mathbb{Z}/\ell )$
. The étale realization functor then is identified with the functor
$\text{D}_{\text{fil}}^{b}(\mathbb{Z}/\ell )$
. The étale realization functor then is identified with the functor
![]() $\unicode[STIX]{x1D70B}:\text{D}_{\text{fil}}^{b}(\mathbb{Z}/\ell )\rightarrow \text{D}^{b}(\mathbb{Z}/\ell )$
, which forgets the filtration.
$\unicode[STIX]{x1D70B}:\text{D}_{\text{fil}}^{b}(\mathbb{Z}/\ell )\rightarrow \text{D}^{b}(\mathbb{Z}/\ell )$
, which forgets the filtration.
In [Reference GallauerGal18, 7.8] we studied the tt-category
![]() $\text{D}_{\text{fil}}^{b}(\mathbb{Z}/\ell )$
, and found that it has a unique non-trivial tt-ideal given by
$\text{D}_{\text{fil}}^{b}(\mathbb{Z}/\ell )$
, and found that it has a unique non-trivial tt-ideal given by
![]() $\ker (\unicode[STIX]{x1D70B})=\langle \operatorname{cone}(\unicode[STIX]{x1D6FD})\rangle$
.Footnote
3
◻
$\ker (\unicode[STIX]{x1D70B})=\langle \operatorname{cone}(\unicode[STIX]{x1D6FD})\rangle$
.Footnote
3
◻
Fix the invertible object
![]() $\mathbb{Z}/\ell (1)$
in
$\mathbb{Z}/\ell (1)$
in
![]() $\text{DTM}_{\text{gm}}(\mathbb{F},\mathbb{Z}/\ell )$
and define the graded central ring
$\text{DTM}_{\text{gm}}(\mathbb{F},\mathbb{Z}/\ell )$
and define the graded central ring
Corollary 8.3.
(1) The graded central ring
 ${\mathcal{R}}_{\ell }^{\bullet }$
is canonically isomorphic to the polynomial ring
${\mathcal{R}}_{\ell }^{\bullet }$
is canonically isomorphic to the polynomial ring
 $\mathbb{Z}/\ell [\unicode[STIX]{x1D6FD}]$
.
$\mathbb{Z}/\ell [\unicode[STIX]{x1D6FD}]$
.(2) The comparison morphism
is an isomorphism of locally ringed spaces. $$\begin{eqnarray}\unicode[STIX]{x1D70C}_{\mathbb{F},\ell }^{\bullet }:\operatorname{Spec}(\text{DTM}_{\text{gm}}(\mathbb{F},\mathbb{Z}/\ell ))\rightarrow \operatorname{Spec}^{\text{h}}(\mathbb{Z}/\ell [\unicode[STIX]{x1D6FD}])\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D70C}_{\mathbb{F},\ell }^{\bullet }:\operatorname{Spec}(\text{DTM}_{\text{gm}}(\mathbb{F},\mathbb{Z}/\ell ))\rightarrow \operatorname{Spec}^{\text{h}}(\mathbb{Z}/\ell [\unicode[STIX]{x1D6FD}])\end{eqnarray}$$
Proof. The first part can be deduced from the Beilinson–Lichtenbaum conjecture, recalled in § 7. For the second part, it suffices to show that the map is a homeomorphism. The map is a bijection by Proposition 8.2. And the only non-trivial open
![]() $\{\langle \operatorname{cone}(\unicode[STIX]{x1D6FD})\rangle \}$
is mapped to the open subset
$\{\langle \operatorname{cone}(\unicode[STIX]{x1D6FD})\rangle \}$
is mapped to the open subset
![]() $U(\unicode[STIX]{x1D6FD})$
.◻
$U(\unicode[STIX]{x1D6FD})$
.◻
Corollary 8.4. The support of
![]() $\mathbb{Z}/\ell (0)$
in
$\mathbb{Z}/\ell (0)$
in
![]() $\operatorname{Spc}(\text{DTM}_{\text{gm}}(\mathbb{F},\mathbb{Z}))$
is the subspace
$\operatorname{Spc}(\text{DTM}_{\text{gm}}(\mathbb{F},\mathbb{Z}))$
is the subspace

where
![]() $\unicode[STIX]{x1D6FE}^{\ast }:\text{DTM}_{\text{gm}}(\mathbb{F},\mathbb{Z})\rightarrow \text{DTM}_{\text{gm}}(\mathbb{F},\mathbb{Z}/\ell )$
is the change of coefficients functor, and the specialization relation is indicated by the line going upward.
$\unicode[STIX]{x1D6FE}^{\ast }:\text{DTM}_{\text{gm}}(\mathbb{F},\mathbb{Z})\rightarrow \text{DTM}_{\text{gm}}(\mathbb{F},\mathbb{Z}/\ell )$
is the change of coefficients functor, and the specialization relation is indicated by the line going upward.
Proof. Since
![]() $\mathbb{Z}/\ell$
is perfect over
$\mathbb{Z}/\ell$
is perfect over
![]() $\mathbb{Z}$
, the corresponding change of coefficients functor
$\mathbb{Z}$
, the corresponding change of coefficients functor
![]() $\unicode[STIX]{x1D6FE}^{\ast }$
has a right adjoint
$\unicode[STIX]{x1D6FE}^{\ast }$
has a right adjoint
![]() $\unicode[STIX]{x1D6FE}_{\ast }$
. By [Reference BalmerBal18, 1.7], the image of
$\unicode[STIX]{x1D6FE}_{\ast }$
. By [Reference BalmerBal18, 1.7], the image of
![]() $\operatorname{Spc}(\unicode[STIX]{x1D6FE}^{\ast })$
is precisely the support of
$\operatorname{Spc}(\unicode[STIX]{x1D6FE}^{\ast })$
is precisely the support of
![]() $\unicode[STIX]{x1D6FE}_{\ast }\unicode[STIX]{x1D6FE}^{\ast }(\mathbb{Z})=\mathbb{Z}/\ell (0)$
.
$\unicode[STIX]{x1D6FE}_{\ast }\unicode[STIX]{x1D6FE}^{\ast }(\mathbb{Z})=\mathbb{Z}/\ell (0)$
.
On the other hand, using Corollary 8.3 we see that the image of
![]() $\operatorname{Spc}(\unicode[STIX]{x1D6FE}^{\ast })$
is the set of primes in the statement. It follows from Lemma B.6 below that the two primes are distinct since
$\operatorname{Spc}(\unicode[STIX]{x1D6FE}^{\ast })$
is the set of primes in the statement. It follows from Lemma B.6 below that the two primes are distinct since
The inclusion
![]() $\ker (\unicode[STIX]{x1D6FE}^{\ast })\subset \ker (\text{Re}_{\ell })$
gives the specialization relation in the statement. (And, of course, there can be no other specialization relation by continuity of
$\ker (\unicode[STIX]{x1D6FE}^{\ast })\subset \ker (\text{Re}_{\ell })$
gives the specialization relation in the statement. (And, of course, there can be no other specialization relation by continuity of
![]() $\operatorname{Spc}(\unicode[STIX]{x1D6FE}^{\ast })$
.)◻
$\operatorname{Spc}(\unicode[STIX]{x1D6FE}^{\ast })$
.)◻
We now have a good understanding of the tt-spectrum of
![]() $\text{DTM}_{\text{gm}}(\mathbb{F},R)$
for coefficients
$\text{DTM}_{\text{gm}}(\mathbb{F},R)$
for coefficients
![]() $R=\mathbb{Z}/\ell$
and
$R=\mathbb{Z}/\ell$
and
![]() $R=\mathbb{Q}$
, and our last step consists in patching these two cases together. For this we will use the results on étale Tate motives in the following form.
$R=\mathbb{Q}$
, and our last step consists in patching these two cases together. For this we will use the results on étale Tate motives in the following form.
Lemma 8.5. Let
![]() $\mathbb{F}$
be a field of exponential characteristic
$\mathbb{F}$
be a field of exponential characteristic
![]() $p$
, and assume that for every
$p$
, and assume that for every
![]() $\ell \neq p$
prime,
$\ell \neq p$
prime,
![]() $\mathbb{F}$
contains a primitive
$\mathbb{F}$
contains a primitive
![]() $\ell$
th root of unity (respectively,
$\ell$
th root of unity (respectively,
![]() $4$
th root of unity if
$4$
th root of unity if
![]() $\ell =2$
). Assume also that
$\ell =2$
). Assume also that
![]() $\mathbb{F}$
satisfies Hypothesis 6.6. Then the étale sheafification induces a map
$\mathbb{F}$
satisfies Hypothesis 6.6. Then the étale sheafification induces a map
which is a homeomorphism onto the subspace
![]() $\{\mathfrak{m}_{0},\mathfrak{e}_{\ell }\mid \ell \neq p\}$
of torsion objects
$\{\mathfrak{m}_{0},\mathfrak{e}_{\ell }\mid \ell \neq p\}$
of torsion objects
![]() $\mathfrak{m}_{0}$
and
$\mathfrak{m}_{0}$
and
![]() $\text{Re}_{\ell }$
-acyclics
$\text{Re}_{\ell }$
-acyclics
![]() $\mathfrak{e}_{\ell }$
.
$\mathfrak{e}_{\ell }$
.
Proof. By Theorem 6.10 and naturality of
![]() $\unicode[STIX]{x1D70C}$
([Reference BalmerBal10a, 5.6]; recalled in Appendix A), the étale sheafification induces a section to
$\unicode[STIX]{x1D70C}$
([Reference BalmerBal10a, 5.6]; recalled in Appendix A), the étale sheafification induces a section to
![]() $\unicode[STIX]{x1D70C}$
on the level of spectra:
$\unicode[STIX]{x1D70C}$
on the level of spectra:
and therefore a homeomorphism onto its image. It is obvious that this image is precisely
![]() $\{\mathfrak{m}_{0},\mathfrak{e}_{\ell }\mid \ell \neq p\}$
.◻
$\{\mathfrak{m}_{0},\mathfrak{e}_{\ell }\mid \ell \neq p\}$
.◻
With this preparation we can now state and easily prove our main result in this section.
Theorem 8.6. Let
![]() $\mathbb{F}$
be an algebraically closed field of exponential characteristic
$\mathbb{F}$
be an algebraically closed field of exponential characteristic
![]() $p$
, which satisfies Hypothesis 6.6. The primes of
$p$
, which satisfies Hypothesis 6.6. The primes of
![]() $\text{DTM}_{\text{gm}}(\mathbb{F},\mathbb{Z}[1/p])$
are depicted in the following diagram, including the specialization relations pointing upward.
$\text{DTM}_{\text{gm}}(\mathbb{F},\mathbb{Z}[1/p])$
are depicted in the following diagram, including the specialization relations pointing upward.

Here,
![]() $\ell$
runs through all prime numbers different from
$\ell$
runs through all prime numbers different from
![]() $p$
, and the prime tensor ideals are defined by the vanishing of the cohomology theories as indicated on the right.
$p$
, and the prime tensor ideals are defined by the vanishing of the cohomology theories as indicated on the right.
Proof. The central ring
![]() ${\mathcal{R}}=\hom _{\text{DTM}_{\text{gm}}(\mathbb{F},\mathbb{Z}[1/p])}(\mathbb{Z}[1/p],\mathbb{Z}[1/p])$
is simply
${\mathcal{R}}=\hom _{\text{DTM}_{\text{gm}}(\mathbb{F},\mathbb{Z}[1/p])}(\mathbb{Z}[1/p],\mathbb{Z}[1/p])$
is simply
![]() $\mathbb{Z}[1/p]$
, and we get a canonical map
$\mathbb{Z}[1/p]$
, and we get a canonical map
which we analyse fiberwise, i.e. we identify the primes in each fiber of
![]() $\unicode[STIX]{x1D70C}$
with the corresponding primes in the statement of the theorem.
$\unicode[STIX]{x1D70C}$
with the corresponding primes in the statement of the theorem.
∙ For a prime
 $\ell \neq p$
we have and therefore we can apply Corollary 8.4.
$\ell \neq p$
we have and therefore we can apply Corollary 8.4. $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D70C}^{-1}(\langle \ell \rangle ) & = & \displaystyle \{\mathfrak{P}\mid \ell \in \unicode[STIX]{x1D70C}(\mathfrak{P})\}\nonumber\\ \displaystyle & = & \displaystyle \{\mathfrak{P}\mid \mathbb{Z}/\ell (0)=\operatorname{cone}(\ell )\notin \mathfrak{P}\}\nonumber\\ \displaystyle & = & \displaystyle \operatorname{supp}(\mathbb{Z}/\ell (0)),\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D70C}^{-1}(\langle \ell \rangle ) & = & \displaystyle \{\mathfrak{P}\mid \ell \in \unicode[STIX]{x1D70C}(\mathfrak{P})\}\nonumber\\ \displaystyle & = & \displaystyle \{\mathfrak{P}\mid \mathbb{Z}/\ell (0)=\operatorname{cone}(\ell )\notin \mathfrak{P}\}\nonumber\\ \displaystyle & = & \displaystyle \operatorname{supp}(\mathbb{Z}/\ell (0)),\nonumber\end{eqnarray}$$
∙ Over the generic point, the fiber is the spectrum of the central localization of
 $\text{DTM}_{\text{gm}}(\mathbb{F},\mathbb{Z}[1/p])$
at
$\text{DTM}_{\text{gm}}(\mathbb{F},\mathbb{Z}[1/p])$
at
 $\mathbb{Z}\backslash 0$
(see [Reference BalmerBal10a, 5.6] or Corollary A.4). Up to idempotent completion, this localization is
$\mathbb{Z}\backslash 0$
(see [Reference BalmerBal10a, 5.6] or Corollary A.4). Up to idempotent completion, this localization is
 $\text{DTM}_{\text{gm}}(\mathbb{F},\mathbb{Q})$
, by Lemma 5.4. The contention now follows from Proposition 6.9.
$\text{DTM}_{\text{gm}}(\mathbb{F},\mathbb{Q})$
, by Lemma 5.4. The contention now follows from Proposition 6.9.
At this point all that remains to be justified is the specialization relation
![]() $\mathfrak{m}_{0}{\rightsquigarrow}\mathfrak{e}_{\ell }$
, for every
$\mathfrak{m}_{0}{\rightsquigarrow}\mathfrak{e}_{\ell }$
, for every
![]() $\ell \neq p$
. This follows from Lemma 8.5.◻
$\ell \neq p$
. This follows from Lemma 8.5.◻
9 Classification of tt-ideals
Convention 9.1. Throughout this section we fix a field
![]() $\mathbb{F}$
as in Theorem 8.6.
$\mathbb{F}$
as in Theorem 8.6.
We determined the prime ideals of
![]() $\text{DTM}_{\text{gm}}(\mathbb{F},\mathbb{Z}[1/p])$
, as well as the specialization relations among these. This is not enough to determine the tt-spectrum as a topological space, nor its Thomason subsets. The goal of this section is to remedy this, and then deduce the classification of the tt-ideals in
$\text{DTM}_{\text{gm}}(\mathbb{F},\mathbb{Z}[1/p])$
, as well as the specialization relations among these. This is not enough to determine the tt-spectrum as a topological space, nor its Thomason subsets. The goal of this section is to remedy this, and then deduce the classification of the tt-ideals in
![]() $\text{DTM}_{\text{gm}}(\mathbb{F},\mathbb{Z}[1/p])$
.
$\text{DTM}_{\text{gm}}(\mathbb{F},\mathbb{Z}[1/p])$
.
The main input we need was already proved in Proposition 5.8. Here is the tt-geometric content of this result.
Proposition 9.2. The topology of
![]() $\operatorname{Spc}(\text{DTM}_{\text{gm}}(\mathbb{F},\mathbb{Z}[1/p]))$
is coarser than the cofinite topology.
$\operatorname{Spc}(\text{DTM}_{\text{gm}}(\mathbb{F},\mathbb{Z}[1/p]))$
is coarser than the cofinite topology.
Proof. Since the sets
![]() $\operatorname{supp}(M)$
with
$\operatorname{supp}(M)$
with
![]() $M\in \text{DTM}_{\text{gm}}(\mathbb{F},\mathbb{Z}[1/p])$
generate the closed subsets for the topology it suffices to show that if
$M\in \text{DTM}_{\text{gm}}(\mathbb{F},\mathbb{Z}[1/p])$
generate the closed subsets for the topology it suffices to show that if
![]() $\operatorname{supp}(M)$
is infinite then it is already the whole space. Lemma 8.5 implies that if
$\operatorname{supp}(M)$
is infinite then it is already the whole space. Lemma 8.5 implies that if
![]() $\operatorname{supp}(M)\cap \{\mathfrak{e}_{\ell }\mid \ell \neq p\}$
is infinite then
$\operatorname{supp}(M)\cap \{\mathfrak{e}_{\ell }\mid \ell \neq p\}$
is infinite then
![]() $\operatorname{supp}(M)$
is the whole space. Otherwise
$\operatorname{supp}(M)$
is the whole space. Otherwise
![]() $\operatorname{supp}(M)\cap \{\mathfrak{m}_{\ell }\mid \ell \neq p\}$
must be infinite, i.e. for infinitely many primes
$\operatorname{supp}(M)\cap \{\mathfrak{m}_{\ell }\mid \ell \neq p\}$
must be infinite, i.e. for infinitely many primes
![]() $\ell$
, the mod-
$\ell$
, the mod-
![]() $\ell$
motivic cohomology of
$\ell$
motivic cohomology of
![]() $M$
is non-trivial. By Proposition 5.8,
$M$
is non-trivial. By Proposition 5.8,
![]() $M$
has non-trivial rational motivic cohomology, i.e.
$M$
has non-trivial rational motivic cohomology, i.e.
![]() $\mathfrak{m}_{0}\in \operatorname{supp}(M)$
, and this shows that
$\mathfrak{m}_{0}\in \operatorname{supp}(M)$
, and this shows that
![]() $\operatorname{supp}(M)$
is the whole space.◻
$\operatorname{supp}(M)$
is the whole space.◻
Corollary 9.3. For a proper subset
![]() $Z\subsetneq \operatorname{Spc}(\text{DTM}_{\text{gm}}(\mathbb{F},\mathbb{Z}[1/p]))$
the following are equivalent:
$Z\subsetneq \operatorname{Spc}(\text{DTM}_{\text{gm}}(\mathbb{F},\mathbb{Z}[1/p]))$
the following are equivalent:
(1)
 $Z$
is closed;
$Z$
is closed;(2)
 $Z$
is finite and specialization closed.
$Z$
is finite and specialization closed.
Corollary 9.4. The topological space
![]() $\operatorname{Spc}(\text{DTM}_{\text{gm}}(\mathbb{F},\mathbb{Z}[1/p]))$
is noetherian.
$\operatorname{Spc}(\text{DTM}_{\text{gm}}(\mathbb{F},\mathbb{Z}[1/p]))$
is noetherian.
We are now in a position to classify the tt-ideals in
![]() $\text{DTM}_{\text{gm}}(\mathbb{F},\mathbb{Z}[1/p])$
. In order to state the classification concisely, let us introduce the following notation:
$\text{DTM}_{\text{gm}}(\mathbb{F},\mathbb{Z}[1/p])$
. In order to state the classification concisely, let us introduce the following notation:
∙
 $\mathbb{P}=\{\text{prime numbers }\ell \text{ different from }p\}$
;
$\mathbb{P}=\{\text{prime numbers }\ell \text{ different from }p\}$
;∙ for every
 $\ell \in \mathbb{P}$
, choose a Bott element
$\ell \in \mathbb{P}$
, choose a Bott element
 $\unicode[STIX]{x1D6FD}_{\ell }:\mathbb{Z}/\ell \rightarrow \mathbb{Z}/\ell (1)$
in
$\unicode[STIX]{x1D6FD}_{\ell }:\mathbb{Z}/\ell \rightarrow \mathbb{Z}/\ell (1)$
in
 $\text{DTM}_{\text{gm}}(\mathbb{F},\mathbb{Z}/\ell )$
, i.e. a primitive
$\text{DTM}_{\text{gm}}(\mathbb{F},\mathbb{Z}/\ell )$
, i.e. a primitive
 $\ell$
th root of unity; we denote abusively by
$\ell$
th root of unity; we denote abusively by
 $\operatorname{cone}(\unicode[STIX]{x1D6FD}_{\ell })$
the image of its cone in
$\operatorname{cone}(\unicode[STIX]{x1D6FD}_{\ell })$
the image of its cone in
 $\text{DTM}_{\text{gm}}(\mathbb{F},\mathbb{Z}[1/p])$
under the right adjoint
$\text{DTM}_{\text{gm}}(\mathbb{F},\mathbb{Z}[1/p])$
under the right adjoint
 $\unicode[STIX]{x1D6FE}_{\ast }$
of the change of coefficients functor.
$\unicode[STIX]{x1D6FE}_{\ast }$
of the change of coefficients functor.
Theorem 9.5. Let
![]() $\mathbb{F}$
be an algebraically closed field of exponential characteristic
$\mathbb{F}$
be an algebraically closed field of exponential characteristic
![]() $p$
, which satisfies Hypothesis 6.6. The following two maps are inverses to each other and set up a bijection
$p$
, which satisfies Hypothesis 6.6. The following two maps are inverses to each other and set up a bijection
 $$\begin{eqnarray}\displaystyle \{\text{proper tt-ideals in }\text{DTM}_{\text{gm}}(\mathbb{F},\mathbb{Z}[1/p])\} & \longleftrightarrow & \displaystyle \{\text{subsets }{\mathcal{E}}\subset {\mathcal{M}}\subset \mathbb{P}\}\nonumber\\ \displaystyle {\mathcal{I}} & \longmapsto & \displaystyle \{\ell \mid \text{H}_{\acute{\text{e}}\text{t}}^{\bullet }({\mathcal{I}},\mathbb{Z}/\ell )\neq 0\}\subset \{\ell \mid \text{H}_{\text{M}}^{\bullet ,\bullet }({\mathcal{I}},\mathbb{Z}/\ell )\neq 0\}\nonumber\\ \displaystyle \langle \operatorname{cone}(\unicode[STIX]{x1D6FD}_{\ell }),\mathbb{Z}/\ell ^{\prime }(0)\mid \ell \in {\mathcal{M}},\ell ^{\prime }\in {\mathcal{E}}\rangle & \longleftarrow & \displaystyle ({\mathcal{E}}\subset {\mathcal{M}}).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \{\text{proper tt-ideals in }\text{DTM}_{\text{gm}}(\mathbb{F},\mathbb{Z}[1/p])\} & \longleftrightarrow & \displaystyle \{\text{subsets }{\mathcal{E}}\subset {\mathcal{M}}\subset \mathbb{P}\}\nonumber\\ \displaystyle {\mathcal{I}} & \longmapsto & \displaystyle \{\ell \mid \text{H}_{\acute{\text{e}}\text{t}}^{\bullet }({\mathcal{I}},\mathbb{Z}/\ell )\neq 0\}\subset \{\ell \mid \text{H}_{\text{M}}^{\bullet ,\bullet }({\mathcal{I}},\mathbb{Z}/\ell )\neq 0\}\nonumber\\ \displaystyle \langle \operatorname{cone}(\unicode[STIX]{x1D6FD}_{\ell }),\mathbb{Z}/\ell ^{\prime }(0)\mid \ell \in {\mathcal{M}},\ell ^{\prime }\in {\mathcal{E}}\rangle & \longleftarrow & \displaystyle ({\mathcal{E}}\subset {\mathcal{M}}).\nonumber\end{eqnarray}$$
Proof. Since
![]() $\operatorname{Spc}(\text{DTM}_{\text{gm}}(\mathbb{F},\mathbb{Z}[1/p]))$
is noetherian (Corollary 9.4), the Thomason subsets are precisely the specialization closed ones. It is then clear that the proper Thomason subsets correspond bijectively to
$\operatorname{Spc}(\text{DTM}_{\text{gm}}(\mathbb{F},\mathbb{Z}[1/p]))$
is noetherian (Corollary 9.4), the Thomason subsets are precisely the specialization closed ones. It is then clear that the proper Thomason subsets correspond bijectively to
![]() $\{\text{subsets }{\mathcal{E}}\subset {\mathcal{M}}\subset \mathbb{P}\}$
. One now applies [Reference BalmerBal05, 4.10].◻
$\{\text{subsets }{\mathcal{E}}\subset {\mathcal{M}}\subset \mathbb{P}\}$
. One now applies [Reference BalmerBal05, 4.10].◻
Example 9.6. The étale sheafification functor
is a non-trivial tt-functor and its kernel therefore a proper tt-ideal. It corresponds to the subsets
![]() $\emptyset ={\mathcal{E}}\subset {\mathcal{M}}=\mathbb{P}$
. We must then have
$\emptyset ={\mathcal{E}}\subset {\mathcal{M}}=\mathbb{P}$
. We must then have
In fact, we will prove in Appendix C that
![]() $a_{\acute{\text{e}}\text{t}}$
is a Verdier localization of the tt-category
$a_{\acute{\text{e}}\text{t}}$
is a Verdier localization of the tt-category
![]() $\text{DTM}_{\text{gm}}(\mathbb{F},\mathbb{Z}[1/p])$
at
$\text{DTM}_{\text{gm}}(\mathbb{F},\mathbb{Z}[1/p])$
at
![]() $\operatorname{cone}(\unicode[STIX]{x1D6FD}_{\ell })$
for all
$\operatorname{cone}(\unicode[STIX]{x1D6FD}_{\ell })$
for all
![]() $\ell \neq p$
.
$\ell \neq p$
.
10 Structure sheaf
Convention 10.1. We continue to denote by
![]() $\mathbb{F}$
an algebraically closed field of exponential characteristic
$\mathbb{F}$
an algebraically closed field of exponential characteristic
![]() $p$
, satisfying Hypothesis 6.6.
$p$
, satisfying Hypothesis 6.6.
At this point we know
![]() $\operatorname{Spec}(\text{DTM}_{\text{gm}}(\mathbb{F},\mathbb{Z}[1/p]))$
as a topological space, and in this last section we want to describe the structure sheaf of this locally ringed space. We denote it simply by
$\operatorname{Spec}(\text{DTM}_{\text{gm}}(\mathbb{F},\mathbb{Z}[1/p]))$
as a topological space, and in this last section we want to describe the structure sheaf of this locally ringed space. We denote it simply by
![]() ${\mathcal{O}}_{\mathbb{F}}$
.
${\mathcal{O}}_{\mathbb{F}}$
.
Proposition 10.2. Let
![]() ${\mathcal{O}}_{\mathbb{F}}^{\acute{\text{e}}\text{t}}$
denote the structure sheaf on
${\mathcal{O}}_{\mathbb{F}}^{\acute{\text{e}}\text{t}}$
denote the structure sheaf on
![]() $\text{DTM}_{\text{gm}}^{\acute{\text{e}}\text{t}}(\mathbb{F},\mathbb{Z}[1/p])$
(which is according to Theorem 6.10 essentially just
$\text{DTM}_{\text{gm}}^{\acute{\text{e}}\text{t}}(\mathbb{F},\mathbb{Z}[1/p])$
(which is according to Theorem 6.10 essentially just
![]() $\mathbb{Z}[1/p]$
). The canonical map
$\mathbb{Z}[1/p]$
). The canonical map
is an isomorphism.
Proof. By Theorem C.4, we know that the functor
![]() $a_{\acute{\text{e}}\text{t}}$
is a Verdier localization, and by Example 9.6, the kernel is
$a_{\acute{\text{e}}\text{t}}$
is a Verdier localization, and by Example 9.6, the kernel is
![]() $\langle \operatorname{cone}(\unicode[STIX]{x1D6FD}_{\ell })\mid \ell \neq p\rangle$
. By Remark A.5, the map in the statement of the proposition is an isomorphism on all stalks in the image of
$\langle \operatorname{cone}(\unicode[STIX]{x1D6FD}_{\ell })\mid \ell \neq p\rangle$
. By Remark A.5, the map in the statement of the proposition is an isomorphism on all stalks in the image of
![]() $\operatorname{Spc}(a_{\acute{\text{e}}\text{t}})$
, i.e. on all non-closed points. For a closed point
$\operatorname{Spc}(a_{\acute{\text{e}}\text{t}})$
, i.e. on all non-closed points. For a closed point
![]() $\mathfrak{m}_{\ell }$
,
$\mathfrak{m}_{\ell }$
,
![]() $\ell \neq p$
, we may localize at
$\ell \neq p$
, we may localize at
![]() $\ell$
and consider the functor
$\ell$
and consider the functor
instead (cf. Corollary A.4). In that case the prime
![]() $\mathfrak{m}_{\ell }$
is the zero ideal (the category
$\mathfrak{m}_{\ell }$
is the zero ideal (the category
![]() $\text{DTM}_{\text{gm}}(\mathbb{F},\mathbb{Z}_{\langle \ell \rangle })$
is local; cf. Example 6.12) hence
$\text{DTM}_{\text{gm}}(\mathbb{F},\mathbb{Z}_{\langle \ell \rangle })$
is local; cf. Example 6.12) hence
Again since the space
![]() $\operatorname{Spc}(\text{DTM}_{\text{gm}}(\mathbb{F},\mathbb{Z}_{\langle \ell \rangle }))$
is local, this is also the stalk of
$\operatorname{Spc}(\text{DTM}_{\text{gm}}(\mathbb{F},\mathbb{Z}_{\langle \ell \rangle }))$
is local, this is also the stalk of
![]() $\operatorname{Spc}(a_{\acute{\text{e}}\text{t}})_{\ast }{\mathcal{O}}_{\mathbb{F}}^{\acute{\text{e}}\text{t}}$
at
$\operatorname{Spc}(a_{\acute{\text{e}}\text{t}})_{\ast }{\mathcal{O}}_{\mathbb{F}}^{\acute{\text{e}}\text{t}}$
at
![]() $\mathfrak{m}_{\ell }$
. The morphism induced between these stalks is clearly an isomorphism, which concludes the proof.◻
$\mathfrak{m}_{\ell }$
. The morphism induced between these stalks is clearly an isomorphism, which concludes the proof.◻
Corollary 10.3. The stalks at the primes are
Corollary 10.4. The locally ringed space
![]() $\operatorname{Spec}(\text{DTM}_{\text{gm}}(\mathbb{F},\mathbb{Z}[1/p]))$
is not a scheme.
$\operatorname{Spec}(\text{DTM}_{\text{gm}}(\mathbb{F},\mathbb{Z}[1/p]))$
is not a scheme.
Proof. The canonical functor from schemes to locally ringed spaces preserves fiber products. Localizing at
![]() $S=\mathbb{Z}\backslash \langle \ell \rangle$
, it would follow from Lemma A.3, that
$S=\mathbb{Z}\backslash \langle \ell \rangle$
, it would follow from Lemma A.3, that
![]() $\operatorname{Spec}(\text{DTM}_{\text{gm}}(\mathbb{F},\mathbb{Z}_{\langle \ell \rangle }))$
is a scheme as well. Since it is local it would have to be affine, the spectrum of
$\operatorname{Spec}(\text{DTM}_{\text{gm}}(\mathbb{F},\mathbb{Z}_{\langle \ell \rangle }))$
is a scheme as well. Since it is local it would have to be affine, the spectrum of
![]() $\mathbb{Z}_{\langle \ell \rangle }$
. But the latter has two, not three, points.◻
$\mathbb{Z}_{\langle \ell \rangle }$
. But the latter has two, not three, points.◻
Acknowledgements
I would like to thank Simon Pepin Lehalleur for bringing [Reference PositselskiPos11] to my attention, which was the starting point for this project. Many thanks to Paul Balmer, Shane Kelly, and Simon Pepin Lehalleur for their valuable input on an earlier version of this article, and to Denis-Charles Cisinski for pointing out a flaw in an argument and the connection to the conservativity of the
![]() $\ell$
-adic realizations. I am also grateful to Joseph Ayoub for an encouraging discussion concerning Appendix C.
$\ell$
-adic realizations. I am also grateful to Joseph Ayoub for an encouraging discussion concerning Appendix C.
Appendix A Some remarks on Balmer’s structure sheaf
Balmer in [Reference BalmerBal05] (see also [Reference BalmerBal10a]) associates to every (small) rigid tt-category
![]() ${\mathcal{T}}$
a locally ringed space
${\mathcal{T}}$
a locally ringed space
![]() $\operatorname{Spec}({\mathcal{T}})$
, its tt-spectrum. It is fairly obvious that this actually extends canonically to a functor satisfying certain good properties. Since we have not seen this explained in the literature and since we need it in the body of the text, let us spell out the details here. For this section only, we assume that all tt-categories are rigid.
$\operatorname{Spec}({\mathcal{T}})$
, its tt-spectrum. It is fairly obvious that this actually extends canonically to a functor satisfying certain good properties. Since we have not seen this explained in the literature and since we need it in the body of the text, let us spell out the details here. For this section only, we assume that all tt-categories are rigid.
Lemma A.1. Balmer’s construction canonically extends to a contravariant functor
![]() $\text{Spec}:\text{tt}\text{Cat}^{\text{rig}}\rightarrow \text{LRS}$
from the category of rigid tt-categories to the category of locally ringed spaces.
$\text{Spec}:\text{tt}\text{Cat}^{\text{rig}}\rightarrow \text{LRS}$
from the category of rigid tt-categories to the category of locally ringed spaces.
Proof. That
![]() $\operatorname{Spc}$
is a contravariant functor
$\operatorname{Spc}$
is a contravariant functor
![]() $\text{tt}\text{Cat}^{\text{rig}}\rightarrow \text{Top}$
is proved in [Reference BalmerBal05, 3.6] so that we need only consider the structure sheaves. Recall that these are defined as the sheafification of a presheaf
$\text{tt}\text{Cat}^{\text{rig}}\rightarrow \text{Top}$
is proved in [Reference BalmerBal05, 3.6] so that we need only consider the structure sheaves. Recall that these are defined as the sheafification of a presheaf
![]() $\text{}_{p}{\mathcal{O}}$
on the canonical base for the topology, whose definition we now recall. Let
$\text{}_{p}{\mathcal{O}}$
on the canonical base for the topology, whose definition we now recall. Let
![]() ${\mathcal{T}}$
be a tt-category, and
${\mathcal{T}}$
be a tt-category, and
![]() $a\in {\mathcal{T}}$
. Sections of
$a\in {\mathcal{T}}$
. Sections of
![]() $\text{}_{p}{\mathcal{O}}_{{\mathcal{T}}}$
over
$\text{}_{p}{\mathcal{O}}_{{\mathcal{T}}}$
over
![]() $U(a)$
are given by endomorphisms of the unit in
$U(a)$
are given by endomorphisms of the unit in
![]() ${\mathcal{T}}/\langle a\rangle$
. Given an inclusion
${\mathcal{T}}/\langle a\rangle$
. Given an inclusion
![]() $U(b)\subset U(a)$
, we have
$U(b)\subset U(a)$
, we have
![]() $\langle a\rangle \subset \langle b\rangle$
from which a functor
$\langle a\rangle \subset \langle b\rangle$
from which a functor
![]() ${\mathcal{T}}/\langle a\rangle \rightarrow {\mathcal{T}}/\langle b\rangle$
and then an induced morphism of rings.
${\mathcal{T}}/\langle a\rangle \rightarrow {\mathcal{T}}/\langle b\rangle$
and then an induced morphism of rings.
We note that the association
![]() $U(a)\mapsto {\mathcal{T}}/\langle a\rangle$
can be made into a functor
$U(a)\mapsto {\mathcal{T}}/\langle a\rangle$
can be made into a functor
![]() ${\mathcal{T}}/-$
with values in
${\mathcal{T}}/-$
with values in
![]() $\text{tt}\text{Cat}^{\text{rig}}$
. We can then compose with the functor
$\text{tt}\text{Cat}^{\text{rig}}$
. We can then compose with the functor
![]() ${\mathcal{R}}_{-}=\operatorname{End}_{-}(\unicode[STIX]{x1D7D9}):\text{tt}\text{Cat}^{\text{rig}}\rightarrow \text{Rng}$
to the category of rings, and this defines the presheaf
${\mathcal{R}}_{-}=\operatorname{End}_{-}(\unicode[STIX]{x1D7D9}):\text{tt}\text{Cat}^{\text{rig}}\rightarrow \text{Rng}$
to the category of rings, and this defines the presheaf
![]() $\text{}_{p}{\mathcal{O}}_{{\mathcal{T}}}$
on the distinguished base for the topology.
$\text{}_{p}{\mathcal{O}}_{{\mathcal{T}}}$
on the distinguished base for the topology.
Given a tt-functor
![]() $F:{\mathcal{T}}\rightarrow {\mathcal{T}}^{\prime }$
, denote its induced continuous map
$F:{\mathcal{T}}\rightarrow {\mathcal{T}}^{\prime }$
, denote its induced continuous map
![]() $\operatorname{Spc}(F)$
by
$\operatorname{Spc}(F)$
by
![]() $f$
. We have
$f$
. We have
![]() $f^{-1}(U(a))=U(Fa)$
and
$f^{-1}(U(a))=U(Fa)$
and
![]() $F:{\mathcal{T}}/\langle a\rangle \rightarrow {\mathcal{T}}^{\prime }/\langle Fa\rangle$
thus a natural transformation
$F:{\mathcal{T}}/\langle a\rangle \rightarrow {\mathcal{T}}^{\prime }/\langle Fa\rangle$
thus a natural transformation
![]() $F/-:{\mathcal{T}}/-\rightarrow {\mathcal{T}}^{\prime }/F(-)$
. Whiskering with
$F/-:{\mathcal{T}}/-\rightarrow {\mathcal{T}}^{\prime }/F(-)$
. Whiskering with
![]() $\operatorname{End}_{-}(\unicode[STIX]{x1D7D9})$
we obtain a morphism of presheaves of rings
$\operatorname{End}_{-}(\unicode[STIX]{x1D7D9})$
we obtain a morphism of presheaves of rings
After sheafifying we clearly obtain a functor
![]() $\text{tt}\text{Cat}^{\text{rig,op}}\rightarrow \text{RS}$
, the category of ringed spaces. The objects are sent to locally ringed spaces, by [Reference BalmerBal10a, 6.6], and it remains to check that the morphisms are local. This can be checked on the level of presheaves. Fix a prime
$\text{tt}\text{Cat}^{\text{rig,op}}\rightarrow \text{RS}$
, the category of ringed spaces. The objects are sent to locally ringed spaces, by [Reference BalmerBal10a, 6.6], and it remains to check that the morphisms are local. This can be checked on the level of presheaves. Fix a prime
![]() $\mathfrak{P}\in \operatorname{Spec}({\mathcal{T}}^{\prime })$
and let
$\mathfrak{P}\in \operatorname{Spec}({\mathcal{T}}^{\prime })$
and let
![]() $\mathfrak{Q}=f(\mathfrak{P})=F^{-1}(\mathfrak{P})$
. Using [Reference BalmerBal10a, 6.5] we see that the morphism on stalks at these two points naturally identifies with the morphism
$\mathfrak{Q}=f(\mathfrak{P})=F^{-1}(\mathfrak{P})$
. Using [Reference BalmerBal10a, 6.5] we see that the morphism on stalks at these two points naturally identifies with the morphism
![]() ${\mathcal{R}}_{{\mathcal{T}}/\mathfrak{Q}}\rightarrow {\mathcal{R}}_{{\mathcal{T}}^{\prime }/\mathfrak{P}}$
induced by
${\mathcal{R}}_{{\mathcal{T}}/\mathfrak{Q}}\rightarrow {\mathcal{R}}_{{\mathcal{T}}^{\prime }/\mathfrak{P}}$
induced by
![]() $F:{\mathcal{T}}/\mathfrak{Q}\rightarrow {\mathcal{T}}^{\prime }/\mathfrak{P}$
. But this functor is conservative by definition, i.e. detects isomorphisms, in particular, automorphisms of
$F:{\mathcal{T}}/\mathfrak{Q}\rightarrow {\mathcal{T}}^{\prime }/\mathfrak{P}$
. But this functor is conservative by definition, i.e. detects isomorphisms, in particular, automorphisms of
![]() $\unicode[STIX]{x1D7D9}$
, and hence
$\unicode[STIX]{x1D7D9}$
, and hence
![]() ${\mathcal{R}}_{{\mathcal{T}}/\mathfrak{Q}}\rightarrow {\mathcal{R}}_{{\mathcal{T}}^{\prime }/\mathfrak{P}}$
is local.◻
${\mathcal{R}}_{{\mathcal{T}}/\mathfrak{Q}}\rightarrow {\mathcal{R}}_{{\mathcal{T}}^{\prime }/\mathfrak{P}}$
is local.◻
Lemma A.2. The comparison morphism
![]() $\unicode[STIX]{x1D70C}:\operatorname{Spec}({\mathcal{T}})\rightarrow \operatorname{Spec}({\mathcal{R}}_{{\mathcal{T}}})$
defines a natural transformation of functors
$\unicode[STIX]{x1D70C}:\operatorname{Spec}({\mathcal{T}})\rightarrow \operatorname{Spec}({\mathcal{R}}_{{\mathcal{T}}})$
defines a natural transformation of functors
![]() $\text{tt}\text{Cat}^{\text{rig,op}}\rightarrow \text{LRS}$
.
$\text{tt}\text{Cat}^{\text{rig,op}}\rightarrow \text{LRS}$
.
Proof. Naturality on the level of topological spaces is [Reference BalmerBal10a, 5.3]. Also,
![]() $\unicode[STIX]{x1D70C}$
is a morphism of locally ringed spaces, by [Reference BalmerBal10a, 6.11]. It remains to check naturality on the level of sheaves, or indeed, presheaves. In other words, for
$\unicode[STIX]{x1D70C}$
is a morphism of locally ringed spaces, by [Reference BalmerBal10a, 6.11]. It remains to check naturality on the level of sheaves, or indeed, presheaves. In other words, for
![]() $F:{\mathcal{T}}\rightarrow {\mathcal{T}}^{\prime }$
we need to show commutativity of the square
$F:{\mathcal{T}}\rightarrow {\mathcal{T}}^{\prime }$
we need to show commutativity of the square

where by definition [Reference BalmerBal10a, 6.10] the vertical arrows are isomorphisms, identifying both rings with
![]() ${\mathcal{R}}_{{\mathcal{T}}^{\prime }}[1/Fr]$
, respectively,
${\mathcal{R}}_{{\mathcal{T}}^{\prime }}[1/Fr]$
, respectively,
![]() ${\mathcal{R}}_{{\mathcal{T}}}[1/r]$
. By the universal property of localization at the level of rings, it suffices to prove that the diagram commutes on the image of
${\mathcal{R}}_{{\mathcal{T}}}[1/r]$
. By the universal property of localization at the level of rings, it suffices to prove that the diagram commutes on the image of
![]() ${\mathcal{R}}_{{\mathcal{T}}}\rightarrow \text{}_{p}{\mathcal{O}}_{{\mathcal{R}}_{{\mathcal{T}}}}(D(r))$
. But for
${\mathcal{R}}_{{\mathcal{T}}}\rightarrow \text{}_{p}{\mathcal{O}}_{{\mathcal{R}}_{{\mathcal{T}}}}(D(r))$
. But for
![]() $s\in {\mathcal{R}}_{{\mathcal{T}}}=\operatorname{End}_{{\mathcal{T}}}(\unicode[STIX]{x1D7D9})$
, the image under both possible paths traversing the square is simply
$s\in {\mathcal{R}}_{{\mathcal{T}}}=\operatorname{End}_{{\mathcal{T}}}(\unicode[STIX]{x1D7D9})$
, the image under both possible paths traversing the square is simply
![]() $\mathit{Fs}$
considered as an endomorphism of
$\mathit{Fs}$
considered as an endomorphism of
![]() $\unicode[STIX]{x1D7D9}\in {\mathcal{T}}^{\prime }/\langle \operatorname{cone}(Fr)\rangle$
.◻
$\unicode[STIX]{x1D7D9}\in {\mathcal{T}}^{\prime }/\langle \operatorname{cone}(Fr)\rangle$
.◻
Lemma A.3. Let
![]() ${\mathcal{T}}$
be a tt-category, and
${\mathcal{T}}$
be a tt-category, and
![]() $S\subset {\mathcal{R}}_{{\mathcal{T}}}$
a multiplicative system. Then the following square is cartesian in
$S\subset {\mathcal{R}}_{{\mathcal{T}}}$
a multiplicative system. Then the following square is cartesian in
![]() $\text{LRS}$
.
$\text{LRS}$
.

(Here
![]() $Q$
denotes the canonical localization functor
$Q$
denotes the canonical localization functor
![]() $Q:{\mathcal{T}}\rightarrow S^{-1}{\mathcal{T}}$
.)
$Q:{\mathcal{T}}\rightarrow S^{-1}{\mathcal{T}}$
.)
Before giving the proof let us recall that for this type of diagram (where the bottom horizontal map is an isomorphism on stalks) the fiber product in the category
![]() $\text{LRS}$
is simple to describe: it coincides with the fiber product in the category
$\text{LRS}$
is simple to describe: it coincides with the fiber product in the category
![]() $\text{RS}$
[Reference GillamGil11, Corollary 11]. So, this result can be made more explicit as follows.
$\text{RS}$
[Reference GillamGil11, Corollary 11]. So, this result can be made more explicit as follows.
Corollary A.4. In the situation of Lemma A.3,
![]() $\operatorname{Spec}(S^{-1}{\mathcal{T}})$
maps homeomorphically onto
$\operatorname{Spec}(S^{-1}{\mathcal{T}})$
maps homeomorphically onto
![]() $\{\mathfrak{P}\in \operatorname{Spec}({\mathcal{T}})\mid \unicode[STIX]{x1D70C}_{{\mathcal{T}}}(\mathfrak{P})\cap S=\emptyset \}$
, and its structure sheaf identifies with the restriction of
$\{\mathfrak{P}\in \operatorname{Spec}({\mathcal{T}})\mid \unicode[STIX]{x1D70C}_{{\mathcal{T}}}(\mathfrak{P})\cap S=\emptyset \}$
, and its structure sheaf identifies with the restriction of
![]() ${\mathcal{O}}_{{\mathcal{T}}}$
to this subset.
${\mathcal{O}}_{{\mathcal{T}}}$
to this subset.
Proof. By the remarks just made, Lemma A.3 and Corollary A.4 are equivalent. Moreover, [Reference BalmerBal10a, 5.6] shows that the square is cartesian on the level of sets. Both
![]() $S^{-1}{\mathcal{T}}$
and
$S^{-1}{\mathcal{T}}$
and
![]() ${\mathcal{T}}$
have the ‘same’ base for the topology, namely
${\mathcal{T}}$
have the ‘same’ base for the topology, namely
![]() $U(a)$
where
$U(a)$
where
![]() $a\in {\mathcal{T}}$
, and we see that the diagram is cartesian on the level of topological spaces as well.
$a\in {\mathcal{T}}$
, and we see that the diagram is cartesian on the level of topological spaces as well.
The square is commutative in
![]() $\text{LRS}$
, by Lemma A.2. Consequently we obtain a canonical morphism of locally ringed spaces
$\text{LRS}$
, by Lemma A.2. Consequently we obtain a canonical morphism of locally ringed spaces
![]() $\operatorname{Spec}(S^{-1}{\mathcal{T}})\rightarrow X$
where
$\operatorname{Spec}(S^{-1}{\mathcal{T}})\rightarrow X$
where
![]() $X$
is the fiber product in
$X$
is the fiber product in
![]() $\text{LRS}$
. To show that it is an isomorphism we check that it is so on stalks. If
$\text{LRS}$
. To show that it is an isomorphism we check that it is so on stalks. If
![]() $\mathfrak{P}\in \operatorname{Spec}({\mathcal{T}})$
such that
$\mathfrak{P}\in \operatorname{Spec}({\mathcal{T}})$
such that
![]() $\unicode[STIX]{x1D70C}_{{\mathcal{T}}}(\mathfrak{P})\cap S=\emptyset$
, and
$\unicode[STIX]{x1D70C}_{{\mathcal{T}}}(\mathfrak{P})\cap S=\emptyset$
, and
![]() $S^{-1}\mathfrak{P}$
is the corresponding prime in
$S^{-1}\mathfrak{P}$
is the corresponding prime in
![]() $S^{-1}{\mathcal{T}}$
, then the stalk of
$S^{-1}{\mathcal{T}}$
, then the stalk of
![]() ${\mathcal{O}}_{S^{-1}{\mathcal{T}}}$
at
${\mathcal{O}}_{S^{-1}{\mathcal{T}}}$
at
![]() $S^{-1}\mathfrak{P}$
is
$S^{-1}\mathfrak{P}$
is
and we conclude. ◻
Remark A.5. The last argument in this proof also shows that for any Verdier localization
![]() ${\mathcal{T}}\rightarrow {\mathcal{T}}/{\mathcal{K}}$
the induced map on spectra (which is a homeomorphism onto its image)
${\mathcal{T}}\rightarrow {\mathcal{T}}/{\mathcal{K}}$
the induced map on spectra (which is a homeomorphism onto its image)
identifies the structure sheaf on the domain with the restriction of the structure sheaf on the codomain.
Appendix B The motivic Bott element and change of coefficients
In this section we will perform some computations regarding how the Bott elements behave under certain changes of coefficients. Our main goal is Corollary B.12, which states that inverting a Bott element of any prime power order is equally good. We fix a field
![]() $\mathbb{F}$
, a localization
$\mathbb{F}$
, a localization
![]() $\mathbb{Z}\subset R\subset \mathbb{Q}$
, and two integers
$\mathbb{Z}\subset R\subset \mathbb{Q}$
, and two integers
![]() $1<n,N$
such that
$1<n,N$
such that
![]() $n\mid N$
and
$n\mid N$
and
![]() $N$
is invertible in
$N$
is invertible in
![]() $\mathbb{F}$
. We also assume that
$\mathbb{F}$
. We also assume that
![]() $\mathbb{F}$
contains a primitive
$\mathbb{F}$
contains a primitive
![]() $N$
th root of unity
$N$
th root of unity
![]() $\unicode[STIX]{x1D701}_{N}$
, and we let
$\unicode[STIX]{x1D701}_{N}$
, and we let
![]() $\unicode[STIX]{x1D701}_{n}=\unicode[STIX]{x1D701}_{N}^{N/n}$
, a primitive
$\unicode[STIX]{x1D701}_{n}=\unicode[STIX]{x1D701}_{N}^{N/n}$
, a primitive
![]() $n$
th root of unity. Finally, we use a subscript
$n$
th root of unity. Finally, we use a subscript
![]() $(-)_{R}$
to denote tensoring with
$(-)_{R}$
to denote tensoring with
![]() $R$
.
$R$
.
For any positive integer
![]() $k$
, the triangle
$k$
, the triangle
gives rise to a long exact sequence
which identifies with
and we see that
![]() $\hom _{\text{DM}_{\text{gm}}(\mathbb{F},R)}(R,R/k(1))=\unicode[STIX]{x1D707}_{k}(\mathbb{F})_{R}$
. By adjunction, also
$\hom _{\text{DM}_{\text{gm}}(\mathbb{F},R)}(R,R/k(1))=\unicode[STIX]{x1D707}_{k}(\mathbb{F})_{R}$
. By adjunction, also
We can therefore interpret the
![]() $N$
th root of unity
$N$
th root of unity
![]() $\unicode[STIX]{x1D701}_{N}$
as a morphism
$\unicode[STIX]{x1D701}_{N}$
as a morphism
![]() $\unicode[STIX]{x1D6FD}_{N}:R/N\rightarrow R/N(1)$
in
$\unicode[STIX]{x1D6FD}_{N}:R/N\rightarrow R/N(1)$
in
![]() $\text{DM}_{\text{gm}}(\mathbb{F},R/N)$
. This is called the motivic Bott element (with
$\text{DM}_{\text{gm}}(\mathbb{F},R/N)$
. This is called the motivic Bott element (with
![]() $R/N$
-coefficients). Similarly we obtain
$R/N$
-coefficients). Similarly we obtain
![]() $\unicode[STIX]{x1D6FD}_{n}:R/n\rightarrow R/n(1)$
in
$\unicode[STIX]{x1D6FD}_{n}:R/n\rightarrow R/n(1)$
in
![]() $\text{DM}_{\text{gm}}(\mathbb{F},R/n)$
.
$\text{DM}_{\text{gm}}(\mathbb{F},R/n)$
.
Fix the following notation
with associated change of coefficients adjunctions
![]() $\unicode[STIX]{x1D6E4}^{\ast }\dashv \unicode[STIX]{x1D6E4}_{\ast }$
,
$\unicode[STIX]{x1D6E4}^{\ast }\dashv \unicode[STIX]{x1D6E4}_{\ast }$
,
![]() $\unicode[STIX]{x1D6FE}^{\ast }\dashv \unicode[STIX]{x1D6FE}_{\ast }$
,
$\unicode[STIX]{x1D6FE}^{\ast }\dashv \unicode[STIX]{x1D6FE}_{\ast }$
,
![]() $\unicode[STIX]{x1D70B}^{\ast }\dashv \unicode[STIX]{x1D70B}_{\ast }$
.
$\unicode[STIX]{x1D70B}^{\ast }\dashv \unicode[STIX]{x1D70B}_{\ast }$
.
Lemma B.1. The following square in
![]() $\text{DM}_{\text{gm}}(\mathbb{F},R)$
commutes.
$\text{DM}_{\text{gm}}(\mathbb{F},R)$
commutes.

Proof. Applying
![]() $\hom _{\text{DM}_{\text{gm}}(\mathbb{F},R)}(-,R/n(1))$
to (BN) we obtain part of a long exact sequence
$\hom _{\text{DM}_{\text{gm}}(\mathbb{F},R)}(-,R/n(1))$
to (BN) we obtain part of a long exact sequence
In particular, it suffices to show commutativity of the square after precomposing with
![]() $\unicode[STIX]{x1D6E4}:R\rightarrow R/N$
. It also shows that
$\unicode[STIX]{x1D6E4}:R\rightarrow R/N$
. It also shows that
![]() $\unicode[STIX]{x1D6FE}_{\ast }\unicode[STIX]{x1D6FD}_{n}\circ \unicode[STIX]{x1D70B}$
corresponds to
$\unicode[STIX]{x1D6FE}_{\ast }\unicode[STIX]{x1D6FD}_{n}\circ \unicode[STIX]{x1D70B}$
corresponds to
![]() $\unicode[STIX]{x1D701}_{n}\in \unicode[STIX]{x1D707}_{n}(\mathbb{F})_{R}$
.
$\unicode[STIX]{x1D701}_{n}\in \unicode[STIX]{x1D707}_{n}(\mathbb{F})_{R}$
.
Now,
![]() $\unicode[STIX]{x1D70B}$
fits into a morphism of triangles
$\unicode[STIX]{x1D70B}$
fits into a morphism of triangles

and applying
![]() $\hom _{\text{DM}_{\text{gm}}(\mathbb{F},R)}(R,-(1))$
we obtain
$\hom _{\text{DM}_{\text{gm}}(\mathbb{F},R)}(R,-(1))$
we obtain

thus
![]() $\unicode[STIX]{x1D70B}\circ \unicode[STIX]{x1D6E4}_{\ast }\unicode[STIX]{x1D6FD}_{N}$
corresponds to
$\unicode[STIX]{x1D70B}\circ \unicode[STIX]{x1D6E4}_{\ast }\unicode[STIX]{x1D6FD}_{N}$
corresponds to
![]() $\unicode[STIX]{x1D701}_{N}^{N/n}=\unicode[STIX]{x1D701}_{n}\in \unicode[STIX]{x1D707}_{n}(\mathbb{F})_{R}$
. This concludes the proof.◻
$\unicode[STIX]{x1D701}_{N}^{N/n}=\unicode[STIX]{x1D701}_{n}\in \unicode[STIX]{x1D707}_{n}(\mathbb{F})_{R}$
. This concludes the proof.◻
Lemma B.2. Let
![]() $m=N/n$
. The following square in
$m=N/n$
. The following square in
![]() $\text{DM}_{\text{gm}}(\mathbb{F},R)$
commutes.
$\text{DM}_{\text{gm}}(\mathbb{F},R)$
commutes.

Proof. We have a morphism of triangles

which implies the commutativity of the bottom half of the following diagram.

The upper half clearly commutes and the vertical arrows are injections. We deduce that
![]() $m\circ \unicode[STIX]{x1D6FE}_{\ast }\unicode[STIX]{x1D6FD}_{n}$
corresponds to
$m\circ \unicode[STIX]{x1D6FE}_{\ast }\unicode[STIX]{x1D6FD}_{n}$
corresponds to
![]() $\unicode[STIX]{x1D701}_{n}\in \mathbb{F}_{R}^{\times }$
.
$\unicode[STIX]{x1D701}_{n}\in \mathbb{F}_{R}^{\times }$
.
Next consider the following diagram.

The commutativity of the upper half again follows from the morphism of triangles above, while the lower half clearly commutes. The vertical arrows are injections and we deduce that
![]() $\unicode[STIX]{x1D6E4}_{\ast }\unicode[STIX]{x1D6FD}_{N}\circ m$
corresponds to
$\unicode[STIX]{x1D6E4}_{\ast }\unicode[STIX]{x1D6FD}_{N}\circ m$
corresponds to
![]() $\unicode[STIX]{x1D701}_{N}^{m}=\unicode[STIX]{x1D701}_{n}$
and thus the claim.◻
$\unicode[STIX]{x1D701}_{N}^{m}=\unicode[STIX]{x1D701}_{n}$
and thus the claim.◻
Lemma B.3. Let
![]() $F\dashv G:{\mathcal{C}}\rightarrow {\mathcal{D}}$
be an adjunction. For any
$F\dashv G:{\mathcal{C}}\rightarrow {\mathcal{D}}$
be an adjunction. For any
![]() $c\in {\mathcal{C}}$
and
$c\in {\mathcal{C}}$
and
![]() $d\in {\mathcal{D}}$
the following map is injective:
$d\in {\mathcal{D}}$
the following map is injective:
Proof. By adjunction, the target is identified with
![]() $\hom _{{\mathcal{D}}}(FGFc,d)$
and under this identification, the map is induced by the counit
$\hom _{{\mathcal{D}}}(FGFc,d)$
and under this identification, the map is induced by the counit
![]() $FGFc\rightarrow Fc$
, which is a split epimorphism (the splitting is given by the unit of the adjunction). Thus the claim is proven.◻
$FGFc\rightarrow Fc$
, which is a split epimorphism (the splitting is given by the unit of the adjunction). Thus the claim is proven.◻
Lemma B.4. For any
![]() $M\in \text{DM}_{\text{gm}}(\mathbb{F},R)$
we have
$M\in \text{DM}_{\text{gm}}(\mathbb{F},R)$
we have
Proof. Tensoring
![]() $M$
with (Bn) and applying
$M$
with (Bn) and applying
![]() $\unicode[STIX]{x1D6FE}^{\ast }$
we obtain a triangle
$\unicode[STIX]{x1D6FE}^{\ast }$
we obtain a triangle
and since the first map is zero (the category
![]() $\text{DM}_{\text{gm}}(\mathbb{F},R/n)$
is
$\text{DM}_{\text{gm}}(\mathbb{F},R/n)$
is
![]() $\mathbb{Z}/n$
-linear), the triangle splits and the lemma follows.◻
$\mathbb{Z}/n$
-linear), the triangle splits and the lemma follows.◻
Lemma B.5. For any
![]() $M\in \text{DM}_{\text{gm}}(\mathbb{F},R/n)$
we have
$M\in \text{DM}_{\text{gm}}(\mathbb{F},R/n)$
we have
Proof. Tensoring
![]() $\unicode[STIX]{x1D6FE}_{\ast }M$
with (Bn) we obtain a triangle
$\unicode[STIX]{x1D6FE}_{\ast }M$
with (Bn) we obtain a triangle
and since the first map is zero the triangle splits and the lemma follows. ◻
Lemma B.6. We have in
![]() $\text{DM}_{\text{gm}}(\mathbb{F},R/n)$
that
$\text{DM}_{\text{gm}}(\mathbb{F},R/n)$
that
Proof. We have
and by Lemma B.4,
![]() $\unicode[STIX]{x1D6FE}^{\ast }\unicode[STIX]{x1D6FE}_{\ast }\unicode[STIX]{x1D6FD}_{n}$
is a morphism between
$\unicode[STIX]{x1D6FE}^{\ast }\unicode[STIX]{x1D6FE}_{\ast }\unicode[STIX]{x1D6FD}_{n}$
is a morphism between
![]() $\unicode[STIX]{x1D6FE}^{\ast }R\oplus \unicode[STIX]{x1D6FE}^{\ast }R[1]$
and
$\unicode[STIX]{x1D6FE}^{\ast }R\oplus \unicode[STIX]{x1D6FE}^{\ast }R[1]$
and
![]() $\unicode[STIX]{x1D6FE}^{\ast }R(1)\oplus \unicode[STIX]{x1D6FE}^{\ast }R(1)[1]$
. Such a morphism is therefore described by a
$\unicode[STIX]{x1D6FE}^{\ast }R(1)\oplus \unicode[STIX]{x1D6FE}^{\ast }R(1)[1]$
. Such a morphism is therefore described by a
![]() $2\times 2$
-matrix, whose diagonal entries ‘are’ elements of
$2\times 2$
-matrix, whose diagonal entries ‘are’ elements of
![]() $\unicode[STIX]{x1D707}_{n}(\mathbb{F})_{R}$
, while the off-diagonal entries necessarily vanish. To describe the non-trivial entries we can do so after applying
$\unicode[STIX]{x1D707}_{n}(\mathbb{F})_{R}$
, while the off-diagonal entries necessarily vanish. To describe the non-trivial entries we can do so after applying
![]() $\unicode[STIX]{x1D6FE}_{\ast }$
, by Lemma B.3. But by Lemma B.5, we have
$\unicode[STIX]{x1D6FE}_{\ast }$
, by Lemma B.3. But by Lemma B.5, we have
![]() $\unicode[STIX]{x1D6FE}_{\ast }\unicode[STIX]{x1D6FE}^{\ast }\unicode[STIX]{x1D6FE}_{\ast }\operatorname{cone}(\unicode[STIX]{x1D6FD}_{n})=\unicode[STIX]{x1D6FE}_{\ast }\operatorname{cone}(\unicode[STIX]{x1D6FD}_{n})\oplus \unicode[STIX]{x1D6FE}_{\ast }\operatorname{cone}(\unicode[STIX]{x1D6FD}_{n})[1]$
, which completes the proof.◻
$\unicode[STIX]{x1D6FE}_{\ast }\unicode[STIX]{x1D6FE}^{\ast }\unicode[STIX]{x1D6FE}_{\ast }\operatorname{cone}(\unicode[STIX]{x1D6FD}_{n})=\unicode[STIX]{x1D6FE}_{\ast }\operatorname{cone}(\unicode[STIX]{x1D6FD}_{n})\oplus \unicode[STIX]{x1D6FE}_{\ast }\operatorname{cone}(\unicode[STIX]{x1D6FD}_{n})[1]$
, which completes the proof.◻
Lemma B.7. We have in
![]() $\text{DM}_{\text{gm}}(\mathbb{F},R/n)$
that
$\text{DM}_{\text{gm}}(\mathbb{F},R/n)$
that
Proof. First, we have
by Lemma B.6. It now suffices to show that
maps
![]() $\unicode[STIX]{x1D6FD}_{N}$
to
$\unicode[STIX]{x1D6FD}_{N}$
to
![]() $\unicode[STIX]{x1D6FD}_{n}$
. This follows easily from Lemma B.1.◻
$\unicode[STIX]{x1D6FD}_{n}$
. This follows easily from Lemma B.1.◻
Lemma B.8. Assume the existence of a primitive
![]() $(N\cdot n)$
th root of unity in
$(N\cdot n)$
th root of unity in
![]() $\mathbb{F}$
. We then have in
$\mathbb{F}$
. We then have in
![]() $\text{DM}_{\text{gm}}(\mathbb{F},R/N)$
that
$\text{DM}_{\text{gm}}(\mathbb{F},R/N)$
that
Proof. More precisely we are going to prove that the cone
![]() $C$
of multiplication by
$C$
of multiplication by
![]() $n$
on
$n$
on
![]() $\operatorname{cone}(\unicode[STIX]{x1D6FD}_{N})$
is
$\operatorname{cone}(\unicode[STIX]{x1D6FD}_{N})$
is
![]() $\operatorname{cone}(\unicode[STIX]{x1D6FD}_{n})\oplus \operatorname{cone}(\unicode[STIX]{x1D6FD}_{n})[1]$
.
$\operatorname{cone}(\unicode[STIX]{x1D6FD}_{n})\oplus \operatorname{cone}(\unicode[STIX]{x1D6FD}_{n})[1]$
.
Consider the following commutative diagram of solid arrows.

We want to prove that
![]() $\unicode[STIX]{x1D6E4}^{\ast }\unicode[STIX]{x1D6FE}_{\ast }\unicode[STIX]{x1D6FD}_{n}$
makes this diagram commutative. Taking cones of the vertical maps and applying the octahedral axiom the lemma would then be proved. We may prove commutativity after applying
$\unicode[STIX]{x1D6E4}^{\ast }\unicode[STIX]{x1D6FE}_{\ast }\unicode[STIX]{x1D6FD}_{n}$
makes this diagram commutative. Taking cones of the vertical maps and applying the octahedral axiom the lemma would then be proved. We may prove commutativity after applying
![]() $\unicode[STIX]{x1D6E4}_{\ast }$
by Lemma B.3. In fact, we will prove that after applying
$\unicode[STIX]{x1D6E4}_{\ast }$
by Lemma B.3. In fact, we will prove that after applying
![]() $\unicode[STIX]{x1D6E4}_{\ast }$
, the morphism
$\unicode[STIX]{x1D6E4}_{\ast }$
, the morphism
![]() $\unicode[STIX]{x1D6E4}^{\ast }\unicode[STIX]{x1D6FE}_{\ast }\unicode[STIX]{x1D6FD}_{n}$
is identified with
$\unicode[STIX]{x1D6E4}^{\ast }\unicode[STIX]{x1D6FE}_{\ast }\unicode[STIX]{x1D6FD}_{n}$
is identified with
![]() $\unicode[STIX]{x1D6FC}$
, the ‘natural’ cone coming from a model. For this we will work in the homotopy category of bounded complexes of Nisnevich sheaves with transfers (i.e. before
$\unicode[STIX]{x1D6FC}$
, the ‘natural’ cone coming from a model. For this we will work in the homotopy category of bounded complexes of Nisnevich sheaves with transfers (i.e. before
![]() $\mathbb{A}^{1}$
-localization). As a model for
$\mathbb{A}^{1}$
-localization). As a model for
![]() $R(1)$
we will use
$R(1)$
we will use
![]() ${\mathcal{O}}_{R}^{\times }[-1]$
. The Bott element
${\mathcal{O}}_{R}^{\times }[-1]$
. The Bott element
![]() $\unicode[STIX]{x1D6FD}_{N}$
can then be modeled by the following morphism of complexes, where the last term is in degree
$\unicode[STIX]{x1D6FD}_{N}$
can then be modeled by the following morphism of complexes, where the last term is in degree
![]() $-1$
.
$-1$
.

Taking the mapping cone of multiplication by
![]() $n$
we obtain the following model for
$n$
we obtain the following model for
![]() $\unicode[STIX]{x1D6FC}$
.
$\unicode[STIX]{x1D6FC}$
.

The last term being in degree
![]() $-1$
.
$-1$
.
Now, since
![]() $n\mid N$
, the domain and the codomain split into direct sums of two-term complexes, and under these identifications,
$n\mid N$
, the domain and the codomain split into direct sums of two-term complexes, and under these identifications,
![]() $\unicode[STIX]{x1D6FC}$
is identified with the following.
$\unicode[STIX]{x1D6FC}$
is identified with the following.

Let
![]() $\unicode[STIX]{x1D701}_{Nn}$
be an
$\unicode[STIX]{x1D701}_{Nn}$
be an
![]() $n$
th root of
$n$
th root of
![]() $\unicode[STIX]{x1D701}_{N}$
, and define the homotopy
$\unicode[STIX]{x1D701}_{N}$
, and define the homotopy
![]() $\unicode[STIX]{x1D701}_{Nn}^{-1}:R\rightarrow {\mathcal{O}}_{R}^{\times }$
. It shows that
$\unicode[STIX]{x1D701}_{Nn}^{-1}:R\rightarrow {\mathcal{O}}_{R}^{\times }$
. It shows that
![]() $\unicode[STIX]{x1D6FC}$
is homotopic to the map
$\unicode[STIX]{x1D6FC}$
is homotopic to the map
![]() $\left(\begin{array}{@{}cc@{}}0 & \unicode[STIX]{x1D701}_{n}\end{array}\right)$
(in degree 1),
$\left(\begin{array}{@{}cc@{}}0 & \unicode[STIX]{x1D701}_{n}\end{array}\right)$
(in degree 1),
![]() $(\!\begin{smallmatrix}\unicode[STIX]{x1D701}_{n}\\ 0\end{smallmatrix}\!)$
(in degree 0), i.e. a model for
$(\!\begin{smallmatrix}\unicode[STIX]{x1D701}_{n}\\ 0\end{smallmatrix}\!)$
(in degree 0), i.e. a model for
![]() $\unicode[STIX]{x1D6E4}_{\ast }\unicode[STIX]{x1D6E4}^{\ast }\unicode[STIX]{x1D6FE}_{\ast }\unicode[STIX]{x1D6FD}_{n}$
. This concludes the proof.◻
$\unicode[STIX]{x1D6E4}_{\ast }\unicode[STIX]{x1D6E4}^{\ast }\unicode[STIX]{x1D6FE}_{\ast }\unicode[STIX]{x1D6FD}_{n}$
. This concludes the proof.◻
For the last two results we specialize to the case
![]() $N=\ell ^{m}$
and
$N=\ell ^{m}$
and
![]() $n=\ell$
for some
$n=\ell$
for some
![]() $m\geqslant 1$
.
$m\geqslant 1$
.
Lemma B.10. We have in
![]() $\text{DM}_{\text{gm}}(\mathbb{F},R)$
that
$\text{DM}_{\text{gm}}(\mathbb{F},R)$
that
Proof. The proof is by induction on
![]() $m$
. Assume
$m$
. Assume
![]() $m>1$
and consider the following diagram in
$m>1$
and consider the following diagram in
![]() $\text{DTM}_{\text{gm}}(\mathbb{F},R)$
.
$\text{DTM}_{\text{gm}}(\mathbb{F},R)$
.

The two rows are triangles thus if the diagram commutes we can take cones of the vertical maps and the induction hypothesis will allow us to conclude.
We now proceed to describe this diagram using the same model as in the previous proof. Commutativity of the first square is Lemma B.2. We may therefore compute the induced morphism on the mapping cones of multiplication by
![]() $\ell$
as follows.
$\ell$
as follows.

The last term being in degree
![]() $-1$
.
$-1$
.
Now, the domain and codomain of this morphism identifies with
![]() $R/\ell$
and
$R/\ell$
and
![]() $R/\ell (1)$
, respectively.
$R/\ell (1)$
, respectively.

The composition is a model for
![]() $\unicode[STIX]{x1D6FD}_{\ell }$
using that
$\unicode[STIX]{x1D6FD}_{\ell }$
using that
![]() $\unicode[STIX]{x1D701}_{\ell ^{m}}^{m-1}=\unicode[STIX]{x1D701}_{\ell }$
.◻
$\unicode[STIX]{x1D701}_{\ell ^{m}}^{m-1}=\unicode[STIX]{x1D701}_{\ell }$
.◻
Corollary B.12. Assume that
![]() $\mathbb{F}$
contains a primitive
$\mathbb{F}$
contains a primitive
![]() $\ell ^{m+1}$
th root of unity. Then in
$\ell ^{m+1}$
th root of unity. Then in
![]() $\text{DM}_{\text{gm}}(\mathbb{F},R)$
we have
$\text{DM}_{\text{gm}}(\mathbb{F},R)$
we have
Proof. The forward inclusion is Lemma B.10. For the reverse inclusion we may invoke Lemma B.8 and obtain that
But
![]() $\unicode[STIX]{x1D6E4}_{\ast }\unicode[STIX]{x1D6E4}^{\ast }\unicode[STIX]{x1D6FE}_{\ast }\operatorname{cone}(\unicode[STIX]{x1D6FD}_{\ell })=\unicode[STIX]{x1D6E4}_{\ast }\unicode[STIX]{x1D6E4}^{\ast }\unicode[STIX]{x1D6E4}_{\ast }\unicode[STIX]{x1D70B}_{\ast }\operatorname{cone}(\unicode[STIX]{x1D6FD}_{\ell })=\unicode[STIX]{x1D6FE}_{\ast }\operatorname{cone}(\unicode[STIX]{x1D6FD}_{\ell })\oplus \unicode[STIX]{x1D6FE}_{\ast }\operatorname{cone}(\unicode[STIX]{x1D6FD}_{\ell })[1]$
by Lemma B.5. We conclude that also
$\unicode[STIX]{x1D6E4}_{\ast }\unicode[STIX]{x1D6E4}^{\ast }\unicode[STIX]{x1D6FE}_{\ast }\operatorname{cone}(\unicode[STIX]{x1D6FD}_{\ell })=\unicode[STIX]{x1D6E4}_{\ast }\unicode[STIX]{x1D6E4}^{\ast }\unicode[STIX]{x1D6E4}_{\ast }\unicode[STIX]{x1D70B}_{\ast }\operatorname{cone}(\unicode[STIX]{x1D6FD}_{\ell })=\unicode[STIX]{x1D6FE}_{\ast }\operatorname{cone}(\unicode[STIX]{x1D6FD}_{\ell })\oplus \unicode[STIX]{x1D6FE}_{\ast }\operatorname{cone}(\unicode[STIX]{x1D6FD}_{\ell })[1]$
by Lemma B.5. We conclude that also
![]() $\unicode[STIX]{x1D6FE}_{\ast }\operatorname{cone}(\unicode[STIX]{x1D6FD}_{\ell })\in \langle \unicode[STIX]{x1D6E4}_{\ast }\operatorname{cone}(\unicode[STIX]{x1D6FD}_{\ell ^{m}})\rangle$
.◻
$\unicode[STIX]{x1D6FE}_{\ast }\operatorname{cone}(\unicode[STIX]{x1D6FD}_{\ell })\in \langle \unicode[STIX]{x1D6E4}_{\ast }\operatorname{cone}(\unicode[STIX]{x1D6FD}_{\ell ^{m}})\rangle$
.◻
Appendix C Inverting the motivic Bott element
In [Reference Hasemeyer and HornbostelHH05], Haesemeyer and Hornbostel prove that under certain assumptions on
![]() $\mathbb{F}$
, the étale sheafification functor
$\mathbb{F}$
, the étale sheafification functor
can be seen as the functor inverting the Bott element
![]() $\unicode[STIX]{x1D6FD}_{n}:\mathbb{Z}/n\rightarrow \mathbb{Z}/n(1)$
. In other words, it induces an identification
$\unicode[STIX]{x1D6FD}_{n}:\mathbb{Z}/n\rightarrow \mathbb{Z}/n(1)$
. In other words, it induces an identification
Our goal in this section is to prove an analogous result with integral coefficients.
We first restate Haesemeyer–Hornbostel’s result in a slightly improved form.
Theorem C.1 [Reference Hasemeyer and HornbostelHH05].
Let
![]() $\mathbb{F}$
be a field, and
$\mathbb{F}$
be a field, and
![]() $n$
an integer. We assume that:
$n$
an integer. We assume that:
∙
 $n$
is prime to the characteristic of
$n$
is prime to the characteristic of
 $\mathbb{F}$
;
$\mathbb{F}$
;∙
 $\mathbb{F}$
contains the
$\mathbb{F}$
contains the
 $n$
th roots of unity (respectively, and the 4th roots of unity if
$n$
th roots of unity (respectively, and the 4th roots of unity if
 $n$
is even);
$n$
is even);∙
 $\mathbb{F}$
has finite étale
$\mathbb{F}$
has finite étale
 $n$
-dimension.
$n$
-dimension.
Then étale sheafification induces equivalences of tensor triangulated categories
 $$\begin{eqnarray}\displaystyle \text{DM}^{\text{eff}}(\mathbb{F},\mathbb{Z}/n)/\langle \operatorname{cone}(\unicode[STIX]{x1D6FD}_{n})\rangle ^{\oplus } & \xrightarrow[{}]{{\sim}} & \displaystyle \text{DM}^{\acute{\text{e}}\text{t},\text{eff}}(\mathbb{F},\mathbb{Z}/n)\nonumber\\ \displaystyle (\text{DM}_{\text{gm}}^{\text{eff}}(\mathbb{F},\mathbb{Z}/n)/\langle \operatorname{cone}(\unicode[STIX]{x1D6FD}_{n})\rangle )^{\natural } & \xrightarrow[{}]{{\sim}} & \displaystyle \text{DM}_{\text{gm}}^{\acute{\text{e}}\text{t},\text{eff}}(\mathbb{F},\mathbb{Z}/n)\nonumber\\ \displaystyle \text{DM}(\mathbb{F},\mathbb{Z}/n)/\langle \operatorname{cone}(\unicode[STIX]{x1D6FD}_{n})\rangle ^{\oplus } & \xrightarrow[{}]{{\sim}} & \displaystyle \text{DM}^{\acute{\text{e}}\text{t}}(\mathbb{F},\mathbb{Z}/n)\nonumber\\ \displaystyle (\text{DM}_{\text{gm}}(\mathbb{F},\mathbb{Z}/n)/\langle \operatorname{cone}(\unicode[STIX]{x1D6FD}_{n})\rangle )^{\natural } & \xrightarrow[{}]{{\sim}} & \displaystyle \text{DM}_{\text{gm}}^{\acute{\text{e}}\text{t}}(\mathbb{F},\mathbb{Z}/n).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \text{DM}^{\text{eff}}(\mathbb{F},\mathbb{Z}/n)/\langle \operatorname{cone}(\unicode[STIX]{x1D6FD}_{n})\rangle ^{\oplus } & \xrightarrow[{}]{{\sim}} & \displaystyle \text{DM}^{\acute{\text{e}}\text{t},\text{eff}}(\mathbb{F},\mathbb{Z}/n)\nonumber\\ \displaystyle (\text{DM}_{\text{gm}}^{\text{eff}}(\mathbb{F},\mathbb{Z}/n)/\langle \operatorname{cone}(\unicode[STIX]{x1D6FD}_{n})\rangle )^{\natural } & \xrightarrow[{}]{{\sim}} & \displaystyle \text{DM}_{\text{gm}}^{\acute{\text{e}}\text{t},\text{eff}}(\mathbb{F},\mathbb{Z}/n)\nonumber\\ \displaystyle \text{DM}(\mathbb{F},\mathbb{Z}/n)/\langle \operatorname{cone}(\unicode[STIX]{x1D6FD}_{n})\rangle ^{\oplus } & \xrightarrow[{}]{{\sim}} & \displaystyle \text{DM}^{\acute{\text{e}}\text{t}}(\mathbb{F},\mathbb{Z}/n)\nonumber\\ \displaystyle (\text{DM}_{\text{gm}}(\mathbb{F},\mathbb{Z}/n)/\langle \operatorname{cone}(\unicode[STIX]{x1D6FD}_{n})\rangle )^{\natural } & \xrightarrow[{}]{{\sim}} & \displaystyle \text{DM}_{\text{gm}}^{\acute{\text{e}}\text{t}}(\mathbb{F},\mathbb{Z}/n).\nonumber\end{eqnarray}$$
Proof. Haesemeyer and Hornbostel prove the first two equivalences under the additional assumption that
![]() $\mathbb{F}$
is perfect and admits resolution of singularities. These assumptions are used to apply Voevodsky’s fundamental results on
$\mathbb{F}$
is perfect and admits resolution of singularities. These assumptions are used to apply Voevodsky’s fundamental results on
![]() $\text{DM}_{\text{gm}}$
. As we are inverting the exponential characteristic of
$\text{DM}_{\text{gm}}$
. As we are inverting the exponential characteristic of
![]() $\mathbb{F}$
, Kelly’s [Reference KellyKel17] allows the removal of the resolution of singularities assumption. Now let
$\mathbb{F}$
, Kelly’s [Reference KellyKel17] allows the removal of the resolution of singularities assumption. Now let
![]() $\mathbb{F}$
be arbitrary and let
$\mathbb{F}$
be arbitrary and let
![]() $\mathbb{F}^{s}$
denote its inseparable closure. Then we have the following commutative square induced by scalar extension and étale sheafification.
$\mathbb{F}^{s}$
denote its inseparable closure. Then we have the following commutative square induced by scalar extension and étale sheafification.

The right vertical arrow is an equivalence since
![]() $\mathbb{F}^{s}$
is perfect, the top horizontal arrow by [Reference Cisinski and DégliseCD15, 8.1], and the bottom horizontal arrow by [Reference Cisinski and DégliseCD16, 6.3.16]. It follows that the left vertical arrow is an equivalence as well. This proves the first equivalence of the theorem, and the second follows by restricting to the compact objects.
$\mathbb{F}^{s}$
is perfect, the top horizontal arrow by [Reference Cisinski and DégliseCD15, 8.1], and the bottom horizontal arrow by [Reference Cisinski and DégliseCD16, 6.3.16]. It follows that the left vertical arrow is an equivalence as well. This proves the first equivalence of the theorem, and the second follows by restricting to the compact objects.
For the third equivalence we notice that both sides are compactly generated and the functor maps onto a set of compact generators. We therefore reduce to prove the 4th equivalence, or indeed that
is fully faithful. For this consider the following commutative square.

The left vertical arrow is fully faithful and the bottom horizontal arrow is an equivalence since
![]() $\mathbb{Z}/n\cong \mathbb{Z}/n(1)$
. It therefore suffices to prove that the top horizontal arrow is an equivalence as well. This follows immediately from
$\mathbb{Z}/n\cong \mathbb{Z}/n(1)$
. It therefore suffices to prove that the top horizontal arrow is an equivalence as well. This follows immediately from
![]() $\text{DM}_{\text{gm}}(\mathbb{F},\mathbb{Z}/n)=\text{DM}_{\text{gm}}^{\text{eff}}(\mathbb{F},\mathbb{Z}/n)[(\otimes \mathbb{Z}/n(1))^{-1}]$
and again the fact that
$\text{DM}_{\text{gm}}(\mathbb{F},\mathbb{Z}/n)=\text{DM}_{\text{gm}}^{\text{eff}}(\mathbb{F},\mathbb{Z}/n)[(\otimes \mathbb{Z}/n(1))^{-1}]$
and again the fact that
![]() $\mathbb{Z}/n\cong \mathbb{Z}/n(1)$
after inverting
$\mathbb{Z}/n\cong \mathbb{Z}/n(1)$
after inverting
![]() $\unicode[STIX]{x1D6FD}_{n}$
.◻
$\unicode[STIX]{x1D6FD}_{n}$
.◻
Remark C.2. The assumption on the cohomological dimension of
![]() $\mathbb{F}$
seems reasonable since, for example, the first equivalence in Theorem C.1 implies that the triangulated category
$\mathbb{F}$
seems reasonable since, for example, the first equivalence in Theorem C.1 implies that the triangulated category
![]() $\text{DM}^{\acute{\text{e}}\text{t},\text{eff}}(\mathbb{F},\mathbb{Z}/n)$
is compactly generated by smooth varieties.
$\text{DM}^{\acute{\text{e}}\text{t},\text{eff}}(\mathbb{F},\mathbb{Z}/n)$
is compactly generated by smooth varieties.
Convention C.3. From now on we fix a field
![]() $\mathbb{F}$
and a set of primes
$\mathbb{F}$
and a set of primes
![]() $S$
containing the exponential characteristic of
$S$
containing the exponential characteristic of
![]() $\mathbb{F}$
. We denote by
$\mathbb{F}$
. We denote by
![]() $R$
the localization
$R$
the localization
![]() $S^{-1}\mathbb{Z}\subset \mathbb{Q}$
.
$S^{-1}\mathbb{Z}\subset \mathbb{Q}$
.
![]() $\mathbb{F}$
is assumed to have finite
$\mathbb{F}$
is assumed to have finite
![]() $\ell$
-cohomological dimension for every prime
$\ell$
-cohomological dimension for every prime
![]() $\ell \notin S$
, and to contain a primitive
$\ell \notin S$
, and to contain a primitive
![]() $\ell ^{n}$
th root of unity for every
$\ell ^{n}$
th root of unity for every
![]() $\ell \notin S$
and every
$\ell \notin S$
and every
![]() $n\geqslant 1$
.
$n\geqslant 1$
.
For any
![]() $\ell \notin S$
, fix a primitive
$\ell \notin S$
, fix a primitive
![]() $\ell$
th root of unity and interpret it as a morphism
$\ell$
th root of unity and interpret it as a morphism
![]() $\unicode[STIX]{x1D6FD}_{\ell }:\mathbb{Z}/\ell \rightarrow \mathbb{Z}/\ell (1)$
in
$\unicode[STIX]{x1D6FD}_{\ell }:\mathbb{Z}/\ell \rightarrow \mathbb{Z}/\ell (1)$
in
![]() $\text{DM}_{\text{gm}}(\mathbb{F},\mathbb{Z}/\ell )$
. We denote (abusively) the image of its cone in
$\text{DM}_{\text{gm}}(\mathbb{F},\mathbb{Z}/\ell )$
. We denote (abusively) the image of its cone in
![]() $\text{DM}_{\text{gm}}(\mathbb{F},R)$
by
$\text{DM}_{\text{gm}}(\mathbb{F},R)$
by
![]() $\unicode[STIX]{x1D6FE}_{\ast }\operatorname{cone}(\unicode[STIX]{x1D6FD}_{\ell })$
.
$\unicode[STIX]{x1D6FE}_{\ast }\operatorname{cone}(\unicode[STIX]{x1D6FD}_{\ell })$
.
Theorem C.4. The étale sheafification functor induces an equivalence of tt-categories
In particular, it induces an equivalence on the level of geometric motives
The same results hold for the effective versions.
Proof. In this proof, we denote by
![]() ${\mathcal{D}}$
the category
${\mathcal{D}}$
the category
![]() $\text{DM}(\mathbb{F},R)$
, by
$\text{DM}(\mathbb{F},R)$
, by
![]() ${\mathcal{D}}^{\acute{\text{e}}\text{t}}$
its étale version, by
${\mathcal{D}}^{\acute{\text{e}}\text{t}}$
its étale version, by
![]() ${\mathcal{B}}$
(respectively,
${\mathcal{B}}$
(respectively,
![]() ${\mathcal{B}}^{c}$
) the localizing (respectively, thick) subcategory of
${\mathcal{B}}^{c}$
) the localizing (respectively, thick) subcategory of
![]() ${\mathcal{D}}$
generated by
${\mathcal{D}}$
generated by
![]() $\unicode[STIX]{x1D6FE}_{\ast }\operatorname{cone}(\unicode[STIX]{x1D6FD}_{\ell })$
,
$\unicode[STIX]{x1D6FE}_{\ast }\operatorname{cone}(\unicode[STIX]{x1D6FD}_{\ell })$
,
![]() $\ell \notin S$
.
$\ell \notin S$
.
![]() ${\mathcal{D}}$
is compactly generated, and the objects
${\mathcal{D}}$
is compactly generated, and the objects
![]() $\unicode[STIX]{x1D6FE}_{\ast }\operatorname{cone}(\unicode[STIX]{x1D6FD}_{\ell })$
are compact. It follows that the full subcategory of compact objects in the localization
$\unicode[STIX]{x1D6FE}_{\ast }\operatorname{cone}(\unicode[STIX]{x1D6FD}_{\ell })$
are compact. It follows that the full subcategory of compact objects in the localization
![]() ${\mathcal{D}}/{\mathcal{B}}$
is canonically identified with the idempotent completion of the localization
${\mathcal{D}}/{\mathcal{B}}$
is canonically identified with the idempotent completion of the localization
![]() ${\mathcal{D}}^{c}/{\mathcal{B}}^{c}$
. Thus the second statement follows from the first.
${\mathcal{D}}^{c}/{\mathcal{B}}^{c}$
. Thus the second statement follows from the first.
The generators
![]() $R^{\acute{\text{e}}\text{t}}(X)(n)$
(
$R^{\acute{\text{e}}\text{t}}(X)(n)$
(
![]() $X$
smooth,
$X$
smooth,
![]() $n\in \mathbb{Z}$
) for
$n\in \mathbb{Z}$
) for
![]() ${\mathcal{D}}^{\acute{\text{e}}\text{t}}$
clearly lie in the image of
${\mathcal{D}}^{\acute{\text{e}}\text{t}}$
clearly lie in the image of
![]() $a_{\acute{\text{e}}\text{t}}$
. It thus suffices to show that the functor in the first statement is fully faithful on compact objects. Let
$a_{\acute{\text{e}}\text{t}}$
. It thus suffices to show that the functor in the first statement is fully faithful on compact objects. Let
![]() $M\in {\mathcal{D}}$
be a geometric motive,
$M\in {\mathcal{D}}$
be a geometric motive,
![]() $N\in {\mathcal{D}}$
an arbitrary motive, and consider the triangle
$N\in {\mathcal{D}}$
an arbitrary motive, and consider the triangle
in
![]() ${\mathcal{D}}/{\mathcal{B}}$
. By the long exact sequence associated to the functor
${\mathcal{D}}/{\mathcal{B}}$
. By the long exact sequence associated to the functor
![]() $\hom _{{\mathcal{D}}/{\mathcal{B}}}(M,-)$
and the 5-lemma, it suffices to show that the following two maps are bijections (for arbitrary
$\hom _{{\mathcal{D}}/{\mathcal{B}}}(M,-)$
and the 5-lemma, it suffices to show that the following two maps are bijections (for arbitrary
![]() $N$
):
$N$
):
For the first map, consider the diagram

where
![]() ${\mathcal{D}}_{\mathbb{Q}}^{(\acute{\text{e}}\text{t})}$
denotes the corresponding category of motives with rational coefficients. The subdiagram with the right adjoints removed is commutative. The left vertical map factors through the localization with respect to
${\mathcal{D}}_{\mathbb{Q}}^{(\acute{\text{e}}\text{t})}$
denotes the corresponding category of motives with rational coefficients. The subdiagram with the right adjoints removed is commutative. The left vertical map factors through the localization with respect to
![]() ${\mathcal{B}}$
, and we obtain another diagram
${\mathcal{B}}$
, and we obtain another diagram

which commutes in the same sense. (Here, the existence of the right adjoint in the second row follows from Brown representability.)
We claim that the following identities hold:
To prove the first identity, let
![]() $A,B\in {\mathcal{D}}$
and consider the following sequence of canonical maps and identifications:
$A,B\in {\mathcal{D}}$
and consider the following sequence of canonical maps and identifications:
 $$\begin{eqnarray}\displaystyle \hom _{{\mathcal{D}}/{\mathcal{B}}}(qA,\overline{\unicode[STIX]{x1D6FE}}_{\ast }\overline{\unicode[STIX]{x1D6FE}}^{\ast }qB) & = & \displaystyle \hom _{{\mathcal{D}}_{\mathbb{Q}}}(\overline{\unicode[STIX]{x1D6FE}}^{\ast }qA,\overline{\unicode[STIX]{x1D6FE}}^{\ast }qB)\nonumber\\ \displaystyle & = & \displaystyle \hom _{{\mathcal{D}}_{\mathbb{Q}}}(\unicode[STIX]{x1D6FE}^{\ast }A,\unicode[STIX]{x1D6FE}^{\ast }B)\nonumber\\ \displaystyle & = & \displaystyle \hom _{{\mathcal{D}}}(A,\unicode[STIX]{x1D6FE}_{\ast }\unicode[STIX]{x1D6FE}^{\ast }B)\nonumber\\ \displaystyle & \rightarrow & \displaystyle \hom _{{\mathcal{D}}/{\mathcal{B}}}(qA,q\unicode[STIX]{x1D6FE}_{\ast }\unicode[STIX]{x1D6FE}^{\ast }B).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \hom _{{\mathcal{D}}/{\mathcal{B}}}(qA,\overline{\unicode[STIX]{x1D6FE}}_{\ast }\overline{\unicode[STIX]{x1D6FE}}^{\ast }qB) & = & \displaystyle \hom _{{\mathcal{D}}_{\mathbb{Q}}}(\overline{\unicode[STIX]{x1D6FE}}^{\ast }qA,\overline{\unicode[STIX]{x1D6FE}}^{\ast }qB)\nonumber\\ \displaystyle & = & \displaystyle \hom _{{\mathcal{D}}_{\mathbb{Q}}}(\unicode[STIX]{x1D6FE}^{\ast }A,\unicode[STIX]{x1D6FE}^{\ast }B)\nonumber\\ \displaystyle & = & \displaystyle \hom _{{\mathcal{D}}}(A,\unicode[STIX]{x1D6FE}_{\ast }\unicode[STIX]{x1D6FE}^{\ast }B)\nonumber\\ \displaystyle & \rightarrow & \displaystyle \hom _{{\mathcal{D}}/{\mathcal{B}}}(qA,q\unicode[STIX]{x1D6FE}_{\ast }\unicode[STIX]{x1D6FE}^{\ast }B).\nonumber\end{eqnarray}$$
We need to show that the last map (induced by the localization) is bijective, which means that
![]() $\unicode[STIX]{x1D6FE}_{\ast }\unicode[STIX]{x1D6FE}^{\ast }B$
is local with respect to the localization, in other words,
$\unicode[STIX]{x1D6FE}_{\ast }\unicode[STIX]{x1D6FE}^{\ast }B$
is local with respect to the localization, in other words,
![]() $\unicode[STIX]{x1D6FE}_{\ast }\unicode[STIX]{x1D6FE}^{\ast }B\in ({\mathcal{B}})^{\bot }$
. But for any prime
$\unicode[STIX]{x1D6FE}_{\ast }\unicode[STIX]{x1D6FE}^{\ast }B\in ({\mathcal{B}})^{\bot }$
. But for any prime
![]() $\ell \notin S$
and any integer
$\ell \notin S$
and any integer
![]() $p$
, we have
$p$
, we have
and thus the claim.
For the second identity, recall that in
![]() ${\mathcal{D}}$
(respectively,
${\mathcal{D}}$
(respectively,
![]() ${\mathcal{D}}^{\acute{\text{e}}\text{t}}$
), the composition
${\mathcal{D}}^{\acute{\text{e}}\text{t}}$
), the composition
![]() $\unicode[STIX]{x1D6FE}_{\ast }\unicode[STIX]{x1D6FE}^{\ast }$
(respectively,
$\unicode[STIX]{x1D6FE}_{\ast }\unicode[STIX]{x1D6FE}^{\ast }$
(respectively,
![]() $\unicode[STIX]{x1D6FE}_{\ast }^{\acute{\text{e}}\text{t}}\unicode[STIX]{x1D6FE}_{\acute{\text{e}}\text{t}}^{\ast }$
) is simply tensoring with
$\unicode[STIX]{x1D6FE}_{\ast }^{\acute{\text{e}}\text{t}}\unicode[STIX]{x1D6FE}_{\acute{\text{e}}\text{t}}^{\ast }$
) is simply tensoring with
![]() $\mathbb{Q}$
. Since
$\mathbb{Q}$
. Since
![]() $a_{\acute{\text{e}}\text{t}}$
is monoidal, we get indeed
$a_{\acute{\text{e}}\text{t}}$
is monoidal, we get indeed
Let us come back to the map in (C.5). It decomposes as the following composition:
 $$\begin{eqnarray}\displaystyle \hom _{{\mathcal{D}}/{\mathcal{B}}}(qM,q\unicode[STIX]{x1D6FE}_{\ast }\unicode[STIX]{x1D6FE}^{\ast }N) & = & \displaystyle \hom _{{\mathcal{D}}/{\mathcal{B}}}(qM,\unicode[STIX]{x1D6FE}_{\ast }\unicode[STIX]{x1D6FE}^{\ast }qN)\nonumber\\ \displaystyle & = & \displaystyle \hom _{{\mathcal{D}}_{\mathbb{Q}}}(\unicode[STIX]{x1D6FE}^{\ast }M,\unicode[STIX]{x1D6FE}^{\ast }N)\nonumber\\ \displaystyle & = & \displaystyle \hom _{{\mathcal{D}}_{\mathbb{ Q}}^{\acute{\text{e}}\text{t}}}(a_{\acute{\text{e}}\text{t}}\unicode[STIX]{x1D6FE}^{\ast }M,a_{\acute{\text{e}}\text{t}}\unicode[STIX]{x1D6FE}^{\ast }N)\nonumber\\ \displaystyle & = & \displaystyle \hom _{{\mathcal{D}}_{\mathbb{ Q}}^{\acute{\text{e}}\text{t}}}(\unicode[STIX]{x1D6FE}_{\acute{\text{e}}\text{t}}^{\ast }a_{\acute{\text{e}}\text{t}}M,\unicode[STIX]{x1D6FE}_{\acute{\text{e}}\text{t}}^{\ast }a_{\acute{\text{e}}\text{t}}N)\nonumber\\ \displaystyle & = & \displaystyle \hom _{{\mathcal{D}}^{\acute{\text{e}}\text{t}}}(a_{\acute{\text{e}}\text{t}}M,\unicode[STIX]{x1D6FE}_{\ast }^{\acute{\text{e}}\text{t}}\unicode[STIX]{x1D6FE}_{\acute{\text{e}}\text{t}}^{\ast }a_{\acute{\text{e}}\text{t}}N)\nonumber\\ \displaystyle & = & \displaystyle \hom _{{\mathcal{D}}^{\acute{\text{e}}\text{t}}}(a_{\acute{\text{e}}\text{t}}M,a_{\acute{\text{e}}\text{t}}\unicode[STIX]{x1D6FE}_{\ast }\unicode[STIX]{x1D6FE}^{\ast }N)\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \hom _{{\mathcal{D}}/{\mathcal{B}}}(qM,q\unicode[STIX]{x1D6FE}_{\ast }\unicode[STIX]{x1D6FE}^{\ast }N) & = & \displaystyle \hom _{{\mathcal{D}}/{\mathcal{B}}}(qM,\unicode[STIX]{x1D6FE}_{\ast }\unicode[STIX]{x1D6FE}^{\ast }qN)\nonumber\\ \displaystyle & = & \displaystyle \hom _{{\mathcal{D}}_{\mathbb{Q}}}(\unicode[STIX]{x1D6FE}^{\ast }M,\unicode[STIX]{x1D6FE}^{\ast }N)\nonumber\\ \displaystyle & = & \displaystyle \hom _{{\mathcal{D}}_{\mathbb{ Q}}^{\acute{\text{e}}\text{t}}}(a_{\acute{\text{e}}\text{t}}\unicode[STIX]{x1D6FE}^{\ast }M,a_{\acute{\text{e}}\text{t}}\unicode[STIX]{x1D6FE}^{\ast }N)\nonumber\\ \displaystyle & = & \displaystyle \hom _{{\mathcal{D}}_{\mathbb{ Q}}^{\acute{\text{e}}\text{t}}}(\unicode[STIX]{x1D6FE}_{\acute{\text{e}}\text{t}}^{\ast }a_{\acute{\text{e}}\text{t}}M,\unicode[STIX]{x1D6FE}_{\acute{\text{e}}\text{t}}^{\ast }a_{\acute{\text{e}}\text{t}}N)\nonumber\\ \displaystyle & = & \displaystyle \hom _{{\mathcal{D}}^{\acute{\text{e}}\text{t}}}(a_{\acute{\text{e}}\text{t}}M,\unicode[STIX]{x1D6FE}_{\ast }^{\acute{\text{e}}\text{t}}\unicode[STIX]{x1D6FE}_{\acute{\text{e}}\text{t}}^{\ast }a_{\acute{\text{e}}\text{t}}N)\nonumber\\ \displaystyle & = & \displaystyle \hom _{{\mathcal{D}}^{\acute{\text{e}}\text{t}}}(a_{\acute{\text{e}}\text{t}}M,a_{\acute{\text{e}}\text{t}}\unicode[STIX]{x1D6FE}_{\ast }\unicode[STIX]{x1D6FE}^{\ast }N)\end{eqnarray}$$
and is therefore a bijection.
We now turn to (C.6). The motive
![]() $\mathbb{Q}/R$
is a sum
$\mathbb{Q}/R$
is a sum
![]() $\oplus _{\ell \notin S}R[\ell ^{\infty }]$
where
$\oplus _{\ell \notin S}R[\ell ^{\infty }]$
where
![]() $R[\ell ^{\infty }]$
is the homotopy colimit of
$R[\ell ^{\infty }]$
is the homotopy colimit of
![]() $(R/\ell ^{n})_{n}$
with transition maps
$(R/\ell ^{n})_{n}$
with transition maps
![]() $R/\ell ^{n}\rightarrow R/\ell ^{n+1}$
given by multiplication by
$R/\ell ^{n}\rightarrow R/\ell ^{n+1}$
given by multiplication by
![]() $\ell$
. As the tensor product commutes with direct sums and homotopy colimits and
$\ell$
. As the tensor product commutes with direct sums and homotopy colimits and
![]() $M$
is compact, we reduce to show that
$M$
is compact, we reduce to show that
is a bijection.
Write
![]() ${\mathcal{D}}_{\ell ^{n}}^{(\acute{\text{e}}\text{t})}$
for the corresponding categories of motives with
${\mathcal{D}}_{\ell ^{n}}^{(\acute{\text{e}}\text{t})}$
for the corresponding categories of motives with
![]() $R/\ell ^{n}$
-coefficients. Let
$R/\ell ^{n}$
-coefficients. Let
![]() ${\mathcal{B}}_{\ell ^{n}}$
be the localizing subcategory of
${\mathcal{B}}_{\ell ^{n}}$
be the localizing subcategory of
![]() ${\mathcal{D}}_{\ell ^{n}}$
generated by
${\mathcal{D}}_{\ell ^{n}}$
generated by
![]() $\operatorname{cone}(\unicode[STIX]{x1D6FD}_{\ell ^{n}})$
. By Lemma B.8,
$\operatorname{cone}(\unicode[STIX]{x1D6FD}_{\ell ^{n}})$
. By Lemma B.8,
![]() $\unicode[STIX]{x1D6FE}^{\ast }$
maps
$\unicode[STIX]{x1D6FE}^{\ast }$
maps
![]() ${\mathcal{B}}$
to
${\mathcal{B}}$
to
![]() ${\mathcal{B}}_{\ell ^{n}}$
so that we obtain a diagram
${\mathcal{B}}_{\ell ^{n}}$
so that we obtain a diagram

as before. The bottom right equivalence follows from Theorem C.1.
We now claim that the analogous identities hold:
The second identity is proved as before, while the first one can be verified as follows. Since
![]() $\unicode[STIX]{x1D6FE}^{\ast }$
preserves compact objects
$\unicode[STIX]{x1D6FE}^{\ast }$
preserves compact objects
![]() $\unicode[STIX]{x1D6FE}_{\ast }$
commutes with small sums, and it follows that
$\unicode[STIX]{x1D6FE}_{\ast }$
commutes with small sums, and it follows that
![]() $\unicode[STIX]{x1D6FE}_{\ast }$
maps
$\unicode[STIX]{x1D6FE}_{\ast }$
maps
![]() ${\mathcal{B}}_{\ell ^{n}}$
to
${\mathcal{B}}_{\ell ^{n}}$
to
![]() ${\mathcal{B}}$
, by Lemma B.10. It follows from Lemma C.9 that
${\mathcal{B}}$
, by Lemma B.10. It follows from Lemma C.9 that
![]() $\overline{\unicode[STIX]{x1D6FE}}^{\ast }$
and
$\overline{\unicode[STIX]{x1D6FE}}^{\ast }$
and
![]() $\overline{\unicode[STIX]{x1D6FE}}_{\ast }$
are simply the functors induced by
$\overline{\unicode[STIX]{x1D6FE}}_{\ast }$
are simply the functors induced by
![]() $\unicode[STIX]{x1D6FE}^{\ast }$
and
$\unicode[STIX]{x1D6FE}^{\ast }$
and
![]() $\unicode[STIX]{x1D6FE}_{\ast }$
, respectively. The first identity follows immediately. The map in (C.8) is now seen to be a bijection precisely as in (C.7).◻
$\unicode[STIX]{x1D6FE}_{\ast }$
, respectively. The first identity follows immediately. The map in (C.8) is now seen to be a bijection precisely as in (C.7).◻
Lemma C.9. Let
![]() ${\mathcal{D}},{\mathcal{D}}^{\prime }$
be two triangulated categories, let
${\mathcal{D}},{\mathcal{D}}^{\prime }$
be two triangulated categories, let
![]() $\unicode[STIX]{x1D6FE}^{\ast }\dashv \unicode[STIX]{x1D6FE}_{\ast }:{\mathcal{D}}\rightarrow {\mathcal{D}}^{\prime }$
be an adjunction, and suppose
$\unicode[STIX]{x1D6FE}^{\ast }\dashv \unicode[STIX]{x1D6FE}_{\ast }:{\mathcal{D}}\rightarrow {\mathcal{D}}^{\prime }$
be an adjunction, and suppose
![]() ${\mathcal{B}}\subset {\mathcal{D}}$
and
${\mathcal{B}}\subset {\mathcal{D}}$
and
![]() ${\mathcal{B}}^{\prime }\subset {\mathcal{D}}^{\prime }$
are thick subcategories such that the corresponding Bousfield localizations exist.
${\mathcal{B}}^{\prime }\subset {\mathcal{D}}^{\prime }$
are thick subcategories such that the corresponding Bousfield localizations exist.
If
![]() $\unicode[STIX]{x1D6FE}^{\ast }{\mathcal{B}}\subset {\mathcal{B}}^{\prime }$
and
$\unicode[STIX]{x1D6FE}^{\ast }{\mathcal{B}}\subset {\mathcal{B}}^{\prime }$
and
![]() $\unicode[STIX]{x1D6FE}_{\ast }{\mathcal{B}}^{\prime }\subset {\mathcal{B}}$
then
$\unicode[STIX]{x1D6FE}_{\ast }{\mathcal{B}}^{\prime }\subset {\mathcal{B}}$
then
![]() $\unicode[STIX]{x1D6FE}^{\ast }$
and
$\unicode[STIX]{x1D6FE}^{\ast }$
and
![]() $\unicode[STIX]{x1D6FE}_{\ast }$
descend to an adjunction on the quotient categories:
$\unicode[STIX]{x1D6FE}_{\ast }$
descend to an adjunction on the quotient categories:
![]() $\unicode[STIX]{x1D6FE}^{\ast }\dashv \unicode[STIX]{x1D6FE}_{\ast }:{\mathcal{D}}/{\mathcal{B}}\rightarrow {\mathcal{D}}^{\prime }/{\mathcal{B}}^{\prime }$
.
$\unicode[STIX]{x1D6FE}^{\ast }\dashv \unicode[STIX]{x1D6FE}_{\ast }:{\mathcal{D}}/{\mathcal{B}}\rightarrow {\mathcal{D}}^{\prime }/{\mathcal{B}}^{\prime }$
.
Proof. By our assumption, these functors do descend to the quotient categories. To see that the induced functors are still adjoint to each other, let us denote by
![]() $L^{\prime }$
the localization functor on
$L^{\prime }$
the localization functor on
![]() ${\mathcal{D}}^{\prime }$
with respect to
${\mathcal{D}}^{\prime }$
with respect to
![]() ${\mathcal{B}}^{\prime }$
, and consider the following sequence of morphisms and canonical identifications, where
${\mathcal{B}}^{\prime }$
, and consider the following sequence of morphisms and canonical identifications, where
![]() $a\in {\mathcal{D}}$
and
$a\in {\mathcal{D}}$
and
![]() $b\in {\mathcal{D}}^{\prime }$
:
$b\in {\mathcal{D}}^{\prime }$
:
 $$\begin{eqnarray}\displaystyle \hom _{{\mathcal{D}}^{\prime }/{\mathcal{B}}^{\prime }}(\unicode[STIX]{x1D6FE}^{\ast }a,b) & = & \displaystyle \hom _{{\mathcal{D}}^{\prime }/{\mathcal{B}}^{\prime }}(\unicode[STIX]{x1D6FE}^{\ast }a,L^{\prime }b)\nonumber\\ \displaystyle & = & \displaystyle \hom _{{\mathcal{D}}^{\prime }}(\unicode[STIX]{x1D6FE}^{\ast }a,L^{\prime }b)\nonumber\\ \displaystyle & = & \displaystyle \hom _{{\mathcal{D}}}(a,\unicode[STIX]{x1D6FE}_{\ast }L^{\prime }b)\nonumber\\ \displaystyle & \rightarrow & \displaystyle \hom _{{\mathcal{D}}/{\mathcal{B}}}(a,\unicode[STIX]{x1D6FE}_{\ast }L^{\prime }b)\nonumber\\ \displaystyle & \leftarrow & \displaystyle \hom _{{\mathcal{D}}/{\mathcal{B}}}(a,\unicode[STIX]{x1D6FE}_{\ast }b).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \hom _{{\mathcal{D}}^{\prime }/{\mathcal{B}}^{\prime }}(\unicode[STIX]{x1D6FE}^{\ast }a,b) & = & \displaystyle \hom _{{\mathcal{D}}^{\prime }/{\mathcal{B}}^{\prime }}(\unicode[STIX]{x1D6FE}^{\ast }a,L^{\prime }b)\nonumber\\ \displaystyle & = & \displaystyle \hom _{{\mathcal{D}}^{\prime }}(\unicode[STIX]{x1D6FE}^{\ast }a,L^{\prime }b)\nonumber\\ \displaystyle & = & \displaystyle \hom _{{\mathcal{D}}}(a,\unicode[STIX]{x1D6FE}_{\ast }L^{\prime }b)\nonumber\\ \displaystyle & \rightarrow & \displaystyle \hom _{{\mathcal{D}}/{\mathcal{B}}}(a,\unicode[STIX]{x1D6FE}_{\ast }L^{\prime }b)\nonumber\\ \displaystyle & \leftarrow & \displaystyle \hom _{{\mathcal{D}}/{\mathcal{B}}}(a,\unicode[STIX]{x1D6FE}_{\ast }b).\nonumber\end{eqnarray}$$
It remains to check that the last two maps are bijections. We know that
![]() $L^{\prime }b\in ({\mathcal{B}}^{\prime })^{\bot }$
and hence for any
$L^{\prime }b\in ({\mathcal{B}}^{\prime })^{\bot }$
and hence for any
![]() $x\in {\mathcal{B}}$
we have
$x\in {\mathcal{B}}$
we have
since
![]() $\unicode[STIX]{x1D6FE}^{\ast }{\mathcal{B}}\subset {\mathcal{B}}^{\prime }$
. In other words
$\unicode[STIX]{x1D6FE}^{\ast }{\mathcal{B}}\subset {\mathcal{B}}^{\prime }$
. In other words
![]() $\unicode[STIX]{x1D6FE}_{\ast }L^{\prime }b\in {\mathcal{B}}^{\bot }$
and the first map above is therefore a bijection. We also know that
$\unicode[STIX]{x1D6FE}_{\ast }L^{\prime }b\in {\mathcal{B}}^{\bot }$
and the first map above is therefore a bijection. We also know that
![]() $b\rightarrow L^{\prime }b$
becomes invertible in
$b\rightarrow L^{\prime }b$
becomes invertible in
![]() ${\mathcal{D}}^{\prime }/{\mathcal{B}}^{\prime }$
, i.e. its cone lies in
${\mathcal{D}}^{\prime }/{\mathcal{B}}^{\prime }$
, i.e. its cone lies in
![]() ${\mathcal{B}}^{\prime }$
. It follows that the cone of
${\mathcal{B}}^{\prime }$
. It follows that the cone of
![]() $\unicode[STIX]{x1D6FE}_{\ast }b\rightarrow \unicode[STIX]{x1D6FE}_{\ast }L^{\prime }b$
lies in
$\unicode[STIX]{x1D6FE}_{\ast }b\rightarrow \unicode[STIX]{x1D6FE}_{\ast }L^{\prime }b$
lies in
![]() $\unicode[STIX]{x1D6FE}_{\ast }{\mathcal{B}}^{\prime }\subset {\mathcal{B}}$
and the second map above is therefore a bijection as well.◻
$\unicode[STIX]{x1D6FE}_{\ast }{\mathcal{B}}^{\prime }\subset {\mathcal{B}}$
and the second map above is therefore a bijection as well.◻