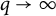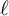1 Introduction
In this paper, we study the unit random walk in finite vector spaces. We also provide a discussion of a related association scheme that was the subject of the first author’s thesis work [Reference Brittenham4] that we latter were informed was previously studied by W. M. Kwok, E. Bannai, O. Shimabukuro, and H. Tanaka in [Reference Bannai, Shimabukuro and Tanaka2, Reference Kwok12]. In [Reference Kwok12], the P-matrix and intersection numbers of this scheme were worked out in terms of the character table of the “Euclidean” group over finite fields but had some errors which were latter corrected in [Reference Bannai, Shimabukuro and Tanaka2] where a connection to Kloosterman sums was also mentioned, including Kloosterman’s original bound. In this paper, we recap these calculations first to connect them more explicitly to our applications which use some deeper distributional data about Kloosterman sums provided by equidistribution results from number theory. (Along the way we also provide an explicit calculation of the planar intersection numbers implicitly described in [Reference Kwok12].)
The books [Reference Brouwer and Haemers5, Reference Godsil and Royle7, Reference Terras17] are good references for the spectral graph theory concepts used in this paper. The book [Reference Brouwer and Haemers5] is a good reference for association schemes. Let
![]() $\mathbb {F}_q$
be a finite field of odd prime power order q, and let
$\mathbb {F}_q$
be a finite field of odd prime power order q, and let
![]() $V=\mathbb {F}_q^d$
be the standard d-dimensional vector space over
$V=\mathbb {F}_q^d$
be the standard d-dimensional vector space over
![]() $\mathbb {F}_q$
. Note that all finite vector spaces of odd characteristic are of this form.
$\mathbb {F}_q$
. Note that all finite vector spaces of odd characteristic are of this form.
Equip V with the standard bilinear dot product associated with the nondegenerate quadratic form
![]() $Q(v)=v_1^2 + \dots + v_d^2$
. The “distance” between two points v and w in V as determined by this quadratic form is given by
$Q(v)=v_1^2 + \dots + v_d^2$
. The “distance” between two points v and w in V as determined by this quadratic form is given by
![]() $Q(v-w),$
which is the standard “Euclidean” distance formula without the square root. The quadratic space
$Q(v-w),$
which is the standard “Euclidean” distance formula without the square root. The quadratic space
![]() $(V,Q)$
will be referred to as d-dimensional Euclidean space over
$(V,Q)$
will be referred to as d-dimensional Euclidean space over
![]() $\mathbb {F}_q$
in this paper. Note that it is known that there are only two nondegenerate quadratic forms up to isometry on any finite vector space (see [Reference Serre16]), besides the one derived from the standard dot product that we are using, the other one is a “Lorentzian” quadratic form with
$\mathbb {F}_q$
in this paper. Note that it is known that there are only two nondegenerate quadratic forms up to isometry on any finite vector space (see [Reference Serre16]), besides the one derived from the standard dot product that we are using, the other one is a “Lorentzian” quadratic form with
![]() $Q_\mathrm{Lorentz}(v)=v_1^2 + \dots + v_{d-1}^2 + \xi v_d^2$
, where
$Q_\mathrm{Lorentz}(v)=v_1^2 + \dots + v_{d-1}^2 + \xi v_d^2$
, where
![]() $\xi $
is any fixed nonsquare element in
$\xi $
is any fixed nonsquare element in
![]() $\mathbb {F}_q$
. Most of what we discuss will also hold for this other quadratic form but we will stick to the dot product in this paper for brevity.
$\mathbb {F}_q$
. Most of what we discuss will also hold for this other quadratic form but we will stick to the dot product in this paper for brevity.
For every
![]() $t \in \mathbb {F}_q$
, we may define the distance-t graph whose vertex set is V and where there is an edge between
$t \in \mathbb {F}_q$
, we may define the distance-t graph whose vertex set is V and where there is an edge between
![]() $v, w \in V$
if and only if
$v, w \in V$
if and only if
![]() $Q(v-w)=t$
and
$Q(v-w)=t$
and
![]() $v \neq w$
. This regular graph has a
$v \neq w$
. This regular graph has a
![]() $q^d \times q^d$
adjacency matrix
$q^d \times q^d$
adjacency matrix
![]() $\mathbb {A}_t$
with respect to some fixed ordering of the vertices of V and common vertex degree
$\mathbb {A}_t$
with respect to some fixed ordering of the vertices of V and common vertex degree
![]() $|S_t|$
, where
$|S_t|$
, where
![]() $S_t=\{ v \in V\setminus \{0\} | Q(v)=t \}$
is the “sphere of radius t” and has order
$S_t=\{ v \in V\setminus \{0\} | Q(v)=t \}$
is the “sphere of radius t” and has order
![]() $q^{d-1}(1+o(1))$
when
$q^{d-1}(1+o(1))$
when
![]() $t \neq 0$
. (The exact order is known but here for brevity, we collect secondary terms in
$t \neq 0$
. (The exact order is known but here for brevity, we collect secondary terms in
![]() $o(1)$
which tends to
$o(1)$
which tends to
![]() $0$
as
$0$
as
![]() $q \to \infty $
.) In fact, this graph is a Cayley graph with connection set
$q \to \infty $
.) In fact, this graph is a Cayley graph with connection set
![]() $S_t$
and hence is in fact vertex-transitive (i.e., there is a graph automorphism taking any vertex to any other vertex). The corresponding Markov chain (see [Reference Levin13] for basic Markov chain terminology) on this graph is called the distance-t random walk in V with the case
$S_t$
and hence is in fact vertex-transitive (i.e., there is a graph automorphism taking any vertex to any other vertex). The corresponding Markov chain (see [Reference Levin13] for basic Markov chain terminology) on this graph is called the distance-t random walk in V with the case
![]() $t=1$
called the unit random walk in V. It corresponds to a situation where at each step, the current state evolves by taking a distance-t step with each such step equally likely. The transition matrix for this Markov chain is
$t=1$
called the unit random walk in V. It corresponds to a situation where at each step, the current state evolves by taking a distance-t step with each such step equally likely. The transition matrix for this Markov chain is
![]() $T_t =\frac {1}{|S_t|}\mathbb {A}_t$
.
$T_t =\frac {1}{|S_t|}\mathbb {A}_t$
.
The matrices
![]() $\{ \mathbb {A}_t | t \in \mathbb {F}_q \}$
determine a symmetric association scheme with corresponding real and complex Bose–Messner algebras. What this means is that we have identities of the form
$\{ \mathbb {A}_t | t \in \mathbb {F}_q \}$
determine a symmetric association scheme with corresponding real and complex Bose–Messner algebras. What this means is that we have identities of the form
where the intersection numbers
![]() $p_{i,j}^k$
correspond to the number of ways that a given “line segment” of length k can be completed to a triangle of side lengths
$p_{i,j}^k$
correspond to the number of ways that a given “line segment” of length k can be completed to a triangle of side lengths
![]() $i,j,$
and k. We call this particular scheme the Euclidean association scheme for the finite field
$i,j,$
and k. We call this particular scheme the Euclidean association scheme for the finite field
![]() $\mathbb {F}_q$
and recompute certain change of basis matrices P and Q (between a geometric and a spectral basis of the Bose–Messner algebra) which are generally important in the theory of such schemes. We also compute this association scheme’s intersection numbers. (In [Reference Kwok12], the higher-dimensional numbers were computed in terms of the planar case which we compute explicitly here.) This first part of the paper’s results appear in the first author’s thesis as well as in [Reference Kwok12] (some errors in [Reference Kwok12] were later corrected in [Reference Bannai, Shimabukuro and Tanaka2] and the connection to Kloosterman sums made more explicit, though these were also already described earlier in [Reference Iosevich and Rudnev9]).
$\mathbb {F}_q$
and recompute certain change of basis matrices P and Q (between a geometric and a spectral basis of the Bose–Messner algebra) which are generally important in the theory of such schemes. We also compute this association scheme’s intersection numbers. (In [Reference Kwok12], the higher-dimensional numbers were computed in terms of the planar case which we compute explicitly here.) This first part of the paper’s results appear in the first author’s thesis as well as in [Reference Kwok12] (some errors in [Reference Kwok12] were later corrected in [Reference Bannai, Shimabukuro and Tanaka2] and the connection to Kloosterman sums made more explicit, though these were also already described earlier in [Reference Iosevich and Rudnev9]).
The eigenvalues of
![]() $\mathbb {A}_t$
are related to twisted Kloosterman sums:
$\mathbb {A}_t$
are related to twisted Kloosterman sums:
 $$ \begin{align*}\tilde{K}_d(a,b) = \sum_{x \in \mathbb{F}_q - \{0\}} \binom{x}{q}^d \chi(ax + \frac{b}{x}), \end{align*} $$
$$ \begin{align*}\tilde{K}_d(a,b) = \sum_{x \in \mathbb{F}_q - \{0\}} \binom{x}{q}^d \chi(ax + \frac{b}{x}), \end{align*} $$
where
![]() $\binom {x}{q}$
is the Legendre symbol and
$\binom {x}{q}$
is the Legendre symbol and
![]() $\chi $
is a fixed nontrivial additive character given by
$\chi $
is a fixed nontrivial additive character given by
![]() $\chi (x) = e^{\frac {2 \pi i \mathrm{Tr}(x)}{p}}$
, Here,
$\chi (x) = e^{\frac {2 \pi i \mathrm{Tr}(x)}{p}}$
, Here,
![]() $q=p^{\ell }$
with p an odd prime and
$q=p^{\ell }$
with p an odd prime and
![]() $\mathrm{Tr}$
is the Galois trace from
$\mathrm{Tr}$
is the Galois trace from
![]() $\mathbb {F}_q$
to
$\mathbb {F}_q$
to
![]() $\mathbb {F}_p$
.
$\mathbb {F}_p$
.
In even dimensions d, the twisting by the Legendre symbol disappears and the eigenvalues are related to Kloosterman sums:
 $$ \begin{align*}K(a,b) = \sum_{x \in \mathbb{F}_q - \{0\}} \chi(ax + \frac{b}{x}). \end{align*} $$
$$ \begin{align*}K(a,b) = \sum_{x \in \mathbb{F}_q - \{0\}} \chi(ax + \frac{b}{x}). \end{align*} $$
In general, the
![]() $K(a,b)$
are real algebraic integers, contained in
$K(a,b)$
are real algebraic integers, contained in
![]() $\mathbb {Q}[e^{\frac {2 \pi i}{p}}]$
, the pth cyclotomic field.
$\mathbb {Q}[e^{\frac {2 \pi i}{p}}]$
, the pth cyclotomic field.
The identities
![]() $K(0,0)=q-1, K(a,b)=K(b,a), K(1,0)=-1$
are trivial to verify via character orthogonality and coordinate changes, as is the identity
$K(0,0)=q-1, K(a,b)=K(b,a), K(1,0)=-1$
are trivial to verify via character orthogonality and coordinate changes, as is the identity
![]() $K(a,b)=K(1,ab)$
when
$K(a,b)=K(1,ab)$
when
![]() $a \neq 0$
. By work of Kloosterman and others (see [Reference Kloosterman11, Reference Weil18]), it is known
$a \neq 0$
. By work of Kloosterman and others (see [Reference Kloosterman11, Reference Weil18]), it is known
![]() $|K(1,\alpha )| \leq 2\sqrt {q}$
when
$|K(1,\alpha )| \leq 2\sqrt {q}$
when
![]() $\alpha \neq 0$
and
$\alpha \neq 0$
and
![]() $q=p$
is an odd prime. One typically writes
$q=p$
is an odd prime. One typically writes
![]() $K(1,\alpha )=2\sqrt {q} \cos (\theta _{\alpha ,q}),$
where
$K(1,\alpha )=2\sqrt {q} \cos (\theta _{\alpha ,q}),$
where
![]() $\theta _{\alpha ,q} \in [0, \pi ]$
. These numbers occur as spectra of various natural Cayley graphs and hence in many combinatorial applications (see [Reference Baker1, Reference Demiroglu6, Reference Hart, Iosevich and Solymosi8]).
$\theta _{\alpha ,q} \in [0, \pi ]$
. These numbers occur as spectra of various natural Cayley graphs and hence in many combinatorial applications (see [Reference Baker1, Reference Demiroglu6, Reference Hart, Iosevich and Solymosi8]).
Nick Katz [Reference Katz10] proved the deep result on “vertical equidistribution of Kloosterman sums” (see [Reference Ping14]) which states that for any
![]() $[a,b] \subseteq [0, \pi ]$
, the proportion of
$[a,b] \subseteq [0, \pi ]$
, the proportion of
![]() $\{\theta _{\alpha , q}, 1 \leq \alpha \leq q-1 \}$
that lie in
$\{\theta _{\alpha , q}, 1 \leq \alpha \leq q-1 \}$
that lie in
![]() $[a,b]$
approaches
$[a,b]$
approaches
![]() $ \frac {2}{\pi }\int _a^b sin^2(\theta ) d\theta $
as
$ \frac {2}{\pi }\int _a^b sin^2(\theta ) d\theta $
as
![]() $q \to \infty $
. This result was obtained by estimating the
$q \to \infty $
. This result was obtained by estimating the
![]() $\ell $
th moment of the Kloosterman numbers
$\ell $
th moment of the Kloosterman numbers
![]() $M_{q,\ell }= \sum _{1 \leq \alpha \leq q-1} |K(1,\alpha )|^{\ell }$
for all positive integers
$M_{q,\ell }= \sum _{1 \leq \alpha \leq q-1} |K(1,\alpha )|^{\ell }$
for all positive integers
![]() $\ell $
reasonably. Useful closed form formulas for these moments are only known for a finite number of
$\ell $
reasonably. Useful closed form formulas for these moments are only known for a finite number of
![]() $\ell $
(see [Reference Ping and Yuan15]).
$\ell $
(see [Reference Ping and Yuan15]).
In this paper, we calculate
![]() $R_{q,\ell ,t}$
(see Theorem 7.1), the probability that you return to the vertex you started from after
$R_{q,\ell ,t}$
(see Theorem 7.1), the probability that you return to the vertex you started from after
![]() $\ell $
-steps in the random distance-t walk, in terms of these moments of Kloosterman sums. We show that this probability is independent of your starting state/vertex and is given by the following.
$\ell $
-steps in the random distance-t walk, in terms of these moments of Kloosterman sums. We show that this probability is independent of your starting state/vertex and is given by the following.
Theorem 1.1 (Probability of return in the distance-t random walk in
 $\mathbb {F}_q$
-planes)
$\mathbb {F}_q$
-planes)
Let q be an odd prime,
![]() $q=3 \text { mod } 4$
. Let
$q=3 \text { mod } 4$
. Let
![]() $R_{q,\ell ,t}$
be the probability that you return to the same vertex after
$R_{q,\ell ,t}$
be the probability that you return to the same vertex after
![]() $\ell $
steps in the distance-t walk where
$\ell $
steps in the distance-t walk where
![]() $t \neq 0$
. Then
$t \neq 0$
. Then
![]() $R_{q,\ell , t}=R_{q,\ell }$
is independent of
$R_{q,\ell , t}=R_{q,\ell }$
is independent of
![]() $t \neq 0$
and initial state. We have
$t \neq 0$
and initial state. We have
 $$ \begin{align*}R_{q,\ell,t}=R_{q,\ell}=\frac{1}{q^2}\left(1 + \frac{(-1)^{\ell}}{(q+1)^{\ell-1}} M_{q,\ell}\right). \end{align*} $$
$$ \begin{align*}R_{q,\ell,t}=R_{q,\ell}=\frac{1}{q^2}\left(1 + \frac{(-1)^{\ell}}{(q+1)^{\ell-1}} M_{q,\ell}\right). \end{align*} $$
Furthermore, as
![]() $q \to \infty $
, we have
$q \to \infty $
, we have
 $$ \begin{align*}R_{q, 2\ell} = \frac{1}{q^2} + \frac{q^{\ell-1}}{(\ell+1)(q+1)^{2\ell-1}}\binom{2\ell}{\ell} (1 + o(1)) = \frac{1}{q^2} + \frac{1}{q^{\ell}(\ell+1)}\binom{2\ell}{\ell}(1+o(1)) \end{align*} $$
$$ \begin{align*}R_{q, 2\ell} = \frac{1}{q^2} + \frac{q^{\ell-1}}{(\ell+1)(q+1)^{2\ell-1}}\binom{2\ell}{\ell} (1 + o(1)) = \frac{1}{q^2} + \frac{1}{q^{\ell}(\ell+1)}\binom{2\ell}{\ell}(1+o(1)) \end{align*} $$
and
 $$ \begin{align*}R_{q, 2\ell+1}=\frac{1}{q^2}\left(1 - \frac{1}{(q+1)^{2\ell}}o(q^{\ell+1.5})\right)=\frac{1}{q^2}\left(1+o(q^{1.5-\ell})\right). \end{align*} $$
$$ \begin{align*}R_{q, 2\ell+1}=\frac{1}{q^2}\left(1 - \frac{1}{(q+1)^{2\ell}}o(q^{\ell+1.5})\right)=\frac{1}{q^2}\left(1+o(q^{1.5-\ell})\right). \end{align*} $$
Note that the first
![]() $\frac {1}{q^2}$
term in these asymptotic formulas is what one would expect if the location after
$\frac {1}{q^2}$
term in these asymptotic formulas is what one would expect if the location after
![]() $\ell $
steps were equally likely to be anywhere in the plane and the second term represents an arithmetic bias against that happening. In particular, we see that for
$\ell $
steps were equally likely to be anywhere in the plane and the second term represents an arithmetic bias against that happening. In particular, we see that for
![]() $\ell \geq 5$
, we have
$\ell \geq 5$
, we have
![]() $\mathbb {R}_{q,\ell }$
is
$\mathbb {R}_{q,\ell }$
is
![]() $\frac {1}{q^2}(1+o(1))$
but for smaller
$\frac {1}{q^2}(1+o(1))$
but for smaller
![]() $\ell $
arithmetic bias is significant and so we need at least five steps to achieve uniformity. Note
$\ell $
arithmetic bias is significant and so we need at least five steps to achieve uniformity. Note
![]() $R_{q,1}=0, R_{q,2}=\frac {1}{q} (1+o(1)), R_{q,4}=\frac {3}{q^2}(1+o(1))$
are all “arithmetically biased.” Similar results hold for
$R_{q,1}=0, R_{q,2}=\frac {1}{q} (1+o(1)), R_{q,4}=\frac {3}{q^2}(1+o(1))$
are all “arithmetically biased.” Similar results hold for
![]() $q=1 \text { mod } 4$
and can be seen in the paper.
$q=1 \text { mod } 4$
and can be seen in the paper.
Though the main terms in these formulas can be derived using just the spectral gap when
![]() $\ell \geq 5$
, the explicit nature of the second-order term requires, and is equivalent to, the deeper vertical equidistribution results.
$\ell \geq 5$
, the explicit nature of the second-order term requires, and is equivalent to, the deeper vertical equidistribution results.
2 Association scheme definitions
See [Reference Brouwer and Haemers5] for a discussion of the essentials of the theory of association schemes. There are various equivalent definitions of association schemes, for us the following is most convenient.
Definition 2.1 (Association scheme)
An association scheme is a set X equipped with a surjective “distance function”
![]() $d: X \to \Delta $
with distance set
$d: X \to \Delta $
with distance set
![]() $\Delta $
which contains a formal zero element
$\Delta $
which contains a formal zero element
![]() $\{ \bar {0} \}$
such that:
$\{ \bar {0} \}$
such that:
(1)
![]() $d(x,y)=\bar {0}$
if and only if
$d(x,y)=\bar {0}$
if and only if
![]() $x=y$
.
$x=y$
.
(2)
![]() $d(x,y)=d(y,x)$
all
$d(x,y)=d(y,x)$
all
![]() $x, y \in X$
.
$x, y \in X$
.
(3) Given
![]() $x,y \in X$
,
$x,y \in X$
,
![]() $k, i, j \in \Delta $
with
$k, i, j \in \Delta $
with
![]() $d(x,y)=k$
, the number
$d(x,y)=k$
, the number
![]() $p_{i,j}^k(x,y)$
of
$p_{i,j}^k(x,y)$
of
![]() $z \in X$
such that
$z \in X$
such that
![]() $d(x,z)=i, d(z,y)=j$
only depends on
$d(x,z)=i, d(z,y)=j$
only depends on
![]() $i, j, k$
and not
$i, j, k$
and not
![]() $x, y$
. Thus,
$x, y$
. Thus,
![]() $p_{i,j}^k(x,y)=p_{i,j}^k$
and these are called the “intersection numbers” of the association scheme.
$p_{i,j}^k(x,y)=p_{i,j}^k$
and these are called the “intersection numbers” of the association scheme.
The best way to think of this last condition is to think of
![]() $x,y$
giving a segment of length k and then noting that (3) states that the number of ways to complete this segment into a “triangle” only depends on the side lengths of the triangle and not the endpoints of the segment itself.
$x,y$
giving a segment of length k and then noting that (3) states that the number of ways to complete this segment into a “triangle” only depends on the side lengths of the triangle and not the endpoints of the segment itself.
Though it is nice to think of an association scheme “geometrically” do note that we do not require the “distance” to satisfy the triangle inequality nor for the set
![]() $\Delta $
to be numerical. The elements of
$\Delta $
to be numerical. The elements of
![]() $\Delta $
can be any objects such as colors, etc.
$\Delta $
can be any objects such as colors, etc.
For any
![]() $x \in X$
and
$x \in X$
and
![]() $j \in \Delta $
, the sphere of radius j about x is denoted
$j \in \Delta $
, the sphere of radius j about x is denoted
Note in any finite association scheme, setting
![]() $x=y$
in
$x=y$
in
![]() $(3),$
we see that
$(3),$
we see that
is independent of x. Here,
![]() $\delta _{i,j}$
is the Kronecker Delta function which is
$\delta _{i,j}$
is the Kronecker Delta function which is
![]() $1$
when
$1$
when
![]() $i=j$
and
$i=j$
and
![]() $0$
otherwise. Furthermore, by (2), we may reverse the role of x and y and so conclude that
$0$
otherwise. Furthermore, by (2), we may reverse the role of x and y and so conclude that
for all
![]() $i,j,k \in \Delta $
.
$i,j,k \in \Delta $
.
Given an association scheme
![]() $(X,d)$
, we define the distance-t graph for any
$(X,d)$
, we define the distance-t graph for any
![]() $t \in \Delta $
as the graph on vertex set X and where two vertices
$t \in \Delta $
as the graph on vertex set X and where two vertices
![]() $x, y \in X$
are adjacent if and only if
$x, y \in X$
are adjacent if and only if
![]() $d(x,y)=t$
. As
$d(x,y)=t$
. As
![]() $|S_t(x)|$
is independent of x, the distance-t graph is
$|S_t(x)|$
is independent of x, the distance-t graph is
![]() $|S_t|$
-regular.
$|S_t|$
-regular.
In the case X is finite, we denote the adjacency matrix of the graph (with respect to some linear ordering of X) as
![]() $\mathbb {A}_t$
. Thus,
$\mathbb {A}_t$
. Thus,
![]() $\mathbb {A}_{\bar {0}} = I$
and
$\mathbb {A}_{\bar {0}} = I$
and
![]() $\sum _{j \in \Delta } \mathbb {A}_j = \mathbb {J}$
, where
$\sum _{j \in \Delta } \mathbb {A}_j = \mathbb {J}$
, where
![]() $\mathbb {J}$
is the all
$\mathbb {J}$
is the all
![]() $1$
matrix. It is easy to check that condition (2) is equivalent to the
$1$
matrix. It is easy to check that condition (2) is equivalent to the
![]() $\mathbb {A}_t$
being symmetric matrices and condition (3) is equivalent to
$\mathbb {A}_t$
being symmetric matrices and condition (3) is equivalent to
As
![]() $p_{i,j}^k=p_{j,i}^k$
, this says the matrices
$p_{i,j}^k=p_{j,i}^k$
, this says the matrices
![]() $\{ \mathbb {A}_i | i \in \Delta \}$
all commute with each other. Note as we require
$\{ \mathbb {A}_i | i \in \Delta \}$
all commute with each other. Note as we require
![]() $d: X \times X \to \Delta $
to be surjective, no
$d: X \times X \to \Delta $
to be surjective, no
![]() $\mathbb {A}_j$
is the zero matrix and so the fact that they sum to
$\mathbb {A}_j$
is the zero matrix and so the fact that they sum to
![]() $\mathbb {J}$
shows that the
$\mathbb {J}$
shows that the
![]() $\{ \mathbb {A}_i | i \in \Delta \}$
are a linearly independent set in
$\{ \mathbb {A}_i | i \in \Delta \}$
are a linearly independent set in
![]() $Mat_{|X|}(\mathbb {R})$
. Condition (3), guarantees that their span is an algebra.
$Mat_{|X|}(\mathbb {R})$
. Condition (3), guarantees that their span is an algebra.
Definition 2.2 (Bose–Messner algebra)
Let
![]() $\mathfrak {A}=(X,d)$
be a finite association scheme with distance set
$\mathfrak {A}=(X,d)$
be a finite association scheme with distance set
![]() $\Delta $
such that
$\Delta $
such that
![]() $|\Delta |=D+1$
. We say
$|\Delta |=D+1$
. We say
![]() $(X,d)$
has D (nonzero) classes. The Bose–Messner algebra of the scheme is defined as
$(X,d)$
has D (nonzero) classes. The Bose–Messner algebra of the scheme is defined as
It is a (
![]() $D+1$
)-dimensional
$D+1$
)-dimensional
![]() $\mathbb {R}$
-commutative algebra with basis
$\mathbb {R}$
-commutative algebra with basis
![]() $\{ \mathbb {A}_j | j \in \Delta \}$
and multiplication determined by the rule
$\{ \mathbb {A}_j | j \in \Delta \}$
and multiplication determined by the rule
![]() $\mathbb {A}_i \mathbb {A}_j = \sum _{k} p_{i,j}^k \mathbb {A}_k$
.
$\mathbb {A}_i \mathbb {A}_j = \sum _{k} p_{i,j}^k \mathbb {A}_k$
.
The complexification of this algebra is called the complex Bose–Messner algebra and consists of the
![]() $\mathbb {C}$
-span of the same
$\mathbb {C}$
-span of the same
![]() $\mathbb {A}_j$
matrices.
$\mathbb {A}_j$
matrices.
Example 2.3 Let
![]() $X=(V,E)$
be a distance regular graph of diameter D, then V equipped with the graph metric is an association scheme on D (nonzero) classes. The theory of association schemes was introduced historically as a generalization of the theory of distance regular graphs.
$X=(V,E)$
be a distance regular graph of diameter D, then V equipped with the graph metric is an association scheme on D (nonzero) classes. The theory of association schemes was introduced historically as a generalization of the theory of distance regular graphs.
The next example is the primary example considered in this paper.
Example 2.4 (Euclidean association scheme)
Let q be an odd prime power,
![]() $n\geq 2$
, and
$n\geq 2$
, and
![]() $V=\mathbb {F}_q^n$
equipped with the “Euclidean” quadratic form
$V=\mathbb {F}_q^n$
equipped with the “Euclidean” quadratic form
![]() $Q(v)=v_1^2+\dots +v_n^2$
and “distance”
$Q(v)=v_1^2+\dots +v_n^2$
and “distance”
![]() $Q(v-w)$
. Then given
$Q(v-w)$
. Then given
![]() $x \neq y,v \neq w \in V$
with
$x \neq y,v \neq w \in V$
with
![]() $Q(x-y)=Q(v-w)$
, Witt’s theorem shows there is a isometry of V (consisting of a composition of a translation and matrix multiplication by A, where
$Q(x-y)=Q(v-w)$
, Witt’s theorem shows there is a isometry of V (consisting of a composition of a translation and matrix multiplication by A, where
![]() $A \in O(n,q)=\{ \mathbb {A} \in Mat_n(\mathbb {F}_q) | A^T A = I \}$
is an “orthogonal” matrix), taking the pair
$A \in O(n,q)=\{ \mathbb {A} \in Mat_n(\mathbb {F}_q) | A^T A = I \}$
is an “orthogonal” matrix), taking the pair
![]() $x,y$
to the pair of
$x,y$
to the pair of
![]() $v,w$
.
$v,w$
.
When
![]() $n \geq 3$
or
$n \geq 3$
or
![]() $n=2$
and
$n=2$
and
![]() $q=1 \text { mod } 4$
, it is possible
$q=1 \text { mod } 4$
, it is possible
![]() $Q(x-y)=0$
but
$Q(x-y)=0$
but
![]() $x \neq y$
and so we distinguish between distance
$x \neq y$
and so we distinguish between distance
![]() $0$
and distance
$0$
and distance
![]() $\bar {0}$
by declaring
$\bar {0}$
by declaring
![]() $d(x,y)=\bar {0}$
if and only if
$d(x,y)=\bar {0}$
if and only if
![]() $x=y$
and
$x=y$
and
![]() $d(x,y)=Q(x-y)$
whenever
$d(x,y)=Q(x-y)$
whenever
![]() $x \neq y$
. Thus in
$x \neq y$
. Thus in
![]() $\mathbb {Z}_5^2$
,
$\mathbb {Z}_5^2$
,
The distance set is
![]() $\Delta =\mathbb {F}_q \cup \{ \bar {0} \}$
when
$\Delta =\mathbb {F}_q \cup \{ \bar {0} \}$
when
![]() $n \geq 3$
or
$n \geq 3$
or
![]() $n=2, q=1 \text { mod } 4$
but when
$n=2, q=1 \text { mod } 4$
but when
![]() $n=2, q=3 \text { mod } 4$
,
$n=2, q=3 \text { mod } 4$
,
![]() $\Delta =(\mathbb {F}_q-\{ 0\})\cup \{ \bar {0} \}$
as
$\Delta =(\mathbb {F}_q-\{ 0\})\cup \{ \bar {0} \}$
as
![]() $Q(x-y) \neq 0$
when
$Q(x-y) \neq 0$
when
![]() $x \neq y$
in that case.
$x \neq y$
in that case.
Witt’s theorem establishes that
![]() $(V,d)$
is an association scheme by establishing property (3).
$(V,d)$
is an association scheme by establishing property (3).
Example 2.5 Let q be an odd prime power,
![]() $q = 3 \text { mod 4}$
, then
$q = 3 \text { mod 4}$
, then
![]() $-1$
is not a square in
$-1$
is not a square in
![]() $\mathbb {F}_q$
and so the Galois extension
$\mathbb {F}_q$
and so the Galois extension
![]() $E=\mathbb {F}_q[i]$
of
$E=\mathbb {F}_q[i]$
of
![]() $\mathbb {F}_q$
is a degree
$\mathbb {F}_q$
is a degree
![]() $2$
extension where i is a root of
$2$
extension where i is a root of
![]() $x^2+1$
. The Galois norm map
$x^2+1$
. The Galois norm map
![]() $N: E^{\times } \to \mathbb {F}_q^{\times }$
has
$N: E^{\times } \to \mathbb {F}_q^{\times }$
has
![]() $N(a+bi)=(a+bi)(a-bi)=a^2+b^2$
and this agrees with the Euclidean quadratic form Q on
$N(a+bi)=(a+bi)(a-bi)=a^2+b^2$
and this agrees with the Euclidean quadratic form Q on
![]() $V=\mathbb {F}_q^2$
and so
$V=\mathbb {F}_q^2$
and so
![]() $Q(x-y)=0 \iff x=y$
in this case. Note as N is a homomorphism,
$Q(x-y)=0 \iff x=y$
in this case. Note as N is a homomorphism,
 $$ \begin{align*}|S_j((0,0))|=|N^{-1}(j)|=\frac{q^2-1}{q-1}=q+1\end{align*} $$
$$ \begin{align*}|S_j((0,0))|=|N^{-1}(j)|=\frac{q^2-1}{q-1}=q+1\end{align*} $$
for all
![]() $j \in \mathbb {F}_q^{\times } = \mathbb {F}_q-\{ 0 \}.$
Thus, in the corresponding association scheme,
$j \in \mathbb {F}_q^{\times } = \mathbb {F}_q-\{ 0 \}.$
Thus, in the corresponding association scheme,
![]() $p_{j,j}^{\bar {0}} = q+1$
whenever
$p_{j,j}^{\bar {0}} = q+1$
whenever
![]() $j \in \mathbb {F}_q^{\times }$
while
$j \in \mathbb {F}_q^{\times }$
while
![]() $p_{\bar {0},\bar {0}}^{\bar {0}}=1$
.
$p_{\bar {0},\bar {0}}^{\bar {0}}=1$
.
Given a finite association scheme
![]() $\mathfrak {A}=(X,d)$
on D classes, the matrices
$\mathfrak {A}=(X,d)$
on D classes, the matrices
![]() $\{ \mathbb {A}_j | j \in \Delta \}$
are a real basis for the corresponding Bose–Messner algebra
$\{ \mathbb {A}_j | j \in \Delta \}$
are a real basis for the corresponding Bose–Messner algebra
![]() $BM(\mathfrak {A})$
. As the matrices are symmetric and as they commute, they can be simultaneously (orthogonally) diagonalized on their action on
$BM(\mathfrak {A})$
. As the matrices are symmetric and as they commute, they can be simultaneously (orthogonally) diagonalized on their action on
![]() $\mathbb {R}^X$
and this vector space splits as an orthogonal direct sum of simultaneous eigenspaces of all the
$\mathbb {R}^X$
and this vector space splits as an orthogonal direct sum of simultaneous eigenspaces of all the
![]() $\mathbb {A}_j$
operators. These simultaneous eigenspaces are called weight spaces. Let
$\mathbb {A}_j$
operators. These simultaneous eigenspaces are called weight spaces. Let
![]() $\{ E_i, i \in \Delta ' \}$
be the collection of orthogonal projection operators to the individual weight spaces. Linear algebra guarantees that each
$\{ E_i, i \in \Delta ' \}$
be the collection of orthogonal projection operators to the individual weight spaces. Linear algebra guarantees that each
![]() $E_i$
is a polynomial expression in the
$E_i$
is a polynomial expression in the
![]() $A_j$
’s and hence lies in the Bose–Messner algebra and thus is a linear combination of the
$A_j$
’s and hence lies in the Bose–Messner algebra and thus is a linear combination of the
![]() $A_j$
. Conversely, as each
$A_j$
. Conversely, as each
![]() $A_j$
is constant on the image of any
$A_j$
is constant on the image of any
![]() $E_i$
, each
$E_i$
, each
![]() $A_j$
can be trivially written as a linear combination of the
$A_j$
can be trivially written as a linear combination of the
![]() $E_i$
. Thus, the
$E_i$
. Thus, the
![]() $\{ E_i | i \in \Delta ' \}$
are a different, “spectral basis” of the Bose–Messner algebra
$\{ E_i | i \in \Delta ' \}$
are a different, “spectral basis” of the Bose–Messner algebra
![]() $BM(\mathfrak {A})$
and hence
$BM(\mathfrak {A})$
and hence
![]() $|\Delta | = |\Delta '|$
. We will refer to the original basis
$|\Delta | = |\Delta '|$
. We will refer to the original basis
![]() $\{ \mathbb {A}_j | j \in \Delta \}$
of
$\{ \mathbb {A}_j | j \in \Delta \}$
of
![]() $BM(\mathfrak {A})$
as the geometric basis of the Bose–Messner algebra as these encode the distances of the scheme.
$BM(\mathfrak {A})$
as the geometric basis of the Bose–Messner algebra as these encode the distances of the scheme.
Many of the main results of association schemes, and distance regular graphs, in particular, arise from the interactions between the geometric and spectral basis of the Bose–Messner algebra of the scheme.
In particular, two fundamental change of basis matrices are defined as follows.
Definition 2.6 Let
![]() $(X,d)$
be a finite association scheme on D (nonzero) classes, and let
$(X,d)$
be a finite association scheme on D (nonzero) classes, and let
![]() $\{ A_j | j \in \Delta \}$
and
$\{ A_j | j \in \Delta \}$
and
![]() $\{ E_i | i \in \Delta '\}$
denote the “geometric” and “spectral” basis of the corresponding Bose–Messner algebra. The
$\{ E_i | i \in \Delta '\}$
denote the “geometric” and “spectral” basis of the corresponding Bose–Messner algebra. The
![]() $(D+1) \times (D+1)$
real matrices P and Q are defined via
$(D+1) \times (D+1)$
real matrices P and Q are defined via
and
 $$ \begin{align*}E_i = \frac{1}{|X|} \sum_{j \in \Delta} Q_{j,i} A_j \text{ for all } i \in \Delta'. \end{align*} $$
$$ \begin{align*}E_i = \frac{1}{|X|} \sum_{j \in \Delta} Q_{j,i} A_j \text{ for all } i \in \Delta'. \end{align*} $$
Thus
![]() $P Q = |X| I = Q P$
.
$P Q = |X| I = Q P$
.
Note that the
![]() $\{ P_{i,j} | i \in \Delta '\}$
are just the eigenvalues of
$\{ P_{i,j} | i \in \Delta '\}$
are just the eigenvalues of
![]() $A_j$
, the adjacency matrix of the distance-j graph of the scheme. Note that
$A_j$
, the adjacency matrix of the distance-j graph of the scheme. Note that
![]() $|\Delta '|=|\Delta |=D+1$
is usually much smaller than
$|\Delta '|=|\Delta |=D+1$
is usually much smaller than
![]() $|X|$
and so the
$|X|$
and so the
![]() $|X| \times |X|$
matrix
$|X| \times |X|$
matrix
![]() $A_j$
has lots of multiplicities in its eigenvalues, encoded by
$A_j$
has lots of multiplicities in its eigenvalues, encoded by
![]() $rank(E_i)$
which is the dimension of the ith weight space.
$rank(E_i)$
which is the dimension of the ith weight space.
Definition 2.7 (Intersection matrices)
Given an association scheme on D (nonzero) classes with intersection numbers
![]() $p_{i,j}^k$
,
$p_{i,j}^k$
,
![]() $i,j,k \in \Delta $
. The
$i,j,k \in \Delta $
. The
![]() $(D+1) \times (D+1)$
intersection matrix
$(D+1) \times (D+1)$
intersection matrix
![]() $L_i$
is defined via
$L_i$
is defined via
![]() $(L_i)_{k,j}=p_{i,j}^k$
for all
$(L_i)_{k,j}=p_{i,j}^k$
for all
![]() $i \in \Delta $
.
$i \in \Delta $
.
It turns out the eigenvalues of
![]() $L_j$
are the same as the eigenvalues of the
$L_j$
are the same as the eigenvalues of the
![]() $|X| \times |X|$
matrix
$|X| \times |X|$
matrix
![]() $A_j$
, i.e., are also
$A_j$
, i.e., are also
![]() $\{ P_{i,j} | i \in \Delta '\}$
.
$\{ P_{i,j} | i \in \Delta '\}$
.
The matrices
![]() $P, Q, L_j, A_i, E_j$
satisfy many interesting identities in an association scheme. For our purpose, we focus on Delsarte’s linear programming bound. Let
$P, Q, L_j, A_i, E_j$
satisfy many interesting identities in an association scheme. For our purpose, we focus on Delsarte’s linear programming bound. Let
![]() $(X,d)$
be a finite association scheme and
$(X,d)$
be a finite association scheme and
![]() $Y \subseteq X$
. For each
$Y \subseteq X$
. For each
![]() $j \in \Delta $
, define
$j \in \Delta $
, define
![]() $a_j=\frac {| \{ (y_1,y_2) \in Y \times Y | d(y_1,y_2)=j \}|}{|Y|} =\frac {\chi _Y^T A_j \chi _Y}{\chi _Y^ T \chi _Y} \in \mathbb {Q}_{\geq 0}$
, where
$a_j=\frac {| \{ (y_1,y_2) \in Y \times Y | d(y_1,y_2)=j \}|}{|Y|} =\frac {\chi _Y^T A_j \chi _Y}{\chi _Y^ T \chi _Y} \in \mathbb {Q}_{\geq 0}$
, where
![]() $\chi _Y$
is the characteristic column vector of Y. Then, the row vector
$\chi _Y$
is the characteristic column vector of Y. Then, the row vector
![]() $a=(a_j)_{j \in \Delta }$
is called the inner distribution of Y as it encodes the frequency of various distances on the pairs in the subset Y. This inner distribution satisfies Delsarte’s linear programming bound condition
$a=(a_j)_{j \in \Delta }$
is called the inner distribution of Y as it encodes the frequency of various distances on the pairs in the subset Y. This inner distribution satisfies Delsarte’s linear programming bound condition
![]() $a Q \geq 0$
as well as
$a Q \geq 0$
as well as
![]() $\sum _{j \in \Delta } a_j = |Y|$
and these conditions give us many constraints on distances induced on subsets Y of the scheme.
$\sum _{j \in \Delta } a_j = |Y|$
and these conditions give us many constraints on distances induced on subsets Y of the scheme.
3 Eigenvalues of the distance-t graphs
For any
![]() $t \in \mathbb {F}_q$
, let
$t \in \mathbb {F}_q$
, let
![]() $X(q,t)$
denote the associated distance-t graph on
$X(q,t)$
denote the associated distance-t graph on
![]() $\mathbb {F}_q^d$
. In this section, we describe the spectrum of the adjacency matrix of this graph,
$\mathbb {F}_q^d$
. In this section, we describe the spectrum of the adjacency matrix of this graph,
![]() $A_t$
, when
$A_t$
, when
![]() $t \neq \bar {0}$
, i.e., for
$t \neq \bar {0}$
, i.e., for
![]() $t \in \mathbb {F}_q$
. This spectrum was previously computed by various authors, for example, in [Reference Iosevich and Rudnev9, Reference Terras17] but we include a brief discussion here to be self-contained.
$t \in \mathbb {F}_q$
. This spectrum was previously computed by various authors, for example, in [Reference Iosevich and Rudnev9, Reference Terras17] but we include a brief discussion here to be self-contained.
Standard spectral theory of finite Cayley graphs over Abelian groups, shows that the complex eigenfunctions of this graph’s adjacency operator
![]() $A_t$
are the characters
$A_t$
are the characters
![]() $\chi _m(x)=\chi (m \cdot x)$
as m ranges over
$\chi _m(x)=\chi (m \cdot x)$
as m ranges over
![]() $\mathbb {F}_q^d$
. Here,
$\mathbb {F}_q^d$
. Here,
![]() $\cdot $
stands for dot product. The corresponding eigenvalue of
$\cdot $
stands for dot product. The corresponding eigenvalue of
![]() $A_t$
on
$A_t$
on
![]() $\chi _m$
which we will denote
$\chi _m$
which we will denote
![]() $\lambda _{m,t,d}$
(recall d is the dimension of V) is given by
$\lambda _{m,t,d}$
(recall d is the dimension of V) is given by
Clearly,
![]() $\lambda _{0,t,d} = |S_{t,d}|$
. The size of these spheres were originally calculated by Minkowski, and there are at most three distinct sphere sizes corresponding to
$\lambda _{0,t,d} = |S_{t,d}|$
. The size of these spheres were originally calculated by Minkowski, and there are at most three distinct sphere sizes corresponding to
![]() $t=0$
, t a nonsquare in
$t=0$
, t a nonsquare in
![]() $\mathbb {F}_q$
, and t a nonzero square in
$\mathbb {F}_q$
, and t a nonzero square in
![]() $\mathbb {F}_q$
. This is because scaling by
$\mathbb {F}_q$
. This is because scaling by
![]() $\lambda \in \mathbb {F}_q^{\times }$
gives a bijection between
$\lambda \in \mathbb {F}_q^{\times }$
gives a bijection between
![]() $S_{t,d}$
and
$S_{t,d}$
and
![]() $S_{\lambda ^2 t, d}$
.
$S_{\lambda ^2 t, d}$
.
When
![]() $m,t$
are both nonzero, these eigenvalues are given by twisted Kloosterman sums. We provide the calculation for the convenience of the reader. First, note that by character orthogonality, we have
$m,t$
are both nonzero, these eigenvalues are given by twisted Kloosterman sums. We provide the calculation for the convenience of the reader. First, note that by character orthogonality, we have
![]() $\frac {1}{q}\sum _{s \in \mathbb {F}_q} \chi (sL)=\delta _{L,0}$
, where
$\frac {1}{q}\sum _{s \in \mathbb {F}_q} \chi (sL)=\delta _{L,0}$
, where
![]() $\delta _{L,0}=1$
if
$\delta _{L,0}=1$
if
![]() $L=0$
and
$L=0$
and
![]() $0$
otherwise. Then we compute, when
$0$
otherwise. Then we compute, when
![]() $t \neq 0$
,
$t \neq 0$
,
 $$ \begin{align*} \lambda_{m,t,d} &= \sum_{\{x | Q(x)=t\}} \chi(m \cdot x) =\frac{1}{q} \sum_{s \in \mathbb{F}_q} \sum_{x \in V} \chi(m \cdot x) \chi(s(Q(x)-t)) \\ &= \frac{1}{q}\sum_{s \in \mathbb{F}_q} \chi(-st) \sum_{x_1,\dots, x_d \in \mathbb{F}_q} \chi(m_1x_1 + \dots + m_dx_d + s(x_1^2 + \dots + x_d^2)) \\ &=\frac{1}{q}\sum_{s \in \mathbb{F}_q} \chi(-st) \prod_{i=1}^d \sum_{x_i \in \mathbb{F}_q} \chi(m_i x_i + sx_i^2) \\ &=q^{d-1} \delta_{m,0} + \frac{1}{q}\sum_{s \neq 0} \chi(-st) \prod_{i=1}^d \sum_{x_i \in \mathbb{F}_q} \chi(m_i x_i + sx_i^2) \\ &=q^{d-1} \delta_{m,0} + \frac{1}{q}\sum_{s \neq 0} \chi(-st) \prod_{i=1}^d \sum_{y_i \in \mathbb{F}_q} \chi(sy_i^2-\frac{m_i^2}{4s}), \end{align*} $$
$$ \begin{align*} \lambda_{m,t,d} &= \sum_{\{x | Q(x)=t\}} \chi(m \cdot x) =\frac{1}{q} \sum_{s \in \mathbb{F}_q} \sum_{x \in V} \chi(m \cdot x) \chi(s(Q(x)-t)) \\ &= \frac{1}{q}\sum_{s \in \mathbb{F}_q} \chi(-st) \sum_{x_1,\dots, x_d \in \mathbb{F}_q} \chi(m_1x_1 + \dots + m_dx_d + s(x_1^2 + \dots + x_d^2)) \\ &=\frac{1}{q}\sum_{s \in \mathbb{F}_q} \chi(-st) \prod_{i=1}^d \sum_{x_i \in \mathbb{F}_q} \chi(m_i x_i + sx_i^2) \\ &=q^{d-1} \delta_{m,0} + \frac{1}{q}\sum_{s \neq 0} \chi(-st) \prod_{i=1}^d \sum_{x_i \in \mathbb{F}_q} \chi(m_i x_i + sx_i^2) \\ &=q^{d-1} \delta_{m,0} + \frac{1}{q}\sum_{s \neq 0} \chi(-st) \prod_{i=1}^d \sum_{y_i \in \mathbb{F}_q} \chi(sy_i^2-\frac{m_i^2}{4s}), \end{align*} $$
where in the last step, we completed the square and substituted
![]() $y_i=x_i+\frac {m_i}{2s}$
. Letting
$y_i=x_i+\frac {m_i}{2s}$
. Letting
![]() $G(s)=\sum _{y \in \mathbb {F}_q} \chi (sy^2)$
denote the corresponding Gauss sum, we conclude that
$G(s)=\sum _{y \in \mathbb {F}_q} \chi (sy^2)$
denote the corresponding Gauss sum, we conclude that
 $$ \begin{align*}\lambda_{m,t,d}=q^{d-1} \delta_{m,0} + \frac{1}{q}\sum_{s \neq 0} \chi\left(-st-\frac{Q(m)}{4s}\right) G(s)^d. \end{align*} $$
$$ \begin{align*}\lambda_{m,t,d}=q^{d-1} \delta_{m,0} + \frac{1}{q}\sum_{s \neq 0} \chi\left(-st-\frac{Q(m)}{4s}\right) G(s)^d. \end{align*} $$
When
![]() $t=0,$
the only correction needed is to exclude
$t=0,$
the only correction needed is to exclude
![]() $x=0$
from the set
$x=0$
from the set
![]() $Q(x)=0$
which results in reducing this quantity by
$Q(x)=0$
which results in reducing this quantity by
![]() $1$
. Thus, we have generally that
$1$
. Thus, we have generally that
 $$ \begin{align*}\lambda_{m,t,d}=q^{d-1} \delta_{m,0} -\delta_{t,0} + \frac{1}{q}\sum_{s \neq 0} \chi\left(-st-\frac{Q(m)}{4s}\right) G(s)^d. \end{align*} $$
$$ \begin{align*}\lambda_{m,t,d}=q^{d-1} \delta_{m,0} -\delta_{t,0} + \frac{1}{q}\sum_{s \neq 0} \chi\left(-st-\frac{Q(m)}{4s}\right) G(s)^d. \end{align*} $$
It is a well-known result of Gauss that
![]() $G(s)=\binom {s}{q} \epsilon (q) \sqrt {q}$
, where
$G(s)=\binom {s}{q} \epsilon (q) \sqrt {q}$
, where
![]() $\binom {s}{q}$
is the Legendre symbol which is
$\binom {s}{q}$
is the Legendre symbol which is
![]() $+1$
when s is a nonzero square modulo q, and
$+1$
when s is a nonzero square modulo q, and
![]() $-1$
when s is a nonsquare modulo q. The quantity
$-1$
when s is a nonsquare modulo q. The quantity
![]() $\epsilon (q)=1$
when
$\epsilon (q)=1$
when
![]() $q \equiv 1 \text { mod } 4$
and
$q \equiv 1 \text { mod } 4$
and
![]() $\epsilon (q)=i$
when
$\epsilon (q)=i$
when
![]() $q \equiv 3 \text { mod } 4$
. Thus, we conclude
$q \equiv 3 \text { mod } 4$
. Thus, we conclude
 $$ \begin{align*}\lambda_{m,t,d}=q^{d-1} \delta_{m,0} -\delta_{t,0} + q^{\frac{d}{2}-1} \epsilon(q)^d \tilde{K}_d\left(-t,-\frac{Q(m)}{4}\right), \end{align*} $$
$$ \begin{align*}\lambda_{m,t,d}=q^{d-1} \delta_{m,0} -\delta_{t,0} + q^{\frac{d}{2}-1} \epsilon(q)^d \tilde{K}_d\left(-t,-\frac{Q(m)}{4}\right), \end{align*} $$
where
![]() $\tilde {K}_d(a,b)=\sum _{s \neq 0} \binom {s}{q}^d \chi (as+\frac {b}{s})$
is a twisted Kloosterman sum. Note that the dependence of
$\tilde {K}_d(a,b)=\sum _{s \neq 0} \binom {s}{q}^d \chi (as+\frac {b}{s})$
is a twisted Kloosterman sum. Note that the dependence of
![]() $\tilde {K}_d(a,b)$
on d is weak and only depends on the parity of d. When d is even,
$\tilde {K}_d(a,b)$
on d is weak and only depends on the parity of d. When d is even,
![]() $\tilde {K}_d(a,b)=K(a,b)=\sum _{s \neq 0} \chi (as+\frac {b}{s})$
is the regular Kloosterman sum. Note that the m-dependence of the eigenvalue
$\tilde {K}_d(a,b)=K(a,b)=\sum _{s \neq 0} \chi (as+\frac {b}{s})$
is the regular Kloosterman sum. Note that the m-dependence of the eigenvalue
![]() $\lambda _{m,t,d}$
is only through
$\lambda _{m,t,d}$
is only through
![]() $Q(m)=||m||=m_1^2+\dots +m_d^2$
and whether m is the origin or not. Following the convention adopted in association schemes, we will write
$Q(m)=||m||=m_1^2+\dots +m_d^2$
and whether m is the origin or not. Following the convention adopted in association schemes, we will write
![]() $Q(m)=\bar {0}$
if
$Q(m)=\bar {0}$
if
![]() $m=0$
and
$m=0$
and
![]() $Q(m)=0$
if
$Q(m)=0$
if
![]() $m \neq 0$
but
$m \neq 0$
but
![]() $m_1^2+\dots +m_d^2=0$
.
$m_1^2+\dots +m_d^2=0$
.
Thus
![]() $Span\{\chi _m | Q(m)=k\}=L_k$
is contained in an eigenspace of
$Span\{\chi _m | Q(m)=k\}=L_k$
is contained in an eigenspace of
![]() $A_t$
for each
$A_t$
for each
![]() $t,k \in \mathbb {F}_q \cup \{ \bar {0} \}$
. The complex vector space
$t,k \in \mathbb {F}_q \cup \{ \bar {0} \}$
. The complex vector space
![]() $\mathbb {C}[V]$
, of all complex functions on V, decomposes as a orthogonal direct sum of the
$\mathbb {C}[V]$
, of all complex functions on V, decomposes as a orthogonal direct sum of the
![]() $L_k$
with respect to the standard Hermitian inner product. The
$L_k$
with respect to the standard Hermitian inner product. The
![]() $L_k$
are simultaneous eigenspaces of all the
$L_k$
are simultaneous eigenspaces of all the
![]() $A_t$
operators and
$A_t$
operators and
![]() $L_0$
is
$L_0$
is
![]() $0$
if and only if
$0$
if and only if
![]() $S_0 = \emptyset $
. Thus, the number of nonzero
$S_0 = \emptyset $
. Thus, the number of nonzero
![]() $L_k$
is the same as the dimension of the corresponding Euclidean association scheme and so the nonzero
$L_k$
is the same as the dimension of the corresponding Euclidean association scheme and so the nonzero
![]() $L_k$
are exactly the weight spaces in the decomposition of the complex Bose–Messner algebra of the scheme. Note that
$L_k$
are exactly the weight spaces in the decomposition of the complex Bose–Messner algebra of the scheme. Note that
![]() $L_{\bar {0}}=Span\{\chi _0\} =Span\{ \mathfrak {1} \}$
consists of the constant functions.
$L_{\bar {0}}=Span\{\chi _0\} =Span\{ \mathfrak {1} \}$
consists of the constant functions.
We record these results in the following theorem.
Theorem 3.1 Let q be an odd prime power and
![]() $\mathbb {F}_q$
the finite field of order q. For d an integer
$\mathbb {F}_q$
the finite field of order q. For d an integer
![]() $\geq 2$
,
$\geq 2$
,
![]() $m \in \mathbb {F}_q^d, t \in \mathbb {F}_q$
we have that the eigenvalue
$m \in \mathbb {F}_q^d, t \in \mathbb {F}_q$
we have that the eigenvalue
![]() $\lambda _{m,t,d}$
of the adjacency matrix
$\lambda _{m,t,d}$
of the adjacency matrix
![]() $A_t$
of the distance-t graph of
$A_t$
of the distance-t graph of
![]() $V=\mathbb {F}_q^d$
on the character
$V=\mathbb {F}_q^d$
on the character
![]() $\chi _m(x)=\chi (m \cdot x)$
is given by
$\chi _m(x)=\chi (m \cdot x)$
is given by
 $$ \begin{align*} \lambda_{m,t,d}=q^{d-1} \delta_{m,0} -\delta_{t,0} + q^{\frac{d}{2}-1} \epsilon(q)^d \tilde{K}_d\left(-t,-\frac{Q(m)}{4}\right), \end{align*} $$
$$ \begin{align*} \lambda_{m,t,d}=q^{d-1} \delta_{m,0} -\delta_{t,0} + q^{\frac{d}{2}-1} \epsilon(q)^d \tilde{K}_d\left(-t,-\frac{Q(m)}{4}\right), \end{align*} $$
where
![]() $\tilde {K}_d(a,b)=\sum _{s \neq 0} \binom {s}{q}^d \chi (as+\frac {b}{s})$
is a twisted Kloosterman sum.
$\tilde {K}_d(a,b)=\sum _{s \neq 0} \binom {s}{q}^d \chi (as+\frac {b}{s})$
is a twisted Kloosterman sum.
If
![]() $W_k=Span\{\chi _m | Q(m)=k\}$
in
$W_k=Span\{\chi _m | Q(m)=k\}$
in
![]() $\mathbb {C}[V]$
, then
$\mathbb {C}[V]$
, then
![]() $\mathbb {C}[V]=\oplus _{k \in \mathbb {F}_q \cup \{ \bar {0} \}} W_k$
is an orthogonal direct sum decomposition of the vector space of complex-valued functions on V into simultaneous eigenspaces of all the
$\mathbb {C}[V]=\oplus _{k \in \mathbb {F}_q \cup \{ \bar {0} \}} W_k$
is an orthogonal direct sum decomposition of the vector space of complex-valued functions on V into simultaneous eigenspaces of all the
![]() $A_t$
operators,
$A_t$
operators,
![]() $t \in \mathbb {F}_q \cup \{ \bar {0}\}$
. The orthogonal projection
$t \in \mathbb {F}_q \cup \{ \bar {0}\}$
. The orthogonal projection
![]() $E_k$
onto the (nonzero)
$E_k$
onto the (nonzero)
![]() $W_k$
give the spectral basis of the complex Bose–Messner algebra of the corresponding Euclidean association scheme.
$W_k$
give the spectral basis of the complex Bose–Messner algebra of the corresponding Euclidean association scheme.
Note it is not hard to see that the complex conjugate of
![]() $\tilde {K}_d(a,b)$
is
$\tilde {K}_d(a,b)$
is
 $$ \begin{align*} \sum_{s \neq 0} \binom{s}{q}^d \chi\left(-as - \frac{b}{s}\right)=\sum_{s \neq 0} \binom{-s}{q}^d \chi\left(as + \frac{b}{s}\right)\end{align*} $$
$$ \begin{align*} \sum_{s \neq 0} \binom{s}{q}^d \chi\left(-as - \frac{b}{s}\right)=\sum_{s \neq 0} \binom{-s}{q}^d \chi\left(as + \frac{b}{s}\right)\end{align*} $$
and so
![]() $\tilde {K}_d(a,b)$
is real if either d is even or
$\tilde {K}_d(a,b)$
is real if either d is even or
![]() $q\equiv 1 \text { mod } 4$
(i.e., when
$q\equiv 1 \text { mod } 4$
(i.e., when
![]() $-1$
is a square modulo q) but is purely imaginary when d is odd and
$-1$
is a square modulo q) but is purely imaginary when d is odd and
![]() $q \equiv 3 \text { mod 4}$
. However, the quantity
$q \equiv 3 \text { mod 4}$
. However, the quantity
![]() $\epsilon (q)^d \tilde {K}_d(a,b)$
and hence
$\epsilon (q)^d \tilde {K}_d(a,b)$
and hence
![]() $\lambda _{m,t,d}$
are real numbers of course as they are eigenvalues of symmetric matrices.
$\lambda _{m,t,d}$
are real numbers of course as they are eigenvalues of symmetric matrices.
4 Some properties of (twisted) Kloosterman sums
Let
![]() $q=p^{\ell }$
be an odd prime power and define
$q=p^{\ell }$
be an odd prime power and define
![]() $\tilde {K}_d(a,b)=\sum _{s \neq 0} \binom {s}{q}^d \chi (as+\frac {b}{s})$
for
$\tilde {K}_d(a,b)=\sum _{s \neq 0} \binom {s}{q}^d \chi (as+\frac {b}{s})$
for
![]() $a,b \in \mathbb {F}_q$
.
$a,b \in \mathbb {F}_q$
.
Let
![]() $\xi _p=e^{\frac {2 \pi i}{p}}$
be a primitive pth root of unity and
$\xi _p=e^{\frac {2 \pi i}{p}}$
be a primitive pth root of unity and
![]() $\mathbb {Q}[\xi _p]$
be the corresponding cyclotomic field. Note as
$\mathbb {Q}[\xi _p]$
be the corresponding cyclotomic field. Note as
![]() $\chi (x)=\xi ^{\mathrm{Tr}(x)}$
, where
$\chi (x)=\xi ^{\mathrm{Tr}(x)}$
, where
![]() $\mathrm{Tr}: \mathbb {F}_q \to \mathbb {F}_p$
is the Galois trace, we have that
$\mathrm{Tr}: \mathbb {F}_q \to \mathbb {F}_p$
is the Galois trace, we have that
![]() $\tilde {K}_d(a,b)$
are elements in the ring of integers of
$\tilde {K}_d(a,b)$
are elements in the ring of integers of
![]() $\mathbb {Q}[\xi _p]$
. Recall that the Galois group
$\mathbb {Q}[\xi _p]$
. Recall that the Galois group
![]() $Gal(\mathbb {Q}[\xi _p]/\mathbb {Q})$
is Abelian of order
$Gal(\mathbb {Q}[\xi _p]/\mathbb {Q})$
is Abelian of order
![]() $p-1$
and contains automorphisms of the form
$p-1$
and contains automorphisms of the form
![]() $\psi _a$
determined by the property that they take
$\psi _a$
determined by the property that they take
![]() $\xi $
to
$\xi $
to
![]() $\xi ^a$
for all
$\xi ^a$
for all
![]() $a \in \mathbb {F}_p^*$
and fix the rational subfield.
$a \in \mathbb {F}_p^*$
and fix the rational subfield.
Proposition 4.1 Let p be an odd prime and
![]() $q=p^{\ell }$
and define
$q=p^{\ell }$
and define
 $$ \begin{align*}\tilde{K}_d(a,b)=\sum_{s \neq 0} \binom{s}{q}^d \chi\left(as+\frac{b}{s}\right)\end{align*} $$
$$ \begin{align*}\tilde{K}_d(a,b)=\sum_{s \neq 0} \binom{s}{q}^d \chi\left(as+\frac{b}{s}\right)\end{align*} $$
for
![]() $a,b \in \mathbb {F}_q$
. These are algebraic integers in the cyclotomic field
$a,b \in \mathbb {F}_q$
. These are algebraic integers in the cyclotomic field
![]() $\mathbb {Q}[\xi _p]$
which satisfy:
$\mathbb {Q}[\xi _p]$
which satisfy:
(1)
![]() $\tilde {K}_d(a,b)=\tilde {K}_d(b,a).$
$\tilde {K}_d(a,b)=\tilde {K}_d(b,a).$
(2)
![]() $\tilde {K}_d(a,b)=\binom {a}{q}^d\tilde {K}_d(1,ab)$
when
$\tilde {K}_d(a,b)=\binom {a}{q}^d\tilde {K}_d(1,ab)$
when
![]() $a \neq 0.$
$a \neq 0.$
(3) The quantity
![]() $\tilde {K}_d(0,0)$
is equal to
$\tilde {K}_d(0,0)$
is equal to
![]() $q-1$
when d is even and equal to
$q-1$
when d is even and equal to
![]() $0$
when d is odd. Thus
$0$
when d is odd. Thus
![]() $\tilde {K}_d(0,0)=(q-1)\frac {(-1)^d+1}{2}$
.
$\tilde {K}_d(0,0)=(q-1)\frac {(-1)^d+1}{2}$
.
(4) The quantity
![]() $\tilde {K}_d(1,0)=\tilde {K}_d(0,1)$
equals
$\tilde {K}_d(1,0)=\tilde {K}_d(0,1)$
equals
![]() $-1$
when d is even and
$-1$
when d is even and
![]() $G(1)$
when d is odd where
$G(1)$
when d is odd where
![]() $G(1)=\sum _{s \in \mathbb {F}_q} \chi (s^2)=\epsilon (q)\sqrt {q}$
is a quadratic Gauss sum.
$G(1)=\sum _{s \in \mathbb {F}_q} \chi (s^2)=\epsilon (q)\sqrt {q}$
is a quadratic Gauss sum.
(5) For
![]() $c \in \mathbb {F}_p^*$
, we have that
$c \in \mathbb {F}_p^*$
, we have that
![]() $\psi _c(\tilde {K}_d(a,b))=\tilde {K}_d(ca,cb),$
where
$\psi _c(\tilde {K}_d(a,b))=\tilde {K}_d(ca,cb),$
where
![]() $\psi _c$
is the Galois automorphism of
$\psi _c$
is the Galois automorphism of
![]() $\mathbb {Q}[\xi _p]$
over
$\mathbb {Q}[\xi _p]$
over
![]() $\mathbb {Q}$
which takes
$\mathbb {Q}$
which takes
![]() $\xi _p$
to
$\xi _p$
to
![]() $\xi _p^c$
.
$\xi _p^c$
.
Proof To prove (1), use the change of variable
![]() $s \to \frac {1}{s}$
. To prove (2), use the change of variable
$s \to \frac {1}{s}$
. To prove (2), use the change of variable
![]() $s'=as$
for nonzero a. (3) follows trivially once one notes that in any finite field, an equal number of elements are nonzero squares as are nonsquares.
$s'=as$
for nonzero a. (3) follows trivially once one notes that in any finite field, an equal number of elements are nonzero squares as are nonsquares.
For (4), first note that when d is even we have
![]() $\tilde {K}_d(1,0)=\sum _{s \neq 0} \chi (s)$
which by character orthogonality is equal to
$\tilde {K}_d(1,0)=\sum _{s \neq 0} \chi (s)$
which by character orthogonality is equal to
![]() $-\chi (0)=-1$
. When d is odd, we have
$-\chi (0)=-1$
. When d is odd, we have
 $\tilde {K}_d(1,0)=\sum _{s \neq 0} \binom {s}{q}\chi (s)=\sum _{s \in \mathbb {F}_q} \binom {s}{q}\chi (s)=\sum _{s \in \mathbb {F}_q} (\binom {s}{q}+1)\chi (s)=\sum _{u \in \mathbb {F}_q} \chi (u^2)=G(1).$
$\tilde {K}_d(1,0)=\sum _{s \neq 0} \binom {s}{q}\chi (s)=\sum _{s \in \mathbb {F}_q} \binom {s}{q}\chi (s)=\sum _{s \in \mathbb {F}_q} (\binom {s}{q}+1)\chi (s)=\sum _{u \in \mathbb {F}_q} \chi (u^2)=G(1).$
Finally, for (5), we note that
![]() $\tilde {K}_d(a,b)=\sum _{s \neq 0} \binom {s}{q}^d \xi _p^{\mathrm{Tr}(as+\frac {b}{s})}$
and apply the Galois automorphism
$\tilde {K}_d(a,b)=\sum _{s \neq 0} \binom {s}{q}^d \xi _p^{\mathrm{Tr}(as+\frac {b}{s})}$
and apply the Galois automorphism
![]() $\psi _c$
to get
$\psi _c$
to get
 $$ \begin{align*}\psi_c(\tilde{K}_d(a,b)) = \sum_{s \neq 0} \binom{s}{q}^d \xi_p^{c\mathrm{Tr}(as+\frac{b}{s})}=\sum_{s \neq 0} \binom{s}{q}^d \xi_p^{\mathrm{Tr}(cas+\frac{cb}{s})}=\tilde{K}_d(ca,cb)\end{align*} $$
$$ \begin{align*}\psi_c(\tilde{K}_d(a,b)) = \sum_{s \neq 0} \binom{s}{q}^d \xi_p^{c\mathrm{Tr}(as+\frac{b}{s})}=\sum_{s \neq 0} \binom{s}{q}^d \xi_p^{\mathrm{Tr}(cas+\frac{cb}{s})}=\tilde{K}_d(ca,cb)\end{align*} $$
as the Galois trace
![]() $\mathrm{Tr}: \mathbb {F}_q \to \mathbb {F}_p$
is
$\mathrm{Tr}: \mathbb {F}_q \to \mathbb {F}_p$
is
![]() $\mathbb {F}_p$
-linear.
$\mathbb {F}_p$
-linear.
Note that when d is even, the
![]() $\tilde {K}_d(a,b)$
coincide with (untwisted) Kloosterman sums
$\tilde {K}_d(a,b)$
coincide with (untwisted) Kloosterman sums
![]() $K(a,b)=\sum _{s \neq 0} \chi (as+\frac {b}{s})$
and the properties above apply to those also. In particular, when
$K(a,b)=\sum _{s \neq 0} \chi (as+\frac {b}{s})$
and the properties above apply to those also. In particular, when
![]() $q=p$
, this implies that the
$q=p$
, this implies that the
![]() $\{ K(1,u) | u \text { a nonzero square} \}$
are all Galois conjugates in
$\{ K(1,u) | u \text { a nonzero square} \}$
are all Galois conjugates in
![]() $\mathbb {Q}[\xi _p]$
. This is because for
$\mathbb {Q}[\xi _p]$
. This is because for
![]() $c \neq 0$
,
$c \neq 0$
,
![]() $\psi _c(K(1,1))=K(c,c)=K(1,c^2)$
.
$\psi _c(K(1,1))=K(c,c)=K(1,c^2)$
.
We will need one more property of these Kloosterman numbers that requires some Fourier analysis. Recall if
![]() $f: V \to \mathbb {C}$
, then we define the Fourier transform
$f: V \to \mathbb {C}$
, then we define the Fourier transform
It is easy to show via character orthogonality that we can recover f via
Note if we let
![]() $S_t$
denote the indicator function of the corresponding t-sphere,
$S_t$
denote the indicator function of the corresponding t-sphere,
![]() $t \in \Delta $
, then
$t \in \Delta $
, then
![]() $q^d \hat {S}_t(m)=\sum _{x \in \mathbb {F}_q^d} S_t(x)\chi (-m \cdot x) = \sum _{x \in S_t} \chi (m \cdot x) = \lambda _{m,t,d}$
from the previous section. (We define
$q^d \hat {S}_t(m)=\sum _{x \in \mathbb {F}_q^d} S_t(x)\chi (-m \cdot x) = \sum _{x \in S_t} \chi (m \cdot x) = \lambda _{m,t,d}$
from the previous section. (We define
![]() $\lambda _{m,\bar {0},d}=1$
to also make it work in that case.) By disjointness of spheres of different radii, it follows that for any
$\lambda _{m,\bar {0},d}=1$
to also make it work in that case.) By disjointness of spheres of different radii, it follows that for any
![]() $i \neq j \in \Delta $
,
$i \neq j \in \Delta $
,
 $$ \begin{align*} 0 = S_i(x)S_j(x) &=\left(\sum_{m \in V} \hat{S}_i(m)\chi(m \cdot x) \right)\left(\sum_{n \in V} \hat{S}_j(n) \chi(n \cdot x)\right) \\ 0 &=\sum_{t \in V} \left(\sum_{m \in V} \hat{S}_i(m)\hat{S}_j(t-m)\right) \chi(t \cdot x). \end{align*} $$
$$ \begin{align*} 0 = S_i(x)S_j(x) &=\left(\sum_{m \in V} \hat{S}_i(m)\chi(m \cdot x) \right)\left(\sum_{n \in V} \hat{S}_j(n) \chi(n \cdot x)\right) \\ 0 &=\sum_{t \in V} \left(\sum_{m \in V} \hat{S}_i(m)\hat{S}_j(t-m)\right) \chi(t \cdot x). \end{align*} $$
By character independence, we conclude that
![]() $\sum _{m \in V} \hat {S}_i(m) \hat {S}_j(t-m) = 0$
for all
$\sum _{m \in V} \hat {S}_i(m) \hat {S}_j(t-m) = 0$
for all
![]() $t \in \mathbb {F}_q^d$
when
$t \in \mathbb {F}_q^d$
when
![]() $i \neq j \in \Delta $
. When
$i \neq j \in \Delta $
. When
![]() $i=j$
, as
$i=j$
, as
![]() $S_i(x)S_i(x)=S_i(x)$
, we instead conclude
$S_i(x)S_i(x)=S_i(x)$
, we instead conclude
![]() $\hat {S}_i(t) = \sum _{m \in V} \hat {S}_i(m) \hat {S}_i(t-m)$
.
$\hat {S}_i(t) = \sum _{m \in V} \hat {S}_i(m) \hat {S}_i(t-m)$
.
Using that
![]() $q^d \hat {S}_t(m)=\lambda _{m,t,d}$
and that
$q^d \hat {S}_t(m)=\lambda _{m,t,d}$
and that
![]() $\hat {S}_t(m)=\hat {S}_t(-m)$
, this becomes the next proposition.
$\hat {S}_t(m)=\hat {S}_t(-m)$
, this becomes the next proposition.
Proposition 4.2 Consider the Euclidean association scheme on
![]() $V=\mathbb {F}_q^d$
with distance set
$V=\mathbb {F}_q^d$
with distance set
![]() $\Delta $
. Let
$\Delta $
. Let
![]() $\lambda _{m,t,d}$
be as in Theorem 3.1 with
$\lambda _{m,t,d}$
be as in Theorem 3.1 with
![]() $\lambda _{m,\bar {0},d}=1$
. Then for any
$\lambda _{m,\bar {0},d}=1$
. Then for any
![]() $i \neq j \in \Delta $
and
$i \neq j \in \Delta $
and
![]() $t \in V$
, we have
$t \in V$
, we have
and, in particular, when
![]() $t=0$
,
$t=0$
,
When
![]() $i=j$
, we instead have
$i=j$
, we instead have
and
5 The P and Q matrices of the Euclidean association scheme
The calculation of the P-matrix of the Euclidean scheme in this section was first done in [Reference Kwok12] with corrections in [Reference Bannai, Shimabukuro and Tanaka2] but we provide the details independently here in language more connected to our applications.
Let
![]() $\Delta $
be the “distance” set of the Euclidean association scheme on
$\Delta $
be the “distance” set of the Euclidean association scheme on
![]() $V=\mathbb {F}_q^d$
. Thus, if
$V=\mathbb {F}_q^d$
. Thus, if
![]() $d \geq 3$
or
$d \geq 3$
or
![]() $(d=2, q=1 \text { mod } 4)$
, we have
$(d=2, q=1 \text { mod } 4)$
, we have
![]() $\Delta =\{ \bar {0} \} \cup \mathbb {F}_q$
whereas when
$\Delta =\{ \bar {0} \} \cup \mathbb {F}_q$
whereas when
![]() $(d=2, q=3 \text {mod } 4)$
, we have
$(d=2, q=3 \text {mod } 4)$
, we have
![]() $\Delta =\{ \bar {0} \} \cup \mathbb {F}_q^{\times }$
.
$\Delta =\{ \bar {0} \} \cup \mathbb {F}_q^{\times }$
.
By Theorem 3.1, it follows that both the spectral and geometric basis of the complex Bose–Messner algebra can be indexed by the distance set
![]() $\Delta $
. Fix a linear ordering of
$\Delta $
. Fix a linear ordering of
![]() $\Delta $
where
$\Delta $
where
![]() $\bar {0}$
comes first and if
$\bar {0}$
comes first and if
![]() $0 \in \Delta $
, it comes second. For example, the ordering
$0 \in \Delta $
, it comes second. For example, the ordering
![]() $\bar {0} < 0 < 1 < \dots < q-1$
works when
$\bar {0} < 0 < 1 < \dots < q-1$
works when
![]() $(d=2, q=1 \text { mod } 4)$
or
$(d=2, q=1 \text { mod } 4)$
or
![]() $d \geq 3$
and when otherwise, i.e., when
$d \geq 3$
and when otherwise, i.e., when
![]() $(d=2, q=3 \text { mod } 4)$
we drop
$(d=2, q=3 \text { mod } 4)$
we drop
![]() $0$
from the list.
$0$
from the list.
Then when
![]() $i, j \in \Delta $
, we have
$i, j \in \Delta $
, we have
![]() $\mathbb {P}_{i,j}$
is by definition the eigenvalue of
$\mathbb {P}_{i,j}$
is by definition the eigenvalue of
![]() $A_j$
on the ith weight space
$A_j$
on the ith weight space
![]() $W_i$
which was denoted
$W_i$
which was denoted
![]() $\lambda _{m,j,d}$
in previous sections where
$\lambda _{m,j,d}$
in previous sections where
![]() $m \in V$
is any vector with
$m \in V$
is any vector with
![]() $Q(m)=i$
. In other words, by definitions, it follows that
$Q(m)=i$
. In other words, by definitions, it follows that
![]() $\lambda _{m,j,d}=\mathbb {P}_{Q(m),j}$
for all
$\lambda _{m,j,d}=\mathbb {P}_{Q(m),j}$
for all
![]() $m \in V, j \in \Delta $
.
$m \in V, j \in \Delta $
.
In particular,
![]() $\mathbb {P}_{\bar {0},t} = \lambda _{0,t,d}=q^d \hat {S}_t(0)=|S_t|$
for all
$\mathbb {P}_{\bar {0},t} = \lambda _{0,t,d}=q^d \hat {S}_t(0)=|S_t|$
for all
![]() $t \in \Delta $
and thus the top row of
$t \in \Delta $
and thus the top row of
![]() $\mathbb {P}$
lists the sphere sizes. Also
$\mathbb {P}$
lists the sphere sizes. Also
![]() $\mathbb {P}_{i,\bar {0}} = \lambda _{m,\bar {0},d}=1$
(here, m is any vector with
$\mathbb {P}_{i,\bar {0}} = \lambda _{m,\bar {0},d}=1$
(here, m is any vector with
![]() $Q(m)=i$
). Thus, the leftmost column of
$Q(m)=i$
). Thus, the leftmost column of
![]() $\mathbb {P}$
is all 1’s (eigenvalues of
$\mathbb {P}$
is all 1’s (eigenvalues of
![]() $\mathbb {A}_{\bar {0}}$
which is the identity operator).
$\mathbb {A}_{\bar {0}}$
which is the identity operator).
On the other hand, if
![]() $0 \in \Delta $
,
$0 \in \Delta $
,
![]() $\mathbb {P}_{0,t} = \lambda _{m,t,d}$
for some nonzero vector m of length
$\mathbb {P}_{0,t} = \lambda _{m,t,d}$
for some nonzero vector m of length
![]() $Q(m)=0$
. By Theorem 3.1,
$Q(m)=0$
. By Theorem 3.1,
![]() $\mathbb {P}_{0,t}=-\delta _{t,0} + q^{\frac {d}{2}-1}\epsilon (q)^d \tilde {K}_d(-t,0)=\mathbb {P}_{\bar {0},t}-q^{d-1}=|S_t|-q^{d-1}$
. Thus, the
$\mathbb {P}_{0,t}=-\delta _{t,0} + q^{\frac {d}{2}-1}\epsilon (q)^d \tilde {K}_d(-t,0)=\mathbb {P}_{\bar {0},t}-q^{d-1}=|S_t|-q^{d-1}$
. Thus, the
![]() $0$
-row (which would be listed second if it occurs) consists of the deviations of sphere sizes from the expected size
$0$
-row (which would be listed second if it occurs) consists of the deviations of sphere sizes from the expected size
![]() $q^{d-1}$
.
$q^{d-1}$
.
Proposition 4.2 can be recast in terms of the entries of
![]() $\mathbb {P}$
as follows: When
$\mathbb {P}$
as follows: When
![]() $i \neq j \in \Delta $
, we have
$i \neq j \in \Delta $
, we have
![]() $\sum _{m \in V} \lambda _{m,i,d} \lambda _{m,j,d} = 0$
. Lumping terms in this sum by the length t of the vector m yields
$\sum _{m \in V} \lambda _{m,i,d} \lambda _{m,j,d} = 0$
. Lumping terms in this sum by the length t of the vector m yields
Similarly, we get when
![]() $i = j \in \Delta $
,
$i = j \in \Delta $
,
![]() $\sum _{t \in \Delta } |S_t| \mathbb {P}_{t,i}^2 = q^d |S_i|$
.
$\sum _{t \in \Delta } |S_t| \mathbb {P}_{t,i}^2 = q^d |S_i|$
.
It follows that
![]() $\mathbb {P}^T D \mathbb {P} = q^d D$
, where D is a diagonal matrix with the sizes of the spheres along the diagonal in the same order as they appear in the top row of
$\mathbb {P}^T D \mathbb {P} = q^d D$
, where D is a diagonal matrix with the sizes of the spheres along the diagonal in the same order as they appear in the top row of
![]() $\mathbb {P}$
.
$\mathbb {P}$
.
As no sphere sizes are zero (we only index distances that occur), D is invertible and it follows that
![]() $\mathbb {P}^{-1} = \frac {1}{q^d} D^{-1} \mathbb {P}^T D$
.
$\mathbb {P}^{-1} = \frac {1}{q^d} D^{-1} \mathbb {P}^T D$
.
As the Q-matrix is defined uniquely (as inverses are unique) by the condition
![]() $PQ=q^d I = QP$
, it follows that
$PQ=q^d I = QP$
, it follows that
![]() $Q=D^{-1} \mathbb {P}^T D$
. We summarize this next in the following.
$Q=D^{-1} \mathbb {P}^T D$
. We summarize this next in the following.
Theorem 5.1 Let q be any odd prime power,
![]() $d \geq 2$
and consider the Euclidean association scheme with distance set
$d \geq 2$
and consider the Euclidean association scheme with distance set
![]() $\Delta $
. Then
$\Delta $
. Then
![]() $|\Delta |=q+1$
, when
$|\Delta |=q+1$
, when
![]() $0 \neq \bar {0} \in \Delta $
and
$0 \neq \bar {0} \in \Delta $
and
![]() $|\Delta |=q$
otherwise when
$|\Delta |=q$
otherwise when
![]() $0 \notin \Delta $
, i.e., when
$0 \notin \Delta $
, i.e., when
![]() $(d=2$
and
$(d=2$
and
![]() $q = 3 \text { mod } 4)$
.
$q = 3 \text { mod } 4)$
.
The
![]() $|\Delta | \times |\Delta |$
matrices
$|\Delta | \times |\Delta |$
matrices
![]() $\mathbb {P}$
and Q of the association scheme (relative to some linear ordering of
$\mathbb {P}$
and Q of the association scheme (relative to some linear ordering of
![]() $\Delta $
for which
$\Delta $
for which
![]() $\bar {0}$
comes first) have:
$\bar {0}$
comes first) have:
![]() $\mathbb {P}_{\bar {0},j} = |S_j|$
for all
$\mathbb {P}_{\bar {0},j} = |S_j|$
for all
![]() $j \in \Delta $
,
$j \in \Delta $
,
![]() $\mathbb {P}_{i,\bar {0}} = 1$
for all
$\mathbb {P}_{i,\bar {0}} = 1$
for all
![]() $i \in \Delta $
and otherwise for
$i \in \Delta $
and otherwise for
![]() $i, j \in \Delta -\{ \bar {0} \}$
we have
$i, j \in \Delta -\{ \bar {0} \}$
we have
where
![]() $\tilde {K}_d(a,b)=\sum _{x \in \mathbb {F}_q^{\times }} \binom {x}{q}^d \chi (ax+\frac {b}{x})$
is a twisted Kloosterman sum and
$\tilde {K}_d(a,b)=\sum _{x \in \mathbb {F}_q^{\times }} \binom {x}{q}^d \chi (ax+\frac {b}{x})$
is a twisted Kloosterman sum and
![]() $\epsilon (q)$
is either
$\epsilon (q)$
is either
![]() $1$
or i depending if q is
$1$
or i depending if q is
![]() $1$
or
$1$
or
![]() $3$
mod
$3$
mod
![]() $4$
.
$4$
.
If D is the diagonal matrix whose diagonals are the sphere sizes (following the chosen linear ordering of
![]() $\Delta $
), then
$\Delta $
), then
![]() $Q=D^{-1}\mathbb {P}^T D$
and
$Q=D^{-1}\mathbb {P}^T D$
and
![]() $Q\mathbb {P}=\mathbb {P}Q=q^d\mathbb {I}$
. Thus
$Q\mathbb {P}=\mathbb {P}Q=q^d\mathbb {I}$
. Thus
![]() $Q_{i,j}=\frac {|S_j|}{|S_i|} P_{j,i}$
.
$Q_{i,j}=\frac {|S_j|}{|S_i|} P_{j,i}$
.
Note that when
![]() $d=2, q=3 \text { mod } 4$
, then
$d=2, q=3 \text { mod } 4$
, then
![]() $0 \notin \Delta $
and
$0 \notin \Delta $
and
![]() $P_{i,j}=-K(-j,\frac {-i}{4})=-K(1,\frac {ij}{4})$
for any
$P_{i,j}=-K(-j,\frac {-i}{4})=-K(1,\frac {ij}{4})$
for any
![]() $i, j \in \Delta -\{ \bar {0} \}$
and so other than the first row and column of
$i, j \in \Delta -\{ \bar {0} \}$
and so other than the first row and column of
![]() $\mathbb {P}$
, the other entries are negatives of Kloosterman numbers. In this case, we also have
$\mathbb {P}$
, the other entries are negatives of Kloosterman numbers. In this case, we also have
![]() $|S_i|=q+1$
for all
$|S_i|=q+1$
for all
![]() $i \neq \bar {0}$
and
$i \neq \bar {0}$
and
![]() $|S_{\bar {0}}|=1$
. If we denote
$|S_{\bar {0}}|=1$
. If we denote
![]() $\mathfrak {1}$
to be the (
$\mathfrak {1}$
to be the (
![]() $q-1$
)-dimensional column vector of all
$q-1$
)-dimensional column vector of all
![]() $1$
s, and K to the symmetric
$1$
s, and K to the symmetric
![]() $(q-1) \times (q-1)$
matrix with
$(q-1) \times (q-1)$
matrix with
![]() $K_{i,j}=K(1,\frac {ij}{4})=K_{j,i}, i,j \in \mathbb {F}_q^{\times }$
, then we have
$K_{i,j}=K(1,\frac {ij}{4})=K_{j,i}, i,j \in \mathbb {F}_q^{\times }$
, then we have
 $$ \begin{align*}\mathbb{P}=\begin{bmatrix} 1 & (q+1)\mathfrak{1}^T \\ \mathfrak{1} & -K \end{bmatrix}=Q.\end{align*} $$
$$ \begin{align*}\mathbb{P}=\begin{bmatrix} 1 & (q+1)\mathfrak{1}^T \\ \mathfrak{1} & -K \end{bmatrix}=Q.\end{align*} $$
Thus,
![]() $\mathbb {P}^2=q^2\mathbb {I}$
for the Euclidean association scheme when
$\mathbb {P}^2=q^2\mathbb {I}$
for the Euclidean association scheme when
![]() $d=2, q = 3 \text { mod } 4.$
$d=2, q = 3 \text { mod } 4.$
On the other hand, when
![]() $d=2, q=1 \text { mod } 4$
, then
$d=2, q=1 \text { mod } 4$
, then
![]() $0 \in \Delta $
,
$0 \in \Delta $
,
![]() $|S_i|=q-1$
if
$|S_i|=q-1$
if
![]() $i \neq 0, \bar {0}$
and
$i \neq 0, \bar {0}$
and
![]() $|S_0|=2q-2, |S_{\bar {0}}|=1$
. With respect to any linear ordering with
$|S_0|=2q-2, |S_{\bar {0}}|=1$
. With respect to any linear ordering with
![]() $\bar {0} < 0 < \mathbb {F}_q^{\times }$
, the
$\bar {0} < 0 < \mathbb {F}_q^{\times }$
, the
![]() $(q+1) \times (q+1)\ \mathbb {P}$
and Q matrices are given in this case by
$(q+1) \times (q+1)\ \mathbb {P}$
and Q matrices are given in this case by
 $$ \begin{align*}\mathbb{P}=\begin{bmatrix} 1 & 2q-2 & (q-1)\mathfrak{1}^T \\ 1 & q-2 & -\mathfrak{1}^T \\ \mathfrak{1} & (-2)\mathfrak{1} & K \end{bmatrix}\end{align*} $$
$$ \begin{align*}\mathbb{P}=\begin{bmatrix} 1 & 2q-2 & (q-1)\mathfrak{1}^T \\ 1 & q-2 & -\mathfrak{1}^T \\ \mathfrak{1} & (-2)\mathfrak{1} & K \end{bmatrix}\end{align*} $$
and again one can verify that
![]() $\mathbb {P}=Q$
using the formulas of the last theorem. Thus again one has
$\mathbb {P}=Q$
using the formulas of the last theorem. Thus again one has
![]() $\mathbb {P}^2=q^2\mathbb {I}$
though the dimensions of
$\mathbb {P}^2=q^2\mathbb {I}$
though the dimensions of
![]() $\mathbb {P}$
are one larger in this case compared to the last one.
$\mathbb {P}$
are one larger in this case compared to the last one.
We record these dimension 2 results in the next proposition.
Proposition 5.2 Let
![]() $\mathbb {F}_q$
be a finite field of odd characteristic and consider the Euclidean association scheme when dimension
$\mathbb {F}_q$
be a finite field of odd characteristic and consider the Euclidean association scheme when dimension
![]() $d=2$
. Let
$d=2$
. Let
![]() $\mathfrak {1}$
to be the (
$\mathfrak {1}$
to be the (
![]() $q-1$
)-dimensional column vector of all
$q-1$
)-dimensional column vector of all
![]() $1$
s, and K be the symmetric
$1$
s, and K be the symmetric
![]() $(q-1) \times (q-1)$
matrix with
$(q-1) \times (q-1)$
matrix with
![]() $K_{i,j}=K(1,\frac {ij}{4})=K_{j,i}, i,j \in \mathbb {F}_q^{\times }$
(with respect to some linear ordering of
$K_{i,j}=K(1,\frac {ij}{4})=K_{j,i}, i,j \in \mathbb {F}_q^{\times }$
(with respect to some linear ordering of
![]() $\mathbb {F}_q^{\times }$
). Order the distance set
$\mathbb {F}_q^{\times }$
). Order the distance set
![]() $\Delta $
via a linear ordering with
$\Delta $
via a linear ordering with
![]() $\bar {0} < 0 < \mathbb {F}_q^{\times }$
.
$\bar {0} < 0 < \mathbb {F}_q^{\times }$
.
Then if
![]() $q=3 \text { mod } 4$
, we have
$q=3 \text { mod } 4$
, we have
 $$ \begin{align*}\mathbb{P}=\begin{bmatrix} 1 & (q+1)\mathfrak{1}^T \\ \mathfrak{1} & -K \end{bmatrix}=Q\end{align*} $$
$$ \begin{align*}\mathbb{P}=\begin{bmatrix} 1 & (q+1)\mathfrak{1}^T \\ \mathfrak{1} & -K \end{bmatrix}=Q\end{align*} $$
are
![]() $q \times q$
matrices.
$q \times q$
matrices.
On the other hand, when
![]() $q=1 \text { mod } 4$
, we have
$q=1 \text { mod } 4$
, we have
 $$ \begin{align*}\mathbb{P}=\begin{bmatrix} 1 & 2q-2 & (q-1)\mathfrak{1}^T \\ 1 & q-2 & -\mathfrak{1}^T \\ \mathfrak{1} & (-2)\mathfrak{1} & K \end{bmatrix}=Q\end{align*} $$
$$ \begin{align*}\mathbb{P}=\begin{bmatrix} 1 & 2q-2 & (q-1)\mathfrak{1}^T \\ 1 & q-2 & -\mathfrak{1}^T \\ \mathfrak{1} & (-2)\mathfrak{1} & K \end{bmatrix}=Q\end{align*} $$
are
![]() $(q+1) \times (q+1)$
matrices.
$(q+1) \times (q+1)$
matrices.
In either case,
![]() $\mathbb {P}^2=q^2\mathbb {I}$
.
$\mathbb {P}^2=q^2\mathbb {I}$
.
The case when
![]() $d \geq 3$
is a bit trickier as the dimension of spheres can vary more. In general, for any
$d \geq 3$
is a bit trickier as the dimension of spheres can vary more. In general, for any
![]() $\lambda \in \mathbb {F}_q^{\times }$
, scaling by
$\lambda \in \mathbb {F}_q^{\times }$
, scaling by
![]() $\lambda $
gives a bijection between the sphere of radius j about the origin and the sphere of radius
$\lambda $
gives a bijection between the sphere of radius j about the origin and the sphere of radius
![]() $\lambda ^2 j$
about the origin. Thus, there are in general four distinct sizes of spheres
$\lambda ^2 j$
about the origin. Thus, there are in general four distinct sizes of spheres
![]() $|S_{\hat {0}}|=1$
,
$|S_{\hat {0}}|=1$
,
![]() $|S_0|$
,
$|S_0|$
,
![]() $|S_{Sq}|$
and
$|S_{Sq}|$
and
![]() $|S_{Sq^c}|$
, where
$|S_{Sq^c}|$
, where
![]() $|S_{Sq}|$
is the common size of
$|S_{Sq}|$
is the common size of
![]() $S_j$
when j is a nonzero square in
$S_j$
when j is a nonzero square in
![]() $\mathbb {F}_q$
and
$\mathbb {F}_q$
and
![]() $|S_{Sq^c}|$
is the common size of
$|S_{Sq^c}|$
is the common size of
![]() $S_j$
when j is a nonsquare in
$S_j$
when j is a nonsquare in
![]() $\mathbb {F}_q$
. As these spheres partition
$\mathbb {F}_q$
. As these spheres partition
![]() $\mathbb {F}_q^d$
, we have
$\mathbb {F}_q^d$
, we have
for all integers
![]() $d \geq 3$
and odd prime powers q.
$d \geq 3$
and odd prime powers q.
Pick a primitive generator
![]() $\theta $
of the multiplicative group of
$\theta $
of the multiplicative group of
![]() $\mathbb {F}_q$
(which is a cyclic group of order
$\mathbb {F}_q$
(which is a cyclic group of order
![]() $q-1$
). Then
$q-1$
). Then
![]() $\theta ^j$
is a square in
$\theta ^j$
is a square in
![]() $\mathbb {F}_q$
if and only if j is even and so the Legendre symbol
$\mathbb {F}_q$
if and only if j is even and so the Legendre symbol
![]() $\binom {\theta ^j}{q}$
is equal to
$\binom {\theta ^j}{q}$
is equal to
![]() $(-1)^j$
for all integers j. We order the distance set
$(-1)^j$
for all integers j. We order the distance set
![]() $\Delta =\{ \bar {0} \} \cup \mathbb {F}_q$
via
$\Delta =\{ \bar {0} \} \cup \mathbb {F}_q$
via
![]() $\bar {0} < 0 < \theta ^0 < \theta ^1 < \theta ^2 < \dots < \theta ^{q-2}$
. Note
$\bar {0} < 0 < \theta ^0 < \theta ^1 < \theta ^2 < \dots < \theta ^{q-2}$
. Note
![]() $4=\theta ^s$
for unique integer s with
$4=\theta ^s$
for unique integer s with
![]() $0 \leq s \leq q-2$
.
$0 \leq s \leq q-2$
.
We define the
![]() $(q-1) \times (q-1)$
matrix
$(q-1) \times (q-1)$
matrix
![]() $\tilde {\mathbb {K}}_d$
(whose rows and columns are indexed by
$\tilde {\mathbb {K}}_d$
(whose rows and columns are indexed by
![]() $\{0,1,\dots , q-2\}$
in the natural order) via
$\{0,1,\dots , q-2\}$
in the natural order) via
 $$ \begin{align*} (\tilde{\mathbb{K}}_d)_{i,j} &= \epsilon(q)^d \tilde{K}_d(-\theta^j, -\frac{\theta^i}{4}) \\ &=\epsilon(q)^d \binom{-\theta^j}{q}^d \tilde{K}_d(1,\frac{\theta^i\theta^j}{4})\\ &=\epsilon(q)^d\binom{-1}{q}^d (-1)^{jd}\tilde{K}_d(1,\theta^{i+j-s}), \end{align*} $$
$$ \begin{align*} (\tilde{\mathbb{K}}_d)_{i,j} &= \epsilon(q)^d \tilde{K}_d(-\theta^j, -\frac{\theta^i}{4}) \\ &=\epsilon(q)^d \binom{-\theta^j}{q}^d \tilde{K}_d(1,\frac{\theta^i\theta^j}{4})\\ &=\epsilon(q)^d\binom{-1}{q}^d (-1)^{jd}\tilde{K}_d(1,\theta^{i+j-s}), \end{align*} $$
where
![]() $\tilde {K}(a,b)$
are the (twisted) Kloosterman sums. The second equality follows from part (2) of Proposition 4.1.
$\tilde {K}(a,b)$
are the (twisted) Kloosterman sums. The second equality follows from part (2) of Proposition 4.1.
This matrix is always a real matrix from the earlier discussion about twisted Kloosterman sums. When d is even, it is symmetric and circulant. Recall, a circulant matrix is one such that each row of the matrix is the cyclic shift of the row above it, one notch to the left. When d is odd, it is no longer circulant or symmetric but is signed-circulant, i.e., each row is the negative of the cyclic shift of the row above it, one notch to the left.
Using these conventions and Theorem 5.1, the following proposition follows by a simple computation with the help of the identities in Proposition 4.1.
Proposition 5.3 Let
![]() $\mathbb {F}_q$
be a finite field of odd characteristic and consider the Euclidean association scheme of dimension
$\mathbb {F}_q$
be a finite field of odd characteristic and consider the Euclidean association scheme of dimension
![]() $d \geq 3$
. Fix a primitive generator
$d \geq 3$
. Fix a primitive generator
![]() $\theta $
of
$\theta $
of
![]() $\mathbb {F}_q^{\times }$
, then
$\mathbb {F}_q^{\times }$
, then
![]() $4=\theta ^s$
for unique integer
$4=\theta ^s$
for unique integer
![]() $0 \leq s \leq q-2$
.
$0 \leq s \leq q-2$
.
Let
![]() $(\tilde {\mathbb {K}}_d)_{i,j} =\epsilon (q)^d\binom {-1}{q}^d (-1)^{jd}\tilde {K}_d(1,\theta ^{i+j-s})$
whose rows and columns are indexed by
$(\tilde {\mathbb {K}}_d)_{i,j} =\epsilon (q)^d\binom {-1}{q}^d (-1)^{jd}\tilde {K}_d(1,\theta ^{i+j-s})$
whose rows and columns are indexed by
![]() $\{0,\dots , q-2\}$
. It is a real, symmetric, and circulant matrix when d is even and it is a real, signed-circulant matrix when d is odd.
$\{0,\dots , q-2\}$
. It is a real, symmetric, and circulant matrix when d is even and it is a real, signed-circulant matrix when d is odd.
Let
![]() $\mathfrak {1}$
be the
$\mathfrak {1}$
be the
![]() $(q-1)$
-dimensional column vector of all ones, and let
$(q-1)$
-dimensional column vector of all ones, and let
![]() $\hat {\eta }$
be the
$\hat {\eta }$
be the
![]() $(q-1)$
-dimensional row vector whose entries alternate between
$(q-1)$
-dimensional row vector whose entries alternate between
![]() $|S_{Sq}|$
and
$|S_{Sq}|$
and
![]() $|S_{Sq^c}|$
, starting with the former. Let
$|S_{Sq^c}|$
, starting with the former. Let
![]() $\hat {\mu }$
be the
$\hat {\mu }$
be the
![]() $(q-1)$
-dimensional column vector whose entries are
$(q-1)$
-dimensional column vector whose entries are
![]() $(-1)^{id}$
as i ranges from
$(-1)^{id}$
as i ranges from
![]() $0$
to
$0$
to
![]() $q-2$
. (So it always starts at
$q-2$
. (So it always starts at
![]() $1$
and alternates sign if d is odd, but is the all one vector when d is even.)
$1$
and alternates sign if d is odd, but is the all one vector when d is even.)
With respect to the ordering
![]() $\bar {0} < 0 < \theta ^0 < \theta ^1 < \theta ^2 < \dots < \theta ^{q-2}$
of the distance set
$\bar {0} < 0 < \theta ^0 < \theta ^1 < \theta ^2 < \dots < \theta ^{q-2}$
of the distance set
![]() $\Delta $
, the P matrix of the Euclidean association scheme is a
$\Delta $
, the P matrix of the Euclidean association scheme is a
![]() $(q+1)\times (q+1)$
matrix given by
$(q+1)\times (q+1)$
matrix given by
 $$ \begin{align*}\mathbb{P}=\begin{bmatrix} 1 & |S_0| & \hat{\eta} \\ 1 & \alpha & \beta\hat{\mu}^T \\ \mathfrak{1} & \beta\hat{\mu}-\mathfrak{1} & q^{\frac{d}{2}-1}\tilde{\mathbb{K}}_d \end{bmatrix}\end{align*} $$
$$ \begin{align*}\mathbb{P}=\begin{bmatrix} 1 & |S_0| & \hat{\eta} \\ 1 & \alpha & \beta\hat{\mu}^T \\ \mathfrak{1} & \beta\hat{\mu}-\mathfrak{1} & q^{\frac{d}{2}-1}\tilde{\mathbb{K}}_d \end{bmatrix}\end{align*} $$
where
![]() $\alpha =-1+q^{\frac {d}{2}-1}\epsilon (q)^d (q-1)\frac {(-1)^d+1}{2}$
and
$\alpha =-1+q^{\frac {d}{2}-1}\epsilon (q)^d (q-1)\frac {(-1)^d+1}{2}$
and
![]() $\beta =-q^{\frac {d}{2}-1}\epsilon (q)^d$
when d even,
$\beta =-q^{\frac {d}{2}-1}\epsilon (q)^d$
when d even,
![]() $\beta =\binom {-1}{q} q^{\frac {d-1}{2}}\epsilon (q)^{d+1}$
when d odd.
$\beta =\binom {-1}{q} q^{\frac {d-1}{2}}\epsilon (q)^{d+1}$
when d odd.
The Q matrix has
![]() $Q_{i,j}=\frac {|S_j|}{|S_i|}P_{j,i}$
. Due to varying sizes of spheres when
$Q_{i,j}=\frac {|S_j|}{|S_i|}P_{j,i}$
. Due to varying sizes of spheres when
![]() $d \geq 3$
, one no longer has
$d \geq 3$
, one no longer has
![]() $Q=P$
in general.
$Q=P$
in general.
The above proposition also works for the
![]() $d=2$
case though in the case
$d=2$
case though in the case
![]() $q=3 \text { mod } 4$
one should throw out the second row and column as the distance
$q=3 \text { mod } 4$
one should throw out the second row and column as the distance
![]() $0$
does not occur.
$0$
does not occur.
6 Equidistribution
Through work of Kloosterman and A. Weil, for any odd prime power q and
![]() $a \in \mathbb {F}_q^{\times }$
, it is known that the Kloosterman numbers
$a \in \mathbb {F}_q^{\times }$
, it is known that the Kloosterman numbers
![]() $K_q(1,a)=\sum _{x \in \mathbb {F}_q^{\times }} \chi (x + \frac {a}{x})$
satisfy
$K_q(1,a)=\sum _{x \in \mathbb {F}_q^{\times }} \chi (x + \frac {a}{x})$
satisfy
for a unique “Kloosterman” angle
![]() $\theta _{q,a} \in [0, \pi ]$
.
$\theta _{q,a} \in [0, \pi ]$
.
Using the sophisticated tools of lisse sheafs and etale cohomology, N. Katz (slightly simplified proofs later by Adolphson), proved the “vertical equidistribution” of these numbers that states that as
![]() $q \to \infty $
, the distribution of these angles approaches the Sato–Tate measure on
$q \to \infty $
, the distribution of these angles approaches the Sato–Tate measure on
![]() $[0,\pi ]$
. We discuss this more carefully next.
$[0,\pi ]$
. We discuss this more carefully next.
Definition 6.1 (Sato–Tate measure)
The Sato–Tate Borel probability measure
![]() $\mu _{ST}$
on
$\mu _{ST}$
on
![]() $[0,\pi ]$
is given by the condition
$[0,\pi ]$
is given by the condition
for all
![]() $0\leq a < b \leq \pi $
.
$0\leq a < b \leq \pi $
.
![]() $\mu _{ST}$
is characterized as the unique Borel measure being absolutely continuous with respect to Lebesgue measure with Radon–Nikodym derivative
$\mu _{ST}$
is characterized as the unique Borel measure being absolutely continuous with respect to Lebesgue measure with Radon–Nikodym derivative
![]() $\frac {2}{\pi } sin^2(\theta )$
.
$\frac {2}{\pi } sin^2(\theta )$
.
For any continuous
![]() $f: [0, \pi ] \to \mathbb {R}$
, we write
$f: [0, \pi ] \to \mathbb {R}$
, we write
for the expectation of f with respect to this probability measure.
Definition 6.2 (Kloosterman angle average)
For any odd prime power q, let
![]() $\theta _{a,q}$
be the Kloosterman angles associated with the Kloosterman sums
$\theta _{a,q}$
be the Kloosterman angles associated with the Kloosterman sums
![]() $K(1,a), a \in \mathbb {F}_q^{\times }$
. Given a continuous function
$K(1,a), a \in \mathbb {F}_q^{\times }$
. Given a continuous function
![]() $f: [0, \pi ] \to \mathbb {R}$
, we let
$f: [0, \pi ] \to \mathbb {R}$
, we let
 $$ \begin{align*}E_{K,q}[f] = \frac{1}{q-1} \sum_{a \in \mathbb{F}_q^{\times}} f(\theta_{q,a}) \end{align*} $$
$$ \begin{align*}E_{K,q}[f] = \frac{1}{q-1} \sum_{a \in \mathbb{F}_q^{\times}} f(\theta_{q,a}) \end{align*} $$
be the “sample average” of f over these Kloosterman angles.
We are now ready to state the deep vertical equidistribution theorem of N. Katz (see [Reference Katz10]).
Theorem 6.3 (Vertical equidistribution of Kloosterman sums)
For any sequence of odd prime powers
![]() $q_n \to \infty $
, and any continuous function
$q_n \to \infty $
, and any continuous function
![]() $f: [0, \pi ] \to \mathbb {R}$
, we have
$f: [0, \pi ] \to \mathbb {R}$
, we have
Next, we will discuss some graph theoretical equivalents to the equidistribution theorem. First, some basic trigonometric facts will be collected.
Proposition 6.4 For any nonnegative integers
![]() $m, n,$
we have:
$m, n,$
we have:
(1)
![]() $\frac {2}{\pi } \int _{0}^{\pi } \cos (m \theta )\cos (n \theta )d\theta = \delta _{m,n}+\delta _{m,n}\delta _{m,0}.$
$\frac {2}{\pi } \int _{0}^{\pi } \cos (m \theta )\cos (n \theta )d\theta = \delta _{m,n}+\delta _{m,n}\delta _{m,0}.$
(2)
![]() $E_{ST}[\cos (n\theta )]=0$
if
$E_{ST}[\cos (n\theta )]=0$
if
![]() $n \neq 0,2$
.
$n \neq 0,2$
.
![]() $E_{ST}[\cos (2\theta )]=-\frac {1}{2}$
.
$E_{ST}[\cos (2\theta )]=-\frac {1}{2}$
.
The Sato–Tate probability measure is characterized by these expectations amongst continuous probability measures on
![]() $[0, \pi ]$
.
$[0, \pi ]$
.
(3) For every
![]() $\ell \geq 1$
, we have
$\ell \geq 1$
, we have
 $$ \begin{align*}2^{2\ell-1}\cos^{2\ell}(\theta)=\sum_{k=0}^{\ell-1} \binom{2\ell}{k} \cos((2\ell-2k)\theta) + \frac{1}{2} \binom{2\ell}{\ell}.\end{align*} $$
$$ \begin{align*}2^{2\ell-1}\cos^{2\ell}(\theta)=\sum_{k=0}^{\ell-1} \binom{2\ell}{k} \cos((2\ell-2k)\theta) + \frac{1}{2} \binom{2\ell}{\ell}.\end{align*} $$
(4) For every
![]() $\ell \geq 1$
, we have
$\ell \geq 1$
, we have
 $$ \begin{align*}2^{2\ell}\cos^{2\ell+1}(\theta)=\sum_{k=0}^{\ell} \binom{2\ell+1}{k} \cos((2\ell+1-2k)\theta).\end{align*} $$
$$ \begin{align*}2^{2\ell}\cos^{2\ell+1}(\theta)=\sum_{k=0}^{\ell} \binom{2\ell+1}{k} \cos((2\ell+1-2k)\theta).\end{align*} $$
(5) For positive integer m, we have
![]() $E_{ST}[\cos ^{2m+1}(\theta )]=0$
and
$E_{ST}[\cos ^{2m+1}(\theta )]=0$
and
Proof Proof of (1): Follows from the trigonometric identity
and simple integration.
Proof of (2): Follows from (1), once one notes that
![]() $\sin ^2(\theta )=\frac {1-\cos (2\theta )}{2}$
. The characterization of Sato–Tate measure from these expectations follows from the density of the algebra generated by the
$\sin ^2(\theta )=\frac {1-\cos (2\theta )}{2}$
. The characterization of Sato–Tate measure from these expectations follows from the density of the algebra generated by the
![]() $cos(n\theta )$
in the ring of continuous real-valued functions on
$cos(n\theta )$
in the ring of continuous real-valued functions on
![]() $[0,\pi ]$
(with the supremum metric) which itself follows from a generalized Stone–Weierstrass theorem, together with the Riesz representation theorem.
$[0,\pi ]$
(with the supremum metric) which itself follows from a generalized Stone–Weierstrass theorem, together with the Riesz representation theorem.
Proof of (3): Write
![]() $2\cos (\theta )=e^{i\theta } + e^{-i\theta }$
and raise both sides to the
$2\cos (\theta )=e^{i\theta } + e^{-i\theta }$
and raise both sides to the
![]() $2\ell $
power to conclude
$2\ell $
power to conclude
 $$ \begin{align*}2^{2\ell} \cos^{2\ell}(\theta)=\sum_{k=0}^{2\ell} \binom{2\ell}{k} (e^{i\theta})^{2\ell-k} (e^{-i\theta})^k = \sum_{k=0}^{2\ell} \binom{2\ell}{k} (e^{i\theta})^{2\ell-2k}. \end{align*} $$
$$ \begin{align*}2^{2\ell} \cos^{2\ell}(\theta)=\sum_{k=0}^{2\ell} \binom{2\ell}{k} (e^{i\theta})^{2\ell-k} (e^{-i\theta})^k = \sum_{k=0}^{2\ell} \binom{2\ell}{k} (e^{i\theta})^{2\ell-2k}. \end{align*} $$
Finish by grouping the
![]() $k=j$
and
$k=j$
and
![]() $k=2\ell -j$
terms for each j.
$k=2\ell -j$
terms for each j.
Proof of (4): Follows the same procedure as for (3).
Proof of (5): Follows from using (3), (4) in (2).
Definition 6.5 (Kloosterman moments)
For any odd prime power q, and positive integer
![]() $\ell $
, let
$\ell $
, let
 $$ \begin{align*}M_{q,\ell} = \sum_{a \in \mathbb{F}_q^{\times}} K_q(1,a)^\ell = 2^{\ell} q^{\frac{\ell}{2}}(q-1) E_{K,q}[cos^{\ell}(\theta)] \end{align*} $$
$$ \begin{align*}M_{q,\ell} = \sum_{a \in \mathbb{F}_q^{\times}} K_q(1,a)^\ell = 2^{\ell} q^{\frac{\ell}{2}}(q-1) E_{K,q}[cos^{\ell}(\theta)] \end{align*} $$
be the
![]() $\ell $
th Kloosterman moment.
$\ell $
th Kloosterman moment.
Using little-oh notation and the trigonometric identities in Proposition 6.4, we find that the vertical equidistribution of Kloosterman sums is equivalent to establishing the following behavior for Kloosterman moments:
and
as
![]() $q \to \infty $
.
$q \to \infty $
.
The quantity
![]() $C_{\ell }=\frac {1}{\ell +1}\binom {2\ell }{\ell }$
in the last limit is the
$C_{\ell }=\frac {1}{\ell +1}\binom {2\ell }{\ell }$
in the last limit is the
![]() $\ell $
th Catalan number which occurs frequently in combinatorics. It is, for example, the number of ways to bracket a given
$\ell $
th Catalan number which occurs frequently in combinatorics. It is, for example, the number of ways to bracket a given
![]() $(\ell +1)$
-fold product in terms of pairwise multiplications.
$(\ell +1)$
-fold product in terms of pairwise multiplications.
Recall, in a graph, two edges are incident if they share a common vertex and a walk of length
![]() $\ell $
is a sequence of
$\ell $
is a sequence of
![]() $\ell $
edges, where each edge is incident to the previous one. If
$\ell $
edges, where each edge is incident to the previous one. If
![]() $\mathbb {A}$
is the adjacency matrix of the graph with respect to some vertex ordering, then the
$\mathbb {A}$
is the adjacency matrix of the graph with respect to some vertex ordering, then the
![]() $(v,w)$
-entry of
$(v,w)$
-entry of
![]() $\mathbb {A}^{\ell }$
is the number of walks of length
$\mathbb {A}^{\ell }$
is the number of walks of length
![]() $\ell $
from vertex v to vertex w in the graph. Such a walk is called closed if
$\ell $
from vertex v to vertex w in the graph. Such a walk is called closed if
![]() $v=w$
. Thus,
$v=w$
. Thus,
![]() $\mathrm{Trace}(\mathbb {A}^{\ell })$
is the number of closed walks of length
$\mathrm{Trace}(\mathbb {A}^{\ell })$
is the number of closed walks of length
![]() $\ell $
in the graph.
$\ell $
in the graph.
Let q be an odd prime power,
![]() $q= 3 \text { mod } 4$
. Fix any
$q= 3 \text { mod } 4$
. Fix any
![]() $t \in \mathbb {F}_q^{\times }$
then we have seen that the spectrum of
$t \in \mathbb {F}_q^{\times }$
then we have seen that the spectrum of
![]() $\mathbb {A}_t$
, the adjacency matrix of the distance-t graph for the plane
$\mathbb {A}_t$
, the adjacency matrix of the distance-t graph for the plane
![]() $\mathbb {F}_q^2$
is the multiset
$\mathbb {F}_q^2$
is the multiset
where the superscripts indicate the multiplicity of each eigenvalue in the multiset.
Thus
On the other hand, when
![]() $q=1 \text { mod } 4$
, the spectrum of
$q=1 \text { mod } 4$
, the spectrum of
![]() $\mathbb {A}_t$
is
$\mathbb {A}_t$
is
and so
 $$ \begin{align*}\mathrm{Trace}(\mathbb{A}_t^{\ell}) &= (q-1)^{\ell} + (2q-2)(-1)^{\ell} + (q-1)\sum_{a \in \mathbb{F}_q^{\times}} K_q(1,a)^{\ell}\\ &= (q-1)^{\ell} + (2q-2)(-1)^{\ell} + (q-1)M_{q,\ell}. \end{align*} $$
$$ \begin{align*}\mathrm{Trace}(\mathbb{A}_t^{\ell}) &= (q-1)^{\ell} + (2q-2)(-1)^{\ell} + (q-1)\sum_{a \in \mathbb{F}_q^{\times}} K_q(1,a)^{\ell}\\ &= (q-1)^{\ell} + (2q-2)(-1)^{\ell} + (q-1)M_{q,\ell}. \end{align*} $$
We record these results in the next proposition.
Proposition 6.6 Let q be an odd prime power, and let
![]() $t \in \mathbb {F}_q^{\times }$
and
$t \in \mathbb {F}_q^{\times }$
and
![]() $\mathbb {A}_t$
be the adjacency matrix of the distance-t graph for the plane
$\mathbb {A}_t$
be the adjacency matrix of the distance-t graph for the plane
![]() $\mathbb {F}_q^2$
. Then if
$\mathbb {F}_q^2$
. Then if
![]() $q = 3 \text { mod } 4$
, we have the number of closed walks of length
$q = 3 \text { mod } 4$
, we have the number of closed walks of length
![]() $\ell $
is
$\ell $
is
If
![]() $q=1 \text { mod } 4$
, we have
$q=1 \text { mod } 4$
, we have
where
![]() $M_{q,\ell }$
is the
$M_{q,\ell }$
is the
![]() $\ell $
th Kloosterman moment.
$\ell $
th Kloosterman moment.
Vertical equidistribution of Kloosterman angles is equivalent to
and
as
![]() $q \to \infty $
.
$q \to \infty $
.
Corollary 6.7 For any odd prime power q, we have
![]() $M_{q,1}=1$
and
$M_{q,1}=1$
and
![]() $M_{q,2}=q^2-q-1$
. Thus, the equidistribution conditions hold for these moments.
$M_{q,2}=q^2-q-1$
. Thus, the equidistribution conditions hold for these moments.
Proof We prove the
![]() $q=3 \text { mod } 4$
case with similar calculations working for the
$q=3 \text { mod } 4$
case with similar calculations working for the
![]() $q=1 \text { mod } 4$
case. Setting
$q=1 \text { mod } 4$
case. Setting
![]() $t=1$
in Proposition 6.6, we see
$t=1$
in Proposition 6.6, we see
![]() $\mathrm{Trace}(\mathbb {A}_1)=0$
as there are no closed walks of length one. Thus
$\mathrm{Trace}(\mathbb {A}_1)=0$
as there are no closed walks of length one. Thus
![]() $(q+1)-(q+1)M_{q,1}=0$
giving
$(q+1)-(q+1)M_{q,1}=0$
giving
![]() $M_{q,1}=1$
. A closed walk of length two consists of walking out using an edge and returning using the same edge and so the number of those is
$M_{q,1}=1$
. A closed walk of length two consists of walking out using an edge and returning using the same edge and so the number of those is
![]() $q^2(q+1)$
as there are
$q^2(q+1)$
as there are
![]() $q^2$
choices of initial vertices and
$q^2$
choices of initial vertices and
![]() $q+1$
many adjacent vertices to walk to. Thus,
$q+1$
many adjacent vertices to walk to. Thus,
![]() $q^2(q+1)=\mathrm{Trace}(\mathbb {A}_1^2)=(q+1)^2 + (q+1)M_{q,2}$
yielding the stated formula for
$q^2(q+1)=\mathrm{Trace}(\mathbb {A}_1^2)=(q+1)^2 + (q+1)M_{q,2}$
yielding the stated formula for
![]() $M_{q,2}$
.
$M_{q,2}$
.
7 An application to the random walk in finite planes of odd order
Fix
![]() $t \neq 0$
in
$t \neq 0$
in
![]() $\mathbb {F}_q$
and let
$\mathbb {F}_q$
and let
![]() $\mathbb {A}_t$
be the adjacency matrix for the distance-t graph in the plane
$\mathbb {A}_t$
be the adjacency matrix for the distance-t graph in the plane
![]() $\mathbb {F}_q^2$
. Define
$\mathbb {F}_q^2$
. Define
![]() $T_t=\frac {1}{|S_t|} \mathbb {A}_t$
to be the transition matrix of the corresponding random walk Markov chain. The
$T_t=\frac {1}{|S_t|} \mathbb {A}_t$
to be the transition matrix of the corresponding random walk Markov chain. The
![]() $(i,j)$
-entry of
$(i,j)$
-entry of
![]() $T_t^{\ell }$
represents the probability of transitioning from the ith vertex to the jth vertex after
$T_t^{\ell }$
represents the probability of transitioning from the ith vertex to the jth vertex after
![]() $\ell $
steps in this Markov chain. As the
$\ell $
steps in this Markov chain. As the
![]() $A_t$
-graph is vertex transitive, the diagonal entries of
$A_t$
-graph is vertex transitive, the diagonal entries of
![]() $T_t^{\ell }$
are all equal as the probability that we return to vertex i after
$T_t^{\ell }$
are all equal as the probability that we return to vertex i after
![]() $\ell $
steps, if we start at vertex i, will be independent of the vertex. Thus
$\ell $
steps, if we start at vertex i, will be independent of the vertex. Thus
![]() $(T_t^{\ell })_{i,i}=\frac {1}{q^2}\mathrm{Trace}(T_t^{\ell })$
for any i.
$(T_t^{\ell })_{i,i}=\frac {1}{q^2}\mathrm{Trace}(T_t^{\ell })$
for any i.
Using Bayesian conditioning, it follows that for any initial probability distribution
![]() $p_i$
on the vertices, the chance that you start and end at the same vertex after
$p_i$
on the vertices, the chance that you start and end at the same vertex after
![]() $\ell $
steps is
$\ell $
steps is
![]() $ \sum _{j=1}^{q^2} (T_t^{\ell })_{j,j}p_j= \frac {1}{q^2} \mathrm{Trace} (T_t^{\ell })\sum _{j=1}^{q^2} p_j =\frac {1}{q^2|S_t|^{\ell }} \mathrm{Trace}(A_t^{\ell })$
is the probability that you return to where you start after
$ \sum _{j=1}^{q^2} (T_t^{\ell })_{j,j}p_j= \frac {1}{q^2} \mathrm{Trace} (T_t^{\ell })\sum _{j=1}^{q^2} p_j =\frac {1}{q^2|S_t|^{\ell }} \mathrm{Trace}(A_t^{\ell })$
is the probability that you return to where you start after
![]() $\ell $
steps (it is independent of initiate state). Let us call this quantity the probability of return and denote it
$\ell $
steps (it is independent of initiate state). Let us call this quantity the probability of return and denote it
![]() $R_{q,\ell ,t}$
. Now
$R_{q,\ell ,t}$
. Now
![]() $|S_t|=q \pm 1$
where the sign depends if q is
$|S_t|=q \pm 1$
where the sign depends if q is
![]() $1$
or
$1$
or
![]() $3$
mod
$3$
mod
![]() $4$
so we find that this probability is
$4$
so we find that this probability is
![]() $R_{q,\ell ,t}=\frac {1}{q^2(q \pm 1)^{\ell }} \mathrm{Trace}(A_t^{\ell })$
.
$R_{q,\ell ,t}=\frac {1}{q^2(q \pm 1)^{\ell }} \mathrm{Trace}(A_t^{\ell })$
.
By Corollary 6, we see that if
![]() $q=3 \text { mod } 4$
, and positive
$q=3 \text { mod } 4$
, and positive
![]() $\ell $
, we have
$\ell $
, we have
 $$ \begin{align*}R_{q,\ell,t}=R_{q,\ell}=\frac{1}{q^2}(1 + \frac{(-1)^{\ell}}{(q+1)^{\ell-1}} M_{q,\ell}) \end{align*} $$
$$ \begin{align*}R_{q,\ell,t}=R_{q,\ell}=\frac{1}{q^2}(1 + \frac{(-1)^{\ell}}{(q+1)^{\ell-1}} M_{q,\ell}) \end{align*} $$
does not depend on
![]() $t \neq 0$
. Note the first
$t \neq 0$
. Note the first
![]() $\frac {1}{q^2}$
term is what one would expect if the location after
$\frac {1}{q^2}$
term is what one would expect if the location after
![]() $\ell $
steps were equally likely to be anywhere in the plane and the second term represents an arithmetic bias against that happening. Vertical equidistribution of Kloosterman sums, tells us furthermore that
$\ell $
steps were equally likely to be anywhere in the plane and the second term represents an arithmetic bias against that happening. Vertical equidistribution of Kloosterman sums, tells us furthermore that
 $$ \begin{align*}R_{q, 2\ell} = \frac{1}{q^2} + \frac{q^{\ell-1}}{(\ell+1)(q+1)^{2\ell-1}}\binom{2\ell}{\ell} (1 + o(1)) = \frac{1}{q^2} + \frac{1}{q^{\ell}(\ell+1)}\binom{2\ell}{\ell}(1+o(1)) \end{align*} $$
$$ \begin{align*}R_{q, 2\ell} = \frac{1}{q^2} + \frac{q^{\ell-1}}{(\ell+1)(q+1)^{2\ell-1}}\binom{2\ell}{\ell} (1 + o(1)) = \frac{1}{q^2} + \frac{1}{q^{\ell}(\ell+1)}\binom{2\ell}{\ell}(1+o(1)) \end{align*} $$
and
as
![]() $q \to \infty $
through such prime powers.
$q \to \infty $
through such prime powers.
Thus we have proven:
Theorem 7.1 (Probability of return in the distance-t random walk in
 $\mathbb {F}_q$
-planes)
$\mathbb {F}_q$
-planes)
Let q be an odd prime,
![]() $q=3 \text { mod } 4$
. Let
$q=3 \text { mod } 4$
. Let
![]() $R_{q,\ell ,t}$
be the probability that you return to the same vertex after
$R_{q,\ell ,t}$
be the probability that you return to the same vertex after
![]() $\ell $
steps in the distance-t walk where
$\ell $
steps in the distance-t walk where
![]() $t \neq 0$
. Then
$t \neq 0$
. Then
![]() $R_{q,\ell , t}=R_{q,\ell }$
is independent of
$R_{q,\ell , t}=R_{q,\ell }$
is independent of
![]() $t \neq 0$
and initial state. We have
$t \neq 0$
and initial state. We have
 $$ \begin{align*}R_{q,\ell,t}=R_{q,\ell}=\frac{1}{q^2}(1 + \frac{(-1)^{\ell}}{(q+1)^{\ell-1}} M_{q,\ell}). \end{align*} $$
$$ \begin{align*}R_{q,\ell,t}=R_{q,\ell}=\frac{1}{q^2}(1 + \frac{(-1)^{\ell}}{(q+1)^{\ell-1}} M_{q,\ell}). \end{align*} $$
Furthermore, as
![]() $q \to \infty $
, we have
$q \to \infty $
, we have
 $$ \begin{align*}R_{q, 2\ell} = \frac{1}{q^2} + \frac{q^{\ell-1}}{(\ell+1)(q+1)^{2\ell-1}}\binom{2\ell}{\ell} (1 + o(1)) = \frac{1}{q^2} + \frac{1}{q^{\ell}(\ell+1)}\binom{2\ell}{\ell}(1+o(1)) \end{align*} $$
$$ \begin{align*}R_{q, 2\ell} = \frac{1}{q^2} + \frac{q^{\ell-1}}{(\ell+1)(q+1)^{2\ell-1}}\binom{2\ell}{\ell} (1 + o(1)) = \frac{1}{q^2} + \frac{1}{q^{\ell}(\ell+1)}\binom{2\ell}{\ell}(1+o(1)) \end{align*} $$
and
8 Intersection numbers and matrices of the scheme
In this section, we calculate the intersection numbers
![]() $p_{i,j}^k$
of the d-dimensional Euclidean association scheme. Recall
$p_{i,j}^k$
of the d-dimensional Euclidean association scheme. Recall
![]() $p_{i,j}^k=p_{j,i}^k$
is the number of ways a pair of points
$p_{i,j}^k=p_{j,i}^k$
is the number of ways a pair of points
![]() $\{x,y\}$
in
$\{x,y\}$
in
![]() $\mathbb {F}_q^d$
with
$\mathbb {F}_q^d$
with
![]() $d(x,y)=k$
can be completed to a triangle
$d(x,y)=k$
can be completed to a triangle
![]() $\{x,y,z\}$
of side lengths
$\{x,y,z\}$
of side lengths
![]() $i,j,k$
. Note
$i,j,k$
. Note
![]() $p_{i,j}^{\bar {0}} =\delta _{i,j} |S_i|$
and
$p_{i,j}^{\bar {0}} =\delta _{i,j} |S_i|$
and
![]() $p_{\bar {0},j}^k =\delta _{j,k}$
so we may assume
$p_{\bar {0},j}^k =\delta _{j,k}$
so we may assume
![]() $i,j,k \in \mathbb {F}_q$
and so are not
$i,j,k \in \mathbb {F}_q$
and so are not
![]() $\bar {0}$
.
$\bar {0}$
.
We will concentrate on the planar,
![]() $d=2$
case as the higher-dimensional cases were reduced to this case in [Reference Kwok12]. This case was partially computed in [Reference Bennet, Iosevich and Pakianathan3] in a different context.
$d=2$
case as the higher-dimensional cases were reduced to this case in [Reference Kwok12]. This case was partially computed in [Reference Bennet, Iosevich and Pakianathan3] in a different context.
Theorem 8.1 (Intersection numbers of planar Euclidean association scheme)
Let q be an odd prime power, and let
![]() $p_{i,j}^k$
be the intersection numbers of the planar (
$p_{i,j}^k$
be the intersection numbers of the planar (
![]() $d=2$
) Euclidean association scheme for
$d=2$
) Euclidean association scheme for
![]() $i,j,k \in \mathbb {F}_q$
not equal to
$i,j,k \in \mathbb {F}_q$
not equal to
![]() $\bar {0}$
.
$\bar {0}$
.
If
![]() $q=1 \text { mod } 4$
, we have
$q=1 \text { mod } 4$
, we have
![]() $p_{i,j}^0=1+(q-2)\delta _{i,j}\delta _{i,0}-\delta _{i,j}$
.
$p_{i,j}^0=1+(q-2)\delta _{i,j}\delta _{i,0}-\delta _{i,j}$
.
Otherwise,
![]() $k \neq 0$
and we have
$k \neq 0$
and we have
 $$ \begin{align*}p_{i,j}^k=\binom{4\sigma_2-\sigma_1^2}{q}+1, \end{align*} $$
$$ \begin{align*}p_{i,j}^k=\binom{4\sigma_2-\sigma_1^2}{q}+1, \end{align*} $$
where
![]() $\binom {x}{q}$
is the usual Legendre symbol,
$\binom {x}{q}$
is the usual Legendre symbol,
![]() $\sigma _1=i+j+k, \sigma _2=ij+jk+ki$
.
$\sigma _1=i+j+k, \sigma _2=ij+jk+ki$
.
Furthermore, when
![]() $i,j,k \in \mathbb {F}_q$
are the distances in a triple of points of
$i,j,k \in \mathbb {F}_q$
are the distances in a triple of points of
![]() $\mathbb {F}_q^2$
, we have
$\mathbb {F}_q^2$
, we have
![]() $4\sigma _2 = \sigma _1^2$
if and only if
$4\sigma _2 = \sigma _1^2$
if and only if
![]() $\{i,j,k\}$
are the distances of a collinear triple of points (a triple of points that lies on an affine line).
$\{i,j,k\}$
are the distances of a collinear triple of points (a triple of points that lies on an affine line).
Proof WLOG we may take
![]() $x=(0,0)$
and Witt’s theorem guarantees
$x=(0,0)$
and Witt’s theorem guarantees
![]() $p_{i,j}^k$
will be independent of
$p_{i,j}^k$
will be independent of
![]() $y=(u_1,v_1) \neq (0,0)$
but only depend on its length
$y=(u_1,v_1) \neq (0,0)$
but only depend on its length
![]() $u_1^2+v_1^2=k$
. We may furthermore assume
$u_1^2+v_1^2=k$
. We may furthermore assume
![]() $u_1 \neq 0$
.
$u_1 \neq 0$
.
Then by definition, any
![]() $z=(u_2,v_2)$
making
$z=(u_2,v_2)$
making
![]() $\{x,y,z\}$
a
$\{x,y,z\}$
a
![]() $i-j-k$
triangle must satisfy
$i-j-k$
triangle must satisfy
![]() $u_2^2+v_2^2=i, (u_2-u_1)^2+(v_2-v_1)^2=j$
. Given
$u_2^2+v_2^2=i, (u_2-u_1)^2+(v_2-v_1)^2=j$
. Given
![]() $u_1, v_1, i, j, k$
, we need to count the number,
$u_1, v_1, i, j, k$
, we need to count the number,
![]() $p_{i,j}^k$
, of
$p_{i,j}^k$
, of
![]() $z=(u_2,v_2)$
that solve these equations. Plugging the first two equations into the last one, we get
$z=(u_2,v_2)$
that solve these equations. Plugging the first two equations into the last one, we get
![]() $u_1u_2+v_1v_2 = \frac {k+i-j}{2}$
. The set of
$u_1u_2+v_1v_2 = \frac {k+i-j}{2}$
. The set of
![]() $(u_2,v_2)$
solving this equation is an affine line (not necessarily through the origin) perpendicular to the line through
$(u_2,v_2)$
solving this equation is an affine line (not necessarily through the origin) perpendicular to the line through
![]() $y=(u_1,v_1)$
. It is not hard to see that in fact
$y=(u_1,v_1)$
. It is not hard to see that in fact
![]() $(u_2,v_2)=(\frac {k+i-j}{2u_1},0) + s(v_1,-u_1)$
for some
$(u_2,v_2)=(\frac {k+i-j}{2u_1},0) + s(v_1,-u_1)$
for some
![]() $s \in \mathbb {F}_q$
. However, we still need
$s \in \mathbb {F}_q$
. However, we still need
![]() $u_2^2+v_2^2=i$
which yields
$u_2^2+v_2^2=i$
which yields
![]() $(\frac {k+i-j}{2u_1}+sv_1)^2 + s^2u_1^2=i$
. This yields the equation
$(\frac {k+i-j}{2u_1}+sv_1)^2 + s^2u_1^2=i$
. This yields the equation
![]() $ks^2 +(k+i-j)\frac {v_1}{u_1}s +((\frac {k+i-j}{2u_1})^2 -i)=0$
which is a quadratic equation unless
$ks^2 +(k+i-j)\frac {v_1}{u_1}s +((\frac {k+i-j}{2u_1})^2 -i)=0$
which is a quadratic equation unless
![]() $k=0$
.
$k=0$
.
When
![]() $k=0$
,
$k=0$
,
![]() $v_1^2=-u_1^2 \neq 0$
so the resultant linear equation has a unique solution for s whenever
$v_1^2=-u_1^2 \neq 0$
so the resultant linear equation has a unique solution for s whenever
![]() $j \neq i$
and
$j \neq i$
and
![]() $p_{i,j}^0=1$
for all
$p_{i,j}^0=1$
for all
![]() $i \neq j \in \mathbb {F}_q$
. When
$i \neq j \in \mathbb {F}_q$
. When
![]() $k=0$
and
$k=0$
and
![]() $i=j$
, the equation cannot hold unless
$i=j$
, the equation cannot hold unless
![]() $i=0$
also in which case any s works as long as
$i=0$
also in which case any s works as long as
![]() $x \neq y$
and
$x \neq y$
and
![]() $x \neq z$
so there are
$x \neq z$
so there are
![]() $(q-2)$
such
$(q-2)$
such
![]() $s.$
(In this case, as
$s.$
(In this case, as
![]() $k=0$
the original line through
$k=0$
the original line through
![]() $y=(u_1,v_1)$
is its own perpendicular and so one must avoid the two choices of s where z coincides with
$y=(u_1,v_1)$
is its own perpendicular and so one must avoid the two choices of s where z coincides with
![]() $x=(0,0)$
or y.) Thus
$x=(0,0)$
or y.) Thus
![]() $p_{i,i}^0=(q-2)\delta _{i,0}$
. Note this
$p_{i,i}^0=(q-2)\delta _{i,0}$
. Note this
![]() $k=0$
case can occur only when
$k=0$
case can occur only when
![]() $q=1 \text { mod } 4$
.
$q=1 \text { mod } 4$
.
Otherwise,
![]() $k \neq 0$
and we get a quadratic equation for s whose discriminant can be calculated to be
$k \neq 0$
and we get a quadratic equation for s whose discriminant can be calculated to be
![]() $ (k+i-j)^2(\frac {v_1}{u_1})^2-4k((\frac {k+i-j}{2u_1})^2 -i)=\frac {1}{u_1^2}((k+i-j)^2v_1^2 -k(k+i-j)^2+4kiu_1^2)$
. Using
$ (k+i-j)^2(\frac {v_1}{u_1})^2-4k((\frac {k+i-j}{2u_1})^2 -i)=\frac {1}{u_1^2}((k+i-j)^2v_1^2 -k(k+i-j)^2+4kiu_1^2)$
. Using
![]() $v_1^2=k-u_1^2$
this becomes
$v_1^2=k-u_1^2$
this becomes
![]() $4ki-(k+i-j)^2=2(ki+ij+jk)-(k^2+i^2+j^2)=4\sigma _2-\sigma _1^2$
.
$4ki-(k+i-j)^2=2(ki+ij+jk)-(k^2+i^2+j^2)=4\sigma _2-\sigma _1^2$
.
Thus, there are
![]() $\binom {4\sigma _2-\sigma _1^2}{q}+1$
solutions for s where
$\binom {4\sigma _2-\sigma _1^2}{q}+1$
solutions for s where
![]() $\binom {x}{q}$
is the usual Legendre symbol.
$\binom {x}{q}$
is the usual Legendre symbol.
For the last statement, let
 $B=\begin {bmatrix} u_1 & u_2 \\ v_1 & v_2 \end {bmatrix}$
and note that
$B=\begin {bmatrix} u_1 & u_2 \\ v_1 & v_2 \end {bmatrix}$
and note that
 $B^TB=\begin {bmatrix} k & \frac {k+i-j}{2} \\ \frac {k+i-j}{2} & i \end {bmatrix}$
by the calculations above. The triple of points
$B^TB=\begin {bmatrix} k & \frac {k+i-j}{2} \\ \frac {k+i-j}{2} & i \end {bmatrix}$
by the calculations above. The triple of points
![]() $\{ (0,0), (u_1,v_1), (u_2,v_2) \}$
is collinear if and only if
$\{ (0,0), (u_1,v_1), (u_2,v_2) \}$
is collinear if and only if
![]() $rank(B) < 2$
if and only if
$rank(B) < 2$
if and only if
![]() $det(B)=0$
if and only if
$det(B)=0$
if and only if
 $det( \begin {bmatrix} k & \frac {k+i-j}{2} \\ \frac {k+i-j}{2} & i \end {bmatrix})=\frac {4\sigma _2-\sigma _1^2}{4}=0$
.
$det( \begin {bmatrix} k & \frac {k+i-j}{2} \\ \frac {k+i-j}{2} & i \end {bmatrix})=\frac {4\sigma _2-\sigma _1^2}{4}=0$
.
We record the following corollary, which exploits the odd behavior of isotropic lines when they exist.
Corollary 8.2 Let q be an odd prime power with
![]() $q=1 \text { mod } 4$
. Let
$q=1 \text { mod } 4$
. Let
![]() $E \subseteq \mathbb {F}_q^2$
have
$E \subseteq \mathbb {F}_q^2$
have
![]() $|E|> q$
and
$|E|> q$
and
![]() $\Delta '(E)$
be the nonzero distances achieved by E. Then
$\Delta '(E)$
be the nonzero distances achieved by E. Then
![]() $|E| \leq q + |\Delta '(E)|(|\Delta '(E)|-1)$
.
$|E| \leq q + |\Delta '(E)|(|\Delta '(E)|-1)$
.
Proof As
![]() $|E|> q$
, there exist two distinct points
$|E|> q$
, there exist two distinct points
![]() $x, y \in E$
with
$x, y \in E$
with
![]() $d(x,y)=0$
. Let
$d(x,y)=0$
. Let
![]() $E'=E \backslash L$
, where L is the line through x and y. This line L is isotropic in the sense that distances between distinct points on the line are always zero. Note that
$E'=E \backslash L$
, where L is the line through x and y. This line L is isotropic in the sense that distances between distinct points on the line are always zero. Note that
![]() $|E'| \geq |E|-q$
.
$|E'| \geq |E|-q$
.
By Theorem 8.1,
![]() $p_{i,j}^0=1$
for all
$p_{i,j}^0=1$
for all
![]() $i,j \in \mathbb {F}_q^{\times }$
with
$i,j \in \mathbb {F}_q^{\times }$
with
![]() $i \neq j$
and
$i \neq j$
and
![]() $p_{i,i}^0=0$
unless
$p_{i,i}^0=0$
unless
![]() $i=0$
. Furthermore, by the collinearity condition
$i=0$
. Furthermore, by the collinearity condition
![]() $4\sigma _2-\sigma _1^2=0$
, it is easy to check that a point
$4\sigma _2-\sigma _1^2=0$
, it is easy to check that a point
![]() $z \neq x, y$
is collinear with x and y if and only if
$z \neq x, y$
is collinear with x and y if and only if
![]() $d(z,x)=d(z,y)=0$
also.
$d(z,x)=d(z,y)=0$
also.
It follows that each point z off the isotropic line L through x and y is uniquely determined in the plane by the pair of unequal, nonzero distances
![]() $i=d(z,x)$
and
$i=d(z,x)$
and
![]() $j=d(z,y)$
. Thus
$j=d(z,y)$
. Thus
![]() $|E|-q \leq |E'| \leq |\Delta '(E)|(|\Delta '(E)|-1)$
from which the corollary follows.
$|E|-q \leq |E'| \leq |\Delta '(E)|(|\Delta '(E)|-1)$
from which the corollary follows.
We now recall the definition of the intersection matrices of an association scheme.
Definition 8.3 (Intersection matrices)
Let
![]() $(V,d)$
be an association scheme with distance set
$(V,d)$
be an association scheme with distance set
![]() $\Delta $
and intersection numbers
$\Delta $
and intersection numbers
![]() $p_{i,j}^k$
. We define
$p_{i,j}^k$
. We define
![]() $|\Delta |$
many
$|\Delta |$
many
![]() $|\Delta | \times |\Delta |$
intersection matrices of the scheme
$|\Delta | \times |\Delta |$
intersection matrices of the scheme
![]() $L_i, i \in \Delta $
via
$L_i, i \in \Delta $
via
In general, these satisfy
![]() $L_{\bar {0}}=\mathbb {I}$
and
$L_{\bar {0}}=\mathbb {I}$
and
![]() $L_i L_j = \sum _{k \in \Delta } p_{i,j}^k L_k$
. Thus the map
$L_i L_j = \sum _{k \in \Delta } p_{i,j}^k L_k$
. Thus the map
is an algebra epimorphism from the Bose–Messner algebra to the real algebra generated by these intersection matrices. Note the dimensions
![]() $|V| \times |V|$
of the
$|V| \times |V|$
of the
![]() $A_i$
matrices are in general quite different than the size of the
$A_i$
matrices are in general quite different than the size of the
![]() $L_i$
matrices.
$L_i$
matrices.
The eigenvalues of the
![]() $L_i$
matrix are the same as that of the
$L_i$
matrix are the same as that of the
![]() $A_i$
matrix but with different multiplicities. In fact the columns of the scheme’s Q matrix are the corresponding simultaneous (right) eigenvectors of the
$A_i$
matrix but with different multiplicities. In fact the columns of the scheme’s Q matrix are the corresponding simultaneous (right) eigenvectors of the
![]() $L_i$
while the rows of the P matrix are the (left) eigenvectors of the
$L_i$
while the rows of the P matrix are the (left) eigenvectors of the
![]() $L_i$
. These facts follow from the identity
$L_i$
. These facts follow from the identity
(see section 11.2 of [Reference Brouwer and Haemers5]).
We now record the intersection matrices for the planar Euclidean association scheme.
Theorem 8.4 Let q be an odd prime power and consider the planar Euclidean association scheme on
![]() $\mathbb {F}_q^2$
. Note
$\mathbb {F}_q^2$
. Note
![]() $L_{\bar {0}}$
is always an identity matrix. Recall when
$L_{\bar {0}}$
is always an identity matrix. Recall when
![]() $q=1 \text { mod } 4$
, we have
$q=1 \text { mod } 4$
, we have
![]() $\bar {0} \neq 0 \in \Delta $
also.
$\bar {0} \neq 0 \in \Delta $
also.
When
![]() $i,j \in \mathbb {F}_q^{\times }$
, we have
$i,j \in \mathbb {F}_q^{\times }$
, we have
![]() $(L_i)_{\bar {0},j}=p_{i,j}^{\bar {0}}=\delta _{i,j}|S_i|=\delta _{i,j}(q-\epsilon _q^2)$
and
$(L_i)_{\bar {0},j}=p_{i,j}^{\bar {0}}=\delta _{i,j}|S_i|=\delta _{i,j}(q-\epsilon _q^2)$
and
![]() $(L_i)_{0,j}=p_{i,j}^{0}=1-\delta _{i,j}$
.
$(L_i)_{0,j}=p_{i,j}^{0}=1-\delta _{i,j}$
.
We have
![]() $(L_i)_{j,\bar {0}}=p_{i,\bar {0}}^j=\delta _{i,j}$
and
$(L_i)_{j,\bar {0}}=p_{i,\bar {0}}^j=\delta _{i,j}$
and
![]() $(L_i)_{\bar {0},\bar {0}}=p^{\bar {0}}_{i,\bar {0}}=0$
.
$(L_i)_{\bar {0},\bar {0}}=p^{\bar {0}}_{i,\bar {0}}=0$
.
When
![]() $i,j \in \mathbb {F}_q$
,
$i,j \in \mathbb {F}_q$
,
![]() $k \in \mathbb {F}_q^{\times }$
, we have
$k \in \mathbb {F}_q^{\times }$
, we have
 $$ \begin{align*}(L_i)_{k,j}=p^k_{i,j}=\binom{4\sigma_2 - \sigma_1^2}{q} + 1 \in \{0,1,2\}, \end{align*} $$
$$ \begin{align*}(L_i)_{k,j}=p^k_{i,j}=\binom{4\sigma_2 - \sigma_1^2}{q} + 1 \in \{0,1,2\}, \end{align*} $$
where
![]() $\sigma _2=ij+jk+ki, \sigma _1=i+j+k$
and
$\sigma _2=ij+jk+ki, \sigma _1=i+j+k$
and
![]() $\binom {x}{q}$
is the Legendre symbol.
$\binom {x}{q}$
is the Legendre symbol.
When
![]() $q=3 \text { mod } 4$
, the spectrum of
$q=3 \text { mod } 4$
, the spectrum of
![]() $L_i$
is
$L_i$
is
![]() $\{\{ (q+1)^{(1)}, -K_q(1,a)^{(1)}, a \in \mathbb {F}_q^{\times } \}\}$
for any
$\{\{ (q+1)^{(1)}, -K_q(1,a)^{(1)}, a \in \mathbb {F}_q^{\times } \}\}$
for any
![]() $i \in \mathbb {F}_q^{\times }$
. Thus
$i \in \mathbb {F}_q^{\times }$
. Thus
![]() $\mathrm{Trace}(L_i^{\ell })=(q+1)^{\ell } + (-1)^{\ell }M_{q,\ell }$
.
$\mathrm{Trace}(L_i^{\ell })=(q+1)^{\ell } + (-1)^{\ell }M_{q,\ell }$
.
When
![]() $q=1 \text { mod } 4$
, the spectrum of
$q=1 \text { mod } 4$
, the spectrum of
![]() $L_i$
is
$L_i$
is
![]() $\{\{ (q-1)^{(1)}, -1^{(1)}, K_q(1,a)^{(1)}, a \in \mathbb {F}_q^{\times } \}\}$
for any
$\{\{ (q-1)^{(1)}, -1^{(1)}, K_q(1,a)^{(1)}, a \in \mathbb {F}_q^{\times } \}\}$
for any
![]() $i \in \mathbb {F}_q^{\times }$
. Thus
$i \in \mathbb {F}_q^{\times }$
. Thus
![]() $\mathrm{Trace}(L_i^{\ell })=(q-1)^{\ell } + (-1)^{\ell } + M_{q,\ell }$
.
$\mathrm{Trace}(L_i^{\ell })=(q-1)^{\ell } + (-1)^{\ell } + M_{q,\ell }$
.
Note that the entries of
![]() $L_i$
keep track of which triangles exist in the plane
$L_i$
keep track of which triangles exist in the plane
![]() $\mathbb {F}_q^2$
and through the last theorem, implicitly determine the Kloosterman moments
$\mathbb {F}_q^2$
and through the last theorem, implicitly determine the Kloosterman moments
![]() $M_{q,\ell }$
for all
$M_{q,\ell }$
for all
![]() $\ell $
. As it is well known that a finite multiset of complex numbers is determined by all its moments, this means the Kloosterman sums as a set are determined by exactly the data of which triangles exist in the plane
$\ell $
. As it is well known that a finite multiset of complex numbers is determined by all its moments, this means the Kloosterman sums as a set are determined by exactly the data of which triangles exist in the plane
![]() $\mathbb {F}_q^2$
.
$\mathbb {F}_q^2$
.