In an article published recently in Microscopy and Microanalysis (Bellido et al., Reference Bellido, Rossouw and Botton2014), the first application of the Richardson–Lucy (RL) algorithm was claimed for the deconvolution of surface plasmon resonances in electron energy-loss spectroscopy (EELS) data obtained with a monochromated electron beam. However, we previously reported such an application (Walther et al., Reference Walther, Schneider, Müller, Carmeli, Richter, Maniv, Cohen and Gerthsen2012, Reference Walther, Müller, Schneider and Gerthsen2013). In this work, we studied cavity modes hybridized with surface plasmon polaritons in submicron slits in a thin Au film. Such cavity modes were reported by Carmeli et al. (Reference Carmeli, Itskovsky, Kauffmann, Shaked, Richter, Maniv and Cohen2012) and strong enhancement of the cavity modes upon introduction of neighboring slits was also demonstrated (Walther et al., Reference Walther, Carmeli, Schneider, Gerthsen, Busch, Matyssek, Shvarzman, Richter and Cohen2014). We performed scanning transmission electron microscopy (STEM) at 300 keV combined with EELS in a FEI Titan3 80–300 (FEI, Hillsboro, OR, USA) with excited Wien-type filter monochromator. Spectra were taken with a high-resolution Gatan Imaging Filter Tridiem 865 (Gatan) using a dispersion of 10 meV/channel. The RL algorithm was adapted to EELS as proposed by Gloter et al. (Reference Gloter, Douiri, Tence and Colliex2003) in a self-written script in Digital Micrograph (Gatan, Pleasanton, CA, USA).
Figure 1 of this letter shows a series of spectra recorded in one slit with a size of 900×180 nm that is arranged in a two-slit system separated by a 100 nm wide metal bar. The spectra are shifted vertically for better visibility. The arrow in the inset high-angle annular dark-field STEM image marks the positions where the spectra were acquired. With decreasing distance to the central metal bar two low-energy peaks are resolved at energy losses ΔE of 0.5 and 1.47 eV in addition to the surface plasmon at 2.3 eV. The two low-energy signals are the fundamental mode and the third harmonic of a cavity standing wave (Carmeli et al., Reference Carmeli, Itskovsky, Kauffmann, Shaked, Richter, Maniv and Cohen2012) along the long slit direction. The second harmonic is missing because it has a node at the position where the spectra were taken. Spectra taken close to the opposite slit wall (e.g., the black spectrum in Fig. 1 taken at 10 nm distance from the outer wall) show these signals only as faint shoulders that do not allow the precise determination of the signal energy. Figure 2a demonstrates how the application of the RL algorithm yields a significant improvement of energy resolution and visibility of these weak signals. With an increasing number of iterations up to seven, the shoulder at ΔE=0.5 eV is clearly resolved as a peak. The most significant effect of the RL algorithm is observed close to the zero-loss peak that is substantially sharpened (inset in Fig. 2a) from a full-width at half-maximum of 120–70 meV. Owing to the tunability of the cavity-mode energies by variation of the slit length, slits are superb objects to evaluate the performance of EELS in the plasmon energy-loss range below 1.5 eV. Figure 2b shows raw and RL-processed EELS spectra taken in a 2.34 μm long slit at 20 nm distance from the slit wall. After seven iterations with the RL algorithm, the fundamental mode at ΔE=0.24 eV is well resolved as well as higher harmonics up to the ninth order. Higher harmonics of even order are missing for symmetry reasons.
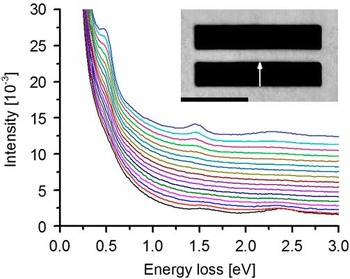
Figure 1 Series of electron energy-loss spectroscopy spectra acquired across one slit of two-slit system. The inset shows a high-angle annular dark-field scanning transmission electron microscopic image of the two-slit structure. The arrow depicts the acquizition direction of the spectra from the outer to the inner wall of one slit in the two-slit system. The black bar indicates 500 nm.
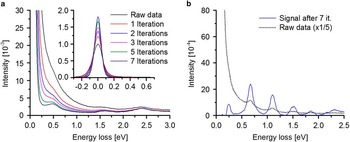
Figure 2 a: Effect of processing with the Richardson–Lucy (RL) algorithm on the bottom-most (black) electron energy-loss spectroscopy spectrum in Figure 1. The faint signal at ΔE=0.5 eV is clearly resolved with increasing number of iterations up to seven. The inset shows the effect of RL processing on the zero-loss peak. b: Raw (dotted line, raw intensity divided by five) and RL processed spectra (solid line) from a 2.34 μm long slit.
The data shown in Figure 2a of this letter was reported in 2013 (Walther et al., Reference Walther, Müller, Schneider and Gerthsen2013). RL processing of similar EELS data obtained from submicron slits were previously presented in 2012 (Walther et al., Reference Walther, Schneider, Müller, Carmeli, Richter, Maniv, Cohen and Gerthsen2012). This demonstrates that RL processing of EELS data acquired under monochromatized beam conditions was introduced before Bellido et al. (Reference Bellido, Rossouw and Botton2014).




