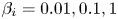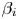1. Introduction
Plasma turbulence plays an important role in the transport of energy throughout the heliosphere, governing the conversion of the energy of large-scale magnetic fields and plasma flows into heat of the plasma species. Under the hot and diffuse conditions typical of heliospheric plasmas, collisionless interactions between the electromagnetic fields and the individual plasma particles govern the rate of damping of the turbulent fluctuations and the resulting particle energization. Landau damping (Landau Reference Landau1946) is one of several collisionless mechanisms that may transfer electromagnetic energy to particle energy in a weakly collisional plasma, and it has been proposed to be of considerable importance in dissipating the turbulent energy in the solar wind (Leamon et al. Reference Leamon, Smith, Ness, Matthaeus and Wong1998, Reference Leamon, Smith, Ness and Wong1999; Quataert Reference Quataert1998; Howes et al. Reference Howes, Cowley, Dorland, Hammett, Quataert and Schekochihin2008a; Schekochihin et al. Reference Schekochihin, Cowley, Dorland, Hammett, Howes, Quataert and Tatsuno2009; Howes Reference Howes2011; Howes, Tenbarge & Dorland Reference Howes, Tenbarge and Dorland2011a; TenBarge & Howes Reference TenBarge and Howes2013; Howes Reference Howes2015; Li et al. Reference Li, Howes, Klein and TenBarge2016). Recent analyses of observations in the Earth's turbulent magnetosheath plasma from the Magnetospheric Multiscale (MMS) mission (Burch et al. Reference Burch, Moore, Torbert and Giles2016) have provided the first in situ evidence of electron Landau damping acting to dissipate turbulence in any space plasma (Chen, Klein & Howes Reference Chen, Klein and Howes2019; Afshari et al. Reference Afshari, Howes, Kletzing, Hartley and Boardsen2021). Understanding how energy is transferred to plasma particles in turbulent dissipation is a major goal in heliophysics, needed to explain the long-standing problem of how the solar corona is heated to temperatures above $1\times 10^6$![]() K (Edlén Reference Edlén1943, Reference Edlén1945) in which turbulence is thought to play a crucial role (Withbroe & Noyes Reference Withbroe and Noyes1977; Heyvaerts & Priest Reference Heyvaerts and Priest1983; Parker Reference Parker1988; Klimchuk Reference Klimchuk2006; Cranmer Reference Cranmer2009; Chandran Reference Chandran2010), or to predict the observed non-adiabatic temperature profile of the expanding solar wind (Richardson & Smith Reference Richardson and Smith2003). A variety of mechanisms are likely to be involved in the dissipation process; descriptions of these can be found in a recent literature review (Verscharen, Klein & Maruca Reference Verscharen, Klein and Maruca2019).
K (Edlén Reference Edlén1943, Reference Edlén1945) in which turbulence is thought to play a crucial role (Withbroe & Noyes Reference Withbroe and Noyes1977; Heyvaerts & Priest Reference Heyvaerts and Priest1983; Parker Reference Parker1988; Klimchuk Reference Klimchuk2006; Cranmer Reference Cranmer2009; Chandran Reference Chandran2010), or to predict the observed non-adiabatic temperature profile of the expanding solar wind (Richardson & Smith Reference Richardson and Smith2003). A variety of mechanisms are likely to be involved in the dissipation process; descriptions of these can be found in a recent literature review (Verscharen, Klein & Maruca Reference Verscharen, Klein and Maruca2019).
In the solar wind, observations show that the incompressible (Alfvénic) component dominates turbulent fluctuations within the inertial range (Bruno & Carbone Reference Bruno and Carbone2005; Alexandrova et al. Reference Alexandrova, Carbone, Veltri and Sorriso-Valvo2008). As the turbulent cascade of Alfvénic fluctuations reaches the ion kinetic length scales, finite Larmor radius effects lead to the development of a non-zero component of the electric field parallel to the local mean magnetic field. Particles with a parallel velocity near the parallel phase velocity of an Alfvén wave can resonantly interact with the parallel electric field of the wave and thereby gain or lose energy. This results in net energization of the particles if, in the region of the resonance, the initial slope of the distribution function is negative (positive) for particles with $v_\parallel > 0$![]() ($v_\parallel < 0$
($v_\parallel < 0$![]() ). This collisionless transfer of energy from the electric field to the particles is entropy conserving and thus reversible. However, in practice arbitrarily weak Coulomb collisions acting on small velocity scales in the particle distribution function serve to thermalize the energy, realizing thermodynamic heating of that plasma species (Howes et al. Reference Howes, Cowley, Dorland, Hammett, Quataert and Schekochihin2006; Howes Reference Howes2008; Schekochihin et al. Reference Schekochihin, Cowley, Dorland, Hammett, Howes, Quataert and Tatsuno2009). Landau damping is capable of energizing ions at perpendicular scales near the ion Larmor radius, $k_\perp \rho _i \sim 1$
). This collisionless transfer of energy from the electric field to the particles is entropy conserving and thus reversible. However, in practice arbitrarily weak Coulomb collisions acting on small velocity scales in the particle distribution function serve to thermalize the energy, realizing thermodynamic heating of that plasma species (Howes et al. Reference Howes, Cowley, Dorland, Hammett, Quataert and Schekochihin2006; Howes Reference Howes2008; Schekochihin et al. Reference Schekochihin, Cowley, Dorland, Hammett, Howes, Quataert and Tatsuno2009). Landau damping is capable of energizing ions at perpendicular scales near the ion Larmor radius, $k_\perp \rho _i \sim 1$![]() , and electrons at smaller perpendicular scales, $k_\perp \rho _i \gtrsim 1$
, and electrons at smaller perpendicular scales, $k_\perp \rho _i \gtrsim 1$![]() (Leamon et al. Reference Leamon, Smith, Ness and Wong1999; Quataert Reference Quataert1998; Howes et al. Reference Howes, Cowley, Dorland, Hammett, Quataert and Schekochihin2008a; Schekochihin et al. Reference Schekochihin, Cowley, Dorland, Hammett, Howes, Quataert and Tatsuno2009; Howes Reference Howes2011; Howes et al. Reference Howes, Tenbarge and Dorland2011a; TenBarge & Howes Reference TenBarge and Howes2013; Howes Reference Howes2015; Kiyani, Osman & Chapman Reference Kiyani, Osman and Chapman2015; Told et al. Reference Told, Jenko, TenBarge, Howes and Hammett2015; Li et al. Reference Li, Howes, Klein and TenBarge2016).
(Leamon et al. Reference Leamon, Smith, Ness and Wong1999; Quataert Reference Quataert1998; Howes et al. Reference Howes, Cowley, Dorland, Hammett, Quataert and Schekochihin2008a; Schekochihin et al. Reference Schekochihin, Cowley, Dorland, Hammett, Howes, Quataert and Tatsuno2009; Howes Reference Howes2011; Howes et al. Reference Howes, Tenbarge and Dorland2011a; TenBarge & Howes Reference TenBarge and Howes2013; Howes Reference Howes2015; Kiyani, Osman & Chapman Reference Kiyani, Osman and Chapman2015; Told et al. Reference Told, Jenko, TenBarge, Howes and Hammett2015; Li et al. Reference Li, Howes, Klein and TenBarge2016).
Recent analyses of burst-mode measurements from the MMS mission (Burch et al. Reference Burch, Moore, Torbert and Giles2016) using the field–particle correlation technique (Klein & Howes Reference Klein and Howes2016; Howes, Klein & Li Reference Howes, Klein and Li2017; Klein, Howes & Tenbarge Reference Klein, Howes and Tenbarge2017) have provided the first direct observational evidence of electron Landau damping acting to damp turbulence in the Earth's magnetosheath plasma (Chen et al. Reference Chen, Klein and Howes2019). Following this groundbreaking study, a survey of the field–particle correlation signatures in 20 MMS intervals was conducted, revealing evidence for electron Landau damping in 19 of the intervals. In one-third of those intervals, the study indicated that this mechanism may be responsible for a dominant fraction of the damping required to terminate the solar wind turbulent cascade (Afshari et al. Reference Afshari, Howes, Kletzing, Hartley and Boardsen2021).
Motivated by these results, we previously used a high-resolution, gyrokinetic simulation to recreate the field–particle correlation signature of electron Landau damping in plasma conditions matching the first MMS interval that yielded an in situ observation of electron Landau damping (Chen et al. Reference Chen, Klein and Howes2019). The study demonstrated that electron Landau damping is observable in gyrokinetic turbulence simulations and confirmed the complex features of Landau damping in the regime of dispersive kinetic Alfvén waves (KAWs) (Horvath, Howes & McCubbin Reference Horvath, Howes and McCubbin2020). In particular, we showed how the bipolar signatures of Landau damping of KAWs at different phase velocities may appear together in velocity-space to produce field–particle correlations with multiple bipolar signatures or with superimposed signatures that create a single, broadened structure. Furthermore, we demonstrated that the broadband frequency content in velocity-space fluctuations increases the difficulty of observing signatures in broadband turbulence due to the inability to choose the correlation interval $\tau$![]() such that it averages over an integer multiple of all of the wave modes represented (Klein & Howes Reference Klein and Howes2016; Howes et al. Reference Howes, Klein and Li2017; Klein et al. Reference Klein, Howes and Tenbarge2017; Horvath et al. Reference Horvath, Howes and McCubbin2020)
such that it averages over an integer multiple of all of the wave modes represented (Klein & Howes Reference Klein and Howes2016; Howes et al. Reference Howes, Klein and Li2017; Klein et al. Reference Klein, Howes and Tenbarge2017; Horvath et al. Reference Horvath, Howes and McCubbin2020)
In this paper, it is our goal to follow up on our previous work by applying the field–particle correlation technique to a suite of gyrokinetic simulations. Through this, we will construct a framework for identifying the presence of electron Landau damping in situ throughout the inner heliosphere. Though the fiducial field–particle correlation signature of ion Landau damping is well understood (Klein & Howes Reference Klein and Howes2016; Klein et al. Reference Klein, Howes and Tenbarge2017), our first study showed that electron Landau damping produces more complicated signatures due to the dispersive nature of KAWs at spatial scales smaller than the ion Larmor radius, $k_\perp \rho _i \gtrsim 1$![]() (Horvath et al. Reference Horvath, Howes and McCubbin2020). Further, the range of wavenumbers and frequencies over which KAWs are dispersive changes with the ion plasma beta $\beta _i= 8 {\rm \pi}n_i T_i/B^2$
(Horvath et al. Reference Horvath, Howes and McCubbin2020). Further, the range of wavenumbers and frequencies over which KAWs are dispersive changes with the ion plasma beta $\beta _i= 8 {\rm \pi}n_i T_i/B^2$![]() – the ratio of the ion thermal to magnetic pressure – and with the ion-to-electron temperature ratio $T_i/T_e$
– the ratio of the ion thermal to magnetic pressure – and with the ion-to-electron temperature ratio $T_i/T_e$![]() . Both of these quantities change throughout the heliosphere. In order to understand how the signature of electron Landau damping will appear at different locations in the inner heliosphere, therefore, we create four high-resolution gyrokinetic simulations at different ion plasma beta $\beta _i$
. Both of these quantities change throughout the heliosphere. In order to understand how the signature of electron Landau damping will appear at different locations in the inner heliosphere, therefore, we create four high-resolution gyrokinetic simulations at different ion plasma beta $\beta _i$![]() values and analyse these simulations with the field–particle correlation technique, described in § 2.1. In addition, we create and analyse a set of single KAW simulations to aid in interpreting the field–particle correlation signatures in turbulence. Both of these simulation types are described in more detail in § 2.2. The insights gained from the single-wave runs are discussed in § 3, and we present results from the turbulent simulations in § 4, and discuss the implications for observing these signatures in situ in § 5.
values and analyse these simulations with the field–particle correlation technique, described in § 2.1. In addition, we create and analyse a set of single KAW simulations to aid in interpreting the field–particle correlation signatures in turbulence. Both of these simulation types are described in more detail in § 2.2. The insights gained from the single-wave runs are discussed in § 3, and we present results from the turbulent simulations in § 4, and discuss the implications for observing these signatures in situ in § 5.
2. Methods
2.1. The field–particle correlation technique
The field–particle correlation technique (Klein & Howes Reference Klein and Howes2016; Howes et al. Reference Howes, Klein and Li2017; Klein et al. Reference Klein, Howes and Tenbarge2017) uses single-point measurements of the velocity distribution function and electromagnetic fields to measure the rate of change of the particle phase-space energy density $w_s ({\boldsymbol x},{\boldsymbol v},t)= \tfrac {1}{2}m_s {\boldsymbol v}^2 f_s({\boldsymbol x},{\boldsymbol v},t)$![]() and to identify particle energization mechanisms in weakly collisional plasmas. Energization mechanisms interact with particles in specific regions of velocity-space, thereby creating characteristic patterns as net energy is transferred between fields and particles. Correlating field and particle data together generates these characteristic velocity-space signatures and, in doing so, makes possible the identification of the physical mechanism at work and determines the net change in phase-space energy density. The field–particle correlation technique has been successfully applied to understand particle energization in a wide range of fundamental plasma physics processes: (i) collisionless damping of electrostatic (Klein & Howes Reference Klein and Howes2016; Howes et al. Reference Howes, Klein and Li2017) and electromagnetic (Howes Reference Howes2017; Klein et al. Reference Klein, Howes and Tenbarge2017; Howes, McCubbin & Klein Reference Howes, McCubbin and Klein2018) plasma waves; (ii) kinetic instabilities (Klein Reference Klein2017); (iii) damping of electromagnetic plasma turbulence through ion Landau damping (Klein et al. Reference Klein, Howes and Tenbarge2017; Howes et al. Reference Howes, McCubbin and Klein2018; Klein et al. Reference Klein, Howes, TenBarge and Valentini2020), ion transit-time damping (Arzamasskiy et al. Reference Arzamasskiy, Kunz, Chandran and Quataert2019; Cerri, Arzamasskiy & Kunz Reference Cerri, Arzamasskiy and Kunz2021), electron Landau damping (Chen et al. Reference Chen, Klein and Howes2019; Horvath et al. Reference Horvath, Howes and McCubbin2020; Afshari et al. Reference Afshari, Howes, Kletzing, Hartley and Boardsen2021; Horvath, Howes & McCubbin Reference Horvath, Howes and McCubbin2022), ion cyclotron damping (Klein et al. Reference Klein, Howes, TenBarge and Valentini2020; Afshari et al. Reference Afshari, Howes, Shuster, Klein, McGinnis, Martinovic, Boardsen, Kletzing and Hartley2023), electron magnetic pumping (Montag & Howes Reference Montag and Howes2022), ion stochastic heating (Arzamasskiy et al. Reference Arzamasskiy, Kunz, Chandran and Quataert2019; Cerri et al. Reference Cerri, Arzamasskiy and Kunz2021); (iv) electron energization in collisionless magnetic reconnection (McCubbin, Howes & TenBarge Reference McCubbin, Howes and TenBarge2022); and (v) ion and electron acceleration in collisionless shocks (Juno et al. Reference Juno, Howes, TenBarge, Wilson, Spitkovsky, Caprioli, Klein and Hakim2021, Reference Juno, Brown, Howes, Haggerty, TenBarge, Wilson, Caprioli and Klein2023; Brown et al. Reference Brown, Juno, Howes, Haggerty and Constantinou2023).
and to identify particle energization mechanisms in weakly collisional plasmas. Energization mechanisms interact with particles in specific regions of velocity-space, thereby creating characteristic patterns as net energy is transferred between fields and particles. Correlating field and particle data together generates these characteristic velocity-space signatures and, in doing so, makes possible the identification of the physical mechanism at work and determines the net change in phase-space energy density. The field–particle correlation technique has been successfully applied to understand particle energization in a wide range of fundamental plasma physics processes: (i) collisionless damping of electrostatic (Klein & Howes Reference Klein and Howes2016; Howes et al. Reference Howes, Klein and Li2017) and electromagnetic (Howes Reference Howes2017; Klein et al. Reference Klein, Howes and Tenbarge2017; Howes, McCubbin & Klein Reference Howes, McCubbin and Klein2018) plasma waves; (ii) kinetic instabilities (Klein Reference Klein2017); (iii) damping of electromagnetic plasma turbulence through ion Landau damping (Klein et al. Reference Klein, Howes and Tenbarge2017; Howes et al. Reference Howes, McCubbin and Klein2018; Klein et al. Reference Klein, Howes, TenBarge and Valentini2020), ion transit-time damping (Arzamasskiy et al. Reference Arzamasskiy, Kunz, Chandran and Quataert2019; Cerri, Arzamasskiy & Kunz Reference Cerri, Arzamasskiy and Kunz2021), electron Landau damping (Chen et al. Reference Chen, Klein and Howes2019; Horvath et al. Reference Horvath, Howes and McCubbin2020; Afshari et al. Reference Afshari, Howes, Kletzing, Hartley and Boardsen2021; Horvath, Howes & McCubbin Reference Horvath, Howes and McCubbin2022), ion cyclotron damping (Klein et al. Reference Klein, Howes, TenBarge and Valentini2020; Afshari et al. Reference Afshari, Howes, Shuster, Klein, McGinnis, Martinovic, Boardsen, Kletzing and Hartley2023), electron magnetic pumping (Montag & Howes Reference Montag and Howes2022), ion stochastic heating (Arzamasskiy et al. Reference Arzamasskiy, Kunz, Chandran and Quataert2019; Cerri et al. Reference Cerri, Arzamasskiy and Kunz2021); (iv) electron energization in collisionless magnetic reconnection (McCubbin, Howes & TenBarge Reference McCubbin, Howes and TenBarge2022); and (v) ion and electron acceleration in collisionless shocks (Juno et al. Reference Juno, Howes, TenBarge, Wilson, Spitkovsky, Caprioli, Klein and Hakim2021, Reference Juno, Brown, Howes, Haggerty, TenBarge, Wilson, Caprioli and Klein2023; Brown et al. Reference Brown, Juno, Howes, Haggerty and Constantinou2023).
The field–particle correlation is derived by multiplying the Vlasov equation for species $s$![]() by $m_sv^2/2$
by $m_sv^2/2$![]() to obtain an equation for the rate of change of phase-space energy density $\partial w_s ({\boldsymbol x},{\boldsymbol v},t)/\partial t$
to obtain an equation for the rate of change of phase-space energy density $\partial w_s ({\boldsymbol x},{\boldsymbol v},t)/\partial t$![]() . Time-averaging the electric field term in the resulting equation over a correlation interval $\tau$
. Time-averaging the electric field term in the resulting equation over a correlation interval $\tau$![]() yields the form of the field–particle correlation. The contribution from the component of the parallel electric field yields the net energy transfer from Landau damping at a given spatial point $\boldsymbol {r}_0$
yields the form of the field–particle correlation. The contribution from the component of the parallel electric field yields the net energy transfer from Landau damping at a given spatial point $\boldsymbol {r}_0$![]() , and is called the parallel field–particle correlation (Howes et al. Reference Howes, Klein and Li2017; Klein et al. Reference Klein, Howes and Tenbarge2017),
, and is called the parallel field–particle correlation (Howes et al. Reference Howes, Klein and Li2017; Klein et al. Reference Klein, Howes and Tenbarge2017),

Taking a cylindrical coordinate system in velocity-space that is aligned with the direction of the local mean magnetic field, $(v_\parallel,v_\perp,\theta )$![]() , we can integrate the parallel correlation over the gyrophase $\theta$
, we can integrate the parallel correlation over the gyrophase $\theta$![]() to obtain the parallel field–particle correlation in gyrotropic phase space, $C_{E_\parallel }(v_\parallel, v_\perp,t)$
to obtain the parallel field–particle correlation in gyrotropic phase space, $C_{E_\parallel }(v_\parallel, v_\perp,t)$![]() , with the correlation (time-averaging) interval $\tau$
, with the correlation (time-averaging) interval $\tau$![]() centred at time $t$
centred at time $t$![]() and taken at a specified spatial location $\boldsymbol {r}_0$
and taken at a specified spatial location $\boldsymbol {r}_0$![]() (e.g. see contour plots in figure 7). Below we suppress the $\boldsymbol {r}_0$
(e.g. see contour plots in figure 7). Below we suppress the $\boldsymbol {r}_0$![]() argument, with the implication that each field–particle correlation is computed using data from a single spatial point. The resulting energy transfer between the parallel electric field and the particles includes two contributions in the case of Landau damping: (i) the conservative, oscillating energy transfer between the waves and the particles that is associated with undamped waves; and (ii) the secular energy transfer from the parallel electric field to the particles that is associated with collisionless damping via the Landau resonance. In the case of plasma turbulence, the oscillatory energy transfer is often larger in amplitude than the secular energy transfer. Applying a time average over a suitably chosen correlation interval cancels out the large-amplitude oscillatory energy transfer to reveal the smaller amplitude signature of the collisionless damping. For turbulence simulations, one may choose a correlation interval $\tau$
argument, with the implication that each field–particle correlation is computed using data from a single spatial point. The resulting energy transfer between the parallel electric field and the particles includes two contributions in the case of Landau damping: (i) the conservative, oscillating energy transfer between the waves and the particles that is associated with undamped waves; and (ii) the secular energy transfer from the parallel electric field to the particles that is associated with collisionless damping via the Landau resonance. In the case of plasma turbulence, the oscillatory energy transfer is often larger in amplitude than the secular energy transfer. Applying a time average over a suitably chosen correlation interval cancels out the large-amplitude oscillatory energy transfer to reveal the smaller amplitude signature of the collisionless damping. For turbulence simulations, one may choose a correlation interval $\tau$![]() that is longer than the period of waves at the simulation domain scale (Klein & Howes Reference Klein and Howes2016; Howes et al. Reference Howes, Klein and Li2017; Klein et al. Reference Klein, Howes and Tenbarge2017). For spacecraft observations, in which there is a broadband frequency spectrum, including wave periods much longer than the MMS burst-mode intervals used for the analysis, one may employ a high-pass filter to the electric field to eliminate the large-amplitude, low frequency contribution to undamped wave motion, isolating the wave periods at kinetic scales where collisionless damping is expected to arise (Chen et al. Reference Chen, Klein and Howes2019; Afshari et al. Reference Afshari, Howes, Kletzing, Hartley and Boardsen2021).
that is longer than the period of waves at the simulation domain scale (Klein & Howes Reference Klein and Howes2016; Howes et al. Reference Howes, Klein and Li2017; Klein et al. Reference Klein, Howes and Tenbarge2017). For spacecraft observations, in which there is a broadband frequency spectrum, including wave periods much longer than the MMS burst-mode intervals used for the analysis, one may employ a high-pass filter to the electric field to eliminate the large-amplitude, low frequency contribution to undamped wave motion, isolating the wave periods at kinetic scales where collisionless damping is expected to arise (Chen et al. Reference Chen, Klein and Howes2019; Afshari et al. Reference Afshari, Howes, Kletzing, Hartley and Boardsen2021).
The velocity-space signatures of the particle energization can be presented in a variety of useful ways. To determine if the signature is coherent over time, $C_{E_\parallel }(v_\parallel, v_\perp, t)$![]() may be integrated over the perpendicular velocity $v_\perp$
may be integrated over the perpendicular velocity $v_\perp$![]() to obtain the reduced parallel correlation $C_{E_\parallel }(v_\parallel, t)$
to obtain the reduced parallel correlation $C_{E_\parallel }(v_\parallel, t)$![]() . This rate of energization versus $v_\parallel$
. This rate of energization versus $v_\parallel$![]() can be plotted as a line plot at a single time $t$
can be plotted as a line plot at a single time $t$![]() (e.g., figure 7, lower subpanels), or the $v_\parallel$
(e.g., figure 7, lower subpanels), or the $v_\parallel$![]() -dependence at each time can be stacked to generate a timestack plot of $C_{E_\parallel }(v_\parallel, t)$
-dependence at each time can be stacked to generate a timestack plot of $C_{E_\parallel }(v_\parallel, t)$![]() (e.g. see figure 8, central contour plots), revealing the persistence of the energization mechanism over time. To determine the net effect of the energization mechanism as a function of $v_\parallel$
(e.g. see figure 8, central contour plots), revealing the persistence of the energization mechanism over time. To determine the net effect of the energization mechanism as a function of $v_\parallel$![]() , integrating the reduced parallel correlation over time yields the time-integrated, reduced parallel correlation $C_{E_\parallel }(v_\parallel )$
, integrating the reduced parallel correlation over time yields the time-integrated, reduced parallel correlation $C_{E_\parallel }(v_\parallel )$![]() (e.g., figure 8, lower subpanels), providing the full time-averaged change in the phase-space energy density $w_s$
(e.g., figure 8, lower subpanels), providing the full time-averaged change in the phase-space energy density $w_s$![]() as a function of $v_\parallel$
as a function of $v_\parallel$![]() . Alternatively, one may instead integrate the reduced parallel correlation over $v_\parallel$
. Alternatively, one may instead integrate the reduced parallel correlation over $v_\parallel$![]() to obtain the total rate of change of spatial energy density at position ${\boldsymbol r}_0$
to obtain the total rate of change of spatial energy density at position ${\boldsymbol r}_0$![]() due to the parallel electric field, $(\partial W_s/\partial t)_{E_\parallel }$
due to the parallel electric field, $(\partial W_s/\partial t)_{E_\parallel }$![]() (e.g., figure 8, left-hand subpanels). Note that $(\partial W_s/\partial t)_{E_\parallel }=j_{e,\parallel } E_\parallel$
(e.g., figure 8, left-hand subpanels). Note that $(\partial W_s/\partial t)_{E_\parallel }=j_{e,\parallel } E_\parallel$![]() is simply the rate of electromagnetic work done by the parallel electric field on the electrons.
is simply the rate of electromagnetic work done by the parallel electric field on the electrons.
2.2. AstroGK simulations
The astrophysical gyrokinetics code, AstoGK (Numata et al. Reference Numata, Howes, Tatsuno, Barnes and Dorland2010), was used to generate a suite of four plasma turbulence simulations spanning expected conditions in the solar wind of the inner heliosphere. These four simulations use a realistic mass ratio, $m_i/m_e = 1836$![]() , in order to properly separate the ion and electron scales within the turbulent cascade, have a unity temperature ratio $T_i/T_e = 1$
, in order to properly separate the ion and electron scales within the turbulent cascade, have a unity temperature ratio $T_i/T_e = 1$![]() and sweep through four different plasma beta values, $\beta _i={0.01,0.1,1,10}$
and sweep through four different plasma beta values, $\beta _i={0.01,0.1,1,10}$![]() . Each AstroGK simulation evolves the complementary, perturbed gyrokinetic distribution function, $g_s(v_\parallel,v_\perp, t)$
. Each AstroGK simulation evolves the complementary, perturbed gyrokinetic distribution function, $g_s(v_\parallel,v_\perp, t)$![]() , where $g_s(v_\parallel,v_\perp ) = h_s(v_\parallel,v_\perp ) - ({q_s F_{0s}}/{T_{0s}}) \langle \phi - \boldsymbol {v}_\perp \boldsymbol {\cdot } \boldsymbol {A}_\perp \rangle _{\boldsymbol {R}_s}$
, where $g_s(v_\parallel,v_\perp ) = h_s(v_\parallel,v_\perp ) - ({q_s F_{0s}}/{T_{0s}}) \langle \phi - \boldsymbol {v}_\perp \boldsymbol {\cdot } \boldsymbol {A}_\perp \rangle _{\boldsymbol {R}_s}$![]() , $h_s$
, $h_s$![]() is the gyrokinetic distribution function and $\langle \rangle _{\boldsymbol {R}_s}$
is the gyrokinetic distribution function and $\langle \rangle _{\boldsymbol {R}_s}$![]() denotes a gyroaverage about a fixed gyrocentre coordinate $\boldsymbol {R}_s$
denotes a gyroaverage about a fixed gyrocentre coordinate $\boldsymbol {R}_s$![]() (Numata et al. Reference Numata, Howes, Tatsuno, Barnes and Dorland2010). We choose $g_s(v_\parallel,v_\perp, t)$
(Numata et al. Reference Numata, Howes, Tatsuno, Barnes and Dorland2010). We choose $g_s(v_\parallel,v_\perp, t)$![]() at a fixed probe position $\boldsymbol {r}_0$
at a fixed probe position $\boldsymbol {r}_0$![]() as the distribution function $f_s(\boldsymbol {r_0},\boldsymbol {v},t)$
as the distribution function $f_s(\boldsymbol {r_0},\boldsymbol {v},t)$![]() in our computation of the parallel field–particle correlation by (2.1).
in our computation of the parallel field–particle correlation by (2.1).
We choose the physical ($x,y,z$![]() ) and velocity ($\lambda, \varepsilon$
) and velocity ($\lambda, \varepsilon$![]() ) space resolution in each simulation to be $(n_x, n_y, n_z, n_\lambda, n_\varepsilon, n_s) = (64, 64, 32, 128, 32, 2)$
) space resolution in each simulation to be $(n_x, n_y, n_z, n_\lambda, n_\varepsilon, n_s) = (64, 64, 32, 128, 32, 2)$![]() , where $n_s$
, where $n_s$![]() is the number of plasma species and velocity-space is partitioned into a gyrotropic grid by pitch angle $\lambda =v_\perp ^2/v^2$
is the number of plasma species and velocity-space is partitioned into a gyrotropic grid by pitch angle $\lambda =v_\perp ^2/v^2$![]() and energy $\varepsilon = v^2$
and energy $\varepsilon = v^2$![]() . Velocity $v$
. Velocity $v$![]() is normalized to the thermal velocity, $v_{ts} = \sqrt {2T_s/m_s}$
is normalized to the thermal velocity, $v_{ts} = \sqrt {2T_s/m_s}$![]() , for each species. Each simulation domain is an elongated three-dimensional Eulerian slab with dimensions $L_\parallel \times L_\perp ^2$
, for each species. Each simulation domain is an elongated three-dimensional Eulerian slab with dimensions $L_\parallel \times L_\perp ^2$![]() , given by $L_\parallel = 2 {\rm \pi}a_0$
, given by $L_\parallel = 2 {\rm \pi}a_0$![]() and $L_\perp = {\rm \pi}\rho _i$
and $L_\perp = {\rm \pi}\rho _i$![]() , where the ion thermal Larmor radius is $\rho _i =v_{ti}/\varOmega _i$
, where the ion thermal Larmor radius is $\rho _i =v_{ti}/\varOmega _i$![]() , and the ion cyclotron frequency is given by $\varOmega _i=q_iB_0/m_ic$
, and the ion cyclotron frequency is given by $\varOmega _i=q_iB_0/m_ic$![]() . The elongation of the simulation domain is characterized by the small gyrokinetic expansion parameter, where $\epsilon \sim \rho _i/a_0\ll 1$
. The elongation of the simulation domain is characterized by the small gyrokinetic expansion parameter, where $\epsilon \sim \rho _i/a_0\ll 1$![]() (Howes et al. Reference Howes, Cowley, Dorland, Hammett, Quataert and Schekochihin2006, Reference Howes, Dorland, Cowley, Hammett, Quataert, Schekochihin and Tatsuno2008b, Reference Howes, Tenbarge, Dorland, Quataert, Schekochihin, Numata and Tatsuno2011b). For these parameters, the fully resolved range of perpendicular scales is given by $2 \le k_\perp \rho _i \le 42$
(Howes et al. Reference Howes, Cowley, Dorland, Hammett, Quataert and Schekochihin2006, Reference Howes, Dorland, Cowley, Hammett, Quataert, Schekochihin and Tatsuno2008b, Reference Howes, Tenbarge, Dorland, Quataert, Schekochihin, Numata and Tatsuno2011b). For these parameters, the fully resolved range of perpendicular scales is given by $2 \le k_\perp \rho _i \le 42$![]() , or $0.05 \lesssim k_\perp \rho _e \lesssim 1$
, or $0.05 \lesssim k_\perp \rho _e \lesssim 1$![]() , capturing a broad range of dispersive KAW frequencies (see figure 2). Note that, for each timeslice, the fields are output at each point on the high-resolution spatial grid but the electron velocity distribution function is output only at $24$
, capturing a broad range of dispersive KAW frequencies (see figure 2). Note that, for each timeslice, the fields are output at each point on the high-resolution spatial grid but the electron velocity distribution function is output only at $24$![]() individual ‘probes’ spread throughout the simulation box. Sixteen are in the midplane ($z=0$
individual ‘probes’ spread throughout the simulation box. Sixteen are in the midplane ($z=0$![]() ) and the remaining eight along the $z$
) and the remaining eight along the $z$![]() -axis ($x=y=0$
-axis ($x=y=0$![]() ), as indicated in figure 2 of Horvath et al. (Reference Horvath, Howes and McCubbin2020).
), as indicated in figure 2 of Horvath et al. (Reference Horvath, Howes and McCubbin2020).
An oscillating Langevin antenna (TenBarge et al. Reference TenBarge, Howes, Dorland and Hammett2014) drives counter-propagating, perpendicularly polarized Alfvén waves with $(k_x\rho _i, k_y\rho _i, k_z a_0) = (2, 0, \pm 1)$![]() and $(0, 2, \pm 1)$
and $(0, 2, \pm 1)$![]() to launch a turbulent cascade for each simulation. The driving frequencies $\omega _0$
to launch a turbulent cascade for each simulation. The driving frequencies $\omega _0$![]() and decorrelation rates $\gamma _0$
and decorrelation rates $\gamma _0$![]() for each driven mode are listed in table 1, where $\bar {\omega }\equiv \omega /k_{\parallel 0} v_A$
for each driven mode are listed in table 1, where $\bar {\omega }\equiv \omega /k_{\parallel 0} v_A$![]() and $k_{\parallel 0}=2 {\rm \pi}/L_\parallel$
and $k_{\parallel 0}=2 {\rm \pi}/L_\parallel$![]() . The amplitude of the driving is chosen in accordance with critically balanced KAW turbulence (Howes et al. Reference Howes, Cowley, Dorland, Hammett, Quataert and Schekochihin2008a, Reference Howes, Tenbarge and Dorland2011a) in order to self-consistently produce a strong turbulent cascade that begins at the driving scale of $k_\perp \rho _i = 2$
. The amplitude of the driving is chosen in accordance with critically balanced KAW turbulence (Howes et al. Reference Howes, Cowley, Dorland, Hammett, Quataert and Schekochihin2008a, Reference Howes, Tenbarge and Dorland2011a) in order to self-consistently produce a strong turbulent cascade that begins at the driving scale of $k_\perp \rho _i = 2$![]() . The turbulent cascade transfers energy to ever smaller length scales, ultimately reaching $k_\perp \rho _i = 42$
. The turbulent cascade transfers energy to ever smaller length scales, ultimately reaching $k_\perp \rho _i = 42$![]() where the resolved electron collisionless damping is sufficiently strong to terminate the cascade, enabling a turbulent steady state to be achieved. To prevent a build-up of fine-scale structure in velocity space that is unresolved by our finite grid, we set non-zero collisionalities for the ions and electrons. This allows the energy that is transferred to the particles via collisionless Landau damping to thermalize. These values may be changed somewhat during the course of a simulation to ensure good conservation of energy. In table 1, we display the final values of the electron and ion collisionalities in normalized units ($\bar {\nu }_{e,f}\equiv \nu _{e,f}/k_{\parallel 0} v_A; \bar {\nu }_{i,f} \equiv \nu _{i,f}/k_{\parallel 0} v_A$
where the resolved electron collisionless damping is sufficiently strong to terminate the cascade, enabling a turbulent steady state to be achieved. To prevent a build-up of fine-scale structure in velocity space that is unresolved by our finite grid, we set non-zero collisionalities for the ions and electrons. This allows the energy that is transferred to the particles via collisionless Landau damping to thermalize. These values may be changed somewhat during the course of a simulation to ensure good conservation of energy. In table 1, we display the final values of the electron and ion collisionalities in normalized units ($\bar {\nu }_{e,f}\equiv \nu _{e,f}/k_{\parallel 0} v_A; \bar {\nu }_{i,f} \equiv \nu _{i,f}/k_{\parallel 0} v_A$![]() ) for each simulation. These values may be compared with the maximum damping rate ($-\bar {\gamma }_{{\rm max}}$
) for each simulation. These values may be compared with the maximum damping rate ($-\bar {\gamma }_{{\rm max}}$![]() , not listed) and the driving-scale wave frequency ($\bar {\omega }_0$
, not listed) and the driving-scale wave frequency ($\bar {\omega }_0$![]() ) to ensure that $\bar {\nu }_{s}$
) to ensure that $\bar {\nu }_{s}$![]() is large enough to dissipate fine-scale structure in velocity space but small enough such that the driving scale remains collisionless.
is large enough to dissipate fine-scale structure in velocity space but small enough such that the driving scale remains collisionless.
Table 1. Parameters of the four turbulent simulations.
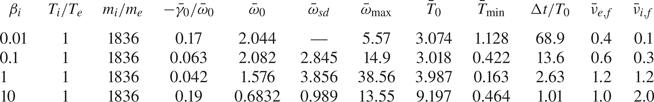
We present the average spectra of the perpendicular magnetic field energy for the four simulations in steady state in figure 1. The spectra have been separated in amplitude in order to highlight the individual power law slopes, and by-eye fits (dashed black lines) are presented alongside the data. At $\beta _i = 10$![]() and $\beta _i = 1$
and $\beta _i = 1$![]() , the slope of the perpendicular magnetic energy spectra agree well with dissipation-range spectra that have been observed in $\beta _i\gtrsim 1$
, the slope of the perpendicular magnetic energy spectra agree well with dissipation-range spectra that have been observed in $\beta _i\gtrsim 1$![]() plasmas near 1 AU, $E_{B_\perp } \propto k_\perp ^{-2.8}$
plasmas near 1 AU, $E_{B_\perp } \propto k_\perp ^{-2.8}$![]() (Sahraoui et al. Reference Sahraoui, Huang, Belmont, Goldstein, Rétino, Robert and De Patoul2013). The simulation spectra steepen as beta decreases, up to $E_{B_\perp } \propto k_\perp ^{-3.5}$
(Sahraoui et al. Reference Sahraoui, Huang, Belmont, Goldstein, Rétino, Robert and De Patoul2013). The simulation spectra steepen as beta decreases, up to $E_{B_\perp } \propto k_\perp ^{-3.5}$![]() at $\beta _i = 0.01$
at $\beta _i = 0.01$![]() . Such low beta plasmas are rarely observed near the Earth (Wilson et al. Reference Wilson, Stevens, Kasper, Klein, Maruca, Bale, Bowen, Pulupa and Salem2018), and dissipation-range simulations of turbulence at this beta are uncommon, though one recent work studying the low-$\beta$
. Such low beta plasmas are rarely observed near the Earth (Wilson et al. Reference Wilson, Stevens, Kasper, Klein, Maruca, Bale, Bowen, Pulupa and Salem2018), and dissipation-range simulations of turbulence at this beta are uncommon, though one recent work studying the low-$\beta$![]() limit of plasma turbulence also finds steep magnetic energy spectra (Zhou, Liu & Loureiro Reference Zhou, Liu and Loureiro2023). Additionally, our steepest spectrum is within the range of early dissipation-range observations (Leamon et al. Reference Leamon, Smith, Ness, Matthaeus and Wong1998) and the trend we observe of the spectra steepening as beta decreases is consistent with the electrons transferring more energy from the turbulence within the dissipation range in the case of more significant damping (Told et al. Reference Told, Jenko, TenBarge, Howes and Hammett2015).
limit of plasma turbulence also finds steep magnetic energy spectra (Zhou, Liu & Loureiro Reference Zhou, Liu and Loureiro2023). Additionally, our steepest spectrum is within the range of early dissipation-range observations (Leamon et al. Reference Leamon, Smith, Ness, Matthaeus and Wong1998) and the trend we observe of the spectra steepening as beta decreases is consistent with the electrons transferring more energy from the turbulence within the dissipation range in the case of more significant damping (Told et al. Reference Told, Jenko, TenBarge, Howes and Hammett2015).
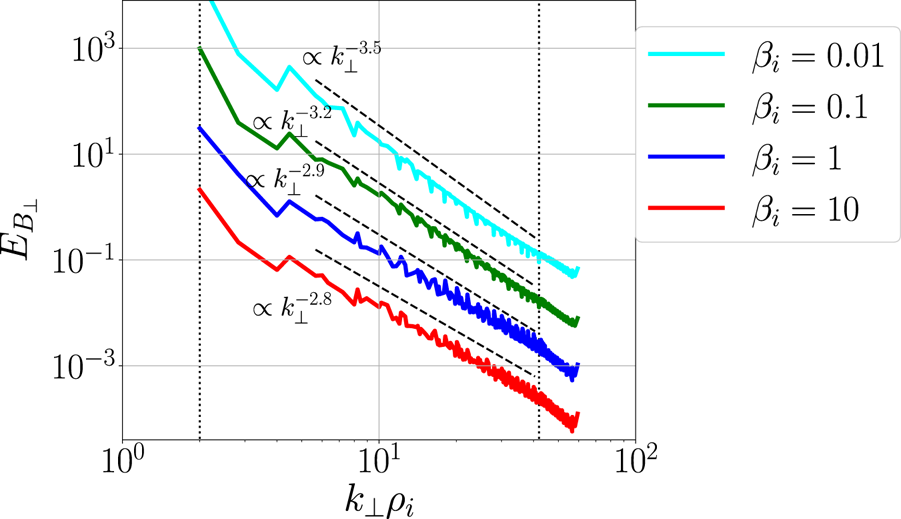
Figure 1. Perpendicular magnetic energy spectra ($E_{B_\perp }$![]() ) of the four simulations, as a function of $k_\perp \rho _i$
) of the four simulations, as a function of $k_\perp \rho _i$![]() , time-averaged over a representative portion of the full simulations. The vertical dotted lines mark the driving scale ($k_\perp \rho _i = 2$
, time-averaged over a representative portion of the full simulations. The vertical dotted lines mark the driving scale ($k_\perp \rho _i = 2$![]() ) and the smallest fully resolved scale ($k_\perp \rho _i = 42$
) and the smallest fully resolved scale ($k_\perp \rho _i = 42$![]() ). By-eye power law fits are shown as references for each spectrum.
). By-eye power law fits are shown as references for each spectrum.
The linear phase velocity normalized to the electron thermal velocity, $\omega /k_\parallel v_{te}$![]() , and the normalized damping rate $-\gamma /\omega$
, and the normalized damping rate $-\gamma /\omega$![]() for the KAWs over the parameter range of each of these four simulations are computed using the linear Vlasov–Maxwell dispersion relation solver PLUME (Klein & Howes Reference Klein and Howes2015) and are presented in figure 2. The normalized frequencies $\bar {\omega }_0 \equiv \omega _0/(k_{\parallel } v_A)$
for the KAWs over the parameter range of each of these four simulations are computed using the linear Vlasov–Maxwell dispersion relation solver PLUME (Klein & Howes Reference Klein and Howes2015) and are presented in figure 2. The normalized frequencies $\bar {\omega }_0 \equiv \omega _0/(k_{\parallel } v_A)$![]() of the domain scale KAWs with wavevector components $k_{\perp 0}\rho _i = 2{\rm \pi} \rho _i /L_\perp = 2$
of the domain scale KAWs with wavevector components $k_{\perp 0}\rho _i = 2{\rm \pi} \rho _i /L_\perp = 2$![]() and $k_{\parallel 0} a_0 = 2{\rm \pi} a_0/L_\parallel =1$
and $k_{\parallel 0} a_0 = 2{\rm \pi} a_0/L_\parallel =1$![]() are listed in table 1. Note that the Alfvén wave and electron thermal velocity normalizations of the frequency are related by $\omega /k_\parallel v_{te} = \bar {\omega }\beta _i^{-1/2}(T_i/T_e)^{1/2} (m_e/m_i)^{1/2}$
are listed in table 1. Note that the Alfvén wave and electron thermal velocity normalizations of the frequency are related by $\omega /k_\parallel v_{te} = \bar {\omega }\beta _i^{-1/2}(T_i/T_e)^{1/2} (m_e/m_i)^{1/2}$![]() . Also, the normalized Alfvén wave frequencies have departed from the magnetohydrodynamic (MHD) limit of $\bar {\omega }=1$
. Also, the normalized Alfvén wave frequencies have departed from the magnetohydrodynamic (MHD) limit of $\bar {\omega }=1$![]() , since we are modelling KAWs with $k_\perp \rho _i > 1$
, since we are modelling KAWs with $k_\perp \rho _i > 1$![]() (figure 2a). The maximum frequency KAW found in each simulation can be determined from figure 2 (listed in table 1 as $\bar {\omega }_{{\rm max}}$
(figure 2a). The maximum frequency KAW found in each simulation can be determined from figure 2 (listed in table 1 as $\bar {\omega }_{{\rm max}}$![]() ), along with the frequency corresponding to the onset of strong damping at $-\gamma /\omega \sim 0.1$
), along with the frequency corresponding to the onset of strong damping at $-\gamma /\omega \sim 0.1$![]() (figure 2b), which is listed as $\bar {\omega }_{sd}$
(figure 2b), which is listed as $\bar {\omega }_{sd}$![]() in table 1 if this frequency is above that of the domain scale.
in table 1 if this frequency is above that of the domain scale.

Figure 2. Linear Vlasov–Maxwell dispersion relation for plasmas with $T_i/T_e = 1$![]() , ${m_i/m_e = 1836}$
, ${m_i/m_e = 1836}$![]() , and $\beta _i = 0.01$
, and $\beta _i = 0.01$![]() (cyan), $0.1$
(cyan), $0.1$![]() (green), $1$
(green), $1$![]() (blue) and $10$
(blue) and $10$![]() (red). (a) Parallel phase velocity normalized to the electron thermal velocity $\omega /k_\parallel v_{te}$
(red). (a) Parallel phase velocity normalized to the electron thermal velocity $\omega /k_\parallel v_{te}$![]() . (b) Normalized damping rate $-\gamma /\omega$
. (b) Normalized damping rate $-\gamma /\omega$![]() , with the onset of strong damping ($-\gamma /\omega \gtrsim 0.1$
, with the onset of strong damping ($-\gamma /\omega \gtrsim 0.1$![]() ) marked by a horizontal dashed line.
) marked by a horizontal dashed line.
The postsaturation length of each of the four simulations, $\Delta t/T_0$![]() , is listed in table 1 in terms of time normalized to the period of the domain-scale KAWs, $T_0=2{\rm \pi} /\omega _0$
, is listed in table 1 in terms of time normalized to the period of the domain-scale KAWs, $T_0=2{\rm \pi} /\omega _0$![]() . Note that the time scale separation between the faster electron thermal velocity and the slower Alfvén velocity, $v_{te}/v_A = \beta _i^{1/2}(T_e/T_i)^{1/2} (m_i/m_e)^{1/2}$
. Note that the time scale separation between the faster electron thermal velocity and the slower Alfvén velocity, $v_{te}/v_A = \beta _i^{1/2}(T_e/T_i)^{1/2} (m_i/m_e)^{1/2}$![]() , decreases for lower values of $\beta _i$
, decreases for lower values of $\beta _i$![]() . Since the maximum time step in AstroGK is determined by the electron thermal velocity, lower $\beta _i$
. Since the maximum time step in AstroGK is determined by the electron thermal velocity, lower $\beta _i$![]() simulations are substantially less computationally costly to run.
simulations are substantially less computationally costly to run.
In addition to the nonlinear turbulence simulations described above, we also use AstroGK to model a total of $20$![]() individually driven, damped KAWs at a single value of $k_\perp \rho _i$
individually driven, damped KAWs at a single value of $k_\perp \rho _i$![]() . For each value of $\beta _i = {0.01, 0.1, 1, 10}$
. For each value of $\beta _i = {0.01, 0.1, 1, 10}$![]() we use the oscillating Langevin antenna to separately drive linear modes at $k_\perp \rho _i = {2, 4, 8, 16, 32}$
we use the oscillating Langevin antenna to separately drive linear modes at $k_\perp \rho _i = {2, 4, 8, 16, 32}$![]() , where $(k_x \rho _i, k_y \rho _i, k_z a_0) = (k_\perp \rho _i, 0, 1)$
, where $(k_x \rho _i, k_y \rho _i, k_z a_0) = (k_\perp \rho _i, 0, 1)$![]() in each case. The parallel spatial grid and velocity-space resolutions for each wave are $(n_z, n_\lambda, n_\varepsilon, n_s) = (32, 128, 32, 2)$
in each case. The parallel spatial grid and velocity-space resolutions for each wave are $(n_z, n_\lambda, n_\varepsilon, n_s) = (32, 128, 32, 2)$![]() , where the variables and normalization are the same as described for the turbulence runs. Each driven, damped linear wave was evolved for a minimum of $10$
, where the variables and normalization are the same as described for the turbulence runs. Each driven, damped linear wave was evolved for a minimum of $10$![]() wave periods.
wave periods.
3. Velocity-space signatures of single KAWs
To develop a framework for interpreting the velocity-space signatures of electron Landau damping in turbulence simulations, we first present the results of applying field–particle correlation analysis to the suite of single KAWs described in § 2. The analysis of single, damped waves eliminates the complications which arise from overlapping bipolar signatures of Landau damping in broadband turbulence, as illustrated in figure 1 of Horvath et al. (Reference Horvath, Howes and McCubbin2020). Thus, we are able to more easily identify trends in the behaviour of the field–particle correlation signatures of this mechanism as the ion plasma $\beta _i$![]() is changed. Later, these clearly identified features will aid our interpretation of signatures in the turbulence simulations, which we present in § 4.
is changed. Later, these clearly identified features will aid our interpretation of signatures in the turbulence simulations, which we present in § 4.
Figure 3(a) shows a gyrotropic signature $C_{E_\parallel }(v_\parallel, v_\perp, t)$![]() and figure 3(b) a timestack plot $C_{E_\parallel }(v_\parallel, t)$
and figure 3(b) a timestack plot $C_{E_\parallel }(v_\parallel, t)$![]() of the field–particle correlation for an individual KAW simulation with $\beta _i = 0.1$
of the field–particle correlation for an individual KAW simulation with $\beta _i = 0.1$![]() and $k_\perp \rho _i = 8$
and $k_\perp \rho _i = 8$![]() . In figure 3(a), the characteristic bipolar form of the field–particle correlation signature of Landau damping (Klein & Howes Reference Klein and Howes2016; Howes et al. Reference Howes, Klein and Li2017; Klein et al. Reference Klein, Howes and Tenbarge2017; Chen et al. Reference Chen, Klein and Howes2019; Horvath et al. Reference Horvath, Howes and McCubbin2020) is clearly visible in both the colourmap plot and in the line plot of the time-integrated, reduced parallel correlation $C_{E_\parallel }(v_\parallel )$
. In figure 3(a), the characteristic bipolar form of the field–particle correlation signature of Landau damping (Klein & Howes Reference Klein and Howes2016; Howes et al. Reference Howes, Klein and Li2017; Klein et al. Reference Klein, Howes and Tenbarge2017; Chen et al. Reference Chen, Klein and Howes2019; Horvath et al. Reference Horvath, Howes and McCubbin2020) is clearly visible in both the colourmap plot and in the line plot of the time-integrated, reduced parallel correlation $C_{E_\parallel }(v_\parallel )$![]() shown below. In this example, the correlation interval $\tau$
shown below. In this example, the correlation interval $\tau$![]() is equal to a full wave period ($\tau /T_0 = 1$
is equal to a full wave period ($\tau /T_0 = 1$![]() ) and the gyrotropic correlation in figure 3(a) is shown centred at time $t/T_0 = 6.75$
) and the gyrotropic correlation in figure 3(a) is shown centred at time $t/T_0 = 6.75$![]() . The significant energy transfer shown in the bipolar velocity-space signature is localized in $v_\parallel$
. The significant energy transfer shown in the bipolar velocity-space signature is localized in $v_\parallel$![]() around the parallel phase velocity of the damped wave (vertical dashed line, $v_{ph, \parallel }/v_{te} = \omega /k_\parallel v_{te} = 0.51$
around the parallel phase velocity of the damped wave (vertical dashed line, $v_{ph, \parallel }/v_{te} = \omega /k_\parallel v_{te} = 0.51$![]() ), with a loss of phase-space energy density (blue) at $v_\parallel < v_{ph, \parallel }$
), with a loss of phase-space energy density (blue) at $v_\parallel < v_{ph, \parallel }$![]() and a gain of of phase-space energy density (red) at $v_\parallel > v_{ph, \parallel }$
and a gain of of phase-space energy density (red) at $v_\parallel > v_{ph, \parallel }$![]() . The dominance of the positive region indicates a net transfer of energy from the parallel electric field to the resonant electrons. As expected for Landau damping, the bipolar structure does not vary in the perpendicular direction apart from an exponential decrease at high perpendicular velocities due to the equilibrium velocity distribution. Therefore, we may integrate over all of $v_\perp$
. The dominance of the positive region indicates a net transfer of energy from the parallel electric field to the resonant electrons. As expected for Landau damping, the bipolar structure does not vary in the perpendicular direction apart from an exponential decrease at high perpendicular velocities due to the equilibrium velocity distribution. Therefore, we may integrate over all of $v_\perp$![]() to yield the total change in $w_s$
to yield the total change in $w_s$![]() as a function of $v_\parallel$
as a function of $v_\parallel$![]() at the spatial point being considered (lower subpanel). This lower subpanel is then calculated for all times and combined to create figure 3(b) a timestack plot of the correlation $C_{E_\parallel }(v_\parallel, t)$
at the spatial point being considered (lower subpanel). This lower subpanel is then calculated for all times and combined to create figure 3(b) a timestack plot of the correlation $C_{E_\parallel }(v_\parallel, t)$![]() . The subpanel beneath the timestack plot is the time-integrated, reduced parallel correlation $C_{E_\parallel, e}(v_\parallel )$
. The subpanel beneath the timestack plot is the time-integrated, reduced parallel correlation $C_{E_\parallel, e}(v_\parallel )$![]() . The left-hand subpanel (to the left of the timestack) is the rate of change of the electron spatial energy density due to the parallel electric field, $(\partial W_e/\partial t)_{E_\parallel }$
. The left-hand subpanel (to the left of the timestack) is the rate of change of the electron spatial energy density due to the parallel electric field, $(\partial W_e/\partial t)_{E_\parallel }$![]() , which is calculated by integrating the correlation over $v_\parallel$
, which is calculated by integrating the correlation over $v_\parallel$![]() and is equal to $j_{e,\parallel } E_\parallel$
and is equal to $j_{e,\parallel } E_\parallel$![]() .
.
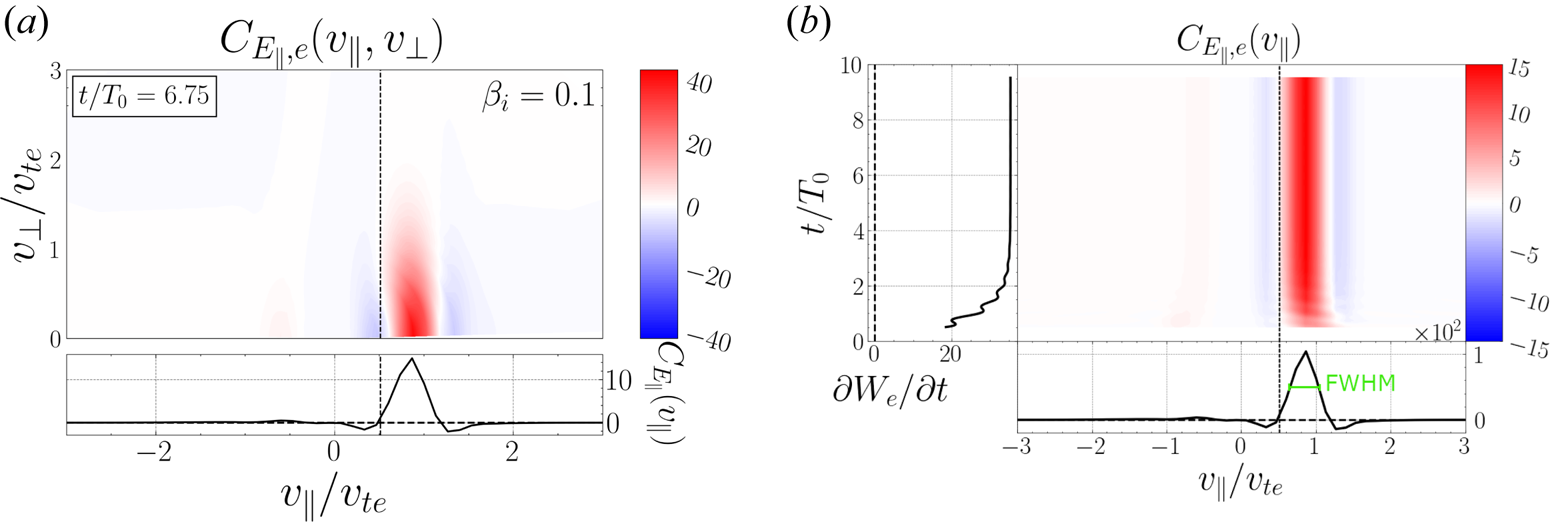
Figure 3. (a) Gyrotropic field–particle correlation signature $C_{E_\parallel }(v_\parallel, v_\perp )$![]() at $t/T_0 = 6.75$
at $t/T_0 = 6.75$![]() and (b) timestack plot $C_{E_\parallel }(v_\parallel, t)$
and (b) timestack plot $C_{E_\parallel }(v_\parallel, t)$![]() of a driven, damped wave simulation with $\beta _i = 0.1$
of a driven, damped wave simulation with $\beta _i = 0.1$![]() , $k_\perp \rho _i = 8$
, $k_\perp \rho _i = 8$![]() and a correlation interval of $\tau /T_0 = 1$
and a correlation interval of $\tau /T_0 = 1$![]() . In the time-integrated subpanel (below) in (b), the full-width at half-maximum (FWHM) of the positive portion of the bipolar signature is indicated.
. In the time-integrated subpanel (below) in (b), the full-width at half-maximum (FWHM) of the positive portion of the bipolar signature is indicated.
3.1. Velocity-space signature location and wave phase velocity
A key feature of a bipolar signature of Landau damping is its concentration in velocity-space about the parallel phase velocity of the damped wave (Klein & Howes Reference Klein and Howes2016). The form of the signature is consistent with flattening of the distribution function around the resonant velocity, as predicted by quasilinear theory of Landau damping, and indicates that a resonant mechanism is producing the energization (Howes et al. Reference Howes, Klein and Li2017). Through the sweep of $\beta _i$![]() and $k_\perp \rho _i$
and $k_\perp \rho _i$![]() parameter space provided by our 20 single-wave simulations, we show here quantitatively that the location of the zero crossing in the bipolar signature of Landau damping (the velocity $v_{\parallel }/v_{te}$
parameter space provided by our 20 single-wave simulations, we show here quantitatively that the location of the zero crossing in the bipolar signature of Landau damping (the velocity $v_{\parallel }/v_{te}$![]() where $C_{E_\parallel }(v_\parallel ) = 0$
where $C_{E_\parallel }(v_\parallel ) = 0$![]() ) is indeed very well correlated with the parallel phase velocity of the damped wave. These two quantities are plotted against each other in figure 4(a), and the results lie almost entirely on the line of $v_\parallel = v_{ph}$
) is indeed very well correlated with the parallel phase velocity of the damped wave. These two quantities are plotted against each other in figure 4(a), and the results lie almost entirely on the line of $v_\parallel = v_{ph}$![]() . The linear Vlasov–Maxwell dispersion relation (Stix Reference Stix1992; Klein & Howes Reference Klein and Howes2015) was used to find $v_{ph}$
. The linear Vlasov–Maxwell dispersion relation (Stix Reference Stix1992; Klein & Howes Reference Klein and Howes2015) was used to find $v_{ph}$![]() for each wavemode, and the zeros are found from gyrotropic plots with correlation interval $\tau /T_0 = 1$
for each wavemode, and the zeros are found from gyrotropic plots with correlation interval $\tau /T_0 = 1$![]() . Note that the exception to the close agreement between $v_\parallel$
. Note that the exception to the close agreement between $v_\parallel$![]() and $v_{ph,\parallel }$
and $v_{ph,\parallel }$![]() occurs for the signatures with $\beta _i = 10$
occurs for the signatures with $\beta _i = 10$![]() (circles). This error likely arises due to a combination of the small KAW phase velocity at high $\beta _i$
(circles). This error likely arises due to a combination of the small KAW phase velocity at high $\beta _i$![]() and the finite $v_\parallel$
and the finite $v_\parallel$![]() -resolution $\Delta v_\parallel /v_{te} = 0.133$
-resolution $\Delta v_\parallel /v_{te} = 0.133$![]() of the simulations. The slight deviation of the other signatures from the $v_\parallel = v_{ph}$
of the simulations. The slight deviation of the other signatures from the $v_\parallel = v_{ph}$![]() line appears to fall within the error due to finite $v_\parallel$
line appears to fall within the error due to finite $v_\parallel$![]() -resolution.
-resolution.
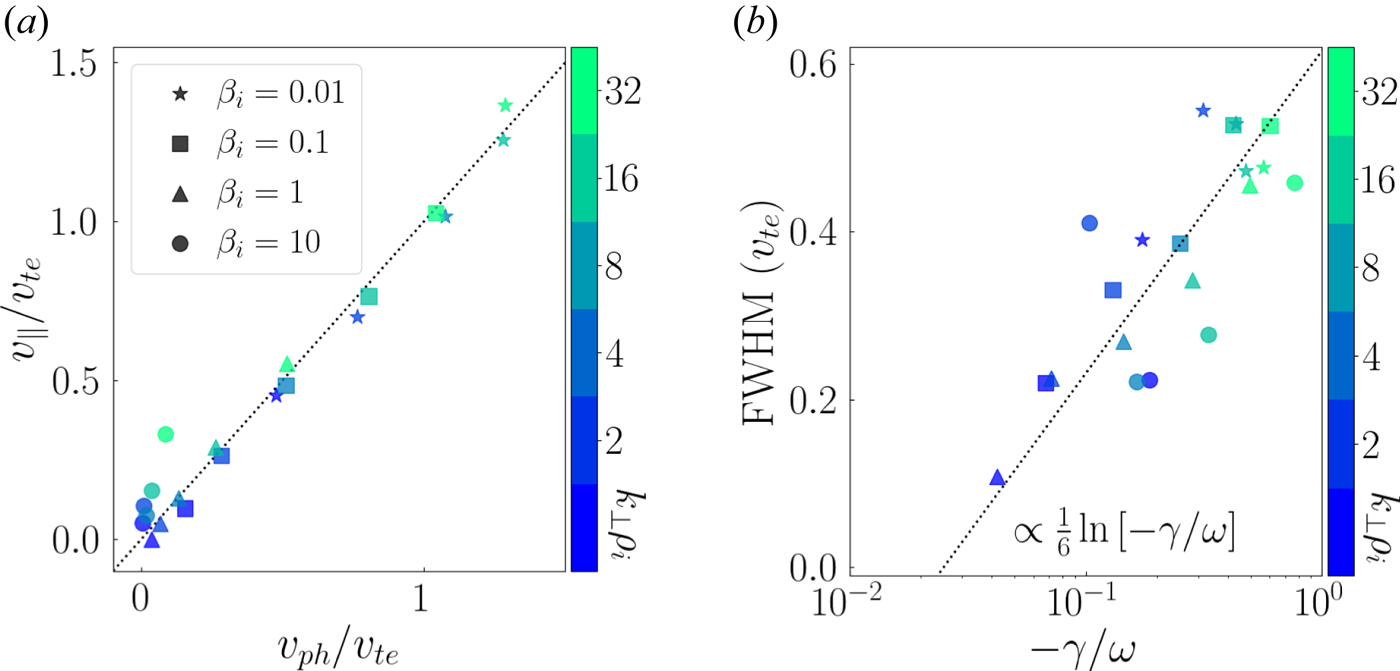
Figure 4. (a) Velocity-space signature location $v_\parallel /v_{te}$![]() versus parallel wave phase velocity $v_{ph,\parallel }/v_{te}$
versus parallel wave phase velocity $v_{ph,\parallel }/v_{te}$![]() for the linear runs. (b) The FWHM value of the bipolar signatures versus the damping rate $-\gamma /\omega$
for the linear runs. (b) The FWHM value of the bipolar signatures versus the damping rate $-\gamma /\omega$![]() of the wave. Plasma $\beta _i$
of the wave. Plasma $\beta _i$![]() and $k_\perp \rho _i$
and $k_\perp \rho _i$![]() are differentiated using marker styles and colour, respectively.
are differentiated using marker styles and colour, respectively.
3.2. Velocity-space signature width and wave damping rate
The second observation we are able to make using the single-wave simulations is that the width of the field–particle correlation signatures changes with both $\beta _i$![]() and $k_\perp \rho _i$
and $k_\perp \rho _i$![]() . The width tends to vary directly with $k_\perp \rho _i$
. The width tends to vary directly with $k_\perp \rho _i$![]() (for instance, see the five single-wave signatures for $\beta _i=1$
(for instance, see the five single-wave signatures for $\beta _i=1$![]() shown in Appendix A) and indirectly with $\beta _i$
shown in Appendix A) and indirectly with $\beta _i$![]() . Similarly, the damping rate of the KAWs increases with $k_\perp \rho _i$
. Similarly, the damping rate of the KAWs increases with $k_\perp \rho _i$![]() and decreases with $\beta _i$
and decreases with $\beta _i$![]() , suggesting a possible relationship. Note that this connection with $k_\perp \rho _i$
, suggesting a possible relationship. Note that this connection with $k_\perp \rho _i$![]() is true specifically for dispersive KAWs, where $v_{ph}$
is true specifically for dispersive KAWs, where $v_{ph}$![]() generally increases monotonically with $k_\perp \rho _i$
generally increases monotonically with $k_\perp \rho _i$![]() . Indeed, when the signature width – quantified by the FWHM of the positive portion of the bipolar structure (e.g. see the lower subpanel of figure 3) – is plotted against the corresponding normalized damping rate of the KAW in the simulation, $-\gamma /\omega$
. Indeed, when the signature width – quantified by the FWHM of the positive portion of the bipolar structure (e.g. see the lower subpanel of figure 3) – is plotted against the corresponding normalized damping rate of the KAW in the simulation, $-\gamma /\omega$![]() , a logarithmic dependence emerges, roughly described by ${\rm FWHM} \propto \tfrac {1}{6} ln(-\gamma /\omega )$
, a logarithmic dependence emerges, roughly described by ${\rm FWHM} \propto \tfrac {1}{6} ln(-\gamma /\omega )$![]() . This relationship is shown in figure 4(b). Though logarithmic dependencies are weak, broadening of the signatures due to increased damping rates has plausible theoretical support. Specifically, it may be analogous to the frequency-space broadening of the Fourier transform of a damped sine wave. A pure sine wave yields a Dirac delta function in frequency space under a Fourier transform, while a damped wave yields a peak of finite width due to its decrease in amplitude over time.
. This relationship is shown in figure 4(b). Though logarithmic dependencies are weak, broadening of the signatures due to increased damping rates has plausible theoretical support. Specifically, it may be analogous to the frequency-space broadening of the Fourier transform of a damped sine wave. A pure sine wave yields a Dirac delta function in frequency space under a Fourier transform, while a damped wave yields a peak of finite width due to its decrease in amplitude over time.
3.3. The effect of weighting by $v_\parallel ^2$ in the parallel field–particle correlation
in the parallel field–particle correlation
Another feature that becomes clear through the suite of single-wave signatures is the effect of $v_\parallel ^2$![]() in the definition of the field–particle correlation, (2.1). Since particle velocities are normalized by the species thermal velocity, this factor enhances the velocity-space signature for $v_\parallel /v_{te}>1$
in the definition of the field–particle correlation, (2.1). Since particle velocities are normalized by the species thermal velocity, this factor enhances the velocity-space signature for $v_\parallel /v_{te}>1$![]() and suppresses the signature for $v_\parallel /v_{te}<1$
and suppresses the signature for $v_\parallel /v_{te}<1$![]() .Footnote 1 This behaviour is due to the mathematical form of the field–particle correlation, which arises from the derivation of the rate of change of phase-space energy density. Therefore, the enhancement or suppression of the energy transfer rate due to $v_\parallel ^2$
.Footnote 1 This behaviour is due to the mathematical form of the field–particle correlation, which arises from the derivation of the rate of change of phase-space energy density. Therefore, the enhancement or suppression of the energy transfer rate due to $v_\parallel ^2$![]() is a physical effect that can hinder the ability to recognize bipolar velocity-space signatures. Specifically, for damped waves that are resonant with particles at low parallel velocities with $v_\parallel /v_{te}<1$
is a physical effect that can hinder the ability to recognize bipolar velocity-space signatures. Specifically, for damped waves that are resonant with particles at low parallel velocities with $v_\parallel /v_{te}<1$![]() , the preferential suppression of signal at small $v_\parallel$
, the preferential suppression of signal at small $v_\parallel$![]() can mask the characteristic bipolar structure that identifies the energization as being due to Landau damping. Figure 5 presents two sketches of this effect, showing the separate magnitudes of the weighting by $v_\parallel ^2/2$
can mask the characteristic bipolar structure that identifies the energization as being due to Landau damping. Figure 5 presents two sketches of this effect, showing the separate magnitudes of the weighting by $v_\parallel ^2/2$![]() (cyan dashed) and the remaining parallel electric field correlation $q_s E_\parallel \partial f/\partial v_\parallel$
(cyan dashed) and the remaining parallel electric field correlation $q_s E_\parallel \partial f/\partial v_\parallel$![]() (blue dot–dashed) along with their product (red solid). The relative magnitudes of the negative and positive regions of the bipolar signature of $C_{E_\parallel }$
(blue dot–dashed) along with their product (red solid). The relative magnitudes of the negative and positive regions of the bipolar signature of $C_{E_\parallel }$![]() when (i) $v_{ph}/v_{te} > 1$
when (i) $v_{ph}/v_{te} > 1$![]() is contrasted with the relative magnitudes when (ii) $v_{ph}/v_{te} < 1$
is contrasted with the relative magnitudes when (ii) $v_{ph}/v_{te} < 1$![]() . For the Landau damping of ions, the wave resonance is typically $v_{ph,\parallel }/v_{ti} \simeq 1$
. For the Landau damping of ions, the wave resonance is typically $v_{ph,\parallel }/v_{ti} \simeq 1$![]() , as in figure 5(a), where the bipolar structure of the signature of Landau damping is easily observed. For electron Landau damping, however, the resonances are typically less than the electron thermal velocity $v_{ph,\parallel }/v_{te} < 1$
, as in figure 5(a), where the bipolar structure of the signature of Landau damping is easily observed. For electron Landau damping, however, the resonances are typically less than the electron thermal velocity $v_{ph,\parallel }/v_{te} < 1$![]() , and asymptotically reach $v_{ph}/v_{te} \rightarrow 1$
, and asymptotically reach $v_{ph}/v_{te} \rightarrow 1$![]() at the smallest spatial scales ($k_\perp \rho _e \rightarrow 1$
at the smallest spatial scales ($k_\perp \rho _e \rightarrow 1$![]() ), as seen in figure 2(a). Additionally, as $\beta _i$
), as seen in figure 2(a). Additionally, as $\beta _i$![]() increases, the parallel phase velocity $\omega /k_\parallel v_{te}$
increases, the parallel phase velocity $\omega /k_\parallel v_{te}$![]() across all dissipation range scales becomes an even smaller fraction of $v_{te}$
across all dissipation range scales becomes an even smaller fraction of $v_{te}$![]() . Therefore, for electron Landau damping signatures in high $\beta _i$
. Therefore, for electron Landau damping signatures in high $\beta _i$![]() plasmas, the resonant velocities are often deep in the centre of the electron distribution function, so the negative portion of the signature can be significantly suppressed and become nearly unobservable, as in figure 5(b). For our 20 single-wave simulations binned in parallel velocity to a resolution of $\Delta v_\parallel = 0.133\ v_{te}$
plasmas, the resonant velocities are often deep in the centre of the electron distribution function, so the negative portion of the signature can be significantly suppressed and become nearly unobservable, as in figure 5(b). For our 20 single-wave simulations binned in parallel velocity to a resolution of $\Delta v_\parallel = 0.133\ v_{te}$![]() , the $v_\parallel ^2$
, the $v_\parallel ^2$![]() -weighting made the negative portion of the bipolar signatures difficult or impossible to observe for resonant waves with $v_{ph} \leq 0.3\ v_{te}$
-weighting made the negative portion of the bipolar signatures difficult or impossible to observe for resonant waves with $v_{ph} \leq 0.3\ v_{te}$![]() : the case for 11 out of the 20 signatures.Footnote 2
: the case for 11 out of the 20 signatures.Footnote 2
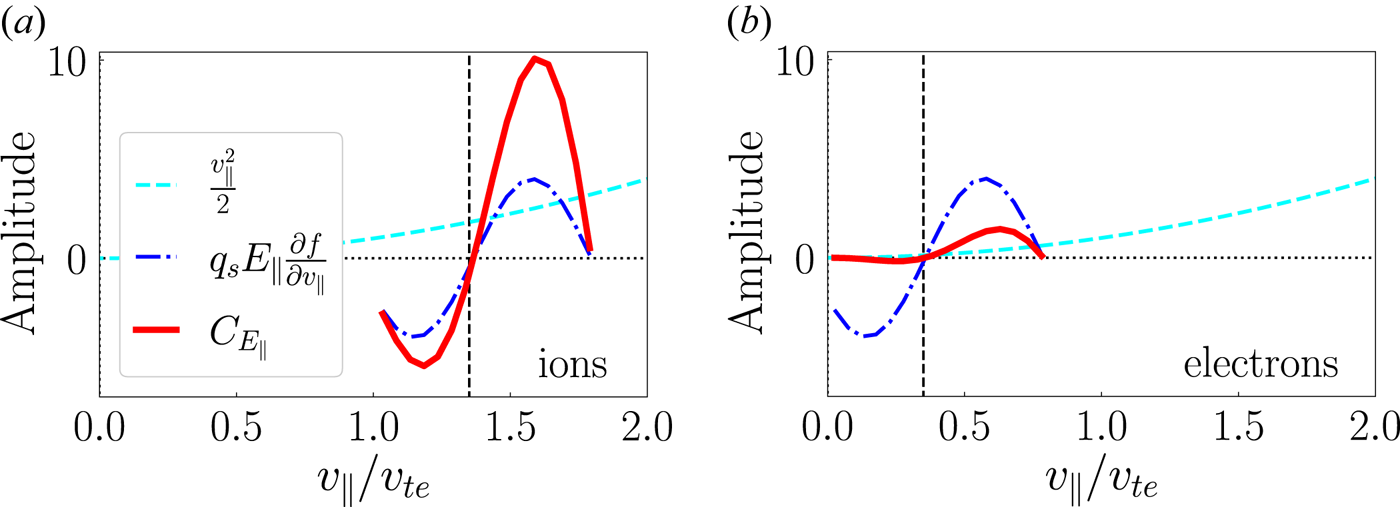
Figure 5. Diagram of the effect of $v_\parallel ^2$![]() -weighting on bipolar signatures of Landau damping.
-weighting on bipolar signatures of Landau damping.
3.4. Non-resonant feature
Finally, we use the single-wave simulations to address a prominent, non-resonant feature that begins to appear in the field–particle correlations for $\beta _i \gtrsim 1$![]() . Specifically, we see a large-amplitude feature across all parallel velocities that is antisymmetric about $v_\parallel = 0$
. Specifically, we see a large-amplitude feature across all parallel velocities that is antisymmetric about $v_\parallel = 0$![]() . Figure 6 shows the non-resonant feature for two individual wave simulations at perpendicular wavenumber $k_\perp \rho _i = 8$
. Figure 6 shows the non-resonant feature for two individual wave simulations at perpendicular wavenumber $k_\perp \rho _i = 8$![]() and $\beta _i = 1$
and $\beta _i = 1$![]() (see figure 6a) and $beta_i =10$
(see figure 6a) and $beta_i =10$![]() (see figure 6b). At $\beta _i=1$
(see figure 6b). At $\beta _i=1$![]() , the non-resonant feature is visible but subdominant to the resonant, bipolar signature which is centred around $v_\parallel /v_{te} = 0.133$
, the non-resonant feature is visible but subdominant to the resonant, bipolar signature which is centred around $v_\parallel /v_{te} = 0.133$![]() . At $\beta _i=10$
. At $\beta _i=10$![]() , however, the amplitude of the non-resonant feature has completely eclipsed the amplitude of the resonant feature, which is centred close to zero at $v_\parallel /v_{te} = 0.018$
, however, the amplitude of the non-resonant feature has completely eclipsed the amplitude of the resonant feature, which is centred close to zero at $v_\parallel /v_{te} = 0.018$![]() .
.
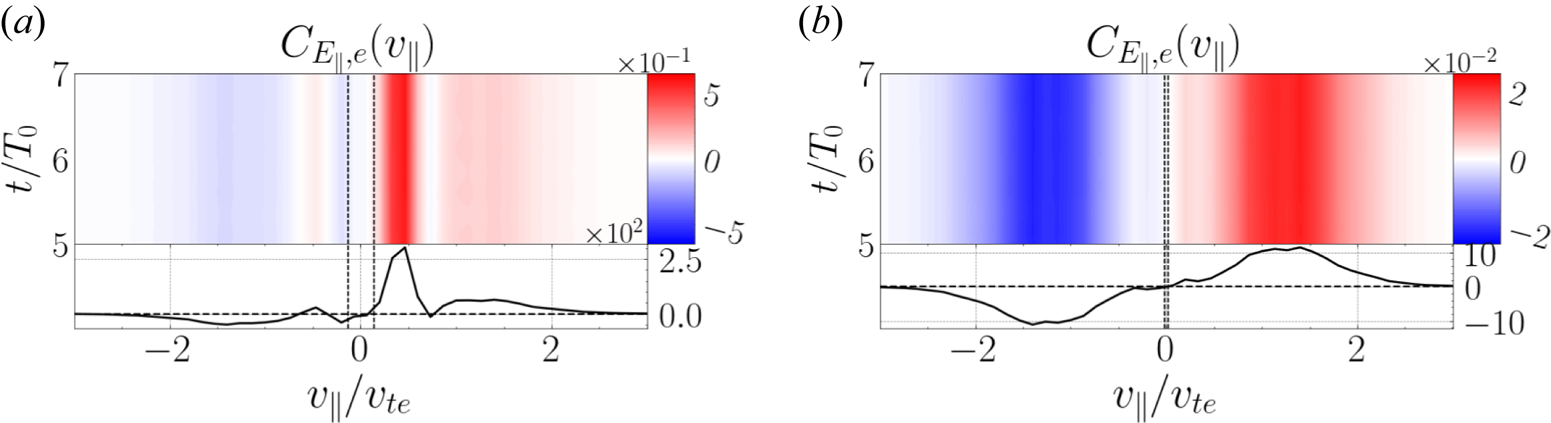
Figure 6. Timestack field–particle correlation of driven, damped KAWs at $k_\perp \rho _i = 8$![]() with (a) $\beta _i = 1$
with (a) $\beta _i = 1$![]() and (b) $\beta = 10$
and (b) $\beta = 10$![]() and $\tau /T_0 = 1$
and $\tau /T_0 = 1$![]() for both. The bipolar signature of Landau damping appears in (a) along with an antisymmetric, non-resonant feature. In (b), the non-resonant feature is dominant.
for both. The bipolar signature of Landau damping appears in (a) along with an antisymmetric, non-resonant feature. In (b), the non-resonant feature is dominant.
Our explanation of the source of this non-resonant feature are electron density oscillations, $\delta n_e$![]() , that arise naturally in the turbulent plasma at $\beta _i \gtrsim 1$
, that arise naturally in the turbulent plasma at $\beta _i \gtrsim 1$![]() . A local spatial density perturbation has a Maxwellian $\delta f$
. A local spatial density perturbation has a Maxwellian $\delta f$![]() , which is even in $v$
, which is even in $v$![]() and therefore contributes an odd variation in $v_\parallel$
and therefore contributes an odd variation in $v_\parallel$![]() to the correlation due to the velocity derivative of the distribution function in (2.1). The effect of a density perturbation on the parallel field–particle correlation is illustrated in a diagram shown in figure 5(b) of McCubbin et al. (Reference McCubbin, Howes and TenBarge2022). The code, AstroGK, evolves the perturbed electron distribution function (Numata et al. Reference Numata, Howes, Tatsuno, Barnes and Dorland2010), which in our KAW simulations contains disturbances due to resonant field–particle interactions and due to non-resonant density oscillations. A density perturbation may appear in the field–particle correlation at high $\beta _i$
to the correlation due to the velocity derivative of the distribution function in (2.1). The effect of a density perturbation on the parallel field–particle correlation is illustrated in a diagram shown in figure 5(b) of McCubbin et al. (Reference McCubbin, Howes and TenBarge2022). The code, AstroGK, evolves the perturbed electron distribution function (Numata et al. Reference Numata, Howes, Tatsuno, Barnes and Dorland2010), which in our KAW simulations contains disturbances due to resonant field–particle interactions and due to non-resonant density oscillations. A density perturbation may appear in the field–particle correlation at high $\beta _i$![]() due to a combination of two factors. First, as $\beta _i$
due to a combination of two factors. First, as $\beta _i$![]() increases, the relative magnitude of the compressive density perturbation to the resonant perturbations grows as the KAWs become more compressible (TenBarge et al. Reference TenBarge, Podesta, Klein and Howes2012; Matteini et al. Reference Matteini, Franci, Alexandrova, Lacombe, Landi, Hellinger, Papini and Verdini2020) and as the phase velocity of the damped KAW decreases and moves deeper into the core of the electron distribution function. Second, in order for the compressive signature to appear in the field–particle correlation, it must have an appropriate phase-offset from the parallel electric field fluctuation. At low $\beta _i$
increases, the relative magnitude of the compressive density perturbation to the resonant perturbations grows as the KAWs become more compressible (TenBarge et al. Reference TenBarge, Podesta, Klein and Howes2012; Matteini et al. Reference Matteini, Franci, Alexandrova, Lacombe, Landi, Hellinger, Papini and Verdini2020) and as the phase velocity of the damped KAW decreases and moves deeper into the core of the electron distribution function. Second, in order for the compressive signature to appear in the field–particle correlation, it must have an appropriate phase-offset from the parallel electric field fluctuation. At low $\beta _i$![]() , $E_\parallel$
, $E_\parallel$![]() and $(\partial f_e/\partial v_\parallel )_{\delta n_e}$
and $(\partial f_e/\partial v_\parallel )_{\delta n_e}$![]() are approximately out of phase, $\phi \simeq {\rm \pi}/2$
are approximately out of phase, $\phi \simeq {\rm \pi}/2$![]() ; as $\beta _i$
; as $\beta _i$![]() increases, the phase offset shifts and the product of $E_\parallel$
increases, the phase offset shifts and the product of $E_\parallel$![]() and $(\partial f_e/\partial v_\parallel )_{\delta n_e}$
and $(\partial f_e/\partial v_\parallel )_{\delta n_e}$![]() contributes more significantly to the field–particle correlation. Appendix B discusses the density perturbation and how it appears in the field–particle correlation in greater detail. In § 5.5.1, we present a technique for removing this feature from the data.
contributes more significantly to the field–particle correlation. Appendix B discusses the density perturbation and how it appears in the field–particle correlation in greater detail. In § 5.5.1, we present a technique for removing this feature from the data.
4. Turbulence analysis
Next, we present the results of the field–particle correlation analysis of the four full turbulence simulations. The features of the bipolar signatures of electron Landau damping that were isolated in the suite of damped individual waves – including variations in signature width, suppression of the negative portion of the bipolar signatures at low resonant velocity, and the presence of a non-resonant feature arising in $\beta _i = 1$![]() and $10$
and $10$![]() – are also present. To illustrate some of the commonly observed features, we present examples of the gyrotropic parallel field–particle correlation $C_{E_\parallel }(v_\parallel, v_\perp, t)$
– are also present. To illustrate some of the commonly observed features, we present examples of the gyrotropic parallel field–particle correlation $C_{E_\parallel }(v_\parallel, v_\perp, t)$![]() in figure 7 and of the timestack plot of $C_{E_\parallel }(v_\parallel, t)$
in figure 7 and of the timestack plot of $C_{E_\parallel }(v_\parallel, t)$![]() in figure 8.
in figure 8.
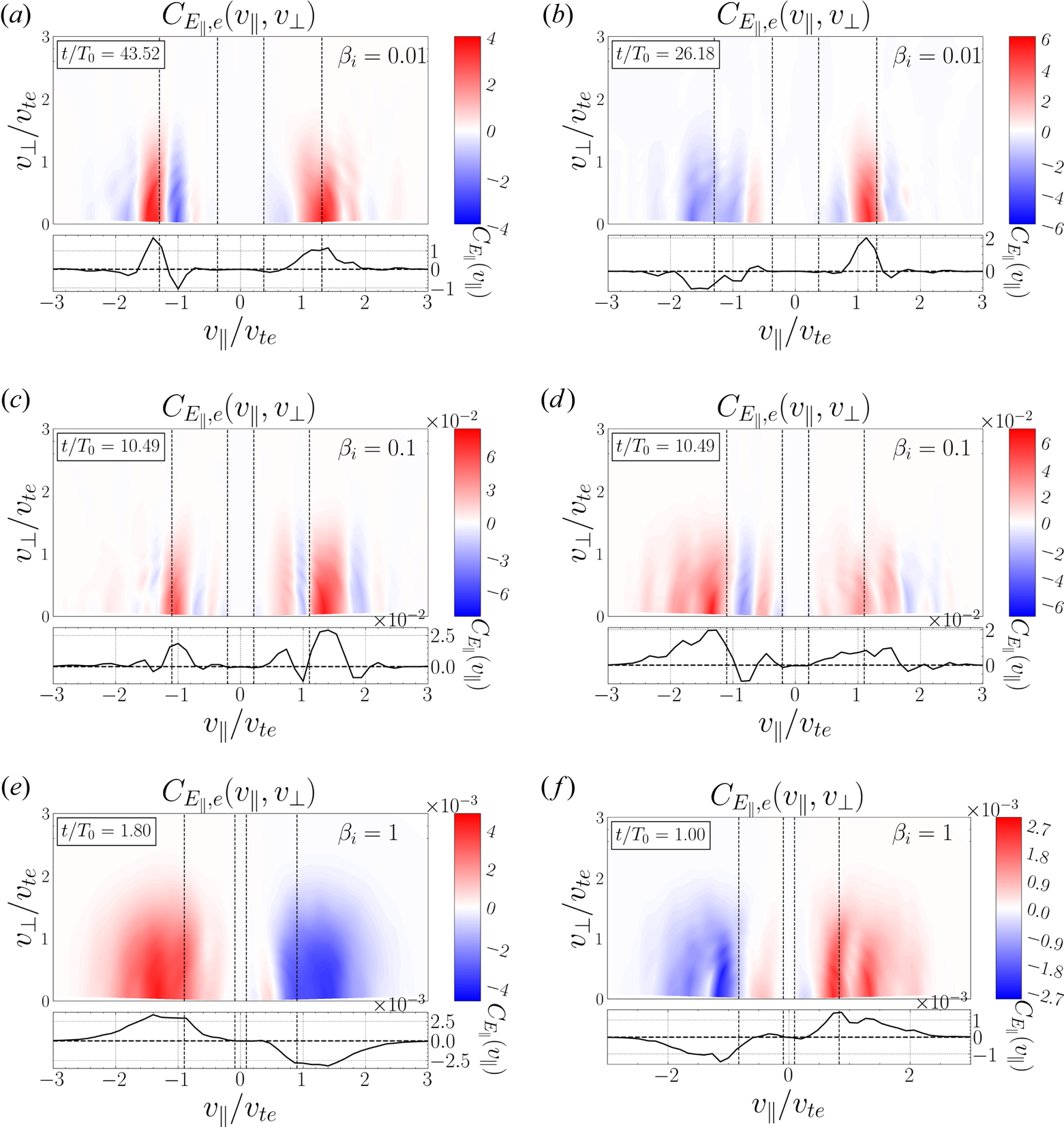
Figure 7. Gyrotropic parallel field–particle correlations $C_{E_\parallel, e}(v_\parallel, v_\perp )$![]() from different probes in the (a,b) $\beta _i = 0.01$
from different probes in the (a,b) $\beta _i = 0.01$![]() ($\tau /T_0 \simeq 17.2, \tau /T_{{\rm min}} \simeq 47.0$
($\tau /T_0 \simeq 17.2, \tau /T_{{\rm min}} \simeq 47.0$![]() ), (c,d) $\beta _i = 0.1$
), (c,d) $\beta _i = 0.1$![]() ($\tau /T_0 \simeq 2.47, \tau /T_{{\rm min}} \simeq 17.7$
($\tau /T_0 \simeq 2.47, \tau /T_{{\rm min}} \simeq 17.7$![]() ) and (e, f) $\beta _i = 1$
) and (e, f) $\beta _i = 1$![]() ($\tau /T_0 \simeq 2.43, \tau /T_{{\rm min}} \simeq 35.0$
($\tau /T_0 \simeq 2.43, \tau /T_{{\rm min}} \simeq 35.0$![]() ) simulations. The features of the velocity-space signatures are described in the text.
) simulations. The features of the velocity-space signatures are described in the text.
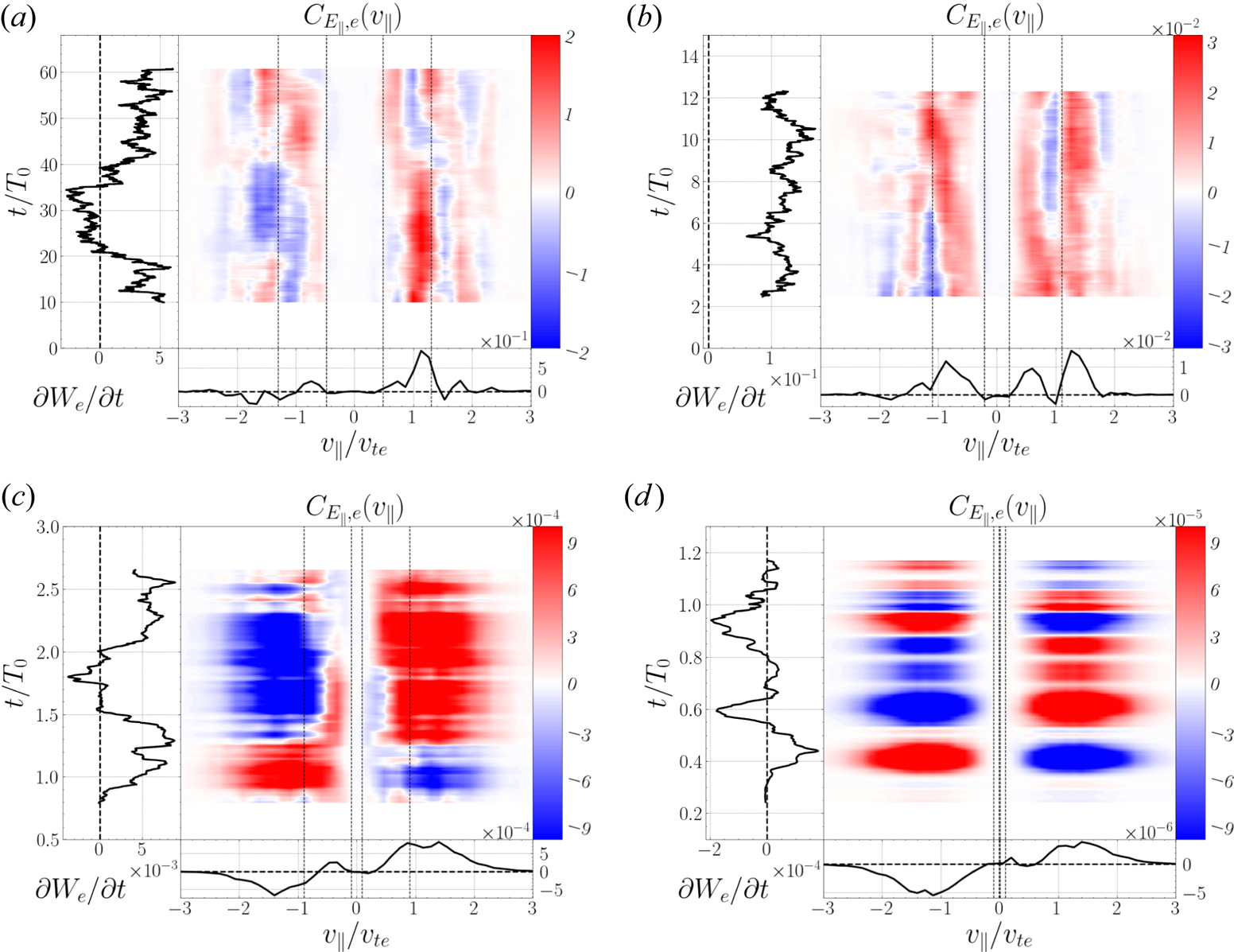
Figure 8. Timestacks of the reduced field–particle correlations $C_{E_\parallel, e}(v_\parallel )$![]() from the simulations with plasma (a) $\beta _i = 0.01$
from the simulations with plasma (a) $\beta _i = 0.01$![]() $(\tau /T_0 \simeq 17.2, \tau /T_{{\rm min}} \simeq 47.0)$
$(\tau /T_0 \simeq 17.2, \tau /T_{{\rm min}} \simeq 47.0)$![]() , (b) $0.1$
, (b) $0.1$![]() $(\tau /T_0 \simeq 4.94, \tau /T_{{\rm min}} \simeq 35.3)$
$(\tau /T_0 \simeq 4.94, \tau /T_{{\rm min}} \simeq 35.3)$![]() , (c) $1$
, (c) $1$![]() $(\tau /T_0 \simeq 1.43,\tau /T_{{\rm min}} \simeq 35.0)$
$(\tau /T_0 \simeq 1.43,\tau /T_{{\rm min}} \simeq 35.0)$![]() and (d) $10$
and (d) $10$![]() $(\tau /T_0 \simeq 0.06, \tau /T_{{\rm min}} \simeq 1.21)$
$(\tau /T_0 \simeq 0.06, \tau /T_{{\rm min}} \simeq 1.21)$![]() . The correlations in panels (a) and (b) are calculated from the same probe points as those in figures 7(b) and 7(c), respectively.
. The correlations in panels (a) and (b) are calculated from the same probe points as those in figures 7(b) and 7(c), respectively.
4.1. Gyrotropic field–particle correlations
Figure 7 shows six example gyrotropic field–particle correlations, two from each of the turbulence simulations at $\beta _i = 0.01, 0.1$![]() and $1$
and $1$![]() . We exclude $\beta _i=10$
. We exclude $\beta _i=10$![]() , since signatures are not easily observed in this case, given that the $v_\parallel$
, since signatures are not easily observed in this case, given that the $v_\parallel$![]() -resolution of our simulations is binned at $\Delta v_\parallel /v_{te} = 0.133$
-resolution of our simulations is binned at $\Delta v_\parallel /v_{te} = 0.133$![]() while the largest fully resolved wave mode in the $\beta _i=10$
while the largest fully resolved wave mode in the $\beta _i=10$![]() simulation has a phase velocity around $v_{ph}/v_{te} \sim 0.1$
simulation has a phase velocity around $v_{ph}/v_{te} \sim 0.1$![]() . Though the positive portion of the damping signature can be seen in some cases, the negative portion is unresolved (and would be strongly suppressed due to the factor of $v_\parallel ^2$
. Though the positive portion of the damping signature can be seen in some cases, the negative portion is unresolved (and would be strongly suppressed due to the factor of $v_\parallel ^2$![]() ). Further, the large relative magnitude of the non-resonant feature dominates the field–particle correlations at $\beta _i=10$
). Further, the large relative magnitude of the non-resonant feature dominates the field–particle correlations at $\beta _i=10$![]() .
.
Each example plot in figure 7 shows a contour map of $C_{E_\parallel, e}(v_\parallel, v_\perp )$![]() , the gyrotropic correlation, that has been averaged over a correlation interval of length $\tau$
, the gyrotropic correlation, that has been averaged over a correlation interval of length $\tau$![]() , included in the caption in terms of both the largest ($T_0$
, included in the caption in terms of both the largest ($T_0$![]() ) and smallest ($T_{{\rm min}}$
) and smallest ($T_{{\rm min}}$![]() ) KAW periods resolved within each simulation, and centred at some time $t/T_0$
) KAW periods resolved within each simulation, and centred at some time $t/T_0$![]() (displayed in the upper left-hand corner). The range of phase velocities at which we expect to see signatures of Landau damping are marked with vertical dotted lines. The inner vertical lines correspond to the magnitude of the phase velocity of the lowest frequency waves in this range: having a period of either $T_0$
(displayed in the upper left-hand corner). The range of phase velocities at which we expect to see signatures of Landau damping are marked with vertical dotted lines. The inner vertical lines correspond to the magnitude of the phase velocity of the lowest frequency waves in this range: having a period of either $T_0$![]() (the driving-scale wave) or $T_{{\rm max}}$
(the driving-scale wave) or $T_{{\rm max}}$![]() (the wave at the onset of strong damping) for $\beta _i \geq 0.1$
(the wave at the onset of strong damping) for $\beta _i \geq 0.1$![]() . This minimum damped frequency occurs when the damping rate reaches a threshold of $-\gamma /\omega = 0.1$
. This minimum damped frequency occurs when the damping rate reaches a threshold of $-\gamma /\omega = 0.1$![]() , which we take to be the onset of strong damping. Figure 2(b) shows that for $\beta _i = 0.1$
, which we take to be the onset of strong damping. Figure 2(b) shows that for $\beta _i = 0.1$![]() and $1$
and $1$![]() , this wave is above the driving-scale wave of $k_\perp \rho _i = 2$
, this wave is above the driving-scale wave of $k_\perp \rho _i = 2$![]() . For $\beta _i = 10$
. For $\beta _i = 10$![]() , the initial peak above $-\gamma /\omega = 0.1$
, the initial peak above $-\gamma /\omega = 0.1$![]() is due to ion Landau damping; therefore, we take the onset of strong electron damping to be around $k_\perp \rho _i \sim 3$
is due to ion Landau damping; therefore, we take the onset of strong electron damping to be around $k_\perp \rho _i \sim 3$![]() . The vertical dotted lines at higher velocities correspond to the highest frequency wave that we expect to undergo Landau damping (with period $T_{{\rm min}}$
. The vertical dotted lines at higher velocities correspond to the highest frequency wave that we expect to undergo Landau damping (with period $T_{{\rm min}}$![]() ), found simply by the taking the peak of the curve in figure 2(a). The phase velocities of these two limiting cases are marked for both upward ($v_\parallel /v_{te} > 0$
), found simply by the taking the peak of the curve in figure 2(a). The phase velocities of these two limiting cases are marked for both upward ($v_\parallel /v_{te} > 0$![]() ) and downward ($v_\parallel /v_{te} < 0$
) and downward ($v_\parallel /v_{te} < 0$![]() ) wave propagation. Each line plot in the lower subpanels of figure 7 displays the reduced correlation integrated over all $v_\perp$
) wave propagation. Each line plot in the lower subpanels of figure 7 displays the reduced correlation integrated over all $v_\perp$![]() , $C_{E_\parallel,e}(v_\parallel )$
, $C_{E_\parallel,e}(v_\parallel )$![]() .
.
Figures 7(a) and 7(b) show gyrotropic correlations from the $\beta _i = 0.01$![]() turbulent simulation. Figures 7(a) is from a probe in the $z=0$
turbulent simulation. Figures 7(a) is from a probe in the $z=0$![]() plane of the simulation box, calculated using a correlation interval of length $\tau \simeq 17.2\ T_0$
plane of the simulation box, calculated using a correlation interval of length $\tau \simeq 17.2\ T_0$![]() ($\tau \simeq 47.0 T_{{\rm min}}$
($\tau \simeq 47.0 T_{{\rm min}}$![]() ) and shown centred at time $t/T_0 = 43.52$
) and shown centred at time $t/T_0 = 43.52$![]() . This example contains a pair of bipolar signatures: one at positive and the other at negative parallel velocity, indicating damping of KAWs propagating in both directions relative to the background magnetic field. As shown in figure 4(a), the location of the zero crossing in the integrated correlation $C_{E_\parallel }(v_\parallel )$
. This example contains a pair of bipolar signatures: one at positive and the other at negative parallel velocity, indicating damping of KAWs propagating in both directions relative to the background magnetic field. As shown in figure 4(a), the location of the zero crossing in the integrated correlation $C_{E_\parallel }(v_\parallel )$![]() in the lower subpanels of figure 8 corresponds to the phase velocity of the damped wave. Thus, the upward-propagating damped wave has a lower phase velocity than the downward propagating damped wave. However, the signature at $v_\parallel /v_{te} > 0$
in the lower subpanels of figure 8 corresponds to the phase velocity of the damped wave. Thus, the upward-propagating damped wave has a lower phase velocity than the downward propagating damped wave. However, the signature at $v_\parallel /v_{te} > 0$![]() is significantly wider than the one at $v_\parallel /v_{te} < 0$
is significantly wider than the one at $v_\parallel /v_{te} < 0$![]() . This seems to contradict the conclusion of figure 4(b), which predicts a direct relationship between phase velocity and signature width for constant $\beta _i$
. This seems to contradict the conclusion of figure 4(b), which predicts a direct relationship between phase velocity and signature width for constant $\beta _i$![]() . However, the $v_\parallel /v_{te} > 0$
. However, the $v_\parallel /v_{te} > 0$![]() signature has a subtle, divided positive peak. This may indicate that the signature is a superposition of the damping signatures of two waves closely spaced in parallel phase velocity such that their individual bipolar signatures cannot be resolved. Instead, the two signatures merge into a single, broadened peak (Horvath et al. Reference Horvath, Howes and McCubbin2020). This interpretation is supported by gyrotropic plots centred at earlier times and by the timestack plot of the correlation at this probe point. The plot in figure 7(b) is an example of an imbalanced signature, which occurs when damping is present for only upward or downward propagating waves at a given time. In this case, an upward-propagating wave produces a bipolar signature but no clear resonant damping signature is visible for $v_\parallel /v_{te} < 0$
signature has a subtle, divided positive peak. This may indicate that the signature is a superposition of the damping signatures of two waves closely spaced in parallel phase velocity such that their individual bipolar signatures cannot be resolved. Instead, the two signatures merge into a single, broadened peak (Horvath et al. Reference Horvath, Howes and McCubbin2020). This interpretation is supported by gyrotropic plots centred at earlier times and by the timestack plot of the correlation at this probe point. The plot in figure 7(b) is an example of an imbalanced signature, which occurs when damping is present for only upward or downward propagating waves at a given time. In this case, an upward-propagating wave produces a bipolar signature but no clear resonant damping signature is visible for $v_\parallel /v_{te} < 0$![]() . This correlation is averaged over the same interval $\tau$
. This correlation is averaged over the same interval $\tau$![]() , but is taken at a probe point along the $z$
, but is taken at a probe point along the $z$![]() -axis ($z \neq 0$
-axis ($z \neq 0$![]() ) and is centred at an earlier time.
) and is centred at an earlier time.
Figures 7(c) and 7(d) contain correlations from the $\beta _i = 0.1$![]() simulation, taken from two different probe points along the $z$
simulation, taken from two different probe points along the $z$![]() -axis ($z \neq 0$
-axis ($z \neq 0$![]() ). Each is averaged over a correlation interval of $\tau = 2.47\ T_0$
). Each is averaged over a correlation interval of $\tau = 2.47\ T_0$![]() ($17.7\ T_{{\rm min}}$
($17.7\ T_{{\rm min}}$![]() ) and is centred at $t/T_0 = 10.49$
) and is centred at $t/T_0 = 10.49$![]() . Note that the velocity range marked by the pairs of vertical dotted lines has shifted towards smaller $v_\parallel$
. Note that the velocity range marked by the pairs of vertical dotted lines has shifted towards smaller $v_\parallel$![]() , reflecting the shift towards smaller parallel phase velocities in the dispersion relation as $\beta _i$
, reflecting the shift towards smaller parallel phase velocities in the dispersion relation as $\beta _i$![]() increases, as shown in figure 2(a). In figure 7(c), the example correlation shows signatures of damped KAWs propagating in both directions along the background magnetic field. For $v_\parallel /v_{te} > 0$
increases, as shown in figure 2(a). In figure 7(c), the example correlation shows signatures of damped KAWs propagating in both directions along the background magnetic field. For $v_\parallel /v_{te} > 0$![]() , there is evidence of two bipolar signatures, spaced far enough apart to be resolved in $v_\parallel$
, there is evidence of two bipolar signatures, spaced far enough apart to be resolved in $v_\parallel$![]() space. The higher-frequency signature is centred around the upper vertical dotted line, indicating that the damped wave is at the maximum phase velocity that we expect in this simulation. This signature is also wider than the signature at smaller $v_\parallel$
space. The higher-frequency signature is centred around the upper vertical dotted line, indicating that the damped wave is at the maximum phase velocity that we expect in this simulation. This signature is also wider than the signature at smaller $v_\parallel$![]() , consistent with our theoretical expectations illustrated in figure 4(b). Note also that the lower resonant-velocity has a significantly suppressed negative portion of its bipolar signature that is difficult to observe at this colour scale, consistent with the effect of $v_\parallel ^2$
, consistent with our theoretical expectations illustrated in figure 4(b). Note also that the lower resonant-velocity has a significantly suppressed negative portion of its bipolar signature that is difficult to observe at this colour scale, consistent with the effect of $v_\parallel ^2$![]() weighting as illustrated in figure 5. For $v_\parallel /v_{te} < 0$
weighting as illustrated in figure 5. For $v_\parallel /v_{te} < 0$![]() , one signature is visible just below the dotted line marking the magnitude of the most highly damped phase-velocity. The relative width of this signature is between that of the two upward-propagating wave signatures, as expected. Figure 7(d) shows an example of another imbalanced signature with a clear velocity-space signature of electron Landau damping for only downward-propagating waves. In this case, there are two bipolar structures: one centred at $v_\parallel /v_{te} \simeq -1$
, one signature is visible just below the dotted line marking the magnitude of the most highly damped phase-velocity. The relative width of this signature is between that of the two upward-propagating wave signatures, as expected. Figure 7(d) shows an example of another imbalanced signature with a clear velocity-space signature of electron Landau damping for only downward-propagating waves. In this case, there are two bipolar structures: one centred at $v_\parallel /v_{te} \simeq -1$![]() and another at $v_\parallel /v_{te} \simeq -0.25$
and another at $v_\parallel /v_{te} \simeq -0.25$![]() . Again, the low-velocity signature is strongly affected by the $v_\parallel ^2$
. Again, the low-velocity signature is strongly affected by the $v_\parallel ^2$![]() weighting; however, this fainter signature is persistent throughout the whole simulation. The structures in the positive velocity region of the plot do not show a clear bipolar signature indicative of electron Landau damping of upward propagating KAWs, but rather may simply be the remnants of oscillatory fluctuations that are poorly cancelled out by the average over our chosen correlation interval $\tau$
weighting; however, this fainter signature is persistent throughout the whole simulation. The structures in the positive velocity region of the plot do not show a clear bipolar signature indicative of electron Landau damping of upward propagating KAWs, but rather may simply be the remnants of oscillatory fluctuations that are poorly cancelled out by the average over our chosen correlation interval $\tau$![]() .Footnote 3
.Footnote 3
Figures 7(e) and 7( f) show gyrotropic correlations from the $\beta _i = 1$![]() simulation, from two different probe points in the midplane ($z = 0$
simulation, from two different probe points in the midplane ($z = 0$![]() ). These correlations are averaged over an interval $\tau = 1.43\ T_0$
). These correlations are averaged over an interval $\tau = 1.43\ T_0$![]() ($\tau = 35.0\ T_{{\rm min}}$
($\tau = 35.0\ T_{{\rm min}}$![]() ). As before, the vertical dotted lines mark out a range of resonant parallel phase velocities that are yet nearer to $v_\parallel = 0$
). As before, the vertical dotted lines mark out a range of resonant parallel phase velocities that are yet nearer to $v_\parallel = 0$![]() . The largest expected velocity is now at $v_\parallel /v_{te} < 1$
. The largest expected velocity is now at $v_\parallel /v_{te} < 1$![]() , meaning that the $v_\parallel ^2$
, meaning that the $v_\parallel ^2$![]() -weighting will act to suppress all of the signatures relative to any incomplete cancellation that appears at $v_\parallel / v_{te}>1$
-weighting will act to suppress all of the signatures relative to any incomplete cancellation that appears at $v_\parallel / v_{te}>1$![]() . These examples show how the non-resonant feature begins to dominate the correlations at $\beta _i \gtrsim 1$
. These examples show how the non-resonant feature begins to dominate the correlations at $\beta _i \gtrsim 1$![]() , and this feature is particularly prominent in figure 7(e). Despite this, a faint bipolar signature of an upward-propagating wave can still be seen in the colour map of this example at the shown scale, though it has become indistinguishable in the reduced correlation due to the overwhelming magnitude of the non-resonant feature. As discussed for the damped individual waves, this feature arises due to the increased compressibility of KAWs at $\beta _i \gtrsim 1$
, and this feature is particularly prominent in figure 7(e). Despite this, a faint bipolar signature of an upward-propagating wave can still be seen in the colour map of this example at the shown scale, though it has become indistinguishable in the reduced correlation due to the overwhelming magnitude of the non-resonant feature. As discussed for the damped individual waves, this feature arises due to the increased compressibility of KAWs at $\beta _i \gtrsim 1$![]() , and due to the changing phase offset $\phi \neq {\rm \pi}/2$
, and due to the changing phase offset $\phi \neq {\rm \pi}/2$![]() between $E_\parallel$
between $E_\parallel$![]() and the compressive density fluctuation in $\partial f/\partial v_\parallel$
and the compressive density fluctuation in $\partial f/\partial v_\parallel$![]() . In many cases, this non-resonant feature hinders the observation of bipolar signatures at $\beta _i \gtrsim 1$
. In many cases, this non-resonant feature hinders the observation of bipolar signatures at $\beta _i \gtrsim 1$![]() , though at times it can be removed so that the signatures may be observed via a folding technique discussed in § 5.5.1. At the time of the correlation in figure 7( f), the non-resonant feature is smaller in amplitude relative to the resonant signatures, and a bipolar structure is visible (with a somewhat attenuated negative portion) at $v_\parallel /v_{te} \simeq 0.3$
, though at times it can be removed so that the signatures may be observed via a folding technique discussed in § 5.5.1. At the time of the correlation in figure 7( f), the non-resonant feature is smaller in amplitude relative to the resonant signatures, and a bipolar structure is visible (with a somewhat attenuated negative portion) at $v_\parallel /v_{te} \simeq 0.3$![]() .
.
In summary, this section presents one of the key results of this paper, the gyrotropic velocity-space signature of electron Landau damping $C_{E_\parallel }(v_\parallel, v_\perp )$![]() , as exemplified for $\beta _i=0.01$
, as exemplified for $\beta _i=0.01$![]() in figure 7(a) at $v_\parallel /v_{te} \simeq -1.2$
in figure 7(a) at $v_\parallel /v_{te} \simeq -1.2$![]() and figure 7(b) at $v_\parallel /v_{te} \simeq +0.75$
and figure 7(b) at $v_\parallel /v_{te} \simeq +0.75$![]() , for $\beta _i=0.1$
, for $\beta _i=0.1$![]() in figure 7(c) at $v_\parallel /v_{te} \simeq -0.8$
in figure 7(c) at $v_\parallel /v_{te} \simeq -0.8$![]() and $+1.1$
and $+1.1$![]() and figure 7(d) at $v_\parallel /v_{te} \simeq -1.0$
and figure 7(d) at $v_\parallel /v_{te} \simeq -1.0$![]() , and for $\beta _i=1$
, and for $\beta _i=1$![]() in figure 7( f) at $v_\parallel /v_{te} \simeq +0.4$
in figure 7( f) at $v_\parallel /v_{te} \simeq +0.4$![]() . These qualitative and quantitative features of the velocity-space signatures as a function of the ion plasma $\beta _i$
. These qualitative and quantitative features of the velocity-space signatures as a function of the ion plasma $\beta _i$![]() provide an essential framework for identifying electron Landau damping in both kinetic turbulence simulations and spacecraft observations.
provide an essential framework for identifying electron Landau damping in both kinetic turbulence simulations and spacecraft observations.
4.2. Timestack plots of the field–particle correlation
To observe how the gyrotropic velocity-space signatures of electron energization in figure 7 evolve over time, we take advantage of the fact that these gyrotropic signatures do not strongly depend on $v_\perp$![]() (other than the exponential decrease with increasing $v_\perp$
(other than the exponential decrease with increasing $v_\perp$![]() , a consequence of the underlying Maxwellian equilibrium velocity distribution) to integrate over $v_\perp$
, a consequence of the underlying Maxwellian equilibrium velocity distribution) to integrate over $v_\perp$![]() and generate a timestack plot of reduced parallel correlation $C_{E_\parallel }(v_\parallel, t)$
and generate a timestack plot of reduced parallel correlation $C_{E_\parallel }(v_\parallel, t)$![]() . These timestack plots are invaluable for determining the persistence of a signature over time and for establishing an overall view of the net energy transfer at a given location. In figure 8, we present one timestack plot from a single probe in each of the four simulations at (figure 8a) $\beta _i=0.01$
. These timestack plots are invaluable for determining the persistence of a signature over time and for establishing an overall view of the net energy transfer at a given location. In figure 8, we present one timestack plot from a single probe in each of the four simulations at (figure 8a) $\beta _i=0.01$![]() , (figure 8b) $0.1$
, (figure 8b) $0.1$![]() , (figure 8c) $1$
, (figure 8c) $1$![]() and (figure 8d) $10$
and (figure 8d) $10$![]() . In each, we integrate over the full duration of the simulation to obtain the time-integrated, reduced parallel correlation $C_{E_\parallel }(v_\parallel )$
. In each, we integrate over the full duration of the simulation to obtain the time-integrated, reduced parallel correlation $C_{E_\parallel }(v_\parallel )$![]() at the probe position (figure 8c and figure 8d); we also integrate over $v_\parallel$
at the probe position (figure 8c and figure 8d); we also integrate over $v_\parallel$![]() to obtain the rate of change of the spatial energy density $(\partial W_s/ \partial t)_{E_\parallel }=j_{e,\parallel } E_\parallel$
to obtain the rate of change of the spatial energy density $(\partial W_s/ \partial t)_{E_\parallel }=j_{e,\parallel } E_\parallel$![]() due to the parallel electric field.
due to the parallel electric field.
In figure 8(a), we show the timestack from the $\beta _i=0.01$![]() simulation at the same probe point as the gyrotropic correlation in figure 7(b) and averaged over the same correlation interval $\tau /T_0 \simeq 17.2, \tau /T_{{\rm min}} \simeq 47.0$
simulation at the same probe point as the gyrotropic correlation in figure 7(b) and averaged over the same correlation interval $\tau /T_0 \simeq 17.2, \tau /T_{{\rm min}} \simeq 47.0$![]() . Note that the $v_\parallel /v_{te} > 0$
. Note that the $v_\parallel /v_{te} > 0$![]() signature observed at $t/T_0 = 26.18$
signature observed at $t/T_0 = 26.18$![]() in the gyrotropic plot was present at the beginning of the averaging interval and persisted for over $30$
in the gyrotropic plot was present at the beginning of the averaging interval and persisted for over $30$![]() domain-scale wave periods. Other signatures (of both upward and downward propagating waves) appear later in the simulation. The proximity of these signatures in velocity-space can make it difficult to distinguish their bipolar form due to overlap with signatures at other parallel phase velocities in addition to the $v_\parallel ^2$
domain-scale wave periods. Other signatures (of both upward and downward propagating waves) appear later in the simulation. The proximity of these signatures in velocity-space can make it difficult to distinguish their bipolar form due to overlap with signatures at other parallel phase velocities in addition to the $v_\parallel ^2$![]() suppression of the bipolar form. The timestack from the $\beta _i=0.1$
suppression of the bipolar form. The timestack from the $\beta _i=0.1$![]() simulation in figure 8(b) is taken from the same probe point as the gyrotropic plot in figure 7(c) but averaged over a longer correlation interval, $\tau /T_0 \simeq 4.94, \tau /T_{{\rm min}} \simeq 35.3$
simulation in figure 8(b) is taken from the same probe point as the gyrotropic plot in figure 7(c) but averaged over a longer correlation interval, $\tau /T_0 \simeq 4.94, \tau /T_{{\rm min}} \simeq 35.3$![]() . At $t/T_0 = 10.49$
. At $t/T_0 = 10.49$![]() – the central time of the correlation interval for the gyrotropic plot – the three signatures seen in the gyrotropic plot are clearly visible. The timestack shows that each of these signatures are present through the whole simulation, but two of the three shift somewhat in velocity, leading to the overlap of signatures at slightly different resonant parallel velocities when integrated over the full simulation (lower subpanel).
– the central time of the correlation interval for the gyrotropic plot – the three signatures seen in the gyrotropic plot are clearly visible. The timestack shows that each of these signatures are present through the whole simulation, but two of the three shift somewhat in velocity, leading to the overlap of signatures at slightly different resonant parallel velocities when integrated over the full simulation (lower subpanel).
In figure 8(c), we plot a timestack from the $\beta _i=1$![]() simulation, taken at a midplane ($z=0$
simulation, taken at a midplane ($z=0$![]() ) probe that is not represented in figure 7, but averaged over the same correlation interval $\tau /T_0 \simeq 1.43, \tau /T_{{\rm min}} \simeq 35.0$
) probe that is not represented in figure 7, but averaged over the same correlation interval $\tau /T_0 \simeq 1.43, \tau /T_{{\rm min}} \simeq 35.0$![]() . At this value of $\beta _i$
. At this value of $\beta _i$![]() , the broad non-resonant feature has become prominent in the correlation, though the lower amplitude resonant signatures can still be seen at small parallel velocities. For instance, at $v_\parallel /v_{te} \simeq -0.2$
, the broad non-resonant feature has become prominent in the correlation, though the lower amplitude resonant signatures can still be seen at small parallel velocities. For instance, at $v_\parallel /v_{te} \simeq -0.2$![]() a signature is visible in the range $1.2 < t/T_0 < 2$
a signature is visible in the range $1.2 < t/T_0 < 2$![]() , which creates an obvious positive region in the lower, time-integrated subpanel. Note that the negative portion of this bipolar signature is not visible in the timestack at this colour scale and does not appear in the time-integrated correlation. At many probe points, such evidence of a damping signature at lower parallel velocities than the non-resonant feature is much more difficult to observe. When $\beta _i$
, which creates an obvious positive region in the lower, time-integrated subpanel. Note that the negative portion of this bipolar signature is not visible in the timestack at this colour scale and does not appear in the time-integrated correlation. At many probe points, such evidence of a damping signature at lower parallel velocities than the non-resonant feature is much more difficult to observe. When $\beta _i$![]() is increased further, these difficulties are exacerbated, as illustrated in figure 8(d) for the $\beta _i=10$
is increased further, these difficulties are exacerbated, as illustrated in figure 8(d) for the $\beta _i=10$![]() simulation. This correlation is taken from a midplane probe, and averaged over a mere $\tau /T_0 \simeq 0.06$
simulation. This correlation is taken from a midplane probe, and averaged over a mere $\tau /T_0 \simeq 0.06$![]() , or $\tau /T_{{\rm min}} \simeq 1.21$
, or $\tau /T_{{\rm min}} \simeq 1.21$![]() . The correlation interval is a very small fraction of the driving scale wave period $T_0$
. The correlation interval is a very small fraction of the driving scale wave period $T_0$![]() , so we would not expect to see bipolar signatures in the timestack due to these waves. The full interval of this simulation is long enough to give $\tau /T_0 \simeq 1.01$
, so we would not expect to see bipolar signatures in the timestack due to these waves. The full interval of this simulation is long enough to give $\tau /T_0 \simeq 1.01$![]() (shown in the lower subpanel), so in order to display a timestack at this plasma beta we have chosen a low value of $\tau /T_0$
(shown in the lower subpanel), so in order to display a timestack at this plasma beta we have chosen a low value of $\tau /T_0$![]() for the contour plot. As in the case of $\beta _i=1$
for the contour plot. As in the case of $\beta _i=1$![]() , at some probe points in the $\beta _i=10$
, at some probe points in the $\beta _i=10$![]() simulation evidence of energization due to Landau damping can be found by observing positive bumps near the range of expected resonant velocities in the time-integrated correlation. However, the increased amplitude of the non-resonant feature with respect to the resonant damping signatures, coupled with the finite resolution of our parallel velocity grid, make damping signatures nearly impossible to observe clearly in correlations for $\beta _i=10$
simulation evidence of energization due to Landau damping can be found by observing positive bumps near the range of expected resonant velocities in the time-integrated correlation. However, the increased amplitude of the non-resonant feature with respect to the resonant damping signatures, coupled with the finite resolution of our parallel velocity grid, make damping signatures nearly impossible to observe clearly in correlations for $\beta _i=10$![]() . It is worthwhile noting here that, at higher ion plasma beta values $\beta _i \gtrsim 1$
. It is worthwhile noting here that, at higher ion plasma beta values $\beta _i \gtrsim 1$![]() , ion Landau and transit-time damping are expected to play a significant role in the dissipation of turbulent energy at scales $k_\perp \rho _i \sim 1$
, ion Landau and transit-time damping are expected to play a significant role in the dissipation of turbulent energy at scales $k_\perp \rho _i \sim 1$![]() (Klein et al. Reference Klein, Howes and Tenbarge2017), so electron Landau damping of turbulent energy that reaches the KAW cascade at $k_\perp \rho _i \gg 1$
(Klein et al. Reference Klein, Howes and Tenbarge2017), so electron Landau damping of turbulent energy that reaches the KAW cascade at $k_\perp \rho _i \gg 1$![]() is expected to be less significant in the overall dissipation of the turbulent cascade.
is expected to be less significant in the overall dissipation of the turbulent cascade.
5. Discussion: features of the velocity-space signatures of electron landau damping as a function of plasma $\beta _i$
In the previous sections, we have demonstrated general qualitative and quantitative features that are present in the velocity-space signatures of electron Landau damping as a function of the ion plasma $\beta _i$![]() for linear KAWs. These indicate the general trends that should be visible in the velocity-space signatures generated by turbulence dissipation measured at different locations throughout the inner heliosphere. Next, we presented example velocity-space signatures from our suite of four kinetic plasma turbulence simulations to illustrate how these general trends appear in the context of broadband turbulent energy dissipation via the mechanism of electron Landau damping. Here, we recap these features and discuss implications for making in situ observations of electron Landau damping.
for linear KAWs. These indicate the general trends that should be visible in the velocity-space signatures generated by turbulence dissipation measured at different locations throughout the inner heliosphere. Next, we presented example velocity-space signatures from our suite of four kinetic plasma turbulence simulations to illustrate how these general trends appear in the context of broadband turbulent energy dissipation via the mechanism of electron Landau damping. Here, we recap these features and discuss implications for making in situ observations of electron Landau damping.
5.1. Imbalanced velocity-space signatures
Since the earliest studies of turbulence in MHD plasmas, it was recognized that the turbulent cascade is mediated by nonlinear interactions between Alfvén wave packets propagating up and down the magnetic field (Iroshnikov Reference Iroshnikov1963; Kraichnan Reference Kraichnan1965; Sridhar & Goldreich Reference Sridhar and Goldreich1994; Goldreich & Sridhar Reference Goldreich and Sridhar1995). These ‘collisions’ between counterpropagating Alfvén wave packets have been invoked as the fundamental building block of astrophysical plasma turbulence, with theoretical (Howes & Nielson Reference Howes and Nielson2013), numerical (Nielson, Howes & Dorland Reference Nielson, Howes and Dorland2013) and experimental (Howes et al. Reference Howes, Drake, Nielson, Carter, Kletzing and Skiff2012, Reference Howes, Nielson, Drake, Schroeder, Skiff, Kletzing and Carter2013; Drake et al. Reference Drake, Schroeder, Howes, Kletzing, Skiff, Carter and Auerbach2013) confirmation of the underlying physics. Further work has illustrated the role of the Alfvén wave collisions in the self-consistent development of current sheets in kinetic plasma turbulence (Howes Reference Howes2016; Verniero, Howes & Klein Reference Verniero, Howes and Klein2018; Verniero & Howes Reference Verniero and Howes2018) and the role of Landau damping in the dissipation of those current sheets (Howes et al. Reference Howes, McCubbin and Klein2018). When the turbulent fluctuations have more Alfvénic energy flux propagating in one direction along the local magnetic field than the other direction – known as imbalanced turbulence (Lithwick & Goldreich Reference Lithwick and Goldreich2003; Lithwick, Goldreich & Sridhar Reference Lithwick, Goldreich and Sridhar2007; Beresnyak & Lazarian Reference Beresnyak and Lazarian2008; Chandran Reference Chandran2008; Markovskii & Vasquez Reference Markovskii and Vasquez2013), or turbulence with non-zero cross-helicity – it is predicted to alter the dynamics of the turbulent cascade (Meyrand et al. Reference Meyrand, Squire, Schekochihin and Dorland2021; Squire et al. Reference Squire, Meyrand, Kunz, Arzamasskiy, Schekochihin and Quataert2022), and therefore will likely also impact the dominant mechanisms of its dissipation.
Even if the turbulence is balanced on longer time scales, during short periods of time local regions of imbalanced turbulence may develop. Averaged over space and time, such imbalanced regions are not thought to affect the overall energy spectra of the turbulent cascade (Perez & Boldyrev Reference Perez and Boldyrev2009). Further, in this work we find that one may measure a local dominance of wave damping in one direction or another even if the turbulence remains relatively balanced locally. The field–particle correlation analysis of our suite of turbulence simulations frequently finds asymmetric signatures of electron Landau damping, e.g. figure 7(b). An inspection of the timestack plots in figure 8 clearly shows that the damping of the turbulent fluctuations varies significantly in time over the evolution of the simulations, with upward- or downward-propagating fluctuations dominating the energy transfer to the electrons over intervals of time from a few to tens of characteristic wave periods. This is consistent with the results of our previous simulations (Horvath et al. Reference Horvath, Howes and McCubbin2020) and with in situ observations in the magnetosheath (Afshari et al. Reference Afshari, Howes, Kletzing, Hartley and Boardsen2021). Using MMS data, Afshari et al. (Reference Afshari, Howes, Kletzing, Hartley and Boardsen2021) connected the imbalance in the wave damping with the dominant direction of the Poynting flux in the data interval. In our suite of simulations presented here, however, we find that the overall flux of electromagnetic energy remains roughly balanced at all times. This is not surprising since the turbulence is driven by approximately equal amplitude, oppositely directed Alfvén waves. Nonetheless, on shorter time scales and at individual probe positions in the simulations, local imbalances of damping arise that lead to the asymmetric signatures that are frequently observed in these simulations and in MMS observations (Afshari et al. Reference Afshari, Howes, Kletzing, Hartley and Boardsen2021).
5.2. Temporal intermittency and the overlap of velocity-space signatures
As was found in previous field–particle correlation studies of electron Landau damping in simulations (Horvath et al. Reference Horvath, Howes and McCubbin2020, Reference Horvath, Howes and McCubbin2022), we find that electron damping signatures in broadband, dispersive KAW turbulence contain more structure than the simple bipolar signature of a single, damped wave. This was illustrated in figure 7(c), where the time-integrated signature at $v_\parallel > 0$![]() is composed of at least two overlapping bipolar signatures, creating a broadened, double-peaked structure. In the timestack plot of figure 8(b), closely spaced signatures overlap in the time-average to create the appearance of a single signature that ‘shifts’ in $v_\parallel$
is composed of at least two overlapping bipolar signatures, creating a broadened, double-peaked structure. In the timestack plot of figure 8(b), closely spaced signatures overlap in the time-average to create the appearance of a single signature that ‘shifts’ in $v_\parallel$![]() . Note that, if the resonant velocities were spaced more closely and were unresolved along $v_\parallel$
. Note that, if the resonant velocities were spaced more closely and were unresolved along $v_\parallel$![]() , this would result in a smoothly broadened signature. The superposition of multiple bipolar signatures creating a complicated final signature was most commonly observed in our lowest beta simulation ($\beta _i=0.01$
, this would result in a smoothly broadened signature. The superposition of multiple bipolar signatures creating a complicated final signature was most commonly observed in our lowest beta simulation ($\beta _i=0.01$![]() ), which has the largest range of expected resonant parallel phase velocities. Additionally, AstroGK evolves low-beta plasmas significantly faster than high-beta plasmas, resulting in a longer time interval over which temporally intermittent wave damping can be observed (see the simulation lengths, $\Delta t/T_0$
), which has the largest range of expected resonant parallel phase velocities. Additionally, AstroGK evolves low-beta plasmas significantly faster than high-beta plasmas, resulting in a longer time interval over which temporally intermittent wave damping can be observed (see the simulation lengths, $\Delta t/T_0$![]() , in table 1). If we continued running the higher beta simulations to create longer time intervals, we would expect to see the effects of signature superposition ubiquitously (with the exception of the $\beta _i = 10$
, in table 1). If we continued running the higher beta simulations to create longer time intervals, we would expect to see the effects of signature superposition ubiquitously (with the exception of the $\beta _i = 10$![]() simulation, in which the $v_\parallel$
simulation, in which the $v_\parallel$![]() resolution is insufficient to resolve multiple signatures in the region of expected damping). In observations, obtaining long time intervals – in terms of the underlying KAW periods – is not a problem. On the other hand, finite instrumental resolution in parallel velocity (Verniero et al. Reference Verniero, Howes, Stewart and Klein2021a,Reference Verniero, Howes, Stewart and Kleinb) is a significant limitation that must be taken into account when interpreting the velocity-space signatures from the field–particle correlation analysis of spacecraft observations.
resolution is insufficient to resolve multiple signatures in the region of expected damping). In observations, obtaining long time intervals – in terms of the underlying KAW periods – is not a problem. On the other hand, finite instrumental resolution in parallel velocity (Verniero et al. Reference Verniero, Howes, Stewart and Klein2021a,Reference Verniero, Howes, Stewart and Kleinb) is a significant limitation that must be taken into account when interpreting the velocity-space signatures from the field–particle correlation analysis of spacecraft observations.
5.3. Velocity-space resolution and weighting by $v_\parallel ^2$
The effects of $v_\parallel ^2$![]() weighting on the velocity-space signatures are visible in the various examples from the turbulence simulations in figures 7 and 8. In particular, we have shown that this weighting may obscure the negative portion of a bipolar signature of electron Landau damping when the parallel resonant phase velocity falls at a sufficiently small value of $v_\parallel /v_{te}$
weighting on the velocity-space signatures are visible in the various examples from the turbulence simulations in figures 7 and 8. In particular, we have shown that this weighting may obscure the negative portion of a bipolar signature of electron Landau damping when the parallel resonant phase velocity falls at a sufficiently small value of $v_\parallel /v_{te}$![]() . From our individual wave simulations in § 3, we found that our binned parallel velocity resolution of $\Delta v_\parallel /v_{te} = 0.133$
. From our individual wave simulations in § 3, we found that our binned parallel velocity resolution of $\Delta v_\parallel /v_{te} = 0.133$![]() , coupled with the $v_\parallel ^2$
, coupled with the $v_\parallel ^2$![]() weighting, resulted in difficulty observing the full bipolar structure of the velocity-space signatures of electron Landau damping at parallel velocities $v_\parallel /v_{te} \le 0.3$
weighting, resulted in difficulty observing the full bipolar structure of the velocity-space signatures of electron Landau damping at parallel velocities $v_\parallel /v_{te} \le 0.3$![]() . The entire dispersive range of parallel phase velocities is above this threshold for the $\beta _i = 0.01$
. The entire dispersive range of parallel phase velocities is above this threshold for the $\beta _i = 0.01$![]() simulations, but as $\beta _i$
simulations, but as $\beta _i$![]() is increased, more and more of the dispersive range of phase velocities falls below this threshold. For in situ signatures, clear bipolar signatures may therefore be more easily observed for a given finite resolution in parallel velocity closer to the Sun, where $\beta _i$
is increased, more and more of the dispersive range of phase velocities falls below this threshold. For in situ signatures, clear bipolar signatures may therefore be more easily observed for a given finite resolution in parallel velocity closer to the Sun, where $\beta _i$![]() may be smaller due to increased local magnetic energy density relative to the plasma thermal energy density. For plasma conditions and velocity resolutions where $v_\parallel ^2$
may be smaller due to increased local magnetic energy density relative to the plasma thermal energy density. For plasma conditions and velocity resolutions where $v_\parallel ^2$![]() does result in obscuring the negative portion of the characteristic bipolar structure, electron Landau damping may still be identified through the timestack correlations. If energization is persistent and localized at a given parallel velocity in a regime where the negative portion is not observed, this still indicates the action of a resonant energization mechanism that may be identified as electron Landau damping.
does result in obscuring the negative portion of the characteristic bipolar structure, electron Landau damping may still be identified through the timestack correlations. If energization is persistent and localized at a given parallel velocity in a regime where the negative portion is not observed, this still indicates the action of a resonant energization mechanism that may be identified as electron Landau damping.
5.4. Variations in velocity-space signature width
As discussed above, in both individual KAW and turbulence simulations, we observe that the velocity-space signature of electron Landau damping varies in width as the perpendicular wavenumber and plasma parameters change. We explain this relationship by showing that the increased width (quantified by the FWHM value of the positive portion of the bipolar signature) is associated with an increased normalized damping rate of KAWs, as shown in figure 4(b). Our simulations indicate that we should expect to observe widths of the velocity-space signatures of electron Landau damping that depend on the local plasma $\beta _i$![]() and the perpendicular scale $k_\perp \rho _i$
and the perpendicular scale $k_\perp \rho _i$![]() of the wave being damped, which is generally a monotonically increasing function of the parallel phase velocity, as shown in dispersion relation plotted in figure 2(a). As observed in the gyrotropic plot of figure 7(a) at $v_\parallel /v_{te}>0$
of the wave being damped, which is generally a monotonically increasing function of the parallel phase velocity, as shown in dispersion relation plotted in figure 2(a). As observed in the gyrotropic plot of figure 7(a) at $v_\parallel /v_{te}>0$![]() , if an unexpectedly wide velocity-space signature is observed, it may indicate the damping of multiple dispersive KAW packets with different characteristic perpendicular wavenumbers $k_\perp \rho _i$
, if an unexpectedly wide velocity-space signature is observed, it may indicate the damping of multiple dispersive KAW packets with different characteristic perpendicular wavenumbers $k_\perp \rho _i$![]() (and therefore multiple resonant parallel phase velocities $\omega /k_\parallel v_{te}$
(and therefore multiple resonant parallel phase velocities $\omega /k_\parallel v_{te}$![]() ). In this case, the overlap of multiple bipolar signatures is expected to lead to a broadened velocity-space signature, as illustrated in figure 1 of Horvath et al. (Reference Horvath, Howes and McCubbin2020).
). In this case, the overlap of multiple bipolar signatures is expected to lead to a broadened velocity-space signature, as illustrated in figure 1 of Horvath et al. (Reference Horvath, Howes and McCubbin2020).
5.5. Non-resonant feature
Finally, here we show that, as the plasma parameters are varied, a non-resonant feature may arise in the field–particle correlation that obscures the signatures of secular particle energization in velocity-space. Our results show, for a constant ion-to-electron temperature ratio, that a non-resonant feature due to electron density oscillations becomes problematic for $\beta _i \geq 1$![]() . This feature is antisymmetric in $v_\parallel$
. This feature is antisymmetric in $v_\parallel$![]() , so it cancels out when the correlation is integrated over parallel velocity, yielding zero net change to the total electron spatial energy density $W_e({\boldsymbol r}, t)$
, so it cancels out when the correlation is integrated over parallel velocity, yielding zero net change to the total electron spatial energy density $W_e({\boldsymbol r}, t)$![]() . However, it is the velocity-space signatures of the rate of change of the phase-space energy density $w_e({\boldsymbol r}, {\boldsymbol v}, t)$
. However, it is the velocity-space signatures of the rate of change of the phase-space energy density $w_e({\boldsymbol r}, {\boldsymbol v}, t)$![]() that are used to distinguish the mechanisms of energy transfer using the field–particle correlation technique. Therefore, this non-resonant feature may hinder the identification of energization mechanisms in high-$\beta _i$
that are used to distinguish the mechanisms of energy transfer using the field–particle correlation technique. Therefore, this non-resonant feature may hinder the identification of energization mechanisms in high-$\beta _i$![]() , KAW turbulence which has non-negligible levels of compressibility and in which the phase offset between $E_\parallel$
, KAW turbulence which has non-negligible levels of compressibility and in which the phase offset between $E_\parallel$![]() and the compressive fluctuation of $\partial f_e/\partial v_\parallel$
and the compressive fluctuation of $\partial f_e/\partial v_\parallel$![]() has shifted away from $\phi \simeq {\rm \pi}/2$
has shifted away from $\phi \simeq {\rm \pi}/2$![]() .
.
5.5.1. Eliminating the non-resonant feature by ‘folding’ parallel velocity-space
At the expense of losing the distinction between signatures of upward ($v_\parallel > 0$![]() ) and downward ($v_\parallel < 0$
) and downward ($v_\parallel < 0$![]() ) propagating waves, the non-resonant feature can be removed by taking advantage of its antisymmetric nature. ‘Folding’ the reduced parallel correlation across $v_\parallel = 0$
) propagating waves, the non-resonant feature can be removed by taking advantage of its antisymmetric nature. ‘Folding’ the reduced parallel correlation across $v_\parallel = 0$![]() , obtaining $C_{E_\parallel }(|v_\parallel |,t)= C_{E_\parallel }(v_\parallel > 0,t)+ C_{E_\parallel }(v_\parallel < 0,t)$
, obtaining $C_{E_\parallel }(|v_\parallel |,t)= C_{E_\parallel }(v_\parallel > 0,t)+ C_{E_\parallel }(v_\parallel < 0,t)$![]() , causes the large-amplitude, non-resonant feature to cancel out, often revealing an underlying bipolar velocity-space signature, as shown in figure 9. In figure 9(a), we plot the timestack correlation $C_{E_\parallel }(v_\parallel, t)$
, causes the large-amplitude, non-resonant feature to cancel out, often revealing an underlying bipolar velocity-space signature, as shown in figure 9. In figure 9(a), we plot the timestack correlation $C_{E_\parallel }(v_\parallel, t)$![]() from the $\beta _i = 1$
from the $\beta _i = 1$![]() simulation, which clearly shows an antisymmetric feature that obscures a portion of the expected velocity-range for Landau damping. When the data in the central and lower panels are folded over $v_\parallel = 0$
simulation, which clearly shows an antisymmetric feature that obscures a portion of the expected velocity-range for Landau damping. When the data in the central and lower panels are folded over $v_\parallel = 0$![]() – like closing a book with $v_\parallel = 0$
– like closing a book with $v_\parallel = 0$![]() as the spine – a bipolar structure is revealed that is persistent throughout the entire simulated interval, shown in figure 9(b). The amplitude of the resulting signature of electron Landau damping has a peak amplitude approximately one-quarter of the amplitude of the broad non-resonant feature. Though by folding the correlation we have lost insight into whether the signature is due to the damping of upward or downward propagating waves, it reveals the structure in velocity-space that is necessary for identifying the mechanism of electron Landau damping. This method of ‘seeing beneath’ the non-resonant feature was effective for our $\beta _i=1$
as the spine – a bipolar structure is revealed that is persistent throughout the entire simulated interval, shown in figure 9(b). The amplitude of the resulting signature of electron Landau damping has a peak amplitude approximately one-quarter of the amplitude of the broad non-resonant feature. Though by folding the correlation we have lost insight into whether the signature is due to the damping of upward or downward propagating waves, it reveals the structure in velocity-space that is necessary for identifying the mechanism of electron Landau damping. This method of ‘seeing beneath’ the non-resonant feature was effective for our $\beta _i=1$![]() simulations, but we note that in our $\beta _i = 10$
simulations, but we note that in our $\beta _i = 10$![]() simulations the Landau resonances with the electrons are so close to $v_\parallel =0$
simulations the Landau resonances with the electrons are so close to $v_\parallel =0$![]() that the velocity-space resolution of the simulation is insufficient for revealing signatures with certainty, even after folding the data.
that the velocity-space resolution of the simulation is insufficient for revealing signatures with certainty, even after folding the data.
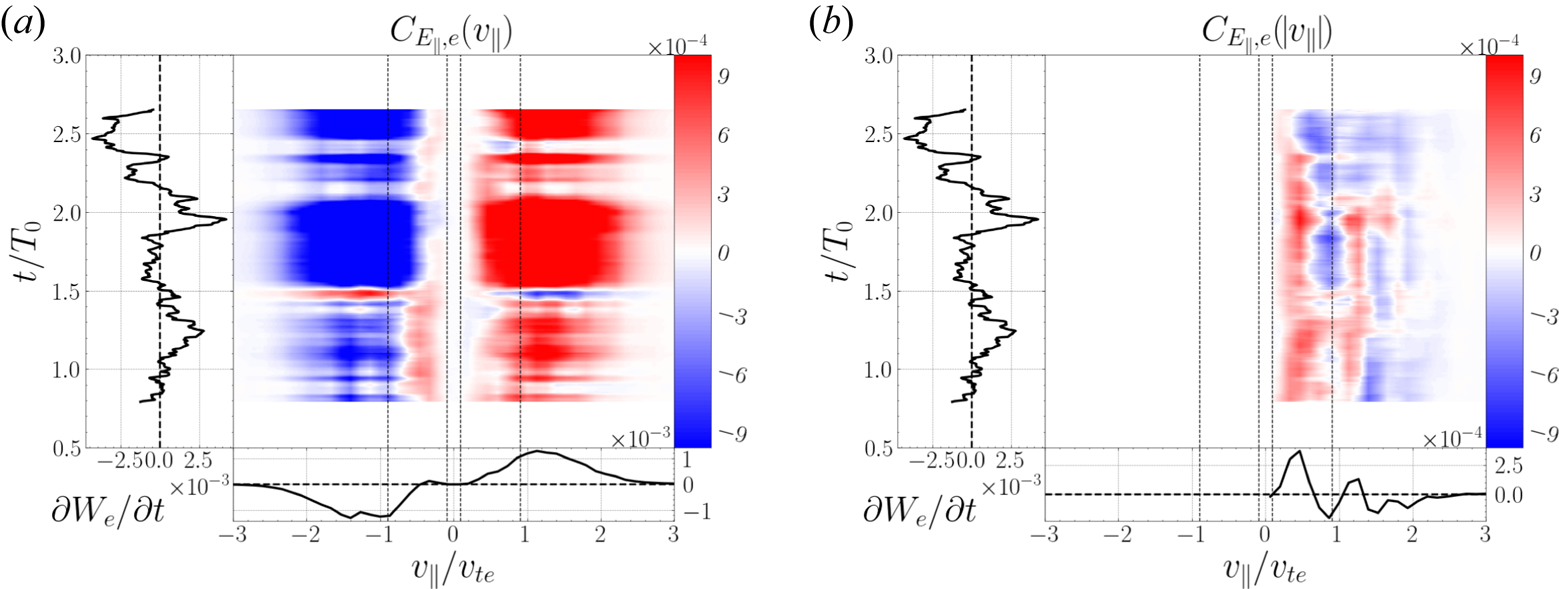
Figure 9. (a) Reduced parallel field–particle correlation $C_{E_\parallel }(v_\parallel, t)$![]() timestack plot in the $\beta _i = 1$
timestack plot in the $\beta _i = 1$![]() turbulence simulation using $\tau = 2.6\ T_{{\rm max}}$
turbulence simulation using $\tau = 2.6\ T_{{\rm max}}$![]() . (b) The same timestack plot in (a) folded across ${v_\parallel =0}$
. (b) The same timestack plot in (a) folded across ${v_\parallel =0}$![]() to obtain $C_{E_\parallel }(|v_\parallel |,t)$
to obtain $C_{E_\parallel }(|v_\parallel |,t)$![]() , showing a clear signature of electron Landau damping at $v_\parallel /v_{te} \sim 0.1$
, showing a clear signature of electron Landau damping at $v_\parallel /v_{te} \sim 0.1$![]() (albeit with the negative region suppressed by the $v_\parallel ^2$
(albeit with the negative region suppressed by the $v_\parallel ^2$![]() weighting) that persists throughout the simulation, with a peak amplitude approximately one quarter of the non-resonant feature.
weighting) that persists throughout the simulation, with a peak amplitude approximately one quarter of the non-resonant feature.
Alternatively, high-pass filtering could be an effective way of removing a low-frequency non-resonant feature while retaining the distinction between the damping of forward and backward propagating waves. We tested this with some success in our simulations, but since the time step in AstroGK simulations varies dynamically in order to satisfy the numerical Courant–Friedrichs–Lewy stability condition, it is unclear if the results of the filtered AstroGK datasets are reliable. We report that applying a fast-Fourier transform, backward and forward high-pass Butterworth filters, and an inverse fast-Fourier transform did remove the non-resonant feature in tests performed on the $\beta _i=1$![]() simulation. Due to the variable time step, however, we did not pursue this method of removing the non-resonant feature in depth.
simulation. Due to the variable time step, however, we did not pursue this method of removing the non-resonant feature in depth.
6. Summary and conclusions
Application of the field–particle correlation technique to measurements of weakly collisional plasma turbulence in space and astrophysical plasma environments generates velocity-space signatures of particle energization. These signatures can be used to identify the specific physical mechanisms that dominate the dissipation of the turbulence. Recent field–particle correlation analyses of MMS observations of turbulence in the Earth's magnetosheath plasma have provided the first direct evidence of electron Landau damping as a significant mechanism for the dissipation of space plasma turbulence (Chen et al. Reference Chen, Klein and Howes2019; Afshari et al. Reference Afshari, Howes, Kletzing, Hartley and Boardsen2021). Here, we employ linear KAW simulations and a suite of four gyrokinetic simulations of turbulence with $\beta _i=0.01,0.1,1,10$![]() and $T_i/T_e=1$
and $T_i/T_e=1$![]() to characterize the qualitative and quantitative features of the velocity-space signature of electron Landau damping in a turbulent space plasma. Linear KAW simulations have demonstrated that the zero-crossing of the bipolar velocity-space signature of electron Landau damping falls at the resonant parallel phase velocity of the wave, and that the width of the signature increases with increasing normalized damping rate. Furthermore, unlike in the case of ion Landau damping where both the negative and positive regions of the bipolar velocity-space signature are clearly observable (Klein et al. Reference Klein, Howes and Tenbarge2017; Howes et al. Reference Howes, McCubbin and Klein2018; Klein et al. Reference Klein, Howes, TenBarge and Valentini2020), for the electron Landau damping of dispersive KAWs, the negative region of the bipolar signature can be suppressed by the $v_\parallel ^2$
to characterize the qualitative and quantitative features of the velocity-space signature of electron Landau damping in a turbulent space plasma. Linear KAW simulations have demonstrated that the zero-crossing of the bipolar velocity-space signature of electron Landau damping falls at the resonant parallel phase velocity of the wave, and that the width of the signature increases with increasing normalized damping rate. Furthermore, unlike in the case of ion Landau damping where both the negative and positive regions of the bipolar velocity-space signature are clearly observable (Klein et al. Reference Klein, Howes and Tenbarge2017; Howes et al. Reference Howes, McCubbin and Klein2018; Klein et al. Reference Klein, Howes, TenBarge and Valentini2020), for the electron Landau damping of dispersive KAWs, the negative region of the bipolar signature can be suppressed by the $v_\parallel ^2$![]() weighting in the field–particle correlation for waves with low parallel phase velocities compared with the electron thermal velocity, $v_{ph, \parallel }/v_{te} \le 0.3$
weighting in the field–particle correlation for waves with low parallel phase velocities compared with the electron thermal velocity, $v_{ph, \parallel }/v_{te} \le 0.3$![]() .
.
A key result of this paper is the characterization of the typical gyrotropic velocity-space signatures $C_{E_\parallel }(v_\parallel,v_\perp )$![]() of electron Landau damping, with typical examples presented in figure 7 for $\beta _i=0.01,0.1$
of electron Landau damping, with typical examples presented in figure 7 for $\beta _i=0.01,0.1$![]() and $1$
and $1$![]() . Similarly, timestack plots of the reduced parallel field–particle correlation $C_{E_\parallel }(v_\parallel,t)$
. Similarly, timestack plots of the reduced parallel field–particle correlation $C_{E_\parallel }(v_\parallel,t)$![]() , shown in figure 8, provide a clear means to determine the electron energization rates as a function of time, showing both temporal intermittency and the overlap of bipolar velocity-space signatures of KAW wave packets with different resonant parallel phase velocities. Furthermore, even in balanced turbulence – characterized by approximately equal wave energy fluxes up and down the local mean magnetic field – over periods of a few to tens of KAW periods, one frequently observes an imbalance of the velocity-space signatures of electron Landau damping of upward and downward propagating KAWs, consistent with previous MMS observations (Afshari et al. Reference Afshari, Howes, Kletzing, Hartley and Boardsen2021). In addition, a significant non-resonant feature that is asymmetric in $v_\parallel$
, shown in figure 8, provide a clear means to determine the electron energization rates as a function of time, showing both temporal intermittency and the overlap of bipolar velocity-space signatures of KAW wave packets with different resonant parallel phase velocities. Furthermore, even in balanced turbulence – characterized by approximately equal wave energy fluxes up and down the local mean magnetic field – over periods of a few to tens of KAW periods, one frequently observes an imbalance of the velocity-space signatures of electron Landau damping of upward and downward propagating KAWs, consistent with previous MMS observations (Afshari et al. Reference Afshari, Howes, Kletzing, Hartley and Boardsen2021). In addition, a significant non-resonant feature that is asymmetric in $v_\parallel$![]() appears due to the plasma density fluctuations associated with KAWs at higher values of plasma beta, $\beta _i \gtrsim 1$
appears due to the plasma density fluctuations associated with KAWs at higher values of plasma beta, $\beta _i \gtrsim 1$![]() . This large-amplitude, non-resonant feature can make it difficult to identify the velocity-space signatures of electron Landau damping, but a method of folding over the correlations in $v_\parallel$
. This large-amplitude, non-resonant feature can make it difficult to identify the velocity-space signatures of electron Landau damping, but a method of folding over the correlations in $v_\parallel$![]() can effectively eliminate the feature, revealing the generally smaller amplitude velocity-space signatures of resonant damping. All of these factors should be taken into consideration when analysing the field–particle correlation signatures of electron Landau damping. It is our hope that these results can provide insight for interpreting future field–particle correlation analysis of in situ spacecraft observations: helping to identify the signatures of electron Landau damping throughout the inner heliosphere and advancing the wider goal of determining the contribution of this mechanism to electron energization in the solar wind and other weakly collisional plasma environments.
can effectively eliminate the feature, revealing the generally smaller amplitude velocity-space signatures of resonant damping. All of these factors should be taken into consideration when analysing the field–particle correlation signatures of electron Landau damping. It is our hope that these results can provide insight for interpreting future field–particle correlation analysis of in situ spacecraft observations: helping to identify the signatures of electron Landau damping throughout the inner heliosphere and advancing the wider goal of determining the contribution of this mechanism to electron energization in the solar wind and other weakly collisional plasma environments.
Acknowledgements
Editor A. Schekochihin thanks the referees for their advice in evaluating this article.
Funding
This work was supported by NASA FINESST grant 80NSSC20K1509 as well as NASA grants 80NSSC18K1217 and 80NSSC18K1371. Numerical simulations were performed using the Extreme Science and Engineering Discovery Environment (XSEDE), which is supported by National Science Foundation grant number ACI-1548562, through allocation TG-PHY090084.
Declaration of interests
The authors report no conflict of interest.
Appendix A. Velocity-space signatures of electron Landau damping of single KAWs
Here (figure 10) we reproduce timestack plots of the field–particle correlations $C_{E_\parallel }(v_\parallel, t)$![]() in steady state for five of the 20 individual KAW simulations. For a $\beta _i = 1$
in steady state for five of the 20 individual KAW simulations. For a $\beta _i = 1$![]() plasma, we plot the cases of a KAW with $k_\perp \rho _i = 2, 4, 8, 16$
plasma, we plot the cases of a KAW with $k_\perp \rho _i = 2, 4, 8, 16$![]() and $32$
and $32$![]() . Each correlation shows clear electron energization due to Landau damping of the wave by the resonant electrons, where the resonant parallel phase velocity for each wave is indicated by the vertical dotted lines. At the parallel velocity-space resolution of the AstroGK simulations, the negative portion of the bipolar damping signature is only visible in the time-integrated panels for the two smallest-scale waves (those at the largest resonant velocities), but all have a clear, localized and persistent energization signature due to the action of Landau damping. The non-resonant feature, antisymmetric in $v_\parallel$
. Each correlation shows clear electron energization due to Landau damping of the wave by the resonant electrons, where the resonant parallel phase velocity for each wave is indicated by the vertical dotted lines. At the parallel velocity-space resolution of the AstroGK simulations, the negative portion of the bipolar damping signature is only visible in the time-integrated panels for the two smallest-scale waves (those at the largest resonant velocities), but all have a clear, localized and persistent energization signature due to the action of Landau damping. The non-resonant feature, antisymmetric in $v_\parallel$![]() , is visible in these correlations. Though the compressibility of the KAWs increases with $k_\perp \rho _i$
, is visible in these correlations. Though the compressibility of the KAWs increases with $k_\perp \rho _i$![]() (Matteini et al. Reference Matteini, Franci, Alexandrova, Lacombe, Landi, Hellinger, Papini and Verdini2020), the non-resonant feature is most clearly visible at lower $k_\perp \rho _i$
(Matteini et al. Reference Matteini, Franci, Alexandrova, Lacombe, Landi, Hellinger, Papini and Verdini2020), the non-resonant feature is most clearly visible at lower $k_\perp \rho _i$![]() in these plots, likely due to the lower damping rate and the resonance's increased proximity to $v_\parallel = 0$
in these plots, likely due to the lower damping rate and the resonance's increased proximity to $v_\parallel = 0$![]() for these larger perpendicular wavelength waves.
for these larger perpendicular wavelength waves.
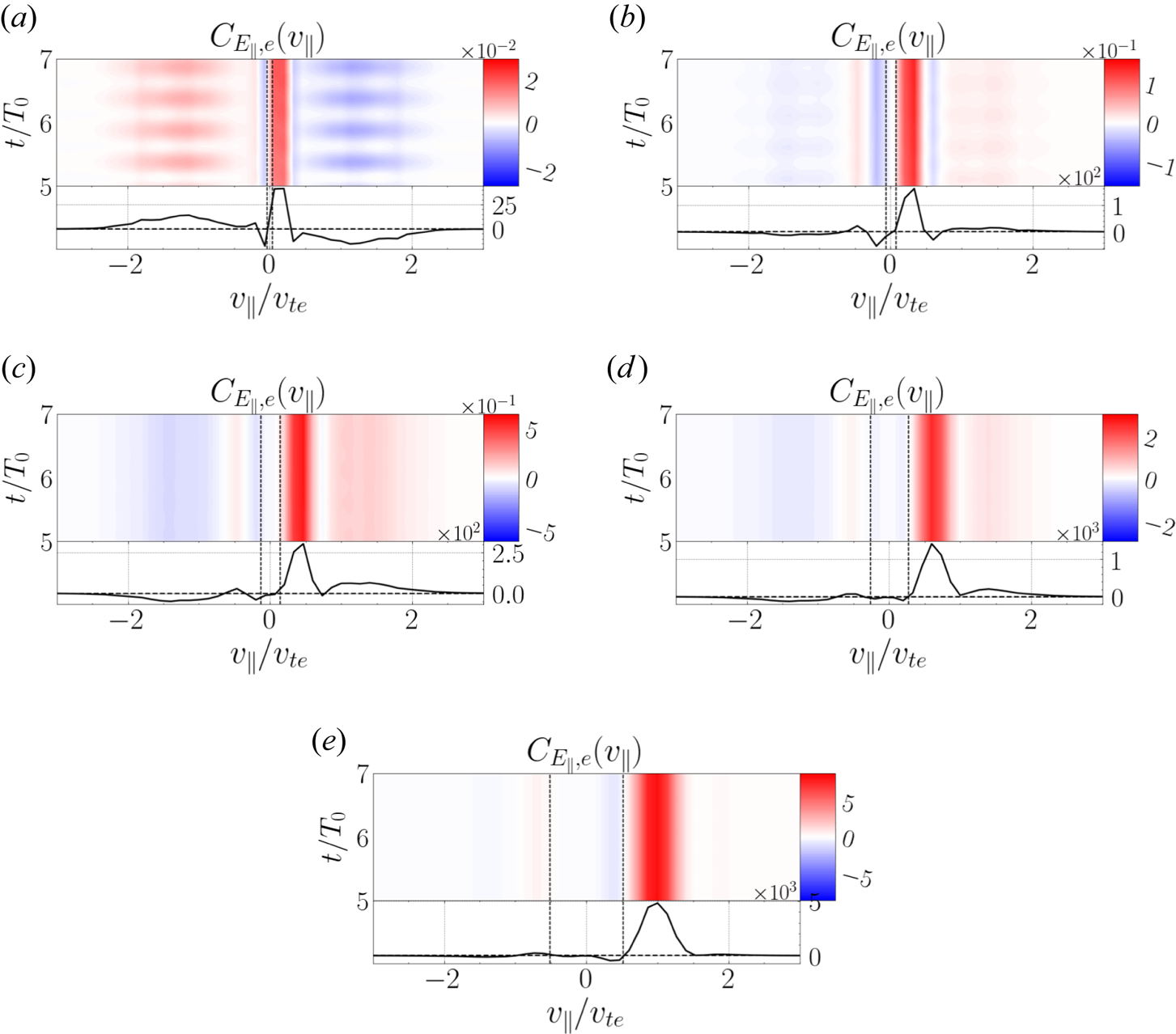
Figure 10. Field–particle correlations of a set of driven, damped KAWs with $\beta _i = 1$![]() and (a) $k_\perp \rho _i = 2$
and (a) $k_\perp \rho _i = 2$![]() , (b) 4, (c) 8, (d) 16 and (e) 32. The zero-crossing of the bipolar signatures correspond to the parallel wave phase velocity (vertical dotted lines), and the width of the signature increases with increasing damping rate as $k_\perp \rho _i$
, (b) 4, (c) 8, (d) 16 and (e) 32. The zero-crossing of the bipolar signatures correspond to the parallel wave phase velocity (vertical dotted lines), and the width of the signature increases with increasing damping rate as $k_\perp \rho _i$![]() increases.
increases.
Appendix B. Non-resonant feature analysis
Here we explore more deeply the antisymmetric, non-resonant feature that appears in the field–particle correlation, which we attribute to the electron density perturbations, $\delta n_e$![]() , that constitute a dynamic part of the KAW. This non-resonant feature arises in the field–particle correlation due to (i) an increase in the amplitude of $\delta n_e$
, that constitute a dynamic part of the KAW. This non-resonant feature arises in the field–particle correlation due to (i) an increase in the amplitude of $\delta n_e$![]() relative to the resonant perturbations and (ii) the relative phase between $E_\parallel$
relative to the resonant perturbations and (ii) the relative phase between $E_\parallel$![]() and $\partial f/\partial v_\parallel$
and $\partial f/\partial v_\parallel$![]() as a function of $v_\parallel$
as a function of $v_\parallel$![]() . The compressive nature of the non-resonant feature, its amplitude, and its dependence on the phase offset $\phi$
. The compressive nature of the non-resonant feature, its amplitude, and its dependence on the phase offset $\phi$![]() are seen clearly when the factors in the mathematical form of the correlation are divided into separate plots, as shown in figure 11.
are seen clearly when the factors in the mathematical form of the correlation are divided into separate plots, as shown in figure 11.

Figure 11. Detail of the density perturbations giving rise to the non-resonant feature in the $E_\parallel$![]() field–particle correlations of high-$\beta _i$
field–particle correlations of high-$\beta _i$![]() plasmas. (a) The parallel electric field–particle correlation $C_{E_\parallel, e}(v_\parallel )$
plasmas. (a) The parallel electric field–particle correlation $C_{E_\parallel, e}(v_\parallel )$![]() ; (b) the perturbed distribution function $g_e$
; (b) the perturbed distribution function $g_e$![]() ; (c) the parallel electric field weighted by parallel velocity factor $E_\parallel v_\parallel ^2$
; (c) the parallel electric field weighted by parallel velocity factor $E_\parallel v_\parallel ^2$![]() ; (d) the parallel velocity derivative of the perturbed distribution function $\partial g_e/\partial v_\parallel$
; (d) the parallel velocity derivative of the perturbed distribution function $\partial g_e/\partial v_\parallel$![]() .
.
The reduced parallel field–particle correlation $C_{E_\parallel }(v_\parallel, t)$![]() is shown in figure 11(a) for the individual wave simulation at $k_\perp \rho _i = 8$
is shown in figure 11(a) for the individual wave simulation at $k_\perp \rho _i = 8$![]() , $\beta _i = 0.1$
, $\beta _i = 0.1$![]() . The reduced, complementary perturbed distribution function $g_e(v_\parallel, t)$
. The reduced, complementary perturbed distribution function $g_e(v_\parallel, t)$![]() (Numata et al. Reference Numata, Howes, Tatsuno, Barnes and Dorland2010) is plotted in figure 11(b). The location of the resonant KAW phase velocity is marked by the vertical dashed line at $v_\parallel /v_{te} = 0.51$
(Numata et al. Reference Numata, Howes, Tatsuno, Barnes and Dorland2010) is plotted in figure 11(b). The location of the resonant KAW phase velocity is marked by the vertical dashed line at $v_\parallel /v_{te} = 0.51$![]() , and the resonant perturbations in $g_e(v_\parallel, t)$
, and the resonant perturbations in $g_e(v_\parallel, t)$![]() peak broadly around this resonant parallel velocity. In the background, at lower amplitude, there is a broad oscillatory signature that is an even function in $v_\parallel$
peak broadly around this resonant parallel velocity. In the background, at lower amplitude, there is a broad oscillatory signature that is an even function in $v_\parallel$![]() and that spans all velocities (fading to zero with the distribution function at large $v_\parallel$
and that spans all velocities (fading to zero with the distribution function at large $v_\parallel$![]() ). This non-resonant, even perturbation in $g_e(v_\parallel, t)$
). This non-resonant, even perturbation in $g_e(v_\parallel, t)$![]() represents compression in the electron density, $\delta n_e$
represents compression in the electron density, $\delta n_e$![]() , when integrated over $v_\parallel$
, when integrated over $v_\parallel$![]() . In figure 11(d), we show the parallel velocity derivative of the reduced perturbed distribution function, $\partial g_e/\partial v_\parallel$
. In figure 11(d), we show the parallel velocity derivative of the reduced perturbed distribution function, $\partial g_e/\partial v_\parallel$![]() . Here, it can be seen that the even function in $g_e$
. Here, it can be seen that the even function in $g_e$![]() , yielding $\delta n_e \neq 0$
, yielding $\delta n_e \neq 0$![]() , turns into an odd function when the derivative with respect to $v_\parallel$
, turns into an odd function when the derivative with respect to $v_\parallel$![]() is computed. Finally, figure 11(c) contains the parallel electric field multiplied by $v_\parallel ^2$
is computed. Finally, figure 11(c) contains the parallel electric field multiplied by $v_\parallel ^2$![]() ; note that $E_\parallel$
; note that $E_\parallel$![]() itself is constant over $v_\parallel$
itself is constant over $v_\parallel$![]() . Upon close inspection, it can be observed that the oscillation in $E_\parallel$
. Upon close inspection, it can be observed that the oscillation in $E_\parallel$![]() and the background oscillation in $\partial g_e/\partial v_\parallel$
and the background oscillation in $\partial g_e/\partial v_\parallel$![]() have the same period but are offset in phase. This phase offset $\phi$
have the same period but are offset in phase. This phase offset $\phi$![]() is ultimately what causes the density oscillation to lead to the odd, non-resonant signature that appears in the field–particle correlation in figure 11(a).
is ultimately what causes the density oscillation to lead to the odd, non-resonant signature that appears in the field–particle correlation in figure 11(a).
In the main body of this paper, we have explained how the relative amplitudes of the resonant and density perturbations to $g_e$![]() change due to the combined effects of increasing compressibility of KAWs and to the decreasing phase-velocity of KAWs as $\beta _i$
change due to the combined effects of increasing compressibility of KAWs and to the decreasing phase-velocity of KAWs as $\beta _i$![]() increases. However, we did not discuss the origin of the phase offset between the density perturbation and the parallel electric field from $\phi \simeq {\rm \pi}/2$
increases. However, we did not discuss the origin of the phase offset between the density perturbation and the parallel electric field from $\phi \simeq {\rm \pi}/2$![]() at low $\beta _i$
at low $\beta _i$![]() to $\phi \neq {\rm \pi}/2$
to $\phi \neq {\rm \pi}/2$![]() at higher $\beta _i$
at higher $\beta _i$![]() . If the electron response is approximately instantaneous, the density perturbation will be exactly ${\rm \pi} /2$
. If the electron response is approximately instantaneous, the density perturbation will be exactly ${\rm \pi} /2$![]() out of phase with the finite $E_\parallel$
out of phase with the finite $E_\parallel$![]() that drives it. In this case, the average acceleration of the particles by $E_\parallel$
that drives it. In this case, the average acceleration of the particles by $E_\parallel$![]() is zero. This is approximately the background phase relationship we observe in the low $\beta _i$
is zero. This is approximately the background phase relationship we observe in the low $\beta _i$![]() ($0.01$
($0.01$![]() and $0.1$
and $0.1$![]() ) single-wave runs.
) single-wave runs.
The phase offset is approximately $\phi \simeq {\rm \pi}/2$![]() at all parallel velocities except those that resonantly interact with the $E_\parallel$
at all parallel velocities except those that resonantly interact with the $E_\parallel$![]() wave around $v_{ph} = \omega /k_\parallel$
wave around $v_{ph} = \omega /k_\parallel$![]() , as shown in figure 12. For small perpendicular wavenumbers at large $\beta _i$
, as shown in figure 12. For small perpendicular wavenumbers at large $\beta _i$![]() ($1$
($1$![]() and $10$
and $10$![]() ) the phase offset is also $\phi \simeq {\rm \pi}/2$
) the phase offset is also $\phi \simeq {\rm \pi}/2$![]() . As $k_\perp \rho _i$
. As $k_\perp \rho _i$![]() increases, however, the phase offset deviates from ${\rm \pi} /2$
increases, however, the phase offset deviates from ${\rm \pi} /2$![]() and moves towards ${\rm \pi}$
and moves towards ${\rm \pi}$![]() or $0$
or $0$![]() , resulting in detectable non-resonant features in the field–particle correlation signatures. As $\beta _i$
, resulting in detectable non-resonant features in the field–particle correlation signatures. As $\beta _i$![]() and $k_\perp \rho _i$
and $k_\perp \rho _i$![]() increase, the compressive wave begins to lag $E_\parallel$
increase, the compressive wave begins to lag $E_\parallel$![]() , shifting the relative phase $\phi$
, shifting the relative phase $\phi$![]() and thereby enabling $E_\parallel$
and thereby enabling $E_\parallel$![]() to do work on the particles, which results in a local non-zero contribution to the change in phase-space energy density. Averaged over parallel velocity, however, the contribution of the non-resonant feature goes to zero, and therefore the compressions do not change the total spatial energy density of the electrons $W_e(\boldsymbol {r},t)$
to do work on the particles, which results in a local non-zero contribution to the change in phase-space energy density. Averaged over parallel velocity, however, the contribution of the non-resonant feature goes to zero, and therefore the compressions do not change the total spatial energy density of the electrons $W_e(\boldsymbol {r},t)$![]() .
.
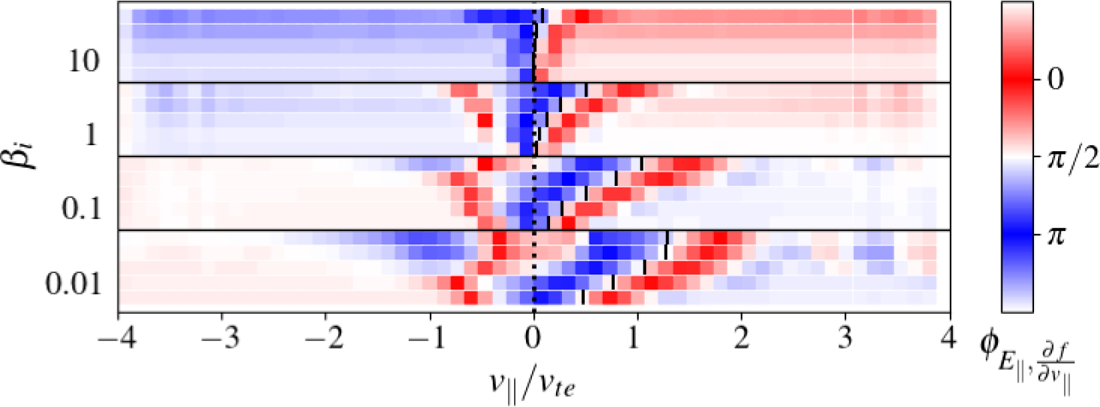
Figure 12. The phase offset $\phi$![]() between $E_\parallel$
between $E_\parallel$![]() and the density oscillation in $\partial g_e/\partial v_\parallel$
and the density oscillation in $\partial g_e/\partial v_\parallel$![]() as a function of $v_\parallel /v_{te}$
as a function of $v_\parallel /v_{te}$![]() . Horizontal sections, separated by black lines, correspond to different $\beta _i$
. Horizontal sections, separated by black lines, correspond to different $\beta _i$![]() . Within each of these sections, there are five separate strips that correspond to a different $k_\perp \rho _i$
. Within each of these sections, there are five separate strips that correspond to a different $k_\perp \rho _i$![]() . Increasing vertically within each section, $k_\perp \rho _i$
. Increasing vertically within each section, $k_\perp \rho _i$![]() cycles through $\{2, 4, 8, 16, 32\}$
cycles through $\{2, 4, 8, 16, 32\}$![]() . The phase velocity of the KAW for each $\beta _i$
. The phase velocity of the KAW for each $\beta _i$![]() , $k_\perp \rho _i$
, $k_\perp \rho _i$![]() pair is marked with a vertical black line.
pair is marked with a vertical black line.