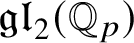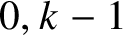1 Introduction
Let p be a rational prime. In his pioneering work [Reference EmertonEme06b], Emerton introduced completed cohomology, which p-adically interpolates automorphic representations, and explained how techniques of locally analytic p-adic representation theory may be applied to study it. In this article, we will focus on the simplest (non-abelian) case: completed cohomology of the modular curves. More precisely, let K be an open subgroup
![]() $\mathrm {GL}_2(\mathbb {A}_f)$
, where
$\mathrm {GL}_2(\mathbb {A}_f)$
, where
![]() $\mathbb {A}_f$
denotes the ring of finite adèles of
$\mathbb {A}_f$
denotes the ring of finite adèles of
![]() $\mathbb {Q}$
. We have the modular curve of level K
$\mathbb {Q}$
. We have the modular curve of level K
 $$ \begin{align*}Y_K(\mathbb{C})=\mathrm{GL}_2(\mathbb{Q})\backslash (\mathbb{H}^{\pm1}\times\mathrm{GL}_2(\mathbb{A}_f)/K),\end{align*} $$
$$ \begin{align*}Y_K(\mathbb{C})=\mathrm{GL}_2(\mathbb{Q})\backslash (\mathbb{H}^{\pm1}\times\mathrm{GL}_2(\mathbb{A}_f)/K),\end{align*} $$
where
![]() $\mathbb {H}^{\pm 1}=\mathbb {C}-\mathbb {R}$
is the union of the usual upper and lower half-planes. Denote by
$\mathbb {H}^{\pm 1}=\mathbb {C}-\mathbb {R}$
is the union of the usual upper and lower half-planes. Denote by
 $\mathbb {A}^p_f$
the prime-to-p part of
$\mathbb {A}^p_f$
the prime-to-p part of
![]() $\mathbb {A}_f$
. For an open subgroup
$\mathbb {A}_f$
. For an open subgroup
![]() $K^p$
of
$K^p$
of
 $\mathrm {GL}_2(\mathbb {A}^p_f)$
, the completed cohomology of tame level
$\mathrm {GL}_2(\mathbb {A}^p_f)$
, the completed cohomology of tame level
![]() $K^p$
is defined as
$K^p$
is defined as
 $$ \begin{align*}\tilde{H}^i(K^p,\mathbb{Z}_p):=\varprojlim_n \varinjlim_{K_p\subset\mathrm{GL}_2(\mathbb{Q}_p)}H^i(Y_{K^pK_p}(\mathbb{C}),\mathbb{Z}/p^n).\end{align*} $$
$$ \begin{align*}\tilde{H}^i(K^p,\mathbb{Z}_p):=\varprojlim_n \varinjlim_{K_p\subset\mathrm{GL}_2(\mathbb{Q}_p)}H^i(Y_{K^pK_p}(\mathbb{C}),\mathbb{Z}/p^n).\end{align*} $$
It is p-adically complete and equipped with a natural continuous action of
![]() $\mathrm {GL}_2(\mathbb {Q}_p)$
. Our main tool to study this will be (p-adic) Hodge theory. Hence, we would like to extend the coefficients
$\mathrm {GL}_2(\mathbb {Q}_p)$
. Our main tool to study this will be (p-adic) Hodge theory. Hence, we would like to extend the coefficients
![]() $\mathbb {Q}_p$
to a complete, algebraically closed field. So let
$\mathbb {Q}_p$
to a complete, algebraically closed field. So let
![]() $C=\mathbb {C}_p$
, the completion of an algebraic closure
$C=\mathbb {C}_p$
, the completion of an algebraic closure
 of
of
![]() $\mathbb {Q}_{p}$
, and
$\mathbb {Q}_{p}$
, and
![]() ${\mathcal {O}_{C}}$
be its ring of integers. Consider
${\mathcal {O}_{C}}$
be its ring of integers. Consider
 $$ \begin{align*}{\tilde{H}^{i}}({K^{p}},{\mathcal{O}_{C}}):={\varprojlim_{n}} {\varinjlim_{{K_{p}}\subset{\mathrm{GL}_{2}}{(\mathbb{Q}_{p})}}}{H^{i}}(Y_{K^{p}K_{p}}(\mathbb{C}),\mathcal{O}_{C}/p^{n}).\end{align*} $$
$$ \begin{align*}{\tilde{H}^{i}}({K^{p}},{\mathcal{O}_{C}}):={\varprojlim_{n}} {\varinjlim_{{K_{p}}\subset{\mathrm{GL}_{2}}{(\mathbb{Q}_{p})}}}{H^{i}}(Y_{K^{p}K_{p}}(\mathbb{C}),\mathcal{O}_{C}/p^{n}).\end{align*} $$
Then
![]() $\tilde {H}^{i}(K^{p},C):=\tilde {H}^{i}(K^{p},\mathcal {O}_{C})\otimes _{\mathcal {O}_{C}} C$
is a
$\tilde {H}^{i}(K^{p},C):=\tilde {H}^{i}(K^{p},\mathcal {O}_{C})\otimes _{\mathcal {O}_{C}} C$
is a
![]() $\mathbb {Q}_{p}$
-Banach space representation of
$\mathbb {Q}_{p}$
-Banach space representation of
![]() $\mathrm {GL}_{2}(\mathbb {Q}_{p})$
. As in [Reference Schneider and TeitelbaumST03], we can consider its locally analytic vectors
$\mathrm {GL}_{2}(\mathbb {Q}_{p})$
. As in [Reference Schneider and TeitelbaumST03], we can consider its locally analytic vectors
![]() $\tilde {H}^i(K^p,C)^{\mathrm {la}}$
. Let
$\tilde {H}^i(K^p,C)^{\mathrm {la}}$
. Let
-
•
 $\mathfrak {g}=C\otimes _{\mathbb {Q}_p}\mathfrak {gl}_2(\mathbb {Q}_p)$
: the ‘complexified’ Lie algebra of
$\mathfrak {g}=C\otimes _{\mathbb {Q}_p}\mathfrak {gl}_2(\mathbb {Q}_p)$
: the ‘complexified’ Lie algebra of
 $\mathrm {GL}_2(\mathbb {Q}_p)$
;
$\mathrm {GL}_2(\mathbb {Q}_p)$
; -
•
 $B\subset \mathrm {GL}_2(\mathbb {Q}_p)$
: the upper-triangular Borel subgroup;
$B\subset \mathrm {GL}_2(\mathbb {Q}_p)$
: the upper-triangular Borel subgroup; -
•
 $\mathfrak {b}\subset \mathfrak {g}$
: the ‘complexified’ Lie algebra of B.
$\mathfrak {b}\subset \mathfrak {g}$
: the ‘complexified’ Lie algebra of B.
The Lie algebra
![]() $\mathfrak {g}$
(in particular
$\mathfrak {g}$
(in particular
![]() $\mathfrak {b}$
) acts naturally on
$\mathfrak {b}$
) acts naturally on
![]() $\tilde {H}^i(K^p,C)^{\mathrm {la}}$
by the infinitesimal action of
$\tilde {H}^i(K^p,C)^{\mathrm {la}}$
by the infinitesimal action of
![]() $\mathrm {GL}_2(\mathbb {Q}_p)$
. Given a character
$\mathrm {GL}_2(\mathbb {Q}_p)$
. Given a character
![]() $\mu :\mathfrak {b}\to C$
, one main goal of this article is to study the
$\mu :\mathfrak {b}\to C$
, one main goal of this article is to study the
![]() $\mu $
-isotypic part
$\mu $
-isotypic part
 $\tilde {H}^i(K^p,C)^{\mathrm {la}}_{\mu }$
. We can pass to the direct limit over all tame levels
$\tilde {H}^i(K^p,C)^{\mathrm {la}}_{\mu }$
. We can pass to the direct limit over all tame levels
![]() $K^p$
:
$K^p$
:
 $$ \begin{align*}\tilde{H}^i(C)^{\mathrm{la}}_{\mu}:=\varinjlim_{K^p\subset\mathrm{GL}_2(\mathbb{A}^p_f)} \tilde{H}^i(K^p,C)^{\mathrm{la}}_{\mu}.\end{align*} $$
$$ \begin{align*}\tilde{H}^i(C)^{\mathrm{la}}_{\mu}:=\varinjlim_{K^p\subset\mathrm{GL}_2(\mathbb{A}^p_f)} \tilde{H}^i(K^p,C)^{\mathrm{la}}_{\mu}.\end{align*} $$
Clearly, there is a natural action of
 $\mathrm {GL}_2(\mathbb {A}^p_f)\times B$
on it.
$\mathrm {GL}_2(\mathbb {A}^p_f)\times B$
on it.
To state our result, we need more notation. The open modular curve
![]() $Y_K(\mathbb {C})$
has a natural compactification
$Y_K(\mathbb {C})$
has a natural compactification
![]() $X_K(\mathbb {C})$
by adding cusps. This complete curve
$X_K(\mathbb {C})$
by adding cusps. This complete curve
![]() $X_K(\mathbb {C})$
has a natural model
$X_K(\mathbb {C})$
has a natural model
![]() $X_{K}$
over
$X_{K}$
over
![]() $\mathbb {Q}$
, and we denote by
$\mathbb {Q}$
, and we denote by
![]() $X_{K,C}$
its base change to C. Let k be an integer. We have the usual automorphic line bundle
$X_{K,C}$
its base change to C. Let k be an integer. We have the usual automorphic line bundle
![]() $\omega ^k$
on
$\omega ^k$
on
![]() $X_{K,C}$
whose global sections correspond to level-K modular forms of weight k (with coefficients in C). Denote by
$X_{K,C}$
whose global sections correspond to level-K modular forms of weight k (with coefficients in C). Denote by
 $$ \begin{align*}M_k:=\varinjlim_{K\subset\mathrm{GL}_2(\mathbb{A}_f)}H^0(X_{K,C},\omega^k),\end{align*} $$
$$ \begin{align*}M_k:=\varinjlim_{K\subset\mathrm{GL}_2(\mathbb{A}_f)}H^0(X_{K,C},\omega^k),\end{align*} $$
 $$ \begin{align*}H^1(\omega^k):=\varinjlim_{K\subset\mathrm{GL}_2(\mathbb{A}_f)}H^1(X_{K,C},\omega^k),\end{align*} $$
$$ \begin{align*}H^1(\omega^k):=\varinjlim_{K\subset\mathrm{GL}_2(\mathbb{A}_f)}H^1(X_{K,C},\omega^k),\end{align*} $$
where both limits are taken over all open compact subgroups of
![]() $\mathrm {GL}_2(\mathbb {A}_f)$
. Both spaces have natural actions of
$\mathrm {GL}_2(\mathbb {A}_f)$
. Both spaces have natural actions of
![]() $\mathrm {GL}_2(\mathbb {A}_f)$
and relate to automorphic representations of
$\mathrm {GL}_2(\mathbb {A}_f)$
and relate to automorphic representations of
![]() $\mathrm {GL}_2(\mathbb {A})$
(after choosing an isomorphism
$\mathrm {GL}_2(\mathbb {A})$
(after choosing an isomorphism
![]() $C\cong \mathbb {C}$
). Here
$C\cong \mathbb {C}$
). Here
![]() $\mathbb {A}$
denotes the ring of adèles of
$\mathbb {A}$
denotes the ring of adèles of
![]() $\mathbb {Q}$
.
$\mathbb {Q}$
.
We also need players which are special in this p-adic story: overconvergent modular forms. This will be slightly different from the usual one in the literature as we want an action of the Borel B. We denote by
![]() $\mathcal {X}_K$
the rigid analytic space associated to
$\mathcal {X}_K$
the rigid analytic space associated to
![]() $X_{K,C}$
. Let
$X_{K,C}$
. Let
![]() $\Gamma (p^n)=1+p^nM_2(\mathbb {Z}_p)\subset \mathrm {GL}_2(\mathbb {Z}_p)$
be the principal congruence subgroup of level
$\Gamma (p^n)=1+p^nM_2(\mathbb {Z}_p)\subset \mathrm {GL}_2(\mathbb {Z}_p)$
be the principal congruence subgroup of level
![]() $n\geq 2$
and let
$n\geq 2$
and let
![]() $K^p$
be a tame level. As explained by Katz–Mazur [Reference Katz and MazurKM85, Theorem 13.7.6],
$K^p$
be a tame level. As explained by Katz–Mazur [Reference Katz and MazurKM85, Theorem 13.7.6],
![]() $X_{K^p\Gamma (p^n),C}$
has a natural integral model over
$X_{K^p\Gamma (p^n),C}$
has a natural integral model over
![]() $\mathcal {O}_C$
, and the irreducible components of its special fibre can be indexed by surjective homomorphisms
$\mathcal {O}_C$
, and the irreducible components of its special fibre can be indexed by surjective homomorphisms
![]() $(\mathbb {Z}/p^n)^{2}\to \mathbb {Z}/p^n$
. We denote by
$(\mathbb {Z}/p^n)^{2}\to \mathbb {Z}/p^n$
. We denote by
![]() $\mathcal {X}_{K^p\Gamma (p^n),c}\subset \mathcal {X}_{K^p\Gamma (p^n)}$
the tubular neighbourhood of the non-supersingular points of irreducible components of indices sending
$\mathcal {X}_{K^p\Gamma (p^n),c}\subset \mathcal {X}_{K^p\Gamma (p^n)}$
the tubular neighbourhood of the non-supersingular points of irreducible components of indices sending
![]() $(1,0)\in (\mathbb {Z}/p^n)^2$
to
$(1,0)\in (\mathbb {Z}/p^n)^2$
to
![]() $0$
. Let
$0$
. Let
 $M^{\dagger }_k(K^p\Gamma (p^n))$
be the space of sections of
$M^{\dagger }_k(K^p\Gamma (p^n))$
be the space of sections of
![]() $\omega ^k$
defined on a strict neighbourhood of
$\omega ^k$
defined on a strict neighbourhood of
![]() $\mathcal {X}_{K^p\Gamma (p^n),c}$
. Overconvergent modular forms of weight k are defined as
$\mathcal {X}_{K^p\Gamma (p^n),c}$
. Overconvergent modular forms of weight k are defined as
 $$ \begin{align*}M^{\dagger}_k:=\varinjlim_{K^p\subset\mathrm{GL}_2(\mathbb{A}^p_f)}\varinjlim_{n} M^{\dagger}_k(K^p\Gamma(p^n)).\end{align*} $$
$$ \begin{align*}M^{\dagger}_k:=\varinjlim_{K^p\subset\mathrm{GL}_2(\mathbb{A}^p_f)}\varinjlim_{n} M^{\dagger}_k(K^p\Gamma(p^n)).\end{align*} $$
One can check that there is a natural action of
 $\mathrm {GL}_2(\mathbb {A}^p_f)\times B$
on it.
$\mathrm {GL}_2(\mathbb {A}^p_f)\times B$
on it.
Since modular curves can be defined over
![]() $\mathbb {Q}_p$
, the absolute Galois group
$\mathbb {Q}_p$
, the absolute Galois group
 acts on C and everything we have defined and commutes with the action of
acts on C and everything we have defined and commutes with the action of
 ${\mathrm {GL}_{2}}(\mathbb {A}^{p}_{f})\times B$
. Our main results describe
${\mathrm {GL}_{2}}(\mathbb {A}^{p}_{f})\times B$
. Our main results describe
 ${\tilde {H}^{i}}{(C)^{\mathrm {la}}_{\mu }}$
as a representation of
${\tilde {H}^{i}}{(C)^{\mathrm {la}}_{\mu }}$
as a representation of
 ${\mathrm {GL}_{2}}{(\mathbb {A}^{p}_{f})}\times B\times {G_{\mathbb {Q}_{p}}}$
.
${\mathrm {GL}_{2}}{(\mathbb {A}^{p}_{f})}\times B\times {G_{\mathbb {Q}_{p}}}$
.
We need the following characters of
 $\mathrm {GL}_2(\mathbb {A}^p_f)\times B$
for stating our result. Denote by
$\mathrm {GL}_2(\mathbb {A}^p_f)\times B$
for stating our result. Denote by
 $\varepsilon :\mathbb {A}_f^{\times }/\mathbb {Q}^{\times }_{>0}\to \mathbb {Z}_p^{\times }$
the p-adic cyclotomic character (via class field theory, which sends a uniformiser
$\varepsilon :\mathbb {A}_f^{\times }/\mathbb {Q}^{\times }_{>0}\to \mathbb {Z}_p^{\times }$
the p-adic cyclotomic character (via class field theory, which sends a uniformiser
![]() $l\neq p$
to a geometric Frobenius). We define
$l\neq p$
to a geometric Frobenius). We define
![]() $t:\mathrm {GL}_2(\mathbb {A}_f)\to \mathbb {Z}_p^{\times }$
as
$t:\mathrm {GL}_2(\mathbb {A}_f)\to \mathbb {Z}_p^{\times }$
as
![]() $\varepsilon \circ \det $
and view it as a character of
$\varepsilon \circ \det $
and view it as a character of
 $\mathrm {GL}_2(\mathbb {A}^p_f)\times B$
by restriction. For
$\mathrm {GL}_2(\mathbb {A}^p_f)\times B$
by restriction. For
![]() $i=1,2$
, we define
$i=1,2$
, we define
![]() $e_i:B\to \mathbb {Q}_p^{\times }$
by sending
$e_i:B\to \mathbb {Q}_p^{\times }$
by sending
 $\begin {pmatrix} a_1 & b \\ 0 & a_2 \end {pmatrix}\in B$
to
$\begin {pmatrix} a_1 & b \\ 0 & a_2 \end {pmatrix}\in B$
to
![]() $a_i$
and view them as characters of
$a_i$
and view them as characters of
 $\mathrm {GL}_2(\mathbb {A}^p_f)\times B$
by projecting onto B. We write
$\mathrm {GL}_2(\mathbb {A}^p_f)\times B$
by projecting onto B. We write
![]() $\cdot $
rather than
$\cdot $
rather than
![]() $\otimes $
when twisting by such a character. One main result of this article is as follows. (This is obtained from Theorem 5.4.2 by taking direct limit over all
$\otimes $
when twisting by such a character. One main result of this article is as follows. (This is obtained from Theorem 5.4.2 by taking direct limit over all
![]() $K^p$
. There is a small difference as we do not put a Galois action on
$K^p$
. There is a small difference as we do not put a Galois action on
![]() $e_1,e_2,t$
here.)
$e_1,e_2,t$
here.)
Theorem 1.0.1. Let
![]() $k\in \mathbb {Z}$
and let
$k\in \mathbb {Z}$
and let
![]() $\mu =\mu _k:\mathfrak {b}\to C$
be the character sending
$\mu =\mu _k:\mathfrak {b}\to C$
be the character sending
 $\begin {pmatrix} a & b \\ 0 & d \end {pmatrix}$
to
$\begin {pmatrix} a & b \\ 0 & d \end {pmatrix}$
to
![]() $kd$
. Assume
$kd$
. Assume
![]() $k\neq 1$
. There is a natural decomposition
$k\neq 1$
. There is a natural decomposition
 $$ \begin{align*}\tilde{H}^1(C)^{\mathrm{la}}_{\mu_k}=N_{k,1}\cdot e_1^{-k}t^{k}\oplus N_{k,w}(k-1)\cdot e_1^{-1}e_2^{k-1}t,\end{align*} $$
$$ \begin{align*}\tilde{H}^1(C)^{\mathrm{la}}_{\mu_k}=N_{k,1}\cdot e_1^{-k}t^{k}\oplus N_{k,w}(k-1)\cdot e_1^{-1}e_2^{k-1}t,\end{align*} $$
where
![]() $(k-1)$
denotes a Tate twist by
$(k-1)$
denotes a Tate twist by
![]() $k-1$
. Moreover, we have the following description of
$k-1$
. Moreover, we have the following description of
![]() $N_{k,1}$
and
$N_{k,1}$
and
![]() $N_{k,w}$
:
$N_{k,w}$
:
-
(1)
 $N_{k,w}\cong M^{\dagger }_{2-k}$
for
$N_{k,w}\cong M^{\dagger }_{2-k}$
for
 $k\neq 2$
. When
$k\neq 2$
. When
 $k=2$
, we have
$k=2$
, we have  $$ \begin{align*}0\to M^{\dagger}_0/M_0 \to N_{k,w} \to M_0\to 0.\end{align*} $$
$$ \begin{align*}0\to M^{\dagger}_0/M_0 \to N_{k,w} \to M_0\to 0.\end{align*} $$
-
(2) If
 $k\leq -1$
, then there is an exact sequence
$k\leq -1$
, then there is an exact sequence  $$ \begin{align*}0\to H^1(\omega^{k})\to N_{k,1}\to M^{\dagger}_{k}\to 0.\end{align*} $$
$$ \begin{align*}0\to H^1(\omega^{k})\to N_{k,1}\to M^{\dagger}_{k}\to 0.\end{align*} $$
-
(3) If
 $k=0$
, then there is an exact sequence
$k=0$
, then there is an exact sequence  $$ \begin{align*}0\to H^1(\omega^0)\to N_{k,1}\to M^{\dagger}_0/M_0\to 0.\end{align*} $$
$$ \begin{align*}0\to H^1(\omega^0)\to N_{k,1}\to M^{\dagger}_0/M_0\to 0.\end{align*} $$
-
(4) If
 $k\geq 2$
, then
$k\geq 2$
, then
 $N_{k,1}\cong M^{\dagger }_k/ M_k$
.
$N_{k,1}\cong M^{\dagger }_k/ M_k$
.
All of the maps and isomorphisms here are
 $\mathrm {GL}_2(\mathbb {A}^p_f)\times B\times G_{\mathbb {Q}_p}$
-equivariant.
$\mathrm {GL}_2(\mathbb {A}^p_f)\times B\times G_{\mathbb {Q}_p}$
-equivariant.
One may view this as a Hodge–Tate decomposition into weight
![]() $0$
and
$0$
and
![]() $1-k$
components. Hence, this is a p-adic analogue of the Shimura isomorphism. Our convention is that the cyclotomic character is of Hodge–Tate weight
$1-k$
components. Hence, this is a p-adic analogue of the Shimura isomorphism. Our convention is that the cyclotomic character is of Hodge–Tate weight
![]() $-1$
. We have a similar (Hodge–Tate–Sen) decomposition if
$-1$
. We have a similar (Hodge–Tate–Sen) decomposition if
![]() $k\notin \mathbb {Z}$
(Theorem 5.4.2). Unfortunately, we can only determine half of the decomposition, which roughly is given by overconvergent modular forms of weight
$k\notin \mathbb {Z}$
(Theorem 5.4.2). Unfortunately, we can only determine half of the decomposition, which roughly is given by overconvergent modular forms of weight
![]() $2-k$
. We will give a definition of this space for nonintegral weights in Definition 5.2.3.
$2-k$
. We will give a definition of this space for nonintegral weights in Definition 5.2.3.
When
![]() $k=1$
, we do not get a decomposition because of the existence of non-Hodge–Tate representations with equal Hodge–Tate–Sen weights. Here is our result (which follows from Theorem 5.4.6 by taking the direct limit over all
$k=1$
, we do not get a decomposition because of the existence of non-Hodge–Tate representations with equal Hodge–Tate–Sen weights. Here is our result (which follows from Theorem 5.4.6 by taking the direct limit over all
![]() $K^p$
).
$K^p$
).
Theorem 1.0.2. Suppose
![]() $\mu =\mu _1:\mathfrak {b}\to C$
sends
$\mu =\mu _1:\mathfrak {b}\to C$
sends
 $\begin {pmatrix} a & b \\ 0 & d \end {pmatrix}$
to d. There is a natural exact sequence
$\begin {pmatrix} a & b \\ 0 & d \end {pmatrix}$
to d. There is a natural exact sequence
 $$ \begin{align*}0\to N_{1}\cdot e_1^{-1}t \to \tilde{H}^1(C)^{\mathrm{la}}_{\mu_1} \to M^{\dagger}_{1}\cdot e_1^{-1}t\to 0,\end{align*} $$
$$ \begin{align*}0\to N_{1}\cdot e_1^{-1}t \to \tilde{H}^1(C)^{\mathrm{la}}_{\mu_1} \to M^{\dagger}_{1}\cdot e_1^{-1}t\to 0,\end{align*} $$
where
![]() $N_{1}$
sits inside an exact sequence:
$N_{1}$
sits inside an exact sequence:
 $$ \begin{align*}0\to M^{\dagger}_1/M_1\to N_{1}\to H^1(\omega)\to 0.\end{align*} $$
$$ \begin{align*}0\to M^{\dagger}_1/M_1\to N_{1}\to H^1(\omega)\to 0.\end{align*} $$
Moreover, let
 $\tilde {H}^1(C)^{\mathrm {la},(1,0)}_{\mu _1}\subset \tilde {H}^1(C)^{\mathrm {la}}_{\mu _1}$
be the pullback of
$\tilde {H}^1(C)^{\mathrm {la},(1,0)}_{\mu _1}\subset \tilde {H}^1(C)^{\mathrm {la}}_{\mu _1}$
be the pullback of
 $M_{1}\cdot e_1^{-1}t\subset M^{\dagger }_{1}\cdot e_1^{-1}t$
, so that there is an exact sequence
$M_{1}\cdot e_1^{-1}t\subset M^{\dagger }_{1}\cdot e_1^{-1}t$
, so that there is an exact sequence
 $$ \begin{align*}0\to N_{1}\cdot e_1^{-1}t \to \tilde{H}^1(C)^{\mathrm{la},(1,0)}_{\mu_1} \to M_{1}\cdot e_1^{-1}t\to 0.\end{align*} $$
$$ \begin{align*}0\to N_{1}\cdot e_1^{-1}t \to \tilde{H}^1(C)^{\mathrm{la},(1,0)}_{\mu_1} \to M_{1}\cdot e_1^{-1}t\to 0.\end{align*} $$
Then
 $(\tilde {H}^1(C)^{\mathrm {la}}_{\mu _1})^{G_{\mathbb {Q}_p}}\subset \tilde {H}^1(C)^{\mathrm {la},(1,0)}_{\mu _1}$
. Again, all of the maps here are
$(\tilde {H}^1(C)^{\mathrm {la}}_{\mu _1})^{G_{\mathbb {Q}_p}}\subset \tilde {H}^1(C)^{\mathrm {la},(1,0)}_{\mu _1}$
. Again, all of the maps here are
 $\mathrm {GL}_2(\mathbb {A}^p_f)\times B\times G_{\mathbb {Q}_p}$
-equivariant.
$\mathrm {GL}_2(\mathbb {A}^p_f)\times B\times G_{\mathbb {Q}_p}$
-equivariant.
In fact, we will generalise the usual Sen operator to this situation in Definition 5.1.5 and then show it is nilpotent on
 $\tilde {H}^1(C)^{\mathrm {la}}_{\mu }$
and factors through the quotient
$\tilde {H}^1(C)^{\mathrm {la}}_{\mu }$
and factors through the quotient
 $M^{\dagger }_{1}\cdot e_1^{-1}t$
and maps it to
$M^{\dagger }_{1}\cdot e_1^{-1}t$
and maps it to
 $M^{\dagger }_1/M_1\cdot e_1^{-1}t\subset N_{1}\cdot e_1^{-1}t$
.
$M^{\dagger }_1/M_1\cdot e_1^{-1}t\subset N_{1}\cdot e_1^{-1}t$
.
Both theorems give a concrete relation between completed cohomology and overconvergent modular forms. As a first application, we are able to prove a classicality result for weight 1 overconvergent eigenforms. Fix a tame level
 $K^p=K^SK_{S\setminus \{p\}}$
for some finite set of primes S containing p and suppose
$K^p=K^SK_{S\setminus \{p\}}$
for some finite set of primes S containing p and suppose
![]() $K^S$
is a maximal open compact subgroup of
$K^S$
is a maximal open compact subgroup of
 $\mathrm {GL}_2(\mathbb {A}_f^S)$
, where
$\mathrm {GL}_2(\mathbb {A}_f^S)$
, where
 $\mathbb {A}_f^S$
is the prime-to-S part of
$\mathbb {A}_f^S$
is the prime-to-S part of
![]() $\mathbb {A}_f$
. Denote by
$\mathbb {A}_f$
. Denote by
 $\mathbb {T}_{K^p}:=\mathbb {Z}_p[\mathrm {GL}_2(\mathbb {A}^S_f)//K^S]$
the abstract Hecke algebra of
$\mathbb {T}_{K^p}:=\mathbb {Z}_p[\mathrm {GL}_2(\mathbb {A}^S_f)//K^S]$
the abstract Hecke algebra of
![]() $K^S$
-bi-invariant compactly supported functions on
$K^S$
-bi-invariant compactly supported functions on
 $\mathrm {GL}_2(\mathbb {A}^S_f)$
, where the Haar measure gives
$\mathrm {GL}_2(\mathbb {A}^S_f)$
, where the Haar measure gives
![]() $K^S$
measure
$K^S$
measure
![]() $1$
. Then
$1$
. Then
![]() $\mathbb {T}_{K^p}$
acts on
$\mathbb {T}_{K^p}$
acts on
 $H^1(Y_{K^pK_p}(\mathbb {C}),\mathbb {Z}_p)$
and we denote its image in
$H^1(Y_{K^pK_p}(\mathbb {C}),\mathbb {Z}_p)$
and we denote its image in
 $\operatorname {\mathrm {End}}_{\mathbb {Z}_p}(H^1(Y_{K^pK_p}(\mathbb {C}),\mathbb {Z}_p))$
by
$\operatorname {\mathrm {End}}_{\mathbb {Z}_p}(H^1(Y_{K^pK_p}(\mathbb {C}),\mathbb {Z}_p))$
by
![]() $\mathbb {T}(K^pK_p)$
and let
$\mathbb {T}(K^pK_p)$
and let
 $\mathbb {T}:=\varprojlim _{K_p}\mathbb {T}(K^pK_p)$
. It can be shown that
$\mathbb {T}:=\varprojlim _{K_p}\mathbb {T}(K^pK_p)$
. It can be shown that
![]() $\mathbb {T}$
is independent of S. Let
$\mathbb {T}$
is independent of S. Let

be a
![]() $\mathbb {Z}_p$
-algebra homomorphism. We can associate to
$\mathbb {Z}_p$
-algebra homomorphism. We can associate to
![]() $\lambda $
a 2-dimensional semi-simple Galois representation
$\lambda $
a 2-dimensional semi-simple Galois representation

satisfying
![]() $\mathrm {tr}(\rho _{\lambda }(\operatorname {\mathrm {Frob}}_l))=\lambda (T_l)l^{-1}$
for
$\mathrm {tr}(\rho _{\lambda }(\operatorname {\mathrm {Frob}}_l))=\lambda (T_l)l^{-1}$
for
![]() $l\notin S$
. Here
$l\notin S$
. Here
 $T_l=[K^S\begin {pmatrix} l & 0 \\ 0 & 1 \end {pmatrix}K^S]$
and
$T_l=[K^S\begin {pmatrix} l & 0 \\ 0 & 1 \end {pmatrix}K^S]$
and
![]() $\operatorname {\mathrm {Frob}}_l$
is a lift of geometric Frobenius at l. See Section 6.1.1 for more details.
$\operatorname {\mathrm {Frob}}_l$
is a lift of geometric Frobenius at l. See Section 6.1.1 for more details.
Let
 $M^{\dagger }_1(K^p)=\varinjlim _{n}M^{\dagger }_1(K^p\Gamma (p^n))$
and
$M^{\dagger }_1(K^p)=\varinjlim _{n}M^{\dagger }_1(K^p\Gamma (p^n))$
and
 $N_0=\begin {pmatrix} 1 & \mathbb {Z}_p \\ 0 & 1 \end {pmatrix}\subset \mathrm {GL}_2(\mathbb {Q}_p)$
. We have the usual
$N_0=\begin {pmatrix} 1 & \mathbb {Z}_p \\ 0 & 1 \end {pmatrix}\subset \mathrm {GL}_2(\mathbb {Q}_p)$
. We have the usual
![]() $U_p$
-operator acting on
$U_p$
-operator acting on
![]() $N_0$
-invariants by
$N_0$
-invariants by
 $$ \begin{align*}U_p:=\sum_{i=0}^{p-1}\begin{pmatrix} p & i \\ 0 & 1 \end{pmatrix}.\end{align*} $$
$$ \begin{align*}U_p:=\sum_{i=0}^{p-1}\begin{pmatrix} p & i \\ 0 & 1 \end{pmatrix}.\end{align*} $$
Since
![]() $\mathbb {T}$
acts on
$\mathbb {T}$
acts on
![]() $\tilde H^1(K^p,\mathbb {Z}_p)$
, it follows from Theorem 1.0.2 that
$\tilde H^1(K^p,\mathbb {Z}_p)$
, it follows from Theorem 1.0.2 that
![]() $\mathbb {T}$
acts on
$\mathbb {T}$
acts on
 $M^{\dagger }_1(K^p)$
. We denote by
$M^{\dagger }_1(K^p)$
. We denote by
![]() $\mathfrak {p}_{\lambda }$
the kernel of
$\mathfrak {p}_{\lambda }$
the kernel of
![]() $\lambda $
and by
$\lambda $
and by
 $M^{\dagger }_1(K^p)[\mathfrak {p}_{\lambda }]$
the
$M^{\dagger }_1(K^p)[\mathfrak {p}_{\lambda }]$
the
![]() $\lambda $
-isotypic part of
$\lambda $
-isotypic part of
 $M^{\dagger }_1(K^p)$
.
$M^{\dagger }_1(K^p)$
.
Theorem 1.0.3 Theorem 6.2.2
Suppose
-
•
 $M^{\dagger }_1(K^p)[\mathfrak {p}_{\lambda }]^{N_0}\neq 0$
has a nonzero
$M^{\dagger }_1(K^p)[\mathfrak {p}_{\lambda }]^{N_0}\neq 0$
has a nonzero
 $U_p$
-eigenvector;
$U_p$
-eigenvector; -
•
 $\rho _{\lambda }|_{G_{\mathbb {Q}_p}}$
is Hodge–Tate of weights
$\rho _{\lambda }|_{G_{\mathbb {Q}_p}}$
is Hodge–Tate of weights
 $0,0$
.
$0,0$
.
Then
![]() $\lambda $
comes from a classical weight 1 eigenform; that is,
$\lambda $
comes from a classical weight 1 eigenform; that is,
![]() $M_1(K^p)[\mathfrak {p}_{\lambda }]\neq 0$
.
$M_1(K^p)[\mathfrak {p}_{\lambda }]\neq 0$
.
In the ordinary case, this reproves a result of Buzzard–Taylor [Reference Buzzard and TaylorBT99]. Note that we do not assume the
![]() $U_p$
-eigenvalue is nonzero. This will allow us to attack the Fontaine–Mazur conjecture in the nonordinary, irregular case.
$U_p$
-eigenvalue is nonzero. This will allow us to attack the Fontaine–Mazur conjecture in the nonordinary, irregular case.
Proof. We give a sketch of the proof here. We may assume
![]() $\rho _{\lambda }$
is irreducible. Let
$\rho _{\lambda }$
is irreducible. Let
![]() $\mu _1$
be as in Theorem 1.0.2 and denote by
$\mu _1$
be as in Theorem 1.0.2 and denote by
 the map which sends
the map which sends
![]() $T_l$
to
$T_l$
to
![]() $\lambda (T_l)l^{-1}$
. The key point is that by the Eichler–Shimura relation,
$\lambda (T_l)l^{-1}$
. The key point is that by the Eichler–Shimura relation,
 for some W. Since
for some W. Since
![]() $\rho _{\lambda }$
is Hodge–Tate of weights
$\rho _{\lambda }$
is Hodge–Tate of weights
![]() $0,0$
, we have
$0,0$
, we have
 $\tilde H^1(K^p,C)^{\mathrm {la}}_{\mu _1}[\mathfrak {p}_{\lambda \cdot t}]=\tilde H^1(C)^{\mathrm {la},(1,0)}_{\mu _1}[\mathfrak {p}_{\lambda \cdot t}]$
. Now assume
$\tilde H^1(K^p,C)^{\mathrm {la}}_{\mu _1}[\mathfrak {p}_{\lambda \cdot t}]=\tilde H^1(C)^{\mathrm {la},(1,0)}_{\mu _1}[\mathfrak {p}_{\lambda \cdot t}]$
. Now assume
![]() $\lambda $
is not classical. Then it follows from the second part of Theorem 1.0.2 that
$\lambda $
is not classical. Then it follows from the second part of Theorem 1.0.2 that
 $$ \begin{align*}(M^{\dagger}_1(K^p)[\mathfrak{p}_{\lambda}]\cdot e_1^{-1}t)^{N_0}=\tilde H^1(C)^{\mathrm{la},(1,0)}_{\mu_1}[\mathfrak{p}_{\lambda\cdot t}]^{N_0}=\tilde H^1(K^p,C)^{\mathrm{la}}_{\mu_1}[\mathfrak{p}_{\lambda\cdot t}]^{N_0}=\rho_{\lambda}\otimes W^{N_0}.\end{align*} $$
$$ \begin{align*}(M^{\dagger}_1(K^p)[\mathfrak{p}_{\lambda}]\cdot e_1^{-1}t)^{N_0}=\tilde H^1(C)^{\mathrm{la},(1,0)}_{\mu_1}[\mathfrak{p}_{\lambda\cdot t}]^{N_0}=\tilde H^1(K^p,C)^{\mathrm{la}}_{\mu_1}[\mathfrak{p}_{\lambda\cdot t}]^{N_0}=\rho_{\lambda}\otimes W^{N_0}.\end{align*} $$
By choosing suitable
![]() $K^p$
and taking suitable eigenvectors of Hecke operators
$K^p$
and taking suitable eigenvectors of Hecke operators
![]() $U_l$
and diamond operators at ramified places, the nonzero
$U_l$
and diamond operators at ramified places, the nonzero
![]() $U_p$
-eigenspace of the first term will be 1-dimensional by the q-expansion principle. However, the corresponding subspace of the last term will always have dimension at least
$U_p$
-eigenspace of the first term will be 1-dimensional by the q-expansion principle. However, the corresponding subspace of the last term will always have dimension at least
![]() $\dim \rho _{\lambda }=2$
if it is nonzero! Contradiction. This shows that
$\dim \rho _{\lambda }=2$
if it is nonzero! Contradiction. This shows that
![]() $\lambda $
has to be classical.
$\lambda $
has to be classical.
Thanks to Emerton’s work on local–global compatibility, we have a good understanding of
![]() $\tilde {H}^1(K^p,C)[\mathfrak {p}_{\lambda }]$
in terms of the p-adic local Langlands correspondence. Colmez’s Kirillov model then shows that a
$\tilde {H}^1(K^p,C)[\mathfrak {p}_{\lambda }]$
in terms of the p-adic local Langlands correspondence. Colmez’s Kirillov model then shows that a
![]() $U_p$
-eigenvector always exists (see Corollary 6.4.6).
$U_p$
-eigenvector always exists (see Corollary 6.4.6).
Theorem 1.0.4 (Theorem 6.4.7)
Suppose
-
•
 $\rho _{\lambda }$
is irreducible;
$\rho _{\lambda }$
is irreducible; -
•
 $\rho _{\lambda }|_{G_{\mathbb {Q}_p}}$
is Hodge–Tate of weight
$\rho _{\lambda }|_{G_{\mathbb {Q}_p}}$
is Hodge–Tate of weight
 $0,0$
.
$0,0$
.
Then
![]() $\lambda $
is classical; that is,
$\lambda $
is classical; that is,
![]() $M_1(K^p)[\mathfrak {p}_{\lambda }]\neq 0$
for some tame level
$M_1(K^p)[\mathfrak {p}_{\lambda }]\neq 0$
for some tame level
![]() $K^p$
.
$K^p$
.
We say a Galois representation
![]() $\rho $
is pro-modular if
$\rho $
is pro-modular if
![]() $\rho =\rho _{\lambda }$
for some
$\rho =\rho _{\lambda }$
for some
![]() $K^p$
and
$K^p$
and
![]() $\lambda $
. Combining Theorem 1.0.4 with work on promodularity of a Galois representation ([Reference EmertonEme11, Theorem 1.2.3], which is based on previous work of Böckle, Diamond–Flach–Guo, Khare–Wintenberger and Kisin), we give a new proof of the Fontaine–Mazur conjecture in the irregular case under some mild hypotheses.
$\lambda $
. Combining Theorem 1.0.4 with work on promodularity of a Galois representation ([Reference EmertonEme11, Theorem 1.2.3], which is based on previous work of Böckle, Diamond–Flach–Guo, Khare–Wintenberger and Kisin), we give a new proof of the Fontaine–Mazur conjecture in the irregular case under some mild hypotheses.
Theorem 1.0.5 (Theorem 6.4.8 and Corollary 6.4.9)
Let
![]() $p>2$
be a prime number and
$p>2$
be a prime number and
 a continuous irreducible 2-dimensional representation. Assume
a continuous irreducible 2-dimensional representation. Assume
-
(1)
 $\rho $
is unramified outside of finitely many primes;
$\rho $
is unramified outside of finitely many primes; -
(2)
 $\det \rho (c)=-1$
for a complex conjugation
$\det \rho (c)=-1$
for a complex conjugation
 ;
; -
(3)
 $\rho |_{G_{\mathbb {Q}_p}}$
is Hodge–Tate of weights
$\rho |_{G_{\mathbb {Q}_p}}$
is Hodge–Tate of weights
 $0,0$
;
$0,0$
; -
(4) the residual representation
 is irreducible;
is irreducible; -
(5)
 $(\bar \rho |_{G_{\mathbb {Q}_p}})^{ss}$
is either irreducible or of the form
$(\bar \rho |_{G_{\mathbb {Q}_p}})^{ss}$
is either irreducible or of the form
 $\eta _1\oplus \eta _2$
for some characters
$\eta _1\oplus \eta _2$
for some characters
 $\eta _1,\eta _2$
satisfying
$\eta _1,\eta _2$
satisfying
 $\eta _1/\eta _2\neq 1,\omega ^{\pm 1}$
.
$\eta _1/\eta _2\neq 1,\omega ^{\pm 1}$
.
Then
![]() $\rho $
is modular in the sense that it is isomorphic to the representation attached to a classical weight 1 cuspidal eigenform by [Reference Deligne and SerreDS74]. In particular,
$\rho $
is modular in the sense that it is isomorphic to the representation attached to a classical weight 1 cuspidal eigenform by [Reference Deligne and SerreDS74]. In particular,
![]() $\rho $
has finite image.
$\rho $
has finite image.
Remark 1.0.6. This result was already known by the work of Pilloni–Stroh [Reference Pilloni and StrohPS16]. Before their work, much work on this problem was done in the ordinary case (Buzzard–Taylor [Reference Buzzard and TaylorBT99], Calegari–Geraghty [Reference Calegari and GeraghtyCG18] and others) and has been generalised to the case of Hilbert modular forms. I hope this article gives a new perspective on this problem.
If the results of this article can also be generalised to Hilbert case, one should be able to remove the last two conditions by invoking our previous work on promodularity [Reference PanPan19].
For overconvergent eigenforms of weight not necessarily
![]() $1$
, we have the following result.
$1$
, we have the following result.
Theorem 1.0.7 (Theorem 6.4.11)
Suppose
![]() $\rho _{\lambda }$
is irreducible and
$\rho _{\lambda }$
is irreducible and
 $M^{\dagger }_k(K^p)[\mathfrak {p}_{\lambda }]\neq 0$
; then
$M^{\dagger }_k(K^p)[\mathfrak {p}_{\lambda }]\neq 0$
; then
 $\rho _{\lambda }|_{G_{\mathbb {Q}_p}}$
has Hodge–Tate–Sen weights
$\rho _{\lambda }|_{G_{\mathbb {Q}_p}}$
has Hodge–Tate–Sen weights
![]() $0,k-1$
. Conversely, suppose
$0,k-1$
. Conversely, suppose
-
•
 $\rho _{\lambda }|_{G_{\mathbb {Q}_p}}$
is irreducible and has Hodge–Tate–Sen weights
$\rho _{\lambda }|_{G_{\mathbb {Q}_p}}$
is irreducible and has Hodge–Tate–Sen weights
 $0,k-1$
;
$0,k-1$
;
then
 $M^{\dagger }_k(K^p)[\mathfrak {p}_{\lambda }]\neq 0$
.
$M^{\dagger }_k(K^p)[\mathfrak {p}_{\lambda }]\neq 0$
.
Remark 1.0.8. As pointed out by a referee, Gouvêa in [Reference GouvêaGou94, Conjecture 4] conjectured that the Hodge–Tate weights of the Galois representation associated to an overconvergent eigenform of weight k are
![]() $0,k-1$
and guessed that this should be an equivalence. Our result confirms his conjecture and his guess under the given hypotheses.
$0,k-1$
and guessed that this should be an equivalence. Our result confirms his conjecture and his guess under the given hypotheses.
We note that Sean Howe also proved Gouvêa’s conjecture in [Reference HoweHow21] independently. Recently, we found a more direct way to prove Gouvêa’s conjecture in [Reference PanPan20] using Scholze’s fake-Hasse invariants. But the method in [Reference PanPan20] does not seem to be enough to give a converse result. Indeed, one key ingredient in our proof of Theorem 1.0.7 here is Colmez’s Kirillov model [Reference ColmezCol10, Chap. VI], which is a deep result in p-adic local Langlands correspondence for
![]() $\mathrm {GL}_2(\mathbb {Q}_p)$
.
$\mathrm {GL}_2(\mathbb {Q}_p)$
.
Now we explain our strategy to compute
 $\tilde {H}^1(C)^{\mathrm {la}}_{\mu }$
. As mentioned before, our main tool is p-adic Hodge theory. Fix a tame level
$\tilde {H}^1(C)^{\mathrm {la}}_{\mu }$
. As mentioned before, our main tool is p-adic Hodge theory. Fix a tame level
![]() $K^p$
. By the work of Scholze [Reference ScholzeSch15], there is an adic space
$K^p$
. By the work of Scholze [Reference ScholzeSch15], there is an adic space
 $\mathcal {X}_{K^p}\sim \varprojlim _{K_p}\mathcal {X}_{K^pK_p}$
(the modular curve at infinite level) with Hodge–Tate period map
$\mathcal {X}_{K^p}\sim \varprojlim _{K_p}\mathcal {X}_{K^pK_p}$
(the modular curve at infinite level) with Hodge–Tate period map
![]() $\pi _{\mathrm {HT}}:\mathcal {X}_{K^p}\to {\mathscr {F}\!\ell }=\mathbb {P}^1$
, where
$\pi _{\mathrm {HT}}:\mathcal {X}_{K^p}\to {\mathscr {F}\!\ell }=\mathbb {P}^1$
, where
![]() ${\mathscr {F}\!\ell }$
denotes the adic space associated to the flag variety of
${\mathscr {F}\!\ell }$
denotes the adic space associated to the flag variety of
![]() $\mathrm {GL}_2/C$
. Let
$\mathrm {GL}_2/C$
. Let
![]() $\mathcal {O}_{K^p}$
be the pushforward of the structure sheaf of
$\mathcal {O}_{K^p}$
be the pushforward of the structure sheaf of
![]() $\mathcal {X}_{K^p}$
along
$\mathcal {X}_{K^p}$
along
![]() $\pi _{\mathrm {HT}}$
. Then Scholze shows that there is a natural isomorphism
$\pi _{\mathrm {HT}}$
. Then Scholze shows that there is a natural isomorphism
where the right-hand side is computed on the analytic site of
![]() ${\mathscr {F}\!\ell }$
. In order to study the (
${\mathscr {F}\!\ell }$
. In order to study the (
![]() $\mathrm {GL}_2(\mathbb {Q}_p)$
-)locally analytic vectors, we consider the subsheaf of locally analytic sections
$\mathrm {GL}_2(\mathbb {Q}_p)$
-)locally analytic vectors, we consider the subsheaf of locally analytic sections
 $\mathcal {O}_{K^p}^{\mathrm {la}}\subset \mathcal {O}_{K^p}$
(Section 4.2.6).
$\mathcal {O}_{K^p}^{\mathrm {la}}\subset \mathcal {O}_{K^p}$
(Section 4.2.6).
Theorem 1.0.9 (Theorem 4.4.6)
There is a natural isomorphism
 $$ \begin{align*}\tilde{H}^i(K^p,C)^{\mathrm{la}}\cong H^i({\mathscr{F}\!\ell},\mathcal{O}^{\mathrm{la}}_{K^p}).\end{align*} $$
$$ \begin{align*}\tilde{H}^i(K^p,C)^{\mathrm{la}}\cong H^i({\mathscr{F}\!\ell},\mathcal{O}^{\mathrm{la}}_{K^p}).\end{align*} $$
Next we need a careful local study of the sheaf
 $\mathcal {O}^{\mathrm {la}}_{K^p}$
. This part is largely inspired by the work of Berger–Colmez [Reference Berger and ColmezBC16]. There are two key ingredients:
$\mathcal {O}^{\mathrm {la}}_{K^p}$
. This part is largely inspired by the work of Berger–Colmez [Reference Berger and ColmezBC16]. There are two key ingredients:
-
(1)
 $\mathcal {O}^{\mathrm {la}}_{K^p}$
satisfies a differential equation on
$\mathcal {O}^{\mathrm {la}}_{K^p}$
satisfies a differential equation on
 ${\mathscr {F}\!\ell }$
;
${\mathscr {F}\!\ell }$
; -
(2) an explicit description of sections of
 $\mathcal {O}^{\mathrm {la}}_{K^p}$
(Theorem 4.3.9).
$\mathcal {O}^{\mathrm {la}}_{K^p}$
(Theorem 4.3.9).
We will only explain the differential equation in detail here. It turns out to be nothing but the horizontal nilpotent subalgebra. To be more precise, we follow some constructions on the flag variety from [Reference Beĭlinson and BernsteinBB83]. Recall
![]() $\mathfrak {g}=\mathfrak {gl}_2(C)$
. For a C-point x of the flag variety
$\mathfrak {g}=\mathfrak {gl}_2(C)$
. For a C-point x of the flag variety
![]() $\mathrm {Fl}$
of
$\mathrm {Fl}$
of
![]() $\mathrm {GL}_2/C$
, let
$\mathrm {GL}_2/C$
, let
![]() $\mathfrak {b}_x,\mathfrak {n}_x\subset \mathfrak {g}$
be its corresponding Borel subalgebra and nilpotent subalgebra. Let
$\mathfrak {b}_x,\mathfrak {n}_x\subset \mathfrak {g}$
be its corresponding Borel subalgebra and nilpotent subalgebra. Let
 $$ \begin{align*} \mathfrak{g}^0&:= \mathcal{O}_{\mathrm{Fl}}\otimes_{C}\mathfrak{g},\\ \mathfrak{b}^0&:= \{f\in \mathfrak{g}^0\,| \, f_x\in \mathfrak{b}_x,\mbox{ for all }x\in\mathrm{Fl}(C)\},\\ \mathfrak{n}^0&:= \{f\in \mathfrak{g}^0\,| \, f_x\in \mathfrak{n}_x,\mbox{ for all }x\in\mathrm{Fl}(C)\}. \end{align*} $$
$$ \begin{align*} \mathfrak{g}^0&:= \mathcal{O}_{\mathrm{Fl}}\otimes_{C}\mathfrak{g},\\ \mathfrak{b}^0&:= \{f\in \mathfrak{g}^0\,| \, f_x\in \mathfrak{b}_x,\mbox{ for all }x\in\mathrm{Fl}(C)\},\\ \mathfrak{n}^0&:= \{f\in \mathfrak{g}^0\,| \, f_x\in \mathfrak{n}_x,\mbox{ for all }x\in\mathrm{Fl}(C)\}. \end{align*} $$
By abuse of notation, we also view these as vector bundles on
![]() ${\mathscr {F}\!\ell }$
. Then
${\mathscr {F}\!\ell }$
. Then
![]() $\mathfrak {g}^0$
acts on
$\mathfrak {g}^0$
acts on
 $\mathcal {O}^{\mathrm {la}}_{K^p}$
in an obvious way.
$\mathcal {O}^{\mathrm {la}}_{K^p}$
in an obvious way.
Theorem 1.0.10 (Theorem 4.2.7)
![]() $\mathfrak {n}^0$
acts trivially on
$\mathfrak {n}^0$
acts trivially on
 $\mathcal {O}^{\mathrm {la}}_{K^p}$
.
$\mathcal {O}^{\mathrm {la}}_{K^p}$
.
In fact, we will show the existence of such a differential equation in a very general setting.
Theorem 1.0.11 (Theorem 3.1.2)
Suppose
-
•
 $X=\operatorname {\mathrm {Spa}}(A,A^+)$
: a 1-dimensional smooth affinoid adic space (over
$X=\operatorname {\mathrm {Spa}}(A,A^+)$
: a 1-dimensional smooth affinoid adic space (over
 $\operatorname {\mathrm {Spa}}(C,\mathcal {O}_C)$
);
$\operatorname {\mathrm {Spa}}(C,\mathcal {O}_C)$
); -
• G: a finite-dimensional compact p-adic Lie group;
-
•
 $\operatorname {\mathrm {Spa}}(B,B^+)$
: a Galois pro-étale perfectoid covering of X with Galois group G.
$\operatorname {\mathrm {Spa}}(B,B^+)$
: a Galois pro-étale perfectoid covering of X with Galois group G.
Then under some smallness assumption on X (cf. Section 3.1.1), there is an element of
![]() $B\otimes _{\mathbb {Q}_p}\operatorname {\mathrm {Lie}}(G)$
that annihilates the G-locally analytic vectors in B. It is nonzero if
$B\otimes _{\mathbb {Q}_p}\operatorname {\mathrm {Lie}}(G)$
that annihilates the G-locally analytic vectors in B. It is nonzero if
![]() $\operatorname {\mathrm {Spa}}(B,B^+)$
is a locally analytic covering in the sense of Definition 3.5.4.
$\operatorname {\mathrm {Spa}}(B,B^+)$
is a locally analytic covering in the sense of Definition 3.5.4.
Remark 1.0.12. This can be viewed as a p-adic analogue of the Cauchy–Riemann equation in classical complex analysis. See also Remarks 3.1.4, 3.1.7 for the relation with classical and relative Sen theory (also called the p-adic Simpson correspondence in the literature). We can also allow some ramification; cf. Theorem 3.1.2.
Example 1.0.13. One simple example is
-
•
 $X=\operatorname {\mathrm {Spa}}(C\langle T^{\pm 1}\rangle , \mathcal {O}_C\langle T^{\pm 1}\rangle )$
, the 1-dimensional torus;
$X=\operatorname {\mathrm {Spa}}(C\langle T^{\pm 1}\rangle , \mathcal {O}_C\langle T^{\pm 1}\rangle )$
, the 1-dimensional torus; -
•
 $\widetilde X=\operatorname {\mathrm {Spa}}(C\langle T^{\pm \frac {1}{p^{\infty }}}\rangle , \mathcal {O}_C\langle T^{\pm \frac {1}{p^{\infty }}}\rangle )$
, the perfectoid inverse limit of
$\widetilde X=\operatorname {\mathrm {Spa}}(C\langle T^{\pm \frac {1}{p^{\infty }}}\rangle , \mathcal {O}_C\langle T^{\pm \frac {1}{p^{\infty }}}\rangle )$
, the perfectoid inverse limit of
 $\operatorname {\mathrm {Spa}}(C\langle T^{\pm \frac {1}{p^{m}}}\rangle , \mathcal {O}_C\langle T^{\pm \frac {1}{p^{m}}}\rangle )$
;
$\operatorname {\mathrm {Spa}}(C\langle T^{\pm \frac {1}{p^{m}}}\rangle , \mathcal {O}_C\langle T^{\pm \frac {1}{p^{m}}}\rangle )$
; -
•
 $G\cong \mathbb {Z}_p$
.
$G\cong \mathbb {Z}_p$
.
In this case, the G-locally analytic vectors in
 $C\langle T^{\pm \frac {1}{p^{\infty }}}\rangle $
are the smooth vectors
$C\langle T^{\pm \frac {1}{p^{\infty }}}\rangle $
are the smooth vectors
 $\bigcup _{m\in \mathbb {N}} C\langle T^{\pm \frac {1}{p^{m}}}\rangle $
. Our differential operator is simply a generator of
$\bigcup _{m\in \mathbb {N}} C\langle T^{\pm \frac {1}{p^{m}}}\rangle $
. Our differential operator is simply a generator of
![]() $\operatorname {\mathrm {Lie}}(G)$
.
$\operatorname {\mathrm {Lie}}(G)$
.
Back to the flag variety. Since
![]() $\mathfrak {n}^0$
acts trivially on
$\mathfrak {n}^0$
acts trivially on
 $\mathcal {O}^{\mathrm {la}}_{K^p}$
, there is an induced action of
$\mathcal {O}^{\mathrm {la}}_{K^p}$
, there is an induced action of
![]() $\mathfrak {b}^0/\mathfrak {n}^0\cong \mathfrak {h}\otimes \mathcal {O}_{{\mathscr {F}\!\ell }}$
, where
$\mathfrak {b}^0/\mathfrak {n}^0\cong \mathfrak {h}\otimes \mathcal {O}_{{\mathscr {F}\!\ell }}$
, where
![]() $\mathfrak {h}$
is a Cartan subalgebra of
$\mathfrak {h}$
is a Cartan subalgebra of
![]() $\mathfrak {g}$
. We choose it as the Levi quotient of
$\mathfrak {g}$
. We choose it as the Levi quotient of
![]() $\mathfrak {b}$
; that is, the diagonal matrices. Hence, we have an (horizontal) action
$\mathfrak {b}$
; that is, the diagonal matrices. Hence, we have an (horizontal) action
![]() $\theta _{\mathfrak {h}}$
of
$\theta _{\mathfrak {h}}$
of
![]() $\mathfrak {h}$
on
$\mathfrak {h}$
on
 $\mathcal {O}^{\mathrm {la}}_{K^p}$
. By Harish–Chandra’s theory, this action is closely related to the action of the centre
$\mathcal {O}^{\mathrm {la}}_{K^p}$
. By Harish–Chandra’s theory, this action is closely related to the action of the centre
![]() $Z(U(\mathfrak {g}))$
(Corollary 4.2.8). In the study of cohomology of locally symmetric spaces, the infinitesimal group action is related to Hodge theory. Our next result gives a p-adic Hodgetheoretic interpretation of
$Z(U(\mathfrak {g}))$
(Corollary 4.2.8). In the study of cohomology of locally symmetric spaces, the infinitesimal group action is related to Hodge theory. Our next result gives a p-adic Hodgetheoretic interpretation of
![]() $\theta _{\mathfrak {h}}$
.
$\theta _{\mathfrak {h}}$
.
Theorem 1.0.14 (Theorem 5.1.11)
 $\theta _{\mathfrak {h}}(\begin {pmatrix}0 & 0\\ 0 & 1 \end {pmatrix})$
is the unique Sen operator on the cohomology
$\theta _{\mathfrak {h}}(\begin {pmatrix}0 & 0\\ 0 & 1 \end {pmatrix})$
is the unique Sen operator on the cohomology
 $H^i({\mathscr {F}\!\ell },\mathcal {O}_{K^p}^{\mathrm {la}})\cong \tilde {H}^i(K^p,C)^{\mathrm {la}}$
for any i.
$H^i({\mathscr {F}\!\ell },\mathcal {O}_{K^p}^{\mathrm {la}})\cong \tilde {H}^i(K^p,C)^{\mathrm {la}}$
for any i.
Remark 1.0.15. Since the usual Sen operator is defined for a finite-dimensional C-semilinear representation of
![]() $G_{\mathbb {Q}_p}$
, we will generalise this notion to this situation in Definition 5.1.5. For example, for any finite-dimensional C-semilinear subrepresentation V of
$G_{\mathbb {Q}_p}$
, we will generalise this notion to this situation in Definition 5.1.5. For example, for any finite-dimensional C-semilinear subrepresentation V of
![]() $G_{\mathbb {Q}_p}$
in
$G_{\mathbb {Q}_p}$
in
![]() $\tilde {H}^i(K^p,C)^{\mathrm {la}}$
, this result implies that
$\tilde {H}^i(K^p,C)^{\mathrm {la}}$
, this result implies that
 $\theta _{\mathfrak {h}}(\begin {pmatrix}0 & 0\\ 0 & 1 \end {pmatrix})$
agrees with usual Sen operator when restricted to V. We also sketch a more direct construction of the Sen operator on
$\theta _{\mathfrak {h}}(\begin {pmatrix}0 & 0\\ 0 & 1 \end {pmatrix})$
agrees with usual Sen operator when restricted to V. We also sketch a more direct construction of the Sen operator on
![]() $\tilde {H}^i(K^p,C)^{\mathrm {la}}$
in Remark 5.1.16.
$\tilde {H}^i(K^p,C)^{\mathrm {la}}$
in Remark 5.1.16.
Remark 1.0.16. In Beilinson–Bernstein’s theory of localisation (see Section C of [Reference BeĭlinsonBeĭ84]),
 $\mathcal {O}^{\mathrm {la}}_{K^p}$
is a
$\mathcal {O}^{\mathrm {la}}_{K^p}$
is a
![]() $\tilde {\mathscr {D}}$
-module. Note that everything here is also
$\tilde {\mathscr {D}}$
-module. Note that everything here is also
![]() $\mathrm {GL}_2(\mathbb {Q}_p)$
-equivariant. Hence, we obtain a
$\mathrm {GL}_2(\mathbb {Q}_p)$
-equivariant. Hence, we obtain a
 $(\tilde {\mathscr {D}},\mathrm {GL}_2(\mathbb {Q}_p))$
-module on
$(\tilde {\mathscr {D}},\mathrm {GL}_2(\mathbb {Q}_p))$
-module on
![]() ${\mathscr {F}\!\ell }$
, which is very similar to the picture in the complex analytic setting (for example, the work of Kashiwara–Schmid [Reference Kashiwara and SchmidKS94]).
${\mathscr {F}\!\ell }$
, which is very similar to the picture in the complex analytic setting (for example, the work of Kashiwara–Schmid [Reference Kashiwara and SchmidKS94]).
As a corollary, this implies that on the locally analytic vectors in the completed cohomology, the infinitesimal character of
![]() $\mathrm {GL}_2(\mathbb {Q}_p)$
(i.e., action of
$\mathrm {GL}_2(\mathbb {Q}_p)$
(i.e., action of
![]() $Z(U(\mathfrak {g}))$
) and the infinitesimal character of
$Z(U(\mathfrak {g}))$
) and the infinitesimal character of
![]() $G_{\mathbb {Q}_p}$
(Sen operator as an element in the centre of ‘
$G_{\mathbb {Q}_p}$
(Sen operator as an element in the centre of ‘
![]() $C\otimes _{\mathbb {Q}_p}\operatorname {\mathrm {Lie}}(G_{\mathbb {Q}_p})$
’) are closely related. This directly implies the (Hodge–Tate) decomposition in Theorem 1.0.1.
$C\otimes _{\mathbb {Q}_p}\operatorname {\mathrm {Lie}}(G_{\mathbb {Q}_p})$
’) are closely related. This directly implies the (Hodge–Tate) decomposition in Theorem 1.0.1.
Remark 1.0.17. The same strategy of this article should give Theorem 1.0.11 for higher dimensional rigid analytic varieties, Theorem 1.0.10 for general Hodge–Tate period maps and Theorem 1.0.14 for Shimura varieties of Hodge type. I plan to report about this in a future paper. We also note that the relation between the action of the centre of the universal enveloping algebra and Sen operator on the locally analytic vectors in the completed cohomology (not necessarily of the modular curves) was already vastly studied by Dospinescu–Paškūnas–Schraen in [Reference Dospinescu, Paškūnas and SchraenDPS20].
After writing up this article, I was informed by Sean Howe that very recently he also obtained some part of Theorem 5.4.2 and the easier direction of Theorem 1.0.7 in [Reference HoweHow21].
For people who are interested in the relation between our work and the higher Coleman theory recently developed by Boxer–Pilloni in [Reference Boxer and PilloniBP21], it is worth pointing out that one can show that the
![]() $N_{k,1}$
(
$N_{k,1}$
(
![]() $k\geq 2$
) in Theorem 1.0.1 and
$k\geq 2$
) in Theorem 1.0.1 and
![]() $N_1$
in Theorem 1.0.2 are nothing but the direct limit of the first cohomology of
$N_1$
in Theorem 1.0.2 are nothing but the direct limit of the first cohomology of
![]() $\omega ^k$
on
$\omega ^k$
on
![]() $\mathcal {X}_{K^p\Gamma (p^n)}$
with support in the closure (in the adic topology) of
$\mathcal {X}_{K^p\Gamma (p^n)}$
with support in the closure (in the adic topology) of
![]() ${\mathcal {X}}_{K^p\Gamma (p^n),c}$
. See also [Reference CamargoCam21, Theorem 1.0.3].
${\mathcal {X}}_{K^p\Gamma (p^n),c}$
. See also [Reference CamargoCam21, Theorem 1.0.3].
This article is organised as follows. We first collect some basic facts about locally analytic vectors in Section 2. One important notion is a derived functor
![]() $R^i\mathfrak {LA}$
of taking locally analytic vectors introduced in Definition 2.2.1.
$R^i\mathfrak {LA}$
of taking locally analytic vectors introduced in Definition 2.2.1.
In Section 3, we explain how to derive the differential equation claimed in Theorem 1.0.11 from relative Sen theory. Along the way, we also prove a vanishing result for
![]() $R^i\mathfrak {LA}$
which later will be used to prove Theorem 1.0.9. Nothing is new in the sense that all of the techniques were probably well-known in Sen’s theory.
$R^i\mathfrak {LA}$
which later will be used to prove Theorem 1.0.9. Nothing is new in the sense that all of the techniques were probably well-known in Sen’s theory.
In Section 4, we apply our theory developed in the previous section to modular curves at infinite level. The computation of the differential equation in this case is a simple reinterpretation of an old result of Faltings. We also give an explicit description of the sections of
 $\mathcal {O}^{\mathrm {la}}_{K^p}$
and use it to prove Theorem 1.0.9.
$\mathcal {O}^{\mathrm {la}}_{K^p}$
and use it to prove Theorem 1.0.9.
In Section 5, we first give a proof of Theorem 1.0.14. Using our explicit description of
 $\mathcal {O}^{\mathrm {la}}_{K^p}$
, it is easy to verify that
$\mathcal {O}^{\mathrm {la}}_{K^p}$
, it is easy to verify that
 $\theta _{\mathfrak {h}}(\begin {pmatrix}0 & 0\\ 0 & 1 \end {pmatrix})$
behaves as a Sen operator on
$\theta _{\mathfrak {h}}(\begin {pmatrix}0 & 0\\ 0 & 1 \end {pmatrix})$
behaves as a Sen operator on
 $\mathcal {O}^{\mathrm {la}}_{K^p}$
and its cohomology. Next we compute
$\mathcal {O}^{\mathrm {la}}_{K^p}$
and its cohomology. Next we compute
 $\tilde {H}^1(K^p,C)^{\mathrm {la}}_{\mu }$
. Fix a character
$\tilde {H}^1(K^p,C)^{\mathrm {la}}_{\mu }$
. Fix a character
![]() $\chi \in \mathfrak {h}^*$
and denote by
$\chi \in \mathfrak {h}^*$
and denote by
 $\mathcal {O}^{\mathrm {la},\chi }_{K^p}$
the
$\mathcal {O}^{\mathrm {la},\chi }_{K^p}$
the
![]() $\theta _{\mathfrak {h}}=\chi $
-isotypic part. Let
$\theta _{\mathfrak {h}}=\chi $
-isotypic part. Let
![]() $\mathfrak {n}$
be the nilpotent subalgebra of
$\mathfrak {n}$
be the nilpotent subalgebra of
![]() $\mathfrak {b}$
. Basically we are reduced to computing the
$\mathfrak {b}$
. Basically we are reduced to computing the
![]() $\mathfrak {n}$
-cohomology of the sheaf
$\mathfrak {n}$
-cohomology of the sheaf
 $\mathcal {O}^{\mathrm {la},\chi }_{K^p}$
and the cohomology of the
$\mathcal {O}^{\mathrm {la},\chi }_{K^p}$
and the cohomology of the
![]() $\mathfrak {n}$
-invariants and
$\mathfrak {n}$
-invariants and
![]() $\mathfrak {n}$
-coinvariants of
$\mathfrak {n}$
-coinvariants of
 $\mathcal {O}^{\mathrm {la},\chi }_{K^p}$
on
$\mathcal {O}^{\mathrm {la},\chi }_{K^p}$
on
![]() ${\mathscr {F}\!\ell }$
(at least for nonsingular weight).
${\mathscr {F}\!\ell }$
(at least for nonsingular weight).
In Section 6, we give the global applications mentioned earlier. To do this, we need Emerton’s work on local–global compatibility and Colmez’s work on Kirillov models. It should be mentioned that we slightly generalise Emerton’s local–global compatibility result so that it is now valid when localised at a Eisenstein maximal ideal.
Notation
Fix an algebraic closure
![]() of
of
![]() $\mathbb {Q}$
. Denote by
$\mathbb {Q}$
. Denote by
![]() $G_{\mathbb {Q}}$
the absolute Galois group
$G_{\mathbb {Q}}$
the absolute Galois group
![]() . For each rational prime l, fix an algebraic closure
. For each rational prime l, fix an algebraic closure
![]() of
of
![]() $\mathbb {Q}_l$
with ring of integers
$\mathbb {Q}_l$
with ring of integers
![]() , an embedding
, an embedding
![]() which determines a decomposition group
which determines a decomposition group
![]() $G_{\mathbb {Q}_l}\subset G_{\mathbb {Q}}$
at l and a lift of geometric Frobenius
$G_{\mathbb {Q}_l}\subset G_{\mathbb {Q}}$
at l and a lift of geometric Frobenius
![]() $\operatorname {\mathrm {Frob}}_l\in G_{\mathbb {Q}_l}$
. Our convention for local class field theory sends a uniformiser to a lift of geometric Frobenius. We denote by
$\operatorname {\mathrm {Frob}}_l\in G_{\mathbb {Q}_l}$
. Our convention for local class field theory sends a uniformiser to a lift of geometric Frobenius. We denote by
![]() $\varepsilon $
the p-adic cyclotomic character
$\varepsilon $
the p-adic cyclotomic character
![]() $G_{\mathbb {Q}}\to \mathbb {Z}_p^{\times }$
and, by abuse of notation, also the corresponding character
$G_{\mathbb {Q}}\to \mathbb {Z}_p^{\times }$
and, by abuse of notation, also the corresponding character
 $\mathbb {A}_f^{\times }/\mathbb {Q}_{>0}^{\times }\to \mathbb {Z}_p^{\times }$
via global class field theory. Similarly, we denote by
$\mathbb {A}_f^{\times }/\mathbb {Q}_{>0}^{\times }\to \mathbb {Z}_p^{\times }$
via global class field theory. Similarly, we denote by
![]() $\varepsilon _p$
the p-adic cyclotomic character
$\varepsilon _p$
the p-adic cyclotomic character
![]() $G_{\mathbb {Q}_p}\to \mathbb {Z}_p^{\times }$
and also the character
$G_{\mathbb {Q}_p}\to \mathbb {Z}_p^{\times }$
and also the character
![]() $\mathbb {Q}_p^{\times }\to \mathbb {Z}_p^{\times }$
sending x to
$\mathbb {Q}_p^{\times }\to \mathbb {Z}_p^{\times }$
sending x to
![]() $x|x|$
. Suppose S is a finite set of rational primes. We denote by
$x|x|$
. Suppose S is a finite set of rational primes. We denote by
![]() $G_{\mathbb {Q},S}$
the the Galois group of the maximal extension of
$G_{\mathbb {Q},S}$
the the Galois group of the maximal extension of
![]() $\mathbb {Q}$
unramified outside S and
$\mathbb {Q}$
unramified outside S and
![]() $\infty $
.
$\infty $
.
All completed tensor products mean ‘p-adically completed tensor product’. For example, if V and W are two
![]() $\mathbb {Q}_p$
-Banach spaces, then
$\mathbb {Q}_p$
-Banach spaces, then
 $V\widehat {\otimes }_{\mathbb {Q}_p}W=(\varprojlim _n (V^o\otimes _{\mathbb {Z}_p}W^o/p^n))\otimes _{\mathbb {Z}_p}\mathbb {Q}_p$
, where
$V\widehat {\otimes }_{\mathbb {Q}_p}W=(\varprojlim _n (V^o\otimes _{\mathbb {Z}_p}W^o/p^n))\otimes _{\mathbb {Z}_p}\mathbb {Q}_p$
, where
![]() $V^o$
and
$V^o$
and
![]() $W^o$
denote the open unit balls of V and W.
$W^o$
denote the open unit balls of V and W.
If
 denotes a continuous representation of a profinite group
denotes a continuous representation of a profinite group
![]() $\Gamma $
, we denote by
$\Gamma $
, we denote by
 the semi-simplification of its residual representation, which is well-defined up to conjugation. If
the semi-simplification of its residual representation, which is well-defined up to conjugation. If
![]() $\bar \rho ^{ss}$
is irreducible, we simply write
$\bar \rho ^{ss}$
is irreducible, we simply write
![]() $\bar \rho $
. Here
$\bar \rho $
. Here
![]() denotes the residue field of
denotes the residue field of
![]() .
.
For an adic space X, an open set
![]() $V\subset X$
and a sheaf
$V\subset X$
and a sheaf
![]() $\mathcal {F}$
on X, we sometimes write
$\mathcal {F}$
on X, we sometimes write
![]() $\mathcal {F}(V)$
instead of
$\mathcal {F}(V)$
instead of
![]() $H^0(\mathcal {V},\mathcal {F})$
. For example,
$H^0(\mathcal {V},\mathcal {F})$
. For example,
![]() $\mathcal {O}_{X}(V)$
denotes analytic functions on V.
$\mathcal {O}_{X}(V)$
denotes analytic functions on V.
For a tuple
![]() $\mathbf {k}=(k_1,\cdots ,k_d)\in \mathbb {N}^d$
, we denote the sum
$\mathbf {k}=(k_1,\cdots ,k_d)\in \mathbb {N}^d$
, we denote the sum
 $\sum _{i=1}^d k_i$
by
$\sum _{i=1}^d k_i$
by
![]() $|\mathbf {k}|$
.
$|\mathbf {k}|$
.
Suppose G is a group and f is a function on G (valued in some group). Let
![]() $g\in G$
. The left translation action of g on f is denoted by
$g\in G$
. The left translation action of g on f is denoted by
![]() ${}^{l}g\cdot f$
, which sends
${}^{l}g\cdot f$
, which sends
![]() $x\in G$
to
$x\in G$
to
![]() $f(g^{-1}x)$
. Similarly, the right translation action of g on f is denoted by
$f(g^{-1}x)$
. Similarly, the right translation action of g on f is denoted by
![]() ${}^{r}g\cdot f$
and sends
${}^{r}g\cdot f$
and sends
![]() $x\in G$
to
$x\in G$
to
![]() $f(xg)$
. Note that both actions are left actions.
$f(xg)$
. Note that both actions are left actions.
2 Locally analytic vectors
In this section, we collect some basic results in the theory of locally analytic representations studied by Schneider and Teitelbaum [Reference Schneider and TeitelbaumST02, Reference Schneider and TeitelbaumST03]. We will first recall the (naive) definition of locally analytic functions on a compact p-adic Lie group, following Subsection 2.1 of [Reference Berger and ColmezBC16]. Then we will introduce a derived functor of taking locally analytic vectors.
2.1 Definition and basic properties
2.1.1. Let G be a p-adic Lie group of dimension d. By Theorem 27.1 of [Reference SchneiderSch11], there exists a compact open subgroup
![]() $G_0$
of G equipped with an integer-valued, saturated p-valuation. As a consequence, there exist
$G_0$
of G equipped with an integer-valued, saturated p-valuation. As a consequence, there exist
![]() $g_1,\cdots ,g_d\in G_0$
(an ordered basis) such that the map
$g_1,\cdots ,g_d\in G_0$
(an ordered basis) such that the map
 $c:\mathbb {Z}_p^d\to G_0$
defined by
$c:\mathbb {Z}_p^d\to G_0$
defined by
 $(x_1,\cdots ,x_d)\mapsto g_1^{x_1}\cdots g_d^{x_d}$
is a homeomorphism. Let
$(x_1,\cdots ,x_d)\mapsto g_1^{x_1}\cdots g_d^{x_d}$
is a homeomorphism. Let
 $G_n=G_0^{p^n}=\{g^{p^n},g\in G_0\}$
for
$G_n=G_0^{p^n}=\{g^{p^n},g\in G_0\}$
for
![]() $n\geq 1$
. This is in fact a subgroup, and
$n\geq 1$
. This is in fact a subgroup, and
![]() $c^{-1}(G_n)=(p^n\mathbb {Z}_p)^d$
. So
$c^{-1}(G_n)=(p^n\mathbb {Z}_p)^d$
. So
![]() $\{G_n\}_n$
forms a fundamental system of open neighbourhoods of the identity element
$\{G_n\}_n$
forms a fundamental system of open neighbourhoods of the identity element
![]() $1$
in G. We will fix such a c in the following discussion, but all of the definitions we make below will not depend on the choice of c. See Section 23 and Section 26 of [Reference SchneiderSch11] for more details.
$1$
in G. We will fix such a c in the following discussion, but all of the definitions we make below will not depend on the choice of c. See Section 23 and Section 26 of [Reference SchneiderSch11] for more details.
If B is a
![]() $\mathbb {Q}_p$
-Banach space with norm
$\mathbb {Q}_p$
-Banach space with norm
![]() $\|\cdot \|$
, we denote by
$\|\cdot \|$
, we denote by
![]() $\mathscr {C}(G_n,B)$
the space of B-valued continuous functions on
$\mathscr {C}(G_n,B)$
the space of B-valued continuous functions on
![]() $G_n$
and by
$G_n$
and by
![]() $\mathscr {C}^{\mathrm {an}}(G_n,B)$
the subspace of B-valued analytic functions. More precisely,
$\mathscr {C}^{\mathrm {an}}(G_n,B)$
the subspace of B-valued analytic functions. More precisely,
![]() $f:G_n\to B$
is analytic if its pullback under c can be written as
$f:G_n\to B$
is analytic if its pullback under c can be written as
 $$ \begin{align*}\mathbf{x}=(x_1,\cdots,x_d)\in (p^n\mathbb{Z}_p)^d\mapsto \sum_{\mathbf{k}=(k_1,\cdots,k_d)\in \mathbb{N}^d} b_{\mathbf{k}} x_1^{k_1}\cdots x_d^{k_d}\end{align*} $$
$$ \begin{align*}\mathbf{x}=(x_1,\cdots,x_d)\in (p^n\mathbb{Z}_p)^d\mapsto \sum_{\mathbf{k}=(k_1,\cdots,k_d)\in \mathbb{N}^d} b_{\mathbf{k}} x_1^{k_1}\cdots x_d^{k_d}\end{align*} $$
for some
![]() $b_{\mathbf {k}}\in B$
such that
$b_{\mathbf {k}}\in B$
such that
![]() $p^{n|\mathbf {k}|}b_{\mathbf {k}}\to 0$
as
$p^{n|\mathbf {k}|}b_{\mathbf {k}}\to 0$
as
![]() $|\mathbf {k}|\to \infty $
. We define
$|\mathbf {k}|\to \infty $
. We define
![]() $\|f\|_{G_n}=\sup _{\mathbf {k}\in \mathbb {N}^d}\|p^{n|\mathbf {k}|}b_{\mathbf {k}}\|$
and
$\|f\|_{G_n}=\sup _{\mathbf {k}\in \mathbb {N}^d}\|p^{n|\mathbf {k}|}b_{\mathbf {k}}\|$
and
![]() $\mathscr {C}^{\mathrm {an}}(G_n,B)$
is a
$\mathscr {C}^{\mathrm {an}}(G_n,B)$
is a
![]() $\mathbb {Q}_p$
-Banach space under this norm. There is a natural norm-preserving isomorphism
$\mathbb {Q}_p$
-Banach space under this norm. There is a natural norm-preserving isomorphism
 $\mathscr {C}^{\mathrm {an}}(G_n,\mathbb {Q}_p) \widehat \otimes _{\mathbb {Q}_p} B\cong \mathscr {C}^{\mathrm {an}}(G_n,B)$
induced by the
$\mathscr {C}^{\mathrm {an}}(G_n,\mathbb {Q}_p) \widehat \otimes _{\mathbb {Q}_p} B\cong \mathscr {C}^{\mathrm {an}}(G_n,B)$
induced by the
![]() $\mathbb {Q}_p$
-linear structure of B. When
$\mathbb {Q}_p$
-linear structure of B. When
![]() $B=\mathbb {Q}_p$
, the usual point-wise multiplication of two functions defines a natural
$B=\mathbb {Q}_p$
, the usual point-wise multiplication of two functions defines a natural
![]() $\mathbb {Q}_p$
-algebra structure on
$\mathbb {Q}_p$
-algebra structure on
![]() $\mathscr {C}^{\mathrm {an}}(G_n,\mathbb {Q}_p)$
.
$\mathscr {C}^{\mathrm {an}}(G_n,\mathbb {Q}_p)$
.
To see this definition is independent of the choice of
![]() $g_1,\cdots ,g_d$
, we introduce another set of coordinates of
$g_1,\cdots ,g_d$
, we introduce another set of coordinates of
![]() $G_n$
given by the the exponential map. These coordinates are called coordinates of the first kind in Section 34 of [Reference SchneiderSch11]. More precisely, let
$G_n$
given by the the exponential map. These coordinates are called coordinates of the first kind in Section 34 of [Reference SchneiderSch11]. More precisely, let
![]() $\operatorname {\mathrm {Lie}}(G)$
be the Lie algebra of G and consider the logarithm map
$\operatorname {\mathrm {Lie}}(G)$
be the Lie algebra of G and consider the logarithm map
which is a homeomorphism onto its image. In fact, its image
![]() $\log (G_0)$
is a free
$\log (G_0)$
is a free
![]() $\mathbb {Z}_p$
-module with a basis
$\mathbb {Z}_p$
-module with a basis
![]() $\log (g_1),\cdots ,\log (g_d)$
. Hence,
$\log (g_1),\cdots ,\log (g_d)$
. Hence,
 $$ \begin{align*}e:\mathbb{Z}_p^{d}\to G_0,\, (y_1,\cdots,y_d)\mapsto \exp(y_1\log(g_1)+\cdots+y_d\log(g_d))\end{align*} $$
$$ \begin{align*}e:\mathbb{Z}_p^{d}\to G_0,\, (y_1,\cdots,y_d)\mapsto \exp(y_1\log(g_1)+\cdots+y_d\log(g_d))\end{align*} $$
defines a homeomorphism. Here
![]() $\exp $
is the inverse of
$\exp $
is the inverse of
![]() $\log $
(exponential map). Under this parametrisation,
$\log $
(exponential map). Under this parametrisation,
![]() $G_n$
is identified with the image of
$G_n$
is identified with the image of
![]() $(p^n\mathbb {Z}_p)^d$
. As before, a function on
$(p^n\mathbb {Z}_p)^d$
. As before, a function on
![]() $G_n$
is called analytic if its pullback under e can be written as a power series in
$G_n$
is called analytic if its pullback under e can be written as a power series in
![]() $y_i$
with certain growth conditions on its coefficients. This definition of analyticity agrees with the previous definition as the transition functions between the coordinates
$y_i$
with certain growth conditions on its coefficients. This definition of analyticity agrees with the previous definition as the transition functions between the coordinates
![]() $(x_1,\cdots ,x_d)$
and
$(x_1,\cdots ,x_d)$
and
![]() $(y_1,\cdots ,y_d)$
are given by convergent power series with coefficients in
$(y_1,\cdots ,y_d)$
are given by convergent power series with coefficients in
![]() $\mathbb {Z}_p$
; cf. Proposition 34.1 of [Reference SchneiderSch11].
$\mathbb {Z}_p$
; cf. Proposition 34.1 of [Reference SchneiderSch11].
Different choices of ordered bases
![]() $g_1,\cdots ,g_d$
give rise to different bases of
$g_1,\cdots ,g_d$
give rise to different bases of
![]() $\log (G_0)$
over
$\log (G_0)$
over
![]() $\mathbb {Z}_p$
(as a
$\mathbb {Z}_p$
(as a
![]() $\mathbb {Z}_p$
-module). It is easy to see now that
$\mathbb {Z}_p$
-module). It is easy to see now that
![]() $\mathscr {C}^{\mathrm {an}}(G_n,B)$
and
$\mathscr {C}^{\mathrm {an}}(G_n,B)$
and
![]() $\|\cdot \|_{G_n}$
are independent of choice of an ordered basis. As a corollary,
$\|\cdot \|_{G_n}$
are independent of choice of an ordered basis. As a corollary,
![]() $\mathscr {C}^{\mathrm {an}}(G_n,B)$
and
$\mathscr {C}^{\mathrm {an}}(G_n,B)$
and
![]() $\|\cdot \|_{G_n}$
are invariant under both the left and right translation actions of
$\|\cdot \|_{G_n}$
are invariant under both the left and right translation actions of
![]() $G_0$
. We sketch a proof for the left translation by
$G_0$
. We sketch a proof for the left translation by
![]() $G_0$
here. The case for right translation and general n will be exactly the same. Let x be a nontrivial element of
$G_0$
here. The case for right translation and general n will be exactly the same. Let x be a nontrivial element of
![]() $G_0$
. It suffices to prove the claim under the assumption that x is not a pth power. Choose an ordered basis
$G_0$
. It suffices to prove the claim under the assumption that x is not a pth power. Choose an ordered basis
![]() $g_1,\cdots ,g_d$
with
$g_1,\cdots ,g_d$
with
![]() $g_1=x$
. This is possible by our assumption on
$g_1=x$
. This is possible by our assumption on
![]() $G_0$
; see Section 26 of [Reference SchneiderSch11]. To compute the left translation action of x, we are essentially reduced to the case
$G_0$
; see Section 26 of [Reference SchneiderSch11]. To compute the left translation action of x, we are essentially reduced to the case
![]() $G_0=\mathbb {Z}_p$
, which can be verified directly. In fact, this argument shows a bit more.
$G_0=\mathbb {Z}_p$
, which can be verified directly. In fact, this argument shows a bit more.
Lemma 2.1.2. For any integer
![]() $n\geq 0$
, let
$n\geq 0$
, let
![]() $\mathscr {C}^{\mathrm {an}}(G_n,\mathbb {Q}_p)^o\subset \mathscr {C}^{\mathrm {an}}(G_n,\mathbb {Q}_p)$
be the unit ball with respect to the norm
$\mathscr {C}^{\mathrm {an}}(G_n,\mathbb {Q}_p)^o\subset \mathscr {C}^{\mathrm {an}}(G_n,\mathbb {Q}_p)$
be the unit ball with respect to the norm
![]() $\|\cdot \|_{G_n}$
. Then both left and right translation actions of
$\|\cdot \|_{G_n}$
. Then both left and right translation actions of
![]() $G_{n+1}$
are trivial on
$G_{n+1}$
are trivial on
![]() $\mathscr {C}^{\mathrm {an}}(G_n,\mathbb {Q}_p)^o/p$
.
$\mathscr {C}^{\mathrm {an}}(G_n,\mathbb {Q}_p)^o/p$
.
Proof. One can reduce to the trivial case
![]() $G_n=\mathbb {Z}_p$
by the same argument.
$G_n=\mathbb {Z}_p$
by the same argument.
The following density result will be used later.
Proposition 2.1.3. For n large enough, there is a dense subspace
 $\varinjlim _{k\in \mathbb {N}} V_k\subset \mathscr {C}^{\mathrm {an}}(G_n,\mathbb {Q}_p)$
, where each
$\varinjlim _{k\in \mathbb {N}} V_k\subset \mathscr {C}^{\mathrm {an}}(G_n,\mathbb {Q}_p)$
, where each
![]() $V_k$
is a finite-dimensional subspace of
$V_k$
is a finite-dimensional subspace of
![]() $\mathscr {C}^{\mathrm {an}}(G_n,\mathbb {Q}_p)$
stable under both the left and right translation actions of
$\mathscr {C}^{\mathrm {an}}(G_n,\mathbb {Q}_p)$
stable under both the left and right translation actions of
![]() $G_n$
and such that for any
$G_n$
and such that for any
![]() $k,l\in \mathbb {N}, f_k\in V_k, f_l\in V_l$
, we have
$k,l\in \mathbb {N}, f_k\in V_k, f_l\in V_l$
, we have
![]() $f_k f_l\in V_{k+l}$
.
$f_k f_l\in V_{k+l}$
.
Proof. This is essentially proved in the proof of Theorem 6.1 of [Reference Berger and ColmezBC16]. We recall their argument here. The rough idea is to reduce to the case
![]() $G=\mathrm {GL}_N(\mathbb {Z}_p)$
, in which case the algebraic functions on
$G=\mathrm {GL}_N(\mathbb {Z}_p)$
, in which case the algebraic functions on
![]() $\mathrm {GL}_N$
are dense in the space of analytic functions.
$\mathrm {GL}_N$
are dense in the space of analytic functions.
For n large enough, we may find an embedding
![]() $G_n$
into
$G_n$
into
![]() $1+p^2 M_N(\mathbb {Z}_p)\subset \mathrm {GL}_N(\mathbb {Z}_p)$
for some N, where
$1+p^2 M_N(\mathbb {Z}_p)\subset \mathrm {GL}_N(\mathbb {Z}_p)$
for some N, where
![]() $M_N(\mathbb {Z}_p)$
denotes the space of
$M_N(\mathbb {Z}_p)$
denotes the space of
![]() $N\times N$
matrices over
$N\times N$
matrices over
![]() $\mathbb {Z}_p$
. We sketch a proof of this well-known result here because it seems to lack a suitable reference. By Ado’s theorem (Section 7,
$\mathbb {Z}_p$
. We sketch a proof of this well-known result here because it seems to lack a suitable reference. By Ado’s theorem (Section 7,
![]() , Theorem 3 of [Reference BourbakiBou60]), there is a faithful representation of
, Theorem 3 of [Reference BourbakiBou60]), there is a faithful representation of
![]() $\operatorname {\mathrm {Lie}}(G)$
over
$\operatorname {\mathrm {Lie}}(G)$
over
 $\mathbb {Q}_p^{\oplus N}$
for some N. Choose n large enough so that
$\mathbb {Q}_p^{\oplus N}$
for some N. Choose n large enough so that
![]() $\log (G_n)$
maps to
$\log (G_n)$
maps to
![]() $p^2 M_N(\mathbb {Z}_p)$
. Then this Lie algebra morphism can be integrated to a group homomorphism
$p^2 M_N(\mathbb {Z}_p)$
. Then this Lie algebra morphism can be integrated to a group homomorphism
![]() $G_n\to 1+p^2 M_N(\mathbb {Z}_p)$
, which is necessarily a closed embedding. This can be deduced from results in Section 31, notably Theorem 31.5 of [Reference SchneiderSch11].
$G_n\to 1+p^2 M_N(\mathbb {Z}_p)$
, which is necessarily a closed embedding. This can be deduced from results in Section 31, notably Theorem 31.5 of [Reference SchneiderSch11].
Fix such an embedding.
![]() $G_n$
is now viewed as a subset of
$G_n$
is now viewed as a subset of
![]() $M_N(\mathbb {Q}_p)$
. For
$M_N(\mathbb {Q}_p)$
. For
![]() $k\in N$
, let
$k\in N$
, let
![]() $V_k$
be the space of
$V_k$
be the space of
![]() $\mathbb {Q}_p$
-valued functions on
$\mathbb {Q}_p$
-valued functions on
![]() $G_n$
that are restrictions of polynomials of degree
$G_n$
that are restrictions of polynomials of degree
![]() $\leq k$
on
$\leq k$
on
![]() $M_N(\mathbb {Q}_p)$
. Here we identify
$M_N(\mathbb {Q}_p)$
. Here we identify
![]() $M_N(\mathbb {Q}_p)$
with an affine space of dimension
$M_N(\mathbb {Q}_p)$
with an affine space of dimension
![]() $N^2$
(over
$N^2$
(over
![]() $\mathbb {Q}_p$
). We claim that the union of all
$\mathbb {Q}_p$
). We claim that the union of all
![]() $V_k$
is dense in
$V_k$
is dense in
![]() $\mathscr {C}^{\mathrm {an}}(G_n,\mathbb {Q}_p)$
. To see this, note that the space of polynomial functions on
$\mathscr {C}^{\mathrm {an}}(G_n,\mathbb {Q}_p)$
. To see this, note that the space of polynomial functions on
![]() $M_N(\mathbb {Q}_p)$
is dense in
$M_N(\mathbb {Q}_p)$
is dense in
![]() $\mathscr {C}^{\mathrm {an}}(1+p^2M_N(\mathbb {Z}_p),\mathbb {Q}_p)$
when restricted to
$\mathscr {C}^{\mathrm {an}}(1+p^2M_N(\mathbb {Z}_p),\mathbb {Q}_p)$
when restricted to
![]() $1+p^2M_N(\mathbb {Z}_p)$
. Hence, its pullback under the exponential map is dense in
$1+p^2M_N(\mathbb {Z}_p)$
. Hence, its pullback under the exponential map is dense in
![]() $\mathscr {C}^{\mathrm {an}}(p^2M_N(\mathbb {Z}_p),\mathbb {Q}_p)$
. As the image of
$\mathscr {C}^{\mathrm {an}}(p^2M_N(\mathbb {Z}_p),\mathbb {Q}_p)$
. As the image of
![]() $\mathscr {C}^{\mathrm {an}}(p^2M_N(\mathbb {Z}_p),\mathbb {Q}_p)\to \mathscr {C}^{\mathrm {an}}(\log (G_n),\mathbb {Q}_p)$
is dense, this implies our claim.
$\mathscr {C}^{\mathrm {an}}(p^2M_N(\mathbb {Z}_p),\mathbb {Q}_p)\to \mathscr {C}^{\mathrm {an}}(\log (G_n),\mathbb {Q}_p)$
is dense, this implies our claim.
It is clear from the construction that all
![]() $V_k$
are stable under left and right translation actions and closed under multiplications.
$V_k$
are stable under left and right translation actions and closed under multiplications.
2.1.4. Now if B is a
![]() $\mathbb {Q}_p$
-Banach space equipped with a continuous action of
$\mathbb {Q}_p$
-Banach space equipped with a continuous action of
![]() $G_n$
, then we denote by
$G_n$
, then we denote by
![]() $B^{G_n-\mathrm {an}}\subset B$
the subset of
$B^{G_n-\mathrm {an}}\subset B$
the subset of
![]() $G_n$
-analytic vectors. One can define this as follows: there is a left action on
$G_n$
-analytic vectors. One can define this as follows: there is a left action on
![]() $\mathscr {C}^{\mathrm {an}}(G_n,B)$
by
$\mathscr {C}^{\mathrm {an}}(G_n,B)$
by
![]() $(g\cdot f)(h)=g(f(g^{-1}h)),g,h\in G_n,f\in \mathscr {C}^{\mathrm {an}}(G_n,B)$
. We define
$(g\cdot f)(h)=g(f(g^{-1}h)),g,h\in G_n,f\in \mathscr {C}^{\mathrm {an}}(G_n,B)$
. We define
![]() $B^{G_n-\mathrm {an}}$
as the image of
$B^{G_n-\mathrm {an}}$
as the image of
![]() $\mathscr {C}^{\mathrm {an}}(G_n,B)^{G_n}\to B$
under the evaluation map at the identity element in
$\mathscr {C}^{\mathrm {an}}(G_n,B)^{G_n}\to B$
under the evaluation map at the identity element in
![]() $G_n$
. Equivalently,
$G_n$
. Equivalently,
![]() $v\in B^{G_n-\mathrm {an}}$
if
$v\in B^{G_n-\mathrm {an}}$
if
![]() $f_v:G_n\to B,~f_v(g)=g\cdot v$
lies in
$f_v:G_n\to B,~f_v(g)=g\cdot v$
lies in
![]() $\mathscr {C}^{\mathrm {an}}(G_n,B)$
. It is clear that
$\mathscr {C}^{\mathrm {an}}(G_n,B)$
. It is clear that
![]() $\|\cdot \|_{G_n}$
induces a norm on
$\|\cdot \|_{G_n}$
induces a norm on
![]() $B^{G_n-\mathrm {an}}$
, which we denote by the same notation. Now
$B^{G_n-\mathrm {an}}$
, which we denote by the same notation. Now
![]() $G_n$
acts on
$G_n$
acts on
![]() $B^{G_n-\mathrm {an}}=\mathscr {C}^{\mathrm {an}}(G_n,B)^{G_n}$
by right translation. One checks easily that this action is unitary and equivariant with respect to the inclusion
$B^{G_n-\mathrm {an}}=\mathscr {C}^{\mathrm {an}}(G_n,B)^{G_n}$
by right translation. One checks easily that this action is unitary and equivariant with respect to the inclusion
![]() $B^{G_n-\mathrm {an}}\subset B$
.
$B^{G_n-\mathrm {an}}\subset B$
.
We say B is an analytic representation of
![]() $G_n$
if
$G_n$
if
![]() $B=B^{G_n-\mathrm {an}}$
.
$B=B^{G_n-\mathrm {an}}$
.
One has the following lemma (cf. Lemme 2.4. of [Reference Berger and ColmezBC16]).
Lemma 2.1.5. Let B be a Banach representation of
![]() $G_n$
. If
$G_n$
. If
![]() $b\in B^{G_n-\mathrm {an}}$
, then
$b\in B^{G_n-\mathrm {an}}$
, then
-
(1)
 $b\in B^{G_{n+1}-\mathrm {an}}$
,
$b\in B^{G_{n+1}-\mathrm {an}}$
, -
(2)
 $\|b\|_{G_{n+1}}\leq \|b\|_{G_n}$
.
$\|b\|_{G_{n+1}}\leq \|b\|_{G_n}$
. -
(3)
 $\|b\|_{G_m}$
agrees with the norm of b in B for m sufficiently large.
$\|b\|_{G_m}$
agrees with the norm of b in B for m sufficiently large.
Definition 2.1.6. Suppose B is a Banach representation of
![]() $G_0$
. The space of locally analytic vectors in B is
$G_0$
. The space of locally analytic vectors in B is
![]() $B^{\mathrm {la}}=\bigcup _{n\geq 0} B^{G_n-\mathrm {an}}$
with the direct limit topology.
$B^{\mathrm {la}}=\bigcup _{n\geq 0} B^{G_n-\mathrm {an}}$
with the direct limit topology.
Remark 2.1.7. If B is a representation of G, then
![]() $B^{\mathrm {la}}$
can be defined by restricting to the action of
$B^{\mathrm {la}}$
can be defined by restricting to the action of
![]() $G_0$
. It is easy to see that
$G_0$
. It is easy to see that
![]() $B^{\mathrm {la}}$
is independent of the choice of
$B^{\mathrm {la}}$
is independent of the choice of
![]() $G_0$
and
$G_0$
and
![]() $B^{\mathrm {la}}$
is G-stable.
$B^{\mathrm {la}}$
is G-stable.
The Lie algebra
![]() $\operatorname {\mathrm {Lie}}(G)$
acts on the locally analytic vectors. One can check this in the universal case
$\operatorname {\mathrm {Lie}}(G)$
acts on the locally analytic vectors. One can check this in the universal case
![]() $\mathscr {C}^{\mathrm {an}}(G_n,\mathbb {Q}_p)$
. Indeed, one writes
$\mathscr {C}^{\mathrm {an}}(G_n,\mathbb {Q}_p)$
. Indeed, one writes
 $B^{G_n-\mathrm {an}}=(\mathscr {C}^{\mathrm {an}}(G_n,\mathbb {Q}_p) \widehat \otimes _{\mathbb {Q}_p} B)^{G_n}$
. The Lie algebra action of
$B^{G_n-\mathrm {an}}=(\mathscr {C}^{\mathrm {an}}(G_n,\mathbb {Q}_p) \widehat \otimes _{\mathbb {Q}_p} B)^{G_n}$
. The Lie algebra action of
![]() $\operatorname {\mathrm {Lie}}(G)$
on
$\operatorname {\mathrm {Lie}}(G)$
on
![]() $B^{G_n-\mathrm {an}}$
comes from the action on
$B^{G_n-\mathrm {an}}$
comes from the action on
![]() $\mathscr {C}^{\mathrm {an}}(G_n,\mathbb {Q}_p)$
induced from the right translation action. The following lemma is Lemme 2.6 of [Reference Berger and ColmezBC16].
$\mathscr {C}^{\mathrm {an}}(G_n,\mathbb {Q}_p)$
induced from the right translation action. The following lemma is Lemme 2.6 of [Reference Berger and ColmezBC16].
Lemma 2.1.8. Suppose B is a Banach representation of
![]() $G_0$
. If
$G_0$
. If
![]() $D\in \operatorname {\mathrm {Lie}}(G)$
and
$D\in \operatorname {\mathrm {Lie}}(G)$
and
![]() $n\geq 1$
, then there exists a constant
$n\geq 1$
, then there exists a constant
![]() $C_{D,n}$
such that
$C_{D,n}$
such that
![]() $\|D(x)\|_{G_n}\leq C_{D,n}\|x\|_{G_n}$
for any
$\|D(x)\|_{G_n}\leq C_{D,n}\|x\|_{G_n}$
for any
![]() $x\in B^{G_n-\mathrm {an}}$
.
$x\in B^{G_n-\mathrm {an}}$
.
The following example will appear naturally later.
Example 2.1.9. Suppose
![]() $G=G_0=\mathbb {Z}_p$
and B is a
$G=G_0=\mathbb {Z}_p$
and B is a
![]() $\mathbb {Q}_p$
-Banach space representation of
$\mathbb {Q}_p$
-Banach space representation of
![]() $\mathbb {Z}_p$
. Let
$\mathbb {Z}_p$
. Let
![]() $B^o$
be the open unit ball of B. Suppose there exists an integer
$B^o$
be the open unit ball of B. Suppose there exists an integer
![]() $m>0$
such that
$m>0$
such that
for any
![]() $\gamma \in \mathbb {Z}_p$
. Then B is an analytic representation of
$\gamma \in \mathbb {Z}_p$
. Then B is an analytic representation of
![]() $p^{h}\mathbb {Z}_p$
for h sufficiently large. To see this, it suffices to prove that B is an analytic representation of
$p^{h}\mathbb {Z}_p$
for h sufficiently large. To see this, it suffices to prove that B is an analytic representation of
![]() $\mathbb {Z}_p$
if
$\mathbb {Z}_p$
if
![]() $(\gamma -1)\cdot (B^o)\subset p^2 B^o$
for any
$(\gamma -1)\cdot (B^o)\subset p^2 B^o$
for any
![]() $\gamma \in \mathbb {Z}_p$
. Let
$\gamma \in \mathbb {Z}_p$
. Let
![]() $\gamma =1\in \mathbb {Z}_p$
. For any
$\gamma =1\in \mathbb {Z}_p$
. For any
![]() $f\in B$
, consider
$f\in B$
, consider
![]() $g:\mathbb {Z}_p\to B$
defined by
$g:\mathbb {Z}_p\to B$
defined by
 $g(x)=\sum _{n=0}^{+\infty }{x\choose {n}}(\gamma -1)^n\cdot f$
. One checks easily that g is analytic and
$g(x)=\sum _{n=0}^{+\infty }{x\choose {n}}(\gamma -1)^n\cdot f$
. One checks easily that g is analytic and
![]() $g(x)=x\cdot f$
. Hence,
$g(x)=x\cdot f$
. Hence,
![]() $f\in B^{\mathbb {Z}_p-\mathrm {an}}$
and
$f\in B^{\mathbb {Z}_p-\mathrm {an}}$
and
![]() $B=B^{\mathbb {Z}_p-\mathrm {an}}$
.
$B=B^{\mathbb {Z}_p-\mathrm {an}}$
.
2.2 Derived functor
Let
![]() $G,G_0,G_n$
be as in the first paragraph of Section 2.1.1 and let B be a
$G,G_0,G_n$
be as in the first paragraph of Section 2.1.1 and let B be a
![]() $\mathbb {Q}_p$
-Banach representation of G. Recall
$\mathbb {Q}_p$
-Banach representation of G. Recall
 $$ \begin{align*}B^{\mathrm{la}}=\varinjlim_{n}B^{G_n-\mathrm{an}}=\varinjlim_{n}(B\widehat{\otimes}_{\mathbb{Q}_p}\mathscr{C}^{\mathrm{an}}(G_n,\mathbb{Q}_p))^{G_n}=\varinjlim_{n}H^0_{\mathrm{cont}}(G_n,B\widehat{\otimes}_{\mathbb{Q}_p}\mathscr{C}^{\mathrm{an}}(G_n,\mathbb{Q}_p)).\end{align*} $$
$$ \begin{align*}B^{\mathrm{la}}=\varinjlim_{n}B^{G_n-\mathrm{an}}=\varinjlim_{n}(B\widehat{\otimes}_{\mathbb{Q}_p}\mathscr{C}^{\mathrm{an}}(G_n,\mathbb{Q}_p))^{G_n}=\varinjlim_{n}H^0_{\mathrm{cont}}(G_n,B\widehat{\otimes}_{\mathbb{Q}_p}\mathscr{C}^{\mathrm{an}}(G_n,\mathbb{Q}_p)).\end{align*} $$
Write
![]() $\mathfrak {LA}(B)=B^{\mathrm {la}}$
. We can also consider the following ‘right derived functor’ of
$\mathfrak {LA}(B)=B^{\mathrm {la}}$
. We can also consider the following ‘right derived functor’ of
![]() $\mathfrak {LA}$
.
$\mathfrak {LA}$
.
Definition 2.2.1. For a
![]() $\mathbb {Q}_p$
-Banach representation B of G, let
$\mathbb {Q}_p$
-Banach representation B of G, let
 $$ \begin{align*}R^i\mathfrak{LA}(B):=\varinjlim_{n}H^i_{\mathrm{cont}}(G_n,B\widehat{\otimes}_{\mathbb{Q}_p}\mathscr{C}^{\mathrm{an}}(G_n,\mathbb{Q}_p)).\end{align*} $$
$$ \begin{align*}R^i\mathfrak{LA}(B):=\varinjlim_{n}H^i_{\mathrm{cont}}(G_n,B\widehat{\otimes}_{\mathbb{Q}_p}\mathscr{C}^{\mathrm{an}}(G_n,\mathbb{Q}_p)).\end{align*} $$
We say B is
-
•
 $\mathfrak {LA}$
-acyclic if
$\mathfrak {LA}$
-acyclic if
 $R^i\mathfrak {LA}(B)=0,i\geq 1$
;
$R^i\mathfrak {LA}(B)=0,i\geq 1$
; -
• strongly
 $\mathfrak {LA}$
-acyclic if the direct systems
$\mathfrak {LA}$
-acyclic if the direct systems
 $\{H^i_{\mathrm {cont}}(G_n,B\widehat {\otimes }_{\mathbb {Q}_p}\mathscr {C}^{\mathrm {an}}(G_n,\mathbb {Q}_p)) \}_n,i\geq 1$
are essentially zero; that is, for any n, the image of
$\{H^i_{\mathrm {cont}}(G_n,B\widehat {\otimes }_{\mathbb {Q}_p}\mathscr {C}^{\mathrm {an}}(G_n,\mathbb {Q}_p)) \}_n,i\geq 1$
are essentially zero; that is, for any n, the image of
 $H^i_{\mathrm {cont}}(G_n,B\widehat {\otimes }_{\mathbb {Q}_p}\mathscr {C}^{\mathrm {an}}(G_n,\mathbb {Q}_p)) \to H^i_{\mathrm {cont}}(G_m,B\widehat {\otimes }_{\mathbb {Q}_p}\mathscr {C}^{\mathrm {an}} (G_m,\mathbb {Q}_p))$
is zero for sufficiently large
$H^i_{\mathrm {cont}}(G_n,B\widehat {\otimes }_{\mathbb {Q}_p}\mathscr {C}^{\mathrm {an}}(G_n,\mathbb {Q}_p)) \to H^i_{\mathrm {cont}}(G_m,B\widehat {\otimes }_{\mathbb {Q}_p}\mathscr {C}^{\mathrm {an}} (G_m,\mathbb {Q}_p))$
is zero for sufficiently large
 $m\geq n$
.
$m\geq n$
.
We put a quotation mark on right derived functor as we do not plan to discuss the abelian category we are working with. Clearly,
![]() $R^i\mathfrak {LA}$
measures the failure of exactness when taking the locally analytic vectors and does not depend on choices of
$R^i\mathfrak {LA}$
measures the failure of exactness when taking the locally analytic vectors and does not depend on choices of
![]() $G_0$
. This ad hoc definition will be enough for our purpose in view of the following simple lemma.
$G_0$
. This ad hoc definition will be enough for our purpose in view of the following simple lemma.
Lemma 2.2.2.
-
(1) Suppose
 $0\to M^0\to M^1\to M^2\to 0$
is a short exact sequence of
$0\to M^0\to M^1\to M^2\to 0$
is a short exact sequence of
 $\mathbb {Q}_p$
-Banach representations of G with G-equivariant continuous homomorphisms (which are necessarily strict by the open mapping theorem). Then there is a long exact sequence:
$\mathbb {Q}_p$
-Banach representations of G with G-equivariant continuous homomorphisms (which are necessarily strict by the open mapping theorem). Then there is a long exact sequence:  $$ \begin{align*}0\to (M^0)^{\mathrm{la}}\to (M^1)^{\mathrm{la}}\to (M^2)^{\mathrm{la}}\to R^1\mathfrak{LA}(M^0)\to R^1\mathfrak{LA}(M^1) \to R^1\mathfrak{LA}(M^2)\to \ldots \end{align*} $$
$$ \begin{align*}0\to (M^0)^{\mathrm{la}}\to (M^1)^{\mathrm{la}}\to (M^2)^{\mathrm{la}}\to R^1\mathfrak{LA}(M^0)\to R^1\mathfrak{LA}(M^1) \to R^1\mathfrak{LA}(M^2)\to \ldots \end{align*} $$
-
(2) Let
 $M^{\bullet }$
be a bounded chain complex of
$M^{\bullet }$
be a bounded chain complex of
 $\mathbb {Q}_p$
-Banach representations of G with G-equivariant strict homomorphisms. If
$\mathbb {Q}_p$
-Banach representations of G with G-equivariant strict homomorphisms. If
 $M^q$
and
$M^q$
and
 $H^q(M^{\bullet })$
are
$H^q(M^{\bullet })$
are
 $\mathfrak {LA}$
-acyclic for any q, then
$\mathfrak {LA}$
-acyclic for any q, then
 $(H^q(M^{\bullet }))^{\mathrm {la}}=H^q((M^{\bullet })^{\mathrm {la}})$
.
$(H^q(M^{\bullet }))^{\mathrm {la}}=H^q((M^{\bullet })^{\mathrm {la}})$
. -
(3) Let
 $0\to B\to M^0\to M^1\to \cdots $
be an exact chain complex of
$0\to B\to M^0\to M^1\to \cdots $
be an exact chain complex of
 $\mathbb {Q}_p$
-Banach representations of G with G-equivariant strict homomorphisms. Assume
$\mathbb {Q}_p$
-Banach representations of G with G-equivariant strict homomorphisms. Assume
 $M^q$
is
$M^q$
is
 $\mathfrak {LA}$
-acyclic for any q. Then
$\mathfrak {LA}$
-acyclic for any q. Then
 $R^i\mathfrak {LA}(B)=H^i((M^{\bullet })^{\mathrm {la}})$
. Moreover, if all
$R^i\mathfrak {LA}(B)=H^i((M^{\bullet })^{\mathrm {la}})$
. Moreover, if all
 $M^q$
are strongly
$M^q$
are strongly
 $\mathfrak {LA}$
-acyclic and the direct systems
$\mathfrak {LA}$
-acyclic and the direct systems
 $\{H^i((M^{\bullet })^{G_n-\mathrm {an}})\}_n,i\geq 1$
are essentially zero, then B is strongly
$\{H^i((M^{\bullet })^{G_n-\mathrm {an}})\}_n,i\geq 1$
are essentially zero, then B is strongly
 $\mathfrak {LA}$
-acyclic.
$\mathfrak {LA}$
-acyclic.
Proof. For the first part, since all of the homomorphisms are strict,
![]() $H^i(M^{\bullet ,o})$
can be killed by a bounded power of p, where
$H^i(M^{\bullet ,o})$
can be killed by a bounded power of p, where
![]() $M^{\bullet ,o}$
denotes the open unit ball of
$M^{\bullet ,o}$
denotes the open unit ball of
![]() $M^{\bullet }$
. Therefore,
$M^{\bullet }$
. Therefore,
 $M^{\bullet }\widehat {\otimes }_{\mathbb {Q}_p}\mathscr {C}^{\mathrm {an}}(G_n,\mathbb {Q}_p)$
remains exact for any n and we obtain the desired long exact sequence by taking
$M^{\bullet }\widehat {\otimes }_{\mathbb {Q}_p}\mathscr {C}^{\mathrm {an}}(G_n,\mathbb {Q}_p)$
remains exact for any n and we obtain the desired long exact sequence by taking
![]() $G_n$
-cohomology and passing to the direct limit over n.
$G_n$
-cohomology and passing to the direct limit over n.
The second and third parts follow from the first part by a simple induction argument. For example, one can prove that the kernel and image of
![]() $M^q\to M^{q+1}$
are
$M^q\to M^{q+1}$
are
![]() $\mathfrak {LA}$
-acyclic by induction on q. This certainly implies that
$\mathfrak {LA}$
-acyclic by induction on q. This certainly implies that
![]() $(H^q(M^{\bullet }))^{\mathrm {la}}=H^q((M^{\bullet })^{\mathrm {la}})$
. We leave the third part as an exercise.
$(H^q(M^{\bullet }))^{\mathrm {la}}=H^q((M^{\bullet })^{\mathrm {la}})$
. We leave the third part as an exercise.
A result of Schneider–Teitelbaum says that admissible representations are
![]() $\mathfrak {LA}$
-acyclic (Theorem 7.1 of [Reference Schneider and TeitelbaumST03]). In fact, their argument also essentially proves strong
$\mathfrak {LA}$
-acyclic (Theorem 7.1 of [Reference Schneider and TeitelbaumST03]). In fact, their argument also essentially proves strong
![]() $\mathfrak {LA}$
-acyclicity.
$\mathfrak {LA}$
-acyclicity.
Theorem 2.2.3. Any admissible
![]() $\mathbb {Q}_p$
-Banach representation B of G is strongly
$\mathbb {Q}_p$
-Banach representation B of G is strongly
![]() $\mathfrak {LA}$
-acyclic.
$\mathfrak {LA}$
-acyclic.
Proof. Since B is admissible, there is a
![]() $G_0$
-equivariant embedding
$G_0$
-equivariant embedding
![]() $B \hookrightarrow \mathscr {C}(G_0,\mathbb {Q}_p)^{\oplus d}$
for some d. Then the quotient C is an admissible
$B \hookrightarrow \mathscr {C}(G_0,\mathbb {Q}_p)^{\oplus d}$
for some d. Then the quotient C is an admissible
![]() $\mathbb {Q}_p$
-Banach representation of
$\mathbb {Q}_p$
-Banach representation of
![]() $G_0$
. Note that
$G_0$
. Note that
![]() $ \mathscr {C}(G_0,\mathbb {Q}_p)\cong \mathscr {C}(G_n,\mathbb {Q}_p)^{\oplus d_n}$
as a representation of
$ \mathscr {C}(G_0,\mathbb {Q}_p)\cong \mathscr {C}(G_n,\mathbb {Q}_p)^{\oplus d_n}$
as a representation of
![]() $G_n$
for some
$G_n$
for some
![]() $d_n$
. It follows from Shapiro’s lemma for continuous cohomology that
$d_n$
. It follows from Shapiro’s lemma for continuous cohomology that
 $H_{\mathrm {cont}}^1(G_n,\mathscr {C}(G_0,\mathbb {Q}_p)\widehat {\otimes }_{\mathbb {Q}_p}\mathscr {C}^{\mathrm {an}}(G_n,\mathbb {Q}_p))=0$
. Hence,
$H_{\mathrm {cont}}^1(G_n,\mathscr {C}(G_0,\mathbb {Q}_p)\widehat {\otimes }_{\mathbb {Q}_p}\mathscr {C}^{\mathrm {an}}(G_n,\mathbb {Q}_p))=0$
. Hence,
 $$ \begin{align*}(\mathscr{C}(G_0,\mathbb{Q}_p)^{\oplus d})^{G_n-\mathrm{an}}\to C^{G_n-\mathrm{an}} \to H^1_{\mathrm{cont}}(G_n,B\widehat{\otimes}_{\mathbb{Q}_p}\mathscr{C}^{\mathrm{an}}(G_n,\mathbb{Q}_p))\to 0.\end{align*} $$
$$ \begin{align*}(\mathscr{C}(G_0,\mathbb{Q}_p)^{\oplus d})^{G_n-\mathrm{an}}\to C^{G_n-\mathrm{an}} \to H^1_{\mathrm{cont}}(G_n,B\widehat{\otimes}_{\mathbb{Q}_p}\mathscr{C}^{\mathrm{an}}(G_n,\mathbb{Q}_p))\to 0.\end{align*} $$
By Corollaire IV.14. of [Reference Colmez and DospinescuCD14], we have an exact sequence
 $$ \begin{align*}0\to B^{(m)}\to (\mathscr{C}(G_0,\mathbb{Q}_p)^{\oplus d})^{(m)}\to C^{(m)}\to 0.\end{align*} $$
$$ \begin{align*}0\to B^{(m)}\to (\mathscr{C}(G_0,\mathbb{Q}_p)^{\oplus d})^{(m)}\to C^{(m)}\to 0.\end{align*} $$
See [Reference Colmez and DospinescuCD14, §IV] for the notation here. One can check
![]() $C^{G_n-\mathrm {an}}\subset C^{(n+2)}\subset C^{G_{n+1}-\mathrm {an}}$
. This means that the image of
$C^{G_n-\mathrm {an}}\subset C^{(n+2)}\subset C^{G_{n+1}-\mathrm {an}}$
. This means that the image of
![]() $(\mathscr {C}(G_0,\mathbb {Q}_p)^{\oplus d})^{G_{n+1}-\mathrm {an}}$
in
$(\mathscr {C}(G_0,\mathbb {Q}_p)^{\oplus d})^{G_{n+1}-\mathrm {an}}$
in
![]() $C^{G_{n+1}-\mathrm {an}}$
contains
$C^{G_{n+1}-\mathrm {an}}$
contains
![]() $C^{G_n-\mathrm {an}}$
. Hence,
$C^{G_n-\mathrm {an}}$
. Hence,
 $H^1_{\mathrm {cont}}(G_n,B\widehat {\otimes }_{\mathbb {Q}_p}\mathscr {C}^{\mathrm {an}}(G_n,\mathbb {Q}_p)) \to H^1_{\mathrm {cont}}(G_{n+1},B\widehat {\otimes }_{\mathbb {Q}_p}\mathscr {C}^{\mathrm {an}}(G_{n+1},\mathbb {Q}_p))$
has zero image. A simple induction on cohomology degree
$H^1_{\mathrm {cont}}(G_n,B\widehat {\otimes }_{\mathbb {Q}_p}\mathscr {C}^{\mathrm {an}}(G_n,\mathbb {Q}_p)) \to H^1_{\mathrm {cont}}(G_{n+1},B\widehat {\otimes }_{\mathbb {Q}_p}\mathscr {C}^{\mathrm {an}}(G_{n+1},\mathbb {Q}_p))$
has zero image. A simple induction on cohomology degree
![]() $i\geq 1$
proves the theorem.
$i\geq 1$
proves the theorem.
We need the following variant for later applications.
Corollary 2.2.4. Let B be an admissible
![]() $\mathbb {Q}_p$
-Banach representation of G and M be a
$\mathbb {Q}_p$
-Banach representation of G and M be a
![]() $\mathbb {Q}_p$
-Banach space with trivial G-action. Then
$\mathbb {Q}_p$
-Banach space with trivial G-action. Then
 $B\widehat {\otimes }_{\mathbb {Q}_p}M$
is strongly
$B\widehat {\otimes }_{\mathbb {Q}_p}M$
is strongly
![]() $\mathfrak {LA}$
-acyclic.
$\mathfrak {LA}$
-acyclic.
Proof. Let
![]() $B^o$
be the unit open ball of B. Take n large enough so that
$B^o$
be the unit open ball of B. Take n large enough so that
![]() $B^o$
is
$B^o$
is
![]() $G_n$
-stable. We claim that
$G_n$
-stable. We claim that
![]() $H^{\bullet }_{\mathrm {cont}}(G_n,B^o)$
is a finitely generated
$H^{\bullet }_{\mathrm {cont}}(G_n,B^o)$
is a finitely generated
![]() $\mathbb {Z}_p$
-module and hence has bounded p-torsion. Indeed, since B is admissible, there exists a
$\mathbb {Z}_p$
-module and hence has bounded p-torsion. Indeed, since B is admissible, there exists a
![]() $\mathbb {Z}_p[G_n]$
-equivariant injection
$\mathbb {Z}_p[G_n]$
-equivariant injection
![]() $B^o \hookrightarrow \mathscr {C}(G_n,\mathbb {Z}_p)^{\oplus d}$
for some d, whose quotient is p-torsion free. An induction argument on i implies the finiteness here. It is well-known that
$B^o \hookrightarrow \mathscr {C}(G_n,\mathbb {Z}_p)^{\oplus d}$
for some d, whose quotient is p-torsion free. An induction argument on i implies the finiteness here. It is well-known that
![]() $H^{\bullet }_{\mathrm {cont}}(G_n,B)$
can be computed by a cochain complex
$H^{\bullet }_{\mathrm {cont}}(G_n,B)$
can be computed by a cochain complex
![]() $(\mathscr {C}(G_n,B)^{\oplus i},d^i)$
. This is a strict complex because
$(\mathscr {C}(G_n,B)^{\oplus i},d^i)$
. This is a strict complex because
![]() $(\mathscr {C}(G_n,B^o)^{\oplus i},d^i)$
computes
$(\mathscr {C}(G_n,B^o)^{\oplus i},d^i)$
computes
![]() $H^{\bullet }_{\mathrm {cont}}(G_n,B^o)$
. Since
$H^{\bullet }_{\mathrm {cont}}(G_n,B^o)$
. Since
 $\mathscr {C}(G_n,B\widehat {\otimes }_{\mathbb {Q}_p}M)\cong \mathscr {C}(G_n,B)\widehat {\otimes }_{\mathbb {Q}_p}M$
, we know that
$\mathscr {C}(G_n,B\widehat {\otimes }_{\mathbb {Q}_p}M)\cong \mathscr {C}(G_n,B)\widehat {\otimes }_{\mathbb {Q}_p}M$
, we know that
 $(\mathscr {C}(G_n,B)^{\oplus i}\widehat {\otimes }_{\mathbb {Q}_p}M,d^i\otimes \mathbf {1})$
computes
$(\mathscr {C}(G_n,B)^{\oplus i}\widehat {\otimes }_{\mathbb {Q}_p}M,d^i\otimes \mathbf {1})$
computes
 $H^{\bullet }_{\mathrm {cont}}(G_n,B\widehat {\otimes }_{\mathbb {Q}_p}M)$
. Therefore,
$H^{\bullet }_{\mathrm {cont}}(G_n,B\widehat {\otimes }_{\mathbb {Q}_p}M)$
. Therefore,
 $$ \begin{align*} H^{\bullet}_{\mathrm{cont}}(G_n,B\widehat{\otimes}_{\mathbb{Q}_p}M)\cong H^{\bullet}_{\mathrm{cont}}(G_n,B)\widehat{\otimes}_{\mathbb{Q}_p}M.\end{align*} $$
$$ \begin{align*} H^{\bullet}_{\mathrm{cont}}(G_n,B\widehat{\otimes}_{\mathbb{Q}_p}M)\cong H^{\bullet}_{\mathrm{cont}}(G_n,B)\widehat{\otimes}_{\mathbb{Q}_p}M.\end{align*} $$
Our claim now follows from the previous theorem.
3 Locally analytic vectors and relative Sen theory
The main goal of this section is to generalise results of Berger and Colmez [Reference Berger and ColmezBC16] and Sen [Reference SenSen81] in the 1-dimensional geometric setting. The main result roughly says that the locally analytic vectors satisfy a differential equation given by a (relative) Sen operator. We claim no originality for most results here. One strong tool in these works is the theory of decompletions. We will review the Tate–Sen formalism of Berger–Colmez [Reference Berger and ColmezBC08], which is flexible enough to handle our situation. As an application, we will show that taking locally analytic vectors is exact under certain conditions.
The results of this section are closely related to the work of Faltings [Reference FaltingsFal05], Abbes–Gros–Tsuji [Reference Abbes, Gros and TsujiAGT16] and Liu–Zhu [Reference Liu and ZhuLZ17] on p-adic Simpson correspondences. See Remark 3.1.7.
3.1 Statement of the main result
3.1.1. Fix a complete algebraically closed non-Archimedean field C of characteristic zero. Recall that a non-Archimedean field is a topological field whose topology is induced by a non-Archimedean norm
![]() $|\cdot |:C\to \mathbb {R}_{\geq 0}$
. It is naturally an extension of
$|\cdot |:C\to \mathbb {R}_{\geq 0}$
. It is naturally an extension of
![]() $\mathbb {Q}_p$
for some p and we assume its norm agrees with the usual p-adic norm
$\mathbb {Q}_p$
for some p and we assume its norm agrees with the usual p-adic norm
 $|\cdot |_p=p^{-\mathrm {val}_p(\cdot )}$
on
$|\cdot |_p=p^{-\mathrm {val}_p(\cdot )}$
on
![]() $\mathbb {Q}_p$
. Let
$\mathbb {Q}_p$
. Let
![]() $\mathcal {O}_C$
be the ring of integers of C. Our setup is as follows:
$\mathcal {O}_C$
be the ring of integers of C. Our setup is as follows:
-
•
 $X=\operatorname {\mathrm {Spa}}(A,A^+)$
: a 1-dimensional smooth affinoid adic space over
$X=\operatorname {\mathrm {Spa}}(A,A^+)$
: a 1-dimensional smooth affinoid adic space over
 $\operatorname {\mathrm {Spa}}(C,\mathcal {O}_C)$
;
$\operatorname {\mathrm {Spa}}(C,\mathcal {O}_C)$
; -
• G: a finite-dimensional compact p-adic Lie group;
-
•
 $\widetilde X=\operatorname {\mathrm {Spa}}(B,B^+)$
: an affinoid perfectoid algebra over
$\widetilde X=\operatorname {\mathrm {Spa}}(B,B^+)$
: an affinoid perfectoid algebra over
 $\operatorname {\mathrm {Spa}}(C,\mathcal {O}_C)$
, which is a ‘log G-Galois pro-étale perfectoid covering’ of X. More precisely, this means that there is a finite set S of classical points in X and
$\operatorname {\mathrm {Spa}}(C,\mathcal {O}_C)$
, which is a ‘log G-Galois pro-étale perfectoid covering’ of X. More precisely, this means that there is a finite set S of classical points in X and
 $\widetilde X\sim \varprojlim _{i\in I} X_i$
in the sense of Definition 7.14 of [Reference ScholzeSch12] for some index set I, where each
$\widetilde X\sim \varprojlim _{i\in I} X_i$
in the sense of Definition 7.14 of [Reference ScholzeSch12] for some index set I, where each
 $X_i=\operatorname {\mathrm {Spa}}(B_i,B_i^+)$
is a finite Galois covering of X unramified outside of S, and
$X_i=\operatorname {\mathrm {Spa}}(B_i,B_i^+)$
is a finite Galois covering of X unramified outside of S, and
 $B^{+}$
is the p-adic completion of
$B^{+}$
is the p-adic completion of
 $\varinjlim _i B_i^{+}$
. Moreover, the inverse limit of the Galois group of
$\varinjlim _i B_i^{+}$
. Moreover, the inverse limit of the Galois group of
 $X_i$
over X is identified with G. When S is nonempty, we further assume for each point s in S, the ramification-index
$X_i$
over X is identified with G. When S is nonempty, we further assume for each point s in S, the ramification-index
 $e_i$
of
$e_i$
of
 $X_i\to X$
at s is a p-power for any i and
$X_i\to X$
at s is a p-power for any i and
 $\{e_i\}_{i\in I}$
is unbounded;
$\{e_i\}_{i\in I}$
is unbounded; -
• assume X is small in the sense that S contains at most one element and there is an étale map
 $X\to \mathbb {T}^1=\operatorname {\mathrm {Spa}}(C\langle T^{\pm 1}\rangle , \mathcal {O}_C\langle T^{\pm 1}\rangle )$
(respectively
$X\to \mathbb {T}^1=\operatorname {\mathrm {Spa}}(C\langle T^{\pm 1}\rangle , \mathcal {O}_C\langle T^{\pm 1}\rangle )$
(respectively
 $X\to \mathbb {B}^1=\operatorname {\mathrm {Spa}}(C\langle T\rangle , \mathcal {O}_C\langle T\rangle )$
mapping S to
$X\to \mathbb {B}^1=\operatorname {\mathrm {Spa}}(C\langle T\rangle , \mathcal {O}_C\langle T\rangle )$
mapping S to
 $0$
) when S is empty (respectively otherwise) which factors as a composite of rational embeddings and finite étale maps.
$0$
) when S is empty (respectively otherwise) which factors as a composite of rational embeddings and finite étale maps.
Note that G acts continuously on the Banach algebra B and we can consider the locally analytic vectors
![]() $B^{\mathrm {la}}\subset B$
. Let
$B^{\mathrm {la}}\subset B$
. Let
![]() $\operatorname {\mathrm {Lie}}(G)$
be the Lie algebra of G. It acts on
$\operatorname {\mathrm {Lie}}(G)$
be the Lie algebra of G. It acts on
![]() $B^{\mathrm {la}}$
, and this action can be extended B-linearly to a map
$B^{\mathrm {la}}$
, and this action can be extended B-linearly to a map
 $B\otimes _{\mathbb {Q}_p}\operatorname {\mathrm {Lie}}(G) \times B^{\mathrm {la}} \to B$
.
$B\otimes _{\mathbb {Q}_p}\operatorname {\mathrm {Lie}}(G) \times B^{\mathrm {la}} \to B$
.
Theorem 3.1.2. Fix an étale map
![]() $X\to \mathbb {T}^1$
(respectively
$X\to \mathbb {T}^1$
(respectively
![]() $X\to \mathbb {B}^1$
) if S is empty (respectively nonempty) as above. For each ‘log G-Galois pro-étale perfectoid covering’
$X\to \mathbb {B}^1$
) if S is empty (respectively nonempty) as above. For each ‘log G-Galois pro-étale perfectoid covering’
![]() $\widetilde {X}$
of X, we can assign an element
$\widetilde {X}$
of X, we can assign an element
![]() $\theta =\theta _{\widetilde {X}}\in B\otimes _{\mathbb {Q}_p}\operatorname {\mathrm {Lie}}(G)$
, satisfying
$\theta =\theta _{\widetilde {X}}\in B\otimes _{\mathbb {Q}_p}\operatorname {\mathrm {Lie}}(G)$
, satisfying
-
(1)
 $\theta $
annihilates
$\theta $
annihilates
 $B^{\mathrm {la}}$
. In other words, locally analytic vectors satisfy certain (first-order) differential equation.
$B^{\mathrm {la}}$
. In other words, locally analytic vectors satisfy certain (first-order) differential equation. -
(2)
 $\theta $
is functorial in
$\theta $
is functorial in
 $(G,\tilde {X})$
: if H is a closed normal subgroup of G so that
$(G,\tilde {X})$
: if H is a closed normal subgroup of G so that
 $\widetilde {X}'=\operatorname {\mathrm {Spa}}(B^H,(B^+)^H)$
is a ‘log
$\widetilde {X}'=\operatorname {\mathrm {Spa}}(B^H,(B^+)^H)$
is a ‘log
 $G/H$
-Galois pro-étale perfectoid covering’ of X, then where
$G/H$
-Galois pro-étale perfectoid covering’ of X, then where $$ \begin{align*}\theta_{\widetilde{X}}\equiv \theta_{\widetilde{X}'}\mod B\otimes_{\mathbb{Q}_p}\operatorname{\mathrm{Lie}}(H),\end{align*} $$
$$ \begin{align*}\theta_{\widetilde{X}}\equiv \theta_{\widetilde{X}'}\mod B\otimes_{\mathbb{Q}_p}\operatorname{\mathrm{Lie}}(H),\end{align*} $$
 $\theta _{\widetilde {X}'}\in B^H\otimes _{\mathbb {Q}_p}\operatorname {\mathrm {Lie}}(G/H)$
is viewed as an element in
$\theta _{\widetilde {X}'}\in B^H\otimes _{\mathbb {Q}_p}\operatorname {\mathrm {Lie}}(G/H)$
is viewed as an element in
 $B\otimes _{\mathbb {Q}_p}\operatorname {\mathrm {Lie}}(G/H)$
.
$B\otimes _{\mathbb {Q}_p}\operatorname {\mathrm {Lie}}(G/H)$
.
-
(3)
 $\theta \neq 0$
if
$\theta \neq 0$
if
 $\widetilde {X}$
is a locally analytic covering in the sense of 3.5.4.
$\widetilde {X}$
is a locally analytic covering in the sense of 3.5.4.
Moreover, if we start with another étale map
![]() $X\to \mathbb {T}^1$
(or étale map
$X\to \mathbb {T}^1$
(or étale map
![]() $X\to \mathbb {B}^1$
), then the element
$X\to \mathbb {B}^1$
), then the element
![]() $\theta '\in B\otimes _{\mathbb {Q}_p}\operatorname {\mathrm {Lie}}(G)$
obtained using this étale map will differ
$\theta '\in B\otimes _{\mathbb {Q}_p}\operatorname {\mathrm {Lie}}(G)$
obtained using this étale map will differ
![]() $\theta $
by a unit of A. In other words,
$\theta $
by a unit of A. In other words,
![]() $A^{\times }\theta \subset B\otimes _{\mathbb {Q}_p}\operatorname {\mathrm {Lie}}(G)$
does not depend on the choice of the étale map.
$A^{\times }\theta \subset B\otimes _{\mathbb {Q}_p}\operatorname {\mathrm {Lie}}(G)$
does not depend on the choice of the étale map.
Remark 3.1.3. From the point of view of differential operators, one may regard
![]() $\theta $
as some p-adic analogue of Cauchy–Riemann operator in the classical complex analysis.
$\theta $
as some p-adic analogue of Cauchy–Riemann operator in the classical complex analysis.
Remark 3.1.4. In the classical p-adic Hodge theory of p-adic Galois representations, this
![]() $\theta $
is nothing but the Sen operator; cf. Theorem 12 of [Reference SenSen81], Théorème 1.9 of [Reference Berger and ColmezBC16]. So it is reasonable to call it relative Sen operator.
$\theta $
is nothing but the Sen operator; cf. Theorem 12 of [Reference SenSen81], Théorème 1.9 of [Reference Berger and ColmezBC16]. So it is reasonable to call it relative Sen operator.
Remark 3.1.5. It is natural to ask whether there is a canonical representative of
![]() $\theta $
so that one can glue them in some global situation. First, it turns out that the natural place for
$\theta $
so that one can glue them in some global situation. First, it turns out that the natural place for
![]() $\theta $
to live is
$\theta $
to live is
 $B\otimes _A\Omega _{A/C}^{1}(S)\otimes _{\mathbb {Q}_p}\operatorname {\mathrm {Lie}}(G)(-1)$
, where
$B\otimes _A\Omega _{A/C}^{1}(S)\otimes _{\mathbb {Q}_p}\operatorname {\mathrm {Lie}}(G)(-1)$
, where
 $\Omega _{A/C}^{1}(S)$
denotes the continuous
$\Omega _{A/C}^{1}(S)$
denotes the continuous
![]() $1$
-forms of A over C with simple poles at S and
$1$
-forms of A over C with simple poles at S and
![]() $(1)$
denotes the usual Tate-twist. So
$(1)$
denotes the usual Tate-twist. So
![]() $\theta $
is viewed as a (log) Higgs field.
$\theta $
is viewed as a (log) Higgs field.
Secondly, if S is empty – that is,
![]() $\widetilde X$
is a G-Galois pro-étale perfectoid covering of X – then we can make this element canonical using the functorial isomorphism
$\widetilde X$
is a G-Galois pro-étale perfectoid covering of X – then we can make this element canonical using the functorial isomorphism
 $\Omega _{A/C}^{1}(-1)\cong H^1_{\mathrm {cont}}(G,B)$
(Proposition 3.23 of [Reference ScholzeSch13b]). Here
$\Omega _{A/C}^{1}(-1)\cong H^1_{\mathrm {cont}}(G,B)$
(Proposition 3.23 of [Reference ScholzeSch13b]). Here
![]() $H^1_{\mathrm {cont}}(G,B)$
denotes the continuous group cohomology group and is identified with
$H^1_{\mathrm {cont}}(G,B)$
denotes the continuous group cohomology group and is identified with
 $H^1(X_{\mathrm {pro\acute {e}t}},\hat {\mathcal {O}}_X)$
by an argument similar to the proof of Lemma 5.6 of [Reference ScholzeSch13a]. By the functorial property, it is enough to pin down this element
$H^1(X_{\mathrm {pro\acute {e}t}},\hat {\mathcal {O}}_X)$
by an argument similar to the proof of Lemma 5.6 of [Reference ScholzeSch13a]. By the functorial property, it is enough to pin down this element
![]() $\theta $
for a particular
$\theta $
for a particular
![]() $\widetilde X$
, provided that
$\widetilde X$
, provided that
![]() $\theta _{\tilde {X}}\neq 0$
. Indeed, if
$\theta _{\tilde {X}}\neq 0$
. Indeed, if
![]() $\widetilde X'$
is a H-Galois pro-étale perfectoid covering of X, we can consider
$\widetilde X'$
is a H-Galois pro-étale perfectoid covering of X, we can consider
![]() $\widetilde X'':=\widetilde X\times _X \widetilde {X}'$
, the fibre product in the category of pro-étale coverings of X. Then
$\widetilde X'':=\widetilde X\times _X \widetilde {X}'$
, the fibre product in the category of pro-étale coverings of X. Then
![]() $\widetilde X''$
is a
$\widetilde X''$
is a
![]() $(G\times H)$
-Galois pro-étale perfectoid covering of X. Once
$(G\times H)$
-Galois pro-étale perfectoid covering of X. Once
![]() $\theta _{\widetilde {X}}$
is determined, so is
$\theta _{\widetilde {X}}$
is determined, so is
![]() $\theta _{\widetilde X''}$
and hence
$\theta _{\widetilde X''}$
and hence
![]() $\theta _{\widetilde X'}$
by the functorial property.
$\theta _{\widetilde X'}$
by the functorial property.
Suppose
![]() $G\cong \mathbb {Z}_p$
. Then there is a canonical isomorphism
$G\cong \mathbb {Z}_p$
. Then there is a canonical isomorphism
 $$ \begin{align*}\Omega_{A/C}^{1}(-1)\otimes_{\mathbb{Q}_p}\operatorname{\mathrm{Lie}}(G)\stackrel{\sim}{\longrightarrow} H^1_{\mathrm{cont}}(G,B)\otimes_{\mathbb{Z}_p} G\stackrel{\sim}{\longrightarrow} B_G,\end{align*} $$
$$ \begin{align*}\Omega_{A/C}^{1}(-1)\otimes_{\mathbb{Q}_p}\operatorname{\mathrm{Lie}}(G)\stackrel{\sim}{\longrightarrow} H^1_{\mathrm{cont}}(G,B)\otimes_{\mathbb{Z}_p} G\stackrel{\sim}{\longrightarrow} B_G,\end{align*} $$
where the first map is induced by the exponential map of G and
![]() $B_G$
denotes the G-coinvariants of B. Under this isomorphism, the canonical
$B_G$
denotes the G-coinvariants of B. Under this isomorphism, the canonical
![]() $\theta $
is given by the image of
$\theta $
is given by the image of
![]() $1\in B$
in
$1\in B$
in
![]() $B_G$
. It can be checked that this is independent of the choice of such a
$B_G$
. It can be checked that this is independent of the choice of such a
![]() $\mathbb {Z}_p$
-covering.
$\mathbb {Z}_p$
-covering.
The proof of Proposition 3.23 of [Reference ScholzeSch13b] crucially uses the fact that when X is defined over some finite extension of
![]() $\mathbb {Q}_p$
, then there is the Faltings’s extension (Corollary 6.14 of [Reference ScholzeSch13a]) which produces this canonical isomorphism. Faltings’s extension has also been generalised to the log case; cf. Corollary 2.4.5 of [Reference Diao, Lan, Liu and ZhuDLLZ18]. Hence, it is conceivable that there is a canonical
$\mathbb {Q}_p$
, then there is the Faltings’s extension (Corollary 6.14 of [Reference ScholzeSch13a]) which produces this canonical isomorphism. Faltings’s extension has also been generalised to the log case; cf. Corollary 2.4.5 of [Reference Diao, Lan, Liu and ZhuDLLZ18]. Hence, it is conceivable that there is a canonical
![]() $\theta $
in general.
$\theta $
in general.
Example 3.1.6.
-
•
 $X=\operatorname {\mathrm {Spa}}(C\langle T^{\pm 1}\rangle , \mathcal {O}_C\langle T^{\pm 1}\rangle )$
, the 1-dimensional torus;
$X=\operatorname {\mathrm {Spa}}(C\langle T^{\pm 1}\rangle , \mathcal {O}_C\langle T^{\pm 1}\rangle )$
, the 1-dimensional torus; -
•
 $\widetilde X=\operatorname {\mathrm {Spa}}(C\langle T^{\pm \frac {1}{p^{\infty }}}\rangle , \mathcal {O}_C\langle T^{\pm \frac {1}{p^{\infty }}}\rangle )$
, the inverse limit of
$\widetilde X=\operatorname {\mathrm {Spa}}(C\langle T^{\pm \frac {1}{p^{\infty }}}\rangle , \mathcal {O}_C\langle T^{\pm \frac {1}{p^{\infty }}}\rangle )$
, the inverse limit of
 $\operatorname {\mathrm {Spa}}(C\langle T^{\pm \frac {1}{p^{m}}}\rangle , \mathcal {O}_C\langle T^{\pm \frac {1}{p^{m}}}\rangle )$
;
$\operatorname {\mathrm {Spa}}(C\langle T^{\pm \frac {1}{p^{m}}}\rangle , \mathcal {O}_C\langle T^{\pm \frac {1}{p^{m}}}\rangle )$
; -
•
 $G=\mathbb {Z}_p$
which acts by
$G=\mathbb {Z}_p$
which acts by
 $k\cdot T^{\frac {1}{p^m}}=\zeta ^{\frac {k}{p^m}}T^{\frac {1}{p^m}},~k\in \mathbb {Z}_p$
where
$k\cdot T^{\frac {1}{p^m}}=\zeta ^{\frac {k}{p^m}}T^{\frac {1}{p^m}},~k\in \mathbb {Z}_p$
where
 $\{\zeta _{p^m}\}_m$
is a choice of compatible system of
$\{\zeta _{p^m}\}_m$
is a choice of compatible system of
 $p^m$
th roots of unity.
$p^m$
th roots of unity.
The locally analytic vectors in
 $C\langle T^{\pm \frac {1}{p^{\infty }}}\rangle $
are just
$C\langle T^{\pm \frac {1}{p^{\infty }}}\rangle $
are just
 $\bigcup _m C\langle T^{\pm \frac {1}{p^{m}}}\rangle $
, the smooth vectors. This can be deduced easily from the existence of Tate’s normalised trace in this situation; that is, there is a continuous left inverse of the inclusion
$\bigcup _m C\langle T^{\pm \frac {1}{p^{m}}}\rangle $
, the smooth vectors. This can be deduced easily from the existence of Tate’s normalised trace in this situation; that is, there is a continuous left inverse of the inclusion
 $C\langle T^{\pm \frac {1}{p^{m}}}\rangle \hookrightarrow C\langle T^{\pm \frac {1}{p^{\infty }}}\rangle $
. See Lemma 3.2.5 or Théorème 3.2 of [Reference Berger and ColmezBC16]. The differential operator
$C\langle T^{\pm \frac {1}{p^{m}}}\rangle \hookrightarrow C\langle T^{\pm \frac {1}{p^{\infty }}}\rangle $
. See Lemma 3.2.5 or Théorème 3.2 of [Reference Berger and ColmezBC16]. The differential operator
![]() $\theta $
in this case is
$\theta $
in this case is
 $\frac {dT}{T}\otimes \mathbf {1}$
, where
$\frac {dT}{T}\otimes \mathbf {1}$
, where
![]() $\mathbf {1}$
is the image of
$\mathbf {1}$
is the image of
 $1\in \mathbb {Z}_p\stackrel {\log }{\longrightarrow } \operatorname {\mathrm {Lie}}(\mathbb {Z}_p)$
under the logarithm. The same result holds for
$1\in \mathbb {Z}_p\stackrel {\log }{\longrightarrow } \operatorname {\mathrm {Lie}}(\mathbb {Z}_p)$
under the logarithm. The same result holds for
![]() $X=\operatorname {\mathrm {Spa}}(C\langle T\rangle , \mathcal {O}_C\langle T\rangle )$
, the 1-dimensional unit ball and
$X=\operatorname {\mathrm {Spa}}(C\langle T\rangle , \mathcal {O}_C\langle T\rangle )$
, the 1-dimensional unit ball and
 $\widetilde X=\operatorname {\mathrm {Spa}}(C\langle T^{ \frac {1}{p^{\infty }}}\rangle , \mathcal {O}_C\langle T^{\frac {1}{p^{\infty }}}\rangle )$
.
$\widetilde X=\operatorname {\mathrm {Spa}}(C\langle T^{ \frac {1}{p^{\infty }}}\rangle , \mathcal {O}_C\langle T^{\frac {1}{p^{\infty }}}\rangle )$
.
Remark 3.1.7. As mentioned in Remark 3.1.5,
![]() $\theta $
should be considered as a log Higgs field. This is closely related to previous work of Faltings [Reference FaltingsFal05], Abbes–Gros–Tsuji [Reference Abbes, Gros and TsujiAGT16] and Liu–Zhu [Reference Liu and ZhuLZ17] on p-adic Simpson correspondences. More precisely, for a finite-dimensional continuous representation V of G, the p-adic Simpson correspondence associates a log Higgs field (after extending the coefficients to B):
$\theta $
should be considered as a log Higgs field. This is closely related to previous work of Faltings [Reference FaltingsFal05], Abbes–Gros–Tsuji [Reference Abbes, Gros and TsujiAGT16] and Liu–Zhu [Reference Liu and ZhuLZ17] on p-adic Simpson correspondences. More precisely, for a finite-dimensional continuous representation V of G, the p-adic Simpson correspondence associates a log Higgs field (after extending the coefficients to B):
 $$ \begin{align*}\phi_V: B\otimes_{\mathbb{Q}_p}V \to \Omega_{A/C}^{1}(S)\otimes_A B\otimes_{\mathbb{Q}_p}V(-1),\end{align*} $$
$$ \begin{align*}\phi_V: B\otimes_{\mathbb{Q}_p}V \to \Omega_{A/C}^{1}(S)\otimes_A B\otimes_{\mathbb{Q}_p}V(-1),\end{align*} $$
which is monoidal in V. Hence, from the Tannakian point of view, this gives rise to a log Higgs field which is nothing but our
![]() $\theta $
. Basically, we will construct
$\theta $
. Basically, we will construct
![]() $\theta $
by taking V as the space of analytic functions on G (after taking a certain limit).
$\theta $
by taking V as the space of analytic functions on G (after taking a certain limit).
To see that
![]() $\theta $
annihilates
$\theta $
annihilates
![]() $B^{\mathrm {la}}$
, we remark that, as a B-module,
$B^{\mathrm {la}}$
, we remark that, as a B-module,
![]() $\ker (\phi _V)$
are generated by the G-smooth vectors in
$\ker (\phi _V)$
are generated by the G-smooth vectors in
![]() $B\otimes _{\mathbb {Q}_p} V$
. Hence, when V is the space of analytic functions on G, it is tautological that
$B\otimes _{\mathbb {Q}_p} V$
. Hence, when V is the space of analytic functions on G, it is tautological that
![]() $B^{\mathrm {la}}$
is in the kernel of
$B^{\mathrm {la}}$
is in the kernel of
![]() $\theta $
. I hope this provides some intuition for the constructions below.
$\theta $
. I hope this provides some intuition for the constructions below.
3.2 Relative Sen theory
In this subsection, we will first define a bigger perfectoid algebra
![]() $B_{\infty }$
containing B and construct (functorially) an operator in the endomorphism group
$B_{\infty }$
containing B and construct (functorially) an operator in the endomorphism group
![]() $\operatorname {\mathrm {End}}_{B_{\infty }}(B_{\infty }\otimes _{\mathbb {Q}_p} V)$
for any continuous finite-dimensional
$\operatorname {\mathrm {End}}_{B_{\infty }}(B_{\infty }\otimes _{\mathbb {Q}_p} V)$
for any continuous finite-dimensional
![]() $\mathbb {Q}_p$
-representation V of G.
$\mathbb {Q}_p$
-representation V of G.
3.2.1. Fix an étale map
![]() $f_1:X\to Y$
which factors as a composite of rational embeddings and finite étale maps, where Y is either
$f_1:X\to Y$
which factors as a composite of rational embeddings and finite étale maps, where Y is either
![]() $\mathbb {T}^1=\operatorname {\mathrm {Spa}}(C\langle T^{\pm 1}\rangle , \mathcal {O}_C\langle T^{\pm 1}\rangle )$
or
$\mathbb {T}^1=\operatorname {\mathrm {Spa}}(C\langle T^{\pm 1}\rangle , \mathcal {O}_C\langle T^{\pm 1}\rangle )$
or
![]() $\mathbb {B}^1=\operatorname {\mathrm {Spa}}(C\langle T\rangle , \mathcal {O}_C\langle T\rangle )$
. In the latter case, we assume the image of S in Y is
$\mathbb {B}^1=\operatorname {\mathrm {Spa}}(C\langle T\rangle , \mathcal {O}_C\langle T\rangle )$
. In the latter case, we assume the image of S in Y is
![]() $0$
. We will fix such a choice of
$0$
. We will fix such a choice of
![]() $f_1:X\to Y$
from now on.
$f_1:X\to Y$
from now on.
For any
![]() $n\in \mathbb {N}$
, when
$n\in \mathbb {N}$
, when
![]() $Y=\mathbb {T}^1$
(respectively
$Y=\mathbb {T}^1$
(respectively
![]() $\mathbb {B}^1$
), let
$\mathbb {B}^1$
), let
 $$ \begin{align*}Y_n=\operatorname{\mathrm{Spa}}(R_n,R_n^+):=\operatorname{\mathrm{Spa}}(C\langle T^{\pm \frac{1}{p^{n}}}\rangle, \mathcal{O}_C\langle T^{\pm\frac{1}{p^{n}}}\rangle)~ (\mbox{respectively } \operatorname{\mathrm{Spa}}(C\langle T^{ \frac{1}{p^{n}}}\rangle, \mathcal{O}_C\langle T^{\frac{1}{p^{n}}}\rangle)),\end{align*} $$
$$ \begin{align*}Y_n=\operatorname{\mathrm{Spa}}(R_n,R_n^+):=\operatorname{\mathrm{Spa}}(C\langle T^{\pm \frac{1}{p^{n}}}\rangle, \mathcal{O}_C\langle T^{\pm\frac{1}{p^{n}}}\rangle)~ (\mbox{respectively } \operatorname{\mathrm{Spa}}(C\langle T^{ \frac{1}{p^{n}}}\rangle, \mathcal{O}_C\langle T^{\frac{1}{p^{n}}}\rangle)),\end{align*} $$
 $$ \begin{align*} Y_{\infty}=\operatorname{\mathrm{Spa}}(R,R^+):=\operatorname{\mathrm{Spa}}(C\langle T^{\pm \frac{1}{p^{\infty}}}\rangle, \mathcal{O}_C\langle T^{\pm\frac{1}{p^{\infty}}}\rangle)~ (\mbox{respectively } \operatorname{\mathrm{Spa}}(C\langle T^{ \frac{1}{p^{\infty}}}\rangle, \mathcal{O}_C\langle T^{\frac{1}{p^{\infty}}}\rangle)).\end{align*} $$
$$ \begin{align*} Y_{\infty}=\operatorname{\mathrm{Spa}}(R,R^+):=\operatorname{\mathrm{Spa}}(C\langle T^{\pm \frac{1}{p^{\infty}}}\rangle, \mathcal{O}_C\langle T^{\pm\frac{1}{p^{\infty}}}\rangle)~ (\mbox{respectively } \operatorname{\mathrm{Spa}}(C\langle T^{ \frac{1}{p^{\infty}}}\rangle, \mathcal{O}_C\langle T^{\frac{1}{p^{\infty}}}\rangle)).\end{align*} $$
This is the example considered in Example 3.1.6. Note that
 $Y_{\infty }\sim \varprojlim _{i\in \mathbb {N}} Y_i$
is a Galois covering of Y and
$Y_{\infty }\sim \varprojlim _{i\in \mathbb {N}} Y_i$
is a Galois covering of Y and
![]() $R^+$
is the p-adic completion of
$R^+$
is the p-adic completion of
 $\varinjlim R^+_n$
. We denote the Galois group by
$\varinjlim R^+_n$
. We denote the Galois group by
![]() $\Gamma $
, which can be identified with
$\Gamma $
, which can be identified with
![]() $\mathbb {Z}_p$
noncanonically. For
$\mathbb {Z}_p$
noncanonically. For
![]() $n\geq m$
, there is the usual trace map
$n\geq m$
, there is the usual trace map
Concretely, it sends
 $T^{\frac {l}{p^k}},(l,p)=1$
to
$T^{\frac {l}{p^k}},(l,p)=1$
to
 $p^{n-m}T^{\frac {l}{p^k}}$
if
$p^{n-m}T^{\frac {l}{p^k}}$
if
![]() $k\leq m$
and
$k\leq m$
and
![]() $0$
otherwise. Clearly,
$0$
otherwise. Clearly,
 $\frac {1}{p^{n-m}}\mathrm {tr}_{Y,n,m}$
are compatible when n varies and extends to a
$\frac {1}{p^{n-m}}\mathrm {tr}_{Y,n,m}$
are compatible when n varies and extends to a
![]() $R_m^+$
-linear map
$R_m^+$
-linear map
 $$ \begin{align*}\overline{\mathrm{tr}}_{Y,m}^+:R^+\to R^+_m,\end{align*} $$
$$ \begin{align*}\overline{\mathrm{tr}}_{Y,m}^+:R^+\to R^+_m,\end{align*} $$
which is a left inverse of the inclusion
![]() $R^+_m\to R^+$
. It commutes with the action of
$R^+_m\to R^+$
. It commutes with the action of
![]() $\Gamma $
as taking traces commutes with the Galois action. Moreover, for any
$\Gamma $
as taking traces commutes with the Galois action. Moreover, for any
![]() $x\in R^+$
,
$x\in R^+$
,
 $$ \begin{align*}\lim_{m\to +\infty}\overline{\mathrm{tr}}_{Y,m}^+(x)=x.\end{align*} $$
$$ \begin{align*}\lim_{m\to +\infty}\overline{\mathrm{tr}}_{Y,m}^+(x)=x.\end{align*} $$
After inverting p, we get a
![]() $R_m$
-linear map
$R_m$
-linear map
![]() $\overline {\mathrm {tr}}_{Y,m} :R\to R_m$
(Tate’s normalised trace). Let
$\overline {\mathrm {tr}}_{Y,m} :R\to R_m$
(Tate’s normalised trace). Let
![]() $\gamma $
be any topological generator of
$\gamma $
be any topological generator of
![]() $p^m\Gamma $
. It is easy to see that
$p^m\Gamma $
. It is easy to see that
![]() $\gamma -1$
is invertible on
$\gamma -1$
is invertible on
![]() $\ker (\overline {\mathrm {tr}}_{Y,m})$
. Moreover, the norm
$\ker (\overline {\mathrm {tr}}_{Y,m})$
. Moreover, the norm
![]() $\|(\gamma -1)^{-1}\|$
on
$\|(\gamma -1)^{-1}\|$
on
![]() $\ker (\overline {\mathrm {tr}}_{Y,m})$
equals
$\ker (\overline {\mathrm {tr}}_{Y,m})$
equals
 $|(\zeta _{p^{m+1}}-1)^{-1}|_p=p^{\frac {1}{p^m(p-1)}}$
, which converges to
$|(\zeta _{p^{m+1}}-1)^{-1}|_p=p^{\frac {1}{p^m(p-1)}}$
, which converges to
![]() $1$
as
$1$
as
![]() $m\to \infty $
.
$m\to \infty $
.
3.2.2. The material here should be a consequence of some general results of Diao–Lan–Liu–Zhu on log affinoid perfectoid spaces. See 5.3 of [Reference Diao, Lan, Liu and ZhuDLLZ19]. For our later applications, we give a more explicit presentation.
Now we base change everything along the map
![]() $X\to Y$
:
$X\to Y$
:
where all of the fibre products are taken in the category of adic spaces over C. We remark that
![]() $X\to Y$
is locally of finite type in the sense of [Reference HuberHub96, Definition 1.2.1] and the fibre product exists by [Reference HuberHub96, Proposition 1.2.2]. All of the fibre products we consider below will exist for the same reason.
$X\to Y$
is locally of finite type in the sense of [Reference HuberHub96, Definition 1.2.1] and the fibre product exists by [Reference HuberHub96, Proposition 1.2.2]. All of the fibre products we consider below will exist for the same reason.

Recall that C is equipped with an non-Archimedean norm
![]() $|\cdot |$
. For any
$|\cdot |$
. For any
![]() $|p|^{c}\in |C^{\times }|\subset \mathbb {R}^{\times }_{\geq 0}$
, we fix a choice of element in C, formally written as
$|p|^{c}\in |C^{\times }|\subset \mathbb {R}^{\times }_{\geq 0}$
, we fix a choice of element in C, formally written as
![]() $p^c$
, with norm
$p^c$
, with norm
![]() $|p|^{c}$
.
$|p|^{c}$
.
Lemma 3.2.3. Let
 $(A_n^+\otimes _{R_n^+} R^+)^{\mathrm {tf},\wedge }$
be the p-adic completion of the p-torsion free quotient of
$(A_n^+\otimes _{R_n^+} R^+)^{\mathrm {tf},\wedge }$
be the p-adic completion of the p-torsion free quotient of
![]() $A_n^+\otimes _{R_n^+} R^+$
.
$A_n^+\otimes _{R_n^+} R^+$
.
-
(1) The natural map
 $(A_n^+\otimes _{R_n^+} R^+)^{\mathrm {tf},\wedge }\to A_{\infty }^+$
is injective and its cokernel is killed by
$(A_n^+\otimes _{R_n^+} R^+)^{\mathrm {tf},\wedge }\to A_{\infty }^+$
is injective and its cokernel is killed by
 $p^{C_n}$
for some constant
$p^{C_n}$
for some constant
 $C_n$
with
$C_n$
with
 $C_n\to 0$
as
$C_n\to 0$
as
 $n\to 0$
.
$n\to 0$
. -
(2)
 $A_{\infty }^+$
is the p-adic completion of
$A_{\infty }^+$
is the p-adic completion of
 $\varinjlim _n A^+_n$
.
$\varinjlim _n A^+_n$
. -
(3)
 $(A_{\infty },A_{\infty }^+)$
is a perfectoid affinoid
$(A_{\infty },A_{\infty }^+)$
is a perfectoid affinoid
 $(C,\mathcal {O}_C)$
-algebra.
$(C,\mathcal {O}_C)$
-algebra.
Proof. As
![]() $X\to Y$
can be written as a composite of rational embeddings and finite étale maps, we may apply Lemma 4.5 of [Reference ScholzeSch13a] here. Strictly speaking, Lemma 4.5 assumes
$X\to Y$
can be written as a composite of rational embeddings and finite étale maps, we may apply Lemma 4.5 of [Reference ScholzeSch13a] here. Strictly speaking, Lemma 4.5 assumes
![]() $Y_n$
is étale over Y, but the same argument works here using that R is a perfectoid C-algebra and
$Y_n$
is étale over Y, but the same argument works here using that R is a perfectoid C-algebra and
![]() $R^+$
is the p-adic completion of
$R^+$
is the p-adic completion of
 $\varinjlim R^+_n$
.
$\varinjlim R^+_n$
.
Hence, we may extend (
![]() $A_m$
-linearly) Tate’s normalised trace
$A_m$
-linearly) Tate’s normalised trace
![]() $\overline {\mathrm {tr}}_{Y,m}$
to
$\overline {\mathrm {tr}}_{Y,m}$
to
![]() $X_{\infty }$
:
$X_{\infty }$
:
which is a continuous
![]() $A_m$
-linear left inverse of the inclusion
$A_m$
-linear left inverse of the inclusion
![]() $A_m\to A_{\infty }$
. Moreover, the image of
$A_m\to A_{\infty }$
. Moreover, the image of
![]() $A_{\infty }^+$
is contained in
$A_{\infty }^+$
is contained in
![]() $p^{-C_m}A_m^+$
for some constant
$p^{-C_m}A_m^+$
for some constant
![]() $C_m$
with
$C_m$
with
![]() $C_m\to 0$
as
$C_m\to 0$
as
![]() $m\to 0$
. For any
$m\to 0$
. For any
![]() $x\in A_{\infty }$
, we still have
$x\in A_{\infty }$
, we still have
 $$ \begin{align*}\lim_{m\to +\infty}\overline{\mathrm{tr}}_{X,m}(x)=x.\end{align*} $$
$$ \begin{align*}\lim_{m\to +\infty}\overline{\mathrm{tr}}_{X,m}(x)=x.\end{align*} $$
Note that
![]() $\Gamma $
acts on
$\Gamma $
acts on
![]() $X_{\infty }$
and commutes with
$X_{\infty }$
and commutes with
![]() $\overline {\mathrm {tr}}_{X,m}$
. For any topological generator
$\overline {\mathrm {tr}}_{X,m}$
. For any topological generator
![]() $\gamma $
of
$\gamma $
of
![]() $p^m\Gamma $
, the action of
$p^m\Gamma $
, the action of
![]() $\gamma -1$
on
$\gamma -1$
on
![]() $\ker (\overline {\mathrm {tr}}_{X,m})$
is invertible. The norm of its inverse
$\ker (\overline {\mathrm {tr}}_{X,m})$
is invertible. The norm of its inverse
![]() $\|(\gamma -1)^{-1}\|$
is bounded by some
$\|(\gamma -1)^{-1}\|$
is bounded by some
![]() $p^{c_m}$
for some constant
$p^{c_m}$
for some constant
![]() $c_m>0$
, and
$c_m>0$
, and
![]() $c_m\to 0$
as
$c_m\to 0$
as
![]() $m\to \infty $
.
$m\to \infty $
.
Remark 3.2.4. These properties of Tate’s normalised trace appear as (TS2), (TS3) in the Tate–Sen conditions formulated by Berger–Colmez; cf. [Reference Berger and ColmezBC08] Définition 3.1.3.
![]() $A_{\infty }$
is a Banach space representation of
$A_{\infty }$
is a Banach space representation of
![]() $\Gamma $
. We can consider its
$\Gamma $
. We can consider its
![]() $\Gamma $
-locally analytic vectors; cf. 2.1.4. The following lemma is a direct consequence of the existence of Tate’s normalised traces. See also Théorème 3.2 of [Reference Berger and ColmezBC16].
$\Gamma $
-locally analytic vectors; cf. 2.1.4. The following lemma is a direct consequence of the existence of Tate’s normalised traces. See also Théorème 3.2 of [Reference Berger and ColmezBC16].
Lemma 3.2.5.
![]() $(A_{\infty })^{p^n\Gamma -\mathrm {an}}=A_n$
for any integer
$(A_{\infty })^{p^n\Gamma -\mathrm {an}}=A_n$
for any integer
![]() $n\geq 0$
. In particular, the subspace of
$n\geq 0$
. In particular, the subspace of
![]() $\,\Gamma $
-locally analytic vectors in
$\,\Gamma $
-locally analytic vectors in
![]() $A_{\infty }$
is
$A_{\infty }$
is
![]() $\bigcup _{n\geq 0}A_n$
.
$\bigcup _{n\geq 0}A_n$
.
Proof. For
![]() $m\geq n$
, as
$m\geq n$
, as
![]() $\overline {\mathrm {tr}}_{X,m}$
is continuous and
$\overline {\mathrm {tr}}_{X,m}$
is continuous and
![]() $\Gamma $
-equivariant, it can be restricted to the
$\Gamma $
-equivariant, it can be restricted to the
![]() $p^n\Gamma $
-analytic vectors
$p^n\Gamma $
-analytic vectors
 $$ \begin{align*}(A_{\infty})^{p^n\Gamma-\mathrm{an}}\xrightarrow{\overline{\mathrm{tr}}_{X,m}} (A_m)^{p^n\Gamma-\mathrm{an}}=(A_m)^{p^n\Gamma}=A_n.\end{align*} $$
$$ \begin{align*}(A_{\infty})^{p^n\Gamma-\mathrm{an}}\xrightarrow{\overline{\mathrm{tr}}_{X,m}} (A_m)^{p^n\Gamma-\mathrm{an}}=(A_m)^{p^n\Gamma}=A_n.\end{align*} $$
Note that the action of
![]() $p^n\Gamma $
on
$p^n\Gamma $
on
![]() $A_m$
is trivial on
$A_m$
is trivial on
![]() $p^m\Gamma $
; hence, the analyticity implies the first equality. Now the lemma follows from
$p^m\Gamma $
; hence, the analyticity implies the first equality. Now the lemma follows from
![]() $\lim _{m\to +\infty }\overline {\mathrm {tr}}_{X,m}(x)=x$
.
$\lim _{m\to +\infty }\overline {\mathrm {tr}}_{X,m}(x)=x$
.
3.2.6. Next we base change the tower
![]() $\{X_n\}_n$
to
$\{X_n\}_n$
to
![]() $\widetilde {X}$
. Suppose
$\widetilde {X}$
. Suppose
![]() $G_0$
is an open subgroup of G. Let
$G_0$
is an open subgroup of G. Let
 $$ \begin{align*}X_{G_0}:=\operatorname{\mathrm{Spa}}(B^{G_0},(B^+)^{G_0})\end{align*} $$
$$ \begin{align*}X_{G_0}:=\operatorname{\mathrm{Spa}}(B^{G_0},(B^+)^{G_0})\end{align*} $$
be the corresponding covering of X. We can take the fibre product in the category of adic spaces over C
 $$ \begin{align*}X^{\prime}_{G_0,n}:=X_{G_0}\times_X X_n=X_{G_0}\times_Y Y_n,\end{align*} $$
$$ \begin{align*}X^{\prime}_{G_0,n}:=X_{G_0}\times_X X_n=X_{G_0}\times_Y Y_n,\end{align*} $$
and take its normalisation
 $$ \begin{align*}X_{G_0,n}=\operatorname{\mathrm{Spa}}(B_{G_0,n},B_{G_0,n}^+).\end{align*} $$
$$ \begin{align*}X_{G_0,n}=\operatorname{\mathrm{Spa}}(B_{G_0,n},B_{G_0,n}^+).\end{align*} $$
Note that by Abhyankar’s lemma for rigid analytic spaces (cf. Lemma 4.2.2, 4.2.3 of [Reference Diao, Lan, Liu and ZhuDLLZ19], which is based on earlier work of Lütkebohmert),
![]() $X_{G_0,n}\to Y_n$
is unramified when n is sufficiently large; hence,
$X_{G_0,n}\to Y_n$
is unramified when n is sufficiently large; hence,
![]() $X_{G_0,n}\to X_n$
is finite étale and
$X_{G_0,n}\to X_n$
is finite étale and
for sufficiently large
![]() $m<n$
. This implies that when n is sufficiently large,
$m<n$
. This implies that when n is sufficiently large,
 $$ \begin{align*}X_{G_0,\infty}=\operatorname{\mathrm{Spa}}(B_{G_0,\infty},B_{G_0,\infty}^+):=X_{G_0,n}\times_{X_n} X_{\infty}=X_{G_0,n}\times_{Y_n} Y_{\infty}\end{align*} $$
$$ \begin{align*}X_{G_0,\infty}=\operatorname{\mathrm{Spa}}(B_{G_0,\infty},B_{G_0,\infty}^+):=X_{G_0,n}\times_{X_n} X_{\infty}=X_{G_0,n}\times_{Y_n} Y_{\infty}\end{align*} $$
is independent of n. Since
![]() $X_{G_0,n}\to Y_n$
can be written as a composite of rational embeddings and finite étale maps, Lemma 3.2.3 still holds in this setting. For example,
$X_{G_0,n}\to Y_n$
can be written as a composite of rational embeddings and finite étale maps, Lemma 3.2.3 still holds in this setting. For example,
 $B_{G_0,\infty }^+$
is the p-adic completion of
$B_{G_0,\infty }^+$
is the p-adic completion of
 $\varinjlim _n B_{G_0,n}^+$
. For sufficiently large n, there exist Tate’s normalised traces
$\varinjlim _n B_{G_0,n}^+$
. For sufficiently large n, there exist Tate’s normalised traces
 $\overline {\mathrm {tr}}_{X_{G_0},n}:B_{G_0,\infty }\to B_{G_0,n}$
with same properties as in the case
$\overline {\mathrm {tr}}_{X_{G_0},n}:B_{G_0,\infty }\to B_{G_0,n}$
with same properties as in the case
![]() $\{X_n\}_n$
. In particular,
$\{X_n\}_n$
. In particular,
![]() $(B_{G_0,\infty })^{p^n\Gamma -\mathrm {an}}=B_{G_0,n}$
for n large enough.
$(B_{G_0,\infty })^{p^n\Gamma -\mathrm {an}}=B_{G_0,n}$
for n large enough.

Suppose
![]() $G^{\prime }_0$
is another open subgroup of G containing
$G^{\prime }_0$
is another open subgroup of G containing
![]() $G_0$
. We have compatible maps
$G_0$
. We have compatible maps
![]() $X_{G_0,n}\to X_{G^{\prime }_0,n}$
which are finite étale when n is sufficiently large. Hence,
$X_{G_0,n}\to X_{G^{\prime }_0,n}$
which are finite étale when n is sufficiently large. Hence,
![]() $X_{G_0,\infty }\to X_{G^{\prime }_0,\infty }$
is a finite étale covering of affinoid perfectoid spaces. Let
$X_{G_0,\infty }\to X_{G^{\prime }_0,\infty }$
is a finite étale covering of affinoid perfectoid spaces. Let
![]() $B_{\infty }^+$
be the p-adic completion of
$B_{\infty }^+$
be the p-adic completion of
 $\varinjlim _{G_0}B_{G_0,\infty }^+$
over all open subgroups
$\varinjlim _{G_0}B_{G_0,\infty }^+$
over all open subgroups
![]() $G_0$
of G and
$G_0$
of G and
 $B_{\infty }=B_{\infty }^+[\frac {1}{p}]$
equipped with the norm induced from
$B_{\infty }=B_{\infty }^+[\frac {1}{p}]$
equipped with the norm induced from
 $B_{G_0,\infty }^+$
. Then
$B_{G_0,\infty }^+$
. Then
![]() $(B_{\infty }, B_{\infty }^+)$
is again an affinoid perfectoid
$(B_{\infty }, B_{\infty }^+)$
is again an affinoid perfectoid
![]() $(C,\mathcal {O}_C)$
-algebra as it is the completion of a direct limit of perfectoid affinoid
$(C,\mathcal {O}_C)$
-algebra as it is the completion of a direct limit of perfectoid affinoid
![]() $(C,\mathcal {O}_C)$
-algebras. We denote
$(C,\mathcal {O}_C)$
-algebras. We denote
![]() $\operatorname {\mathrm {Spa}}(B_{\infty }, B_{\infty }^+)$
by
$\operatorname {\mathrm {Spa}}(B_{\infty }, B_{\infty }^+)$
by
![]() $\widetilde X_{\infty }$
. Note that
$\widetilde X_{\infty }$
. Note that
![]() $\widetilde {X}_{\infty }$
also agrees with the fibre product of
$\widetilde {X}_{\infty }$
also agrees with the fibre product of
 $\tilde {X}=\varprojlim X_{G_0}$
and
$\tilde {X}=\varprojlim X_{G_0}$
and
 $X_{\infty }=\varprojlim X_n$
in the pro-Kummer étale site of X equipped with the natural log structure defined by S; cf. [Reference Diao, Lan, Liu and ZhuDLLZ18].
$X_{\infty }=\varprojlim X_n$
in the pro-Kummer étale site of X equipped with the natural log structure defined by S; cf. [Reference Diao, Lan, Liu and ZhuDLLZ18].
Clearly,
![]() $G\times \Gamma $
acts on
$G\times \Gamma $
acts on
![]() $B_{\infty }^+$
and
$B_{\infty }^+$
and
![]() $B_{\infty }$
. Then it follows from Faltings’s almost purity theorem (cf. [Reference ScholzeSch12, Theorem 7.9 (iii)]) that
$B_{\infty }$
. Then it follows from Faltings’s almost purity theorem (cf. [Reference ScholzeSch12, Theorem 7.9 (iii)]) that
![]() $(B_{\infty }^+/(p))^{G_0}$
almost equals
$(B_{\infty }^+/(p))^{G_0}$
almost equals
 $B^{+}_{G_0,\infty }/(p)$
. Hence,
$B^{+}_{G_0,\infty }/(p)$
. Hence,
![]() $(B_{\infty })^{G_0}=B_{G_0,\infty }$
and
$(B_{\infty })^{G_0}=B_{G_0,\infty }$
and
![]() $(B_{\infty }^+)^{G_0}$
almost equals
$(B_{\infty }^+)^{G_0}$
almost equals
 $B_{G_0,\infty }^+$
.
$B_{G_0,\infty }^+$
.
Proposition 3.2.7.
![]() $B_{\infty }$
satisfies the Tate–Sen conditions formulated by Berger–Colmez in [Reference Berger and ColmezBC08, Définition 3.1.3] with
$B_{\infty }$
satisfies the Tate–Sen conditions formulated by Berger–Colmez in [Reference Berger and ColmezBC08, Définition 3.1.3] with
-
•
 $S=\mathbb {Q}_p$
;
$S=\mathbb {Q}_p$
; -
•
 $\tilde \Lambda =B_{\infty }$
equipped with the valuation induced by its norm;
$\tilde \Lambda =B_{\infty }$
equipped with the valuation induced by its norm; -
•
 $G_0=G\times \Gamma $
,
$G_0=G\times \Gamma $
,
 $H_0=G\times \{1\}$
as a subgroup of
$H_0=G\times \{1\}$
as a subgroup of
 $G\times \Gamma $
;
$G\times \Gamma $
; -
•
 $\Lambda _{H,n}=B_{H,n}, R_{H,n}=\overline {\mathrm {tr}}_{X_H,n}$
for any open subgroup H of
$\Lambda _{H,n}=B_{H,n}, R_{H,n}=\overline {\mathrm {tr}}_{X_H,n}$
for any open subgroup H of
 $H_0=G$
.
$H_0=G$
.
Proof. To see (TS1), for any open subgroups
![]() $H_1\subset H_2$
of G, we know that
$H_1\subset H_2$
of G, we know that
![]() $(B_{\infty })^{H_2}=B_{H_2,\infty }\to (B_{\infty })^{H_1}=B_{H_1,\infty }$
is a finite étale map between perfectoid algebras; hence, by Faltings’s almost purity theorem,
$(B_{\infty })^{H_2}=B_{H_2,\infty }\to (B_{\infty })^{H_1}=B_{H_1,\infty }$
is a finite étale map between perfectoid algebras; hence, by Faltings’s almost purity theorem,
 $B_{H_2,\infty }^+\to B_{H_1,\infty }^+$
is almost finite étale. All of the claims in (TS2), (TS3) are essentially verified in 3.2.2 and the above discussion.
$B_{H_2,\infty }^+\to B_{H_1,\infty }^+$
is almost finite étale. All of the claims in (TS2), (TS3) are essentially verified in 3.2.2 and the above discussion.
Remark 3.2.8. It follows from the definition directly that
![]() $B_{\infty }$
satisfies the Tate–Sen conditions with respect to the action of
$B_{\infty }$
satisfies the Tate–Sen conditions with respect to the action of
![]() $G_0\times \Gamma $
for any open subgroup
$G_0\times \Gamma $
for any open subgroup
![]() $G_0$
of G.
$G_0$
of G.
Lemma 3.2.9.
![]() $(B_{\infty })^{\Gamma }=B$
.
$(B_{\infty })^{\Gamma }=B$
.
Proof. Recall that
![]() $\widetilde {X}=\operatorname {\mathrm {Spa}}(B,B^+)$
is perfectoid and
$\widetilde {X}=\operatorname {\mathrm {Spa}}(B,B^+)$
is perfectoid and
![]() $B^+$
is the p-adic completion of the direct limit
$B^+$
is the p-adic completion of the direct limit
 $\varinjlim _{G_0} B^+_{G_0,0}$
over all open subgroups
$\varinjlim _{G_0} B^+_{G_0,0}$
over all open subgroups
![]() $G_0$
of G. Let n be a positive integer. Note that by our assumption on the ramification-index in Section 3.1.1 and Abhyankar’s lemma (cf. Lemma 4.2.2, 4.2.3 of [Reference Diao, Lan, Liu and ZhuDLLZ19]),
$G_0$
of G. Let n be a positive integer. Note that by our assumption on the ramification-index in Section 3.1.1 and Abhyankar’s lemma (cf. Lemma 4.2.2, 4.2.3 of [Reference Diao, Lan, Liu and ZhuDLLZ19]),
![]() $X_{G_0,n}\to X_{G_0,0}$
is finite étale for sufficiently small
$X_{G_0,n}\to X_{G_0,0}$
is finite étale for sufficiently small
![]() $G_0$
. Hence, for a sufficiently small subgroup
$G_0$
. Hence, for a sufficiently small subgroup
![]() $G_0$
, the fibre product
$G_0$
, the fibre product
 $$ \begin{align*}\widetilde{X}_n=\operatorname{\mathrm{Spa}}(B_n,B_n^+):=\widetilde{X}\times_{X_{G_0,0}} X_{G_0,n}\end{align*} $$
$$ \begin{align*}\widetilde{X}_n=\operatorname{\mathrm{Spa}}(B_n,B_n^+):=\widetilde{X}\times_{X_{G_0,0}} X_{G_0,n}\end{align*} $$
is independent of the choice of
![]() $G_0$
and
$G_0$
and
![]() $\widetilde {X}_n\to \widetilde {X}$
is a finite étale map between affinoid perfectoid spaces. By the same argument as in the proof of Lemma 3.2.3,
$\widetilde {X}_n\to \widetilde {X}$
is a finite étale map between affinoid perfectoid spaces. By the same argument as in the proof of Lemma 3.2.3,
![]() $B^+_n$
is the p-adic completion of
$B^+_n$
is the p-adic completion of
 $\varinjlim _{G_0} B^+_{G_0,n}$
. Hence, it follows from our discussion in Section 3.2.6 that
$\varinjlim _{G_0} B^+_{G_0,n}$
. Hence, it follows from our discussion in Section 3.2.6 that
![]() $B_{\infty }^+$
is the p-adic completion of
$B_{\infty }^+$
is the p-adic completion of
 $\varinjlim _n B^+_n$
. By Faltings’s almost purity theorem, we see that
$\varinjlim _n B^+_n$
. By Faltings’s almost purity theorem, we see that
![]() $(B^+_{\infty })^{\Gamma }$
is almost
$(B^+_{\infty })^{\Gamma }$
is almost
![]() $B^+$
and
$B^+$
and
![]() $(B_{\infty })^{\Gamma }=B$
.
$(B_{\infty })^{\Gamma }=B$
.
3.2.10. Now suppose V is a finite-dimensional continuous representation of G over
![]() $\mathbb {Q}_p$
. We are going to construct a morphism:
$\mathbb {Q}_p$
. We are going to construct a morphism:
![]() $\operatorname {\mathrm {Lie}}(\Gamma )\to \operatorname {\mathrm {End}}_{B_{\infty }}(B_{\infty }\otimes _{\mathbb {Q}_p}V)$
; that is, a Lie algebra representation of
$\operatorname {\mathrm {Lie}}(\Gamma )\to \operatorname {\mathrm {End}}_{B_{\infty }}(B_{\infty }\otimes _{\mathbb {Q}_p}V)$
; that is, a Lie algebra representation of
![]() $\operatorname {\mathrm {Lie}}(\Gamma )$
on
$\operatorname {\mathrm {Lie}}(\Gamma )$
on
![]() $B_{\infty }\otimes _{\mathbb {Q}_p}V$
.
$B_{\infty }\otimes _{\mathbb {Q}_p}V$
.
As G is compact, there exists a G-stable
![]() $\mathbb {Z}_p$
-lattice
$\mathbb {Z}_p$
-lattice
![]() $T\subset V$
. Let
$T\subset V$
. Let
![]() $(B_{\infty })^{\circ }\subset B_{\infty }$
be the subset of power-bounded elements (equivalently elements with spectral norm at most
$(B_{\infty })^{\circ }\subset B_{\infty }$
be the subset of power-bounded elements (equivalently elements with spectral norm at most
![]() $1$
). Note that
$1$
). Note that
![]() $(B_{\infty })^{\circ }\otimes _{\mathbb {Z}_p}T$
carries a diagonal action of G and an action of
$(B_{\infty })^{\circ }\otimes _{\mathbb {Z}_p}T$
carries a diagonal action of G and an action of
![]() $\Gamma $
on the first factor. This defines an action of
$\Gamma $
on the first factor. This defines an action of
![]() $G\times \Gamma $
on
$G\times \Gamma $
on
![]() $(B_{\infty })^{\circ }\otimes _{\mathbb {Z}_p}T$
.
$(B_{\infty })^{\circ }\otimes _{\mathbb {Z}_p}T$
.
Proposition 3.2.11. Fix a constant
 $c<\frac {1}{2}$
inside
$c<\frac {1}{2}$
inside
![]() $|C^{\times }|\subset \mathbb {R}^{\times }_{\geq 0}$
. Suppose
$|C^{\times }|\subset \mathbb {R}^{\times }_{\geq 0}$
. Suppose
![]() $G_0$
is an open subgroup of G acting trivially on
$G_0$
is an open subgroup of G acting trivially on
![]() $T/pT$
. Then there exists a constant
$T/pT$
. Then there exists a constant
![]() $n(G_0)$
, which is independent of T and only depends on c, such that for any integer
$n(G_0)$
, which is independent of T and only depends on c, such that for any integer
![]() $n\geq n(G_0)$
, the tensor product
$n\geq n(G_0)$
, the tensor product
![]() $(B_{\infty })^{\circ }\otimes _{\mathbb {Z}_p}T$
has a unique free
$(B_{\infty })^{\circ }\otimes _{\mathbb {Z}_p}T$
has a unique free
 $B_{G_0,n}^{+}$
-submodule
$B_{G_0,n}^{+}$
-submodule
 $D_{G_0,n}^{+}(T)$
of rank
$D_{G_0,n}^{+}(T)$
of rank
![]() $\dim _{\mathbb {Q}_p}V$
with the following properties:
$\dim _{\mathbb {Q}_p}V$
with the following properties:
-
(1)
 $D_{G_0,n}^{+}(T)$
is fixed by
$D_{G_0,n}^{+}(T)$
is fixed by
 $G_0$
and
$G_0$
and
 $G\times \Gamma $
-stable;
$G\times \Gamma $
-stable; -
(2) the natural morphism
 $(B_{\infty })^{\circ }\otimes _{B_{G_0,n}^{+}} D_{G_0,n}^{+}(T)\to (B_{\infty })^{\circ }\otimes _{\mathbb {Z}_p}T$
is an isomorphism;
$(B_{\infty })^{\circ }\otimes _{B_{G_0,n}^{+}} D_{G_0,n}^{+}(T)\to (B_{\infty })^{\circ }\otimes _{\mathbb {Z}_p}T$
is an isomorphism; -
(3) there exists a basis
 $\mathfrak {B}$
of
$\mathfrak {B}$
of
 $D_{G_0,n}^{+}(T)$
over
$D_{G_0,n}^{+}(T)$
over
 $B_{G_0,n}^{+}$
such that
$B_{G_0,n}^{+}$
such that
 $(\gamma -1)(\mathfrak {B})\subset p^c D_{G_0,n}^{+}(T)$
for any
$(\gamma -1)(\mathfrak {B})\subset p^c D_{G_0,n}^{+}(T)$
for any
 $\gamma \in \Gamma $
;
$\gamma \in \Gamma $
; -
(4)
 $(\gamma -1)^m (D_{G_0,n}^{+}(T))\subset p D_{G_0,n}^{+}(T)$
for any
$(\gamma -1)^m (D_{G_0,n}^{+}(T))\subset p D_{G_0,n}^{+}(T)$
for any
 $\gamma \in \Gamma $
and
$\gamma \in \Gamma $
and
 $m\geq m(c,n)$
, a constant only depending on
$m\geq m(c,n)$
, a constant only depending on
 $c,n$
.
$c,n$
.
Proof. This follows from Proposition 3.3.1 of [Reference Berger and ColmezBC08] by choosing
![]() $c_3=c$
and
$c_3=c$
and
![]() $c_1,c_2$
sufficiently small such that
$c_1,c_2$
sufficiently small such that
![]() $c_1+2c_2+2c_3< 1$
. Note that in our setup, we may choose the constants
$c_1+2c_2+2c_3< 1$
. Note that in our setup, we may choose the constants
![]() $c_1,c_2,c_3$
in the Tate–Sen conditions to be arbitrarily small. The first three parts are the same as [Reference Berger and ColmezBC08, 3.3.1]. The last part is a consequence of the third one.
$c_1,c_2,c_3$
in the Tate–Sen conditions to be arbitrarily small. The first three parts are the same as [Reference Berger and ColmezBC08, 3.3.1]. The last part is a consequence of the third one.
Now we construct an action of
![]() $\operatorname {\mathrm {Lie}}(\Gamma )$
on
$\operatorname {\mathrm {Lie}}(\Gamma )$
on
![]() $B_{\infty }\otimes _{\mathbb {Q}_p}V$
. Choose a constant c, a sufficiently small open subgroup
$B_{\infty }\otimes _{\mathbb {Q}_p}V$
. Choose a constant c, a sufficiently small open subgroup
![]() $G_0$
and
$G_0$
and
![]() $n\geq n(G_0)$
as in the proposition. By Amice’s result (see Example 2.1.9), the last part of the proposition implies that the action of
$n\geq n(G_0)$
as in the proposition. By Amice’s result (see Example 2.1.9), the last part of the proposition implies that the action of
![]() $p^m\Gamma $
on
$p^m\Gamma $
on
 $D_{G_0,n}^{+}(T)\otimes _{\mathbb {Z}_p} \mathbb {Q}_p$
is analytic for sufficiently large m. Thus,
$D_{G_0,n}^{+}(T)\otimes _{\mathbb {Z}_p} \mathbb {Q}_p$
is analytic for sufficiently large m. Thus,
![]() $\operatorname {\mathrm {Lie}}(\Gamma )$
acts on
$\operatorname {\mathrm {Lie}}(\Gamma )$
acts on
 $D_{G_0,n}^{+}(T)\otimes _{\mathbb {Z}_p} \mathbb {Q}_p$
. Since
$D_{G_0,n}^{+}(T)\otimes _{\mathbb {Z}_p} \mathbb {Q}_p$
. Since
![]() $B_{G_0,n}$
is fixed by
$B_{G_0,n}$
is fixed by
![]() $p^n\Gamma $
, this action of
$p^n\Gamma $
, this action of
![]() $\operatorname {\mathrm {Lie}}(\Gamma )$
is
$\operatorname {\mathrm {Lie}}(\Gamma )$
is
![]() $B_{G_0,n}$
-linear. By the second part of the proposition, we may extend it
$B_{G_0,n}$
-linear. By the second part of the proposition, we may extend it
![]() $B_{\infty }$
-linearly to an action of
$B_{\infty }$
-linearly to an action of
![]() $\operatorname {\mathrm {Lie}}(\Gamma )$
on
$\operatorname {\mathrm {Lie}}(\Gamma )$
on
![]() $(B_{\infty })^{\circ }\otimes _{\mathbb {Z}_p}T\otimes \mathbb {Q}_p=B_{\infty }\otimes _{\mathbb {Q}_p}V$
. This action commutes with the action of
$(B_{\infty })^{\circ }\otimes _{\mathbb {Z}_p}T\otimes \mathbb {Q}_p=B_{\infty }\otimes _{\mathbb {Q}_p}V$
. This action commutes with the action of
![]() $G\times \Gamma $
as the two actions commute when restricted to
$G\times \Gamma $
as the two actions commute when restricted to
 $D_{G_0,n}^{+}(T)\otimes \mathbb {Q}_p$
.
$D_{G_0,n}^{+}(T)\otimes \mathbb {Q}_p$
.
Note that the second part of Proposition 3.2.11 implies that
 $$ \begin{align*}(B_{\infty}\otimes_{\mathbb{Q}_p} V)^{G_0}=(B_{\infty})^{G_0}\otimes_{B_{G_0,n}^{+}} D_{G_0,n}^{+}(T)=B_{G_0,\infty}\otimes_{B_{G_0,n}^{+}} D_{G_0,n}^{+}(T).\end{align*} $$
$$ \begin{align*}(B_{\infty}\otimes_{\mathbb{Q}_p} V)^{G_0}=(B_{\infty})^{G_0}\otimes_{B_{G_0,n}^{+}} D_{G_0,n}^{+}(T)=B_{G_0,\infty}\otimes_{B_{G_0,n}^{+}} D_{G_0,n}^{+}(T).\end{align*} $$
Lemma 3.2.12. For any
![]() $m\geq m(c,n)$
, the subspace of
$m\geq m(c,n)$
, the subspace of
![]() $p^m\Gamma $
-analytic vectors in
$p^m\Gamma $
-analytic vectors in
![]() $(B_{\infty }\otimes V)^{G_0}$
is
$(B_{\infty }\otimes V)^{G_0}$
is
 $B_{G_0,m}\otimes _{B_{G_0,n}^{+}} D_{G_0,n}^{+}(T)$
. In particular, the second part of Proposition 3.2.11 implies that there is a natural isomorphism
$B_{G_0,m}\otimes _{B_{G_0,n}^{+}} D_{G_0,n}^{+}(T)$
. In particular, the second part of Proposition 3.2.11 implies that there is a natural isomorphism
 $$ \begin{align*}(B_{\infty}\otimes_{\mathbb{Q}_p}V)^{G_0,p^m\Gamma-\mathrm{an}}\otimes_{B_{G_0,m}}B_{\infty}\cong B_{\infty}\otimes_{\mathbb{Q}_p}V. \end{align*} $$
$$ \begin{align*}(B_{\infty}\otimes_{\mathbb{Q}_p}V)^{G_0,p^m\Gamma-\mathrm{an}}\otimes_{B_{G_0,m}}B_{\infty}\cong B_{\infty}\otimes_{\mathbb{Q}_p}V. \end{align*} $$
Proof. For any
![]() $k\geq m$
, the normalised trace
$k\geq m$
, the normalised trace
 $\overline {\mathrm {tr}}_{X_{G_0},k}:B_{G_0,\infty }\to B_{G_0,k}$
induces a map
$\overline {\mathrm {tr}}_{X_{G_0},k}:B_{G_0,\infty }\to B_{G_0,k}$
induces a map
 $$ \begin{align*}(B_{\infty}\otimes_{\mathbb{Q}_p} V)^{G_0,p^m\Gamma-\mathrm{an}}=(B_{G_0,\infty}\otimes_{B_{G_0,n}^{+}} D_{G_0,n}^{+}(T))^{p^m\Gamma-\mathrm{an}}\to (B_{G_0,k}\otimes_{B_{G_0,n}^{+}} D_{G_0,n}^{+}(T))^{p^m\Gamma-\mathrm{an}}.\end{align*} $$
$$ \begin{align*}(B_{\infty}\otimes_{\mathbb{Q}_p} V)^{G_0,p^m\Gamma-\mathrm{an}}=(B_{G_0,\infty}\otimes_{B_{G_0,n}^{+}} D_{G_0,n}^{+}(T))^{p^m\Gamma-\mathrm{an}}\to (B_{G_0,k}\otimes_{B_{G_0,n}^{+}} D_{G_0,n}^{+}(T))^{p^m\Gamma-\mathrm{an}}.\end{align*} $$
As the action of
![]() $p^m\Gamma $
on
$p^m\Gamma $
on
![]() $B_{G_0,k}$
is trivial on
$B_{G_0,k}$
is trivial on
![]() $p^k\Gamma $
, we have a natural decomposition
$p^k\Gamma $
, we have a natural decomposition
 $$ \begin{align*}B_{G_0,k}=\bigoplus_{\chi: p^m\Gamma/p^k\Gamma\to C^{\times}}B_{G_0,k}[\chi]\end{align*} $$
$$ \begin{align*}B_{G_0,k}=\bigoplus_{\chi: p^m\Gamma/p^k\Gamma\to C^{\times}}B_{G_0,k}[\chi]\end{align*} $$
into the direct sum of
![]() $\chi $
-isotypic components, where
$\chi $
-isotypic components, where
![]() $\chi $
runs through all characters of
$\chi $
runs through all characters of
![]() $p^m\Gamma /p^k\Gamma $
. Note that
$p^m\Gamma /p^k\Gamma $
. Note that
![]() $\chi $
is an analytic function on
$\chi $
is an analytic function on
![]() $p^m\Gamma $
only when
$p^m\Gamma $
only when
![]() $\chi $
is trivial. Hence,
$\chi $
is trivial. Hence,
 $$ \begin{align*}(B_{G_0,k}\otimes_{B_{G_0,n}^{+}} D_{G_0,n}^{+}(T))^{p^m\Gamma-\mathrm{an}}=(B_{G_0,k})^{p^m\Gamma}\otimes_{B_{G_0,n}^{+}} D_{G_0,n}^{+}(T)=B_{G_0,m}\otimes_{B_{G_0,n}^{+}} D_{G_0,n}^{+}(T).\end{align*} $$
$$ \begin{align*}(B_{G_0,k}\otimes_{B_{G_0,n}^{+}} D_{G_0,n}^{+}(T))^{p^m\Gamma-\mathrm{an}}=(B_{G_0,k})^{p^m\Gamma}\otimes_{B_{G_0,n}^{+}} D_{G_0,n}^{+}(T)=B_{G_0,m}\otimes_{B_{G_0,n}^{+}} D_{G_0,n}^{+}(T).\end{align*} $$
The rest of the proof is the same as the one of Lemma 3.2.5.
If
![]() $G_0$
is moreover a normal subgroup of G, we may choose n large enough so that
$G_0$
is moreover a normal subgroup of G, we may choose n large enough so that
![]() $B_{G,n}\to B_{G_0,n}$
is finite étale. Then by Galois descent, there is a
$B_{G,n}\to B_{G_0,n}$
is finite étale. Then by Galois descent, there is a
![]() $\Gamma $
-equivariant isomorphism
$\Gamma $
-equivariant isomorphism
 $$ \begin{align*}(D_{G_0,n}^{+}(T)\otimes_{\mathbb{Z}_p} \mathbb{Q}_p)^G\otimes_{B_{G,n}}B_{G_0,n}=D_{G_0,n}^{+}(T)\otimes_{\mathbb{Z}_p} \mathbb{Q}_p.\end{align*} $$
$$ \begin{align*}(D_{G_0,n}^{+}(T)\otimes_{\mathbb{Z}_p} \mathbb{Q}_p)^G\otimes_{B_{G,n}}B_{G_0,n}=D_{G_0,n}^{+}(T)\otimes_{\mathbb{Z}_p} \mathbb{Q}_p.\end{align*} $$
Let
 $D_{G,n}(V)= (D_{G_0,n}^{+}(T)\otimes _{\mathbb {Z}_p} \mathbb {Q}_p)^G$
. By the second part of Proposition 3.2.11, there is a natural isomorphism
$D_{G,n}(V)= (D_{G_0,n}^{+}(T)\otimes _{\mathbb {Z}_p} \mathbb {Q}_p)^G$
. By the second part of Proposition 3.2.11, there is a natural isomorphism
and one can repeat all of the above discussion with
![]() $G_0$
replaced by G. Hence, we may reformulate the above construction into the following form, which clearly is independent of the choice of
$G_0$
replaced by G. Hence, we may reformulate the above construction into the following form, which clearly is independent of the choice of
![]() $T,c,G_0,n$
.
$T,c,G_0,n$
.
Proposition 3.2.13. For each finite-dimensional continuous representation V of G over
![]() $\mathbb {Q}_p$
, there exists a (necessarily unique)
$\mathbb {Q}_p$
, there exists a (necessarily unique)
![]() $B_{\infty }$
-linear action of
$B_{\infty }$
-linear action of
![]() $\operatorname {\mathrm {Lie}}(\Gamma )$
on
$\operatorname {\mathrm {Lie}}(\Gamma )$
on
![]() $B_{\infty }\otimes _{\mathbb {Q}_p}V$
$B_{\infty }\otimes _{\mathbb {Q}_p}V$
extending the natural action of
![]() $\operatorname {\mathrm {Lie}}(\Gamma )$
on the
$\operatorname {\mathrm {Lie}}(\Gamma )$
on the
![]() $\Gamma $
-locally analytic vectors in
$\Gamma $
-locally analytic vectors in
 $(B_{\infty }\otimes _{\mathbb {Q}_p}V)^G$
. Moreover, it satisfies the following properties:
$(B_{\infty }\otimes _{\mathbb {Q}_p}V)^G$
. Moreover, it satisfies the following properties:
-
(1)
 $\phi _V$
commutes with the action of
$\phi _V$
commutes with the action of
 $G\times \Gamma $
;
$G\times \Gamma $
; -
(2)
 $\phi _V$
is functorial in V; that is, suppose
$\phi _V$
is functorial in V; that is, suppose
 $\psi :V\to W$
is a G-equivariant map between G-representations, then
$\psi :V\to W$
is a G-equivariant map between G-representations, then
 $\mathbf {1}\otimes \psi : B_{\infty }\otimes V\to B_{\infty }\otimes W$
intertwines
$\mathbf {1}\otimes \psi : B_{\infty }\otimes V\to B_{\infty }\otimes W$
intertwines
 $\phi _V$
and
$\phi _V$
and
 $\phi _W$
.
$\phi _W$
. -
(3)
 $\phi _V$
commutes with tensor products; that is, suppose
$\phi _V$
commutes with tensor products; that is, suppose
 $V_1,V_2$
are two finite-dimensional representations of G, then
$V_1,V_2$
are two finite-dimensional representations of G, then
 $\phi _{V_1}\otimes \mathbf {1}+\mathbf {1}\otimes \phi _{V_2}=\phi _{V_1\otimes _{\mathbb {Q}_p}V_2}$
on
$\phi _{V_1}\otimes \mathbf {1}+\mathbf {1}\otimes \phi _{V_2}=\phi _{V_1\otimes _{\mathbb {Q}_p}V_2}$
on
 $(B_{\infty }\otimes _{\mathbb {Q}_p} V_1)\otimes _{B_{\infty }}(B_{\infty }\otimes _{\mathbb {Q}_p} V_2)=B_{\infty }\otimes _{\mathbb {Q}_p}(V_1\otimes _{\mathbb {Q}_p} V_2)$
.
$(B_{\infty }\otimes _{\mathbb {Q}_p} V_1)\otimes _{B_{\infty }}(B_{\infty }\otimes _{\mathbb {Q}_p} V_2)=B_{\infty }\otimes _{\mathbb {Q}_p}(V_1\otimes _{\mathbb {Q}_p} V_2)$
.
Proof. It is easy to check all these properties on the
![]() $\Gamma $
-locally analytic vectors in
$\Gamma $
-locally analytic vectors in
 $(B_{\infty }\otimes _{\mathbb {Q}_p}V)^G$
. We omit the details here.
$(B_{\infty }\otimes _{\mathbb {Q}_p}V)^G$
. We omit the details here.
If we fix a generator of
![]() $\operatorname {\mathrm {Lie}}(\Gamma )$
, then this proposition becomes the form claimed in the beginning of this subsection.
$\operatorname {\mathrm {Lie}}(\Gamma )$
, then this proposition becomes the form claimed in the beginning of this subsection.
Suppose
![]() $G_0$
is an open subgroup of G. As
$G_0$
is an open subgroup of G. As
![]() $B_{\infty }$
satisfies the Tate–Sen conditions with respect to
$B_{\infty }$
satisfies the Tate–Sen conditions with respect to
![]() $G_0\times \Gamma $
(see Remark 3.2.8), Proposition 3.2.13 still holds with all G replaced by
$G_0\times \Gamma $
(see Remark 3.2.8), Proposition 3.2.13 still holds with all G replaced by
![]() $G_0$
. Thus, Proposition 3.2.13 can be generalised as follows.
$G_0$
. Thus, Proposition 3.2.13 can be generalised as follows.
Proposition 3.2.14. For each finite-dimensional continuous representation V of G over
![]() $\mathbb {Q}_p$
, there exists a (necessarily unique)
$\mathbb {Q}_p$
, there exists a (necessarily unique)
![]() $B_{\infty }$
-linear action of
$B_{\infty }$
-linear action of
![]() $\operatorname {\mathrm {Lie}}(\Gamma )$
on
$\operatorname {\mathrm {Lie}}(\Gamma )$
on
![]() $B_{\infty }\otimes _{\mathbb {Q}_p}V$
, extending its natural action on the G-smooth,
$B_{\infty }\otimes _{\mathbb {Q}_p}V$
, extending its natural action on the G-smooth,
![]() $\Gamma $
-locally analytic vectors in
$\Gamma $
-locally analytic vectors in
![]() $B_{\infty }\otimes _{\mathbb {Q}_p}V$
. Here an element in
$B_{\infty }\otimes _{\mathbb {Q}_p}V$
. Here an element in
![]() $B_{\infty }\otimes _{\mathbb {Q}_p}V$
is called G-smooth if it is fixed by some open subgroup of G. Moreover, this action satisfies all three properties as in the previous proposition.
$B_{\infty }\otimes _{\mathbb {Q}_p}V$
is called G-smooth if it is fixed by some open subgroup of G. Moreover, this action satisfies all three properties as in the previous proposition.
Hence, this action of
![]() $\operatorname {\mathrm {Lie}}(\Gamma )$
on
$\operatorname {\mathrm {Lie}}(\Gamma )$
on
![]() $B_{\infty }\otimes _{\mathbb {Q}_p}V$
only depends on the restriction of the representation to any open subgroup of G. As it commutes with
$B_{\infty }\otimes _{\mathbb {Q}_p}V$
only depends on the restriction of the representation to any open subgroup of G. As it commutes with
![]() $\Gamma $
, it induces a B-linear action of
$\Gamma $
, it induces a B-linear action of
![]() $\operatorname {\mathrm {Lie}}(\Gamma )$
on
$\operatorname {\mathrm {Lie}}(\Gamma )$
on
 $(B_{\infty }\otimes _{\mathbb {Q}_p} V)^{\Gamma }=B\otimes _{\mathbb {Q}_p} V$
by Lemma 3.2.9.
$(B_{\infty }\otimes _{\mathbb {Q}_p} V)^{\Gamma }=B\otimes _{\mathbb {Q}_p} V$
by Lemma 3.2.9.
3.3 Proof of the main result I: construction
3.3.1. We will first show that the action in Proposition 3.2.13 factors through
![]() $B\otimes \operatorname {\mathrm {Lie}}(G)$
. As a byproduct, this will imply Theorem 3.1.2. The strategy is to apply Proposition 3.2.13 to
$B\otimes \operatorname {\mathrm {Lie}}(G)$
. As a byproduct, this will imply Theorem 3.1.2. The strategy is to apply Proposition 3.2.13 to
![]() $V=\mathscr {C}^{\mathrm {an}}(G,\mathbb {Q}_p)$
, the space of analytic functions on G. However, as this is an infinite-dimensional vector space over
$V=\mathscr {C}^{\mathrm {an}}(G,\mathbb {Q}_p)$
, the space of analytic functions on G. However, as this is an infinite-dimensional vector space over
![]() $\mathbb {Q}_p$
, it requires a limiting argument plus some extra work.
$\mathbb {Q}_p$
, it requires a limiting argument plus some extra work.
Let
![]() $G_0\subset G$
be a compact open subgroup equipped with an integer-valued, saturated p-valuation as in Section 2.1.1. By Proposition 2.1.3, we may replace
$G_0\subset G$
be a compact open subgroup equipped with an integer-valued, saturated p-valuation as in Section 2.1.1. By Proposition 2.1.3, we may replace
![]() $G_0$
by a smaller subgroup and assume that there is a dense sub-algebra
$G_0$
by a smaller subgroup and assume that there is a dense sub-algebra
 $\varinjlim _{k\in \mathbb {N}} V_k\subset \mathscr {C}^{\mathrm {an}}(G_0,\mathbb {Q}_p)$
, where each
$\varinjlim _{k\in \mathbb {N}} V_k\subset \mathscr {C}^{\mathrm {an}}(G_0,\mathbb {Q}_p)$
, where each
![]() $V_k$
is a finite-dimensional subspace of
$V_k$
is a finite-dimensional subspace of
![]() $\mathscr {C}^{\mathrm {an}}(G_0,\mathbb {Q}_p)$
stable under both the left and right translation actions of
$\mathscr {C}^{\mathrm {an}}(G_0,\mathbb {Q}_p)$
stable under both the left and right translation actions of
![]() $G_0$
. We will always view
$G_0$
. We will always view
![]() $V_k$
as a representation of
$V_k$
as a representation of
![]() $G_0$
using the left translation action.
$G_0$
using the left translation action.
Let
![]() $\mathscr {C}^{\mathrm {an}}(G_0,\mathbb {Q}_p)^o$
be the unit ball of
$\mathscr {C}^{\mathrm {an}}(G_0,\mathbb {Q}_p)^o$
be the unit ball of
![]() $\mathscr {C}^{\mathrm {an}}(G_0,\mathbb {Q}_p)$
with respect to the norm
$\mathscr {C}^{\mathrm {an}}(G_0,\mathbb {Q}_p)$
with respect to the norm
![]() $\|\cdot \|_{G_0}$
(see Section 2.1.1 for the notation here). Then
$\|\cdot \|_{G_0}$
(see Section 2.1.1 for the notation here). Then
is a
![]() $G_0$
-stable lattice. Moreover, it follows from Lemma 2.1.2 that
$G_0$
-stable lattice. Moreover, it follows from Lemma 2.1.2 that
![]() $V_k^o/p$
is fixed by an open subgroup
$V_k^o/p$
is fixed by an open subgroup
![]() $G_1$
of
$G_1$
of
![]() $G_0$
for all k. Now we apply Proposition 3.2.11 to
$G_0$
for all k. Now we apply Proposition 3.2.11 to
![]() $V_k$
, with
$V_k$
, with
![]() $G=G_0$
: fix a constant c as in the proposition and
$G=G_0$
: fix a constant c as in the proposition and
![]() $n\geq n(G_1)$
. There is
$n\geq n(G_1)$
. There is
 $D^+_{G_1,n}(V_k^o)\subset (B_{\infty })^o\otimes V_k^o$
such that
$D^+_{G_1,n}(V_k^o)\subset (B_{\infty })^o\otimes V_k^o$
such that
 $$ \begin{align*}(B_{\infty})^{\circ}\otimes_{B_{G_1,n}^{+}} D_{G_1,n}^{+}(V_k^o)=(B_{\infty})^{\circ}\otimes_{\mathbb{Z}_p}V_k^o.\end{align*} $$
$$ \begin{align*}(B_{\infty})^{\circ}\otimes_{B_{G_1,n}^{+}} D_{G_1,n}^{+}(V_k^o)=(B_{\infty})^{\circ}\otimes_{\mathbb{Z}_p}V_k^o.\end{align*} $$
By the uniqueness of
 $D_{G_1,n}^{+}(V_k^o)$
, these
$D_{G_1,n}^{+}(V_k^o)$
, these
 $\{D_{G_1,n}^{+}(V_k^o)\}_k$
form a direct system. Hence, we may take the direct limit of this equality over k:
$\{D_{G_1,n}^{+}(V_k^o)\}_k$
form a direct system. Hence, we may take the direct limit of this equality over k:
 $$ \begin{align*}(B_{\infty})^{\circ}\otimes_{B_{G_1,n}^{+}} \varinjlim_k D_{G_1,n}^{+}(V_k^o)=(B_{\infty})^{\circ}\otimes_{\mathbb{Z}_p}\varinjlim_k V_k^o.\end{align*} $$
$$ \begin{align*}(B_{\infty})^{\circ}\otimes_{B_{G_1,n}^{+}} \varinjlim_k D_{G_1,n}^{+}(V_k^o)=(B_{\infty})^{\circ}\otimes_{\mathbb{Z}_p}\varinjlim_k V_k^o.\end{align*} $$
By taking the p-adic completion and inverting p, we obtain
 $$ \begin{align*}B_{\infty}\widehat{\otimes}_{B_{G_1,n}} D_{G_1,n}=B_{\infty}\widehat{\otimes}_{\mathbb{Q}_p}\mathscr{C}^{\mathrm{an}}(G_0,\mathbb{Q}_p).\end{align*} $$
$$ \begin{align*}B_{\infty}\widehat{\otimes}_{B_{G_1,n}} D_{G_1,n}=B_{\infty}\widehat{\otimes}_{\mathbb{Q}_p}\mathscr{C}^{\mathrm{an}}(G_0,\mathbb{Q}_p).\end{align*} $$
Here
 $D^+_{G_1,n}$
is the p-adic completion of
$D^+_{G_1,n}$
is the p-adic completion of
 $\varinjlim _k D_{G_1,n}^{+}(V_k^o)$
and
$\varinjlim _k D_{G_1,n}^{+}(V_k^o)$
and
 $D_{G_1,n}=D^+_{G_1,n}\otimes _{\mathbb {Z}_p}\mathbb {Q}_p$
equipped with the p-adic topology. The right-hand side becomes
$D_{G_1,n}=D^+_{G_1,n}\otimes _{\mathbb {Z}_p}\mathbb {Q}_p$
equipped with the p-adic topology. The right-hand side becomes
![]() $\mathscr {C}^{\mathrm {an}}(G_0,\mathbb {Q}_p)$
as
$\mathscr {C}^{\mathrm {an}}(G_0,\mathbb {Q}_p)$
as
 $\varinjlim _k V_k$
is dense inside of it.
$\varinjlim _k V_k$
is dense inside of it.
Now we can construct an action of
![]() $\operatorname {\mathrm {Lie}}(\Gamma )$
as before: there is an integer
$\operatorname {\mathrm {Lie}}(\Gamma )$
as before: there is an integer
![]() $m\geq 0$
such that
$m\geq 0$
such that
 $(\gamma -1)^mD^+_{G_1,n}(V_k^o)\subset pD^+_{G_1,n}(V_k^o)$
for all
$(\gamma -1)^mD^+_{G_1,n}(V_k^o)\subset pD^+_{G_1,n}(V_k^o)$
for all
![]() $k\geq 0$
and
$k\geq 0$
and
![]() $\gamma \in \Gamma $
. Hence,
$\gamma \in \Gamma $
. Hence,
 $$ \begin{align*}(\gamma-1)^mD^+_{G_1,n}\subset pD^+_{G_1,n}\end{align*} $$
$$ \begin{align*}(\gamma-1)^mD^+_{G_1,n}\subset pD^+_{G_1,n}\end{align*} $$
for any
![]() $\gamma \in \Gamma $
. By Example 2.1.9, the action of
$\gamma \in \Gamma $
. By Example 2.1.9, the action of
![]() $\Gamma $
on
$\Gamma $
on
![]() $D_{G_1,n}$
is locally analytic. Its Lie algebra action can be extended
$D_{G_1,n}$
is locally analytic. Its Lie algebra action can be extended
![]() $B_{\infty }$
-linearly to an action on
$B_{\infty }$
-linearly to an action on
 $B_{\infty }\widehat {\otimes }_{B_{G_1,n}} D_{G_1,n}=B_{\infty }\widehat {\otimes }_{\mathbb {Q}_p}\mathscr {C}^{\mathrm {an}}(G_0,\mathbb {Q}_p)$
:
$B_{\infty }\widehat {\otimes }_{B_{G_1,n}} D_{G_1,n}=B_{\infty }\widehat {\otimes }_{\mathbb {Q}_p}\mathscr {C}^{\mathrm {an}}(G_0,\mathbb {Q}_p)$
:
 $$ \begin{align*}\phi_{G_0}:\operatorname{\mathrm{Lie}}(\Gamma)\to\operatorname{\mathrm{End}}_{B_{\infty}}(B_{\infty}\widehat{\otimes}_{\mathbb{Q}_p}\mathscr{C}^{\mathrm{an}}(G_0,\mathbb{Q}_p)).\end{align*} $$
$$ \begin{align*}\phi_{G_0}:\operatorname{\mathrm{Lie}}(\Gamma)\to\operatorname{\mathrm{End}}_{B_{\infty}}(B_{\infty}\widehat{\otimes}_{\mathbb{Q}_p}\mathscr{C}^{\mathrm{an}}(G_0,\mathbb{Q}_p)).\end{align*} $$
Again this action uniquely extends the natural action of
![]() $\operatorname {\mathrm {Lie}}(\Gamma )$
on the
$\operatorname {\mathrm {Lie}}(\Gamma )$
on the
![]() $\Gamma $
-locally analytic vectors in
$\Gamma $
-locally analytic vectors in
 $(B_{\infty }\widehat {\otimes }_{\mathbb {Q}_p}\mathscr {C}^{\mathrm {an}}(G_0,\mathbb {Q}_p))^{G_0}$
, where
$(B_{\infty }\widehat {\otimes }_{\mathbb {Q}_p}\mathscr {C}^{\mathrm {an}}(G_0,\mathbb {Q}_p))^{G_0}$
, where
![]() $G_0$
acts diagonally on
$G_0$
acts diagonally on
![]() $B_{\infty }$
and
$B_{\infty }$
and
![]() $\mathscr {C}^{\mathrm {an}}(G_0,\mathbb {Q}_p)$
. In fact, let
$\mathscr {C}^{\mathrm {an}}(G_0,\mathbb {Q}_p)$
. In fact, let
 $D_{G_0,n}^{+}=(D_{G_1,n}^{+})^{G_0}$
and
$D_{G_0,n}^{+}=(D_{G_1,n}^{+})^{G_0}$
and
 $D_{G_0,n}=(D_{G_1,n})^{G_0}=D_{G_0,n}^{+}\otimes _{\mathbb {Z}_p}{\mathbb {Q}_p}$
. Then by arguments similar to Lemma 3.2.12 and the paragraph below it, we have the following lemma.
$D_{G_0,n}=(D_{G_1,n})^{G_0}=D_{G_0,n}^{+}\otimes _{\mathbb {Z}_p}{\mathbb {Q}_p}$
. Then by arguments similar to Lemma 3.2.12 and the paragraph below it, we have the following lemma.
Lemma 3.3.2. For n sufficiently large,
![]() $D_{G_0,n}$
is the subspace of
$D_{G_0,n}$
is the subspace of
![]() $p^n\Gamma $
-analytic vectors in
$p^n\Gamma $
-analytic vectors in
 $(B_{\infty }\widehat {\otimes }_{\mathbb {Q}_p}\mathscr {C}^{\mathrm {an}}(G_0,\mathbb {Q}_p))^{G_0}=(B_{\infty })^{G_0-\mathrm {an}}$
, and
$(B_{\infty }\widehat {\otimes }_{\mathbb {Q}_p}\mathscr {C}^{\mathrm {an}}(G_0,\mathbb {Q}_p))^{G_0}=(B_{\infty })^{G_0-\mathrm {an}}$
, and
 $B_{\infty }\widehat {\otimes }_{B_{G_0,n}} D_{G_0,n}=B_{\infty }\widehat {\otimes }_{\mathbb {Q}_p}\mathscr {C}^{\mathrm {an}}(G_0,\mathbb {Q}_p)$
.
$B_{\infty }\widehat {\otimes }_{B_{G_0,n}} D_{G_0,n}=B_{\infty }\widehat {\otimes }_{\mathbb {Q}_p}\mathscr {C}^{\mathrm {an}}(G_0,\mathbb {Q}_p)$
.
The action of
![]() $\operatorname {\mathrm {Lie}}(\Gamma )$
via
$\operatorname {\mathrm {Lie}}(\Gamma )$
via
![]() $\phi _{G_0}$
commutes with
$\phi _{G_0}$
commutes with
![]() $\Gamma $
as both actions commute on
$\Gamma $
as both actions commute on
![]() $D_{G_1,n}$
. Moreover, it follows from the functorial property of
$D_{G_1,n}$
. Moreover, it follows from the functorial property of
![]() $\phi _{V_k}$
in Proposition 3.2.13 that the action of
$\phi _{V_k}$
in Proposition 3.2.13 that the action of
![]() $\operatorname {\mathrm {Lie}}(\Gamma )$
on
$\operatorname {\mathrm {Lie}}(\Gamma )$
on
 $D_{G_1,n}^{+}(V_k^o)\otimes \mathbb {Q}_p$
commutes with the right translation action of
$D_{G_1,n}^{+}(V_k^o)\otimes \mathbb {Q}_p$
commutes with the right translation action of
![]() $G_0$
. By passing to the limit, we see that
$G_0$
. By passing to the limit, we see that
![]() $\phi _{G_0}$
also commutes with the right translation action of
$\phi _{G_0}$
also commutes with the right translation action of
![]() $G_0$
. Recall that the multiplication structure on
$G_0$
. Recall that the multiplication structure on
![]() $\mathscr {C}^{\mathrm {an}}(G_0,\mathbb {Q}_p)$
induces maps
$\mathscr {C}^{\mathrm {an}}(G_0,\mathbb {Q}_p)$
induces maps
![]() $V_k\otimes V_l\to V_{k+l}$
; cf. Proposition 2.1.3. Hence, the last part of Proposition 3.2.13 implies that for any
$V_k\otimes V_l\to V_{k+l}$
; cf. Proposition 2.1.3. Hence, the last part of Proposition 3.2.13 implies that for any
![]() $\theta \in \phi _{G_0}(\operatorname {\mathrm {Lie}}(\Gamma )), f_1,f_2\in \mathscr {C}^{\mathrm {an}}(G_0,\mathbb {Q}_p)$
,
$\theta \in \phi _{G_0}(\operatorname {\mathrm {Lie}}(\Gamma )), f_1,f_2\in \mathscr {C}^{\mathrm {an}}(G_0,\mathbb {Q}_p)$
,
that is,
![]() $\theta $
is a derivation. Hence, we have proved the following.
$\theta $
is a derivation. Hence, we have proved the following.
Proposition 3.3.3.
![]() $\phi _{G_0}(x)$
acts as a
$\phi _{G_0}(x)$
acts as a
![]() $G_0$
-right-invariant derivation on
$G_0$
-right-invariant derivation on
 $B_{\infty }\widehat {\otimes }_{\mathbb {Q}_p}\mathscr {C}^{\mathrm {an}}(G_0,\mathbb {Q}_p)$
for any
$B_{\infty }\widehat {\otimes }_{\mathbb {Q}_p}\mathscr {C}^{\mathrm {an}}(G_0,\mathbb {Q}_p)$
for any
![]() $x\in \operatorname {\mathrm {Lie}}(\Gamma )$
. Moreover, it commutes with
$x\in \operatorname {\mathrm {Lie}}(\Gamma )$
. Moreover, it commutes with
![]() $\Gamma $
.
$\Gamma $
.
Corollary 3.3.4.
![]() $\phi _{G_0}$
factors through
$\phi _{G_0}$
factors through
 $B\otimes _{\mathbb {Q}_p}\operatorname {\mathrm {Lie}}(G_0)\subset \operatorname {\mathrm {End}}_{B_{\infty }}(B_{\infty }\widehat {\otimes }_{\mathbb {Q}_p}\mathscr {C}^{\mathrm {an}}(G_0,\mathbb {Q}_p))$
. Here
$B\otimes _{\mathbb {Q}_p}\operatorname {\mathrm {Lie}}(G_0)\subset \operatorname {\mathrm {End}}_{B_{\infty }}(B_{\infty }\widehat {\otimes }_{\mathbb {Q}_p}\mathscr {C}^{\mathrm {an}}(G_0,\mathbb {Q}_p))$
. Here
![]() $\operatorname {\mathrm {Lie}}(G_0)$
acts on
$\operatorname {\mathrm {Lie}}(G_0)$
acts on
![]() $\mathscr {C}^{\mathrm {an}}(G_0,\mathbb {Q}_p)$
by the infinitesimal action of the left translation of
$\mathscr {C}^{\mathrm {an}}(G_0,\mathbb {Q}_p)$
by the infinitesimal action of the left translation of
![]() $G_0$
, and we extend it
$G_0$
, and we extend it
![]() $B_{\infty }$
-linearly to an action of
$B_{\infty }$
-linearly to an action of
![]() $B\otimes _{\mathbb {Q}_p}\operatorname {\mathrm {Lie}}(G_0)$
on
$B\otimes _{\mathbb {Q}_p}\operatorname {\mathrm {Lie}}(G_0)$
on
 $B_{\infty }\widehat {\otimes }_{\mathbb {Q}_p}\mathscr {C}^{\mathrm {an}}(G_0,\mathbb {Q}_p)$
.
$B_{\infty }\widehat {\otimes }_{\mathbb {Q}_p}\mathscr {C}^{\mathrm {an}}(G_0,\mathbb {Q}_p)$
.
Proof. Clearly,
![]() $\phi _{G_0}$
factors through
$\phi _{G_0}$
factors through
![]() $B_{\infty }\otimes _{\mathbb {Q}_p}\operatorname {\mathrm {Lie}}(G_0)$
. As it commutes with
$B_{\infty }\otimes _{\mathbb {Q}_p}\operatorname {\mathrm {Lie}}(G_0)$
. As it commutes with
![]() $\Gamma $
, it also factors through
$\Gamma $
, it also factors through
 $(B_{\infty }\otimes _{\mathbb {Q}_p}\operatorname {\mathrm {Lie}}(G_0))^{\Gamma }=B\otimes _{\mathbb {Q}_p}\operatorname {\mathrm {Lie}}(G_0)$
by Lemma 3.2.9.
$(B_{\infty }\otimes _{\mathbb {Q}_p}\operatorname {\mathrm {Lie}}(G_0))^{\Gamma }=B\otimes _{\mathbb {Q}_p}\operatorname {\mathrm {Lie}}(G_0)$
by Lemma 3.2.9.
By abuse of notation, we also denote by
![]() $\phi _{G_0}:\operatorname {\mathrm {Lie}}(\Gamma )\to B\otimes _{\mathbb {Q}_p}\operatorname {\mathrm {Lie}}(G_0)$
. Suppose we replace
$\phi _{G_0}:\operatorname {\mathrm {Lie}}(\Gamma )\to B\otimes _{\mathbb {Q}_p}\operatorname {\mathrm {Lie}}(G_0)$
. Suppose we replace
![]() $G_0$
by a smaller subgroup
$G_0$
by a smaller subgroup
![]() $G_0'$
and consider the restriction of
$G_0'$
and consider the restriction of
![]() $\mathscr {C}^{\mathrm {an}}(G_0,\mathbb {Q}_p)\to \mathscr {C}^{\mathrm {an}}(G_0',\mathbb {Q}_p)$
. It is easy to see that
$\mathscr {C}^{\mathrm {an}}(G_0,\mathbb {Q}_p)\to \mathscr {C}^{\mathrm {an}}(G_0',\mathbb {Q}_p)$
. It is easy to see that
![]() $\phi _{G_0}=\phi _{G_0'}$
once we identify
$\phi _{G_0}=\phi _{G_0'}$
once we identify
![]() $\operatorname {\mathrm {Lie}}(G_0)=\operatorname {\mathrm {Lie}}(G)=\operatorname {\mathrm {Lie}}(G_0')$
. Hence,
$\operatorname {\mathrm {Lie}}(G_0)=\operatorname {\mathrm {Lie}}(G)=\operatorname {\mathrm {Lie}}(G_0')$
. Hence,
![]() $\phi _{G_0}$
is independent of the choice of
$\phi _{G_0}$
is independent of the choice of
![]() $G_0$
and we denote it by
$G_0$
and we denote it by
Corollary 3.3.5. The image of
![]() $\phi _{\widetilde {X}}$
acts trivially on the G-locally analytic vectors in B.
$\phi _{\widetilde {X}}$
acts trivially on the G-locally analytic vectors in B.
Proof. Recall that (see Section 2.1.1)
 $$ \begin{align*}B^{G_0-\mathrm{an}}=(B\widehat{\otimes}_{\mathbb{Q}_p}\mathscr{C}^{\mathrm{an}}(G_0,\mathbb{Q}_p))^{G_0}=(B_{\infty}\widehat{\otimes}_{\mathbb{Q}_p}\mathscr{C}^{\mathrm{an}}(G_0,\mathbb{Q}_p))^{G_0\times\Gamma},\end{align*} $$
$$ \begin{align*}B^{G_0-\mathrm{an}}=(B\widehat{\otimes}_{\mathbb{Q}_p}\mathscr{C}^{\mathrm{an}}(G_0,\mathbb{Q}_p))^{G_0}=(B_{\infty}\widehat{\otimes}_{\mathbb{Q}_p}\mathscr{C}^{\mathrm{an}}(G_0,\mathbb{Q}_p))^{G_0\times\Gamma},\end{align*} $$
where the second equality follows from Lemma 3.2.9. Hence, by our construction of
![]() $\phi _{G_0}$
, the action of
$\phi _{G_0}$
, the action of
![]() $\operatorname {\mathrm {Lie}}(\Gamma )$
is trivial on
$\operatorname {\mathrm {Lie}}(\Gamma )$
is trivial on
![]() $B^{G_0-\mathrm {an}}$
. An easy computation shows that this action is nothing but
$B^{G_0-\mathrm {an}}$
. An easy computation shows that this action is nothing but
![]() $\phi _{\widetilde {X}}$
. Note that this argument works for all sufficiently small
$\phi _{\widetilde {X}}$
. Note that this argument works for all sufficiently small
![]() $G_0$
, which clearly implies the claim in the corollary.
$G_0$
, which clearly implies the claim in the corollary.
Now if we fix a generator of
![]() $\operatorname {\mathrm {Lie}}(\Gamma )$
and denote by
$\operatorname {\mathrm {Lie}}(\Gamma )$
and denote by
![]() $\theta _{\widetilde {X}}$
its image in
$\theta _{\widetilde {X}}$
its image in
![]() $B\otimes _{\mathbb {Q}_p}\operatorname {\mathrm {Lie}}(G)$
under
$B\otimes _{\mathbb {Q}_p}\operatorname {\mathrm {Lie}}(G)$
under
![]() $\phi _{\widetilde {X}}$
, then we obtain the form claimed in the first part of Theorem 3.1.2.
$\phi _{\widetilde {X}}$
, then we obtain the form claimed in the first part of Theorem 3.1.2.
Our next result implies that
![]() $\phi _{\widetilde {X}}$
is universal. Let V be a finite-dimensional representation of G over
$\phi _{\widetilde {X}}$
is universal. Let V be a finite-dimensional representation of G over
![]() $\mathbb {Q}_p$
. The action of G on V is locally analytic; hence, there is a natural
$\mathbb {Q}_p$
. The action of G on V is locally analytic; hence, there is a natural
![]() $B_{\infty }$
-linear action of
$B_{\infty }$
-linear action of
![]() $B_{\infty }\otimes _{\mathbb {Q}_p}\operatorname {\mathrm {Lie}}(G)$
on
$B_{\infty }\otimes _{\mathbb {Q}_p}\operatorname {\mathrm {Lie}}(G)$
on
![]() $B_{\infty }\otimes _{\mathbb {Q}_p}V$
. Therefore,
$B_{\infty }\otimes _{\mathbb {Q}_p}V$
. Therefore,
![]() $\phi _{\widetilde {X}}$
gives an action of
$\phi _{\widetilde {X}}$
gives an action of
![]() $\operatorname {\mathrm {Lie}}(\Gamma )$
on
$\operatorname {\mathrm {Lie}}(\Gamma )$
on
![]() $B_{\infty }\otimes _{\mathbb {Q}_p}V$
. On the other hand, we defined another action of
$B_{\infty }\otimes _{\mathbb {Q}_p}V$
. On the other hand, we defined another action of
![]() $\operatorname {\mathrm {Lie}}(\Gamma )$
called
$\operatorname {\mathrm {Lie}}(\Gamma )$
called
![]() $\phi _V$
in Proposition 3.2.13.
$\phi _V$
in Proposition 3.2.13.
Corollary 3.3.6.
![]() $\phi _V$
agrees with
$\phi _V$
agrees with
![]() $\phi _{\widetilde {X}}$
for any V.
$\phi _{\widetilde {X}}$
for any V.
Proof. Let
![]() $G_0$
be a sufficiently small open subgroup of G as in the beginning of Section 3.3.1. Moreover, we may assume V is a
$G_0$
be a sufficiently small open subgroup of G as in the beginning of Section 3.3.1. Moreover, we may assume V is a
![]() $G_0$
-analytic representation. Let
$G_0$
-analytic representation. Let
![]() $V^*$
be the dual vector space of V. Then taking the matrix coefficients of V induces a map
$V^*$
be the dual vector space of V. Then taking the matrix coefficients of V induces a map
This map is
![]() $G_0$
-equivariant where
$G_0$
-equivariant where
![]() $G_0$
acts only on the first factor of
$G_0$
acts only on the first factor of
![]() $V\otimes V^*$
and acts via the left translation on
$V\otimes V^*$
and acts via the left translation on
![]() $\mathscr {C}^{\mathrm {an}}(G_0,\mathbb {Q}_p)$
. The induced map
$\mathscr {C}^{\mathrm {an}}(G_0,\mathbb {Q}_p)$
. The induced map
 $$ \begin{align*}\mathbf{1}_{B_{\infty}}\otimes m_V:B_{\infty}\otimes_{\mathbb{Q}_p}V\otimes_{\mathbb{Q}_p}V^*\to B_{\infty}\widehat{\otimes}_{\mathbb{Q}_p}\mathscr{C}^{\mathrm{an}}(G_0,\mathbb{Q}_p)\end{align*} $$
$$ \begin{align*}\mathbf{1}_{B_{\infty}}\otimes m_V:B_{\infty}\otimes_{\mathbb{Q}_p}V\otimes_{\mathbb{Q}_p}V^*\to B_{\infty}\widehat{\otimes}_{\mathbb{Q}_p}\mathscr{C}^{\mathrm{an}}(G_0,\mathbb{Q}_p)\end{align*} $$
intertwines
![]() $\phi _{V\otimes V^*}=\phi _V\otimes \mathbf {1}_{V^*}$
and
$\phi _{V\otimes V^*}=\phi _V\otimes \mathbf {1}_{V^*}$
and
![]() $\phi _{G_0}=\phi _{\widetilde {X}}$
. One can check this on the
$\phi _{G_0}=\phi _{\widetilde {X}}$
. One can check this on the
![]() $G_0$
-fixed,
$G_0$
-fixed,
![]() $\Gamma $
-locally analytic vectors. Trivially, this map also intertwines
$\Gamma $
-locally analytic vectors. Trivially, this map also intertwines
![]() $\phi _{\widetilde {X}}\otimes \mathbf {1}_{V^*}$
and
$\phi _{\widetilde {X}}\otimes \mathbf {1}_{V^*}$
and
![]() $\phi _{\widetilde {X}}$
. Now for any nonzero
$\phi _{\widetilde {X}}$
. Now for any nonzero
![]() $v\in V$
, there exists
$v\in V$
, there exists
![]() $l\in V^*$
such that
$l\in V^*$
such that
![]() $m_V(v\otimes l)\neq 0$
. From this, it is easy to see that
$m_V(v\otimes l)\neq 0$
. From this, it is easy to see that
![]() $\phi _V$
has to factor through
$\phi _V$
has to factor through
![]() $\phi _{\widetilde {X}}$
.
$\phi _{\widetilde {X}}$
.
Remark 3.3.7. This corollary gives a ‘practical way’ to compute
![]() $\phi _{\widetilde {X}}$
: choose a faithful representation V of an open subgroup of G. Then
$\phi _{\widetilde {X}}$
: choose a faithful representation V of an open subgroup of G. Then
![]() $\phi _V$
completely determines
$\phi _V$
completely determines
![]() $\phi _{\widetilde {X}}$
.
$\phi _{\widetilde {X}}$
.
Remark 3.3.8.
![]() $B\otimes _{\mathbb {Q}_p}\operatorname {\mathrm {Lie}}(G)$
acts naturally on the G-locally analytic vectors
$B\otimes _{\mathbb {Q}_p}\operatorname {\mathrm {Lie}}(G)$
acts naturally on the G-locally analytic vectors
 $(B\otimes _{\mathbb {Q}_p} V)^{\mathrm {la}}$
of
$(B\otimes _{\mathbb {Q}_p} V)^{\mathrm {la}}$
of
![]() $B\otimes _{\mathbb {Q}_p} V$
. Hence,
$B\otimes _{\mathbb {Q}_p} V$
. Hence,
![]() $\phi _{\widetilde {X}}:\operatorname {\mathrm {Lie}}(\Gamma )\to B\otimes _{\mathbb {Q}_p}\operatorname {\mathrm {Lie}}(G)$
induces an action of
$\phi _{\widetilde {X}}:\operatorname {\mathrm {Lie}}(\Gamma )\to B\otimes _{\mathbb {Q}_p}\operatorname {\mathrm {Lie}}(G)$
induces an action of
![]() $\operatorname {\mathrm {Lie}}(\Gamma )$
on
$\operatorname {\mathrm {Lie}}(\Gamma )$
on
 $(B\otimes _{\mathbb {Q}_p} V)^{\mathrm {la}}$
. Combining Corollaries 3.3.5 and 3.3.6, it is easy to see that this action is nothing but
$(B\otimes _{\mathbb {Q}_p} V)^{\mathrm {la}}$
. Combining Corollaries 3.3.5 and 3.3.6, it is easy to see that this action is nothing but
![]() $\phi _V$
.
$\phi _V$
.
Corollary 3.3.9.
![]() $\phi _{\widetilde {X}}$
is functorial in the pair
$\phi _{\widetilde {X}}$
is functorial in the pair
![]() $(B,G)$
; that is, suppose that H is a closed normal subgroup of G such that
$(B,G)$
; that is, suppose that H is a closed normal subgroup of G such that
![]() $\widetilde {X}'=\operatorname {\mathrm {Spa}}(B^H,(B^+)^H)$
is a ‘log
$\widetilde {X}'=\operatorname {\mathrm {Spa}}(B^H,(B^+)^H)$
is a ‘log
![]() $G/H$
-Galois pro-étale perfectoid covering’ of X as in 3.1.1, then
$G/H$
-Galois pro-étale perfectoid covering’ of X as in 3.1.1, then
 $\phi _{\widetilde {X}'}:\operatorname {\mathrm {Lie}}(\Gamma )\to B^H\otimes _{\mathbb {Q}_p}\operatorname {\mathrm {Lie}}(G/H)\subset B\otimes _{\mathbb {Q}_p}\operatorname {\mathrm {Lie}}(G/H)$
can be identified with the composite
$\phi _{\widetilde {X}'}:\operatorname {\mathrm {Lie}}(\Gamma )\to B^H\otimes _{\mathbb {Q}_p}\operatorname {\mathrm {Lie}}(G/H)\subset B\otimes _{\mathbb {Q}_p}\operatorname {\mathrm {Lie}}(G/H)$
can be identified with the composite
 $$ \begin{align*}\operatorname{\mathrm{Lie}}(\Gamma)\xrightarrow{\phi_{\widetilde{X}}} B\otimes_{\mathbb{Q}_p}\operatorname{\mathrm{Lie}}(G)\xrightarrow{\mod B\otimes_{\mathbb{Q}_p}\operatorname{\mathrm{Lie}}(H)}B\otimes_{\mathbb{Q}_p}\operatorname{\mathrm{Lie}}(G/H).\end{align*} $$
$$ \begin{align*}\operatorname{\mathrm{Lie}}(\Gamma)\xrightarrow{\phi_{\widetilde{X}}} B\otimes_{\mathbb{Q}_p}\operatorname{\mathrm{Lie}}(G)\xrightarrow{\mod B\otimes_{\mathbb{Q}_p}\operatorname{\mathrm{Lie}}(H)}B\otimes_{\mathbb{Q}_p}\operatorname{\mathrm{Lie}}(G/H).\end{align*} $$
Proof. It is enough to check that the formulation of
![]() $\phi _V$
in Proposition 3.2.13 is functorial in a similar sense. But this basically follows from the construction. We omit the details here.
$\phi _V$
in Proposition 3.2.13 is functorial in a similar sense. But this basically follows from the construction. We omit the details here.
We mention the following results concerning the uniqueness of our differential equation. Note that
![]() $\widetilde {X}_{\infty }=\operatorname {\mathrm {Spa}}(B_{\infty },B_{\infty }^+)$
is a ‘log
$\widetilde {X}_{\infty }=\operatorname {\mathrm {Spa}}(B_{\infty },B_{\infty }^+)$
is a ‘log
![]() $G\times \Gamma $
-Galois pro-étale perfectoid covering’ of X. Let
$G\times \Gamma $
-Galois pro-étale perfectoid covering’ of X. Let
![]() $B_{\infty }^{\mathrm {la}}$
be the
$B_{\infty }^{\mathrm {la}}$
be the
![]() $G\times \Gamma $
-locally analytic vectors in
$G\times \Gamma $
-locally analytic vectors in
![]() $B_{\infty }$
.
$B_{\infty }$
.
Proposition 3.3.10. If
![]() $D\in B_{\infty }\otimes _{\mathbb {Q}_p}\operatorname {\mathrm {Lie}}(G)$
and
$D\in B_{\infty }\otimes _{\mathbb {Q}_p}\operatorname {\mathrm {Lie}}(G)$
and
![]() $D(v)=0$
for any
$D(v)=0$
for any
![]() $v\in B_{\infty }^{\mathrm {la}}$
, then
$v\in B_{\infty }^{\mathrm {la}}$
, then
![]() $D=0$
.
$D=0$
.
Proof. We will freely use notation introduced in Section 3.3.1. Let
![]() $G_0$
be a compact open subgroup of G considered there. By Lemma 3.3.2, we have an isomorphism for sufficiently large n
$G_0$
be a compact open subgroup of G considered there. By Lemma 3.3.2, we have an isomorphism for sufficiently large n
 $$ \begin{align*}B_{\infty}\widehat{\otimes}_{B_{G_0,n}} (B_{\infty})^{G_0-\mathrm{an},p^n\Gamma-\mathrm{an}}=B_{\infty}\widehat{\otimes}_{\mathbb{Q}_p}\mathscr{C}^{\mathrm{an}}(G_0,\mathbb{Q}_p).\end{align*} $$
$$ \begin{align*}B_{\infty}\widehat{\otimes}_{B_{G_0,n}} (B_{\infty})^{G_0-\mathrm{an},p^n\Gamma-\mathrm{an}}=B_{\infty}\widehat{\otimes}_{\mathbb{Q}_p}\mathscr{C}^{\mathrm{an}}(G_0,\mathbb{Q}_p).\end{align*} $$
It follows from Section 2.1.4 that this is equivariant with respect to the following actions of
![]() $G_0$
: the natural action on
$G_0$
: the natural action on
![]() $(B_{\infty })^{G_0-\mathrm {an},p^n\Gamma -\mathrm {an}}$
, the right translation action on
$(B_{\infty })^{G_0-\mathrm {an},p^n\Gamma -\mathrm {an}}$
, the right translation action on
![]() $\mathscr {C}^{\mathrm {an}}(G_0,\mathbb {Q}_p)$
and trivial actions on both
$\mathscr {C}^{\mathrm {an}}(G_0,\mathbb {Q}_p)$
and trivial actions on both
![]() $B_{\infty }$
. Using this action of
$B_{\infty }$
. Using this action of
![]() $G_0$
, we get
$G_0$
, we get
![]() $B_{\infty }$
-linear actions of
$B_{\infty }$
-linear actions of
![]() $B_{\infty }\otimes _{\mathbb {Q}_p}\operatorname {\mathrm {Lie}}(G)$
on both sides. In particular, D annihilates both sides. However, if
$B_{\infty }\otimes _{\mathbb {Q}_p}\operatorname {\mathrm {Lie}}(G)$
on both sides. In particular, D annihilates both sides. However, if
![]() $D\neq 0$
, we can always find a
$D\neq 0$
, we can always find a
![]() $B_{\infty }$
-valued analytic function on
$B_{\infty }$
-valued analytic function on
![]() $G_0$
which is not annihilated by D. Contradiction. This proves our claim.
$G_0$
which is not annihilated by D. Contradiction. This proves our claim.
Corollary 3.3.11. Suppose
![]() $D\in B_{\infty }\otimes _{\mathbb {Q}_p}\operatorname {\mathrm {Lie}}(G\times \Gamma )$
annihilates
$D\in B_{\infty }\otimes _{\mathbb {Q}_p}\operatorname {\mathrm {Lie}}(G\times \Gamma )$
annihilates
![]() $B_{\infty }^{\mathrm {la}}$
. Then D can be written as
$B_{\infty }^{\mathrm {la}}$
. Then D can be written as
where
![]() $b\in B_{\infty }$
and
$b\in B_{\infty }$
and
![]() $d\in \phi _{\widetilde {X}\infty }(\operatorname {\mathrm {Lie}}(\Gamma ))$
.
$d\in \phi _{\widetilde {X}\infty }(\operatorname {\mathrm {Lie}}(\Gamma ))$
.
Proof. We note that by the functorial property Corollary 3.3.9,
![]() $\phi _{\widetilde {X}_{\infty }}\equiv \phi _{{X}_{\infty }}\mod B_{\infty }\otimes _{\mathbb {Q}_p}\operatorname {\mathrm {Lie}}(G)$
; hence, the composite of
$\phi _{\widetilde {X}_{\infty }}\equiv \phi _{{X}_{\infty }}\mod B_{\infty }\otimes _{\mathbb {Q}_p}\operatorname {\mathrm {Lie}}(G)$
; hence, the composite of
![]() $\phi _{\widetilde {X}_{\infty }}$
and the projection map
$\phi _{\widetilde {X}_{\infty }}$
and the projection map
 $$ \begin{align*}\operatorname{\mathrm{Lie}}(\Gamma)\xrightarrow{\phi_{\widetilde{X}_{\infty}}}B_{\infty}\otimes_{\mathbb{Q}_p}\operatorname{\mathrm{Lie}}(G\times\Gamma)\to B_{\infty}\otimes_{\mathbb{Q}_p}\operatorname{\mathrm{Lie}}(\Gamma)\end{align*} $$
$$ \begin{align*}\operatorname{\mathrm{Lie}}(\Gamma)\xrightarrow{\phi_{\widetilde{X}_{\infty}}}B_{\infty}\otimes_{\mathbb{Q}_p}\operatorname{\mathrm{Lie}}(G\times\Gamma)\to B_{\infty}\otimes_{\mathbb{Q}_p}\operatorname{\mathrm{Lie}}(\Gamma)\end{align*} $$
is simply the identity map. In particular, we can find
![]() $b\in B_{\infty }$
and
$b\in B_{\infty }$
and
![]() $d\in \phi _{\widetilde {X}\infty }(\operatorname {\mathrm {Lie}}(\Gamma ))$
such that
$d\in \phi _{\widetilde {X}\infty }(\operatorname {\mathrm {Lie}}(\Gamma ))$
such that
![]() $D-bd\in B_{\infty }\otimes _{\mathbb {Q}_p}\operatorname {\mathrm {Lie}}(G)$
. The rest follows from Corollary 3.3.5 and Proposition 3.3.10.
$D-bd\in B_{\infty }\otimes _{\mathbb {Q}_p}\operatorname {\mathrm {Lie}}(G)$
. The rest follows from Corollary 3.3.5 and Proposition 3.3.10.
3.4 Proof of the main result II: uniqueness
3.4.1. In the previous section, we proved the existence of
![]() $\theta $
in Theorem 3.1.2. Note that the construction depends on a choice of an étale map
$\theta $
in Theorem 3.1.2. Note that the construction depends on a choice of an étale map
![]() $f_1:X\to Y=\mathbb {T}^1$
or
$f_1:X\to Y=\mathbb {T}^1$
or
![]() $\mathbb {B}^1$
in Section 3.2.1. In this section, we will show that in fact
$\mathbb {B}^1$
in Section 3.2.1. In this section, we will show that in fact
![]() $\theta $
is well-defined up to
$\theta $
is well-defined up to
![]() $A^{\times }$
. People who are interested in global applications can skip reading this part as this part will not play any role later.
$A^{\times }$
. People who are interested in global applications can skip reading this part as this part will not play any role later.
3.4.2. Consider another étale map
![]() $f_2:X\to Y$
which factors as a composite of rational embeddings and finite étale maps. Let
$f_2:X\to Y$
which factors as a composite of rational embeddings and finite étale maps. Let
 $$ \begin{align*}\widetilde{X}':=X\times_{f_2,Y}Y_{\infty}\end{align*} $$
$$ \begin{align*}\widetilde{X}':=X\times_{f_2,Y}Y_{\infty}\end{align*} $$
be the pullback of the profinite covering
![]() $Y_{\infty }$
along
$Y_{\infty }$
along
![]() $f_2$
. See Section 3.2.1 for the definition of
$f_2$
. See Section 3.2.1 for the definition of
![]() $Y_{\infty }$
. In the notation below, we put a superscript
$Y_{\infty }$
. In the notation below, we put a superscript
![]() $'$
for everything constructed using
$'$
for everything constructed using
![]() $f_2$
instead of
$f_2$
instead of
![]() $f_1$
. For example,
$f_1$
. For example,
![]() $\widetilde X'=\operatorname {\mathrm {Spa}}(B',B^{\prime +})$
is an affinoid ‘log
$\widetilde X'=\operatorname {\mathrm {Spa}}(B',B^{\prime +})$
is an affinoid ‘log
![]() $G'$
-Galois pro-étale perfectoid covering’ of X with
$G'$
-Galois pro-étale perfectoid covering’ of X with
![]() $G'=\Gamma $
. We would like to compute
$G'=\Gamma $
. We would like to compute
![]() $\phi _{\widetilde {X}'}:\operatorname {\mathrm {Lie}}(\Gamma )\to B'\otimes _{\mathbb {Q}_p}\operatorname {\mathrm {Lie}}(G')=B'\otimes _{\mathbb {Q}_p}\operatorname {\mathrm {Lie}}(\Gamma )$
first. In general, we will use the functorial property to reduce to this computation.
$\phi _{\widetilde {X}'}:\operatorname {\mathrm {Lie}}(\Gamma )\to B'\otimes _{\mathbb {Q}_p}\operatorname {\mathrm {Lie}}(G')=B'\otimes _{\mathbb {Q}_p}\operatorname {\mathrm {Lie}}(\Gamma )$
first. In general, we will use the functorial property to reduce to this computation.
We will freely use the notation introduced in the previous subsections. In particular,
![]() $\widetilde {X}_{\infty }'=\operatorname {\mathrm {Spa}}(B_{\infty }',B_{\infty }^{\prime +})$
is a
$\widetilde {X}_{\infty }'=\operatorname {\mathrm {Spa}}(B_{\infty }',B_{\infty }^{\prime +})$
is a
![]() $G'\times \Gamma $
-covering of X. It is also a
$G'\times \Gamma $
-covering of X. It is also a
![]() $G'$
-covering of
$G'$
-covering of
![]() $X_{\infty }=\operatorname {\mathrm {Spa}}(A_{\infty },A_{\infty }^+)$
and a
$X_{\infty }=\operatorname {\mathrm {Spa}}(A_{\infty },A_{\infty }^+)$
and a
![]() $\Gamma $
-covering of
$\Gamma $
-covering of
![]() $\widetilde {X}'=\operatorname {\mathrm {Spa}}(B',B^{\prime +})$
. Note that by Abhyankar’s lemma, both coverings are profinite étale of perfectoid algebras. By the Hochschild–Serre spectral sequence, we have
$\widetilde {X}'=\operatorname {\mathrm {Spa}}(B',B^{\prime +})$
. Note that by Abhyankar’s lemma, both coverings are profinite étale of perfectoid algebras. By the Hochschild–Serre spectral sequence, we have
 $$ \begin{align*}H^1_{\mathrm{cont}}(G'\times\Gamma,B_{\infty}')\cong H^1_{\mathrm{cont}}(\Gamma,(B_{\infty}')^{G'\times{\{\mathbf{1}\}}})=H^1_{\mathrm{cont}}(\Gamma,A_{\infty})\cong H^1_{\mathrm{cont}}(\Gamma,A).\end{align*} $$
$$ \begin{align*}H^1_{\mathrm{cont}}(G'\times\Gamma,B_{\infty}')\cong H^1_{\mathrm{cont}}(\Gamma,(B_{\infty}')^{G'\times{\{\mathbf{1}\}}})=H^1_{\mathrm{cont}}(\Gamma,A_{\infty})\cong H^1_{\mathrm{cont}}(\Gamma,A).\end{align*} $$
The first isomorphism follows from
![]() $H^1_{\mathrm {cont}}(G'\times \{\mathbf {1}\},B_{\infty }')=0$
, which is a consequence of the almost purity theorem. The last isomorphism follows from the existence and properties of the Tate normalised trace
$H^1_{\mathrm {cont}}(G'\times \{\mathbf {1}\},B_{\infty }')=0$
, which is a consequence of the almost purity theorem. The last isomorphism follows from the existence and properties of the Tate normalised trace
![]() $\overline {\mathrm {tr}}_{X,0}:A_{\infty }\to A$
. We denote by
$\overline {\mathrm {tr}}_{X,0}:A_{\infty }\to A$
. We denote by
![]() $\tau _1$
the composite isomorphism
$\tau _1$
the composite isomorphism
 $H^1_{\mathrm {cont}}(G'\times \Gamma ,B_{\infty }')\xrightarrow {\sim } H^1_{\mathrm {cont}}(\Gamma ,A)$
.
$H^1_{\mathrm {cont}}(G'\times \Gamma ,B_{\infty }')\xrightarrow {\sim } H^1_{\mathrm {cont}}(\Gamma ,A)$
.
Symmetrically, we can get another isomorphism
 $\tau _2:H^1_{\mathrm {cont}}(G'\times \Gamma ,B_{\infty }')\xrightarrow {\sim }H^1_{\mathrm {cont}}(\Gamma ,A)$
by
$\tau _2:H^1_{\mathrm {cont}}(G'\times \Gamma ,B_{\infty }')\xrightarrow {\sim }H^1_{\mathrm {cont}}(\Gamma ,A)$
by
 $$ \begin{align*}H^1_{\mathrm{cont}}(G'\times\Gamma,B_{\infty}')\cong H^1_{\mathrm{cont}}(G',(B_{\infty}')^{{\{\mathbf{1}\}}\times\Gamma})=H^1_{\mathrm{cont}}(G',B')=H^1_{\mathrm{cont}}(\Gamma,B')\cong H^1_{\mathrm{cont}}(\Gamma,A).\end{align*} $$
$$ \begin{align*}H^1_{\mathrm{cont}}(G'\times\Gamma,B_{\infty}')\cong H^1_{\mathrm{cont}}(G',(B_{\infty}')^{{\{\mathbf{1}\}}\times\Gamma})=H^1_{\mathrm{cont}}(G',B')=H^1_{\mathrm{cont}}(\Gamma,B')\cong H^1_{\mathrm{cont}}(\Gamma,A).\end{align*} $$
As
![]() $H^1_{\mathrm {cont}}(\Gamma ,A)$
is a free A-module of rank 1, the composite
$H^1_{\mathrm {cont}}(\Gamma ,A)$
is a free A-module of rank 1, the composite
 $\tau _1\circ \tau _2^{-1}\in \operatorname {\mathrm {End}}_A(H^1_{\mathrm {cont}}(\Gamma ,A))=A$
is given by an element
$\tau _1\circ \tau _2^{-1}\in \operatorname {\mathrm {End}}_A(H^1_{\mathrm {cont}}(\Gamma ,A))=A$
is given by an element
![]() $a\in A^{\times }$
.
$a\in A^{\times }$
.
Lemma 3.4.3.
![]() $\phi _{\widetilde {X}'}:\operatorname {\mathrm {Lie}}(\Gamma )\to B'\otimes _{\mathbb {Q} _p}\operatorname {\mathrm {Lie}}(\Gamma )$
is multiplication by a.
$\phi _{\widetilde {X}'}:\operatorname {\mathrm {Lie}}(\Gamma )\to B'\otimes _{\mathbb {Q} _p}\operatorname {\mathrm {Lie}}(\Gamma )$
is multiplication by a.
Proof. Fix a topological generator
![]() $\gamma $
of
$\gamma $
of
![]() $\Gamma $
. Unravelling all of the isomorphisms above, we can find an element
$\Gamma $
. Unravelling all of the isomorphisms above, we can find an element
![]() $b\in B_{\infty }'$
such that
$b\in B_{\infty }'$
such that
Here
![]() $(\gamma ,\mathbf {1}), (\mathbf {1},\gamma )$
are elements in
$(\gamma ,\mathbf {1}), (\mathbf {1},\gamma )$
are elements in
![]() $G'\times \Gamma =\Gamma \times \Gamma $
. In particular, both actions of
$G'\times \Gamma =\Gamma \times \Gamma $
. In particular, both actions of
![]() $\Gamma $
on b are analytic.
$\Gamma $
on b are analytic.
As pointed out in Remark 3.3.7, in order to compute
![]() $\phi _{\widetilde {X}'}$
, we choose a faithful representation of
$\phi _{\widetilde {X}'}$
, we choose a faithful representation of
![]() $G'=\Gamma $
on
$G'=\Gamma $
on
 $V=\mathbb {Q}_p^{\oplus 2}$
:
$V=\mathbb {Q}_p^{\oplus 2}$
:
 $$ \begin{align*}\Gamma\to\mathrm{GL}_2(\mathbb{Q}_p),\, \gamma\mapsto \begin{pmatrix} 1 & 1 \\ 0 &1 \end{pmatrix}.\end{align*} $$
$$ \begin{align*}\Gamma\to\mathrm{GL}_2(\mathbb{Q}_p),\, \gamma\mapsto \begin{pmatrix} 1 & 1 \\ 0 &1 \end{pmatrix}.\end{align*} $$
Then
 $B_{\infty }'\otimes _{\mathbb {Q}_p} V=(B_{\infty }')^{\oplus 2}$
has a
$B_{\infty }'\otimes _{\mathbb {Q}_p} V=(B_{\infty }')^{\oplus 2}$
has a
![]() $G'$
-fixed basis over
$G'$
-fixed basis over
![]() $B_{\infty }'$
:
$B_{\infty }'$
:
Moreover, it is easy to see that the action of
![]() $\Gamma $
on this basis is (locally) analytic. Therefore,
$\Gamma $
on this basis is (locally) analytic. Therefore,
![]() $\phi _V$
is obtained by
$\phi _V$
is obtained by
![]() $B_{\infty }'$
-linearly extending the action of
$B_{\infty }'$
-linearly extending the action of
![]() $\operatorname {\mathrm {Lie}}(\Gamma )$
on
$\operatorname {\mathrm {Lie}}(\Gamma )$
on
![]() $e_1,e_2$
. Let
$e_1,e_2$
. Let
![]() $t\in \operatorname {\mathrm {Lie}}(\Gamma )$
be the logarithm of
$t\in \operatorname {\mathrm {Lie}}(\Gamma )$
be the logarithm of
![]() $\gamma $
. Then
$\gamma $
. Then
![]() $t\cdot e_1=0$
and it follows from Equation (3.4.2) that
$t\cdot e_1=0$
and it follows from Equation (3.4.2) that
![]() $t\cdot e_2=ae_1$
. Hence,
$t\cdot e_2=ae_1$
. Hence,
 $$ \begin{align*}t\mapsto \begin{pmatrix} 0 & a \\ 0 &0 \end{pmatrix}.\end{align*} $$
$$ \begin{align*}t\mapsto \begin{pmatrix} 0 & a \\ 0 &0 \end{pmatrix}.\end{align*} $$
Comparing this with the definition of V, we see that
![]() $\phi _{\widetilde {X}'}$
is just multiplication by a.
$\phi _{\widetilde {X}'}$
is just multiplication by a.
3.4.4. Now we are ready to prove
![]() $\phi _{\widetilde {X}}$
is well-defined up to
$\phi _{\widetilde {X}}$
is well-defined up to
![]() $A^{\times }$
. We will keep using the notation introduced in Section 3.4.2. Suppose
$A^{\times }$
. We will keep using the notation introduced in Section 3.4.2. Suppose
![]() $\widetilde {X}$
is ‘log G-Galois pro-étale perfectoid covering’ of X. Now using
$\widetilde {X}$
is ‘log G-Galois pro-étale perfectoid covering’ of X. Now using
![]() $f_2:X\to Y$
instead of
$f_2:X\to Y$
instead of
![]() $f_1:X\to Y$
in the setup Section 3.2.1 and redoing everything before, then rather than
$f_1:X\to Y$
in the setup Section 3.2.1 and redoing everything before, then rather than
![]() $\phi _{\widetilde {X}}$
, we get
$\phi _{\widetilde {X}}$
, we get
 $$ \begin{align*}\phi^{\prime}_{\widetilde{X}}:\operatorname{\mathrm{Lie}}(\Gamma)\to B\otimes_{\mathbb{Q}_p}\operatorname{\mathrm{Lie}}(G).\end{align*} $$
$$ \begin{align*}\phi^{\prime}_{\widetilde{X}}:\operatorname{\mathrm{Lie}}(\Gamma)\to B\otimes_{\mathbb{Q}_p}\operatorname{\mathrm{Lie}}(G).\end{align*} $$
Proposition 3.4.5.
 $a\phi ^{\prime }_{\widetilde {X}}(x)=\phi _{\widetilde {X}}(x)$
, for any
$a\phi ^{\prime }_{\widetilde {X}}(x)=\phi _{\widetilde {X}}(x)$
, for any
![]() $x\in \operatorname {\mathrm {Lie}}(\Gamma )$
. In particular,
$x\in \operatorname {\mathrm {Lie}}(\Gamma )$
. In particular,
![]() $\phi ^{\prime }_{\widetilde {X}}$
and
$\phi ^{\prime }_{\widetilde {X}}$
and
![]() $\phi _{\widetilde {X}}$
differ by a unit of A.
$\phi _{\widetilde {X}}$
differ by a unit of A.
Proof. First note that the special case
![]() $\widetilde {X}=X_{\infty }=\operatorname {\mathrm {Spa}}(A_{\infty },A_{\infty }^+)$
is essentially proved by the same computation as above (after switching the role of
$\widetilde {X}=X_{\infty }=\operatorname {\mathrm {Spa}}(A_{\infty },A_{\infty }^+)$
is essentially proved by the same computation as above (after switching the role of
![]() $f_1$
and
$f_1$
and
![]() $f_2$
). In general, let V be a finite-dimensional continuous representation of G over
$f_2$
). In general, let V be a finite-dimensional continuous representation of G over
![]() $\mathbb {Q}_p$
. It is enough to show that
$\mathbb {Q}_p$
. It is enough to show that
![]() $a^{-1}\phi _V$
on
$a^{-1}\phi _V$
on
![]() $B_{\infty }\otimes _{\mathbb {Q}_p} V$
agrees with the action of
$B_{\infty }\otimes _{\mathbb {Q}_p} V$
agrees with the action of
![]() $\operatorname {\mathrm {Lie}}(\Gamma )$
induced from
$\operatorname {\mathrm {Lie}}(\Gamma )$
induced from
![]() $\phi ^{\prime }_{\widetilde {X}}$
. Consider
$\phi ^{\prime }_{\widetilde {X}}$
. Consider
![]() $\widetilde {X}_{\infty }:=\operatorname {\mathrm {Spa}}(B_{\infty },B_{\infty }^+)$
. This is a ‘log
$\widetilde {X}_{\infty }:=\operatorname {\mathrm {Spa}}(B_{\infty },B_{\infty }^+)$
. This is a ‘log
![]() $G\times \Gamma $
-Galois pro-étale perfectoid covering’ of X. Then by the functorial property Corollary 3.3.9,
$G\times \Gamma $
-Galois pro-étale perfectoid covering’ of X. Then by the functorial property Corollary 3.3.9,
 $$ \begin{align*}\phi^{\prime}_{\widetilde{X}}\equiv \phi^{\prime}_{\widetilde{X}_{\infty}} \mod B_{\infty}\otimes_{\mathbb{Q}_p}\operatorname{\mathrm{Lie}}(\Gamma).\end{align*} $$
$$ \begin{align*}\phi^{\prime}_{\widetilde{X}}\equiv \phi^{\prime}_{\widetilde{X}_{\infty}} \mod B_{\infty}\otimes_{\mathbb{Q}_p}\operatorname{\mathrm{Lie}}(\Gamma).\end{align*} $$
Hence, the actions of
![]() $\operatorname {\mathrm {Lie}}(\Gamma )$
on
$\operatorname {\mathrm {Lie}}(\Gamma )$
on
![]() $B_{\infty }\otimes _{\mathbb {Q}_p} V$
induced from
$B_{\infty }\otimes _{\mathbb {Q}_p} V$
induced from
![]() $\phi ^{\prime }_{\widetilde {X}}$
and
$\phi ^{\prime }_{\widetilde {X}}$
and
 $\phi ^{\prime }_{\widetilde {X}_{\infty }}$
are the same because
$\phi ^{\prime }_{\widetilde {X}_{\infty }}$
are the same because
![]() $\Gamma $
acts trivially on V. So it suffices to compare
$\Gamma $
acts trivially on V. So it suffices to compare
![]() $a^{-1}\phi _V$
and
$a^{-1}\phi _V$
and
 $\phi ^{\prime }_{\widetilde {X}_{\infty }}$
.
$\phi ^{\prime }_{\widetilde {X}_{\infty }}$
.
Since both actions are
![]() $B_{\infty }$
-linear, it follows from Proposition 3.2.11 that we only need to compare two actions on the
$B_{\infty }$
-linear, it follows from Proposition 3.2.11 that we only need to compare two actions on the
![]() $\Gamma $
-locally analytic vectors in
$\Gamma $
-locally analytic vectors in
 $(B_{\infty }\otimes _{\mathbb {Q}_p} V)^{G}$
. Now on this G-fixed subspace,
$(B_{\infty }\otimes _{\mathbb {Q}_p} V)^{G}$
. Now on this G-fixed subspace,
![]() $\phi _V$
acts by the natural Lie algebra action of
$\phi _V$
acts by the natural Lie algebra action of
![]() $\operatorname {\mathrm {Lie}}(\Gamma )$
, while by Remark 3.3.8 and the functorial property Corollary 3.3.9,
$\operatorname {\mathrm {Lie}}(\Gamma )$
, while by Remark 3.3.8 and the functorial property Corollary 3.3.9,
 $$ \begin{align*}\phi^{\prime}_{\widetilde{X}_{\infty}}\equiv\phi^{\prime}_{X_{\infty}}\mod B_{\infty}\otimes_{\mathbb{Q}_p}\operatorname{\mathrm{Lie}}(G),\end{align*} $$
$$ \begin{align*}\phi^{\prime}_{\widetilde{X}_{\infty}}\equiv\phi^{\prime}_{X_{\infty}}\mod B_{\infty}\otimes_{\mathbb{Q}_p}\operatorname{\mathrm{Lie}}(G),\end{align*} $$
the action on
 $(B_{\infty }\otimes _{\mathbb {Q}_p} V)^{G,\Gamma -\mathrm {la}}$
induced by
$(B_{\infty }\otimes _{\mathbb {Q}_p} V)^{G,\Gamma -\mathrm {la}}$
induced by
 $\phi ^{\prime }_{\widetilde {X}_{\infty }}$
is just
$\phi ^{\prime }_{\widetilde {X}_{\infty }}$
is just
![]() $\phi ^{\prime }_{X_{\infty }}$
. Hence, the desired equality is a direct consequence of the special case
$\phi ^{\prime }_{X_{\infty }}$
. Hence, the desired equality is a direct consequence of the special case
![]() $\widetilde {X}=X_{\infty }$
.
$\widetilde {X}=X_{\infty }$
.
Remark 3.4.6. One can also use Corollary 3.3.11 to reduce the general case to the special case
![]() $\widetilde {X}=X_{\infty }$
.
$\widetilde {X}=X_{\infty }$
.
3.5 Locally analytic covering
3.5.1. The goal of this subsection is to give a sufficient condition for
![]() $\theta $
to be nonzero. We will continue using the notation introduced before. In particular, there is a fixed étale map
$\theta $
to be nonzero. We will continue using the notation introduced before. In particular, there is a fixed étale map
![]() $f_1:X\to Y$
as in Section 3.2.1. First, let’s recall Faltings’s extension in the rigid analytic variety setting; cf. Corollary 6.14 of [Reference ScholzeSch13a], Corollary 2.4.5 of [Reference Diao, Lan, Liu and ZhuDLLZ18]. However, as both references assume X is defined over a discretely valued complete non-Archimedean extension of
$f_1:X\to Y$
as in Section 3.2.1. First, let’s recall Faltings’s extension in the rigid analytic variety setting; cf. Corollary 6.14 of [Reference ScholzeSch13a], Corollary 2.4.5 of [Reference Diao, Lan, Liu and ZhuDLLZ18]. However, as both references assume X is defined over a discretely valued complete non-Archimedean extension of
![]() $\mathbb {Q}_p$
, we give a rather ad hoc definition here which will be sufficient for our purpose.
$\mathbb {Q}_p$
, we give a rather ad hoc definition here which will be sufficient for our purpose.
Fix a generator
![]() $\gamma $
of
$\gamma $
of
![]() $\Gamma $
from now on and consider the following unipotent representation of
$\Gamma $
from now on and consider the following unipotent representation of
![]() $\Gamma $
on
$\Gamma $
on
 $V=\mathbb {Q}_p^{\oplus 2}$
:
$V=\mathbb {Q}_p^{\oplus 2}$
:
 $$ \begin{align*}\Gamma\to\mathrm{GL}_2(\mathbb{Q}_p):~\gamma\mapsto \begin{pmatrix} 1 & 1 \\ 0 &1 \end{pmatrix}.\end{align*} $$
$$ \begin{align*}\Gamma\to\mathrm{GL}_2(\mathbb{Q}_p):~\gamma\mapsto \begin{pmatrix} 1 & 1 \\ 0 &1 \end{pmatrix}.\end{align*} $$
Clearly, V is an extension of the trivial representation by itself:
Tensor this exact sequence with
![]() $B_{\infty }$
over
$B_{\infty }$
over
![]() $\mathbb {Q}_p$
and take
$\mathbb {Q}_p$
and take
![]() $\Gamma $
-invariants with respect to the diagonal actions:
$\Gamma $
-invariants with respect to the diagonal actions:
 $$ \begin{align} 0\to B\to (B_{\infty}\otimes_{\mathbb{Q}_p} V)^{\Gamma}\to B\to 0. \end{align} $$
$$ \begin{align} 0\to B\to (B_{\infty}\otimes_{\mathbb{Q}_p} V)^{\Gamma}\to B\to 0. \end{align} $$
Note that this G-equivariant sequence is exact by the almost purity theorem. It follows from the discussion in 3.4.2 that its extension class is independent of the choice of
![]() $f_1$
up to multiplication by a unit of A.
$f_1$
up to multiplication by a unit of A.
The norm on
![]() $B_{\infty }$
induces norms on
$B_{\infty }$
induces norms on
![]() $B_{\infty }\otimes V=(B_{\infty })^{\oplus 2}$
and its subspaces, and (FE) is continuous with respect to this topology. One important property of (FE) is that if we take the continuous G-cohomology, the following connecting homomorphism of the long exact sequence is an isomorphism:
$B_{\infty }\otimes V=(B_{\infty })^{\oplus 2}$
and its subspaces, and (FE) is continuous with respect to this topology. One important property of (FE) is that if we take the continuous G-cohomology, the following connecting homomorphism of the long exact sequence is an isomorphism:
 $$ \begin{align*}A=B^G\xrightarrow{\sim} H^1_{\mathrm{cont}}(G,B).\end{align*} $$
$$ \begin{align*}A=B^G\xrightarrow{\sim} H^1_{\mathrm{cont}}(G,B).\end{align*} $$
This can be seen by identifying
where the first two isomorphisms follow from the almost purity theorem and the last isomorphism is a consequence of the Tate’s normalised trace. Then it is easy to compute the connecting homomorphism.
In fact, this holds for any open subgroup
![]() $G_0$
of G; that is, if we take the continuous
$G_0$
of G; that is, if we take the continuous
![]() $G_0$
-cohomology of (FE), the connecting homomorphism
$G_0$
-cohomology of (FE), the connecting homomorphism
![]() $B^{G_0}\to H^1_{\mathrm {cont}}(G_0,B)$
is an isomorphism. To see this, note that
$B^{G_0}\to H^1_{\mathrm {cont}}(G_0,B)$
is an isomorphism. To see this, note that
![]() $\operatorname {\mathrm {Spa}}(B,B^+)$
is a ‘log
$\operatorname {\mathrm {Spa}}(B,B^+)$
is a ‘log
![]() $G_0$
-Galois pro-étale perfectoid covering’ of
$G_0$
-Galois pro-étale perfectoid covering’ of
![]() $\operatorname {\mathrm {Spa}}(B^{G_0},(B^+)^{G_0})$
. Hence,
$\operatorname {\mathrm {Spa}}(B^{G_0},(B^+)^{G_0})$
. Hence,
![]() $H^1_{\mathrm {cont}}(G_0,B)$
is also a free rank 1
$H^1_{\mathrm {cont}}(G_0,B)$
is also a free rank 1
![]() $B^{G_0}$
-module. So in view of what we have proved, the claim follows from the fact that the natural map
$B^{G_0}$
-module. So in view of what we have proved, the claim follows from the fact that the natural map
![]() $B^{G_0}\otimes _{A} H^1_{\mathrm {cont}}(G,B)\to H^1_{\mathrm {cont}}(G_0,B)$
is an isomorphism.
$B^{G_0}\otimes _{A} H^1_{\mathrm {cont}}(G,B)\to H^1_{\mathrm {cont}}(G_0,B)$
is an isomorphism.
Remark 3.5.2. If X is defined over a finite extension of
![]() $\mathbb {Q}_p$
, then (FE) recovers (log) Faltings’s extension on
$\mathbb {Q}_p$
, then (FE) recovers (log) Faltings’s extension on
![]() $\tilde {X}$
defined in [Reference ScholzeSch13a, Reference Diao, Lan, Liu and ZhuDLLZ18] by identifying the quotient B with
$\tilde {X}$
defined in [Reference ScholzeSch13a, Reference Diao, Lan, Liu and ZhuDLLZ18] by identifying the quotient B with
 $B\otimes _{A}\Omega _{A/C}^{1}(S)$
sending
$B\otimes _{A}\Omega _{A/C}^{1}(S)$
sending
![]() $1\in B$
to
$1\in B$
to
 $f_1^*(\frac {dT}{T})$
, where
$f_1^*(\frac {dT}{T})$
, where
 $\Omega _{A/C}^{1}(S)$
denotes the continuous
$\Omega _{A/C}^{1}(S)$
denotes the continuous
![]() $1$
-forms of A over C with a simple pole at S. See Proposition 2.3.15 and proof of Corollary 2.4.2 of [Reference Diao, Lan, Liu and ZhuDLLZ18]. Here
$1$
-forms of A over C with a simple pole at S. See Proposition 2.3.15 and proof of Corollary 2.4.2 of [Reference Diao, Lan, Liu and ZhuDLLZ18]. Here
![]() $\tilde {X}$
is viewed as an open set in the pro-Kummer étale site of X equipped with the natural log structure defined by S (cf. Example 2.1.2 of [Reference Diao, Lan, Liu and ZhuDLLZ18]).
$\tilde {X}$
is viewed as an open set in the pro-Kummer étale site of X equipped with the natural log structure defined by S (cf. Example 2.1.2 of [Reference Diao, Lan, Liu and ZhuDLLZ18]).
Proposition 3.5.3. The following conditions are equivalent:
-
(1) (FE) remains exact after taking
 $G_0$
-analytic vectors for some open subgroup
$G_0$
-analytic vectors for some open subgroup
 $G_0$
of G equipped with an integer-valued, saturated p-valuation as in Section 2.1.1.
$G_0$
of G equipped with an integer-valued, saturated p-valuation as in Section 2.1.1. -
(2) (FE) remains exact after taking G-locally analytic vectors of each term.
-
(3) There exists a G-locally analytic vector
 $z\in B_{\infty }$
such that
$z\in B_{\infty }$
such that
 $\gamma (z)=z-1$
.
$\gamma (z)=z-1$
.
Proof. The first two parts are clearly equivalent with existence of a G-locally analytic vector
 $x\in (B_{\infty }\otimes _{\mathbb {Q}_p} V)^{\Gamma }$
mapping to
$x\in (B_{\infty }\otimes _{\mathbb {Q}_p} V)^{\Gamma }$
mapping to
![]() $1\in B$
in (FE). Write
$1\in B$
in (FE). Write
 $B_{\infty }\otimes _{\mathbb {Q}_p} V=(B_{\infty })^{\oplus 2}$
. Then
$B_{\infty }\otimes _{\mathbb {Q}_p} V=(B_{\infty })^{\oplus 2}$
. Then
![]() $x=(z,1)$
for some
$x=(z,1)$
for some
![]() $z\in B_{\infty }$
which is G-locally analytic and satisfies
$z\in B_{\infty }$
which is G-locally analytic and satisfies
![]() $\gamma (z)=z-1$
. This proves the equivalence between these three conditions.
$\gamma (z)=z-1$
. This proves the equivalence between these three conditions.
Definition 3.5.4. We say
![]() $\widetilde {X}$
is a locally analytic covering of X if one of the conditions in Proposition 3.5.3 holds.
$\widetilde {X}$
is a locally analytic covering of X if one of the conditions in Proposition 3.5.3 holds.
Remark 3.5.5. An analysis similar to Section 3.4.2 shows that this definition is independent of the choice of
![]() $f_1:X\to Y$
. There is another intrinsic definition:
$f_1:X\to Y$
. There is another intrinsic definition:
![]() $\widetilde {X}$
is a locally analytic covering of X if and only if the natural map
$\widetilde {X}$
is a locally analytic covering of X if and only if the natural map
![]() $H^1_{\mathrm {cont}}(G,B^{\mathrm {la}})\to H_{\mathrm {cont}}^1(G,B)$
is an isomorphism. We sketch a proof here. It follows from Tate’s normalised trace that
$H^1_{\mathrm {cont}}(G,B^{\mathrm {la}})\to H_{\mathrm {cont}}^1(G,B)$
is an isomorphism. We sketch a proof here. It follows from Tate’s normalised trace that
![]() $H^1_{\mathrm {cont}}(\Gamma ,(A_{\infty })^{\mathrm {la}})\cong H^1(\Gamma ,A_{\infty })$
. Note that
$H^1_{\mathrm {cont}}(\Gamma ,(A_{\infty })^{\mathrm {la}})\cong H^1(\Gamma ,A_{\infty })$
. Note that
![]() $A_{\infty }=(B_{\infty })^{G}$
. We claim that there are natural isomorphisms
$A_{\infty }=(B_{\infty })^{G}$
. We claim that there are natural isomorphisms
 $$ \begin{align*}H^1_{\mathrm{cont}}(G\times\Gamma,(B_{\infty})^{\mathrm{la}})\cong H^1_{\mathrm{cont}}(\Gamma,(A_{\infty})^{\mathrm{la}})\cong H^1_{\mathrm{cont}}(\Gamma,A_{\infty})\cong H^1_{\mathrm{cont}}(G\times\Gamma, B_{\infty}).\end{align*} $$
$$ \begin{align*}H^1_{\mathrm{cont}}(G\times\Gamma,(B_{\infty})^{\mathrm{la}})\cong H^1_{\mathrm{cont}}(\Gamma,(A_{\infty})^{\mathrm{la}})\cong H^1_{\mathrm{cont}}(\Gamma,A_{\infty})\cong H^1_{\mathrm{cont}}(G\times\Gamma, B_{\infty}).\end{align*} $$
The first and third isomorphisms follow from the Hochschild–Serre spectral sequence and
![]() $H^1_{\mathrm {cont}}(G,B_{\infty })=H^1_{\mathrm {cont}}(G,(B_{\infty })^{\mathrm {la}})=0$
. The vanishing of
$H^1_{\mathrm {cont}}(G,B_{\infty })=H^1_{\mathrm {cont}}(G,(B_{\infty })^{\mathrm {la}})=0$
. The vanishing of
![]() $H^1_{\mathrm {cont}}(G,B_{\infty })$
is clear by the almost purity theorem. For the vanishing of
$H^1_{\mathrm {cont}}(G,B_{\infty })$
is clear by the almost purity theorem. For the vanishing of
![]() $H^1_{\mathrm {cont}}(G,(B_{\infty })^{\mathrm {la}})$
, using Lemma 3.3.2, it suffices to show that
$H^1_{\mathrm {cont}}(G,(B_{\infty })^{\mathrm {la}})$
, using Lemma 3.3.2, it suffices to show that
 $\varinjlim _nH^1(G_n,\mathscr {C}^{\mathrm {an}}(G_n,\mathbb {Q}_p))=0$
, which is true. Now we apply the Hochschild–Serre spectral sequence to the subgroup
$\varinjlim _nH^1(G_n,\mathscr {C}^{\mathrm {an}}(G_n,\mathbb {Q}_p))=0$
, which is true. Now we apply the Hochschild–Serre spectral sequence to the subgroup
![]() $\{\mathbf {1}\}\times \Gamma \subset G\times \Gamma $
in the computation of
$\{\mathbf {1}\}\times \Gamma \subset G\times \Gamma $
in the computation of
![]() $H^1_{\mathrm {cont}}(G\times \Gamma ,(B_{\infty })^{\mathrm {la}})$
and
$H^1_{\mathrm {cont}}(G\times \Gamma ,(B_{\infty })^{\mathrm {la}})$
and
![]() $H^1_{\mathrm {cont}}(G\times \Gamma , B_{\infty })$
. Since
$H^1_{\mathrm {cont}}(G\times \Gamma , B_{\infty })$
. Since
![]() $H^1_{\mathrm {cont}}(\Gamma ,B_{\infty })=0$
, it is easy to see that
$H^1_{\mathrm {cont}}(\Gamma ,B_{\infty })=0$
, it is easy to see that
![]() $H^1_{\mathrm {cont}}(G,B^{\mathrm {la}})\cong H_{\mathrm {cont}}^1(G,B)$
is equivalent with
$H^1_{\mathrm {cont}}(G,B^{\mathrm {la}})\cong H_{\mathrm {cont}}^1(G,B)$
is equivalent with
that is, the
![]() $\Gamma $
-coinvariants of
$\Gamma $
-coinvariants of
![]() $(B_{\infty })^{\mathrm {la}}$
have no G-invariants. Note that
$(B_{\infty })^{\mathrm {la}}$
have no G-invariants. Note that
![]() $1\in (B_{\infty })^{\mathrm {la}}$
is fixed by G. Hence, the vanishing of
$1\in (B_{\infty })^{\mathrm {la}}$
is fixed by G. Hence, the vanishing of
![]() $H^1(\Gamma ,(B_{\infty })^{\mathrm {la}})^G$
certainly implies the existence of element z in the third part of Proposition 3.5.3. On the other hand, if there exists such an element z, the argument in Section 3.6.7 will imply that
$H^1(\Gamma ,(B_{\infty })^{\mathrm {la}})^G$
certainly implies the existence of element z in the third part of Proposition 3.5.3. On the other hand, if there exists such an element z, the argument in Section 3.6.7 will imply that
![]() $H^1(\Gamma ,(B_{\infty })^{\mathrm {la}})=0$
. This finishes the proof.
$H^1(\Gamma ,(B_{\infty })^{\mathrm {la}})=0$
. This finishes the proof.
Proposition 3.5.6.
![]() $\phi _{\widetilde {X}}:\operatorname {\mathrm {Lie}}(\Gamma )\to B\otimes _{\mathbb {Q}_p}\operatorname {\mathrm {Lie}}(G)$
is nonzero if
$\phi _{\widetilde {X}}:\operatorname {\mathrm {Lie}}(\Gamma )\to B\otimes _{\mathbb {Q}_p}\operatorname {\mathrm {Lie}}(G)$
is nonzero if
![]() $\widetilde {X}$
is a locally analytic covering of X.
$\widetilde {X}$
is a locally analytic covering of X.
Proof. We need results established in Section 3.3.1. Let
![]() $G_0$
an open subgroup as in Section 3.3.1. Suppose
$G_0$
an open subgroup as in Section 3.3.1. Suppose
![]() $\phi _{\widetilde {X}}=0$
. It follows from our construction there and Lemma 3.3.2 that
$\phi _{\widetilde {X}}=0$
. It follows from our construction there and Lemma 3.3.2 that
![]() $\operatorname {\mathrm {Lie}}(\Gamma )$
is acting trivially on the
$\operatorname {\mathrm {Lie}}(\Gamma )$
is acting trivially on the
![]() $\Gamma $
-locally analytic vectors in
$\Gamma $
-locally analytic vectors in
![]() $(B_{\infty })^{G_0-\mathrm {an}}$
. Hence, there does not exist an element
$(B_{\infty })^{G_0-\mathrm {an}}$
. Hence, there does not exist an element
![]() $z\in (B_{\infty })^{G_0-\mathrm {an}}$
such that
$z\in (B_{\infty })^{G_0-\mathrm {an}}$
such that
![]() $\gamma (z)=z-1$
. As
$\gamma (z)=z-1$
. As
![]() $G_0$
can be taken arbitrarily small, part (3) of Proposition 3.5.3 implies that
$G_0$
can be taken arbitrarily small, part (3) of Proposition 3.5.3 implies that
![]() $\widetilde {X}$
is not a locally analytic covering of X.
$\widetilde {X}$
is not a locally analytic covering of X.
3.6 Application: acyclicity of taking locally analytic vectors of B
We keep the notation and setup from Section 3.1.1. Our main result of this subsection gives an equivalent condition for B being
![]() $\mathfrak {LA}$
-acyclic. See Subsection 2.2 for more details about this notion.
$\mathfrak {LA}$
-acyclic. See Subsection 2.2 for more details about this notion.
Theorem 3.6.1. Suppose
![]() $\widetilde X=\operatorname {\mathrm {Spa}}(B,B^+)$
is a ‘log G-Galois pro-étale perfectoid covering’ of X and X is small. Then
$\widetilde X=\operatorname {\mathrm {Spa}}(B,B^+)$
is a ‘log G-Galois pro-étale perfectoid covering’ of X and X is small. Then
![]() $R^i\mathfrak {LA}(B)=0$
for all
$R^i\mathfrak {LA}(B)=0$
for all
![]() $i\geq 1$
if and only if
$i\geq 1$
if and only if
![]() $\widetilde X$
is a locally analytic covering of X (see Definition 3.5.4). When this happens, B is strongly
$\widetilde X$
is a locally analytic covering of X (see Definition 3.5.4). When this happens, B is strongly
![]() $\mathfrak {LA}$
-acyclic.
$\mathfrak {LA}$
-acyclic.
3.6.2. One direction is clear. Suppose
![]() $R^i\mathfrak {LA}(B)=0$
,
$R^i\mathfrak {LA}(B)=0$
,
![]() $i\geq 1$
. Take completed tensor products of (FE) with
$i\geq 1$
. Take completed tensor products of (FE) with
![]() $\mathscr {C}^{\mathrm {an}}(G_n,\mathbb {Q}_p)$
over
$\mathscr {C}^{\mathrm {an}}(G_n,\mathbb {Q}_p)$
over
![]() $\mathbb {Q}_p$
and take the continuous
$\mathbb {Q}_p$
and take the continuous
![]() $G_n$
-cohomology
$G_n$
-cohomology
 $$ \begin{align*}0\to B^{G_n-\mathrm{an}}\to (B_{\infty}\otimes_{\mathbb{Q}_p} V)^{\Gamma,G_n-\mathrm{an}}\to B^{G_n-\mathrm{an}}\to H^1_{\mathrm{cont}}(G_n, \mathscr{C}^{\mathrm{an}}(G_n,\mathbb{Q}_p)\widehat\otimes_{\mathbb{Q}_p} B).\end{align*} $$
$$ \begin{align*}0\to B^{G_n-\mathrm{an}}\to (B_{\infty}\otimes_{\mathbb{Q}_p} V)^{\Gamma,G_n-\mathrm{an}}\to B^{G_n-\mathrm{an}}\to H^1_{\mathrm{cont}}(G_n, \mathscr{C}^{\mathrm{an}}(G_n,\mathbb{Q}_p)\widehat\otimes_{\mathbb{Q}_p} B).\end{align*} $$
Then by passing to the direct limit with
![]() $n\to \infty $
, we see that the last term vanishes. Hence, (FE) remains exact when taking G-locally analytic vectors.
$n\to \infty $
, we see that the last term vanishes. Hence, (FE) remains exact when taking G-locally analytic vectors.
3.6.3. The proof of the other direction goes as follows: first
 $H^i_{\mathrm {cont}}(G_n,B\widehat {\otimes }_{\mathbb {Q}_p}\mathscr {C}^{\mathrm {an}}(G_n,\mathbb {Q}_p))$
will be identified with a certain group cohomology of
$H^i_{\mathrm {cont}}(G_n,B\widehat {\otimes }_{\mathbb {Q}_p}\mathscr {C}^{\mathrm {an}}(G_n,\mathbb {Q}_p))$
will be identified with a certain group cohomology of
![]() $\Gamma $
and then we construct explicit elements to kill these cohomology groups. In particular, it implies strongly
$\Gamma $
and then we construct explicit elements to kill these cohomology groups. In particular, it implies strongly
![]() $\mathfrak {LA}$
-acyclicity. We remark that this is a standard technique in the theory of
$\mathfrak {LA}$
-acyclicity. We remark that this is a standard technique in the theory of
![]() $(\varphi ,\Gamma )$
-modules for studying Galois cohomology of p-adic Galois representations.
$(\varphi ,\Gamma )$
-modules for studying Galois cohomology of p-adic Galois representations.
Keep the notation introduced in Section 3.2.1. Let
![]() $G_0$
be an open subgroup considered in Section 3.3.1. We can consider
$G_0$
be an open subgroup considered in Section 3.3.1. We can consider
 $H^i_{\mathrm {cont}}(G_0\times \Gamma ,B_{\infty }\widehat {\otimes }_{\mathbb {Q}_p}\mathscr {C}^{\mathrm {an}}(G_0,\mathbb {Q}_p))$
. On the one hand, by the almost purity theorem,
$H^i_{\mathrm {cont}}(G_0\times \Gamma ,B_{\infty }\widehat {\otimes }_{\mathbb {Q}_p}\mathscr {C}^{\mathrm {an}}(G_0,\mathbb {Q}_p))$
. On the one hand, by the almost purity theorem,
 $H^i_{\mathrm {cont}}(\Gamma ,B_{\infty }^+\otimes _{\mathbb {Z}_p} \mathscr {C}^{\mathrm {an}}(G_0,\mathbb {Q}_p)^\circ /p)$
almost vanishes for
$H^i_{\mathrm {cont}}(\Gamma ,B_{\infty }^+\otimes _{\mathbb {Z}_p} \mathscr {C}^{\mathrm {an}}(G_0,\mathbb {Q}_p)^\circ /p)$
almost vanishes for
![]() $i\geq 1$
; hence,
$i\geq 1$
; hence,
 $$ \begin{align*}H^i_{\mathrm{cont}}(\Gamma,B_{\infty}\widehat{\otimes}_{\mathbb{Q}_p}\mathscr{C}^{\mathrm{an}}(G_0,\mathbb{Q}_p))=0.\end{align*} $$
$$ \begin{align*}H^i_{\mathrm{cont}}(\Gamma,B_{\infty}\widehat{\otimes}_{\mathbb{Q}_p}\mathscr{C}^{\mathrm{an}}(G_0,\mathbb{Q}_p))=0.\end{align*} $$
Applying the Hochschild–Serre spectral sequence to
![]() $\{\mathbf {1}\}\times \Gamma \subset G_0\times \Gamma $
and using Lemma 3.2.9, we get
$\{\mathbf {1}\}\times \Gamma \subset G_0\times \Gamma $
and using Lemma 3.2.9, we get
 $$ \begin{align*}H^i_{\mathrm{cont}}(G_0,B\widehat{\otimes}_{\mathbb{Q}_p}\mathscr{C}^{\mathrm{an}}(G_0,\mathbb{Q}_p))\xrightarrow{\sim}H^i_{\mathrm{cont}}(G_0\times \Gamma,B_{\infty}\widehat{\otimes}_{\mathbb{Q}_p}\mathscr{C}^{\mathrm{an}}(G_0,\mathbb{Q}_p)).\end{align*} $$
$$ \begin{align*}H^i_{\mathrm{cont}}(G_0,B\widehat{\otimes}_{\mathbb{Q}_p}\mathscr{C}^{\mathrm{an}}(G_0,\mathbb{Q}_p))\xrightarrow{\sim}H^i_{\mathrm{cont}}(G_0\times \Gamma,B_{\infty}\widehat{\otimes}_{\mathbb{Q}_p}\mathscr{C}^{\mathrm{an}}(G_0,\mathbb{Q}_p)).\end{align*} $$
On the other hand, if we apply the Hochschild–Serre spectral sequence to
![]() $G_0\times \{\mathbf {1}\} \subset G_0\times \Gamma $
and note that
$G_0\times \{\mathbf {1}\} \subset G_0\times \Gamma $
and note that
 $(B_{\infty }\widehat {\otimes }_{\mathbb {Q}_p}\mathscr {C}^{\mathrm {an}}(G_0,\mathbb {Q}_p))^{G_0}=(B_{\infty })^{G_0-\mathrm {an}}$
, we get
$(B_{\infty }\widehat {\otimes }_{\mathbb {Q}_p}\mathscr {C}^{\mathrm {an}}(G_0,\mathbb {Q}_p))^{G_0}=(B_{\infty })^{G_0-\mathrm {an}}$
, we get
 $$ \begin{align*}H^i_{\mathrm{cont}}(\Gamma,(B_{\infty})^{G_0-\mathrm{an}})\xrightarrow{\sim}H^i_{\mathrm{cont}}(G_0\times \Gamma,B_{\infty}\widehat{\otimes}_{\mathbb{Q}_p}\mathscr{C}^{\mathrm{an}}(G_0,\mathbb{Q}_p)).\end{align*} $$
$$ \begin{align*}H^i_{\mathrm{cont}}(\Gamma,(B_{\infty})^{G_0-\mathrm{an}})\xrightarrow{\sim}H^i_{\mathrm{cont}}(G_0\times \Gamma,B_{\infty}\widehat{\otimes}_{\mathbb{Q}_p}\mathscr{C}^{\mathrm{an}}(G_0,\mathbb{Q}_p)).\end{align*} $$
All of these isomorphism are functorial in
![]() $G_0$
. Therefore,
$G_0$
. Therefore,
Lemma 3.6.4. There is a natural isomorphism
 $$ \begin{align*}H^i_{\mathrm{cont}}(G_0,B\widehat{\otimes}_{\mathbb{Q}_p}\mathscr{C}^{\mathrm{an}}(G_0,\mathbb{Q}_p))\cong H^i_{\mathrm{cont}}(\Gamma,(B_{\infty})^{G_0-\mathrm{an}})\end{align*} $$
$$ \begin{align*}H^i_{\mathrm{cont}}(G_0,B\widehat{\otimes}_{\mathbb{Q}_p}\mathscr{C}^{\mathrm{an}}(G_0,\mathbb{Q}_p))\cong H^i_{\mathrm{cont}}(\Gamma,(B_{\infty})^{G_0-\mathrm{an}})\end{align*} $$
functorial in
![]() $G_0$
.
$G_0$
.
3.6.5. From this, it is clear that
 $H^i_{\mathrm {cont}}(G_0,B\widehat {\otimes }_{\mathbb {Q}_p}\mathscr {C}^{\mathrm {an}}(G_0,\mathbb {Q}_p))=0,i\geq 2$
as
$H^i_{\mathrm {cont}}(G_0,B\widehat {\otimes }_{\mathbb {Q}_p}\mathscr {C}^{\mathrm {an}}(G_0,\mathbb {Q}_p))=0,i\geq 2$
as
![]() $\Gamma $
is 1-dimensional. So we assume
$\Gamma $
is 1-dimensional. So we assume
![]() $i=1$
from now on. Our next step is to replace
$i=1$
from now on. Our next step is to replace
![]() $(B_{\infty })^{G_0-\mathrm {an}}$
on the right-hand side by a smaller space. Let
$(B_{\infty })^{G_0-\mathrm {an}}$
on the right-hand side by a smaller space. Let
![]() $D_{G_0,n}$
be the subspace of
$D_{G_0,n}$
be the subspace of
![]() $p^n\Gamma $
-analytic vectors in
$p^n\Gamma $
-analytic vectors in
![]() $(B_{\infty })^{G_0-\mathrm {an}}$
; that is,
$(B_{\infty })^{G_0-\mathrm {an}}$
; that is,
![]() $(B_{\infty })^{G_0\times p^n\Gamma -\mathrm {an}}$
. It follows from Lemma 3.3.2 that for sufficiently large n,
$(B_{\infty })^{G_0\times p^n\Gamma -\mathrm {an}}$
. It follows from Lemma 3.3.2 that for sufficiently large n,
 $$ \begin{align*}(B_{\infty})^{G_0-\mathrm{an}}=B_{G_0,\infty}\widehat{\otimes}_{B_{G_0,n}}D_{G_0,n}.\end{align*} $$
$$ \begin{align*}(B_{\infty})^{G_0-\mathrm{an}}=B_{G_0,\infty}\widehat{\otimes}_{B_{G_0,n}}D_{G_0,n}.\end{align*} $$
Moreover, let
 $D_{G_0,n}^{+}=B_{\infty }^{+}\cap D_{G_0,n}$
; then by our construction in Section 3.3.1,
$D_{G_0,n}^{+}=B_{\infty }^{+}\cap D_{G_0,n}$
; then by our construction in Section 3.3.1,
 $$ \begin{align*}(\gamma-1)^m(D_{G_0,n}^{+})\subset pD_{G_0,n}^{+}\end{align*} $$
$$ \begin{align*}(\gamma-1)^m(D_{G_0,n}^{+})\subset pD_{G_0,n}^{+}\end{align*} $$
for some m depending on n. Fix such n and m for the moment. Recall that from results in Section 3.2.6, for k large enough, there is Tate’s normalised trace
 $\overline {\mathrm {tr}}_{X_{G_0,k}}:B_{G_0,\infty }\to B_{G_0,k}$
and
$\overline {\mathrm {tr}}_{X_{G_0,k}}:B_{G_0,\infty }\to B_{G_0,k}$
and
![]() $\gamma -1$
is invertible on
$\gamma -1$
is invertible on
 $\ker (\overline {\mathrm {tr}}_{X_{G_0,k}})$
with the norm of its inverse
$\ker (\overline {\mathrm {tr}}_{X_{G_0,k}})$
with the norm of its inverse
 $\|(\gamma -1)^{-1}\|<p^{\frac {1}{2m}}$
. We claim that
$\|(\gamma -1)^{-1}\|<p^{\frac {1}{2m}}$
. We claim that
 $H^1_{\mathrm {cont}} (\Gamma ,\ker (\overline {\mathrm {tr}}_{X_{G_0,k}})\widehat {\otimes }_{B_{G_0,n}}D_{G_0,n})=0$
for such k. Assuming this, as
$H^1_{\mathrm {cont}} (\Gamma ,\ker (\overline {\mathrm {tr}}_{X_{G_0,k}})\widehat {\otimes }_{B_{G_0,n}}D_{G_0,n})=0$
for such k. Assuming this, as
![]() $D_{G_0,k}=B_{G_n,k}\otimes _{B_{G_0,n}}D_{G_0,n}$
, we get
$D_{G_0,k}=B_{G_n,k}\otimes _{B_{G_0,n}}D_{G_0,n}$
, we get
 $$ \begin{align*}H^1_{\mathrm{cont}}(\Gamma,(B_{\infty})^{G_0-\mathrm{an}})=H^1_{\mathrm{cont}}(\Gamma,D_{G_0,k})=H^1_{\mathrm{cont}}(\Gamma,(B_{\infty})^{(G_0\times p^k\Gamma)-\mathrm{an}})\end{align*} $$
$$ \begin{align*}H^1_{\mathrm{cont}}(\Gamma,(B_{\infty})^{G_0-\mathrm{an}})=H^1_{\mathrm{cont}}(\Gamma,D_{G_0,k})=H^1_{\mathrm{cont}}(\Gamma,(B_{\infty})^{(G_0\times p^k\Gamma)-\mathrm{an}})\end{align*} $$
for k sufficiently large. Therefore,
 $$ \begin{align*}R^1\mathfrak{LA}(B)=\varinjlim_{n,k}H^1_{\mathrm{cont}}(\Gamma,(B_{\infty})^{(G_n\times p^k\Gamma)-\mathrm{an}}).\end{align*} $$
$$ \begin{align*}R^1\mathfrak{LA}(B)=\varinjlim_{n,k}H^1_{\mathrm{cont}}(\Gamma,(B_{\infty})^{(G_n\times p^k\Gamma)-\mathrm{an}}).\end{align*} $$
The vanishing of
 $H^1_{\mathrm {cont}}(\Gamma ,\ker (\overline {\mathrm {tr}}_{X_{G_0,k}})\widehat {\otimes }_{B_{G_0,n}}D_{G_0,n})$
is a consequence of the following easy lemma.
$H^1_{\mathrm {cont}}(\Gamma ,\ker (\overline {\mathrm {tr}}_{X_{G_0,k}})\widehat {\otimes }_{B_{G_0,n}}D_{G_0,n})$
is a consequence of the following easy lemma.
Lemma 3.6.6. For any
 $a\in \ker (\overline {\mathrm {tr}}_{X_{G_0,k}})^{+}:=\ker (\overline {\mathrm {tr}}_{X_{G_0,k}})\cap B_{\infty }^{+}$
and
$a\in \ker (\overline {\mathrm {tr}}_{X_{G_0,k}})^{+}:=\ker (\overline {\mathrm {tr}}_{X_{G_0,k}})\cap B_{\infty }^{+}$
and
 $b\in D_{G_0,n}^{+}$
, we have
$b\in D_{G_0,n}^{+}$
, we have
 $pa\otimes b\in (\gamma -1)(\ker (\overline {\mathrm {tr}}_{X_{G_0,k}})^+\widehat {\otimes }_{B_{G_0,k}^{+}}D_{G_0,n}^{+})$
.
$pa\otimes b\in (\gamma -1)(\ker (\overline {\mathrm {tr}}_{X_{G_0,k}})^+\widehat {\otimes }_{B_{G_0,k}^{+}}D_{G_0,n}^{+})$
.
Proof. Let
 $c=(\gamma -1)^{-1}(pa)\in \ker (\overline {\mathrm {tr}}_{X_{G_0,k}})^{+}$
. Consider the series
$c=(\gamma -1)^{-1}(pa)\in \ker (\overline {\mathrm {tr}}_{X_{G_0,k}})^{+}$
. Consider the series
 $$ \begin{align*}\sum^{+\infty}_{l=0} (\gamma^{-1}-1)^{-l}(c)\otimes (\gamma-1)^{l}(b)=\sum^{+\infty}_{l=0} \gamma^l(1-\gamma)^{-l}(c)\otimes (\gamma-1)^{l}(b)\end{align*} $$
$$ \begin{align*}\sum^{+\infty}_{l=0} (\gamma^{-1}-1)^{-l}(c)\otimes (\gamma-1)^{l}(b)=\sum^{+\infty}_{l=0} \gamma^l(1-\gamma)^{-l}(c)\otimes (\gamma-1)^{l}(b)\end{align*} $$
which by our assumption converges to an element
 $x\in \ker (\overline {\mathrm {tr}}_{X_{G_0,k}})^+\widehat {\otimes }_{B_{G_0,k}^{+}}D_{G_0,n}^{+}$
. A direct computation gives
$x\in \ker (\overline {\mathrm {tr}}_{X_{G_0,k}})^+\widehat {\otimes }_{B_{G_0,k}^{+}}D_{G_0,n}^{+}$
. A direct computation gives
![]() $(\gamma -1)(x)=pa\otimes b$
. Indeed, let
$(\gamma -1)(x)=pa\otimes b$
. Indeed, let
Then
![]() $(\gamma -1)(y_l)=-\gamma (y_{l-1}), (\gamma -1)(z_l)=z_{l+1}$
. Hence,
$(\gamma -1)(y_l)=-\gamma (y_{l-1}), (\gamma -1)(z_l)=z_{l+1}$
. Hence,
When taking the summation of l from
![]() $0$
to
$0$
to
![]() $+\infty $
, only
$+\infty $
, only
![]() $-\gamma (y_{-1})\otimes z_0$
is not cancelled out. But this is just
$-\gamma (y_{-1})\otimes z_0$
is not cancelled out. But this is just
![]() $(\gamma -1)(c)\otimes b=pa\otimes b$
.
$(\gamma -1)(c)\otimes b=pa\otimes b$
.
3.6.7. Now it suffices to show that for any element
 $x\in (B_{\infty })^{(G_0\times p^k\Gamma )-\mathrm {an}}$
, we can find
$x\in (B_{\infty })^{(G_0\times p^k\Gamma )-\mathrm {an}}$
, we can find
![]() $n>0$
and
$n>0$
and
![]() $l\geq k$
such that
$l\geq k$
such that
 $$ \begin{align*}x\in(\gamma-1)((B_{\infty})^{(G_n\times p^l\Gamma)-\mathrm{an}}).\end{align*} $$
$$ \begin{align*}x\in(\gamma-1)((B_{\infty})^{(G_n\times p^l\Gamma)-\mathrm{an}}).\end{align*} $$
Fix such
![]() $k,x$
. Let
$k,x$
. Let
![]() $\phi _{\gamma }\in \operatorname {\mathrm {Lie}}(\Gamma )$
be the logarithm of
$\phi _{\gamma }\in \operatorname {\mathrm {Lie}}(\Gamma )$
be the logarithm of
![]() $\gamma $
. Then by Lemma 2.1.8, there exists a constant
$\gamma $
. Then by Lemma 2.1.8, there exists a constant
![]() $C>0$
such that
$C>0$
such that
Recall that
![]() $\|\cdot \|_{G_0\times p^k\Gamma }$
is a norm on the
$\|\cdot \|_{G_0\times p^k\Gamma }$
is a norm on the
![]() $G_0\times p^k\Gamma $
-analytic vectors introduced in Section 2.1.1.
$G_0\times p^k\Gamma $
-analytic vectors introduced in Section 2.1.1.
Recall that we assume
![]() $\widetilde {X}$
is a locally analytic covering of X. Hence, by part (3) of Proposition 3.5.3, we may find an element
$\widetilde {X}$
is a locally analytic covering of X. Hence, by part (3) of Proposition 3.5.3, we may find an element
![]() $z\in (B_{\infty })^{\mathrm {la}}$
such that
$z\in (B_{\infty })^{\mathrm {la}}$
such that
![]() $\gamma (z)=z-1$
. By our construction of
$\gamma (z)=z-1$
. By our construction of
![]() $B_{\infty }$
in Section 3.2.6,
$B_{\infty }$
in Section 3.2.6,
![]() $\bigcup _{n,l} B_{G_n,l}$
is dense in
$\bigcup _{n,l} B_{G_n,l}$
is dense in
![]() $B_{\infty }$
. Hence, there exists an element
$B_{\infty }$
. Hence, there exists an element
![]() $z_0\in B_{G_n,l}$
for some
$z_0\in B_{G_n,l}$
for some
![]() $n,l$
such that
$n,l$
such that
 $z\in (B_{\infty })^{(G_n\times p^l\Gamma )-\mathrm {an}}$
and the norm of
$z\in (B_{\infty })^{(G_n\times p^l\Gamma )-\mathrm {an}}$
and the norm of
![]() $z-z_0$
(as an element in
$z-z_0$
(as an element in
![]() $B_{\infty }$
) satisfies
$B_{\infty }$
) satisfies
 $$ \begin{align*}\|z-z_0\|\leq \frac{1}{2Cp^{1/(p-1)}}.\end{align*} $$
$$ \begin{align*}\|z-z_0\|\leq \frac{1}{2Cp^{1/(p-1)}}.\end{align*} $$
Enlarging
![]() $n,l$
if necessary, we may assume
$n,l$
if necessary, we may assume
![]() $\|z-z_0\|_{G_n\times p^l\Gamma }=\|z-z_0\|$
by Lemma 2.1.8. Now consider the series
$\|z-z_0\|_{G_n\times p^l\Gamma }=\|z-z_0\|$
by Lemma 2.1.8. Now consider the series
 $$ \begin{align*} -\sum_{m=0}^{+\infty} \frac{\phi_{\gamma}^{(m)}(x)}{(m+1)!}(z-z_0)^{m+1}. \end{align*} $$
$$ \begin{align*} -\sum_{m=0}^{+\infty} \frac{\phi_{\gamma}^{(m)}(x)}{(m+1)!}(z-z_0)^{m+1}. \end{align*} $$
It is easy to see that
 $\|\frac {\phi _\gamma ^{(m)}(x)}{(m+1)!}(z-z_0)^{m+1}\|_{G_n\times p^l\Gamma }\leq \frac {\|x\|_{G_0\times p^k\Gamma }}{2^{m+1}C}$
. So this series converges (with respect to
$\|\frac {\phi _\gamma ^{(m)}(x)}{(m+1)!}(z-z_0)^{m+1}\|_{G_n\times p^l\Gamma }\leq \frac {\|x\|_{G_0\times p^k\Gamma }}{2^{m+1}C}$
. So this series converges (with respect to
![]() $\|\cdot \|_{G_n\times p^l\Gamma }$
) to an element
$\|\cdot \|_{G_n\times p^l\Gamma }$
) to an element
 $y\in (B_{\infty })^{(G_n\times p^l\Gamma )-\mathrm {an}}$
. Note that
$y\in (B_{\infty })^{(G_n\times p^l\Gamma )-\mathrm {an}}$
. Note that
![]() $\phi _{\gamma }(z-z_0)=\phi _{\gamma }(z)=-1$
. A direct computation shows
$\phi _{\gamma }(z-z_0)=\phi _{\gamma }(z)=-1$
. A direct computation shows
After replacing l by a larger integer, we may assume
 $(\gamma -1)^m(D_{G_n,l}^+)\subset pD_{G_n,l}^+$
for some
$(\gamma -1)^m(D_{G_n,l}^+)\subset pD_{G_n,l}^+$
for some
![]() $m>0$
by our construction in Section 3.3.1. Recall that
$m>0$
by our construction in Section 3.3.1. Recall that
 $D_{G_n,l}^+=(B_{\infty })^{(G_n\times p^l\Gamma )-\mathrm {an}}\cap B_{\infty }^+$
. From this and
$D_{G_n,l}^+=(B_{\infty })^{(G_n\times p^l\Gamma )-\mathrm {an}}\cap B_{\infty }^+$
. From this and
![]() $\phi _{\gamma }(y)=x$
, we conclude
$\phi _{\gamma }(y)=x$
, we conclude
 $x\in (\gamma -1)((B_{\infty })^{(G_n\times p^l\Gamma )-\mathrm {an}})$
by the following simple lemma.
$x\in (\gamma -1)((B_{\infty })^{(G_n\times p^l\Gamma )-\mathrm {an}})$
by the following simple lemma.
Lemma 3.6.8. Let M be a unitary
![]() $\mathbb {Q}_p$
-Banach representation of
$\mathbb {Q}_p$
-Banach representation of
![]() $\Gamma $
and
$\Gamma $
and
![]() $M^o$
be its unit ball. Suppose
$M^o$
be its unit ball. Suppose
![]() $(\gamma -1)^mM^o \subset pM^o$
for some
$(\gamma -1)^mM^o \subset pM^o$
for some
![]() $m\geq 0$
. Then
$m\geq 0$
. Then
![]() $\phi _{\gamma }(M)\subset (\gamma -1)(M)$
.
$\phi _{\gamma }(M)\subset (\gamma -1)(M)$
.
Proof. The argument here was pointed out by a referee and is much simpler than my previous argument. One only needs to observe that
![]() $\phi _\gamma $
is the logarithm of
$\phi _\gamma $
is the logarithm of
![]() $\gamma $
; hence,
$\gamma $
; hence,
 $$ \begin{align*}\phi_\gamma=(\gamma-1)\sum_{m=0}(-1)^m\frac{(\gamma-1)^{m}}{m+1},\end{align*} $$
$$ \begin{align*}\phi_\gamma=(\gamma-1)\sum_{m=0}(-1)^m\frac{(\gamma-1)^{m}}{m+1},\end{align*} $$
and the second series converges to an operator on M by our assumption.
Remark 3.6.9. The argument of this subsection is basically the same as the proof of Théorème 3.4 of [Reference Berger and ColmezBC16]. Note that in their setting, the assumption ‘locally analytic’ always holds by Lemme 3.6 of [Reference Berger and ColmezBC16].
For later applications, it will be useful to remove the smallness assumption on X in Theorem 3.6.1. Unfortunately, we have to make some assumption in order to do this. Let
![]() $\widetilde X=\operatorname {\mathrm {Spa}}(B,B^+)$
be a ‘log G-Galois pro-étale perfectoid covering’ of
$\widetilde X=\operatorname {\mathrm {Spa}}(B,B^+)$
be a ‘log G-Galois pro-étale perfectoid covering’ of
![]() $X=\operatorname {\mathrm {Spa}}(A,A^+)$
as in Section 3.1.1 except that we do not require X to be small anymore. Denote by
$X=\operatorname {\mathrm {Spa}}(A,A^+)$
as in Section 3.1.1 except that we do not require X to be small anymore. Denote by
![]() $\pi :\widetilde X \to X$
and
$\pi :\widetilde X \to X$
and
 $\widetilde {\mathcal {O}}=\pi _*\mathcal {O}_{\widetilde X}$
. Then we can consider subsheaf
$\widetilde {\mathcal {O}}=\pi _*\mathcal {O}_{\widetilde X}$
. Then we can consider subsheaf
 $\widetilde {\mathcal {O}}^{\mathrm {la}}\subset \widetilde {\mathcal {O}}$
of G-locally analytic sections and subsheaves
$\widetilde {\mathcal {O}}^{\mathrm {la}}\subset \widetilde {\mathcal {O}}$
of G-locally analytic sections and subsheaves
![]() $\widetilde {\mathcal {O}}^{n}\subset \widetilde {\mathcal {O}}$
of
$\widetilde {\mathcal {O}}^{n}\subset \widetilde {\mathcal {O}}$
of
![]() $G_n$
-analytic sections. Clearly,
$G_n$
-analytic sections. Clearly,
 $\varinjlim _n \widetilde {\mathcal {O}}^{n}=\mathcal {O}^{\mathrm {la}}$
.
$\varinjlim _n \widetilde {\mathcal {O}}^{n}=\mathcal {O}^{\mathrm {la}}$
.
Corollary 3.6.10. Suppose
![]() $\widetilde X=\operatorname {\mathrm {Spa}}(B,B^+)$
is a ‘log G-Galois pro-étale perfectoid covering’ of
$\widetilde X=\operatorname {\mathrm {Spa}}(B,B^+)$
is a ‘log G-Galois pro-étale perfectoid covering’ of
![]() $X=\operatorname {\mathrm {Spa}}(A,A^+)$
and X can be covered by small rational open subsets
$X=\operatorname {\mathrm {Spa}}(A,A^+)$
and X can be covered by small rational open subsets
![]() $X_i,i=1,\cdots ,k$
, whose preimage
$X_i,i=1,\cdots ,k$
, whose preimage
![]() $\widetilde {X}_i$
in
$\widetilde {X}_i$
in
![]() $\tilde X$
is a locally analytic covering of
$\tilde X$
is a locally analytic covering of
![]() $X_i$
. Then
$X_i$
. Then
-
(1)
 $R^i\mathfrak {LA}(B)=H^i(X,\widetilde {\mathcal {O}}^{\mathrm {la}})=\check {H}^i(X,\widetilde {\mathcal {O}}^{\mathrm {la}})$
for any i, where
$R^i\mathfrak {LA}(B)=H^i(X,\widetilde {\mathcal {O}}^{\mathrm {la}})=\check {H}^i(X,\widetilde {\mathcal {O}}^{\mathrm {la}})$
for any i, where
 $\check {H}^i(X,\widetilde {\mathcal {O}}^{\mathrm {la}})$
denotes the Čech cohomology. In particular, B is
$\check {H}^i(X,\widetilde {\mathcal {O}}^{\mathrm {la}})$
denotes the Čech cohomology. In particular, B is
 $\mathfrak {LA}$
-acyclic if and only if
$\mathfrak {LA}$
-acyclic if and only if  $$ \begin{align*}\check{H}^i(X,\widetilde{\mathcal{O}}^{\mathrm{la}})=0,\,i\geq 1.\end{align*} $$
$$ \begin{align*}\check{H}^i(X,\widetilde{\mathcal{O}}^{\mathrm{la}})=0,\,i\geq 1.\end{align*} $$
-
(2) Write
 $\mathfrak {U}_0=\{X_1,\cdots ,X_k\}$
. For any sheaf F on X, denote by
$\mathfrak {U}_0=\{X_1,\cdots ,X_k\}$
. For any sheaf F on X, denote by
 $\check {H}^i(\mathfrak {U}_0,F)$
the Čech cohomology of F with respect to the cover
$\check {H}^i(\mathfrak {U}_0,F)$
the Čech cohomology of F with respect to the cover
 $\mathfrak {U}_0$
. Suppose the direct system
$\mathfrak {U}_0$
. Suppose the direct system
 $\{\check {H}^i(\mathfrak {U}_0,\widetilde {\mathcal {O}}^{n})\}_{n}$
is essentially zero for any
$\{\check {H}^i(\mathfrak {U}_0,\widetilde {\mathcal {O}}^{n})\}_{n}$
is essentially zero for any
 $i>0$
. Then B is strongly
$i>0$
. Then B is strongly
 $\mathfrak {LA}$
-acyclic.
$\mathfrak {LA}$
-acyclic.
Proof. The argument here is a standard application of Čech cohomology. Let
![]() $\mathfrak {B}$
be the set of small rational open subsets of X contained in some
$\mathfrak {B}$
be the set of small rational open subsets of X contained in some
![]() $X_i$
. It is easy to see that
$X_i$
. It is easy to see that
![]() $\mathfrak {B}$
is closed under finite intersections and forms a basis of open subsets of X. Moreover, for any
$\mathfrak {B}$
is closed under finite intersections and forms a basis of open subsets of X. Moreover, for any
![]() $U\in \mathfrak {B}$
,
$U\in \mathfrak {B}$
,
![]() $\pi ^{-1}(U)$
is a locally analytic covering of U. We claim that for any
$\pi ^{-1}(U)$
is a locally analytic covering of U. We claim that for any
![]() $i\geq 1, U\in \mathfrak {B}$
, the Čech cohomology
$i\geq 1, U\in \mathfrak {B}$
, the Čech cohomology
 $$ \begin{align*}\check{H}^i(U,\widetilde{\mathcal{O}}^{\mathrm{la}})=0.\end{align*} $$
$$ \begin{align*}\check{H}^i(U,\widetilde{\mathcal{O}}^{\mathrm{la}})=0.\end{align*} $$
To see this, since U is quasi-compact, any open cover of U can be refined to a finite cover
![]() $\mathfrak {U}\subset \mathfrak {B}$
. Let
$\mathfrak {U}\subset \mathfrak {B}$
. Let
 $C^{\bullet }(\mathfrak {U},\widetilde {\mathcal {O}}),C^{\bullet }(\mathfrak {U},\widetilde {\mathcal {O}}^{\mathrm {la}})$
be the Čech complex for
$C^{\bullet }(\mathfrak {U},\widetilde {\mathcal {O}}),C^{\bullet }(\mathfrak {U},\widetilde {\mathcal {O}}^{\mathrm {la}})$
be the Čech complex for
![]() $\widetilde {\mathcal {O}}$
and
$\widetilde {\mathcal {O}}$
and
 $\widetilde {\mathcal {O}}^{\mathrm {la}}$
with respect to this cover. Then
$\widetilde {\mathcal {O}}^{\mathrm {la}}$
with respect to this cover. Then
![]() $B\to C^{\bullet }(\mathfrak {U},\widetilde {\mathcal {O}})$
is strictly exact by the almost vanishing of higher cohomology (Theorem 1.8.(iv) of [Reference ScholzeSch12]). Note that each term in this complex is
$B\to C^{\bullet }(\mathfrak {U},\widetilde {\mathcal {O}})$
is strictly exact by the almost vanishing of higher cohomology (Theorem 1.8.(iv) of [Reference ScholzeSch12]). Note that each term in this complex is
![]() $\mathfrak {LA}$
-acyclic by Theorem 3.6.1. Passing to locally analytic vectors, we see that
$\mathfrak {LA}$
-acyclic by Theorem 3.6.1. Passing to locally analytic vectors, we see that
 $B^{\mathrm {la}}\to C^{\bullet }(\mathfrak {U},\widetilde {\mathcal {O}}^{\mathrm {la}})$
is also exact by the second part of Lemma 2.2.2. Hence,
$B^{\mathrm {la}}\to C^{\bullet }(\mathfrak {U},\widetilde {\mathcal {O}}^{\mathrm {la}})$
is also exact by the second part of Lemma 2.2.2. Hence,
 $\check {H}^i(U,\widetilde {\mathcal {O}}^{\mathrm {la}})=0,i\geq 1$
.
$\check {H}^i(U,\widetilde {\mathcal {O}}^{\mathrm {la}})=0,i\geq 1$
.
Now by Corollaire 4, p. 176 of [Reference GrothendieckGro57], the vanishing of higher Čech cohomology for any
![]() $U\in \mathfrak {B}$
implies that
$U\in \mathfrak {B}$
implies that
 $H^i(U,\widetilde {\mathcal {O}}^{\mathrm {la}})=0,i\geq 1$
and
$H^i(U,\widetilde {\mathcal {O}}^{\mathrm {la}})=0,i\geq 1$
and
 ${H}^i(X,\widetilde {\mathcal {O}}^{\mathrm {la}})=\check {H}^i(X,\widetilde {\mathcal {O}}^{\mathrm {la}})$
. Hence, we can compute
${H}^i(X,\widetilde {\mathcal {O}}^{\mathrm {la}})=\check {H}^i(X,\widetilde {\mathcal {O}}^{\mathrm {la}})$
. Hence, we can compute
 ${H}^i(X,\widetilde {\mathcal {O}}^{\mathrm {la}})$
using a Čech complex with respect to a finite cover in
${H}^i(X,\widetilde {\mathcal {O}}^{\mathrm {la}})$
using a Čech complex with respect to a finite cover in
![]() $\mathfrak {B}$
. We can use
$\mathfrak {B}$
. We can use
![]() $\mathfrak {U}_0$
here. All of the claims in the corollary follow on applying the third part of Lemma 2.2.2 to
$\mathfrak {U}_0$
here. All of the claims in the corollary follow on applying the third part of Lemma 2.2.2 to
![]() $B\to C^{\bullet }(\mathfrak {U}_0,\widetilde {\mathcal {O}})$
.
$B\to C^{\bullet }(\mathfrak {U}_0,\widetilde {\mathcal {O}})$
.
4 Locally analytic functions on perfectoid modular curves
Now we apply the previous general theory to the case of modular curves of infinite level at p. It turns out that in this case, the differential operator in Theorem 3.1.2 is very classical (see Theorem 4.2.7) and (twisted)
![]() $\mathscr {D}$
-modules on the flag variety appear naturally in this setup. Following Berger–Colmez [Reference Berger and ColmezBC16], we also give explicit descriptions of the
$\mathscr {D}$
-modules on the flag variety appear naturally in this setup. Following Berger–Colmez [Reference Berger and ColmezBC16], we also give explicit descriptions of the
![]() $\mathrm {GL}_2(\mathbb {Q}_p)$
-locally analytic functions on the infinite level modular curve. This will be important for our calculations in the next section.
$\mathrm {GL}_2(\mathbb {Q}_p)$
-locally analytic functions on the infinite level modular curve. This will be important for our calculations in the next section.
In the first subsection, we will collect some basic facts about modular curves of infinite level at p and the Hodge–Tate period map. This is the simplest case in the theory of perfectoid Shimura varieties developed by Scholze in [Reference ScholzeSch15].
4.1 Modular curves and the Hodge–Tate period map
4.1.1. We define modular curves adèlically. Fix a neat open compact subgroup
![]() $K\subset \mathrm {GL}_2(\mathbb {A}_f)$
and let
$K\subset \mathrm {GL}_2(\mathbb {A}_f)$
and let
![]() $Y_{K}/\mathbb {Q}$
be the moduli space of elliptic curves with level-K structure. Let
$Y_{K}/\mathbb {Q}$
be the moduli space of elliptic curves with level-K structure. Let
![]() $\mathbb {H}^{\pm 1}$
be the union of upper and lower half-planes. The complex points of
$\mathbb {H}^{\pm 1}$
be the union of upper and lower half-planes. The complex points of
![]() $Y_{K}$
are given by the usual double quotient
$Y_{K}$
are given by the usual double quotient
 $$ \begin{align*}Y_{K}(\mathbb{C})=\mathrm{GL}_2(\mathbb{Q})\backslash (\mathbb{H}^{\pm1}\times\mathrm{GL}_2(\mathbb{A}_f)/K).\end{align*} $$
$$ \begin{align*}Y_{K}(\mathbb{C})=\mathrm{GL}_2(\mathbb{Q})\backslash (\mathbb{H}^{\pm1}\times\mathrm{GL}_2(\mathbb{A}_f)/K).\end{align*} $$
![]() $Y_{K}$
admits a natural compactification
$Y_{K}$
admits a natural compactification
![]() $X_K/\mathbb {Q}$
by adding finitely many cusps. The universal elliptic curve over
$X_K/\mathbb {Q}$
by adding finitely many cusps. The universal elliptic curve over
![]() $Y_{K}$
extends to a semi-abelian variety over
$Y_{K}$
extends to a semi-abelian variety over
![]() $X_K$
and we denote by
$X_K$
and we denote by
![]() $\omega $
the sheaf of its invariant differentials. On the complex points,
$\omega $
the sheaf of its invariant differentials. On the complex points,
![]() $\omega $
is the canonical extension of
$\omega $
is the canonical extension of
![]() $\omega |_{Y_K(\mathbb {C})}$
as defined in Main Theorem 3.1 of [Reference MumfordMum77].
$\omega |_{Y_K(\mathbb {C})}$
as defined in Main Theorem 3.1 of [Reference MumfordMum77].
Fix a complete algebraically closed non-Archimedean field extension C of
![]() $\mathbb {Q}_p$
as in Section 3.1.1. Denote by
$\mathbb {Q}_p$
as in Section 3.1.1. Denote by
![]() $\mathcal {X}_{K}$
(respectively
$\mathcal {X}_{K}$
(respectively
![]() $\mathcal {Y}_K$
) the adic space associated to
$\mathcal {Y}_K$
) the adic space associated to
![]() $X_{K}\times _{\mathbb {Q}}C$
(respectively
$X_{K}\times _{\mathbb {Q}}C$
(respectively
![]() $Y_{K}\times _{\mathbb {Q}}C$
).
$Y_{K}\times _{\mathbb {Q}}C$
).
Theorem 4.1.2. For any tame level
 $K^p\subset \mathrm {GL}_2(\mathbb {A}^p_f)$
contained in the level-N subgroup
$K^p\subset \mathrm {GL}_2(\mathbb {A}^p_f)$
contained in the level-N subgroup
 $\{g\in \mathrm {GL}_2(\hat {\mathbb {Z}}^p)=\prod _{l\neq p}\mathrm {GL}_2(\mathbb {Z}_l)\,\vert \, g\equiv 1\mod N\}$
for some
$\{g\in \mathrm {GL}_2(\hat {\mathbb {Z}}^p)=\prod _{l\neq p}\mathrm {GL}_2(\mathbb {Z}_l)\,\vert \, g\equiv 1\mod N\}$
for some
![]() $N\geq 3$
prime to p, there exists a unique perfectoid space
$N\geq 3$
prime to p, there exists a unique perfectoid space
![]() $\mathcal {X}_{K^p}$
over C such that
$\mathcal {X}_{K^p}$
over C such that
 $$ \begin{align*}\mathcal{X}_{K^p}\sim\varprojlim_{K_p\subset\mathrm{GL}_2(\mathbb{Q}_p)}\mathcal{X}_{K^pK_p},\end{align*} $$
$$ \begin{align*}\mathcal{X}_{K^p}\sim\varprojlim_{K_p\subset\mathrm{GL}_2(\mathbb{Q}_p)}\mathcal{X}_{K^pK_p},\end{align*} $$
where
![]() $K_p$
runs through all open compact subgroups of
$K_p$
runs through all open compact subgroups of
![]() $\mathrm {GL}_2(\mathbb {Q}_p)$
. Therefore, there is a natural right action of
$\mathrm {GL}_2(\mathbb {Q}_p)$
. Therefore, there is a natural right action of
![]() $\mathrm {GL}_2(\mathbb {Q}_p)$
on
$\mathrm {GL}_2(\mathbb {Q}_p)$
on
![]() $\mathcal {X}_{K^p}$
. Moreover, for any open compact subgroup
$\mathcal {X}_{K^p}$
. Moreover, for any open compact subgroup
![]() $K_p$
of
$K_p$
of
![]() $\mathrm {GL}_2(\mathbb {Q}_p)$
, there is a basis consisting of open affinoid subsets U of
$\mathrm {GL}_2(\mathbb {Q}_p)$
, there is a basis consisting of open affinoid subsets U of
![]() $\mathcal {X}_{K^pK_p}$
with affinoid perfectoid preimage
$\mathcal {X}_{K^pK_p}$
with affinoid perfectoid preimage
![]() $U_{\infty }$
in
$U_{\infty }$
in
![]() $\mathcal {X}_{K^p}$
, and the map
$\mathcal {X}_{K^p}$
, and the map
 $$ \begin{align*}\varinjlim_{K_p'\subset K_p}H^0(U_{K_p'},\mathcal{O}_{\mathcal{X}_{K^pK_p'}})\to H^0(U_{\infty},\mathcal{O}_{\mathcal{X}_{K^p}})\end{align*} $$
$$ \begin{align*}\varinjlim_{K_p'\subset K_p}H^0(U_{K_p'},\mathcal{O}_{\mathcal{X}_{K^pK_p'}})\to H^0(U_{\infty},\mathcal{O}_{\mathcal{X}_{K^p}})\end{align*} $$
has dense image. Here
![]() $U_{K_p'}$
denotes the preimage of U in
$U_{K_p'}$
denotes the preimage of U in
![]() $\mathcal {X}_{K^pK_p'}$
.
$\mathcal {X}_{K^pK_p'}$
.
Proof. The existence of
![]() $\mathcal {X}_{K^p}$
basically follows from Theorem III.1.2 of [Reference ScholzeSch15] by taking connected components into account. For the existence of a basis of open subsets of
$\mathcal {X}_{K^p}$
basically follows from Theorem III.1.2 of [Reference ScholzeSch15] by taking connected components into account. For the existence of a basis of open subsets of
![]() $\mathcal {X}_{K^pK_p}$
, by part (iii) of Theorem III.1.2 of [Reference ScholzeSch15], for sufficiently small
$\mathcal {X}_{K^pK_p}$
, by part (iii) of Theorem III.1.2 of [Reference ScholzeSch15], for sufficiently small
![]() $K_p$
, we can find an open cover of
$K_p$
, we can find an open cover of
![]() $\mathcal {X}_{K^pK_p}$
with the desired density property. As taking rational subsets preserves this density property by Lemma 4.5 of [Reference ScholzeSch13a], we may find such a basis
$\mathcal {X}_{K^pK_p}$
with the desired density property. As taking rational subsets preserves this density property by Lemma 4.5 of [Reference ScholzeSch13a], we may find such a basis
![]() $\mathfrak {B}_{K_p}$
of open affinoid subsets for sufficiently small
$\mathfrak {B}_{K_p}$
of open affinoid subsets for sufficiently small
![]() $K_p$
. In general, we can descend this property to any
$K_p$
. In general, we can descend this property to any
![]() $K_p$
. To see this, it is enough to find an affinoid cover of
$K_p$
. To see this, it is enough to find an affinoid cover of
![]() $\mathcal {X}_{K^pK_p}$
with the desired properties. We may assume
$\mathcal {X}_{K^pK_p}$
with the desired properties. We may assume
![]() $K_p$
is a subgroup of
$K_p$
is a subgroup of
![]() $\mathrm {GL}_2(\mathbb {Z}_p)$
. Take an
$\mathrm {GL}_2(\mathbb {Z}_p)$
. Take an
![]() $\mathrm {GL}_2(\mathbb {Z}_p)$
-invariant affinoid cover of
$\mathrm {GL}_2(\mathbb {Z}_p)$
-invariant affinoid cover of
![]() ${\mathscr {F}\!\ell }$
. Then Scholze’s result implies that this cover comes from an affinoid cover of
${\mathscr {F}\!\ell }$
. Then Scholze’s result implies that this cover comes from an affinoid cover of
![]() $\mathcal {X}_{K^pK_p'}$
for some
$\mathcal {X}_{K^pK_p'}$
for some
![]() $K^{\prime }_p$
sufficiently small. We may assume
$K^{\prime }_p$
sufficiently small. We may assume
![]() $K^{\prime }_p$
is a normal subgroup of
$K^{\prime }_p$
is a normal subgroup of
![]() $K_p$
. Hence,
$K_p$
. Hence,
![]() $\mathcal {X}_{K^pK_p}$
can be viewed as the quotient of
$\mathcal {X}_{K^pK_p}$
can be viewed as the quotient of
![]() $\mathcal {X}_{K^pK_p'}$
by
$\mathcal {X}_{K^pK_p'}$
by
![]() $K_p/K^{\prime }_p$
and we can descend this cover to
$K_p/K^{\prime }_p$
and we can descend this cover to
![]() $\mathcal {X}_{K^pK_p}$
by [Reference HansenHan16, Theorem 1.3].
$\mathcal {X}_{K^pK_p}$
by [Reference HansenHan16, Theorem 1.3].
4.1.3. One powerful tool to study the geometry of
![]() $\mathcal {X}_{K^p}$
is the Hodge–Tate period map introduced in Theorem III.1.2 of [Reference ScholzeSch15]. We will give an equivalent definition in our setup.
$\mathcal {X}_{K^p}$
is the Hodge–Tate period map introduced in Theorem III.1.2 of [Reference ScholzeSch15]. We will give an equivalent definition in our setup.
Fix a
![]() $K^p$
as in the theorem and an open subgroup
$K^p$
as in the theorem and an open subgroup
![]() $K_p$
of
$K_p$
of
![]() $\mathrm {GL}_2(\mathbb {Z}_p)$
. Let
$\mathrm {GL}_2(\mathbb {Z}_p)$
. Let
![]() $\mathcal {X}=\mathcal {X}_{K},\mathcal {Y}=\mathcal {Y}_{K}$
with
$\mathcal {X}=\mathcal {X}_{K},\mathcal {Y}=\mathcal {Y}_{K}$
with
![]() $K=K^pK_p$
and let
$K=K^pK_p$
and let
![]() $f:\mathcal {E}\to \mathcal {Y}$
be the universal elliptic curve. Then
$f:\mathcal {E}\to \mathcal {Y}$
be the universal elliptic curve. Then
![]() $R^1f_*\mathbb {Z}_p$
defines a rank 2 étale
$R^1f_*\mathbb {Z}_p$
defines a rank 2 étale
![]() $\mathbb {Z}_p$
-local system
$\mathbb {Z}_p$
-local system
![]() $\underline {V}$
. Our normalisation is that
$\underline {V}$
. Our normalisation is that
-
•
 $\underline {V}$
corresponds to the standard representation of
$\underline {V}$
corresponds to the standard representation of
 $K_p\subset \mathrm {GL}_2(\mathbb {Z}_p)$
. See, for example, Subsection 2.4 of [Reference EmertonEme06a].
$K_p\subset \mathrm {GL}_2(\mathbb {Z}_p)$
. See, for example, Subsection 2.4 of [Reference EmertonEme06a].
This
![]() $\mathbb {Z}_p$
-local system
$\mathbb {Z}_p$
-local system
![]() $\underline {V}$
induces a
$\underline {V}$
induces a
![]() $\hat {\mathbb {Z}}_p$
-local system
$\hat {\mathbb {Z}}_p$
-local system
![]() $\hat {\underline {V}}$
on
$\hat {\underline {V}}$
on
![]() $\mathcal {Y}_{\mathrm {pro\acute {e}t}}$
, the pro-étale site of
$\mathcal {Y}_{\mathrm {pro\acute {e}t}}$
, the pro-étale site of
![]() $\mathcal {Y}$
; see 8.1, 8.2 of [Reference ScholzeSch13a] for the notation here. On the other hand, we denote by
$\mathcal {Y}$
; see 8.1, 8.2 of [Reference ScholzeSch13a] for the notation here. On the other hand, we denote by
![]() $D_{\mathrm {dR}}$
the relative de Rham cohomology of
$D_{\mathrm {dR}}$
the relative de Rham cohomology of
![]() $\mathcal {E}$
over
$\mathcal {E}$
over
![]() $\mathcal {Y}$
. This is a rank 2 vector bundle on
$\mathcal {Y}$
. This is a rank 2 vector bundle on
![]() $\mathcal {Y}$
equipped with a (decreasing) Hodge filtration
$\mathcal {Y}$
equipped with a (decreasing) Hodge filtration
![]() $\operatorname {\mathrm {Fil}}^{\bullet }$
and Gauss–Manin connection
$\operatorname {\mathrm {Fil}}^{\bullet }$
and Gauss–Manin connection
![]() $\nabla _{\underline {V}}$
. Its graded components are given by
$\nabla _{\underline {V}}$
. Its graded components are given by
 $$ \begin{align*}\operatorname{\mathrm{gr}}^n(D_{\mathrm{dR}})\cong\left\{ \begin{array}{lll} \omega^{-1}|_{\mathcal{Y}},~n=0\\ \omega|_{\mathcal{Y}},~n=1\\ 0,~n\neq 0,1 \end{array}.\right.\end{align*} $$
$$ \begin{align*}\operatorname{\mathrm{gr}}^n(D_{\mathrm{dR}})\cong\left\{ \begin{array}{lll} \omega^{-1}|_{\mathcal{Y}},~n=0\\ \omega|_{\mathcal{Y}},~n=1\\ 0,~n\neq 0,1 \end{array}.\right.\end{align*} $$
Here implicitly we choose a polarisation of
![]() $\mathcal {E}$
– that is, an isomorphism
$\mathcal {E}$
– that is, an isomorphism
![]() $\wedge ^2 D_{\mathrm {dR}}\cong \mathcal {O}_{\mathcal {Y}}$
– and we will fix this choice from now on. Recall that there is the structural de Rham sheaf
$\wedge ^2 D_{\mathrm {dR}}\cong \mathcal {O}_{\mathcal {Y}}$
– and we will fix this choice from now on. Recall that there is the structural de Rham sheaf
![]() $\mathcal {O}\mathbb {B}_{\mathrm {dR}}$
on
$\mathcal {O}\mathbb {B}_{\mathrm {dR}}$
on
![]() $\mathcal {Y}_{\mathrm {pro\acute {e}t}}$
also equipped with a decreasing filtration and a
$\mathcal {Y}_{\mathrm {pro\acute {e}t}}$
also equipped with a decreasing filtration and a
![]() $\mathbb {B}_{\mathrm {dR}}$
-linear connection; cf. §6 of [Reference ScholzeSch13a] and [Reference ScholzeSch16]. By the relative de Rham comparison theorem (Theorem 8.8 of [Reference ScholzeSch13a]), there is a natural isomorphism
$\mathbb {B}_{\mathrm {dR}}$
-linear connection; cf. §6 of [Reference ScholzeSch13a] and [Reference ScholzeSch16]. By the relative de Rham comparison theorem (Theorem 8.8 of [Reference ScholzeSch13a]), there is a natural isomorphism
 $$ \begin{align*}\hat{\underline{V}}\otimes_{\hat{\mathbb{Z}}_p}\mathcal{O}\mathbb{B}_{\mathrm{dR}}\cong D_{\mathrm{dR}}\otimes_{\mathcal{O}_{\mathcal{Y}}}\mathcal{O}\mathbb{B}_{\mathrm{dR}}\end{align*} $$
$$ \begin{align*}\hat{\underline{V}}\otimes_{\hat{\mathbb{Z}}_p}\mathcal{O}\mathbb{B}_{\mathrm{dR}}\cong D_{\mathrm{dR}}\otimes_{\mathcal{O}_{\mathcal{Y}}}\mathcal{O}\mathbb{B}_{\mathrm{dR}}\end{align*} $$
compatible with the filtrations and connections. Here, by abuse of notation,
![]() $D_{\mathrm {dR}}$
is viewed as a sheaf on
$D_{\mathrm {dR}}$
is viewed as a sheaf on
![]() $\mathcal {Y}_{\mathrm {pro\acute {e}t}}$
by Lemma 7.3 of [Reference ScholzeSch13a].
$\mathcal {Y}_{\mathrm {pro\acute {e}t}}$
by Lemma 7.3 of [Reference ScholzeSch13a].
Next, we extend these results to
![]() $\mathcal {X}$
using the theory of log adic spaces. See [Reference Diao, Lan, Liu and ZhuDLLZ19, Reference Diao, Lan, Liu and ZhuDLLZ18] for more details here. We will view
$\mathcal {X}$
using the theory of log adic spaces. See [Reference Diao, Lan, Liu and ZhuDLLZ19, Reference Diao, Lan, Liu and ZhuDLLZ18] for more details here. We will view
![]() $\mathcal {X}$
as a log adic space by equipping it with the natural log structure defined by the cusps
$\mathcal {X}$
as a log adic space by equipping it with the natural log structure defined by the cusps
![]() $\mathcal {C}:=\mathcal {X}-\mathcal {Y}$
; cf. Example 2.1.2 of [Reference Diao, Lan, Liu and ZhuDLLZ18]. Then
$\mathcal {C}:=\mathcal {X}-\mathcal {Y}$
; cf. Example 2.1.2 of [Reference Diao, Lan, Liu and ZhuDLLZ18]. Then
![]() $\hat {\underline {V}}$
defines a rank 2
$\hat {\underline {V}}$
defines a rank 2
![]() $\hat {\mathbb {Z}}_p$
-local system
$\hat {\mathbb {Z}}_p$
-local system
 $\hat {\underline {V}}_{\log }$
on
$\hat {\underline {V}}_{\log }$
on
![]() $\mathcal {X}_{\mathrm {prok\acute {e}t}}$
, the pro-Kummer étale site of
$\mathcal {X}_{\mathrm {prok\acute {e}t}}$
, the pro-Kummer étale site of
![]() $\mathcal {X}$
. There is also the structural de Rham sheaf
$\mathcal {X}$
. There is also the structural de Rham sheaf
![]() $\mathcal {O}\mathbb {B}_{\mathrm {dR},\log }$
on
$\mathcal {O}\mathbb {B}_{\mathrm {dR},\log }$
on
![]() $\mathcal {X}_{\mathrm {prok\acute {e}t}}$
equipped with a decreasing filtration and a logarithmic connection:
$\mathcal {X}_{\mathrm {prok\acute {e}t}}$
equipped with a decreasing filtration and a logarithmic connection:
 $$ \begin{align*}\nabla:\mathcal{O}\mathbb{B}_{\mathrm{dR},\log}\to\mathcal{O}\mathbb{B}_{\mathrm{dR},\log}\otimes_{\mathcal{O}_{\mathcal{X}}}\Omega^1_{\mathcal{X}}(\mathcal{C}).\end{align*} $$
$$ \begin{align*}\nabla:\mathcal{O}\mathbb{B}_{\mathrm{dR},\log}\to\mathcal{O}\mathbb{B}_{\mathrm{dR},\log}\otimes_{\mathcal{O}_{\mathcal{X}}}\Omega^1_{\mathcal{X}}(\mathcal{C}).\end{align*} $$
Here
 $\Omega ^1_{\mathcal {X}}(\mathcal {C})$
as usual denotes the sheaf of differentials on
$\Omega ^1_{\mathcal {X}}(\mathcal {C})$
as usual denotes the sheaf of differentials on
![]() $\mathcal {X}$
with simple poles at
$\mathcal {X}$
with simple poles at
![]() $\mathcal {C}$
. As the monodromy of
$\mathcal {C}$
. As the monodromy of
![]() ${\underline {V}}$
along each cusp is unipotent, we have the following relative log de Rham comparison isomorphism (Theorem 3.2.12 and its proof of [Reference Diao, Lan, Liu and ZhuDLLZ18]):
${\underline {V}}$
along each cusp is unipotent, we have the following relative log de Rham comparison isomorphism (Theorem 3.2.12 and its proof of [Reference Diao, Lan, Liu and ZhuDLLZ18]):
 $$ \begin{align} \hat{\underline{V}}_{\log}\otimes_{\hat{\mathbb{Z}}_p}\mathcal{O}\mathbb{B}_{\mathrm{dR},\log}\cong D_{\mathrm{dR},\log}\otimes_{\mathcal{O}_{\mathcal{X}}}\mathcal{O}\mathbb{B}_{\mathrm{dR},\log} \end{align} $$
$$ \begin{align} \hat{\underline{V}}_{\log}\otimes_{\hat{\mathbb{Z}}_p}\mathcal{O}\mathbb{B}_{\mathrm{dR},\log}\cong D_{\mathrm{dR},\log}\otimes_{\mathcal{O}_{\mathcal{X}}}\mathcal{O}\mathbb{B}_{\mathrm{dR},\log} \end{align} $$
compatible with the filtrations and logarithmic connections, where
![]() $D_{\mathrm {dR},\log }$
is a filtered vector bundle equipped with a logarithmic connection
$D_{\mathrm {dR},\log }$
is a filtered vector bundle equipped with a logarithmic connection
![]() $\nabla _{\underline {V}}$
. In fact, by Theorem 1.7 of [Reference Diao, Lan, Liu and ZhuDLLZ18],
$\nabla _{\underline {V}}$
. In fact, by Theorem 1.7 of [Reference Diao, Lan, Liu and ZhuDLLZ18],
![]() $(D_{\mathrm {dR},\log },\nabla _{\underline {V}})$
is the canonical extension of
$(D_{\mathrm {dR},\log },\nabla _{\underline {V}})$
is the canonical extension of
![]() $(D_{\mathrm {dR}},\nabla _{\underline {V}})$
. Hence, in particular,
$(D_{\mathrm {dR}},\nabla _{\underline {V}})$
. Hence, in particular,
 $$ \begin{align*}\operatorname{\mathrm{gr}}^n(D_{\mathrm{dR},\log})\cong\left\{ \begin{array}{lll} \omega^{-1},~n=0\\ \omega,~n=1\\ 0,~n\neq 0,1 \end{array}.\right.\end{align*} $$
$$ \begin{align*}\operatorname{\mathrm{gr}}^n(D_{\mathrm{dR},\log})\cong\left\{ \begin{array}{lll} \omega^{-1},~n=0\\ \omega,~n=1\\ 0,~n\neq 0,1 \end{array}.\right.\end{align*} $$
Now we have a decreasing filtration (the relative Hodge–Tate filtration) on
 $\hat {\underline {V}}_{\log }\otimes _{\hat {\mathbb {Z}}_p}\hat {\mathcal {O}}_{\mathcal {X}}$
as in Subsection 2.2. of [Reference Caraiani and ScholzeCS17]. More precisely, let
$\hat {\underline {V}}_{\log }\otimes _{\hat {\mathbb {Z}}_p}\hat {\mathcal {O}}_{\mathcal {X}}$
as in Subsection 2.2. of [Reference Caraiani and ScholzeCS17]. More precisely, let
 $\mathcal {O}\mathbb {B}_{\mathrm {dR},\log }^+$
be the positive structural de Rham sheaf on
$\mathcal {O}\mathbb {B}_{\mathrm {dR},\log }^+$
be the positive structural de Rham sheaf on
![]() $\mathcal {X}_{\mathrm {prok\acute {e}t}}$
(the geometric de Rham period sheaf in Definition 2.2.10 of [Reference Diao, Lan, Liu and ZhuDLLZ18]) which also admits a logarithmic connection. Consider
$\mathcal {X}_{\mathrm {prok\acute {e}t}}$
(the geometric de Rham period sheaf in Definition 2.2.10 of [Reference Diao, Lan, Liu and ZhuDLLZ18]) which also admits a logarithmic connection. Consider
 $$ \begin{align*}\mathbb{M}_0=(D_{\mathrm{dR},\log}\otimes_{\mathcal{O}_{\mathcal{X}}}\mathcal{O}\mathbb{B}_{\mathrm{dR},\log}^+)^{\nabla=0}.\end{align*} $$
$$ \begin{align*}\mathbb{M}_0=(D_{\mathrm{dR},\log}\otimes_{\mathcal{O}_{\mathcal{X}}}\mathcal{O}\mathbb{B}_{\mathrm{dR},\log}^+)^{\nabla=0}.\end{align*} $$
Recall that there is the positive de Rham sheaf
![]() $\mathbb {B}_{\mathrm {dR}}^+$
on
$\mathbb {B}_{\mathrm {dR}}^+$
on
![]() $\mathcal {X}_{\mathrm {prok\acute {e}t}}$
(Definition 2.2.3.(2) of [Reference Diao, Lan, Liu and ZhuDLLZ18]) and the usual surjective map:
$\mathcal {X}_{\mathrm {prok\acute {e}t}}$
(Definition 2.2.3.(2) of [Reference Diao, Lan, Liu and ZhuDLLZ18]) and the usual surjective map:
 $\theta :\mathbb {B}_{\mathrm {dR}}^+\to \hat {\mathcal {O}}_{\mathcal {X}}$
. Then Proposition 7.9 of [Reference ScholzeSch13a] implies
$\theta :\mathbb {B}_{\mathrm {dR}}^+\to \hat {\mathcal {O}}_{\mathcal {X}}$
. Then Proposition 7.9 of [Reference ScholzeSch13a] implies
 $$ \begin{align} \hat{\underline{V}}_{\log}\otimes_{\hat{\mathbb{Z}}_p}\mathbb{B}_{\mathrm{dR},\log}^+\supseteq \mathbb{M}_0 \supseteq \hat{\underline{V}}_{\log}\otimes_{\hat{\mathbb{Z}}_p}\ker(\theta). \end{align} $$
$$ \begin{align} \hat{\underline{V}}_{\log}\otimes_{\hat{\mathbb{Z}}_p}\mathbb{B}_{\mathrm{dR},\log}^+\supseteq \mathbb{M}_0 \supseteq \hat{\underline{V}}_{\log}\otimes_{\hat{\mathbb{Z}}_p}\ker(\theta). \end{align} $$
Hence, we obtain a filtration on
 $\hat {\underline {V}}_{\log }\otimes _{\hat {\mathbb {Z}}_p}\mathbb {B}_{\mathrm {dR}}^+/(\ker \theta )=\hat {\underline {V}}_{\log }\otimes _{\hat {\mathbb {Z}}_p}\hat {\mathcal {O}}_{\mathcal {X}}$
, which again by Proposition 7.9 of [Reference ScholzeSch13a] can be identified with
$\hat {\underline {V}}_{\log }\otimes _{\hat {\mathbb {Z}}_p}\mathbb {B}_{\mathrm {dR}}^+/(\ker \theta )=\hat {\underline {V}}_{\log }\otimes _{\hat {\mathbb {Z}}_p}\hat {\mathcal {O}}_{\mathcal {X}}$
, which again by Proposition 7.9 of [Reference ScholzeSch13a] can be identified with
 $$ \begin{align*}0\to \operatorname{\mathrm{gr}}^0(D_{\mathrm{dR},\log})\otimes_{\mathcal{O}_{\mathcal{X}}}\hat{\mathcal{O}}_{\mathcal{X}}\to \hat{\underline{V}}_{\log}\otimes_{\hat{\mathbb{Z}}_p}\hat{\mathcal{O}}_{\mathcal{X}} \to \operatorname{\mathrm{gr}}^1(D_{\mathrm{dR},\log})\otimes_{\mathcal{O}_{\mathcal{X}}}\hat{\mathcal{O}}_{\mathcal{X}}(-1)\to 0.\end{align*} $$
$$ \begin{align*}0\to \operatorname{\mathrm{gr}}^0(D_{\mathrm{dR},\log})\otimes_{\mathcal{O}_{\mathcal{X}}}\hat{\mathcal{O}}_{\mathcal{X}}\to \hat{\underline{V}}_{\log}\otimes_{\hat{\mathbb{Z}}_p}\hat{\mathcal{O}}_{\mathcal{X}} \to \operatorname{\mathrm{gr}}^1(D_{\mathrm{dR},\log})\otimes_{\mathcal{O}_{\mathcal{X}}}\hat{\mathcal{O}}_{\mathcal{X}}(-1)\to 0.\end{align*} $$
In other words, we get the following exact sequence of locally free
![]() $\hat {\mathcal {O}}_{\mathcal {X}}$
-modules on
$\hat {\mathcal {O}}_{\mathcal {X}}$
-modules on
![]() $\mathcal {X}_{\mathrm {prok\acute {e}t}}$
(relative Hodge–Tate filtration of
$\mathcal {X}_{\mathrm {prok\acute {e}t}}$
(relative Hodge–Tate filtration of
 $ \hat {\underline {V}}_{\log }\otimes _{\hat {\mathbb {Z}}_p}\hat {\mathcal {O}}_{\mathcal {X}}$
):
$ \hat {\underline {V}}_{\log }\otimes _{\hat {\mathbb {Z}}_p}\hat {\mathcal {O}}_{\mathcal {X}}$
):
 $$ \begin{align} 0\to \omega^{-1}\otimes_{\mathcal{O}_{\mathcal{X}}}\hat{\mathcal{O}}_{\mathcal{X}}(1) \to \hat{\underline{V}}_{\log}(1)\otimes_{\hat{\mathbb{Z}}_p}\hat{\mathcal{O}}_{\mathcal{X}} \to \omega\otimes_{\mathcal{O}_{\mathcal{X}}}\hat{\mathcal{O}}_{\mathcal{X}}\to 0. \end{align} $$
$$ \begin{align} 0\to \omega^{-1}\otimes_{\mathcal{O}_{\mathcal{X}}}\hat{\mathcal{O}}_{\mathcal{X}}(1) \to \hat{\underline{V}}_{\log}(1)\otimes_{\hat{\mathbb{Z}}_p}\hat{\mathcal{O}}_{\mathcal{X}} \to \omega\otimes_{\mathcal{O}_{\mathcal{X}}}\hat{\mathcal{O}}_{\mathcal{X}}\to 0. \end{align} $$
Remark 4.1.4. Strictly speaking, Proposition 7.9 of [Reference ScholzeSch13a] is only proved when there is no log structure. However, all of the arguments work here with the input replaced by the corresponding results in Section 2 of [Reference Diao, Lan, Liu and ZhuDLLZ18]. For example, the local structure of
 $\mathcal {O}\mathbb {B}_{\mathrm {dR},\log }^+$
in Proposition 6.10 is now replaced by Proposition 2.3.15 of [Reference Diao, Lan, Liu and ZhuDLLZ18].
$\mathcal {O}\mathbb {B}_{\mathrm {dR},\log }^+$
in Proposition 6.10 is now replaced by Proposition 2.3.15 of [Reference Diao, Lan, Liu and ZhuDLLZ18].
There is one minor subtlety here: compared with the definition of
![]() $\mathcal {O}\mathbb {B}_{\mathrm {dR}}$
in [Reference ScholzeSch13a], there is an extra completion of
$\mathcal {O}\mathbb {B}_{\mathrm {dR}}$
in [Reference ScholzeSch13a], there is an extra completion of
 $\mathcal {O}\mathbb {B}_{\mathrm {dR},\log }^+[t^{-1}]$
in Definition 2.2.10 of [Reference Diao, Lan, Liu and ZhuDLLZ18], where
$\mathcal {O}\mathbb {B}_{\mathrm {dR},\log }^+[t^{-1}]$
in Definition 2.2.10 of [Reference Diao, Lan, Liu and ZhuDLLZ18], where
![]() $t\in \mathbb {B}_{\mathrm {dR}}^+$
is a generator of
$t\in \mathbb {B}_{\mathrm {dR}}^+$
is a generator of
![]() $\ker (\theta )$
. I claim that such a completion is unnecessary in our case; that is, the isomorphism (4.1.1) can be restricted to
$\ker (\theta )$
. I claim that such a completion is unnecessary in our case; that is, the isomorphism (4.1.1) can be restricted to
 $$ \begin{align*}\hat{\underline{V}}_{\log}\otimes_{\hat{\mathbb{Z}}_p}\mathcal{O}\mathbb{B}_{\mathrm{dR},\log}^+[t^{-1}]\cong D_{\mathrm{dR},\log}\otimes_{\mathcal{O}_{\mathcal{X}}}\mathcal{O}\mathbb{B}_{\mathrm{dR},\log}^+[t^{-1}].\end{align*} $$
$$ \begin{align*}\hat{\underline{V}}_{\log}\otimes_{\hat{\mathbb{Z}}_p}\mathcal{O}\mathbb{B}_{\mathrm{dR},\log}^+[t^{-1}]\cong D_{\mathrm{dR},\log}\otimes_{\mathcal{O}_{\mathcal{X}}}\mathcal{O}\mathbb{B}_{\mathrm{dR},\log}^+[t^{-1}].\end{align*} $$
In fact, using the local structure of
 $\mathcal {O}\mathbb {B}_{\mathrm {dR},\log }^+$
, we may argue as in Theorem 7.2 of [Reference ScholzeSch13a] that
$\mathcal {O}\mathbb {B}_{\mathrm {dR},\log }^+$
, we may argue as in Theorem 7.2 of [Reference ScholzeSch13a] that
![]() $\mathbb {M}_0$
is a
$\mathbb {M}_0$
is a
![]() $\mathbb {B}_{\mathrm {dR}}^+$
-lattice of
$\mathbb {B}_{\mathrm {dR}}^+$
-lattice of
 $(\hat {\underline {V}}_{\log }\otimes _{\hat {\mathbb {Z}}_p}\mathcal {O}\mathbb {B}_{\mathrm {dR},\log })^{\nabla =0}=\hat {\underline {V}}_{\log }\otimes _{\hat {\mathbb {Z}}_p}\mathbb {B}_{\mathrm {dR}}$
by the Poincaré lemma (Corollary 2.4.2 of [Reference Diao, Lan, Liu and ZhuDLLZ18]). This is enough to deduce our claim.
$(\hat {\underline {V}}_{\log }\otimes _{\hat {\mathbb {Z}}_p}\mathcal {O}\mathbb {B}_{\mathrm {dR},\log })^{\nabla =0}=\hat {\underline {V}}_{\log }\otimes _{\hat {\mathbb {Z}}_p}\mathbb {B}_{\mathrm {dR}}$
by the Poincaré lemma (Corollary 2.4.2 of [Reference Diao, Lan, Liu and ZhuDLLZ18]). This is enough to deduce our claim.
4.1.5. Now we take
![]() $K_p=\mathrm {GL}_2(\mathbb {Z}_p)$
. Hence,
$K_p=\mathrm {GL}_2(\mathbb {Z}_p)$
. Hence,
![]() $\mathcal {X}=\mathcal {X}_{K^p\mathrm {GL}_2(\mathbb {Z}_p)}$
. As
$\mathcal {X}=\mathcal {X}_{K^p\mathrm {GL}_2(\mathbb {Z}_p)}$
. As
 $\varprojlim _{K_p\subset \mathrm {GL}_2(\mathbb {Q}_p)}\mathcal {X}_{K^pK_p}$
(equipped with log structures defined by cusps) can be viewed as an open covering of
$\varprojlim _{K_p\subset \mathrm {GL}_2(\mathbb {Q}_p)}\mathcal {X}_{K^pK_p}$
(equipped with log structures defined by cusps) can be viewed as an open covering of
![]() $\mathcal {X}$
in
$\mathcal {X}$
in
![]() $\mathcal {X}_{\mathrm {prok\acute {e}t}}$
, we can evaluate the exact sequence (4.1.3) on
$\mathcal {X}_{\mathrm {prok\acute {e}t}}$
, we can evaluate the exact sequence (4.1.3) on
 $\varprojlim _{K_p}\mathcal {X}_{K^pK_p}$
. Note that
$\varprojlim _{K_p}\mathcal {X}_{K^pK_p}$
. Note that
![]() $\mathcal {X}_{K^p}$
trivialises the universal Tate module; hence, by Theorem 4.1.2, we obtain the following exact sequence of vector bundles on
$\mathcal {X}_{K^p}$
trivialises the universal Tate module; hence, by Theorem 4.1.2, we obtain the following exact sequence of vector bundles on
![]() $\mathcal {X}_{K^p}$
.
$\mathcal {X}_{K^p}$
.
Theorem 4.1.6.
 $$ \begin{align*}0\to\omega_{K^p}^{-1}(1)\to V(1)\otimes_{\mathbb{Q}_p} \mathcal{O}_{\mathcal{X}_{K^p}} \to \omega_{K^p}\to 0,\end{align*} $$
$$ \begin{align*}0\to\omega_{K^p}^{-1}(1)\to V(1)\otimes_{\mathbb{Q}_p} \mathcal{O}_{\mathcal{X}_{K^p}} \to \omega_{K^p}\to 0,\end{align*} $$
where
![]() $\omega _{K^p}$
is the pullback of
$\omega _{K^p}$
is the pullback of
![]() $\omega $
as a coherent sheaf from
$\omega $
as a coherent sheaf from
![]() $\mathcal {X}$
to
$\mathcal {X}$
to
![]() $\mathcal {X}_{K^p}$
and
$\mathcal {X}_{K^p}$
and
 $V=\mathbb {Q}_p^{\oplus 2}$
is the standard representation of
$V=\mathbb {Q}_p^{\oplus 2}$
is the standard representation of
![]() $\mathrm {GL}_2(\mathbb {Q}_p)$
and viewed as a constant sheaf on
$\mathrm {GL}_2(\mathbb {Q}_p)$
and viewed as a constant sheaf on
![]() $\mathcal {X}_{K^p}$
. This exact sequence is
$\mathcal {X}_{K^p}$
. This exact sequence is
![]() $\mathrm {GL}_2(\mathbb {Z}_p)$
-equivariant.
$\mathrm {GL}_2(\mathbb {Z}_p)$
-equivariant.
Clearly, the position of
 $\omega _{K^p}^{-1}$
in
$\omega _{K^p}^{-1}$
in
![]() $V\otimes _{\mathbb {Q}_p} \mathcal {O}_{\mathcal {X}_{K^p}}$
induces a map (Hodge–Tate period map)
$V\otimes _{\mathbb {Q}_p} \mathcal {O}_{\mathcal {X}_{K^p}}$
induces a map (Hodge–Tate period map)
where
![]() ${\mathscr {F}\!\ell }$
is the adic space over C associated to the usual flag variety for
${\mathscr {F}\!\ell }$
is the adic space over C associated to the usual flag variety for
![]() $\mathrm {GL}_2$
. One can check that our definition of
$\mathrm {GL}_2$
. One can check that our definition of
![]() $\pi _{\mathrm {HT}}$
agrees with the one defined in III.3 of [Reference ScholzeSch15],Footnote
1
using Lemma III.3.4 and Corollary III.3.17 in the reference.
$\pi _{\mathrm {HT}}$
agrees with the one defined in III.3 of [Reference ScholzeSch15],Footnote
1
using Lemma III.3.4 and Corollary III.3.17 in the reference.
There is a right action of
![]() $\mathrm {GL}_2(\mathbb {Q}_p)$
on
$\mathrm {GL}_2(\mathbb {Q}_p)$
on
![]() ${\mathscr {F}\!\ell }$
by acting on the total space (rather than the position of the flag). We will always use this right action.
${\mathscr {F}\!\ell }$
by acting on the total space (rather than the position of the flag). We will always use this right action.
Theorem III.3.18 of [Reference ScholzeSch15] provides an affinoid cover
![]() $\{U_1,U_2\}$
of
$\{U_1,U_2\}$
of
![]() ${\mathscr {F}\!\ell }$
. In our case,
${\mathscr {F}\!\ell }$
. In our case,
![]() ${\mathscr {F}\!\ell }=\mathbb {P}^1$
and
${\mathscr {F}\!\ell }=\mathbb {P}^1$
and
![]() $U_1=\{[x_1:x_2],\|x_1\|\geq \|x_2\|\},U_2=\{[x_1:x_2],\|x_2\|\geq \|x_1\|\}$
.
$U_1=\{[x_1:x_2],\|x_1\|\geq \|x_2\|\},U_2=\{[x_1:x_2],\|x_2\|\geq \|x_1\|\}$
.
Theorem 4.1.7.
![]() $\pi _{\mathrm {HT}}$
is
$\pi _{\mathrm {HT}}$
is
![]() $\mathrm {GL}_2(\mathbb {Q}_p)$
-equivariant and commutes with Hecke operators away from p (when changing
$\mathrm {GL}_2(\mathbb {Q}_p)$
-equivariant and commutes with Hecke operators away from p (when changing
![]() $K^p$
), for the trivial action of these Hecke operators on
$K^p$
), for the trivial action of these Hecke operators on
![]() ${\mathscr {F}\!\ell }$
. Moreover, let
${\mathscr {F}\!\ell }$
. Moreover, let
![]() $\mathfrak {B}$
be the set of finite intersections of rational subsets of
$\mathfrak {B}$
be the set of finite intersections of rational subsets of
![]() $U_1,U_2$
. Then
$U_1,U_2$
. Then
![]() $\mathfrak {B}$
is a basis of open affinoid subsets of
$\mathfrak {B}$
is a basis of open affinoid subsets of
![]() ${\mathscr {F}\!\ell }$
stable under finite intersections and each
${\mathscr {F}\!\ell }$
stable under finite intersections and each
![]() $U\in \mathfrak {B}$
has the following properties:
$U\in \mathfrak {B}$
has the following properties:
-
• its preimage
 $V_{\infty }=\pi _{\mathrm {HT}}^{-1}(U)$
is affinoid perfectoid;
$V_{\infty }=\pi _{\mathrm {HT}}^{-1}(U)$
is affinoid perfectoid; -
•
 $V_{\infty }$
is the preimage of an affinoid subset
$V_{\infty }$
is the preimage of an affinoid subset
 $V_{K_p}\subset \mathcal {X}_{K^pK_p}$
for sufficiently small open subgroup
$V_{K_p}\subset \mathcal {X}_{K^pK_p}$
for sufficiently small open subgroup
 $K_p$
of
$K_p$
of
 $\mathrm {GL}_2(\mathbb {Q}_p)$
;
$\mathrm {GL}_2(\mathbb {Q}_p)$
; -
• the map
 $\varinjlim _{K_p}H^0(V_{K_p},\mathcal {O}_{\mathcal {X}_{K^pK_p}})\to H^0(V_{\infty },\mathcal {O}_{\mathcal {X}_{K^p}})$
has dense image;
$\varinjlim _{K_p}H^0(V_{K_p},\mathcal {O}_{\mathcal {X}_{K^pK_p}})\to H^0(V_{\infty },\mathcal {O}_{\mathcal {X}_{K^p}})$
has dense image; -
• U does not contain all
 $\mathbb {Q}_p$
-rational points of
$\mathbb {Q}_p$
-rational points of
 ${\mathscr {F}\!\ell }$
.
${\mathscr {F}\!\ell }$
.
Proof. See Theorem III.1.2 of [Reference ScholzeSch15] and Theorem III.3.18 of [Reference ScholzeSch15].
4.2 Faltings’s extension and computation of
 $\theta $
$\theta $
Let
![]() $K_p\subset \mathrm {GL}_2(\mathbb {Q}_p)$
be an open subgroup and X an affinoid subset of
$K_p\subset \mathrm {GL}_2(\mathbb {Q}_p)$
be an open subgroup and X an affinoid subset of
![]() $\mathcal {X}=\mathcal {X}_{K^pK_p}$
containing at most one cusp. Suppose its preimage
$\mathcal {X}=\mathcal {X}_{K^pK_p}$
containing at most one cusp. Suppose its preimage
![]() $\tilde {X}$
in
$\tilde {X}$
in
![]() $\mathcal {X}_{K^p}$
is a ‘log
$\mathcal {X}_{K^p}$
is a ‘log
![]() $K_p$
-Galois pro-étale perfectoid covering’ of X and X is small in the sense of Section 3.1.1. Note that by Theorem 4.1.2 and Lemma 5.2 (and its proof) of [Reference ScholzeSch15], such X form a basis of open subsets of
$K_p$
-Galois pro-étale perfectoid covering’ of X and X is small in the sense of Section 3.1.1. Note that by Theorem 4.1.2 and Lemma 5.2 (and its proof) of [Reference ScholzeSch15], such X form a basis of open subsets of
![]() $\mathcal {X}$
.
$\mathcal {X}$
.
The goal of this subsection is to compute the differential operator
![]() $\theta $
in Theorem 3.1.2 for this Galois covering. It turns out that this follows from a classical result of Faltings which (up to a twist) identifies the relative Hodge–Tate filtration sequence in Theorem 4.1.6 with (log) Faltings’s extension; cf. Theorem 5 of [Reference FaltingsFal87]. We will give a proof of this result (Theorem 4.2.2) in our setup below. A more conceptual computation of
$\theta $
in Theorem 3.1.2 for this Galois covering. It turns out that this follows from a classical result of Faltings which (up to a twist) identifies the relative Hodge–Tate filtration sequence in Theorem 4.1.6 with (log) Faltings’s extension; cf. Theorem 5 of [Reference FaltingsFal87]. We will give a proof of this result (Theorem 4.2.2) in our setup below. A more conceptual computation of
![]() $\theta $
in terms of the p-adic Simpson correspondence is given in Remark 4.2.5.
$\theta $
in terms of the p-adic Simpson correspondence is given in Remark 4.2.5.
4.2.1. We use notation introduced in the previous subsection. First we recall the log Faltings’s extension as defined in Corollary 6.14 of [Reference ScholzeSch13a] and Corollary 2.4.5 of [Reference Diao, Lan, Liu and ZhuDLLZ18]. Taking the first graded piece of the Poincaré lemma sequence (Corollary 2.4.2 of [Reference Diao, Lan, Liu and ZhuDLLZ18]):
 $$ \begin{align} 0\to \mathbb{B}^+_{\mathrm{dR}}\to \mathcal{O}\mathbb{B}_{\mathrm{dR},\log}^+ \xrightarrow{\nabla} \mathcal{O}\mathbb{B}_{\mathrm{dR},\log}^+\otimes_{\mathcal{O}_{\mathcal{X}}}\Omega^1_{\mathcal{X}}(\mathcal{C})\to 0, \end{align} $$
$$ \begin{align} 0\to \mathbb{B}^+_{\mathrm{dR}}\to \mathcal{O}\mathbb{B}_{\mathrm{dR},\log}^+ \xrightarrow{\nabla} \mathcal{O}\mathbb{B}_{\mathrm{dR},\log}^+\otimes_{\mathcal{O}_{\mathcal{X}}}\Omega^1_{\mathcal{X}}(\mathcal{C})\to 0, \end{align} $$
we obtain an exact sequence of
![]() $\hat {\mathcal {O}}_{\mathcal {X}}$
-modules on
$\hat {\mathcal {O}}_{\mathcal {X}}$
-modules on
![]() $\mathcal {X}_{\mathrm {prok\acute {e}t}}$
(the log Faltings’s extension):
$\mathcal {X}_{\mathrm {prok\acute {e}t}}$
(the log Faltings’s extension):
 $$ \begin{align*}0\to \hat{\mathcal{O}}_{\mathcal{X}}(1)\to \operatorname{\mathrm{gr}}^1\mathcal{O}\mathbb{B}_{\mathrm{dR},\log}^+\xrightarrow{\nabla} \hat{\mathcal{O}}_{\mathcal{X}}\otimes_{\mathcal{O}_{\mathcal{X}}}\Omega^1_{\mathcal{X}}(\mathcal{C})\to 0.\end{align*} $$
$$ \begin{align*}0\to \hat{\mathcal{O}}_{\mathcal{X}}(1)\to \operatorname{\mathrm{gr}}^1\mathcal{O}\mathbb{B}_{\mathrm{dR},\log}^+\xrightarrow{\nabla} \hat{\mathcal{O}}_{\mathcal{X}}\otimes_{\mathcal{O}_{\mathcal{X}}}\Omega^1_{\mathcal{X}}(\mathcal{C})\to 0.\end{align*} $$
Its tensor product with
![]() $\omega ^{-1}$
becomes
$\omega ^{-1}$
becomes
 $$ \begin{align*}0\to \omega^{-1}\otimes_{\mathcal{O}_{\mathcal{X}}}\hat{\mathcal{O}}_{\mathcal{X}}(1)\to \omega^{-1}\otimes_{\mathcal{O}_{\mathcal{X}}}\operatorname{\mathrm{gr}}^1\mathcal{O}\mathbb{B}_{\mathrm{dR},\log}^+\to \omega^{-1}\otimes_{\mathcal{O}_{\mathcal{X}}}\Omega^1_{\mathcal{X}}(\mathcal{C})\otimes_{\mathcal{O}_{\mathcal{X}}}\hat{\mathcal{O}}_{\mathcal{X}}\to 0.\end{align*} $$
$$ \begin{align*}0\to \omega^{-1}\otimes_{\mathcal{O}_{\mathcal{X}}}\hat{\mathcal{O}}_{\mathcal{X}}(1)\to \omega^{-1}\otimes_{\mathcal{O}_{\mathcal{X}}}\operatorname{\mathrm{gr}}^1\mathcal{O}\mathbb{B}_{\mathrm{dR},\log}^+\to \omega^{-1}\otimes_{\mathcal{O}_{\mathcal{X}}}\Omega^1_{\mathcal{X}}(\mathcal{C})\otimes_{\mathcal{O}_{\mathcal{X}}}\hat{\mathcal{O}}_{\mathcal{X}}\to 0.\end{align*} $$
Recall that there is a Kodaira–Spencer map
 $\omega \to \omega ^{-1}\otimes _{\mathcal {O}_{\mathcal {X}}}\Omega ^1_{\mathcal {X}}(\mathcal {C})$
of coherent sheaves on
$\omega \to \omega ^{-1}\otimes _{\mathcal {O}_{\mathcal {X}}}\Omega ^1_{\mathcal {X}}(\mathcal {C})$
of coherent sheaves on
![]() $\mathcal {X}$
defined as the composite
$\mathcal {X}$
defined as the composite
 $$ \begin{align*}\omega=\operatorname{\mathrm{Fil}}^1 D_{\mathrm{dR},\log}\subset D_{\mathrm{dR},\log}\xrightarrow{\nabla}D_{\mathrm{dR},\log}\otimes_{\mathcal{O}_{\mathcal{X}}}\Omega^1_{\mathcal{X}}(\mathcal{C})\to \operatorname{\mathrm{gr}}^0 D_{\mathrm{dR},\log}\otimes_{\mathcal{O}_{\mathcal{X}}}\Omega^1_{\mathcal{X}}(\mathcal{C})=\omega^{-1}\otimes_{\mathcal{O}_{\mathcal{X}}}\Omega^1_{\mathcal{X}}(\mathcal{C}).\end{align*} $$
$$ \begin{align*}\omega=\operatorname{\mathrm{Fil}}^1 D_{\mathrm{dR},\log}\subset D_{\mathrm{dR},\log}\xrightarrow{\nabla}D_{\mathrm{dR},\log}\otimes_{\mathcal{O}_{\mathcal{X}}}\Omega^1_{\mathcal{X}}(\mathcal{C})\to \operatorname{\mathrm{gr}}^0 D_{\mathrm{dR},\log}\otimes_{\mathcal{O}_{\mathcal{X}}}\Omega^1_{\mathcal{X}}(\mathcal{C})=\omega^{-1}\otimes_{\mathcal{O}_{\mathcal{X}}}\Omega^1_{\mathcal{X}}(\mathcal{C}).\end{align*} $$
It is well-known that this is an isomorphism:
 $\omega \xrightarrow {\sim } \omega ^{-1}\otimes _{\mathcal {O}_{\mathcal {X}}}\Omega ^1_{\mathcal {X}}(\mathcal {C})$
. Under this isomorphism,
$\omega \xrightarrow {\sim } \omega ^{-1}\otimes _{\mathcal {O}_{\mathcal {X}}}\Omega ^1_{\mathcal {X}}(\mathcal {C})$
. Under this isomorphism,
 $\omega ^{-1}\otimes _{\mathcal {O}_{\mathcal {X}}}\operatorname {\mathrm {gr}}^1\mathcal {O}\mathbb {B}_{\mathrm {dR},\log }^+$
can be viewed as an element of
$\omega ^{-1}\otimes _{\mathcal {O}_{\mathcal {X}}}\operatorname {\mathrm {gr}}^1\mathcal {O}\mathbb {B}_{\mathrm {dR},\log }^+$
can be viewed as an element of
 $$ \begin{align*}\operatorname{\mathrm{Ext}}^1_{\mathcal{X}_{\mathrm{prok\acute{e}t}}}(\omega\otimes_{\mathcal{O}_{\mathcal{X}}}\hat{\mathcal{O}}_{\mathcal{X}},\omega^{-1}\otimes_{\mathcal{O}_{\mathcal{X}}}\hat{\mathcal{O}}_{\mathcal{X}}(1)).\end{align*} $$
$$ \begin{align*}\operatorname{\mathrm{Ext}}^1_{\mathcal{X}_{\mathrm{prok\acute{e}t}}}(\omega\otimes_{\mathcal{O}_{\mathcal{X}}}\hat{\mathcal{O}}_{\mathcal{X}},\omega^{-1}\otimes_{\mathcal{O}_{\mathcal{X}}}\hat{\mathcal{O}}_{\mathcal{X}}(1)).\end{align*} $$
On the other hand, recall that
 $\hat {\underline {V}}_{\log }\otimes _{\hat {\mathbb {Z}}_p}\hat {\mathcal {O}}_{\mathcal {X}}$
also defines an element in this extension group by the relative Hodge–Tate filtration (4.1.3).
$\hat {\underline {V}}_{\log }\otimes _{\hat {\mathbb {Z}}_p}\hat {\mathcal {O}}_{\mathcal {X}}$
also defines an element in this extension group by the relative Hodge–Tate filtration (4.1.3).
Theorem 4.2.2. There is an isomorphism between
 $\omega ^{-1}\otimes _{\mathcal {O}_{\mathcal {X}}}\operatorname {\mathrm {gr}}^1\mathcal {O}\mathbb {B}_{\mathrm {dR},\log }^+$
and
$\omega ^{-1}\otimes _{\mathcal {O}_{\mathcal {X}}}\operatorname {\mathrm {gr}}^1\mathcal {O}\mathbb {B}_{\mathrm {dR},\log }^+$
and
 $\hat {\underline {V}}_{\log }(1)\otimes _{\hat {\mathbb {Z}}_p}\hat {\mathcal {O}}_{\mathcal {X}}$
as
$\hat {\underline {V}}_{\log }(1)\otimes _{\hat {\mathbb {Z}}_p}\hat {\mathcal {O}}_{\mathcal {X}}$
as
![]() $\hat {\mathcal {O}}_{\mathcal {X}}$
-modules such that as extension classes, they differ by
$\hat {\mathcal {O}}_{\mathcal {X}}$
-modules such that as extension classes, they differ by
![]() $-1$
.
$-1$
.
Proof. Consider the first graded piece of the tensor product of
 $\hat {\underline {V}}_{\log }$
and the Poincaré lemma sequence (4.2.1) over
$\hat {\underline {V}}_{\log }$
and the Poincaré lemma sequence (4.2.1) over
![]() $\hat {\mathbb {Z}}_p$
; that is, the tensor product of
$\hat {\mathbb {Z}}_p$
; that is, the tensor product of
 $\hat {\underline {V}}_{\log }$
with the log Faltings’s extension:
$\hat {\underline {V}}_{\log }$
with the log Faltings’s extension:
 $$ \begin{align*}0\to \hat{\underline{V}}_{\log}(1)\otimes_{\hat{\mathbb{Z}}_p} \hat{\mathcal{O}}_{\mathcal{X}}\to \hat{\underline{V}}_{\log}\otimes_{\hat{\mathbb{Z}}_p} \operatorname{\mathrm{gr}}^1\mathcal{O}\mathbb{B}_{\mathrm{dR},\log}^+ \xrightarrow{\nabla} \hat{\underline{V}}_{\log}\otimes_{\hat{\mathbb{Z}}_p}\hat{\mathcal{O}}_{\mathcal{X}}\otimes_{\mathcal{O}_{\mathcal{X}}}\Omega^1_{\mathcal{X}}(\mathcal{C})\to 0.\end{align*} $$
$$ \begin{align*}0\to \hat{\underline{V}}_{\log}(1)\otimes_{\hat{\mathbb{Z}}_p} \hat{\mathcal{O}}_{\mathcal{X}}\to \hat{\underline{V}}_{\log}\otimes_{\hat{\mathbb{Z}}_p} \operatorname{\mathrm{gr}}^1\mathcal{O}\mathbb{B}_{\mathrm{dR},\log}^+ \xrightarrow{\nabla} \hat{\underline{V}}_{\log}\otimes_{\hat{\mathbb{Z}}_p}\hat{\mathcal{O}}_{\mathcal{X}}\otimes_{\mathcal{O}_{\mathcal{X}}}\Omega^1_{\mathcal{X}}(\mathcal{C})\to 0.\end{align*} $$
Then the inclusion
 $\operatorname {\mathrm {gr}}^1(D_{\mathrm {dR},\log }\otimes _{\mathcal {O}_{\mathcal {X}}} \mathcal {O}\mathbb {B}_{\mathrm {dR},\log }^+)\subset \operatorname {\mathrm {gr}}^1(\hat {\underline {V}}_{\log }\otimes _{\hat {\mathbb {Z}}_p}\mathcal {O}\mathbb {B}_{\mathrm {dR},\log }^+)$
induces
$\operatorname {\mathrm {gr}}^1(D_{\mathrm {dR},\log }\otimes _{\mathcal {O}_{\mathcal {X}}} \mathcal {O}\mathbb {B}_{\mathrm {dR},\log }^+)\subset \operatorname {\mathrm {gr}}^1(\hat {\underline {V}}_{\log }\otimes _{\hat {\mathbb {Z}}_p}\mathcal {O}\mathbb {B}_{\mathrm {dR},\log }^+)$
induces
 $$ \begin{align*}0\to \hat{\underline{V}}_{\log}(1)\otimes_{\hat{\mathbb{Z}}_p} \hat{\mathcal{O}}_{\mathcal{X}}\to \operatorname{\mathrm{gr}}^1(D_{\mathrm{dR},\log}\otimes_{\mathcal{O}_{\mathcal{X}}} \mathcal{O}\mathbb{B}_{\mathrm{dR},\log}^+) \xrightarrow{\nabla} \operatorname{\mathrm{gr}}^0 D_{\mathrm{dR},\log}\otimes_{\mathcal{O}_{\mathcal{X}}}\hat{\mathcal{O}}_{\mathcal{X}}\otimes_{\mathcal{O}_{\mathcal{X}}}\Omega^1_{\mathcal{X}}(\mathcal{C}), \end{align*} $$
$$ \begin{align*}0\to \hat{\underline{V}}_{\log}(1)\otimes_{\hat{\mathbb{Z}}_p} \hat{\mathcal{O}}_{\mathcal{X}}\to \operatorname{\mathrm{gr}}^1(D_{\mathrm{dR},\log}\otimes_{\mathcal{O}_{\mathcal{X}}} \mathcal{O}\mathbb{B}_{\mathrm{dR},\log}^+) \xrightarrow{\nabla} \operatorname{\mathrm{gr}}^0 D_{\mathrm{dR},\log}\otimes_{\mathcal{O}_{\mathcal{X}}}\hat{\mathcal{O}}_{\mathcal{X}}\otimes_{\mathcal{O}_{\mathcal{X}}}\Omega^1_{\mathcal{X}}(\mathcal{C}), \end{align*} $$
where the first inclusion follows from the sequence (4.1.2) and the image of
![]() $\nabla $
lies in
$\nabla $
lies in
 $\operatorname {\mathrm {gr}}^0 D_{\mathrm {dR},\log }\otimes _{\mathcal {O}_{\mathcal {X}}}\hat {\mathcal {O}}_{\mathcal {X}}\otimes _{\mathcal {O}_{\mathcal {X}}}\Omega ^1_{\mathcal {X}}(\mathcal {C})$
by Griffiths transversality. I claim that
$\operatorname {\mathrm {gr}}^0 D_{\mathrm {dR},\log }\otimes _{\mathcal {O}_{\mathcal {X}}}\hat {\mathcal {O}}_{\mathcal {X}}\otimes _{\mathcal {O}_{\mathcal {X}}}\Omega ^1_{\mathcal {X}}(\mathcal {C})$
by Griffiths transversality. I claim that
![]() $\nabla $
is in fact surjective as it has a left inverse: the composite map
$\nabla $
is in fact surjective as it has a left inverse: the composite map
 $$ \begin{align*}\operatorname{\mathrm{gr}}^1(D_{\mathrm{dR},\log})\otimes_{\mathcal{O}_{\mathcal{X}}} \hat{\mathcal{O}}_{\mathcal{X}}\subset \operatorname{\mathrm{gr}}^1(D_{\mathrm{dR},\log}\otimes_{\mathcal{O}_{\mathcal{X}}} \mathcal{O}\mathbb{B}_{\mathrm{dR},\log}^+) \xrightarrow{\nabla} \operatorname{\mathrm{gr}}^0 D_{\mathrm{dR},\log}\otimes_{\mathcal{O}_{\mathcal{X}}}\hat{\mathcal{O}}_{\mathcal{X}}\otimes_{\mathcal{O}_{\mathcal{X}}}\Omega^1_{\mathcal{X}}(\mathcal{C})\end{align*} $$
$$ \begin{align*}\operatorname{\mathrm{gr}}^1(D_{\mathrm{dR},\log})\otimes_{\mathcal{O}_{\mathcal{X}}} \hat{\mathcal{O}}_{\mathcal{X}}\subset \operatorname{\mathrm{gr}}^1(D_{\mathrm{dR},\log}\otimes_{\mathcal{O}_{\mathcal{X}}} \mathcal{O}\mathbb{B}_{\mathrm{dR},\log}^+) \xrightarrow{\nabla} \operatorname{\mathrm{gr}}^0 D_{\mathrm{dR},\log}\otimes_{\mathcal{O}_{\mathcal{X}}}\hat{\mathcal{O}}_{\mathcal{X}}\otimes_{\mathcal{O}_{\mathcal{X}}}\Omega^1_{\mathcal{X}}(\mathcal{C})\end{align*} $$
is nothing but the tensor product of Kodaira–Spencer map with
![]() $\hat {\mathcal {O}}_{\mathcal {X}}$
and, hence, an isomorphism. This implies that
$\hat {\mathcal {O}}_{\mathcal {X}}$
and, hence, an isomorphism. This implies that
 $$ \begin{align*}\hat{\underline{V}}_{\log}(1)\otimes_{\hat{\mathbb{Z}}_p} \hat{\mathcal{O}}_{\mathcal{X}} \xrightarrow{\sim} \operatorname{\mathrm{gr}}^1(D_{\mathrm{dR},\log}\otimes_{\mathcal{O}_{\mathcal{X}}} \mathcal{O}\mathbb{B}_{\mathrm{dR},\log}^+) / \operatorname{\mathrm{gr}}^1(D_{\mathrm{dR},\log})\otimes_{\mathcal{O}_{\mathcal{X}}} \hat{\mathcal{O}}_{\mathcal{X}}.\end{align*} $$
$$ \begin{align*}\hat{\underline{V}}_{\log}(1)\otimes_{\hat{\mathbb{Z}}_p} \hat{\mathcal{O}}_{\mathcal{X}} \xrightarrow{\sim} \operatorname{\mathrm{gr}}^1(D_{\mathrm{dR},\log}\otimes_{\mathcal{O}_{\mathcal{X}}} \mathcal{O}\mathbb{B}_{\mathrm{dR},\log}^+) / \operatorname{\mathrm{gr}}^1(D_{\mathrm{dR},\log})\otimes_{\mathcal{O}_{\mathcal{X}}} \hat{\mathcal{O}}_{\mathcal{X}}.\end{align*} $$
Note that this right-hand side can be identified with
 $\operatorname {\mathrm {gr}}^0(D_{\mathrm {dR},\log })\otimes _{\mathcal {O}_{\mathcal {X}}}\operatorname {\mathrm {gr}}^1\mathcal {O}\mathbb {B}_{\mathrm {dR},\log }^+=\omega ^{-1}\otimes _{\mathcal {O}_{\mathcal {X}}}\operatorname {\mathrm {gr}}^1\mathcal {O}\mathbb {B}_{\mathrm {dR},\log }^+$
as there is a canonical decomposition
$\operatorname {\mathrm {gr}}^0(D_{\mathrm {dR},\log })\otimes _{\mathcal {O}_{\mathcal {X}}}\operatorname {\mathrm {gr}}^1\mathcal {O}\mathbb {B}_{\mathrm {dR},\log }^+=\omega ^{-1}\otimes _{\mathcal {O}_{\mathcal {X}}}\operatorname {\mathrm {gr}}^1\mathcal {O}\mathbb {B}_{\mathrm {dR},\log }^+$
as there is a canonical decomposition
 $$ \begin{align*}\operatorname{\mathrm{gr}}^1(D_{\mathrm{dR},\log}\otimes_{\mathcal{O}_{\mathcal{X}}} \mathcal{O}\mathbb{B}_{\mathrm{dR},\log}^+) = \operatorname{\mathrm{gr}}^1(D_{\mathrm{dR},\log})\otimes_{\mathcal{O}_{\mathcal{X}}} \hat{\mathcal{O}}_{\mathcal{X}} \oplus \operatorname{\mathrm{gr}}^0(D_{\mathrm{dR},\log})\otimes_{\mathcal{O}_{\mathcal{X}}}\operatorname{\mathrm{gr}}^1\mathcal{O}\mathbb{B}_{\mathrm{dR},\log}^+.\end{align*} $$
$$ \begin{align*}\operatorname{\mathrm{gr}}^1(D_{\mathrm{dR},\log}\otimes_{\mathcal{O}_{\mathcal{X}}} \mathcal{O}\mathbb{B}_{\mathrm{dR},\log}^+) = \operatorname{\mathrm{gr}}^1(D_{\mathrm{dR},\log})\otimes_{\mathcal{O}_{\mathcal{X}}} \hat{\mathcal{O}}_{\mathcal{X}} \oplus \operatorname{\mathrm{gr}}^0(D_{\mathrm{dR},\log})\otimes_{\mathcal{O}_{\mathcal{X}}}\operatorname{\mathrm{gr}}^1\mathcal{O}\mathbb{B}_{\mathrm{dR},\log}^+.\end{align*} $$
Hence, we obtain an isomorphism
 $\hat {\underline {V}}_{\log }(1)\otimes _{\hat {\mathbb {Z}}_p} \hat {\mathcal {O}}_{\mathcal {X}} \cong \omega ^{-1}\otimes _{\mathcal {O}_{\mathcal {X}}}\operatorname {\mathrm {gr}}^1\mathcal {O}\mathbb {B}_{\mathrm {dR},\log }^+$
as claimed in the theorem. To check their relation as extension classes, one useful observation is that the surjection
$\hat {\underline {V}}_{\log }(1)\otimes _{\hat {\mathbb {Z}}_p} \hat {\mathcal {O}}_{\mathcal {X}} \cong \omega ^{-1}\otimes _{\mathcal {O}_{\mathcal {X}}}\operatorname {\mathrm {gr}}^1\mathcal {O}\mathbb {B}_{\mathrm {dR},\log }^+$
as claimed in the theorem. To check their relation as extension classes, one useful observation is that the surjection
 $\hat {\underline {V}}_{\log }(1)\otimes _{\hat {\mathbb {Z}}_p} \hat {\mathcal {O}}_{\mathcal {X}}\to \omega ^{1}\otimes _{\mathcal {O}_{\mathcal {X}}}\hat {\mathcal {O}}_{\mathcal {X}}$
in the exact sequence (4.1.3) agrees with the composite map
$\hat {\underline {V}}_{\log }(1)\otimes _{\hat {\mathbb {Z}}_p} \hat {\mathcal {O}}_{\mathcal {X}}\to \omega ^{1}\otimes _{\mathcal {O}_{\mathcal {X}}}\hat {\mathcal {O}}_{\mathcal {X}}$
in the exact sequence (4.1.3) agrees with the composite map
 $$ \begin{align*} \hat{\underline{V}}_{\log}(1)\otimes_{\hat{\mathbb{Z}}_p} \hat{\mathcal{O}}_{\mathcal{X}}\subset \operatorname{\mathrm{gr}}^1(D_{\mathrm{dR},\log}\otimes_{\mathcal{O}_{\mathcal{X}}} \mathcal{O}\mathbb{B}_{\mathrm{dR},\log}^+) \to \operatorname{\mathrm{gr}}^1(D_{\mathrm{dR},\log})\otimes_{\mathcal{O}_{\mathcal{X}}} \hat{\mathcal{O}}_{\mathcal{X}}, \end{align*} $$
$$ \begin{align*} \hat{\underline{V}}_{\log}(1)\otimes_{\hat{\mathbb{Z}}_p} \hat{\mathcal{O}}_{\mathcal{X}}\subset \operatorname{\mathrm{gr}}^1(D_{\mathrm{dR},\log}\otimes_{\mathcal{O}_{\mathcal{X}}} \mathcal{O}\mathbb{B}_{\mathrm{dR},\log}^+) \to \operatorname{\mathrm{gr}}^1(D_{\mathrm{dR},\log})\otimes_{\mathcal{O}_{\mathcal{X}}} \hat{\mathcal{O}}_{\mathcal{X}}, \end{align*} $$
where the second map is the projection using the above decomposition. Hence, it differs by
![]() $-1$
with the composite
$-1$
with the composite
 $$ \begin{align*} \hat{\underline{V}}_{\log}(1)\otimes_{\hat{\mathbb{Z}}_p} \hat{\mathcal{O}}_{\mathcal{X}}\to \operatorname{\mathrm{gr}}^1(D_{\mathrm{dR},\log}\otimes_{\mathcal{O}_{\mathcal{X}}} \mathcal{O}\mathbb{B}_{\mathrm{dR},\log}^+) \to \operatorname{\mathrm{gr}}^0(D_{\mathrm{dR},\log})\otimes_{\mathcal{O}_{\mathcal{X}}}\operatorname{\mathrm{gr}}^1\mathcal{O}\mathbb{B}_{\mathrm{dR},\log}^+\end{align*} $$
$$ \begin{align*} \hat{\underline{V}}_{\log}(1)\otimes_{\hat{\mathbb{Z}}_p} \hat{\mathcal{O}}_{\mathcal{X}}\to \operatorname{\mathrm{gr}}^1(D_{\mathrm{dR},\log}\otimes_{\mathcal{O}_{\mathcal{X}}} \mathcal{O}\mathbb{B}_{\mathrm{dR},\log}^+) \to \operatorname{\mathrm{gr}}^0(D_{\mathrm{dR},\log})\otimes_{\mathcal{O}_{\mathcal{X}}}\operatorname{\mathrm{gr}}^1\mathcal{O}\mathbb{B}_{\mathrm{dR},\log}^+\end{align*} $$
 $$ \begin{align*}\xrightarrow{\nabla} \operatorname{\mathrm{gr}}^0 D_{\mathrm{dR},\log}\otimes_{\mathcal{O}_{\mathcal{X}}}\hat{\mathcal{O}}_{\mathcal{X}}\otimes_{\mathcal{O}_{\mathcal{X}}}\Omega^1_{\mathcal{X}}(\mathcal{C}) \xleftarrow{\sim} \operatorname{\mathrm{gr}}^1(D_{\mathrm{dR},\log})\otimes_{\mathcal{O}_{\mathcal{X}}} \hat{\mathcal{O}}_{\mathcal{X}}, \end{align*} $$
$$ \begin{align*}\xrightarrow{\nabla} \operatorname{\mathrm{gr}}^0 D_{\mathrm{dR},\log}\otimes_{\mathcal{O}_{\mathcal{X}}}\hat{\mathcal{O}}_{\mathcal{X}}\otimes_{\mathcal{O}_{\mathcal{X}}}\Omega^1_{\mathcal{X}}(\mathcal{C}) \xleftarrow{\sim} \operatorname{\mathrm{gr}}^1(D_{\mathrm{dR},\log})\otimes_{\mathcal{O}_{\mathcal{X}}} \hat{\mathcal{O}}_{\mathcal{X}}, \end{align*} $$
where the second map is the other projection and the last isomorphism is given by Kodaira–Spencer map. Note that the composite of the first row is the isomorphism constructed before. This finishes the proof of theorem.
Corollary 4.2.3. Let
![]() $X,\tilde {X}$
be as in the beginning of this subsection. Moreover, we assume
$X,\tilde {X}$
be as in the beginning of this subsection. Moreover, we assume
![]() $\pi _{\mathrm {HT}}(\tilde {X})$
is contained in an affinoid open subset of
$\pi _{\mathrm {HT}}(\tilde {X})$
is contained in an affinoid open subset of
![]() ${\mathscr {F}\!\ell }$
. Then
${\mathscr {F}\!\ell }$
. Then
![]() $\widetilde {X}$
is a locally analytic covering of X in the sense of Definition 3.5.4.
$\widetilde {X}$
is a locally analytic covering of X in the sense of Definition 3.5.4.
Proof. By Proposition 3.5.3, one equivalent definition of locally analytic covering is that if we take the global sections of Faltings’s extension on
![]() $\tilde {X}$
(viewed as open set in
$\tilde {X}$
(viewed as open set in
![]() $\mathcal {X}_{\mathrm {prok\acute {e}t}}$
by abuse of notation), it remains exact after taking
$\mathcal {X}_{\mathrm {prok\acute {e}t}}$
by abuse of notation), it remains exact after taking
![]() $K_p$
-locally analytic vectors. First consider taking the global sections of relative Hodge–Tate filtration (4.1.3) on
$K_p$
-locally analytic vectors. First consider taking the global sections of relative Hodge–Tate filtration (4.1.3) on
![]() $\tilde {X}$
:
$\tilde {X}$
:
 $$ \begin{align} \;\;\;\;\;\;\;0\to H^0(\tilde{X},\omega^{-1}\otimes\hat{\mathcal{O}}_{\mathcal{X}}(1)) \to H^0(\tilde{X},\hat{\underline{V}}_{\log}(1)\otimes\hat{\mathcal{O}}_{\mathcal{X}}) \to H^0(\tilde{X},\omega\otimes\hat{\mathcal{O}}_{\mathcal{X}})\to 0. \end{align} $$
$$ \begin{align} \;\;\;\;\;\;\;0\to H^0(\tilde{X},\omega^{-1}\otimes\hat{\mathcal{O}}_{\mathcal{X}}(1)) \to H^0(\tilde{X},\hat{\underline{V}}_{\log}(1)\otimes\hat{\mathcal{O}}_{\mathcal{X}}) \to H^0(\tilde{X},\omega\otimes\hat{\mathcal{O}}_{\mathcal{X}})\to 0. \end{align} $$
This is exact as
![]() $H^1(\tilde {X},\omega ^{-1}\otimes _{\mathcal {O}_{\mathcal {X}}}\hat {\mathcal {O}}_{\mathcal {X}}(1))=0$
by Theorem 5.4.3 of [Reference Diao, Lan, Liu and ZhuDLLZ19]. Note that
$H^1(\tilde {X},\omega ^{-1}\otimes _{\mathcal {O}_{\mathcal {X}}}\hat {\mathcal {O}}_{\mathcal {X}}(1))=0$
by Theorem 5.4.3 of [Reference Diao, Lan, Liu and ZhuDLLZ19]. Note that
 $\hat {\underline {V}}_{\log }$
becomes a trivial local system on
$\hat {\underline {V}}_{\log }$
becomes a trivial local system on
![]() $\tilde {X}$
; hence, the middle term is naturally isomorphic to
$\tilde {X}$
; hence, the middle term is naturally isomorphic to
 $V(1)\otimes _{\mathbb {Q}_p} H^0(\tilde {X},\hat {\mathcal {O}}_{\mathcal {X}})$
where
$V(1)\otimes _{\mathbb {Q}_p} H^0(\tilde {X},\hat {\mathcal {O}}_{\mathcal {X}})$
where
 $V=\mathbb {Q}_p^{\oplus 2}$
is the standard representation of
$V=\mathbb {Q}_p^{\oplus 2}$
is the standard representation of
![]() $K_p\subset \mathrm {GL}_2(\mathbb {Q}_p)$
. By our assumption on
$K_p\subset \mathrm {GL}_2(\mathbb {Q}_p)$
. By our assumption on
![]() $\pi _{\mathrm {HT}}(\tilde {X})$
, there exists an element
$\pi _{\mathrm {HT}}(\tilde {X})$
, there exists an element
 $\mathbf {e}\in V(1)\otimes _{\mathbb {Q}_p} C\subset V(1)\otimes _{\mathbb {Q}_p} H^0(\tilde {X},\hat {\mathcal {O}}_{\mathcal {X}})$
whose image
$\mathbf {e}\in V(1)\otimes _{\mathbb {Q}_p} C\subset V(1)\otimes _{\mathbb {Q}_p} H^0(\tilde {X},\hat {\mathcal {O}}_{\mathcal {X}})$
whose image
![]() $e\in H^0(\tilde {X},\omega \otimes _{\mathcal {O}_{\mathcal {X}}}\hat {\mathcal {O}}_{\mathcal {X}})$
is a basis of
$e\in H^0(\tilde {X},\omega \otimes _{\mathcal {O}_{\mathcal {X}}}\hat {\mathcal {O}}_{\mathcal {X}})$
is a basis of
![]() $H^0(\tilde {X},\omega \otimes _{\mathcal {O}_{\mathcal {X}}}\hat {\mathcal {O}}_{\mathcal {X}})$
as a
$H^0(\tilde {X},\omega \otimes _{\mathcal {O}_{\mathcal {X}}}\hat {\mathcal {O}}_{\mathcal {X}})$
as a
![]() $H^0(\tilde {X},\hat {\mathcal {O}}_{\mathcal {X}})$
-module.
$H^0(\tilde {X},\hat {\mathcal {O}}_{\mathcal {X}})$
-module.
As the action of
![]() $K_p$
on V is analytic (even algebraic), we conclude that the short exact sequence (4.2.2) remains exact after passing to the
$K_p$
on V is analytic (even algebraic), we conclude that the short exact sequence (4.2.2) remains exact after passing to the
![]() $K_p$
-locally analytic vectors. The same holds when taking global sections of the tensor product of the exact sequence (4.1.3) and
$K_p$
-locally analytic vectors. The same holds when taking global sections of the tensor product of the exact sequence (4.1.3) and
![]() $\omega $
, which is equivalent to multiplying the sequence (4.2.2) by
$\omega $
, which is equivalent to multiplying the sequence (4.2.2) by
![]() ${e}$
. Now the corollary follows by identifying this exact sequence with Faltings’s extension (up to
${e}$
. Now the corollary follows by identifying this exact sequence with Faltings’s extension (up to
![]() $-1$
).
$-1$
).
Now we are ready to calculate
![]() $\theta $
. We will give an explicit description first and rewrite in a coordinate-free way later. We
$\theta $
. We will give an explicit description first and rewrite in a coordinate-free way later. We
-
• fix a generator of
 $\mathbb {Z}_p(1)$
from now on; that is, an isomorphism
$\mathbb {Z}_p(1)$
from now on; that is, an isomorphism
 $\mathbb {Z}_p(1)\cong \mathbb {Z}_p$
.
$\mathbb {Z}_p(1)\cong \mathbb {Z}_p$
.
Let
![]() $\mathbf {e}_1=(1,0),\mathbf {e}_2=(0,1)$
be the standard basis of
$\mathbf {e}_1=(1,0),\mathbf {e}_2=(0,1)$
be the standard basis of
 $V=\mathbb {Q}_p^{\oplus 2}$
and denote their images by
$V=\mathbb {Q}_p^{\oplus 2}$
and denote their images by
![]() $e_1,e_2\in H^0(\mathcal {X}_{K^p}, \omega _{K^p})$
(fake-Hasse invariants) using the surjective map in the exact sequence in Theorem 4.1.6 and the chosen generator of
$e_1,e_2\in H^0(\mathcal {X}_{K^p}, \omega _{K^p})$
(fake-Hasse invariants) using the surjective map in the exact sequence in Theorem 4.1.6 and the chosen generator of
![]() $\mathbb {Z}_p(1)$
. We remark that
$\mathbb {Z}_p(1)$
. We remark that
![]() $\mathrm {Aut}(C/\mathbb {Q}_p)$
acts on
$\mathrm {Aut}(C/\mathbb {Q}_p)$
acts on
![]() $e_1,e_2$
via the cyclotomic character because of the Tate-twist in
$e_1,e_2$
via the cyclotomic character because of the Tate-twist in
![]() $V(1)$
.
$V(1)$
.
Let
![]() $X,\tilde {X}$
be as in the previous corollary. In particular,
$X,\tilde {X}$
be as in the previous corollary. In particular,
![]() $\omega _{K^p}|_{\tilde X}$
is trivial and generated by some section e. Hence, we may view
$\omega _{K^p}|_{\tilde X}$
is trivial and generated by some section e. Hence, we may view
![]() $\frac {e_1}{e},\frac {e_2}{e}$
as elements in
$\frac {e_1}{e},\frac {e_2}{e}$
as elements in
![]() $\mathcal {O}_{\mathcal {X}_{K^p}}(\tilde X)$
.
$\mathcal {O}_{\mathcal {X}_{K^p}}(\tilde X)$
.
Theorem 4.2.4. The differential operator
![]() $\theta $
associated to
$\theta $
associated to
![]() $(K_p,\tilde {X})$
in Theorem 3.1.2 is, up to a unit of
$(K_p,\tilde {X})$
in Theorem 3.1.2 is, up to a unit of
![]() $\mathcal {O}_{\mathcal {X}_{K^p}}(\tilde X)$
,
$\mathcal {O}_{\mathcal {X}_{K^p}}(\tilde X)$
,
 $$ \begin{align*}\frac{1}{e^2}\begin{pmatrix}e_1e_2 & e_2^2\\ -e_1^2 & -e_1e_2\end{pmatrix}\in \mathfrak{gl}_2(\mathcal{O}_{\mathcal{X}_{K^p}}(\tilde X))=\mathcal{O}_{\mathcal{X}_{K^p}}(\tilde X)\otimes_{\mathbb{Q}_p} \operatorname{\mathrm{Lie}}(K_p).\end{align*} $$
$$ \begin{align*}\frac{1}{e^2}\begin{pmatrix}e_1e_2 & e_2^2\\ -e_1^2 & -e_1e_2\end{pmatrix}\in \mathfrak{gl}_2(\mathcal{O}_{\mathcal{X}_{K^p}}(\tilde X))=\mathcal{O}_{\mathcal{X}_{K^p}}(\tilde X)\otimes_{\mathbb{Q}_p} \operatorname{\mathrm{Lie}}(K_p).\end{align*} $$
Remark 4.2.5. As mentioned in Remark 3.1.7, it is better to view
![]() $\theta $
as a log Higgs field. The computation of
$\theta $
as a log Higgs field. The computation of
![]() $\theta $
here is just computing the Higgs bundle associated to
$\theta $
here is just computing the Higgs bundle associated to
 $\underline {\hat {V}}_{\log }$
under the p-adic Simpson correspondence, which can be deduced from
$\underline {\hat {V}}_{\log }$
under the p-adic Simpson correspondence, which can be deduced from
![]() $(D_{\mathrm {dR},\log },\nabla )$
, the other side of the de Rham comparison. This was pointed out to me by Michael Harris.
$(D_{\mathrm {dR},\log },\nabla )$
, the other side of the de Rham comparison. This was pointed out to me by Michael Harris.
Proof. We will freely use the notation and constructions introduced in Section 3. Hence,
![]() $X=\operatorname {\mathrm {Spa}}(A,A^+),\tilde {X}=\operatorname {\mathrm {Spa}}(B,B^+)$
. Fix an étale map
$X=\operatorname {\mathrm {Spa}}(A,A^+),\tilde {X}=\operatorname {\mathrm {Spa}}(B,B^+)$
. Fix an étale map
![]() $X\to Y$
as in Section 3.2.1. Let
$X\to Y$
as in Section 3.2.1. Let
![]() $X_{\infty }=\operatorname {\mathrm {Spa}}(A_{\infty },A_{\infty }^+)$
(respectively
$X_{\infty }=\operatorname {\mathrm {Spa}}(A_{\infty },A_{\infty }^+)$
(respectively
![]() $\tilde {X}_{\infty }=\operatorname {\mathrm {Spa}}(B_{\infty },B_{\infty }^+)$
) be the pullback of the perfectoid covering
$\tilde {X}_{\infty }=\operatorname {\mathrm {Spa}}(B_{\infty },B_{\infty }^+)$
) be the pullback of the perfectoid covering
![]() $Y_{\infty }$
to X (respectively
$Y_{\infty }$
to X (respectively
![]() $\tilde X$
); cf. Section 3.2.2 (respectively 3.2.6).
$\tilde X$
); cf. Section 3.2.2 (respectively 3.2.6).
To compute
![]() $\theta $
, we follow Remark 3.3.7. Recall that V is the standard 2-dimensional
$\theta $
, we follow Remark 3.3.7. Recall that V is the standard 2-dimensional
![]() $\mathbb {Q}_p$
-representation of
$\mathbb {Q}_p$
-representation of
![]() $K_p\subset \mathrm {GL}_2(\mathbb {Q}_p)$
. We need to compute
$K_p\subset \mathrm {GL}_2(\mathbb {Q}_p)$
. We need to compute
![]() $\phi _{V}:\operatorname {\mathrm {Lie}}(\Gamma )\to B_{\infty }\otimes _{\mathbb {Q}_p}V$
in Proposition 3.2.13, which agrees with the natural action of
$\phi _{V}:\operatorname {\mathrm {Lie}}(\Gamma )\to B_{\infty }\otimes _{\mathbb {Q}_p}V$
in Proposition 3.2.13, which agrees with the natural action of
![]() $\operatorname {\mathrm {Lie}}(\Gamma )$
when restricted to
$\operatorname {\mathrm {Lie}}(\Gamma )$
when restricted to
 $(B_{\infty }\otimes _{\mathbb {Q}_p}V)^{K_p,\Gamma -\mathrm {la}}$
. By Theorem 4.1.6, ignoring the Tate-twist, we have
$(B_{\infty }\otimes _{\mathbb {Q}_p}V)^{K_p,\Gamma -\mathrm {la}}$
. By Theorem 4.1.6, ignoring the Tate-twist, we have
 $$ \begin{align*}0\to B\cdot e^{-1}\to B\otimes_{\mathbb{Q}_p} V\to B\cdot e \to 0,\end{align*} $$
$$ \begin{align*}0\to B\cdot e^{-1}\to B\otimes_{\mathbb{Q}_p} V\to B\cdot e \to 0,\end{align*} $$
where
 $e^{-1}\in H^0(\tilde {X},\omega _{K^p}^{-1})$
is dual to
$e^{-1}\in H^0(\tilde {X},\omega _{K^p}^{-1})$
is dual to
![]() $e\in H^0(\tilde {X},\omega _{K^p})$
. Take the tensor product with
$e\in H^0(\tilde {X},\omega _{K^p})$
. Take the tensor product with
![]() $B_{\infty }$
over B and then take the
$B_{\infty }$
over B and then take the
![]() $K_p$
-invariants:
$K_p$
-invariants:
To compute the action of
![]() $\operatorname {\mathrm {Lie}}(\Gamma )$
on
$\operatorname {\mathrm {Lie}}(\Gamma )$
on
![]() $(B_{\infty }\otimes V)^{K_p,\Gamma -\mathrm {la}}$
, by Theorem 4.2.2, this sequence can be identified with the global sections of Faltings’s extension on
$(B_{\infty }\otimes V)^{K_p,\Gamma -\mathrm {la}}$
, by Theorem 4.2.2, this sequence can be identified with the global sections of Faltings’s extension on
![]() $X_{\infty }$
(viewed as an open set in
$X_{\infty }$
(viewed as an open set in
![]() $\mathcal {X}_{\mathrm {prok\acute {e}t}}$
), up to
$\mathcal {X}_{\mathrm {prok\acute {e}t}}$
), up to
![]() $-1$
. Hence, by results in Section 2 of [Reference Diao, Lan, Liu and ZhuDLLZ18] (in particular, Proposition 2.3.15 and proof of Corollary 2.4.2), the sequence (4.2.3) is
$-1$
. Hence, by results in Section 2 of [Reference Diao, Lan, Liu and ZhuDLLZ18] (in particular, Proposition 2.3.15 and proof of Corollary 2.4.2), the sequence (4.2.3) is
![]() $A_{\infty }$
-linearly and
$A_{\infty }$
-linearly and
![]() $\Gamma $
-equivariant isomorphic to the tensor product over
$\Gamma $
-equivariant isomorphic to the tensor product over
![]() $\mathbb {Q}_p$
of
$\mathbb {Q}_p$
of
![]() $A_{\infty }$
with a nontrivial self extension of trivial representation of
$A_{\infty }$
with a nontrivial self extension of trivial representation of
![]() $\Gamma $
:
$\Gamma $
:
which we essentially write down in Section 3.5.1. Clearly,
![]() $\operatorname {\mathrm {Lie}}(\Gamma )$
acts trivially on
$\operatorname {\mathrm {Lie}}(\Gamma )$
acts trivially on
![]() $(B_{\infty }\cdot e^{-1})^{K_p,\Gamma -\mathrm {la}}\cong (A_{\infty })^{\Gamma -\mathrm {la}}$
, and if we fix a generator x of
$(B_{\infty }\cdot e^{-1})^{K_p,\Gamma -\mathrm {la}}\cong (A_{\infty })^{\Gamma -\mathrm {la}}$
, and if we fix a generator x of
![]() $\operatorname {\mathrm {Lie}}(\Gamma )$
, it maps the quotient
$\operatorname {\mathrm {Lie}}(\Gamma )$
, it maps the quotient
![]() $(B_{\infty }\cdot e)^{K_p,\Gamma -\mathrm {la}}$
isomorphically to
$(B_{\infty }\cdot e)^{K_p,\Gamma -\mathrm {la}}$
isomorphically to
![]() $(B_{\infty }\cdot e^{-1})^{K_p,\Gamma -\mathrm {la}}$
. Therefore,
$(B_{\infty }\cdot e^{-1})^{K_p,\Gamma -\mathrm {la}}$
. Therefore,
![]() $\phi _V(x)$
is zero on
$\phi _V(x)$
is zero on
![]() $B\cdot e^{-1}$
and
$B\cdot e^{-1}$
and
![]() $\phi _V(x)(B\otimes V)=B\cdot e^{-1}$
.
$\phi _V(x)(B\otimes V)=B\cdot e^{-1}$
.
The rest is to write this as an element of
![]() $B\otimes _{\mathbb {Q}_p}\operatorname {\mathrm {Lie}}(K_p)$
up to
$B\otimes _{\mathbb {Q}_p}\operatorname {\mathrm {Lie}}(K_p)$
up to
![]() $B^{\times }$
. It is easy to see that
$B^{\times }$
. It is easy to see that
![]() $\mathbf {f}=\frac {e_2}{e}\mathbf {e_1}-\frac {e_1}{e}\mathbf {e_2}\in B\otimes _{\mathbb {Q}_p} V$
generates
$\mathbf {f}=\frac {e_2}{e}\mathbf {e_1}-\frac {e_1}{e}\mathbf {e_2}\in B\otimes _{\mathbb {Q}_p} V$
generates
![]() $B\cdot e^{-1}$
. As
$B\cdot e^{-1}$
. As
![]() $\phi _V(x)|_{B\otimes V}$
factors through
$\phi _V(x)|_{B\otimes V}$
factors through
![]() $B\cdot e$
, we may assume it sends e to
$B\cdot e$
, we may assume it sends e to
![]() $\mathbf {f}$
. A direct computation gives the matrix in the theorem.
$\mathbf {f}$
. A direct computation gives the matrix in the theorem.
4.2.6. To rewrite this theorem in a coordinate-free way, it is better to work with sheaves. Consider the pushforward of
![]() $\mathcal {O}_{\mathcal {X}_{K^p}}$
along
$\mathcal {O}_{\mathcal {X}_{K^p}}$
along
![]() $\pi _{\mathrm {HT}}:\mathcal {X}_{K^p}\to {\mathscr {F}\!\ell }$
$\pi _{\mathrm {HT}}:\mathcal {X}_{K^p}\to {\mathscr {F}\!\ell }$
We define a subsheaf
 $$ \begin{align*}\mathcal{O}_{K^p}^{\mathrm{la}}\subset\mathcal{O}_{K^p}\end{align*} $$
$$ \begin{align*}\mathcal{O}_{K^p}^{\mathrm{la}}\subset\mathcal{O}_{K^p}\end{align*} $$
as follows: for any quasi-compact open set U of
![]() ${\mathscr {F}\!\ell }$
,
${\mathscr {F}\!\ell }$
,
 $H^0(U,\mathcal {O}_{K^p}^{\mathrm {la}})$
is the subspace of
$H^0(U,\mathcal {O}_{K^p}^{\mathrm {la}})$
is the subspace of
![]() $K_p$
-locally analytic vectors in
$K_p$
-locally analytic vectors in
![]() $H^0(U,\mathcal {O}_{K^p})$
, where
$H^0(U,\mathcal {O}_{K^p})$
, where
![]() $K_p$
is an open subgroup of
$K_p$
is an open subgroup of
![]() $\mathrm {GL}_2(\mathbb {Q}_p)$
stabilising U. Note that such
$\mathrm {GL}_2(\mathbb {Q}_p)$
stabilising U. Note that such
![]() $K_p$
always exists by the compactness of U and
$K_p$
always exists by the compactness of U and
 $H^0(U,\mathcal {O}_{K^p}^{\mathrm {la}})$
is independent of choice of
$H^0(U,\mathcal {O}_{K^p}^{\mathrm {la}})$
is independent of choice of
![]() $K_p$
. Since taking locally analytic vectors is a left-exact process (see the construction in Section 2) and
$K_p$
. Since taking locally analytic vectors is a left-exact process (see the construction in Section 2) and
 ${\pi _{\mathrm {HT}}}_*\mathcal {O}^+_{\mathcal {X}_{K^p}}$
is a sheaf,
${\pi _{\mathrm {HT}}}_*\mathcal {O}^+_{\mathcal {X}_{K^p}}$
is a sheaf,
 $\mathcal {O}_{K^p}^{\mathrm {la}}$
indeed defines a sheaf on
$\mathcal {O}_{K^p}^{\mathrm {la}}$
indeed defines a sheaf on
![]() ${\mathscr {F}\!\ell }$
.
${\mathscr {F}\!\ell }$
.
Clearly,
 $\mathcal {O}^{\mathrm {la}}_{K^p}$
is
$\mathcal {O}^{\mathrm {la}}_{K^p}$
is
![]() $\mathrm {GL}_2(\mathbb {Q}_p)$
-equivariant and there is a natural action of the Lie algebra of
$\mathrm {GL}_2(\mathbb {Q}_p)$
-equivariant and there is a natural action of the Lie algebra of
![]() $\mathrm {GL}_2(\mathbb {Q}_p)$
on
$\mathrm {GL}_2(\mathbb {Q}_p)$
on
 $\mathcal {O}^{\mathrm {la}}_{K^p}$
. Hecke operators away from p act on it naturally as we only use the action at p in the construction.
$\mathcal {O}^{\mathrm {la}}_{K^p}$
. Hecke operators away from p act on it naturally as we only use the action at p in the construction.
We claim that the natural map
![]() $\mathcal {O}_{{\mathscr {F}\!\ell }}\to \mathcal {O}_{K^p}$
has image in
$\mathcal {O}_{{\mathscr {F}\!\ell }}\to \mathcal {O}_{K^p}$
has image in
 $\mathcal {O}_{K^p}^{\mathrm {la}}$
. It is enough to check this for a basis of affinoid open subsets U of
$\mathcal {O}_{K^p}^{\mathrm {la}}$
. It is enough to check this for a basis of affinoid open subsets U of
![]() ${\mathscr {F}\!\ell }$
. Since
${\mathscr {F}\!\ell }$
. Since
![]() ${\mathscr {F}\!\ell }$
is an adic space associated to a variety over C of finite type, we may consider all affinoid subsets U such that
${\mathscr {F}\!\ell }$
is an adic space associated to a variety over C of finite type, we may consider all affinoid subsets U such that
![]() $\mathcal {O}_{{\mathscr {F}\!\ell }}(U)$
can be written as a continuous quotient of
$\mathcal {O}_{{\mathscr {F}\!\ell }}(U)$
can be written as a continuous quotient of
![]() $C\langle T_1\cdots ,T_m\rangle $
for some m and the quotient topology on
$C\langle T_1\cdots ,T_m\rangle $
for some m and the quotient topology on
![]() $\mathcal {O}_{{\mathscr {F}\!\ell }}(U)$
agrees with its natural topology. Fix such a U; then there exists an open subgroup
$\mathcal {O}_{{\mathscr {F}\!\ell }}(U)$
agrees with its natural topology. Fix such a U; then there exists an open subgroup
![]() $K_p\subset \mathrm {GL}_2(\mathbb {Q}_p)$
stabilising U and acting trivially on
$K_p\subset \mathrm {GL}_2(\mathbb {Q}_p)$
stabilising U and acting trivially on
![]() $\mathcal {O}^+_{{\mathscr {F}\!\ell }}(U)/p$
. From this, we see that the action of
$\mathcal {O}^+_{{\mathscr {F}\!\ell }}(U)/p$
. From this, we see that the action of
![]() $K_p$
on
$K_p$
on
![]() $\mathcal {O}_{{\mathscr {F}\!\ell }}(U)$
is locally analytic (using arguments in Example 2.1.9, for example).
$\mathcal {O}_{{\mathscr {F}\!\ell }}(U)$
is locally analytic (using arguments in Example 2.1.9, for example).
We follow some constructions on the flag variety in [Reference Beĭlinson and BernsteinBB83]. Denote by
![]() $\mathfrak {g}$
the tensor product of the Lie algebra of
$\mathfrak {g}$
the tensor product of the Lie algebra of
![]() $\mathrm {GL}_2(\mathbb {Q}_p)$
with C; that is,
$\mathrm {GL}_2(\mathbb {Q}_p)$
with C; that is,
![]() $\mathfrak {gl}_2(C)$
. For a C-point x of the flag variety
$\mathfrak {gl}_2(C)$
. For a C-point x of the flag variety
![]() $\mathrm {Fl}$
of
$\mathrm {Fl}$
of
![]() $\mathrm {GL}_2/C$
, let
$\mathrm {GL}_2/C$
, let
![]() $\mathfrak {b}_x,\mathfrak {n}_x\subset \mathfrak {g}$
be its corresponding Borel subalgebra and nilpotent subalgebra. Let
$\mathfrak {b}_x,\mathfrak {n}_x\subset \mathfrak {g}$
be its corresponding Borel subalgebra and nilpotent subalgebra. Let
 $$ \begin{align*} \mathfrak{g}^0&:= \mathcal{O}_{\mathrm{Fl}}\otimes_{C}\mathfrak{g},\\ \mathfrak{b}^0&:= \{f\in \mathfrak{g}^0\,| \, f_x\in \mathfrak{b}_x,\mbox{ for all }x\in\mathrm{Fl}(C)\},\\ \mathfrak{n}^0&:= \{f\in \mathfrak{g}^0\,| \, f_x\in \mathfrak{n}_x,\mbox{ for all }x\in\mathrm{Fl}(C)\} \end{align*} $$
$$ \begin{align*} \mathfrak{g}^0&:= \mathcal{O}_{\mathrm{Fl}}\otimes_{C}\mathfrak{g},\\ \mathfrak{b}^0&:= \{f\in \mathfrak{g}^0\,| \, f_x\in \mathfrak{b}_x,\mbox{ for all }x\in\mathrm{Fl}(C)\},\\ \mathfrak{n}^0&:= \{f\in \mathfrak{g}^0\,| \, f_x\in \mathfrak{n}_x,\mbox{ for all }x\in\mathrm{Fl}(C)\} \end{align*} $$
be
![]() $\mathrm {GL}_2$
-equivariant vector bundles on
$\mathrm {GL}_2$
-equivariant vector bundles on
![]() $\mathrm {Fl}$
, where
$\mathrm {Fl}$
, where
![]() $\mathrm {GL}_2$
acts by conjugation on
$\mathrm {GL}_2$
acts by conjugation on
![]() $\mathfrak {g}$
. By abuse of notation, we also view these as vector bundles on
$\mathfrak {g}$
. By abuse of notation, we also view these as vector bundles on
![]() ${\mathscr {F}\!\ell }$
, the associated adic space of
${\mathscr {F}\!\ell }$
, the associated adic space of
![]() $\mathrm {Fl}$
. Then we have a natural action of
$\mathrm {Fl}$
. Then we have a natural action of
![]() $\mathfrak {g}^0$
on
$\mathfrak {g}^0$
on
 $\mathcal {O}^{\mathrm {la}}_{K^p}$
: for
$\mathcal {O}^{\mathrm {la}}_{K^p}$
: for
 $f\in \mathcal {O}_{{\mathscr {F}\!\ell }},z\in \mathfrak {g},s\in \mathcal {O}^{\mathrm {la}}_{K^p}$
,
$f\in \mathcal {O}_{{\mathscr {F}\!\ell }},z\in \mathfrak {g},s\in \mathcal {O}^{\mathrm {la}}_{K^p}$
,
Theorem 4.2.7.
![]() $\mathfrak {n}^0$
acts trivially on
$\mathfrak {n}^0$
acts trivially on
 $\mathcal {O}^{\mathrm {la}}_{K^p}$
.
$\mathcal {O}^{\mathrm {la}}_{K^p}$
.
Proof. Its enough to check this on open subsets as in Theorem 4.1.7, for which we may invoke Theorem 4.2.4 and our claim follows immediately. In fact, it follows from the proof of Theorem 4.2.4 that the action of
![]() $\phi _V$
on
$\phi _V$
on
![]() $V(1)\otimes _{\mathbb {Q}_p} \mathcal {O}_{\mathcal {X}_{K^p}}$
is trivial on
$V(1)\otimes _{\mathbb {Q}_p} \mathcal {O}_{\mathcal {X}_{K^p}}$
is trivial on
 $\omega ^{-1}_{K^p}(1)$
and induces an isomorphism
$\omega ^{-1}_{K^p}(1)$
and induces an isomorphism
 $\omega _{K^p}\xrightarrow {\sim } \omega ^{-1}_{K^p}(1)$
. Since
$\omega _{K^p}\xrightarrow {\sim } \omega ^{-1}_{K^p}(1)$
. Since
![]() $\pi _{\mathrm {HT}}$
is defined by the position of
$\pi _{\mathrm {HT}}$
is defined by the position of
 $\omega ^{-1}_{K^p}(1)$
in
$\omega ^{-1}_{K^p}(1)$
in
![]() $V(1)\otimes _{\mathbb {Q}_p} \mathcal {O}_{\mathcal {X}_{K^p}}$
, it is tautological that
$V(1)\otimes _{\mathbb {Q}_p} \mathcal {O}_{\mathcal {X}_{K^p}}$
, it is tautological that
![]() $\mathcal {O}_{\mathcal {X}_{K^p}}\theta \subset \mathcal {O}_{\mathcal {X}_{K^p}}\otimes _C \mathfrak {g}$
contains
$\mathcal {O}_{\mathcal {X}_{K^p}}\theta \subset \mathcal {O}_{\mathcal {X}_{K^p}}\otimes _C \mathfrak {g}$
contains
![]() $\mathfrak {n}^0$
.
$\mathfrak {n}^0$
.
Fix a rational Borel subalgebra
 $\mathfrak {b}:=\{\begin {pmatrix} * & * \\ 0 & * \end {pmatrix}\}$
and a Cartan subalgebra
$\mathfrak {b}:=\{\begin {pmatrix} * & * \\ 0 & * \end {pmatrix}\}$
and a Cartan subalgebra
 $\mathfrak {h}:=\{\begin {pmatrix} * & 0 \\ 0 & * \end {pmatrix}\}$
of
$\mathfrak {h}:=\{\begin {pmatrix} * & 0 \\ 0 & * \end {pmatrix}\}$
of
![]() $\mathfrak {g}$
and let W be the Weyl group. Recall the Harish–Chandra isomorphism
$\mathfrak {g}$
and let W be the Weyl group. Recall the Harish–Chandra isomorphism
![]() $Z(U(\mathfrak {g}))\cong S(\mathfrak {h})^W$
, where
$Z(U(\mathfrak {g}))\cong S(\mathfrak {h})^W$
, where
![]() $Z(U(\mathfrak {g}))$
is the centre of the universal enveloping algebra
$Z(U(\mathfrak {g}))$
is the centre of the universal enveloping algebra
![]() $U(\mathfrak {g})$
of
$U(\mathfrak {g})$
of
![]() $\mathfrak {g}$
and
$\mathfrak {g}$
and
![]() $S(\mathfrak {h})$
is the symmetric algebra of
$S(\mathfrak {h})$
is the symmetric algebra of
![]() $\mathfrak {h}$
equipped with the dot action of W:
$\mathfrak {h}$
equipped with the dot action of W:
![]() $w\cdot \mu =w(\mu +\rho )-\rho ,\mu \in \mathfrak {h}^*$
. Here
$w\cdot \mu =w(\mu +\rho )-\rho ,\mu \in \mathfrak {h}^*$
. Here
![]() $\rho $
is the half sum of positive roots as usual. Let
$\rho $
is the half sum of positive roots as usual. Let
![]() $\mathfrak {g}_0:=\mathfrak {sl}_2(C)\subset \mathfrak {g}$
and
$\mathfrak {g}_0:=\mathfrak {sl}_2(C)\subset \mathfrak {g}$
and
![]() $\mathfrak {h}_0=\mathfrak {h}\cap \mathfrak {g}_0$
. Then, similarly,
$\mathfrak {h}_0=\mathfrak {h}\cap \mathfrak {g}_0$
. Then, similarly,
![]() $Z(U(\mathfrak {g_0}))\cong S(\mathfrak {h_0})^W$
. We also denote by
$Z(U(\mathfrak {g_0}))\cong S(\mathfrak {h_0})^W$
. We also denote by
 $\mathfrak {z}:=\{\begin {pmatrix} a & 0 \\ 0 & a \end {pmatrix}\}\subset \mathfrak {g}$
the centre of
$\mathfrak {z}:=\{\begin {pmatrix} a & 0 \\ 0 & a \end {pmatrix}\}\subset \mathfrak {g}$
the centre of
![]() $\mathfrak {g}$
.
$\mathfrak {g}$
.
It is clear that
![]() $\mathfrak {b}^0/\mathfrak {n}^0=\mathcal {O}_{\mathrm {{\mathscr {F}\!\ell }}}\otimes _{C}\mathfrak {h}$
by identifying global sections of
$\mathfrak {b}^0/\mathfrak {n}^0=\mathcal {O}_{\mathrm {{\mathscr {F}\!\ell }}}\otimes _{C}\mathfrak {h}$
by identifying global sections of
![]() $\mathfrak {b}^0/\mathfrak {n}^0$
with
$\mathfrak {b}^0/\mathfrak {n}^0$
with
![]() $\mathfrak {h}$
. So we have a a natural embedding
$\mathfrak {h}$
. So we have a a natural embedding
![]() $\mathfrak {h}\to \mathfrak {b}^0/\mathfrak {n}^0$
.
$\mathfrak {h}\to \mathfrak {b}^0/\mathfrak {n}^0$
.
Corollary 4.2.8. There is a natural (horizontal) action
![]() $\theta _{\mathfrak {h}}$
of
$\theta _{\mathfrak {h}}$
of
![]() $\mathfrak {h}$
on
$\mathfrak {h}$
on
 $\mathcal {O}^{\mathrm {la}}_{K^p}$
commuting with
$\mathcal {O}^{\mathrm {la}}_{K^p}$
commuting with
![]() $\mathfrak {g}$
. In fact,
$\mathfrak {g}$
. In fact,
![]() $-\theta _{\mathfrak {h}}$
induces an action of
$-\theta _{\mathfrak {h}}$
induces an action of
![]() $S(\mathfrak {h_0})$
extending the one of
$S(\mathfrak {h_0})$
extending the one of
![]() $Z(U(\mathfrak {g_0}))$
and
$Z(U(\mathfrak {g_0}))$
and
![]() $\theta _{\mathfrak {h}}|_{\mathfrak {z}}$
agrees with the action of
$\theta _{\mathfrak {h}}|_{\mathfrak {z}}$
agrees with the action of
![]() $\mathfrak {z}\subset \mathfrak {g}$
.
$\mathfrak {z}\subset \mathfrak {g}$
.
Proof. The first part follows from the fact that
![]() $H^0({\mathscr {F}\!\ell },\mathfrak {b}^0/\mathfrak {n}^0)$
is
$H^0({\mathscr {F}\!\ell },\mathfrak {b}^0/\mathfrak {n}^0)$
is
![]() $\mathrm {GL}_2$
-invariant. The second part essentially follows from Harish–Chandra’s theorem. Note that there is a sign here since this construction studies the
$\mathrm {GL}_2$
-invariant. The second part essentially follows from Harish–Chandra’s theorem. Note that there is a sign here since this construction studies the
![]() $\mathfrak {n}_x$
-coinvariants rather than invariants. See Section 2 and Section 3 of [Reference Beĭlinson and BernsteinBB83].
$\mathfrak {n}_x$
-coinvariants rather than invariants. See Section 2 and Section 3 of [Reference Beĭlinson and BernsteinBB83].
Remark 4.2.9. See Theorem 5.1.8, 5.1.11 for an interpretation of this action in terms of the classical Sen operator arising from the action of
![]() $G_{\mathbb {Q}_p}$
.
$G_{\mathbb {Q}_p}$
.
Remark 4.2.10. In Beilinson–Bernstein’s theory of localisation (see, for example, Section C of [Reference BeĭlinsonBeĭ84]),
 $\mathcal {O}^{\mathrm {la}}_{K^p}$
is a
$\mathcal {O}^{\mathrm {la}}_{K^p}$
is a
![]() $\tilde {\mathscr {D}}$
-module in this analytic setting. Similarly, fix a weight
$\tilde {\mathscr {D}}$
-module in this analytic setting. Similarly, fix a weight
![]() $\chi $
of
$\chi $
of
![]() $\mathfrak {h}$
. We denote by
$\mathfrak {h}$
. We denote by
 $\mathcal {O}^{\mathrm {la},\chi }_{K^p}$
the
$\mathcal {O}^{\mathrm {la},\chi }_{K^p}$
the
![]() $\chi $
-component of
$\chi $
-component of
 $\mathcal {O}^{\mathrm {la}}_{K^p}$
; that is, the subsheaf of sections of weight
$\mathcal {O}^{\mathrm {la}}_{K^p}$
; that is, the subsheaf of sections of weight
![]() $\chi $
. Then
$\chi $
. Then
 $\mathcal {O}^{\mathrm {la},\chi }_{K^p}$
is a
$\mathcal {O}^{\mathrm {la},\chi }_{K^p}$
is a
 $\tilde {\mathscr {D}}_{\chi }$
-module. Recall that
$\tilde {\mathscr {D}}_{\chi }$
-module. Recall that
 $\tilde {\mathscr {D}}_{\chi }$
is a ring of twisted differential operators on the flag variety. Everything here is also
$\tilde {\mathscr {D}}_{\chi }$
is a ring of twisted differential operators on the flag variety. Everything here is also
![]() $\mathrm {GL}_2(\mathbb {Q}_p)$
-equivariant. Hence, we obtain a
$\mathrm {GL}_2(\mathbb {Q}_p)$
-equivariant. Hence, we obtain a
 $(\tilde {\mathscr {D}}_{\chi },\mathrm {GL}_2(\mathbb {Q}_p))$
-module on
$(\tilde {\mathscr {D}}_{\chi },\mathrm {GL}_2(\mathbb {Q}_p))$
-module on
![]() ${\mathscr {F}\!\ell }$
, which is very similar to the picture in the complex analytic setting.
${\mathscr {F}\!\ell }$
, which is very similar to the picture in the complex analytic setting.
In a series of works (see, for example, [Reference ArdakovArd17]), Ardakov proved a p-adic analogue of Beilinson–Bernstein’s localisation theorem. Roughly speaking, he showed that one can realise the dual of an admissible locally analytic representation of
![]() $\mathrm {GL}_2(\mathbb {Q}_p)$
as global sections of certain
$\mathrm {GL}_2(\mathbb {Q}_p)$
as global sections of certain
![]() $\mathrm {GL}_2(\mathbb {Q}_p)$
-equivariant
$\mathrm {GL}_2(\mathbb {Q}_p)$
-equivariant
![]() $\mathscr {D}$
-modules on
$\mathscr {D}$
-modules on
![]() ${\mathscr {F}\!\ell }$
. It is very natural to ask whether there is some form of duality relating his construction with
${\mathscr {F}\!\ell }$
. It is very natural to ask whether there is some form of duality relating his construction with
 $\mathcal {O}^{\mathrm {la},\chi }_{K^p}$
here.
$\mathcal {O}^{\mathrm {la},\chi }_{K^p}$
here.
4.3 Local structure of
 $\mathcal {O}^{\mathrm {la}}_{K^p}$
$\mathcal {O}^{\mathrm {la}}_{K^p}$
So far,
 $\mathcal {O}^{\mathrm {la}}_{K^p}$
is defined in an abstract way. We give an explicit description of its sections in this subsection. This is largely inspired by the calculations of Berger–Colmez in Section 4 and Section 5 of [Reference Berger and ColmezBC16]. We will follow their arguments and combine with our differential equation
$\mathcal {O}^{\mathrm {la}}_{K^p}$
is defined in an abstract way. We give an explicit description of its sections in this subsection. This is largely inspired by the calculations of Berger–Colmez in Section 4 and Section 5 of [Reference Berger and ColmezBC16]. We will follow their arguments and combine with our differential equation
![]() $\theta =0$
. To do this, one needs enough sections of
$\theta =0$
. To do this, one needs enough sections of
 $\mathcal {O}^{\mathrm {la}}_{K^p}$
.
$\mathcal {O}^{\mathrm {la}}_{K^p}$
.
4.3.1. Let
![]() $\Gamma (p^n)=1+p^n M_2(\mathbb {Z}_p)$
. Recall that
$\Gamma (p^n)=1+p^n M_2(\mathbb {Z}_p)$
. Recall that
![]() $\mathcal {Y}_{K^p\Gamma (p^n)}$
parametrises elliptic curves with certain level structures away from p and a trivialisation of its
$\mathcal {Y}_{K^p\Gamma (p^n)}$
parametrises elliptic curves with certain level structures away from p and a trivialisation of its
![]() $p^n$
-torsion points. In particular, the Weil pairing induces a trivialisation of
$p^n$
-torsion points. In particular, the Weil pairing induces a trivialisation of
![]() $\mu _{p^n}(C)$
. This defines a map
$\mu _{p^n}(C)$
. This defines a map
![]() $\mathcal {Y}_{K^p\Gamma (p^n)}\to \mathrm {Isom}(\mathbb {Z}/p^n,\mu _{p^n}(C))$
, which extends to its compactification
$\mathcal {Y}_{K^p\Gamma (p^n)}\to \mathrm {Isom}(\mathbb {Z}/p^n,\mu _{p^n}(C))$
, which extends to its compactification
![]() $\mathcal {X}_{K^p\Gamma (p^n)}\to \mathrm {Isom}(\mathbb {Z}/p^n,\mu _{p^n}(C))$
. Classically, this map can be obtained by looking at the connected components. Taking inverse limits, we obtain
$\mathcal {X}_{K^p\Gamma (p^n)}\to \mathrm {Isom}(\mathbb {Z}/p^n,\mu _{p^n}(C))$
. Classically, this map can be obtained by looking at the connected components. Taking inverse limits, we obtain
![]() $\mathcal {X}_{K^p}\to \mathrm {Isom}(\mathbb {Z}_p,\mathbb {Z}_p(1))$
, where
$\mathcal {X}_{K^p}\to \mathrm {Isom}(\mathbb {Z}_p,\mathbb {Z}_p(1))$
, where
![]() $\mathrm {Isom}(\mathbb {Z}_p,\mathbb {Z}_p(1))$
is identified as
$\mathrm {Isom}(\mathbb {Z}_p,\mathbb {Z}_p(1))$
is identified as
![]() $\operatorname {\mathrm {Spa}}(\mathscr {C}(\mathrm {Isom}(\mathbb {Z}_p,\mathbb {Z}_p(1)),C),\mathscr {C}(\mathrm {Isom}(\mathbb {Z}_p,\mathbb {Z}_p(1)),\mathcal {O}_C))$
. Recall that we have chosen a basis of
$\operatorname {\mathrm {Spa}}(\mathscr {C}(\mathrm {Isom}(\mathbb {Z}_p,\mathbb {Z}_p(1)),C),\mathscr {C}(\mathrm {Isom}(\mathbb {Z}_p,\mathbb {Z}_p(1)),\mathcal {O}_C))$
. Recall that we have chosen a basis of
![]() $\mathbb {Z}_p(1)$
before Theorem 4.2.4; that is, an isomorphism
$\mathbb {Z}_p(1)$
before Theorem 4.2.4; that is, an isomorphism
![]() $\mathrm {Isom}(\mathbb {Z}_p,\mathbb {Z}_p(1))\cong \mathbb {Z}_p^{\times }$
. Then
$\mathrm {Isom}(\mathbb {Z}_p,\mathbb {Z}_p(1))\cong \mathbb {Z}_p^{\times }$
. Then
![]() $\mathcal {X}_{K^p}\to \mathrm {Isom}(\mathbb {Z}_p,\mathbb {Z}_p(1))\cong \mathbb {Z}_p^{\times }$
defines a function
$\mathcal {X}_{K^p}\to \mathrm {Isom}(\mathbb {Z}_p,\mathbb {Z}_p(1))\cong \mathbb {Z}_p^{\times }$
defines a function
 $$ \begin{align*}t\in H^0(\mathcal{X}_{K^p},\mathcal{O}_{\mathcal{X}_{K^p}}),\end{align*} $$
$$ \begin{align*}t\in H^0(\mathcal{X}_{K^p},\mathcal{O}_{\mathcal{X}_{K^p}}),\end{align*} $$
which is well-defined up to
![]() $\mathbb {Z}_p^{\times }$
. See also (4.2) of [Reference EmertonEme06b] for another description. We remark that
$\mathbb {Z}_p^{\times }$
. See also (4.2) of [Reference EmertonEme06b] for another description. We remark that
![]() $G_{\mathbb {Q}_p}$
acts on t via the cyclotomic character because it is essentially an element of
$G_{\mathbb {Q}_p}$
acts on t via the cyclotomic character because it is essentially an element of
![]() $\mathbb {Z}_p(1)$
. The group
$\mathbb {Z}_p(1)$
. The group
![]() $\mathrm {GL}_2(\mathbb {Q}_p)$
acts on t via
$\mathrm {GL}_2(\mathbb {Q}_p)$
acts on t via
![]() $\varepsilon _p\circ \det $
, where
$\varepsilon _p\circ \det $
, where
![]() $\varepsilon _p:\mathbb {Q}_p^{\times }\to \mathbb {Z}_p^{\times }$
sends x to
$\varepsilon _p:\mathbb {Q}_p^{\times }\to \mathbb {Z}_p^{\times }$
sends x to
![]() $x|x|$
; hence, the action of
$x|x|$
; hence, the action of
![]() $\mathfrak {g}=\mathfrak {gl}_2(\mathbb {Q}_p)$
on t is the trace map
$\mathfrak {g}=\mathfrak {gl}_2(\mathbb {Q}_p)$
on t is the trace map
 $$ \begin{align*}\begin{pmatrix} a & b \\ c & d \end{pmatrix}\cdot t=(a+d)t,\, \begin{pmatrix} a & b \\ c & d \end{pmatrix}\in \mathfrak{g}.\end{align*} $$
$$ \begin{align*}\begin{pmatrix} a & b \\ c & d \end{pmatrix}\cdot t=(a+d)t,\, \begin{pmatrix} a & b \\ c & d \end{pmatrix}\in \mathfrak{g}.\end{align*} $$
If we take the direct limit over all tame levels
![]() $K^p$
:
$K^p$
:
 $\tilde {H}^0(C):=\varinjlim _{K^p}H^0(\mathcal {X}_{K^p},\mathcal {O}_{\mathcal {X}_{K^p}})$
, then
$\tilde {H}^0(C):=\varinjlim _{K^p}H^0(\mathcal {X}_{K^p},\mathcal {O}_{\mathcal {X}_{K^p}})$
, then
![]() $\mathrm {GL}_2(\mathbb {A}_f)$
acts naturally on
$\mathrm {GL}_2(\mathbb {A}_f)$
acts naturally on
![]() $\tilde {H}^0(C)$
and acts on t via
$\tilde {H}^0(C)$
and acts on t via
![]() $\varepsilon \circ \det $
. See Notation in the beginning of this article for the definition of
$\varepsilon \circ \det $
. See Notation in the beginning of this article for the definition of
![]() $\varepsilon $
. Using this observation, it is easy to figure out how Hecke operators away from p change when multiplying by a power of t.
$\varepsilon $
. Using this observation, it is easy to figure out how Hecke operators away from p change when multiplying by a power of t.
For
![]() $n\geq 1$
, we fix
$n\geq 1$
, we fix
 $t_n\in H^0(\mathcal {X}_{K^p\Gamma (p^n)},\mathcal {O}_{\mathcal {X}_{K^p\Gamma (p^n)}})$
so that
$t_n\in H^0(\mathcal {X}_{K^p\Gamma (p^n)},\mathcal {O}_{\mathcal {X}_{K^p\Gamma (p^n)}})$
so that
![]() $\|t-t_n\|\leq p^{-n}$
.
$\|t-t_n\|\leq p^{-n}$
.
4.3.2 A consequence of
 $\theta =0$
$\theta =0$
We introduced a basis
![]() $\mathfrak {B}$
of affinoid open subsets of
$\mathfrak {B}$
of affinoid open subsets of
![]() ${\mathscr {F}\!\ell }$
in Theorem 4.1.7. Fix
${\mathscr {F}\!\ell }$
in Theorem 4.1.7. Fix
![]() $U\in \mathfrak {B}$
from now on. Then by our construction,
$U\in \mathfrak {B}$
from now on. Then by our construction,
 $V_{\infty }:=\pi _{\mathrm {HT}}^{-1}(U)$
is affinoid perfectoid and is the preimage of an affinoid subset
$V_{\infty }:=\pi _{\mathrm {HT}}^{-1}(U)$
is affinoid perfectoid and is the preimage of an affinoid subset
![]() $V_{K_p}\subset \mathcal {X}_{K^pK_p}$
. Recall that we have fake-Hasse invariants
$V_{K_p}\subset \mathcal {X}_{K^pK_p}$
. Recall that we have fake-Hasse invariants
![]() $e_1,e_2\in H^0(\mathcal {X}_{K^p}, \omega _{K^p})$
. Throughout this subsection, we assume
$e_1,e_2\in H^0(\mathcal {X}_{K^p}, \omega _{K^p})$
. Throughout this subsection, we assume
-
•
 $e_1$
generates
$e_1$
generates
 $H^0(V_{\infty }, \omega _{K^p})$
.
$H^0(V_{\infty }, \omega _{K^p})$
.
In our later computations, we will always assume one of
![]() $e_1,e_2$
generates
$e_1,e_2$
generates
![]() $H^0(V_{\infty }, \omega _{K^p})$
. When
$H^0(V_{\infty }, \omega _{K^p})$
. When
![]() $e_2$
generates
$e_2$
generates
![]() $H^0(V_{\infty }, \omega _{K^p})$
, one can use the action of
$H^0(V_{\infty }, \omega _{K^p})$
, one can use the action of
 $\begin {pmatrix} 0 & 1 \\ 1 & 0\end {pmatrix}$
to reduce to the above case. When
$\begin {pmatrix} 0 & 1 \\ 1 & 0\end {pmatrix}$
to reduce to the above case. When
![]() $e_1$
is a basis, we can take
$e_1$
is a basis, we can take
![]() $e=e_1$
in Theorem 4.2.4. Hence, up to a unit,
$e=e_1$
in Theorem 4.2.4. Hence, up to a unit,
![]() $\theta $
on
$\theta $
on
![]() $V_{\infty }$
is
$V_{\infty }$
is
 $$ \begin{align*}\begin{pmatrix} x & x^2\\ -1 & -x \end{pmatrix}\in\mathfrak{gl}_2(\mathcal{O}_{K^p}(U)),\end{align*} $$
$$ \begin{align*}\begin{pmatrix} x & x^2\\ -1 & -x \end{pmatrix}\in\mathfrak{gl}_2(\mathcal{O}_{K^p}(U)),\end{align*} $$
where
 $x:=\frac {e_2}{e_1}\in \mathcal {O}_{{\mathscr {F}\!\ell }}(U)$
, a standard coordinate on
$x:=\frac {e_2}{e_1}\in \mathcal {O}_{{\mathscr {F}\!\ell }}(U)$
, a standard coordinate on
![]() ${\mathscr {F}\!\ell }=\mathbb {P}^1$
. In particular, we have the following important lemma.
${\mathscr {F}\!\ell }=\mathbb {P}^1$
. In particular, we have the following important lemma.
Lemma 4.3.3. Suppose
 $f\in \mathcal {O}^{\mathrm {la}}_{K^p}(U)$
is annihilated by
$f\in \mathcal {O}^{\mathrm {la}}_{K^p}(U)$
is annihilated by
 $\mathfrak {b}=\{\begin {pmatrix} * & * \\ 0 & * \end {pmatrix}\}\subset \mathfrak {gl}_2(\mathbb {Q}_p)$
. Then f is annihilated by
$\mathfrak {b}=\{\begin {pmatrix} * & * \\ 0 & * \end {pmatrix}\}\subset \mathfrak {gl}_2(\mathbb {Q}_p)$
. Then f is annihilated by
![]() $\mathfrak {gl}_2(\mathbb {Q}_p)$
; that is, f is fixed by an open subgroup of
$\mathfrak {gl}_2(\mathbb {Q}_p)$
; that is, f is fixed by an open subgroup of
![]() $\mathrm {GL}_2(\mathbb {Q}_p)$
.
$\mathrm {GL}_2(\mathbb {Q}_p)$
.
Proof. By Theorem 3.1.2,
![]() $\theta (f)=0$
. But
$\theta (f)=0$
. But
![]() $\mathfrak {b}\cdot f=0$
. Hence,
$\mathfrak {b}\cdot f=0$
. Hence,
 $\theta (f)=\begin {pmatrix} 0 & 0 \\ -1 & 0\end {pmatrix}\cdot f=0$
. Thus,
$\theta (f)=\begin {pmatrix} 0 & 0 \\ -1 & 0\end {pmatrix}\cdot f=0$
. Thus,
![]() $\mathfrak {gl}_2(\mathbb {Q}_p)\cdot f=0$
.
$\mathfrak {gl}_2(\mathbb {Q}_p)\cdot f=0$
.
Remark 4.3.4. Here is a sketch of another proof without using
![]() $\theta $
. By using the action of
$\theta $
. By using the action of
 $\begin {pmatrix} p & 0 \\ 0 & 1\end {pmatrix}$
, one may assume
$\begin {pmatrix} p & 0 \\ 0 & 1\end {pmatrix}$
, one may assume
![]() $V_{\infty }$
is a rational open subset of some
$V_{\infty }$
is a rational open subset of some
![]() $\epsilon $
-neighbourhood of the anticanonical locus
$\epsilon $
-neighbourhood of the anticanonical locus
 $\mathcal {X}^*_{\Gamma (p^\infty )}(\epsilon )_a$
for some
$\mathcal {X}^*_{\Gamma (p^\infty )}(\epsilon )_a$
for some
![]() $\epsilon \in (0,1/2)$
. See Chapter III of [Reference ScholzeSch15] for notation here. Since f is annihilated by
$\epsilon \in (0,1/2)$
. See Chapter III of [Reference ScholzeSch15] for notation here. Since f is annihilated by
![]() $\mathfrak {b}$
, it is fixed by an open subgroup
$\mathfrak {b}$
, it is fixed by an open subgroup
![]() $\Gamma ^{\prime }_0$
of the upper-triangular Borel in
$\Gamma ^{\prime }_0$
of the upper-triangular Borel in
![]() $\mathrm {GL}_2(\mathbb {Q}_p)$
. We may assume
$\mathrm {GL}_2(\mathbb {Q}_p)$
. We may assume
![]() $\Gamma ^{\prime }_0\subset K_p$
and denote by
$\Gamma ^{\prime }_0\subset K_p$
and denote by
![]() $V_{\Gamma ^{\prime }_0}$
the preimage of
$V_{\Gamma ^{\prime }_0}$
the preimage of
![]() $V_{K_p}$
in
$V_{K_p}$
in
 $\mathcal {X}^*_{\Gamma ^{\prime }_0}(\epsilon )_a$
. Then f comes from a section in
$\mathcal {X}^*_{\Gamma ^{\prime }_0}(\epsilon )_a$
. Then f comes from a section in
 $\mathcal {O}_{\mathcal {X}^*_{\Gamma ^{\prime }_0}(\epsilon )_a}(V_{\Gamma ^{\prime }_0})$
. The key point here is that by Corollary III.2.23 of [Reference ScholzeSch15], there exist Tate’s normalised traces from
$\mathcal {O}_{\mathcal {X}^*_{\Gamma ^{\prime }_0}(\epsilon )_a}(V_{\Gamma ^{\prime }_0})$
. The key point here is that by Corollary III.2.23 of [Reference ScholzeSch15], there exist Tate’s normalised traces from
 $\mathcal {O}_{\mathcal {X}^*_{\Gamma ^{\prime }_0}(\epsilon )_a}$
to sections on finite levels. Hence, a standard argument shows that f comes from some finite level by analyticity; cf. the proof of Lemma 3.2.5 or [Reference Berger and ColmezBC16, Théorème 3.2]. Thus, f is fixed by some open subgroup of
$\mathcal {O}_{\mathcal {X}^*_{\Gamma ^{\prime }_0}(\epsilon )_a}$
to sections on finite levels. Hence, a standard argument shows that f comes from some finite level by analyticity; cf. the proof of Lemma 3.2.5 or [Reference Berger and ColmezBC16, Théorème 3.2]. Thus, f is fixed by some open subgroup of
![]() $\mathrm {GL}_2(\mathbb {Q}_p)$
.
$\mathrm {GL}_2(\mathbb {Q}_p)$
.
4.3.5. Now we can give an explicit description of
 $\mathcal {O}^{\mathrm {la}}_{K^p}(U)$
, following Subsection 4.2, 5.2 of [Reference Berger and ColmezBC16]. The basic idea is to find ‘power series expansions along
$\mathcal {O}^{\mathrm {la}}_{K^p}(U)$
, following Subsection 4.2, 5.2 of [Reference Berger and ColmezBC16]. The basic idea is to find ‘power series expansions along
![]() $e_1,e_2,t$
’. Note that the actions of
$e_1,e_2,t$
’. Note that the actions of
![]() $K_p$
on these elements are analytic. Our setup is as follows. Fix a compact open subgroup
$K_p$
on these elements are analytic. Our setup is as follows. Fix a compact open subgroup
![]() $G_0$
of
$G_0$
of
![]() $K_p$
equipped with an integer-valued, saturated p-valuation. For example, one can take
$K_p$
equipped with an integer-valued, saturated p-valuation. For example, one can take
![]() $1+p^m M_2(\mathbb {Z}_p)$
for sufficiently large m. Then we have
$1+p^m M_2(\mathbb {Z}_p)$
for sufficiently large m. Then we have
 $G_n=G_0^{p^n}$
as in Section 2.1.1. Let
$G_n=G_0^{p^n}$
as in Section 2.1.1. Let
![]() $V_{G_n}\subset \mathcal {X}_{K^pG_n}$
be the preimage of
$V_{G_n}\subset \mathcal {X}_{K^pG_n}$
be the preimage of
![]() $V_{K_p}$
. By our choice of U (cf. Theorem 4.1.7), the direct limit
$V_{K_p}$
. By our choice of U (cf. Theorem 4.1.7), the direct limit
 $\varinjlim _n H^0(V_{G_n},\mathcal {O}_{\mathcal {X}_{K^pG_n}})\to H^0(V_{\infty },\mathcal {O}_{\mathcal {X}_{K^p}})$
has dense image. Hence, for any
$\varinjlim _n H^0(V_{G_n},\mathcal {O}_{\mathcal {X}_{K^pG_n}})\to H^0(V_{\infty },\mathcal {O}_{\mathcal {X}_{K^p}})$
has dense image. Hence, for any
![]() $n\geq 0$
, we can find (cf. Section 2.1.4 and Lemma 2.1.5)
$n\geq 0$
, we can find (cf. Section 2.1.4 and Lemma 2.1.5)
-
• an integer
 $r(n)>r(n-1)>0$
;
$r(n)>r(n-1)>0$
; -
•
 $x_n\in H^0(V_{G_{r(n)}},\mathcal {O}_{\mathcal {X}_{K^pG_{r(n)}}})$
such that
$x_n\in H^0(V_{G_{r(n)}},\mathcal {O}_{\mathcal {X}_{K^pG_{r(n)}}})$
such that
 $\|x-x_n\|_{G_{r(n)}}=\|x-x_n\|\leq p^{-n}$
in
$\|x-x_n\|_{G_{r(n)}}=\|x-x_n\|\leq p^{-n}$
in
 $H^0(V_{\infty },\mathcal {O}_{\mathcal {X}_{K^p}})$
.
$H^0(V_{\infty },\mathcal {O}_{\mathcal {X}_{K^p}})$
.
As in Section 4.3.1, we can find (after replacing
![]() $r(n)$
by a larger number if necessary)
$r(n)$
by a larger number if necessary)
-
•
 $t_n\in \mathcal {O}_{\mathcal {X}_{K^pG_{r(n)}}}(\mathcal {X}_{K^pG_{r(n)}})$
such that
$t_n\in \mathcal {O}_{\mathcal {X}_{K^pG_{r(n)}}}(\mathcal {X}_{K^pG_{r(n)}})$
such that
 $\|t-t_n\|_{G_{r(n)}}=\|t-t_n\|\leq p^{-n}$
in
$\|t-t_n\|_{G_{r(n)}}=\|t-t_n\|\leq p^{-n}$
in
 $H^0(\mathcal {X}_{K^p},\mathcal {O}_{\mathcal {X}_{K^p}})$
.
$H^0(\mathcal {X}_{K^p},\mathcal {O}_{\mathcal {X}_{K^p}})$
.
We can define a norm on
![]() $H^0(V_{\infty },\omega _{K^p})$
by identifying it with
$H^0(V_{\infty },\omega _{K^p})$
by identifying it with
![]() $H^0(V_{\infty },\mathcal {O}_{\mathcal {X}_{K^p}})$
using
$H^0(V_{\infty },\mathcal {O}_{\mathcal {X}_{K^p}})$
using
![]() $e_1$
. It is easy to see
$e_1$
. It is easy to see
 $\varinjlim _n H^0(V_{G_n},\omega )\to H^0(V_{\infty },\omega _{K^p})$
also has dense image. Here, by abuse of notation,
$\varinjlim _n H^0(V_{G_n},\omega )\to H^0(V_{\infty },\omega _{K^p})$
also has dense image. Here, by abuse of notation,
![]() $\omega $
denotes ‘the
$\omega $
denotes ‘the
![]() $\omega $
on
$\omega $
on
![]() $\mathcal {X}_{K^pK_p}$
’. Hence, we can also find (after enlarging
$\mathcal {X}_{K^pK_p}$
’. Hence, we can also find (after enlarging
![]() $r(n)$
if necessary)
$r(n)$
if necessary)
-
•
 $e_{1,n}\in H^0(V_{G_{r(n)}},\omega )$
such that
$e_{1,n}\in H^0(V_{G_{r(n)}},\omega )$
such that
 $\|e_1-e_{1,n}\|_{G_{r(n)}}=\|e_1-e_{1,n}\|\leq p^{-n}$
in
$\|e_1-e_{1,n}\|_{G_{r(n)}}=\|e_1-e_{1,n}\|\leq p^{-n}$
in
 $H^0(V_{\infty },\omega _{K^p})$
.
$H^0(V_{\infty },\omega _{K^p})$
.
Note that
![]() $e_{1,n}$
is also a basis of
$e_{1,n}$
is also a basis of
![]() $H^0(V_{\infty },\omega _{K^p})$
, if
$H^0(V_{\infty },\omega _{K^p})$
, if
![]() $n>0$
.
$n>0$
.
As before, we denote by
 $\mathfrak {b}=\{\begin {pmatrix} * & * \\ 0 & * \end {pmatrix}\}\subset \mathfrak {gl}_2(\mathbb {Q}_p)$
the Lie algebra of the upper-triangular Borel subgroup and by
$\mathfrak {b}=\{\begin {pmatrix} * & * \\ 0 & * \end {pmatrix}\}\subset \mathfrak {gl}_2(\mathbb {Q}_p)$
the Lie algebra of the upper-triangular Borel subgroup and by
![]() $\mathfrak {n}$
its nilpotent subalgebra. Let
$\mathfrak {n}$
its nilpotent subalgebra. Let
 $$ \begin{align*}u^+=\begin{pmatrix} 0 & 1 \\ 0 & 0 \end{pmatrix},\,h=\begin{pmatrix} 1 & 0 \\ 0 & -1 \end{pmatrix},\,z=\begin{pmatrix} 1 & 0 \\ 0 & 1 \end{pmatrix}\end{align*} $$
$$ \begin{align*}u^+=\begin{pmatrix} 0 & 1 \\ 0 & 0 \end{pmatrix},\,h=\begin{pmatrix} 1 & 0 \\ 0 & -1 \end{pmatrix},\,z=\begin{pmatrix} 1 & 0 \\ 0 & 1 \end{pmatrix}\end{align*} $$
be a basis of
![]() $\mathfrak {b}$
. Then
$\mathfrak {b}$
. Then
 $u^+\cdot x= u^+\cdot \frac {e_2}{e_1}=1$
and
$u^+\cdot x= u^+\cdot \frac {e_2}{e_1}=1$
and
![]() $h\cdot e_1=e_1$
and
$h\cdot e_1=e_1$
and
![]() $z\cdot t=2t$
.
$z\cdot t=2t$
.
4.3.6 Expansion along
 $\mathfrak {n}$
$\mathfrak {n}$
Fix
 $f\in \mathcal {O}^{\mathrm {la}}_{K^p}(U)$
. We are going to write f as a power series. Suppose
$f\in \mathcal {O}^{\mathrm {la}}_{K^p}(U)$
. We are going to write f as a power series. Suppose
![]() $f\in \mathcal {O}_{K^p}(U)^{G_m-\mathrm {an}}$
. By Lemma 2.1.8, there is a constant
$f\in \mathcal {O}_{K^p}(U)^{G_m-\mathrm {an}}$
. By Lemma 2.1.8, there is a constant
![]() $C_1$
such that
$C_1$
such that
![]() $\|u^+ \cdot s\|_{G_m}\leq p^{C_1}\|s\|_{G_m}$
, for any
$\|u^+ \cdot s\|_{G_m}\leq p^{C_1}\|s\|_{G_m}$
, for any
![]() $s\in \mathcal {O}_{K^p}(U)^{G_m-\mathrm {an}}$
. Choose
$s\in \mathcal {O}_{K^p}(U)^{G_m-\mathrm {an}}$
. Choose
![]() $n''\geq \max (C_1+1/(p-1)+1,m)$
. Then
$n''\geq \max (C_1+1/(p-1)+1,m)$
. Then
 $$ \begin{align*}\|(x-x_{n''})^l\frac{(u^+)^l\cdot s}{l!}\|_{G_{r(n'')}}\leq p^{-l}\|s\|_{G_{r(m)}}\end{align*} $$
$$ \begin{align*}\|(x-x_{n''})^l\frac{(u^+)^l\cdot s}{l!}\|_{G_{r(n'')}}\leq p^{-l}\|s\|_{G_{r(m)}}\end{align*} $$
for any
![]() $l\geq 0$
and
$l\geq 0$
and
![]() $s\in \mathcal {O}_{K^p}(U)^{G_m-\mathrm {an}}$
by a simple calculation. Hence,
$s\in \mathcal {O}_{K^p}(U)^{G_m-\mathrm {an}}$
by a simple calculation. Hence,
 $$ \begin{align*}D_x(s):=\sum_{l= 0}^{+\infty}(-1)^l (x-x_{n''})^l\frac{(u^+)^{l}\cdot s}{l!}\end{align*} $$
$$ \begin{align*}D_x(s):=\sum_{l= 0}^{+\infty}(-1)^l (x-x_{n''})^l\frac{(u^+)^{l}\cdot s}{l!}\end{align*} $$
defines a bounded map
![]() $D_x:\mathcal {O}_{K^p}(U)^{G_{m}-\mathrm {an}}\to \mathcal {O}_{K^p}(U)^{G_{r(n'')}-\mathrm {an}}$
with norm
$D_x:\mathcal {O}_{K^p}(U)^{G_{m}-\mathrm {an}}\to \mathcal {O}_{K^p}(U)^{G_{r(n'')}-\mathrm {an}}$
with norm
![]() $\leq 1$
. Moreover, since
$\leq 1$
. Moreover, since
![]() $u^+\cdot (x-x_{n''})=1$
, one checks easily
$u^+\cdot (x-x_{n''})=1$
, one checks easily
![]() $u^+\circ D_x=0$
. Let
$u^+\circ D_x=0$
. Let
 $$ \begin{align*}a_i:=D_x\left(\frac{(u^+)^i\cdot f}{i!}\right)=\sum_{l= 0}^{+\infty}(-1)^l (x-x_{n''})^l\frac{(u^+)^{l+i}\cdot f}{l!i!}\in \mathcal{O}_{K^p}(U)^{G_{r(n'')}-\mathrm{an}}.\end{align*} $$
$$ \begin{align*}a_i:=D_x\left(\frac{(u^+)^i\cdot f}{i!}\right)=\sum_{l= 0}^{+\infty}(-1)^l (x-x_{n''})^l\frac{(u^+)^{l+i}\cdot f}{l!i!}\in \mathcal{O}_{K^p}(U)^{G_{r(n'')}-\mathrm{an}}.\end{align*} $$
Its norm
 $\|a_i\|_{G_{r(n'')}}\leq \|\frac {(u^+)^i\cdot f}{i!}\|_{G_{m}}\leq p^{(n''-1)i}\|f\|_{G_{m}}$
. Thus,
$\|a_i\|_{G_{r(n'')}}\leq \|\frac {(u^+)^i\cdot f}{i!}\|_{G_{m}}\leq p^{(n''-1)i}\|f\|_{G_{m}}$
. Thus,
![]() $\sum _{i\geq 0}a_i(x-x_{n''})^i$
is convergent in
$\sum _{i\geq 0}a_i(x-x_{n''})^i$
is convergent in
![]() $\mathcal {O}_{K^p}(U)^{G_{r(n'')}-\mathrm {an}}$
and a direct computation shows (using
$\mathcal {O}_{K^p}(U)^{G_{r(n'')}-\mathrm {an}}$
and a direct computation shows (using
 $\sum _{i=0}^l (-1)^i \frac {1}{i!(l-i)!}=0$
if
$\sum _{i=0}^l (-1)^i \frac {1}{i!(l-i)!}=0$
if
![]() $l\geq 1$
) that in fact
$l\geq 1$
) that in fact
 $$ \begin{align*}f=\sum_{i= 0}^{+\infty}a_i(x-x_{n''})^i\end{align*} $$
$$ \begin{align*}f=\sum_{i= 0}^{+\infty}a_i(x-x_{n''})^i\end{align*} $$
in
![]() $\mathcal {O}_{K^p}(U)^{G_{r(n'')}-\mathrm {an}}$
. Note that
$\mathcal {O}_{K^p}(U)^{G_{r(n'')}-\mathrm {an}}$
. Note that
![]() $u^+\cdot a_i=0$
for any i by our construction.
$u^+\cdot a_i=0$
for any i by our construction.
4.3.7 Expansion along h
Next we write
![]() $a_i$
as a power series. Note that
$a_i$
as a power series. Note that
 $\|e_1-e_{1,l}\|_{G_{r(l)}}=\|e_1-e_{1,l}\|\leq p^{-l}$
. Hence,
$\|e_1-e_{1,l}\|_{G_{r(l)}}=\|e_1-e_{1,l}\|\leq p^{-l}$
. Hence,
![]() $\|e_{1,l}\|_{G_{r(l)}}=\|e_1\|_{G_{r(l)}}=1$
. For
$\|e_{1,l}\|_{G_{r(l)}}=\|e_1\|_{G_{r(l)}}=1$
. For
![]() $j\geq 1$
, the series
$j\geq 1$
, the series
 $$ \begin{align*}\log(\frac{e_1}{e_{1,l}})=\log\left(1+\frac{e_1-e_{1,l}}{e_{1,l}}\right):=-\sum_{j=1}^{+\infty} (-1)^{j}\frac{1}{j}(\frac{e_1}{e_{1,l}}-1)^j\end{align*} $$
$$ \begin{align*}\log(\frac{e_1}{e_{1,l}})=\log\left(1+\frac{e_1-e_{1,l}}{e_{1,l}}\right):=-\sum_{j=1}^{+\infty} (-1)^{j}\frac{1}{j}(\frac{e_1}{e_{1,l}}-1)^j\end{align*} $$
converges in
![]() $\mathcal {O}_{K^p}(U)^{G_{r(l)}-\mathrm {an}}$
and has norm
$\mathcal {O}_{K^p}(U)^{G_{r(l)}-\mathrm {an}}$
and has norm
 $\|\log (\frac {e_1}{e_{1,l}})\|_{G_{r(l)}}\leq p^{-l}$
. Moreover, since
$\|\log (\frac {e_1}{e_{1,l}})\|_{G_{r(l)}}\leq p^{-l}$
. Moreover, since
![]() $u^+\cdot e_1=0,h\cdot e_1=e_1$
, it follows that
$u^+\cdot e_1=0,h\cdot e_1=e_1$
, it follows that
 $u^+\cdot \log (\frac {e_1}{e_{1,l}})=0, h\cdot \log (\frac {e_1}{e_{1,l}})=1$
. Hence, we can repeat the previous process with
$u^+\cdot \log (\frac {e_1}{e_{1,l}})=0, h\cdot \log (\frac {e_1}{e_{1,l}})=1$
. Hence, we can repeat the previous process with
![]() $u^+,x-x_{n''}$
replaced by
$u^+,x-x_{n''}$
replaced by
 $h, \log (\frac {e_1}{e_{1,n'}})$
: by Lemma 2.1.8, there is a constant
$h, \log (\frac {e_1}{e_{1,n'}})$
: by Lemma 2.1.8, there is a constant
![]() $C_2$
such that
$C_2$
such that
 $\|h \cdot s\|_{G_{r(n'')}}\leq p^{C_2}\|s\|_{G_{r(n'')}},s\in \mathcal {O}_{K^p}(U)^{G_{r(n'')}-\mathrm {an}}$
. Choose
$\|h \cdot s\|_{G_{r(n'')}}\leq p^{C_2}\|s\|_{G_{r(n'')}},s\in \mathcal {O}_{K^p}(U)^{G_{r(n'')}-\mathrm {an}}$
. Choose
![]() $n'\geq \max \left (C_2+1/(p-1)+1,r(n'')\right )$
. Then we have
$n'\geq \max \left (C_2+1/(p-1)+1,r(n'')\right )$
. Then we have
 $$ \begin{align*}a_i=\sum_{j=0}^{+\infty}b_{i,j}\left(\log(\frac{e_1}{e_{1,n'}})\right)^j\end{align*} $$
$$ \begin{align*}a_i=\sum_{j=0}^{+\infty}b_{i,j}\left(\log(\frac{e_1}{e_{1,n'}})\right)^j\end{align*} $$
in
![]() $\mathcal {O}_{K^p}(U)^{G_{r(n')}-\mathrm {an}}$
, where
$\mathcal {O}_{K^p}(U)^{G_{r(n')}-\mathrm {an}}$
, where
 $$ \begin{align*}b_{i,j}=\sum_{l= 0}^{+\infty}(-1)^l \left(\log(\frac{e_1}{e_{1,n'}})\right)^l\frac{h^{l+j}\cdot a_i}{l!j!}\end{align*} $$
$$ \begin{align*}b_{i,j}=\sum_{l= 0}^{+\infty}(-1)^l \left(\log(\frac{e_1}{e_{1,n'}})\right)^l\frac{h^{l+j}\cdot a_i}{l!j!}\end{align*} $$
is convergent in
![]() $\mathcal {O}_{K^p}(U)^{G_{r(n')}-\mathrm {an}}$
and has norm
$\mathcal {O}_{K^p}(U)^{G_{r(n')}-\mathrm {an}}$
and has norm
 $\|b_{i,j}\|_{G_{r(n')}}\leq p^{(n'-1)j+(n''-1)i}\|f\|_{G_{m}}$
. Also, since
$\|b_{i,j}\|_{G_{r(n')}}\leq p^{(n'-1)j+(n''-1)i}\|f\|_{G_{m}}$
. Also, since
![]() $[h,u^+]=2u^+$
and
$[h,u^+]=2u^+$
and
![]() $u^+\cdot a_i=0$
, we have
$u^+\cdot a_i=0$
, we have
4.3.8 Expansion along z
Finally, we can expand
![]() $b_{i,j}$
using z. This is almost the same as in Section 4.3.7. Note that t is invertible with norm
$b_{i,j}$
using z. This is almost the same as in Section 4.3.7. Note that t is invertible with norm
![]() $1$
; hence,
$1$
; hence,
![]() $t_l$
is also invertible. Thus,
$t_l$
is also invertible. Thus,
 $\log (\frac {t}{t_l})$
converges in
$\log (\frac {t}{t_l})$
converges in
![]() $\mathcal {O}_{K^p}(U)^{G_{r(l)}-\mathrm {an}}$
with norm
$\mathcal {O}_{K^p}(U)^{G_{r(l)}-\mathrm {an}}$
with norm
![]() $\leq p^{-l}$
. It satisfies
$\leq p^{-l}$
. It satisfies
 $u^+\cdot \log (\frac {t}{t_l})=h\cdot \log (\frac {t}{t_l})=0$
and
$u^+\cdot \log (\frac {t}{t_l})=h\cdot \log (\frac {t}{t_l})=0$
and
 $z\cdot \log (\frac {t}{t_l})=2$
. Then for any sufficiently large integer
$z\cdot \log (\frac {t}{t_l})=2$
. Then for any sufficiently large integer
![]() $n\geq r(n')$
, we have
$n\geq r(n')$
, we have
 $$ \begin{align*}b_{i,j}=\sum_{k=0}^{+\infty}c_{i,j,k}\left(\log(\frac{t}{t_{n}})\right)^k\end{align*} $$
$$ \begin{align*}b_{i,j}=\sum_{k=0}^{+\infty}c_{i,j,k}\left(\log(\frac{t}{t_{n}})\right)^k\end{align*} $$
converges in
![]() $\mathcal {O}_{K^p}(U)^{G_{r(n)}-\mathrm {an}}$
, where
$\mathcal {O}_{K^p}(U)^{G_{r(n)}-\mathrm {an}}$
, where
 $$ \begin{align*}c_{i,j,k}=\frac{1}{2^k}\sum_{l= 0}^{+\infty}(-1)^l (\frac{1}{2}\log(\frac{t}{t_{n}}))^l\frac{z^{l+k}\cdot b_{i,j}}{l!k!}\end{align*} $$
$$ \begin{align*}c_{i,j,k}=\frac{1}{2^k}\sum_{l= 0}^{+\infty}(-1)^l (\frac{1}{2}\log(\frac{t}{t_{n}}))^l\frac{z^{l+k}\cdot b_{i,j}}{l!k!}\end{align*} $$
and has norm
 $$ \begin{align*}\|c_{i,j,k}\|_{G_{r(n)}}\leq p^{(n-1)k+(n'-1)j+(n''-1)i}\|f\|_{G_{m}}.\end{align*} $$
$$ \begin{align*}\|c_{i,j,k}\|_{G_{r(n)}}\leq p^{(n-1)k+(n'-1)j+(n''-1)i}\|f\|_{G_{m}}.\end{align*} $$
Since z commutes with
![]() $u^+,h$
, it follows that
$u^+,h$
, it follows that
that is,
![]() $c_{i,j,k}$
is annihilated by
$c_{i,j,k}$
is annihilated by
![]() $\mathfrak {b}$
. By Lemma 4.3.3, this implies
$\mathfrak {b}$
. By Lemma 4.3.3, this implies
![]() $c_{i,j,k}$
is fixed
$c_{i,j,k}$
is fixed
![]() $G_{r(n)}$
. Therefore,
$G_{r(n)}$
. Therefore,
 $$ \begin{align*}c_{i,j,k}\in H^0(V_{G_{r(n)}},\mathcal{O}_{\mathcal{X}_{K^pG_{r(n)}}}).\end{align*} $$
$$ \begin{align*}c_{i,j,k}\in H^0(V_{G_{r(n)}},\mathcal{O}_{\mathcal{X}_{K^pG_{r(n)}}}).\end{align*} $$
In particular,
![]() $\|c_{i,j,k}\|_{G_{r(n)}}=\|c_{i,j,k}\|$
.
$\|c_{i,j,k}\|_{G_{r(n)}}=\|c_{i,j,k}\|$
.
Theorem 4.3.9. Keep the notation in Section 4.3.5. For any
 $f\in \mathcal {O}^{\mathrm {la}}_{K^p}(U)$
which is
$f\in \mathcal {O}^{\mathrm {la}}_{K^p}(U)$
which is
![]() $G_m$
-analytic, there exist an integer
$G_m$
-analytic, there exist an integer
![]() $N=N(f)$
, bounded above by some constant only depending on m, and unique elements
$N=N(f)$
, bounded above by some constant only depending on m, and unique elements
 $c^{(n)}_{i,j,k}(f)\in H^0(V_{G_{r(n)}},\mathcal {O}_{\mathcal {X}_{K^pG_{r(n)}}})$
for
$c^{(n)}_{i,j,k}(f)\in H^0(V_{G_{r(n)}},\mathcal {O}_{\mathcal {X}_{K^pG_{r(n)}}})$
for
![]() $i,j,k\geq 0,n\geq N$
with norm
$i,j,k\geq 0,n\geq N$
with norm
 $\|c^{(n)}_{i,j,k}(f)\|\leq p^{(n-1)(i+j+k)}\|f\|_{G_m}$
for which
$\|c^{(n)}_{i,j,k}(f)\|\leq p^{(n-1)(i+j+k)}\|f\|_{G_m}$
for which
 $$ \begin{align*}f=\sum_{i,j,k\geq0}c^{(n)}_{i,j,k}(f)(x-x_n)^i\left(\log(\frac{e_1}{e_{1,n}})\right)^j\left(\log(\frac{t}{t_{n}})\right)^k\end{align*} $$
$$ \begin{align*}f=\sum_{i,j,k\geq0}c^{(n)}_{i,j,k}(f)(x-x_n)^i\left(\log(\frac{e_1}{e_{1,n}})\right)^j\left(\log(\frac{t}{t_{n}})\right)^k\end{align*} $$
holds in
![]() $\mathcal {O}_{K^p}(U)^{G_{r(n)}-\mathrm {an}}$
. Conversely, given
$\mathcal {O}_{K^p}(U)^{G_{r(n)}-\mathrm {an}}$
. Conversely, given
![]() $n>0$
and
$n>0$
and
 $\mathrm {c}_{i,j,k}\in H^0(V_{G_{r(n)}},\mathcal {O}_{\mathcal {X}_{K^pG_{r(n)}}}),i,j,k\geq 0$
such that
$\mathrm {c}_{i,j,k}\in H^0(V_{G_{r(n)}},\mathcal {O}_{\mathcal {X}_{K^pG_{r(n)}}}),i,j,k\geq 0$
such that
 $\|\mathrm {c}_{i,j,k}\|\leq p^{(n-1)(i+j+k)}C'$
holds for a uniform constant
$\|\mathrm {c}_{i,j,k}\|\leq p^{(n-1)(i+j+k)}C'$
holds for a uniform constant
![]() $C'$
,
$C'$
,
 $$ \begin{align*}f':=\sum_{i,j,k\geq0}\mathrm{c}_{i,j,k}(x-x_n)^i\left(\log(\frac{e_1}{e_{1,n}})\right)^j\left(\log(\frac{t}{t_{n}})\right)^k\end{align*} $$
$$ \begin{align*}f':=\sum_{i,j,k\geq0}\mathrm{c}_{i,j,k}(x-x_n)^i\left(\log(\frac{e_1}{e_{1,n}})\right)^j\left(\log(\frac{t}{t_{n}})\right)^k\end{align*} $$
defines an element in
![]() $\mathcal {O}_{K^p}(U)^{G_{r(n)}-\mathrm {an}}$
. We can take
$\mathcal {O}_{K^p}(U)^{G_{r(n)}-\mathrm {an}}$
. We can take
![]() $N(f')=n$
; hence,
$N(f')=n$
; hence,
 $c^{(n)}_{i,j,k}(f')=\mathrm {c}_{i,j,k}$
.
$c^{(n)}_{i,j,k}(f')=\mathrm {c}_{i,j,k}$
.
Proof. We have written
 $f=\sum _{i,j,k\geq 0} c_{i,j,k} (x-x_{n''})^i\left (\log (\frac {e_1}{e_{1,n'}})\right )^j\left (\log (\frac {t}{t_{n}})\right )^k$
with
$f=\sum _{i,j,k\geq 0} c_{i,j,k} (x-x_{n''})^i\left (\log (\frac {e_1}{e_{1,n'}})\right )^j\left (\log (\frac {t}{t_{n}})\right )^k$
with
 $\|c_{i,j,k}\|_{G_{r(n)}}\leq p^{(n-1)k+(n'-1)j+(n''-1)i}\|f\|_{G_m}$
. The rest is to change the coordinates from
$\|c_{i,j,k}\|_{G_{r(n)}}\leq p^{(n-1)k+(n'-1)j+(n''-1)i}\|f\|_{G_m}$
. The rest is to change the coordinates from
![]() $x-x_{n''}$
to
$x-x_{n''}$
to
![]() $x-x_{n}$
and from
$x-x_{n}$
and from
 $\log (\frac {e_1}{e_{1,n'}})$
to
$\log (\frac {e_1}{e_{1,n'}})$
to
 $\log (\frac {e_1}{e_{1,n}})$
. By our construction, both
$\log (\frac {e_1}{e_{1,n}})$
. By our construction, both
 $(x-x_n)-(x-x_{n''}), \log (\frac {e_1}{e_{1,n}})-\log (\frac {e_1}{e_{1,n'}})\in H^0(V_{G_{r(n)}},\mathcal {O}_{\mathcal {X}_{K^pG_{r(n)}}})$
and
$(x-x_n)-(x-x_{n''}), \log (\frac {e_1}{e_{1,n}})-\log (\frac {e_1}{e_{1,n'}})\in H^0(V_{G_{r(n)}},\mathcal {O}_{\mathcal {X}_{K^pG_{r(n)}}})$
and
 $$ \begin{align*}\|(x-x_n)-(x-x_{n''})\|\leq p^{-n''},\, \|\log(\frac{e_1}{e_{1,n}})-\log(\frac{e_1}{e_{1,n'}})\|\leq p^{-n'}.\end{align*} $$
$$ \begin{align*}\|(x-x_n)-(x-x_{n''})\|\leq p^{-n''},\, \|\log(\frac{e_1}{e_{1,n}})-\log(\frac{e_1}{e_{1,n'}})\|\leq p^{-n'}.\end{align*} $$
Hence, if we write
 $$ \begin{align*}\sum_{i,j,k\geq 0} c_{i,j,k} (x-x_{n''})^i\left(\log(\frac{e_1}{e_{1,n'}})\right)^j\left(\log(\frac{t}{t_{n}})\right)^k=\sum_{i,j,k\geq 0} c^{(n)}_{i,j,k}(f) (x-x_{n})^i\left(\log(\frac{e_1}{e_{1,n}})\right)^j\left(\log(\frac{t}{t_{n}})\right)^k\end{align*} $$
$$ \begin{align*}\sum_{i,j,k\geq 0} c_{i,j,k} (x-x_{n''})^i\left(\log(\frac{e_1}{e_{1,n'}})\right)^j\left(\log(\frac{t}{t_{n}})\right)^k=\sum_{i,j,k\geq 0} c^{(n)}_{i,j,k}(f) (x-x_{n})^i\left(\log(\frac{e_1}{e_{1,n}})\right)^j\left(\log(\frac{t}{t_{n}})\right)^k\end{align*} $$
for some
 $c^{(n)}_{i,j,k}(f)\in H^0(V_{G_{r(n)}},\mathcal {O}_{\mathcal {X}_{K^pG_{r(n)}}})$
, a simple computation gives
$c^{(n)}_{i,j,k}(f)\in H^0(V_{G_{r(n)}},\mathcal {O}_{\mathcal {X}_{K^pG_{r(n)}}})$
, a simple computation gives
 $$ \begin{align*}\|c^{(n)}_{i,j,k}(f)\|_{G_{r(n)}}\leq p^{(n-1)k+(n'-1)j+(n''-1)i}\|f\|_{G_m}\leq p^{(n-1)(i+j+k)}\|f\|_{G_m}\end{align*} $$
$$ \begin{align*}\|c^{(n)}_{i,j,k}(f)\|_{G_{r(n)}}\leq p^{(n-1)k+(n'-1)j+(n''-1)i}\|f\|_{G_m}\leq p^{(n-1)(i+j+k)}\|f\|_{G_m}\end{align*} $$
as
![]() $n\geq n'\geq n''$
. For the uniqueness and the converse part, using the bounds on
$n\geq n'\geq n''$
. For the uniqueness and the converse part, using the bounds on
 $c^{(n)}_{i,j,k}(f)$
, we can repeat our construction (with
$c^{(n)}_{i,j,k}(f)$
, we can repeat our construction (with
![]() $n''=n'=n$
this time) and recover
$n''=n'=n$
this time) and recover
 $c^{(n)}_{i,j,k}(f)$
from f. We omit the details here.
$c^{(n)}_{i,j,k}(f)$
from f. We omit the details here.
Definition 4.3.10. Keep the notation in Section 4.3.5. For any
![]() $n>0$
, we define
$n>0$
, we define
 $\mathcal {O}^{n}(U)\{x,e_1,t\}\subset \mathcal {O}^{\mathrm {la}}_{K^p}(U)$
to be the subset of f, which can be written as
$\mathcal {O}^{n}(U)\{x,e_1,t\}\subset \mathcal {O}^{\mathrm {la}}_{K^p}(U)$
to be the subset of f, which can be written as
 $$ \begin{align*}f=\sum_{i,j,k\geq0}{c}_{i,j,k}(x-x_n)^i\left(\log(\frac{e_1}{e_{1,n}})\right)^j\left(\log(\frac{t}{t_{n}})\right)^k\end{align*} $$
$$ \begin{align*}f=\sum_{i,j,k\geq0}{c}_{i,j,k}(x-x_n)^i\left(\log(\frac{e_1}{e_{1,n}})\right)^j\left(\log(\frac{t}{t_{n}})\right)^k\end{align*} $$
with
 ${c}_{i,j,k}\in H^0(V_{G_{r(n)}},\mathcal {O}_{\mathcal {X}_{K^pG_{r(n)}}}),i,j,k\geq 0$
such that
${c}_{i,j,k}\in H^0(V_{G_{r(n)}},\mathcal {O}_{\mathcal {X}_{K^pG_{r(n)}}}),i,j,k\geq 0$
such that
 $\|{c}_{i,j,k}\|\leq p^{(n-1)(i+j+k)}C'$
holds for some uniform constant
$\|{c}_{i,j,k}\|\leq p^{(n-1)(i+j+k)}C'$
holds for some uniform constant
![]() $C'$
. It is a Banach algebra over C with norm
$C'$
. It is a Banach algebra over C with norm
 $$ \begin{align*}\|f\|_n:=\sup_{i,j,k\geq 0}\|c^{(n)}_{i,j,k}(f)p^{(n-1)(i+j+k)}\|.\end{align*} $$
$$ \begin{align*}\|f\|_n:=\sup_{i,j,k\geq 0}\|c^{(n)}_{i,j,k}(f)p^{(n-1)(i+j+k)}\|.\end{align*} $$
Let
![]() $\mathcal {O}^{n}(U)^+\{x,e_1,t\}$
be its open unit ball. By Theorem 4.3.9, sending f to
$\mathcal {O}^{n}(U)^+\{x,e_1,t\}$
be its open unit ball. By Theorem 4.3.9, sending f to
 $c^{(n)}_{i,j,k}(f)p^{(n-1)(i+j+k)}$
induces an isomorphism of topological
$c^{(n)}_{i,j,k}(f)p^{(n-1)(i+j+k)}$
induces an isomorphism of topological
![]() $\mathbb {Z}_p$
-modules
$\mathbb {Z}_p$
-modules
 $$ \begin{align*}\mathcal{O}^{n}(U)^+\{x,e_1,t\}\cong\prod_{i,j,k\geq 0}H^0(V_{G_{r(n)}},\mathcal{O}^+_{\mathcal{X}_{K^pG_{r(n)}}}).\end{align*} $$
$$ \begin{align*}\mathcal{O}^{n}(U)^+\{x,e_1,t\}\cong\prod_{i,j,k\geq 0}H^0(V_{G_{r(n)}},\mathcal{O}^+_{\mathcal{X}_{K^pG_{r(n)}}}).\end{align*} $$
Remark 4.3.11. It is clear from the proof of Theorem 4.3.9 that
![]() $\mathcal {O}^{n}(U)\{x,e_1,t\}$
is independent of the choice of
$\mathcal {O}^{n}(U)\{x,e_1,t\}$
is independent of the choice of
![]() $x_n,e_{1,n},t_n$
.
$x_n,e_{1,n},t_n$
.
Remark 4.3.12. For any
![]() $m>0$
, by Theorem 4.3.9, we can find n such that there are continuous embeddings (of Banach spaces)
$m>0$
, by Theorem 4.3.9, we can find n such that there are continuous embeddings (of Banach spaces)
Hence,
 $\varinjlim _n \mathcal {O}_{K^p}(U)^{G_n-\mathrm {an}}\cong \varinjlim _n\mathcal {O}^{n}(U)\{x,e_1,t\}$
as topological spaces. It will be clear later that
$\varinjlim _n \mathcal {O}_{K^p}(U)^{G_n-\mathrm {an}}\cong \varinjlim _n\mathcal {O}^{n}(U)\{x,e_1,t\}$
as topological spaces. It will be clear later that
![]() $\mathcal {O}^{n}(U)\{x,e_1,t\}$
behaves a lot better in applications.
$\mathcal {O}^{n}(U)\{x,e_1,t\}$
behaves a lot better in applications.
4.3.13. Theorem 4.3.9 can be rephrased sheaf-theoretically. Recall some construction in the paragraph above Corollary 3.6.10. We denote by
 $\mathcal {O}^+_{r(n)}$
the pushforward of
$\mathcal {O}^+_{r(n)}$
the pushforward of
 $\mathcal {O}^+_{V_{G_{r(n)}}}$
from
$\mathcal {O}^+_{V_{G_{r(n)}}}$
from
![]() $V_{G_{r(n)}}$
to
$V_{G_{r(n)}}$
to
![]() $V_{K_p}$
, by
$V_{K_p}$
, by
![]() $\widetilde {\mathcal {O}}$
the pushforward of
$\widetilde {\mathcal {O}}$
the pushforward of
![]() $\mathcal {O}_{V_{\infty }}$
from
$\mathcal {O}_{V_{\infty }}$
from
![]() $V_{\infty }$
to
$V_{\infty }$
to
![]() $V_{K_p}$
, by
$V_{K_p}$
, by
![]() $\widetilde {\mathcal {O}}^{n}\subset \widetilde {\mathcal {O}}$
the subsheaf of
$\widetilde {\mathcal {O}}^{n}\subset \widetilde {\mathcal {O}}$
the subsheaf of
![]() $G_n$
-analytic sections and by
$G_n$
-analytic sections and by
 $\widetilde {\mathcal {O}}^{\mathrm {la}}\subset \widetilde {\mathcal {O}}$
the subsheaf of
$\widetilde {\mathcal {O}}^{\mathrm {la}}\subset \widetilde {\mathcal {O}}$
the subsheaf of
![]() $K_p$
-locally analytic sections. For each
$K_p$
-locally analytic sections. For each
![]() $n>0$
, we can define a map
$n>0$
, we can define a map
 $$ \begin{align*}\phi^+_n: \prod_{(i,j,k)\in\mathbb{N}^3} \mathcal{O}^+_{r(n)}\to \widetilde{\mathcal{O}}^{\mathrm{la}}\end{align*} $$
$$ \begin{align*}\phi^+_n: \prod_{(i,j,k)\in\mathbb{N}^3} \mathcal{O}^+_{r(n)}\to \widetilde{\mathcal{O}}^{\mathrm{la}}\end{align*} $$
sending
 $(a_{i,j,k})\in \prod _{i,j,k\geq 0} \mathcal {O}^+_{r(n)}(W)$
to
$(a_{i,j,k})\in \prod _{i,j,k\geq 0} \mathcal {O}^+_{r(n)}(W)$
to
 $$ \begin{align*}\sum_{i,j,k\geq0}p^{-(n-1)(i+j+k)}a_{i,j,k}(x-x_n)^i\left(\log(\frac{e_1}{e_{1,n}})\right)^j\left(\log(\frac{t}{t_{n}})\right)^k\in \widetilde{\mathcal{O}}^{\mathrm{la}}(W),\end{align*} $$
$$ \begin{align*}\sum_{i,j,k\geq0}p^{-(n-1)(i+j+k)}a_{i,j,k}(x-x_n)^i\left(\log(\frac{e_1}{e_{1,n}})\right)^j\left(\log(\frac{t}{t_{n}})\right)^k\in \widetilde{\mathcal{O}}^{\mathrm{la}}(W),\end{align*} $$
for any open set W of
![]() $V_{K_p}$
. Let
$V_{K_p}$
. Let
 $\phi _n:(\prod _{(i,j,k)\in \mathbb {N}^3} \mathcal {O}^+_{r(n)})\otimes _{\mathbb {Z}_p}\mathbb {Q}_p\to \widetilde {\mathcal {O}}^{\mathrm {la}}$
be
$\phi _n:(\prod _{(i,j,k)\in \mathbb {N}^3} \mathcal {O}^+_{r(n)})\otimes _{\mathbb {Z}_p}\mathbb {Q}_p\to \widetilde {\mathcal {O}}^{\mathrm {la}}$
be
![]() $\phi ^+_n\otimes \mathbb {Q}_p$
. Then Theorem 4.3.9 implies that
$\phi ^+_n\otimes \mathbb {Q}_p$
. Then Theorem 4.3.9 implies that
![]() $\phi _n$
is an isomorphism onto its image
$\phi _n$
is an isomorphism onto its image
![]() $\operatorname {\mathrm {im}}(\phi _n)$
and for any
$\operatorname {\mathrm {im}}(\phi _n)$
and for any
![]() $m>0$
, we have
$m>0$
, we have
 $\widetilde {\mathcal {O}}^{m}\subset \operatorname {\mathrm {im}}(\phi _n)\subset \widetilde {\mathcal {O}}^{r(n)}$
for some n. A direct consequence is the following.
$\widetilde {\mathcal {O}}^{m}\subset \operatorname {\mathrm {im}}(\phi _n)\subset \widetilde {\mathcal {O}}^{r(n)}$
for some n. A direct consequence is the following.
Lemma 4.3.14. Let
![]() $\mathfrak {U}$
be a finite cover of
$\mathfrak {U}$
be a finite cover of
![]() $V_{K^p}$
by rational open subsets. We have the following assertions for Čech cohomology with respect to
$V_{K^p}$
by rational open subsets. We have the following assertions for Čech cohomology with respect to
![]() $\mathfrak {U}$
.
$\mathfrak {U}$
.
-
(1)
 $\check {H}^i(\mathfrak {U},\prod _{(i,j,k)\in \mathbb {N}^3}\mathcal {O}^+_{r(n)})\otimes _{\mathbb {Z}_p}\mathbb {Q}_p=0, i\geq 1$
.
$\check {H}^i(\mathfrak {U},\prod _{(i,j,k)\in \mathbb {N}^3}\mathcal {O}^+_{r(n)})\otimes _{\mathbb {Z}_p}\mathbb {Q}_p=0, i\geq 1$
. -
(2) The direct system
 $\{\check {H}^i(\mathfrak {U},\widetilde {\mathcal {O}}^{n})\}_n$
is essentially zero for any
$\{\check {H}^i(\mathfrak {U},\widetilde {\mathcal {O}}^{n})\}_n$
is essentially zero for any
 $i\geq 1$
.
$i\geq 1$
.
Proof. Let
 $C^{\bullet }(\mathfrak {U},\mathcal {O}^+_{r(n)})$
be the Čech complex for
$C^{\bullet }(\mathfrak {U},\mathcal {O}^+_{r(n)})$
be the Čech complex for
 $\mathcal {O}^+_{r(n)}$
with respect to
$\mathcal {O}^+_{r(n)}$
with respect to
![]() $\mathfrak {U}$
. Note that if we denote by
$\mathfrak {U}$
. Note that if we denote by
![]() $\mathfrak {U'}$
the pullback of
$\mathfrak {U'}$
the pullback of
![]() $\mathfrak {U}$
to
$\mathfrak {U}$
to
![]() $V_{G_{r(n)}}$
, then
$V_{G_{r(n)}}$
, then
 $C^{\bullet }(\mathfrak {U},\mathcal {O}^+_{r(n)})$
is nothing but the Čech complex for
$C^{\bullet }(\mathfrak {U},\mathcal {O}^+_{r(n)})$
is nothing but the Čech complex for
 $\mathcal {O}^+_{V_{G_{r(n)}}}$
with respect to
$\mathcal {O}^+_{V_{G_{r(n)}}}$
with respect to
![]() $\mathfrak {U}'$
. Hence, Tate’s acyclicity result implies that
$\mathfrak {U}'$
. Hence, Tate’s acyclicity result implies that
 $H^i(C^{\bullet }(\mathfrak {U},\mathcal {O}^+_{r(n)}))\otimes _{\mathbb {Z}_p}\mathbb {Q}_p=0,i\geq 1$
. Therefore,
$H^i(C^{\bullet }(\mathfrak {U},\mathcal {O}^+_{r(n)}))\otimes _{\mathbb {Z}_p}\mathbb {Q}_p=0,i\geq 1$
. Therefore,
 $H^i(C^{\bullet }(\mathfrak {U},\mathcal {O}^+_{r(n)})),i\geq 1$
is annihilated by some
$H^i(C^{\bullet }(\mathfrak {U},\mathcal {O}^+_{r(n)})),i\geq 1$
is annihilated by some
![]() $p^k$
by open mapping theorem. From this, we get
$p^k$
by open mapping theorem. From this, we get
 $H^i(C^{\bullet }(\mathfrak {U},\prod _{(i,j,k)\in \mathbb {N}^3}\mathcal {O}^+_{r(n)}))\otimes _{\mathbb {Z}_p}\mathbb {Q}_p=0,i\geq 1$
, which is exactly what we want.
$H^i(C^{\bullet }(\mathfrak {U},\prod _{(i,j,k)\in \mathbb {N}^3}\mathcal {O}^+_{r(n)}))\otimes _{\mathbb {Z}_p}\mathbb {Q}_p=0,i\geq 1$
, which is exactly what we want.
The second part is a direct consequence of the first one and the inclusion
 $\widetilde {\mathcal {O}}^{m}\subset \operatorname {\mathrm {im}}(\phi _n)\subset \widetilde {\mathcal {O}}^{r(n)}$
.
$\widetilde {\mathcal {O}}^{m}\subset \operatorname {\mathrm {im}}(\phi _n)\subset \widetilde {\mathcal {O}}^{r(n)}$
.
Since
![]() $\mathcal {O}_{K^p}(U)$
is a Banach space representation of
$\mathcal {O}_{K^p}(U)$
is a Banach space representation of
![]() $K_p$
, we can talk about its (strongly)
$K_p$
, we can talk about its (strongly)
![]() $\mathfrak {LA}$
-acyclicity (with respect to
$\mathfrak {LA}$
-acyclicity (with respect to
![]() $K_p$
). See Subsection 2.2 for more details.
$K_p$
). See Subsection 2.2 for more details.
Proposition 4.3.15.
![]() $\mathcal {O}_{K^p}(U)$
is strongly
$\mathcal {O}_{K^p}(U)$
is strongly
![]() $\mathfrak {LA}$
-acyclic for any
$\mathfrak {LA}$
-acyclic for any
![]() $U\in \mathfrak {B}$
.
$U\in \mathfrak {B}$
.
Proof. By Lemma 5.2 and its proof of [Reference ScholzeSch13a], we can find a cover of
![]() $V_{K_p}$
by finitely many rational subsets
$V_{K_p}$
by finitely many rational subsets
![]() $U_1,\cdots ,U_m$
such that each
$U_1,\cdots ,U_m$
such that each
![]() $U_i$
is small in the sense of Section 3.1.1 with
$U_i$
is small in the sense of Section 3.1.1 with
![]() $S=\{\mbox {cusp in }U_i\}$
. By Corollary 4.2.3, the preimage of
$S=\{\mbox {cusp in }U_i\}$
. By Corollary 4.2.3, the preimage of
![]() $U_i$
in
$U_i$
in
![]() $V_{\infty }$
is a locally analytic covering of
$V_{\infty }$
is a locally analytic covering of
![]() $U_i$
. The proposition now follows from Corollary 3.6.10 and Lemma 4.3.14.
$U_i$
. The proposition now follows from Corollary 3.6.10 and Lemma 4.3.14.
4.4 Cohomology of
 $\mathcal {O}^{\mathrm {la}}_{K^p}$
and completed cohomology
$\mathcal {O}^{\mathrm {la}}_{K^p}$
and completed cohomology
In this subsection, we compare the coherent cohomology of
 $\mathcal {O}^{\mathrm {la}}_{K^p}$
(on
$\mathcal {O}^{\mathrm {la}}_{K^p}$
(on
![]() ${\mathscr {F}\!\ell }$
) and
${\mathscr {F}\!\ell }$
) and
![]() $\mathcal {O}_{\mathcal {X}_{K^p}}$
(on
$\mathcal {O}_{\mathcal {X}_{K^p}}$
(on
![]() $\mathcal {X}_{K^p}$
). By Scholze’s result [Reference ScholzeSch15], the latter one is closely related to the completed cohomology of modular curves introduced earlier by Emerton [Reference EmertonEme06b]. The main result is that the cohomology of
$\mathcal {X}_{K^p}$
). By Scholze’s result [Reference ScholzeSch15], the latter one is closely related to the completed cohomology of modular curves introduced earlier by Emerton [Reference EmertonEme06b]. The main result is that the cohomology of
 $\mathcal {O}^{\mathrm {la}}_{K^p}$
is more or less the subspace of locally analytic vectors in completed cohomology.
$\mathcal {O}^{\mathrm {la}}_{K^p}$
is more or less the subspace of locally analytic vectors in completed cohomology.
4.4.1. First recall the construction of completed cohomology. See, for example, [Reference EmertonEme06b, Reference Calegari and EmertonCE12]. For a tame level
 $K^p\subset \mathrm {GL}_2(\mathbb {A}^p_f)$
, let
$K^p\subset \mathrm {GL}_2(\mathbb {A}^p_f)$
, let
 $$ \begin{align*}\tilde{H}^i(K^p,\mathbb{Z}/p^n):=\varinjlim_{K_p\subset\mathrm{GL}_2(\mathbb{Q}_p)}H^i(Y_{K^pK_p}(\mathbb{C}),\mathbb{Z}/p^n).\end{align*} $$
$$ \begin{align*}\tilde{H}^i(K^p,\mathbb{Z}/p^n):=\varinjlim_{K_p\subset\mathrm{GL}_2(\mathbb{Q}_p)}H^i(Y_{K^pK_p}(\mathbb{C}),\mathbb{Z}/p^n).\end{align*} $$
Since
![]() $Y_{K^pK_p}(\mathbb {C})$
is affine,
$Y_{K^pK_p}(\mathbb {C})$
is affine,
![]() $\tilde {H}^i=0,i\geq 2$
. Note that
$\tilde {H}^i=0,i\geq 2$
. Note that
![]() $\tilde {H}^i(K^p,\mathbb {Z}/p^n)$
can also be defined using the compactified modular curves; that is, the natural restriction map
$\tilde {H}^i(K^p,\mathbb {Z}/p^n)$
can also be defined using the compactified modular curves; that is, the natural restriction map
 $$ \begin{align*}\varinjlim_{K_p}H^i(X_{K^pK_p}(\mathbb{C}),\mathbb{Z}/p^n)\to\varinjlim_{K_p}H^i(Y_{K^pK_p}(\mathbb{C}),\mathbb{Z}/p^n)\end{align*} $$
$$ \begin{align*}\varinjlim_{K_p}H^i(X_{K^pK_p}(\mathbb{C}),\mathbb{Z}/p^n)\to\varinjlim_{K_p}H^i(Y_{K^pK_p}(\mathbb{C}),\mathbb{Z}/p^n)\end{align*} $$
is an isomorphism. This is clear when
![]() $i=0$
. When
$i=0$
. When
![]() $i=2$
, both sides are zero. When
$i=2$
, both sides are zero. When
![]() $i=1$
, the cokernel of above comes from cohomology of top degree around each cusp, which vanishes as the ramification degree of each cusp is divisible by arbitrary power of p.
$i=1$
, the cokernel of above comes from cohomology of top degree around each cusp, which vanishes as the ramification degree of each cusp is divisible by arbitrary power of p.
The completed cohomology of tame level
![]() $K^p$
is defined as
$K^p$
is defined as
 $$ \begin{align*}\tilde{H}^i(K^p,\mathbb{Z}_p):=\varprojlim_{n}\tilde{H}^i(K^p,\mathbb{Z}/p^n).\end{align*} $$
$$ \begin{align*}\tilde{H}^i(K^p,\mathbb{Z}_p):=\varprojlim_{n}\tilde{H}^i(K^p,\mathbb{Z}/p^n).\end{align*} $$
It has a natural admissible continuous action of
![]() $\mathrm {GL}_2(\mathbb {Q}_p)$
; that is,
$\mathrm {GL}_2(\mathbb {Q}_p)$
; that is,
![]() $\tilde {H}^i(K^p,\mathbb {Z}_p)/p$
is a smooth admissible representation of
$\tilde {H}^i(K^p,\mathbb {Z}_p)/p$
is a smooth admissible representation of
![]() $\mathrm {GL}_2(\mathbb {Q}_p)$
over
$\mathrm {GL}_2(\mathbb {Q}_p)$
over
![]() $\mathbb {F}_p$
; cf. [Reference Calegari and EmertonCE12, Theorem 1.16]. As a consequence,
$\mathbb {F}_p$
; cf. [Reference Calegari and EmertonCE12, Theorem 1.16]. As a consequence,
![]() $\tilde {H}^i(K^p,\mathbb {Z}_p)$
has bounded p-torsion; that is, p-power torsion classes in
$\tilde {H}^i(K^p,\mathbb {Z}_p)$
has bounded p-torsion; that is, p-power torsion classes in
![]() $\tilde {H}^i(K^p,\mathbb {Z}_p)$
have bounded exponent.
$\tilde {H}^i(K^p,\mathbb {Z}_p)$
have bounded exponent.
The following result (essentially due to Scholze) relates completed cohomology and the cohomology of
 $\mathcal {O}_{\mathcal {X}_{K^p}}^+$
. Here we say a map is Hecke-equivariant if it commutes with Hecke operators away from p.
$\mathcal {O}_{\mathcal {X}_{K^p}}^+$
. Here we say a map is Hecke-equivariant if it commutes with Hecke operators away from p.
Theorem 4.4.2. There is a natural
![]() $\mathrm {GL}_2(\mathbb {Q}_p)$
and Hecke-equivariant isomorphism of almost
$\mathrm {GL}_2(\mathbb {Q}_p)$
and Hecke-equivariant isomorphism of almost
![]() $\mathcal {O}_{C}$
-modules
$\mathcal {O}_{C}$
-modules
 $$ \begin{align*}\tilde{H}^i(K^p,\mathbb{Z}/p^n)\otimes_{\mathbb{Z}_p/p^n}\mathcal{O}_{C}/p^n\cong H^i(\mathcal{X}_{K^p},\mathcal{O}_{\mathcal{X}_{K^p}}^+/p^n),\end{align*} $$
$$ \begin{align*}\tilde{H}^i(K^p,\mathbb{Z}/p^n)\otimes_{\mathbb{Z}_p/p^n}\mathcal{O}_{C}/p^n\cong H^i(\mathcal{X}_{K^p},\mathcal{O}_{\mathcal{X}_{K^p}}^+/p^n),\end{align*} $$
where the right-hand side is computed using the analytic topology of
![]() $\mathcal {X}_{K^p}$
.
$\mathcal {X}_{K^p}$
.
Proof. Basically the same proof of Theorem IV.2.1 of [Reference ScholzeSch15] works here: first we may identify
 $H^i(X_{K^pK_p}(\mathbb {C}),\mathbb {Z}/p^n)$
with
$H^i(X_{K^pK_p}(\mathbb {C}),\mathbb {Z}/p^n)$
with
 $H^i_{\mathrm {\acute {e}t}}(\mathcal {X}_{K^pK_p},\mathbb {Z}/p^n)$
by the comparison theorem; then, using the primitive comparison theorem (Theorem 1.3 of [Reference ScholzeSch13a]) and taking the direct limit over all
$H^i_{\mathrm {\acute {e}t}}(\mathcal {X}_{K^pK_p},\mathbb {Z}/p^n)$
by the comparison theorem; then, using the primitive comparison theorem (Theorem 1.3 of [Reference ScholzeSch13a]) and taking the direct limit over all
![]() $K_p$
, we obtain the desired almost isomorphism.
$K_p$
, we obtain the desired almost isomorphism.
Corollary 4.4.3. There is a natural
![]() $\mathrm {GL}_2(\mathbb {Q}_p)$
and Hecke-equivariant isomorphism of almost
$\mathrm {GL}_2(\mathbb {Q}_p)$
and Hecke-equivariant isomorphism of almost
![]() $\mathcal {O}_{C}$
-modules
$\mathcal {O}_{C}$
-modules
 $$ \begin{align*}\tilde{H}^i(K^p,\mathbb{Z}_p)\widehat\otimes_{\mathbb{Z}_p}\mathcal{O}_{C}\cong H^i(\mathcal{X}_{K^p},\mathcal{O}_{\mathcal{X}_{K^p}}^+).\end{align*} $$
$$ \begin{align*}\tilde{H}^i(K^p,\mathbb{Z}_p)\widehat\otimes_{\mathbb{Z}_p}\mathcal{O}_{C}\cong H^i(\mathcal{X}_{K^p},\mathcal{O}_{\mathcal{X}_{K^p}}^+).\end{align*} $$
Proof. Since the higher cohomology of
 $\mathcal {O}_{\mathcal {X}_{K^p}}^+$
almost vanishes on any affinoid perfectoid open subset (Theorem 1.8.(iv) of [Reference ScholzeSch12]), we can compute
$\mathcal {O}_{\mathcal {X}_{K^p}}^+$
almost vanishes on any affinoid perfectoid open subset (Theorem 1.8.(iv) of [Reference ScholzeSch12]), we can compute
 $H^i(\mathcal {X}_{K^p},\mathcal {O}_{\mathcal {X}_{K^p}}^+)$
and
$H^i(\mathcal {X}_{K^p},\mathcal {O}_{\mathcal {X}_{K^p}}^+)$
and
 $H^i(\mathcal {X}_{K^p},\mathcal {O}_{\mathcal {X}_{K^p}}^+/p^n)$
by Čech cohomology. Take a finite affinoid perfectoid cover of
$H^i(\mathcal {X}_{K^p},\mathcal {O}_{\mathcal {X}_{K^p}}^+/p^n)$
by Čech cohomology. Take a finite affinoid perfectoid cover of
![]() $\mathcal {X}_{K^p}$
and let
$\mathcal {X}_{K^p}$
and let
![]() $M^{\bullet }$
be the Čech complex for
$M^{\bullet }$
be the Čech complex for
 $\mathcal {O}_{\mathcal {X}_{K^p}}^+$
with respect to this cover. Then as almost
$\mathcal {O}_{\mathcal {X}_{K^p}}^+$
with respect to this cover. Then as almost
![]() $\mathcal {O}_C$
-modules,
$\mathcal {O}_C$
-modules,
 $H^i(M^{\bullet })=H^i(\mathcal {X}_{K^p},\mathcal {O}_{\mathcal {X}_{K^p}}^+)$
and
$H^i(M^{\bullet })=H^i(\mathcal {X}_{K^p},\mathcal {O}_{\mathcal {X}_{K^p}}^+)$
and
 $H^i(M^{\bullet }/p^n)=H^i(\mathcal {X}_{K^p},\mathcal {O}_{\mathcal {X}_{K^p}}^+/p^n)$
. In view of the previous theorem, the corollary above is reduced to the following lemma.
$H^i(M^{\bullet }/p^n)=H^i(\mathcal {X}_{K^p},\mathcal {O}_{\mathcal {X}_{K^p}}^+/p^n)$
. In view of the previous theorem, the corollary above is reduced to the following lemma.
Lemma 4.4.4. Let
![]() $M^{\bullet }$
be a bounded above chain complex of p-adically complete, p-torsion-free
$M^{\bullet }$
be a bounded above chain complex of p-adically complete, p-torsion-free
![]() $\mathbb {Z}_p$
-modules. Assume that
$\mathbb {Z}_p$
-modules. Assume that
 $\varprojlim _{n}H^i(M^{\bullet }/p^n)$
has bounded p-torsion for any i. Then we have natural isomorphisms
$\varprojlim _{n}H^i(M^{\bullet }/p^n)$
has bounded p-torsion for any i. Then we have natural isomorphisms
 $$ \begin{align*}H^i(M^{\bullet})\xrightarrow{\sim}\varprojlim_{n}H^i(M^{\bullet})/p^n\xrightarrow{\sim}\varprojlim_{n}H^i(M^{\bullet}/p^n).\end{align*} $$
$$ \begin{align*}H^i(M^{\bullet})\xrightarrow{\sim}\varprojlim_{n}H^i(M^{\bullet})/p^n\xrightarrow{\sim}\varprojlim_{n}H^i(M^{\bullet}/p^n).\end{align*} $$
Proof. Since
![]() $M^{\bullet }$
is p-adically complete and p-torsion free, we know that
$M^{\bullet }$
is p-adically complete and p-torsion free, we know that
![]() $H^i(M^{\bullet })$
is derived p-adically complete. See [Sta20, Tag 091N] for more details. In particular,
$H^i(M^{\bullet })$
is derived p-adically complete. See [Sta20, Tag 091N] for more details. In particular,
 $$ \begin{align*}\operatorname{\mathrm{Hom}}_{\mathbb{Z}_p}(\mathbb{Q}_p,H^i(M^{\bullet}))=0.\end{align*} $$
$$ \begin{align*}\operatorname{\mathrm{Hom}}_{\mathbb{Z}_p}(\mathbb{Q}_p,H^i(M^{\bullet}))=0.\end{align*} $$
For the reader’s convenience, we recall the argument here. Suppose
 $\operatorname {\mathrm {Hom}}_{\mathbb {Z}_p}(\mathbb {Q}_p,H^i(M^{\bullet }))\neq 0$
. We can find
$\operatorname {\mathrm {Hom}}_{\mathbb {Z}_p}(\mathbb {Q}_p,H^i(M^{\bullet }))\neq 0$
. We can find
![]() $x_n\in H^i(M^{\bullet }),n=0,1,2,\cdots $
satisfying
$x_n\in H^i(M^{\bullet }),n=0,1,2,\cdots $
satisfying
![]() $px_n=x_{n-1}$
and
$px_n=x_{n-1}$
and
![]() $x_0\neq 0$
. Let
$x_0\neq 0$
. Let
![]() $\tilde {x}_n\in M^i$
be a lift of
$\tilde {x}_n\in M^i$
be a lift of
![]() $x_n$
. Then there exist
$x_n$
. Then there exist
![]() $y_n\in M^{i-1}$
such that
$y_n\in M^{i-1}$
such that
![]() $dy_n=\tilde {x}_{n-1}-p\tilde {x}_n$
. Define
$dy_n=\tilde {x}_{n-1}-p\tilde {x}_n$
. Define
![]() $y=y_1+py_2+p^2y_3+\cdots \in M^{i-1}$
. One checks easily
$y=y_1+py_2+p^2y_3+\cdots \in M^{i-1}$
. One checks easily
![]() $dy=\tilde {x}_0$
. Hence,
$dy=\tilde {x}_0$
. Hence,
![]() $x_0=0$
, a contradiction.
$x_0=0$
, a contradiction.
Thus,
 $\operatorname {\mathrm {Hom}}_{\mathbb {Z}_p}(\mathbb {Q}_p/\mathbb {Z}_p,H^i(M^{\bullet }))=0$
. Now by the universal coefficient theorem, we have
$\operatorname {\mathrm {Hom}}_{\mathbb {Z}_p}(\mathbb {Q}_p/\mathbb {Z}_p,H^i(M^{\bullet }))=0$
. Now by the universal coefficient theorem, we have
When n varies, the transition map
![]() $H^{i+1}(M^{\bullet })[p^{n+1}]\to H^{i+1}(M^{\bullet })[p^n]$
is multiplication by p. Hence,
$H^{i+1}(M^{\bullet })[p^{n+1}]\to H^{i+1}(M^{\bullet })[p^n]$
is multiplication by p. Hence,
 $\varprojlim _n H^{i+1}(M^{\bullet })[p^n]=\operatorname {\mathrm {Hom}}_{\mathbb {Z}_p}(\mathbb {Q}_p/\mathbb {Z}_p,H^i(M^{\bullet }))=0$
. We get
$\varprojlim _n H^{i+1}(M^{\bullet })[p^n]=\operatorname {\mathrm {Hom}}_{\mathbb {Z}_p}(\mathbb {Q}_p/\mathbb {Z}_p,H^i(M^{\bullet }))=0$
. We get
 $\varprojlim _{n}H^i(M^{\bullet })/p^n\xrightarrow {\sim }\varprojlim _{n}H^i(M^{\bullet }/p^n)$
by passing to the limit over n of the above exact sequence.
$\varprojlim _{n}H^i(M^{\bullet })/p^n\xrightarrow {\sim }\varprojlim _{n}H^i(M^{\bullet }/p^n)$
by passing to the limit over n of the above exact sequence.
It remains to show that
 $H^i(M^{\bullet })\to \varprojlim _{n}H^i(M^{\bullet })/p^n$
is an isomorphism. This is clearly surjective as
$H^i(M^{\bullet })\to \varprojlim _{n}H^i(M^{\bullet })/p^n$
is an isomorphism. This is clearly surjective as
![]() $H^i(M^{\bullet })$
is a quotient of
$H^i(M^{\bullet })$
is a quotient of
 $\ker (M^i\xrightarrow {d} M^{i+1})$
, which is p-adically complete. Let K be the kernel of this map. By our assumption, all of the torsion in
$\ker (M^i\xrightarrow {d} M^{i+1})$
, which is p-adically complete. Let K be the kernel of this map. By our assumption, all of the torsion in
 $\varprojlim _{n}H^i(M^{\bullet })/p^n$
can be annihilated by
$\varprojlim _{n}H^i(M^{\bullet })/p^n$
can be annihilated by
![]() $p^k$
for some k. For any
$p^k$
for some k. For any
![]() $x\in K$
, we can find
$x\in K$
, we can find
![]() $x'\in H^i(M^{\bullet })$
satisfying
$x'\in H^i(M^{\bullet })$
satisfying
![]() $p^{k+1}x'=x$
. Then
$p^{k+1}x'=x$
. Then
![]() $x'$
maps to a torsion element in
$x'$
maps to a torsion element in
 $\varprojlim _{n}H^i(M^{\bullet })/p^n$
. Hence,
$\varprojlim _{n}H^i(M^{\bullet })/p^n$
. Hence,
![]() $y=p^kx'\in K$
and
$y=p^kx'\in K$
and
![]() $py=x$
. Therefore,
$py=x$
. Therefore,
![]() $pK=K$
, which implies
$pK=K$
, which implies
![]() $K=0$
as
$K=0$
as
 $\operatorname {\mathrm {Hom}}_{\mathbb {Z}_p}(\mathbb {Q}_p,H^i(M^{\bullet }))=0$
.
$\operatorname {\mathrm {Hom}}_{\mathbb {Z}_p}(\mathbb {Q}_p,H^i(M^{\bullet }))=0$
.
Remark 4.4.5. In fact, it is well-known that
![]() $\tilde {H}^i(K^p,\mathbb {Z}_p)$
is p-torsion free because the p-adic étale cohomology of curves has no torsion. Hence, the proof of Corollary 4.4.3 can be greatly simplified in this case. We decide to present this complicated proof here because it works in more general settings.
$\tilde {H}^i(K^p,\mathbb {Z}_p)$
is p-torsion free because the p-adic étale cohomology of curves has no torsion. Hence, the proof of Corollary 4.4.3 can be greatly simplified in this case. We decide to present this complicated proof here because it works in more general settings.
We write
 $\tilde {H}^i(K^p,\mathcal {O}_C)=\tilde {H}^i(K^p,\mathbb {Z}_p)\widehat \otimes _{\mathbb {Z}_p}\mathcal {O}_{C}$
and
$\tilde {H}^i(K^p,\mathcal {O}_C)=\tilde {H}^i(K^p,\mathbb {Z}_p)\widehat \otimes _{\mathbb {Z}_p}\mathcal {O}_{C}$
and
 $\tilde {H}^i(K^p,C)=\tilde {H}^i(K^p,\mathbb {Z}_p)\widehat \otimes _{\mathbb {Z}_p}C$
. Then
$\tilde {H}^i(K^p,C)=\tilde {H}^i(K^p,\mathbb {Z}_p)\widehat \otimes _{\mathbb {Z}_p}C$
. Then
 $$ \begin{align*}\tilde{H}^i(K^p,C)\cong H^i(\mathcal{X}_{K^p},\mathcal{O}_{\mathcal{X}_{K^p}})\end{align*} $$
$$ \begin{align*}\tilde{H}^i(K^p,C)\cong H^i(\mathcal{X}_{K^p},\mathcal{O}_{\mathcal{X}_{K^p}})\end{align*} $$
is a
![]() $\mathbb {Q}_p$
-Banach representation of
$\mathbb {Q}_p$
-Banach representation of
![]() $\mathrm {GL}_2(\mathbb {Q}_p)$
. Our main result here identifies its subspace of
$\mathrm {GL}_2(\mathbb {Q}_p)$
. Our main result here identifies its subspace of
![]() $\mathrm {GL}_2(\mathbb {Q}_p)$
-locally analytic vectors.
$\mathrm {GL}_2(\mathbb {Q}_p)$
-locally analytic vectors.
Theorem 4.4.6. For any
![]() $i\geq 0$
, there are natural
$i\geq 0$
, there are natural
![]() $\mathrm {GL}_2(\mathbb {Q}_p)$
and Hecke-equivariant isomorphisms
$\mathrm {GL}_2(\mathbb {Q}_p)$
and Hecke-equivariant isomorphisms
-
•
 $\tilde {H}^i(K^p,C)\cong H^i({\mathscr {F}\!\ell },\mathcal {O}_{K^p})$
,
$\tilde {H}^i(K^p,C)\cong H^i({\mathscr {F}\!\ell },\mathcal {O}_{K^p})$
, -
•
 $\tilde {H}^i(K^p,C)^{\mathrm {la}}\cong H^i({\mathscr {F}\!\ell },\mathcal {O}^{\mathrm {la}}_{K^p})$
.
$\tilde {H}^i(K^p,C)^{\mathrm {la}}\cong H^i({\mathscr {F}\!\ell },\mathcal {O}^{\mathrm {la}}_{K^p})$
.
Proof. First note that all higher direct images
![]() $R^j{\pi _{\mathrm {HT}}}_*\mathcal {O}_{\mathcal {X}_{K^p}}=0$
,
$R^j{\pi _{\mathrm {HT}}}_*\mathcal {O}_{\mathcal {X}_{K^p}}=0$
,
![]() $j>0$
. One can check this on a basis
$j>0$
. One can check this on a basis
![]() $\mathfrak {B}$
of open subsets of
$\mathfrak {B}$
of open subsets of
![]() ${\mathscr {F}\!\ell }$
in Theorem 4.1.7 and invoke the acyclicity result on affinoid perfectoid spaces; cf. Theorem 1.8.(iv) of [Reference ScholzeSch12]. Hence,
${\mathscr {F}\!\ell }$
in Theorem 4.1.7 and invoke the acyclicity result on affinoid perfectoid spaces; cf. Theorem 1.8.(iv) of [Reference ScholzeSch12]. Hence,
 $$ \begin{align*}H^i(\mathcal{X}_{K^p},\mathcal{O}_{\mathcal{X}_{K^p}})=H^i({\mathscr{F}\!\ell},{\pi_{\mathrm{HT}}}_*\mathcal{O}_{\mathcal{X}_{K^p}})=H^i({\mathscr{F}\!\ell},\mathcal{O}_{K^p}).\end{align*} $$
$$ \begin{align*}H^i(\mathcal{X}_{K^p},\mathcal{O}_{\mathcal{X}_{K^p}})=H^i({\mathscr{F}\!\ell},{\pi_{\mathrm{HT}}}_*\mathcal{O}_{\mathcal{X}_{K^p}})=H^i({\mathscr{F}\!\ell},\mathcal{O}_{K^p}).\end{align*} $$
This proves the first isomorphism in the theorem and shows that
![]() $H^i({\mathscr {F}\!\ell },\mathcal {O}_{K^p})$
can be computed by the Čech complex of a finite cover of
$H^i({\mathscr {F}\!\ell },\mathcal {O}_{K^p})$
can be computed by the Čech complex of a finite cover of
![]() ${\mathscr {F}\!\ell }$
of open subsets in
${\mathscr {F}\!\ell }$
of open subsets in
![]() $\mathfrak {B}$
. We claim the same is true for
$\mathfrak {B}$
. We claim the same is true for
 $\mathcal {O}_{K^p}^{\mathrm {la}}$
; that is,
$\mathcal {O}_{K^p}^{\mathrm {la}}$
; that is,
 $$ \begin{align*}H^j(U,\mathcal{O}_{K^p}^{\mathrm{la}})=0\end{align*} $$
$$ \begin{align*}H^j(U,\mathcal{O}_{K^p}^{\mathrm{la}})=0\end{align*} $$
for any
![]() $U\in \mathfrak {B}$
and
$U\in \mathfrak {B}$
and
![]() $j>0$
. Therefore,
$j>0$
. Therefore,
 $H^i({\mathscr {F}\!\ell },\mathcal {O}_{K^p}^{\mathrm {la}})$
can also be computed using Čech cohomology. Recall that
$H^i({\mathscr {F}\!\ell },\mathcal {O}_{K^p}^{\mathrm {la}})$
can also be computed using Čech cohomology. Recall that
![]() $\mathfrak {B}$
is stable under finite intersections. By Corollaire 4, p. 176 of [Reference GrothendieckGro57], it suffices to show the Čech cohomology
$\mathfrak {B}$
is stable under finite intersections. By Corollaire 4, p. 176 of [Reference GrothendieckGro57], it suffices to show the Čech cohomology
 $\check {H}^j(U,\mathcal {O}_{K^p}^{\mathrm {la}})=0$
for any
$\check {H}^j(U,\mathcal {O}_{K^p}^{\mathrm {la}})=0$
for any
![]() $U\in \mathfrak {B}$
and
$U\in \mathfrak {B}$
and
![]() $j>0$
. This can be proved in exactly the same way as in the first paragraph of the proof of Corollary 3.6.10 using the acyclicity result in Proposition 4.3.15.
$j>0$
. This can be proved in exactly the same way as in the first paragraph of the proof of Corollary 3.6.10 using the acyclicity result in Proposition 4.3.15.
Now let
![]() $\mathfrak {U}\subset \mathfrak {B}$
be a finite cover of
$\mathfrak {U}\subset \mathfrak {B}$
be a finite cover of
![]() ${\mathscr {F}\!\ell }$
and
${\mathscr {F}\!\ell }$
and
 $C^{\bullet }(\mathfrak {U},\mathcal {O}_{K^p}),C^{\bullet }(\mathfrak {U},\mathcal {O}_{K^p}^{\mathrm {la}})$
be the Čech complexes for
$C^{\bullet }(\mathfrak {U},\mathcal {O}_{K^p}),C^{\bullet }(\mathfrak {U},\mathcal {O}_{K^p}^{\mathrm {la}})$
be the Čech complexes for
 $\mathcal {O}_{K^p},\mathcal {O}_{K^p}^{\mathrm {la}}$
using this cover. Then
$\mathcal {O}_{K^p},\mathcal {O}_{K^p}^{\mathrm {la}}$
using this cover. Then
![]() $C^{\bullet }(\mathfrak {U},\mathcal {O}_{K^p})$
is a strict complex because
$C^{\bullet }(\mathfrak {U},\mathcal {O}_{K^p})$
is a strict complex because
 $H^i(C^{\bullet }(\mathfrak {U},\mathcal {O}^+_{K^p}))\cong H^i(\mathcal {X}_{K^p},\mathcal {O}^+_{\mathcal {X}_{K^p}})\cong \tilde {H}^i(K^p,\mathcal {O}_C)$
(as almost
$H^i(C^{\bullet }(\mathfrak {U},\mathcal {O}^+_{K^p}))\cong H^i(\mathcal {X}_{K^p},\mathcal {O}^+_{\mathcal {X}_{K^p}})\cong \tilde {H}^i(K^p,\mathcal {O}_C)$
(as almost
![]() $\mathcal {O}_C$
-modules) has bounded p-power torsion, where
$\mathcal {O}_C$
-modules) has bounded p-power torsion, where
 $\mathcal {O}^+_{K^p}={\pi _{\mathrm {HT}}}_*\mathcal {O}^+_{\mathcal {X}_{K^p}}$
. Moreover, each
$\mathcal {O}^+_{K^p}={\pi _{\mathrm {HT}}}_*\mathcal {O}^+_{\mathcal {X}_{K^p}}$
. Moreover, each
![]() $C^{i}(\mathfrak {U},\mathcal {O}_{K^p})$
is
$C^{i}(\mathfrak {U},\mathcal {O}_{K^p})$
is
![]() $\mathfrak {LA}$
-acyclic by Proposition 4.3.15 and
$\mathfrak {LA}$
-acyclic by Proposition 4.3.15 and
![]() $H^i(C^{\bullet }(\mathfrak {U},\mathcal {O}_{K^p}))=\tilde {H}^i(K^p,C)$
is
$H^i(C^{\bullet }(\mathfrak {U},\mathcal {O}_{K^p}))=\tilde {H}^i(K^p,C)$
is
![]() $\mathfrak {LA}$
-acyclic because
$\mathfrak {LA}$
-acyclic because
![]() $\tilde {H}^i(K^p,\mathbb {Z}_p)$
is an admissible representation of
$\tilde {H}^i(K^p,\mathbb {Z}_p)$
is an admissible representation of
![]() $\mathrm {GL}_2(\mathbb {Q}_p)$
and we can apply the result of Schneider–Teitelbaum; cf. Corollary 2.2.4. Hence, the theorem follows from the second part of Lemma 2.2.2 as
$\mathrm {GL}_2(\mathbb {Q}_p)$
and we can apply the result of Schneider–Teitelbaum; cf. Corollary 2.2.4. Hence, the theorem follows from the second part of Lemma 2.2.2 as
 $(C^{\bullet }(\mathfrak {U},\mathcal {O}_{K^p}))^{\mathrm {la}}=C^{\bullet }(\mathfrak {U},\mathcal {O}_{K^p}^{\mathrm {la}})$
.
$(C^{\bullet }(\mathfrak {U},\mathcal {O}_{K^p}))^{\mathrm {la}}=C^{\bullet }(\mathfrak {U},\mathcal {O}_{K^p}^{\mathrm {la}})$
.
5
 $\mu $
-isotypic part of completed cohomology
$\mu $
-isotypic part of completed cohomology
The goal of this section is to determine the
![]() $\mu $
-isotypic part of
$\mu $
-isotypic part of
![]() $\tilde {H}^i(K^p,C)^{\mathrm {la}}$
. We will give a complete answer for integral weights as described in the Introduction. Roughly speaking, the answer is a mixture of coherent cohomology groups of modular curves at finite level and overconvergent modular forms. Also, we will give a p-adic Hodge-theoretic interpretation of the horizontal action
$\tilde {H}^i(K^p,C)^{\mathrm {la}}$
. We will give a complete answer for integral weights as described in the Introduction. Roughly speaking, the answer is a mixture of coherent cohomology groups of modular curves at finite level and overconvergent modular forms. Also, we will give a p-adic Hodge-theoretic interpretation of the horizontal action
![]() $\theta _{\mathfrak {h}}$
.
$\theta _{\mathfrak {h}}$
.
From now on, we assume
![]() $C=\mathbb {C}_p$
is the completion of
$C=\mathbb {C}_p$
is the completion of
 $\overline {\mathbb {Q}}_p$
. Then
$\overline {\mathbb {Q}}_p$
. Then
![]() $G_{\mathbb {Q}_p}$
acts continuously on
$G_{\mathbb {Q}_p}$
acts continuously on
![]() $C,\tilde {H}^i(K^p,\mathbb {Z}_p),\tilde {H}^i(K^p,C)$
and commutes with the action of
$C,\tilde {H}^i(K^p,\mathbb {Z}_p),\tilde {H}^i(K^p,C)$
and commutes with the action of
![]() $\mathrm {GL}_2(\mathbb {Q}_p)$
and Hecke operators away from p.
$\mathrm {GL}_2(\mathbb {Q}_p)$
and Hecke operators away from p.
5.1 A p-adic Hodge-theoretic interpretation of
 $\theta _{\mathfrak {h}}$
$\theta _{\mathfrak {h}}$
5.1.1. We would like to write down the action
![]() $\theta _{\mathfrak {h}}$
introduced in Corollary 4.2.8 on
$\theta _{\mathfrak {h}}$
introduced in Corollary 4.2.8 on
 $\mathcal {O}^{\mathrm {la}}_{K^p}$
using the explicit description in Theorem 4.3.9. So keep the notation in Subsection 4.3. In particular,
$\mathcal {O}^{\mathrm {la}}_{K^p}$
using the explicit description in Theorem 4.3.9. So keep the notation in Subsection 4.3. In particular,
![]() $e_1$
generates
$e_1$
generates
![]() $H^0(V, \omega _{K^p})$
. Then for any
$H^0(V, \omega _{K^p})$
. Then for any
 $f\in \mathcal {O}^{\mathrm {la}}_{K^p}(U)$
, we can write
$f\in \mathcal {O}^{\mathrm {la}}_{K^p}(U)$
, we can write
 $$ \begin{align*}f=\sum_{i,j,k\geq0}c^{(n)}_{i,j,k}(f)(x-x_n)^i\left(\log(\frac{e_1}{e_{1,n}})\right)^j\left(\log(\frac{t}{t_{n}})\right)^k\end{align*} $$
$$ \begin{align*}f=\sum_{i,j,k\geq0}c^{(n)}_{i,j,k}(f)(x-x_n)^i\left(\log(\frac{e_1}{e_{1,n}})\right)^j\left(\log(\frac{t}{t_{n}})\right)^k\end{align*} $$
for sufficiently large n (as in Theorem 4.3.9). By our construction in Corollary 4.2.8, a direct computation shows that
 $\theta _{\mathfrak {h}}(\begin {pmatrix}a & 0\\ 0 & d \end {pmatrix})$
acts on
$\theta _{\mathfrak {h}}(\begin {pmatrix}a & 0\\ 0 & d \end {pmatrix})$
acts on
 $\mathcal {O}^{\mathrm {la}}_{K^p}(U)$
as
$\mathcal {O}^{\mathrm {la}}_{K^p}(U)$
as
 $\begin {pmatrix} d & (d-a)x \\ 0 & a \end {pmatrix}\in \mathcal {O}_{{\mathscr {F}\!\ell }}(U)\otimes _C\mathfrak {g}$
. (To see this, recall that
$\begin {pmatrix} d & (d-a)x \\ 0 & a \end {pmatrix}\in \mathcal {O}_{{\mathscr {F}\!\ell }}(U)\otimes _C\mathfrak {g}$
. (To see this, recall that
 $\begin {pmatrix} x & x^2\\ -1 & -x \end {pmatrix}$
is a generator of
$\begin {pmatrix} x & x^2\\ -1 & -x \end {pmatrix}$
is a generator of
![]() $H^0(U,\mathfrak {n}^0)$
; cf. Section 4.3.2. One computes directly that
$H^0(U,\mathfrak {n}^0)$
; cf. Section 4.3.2. One computes directly that
 $[\begin {pmatrix}d & (d-a)x\\ 0 & a \end {pmatrix},\begin {pmatrix} x & x^2\\ -1 & -x \end {pmatrix}]=(a-d)\begin {pmatrix} x & x^2\\ -1 & -x \end {pmatrix}$
, and this
$[\begin {pmatrix}d & (d-a)x\\ 0 & a \end {pmatrix},\begin {pmatrix} x & x^2\\ -1 & -x \end {pmatrix}]=(a-d)\begin {pmatrix} x & x^2\\ -1 & -x \end {pmatrix}$
, and this
![]() $(a-d)$
agrees with
$(a-d)$
agrees with
 $[\begin {pmatrix}a & 0\\ 0 & d \end {pmatrix},\begin {pmatrix} 0 & 1\\ 0 & 0\end {pmatrix}]=(a-d)\begin {pmatrix} 0 & 1\\ 0 & 0\end {pmatrix}$
.) Hence,
$[\begin {pmatrix}a & 0\\ 0 & d \end {pmatrix},\begin {pmatrix} 0 & 1\\ 0 & 0\end {pmatrix}]=(a-d)\begin {pmatrix} 0 & 1\\ 0 & 0\end {pmatrix}$
.) Hence,
 $$ \begin{align*}c^{(n)}_{i,j,k}(\theta_{\mathfrak{h}}(\begin{pmatrix}a & 0\\ 0 & d \end{pmatrix})\cdot f)=d(j+1)c^{(n)}_{i,j+1,k}(f)+(a+d)(k+1)c^{(n)}_{i,j,k+1}(f).\end{align*} $$
$$ \begin{align*}c^{(n)}_{i,j,k}(\theta_{\mathfrak{h}}(\begin{pmatrix}a & 0\\ 0 & d \end{pmatrix})\cdot f)=d(j+1)c^{(n)}_{i,j+1,k}(f)+(a+d)(k+1)c^{(n)}_{i,j,k+1}(f).\end{align*} $$
Let
![]() $\chi $
be a weight of
$\chi $
be a weight of
![]() $\mathfrak {h}$
; that is, a C-linear map
$\mathfrak {h}$
; that is, a C-linear map
![]() $\chi :\mathfrak {h}\to C$
. We can write
$\chi :\mathfrak {h}\to C$
. We can write
 $\chi (\begin {pmatrix}a & 0\\ 0 & d \end {pmatrix})=an_1+dn_2$
for some
$\chi (\begin {pmatrix}a & 0\\ 0 & d \end {pmatrix})=an_1+dn_2$
for some
![]() $n_1,n_2\in C$
. Fix N sufficiently large so that
$n_1,n_2\in C$
. Fix N sufficiently large so that
 $$ \begin{align*}(\frac{t}{t_{N}})^{n_1}:=\sum_{l\geq0}{n_1\choose{l}}(\frac{t}{t_N}-1)^l,\end{align*} $$
$$ \begin{align*}(\frac{t}{t_{N}})^{n_1}:=\sum_{l\geq0}{n_1\choose{l}}(\frac{t}{t_N}-1)^l,\end{align*} $$
 $$ \begin{align*}(\frac{e_1}{e_{1,N}})^{n_2-n_1}:=\sum_{l\geq0}{n_2-n_1\choose{l}}(\frac{e_1}{e_{1,N}}-1)^l\end{align*} $$
$$ \begin{align*}(\frac{e_1}{e_{1,N}})^{n_2-n_1}:=\sum_{l\geq0}{n_2-n_1\choose{l}}(\frac{e_1}{e_{1,N}}-1)^l\end{align*} $$
converge in
 $\mathcal {O}_{K^p}^{G_{r(N)}-\mathrm {an}}$
. One checks easily that
$\mathcal {O}_{K^p}^{G_{r(N)}-\mathrm {an}}$
. One checks easily that
 $\theta _{\mathfrak {h}}(\begin {pmatrix}a & 0\\ 0 & d \end {pmatrix})$
acts as
$\theta _{\mathfrak {h}}(\begin {pmatrix}a & 0\\ 0 & d \end {pmatrix})$
acts as
![]() $\chi $
on
$\chi $
on
 $(\frac {t}{t_{N}})^{n_1}(\frac {e_1}{e_{1,N}})^{n_2-n_1}$
. Denote by
$(\frac {t}{t_{N}})^{n_1}(\frac {e_1}{e_{1,N}})^{n_2-n_1}$
. Denote by
 $\mathcal {O}^{\mathrm {la},\chi }_{K^p}\subset \mathcal {O}^{\mathrm {la}}_{K^p}$
the subsheaf of sections of weight
$\mathcal {O}^{\mathrm {la},\chi }_{K^p}\subset \mathcal {O}^{\mathrm {la}}_{K^p}$
the subsheaf of sections of weight
![]() $\chi $
.
$\chi $
.
Lemma 5.1.2. For any weight
![]() $\chi $
and
$\chi $
and
![]() $U\in \mathfrak {B}$
,
$U\in \mathfrak {B}$
,
-
(1)
 $H^i(\mathfrak {h},\mathcal {O}^{\mathrm {la}}_{K^p}(U)\otimes \chi )=0,i\geq 1$
.
$H^i(\mathfrak {h},\mathcal {O}^{\mathrm {la}}_{K^p}(U)\otimes \chi )=0,i\geq 1$
. -
(2) Suppose
 $e_1$
is a generator on
$e_1$
is a generator on
 $V=\pi _{\mathrm {HT}}^{-1}(U)$
; then any
$V=\pi _{\mathrm {HT}}^{-1}(U)$
; then any
 $f\in \mathcal {O}^{\mathrm {la},\chi }_{K^p}(U)$
can be written as for some
$f\in \mathcal {O}^{\mathrm {la},\chi }_{K^p}(U)$
can be written as for some $$ \begin{align*}f=(\frac{t}{t_{N}})^{n_1}(\frac{e_1}{e_{1,N}})^{n_2-n_1}\sum_{i\geq0} c^{(n)}_i(f) (x-x_n)^i \end{align*} $$
$$ \begin{align*}f=(\frac{t}{t_{N}})^{n_1}(\frac{e_1}{e_{1,N}})^{n_2-n_1}\sum_{i\geq0} c^{(n)}_i(f) (x-x_n)^i \end{align*} $$
 $n>N$
sufficiently large and
$n>N$
sufficiently large and
 $c^{(n)}_i(f)\in H^0(V_{G_{r(n)}},\mathcal {O}_{\mathcal {X}_{K^pG_{r(n)}}})$
with bound
$c^{(n)}_i(f)\in H^0(V_{G_{r(n)}},\mathcal {O}_{\mathcal {X}_{K^pG_{r(n)}}})$
with bound
 $\|c^{(n)}_i(f)\|\leq C'p^{(n-1)i}$
for a uniform
$\|c^{(n)}_i(f)\|\leq C'p^{(n-1)i}$
for a uniform
 $C'$
.
$C'$
.
Proof. Using the action of
![]() $\mathrm {GL}_2(\mathbb {Q}_p)$
, we can reduce to the case considered above; that is, that
$\mathrm {GL}_2(\mathbb {Q}_p)$
, we can reduce to the case considered above; that is, that
![]() $e_1$
generates
$e_1$
generates
![]() $H^0(V, \omega _{K^p})$
. Note that
$H^0(V, \omega _{K^p})$
. Note that
 $(\frac {t}{t_{N}})^{n_1}(\frac {e_1}{e_{1,N}})^{n_2-n_1}$
is invertible. Hence, multiplication by it induces an
$(\frac {t}{t_{N}})^{n_1}(\frac {e_1}{e_{1,N}})^{n_2-n_1}$
is invertible. Hence, multiplication by it induces an
![]() $\mathfrak {h}$
-equivariant isomorphism
$\mathfrak {h}$
-equivariant isomorphism
 $\mathcal {O}^{\mathrm {la}}_{K^p}(U)\otimes \chi \xrightarrow {\sim }\mathcal {O}^{\mathrm {la}}_{K^p}(U)$
. Therefore, it is enough to prove the case
$\mathcal {O}^{\mathrm {la}}_{K^p}(U)\otimes \chi \xrightarrow {\sim }\mathcal {O}^{\mathrm {la}}_{K^p}(U)$
. Therefore, it is enough to prove the case
![]() $\chi =0$
. The second part is clear in view of the explicit formula for
$\chi =0$
. The second part is clear in view of the explicit formula for
 $c^{(n)}_{i,j,k}(\theta _{\mathfrak {h}}(\begin {pmatrix}a & 0\\ 0 & d \end {pmatrix})\cdot f)$
above. To see the first part, write
$c^{(n)}_{i,j,k}(\theta _{\mathfrak {h}}(\begin {pmatrix}a & 0\\ 0 & d \end {pmatrix})\cdot f)$
above. To see the first part, write
 $\mathfrak {a}=\{\begin {pmatrix} * & 0 \\ 0 & 0 \end {pmatrix}\}\subset \mathfrak {h}$
. We claim
$\mathfrak {a}=\{\begin {pmatrix} * & 0 \\ 0 & 0 \end {pmatrix}\}\subset \mathfrak {h}$
. We claim
-
(1)
 $H^1(\mathfrak {a},\mathcal {O}^{\mathrm {la}}_{K^p}(U))=0$
;
$H^1(\mathfrak {a},\mathcal {O}^{\mathrm {la}}_{K^p}(U))=0$
; -
(2)
 $H^0(\mathfrak {a},\mathcal {O}^{\mathrm {la}}_{K^p}(U))\subset \mathcal {O}^{\mathrm {la}}_{K^p}(U)$
is the subset of f such that
$H^0(\mathfrak {a},\mathcal {O}^{\mathrm {la}}_{K^p}(U))\subset \mathcal {O}^{\mathrm {la}}_{K^p}(U)$
is the subset of f such that
 $c^{(n)}_{i,j,k}(f)=0,k\geq 1$
.
$c^{(n)}_{i,j,k}(f)=0,k\geq 1$
.
Again, the second claim is clear by our explicit formula. For the first claim, suppose
 $f\in \mathcal {O}^{\mathrm {la}}_{K^p}(U)$
has an expansion as in Theorem 4.3.9. For any
$f\in \mathcal {O}^{\mathrm {la}}_{K^p}(U)$
has an expansion as in Theorem 4.3.9. For any
![]() $i,j,k\geq 0$
, let
$i,j,k\geq 0$
, let
 $c^{\prime }_{i,j,k+1}=\frac {1}{k+1}c^{(n)}_{i,j,k}(f)$
. Then
$c^{\prime }_{i,j,k+1}=\frac {1}{k+1}c^{(n)}_{i,j,k}(f)$
. Then
 $\|c^{\prime }_{i,j,k}\|\leq C''p^{(n-0.5)(i+j+k)}$
for some uniform
$\|c^{\prime }_{i,j,k}\|\leq C''p^{(n-0.5)(i+j+k)}$
for some uniform
![]() $C''$
. Hence,
$C''$
. Hence,
 $$ \begin{align*}f'=\sum_{i,j\geq 0,k\geq1}c^{\prime}_{i,j,k}(x-x_n)^i\left(\log(\frac{e_1}{e_{1,n}})\right)^j\left(\log(\frac{t}{t_{n}})\right)^k\end{align*} $$
$$ \begin{align*}f'=\sum_{i,j\geq 0,k\geq1}c^{\prime}_{i,j,k}(x-x_n)^i\left(\log(\frac{e_1}{e_{1,n}})\right)^j\left(\log(\frac{t}{t_{n}})\right)^k\end{align*} $$
converges in
 $\mathcal {O}_{K^p}^{G_{r(n)}-\mathrm {an}}$
. One checks easily
$\mathcal {O}_{K^p}^{G_{r(n)}-\mathrm {an}}$
. One checks easily
 $\theta _{\mathfrak {h}}(\begin {pmatrix}1 & 0\\ 0 & 0 \end {pmatrix})\cdot f'=f$
. This proves the vanishing of
$\theta _{\mathfrak {h}}(\begin {pmatrix}1 & 0\\ 0 & 0 \end {pmatrix})\cdot f'=f$
. This proves the vanishing of
 $H^1(\mathfrak {a},\mathcal {O}^{\mathrm {la}}_{K^p}(U))$
. The same argument also gives
$H^1(\mathfrak {a},\mathcal {O}^{\mathrm {la}}_{K^p}(U))$
. The same argument also gives
 $H^1(\mathfrak {h}/\mathfrak {a},H^0(\mathfrak {a},\mathcal {O}^{\mathrm {la}}_{K^p}(U)))=0$
. By the Hochschild–Serre spectral sequence, we deduce our claim in the lemma.
$H^1(\mathfrak {h}/\mathfrak {a},H^0(\mathfrak {a},\mathcal {O}^{\mathrm {la}}_{K^p}(U)))=0$
. By the Hochschild–Serre spectral sequence, we deduce our claim in the lemma.
We denote by
 $H^i({\mathscr {F}\!\ell },\mathcal {O}^{\mathrm {la}}_{K^p})^{\chi }$
the subspace of
$H^i({\mathscr {F}\!\ell },\mathcal {O}^{\mathrm {la}}_{K^p})^{\chi }$
the subspace of
 $H^i({\mathscr {F}\!\ell },\mathcal {O}^{\mathrm {la}}_{K^p})$
where
$H^i({\mathscr {F}\!\ell },\mathcal {O}^{\mathrm {la}}_{K^p})$
where
![]() $\theta _{\mathfrak {h}}$
acts by
$\theta _{\mathfrak {h}}$
acts by
![]() $\chi $
. Then
$\chi $
. Then
 $H^0({\mathscr {F}\!\ell },\mathcal {O}^{\mathrm {la},\chi }_{K^p})=H^0({\mathscr {F}\!\ell },\mathcal {O}^{\mathrm {la}}_{K^p})^{\chi }$
.
$H^0({\mathscr {F}\!\ell },\mathcal {O}^{\mathrm {la},\chi }_{K^p})=H^0({\mathscr {F}\!\ell },\mathcal {O}^{\mathrm {la}}_{K^p})^{\chi }$
.
Corollary 5.1.3.
-
(1)
 $\theta _{\mathfrak {h}}(h)\cdot f=0,\,\theta _{\mathfrak {h}}(z)\cdot f=z\cdot f,\,f\in H^0({\mathscr {F}\!\ell },\mathcal {O}^{\mathrm {la}}_{K^p})$
. In particular,
$\theta _{\mathfrak {h}}(h)\cdot f=0,\,\theta _{\mathfrak {h}}(z)\cdot f=z\cdot f,\,f\in H^0({\mathscr {F}\!\ell },\mathcal {O}^{\mathrm {la}}_{K^p})$
. In particular,
 $H^0({\mathscr {F}\!\ell },\mathcal {O}^{\mathrm {la},\chi }_{K^p})=0$
if
$H^0({\mathscr {F}\!\ell },\mathcal {O}^{\mathrm {la},\chi }_{K^p})=0$
if
 $\chi (h)\neq 0$
.
$\chi (h)\neq 0$
. -
(2) If
 $\chi (h)\neq 0$
, then
$\chi (h)\neq 0$
, then
 $H^1({\mathscr {F}\!\ell },\mathcal {O}^{\mathrm {la},\chi }_{K^p})=H^1({\mathscr {F}\!\ell },\mathcal {O}^{\mathrm {la}}_{K^p})^{\chi }$
. If
$H^1({\mathscr {F}\!\ell },\mathcal {O}^{\mathrm {la},\chi }_{K^p})=H^1({\mathscr {F}\!\ell },\mathcal {O}^{\mathrm {la}}_{K^p})^{\chi }$
. If
 $\chi (h)=0$
, there is a
$\chi (h)=0$
, there is a
 $\mathfrak {g}$
-equivariant exact sequence where
$\mathfrak {g}$
-equivariant exact sequence where $$ \begin{align*}0\to \varinjlim_{K_p\subset \mathrm{GL}_2(\mathbb{Q}_p)}H^0(\mathcal{X}_{K^pK_p},\mathcal{O}_{\mathcal{X}_{K^pK_p}})\cdot(\frac{t}{t_N})^{n_1}\to H^1({\mathscr{F}\!\ell},\mathcal{O}^{\mathrm{la},\chi}_{K^p}) \to H^1({\mathscr{F}\!\ell},\mathcal{O}^{\mathrm{la}}_{K^p})^{\chi}\to 0,\end{align*} $$
$$ \begin{align*}0\to \varinjlim_{K_p\subset \mathrm{GL}_2(\mathbb{Q}_p)}H^0(\mathcal{X}_{K^pK_p},\mathcal{O}_{\mathcal{X}_{K^pK_p}})\cdot(\frac{t}{t_N})^{n_1}\to H^1({\mathscr{F}\!\ell},\mathcal{O}^{\mathrm{la},\chi}_{K^p}) \to H^1({\mathscr{F}\!\ell},\mathcal{O}^{\mathrm{la}}_{K^p})^{\chi}\to 0,\end{align*} $$
 $n_1=\chi (\begin {pmatrix} 1 & 0 \\ 0 & 0 \end {pmatrix})$
and
$n_1=\chi (\begin {pmatrix} 1 & 0 \\ 0 & 0 \end {pmatrix})$
and
 $t_N\in H^0(\mathcal {X}_{K^pK_p},\mathcal {O}_{\mathcal {X}_{K^pK_p}})$
sufficiently close to t for some
$t_N\in H^0(\mathcal {X}_{K^pK_p},\mathcal {O}_{\mathcal {X}_{K^pK_p}})$
sufficiently close to t for some
 $K_p$
.
$K_p$
.
Proof. The action of
![]() $\mathrm {GL}_2(\mathbb {Q}_p)$
on
$\mathrm {GL}_2(\mathbb {Q}_p)$
on
![]() $\tilde {H}^0(K^p,C)^{\mathrm {la}}$
factors through the determinant map; hence, for any global section
$\tilde {H}^0(K^p,C)^{\mathrm {la}}$
factors through the determinant map; hence, for any global section
 $f\in H^0({\mathscr {F}\!\ell },\mathcal {O}_{K^p}^{\mathrm {la}})\cong \tilde {H}^0(K^p,C)^{\mathrm {la}}$
, we have
$f\in H^0({\mathscr {F}\!\ell },\mathcal {O}_{K^p}^{\mathrm {la}})\cong \tilde {H}^0(K^p,C)^{\mathrm {la}}$
, we have
![]() $\theta _{\mathfrak {h}}(h)\cdot f=0$
and
$\theta _{\mathfrak {h}}(h)\cdot f=0$
and
![]() $\theta _{\mathfrak {h}}(z)\cdot f={z}\cdot f$
by the explicit expression of
$\theta _{\mathfrak {h}}(z)\cdot f={z}\cdot f$
by the explicit expression of
![]() $\theta _{\mathfrak {h}}$
in Section 5.1.1. This also shows that the horizontal action
$\theta _{\mathfrak {h}}$
in Section 5.1.1. This also shows that the horizontal action
![]() $\theta _{\mathfrak {h}}$
of
$\theta _{\mathfrak {h}}$
of
![]() $\mathfrak {h}$
agrees with the constant action of
$\mathfrak {h}$
agrees with the constant action of
![]() $\mathfrak {h}\subset \mathfrak {g}$
on
$\mathfrak {h}\subset \mathfrak {g}$
on
![]() $\tilde {H}^0(K^p,C)^{\mathrm {la}}$
.
$\tilde {H}^0(K^p,C)^{\mathrm {la}}$
.
For the second part, it follows from the first part of Lemma 5.1.2 that there is a spectral sequence
 $$ \begin{align*}E_2^{pq}= \operatorname{\mathrm{Ext}}^p_{C[\mathfrak{h}]}(\chi,H^q({\mathscr{F}\!\ell},\mathcal{O}^{\mathrm{la}}_{K^p}))\Rightarrow H^{p+q}({\mathscr{F}\!\ell},\mathcal{O}^{\mathrm{la},\chi}_{K^p}).\end{align*} $$
$$ \begin{align*}E_2^{pq}= \operatorname{\mathrm{Ext}}^p_{C[\mathfrak{h}]}(\chi,H^q({\mathscr{F}\!\ell},\mathcal{O}^{\mathrm{la}}_{K^p}))\Rightarrow H^{p+q}({\mathscr{F}\!\ell},\mathcal{O}^{\mathrm{la},\chi}_{K^p}).\end{align*} $$
The exact sequence of low degrees readsFootnote 2
 $$ \begin{align*}0\to \operatorname{\mathrm{Ext}}^1_{C[\mathfrak{h}]}(\chi,H^0({\mathscr{F}\!\ell},\mathcal{O}^{\mathrm{la}}_{K^p}))\to H^1({\mathscr{F}\!\ell},\mathcal{O}^{\mathrm{la},\chi}_{K^p}) \to H^1({\mathscr{F}\!\ell},\mathcal{O}^{\mathrm{la}}_{K^p})^{\chi}\to \operatorname{\mathrm{Ext}}^2_{C[\mathfrak{h}]}(\chi,H^0({\mathscr{F}\!\ell},\mathcal{O}^{\mathrm{la}}_{K^p})).\end{align*} $$
$$ \begin{align*}0\to \operatorname{\mathrm{Ext}}^1_{C[\mathfrak{h}]}(\chi,H^0({\mathscr{F}\!\ell},\mathcal{O}^{\mathrm{la}}_{K^p}))\to H^1({\mathscr{F}\!\ell},\mathcal{O}^{\mathrm{la},\chi}_{K^p}) \to H^1({\mathscr{F}\!\ell},\mathcal{O}^{\mathrm{la}}_{K^p})^{\chi}\to \operatorname{\mathrm{Ext}}^2_{C[\mathfrak{h}]}(\chi,H^0({\mathscr{F}\!\ell},\mathcal{O}^{\mathrm{la}}_{K^p})).\end{align*} $$
When
![]() $\chi (h)\neq 0$
, both
$\chi (h)\neq 0$
, both
![]() $\operatorname {\mathrm {Ext}}^1$
and
$\operatorname {\mathrm {Ext}}^1$
and
![]() $\operatorname {\mathrm {Ext}}^2$
vanish because
$\operatorname {\mathrm {Ext}}^2$
vanish because
![]() $\theta _{\mathfrak {h}}(h)$
acts via zero on
$\theta _{\mathfrak {h}}(h)$
acts via zero on
 $H^0({\mathscr {F}\!\ell },\mathcal {O}^{\mathrm {la}}_{K^p})$
. Now assume
$H^0({\mathscr {F}\!\ell },\mathcal {O}^{\mathrm {la}}_{K^p})$
. Now assume
![]() $\chi (h)=0$
. After multiplying by
$\chi (h)=0$
. After multiplying by
 $(\frac {t}{t_N})^{-n_1}\in H^0({\mathscr {F}\!\ell },\mathcal {O}^{\mathrm {la}}_{K^p})^{-\chi }$
, we may assume
$(\frac {t}{t_N})^{-n_1}\in H^0({\mathscr {F}\!\ell },\mathcal {O}^{\mathrm {la}}_{K^p})^{-\chi }$
, we may assume
![]() $\chi =0$
. It suffices to show
$\chi =0$
. It suffices to show
-
•
 $H^1(\mathfrak {h},H^0({\mathscr {F}\!\ell },\mathcal {O}^{\mathrm {la}}_{K^p}))\cong \varinjlim _{K_p\subset \mathrm {GL}_2(\mathbb {Q}_p)}H^0(\mathcal {X}_{K^pK_p},\mathcal {O}_{\mathcal {X}_{K^pK_p}})$
.
$H^1(\mathfrak {h},H^0({\mathscr {F}\!\ell },\mathcal {O}^{\mathrm {la}}_{K^p}))\cong \varinjlim _{K_p\subset \mathrm {GL}_2(\mathbb {Q}_p)}H^0(\mathcal {X}_{K^pK_p},\mathcal {O}_{\mathcal {X}_{K^pK_p}})$
. -
•
 $H^2(\mathfrak {h},H^0({\mathscr {F}\!\ell },\mathcal {O}^{\mathrm {la}}_{K^p}))=0$
.
$H^2(\mathfrak {h},H^0({\mathscr {F}\!\ell },\mathcal {O}^{\mathrm {la}}_{K^p}))=0$
.
Both claims follow from the Hochschild–Serre spectral sequence and
-
•
 $H^1(\mathfrak {a},\tilde {H}^0(K^p,C)^{\mathrm {la}})=0$
;
$H^1(\mathfrak {a},\tilde {H}^0(K^p,C)^{\mathrm {la}})=0$
; -
•
 $H^0(\mathfrak {a},\tilde {H}^0(K^p,C)^{\mathrm {la}})=H^0(\mathfrak {g},\tilde {H}^0(K^p,C)^{\mathrm {la}})=\varinjlim _{K_p\subset \mathrm {GL}_2(\mathbb {Q}_p)}H^0(\mathcal {X}_{K^pK_p},\mathcal {O}_{\mathcal {X}_{K^pK_p}})$
$H^0(\mathfrak {a},\tilde {H}^0(K^p,C)^{\mathrm {la}})=H^0(\mathfrak {g},\tilde {H}^0(K^p,C)^{\mathrm {la}})=\varinjlim _{K_p\subset \mathrm {GL}_2(\mathbb {Q}_p)}H^0(\mathcal {X}_{K^pK_p},\mathcal {O}_{\mathcal {X}_{K^pK_p}})$
by the explicit description of
![]() $\tilde {H}^0(K^p,C)$
in [Reference EmertonEme06b, (4.2)].
$\tilde {H}^0(K^p,C)$
in [Reference EmertonEme06b, (4.2)].
5.1.4. It is interesting to investigate the p-adic Hodge-theoretic meaning of
![]() $\theta _{\mathfrak {h}}$
. First, we generalise the classical notion of the Sen operator.
$\theta _{\mathfrak {h}}$
. First, we generalise the classical notion of the Sen operator.
Definition 5.1.5. Suppose W is a C-Banach space equipped with a semi-linear continuous action of an open subgroup of
![]() $G_{\mathbb {Q}_p}$
, say
$G_{\mathbb {Q}_p}$
, say
![]() $G_K$
. We say a continuous C-linear endomorphism
$G_K$
. We say a continuous C-linear endomorphism
![]() $\theta _{\mathrm {Sen}}\in \operatorname {\mathrm {End}}_C(W)$
is a Sen operator if it extends the natural action of
$\theta _{\mathrm {Sen}}\in \operatorname {\mathrm {End}}_C(W)$
is a Sen operator if it extends the natural action of
![]() $1\in \mathbb {Q}_p\cong \operatorname {\mathrm {Lie}}(\operatorname {\mathrm {Gal}}(\mathbb {Q}_p(\mu _{p^\infty })/\mathbb {Q}_p))$
on the
$1\in \mathbb {Q}_p\cong \operatorname {\mathrm {Lie}}(\operatorname {\mathrm {Gal}}(\mathbb {Q}_p(\mu _{p^\infty })/\mathbb {Q}_p))$
on the
![]() $G_{K(\mu _{p^\infty })}$
-smooth,
$G_{K(\mu _{p^\infty })}$
-smooth,
![]() $G_K$
-locally analytic vectors of W (viewed as a
$G_K$
-locally analytic vectors of W (viewed as a
![]() $\mathbb {Q}_p$
-Banach space).
$\mathbb {Q}_p$
-Banach space).
If
 $W=\varinjlim _n W_n$
is an increasing union of C-Banach spaces
$W=\varinjlim _n W_n$
is an increasing union of C-Banach spaces
![]() $W_n$
equipped with a semi-linear continuous action of an open subgroup of
$W_n$
equipped with a semi-linear continuous action of an open subgroup of
![]() $G_{\mathbb {Q}_p}$
, then we say
$G_{\mathbb {Q}_p}$
, then we say
![]() $\theta \in \operatorname {\mathrm {End}}_C(W)$
is a Sen operator if
$\theta \in \operatorname {\mathrm {End}}_C(W)$
is a Sen operator if
![]() $\theta $
preserves each
$\theta $
preserves each
![]() $W_n$
and acts as a Sen operator on it. We also say W has pure Hodge–Tate–Sen weight
$W_n$
and acts as a Sen operator on it. We also say W has pure Hodge–Tate–Sen weight
![]() $k\in C$
if multiplication by
$k\in C$
if multiplication by
![]() $-k$
is a Sen operator on W.
$-k$
is a Sen operator on W.
Remark 5.1.6. The first part of the definition makes sense as for any
![]() $G_{K(\mu _{p^\infty })}$
-smooth vector v, the action of
$G_{K(\mu _{p^\infty })}$
-smooth vector v, the action of
![]() $G_K$
on v factors through a finite-dimensional p-adic Lie group which has an open subgroup naturally isomorphic to an open subgroup of
$G_K$
on v factors through a finite-dimensional p-adic Lie group which has an open subgroup naturally isomorphic to an open subgroup of
![]() $\operatorname {\mathrm {Gal}}(\mathbb {Q}_p(\mu _{p^\infty })/\mathbb {Q}_p)$
. Also, it is clear that this definition is independent of the choice of K.
$\operatorname {\mathrm {Gal}}(\mathbb {Q}_p(\mu _{p^\infty })/\mathbb {Q}_p)$
. Also, it is clear that this definition is independent of the choice of K.
Remark 5.1.7. If W is a finite-dimensional C-vector space, then in [Reference SenSen81] Sen proves that
![]() $\theta _{\mathrm {Sen}}$
exists and is unique. However, for a general W, to what extent
$\theta _{\mathrm {Sen}}$
exists and is unique. However, for a general W, to what extent
![]() $\theta _{\mathrm {Sen}}$
exists uniquely is not known to the author.
$\theta _{\mathrm {Sen}}$
exists uniquely is not known to the author.
In our case, we will take
![]() $W=\mathcal {O}_{K^p}(U)^{\mathrm {la}}$
and
$W=\mathcal {O}_{K^p}(U)^{\mathrm {la}}$
and
![]() $\tilde {H}^i(K^p,C)^{\mathrm {la}}$
. Note that
$\tilde {H}^i(K^p,C)^{\mathrm {la}}$
. Note that
![]() $V_{K_p}$
can be defined over a finite extension K of
$V_{K_p}$
can be defined over a finite extension K of
![]() $\mathbb {Q}_p$
so
$\mathbb {Q}_p$
so
![]() $\mathcal {O}_{K^p}(U)^{\mathrm {la}}$
has a natural action of
$\mathcal {O}_{K^p}(U)^{\mathrm {la}}$
has a natural action of
![]() $G_K$
.
$G_K$
.
Theorem 5.1.8.
 $\theta _{\mathfrak {h}}(\begin {pmatrix}0 & 0\\ 0 & 1 \end {pmatrix})$
is the unique Sen operator on
$\theta _{\mathfrak {h}}(\begin {pmatrix}0 & 0\\ 0 & 1 \end {pmatrix})$
is the unique Sen operator on
![]() $\mathcal {O}_{K^p}(U)^{\mathrm {la}}$
.
$\mathcal {O}_{K^p}(U)^{\mathrm {la}}$
.
Remark 5.1.9. Roughly speaking, this result relates an operator in p-adic Hodge theory on (the infinite level) modular curves with some group-theoretic operator (
![]() $\theta _{\mathfrak {h}}$
). This is very classical in the study of the cohomology of locally symmetric spaces using complex Hodge theory. See, for example, Chapter II, Section 4 of [Reference Borel and WallachBW00].
$\theta _{\mathfrak {h}}$
). This is very classical in the study of the cohomology of locally symmetric spaces using complex Hodge theory. See, for example, Chapter II, Section 4 of [Reference Borel and WallachBW00].
Remark 5.1.10. This result and Theorem 5.1.11 are all obtained by explicit calculations. It should be possible to avoid these calculations by further decompleting
![]() $\mathcal {O}_{K^p}(U)^{\mathrm {la}}$
with respect to the action of
$\mathcal {O}_{K^p}(U)^{\mathrm {la}}$
with respect to the action of
![]() $G_K$
(i.e., usual Sen theory). I plan to come back to this in a future work.
$G_K$
(i.e., usual Sen theory). I plan to come back to this in a future work.
Proof. By Theorem 4.3.9, for each m, we have continuous embeddings
for some n. See Definition 4.3.10. Since elements defined over a finite extension of K are dense in
 $H^0(V_{G_{r(n)}},\mathcal {O}_{\mathcal {X}_{K^pG_{r(n)}}})$
, we may assume
$H^0(V_{G_{r(n)}},\mathcal {O}_{\mathcal {X}_{K^pG_{r(n)}}})$
, we may assume
![]() $x_n,e_{1,n},t_n$
defined over K after enlarging K if necessary. Hence,
$x_n,e_{1,n},t_n$
defined over K after enlarging K if necessary. Hence,
![]() $G_K$
preserves
$G_K$
preserves
![]() $\mathcal {O}^{n}(U)\{x,e_1,t\}$
and it is enough to show that the action of
$\mathcal {O}^{n}(U)\{x,e_1,t\}$
and it is enough to show that the action of
 $\theta _{\mathfrak {h}}(\begin {pmatrix}0 & 0\\ 0 & 1 \end {pmatrix})$
is a Sen operator on
$\theta _{\mathfrak {h}}(\begin {pmatrix}0 & 0\\ 0 & 1 \end {pmatrix})$
is a Sen operator on
![]() $\mathcal {O}^{n}(U)\{x,e_1,t\}$
and is the unique one.
$\mathcal {O}^{n}(U)\{x,e_1,t\}$
and is the unique one.
For simplicity, we write M for
![]() $\mathcal {O}^{n}(U)\{x,e_1,t\}$
, and for any finite extension
$\mathcal {O}^{n}(U)\{x,e_1,t\}$
, and for any finite extension
![]() $K'$
of K, we denote by
$K'$
of K, we denote by
![]() $M_{K'}\subset M$
the subspace of f with all
$M_{K'}\subset M$
the subspace of f with all
 $c^{(n)}_{i,j,k}(f)$
defined over
$c^{(n)}_{i,j,k}(f)$
defined over
![]() $K'$
. It is clear that
$K'$
. It is clear that
One useful fact is
-
•
 $G_{\mathbb {Q}_p}$
acts trivially on x and acts via cyclotomic character on
$G_{\mathbb {Q}_p}$
acts trivially on x and acts via cyclotomic character on
 $e_1,t$
.
$e_1,t$
.
From this, one can check that
![]() $M_{K'}$
is
$M_{K'}$
is
![]() $G_{K'(\mu _{p^\infty })}$
-fixed and
$G_{K'(\mu _{p^\infty })}$
-fixed and
![]() $G_{K'}$
acts analytically on it. Conversely, any such element f of M is contained in
$G_{K'}$
acts analytically on it. Conversely, any such element f of M is contained in
![]() $M_{K'}$
because
$M_{K'}$
because
 $c^{(n)}_{i,j,k}(f)$
can be computed from f using the action of
$c^{(n)}_{i,j,k}(f)$
can be computed from f using the action of
![]() $\mathfrak {g}$
as in Subsection 4.3; hence, is
$\mathfrak {g}$
as in Subsection 4.3; hence, is
![]() $G_{K'}$
-analytic and an argument using Tate’s normalised trace implies that it is in fact fixed by
$G_{K'}$
-analytic and an argument using Tate’s normalised trace implies that it is in fact fixed by
![]() $G_{K'}$
. Now a direct computation (using results in Section 5.1.1) shows that
$G_{K'}$
. Now a direct computation (using results in Section 5.1.1) shows that
 $\theta _{\mathfrak {h}}(\begin {pmatrix}0 & 0\\ 0 & 1 \end {pmatrix})$
agrees with the natural action of
$\theta _{\mathfrak {h}}(\begin {pmatrix}0 & 0\\ 0 & 1 \end {pmatrix})$
agrees with the natural action of
![]() $1\in \mathbb {Q}_p\cong \operatorname {\mathrm {Lie}}(\operatorname {\mathrm {Gal}}(\mathbb {Q}_p(\mu _{p^\infty })/\mathbb {Q}_p))$
on
$1\in \mathbb {Q}_p\cong \operatorname {\mathrm {Lie}}(\operatorname {\mathrm {Gal}}(\mathbb {Q}_p(\mu _{p^\infty })/\mathbb {Q}_p))$
on
![]() $M_{K'}$
. The uniqueness follows from
$M_{K'}$
. The uniqueness follows from
![]() $M\cong M_{K'}\widehat {\otimes }_{K'} C$
.
$M\cong M_{K'}\widehat {\otimes }_{K'} C$
.
Theorem 5.1.11.
 $\theta _{\mathfrak {h}}(\begin {pmatrix}0 & 0\\ 0 & 1 \end {pmatrix})$
is the unique Sen operator on
$\theta _{\mathfrak {h}}(\begin {pmatrix}0 & 0\\ 0 & 1 \end {pmatrix})$
is the unique Sen operator on
 $H^i({\mathscr {F}\!\ell },\mathcal {O}_{K^p}^{\mathrm {la}})=\tilde {H}^i(K^p,C)^{\mathrm {la}}$
for any i.
$H^i({\mathscr {F}\!\ell },\mathcal {O}_{K^p}^{\mathrm {la}})=\tilde {H}^i(K^p,C)^{\mathrm {la}}$
for any i.
5.1.12. The case
![]() $i=0$
follows from Theorem 5.1.8. So it suffices to prove the case
$i=0$
follows from Theorem 5.1.8. So it suffices to prove the case
![]() $i=1$
. We introduce some notation first.
$i=1$
. We introduce some notation first.
We have shown in the proof of Theorem 4.4.6 that
 $H^i({\mathscr {F}\!\ell },\mathcal {O}^{\mathrm {la}}_{K^p})$
can be computed by Čech cohomology using a finite cover of
$H^i({\mathscr {F}\!\ell },\mathcal {O}^{\mathrm {la}}_{K^p})$
can be computed by Čech cohomology using a finite cover of
![]() ${\mathscr {F}\!\ell }$
in
${\mathscr {F}\!\ell }$
in
![]() $\mathfrak {B}$
. In particular, we can use the cover
$\mathfrak {B}$
. In particular, we can use the cover
![]() $\{U_1,U_2\}$
, where
$\{U_1,U_2\}$
, where
![]() $U_1$
(respectively
$U_1$
(respectively
![]() $U_2$
) is the subset
$U_2$
) is the subset
![]() $|x|\leq 1$
(respectively
$|x|\leq 1$
(respectively
![]() $|x|\geq 1$
). See Theorem 4.1.7. Denote by
$|x|\geq 1$
). See Theorem 4.1.7. Denote by
![]() $U_{12}=U_1\cap U_2$
. Then
$U_{12}=U_1\cap U_2$
. Then
 $$ \begin{align*}\mathcal{O}_{K^p}^{\mathrm{la}}(U_1)\oplus \mathcal{O}_{K^p}^{\mathrm{la}}(U_2)\to \mathcal{O}_{K^p}^{\mathrm{la}}(U_{12})\end{align*} $$
$$ \begin{align*}\mathcal{O}_{K^p}^{\mathrm{la}}(U_1)\oplus \mathcal{O}_{K^p}^{\mathrm{la}}(U_2)\to \mathcal{O}_{K^p}^{\mathrm{la}}(U_{12})\end{align*} $$
computes
 $H^i({\mathscr {F}\!\ell },\mathcal {O}_{K^p}^{\mathrm {la}})$
. Denote by
$H^i({\mathscr {F}\!\ell },\mathcal {O}_{K^p}^{\mathrm {la}})$
. Denote by
 $V_?=\pi _{\mathrm {HT}}^{-1}(U_?)$
with
$V_?=\pi _{\mathrm {HT}}^{-1}(U_?)$
with
![]() $?=1,2,12$
. Fix an open subgroup
$?=1,2,12$
. Fix an open subgroup
![]() $G_0=1+p^lM_2(\mathbb {Z}_p)$
for some sufficiently large
$G_0=1+p^lM_2(\mathbb {Z}_p)$
for some sufficiently large
![]() $l\geq 2$
so that
$l\geq 2$
so that
![]() $V_?$
is the preimage of some affinoid subset
$V_?$
is the preimage of some affinoid subset
![]() $V_{?,G_0}$
of
$V_{?,G_0}$
of
![]() $\mathcal {X}_{K^pG_0}$
. As before, we write
$\mathcal {X}_{K^pG_0}$
. As before, we write
 $G_n=G_0^{p^n}$
. Since
$G_n=G_0^{p^n}$
. Since
![]() $e_1$
is a basis on
$e_1$
is a basis on
![]() $U_1$
, we can find
$U_1$
, we can find
![]() $x_n,e_{1,n},t_n$
as in Section 4.3.5 and define
$x_n,e_{1,n},t_n$
as in Section 4.3.5 and define
![]() $\mathcal {O}^{n}(U_1)\{x,e_1,t\}$
as in Definition 4.3.10. Note that by restricting
$\mathcal {O}^{n}(U_1)\{x,e_1,t\}$
as in Definition 4.3.10. Note that by restricting
![]() $x_n,e_{1,n},t_n$
on
$x_n,e_{1,n},t_n$
on
![]() $U_{12}$
, we can define
$U_{12}$
, we can define
![]() $\mathcal {O}^{n}(U_{12})\{x,e_1,t\}$
similarly with unit ball
$\mathcal {O}^{n}(U_{12})\{x,e_1,t\}$
similarly with unit ball
![]() $\mathcal {O}^{n}(U_{12})^+\{x,e_1,t\}$
. Now
$\mathcal {O}^{n}(U_{12})^+\{x,e_1,t\}$
. Now
![]() $e_1$
is not a basis on
$e_1$
is not a basis on
![]() $U_2$
. So we work with
$U_2$
. So we work with
 $\frac {1}{x},e_2,t$
instead of
$\frac {1}{x},e_2,t$
instead of
![]() $x,e_1,t$
. Write
$x,e_1,t$
. Write
 $y=\frac {1}{x}=\frac {e_1}{e_2}$
. Since the action of
$y=\frac {1}{x}=\frac {e_1}{e_2}$
. Since the action of
 $w=\begin {pmatrix} 0 & 1 \\ 1 & 0\end {pmatrix}$
interchanges
$w=\begin {pmatrix} 0 & 1 \\ 1 & 0\end {pmatrix}$
interchanges
![]() $U_1,U_2$
, we obtain
$U_1,U_2$
, we obtain
![]() $y_n:=w^*x_n,e_{2,n}:=w^*e_{1,n}$
on
$y_n:=w^*x_n,e_{2,n}:=w^*e_{1,n}$
on
![]() $U_2$
. Using
$U_2$
. Using
![]() $y_n,e_{2,n},t_n$
, we can define
$y_n,e_{2,n},t_n$
, we can define
 $\mathcal {O}^{n}(U_2)\{y,e_2,t\}\subset \mathcal {O}^{\mathrm {la}}_{K^p}(U_2)$
on
$\mathcal {O}^{n}(U_2)\{y,e_2,t\}\subset \mathcal {O}^{\mathrm {la}}_{K^p}(U_2)$
on
![]() $U_2$
.
$U_2$
.
Lemma 5.1.13. For any
![]() $n>2$
, the restriction from
$n>2$
, the restriction from
![]() $U_2$
to
$U_2$
to
![]() $U_{12}$
induces a map
$U_{12}$
induces a map
preserving norms of
![]() $y-y_n$
and
$y-y_n$
and
 $\log (\frac {e_2}{e_{2,n}})$
. See Definition 4.3.10 for the definition of norm
$\log (\frac {e_2}{e_{2,n}})$
. See Definition 4.3.10 for the definition of norm
![]() $\|\cdot \|_n$
.
$\|\cdot \|_n$
.
Proof. On
![]() $U_{12}$
, we have
$U_{12}$
, we have
 $$ \begin{align*}y-y_n=\frac{1}{x}-y_n=\frac{1}{x_n}\cdot\frac{1}{1+\frac{x-x_n}{x_n}}-y_n=(\frac{1}{x_n}-y_n)-\sum_{i\geq 1}\frac{1}{(-x_n)^{i+1}}(x-x_n)^i.\end{align*} $$
$$ \begin{align*}y-y_n=\frac{1}{x}-y_n=\frac{1}{x_n}\cdot\frac{1}{1+\frac{x-x_n}{x_n}}-y_n=(\frac{1}{x_n}-y_n)-\sum_{i\geq 1}\frac{1}{(-x_n)^{i+1}}(x-x_n)^i.\end{align*} $$
Since
![]() $\|x_n\|=\|x\|=1$
and
$\|x_n\|=\|x\|=1$
and
 $\frac {1}{x_n}-y_n=(\frac {1}{x_n}-\frac {1}{x})+(y-y_n)$
has norm
$\frac {1}{x_n}-y_n=(\frac {1}{x_n}-\frac {1}{x})+(y-y_n)$
has norm
![]() $\leq p^{-n}$
on
$\leq p^{-n}$
on
![]() $U_{12}$
; hence,
$U_{12}$
; hence,
 $$ \begin{align*}p^{-(n-1)}(y-y_n)\in -\frac{1}{x_n^2}p^{-(n-1)}(x-x_n)+ p\mathcal{O}^{n}(U_{12})^+\{x,e_1,t\}.\end{align*} $$
$$ \begin{align*}p^{-(n-1)}(y-y_n)\in -\frac{1}{x_n^2}p^{-(n-1)}(x-x_n)+ p\mathcal{O}^{n}(U_{12})^+\{x,e_1,t\}.\end{align*} $$
The claim for
 $\log (\frac {e_2}{e_{2,n}})$
can be proved in a similar way.
$\log (\frac {e_2}{e_{2,n}})$
can be proved in a similar way.
Proof of Theorem 5.1.11
Fix an integer
![]() $m>2$
. Recall that
$m>2$
. Recall that
![]() $\tilde {H}^1(K^p,C)= \operatorname {\mathrm {coker}}(\mathcal {O}_{K^p}(U_1)\oplus \mathcal {O}_{K^p}(U_2)\to \mathcal {O}_{K^p}(U_{12}))$
. By Proposition 4.3.15 and Corollary 2.2.4, all of the terms in the following exact sequence
$\tilde {H}^1(K^p,C)= \operatorname {\mathrm {coker}}(\mathcal {O}_{K^p}(U_1)\oplus \mathcal {O}_{K^p}(U_2)\to \mathcal {O}_{K^p}(U_{12}))$
. By Proposition 4.3.15 and Corollary 2.2.4, all of the terms in the following exact sequence
are strongly
![]() $\mathfrak {LA}$
-acyclic with respect to the action of
$\mathfrak {LA}$
-acyclic with respect to the action of
![]() $G_0$
. From this, it is easy to see that there exists an integer
$G_0$
. From this, it is easy to see that there exists an integer
![]() $m'\geq m$
such that
$m'\geq m$
such that
![]() $\tilde {H}^1(K^p,C)^{G_{m}-\mathrm {an}}$
is contained in the image of
$\tilde {H}^1(K^p,C)^{G_{m}-\mathrm {an}}$
is contained in the image of
![]() $\mathcal {O}_{K^p}(U_{12})^{G_{m'}-\mathrm {an}}$
. Then by Theorem 4.3.9, we can find
$\mathcal {O}_{K^p}(U_{12})^{G_{m'}-\mathrm {an}}$
. Then by Theorem 4.3.9, we can find
![]() $n\geq m'$
so that
$n\geq m'$
so that
![]() $\mathcal {O}_{K^p}(U_{12})^{G_{m'}-\mathrm {an}}\subset \mathcal {O}^n(U_{12})\{x,e_1,t\}\subset \mathcal {O}_{K^p}(U_{12})^{G_{r(n)}-\mathrm {an}}$
. As a consequence, the inclusion
$\mathcal {O}_{K^p}(U_{12})^{G_{m'}-\mathrm {an}}\subset \mathcal {O}^n(U_{12})\{x,e_1,t\}\subset \mathcal {O}_{K^p}(U_{12})^{G_{r(n)}-\mathrm {an}}$
. As a consequence, the inclusion
![]() $\tilde {H}^1(K^p,C)^{G_m-\mathrm {an}}\subset \tilde {H}^1(K^p,C)^{G_{r(n)}-\mathrm {an}}$
factors through the largest separated quotient
$\tilde {H}^1(K^p,C)^{G_m-\mathrm {an}}\subset \tilde {H}^1(K^p,C)^{G_{r(n)}-\mathrm {an}}$
factors through the largest separated quotient
![]() $M^n$
of
$M^n$
of
(using the quotient topology on the cokernel). It suffices to show that
 $\theta _{\mathfrak {h}}(\begin {pmatrix} 0 & 0 \\ 0 & 1 \end {pmatrix})$
acts as the unique Sen operator on
$\theta _{\mathfrak {h}}(\begin {pmatrix} 0 & 0 \\ 0 & 1 \end {pmatrix})$
acts as the unique Sen operator on
![]() $M^n$
.
$M^n$
.
Now let K be a finite extension of
![]() $\mathbb {Q}_p$
so that
$\mathbb {Q}_p$
so that
![]() $V_{1,G_0},x_n,e_{1,n},t_n$
are all defined over K. Denote by
$V_{1,G_0},x_n,e_{1,n},t_n$
are all defined over K. Denote by
![]() $M_1\subset \mathcal {O}^{n}(U_{1})\{x,e_1,t\}$
the subspace of
$M_1\subset \mathcal {O}^{n}(U_{1})\{x,e_1,t\}$
the subspace of
![]() $G_{K(\mu _{p^\infty })}$
-fixed,
$G_{K(\mu _{p^\infty })}$
-fixed,
![]() $G_{K}$
-analytic vectors. This is a K-Banach algebra with norm
$G_{K}$
-analytic vectors. This is a K-Banach algebra with norm
![]() $\|\cdot \|_n$
, and we denote its unit ball by
$\|\cdot \|_n$
, and we denote its unit ball by
![]() $M_1^o$
. Similarly, we can define
$M_1^o$
. Similarly, we can define
![]() $M_2\subset \mathcal {O}^{n}(U_{2})\{y,e_2,t\}$
and
$M_2\subset \mathcal {O}^{n}(U_{2})\{y,e_2,t\}$
and
![]() $M_{12}\subset \mathcal {O}^{n}(U_{12})\{x,e_1,t\}$
and their unit balls
$M_{12}\subset \mathcal {O}^{n}(U_{12})\{x,e_1,t\}$
and their unit balls
![]() $M^o_2,M^o_{12}$
. Then as in the proof of Theorem 5.1.8, we have
$M^o_2,M^o_{12}$
. Then as in the proof of Theorem 5.1.8, we have
 $M^o_1\widehat \otimes _{\mathcal {O}_K} C\cong \mathcal {O}^{n}(U_{1})\{x,e_1,t\}$
, and similar results hold for
$M^o_1\widehat \otimes _{\mathcal {O}_K} C\cong \mathcal {O}^{n}(U_{1})\{x,e_1,t\}$
, and similar results hold for
![]() $M_{12}$
and
$M_{12}$
and
![]() $M_2$
. The previous lemma implies that
$M_2$
. The previous lemma implies that
 $\mathcal {O}_{K^p}^{\mathrm {la}}(U_1)\oplus \mathcal {O}_{K^p}^{\mathrm {la}}(U_2)\to \mathcal {O}_{K^p}^{\mathrm {la}}(U_{12})$
has a subcomplex
$\mathcal {O}_{K^p}^{\mathrm {la}}(U_1)\oplus \mathcal {O}_{K^p}^{\mathrm {la}}(U_2)\to \mathcal {O}_{K^p}^{\mathrm {la}}(U_{12})$
has a subcomplex
![]() $M_1^o\oplus M_2^o\to M_{12}^o$
. Moreover, let
$M_1^o\oplus M_2^o\to M_{12}^o$
. Moreover, let
![]() $M^o$
be the quotient of
$M^o$
be the quotient of
![]() $\operatorname {\mathrm {coker}}(M_1^o\oplus M_2^o\to M_{12}^o)$
by its torsion subgroup. Then
$\operatorname {\mathrm {coker}}(M_1^o\oplus M_2^o\to M_{12}^o)$
by its torsion subgroup. Then
and
![]() $M=M^o\otimes _{\mathbb {Z}_p} \mathbb {Q}_p$
is the subspace of
$M=M^o\otimes _{\mathbb {Z}_p} \mathbb {Q}_p$
is the subspace of
![]() $G_{K(\mu _{p^\infty })}$
-fixed
$G_{K(\mu _{p^\infty })}$
-fixed
![]() $G_K$
-analytic vectors in
$G_K$
-analytic vectors in
![]() $M^n$
. As in the proof of Theorem 5.1.8, we know that
$M^n$
. As in the proof of Theorem 5.1.8, we know that
 $\theta _{\mathfrak {h}}(\begin {pmatrix} 0 & 0 \\ 0 & 1 \end {pmatrix})$
agrees with
$\theta _{\mathfrak {h}}(\begin {pmatrix} 0 & 0 \\ 0 & 1 \end {pmatrix})$
agrees with
![]() $1\in \operatorname {\mathrm {Lie}}(\operatorname {\mathrm {Gal}}(\mathbb {Q}_p(\mu _{p^\infty })/\mathbb {Q}_p))$
on
$1\in \operatorname {\mathrm {Lie}}(\operatorname {\mathrm {Gal}}(\mathbb {Q}_p(\mu _{p^\infty })/\mathbb {Q}_p))$
on
![]() $M_{12}$
and hence also agrees on its quotient M. This verifies our definition of Sen operator.
$M_{12}$
and hence also agrees on its quotient M. This verifies our definition of Sen operator.
Remark 5.1.14. It can be proved by explicit calculations that
![]() $\operatorname {\mathrm {coker}}(M_1^o\oplus M_2^o\to M_{12}^o)$
is already torsion-free, so taking the largest separated quotient is in fact unnecessary.
$\operatorname {\mathrm {coker}}(M_1^o\oplus M_2^o\to M_{12}^o)$
is already torsion-free, so taking the largest separated quotient is in fact unnecessary.
Remark 5.1.15. It is clear from the proof that there is a close relation between two analytic aspects of the completed cohomology: one comes from the group action of
![]() $\mathrm {GL}_2(\mathbb {Q}_p)$
, and one comes from the Galois action of
$\mathrm {GL}_2(\mathbb {Q}_p)$
, and one comes from the Galois action of
![]() $G_{\mathbb {Q}_p}$
. Also, Theorem 5.1.11 implies that the two infinitesimal characters are closely related. Both are actually deep theorems in the p-adic local Langlands for
$G_{\mathbb {Q}_p}$
. Also, Theorem 5.1.11 implies that the two infinitesimal characters are closely related. Both are actually deep theorems in the p-adic local Langlands for
![]() $\mathrm {GL}_2(\mathbb {Q}_p)$
. See Théorème V.3 of [Reference Colmez and DospinescuCD14] and Théorème 1.2 of [Reference DospinescuDos12].
$\mathrm {GL}_2(\mathbb {Q}_p)$
. See Théorème V.3 of [Reference Colmez and DospinescuCD14] and Théorème 1.2 of [Reference DospinescuDos12].
Remark 5.1.16. It is natural to ask whether we can show the existence of the Sen operator on
![]() $\tilde {H}^i(K^p,C)^{\mathrm {la}}$
in a more direct way. The answer is affirmative. We sketch a construction here based on the Tate–Sen formalism of Berger–Colmez [Reference Berger and ColmezBC08]. Let
$\tilde {H}^i(K^p,C)^{\mathrm {la}}$
in a more direct way. The answer is affirmative. We sketch a construction here based on the Tate–Sen formalism of Berger–Colmez [Reference Berger and ColmezBC08]. Let
![]() $G=G_n$
for some n. The key point here is that
$G=G_n$
for some n. The key point here is that
-
• the action of
 $G_{\mathbb {Q}_p}$
on
$G_{\mathbb {Q}_p}$
on
 $\tilde {H}^i(K^p,\mathbb {Q}_p)^{G-\mathrm {an},o}/p$
is trivial on an open subgroup; that is, the image of
$\tilde {H}^i(K^p,\mathbb {Q}_p)^{G-\mathrm {an},o}/p$
is trivial on an open subgroup; that is, the image of
 $G_{\mathbb {Q}_p}\to \operatorname {\mathrm {End}}\left ((\tilde {H}^i(K^p,\mathbb {Q}_p)^{G-\mathrm {an}})^{o}/p\right )$
is finite, where
$G_{\mathbb {Q}_p}\to \operatorname {\mathrm {End}}\left ((\tilde {H}^i(K^p,\mathbb {Q}_p)^{G-\mathrm {an}})^{o}/p\right )$
is finite, where
 $\tilde {H}^i(K^p,\mathbb {Q}_p)^{G-\mathrm {an},o}$
denotes the unit open ball of
$\tilde {H}^i(K^p,\mathbb {Q}_p)^{G-\mathrm {an},o}$
denotes the unit open ball of
 $\tilde {H}^i(K^p,\mathbb {Q}_p)^{G-\mathrm {an}}$
.
$\tilde {H}^i(K^p,\mathbb {Q}_p)^{G-\mathrm {an}}$
.
The argument is almost the same as the proof of [Reference PanPan20, Theorem 6.1]. Let
![]() $W^o$
be the unit open ball of
$W^o$
be the unit open ball of
![]() $\tilde {H}^i(K^p,\mathbb {Q}_p)$
. Then
$\tilde {H}^i(K^p,\mathbb {Q}_p)$
. Then
 $$ \begin{align*} \tilde{H}^i(K^p,\mathbb{Q}_p)^{G-\mathrm{an},o}/p&= \left(W^o\widehat{\otimes}_{\mathbb{Z}_p}\mathscr{C}^{\mathrm{an}}(G_n,\mathbb{Q}_p)^o\right)^{G_n}/p\\ &\subseteq \left(W^o\otimes_{\mathbb{Z}_p}\mathscr{C}^{\mathrm{an}}(G_n,\mathbb{Q}_p)^o/p\right)^{G_n}\\ &\subseteq \left(W^o/pW^o\otimes_{\mathbb{F}_p}\mathscr{C}^{\mathrm{an}}(G_n,\mathbb{Q}_p)^o/p\right)^{G_{n+1}}\\ &= (W^o/pW^o)^{G_{n+1}} \otimes_{\mathbb{F}_p}\mathscr{C}^{\mathrm{an}}(G_n,\mathbb{Q}_p)^o/p, \end{align*} $$
$$ \begin{align*} \tilde{H}^i(K^p,\mathbb{Q}_p)^{G-\mathrm{an},o}/p&= \left(W^o\widehat{\otimes}_{\mathbb{Z}_p}\mathscr{C}^{\mathrm{an}}(G_n,\mathbb{Q}_p)^o\right)^{G_n}/p\\ &\subseteq \left(W^o\otimes_{\mathbb{Z}_p}\mathscr{C}^{\mathrm{an}}(G_n,\mathbb{Q}_p)^o/p\right)^{G_n}\\ &\subseteq \left(W^o/pW^o\otimes_{\mathbb{F}_p}\mathscr{C}^{\mathrm{an}}(G_n,\mathbb{Q}_p)^o/p\right)^{G_{n+1}}\\ &= (W^o/pW^o)^{G_{n+1}} \otimes_{\mathbb{F}_p}\mathscr{C}^{\mathrm{an}}(G_n,\mathbb{Q}_p)^o/p, \end{align*} $$
where the last equality follows from Lemma 2.1.2. All maps are
![]() $G_{\mathbb {Q}_p}$
-equivariant. Note that
$G_{\mathbb {Q}_p}$
-equivariant. Note that
![]() $(W^o/pW^o)^{G_{n+1}}$
is a finite-dimensional
$(W^o/pW^o)^{G_{n+1}}$
is a finite-dimensional
![]() $\mathbb {F}_p$
-vector space by the admissibility of the completed cohomology. Hence, the action of
$\mathbb {F}_p$
-vector space by the admissibility of the completed cohomology. Hence, the action of
![]() $G_{\mathbb {Q}_p}$
on
$G_{\mathbb {Q}_p}$
on
![]() $\tilde {H}^i(K^p,\mathbb {Q}_p)^{G-\mathrm {an},o}/p$
necessarily factors through a finite quotient of
$\tilde {H}^i(K^p,\mathbb {Q}_p)^{G-\mathrm {an},o}/p$
necessarily factors through a finite quotient of
![]() $G_{\mathbb {Q}_p}$
.
$G_{\mathbb {Q}_p}$
.
Now we can apply Proposition 3.3.1 of [Reference Berger and ColmezBC08] (with
![]() $G_0=G_{\mathbb {Q}_p}, H_0=G_{\mathbb {Q}_p(\mu _{p^\infty })}$
) to obtain the Sen operator on
$G_0=G_{\mathbb {Q}_p}, H_0=G_{\mathbb {Q}_p(\mu _{p^\infty })}$
) to obtain the Sen operator on
 $\tilde {H}^i(K^p,\mathbb {Q}_p)^{G-\mathrm {an}}\widehat \otimes _{\mathbb {Q}_p}C$
except that
$\tilde {H}^i(K^p,\mathbb {Q}_p)^{G-\mathrm {an}}\widehat \otimes _{\mathbb {Q}_p}C$
except that
![]() $\tilde {H}^i(K^p,\mathbb {Q}_p)^{G-\mathrm {an}}$
is not finite-dimensional. To get around this, one can argue in a similar way to Section 3.3.1 by finding a dense subspace of
$\tilde {H}^i(K^p,\mathbb {Q}_p)^{G-\mathrm {an}}$
is not finite-dimensional. To get around this, one can argue in a similar way to Section 3.3.1 by finding a dense subspace of
![]() $\tilde {H}^i(K^p,\mathbb {Q}_p)^{G-\mathrm {an}}$
which can be written as a union of finite-dimensional
$\tilde {H}^i(K^p,\mathbb {Q}_p)^{G-\mathrm {an}}$
which can be written as a union of finite-dimensional
![]() $G_{\mathbb {Q}_p}$
-invariant subspaces. For example, one can take the subspace of
$G_{\mathbb {Q}_p}$
-invariant subspaces. For example, one can take the subspace of
![]() $\mathrm {GL}_2(\mathbb {Z}_p)$
-algebraic vectors. Indeed, the density is clear when
$\mathrm {GL}_2(\mathbb {Z}_p)$
-algebraic vectors. Indeed, the density is clear when
![]() $i=0$
. When
$i=0$
. When
![]() $i=1$
, the proof of Lemma 6.3.8 implies that
$i=1$
, the proof of Lemma 6.3.8 implies that
![]() $\mathrm {GL}_2(\mathbb {Z}_p)$
-algebraic vectors are dense in
$\mathrm {GL}_2(\mathbb {Z}_p)$
-algebraic vectors are dense in
![]() $\tilde {H}^i(K^p,\mathbb {Q}_p)$
and hence also dense in
$\tilde {H}^i(K^p,\mathbb {Q}_p)$
and hence also dense in
![]() $\tilde {H}^i(K^p,\mathbb {Q}_p)^{G-\mathrm {an}}$
. Therefore, one gets the desired unique Sen operator on
$\tilde {H}^i(K^p,\mathbb {Q}_p)^{G-\mathrm {an}}$
. Therefore, one gets the desired unique Sen operator on
 $\tilde {H}^i(K^p,\mathbb {Q}_p)^{G-\mathrm {an}}\widehat \otimes _{\mathbb {Q}_p}C$
. This defines the Sen operator on
$\tilde {H}^i(K^p,\mathbb {Q}_p)^{G-\mathrm {an}}\widehat \otimes _{\mathbb {Q}_p}C$
. This defines the Sen operator on
 $$ \begin{align*}\varinjlim_n\left(\tilde{H}^i(K^p,\mathbb{Q}_p)^{G_n-\mathrm{an}}\widehat\otimes_{\mathbb{Q}_p}C\right)\cong \tilde{H}^i(K^p,C)^{\mathrm{la}}.\end{align*} $$
$$ \begin{align*}\varinjlim_n\left(\tilde{H}^i(K^p,\mathbb{Q}_p)^{G_n-\mathrm{an}}\widehat\otimes_{\mathbb{Q}_p}C\right)\cong \tilde{H}^i(K^p,C)^{\mathrm{la}}.\end{align*} $$
To see this isomorphism as LB-spaces, we claim that
 $\varinjlim _n \left (W^{G_n-\mathrm {an}}\widehat \otimes _{\mathbb {Q}_p}C\right )\cong (W\widehat \otimes _{\mathbb {Q}_p}C)^{\mathrm {la}}$
for any admissible
$\varinjlim _n \left (W^{G_n-\mathrm {an}}\widehat \otimes _{\mathbb {Q}_p}C\right )\cong (W\widehat \otimes _{\mathbb {Q}_p}C)^{\mathrm {la}}$
for any admissible
![]() $\mathbb {Q}_p$
-Banach representation W of
$\mathbb {Q}_p$
-Banach representation W of
![]() $G_0$
. This is clear for
$G_0$
. This is clear for
![]() $W=\mathscr {C}(G_0,\mathbb {Q}_p)$
because we even have
$W=\mathscr {C}(G_0,\mathbb {Q}_p)$
because we even have
 $(W\widehat \otimes _{\mathbb {Q}_p}C)^{G_n-\mathrm {an}}\cong W^{G_n-\mathrm {an}}\widehat \otimes _{\mathbb {Q}_p}C$
in this case. The general case can be proved by embedding W into
$(W\widehat \otimes _{\mathbb {Q}_p}C)^{G_n-\mathrm {an}}\cong W^{G_n-\mathrm {an}}\widehat \otimes _{\mathbb {Q}_p}C$
in this case. The general case can be proved by embedding W into
![]() $\mathscr {C}(G_0,\mathbb {Q}_p)^{\oplus d}$
for some d and applying the acyclicity result Corollary 2.2.4. We omit the details here.
$\mathscr {C}(G_0,\mathbb {Q}_p)^{\oplus d}$
for some d and applying the acyclicity result Corollary 2.2.4. We omit the details here.
5.2
 $\mathfrak {n}$
-cohomology (I)
$\mathfrak {n}$
-cohomology (I)
5.2.1. We start to compute the
![]() $\mathfrak {n}$
-cohomology of
$\mathfrak {n}$
-cohomology of
 $H^1({\mathscr {F}\!\ell },\mathcal {O}_{K^p}^{\mathrm {la},\chi })$
. Since
$H^1({\mathscr {F}\!\ell },\mathcal {O}_{K^p}^{\mathrm {la},\chi })$
. Since
![]() $\mathfrak {n}$
is 1-dimensional,
$\mathfrak {n}$
is 1-dimensional,
![]() $H^0(\mathfrak {n},\bullet )$
(respectively
$H^0(\mathfrak {n},\bullet )$
(respectively
![]() $H^1(\mathfrak {n},\bullet )$
) are the
$H^1(\mathfrak {n},\bullet )$
) are the
![]() $\mathfrak {n}$
-invariants (respectively
$\mathfrak {n}$
-invariants (respectively
![]() $\mathfrak {n}$
-coinvariants). Denote by
$\mathfrak {n}$
-coinvariants). Denote by
 $\mathcal {O}_{K^p}^{\mathrm {la},\chi ,\mathfrak {n}}$
(respectively
$\mathcal {O}_{K^p}^{\mathrm {la},\chi ,\mathfrak {n}}$
(respectively
 $(\mathcal {O}_{K^p}^{\mathrm {la},\chi })_{\mathfrak {n}}$
) the
$(\mathcal {O}_{K^p}^{\mathrm {la},\chi })_{\mathfrak {n}}$
) the
![]() $\mathfrak {n}$
-invariants (respectively
$\mathfrak {n}$
-invariants (respectively
![]() $\mathfrak {n}$
-coinvariants) of
$\mathfrak {n}$
-coinvariants) of
 $\mathcal {O}_{K^p}^{\mathrm {la},\chi }$
. For the purpose of introduction, we assume
$\mathcal {O}_{K^p}^{\mathrm {la},\chi }$
. For the purpose of introduction, we assume
![]() $\chi (h)\neq 0$
. Then
$\chi (h)\neq 0$
. Then
 $H^0({\mathscr {F}\!\ell },\mathcal {O}^{\mathrm {la},\chi }_{K^p})=0$
and we have B-equivariant mapsFootnote
3
$H^0({\mathscr {F}\!\ell },\mathcal {O}^{\mathrm {la},\chi }_{K^p})=0$
and we have B-equivariant mapsFootnote
3
 $$ \begin{align} 0\to H^1({\mathscr{F}\!\ell},\mathcal{O}_{K^p}^{\mathrm{la},\chi,\mathfrak{n}})\to H^1({\mathscr{F}\!\ell},\mathcal{O}_{K^p}^{\mathrm{la},\chi})^{\mathfrak{n}}&\to H^0({\mathscr{F}\!\ell},(\mathcal{O}_{K^p}^{\mathrm{la},\chi})_{\mathfrak{n}})\otimes_{C} \mathfrak{n}^*\to 0, \end{align} $$
$$ \begin{align} 0\to H^1({\mathscr{F}\!\ell},\mathcal{O}_{K^p}^{\mathrm{la},\chi,\mathfrak{n}})\to H^1({\mathscr{F}\!\ell},\mathcal{O}_{K^p}^{\mathrm{la},\chi})^{\mathfrak{n}}&\to H^0({\mathscr{F}\!\ell},(\mathcal{O}_{K^p}^{\mathrm{la},\chi})_{\mathfrak{n}})\otimes_{C} \mathfrak{n}^*\to 0, \end{align} $$
 $$ \begin{align} H^1({\mathscr{F}\!\ell},\mathcal{O}_{K^p}^{\mathrm{la},\chi})_{\mathfrak{n}}&\cong H^1({\mathscr{F}\!\ell},(\mathcal{O}_{K^p}^{\mathrm{la},\chi})_{\mathfrak{n}}). \end{align} $$
$$ \begin{align} H^1({\mathscr{F}\!\ell},\mathcal{O}_{K^p}^{\mathrm{la},\chi})_{\mathfrak{n}}&\cong H^1({\mathscr{F}\!\ell},(\mathcal{O}_{K^p}^{\mathrm{la},\chi})_{\mathfrak{n}}). \end{align} $$
Here
![]() $\mathfrak {n}^*=\operatorname {\mathrm {Hom}}_C(\mathfrak {n},C)$
. We will compute
$\mathfrak {n}^*=\operatorname {\mathrm {Hom}}_C(\mathfrak {n},C)$
. We will compute
 $\mathcal {O}_{K^p}^{\mathrm {la},\chi ,\mathfrak {n}},(\mathcal {O}_{K^p}^{\mathrm {la},\chi })_{\mathfrak {n}}$
in this subsection.
$\mathcal {O}_{K^p}^{\mathrm {la},\chi ,\mathfrak {n}},(\mathcal {O}_{K^p}^{\mathrm {la},\chi })_{\mathfrak {n}}$
in this subsection.
5.2.2. For a weight
![]() $\chi $
, we write
$\chi $
, we write
 $\chi (\begin {pmatrix} a & 0\\ 0 & d \end {pmatrix}) =n_1a+n_2d$
for some
$\chi (\begin {pmatrix} a & 0\\ 0 & d \end {pmatrix}) =n_1a+n_2d$
for some
![]() $n_1,n_2\in C$
and sometimes identify
$n_1,n_2\in C$
and sometimes identify
![]() $\chi $
with an ordered pair
$\chi $
with an ordered pair
![]() $(n_1,n_2)\in C^2$
.
$(n_1,n_2)\in C^2$
.
First we compute
 $(\mathcal {O}_{K^p}^{\mathrm {la},\chi })_{\mathfrak {n}}$
. It turns out that for generic
$(\mathcal {O}_{K^p}^{\mathrm {la},\chi })_{\mathfrak {n}}$
. It turns out that for generic
![]() $\chi $
, this is essentially the space of overconvergent modular forms. We need some notation here. Let
$\chi $
, this is essentially the space of overconvergent modular forms. We need some notation here. Let
![]() $\infty \in {\mathscr {F}\!\ell }$
be the point where
$\infty \in {\mathscr {F}\!\ell }$
be the point where
![]() $e_1$
vanishes. We can consider the fibre of
$e_1$
vanishes. We can consider the fibre of
 $\mathcal {O}_{K^p}^{\mathrm {la},\chi }$
at
$\mathcal {O}_{K^p}^{\mathrm {la},\chi }$
at
![]() $\infty $
(as a sheaf of
$\infty $
(as a sheaf of
![]() $\mathcal {O}_{{\mathscr {F}\!\ell }}$
-modules); that is,
$\mathcal {O}_{{\mathscr {F}\!\ell }}$
-modules); that is,
 $\mathcal {O}_{K^p}^{\mathrm {la},\chi }/\mathfrak {m}_{\infty }\mathcal {O}_{K^p}^{\mathrm {la},\chi }$
. Here
$\mathcal {O}_{K^p}^{\mathrm {la},\chi }/\mathfrak {m}_{\infty }\mathcal {O}_{K^p}^{\mathrm {la},\chi }$
. Here
![]() $\mathfrak {m}_{\infty }$
denotes the ideal sheaf defined by
$\mathfrak {m}_{\infty }$
denotes the ideal sheaf defined by
![]() $\infty $
.
$\infty $
.
Definition 5.2.3. For a weight
![]() $\chi $
, we define
$\chi $
, we define
 $$ \begin{align*}M_\chi^{\dagger}(K^p):=H^0({\mathscr{F}\!\ell},\mathcal{O}_{K^p}^{\mathrm{la},\chi}/\mathfrak{m}_{\infty}\mathcal{O}_{K^p}^{\mathrm{la},\chi}),\end{align*} $$
$$ \begin{align*}M_\chi^{\dagger}(K^p):=H^0({\mathscr{F}\!\ell},\mathcal{O}_{K^p}^{\mathrm{la},\chi}/\mathfrak{m}_{\infty}\mathcal{O}_{K^p}^{\mathrm{la},\chi}),\end{align*} $$
the fibre of
 $\mathcal {O}_{K^p}^{\mathrm {la},\chi }$
at
$\mathcal {O}_{K^p}^{\mathrm {la},\chi }$
at
![]() $\infty $
, and call it the space of overconvergent modular forms of weight
$\infty $
, and call it the space of overconvergent modular forms of weight
![]() $\chi $
of tame level
$\chi $
of tame level
![]() $K^p$
. There are natural actions of
$K^p$
. There are natural actions of
![]() $G_{\mathbb {Q}_p}$
, the Borel subgroup B and Hecke operators away from p on this space.
$G_{\mathbb {Q}_p}$
, the Borel subgroup B and Hecke operators away from p on this space.
5.2.4. To justify its name, we can compare this definition with other existing definitions of overconvergent modular forms in the literature [Reference KatzKat73, Reference Coleman and MazurCM98, Reference PilloniPil13, Reference Andreatta, Iovita and StevensAIS14, Reference Chojecki, Hansen and JohanssonCHJ17]. We will only focus on integral weights to illustrate the main difference here.
Let k be an integer. We first introduce overconvergent modular forms with full level at p. Let
![]() $\Gamma (p^n)=1+p^nM_2(\mathbb {Z}_p)$
. We define the canonical locus
$\Gamma (p^n)=1+p^nM_2(\mathbb {Z}_p)$
. We define the canonical locus
![]() $\mathcal {X}_{K^p\Gamma (p^n),c}\subset \mathcal {X}_{K^p\Gamma (p^n)}$
as follows: using the integral model and the index of Igusa components in Theorem 13.7.6 of [Reference Katz and MazurKM85],
$\mathcal {X}_{K^p\Gamma (p^n),c}\subset \mathcal {X}_{K^p\Gamma (p^n)}$
as follows: using the integral model and the index of Igusa components in Theorem 13.7.6 of [Reference Katz and MazurKM85],
![]() $\mathcal {X}_{K^p\Gamma (p^n),c}$
is the tubular neighbourhood of the nonsingular points (
$\mathcal {X}_{K^p\Gamma (p^n),c}$
is the tubular neighbourhood of the nonsingular points (
![]() $=$
non-supersingular points) of irreducible components of indices
$=$
non-supersingular points) of irreducible components of indices
![]() $(\mathbb {Z}/p^n)^{2}\to \mathbb {Z}/p^n,~(1,0)\mapsto 0$
. Equivalently, on the ordinary locus of these irreducible components, the canonical subgroup (of level n) corresponds to
$(\mathbb {Z}/p^n)^{2}\to \mathbb {Z}/p^n,~(1,0)\mapsto 0$
. Equivalently, on the ordinary locus of these irreducible components, the canonical subgroup (of level n) corresponds to
![]() $(*,0)\subset (\mathbb {Z}/p^n)^2$
under the level structure. Sections of
$(*,0)\subset (\mathbb {Z}/p^n)^2$
under the level structure. Sections of
![]() $\omega ^k$
on any strict neighbourhood of
$\omega ^k$
on any strict neighbourhood of
![]() $\mathcal {X}_{K^p\Gamma (p^n),c}$
are called overconvergent modular forms of weight k of level
$\mathcal {X}_{K^p\Gamma (p^n),c}$
are called overconvergent modular forms of weight k of level
![]() $K^p\Gamma (p^n)$
, which we denote by
$K^p\Gamma (p^n)$
, which we denote by
 $M_k^{\dagger }(K^p\Gamma (p^n))$
. Here a strict neighbourhood of
$M_k^{\dagger }(K^p\Gamma (p^n))$
. Here a strict neighbourhood of
![]() $\mathcal {X}_{K^p\Gamma (p^n),c}$
means an open set containing the closure
$\mathcal {X}_{K^p\Gamma (p^n),c}$
means an open set containing the closure
 $\bar {\mathcal {X}}_{K^p\Gamma (p^n),c}$
. Clearly,
$\bar {\mathcal {X}}_{K^p\Gamma (p^n),c}$
. Clearly,
 $M_k^{\dagger }(K^p\Gamma (p^n))$
forms a direct system when n varies.
$M_k^{\dagger }(K^p\Gamma (p^n))$
forms a direct system when n varies.
Definition 5.2.5. Let
![]() $k\in \mathbb {Z}$
. We define the space of overconvergent modular forms of weight k of tame level
$k\in \mathbb {Z}$
. We define the space of overconvergent modular forms of weight k of tame level
![]() $K^p$
as
$K^p$
as
 $$ \begin{align*}M^{\dagger}_k(K^p):=\varinjlim_n M_k^{\dagger}(K^p\Gamma(p^n)).\end{align*} $$
$$ \begin{align*}M^{\dagger}_k(K^p):=\varinjlim_n M_k^{\dagger}(K^p\Gamma(p^n)).\end{align*} $$
The Galois group
![]() $G_{\mathbb {Q}_p}$
, Borel subgroup B and Hecke operators away from p act naturally on it.
$G_{\mathbb {Q}_p}$
, Borel subgroup B and Hecke operators away from p act naturally on it.
Recall that classical overconvergent modular forms are defined as follows. Let
 $\Gamma _1(p^n)=\{\begin {pmatrix} a & b \\ c & d \end {pmatrix}\in \mathrm {GL}_2(\mathbb {Z}_p)~|~a-1,d-1,c\in p^n\mathbb {Z}_p\}$
. Then we have the canonical locus
$\Gamma _1(p^n)=\{\begin {pmatrix} a & b \\ c & d \end {pmatrix}\in \mathrm {GL}_2(\mathbb {Z}_p)~|~a-1,d-1,c\in p^n\mathbb {Z}_p\}$
. Then we have the canonical locus
![]() $\mathcal {X}_{K^p\Gamma _1(p^n),c}\subset \mathcal {X}_{K^p\Gamma _1(p^n)}$
, which is defined as the image of
$\mathcal {X}_{K^p\Gamma _1(p^n),c}\subset \mathcal {X}_{K^p\Gamma _1(p^n)}$
, which is defined as the image of
![]() $\mathcal {X}_{K^p\Gamma (p^n),c}$
under the natural map
$\mathcal {X}_{K^p\Gamma (p^n),c}$
under the natural map
![]() $\mathcal {X}_{K^p\Gamma (p^n)}\to \mathcal {X}_{K^p\Gamma _1(p^n)}$
. Using Katz–Mazur’s integral model, this can also be defined as tubular neighbourhood of non-supersingular points of irreducible components whose ordinary points classify ordinary elliptic curves with level structure at p given by the canonical subgroup (of level n). We define
$\mathcal {X}_{K^p\Gamma (p^n)}\to \mathcal {X}_{K^p\Gamma _1(p^n)}$
. Using Katz–Mazur’s integral model, this can also be defined as tubular neighbourhood of non-supersingular points of irreducible components whose ordinary points classify ordinary elliptic curves with level structure at p given by the canonical subgroup (of level n). We define
 $M_k^{\dagger }(K^p\Gamma _1(p^n))$
similarly as sections defined in a strict neighbourhood of
$M_k^{\dagger }(K^p\Gamma _1(p^n))$
similarly as sections defined in a strict neighbourhood of
![]() $\mathcal {X}_{K^p\Gamma _1(p^n),c}$
. Note that this is slightly different from the usual definition as
$\mathcal {X}_{K^p\Gamma _1(p^n),c}$
. Note that this is slightly different from the usual definition as
![]() $\mathcal {X}_{K^p\Gamma _1(p^n)}$
is not connected.
$\mathcal {X}_{K^p\Gamma _1(p^n)}$
is not connected.
We can obtain
 $M^{\dagger }_k(K^p)$
from
$M^{\dagger }_k(K^p)$
from
 $\varinjlim _n M_k^{\dagger }(K^p\Gamma _1(p^n))$
by inverting the action of
$\varinjlim _n M_k^{\dagger }(K^p\Gamma _1(p^n))$
by inverting the action of
 $\begin {pmatrix} p^{-1} & 0 \\ 0 & 1 \end {pmatrix}$
. We can also recover
$\begin {pmatrix} p^{-1} & 0 \\ 0 & 1 \end {pmatrix}$
. We can also recover
 $\varinjlim _n M_k^{\dagger }(K^p\Gamma _1(p^n))$
from
$\varinjlim _n M_k^{\dagger }(K^p\Gamma _1(p^n))$
from
 $M^{\dagger }_k(K^p)$
by taking invariants of
$M^{\dagger }_k(K^p)$
by taking invariants of
 $N_0=\begin {pmatrix} 1 & \mathbb {Z}_p\\ 0 & 1 \end {pmatrix}$
:
$N_0=\begin {pmatrix} 1 & \mathbb {Z}_p\\ 0 & 1 \end {pmatrix}$
:
 $$ \begin{align*}\varinjlim_n M_k^{\dagger}(K^p\Gamma_1(p^n))=M^{\dagger}_k(K^p)^{N_0}.\end{align*} $$
$$ \begin{align*}\varinjlim_n M_k^{\dagger}(K^p\Gamma_1(p^n))=M^{\dagger}_k(K^p)^{N_0}.\end{align*} $$
Proposition 5.2.6. Suppose
 $\chi (\begin {pmatrix} a & 0 \\ 0 & d \end {pmatrix})=n_1a+n_2d$
with
$\chi (\begin {pmatrix} a & 0 \\ 0 & d \end {pmatrix})=n_1a+n_2d$
with
![]() $n_1,n_2\in \mathbb {Z}$
. Let
$n_1,n_2\in \mathbb {Z}$
. Let
![]() $k=\chi (h)=n_1-n_2$
. There is a canonical isomorphism induced by multiplication by
$k=\chi (h)=n_1-n_2$
. There is a canonical isomorphism induced by multiplication by
 $e_2^{-k}t^{n_1}$
:
$e_2^{-k}t^{n_1}$
:
 $$ \begin{align*}\phi_\chi:M^{\dagger}_k(K^p) \xrightarrow{\sim} M_\chi^{\dagger}(K^p)\end{align*} $$
$$ \begin{align*}\phi_\chi:M^{\dagger}_k(K^p) \xrightarrow{\sim} M_\chi^{\dagger}(K^p)\end{align*} $$
satisfying
 $$ \begin{align*}(g_1,g_2)\cdot\phi_{\chi}(f)=\phi_{\chi}\left((g_1,g_2)\cdot f\right)d^{-k}\varepsilon_p(ad)^{n_1}\varepsilon_p(g_2)^{n_1-k},\end{align*} $$
$$ \begin{align*}(g_1,g_2)\cdot\phi_{\chi}(f)=\phi_{\chi}\left((g_1,g_2)\cdot f\right)d^{-k}\varepsilon_p(ad)^{n_1}\varepsilon_p(g_2)^{n_1-k},\end{align*} $$
 $f\in M^{\dagger }_k(K^p),~g_1=\begin {pmatrix} a & b \\ 0 & d \end {pmatrix}\in B,~g_2\in G_{\mathbb {Q}_p}$
. Recall that
$f\in M^{\dagger }_k(K^p),~g_1=\begin {pmatrix} a & b \\ 0 & d \end {pmatrix}\in B,~g_2\in G_{\mathbb {Q}_p}$
. Recall that
![]() $\varepsilon _p:G_{\mathbb {Q}_p}\to \mathbb {Z}_p^{\times }$
is the p-adic cyclotomic character and regarded as a character
$\varepsilon _p:G_{\mathbb {Q}_p}\to \mathbb {Z}_p^{\times }$
is the p-adic cyclotomic character and regarded as a character
![]() $\mathbb {Q}_p^{\times }\to \mathbb {Z}_p^{\times }$
sending x to
$\mathbb {Q}_p^{\times }\to \mathbb {Z}_p^{\times }$
sending x to
![]() $x|x|$
via local class field theory.
$x|x|$
via local class field theory.
Remark 5.2.7. For a
![]() $B\times G_{\mathbb {Q}_p}$
-representation W and integers
$B\times G_{\mathbb {Q}_p}$
-representation W and integers
![]() $i,j,k$
, we write
$i,j,k$
, we write
 $W\cdot e_1^ie_2^jt^k$
to denote the twist of W by the character sending
$W\cdot e_1^ie_2^jt^k$
to denote the twist of W by the character sending
 $(\begin {pmatrix} a & b\\ 0 & d \end {pmatrix},g)\in B\times G_{\mathbb {Q}_p}$
to
$(\begin {pmatrix} a & b\\ 0 & d \end {pmatrix},g)\in B\times G_{\mathbb {Q}_p}$
to
![]() $a^id^j\varepsilon _p(ad)^k\varepsilon _p(g)^{i+j+k}$
. Therefore, we can rewrite the isomorphism in Proposition 5.2.6 as
$a^id^j\varepsilon _p(ad)^k\varepsilon _p(g)^{i+j+k}$
. Therefore, we can rewrite the isomorphism in Proposition 5.2.6 as
 $$ \begin{align*}M^{\dagger}_k(K^p)\cdot e_2^{-k}t^{n_1}\cong M_\chi^{\dagger}(K^p).\end{align*} $$
$$ \begin{align*}M^{\dagger}_k(K^p)\cdot e_2^{-k}t^{n_1}\cong M_\chi^{\dagger}(K^p).\end{align*} $$
Proof. For any
![]() $U\in \mathfrak {B}$
, a neighbourhood of
$U\in \mathfrak {B}$
, a neighbourhood of
![]() $\infty $
not containing the zero of x, since
$\infty $
not containing the zero of x, since
![]() $e_1$
is not a basis now, as in Section 5.1.12, we can use
$e_1$
is not a basis now, as in Section 5.1.12, we can use
![]() $e_2$
instead. More precisely, let
$e_2$
instead. More precisely, let
 $y=\frac {1}{x}=\frac {e_1}{e_2}$
. We can find
$y=\frac {1}{x}=\frac {e_1}{e_2}$
. We can find
![]() $y_n,e_{2,n},t_n$
as in Section 4.3.5 and define
$y_n,e_{2,n},t_n$
as in Section 4.3.5 and define
![]() $\mathcal {O}^n(U)\{y,e_2,t\}$
. Denote by
$\mathcal {O}^n(U)\{y,e_2,t\}$
. Denote by
![]() $\mathcal {O}^n(U)\{y\}\subset \mathcal {O}^n(U)\{y,e_2,t\}$
the subset on which
$\mathcal {O}^n(U)\{y\}\subset \mathcal {O}^n(U)\{y,e_2,t\}$
the subset on which
![]() $\theta _{\mathfrak {h}}$
acts by zero. Then
$\theta _{\mathfrak {h}}$
acts by zero. Then
 $\mathcal {O}^{\mathrm {la},\chi }_{K^p}(U)=\varinjlim _n \mathcal {O}^n(U)\{y\}\cdot {t}^{n_1}(\frac {e_2}{e_{2,n}})^{n_2-n_1}$
. Equivalently, as in Lemma 5.1.2, any element in
$\mathcal {O}^{\mathrm {la},\chi }_{K^p}(U)=\varinjlim _n \mathcal {O}^n(U)\{y\}\cdot {t}^{n_1}(\frac {e_2}{e_{2,n}})^{n_2-n_1}$
. Equivalently, as in Lemma 5.1.2, any element in
 $\mathcal {O}^n(U)\{y\}\cdot {t}^{n_1}(\frac {e_2}{e_{2,n}})^{n_2-n_1}$
can be written as
$\mathcal {O}^n(U)\{y\}\cdot {t}^{n_1}(\frac {e_2}{e_{2,n}})^{n_2-n_1}$
can be written as
 $$ \begin{align*}{t}^{n_1}(\frac{e_2}{e_{2,n}})^{n_2-n_1}\sum_{i\geq0} c_i (y-y_n)^i, \end{align*} $$
$$ \begin{align*}{t}^{n_1}(\frac{e_2}{e_{2,n}})^{n_2-n_1}\sum_{i\geq0} c_i (y-y_n)^i, \end{align*} $$
where
 $c_i\in H^0(V_{G_{r(n)}},\mathcal {O}_{\mathcal {X}_{K^pG_{r(n)}}})$
with bound
$c_i\in H^0(V_{G_{r(n)}},\mathcal {O}_{\mathcal {X}_{K^pG_{r(n)}}})$
with bound
![]() $\|c_i\|\leq C'p^{(n-1)i}$
for a uniform
$\|c_i\|\leq C'p^{(n-1)i}$
for a uniform
![]() $C'$
. There is no need to put
$C'$
. There is no need to put
![]() $t_n^{n_1}$
here because
$t_n^{n_1}$
here because
![]() $n_1$
is an integer.
$n_1$
is an integer.
We can take
![]() $G_{r(n)}$
to be some
$G_{r(n)}$
to be some
![]() $\Gamma (p^m)$
. We claim
$\Gamma (p^m)$
. We claim
-
•
 $V_{G_{r(n)}}$
is a strict neighbourhood of
$V_{G_{r(n)}}$
is a strict neighbourhood of
 $\mathcal {X}_{K^pG_{r(n)},c}$
.
$\mathcal {X}_{K^pG_{r(n)},c}$
.
Since both are affinoid subsets, it is enough to check that
![]() $V_{G_{r(n)}}$
contains the closure of the non-cusp classical points of
$V_{G_{r(n)}}$
contains the closure of the non-cusp classical points of
![]() $\mathcal {X}_{K^pG_{r(n)},c}$
. We check this relation for their preimages in
$\mathcal {X}_{K^pG_{r(n)},c}$
. We check this relation for their preimages in
![]() $\mathcal {X}_{K^p}$
. Note that U is a
$\mathcal {X}_{K^p}$
. Note that U is a
![]() $G_{r(n)}$
-invariant open neighbourhood of
$G_{r(n)}$
-invariant open neighbourhood of
![]() $\infty $
. In particular, U contains
$\infty $
. In particular, U contains
![]() $G_{r(n)}\cdot \infty $
and
$G_{r(n)}\cdot \infty $
and
![]() $V_{\infty }$
contains the closed set
$V_{\infty }$
contains the closed set
 $\pi ^{-1}_{\mathrm {HT}}(G_{r(n)}\cdot \infty )$
. Our claim follows from the following lemma.
$\pi ^{-1}_{\mathrm {HT}}(G_{r(n)}\cdot \infty )$
. Our claim follows from the following lemma.
Lemma 5.2.8. The preimages of non-cusp points of
![]() $\mathcal {X}_{K^p\Gamma (p^m),c}$
in
$\mathcal {X}_{K^p\Gamma (p^m),c}$
in
![]() $\mathcal {X}_{K^p}$
map to
$\mathcal {X}_{K^p}$
map to
![]() $\Gamma (p^m)\cdot \infty $
under the Hodge–Tate period map for any
$\Gamma (p^m)\cdot \infty $
under the Hodge–Tate period map for any
![]() $m\geq 1$
.
$m\geq 1$
.
Proof. If
![]() $m=1$
, this follows from Lemma III.3.14 of [Reference ScholzeSch15] by noting our canonical locus
$m=1$
, this follows from Lemma III.3.14 of [Reference ScholzeSch15] by noting our canonical locus
![]() $\mathcal {X}_{K^p\Gamma (p),c}$
does not intersect the anticanonical locus in the reference. The general case
$\mathcal {X}_{K^p\Gamma (p),c}$
does not intersect the anticanonical locus in the reference. The general case
![]() $m\geq 2$
can be reduced to this case by using the action of
$m\geq 2$
can be reduced to this case by using the action of
 $\begin {pmatrix} p^{m-1} & 0 \\ 0 & 1 \end {pmatrix}$
.
$\begin {pmatrix} p^{m-1} & 0 \\ 0 & 1 \end {pmatrix}$
.
Now fix such a U. Note that
![]() $\infty $
is defined by
$\infty $
is defined by
![]() $y=0$
. We need to construct an isomorphism
$y=0$
. We need to construct an isomorphism
 $$ \begin{align*}\mathcal{O}^{\mathrm{la},\chi}_{K^p}(U)/(y)\xrightarrow{\sim}\varinjlim_n M_k^{\dagger}(K^p\Gamma(p^n)).\end{align*} $$
$$ \begin{align*}\mathcal{O}^{\mathrm{la},\chi}_{K^p}(U)/(y)\xrightarrow{\sim}\varinjlim_n M_k^{\dagger}(K^p\Gamma(p^n)).\end{align*} $$
Since
 $\mathcal {O}^n(U)\{y\}\cong \mathcal {O}_{V_{G_{r(n)}}}^+(V_{G_{r(n)}})[[p^{-(n-1)}(y-y_n)]]\otimes _{\mathbb {Z}_p}\mathbb {Q}_p$
, there is a natural
$\mathcal {O}^n(U)\{y\}\cong \mathcal {O}_{V_{G_{r(n)}}}^+(V_{G_{r(n)}})[[p^{-(n-1)}(y-y_n)]]\otimes _{\mathbb {Z}_p}\mathbb {Q}_p$
, there is a natural
 $\mathcal {O}_{V_{G_{r(n)}}}(V_{G_{r(n)}})$
-algebra homomorphism
$\mathcal {O}_{V_{G_{r(n)}}}(V_{G_{r(n)}})$
-algebra homomorphism
 $$ \begin{align*}\varphi_n:\mathcal{O}^n(U)\{y\}/(y)\to\mathcal{O}_{V_{G_{r(n)}}}(V^{\prime\prime}_{G_{r(n)}})\end{align*} $$
$$ \begin{align*}\varphi_n:\mathcal{O}^n(U)\{y\}/(y)\to\mathcal{O}_{V_{G_{r(n)}}}(V^{\prime\prime}_{G_{r(n)}})\end{align*} $$
sending
![]() $p^{-(n-1)}(y-y_n)$
to
$p^{-(n-1)}(y-y_n)$
to
 $-p^{-(n-1)}y_n\in \mathcal {O}_{V_{G_{r(n)}}}(V^{\prime \prime }_{G_{r(n)}})$
, where
$-p^{-(n-1)}y_n\in \mathcal {O}_{V_{G_{r(n)}}}(V^{\prime \prime }_{G_{r(n)}})$
, where
 $V^{\prime \prime }_{G_{r(n)}}\subset V_{G_{r(n)}}$
is the rational subset defined by
$V^{\prime \prime }_{G_{r(n)}}\subset V_{G_{r(n)}}$
is the rational subset defined by
![]() $|p^{-n}y_n|\leq 1$
. The same argument as above shows that
$|p^{-n}y_n|\leq 1$
. The same argument as above shows that
 $V^{\prime \prime }_{G_{r(n)}}$
is a strict neighbourhood of
$V^{\prime \prime }_{G_{r(n)}}$
is a strict neighbourhood of
![]() $\mathcal {X}_{K^pG_{r(n)},c}$
. Let
$\mathcal {X}_{K^pG_{r(n)},c}$
. Let
 $V^{\prime }_{G_{r(n)}}\subset V_{G_{r(n)}}$
defined by
$V^{\prime }_{G_{r(n)}}\subset V_{G_{r(n)}}$
defined by
![]() $|p^{-(n-1)}y_n|\leq 1$
. We claim that
$|p^{-(n-1)}y_n|\leq 1$
. We claim that
-
• the image of
 $\varphi _n$
contains analytic functions convergent on
$\varphi _n$
contains analytic functions convergent on
 $V^{\prime }_{G_{r(n)}}$
.
$V^{\prime }_{G_{r(n)}}$
.
Indeed, since
 $\mathcal {O}_{V_{G_{r(n)}}}(V^{\prime }_{G_{r(n)}})\cong \mathcal {O}_{V_{G_{r(n)}}}(V_{G_{r(n)}})\langle p^{-(n-1)}y_n\rangle $
, this claim is clear in view of the definition of
$\mathcal {O}_{V_{G_{r(n)}}}(V^{\prime }_{G_{r(n)}})\cong \mathcal {O}_{V_{G_{r(n)}}}(V_{G_{r(n)}})\langle p^{-(n-1)}y_n\rangle $
, this claim is clear in view of the definition of
![]() $\varphi _n$
.
$\varphi _n$
.
Hence, we have a map
 $$ \begin{align*}\mathcal{O}^n(U)\{y\}\cdot t^{n_1}(\frac{e_2}{e_{2,n}})^{n_2-n_1} /(y) \to \omega^k(V^{\prime\prime}_{G_{r(n)}})\end{align*} $$
$$ \begin{align*}\mathcal{O}^n(U)\{y\}\cdot t^{n_1}(\frac{e_2}{e_{2,n}})^{n_2-n_1} /(y) \to \omega^k(V^{\prime\prime}_{G_{r(n)}})\end{align*} $$
by sending
 $ft^{n_1}(\frac {e_2}{e_{2,n}})^{n_2-n_1} $
to
$ft^{n_1}(\frac {e_2}{e_{2,n}})^{n_2-n_1} $
to
 $\varphi _n(f)e_{2,n}^{n_1-n_2}$
; that is, multiplication by
$\varphi _n(f)e_{2,n}^{n_1-n_2}$
; that is, multiplication by
![]() $t^{-n_1}e_2^{n_1-n_2}$
. Clearly, this map is compatible when n varies and induces a map
$t^{-n_1}e_2^{n_1-n_2}$
. Clearly, this map is compatible when n varies and induces a map
 $\mathcal {O}^{\mathrm {la},\chi }_{K^p}(U)/(y)\to \varinjlim _n M_k^{\dagger }(K^p\Gamma (p^n))$
.
$\mathcal {O}^{\mathrm {la},\chi }_{K^p}(U)/(y)\to \varinjlim _n M_k^{\dagger }(K^p\Gamma (p^n))$
.
To prove this is an isomorphism, it suffices to show that for any n and strict neighbourhood W of
![]() $\mathcal {X}_{K^p\Gamma (p^n),c}$
, we can find
$\mathcal {X}_{K^p\Gamma (p^n),c}$
, we can find
![]() $m\geq n$
such that the preimage of W in
$m\geq n$
such that the preimage of W in
![]() $\mathcal {X}_{K^pG_{r(m)}}$
contains
$\mathcal {X}_{K^pG_{r(m)}}$
contains
 $V^{\prime }_{G_{r(m)}}$
. Let
$V^{\prime }_{G_{r(m)}}$
. Let
![]() $\tilde {W}$
be the preimage of W in
$\tilde {W}$
be the preimage of W in
![]() $\mathcal {X}_{K^p}$
. Then it is an open neighbourhood of
$\mathcal {X}_{K^p}$
. Then it is an open neighbourhood of
 $\pi _{\mathrm {HT}}^{-1}(\infty )=\{x\in \mathcal {X}_{K^p}\,|\,|y(x)|=0\}$
. Therefore,
$\pi _{\mathrm {HT}}^{-1}(\infty )=\{x\in \mathcal {X}_{K^p}\,|\,|y(x)|=0\}$
. Therefore,
![]() $\{x\in \mathcal {X}_{K^p}\,|\,|p^{-m}y(x)|\geq 1\},m=0,1,\cdots $
and
$\{x\in \mathcal {X}_{K^p}\,|\,|p^{-m}y(x)|\geq 1\},m=0,1,\cdots $
and
![]() $\tilde {W}$
form an open cover of
$\tilde {W}$
form an open cover of
![]() $V_{\infty }$
. Note that
$V_{\infty }$
. Note that
![]() $V_{\infty }$
is quasi-compact because it is affinoid; hence,
$V_{\infty }$
is quasi-compact because it is affinoid; hence,
![]() $\{z\in V_{\infty }\,|\,|p^{-(m-1)}y(z)|\leq 1\}\subset \tilde {W}$
for some m. Using
$\{z\in V_{\infty }\,|\,|p^{-(m-1)}y(z)|\leq 1\}\subset \tilde {W}$
for some m. Using
![]() $\|y-y_m\|\leq p^{-m}$
on
$\|y-y_m\|\leq p^{-m}$
on
![]() $V_{\infty }$
, it is easy to see that this m works here.
$V_{\infty }$
, it is easy to see that this m works here.
The claim for the B-action follows from the construction and the fact that
 $$ \begin{align*}\begin{pmatrix} a & b\\ 0 & d \end{pmatrix}\cdot e_2=be_1+d e_2,\end{align*} $$
$$ \begin{align*}\begin{pmatrix} a & b\\ 0 & d \end{pmatrix}\cdot e_2=be_1+d e_2,\end{align*} $$
whose reduction modulo
![]() $\mathfrak {m}_{\infty }$
is
$\mathfrak {m}_{\infty }$
is
![]() $de_2$
and that
$de_2$
and that
 $\begin {pmatrix} a & b\\ 0 & d \end {pmatrix}\cdot t=ad|ad|$
. The claim for
$\begin {pmatrix} a & b\\ 0 & d \end {pmatrix}\cdot t=ad|ad|$
. The claim for
![]() $G_{\mathbb {Q}_p}$
-action is clear as
$G_{\mathbb {Q}_p}$
-action is clear as
![]() $G_{\mathbb {Q}_p}$
acts via the cyclotomic character on
$G_{\mathbb {Q}_p}$
acts via the cyclotomic character on
![]() $e_2,t$
.
$e_2,t$
.
We record the following result obtained in this proof.
Lemma 5.2.9. Given an open subset U of
![]() ${\mathscr {F}\!\ell }$
containing
${\mathscr {F}\!\ell }$
containing
![]() $\infty $
, there exists a strict neighbourhood of
$\infty $
, there exists a strict neighbourhood of
![]() $\mathcal {X}_{K^p\Gamma (p^n),c}$
for some n whose preimage in
$\mathcal {X}_{K^p\Gamma (p^n),c}$
for some n whose preimage in
![]() $\mathcal {X}_{K^p}$
is contained in
$\mathcal {X}_{K^p}$
is contained in
 $\pi _{\mathrm {HT}}^{-1}(U)$
. Conversely, for any
$\pi _{\mathrm {HT}}^{-1}(U)$
. Conversely, for any
![]() $n>0$
and any strict neighbourhood W of
$n>0$
and any strict neighbourhood W of
![]() $\mathcal {X}_{K^p\Gamma (p^n),c}$
, there exists an open subset of
$\mathcal {X}_{K^p\Gamma (p^n),c}$
, there exists an open subset of
![]() ${\mathscr {F}\!\ell }$
containing
${\mathscr {F}\!\ell }$
containing
![]() $\infty $
whose preimage in
$\infty $
whose preimage in
![]() $\mathcal {X}_{K^p}$
is contained in the preimage of W.
$\mathcal {X}_{K^p}$
is contained in the preimage of W.
Proof. For the first claim, we may assume
![]() $U\in \mathfrak {B}$
. Then this was proved around Lemma 5.2.8. The second claim follows from the argument in the second to last paragraph of the proof of Theorem 5.2.6.
$U\in \mathfrak {B}$
. Then this was proved around Lemma 5.2.8. The second claim follows from the argument in the second to last paragraph of the proof of Theorem 5.2.6.
We are going to compare
 $M^{\dagger }_\chi (K^p)$
with the
$M^{\dagger }_\chi (K^p)$
with the
![]() $\mathfrak {n}$
-coinvariants
$\mathfrak {n}$
-coinvariants
 $(\mathcal {O}_{K^p}^{\mathrm {la},\chi })_{\mathfrak {n}}$
of
$(\mathcal {O}_{K^p}^{\mathrm {la},\chi })_{\mathfrak {n}}$
of
 $\mathcal {O}^{\mathrm {la},\chi }_{K^p}$
. Note that there is a natural action of
$\mathcal {O}^{\mathrm {la},\chi }_{K^p}$
. Note that there is a natural action of
![]() $\mathfrak {h}$
on
$\mathfrak {h}$
on
 $(\mathcal {O}_{K^p}^{\mathrm {la},\chi })_{\mathfrak {n}}$
induced from the action of
$(\mathcal {O}_{K^p}^{\mathrm {la},\chi })_{\mathfrak {n}}$
induced from the action of
![]() $\mathfrak {b}$
. We will always use this constant
$\mathfrak {b}$
. We will always use this constant
![]() $\mathfrak {h}$
-action from now on, unless otherwise specified (to distinguish with the horizontal action
$\mathfrak {h}$
-action from now on, unless otherwise specified (to distinguish with the horizontal action
![]() $\theta _{\mathfrak {h}}$
). Since
$\theta _{\mathfrak {h}}$
). Since
 $M^{\dagger }_\chi (K^p)$
is the fibre of
$M^{\dagger }_\chi (K^p)$
is the fibre of
 $\mathcal {O}_{K^p}^{\mathrm {la},\chi }$
at
$\mathcal {O}_{K^p}^{\mathrm {la},\chi }$
at
![]() $\infty $
, the action of
$\infty $
, the action of
![]() $\mathfrak {b}$
on it factors through
$\mathfrak {b}$
on it factors through
![]() $\mathfrak {h}$
. It is easy to see that
$\mathfrak {h}$
. It is easy to see that
-
•
 $\mathfrak {h}$
acts on
$\mathfrak {h}$
acts on
 $M^{\dagger }_\chi (K^p)$
via
$M^{\dagger }_\chi (K^p)$
via
 $\chi $
.
$\chi $
.
We denote by
![]() $i_{\infty }$
the natural embedding
$i_{\infty }$
the natural embedding
![]() $\infty \hookrightarrow {\mathscr {F}\!\ell }$
.
$\infty \hookrightarrow {\mathscr {F}\!\ell }$
.
Proposition 5.2.10. Let
![]() $\chi =(n_1,n_2)$
be a weight.
$\chi =(n_1,n_2)$
be a weight.
-
(1)
 $(\mathcal {O}_{K^p}^{\mathrm {la},\chi })_{\mathfrak {n}}$
is a skyscraper sheaf supported at
$(\mathcal {O}_{K^p}^{\mathrm {la},\chi })_{\mathfrak {n}}$
is a skyscraper sheaf supported at
 $\infty $
and hence has no
$\infty $
and hence has no
 $H^1$
.
$H^1$
. -
(2)
 $\mathfrak {n}(\mathcal {O}_{K^p}^{\mathrm {la},\chi })\subset \mathfrak {m}_{\infty }\mathcal {O}_{K^p}^{\mathrm {la},\chi }$
. Thus, we get a natural exact sequence for some
$\mathfrak {n}(\mathcal {O}_{K^p}^{\mathrm {la},\chi })\subset \mathfrak {m}_{\infty }\mathcal {O}_{K^p}^{\mathrm {la},\chi }$
. Thus, we get a natural exact sequence for some $$ \begin{align*}0\to (i_{\infty})_*N^{\chi}\to (\mathcal{O}_{K^p}^{\mathrm{la},\chi})_{\mathfrak{n}}\to (i_{\infty})_*M^{\dagger}_\chi(K^p)\to 0\end{align*} $$
$$ \begin{align*}0\to (i_{\infty})_*N^{\chi}\to (\mathcal{O}_{K^p}^{\mathrm{la},\chi})_{\mathfrak{n}}\to (i_{\infty})_*M^{\dagger}_\chi(K^p)\to 0\end{align*} $$
 $N^\chi $
. Moreover,
$N^\chi $
. Moreover,
 $\mathfrak {h}$
acts on
$\mathfrak {h}$
acts on
 $N^\chi $
via
$N^\chi $
via
 $(n_2+1,n_1-1)$
. In particular, this exact sequence splits naturally if
$(n_2+1,n_1-1)$
. In particular, this exact sequence splits naturally if
 $\chi (h)\neq 1$
; that is,
$\chi (h)\neq 1$
; that is,
 $\chi |_{\mathfrak {h}_0}\neq \rho |_{\mathfrak {h}_0}$
. Recall that
$\chi |_{\mathfrak {h}_0}\neq \rho |_{\mathfrak {h}_0}$
. Recall that
 $\rho $
denotes the half-sum of positive roots.
$\rho $
denotes the half-sum of positive roots.
-
(3)
 $(\mathcal {O}_{K^p}^{\mathrm {la},\chi })_{\mathfrak {n}}=(i_{\infty })_*M^{\dagger }_\chi (K^p)$
; that is,
$(\mathcal {O}_{K^p}^{\mathrm {la},\chi })_{\mathfrak {n}}=(i_{\infty })_*M^{\dagger }_\chi (K^p)$
; that is,
 $N^\chi =0$
if
$N^\chi =0$
if
 $\chi (h)\neq 0,-1,-2,\cdots $
and is p-adically non-Liouville (see Remark 5.2.11 for a definition).
$\chi (h)\neq 0,-1,-2,\cdots $
and is p-adically non-Liouville (see Remark 5.2.11 for a definition). -
(4)
 $(\mathcal {O}_{K^p}^{\mathrm {la},\chi })_{\mathfrak {n}}\cong (i_{\infty })_*M^{\dagger }_\chi (K^p)\oplus (i_{\infty })_*M^{\dagger }_\chi (K^p)\cdot (e_1/e_2)^{1-\chi (h)}$
if
$(\mathcal {O}_{K^p}^{\mathrm {la},\chi })_{\mathfrak {n}}\cong (i_{\infty })_*M^{\dagger }_\chi (K^p)\oplus (i_{\infty })_*M^{\dagger }_\chi (K^p)\cdot (e_1/e_2)^{1-\chi (h)}$
if
 $\chi (h)\in \{0,-1,-2,\cdots \}$
.
$\chi (h)\in \{0,-1,-2,\cdots \}$
.
Remark 5.2.11. Recall that according to Clark [Reference ClarkCla66], we say
![]() $\alpha \in C$
is p-adically non-Liouville if
$\alpha \in C$
is p-adically non-Liouville if
 $$ \begin{align*}\lim\inf_{n\to\infty}|\alpha+n|^{1/n}>0;\end{align*} $$
$$ \begin{align*}\lim\inf_{n\to\infty}|\alpha+n|^{1/n}>0;\end{align*} $$
that is, it cannot be well approximated by rational integers. It appears naturally in the study of p-adic differential equations. Suppose
![]() $\alpha \notin \mathbb {Z}$
and consider the inhomogeneous differential equation around
$\alpha \notin \mathbb {Z}$
and consider the inhomogeneous differential equation around
![]() $x=0$
,
$x=0$
,
 $$ \begin{align*}(x\frac{d}{dx}+\alpha)y=\frac{1}{1-x}.\end{align*} $$
$$ \begin{align*}(x\frac{d}{dx}+\alpha)y=\frac{1}{1-x}.\end{align*} $$
It has a unique formal power series solution
 $\sum _{n\geq 0}\frac {1}{n+\alpha }x^n$
, whose convergence is equivalent with
$\sum _{n\geq 0}\frac {1}{n+\alpha }x^n$
, whose convergence is equivalent with
![]() $\alpha $
being non-Liouville. In fact, it will be clear to the reader that a variant of this differential equation will show up in our case.
$\alpha $
being non-Liouville. In fact, it will be clear to the reader that a variant of this differential equation will show up in our case.
Proof. Let
![]() $U\in \mathfrak {B}$
. We first show
$U\in \mathfrak {B}$
. We first show
 $(\mathcal {O}_{K^p}^{\mathrm {la},\chi }(U))_{\mathfrak {n}}=0$
if
$(\mathcal {O}_{K^p}^{\mathrm {la},\chi }(U))_{\mathfrak {n}}=0$
if
![]() $e_1$
is a basis on U. Clearly, this implies that
$e_1$
is a basis on U. Clearly, this implies that
 $(\mathcal {O}_{K^p}^{\mathrm {la},\chi })_{\mathfrak {n}}$
is supported at
$(\mathcal {O}_{K^p}^{\mathrm {la},\chi })_{\mathfrak {n}}$
is supported at
![]() $\infty $
. On such a U, using the notation in Lemma 5.1.2, any element in
$\infty $
. On such a U, using the notation in Lemma 5.1.2, any element in
 $f\in \mathcal {O}_{K^p}^{\mathrm {la},\chi }(U)$
can be written as
$f\in \mathcal {O}_{K^p}^{\mathrm {la},\chi }(U)$
can be written as
 $$ \begin{align*}f=(\frac{t}{t_{N}})^{n_1}(\frac{e_1}{e_{1,N}})^{n_2-n_1}\sum_{i\geq0} c^{(n)}_i(f) (x-x_n)^i .\end{align*} $$
$$ \begin{align*}f=(\frac{t}{t_{N}})^{n_1}(\frac{e_1}{e_{1,N}})^{n_2-n_1}\sum_{i\geq0} c^{(n)}_i(f) (x-x_n)^i .\end{align*} $$
Since
![]() $u^+\in \mathfrak {n}$
acts trivially on
$u^+\in \mathfrak {n}$
acts trivially on
![]() $e_1,t$
and acts as the usual derivation on
$e_1,t$
and acts as the usual derivation on
![]() $(x-x_n)$
, an argument similar to the proof of Lemma 5.1.2 shows that
$(x-x_n)$
, an argument similar to the proof of Lemma 5.1.2 shows that
![]() $\mathfrak {n}$
is a surjection on
$\mathfrak {n}$
is a surjection on
 $\mathcal {O}_{K^p}^{\mathrm {la},\chi }(U)$
.
$\mathcal {O}_{K^p}^{\mathrm {la},\chi }(U)$
.
Now let
![]() $U\in \mathfrak {B}$
containing
$U\in \mathfrak {B}$
containing
![]() $\infty $
and on which
$\infty $
and on which
![]() $e_2$
is a basis. As in the proof of Proposition 5.2.6, any
$e_2$
is a basis. As in the proof of Proposition 5.2.6, any
 $f\in \mathcal {O}_{K^p}^{\mathrm {la},\chi }(U)$
can be written as
$f\in \mathcal {O}_{K^p}^{\mathrm {la},\chi }(U)$
can be written as
 $$ \begin{align*}f=(\frac{t}{t_{N}})^{n_1}(\frac{e_2}{e_{2,N}})^{n_2-n_1}\sum_{i\geq0} c_i (y-y_n)^i\end{align*} $$
$$ \begin{align*}f=(\frac{t}{t_{N}})^{n_1}(\frac{e_2}{e_{2,N}})^{n_2-n_1}\sum_{i\geq0} c_i (y-y_n)^i\end{align*} $$
for some n and
![]() $c_i$
. Using
$c_i$
. Using
![]() $u^+\cdot e_2=e_1=ye_2$
and
$u^+\cdot e_2=e_1=ye_2$
and
![]() $u^+\cdot y=-y^2$
, we get
$u^+\cdot y=-y^2$
, we get
 $$ \begin{align*} u^+\cdot f&= y(\frac{t}{t_{N}})^{n_1}(\frac{e_2}{e_{2,N}})^{n_2-n_1}(\sum_{i\geq0} (n_2-n_1)c_i(y-y_n)^i -y\sum_{i\geq 1}ic_i (y-y_n)^{i-1})\\ &= y(\frac{t}{t_{N}})^{n_1}(\frac{e_2}{e_{2,N}})^{n_2-n_1}\sum_{i\geq0} ((n_2-n_1-i)c_i-(i+1)c_{i+1}y_n ) (y-y_n)^i\in y\mathcal{O}_{K^p}^{\mathrm{la},\chi}(U). \end{align*} $$
$$ \begin{align*} u^+\cdot f&= y(\frac{t}{t_{N}})^{n_1}(\frac{e_2}{e_{2,N}})^{n_2-n_1}(\sum_{i\geq0} (n_2-n_1)c_i(y-y_n)^i -y\sum_{i\geq 1}ic_i (y-y_n)^{i-1})\\ &= y(\frac{t}{t_{N}})^{n_1}(\frac{e_2}{e_{2,N}})^{n_2-n_1}\sum_{i\geq0} ((n_2-n_1-i)c_i-(i+1)c_{i+1}y_n ) (y-y_n)^i\in y\mathcal{O}_{K^p}^{\mathrm{la},\chi}(U). \end{align*} $$
Hence,
 $\mathfrak {n}(\mathcal {O}_{K^p}^{\mathrm {la},\chi })\subset \mathfrak {m}_{\infty }\mathcal {O}_{K^p}^{\mathrm {la},\chi }$
and we can define
$\mathfrak {n}(\mathcal {O}_{K^p}^{\mathrm {la},\chi })\subset \mathfrak {m}_{\infty }\mathcal {O}_{K^p}^{\mathrm {la},\chi }$
and we can define
![]() $N^{\chi }$
as in the lemma. Moreover, one can compute
$N^{\chi }$
as in the lemma. Moreover, one can compute
 $$ \begin{align*} (h-(n_2-n_1+2))\cdot(yf)&= y(\frac{t}{t_{N}})^{n_1}(\frac{e_2}{e_{2,N}})^{n_2-n_1}(h+2(n_1-n_2))\cdot(\sum_{i\geq 0}c_i(y-y_n)^i)\\ &= -2u^+\cdot f. \end{align*} $$
$$ \begin{align*} (h-(n_2-n_1+2))\cdot(yf)&= y(\frac{t}{t_{N}})^{n_1}(\frac{e_2}{e_{2,N}})^{n_2-n_1}(h+2(n_1-n_2))\cdot(\sum_{i\geq 0}c_i(y-y_n)^i)\\ &= -2u^+\cdot f. \end{align*} $$
Also, it is easy to check that z acts on everything via
![]() $\chi (z)=n_1+n_2$
. Hence, we conclude that
$\chi (z)=n_1+n_2$
. Hence, we conclude that
![]() $\mathfrak {h}$
acts via
$\mathfrak {h}$
acts via
![]() $(n_2+1,n_1-1)$
on
$(n_2+1,n_1-1)$
on
![]() $N^\chi $
.
$N^\chi $
.
The last two claims require a bit more work. We denote by
![]() $U_n\subset U$
the rational subset defined by
$U_n\subset U$
the rational subset defined by
![]() $|p^{-n}y|\leq 1$
. Then
$|p^{-n}y|\leq 1$
. Then
![]() $U_n\in \mathfrak {B}$
and contains
$U_n\in \mathfrak {B}$
and contains
![]() $\infty $
. Note that
$\infty $
. Note that
 $\pi _{\mathrm {HT}}^{-1}(U_n)$
is also the preimage of
$\pi _{\mathrm {HT}}^{-1}(U_n)$
is also the preimage of
 $V^{\prime \prime }_{G_{r(n)}}=\{x\in V_{G_{r(n)}},\,|y_n(x)p^{-n}|\leq 1\}$
because
$V^{\prime \prime }_{G_{r(n)}}=\{x\in V_{G_{r(n)}},\,|y_n(x)p^{-n}|\leq 1\}$
because
![]() $\|y-y_n\|\leq p^{-n}$
. For n sufficiently large so that both
$\|y-y_n\|\leq p^{-n}$
. For n sufficiently large so that both
 $(\frac {t}{t_n})^{n_1}$
,
$(\frac {t}{t_n})^{n_1}$
,
 $(\frac {e_2}{e_{2,n}})^{n_2-n_1}$
converge, we denote by
$(\frac {e_2}{e_{2,n}})^{n_2-n_1}$
converge, we denote by
 $C_n\subset \mathcal {O}_{K^p}^{\mathrm {la}}(U_n)$
the subset of elements of the form
$C_n\subset \mathcal {O}_{K^p}^{\mathrm {la}}(U_n)$
the subset of elements of the form
 $$ \begin{align*}(\frac{t}{t_n})^{n_1}(\frac{e_2}{e_{2,n}})^{n_2-n_1}\sum_{i\geq0} c_i y^i, \end{align*} $$
$$ \begin{align*}(\frac{t}{t_n})^{n_1}(\frac{e_2}{e_{2,n}})^{n_2-n_1}\sum_{i\geq0} c_i y^i, \end{align*} $$
where
 $c_i\in H^0(V^{\prime \prime }_{G_{r(n)}},\mathcal {O}_{\mathcal {X}_{K^pG_{r(n)}}})$
with bound
$c_i\in H^0(V^{\prime \prime }_{G_{r(n)}},\mathcal {O}_{\mathcal {X}_{K^pG_{r(n)}}})$
with bound
![]() $\|c_i\|\leq C'p^{(n-1)i}$
for a uniform
$\|c_i\|\leq C'p^{(n-1)i}$
for a uniform
![]() $C'$
. Note that as
$C'$
. Note that as
![]() $\|y\|\leq p^{-n}$
in
$\|y\|\leq p^{-n}$
in
 $H^0(\pi _{\mathrm {HT}}^{-1}(U_n),\mathcal {O}_{\mathcal {X}_{K^p}})$
, we can choose
$H^0(\pi _{\mathrm {HT}}^{-1}(U_n),\mathcal {O}_{\mathcal {X}_{K^p}})$
, we can choose
![]() $y_n=0$
here. As before,
$y_n=0$
here. As before,
![]() $p^{(n-1)i}c_i$
defines an isomorphism
$p^{(n-1)i}c_i$
defines an isomorphism
 $C_n\cong (\prod _{i\geq 0}H^0(V^{\prime \prime }_{G_{r(n)}},\mathcal {O}^+_{\mathcal {X}_{K^pG_{r(n)}}}))\otimes _{\mathbb {Z}_p}\mathbb {Q}_p$
and
$C_n\cong (\prod _{i\geq 0}H^0(V^{\prime \prime }_{G_{r(n)}},\mathcal {O}^+_{\mathcal {X}_{K^pG_{r(n)}}}))\otimes _{\mathbb {Z}_p}\mathbb {Q}_p$
and
![]() $C_n$
forms a direct system when n varies. It is easy to see that
$C_n$
forms a direct system when n varies. It is easy to see that
 $$ \begin{align*}(\mathcal{O}_{K^p}^{\mathrm{la},\chi})_{\mathfrak{n}}=(i_{\infty})_*(\varinjlim_n (C_n)_{\mathfrak{n}}).\end{align*} $$
$$ \begin{align*}(\mathcal{O}_{K^p}^{\mathrm{la},\chi})_{\mathfrak{n}}=(i_{\infty})_*(\varinjlim_n (C_n)_{\mathfrak{n}}).\end{align*} $$
Assume that
![]() $n_1-n_2=\chi (h)\neq 0,-1,-2,\cdots $
and is p-adically non-Liouville. For any
$n_1-n_2=\chi (h)\neq 0,-1,-2,\cdots $
and is p-adically non-Liouville. For any
![]() $f\in C_n$
and n sufficiently large, we need to show that
$f\in C_n$
and n sufficiently large, we need to show that
![]() $yf\in u^+(C_m)$
for some
$yf\in u^+(C_m)$
for some
![]() $m\geq n$
. Write
$m\geq n$
. Write
 $$ \begin{align*}f=(\frac{t}{t_n})^{n_1}(\frac{e_2}{e_{2,n}})^{n_2-n_1}\sum_{i\geq0} c_i y^i\end{align*} $$
$$ \begin{align*}f=(\frac{t}{t_n})^{n_1}(\frac{e_2}{e_{2,n}})^{n_2-n_1}\sum_{i\geq0} c_i y^i\end{align*} $$
for some
 $c_i\in H^0(V^{\prime \prime }_{G_{r(n)}},\mathcal {O}_{\mathcal {X}_{K^pG_{r(n)}}})$
and
$c_i\in H^0(V^{\prime \prime }_{G_{r(n)}},\mathcal {O}_{\mathcal {X}_{K^pG_{r(n)}}})$
and
![]() $\|c_i\|\leq C'p^{(n-1)i}$
for some
$\|c_i\|\leq C'p^{(n-1)i}$
for some
![]() $C'$
. By our assumption, we can find
$C'$
. By our assumption, we can find
![]() $m\geq n$
such that
$m\geq n$
such that
for i sufficiently large. Then
 $\|\frac {c_i}{-n_1+n_2-i}\|\leq C'p^{(m-1)i}$
for i large enough and
$\|\frac {c_i}{-n_1+n_2-i}\|\leq C'p^{(m-1)i}$
for i large enough and
 $$ \begin{align*}(\frac{t}{t_n})^{n_1}(\frac{e_2}{e_{2,n}})^{n_2-n_1}\sum_{i\geq0} \frac{c_i}{-n_1+n_2-i} y^i\end{align*} $$
$$ \begin{align*}(\frac{t}{t_n})^{n_1}(\frac{e_2}{e_{2,n}})^{n_2-n_1}\sum_{i\geq0} \frac{c_i}{-n_1+n_2-i} y^i\end{align*} $$
defines an element
![]() $g\in C_m$
. A simple computation gives that
$g\in C_m$
. A simple computation gives that
![]() $u^+\cdot g=yf$
. Hence,
$u^+\cdot g=yf$
. Hence,
![]() $N^\chi =0$
and
$N^\chi =0$
and
 $(\mathcal {O}_{K^p}^{\mathrm {la},\chi })_{\mathfrak {n}}=(i_{\infty })_*M^{\dagger }_\chi (K^p)$
in this case.
$(\mathcal {O}_{K^p}^{\mathrm {la},\chi })_{\mathfrak {n}}=(i_{\infty })_*M^{\dagger }_\chi (K^p)$
in this case.
Now assume
![]() $n_1-n_2=\chi (h)\in \{0,-1,-2,\cdots \}$
. Recall that for
$n_1-n_2=\chi (h)\in \{0,-1,-2,\cdots \}$
. Recall that for
![]() $f\in C_n$
as above, we have
$f\in C_n$
as above, we have
 $$ \begin{align*}u^+\cdot f=(\frac{t}{t_n})^{n_1}(\frac{e_2}{e_{2,n}})^{n_2-n_1}\sum_{i\geq0} (n_2-n_1-i)c_i y^{i+1}.\end{align*} $$
$$ \begin{align*}u^+\cdot f=(\frac{t}{t_n})^{n_1}(\frac{e_2}{e_{2,n}})^{n_2-n_1}\sum_{i\geq0} (n_2-n_1-i)c_i y^{i+1}.\end{align*} $$
Hence, the
![]() $y^{n_2-n_1+1}$
term in the summation always has zero coefficient. Conversely, if
$y^{n_2-n_1+1}$
term in the summation always has zero coefficient. Conversely, if
 $f=(\frac {t}{t_n})^{n_1}(\frac {e_2}{e_{2,n}})^{n_2-n_1}\sum _{i\geq 0} c_i y^i\in C_n$
with
$f=(\frac {t}{t_n})^{n_1}(\frac {e_2}{e_{2,n}})^{n_2-n_1}\sum _{i\geq 0} c_i y^i\in C_n$
with
![]() $c_{n_2-n_1}=0$
, we have
$c_{n_2-n_1}=0$
, we have
![]() $|n_2-n_1-i|\geq p^{-i}$
for i sufficiently large and
$|n_2-n_1-i|\geq p^{-i}$
for i sufficiently large and
 $(\frac {t}{t_n})^{n_1}(\frac {e_2}{e_{2,n}})^{n_2-n_1}\sum _{0\leq i\neq n_2-n_1} \frac {c_i}{n_2-n_1-i} y^i$
converges to an element
$(\frac {t}{t_n})^{n_1}(\frac {e_2}{e_{2,n}})^{n_2-n_1}\sum _{0\leq i\neq n_2-n_1} \frac {c_i}{n_2-n_1-i} y^i$
converges to an element
![]() $g\in C_{n+1}$
. Again, it is easy to check that
$g\in C_{n+1}$
. Again, it is easy to check that
![]() $yf=u^+\cdot g$
. Thus, we can define an isomorphism
$yf=u^+\cdot g$
. Thus, we can define an isomorphism
 $$ \begin{align*}M^{\dagger}_\chi(U^p)\xrightarrow{\sim} N^\chi\end{align*} $$
$$ \begin{align*}M^{\dagger}_\chi(U^p)\xrightarrow{\sim} N^\chi\end{align*} $$
by sending f to
![]() $\tilde fy^{n_2-n_1+1}$
, where
$\tilde fy^{n_2-n_1+1}$
, where
 $\tilde f\in \mathcal {O}_{K^p}^{\mathrm {la},\chi }(U)$
is a lifting of
$\tilde f\in \mathcal {O}_{K^p}^{\mathrm {la},\chi }(U)$
is a lifting of
 $f\in \mathcal {O}_{K^p}^{\mathrm {la},\chi }(U)/(y)$
. Since
$f\in \mathcal {O}_{K^p}^{\mathrm {la},\chi }(U)/(y)$
. Since
![]() $y=e_1/e_2$
, this isomorphism becomes B-equivariant if we twist the left-hand side by
$y=e_1/e_2$
, this isomorphism becomes B-equivariant if we twist the left-hand side by
![]() $(e_1/e_2)^{1-n_1+n_2}$
.
$(e_1/e_2)^{1-n_1+n_2}$
.
Next we compute
 $\mathcal {O}^{\mathrm {la},\chi ,\mathfrak {n}}_{K^p}$
, the
$\mathcal {O}^{\mathrm {la},\chi ,\mathfrak {n}}_{K^p}$
, the
![]() $\mathfrak {n}$
-invariants of
$\mathfrak {n}$
-invariants of
 $\mathcal {O}^{\mathrm {la},\chi }_{K^p}$
.
$\mathcal {O}^{\mathrm {la},\chi }_{K^p}$
.
Proposition 5.2.12.
-
(1) Suppose U does not contain
 $\infty $
; that is,
$\infty $
; that is,
 $e_1$
is a basis on U. Fix N large enough so that
$e_1$
is a basis on U. Fix N large enough so that
 $(\frac {t}{t_{N}})^{n_1},(\frac {e_1}{e_{1,N}})^{n_2-n_1}$
converge. Then any
$(\frac {t}{t_{N}})^{n_1},(\frac {e_1}{e_{1,N}})^{n_2-n_1}$
converge. Then any
 $f\in \mathcal {O}^{\mathrm {la},\chi ,\mathfrak {n}}_{K^p}(U)$
can be written as for some
$f\in \mathcal {O}^{\mathrm {la},\chi ,\mathfrak {n}}_{K^p}(U)$
can be written as for some $$ \begin{align*}f=(\frac{t}{t_{N}})^{n_1}(\frac{e_1}{e_{1,N}})^{n_2-n_1}c \end{align*} $$
$$ \begin{align*}f=(\frac{t}{t_{N}})^{n_1}(\frac{e_1}{e_{1,N}})^{n_2-n_1}c \end{align*} $$
 $n\geq N$
sufficiently large and
$n\geq N$
sufficiently large and
 $c\in H^0(V_{G_{r(n)}},\mathcal {O}_{\mathcal {X}_{K^pG_{r(n)}}})$
.
$c\in H^0(V_{G_{r(n)}},\mathcal {O}_{\mathcal {X}_{K^pG_{r(n)}}})$
.
-
(2) Suppose
 $e_2$
is a basis on
$e_2$
is a basis on
 $U\in \mathfrak {B}$
and
$U\in \mathfrak {B}$
and
 $\chi (h)=n_1-n_2\in \{0,-1,-2,\cdots \}$
. Fix N large enough so that
$\chi (h)=n_1-n_2\in \{0,-1,-2,\cdots \}$
. Fix N large enough so that
 $(\frac {t}{t_{N}})^{n_1}$
converges. Then any
$(\frac {t}{t_{N}})^{n_1}$
converges. Then any
 $f\in \mathcal {O}^{\mathrm {la},\chi ,\mathfrak {n}}_{K^p}(U)$
can be written as for some
$f\in \mathcal {O}^{\mathrm {la},\chi ,\mathfrak {n}}_{K^p}(U)$
can be written as for some $$ \begin{align*}f=(\frac{t}{t_{N}})^{n_1}(\frac{e_2}{e_{2,N}})^{n_2-n_1}cy^{n_2-n_1}=(\frac{t}{t_{N}})^{n_1}(\frac{e_1}{e_{2,N}})^{n_2-n_1}c \end{align*} $$
$$ \begin{align*}f=(\frac{t}{t_{N}})^{n_1}(\frac{e_2}{e_{2,N}})^{n_2-n_1}cy^{n_2-n_1}=(\frac{t}{t_{N}})^{n_1}(\frac{e_1}{e_{2,N}})^{n_2-n_1}c \end{align*} $$
 $n\geq N$
and
$n\geq N$
and
 $c\in H^0(V_{G_{r(n)}},\mathcal {O}_{\mathcal {X}_{K^pG_{r(n)}}})$
.
$c\in H^0(V_{G_{r(n)}},\mathcal {O}_{\mathcal {X}_{K^pG_{r(n)}}})$
.
-
(3)
 $\mathfrak {h}$
acts on
$\mathfrak {h}$
acts on
 $\mathcal {O}^{\mathrm {la},\chi ,\mathfrak {n}}_{K^p}(U)$
via
$\mathcal {O}^{\mathrm {la},\chi ,\mathfrak {n}}_{K^p}(U)$
via
 $(n_2,n_1)$
for any open subset
$(n_2,n_1)$
for any open subset
 $U\subset {\mathscr {F}\!\ell }$
.
$U\subset {\mathscr {F}\!\ell }$
. -
(4) Suppose
 $\chi (h)\neq 0,-1,-2,\cdots $
. Then that is, the stalk of
$\chi (h)\neq 0,-1,-2,\cdots $
. Then that is, the stalk of $$ \begin{align*}\varinjlim_{U\ni\infty} \mathcal{O}^{\mathrm{la},\chi,\mathfrak{n}}_{K^p}(U)=0;\end{align*} $$
$$ \begin{align*}\varinjlim_{U\ni\infty} \mathcal{O}^{\mathrm{la},\chi,\mathfrak{n}}_{K^p}(U)=0;\end{align*} $$
 $\mathcal {O}^{\mathrm {la},\chi ,\mathfrak {n}}_{K^p}$
at
$\mathcal {O}^{\mathrm {la},\chi ,\mathfrak {n}}_{K^p}$
at
 $\infty $
is zero.
$\infty $
is zero.
Remark 5.2.13. The overconvergent modular forms of weight
![]() $\chi $
introduced in [Reference PilloniPil13, Reference Andreatta, Iovita and StevensAIS14, Reference Chojecki, Hansen and JohanssonCHJ17] are essentially the stalk of
$\chi $
introduced in [Reference PilloniPil13, Reference Andreatta, Iovita and StevensAIS14, Reference Chojecki, Hansen and JohanssonCHJ17] are essentially the stalk of
 $\mathcal {O}^{\mathrm {la},\chi ,\mathfrak {n}}_{K^p}$
at a
$\mathcal {O}^{\mathrm {la},\chi ,\mathfrak {n}}_{K^p}$
at a
![]() $\mathbb {Q}_p$
-rational point of
$\mathbb {Q}_p$
-rational point of
![]() ${\mathscr {F}\!\ell }\setminus \{\infty \}$
. For example, the
${\mathscr {F}\!\ell }\setminus \{\infty \}$
. For example, the
![]() $\infty $
in [Reference Chojecki, Hansen and JohanssonCHJ17, Theorem 1.1] corresponds to the locus where
$\infty $
in [Reference Chojecki, Hansen and JohanssonCHJ17, Theorem 1.1] corresponds to the locus where
![]() $e_2=0$
; that is,
$e_2=0$
; that is,
![]() $x=0$
in our setup.
$x=0$
in our setup.
Proof. For the first part, as in Lemma 5.1.2, any
 $f\in \mathcal {O}_{K^p}^{\mathrm {la},\chi }(U)$
can be written as
$f\in \mathcal {O}_{K^p}^{\mathrm {la},\chi }(U)$
can be written as
 $$ \begin{align*}f=(\frac{t}{t_{N}})^{n_1}(\frac{e_1}{e_{1,N}})^{n_2-n_1}\sum_{i\geq0} c^{(n)}_i(f) (x-x_n)^i \end{align*} $$
$$ \begin{align*}f=(\frac{t}{t_{N}})^{n_1}(\frac{e_1}{e_{1,N}})^{n_2-n_1}\sum_{i\geq0} c^{(n)}_i(f) (x-x_n)^i \end{align*} $$
for some n and
 $c^{(n)}_i(f)$
are unique for such a n. Since
$c^{(n)}_i(f)$
are unique for such a n. Since
![]() $u^+$
acts as the usual derivation on
$u^+$
acts as the usual derivation on
![]() $(x-x_n)$
, we see that
$(x-x_n)$
, we see that
![]() $u^+\cdot f=0$
if and only if
$u^+\cdot f=0$
if and only if
 $c^{(n)}_i(f)=0$
,
$c^{(n)}_i(f)=0$
,
![]() $i>0$
. This proves the first part.
$i>0$
. This proves the first part.
Suppose
![]() $\infty \in U$
and
$\infty \in U$
and
![]() $e_2$
is a basis on U. As in the proof of Proposition 5.2.10, for any
$e_2$
is a basis on U. As in the proof of Proposition 5.2.10, for any
 $f\in \mathcal {O}_{K^p}^{\mathrm {la},\chi }(U)$
, we can find n so that
$f\in \mathcal {O}_{K^p}^{\mathrm {la},\chi }(U)$
, we can find n so that
![]() $f|_{U_n}$
can be written as
$f|_{U_n}$
can be written as
 $f=(\frac {t}{t_{N}})^{n_1}(\frac {e_2}{e_{2,N}})^{n_2-n_1}\sum _{i\geq 0} c_i y^i$
for some
$f=(\frac {t}{t_{N}})^{n_1}(\frac {e_2}{e_{2,N}})^{n_2-n_1}\sum _{i\geq 0} c_i y^i$
for some
 $c_i \in H^0(V^{\prime \prime }_{G_{r(n)}},\mathcal {O}_{\mathcal {X}_{K^pG_{r(n)}}})$
. Then
$c_i \in H^0(V^{\prime \prime }_{G_{r(n)}},\mathcal {O}_{\mathcal {X}_{K^pG_{r(n)}}})$
. Then
 $$ \begin{align*}u^+\cdot f = (\frac{t}{t_{N}})^{n_1}(\frac{e_2}{e_{2,N}})^{n_2-n_1}\sum_{i\geq0} (n_2-n_1-i)c_i y^{i+1}.\end{align*} $$
$$ \begin{align*}u^+\cdot f = (\frac{t}{t_{N}})^{n_1}(\frac{e_2}{e_{2,N}})^{n_2-n_1}\sum_{i\geq0} (n_2-n_1-i)c_i y^{i+1}.\end{align*} $$
Hence, that
![]() $u^+\cdot f=0$
is equivalent with
$u^+\cdot f=0$
is equivalent with
This implies all
![]() $c_i=0$
; that is,
$c_i=0$
; that is,
![]() $f|_{U_n}=0$
if
$f|_{U_n}=0$
if
![]() $\chi (h)=n_1-n_2\neq 0, -1,-2,\cdots $
. When
$\chi (h)=n_1-n_2\neq 0, -1,-2,\cdots $
. When
![]() $\chi (h)\in \{0, -1,-2,\cdots \}$
, we see that all
$\chi (h)\in \{0, -1,-2,\cdots \}$
, we see that all
![]() $c_i=0$
except
$c_i=0$
except
![]() $i=n_2-n_1$
and
$i=n_2-n_1$
and
 $$ \begin{align*}y|_{U_n}=(\frac{t}{t_{N}})^{n_1}(\frac{e_2}{e_{2,N}})^{n_2-n_1}c_iy^{n_2-n_1}=(\frac{t}{t_{N}})^{n_1}(\frac{e_1}{e_{2,N}})^{n_2-n_1}c_i.\end{align*} $$
$$ \begin{align*}y|_{U_n}=(\frac{t}{t_{N}})^{n_1}(\frac{e_2}{e_{2,N}})^{n_2-n_1}c_iy^{n_2-n_1}=(\frac{t}{t_{N}})^{n_1}(\frac{e_1}{e_{2,N}})^{n_2-n_1}c_i.\end{align*} $$
We have shown that f on
![]() $U^n:=\{z\in U\,|\, |y(z)p^{-n}|\geq 1\}$
has the form
$U^n:=\{z\in U\,|\, |y(z)p^{-n}|\geq 1\}$
has the form
 $(\frac {t}{t_{N}})^{n_1}(\frac {e_1}{e_{2,N}})^{n_2-n_1}c^{\prime }_i$
for some
$(\frac {t}{t_{N}})^{n_1}(\frac {e_1}{e_{2,N}})^{n_2-n_1}c^{\prime }_i$
for some
 $c^{\prime }_i\in H^0(V^{\prime \prime \prime }_{G_{r(n)}},\mathcal {O}_{\mathcal {X}_{K^pG_{r(n)}}})$
, where
$c^{\prime }_i\in H^0(V^{\prime \prime \prime }_{G_{r(n)}},\mathcal {O}_{\mathcal {X}_{K^pG_{r(n)}}})$
, where
 $V^{\prime \prime \prime }_{G_{r(n)}}\subset V_{G_{r(n)}}$
is defined by
$V^{\prime \prime \prime }_{G_{r(n)}}\subset V_{G_{r(n)}}$
is defined by
![]() $|y_np^{-n}|\geq 1$
. It is clear that
$|y_np^{-n}|\geq 1$
. It is clear that
![]() $c_i,c^{\prime }_i$
can glue to a section
$c_i,c^{\prime }_i$
can glue to a section
 $c\in H^0(V_{G_{r(n)}},\mathcal {O}_{\mathcal {X}_{K^pG_{r(n)}}})$
and
$c\in H^0(V_{G_{r(n)}},\mathcal {O}_{\mathcal {X}_{K^pG_{r(n)}}})$
and
 $f=(\frac {t}{t_{N}})^{n_1}(\frac {e_1}{e_{2,N}})^{n_2-n_1}c$
. This proves the second and fourth parts of the proposition.
$f=(\frac {t}{t_{N}})^{n_1}(\frac {e_1}{e_{2,N}})^{n_2-n_1}c$
. This proves the second and fourth parts of the proposition.
The third part follows directly from the first two parts.
Remark 5.2.14. One can reinterpret these computations from the point of view of spectral theory. Consider the stalk of
 $\mathcal {O}^{\mathrm {la},\chi }_{K^p}$
at
$\mathcal {O}^{\mathrm {la},\chi }_{K^p}$
at
![]() $\infty $
:
$\infty $
:
 $$ \begin{align*}A^{\chi}:=\varinjlim_{U\ni\infty} \mathcal{O}^{\mathrm{la},\chi}_{K^p}(U),\end{align*} $$
$$ \begin{align*}A^{\chi}:=\varinjlim_{U\ni\infty} \mathcal{O}^{\mathrm{la},\chi}_{K^p}(U),\end{align*} $$
where the direct limit runs through all open subsets U containing
![]() $\infty $
. We equip
$\infty $
. We equip
![]() $A^\chi $
with the direct limit topology. Note that if we fix
$A^\chi $
with the direct limit topology. Note that if we fix
![]() $U\in \mathfrak {B}$
containing
$U\in \mathfrak {B}$
containing
![]() $\infty $
and
$\infty $
and
 $(\frac {t}{t_n})^{n_1}(\frac {e_2}{e_{2,n}})^{-\chi (h)}\in \mathcal {O}^{\mathrm {la},\chi }_{K^p}(U)$
, then multiplication by
$(\frac {t}{t_n})^{n_1}(\frac {e_2}{e_{2,n}})^{-\chi (h)}\in \mathcal {O}^{\mathrm {la},\chi }_{K^p}(U)$
, then multiplication by
 $(\frac {t}{t_n})^{-n_1}(\frac {e_2}{e_{2,n}})^{\chi (h)}$
induces an isomorphism
$(\frac {t}{t_n})^{-n_1}(\frac {e_2}{e_{2,n}})^{\chi (h)}$
induces an isomorphism
![]() $A^\chi \xrightarrow {\sim }A^0$
. Here
$A^\chi \xrightarrow {\sim }A^0$
. Here
![]() $0$
denotes the weight
$0$
denotes the weight
![]() $0$
. Clearly, this is not
$0$
. Clearly, this is not
![]() $\mathfrak {n}$
-equivariant and a simple computation shows that the action of
$\mathfrak {n}$
-equivariant and a simple computation shows that the action of
![]() $u^+$
on
$u^+$
on
![]() $A^\chi $
becomes
$A^\chi $
becomes
Now Proposition 5.2.10 and Proposition 5.2.12 can be rephrased as follows:
-
(1)
 $u^+/y$
is a well-defined operator on
$u^+/y$
is a well-defined operator on
 $A^0$
.
$A^0$
. -
(2) (outside of spectrum)
 $u^+/y-\chi (h)$
is invertible if
$u^+/y-\chi (h)$
is invertible if
 $\chi (h)\neq 0,-1,-2,\cdots $
and is p-adically non-Liouville.
$\chi (h)\neq 0,-1,-2,\cdots $
and is p-adically non-Liouville. -
(3) (continuous spectrum)
 $u^+/y-\chi (h)$
is injective and has dense image if
$u^+/y-\chi (h)$
is injective and has dense image if
 $\chi (h)$
is p-adically Liouville.
$\chi (h)$
is p-adically Liouville. -
(4) (point spectrum)
 $u^+/y-\chi (h)$
has kernel the stalk of
$u^+/y-\chi (h)$
has kernel the stalk of
 $\mathcal {O}^{\mathrm {la},\chi ,\mathfrak {n}}_{K^p}$
at
$\mathcal {O}^{\mathrm {la},\chi ,\mathfrak {n}}_{K^p}$
at
 $\infty $
if
$\infty $
if
 $-\chi (h)\in \mathbb {N}$
,
$-\chi (h)\in \mathbb {N}$
,
summarising the results we have obtained so far.
Theorem 5.2.15. Let
![]() $\chi =(n_1,n_2)$
be a weight. Then
$\chi =(n_1,n_2)$
be a weight. Then
-
(1)
 $(H^1({\mathscr {F}\!\ell },\mathcal {O}^{\mathrm {la}}_{K^p})^{\chi })_{\mathfrak {n}}=H^1({\mathscr {F}\!\ell },\mathcal {O}^{\mathrm {la},\chi }_{K^p})_{\mathfrak {n}}=0$
if
$(H^1({\mathscr {F}\!\ell },\mathcal {O}^{\mathrm {la}}_{K^p})^{\chi })_{\mathfrak {n}}=H^1({\mathscr {F}\!\ell },\mathcal {O}^{\mathrm {la},\chi }_{K^p})_{\mathfrak {n}}=0$
if
 $\chi (h)\neq 0$
.
$\chi (h)\neq 0$
. -
(2) Suppose
 $\chi (h)\neq 0 ,1$
. There is a natural Hecke-equivariant weight decomposition of
$\chi (h)\neq 0 ,1$
. There is a natural Hecke-equivariant weight decomposition of
 $C[B]$
-modules where
$C[B]$
-modules where $$ \begin{align*}H^1({\mathscr{F}\!\ell},\mathcal{O}^{\mathrm{la}}_{K^p})^{\chi,\mathfrak{n}}=H^1({\mathscr{F}\!\ell},\mathcal{O}^{\mathrm{la},\chi}_{K^p})^{\mathfrak{n}}=M^{\dagger}_{\chi}(K^p)\otimes_{C}\mathfrak{n}^*\oplus W_2,\end{align*} $$
$$ \begin{align*}H^1({\mathscr{F}\!\ell},\mathcal{O}^{\mathrm{la}}_{K^p})^{\chi,\mathfrak{n}}=H^1({\mathscr{F}\!\ell},\mathcal{O}^{\mathrm{la},\chi}_{K^p})^{\mathfrak{n}}=M^{\dagger}_{\chi}(K^p)\otimes_{C}\mathfrak{n}^*\oplus W_2,\end{align*} $$
 $W_2$
has weight
$W_2$
has weight
 $(n_2,n_1)$
and
$(n_2,n_1)$
and
 $M^{\dagger }_{\chi }(K^p)\otimes _C \mathfrak {n}^*$
has weight
$M^{\dagger }_{\chi }(K^p)\otimes _C \mathfrak {n}^*$
has weight
 $(n_1-1,n_2+1)$
.
$(n_1-1,n_2+1)$
.
Proof. Assume
![]() $\chi (h)\neq 0$
. Then by our discussion in the beginning of this subsection Equation (5.2.2),
$\chi (h)\neq 0$
. Then by our discussion in the beginning of this subsection Equation (5.2.2),
 $H^1({\mathscr {F}\!\ell },\mathcal {O}_{K^p}^{\mathrm {la},\chi })_{\mathfrak {n}}\cong H^1({\mathscr {F}\!\ell },(\mathcal {O}_{K^p}^{\mathrm {la},\chi })_{\mathfrak {n}})$
, which is zero, as pointed out in Proposition 5.2.10.
$H^1({\mathscr {F}\!\ell },\mathcal {O}_{K^p}^{\mathrm {la},\chi })_{\mathfrak {n}}\cong H^1({\mathscr {F}\!\ell },(\mathcal {O}_{K^p}^{\mathrm {la},\chi })_{\mathfrak {n}})$
, which is zero, as pointed out in Proposition 5.2.10.
Suppose
![]() $\chi (h)\neq 1$
, then
$\chi (h)\neq 1$
, then
![]() $-\chi (h)\neq w\cdot (-\chi )(h)$
. It follows from Corollary 4.2.8 that
$-\chi (h)\neq w\cdot (-\chi )(h)$
. It follows from Corollary 4.2.8 that
![]() $(h+\chi (h))(h-w\cdot (-\chi )(h))=0$
on
$(h+\chi (h))(h-w\cdot (-\chi )(h))=0$
on
 $H^1({\mathscr {F}\!\ell },\mathcal {O}^{\mathrm {la},\chi }_{K^p})^{\mathfrak {n}}$
. Therefore, we have a natural weight decomposition
$H^1({\mathscr {F}\!\ell },\mathcal {O}^{\mathrm {la},\chi }_{K^p})^{\mathfrak {n}}$
. Therefore, we have a natural weight decomposition
 $H^1({\mathscr {F}\!\ell },\mathcal {O}^{\mathrm {la},\chi }_{K^p})^{\mathfrak {n}}=W_1\oplus W_2$
such that
$H^1({\mathscr {F}\!\ell },\mathcal {O}^{\mathrm {la},\chi }_{K^p})^{\mathfrak {n}}=W_1\oplus W_2$
such that
![]() $\mathfrak {h}$
acts on
$\mathfrak {h}$
acts on
![]() $W_1$
(respectively
$W_1$
(respectively
![]() $W_2$
) via
$W_2$
) via
![]() $(n_1-1,n_2+1)$
(respectively
$(n_1-1,n_2+1)$
(respectively
![]() $(n_2,n_1)$
). Since
$(n_2,n_1)$
). Since
 $H^1({\mathscr {F}\!\ell },\mathcal {O}^{\mathrm {la},\chi ,\mathfrak {n}}_{K^p})$
has no weight-
$H^1({\mathscr {F}\!\ell },\mathcal {O}^{\mathrm {la},\chi ,\mathfrak {n}}_{K^p})$
has no weight-
![]() $(n_1-1,n_2+1)$
part by Proposition 5.2.12 and the weight-
$(n_1-1,n_2+1)$
part by Proposition 5.2.12 and the weight-
![]() $(n_1-1,n_2+1)$
part of
$(n_1-1,n_2+1)$
part of
 $H^0({\mathscr {F}\!\ell },(\mathcal {O}^{\mathrm {la},\chi }_{K^p})_{\mathfrak {n}})\otimes _C \mathfrak {n}^*$
is
$H^0({\mathscr {F}\!\ell },(\mathcal {O}^{\mathrm {la},\chi }_{K^p})_{\mathfrak {n}})\otimes _C \mathfrak {n}^*$
is
 $M^{\dagger }_\chi (K^p)\otimes _C \mathfrak {n}^*$
by Proposition 5.2.10, our claim for
$M^{\dagger }_\chi (K^p)\otimes _C \mathfrak {n}^*$
by Proposition 5.2.10, our claim for
![]() $W_1$
now follows from the short exact sequence (5.2.1).
$W_1$
now follows from the short exact sequence (5.2.1).
The case
![]() $\chi (h)=0$
or
$\chi (h)=0$
or
![]() $1$
will be treated in the next subsection.
$1$
will be treated in the next subsection.
5.3
 $\mathfrak {n}$
-cohomology (II)
$\mathfrak {n}$
-cohomology (II)
5.3.1. In this subsection, we completely determine the
![]() $\mathfrak {n}$
-cohomology of
$\mathfrak {n}$
-cohomology of
 $H^1({\mathscr {F}\!\ell },\mathcal {O}^{\mathrm {la},\chi }_{K^p})$
for integral weight; that is,
$H^1({\mathscr {F}\!\ell },\mathcal {O}^{\mathrm {la},\chi }_{K^p})$
for integral weight; that is,
![]() $\chi (h)\in \mathbb {Z}$
. Write
$\chi (h)\in \mathbb {Z}$
. Write
![]() $k=\chi (h)$
. We will distinguish
$k=\chi (h)$
. We will distinguish
![]() $4$
cases:
$4$
cases:
-
(1)
 $k\geq 2$
;
$k\geq 2$
; -
(2)
 $k=1$
;
$k=1$
; -
(3)
 $k=0$
;
$k=0$
; -
(4)
 $k\leq -1$
.
$k\leq -1$
.
One key step is to understand
 $H^1({\mathscr {F}\!\ell },\mathcal {O}^{\mathrm {la},\chi ,\mathfrak {n}}_{K^p})$
. To do this, we need to introduce some auxiliary sheaves. Recall that
$H^1({\mathscr {F}\!\ell },\mathcal {O}^{\mathrm {la},\chi ,\mathfrak {n}}_{K^p})$
. To do this, we need to introduce some auxiliary sheaves. Recall that
![]() $\omega _{K^p}$
is defined as the pullback of
$\omega _{K^p}$
is defined as the pullback of
![]() $\omega $
(as a coherent sheaf) from some finite level to the infinite level. For an integer k, we write
$\omega $
(as a coherent sheaf) from some finite level to the infinite level. For an integer k, we write
 $\omega _{K^p}^{k}:=\omega _{K^p}^{\otimes k}$
.
$\omega _{K^p}^{k}:=\omega _{K^p}^{\otimes k}$
.
Definition 5.3.2. We define
 $\omega ^{k,\mathrm {sm}}_{K^p}\subset {\pi _{\mathrm {HT}}}_{*} \omega _{K^p}^{k}$
as the subsheaf of
$\omega ^{k,\mathrm {sm}}_{K^p}\subset {\pi _{\mathrm {HT}}}_{*} \omega _{K^p}^{k}$
as the subsheaf of
![]() $\mathrm {GL}_2(\mathbb {Q}_p)$
-smooth sections. More precisely, for any quasi-compact open subset
$\mathrm {GL}_2(\mathbb {Q}_p)$
-smooth sections. More precisely, for any quasi-compact open subset
![]() $U\subset {\mathscr {F}\!\ell }$
, we can find an open subgroup
$U\subset {\mathscr {F}\!\ell }$
, we can find an open subgroup
![]() $K_p$
of
$K_p$
of
![]() $\mathrm {GL}_2(\mathbb {Q}_p)$
stabilising U. Then
$\mathrm {GL}_2(\mathbb {Q}_p)$
stabilising U. Then
 $\omega ^{k,\mathrm {sm}}_{K^p}(U)\subset \omega _{K^p}^{k}(\pi _{\mathrm {HT}}^{-1}(U))$
is the subspace of
$\omega ^{k,\mathrm {sm}}_{K^p}(U)\subset \omega _{K^p}^{k}(\pi _{\mathrm {HT}}^{-1}(U))$
is the subspace of
![]() $K_p$
-smooth vectors; that is, vectors fixed by some open subgroup of
$K_p$
-smooth vectors; that is, vectors fixed by some open subgroup of
![]() $K_p$
. It is easy to see that this definition is independent of the choice of
$K_p$
. It is easy to see that this definition is independent of the choice of
![]() $K_p$
.
$K_p$
.
Remark 5.3.3. For
![]() $U\in \mathfrak {B}$
, using the notation in Theorem 4.1.7, we have
$U\in \mathfrak {B}$
, using the notation in Theorem 4.1.7, we have
 $$ \begin{align*}\omega^{k,\mathrm{sm}}_{K^p}(U)=\varinjlim_{K_p}\omega^{k}(V_{K_p}).\end{align*} $$
$$ \begin{align*}\omega^{k,\mathrm{sm}}_{K^p}(U)=\varinjlim_{K_p}\omega^{k}(V_{K_p}).\end{align*} $$
Hence, compared with Proposition 5.2.12, it is clear that
 $$ \begin{align*}\omega^{0,\mathrm{sm}}_{K^p}=\mathcal{O}^{\mathrm{la},0,\mathfrak{n}}_{K^p}.\end{align*} $$
$$ \begin{align*}\omega^{0,\mathrm{sm}}_{K^p}=\mathcal{O}^{\mathrm{la},0,\mathfrak{n}}_{K^p}.\end{align*} $$
From the point of view of classical Riemann–Hilbert correspondence, it seems better to think of
 $\omega ^{k,\mathrm {sm}}_{K^p}$
as ‘local system on the analytic site of
$\omega ^{k,\mathrm {sm}}_{K^p}$
as ‘local system on the analytic site of
![]() ${\mathscr {F}\!\ell }$
’.
${\mathscr {F}\!\ell }$
’.
Remark 5.3.4. An equivalent definition is
 $\omega ^{k,\mathrm {sm}}_{K^p}={\pi _{\mathrm {HT}}}_{*} (\varinjlim _{K_p\subset \mathrm {GL}_2(\mathbb {Q}_p)}(\pi _{K_p})^{-1} \omega ^{ k})$
. Here
$\omega ^{k,\mathrm {sm}}_{K^p}={\pi _{\mathrm {HT}}}_{*} (\varinjlim _{K_p\subset \mathrm {GL}_2(\mathbb {Q}_p)}(\pi _{K_p})^{-1} \omega ^{ k})$
. Here
![]() $\pi _{K_p}:\mathcal {X}_{K^p}\to \mathcal {X}_{K^pK_p}$
denotes the natural projection and
$\pi _{K_p}:\mathcal {X}_{K^p}\to \mathcal {X}_{K^pK_p}$
denotes the natural projection and
 $\pi _{K_p}^{-1}$
denotes pullback as sheaf of abelian groups. In fact, the cohomology of
$\pi _{K_p}^{-1}$
denotes pullback as sheaf of abelian groups. In fact, the cohomology of
 $\omega ^{k,\mathrm {sm}}_{K^p}$
is closely related to the cohomology of
$\omega ^{k,\mathrm {sm}}_{K^p}$
is closely related to the cohomology of
![]() $\omega ^{k}$
.
$\omega ^{k}$
.
Lemma 5.3.5. There is a natural isomorphism
 $$ \begin{align*}H^i({\mathscr{F}\!\ell},\omega^{k,\mathrm{sm}}_{K^p})\cong \varinjlim_{K_p\subset\mathrm{GL}_2(\mathbb{Q}_p)}H^i(\mathcal{X}_{K^pK_p},\omega^k).\end{align*} $$
$$ \begin{align*}H^i({\mathscr{F}\!\ell},\omega^{k,\mathrm{sm}}_{K^p})\cong \varinjlim_{K_p\subset\mathrm{GL}_2(\mathbb{Q}_p)}H^i(\mathcal{X}_{K^pK_p},\omega^k).\end{align*} $$
Proof. The rough idea is that the Hodge–Tate period map
![]() $\pi _{\mathrm {HT}}$
behaves as a finite map. Let
$\pi _{\mathrm {HT}}$
behaves as a finite map. Let
![]() $\mathfrak {U}=\{U_1,\cdots ,U_r\}$
be a subset of
$\mathfrak {U}=\{U_1,\cdots ,U_r\}$
be a subset of
![]() $\mathfrak {B}$
(not necessarily a cover of
$\mathfrak {B}$
(not necessarily a cover of
![]() ${\mathscr {F}\!\ell }$
); then for sufficiently small
${\mathscr {F}\!\ell }$
); then for sufficiently small
![]() $K_p$
and any
$K_p$
and any
![]() $i=1,\cdots ,r$
, we know that
$i=1,\cdots ,r$
, we know that
 $\pi _{\mathrm {HT}}^{-1}(U_i)$
is the preimage of an affinoid open subset
$\pi _{\mathrm {HT}}^{-1}(U_i)$
is the preimage of an affinoid open subset
![]() $V_{i,K_p}\subset \mathcal {X}_{K^pK_p}$
. Denote by
$V_{i,K_p}\subset \mathcal {X}_{K^pK_p}$
. Denote by
![]() $\mathfrak {V}_{K_p}=\{V_{1,K_p},\cdots ,V_{r,K_p}\}$
. Let
$\mathfrak {V}_{K_p}=\{V_{1,K_p},\cdots ,V_{r,K_p}\}$
. Let
 $C^{\bullet }(\mathfrak {U},\omega ^{k,\mathrm {sm}}_{K^p})$
be the Čech complex of
$C^{\bullet }(\mathfrak {U},\omega ^{k,\mathrm {sm}}_{K^p})$
be the Čech complex of
 $\omega ^{k,\mathrm {sm}}_{K^p}$
with respect to
$\omega ^{k,\mathrm {sm}}_{K^p}$
with respect to
![]() $\mathfrak {U}$
and define
$\mathfrak {U}$
and define
 $C^{\bullet }(\mathfrak {V}_{K_p},\omega ^k)$
in a similar way. Clearly,
$C^{\bullet }(\mathfrak {V}_{K_p},\omega ^k)$
in a similar way. Clearly,
 $$ \begin{align*}C^{\bullet}(\mathfrak{U},\omega^{k,\mathrm{sm}}_{K^p})=\varinjlim_{K_p} C^{\bullet}(\mathfrak{V}_{K_p},\omega^k).\end{align*} $$
$$ \begin{align*}C^{\bullet}(\mathfrak{U},\omega^{k,\mathrm{sm}}_{K^p})=\varinjlim_{K_p} C^{\bullet}(\mathfrak{V}_{K_p},\omega^k).\end{align*} $$
In particular, if
![]() $\mathfrak {U}$
is an open cover of some
$\mathfrak {U}$
is an open cover of some
![]() $U\in \mathfrak {B}$
, we conclude from the usual Tate acyclicity result that
$U\in \mathfrak {B}$
, we conclude from the usual Tate acyclicity result that
 $H^i(C^{\bullet }(\mathfrak {U},\omega ^{k,\mathrm {sm}}_{K^p}))=0,i\geq 1$
. Hence, by Corollaire 4, p. 176 of [Reference GrothendieckGro57], we have
$H^i(C^{\bullet }(\mathfrak {U},\omega ^{k,\mathrm {sm}}_{K^p}))=0,i\geq 1$
. Hence, by Corollaire 4, p. 176 of [Reference GrothendieckGro57], we have
 $H^i(U,\omega ^{k,\mathrm {sm}}_{K^p})=0,i\geq 1$
and
$H^i(U,\omega ^{k,\mathrm {sm}}_{K^p})=0,i\geq 1$
and
 $H^i({\mathscr {F}\!\ell },\omega ^{k,\mathrm {sm}}_{K^p})$
can be computed by Čech complex. Now taking
$H^i({\mathscr {F}\!\ell },\omega ^{k,\mathrm {sm}}_{K^p})$
can be computed by Čech complex. Now taking
![]() $\mathfrak {U}$
as a cover of
$\mathfrak {U}$
as a cover of
![]() ${\mathscr {F}\!\ell }$
, we get our claim.
${\mathscr {F}\!\ell }$
, we get our claim.
Corollary 5.3.6.
 $H^1({\mathscr {F}\!\ell },\omega ^{k,\mathrm {sm}}_{K^p})=0$
if
$H^1({\mathscr {F}\!\ell },\omega ^{k,\mathrm {sm}}_{K^p})=0$
if
![]() $k\geq 2$
.
$k\geq 2$
.
Proof. By our previous lemma, it suffices to prove
 $H^1(\mathcal {X}_{K^pK_p},\omega ^k)=0$
when
$H^1(\mathcal {X}_{K^pK_p},\omega ^k)=0$
when
![]() $k\geq 2$
. This follows from the positivity of
$k\geq 2$
. This follows from the positivity of
![]() $\omega $
and the Kodaira–Spencer isomorphism
$\omega $
and the Kodaira–Spencer isomorphism
 $\omega ^2\cong \Omega ^1_{\mathcal {X}_{K^pK_p}}(\mathcal {C})$
, where
$\omega ^2\cong \Omega ^1_{\mathcal {X}_{K^pK_p}}(\mathcal {C})$
, where
![]() $\mathcal {C}$
denotes the cusps in
$\mathcal {C}$
denotes the cusps in
![]() $\mathcal {X}_{K^pK_p}$
and is nonempty.
$\mathcal {X}_{K^pK_p}$
and is nonempty.
The following lemma implies that the stalk of
 $\omega ^{k,\mathrm {sm}}_{K^p}$
at
$\omega ^{k,\mathrm {sm}}_{K^p}$
at
![]() $\infty $
is the space of overconvergent forms of weight k introduced in Definition 5.2.5.
$\infty $
is the space of overconvergent forms of weight k introduced in Definition 5.2.5.
Lemma 5.3.7.
 $\varinjlim _{U\ni \infty }\omega ^{k,\mathrm {sm}}_{K^p}(U)=M^{\dagger }_k(K^p)$
.
$\varinjlim _{U\ni \infty }\omega ^{k,\mathrm {sm}}_{K^p}(U)=M^{\dagger }_k(K^p)$
.
Proof. This follows from Lemma 5.2.9 directly.
Definition 5.3.8. We denote by
 $$ \begin{align*}M_k(K^p):=H^0({\mathscr{F}\!\ell},\omega^{k,\mathrm{sm}}_{K^p})= \varinjlim_{K_p\subset\mathrm{GL}_2(\mathbb{Q}_p)}H^0(\mathcal{X}_{K^pK_p},\omega^k)\end{align*} $$
$$ \begin{align*}M_k(K^p):=H^0({\mathscr{F}\!\ell},\omega^{k,\mathrm{sm}}_{K^p})= \varinjlim_{K_p\subset\mathrm{GL}_2(\mathbb{Q}_p)}H^0(\mathcal{X}_{K^pK_p},\omega^k)\end{align*} $$
the space of classical weight k modular forms of tame level
![]() $K^p$
.
$K^p$
.
5.3.9 nonintegral powers of t
Recall that in Section 4.3.1, we defined t as the coordinate function on
![]() $\mathrm {Isom}(\mathbb {Z}_p,\mathbb {Z}_p(1))\cong \mathbb {Z}_p^{\times }$
by choosing a basis of
$\mathrm {Isom}(\mathbb {Z}_p,\mathbb {Z}_p(1))\cong \mathbb {Z}_p^{\times }$
by choosing a basis of
![]() $\mathbb {Z}_p(1)$
. For any
$\mathbb {Z}_p(1)$
. For any
![]() $n_1\in C$
, we can find a continuous character
$n_1\in C$
, we can find a continuous character
![]() $\mathbb {Z}_p^{\times }\to C^{\times }$
whose derivative sends
$\mathbb {Z}_p^{\times }\to C^{\times }$
whose derivative sends
![]() $1\in \mathbb {Q}_p=\operatorname {\mathrm {Lie}}(\mathbb {Z}_p^{\times })$
to
$1\in \mathbb {Q}_p=\operatorname {\mathrm {Lie}}(\mathbb {Z}_p^{\times })$
to
![]() $n_1\in C=\operatorname {\mathrm {Lie}}(C^{\times })$
. When
$n_1\in C=\operatorname {\mathrm {Lie}}(C^{\times })$
. When
![]() $n_1$
is an integer, we can simply take
$n_1$
is an integer, we can simply take
![]() $t^{n_1}$
. For noninteger
$t^{n_1}$
. For noninteger
![]() $n_1$
, we fix one choice from now on and denote it by
$n_1$
, we fix one choice from now on and denote it by
![]() $t^{n_1}$
and view it as an invertible element of
$t^{n_1}$
and view it as an invertible element of
![]() $H^0(\mathcal {X}_{K^p},\mathcal {O}_{\mathcal {X}_{K^p}})^{\mathrm {la}}$
by abuse of notation. It follows from the discussion in Section 4.3.1 that
$H^0(\mathcal {X}_{K^p},\mathcal {O}_{\mathcal {X}_{K^p}})^{\mathrm {la}}$
by abuse of notation. It follows from the discussion in Section 4.3.1 that
![]() $\mathrm {GL}_2(\mathbb {A}_f)$
acts on
$\mathrm {GL}_2(\mathbb {A}_f)$
acts on
![]() $t^{n_1}$
via
$t^{n_1}$
via
![]() $t^{n_1}\circ \varepsilon \circ \det $
and
$t^{n_1}\circ \varepsilon \circ \det $
and
![]() $G_{\mathbb {Q}_p}$
acts on it via
$G_{\mathbb {Q}_p}$
acts on it via
![]() $t^{n_1}\circ \varepsilon _p$
. Hence, we can allow nonintegral power of t in Remark 5.2.7.
$t^{n_1}\circ \varepsilon _p$
. Hence, we can allow nonintegral power of t in Remark 5.2.7.
Let
![]() $\chi =(n_1,n_2)$
. Then multiplication by
$\chi =(n_1,n_2)$
. Then multiplication by
![]() $t^{-n_1}$
induces an isomorphism
$t^{-n_1}$
induces an isomorphism
 $\mathcal {O}^{\mathrm {la},\chi }_{K^p}\xrightarrow {\sim } \mathcal {O}^{\mathrm {la},\chi '}_{K^p}$
, where
$\mathcal {O}^{\mathrm {la},\chi }_{K^p}\xrightarrow {\sim } \mathcal {O}^{\mathrm {la},\chi '}_{K^p}$
, where
![]() $\chi '=(0,n_2-n_1)$
. It is easy to see how the actions of
$\chi '=(0,n_2-n_1)$
. It is easy to see how the actions of
![]() $\mathrm {GL}_2(\mathbb {Q}_p)\times G_{\mathbb {Q}_p}$
and Hecke operators away from p change accordingly. From this, we can reduce computations to the case
$\mathrm {GL}_2(\mathbb {Q}_p)\times G_{\mathbb {Q}_p}$
and Hecke operators away from p change accordingly. From this, we can reduce computations to the case
![]() $n_1=0$
.
$n_1=0$
.
5.3.10
 $k\geq 2$
$k\geq 2$
Now we are ready to treat the case
![]() $n_1-n_2=k\geq 2$
. By Proposition 5.2.10, we have
$n_1-n_2=k\geq 2$
. By Proposition 5.2.10, we have
 $(\mathcal {O}_{K^p}^{\mathrm {la},\chi })_{\mathfrak {n}}\cong (i_{\infty })_*M^{\dagger }_\chi (K^p)$
in this case and it suffices to determine
$(\mathcal {O}_{K^p}^{\mathrm {la},\chi })_{\mathfrak {n}}\cong (i_{\infty })_*M^{\dagger }_\chi (K^p)$
in this case and it suffices to determine
 $H^1({\mathscr {F}\!\ell },\mathcal {O}^{\mathrm {la},\chi ,\mathfrak {n}}_{K^p})$
. Note that multiplication by
$H^1({\mathscr {F}\!\ell },\mathcal {O}^{\mathrm {la},\chi ,\mathfrak {n}}_{K^p})$
. Note that multiplication by
 ${t}^{-n_1}e_1^{k}$
induces an injection
${t}^{-n_1}e_1^{k}$
induces an injection
 $$ \begin{align*}\mathcal{O}^{\mathrm{la},\chi,\mathfrak{n}}_{K^p}\to\omega^{k,\mathrm{sm}}_{K^p}.\end{align*} $$
$$ \begin{align*}\mathcal{O}^{\mathrm{la},\chi,\mathfrak{n}}_{K^p}\to\omega^{k,\mathrm{sm}}_{K^p}.\end{align*} $$
More precisely, since the stalk of
 $\mathcal {O}^{\mathrm {la},\chi ,\mathfrak {n}}_{K^p}$
at
$\mathcal {O}^{\mathrm {la},\chi ,\mathfrak {n}}_{K^p}$
at
![]() $\infty $
is zero, it is enough to define this map outside of
$\infty $
is zero, it is enough to define this map outside of
![]() $\infty $
. So let
$\infty $
. So let
![]() $U\in \mathfrak {B}$
be an open subset not containing
$U\in \mathfrak {B}$
be an open subset not containing
![]() $\infty $
. It follows from the first part of Proposition 5.2.12 that this map is nothing but sending
$\infty $
. It follows from the first part of Proposition 5.2.12 that this map is nothing but sending
 $f={t}^{n_1}(\frac {e_1}{e_{1,N}})^{n_2-n_1}c\in \mathcal {O}^{\mathrm {la},\chi ,\mathfrak {n}}_{K^p}(U)$
to
$f={t}^{n_1}(\frac {e_1}{e_{1,N}})^{n_2-n_1}c\in \mathcal {O}^{\mathrm {la},\chi ,\mathfrak {n}}_{K^p}(U)$
to
 $e_{1,N}^{k}c\in \omega ^{k,\mathrm {sm}}_{K^p}(U)$
. This is, in fact, an isomorphism
$e_{1,N}^{k}c\in \omega ^{k,\mathrm {sm}}_{K^p}(U)$
. This is, in fact, an isomorphism
 $\mathcal {O}^{\mathrm {la},\chi ,\mathfrak {n}}_{K^p}(U)\xrightarrow {\sim }\omega ^{k,\mathrm {sm}}_{K^p}(U)$
. Hence, the quotient of
$\mathcal {O}^{\mathrm {la},\chi ,\mathfrak {n}}_{K^p}(U)\xrightarrow {\sim }\omega ^{k,\mathrm {sm}}_{K^p}(U)$
. Hence, the quotient of
 $\mathcal {O}^{\mathrm {la},\chi ,\mathfrak {n}}_{K^p}\to \omega ^{k,\mathrm {sm}}_{K^p}$
is simply the stalk of
$\mathcal {O}^{\mathrm {la},\chi ,\mathfrak {n}}_{K^p}\to \omega ^{k,\mathrm {sm}}_{K^p}$
is simply the stalk of
 $\omega ^{k,\mathrm {sm}}_{K^p}$
at
$\omega ^{k,\mathrm {sm}}_{K^p}$
at
![]() $\infty $
; that is,
$\infty $
; that is,
 $$ \begin{align*}0\to \mathcal{O}^{\mathrm{la},\chi,\mathfrak{n}}_{K^p}\xrightarrow{\times{t}^{-n_1}e_1^{k}}\omega^{k,\mathrm{sm}}_{K^p}\to (i_{\infty})_*M^{\dagger}_k(K^p)\to 0.\end{align*} $$
$$ \begin{align*}0\to \mathcal{O}^{\mathrm{la},\chi,\mathfrak{n}}_{K^p}\xrightarrow{\times{t}^{-n_1}e_1^{k}}\omega^{k,\mathrm{sm}}_{K^p}\to (i_{\infty})_*M^{\dagger}_k(K^p)\to 0.\end{align*} $$
Take the cohomology of this exact sequence. It follows from Corollary 5.3.6 and Lemma 5.3.5 that
 $$ \begin{align*}0\to M_k(K^p)\to M^{\dagger}_k(K^p)\to H^1({\mathscr{F}\!\ell},\mathcal{O}^{\mathrm{la},\chi,\mathfrak{n}}_{K^p})\to 0. \end{align*} $$
$$ \begin{align*}0\to M_k(K^p)\to M^{\dagger}_k(K^p)\to H^1({\mathscr{F}\!\ell},\mathcal{O}^{\mathrm{la},\chi,\mathfrak{n}}_{K^p})\to 0. \end{align*} $$
Hence,
 $H^1({\mathscr {F}\!\ell },\mathcal {O}^{\mathrm {la},\chi ,\mathfrak {n}}_{K^p})\cong M^{\dagger }_k(K^p)/ M_k(K^p)$
; that is, the quotient of overconvergent modular forms of weight k by classical forms.
$H^1({\mathscr {F}\!\ell },\mathcal {O}^{\mathrm {la},\chi ,\mathfrak {n}}_{K^p})\cong M^{\dagger }_k(K^p)/ M_k(K^p)$
; that is, the quotient of overconvergent modular forms of weight k by classical forms.
Theorem 5.3.11. Suppose
![]() $\chi (h)=k\in \{2,3,\cdots \}$
. There is a Hecke and
$\chi (h)=k\in \{2,3,\cdots \}$
. There is a Hecke and
![]() $B\times G_{\mathbb {Q}_p}$
-equivariant weight decomposition (into weight
$B\times G_{\mathbb {Q}_p}$
-equivariant weight decomposition (into weight
![]() $(n_1-1,n_2+1)$
and
$(n_1-1,n_2+1)$
and
![]() $(n_2,n_1)$
components):
$(n_2,n_1)$
components):
 $$ \begin{align*}H^1({\mathscr{F}\!\ell},\mathcal{O}^{\mathrm{la}}_{K^p})^{\chi,\mathfrak{n}}=H^1({\mathscr{F}\!\ell},\mathcal{O}^{\mathrm{la},\chi}_{K^p})^{\mathfrak{n}}=M^{\dagger}_k(K^p)\cdot e_1^{-1}e_2^{-k+1}t^{n_1} \oplus (M^{\dagger}_k(K^p)/ M_k(K^p))\cdot e_1^{-k}t^{n_1}.\end{align*} $$
$$ \begin{align*}H^1({\mathscr{F}\!\ell},\mathcal{O}^{\mathrm{la}}_{K^p})^{\chi,\mathfrak{n}}=H^1({\mathscr{F}\!\ell},\mathcal{O}^{\mathrm{la},\chi}_{K^p})^{\mathfrak{n}}=M^{\dagger}_k(K^p)\cdot e_1^{-1}e_2^{-k+1}t^{n_1} \oplus (M^{\dagger}_k(K^p)/ M_k(K^p))\cdot e_1^{-k}t^{n_1}.\end{align*} $$
Proof. We can multiply
![]() $t^{-n_1}$
to reduce to the case
$t^{-n_1}$
to reduce to the case
![]() $n_1=0$
. Assume
$n_1=0$
. Assume
![]() $n_1=0$
. Note that
$n_1=0$
. Note that
 $\mathfrak {n}^*=e_1^{-1}e_2$
as B-representations. Hence, by Proposition 5.2.6, the weight
$\mathfrak {n}^*=e_1^{-1}e_2$
as B-representations. Hence, by Proposition 5.2.6, the weight
![]() $(-1,-k+1)$
-part is isomorphic to
$(-1,-k+1)$
-part is isomorphic to
 $M^{\dagger }_k(K^p)\cdot e_1^{-1}e_2^{-k+1}$
. Since the isomorphism
$M^{\dagger }_k(K^p)\cdot e_1^{-1}e_2^{-k+1}$
. Since the isomorphism
 $H^1({\mathscr {F}\!\ell },\mathcal {O}^{\mathrm {la},\chi ,\mathfrak {n}}_{K^p})\cong M^{\dagger }_k(K^p)/ M_k(K^p)$
is essentially induced by
$H^1({\mathscr {F}\!\ell },\mathcal {O}^{\mathrm {la},\chi ,\mathfrak {n}}_{K^p})\cong M^{\dagger }_k(K^p)/ M_k(K^p)$
is essentially induced by
 $\times e_1^k$
, we can twist by
$\times e_1^k$
, we can twist by
 $e_1^{-k}$
to make it
$e_1^{-k}$
to make it
![]() $B\times G_{\mathbb {Q}_p}$
-equivariant.
$B\times G_{\mathbb {Q}_p}$
-equivariant.
5.3.12
 $k\leq -1$
$k\leq -1$
Another relatively simple case is when
![]() $\chi (h)=k\leq -1$
. In this case, Proposition 5.2.12 implies that multiplication by
$\chi (h)=k\leq -1$
. In this case, Proposition 5.2.12 implies that multiplication by
 $t^{-n_1}e_1^{k}$
induces an isomorphism
$t^{-n_1}e_1^{k}$
induces an isomorphism
 $$ \begin{align*}\mathcal{O}^{\mathrm{la},\chi,\mathfrak{n}}_{K^p}\xrightarrow{\sim}\omega^{k,\mathrm{sm}}_{K^p}.\end{align*} $$
$$ \begin{align*}\mathcal{O}^{\mathrm{la},\chi,\mathfrak{n}}_{K^p}\xrightarrow{\sim}\omega^{k,\mathrm{sm}}_{K^p}.\end{align*} $$
Therefore, by Lemma 5.3.5,
 $H^1({\mathscr {F}\!\ell },\mathcal {O}^{\mathrm {la},\chi ,\mathfrak {n}}_{K^p})\cong \varinjlim _{K_p} H^1(\mathcal {X}_{K^pK_p},\omega ^{k})$
. Combining this with Proposition 5.2.10, we get the following.
$H^1({\mathscr {F}\!\ell },\mathcal {O}^{\mathrm {la},\chi ,\mathfrak {n}}_{K^p})\cong \varinjlim _{K_p} H^1(\mathcal {X}_{K^pK_p},\omega ^{k})$
. Combining this with Proposition 5.2.10, we get the following.
Theorem 5.3.13. Suppose
![]() $\chi (h)=k\in \{-1,-2,\cdots \}$
. There is a weight decomposition (into weight
$\chi (h)=k\in \{-1,-2,\cdots \}$
. There is a weight decomposition (into weight
![]() $(n_1-1,n_2+1)$
and
$(n_1-1,n_2+1)$
and
![]() $(n_2,n_1)$
components):
$(n_2,n_1)$
components):
 $$ \begin{align*}H^1({\mathscr{F}\!\ell},\mathcal{O}^{\mathrm{la},\chi}_{K^p})^{\mathfrak{n}}=M^{\dagger}_k(K^p)\cdot e_1^{-1}e_2^{-k+1}t^{n_1} \oplus N_{k,1}\cdot e_1^{-k}t^{n_1},\end{align*} $$
$$ \begin{align*}H^1({\mathscr{F}\!\ell},\mathcal{O}^{\mathrm{la},\chi}_{K^p})^{\mathfrak{n}}=M^{\dagger}_k(K^p)\cdot e_1^{-1}e_2^{-k+1}t^{n_1} \oplus N_{k,1}\cdot e_1^{-k}t^{n_1},\end{align*} $$
where
![]() $N_{k,1}$
sits inside the exact sequence
$N_{k,1}$
sits inside the exact sequence
 $$ \begin{align*}0\to\varinjlim_{K_p} H^1(\mathcal{X}_{K^pK_p},\omega^{k})\to N_{k,1}\to M^{\dagger}_{k}(K^p)\to 0.\end{align*} $$
$$ \begin{align*}0\to\varinjlim_{K_p} H^1(\mathcal{X}_{K^pK_p},\omega^{k})\to N_{k,1}\to M^{\dagger}_{k}(K^p)\to 0.\end{align*} $$
All of the maps are Hecke and
![]() $B\times G_{\mathbb {Q}_p}$
-equivariant.
$B\times G_{\mathbb {Q}_p}$
-equivariant.
5.3.14
 $k=0$
$k=0$
Now we consider the case
![]() $\chi (h)=0$
. As before, we can multiply by
$\chi (h)=0$
. As before, we can multiply by
![]() $t^{-n_1}$
and assume
$t^{-n_1}$
and assume
![]() $n_1=0$
; that is,
$n_1=0$
; that is,
![]() $\chi =0$
. First we determine
$\chi =0$
. First we determine
 $H^1({\mathscr {F}\!\ell },\mathcal {O}^{\mathrm {la},0}_{K^p})^{\mathfrak {n}}$
. Let
$H^1({\mathscr {F}\!\ell },\mathcal {O}^{\mathrm {la},0}_{K^p})^{\mathfrak {n}}$
. Let
![]() $\mathcal {F}$
be
$\mathcal {F}$
be
 $\mathfrak {n}(\mathcal {O}^{\mathrm {la},0}_{K^p})\subset \mathcal {O}^{\mathrm {la},0}_{K^p}$
. Hence, the composite
$\mathfrak {n}(\mathcal {O}^{\mathrm {la},0}_{K^p})\subset \mathcal {O}^{\mathrm {la},0}_{K^p}$
. Hence, the composite
 $$ \begin{align*}H^1({\mathscr{F}\!\ell},\mathcal{O}^{\mathrm{la},0}_{K^p})\xrightarrow{u^+}H^1({\mathscr{F}\!\ell},\mathcal{F})\otimes\mathfrak{n}^*\to H^1({\mathscr{F}\!\ell},\mathcal{O}^{\mathrm{la},0}_{K^p})\otimes\mathfrak{n}^*\end{align*} $$
$$ \begin{align*}H^1({\mathscr{F}\!\ell},\mathcal{O}^{\mathrm{la},0}_{K^p})\xrightarrow{u^+}H^1({\mathscr{F}\!\ell},\mathcal{F})\otimes\mathfrak{n}^*\to H^1({\mathscr{F}\!\ell},\mathcal{O}^{\mathrm{la},0}_{K^p})\otimes\mathfrak{n}^*\end{align*} $$
is the endomorphism
![]() $u^+$
on
$u^+$
on
 $H^1({\mathscr {F}\!\ell },\mathcal {O}^{\mathrm {la},0}_{K^p})$
and it suffices to determine the kernels of both maps. Consider
$H^1({\mathscr {F}\!\ell },\mathcal {O}^{\mathrm {la},0}_{K^p})$
and it suffices to determine the kernels of both maps. Consider
 $$ \begin{align*}0\to \mathcal{O}^{\mathrm{la},0,\mathfrak{n}}_{K^p}\to \mathcal{O}^{\mathrm{la},0}_{K^p}\xrightarrow{u^+}\mathcal{F}\otimes \mathfrak{n}^*\to 0.\end{align*} $$
$$ \begin{align*}0\to \mathcal{O}^{\mathrm{la},0,\mathfrak{n}}_{K^p}\to \mathcal{O}^{\mathrm{la},0}_{K^p}\xrightarrow{u^+}\mathcal{F}\otimes \mathfrak{n}^*\to 0.\end{align*} $$
By Proposition 5.2.10, we know that
 $\mathcal {F}\subset \mathfrak {m}_{\infty }\mathcal {O}^{\mathrm {la},0}_{K^p}$
. Hence,
$\mathcal {F}\subset \mathfrak {m}_{\infty }\mathcal {O}^{\mathrm {la},0}_{K^p}$
. Hence,
![]() $H^0({\mathscr {F}\!\ell },\mathcal {F})=0$
because the global sections of
$H^0({\mathscr {F}\!\ell },\mathcal {F})=0$
because the global sections of
 $\mathcal {O}^{\mathrm {la},0}_{K^p}$
are
$\mathcal {O}^{\mathrm {la},0}_{K^p}$
are
 $\varinjlim _{K_p\subset \mathrm {GL}_2(\mathbb {Q}_p)}H^0(\mathcal {X}_{K^pK_p},\mathcal {O}_{\mathcal {X}_{K^pK_p}})$
. Therefore,
$\varinjlim _{K_p\subset \mathrm {GL}_2(\mathbb {Q}_p)}H^0(\mathcal {X}_{K^pK_p},\mathcal {O}_{\mathcal {X}_{K^pK_p}})$
. Therefore,
 $$ \begin{align*}H^1({\mathscr{F}\!\ell},\mathcal{O}^{\mathrm{la},0,\mathfrak{n}}_{K^p})=\ker(H^1({\mathscr{F}\!\ell},\mathcal{O}^{\mathrm{la},0}_{K^p})\xrightarrow{u^+}H^1({\mathscr{F}\!\ell},\mathcal{F})\otimes \mathfrak{n}^*)\end{align*} $$
$$ \begin{align*}H^1({\mathscr{F}\!\ell},\mathcal{O}^{\mathrm{la},0,\mathfrak{n}}_{K^p})=\ker(H^1({\mathscr{F}\!\ell},\mathcal{O}^{\mathrm{la},0}_{K^p})\xrightarrow{u^+}H^1({\mathscr{F}\!\ell},\mathcal{F})\otimes \mathfrak{n}^*)\end{align*} $$
and
 $H^1({\mathscr {F}\!\ell },\mathcal {O}^{\mathrm {la},0}_{K^p})\xrightarrow {u^+}H^1({\mathscr {F}\!\ell },\mathcal {F})\otimes \mathfrak {n}^*$
is surjective because
$H^1({\mathscr {F}\!\ell },\mathcal {O}^{\mathrm {la},0}_{K^p})\xrightarrow {u^+}H^1({\mathscr {F}\!\ell },\mathcal {F})\otimes \mathfrak {n}^*$
is surjective because
![]() ${\mathscr {F}\!\ell }$
is 1-dimensional. Note that
${\mathscr {F}\!\ell }$
is 1-dimensional. Note that
 $\mathcal {O}^{\mathrm {la},0,\mathfrak {n}}_{K^p}=\omega ^{0,\mathrm {sm}}_{K^p}$
. Hence, its
$\mathcal {O}^{\mathrm {la},0,\mathfrak {n}}_{K^p}=\omega ^{0,\mathrm {sm}}_{K^p}$
. Hence, its
![]() $H^1$
is
$H^1$
is
 $\varinjlim _{K_p}H^1(\mathcal {X}_{K^pK_p},\mathcal {O}_{\mathcal {X}_{K^pK_p}})$
. On the other hand, consider
$\varinjlim _{K_p}H^1(\mathcal {X}_{K^pK_p},\mathcal {O}_{\mathcal {X}_{K^pK_p}})$
. On the other hand, consider
 $$ \begin{align*}0\to\mathcal{F}\to \mathcal{O}^{\mathrm{la},0}_{K^p}\to(\mathcal{O}^{\mathrm{la},0}_{K^p})_{\mathfrak{n}}\to 0.\end{align*} $$
$$ \begin{align*}0\to\mathcal{F}\to \mathcal{O}^{\mathrm{la},0}_{K^p}\to(\mathcal{O}^{\mathrm{la},0}_{K^p})_{\mathfrak{n}}\to 0.\end{align*} $$
By Proposition 5.2.10,
 $H^0({\mathscr {F}\!\ell },(\mathcal {O}^{\mathrm {la},0}_{K^p})_{\mathfrak {n}})\cong M^{\dagger }_0(K^p)\oplus M^{\dagger }_0(K^p)\otimes _C\mathfrak {n}$
. It is easy to see that
$H^0({\mathscr {F}\!\ell },(\mathcal {O}^{\mathrm {la},0}_{K^p})_{\mathfrak {n}})\cong M^{\dagger }_0(K^p)\oplus M^{\dagger }_0(K^p)\otimes _C\mathfrak {n}$
. It is easy to see that
 $H^0({\mathscr {F}\!\ell },\mathcal {O}^{\mathrm {la},0}_{K^p})=M_0(K^p)$
maps to the first factor. Hence,
$H^0({\mathscr {F}\!\ell },\mathcal {O}^{\mathrm {la},0}_{K^p})=M_0(K^p)$
maps to the first factor. Hence,
 $$ \begin{align*}\ker(H^1({\mathscr{F}\!\ell},\mathcal{F})\to H^1({\mathscr{F}\!\ell},\mathcal{O}^{\mathrm{la},0}_{K^p}))\cong M^{\dagger}_0(K^p)/M_0(K^p)\oplus M^{\dagger}_0(K^p)\otimes_C\mathfrak{n}.\end{align*} $$
$$ \begin{align*}\ker(H^1({\mathscr{F}\!\ell},\mathcal{F})\to H^1({\mathscr{F}\!\ell},\mathcal{O}^{\mathrm{la},0}_{K^p}))\cong M^{\dagger}_0(K^p)/M_0(K^p)\oplus M^{\dagger}_0(K^p)\otimes_C\mathfrak{n}.\end{align*} $$
Also, since
 $(\mathcal {O}^{\mathrm {la},0}_{K^p})_{\mathfrak {n}}$
has no
$(\mathcal {O}^{\mathrm {la},0}_{K^p})_{\mathfrak {n}}$
has no
![]() $H^1$
, we have
$H^1$
, we have
 $H^1({\mathscr {F}\!\ell },\mathcal {F})\to H^1({\mathscr {F}\!\ell },\mathcal {O}^{\mathrm {la},0}_{K^p})$
is surjective. Summarising our discussions, we have the following result.
$H^1({\mathscr {F}\!\ell },\mathcal {F})\to H^1({\mathscr {F}\!\ell },\mathcal {O}^{\mathrm {la},0}_{K^p})$
is surjective. Summarising our discussions, we have the following result.
Proposition 5.3.15. Suppose
![]() $\chi =0$
. Then
$\chi =0$
. Then
-
(1)
 $H^1({\mathscr {F}\!\ell },\mathcal {O}^{\mathrm {la},0}_{K^p})_{\mathfrak {n}}=0$
;
$H^1({\mathscr {F}\!\ell },\mathcal {O}^{\mathrm {la},0}_{K^p})_{\mathfrak {n}}=0$
; -
(2) there is a Hecke and
 $B\times G_{\mathbb {Q}_p}$
-equivariant exact sequence:
$B\times G_{\mathbb {Q}_p}$
-equivariant exact sequence:  $$ \begin{align*}0\to \varinjlim_{K_p}H^1(\mathcal{X}_{K^pK_p},\mathcal{O}_{\mathcal{X}_{K^pK_p}})\to H^1({\mathscr{F}\!\ell},\mathcal{O}^{\mathrm{la},0}_{K^p})^{\mathfrak{n}}\to \mathfrak{n}^*\otimes M^{\dagger}_0(K^p)/M_0(K^p)\oplus M^{\dagger}_0(K^p)\to 0.\end{align*} $$
$$ \begin{align*}0\to \varinjlim_{K_p}H^1(\mathcal{X}_{K^pK_p},\mathcal{O}_{\mathcal{X}_{K^pK_p}})\to H^1({\mathscr{F}\!\ell},\mathcal{O}^{\mathrm{la},0}_{K^p})^{\mathfrak{n}}\to \mathfrak{n}^*\otimes M^{\dagger}_0(K^p)/M_0(K^p)\oplus M^{\dagger}_0(K^p)\to 0.\end{align*} $$
By Corollary 5.1.3, there is an exact sequence
 $$ \begin{align} 0\to M_0(K^p)\to H^1({\mathscr{F}\!\ell},\mathcal{O}^{\mathrm{la},0}_{K^p}) \to H^1({\mathscr{F}\!\ell},\mathcal{O}^{\mathrm{la}}_{K^p})^{0}\to 0. \end{align} $$
$$ \begin{align} 0\to M_0(K^p)\to H^1({\mathscr{F}\!\ell},\mathcal{O}^{\mathrm{la},0}_{K^p}) \to H^1({\mathscr{F}\!\ell},\mathcal{O}^{\mathrm{la}}_{K^p})^{0}\to 0. \end{align} $$
Note that
![]() $M_0(K^p)$
has trivial
$M_0(K^p)$
has trivial
![]() $\mathfrak {n}$
-action. It is crucial to know its image in
$\mathfrak {n}$
-action. It is crucial to know its image in
 $H^1({\mathscr {F}\!\ell },\mathcal {O}^{\mathrm {la},0}_{K^p})^{\mathfrak {n}}$
. A direct computation shows that the composite of
$H^1({\mathscr {F}\!\ell },\mathcal {O}^{\mathrm {la},0}_{K^p})^{\mathfrak {n}}$
. A direct computation shows that the composite of
 $$ \begin{align*}M_0(K^p)\to H^1({\mathscr{F}\!\ell},\mathcal{O}^{\mathrm{la},0}_{K^p})^{\mathfrak{n}}\to \mathfrak{n}^*\otimes M^{\dagger}_0(K^p)/M_0(K^p)\oplus M^{\dagger}_0(K^p)\end{align*} $$
$$ \begin{align*}M_0(K^p)\to H^1({\mathscr{F}\!\ell},\mathcal{O}^{\mathrm{la},0}_{K^p})^{\mathfrak{n}}\to \mathfrak{n}^*\otimes M^{\dagger}_0(K^p)/M_0(K^p)\oplus M^{\dagger}_0(K^p)\end{align*} $$
is the natural inclusion
 $M_0(K^p)\to M^{\dagger }_0(K^p)$
(up to a sign). Here the second map comes from the previous proposition. From this, taking the
$M_0(K^p)\to M^{\dagger }_0(K^p)$
(up to a sign). Here the second map comes from the previous proposition. From this, taking the
![]() $\mathfrak {n}$
-cohomology of the sequence (5.3.1), we obtain the following description in the case
$\mathfrak {n}$
-cohomology of the sequence (5.3.1), we obtain the following description in the case
![]() $\chi (h)=0$
.
$\chi (h)=0$
.
Theorem 5.3.16. Suppose
![]() $\chi =(n_1,n_1)$
; that is,
$\chi =(n_1,n_1)$
; that is,
![]() $k=0$
. Then
$k=0$
. Then
-
(1)
 $(H^1({\mathscr {F}\!\ell },\mathcal {O}^{\mathrm {la}}_{K^p})^\chi )_{\mathfrak {n}}=0$
;
$(H^1({\mathscr {F}\!\ell },\mathcal {O}^{\mathrm {la}}_{K^p})^\chi )_{\mathfrak {n}}=0$
; -
(2) there is a weight decomposition (into weight
 $(n_1-1,n_1+1)$
and
$(n_1-1,n_1+1)$
and
 $(n_1,n_1)$
components): where
$(n_1,n_1)$
components): where $$ \begin{align*}H^1({\mathscr{F}\!\ell},\mathcal{O}^{\mathrm{la}}_{K^p})^{\chi,\mathfrak{n}}=N_{2,w}\cdot e_1^{-1}e_2t^{n_1}\oplus N_{0,1}\cdot t^{n_1},\end{align*} $$
$$ \begin{align*}H^1({\mathscr{F}\!\ell},\mathcal{O}^{\mathrm{la}}_{K^p})^{\chi,\mathfrak{n}}=N_{2,w}\cdot e_1^{-1}e_2t^{n_1}\oplus N_{0,1}\cdot t^{n_1},\end{align*} $$
 $N_{2,w}$
and
$N_{2,w}$
and
 $N_{0,1}$
sit inside exact sequences
$N_{0,1}$
sit inside exact sequences  $$ \begin{align*}0\to M^{\dagger}_0(K^p)/M_0(K^p) \to N_{2,w} \to M_0(K^p)\to 0,\end{align*} $$
All of the maps are Hecke and
$$ \begin{align*}0\to M^{\dagger}_0(K^p)/M_0(K^p) \to N_{2,w} \to M_0(K^p)\to 0,\end{align*} $$
All of the maps are Hecke and $$ \begin{align*}0\to \varinjlim_{K_p}H^1(\mathcal{X}_{K^pK_p},\mathcal{O}_{\mathcal{X}_{K^pK_p}})\to N_{0,1}\to M^{\dagger}_0(K^p)/M_0(K^p)\to 0.\end{align*} $$
$$ \begin{align*}0\to \varinjlim_{K_p}H^1(\mathcal{X}_{K^pK_p},\mathcal{O}_{\mathcal{X}_{K^pK_p}})\to N_{0,1}\to M^{\dagger}_0(K^p)/M_0(K^p)\to 0.\end{align*} $$
 $B\times G_{\mathbb {Q}_p}$
-equivariant.
$B\times G_{\mathbb {Q}_p}$
-equivariant.
5.3.17
 $k=1$
$k=1$
Finally, we treat the case of singular weight; that is,
![]() $\chi (h)=1$
. Again we may assume
$\chi (h)=1$
. Again we may assume
![]() $n_1=0$
by a twist. Note that by Proposition 5.2.10, we have
$n_1=0$
by a twist. Note that by Proposition 5.2.10, we have
 $(\mathcal {O}_{K^p}^{\mathrm {la},\chi })_{\mathfrak {n}}=(i_{\infty })_*M^{\dagger }_\chi (K^p)$
. Similar to the case
$(\mathcal {O}_{K^p}^{\mathrm {la},\chi })_{\mathfrak {n}}=(i_{\infty })_*M^{\dagger }_\chi (K^p)$
. Similar to the case
![]() $k\geq 2$
in 5.3.10, there is an exact sequence
$k\geq 2$
in 5.3.10, there is an exact sequence
 $$ \begin{align*}0\to \mathcal{O}^{\mathrm{la},\chi,\mathfrak{n}}_{K^p}\xrightarrow{\times e_1}\omega^{1,\mathrm{sm}}_{K^p}\to (i_{\infty})_*M^{\dagger}_1(K^p)\to 0\end{align*} $$
$$ \begin{align*}0\to \mathcal{O}^{\mathrm{la},\chi,\mathfrak{n}}_{K^p}\xrightarrow{\times e_1}\omega^{1,\mathrm{sm}}_{K^p}\to (i_{\infty})_*M^{\dagger}_1(K^p)\to 0\end{align*} $$
induced by multiplication by
![]() $e_1$
. The difference here is that
$e_1$
. The difference here is that
 $\omega ^{1,\mathrm {sm}}_{K^p}$
have both nontrivial
$\omega ^{1,\mathrm {sm}}_{K^p}$
have both nontrivial
![]() $H^0$
and
$H^0$
and
![]() $H^1$
. More precisely, taking the cohomology of this exact sequence, we get
$H^1$
. More precisely, taking the cohomology of this exact sequence, we get
 $$ \begin{align*}0\to M_1(K^p)\to M^{\dagger}_1(K^p)\to H^1({\mathscr{F}\!\ell},\mathcal{O}^{\mathrm{la},\chi,\mathfrak{n}}_{K^p})\to \varinjlim_{K_p}H^1(\mathcal{X}_{K^pK_p}, \omega^{1})\to 0.\end{align*} $$
$$ \begin{align*}0\to M_1(K^p)\to M^{\dagger}_1(K^p)\to H^1({\mathscr{F}\!\ell},\mathcal{O}^{\mathrm{la},\chi,\mathfrak{n}}_{K^p})\to \varinjlim_{K_p}H^1(\mathcal{X}_{K^pK_p}, \omega^{1})\to 0.\end{align*} $$
Then by our discussion in Section 5.2.1, we have the following result.
Theorem 5.3.18. Suppose
![]() $\chi =(n_1,n_1-1)$
; that is,
$\chi =(n_1,n_1-1)$
; that is,
![]() $\chi (h)=1$
. All of the maps below are Hecke and
$\chi (h)=1$
. All of the maps below are Hecke and
![]() $B\times G_{\mathbb {Q}_p}$
-equivariant.
$B\times G_{\mathbb {Q}_p}$
-equivariant.
-
(1) There is a short exact sequence
(5.3.2)where $$ \begin{align} 0\to N_1\cdot e_1^{-1}t^{n_1}\to H^1({\mathscr{F}\!\ell},\mathcal{O}^{\mathrm{la}}_{K^p})^{\chi,\mathfrak{n}}\to M^{\dagger}_1(K^p)\cdot e_1^{-1}t^{n_1}\to 0, \end{align} $$
$$ \begin{align} 0\to N_1\cdot e_1^{-1}t^{n_1}\to H^1({\mathscr{F}\!\ell},\mathcal{O}^{\mathrm{la}}_{K^p})^{\chi,\mathfrak{n}}\to M^{\dagger}_1(K^p)\cdot e_1^{-1}t^{n_1}\to 0, \end{align} $$
 $N_1$
sits inside the exact sequence
$N_1$
sits inside the exact sequence  $$ \begin{align*}0\to M^{\dagger}_1(K^p)/M_1(K^p)\to N_1\to \varinjlim_{K_p}H^1(\mathcal{X}_{K^pK_p}, \omega^{1})\to 0.\end{align*} $$
$$ \begin{align*}0\to M^{\dagger}_1(K^p)/M_1(K^p)\to N_1\to \varinjlim_{K_p}H^1(\mathcal{X}_{K^pK_p}, \omega^{1})\to 0.\end{align*} $$
-
(2) Under (5.3.2), the weight-
 $(n_1-1,n_1)$
part
$(n_1-1,n_1)$
part
 $H^1({\mathscr {F}\!\ell },\mathcal {O}^{\mathrm {la}}_{K^p})^{\chi ,\mathfrak {n}}_{(n_1-1,n_1)}$
of
$H^1({\mathscr {F}\!\ell },\mathcal {O}^{\mathrm {la}}_{K^p})^{\chi ,\mathfrak {n}}_{(n_1-1,n_1)}$
of
 $H^1({\mathscr {F}\!\ell },\mathcal {O}^{\mathrm {la}}_{K^p})^{\chi ,\mathfrak {n}}$
is the pullback of
$H^1({\mathscr {F}\!\ell },\mathcal {O}^{\mathrm {la}}_{K^p})^{\chi ,\mathfrak {n}}$
is the pullback of
 $M_1(K^p)\cdot e_1^{-1}t^{n_1}\subset M^{\dagger }_1(K^p)\cdot e_1^{-1}t^{n_1}$
; that is, it sits inside the exact sequence
$M_1(K^p)\cdot e_1^{-1}t^{n_1}\subset M^{\dagger }_1(K^p)\cdot e_1^{-1}t^{n_1}$
; that is, it sits inside the exact sequence  $$ \begin{align*}0\to N_1\cdot e_1^{-1}t^{n_1}\to H^1({\mathscr{F}\!\ell},\mathcal{O}^{\mathrm{la}}_{K^p})^{\chi,\mathfrak{n}}_{(n_1-1,n_1)}\to M_1(K^p)\cdot e_1^{-1}t^{n_1}\to 0.\end{align*} $$
$$ \begin{align*}0\to N_1\cdot e_1^{-1}t^{n_1}\to H^1({\mathscr{F}\!\ell},\mathcal{O}^{\mathrm{la}}_{K^p})^{\chi,\mathfrak{n}}_{(n_1-1,n_1)}\to M_1(K^p)\cdot e_1^{-1}t^{n_1}\to 0.\end{align*} $$
Proof. Only the second part requires extra explanation. To see this, we tensor the sequence (5.3.2) with
![]() $e_1t^{-n_1}$
and take
$e_1t^{-n_1}$
and take
![]() $\mathfrak {h}_0$
-cohomology. Recall that
$\mathfrak {h}_0$
-cohomology. Recall that
![]() $\mathfrak {h}_0\subset \mathfrak {h}$
is the subalgebra of elements with trace zero. Again, we may assume
$\mathfrak {h}_0\subset \mathfrak {h}$
is the subalgebra of elements with trace zero. Again, we may assume
![]() $n_1=0$
. We need to understand the kernel of the connecting homomorphism
$n_1=0$
. We need to understand the kernel of the connecting homomorphism
 $$ \begin{align*}\delta_1:M^{\dagger}_1(K^p)\to (N_1)_{\mathfrak{h}_0}\cong N_1.\end{align*} $$
$$ \begin{align*}\delta_1:M^{\dagger}_1(K^p)\to (N_1)_{\mathfrak{h}_0}\cong N_1.\end{align*} $$
Let
 $f\in M^{\dagger }_1(K^p)$
. Since
$f\in M^{\dagger }_1(K^p)$
. Since
 $H^1({\mathscr {F}\!\ell },\mathcal {O}^{\mathrm {la}}_{K^p})$
can be computed by Čech complex, we can take a cover
$H^1({\mathscr {F}\!\ell },\mathcal {O}^{\mathrm {la}}_{K^p})$
can be computed by Čech complex, we can take a cover
![]() $\{U^{\prime }_0,U^{\prime }_1\}\subset \mathfrak {B}$
of
$\{U^{\prime }_0,U^{\prime }_1\}\subset \mathfrak {B}$
of
![]() ${\mathscr {F}\!\ell }$
such that only
${\mathscr {F}\!\ell }$
such that only
![]() $U^{\prime }_1$
contains
$U^{\prime }_1$
contains
![]() $\infty $
and the pullback of f to
$\infty $
and the pullback of f to
![]() $\mathcal {X}_{K^p}$
is defined on
$\mathcal {X}_{K^p}$
is defined on
 $\pi _{\mathrm {HT}}^{-1}(U^{\prime }_1)$
. On
$\pi _{\mathrm {HT}}^{-1}(U^{\prime }_1)$
. On
![]() $U^{\prime }_{01}:=U^{\prime }_0\cap U^{\prime }_1$
, we can find
$U^{\prime }_{01}:=U^{\prime }_0\cap U^{\prime }_1$
, we can find
 $g\in \mathcal {O}^{\mathrm {la},\chi }_{K^p}(U^{\prime }_{01})$
such that
$g\in \mathcal {O}^{\mathrm {la},\chi }_{K^p}(U^{\prime }_{01})$
such that
 $u^+\cdot g=fe_2^{-1}$
. Then
$u^+\cdot g=fe_2^{-1}$
. Then
![]() $-g$
can be viewed as a
$-g$
can be viewed as a
![]() $1$
-cocycle of the Čech complex of
$1$
-cocycle of the Čech complex of
 $\mathcal {O}^{\mathrm {la},\chi }_{K^p}$
with respect to the cover
$\mathcal {O}^{\mathrm {la},\chi }_{K^p}$
with respect to the cover
![]() $\{U^{\prime }_0,U^{\prime }_1\}$
, and it maps to
$\{U^{\prime }_0,U^{\prime }_1\}$
, and it maps to
 $f\otimes 1\in M^{\dagger }_1(K^p)\otimes e_1^{-1}=M^{\dagger }_1(K^p)\cdot e_1^{-1}$
in the sequence (5.3.2). (Here we view
$f\otimes 1\in M^{\dagger }_1(K^p)\otimes e_1^{-1}=M^{\dagger }_1(K^p)\cdot e_1^{-1}$
in the sequence (5.3.2). (Here we view
![]() $e_1=C$
as a character of B.) Using the notation in Lemma 5.1.2, we can take g of the form
$e_1=C$
as a character of B.) Using the notation in Lemma 5.1.2, we can take g of the form
 $$ \begin{align*}g=\frac{f}{e_1}\log(\frac{x}{x_n}).\end{align*} $$
$$ \begin{align*}g=\frac{f}{e_1}\log(\frac{x}{x_n}).\end{align*} $$
If we view
![]() $g\otimes 1$
as an element of
$g\otimes 1$
as an element of
 $\mathcal {O}^{\mathrm {la},\chi }_{K^p}(U^{\prime }_{01})\otimes e_1$
, then
$\mathcal {O}^{\mathrm {la},\chi }_{K^p}(U^{\prime }_{01})\otimes e_1$
, then
 $$ \begin{align*}h\cdot (g\otimes 1)= h\cdot g\otimes 1+g\otimes 1=(-g\otimes 1-\frac{2f}{e_1}\otimes 1)+g\otimes 1=-\frac{2f}{e_1}\otimes 1.\end{align*} $$
$$ \begin{align*}h\cdot (g\otimes 1)= h\cdot g\otimes 1+g\otimes 1=(-g\otimes 1-\frac{2f}{e_1}\otimes 1)+g\otimes 1=-\frac{2f}{e_1}\otimes 1.\end{align*} $$
In view of the discussion in Section 5.3.17, this means
 $\delta _1(f)=-2f\in M^{\dagger }_1(K^p)/M_1(K^p)\subset N_1$
. Hence,
$\delta _1(f)=-2f\in M^{\dagger }_1(K^p)/M_1(K^p)\subset N_1$
. Hence,
![]() $\delta _1(f)=0$
if and only if
$\delta _1(f)=0$
if and only if
![]() $f\in M_1(K^p)$
. From this, we easily deduce our claim in the Theorem.
$f\in M_1(K^p)$
. From this, we easily deduce our claim in the Theorem.
5.4
 $\mu $
-isotypic part
$\mu $
-isotypic part
5.4.1. Let
![]() $\mu \in \mathfrak {h}^*$
be a weight, viewed as a character of
$\mu \in \mathfrak {h}^*$
be a weight, viewed as a character of
![]() $\mathfrak {b}$
. The goal of this subsection is to determine the
$\mathfrak {b}$
. The goal of this subsection is to determine the
![]() $\mu $
-isotypic part of
$\mu $
-isotypic part of
 $\tilde {H}^1(K^p,C)^{\mathrm {la}}\cong H^1({\mathscr {F}\!\ell },\mathcal {O}^{\mathrm {la}}_{K^p})$
, which we denote by
$\tilde {H}^1(K^p,C)^{\mathrm {la}}\cong H^1({\mathscr {F}\!\ell },\mathcal {O}^{\mathrm {la}}_{K^p})$
, which we denote by
 $$ \begin{align*}\tilde{H}^1(K^p,C)^{\mathrm{la}}_{\mu}\cong H^1({\mathscr{F}\!\ell},\mathcal{O}^{\mathrm{la}}_{K^p})_{\mu}. \end{align*} $$
$$ \begin{align*}\tilde{H}^1(K^p,C)^{\mathrm{la}}_{\mu}\cong H^1({\mathscr{F}\!\ell},\mathcal{O}^{\mathrm{la}}_{K^p})_{\mu}. \end{align*} $$
Write
![]() $\mu =(k_1,k_2)$
. Then by Corollary 4.2.8 and Harish–Chandra’s theory,Footnote
4
we have
$\mu =(k_1,k_2)$
. Then by Corollary 4.2.8 and Harish–Chandra’s theory,Footnote
4
we have
 $$ \begin{align*}H^1({\mathscr{F}\!\ell},\mathcal{O}^{\mathrm{la}}_{K^p})_{\mu}=H^1({\mathscr{F}\!\ell},\mathcal{O}^{\mathrm{la}}_{K^p})^{(k_2,k_1)}_{\mu}\oplus H^1({\mathscr{F}\!\ell},\mathcal{O}^{\mathrm{la}}_{K^p})^{(k_1+1,k_2-1)}_{\mu}\end{align*} $$
$$ \begin{align*}H^1({\mathscr{F}\!\ell},\mathcal{O}^{\mathrm{la}}_{K^p})_{\mu}=H^1({\mathscr{F}\!\ell},\mathcal{O}^{\mathrm{la}}_{K^p})^{(k_2,k_1)}_{\mu}\oplus H^1({\mathscr{F}\!\ell},\mathcal{O}^{\mathrm{la}}_{K^p})^{(k_1+1,k_2-1)}_{\mu}\end{align*} $$
if
![]() $(k_2,k_1)\neq (k_1+1,k_2-1)$
; that is,
$(k_2,k_1)\neq (k_1+1,k_2-1)$
; that is,
![]() $\mu (h)\neq -1$
. (This is opposite to the singular weight in the previous section as there is a sign in Corollary 4.2.8.) Since the right-hand side is computed in Theorems 5.2.15, 5.3.11, 5.3.13, 5.3.16 (which is complete in the integral weight case), we obtain the following theorem by writing
$\mu (h)\neq -1$
. (This is opposite to the singular weight in the previous section as there is a sign in Corollary 4.2.8.) Since the right-hand side is computed in Theorems 5.2.15, 5.3.11, 5.3.13, 5.3.16 (which is complete in the integral weight case), we obtain the following theorem by writing
 $$ \begin{align*}M_{\mu,1}:=H^1({\mathscr{F}\!\ell},\mathcal{O}^{\mathrm{la}}_{K^p})^{(k_2,k_1)}_{\mu}, M_{\mu,w}:=H^1({\mathscr{F}\!\ell},\mathcal{O}^{\mathrm{la}}_{K^p})^{(k_1+1,k_2-1)}_{\mu}.\end{align*} $$
$$ \begin{align*}M_{\mu,1}:=H^1({\mathscr{F}\!\ell},\mathcal{O}^{\mathrm{la}}_{K^p})^{(k_2,k_1)}_{\mu}, M_{\mu,w}:=H^1({\mathscr{F}\!\ell},\mathcal{O}^{\mathrm{la}}_{K^p})^{(k_1+1,k_2-1)}_{\mu}.\end{align*} $$
Note that by Theorem 5.1.11, the horizontal action
![]() $\theta _{\mathfrak {h}}$
of
$\theta _{\mathfrak {h}}$
of
![]() $\mathfrak {h}$
essentially agrees with the Sen operator. Hence,
$\mathfrak {h}$
essentially agrees with the Sen operator. Hence,
![]() $M_{\mu ,1}$
has pure Hodge–Tate–Sen weight
$M_{\mu ,1}$
has pure Hodge–Tate–Sen weight
![]() $-k_1$
and
$-k_1$
and
![]() $M_{\mu ,w}$
has pure Hodge–Tate–Sen weight
$M_{\mu ,w}$
has pure Hodge–Tate–Sen weight
![]() $1-k_2$
in the sense of Definition 5.1.5. Our convention is that cyclotomic character has Hodge–Tate weight
$1-k_2$
in the sense of Definition 5.1.5. Our convention is that cyclotomic character has Hodge–Tate weight
![]() $-1$
.
$-1$
.
Theorem 5.4.2. Suppose
![]() $\mu =(k_1,k_2)\in \mathfrak {h}^*$
and
$\mu =(k_1,k_2)\in \mathfrak {h}^*$
and
![]() $k:=-\mu (h)\neq 1$
. There is a natural (Hodge)-decomposition
$k:=-\mu (h)\neq 1$
. There is a natural (Hodge)-decomposition
 $$ \begin{align*}\tilde{H}^1(K^p,C)^{\mathrm{la}}_{\mu}=M_{\mu,1}\oplus M_{\mu,w},\end{align*} $$
$$ \begin{align*}\tilde{H}^1(K^p,C)^{\mathrm{la}}_{\mu}=M_{\mu,1}\oplus M_{\mu,w},\end{align*} $$
into Hodge–Tate–Sen weight
![]() $-k_1$
and
$-k_1$
and
![]() $1-k_2$
components. We have
$1-k_2$
components. We have
 $M_{\mu ,w}= M^{\dagger }_{\mu +2\rho }(K^p)\otimes _C \mathfrak {n}^*$
unless
$M_{\mu ,w}= M^{\dagger }_{\mu +2\rho }(K^p)\otimes _C \mathfrak {n}^*$
unless
![]() $k=2$
. Moreover, if
$k=2$
. Moreover, if
![]() $k\in \mathbb {Z}$
and
$k\in \mathbb {Z}$
and
 $$ \begin{align*}M_{\mu,1}=N_{k,1}\cdot e_1^{-k}t^{k_2},\end{align*} $$
$$ \begin{align*}M_{\mu,1}=N_{k,1}\cdot e_1^{-k}t^{k_2},\end{align*} $$
 $$ \begin{align*}M_{\mu,w}=N_{k,w}\cdot e_1^{-1}e_2^{k-1}t^{k_1+1},\end{align*} $$
$$ \begin{align*}M_{\mu,w}=N_{k,w}\cdot e_1^{-1}e_2^{k-1}t^{k_1+1},\end{align*} $$
we have the following description of
![]() $N_{k,1},N_{k,w}$
. All of the isomorphisms and maps below are Hecke and
$N_{k,1},N_{k,w}$
. All of the isomorphisms and maps below are Hecke and
![]() $B\times G_{\mathbb {Q}_p}$
-equivariant.
$B\times G_{\mathbb {Q}_p}$
-equivariant.
-
(1)
 $N_{k,w}\cong M^{\dagger }_{2-k}(K^p)$
unless
$N_{k,w}\cong M^{\dagger }_{2-k}(K^p)$
unless
 $k\neq 2$
. When
$k\neq 2$
. When
 $k=2$
, we have
$k=2$
, we have  $$ \begin{align*}0\to M^{\dagger}_0(K^p)/M_0(K^p) \to N_{2,w} \to M_0(K^p)\to 0.\end{align*} $$
$$ \begin{align*}0\to M^{\dagger}_0(K^p)/M_0(K^p) \to N_{2,w} \to M_0(K^p)\to 0.\end{align*} $$
-
(2) If
 $k\leq -1$
, then there is an exact sequence
$k\leq -1$
, then there is an exact sequence  $$ \begin{align*}0\to\varinjlim_{K_p} H^1(\mathcal{X}_{K^pK_p},\omega^{k})\to N_{k,1}\to M^{\dagger}_{k}(K^p)\to 0.\end{align*} $$
$$ \begin{align*}0\to\varinjlim_{K_p} H^1(\mathcal{X}_{K^pK_p},\omega^{k})\to N_{k,1}\to M^{\dagger}_{k}(K^p)\to 0.\end{align*} $$
-
(3) If
 $k=0$
, then there is an exact sequence
$k=0$
, then there is an exact sequence  $$ \begin{align*}0\to \varinjlim_{K_p}H^1(\mathcal{X}_{K^pK_p},\mathcal{O}_{\mathcal{X}_{K^pK_p}})\to N_{0,1}\to M^{\dagger}_0(K^p)/M_0(K^p)\to 0.\end{align*} $$
$$ \begin{align*}0\to \varinjlim_{K_p}H^1(\mathcal{X}_{K^pK_p},\mathcal{O}_{\mathcal{X}_{K^pK_p}})\to N_{0,1}\to M^{\dagger}_0(K^p)/M_0(K^p)\to 0.\end{align*} $$
-
(4) If
 $k\geq 2$
, then
$k\geq 2$
, then
 $N_{k,1}\cong M^{\dagger }_k(K^p)/ M_k(K^p)$
.
$N_{k,1}\cong M^{\dagger }_k(K^p)/ M_k(K^p)$
.
5.4.3. Now assume
![]() $\mu (h)=-1$
. Write
$\mu (h)=-1$
. Write
![]() $\mu =(k_1,k_1+1)$
. In this case, it follows from Corollary 4.2.8 that
$\mu =(k_1,k_1+1)$
. In this case, it follows from Corollary 4.2.8 that
 $$ \begin{align*}H^1({\mathscr{F}\!\ell},\mathcal{O}^{\mathrm{la}}_{K^p})_{\mu}=H^1({\mathscr{F}\!\ell},\mathcal{O}^{\mathrm{la},(k_1+1,k_1)^2}_{K^p})_{\mu}\end{align*} $$
$$ \begin{align*}H^1({\mathscr{F}\!\ell},\mathcal{O}^{\mathrm{la}}_{K^p})_{\mu}=H^1({\mathscr{F}\!\ell},\mathcal{O}^{\mathrm{la},(k_1+1,k_1)^2}_{K^p})_{\mu}\end{align*} $$
by considering the action of the centre of
![]() $U(\mathfrak {g})$
. Here
$U(\mathfrak {g})$
. Here
 $\mathcal {O}^{\mathrm {la},(k_1+1,k_1)^2}_{K^p}\subset \mathcal {O}^{\mathrm {la}}_{K^p}$
is the subsheaf of sections annihilated by
$\mathcal {O}^{\mathrm {la},(k_1+1,k_1)^2}_{K^p}\subset \mathcal {O}^{\mathrm {la}}_{K^p}$
is the subsheaf of sections annihilated by
![]() $(\theta _{\mathfrak {h}}(h)-1)^2$
and
$(\theta _{\mathfrak {h}}(h)-1)^2$
and
![]() $\theta _{\mathfrak {h}}(z)-\mu (z)=z-(2k_1+1)$
. We compute the
$\theta _{\mathfrak {h}}(z)-\mu (z)=z-(2k_1+1)$
. We compute the
![]() $\mathfrak {n}$
-invariants of
$\mathfrak {n}$
-invariants of
 $H^1({\mathscr {F}\!\ell },\mathcal {O}^{\mathrm {la},(k_1+1,k_1)^2}_{K^p})$
first and then determine the
$H^1({\mathscr {F}\!\ell },\mathcal {O}^{\mathrm {la},(k_1+1,k_1)^2}_{K^p})$
first and then determine the
![]() $\mu $
-component. Note that
$\mu $
-component. Note that
![]() $\theta _{\mathfrak {h}}(h)-1$
induces an exact sequence
$\theta _{\mathfrak {h}}(h)-1$
induces an exact sequence
 $$ \begin{align*}0\to\mathcal{O}^{\mathrm{la},(k_1+1,k_1)}_{K^p}\to\mathcal{O}^{\mathrm{la},(k_1+1,k_1)^2}_{K^p}\xrightarrow{\theta_{\mathfrak{h}}(h)-1} \mathcal{O}^{\mathrm{la},(k_1+1,k_1)}_{K^p} \to 0,\end{align*} $$
$$ \begin{align*}0\to\mathcal{O}^{\mathrm{la},(k_1+1,k_1)}_{K^p}\to\mathcal{O}^{\mathrm{la},(k_1+1,k_1)^2}_{K^p}\xrightarrow{\theta_{\mathfrak{h}}(h)-1} \mathcal{O}^{\mathrm{la},(k_1+1,k_1)}_{K^p} \to 0,\end{align*} $$
where the third map is surjective by the first part of Lemma 5.1.2. For simplicity, we write
 $\mathcal {F}_1=\mathcal {O}^{\mathrm {la},(k_1+1,k_1)}_{K^p}$
and
$\mathcal {F}_1=\mathcal {O}^{\mathrm {la},(k_1+1,k_1)}_{K^p}$
and
 $\mathcal {F}_2=\mathcal {O}^{\mathrm {la},(k_1+1,k_1)^2}_{K^p}$
. Then
$\mathcal {F}_2=\mathcal {O}^{\mathrm {la},(k_1+1,k_1)^2}_{K^p}$
. Then
![]() $\mathcal {F}_2$
has no
$\mathcal {F}_2$
has no
![]() $H^0$
because
$H^0$
because
![]() $\mathcal {F}_1$
has no global section (Corollary 5.1.3). Hence,
$\mathcal {F}_1$
has no global section (Corollary 5.1.3). Hence,
By Propositions 5.2.10 and 5.2.12, we know that the supports of
![]() $(\mathcal {F}_1)^{\mathfrak {n}}$
and
$(\mathcal {F}_1)^{\mathfrak {n}}$
and
![]() $(\mathcal {F}_1)_{\mathfrak {n}}$
do not intersect. Therefore,
$(\mathcal {F}_1)_{\mathfrak {n}}$
do not intersect. Therefore,
![]() $\theta _{\mathfrak {h}}(h)-1$
induces exact sequences
$\theta _{\mathfrak {h}}(h)-1$
induces exact sequences
 $$ \begin{align*}0\to (\mathcal{F}_1)^{\mathfrak{n}}\to (\mathcal{F}_2)^{\mathfrak{n}}\xrightarrow{\theta_{\mathfrak{h}}(h)-1}(\mathcal{F}_1)^{\mathfrak{n}}\to 0;\end{align*} $$
$$ \begin{align*}0\to (\mathcal{F}_1)^{\mathfrak{n}}\to (\mathcal{F}_2)^{\mathfrak{n}}\xrightarrow{\theta_{\mathfrak{h}}(h)-1}(\mathcal{F}_1)^{\mathfrak{n}}\to 0;\end{align*} $$
 $$ \begin{align*}0\to (\mathcal{F}_1)_{\mathfrak{n}}\to (\mathcal{F}_2)_{\mathfrak{n}}\xrightarrow{\theta_{\mathfrak{h}}(h)-1}(\mathcal{F}_1)_{\mathfrak{n}}\to 0.\end{align*} $$
$$ \begin{align*}0\to (\mathcal{F}_1)_{\mathfrak{n}}\to (\mathcal{F}_2)_{\mathfrak{n}}\xrightarrow{\theta_{\mathfrak{h}}(h)-1}(\mathcal{F}_1)_{\mathfrak{n}}\to 0.\end{align*} $$
Taking
![]() $H^1$
of the first sequence, we obtain
$H^1$
of the first sequence, we obtain
 $$ \begin{align*}0\to H^1({\mathscr{F}\!\ell},(\mathcal{F}_1)^{\mathfrak{n}})\to H^1({\mathscr{F}\!\ell},(\mathcal{F}_2)^{\mathfrak{n}})\xrightarrow{\theta_{\mathfrak{h}}(h)-1}H^1({\mathscr{F}\!\ell},(\mathcal{F}_1)^{\mathfrak{n}})\to 0\end{align*} $$
$$ \begin{align*}0\to H^1({\mathscr{F}\!\ell},(\mathcal{F}_1)^{\mathfrak{n}})\to H^1({\mathscr{F}\!\ell},(\mathcal{F}_2)^{\mathfrak{n}})\xrightarrow{\theta_{\mathfrak{h}}(h)-1}H^1({\mathscr{F}\!\ell},(\mathcal{F}_1)^{\mathfrak{n}})\to 0\end{align*} $$
as
![]() $(\mathcal {F}_1)^{\mathfrak {n}}\subset \mathcal {F}_1$
has no
$(\mathcal {F}_1)^{\mathfrak {n}}\subset \mathcal {F}_1$
has no
![]() $H^0$
. Note that h acts as
$H^0$
. Note that h acts as
![]() $-1$
on
$-1$
on
![]() $H^1({\mathscr {F}\!\ell },(\mathcal {F}_1)^{\mathfrak {n}})$
by Proposition 5.2.12.
$H^1({\mathscr {F}\!\ell },(\mathcal {F}_1)^{\mathfrak {n}})$
by Proposition 5.2.12.
Lemma 5.4.4.
![]() $\theta _{\mathfrak {h}}(h)-1=-(h+1)$
on
$\theta _{\mathfrak {h}}(h)-1=-(h+1)$
on
![]() $(\mathcal {F}_2)^{\mathfrak {n}}$
. In particular, the kernel of
$(\mathcal {F}_2)^{\mathfrak {n}}$
. In particular, the kernel of
![]() $h+1$
on
$h+1$
on
![]() $H^1({\mathscr {F}\!\ell },(\mathcal {F}_2)^{\mathfrak {n}})$
is
$H^1({\mathscr {F}\!\ell },(\mathcal {F}_2)^{\mathfrak {n}})$
is
![]() $H^1({\mathscr {F}\!\ell },(\mathcal {F}_1)^{\mathfrak {n}})$
and
$H^1({\mathscr {F}\!\ell },(\mathcal {F}_1)^{\mathfrak {n}})$
and
![]() $h+1$
induces an isomorphism
$h+1$
induces an isomorphism
Proof. This is proved by explicit computation. We only need to check
![]() $U\in \mathfrak {B}$
not containing
$U\in \mathfrak {B}$
not containing
![]() $\infty $
since the stalk of
$\infty $
since the stalk of
![]() $(\mathcal {F}_1)^{\mathfrak {n}}$
, hence also
$(\mathcal {F}_1)^{\mathfrak {n}}$
, hence also
![]() $(\mathcal {F}_2)^{\mathfrak {n}}$
, at
$(\mathcal {F}_2)^{\mathfrak {n}}$
, at
![]() $\infty $
is zero. Using the notation in Section 4.3.7, we have
$\infty $
is zero. Using the notation in Section 4.3.7, we have
 $$ \begin{align*}(\mathcal{F}_2)^{\mathfrak{n}}(U)=(\mathcal{F}_1)^{\mathfrak{n}}(U)+(\mathcal{F}_1)^{\mathfrak{n}}(U)\cdot\log(\frac{e_1}{e_{1,N}})\end{align*} $$
$$ \begin{align*}(\mathcal{F}_2)^{\mathfrak{n}}(U)=(\mathcal{F}_1)^{\mathfrak{n}}(U)+(\mathcal{F}_1)^{\mathfrak{n}}(U)\cdot\log(\frac{e_1}{e_{1,N}})\end{align*} $$
for some
![]() $e_{1,N}$
. Since
$e_{1,N}$
. Since
![]() $\theta _{\mathfrak {h}}(h)$
acts as
$\theta _{\mathfrak {h}}(h)$
acts as
 $\begin {pmatrix} -1 & -2x \\ 0& 1 \end {pmatrix}$
on U (cf. 5.1.1), for
$\begin {pmatrix} -1 & -2x \\ 0& 1 \end {pmatrix}$
on U (cf. 5.1.1), for
![]() $f\in (\mathcal {F}_1)^{\mathfrak {n}}(U)$
,
$f\in (\mathcal {F}_1)^{\mathfrak {n}}(U)$
,
 $$ \begin{align*}(\theta_{\mathfrak{h}}(h)-1)\cdot (f\log(\frac{e_1}{e_{1,N}}))=\log(\frac{e_1}{e_{1,N}})(\theta_{\mathfrak{h}}(h)-1)\cdot f+f\theta_{\mathfrak{h}}(h)\cdot \log(\frac{e_1}{e_{1,N}})=-f.\end{align*} $$
$$ \begin{align*}(\theta_{\mathfrak{h}}(h)-1)\cdot (f\log(\frac{e_1}{e_{1,N}}))=\log(\frac{e_1}{e_{1,N}})(\theta_{\mathfrak{h}}(h)-1)\cdot f+f\theta_{\mathfrak{h}}(h)\cdot \log(\frac{e_1}{e_{1,N}})=-f.\end{align*} $$
On the other hand, by Proposition 5.2.12, we know that
![]() $(h+1)\cdot f=0$
. Therefore,
$(h+1)\cdot f=0$
. Therefore,
 $$ \begin{align*}(h+1)\cdot (f\log(\frac{e_1}{e_{1,N}}))=f h\cdot \log(\frac{e_1}{e_{1,N}})=f.\end{align*} $$
$$ \begin{align*}(h+1)\cdot (f\log(\frac{e_1}{e_{1,N}}))=f h\cdot \log(\frac{e_1}{e_{1,N}})=f.\end{align*} $$
Hence,
![]() $\theta _{\mathfrak {h}}(h)-1=-(h+1)$
on
$\theta _{\mathfrak {h}}(h)-1=-(h+1)$
on
![]() $(\mathcal {F}_2)^{\mathfrak {n}}(U)$
.
$(\mathcal {F}_2)^{\mathfrak {n}}(U)$
.
5.4.5. Similarly, we consider
 $$ \begin{align*}0\to H^0({\mathscr{F}\!\ell},(\mathcal{F}_1)_{\mathfrak{n}})\to H^0({\mathscr{F}\!\ell},(\mathcal{F}_2)_{\mathfrak{n}})\xrightarrow{\theta_{\mathfrak{h}}(h)-1}H^0({\mathscr{F}\!\ell},(\mathcal{F}_1)_{\mathfrak{n}})\to 0.\end{align*} $$
$$ \begin{align*}0\to H^0({\mathscr{F}\!\ell},(\mathcal{F}_1)_{\mathfrak{n}})\to H^0({\mathscr{F}\!\ell},(\mathcal{F}_2)_{\mathfrak{n}})\xrightarrow{\theta_{\mathfrak{h}}(h)-1}H^0({\mathscr{F}\!\ell},(\mathcal{F}_1)_{\mathfrak{n}})\to 0.\end{align*} $$
Recall that
 $(\mathcal {F}_1)_{\mathfrak {n}}\cong (i_{\infty })_*M^{\dagger }_{(k_1+1,k_1)}(K^p)$
in this case, and we may identify
$(\mathcal {F}_1)_{\mathfrak {n}}\cong (i_{\infty })_*M^{\dagger }_{(k_1+1,k_1)}(K^p)$
in this case, and we may identify
 $$ \begin{align*}(\mathcal{F}_2)_{\mathfrak{n}}=(i_{\infty})_*(M^{\dagger}_{(k_1+1,k_1)}(K^p)\oplus M^{\dagger}_{(k_1+1,k_1)}(K^p)\cdot \log(\frac{e_2}{e_{2,N}}))\end{align*} $$
$$ \begin{align*}(\mathcal{F}_2)_{\mathfrak{n}}=(i_{\infty})_*(M^{\dagger}_{(k_1+1,k_1)}(K^p)\oplus M^{\dagger}_{(k_1+1,k_1)}(K^p)\cdot \log(\frac{e_2}{e_{2,N}}))\end{align*} $$
for some
![]() $e_{2,N}$
. Then a similar computation shows that
$e_{2,N}$
. Then a similar computation shows that
![]() $\theta _{\mathfrak {h}}(h)-1=h-1$
on
$\theta _{\mathfrak {h}}(h)-1=h-1$
on
![]() $(\mathcal {F}_2)_{\mathfrak {n}}$
. Hence, the kernel of
$(\mathcal {F}_2)_{\mathfrak {n}}$
. Hence, the kernel of
![]() $h+1$
on
$h+1$
on
![]() $H^0({\mathscr {F}\!\ell },(\mathcal {F}_2)_{\mathfrak {n}})\otimes _{C} \mathfrak {n}^*$
is
$H^0({\mathscr {F}\!\ell },(\mathcal {F}_2)_{\mathfrak {n}})\otimes _{C} \mathfrak {n}^*$
is
![]() $H^0({\mathscr {F}\!\ell },(\mathcal {F}_1)_{\mathfrak {n}})\otimes _{C} \mathfrak {n}^*\subset H^0({\mathscr {F}\!\ell },(\mathcal {F}_2)_{\mathfrak {n}})\otimes _{C} \mathfrak {n}^*$
.
$H^0({\mathscr {F}\!\ell },(\mathcal {F}_1)_{\mathfrak {n}})\otimes _{C} \mathfrak {n}^*\subset H^0({\mathscr {F}\!\ell },(\mathcal {F}_2)_{\mathfrak {n}})\otimes _{C} \mathfrak {n}^*$
.
Now to determine the kernel of
![]() $h+1$
on
$h+1$
on
![]() $H^1({\mathscr {F}\!\ell },\mathcal {F}_2)^{\mathfrak {n}}$
, we claim that the surjection
$H^1({\mathscr {F}\!\ell },\mathcal {F}_2)^{\mathfrak {n}}$
, we claim that the surjection
remains surjective when passing to the kernel of
![]() $h+1$
; that is, there is an exact sequence
$h+1$
; that is, there is an exact sequence
 $$ \begin{align*}0\to H^1({\mathscr{F}\!\ell},(\mathcal{F}_2)^{\mathfrak{n}})_{\mu} \to H^1({\mathscr{F}\!\ell},\mathcal{F}_2)^{\mathfrak{n}}_{\mu}\to (H^0({\mathscr{F}\!\ell},(\mathcal{F}_2)_{\mathfrak{n}})\otimes_{C} \mathfrak{n}^*)_{\mu}\to 0. \end{align*} $$
$$ \begin{align*}0\to H^1({\mathscr{F}\!\ell},(\mathcal{F}_2)^{\mathfrak{n}})_{\mu} \to H^1({\mathscr{F}\!\ell},\mathcal{F}_2)^{\mathfrak{n}}_{\mu}\to (H^0({\mathscr{F}\!\ell},(\mathcal{F}_2)_{\mathfrak{n}})\otimes_{C} \mathfrak{n}^*)_{\mu}\to 0. \end{align*} $$
In fact, this is really a formal consequence of the previous lemma. Consider the following commutative diagram:

Let
![]() $f\in H^0({\mathscr {F}\!\ell },(\mathcal {F}_1)_{\mathfrak {n}})\otimes _{C} \mathfrak {n}^*\subset H^0({\mathscr {F}\!\ell },(\mathcal {F}_2)_{\mathfrak {n}})\otimes _{C} \mathfrak {n}^*$
. We can find a preimage
$f\in H^0({\mathscr {F}\!\ell },(\mathcal {F}_1)_{\mathfrak {n}})\otimes _{C} \mathfrak {n}^*\subset H^0({\mathscr {F}\!\ell },(\mathcal {F}_2)_{\mathfrak {n}})\otimes _{C} \mathfrak {n}^*$
. We can find a preimage
![]() $\tilde {f}\in H^1({\mathscr {F}\!\ell },\mathcal {F}_1)^{\mathfrak {n}}$
. Then
$\tilde {f}\in H^1({\mathscr {F}\!\ell },\mathcal {F}_1)^{\mathfrak {n}}$
. Then
![]() $(h+1)\cdot \tilde f\in H^1({\mathscr {F}\!\ell },(\mathcal {F}_1)^{\mathfrak {n}})$
. By Lemma 5.4.4, there exists
$(h+1)\cdot \tilde f\in H^1({\mathscr {F}\!\ell },(\mathcal {F}_1)^{\mathfrak {n}})$
. By Lemma 5.4.4, there exists
![]() $\tilde {g}\in H^1({\mathscr {F}\!\ell },(\mathcal {F}_2)^{\mathfrak {n}})$
such that
$\tilde {g}\in H^1({\mathscr {F}\!\ell },(\mathcal {F}_2)^{\mathfrak {n}})$
such that
![]() $(h+1)\cdot \tilde {g}=(h+1)\cdot \tilde f$
. Now
$(h+1)\cdot \tilde {g}=(h+1)\cdot \tilde f$
. Now
![]() $g:=\tilde {f}-\tilde {g}$
defines an element in
$g:=\tilde {f}-\tilde {g}$
defines an element in
![]() $H^1({\mathscr {F}\!\ell },\mathcal {F}_2)^{\mathfrak {n}}$
lifting f and annihilated by
$H^1({\mathscr {F}\!\ell },\mathcal {F}_2)^{\mathfrak {n}}$
lifting f and annihilated by
![]() $h+1$
.
$h+1$
.
Since
![]() $H^1({\mathscr {F}\!\ell },\mathcal {F}_1)^{\mathfrak {n}}$
is computed in Section 5.3.17, we obtain the following result. The last part is a restatement of Theorem 5.3.18.
$H^1({\mathscr {F}\!\ell },\mathcal {F}_1)^{\mathfrak {n}}$
is computed in Section 5.3.17, we obtain the following result. The last part is a restatement of Theorem 5.3.18.
Theorem 5.4.6. Suppose
![]() $\mu =(k_1,k_1+1)$
; that is,
$\mu =(k_1,k_1+1)$
; that is,
![]() $\mu (h)=-1$
. There exists an exact sequence
$\mu (h)=-1$
. There exists an exact sequence
 $$ \begin{align*}0\to N_{1}\cdot e_1^{-1}t^{k_1+1} \to \tilde{H}^1(K^p,C)^{\mathrm{la}}_{\mu} \to M^{\dagger}_{1}(K^p)\cdot e_1^{-1}t^{k_1+1}\to 0,\end{align*} $$
$$ \begin{align*}0\to N_{1}\cdot e_1^{-1}t^{k_1+1} \to \tilde{H}^1(K^p,C)^{\mathrm{la}}_{\mu} \to M^{\dagger}_{1}(K^p)\cdot e_1^{-1}t^{k_1+1}\to 0,\end{align*} $$
where
![]() $N_{1}$
sits inside the exact sequence
$N_{1}$
sits inside the exact sequence
 $$ \begin{align*}0\to M^{\dagger}_1(K^p)/M_1(K^p)\to N_{1}\to \varinjlim_{K_p}H^1(\mathcal{X}_{K^pK_p}, \omega^{1})\to 0.\end{align*} $$
$$ \begin{align*}0\to M^{\dagger}_1(K^p)/M_1(K^p)\to N_{1}\to \varinjlim_{K_p}H^1(\mathcal{X}_{K^pK_p}, \omega^{1})\to 0.\end{align*} $$
Moreover,
 $\tilde {H}^1(K^p,C)^{\mathrm {la},(k_1+1,k_1)}_{\mu }\subset \tilde {H}^1(K^p,C)^{\mathrm {la}}_{\mu }$
is identified with the pullback of
$\tilde {H}^1(K^p,C)^{\mathrm {la},(k_1+1,k_1)}_{\mu }\subset \tilde {H}^1(K^p,C)^{\mathrm {la}}_{\mu }$
is identified with the pullback of
 $M_{1}(K^p)\cdot e_1^{-1}t^{k_1+1}\subset M^{\dagger }_{1}(K^p)\cdot e_1^{-1}t^{k_1+1}$
; that is, there is an exact sequence
$M_{1}(K^p)\cdot e_1^{-1}t^{k_1+1}\subset M^{\dagger }_{1}(K^p)\cdot e_1^{-1}t^{k_1+1}$
; that is, there is an exact sequence
 $$ \begin{align*}0\to N_{1}\cdot e_1^{-1}t^{k_1+1} \to \tilde{H}^1(K^p,C)^{\mathrm{la},(k_1+1,k_1)}_{\mu} \to M_{1}(K^p)\cdot e_1^{-1}t^{k_1+1}\to 0.\end{align*} $$
$$ \begin{align*}0\to N_{1}\cdot e_1^{-1}t^{k_1+1} \to \tilde{H}^1(K^p,C)^{\mathrm{la},(k_1+1,k_1)}_{\mu} \to M_{1}(K^p)\cdot e_1^{-1}t^{k_1+1}\to 0.\end{align*} $$
All of the maps are Hecke and
![]() $B\times G_{\mathbb {Q}_p}$
-equivariant.
$B\times G_{\mathbb {Q}_p}$
-equivariant.
6 Applications
In this section, we present several applications of the main results of previous section to the study of overconvergent modular forms and the Fontaine–Mazur conjecture in the irregular case. One main ingredient is Emerton’s local–global compatibility result, which allows us to study completed cohomology using the (p-adic) representation theory of
![]() $\mathrm {GL}_2(\mathbb {Q}_p)$
.
$\mathrm {GL}_2(\mathbb {Q}_p)$
.
6.1 Hecke algebra
6.1.1. First we recall the definition of the (big) Hecke algebra associated to completed cohomology. Let
 $K^p=\prod _{l\neq p} K_l\subset \mathrm {GL}_2(\mathbb {A}_f^p)$
be a tame level and S a finite set of rational primes containing p and all places l for which
$K^p=\prod _{l\neq p} K_l\subset \mathrm {GL}_2(\mathbb {A}_f^p)$
be a tame level and S a finite set of rational primes containing p and all places l for which
![]() $K_l$
is not maximal. As usual, we denote the double coset action of
$K_l$
is not maximal. As usual, we denote the double coset action of
 $$ \begin{align*}[K_l\begin{pmatrix}l&0\\0&1\end{pmatrix}K_l]\end{align*} $$
$$ \begin{align*}[K_l\begin{pmatrix}l&0\\0&1\end{pmatrix}K_l]\end{align*} $$
by
![]() $T_l$
and the double coset action of
$T_l$
and the double coset action of
 $$ \begin{align*}[K_l\begin{pmatrix}l&0\\0&l\end{pmatrix}K_l]\end{align*} $$
$$ \begin{align*}[K_l\begin{pmatrix}l&0\\0&l\end{pmatrix}K_l]\end{align*} $$
by
![]() $S_l$
. For any open compact subgroup
$S_l$
. For any open compact subgroup
![]() $K_p$
of
$K_p$
of
![]() $\mathrm {GL}_2(\mathbb {Q}_p)$
, we define
$\mathrm {GL}_2(\mathbb {Q}_p)$
, we define
 $$ \begin{align*}\mathbb{T}(K^pK_p)\subset \operatorname{\mathrm{End}}_{\mathbb{Z}_p} (H^1_{\mathrm{\acute{e}t}}(\mathcal{Y}_{K^pK_p},\mathbb{Z}_p))\end{align*} $$
$$ \begin{align*}\mathbb{T}(K^pK_p)\subset \operatorname{\mathrm{End}}_{\mathbb{Z}_p} (H^1_{\mathrm{\acute{e}t}}(\mathcal{Y}_{K^pK_p},\mathbb{Z}_p))\end{align*} $$
as the
![]() $\mathbb {Z}_p$
-subalgebra generated by Hecke operators
$\mathbb {Z}_p$
-subalgebra generated by Hecke operators
 $T_l,S_l^{\pm 1}$
at places
$T_l,S_l^{\pm 1}$
at places
![]() $l\notin S$
. As the notation suggests, this does not depend on the choice of S because of the existence of continuous
$l\notin S$
. As the notation suggests, this does not depend on the choice of S because of the existence of continuous
![]() $2$
-dimensional determinants of
$2$
-dimensional determinants of
![]() $G_{\mathbb {Q},S}$
over
$G_{\mathbb {Q},S}$
over
![]() $\mathbb {T}(K^pK_p)$
and Chebatorev’s density theorem. Now we define the Hecke algebra of tame level
$\mathbb {T}(K^pK_p)$
and Chebatorev’s density theorem. Now we define the Hecke algebra of tame level
![]() $K^p$
as
$K^p$
as
 $$ \begin{align*}\mathbb{T}(K^p):=\varprojlim_{K_p\subset\mathrm{GL}_2(\mathbb{Q}_p)}\mathbb{T}(K^pK_p).\end{align*} $$
$$ \begin{align*}\mathbb{T}(K^p):=\varprojlim_{K_p\subset\mathrm{GL}_2(\mathbb{Q}_p)}\mathbb{T}(K^pK_p).\end{align*} $$
This is a complete semi-local
![]() $\mathbb {Z}_p$
-algebra and
$\mathbb {Z}_p$
-algebra and
![]() $\mathbb {T}(K^p)/\mathfrak {m}$
is a finite field for any maximal ideal
$\mathbb {T}(K^p)/\mathfrak {m}$
is a finite field for any maximal ideal
![]() $\mathfrak {m}$
. It acts faithfully on
$\mathfrak {m}$
. It acts faithfully on
![]() $\tilde {H}^1(K^p,\mathbb {Z}_p)$
and commutes with the action of
$\tilde {H}^1(K^p,\mathbb {Z}_p)$
and commutes with the action of
![]() $\mathrm {GL}_2(\mathbb {Q}_p)\times G_{\mathbb {Q}_p}$
. Moreover, there is a continuous
$\mathrm {GL}_2(\mathbb {Q}_p)\times G_{\mathbb {Q}_p}$
. Moreover, there is a continuous
![]() $2$
-dimensional determinant
$2$
-dimensional determinant
![]() $D_S$
of
$D_S$
of
![]() $G_{\mathbb {Q},S}$
valued in
$G_{\mathbb {Q},S}$
valued in
![]() $\mathbb {T}(K^p)$
in the sense of Chenevier [Reference ChenevierChe14] satisfying the following propertyFootnote
5
: for any
$\mathbb {T}(K^p)$
in the sense of Chenevier [Reference ChenevierChe14] satisfying the following propertyFootnote
5
: for any
![]() $l\notin S$
, the characteristic polynomial of
$l\notin S$
, the characteristic polynomial of
![]() $D_S(\operatorname {\mathrm {Frob}}_l)$
is
$D_S(\operatorname {\mathrm {Frob}}_l)$
is
Note that its twist by inverse of the cyclotomic character is also the Eichler–Shimura congruence relation ([Reference DeligneDel71, Théorème 4.9]); that is,
 $$ \begin{align*}\operatorname{\mathrm{Frob}}_l^2-T_l\operatorname{\mathrm{Frob}}_l+lS_l=0\end{align*} $$
$$ \begin{align*}\operatorname{\mathrm{Frob}}_l^2-T_l\operatorname{\mathrm{Frob}}_l+lS_l=0\end{align*} $$
on
![]() $\tilde {H}^1(K^p,\mathbb {Z}_p)$
. This can be checked first on finite levels and then by passing to the limit over
$\tilde {H}^1(K^p,\mathbb {Z}_p)$
. This can be checked first on finite levels and then by passing to the limit over
![]() $K_p$
. Note that
$K_p$
. Note that
 $T_l,S_l^{\pm 1},l\notin S$
generate
$T_l,S_l^{\pm 1},l\notin S$
generate
![]() $\mathbb {T}(K^p)$
topologically.
$\mathbb {T}(K^p)$
topologically.
Let

be a
![]() $\mathbb {Z}_p$
-algebra homomorphism. We can associate an odd semi-simple Galois representation (unique up to conjugation)
$\mathbb {Z}_p$
-algebra homomorphism. We can associate an odd semi-simple Galois representation (unique up to conjugation)

whose determinant is
![]() $\lambda \circ D_S$
. Here odd means
$\lambda \circ D_S$
. Here odd means
![]() $\det (\rho _{\lambda }(c))=-1$
for any complex conjugation
$\det (\rho _{\lambda }(c))=-1$
for any complex conjugation
![]() $c\in G_{\mathbb {Q},S}$
. Let
$c\in G_{\mathbb {Q},S}$
. Let

and let

. If
![]() $\rho _{\lambda }$
is irreducible, by the Eichler–Shimura relation, we have
$\rho _{\lambda }$
is irreducible, by the Eichler–Shimura relation, we have

where
![]() $\rho _{\lambda }(-1)=\rho _{\lambda }\otimes \varepsilon ^{-1}$
is the twist of
$\rho _{\lambda }(-1)=\rho _{\lambda }\otimes \varepsilon ^{-1}$
is the twist of
![]() $\rho _{\lambda }$
by inverse of the p-adic cyclotomic character and
$\rho _{\lambda }$
by inverse of the p-adic cyclotomic character and

denotes the
![]() $\lambda $
-isotypic subspace. By the main result of [Reference Boston, Lenstra and RibetBLR91],
$\lambda $
-isotypic subspace. By the main result of [Reference Boston, Lenstra and RibetBLR91],

is
![]() $\rho _{\lambda }(-1)$
-isotypic in the sense that
$\rho _{\lambda }(-1)$
-isotypic in the sense that

We remark that the centre
 $\mathbb {A}_f^{\times }$
of
$\mathbb {A}_f^{\times }$
of
![]() $\mathrm {GL}_2(\mathbb {A}_f)$
acts via
$\mathrm {GL}_2(\mathbb {A}_f)$
acts via
![]() $\det (\rho _{\lambda })\varepsilon ^{-1}$
on
$\det (\rho _{\lambda })\varepsilon ^{-1}$
on

via global class field theory.
Definition 6.1.2. Let
 $$ \begin{align*}\rho:G_{\mathbb{Q}}\to\mathrm{GL}_2(\overline{\mathbb{Q}}_p)\end{align*} $$
$$ \begin{align*}\rho:G_{\mathbb{Q}}\to\mathrm{GL}_2(\overline{\mathbb{Q}}_p)\end{align*} $$
be a continuous 2-dimensional p-adic Galois representation. We say
![]() $\rho $
is
$\rho $
is
-
• pro-modular if there exists a tame level
 $K^p$
and
$K^p$
and
 such that
such that
 $\rho \cong \rho _{\lambda }$
;
$\rho \cong \rho _{\lambda }$
; -
• pro-cohomological if
 for some tame level
for some tame level
 $K^p$
.
$K^p$
.
Clearly,
![]() $\rho $
is pro-modular if it is pro-cohomological and irreducible by our previous discussion. Conversely, we have the following result.
$\rho $
is pro-modular if it is pro-cohomological and irreducible by our previous discussion. Conversely, we have the following result.
Lemma 6.1.3. Let
![]() $\rho =\rho _{\lambda }$
be an irreducible pro-modular representation for some
$\rho =\rho _{\lambda }$
be an irreducible pro-modular representation for some
![]() $K^p$
and
$K^p$
and
![]() $\lambda $
. The following statements are equivalent:
$\lambda $
. The following statements are equivalent:
-
(1)
 $\rho $
is pro-cohomological.
$\rho $
is pro-cohomological. -
(2)
 .
. -
(3)
 $\tilde {H}^1(K^p,C)[\mathfrak {p}_{\lambda }]\neq 0$
.
$\tilde {H}^1(K^p,C)[\mathfrak {p}_{\lambda }]\neq 0$
.
Proof. The first two are equivalent by the Eichler–Shimura relation. The equivalence between the last two is a consequence of the following lemma.
Lemma 6.1.4. Let
![]() $\rho =\rho _{\lambda }$
be a pro-modular representation for some
$\rho =\rho _{\lambda }$
be a pro-modular representation for some
![]() $K^p$
and
$K^p$
and
![]() $\lambda $
. Then
$\lambda $
. Then

where

is endowed with a norm with unit ball

.
Proof. Choose generators
![]() $g_1,\cdots ,g_s$
of
$g_1,\cdots ,g_s$
of
![]() $\mathfrak {p}_{\lambda }$
as a
$\mathfrak {p}_{\lambda }$
as a

-module. We have an exact sequence

which is continuous with respect to the p-adic topology; that is, defined by the unit open ball

. Note that the second map is strict. This sequence remains exact after taking p-adic completion, which is exactly what we want.
We conclude this subsection by the following result on infinitesimal characters.
Proposition 6.1.5. Suppose
![]() $\rho =\rho _{\lambda }$
is pro-cohomological and irreducible and has Hodge–Tate–Sen weights
$\rho =\rho _{\lambda }$
is pro-cohomological and irreducible and has Hodge–Tate–Sen weights
![]() $(a,b)$
. Then as a representation of
$(a,b)$
. Then as a representation of
![]() $\mathrm {GL}_2(\mathbb {Q}_p)$
, the locally analytic vectors
$\mathrm {GL}_2(\mathbb {Q}_p)$
, the locally analytic vectors
![]() $\tilde {H}^1(K^p,C)^{\mathrm {la}}[\mathfrak {p}_{\lambda }]\neq 0$
and have infinitesimal character
$\tilde {H}^1(K^p,C)^{\mathrm {la}}[\mathfrak {p}_{\lambda }]\neq 0$
and have infinitesimal character
![]() $\{(-a-1,-b),(-b-1,-a)\}\subset \mathfrak {h}^*$
.
$\{(-a-1,-b),(-b-1,-a)\}\subset \mathfrak {h}^*$
.
Proof. Note that
![]() $\rho $
can be defined over a finite extension E of
$\rho $
can be defined over a finite extension E of
![]() $\mathbb {Q}_p$
. Hence,
$\mathbb {Q}_p$
. Hence,
 and is an admissible representation of
and is an admissible representation of
![]() $\mathrm {GL}_2(\mathbb {Q}_p)$
. It has nonzero locally analytic vectors by the main result of [Reference Schneider and TeitelbaumST03]. Since
$\mathrm {GL}_2(\mathbb {Q}_p)$
. It has nonzero locally analytic vectors by the main result of [Reference Schneider and TeitelbaumST03]. Since
![]() $\det \rho $
has Hodge–Tate–Sen weight
$\det \rho $
has Hodge–Tate–Sen weight
![]() $a+b$
, the centre
$a+b$
, the centre
![]() $Cz$
of
$Cz$
of
![]() $\mathfrak {g}$
acts on
$\mathfrak {g}$
acts on
![]() $\tilde {H}^1(K^p,C)^{\mathrm {la}}[\mathfrak {p}_{\lambda }]$
via
$\tilde {H}^1(K^p,C)^{\mathrm {la}}[\mathfrak {p}_{\lambda }]$
via
![]() $z\mapsto -(a+b)-1$
. Now the claim for infinitesimal character follows directly from Corollary 4.2.8 and Theorem 5.1.11.
$z\mapsto -(a+b)-1$
. Now the claim for infinitesimal character follows directly from Corollary 4.2.8 and Theorem 5.1.11.
Remark 6.1.6. A higher dimensional generalisation of this result was obtained by Dospinescu–Paškūnas–Schraen in [Reference Dospinescu, Paškūnas and SchraenDPS20, Theorem 1.4].
6.2 A classicality result for overconvergent weight 1 forms
6.2.1. Suppose
![]() $\rho =\rho _{\lambda }$
has equal Hodge–Tate–Sen weights
$\rho =\rho _{\lambda }$
has equal Hodge–Tate–Sen weights
![]() $0,0$
. (It is easy to reduce to this case by twisting by a character if weights are
$0,0$
. (It is easy to reduce to this case by twisting by a character if weights are
![]() $a,a$
.) There are two possibilities for
$a,a$
.) There are two possibilities for
![]() $\rho $
: either
$\rho $
: either
 $\rho |_{G_{\mathbb {Q}_p}}$
is Hodge–Tate, or not. In other words,
$\rho |_{G_{\mathbb {Q}_p}}$
is Hodge–Tate, or not. In other words,
 $(\rho \otimes _{\mathbb {Q}_p} C)^{G_{\mathbb {Q}_p}}$
is a
$(\rho \otimes _{\mathbb {Q}_p} C)^{G_{\mathbb {Q}_p}}$
is a
![]() -vector space of dimension
-vector space of dimension
![]() $2$
or
$2$
or
![]() $1$
. Recall that by Deligne–Serre [Reference Deligne and SerreDS74], the
$1$
. Recall that by Deligne–Serre [Reference Deligne and SerreDS74], the
![]() $2$
-dimensional Galois representation associated to a classical weight
$2$
-dimensional Galois representation associated to a classical weight
![]() $1$
eigenform is Hodge–Tate at p. The main result of this subsection gives a converse.
$1$
eigenform is Hodge–Tate at p. The main result of this subsection gives a converse.
Recall that there is a natural action of B on
 $M^{\dagger }_{1}(K^p)$
. Let
$M^{\dagger }_{1}(K^p)$
. Let
![]() $N_0\subset B$
be
$N_0\subset B$
be
 $\begin {pmatrix} 1 & \mathbb {Z}_p\\ 0 & 1 \end {pmatrix}$
. Then we have the usual operator
$\begin {pmatrix} 1 & \mathbb {Z}_p\\ 0 & 1 \end {pmatrix}$
. Then we have the usual operator
 $$ \begin{align*}U_p:=\sum_{i=0}^{p-1}\begin{pmatrix} p & i \\ 0 & 1 \end{pmatrix}\end{align*} $$
$$ \begin{align*}U_p:=\sum_{i=0}^{p-1}\begin{pmatrix} p & i \\ 0 & 1 \end{pmatrix}\end{align*} $$
acting on
 $M^{\dagger }_{1}(K^p)^{N_0}$
. Note that Theorem 5.4.2 implies that Hecke algebra
$M^{\dagger }_{1}(K^p)^{N_0}$
. Note that Theorem 5.4.2 implies that Hecke algebra
![]() $\mathbb {T}(K^p)$
also acts on the space of overconvergent modular forms.
$\mathbb {T}(K^p)$
also acts on the space of overconvergent modular forms.
Theorem 6.2.2. Suppose
![]() $\rho =\rho _{\lambda }$
is pro-modular for some tame level
$\rho =\rho _{\lambda }$
is pro-modular for some tame level
![]() $K^p$
. If
$K^p$
. If
 $M^{\dagger }_{1}(K^p)^{N_0}[\mathfrak {p}_{\lambda }]$
has a nonzero
$M^{\dagger }_{1}(K^p)^{N_0}[\mathfrak {p}_{\lambda }]$
has a nonzero
![]() $U_p$
-eigenvector and
$U_p$
-eigenvector and
 $\rho |_{G_{\mathbb {Q}_p}}$
is Hodge–Tate of weights
$\rho |_{G_{\mathbb {Q}_p}}$
is Hodge–Tate of weights
![]() $0,0$
, then
$0,0$
, then
![]() $\rho $
comes from a classical weight
$\rho $
comes from a classical weight
![]() $1$
eigenform; that is,
$1$
eigenform; that is,
![]() $M_1(K^p)[\mathfrak {p}_{\lambda }]\neq 0$
.
$M_1(K^p)[\mathfrak {p}_{\lambda }]\neq 0$
.
Remark 6.2.3. Theorem 6.2.2 implies that an overconvergent weight 1 modular form of finite slope is classical if its associated Galois representation is Hodge–Tate. In particular, this gives a different proof of the main result of Buzzard–Taylor [Reference Buzzard and TaylorBT99] in the ordinary case.
Note that we do not assume the eigenvalue of
![]() $U_p$
is nonzero. In fact, using Colmez’s Kirillov model, we will see that the kernel of
$U_p$
is nonzero. In fact, using Colmez’s Kirillov model, we will see that the kernel of
![]() $U_p$
is always nonzero if we know the local–global compatibility at p (in the sense of Emerton).
$U_p$
is always nonzero if we know the local–global compatibility at p (in the sense of Emerton).
6.2.4. The rest of this subsection is devoted to the proof of Theorem 6.2.2. As mentioned in the Introduction, we will need Hecke operators at bad places in the proof. After making a right translation by some element in
 $\mathrm {GL}_2(\mathbb {A}^p_f)$
and shrinking the level, we can find a finite set of rational primes S containing p and an integer
$\mathrm {GL}_2(\mathbb {A}^p_f)$
and shrinking the level, we can find a finite set of rational primes S containing p and an integer
![]() $m>0$
and assume the following:
$m>0$
and assume the following:
![]() $K^p=\prod _{l\neq p} K_l\subset \prod _{l\neq p}\mathrm {GL}_2(\mathbb {Z}_l)$
, where
$K^p=\prod _{l\neq p} K_l\subset \prod _{l\neq p}\mathrm {GL}_2(\mathbb {Z}_l)$
, where
![]() $K_l=\mathrm {GL}_2(\mathbb {Z}_l)$
for
$K_l=\mathrm {GL}_2(\mathbb {Z}_l)$
for
![]() $l\notin S$
, and
$l\notin S$
, and
 $$ \begin{align*}K_l=\Gamma_1(l^m)=\{\begin{pmatrix} a & b \\ c & d \end{pmatrix},~a-1,c,d-1\in l^m\mathbb{Z}_l\},\,l\in S\setminus \{p\}.\end{align*} $$
$$ \begin{align*}K_l=\Gamma_1(l^m)=\{\begin{pmatrix} a & b \\ c & d \end{pmatrix},~a-1,c,d-1\in l^m\mathbb{Z}_l\},\,l\in S\setminus \{p\}.\end{align*} $$
Moreover,
 $M^{\dagger }_{1}(K^p\Gamma _1(p^m))[\mathfrak {p}_{\lambda }]$
has a nonzero eigenvector of
$M^{\dagger }_{1}(K^p\Gamma _1(p^m))[\mathfrak {p}_{\lambda }]$
has a nonzero eigenvector of
![]() $U_p$
. See Section 5.2.4 for the notation here. Let
$U_p$
. See Section 5.2.4 for the notation here. Let
![]() $K_p=\Gamma _1(p^n)$
for some
$K_p=\Gamma _1(p^n)$
for some
![]() $n\geq m$
and
$n\geq m$
and
![]() $K=K^pK_p$
. Let
$K=K^pK_p$
. Let
![]() $A_S=\prod _{l\in S}\mathbb {Z}_l^{\times }\subset \prod _{l\in S}\mathrm {GL}_2(\mathbb {Z}_l)$
be the subgroup of the form
$A_S=\prod _{l\in S}\mathbb {Z}_l^{\times }\subset \prod _{l\in S}\mathrm {GL}_2(\mathbb {Z}_l)$
be the subgroup of the form
 $\begin {pmatrix} * & 0 \\ 0 & 1 \end {pmatrix}$
. Then
$\begin {pmatrix} * & 0 \\ 0 & 1 \end {pmatrix}$
. Then
![]() $A_S$
is in the normaliser of
$A_S$
is in the normaliser of
![]() $\prod _{l\in S}K_l$
; hence,
$\prod _{l\in S}K_l$
; hence,
![]() $A_S$
acts on
$A_S$
acts on
![]() $\mathcal {X}_{K}$
by right translation, which induces an action of
$\mathcal {X}_{K}$
by right translation, which induces an action of
![]() $A_S$
on
$A_S$
on
 $M^{\dagger }_{1}(K)$
. Clearly, this action factors through a finite group and we can find a (finite-order) character
$M^{\dagger }_{1}(K)$
. Clearly, this action factors through a finite group and we can find a (finite-order) character
 such that the
such that the
![]() $\psi $
-isotypic component
$\psi $
-isotypic component
 $$ \begin{align*}M^{\dagger}_{1}(K)^{\psi}[\mathfrak{p}_{\lambda}]\end{align*} $$
$$ \begin{align*}M^{\dagger}_{1}(K)^{\psi}[\mathfrak{p}_{\lambda}]\end{align*} $$
contains a nonzero eigenvector of
![]() $U_p$
. For
$U_p$
. For
![]() $l\in S$
, we denote by
$l\in S$
, we denote by
![]() $U_l$
the abstract double coset action of
$U_l$
the abstract double coset action of
 $$ \begin{align*}[K_l\begin{pmatrix}l&0\\0&1\end{pmatrix}K_l].\end{align*} $$
$$ \begin{align*}[K_l\begin{pmatrix}l&0\\0&1\end{pmatrix}K_l].\end{align*} $$
These operators act naturally on
 $M^{\dagger }_{1}(K)$
. If, moreover,
$M^{\dagger }_{1}(K)$
. If, moreover,
![]() $l\neq p$
, then
$l\neq p$
, then
![]() $U_l$
acts naturally on
$U_l$
acts naturally on
![]() $\tilde {H}^1(K^p,C)$
. We denote by
$\tilde {H}^1(K^p,C)$
. We denote by
the
![]() $\mathbb {T}(K^p)$
-subalgebra generated by
$\mathbb {T}(K^p)$
-subalgebra generated by
![]() $U_l,l\in S\setminus \{p\}$
.
$U_l,l\in S\setminus \{p\}$
.
Lemma 6.2.5.
![]() $\tilde {\mathbb {T}}(K^p)$
is a finite
$\tilde {\mathbb {T}}(K^p)$
is a finite
![]() $\mathbb {T}(K^p)$
-module; that is, each
$\mathbb {T}(K^p)$
-module; that is, each
![]() $U_l$
is integral over
$U_l$
is integral over
![]() $\mathbb {T}(K^p)$
,
$\mathbb {T}(K^p)$
,
![]() $l\in S\setminus \{p\}$
.
$l\in S\setminus \{p\}$
.
Proof. Fix
![]() $l\in S\setminus \{p\}$
. Since
$l\in S\setminus \{p\}$
. Since
 $\varinjlim _{K^{\prime }_p}H^1_{\mathrm {\acute {e}t}}(\mathcal {X}_{K^pK^{\prime }_p},\mathbb {Q}_p)$
is dense in
$\varinjlim _{K^{\prime }_p}H^1_{\mathrm {\acute {e}t}}(\mathcal {X}_{K^pK^{\prime }_p},\mathbb {Q}_p)$
is dense in
![]() $\tilde {H}^1(K^p,\mathbb {Q}_p)$
(Theorem 2.2.16 (iv) of [Reference EmertonEme06b]), it suffices to find a monic polynomial
$\tilde {H}^1(K^p,\mathbb {Q}_p)$
(Theorem 2.2.16 (iv) of [Reference EmertonEme06b]), it suffices to find a monic polynomial
![]() $P_l(X)\in \mathbb {T}(K^p)[X]$
such that
$P_l(X)\in \mathbb {T}(K^p)[X]$
such that
![]() $P_l(U_l)$
acts as zero on
$P_l(U_l)$
acts as zero on
 $H^1_{\mathrm {\acute {e}t}}(\mathcal {X}_{K^pK^{\prime }_p},\mathbb {Q}_p)$
for any open subgroup
$H^1_{\mathrm {\acute {e}t}}(\mathcal {X}_{K^pK^{\prime }_p},\mathbb {Q}_p)$
for any open subgroup
![]() $K^{\prime }_p$
of
$K^{\prime }_p$
of
![]() $\mathrm {GL}_2(\mathbb {Q}_p)$
. Fix a lift of geometric Frobenius
$\mathrm {GL}_2(\mathbb {Q}_p)$
. Fix a lift of geometric Frobenius
![]() $\operatorname {\mathrm {Frob}}_l\in G_{\mathbb {Q}_l}$
whose image in
$\operatorname {\mathrm {Frob}}_l\in G_{\mathbb {Q}_l}$
whose image in
 $G_{\mathbb {Q}_l}^{\mathrm {ab}}$
corresponds to
$G_{\mathbb {Q}_l}^{\mathrm {ab}}$
corresponds to
![]() $l\in \mathbb {Q}^{\times }_l$
via the local Artin map. Recall that there is a determinant
$l\in \mathbb {Q}^{\times }_l$
via the local Artin map. Recall that there is a determinant
![]() $D_S$
of
$D_S$
of
![]() $G_{\mathbb {Q},S}$
valued in
$G_{\mathbb {Q},S}$
valued in
![]() $\mathbb {T}(K^p)$
. We denote by
$\mathbb {T}(K^p)$
. We denote by
![]() $Q_l(X)\in \mathbb {T}(K^p)[X]$
the characteristic polynomial of
$Q_l(X)\in \mathbb {T}(K^p)[X]$
the characteristic polynomial of
![]() $l\operatorname {\mathrm {Frob}}_l\in \mathbb {T}(K^p)[G_{\mathbb {Q},S}]$
. We claim that
$l\operatorname {\mathrm {Frob}}_l\in \mathbb {T}(K^p)[G_{\mathbb {Q},S}]$
. We claim that
works. To see this, since
 can be decomposed as a direct sum of
can be decomposed as a direct sum of
 $(\pi _f)^{K^pK^{\prime }_p}$
for some cuspidal automorphic representations
$(\pi _f)^{K^pK^{\prime }_p}$
for some cuspidal automorphic representations
![]() $\pi =\pi _f\otimes \pi _{\infty }$
on
$\pi =\pi _f\otimes \pi _{\infty }$
on
![]() $\mathrm {GL}_2(\mathbb {A})$
, it is enough to show
$\mathrm {GL}_2(\mathbb {A})$
, it is enough to show
![]() $P_l(U_l)=0$
on each nonzero
$P_l(U_l)=0$
on each nonzero
 $(\pi _f)^{K^pK^{\prime }_p}$
. By the theory of newforms,
$(\pi _f)^{K^pK^{\prime }_p}$
. By the theory of newforms,
![]() $(\pi _l)^{K_l}$
has dimension at most
$(\pi _l)^{K_l}$
has dimension at most
![]() $m+1$
and
$m+1$
and
![]() $U_l$
is not nilpotent only when
$U_l$
is not nilpotent only when
![]() $\pi _l$
is special or a principal series. Moreover,
$\pi _l$
is special or a principal series. Moreover,
![]() $U_l$
acts semi-simply on generalised eigenspaces associated to nonzero eigenvalues. See, for example, Corollary 2.2 of [Reference HidaHid89]. The local–global compatibility then implies that a nonzero eigenvalue of
$U_l$
acts semi-simply on generalised eigenspaces associated to nonzero eigenvalues. See, for example, Corollary 2.2 of [Reference HidaHid89]. The local–global compatibility then implies that a nonzero eigenvalue of
![]() $U_l$
must be a root of
$U_l$
must be a root of
![]() $Q_l(X)$
. Hence,
$Q_l(X)$
. Hence,
![]() $P_l(U_l)=0$
on
$P_l(U_l)=0$
on
 $(\pi _f)^{K^pK^{\prime }_p}$
.
$(\pi _f)^{K^pK^{\prime }_p}$
.
Now we consider the action of
![]() $\tilde {\mathbb {T}}(K^p)[U_p]$
on
$\tilde {\mathbb {T}}(K^p)[U_p]$
on
 $M^{\dagger }_{1}(K)^{\psi }$
.
$M^{\dagger }_{1}(K)^{\psi }$
.
Lemma 6.2.6.
 can be extended to
can be extended to
![]() $\lambda ':\tilde {\mathbb {T}}(K^p)[U_p]\to C$
such that
$\lambda ':\tilde {\mathbb {T}}(K^p)[U_p]\to C$
such that
 $$ \begin{align*}M^{\dagger}_{1}(K^p\Gamma_1(p^n))^{\psi}[\mathfrak{p}_{\lambda'}]\neq 0,\end{align*} $$
$$ \begin{align*}M^{\dagger}_{1}(K^p\Gamma_1(p^n))^{\psi}[\mathfrak{p}_{\lambda'}]\neq 0,\end{align*} $$
where
![]() $\mathfrak {p}_{\lambda '}$
denotes the kernel of
$\mathfrak {p}_{\lambda '}$
denotes the kernel of
![]() $\lambda '$
. Moreover, for any such
$\lambda '$
. Moreover, for any such
![]() $\lambda '$
, we have
$\lambda '$
, we have
 $$ \begin{align*}\dim_C M^{\dagger}_{1}(K^p\Gamma_1(p^n))^{\psi}[\mathfrak{p}_{\lambda'}]=1.\end{align*} $$
$$ \begin{align*}\dim_C M^{\dagger}_{1}(K^p\Gamma_1(p^n))^{\psi}[\mathfrak{p}_{\lambda'}]=1.\end{align*} $$
In particular, we obtain the following after taking direct limit over all n:
 $$ \begin{align*}\dim_C \varinjlim_n M^{\dagger}_{1}(K^p\Gamma_1(p^n))^{\psi}[\mathfrak{p}_{\lambda'}]=\dim_C M^{\dagger}_{1}(K^p)^{\psi,N_0}[\mathfrak{p}_{\lambda'}]=1.\end{align*} $$
$$ \begin{align*}\dim_C \varinjlim_n M^{\dagger}_{1}(K^p\Gamma_1(p^n))^{\psi}[\mathfrak{p}_{\lambda'}]=\dim_C M^{\dagger}_{1}(K^p)^{\psi,N_0}[\mathfrak{p}_{\lambda'}]=1.\end{align*} $$
Proof. Let
![]() $\alpha \in C$
be an eigenvalue of
$\alpha \in C$
be an eigenvalue of
![]() $U_p$
on
$U_p$
on
 $M^{\dagger }_{1}(K)^{\psi }[\mathfrak {p}_{\lambda }]$
. Then
$M^{\dagger }_{1}(K)^{\psi }[\mathfrak {p}_{\lambda }]$
. Then
![]() $\tilde {\mathbb {T}}(K^p)/(\mathfrak {p}_{\lambda })$
acts on the
$\tilde {\mathbb {T}}(K^p)/(\mathfrak {p}_{\lambda })$
acts on the
![]() $\alpha $
-eigenspace of
$\alpha $
-eigenspace of
 $M^{\dagger }_{1}(K)^{\psi }[\mathfrak {p}_{\lambda }]$
. Since
$M^{\dagger }_{1}(K)^{\psi }[\mathfrak {p}_{\lambda }]$
. Since
![]() $\tilde {\mathbb {T}}(K^p)/(\mathfrak {p}_{\lambda })$
is Artinian by our previous lemma, we can find
$\tilde {\mathbb {T}}(K^p)/(\mathfrak {p}_{\lambda })$
is Artinian by our previous lemma, we can find
![]() $\lambda ':\tilde {\mathbb {T}}(K^p)[U_p]\to C$
which sends
$\lambda ':\tilde {\mathbb {T}}(K^p)[U_p]\to C$
which sends
![]() $U_p$
to
$U_p$
to
![]() $\alpha $
and extends
$\alpha $
and extends
![]() $\lambda $
and
$\lambda $
and
 $M^{\dagger }_{1}(K)^{\psi }[\mathfrak {p}_{\lambda '}]\neq 0$
. To see the multiplicity 1 claim, we remark that
$M^{\dagger }_{1}(K)^{\psi }[\mathfrak {p}_{\lambda '}]\neq 0$
. To see the multiplicity 1 claim, we remark that
![]() $A_S$
acts transitively on all connected components of
$A_S$
acts transitively on all connected components of
![]() $\mathcal {X}_K$
. Hence, any element of
$\mathcal {X}_K$
. Hence, any element of
 $M^{\dagger }_{1}(K)^{\psi }$
is determined by its value on one component. Since elements in
$M^{\dagger }_{1}(K)^{\psi }$
is determined by its value on one component. Since elements in
 $M^{\dagger }_{1}(K)^{\psi }[\mathfrak {p}_{\lambda '}]$
are eigenvectors of
$M^{\dagger }_{1}(K)^{\psi }[\mathfrak {p}_{\lambda '}]$
are eigenvectors of
![]() $T_l,S_l,l\notin S$
and
$T_l,S_l,l\notin S$
and
![]() $U_l,l\in S$
, we conclude from usual q-expansion principle that this space has dimension 1.
$U_l,l\in S$
, we conclude from usual q-expansion principle that this space has dimension 1.
Proof of Theorem 6.2.2
If
![]() $\rho $
is reducible, then it is a sum of two finite-order characters. The theory of Eisenstein series shows that it comes from a classical modular form. Hence, we may assume
$\rho $
is reducible, then it is a sum of two finite-order characters. The theory of Eisenstein series shows that it comes from a classical modular form. Hence, we may assume
![]() $\rho $
is irreducible.
$\rho $
is irreducible.
Assume
![]() $\rho $
is not classical; that is,
$\rho $
is not classical; that is,
![]() $M^1(K^p)[\mathfrak {p}_{\lambda }]=0$
. Since
$M^1(K^p)[\mathfrak {p}_{\lambda }]=0$
. Since
 $M^1(K^p)=\varinjlim _{K^{\prime }_p}H^0(\mathcal {X}_{K^pK^{\prime }_p},\omega )$
is a direct sum of
$M^1(K^p)=\varinjlim _{K^{\prime }_p}H^0(\mathcal {X}_{K^pK^{\prime }_p},\omega )$
is a direct sum of
![]() $(\pi _f)^{K^p}$
for some automorphic representations
$(\pi _f)^{K^p}$
for some automorphic representations
![]() $\pi $
of
$\pi $
of
![]() $\mathrm {GL}_2(\mathbb {A})$
, the localisation
$\mathrm {GL}_2(\mathbb {A})$
, the localisation
 $$ \begin{align*}M^1(K^p)_{\mathfrak{p}_{\lambda}}=0.\end{align*} $$
$$ \begin{align*}M^1(K^p)_{\mathfrak{p}_{\lambda}}=0.\end{align*} $$
Similarly, by Serre duality and the Kodaira–Spencer isomorphism, we also have
 $$ \begin{align*}(\varinjlim_{K^{\prime}_p}H^1(\mathcal{X}_{K^pK^{\prime}_p}, \omega^{1}))_{\mathfrak{p}_{\lambda}}=0.\end{align*} $$
$$ \begin{align*}(\varinjlim_{K^{\prime}_p}H^1(\mathcal{X}_{K^pK^{\prime}_p}, \omega^{1}))_{\mathfrak{p}_{\lambda}}=0.\end{align*} $$
Hence, by the second part of Theorem 5.4.6,
 $(\tilde {H}^1(K^p,C)^{\mathrm {la},(1,0)}_{(0,1)})_{\mathfrak {p}_{\lambda \cdot t}}=M^{\dagger }_{1}(K^p)_{\mathfrak {p}_{\lambda }}\cdot e_1^{-1}t$
and therefore
$(\tilde {H}^1(K^p,C)^{\mathrm {la},(1,0)}_{(0,1)})_{\mathfrak {p}_{\lambda \cdot t}}=M^{\dagger }_{1}(K^p)_{\mathfrak {p}_{\lambda }}\cdot e_1^{-1}t$
and therefore
 $$ \begin{align*}\tilde{H}^1(K^p,C)^{\mathrm{la},(1,0)}_{(0,1)}[\mathfrak{p}_{\lambda\cdot t}]=M^{\dagger}_{1}(K^p)[{\mathfrak{p}_{\lambda}}]\cdot e_1^{-1}t,\end{align*} $$
$$ \begin{align*}\tilde{H}^1(K^p,C)^{\mathrm{la},(1,0)}_{(0,1)}[\mathfrak{p}_{\lambda\cdot t}]=M^{\dagger}_{1}(K^p)[{\mathfrak{p}_{\lambda}}]\cdot e_1^{-1}t,\end{align*} $$
where

denotes ‘the twist of
![]() $\lambda $
by t’; that is, sends
$\lambda $
by t’; that is, sends
![]() $T_l$
to
$T_l$
to
![]() $\lambda (T_l)l^{-1}$
. It can be checked that
$\lambda (T_l)l^{-1}$
. It can be checked that
![]() $\rho _{\lambda \cdot t}(-1)=\rho _{\lambda }$
. Hence,
$\rho _{\lambda \cdot t}(-1)=\rho _{\lambda }$
. Hence,

is
![]() $\rho $
-isotypic. On the other hand, by our assumption that
$\rho $
-isotypic. On the other hand, by our assumption that
![]() $\rho $
is Hodge–Tate and Theorem 5.1.11, we have
$\rho $
is Hodge–Tate and Theorem 5.1.11, we have
 $$ \begin{align*}\tilde{H}^1(K^p,C)^{\mathrm{la}}_{(0,1)}[\mathfrak{p}_{\lambda\cdot t}]=\tilde{H}^1(K^p,C)^{\mathrm{la},(1,0)}_{(0,1)}[\mathfrak{p}_{\lambda\cdot t}].\end{align*} $$
$$ \begin{align*}\tilde{H}^1(K^p,C)^{\mathrm{la}}_{(0,1)}[\mathfrak{p}_{\lambda\cdot t}]=\tilde{H}^1(K^p,C)^{\mathrm{la},(1,0)}_{(0,1)}[\mathfrak{p}_{\lambda\cdot t}].\end{align*} $$
If we write

, then by Lemma 6.1.4 and our discussion in Section 6.1.1,

where W is endowed a norm with unit ball

and
![]() $\rho ^o\subset \rho $
is any
$\rho ^o\subset \rho $
is any
![]() $G_{\mathbb {Q}}$
-stable lattice. Note that
$G_{\mathbb {Q}}$
-stable lattice. Note that
![]() $A_S\times \tilde {\mathbb {T}}(K^p)$
acts naturally on W and
$A_S\times \tilde {\mathbb {T}}(K^p)$
acts naturally on W and
![]() $U_p$
acts on its
$U_p$
acts on its
![]() $N_0$
-fixed vectors. Fix
$N_0$
-fixed vectors. Fix
![]() $\lambda '$
as in Lemma 6.2.6 and consider its ‘twist by
$\lambda '$
as in Lemma 6.2.6 and consider its ‘twist by
 $e_1^{-1}t$
’
$e_1^{-1}t$
’
which sends
![]() $T_l$
to
$T_l$
to
![]() $\lambda '(T_l)l^{-1}$
for
$\lambda '(T_l)l^{-1}$
for
![]() $l\notin S$
and sends
$l\notin S$
and sends
![]() $U_l$
to
$U_l$
to
![]() $\lambda '(U_l)l^{-1}$
for
$\lambda '(U_l)l^{-1}$
for
![]() $l\in S$
. Then we have
$l\in S$
. Then we have

The left-hand side has dimension
![]() $1$
over C by Lemma 6.2.6. However, the last term in the equality has dimension at least 2 because
$1$
over C by Lemma 6.2.6. However, the last term in the equality has dimension at least 2 because
![]() $\rho $
is
$\rho $
is
![]() $2$
-dimensional! Thus, we get a contradiction. This proves that
$2$
-dimensional! Thus, we get a contradiction. This proves that
![]() $\rho $
has to be classical.
$\rho $
has to be classical.
6.3 Local–global compatibility
6.3.1. In order to better understand
 for a pro-modular
for a pro-modular
![]() $\lambda $
, we need Emerton’s local–global compatibility conjecture, which gives a description of
$\lambda $
, we need Emerton’s local–global compatibility conjecture, which gives a description of
 in terms of p-adic local Langlands for
in terms of p-adic local Langlands for
![]() $\mathrm {GL}_2(\mathbb {Q}_p)$
as established by Breuil, Colmez, Berger, Kisin, Paškūnas. In [Reference EmertonEme11, Reference EmertonEme06a], Emerton formulated and proved his conjecture assuming the residual representation is irreducible and generic. Building upon the work of Paškūnas, we gave a proof (which is complete when
$\mathrm {GL}_2(\mathbb {Q}_p)$
as established by Breuil, Colmez, Berger, Kisin, Paškūnas. In [Reference EmertonEme11, Reference EmertonEme06a], Emerton formulated and proved his conjecture assuming the residual representation is irreducible and generic. Building upon the work of Paškūnas, we gave a proof (which is complete when
![]() $p\geq 5$
) in [Reference PanPan19] in the case of definite quaternion algebras. We will mostly follow the argument in Section 3 of [Reference PanPan19] and also Section 5 of [Reference PaskunasPas18]. One key step is to prove the density of algebraic vectors when we are localising at an Eisenstein maximal ideal. This part might be of some independent interest.
$p\geq 5$
) in [Reference PanPan19] in the case of definite quaternion algebras. We will mostly follow the argument in Section 3 of [Reference PanPan19] and also Section 5 of [Reference PaskunasPas18]. One key step is to prove the density of algebraic vectors when we are localising at an Eisenstein maximal ideal. This part might be of some independent interest.
6.3.2. We begin by recalling work of Paškūnas on representations of
![]() $\mathrm {GL}_2(\mathbb {Q}_p)$
. See [Reference PaškūnasPaš13] and also the introduction of [Reference PaškūnasPaš16]. Fix E a finite extension of
$\mathrm {GL}_2(\mathbb {Q}_p)$
. See [Reference PaškūnasPaš13] and also the introduction of [Reference PaškūnasPaš16]. Fix E a finite extension of
![]() $\mathbb {Q}_p$
with ring of integers
$\mathbb {Q}_p$
with ring of integers
![]() $\mathcal {O}$
, residue field
$\mathcal {O}$
, residue field
![]() $\mathbb {F}$
, and fix a uniformiser
$\mathbb {F}$
, and fix a uniformiser
![]() $\varpi $
. Write
$\varpi $
. Write
![]() $G=\mathrm {GL}_2(\mathbb {Q}_p) $
and let
$G=\mathrm {GL}_2(\mathbb {Q}_p) $
and let
 $\zeta :\mathbb {Q}_p^{\times }\to \mathcal {O}^{\times }$
be a continuous character. Following Paškūnas, we denote by
$\zeta :\mathbb {Q}_p^{\times }\to \mathcal {O}^{\times }$
be a continuous character. Following Paškūnas, we denote by
 $\mathrm {Mod}^{\mathrm {l\, adm}}_{G,\zeta }(\mathcal {O})$
the category of smooth, locally admissible G-representations on
$\mathrm {Mod}^{\mathrm {l\, adm}}_{G,\zeta }(\mathcal {O})$
the category of smooth, locally admissible G-representations on
![]() $\mathcal {O}$
-torsion modules with central character
$\mathcal {O}$
-torsion modules with central character
![]() $\zeta $
.
$\zeta $
.
Let
 $\mathrm {Irr}^{\mathrm {adm}}_G$
be the set of G-irreducible representations in
$\mathrm {Irr}^{\mathrm {adm}}_G$
be the set of G-irreducible representations in
 $\mathrm {Mod}^{\mathrm {l\, adm}}_{G,\zeta }(\mathcal {O})$
. There is a natural equivalence relation
$\mathrm {Mod}^{\mathrm {l\, adm}}_{G,\zeta }(\mathcal {O})$
. There is a natural equivalence relation
![]() $\sim $
on
$\sim $
on
 $\mathrm {Irr}^{\mathrm {adm}}_G$
defined as follows:
$\mathrm {Irr}^{\mathrm {adm}}_G$
defined as follows:
![]() $\pi \sim \tau $
if
$\pi \sim \tau $
if
![]() $\pi =\tau $
or there exists a sequence
$\pi =\tau $
or there exists a sequence
 $\pi _0=\pi ,\cdots ,\pi _n=\tau \in \mathrm {Irr}^{\mathrm {adm}}_G$
such that
$\pi _0=\pi ,\cdots ,\pi _n=\tau \in \mathrm {Irr}^{\mathrm {adm}}_G$
such that
![]() $\operatorname {\mathrm {Ext}}^1(\pi _i,\pi _{i+1})\neq 0$
or
$\operatorname {\mathrm {Ext}}^1(\pi _i,\pi _{i+1})\neq 0$
or
![]() $\operatorname {\mathrm {Ext}}^1(\pi _{i+1},\pi _{i})\neq 0$
. An equivalence class
$\operatorname {\mathrm {Ext}}^1(\pi _{i+1},\pi _{i})\neq 0$
. An equivalence class
 $\mathfrak {B}\in \mathrm {Irr}^{\mathrm {adm}}_G/\sim $
is called a block of
$\mathfrak {B}\in \mathrm {Irr}^{\mathrm {adm}}_G/\sim $
is called a block of
 $\mathrm {Mod}^{\mathrm {l\, adm}}_{G,\zeta }(\mathcal {O})$
. There is a natural decomposition
$\mathrm {Mod}^{\mathrm {l\, adm}}_{G,\zeta }(\mathcal {O})$
. There is a natural decomposition
 $$ \begin{align*}\mathrm{Mod}^{\mathrm{l\, adm}}_{G,\zeta}(\mathcal{O})\cong\prod_{\mathfrak{B}\in \mathrm{Irr}^{\mathrm{adm}}_G/\sim}\mathrm{Mod}^{\mathrm{l\, adm}}_{G,\zeta}(\mathcal{O})[\mathfrak{B}],\end{align*} $$
$$ \begin{align*}\mathrm{Mod}^{\mathrm{l\, adm}}_{G,\zeta}(\mathcal{O})\cong\prod_{\mathfrak{B}\in \mathrm{Irr}^{\mathrm{adm}}_G/\sim}\mathrm{Mod}^{\mathrm{l\, adm}}_{G,\zeta}(\mathcal{O})[\mathfrak{B}],\end{align*} $$
where
 $\mathrm {Mod}^{\mathrm {l\, adm}}_{G,\zeta }(\mathcal {O})[\mathfrak {B}]$
denotes the full subcategory of representations with irreducible constituents in
$\mathrm {Mod}^{\mathrm {l\, adm}}_{G,\zeta }(\mathcal {O})[\mathfrak {B}]$
denotes the full subcategory of representations with irreducible constituents in
![]() $\mathfrak {B}$
. A complete list of blocks containing an absolutely irreducible representation can be found on the beginning of p. 3 of [Reference PaškūnasPaš16].
$\mathfrak {B}$
. A complete list of blocks containing an absolutely irreducible representation can be found on the beginning of p. 3 of [Reference PaškūnasPaš16].
The semi-simple mod p correspondence gives a bijection between isomorphism classes of 2-dimensional absolutely semi-simple
![]() $\mathbb {F}$
-representations
$\mathbb {F}$
-representations
![]() $\bar \rho _{\mathfrak {B}}$
of
$\bar \rho _{\mathfrak {B}}$
of
![]() $G_{\mathbb {Q}_p}$
and blocks containing an absolutely irreducible representation. It should be mentioned that
$G_{\mathbb {Q}_p}$
and blocks containing an absolutely irreducible representation. It should be mentioned that
![]() $\det \bar \rho _{\mathfrak {B}}\equiv \zeta \varepsilon _p\mod \varpi $
. Let
$\det \bar \rho _{\mathfrak {B}}\equiv \zeta \varepsilon _p\mod \varpi $
. Let
 $R^{\mathrm {ps},\zeta \varepsilon _p}_{\bar \rho _{\mathfrak {B}}}$
be the deformation ring parametrising all of the
$R^{\mathrm {ps},\zeta \varepsilon _p}_{\bar \rho _{\mathfrak {B}}}$
be the deformation ring parametrising all of the
![]() $2$
-dimensional continuous determinants (in the sense of [Reference ChenevierChe14]) of
$2$
-dimensional continuous determinants (in the sense of [Reference ChenevierChe14]) of
![]() $G_{\mathbb {Q}_p}$
lifting
$G_{\mathbb {Q}_p}$
lifting
![]() $(\mathrm {tr}\bar \rho _{\mathfrak {B}},\det \bar \rho _{\mathfrak {B}})$
with (usual) determinant
$(\mathrm {tr}\bar \rho _{\mathfrak {B}},\det \bar \rho _{\mathfrak {B}})$
with (usual) determinant
![]() $\zeta \varepsilon _p$
. Here is a summary of results of Paškūnas and Paškūnas–Tung that we will use later.
$\zeta \varepsilon _p$
. Here is a summary of results of Paškūnas and Paškūnas–Tung that we will use later.
Theorem 6.3.3. Suppose
![]() $\mathfrak {B}$
contains an absolutely irreducible representation. Let
$\mathfrak {B}$
contains an absolutely irreducible representation. Let
![]() $Z_{\mathfrak {B}}$
be the Bernstein centre of
$Z_{\mathfrak {B}}$
be the Bernstein centre of
 $\mathrm {Mod}^{\mathrm {l\, adm}}_{G,\zeta }(\mathcal {O})[\mathfrak {B}]$
.
$\mathrm {Mod}^{\mathrm {l\, adm}}_{G,\zeta }(\mathcal {O})[\mathfrak {B}]$
.
-
(1) There is a finite
 $\mathcal {O}$
-algebra homomorphism compatible with Colmez’s functor (see [Reference Paškūnas and TungPT21, Theorem 1.2] for the precise statement). Hence,
$\mathcal {O}$
-algebra homomorphism compatible with Colmez’s functor (see [Reference Paškūnas and TungPT21, Theorem 1.2] for the precise statement). Hence, $$ \begin{align*}R^{\mathrm{ps},\zeta\varepsilon_p}_{\bar\rho_{\mathfrak{B}}}\to Z_{\mathfrak{B}}\end{align*} $$
$$ \begin{align*}R^{\mathrm{ps},\zeta\varepsilon_p}_{\bar\rho_{\mathfrak{B}}}\to Z_{\mathfrak{B}}\end{align*} $$
 $\mathrm {Mod}^{\mathrm {l\, adm}}_{G,\zeta }(\mathcal {O})[\mathfrak {B}]$
admits a
$\mathrm {Mod}^{\mathrm {l\, adm}}_{G,\zeta }(\mathcal {O})[\mathfrak {B}]$
admits a
 $R^{\mathrm {ps},\zeta \varepsilon _p}_{\bar \rho _{\mathfrak {B}}}$
-module structure from this map.
$R^{\mathrm {ps},\zeta \varepsilon _p}_{\bar \rho _{\mathfrak {B}}}$
-module structure from this map.
-
(2) There is a faithful
 $R^{\mathrm {ps},\zeta \varepsilon _p}_{\bar \rho _{\mathfrak {B}}}$
-linear contravariant exact functor
$R^{\mathrm {ps},\zeta \varepsilon _p}_{\bar \rho _{\mathfrak {B}}}$
-linear contravariant exact functor
 $\mathrm {m}$
from
$\mathrm {m}$
from
 $\mathrm {Mod}^{\mathrm {l\, adm}}_{G,\zeta }(\mathcal {O})[\mathfrak {B}]$
to the category of
$\mathrm {Mod}^{\mathrm {l\, adm}}_{G,\zeta }(\mathcal {O})[\mathfrak {B}]$
to the category of
 $R^{\mathrm {ps},\zeta \varepsilon _p}_{\bar \rho _{\mathfrak {B}}}$
-modules sending admissible representations to finitely generated
$R^{\mathrm {ps},\zeta \varepsilon _p}_{\bar \rho _{\mathfrak {B}}}$
-modules sending admissible representations to finitely generated
 $R^{\mathrm {ps},\zeta \varepsilon _p}_{\bar \rho _{\mathfrak {B}}}$
-modules.
$R^{\mathrm {ps},\zeta \varepsilon _p}_{\bar \rho _{\mathfrak {B}}}$
-modules.
Proof. Both claims follow from [Reference Paškūnas and TungPT21, Theorem 1.2, 1.3]. In fact, Paškūnas and Tung show that
 $\mathrm {Mod}^{\mathrm {l\, adm}}_{G,\zeta }(\mathcal {O})[\mathfrak {B}]$
is anti-equivalent to the category of right pseudo-compact
$\mathrm {Mod}^{\mathrm {l\, adm}}_{G,\zeta }(\mathcal {O})[\mathfrak {B}]$
is anti-equivalent to the category of right pseudo-compact
![]() $E_{\mathfrak {B}}$
-modules for some pseudo-compact ring
$E_{\mathfrak {B}}$
-modules for some pseudo-compact ring
![]() $E_{\mathfrak {B}}$
and construct a map
$E_{\mathfrak {B}}$
and construct a map
 $R^{\mathrm {ps},\zeta \varepsilon _p}_{\bar \rho _{\mathfrak {B}}}\to Z_{\mathfrak {B}}\subseteq E_{\mathfrak {B}}$
which makes
$R^{\mathrm {ps},\zeta \varepsilon _p}_{\bar \rho _{\mathfrak {B}}}\to Z_{\mathfrak {B}}\subseteq E_{\mathfrak {B}}$
which makes
![]() $E_{\mathfrak {B}}$
into a finitely generated
$E_{\mathfrak {B}}$
into a finitely generated
 $R^{\mathrm {ps},\zeta \varepsilon _p}_{\bar \rho _{\mathfrak {B}}}$
-module. The functor
$R^{\mathrm {ps},\zeta \varepsilon _p}_{\bar \rho _{\mathfrak {B}}}$
-module. The functor
![]() $\mathrm {m}$
is defined by passing the action of
$\mathrm {m}$
is defined by passing the action of
![]() $E_{\mathfrak {B}}$
to
$E_{\mathfrak {B}}$
to
 $R^{\mathrm {ps},\zeta \varepsilon _p}_{\bar \rho _{\mathfrak {B}}}$
.
$R^{\mathrm {ps},\zeta \varepsilon _p}_{\bar \rho _{\mathfrak {B}}}$
.
6.3.4. Next we turn to the global side. Fix a tame level
![]() $K^p$
from now on. Let
$K^p$
from now on. Let
![]() $\mathfrak {m}$
be a maximal ideal of
$\mathfrak {m}$
be a maximal ideal of
![]() $\mathbb {T}(K^p)\otimes _{\mathbb {Z}_p}\mathcal {O}$
. We may assume the residue field of
$\mathbb {T}(K^p)\otimes _{\mathbb {Z}_p}\mathcal {O}$
. We may assume the residue field of
![]() $\mathfrak {m}$
is
$\mathfrak {m}$
is
![]() $\mathbb {F}$
by enlarging E. Recall that there is a
$\mathbb {F}$
by enlarging E. Recall that there is a
![]() $2$
-dimensional determinant of
$2$
-dimensional determinant of
![]() $G_{\mathbb {Q}}$
valued in
$G_{\mathbb {Q}}$
valued in
![]() $\mathbb {T}(K^p)$
and we extend it to a determinant valued in
$\mathbb {T}(K^p)$
and we extend it to a determinant valued in
![]() $\mathbb {T}(K^p)\otimes _{\mathbb {Z}_p}\mathcal {O}$
. Denote by
$\mathbb {T}(K^p)\otimes _{\mathbb {Z}_p}\mathcal {O}$
. Denote by
![]() $D_p$
its restriction to
$D_p$
its restriction to
![]() $G_{\mathbb {Q}_p}$
and by
$G_{\mathbb {Q}_p}$
and by
![]() $\bar {D}_p$
its reduction modulo
$\bar {D}_p$
its reduction modulo
![]() $\mathfrak {m}$
. Again enlarging E if necessary, we may assume that
$\mathfrak {m}$
. Again enlarging E if necessary, we may assume that
![]() $\bar {D}_p$
arises from a
$\bar {D}_p$
arises from a
![]() $2$
-dimensional semi-simple representation
$2$
-dimensional semi-simple representation
![]() ${\bar \rho _{\mathfrak {m},p}:G_{\mathbb {Q}_p}\to \mathrm {GL}_2(\mathbb {F})}$
. Fix a continuous character
${\bar \rho _{\mathfrak {m},p}:G_{\mathbb {Q}_p}\to \mathrm {GL}_2(\mathbb {F})}$
. Fix a continuous character
 $\zeta ':\mathbb {A}_f^{\times }/\det (K^p)\mathbb {Q}^{\times }_{>0}\to \mathcal {O}^{\times }$
such that
$\zeta ':\mathbb {A}_f^{\times }/\det (K^p)\mathbb {Q}^{\times }_{>0}\to \mathcal {O}^{\times }$
such that
 $\zeta =\zeta '|_{\mathbb {Q}_p^{\times }}:\mathbb {Q}_p^{\times }\to \mathcal {O}^{\times }$
is congruent to
$\zeta =\zeta '|_{\mathbb {Q}_p^{\times }}:\mathbb {Q}_p^{\times }\to \mathcal {O}^{\times }$
is congruent to
![]() $(\det \bar \rho _{\mathfrak {m},p})\omega ^{-1}$
modulo
$(\det \bar \rho _{\mathfrak {m},p})\omega ^{-1}$
modulo
![]() $\varpi $
via local class field theory. For
$\varpi $
via local class field theory. For
![]() $?=E,\mathcal {O},E/\mathcal {O}$
, let
$?=E,\mathcal {O},E/\mathcal {O}$
, let
![]() $\tilde {H}^1(K^p,?)_{\zeta ',\mathfrak {m}}$
be the subspace of
$\tilde {H}^1(K^p,?)_{\zeta ',\mathfrak {m}}$
be the subspace of
 $(\tilde {H}^1(K^p,\mathbb {Z}_p)\otimes _{\mathbb {Z}_p} ?)_{\mathfrak {m}}$
on which the centre
$(\tilde {H}^1(K^p,\mathbb {Z}_p)\otimes _{\mathbb {Z}_p} ?)_{\mathfrak {m}}$
on which the centre
 $\mathbb {A}_f^{\times }$
acts via
$\mathbb {A}_f^{\times }$
acts via
![]() $\zeta '$
and let
$\zeta '$
and let
![]() $\mathbb {T}$
be the image of
$\mathbb {T}$
be the image of
![]() $(\mathbb {T}(K^p)\otimes \mathcal {O})_{\mathfrak {m}}$
inside
$(\mathbb {T}(K^p)\otimes \mathcal {O})_{\mathfrak {m}}$
inside
![]() $\operatorname {\mathrm {End}}(\tilde {H}^1(K^p,E/\mathcal {O})_{\zeta ',\mathfrak {m}})$
. Then
$\operatorname {\mathrm {End}}(\tilde {H}^1(K^p,E/\mathcal {O})_{\zeta ',\mathfrak {m}})$
. Then
![]() $D_p$
induces a natural map
$D_p$
induces a natural map
 $$ \begin{align*}R^{\mathrm{ps},\zeta\varepsilon_p}_{\bar\rho_{\mathfrak{m},p}}\to\mathbb{T}.\end{align*} $$
$$ \begin{align*}R^{\mathrm{ps},\zeta\varepsilon_p}_{\bar\rho_{\mathfrak{m},p}}\to\mathbb{T}.\end{align*} $$
Hence, the faithful Hecke action of
![]() $\mathbb {T}$
induces an action of
$\mathbb {T}$
induces an action of
 $R^{\mathrm {ps},\zeta \varepsilon _p}_{\bar \rho _{\mathfrak {m},p}}$
on
$R^{\mathrm {ps},\zeta \varepsilon _p}_{\bar \rho _{\mathfrak {m},p}}$
on
![]() $\tilde {H}^1(K^p,E/\mathcal {O})_{\zeta ',\mathfrak {m}}$
by our discussion. We denote this action by
$\tilde {H}^1(K^p,E/\mathcal {O})_{\zeta ',\mathfrak {m}}$
by our discussion. We denote this action by
![]() $\tau ^{p}$
.
$\tau ^{p}$
.
On the other hand,
![]() $\bar \rho _{\mathfrak {m},p}$
determines a block
$\bar \rho _{\mathfrak {m},p}$
determines a block
![]() $\mathfrak {B}_{\mathfrak {m}}$
of
$\mathfrak {B}_{\mathfrak {m}}$
of
 $\mathrm {Mod}^{\mathrm {l\, adm}}_{G,\zeta }(\mathcal {O})$
. Now we can state the main result of this subsection.
$\mathrm {Mod}^{\mathrm {l\, adm}}_{G,\zeta }(\mathcal {O})$
. Now we can state the main result of this subsection.
Theorem 6.3.5. Let
![]() $\mathfrak {m}$
be a maximal ideal of
$\mathfrak {m}$
be a maximal ideal of
![]() $\mathbb {T}(K^p)\otimes _{\mathbb {Z}_p}\mathcal {O}$
.
$\mathbb {T}(K^p)\otimes _{\mathbb {Z}_p}\mathcal {O}$
.
-
(1)
 $\tilde {H}^1(K^p,E/\mathcal {O})_{\zeta ',\mathfrak {m}}\in \mathrm {Mod}^{\mathrm {l\, adm}}_{G,\zeta }(\mathcal {O})[\mathfrak {B}_{\mathfrak {m}}]$
. Hence, by Theorem 6.3.3, there is a natural action
$\tilde {H}^1(K^p,E/\mathcal {O})_{\zeta ',\mathfrak {m}}\in \mathrm {Mod}^{\mathrm {l\, adm}}_{G,\zeta }(\mathcal {O})[\mathfrak {B}_{\mathfrak {m}}]$
. Hence, by Theorem 6.3.3, there is a natural action
 $\tau _p$
of
$\tau _p$
of
 $R^{\mathrm {ps},\zeta \varepsilon _p}_{\bar \rho _{\mathfrak {B_{\mathfrak {m}}}}}=R^{\mathrm {ps},\zeta \varepsilon _p}_{\bar \rho _{\mathfrak {m},p}}$
on
$R^{\mathrm {ps},\zeta \varepsilon _p}_{\bar \rho _{\mathfrak {B_{\mathfrak {m}}}}}=R^{\mathrm {ps},\zeta \varepsilon _p}_{\bar \rho _{\mathfrak {m},p}}$
on
 $\tilde {H}^1(K^p,E/\mathcal {O})_{\zeta ',\mathfrak {m}}$
.
$\tilde {H}^1(K^p,E/\mathcal {O})_{\zeta ',\mathfrak {m}}$
. -
(2) Two actions
 $\tau ^p$
and
$\tau ^p$
and
 $\tau _p$
of
$\tau _p$
of
 $R^{\mathrm {ps},\zeta \varepsilon _p}_{\bar \rho _{\mathfrak {m},p}}$
are the same.
$R^{\mathrm {ps},\zeta \varepsilon _p}_{\bar \rho _{\mathfrak {m},p}}$
are the same.
Before giving a proof, we show that this result implies a (weak) form of local–global compatibility which will be enough for our applications. Recall that by [Reference Colmez, Dospinescu and PaškūnasCDP14, Theorem 1.1], there is a bijection between the isomorphism classes of the following two sets:
-
•
 $2$
-dimensional absolutely irreducible representation of
$2$
-dimensional absolutely irreducible representation of
 $G_{\mathbb {Q}_p}$
over E;
$G_{\mathbb {Q}_p}$
over E; -
• nonordinary admissible unitary E-Banach representations of
 $\mathrm {GL}_2(\mathbb {Q}_p)$
.
$\mathrm {GL}_2(\mathbb {Q}_p)$
.
Here, a Banach representation is nonordinary if it is not a subquotient of a parabolic induction of a unitary character. This bijection is compatible with taking finite extensions of E. Hence, we can extend this bijection
![]() -linearly to a map (not bijection) from the isomorphism classes of
-linearly to a map (not bijection) from the isomorphism classes of
![]() $2$
-dimensional irreducible representation of
$2$
-dimensional irreducible representation of
![]() $G_{\mathbb {Q}_p}$
over
$G_{\mathbb {Q}_p}$
over
![]() to the isomorphism classes of
to the isomorphism classes of
![]() -representations of
-representations of
![]() $\mathrm {GL}_2(\mathbb {Q}_p)$
. We denote this map by
$\mathrm {GL}_2(\mathbb {Q}_p)$
. We denote this map by
![]() $\rho \mapsto \Pi (\rho )$
.
$\rho \mapsto \Pi (\rho )$
.
Corollary 6.3.6. Suppose
![]() $\rho =\rho _{\lambda }$
is pro-modular and irreducible for some tame level
$\rho =\rho _{\lambda }$
is pro-modular and irreducible for some tame level
![]() $K^p$
. Then
$K^p$
. Then
 ; that is,
; that is,
![]() $\rho $
is pro-cohomological. Moreover, we have the following description of
$\rho $
is pro-cohomological. Moreover, we have the following description of
 as a representation of
as a representation of
![]() $\mathrm {GL}_2(\mathbb {Q}_p)$
:
$\mathrm {GL}_2(\mathbb {Q}_p)$
:
-
• If
 $\rho |_{G_{\mathbb {Q}_p}}$
is irreducible, then
$\rho |_{G_{\mathbb {Q}_p}}$
is irreducible, then
 for some d.
for some d. -
• If
 $\rho |_{G_{\mathbb {Q}_p}}$
is reducible, then
$\rho |_{G_{\mathbb {Q}_p}}$
is reducible, then
 has an ordinary subrepresentation.
has an ordinary subrepresentation.
Remark 6.3.7. For later application (Theorem 6.4.7), all we need is that
 is nonzero and contains an irreducible admissible representation.
is nonzero and contains an irreducible admissible representation.
Proof. We denote by
![]() $\mathrm {m}_0$
the
$\mathrm {m}_0$
the
 $R^{\mathrm {ps},\zeta \varepsilon }_{\bar \rho _{\mathfrak {m},p}}$
-module obtained by applying the faithful functor
$R^{\mathrm {ps},\zeta \varepsilon }_{\bar \rho _{\mathfrak {m},p}}$
-module obtained by applying the faithful functor
![]() $\mathrm {m}$
in Theorem 6.3.3 to
$\mathrm {m}$
in Theorem 6.3.3 to
![]() $\tilde {H}^1(K^p,E/\mathcal {O})_{\zeta ',\mathfrak {m}}$
. Then the admissibility of
$\tilde {H}^1(K^p,E/\mathcal {O})_{\zeta ',\mathfrak {m}}$
. Then the admissibility of
![]() $\tilde {H}^1(K^p,E/\mathcal {O})_{\zeta ',\mathfrak {m}}$
implies that
$\tilde {H}^1(K^p,E/\mathcal {O})_{\zeta ',\mathfrak {m}}$
implies that
![]() $\mathrm {m}_0$
is a finitely generated
$\mathrm {m}_0$
is a finitely generated
 $R^{\mathrm {ps},\zeta \varepsilon }_{\bar \rho _{\mathfrak {m},p}}$
-module. Since the action
$R^{\mathrm {ps},\zeta \varepsilon }_{\bar \rho _{\mathfrak {m},p}}$
-module. Since the action
![]() $\tau _p$
agrees with
$\tau _p$
agrees with
![]() $\tau ^p$
which factors through
$\tau ^p$
which factors through
![]() $\mathbb {T}$
by Theorem 6.3.5, we conclude that
$\mathbb {T}$
by Theorem 6.3.5, we conclude that
![]() $\mathrm {m}_0$
is a faithful finitely generated
$\mathrm {m}_0$
is a faithful finitely generated
![]() $\mathbb {T}$
-module. In particular,
$\mathbb {T}$
-module. In particular,
![]() $\mathrm {m}_0\otimes _{\mathbb {T}} k(\mathfrak {p})\neq 0$
for any
$\mathrm {m}_0\otimes _{\mathbb {T}} k(\mathfrak {p})\neq 0$
for any
![]() $\mathfrak {p}\in \operatorname {\mathrm {Spec}}\mathbb {T}$
, where
$\mathfrak {p}\in \operatorname {\mathrm {Spec}}\mathbb {T}$
, where
![]() $k(\mathfrak {p})$
denotes the residue field of
$k(\mathfrak {p})$
denotes the residue field of
![]() $\mathfrak {p}$
. From this, we easily deduce
$\mathfrak {p}$
. From this, we easily deduce
 in the corollary. Using
in the corollary. Using
![]() $\tau ^p=\tau _p$
, our description of
$\tau ^p=\tau _p$
, our description of
 follows from Paškūnas’s work on Banach representations [Reference PaškūnasPaš13, Theorem 1.10, 1.11], [Reference PaškūnasPaš16, Corollary 2.24].
follows from Paškūnas’s work on Banach representations [Reference PaškūnasPaš13, Theorem 1.10, 1.11], [Reference PaškūnasPaš16, Corollary 2.24].
Proof of Theorem 6.3.5
We can replace
![]() $K^p$
by an open subgroup and assume
$K^p$
by an open subgroup and assume
![]() $K^p\mathrm {GL}_2(\mathbb {Z}_p)$
is sufficiently small. After twisting a character of
$K^p\mathrm {GL}_2(\mathbb {Z}_p)$
is sufficiently small. After twisting a character of
 $\mathbb {A}_f^{\times }/\mathbb {Q}^{\times }_{>0}$
, we may assume
$\mathbb {A}_f^{\times }/\mathbb {Q}^{\times }_{>0}$
, we may assume
 $\zeta (x)=x^k,x\in \mathbb {Z}_p^{\times }$
for some integer k. We denote by
$\zeta (x)=x^k,x\in \mathbb {Z}_p^{\times }$
for some integer k. We denote by
![]() $\tilde {H}^1(K^p,\mathbb {Q}_p)_k\subset \tilde {H}^1(K^p,\mathbb {Q}_p)$
the subspace on which the centre
$\tilde {H}^1(K^p,\mathbb {Q}_p)_k\subset \tilde {H}^1(K^p,\mathbb {Q}_p)$
the subspace on which the centre
![]() $\mathbb {Z}_p^{\times }\subset \mathrm {GL}_2(\mathbb {Q}_p)$
acts via kth power. It has a norm induced from
$\mathbb {Z}_p^{\times }\subset \mathrm {GL}_2(\mathbb {Q}_p)$
acts via kth power. It has a norm induced from
![]() $\tilde {H}^1(K^p,\mathbb {Z}_p)$
. Then after enlarging E if necessary, there is a natural decomposition
$\tilde {H}^1(K^p,\mathbb {Z}_p)$
. Then after enlarging E if necessary, there is a natural decomposition
 $$ \begin{align*}\tilde{H}^1(K^p,\mathbb{Q}_p)_k\otimes_{\mathbb{Q}_p} E=\bigoplus_{(\mathfrak{m}',\zeta'')}\tilde{H}^1(K^p,E)_{\zeta'',\mathfrak{m}'},\end{align*} $$
$$ \begin{align*}\tilde{H}^1(K^p,\mathbb{Q}_p)_k\otimes_{\mathbb{Q}_p} E=\bigoplus_{(\mathfrak{m}',\zeta'')}\tilde{H}^1(K^p,E)_{\zeta'',\mathfrak{m}'},\end{align*} $$
where
![]() $\mathfrak {m}'$
runs through all maximal ideals of
$\mathfrak {m}'$
runs through all maximal ideals of
![]() $\mathbb {T}(K^p)\otimes \mathcal {O}$
and
$\mathbb {T}(K^p)\otimes \mathcal {O}$
and
 $\zeta '':\mathbb {A}_f^{\times }/\det (K^p)\mathbb {Q}^{\times }_{>0}$
runs through all continuous characters satisfying
$\zeta '':\mathbb {A}_f^{\times }/\det (K^p)\mathbb {Q}^{\times }_{>0}$
runs through all continuous characters satisfying
 $\zeta ''(x)=x^k,x\in \mathbb {Z}_p^{\times }$
. In particular,
$\zeta ''(x)=x^k,x\in \mathbb {Z}_p^{\times }$
. In particular,
![]() $(\mathfrak {m},\zeta ')$
appears inside this decomposition. Note that there are only finitely many
$(\mathfrak {m},\zeta ')$
appears inside this decomposition. Note that there are only finitely many
![]() $(\mathfrak {m}',\zeta '')$
.
$(\mathfrak {m}',\zeta '')$
.
Lemma 6.3.8. The
![]() $\mathrm {GL}_2(\mathbb {Z}_p)$
-algebraic vectors in
$\mathrm {GL}_2(\mathbb {Z}_p)$
-algebraic vectors in
![]() $\tilde {H}^1(K^p,\mathbb {Q}_p)_k$
are dense in
$\tilde {H}^1(K^p,\mathbb {Q}_p)_k$
are dense in
![]() $\tilde {H}^1(K^p,\mathbb {Q}_p)_k$
.
$\tilde {H}^1(K^p,\mathbb {Q}_p)_k$
.
Lemma 6.3.9. The Hecke action of
![]() $\mathbb {T}(K^p)$
on the
$\mathbb {T}(K^p)$
on the
![]() $\mathrm {GL}_2(\mathbb {Z}_p)$
-algebraic vectors in
$\mathrm {GL}_2(\mathbb {Z}_p)$
-algebraic vectors in
![]() $\tilde {H}^1(K^p,\mathbb {Q}_p)$
is semi-simple.
$\tilde {H}^1(K^p,\mathbb {Q}_p)$
is semi-simple.
We will give proofs of both lemmas at the end. Assuming these results, we deduce from the natural decomposition above that the
![]() $\mathrm {GL}_2(\mathbb {Z}_p)$
-algebraic vectors in
$\mathrm {GL}_2(\mathbb {Z}_p)$
-algebraic vectors in
![]() $\tilde {H}^1(K^p,E)_{\zeta ',\mathfrak {m}}$
are dense. Now one can argue in exactly the same way as proof of Proposition 5.5 of [Reference PaskunasPas18]. We only give a sketch here. It should be mentioned that these algebraic vectors correspond to cohomology of certain standard local systems on
$\tilde {H}^1(K^p,E)_{\zeta ',\mathfrak {m}}$
are dense. Now one can argue in exactly the same way as proof of Proposition 5.5 of [Reference PaskunasPas18]. We only give a sketch here. It should be mentioned that these algebraic vectors correspond to cohomology of certain standard local systems on
![]() $\mathcal {Y}_{K^p\mathrm {GL}_2(\mathbb {Z}_p)}$
. Let
$\mathcal {Y}_{K^p\mathrm {GL}_2(\mathbb {Z}_p)}$
. Let
 $\mathcal {S}\subset \operatorname {\mathrm {Spec}}\mathbb {T}[\frac {1}{p}]$
be the subset of maximal ideals
$\mathcal {S}\subset \operatorname {\mathrm {Spec}}\mathbb {T}[\frac {1}{p}]$
be the subset of maximal ideals
![]() $\mathfrak {p}$
for which
$\mathfrak {p}$
for which
![]() $\tilde {H}^1(K^p,E)_{\zeta ',\mathfrak {m}}[\mathfrak {p}]$
has nonzero
$\tilde {H}^1(K^p,E)_{\zeta ',\mathfrak {m}}[\mathfrak {p}]$
has nonzero
![]() $\mathrm {GL}_2(\mathbb {Z}_p)$
-algebraic vectors. We write
$\mathrm {GL}_2(\mathbb {Z}_p)$
-algebraic vectors. We write
![]() $\Pi (\mathfrak {p})$
as the smallest
$\Pi (\mathfrak {p})$
as the smallest
![]() $E[G]$
-stable closed subspace containing the
$E[G]$
-stable closed subspace containing the
![]() $\mathrm {GL}_2(\mathbb {Z}_p)$
-algebraic vectors in
$\mathrm {GL}_2(\mathbb {Z}_p)$
-algebraic vectors in
![]() $\tilde {H}^1(K^p,E)_{\zeta ',\mathfrak {m}}[\mathfrak {p}]$
. Let
$\tilde {H}^1(K^p,E)_{\zeta ',\mathfrak {m}}[\mathfrak {p}]$
. Let
![]() $\Pi (\mathfrak {p})^o\subset \Pi (\mathfrak {p})$
be its open unit ball. By our density result and the semi-simplicity of Hecke action on the
$\Pi (\mathfrak {p})^o\subset \Pi (\mathfrak {p})$
be its open unit ball. By our density result and the semi-simplicity of Hecke action on the
![]() $\mathrm {GL}_2(\mathbb {Z}_p)$
-algebraic vectors in
$\mathrm {GL}_2(\mathbb {Z}_p)$
-algebraic vectors in
![]() $\tilde {H}^1(K^p,E)_{\zeta ',\mathfrak {m}}$
, it suffices to prove that for any
$\tilde {H}^1(K^p,E)_{\zeta ',\mathfrak {m}}$
, it suffices to prove that for any
![]() $\mathfrak {p}\in \mathcal {S}$
,
$\mathfrak {p}\in \mathcal {S}$
,
 $$ \begin{align*}\Pi(\mathfrak{p})/\Pi(\mathfrak{p})^o\in \mathrm{Mod}^{\mathrm{l\, adm}}_{G,\zeta}(\mathcal{O})[\mathfrak{B}_{\mathfrak{m}}]\end{align*} $$
$$ \begin{align*}\Pi(\mathfrak{p})/\Pi(\mathfrak{p})^o\in \mathrm{Mod}^{\mathrm{l\, adm}}_{G,\zeta}(\mathcal{O})[\mathfrak{B}_{\mathfrak{m}}]\end{align*} $$
and both actions
![]() $\tau ^p,\tau _p$
are the same on it. Both claims are really formal consequences of classical local–global compatibility and uniqueness of the universal unitary completion in this case ([Reference Berger and BreuilBB10, Corollarie 5.3.4], [Reference Breuil and EmertonBE10, Proposition 2.2.1]) and the compatibility between p-adic and classical local Langlands correspondence [Reference Colmez, Dospinescu and PaškūnasCDP14, Theorem 1.3]. This finishes the proof of Theorem 6.3.5.
$\tau ^p,\tau _p$
are the same on it. Both claims are really formal consequences of classical local–global compatibility and uniqueness of the universal unitary completion in this case ([Reference Berger and BreuilBB10, Corollarie 5.3.4], [Reference Breuil and EmertonBE10, Proposition 2.2.1]) and the compatibility between p-adic and classical local Langlands correspondence [Reference Colmez, Dospinescu and PaškūnasCDP14, Theorem 1.3]. This finishes the proof of Theorem 6.3.5.
Proof of Lemma 6.3.8
As pointed out by a referee, the following argument was sketched by Matthew Emerton in [Reference EmertonEme11, Remark 5.4.2].
We begin the proof by recalling a complex computing
![]() $\tilde {H}^{i}(K^p,\mathbb {Q}_p)$
. Let
$\tilde {H}^{i}(K^p,\mathbb {Q}_p)$
. Let
![]() $\tilde {H}_c^i(K^p,\mathbb {Z}_p)$
be the completed cohomology with compact support, which is defined by
$\tilde {H}_c^i(K^p,\mathbb {Z}_p)$
be the completed cohomology with compact support, which is defined by
 $$ \begin{align*}\tilde{H}_c^i(K^p,\mathbb{Z}_p):=\varprojlim_n\varinjlim_{K_p} H^i_c(Y_{K^pK_p}(\mathbb{C}),\mathbb{Z}/p^n).\end{align*} $$
$$ \begin{align*}\tilde{H}_c^i(K^p,\mathbb{Z}_p):=\varprojlim_n\varinjlim_{K_p} H^i_c(Y_{K^pK_p}(\mathbb{C}),\mathbb{Z}/p^n).\end{align*} $$
Since
![]() $Y_{K^pK_p}$
is a noncompact Riemann surface, it is easy to see that
$Y_{K^pK_p}$
is a noncompact Riemann surface, it is easy to see that
![]() $\tilde {H}_c^i(K^p,\mathbb {Z}_p)=0,i\neq 1$
. There is a spectral sequence (coming from the Poincaré duality) relating
$\tilde {H}_c^i(K^p,\mathbb {Z}_p)=0,i\neq 1$
. There is a spectral sequence (coming from the Poincaré duality) relating
![]() $\tilde {H}^{\bullet }$
and
$\tilde {H}^{\bullet }$
and
![]() $\tilde {H}^1_c$
(Subsection 1.3 of [Reference Calegari and EmertonCE12]) as follows. Let
$\tilde {H}^1_c$
(Subsection 1.3 of [Reference Calegari and EmertonCE12]) as follows. Let
![]() $\Lambda $
be the completed group ring
$\Lambda $
be the completed group ring
![]() $\mathbb {Z}_p[[\mathrm {GL}_2(\mathbb {Z}_p)]]$
. Then
$\mathbb {Z}_p[[\mathrm {GL}_2(\mathbb {Z}_p)]]$
. Then
 $\tilde {H}_c^1(K^p,\mathbb {Z}_p)^d:=\operatorname {\mathrm {Hom}}_{\mathbb {Z}_p}(\tilde {H}_c^1(K^p,\mathbb {Z}_p),\mathbb {Z}_p)$
admits a resolution by finite free
$\tilde {H}_c^1(K^p,\mathbb {Z}_p)^d:=\operatorname {\mathrm {Hom}}_{\mathbb {Z}_p}(\tilde {H}_c^1(K^p,\mathbb {Z}_p),\mathbb {Z}_p)$
admits a resolution by finite free
![]() $\Lambda $
-modules:
$\Lambda $
-modules:
 $$ \begin{align*}\cdots\to \Lambda^{\oplus d_{-1}}\to \Lambda^{\oplus d_0}\to \Lambda^{\oplus d_1}\to \tilde{H}_c^1(K^p,\mathbb{Z}_p)^d\to 0.\end{align*} $$
$$ \begin{align*}\cdots\to \Lambda^{\oplus d_{-1}}\to \Lambda^{\oplus d_0}\to \Lambda^{\oplus d_1}\to \tilde{H}_c^1(K^p,\mathbb{Z}_p)^d\to 0.\end{align*} $$
Taking
![]() $\operatorname {\mathrm {Hom}}_{\Lambda }(\bullet ,\Lambda )$
of this resolution, where
$\operatorname {\mathrm {Hom}}_{\Lambda }(\bullet ,\Lambda )$
of this resolution, where
![]() $\Lambda $
is viewed as a left module of itself, we obtain a complex of right
$\Lambda $
is viewed as a left module of itself, we obtain a complex of right
![]() $\Lambda $
-modules (using the right
$\Lambda $
-modules (using the right
![]() $\Lambda $
-module structure of
$\Lambda $
-module structure of
![]() $\Lambda $
)
$\Lambda $
)
We can view this sequence as a complex of left
![]() $\Lambda $
-modules by applying the main involution
$\Lambda $
-modules by applying the main involution
![]() $g\mapsto g^{-1}$
of
$g\mapsto g^{-1}$
of
![]() $\Lambda $
. Now taking
$\Lambda $
. Now taking
 $\operatorname {\mathrm {Hom}}^{\mathrm {cont}}_{\mathbb {Z}_p}(\bullet ,\mathbb {Q}_p)$
, we get a
$\operatorname {\mathrm {Hom}}^{\mathrm {cont}}_{\mathbb {Z}_p}(\bullet ,\mathbb {Q}_p)$
, we get a
![]() $\mathrm {GL}_2(\mathbb {Z}_p)$
-equivariant complex
$\mathrm {GL}_2(\mathbb {Z}_p)$
-equivariant complex
 $$ \begin{align*}C^{\bullet}=\cdots\to \mathscr{C}(\mathrm{GL}_2(\mathbb{Z}_p),\mathbb{Q}_p)^{\oplus d_{-1}}\to \mathscr{C}(\mathrm{GL}_2(\mathbb{Z}_p),\mathbb{Q}_p)^{\oplus d_0}\to \mathscr{C}(\mathrm{GL}_2(\mathbb{Z}_p),\mathbb{Q}_p)^{\oplus d_1},\end{align*} $$
$$ \begin{align*}C^{\bullet}=\cdots\to \mathscr{C}(\mathrm{GL}_2(\mathbb{Z}_p),\mathbb{Q}_p)^{\oplus d_{-1}}\to \mathscr{C}(\mathrm{GL}_2(\mathbb{Z}_p),\mathbb{Q}_p)^{\oplus d_0}\to \mathscr{C}(\mathrm{GL}_2(\mathbb{Z}_p),\mathbb{Q}_p)^{\oplus d_1},\end{align*} $$
where
![]() $\mathscr {C}(\mathrm {GL}_2(\mathbb {Z}_p),\mathbb {Q}_p)$
denotes the space of
$\mathscr {C}(\mathrm {GL}_2(\mathbb {Z}_p),\mathbb {Q}_p)$
denotes the space of
![]() $\mathbb {Q}_p$
-valued continuous functions on
$\mathbb {Q}_p$
-valued continuous functions on
![]() $\mathrm {GL}_2(\mathbb {Z}_p)$
. The result in Subsection 1.3 of [Reference Calegari and EmertonCE12] says that this complex computes
$\mathrm {GL}_2(\mathbb {Z}_p)$
. The result in Subsection 1.3 of [Reference Calegari and EmertonCE12] says that this complex computes
![]() $\tilde {H}^{i}(K^p,\mathbb {Q}_p)$
as a
$\tilde {H}^{i}(K^p,\mathbb {Q}_p)$
as a
![]() $\mathrm {GL}_2(\mathbb {Z}_p)$
-representation. For a
$\mathrm {GL}_2(\mathbb {Z}_p)$
-representation. For a
![]() $\mathbb {Z}_p[\mathrm {GL}_2(\mathbb {Z}_p)]$
-module M, we denote by
$\mathbb {Z}_p[\mathrm {GL}_2(\mathbb {Z}_p)]$
-module M, we denote by
![]() $M_k$
the subspace on which the centre
$M_k$
the subspace on which the centre
![]() $\mathbb {Z}_p^{\times }$
acts via kth power. We claim that
$\mathbb {Z}_p^{\times }$
acts via kth power. We claim that
 $$ \begin{align*}C^{\bullet}_k=\cdots\to \mathscr{C}(\mathrm{GL}_2(\mathbb{Z}_p),\mathbb{Q}_p)_k^{\oplus d_{-1}}\to \mathscr{C}(\mathrm{GL}_2(\mathbb{Z}_p),\mathbb{Q}_p)_k^{\oplus d_0}\to \mathscr{C}(\mathrm{GL}_2(\mathbb{Z}_p),\mathbb{Q}_p)_k^{\oplus d_1}\end{align*} $$
$$ \begin{align*}C^{\bullet}_k=\cdots\to \mathscr{C}(\mathrm{GL}_2(\mathbb{Z}_p),\mathbb{Q}_p)_k^{\oplus d_{-1}}\to \mathscr{C}(\mathrm{GL}_2(\mathbb{Z}_p),\mathbb{Q}_p)_k^{\oplus d_0}\to \mathscr{C}(\mathrm{GL}_2(\mathbb{Z}_p),\mathbb{Q}_p)_k^{\oplus d_1}\end{align*} $$
computes
![]() $\tilde {H}^{i}(K^p,\mathbb {Q}_p)_k$
. Assuming this,
$\tilde {H}^{i}(K^p,\mathbb {Q}_p)_k$
. Assuming this,
![]() $\tilde {H}^{1}(K^p,\mathbb {Q}_p)_k$
is a
$\tilde {H}^{1}(K^p,\mathbb {Q}_p)_k$
is a
![]() $\mathrm {GL}_2(\mathbb {Z}_p)$
-equivariant quotient of
$\mathrm {GL}_2(\mathbb {Z}_p)$
-equivariant quotient of
 $\mathscr {C}(\mathrm {GL}_2(\mathbb {Z}_p),\mathbb {Q}_p)_k^{\oplus d_1}$
. Hence, we get the density statement in Lemma 6.3.8 because
$\mathscr {C}(\mathrm {GL}_2(\mathbb {Z}_p),\mathbb {Q}_p)_k^{\oplus d_1}$
. Hence, we get the density statement in Lemma 6.3.8 because
![]() $\mathrm {GL}_2(\mathbb {Z}_p)$
-algebraic vectors are dense in
$\mathrm {GL}_2(\mathbb {Z}_p)$
-algebraic vectors are dense in
![]() $\mathscr {C}(\mathrm {GL}_2(\mathbb {Z}_p),\mathbb {Q}_p)_k$
([Reference PanPan19, Proposition 3.2.9]).
$\mathscr {C}(\mathrm {GL}_2(\mathbb {Z}_p),\mathbb {Q}_p)_k$
([Reference PanPan19, Proposition 3.2.9]).
To see that
![]() $C^{\bullet }_k$
computes
$C^{\bullet }_k$
computes
![]() $\tilde {H}^{i}(K^p,\mathbb {Q}_p)_k$
, it is enough to show that
$\tilde {H}^{i}(K^p,\mathbb {Q}_p)_k$
, it is enough to show that
 $$ \begin{align*}H_{\mathrm{cont}}^j(\mathbb{Z}_p^{\times},\mathscr{C}(\mathrm{GL}_2(\mathbb{Z}_p),\mathbb{Q}_p)\otimes z^{-k})=H_{\mathrm{cont}}^j(\mathbb{Z}_p^{\times},\tilde{H}^{0}(K^p,\mathbb{Q}_p)\otimes z^{-k})=0,\,j\geq1,\end{align*} $$
$$ \begin{align*}H_{\mathrm{cont}}^j(\mathbb{Z}_p^{\times},\mathscr{C}(\mathrm{GL}_2(\mathbb{Z}_p),\mathbb{Q}_p)\otimes z^{-k})=H_{\mathrm{cont}}^j(\mathbb{Z}_p^{\times},\tilde{H}^{0}(K^p,\mathbb{Q}_p)\otimes z^{-k})=0,\,j\geq1,\end{align*} $$
where
![]() $z^{-k}=\mathbb {Q}_p$
with
$z^{-k}=\mathbb {Q}_p$
with
![]() $\mathbb {Z}_p^{\times }$
acting via (
$\mathbb {Z}_p^{\times }$
acting via (
![]() $-k$
)th power. Since everything is over a characteristic zero field, it suffices to prove this after replacing
$-k$
)th power. Since everything is over a characteristic zero field, it suffices to prove this after replacing
![]() $\mathbb {Z}_p^{\times }$
by an open subgroup. Let
$\mathbb {Z}_p^{\times }$
by an open subgroup. Let
 $H=1+p^2\mathbb {Z}_p\subset \mathbb {Z}_p^{\times }$
. Using the description of
$H=1+p^2\mathbb {Z}_p\subset \mathbb {Z}_p^{\times }$
. Using the description of
![]() $\tilde {H}^{0}(K^p,\mathbb {Q}_p)$
in [Reference EmertonEme06b, 4.2], it is easy to see that as Banach representations of H, both
$\tilde {H}^{0}(K^p,\mathbb {Q}_p)$
in [Reference EmertonEme06b, 4.2], it is easy to see that as Banach representations of H, both
![]() $\mathscr {C}(\mathrm {GL}_2(\mathbb {Z}_p),\mathbb {Q}_p)$
and
$\mathscr {C}(\mathrm {GL}_2(\mathbb {Z}_p),\mathbb {Q}_p)$
and
![]() $\tilde {H}^{0}(K^p,\mathbb {Q}_p)$
are of the form
$\tilde {H}^{0}(K^p,\mathbb {Q}_p)$
are of the form
![]() $\mathscr {C}(H\times R,\mathbb {Q}_p)$
for some profinite set R with trivial H-action. Hence, their tensor products with
$\mathscr {C}(H\times R,\mathbb {Q}_p)$
for some profinite set R with trivial H-action. Hence, their tensor products with
![]() $z^{-k}$
have no higher cohomology.
$z^{-k}$
have no higher cohomology.
Proof of Lemma 6.3.9
By Emerton’s description [Reference EmertonEme06b, 4.3.4] of the
![]() $\mathrm {GL}_2(\mathbb {Z}_p)$
-algebraic vectors in
$\mathrm {GL}_2(\mathbb {Z}_p)$
-algebraic vectors in
![]() $\tilde {H}^1(K^p,\mathbb {Q}_p)$
, it suffices to show that the Hecke action on
$\tilde {H}^1(K^p,\mathbb {Q}_p)$
, it suffices to show that the Hecke action on
 $H^1(Y_{K^p\textrm {GL}_2(\mathbb {Z}_p)}(\mathbb {C}),\mathcal {V}_{\mathcal{W}})$
is semi-simple for any irreducible algebraic representation W of
$H^1(Y_{K^p\textrm {GL}_2(\mathbb {Z}_p)}(\mathbb {C}),\mathcal {V}_{\mathcal{W}})$
is semi-simple for any irreducible algebraic representation W of
![]() $\mathrm {GL}_2$
over
$\mathrm {GL}_2$
over
![]() $\mathbb {Q}_p$
, where
$\mathbb {Q}_p$
, where
![]() $\mathcal {V}_{\mathcal{W}}$
denotes the local system corresponding to W. This result is presumably well-known for experts. We sketch a proof here. We may change the coefficient field of the local system to
$\mathcal {V}_{\mathcal{W}}$
denotes the local system corresponding to W. This result is presumably well-known for experts. We sketch a proof here. We may change the coefficient field of the local system to
![]() $\mathbb {C}$
. Then using the Shimura isomorphism, it suffices to prove the semi-simplicity of the Hecke action on the space of classical modular forms. This is clear for cusp forms because
$\mathbb {C}$
. Then using the Shimura isomorphism, it suffices to prove the semi-simplicity of the Hecke action on the space of classical modular forms. This is clear for cusp forms because
![]() $T_l,\,l\notin S$
are normal operators with respect to the Petersson inner product. The theory of Eisenstein series then provides an eigenbasis for the orthogonal complement of cusp forms. See, for example, Weisinger’s thesis [Reference WeisingerWei77, Chap. 1].
$T_l,\,l\notin S$
are normal operators with respect to the Petersson inner product. The theory of Eisenstein series then provides an eigenbasis for the orthogonal complement of cusp forms. See, for example, Weisinger’s thesis [Reference WeisingerWei77, Chap. 1].
Here is a more conceptual argument suggested to me by Matthew Emerton using polarisations. For simplicity, we assume W is the trivial local system. But the argument can be generalised for any W. Let
![]() $Y=Y_{K^p\mathrm {GL}_2(\mathbb {Z}_p)}(\mathbb {C})$
and
$Y=Y_{K^p\mathrm {GL}_2(\mathbb {Z}_p)}(\mathbb {C})$
and
![]() $X=X_{K^p\mathrm {GL}_2(\mathbb {Z}_p)}(\mathbb {C})$
. By the Poincaré duality, it is enough to consider
$X=X_{K^p\mathrm {GL}_2(\mathbb {Z}_p)}(\mathbb {C})$
. By the Poincaré duality, it is enough to consider
![]() $H^1_c(Y,\mathbb {C})$
. There is a natural exact sequence
$H^1_c(Y,\mathbb {C})$
. There is a natural exact sequence
 $$ \begin{align*}\mathbb{C}^{\oplus |\mathcal{C}|}\to H^1_c(Y,\mathbb{C})\to H^1(X,\mathbb{C})\to 0.\end{align*} $$
$$ \begin{align*}\mathbb{C}^{\oplus |\mathcal{C}|}\to H^1_c(Y,\mathbb{C})\to H^1(X,\mathbb{C})\to 0.\end{align*} $$
(Recall that
![]() $\mathcal {C}$
denotes the set of cusps in X.) The Hecke operators
$\mathcal {C}$
denotes the set of cusps in X.) The Hecke operators
![]() $T_l,l\notin S$
are normal on
$T_l,l\notin S$
are normal on
![]() $H^1(X,\mathbb {C})$
(respectively
$H^1(X,\mathbb {C})$
(respectively
![]() $\mathbb {C}^{\oplus |\mathcal {C}|}$
) with respect to the Riemann form (respectively standard Hermitian form on
$\mathbb {C}^{\oplus |\mathcal {C}|}$
) with respect to the Riemann form (respectively standard Hermitian form on
![]() $\mathbb {C}^{\oplus |\mathcal {C}|}$
). Hence, the Hecke actions of
$\mathbb {C}^{\oplus |\mathcal {C}|}$
). Hence, the Hecke actions of
![]() $\mathbb {T}(K^p)$
on both spaces are semi-simple. Now our claim follows from the Manin–Drinfeld theorem as it implies that
$\mathbb {T}(K^p)$
on both spaces are semi-simple. Now our claim follows from the Manin–Drinfeld theorem as it implies that
![]() $H^1_c(Y,\mathbb {C})\to H^1(X,\mathbb {C})$
has a natural splitting; cf. [Reference ElkikElk90].
$H^1_c(Y,\mathbb {C})\to H^1(X,\mathbb {C})$
has a natural splitting; cf. [Reference ElkikElk90].
6.4 Colmez’s Kirillov model
6.4.1. Let
![]() $\rho =\rho _{\lambda }$
be as in Corollary 6.3.6. Suppose L is a finite extension of
$\rho =\rho _{\lambda }$
be as in Corollary 6.3.6. Suppose L is a finite extension of
![]() $\mathbb {Q}_p$
containing
$\mathbb {Q}_p$
containing
![]() $\lambda (\mathbb {T}(K^p))$
. Then Corollary 6.3.6 implies that
$\lambda (\mathbb {T}(K^p))$
. Then Corollary 6.3.6 implies that
 contains an irreducible admissible Banach representation
contains an irreducible admissible Banach representation
![]() $\Pi $
of
$\Pi $
of
![]() $\mathrm {GL}_2(\mathbb {Q}_p)$
over L. To apply our previous results (Theorem 5.4.2, Theorem 6.2.2), it is crucial to know whether its locally analytic vectors
$\mathrm {GL}_2(\mathbb {Q}_p)$
over L. To apply our previous results (Theorem 5.4.2, Theorem 6.2.2), it is crucial to know whether its locally analytic vectors
![]() $\Pi ^{\mathrm {la}}$
admit nonzero
$\Pi ^{\mathrm {la}}$
admit nonzero
![]() $\mathfrak {n}$
-invariants and whether its
$\mathfrak {n}$
-invariants and whether its
![]() $N_0$
-invariants have a
$N_0$
-invariants have a
![]() $U_p$
-eigenvector. Thanks to the beautiful work of Colmez, both questions have affirmative answers by his Kirillov model [Reference ColmezCol10, Chap. VI]. We first give a brief review of his work. A nice summary can be found in Subsections 7.3 and 7.4 of [Reference Dospinescu and Le BrasDLB17]. I would like to thank Matthew Emerton for sharing his unpublished notes [Reference Emerton, Pollack and WestonEPW] with Robert Pollack and Tom Weston on this subject.
$U_p$
-eigenvector. Thanks to the beautiful work of Colmez, both questions have affirmative answers by his Kirillov model [Reference ColmezCol10, Chap. VI]. We first give a brief review of his work. A nice summary can be found in Subsections 7.3 and 7.4 of [Reference Dospinescu and Le BrasDLB17]. I would like to thank Matthew Emerton for sharing his unpublished notes [Reference Emerton, Pollack and WestonEPW] with Robert Pollack and Tom Weston on this subject.
6.4.2. Let E be a finite extension of
![]() $\mathbb {Q}_p$
and V a 2-dimensional representation of
$\mathbb {Q}_p$
and V a 2-dimensional representation of
![]() $G_{\mathbb {Q}_p}$
over E. By Fontaine’s work [Reference FontaineFon04], we can study
$G_{\mathbb {Q}_p}$
over E. By Fontaine’s work [Reference FontaineFon04], we can study
![]() $V\otimes _{\mathbb {Q}_p}B_{\mathrm {dR}}^+$
by Sen’s method. As a result, we obtain a free
$V\otimes _{\mathbb {Q}_p}B_{\mathrm {dR}}^+$
by Sen’s method. As a result, we obtain a free
![]() $E[[t]]\otimes _{\mathbb {Q}_p}\mathbb {Q}_p(\mu _{p^\infty })$
-module
$E[[t]]\otimes _{\mathbb {Q}_p}\mathbb {Q}_p(\mu _{p^\infty })$
-module
![]() $D^+_{\mathrm {dif}}(V)$
of rank
$D^+_{\mathrm {dif}}(V)$
of rank
![]() $2$
equipped with a semi-linear action of
$2$
equipped with a semi-linear action of
![]() $\Gamma =\operatorname {\mathrm {Gal}}(\mathbb {Q}_p(\mu _{p^\infty })/\mathbb {Q}_p)$
. Let
$\Gamma =\operatorname {\mathrm {Gal}}(\mathbb {Q}_p(\mu _{p^\infty })/\mathbb {Q}_p)$
. Let
 $D_{\mathrm {dif}}(V):=D^+_{\mathrm {dif}}(V)[\frac {1}{t}]$
and
$D_{\mathrm {dif}}(V):=D^+_{\mathrm {dif}}(V)[\frac {1}{t}]$
and
a torsion
![]() $\mathbb {Q}_p(\mu _{p^\infty })[t]$
-module. We denote by
$\mathbb {Q}_p(\mu _{p^\infty })[t]$
-module. We denote by
 $\mathscr {C}_c(\mathbb {Q}_p^{\times },D^-_{\mathrm {dif}}(V))^{\Gamma }$
the space of functions
$\mathscr {C}_c(\mathbb {Q}_p^{\times },D^-_{\mathrm {dif}}(V))^{\Gamma }$
the space of functions
![]() $\phi :\mathbb {Q}_p^{\times }\to D^-_{\mathrm {dif}}(V)$
with compact support satisfying
$\phi :\mathbb {Q}_p^{\times }\to D^-_{\mathrm {dif}}(V)$
with compact support satisfying
 $$ \begin{align*}\phi(ax)=\sigma_a(\phi(x)),a\in\mathbb{Z}_p^{\times},\,x\in\mathbb{Q}_p^{\times},\end{align*} $$
$$ \begin{align*}\phi(ax)=\sigma_a(\phi(x)),a\in\mathbb{Z}_p^{\times},\,x\in\mathbb{Q}_p^{\times},\end{align*} $$
where
![]() $\sigma _a\in \Gamma $
is inverse image of a under
$\sigma _a\in \Gamma $
is inverse image of a under
 $\varepsilon _p:\Gamma \xrightarrow {\sim }\mathbb {Z}_p^{\times }$
. In particular,
$\varepsilon _p:\Gamma \xrightarrow {\sim }\mathbb {Z}_p^{\times }$
. In particular,
![]() $\phi $
is completely determined by
$\phi $
is completely determined by
![]() $\{\phi (p^n)\}_{n\in \mathbb {Z}}$
. Let
$\{\phi (p^n)\}_{n\in \mathbb {Z}}$
. Let
 $P=\begin {pmatrix} \mathbb {Q}_p^{\times } & \mathbb {Q}_p \\ 0 & 1\end {pmatrix}$
, the mirabolic subgroup of
$P=\begin {pmatrix} \mathbb {Q}_p^{\times } & \mathbb {Q}_p \\ 0 & 1\end {pmatrix}$
, the mirabolic subgroup of
![]() $\mathrm {GL}_2(\mathbb {Q}_p)$
. One can define an action of P on
$\mathrm {GL}_2(\mathbb {Q}_p)$
. One can define an action of P on
 $\mathscr {C}_c(\mathbb {Q}_p^{\times },D^-_{\mathrm {dif}}(V))^{\Gamma }$
by the formula
$\mathscr {C}_c(\mathbb {Q}_p^{\times },D^-_{\mathrm {dif}}(V))^{\Gamma }$
by the formula
 $$ \begin{align*}(\begin{pmatrix} a & b \\ 0 & 1\end{pmatrix}\phi)(x)=\varepsilon'(bx)e^{tbx}\phi(ax),\end{align*} $$
$$ \begin{align*}(\begin{pmatrix} a & b \\ 0 & 1\end{pmatrix}\phi)(x)=\varepsilon'(bx)e^{tbx}\phi(ax),\end{align*} $$
where
![]() $\varepsilon ':\mathbb {Q}_p\to \mu _{p^\infty }$
is an additive character with kernel
$\varepsilon ':\mathbb {Q}_p\to \mu _{p^\infty }$
is an additive character with kernel
![]() $\mathbb {Z}_p$
and
$\mathbb {Z}_p$
and
![]() $e^{tbx}$
is understood as
$e^{tbx}$
is understood as
 $\sum _{n\geq 0}\frac {(bx)^n}{n!}t^n$
. (One can view
$\sum _{n\geq 0}\frac {(bx)^n}{n!}t^n$
. (One can view
![]() $\mathbb {Q}_p\to (\mathbb {Q}_p[[t]]\otimes _{\mathbb {Q}_p}\mathbb {Q}_p(\mu _{p^\infty }))^{\times },\,x\mapsto \varepsilon '(x)e^{tx}$
as an additive character.) This is Colmez’s Kirillov model.
$\mathbb {Q}_p\to (\mathbb {Q}_p[[t]]\otimes _{\mathbb {Q}_p}\mathbb {Q}_p(\mu _{p^\infty }))^{\times },\,x\mapsto \varepsilon '(x)e^{tx}$
as an additive character.) This is Colmez’s Kirillov model.
Now we assume
-
• V is absolutely irreducible.
We denote by
![]() $\Pi (V)_E$
the irreducible unitary E-Banach representation of
$\Pi (V)_E$
the irreducible unitary E-Banach representation of
![]() $\mathrm {GL}_2(\mathbb {Q}_p)$
associated to V via the p-adic local Langlands correspondence ([Reference Colmez, Dospinescu and PaškūnasCDP14, Theorem 1.1]) and by
$\mathrm {GL}_2(\mathbb {Q}_p)$
associated to V via the p-adic local Langlands correspondence ([Reference Colmez, Dospinescu and PaškūnasCDP14, Theorem 1.1]) and by
 $\Pi (V)_E^{\mathrm {la}}$
its locally analytic vectors.
$\Pi (V)_E^{\mathrm {la}}$
its locally analytic vectors.
Theorem 6.4.3. There is a P-equivariant embedding
 $\mathscr {C}_c(\mathbb {Q}_p^{\times },D^-_{\mathrm {dif}}(V))^{\Gamma }\to \Pi (V)_E^{\mathrm {la}}$
.
$\mathscr {C}_c(\mathbb {Q}_p^{\times },D^-_{\mathrm {dif}}(V))^{\Gamma }\to \Pi (V)_E^{\mathrm {la}}$
.
Proof. See Proposition 7.6 of [Reference Dospinescu and Le BrasDLB17].
The following corollary and remark were first pointed out to me by Matthew Emerton.
Corollary 6.4.4.
 $\Pi (V)_E^{\mathrm {la},N_0}\neq 0$
and has a nonzero vector annihilated by
$\Pi (V)_E^{\mathrm {la},N_0}\neq 0$
and has a nonzero vector annihilated by
![]() $U_p$
.
$U_p$
.
Proof. This is a standard formal consequence of the Kirillov model. More precisely, let
![]() $v\in D^-_{\mathrm {dif}}(V)$
be a nonzero element annihilated by t. Consider
$v\in D^-_{\mathrm {dif}}(V)$
be a nonzero element annihilated by t. Consider
 $\phi \in \mathscr {C}_c(\mathbb {Q}_p^{\times },D^-_{\mathrm {dif}}(V))^{\Gamma }$
defined by
$\phi \in \mathscr {C}_c(\mathbb {Q}_p^{\times },D^-_{\mathrm {dif}}(V))^{\Gamma }$
defined by
![]() $\phi (1)=v$
and
$\phi (1)=v$
and
![]() $\phi (x)=0,x\notin \mathbb {Z}_p^{\times }$
. Clearly,
$\phi (x)=0,x\notin \mathbb {Z}_p^{\times }$
. Clearly,
![]() $\phi $
is fixed by
$\phi $
is fixed by
 $\begin {pmatrix} 1 & 1 \\ 0 & 1 \end {pmatrix}$
. Moreover,
$\begin {pmatrix} 1 & 1 \\ 0 & 1 \end {pmatrix}$
. Moreover,
 $$ \begin{align*}(U_p\cdot \phi)(x)=\sum_{i=0}^{p-1}(\begin{pmatrix} p & i \\ 0 & 1\end{pmatrix}\phi)(x)=\sum_{i=0}^{p-1}\varepsilon'(ix)\phi(px).\end{align*} $$
$$ \begin{align*}(U_p\cdot \phi)(x)=\sum_{i=0}^{p-1}(\begin{pmatrix} p & i \\ 0 & 1\end{pmatrix}\phi)(x)=\sum_{i=0}^{p-1}\varepsilon'(ix)\phi(px).\end{align*} $$
If
![]() $px\notin \mathbb {Z}_p^{\times }$
, this is zero for trivial reason. If
$px\notin \mathbb {Z}_p^{\times }$
, this is zero for trivial reason. If
 $x=\frac {1}{p}$
, this is essentially the sum over all pth roots of unity, which is again zero. Hence,
$x=\frac {1}{p}$
, this is essentially the sum over all pth roots of unity, which is again zero. Hence,
![]() $\phi $
is annihilated by
$\phi $
is annihilated by
![]() $U_p$
.
$U_p$
.
Remark 6.4.5. It is easy to see that all the vectors in
 $\mathscr {C}_c(\mathbb {Q}_p^{\times },D^-_{\mathrm {dif}}(V))^{\Gamma ,N_0}$
annihilated by
$\mathscr {C}_c(\mathbb {Q}_p^{\times },D^-_{\mathrm {dif}}(V))^{\Gamma ,N_0}$
annihilated by
![]() $U_p$
(which we denote by
$U_p$
(which we denote by
 $\mathscr {C}_c(\mathbb {Q}_p^{\times },D^-_{\mathrm {dif}}(V))^{\Gamma ,N_0,U_p=0}$
) are of this form; that is,
$\mathscr {C}_c(\mathbb {Q}_p^{\times },D^-_{\mathrm {dif}}(V))^{\Gamma ,N_0,U_p=0}$
) are of this form; that is,
 $$ \begin{align*}\mathscr{C}_c(\mathbb{Q}_p^{\times},D^-_{\mathrm{dif}}(V))^{\Gamma,N_0,U_p=0}=D^+_{\mathrm{dif}}(V)\cdot\frac{1}{t}/D^+_{\mathrm{dif}}(V)=D_{\mathrm{Sen}}(V(-1)).\end{align*} $$
$$ \begin{align*}\mathscr{C}_c(\mathbb{Q}_p^{\times},D^-_{\mathrm{dif}}(V))^{\Gamma,N_0,U_p=0}=D^+_{\mathrm{dif}}(V)\cdot\frac{1}{t}/D^+_{\mathrm{dif}}(V)=D_{\mathrm{Sen}}(V(-1)).\end{align*} $$
Here
![]() $D_{\mathrm {Sen}}(V(-1))$
is a free
$D_{\mathrm {Sen}}(V(-1))$
is a free
![]() $E\otimes _{\mathbb {Q}_p}\mathbb {Q}_p(\mu _{p^\infty })$
-module of rank
$E\otimes _{\mathbb {Q}_p}\mathbb {Q}_p(\mu _{p^\infty })$
-module of rank
![]() $2$
equipped with a semi-linear action of
$2$
equipped with a semi-linear action of
![]() $\Gamma $
associated to
$\Gamma $
associated to
![]() $V(-1)$
in Sen’s theory.
$V(-1)$
in Sen’s theory.
In Colmez’s work, it is also possible to describe the image of
 $\mathscr {C}_c(\mathbb {Q}_p^{\times },D^-_{\mathrm {dif}}(V))^{\Gamma }$
inside
$\mathscr {C}_c(\mathbb {Q}_p^{\times },D^-_{\mathrm {dif}}(V))^{\Gamma }$
inside
 $\Pi (V)_E^{\mathrm {la}}$
. In fact, one can show that this image contains
$\Pi (V)_E^{\mathrm {la}}$
. In fact, one can show that this image contains
 $(\Pi (V)_E^{\mathrm {la}})^{N_0,U_p=0}$
. Hence,
$(\Pi (V)_E^{\mathrm {la}})^{N_0,U_p=0}$
. Hence,
 $$ \begin{align*}\Pi(V)_E^{\mathrm{la},N_0,U_p=0}\cong D_{\mathrm{Sen}}(V(-1)),\end{align*} $$
$$ \begin{align*}\Pi(V)_E^{\mathrm{la},N_0,U_p=0}\cong D_{\mathrm{Sen}}(V(-1)),\end{align*} $$
which identifies the action of
 $\begin {pmatrix} \mathbb {Z}_p^{\times } & 0 \\ 0 & 1 \end {pmatrix}$
on the left-hand side with the action of
$\begin {pmatrix} \mathbb {Z}_p^{\times } & 0 \\ 0 & 1 \end {pmatrix}$
on the left-hand side with the action of
![]() $\Gamma $
on the right-hand side. Therefore, let
$\Gamma $
on the right-hand side. Therefore, let
![]() $a,b$
be the Hodge–Tate–Sen weights of V. Since
$a,b$
be the Hodge–Tate–Sen weights of V. Since
![]() $\Pi (V)$
has central character
$\Pi (V)$
has central character
 $\det (V)\varepsilon _p^{-1}$
([Reference Colmez, Dospinescu and PaškūnasCDP14, Corollary 1.2]), we conclude that both
$\det (V)\varepsilon _p^{-1}$
([Reference Colmez, Dospinescu and PaškūnasCDP14, Corollary 1.2]), we conclude that both
 $$ \begin{align*}(\Pi(V)_E^{\mathrm{la}})_{(-a-1,-b)},(\Pi(V)_E^{\mathrm{la}})_{(-b-1,-a)}\end{align*} $$
$$ \begin{align*}(\Pi(V)_E^{\mathrm{la}})_{(-a-1,-b)},(\Pi(V)_E^{\mathrm{la}})_{(-b-1,-a)}\end{align*} $$
are nonzero. Moreover, let
 $P_0=\begin {pmatrix} \mathbb {Z}_p^{\times } & \mathbb {Z}_p \\ 0 & 1 \end {pmatrix}$
. We have
$P_0=\begin {pmatrix} \mathbb {Z}_p^{\times } & \mathbb {Z}_p \\ 0 & 1 \end {pmatrix}$
. We have
 $$ \begin{align*}\dim_E \Pi(V)_E^{\mathrm{la},P_0,U_p=0}=\dim_E (V(-1)\otimes_{\mathbb{Q}_p}C)^{G_{\mathbb{Q}_p}},\end{align*} $$
$$ \begin{align*}\dim_E \Pi(V)_E^{\mathrm{la},P_0,U_p=0}=\dim_E (V(-1)\otimes_{\mathbb{Q}_p}C)^{G_{\mathbb{Q}_p}},\end{align*} $$
which gives a representation-theoretic way to determine whether
![]() $V(-1)$
is Hodge–Tate of weight
$V(-1)$
is Hodge–Tate of weight
![]() $0,0$
or not. We will use this to give another proof of Corollary 6.4.9.
$0,0$
or not. We will use this to give another proof of Corollary 6.4.9.
Corollary 6.4.6. Suppose
![]() $\Pi $
is an irreducible admissible unitary Banach representation of
$\Pi $
is an irreducible admissible unitary Banach representation of
![]() $\mathrm {GL}_2(\mathbb {Q}_p)$
over some finite extension of
$\mathrm {GL}_2(\mathbb {Q}_p)$
over some finite extension of
![]() $\mathbb {Q}_p$
. Then
$\mathbb {Q}_p$
. Then
![]() $\Pi ^{\mathrm {la},N_0}\neq 0$
and has a nonzero
$\Pi ^{\mathrm {la},N_0}\neq 0$
and has a nonzero
![]() $U_p$
-eigenvector.
$U_p$
-eigenvector.
Proof. We may enlarge the field of coefficients E and assume that
![]() $\Pi $
is absolutely irreducible by [Reference Dospinescu and SchraenDS13, Theorem 1.1]. If
$\Pi $
is absolutely irreducible by [Reference Dospinescu and SchraenDS13, Theorem 1.1]. If
![]() $\Pi $
is nonordinary, then this follows Corollary 6.4.4 as
$\Pi $
is nonordinary, then this follows Corollary 6.4.4 as
![]() $\Pi =\Pi (V)_E$
for some absolutely irreducible Galois representation V by [Reference Colmez, Dospinescu and PaškūnasCDP14, Theorem 1.1]. If
$\Pi =\Pi (V)_E$
for some absolutely irreducible Galois representation V by [Reference Colmez, Dospinescu and PaškūnasCDP14, Theorem 1.1]. If
![]() $\Pi $
is ordinary – that is, a subquotient of a parabolic induction of a unitary character – then up to twist by a character
$\Pi $
is ordinary – that is, a subquotient of a parabolic induction of a unitary character – then up to twist by a character
![]() $\eta \circ \det $
, the representation
$\eta \circ \det $
, the representation
![]() $\Pi $
is either trivial representation
$\Pi $
is either trivial representation
![]() $\mathbf {1}$
, unitary Steinberg representation
$\mathbf {1}$
, unitary Steinberg representation
![]() $\widehat {\mathrm {St}}$
or
$\widehat {\mathrm {St}}$
or
![]() $\Pi $
is a unitary parabolic induction of a unitary character. Recall that
$\Pi $
is a unitary parabolic induction of a unitary character. Recall that
 $\widehat {\mathrm {St}}=(\mathrm {Ind}^{\mathrm {GL}_2(\mathbb {Q}_p)}_B\mathbf {1})/\mathbf {1}$
, the universal unitary completion of the usual Steinberg representation. In all of these cases, it is easy to check that
$\widehat {\mathrm {St}}=(\mathrm {Ind}^{\mathrm {GL}_2(\mathbb {Q}_p)}_B\mathbf {1})/\mathbf {1}$
, the universal unitary completion of the usual Steinberg representation. In all of these cases, it is easy to check that
![]() $\Pi ^{\mathrm {la},N_0}\neq 0$
and has a nonzero
$\Pi ^{\mathrm {la},N_0}\neq 0$
and has a nonzero
![]() $U_p$
-eigenvector.
$U_p$
-eigenvector.
We obtain the following classicality result by combining Corollary 6.4.6, Corollary 6.3.6 and Theorem 6.2.2.
Theorem 6.4.7. Suppose
![]() $\rho =\rho _{\lambda }$
is pro-modular and irreducible. Assume
$\rho =\rho _{\lambda }$
is pro-modular and irreducible. Assume
-
•
 $\rho |_{G_{\mathbb {Q}_p}}$
is Hodge–Tate of weight
$\rho |_{G_{\mathbb {Q}_p}}$
is Hodge–Tate of weight
 $0,0$
.
$0,0$
.
Then
![]() $\rho $
is classical; that is,
$\rho $
is classical; that is,
![]() $M_1(K^p)[\mathfrak {p}_{\lambda }]\neq 0$
for some tame level
$M_1(K^p)[\mathfrak {p}_{\lambda }]\neq 0$
for some tame level
![]() $K^p$
.
$K^p$
.
Proof. Suppose
![]() $\rho $
is pro-modular for some tame level
$\rho $
is pro-modular for some tame level
![]() $K^p$
. We have
$K^p$
. We have

by Corollary 6.3.6. Recall that
![]() $t\in \tilde {H}^0(K^p,\mathbb {Z}_p)$
is an invertible function, so
$t\in \tilde {H}^0(K^p,\mathbb {Z}_p)$
is an invertible function, so

is understood as a subspace of

. Here
![]() $\lambda \cdot t$
was defined in proof of Theorem 6.2.2. Corollary 6.4.6 then implies that
$\lambda \cdot t$
was defined in proof of Theorem 6.2.2. Corollary 6.4.6 then implies that
![]() $\tilde {H}^1(K^p,C)^{\mathrm {la}}[\mathfrak {p}_{\lambda \cdot t}]^{N_0,U_p=\alpha }\neq 0$
for some
$\tilde {H}^1(K^p,C)^{\mathrm {la}}[\mathfrak {p}_{\lambda \cdot t}]^{N_0,U_p=\alpha }\neq 0$
for some

. By our result on the infinitesimal character (Proposition 6.1.5),
![]() $(h+1)^2=0$
on this space. Hence, the weight-
$(h+1)^2=0$
on this space. Hence, the weight-
![]() $(0,1)$
subspace
$(0,1)$
subspace
 $$ \begin{align*}\tilde{H}^1(K^p,C)^{\mathrm{la}}_{(0,1)}[\mathfrak{p}_{\lambda\cdot t}]^{N_0,U_p=\alpha}\neq 0.\end{align*} $$
$$ \begin{align*}\tilde{H}^1(K^p,C)^{\mathrm{la}}_{(0,1)}[\mathfrak{p}_{\lambda\cdot t}]^{N_0,U_p=\alpha}\neq 0.\end{align*} $$
Now assume
![]() $\rho $
is not classical. As in the proof of Theorem 6.2.2, we have
$\rho $
is not classical. As in the proof of Theorem 6.2.2, we have
 $$ \begin{align*}\tilde{H}^1(K^p,C)^{\mathrm{la}}_{(0,1)}[\mathfrak{p}_{\lambda\cdot t}]=M^{\dagger}_{1}(K^p)[{\mathfrak{p}_{\lambda}}]\cdot e_1^{-1}t.\end{align*} $$
$$ \begin{align*}\tilde{H}^1(K^p,C)^{\mathrm{la}}_{(0,1)}[\mathfrak{p}_{\lambda\cdot t}]=M^{\dagger}_{1}(K^p)[{\mathfrak{p}_{\lambda}}]\cdot e_1^{-1}t.\end{align*} $$
However, this means that
 $M^{\dagger }_{1}(K^p)[{\mathfrak {p}_{\lambda }}]^{N_0,U_p=p\alpha }\neq 0$
, which contradicts Theorem 6.2.2. Hence,
$M^{\dagger }_{1}(K^p)[{\mathfrak {p}_{\lambda }}]^{N_0,U_p=p\alpha }\neq 0$
, which contradicts Theorem 6.2.2. Hence,
![]() $\rho $
has to be classical.
$\rho $
has to be classical.
We quote the following result ([Reference EmertonEme11, Theorem 1.2.3], which is based on previous work of Böckle, Diamond–Flach–Guo, Khare–Wintenberger, Kisin) on promodularity of a Galois representation. For simplicity, we exclude the case
 $\bar \rho |_{G_{\mathbb {Q}_p}}\cong \eta \otimes \begin {pmatrix} \omega & * \\ 0 & 1 \end {pmatrix}$
, a nonsplit extension. As a corollary, we give a new proof of the Fontaine–Mazur conjecture in the irregular case under conditions below.
$\bar \rho |_{G_{\mathbb {Q}_p}}\cong \eta \otimes \begin {pmatrix} \omega & * \\ 0 & 1 \end {pmatrix}$
, a nonsplit extension. As a corollary, we give a new proof of the Fontaine–Mazur conjecture in the irregular case under conditions below.
Theorem 6.4.8. Let
![]() $p>2$
be a prime number and
$p>2$
be a prime number and
 be a continuous 2-dimensional irreducible odd representation which is unramified outside of finitely many primes. Assume
be a continuous 2-dimensional irreducible odd representation which is unramified outside of finitely many primes. Assume
-
(1)
 $\bar \rho |_{G_{\mathbb {Q}(\mu _p)}}$
is irreducible;
$\bar \rho |_{G_{\mathbb {Q}(\mu _p)}}$
is irreducible; -
(2)
 $(\bar \rho |_{G_{\mathbb {Q}_p}})^{ss}$
is either irreducible or of the form
$(\bar \rho |_{G_{\mathbb {Q}_p}})^{ss}$
is either irreducible or of the form
 $\eta _1\oplus \eta _2$
for some characters
$\eta _1\oplus \eta _2$
for some characters
 $\eta _1,\eta _2$
satisfying
$\eta _1,\eta _2$
satisfying
 $\eta _1/\eta _2\neq 1,\omega ^{\pm 1}$
.
$\eta _1/\eta _2\neq 1,\omega ^{\pm 1}$
.
Then
![]() $\rho $
is pro-modular.
$\rho $
is pro-modular.
Corollary 6.4.9. Let
![]() $\rho $
be as in Theorem 6.4.8. If
$\rho $
be as in Theorem 6.4.8. If
![]() $\rho $
is Hodge–Tate of weight
$\rho $
is Hodge–Tate of weight
![]() $0,0$
, then
$0,0$
, then
![]() $\rho $
comes from a cuspidal eigenform of weight 1.
$\rho $
comes from a cuspidal eigenform of weight 1.
Proof. A combination of the previous two results.
Remark 6.4.10. The assumptions in this result could possibly be removed in the following way. Let
![]() $\rho $
be a continuous 2-dimensional irreducible odd representation
$\rho $
be a continuous 2-dimensional irreducible odd representation
 which is unramified outside of finitely many primes. In [Reference PanPan19], it is proved that
which is unramified outside of finitely many primes. In [Reference PanPan19], it is proved that
![]() $\rho |_{G_F}$
is irreducible and pro-modular for a solvable totally real field extension
$\rho |_{G_F}$
is irreducible and pro-modular for a solvable totally real field extension
![]() $F/\mathbb {Q}$
in which p completely splits, under the assumption
$F/\mathbb {Q}$
in which p completely splits, under the assumption
-
•
 $p>2$
;
$p>2$
; -
• If
 $p=3$
, then
$p=3$
, then
 $(\bar \rho |_{G_{\mathbb {Q}_p}})^{ss}$
is not of the form
$(\bar \rho |_{G_{\mathbb {Q}_p}})^{ss}$
is not of the form
 $\eta \oplus \eta \omega $
.
$\eta \oplus \eta \omega $
.
Hence, one can prove Corollary 6.4.9 under these assumptions, if Theorem 6.4.7 can be extended to the case of Hilbert modular variety over a totally real field F in which p completely splits. It seems (at least to me) that it is reasonable to expect such a generalisation.
We can also determine the possible systems of Hecke eigenvalues appearing in spaces of overconvergent modular forms.
Theorem 6.4.11. Suppose
![]() $\rho =\rho _{\lambda }$
is irreducible and pro-modular for some tame level
$\rho =\rho _{\lambda }$
is irreducible and pro-modular for some tame level
![]() $K^p$
. Let
$K^p$
. Let
![]() $a,b$
be the Hodge–Tate–Sen weights of
$a,b$
be the Hodge–Tate–Sen weights of
 $\rho |_{G_{\mathbb {Q}_p}}$
.
$\rho |_{G_{\mathbb {Q}_p}}$
.
-
(1) If
 $M^{\dagger }_{(n_1,n_2)}(K^p)[\mathfrak {p}_{\lambda }]\neq 0$
, then
$M^{\dagger }_{(n_1,n_2)}(K^p)[\mathfrak {p}_{\lambda }]\neq 0$
, then
 $(n_1,n_2)=(-a,-b-1)$
or
$(n_1,n_2)=(-a,-b-1)$
or
 $(-b,-a-1)$
. In particular, if
$(-b,-a-1)$
. In particular, if
 $M^{\dagger }_k(K^p)[\mathfrak {p}_{\lambda }]\neq 0$
for some
$M^{\dagger }_k(K^p)[\mathfrak {p}_{\lambda }]\neq 0$
for some
 $k\in \mathbb {Z}$
, then
$k\in \mathbb {Z}$
, then
 $\{a,b\}=\{0,k-1\}$
.
$\{a,b\}=\{0,k-1\}$
. -
(2) Conversely, if
 $\rho |_{G_{\mathbb {Q}_p}}$
is irreducible, then
$\rho |_{G_{\mathbb {Q}_p}}$
is irreducible, then
 $M^{\dagger }_{(n_1,n_2)}(K^p)[\mathfrak {p}_{\lambda }]\neq 0$
for
$M^{\dagger }_{(n_1,n_2)}(K^p)[\mathfrak {p}_{\lambda }]\neq 0$
for
 $(n_1,n_2)=(-a,-b-1)$
and
$(n_1,n_2)=(-a,-b-1)$
and
 $(-b,-a-1)$
.
$(-b,-a-1)$
.
Proof. To see the first part, if
 $M^{\dagger }_{(n_1,n_2)}(K^p)[\mathfrak {p}_{\lambda }]\neq 0$
and
$M^{\dagger }_{(n_1,n_2)}(K^p)[\mathfrak {p}_{\lambda }]\neq 0$
and
![]() $n_1\neq n_2+1$
, then by Theorem 5.4.2, we have
$n_1\neq n_2+1$
, then by Theorem 5.4.2, we have
 $\tilde {H}^1(K^p,C)^{\mathrm {la}}_{(n_1-1,n_2+1)}[\mathfrak {p}_{\lambda }]\neq 0$
. Hence, Proposition 6.1.5 implies that
$\tilde {H}^1(K^p,C)^{\mathrm {la}}_{(n_1-1,n_2+1)}[\mathfrak {p}_{\lambda }]\neq 0$
. Hence, Proposition 6.1.5 implies that
![]() $\rho _{\lambda }$
has Hodge–Tate–Sen weights
$\rho _{\lambda }$
has Hodge–Tate–Sen weights
![]() $-n_1,-1-n_2$
. The case
$-n_1,-1-n_2$
. The case
![]() $n_1=n_2+1$
can be proved in a similar way. We omit the details here.
$n_1=n_2+1$
can be proved in a similar way. We omit the details here.
For the second part, if
![]() $a=b=0$
, the proof of Theorem 6.4.7 shows that
$a=b=0$
, the proof of Theorem 6.4.7 shows that
 $M^{\dagger }_{(0,-1)}(K^p)[\mathfrak {p}_{\lambda }]\neq 0$
. For the general case
$M^{\dagger }_{(0,-1)}(K^p)[\mathfrak {p}_{\lambda }]\neq 0$
. For the general case
![]() $a=b$
, one can twist by some
$a=b$
, one can twist by some
![]() $t^a$
as in Section 5.3.9 to reduce to the case
$t^a$
as in Section 5.3.9 to reduce to the case
![]() $a=0$
.
$a=0$
.
Now assume
![]() $a\neq b$
. By Theorem 6.3.6 and Remark 6.4.5, both
$a\neq b$
. By Theorem 6.3.6 and Remark 6.4.5, both
 $$ \begin{align*}\tilde{H}^1(K^p,C)^{\mathrm{la}}_{(-a-1,-b)}[\mathfrak{p}_{\lambda}]\;\mbox{and}\;\tilde{H}^1(K^p,C)^{\mathrm{la}}_{(-b-1,-a)}[\mathfrak{p}_{\lambda}]\end{align*} $$
$$ \begin{align*}\tilde{H}^1(K^p,C)^{\mathrm{la}}_{(-a-1,-b)}[\mathfrak{p}_{\lambda}]\;\mbox{and}\;\tilde{H}^1(K^p,C)^{\mathrm{la}}_{(-b-1,-a)}[\mathfrak{p}_{\lambda}]\end{align*} $$
are nonzero. By symmetry, it is enough to consider
 $\tilde {H}^1(K^p,C)^{\mathrm {la}}_{(-a-1,-b)}[\mathfrak {p}_{\lambda }]$
. Theorem 5.4.2 provides a natural decomposition of this space according to the Hodge–Tate–Sen weights. Since
$\tilde {H}^1(K^p,C)^{\mathrm {la}}_{(-a-1,-b)}[\mathfrak {p}_{\lambda }]$
. Theorem 5.4.2 provides a natural decomposition of this space according to the Hodge–Tate–Sen weights. Since
 is
is
![]() $\rho _{\lambda }(-1)$
-isotypic, the Hodge–Tate–Sen weight-
$\rho _{\lambda }(-1)$
-isotypic, the Hodge–Tate–Sen weight-
![]() $(b+1)$
component of
$(b+1)$
component of
 $\tilde {H}^1(K^p,C)^{\mathrm {la}}_{(-a-1,-b)}[\mathfrak {p}_{\lambda }]$
is nonzero. Hence,
$\tilde {H}^1(K^p,C)^{\mathrm {la}}_{(-a-1,-b)}[\mathfrak {p}_{\lambda }]$
is nonzero. Hence,
 $M^{\dagger }_{(-a,-b-1)}(K^p)[\mathfrak {p}_{\lambda }]\neq 0$
if
$M^{\dagger }_{(-a,-b-1)}(K^p)[\mathfrak {p}_{\lambda }]\neq 0$
if
![]() $-a\neq -b-1$
by Theorem 5.4.2 (i.e.,
$-a\neq -b-1$
by Theorem 5.4.2 (i.e.,
![]() $k\neq 2$
). If
$k\neq 2$
). If
![]() $-a=-b-1$
, then we claim we still have
$-a=-b-1$
, then we claim we still have
 $M_{(-a-1,-b),w}[\mathfrak {p}_{\lambda }]\cong M^{\dagger }_{(-a,-b-1)}(K^p)[\mathfrak {p}_{\lambda }]$
(as
$M_{(-a-1,-b),w}[\mathfrak {p}_{\lambda }]\cong M^{\dagger }_{(-a,-b-1)}(K^p)[\mathfrak {p}_{\lambda }]$
(as
![]() $\mathbb {T}(K^p)$
-modules). This is because the difference between
$\mathbb {T}(K^p)$
-modules). This is because the difference between
![]() $M_{(-a-1,-b),w}$
and
$M_{(-a-1,-b),w}$
and
 $M^{\dagger }_{(-a,-b-1)}(K^p)$
is essentially
$M^{\dagger }_{(-a,-b-1)}(K^p)$
is essentially
![]() $M_0(K^p)\cdot t^{-a}$
, which can be decomposed as
$M_0(K^p)\cdot t^{-a}$
, which can be decomposed as
 $$ \begin{align*}\bigoplus_{\mathfrak{q}\in\mathrm{Max}(\mathbb{T}(K^p)[\frac{1}{p}])} M_0(K^p)\cdot t^{-a}[\mathfrak{q}]\end{align*} $$
$$ \begin{align*}\bigoplus_{\mathfrak{q}\in\mathrm{Max}(\mathbb{T}(K^p)[\frac{1}{p}])} M_0(K^p)\cdot t^{-a}[\mathfrak{q}]\end{align*} $$
as a Hecke-module, and
![]() $M_0(K^p)\cdot t^{-a}[\mathfrak {p}_{\lambda }]=0$
since
$M_0(K^p)\cdot t^{-a}[\mathfrak {p}_{\lambda }]=0$
since
![]() $M_0(K^p)\cdot t^{-a}[\mathfrak {p}_{\lambda '}]\neq 0$
only when
$M_0(K^p)\cdot t^{-a}[\mathfrak {p}_{\lambda '}]\neq 0$
only when
![]() $\rho _{\lambda '}$
is reducible. This proves the second part.
$\rho _{\lambda '}$
is reducible. This proves the second part.
Remark 6.4.12. We sketch another proof of Theorem 6.4.7 in the nonordinary case (i.e.,
 $\rho |_{G_{\mathbb {Q}_p}}$
is irreducible) without using our work on the Sen operator (Theorem 5.1.11). Suppose
$\rho |_{G_{\mathbb {Q}_p}}$
is irreducible) without using our work on the Sen operator (Theorem 5.1.11). Suppose
![]() $\rho $
is not classical. Then as in the proof of Theorem 6.2.2, we have the following exact sequence by Theorem 5.4.6:
$\rho $
is not classical. Then as in the proof of Theorem 6.2.2, we have the following exact sequence by Theorem 5.4.6:
 $$ \begin{align*}0\to M^{\dagger}_1(K^p)[\mathfrak{p}_{\lambda}]\cdot e_1^{-1}t\to \tilde{H}^1(K^p,C)_{(0,1)}^{\mathrm{la}}[\mathfrak{p}_{\lambda\cdot t}]\to M^{\dagger}_1(K^p)[\mathfrak{p}_{\lambda}]\cdot e_1^{-1}t.\end{align*} $$
$$ \begin{align*}0\to M^{\dagger}_1(K^p)[\mathfrak{p}_{\lambda}]\cdot e_1^{-1}t\to \tilde{H}^1(K^p,C)_{(0,1)}^{\mathrm{la}}[\mathfrak{p}_{\lambda\cdot t}]\to M^{\dagger}_1(K^p)[\mathfrak{p}_{\lambda}]\cdot e_1^{-1}t.\end{align*} $$
For simplicity, let us assume
![]() $K^p=\prod _{l\neq p}\mathrm {GL}_2(\mathbb {Z}_l)$
. In general, we can use Hecke operators at ramified places as in Lemma 6.2.6. Now the key point is that
$K^p=\prod _{l\neq p}\mathrm {GL}_2(\mathbb {Z}_l)$
. In general, we can use Hecke operators at ramified places as in Lemma 6.2.6. Now the key point is that
![]() $\tilde {H}^1(K^p,C)[\mathfrak {p}_{\lambda \cdot t}]$
contains a copy of
$\tilde {H}^1(K^p,C)[\mathfrak {p}_{\lambda \cdot t}]$
contains a copy of
![]() $\rho \otimes \Pi (\rho (1))$
. Hence, by Remark 6.4.5 (with
$\rho \otimes \Pi (\rho (1))$
. Hence, by Remark 6.4.5 (with
![]() $V(-1)=\rho $
here),
$V(-1)=\rho $
here),
 $$ \begin{align*}\tilde{H}^1(K^p,C)_{(0,1)}^{\mathrm{la}}[\mathfrak{p}_{\lambda}]^{P_0,U_p=0}=\tilde{H}^1(K^p,C)^{\mathrm{la}}[\mathfrak{p}_{\lambda}]^{P_0,U_p=0}\end{align*} $$
$$ \begin{align*}\tilde{H}^1(K^p,C)_{(0,1)}^{\mathrm{la}}[\mathfrak{p}_{\lambda}]^{P_0,U_p=0}=\tilde{H}^1(K^p,C)^{\mathrm{la}}[\mathfrak{p}_{\lambda}]^{P_0,U_p=0}\end{align*} $$
has dimension (over C) at least
 . But this contradicts the exact sequence above as
. But this contradicts the exact sequence above as
 $\dim _C (M^{\dagger }_1(K^p)[\mathfrak {p}_{\lambda }]\cdot e_1^{-1}t)^{P_0,U_p=0}=1$
by q-expansion principle and taking
$\dim _C (M^{\dagger }_1(K^p)[\mathfrak {p}_{\lambda }]\cdot e_1^{-1}t)^{P_0,U_p=0}=1$
by q-expansion principle and taking
![]() $P_0$
-invariants and kernel of
$P_0$
-invariants and kernel of
![]() $U_p$
are left-exact. Hence,
$U_p$
are left-exact. Hence,
![]() $\rho $
has to be classical.
$\rho $
has to be classical.
Acknowledgement
I thank Matthew Emerton for useful discussions and suggesting the possibility of applying Colmez’s Kirillov model to the problem of modularity of weight 1 forms. I thank Richard Taylor for a key conversation on possible structure in Theorem 1.0.2. I also thank Tsao-Hsien Chen, Pierre Colmez, Weibo Fu, Kai-Wen Lan, Ruochuan Liu, Jun Su and Xinwen Zhu for answering my questions and helpful discussions. Further, I thank Michael Harris and Kai-Wen Lan for several comments and corrections on an earlier version of this article. Finally, I am very grateful to the anonymous referees for their detailed comments on this article. I am supported by a Simons Junior Faculty Fellows award from the Simons Foundation.
Financial Support
I am supported by a Simons Junior Faculty Fellows award from the Simons Foundation.
Conflict of interest:
None.