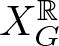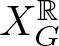1. Introduction
A convex polytope of dimension n is simple if there are exactly n facets intersecting at each vertex. A simple convex polytope P is smooth (or Delzant) if the normal fan of P is unimodular, that is, each cone in the fan is spanned by an integral basis. The importance of smooth polytopes stems from the fact that each smooth polytope P corresponds to a projective smooth toric variety XP, see [Reference Cox, Little and Schenck11]. Taking the real locus of a projective smooth toric variety XP, we obtain a smooth manifold ![]() $X^{\mathbb{R}}_P$ of dimension n, which is also known as a projective smooth real toric variety.
$X^{\mathbb{R}}_P$ of dimension n, which is also known as a projective smooth real toric variety.
In the late 1970s, it was known that the cohomology of a smooth compact toric variety is torsion-free and the integral cohomology ring ![]() $H^\ast(X_P;\mathbb{Z})$ of a projective smooth toric variety XP can be explicitly described by the corresponding smooth polytope P, see [Reference Jurkiewicz13]. On the other hand, the topology of the real locus
$H^\ast(X_P;\mathbb{Z})$ of a projective smooth toric variety XP can be explicitly described by the corresponding smooth polytope P, see [Reference Jurkiewicz13]. On the other hand, the topology of the real locus ![]() $X^{\mathbb{R}}_P$ is much more complicated than that of XP in general. In 1985, Jurkiewicz [Reference Jurkiewicz14] showed that
$X^{\mathbb{R}}_P$ is much more complicated than that of XP in general. In 1985, Jurkiewicz [Reference Jurkiewicz14] showed that ![]() $H^\ast(X^{\mathbb{R}}_P;\mathbb{Z}_2)$ can be explicitly formulated via P just as
$H^\ast(X^{\mathbb{R}}_P;\mathbb{Z}_2)$ can be explicitly formulated via P just as ![]() $H^\ast(X_P;\mathbb{Z})$. Yet,
$H^\ast(X_P;\mathbb{Z})$. Yet, ![]() $X^{\mathbb{R}}_P$ may have p-torsion for arbitrary p > 1 in its cohomology in general, and for that reason, there was no significant progress in this direction for a long time. Recently, there have been some attempts to computing the integral cohomology of a real toric variety [Reference Cai and Choi5, Reference Choi and Park10, Reference Trevisan19].
$X^{\mathbb{R}}_P$ may have p-torsion for arbitrary p > 1 in its cohomology in general, and for that reason, there was no significant progress in this direction for a long time. Recently, there have been some attempts to computing the integral cohomology of a real toric variety [Reference Cai and Choi5, Reference Choi and Park10, Reference Trevisan19].
Let P be a smooth polytope of dimension n and ![]() $\mathcal{F}(P)=\{F_1,\ldots,F_m\}$ the set of all the facets of P. In the normal fan of P, each one-dimensional cone is generated by the primitive integral vector nj normal to a facet
$\mathcal{F}(P)=\{F_1,\ldots,F_m\}$ the set of all the facets of P. In the normal fan of P, each one-dimensional cone is generated by the primitive integral vector nj normal to a facet ![]() $F_j, j=1,\ldots,m$. Define a map
$F_j, j=1,\ldots,m$. Define a map ![]() $\lambda \colon \mathcal{F}(P) \to \mathbb{Z}_2^n$ by taking
$\lambda \colon \mathcal{F}(P) \to \mathbb{Z}_2^n$ by taking ![]() $\lambda(F_j)\equiv \mathbf{n}_j\pmod{2}$. Then λ can be represented by a
$\lambda(F_j)\equiv \mathbf{n}_j\pmod{2}$. Then λ can be represented by a ![]() $\mathbb{Z}_2$-matrix of size n × m as follows:
$\mathbb{Z}_2$-matrix of size n × m as follows:
 \begin{equation*}
\Lambda_P = \begin{pmatrix}
\lambda(F_1) & \cdots & \lambda(F_m)
\end{pmatrix}.
\end{equation*}
\begin{equation*}
\Lambda_P = \begin{pmatrix}
\lambda(F_1) & \cdots & \lambda(F_m)
\end{pmatrix}.
\end{equation*} For ![]() $\omega \in \mathbb{Z}_2^m$, let Pω be the union of facets Fj such that the jth entry of ω is nonzero. For each
$\omega \in \mathbb{Z}_2^m$, let Pω be the union of facets Fj such that the jth entry of ω is nonzero. For each ![]() $S\subset [n]$, by summing the ith rows of
$S\subset [n]$, by summing the ith rows of ![]() $\Lambda_P$ for all
$\Lambda_P$ for all ![]() $i\in S$, we obtain the vector
$i\in S$, we obtain the vector ![]() $\omega_S\in\mathbb{Z}_2^m$. Let KP denote the simplicial complex dual to P and
$\omega_S\in\mathbb{Z}_2^m$. Let KP denote the simplicial complex dual to P and ![]() $K_{P,S}$ denote the simplicial subcomplex of KP dual to
$K_{P,S}$ denote the simplicial subcomplex of KP dual to ![]() $P_{\omega_S}$. That is,
$P_{\omega_S}$. That is,
![]() $K_{P,S}$ is the simplicial complex on
$K_{P,S}$ is the simplicial complex on ![]() $\{j\in[m]\mid \text{the $j$th entry of $\omega_S$ is nonzero}\}$ such that
$\{j\in[m]\mid \text{the $j$th entry of $\omega_S$ is nonzero}\}$ such that ![]() $\sigma=\{j_1,\ldots,j_k\}\in K_{P,S}$ if and only if
$\sigma=\{j_1,\ldots,j_k\}\in K_{P,S}$ if and only if ![]() $F_{j_1}\cap \cdots \cap F_{j_k}\neq \emptyset$ in
$F_{j_1}\cap \cdots \cap F_{j_k}\neq \emptyset$ in ![]() $P_{\omega_S}$.
$P_{\omega_S}$.
Recently, Cai and Choi [Reference Cai and Choi5, Theorem 1.1] showed that the integral cohomology of ![]() $X^{\mathbb{R}}_P$ is completely determined by the reduced integral cohomology of
$X^{\mathbb{R}}_P$ is completely determined by the reduced integral cohomology of ![]() $K_{P,S}$ (
$K_{P,S}$ (![]() $S\subset [n]$) and the h-vector of P. Their formulation says that the integral cohomology of
$S\subset [n]$) and the h-vector of P. Their formulation says that the integral cohomology of ![]() $X^{\mathbb{R}}_P$ is torsion-free or has only 2-torsion if and only if the integral cohomology of
$X^{\mathbb{R}}_P$ is torsion-free or has only 2-torsion if and only if the integral cohomology of ![]() $K_{P,S}$ is torsion-free for each
$K_{P,S}$ is torsion-free for each ![]() $S\subset [n]$. Moreover, the reduced Betti numbers of
$S\subset [n]$. Moreover, the reduced Betti numbers of ![]() $K_{P,S}$ (
$K_{P,S}$ (![]() $S\subset [n]$) and the h-vector of P completely determine the integral cohomology of
$S\subset [n]$) and the h-vector of P completely determine the integral cohomology of ![]() $X^{\mathbb{R}}_P$ if the integral reduced cohomology of
$X^{\mathbb{R}}_P$ if the integral reduced cohomology of ![]() $K_{P,S}$ is torsion-free for every
$K_{P,S}$ is torsion-free for every ![]() $S\subset[n]$. In particular, the reduced Betti numbers of
$S\subset[n]$. In particular, the reduced Betti numbers of ![]() $K_{P,S}$ (
$K_{P,S}$ (![]() $S\subset [n]$) determine the Betti numbers of
$S\subset [n]$) determine the Betti numbers of ![]() $X^{\mathbb{R}}_P$. Naturally, the following question arises:
$X^{\mathbb{R}}_P$. Naturally, the following question arises:
Question 1.1.
Find a family of smooth polytopes P such that the integral cohomology of ![]() $K_{P,S}$ is torsion-free for every
$K_{P,S}$ is torsion-free for every ![]() $S\subset [n]$, where
$S\subset [n]$, where ![]() $n=\dim P$. (This is equivalent to finding a family of projective smooth real toric varieties
$n=\dim P$. (This is equivalent to finding a family of projective smooth real toric varieties ![]() $X^{\mathbb{R}}$ such that
$X^{\mathbb{R}}$ such that ![]() $H^\ast(X^{\mathbb{R}};\mathbb{Z})$ is torsion-free or has only 2-torsion.)
$H^\ast(X^{\mathbb{R}};\mathbb{Z})$ is torsion-free or has only 2-torsion.)
Given a simplicial complex K, it is not easy to determine whether ![]() $H^\ast(K;\mathbb{Z})$ is torsion-free or not. Furthermore,
$H^\ast(K;\mathbb{Z})$ is torsion-free or not. Furthermore, ![]() $H^\ast(K_{P,S};\mathbb{Z})$ may have p-torsion for arbitrary p > 1, see [Reference Choi and Park10]. Thus, the above question seems to cover a wide scope.
$H^\ast(K_{P,S};\mathbb{Z})$ may have p-torsion for arbitrary p > 1, see [Reference Choi and Park10]. Thus, the above question seems to cover a wide scope.
Shellability is a combinatorial property of simplicial complexes with strong topological consequences. A simplicial complex K is shellable if its maximal simplices can be arranged in a linear order ![]() $F_1, F_2, \ldots ,F_t$ such that the subcomplex
$F_1, F_2, \ldots ,F_t$ such that the subcomplex  $(\sum_{i=1}^{k-1} {F_i})\cap {F_k}$ is pure and
$(\sum_{i=1}^{k-1} {F_i})\cap {F_k}$ is pure and ![]() $(\dim {F_k}-1)$-dimensional for all
$(\dim {F_k}-1)$-dimensional for all ![]() $k = 2, \ldots, t$. It was shown in [Reference Björner and Wachs3] that a shellable simplicial complex is homotopy equivalent to a wedge of spheres (in varying dimensions). It follows that the integral cohomology of a shellable simplicial complex is torsion-free. Thus, we can ask to find a family of smooth polytopes P such that
$k = 2, \ldots, t$. It was shown in [Reference Björner and Wachs3] that a shellable simplicial complex is homotopy equivalent to a wedge of spheres (in varying dimensions). It follows that the integral cohomology of a shellable simplicial complex is torsion-free. Thus, we can ask to find a family of smooth polytopes P such that ![]() $K_{P,S}$ is shellable for every subset S in the set
$K_{P,S}$ is shellable for every subset S in the set ![]() $\{1,2,\ldots,\dim(P)\}$.
$\{1,2,\ldots,\dim(P)\}$.
Now we restrict our attention to the real toric varieties arising from graphs. Throughout this paper, a graph permits multiple edges but no loops. A graph is simple if it does not have multiple edges. A bundle is a maximal set of multiple edges with the same pair of endpoints.
For a graph G, the pseudograph associahedron PG is a smooth polytope, and hence we have the projective smooth toric variety ![]() $X_{P_G}$ and the projective smooth real toric variety
$X_{P_G}$ and the projective smooth real toric variety  $X^{\mathbb{R}}_{P_G}$ as well. See §3.2 for the construction of PG. For convenience, we use the notation
$X^{\mathbb{R}}_{P_G}$ as well. See §3.2 for the construction of PG. For convenience, we use the notation ![]() $X_G=X_{P_G}$ and
$X_G=X_{P_G}$ and  $X_G^{\mathbb{R}}=X_{P_G}^{\mathbb{R}}$. We also refer the readers to [Reference Choi, Park and Park8, §2] for a more detailed description of PG.
$X_G^{\mathbb{R}}=X_{P_G}^{\mathbb{R}}$. We also refer the readers to [Reference Choi, Park and Park8, §2] for a more detailed description of PG.
For a simple graph G, it was shown in [Reference Choi and Park9] that  $\widetilde{H}^\ast(K_{P_G,S};\mathbb{Z})$ is torsion-free for every subset S in the set
$\widetilde{H}^\ast(K_{P_G,S};\mathbb{Z})$ is torsion-free for every subset S in the set ![]() $\{1,2,\ldots,\dim(P_{G})\}$, which implies that the polytope PG belongs to the family to be found in Question 1.1. The main contribution of their result is finding a pure shellable poset
$\{1,2,\ldots,\dim(P_{G})\}$, which implies that the polytope PG belongs to the family to be found in Question 1.1. The main contribution of their result is finding a pure shellable poset ![]() $\mathcal{P}_{H}^{\mathrm{even}}$ such that
$\mathcal{P}_{H}^{\mathrm{even}}$ such that ![]() $\Delta(\overline{\mathcal{P}_{H}^{\mathrm{even}}})$, the order complex of the proper part of
$\Delta(\overline{\mathcal{P}_{H}^{\mathrm{even}}})$, the order complex of the proper part of ![]() $\mathcal{P}_{H}^{\mathrm{even}}$, is homotopy equivalent to the complement
$\mathcal{P}_{H}^{\mathrm{even}}$, is homotopy equivalent to the complement ![]() $K_{P_G}\setminus K_{P_G,S}$. Here, H is the subgraph of G determined by S (see [Reference Choi and Park9, §4]), and
$K_{P_G}\setminus K_{P_G,S}$. Here, H is the subgraph of G determined by S (see [Reference Choi and Park9, §4]), and ![]() $\mathcal{P}_{H}^{\mathrm{even}}$ is a poset consisting of the induced subgraphs of H whose connected components are of even order, including
$\mathcal{P}_{H}^{\mathrm{even}}$ is a poset consisting of the induced subgraphs of H whose connected components are of even order, including ![]() $\emptyset$ and H, ordered by the subgraph containment. Note that the reduced cohomology groups of
$\emptyset$ and H, ordered by the subgraph containment. Note that the reduced cohomology groups of ![]() $K_{P_G,S}$ are determined by the reduced homology groups of
$K_{P_G,S}$ are determined by the reduced homology groups of ![]() $\Delta(\overline{\mathcal{P}_{H}^{\mathrm{even}}})$ by the Alexander duality since
$\Delta(\overline{\mathcal{P}_{H}^{\mathrm{even}}})$ by the Alexander duality since ![]() $K_{P_G}$ is homeomorphic to a sphere.
$K_{P_G}$ is homeomorphic to a sphere.
The work of [Reference Choi and Park9] on simple graphs was generalized to graphs (allowing multiple edges) in [Reference Choi, Park and Park8]. Namely, for each simplicial complex ![]() $K_{P_G,S}$, there is a poset
$K_{P_G,S}$, there is a poset ![]() $\mathcal{P}_{H,A}^{\mathrm{even}}$ such that
$\mathcal{P}_{H,A}^{\mathrm{even}}$ such that  $\Delta(\overline{\mathcal{P}_{G,A}^{\mathrm{even}}})$ is homotopy equivalent to the complement
$\Delta(\overline{\mathcal{P}_{G,A}^{\mathrm{even}}})$ is homotopy equivalent to the complement ![]() $K_{P_G}\setminus K_{P_G,S}$. Here, H is a graph determined by S, obtained from G by deleting some vertices and replacing some bundles with simple edges, and A is a set of vertices and multiple edges of H such that
$K_{P_G}\setminus K_{P_G,S}$. Here, H is a graph determined by S, obtained from G by deleting some vertices and replacing some bundles with simple edges, and A is a set of vertices and multiple edges of H such that ![]() $|A\cap V(H^{\prime})|\equiv 0\pmod{2}$ for each connected component Hʹ of H with the following properties:
$|A\cap V(H^{\prime})|\equiv 0\pmod{2}$ for each connected component Hʹ of H with the following properties:
(1) each vertex that is incident to only simple edges of H is contained in A, and
(2)
 $B\cap A\neq \emptyset$ and
$B\cap A\neq \emptyset$ and  $|B\cap A|\equiv 0\pmod{2}$ for each bundle B of H.
$|B\cap A|\equiv 0\pmod{2}$ for each bundle B of H.
We call A an admissible collection of H. The poset ![]() $\mathcal{P}_{H,A}^{\mathrm{even}}$ is defined to be a poset consisting of all the subgraphs I of H such that I includes at least one edge between every pair of vertices in I if such edges exist in H, and each connected component of I has an even number of elements in A, including both
$\mathcal{P}_{H,A}^{\mathrm{even}}$ is defined to be a poset consisting of all the subgraphs I of H such that I includes at least one edge between every pair of vertices in I if such edges exist in H, and each connected component of I has an even number of elements in A, including both ![]() $\emptyset$ and H, ordered by the subgraph containment. All definitions are elaborated in §3.
$\emptyset$ and H, ordered by the subgraph containment. All definitions are elaborated in §3.
Now we let ![]() $\mathcal{A}^\ast(G)$ be the set of all pairs (H, A), where H is a graph obtained from G by deleting some vertices and replacing some bundles with simple edges, and A is an admissible collection of H. In order to show
$\mathcal{A}^\ast(G)$ be the set of all pairs (H, A), where H is a graph obtained from G by deleting some vertices and replacing some bundles with simple edges, and A is an admissible collection of H. In order to show ![]() $K_{P_G,S}$ is torsion-free for every S, it is sufficient to check
$K_{P_G,S}$ is torsion-free for every S, it is sufficient to check  $\Delta(\overline{\mathcal{P}_{H,A}^{\mathrm{even}}})$ for every
$\Delta(\overline{\mathcal{P}_{H,A}^{\mathrm{even}}})$ for every ![]() $(H,A)\in\mathcal{A}^\ast(G)$. Unlike simple graphs, for a non-simple graph H, the poset
$(H,A)\in\mathcal{A}^\ast(G)$. Unlike simple graphs, for a non-simple graph H, the poset ![]() $\mathcal{P}_{H,A}^{\mathrm{even}}$ is neither pure nor shellable in general, see §4. Hence, it is natural to ask the following, which is a subproblem of Question 1.1.
$\mathcal{P}_{H,A}^{\mathrm{even}}$ is neither pure nor shellable in general, see §4. Hence, it is natural to ask the following, which is a subproblem of Question 1.1.
Question 1.2. [Reference Choi, Park and Park8]
Find all graphs G such that ![]() $\mathcal{P}_{H,A}^{\mathrm{even}}$ is shellable for every
$\mathcal{P}_{H,A}^{\mathrm{even}}$ is shellable for every ![]() $(H,A) \in \mathcal{A}^{\ast}(G)$.
$(H,A) \in \mathcal{A}^{\ast}(G)$.
Our main result is the following, which answers Question 1.2.
Theorem 1.3. Let G be a graph. Then ![]() $\mathcal{P}_{H,A}^{\mathrm{even}}$ is shellable for every
$\mathcal{P}_{H,A}^{\mathrm{even}}$ is shellable for every ![]() $(H,A)\in A^\ast(G)$ if and only if each connected component of G is a simple graph or one of the graphs in the following figure.
$(H,A)\in A^\ast(G)$ if and only if each connected component of G is a simple graph or one of the graphs in the following figure.
To show the main theorem, we use the notion of chain-lexicographic shellability (CL-shellability for short) of posets; this tool is based on labelling the edges of the Hasse diagram of a poset in a certain way. Note that CL-shellability is stronger than shellability, and there is an example of a shellable poset with no CL-shelling, see [Reference Walker21]. We refer the readers to [Reference Wachs, Miller, Reiner and Sturmfels20] and references therein regarding lexicographic shellability, but we lay out some basic facts in §2.
Björner and Wachs [Reference Björner and Wachs2] proved that if a bounded poset ![]() $\mathcal{P}$ is CL-shellable, then the homotopy type of
$\mathcal{P}$ is CL-shellable, then the homotopy type of ![]() $\Delta(\overline{\mathcal{P}})$, the order complex of the proper part of
$\Delta(\overline{\mathcal{P}})$, the order complex of the proper part of ![]() $\mathcal{P}$, is determined by the information of the falling chains of
$\mathcal{P}$, is determined by the information of the falling chains of ![]() $\mathcal{P}$ with a CL-labelling. Hence, our results give a way to compute the homotopy type of
$\mathcal{P}$ with a CL-labelling. Hence, our results give a way to compute the homotopy type of ![]() $K_{P_G,S}$, and hence we can compute the integral cohomology groups of
$K_{P_G,S}$, and hence we can compute the integral cohomology groups of ![]() $X^{\mathbb{R}}_G$ explicitly for a graph G in Theorem 1.3.
$X^{\mathbb{R}}_G$ explicitly for a graph G in Theorem 1.3.
This paper is organized as follows. Section 2 collects some basic definitions and important facts about a poset and its shellability. In §3, we provide our motivation from the cohomology of real toric varieties associated with a graph. We also explain Theorem 1.3, which is the main theorem. Section 4 proves the necessary condition of Theorem 1.3, which gives a possible list of graphs G such that ![]() $\mathcal{P}_{H,A}^{\mathrm{even}}$ is shellable for every
$\mathcal{P}_{H,A}^{\mathrm{even}}$ is shellable for every ![]() $(H,A)\in \mathcal{A}^{\ast}(G)$. Section 5 proves the sufficient condition of Theorem 1.3, which shows the CL-shellability of each poset
$(H,A)\in \mathcal{A}^{\ast}(G)$. Section 5 proves the sufficient condition of Theorem 1.3, which shows the CL-shellability of each poset ![]() $\mathcal{P}_{H,A}^{\mathrm{even}}$ for a graph G in the list and
$\mathcal{P}_{H,A}^{\mathrm{even}}$ for a graph G in the list and ![]() $(H,A)\in\mathcal{A}^{\ast}(G)$. In Section 6, we determine the homotopy type of
$(H,A)\in\mathcal{A}^{\ast}(G)$. In Section 6, we determine the homotopy type of  $\Delta(\overline{\mathcal{P}_{G,A}^{\mathrm{even}}})$ by considering the falling chains of
$\Delta(\overline{\mathcal{P}_{G,A}^{\mathrm{even}}})$ by considering the falling chains of ![]() $\mathcal{P}_{G,A}^{\mathrm{even}}$ for a graph G in Figure 1.1. In §7, as an application of our result, we compute the Betti numbers of the projective smooth real toric variety associated with the graph
$\mathcal{P}_{G,A}^{\mathrm{even}}$ for a graph G in Figure 1.1. In §7, as an application of our result, we compute the Betti numbers of the projective smooth real toric variety associated with the graph  $\widetilde{P}_{n,2}$. In Appendix 1, we add a sketch of the proof of Proposition 3.4, which is obtained by combining several results from [Reference Choi, Park and Park8].
$\widetilde{P}_{n,2}$. In Appendix 1, we add a sketch of the proof of Proposition 3.4, which is obtained by combining several results from [Reference Choi, Park and Park8].

Figure 1.1. Non-simple connected graphs with n vertices and m multiple edges (![]() $m\ge 2$).
$m\ge 2$).
2. Preliminaries: Shellability of a poset
In this section, we prepare some notions and basic facts about a poset and its shellability. See [Reference Wachs, Miller, Reiner and Sturmfels20] for a more detailed explanation about this section.
We only consider a finite poset in this paper. Let ![]() $\mathcal{P}$ be a poset (partially ordered set). For two elements
$\mathcal{P}$ be a poset (partially ordered set). For two elements ![]() $x,y\in\mathcal{P}$, we say y covers x, denoted by
$x,y\in\mathcal{P}$, we say y covers x, denoted by ![]() $x\lessdot y$, if x < y, and there is no z such that
$x\lessdot y$, if x < y, and there is no z such that ![]() $x \lt z \lt y$. We also call it a cover
$x \lt z \lt y$. We also call it a cover ![]() $x\lessdot y$. One represents
$x\lessdot y$. One represents ![]() $\mathcal{P}$ as a mathematical diagram, called a Hasse diagram, in a way that a point in the plane is drawn for each element of
$\mathcal{P}$ as a mathematical diagram, called a Hasse diagram, in a way that a point in the plane is drawn for each element of ![]() $\mathcal{P}$, and a line segment or curve is drawn upward from x to y whenever y covers x. A chain of
$\mathcal{P}$, and a line segment or curve is drawn upward from x to y whenever y covers x. A chain of ![]() $\mathcal{P}$ is a totally ordered subset σ of
$\mathcal{P}$ is a totally ordered subset σ of ![]() $\mathcal{P}$, and we say the length
$\mathcal{P}$, and we say the length ![]() $\ell(\sigma)$ of σ is
$\ell(\sigma)$ of σ is ![]() $|\sigma|-1$. We say
$|\sigma|-1$. We say ![]() $\mathcal{P}$ is pure if all maximal chains have the same length. The length
$\mathcal{P}$ is pure if all maximal chains have the same length. The length ![]() $\ell(\mathcal{P})$ of
$\ell(\mathcal{P})$ of ![]() $\mathcal{P}$ is the length of a longest chain of
$\mathcal{P}$ is the length of a longest chain of ![]() $\mathcal{P}$. For
$\mathcal{P}$. For ![]() $x \leq y$ in
$x \leq y$ in ![]() $\mathcal{P}$, let
$\mathcal{P}$, let ![]() $[x,y]$ denote the (closed) interval
$[x,y]$ denote the (closed) interval ![]() $\{z\in \mathcal{P}\colon x \le z \le y\}$. We say
$\{z\in \mathcal{P}\colon x \le z \le y\}$. We say ![]() $\mathcal{P}$ is semimodular if for all
$\mathcal{P}$ is semimodular if for all ![]() $x,y\in \mathcal{P}$ that cover
$x,y\in \mathcal{P}$ that cover ![]() $a\in \mathcal{P}$, there is an element
$a\in \mathcal{P}$, there is an element ![]() $b\in \mathcal{P}$ that covers both x and y. If every closed interval of
$b\in \mathcal{P}$ that covers both x and y. If every closed interval of ![]() $\mathcal{P}$ is semimodular, then
$\mathcal{P}$ is semimodular, then ![]() $\mathcal{P}$ is totally semimodular. If
$\mathcal{P}$ is totally semimodular. If ![]() $\mathcal{P}$ has a unique minimum element, it is usually denoted by
$\mathcal{P}$ has a unique minimum element, it is usually denoted by ![]() $\hat{0}$ and referred to as the bottom element. Similarly, the unique maximum element, if it exists, is denoted by
$\hat{0}$ and referred to as the bottom element. Similarly, the unique maximum element, if it exists, is denoted by ![]() $\hat{1}$ and referred to as the top element. An element of
$\hat{1}$ and referred to as the top element. An element of ![]() $\mathcal{P}$ that covers the bottom element is called an atom. We say
$\mathcal{P}$ that covers the bottom element is called an atom. We say ![]() $\mathcal{P}$ is bounded if it has the elements
$\mathcal{P}$ is bounded if it has the elements ![]() $\hat{0}$ and
$\hat{0}$ and ![]() $\hat{1}$. The order complex of
$\hat{1}$. The order complex of ![]() $\mathcal{P}$, denoted by
$\mathcal{P}$, denoted by ![]() $\Delta(\mathcal{P})$, is an abstract simplicial complex whose faces are the chains of
$\Delta(\mathcal{P})$, is an abstract simplicial complex whose faces are the chains of ![]() $\mathcal{P}$. Note that if
$\mathcal{P}$. Note that if ![]() $\mathcal{P}$ has either
$\mathcal{P}$ has either ![]() $\hat{0}$ or
$\hat{0}$ or ![]() $\hat{1}$, then
$\hat{1}$, then ![]() $\Delta(\mathcal{P})$ is contractible; hence, we usually remove the top and bottom elements, and then study the topology of the remaining part. The proper part of a bounded poset
$\Delta(\mathcal{P})$ is contractible; hence, we usually remove the top and bottom elements, and then study the topology of the remaining part. The proper part of a bounded poset ![]() $\mathcal{P}$ with length at least one is defined to be the poset
$\mathcal{P}$ with length at least one is defined to be the poset ![]() $\overline{\mathcal{P}}:=\mathcal{P}\setminus\{\hat{0},\,\hat{1}\}$.
$\overline{\mathcal{P}}:=\mathcal{P}\setminus\{\hat{0},\,\hat{1}\}$.
The notion of shellability first appeared in the middle of the nineteenth century in the computation of the Euler characteristic of a convex polytope [Reference Schläfli16]. A simplicial complex K is shellable if its maximal simplices can be arranged in a linear order ![]() $F_1, F_2, \ldots ,F_t$ in such a way that the subcomplex
$F_1, F_2, \ldots ,F_t$ in such a way that the subcomplex  $(\sum_{i=1}^{k-1} {F_i})\cap{F_k}$ is pure and
$(\sum_{i=1}^{k-1} {F_i})\cap{F_k}$ is pure and ![]() $(\dim {F_k}-1)$-dimensional for all
$(\dim {F_k}-1)$-dimensional for all ![]() $k = 2, \ldots, t$. Such an ordering of the facets is called a shelling. A poset
$k = 2, \ldots, t$. Such an ordering of the facets is called a shelling. A poset ![]() $\mathcal{P}$ is shellable if its order complex
$\mathcal{P}$ is shellable if its order complex ![]() $\Delta(\mathcal{P})$ is shellable.
$\Delta(\mathcal{P})$ is shellable.
The idea of lexicographic shellability is based on a technique introduced by Stanley [Reference Stanley17, Reference Stanley18] for showing that the Möbius function of rank-selected subposets of certain posets alternates in sign. This technique involved labelling the edges of the Hasse diagram of the poset in a certain way. Stanley conjectured that the posets that he was considering were topological and algebraic properties of simplicial complexes implied by shellability. This conjecture was proved by Björner [Reference Björner1] by finding a condition on edge labellings, which implies shellability of the poset, and then the theory of lexicographic shellability was further developed in a series of papers by Björner and Wachs [Reference Björner and Wachs2–Reference Björner and Wachs4]. In this paper, we consider CL-shellability. CL-shellability was introduced to establish the shellability of Bruhat order on a Coxeter group [Reference Björner and Wachs2]. It is known that every CL-shellable poset is a shellable poset, but the converse is not true in general; see [Reference Walker21]. We refer to the readers [Reference Wachs, Miller, Reiner and Sturmfels20, Lecture 4] and the references therein.
Let ![]() $\mathcal{P}$ be a bounded poset and
$\mathcal{P}$ be a bounded poset and ![]() $\mathcal{ME}(\mathcal{P})$ the set of pairs
$\mathcal{ME}(\mathcal{P})$ the set of pairs ![]() $(\sigma,x \lessdot y)$ consisting of a maximal chain σ and a cover
$(\sigma,x \lessdot y)$ consisting of a maximal chain σ and a cover ![]() $x\lessdot y$ along that chain. For
$x\lessdot y$ along that chain. For ![]() $x,y\in\mathcal{P}$ and a maximal chain r of
$x,y\in\mathcal{P}$ and a maximal chain r of ![]() $[\hat{0},x]$, the closed rooted interval
$[\hat{0},x]$, the closed rooted interval ![]() $[x,y]_r$ of
$[x,y]_r$ of ![]() $\mathcal{P}$ is a subposet of
$\mathcal{P}$ is a subposet of ![]() $\mathcal{P}$ obtained from
$\mathcal{P}$ obtained from ![]() $[x,y]$ adding the chain r. A chain-edge labelling of
$[x,y]$ adding the chain r. A chain-edge labelling of ![]() $\mathcal{P}$ is a map
$\mathcal{P}$ is a map ![]() $\rho\colon \mathcal{ME}(\mathcal{P}) \rightarrow L$ satisfying the following: if two maximal chains coincide along their bottom d covers, then their labels also coincide along these covers. Here, L is a poset. A chain-lexicographic labelling (CL-labelling for short) of a bounded poset
$\rho\colon \mathcal{ME}(\mathcal{P}) \rightarrow L$ satisfying the following: if two maximal chains coincide along their bottom d covers, then their labels also coincide along these covers. Here, L is a poset. A chain-lexicographic labelling (CL-labelling for short) of a bounded poset ![]() $\mathcal{P}$ is a chain-edge labelling such that for each closed rooted interval
$\mathcal{P}$ is a chain-edge labelling such that for each closed rooted interval ![]() $[x,y]_r$ of
$[x,y]_r$ of ![]() $\mathcal{P}$, there is a unique strictly increasing maximal chain, which lexicographically precedes all other maximal chains of
$\mathcal{P}$, there is a unique strictly increasing maximal chain, which lexicographically precedes all other maximal chains of ![]() $[x,y]_r$. A poset that admits a CL-labelling is CL-shellable. Figure 2.1 shows an example of a CL-shellable poset.
$[x,y]_r$. A poset that admits a CL-labelling is CL-shellable. Figure 2.1 shows an example of a CL-shellable poset.

Figure 2.1. A CL-labelling of a poset with four maximal chains (same example in [Reference Wachs, Miller, Reiner and Sturmfels20]).
We recall well-known properties on shellability which we will use. The product ![]() $\mathcal{P}\times \mathcal{Q}$ of two posets
$\mathcal{P}\times \mathcal{Q}$ of two posets ![]() $\mathcal{P}$ and
$\mathcal{P}$ and ![]() $\mathcal{Q}$ is the new poset with partial order given by
$\mathcal{Q}$ is the new poset with partial order given by ![]() $(a,b) \le (c,d)$ if and only if
$(a,b) \le (c,d)$ if and only if ![]() $a \le c$ (in
$a \le c$ (in ![]() $\mathcal{P}$) and
$\mathcal{P}$) and ![]() $b \le d$ (in
$b \le d$ (in ![]() $\mathcal{Q}$).
$\mathcal{Q}$).
Theorem 2.1. ([Reference Björner1, Reference Björner and Wachs3, Reference Björner and Wachs4])
The following statements hold:
(1) Every (closed) interval of a shellable (respectively, CL-shellable) poset is shellable (respectively, CL-shellable).
(2) The product of bounded posets is shellable (respectively, CL-shellable) if and only if each of the posets is shellable (respectively, CL-shellable).
(3) If a bounded poset is pure and totally semimodular, then it is CL-shellable.
For a bounded poset ![]() $\mathcal{P}$ with a CL-labelling
$\mathcal{P}$ with a CL-labelling ![]() $\rho\colon\mathcal{ME}(\mathcal{P}) \rightarrow \mathbb{Z}$, a chain
$\rho\colon\mathcal{ME}(\mathcal{P}) \rightarrow \mathbb{Z}$, a chain ![]() $\sigma:x_0\lessdot x_1\lessdot\cdots\lessdot x_{\ell}$ of
$\sigma:x_0\lessdot x_1\lessdot\cdots\lessdot x_{\ell}$ of ![]() $\mathcal{P}$ is called a falling chain if it is a maximal chain such that
$\mathcal{P}$ is called a falling chain if it is a maximal chain such that ![]() $\rho(\sigma,x_{i-1}\lessdot x_i) \not \lt _{L} \rho(\sigma,x_{i}\lessdot x_{i+1})$ for every
$\rho(\sigma,x_{i-1}\lessdot x_i) \not \lt _{L} \rho(\sigma,x_{i}\lessdot x_{i+1})$ for every ![]() $1\leq i \lt {\ell}$.
$1\leq i \lt {\ell}$.
Theorem 2.2. ([Reference Björner and Wachs3])
If a bounded poset ![]() $\mathcal{P}$ is CL-shellable, then the order complex of the proper part of
$\mathcal{P}$ is CL-shellable, then the order complex of the proper part of ![]() $\mathcal{P}, \Delta(\overline{\mathcal{P}})$, is homotopy equivalent to a wedge of spheres. Furthermore, for every fixed CL-labelling, the ith reduced BettiFootnote 1 number of
$\mathcal{P}, \Delta(\overline{\mathcal{P}})$, is homotopy equivalent to a wedge of spheres. Furthermore, for every fixed CL-labelling, the ith reduced BettiFootnote 1 number of ![]() $\Delta(\overline{\mathcal{P}})$ is equal to the number of falling chains of
$\Delta(\overline{\mathcal{P}})$ is equal to the number of falling chains of ![]() $\mathcal{P}$ of length
$\mathcal{P}$ of length ![]() $(i+2)$.
$(i+2)$.
The poset in Figure 2.1 has exactly one falling chain ![]() $a \lt c \lt d \lt f$. On the other hand, the order complex of the proper part of the poset is homotopy equivalent to S 1 whose first reduced Betti number is 1.
$a \lt c \lt d \lt f$. On the other hand, the order complex of the proper part of the poset is homotopy equivalent to S 1 whose first reduced Betti number is 1.
A recursive atom ordering is an alternative approach to lexicographic shellability, which is known to be an equivalent concept of CL-shellability.
Definition 2.3. A bounded poset ![]() $\mathcal{P}$ is said to admit a recursive atom ordering if its length
$\mathcal{P}$ is said to admit a recursive atom ordering if its length ![]() $\ell(\mathcal{P})$ is 1, or
$\ell(\mathcal{P})$ is 1, or ![]() $\ell(\mathcal{P}) \gt 1$, and there is an ordering
$\ell(\mathcal{P}) \gt 1$, and there is an ordering ![]() $\alpha_1,\ldots,\alpha_t$ of the atoms of
$\alpha_1,\ldots,\alpha_t$ of the atoms of ![]() $\mathcal{P}$ satisfying the following:
$\mathcal{P}$ satisfying the following:
(1) For all
 $j=1,\ldots,t$, the interval
$j=1,\ldots,t$, the interval  $[\alpha_j,\hat{1}]$ admits a recursive atom ordering in which the atoms of
$[\alpha_j,\hat{1}]$ admits a recursive atom ordering in which the atoms of  $[\alpha_j,\hat{1}]$ that belong to
$[\alpha_j,\hat{1}]$ that belong to  $[\alpha_i,\hat{1}]$ for some i < j come first.
$[\alpha_i,\hat{1}]$ for some i < j come first.(2) For all
 $i,j$ with
$i,j$ with  $1\le i \lt j \le t$, if
$1\le i \lt j \le t$, if  $\alpha_i,\alpha_j \lt y$, then there exist an integer k and an atom z of
$\alpha_i,\alpha_j \lt y$, then there exist an integer k and an atom z of  $[\alpha_j,\hat{1}]$ such that
$[\alpha_j,\hat{1}]$ such that  $1\le k \lt j$ and
$1\le k \lt j$ and  $\alpha_k \lt z\leq y$.
$\alpha_k \lt z\leq y$.
For example, for the poset in Figure 2.1, if we order the atoms of each interval by alphabetical order (for the atoms of ![]() $[a,f]$, the ordering is
$[a,f]$, the ordering is ![]() $b\prec c$; for the atoms of
$b\prec c$; for the atoms of ![]() $[b,f]$, the ordering is
$[b,f]$, the ordering is ![]() $d\prec e$; and for the atoms of
$d\prec e$; and for the atoms of ![]() $[c,f]$, the ordering is
$[c,f]$, the ordering is ![]() $d\prec e$), then it is a recursive atom ordering.
$d\prec e$), then it is a recursive atom ordering.
We note that any atom ordering of a pure totally semimodular bounded poset is a recursive atom ordering, which implies (3) of Theorem 2.1. We finish the section by introducing a sketch of the proof shown in [Reference Björner and Wachs3] that the existence of a recursive atom ordering implies CL-shellability.
Theorem 2.4. ([Reference Björner and Wachs3])
A bounded poset admits a recursive atom ordering if and only if it is CL-shellable.
Sketch of proof of the ‘only if’ part
Suppose that a bounded poset ![]() $\mathcal{P}$ admits a recursive atom ordering, and let the atoms of
$\mathcal{P}$ admits a recursive atom ordering, and let the atoms of ![]() $\mathcal{P}$ be ordered as
$\mathcal{P}$ be ordered as ![]() $\alpha_1, \ldots, \alpha_t$. Let us give an integer labelling ρ of the bottom covers of
$\alpha_1, \ldots, \alpha_t$. Let us give an integer labelling ρ of the bottom covers of ![]() $\mathcal{P}$ such that
$\mathcal{P}$ such that  $\rho(\hat{0},\alpha_i) \lt \rho(\hat{0},\alpha_j)$ for all i < j. For each j, let
$\rho(\hat{0},\alpha_i) \lt \rho(\hat{0},\alpha_j)$ for all i < j. For each j, let ![]() $F(\alpha_j)$ be the set of all atoms of
$F(\alpha_j)$ be the set of all atoms of  $[\alpha_j,\hat{1}]$ that cover some αi, where i < j. We label the bottom covers of
$[\alpha_j,\hat{1}]$ that cover some αi, where i < j. We label the bottom covers of  $[\alpha_j,\hat{1}]$ consistently with the atom ordering of
$[\alpha_j,\hat{1}]$ consistently with the atom ordering of  $[\alpha_j,\hat{1}]$ and satisfying
$[\alpha_j,\hat{1}]$ and satisfying
 \begin{equation*}x\in F(\alpha_j) \Rightarrow \rho(\alpha_j,x) \lt \rho(\hat{0},\alpha_j)\quad \text{and}\quad
x\not\in F(\alpha_j) \Rightarrow \rho(\alpha_j,x) \gt \rho(\hat{0},\alpha_j),
\end{equation*}
\begin{equation*}x\in F(\alpha_j) \Rightarrow \rho(\alpha_j,x) \lt \rho(\hat{0},\alpha_j)\quad \text{and}\quad
x\not\in F(\alpha_j) \Rightarrow \rho(\alpha_j,x) \gt \rho(\hat{0},\alpha_j),
\end{equation*} where ρ denotes the labelling of the bottom covers of  $[\alpha_j,\hat{1}]$ as well as the original labelling of the bottom covers of
$[\alpha_j,\hat{1}]$ as well as the original labelling of the bottom covers of ![]() $\mathcal{P}$. This labelling inductively extends to an integer CL-labelling of
$\mathcal{P}$. This labelling inductively extends to an integer CL-labelling of  $[\alpha_j,\hat{1}]$. Choosing such an extension at each αj, we obtain a chain-edge labelling ρ of
$[\alpha_j,\hat{1}]$. Choosing such an extension at each αj, we obtain a chain-edge labelling ρ of ![]() $\mathcal{P}$, which is a CL-labelling of
$\mathcal{P}$, which is a CL-labelling of  $[\alpha_j, \hat{1}]$ for all
$[\alpha_j, \hat{1}]$ for all ![]() $j = 1,\ldots ,t$, and hence for every rooted interval whose bottom element is not
$j = 1,\ldots ,t$, and hence for every rooted interval whose bottom element is not ![]() $\hat{0}$, and which extends the original labelling of the bottom covers of
$\hat{0}$, and which extends the original labelling of the bottom covers of ![]() $\mathcal{P}$. Then one can show that the unique lexicographically first maximal chain of each interval
$\mathcal{P}$. Then one can show that the unique lexicographically first maximal chain of each interval ![]() $[0, y]$ is the only increasing maximal chain of that interval. Hence, the labelling ρ is an integer CL-labellling on
$[0, y]$ is the only increasing maximal chain of that interval. Hence, the labelling ρ is an integer CL-labellling on ![]() $\mathcal{P}$.
$\mathcal{P}$.
3. Real toric variety arising from a graph G and a poset  $\mathcal{P}_{G,A}^{\mathrm{even}}$
$\mathcal{P}_{G,A}^{\mathrm{even}}$
In this section, we first introduce the integral cohomology of a projective smooth real toric variety and then restrict our attention to projective smooth real toric varieties arising from graphs. For a graph G, we construct the pseudograph associahedron PG, which defines the projective smooth real toric variety ![]() $X^{\mathbb{R}}_G$. We describe the cohomology of
$X^{\mathbb{R}}_G$. We describe the cohomology of ![]() $X^{\mathbb{R}}_G$ in terms of posets of even subgraphs of G, and then introduce our main result.
$X^{\mathbb{R}}_G$ in terms of posets of even subgraphs of G, and then introduce our main result.
3.1. Cohomology of a real toric variety
A toric variety of complex dimension n is a normal algebraic variety containing an algebraic torus ![]() $(\mathbb{C}^\ast)^n$ as a Zariski open dense subset such that the action of the torus on itself extends to the whole variety. A real toric variety is the real locus of a toric variety. The fundamental theorem of toric geometry says that there is a one-to-one correspondence between the class of toric varieties of complex dimension n and the class of fans in
$(\mathbb{C}^\ast)^n$ as a Zariski open dense subset such that the action of the torus on itself extends to the whole variety. A real toric variety is the real locus of a toric variety. The fundamental theorem of toric geometry says that there is a one-to-one correspondence between the class of toric varieties of complex dimension n and the class of fans in ![]() $\mathbb{R}^n$. In particular, for a complete smooth toric variety X, the corresponding fan
$\mathbb{R}^n$. In particular, for a complete smooth toric variety X, the corresponding fan ![]() $\Sigma_X$ is complete and smooth. Furthermore, a complete smooth toric variety X is projective if and only if
$\Sigma_X$ is complete and smooth. Furthermore, a complete smooth toric variety X is projective if and only if ![]() $\Sigma_X$ can be realized as the normal fan of a smooth polytope in
$\Sigma_X$ can be realized as the normal fan of a smooth polytope in ![]() $\mathbb{R}^n$.
$\mathbb{R}^n$.
Although the integral cohomology ring of a complete smooth toric variety was studied by Danilov [Reference Danilov12] and Jurkiewicz [Reference Jurkiewicz13] in the late 1970s, only little is known about the cohomology of complete smooth real toric varieties. For a complete smooth toric variety X and its real locus ![]() $X^{\mathbb{R}}$, the cohomology ring
$X^{\mathbb{R}}$, the cohomology ring ![]() $H^\ast(X^{\mathbb{R}};\mathbb{Z}_2)$ was computed by Jurkiewicz [Reference Jurkiewicz14] in 1985, and it has a similar form to the integral cohomology ring
$H^\ast(X^{\mathbb{R}};\mathbb{Z}_2)$ was computed by Jurkiewicz [Reference Jurkiewicz14] in 1985, and it has a similar form to the integral cohomology ring ![]() $H^\ast(X;\mathbb{Z})$. Note that the dimension of
$H^\ast(X;\mathbb{Z})$. Note that the dimension of ![]() $H^i(X^{\mathbb{R}};\mathbb{Z}_2)$ as a vector space over
$H^i(X^{\mathbb{R}};\mathbb{Z}_2)$ as a vector space over ![]() $\mathbb{Z}_2$ is equal to hi, where
$\mathbb{Z}_2$ is equal to hi, where ![]() $(h_0,h_1,\ldots,h_n)$ is the h-vector of KX, the underlying simplicial sphere of the fan
$(h_0,h_1,\ldots,h_n)$ is the h-vector of KX, the underlying simplicial sphere of the fan ![]() $\Sigma_X$.
$\Sigma_X$.
Recently, there were several efforts to compute the integral cohomology of a real toric variety. Let P be a smooth polytope of dimension n and let ![]() $\mathcal{F}(P)=\{F_1,\ldots,F_m\}$ be the set of facets of P. Then the primitive outward normal vectors of P can be understood as a function ϕ from
$\mathcal{F}(P)=\{F_1,\ldots,F_m\}$ be the set of facets of P. Then the primitive outward normal vectors of P can be understood as a function ϕ from ![]() $\mathcal{F}(P)$ to
$\mathcal{F}(P)$ to ![]() $\mathbb{Z}^n$, and the composition map
$\mathbb{Z}^n$, and the composition map  $\lambda \colon \mathcal{F}(P) \stackrel{\phi}{\rightarrow} \mathbb{Z}^n \stackrel{\text{mod $2$}}{\longrightarrow} \mathbb{Z}_2^n$ is called the (mod 2) characteristic function over P. Note that λ can be represented by a
$\lambda \colon \mathcal{F}(P) \stackrel{\phi}{\rightarrow} \mathbb{Z}^n \stackrel{\text{mod $2$}}{\longrightarrow} \mathbb{Z}_2^n$ is called the (mod 2) characteristic function over P. Note that λ can be represented by a ![]() $\mathbb{Z}_2$-matrix
$\mathbb{Z}_2$-matrix ![]() $\Lambda_P$ of size n × m as
$\Lambda_P$ of size n × m as
 \begin{equation*}
\Lambda_P = \begin{pmatrix}
\lambda(F_1) & \cdots & \lambda(F_m)
\end{pmatrix},
\end{equation*}
\begin{equation*}
\Lambda_P = \begin{pmatrix}
\lambda(F_1) & \cdots & \lambda(F_m)
\end{pmatrix},
\end{equation*} where the ith column of ![]() $\Lambda_P$ is
$\Lambda_P$ is ![]() $\lambda(F_i) \in \mathbb{Z}_2^n$. For
$\lambda(F_i) \in \mathbb{Z}_2^n$. For ![]() $\omega \in \mathbb{Z}_2^m$, we define Pω to be the union of facets Fj such that the jth entry of ω is nonzero. Then the following holds:
$\omega \in \mathbb{Z}_2^m$, we define Pω to be the union of facets Fj such that the jth entry of ω is nonzero. Then the following holds:
Theorem 3.1. ([Reference Choi and Park10, Reference Trevisan19])
Let P be a smooth polytope of dimension n and ![]() $X^{\mathbb{R}}_P$ the projective smooth real toric variety associated with P. Then the Betti numbers of
$X^{\mathbb{R}}_P$ the projective smooth real toric variety associated with P. Then the Betti numbers of ![]() $X^{\mathbb{R}}_P$ is given as follows:
$X^{\mathbb{R}}_P$ is given as follows:
 \begin{equation}
\beta^i(X^{\mathbb{R}}_P) = \sum_{S\subset [n]} \widetilde{\beta}^{i-1}(P_{\omega_S}),
\end{equation}
\begin{equation}
\beta^i(X^{\mathbb{R}}_P) = \sum_{S\subset [n]} \widetilde{\beta}^{i-1}(P_{\omega_S}),
\end{equation} where ωS is the sum of the kth rows of ![]() $\Lambda_P$ for all
$\Lambda_P$ for all ![]() $k\in S$.
$k\in S$.
For ![]() $S\subset [n]$, let
$S\subset [n]$, let ![]() $K_{P,S}$ be the simplicial subcomplex of KP dual to
$K_{P,S}$ be the simplicial subcomplex of KP dual to ![]() $P_{\omega_S}$. Note that
$P_{\omega_S}$. Note that ![]() $K_{P,S}$ and
$K_{P,S}$ and ![]() $P_{\omega_S}$ have the same homotopy type. Hence, we can rewrite Equation (3.1) by using
$P_{\omega_S}$ have the same homotopy type. Hence, we can rewrite Equation (3.1) by using ![]() $K_{P,S}$:
$K_{P,S}$:
 \begin{equation}
\beta^i(X^{\mathbb{R}}_P) =\sum_{S\subset [n]} \widetilde{\beta}^{i-1}(K_{P,S}).
\end{equation}
\begin{equation}
\beta^i(X^{\mathbb{R}}_P) =\sum_{S\subset [n]} \widetilde{\beta}^{i-1}(K_{P,S}).
\end{equation} In general, the integral cohomology of ![]() $K_{P,S}$ may have p-torsion for arbitrary p > 1, and hence it is not easy to compute. Furthermore, the torsion of
$K_{P,S}$ may have p-torsion for arbitrary p > 1, and hence it is not easy to compute. Furthermore, the torsion of ![]() $H^\ast(K_{P,S};\mathbb{Z})$ influences the torsion of
$H^\ast(K_{P,S};\mathbb{Z})$ influences the torsion of ![]() $H^\ast(X^{\mathbb{R}}_P;\mathbb{Z})$.
$H^\ast(X^{\mathbb{R}}_P;\mathbb{Z})$.
Theorem 3.2. ([Reference Cai and Choi5])
Let P be a smooth polytope of dimension n and ![]() $X^{\mathbb{R}}_P$ the projective smooth real toric variety associated with P. Then the integral cohomology of
$X^{\mathbb{R}}_P$ the projective smooth real toric variety associated with P. Then the integral cohomology of ![]() $X^{\mathbb{R}}_P$ is completely determined by the reduced cohomology group of
$X^{\mathbb{R}}_P$ is completely determined by the reduced cohomology group of ![]() $K_{P,S}$ (for
$K_{P,S}$ (for ![]() $S\subset [n]$) and the h-vector of P. Moreover, the following are equivalent:
$S\subset [n]$) and the h-vector of P. Moreover, the following are equivalent:
(1)
 $H^\ast(X^{\mathbb{R}}_P;\mathbb{Z})$ has no p-torsion for every p > 2.
$H^\ast(X^{\mathbb{R}}_P;\mathbb{Z})$ has no p-torsion for every p > 2.(2)
 $\widetilde{H}^\ast(K_{P,S};\mathbb{Z})$ is torsion-free for every
$\widetilde{H}^\ast(K_{P,S};\mathbb{Z})$ is torsion-free for every  $S\subset [n]$.
$S\subset [n]$.
See Theorem 1.1 and Corollary 1.2 of [Reference Cai and Choi5] for more details of the above theorem.
3.2. Real toric variety arising from a graph
Given a graph G, the pseudograph associahedron PG is first introduced in [Reference Carr, Devadoss and Forcey7] as a generalization of a graph associahedron in [Reference Carr and Devadoss6]. In this paper, we use the construction of a pseudograph associahedron in [Reference Choi, Park and Park8], slightly different from [Reference Carr, Devadoss and Forcey7]. When G is connected, our pseudograph associahedron PG is the same as the pseudograph associahedron ![]() $\mathcal{K}G$ in [Reference Carr, Devadoss and Forcey7], but if G is disconnected, we get a different polytope. In our constructon, if G consists of connected components
$\mathcal{K}G$ in [Reference Carr, Devadoss and Forcey7], but if G is disconnected, we get a different polytope. In our constructon, if G consists of connected components ![]() $G_1,\dots,G_k$, then PG is defined to be the product
$G_1,\dots,G_k$, then PG is defined to be the product ![]() $P_{G_1}\times\dots\times P_{G_k}.$Footnote 2 We introduce the construction of PG briefly.
$P_{G_1}\times\dots\times P_{G_k}.$Footnote 2 We introduce the construction of PG briefly.
For a graph G, we label the vertices and the multiple edges of G. We write a subgraph H of G as the set of the vertices of H and the edges of H in a bundle of G. For simplicity, we omit the braces and commas to represent a subset of ![]() $\mathcal{C}_G$ and we always denote it in a way that the vertices precede the multiple edges. We say that a subgraph H of G is induced (respectively, semi-induced) if H is a subgraph that includes all edges (respectively, at least one edge) between every pair of vertices in H, if such edges exist in G. For instance, in Figure 3.1, the four subgraphs
$\mathcal{C}_G$ and we always denote it in a way that the vertices precede the multiple edges. We say that a subgraph H of G is induced (respectively, semi-induced) if H is a subgraph that includes all edges (respectively, at least one edge) between every pair of vertices in H, if such edges exist in G. For instance, in Figure 3.1, the four subgraphs ![]() $12a, 12b, 123a, 123b$ are semi-induced but not induced subgraphs of G. It should be noted that our set expression makes sense for a semi-induced subgraph because semi-induced subgraphs of a given graph G can be distinguishable by the corresponding set.
$12a, 12b, 123a, 123b$ are semi-induced but not induced subgraphs of G. It should be noted that our set expression makes sense for a semi-induced subgraph because semi-induced subgraphs of a given graph G can be distinguishable by the corresponding set.

Figure 3.1. The proper connected semi-induced subgraphs of G and the facets of PG
We remark that when we consider a subgraph H of a graph G, the labels of H are inherited from the labels of G. Thus, if a graph H is considered as a subgraph of a graph G, then H may have a labelled simple edge, which is not in a bundle of H (actually, it is in a bundle of G). Note that for the graph G in Figure 3.1, 12a and 12b are different objects if they are considered as semi-induced subgraphs of G.
Let G be a connected graph on the vertex set ![]() $V=[n]$ and with exactly k bundles
$V=[n]$ and with exactly k bundles ![]() $B_1,\dots, B_k$. Let
$B_1,\dots, B_k$. Let ![]() $\Delta_V$ be the simplex
$\Delta_V$ be the simplex ![]() $\Delta^{|V|-1}$ whose facets are labelled with the vertices of G. Then each face of
$\Delta^{|V|-1}$ whose facets are labelled with the vertices of G. Then each face of ![]() $\Delta_V$ corresponds to a proper subset of vertices of G, defined by the intersection of the facets associated with those vertices.Footnote 3 For each
$\Delta_V$ corresponds to a proper subset of vertices of G, defined by the intersection of the facets associated with those vertices.Footnote 3 For each ![]() $i=1,\ldots,k$, let
$i=1,\ldots,k$, let ![]() $\Delta_{B_i}$ be the simplex
$\Delta_{B_i}$ be the simplex ![]() $\Delta^{|B_i|-1}$ whose vertices are labelled with the multiple edges in Bi. Then each face of
$\Delta^{|B_i|-1}$ whose vertices are labelled with the multiple edges in Bi. Then each face of ![]() $\Delta_{B_i}$ corresponds to a subset of Bi defined by the vertices spanning the face.Footnote 4 Now we define
$\Delta_{B_i}$ corresponds to a subset of Bi defined by the vertices spanning the face.Footnote 4 Now we define ![]() $\Delta_G$ as the product of simplices
$\Delta_G$ as the product of simplices
endowed with the labels naturally induced from the labelling on ![]() $\Delta_V$ and
$\Delta_V$ and ![]() $\Delta_{B_i}$ (
$\Delta_{B_i}$ (![]() $1\leq i\leq k$). Then the pseudograph associahedron PG is obtained from
$1\leq i\leq k$). Then the pseudograph associahedron PG is obtained from ![]() $\Delta_G$ by truncating the faces corresponding to the proper connected semi-induced subgraphs of G in increasing order of dimension.Footnote 5 See Figure 3.1. Then the following hold:
$\Delta_G$ by truncating the faces corresponding to the proper connected semi-induced subgraphs of G in increasing order of dimension.Footnote 5 See Figure 3.1. Then the following hold:
(1) There is a one-to-one correspondence between the facets FI of PG and the proper connected semi-induced subgraphs I of G.
(2) Two facets FH and
 $F_{H^{\prime}}$ of PG intersect if and only if H and Hʹ are disjoint and cannot be connected by an edge of G, or one contains the other.
$F_{H^{\prime}}$ of PG intersect if and only if H and Hʹ are disjoint and cannot be connected by an edge of G, or one contains the other.
If ![]() $G_1,\ldots,G_\ell$ are the connected components of G, then
$G_1,\ldots,G_\ell$ are the connected components of G, then ![]() $P_G=P_{G_1}\times\cdots\times P_{G_\ell}$ and the dimension of PG is
$P_G=P_{G_1}\times\cdots\times P_{G_\ell}$ and the dimension of PG is
 \begin{equation*}
\dim P_{G}=|V(G)|-\ell+\sum_{i=1}^k(|B_i|-1),
\end{equation*}
\begin{equation*}
\dim P_{G}=|V(G)|-\ell+\sum_{i=1}^k(|B_i|-1),
\end{equation*}where Bi’s are all the bundles of G. See [Reference Choi, Park and Park8, §2], where the readers may find examples, definitions and a much more detailed account of results for pseudograph associahedra.
Note that
• a product of smooth polytopes is a smooth polytope,
• any face of a smooth polytope is a smooth polytope, and
• for a smooth polytope P and a proper face F, there is a canonical truncation of P along F such that the result is a smooth polytope. (See [Reference Choi, Park and Park8, Lemma 2.5].)
For a connected graph G, since ![]() $\Delta_G$ is a smooth polytope, the pseudograph associahedron PG can be realized as a smooth polytope canonically. In particular, the normal vector of the facet corresponding to a proper connected semi-induced subgraph H of G is determined by the label of H. Hence, under the canonical smooth realization, we get the projective smooth toric variety
$\Delta_G$ is a smooth polytope, the pseudograph associahedron PG can be realized as a smooth polytope canonically. In particular, the normal vector of the facet corresponding to a proper connected semi-induced subgraph H of G is determined by the label of H. Hence, under the canonical smooth realization, we get the projective smooth toric variety ![]() $X_G:=X_{P_G}$ and the projective smooth real toric variety
$X_G:=X_{P_G}$ and the projective smooth real toric variety  $X^{\mathbb{R}}_G:=X_{P_G}^{\mathbb{R}}$, associated with a graph G. For example, it is known that if G is the simple path graph P 3, then the polytope PG is a pentagon. Hence, XG is
$X^{\mathbb{R}}_G:=X_{P_G}^{\mathbb{R}}$, associated with a graph G. For example, it is known that if G is the simple path graph P 3, then the polytope PG is a pentagon. Hence, XG is ![]() $\mathbb{C} P^2\#2\overline{\mathbb{C} P^2}$, obtained from
$\mathbb{C} P^2\#2\overline{\mathbb{C} P^2}$, obtained from ![]() $\mathbb{C} P^2$ by blowing up two fixed points;
$\mathbb{C} P^2$ by blowing up two fixed points; ![]() $X^{\mathbb{R}}_G$ is
$X^{\mathbb{R}}_G$ is ![]() $\#3\mathbb{R}P^2$, the connected sum of three copies of the real projective plane
$\#3\mathbb{R}P^2$, the connected sum of three copies of the real projective plane ![]() $\mathbb{R}P^2$. If G is the graph with two vertices and two multiple edges, then XG is
$\mathbb{R}P^2$. If G is the graph with two vertices and two multiple edges, then XG is ![]() $\mathbb{C} P^1\times \mathbb{C} P^1$ and
$\mathbb{C} P^1\times \mathbb{C} P^1$ and ![]() $X_G^{\mathbb{R}}$ is
$X_G^{\mathbb{R}}$ is ![]() $\mathbb{R} P^1\times \mathbb{R} P^1$.Footnote 6
$\mathbb{R} P^1\times \mathbb{R} P^1$.Footnote 6
3.3. A poset of even subgraphs
For a graph G, a graph H is a partial underlying graph of G if H can be obtained from G by replacing some bundles with simple edges, that is, the set of all the bundles of H is a subset of G. A graph H is a partial underlying induced graph (PI-graph for short) of G if H is an induced subgraph of some partial underlying graph of G. Note that a graph is a PI-graph of itself. For instance, for the graph G with two bundles ![]() $\{a,b\}$ and
$\{a,b\}$ and ![]() $\{c,d,e\}$ in Figure 3.2,
$\{c,d,e\}$ in Figure 3.2,
•
 $H_1, H_2$ and H 3 are partial underlying graphs of G, and
$H_1, H_2$ and H 3 are partial underlying graphs of G, and• all Hi’s are PI-graphs of G.

Figure 3.2. Examples for PI-graphs of G and the posets ![]() $\mathcal{P}_{H,A}^{\mathrm{even}}$.
$\mathcal{P}_{H,A}^{\mathrm{even}}$.
For a graph G, we let ![]() $\mathcal{C}_G$ be the set of all labels of G, i.e.,
$\mathcal{C}_G$ be the set of all labels of G, i.e., ![]() $\mathcal{C}_G=V(G)\cup B_1\cup \cdots \cup B_k$, where
$\mathcal{C}_G=V(G)\cup B_1\cup \cdots \cup B_k$, where ![]() $B_1,\ldots,B_k$ are the bundles of G. For instance,
$B_1,\ldots,B_k$ are the bundles of G. For instance, ![]() $\mathcal{C}_G=\{1,2,3,4,a,b,c,d,e\} $ and
$\mathcal{C}_G=\{1,2,3,4,a,b,c,d,e\} $ and ![]() $\mathcal{C}_{H_3}=\{1,2,3,4,c,d,e\}$ for the graphs G and H 3 in Figure 3.2.
$\mathcal{C}_{H_3}=\{1,2,3,4,c,d,e\}$ for the graphs G and H 3 in Figure 3.2.
Definition 3.3. For a graph H, a subset A of ![]() $\mathcal{C}_H$ is called an admissible collection of H if
$\mathcal{C}_H$ is called an admissible collection of H if ![]() $|A\cap V(H^{\prime})|\equiv 0\pmod{2}$ for every connected component Hʹ of H with the following properties:
$|A\cap V(H^{\prime})|\equiv 0\pmod{2}$ for every connected component Hʹ of H with the following properties:
(1) each vertex that is incident to only simple edges of H is contained in A, and
(2)
 $B\cap A\neq \emptyset$ and
$B\cap A\neq \emptyset$ and  $|B\cap A|\equiv 0\pmod{2}$ for each bundle B of H.
$|B\cap A|\equiv 0\pmod{2}$ for each bundle B of H.
Let ![]() $\mathcal{A}(H)$ denote the set of all the admissible collections of H. The set of admissible collections each of the graphs Hi’s in Figure 3.2 are as follows:
$\mathcal{A}(H)$ denote the set of all the admissible collections of H. The set of admissible collections each of the graphs Hi’s in Figure 3.2 are as follows:
 \begin{equation*}\begin{array}{lll}
\mathcal{A}(H_1)=\{1234\}, &\mathcal{A}(H_2)=\{34ab, 1234ab\},&\mathcal{A}(H_3)=\left\{14cd, 14ce, 14de, 1234cd,\right.\\
&& \qquad \qquad \left.1234ce, 1234de\right\},\\
\mathcal{A}(H_4)=\emptyset, &\mathcal{A}(H_5)=\{13ab, 23ab\},
&\mathcal{A}(H_6)=\left\{12cd, 12ce, 12de, 13cd,\right.\\
&& \qquad \qquad \left. 13ce, 13de\right\},\\
\end{array}\end{equation*}
\begin{equation*}\begin{array}{lll}
\mathcal{A}(H_1)=\{1234\}, &\mathcal{A}(H_2)=\{34ab, 1234ab\},&\mathcal{A}(H_3)=\left\{14cd, 14ce, 14de, 1234cd,\right.\\
&& \qquad \qquad \left.1234ce, 1234de\right\},\\
\mathcal{A}(H_4)=\emptyset, &\mathcal{A}(H_5)=\{13ab, 23ab\},
&\mathcal{A}(H_6)=\left\{12cd, 12ce, 12de, 13cd,\right.\\
&& \qquad \qquad \left. 13ce, 13de\right\},\\
\end{array}\end{equation*} Let ![]() $A\subset \mathcal{C}_H$. We say that a semi-induced subgraph I of H is A-even (respectively, A-odd) if
$A\subset \mathcal{C}_H$. We say that a semi-induced subgraph I of H is A-even (respectively, A-odd) if ![]() $|A\cap I^{\prime}|$ is even (respectively, odd) for every connected component Iʹ of I.Footnote 7 Then we define the poset
$|A\cap I^{\prime}|$ is even (respectively, odd) for every connected component Iʹ of I.Footnote 7 Then we define the poset ![]() $\mathcal{P}_{H,A}^{\mathrm{even}}$ as follows. If
$\mathcal{P}_{H,A}^{\mathrm{even}}$ as follows. If ![]() $A \in \mathcal{A}(H)$, then the poset
$A \in \mathcal{A}(H)$, then the poset ![]() $\mathcal{P}_{H,A}^{\mathrm{even}}$ is defined to be the poset consisting of all A-even semi-induced subgraphs of H ordered by the subgraph containment, including both
$\mathcal{P}_{H,A}^{\mathrm{even}}$ is defined to be the poset consisting of all A-even semi-induced subgraphs of H ordered by the subgraph containment, including both ![]() $\emptyset$ and H. Hence,
$\emptyset$ and H. Hence, ![]() $\mathcal{P}_{H,A}^{\mathrm{even}}$ is a bounded poset. If
$\mathcal{P}_{H,A}^{\mathrm{even}}$ is a bounded poset. If ![]() $A\not \in \mathcal{A}(H)$, then we define
$A\not \in \mathcal{A}(H)$, then we define ![]() $\mathcal{P}_{H,A}^{\mathrm{even}}$ by the null poset. Figure 3.2 shows (the Hasse diagram of) the posets
$\mathcal{P}_{H,A}^{\mathrm{even}}$ by the null poset. Figure 3.2 shows (the Hasse diagram of) the posets  $\mathcal{P}_{H_1,1234}^{\mathrm{even}}, \mathcal{P}_{H_2,1234ab}^{\mathrm{even}}$ and
$\mathcal{P}_{H_1,1234}^{\mathrm{even}}, \mathcal{P}_{H_2,1234ab}^{\mathrm{even}}$ and  $\mathcal{P}_{H_3,1234cd}^{\mathrm{even}}$. Note that the first two posets are shellable but the last is not. For more examples of
$\mathcal{P}_{H_3,1234cd}^{\mathrm{even}}$. Note that the first two posets are shellable but the last is not. For more examples of ![]() $\mathcal{P}_{H,A}^\mathrm{even}$, see also Figure 5.3.
$\mathcal{P}_{H,A}^\mathrm{even}$, see also Figure 5.3.
Combining Lemma 4.5 with Proposition 4.7 of [Reference Choi, Park and Park8], it holds the following.
Proposition 3.4. ([Reference Choi, Park and Park8])
Let G be a graph.
(1) For every subset S in the set of integers
 $\{1,2,\dots,\dim P_{G}\}$, the simplicial complex
$\{1,2,\dots,\dim P_{G}\}$, the simplicial complex  $K_{P_G,S}$ is contractible or there exist a PI-graph H of G and
$K_{P_G,S}$ is contractible or there exist a PI-graph H of G and  $A\in\mathcal{A}(H)$ such that
$A\in\mathcal{A}(H)$ such that  $K_{P_G,S}$ is homotopy equivalent to the order complex of the proper part of
$K_{P_G,S}$ is homotopy equivalent to the order complex of the proper part of  $\mathcal{P}^\mathrm{odd}_{H,A}$.
$\mathcal{P}^\mathrm{odd}_{H,A}$.(2) The ith Betti number of
 $X_G^{\mathbb{R}}$ is
$X_G^{\mathbb{R}}$ is
 \begin{equation*}
\beta^{i}(X^{\mathbb{R}}_G) = \sum_{H:\text{PI-graph}\atop\text{of }G}\sum_{A\in\mathcal{A}(H)} \tilde{\beta}^{i-1}\left(\Delta\left(\overline{\mathcal{P}_{H,A}^{\mathrm{odd}}}\right)\right).
\end{equation*}
\begin{equation*}
\beta^{i}(X^{\mathbb{R}}_G) = \sum_{H:\text{PI-graph}\atop\text{of }G}\sum_{A\in\mathcal{A}(H)} \tilde{\beta}^{i-1}\left(\Delta\left(\overline{\mathcal{P}_{H,A}^{\mathrm{odd}}}\right)\right).
\end{equation*}
For the sake of convenience, we put a sketch of the proof of Proposition 3.4 in Appendix.
For a graph H, it was also noted in [Reference Choi, Park and Park8, §5] that  $\Delta(\overline{\mathcal{P}_{H,A}^{\mathrm{even}}})$ (respectively,
$\Delta(\overline{\mathcal{P}_{H,A}^{\mathrm{even}}})$ (respectively,  $\Delta(\overline{\mathcal{P}_{H,A}^{\mathrm{odd}}})$) is a geometric subdivision of the simplicial complex dual to the union of the facets FI of the polytope PH such that
$\Delta(\overline{\mathcal{P}_{H,A}^{\mathrm{odd}}})$) is a geometric subdivision of the simplicial complex dual to the union of the facets FI of the polytope PH such that ![]() $|I\cap A|$ is even (respectively, odd). Hence, from the Alexander duality, we have
$|I\cap A|$ is even (respectively, odd). Hence, from the Alexander duality, we have
 \begin{equation}
\widetilde{H}^{i}\left(\Delta\left(\overline{\mathcal{P}_{H,A}^{\mathrm{odd}}}\right);\mathbb{Z}\right) \cong\widetilde{H}_{\dim(P_H)-i-2}\left(\Delta\left(\overline{\mathcal{P}_{H,A}^{\mathrm{even}}}\right);\mathbb{Z}\right).
\end{equation}
\begin{equation}
\widetilde{H}^{i}\left(\Delta\left(\overline{\mathcal{P}_{H,A}^{\mathrm{odd}}}\right);\mathbb{Z}\right) \cong\widetilde{H}_{\dim(P_H)-i-2}\left(\Delta\left(\overline{\mathcal{P}_{H,A}^{\mathrm{even}}}\right);\mathbb{Z}\right).
\end{equation} Therefore, if ![]() $K_{P_G,S}$ is homotopy equivalent to
$K_{P_G,S}$ is homotopy equivalent to  $\Delta(\overline{\mathcal{P}_{H,A}^{\mathrm{odd}}})$ and
$\Delta(\overline{\mathcal{P}_{H,A}^{\mathrm{odd}}})$ and ![]() $\mathcal{P}_{H,A}^{\mathrm{even}}$ is shellable, then
$\mathcal{P}_{H,A}^{\mathrm{even}}$ is shellable, then  $\widetilde{H}^\ast(K_{P_G,S};\mathbb{Z})$ is torsion-free.
$\widetilde{H}^\ast(K_{P_G,S};\mathbb{Z})$ is torsion-free.
Let H be a simple graph. Then ![]() $\mathcal{A}(H)=\{H\}$ if each connected component of H has an even number of vertices, and
$\mathcal{A}(H)=\{H\}$ if each connected component of H has an even number of vertices, and ![]() $\mathcal{A}(H)=\emptyset$ otherwise. Thus, we write
$\mathcal{A}(H)=\emptyset$ otherwise. Thus, we write ![]() $\mathcal{P}_H^{\mathrm{even}}$ instead of
$\mathcal{P}_H^{\mathrm{even}}$ instead of ![]() $\mathcal{P}_{H,H}^{\mathrm{even}}$.
$\mathcal{P}_{H,H}^{\mathrm{even}}$.
Theorem 3.5. ([Reference Choi and Park9, Proposition 4.9])
For a simple graph H, ![]() $\mathcal{P}_H^{\mathrm{even}}$ is pure and totally semimodular, so it is shellable.
$\mathcal{P}_H^{\mathrm{even}}$ is pure and totally semimodular, so it is shellable.
Recall that a pure and totally semimodular poset is CL-shellable by Theorem 2.1-(3). Hence, ![]() $\mathcal{P}_H^{\mathrm{even}}$ is CL-shellable for every simple graph H.
$\mathcal{P}_H^{\mathrm{even}}$ is CL-shellable for every simple graph H.
In [Reference Choi, Park and Park8], there was an effort to extend results of [Reference Choi and Park9] for a simple graph to a graph allowing multiple edges. Almost all results of [Reference Choi and Park9] except for Theorem 3.5 were well-extended by using ![]() $\mathcal{P}_{H,A}^{\mathrm{even}}$, where H is a PI-graph of G and
$\mathcal{P}_{H,A}^{\mathrm{even}}$, where H is a PI-graph of G and ![]() $A\in\mathcal{A}(H)$. In fact, since the poset
$A\in\mathcal{A}(H)$. In fact, since the poset  $\mathcal{P}_{H_3,1234cd}^{\mathrm{even}}$ in Figure 3.2 is not shellable, Theorem 3.5 cannot be generalized to
$\mathcal{P}_{H_3,1234cd}^{\mathrm{even}}$ in Figure 3.2 is not shellable, Theorem 3.5 cannot be generalized to ![]() $\mathcal{P}_{H,A}^{\mathrm{even}}$. Hence, it is natural to ask which
$\mathcal{P}_{H,A}^{\mathrm{even}}$. Hence, it is natural to ask which ![]() $\mathcal{P}_{H,A}^{\mathrm{even}}$ is shellable. Taking an interest in a projective smooth real toric variety associated with a graph, the following Question 1.2 was asked in [Reference Choi, Park and Park8]. For a graph G, let
$\mathcal{P}_{H,A}^{\mathrm{even}}$ is shellable. Taking an interest in a projective smooth real toric variety associated with a graph, the following Question 1.2 was asked in [Reference Choi, Park and Park8]. For a graph G, let ![]() $\mathcal{A}^\ast(G)=\{(H,A)\mid H \text{is a PI-graph of $G$ and }A\in \mathcal{A}(H) \}.$
$\mathcal{A}^\ast(G)=\{(H,A)\mid H \text{is a PI-graph of $G$ and }A\in \mathcal{A}(H) \}.$
Question 1.2. ([Reference Choi, Park and Park8]) Find all graphs G such that ![]() $\mathcal{P}_{H,A}^{\mathrm{even}}$ is shellable for every
$\mathcal{P}_{H,A}^{\mathrm{even}}$ is shellable for every ![]() $(H,A) \in \mathcal{A}^{\ast}(G)$.
$(H,A) \in \mathcal{A}^{\ast}(G)$.
For simplicity, throughout the paper, let ![]() $\mathcal{G}^{\ast}$ be the family of all graphs G such that
$\mathcal{G}^{\ast}$ be the family of all graphs G such that ![]() $\mathcal{P}_{H,A}^{\mathrm{even}}$ is shellable for every
$\mathcal{P}_{H,A}^{\mathrm{even}}$ is shellable for every ![]() $(H,A) \in \mathcal{A}^{\ast}(G)$. Clearly, the family
$(H,A) \in \mathcal{A}^{\ast}(G)$. Clearly, the family ![]() $\mathcal{G}^\ast$ contains all simple graphs by Theorem 3.5. The answer to Question 1.2 is the following, which restates Theorem 1.3.
$\mathcal{G}^\ast$ contains all simple graphs by Theorem 3.5. The answer to Question 1.2 is the following, which restates Theorem 1.3.
Theorem 1.3. A graph G is in ![]() $\mathcal{G}^*$ if and only if each connected component of G is either a simple graph or one of the graphs in Figure 1.1.
$\mathcal{G}^*$ if and only if each connected component of G is either a simple graph or one of the graphs in Figure 1.1.
By Theorem 1.3, for every ![]() $G\in\mathcal{G}^\ast$, each poset
$G\in\mathcal{G}^\ast$, each poset ![]() $\mathcal{P}_{H,A}^{\mathrm{even}}$ is shellable, and hence
$\mathcal{P}_{H,A}^{\mathrm{even}}$ is shellable, and hence  $\Delta(\overline{\mathcal{P}_{H,A}^{\mathrm{even}}})$ is homotopy equivalent to a wedge of spheres. Thus,
$\Delta(\overline{\mathcal{P}_{H,A}^{\mathrm{even}}})$ is homotopy equivalent to a wedge of spheres. Thus,  $\widetilde{H}^\ast(K_{P_G,S};\mathbb{Z})$ is torsion-free for every subset S of the set of integers
$\widetilde{H}^\ast(K_{P_G,S};\mathbb{Z})$ is torsion-free for every subset S of the set of integers ![]() $\{1,2,\dots,\dim P_{G}\}$, and we get the following from [Reference Cai and Choi5, Corollary 1.2].
$\{1,2,\dots,\dim P_{G}\}$, and we get the following from [Reference Cai and Choi5, Corollary 1.2].
Corollary 3.6. For a graph ![]() $G\in\mathcal{G}^\ast$, the integral cohomology of the projective smooth real toric variety
$G\in\mathcal{G}^\ast$, the integral cohomology of the projective smooth real toric variety ![]() $X^{\mathbb{R}}_G$ is torsion-free or has only 2-torsion elements:
$X^{\mathbb{R}}_G$ is torsion-free or has only 2-torsion elements:
 \begin{equation*}H^i\left(X^{\mathbb{R}}_G;\mathbb{Z}\right)=\mathbb{Z}^{\beta^i}\oplus\mathbb{Z}_2^{h_i-\beta^i},\end{equation*}
\begin{equation*}H^i\left(X^{\mathbb{R}}_G;\mathbb{Z}\right)=\mathbb{Z}^{\beta^i}\oplus\mathbb{Z}_2^{h_i-\beta^i},\end{equation*} where ![]() $\beta^i=\beta^i(X^{\mathbb{R}}_G)$ and
$\beta^i=\beta^i(X^{\mathbb{R}}_G)$ and ![]() $h_i=h_i(P_G)$.
$h_i=h_i(P_G)$.
As an immediate consequence of the proof in §5, we also get the following:
Theorem 3.7. For every ![]() $G\in \mathcal{G}^\ast$, each
$G\in \mathcal{G}^\ast$, each ![]() $\mathcal{P}_{H,A}^{\mathrm{even}}$ is CL-shellable for every
$\mathcal{P}_{H,A}^{\mathrm{even}}$ is CL-shellable for every ![]() $(H,A)\in\mathcal{A}^{\ast}(G)$.
$(H,A)\in\mathcal{A}^{\ast}(G)$.
We finish the section by giving a remark that it is sufficient to consider a connected graph to prove Theorem 1.3 and Theorem 3.7. To see why, let ![]() $G_1, \ldots, G_k$ be the connected components of a graph G. Note that for a subgraph H of G and
$G_1, \ldots, G_k$ be the connected components of a graph G. Note that for a subgraph H of G and ![]() $A\in\mathcal{C}_H, (H,A)\in\mathcal{A}^{\ast}(G)$ if and only if
$A\in\mathcal{C}_H, (H,A)\in\mathcal{A}^{\ast}(G)$ if and only if ![]() $(H\cap G_i, A\cap \mathcal{C}_{G_i})\in \mathcal{A}^\ast(G_i)$ for each i. Thus, for each
$(H\cap G_i, A\cap \mathcal{C}_{G_i})\in \mathcal{A}^\ast(G_i)$ for each i. Thus, for each ![]() $(H,A)\in\mathcal{A}^{\ast}(G)$,
$(H,A)\in\mathcal{A}^{\ast}(G)$, ![]() $\mathcal{P}_{H,A}^{\mathrm{even}}$ is isomorphic to the product
$\mathcal{P}_{H,A}^{\mathrm{even}}$ is isomorphic to the product  $\mathcal{P}_{H_1,A_1}^{\mathrm{even}}\times \cdots \times \mathcal{P}_{H_k,A_k}^{\mathrm{even}}$, where
$\mathcal{P}_{H_1,A_1}^{\mathrm{even}}\times \cdots \times \mathcal{P}_{H_k,A_k}^{\mathrm{even}}$, where ![]() $H_i=H\cap G_i$ and
$H_i=H\cap G_i$ and ![]() $A_i=A\cap \mathcal{C}_{G_i}$ for each i. By (2) of Theorem 2.1,
$A_i=A\cap \mathcal{C}_{G_i}$ for each i. By (2) of Theorem 2.1, ![]() $\mathcal{P}_{H,A}^{\mathrm{even}}$ is shellable if and only if
$\mathcal{P}_{H,A}^{\mathrm{even}}$ is shellable if and only if  $\mathcal{P}_{H_i,A_i}^{\mathrm{even}}$ is shellable for each i. Thus,
$\mathcal{P}_{H_i,A_i}^{\mathrm{even}}$ is shellable for each i. Thus, ![]() $G\in \mathcal{G}^\ast$ if and only if
$G\in \mathcal{G}^\ast$ if and only if ![]() $G_i\in \mathcal{G}^\ast$ for each i.
$G_i\in \mathcal{G}^\ast$ for each i.
4. Graphs that admit a non-shellable poset  $\mathcal{P}_{H,A}^{\mathrm{even}}$
$\mathcal{P}_{H,A}^{\mathrm{even}}$
In this section, we give the ‘only if’ part of Theorem 1.3. We will see that almost all graphs do not belong to the family ![]() $\mathcal{G}^{\ast}$. The result of this section is based on the following basic observation.
$\mathcal{G}^{\ast}$. The result of this section is based on the following basic observation.
Lemma 4.1. Let ![]() $\mathcal{P}_0$ be the poset in Figure 4.1 and let
$\mathcal{P}_0$ be the poset in Figure 4.1 and let ![]() $\mathcal{Q}$ be any subposet that has at least two chains of length 3, with one containing a or b and another containing aʹ or bʹ. Then
$\mathcal{Q}$ be any subposet that has at least two chains of length 3, with one containing a or b and another containing aʹ or bʹ. Then ![]() $\mathcal{Q}$ is not shellable.
$\mathcal{Q}$ is not shellable.

Figure 4.1. The poset ![]() $\mathcal{P}_0$.
$\mathcal{P}_0$.
Theorem 4.2. Let G be a connected non-simple graph in ![]() $\mathcal{G}^\ast$. Then G is one of the graphs in Figure 1.1.
$\mathcal{G}^\ast$. Then G is one of the graphs in Figure 1.1.
Before starting the proof, recall that we often drop the braces and commas to denote a subset of ![]() $\mathcal{C}_G$.
$\mathcal{C}_G$.
Proof. Suppose that G is a connected non-simple graph in ![]() $\mathcal{G}^\ast$. If
$\mathcal{G}^\ast$. If ![]() $|V(G)|=2$, then
$|V(G)|=2$, then  $G=\widetilde{P}_{2,m}$ in Figure 1.1 for some m. Assume that
$G=\widetilde{P}_{2,m}$ in Figure 1.1 for some m. Assume that ![]() $|V(G)|\ge 3$ and G has a bundle B whose endpoints are 1 and 2.
$|V(G)|\ge 3$ and G has a bundle B whose endpoints are 1 and 2.
Claim 4.3.
The graph G has exactly one bundle B.
Proof of Claim 4.3
Suppose that G has a bundle Bʹ other than B. Take a shortest path in G whose starting vertex is an endpoint of B and whose terminal vertex is an endpoint of Bʹ. We denote the path by Q. Note that Q does not contain a multiple edge. Let ![]() $Q:=(v_1,\ldots, v_k)$, where
$Q:=(v_1,\ldots, v_k)$, where ![]() $k\ge 1$, and let
$k\ge 1$, and let ![]() $v_1=2$ without loss of generality. Let H be a PI-graph of G such that
$v_1=2$ without loss of generality. Let H be a PI-graph of G such that ![]() $V(H)=V(Q)\cup\{1,2\}\cup\{\text{endpoints of }B^{\prime}\}$ and H has exactly two bundles B and Bʹ. Let
$V(H)=V(Q)\cup\{1,2\}\cup\{\text{endpoints of }B^{\prime}\}$ and H has exactly two bundles B and Bʹ. Let ![]() $a,b\in B$ and
$a,b\in B$ and ![]() $a^{\prime},b^{\prime}\in B^{\prime}$.
$a^{\prime},b^{\prime}\in B^{\prime}$.
(Case 1) Suppose that k = 1. Then ![]() $|V(H)|=3$, so we set
$|V(H)|=3$, so we set ![]() $V(H)=\{1,2,3\}$. Then
$V(H)=\{1,2,3\}$. Then ![]() $A:=23aba^{\prime}b^{\prime}$ belongs to
$A:=23aba^{\prime}b^{\prime}$ belongs to ![]() $\mathcal{A}(H)$. Setting
$\mathcal{A}(H)$. Setting ![]() $I=123aba^{\prime}b^{\prime}$ (the dashed edge in Figure 4.2 is a simple edge or does not exist), we see
$I=123aba^{\prime}b^{\prime}$ (the dashed edge in Figure 4.2 is a simple edge or does not exist), we see ![]() $I\cap A=A$, and hence I is an element of
$I\cap A=A$, and hence I is an element of ![]() $\mathcal{P}_{H,A}^{\mathrm{even}}$. Let
$\mathcal{P}_{H,A}^{\mathrm{even}}$. Let ![]() $I^{\prime}=1$ and consider the interval
$I^{\prime}=1$ and consider the interval ![]() $\mathcal{I}=[I^{\prime},I]$ of
$\mathcal{I}=[I^{\prime},I]$ of ![]() $\mathcal{P}_{H,A}^{\mathrm{even}}$, see Figure 4.2. Then
$\mathcal{P}_{H,A}^{\mathrm{even}}$, see Figure 4.2. Then ![]() $\mathcal{I}$ is isomorphic to a subposet of
$\mathcal{I}$ is isomorphic to a subposet of ![]() $\mathcal{P}_0$ in Figure 4.1. By Lemma 4.1,
$\mathcal{P}_0$ in Figure 4.1. By Lemma 4.1, ![]() $\mathcal{I}$ is not shellable, a contradiction to (1) of Theorem 2.1.
$\mathcal{I}$ is not shellable, a contradiction to (1) of Theorem 2.1.

Figure 4.2. A graph I and the interval ![]() $\mathcal{I}$.
$\mathcal{I}$.
(Case 2) Suppose that ![]() $k\ge 2$. Let the endpoints of Bʹ be labelled by 3 and 4, and
$k\ge 2$. Let the endpoints of Bʹ be labelled by 3 and 4, and ![]() $v_k=3$. Let
$v_k=3$. Let
 \begin{equation*}A=\begin{cases}
(V(H)\setminus\{1\}) \cup a b a^{\prime} b^{\prime} &\text{if }k\text{ is odd}; \\
(V(H)\setminus\{1,2\}) \cup aba^{\prime}b^{\prime} &\text{if }k\text{ is even}.\end{cases}\end{equation*}
\begin{equation*}A=\begin{cases}
(V(H)\setminus\{1\}) \cup a b a^{\prime} b^{\prime} &\text{if }k\text{ is odd}; \\
(V(H)\setminus\{1,2\}) \cup aba^{\prime}b^{\prime} &\text{if }k\text{ is even}.\end{cases}\end{equation*} Note that ![]() $A\in\mathcal{A}(H)$. Let
$A\in\mathcal{A}(H)$. Let ![]() $I^{\prime}=V(Q)\setminus\{v_k\}$ and
$I^{\prime}=V(Q)\setminus\{v_k\}$ and ![]() $I=I^{\prime}\cup 134aba^{\prime}b^{\prime}$. Then
$I=I^{\prime}\cup 134aba^{\prime}b^{\prime}$. Then ![]() $I^{\prime}\cap A=\{v_1,\ldots,v_{k-1}\}$ (if k is odd) or
$I^{\prime}\cap A=\{v_1,\ldots,v_{k-1}\}$ (if k is odd) or ![]() $I^{\prime}\cap A=\{v_2,\ldots,v_{k-1}\}$ (if k is even). Then they have the form in Figure 4.3 (the dashed edges are simple edges or do not exist), and both Iʹ and I are elements of
$I^{\prime}\cap A=\{v_2,\ldots,v_{k-1}\}$ (if k is even). Then they have the form in Figure 4.3 (the dashed edges are simple edges or do not exist), and both Iʹ and I are elements of ![]() $\mathcal{P}_{H,A}^{\mathrm{even}}$. Consider the interval
$\mathcal{P}_{H,A}^{\mathrm{even}}$. Consider the interval ![]() $\mathcal{I}=[I^{\prime},I]$ in
$\mathcal{I}=[I^{\prime},I]$ in ![]() $\mathcal{P}_{H,A}^{\mathrm{even}}$, see Figure 4.3. Thus,
$\mathcal{P}_{H,A}^{\mathrm{even}}$, see Figure 4.3. Thus, ![]() $\mathcal{I}$ is isomorphic to a subposet of
$\mathcal{I}$ is isomorphic to a subposet of ![]() $\mathcal{P}_0$ in Figure 4.1. Note that
$\mathcal{P}_0$ in Figure 4.1. Note that ![]() $I^{\prime}\cup 134aa^{\prime}$,
$I^{\prime}\cup 134aa^{\prime}$, ![]() $I^{\prime}\cup 134ab^{\prime}, I^{\prime}\cup 134ba^{\prime}, I^{\prime}\cup 134bb^{\prime}$ are elements in
$I^{\prime}\cup 134ab^{\prime}, I^{\prime}\cup 134ba^{\prime}, I^{\prime}\cup 134bb^{\prime}$ are elements in ![]() $\mathcal{I}$, and both
$\mathcal{I}$, and both ![]() $I^{\prime}\cup 13a$ and
$I^{\prime}\cup 13a$ and ![]() $I^{\prime}\cup 13b$ are also elements in
$I^{\prime}\cup 13b$ are also elements in ![]() $\mathcal{I}$. The elements
$\mathcal{I}$. The elements ![]() $I^{\prime}\cup14a$ and
$I^{\prime}\cup14a$ and ![]() $I^{\prime}\cup 14b$ in the dashed boxes of Figure 4.3 are in
$I^{\prime}\cup 14b$ in the dashed boxes of Figure 4.3 are in ![]() $\mathcal{I}$ if there is an edge between the vertex 4 and a vertex in Iʹ. By Lemma 4.1,
$\mathcal{I}$ if there is an edge between the vertex 4 and a vertex in Iʹ. By Lemma 4.1, ![]() $\mathcal{I}$ is not shellable, a contradiction to (1) of Theorem 2.1.
$\mathcal{I}$ is not shellable, a contradiction to (1) of Theorem 2.1.

Figure 4.3. A graph I and the interval ![]() $\mathcal{I}$ where the dashed boxes may be in
$\mathcal{I}$ where the dashed boxes may be in ![]() $\mathcal{I}$.
$\mathcal{I}$.
Hence, G has only one bundle B. If ![]() $|V(G)|=3$, then clearly G is one of the graphs in Figure 1.1. Now assume that
$|V(G)|=3$, then clearly G is one of the graphs in Figure 1.1. Now assume that ![]() $|V(G)|\ge 4$. For each vertex i, we let
$|V(G)|\ge 4$. For each vertex i, we let ![]() $N^{\ast}(i)=N_G(i)\setminus\{1,2\}$, where
$N^{\ast}(i)=N_G(i)\setminus\{1,2\}$, where ![]() $N_G(i)$ is the set of vertices which are adjacent to i in G.
$N_G(i)$ is the set of vertices which are adjacent to i in G.
Claim 4.4.
![]() $|N^{\ast}(1)\cup N^\ast(2)|= 1$.
$|N^{\ast}(1)\cup N^\ast(2)|= 1$.
Proof of Claim 4.4
Since ![]() $|V(G)|\ge 3$ and G is connected,
$|V(G)|\ge 3$ and G is connected, ![]() $|N^{\ast}(1)\cup N^\ast(2)| \ge 1$. Suppose that
$|N^{\ast}(1)\cup N^\ast(2)| \ge 1$. Suppose that ![]() $|N^{\ast}(1)\cup N^\ast(2)| \ge 2$, and
$|N^{\ast}(1)\cup N^\ast(2)| \ge 2$, and ![]() $ 3,4\in N^{\ast}(1)\cup N^\ast(2)$. Let H be a PI-graph of G such that
$ 3,4\in N^{\ast}(1)\cup N^\ast(2)$. Let H be a PI-graph of G such that ![]() $V(H)=\{1,2,3,4\}$ and H has the bundle B. Let
$V(H)=\{1,2,3,4\}$ and H has the bundle B. Let ![]() $A=1234ab$ for some
$A=1234ab$ for some ![]() $a,b\in B$. Note that
$a,b\in B$. Note that ![]() $A\in\mathcal{A}(H)$. Let
$A\in\mathcal{A}(H)$. Let ![]() $I=1234ab$, and consider the interval
$I=1234ab$, and consider the interval ![]() $\mathcal{I}=[\emptyset, I]$ in
$\mathcal{I}=[\emptyset, I]$ in ![]() $\mathcal{P}_{H,A}^{\mathrm{even}}$, see Figure 4.4. Then I is a subgraph of a complete graph of four vertices with exactly one bundle of size two, and
$\mathcal{P}_{H,A}^{\mathrm{even}}$, see Figure 4.4. Then I is a subgraph of a complete graph of four vertices with exactly one bundle of size two, and ![]() $\mathcal{I}$ is isomorphic to a subposet of
$\mathcal{I}$ is isomorphic to a subposet of ![]() $\mathcal{P}_0$. Note 123a, 123b, 124a and 124b are elements of
$\mathcal{P}_0$. Note 123a, 123b, 124a and 124b are elements of ![]() $\mathcal{I}$. Since the vertex 3 is a neighbour of 1 or 2, at least one of 13 and 23 is an element of
$\mathcal{I}$. Since the vertex 3 is a neighbour of 1 or 2, at least one of 13 and 23 is an element of ![]() $\mathcal{I}$ (the elements 13 and 23 are drawn in a dotted box in Figure 4.4). Similarly, since the vertex 4 is also a neighbour of 1 or 2, at least one of 14 and 24 is an element of
$\mathcal{I}$ (the elements 13 and 23 are drawn in a dotted box in Figure 4.4). Similarly, since the vertex 4 is also a neighbour of 1 or 2, at least one of 14 and 24 is an element of ![]() $\mathcal{I}$ (the elements 14 and 24 are drawn in a dotted box in Figure 4.4). By Lemma 4.1,
$\mathcal{I}$ (the elements 14 and 24 are drawn in a dotted box in Figure 4.4). By Lemma 4.1, ![]() $\mathcal{I}$ is not shellable, a contradiction to (1) of Theorem 2.1.
$\mathcal{I}$ is not shellable, a contradiction to (1) of Theorem 2.1.

Figure 4.4. A graph containing I and the interval ![]() $\mathcal{I}$, where at least one of the elements in each dotted box is in
$\mathcal{I}$, where at least one of the elements in each dotted box is in ![]() $\mathcal{I}$, and the dashed box 34 may be in
$\mathcal{I}$, and the dashed box 34 may be in ![]() $\mathcal{I}$.
$\mathcal{I}$.
From now on, we set ![]() $N^{\ast}(1)\cup N^\ast(2)=N^\ast(2)=\{3\}$.
$N^{\ast}(1)\cup N^\ast(2)=N^\ast(2)=\{3\}$.
Claim 4.5.
For each vertex i other than 1 or 2, let Qi be the shortest path of G from 3 to i. Then
where the equality holds if and only if ![]() $|V(Q_i)|$ is odd and
$|V(Q_i)|$ is odd and ![]() $V(G)=V(Q_i)\cup\{1,2\}\cup N^\ast(i)$.
$V(G)=V(Q_i)\cup\{1,2\}\cup N^\ast(i)$.
Proof of Claim 4.5
Suppose that there is a vertex ![]() $i\in V(G)\setminus\{1,2\}$ satisfying one of the following:
$i\in V(G)\setminus\{1,2\}$ satisfying one of the following:
(1)
 $|N^\ast(i)\setminus V(Q_i) |\ge 3$,
$|N^\ast(i)\setminus V(Q_i) |\ge 3$,(2)
 $|N^\ast(i)\setminus V(Q_i)|=2$ and
$|N^\ast(i)\setminus V(Q_i)|=2$ and  $|V(Q_i)|$ is even, and
$|V(Q_i)|$ is even, and(3)
 $|N^\ast(i)\setminus V(Q_i)|=2, |V(Q_i)|$ is odd, and
$|N^\ast(i)\setminus V(Q_i)|=2, |V(Q_i)|$ is odd, and  $V(G)\neq V(Q_i)\cup\{1,2\}\cup N^\ast(i)$.
$V(G)\neq V(Q_i)\cup\{1,2\}\cup N^\ast(i)$.
If ![]() $|V(Q_i)|$ is even, then it is the case of (1) or (2), so we set
$|V(Q_i)|$ is even, then it is the case of (1) or (2), so we set ![]() $I^{\prime}=Q_i$ and take two vertices x and y in
$I^{\prime}=Q_i$ and take two vertices x and y in ![]() $N^\ast(i)\setminus V(Q_i)$. Suppose that
$N^\ast(i)\setminus V(Q_i)$. Suppose that ![]() $|V(Q_i)|$ is odd. Then it is the case of (1) or (3). In case (1), we take three vertices
$|V(Q_i)|$ is odd. Then it is the case of (1) or (3). In case (1), we take three vertices ![]() $w,x,y\in N^\ast(i)\setminus V(Q_i)$ and set
$w,x,y\in N^\ast(i)\setminus V(Q_i)$ and set ![]() $I^{\prime}=Q_i\cup w$. Otherwise, we take a vertex
$I^{\prime}=Q_i\cup w$. Otherwise, we take a vertex ![]() $w\in N^\ast(i)\setminus V(Q_i)$ and a vertex
$w\in N^\ast(i)\setminus V(Q_i)$ and a vertex ![]() $y\in V(G)\setminus \left( V(Q_i)\cup\{1,2\}\cup N^\ast(i)\right)$ so that
$y\in V(G)\setminus \left( V(Q_i)\cup\{1,2\}\cup N^\ast(i)\right)$ so that ![]() $Q_i\cup wy$ is connected. Then we set
$Q_i\cup wy$ is connected. Then we set ![]() $I^{\prime}=Q_i\cup w$ and take x as a vertex in
$I^{\prime}=Q_i\cup w$ and take x as a vertex in ![]() $N^\ast(i)\setminus V(Q_i)$ other than w. For any case, note that
$N^\ast(i)\setminus V(Q_i)$ other than w. For any case, note that ![]() $3\in I^{\prime}, I^{\prime}\cap\{1,2\}=\emptyset$,
$3\in I^{\prime}, I^{\prime}\cap\{1,2\}=\emptyset$, ![]() $|I^{\prime}|$ is even, and each of Iʹ,
$|I^{\prime}|$ is even, and each of Iʹ, ![]() $I^{\prime}\cup x $ and
$I^{\prime}\cup x $ and ![]() $I^{\prime}\cup y$ is a connected subgraph of G.
$I^{\prime}\cup y$ is a connected subgraph of G.
Let H be a PI-graph such that ![]() $V(H)=I^{\prime} \cup 12xy$ and B is the bundle of H. Let
$V(H)=I^{\prime} \cup 12xy$ and B is the bundle of H. Let ![]() $A=V(H)\cup ab$ and I = A for some
$A=V(H)\cup ab$ and I = A for some ![]() $a,b\in B$. Note that
$a,b\in B$. Note that ![]() $A\in\mathcal{A}(H)$ and I is the graph in the left of Figure 5.1 (the dashed edges are simple edges or do not exist). Consider the interval
$A\in\mathcal{A}(H)$ and I is the graph in the left of Figure 5.1 (the dashed edges are simple edges or do not exist). Consider the interval ![]() $\mathcal{I}=[I^{\prime},I]$ in
$\mathcal{I}=[I^{\prime},I]$ in ![]() $\mathcal{P}_{H,A}^{\mathrm{even}}$, see Figure 5.1. Then
$\mathcal{P}_{H,A}^{\mathrm{even}}$, see Figure 5.1. Then ![]() $\mathcal{I}$ is isomorphic to a subposet of
$\mathcal{I}$ is isomorphic to a subposet of ![]() $\mathcal{P}_0$. Note that
$\mathcal{P}_0$. Note that ![]() $I^{\prime}\cup 12xa$,
$I^{\prime}\cup 12xa$, ![]() $I^{\prime}\cup 12xb$,
$I^{\prime}\cup 12xb$, ![]() $I^{\prime}\cup 12ya$ and
$I^{\prime}\cup 12ya$ and ![]() $I^{\prime}\cup 12yb$ are elements in
$I^{\prime}\cup 12yb$ are elements in ![]() $\mathcal{I}$. Moreover, both
$\mathcal{I}$. Moreover, both ![]() $I^{\prime}\cup 2x$ and
$I^{\prime}\cup 2x$ and ![]() $I^{\prime}\cup 2y$ are in
$I^{\prime}\cup 2y$ are in ![]() $\mathcal{I}$. The elements
$\mathcal{I}$. The elements ![]() $I^{\prime}\cup1x$ and
$I^{\prime}\cup1x$ and ![]() $I^{\prime}\cup 1y$ in the dashed boxes of Figure 5.1 are in
$I^{\prime}\cup 1y$ in the dashed boxes of Figure 5.1 are in ![]() $\mathcal{I}$ if there is an edge between the vertex 1 and a vertex in Iʹ. By Lemma 4.1,
$\mathcal{I}$ if there is an edge between the vertex 1 and a vertex in Iʹ. By Lemma 4.1, ![]() $\mathcal{I}$ is not shellable, a contradiction to (1) of Theorem 2.1.
$\mathcal{I}$ is not shellable, a contradiction to (1) of Theorem 2.1.
Proof. Since ![]() $|V(G)|\ge 4$, we have
$|V(G)|\ge 4$, we have ![]() $|N^\ast(3)|\ge 1$. Since
$|N^\ast(3)|\ge 1$. Since ![]() $N^\ast(3)\setminus V(Q_3)=N^\ast(3)$, we see
$N^\ast(3)\setminus V(Q_3)=N^\ast(3)$, we see ![]() $|N^\ast(3)|\le 2$ by Claim 4.5. If
$|N^\ast(3)|\le 2$ by Claim 4.5. If ![]() $|N^\ast(3)|=2$, then the equality part of Claim 4.5 says that G is one of
$|N^\ast(3)|=2$, then the equality part of Claim 4.5 says that G is one of  $\widetilde{S}_{5,m}$,
$\widetilde{S}_{5,m}$,  $\widetilde{S}^{\prime}_{5,m}$,
$\widetilde{S}^{\prime}_{5,m}$,  $\widetilde{T}_{5,m}$ and
$\widetilde{T}_{5,m}$ and  $\widetilde{T}^{\prime}_{5,m}$ in Figure 1.1 for some m. Suppose that
$\widetilde{T}^{\prime}_{5,m}$ in Figure 1.1 for some m. Suppose that ![]() $|N^\ast(3)|=1$, and let
$|N^\ast(3)|=1$, and let ![]() $N^\ast(3)=\{4\}$. Since
$N^\ast(3)=\{4\}$. Since ![]() $N^\ast(4)\setminus V(Q_4)=N^\ast(4)\setminus\{3\}$, we see
$N^\ast(4)\setminus V(Q_4)=N^\ast(4)\setminus\{3\}$, we see ![]() $|N^\ast(4)\setminus\{3\}|\le 1$ by Claim 4.5. If
$|N^\ast(4)\setminus\{3\}|\le 1$ by Claim 4.5. If ![]() $|N^\ast(4)\setminus\{3\}|=0$, then G is one of
$|N^\ast(4)\setminus\{3\}|=0$, then G is one of  $\widetilde{P}_{4,m}$, and
$\widetilde{P}_{4,m}$, and  $\widetilde{P}^{\prime}_{4,m}$ in Figure 1.1 for some m. Suppose that
$\widetilde{P}^{\prime}_{4,m}$ in Figure 1.1 for some m. Suppose that ![]() $|N^\ast(4)\setminus\{3\}|=1$, and let
$|N^\ast(4)\setminus\{3\}|=1$, and let ![]() $N^\ast(4)\setminus\{3\}=\{5\}$. Then consider
$N^\ast(4)\setminus\{3\}=\{5\}$. Then consider ![]() $N^\ast(5)\setminus V(Q_5)$. Repeating the argument through the vertices one by one completes the proof.
$N^\ast(5)\setminus V(Q_5)$. Repeating the argument through the vertices one by one completes the proof.
5. CL-shellability of  $\mathcal{P}_{G,A}^{\mathrm{even}}$
$\mathcal{P}_{G,A}^{\mathrm{even}}$
In this section, we show that the poset ![]() $\mathcal{P}_{H,A}^{\mathrm{even}}$ is CL-shellable for every
$\mathcal{P}_{H,A}^{\mathrm{even}}$ is CL-shellable for every ![]() $(H,A)\in\mathcal{A}^\ast(G)$ if G is a graph in Figure 1.1. Note that a connected PI-graph of G in Figure 1.1 is a simple graph or a graph in Figure 1.1. Thus, it is sufficient to show that when G is a graph in Figure 1.1,
$(H,A)\in\mathcal{A}^\ast(G)$ if G is a graph in Figure 1.1. Note that a connected PI-graph of G in Figure 1.1 is a simple graph or a graph in Figure 1.1. Thus, it is sufficient to show that when G is a graph in Figure 1.1, ![]() $\mathcal{P}_{G,A}^{\mathrm{even}}$ is shellable for every
$\mathcal{P}_{G,A}^{\mathrm{even}}$ is shellable for every ![]() $A\in\mathcal{A}(G)$. From now on, throughout this section, we fix a graph G with n vertices and m multiple edges in Figure 1.1, and an admissible collection
$A\in\mathcal{A}(G)$. From now on, throughout this section, we fix a graph G with n vertices and m multiple edges in Figure 1.1, and an admissible collection ![]() $A\in\mathcal{A}(G)$.
$A\in\mathcal{A}(G)$.

Figure 5.1. A graph containing I and the poset containing ![]() $\mathcal{I}$, where the dashed boxes may be in
$\mathcal{I}$, where the dashed boxes may be in ![]() $\mathcal{I}$.
$\mathcal{I}$.
5.1. Definition of an ordering  $\prec_{\tiny\text{atm}}^{I}$ for the atoms of
$\prec_{\tiny\text{atm}}^{I}$ for the atoms of  $[I,G]$
$[I,G]$
We let ![]() $V=\{1,2,\ldots,n\}$
$V=\{1,2,\ldots,n\}$ ![]() $(n\ge 2)$ be the set of vertices of G, and 1 and 2 be the endpoints of the bundle B. By the definition of an admissible collection, note that
$(n\ge 2)$ be the set of vertices of G, and 1 and 2 be the endpoints of the bundle B. By the definition of an admissible collection, note that ![]() $\{3,\ldots,n\} \subset A$,
$\{3,\ldots,n\} \subset A$, ![]() $A\cap B\neq\emptyset$ and
$A\cap B\neq\emptyset$ and ![]() $|A\cap B|$ is even, so we let
$|A\cap B|$ is even, so we let ![]() $B\cap A=\{a_1,\ldots,a_{2m}\}$ (
$B\cap A=\{a_1,\ldots,a_{2m}\}$ (![]() $m\ge 1$) and
$m\ge 1$) and ![]() $B\setminus A=\{b_1,\ldots,b_\ell\}$. Here,
$B\setminus A=\{b_1,\ldots,b_\ell\}$. Here, ![]() $B\setminus A$ may be the empty set. There are three cases:
$B\setminus A$ may be the empty set. There are three cases:
•
 $|V|$ is odd and
$|V|$ is odd and  $ V\cap A = V \setminus \{w\} $ for some
$ V\cap A = V \setminus \{w\} $ for some  $w\in\{1,2\}$;
$w\in\{1,2\}$;•
 $|V|$ is even and
$|V|$ is even and  $ V\cap A = V \setminus \{1,2\}$;
$ V\cap A = V \setminus \{1,2\}$;•
 $|V|$ is even and
$|V|$ is even and  $ V\cap A = V$.
$ V\cap A = V$.
We label the vertices that are not the endpoints of B so that for each ![]() $i\in \{3,\ldots,n\}$, the vertex i is closest to the vertex i − 1. We relabel the endpoints of B so that
$i\in \{3,\ldots,n\}$, the vertex i is closest to the vertex i − 1. We relabel the endpoints of B so that ![]() $1\not\in A$ if
$1\not\in A$ if ![]() $|V|$ is odd and 13 is an edge if
$|V|$ is odd and 13 is an edge if ![]() $|V|$ is even. See (i) of Figure 5.2 for all the possible labellings when
$|V|$ is even. See (i) of Figure 5.2 for all the possible labellings when ![]() $|V|$ is odd. We illustrate all the possible labellings when
$|V|$ is odd. We illustrate all the possible labellings when ![]() $|V|$ is even in (ii) of Figure 5.2. See Figure 5.3 for examples of
$|V|$ is even in (ii) of Figure 5.2. See Figure 5.3 for examples of ![]() $\mathcal{P}_{G,A}^{\mathrm{even}}$ under this labelling. We also assume that there is a total ordering between the vertices:
$\mathcal{P}_{G,A}^{\mathrm{even}}$ under this labelling. We also assume that there is a total ordering between the vertices: ![]() $1\prec 2 \prec \cdots \prec n$. Thus, for
$1\prec 2 \prec \cdots \prec n$. Thus, for ![]() $I\subset V$, the minimum of I, denoted by
$I\subset V$, the minimum of I, denoted by ![]() $\min(I)$, means the frontmost one in the ordering.
$\min(I)$, means the frontmost one in the ordering.

Figure 5.2. Labelling of the vertices.

Figure 5.3. Examples of posets ![]() $\mathcal{P}_{G,A}^{\mathrm{even}}.$
$\mathcal{P}_{G,A}^{\mathrm{even}}.$
Note that given a cover ![]() $I\lessdot J$ in
$I\lessdot J$ in ![]() $\mathcal{P}_{G,A}^{\mathrm{even}}$, if
$\mathcal{P}_{G,A}^{\mathrm{even}}$, if ![]() $(J\setminus I)\cap B\neq\emptyset$, then either
$(J\setminus I)\cap B\neq\emptyset$, then either ![]() $(J\setminus I)\cap (B\cap A)=\emptyset$ or
$(J\setminus I)\cap (B\cap A)=\emptyset$ or ![]() $(J\setminus I)\cap (B\setminus A)=\emptyset$. Suppose not, that is,
$(J\setminus I)\cap (B\setminus A)=\emptyset$. Suppose not, that is, ![]() $(J\setminus I)\cap (B\cap A)\neq\emptyset$ and
$(J\setminus I)\cap (B\cap A)\neq\emptyset$ and ![]() $(J\setminus I)\cap (B\setminus A)\neq\emptyset$. Then
$(J\setminus I)\cap (B\setminus A)\neq\emptyset$. Then ![]() $K:=J\setminus \{(J\setminus I)\cap (B\setminus A)\}$ satisfies that
$K:=J\setminus \{(J\setminus I)\cap (B\setminus A)\}$ satisfies that ![]() $I \lt K \lt J$ and
$I \lt K \lt J$ and ![]() $|(K\setminus I)\cap A|\equiv|(J\setminus I)\cap A|$, a contradiction to
$|(K\setminus I)\cap A|\equiv|(J\setminus I)\cap A|$, a contradiction to ![]() $I\lessdot J$. Hence, we can define the type of a cover
$I\lessdot J$. Hence, we can define the type of a cover ![]() $I\lessdot J$ in
$I\lessdot J$ in ![]() $\mathcal{P}_{G,A}^{\mathrm{even}}$ according to the size of
$\mathcal{P}_{G,A}^{\mathrm{even}}$ according to the size of ![]() $J\setminus I$ and the intersection with
$J\setminus I$ and the intersection with ![]() $B\setminus A$. A cover
$B\setminus A$. A cover ![]() $I\lessdot J$ has type (Ei) if
$I\lessdot J$ has type (Ei) if ![]() $|J\setminus I|=i$ and
$|J\setminus I|=i$ and ![]() $J\setminus I$ has no element of
$J\setminus I$ has no element of ![]() $B\setminus A$;
$B\setminus A$; ![]() $I\lessdot J$ has type (E
$I\lessdot J$ has type (E![]() ${i}^{\prime}$) if
${i}^{\prime}$) if ![]() $|J\setminus I|=i$ and
$|J\setminus I|=i$ and ![]() $J\setminus I$ contains some elements of
$J\setminus I$ contains some elements of ![]() $B\setminus A$. Hence, (E
$B\setminus A$. Hence, (E![]() $i{}^\prime$) can occur only when
$i{}^\prime$) can occur only when ![]() $B\setminus A\neq \emptyset$.
$B\setminus A\neq \emptyset$.
Lemma 5.1. Let ![]() $I\lessdot J$ be a cover in
$I\lessdot J$ be a cover in ![]() $\mathcal{P}_{G,A}^{\mathrm{even}}$. Then
$\mathcal{P}_{G,A}^{\mathrm{even}}$. Then ![]() $J\setminus I$ is one of the sets represented in Table 1.
$J\setminus I$ is one of the sets represented in Table 1.
Table 1. Types of ![]() $I\lessdot J$ in
$I\lessdot J$ in ![]() $\mathcal{P}_{G,A}^{\mathrm{even}}$, where
$\mathcal{P}_{G,A}^{\mathrm{even}}$, where ![]() $a,\,a^{\prime}\in B\cap A$,
$a,\,a^{\prime}\in B\cap A$, ![]() $b\in (B\setminus A)$, c,
$b\in (B\setminus A)$, c, ![]() $c^{\prime}\in A$,
$c^{\prime}\in A$, ![]() $v=\min(V\setminus (I\cup\{1,2\}))$
$v=\min(V\setminus (I\cup\{1,2\}))$

For the case of (E3), ![]() $c\in B\cap A$ or
$c\in B\cap A$ or ![]() $c=\min(V\setminus (I\cup\{1,2\}))$.
$c=\min(V\setminus (I\cup\{1,2\}))$.
Proof. It follows from the fact that for a cover ![]() $I\lessdot J$ in
$I\lessdot J$ in ![]() $\mathcal{P}_{G,A}^{\mathrm{even}}$, each of
$\mathcal{P}_{G,A}^{\mathrm{even}}$, each of ![]() $|I\cap A|$,
$|I\cap A|$, ![]() $|J\cap A|$ and
$|J\cap A|$ and ![]() $|(J\setminus I)\cap A|$ is even, and
$|(J\setminus I)\cap A|$ is even, and ![]() $J\setminus I$ satisfies the following condition, which we will call (
$J\setminus I$ satisfies the following condition, which we will call (![]() $\dagger$).
$\dagger$).
(†) The elements in
 $J\setminus I$ belong to the same connected component of J.
$J\setminus I$ belong to the same connected component of J.
When ![]() $I\lessdot J$ is of (E3
$I\lessdot J$ is of (E3![]() ${}^\prime$), as in Table 1, we divide the type (E3
${}^\prime$), as in Table 1, we divide the type (E3![]() ${}^\prime$) into two subtypes according to the size of
${}^\prime$) into two subtypes according to the size of ![]() $(J\setminus I)\cap \{1,2\}$:
$(J\setminus I)\cap \{1,2\}$:
•
 $I\lessdot J$ has type (E3
$I\lessdot J$ has type (E3 ${}^{\prime}$-1) if
${}^{\prime}$-1) if  $I\lessdot J$ has type (E3
$I\lessdot J$ has type (E3 ${}^{\prime}$) and
${}^{\prime}$) and  $|(J\setminus I)\cap \{1,2\}|=1$;
$|(J\setminus I)\cap \{1,2\}|=1$;•
 $I\lessdot J$ has type (E3
$I\lessdot J$ has type (E3 ${}^{\prime}$-2) if
${}^{\prime}$-2) if  $I\lessdot J$ has type (E3
$I\lessdot J$ has type (E3 ${}^{\prime}$) and
${}^{\prime}$) and  $|(J\setminus I)\cap \{1,2\}|=2$.
$|(J\setminus I)\cap \{1,2\}|=2$.
We can also show that when ![]() $I\lessdot J$ is of (E3
$I\lessdot J$ is of (E3![]() ${}^{\prime}$-1),
${}^{\prime}$-1), ![]() $J\setminus I$ contains the vertex
$J\setminus I$ contains the vertex ![]() $\min(V\setminus (I\cup\{1,2\}))$.
$\min(V\setminus (I\cup\{1,2\}))$.
Proposition 5.2. The lengths of maximal chains of ![]() $\mathcal{P}_{G,A}^{\mathrm{even}}$ are
$\mathcal{P}_{G,A}^{\mathrm{even}}$ are
 \begin{equation*}\begin{cases}
\frac{|A|}{2}+|B\setminus A|+1 \ \text{or }\ \frac{|A|}{2}+ |B\setminus A| & \text{if }|V|\text{is odd,}\\
\frac{|A|}{2}+|B\setminus A|+1 & \text{if }|V|\text{is even and }A\cap V\neq V, {and}\\
\frac{|A|}{2}+|B\setminus A| \ \text{or }\ \frac{|A|}{2}+|B\setminus A|-1& \text{if }|V|\text{is even and }A\cap V = V.
\end{cases} \end{equation*}
\begin{equation*}\begin{cases}
\frac{|A|}{2}+|B\setminus A|+1 \ \text{or }\ \frac{|A|}{2}+ |B\setminus A| & \text{if }|V|\text{is odd,}\\
\frac{|A|}{2}+|B\setminus A|+1 & \text{if }|V|\text{is even and }A\cap V\neq V, {and}\\
\frac{|A|}{2}+|B\setminus A| \ \text{or }\ \frac{|A|}{2}+|B\setminus A|-1& \text{if }|V|\text{is even and }A\cap V = V.
\end{cases} \end{equation*} Moreover, if ![]() $|V|$ is odd, 2 and 3 are not adjacent in G and
$|V|$ is odd, 2 and 3 are not adjacent in G and ![]() $B\subset A$, then
$B\subset A$, then ![]() $\mathcal{P}_{G,A}^{\mathrm{even}}$ is pure and its length is
$\mathcal{P}_{G,A}^{\mathrm{even}}$ is pure and its length is  $\frac{|A|}{2}+1$.
$\frac{|A|}{2}+1$.
Proof. Recall that ![]() $|V|=n, |B\cap A|=2m$ and
$|V|=n, |B\cap A|=2m$ and ![]() $|B\setminus A|=\ell$. Note that
$|B\setminus A|=\ell$. Note that ![]() $2m+n\ge 4$. Let
$2m+n\ge 4$. Let ![]() $\sigma\colon I_0\lessdot I_1\lessdot\cdots\lessdot I_p$ be a maximal chain of
$\sigma\colon I_0\lessdot I_1\lessdot\cdots\lessdot I_p$ be a maximal chain of ![]() $\mathcal{P}_{G,A}^{\mathrm{even}}$. Note that
$\mathcal{P}_{G,A}^{\mathrm{even}}$. Note that ![]() $\{I_i\setminus I_{i-1} \mid i=1,\ldots,p \}$ is a partition of
$\{I_i\setminus I_{i-1} \mid i=1,\ldots,p \}$ is a partition of ![]() $V\cup B$.
$V\cup B$.
Let k be the smallest index such that ![]() $I_{k}\setminus I_{k-1}$ contains an element in B, that is, Ik is the first element of σ containing a multiple edge. Then
$I_{k}\setminus I_{k-1}$ contains an element in B, that is, Ik is the first element of σ containing a multiple edge. Then ![]() $\{1,2\}\subset I_k$ and
$\{1,2\}\subset I_k$ and ![]() $\{1,2\}\not\subset I_{k-1}$. Together with Table 1, we see that for each cover
$\{1,2\}\not\subset I_{k-1}$. Together with Table 1, we see that for each cover ![]() $I_{i-1}\lessdot I_i$ of σ, except the cover
$I_{i-1}\lessdot I_i$ of σ, except the cover ![]() $I_{k-1}\lessdot I_k$, it holds that
$I_{k-1}\lessdot I_k$, it holds that ![]() $|I_{i}\setminus I_{i-1}|=1$ or 2. For each
$|I_{i}\setminus I_{i-1}|=1$ or 2. For each ![]() $j\in\{1,2\}$, let tj be the number of covers
$j\in\{1,2\}$, let tj be the number of covers ![]() $I_{i-1}\lessdot I_i$ of σ, except the cover
$I_{i-1}\lessdot I_i$ of σ, except the cover ![]() $I_{k-1}\lessdot I_k$, such that
$I_{k-1}\lessdot I_k$, such that ![]() $|I_{i}\setminus I_{i-1}|=j$. Then the number of covers of σ, which is equal to
$|I_{i}\setminus I_{i-1}|=j$. Then the number of covers of σ, which is equal to ![]() $\ell(\sigma)$, is
$\ell(\sigma)$, is ![]() $1+t_1+t_2$. Since
$1+t_1+t_2$. Since ![]() $\{I_i\setminus I_{i-1} \mid i=1,\ldots,p \}$ is a partition of
$\{I_i\setminus I_{i-1} \mid i=1,\ldots,p \}$ is a partition of ![]() $V\cup B$, we have
$V\cup B$, we have
or  $t_2=\frac{(n+2m+\ell)-t_1-|I_k\setminus I_{k-1}|}{2}$. Therefore,
$t_2=\frac{(n+2m+\ell)-t_1-|I_k\setminus I_{k-1}|}{2}$. Therefore,
 \begin{eqnarray}
&&\ell(\sigma)=1+t_1+t_2 = \frac{(n+2m+\ell)+2+t_1-|I_k\setminus I_{k-1}|}{2}.
\end{eqnarray}
\begin{eqnarray}
&&\ell(\sigma)=1+t_1+t_2 = \frac{(n+2m+\ell)+2+t_1-|I_k\setminus I_{k-1}|}{2}.
\end{eqnarray} Note that σ has exactly ![]() $ |B\setminus (A\cup I_k)|$ covers of (E1
$ |B\setminus (A\cup I_k)|$ covers of (E1![]() ${}^{\prime}$) and at most one cover of (E1). In addition, σ has one cover of (E1) if and only if
${}^{\prime}$) and at most one cover of (E1). In addition, σ has one cover of (E1) if and only if ![]() $I_{k-1}$ contains a vertex in
$I_{k-1}$ contains a vertex in ![]() $\{1,2\}\setminus A$. Since t 1 is the sum of the number of covers of (E1) and the number of covers of (E1
$\{1,2\}\setminus A$. Since t 1 is the sum of the number of covers of (E1) and the number of covers of (E1![]() ${}^{\prime}$), we get
${}^{\prime}$), we get
 \begin{eqnarray}
&&t_1=\begin{cases}
1+|B\setminus (A\cup I_k)| &\text{if }I_{k-1} \text{ contains a vertex in }\{1,2\}\setminus A,\\
|B\setminus (A\cup I_k)| &\text{otherwise}.
\end{cases}
\end{eqnarray}
\begin{eqnarray}
&&t_1=\begin{cases}
1+|B\setminus (A\cup I_k)| &\text{if }I_{k-1} \text{ contains a vertex in }\{1,2\}\setminus A,\\
|B\setminus (A\cup I_k)| &\text{otherwise}.
\end{cases}
\end{eqnarray} Suppose that ![]() $|V|$ is odd. Then
$|V|$ is odd. Then ![]() $|A|=2m+n-1$. By Table 1 again,
$|A|=2m+n-1$. By Table 1 again, ![]() $I_{k-1}\lessdot I_{k}$ has one of types (E2), (E3), (E2
$I_{k-1}\lessdot I_{k}$ has one of types (E2), (E3), (E2![]() ${}^{\prime}$) and (E3
${}^{\prime}$) and (E3![]() ${}^{\prime}$-1). By Equations (5.1) and (5.2),
${}^{\prime}$-1). By Equations (5.1) and (5.2),
 \begin{equation*}\ell(\sigma)=\begin{cases}
\frac{(n+2m+\ell)+2+(1+\ell)-2}{2} = \ell+1+\frac{n+2m-1}{2}=\ell+1+\frac{|A|}{2} &\text{if }I_{k-1}\lessdot I_{k} \text{ is of (E2)},\\
\frac{(n+2m+\ell)+2+\ell-3}{2}=\ell+\frac{n+2m-1}{2} =\ell +\frac{|A|}{2} &\text{if }I_{k-1}\lessdot I_{k} \text{ is of (E3)},\\
\frac{(n+2m+\ell)+2+(\ell-1)-2}{2}=\ell+\frac{n+2m-1}{2}=\ell +\frac{|A|}{2} &\text{if }I_{k-1}\lessdot I_{k} \text{ is of (E2${}^{\prime}$)},\\
\frac{(n+2m+\ell)+2+(1+(\ell-1))-3}{2}=\ell+\frac{n+2m-1}{2}=\ell +\frac{|A|}{2} & \text{if }I_{k-1}\lessdot I_{k} \text{ is of (E3${}^{\prime}$-1)}.
\end{cases}\end{equation*}
\begin{equation*}\ell(\sigma)=\begin{cases}
\frac{(n+2m+\ell)+2+(1+\ell)-2}{2} = \ell+1+\frac{n+2m-1}{2}=\ell+1+\frac{|A|}{2} &\text{if }I_{k-1}\lessdot I_{k} \text{ is of (E2)},\\
\frac{(n+2m+\ell)+2+\ell-3}{2}=\ell+\frac{n+2m-1}{2} =\ell +\frac{|A|}{2} &\text{if }I_{k-1}\lessdot I_{k} \text{ is of (E3)},\\
\frac{(n+2m+\ell)+2+(\ell-1)-2}{2}=\ell+\frac{n+2m-1}{2}=\ell +\frac{|A|}{2} &\text{if }I_{k-1}\lessdot I_{k} \text{ is of (E2${}^{\prime}$)},\\
\frac{(n+2m+\ell)+2+(1+(\ell-1))-3}{2}=\ell+\frac{n+2m-1}{2}=\ell +\frac{|A|}{2} & \text{if }I_{k-1}\lessdot I_{k} \text{ is of (E3${}^{\prime}$-1)}.
\end{cases}\end{equation*} Hence, every maximal chain has a length of either  ${\frac{|A|}{2}+\ell+1}$ or
${\frac{|A|}{2}+\ell+1}$ or  ${\frac{|A|}{2}+\ell}$, and hence the poset
${\frac{|A|}{2}+\ell}$, and hence the poset ![]() $\mathcal{P}_{G,A}^{\mathrm{even}}$ is nonpure. Note that if 2 and 3 are not adjacent in G, then there is no cover of (E3), and if
$\mathcal{P}_{G,A}^{\mathrm{even}}$ is nonpure. Note that if 2 and 3 are not adjacent in G, then there is no cover of (E3), and if ![]() $B\subset A$, then
$B\subset A$, then ![]() $B\setminus A=\emptyset$ and then there is no cover of (E2
$B\setminus A=\emptyset$ and then there is no cover of (E2![]() ${}^\prime$) or (E3
${}^\prime$) or (E3![]() ${}^\prime$). Hence, if 2 and 3 are not adjacent in G and
${}^\prime$). Hence, if 2 and 3 are not adjacent in G and ![]() $B\subset A$, then
$B\subset A$, then ![]() $\mathcal{P}_{G,A}^{\mathrm{even}}$ is a pure poset of length
$\mathcal{P}_{G,A}^{\mathrm{even}}$ is a pure poset of length  ${\frac{|A|}{2}+1}$. We summarize in the following table:
${\frac{|A|}{2}+1}$. We summarize in the following table:

Suppose that ![]() $|V|$ is even. When
$|V|$ is even. When ![]() $A\cap \{1,2\}=\emptyset$, it holds that
$A\cap \{1,2\}=\emptyset$, it holds that ![]() $|A|=2m+n-2$ and
$|A|=2m+n-2$ and ![]() $I_{k-1}\lessdot I_{k}$ is of (E3) or (E2
$I_{k-1}\lessdot I_{k}$ is of (E3) or (E2![]() ${}^{\prime}$). By Equations (5.1) and (5.2),
${}^{\prime}$). By Equations (5.1) and (5.2),
 \begin{equation*}\ell(\sigma)=\begin{cases}
\frac{(n+2m+\ell)+2+(1+\ell)-3}{2} = \ell+1+\frac{n+2m-2}{2}=\ell+1+\frac{|A|}{2} &\text{if }I_{k-1}\lessdot I_{k} \text{ is of (E3)},\\
\frac{(n+2m+\ell)+2+(1+(\ell-1))-2}{2}=\ell+1+\frac{n+2m-2}{2} =\ell +1+\frac{|A|}{2} &\text{if }I_{k-1}\lessdot I_{k} \text{ is of (E2${}^{\prime}$)}.
\end{cases}\end{equation*}
\begin{equation*}\ell(\sigma)=\begin{cases}
\frac{(n+2m+\ell)+2+(1+\ell)-3}{2} = \ell+1+\frac{n+2m-2}{2}=\ell+1+\frac{|A|}{2} &\text{if }I_{k-1}\lessdot I_{k} \text{ is of (E3)},\\
\frac{(n+2m+\ell)+2+(1+(\ell-1))-2}{2}=\ell+1+\frac{n+2m-2}{2} =\ell +1+\frac{|A|}{2} &\text{if }I_{k-1}\lessdot I_{k} \text{ is of (E2${}^{\prime}$)}.
\end{cases}\end{equation*} Hence, every maximal chain has length  $\frac{|A|}{2}+\ell+1$.
$\frac{|A|}{2}+\ell+1$.
When A contains ![]() $\{1,2\}$, it holds that
$\{1,2\}$, it holds that ![]() $|A|=2m+n$ and
$|A|=2m+n$ and ![]() $I_{k-1}\lessdot I_{k}$ is one of (E2), (E4) and (E3
$I_{k-1}\lessdot I_{k}$ is one of (E2), (E4) and (E3![]() ${}^{\prime}$). By Equation (5.1) and (5.2),
${}^{\prime}$). By Equation (5.1) and (5.2),
 \begin{equation*}\ell(\sigma)=\begin{cases}
\frac{(n+2m+\ell)+2+\ell-2}{2} = \ell+\frac{n+2m}{2}=\ell+\frac{|A|}{2} &\text{if }I_{k-1}\lessdot I_{k} \text{ is of (E2)},\\
\frac{(n+2m+\ell)+2+\ell-4}{2} = \ell-1+\frac{n+2m}{2}=\ell-1+\frac{|A|}{2} &\text{if }I_{k-1}\lessdot I_{k} \text{ is of (E4)},\\
\frac{(n+2m+\ell)+2+(\ell-1)-3}{2}=\ell-1+\frac{n+2m}{2} =\ell-1+\frac{|A|}{2} &\text{if }I_{k-1}\lessdot I_{k} \text{ is of (E3${}^{\prime}$)}.
\end{cases}\end{equation*}
\begin{equation*}\ell(\sigma)=\begin{cases}
\frac{(n+2m+\ell)+2+\ell-2}{2} = \ell+\frac{n+2m}{2}=\ell+\frac{|A|}{2} &\text{if }I_{k-1}\lessdot I_{k} \text{ is of (E2)},\\
\frac{(n+2m+\ell)+2+\ell-4}{2} = \ell-1+\frac{n+2m}{2}=\ell-1+\frac{|A|}{2} &\text{if }I_{k-1}\lessdot I_{k} \text{ is of (E4)},\\
\frac{(n+2m+\ell)+2+(\ell-1)-3}{2}=\ell-1+\frac{n+2m}{2} =\ell-1+\frac{|A|}{2} &\text{if }I_{k-1}\lessdot I_{k} \text{ is of (E3${}^{\prime}$)}.
\end{cases}\end{equation*} Hence, every maximal chain has length  $\ell+\frac{|A|}{2} $ or
$\ell+\frac{|A|}{2} $ or  $\ell-1+\frac{|A|}{2}$. We summarize in the following table:
$\ell-1+\frac{|A|}{2}$. We summarize in the following table:

We shall show that ![]() $\mathcal{P}_{G,A}^{\mathrm{even}}$ admits a recursive atom ordering. We first define the lexicographic order
$\mathcal{P}_{G,A}^{\mathrm{even}}$ admits a recursive atom ordering. We first define the lexicographic order ![]() $\prec_{\tiny\text{lex}}^{I}$ on
$\prec_{\tiny\text{lex}}^{I}$ on ![]() $V\cup B$ for each
$V\cup B$ for each ![]() $I\in \mathcal{P}_{G,A}^{\mathrm{even}}$ and then define the atom ordering
$I\in \mathcal{P}_{G,A}^{\mathrm{even}}$ and then define the atom ordering ![]() $\prec_{\tiny\text{atm}}^{I}$ for
$\prec_{\tiny\text{atm}}^{I}$ for ![]() $[I,G]$.
$[I,G]$.
Definition 5.3. Let ![]() $I\in \mathcal{P}_{G,A}^{\mathrm{even}}$. We define the lexicographic order
$I\in \mathcal{P}_{G,A}^{\mathrm{even}}$. We define the lexicographic order ![]() $\prec_{\tiny\text{lex}}^{I}$ on
$\prec_{\tiny\text{lex}}^{I}$ on ![]() $V\cup B$ as follows:
$V\cup B$ as follows:
• If
 $B\cap I=\emptyset$, then
$B\cap I=\emptyset$, then
 \begin{equation*}\prec_{\tiny\text{lex}}^{I}: \ 1,2,3,\ldots,{n},a_1,\ldots,a_{2m},b_1,\ldots,b_\ell.\end{equation*}
\begin{equation*}\prec_{\tiny\text{lex}}^{I}: \ 1,2,3,\ldots,{n},a_1,\ldots,a_{2m},b_1,\ldots,b_\ell.\end{equation*}• If
 $B\cap I\neq\emptyset$ and
$B\cap I\neq\emptyset$ and  $(B\setminus A)\cap I= \emptyset$, then let
$(B\setminus A)\cap I= \emptyset$, then let  $k:=\max\{i\mid a_i\in B\cap A\cap I\}$ and
$k:=\max\{i\mid a_i\in B\cap A\cap I\}$ and
 \begin{equation*}\prec_{\tiny\text{lex}}^{I}: \ 1,2,a_1,\ldots,a_{k},3,\ldots,n,a_{k+1},\ldots,a_{2m}, b_1,\ldots,b_{\ell}.\end{equation*}
\begin{equation*}\prec_{\tiny\text{lex}}^{I}: \ 1,2,a_1,\ldots,a_{k},3,\ldots,n,a_{k+1},\ldots,a_{2m}, b_1,\ldots,b_{\ell}.\end{equation*}• If
 $(B\setminus A)\cap I \neq \emptyset$, then let
$(B\setminus A)\cap I \neq \emptyset$, then let  $k:=\max\{i\mid b_i\in (B\setminus A)\cap I\}$ and
$k:=\max\{i\mid b_i\in (B\setminus A)\cap I\}$ and
 \begin{equation*}\prec_{\tiny\text{lex}}^{I}: \ 1,2,a_1,\ldots,a_{2m},b_1,\ldots,b_{k},3,\ldots,n,b_{k+1},\ldots,b_{\ell}.\end{equation*}
\begin{equation*}\prec_{\tiny\text{lex}}^{I}: \ 1,2,a_1,\ldots,a_{2m},b_1,\ldots,b_{k},3,\ldots,n,b_{k+1},\ldots,b_{\ell}.\end{equation*}
Then for two atoms J and Jʹ of ![]() $[I,G]$, we define
$[I,G]$, we define ![]() $J\prec_{\tiny\text{atm}}^{I} J^{\prime}$ if
$J\prec_{\tiny\text{atm}}^{I} J^{\prime}$ if
(O1)
 $|(J\setminus I)\cap\{1,2\}|=1$ and
$|(J\setminus I)\cap\{1,2\}|=1$ and  $|(J^{\prime}\setminus I)\cap \{1,2\}|=2$, or
$|(J^{\prime}\setminus I)\cap \{1,2\}|=2$, or(O2) (O1) does not hold and
 $J\setminus I \prec_{\tiny\text{lex}}^{I} J^{\prime}\setminus I$, where we compare lexicographic order induced by
$J\setminus I \prec_{\tiny\text{lex}}^{I} J^{\prime}\setminus I$, where we compare lexicographic order induced by  $\prec_{\tiny\text{lex}}^{I}$, that is, we sort the elements in each of
$\prec_{\tiny\text{lex}}^{I}$, that is, we sort the elements in each of  $J\setminus I$ and
$J\setminus I$ and  $J^{\prime}\setminus I$ in ascending order by
$J^{\prime}\setminus I$ in ascending order by  $\prec_{\tiny\text{lex}}^{I}$ and compare them by the lexicographic order
$\prec_{\tiny\text{lex}}^{I}$ and compare them by the lexicographic order  $\prec_{\tiny\text{lex}}^{I}$.
$\prec_{\tiny\text{lex}}^{I}$.
In the above, we check (O1) first, and if (O1) does not hold, we check whether (O2) holds. Note that (O1) is considered only when ![]() $\mathcal{P}_{G,A}^{\mathrm{even}}$ admits a cover of (E4) or (E3
$\mathcal{P}_{G,A}^{\mathrm{even}}$ admits a cover of (E4) or (E3![]() ${}^\prime$-2), that is,
${}^\prime$-2), that is, ![]() $|V|$ is even and A contains
$|V|$ is even and A contains ![]() $\{1,2\}$.
$\{1,2\}$.
Here is an example. Let G be the graph  $\widetilde{P}_{6,5}$ in Figure 1.1. Suppose that
$\widetilde{P}_{6,5}$ in Figure 1.1. Suppose that ![]() $A=V \cup \{a_1,a_2,a_3,a_4\}$. Then the atoms of
$A=V \cup \{a_1,a_2,a_3,a_4\}$. Then the atoms of ![]() $\mathcal{P}_{G,A}^{\mathrm{even}}$ are ordered as follows:
$\mathcal{P}_{G,A}^{\mathrm{even}}$ are ordered as follows:
 \begin{equation*}\prec_{\tiny\text{atm}}^{\emptyset}: \ 13, \ 12a_1a_2, \ 12a_1a_3 , \ 12a_1a_4, \ 12a_2a_3, \ 12a_2a_4
, \ 12a_3a_4, \ 12b_1, \ 34, \ 45, \ 56.\end{equation*}
\begin{equation*}\prec_{\tiny\text{atm}}^{\emptyset}: \ 13, \ 12a_1a_2, \ 12a_1a_3 , \ 12a_1a_4, \ 12a_2a_3, \ 12a_2a_4
, \ 12a_3a_4, \ 12b_1, \ 34, \ 45, \ 56.\end{equation*} For ![]() $I=12a_1a_3$,
$I=12a_1a_3$, ![]() $\prec_{\tiny\text{lex}}^{I}: 1, 2,a_1,{\bf a_2},a_3,{\bf 3},{\bf 4},{\bf 5},{\bf 6},{\bf a_4},{\bf b_1}$, and the atoms of
$\prec_{\tiny\text{lex}}^{I}: 1, 2,a_1,{\bf a_2},a_3,{\bf 3},{\bf 4},{\bf 5},{\bf 6},{\bf a_4},{\bf b_1}$, and the atoms of ![]() $[I,G]$ are ordered as follows:
$[I,G]$ are ordered as follows:
because ![]() $a_23\prec_{\tiny\text{lex}}^{I}a_2a_4\prec_{\tiny\text{lex}}^{I}34\prec_{\tiny\text{lex}}^{I}3a_4\prec_{\tiny\text{lex}}^{I}45\prec_{\tiny\text{lex}}^{I}56\prec_{\tiny\text{lex}}^{I}b_1$, where the bold letters indicate the elements not in I.
$a_23\prec_{\tiny\text{lex}}^{I}a_2a_4\prec_{\tiny\text{lex}}^{I}34\prec_{\tiny\text{lex}}^{I}3a_4\prec_{\tiny\text{lex}}^{I}45\prec_{\tiny\text{lex}}^{I}56\prec_{\tiny\text{lex}}^{I}b_1$, where the bold letters indicate the elements not in I.
The following is the main theorem of this section, whose proof is given in §5.2.
Theorem 5.4. Let G be a connected graph in Figure 1.1, and A be an admissible collection of G. Then the poset ![]() $\mathcal{P}_{G,A}^{\mathrm{even}}$ admits a recursive atom ordering, and hence
$\mathcal{P}_{G,A}^{\mathrm{even}}$ admits a recursive atom ordering, and hence ![]() $\mathcal{P}_{G,A}^{\mathrm{even}}$ is CL-shellable.
$\mathcal{P}_{G,A}^{\mathrm{even}}$ is CL-shellable.
Remark. We insist that the ordering ![]() $\prec_{\tiny\text{atm}}^{I}$ is essential. Suppose that we consider the lexicographic order
$\prec_{\tiny\text{atm}}^{I}$ is essential. Suppose that we consider the lexicographic order ![]() $\prec^\ast$ given by
$\prec^\ast$ given by ![]() $1,2,a_1,a_2,\ldots,a_{2m},3,4,\ldots,n,b_1,\ldots, b_\ell$ and define
$1,2,a_1,a_2,\ldots,a_{2m},3,4,\ldots,n,b_1,\ldots, b_\ell$ and define ![]() $\prec_{\tiny\text{atm}}^{\ast}$ by an ordering obtained by replacing
$\prec_{\tiny\text{atm}}^{\ast}$ by an ordering obtained by replacing ![]() $\prec_{\tiny\text{lex}}^{I}$ in (O2) of Definition 5.3 with the fixed ordering
$\prec_{\tiny\text{lex}}^{I}$ in (O2) of Definition 5.3 with the fixed ordering ![]() $\prec^*$. For the posets in Figure 5.3,
$\prec^*$. For the posets in Figure 5.3, ![]() $\prec_{\tiny\text{atm}}^{\ast}$ gives a recursive atom ordering. However, it fails to be a recursive atom ordering in general. For example, let G be a graph in Figure 1.1 with
$\prec_{\tiny\text{atm}}^{\ast}$ gives a recursive atom ordering. However, it fails to be a recursive atom ordering in general. For example, let G be a graph in Figure 1.1 with ![]() $|V|= 4$ and
$|V|= 4$ and ![]() $|B|= 6$, and let
$|B|= 6$, and let ![]() $A=V\cup B$. Then
$A=V\cup B$. Then ![]() $A\in\mathcal{A}(G)$. Let
$A\in\mathcal{A}(G)$. Let ![]() $I=12a_1a_3$, and consider the atoms
$I=12a_1a_3$, and consider the atoms ![]() $J_1= 12 a_1 a_3{\bf a_5}{\bf a_6}$ and
$J_1= 12 a_1 a_3{\bf a_5}{\bf a_6}$ and ![]() $J_2= 12{\bf 3}a_1 a_3{\bf a_5}$ of
$J_2= 12{\bf 3}a_1 a_3{\bf a_5}$ of ![]() $[I,G]$, where the bold letters indicate the elements not in I. Then the atoms of
$[I,G]$, where the bold letters indicate the elements not in I. Then the atoms of ![]() $[\emptyset,G]$ preceding I in
$[\emptyset,G]$ preceding I in ![]() $\prec_{\tiny\text{atm}}^{\ast}$ are 13 and
$\prec_{\tiny\text{atm}}^{\ast}$ are 13 and ![]() $ 12a_1a_2$. However,
$ 12a_1a_2$. However, ![]() $J_1 \prec_{\tiny\text{atm}}^{\ast} J_2, J_2$ contains the atom 13, and J 1 does not contain any atom of
$J_1 \prec_{\tiny\text{atm}}^{\ast} J_2, J_2$ contains the atom 13, and J 1 does not contain any atom of ![]() $[\emptyset,G]$ preceding I. Thus, (2) of Definition 2.3 fails.
$[\emptyset,G]$ preceding I. Thus, (2) of Definition 2.3 fails.
5.2. Proof of Theorem 5.4
For a subset ![]() $X\subset V\cup B$,
$X\subset V\cup B$, ![]() $\min^{I}(X)$ and
$\min^{I}(X)$ and ![]() $\max^{I}(X)$ denote the minimum and the maximum of X with respect to
$\max^{I}(X)$ denote the minimum and the maximum of X with respect to ![]() $\prec_{\tiny\text{lex}}^{I}$, respectively. We will show that the ordering
$\prec_{\tiny\text{lex}}^{I}$, respectively. We will show that the ordering ![]() $\prec_{\tiny\text{atm}}^{I}$ (
$\prec_{\tiny\text{atm}}^{I}$ (![]() $I\in \mathcal{P}_{G,A}^{\mathrm{even}}$) is a recursive atom ordering. We first check Condition (2) of Definition 2.3.
$I\in \mathcal{P}_{G,A}^{\mathrm{even}}$) is a recursive atom ordering. We first check Condition (2) of Definition 2.3.
Lemma 5.5. Let Ii and Ij be atoms of ![]() $[I,G]$ such that
$[I,G]$ such that ![]() $I_i\prec_{\tiny\text{atm}}^{I} I_j$. If there is an element K of
$I_i\prec_{\tiny\text{atm}}^{I} I_j$. If there is an element K of ![]() $[I,G]$ such that
$[I,G]$ such that ![]() $I_i, I_j \lt K$, then there exists an atom
$I_i, I_j \lt K$, then there exists an atom ![]() $K_\ast$ of
$K_\ast$ of ![]() $[I_j,G]$ and an atom
$[I_j,G]$ and an atom ![]() $I_\ast$ of
$I_\ast$ of ![]() $[I,G]$ such that
$[I,G]$ such that
 \begin{equation*}K_\ast\le K, \quad K_\ast\in [I_\ast,G],\quad\text{and }\quad I_\ast\prec_{\tiny\text{atm}}^{I} I_j.\end{equation*}
\begin{equation*}K_\ast\le K, \quad K_\ast\in [I_\ast,G],\quad\text{and }\quad I_\ast\prec_{\tiny\text{atm}}^{I} I_j.\end{equation*}Proof. Let ![]() $K_0=I_i\cup I_j$ for simplicity. Note that
$K_0=I_i\cup I_j$ for simplicity. Note that ![]() $K_0\subset K$, and one can check from Lemma 5.1 that there is no element
$K_0\subset K$, and one can check from Lemma 5.1 that there is no element ![]() $L\in \mathcal{P}_{G,A}^{\mathrm{even}}$ such that
$L\in \mathcal{P}_{G,A}^{\mathrm{even}}$ such that ![]() $I_j \subsetneq L \subsetneq K_0$.
$I_j \subsetneq L \subsetneq K_0$.
(Case 1) K 0 is not a semi-induced subgraph of G. Note that a subset of ![]() $V\cup B$ is not a semi-induced subgraph if and only if it contains
$V\cup B$ is not a semi-induced subgraph if and only if it contains ![]() $\{1,2\}$ and has no element in B. Then
$\{1,2\}$ and has no element in B. Then ![]() $I_i\setminus I$ and
$I_i\setminus I$ and ![]() $I_j\setminus I$ contain exactly one of the endpoints of B, not the same. More precisely, letting
$I_j\setminus I$ contain exactly one of the endpoints of B, not the same. More precisely, letting ![]() $v=\min(V\setminus (I\cup\{1,2\}))$, one of the following holds:
$v=\min(V\setminus (I\cup\{1,2\}))$, one of the following holds:
 \begin{equation*} \begin{array}{lll}
I_i\setminus I=1 &\text{and }\quad I_j\setminus I=2v &\text{if }A\cap\{1,2\}=\{2\},\\
I_i\setminus I=1 &\text{and }\quad I_j\setminus I=2 &\text{if }A\cap\{1,2\}=\emptyset,\\
I_i\setminus I=1v &\text{and }\quad I_j\setminus I=2v &\text{if }A\cap\{1,2\}=\{1,2\}.\\
\end{array}\end{equation*}
\begin{equation*} \begin{array}{lll}
I_i\setminus I=1 &\text{and }\quad I_j\setminus I=2v &\text{if }A\cap\{1,2\}=\{2\},\\
I_i\setminus I=1 &\text{and }\quad I_j\setminus I=2 &\text{if }A\cap\{1,2\}=\emptyset,\\
I_i\setminus I=1v &\text{and }\quad I_j\setminus I=2v &\text{if }A\cap\{1,2\}=\{1,2\}.\\
\end{array}\end{equation*} Note that ![]() $I_j\setminus I=2v$ occurs only when 2 and 3 are adjacent in G. Moreover, if
$I_j\setminus I=2v$ occurs only when 2 and 3 are adjacent in G. Moreover, if ![]() $I_i\setminus I=1v_1$ and
$I_i\setminus I=1v_1$ and ![]() $I_j\setminus I=2v_2$ hold, then I is a simple connected graph with even number of vertices, so
$I_j\setminus I=2v_2$ hold, then I is a simple connected graph with even number of vertices, so ![]() $v_1=v_2=v$. Indeed, if G is
$v_1=v_2=v$. Indeed, if G is  $\tilde{P}^{\prime}_{n,m}$, then
$\tilde{P}^{\prime}_{n,m}$, then ![]() $v_1=v_2=v$ by the structure of a path. If G is
$v_1=v_2=v$ by the structure of a path. If G is  $ \tilde{S^{\prime}}_{n,m}$ or
$ \tilde{S^{\prime}}_{n,m}$ or  $\tilde{T}^{\prime}_{n,m}$ (
$\tilde{T}^{\prime}_{n,m}$ (![]() $n\geq 5$, odd), then
$n\geq 5$, odd), then ![]() $v_1\neq v_2$ only when
$v_1\neq v_2$ only when ![]() $I=V\setminus\{1,2,n-1,n\}$. However, since n is odd, I has an odd number of vertices. This is a contradiction. In addition,
$I=V\setminus\{1,2,n-1,n\}$. However, since n is odd, I has an odd number of vertices. This is a contradiction. In addition, ![]() $1\not\in A$ if and only if
$1\not\in A$ if and only if ![]() $|K_0\cap A|\equiv |(K_0\setminus I)\cap A|\equiv 0\pmod{2}$. Since K has both 1 and 2, it should have a multiple edge e. We find
$|K_0\cap A|\equiv |(K_0\setminus I)\cap A|\equiv 0\pmod{2}$. Since K has both 1 and 2, it should have a multiple edge e. We find ![]() $K_\ast$ and
$K_\ast$ and ![]() $I_\ast$ according to the parity of
$I_\ast$ according to the parity of ![]() $|A\cap\{1,e\}|$.
$|A\cap\{1,e\}|$.
(Subcase 1) ![]() $\underline{|A\cap\{1,e\}|\equiv 0\pmod{2}}$. In this case,
$\underline{|A\cap\{1,e\}|\equiv 0\pmod{2}}$. In this case, ![]() $K_\ast=K_0\cup e=I_j\cup 1e$ and
$K_\ast=K_0\cup e=I_j\cup 1e$ and ![]() $I_\ast=I_i$.
$I_\ast=I_i$.
(Subcase 2) ![]() $\underline{|A\cap\{1,e\}|=1}$. We consider the connected component H of K containing e. Since
$\underline{|A\cap\{1,e\}|=1}$. We consider the connected component H of K containing e. Since ![]() $e\in H\setminus K_0$,
$e\in H\setminus K_0$, ![]() $|K_0\cap A|\equiv|H\cap K_0\cap A|\equiv|(H\setminus K_0)\cap A|$, where the first equivalence follows from the definition of H and the second equivalence comes from
$|K_0\cap A|\equiv|H\cap K_0\cap A|\equiv|(H\setminus K_0)\cap A|$, where the first equivalence follows from the definition of H and the second equivalence comes from ![]() $|H\cap A|\equiv 0\pmod{2}$. Hence,
$|H\cap A|\equiv 0\pmod{2}$. Hence, ![]() $1\not\in A$ if and only if
$1\not\in A$ if and only if ![]() $|(H\setminus K_0)\cap A|$ is even. Let
$|(H\setminus K_0)\cap A|$ is even. Let ![]() $X=(H\setminus K_0)\cap A$ for simplicity. If
$X=(H\setminus K_0)\cap A$ for simplicity. If ![]() $|X|$ is even, then
$|X|$ is even, then ![]() $1\not\in A$ and
$1\not\in A$ and ![]() $e\in A$, and therefore,
$e\in A$, and therefore, ![]() $|X\setminus\{e\}|\geq 1$. If
$|X\setminus\{e\}|\geq 1$. If ![]() $|X|$ is odd, then
$|X|$ is odd, then ![]() $1\in A$ and
$1\in A$ and ![]() $e\not\in A$, and therefore,
$e\not\in A$, and therefore, ![]() $|X\setminus \{e\}|=|X|\geq 1$. Hence, in any case, we can take an element
$|X\setminus \{e\}|=|X|\geq 1$. Hence, in any case, we can take an element ![]() $c\in X\setminus\{e\}$ so that
$c\in X\setminus\{e\}$ so that ![]() $K_\ast=K_0\cup ce=I_j\cup 1ce$ and
$K_\ast=K_0\cup ce=I_j\cup 1ce$ and ![]() $I_\ast=I_i$. More precisely, either c is the vertex
$I_\ast=I_i$. More precisely, either c is the vertex ![]() $\min(V\setminus (I_j\cup\{1,2\}))$ or belongs to
$\min(V\setminus (I_j\cup\{1,2\}))$ or belongs to ![]() $(B\cap A)\setminus{e}$.
$(B\cap A)\setminus{e}$.
(Case 2)K 0 is a semi-induced subgraph of G. Note that ![]() $(I_i\setminus I) \cap (I_j\setminus I)\cap A$ is nonempty and has at most three elements.
$(I_i\setminus I) \cap (I_j\setminus I)\cap A$ is nonempty and has at most three elements.
(Subcase 1)  $\underline{|(I_i\setminus I) \cap (I_j\setminus I)\cap A|}$ is even. In this case,
$\underline{|(I_i\setminus I) \cap (I_j\setminus I)\cap A|}$ is even. In this case,
and therefore ![]() $|K_0\cap A|$ is even. By (
$|K_0\cap A|$ is even. By (![]() $\dagger$) in the proof of Lemma 5.1,
$\dagger$) in the proof of Lemma 5.1, ![]() $K_0=I_j\cup (I_i\setminus I_j)$ is an atom of
$K_0=I_j\cup (I_i\setminus I_j)$ is an atom of ![]() $[I_j,G]$, so
$[I_j,G]$, so ![]() $K_{\ast}=K_0$ and
$K_{\ast}=K_0$ and ![]() $I_{\ast}=I_i$.
$I_{\ast}=I_i$.
(Subcase 2)  $\underline{|(I_i\setminus I) \cap (I_j\setminus I)\cap A|}$ is odd. Then
$\underline{|(I_i\setminus I) \cap (I_j\setminus I)\cap A|}$ is odd. Then ![]() $|(I_i\setminus I) \cap (I_j\setminus I)\cap A|$ is one or three. Since
$|(I_i\setminus I) \cap (I_j\setminus I)\cap A|$ is one or three. Since ![]() $(I_i\setminus I) \cap (I_j\setminus I)\cap A \neq \emptyset$, the elements in
$(I_i\setminus I) \cap (I_j\setminus I)\cap A \neq \emptyset$, the elements in ![]() $K_0\setminus I$ lie on the same connected component of K 0 by (
$K_0\setminus I$ lie on the same connected component of K 0 by (![]() $\dagger$). Thus, K 0 has exactly one connected component H 0 such that
$\dagger$). Thus, K 0 has exactly one connected component H 0 such that ![]() $|H_0\cap A|$ is odd. Note that for the connected component H of K containing H 0, we have
$|H_0\cap A|$ is odd. Note that for the connected component H of K containing H 0, we have ![]() $|(H\setminus H_0)\cap A| \ge 1$ since
$|(H\setminus H_0)\cap A| \ge 1$ since ![]() $|H\cap A|$ is even.
$|H\cap A|$ is even.
(i) If H 0 contains a multiple edge, then there exists an element ![]() $c\in (H\setminus H_0)\cap A$ such that
$c\in (H\setminus H_0)\cap A$ such that ![]() $K_\ast=K_0 {\cup c}$ and
$K_\ast=K_0 {\cup c}$ and ![]() $I_\ast=I_i$. More precisely, if
$I_\ast=I_i$. More precisely, if ![]() $(H\setminus H_0)\cap B\cap A\neq\emptyset$, then
$(H\setminus H_0)\cap B\cap A\neq\emptyset$, then ![]() $c\in B\cap A$; otherwise, c is the vertex
$c\in B\cap A$; otherwise, c is the vertex ![]() $\min(V\setminus H_0)$.
$\min(V\setminus H_0)$.
(ii) Suppose that H 0 has no multiple edges. Then both ![]() $I_i\setminus I$ and
$I_i\setminus I$ and ![]() $I_j\setminus I$ consist of two vertices in A, and
$I_j\setminus I$ consist of two vertices in A, and ![]() $|(I_i\setminus I)\cap (I_j\setminus I)\cap A|=1$. Since H 0 is a semi-induced subgraph of G and
$|(I_i\setminus I)\cap (I_j\setminus I)\cap A|=1$. Since H 0 is a semi-induced subgraph of G and ![]() $|H_0\cap A|$ is odd,
$|H_0\cap A|$ is odd, ![]() $(H\setminus H_0)\cap V\neq \emptyset$. If
$(H\setminus H_0)\cap V\neq \emptyset$. If ![]() $(H\setminus H_0)\cap V$ has a vertex in
$(H\setminus H_0)\cap V$ has a vertex in ![]() $\{3,\ldots,n\}$, then by the structure of G, it is easy to see that there is a vertex v in
$\{3,\ldots,n\}$, then by the structure of G, it is easy to see that there is a vertex v in ![]() $(H\setminus H_0)\cap \{3,\ldots,n\}$ such that
$(H\setminus H_0)\cap \{3,\ldots,n\}$ such that ![]() $K_{\ast}=K_0\cup v$ and
$K_{\ast}=K_0\cup v$ and ![]() $I_{\ast}=I_i$. Hence, we only need to consider the case in which
$I_{\ast}=I_i$. Hence, we only need to consider the case in which ![]() ${(H\setminus H_0)\cap V}\subset\{1,2\}$. If
${(H\setminus H_0)\cap V}\subset\{1,2\}$. If ![]() ${(H\setminus H_0)\cap V}=\{1,2\}$, then
${(H\setminus H_0)\cap V}=\{1,2\}$, then
 \begin{equation*}\begin{cases}
K_\ast=I_j\cup 1 \text{ and } I_\ast=I\cup 1&\text{if }1\not\in A\\
K_\ast=K_0\cup 1 \text{ and } I_\ast=I_i &\text{if }1\in A.
\end{cases}\end{equation*}
\begin{equation*}\begin{cases}
K_\ast=I_j\cup 1 \text{ and } I_\ast=I\cup 1&\text{if }1\not\in A\\
K_\ast=K_0\cup 1 \text{ and } I_\ast=I_i &\text{if }1\in A.
\end{cases}\end{equation*} It remains to consider the case where ![]() $(H\setminus H_0)\cap V=\{1\}$ or
$(H\setminus H_0)\cap V=\{1\}$ or ![]() $\{2\}$. Let
$\{2\}$. Let ![]() $(H\setminus H_0)\cap V=\{w_1\}$, and let w 2 be the other vertex in
$(H\setminus H_0)\cap V=\{w_1\}$, and let w 2 be the other vertex in ![]() $\{1,2\}$. If H 0 does not contain w 2, then
$\{1,2\}$. If H 0 does not contain w 2, then ![]() $H=H_0\cup w_1$ and
$H=H_0\cup w_1$ and ![]() $w_1\in A$ (and therefore, w 1 must be a neighbour of 3 since H is an element of
$w_1\in A$ (and therefore, w 1 must be a neighbour of 3 since H is an element of ![]() $\mathcal{P}_{G,A}^{\mathrm{even}}$), and hence
$\mathcal{P}_{G,A}^{\mathrm{even}}$), and hence ![]() $K_\ast=K_0\cup w_1$ and
$K_\ast=K_0\cup w_1$ and ![]() $I_\ast=I_i$. The remaining case is that H 0 contains w 2. Then H contains a multiple edge, that is,
$I_\ast=I_i$. The remaining case is that H 0 contains w 2. Then H contains a multiple edge, that is, ![]() $(H\setminus H_0) \cap B=H\cap B\neq \emptyset$. Hence,
$(H\setminus H_0) \cap B=H\cap B\neq \emptyset$. Hence,
Since ![]() $|(H\setminus H_0)\cap A|$ is odd and
$|(H\setminus H_0)\cap A|$ is odd and
we see
 \begin{equation*}\begin{cases}
|H\cap B\cap A|\ge 1 &\text{if } w_1\not\in A,\\
|H\cap B\cap A|\ge 2 &\text{if } w_1\in A \text{ and } H\cap (B\setminus A)=\emptyset\\
|H\cap (B\setminus A)|\ge 1 &\text{otherwise.}
\end{cases}\end{equation*}
\begin{equation*}\begin{cases}
|H\cap B\cap A|\ge 1 &\text{if } w_1\not\in A,\\
|H\cap B\cap A|\ge 2 &\text{if } w_1\in A \text{ and } H\cap (B\setminus A)=\emptyset\\
|H\cap (B\setminus A)|\ge 1 &\text{otherwise.}
\end{cases}\end{equation*} Now there are two possibilities: (a) ![]() $w_1\not\in A$ and (b)
$w_1\not\in A$ and (b) ![]() $w_1\in A$. In (a), it easily follows that
$w_1\in A$. In (a), it easily follows that ![]() $K_\ast=K_0\cup w_1a$ and
$K_\ast=K_0\cup w_1a$ and ![]() $I_\ast=I_i$ for some
$I_\ast=I_i$ for some ![]() $a\in H\cap B\cap A$. In (b), we prove it by dividing two subcases whether
$a\in H\cap B\cap A$. In (b), we prove it by dividing two subcases whether ![]() $w_2\in I$ or not. If
$w_2\in I$ or not. If ![]() $w_2\in I$, then
$w_2\in I$, then
 \begin{equation*}\begin{cases}
K_\ast=I_j\cup w_1aa^{\prime} \text{ and } I_\ast=I\cup w_1a \text{ for some } a,a^{\prime}\in H\cap B\cap A&\text{if } {H}\cap (B\setminus A)=\emptyset,\\
K_\ast=K_0\cup w_1b \text{ and } I_\ast=I_i \text{ for some }b\in H\cap(B\setminus A)&\text{if } {H}\cap(B\setminus A)\neq\emptyset.
\end{cases}\end{equation*}
\begin{equation*}\begin{cases}
K_\ast=I_j\cup w_1aa^{\prime} \text{ and } I_\ast=I\cup w_1a \text{ for some } a,a^{\prime}\in H\cap B\cap A&\text{if } {H}\cap (B\setminus A)=\emptyset,\\
K_\ast=K_0\cup w_1b \text{ and } I_\ast=I_i \text{ for some }b\in H\cap(B\setminus A)&\text{if } {H}\cap(B\setminus A)\neq\emptyset.
\end{cases}\end{equation*} If ![]() $w_2\not\in I$, then
$w_2\not\in I$, then ![]() $w_2\in (I_i\setminus I) \cup (I_j\setminus I)$. Since
$w_2\in (I_i\setminus I) \cup (I_j\setminus I)$. Since ![]() $I_i\prec_{\tiny\text{atm}}^{I} I_j, w_2\in I_i$. Moreover, by the structure of G,
$I_i\prec_{\tiny\text{atm}}^{I} I_j, w_2\in I_i$. Moreover, by the structure of G, ![]() $I_i\setminus I=w_2v$ and
$I_i\setminus I=w_2v$ and ![]() $I_j\setminus I=vv^{\prime}$ for
$I_j\setminus I=vv^{\prime}$ for ![]() $v=\min(V\setminus (I\cup \{1,2\} ))$ and
$v=\min(V\setminus (I\cup \{1,2\} ))$ and ![]() $v^{\prime}=\min(V\setminus (I\cup\{1,2,v\}))$. Hence,
$v^{\prime}=\min(V\setminus (I\cup\{1,2,v\}))$. Hence,
 \begin{equation*}\begin{cases}
K_\ast=I_j\cup 12aa^{\prime} \text{ and }I_\ast=I \cup 12aa^{\prime} \text{ for some } a,a^{\prime}\in H\cap B\cap A& \text{if } H\cap (B\setminus A)=\emptyset,\\
K_\ast=I_j\cup 12b \text{ and }I_\ast=I \cup 12b \text{ for some }b\in H\cap (B\setminus A)& \text{if }H\cap (B\setminus A)\neq\emptyset.
\end{cases}\end{equation*}
\begin{equation*}\begin{cases}
K_\ast=I_j\cup 12aa^{\prime} \text{ and }I_\ast=I \cup 12aa^{\prime} \text{ for some } a,a^{\prime}\in H\cap B\cap A& \text{if } H\cap (B\setminus A)=\emptyset,\\
K_\ast=I_j\cup 12b \text{ and }I_\ast=I \cup 12b \text{ for some }b\in H\cap (B\setminus A)& \text{if }H\cap (B\setminus A)\neq\emptyset.
\end{cases}\end{equation*}This completes the proof.
For an element I of ![]() $\mathcal{P}_{G,A}^{\mathrm{even}}$, a multiple edge e is called a big (respectively, small) edge of I if
$\mathcal{P}_{G,A}^{\mathrm{even}}$, a multiple edge e is called a big (respectively, small) edge of I if ![]() $e \succ^{I}_{\mathrm{lex}} n$ (respectively,
$e \succ^{I}_{\mathrm{lex}} n$ (respectively, ![]() $e\preceq_{\tiny\text{lex}}^{I} n$). Note that if e is a small edge of I, then
$e\preceq_{\tiny\text{lex}}^{I} n$). Note that if e is a small edge of I, then ![]() $e\prec_{\tiny\text{lex}}^{I} 3$. Now we check that
$e\prec_{\tiny\text{lex}}^{I} 3$. Now we check that ![]() $\prec_{\tiny\text{atm}}^{I}$ satisfies Condition (1) of Definition 2.3.
$\prec_{\tiny\text{atm}}^{I}$ satisfies Condition (1) of Definition 2.3.
For an atom Ij of ![]() $[I,G]$, suppose that an atom J of
$[I,G]$, suppose that an atom J of ![]() $[I_j,G]$ belongs to
$[I_j,G]$ belongs to ![]() $[I_\ast,G]$ for some atom
$[I_\ast,G]$ for some atom ![]() $I_\ast$ of
$I_\ast$ of ![]() $[I,G]$ with
$[I,G]$ with ![]() $I_\ast\prec_{\tiny\text{atm}}^{I} I_j$ if and only if
$I_\ast\prec_{\tiny\text{atm}}^{I} I_j$ if and only if  $\min^{I_j}(J\setminus I_j) \prec_{\tiny\text{lex}}^{I_j} z$ for some
$\min^{I_j}(J\setminus I_j) \prec_{\tiny\text{lex}}^{I_j} z$ for some ![]() $z\in V\cup B$. Then the atoms J belonging to
$z\in V\cup B$. Then the atoms J belonging to ![]() $[I_\ast,G]$ for some atom
$[I_\ast,G]$ for some atom ![]() $I_\ast$ of
$I_\ast$ of ![]() $[I,G]$ with
$[I,G]$ with ![]() $I_\ast\prec_{\tiny\text{atm}}^{I} I_j$ come first in the order
$I_\ast\prec_{\tiny\text{atm}}^{I} I_j$ come first in the order  $\prec^{I_j}_{\mathrm{atm}}$. Hence, the following lemma says that
$\prec^{I_j}_{\mathrm{atm}}$. Hence, the following lemma says that ![]() $\prec_{\tiny\text{atm}}^{I}$ satisfies Condition (1) of Definition 2.3.
$\prec_{\tiny\text{atm}}^{I}$ satisfies Condition (1) of Definition 2.3.
Lemma 5.6. Let Ij be an atom of ![]() $[I,G]$, not the first in
$[I,G]$, not the first in ![]() $\prec_{\tiny\text{atm}}^{I}$. Then an atom J of
$\prec_{\tiny\text{atm}}^{I}$. Then an atom J of ![]() $[I_j,G]$ belongs to
$[I_j,G]$ belongs to ![]() $[I_\ast,G]$ for some atom
$[I_\ast,G]$ for some atom ![]() $I_\ast$ of
$I_\ast$ of ![]() $[I,G]$ with
$[I,G]$ with ![]() $I_\ast\prec_{\tiny\text{atm}}^{I} I_j$ if and only if
$I_\ast\prec_{\tiny\text{atm}}^{I} I_j$ if and only if  $\min^{I_j}(J\setminus I_j)$ satisfies one of the following:
$\min^{I_j}(J\setminus I_j)$ satisfies one of the following:
(1)
 $\min^{I_j}(J\setminus I_j) \prec_{\tiny\text{lex}}^{I_j} 2$ if
$\min^{I_j}(J\setminus I_j) \prec_{\tiny\text{lex}}^{I_j} 2$ if  $I_j\setminus I\subset V$ and
$I_j\setminus I\subset V$ and  $(I_j\setminus I)\cap\{1,2\}\neq\emptyset$;
$(I_j\setminus I)\cap\{1,2\}\neq\emptyset$;(2)
 $\min^{I_j}(J\setminus I_j) \prec_{\tiny\text{lex}}^{I_j}\min^{I_j}\{v,b_1\}$ if
$\min^{I_j}(J\setminus I_j) \prec_{\tiny\text{lex}}^{I_j}\min^{I_j}\{v,b_1\}$ if  $I_j\setminus I=va$ for
$I_j\setminus I=va$ for  $v\in V$ and a small edge a of I in
$v\in V$ and a small edge a of I in  $B\cap A$;
$B\cap A$;(3)
 $\min^{I_j}(J\setminus I_j) \preceq^{I_j}_{\mathrm{lex}} n$ if
$\min^{I_j}(J\setminus I_j) \preceq^{I_j}_{\mathrm{lex}} n$ if  $I_j\setminus I$ consists of only big edges of I;
$I_j\setminus I$ consists of only big edges of I;(4)
 $\min^{I_j}(J\setminus I_j) \preceq^{I_j}_{\mathrm{lex}} {\min(V\setminus I_j)}$ if
$\min^{I_j}(J\setminus I_j) \preceq^{I_j}_{\mathrm{lex}} {\min(V\setminus I_j)}$ if  $V\setminus I_j\neq\emptyset$,
$V\setminus I_j\neq\emptyset$,  $I_j\setminus I$ has an element
$I_j\setminus I$ has an element  $c\preceq_{\tiny\text{lex}}^{I}n$ and a big edge of I, and
$c\preceq_{\tiny\text{lex}}^{I}n$ and a big edge of I, and  $|(I_j\setminus I) \cap \{1,2\}|\equiv 0\pmod{2}$; and
$|(I_j\setminus I) \cap \{1,2\}|\equiv 0\pmod{2}$; and(5)
 $\min^{I_j}(J\setminus I_j) \prec_{\tiny\text{lex}}^{I_j}\max^{I_j}(I_j\setminus I)$ otherwise.
$\min^{I_j}(J\setminus I_j) \prec_{\tiny\text{lex}}^{I_j}\max^{I_j}(I_j\setminus I)$ otherwise.
Proof. In each case, when we show the ‘if’ part, we show that there exists an atom ![]() $I_\ast$
$I_\ast$ ![]() $[I,G]$ such that
$[I,G]$ such that ![]() $J\in [I_\ast,G]$ and
$J\in [I_\ast,G]$ and ![]() $I_\ast\prec_{\tiny\text{atm}}^{I} I_j$. On the other hand, we prove the ‘only if’ part by contradiction. Set
$I_\ast\prec_{\tiny\text{atm}}^{I} I_j$. On the other hand, we prove the ‘only if’ part by contradiction. Set  $x=\min^{I_j}(J\setminus I_j)$.
$x=\min^{I_j}(J\setminus I_j)$.
(1) Suppose that ![]() $I_j\setminus I\subset V$ and
$I_j\setminus I\subset V$ and ![]() $(I_j\setminus I)\cap\{1,2\}\neq\emptyset$. Note that
$(I_j\setminus I)\cap\{1,2\}\neq\emptyset$. Note that
Since we assumed Ij is not the first atom of ![]() $[I,G]$, we have
$[I,G]$, we have ![]() $(I_j\setminus I)\cap\{1,2\}=\{2\}$. Suppose that
$(I_j\setminus I)\cap\{1,2\}=\{2\}$. Suppose that  $x\prec_{\tiny\text{lex}}^{I_j} 2$. Then x = 1, and
$x\prec_{\tiny\text{lex}}^{I_j} 2$. Then x = 1, and
 \begin{equation*} J\setminus I_j = \left\{\begin{array}{ll}
1ac\text{ or }1b, &\text{if }1\not\in A,\\
1a\text{ or }1{v}b & \text{if }1\in A,
\end{array}\right. \end{equation*}
\begin{equation*} J\setminus I_j = \left\{\begin{array}{ll}
1ac\text{ or }1b, &\text{if }1\not\in A,\\
1a\text{ or }1{v}b & \text{if }1\in A,
\end{array}\right. \end{equation*} where ![]() $a\in B\cap A$,
$a\in B\cap A$, ![]() $c\in A$,
$c\in A$, ![]() $b\in B\setminus A$ and
$b\in B\setminus A$ and ![]() ${v}=\min(V\setminus (I_j\cup\{1\}))$. Then
${v}=\min(V\setminus (I_j\cup\{1\}))$. Then ![]() $I_\ast$ is either
$I_\ast$ is either ![]() $I\cup 1$ or
$I\cup 1$ or ![]() $I\cup 1v$, which proves the ‘if’ part.
$I\cup 1v$, which proves the ‘if’ part.
Suppose that  $x\succeq_{\mathrm{lex}}^{I_j} 2$. Then
$x\succeq_{\mathrm{lex}}^{I_j} 2$. Then ![]() $1\not\in J\setminus I_j$, so
$1\not\in J\setminus I_j$, so ![]() $J\setminus I_j$ cannot have a multiple edge. Thus,
$J\setminus I_j$ cannot have a multiple edge. Thus, ![]() $J\setminus I_j$ consists of vertices greater than
$J\setminus I_j$ consists of vertices greater than ![]() $\max^{I}(I_j\setminus I)$ by (
$\max^{I}(I_j\setminus I)$ by (![]() $\dagger$) in the proof of Lemma 5.1. Then Ij is the first atom of
$\dagger$) in the proof of Lemma 5.1. Then Ij is the first atom of ![]() $[I,G]$, which is a contradiction to the assumption.
$[I,G]$, which is a contradiction to the assumption.
(2) Suppose ![]() $I_j\setminus I=va$ for
$I_j\setminus I=va$ for ![]() $v\in V$ and a small edge a of I in
$v\in V$ and a small edge a of I in ![]() $B\cap A$. The existence of a small edge of I implies
$B\cap A$. The existence of a small edge of I implies ![]() $\{1,2\}\subset I$ and
$\{1,2\}\subset I$ and ![]() $v={\min(V\setminus I)}$. Hence,
$v={\min(V\setminus I)}$. Hence,  $\prec_{\tiny\text{lex}}^{I}=\prec_{\tiny\text{lex}}^{I_j}$, and they are either
$\prec_{\tiny\text{lex}}^{I}=\prec_{\tiny\text{lex}}^{I_j}$, and they are either
 \begin{eqnarray*}
&&\prec_{\tiny\text{lex}}^{I}=\prec_{\tiny\text{lex}}^{I_j}: \ 1,2,a_1,a_2,\ldots,a_{k},3, \ldots,n, a_{k+1},\ldots,a_{2m},b_1,\ldots,b_\ell, \quad \text{or}\\
&&\prec_{\tiny\text{lex}}^{I}=\prec_{\tiny\text{lex}}^{I_j}: \ 1,2,a_1,a_2,\ldots,a_{2m},b_1,\ldots,b_{k},3,\ldots,n, b_{k+1},\ldots,b_\ell.
\end{eqnarray*}
\begin{eqnarray*}
&&\prec_{\tiny\text{lex}}^{I}=\prec_{\tiny\text{lex}}^{I_j}: \ 1,2,a_1,a_2,\ldots,a_{k},3, \ldots,n, a_{k+1},\ldots,a_{2m},b_1,\ldots,b_\ell, \quad \text{or}\\
&&\prec_{\tiny\text{lex}}^{I}=\prec_{\tiny\text{lex}}^{I_j}: \ 1,2,a_1,a_2,\ldots,a_{2m},b_1,\ldots,b_{k},3,\ldots,n, b_{k+1},\ldots,b_\ell.
\end{eqnarray*} Suppose  $x\prec_{\tiny\text{lex}}^{I_j} \min^{I_j}\{v,b_1\}$. Then
$x\prec_{\tiny\text{lex}}^{I_j} \min^{I_j}\{v,b_1\}$. Then ![]() $J\setminus I_j$ has an element
$J\setminus I_j$ has an element  $a^{\prime}\prec_{\tiny\text{lex}}^{I_j} \min^{I_j}\{v,b_1\}$. Hence,
$a^{\prime}\prec_{\tiny\text{lex}}^{I_j} \min^{I_j}\{v,b_1\}$. Hence, ![]() $a^{\prime}\in B\cap A$ and
$a^{\prime}\in B\cap A$ and ![]() $I_\ast=I \cup aa^{\prime}$, which proves the ‘if’ part.
$I_\ast=I \cup aa^{\prime}$, which proves the ‘if’ part.
Suppose  $x \succeq_{\mathrm{lex}}^{I_j} \min^{I_j}\{v,b_1\}$. Then
$x \succeq_{\mathrm{lex}}^{I_j} \min^{I_j}\{v,b_1\}$. Then ![]() $I_j\lessdot J$ is of type (E1ʹ) or (E2). If
$I_j\lessdot J$ is of type (E1ʹ) or (E2). If ![]() $J\setminus I_j=b$ for some
$J\setminus I_j=b$ for some ![]() $b\in B\setminus A$, then
$b\in B\setminus A$, then ![]() $[I,J]$ has only two atoms Ij and
$[I,J]$ has only two atoms Ij and ![]() $I\cup b$, so Ij is the first. If
$I\cup b$, so Ij is the first. If ![]() $J\setminus I_j=cc^{\prime}\subset A$ for some
$J\setminus I_j=cc^{\prime}\subset A$ for some  $c,c^{\prime}\succeq_{\mathrm{lex}}^{I_j} v$, then
$c,c^{\prime}\succeq_{\mathrm{lex}}^{I_j} v$, then ![]() $I_j\setminus I$ consists of the first two smallest elements of
$I_j\setminus I$ consists of the first two smallest elements of ![]() $J\setminus I$, so Ij is the first. Then, in any case, Ij is the first atom of
$J\setminus I$, so Ij is the first. Then, in any case, Ij is the first atom of ![]() $[I,J]$, which is a contradiction to the assumption.
$[I,J]$, which is a contradiction to the assumption.
(3) Suppose that ![]() $I_j\setminus I$ consists of only big edges of I. Then
$I_j\setminus I$ consists of only big edges of I. Then ![]() $I\cap B\neq\emptyset$ and either
$I\cap B\neq\emptyset$ and either ![]() $I_j\setminus I=aa^{\prime}$ or
$I_j\setminus I=aa^{\prime}$ or ![]() $I_j\setminus I=b$, where
$I_j\setminus I=b$, where ![]() $a,a^{\prime}\in B\cap A$ and
$a,a^{\prime}\in B\cap A$ and ![]() $b\in B\setminus A$.
$b\in B\setminus A$.
(Case 1)  $\underline{I_j\setminus I=aa^{\prime}}$. The existence of a big edge of I in
$\underline{I_j\setminus I=aa^{\prime}}$. The existence of a big edge of I in ![]() $B\cap A$ implies that
$B\cap A$ implies that ![]() $I\cap (B\setminus A)=\emptyset$, so the lexicographic orders
$I\cap (B\setminus A)=\emptyset$, so the lexicographic orders ![]() $\prec_{\tiny\text{lex}}^{I}$ and
$\prec_{\tiny\text{lex}}^{I}$ and  $\prec_{\tiny\text{lex}}^{I_j}$ are as follows:
$\prec_{\tiny\text{lex}}^{I_j}$ are as follows:
 \begin{eqnarray*}
\prec_{\tiny\text{lex}}^{I}:&& 1,2,a_1,\ldots,a_{k},3,\ldots,n, a_{k+1},\ldots,a,\ldots,a^{\prime}(=a_t),\ldots, a_{2m},b_{1},\ldots,b_\ell\\
\prec_{\tiny\text{lex}}^{I_j}:&& 1,2,a_1,\ldots,a_{k},\ldots,a,\ldots,a^{\prime}(=a_t),3,\ldots,n, a_{t+1},\ldots, a_{2m},b_{1},\ldots,b_\ell.
\end{eqnarray*}
\begin{eqnarray*}
\prec_{\tiny\text{lex}}^{I}:&& 1,2,a_1,\ldots,a_{k},3,\ldots,n, a_{k+1},\ldots,a,\ldots,a^{\prime}(=a_t),\ldots, a_{2m},b_{1},\ldots,b_\ell\\
\prec_{\tiny\text{lex}}^{I_j}:&& 1,2,a_1,\ldots,a_{k},\ldots,a,\ldots,a^{\prime}(=a_t),3,\ldots,n, a_{t+1},\ldots, a_{2m},b_{1},\ldots,b_\ell.
\end{eqnarray*} Suppose that  $x\preceq_{\tiny\text{lex}}^{I_j} n$. Then
$x\preceq_{\tiny\text{lex}}^{I_j} n$. Then ![]() $x \prec_{\tiny\text{lex}}^{I} a^{\prime}$ and
$x \prec_{\tiny\text{lex}}^{I} a^{\prime}$ and ![]() $I_j\lessdot J$ is of (E2). Hence, we can set
$I_j\lessdot J$ is of (E2). Hence, we can set ![]() $J\setminus I_j=xx^{\prime} \subset A$, where
$J\setminus I_j=xx^{\prime} \subset A$, where  $x\prec_{\tiny\text{lex}}^{I_j}x^{\prime}$. If
$x\prec_{\tiny\text{lex}}^{I_j}x^{\prime}$. If  $x\preceq_{\tiny\text{lex}}^{I_j} {\min(V\setminus I)}$, then
$x\preceq_{\tiny\text{lex}}^{I_j} {\min(V\setminus I)}$, then ![]() $I_\ast=I\cup ax$. If
$I_\ast=I\cup ax$. If  $ {\min(V\setminus I)}\prec_{\tiny\text{lex}}^{I_j} x$, then both x and xʹ are vertices and
$ {\min(V\setminus I)}\prec_{\tiny\text{lex}}^{I_j} x$, then both x and xʹ are vertices and ![]() $I_\ast=I\cup xx^{\prime}$. This proves the ‘if’ part.
$I_\ast=I\cup xx^{\prime}$. This proves the ‘if’ part.
Suppose that  $x \succ_{\mathrm{lex}}^{I_j} n$. Then either
$x \succ_{\mathrm{lex}}^{I_j} n$. Then either ![]() $J\setminus I_j=xx^{\prime}\subset B\cap A$ or
$J\setminus I_j=xx^{\prime}\subset B\cap A$ or ![]() $J\setminus I_j=x\in B\setminus A$. Since
$J\setminus I_j=x\in B\setminus A$. Since ![]() $a\prec_{\tiny\text{lex}}^{I} a^{\prime} \prec_{\tiny\text{lex}}^{I} x$, Ij is the first atom of
$a\prec_{\tiny\text{lex}}^{I} a^{\prime} \prec_{\tiny\text{lex}}^{I} x$, Ij is the first atom of ![]() $[I,J]$ in
$[I,J]$ in ![]() $\prec_{\tiny\text{atm}}^{I}$. This is a contradiction to the assumption.
$\prec_{\tiny\text{atm}}^{I}$. This is a contradiction to the assumption.
(Case 2)  $\underline{I_j\setminus I=b}$. In this case, the lexicographic order
$\underline{I_j\setminus I=b}$. In this case, the lexicographic order  $\prec_{\tiny\text{lex}}^{I_j}$ is given as follows:
$\prec_{\tiny\text{lex}}^{I_j}$ is given as follows:
 \begin{equation*}\prec_{\tiny\text{lex}}^{I_j}: 1,2,a_1,a_2,\ldots,a_{2m},b_1,\ldots,b(=b_k),3,4,\ldots,n,b_{k+1},\ldots,b_{\ell}.\end{equation*}
\begin{equation*}\prec_{\tiny\text{lex}}^{I_j}: 1,2,a_1,a_2,\ldots,a_{2m},b_1,\ldots,b(=b_k),3,4,\ldots,n,b_{k+1},\ldots,b_{\ell}.\end{equation*} Suppose that ![]() $J\setminus I_j$ contains an element x with
$J\setminus I_j$ contains an element x with  ${x}\preceq_{\tiny\text{lex}}^{I_j} n$. Note that
${x}\preceq_{\tiny\text{lex}}^{I_j} n$. Note that ![]() ${x}\prec_{\tiny\text{lex}}^{I} b$. If x is a vertex, then
${x}\prec_{\tiny\text{lex}}^{I} b$. If x is a vertex, then ![]() $J\setminus I_j$ consists of two vertices, and
$J\setminus I_j$ consists of two vertices, and ![]() $I_\ast= I\cup (J\setminus I_j)$. Now let x be a multiple edge e. If
$I_\ast= I\cup (J\setminus I_j)$. Now let x be a multiple edge e. If ![]() $e\in B\setminus A$, then
$e\in B\setminus A$, then ![]() $I_\ast=I_j\cup e$. If
$I_\ast=I_j\cup e$. If ![]() $e\in B\cap A$, then
$e\in B\cap A$, then ![]() $J\setminus I_j=ec$ for some
$J\setminus I_j=ec$ for some ![]() $c\in A$, which implies that
$c\in A$, which implies that ![]() $I_\ast=I\cup ec$. This proves the ‘if’ part.
$I_\ast=I\cup ec$. This proves the ‘if’ part.
If  $x \succeq_{\mathrm{lex}}^{I_j} n$, then
$x \succeq_{\mathrm{lex}}^{I_j} n$, then ![]() $J\setminus I_j=\{b^{\prime}\}$ for some
$J\setminus I_j=\{b^{\prime}\}$ for some ![]() $b^{\prime}\in B\setminus A$ with
$b^{\prime}\in B\setminus A$ with  $b\prec_{\tiny\text{lex}}^{I_j} b^{\prime}$, and hence
$b\prec_{\tiny\text{lex}}^{I_j} b^{\prime}$, and hence ![]() $[I,J]$ has only two atoms Ij and
$[I,J]$ has only two atoms Ij and ![]() $I\cup b^{\prime}$, where Ij is the first atom in
$I\cup b^{\prime}$, where Ij is the first atom in ![]() $\prec_{\tiny\text{atm}}^{I}$. This is a contradiction to the assumption.
$\prec_{\tiny\text{atm}}^{I}$. This is a contradiction to the assumption.
In order to show (4) and (5), we need to show the following claim.
Claim 5.7.
Suppose that ![]() $I\cap (B\setminus A)$ is empty,
$I\cap (B\setminus A)$ is empty, ![]() $I_j\setminus I$ has both an element
$I_j\setminus I$ has both an element ![]() $c\preceq_{\tiny\text{lex}}^{I} n$ and a big edge of I, and
$c\preceq_{\tiny\text{lex}}^{I} n$ and a big edge of I, and ![]() $|(I_j\setminus I) \cap \{1,2\}|{\equiv 0\pmod{2}}$. Then an atom J of
$|(I_j\setminus I) \cap \{1,2\}|{\equiv 0\pmod{2}}$. Then an atom J of ![]() $[I_j,G]$ belongs to
$[I_j,G]$ belongs to ![]() $[I_\ast,G]$ for some atom
$[I_\ast,G]$ for some atom ![]() $I_\ast$ of
$I_\ast$ of ![]() $[I,G]$ with
$[I,G]$ with ![]() $I_\ast\prec_{\tiny\text{atm}}^{I} I_j$ if and only if one of the following holds:
$I_\ast\prec_{\tiny\text{atm}}^{I} I_j$ if and only if one of the following holds:
(i)
 $x\preceq_{\tiny\text{lex}}^{I_j} {\min(V\setminus I_j)}$ if
$x\preceq_{\tiny\text{lex}}^{I_j} {\min(V\setminus I_j)}$ if  $V\setminus I_j\neq \emptyset$,
$V\setminus I_j\neq \emptyset$,(ii)
 $x\prec_{\tiny\text{lex}}^{I_j}\max^{I_j}(I_j\setminus I)$ if
$x\prec_{\tiny\text{lex}}^{I_j}\max^{I_j}(I_j\setminus I)$ if  $V\setminus I_j= \emptyset$.
$V\setminus I_j= \emptyset$.
Proof of Claim 5.7
From the hypotheses, we need to consider the following four cases ①∼④ in the table below, where ![]() $a,a^{\prime}\in B\cap A$ with
$a,a^{\prime}\in B\cap A$ with ![]() $a^{\prime}\prec_{\tiny\text{lex}}^{I} a$,
$a^{\prime}\prec_{\tiny\text{lex}}^{I} a$, ![]() $b\in B\setminus A$, and
$b\in B\setminus A$, and ![]() $v=\min(V\setminus I)$:
$v=\min(V\setminus I)$:

Note that cases ① and ② occur only when ![]() $\{1,2\}\subset A$. Let
$\{1,2\}\subset A$. Let ![]() $v_\ast:={\min(V\setminus I_j)}$, provided
$v_\ast:={\min(V\setminus I_j)}$, provided ![]() $V\setminus I_j\neq\emptyset$. In cases ①∼④, if
$V\setminus I_j\neq\emptyset$. In cases ①∼④, if ![]() $v_\ast\in J\setminus I_j$, then
$v_\ast\in J\setminus I_j$, then ![]() $I_\ast$’s are
$I_\ast$’s are ![]() $I\cup 1v_\ast$,
$I\cup 1v_\ast$, ![]() $I\cup 1v_\ast$,
$I\cup 1v_\ast$, ![]() $I\cup vv_\ast$ and
$I\cup vv_\ast$ and ![]() $I\cup a^{\prime}v_\ast$, respectively. Note that when
$I\cup a^{\prime}v_\ast$, respectively. Note that when ![]() $v_{\ast}\not\in J\setminus I_j$, it holds that
$v_{\ast}\not\in J\setminus I_j$, it holds that  $x\preceq_{\tiny\text{lex}}^{I_j} v_\ast$ if and only if
$x\preceq_{\tiny\text{lex}}^{I_j} v_\ast$ if and only if  $x\prec_{\tiny\text{lex}}^{I_j}\max^{I_j}(I_j\setminus I)$. Now we assume that
$x\prec_{\tiny\text{lex}}^{I_j}\max^{I_j}(I_j\setminus I)$. Now we assume that ![]() $v_{\ast}\not\in J\setminus I_j$ and
$v_{\ast}\not\in J\setminus I_j$ and  $x\prec_{\tiny\text{lex}}^{I_j}\max^{I_j}(I_j\setminus I)$. Since x is a small edge of Ij, x is also a multiple edge, and hence
$x\prec_{\tiny\text{lex}}^{I_j}\max^{I_j}(I_j\setminus I)$. Since x is a small edge of Ij, x is also a multiple edge, and hence ![]() $J\setminus I_j$ consists of multiple edges. In case ②,
$J\setminus I_j$ consists of multiple edges. In case ②, ![]() $I_\ast=I\cup 12 \cup(J\setminus I_j)$. For the other cases,
$I_\ast=I\cup 12 \cup(J\setminus I_j)$. For the other cases, ![]() $x\prec_{\tiny\text{lex}}^{I}a$ and
$x\prec_{\tiny\text{lex}}^{I}a$ and ![]() $x,a\in B\cap A$. Hence,
$x,a\in B\cap A$. Hence, ![]() $I_\ast$ is obtained from Ij by replacing a with x. This proves the ‘if’ part.
$I_\ast$ is obtained from Ij by replacing a with x. This proves the ‘if’ part.
To prove the ‘only if’ part, first suppose that ![]() $V\setminus I_j\neq\emptyset$ and
$V\setminus I_j\neq\emptyset$ and  $x\succ_{\mathrm{lex}}^{I_j}v_\ast$. Then x is either a vertex greater than
$x\succ_{\mathrm{lex}}^{I_j}v_\ast$. Then x is either a vertex greater than ![]() $v_\ast$ or a big edge of Ij. Hence,
$v_\ast$ or a big edge of Ij. Hence, ![]() $J\setminus I_j$ consists of either two vertices greater than
$J\setminus I_j$ consists of either two vertices greater than ![]() $v_\ast$ or only big edges of Ij. Note that a big edge of Ij is also a big edge of I. Then Ij is the first atom of
$v_\ast$ or only big edges of Ij. Note that a big edge of Ij is also a big edge of I. Then Ij is the first atom of ![]() $[I,J]$ in
$[I,J]$ in ![]() $\prec_{\tiny\text{atm}}^{I}$, which is a contradiction to the assumption. If
$\prec_{\tiny\text{atm}}^{I}$, which is a contradiction to the assumption. If ![]() $V\setminus I_j=\emptyset$ and
$V\setminus I_j=\emptyset$ and  $x\succ_{\mathrm{lex}}^{I_j}\max^{I_j}(I_j\setminus I)$, then x is a big edge of Ij, and hence
$x\succ_{\mathrm{lex}}^{I_j}\max^{I_j}(I_j\setminus I)$, then x is a big edge of Ij, and hence ![]() $I_j\setminus I$ consists of only big edges of Ij. Then Ij is the first atom of
$I_j\setminus I$ consists of only big edges of Ij. Then Ij is the first atom of ![]() $[I,J]$ in
$[I,J]$ in ![]() $\prec_{\tiny\text{atm}}^{I}$, which is a contradiction to the assumption.
$\prec_{\tiny\text{atm}}^{I}$, which is a contradiction to the assumption.
From Claim 5.7, (4) follows and (5) partially follows. We exclude the cases of (1)–(4) and the case shown by Claim 5.7. We divide the remaining part into two cases according to the existence of a big edge of I in ![]() $I_j\setminus I$.
$I_j\setminus I$.
(Case 1)  $\underline{I_j\setminus I}$ has no big edge of I. By excluding (1) and (2), we get one of the following:
$\underline{I_j\setminus I}$ has no big edge of I. By excluding (1) and (2), we get one of the following:
①
 $I_j\setminus I=b$, where
$I_j\setminus I=b$, where  $b\in B\setminus A$ and b is a small edge of I;
$b\in B\setminus A$ and b is a small edge of I;②
 $I_j\setminus I=aa^{\prime}$, where both
$I_j\setminus I=aa^{\prime}$, where both  $a,a^{\prime}\in B\cap A$ are small edges of I; or
$a,a^{\prime}\in B\cap A$ are small edges of I; or③
 $I_j\setminus I=vv^{\prime}$, where
$I_j\setminus I=vv^{\prime}$, where  $v, v^{\prime}\in V\setminus\{1,2\}$.
$v, v^{\prime}\in V\setminus\{1,2\}$.
In each case, the ‘only if’ part easily follows, that is, if  $x\succ_{\mathrm{lex}}^{I_j} \max^{I_j}(I_j\setminus I)$, then
$x\succ_{\mathrm{lex}}^{I_j} \max^{I_j}(I_j\setminus I)$, then ![]() $I_j\setminus I$ has the first
$I_j\setminus I$ has the first ![]() $|I_j\setminus I|$ smallest elements of
$|I_j\setminus I|$ smallest elements of ![]() $J\setminus I$ (in
$J\setminus I$ (in ![]() $\prec_{\tiny\text{lex}}^{I}$), so Ij is the first atom of
$\prec_{\tiny\text{lex}}^{I}$), so Ij is the first atom of ![]() $[I,J]$ in
$[I,J]$ in ![]() $\prec_{\tiny\text{atm}}^{I}$. Let us prove the ‘if’ part of each case. We assume that
$\prec_{\tiny\text{atm}}^{I}$. Let us prove the ‘if’ part of each case. We assume that  $x \prec_{\tiny\text{lex}}^{I_j} \max^{I_j}(I_j\setminus I)$ and note that
$x \prec_{\tiny\text{lex}}^{I_j} \max^{I_j}(I_j\setminus I)$ and note that  $\prec_{\tiny\text{lex}}^{I}=\prec_{\tiny\text{lex}}^{I_j}$.
$\prec_{\tiny\text{lex}}^{I}=\prec_{\tiny\text{lex}}^{I_j}$.
① From the existence of a small edge in ![]() $B\setminus A$, it follows that
$B\setminus A$, it follows that ![]() $I\cap(B\setminus A)\neq\emptyset$ and
$I\cap(B\setminus A)\neq\emptyset$ and
 \begin{equation*}\prec_{\tiny\text{lex}}^{I}=\prec_{\tiny\text{lex}}^{I_j}: 1,2,a_1,a_2,\ldots,a_{2m},b_1,\ldots,b,\ldots,b_k,3,\ldots,n,b_{k+1},\ldots,b_{\ell}.\end{equation*}
\begin{equation*}\prec_{\tiny\text{lex}}^{I}=\prec_{\tiny\text{lex}}^{I_j}: 1,2,a_1,a_2,\ldots,a_{2m},b_1,\ldots,b,\ldots,b_k,3,\ldots,n,b_{k+1},\ldots,b_{\ell}.\end{equation*} If  $x\prec_{\tiny\text{lex}}^{I_j} b$, then
$x\prec_{\tiny\text{lex}}^{I_j} b$, then ![]() $I_\ast=I\cup (J\setminus I_j)$.
$I_\ast=I\cup (J\setminus I_j)$.
② Assume  $a \prec_{\tiny\text{lex}}^{I_j} a^{\prime}$. Then
$a \prec_{\tiny\text{lex}}^{I_j} a^{\prime}$. Then  $a^{\prime}=\max^{I_j}(J\setminus I_j)$. The assumption
$a^{\prime}=\max^{I_j}(J\setminus I_j)$. The assumption  $x\prec_{\tiny\text{lex}}^{I_j} a^{\prime}$ implies that
$x\prec_{\tiny\text{lex}}^{I_j} a^{\prime}$ implies that ![]() $J\setminus I$ contains a multiple edge a ʹʹ with
$J\setminus I$ contains a multiple edge a ʹʹ with ![]() $a^{\prime\prime}\prec_{\tiny\text{lex}}^{I} a^{\prime}$, so
$a^{\prime\prime}\prec_{\tiny\text{lex}}^{I} a^{\prime}$, so ![]() $I_\ast= I\cup aa^{\prime\prime}$.
$I_\ast= I\cup aa^{\prime\prime}$.
③ Assume  $v \prec_{\tiny\text{lex}}^{I_j} v^{\prime}$. Then
$v \prec_{\tiny\text{lex}}^{I_j} v^{\prime}$. Then  $v^{\prime}=\max^{I_j}(I_j\setminus I)$, so
$v^{\prime}=\max^{I_j}(I_j\setminus I)$, so  $x\prec_{\tiny\text{lex}}^{I_j} v^{\prime}$. If
$x\prec_{\tiny\text{lex}}^{I_j} v^{\prime}$. If ![]() $J\setminus I_j \subset V$, then
$J\setminus I_j \subset V$, then ![]() $J\setminus I \subset V$ and
$J\setminus I \subset V$ and ![]() $I_\ast=I\cup xy$, where x and y are the first two smallest elements of
$I_\ast=I\cup xy$, where x and y are the first two smallest elements of ![]() $J\setminus I$. When
$J\setminus I$. When ![]() $J\setminus I_j \not\subset V$, Table 2 shows how to obtain
$J\setminus I_j \not\subset V$, Table 2 shows how to obtain ![]() $I_{\ast}$:
$I_{\ast}$:
Table 2. ![]() $I_\ast$, where
$I_\ast$, where ![]() $b\in B\setminus A, a,a^{\prime}\in A\cap B, v^{\prime\prime}=\min V\setminus(I_j \cup x)$,
$b\in B\setminus A, a,a^{\prime}\in A\cap B, v^{\prime\prime}=\min V\setminus(I_j \cup x)$, ![]() $v_\ast=\min\{v,v^{\prime\prime}\}$ and
$v_\ast=\min\{v,v^{\prime\prime}\}$ and  $c_\ast=\min_{I_j}\{v,c\}$
$c_\ast=\min_{I_j}\{v,c\}$

(Case 2)  $\underline{I_j\setminus I}$ has a big edge of I. Excluding (3) and (4), we get the following five cases ①∼⑤ in the table, where
$\underline{I_j\setminus I}$ has a big edge of I. Excluding (3) and (4), we get the following five cases ①∼⑤ in the table, where ![]() $w\in \{1,2\}, a,a^{\prime}\in B\cap A$ with
$w\in \{1,2\}, a,a^{\prime}\in B\cap A$ with  $a^{\prime} \prec_{\tiny\text{lex}}^{I_j} a$,
$a^{\prime} \prec_{\tiny\text{lex}}^{I_j} a$, ![]() $b\in B\setminus A$, and
$b\in B\setminus A$, and ![]() $v=\min(V\setminus (I\cup\{1,2\}))$:
$v=\min(V\setminus (I\cup\{1,2\}))$:

Note that, in any case, the lexicographic ordering ![]() $\prec_{\tiny\text{lex}}^{I}$ on
$\prec_{\tiny\text{lex}}^{I}$ on ![]() $V\cup B$ is given by
$V\cup B$ is given by
and any atom of ![]() $[I,J]$ containing the element w has a multiple edge. If
$[I,J]$ containing the element w has a multiple edge. If  $x\succ_{\mathrm{lex}}^{I_j}\max^{I_j}(I_j\setminus I)$, then
$x\succ_{\mathrm{lex}}^{I_j}\max^{I_j}(I_j\setminus I)$, then ![]() $J\setminus I_j$ cannot have a multiple edge less than
$J\setminus I_j$ cannot have a multiple edge less than ![]() $\max^I(B\cap(I_j\setminus I))$ in
$\max^I(B\cap(I_j\setminus I))$ in ![]() $\prec_{\tiny\text{lex}}^{I}$. Then Ij is the first atom of
$\prec_{\tiny\text{lex}}^{I}$. Then Ij is the first atom of ![]() $[I,J]$ in
$[I,J]$ in ![]() $\prec_{\tiny\text{atm}}^{I}$, which is a contradiction to the assumption.
$\prec_{\tiny\text{atm}}^{I}$, which is a contradiction to the assumption.
Proof. Suppose that  $x\prec_{\tiny\text{lex}}^{I_j} \max^{I_j}(I_j\setminus I)$. In cases ①, ② and ④,
$x\prec_{\tiny\text{lex}}^{I_j} \max^{I_j}(I_j\setminus I)$. In cases ①, ② and ④, ![]() $J\setminus I_j$ contains a multiple edge a ʹʹ with
$J\setminus I_j$ contains a multiple edge a ʹʹ with  $a^{\prime\prime}\prec_{\tiny\text{lex}}^{I_j} a$, which implies that
$a^{\prime\prime}\prec_{\tiny\text{lex}}^{I_j} a$, which implies that ![]() $I_\ast$ can be obtained from Ij by replacing a with a ʹʹ. In cases ③ and ⑤,
$I_\ast$ can be obtained from Ij by replacing a with a ʹʹ. In cases ③ and ⑤, ![]() $I_j\setminus I$ contains a multiple edge
$I_j\setminus I$ contains a multiple edge  ${e}\prec_{\tiny\text{lex}}^{I_j}b$. If
${e}\prec_{\tiny\text{lex}}^{I_j}b$. If ![]() ${e}\in A$, then
${e}\in A$, then ![]() $J\setminus I_j$ is
$J\setminus I_j$ is ![]() ${e}c$ for some
${e}c$ for some ![]() $c\in A$, and hence
$c\in A$, and hence ![]() $I_\ast$’s are
$I_\ast$’s are ![]() $I\cup w{e}c$ and
$I\cup w{e}c$ and ![]() $I\cup w{e}$, respectively. If
$I\cup w{e}$, respectively. If ![]() ${e}\not\in A$, then
${e}\not\in A$, then ![]() $I_\ast$’s are
$I_\ast$’s are ![]() $I\cup w{e}$ and
$I\cup w{e}$ and ![]() $I\cup wv{e}$, respectively. This proves the ‘if’ part.
$I\cup wv{e}$, respectively. This proves the ‘if’ part.
Lemmas 5.5 and 5.6 imply that the ordering ![]() $\prec^I_{\mathrm{atm}}$ satisfies Definition 2.3. This proves Theorem 5.4.
$\prec^I_{\mathrm{atm}}$ satisfies Definition 2.3. This proves Theorem 5.4.
6. Falling chains of  $\mathcal{P}_{H,A}^{\mathrm{even}}$
$\mathcal{P}_{H,A}^{\mathrm{even}}$
In this section, for a graph H in Figure 1.1 and its admissible collection A, we study the falling chains of our CL-shelling on ![]() $\mathcal{P}_{H,A}^{\mathrm{even}}$, which let us know the homotopy type of the order complex of the proper part
$\mathcal{P}_{H,A}^{\mathrm{even}}$, which let us know the homotopy type of the order complex of the proper part  $\Delta(\overline{\mathcal{P}_{H,A}^{\mathrm{even}}})$. Throughout the section, the labelling of the vertices follows the way in Figure 5.2, so that the labels of the endpoints of the bundle are changed according to A. We always let V and B be the vertex set and the bundle of G, respectively.
$\Delta(\overline{\mathcal{P}_{H,A}^{\mathrm{even}}})$. Throughout the section, the labelling of the vertices follows the way in Figure 5.2, so that the labels of the endpoints of the bundle are changed according to A. We always let V and B be the vertex set and the bundle of G, respectively.
Recall that if a bounded poset ![]() $\mathcal{P}$ admits a recursive atom ordering, then we can find a CL-labelling ρ as in the sketch of the proof of Theorem 2.4. Furthermore, the ith reduced Betti number of the order complex
$\mathcal{P}$ admits a recursive atom ordering, then we can find a CL-labelling ρ as in the sketch of the proof of Theorem 2.4. Furthermore, the ith reduced Betti number of the order complex ![]() $\Delta(\overline{\mathcal{P}})$ equals the number of falling chains of length i + 2 from Theorem 2.2. For a graph
$\Delta(\overline{\mathcal{P}})$ equals the number of falling chains of length i + 2 from Theorem 2.2. For a graph ![]() $G\in\mathcal{G}^\ast$, if G is simple, then the homotopy type of
$G\in\mathcal{G}^\ast$, if G is simple, then the homotopy type of ![]() $\Delta(\overline{\mathcal{P}_{G}^{\mathrm{even}}})$ is completely determined by the length
$\Delta(\overline{\mathcal{P}_{G}^{\mathrm{even}}})$ is completely determined by the length ![]() $\ell(\mathcal{P}_{G}^{\mathrm{even}})$ and the Möbius invariant
$\ell(\mathcal{P}_{G}^{\mathrm{even}})$ and the Möbius invariant ![]() $\mu(\mathcal{P}_{G}^{\mathrm{even}})$, see [Reference Choi and Park9]. If G is a graph in Figure 1.1, then as we saw in §5, the order
$\mu(\mathcal{P}_{G}^{\mathrm{even}})$, see [Reference Choi and Park9]. If G is a graph in Figure 1.1, then as we saw in §5, the order ![]() $\prec_{\tiny\text{atm}}^{I}$ in Definition 5.3 gives a recursive atom ordering of
$\prec_{\tiny\text{atm}}^{I}$ in Definition 5.3 gives a recursive atom ordering of ![]() $\mathcal{P}_{G,A}^{\mathrm{even}}$ for every
$\mathcal{P}_{G,A}^{\mathrm{even}}$ for every ![]() $A\in\mathcal{A}(G)$. Hence, we can determine the homotopy type of
$A\in\mathcal{A}(G)$. Hence, we can determine the homotopy type of  $\Delta(\overline{\mathcal{P}_{G,A}^{\mathrm{even}}})$ by considering the CL-labelling ρ obtained from the recursive atom order on
$\Delta(\overline{\mathcal{P}_{G,A}^{\mathrm{even}}})$ by considering the CL-labelling ρ obtained from the recursive atom order on ![]() $\mathcal{P}_{G,A}^{\mathrm{even}}$.
$\mathcal{P}_{G,A}^{\mathrm{even}}$.
Proposition 6.1. Let (G, A) be a pair of a graph G and its admissible collection A illustrated in Figure 5.2. Then ![]() $\mathcal{P}_{G,A}^{\mathrm{even}}$ has a falling chain if and only if one of the following holds: (a) 2 and 3 are adjacent, and (b)
$\mathcal{P}_{G,A}^{\mathrm{even}}$ has a falling chain if and only if one of the following holds: (a) 2 and 3 are adjacent, and (b) ![]() $|V|$ is even.
$|V|$ is even.
Proof. We show the ‘only if’ part first. Let ![]() $\sigma:I_0\lessdot I_1\lessdot \cdots \lessdot I_{p}$ be a falling chain of
$\sigma:I_0\lessdot I_1\lessdot \cdots \lessdot I_{p}$ be a falling chain of ![]() $\mathcal{P}_{G,A}^{\mathrm{even}}$ and let
$\mathcal{P}_{G,A}^{\mathrm{even}}$ and let ![]() $I_{k-1}\lessdot I_k$ be the cover such that
$I_{k-1}\lessdot I_k$ be the cover such that ![]() $I_k\setminus I_{k-1}$ contains the vertex 1. Suppose that the vertices 2 and 3 are not adjacent and
$I_k\setminus I_{k-1}$ contains the vertex 1. Suppose that the vertices 2 and 3 are not adjacent and ![]() $|V|$ is odd. Then
$|V|$ is odd. Then ![]() $A\cap V\neq V$ and
$A\cap V\neq V$ and ![]() $1\not\in A$. Note that there is no cover
$1\not\in A$. Note that there is no cover ![]() $I\lessdot J$ such that
$I\lessdot J$ such that ![]() $J\setminus I$ contains
$J\setminus I$ contains ![]() $\{1,2\}$, and therefore,
$\{1,2\}$, and therefore, ![]() $2\not\in I_k\setminus I_{k-1}$. Since
$2\not\in I_k\setminus I_{k-1}$. Since ![]() $1\not\in I_{k-1}$ and (a) fails, it follows that
$1\not\in I_{k-1}$ and (a) fails, it follows that ![]() $2\not\in I_{k-1}$, so
$2\not\in I_{k-1}$, so ![]() $2\not\in I_k$. Thus,
$2\not\in I_k$. Thus, ![]() $I_k=I_{k-1}\cup 1$ and hence
$I_k=I_{k-1}\cup 1$ and hence ![]() $I_{k-1}\lessdot I_k$ is the first atom of
$I_{k-1}\lessdot I_k$ is the first atom of ![]() $[I_{k-1},G]$, which implies that σ cannot be a falling chain, a contradiction.
$[I_{k-1},G]$, which implies that σ cannot be a falling chain, a contradiction.
To show the ‘if’ part, recall that ![]() $A=\{a_1,\ldots,a_m\}$ and
$A=\{a_1,\ldots,a_m\}$ and ![]() $B\setminus A=\{b_1,b_2,\ldots, b_{\ell}\}$ as long as
$B\setminus A=\{b_1,b_2,\ldots, b_{\ell}\}$ as long as ![]() $B\setminus A\neq\emptyset$. We fix a falling chain σE of an interval of
$B\setminus A\neq\emptyset$. We fix a falling chain σE of an interval of ![]() $\mathcal{P}_{G,A}^{\mathrm{even}}$ as follows. If
$\mathcal{P}_{G,A}^{\mathrm{even}}$ as follows. If ![]() $B\setminus A\neq \emptyset$, then let σE be a falling chain of
$B\setminus A\neq \emptyset$, then let σE be a falling chain of ![]() $[V\cup b_{\ell}, G]$ defined by
$[V\cup b_{\ell}, G]$ defined by
If ![]() $B\subset A$, then let σE be a falling chain of
$B\subset A$, then let σE be a falling chain of ![]() $[V\cup a_{m-1}a_m, G]$ defined by
$[V\cup a_{m-1}a_m, G]$ defined by
Note that there is a falling chain ![]() $\sigma_\ast$ of
$\sigma_\ast$ of ![]() $[\emptyset,I]$, where
$[\emptyset,I]$, where
 \begin{equation*}I=\begin{cases}
34\cdots n & \text{if }n \text{ is even};\\
4\cdots n & \text{if }n \text{ is odd and }n\ge 5; \\
\emptyset & \text{if }n= 3. \\
\end{cases}\end{equation*}
\begin{equation*}I=\begin{cases}
34\cdots n & \text{if }n \text{ is even};\\
4\cdots n & \text{if }n \text{ is odd and }n\ge 5; \\
\emptyset & \text{if }n= 3. \\
\end{cases}\end{equation*} Suppose that (a) or (b) is true. We will show that ![]() $\sigma_\ast$ and σE are extended to a falling chain of
$\sigma_\ast$ and σE are extended to a falling chain of ![]() $\mathcal{P}_{G,A}^{\mathrm{even}}$. When
$\mathcal{P}_{G,A}^{\mathrm{even}}$. When ![]() $\{1,2\}\subset A$, the chain σ obtained by concatenating
$\{1,2\}\subset A$, the chain σ obtained by concatenating ![]() $\sigma_\ast$, σ 0 and σE is a falling chain of
$\sigma_\ast$, σ 0 and σE is a falling chain of ![]() $\mathcal{P}_{G,A}^{\mathrm{even}}$, where
$\mathcal{P}_{G,A}^{\mathrm{even}}$, where
 \begin{equation*} \sigma_0=\begin{cases}
I\lessdot I\cup 12b_{\ell} &\text{if }B\setminus A\neq\emptyset, \\
I\lessdot I\cup 12a_{m-1}a_m &\text{if }B\subset A.
\end{cases} \end{equation*}
\begin{equation*} \sigma_0=\begin{cases}
I\lessdot I\cup 12b_{\ell} &\text{if }B\setminus A\neq\emptyset, \\
I\lessdot I\cup 12a_{m-1}a_m &\text{if }B\subset A.
\end{cases} \end{equation*} When ![]() $A\cap \{1,2\}=\emptyset$, the chain σ obtained by concatenating
$A\cap \{1,2\}=\emptyset$, the chain σ obtained by concatenating ![]() $\sigma_\ast, I\lessdot I\cup 2\lessdot I\cup 1b_{\ell}$ and σE is a falling chain of
$\sigma_\ast, I\lessdot I\cup 2\lessdot I\cup 1b_{\ell}$ and σE is a falling chain of ![]() $\mathcal{P}_{G,A}^{\mathrm{even}}$. If
$\mathcal{P}_{G,A}^{\mathrm{even}}$. If ![]() $A\cap \{1,2\}=\{2\}$, then (a) is true, and hence the chain σ obtained by concatenating
$A\cap \{1,2\}=\{2\}$, then (a) is true, and hence the chain σ obtained by concatenating ![]() $\sigma_\ast$, σ 0 and σE is a falling chain of
$\sigma_\ast$, σ 0 and σE is a falling chain of ![]() $\mathcal{P}_{G,A}^{\mathrm{even}}$, where
$\mathcal{P}_{G,A}^{\mathrm{even}}$, where
 \begin{equation*} \sigma_0=\begin{cases}
I\lessdot I\cup 23 \lessdot 1 b_{\ell} &\text{if }B\setminus A\neq\emptyset, \\
I\lessdot I\cup 23 \lessdot 1 a_{m-1}a_m &\text{if }B\subset A.
\end{cases}\end{equation*}
\begin{equation*} \sigma_0=\begin{cases}
I\lessdot I\cup 23 \lessdot 1 b_{\ell} &\text{if }B\setminus A\neq\emptyset, \\
I\lessdot I\cup 23 \lessdot 1 a_{m-1}a_m &\text{if }B\subset A.
\end{cases}\end{equation*}Proposition 6.2. Let (G, A) be a pair of a graph G and its admissible collection A illustrated in Figure 5.2. Let ![]() $\sigma:I_0\lessdot I_1\lessdot \cdots \lessdot I_{p+1}$ be a falling chain of
$\sigma:I_0\lessdot I_1\lessdot \cdots \lessdot I_{p+1}$ be a falling chain of ![]() $\mathcal{P}_{G,A}^{\mathrm{even}}$, and
$\mathcal{P}_{G,A}^{\mathrm{even}}$, and ![]() $I_{k-1}\lessdot I_k$ be the cover satisfying
$I_{k-1}\lessdot I_k$ be the cover satisfying ![]() $1\in I_k\setminus I_{k-1}$. Then the possible values of length
$1\in I_k\setminus I_{k-1}$. Then the possible values of length ![]() $\ell(\sigma)$ and the set
$\ell(\sigma)$ and the set ![]() $I_k\setminus I_{k-1}$ are represented in Table 3.
$I_k\setminus I_{k-1}$ are represented in Table 3.
Table 3. Each cell represents ![]() $\ell(\sigma)$ and
$\ell(\sigma)$ and ![]() $I_k\setminus I_{k-1}$, where
$I_k\setminus I_{k-1}$, where ![]() $a,a^{\prime}\in A\cap B$,
$a,a^{\prime}\in A\cap B$, ![]() $b\in B\setminus A$ and
$b\in B\setminus A$ and ![]() $v\in V\setminus\{1,2\}$.
$v\in V\setminus\{1,2\}$.

Proof. We first prove the case where ![]() $A\cap V\neq V$. Then
$A\cap V\neq V$. Then ![]() $1\not\in A$ by the way of labelling. If
$1\not\in A$ by the way of labelling. If ![]() $I_k=I_{k-1}\cup 1$, then
$I_k=I_{k-1}\cup 1$, then ![]() $I_{k-1}\cup 1$ is the first atom of
$I_{k-1}\cup 1$ is the first atom of ![]() $[I_{k-1},G]$, so the chain σ cannot be a falling chain. Hence,
$[I_{k-1},G]$, so the chain σ cannot be a falling chain. Hence, ![]() $I_k\neq I_{k-1}\cup 1$ and
$I_k\neq I_{k-1}\cup 1$ and ![]() $2\in I_{k-1}$. Then the vertices 2 and 3 are adjacent. By Proposition 5.2, if
$2\in I_{k-1}$. Then the vertices 2 and 3 are adjacent. By Proposition 5.2, if ![]() $|V|$ is even, then
$|V|$ is even, then ![]() $\mathcal{P}_{G,A}^{\mathrm{even}}$ is pure and
$\mathcal{P}_{G,A}^{\mathrm{even}}$ is pure and  $\ell(\sigma)=\frac{|A|}{2}+|B\setminus A|+1$; if
$\ell(\sigma)=\frac{|A|}{2}+|B\setminus A|+1$; if ![]() $|V|$ is odd, then σ is not a longest chain, so
$|V|$ is odd, then σ is not a longest chain, so  $\ell(\sigma)=\frac{|A|}{2}+|B\setminus A|$. If
$\ell(\sigma)=\frac{|A|}{2}+|B\setminus A|$. If ![]() $B\setminus A\neq\emptyset$, then we let q be the first index such that
$B\setminus A\neq\emptyset$, then we let q be the first index such that ![]() $I_{q}\setminus I_{q-1}$ contains an element b in
$I_{q}\setminus I_{q-1}$ contains an element b in ![]() $B\setminus A$. Since
$B\setminus A$. Since ![]() $I_{q-2}\lessdot I_{q-1}\lessdot I_q$ is falling, we get k = q, that is,
$I_{q-2}\lessdot I_{q-1}\lessdot I_q$ is falling, we get k = q, that is, ![]() $I_k\setminus I_{k-1}= 1b$. If
$I_k\setminus I_{k-1}= 1b$. If ![]() $B\subset A$, then
$B\subset A$, then ![]() $I_k\setminus I_{k-1}= 1aa^{\prime}$ or 1av for some
$I_k\setminus I_{k-1}= 1aa^{\prime}$ or 1av for some ![]() $a,a^{\prime}\in B\cap A$ and
$a,a^{\prime}\in B\cap A$ and ![]() $v\in V\setminus\{1,2\}$.
$v\in V\setminus\{1,2\}$.
Now we assume ![]() $A\cap V=V$. Then
$A\cap V=V$. Then ![]() $|V|$ is even. If
$|V|$ is even. If ![]() $2\not\in I_k$, then
$2\not\in I_k$, then ![]() $I_k=I_{k-1}\cup 1v$ for some
$I_k=I_{k-1}\cup 1v$ for some ![]() $v\in V\setminus\{1,2\}$. Then σ cannot be a falling chain since
$v\in V\setminus\{1,2\}$. Then σ cannot be a falling chain since ![]() $I_{k-1}\cup 1v$ is the first atom of
$I_{k-1}\cup 1v$ is the first atom of ![]() $[I_{k-1},G]$. Thus,
$[I_{k-1},G]$. Thus, ![]() $2\in I_{k}$.
$2\in I_{k}$.
Suppose that ![]() $B\setminus A\neq\emptyset$. We let q be the first index such that
$B\setminus A\neq\emptyset$. We let q be the first index such that ![]() $I_{q}\setminus I_{q-1}$ contains an element b in
$I_{q}\setminus I_{q-1}$ contains an element b in ![]() $B\setminus A$. Since
$B\setminus A$. Since ![]() $I_{q-2}\lessdot I_{q-1}\lessdot I_q$ is a falling chain of
$I_{q-2}\lessdot I_{q-1}\lessdot I_q$ is a falling chain of ![]() $[I_{q-2}, I_q]$, we have k = q, that is,
$[I_{q-2}, I_q]$, we have k = q, that is, ![]() $b\in I_k$. Then
$b\in I_k$. Then
 \begin{equation*}I_k\setminus I_{k-1}=\begin{cases}
1vb & \text{if }2\in I_{k-1};\\
12b & \text{if }2\in I_{k}\setminus I_{k-1}.
\end{cases}\end{equation*}
\begin{equation*}I_k\setminus I_{k-1}=\begin{cases}
1vb & \text{if }2\in I_{k-1};\\
12b & \text{if }2\in I_{k}\setminus I_{k-1}.
\end{cases}\end{equation*} Thus, σ is not a longest chain, so  $\ell(\sigma)= \frac{|A|}{2}+|B\setminus A|-1$ by Proposition 5.2.
$\ell(\sigma)= \frac{|A|}{2}+|B\setminus A|-1$ by Proposition 5.2.
Suppose that ![]() $B\subset A$. Suppose that the vertices 2 and 3 are not adjacent. Then
$B\subset A$. Suppose that the vertices 2 and 3 are not adjacent. Then ![]() $2\not\in I_{k-1}$, so
$2\not\in I_{k-1}$, so ![]() $2\in I_{k-1}$. Thus,
$2\in I_{k-1}$. Thus, ![]() $I_k\setminus I_{k-1}=12aa^{\prime}$ for some
$I_k\setminus I_{k-1}=12aa^{\prime}$ for some ![]() $a,a^{\prime}\in B$, which implies that σ is not a longest chain. Hence,
$a,a^{\prime}\in B$, which implies that σ is not a longest chain. Hence,  $\ell(\sigma)= \frac{|A|}{2}+|B\setminus A|-1$ by Proposition 5.2. If the vertices 2 and 3 are adjacent, then by Proposition 5.2,
$\ell(\sigma)= \frac{|A|}{2}+|B\setminus A|-1$ by Proposition 5.2. If the vertices 2 and 3 are adjacent, then by Proposition 5.2,  $\ell(\sigma)=\frac{|A|}{2}-1$ or
$\ell(\sigma)=\frac{|A|}{2}-1$ or ![]() $\frac{|A|}{2}$, and it holds that
$\frac{|A|}{2}$, and it holds that
 \begin{equation*}I_k\setminus I_{k-1}=\begin{cases}
1a & \text{if }2\in I_{k-1};\\
12aa^{\prime} & \text{if }2\in I_{k}\setminus I_{k-1}.
\end{cases}\end{equation*}
\begin{equation*}I_k\setminus I_{k-1}=\begin{cases}
1a & \text{if }2\in I_{k-1};\\
12aa^{\prime} & \text{if }2\in I_{k}\setminus I_{k-1}.
\end{cases}\end{equation*}By Theorem 2.2 and Propositions 6.1 and 6.2, the following hold:
Corollary 6.3. Let (G, A) be a pair of a graph G and its admissible collection A illustrated in Figure 5.2. If neither (a) nor (b) of Proposition 6.1 holds, then  $\Delta(\overline{\mathcal{P}_{G,A}^{\mathrm{even}}})$ is contractible. If not, the order complex
$\Delta(\overline{\mathcal{P}_{G,A}^{\mathrm{even}}})$ is contractible. If not, the order complex  $\Delta(\overline{\mathcal{P}_{G,A}^{\mathrm{even}}})$ is homotopy equivalent to a wedge of spheres of dimensions
$\Delta(\overline{\mathcal{P}_{G,A}^{\mathrm{even}}})$ is homotopy equivalent to a wedge of spheres of dimensions
 \begin{equation*}\begin{cases}
\frac{|A|}{2}+ |B\setminus A|-2 & \text{if }|V|\text{is odd},\\
\frac{|A|}{2}+ |B\setminus A|-1 & \text{if }|V|\text{is even and }A\cap V\neq V,\\
\frac{|A|}{2}-1 \text{ or } \frac{|A|}{2} & \text{if } A=V\cup B \text{ and the vertices 2 and 3 are adjacent}, and\\
\frac{|A|}{2}+|B\setminus A|-3& \text{otherwise}.\end{cases} \end{equation*}
\begin{equation*}\begin{cases}
\frac{|A|}{2}+ |B\setminus A|-2 & \text{if }|V|\text{is odd},\\
\frac{|A|}{2}+ |B\setminus A|-1 & \text{if }|V|\text{is even and }A\cap V\neq V,\\
\frac{|A|}{2}-1 \text{ or } \frac{|A|}{2} & \text{if } A=V\cup B \text{ and the vertices 2 and 3 are adjacent}, and\\
\frac{|A|}{2}+|B\setminus A|-3& \text{otherwise}.\end{cases} \end{equation*}Example 6.4. See the posets ![]() $\mathcal{P}_{G,A}^{\mathrm{even}}$ in Figure 5.3. The posets in (i) and (iii) are nonpure but none of the longest maximal chains of (i) and (iii) are falling chains. In (i), (ii) and (iii), there are four, three and four falling chains, respectively:
$\mathcal{P}_{G,A}^{\mathrm{even}}$ in Figure 5.3. The posets in (i) and (iii) are nonpure but none of the longest maximal chains of (i) and (iii) are falling chains. In (i), (ii) and (iii), there are four, three and four falling chains, respectively:
 \begin{equation*}\begin{array}{lll}
\hspace{-.2cm}(i)&\emptyset \lt \bf{23} \lt \bf{1}{23}\bf{{b_1}} \lt {123}\bf{4a_1}{b_1} \lt {1234}\bf{5}{a_1}\bf{a_2}{b_1}\\
&\emptyset \lt \bf{23} \lt \bf{1}{23}\bf{b_1} \lt {123}\bf{4a_2}{b_1} \lt {1234}\bf{5a_1}{a_2b_1}\\
&\emptyset \lt \bf{34} \lt \bf{2}{34}\bf{5} \lt \bf{1}2345\bf{b_1} \lt 12345\bf{a_1a_2}b_1\\
&\emptyset \lt \bf{45} \lt \bf{23}45 \lt \bf{1}2345\bf{b_1} \lt 12345\bf{a_1a_2}b_1\\
\hspace{-.2cm}(ii)&\emptyset \lt \bf{2} \lt \bf{1} 2 \bf{b_2} \lt 12\bf{b_1}b_2 \lt 12\bf{3a_1}b_1b_2 \lt 123\bf{4}a_1\bf{a_2}b_1b_2\\
&\emptyset \lt \bf{2} \lt \bf{1}2\bf{b_2} \lt 12\bf{b_1}b_2 \lt 12\bf{3a_2}b_1b_2 \lt 123\bf{4a_1}a_2b_1b_2 \\
&\emptyset \lt \bf{34} \lt \bf{2}34 \lt \bf{1}234\bf{b_2} \lt 1234\bf{b_1} b_2 \lt 1234\bf{a_1a_2}b_1b_2&\\
\hspace{-.2cm}(iii)& \emptyset \lt \bf{12b_2} \lt 12\bf{a_1a_2}b_2 \lt 12a_1a_2\bf{b_1}b_2 \lt 12\bf{34}a_1a_2b_1b_2\\
&\emptyset \lt \bf{34} \lt \bf{12}34\bf{b_2} \lt 1234\bf{b_1}b_2 \lt 1234\bf{a_1a_2}b_1b_2\\
& \emptyset \lt \bf{12b_2} \lt 12\bf{b_1}b_2 \lt 12\bf{3a_1}b_1b_2 \lt 123\bf{4}a_1\bf{a_2}b_1b_2\\
& \emptyset \lt \bf{12b_2} \lt 12\bf{b_1}b_2 \lt 12\bf{3a_2}b_1b_2 \lt 123\bf{4a_1}a_2b_1b_2
\end{array}\end{equation*}
\begin{equation*}\begin{array}{lll}
\hspace{-.2cm}(i)&\emptyset \lt \bf{23} \lt \bf{1}{23}\bf{{b_1}} \lt {123}\bf{4a_1}{b_1} \lt {1234}\bf{5}{a_1}\bf{a_2}{b_1}\\
&\emptyset \lt \bf{23} \lt \bf{1}{23}\bf{b_1} \lt {123}\bf{4a_2}{b_1} \lt {1234}\bf{5a_1}{a_2b_1}\\
&\emptyset \lt \bf{34} \lt \bf{2}{34}\bf{5} \lt \bf{1}2345\bf{b_1} \lt 12345\bf{a_1a_2}b_1\\
&\emptyset \lt \bf{45} \lt \bf{23}45 \lt \bf{1}2345\bf{b_1} \lt 12345\bf{a_1a_2}b_1\\
\hspace{-.2cm}(ii)&\emptyset \lt \bf{2} \lt \bf{1} 2 \bf{b_2} \lt 12\bf{b_1}b_2 \lt 12\bf{3a_1}b_1b_2 \lt 123\bf{4}a_1\bf{a_2}b_1b_2\\
&\emptyset \lt \bf{2} \lt \bf{1}2\bf{b_2} \lt 12\bf{b_1}b_2 \lt 12\bf{3a_2}b_1b_2 \lt 123\bf{4a_1}a_2b_1b_2 \\
&\emptyset \lt \bf{34} \lt \bf{2}34 \lt \bf{1}234\bf{b_2} \lt 1234\bf{b_1} b_2 \lt 1234\bf{a_1a_2}b_1b_2&\\
\hspace{-.2cm}(iii)& \emptyset \lt \bf{12b_2} \lt 12\bf{a_1a_2}b_2 \lt 12a_1a_2\bf{b_1}b_2 \lt 12\bf{34}a_1a_2b_1b_2\\
&\emptyset \lt \bf{34} \lt \bf{12}34\bf{b_2} \lt 1234\bf{b_1}b_2 \lt 1234\bf{a_1a_2}b_1b_2\\
& \emptyset \lt \bf{12b_2} \lt 12\bf{b_1}b_2 \lt 12\bf{3a_1}b_1b_2 \lt 123\bf{4}a_1\bf{a_2}b_1b_2\\
& \emptyset \lt \bf{12b_2} \lt 12\bf{b_1}b_2 \lt 12\bf{3a_2}b_1b_2 \lt 123\bf{4a_1}a_2b_1b_2
\end{array}\end{equation*} Hence, the order complexes  $\Delta(\overline{\mathcal{P}_{G,A}^{\mathrm{even}}})$ of the proper parts of the posets in Figure 5.3 are homotopy equivalent to
$\Delta(\overline{\mathcal{P}_{G,A}^{\mathrm{even}}})$ of the proper parts of the posets in Figure 5.3 are homotopy equivalent to  ${\tiny{\displaystyle\bigvee_{4}}} S^2$,
${\tiny{\displaystyle\bigvee_{4}}} S^2$,  ${\tiny{\displaystyle\bigvee_{3}}} S^3$ and
${\tiny{\displaystyle\bigvee_{3}}} S^3$ and  ${\tiny{\displaystyle\bigvee_{4}}} S^2$, respectively.
${\tiny{\displaystyle\bigvee_{4}}} S^2$, respectively.
7. Betti numbers of the real toric variety associated with  $\widetilde{P}_{n,2}$
$\widetilde{P}_{n,2}$
In this section, we consider the graph  $G_n=\widetilde{P}_{n,2}$ in Figure 1.1. We count the number of falling chains of
$G_n=\widetilde{P}_{n,2}$ in Figure 1.1. We count the number of falling chains of ![]() $\mathcal{P}_{G_n,A}^{\mathrm{even}}$ for
$\mathcal{P}_{G_n,A}^{\mathrm{even}}$ for ![]() $A\in\mathcal{A}(G_n)$ and then compute the Betti numbers of the projective smooth real toric variety
$A\in\mathcal{A}(G_n)$ and then compute the Betti numbers of the projective smooth real toric variety  $X^{\mathbb{R}}_{G_n}$.
$X^{\mathbb{R}}_{G_n}$.
Proposition 7.1. Let  $G_n=\widetilde{P}_{n,2}$ in Figure 1.1. For
$G_n=\widetilde{P}_{n,2}$ in Figure 1.1. For ![]() $A\in\mathcal{A}(G_n)$, the number of falling chains of
$A\in\mathcal{A}(G_n)$, the number of falling chains of ![]() $\mathcal{P}_{G_n,A}^{\mathrm{even}}$ is
$\mathcal{P}_{G_n,A}^{\mathrm{even}}$ is
 \begin{equation*}\begin{cases}
C_k&\text{if }n=2k\text{ for some }k\ge1\\
C_{k+1}-C_k&\text{if }n=2k+1\text{ for some }k\ge1\text{ and } {A\cap V} \text{itself induces a connected graph},\\
0 &\text{otherwise},
\end{cases}\end{equation*}
\begin{equation*}\begin{cases}
C_k&\text{if }n=2k\text{ for some }k\ge1\\
C_{k+1}-C_k&\text{if }n=2k+1\text{ for some }k\ge1\text{ and } {A\cap V} \text{itself induces a connected graph},\\
0 &\text{otherwise},
\end{cases}\end{equation*}where Ck is the kth Catalan number.
Proof. Let V be the set of vertices and ![]() $B=\{a_1,a_2\}$ be the bundle of Gn. Recall that we follow the labelling of the vertices shown in Figure 5.2. Note that
$B=\{a_1,a_2\}$ be the bundle of Gn. Recall that we follow the labelling of the vertices shown in Figure 5.2. Note that ![]() $A=V\cup B$ or
$A=V\cup B$ or ![]() $(V\cup B)\setminus 1$ or
$(V\cup B)\setminus 1$ or ![]() $(V\cup B)\setminus \{1,2\}$.
$(V\cup B)\setminus \{1,2\}$.
Suppose that ![]() $A=V\cup B$. Then
$A=V\cup B$. Then ![]() $|V|$ is even, and by the way of labelling, the vertices 2 and 3 are not adjacent. Let
$|V|$ is even, and by the way of labelling, the vertices 2 and 3 are not adjacent. Let ![]() $\sigma:I_0\lessdot I_1\lessdot \cdots \lessdot I_{p+1}$ be a falling chain of
$\sigma:I_0\lessdot I_1\lessdot \cdots \lessdot I_{p+1}$ be a falling chain of ![]() $\mathcal{P}_{G_n,A}^{\mathrm{even}}$, and
$\mathcal{P}_{G_n,A}^{\mathrm{even}}$, and ![]() $I_{k-1}\lessdot I_k$ be the cover such that
$I_{k-1}\lessdot I_k$ be the cover such that ![]() $I_k\setminus I_{k-1}$ contains the vertex 1. By Proposition 6.2,
$I_k\setminus I_{k-1}$ contains the vertex 1. By Proposition 6.2, ![]() $I_{k}\setminus I_{k-1}=12a_1a_2$ and the number of falling chains of
$I_{k}\setminus I_{k-1}=12a_1a_2$ and the number of falling chains of ![]() $\mathcal{P}_{G_n,A}^{\mathrm{even}}$ is equal to
$\mathcal{P}_{G_n,A}^{\mathrm{even}}$ is equal to
 \begin{equation}
\begin{split}
& \sum_{I\subset V\setminus\{1,2\}} \!\!\!\!\!\!\! (\#\text{falling chains of } [I\cup 12a_1a_2,G_n] ) \times(\#\text{falling chains of }[\emptyset, I]) .\\
\end{split}
\end{equation}
\begin{equation}
\begin{split}
& \sum_{I\subset V\setminus\{1,2\}} \!\!\!\!\!\!\! (\#\text{falling chains of } [I\cup 12a_1a_2,G_n] ) \times(\#\text{falling chains of }[\emptyset, I]) .\\
\end{split}
\end{equation} Since ![]() $|V|$ is even, we can set
$|V|$ is even, we can set ![]() $|V|=2k$ for some
$|V|=2k$ for some ![]() $k\ge 1$. If k = 1, then it is clear. Suppose that
$k\ge 1$. If k = 1, then it is clear. Suppose that ![]() $k\ge 2$. From Equation (7.1), the number of falling chains of
$k\ge 2$. From Equation (7.1), the number of falling chains of ![]() $\mathcal{P}_{G_n,A}^{\mathrm{even}}$ is
$\mathcal{P}_{G_n,A}^{\mathrm{even}}$ is
 \begin{align*}&\sum_{q=1}^{2} (\#{{\rm falling} \ {\rm chains} \ {\rm of}\ } \mathcal{P}_{2q}{ \ {\rm starting} \ {\rm with}\ } 12a_1a_2)\\ & \quad\quad \times \!\!\sum_{\ |I|=2k-2q \atop \quad I\subset \{3,4,\ldots,2k\} } (\#{{\rm falling} \ {\rm chains} \ {\rm of}\ }[\emptyset, I])\\&\quad=C_{k-1} \!+ \! (\#{{\rm falling} \ {\rm chains} \ {\rm of}\ } \mathcal{P}_{4}{ \ {\rm starting} \ {\rm with}} 12a_1a_2 )\\ & \quad\quad \times \!\! \!\! \sum_{\ |I|=2k-4 \atop \quad I\subset V\setminus \{1,2\} } \!\! \!\! (\#{{\rm falling} \ {\rm chains} \ {\rm of}\ }[\emptyset, I]),\end{align*}
\begin{align*}&\sum_{q=1}^{2} (\#{{\rm falling} \ {\rm chains} \ {\rm of}\ } \mathcal{P}_{2q}{ \ {\rm starting} \ {\rm with}\ } 12a_1a_2)\\ & \quad\quad \times \!\!\sum_{\ |I|=2k-2q \atop \quad I\subset \{3,4,\ldots,2k\} } (\#{{\rm falling} \ {\rm chains} \ {\rm of}\ }[\emptyset, I])\\&\quad=C_{k-1} \!+ \! (\#{{\rm falling} \ {\rm chains} \ {\rm of}\ } \mathcal{P}_{4}{ \ {\rm starting} \ {\rm with}} 12a_1a_2 )\\ & \quad\quad \times \!\! \!\! \sum_{\ |I|=2k-4 \atop \quad I\subset V\setminus \{1,2\} } \!\! \!\! (\#{{\rm falling} \ {\rm chains} \ {\rm of}\ }[\emptyset, I]),\end{align*} where ![]() $\mathcal{P}_{2q}$ means the poset
$\mathcal{P}_{2q}$ means the poset  $\mathcal{P}_{G_{2q},G_{2q}}^{\mathrm{even}}$ for
$\mathcal{P}_{G_{2q},G_{2q}}^{\mathrm{even}}$ for ![]() $q\leq \lfloor\frac{n}{2}\rfloor$, and the second summation is over the vertices I of
$q\leq \lfloor\frac{n}{2}\rfloor$, and the second summation is over the vertices I of ![]() $\mathcal{P}_{G_n,A}^{\mathrm{even}}$. Since the number of falling chains of
$\mathcal{P}_{G_n,A}^{\mathrm{even}}$. Since the number of falling chains of ![]() $\mathcal{P}_{4}$ starting with
$\mathcal{P}_{4}$ starting with ![]() $12a_1a_2$ is only one (see the second poset of Figure 3.2), the number of falling chains is
$12a_1a_2$ is only one (see the second poset of Figure 3.2), the number of falling chains is ![]() $C_{k-1}+s$, where
$C_{k-1}+s$, where
 \begin{equation*}{s= \sum_{ \ |I|=2k-4 \atop \quad I\subset V\setminus \{1,2\} } \!\!\!\! (\#\text{falling chains of }[\emptyset, I])}.\end{equation*}
\begin{equation*}{s= \sum_{ \ |I|=2k-4 \atop \quad I\subset V\setminus \{1,2\} } \!\!\!\! (\#\text{falling chains of }[\emptyset, I])}.\end{equation*} Let ![]() $I\subset\{3,4,\ldots,2k\}$ be an element of
$I\subset\{3,4,\ldots,2k\}$ be an element of ![]() $\mathcal{P}_{G_n,A}^{\mathrm{even}}$ with
$\mathcal{P}_{G_n,A}^{\mathrm{even}}$ with ![]() $2k-4$ vertices. Then
$2k-4$ vertices. Then ![]() $V\setminus I=\{1,2, v_1,v_2\}$, where
$V\setminus I=\{1,2, v_1,v_2\}$, where ![]() $v_1 \lt v_2$. Since each connected component of I has an even number of vertices, v 1 is odd and v 2 is even. Thus, the number of falling chains of
$v_1 \lt v_2$. Since each connected component of I has an even number of vertices, v 1 is odd and v 2 is even. Thus, the number of falling chains of ![]() $[\emptyset, I]$ is
$[\emptyset, I]$ is  $C_{\frac{v_1-3}{2}} C_{\frac{v_2-v_1-1}{2}} C_{\frac{2n-v_{2}}{2}}$. By a recursion of the Catalan numbers,
$C_{\frac{v_1-3}{2}} C_{\frac{v_2-v_1-1}{2}} C_{\frac{2n-v_{2}}{2}}$. By a recursion of the Catalan numbers,
 \begin{equation}
s=\sum_{v_1=3\atop v_1:{\rm odd}}^{2k-1}\! \sum_{v_2=v_1+1 \atop v_2:{\rm even}}^{2k}\!\! C_{\frac{v_1-3}{2}} C_{\frac{v_2-v_1-1}{2}} C_{\frac{2k-v_{2}}{2}} = \sum_{v_1=3\atop v_1:{\rm odd}}^{2k-1} \!\! C_{\frac{v_1-3}{2}} C_{\frac{2k-v_1+1}{2}} = C_k-C_{k-1}.
\end{equation}
\begin{equation}
s=\sum_{v_1=3\atop v_1:{\rm odd}}^{2k-1}\! \sum_{v_2=v_1+1 \atop v_2:{\rm even}}^{2k}\!\! C_{\frac{v_1-3}{2}} C_{\frac{v_2-v_1-1}{2}} C_{\frac{2k-v_{2}}{2}} = \sum_{v_1=3\atop v_1:{\rm odd}}^{2k-1} \!\! C_{\frac{v_1-3}{2}} C_{\frac{2k-v_1+1}{2}} = C_k-C_{k-1}.
\end{equation} Hence, the number of falling chains is ![]() $C_{k-1}+s=C_k$ when
$C_{k-1}+s=C_k$ when ![]() $n=2k$ (
$n=2k$ (![]() $k\ge 1$).
$k\ge 1$).
Now we suppose that ![]() $A\cap V\neq V$. Then A is either
$A\cap V\neq V$. Then A is either ![]() $(V\cup B)\setminus 1$ or
$(V\cup B)\setminus 1$ or ![]() $(V\cup B)\setminus \{1,2\}$. Then
$(V\cup B)\setminus \{1,2\}$. Then ![]() $I_{k}\setminus I_{k-1}=1a_1a_2$ or 1av by Proposition 6.2, where
$I_{k}\setminus I_{k-1}=1a_1a_2$ or 1av by Proposition 6.2, where ![]() $a\in B$ and
$a\in B$ and ![]() $v\in V\setminus\{1,2\}$. Thus, the number of falling chains of
$v\in V\setminus\{1,2\}$. Thus, the number of falling chains of ![]() $\mathcal{P}_{G_n,A}^{\mathrm{even}}$ is equal to
$\mathcal{P}_{G_n,A}^{\mathrm{even}}$ is equal to
 \begin{align}
& \sum_{I\subset V\setminus\{1\} \atop 2\in I} \!\!\!\!\!\! (\#\text{falling chains of } [I\cup 1ac,G_n]\text{ for some }a\in B, c\in A)\\ & \qquad \times (\#\text{falling chains of }[\emptyset, I]).\end{align}
\begin{align}
& \sum_{I\subset V\setminus\{1\} \atop 2\in I} \!\!\!\!\!\! (\#\text{falling chains of } [I\cup 1ac,G_n]\text{ for some }a\in B, c\in A)\\ & \qquad \times (\#\text{falling chains of }[\emptyset, I]).\end{align} Note that it follows from Proposition 6.2 that there is no falling chain of ![]() $\mathcal{P}_{G_n,A}^{\mathrm{even}}$ if
$\mathcal{P}_{G_n,A}^{\mathrm{even}}$ if ![]() $|V|$ is odd and
$|V|$ is odd and ![]() ${A\cap V}$ does not induce a connected graph. Hence, we need to consider the case where
${A\cap V}$ does not induce a connected graph. Hence, we need to consider the case where ![]() $|V|$ is even or
$|V|$ is even or ![]() ${A\cap V}$ induces a connected graph. In Equation (7.3), a falling chain of
${A\cap V}$ induces a connected graph. In Equation (7.3), a falling chain of ![]() $[I\cup 1a_ic,G_n]$ for some
$[I\cup 1a_ic,G_n]$ for some ![]() $a_i\in B$ and
$a_i\in B$ and ![]() $c\in A$ is either
$c\in A$ is either ![]() $I\lessdot I\cup 1a_2v \lessdot G_n$ (
$I\lessdot I\cup 1a_2v \lessdot G_n$ (![]() $v\in V$) or
$v\in V$) or ![]() $I\lessdot I\cup 1a_1a_2=G_n$. In each of the cases, it is uniquely determined. Hence, the number of falling chains is equal to
$I\lessdot I\cup 1a_1a_2=G_n$. In each of the cases, it is uniquely determined. Hence, the number of falling chains is equal to ![]() $s_1+s_2$, where
$s_1+s_2$, where
 \begin{equation*}s_1= (\#{{\rm falling} \ {\rm chains} \ {\rm of}\ } [\emptyset, G_n\setminus (1\cup B) ]),\qquad s_2= \sum_{|I|=n-3\atop I\subset V\setminus\{1\}, \ 2\in I} \!\!\!\! (\#{{\rm falling} \ {\rm chains} \ {\rm of}\ } [\emptyset, I]).\end{equation*}
\begin{equation*}s_1= (\#{{\rm falling} \ {\rm chains} \ {\rm of}\ } [\emptyset, G_n\setminus (1\cup B) ]),\qquad s_2= \sum_{|I|=n-3\atop I\subset V\setminus\{1\}, \ 2\in I} \!\!\!\! (\#{{\rm falling} \ {\rm chains} \ {\rm of}\ } [\emptyset, I]).\end{equation*} Let us compute ![]() $s_1+s_2$. First, suppose
$s_1+s_2$. First, suppose ![]() $n=2k$ and
$n=2k$ and ![]() $k\ge 1$. Then s 1 is equal to
$k\ge 1$. Then s 1 is equal to ![]() $C_{k-1}$, the number of falling chains of
$C_{k-1}$, the number of falling chains of  $\mathcal{P}_{P_{2k-2}}^{\mathrm{even}}$. If k = 1, then
$\mathcal{P}_{P_{2k-2}}^{\mathrm{even}}$. If k = 1, then ![]() $s_2=0$, so the number of falling chains is C 1 (since
$s_2=0$, so the number of falling chains is C 1 (since ![]() $C_0=C_1=1$). Suppose that
$C_0=C_1=1$). Suppose that ![]() $k \ge2 $. Let
$k \ge2 $. Let ![]() $I\subset\{2,3,\ldots,2k\}$ be an element of
$I\subset\{2,3,\ldots,2k\}$ be an element of ![]() $\mathcal{P}_{G_n,A}^{\mathrm{even}}$ with
$\mathcal{P}_{G_n,A}^{\mathrm{even}}$ with ![]() $2k-3$ vertices containing the vertex 2. Then
$2k-3$ vertices containing the vertex 2. Then ![]() $V\setminus I=\{1,v_1,v_2\}$, where
$V\setminus I=\{1,v_1,v_2\}$, where ![]() $2 \lt v_1 \lt v_2$. Since each connected component of I has an even number of vertices and
$2 \lt v_1 \lt v_2$. Since each connected component of I has an even number of vertices and ![]() $2\not\in A$, v 1 is odd and v 2 is even. Since s 2 has the same equation as in Equation (7.2),
$2\not\in A$, v 1 is odd and v 2 is even. Since s 2 has the same equation as in Equation (7.2), ![]() $s_1+ s_2=C_{k-1}+(C_{k}-C_{k-1})=C_k$. Hence, the number of falling chains is Ck if
$s_1+ s_2=C_{k-1}+(C_{k}-C_{k-1})=C_k$. Hence, the number of falling chains is Ck if ![]() $n=2k$.
$n=2k$.
Suppose ![]() $n=2k+1$ and
$n=2k+1$ and ![]() $k\ge 1$. Then s 1 is equal to Ck, the number of falling chains of
$k\ge 1$. Then s 1 is equal to Ck, the number of falling chains of  $\mathcal{P}_{P_{2k}}^{\mathrm{even}}$. If k = 1, then
$\mathcal{P}_{P_{2k}}^{\mathrm{even}}$. If k = 1, then ![]() $s_2=1$, so the number of falling chains is
$s_2=1$, so the number of falling chains is ![]() $C_2-C_1$ (note
$C_2-C_1$ (note ![]() $C_2=2$ and
$C_2=2$ and ![]() $C_1=1$). Suppose
$C_1=1$). Suppose ![]() $k\ge 2$. Let
$k\ge 2$. Let ![]() $I\subset\{2,3,\ldots,2k+1\}$ be an element of
$I\subset\{2,3,\ldots,2k+1\}$ be an element of ![]() $\mathcal{P}_{G_n,A}^{\mathrm{even}}$ with
$\mathcal{P}_{G_n,A}^{\mathrm{even}}$ with ![]() $2k-3$ vertices containing the vertex 2. Then
$2k-3$ vertices containing the vertex 2. Then ![]() $V\setminus I=\{1,v_1,v_2\}$, where
$V\setminus I=\{1,v_1,v_2\}$, where ![]() $2 \lt v_1 \lt v_2$. Since each connected component of I has an even number of vertices and
$2 \lt v_1 \lt v_2$. Since each connected component of I has an even number of vertices and ![]() $2\in A$, v 1 is even and v 2 is odd. Thus,
$2\in A$, v 1 is even and v 2 is odd. Thus, ![]() $s_1+ s_2=C_k+(C_{k+1}-2C_k)=C_{k+1}-C_k$ since
$s_1+ s_2=C_k+(C_{k+1}-2C_k)=C_{k+1}-C_k$ since
 \begin{equation*}\begin{split}
s_2& =\sum_{v_1=4\atop v_1:\text{even}}^{2k} \sum_{v_2=v_1+1 \atop v_2:\text{odd}}^{2k+1} C_{\frac{v_1-2}{2}} C_{\frac{v_2-v_1-1}{2}} C_{\frac{2k+1-v_{2}}{2}}= \sum_{v_1=4\atop v_1:\text{even}}^{2k}
C_{\frac{v_1-2}{2}} C_{\frac{2k-v_1+2}{2}}= C_{k+1}-2C_{k}.
\end{split}\end{equation*}
\begin{equation*}\begin{split}
s_2& =\sum_{v_1=4\atop v_1:\text{even}}^{2k} \sum_{v_2=v_1+1 \atop v_2:\text{odd}}^{2k+1} C_{\frac{v_1-2}{2}} C_{\frac{v_2-v_1-1}{2}} C_{\frac{2k+1-v_{2}}{2}}= \sum_{v_1=4\atop v_1:\text{even}}^{2k}
C_{\frac{v_1-2}{2}} C_{\frac{2k-v_1+2}{2}}= C_{k+1}-2C_{k}.
\end{split}\end{equation*} Thus, the number of falling chains is ![]() $C_{k+1}-C_{k}$. It completes the proof.
$C_{k+1}-C_{k}$. It completes the proof.
From Corollary 6.3 and Proposition 7.1, we can compute the homotopy types of  $\Delta(\overline{\mathcal{P}_{G_n,A}^{\mathrm{even}}})$ when
$\Delta(\overline{\mathcal{P}_{G_n,A}^{\mathrm{even}}})$ when  $G_n=\widetilde{P}_{n,2}$ and A is an admissible collection of Gn, as in Table 4. One may formulate the number of falling chains of
$G_n=\widetilde{P}_{n,2}$ and A is an admissible collection of Gn, as in Table 4. One may formulate the number of falling chains of ![]() $\mathcal{P}_{G,A}^{\mathrm{even}}$, when
$\mathcal{P}_{G,A}^{\mathrm{even}}$, when  $G=\widetilde{P}_{n,m}$, in terms of the Catalan numbers (or the secant numbers), and it would be interesting to explain the formula by using other combinatorial objects.
$G=\widetilde{P}_{n,m}$, in terms of the Catalan numbers (or the secant numbers), and it would be interesting to explain the formula by using other combinatorial objects.
Table 4. The homotopy types of  $\overline{\mathcal{P}_{G_n,A}^{\mathrm{even}}}$ for
$\overline{\mathcal{P}_{G_n,A}^{\mathrm{even}}}$ for ![]() $A\in\mathcal{A}^\ast(G_n)$ and
$A\in\mathcal{A}^\ast(G_n)$ and  $G_n=\widetilde{P}_{n,2}$
$G_n=\widetilde{P}_{n,2}$

The last row of the table is true only when ![]() ${A\cap V}$ induces a connected graph.
${A\cap V}$ induces a connected graph.
Now we are ready to compute the Betti numbers of the projective smooth real toric variety  $X^{\mathbb{R}}_{G_n}$ associated with the graph Gn. It was shown in [Reference Choi and Park9, Theorem 2.5] that, for the simple path Pn with n vertices,
$X^{\mathbb{R}}_{G_n}$ associated with the graph Gn. It was shown in [Reference Choi and Park9, Theorem 2.5] that, for the simple path Pn with n vertices,  $\Delta(\overline{\mathcal{P}_{P_n}^{\mathrm{even}}})$ is homotopy equivalent to
$\Delta(\overline{\mathcal{P}_{P_n}^{\mathrm{even}}})$ is homotopy equivalent to  ${\tiny{\displaystyle\bigvee_{C_k}}} S^{k-1}$ for
${\tiny{\displaystyle\bigvee_{C_k}}} S^{k-1}$ for ![]() $n=2k$ and it is contractible for an odd integer n. In addition, for an integer
$n=2k$ and it is contractible for an odd integer n. In addition, for an integer ![]() $n\ge 1$, we have
$n\ge 1$, we have
 \begin{eqnarray}
\beta^{i}(X^{\mathbb{R}}_{P_n}) =
\begin{cases}
{n \choose i}-{n\choose i-1} & \text{if } n\geq 2\text{ and }0\le i\le \lfloor \frac{n}{2}\rfloor,\\
1&\text{if }n=1\text{ and }i=0,\\
0& \text{otherwise.}
\end{cases}
\end{eqnarray}
\begin{eqnarray}
\beta^{i}(X^{\mathbb{R}}_{P_n}) =
\begin{cases}
{n \choose i}-{n\choose i-1} & \text{if } n\geq 2\text{ and }0\le i\le \lfloor \frac{n}{2}\rfloor,\\
1&\text{if }n=1\text{ and }i=0,\\
0& \text{otherwise.}
\end{cases}
\end{eqnarray} For a non-simple connected graph Gk (k > 0) in Table 4, since the pseudograph associahedron ![]() $P_{G_k}$ is k-dimensional, it follows from Equation (3.3) that
$P_{G_k}$ is k-dimensional, it follows from Equation (3.3) that
 \begin{equation}
\sum_{A\in\mathcal{A}(G_k)}\widetilde{\beta}^{i}\left(\Delta\left(\overline{\mathcal{P}_{G_k,A}^{\mathrm{odd}}}\right)\right)=
\begin{cases} C_{\frac{k}{2}}&\text{if }i=\frac{k}{2} \text{or }\frac{k}{2}-1\text{ for even }k\\
C_{\frac{k+1}{2}}-C_{\frac{k-1}{2}} &\text{if }i=\frac{k-1}{2}\text{ for odd }k\\
0&\text{otherwise}.
\end{cases}
\end{equation}
\begin{equation}
\sum_{A\in\mathcal{A}(G_k)}\widetilde{\beta}^{i}\left(\Delta\left(\overline{\mathcal{P}_{G_k,A}^{\mathrm{odd}}}\right)\right)=
\begin{cases} C_{\frac{k}{2}}&\text{if }i=\frac{k}{2} \text{or }\frac{k}{2}-1\text{ for even }k\\
C_{\frac{k+1}{2}}-C_{\frac{k-1}{2}} &\text{if }i=\frac{k-1}{2}\text{ for odd }k\\
0&\text{otherwise}.
\end{cases}
\end{equation} Note that for a connected graph Gn and ![]() $(H,A)\in \mathcal{A}^*(G_n)$, if H 1 is a connected component of H and
$(H,A)\in \mathcal{A}^*(G_n)$, if H 1 is a connected component of H and ![]() $A_1=A\cap \mathcal{C}_{H_1}$ for
$A_1=A\cap \mathcal{C}_{H_1}$ for ![]() $A\in\mathcal{A}(H)$, then
$A\in\mathcal{A}(H)$, then  $\mathcal{P}_{H,A}^{\mathrm{odd}}$ is isomorphic to the join
$\mathcal{P}_{H,A}^{\mathrm{odd}}$ is isomorphic to the join  $\mathcal{P}_{H_1,A_1}^{\mathrm{odd}}\ast \mathcal{P}_{H_2,A_2}^{\mathrm{odd}} $, where
$\mathcal{P}_{H_1,A_1}^{\mathrm{odd}}\ast \mathcal{P}_{H_2,A_2}^{\mathrm{odd}} $, where ![]() $H_2=H\setminus H_1$ and
$H_2=H\setminus H_1$ and ![]() $A_2=A\setminus A_1$, see [Reference Choi, Park and Park8, Lemma 4.5], and therefore the following holds:
$A_2=A\setminus A_1$, see [Reference Choi, Park and Park8, Lemma 4.5], and therefore the following holds:
 \begin{eqnarray}
&&\widetilde{\beta}^{i-1}\left(\Delta\left(\overline{\mathcal{P}_{H,C}^{\mathrm{odd}}}\right)\right)= \sum_{\ell} \widetilde{\beta}^{\ell}\left(\Delta\left(\overline{\mathcal{P}_{H_1,C_1}^{\mathrm{odd}}}\right)\right) \times \widetilde{\beta}^{i-\ell-2}\left(\Delta\left(\overline{\mathcal{P}_{H_2,C_2}^{\mathrm{odd}}}\right)\right).
\end{eqnarray}
\begin{eqnarray}
&&\widetilde{\beta}^{i-1}\left(\Delta\left(\overline{\mathcal{P}_{H,C}^{\mathrm{odd}}}\right)\right)= \sum_{\ell} \widetilde{\beta}^{\ell}\left(\Delta\left(\overline{\mathcal{P}_{H_1,C_1}^{\mathrm{odd}}}\right)\right) \times \widetilde{\beta}^{i-\ell-2}\left(\Delta\left(\overline{\mathcal{P}_{H_2,C_2}^{\mathrm{odd}}}\right)\right).
\end{eqnarray} Now we are ready to explain how to compute  $\beta^i(X^{\mathbb{R}}_{G_n})$ from Equations (7.4), (7.5) and (7.6). Assume that i > 0. Let
$\beta^i(X^{\mathbb{R}}_{G_n})$ from Equations (7.4), (7.5) and (7.6). Assume that i > 0. Let ![]() $\mathcal{H}_1$ be the set of all simple PI-graphs of Gn and
$\mathcal{H}_1$ be the set of all simple PI-graphs of Gn and ![]() $\mathcal{H}_2$ the set of all non-simple PI-graphs of Gn. By Proposition 3.4,
$\mathcal{H}_2$ the set of all non-simple PI-graphs of Gn. By Proposition 3.4,  $\beta^i(X^{\mathbb{R}}_{G_n})=s^i_1(G_n)+s^i_2(G_n)$, where
$\beta^i(X^{\mathbb{R}}_{G_n})=s^i_1(G_n)+s^i_2(G_n)$, where
 \begin{align*}s_1^i(G_n)&=\sum_{H\in{\mathcal H}_1}\sum_{A\in\mathcal A(H)}\widetilde\beta^{i-1}{(\mathrm\Delta{(\overline{\mathcal P_{H,A}^{\mathrm o\mathrm d\mathrm d}})})}\hspace{1em}\text{and}\\s_2^i(G_n)&=\sum_{H\in{\mathcal H}_2}\sum_{A\in\mathcal A(H)}\widetilde\beta^{i-1}{(\mathrm\Delta{(\overline{\mathcal P_{H,A}^{\mathrm o\mathrm d\mathrm d}})})}.\end{align*}
\begin{align*}s_1^i(G_n)&=\sum_{H\in{\mathcal H}_1}\sum_{A\in\mathcal A(H)}\widetilde\beta^{i-1}{(\mathrm\Delta{(\overline{\mathcal P_{H,A}^{\mathrm o\mathrm d\mathrm d}})})}\hspace{1em}\text{and}\\s_2^i(G_n)&=\sum_{H\in{\mathcal H}_2}\sum_{A\in\mathcal A(H)}\widetilde\beta^{i-1}{(\mathrm\Delta{(\overline{\mathcal P_{H,A}^{\mathrm o\mathrm d\mathrm d}})})}.\end{align*} As ![]() $\mathcal{H}_1$ is the set of PI-graphs of the simple graph
$\mathcal{H}_1$ is the set of PI-graphs of the simple graph  $P_n, s^i_1(G_n)=\beta^{i}(X^{\mathbb{R}}_{P_n})$. By Proposition 3.4 and Equation (7.6),
$P_n, s^i_1(G_n)=\beta^{i}(X^{\mathbb{R}}_{P_n})$. By Proposition 3.4 and Equation (7.6),
 \begin{align*} s^i_2(G_n)
&=
\sum_{m=2}^{n-1} \sum_{\ell=0}^{\lfloor\frac{m}{2}\rfloor} \sum_{A\in\mathcal{A}(G_m)} \widetilde{\beta}^{\ell}\left(\Delta\left(\overline{\mathcal{P}_{G_m,A}^{\mathrm{odd}}}\right)\right) \times \beta^{i-\ell-1}\left(X^{\mathbb{R}}_{P_{n-m-1}}\right)\nonumber \\ & +\sum_{A\in\mathcal{A}(G_n)} \widetilde{\beta}^{i-1}\left(\Delta\left(\overline{\mathcal{P}_{G_n,A}^{\mathrm{odd}}}\right)\right).
\end{align*}
\begin{align*} s^i_2(G_n)
&=
\sum_{m=2}^{n-1} \sum_{\ell=0}^{\lfloor\frac{m}{2}\rfloor} \sum_{A\in\mathcal{A}(G_m)} \widetilde{\beta}^{\ell}\left(\Delta\left(\overline{\mathcal{P}_{G_m,A}^{\mathrm{odd}}}\right)\right) \times \beta^{i-\ell-1}\left(X^{\mathbb{R}}_{P_{n-m-1}}\right)\nonumber \\ & +\sum_{A\in\mathcal{A}(G_n)} \widetilde{\beta}^{i-1}\left(\Delta\left(\overline{\mathcal{P}_{G_n,A}^{\mathrm{odd}}}\right)\right).
\end{align*}Note that
 \begin{equation}
\beta^{i-1}(X^{\mathbb{R}}_{P_n})+\beta^i(X^{\mathbb{R}}_{P_n})=\beta^i(X^{\mathbb{R}}_{P_{n+1}})\quad \text{ for }1\leq i \lt \frac{n}{2},
\end{equation}
\begin{equation}
\beta^{i-1}(X^{\mathbb{R}}_{P_n})+\beta^i(X^{\mathbb{R}}_{P_n})=\beta^i(X^{\mathbb{R}}_{P_{n+1}})\quad \text{ for }1\leq i \lt \frac{n}{2},
\end{equation} that is, ![]() $s_1^{i-1}(G_n)+s_1^i(G_n)=s_1^i(G_{n+1})$ for
$s_1^{i-1}(G_n)+s_1^i(G_n)=s_1^i(G_{n+1})$ for ![]() $1\leq i \lt \frac{n}{2}$. Using Equations (7.5) and (7.7), we also have
$1\leq i \lt \frac{n}{2}$. Using Equations (7.5) and (7.7), we also have ![]() $s_2^{i-1}(G_n)+s_2^i(G_n)=s_2^i(G_{n+1})$ for
$s_2^{i-1}(G_n)+s_2^i(G_n)=s_2^i(G_{n+1})$ for ![]() $1\leq i \lt \frac{n}{2}.$ Hence, for
$1\leq i \lt \frac{n}{2}.$ Hence, for ![]() $1\leq i \lt \frac{n}{2}$, we have
$1\leq i \lt \frac{n}{2}$, we have
 \begin{equation}
\beta^{i-1}(X^{\mathbb{R}}_{G_{n}})+\beta^i(X^{\mathbb{R}}_{G_{n}})=\beta^i(X^{\mathbb{R}}_{G_{n+1}}).
\end{equation}
\begin{equation}
\beta^{i-1}(X^{\mathbb{R}}_{G_{n}})+\beta^i(X^{\mathbb{R}}_{G_{n}})=\beta^i(X^{\mathbb{R}}_{G_{n+1}}).
\end{equation} For ![]() $k=\lfloor \frac{n}{2}\rfloor$, plugging Equations (7.4) and (7.5) into
$k=\lfloor \frac{n}{2}\rfloor$, plugging Equations (7.4) and (7.5) into ![]() $s_1^k(G_n)+s_2^k(G_n)$, we see that
$s_1^k(G_n)+s_2^k(G_n)$, we see that
 \begin{equation}
\beta^{k}\left(X^{\mathbb{R}}_{G_{2k}}\right)=\beta^{k+1}\left(X^{\mathbb{R}}_{G_{2k+1}}\right)=\frac{6k}{k+2}C_k,
\end{equation}
\begin{equation}
\beta^{k}\left(X^{\mathbb{R}}_{G_{2k}}\right)=\beta^{k+1}\left(X^{\mathbb{R}}_{G_{2k+1}}\right)=\frac{6k}{k+2}C_k,
\end{equation} which is known as the total number of nonempty subtrees over all binary trees having k + 1 internal vertices, see[22, A071721]. Table 5 shows the Betti numbers of  $X^{\mathbb{R}}_{G_{n}}$ for some small integers n.
$X^{\mathbb{R}}_{G_{n}}$ for some small integers n.
Table 5. The Betti numbers  $\beta^i(X^{\mathbb{R}}_{\widetilde{P}_{n,2}})$ for small n
$\beta^i(X^{\mathbb{R}}_{\widetilde{P}_{n,2}})$ for small n

On the other hand, it is not difficult to check  $\{\beta^i(X^{\mathbb{R}}_{P_n})\}_{i\geq 0}$ in Equation (7.4) is log-concave, and hence unimodal. For
$\{\beta^i(X^{\mathbb{R}}_{P_n})\}_{i\geq 0}$ in Equation (7.4) is log-concave, and hence unimodal. For  $\widetilde{P}_{n,2}$, we can also see that
$\widetilde{P}_{n,2}$, we can also see that  $\{\beta^i(X^{\mathbb{R}}_{\widetilde{P}_{n,2}})\}_{i\geq 0}$ is unimodal from Equations (7.7) and (7.9). We remain the unimodality of
$\{\beta^i(X^{\mathbb{R}}_{\widetilde{P}_{n,2}})\}_{i\geq 0}$ is unimodal from Equations (7.7) and (7.9). We remain the unimodality of  $\beta^i(X^{\mathbb{R}}_{\widetilde{P}_{n,m}})$ for general n and m, as an open problem.
$\beta^i(X^{\mathbb{R}}_{\widetilde{P}_{n,m}})$ for general n and m, as an open problem.
Funding Statement
Boram Park was supported by the Basic Science Research Program through the National Research Foundation of Korea (NRF-2022R1F1A1069500). Seonjeong Park was supported by the National Research Foundation of Korea (NRF-2020R1A2C1A01011045).
Appendix 1. Appendix: Proof of Proposition 3.4
In this appendix, we give a sketch of Proposition 3.4. Since the notation given in [Reference Choi, Park and Park8] is not the same as this paper, we give the definitions used in [Reference Choi, Park and Park8].
Proof of Proposition 3.4
Let G be a graph and
 \begin{eqnarray*}
2^{\mathcal{C}_G}_{\mathrm{even}} &=& \{C\subset \mathcal{C}_G\mid |C\cap V|\text{is even, } |C\cap B|\text{is even for every bundle }B\text{ of }G\}.
\end{eqnarray*}
\begin{eqnarray*}
2^{\mathcal{C}_G}_{\mathrm{even}} &=& \{C\subset \mathcal{C}_G\mid |C\cap V|\text{is even, } |C\cap B|\text{is even for every bundle }B\text{ of }G\}.
\end{eqnarray*} Section 3 of [Reference Choi, Park and Park8] is devoted to show that for each subset S in the set ![]() $\{1,2,\dots,\dim P_{G}\}$, there exists
$\{1,2,\dots,\dim P_{G}\}$, there exists  $C\in 2^{\mathcal{C}_G}_{\mathrm{even}}$ such that
$C\in 2^{\mathcal{C}_G}_{\mathrm{even}}$ such that  $K_{P_G,S}=K_{C,G}^{\mathrm{odd}}$. Hence, Equation (3.2) becomes
$K_{P_G,S}=K_{C,G}^{\mathrm{odd}}$. Hence, Equation (3.2) becomes
 \begin{equation}
\beta^i(X^{\mathbb{R}}_G) =\sum_{C\in 2^{{\mathcal{C}}_G}_{\mathrm{even}}} \tilde{\beta}^{i-1}( K_{C,G}^{\mathrm{odd}} ),
\end{equation}
\begin{equation}
\beta^i(X^{\mathbb{R}}_G) =\sum_{C\in 2^{{\mathcal{C}}_G}_{\mathrm{even}}} \tilde{\beta}^{i-1}( K_{C,G}^{\mathrm{odd}} ),
\end{equation} where  $K_{C,G}^{\mathrm{odd}}$ is the dual complex of the union of all facets FI of PG such that
$K_{C,G}^{\mathrm{odd}}$ is the dual complex of the union of all facets FI of PG such that ![]() $|I\cap c$ is odd. Then, for
$|I\cap c$ is odd. Then, for  $C\in 2^{\mathcal{C}_G}_{\mathrm{even}}$, we define
$C\in 2^{\mathcal{C}_G}_{\mathrm{even}}$, we define  $\widetilde\Gamma_G(C)$ as the subgraph of G induced by the set
$\widetilde\Gamma_G(C)$ as the subgraph of G induced by the set
Lemma 1.1. ([Reference Choi, Park and Park8, Lemmas 4.3 and 4.4])
Let ![]() $K^{\prime\prime}_{C,G}$ be the subcomplex of
$K^{\prime\prime}_{C,G}$ be the subcomplex of  $K_{C,G}^{\mathrm{odd}}$ whose vertex set consists of vertices I satisfying the following:
$K_{C,G}^{\mathrm{odd}}$ whose vertex set consists of vertices I satisfying the following:
(1)
 $I\subset \widetilde{\Gamma}_G(C)$ and
$I\subset \widetilde{\Gamma}_G(C)$ and  $|I\cap C|$ is odd.
$|I\cap C|$ is odd.(2) For each bundle B of
 $\widetilde{\Gamma}_G(C)$ such that
$\widetilde{\Gamma}_G(C)$ such that  $B \cap C =\emptyset$, if the endpoints of B are in I, then
$B \cap C =\emptyset$, if the endpoints of B are in I, then  $B\subset I$.
$B\subset I$.
Then  $K_{C,G}^{\mathrm{odd}}$ is homotopy equivalent to
$K_{C,G}^{\mathrm{odd}}$ is homotopy equivalent to ![]() $K^{\prime\prime}_{C,G}$.
$K^{\prime\prime}_{C,G}$.
Then we get the following formula from Equation (A.1),
 \begin{equation}
\beta^i(X^{\mathbb{R}}_G) =\sum_{C\in 2^{{\mathcal{C}}_G}_{\mathrm{even}}} \tilde{\beta}^{i-1}( K^{\prime\prime}_{C,G} ).
\end{equation}
\begin{equation}
\beta^i(X^{\mathbb{R}}_G) =\sum_{C\in 2^{{\mathcal{C}}_G}_{\mathrm{even}}} \tilde{\beta}^{i-1}( K^{\prime\prime}_{C,G} ).
\end{equation}Lemma 1.2. ([Reference Choi, Park and Park8, Lemma 4.5(i)])
For  $C\in 2^{\mathcal{C}_G}_{\mathrm{even}}$, if
$C\in 2^{\mathcal{C}_G}_{\mathrm{even}}$, if ![]() $|I\cap C|$ is odd for some connected component I of
$|I\cap C|$ is odd for some connected component I of  $\widetilde\Gamma_G(C)$, then
$\widetilde\Gamma_G(C)$, then ![]() $K^{\prime\prime}_{C,G}$ is contractible.
$K^{\prime\prime}_{C,G}$ is contractible.
The above lemma implies that, to compute ![]() $\beta^i(X_G^{\mathbb{R}})$, it is enough to consider the collection C in
$\beta^i(X_G^{\mathbb{R}})$, it is enough to consider the collection C in  $2^{\mathcal{C}_G}_{\mathrm{even}}$ such that the intersection of C and each of the connected components of
$2^{\mathcal{C}_G}_{\mathrm{even}}$ such that the intersection of C and each of the connected components of  $\widetilde\Gamma_G(C)$ belongs to
$\widetilde\Gamma_G(C)$ belongs to  $2^{\mathcal{C}_G}_{\mathrm{even}}$. Thus, we define
$2^{\mathcal{C}_G}_{\mathrm{even}}$. Thus, we define
 \begin{equation*}2^{\mathcal{C}_G}_{\mathrm{even}\ast} := \{C \in 2^{\mathcal{C}_G}_{\mathrm{even}} \mid \text{each connected component of }\widetilde\Gamma_G(C)\text{ is even with respect to }C \}.\end{equation*}
\begin{equation*}2^{\mathcal{C}_G}_{\mathrm{even}\ast} := \{C \in 2^{\mathcal{C}_G}_{\mathrm{even}} \mid \text{each connected component of }\widetilde\Gamma_G(C)\text{ is even with respect to }C \}.\end{equation*} Note that for a collection C not in  $2^{\mathcal{C}_G}_{\mathrm{even}\ast}$,
$2^{\mathcal{C}_G}_{\mathrm{even}\ast}$,  $K_{C,G}^{\mathrm{odd}}$ is contractible. For
$K_{C,G}^{\mathrm{odd}}$ is contractible. For  $C\in 2^{\mathcal{C}_G}_{\mathrm{even}\ast}$, we let
$C\in 2^{\mathcal{C}_G}_{\mathrm{even}\ast}$, we let ![]() $\Gamma_G(C)$ be the graph from
$\Gamma_G(C)$ be the graph from  $\widetilde\Gamma_G(C)$ by replacing each bundle B of
$\widetilde\Gamma_G(C)$ by replacing each bundle B of  $\widetilde\Gamma_G(C)$, satisfying
$\widetilde\Gamma_G(C)$, satisfying ![]() $C\cap B=\emptyset$ with an (unlabelled) simple edge.
$C\cap B=\emptyset$ with an (unlabelled) simple edge.
Proposition 1.3. ([Reference Choi, Park and Park8, Proposition 4.7])
For  $C\in 2^{\mathcal{C}_G}_{\mathrm{even}\ast}$,
$C\in 2^{\mathcal{C}_G}_{\mathrm{even}\ast}$,  $K^{\mathrm{odd}}_{C,G}$ is homotopy equivalent to
$K^{\mathrm{odd}}_{C,G}$ is homotopy equivalent to  $K^{\mathrm{odd}}_{C,\Gamma_G(C)}$, and hence, the ith rational Betti number of
$K^{\mathrm{odd}}_{C,\Gamma_G(C)}$, and hence, the ith rational Betti number of ![]() $X_G^{\mathbb{R}}$ is
$X_G^{\mathbb{R}}$ is
 \begin{equation}
\beta^i(X_G^{\mathbb{R}})=\sum_{C\in 2^{\mathcal{C}_G}_{\mathrm{even}\ast}} \tilde{\beta}^{i-1}\left(K^{\mathrm{odd}}_{C,\Gamma_G(C)}\right),
\end{equation}
\begin{equation}
\beta^i(X_G^{\mathbb{R}})=\sum_{C\in 2^{\mathcal{C}_G}_{\mathrm{even}\ast}} \tilde{\beta}^{i-1}\left(K^{\mathrm{odd}}_{C,\Gamma_G(C)}\right),
\end{equation}Proof. Note that ![]() $\Gamma_G(C)$ is a PI-graph of G. Moreover, by definition, it holds that for a PI-graph H of G,
$\Gamma_G(C)$ is a PI-graph of G. Moreover, by definition, it holds that for a PI-graph H of G, ![]() $C\in \mathcal{A}(H)$ if and only if
$C\in \mathcal{A}(H)$ if and only if ![]() $H=\Gamma_G(C)$. Thus,
$H=\Gamma_G(C)$. Thus,
 \begin{equation*}
\beta^i(X_G^{\mathbb{R}})=\sum_{H:\text{PI-graph}\atop\text{of }G}\sum_{A\in\mathcal{A}(H)} \tilde{\beta}^{i-1}(K^{\mathrm{odd}}_{A,H}).
\end{equation*}
\begin{equation*}
\beta^i(X_G^{\mathbb{R}})=\sum_{H:\text{PI-graph}\atop\text{of }G}\sum_{A\in\mathcal{A}(H)} \tilde{\beta}^{i-1}(K^{\mathrm{odd}}_{A,H}).
\end{equation*} It was also shown in [Reference Choi, Park and Park8, §5] that for each admissible collection ![]() $A\in\mathcal{A}(H)$, the simplicial complex
$A\in\mathcal{A}(H)$, the simplicial complex  $K_{A,H}^{\mathrm{odd}}$ is homotopy equivalent to the order complex of the proper part of the poset
$K_{A,H}^{\mathrm{odd}}$ is homotopy equivalent to the order complex of the proper part of the poset  $\mathcal{P}_{H,A}^{\mathrm{odd}}.$Footnote 8 This proves Proposition 3.4.
$\mathcal{P}_{H,A}^{\mathrm{odd}}.$Footnote 8 This proves Proposition 3.4.