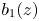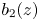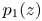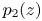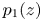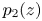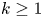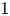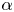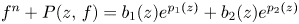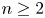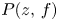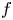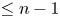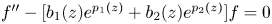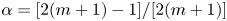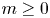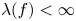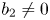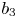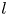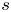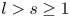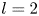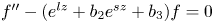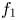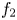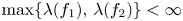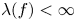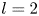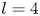1. Introduction
In the last several decades, the growth and value distribution of meromorphic solutions of complex differential equations have attracted much interest; see [Reference Laine23] and references therein. One of the main tools in this subject is Nevanlinna theory; see, e.g., [Reference Hayman14, Reference Laine23] for the standard notation and basic results of Nevanlinna theory. Bank and Laine [Reference Bank and Laine2, Reference Bank and Laine3] initiated the study on the oscillation of the second-order linear differential equation
where $A(z)$![]() is an entire function. It is well-known that all solutions of equation (1.1) are entire. For an entire function $f$
is an entire function. It is well-known that all solutions of equation (1.1) are entire. For an entire function $f$![]() , denote by $\sigma (f)$
, denote by $\sigma (f)$![]() the order of $f$
the order of $f$![]() which is defined as
which is defined as
where $M(r,\,f)$![]() is the maximum modulus of $f$
is the maximum modulus of $f$![]() on the circle $|z|=r$
on the circle $|z|=r$![]() . When $A$
. When $A$![]() is transcendental, an application of the lemma on the logarithmic derivative easily yields that all nontrivial solutions of (1.1) satisfy $\sigma (f)=\infty$
is transcendental, an application of the lemma on the logarithmic derivative easily yields that all nontrivial solutions of (1.1) satisfy $\sigma (f)=\infty$![]() . Denote by $\lambda (f)$
. Denote by $\lambda (f)$![]() the exponent of convergence of zeros of $f$
the exponent of convergence of zeros of $f$![]() which is defined as
which is defined as
where $n(r,\,f)$![]() denotes the number of zeros of $f$
denotes the number of zeros of $f$![]() in the disc $\{z: |z|< r\}$
in the disc $\{z: |z|< r\}$![]() . Concerning the zero distribution of solutions of equation (1.1), Bank and Laine [Reference Bank and Laine2, Reference Bank and Laine3] proved: Let $f_1$
. Concerning the zero distribution of solutions of equation (1.1), Bank and Laine [Reference Bank and Laine2, Reference Bank and Laine3] proved: Let $f_1$![]() and $f_2$
and $f_2$![]() be two linearly independent solutions of (1.1). If $\sigma (A)$
be two linearly independent solutions of (1.1). If $\sigma (A)$![]() is not an integer, then $\max \{\lambda (f_1),\,\lambda (f_2)\}\geq \sigma (A)$
is not an integer, then $\max \{\lambda (f_1),\,\lambda (f_2)\}\geq \sigma (A)$![]() ; if $\sigma (A)<1/2$
; if $\sigma (A)<1/2$![]() , then $\max \{\lambda (f_1),\,\lambda (f_2)\}=\infty$
, then $\max \{\lambda (f_1),\,\lambda (f_2)\}=\infty$![]() . Later, Shen [Reference Shen29] and Rossi [Reference Rossi28] relaxed the condition $\sigma (A)<1/2$
. Later, Shen [Reference Shen29] and Rossi [Reference Rossi28] relaxed the condition $\sigma (A)<1/2$![]() to the case $\sigma (A)=1/2$
to the case $\sigma (A)=1/2$![]() . Based on these results, Bank and Laine conjectured that $\max \{\lambda (f_1),\,\lambda (f_2)\}=\infty$
. Based on these results, Bank and Laine conjectured that $\max \{\lambda (f_1),\,\lambda (f_2)\}=\infty$![]() whenever $\sigma (A)$
whenever $\sigma (A)$![]() is not an integer. This conjecture is known as the Bank–Laine conjecture and has attracted much interest; see the surveys [Reference Gundersen13, Reference Laine and Tohge24] and references therein. Recently, this conjecture was disproved by Bergweiler and Eremenko [Reference Bergweiler and Eremenko7, Reference Bergweiler and Eremenko8]. They constructed counterexamples for the coefficient $A$
is not an integer. This conjecture is known as the Bank–Laine conjecture and has attracted much interest; see the surveys [Reference Gundersen13, Reference Laine and Tohge24] and references therein. Recently, this conjecture was disproved by Bergweiler and Eremenko [Reference Bergweiler and Eremenko7, Reference Bergweiler and Eremenko8]. They constructed counterexamples for the coefficient $A$![]() such that $\sigma (A)$
such that $\sigma (A)$![]() is not an integer and equation (1.1) admits two linearly independent solutions such that $\max \{\lambda (f_1),\,\lambda (f_2)\}<\infty$
is not an integer and equation (1.1) admits two linearly independent solutions such that $\max \{\lambda (f_1),\,\lambda (f_2)\}<\infty$![]() . In particular, one of the solutions is free of zeros. In their constructions, they used the solutions of (1.1) with $A$
. In particular, one of the solutions is free of zeros. In their constructions, they used the solutions of (1.1) with $A$![]() being a polynomial of $e^z$
being a polynomial of $e^z$![]() of degree 2, namely $A(z)=a_1e^{2z}+a_2e^z+a_3$
of degree 2, namely $A(z)=a_1e^{2z}+a_2e^z+a_3$![]() with certain coefficients $a_1$
with certain coefficients $a_1$![]() , $a_2$
, $a_2$![]() and $a_3$
and $a_3$![]() .
.
On the other hand, it is natural to give explicit solutions of (1.1) such that $\lambda (f)<\infty$![]() when $A$
when $A$![]() is a periodic entire function of the form
is a periodic entire function of the form
For such solutions, a remarkable result in [Reference Bank and Laine4, Reference Chiang9] states that there exist complex constants $c$![]() , $c_j$
, $c_j$![]() and a polynomial $P(z)$
and a polynomial $P(z)$![]() with simple roots only such that if $l$
with simple roots only such that if $l$![]() is an odd positive integer, then
is an odd positive integer, then

where $c_j=0$![]() whenever $j$
whenever $j$![]() is even; while if $l$
is even; while if $l$![]() is an even positive integer, then
is an even positive integer, then

However, it seems difficult to determine explicitly $c_j$![]() and also the polynomial $P(z)$
and also the polynomial $P(z)$![]() in the above two expressions and, until now, they are only known in some special cases. For example, Bank and Laine [Reference Bank and Laine4] gave a precise characterization of all nontrivial solutions such that $\lambda (f)<\infty$
in the above two expressions and, until now, they are only known in some special cases. For example, Bank and Laine [Reference Bank and Laine4] gave a precise characterization of all nontrivial solutions such that $\lambda (f)<\infty$![]() of (1.1) when $A(z)=e^{z}-b$
of (1.1) when $A(z)=e^{z}-b$![]() for some constant $b$
for some constant $b$![]() ; see also [Reference Laine23, theorem 5.22]. Bank and Laine [Reference Bank and Laine4] also characterized entire solutions such that $\lambda (f)<\infty$
; see also [Reference Laine23, theorem 5.22]. Bank and Laine [Reference Bank and Laine4] also characterized entire solutions such that $\lambda (f)<\infty$![]() of equation (1.1) when $A(z)=-(1/4)e^{-2z}+(1/2)e^{-z}+b$
of equation (1.1) when $A(z)=-(1/4)e^{-2z}+(1/2)e^{-z}+b$![]() for some constant $b$
for some constant $b$![]() . For these two coefficients, Chiang and Ismail [Reference Chiang and Ismail10] expressed all solutions of (1.1) in terms of some special functions and give a complete characterization of the zero distribution of these solutions.
. For these two coefficients, Chiang and Ismail [Reference Chiang and Ismail10] expressed all solutions of (1.1) in terms of some special functions and give a complete characterization of the zero distribution of these solutions.
In [Reference Bank1], Bank developed a method to find entire solutions such that $\lambda (f)<\infty$![]() of equation (1.1), but the manipulation of this method seems complicated. One of the main purposes of this paper is to give a more precise description of the oscillation of equation (1.1) when $A(z)$
of equation (1.1), but the manipulation of this method seems complicated. One of the main purposes of this paper is to give a more precise description of the oscillation of equation (1.1) when $A(z)$![]() contains two exponential terms, i.e.,
contains two exponential terms, i.e.,
or
In particular, this provides a different approach from that in [Reference Chiang and Ismail10] and also leads to a complete characterization of all solutions such that $\lambda (f)<\infty$![]() of (1.1) when $A(z)$
of (1.1) when $A(z)$![]() is an arbitrary polynomial in $e^z$
is an arbitrary polynomial in $e^z$![]() of degree $2$
of degree $2$![]() ; see theorem 4.4 in § 4. This work is a continuation of [Reference Zhang33], where the present author found all nontrivial solutions such that $\lambda (f)< k$
; see theorem 4.4 in § 4. This work is a continuation of [Reference Zhang33], where the present author found all nontrivial solutions such that $\lambda (f)< k$![]() of the differential equation
of the differential equation
where $b_1(z)$![]() , $b_2(z)$
, $b_2(z)$![]() and $b_3(z)$
and $b_3(z)$![]() are three polynomials such that $b_1(z)b_2(z)\not \equiv 0$
are three polynomials such that $b_1(z)b_2(z)\not \equiv 0$![]() and $p_1(z)$
and $p_1(z)$![]() and $p_2(z)$
and $p_2(z)$![]() are two polynomials of the same degree $k\geq 1$
are two polynomials of the same degree $k\geq 1$![]() with distinct leading coefficients $1$
with distinct leading coefficients $1$![]() and $\alpha$
and $\alpha$![]() , respectively.
, respectively.
Theorem 1.1 see [Reference Zhang33]
Let $b_1$![]() , $b_2$
, $b_2$![]() and $b_3$
and $b_3$![]() be polynomials such that $b_1b_2\not \equiv 0$
be polynomials such that $b_1b_2\not \equiv 0$![]() and $p_1$
and $p_1$![]() , $p_2$
, $p_2$![]() be two polynomials of degree $k\geq 1$
be two polynomials of degree $k\geq 1$![]() with distinct leading coefficients $1$
with distinct leading coefficients $1$![]() and $\alpha$
and $\alpha$![]() , respectively, and $p_1(0)=p_2(0)=0$
, respectively, and $p_1(0)=p_2(0)=0$![]() . Suppose that (1.7) admits a nontrivial solution such that $\lambda (f)< k$
. Suppose that (1.7) admits a nontrivial solution such that $\lambda (f)< k$![]() . Then $\alpha =1/2$
. Then $\alpha =1/2$![]() or $\alpha =3/4$
or $\alpha =3/4$![]() . Moreover,
. Moreover,
(1) if $\alpha =1/2,$
 then $p_2=p_1/2,$
then $p_2=p_1/2,$ $f=\kappa e^{h},$
$f=\kappa e^{h},$ where $\kappa$
where $\kappa$ is a polynomial with simple roots only and $h$
is a polynomial with simple roots only and $h$ satisfies $h'=\gamma _1e^{p_1/2}+\gamma$
satisfies $h'=\gamma _1e^{p_1/2}+\gamma$ with $\gamma _1$
with $\gamma _1$ and $\gamma$
and $\gamma$ being two polynomials such that $\gamma _1^2=b_1$
being two polynomials such that $\gamma _1^2=b_1$ , $2\gamma _1\gamma +\gamma _1'+\gamma _1p_1'/2+2\kappa '/\kappa \gamma _1=b_2$
, $2\gamma _1\gamma +\gamma _1'+\gamma _1p_1'/2+2\kappa '/\kappa \gamma _1=b_2$ and $\gamma ^2+\gamma '+2\gamma \kappa '/\kappa +\kappa ''/\kappa =b_3$
and $\gamma ^2+\gamma '+2\gamma \kappa '/\kappa +\kappa ''/\kappa =b_3$ ;
;(2) if $\alpha =3/4,$
 then $p_1=z,$
then $p_1=z,$ $p_2=3z/4$
$p_2=3z/4$ and $f=e^{h},$
and $f=e^{h},$ where $h$
where $h$ satisfies $h'=-4c^2e^{z/2}+ce^{z/4}-1/8$
satisfies $h'=-4c^2e^{z/2}+ce^{z/4}-1/8$ and $A=-(16c^2e^{z}-8c^3e^{3z/4}+1/64),$
and $A=-(16c^2e^{z}-8c^3e^{3z/4}+1/64),$ where $c$
where $c$ is a nonzero constant.
is a nonzero constant.
The proof of theorem 1.1 is based on a development of the Tumura–Clunie method; see [Reference Hayman14, chapter 4]. Define a differential polynomial $P(z,\,g)$![]() in $g$
in $g$![]() to be a finite sum of monomials in $g$
to be a finite sum of monomials in $g$![]() and its derivatives of the form $P(z,\,g)=\sum _{l=1}^{m}a_{l}g^{n_{l0}}(g')^{n_{l1}}\cdots (g^{(s)})^{n_{ls}}$
and its derivatives of the form $P(z,\,g)=\sum _{l=1}^{m}a_{l}g^{n_{l0}}(g')^{n_{l1}}\cdots (g^{(s)})^{n_{ls}}$![]() , where $n_{l0},\,\cdots,\,n_{ls}\in \mathbb {N}$
, where $n_{l0},\,\cdots,\,n_{ls}\in \mathbb {N}$![]() and the coefficients $a_l$
and the coefficients $a_l$![]() are meromorphic functions of order less than $\sigma (g)$
are meromorphic functions of order less than $\sigma (g)$![]() . Define the degree of $P(z,\,g)$
. Define the degree of $P(z,\,g)$![]() to be the greatest integer of $d_l:=\sum _{t=0}^sn_{lt}$
to be the greatest integer of $d_l:=\sum _{t=0}^sn_{lt}$![]() , $l=1,\,\cdots,\,m$
, $l=1,\,\cdots,\,m$![]() , and denote it by $\deg _g(P(z,\,g))$
, and denote it by $\deg _g(P(z,\,g))$![]() . Consider the equation
. Consider the equation
where $n\geq 2$![]() and $P(z,\,g)$
and $P(z,\,g)$![]() is a differential polynomial in $g$
is a differential polynomial in $g$![]() of degree $\leq n-1$
of degree $\leq n-1$![]() with meromorphic functions of order less than $k$
with meromorphic functions of order less than $k$![]() as coefficients. If equation (1.7) admits an entire solution such that $\lambda (f)< k$
as coefficients. If equation (1.7) admits an entire solution such that $\lambda (f)< k$![]() , then equation (1.7) reduces to an equation of the form in (1.8) with $n=2$
, then equation (1.7) reduces to an equation of the form in (1.8) with $n=2$![]() . It is shown in [Reference Zhang33, theorem 2.1] that if equation (1.8) admits an entire solution, then either $\alpha =-1$
. It is shown in [Reference Zhang33, theorem 2.1] that if equation (1.8) admits an entire solution, then either $\alpha =-1$![]() or $\alpha$
or $\alpha$![]() is positive rational number and in either case $g$
is positive rational number and in either case $g$![]() is a linear combination of certain exponential functions plus some function of order less than $k$
is a linear combination of certain exponential functions plus some function of order less than $k$![]() . However, to solve entire solutions of (1.7) such that $\lambda (f)<\infty$
. However, to solve entire solutions of (1.7) such that $\lambda (f)<\infty$![]() , [Reference Zhang33, theorem 2.1] fails to work since in this case the coefficients of $P(z,\,g)$
, [Reference Zhang33, theorem 2.1] fails to work since in this case the coefficients of $P(z,\,g)$![]() shall contain some logarithmic derivatives which have order no less than $k$
shall contain some logarithmic derivatives which have order no less than $k$![]() .
.
The remainder of this paper is organized in the following way. Denote by $\mathcal {R}$![]() the set of rational functions and by $\mathcal {L}$
the set of rational functions and by $\mathcal {L}$![]() the set of functions $a(z)$
the set of functions $a(z)$![]() such that $a(z)=h^{(l)}(z)/h(z)$
such that $a(z)=h^{(l)}(z)/h(z)$![]() , $l\geq 1$
, $l\geq 1$![]() , for some meromorphic function $h(z)$
, for some meromorphic function $h(z)$![]() of finite order, respectively. In § 2, we further develop the Tumura–Clunie method by solving entire solutions of equation (1.8), where $P(z,\,g)$
of finite order, respectively. In § 2, we further develop the Tumura–Clunie method by solving entire solutions of equation (1.8), where $P(z,\,g)$![]() is now a differential polynomial in $g$
is now a differential polynomial in $g$![]() with coefficients that are combinations of functions in the set $\mathcal {S}=\mathcal {R}\cup \mathcal {L}$
with coefficients that are combinations of functions in the set $\mathcal {S}=\mathcal {R}\cup \mathcal {L}$![]() . For equation (1.8) with such coefficients, we can also write the entire solution as a linear combination of exponential functions with certain constant coefficients, but unlike in [Reference Zhang33, theorem 2.1], it is impossible to determine whether $\alpha$
. For equation (1.8) with such coefficients, we can also write the entire solution as a linear combination of exponential functions with certain constant coefficients, but unlike in [Reference Zhang33, theorem 2.1], it is impossible to determine whether $\alpha$![]() is a rational number; see theorem 2.1. In § 3, we apply our results on equation (1.8) to study the oscillation of equation (1.7) and prove that $\alpha =[2(m+1)-1]/[2(m+1)$
is a rational number; see theorem 2.1. In § 3, we apply our results on equation (1.8) to study the oscillation of equation (1.7) and prove that $\alpha =[2(m+1)-1]/[2(m+1)$![]() ] for some integer $m\geq 0$
] for some integer $m\geq 0$![]() provided that equation (1.7) with $b_3\equiv 0$
provided that equation (1.7) with $b_3\equiv 0$![]() admits a nontrivial solution such that $\lambda (f)<\infty$
admits a nontrivial solution such that $\lambda (f)<\infty$![]() ; see theorem 3.1. This gives a partial answer to a question of Ishizaki [Reference Ishizaki19]. In § 4, we consider the equation $f''-(b_1e^{lz}+b_2e^{sz}+b_3)f=0$
; see theorem 3.1. This gives a partial answer to a question of Ishizaki [Reference Ishizaki19]. In § 4, we consider the equation $f''-(b_1e^{lz}+b_2e^{sz}+b_3)f=0$![]() , where $l,\,s$
, where $l,\,s$![]() are relatively prime integers such that $l>s\geq 1$
are relatively prime integers such that $l>s\geq 1$![]() and $b_i$
and $b_i$![]() are constants such that $b_1b_2\not =0$
are constants such that $b_1b_2\not =0$![]() . We prove that $l=2$
. We prove that $l=2$![]() if this equation admits two linearly independent solutions $f_1$
if this equation admits two linearly independent solutions $f_1$![]() and $f_2$
and $f_2$![]() such that $\max \{\lambda (f_1),\,\lambda (f_2)\}<\infty$
such that $\max \{\lambda (f_1),\,\lambda (f_2)\}<\infty$![]() . In particular, when $l=2$
. In particular, when $l=2$![]() or $l=4$
or $l=4$![]() , we determine the polynomial $P(z)$
, we determine the polynomial $P(z)$![]() and the coefficients $c_j$
and the coefficients $c_j$![]() and $c$
and $c$![]() in (1.4) precisely. Finally, in § 5, we give some remarks on our results.
in (1.4) precisely. Finally, in § 5, we give some remarks on our results.
2. Tumura–clunie differential equations
Let $b_1(z)$![]() and $b_2(z)$
and $b_2(z)$![]() be two nonzero polynomials and $p_1(z)$
be two nonzero polynomials and $p_1(z)$![]() and $p_2(z)$
and $p_2(z)$![]() be two polynomials of the same degree $k\geq 1$
be two polynomials of the same degree $k\geq 1$![]() with distinct leading coefficients $1$
with distinct leading coefficients $1$![]() and $\alpha$
and $\alpha$![]() , respectively, and $p_1(0)=p_2(0)=0$
, respectively, and $p_1(0)=p_2(0)=0$![]() . Without loss of generality, we may suppose that $0<|\alpha |\leq 1$
. Without loss of generality, we may suppose that $0<|\alpha |\leq 1$![]() . In this section, we solve entire solutions of the differential equation
. In this section, we solve entire solutions of the differential equation
where $n\geq 2$![]() and $P(z,\,f)$
and $P(z,\,f)$![]() is a differential polynomial in $f$
is a differential polynomial in $f$![]() of degree $\leq n-1$
of degree $\leq n-1$![]() with coefficients being combinations of functions in $\mathcal {S}$
with coefficients being combinations of functions in $\mathcal {S}$![]() . In the following, a differential polynomial in $f$
. In the following, a differential polynomial in $f$![]() will always have coefficients which are combinations of functions in $\mathcal {S}$
will always have coefficients which are combinations of functions in $\mathcal {S}$![]() and thus we will omit mentioning this from now on.
and thus we will omit mentioning this from now on.
To state our results, we first set up some notation: Let $p(z)$![]() be a polynomial of degree $k\geq 1$
be a polynomial of degree $k\geq 1$![]() . We write $p(z)=(a+ib)z^{k}+q(z)$
. We write $p(z)=(a+ib)z^{k}+q(z)$![]() , where $a,\,b$
, where $a,\,b$![]() are real and $a+ib\not =0$
are real and $a+ib\not =0$![]() and $q(z)$
and $q(z)$![]() is a polynomial of degree at most $k-1$
is a polynomial of degree at most $k-1$![]() . Denote
. Denote
Then on the ray $z=re^{i\theta }$![]() , $r\geq 0$
, $r\geq 0$![]() , from [Reference Bank and Langley6] (or [Reference Laine23, lemma 5.14]) we know that:
, from [Reference Bank and Langley6] (or [Reference Laine23, lemma 5.14]) we know that:
1. if $\delta (p,\,\theta )>0$
 , then there exists an $r_0=r_0(\theta )$
, then there exists an $r_0=r_0(\theta )$ such that $\log |e^{p(z)}|$
such that $\log |e^{p(z)}|$ is increasing on $[r_0,\,\infty )$
is increasing on $[r_0,\,\infty )$ and $|e^{p(z)}|\geq e^{\delta (p,\theta )r^{n}/2}$
and $|e^{p(z)}|\geq e^{\delta (p,\theta )r^{n}/2}$ there;
there;2. if $\delta (p,\,\theta )<0$
 , then there exists an $r_0=r_0(\theta )$
, then there exists an $r_0=r_0(\theta )$ such that $\log |e^{p(z)}|$
such that $\log |e^{p(z)}|$ is decreasing on $[r_0,\,\infty )$
is decreasing on $[r_0,\,\infty )$ and $|e^{p(z)}|\leq e^{\delta (p,\theta )r^{n}/2}$
and $|e^{p(z)}|\leq e^{\delta (p,\theta )r^{n}/2}$ there.
there.
Let $\theta _1,\, \theta _2,\, \cdots,\, \theta _{2k}\in [0,\,2\pi )$![]() be such that $\delta (p,\,\theta _j)=0$
be such that $\delta (p,\,\theta _j)=0$![]() , $j=1,\,2,\,\cdots,\,2k$
, $j=1,\,2,\,\cdots,\,2k$![]() . We may suppose that $\theta _1< \pi$
. We may suppose that $\theta _1< \pi$![]() and $\theta _j=\theta _1+(j-1)\pi /k$
and $\theta _j=\theta _1+(j-1)\pi /k$![]() . Denoting $\theta _{2k+1}=\theta _1+2\pi$
. Denoting $\theta _{2k+1}=\theta _1+2\pi$![]() , then $\theta _1$
, then $\theta _1$![]() , $\theta _2$
, $\theta _2$![]() , $\cdots$
, $\cdots$![]() , $\theta _{2k}$
, $\theta _{2k}$![]() divides the complex plane $\mathbb {C}$
divides the complex plane $\mathbb {C}$![]() into $2k$
into $2k$![]() sectors $S_j$
sectors $S_j$![]() , namely
, namely
Throughout this paper, we let $\epsilon >0$![]() be an arbitrary constant. We also denote
be an arbitrary constant. We also denote
Denote by $\overline {S}_j$![]() and $\overline {S}_{j,\epsilon }$
and $\overline {S}_{j,\epsilon }$![]() the closure of $S_j$
the closure of $S_j$![]() and $S_{j,\epsilon }$
and $S_{j,\epsilon }$![]() , respectively. For $p_1$
, respectively. For $p_1$![]() in (2.1), we choose $\theta _1=-\pi /(2k)$
in (2.1), we choose $\theta _1=-\pi /(2k)$![]() and thus $\delta (p_1,\,\theta )>0$
and thus $\delta (p_1,\,\theta )>0$![]() in the sectors $S_j$
in the sectors $S_j$![]() when $j$
when $j$![]() is odd, and $\delta (p_1,\,\theta )<0$
is odd, and $\delta (p_1,\,\theta )<0$![]() in the sectors $S_j$
in the sectors $S_j$![]() when $j$
when $j$![]() is even. Denote by $J_1$
is even. Denote by $J_1$![]() and $J_2$
and $J_2$![]() the subsets of odd and even integers in the set $J=\{1,\,2\cdots,\,2k\}$
the subsets of odd and even integers in the set $J=\{1,\,2\cdots,\,2k\}$![]() , respectively, i.e., $J_1=\{1,\,3,\,\cdots,\,2k-1\}$
, respectively, i.e., $J_1=\{1,\,3,\,\cdots,\,2k-1\}$![]() and $J_2=\{2,\,4,\,\cdots,\,2k\}$
and $J_2=\{2,\,4,\,\cdots,\,2k\}$![]() . We prove the following
. We prove the following
Theorem 2.1 Let $n\geq 2$![]() be an integer and $P(z,\,f)$
be an integer and $P(z,\,f)$![]() be a differential polynomial in $f$
be a differential polynomial in $f$![]() of degree $\leq {n-1}$
of degree $\leq {n-1}$![]() . Suppose that (2.1) admits an entire solution $f$
. Suppose that (2.1) admits an entire solution $f$![]() . Then $\alpha$
. Then $\alpha$![]() is real. Moreover,
is real. Moreover,
(1) if $-1\leq \alpha <0,$
 then $f=\gamma _1e^{p_1/n}+\gamma _2e^{p_2/n}+\eta,$
then $f=\gamma _1e^{p_1/n}+\gamma _2e^{p_2/n}+\eta,$ where $\gamma _1,$
where $\gamma _1,$ $\gamma _2$
$\gamma _2$ are two polynomials such that $\gamma _1^n=b_1,$
are two polynomials such that $\gamma _1^n=b_1,$ $\gamma _2^n=b_2$
$\gamma _2^n=b_2$ and $\eta$
and $\eta$ is an entire function such that $\eta =(\mu _{1,j}-1)\gamma _1e^{p_1/n}+(\mu _{2,j}-1)\gamma _2e^{p_2/n}+\eta _j,$
is an entire function such that $\eta =(\mu _{1,j}-1)\gamma _1e^{p_1/n}+(\mu _{2,j}-1)\gamma _2e^{p_2/n}+\eta _j,$ where $\mu _{1,j}$
where $\mu _{1,j}$ and $\mu _{2,j}$
and $\mu _{2,j}$ are the $n$
are the $n$ -th roots of $1$
-th roots of $1$ such that $\mu _{1,j}=1$
such that $\mu _{1,j}=1$ when $j\in \{1\}\cup J_2$
when $j\in \{1\}\cup J_2$ and $\mu _{2,j}=1$
and $\mu _{2,j}=1$ when $j\in \{2\}\cup J_1,$
when $j\in \{2\}\cup J_1,$ and there is an integer $N$
and there is an integer $N$ such that $|\eta _j|=O(r^N)$
such that $|\eta _j|=O(r^N)$ uniformly in $\overline {S}_{j,\epsilon };$
uniformly in $\overline {S}_{j,\epsilon };$ in particular, when $k=1,$
in particular, when $k=1,$ $\eta$
$\eta$ is a polynomial;
is a polynomial;(2) if $0<\alpha <1,$
 letting $m$
letting $m$ be the smallest integer such that $\alpha \leq [(m+1)n-1]/[(m+1)n],$
be the smallest integer such that $\alpha \leq [(m+1)n-1]/[(m+1)n],$ then $f=\gamma _1\sum _{j=0}^mc_j(b_2/b_1)^je^{[jn(\alpha -1)+1]p_1/n}+\eta$
then $f=\gamma _1\sum _{j=0}^mc_j(b_2/b_1)^je^{[jn(\alpha -1)+1]p_1/n}+\eta$ , where $\gamma _1$
, where $\gamma _1$ is a polynomial such that $\gamma _1^n=b_1$
is a polynomial such that $\gamma _1^n=b_1$ and $c_0,$
and $c_0,$ $\cdots,$
$\cdots,$ $c_m$
$c_m$ are constants such that $c_0^{n}=1$
are constants such that $c_0^{n}=1$ when $m=0,$
when $m=0,$ and $c_0^{n}=nc_0^{n-1}c_1=1$
and $c_0^{n}=nc_0^{n-1}c_1=1$ when $m=1$
when $m=1$ , and $c_0^{n}=nc_0^{n-1}c_1=1$
, and $c_0^{n}=nc_0^{n-1}c_1=1$ and $\sum _{\substack {j_0+\cdots +j_m=n,\\ j_1+\cdots +mj_m=k_0}}\frac {n!}{j_0!j_1!\cdots j_m!}c_0^{j_0}c_1^{j_1}\cdots c_m^{j_m}=0,$
and $\sum _{\substack {j_0+\cdots +j_m=n,\\ j_1+\cdots +mj_m=k_0}}\frac {n!}{j_0!j_1!\cdots j_m!}c_0^{j_0}c_1^{j_1}\cdots c_m^{j_m}=0,$ $k_0=2,\,\cdots,\,m,$
$k_0=2,\,\cdots,\,m,$ when $m\geq 2,$
when $m\geq 2,$ and $\eta$
and $\eta$ is a meromorphic function with at most finitely many poles such that $\eta =\gamma _1\sum _{l=0}^m(\mu _j-1)c_{j}(b_2/b_1)^je^{[jn(\alpha -1)+1]p_1/n}+\eta _{j},$
is a meromorphic function with at most finitely many poles such that $\eta =\gamma _1\sum _{l=0}^m(\mu _j-1)c_{j}(b_2/b_1)^je^{[jn(\alpha -1)+1]p_1/n}+\eta _{j},$ where $\mu _j$
where $\mu _j$ are the $n$
are the $n$ -th roots of $1$
-th roots of $1$ such that $\mu _j=1$
such that $\mu _j=1$ when $j\in \{1\}\cup J_2,$
when $j\in \{1\}\cup J_2,$ and there is an integer $N$
and there is an integer $N$ such that $|\eta _j|=O(r^N)$
such that $|\eta _j|=O(r^N)$ uniformly in $\overline {S}_{j,\epsilon };$
uniformly in $\overline {S}_{j,\epsilon };$ moreover, we have $p_2=\alpha p_1$
moreover, we have $p_2=\alpha p_1$ when $m\geq 1;$
when $m\geq 1;$ in particular, when $k=1,$
in particular, when $k=1,$ $\eta$
$\eta$ is a rational function.
is a rational function.
In theorem 2.1, if all coefficients of the monomials in $P(z,\,f)$![]() of degree $n-1$
of degree $n-1$![]() are rational functions, then we may use the method in the proof of [Reference Zhang33, theorem 2.1] to show that $\eta$
are rational functions, then we may use the method in the proof of [Reference Zhang33, theorem 2.1] to show that $\eta$![]() is a polynomial or a rational function. We also remark that, by using the method in the proof of theorem 2.1 for the case $-1\leq \alpha <0$
is a polynomial or a rational function. We also remark that, by using the method in the proof of theorem 2.1 for the case $-1\leq \alpha <0$![]() together with the method in [Reference Zhang, Gao and Zhang34], we may extend [Reference Zhang33, theorem 2.1] to the case $P(z,\,f)$
together with the method in [Reference Zhang, Gao and Zhang34], we may extend [Reference Zhang33, theorem 2.1] to the case $P(z,\,f)$![]() is a delay–differential polynomial in $f$
is a delay–differential polynomial in $f$![]() with meromorphic functions of order less than $k$
with meromorphic functions of order less than $k$![]() as coefficients; see [Reference Zhang, Gao and Zhang34] for the definition of a delay–differential polynomial.
as coefficients; see [Reference Zhang, Gao and Zhang34] for the definition of a delay–differential polynomial.
As in the proof of theorems [Reference Zhang, Gao and Zhang34, theorem 1.1] and [Reference Zhang33, theorem 2.1], we also start from analysing first-order linear differential equation $f'-uf=w$![]() , where $u$
, where $u$![]() is a nonzero polynomial and $w$
is a nonzero polynomial and $w$![]() is a meromorphic function with at most finitely many poles. Let $p(z)$
is a meromorphic function with at most finitely many poles. Let $p(z)$![]() be a primitive function of $u$
be a primitive function of $u$![]() and suppose that $\deg (p(z))=k\geq 1$
and suppose that $\deg (p(z))=k\geq 1$![]() . If $f$
. If $f$![]() is meromorphic, then there is a rational function $v(z)$
is meromorphic, then there is a rational function $v(z)$![]() such that $v(z)\to 0$
such that $v(z)\to 0$![]() as $z\to \infty$
as $z\to \infty$![]() and $h(z)=f(z)-v(z)$
and $h(z)=f(z)-v(z)$![]() is entire. It follows that $f(z)=h(z)+v(z)$
is entire. It follows that $f(z)=h(z)+v(z)$![]() and $h$
and $h$![]() satisfies $h'-uh=w-(v'-uv)$
satisfies $h'-uh=w-(v'-uv)$![]() and $w-(v'-uv)$
and $w-(v'-uv)$![]() is an entire function. By elementary integration, the meromorphic solutions of $f'-uf=w$
is an entire function. By elementary integration, the meromorphic solutions of $f'-uf=w$![]() are $f=ce^{p(z)}+H(z)$
are $f=ce^{p(z)}+H(z)$![]() , where
, where
To study the growth behaviour of this function, a useful tool is the Phragmén–Lindelöf theorem (see [Reference Holland18, theorem 7.3]): Let $f(z)$![]() be an analytic function, regular in a region $D$
be an analytic function, regular in a region $D$![]() between two straight lines making an angle $\pi /\tau _1$
between two straight lines making an angle $\pi /\tau _1$![]() at the origin, and on the lines themselves. Suppose that $|f(z)|\leq M$
at the origin, and on the lines themselves. Suppose that $|f(z)|\leq M$![]() on the line, and that, as $r\to \infty$
on the line, and that, as $r\to \infty$![]() $|f(z)|=O(e^{r^{\tau _2}})$
$|f(z)|=O(e^{r^{\tau _2}})$![]() , where $\tau _2<\tau _1$
, where $\tau _2<\tau _1$![]() , uniformly in the angle. Then actually $|f(z)|\leq M$
, uniformly in the angle. Then actually $|f(z)|\leq M$![]() holds throughout the region. Moreover, if $f(z)\to c_1$
holds throughout the region. Moreover, if $f(z)\to c_1$![]() and $f(z)\to c_2$
and $f(z)\to c_2$![]() as $z\to \infty$
as $z\to \infty$![]() along the two lines, respectively, then $c_1=c_2$
along the two lines, respectively, then $c_1=c_2$![]() and $f(z)\to c_1$
and $f(z)\to c_1$![]() uniformly as $z\to \infty$
uniformly as $z\to \infty$![]() in $D$
in $D$![]() . Using the Phragmén–Lindelöf theorem, the present author proved the following
. Using the Phragmén–Lindelöf theorem, the present author proved the following
Lemma 2.2 see [Reference Zhang33, Reference Zhang, Gao and Zhang34]
Let $p(z)$![]() be a polynomial with degree $k\geq 1$
be a polynomial with degree $k\geq 1$![]() and $w$
and $w$![]() be a nonzero polynomial. Then there is an integer $N$
be a nonzero polynomial. Then there is an integer $N$![]() such that for each $S_j$
such that for each $S_j$![]() where $\delta (p,\,\theta )>0$
where $\delta (p,\,\theta )>0$![]() , there is a constant $a_j$
, there is a constant $a_j$![]() such that $|H(re^{i\theta })-a_je^{p(re^{i\theta })}|= O(r^N)$
such that $|H(re^{i\theta })-a_je^{p(re^{i\theta })}|= O(r^N)$![]() uniformly in $\overline {S}_{j,\epsilon }$
uniformly in $\overline {S}_{j,\epsilon }$![]() , and for each $S_j$
, and for each $S_j$![]() where $\delta (p,\,\theta )<0$
where $\delta (p,\,\theta )<0$![]() and any constant $a$
and any constant $a$![]() , $|H(re^{i\theta })-ae^{p(re^{i\theta })}|= O(r^N)$
, $|H(re^{i\theta })-ae^{p(re^{i\theta })}|= O(r^N)$![]() uniformly in $\overline {S}_{j,\epsilon }$
uniformly in $\overline {S}_{j,\epsilon }$![]() .
.
Most arguments we use below are the same as that in the proof of [Reference Zhang33, theorem 2.1]. We also first introduce the definition of $R$![]() –set: An $R$
–set: An $R$![]() –set in the complex plane is a countable union of discs whose radii have finite sum. Let $f(z)$
–set in the complex plane is a countable union of discs whose radii have finite sum. Let $f(z)$![]() be an entire solution of (2.1). We denote the union of all $R$
be an entire solution of (2.1). We denote the union of all $R$![]() –sets associated with $f(z)$
–sets associated with $f(z)$![]() and each coefficient of $P(z,\,f)$
and each coefficient of $P(z,\,f)$![]() by $\tilde {R}$
by $\tilde {R}$![]() from now on. In the proof of theorem 2.1, after taking the derivatives on both sides of equation (2.1), there may be some new coefficients appearing in the resulting equations. We will always assume that $\tilde {R}$
from now on. In the proof of theorem 2.1, after taking the derivatives on both sides of equation (2.1), there may be some new coefficients appearing in the resulting equations. We will always assume that $\tilde {R}$![]() also contains those $R$
also contains those $R$![]() -sets associated with these new coefficients.
-sets associated with these new coefficients.
As in the proof of [Reference Zhang33, theorem 2.1], we first reduce (2.1) into a non-homogeneous linear differential equation with rational coefficients. Now, with all coefficients of $P(z,\,f)$![]() being combinations of functions in $\mathcal {S}$
being combinations of functions in $\mathcal {S}$![]() , the key lemma for this aim is the following
, the key lemma for this aim is the following
Lemma 2.3 Under the assumptions of theorem 2.1 , $\sigma (f)=k$![]() and $\alpha$
and $\alpha$![]() is real. Moreover, for any $\theta \in [0,\,2\pi )$
is real. Moreover, for any $\theta \in [0,\,2\pi )$![]() such that the ray $z=re^{i\theta }$
such that the ray $z=re^{i\theta }$![]() meets finitely discs in $\tilde {R},$
meets finitely discs in $\tilde {R},$![]()
(1) when $-1\!\leq\! \alpha <0,$
 if $\delta (p_1,\,\theta )\!>\!0,$
if $\delta (p_1,\,\theta )\!>\!0,$ then $|f(re^{i\theta })^n|=(1+o(1)) |b_1(re^{i\theta })e^{p_1(re^{i\theta })}|,$
then $|f(re^{i\theta })^n|=(1+o(1)) |b_1(re^{i\theta })e^{p_1(re^{i\theta })}|,$ $r\to \infty ;$
$r\to \infty ;$ if $\delta (p_2,\,\theta )>0,$
if $\delta (p_2,\,\theta )>0,$ then $|f(re^{i\theta })^n|=(1+o(1))|b_2(re^{i\theta })e^{p_2(re^{i\theta })}|,$
then $|f(re^{i\theta })^n|=(1+o(1))|b_2(re^{i\theta })e^{p_2(re^{i\theta })}|,$ $r\to \infty ;$
$r\to \infty ;$
(2) when $0<\alpha <1,$
 if $\delta (p_1,\,\theta )>0,$
if $\delta (p_1,\,\theta )>0,$ then $|f(re^{i\theta })^n|=(1+o(1)) |b_1(re^{i\theta })e^{p_1(re^{i\theta })}|,$
then $|f(re^{i\theta })^n|=(1+o(1)) |b_1(re^{i\theta })e^{p_1(re^{i\theta })}|,$ $r\to \infty ;$
$r\to \infty ;$ if $\delta (p_1,\,\theta )<0,$
if $\delta (p_1,\,\theta )<0,$ then there is an integer $N$
then there is an integer $N$ such that $|f(re^{i\theta })|\leq r^N$
such that $|f(re^{i\theta })|\leq r^N$ for all large $r$
for all large $r$ .
.
Proof of lemma 2.3. Since $\alpha \not =1$![]() , then by Steinmetz's result [Reference Steinmetz30] for exponential polynomials, we have $T(r,\,b_1e^{p_1}+b_2e^{p_2})=K(1+o(1))r^k$
, then by Steinmetz's result [Reference Steinmetz30] for exponential polynomials, we have $T(r,\,b_1e^{p_1}+b_2e^{p_2})=K(1+o(1))r^k$![]() for some nonzero constant $K$
for some nonzero constant $K$![]() depending only on $\alpha$
depending only on $\alpha$![]() . Recall that the coefficients of equation (2.1) are combinations of functions in $\mathcal {S}$
. Recall that the coefficients of equation (2.1) are combinations of functions in $\mathcal {S}$![]() . By the lemma on the logarithmic derivative, we deduce from equation (2.1) that
. By the lemma on the logarithmic derivative, we deduce from equation (2.1) that
Therefore, $f$![]() is transcendental and $T(r,\,f)\geq K_1 r^k$
is transcendental and $T(r,\,f)\geq K_1 r^k$![]() for some positive constant $K_1$
for some positive constant $K_1$![]() . On the other hand, by the lemma on the logarithmic derivative we also have from equation (2.1) that
. On the other hand, by the lemma on the logarithmic derivative we also have from equation (2.1) that

which yields that $T(r,\,f)\leq K_2 r^k$![]() for some positive constant $K_2$
for some positive constant $K_2$![]() . This together with $T(r,\,f)\geq K_1 r^k$
. This together with $T(r,\,f)\geq K_1 r^k$![]() yields $\sigma (f)=k$
yields $\sigma (f)=k$![]() . Then by definition of $\mathcal {S}$
. Then by definition of $\mathcal {S}$![]() and looking at the proof of [Reference Zhang33, theorem 2.1], we see that $\alpha$
and looking at the proof of [Reference Zhang33, theorem 2.1], we see that $\alpha$![]() is real. Now, $-1\leq \alpha <0$
is real. Now, $-1\leq \alpha <0$![]() or $0<\alpha <1$
or $0<\alpha <1$![]() .
.
Recall that $\theta _1=-\pi /(2k)$![]() and from (2.2) that $\delta (p_1,\,\theta )=\cos k\theta$
and from (2.2) that $\delta (p_1,\,\theta )=\cos k\theta$![]() and $\delta (p_2,\,\theta )=\alpha \cos k\theta$
and $\delta (p_2,\,\theta )=\alpha \cos k\theta$![]() . When $\alpha <0$
. When $\alpha <0$![]() , we see that $\delta (p_1,\,\theta )$
, we see that $\delta (p_1,\,\theta )$![]() and $\delta (p_2,\,\theta )$
and $\delta (p_2,\,\theta )$![]() have opposite signs for each $\theta$
have opposite signs for each $\theta$![]() in the sectors $S_j$
in the sectors $S_j$![]() defined in (2.3) for $p_1$
defined in (2.3) for $p_1$![]() and $\delta (p_1,\,\theta )>0$
and $\delta (p_1,\,\theta )>0$![]() for $\theta$
for $\theta$![]() in the sectors $S_{j}$
in the sectors $S_{j}$![]() where $j\in J_1$
where $j\in J_1$![]() ; when $\alpha >0$
; when $\alpha >0$![]() , we see that $\delta (p_1,\,\theta )>0$
, we see that $\delta (p_1,\,\theta )>0$![]() and $\delta (p_2,\,\theta )>0$
and $\delta (p_2,\,\theta )>0$![]() simultaneously for each $\theta$
simultaneously for each $\theta$![]() in the sectors $S_{j}$
in the sectors $S_{j}$![]() where $j\in J_1$
where $j\in J_1$![]() and $\delta (p_1,\,\theta )<0$
and $\delta (p_1,\,\theta )<0$![]() and $\delta (p_2,\,\theta )<0$
and $\delta (p_2,\,\theta )<0$![]() simultaneously for each $\theta$
simultaneously for each $\theta$![]() in the sectors $S_{j}$
in the sectors $S_{j}$![]() where $j\in J_2$
where $j\in J_2$![]() . Then we see that the assertion (1) and the assertion (2) for the case that $\delta (p_1,\,\theta )>0$
. Then we see that the assertion (1) and the assertion (2) for the case that $\delta (p_1,\,\theta )>0$![]() can be obtained by directly following the proof of [Reference Zhang, Gao and Zhang34, lemma 2.5].
can be obtained by directly following the proof of [Reference Zhang, Gao and Zhang34, lemma 2.5].
Now we consider the growth behaviour of $f(z)$![]() along the ray $z=re^{i\theta }$
along the ray $z=re^{i\theta }$![]() such that $\delta (p_1,\,\theta )<0$
such that $\delta (p_1,\,\theta )<0$![]() when $0<\alpha <1$
when $0<\alpha <1$![]() . Let $\varepsilon >0$
. Let $\varepsilon >0$![]() be given. By [Reference Gundersen12, corollary 1], there exists a constant $r_0=r_0(\theta )>1$
be given. By [Reference Gundersen12, corollary 1], there exists a constant $r_0=r_0(\theta )>1$![]() such that for all $z$
such that for all $z$![]() on the ray $z=re^{i\theta }$
on the ray $z=re^{i\theta }$![]() which does not meet $\tilde {R}$
which does not meet $\tilde {R}$![]() when $r\geq r_0$
when $r\geq r_0$![]() , and for all positive integers $j$
, and for all positive integers $j$![]() ,
,
Since all coefficients of $P(z,\,f)$![]() are combinations of functions in $\mathcal {S}$
are combinations of functions in $\mathcal {S}$![]() , then for each coefficient of $P(z,\,f)$
, then for each coefficient of $P(z,\,f)$![]() , say $a_l$
, say $a_l$![]() , by [Reference Gundersen12, corollary 1], we also have, along the ray $z=re^{i\theta }$
, by [Reference Gundersen12, corollary 1], we also have, along the ray $z=re^{i\theta }$![]() , that
, that
for sufficiently large $r$![]() and some large integer $M$
and some large integer $M$![]() . Recalling from the introduction that $P(z,\,f)=\sum ^{m}_{l=1}a_{l}f^{n_{l0}}(f')^{n_{l1}}\cdots (f^{(s)})^{n_{ls}}$
. Recalling from the introduction that $P(z,\,f)=\sum ^{m}_{l=1}a_{l}f^{n_{l0}}(f')^{n_{l1}}\cdots (f^{(s)})^{n_{ls}}$![]() , where $m$
, where $m$![]() is an integer and $n_{l0}+n_{l1}+\cdots n_{ls}\leq n-1$
is an integer and $n_{l0}+n_{l1}+\cdots n_{ls}\leq n-1$![]() , we may write
, we may write

with the new coefficients $\hat {a}_l=a_l(f'/f)^{n_{l1}}\cdots (f^{(s)}/f)^{n_{ls}}$![]() , where $n_{l0},\,\cdots,\,n_{ls}$
, where $n_{l0},\,\cdots,\,n_{ls}$![]() are nonnegative integers. Note that the greatest order of the derivatives of $f$
are nonnegative integers. Note that the greatest order of the derivatives of $f$![]() in $P(z,\,f)$
in $P(z,\,f)$![]() is equal to $s\geq 0$
is equal to $s\geq 0$![]() . Suppose now that $|f(r_je^{i\theta })|\geq r_j^{N}$
. Suppose now that $|f(r_je^{i\theta })|\geq r_j^{N}$![]() for some infinite sequence $z_j=r_je^{i\theta }$
for some infinite sequence $z_j=r_je^{i\theta }$![]() and some large $N\geq M+s(k-1+\varepsilon )$
and some large $N\geq M+s(k-1+\varepsilon )$![]() . Then, from (2.1), (2.8), (2.9) and (2.10) we have
. Then, from (2.1), (2.8), (2.9) and (2.10) we have

which is impossible when $r_j$![]() is large since $b_1(r_je^{i\theta })e^{p_1(r_je^{i\theta })}+b_2(r_je^{i\theta })e^{p_2(r_je^{i\theta })}\to 0$
is large since $b_1(r_je^{i\theta })e^{p_1(r_je^{i\theta })}+b_2(r_je^{i\theta })e^{p_2(r_je^{i\theta })}\to 0$![]() as $z_j\to \infty$
as $z_j\to \infty$![]() . Therefore, along the ray $z=re^{i\theta }$
. Therefore, along the ray $z=re^{i\theta }$![]() such that $\delta (p_1,\,\theta )<0$
such that $\delta (p_1,\,\theta )<0$![]() we must have $|f(re^{i\theta })|\leq r^{N}$
we must have $|f(re^{i\theta })|\leq r^{N}$![]() for all large $r$
for all large $r$![]() and some integer $N$
and some integer $N$![]() . Thus our second assertion follows.
. Thus our second assertion follows.
Now we begin to prove theorem 2.1.
Proof of theorem 2.1. For simplicity, we denote $P=P(z,\,f)$![]() . By taking the derivatives on both sides of (2.1) and eliminating $e^{p_2}$
. By taking the derivatives on both sides of (2.1) and eliminating $e^{p_2}$![]() and $e^{p_1}$
and $e^{p_1}$![]() from (2.1) and the resulting equation, respectively, we get the following two equations:
from (2.1) and the resulting equation, respectively, we get the following two equations:
where $B_1=b_1'/b_1+p_1'$![]() , $B_2=b_2'/b_2+p_2'$
, $B_2=b_2'/b_2+p_2'$![]() and $A_1=b_1b_2(B_2-B_1)$
and $A_1=b_1b_2(B_2-B_1)$![]() . Note that $B_1B_2A_1\not \equiv 0$
. Note that $B_1B_2A_1\not \equiv 0$![]() . By differentiating on both sides of (2.12) and then eliminating $e^{p_1}$
. By differentiating on both sides of (2.12) and then eliminating $e^{p_1}$![]() from (2.12) and the resulting equation, we get
from (2.12) and the resulting equation, we get
where $h_1=b_2B_2(A_1'+p_1'A_1)-(b_2B_2)'A_1$![]() , $h_2=-n b_2A_1(p_1'+p_2')-nb_2A_1'$
, $h_2=-n b_2A_1(p_1'+p_2')-nb_2A_1'$![]() , $h_3=n(n-1)b_2A_1$
, $h_3=n(n-1)b_2A_1$![]() , $h_4=nb_2A_1$
, $h_4=nb_2A_1$![]() , and $P_1=(A_1'+p_1'A_1)(b_2B_2P-b_2P')-A_1(b_2B_2P-b_2P')'$
, and $P_1=(A_1'+p_1'A_1)(b_2B_2P-b_2P')-A_1(b_2B_2P-b_2P')'$![]() is a differential polynomial in $f$
is a differential polynomial in $f$![]() of degree $\leq n-1$
of degree $\leq n-1$![]() . By lemma 2.3 and our assumption, $\alpha$
. By lemma 2.3 and our assumption, $\alpha$![]() is a nonzero real number such that $-1\leq \alpha < 1$
is a nonzero real number such that $-1\leq \alpha < 1$![]() . Below we consider the two cases where $-1\leq \alpha < 0$
. Below we consider the two cases where $-1\leq \alpha < 0$![]() and $0<\alpha <1$
and $0<\alpha <1$![]() , respectively.
, respectively.
Case 1: $-1\leq \alpha < 0$![]() . We multiply both sides of equations (2.12) and (2.13) and obtain
. We multiply both sides of equations (2.12) and (2.13) and obtain
where $g_1=b_1b_2B_1B_2$![]() , $g_2=-nb_1b_2(B_1+B_2)$
, $g_2=-nb_1b_2(B_1+B_2)$![]() , $g_3=n^2b_1b_2$
, $g_3=n^2b_1b_2$![]() and $P_2=b_1b_2(B_2f^n-nf^{n-1}f')(B_1P-P')+b_1b_2(B_1f^n-nf^{n-1}f')$
and $P_2=b_1b_2(B_2f^n-nf^{n-1}f')(B_1P-P')+b_1b_2(B_1f^n-nf^{n-1}f')$![]() $(B_2P-P')+b_1b_2(B_1P-P')(B_2P-P')$
$(B_2P-P')+b_1b_2(B_1P-P')(B_2P-P')$![]() is a differential polynomial in $f$
is a differential polynomial in $f$![]() of degree $\leq 2n-1$
of degree $\leq 2n-1$![]() . By eliminating $(f')^2$
. By eliminating $(f')^2$![]() from (2.14) and (2.15), we get
from (2.14) and (2.15), we get
where $P_3=g_3f^nP_1-h_3P_2$![]() is a differential polynomial in $f$
is a differential polynomial in $f$![]() of degree $\leq 2n-1$
of degree $\leq 2n-1$![]() . For simplicity, we denote
. For simplicity, we denote
Recalling $B_1=b_1'/b_1+p_1'$![]() and $B_2=b_2'/b_2+p_2'$
and $B_2=b_2'/b_2+p_2'$![]() , we get from equation (2.16) that
, we get from equation (2.16) that
where

Now we prove that $\varphi$![]() is a rational function. Recall that $b_1,\,b_2,\,p_1,\,p_2$
is a rational function. Recall that $b_1,\,b_2,\,p_1,\,p_2$![]() are all polynomials and $B_1=b_1'/b_1+p_1'$
are all polynomials and $B_1=b_1'/b_1+p_1'$![]() , $B_2=b_2'/b_2+p_2'$
, $B_2=b_2'/b_2+p_2'$![]() and $A_1=b_1b_2(B_2-B_1)$
and $A_1=b_1b_2(B_2-B_1)$![]() . Since $f$
. Since $f$![]() is entire, we see that $\varphi$
is entire, we see that $\varphi$![]() has only finitely many poles. By lemma 2.3, $\sigma (f)=k$
has only finitely many poles. By lemma 2.3, $\sigma (f)=k$![]() . By the lemma on the logarithmic derivative, we deduce from (2.18) that
. By the lemma on the logarithmic derivative, we deduce from (2.18) that
Therefore, $\sigma (\varphi )\leq k$![]() . Now let $\theta \in [0,\,2\pi )$
. Now let $\theta \in [0,\,2\pi )$![]() be such that $\delta (p_1,\,\theta )\not =0$
be such that $\delta (p_1,\,\theta )\not =0$![]() and $z=re^{i\theta }$
and $z=re^{i\theta }$![]() is a ray that meets only finitely discs in $\tilde {R}$
is a ray that meets only finitely discs in $\tilde {R}$![]() . Since $\alpha <0$
. Since $\alpha <0$![]() , then by lemma 2.3 (1) we see that in both cases that $\delta (p_1,\,\theta )>0$
, then by lemma 2.3 (1) we see that in both cases that $\delta (p_1,\,\theta )>0$![]() and $\delta (p_1,\,\theta )<0$
and $\delta (p_1,\,\theta )<0$![]() we always have $|e^{p_1(re^{i\theta })+p_2(re^{i\theta })}/f(re^{i\theta })^{2n-1}|\to 0$
we always have $|e^{p_1(re^{i\theta })+p_2(re^{i\theta })}/f(re^{i\theta })^{2n-1}|\to 0$![]() as $r\to \infty$
as $r\to \infty$![]() along the ray $z=re^{i\theta }$
along the ray $z=re^{i\theta }$![]() . Together with [Reference Gundersen12, corollary 1] we see from (2.17) that there is some integer $N$
. Together with [Reference Gundersen12, corollary 1] we see from (2.17) that there is some integer $N$![]() such that $|\varphi (re^{i\theta })|\leq r^{N}$
such that $|\varphi (re^{i\theta })|\leq r^{N}$![]() for all large $r$
for all large $r$![]() . Then by the Phragmén–Lindelöf theorem we see that $|\varphi |\leq r^{N}$
. Then by the Phragmén–Lindelöf theorem we see that $|\varphi |\leq r^{N}$![]() uniformly in each $\overline {S}_{j,\epsilon }$
uniformly in each $\overline {S}_{j,\epsilon }$![]() , $j=1,\,2,\,\cdots,\,2k$
, $j=1,\,2,\,\cdots,\,2k$![]() , for some integer $N=N(j)$
, for some integer $N=N(j)$![]() . Since $\epsilon$
. Since $\epsilon$![]() can be arbitrarily small, then by the Phragmén–Lindelöf theorem again we conclude that $\varphi$
can be arbitrarily small, then by the Phragmén–Lindelöf theorem again we conclude that $\varphi$![]() is a rational function. From now on we fix one large $N$
is a rational function. From now on we fix one large $N$![]() .
.
Recall that $B_2=b_2'/b_2+p_2'$![]() . Denote $F_1=f'-(B_1/n)f$
. Denote $F_1=f'-(B_1/n)f$![]() . Then by simple computations we obtain from (2.18) that
. Then by simple computations we obtain from (2.18) that
Denote $\xi _1=p_2'/n-b_1'/b_1-(n-1)b_2'/nb_2+A_1'/A_1$![]() . Then the general solution of the homogeneous equation $F_1'-\xi _1 F_1=0$
. Then the general solution of the homogeneous equation $F_1'-\xi _1 F_1=0$![]() is defined on a finite-sheeted Riemann surface and is of the form $F_1=C_2b_2^{1/n}A_1/(b_1b_2)e^{p_2/n}$
is defined on a finite-sheeted Riemann surface and is of the form $F_1=C_2b_2^{1/n}A_1/(b_1b_2)e^{p_2/n}$![]() , where $C_2$
, where $C_2$![]() is a constant and $b_2^{1/n}$
is a constant and $b_2^{1/n}$![]() is in general an algebraic function (see [Reference Katajamäki21] for the theory of algebroid functions). Suppose that $\Gamma _2$
is in general an algebraic function (see [Reference Katajamäki21] for the theory of algebroid functions). Suppose that $\Gamma _2$![]() is a particular solution of $F_1'-\xi _1F_1=\varphi$
is a particular solution of $F_1'-\xi _1F_1=\varphi$![]() . We may write the meromorphic solution of this equation as $F_1=C_2b_2^{1/n}A_1/(b_1b_2)e^{p_2/n}+\Gamma _2$
. We may write the meromorphic solution of this equation as $F_1=C_2b_2^{1/n}A_1/(b_1b_2)e^{p_2/n}+\Gamma _2$![]() . By an elementary series expansion analysis around the zeros of $b_2$
. By an elementary series expansion analysis around the zeros of $b_2$![]() , we conclude that $\Gamma _2/b_2^{1/n}$
, we conclude that $\Gamma _2/b_2^{1/n}$![]() is a meromorphic function. This implies that $b_2$
is a meromorphic function. This implies that $b_2$![]() is an $n$
is an $n$![]() -square of some polynomial. Then by lemma 2.2 we integrate the equation (2.21) along the ray $z=re^{i\theta }$
-square of some polynomial. Then by lemma 2.2 we integrate the equation (2.21) along the ray $z=re^{i\theta }$![]() in $S_2$
in $S_2$![]() such that $\delta (p_2,\,\theta )>0$
such that $\delta (p_2,\,\theta )>0$![]() and obtain
and obtain
where

where $a_{2,2}=a_{2,2}(\theta )$![]() is a constant such that $|\Gamma _2|=O(r^N)$
is a constant such that $|\Gamma _2|=O(r^N)$![]() along the ray $z=re^{i\theta }$
along the ray $z=re^{i\theta }$![]() in $S_2$
in $S_2$![]() . Now, for $z\in S_{j,\epsilon }$
. Now, for $z\in S_{j,\epsilon }$![]() where $j\in J_2$
where $j\in J_2$![]() , we have $\delta (p_2,\,\theta )>0$
, we have $\delta (p_2,\,\theta )>0$![]() and so $\Gamma _2=(c_2d_{2,j}/n)b_2^{1/n}A_1/(b_1b_2)e^{p_2/n}+\gamma _{2,j}$
and so $\Gamma _2=(c_2d_{2,j}/n)b_2^{1/n}A_1/(b_1b_2)e^{p_2/n}+\gamma _{2,j}$![]() , where $d_{2,j}$
, where $d_{2,j}$![]() are some constants related to a sector $S_{j,\epsilon }$
are some constants related to a sector $S_{j,\epsilon }$![]() and $|\gamma _{2,j}|=O(r^N)$
and $|\gamma _{2,j}|=O(r^N)$![]() uniformly in $\overline {S}_{j,\epsilon }$
uniformly in $\overline {S}_{j,\epsilon }$![]() . Of course, for $j=2$
. Of course, for $j=2$![]() , we have $d_{2,2}=0$
, we have $d_{2,2}=0$![]() . Furthermore, $|\Gamma _2|=O(r^N)$
. Furthermore, $|\Gamma _2|=O(r^N)$![]() uniformly in $\overline {S}_{j,\epsilon }$
uniformly in $\overline {S}_{j,\epsilon }$![]() where $j\in J_1$
where $j\in J_1$![]() . We then define $d_{2,j}=0$
. We then define $d_{2,j}=0$![]() for $j\in J_1$
for $j\in J_1$![]() .
.
Similarly, denoting that $\xi _2=p_1'/n-b_2'/b_2-(n-1)b_1'/nb_1+A_1'/A_1$![]() we also have $F_2'-\xi _2F_2=\varphi$
we also have $F_2'-\xi _2F_2=\varphi$![]() and it follows by integration that $F_2=-(c_1/n)b_1^{1/n}A_1/(b_1b_2)e^{p_1/n}+\Gamma _1$
and it follows by integration that $F_2=-(c_1/n)b_1^{1/n}A_1/(b_1b_2)e^{p_1/n}+\Gamma _1$![]() , where $\Gamma _1=-(c_1d_{1,j}/n)b_1^{1/n}A_1/(b_1b_2)e^{p_1/n}+\gamma _{1,j}$
, where $\Gamma _1=-(c_1d_{1,j}/n)b_1^{1/n}A_1/(b_1b_2)e^{p_1/n}+\gamma _{1,j}$![]() , where $d_{l,j}$
, where $d_{l,j}$![]() are some constants related to a sector $S_{j,\epsilon }$
are some constants related to a sector $S_{j,\epsilon }$![]() and $|\gamma _{1,j}|=O(r^N)$
and $|\gamma _{1,j}|=O(r^N)$![]() uniformly in $\overline {S}_{j,\epsilon }$
uniformly in $\overline {S}_{j,\epsilon }$![]() for $j\in J_1$
for $j\in J_1$![]() . Of course, for $j=1$
. Of course, for $j=1$![]() , we have $d_{1,1}=0$
, we have $d_{1,1}=0$![]() . Furthermore, $|\Gamma _1|=O(r^N)$
. Furthermore, $|\Gamma _1|=O(r^N)$![]() uniformly in $\overline {S}_{j,\epsilon }$
uniformly in $\overline {S}_{j,\epsilon }$![]() where $j\in J_2$
where $j\in J_2$![]() . We then define $d_{1,j}=0$
. We then define $d_{1,j}=0$![]() for $j\in J_2$
for $j\in J_2$![]() .
.
Denoting $B=n/(B_2-B_1)$![]() , we have $f=B(F_1-F_2)$
, we have $f=B(F_1-F_2)$![]() . Together with the relation $A_1=b_1b_2(B_2-B_1)$
. Together with the relation $A_1=b_1b_2(B_2-B_1)$![]() , we have $f=c_1b_1^{1/n}e^{p_1/n}+c_2b_2^{1/n}e^{p_2/n}+\eta$
, we have $f=c_1b_1^{1/n}e^{p_1/n}+c_2b_2^{1/n}e^{p_2/n}+\eta$![]() with an entire function $\eta =B(\Gamma _2-\Gamma _1)$
with an entire function $\eta =B(\Gamma _2-\Gamma _1)$![]() . We see that $\eta =c_2d_{2,j}b_2^{1/n}e^{p_2/n}+B(\gamma _{2,j}-\gamma _{1,j})$
. We see that $\eta =c_2d_{2,j}b_2^{1/n}e^{p_2/n}+B(\gamma _{2,j}-\gamma _{1,j})$![]() when $j\in J_1$
when $j\in J_1$![]() and $\eta =c_1d_{1,j}b_1^{1/n}e^{p_1/n}+B(\gamma _{2,j}-\gamma _{1,j})$
and $\eta =c_1d_{1,j}b_1^{1/n}e^{p_1/n}+B(\gamma _{2,j}-\gamma _{1,j})$![]() when $j\in J_2$
when $j\in J_2$![]() .
.
Now we determine $d_{1,j}$![]() and $d_{2,j}$
and $d_{2,j}$![]() . By [Reference Gundersen12, corollary 1], we may suppose that along the ray $z=re^{i\theta }$
. By [Reference Gundersen12, corollary 1], we may suppose that along the ray $z=re^{i\theta }$![]() we have $|f^{(j)}(re^{i\theta })/f(re^{i\theta })|=r^{j(k-1+\varepsilon )}$
we have $|f^{(j)}(re^{i\theta })/f(re^{i\theta })|=r^{j(k-1+\varepsilon )}$![]() for all $j>0$
for all $j>0$![]() for all sufficiently large $r$
for all sufficiently large $r$![]() and thus write $P$
and thus write $P$![]() in the form in (2.10) with the new coefficients $\hat {a}_l=a_l(f'/f)^{n_{l1}}\cdots (f^{(s)}/f)^{n_{ls}}$
in the form in (2.10) with the new coefficients $\hat {a}_l=a_l(f'/f)^{n_{l1}}\cdots (f^{(s)}/f)^{n_{ls}}$![]() , where $n_{l1},\,\cdots,\,n_{ls}$
, where $n_{l1},\,\cdots,\,n_{ls}$![]() are nonnegative integers. For simplicity, denote $D_{1,j}=c_1+c_1d_{1,j}$
are nonnegative integers. For simplicity, denote $D_{1,j}=c_1+c_1d_{1,j}$![]() . By substituting $f=c_1b_1^{1/n}e^{p_1/n}+c_2b_2^{1/n}e^{p_2/n}+\eta$
. By substituting $f=c_1b_1^{1/n}e^{p_1/n}+c_2b_2^{1/n}e^{p_2/n}+\eta$![]() into (2.1), we obtain, for $z=re^{i\theta }$
into (2.1), we obtain, for $z=re^{i\theta }$![]() for a $\theta$
for a $\theta$![]() in $S_j$
in $S_j$![]() and $j\in J_1$
and $j\in J_1$![]() ,
,

where $\alpha _{s,k_s}$![]() , $s=1,\,\cdots,\,n$
, $s=1,\,\cdots,\,n$![]() , $k_s=0,\,\cdots,\,n-s$
, $k_s=0,\,\cdots,\,n-s$![]() , are functions satisfying $|\alpha _{s,k_s}(re^{i\theta })|=O(r^N)$
, are functions satisfying $|\alpha _{s,k_s}(re^{i\theta })|=O(r^N)$![]() along the ray $z=re^{i\theta }$
along the ray $z=re^{i\theta }$![]() . By letting $r\to \infty$
. By letting $r\to \infty$![]() along the above ray $z=re^{i\theta }$
along the above ray $z=re^{i\theta }$![]() such that $\delta (p_1,\,\theta )>0$
such that $\delta (p_1,\,\theta )>0$![]() and comparing the growth on both sides of the above equation we conclude that $c_1^n(1+d_{1,j})^n=1$
and comparing the growth on both sides of the above equation we conclude that $c_1^n(1+d_{1,j})^n=1$![]() . Since $d_{1,1}=0$
. Since $d_{1,1}=0$![]() , we have $c_1^n=1$
, we have $c_1^n=1$![]() and $d_{1,j}=\mu _{1,j}-1$
and $d_{1,j}=\mu _{1,j}-1$![]() for some $\mu _{1,j}$
for some $\mu _{1,j}$![]() such that $\mu _{1,j}^n=1$
such that $\mu _{1,j}^n=1$![]() . Similarly, we can prove that $d_{2,j}=\mu _{2,j}-1$
. Similarly, we can prove that $d_{2,j}=\mu _{2,j}-1$![]() for some $\mu _{2,j}$
for some $\mu _{2,j}$![]() such that $\mu _{2,j}^n=1$
such that $\mu _{2,j}^n=1$![]() . In particular, when $k=1$
. In particular, when $k=1$![]() , since $d_{1,1}=d_{2,2}=0$
, since $d_{1,1}=d_{2,2}=0$![]() and $|\eta _j|=O(r^N)$
and $|\eta _j|=O(r^N)$![]() uniformly in the sectors $\overline {S}_{j,\epsilon }$
uniformly in the sectors $\overline {S}_{j,\epsilon }$![]() , $j=1,\,2$
, $j=1,\,2$![]() and since $\epsilon$
and since $\epsilon$![]() can be arbitrarily small, by the Phragmén–Lindelöf theorem we conclude that $\eta$
can be arbitrarily small, by the Phragmén–Lindelöf theorem we conclude that $\eta$![]() is a polynomial. Thus our first assertion follows.
is a polynomial. Thus our first assertion follows.
Case 2: $0<\alpha <1$![]() .
.
As in the proof of [Reference Zhang33, theorem 2.1], we first define some functions in the following way: We let $m$![]() be the smallest integer such that $\alpha \leq [(m+1)n-1]/[(m+1)n]$
be the smallest integer such that $\alpha \leq [(m+1)n-1]/[(m+1)n]$![]() and ${\iota _0,\,\cdots,\,\iota _m}$
and ${\iota _0,\,\cdots,\,\iota _m}$![]() be a finite sequence of functions such that
be a finite sequence of functions such that

Recall that $B_1=b_1'/b_1+p_1'$![]() . We also let ${\kappa _0,\,\cdots,\,\kappa _m}$
. We also let ${\kappa _0,\,\cdots,\,\kappa _m}$![]() be a finite sequence of functions defined in the following way:
be a finite sequence of functions defined in the following way:

Then we define $m+1$![]() functions $G_0$
functions $G_0$![]() , $G_1$
, $G_1$![]() , $\cdots$
, $\cdots$![]() , $G_m$
, $G_m$![]() in the way that $G_0=f'-\kappa _0f$
in the way that $G_0=f'-\kappa _0f$![]() , $G_{1}=G_{0}'-\kappa _1G_{0}$
, $G_{1}=G_{0}'-\kappa _1G_{0}$![]() , $\cdots$
, $\cdots$![]() , $G_{m}=G_{m-1}'-\kappa _mG_{m-1}$
, $G_{m}=G_{m-1}'-\kappa _mG_{m-1}$![]() . Now we have equation (2.13) and it follows that
. Now we have equation (2.13) and it follows that
where $W_0=-(B_1P-P')/(nf^{n-1})$![]() . Moreover, when $m\geq 1$
. Moreover, when $m\geq 1$![]() , by simple computations we obtain
, by simple computations we obtain

and by induction we obtain
For an integer $l\geq 0$![]() , by elementary computations it is easy to show that $W_0^{(l)}=W_{0l}/f^{n+l-1}$
, by elementary computations it is easy to show that $W_0^{(l)}=W_{0l}/f^{n+l-1}$![]() , where $W_{0l}=W_{0l}(z,\,f)$
, where $W_{0l}=W_{0l}(z,\,f)$![]() is a differential polynomial in $f$
is a differential polynomial in $f$![]() of degree $\leq n+l-1$
of degree $\leq n+l-1$![]() , and also that $(e^{p_2}/f^{n})^{(l)}=e^{p_2}W_{1l}/f^{n+l}$
, and also that $(e^{p_2}/f^{n})^{(l)}=e^{p_2}W_{1l}/f^{n+l}$![]() , where $W_{1l}=W_{1l}(z,\,f)$
, where $W_{1l}=W_{1l}(z,\,f)$![]() is a differential polynomial in $f$
is a differential polynomial in $f$![]() of degree $\leq n+l$
of degree $\leq n+l$![]() . We see that $W_j$
. We see that $W_j$![]() , $1\leq j\leq m$
, $1\leq j\leq m$![]() , is formulated in terms of $W_0$
, is formulated in terms of $W_0$![]() and $e^{p_2}/f^{n}$
and $e^{p_2}/f^{n}$![]() and their derivatives. We may write
and their derivatives. We may write
where $F(W_0,\,e^{p_2}/f^{n})$![]() is a combination of $W_0$
is a combination of $W_0$![]() and $e^{p_2}/f^{n}$
and $e^{p_2}/f^{n}$![]() and their derivatives with functions being combinations of functions in $\mathcal {S}$
and their derivatives with functions being combinations of functions in $\mathcal {S}$![]() . Moreover, from the recursion formula $G_j=G_{j-1}'-\kappa _jG_{j-1}$
. Moreover, from the recursion formula $G_j=G_{j-1}'-\kappa _jG_{j-1}$![]() , $j\geq 1$
, $j\geq 1$![]() , and $G_0=f'-\kappa _0f$
, and $G_0=f'-\kappa _0f$![]() , we easily deduce that $f$
, we easily deduce that $f$![]() satisfies the linear differential equation
satisfies the linear differential equation
where $\hat {t}_m$![]() , $\hat {t}_{m-1}$
, $\hat {t}_{m-1}$![]() , $\cdots$
, $\cdots$![]() , $\hat {t}_0$
, $\hat {t}_0$![]() are functions formulated in terms of $\kappa _0$
are functions formulated in terms of $\kappa _0$![]() , $\cdots$
, $\cdots$![]() , $\kappa _m$
, $\kappa _m$![]() and their derivatives.
and their derivatives.
Now we prove that $G_m$![]() is a rational function. Recall that $b_1,\,b_2,\,p_1,\,p_2$
is a rational function. Recall that $b_1,\,b_2,\,p_1,\,p_2$![]() are all polynomials. Since $f$
are all polynomials. Since $f$![]() is entire, then by the definitions of $\kappa _0$
is entire, then by the definitions of $\kappa _0$![]() and $\kappa _j$
and $\kappa _j$![]() in (2.26), we see that $G_m$
in (2.26), we see that $G_m$![]() has only finitely many poles. With an application of the lemma on the logarithmic derivative as in previous case, we deduce from (2.31) that $\sigma (G_m)\leq \sigma (f)=k$
has only finitely many poles. With an application of the lemma on the logarithmic derivative as in previous case, we deduce from (2.31) that $\sigma (G_m)\leq \sigma (f)=k$![]() . Now let $\theta \in [0,\,2\pi )$
. Now let $\theta \in [0,\,2\pi )$![]() be such that $\delta (p_1,\,\theta )\not =0$
be such that $\delta (p_1,\,\theta )\not =0$![]() and $z=re^{i\theta }$
and $z=re^{i\theta }$![]() be a ray that meets only finitely may discs in $\tilde {R}$
be a ray that meets only finitely may discs in $\tilde {R}$![]() . By [Reference Gundersen12, corollary 1] and lemma 2.3 (2), we see from (2.31) that there is some integer $N$
. By [Reference Gundersen12, corollary 1] and lemma 2.3 (2), we see from (2.31) that there is some integer $N$![]() such that $|G_m(re^{i\theta })|\leq r^{N}$
such that $|G_m(re^{i\theta })|\leq r^{N}$![]() for all large $r$
for all large $r$![]() along the ray $z=re^{i\theta }$
along the ray $z=re^{i\theta }$![]() such that $\delta (p_1,\,\theta )<0$
such that $\delta (p_1,\,\theta )<0$![]() . On the other hand, by lemma 2.3 (2) there is some integer $N$
. On the other hand, by lemma 2.3 (2) there is some integer $N$![]() such that
such that
(1) if $\alpha <[(m+1)n-1]/[(m+1)n]$
 , then $|e^{(m+1)p_2(re^{i\theta })}/f(re^{i\theta })^{(m+1)n-1}|\to 0$
, then $|e^{(m+1)p_2(re^{i\theta })}/f(re^{i\theta })^{(m+1)n-1}|\to 0$ as $r\to \infty$
as $r\to \infty$ along the ray $z=re^{i\theta }$
along the ray $z=re^{i\theta }$ such that $\delta (p_1,\,\theta )>0$
such that $\delta (p_1,\,\theta )>0$ ;
;(2) if $\alpha =[(m+1)n-1]/[(m+1)n]$
 , then $|e^{(m+1)p_2(re^{i\theta })}/f(re^{i\theta })^{(m+1)n-1}|\leq e^{Nr^{k-1}}$
, then $|e^{(m+1)p_2(re^{i\theta })}/f(re^{i\theta })^{(m+1)n-1}|\leq e^{Nr^{k-1}}$ for all large $r$
for all large $r$ along the ray $z=re^{i\theta }$
along the ray $z=re^{i\theta }$ such that $\delta (p_1,\,\theta )>0$
such that $\delta (p_1,\,\theta )>0$ .
.
Note that $e^{p_2(re^{i\theta })}/f(re^{i\theta })^{n}\to 0$![]() as $r\to \infty$
as $r\to \infty$![]() along the ray $z=re^{i\theta }$
along the ray $z=re^{i\theta }$![]() such that $\delta (p_1,\,\theta )>0$
such that $\delta (p_1,\,\theta )>0$![]() . In case (1), together with [Reference Gundersen12, corollary 1] we see from (2.30) that $|G_m(re^{i\theta })|\leq r^{N}$
. In case (1), together with [Reference Gundersen12, corollary 1] we see from (2.30) that $|G_m(re^{i\theta })|\leq r^{N}$![]() for all large $r$
for all large $r$![]() and thus by the Phragmén–Lindelöf theorem we see that $|G_m|\leq r^{N}$
and thus by the Phragmén–Lindelöf theorem we see that $|G_m|\leq r^{N}$![]() uniformly in each $\overline {S}_{j,\epsilon }$
uniformly in each $\overline {S}_{j,\epsilon }$![]() , $j\in J_2$
, $j\in J_2$![]() , for some integer $N=N(j)$
, for some integer $N=N(j)$![]() ; in case (2), together with [Reference Gundersen12, corollary 1] we see from (2.30) that $|G_m(re^{i\theta })|\leq e^{Nr^{k-1}}$
; in case (2), together with [Reference Gundersen12, corollary 1] we see from (2.30) that $|G_m(re^{i\theta })|\leq e^{Nr^{k-1}}$![]() for all large $r$
for all large $r$![]() and, since the set of rays $z=re^{i\theta }$
and, since the set of rays $z=re^{i\theta }$![]() meeting infinitely many discs in $\tilde {R}$
meeting infinitely many discs in $\tilde {R}$![]() has zero linear measure, then by the Phragmén–Lindelöf theorem we see that $|G_m|\leq e^{Nr^{k-1}}$
has zero linear measure, then by the Phragmén–Lindelöf theorem we see that $|G_m|\leq e^{Nr^{k-1}}$![]() uniformly in each $\overline {S}_{j,\epsilon }$
uniformly in each $\overline {S}_{j,\epsilon }$![]() , $j\in J_2$
, $j\in J_2$![]() , for some integer $N=N(j)$
, for some integer $N=N(j)$![]() . Since $\epsilon$
. Since $\epsilon$![]() can be arbitrarily small, then in either case of (1) and (2) by the Phragmén–Lindelöf theorem again we conclude that $G_m$
can be arbitrarily small, then in either case of (1) and (2) by the Phragmén–Lindelöf theorem again we conclude that $G_m$![]() is a rational function. From now on we fix one large $N$
is a rational function. From now on we fix one large $N$![]() .
.
We denote $D_0=b_1^{1/n}$![]() and $D_j=\iota _{j-1}b_1^{-j}b_1^{1/n}$
and $D_j=\iota _{j-1}b_1^{-j}b_1^{1/n}$![]() , $j=1,\,\cdots,\,m$
, $j=1,\,\cdots,\,m$![]() . Now we choose one $\theta$
. Now we choose one $\theta$![]() such that $\delta (p_1,\,\theta )>0$
such that $\delta (p_1,\,\theta )>0$![]() and let $z=re^{i\theta }\in S_1$
and let $z=re^{i\theta }\in S_1$![]() . Let $t_0=1/n$
. Let $t_0=1/n$![]() , $t_1=(\alpha -1)+1/n$
, $t_1=(\alpha -1)+1/n$![]() , $\cdots$
, $\cdots$![]() , $t_m=m(\alpha -1)+1/n$
, $t_m=m(\alpha -1)+1/n$![]() . Similarly as in the proof of [Reference Zhang33, theorem 2.1], we may use lemma 2.2 to integrate the recursion formulas $G_j=G_{j-1}'-\kappa _jG_{j-1}$
. Similarly as in the proof of [Reference Zhang33, theorem 2.1], we may use lemma 2.2 to integrate the recursion formulas $G_j=G_{j-1}'-\kappa _jG_{j-1}$![]() from $j=m$
from $j=m$![]() to $j=1$
to $j=1$![]() along the above ray $z=re^{i\theta }$
along the above ray $z=re^{i\theta }$![]() such that $\delta (p_1,\,\theta )>0$
such that $\delta (p_1,\,\theta )>0$![]() inductively and finally integrating $G_0=f'-\kappa _0f$
inductively and finally integrating $G_0=f'-\kappa _0f$![]() along this ray $z=re^{i\theta }$
along this ray $z=re^{i\theta }$![]() to obtain
to obtain

where $c_0$![]() , $\cdots$
, $\cdots$![]() , $c_m$
, $c_m$![]() are constants and
are constants and
where $a_0=a_{0}(\theta )$![]() is a constant such that $|H_0|=O(r^N)$
is a constant such that $|H_0|=O(r^N)$![]() along the ray $z=re^{i\theta }$
along the ray $z=re^{i\theta }$![]() .
.
As is shown in the proof of [Reference Zhang33, theorem 2.1], $b_1$![]() is an $n$
is an $n$![]() -square of some polynomial and we may write the entire solution of (2.1) as $f=\gamma _1\sum _{j=0}^mc_j(b_2/b_1)^je^{t_jp_1}+\eta$
-square of some polynomial and we may write the entire solution of (2.1) as $f=\gamma _1\sum _{j=0}^mc_j(b_2/b_1)^je^{t_jp_1}+\eta$![]() , where $\gamma _1$
, where $\gamma _1$![]() is a polynomial such that $\gamma _1^n=b_1$
is a polynomial such that $\gamma _1^n=b_1$![]() and $\eta$
and $\eta$![]() is a meromorphic function with at most finitely many poles. Then we can integrate $G_j=G_{j-1}'-\kappa _jG_{j-1}$
is a meromorphic function with at most finitely many poles. Then we can integrate $G_j=G_{j-1}'-\kappa _jG_{j-1}$![]() from $j=m$
from $j=m$![]() to $j=1$
to $j=1$![]() inductively and finally integrate $G_0=f'-\kappa _0f$
inductively and finally integrate $G_0=f'-\kappa _0f$![]() to obtain that $H_0$
to obtain that $H_0$![]() is a meromorphic function with at most finitely many poles. We choose $\eta =H_0$
is a meromorphic function with at most finitely many poles. We choose $\eta =H_0$![]() . Recall that along the ray $z=re^{i\theta }$
. Recall that along the ray $z=re^{i\theta }$![]() such that $\delta (p_1,\,\theta )>0$
such that $\delta (p_1,\,\theta )>0$![]() and $z=re^{i\theta }\in S_1$
and $z=re^{i\theta }\in S_1$![]() , we have $|H_0|=O(r^N)$
, we have $|H_0|=O(r^N)$![]() . Denote $g=b_1^{1/n}\sum _{i=0}^mc_i(b_2/b_1)^ie^{t_ip_1}$
. Denote $g=b_1^{1/n}\sum _{i=0}^mc_i(b_2/b_1)^ie^{t_ip_1}$![]() . Then
. Then

where

By [Reference Gundersen12, corollary 1], we may suppose that along the ray $z=re^{i\theta }$![]() we have $|f(re^{i\theta })^{(j)}/f(re^{i\theta })|=r^{j(k-1+\varepsilon )}$
we have $|f(re^{i\theta })^{(j)}/f(re^{i\theta })|=r^{j(k-1+\varepsilon )}$![]() for all $j>0$
for all $j>0$![]() and all sufficiently large $r$
and all sufficiently large $r$![]() . By writing $P$
. By writing $P$![]() in the form in (2.10) with the new coefficients $\hat {a}_l=a_l(f'/f)^{n_{l1}}\cdots (f^{(s)}/f)^{n_{ls}}$
in the form in (2.10) with the new coefficients $\hat {a}_l=a_l(f'/f)^{n_{l1}}\cdots (f^{(s)}/f)^{n_{ls}}$![]() , where $n_{l1},\,\cdots,\,n_{ls}$
, where $n_{l1},\,\cdots,\,n_{ls}$![]() are nonnegative integers, and using [Reference Gundersen12, corollary 1], we see that each term in $P(z,\,f)$
are nonnegative integers, and using [Reference Gundersen12, corollary 1], we see that each term in $P(z,\,f)$![]() of degree $n-j$
of degree $n-j$![]() , $1\leq j\leq n-1$
, $1\leq j\leq n-1$![]() , equals a linear combination of exponential functions of the form $e^{[nk_{j}(\alpha -1)+n-j]p_1/n}$
, equals a linear combination of exponential functions of the form $e^{[nk_{j}(\alpha -1)+n-j]p_1/n}$![]() , $0\leq k_{j}\leq (n-j)m$
, $0\leq k_{j}\leq (n-j)m$![]() , with coefficients $\beta _j$
, with coefficients $\beta _j$![]() having polynomial growth along the ray $z=re^{i\theta }$
having polynomial growth along the ray $z=re^{i\theta }$![]() . Therefore, by substituting $f=g+H_0$
. Therefore, by substituting $f=g+H_0$![]() into (2.1) we obtain by the same arguments in the proof of [Reference Zhang33, theorem 2.1] that $c_0^n=1$
into (2.1) we obtain by the same arguments in the proof of [Reference Zhang33, theorem 2.1] that $c_0^n=1$![]() when $m=0$
when $m=0$![]() , and $c_0^{n}=1$
, and $c_0^{n}=1$![]() , $nc_0^{n-1}c_1=1$
, $nc_0^{n-1}c_1=1$![]() and $p_2=\alpha p_1$
and $p_2=\alpha p_1$![]() when $m=1$
when $m=1$![]() and further that $C_{k_0}\equiv 0$
and further that $C_{k_0}\equiv 0$![]() for all $2\leq k_0\leq m$
for all $2\leq k_0\leq m$![]() when $m\geq 2$
when $m\geq 2$![]() .
.
Now, $b_1^{1/n}$![]() denotes a polynomial. By the definition of $\iota _j$
denotes a polynomial. By the definition of $\iota _j$![]() and $D_j$
and $D_j$![]() , we see that $D_j$
, we see that $D_j$![]() are rational functions. Recall that $G_m$
are rational functions. Recall that $G_m$![]() is a rational function. By lemma 2.2 and looking at the calculations to obtain $H_0$
is a rational function. By lemma 2.2 and looking at the calculations to obtain $H_0$![]() in (2.33), we have, for $z\in S_{j,\epsilon }$
in (2.33), we have, for $z\in S_{j,\epsilon }$![]() , $j\in J_1$
, $j\in J_1$![]() , such that $\delta (p_1,\,\theta )>0$
, such that $\delta (p_1,\,\theta )>0$![]() , $H_0=\gamma _1\sum _{l=0}^md_{l,j}(b_2/b_1)^je^{t_jp_1}+\eta _{j}$
, $H_0=\gamma _1\sum _{l=0}^md_{l,j}(b_2/b_1)^je^{t_jp_1}+\eta _{j}$![]() , where $d_{l,j}$
, where $d_{l,j}$![]() , $l=0,\,\cdots,\,m$
, $l=0,\,\cdots,\,m$![]() , are some constants related to a sector $S_{j,\epsilon }$
, are some constants related to a sector $S_{j,\epsilon }$![]() and $|\eta _j|=O(r^N)$
and $|\eta _j|=O(r^N)$![]() uniformly in $\overline {S}_{j,\epsilon }$
uniformly in $\overline {S}_{j,\epsilon }$![]() , $j\in J_1$
, $j\in J_1$![]() . Of course, for $j=1$
. Of course, for $j=1$![]() , we have $d_{l,1}=0$
, we have $d_{l,1}=0$![]() for all $l$
for all $l$![]() . Since $c_0^{n}=1$
. Since $c_0^{n}=1$![]() when $m=0$
when $m=0$![]() , $c_0^{n}=nc_0^{n-1}c_1=1$
, $c_0^{n}=nc_0^{n-1}c_1=1$![]() when $m=1$
when $m=1$![]() , and $c_0^{n}=nc_0^{n-1}c_1=1$
, and $c_0^{n}=nc_0^{n-1}c_1=1$![]() and $C_{k_0}=0$
and $C_{k_0}=0$![]() for all $2\leq k_0\leq m$
for all $2\leq k_0\leq m$![]() when $m\geq 2$
when $m\geq 2$![]() , then by simple computations, we deduce that $c_j=s_jc_0$
, then by simple computations, we deduce that $c_j=s_jc_0$![]() for some nonzero rational numbers $s_j$
for some nonzero rational numbers $s_j$![]() , $j=0,\,1,\,\cdots,\,m$
, $j=0,\,1,\,\cdots,\,m$![]() . Therefore, by considering the growth of $f$
. Therefore, by considering the growth of $f$![]() along the ray $z=re^{i\theta }$
along the ray $z=re^{i\theta }$![]() such that $z\in S_{j,\epsilon }$
such that $z\in S_{j,\epsilon }$![]() , $j\in J_1$
, $j\in J_1$![]() , as for the ray $z=re^{i\theta }\in S_1$
, as for the ray $z=re^{i\theta }\in S_1$![]() , we have $(c_0+d_{0,j})^n=1$
, we have $(c_0+d_{0,j})^n=1$![]() when $m=0$
when $m=0$![]() , $(c_0+d_{0,j})^n=n(c_0+d_{0,j})^{n-1}(c_1+d_{1,j})=1$
, $(c_0+d_{0,j})^n=n(c_0+d_{0,j})^{n-1}(c_1+d_{1,j})=1$![]() when $m=1$
when $m=1$![]() and further that $\hat {C}_{k_0}=\sum _{\substack {j_0+\cdots +j_m=n,\\j_1+\cdots +mj_m=k_0}}\frac {n!}{j_0!j_1!\cdots j_m!}(c_0+d_{0,j})^{j_0}(c_1+d_{1,j})^{j_1}\cdots (c_m+d_{m,j})^{j_m}=0$
and further that $\hat {C}_{k_0}=\sum _{\substack {j_0+\cdots +j_m=n,\\j_1+\cdots +mj_m=k_0}}\frac {n!}{j_0!j_1!\cdots j_m!}(c_0+d_{0,j})^{j_0}(c_1+d_{1,j})^{j_1}\cdots (c_m+d_{m,j})^{j_m}=0$![]() for $k_0=2,\,\cdots,\,m$
for $k_0=2,\,\cdots,\,m$![]() when $m\geq 2$
when $m\geq 2$![]() . Therefore, for each $j\in J_1$
. Therefore, for each $j\in J_1$![]() , there is a $\mu _j$
, there is a $\mu _j$![]() satisfying $\mu _j^n=1$
satisfying $\mu _j^n=1$![]() such that $c_l+a_{l,j}=\mu _j c_l$
such that $c_l+a_{l,j}=\mu _j c_l$![]() for all $l$
for all $l$![]() . Note that $\mu _{1}=1$
. Note that $\mu _{1}=1$![]() . Also, we have $|\eta |=O(r^N)$
. Also, we have $|\eta |=O(r^N)$![]() uniformly in the sectors $\overline {S}_{j,\epsilon }$
uniformly in the sectors $\overline {S}_{j,\epsilon }$![]() , $j\in J_2$
, $j\in J_2$![]() . In conclusion, we may write $\eta =\gamma _1\sum _{l=0}^m(\mu _j-1)c_{j}(b_2/b_1)^je^{[jn(\alpha -1)+1]p_1/n}+\eta _{j}$
. In conclusion, we may write $\eta =\gamma _1\sum _{l=0}^m(\mu _j-1)c_{j}(b_2/b_1)^je^{[jn(\alpha -1)+1]p_1/n}+\eta _{j}$![]() , where $\mu _j$
, where $\mu _j$![]() are the $n$
are the $n$![]() -th roots of $1$
-th roots of $1$![]() such that $\mu _j=1$
such that $\mu _j=1$![]() , $j=\{1\}\cup \in J_2$
, $j=\{1\}\cup \in J_2$![]() , and $|\eta _j|=O(r^N)$
, and $|\eta _j|=O(r^N)$![]() uniformly in the sector $\overline {S}_{j,\epsilon }$
uniformly in the sector $\overline {S}_{j,\epsilon }$![]() . In particular, when $k=1$
. In particular, when $k=1$![]() , since $\epsilon$
, since $\epsilon$![]() can be arbitrarily small, then by the Phragmén–Lindelöf theorem we conclude that $\eta$
can be arbitrarily small, then by the Phragmén–Lindelöf theorem we conclude that $\eta$![]() is a rational function. This completes the proof.
is a rational function. This completes the proof.
3. An oscillation question of Ishizaki
Let $b_1(z)$![]() , $b_2(z)$
, $b_2(z)$![]() and $b_3(z)$
and $b_3(z)$![]() be three polynomials such that $b_1b_2\not \equiv 0$
be three polynomials such that $b_1b_2\not \equiv 0$![]() and $p_1(z)$
and $p_1(z)$![]() and $p_2(z)$
and $p_2(z)$![]() be two polynomials of the same degree $k\geq 1$
be two polynomials of the same degree $k\geq 1$![]() with distinct leading coefficients $1$
with distinct leading coefficients $1$![]() and $\alpha$
and $\alpha$![]() , respectively, and $p_1(0)=p_2(0)=0$
, respectively, and $p_1(0)=p_2(0)=0$![]() . In this section, we use theorem 2.1 to investigate the oscillation of the second-order linear differential equation:
. In this section, we use theorem 2.1 to investigate the oscillation of the second-order linear differential equation:
There have been several results about the oscillation of equation (3.1) and recently second-order linear differential equations with exponential polynomials are taken into more consideration in [Reference Heittokangas, Ishizaki, Laine and Tohge15, Reference Heittokangas, Ishizaki, Laine and Tohge16]. The results of Bank, Laine and langely [Reference Bank., Laine and Langley5], Ishizaki and Kazuya [Reference Ishizaki and Tohge20] and Ishizaki [Reference Ishizaki19] can be summarized as follows:
(1) if $\alpha$
 is non-real, then all nontrivial solutions of (3.1) satisfy $\lambda (f)=\infty$
is non-real, then all nontrivial solutions of (3.1) satisfy $\lambda (f)=\infty$ ;
;(2) if $\alpha$
 is negative, then all nontrivial solutions of (3.1) satisfy $\lambda (f)=\infty$
is negative, then all nontrivial solutions of (3.1) satisfy $\lambda (f)=\infty$ ;
;(3) if $0<\alpha <1/2$
 or if $b_3\equiv 0$
or if $b_3\equiv 0$ and $3/4<\alpha <1$
and $3/4<\alpha <1$ , then all nontrivial solutions of (3.1) satisfy $\lambda (f)\geq k$
, then all nontrivial solutions of (3.1) satisfy $\lambda (f)\geq k$ .
.
Theorem 1.1 shows that the condition $b_3\equiv 0$![]() in the third result can be removed. Ishizaki [Reference Ishizaki19] asked if the third result $\lambda (f)\geq k$
in the third result can be removed. Ishizaki [Reference Ishizaki19] asked if the third result $\lambda (f)\geq k$![]() above can be replaced by $\lambda (f)=\infty$
above can be replaced by $\lambda (f)=\infty$![]() . With theorem 2.1 at our disposal, we are able to answer this question partially. We prove the following
. With theorem 2.1 at our disposal, we are able to answer this question partially. We prove the following
Theorem 3.1 Let $0<\alpha <1$![]() and $m$
and $m$![]() be the smallest integer such that $\alpha \leq [2(m+1) -1]/[2(m+1)]$
be the smallest integer such that $\alpha \leq [2(m+1) -1]/[2(m+1)]$![]() . Suppose that $b_3\equiv 0$
. Suppose that $b_3\equiv 0$![]() in (3.1). If (3.1) admits a nontrivial solution $f$
in (3.1). If (3.1) admits a nontrivial solution $f$![]() such that $\lambda (f)<\infty,$
such that $\lambda (f)<\infty,$![]() then $\alpha =[2(m+1)-1]/[2(m+1)]$
then $\alpha =[2(m+1)-1]/[2(m+1)]$![]() and $p_2=\alpha p_1$
and $p_2=\alpha p_1$![]() .
.
We will mainly use the techniques in [Reference Bank and Langley6] (see also [Reference Laine23, theorem 5.7]) to prove theorem 3.1. Since $\alpha$![]() is a positive number, we have $\int _{1}^{\infty }r|A(re^{i\theta })|dr<\infty$
is a positive number, we have $\int _{1}^{\infty }r|A(re^{i\theta })|dr<\infty$![]() along the ray $z=re^{i\theta }$
along the ray $z=re^{i\theta }$![]() such that $\delta (p_1,\,\theta )<0$
such that $\delta (p_1,\,\theta )<0$![]() . The following lemma can be proved similarly as in [Reference Laine23, lemma 5.16] by using Gronwall's lemma (see [Reference Laine23, p. 86]).
. The following lemma can be proved similarly as in [Reference Laine23, lemma 5.16] by using Gronwall's lemma (see [Reference Laine23, p. 86]).
Lemma 3.2 Under the assumptions of theorem 3.1, all solutions of equation (3.1) satisfy $|f(re^{i\theta })|=O(r)$![]() as $r\to \infty$
as $r\to \infty$![]() along the ray $z=re^{i\theta }$
along the ray $z=re^{i\theta }$![]() such that $\delta (p_1,\,\theta )<0$
such that $\delta (p_1,\,\theta )<0$![]() .
.
Now we begin to prove theorem 3.1.
Proof of theorem 3.1. Let $f$![]() be a nontrivial solution of equation (3.1) such that $\lambda (f)<\infty$
be a nontrivial solution of equation (3.1) such that $\lambda (f)<\infty$![]() . By Hadamard's factorization theorem we may write $f=\kappa e^{h}$
. By Hadamard's factorization theorem we may write $f=\kappa e^{h}$![]() , where $h$
, where $h$![]() is an entire function and $\kappa$
is an entire function and $\kappa$![]() is the canonical product from the zeros of $f$
is the canonical product from the zeros of $f$![]() satisfying $\rho (\kappa )=\lambda (\kappa )<\infty$
satisfying $\rho (\kappa )=\lambda (\kappa )<\infty$![]() . Denoting $g=h'$
. Denoting $g=h'$![]() , then from (3.1) we have
, then from (3.1) we have
Below we consider the two cases where $0<\alpha \leq 1/2$![]() and $(2m-1)/(2m)< \alpha \leq [2(m+1)-1]/[2(m+1)]$
and $(2m-1)/(2m)< \alpha \leq [2(m+1)-1]/[2(m+1)]$![]() , $m\geq 1$
, $m\geq 1$![]() , respectively.
, respectively.
Case 1: $0<\alpha \leq 1/2$![]() .
.
By theorem 2.1, we may write $g=\gamma _1e^{p_1/2}+\eta$![]() , where $\gamma _1$
, where $\gamma _1$![]() is a polynomial such that $\gamma _1^2=b_1$
is a polynomial such that $\gamma _1^2=b_1$![]() and $\eta$
and $\eta$![]() is an entire function such that $|\eta |=O(r^N)$
is an entire function such that $|\eta |=O(r^N)$![]() uniformly in $\overline {S}_{1,\epsilon }$
uniformly in $\overline {S}_{1,\epsilon }$![]() and $\overline {S}_{2,\epsilon }$
and $\overline {S}_{2,\epsilon }$![]() . By substituting this expression into equation (3.2), we obtain
. By substituting this expression into equation (3.2), we obtain
Suppose that $0<\alpha <1/2$![]() . We define
. We define
where $z_0$![]() is chosen so that $|z_0|$
is chosen so that $|z_0|$![]() is large. Then $w$
is large. Then $w$![]() is analytic outside a finite disc centred at $0$
is analytic outside a finite disc centred at $0$![]() and satisfy
and satisfy
Dividing by $2\gamma _1e^{p_1/2}$![]() on both sides of equation (3.3) and then considering the growth of $w'/w$
on both sides of equation (3.3) and then considering the growth of $w'/w$![]() along the ray $z=re^{i(\theta _2-\epsilon )}$
along the ray $z=re^{i(\theta _2-\epsilon )}$![]() such that $w$
such that $w$![]() has no zero around the neighbourhood of the ray $z=re^{i(\theta _2-\epsilon )}$
has no zero around the neighbourhood of the ray $z=re^{i(\theta _2-\epsilon )}$![]() , we have by [Reference Gundersen12, corollary 1] that $|w'(re^{i\theta })/w(re^{i\theta })|=O(r^{-2})$
, we have by [Reference Gundersen12, corollary 1] that $|w'(re^{i\theta })/w(re^{i\theta })|=O(r^{-2})$![]() as $r\to \infty$
as $r\to \infty$![]() . By integration, we obtain that $w(re^{i(\theta _2-\epsilon )})\to a$
. By integration, we obtain that $w(re^{i(\theta _2-\epsilon )})\to a$![]() as $r\to \infty$
as $r\to \infty$![]() along the ray $z=re^{i(\theta _2-\epsilon )}$
along the ray $z=re^{i(\theta _2-\epsilon )}$![]() for some nonzero constant $a=a(\theta _2,\,\epsilon )$
for some nonzero constant $a=a(\theta _2,\,\epsilon )$![]() . On the other hand, by applying lemma 3.2 to equation (3.1) we have $|f(re^{i(\theta _2+\epsilon )})|=O(r)$
. On the other hand, by applying lemma 3.2 to equation (3.1) we have $|f(re^{i(\theta _2+\epsilon )})|=O(r)$![]() along the ray $z=re^{i(\theta _2+\epsilon )}$
along the ray $z=re^{i(\theta _2+\epsilon )}$![]() . Recalling that $f=\kappa e^{h}$
. Recalling that $f=\kappa e^{h}$![]() and $g=h'=\gamma _1e^{p_1/2}+\eta$
and $g=h'=\gamma _1e^{p_1/2}+\eta$![]() , we may write
, we may write
Since $\delta (p_1,\,\theta _2+\epsilon )<0$![]() and thus along the ray $z=re^{i(\theta _2+\epsilon )}$
and thus along the ray $z=re^{i(\theta _2+\epsilon )}$![]() we have $\int _{z_0}^z \gamma _1e^{p_1/2}\,{\rm d}t\to c$
we have $\int _{z_0}^z \gamma _1e^{p_1/2}\,{\rm d}t\to c$![]() for some constant $c=c(\theta _2,\,\epsilon )$
for some constant $c=c(\theta _2,\,\epsilon )$![]() , we see from (3.6) that $w$
, we see from (3.6) that $w$![]() defined in (3.4) satisfies $w(re^{i(\theta +\epsilon )})\to 0$
defined in (3.4) satisfies $w(re^{i(\theta +\epsilon )})\to 0$![]() as $r\to \infty$
as $r\to \infty$![]() . Denote
. Denote
By choosing $\epsilon$![]() to be small and applying the Phragmén–Lindelöf theorem to $w$
to be small and applying the Phragmén–Lindelöf theorem to $w$![]() defined in (3.4) in the sector in (3.7), we get $a=0$
defined in (3.4) in the sector in (3.7), we get $a=0$![]() , a contradiction. Therefore, we must have $\alpha =1/2$
, a contradiction. Therefore, we must have $\alpha =1/2$![]() when $b_3\equiv 0$
when $b_3\equiv 0$![]() .
.
Now, if $k=1$![]() , then obviously $p_2=p_1/2$
, then obviously $p_2=p_1/2$![]() since we have assumed $p_1(0)=p_2(0)=0$
since we have assumed $p_1(0)=p_2(0)=0$![]() . If $k>1$
. If $k>1$![]() , then by theorem 2.1 we have $g=\mu _j\gamma _1e^{p_1/2}+\eta _j$
, then by theorem 2.1 we have $g=\mu _j\gamma _1e^{p_1/2}+\eta _j$![]() , where $\mu _j^n=1$
, where $\mu _j^n=1$![]() , $\gamma _1$
, $\gamma _1$![]() is a polynomial such that $\gamma _1^2=b_1$
is a polynomial such that $\gamma _1^2=b_1$![]() and $\eta _j$
and $\eta _j$![]() is an entire function such that $|\eta _j|=O(r^N)$
is an entire function such that $|\eta _j|=O(r^N)$![]() uniformly in $\overline {S}_{j,\epsilon }$
uniformly in $\overline {S}_{j,\epsilon }$![]() . Note that $\eta _j$
. Note that $\eta _j$![]() has finite order. Denoting $p_3=p_2-p_1/2$
has finite order. Denoting $p_3=p_2-p_1/2$![]() , we rewrite equation (3.3) as
, we rewrite equation (3.3) as
If $p_2\not \equiv p_1/2$![]() , then $p_3$
, then $p_3$![]() is a nonconstant polynomial such that $\deg (p_3)\leq \deg (p_2)-1$
is a nonconstant polynomial such that $\deg (p_3)\leq \deg (p_2)-1$![]() . By the definition of $S_j$
. By the definition of $S_j$![]() in (2.3), we may choose a $\theta \in [0,\,2\pi )$
in (2.3), we may choose a $\theta \in [0,\,2\pi )$![]() so that the ray $z=re^{i\theta }$
so that the ray $z=re^{i\theta }$![]() meets only finitely discs in $\tilde {R}$
meets only finitely discs in $\tilde {R}$![]() and also that $\log |e^{p_1/2}|$
and also that $\log |e^{p_1/2}|$![]() and $\log |e^{p_2-p_1/2}|$
and $\log |e^{p_2-p_1/2}|$![]() both increase along the ray $z=re^{i\theta }$
both increase along the ray $z=re^{i\theta }$![]() . By [Reference Gundersen12, corollary 1] we see that $\kappa '/\kappa +\gamma _1'/2\gamma _1+p_1'/4+\eta _j$
. By [Reference Gundersen12, corollary 1] we see that $\kappa '/\kappa +\gamma _1'/2\gamma _1+p_1'/4+\eta _j$![]() and $\kappa ''/\kappa +2\eta _j\kappa '/\kappa +\eta _j^2+\eta _j'-b_3$
and $\kappa ''/\kappa +2\eta _j\kappa '/\kappa +\eta _j^2+\eta _j'-b_3$![]() both have polynomial growth along the ray $z=re^{i\theta }$
both have polynomial growth along the ray $z=re^{i\theta }$![]() . Then by comparing the growth on both sides of equation (3.8) along the ray $z=re^{i\theta }$
. Then by comparing the growth on both sides of equation (3.8) along the ray $z=re^{i\theta }$![]() , we get a contradiction. Therefore, we must have $p_2\equiv p_1/2$
, we get a contradiction. Therefore, we must have $p_2\equiv p_1/2$![]() when $\alpha =1/2$
when $\alpha =1/2$![]() .
.
Case 2: $(2m-1)/(2m)<\alpha \leq [2(m+1)-1]/[2(m+1)]$![]() , $m\geq 1$
, $m\geq 1$![]() .
.
In this case, by theorem 2.1 we already have $p_2=\alpha p_1$![]() and we may write $g=\gamma _1\sum _{j=0}^mc_j(b_2/b_1)^je^{[2j(\alpha -1)+1]p_1/2}+\eta$
and we may write $g=\gamma _1\sum _{j=0}^mc_j(b_2/b_1)^je^{[2j(\alpha -1)+1]p_1/2}+\eta$![]() , where $m\geq 1$
, where $m\geq 1$![]() , $\gamma _1$
, $\gamma _1$![]() is a polynomial such that $\gamma _1^2=b_1$
is a polynomial such that $\gamma _1^2=b_1$![]() and $\eta$
and $\eta$![]() is a mermorphic function with at most finitely many poles such that $|\eta |=O(r^N)$
is a mermorphic function with at most finitely many poles such that $|\eta |=O(r^N)$![]() uniformly in $\overline {S}_{1,\epsilon }$
uniformly in $\overline {S}_{1,\epsilon }$![]() and $\overline {S}_{2,\epsilon }$
and $\overline {S}_{2,\epsilon }$![]() . By substituting this expression into equation (3.2), we obtain
. By substituting this expression into equation (3.2), we obtain

where $L_j=[2j(\alpha -1)+1]/2$![]() , $M_{k_0}=k_0\alpha -k_0+1$
, $M_{k_0}=k_0\alpha -k_0+1$![]() and the coefficients $C_{k_0}=\sum _{\substack {j_0+\cdots +j_m=2,\\j_1+\cdots +mj_m=k_0}}\frac {2!}{j_0!j_1!\cdots j_m!}c_0^{j_0}c_1^{j_1}\cdots c_m^{j_m}$
and the coefficients $C_{k_0}=\sum _{\substack {j_0+\cdots +j_m=2,\\j_1+\cdots +mj_m=k_0}}\frac {2!}{j_0!j_1!\cdots j_m!}c_0^{j_0}c_1^{j_1}\cdots c_m^{j_m}$![]() , $k_0=m+1,\,\cdots,\,2\,m$
, $k_0=m+1,\,\cdots,\,2\,m$![]() . Suppose that $\alpha <[2(m+1)-1]/2(m+1)$
. Suppose that $\alpha <[2(m+1)-1]/2(m+1)$![]() . Then, for $k_0=m+1+j$
. Then, for $k_0=m+1+j$![]() , $j=0,\,1,\,\cdots,\,m-1$
, $j=0,\,1,\,\cdots,\,m-1$![]() , we have $L_{j+1}< k_0\alpha -\alpha +1< L_j$
, we have $L_{j+1}< k_0\alpha -\alpha +1< L_j$![]() . As in previous case, we also define the function $w$
. As in previous case, we also define the function $w$![]() in (3.4), where $z_0$
in (3.4), where $z_0$![]() is chosen so that $|z_0|$
is chosen so that $|z_0|$![]() is large and $w$
is large and $w$![]() is analytic outside a finite disc centred at $0$
is analytic outside a finite disc centred at $0$![]() . It follows that $w'/w$
. It follows that $w'/w$![]() has the form in (3.5). Similarly as in previous case, we first divide by $2c_0\gamma _1e^{p_1/2}$
has the form in (3.5). Similarly as in previous case, we first divide by $2c_0\gamma _1e^{p_1/2}$![]() on both sides of equation (3.9) and conclude that $w(re^{i(\theta _2-\epsilon )})\to a$
on both sides of equation (3.9) and conclude that $w(re^{i(\theta _2-\epsilon )})\to a$![]() as $r\to \infty$
as $r\to \infty$![]() along the ray $z=re^{i(\theta _2-\epsilon )}$
along the ray $z=re^{i(\theta _2-\epsilon )}$![]() for some nonzero constant $a=a(\theta _2,\,\epsilon )$
for some nonzero constant $a=a(\theta _2,\,\epsilon )$![]() ; then we use the expression $g=h'=\gamma _1\sum _{j=0}^mc_j(b_2/b_1)^je^{[2j(\alpha -1)+1]p_1/2}+\eta$
; then we use the expression $g=h'=\gamma _1\sum _{j=0}^mc_j(b_2/b_1)^je^{[2j(\alpha -1)+1]p_1/2}+\eta$![]() to derive from (3.4) that $w(re^{i(\theta +\epsilon )})\to 0$
to derive from (3.4) that $w(re^{i(\theta +\epsilon )})\to 0$![]() as $r\to \infty$
as $r\to \infty$![]() along the ray $z=re^{i(\theta _2+\epsilon )}$
along the ray $z=re^{i(\theta _2+\epsilon )}$![]() . An application of the Phragmén–Lindelöf theorem to $w$
. An application of the Phragmén–Lindelöf theorem to $w$![]() in the sector in (3.7) then yields a contradiction. We omit those details. Therefore, we must have $\alpha =[2(m+1)-1]/2(m+1)$
in the sector in (3.7) then yields a contradiction. We omit those details. Therefore, we must have $\alpha =[2(m+1)-1]/2(m+1)$![]() . We complete the proof.
. We complete the proof.
4. Equation (1.1) with periodic coefficients in (1.6)
As mentioned in the introduction, all nontrivial solutions of the second-order linear differential equation $f''+(e^z-b)f=0$![]() such that $\lambda (f)<\infty$
such that $\lambda (f)<\infty$![]() are given explicit expressions. In this section we solve nontrivial solutions such that $\lambda (f)<\infty$
are given explicit expressions. In this section we solve nontrivial solutions such that $\lambda (f)<\infty$![]() of the second-order linear differential equation:
of the second-order linear differential equation:
where $l$![]() and $s$
and $s$![]() are relatively prime integers such that $l>s\geq 1$
are relatively prime integers such that $l>s\geq 1$![]() , $b_2$
, $b_2$![]() and $b_3$
and $b_3$![]() are constants and $b_2\not =0$
are constants and $b_2\not =0$![]() . We remark that by using the method in [Reference Langley25], we may prove that all nontrivial solutions of equation (4.1) satisfy $\lambda (f)=\infty$
. We remark that by using the method in [Reference Langley25], we may prove that all nontrivial solutions of equation (4.1) satisfy $\lambda (f)=\infty$![]() when $b_3$
when $b_3$![]() is replaced by a nonconstant polynomial.
is replaced by a nonconstant polynomial.
Suppose that equation (4.1) admits a nontrivial solution such that $\lambda (f)<\infty$![]() . Then $f$
. Then $f$![]() has the form in (1.3) or (1.4). Also, we may write $f=\kappa e^{h}$
has the form in (1.3) or (1.4). Also, we may write $f=\kappa e^{h}$![]() , where $h$
, where $h$![]() is an entire function and $\kappa$
is an entire function and $\kappa$![]() is the canonical product from the zeros of $f$
is the canonical product from the zeros of $f$![]() satisfying $\sigma (\kappa )=\lambda (\kappa )<\infty$
satisfying $\sigma (\kappa )=\lambda (\kappa )<\infty$![]() . Thus we may suppose that $\kappa$
. Thus we may suppose that $\kappa$![]() equals a polynomial in $e^{z/2}$
equals a polynomial in $e^{z/2}$![]() or $e^{z}$
or $e^{z}$![]() and $h'$
and $h'$![]() equals a polynomial in $e^{z/2}$
equals a polynomial in $e^{z/2}$![]() or $e^{z}$
or $e^{z}$![]() . By denoting $g=h'$
. By denoting $g=h'$![]() , from (4.1) we have
, from (4.1) we have
By theorem 2.1, we may determine the coefficients $c_j$![]() in (1.3) or (1.4) from equation (4.2). Our main result is the following
in (1.3) or (1.4) from equation (4.2). Our main result is the following
Theorem 4.1 Let $b_2$![]() and $b_3$
and $b_3$![]() be constants such that $b_2\not =0$
be constants such that $b_2\not =0$![]() and $l,$
and $l,$![]() $s$
$s$![]() be relatively prime integers such that $l>s\geq 1$
be relatively prime integers such that $l>s\geq 1$![]() . Suppose that (4.1) admits two linearly independent solutions $f_1$
. Suppose that (4.1) admits two linearly independent solutions $f_1$![]() and $f_2$
and $f_2$![]() such that $\max \{\lambda (f_1),\,\lambda (f_2)\}<\infty$
such that $\max \{\lambda (f_1),\,\lambda (f_2)\}<\infty$![]() . Then $s=1$
. Then $s=1$![]() and $l=2$
and $l=2$![]() .
.
Recall the following well-known result due to Wittich [Reference Wittich32]. We say that a function $f$![]() is subnormal if $\limsup _{r\to \infty } \log T(r,\,f)/r=0$
is subnormal if $\limsup _{r\to \infty } \log T(r,\,f)/r=0$![]() . This lemma gives the form of subnormal solutions of second-order linear differential equations with certain periodic functions as coefficients.
. This lemma gives the form of subnormal solutions of second-order linear differential equations with certain periodic functions as coefficients.
Lemma 4.2 Let $P(z)$![]() and $Q(z)$
and $Q(z)$![]() be polynomials in $z$
be polynomials in $z$![]() and not both constants. If $w\not \equiv 0$
and not both constants. If $w\not \equiv 0$![]() is a subnormal solution of equation
is a subnormal solution of equation
then $w$![]() must have the form $w=e^{cz}(a_0+a_1e^{z}+\cdots +a_ke^{kz})$
must have the form $w=e^{cz}(a_0+a_1e^{z}+\cdots +a_ke^{kz})$![]() , where $k\geq 0$
, where $k\geq 0$![]() is an integer and $c$
is an integer and $c$![]() , $a_0$
, $a_0$![]() , $\cdots$
, $\cdots$![]() , $a_k$
, $a_k$![]() are constants with $a_0\not =0$
are constants with $a_0\not =0$![]() and $a_k\not =0$
and $a_k\not =0$![]() . Moreover, we have $c^2+cP(0)+Q(0)=0$
. Moreover, we have $c^2+cP(0)+Q(0)=0$![]() .
.
Proof of lemma 4.2. By Wittich [Reference Wittich32], we have $w=e^{cz}(a_0+a_1e^{z}+\cdots +a_ke^{kz})$![]() . By taking the derivatives of $w$
. By taking the derivatives of $w$![]() and then dividing $w'$
and then dividing $w'$![]() and $w''$
and $w''$![]() by $w$
by $w$![]() , respectively, we get
, respectively, we get


We write equation (4.3) as $Q(e^z)=-w''/w-P(e^z)w'/w$![]() . Since $w$
. Since $w$![]() is of finite order, then an application of the lemma on the logarithmic derivative yields $\deg (Q(z))m(r,\,e^z)\leq \deg (P(z))m(r,\,e^z)+O(\log r)$
is of finite order, then an application of the lemma on the logarithmic derivative yields $\deg (Q(z))m(r,\,e^z)\leq \deg (P(z))m(r,\,e^z)+O(\log r)$![]() , i.e., $[\deg (Q(z))-\deg (P(z))]T(r,\,e^z)\leq O(\log r)$
, i.e., $[\deg (Q(z))-\deg (P(z))]T(r,\,e^z)\leq O(\log r)$![]() . Therefore, $\deg (Q(z))\leq \deg (P(z))$
. Therefore, $\deg (Q(z))\leq \deg (P(z))$![]() and thus $P(z)$
and thus $P(z)$![]() is nonconstant. Together with equations (4.4) and (4.5), we rewrite equation (4.3) as
is nonconstant. Together with equations (4.4) and (4.5), we rewrite equation (4.3) as

Since along a ray $z=re^{i\theta }$![]() such that $\cos \theta <0$
such that $\cos \theta <0$![]() , we have $e^{z}\to 0$
, we have $e^{z}\to 0$![]() as $r\to \infty$
as $r\to \infty$![]() , then by letting $r\to \infty$
, then by letting $r\to \infty$![]() along the ray $z=re^{i\theta }$
along the ray $z=re^{i\theta }$![]() , we obtain from equation (4.6) that $c^2+cP(0)+Q(0)=0$
, we obtain from equation (4.6) that $c^2+cP(0)+Q(0)=0$![]() . This completes the proof.
. This completes the proof.
Unlike in § 2 and 3 where Nevanlinna theory plays the central role in proving theorems 2.1 and 3.1, the proof of theorem 4.1 will, however, mainly rely on the Lommel transformation for the generalized Bessel equation:

Recall the Bessel equation: $x^2y''+xy'+(x^2-\nu ^2)y=0$![]() , where $\nu$
, where $\nu$![]() is a nonzero constant. Lommel [Reference Lommel26] and Pearson [Reference Pearson27] independently (see also [Reference Watson31]) studied the following transformation given by:
is a nonzero constant. Lommel [Reference Lommel26] and Pearson [Reference Pearson27] independently (see also [Reference Watson31]) studied the following transformation given by:
where $\alpha$![]() , $\beta$
, $\beta$![]() and $\gamma$
and $\gamma$![]() are constants and applied to the Bessel equation. By using the above transformation to equation (4.7) and by computing the derivatives of $x$
are constants and applied to the Bessel equation. By using the above transformation to equation (4.7) and by computing the derivatives of $x$![]() and $y$
and $y$![]() , we get
, we get

A further change of variable such that
leads to an equation of the form

In the case of equation (4.1), by Lommel's transformation we have
where $d_1$![]() , $d_2$
, $d_2$![]() and $d_3$
and $d_3$![]() are some constants. By comparing the coefficients of equation (4.1) and (4.11), we deduce that $2\gamma p=0$
are some constants. By comparing the coefficients of equation (4.1) and (4.11), we deduce that $2\gamma p=0$![]() , $\beta p=1$
, $\beta p=1$![]() , $\alpha ^{l}d_1=1$
, $\alpha ^{l}d_1=1$![]() , $\alpha ^{s}d_2=b_2$
, $\alpha ^{s}d_2=b_2$![]() and $d_3=b_3$
and $d_3=b_3$![]() . Further, for equation (4.12), it is well-known that the transformation $y=x^{-1/2}u$
. Further, for equation (4.12), it is well-known that the transformation $y=x^{-1/2}u$![]() leads to an equation of the form
leads to an equation of the form
In the case $l=4$![]() , it has been shown by Chiang and Yu [Reference Chiang and Yu11] that there is a full correspondence between solutions of (4.1) such that $\lambda (f)<\infty$
, it has been shown by Chiang and Yu [Reference Chiang and Yu11] that there is a full correspondence between solutions of (4.1) such that $\lambda (f)<\infty$![]() and Liouvillian solutions of (4.13). The only possible singular point of equation (4.13) is $x=0$
and Liouvillian solutions of (4.13). The only possible singular point of equation (4.13) is $x=0$![]() . Concerning the local solutions around a singular point of a second-order linear differential equation, we have the following elementary lemma 4.3; see [Reference Herold17] or in [Reference Laine23, lemma 6.6].
. Concerning the local solutions around a singular point of a second-order linear differential equation, we have the following elementary lemma 4.3; see [Reference Herold17] or in [Reference Laine23, lemma 6.6].
Lemma 4.3 [Reference Herold17, Reference Laine23]
Suppose that $h$![]() is analytic in $|z|< R,$
is analytic in $|z|< R,$![]() $R>0,$
$R>0,$![]() and consider the differential equation
and consider the differential equation
in the disc $|z|< R$![]() . Let $\rho _1$
. Let $\rho _1$![]() and $\rho _2$
and $\rho _2$![]() be the roots of
be the roots of
Denote by $D=D(r)$![]() the slit disc $D:=\{z:|z|< r\}\setminus \{t \ | \ 0\leq t< r\}$
the slit disc $D:=\{z:|z|< r\}\setminus \{t \ | \ 0\leq t< r\}$![]() . Then
. Then
(1) if $\rho _1-\rho _2\in \mathbb {Z}\setminus \{0\}$
 , then equation (4.14) admits in some slit disc $D=D(r)$
, then equation (4.14) admits in some slit disc $D=D(r)$ , $r\leq R$
, $r\leq R$ , two linearly independent solutions $u_1$
, two linearly independent solutions $u_1$ and $u_2$
and $u_2$ of the form:
(4.16)\begin{equation} \begin{aligned} u_1(z) & =z^{\rho_1}\sum_{i=0}^{\infty}a_iz^i, \quad a_0\not=0, \\ u_2(z) & =u_1(z)d\log z+z^{\rho_2}\sum_{i=0}^{\infty}b_iz^i, \end{aligned} \end{equation}where $d=0$
of the form:
(4.16)\begin{equation} \begin{aligned} u_1(z) & =z^{\rho_1}\sum_{i=0}^{\infty}a_iz^i, \quad a_0\not=0, \\ u_2(z) & =u_1(z)d\log z+z^{\rho_2}\sum_{i=0}^{\infty}b_iz^i, \end{aligned} \end{equation}where $d=0$
 or $d=1$
or $d=1$ ;
;(2) if $\rho _1-\rho _2\not \in \mathbb {Z},$
 then equation (4.14) admits in some slit disc $D=D(r),$
then equation (4.14) admits in some slit disc $D=D(r),$ $r\leq R,$
$r\leq R,$ two linearly independent solutions $u_1$
two linearly independent solutions $u_1$ and $u_2$
and $u_2$ of the form:
(4.17)\begin{equation} \begin{aligned} u_1(z) & =z^{\rho_1}\sum_{i=0}^{\infty}a_iz^i, \quad a_0\not=0, \\ u_2(z) & =z^{\rho_2}\sum_{i=0}^{\infty}b_iz^i, \quad b_0\not=0; \end{aligned} \end{equation}
of the form:
(4.17)\begin{equation} \begin{aligned} u_1(z) & =z^{\rho_1}\sum_{i=0}^{\infty}a_iz^i, \quad a_0\not=0, \\ u_2(z) & =z^{\rho_2}\sum_{i=0}^{\infty}b_iz^i, \quad b_0\not=0; \end{aligned} \end{equation}
(3) if $\rho _1-\rho _2=0,$
 then equation (4.14) admits in some slit disc $D=D(r),$
then equation (4.14) admits in some slit disc $D=D(r),$ $r\leq R,$
$r\leq R,$ two linearly independent solutions $u_1$
two linearly independent solutions $u_1$ and $u_2$
and $u_2$ of the form:
(4.18)\begin{equation} \begin{aligned} u_1(z) & =z^{\rho_1}\sum_{i=0}^{\infty}a_iz^i, \quad a_0\not=0, \\ u_2(z) & =u_1(z)\log z+z^{\rho_2}\sum_{i=0}^{\infty}b_iz^i. \end{aligned} \end{equation}
of the form:
(4.18)\begin{equation} \begin{aligned} u_1(z) & =z^{\rho_1}\sum_{i=0}^{\infty}a_iz^i, \quad a_0\not=0, \\ u_2(z) & =u_1(z)\log z+z^{\rho_2}\sum_{i=0}^{\infty}b_iz^i. \end{aligned} \end{equation}
For the solution $u_2$![]() in (4.16), if $d=0$
in (4.16), if $d=0$![]() , then from the proof of [Reference Laine23, lemma 6.6] we know that $b_0\not =0$
, then from the proof of [Reference Laine23, lemma 6.6] we know that $b_0\not =0$![]() .
.
Now, by elementary theory of ordinary differential equation (see [Reference Herold17]), lemma 4.3 shows that equation (4.13) admits two linearly independent solutions $u_1$![]() and $u_2$
and $u_2$![]() in the broken plane $\mathbb {C}^{-}=\mathbb {C}\setminus \{x \ | \ 0\leq x<\infty \}$
in the broken plane $\mathbb {C}^{-}=\mathbb {C}\setminus \{x \ | \ 0\leq x<\infty \}$![]() . When $p=1$
. When $p=1$![]() in (4.10), by the Lommel transformation and analytic continuation principle, the general solution of (4.1) is thus given by
in (4.10), by the Lommel transformation and analytic continuation principle, the general solution of (4.1) is thus given by
where $E_1$![]() and $E_2$
and $E_2$![]() are two arbitrary constants. Note that the above solution is independent from the choice of the branches of $u_1$
are two arbitrary constants. Note that the above solution is independent from the choice of the branches of $u_1$![]() and $u_2$
and $u_2$![]() in lemma 4.3. This is the key observation for the proof of theorem 4.1.
in lemma 4.3. This is the key observation for the proof of theorem 4.1.
Now we begin to prove theorem 4.1.
Proof of theorem 4.1. We first suppose that $f$![]() is a nontrivial solution such that $\lambda (f)<\infty$
is a nontrivial solution such that $\lambda (f)<\infty$![]() of equation (4.1) and use the expressions in (1.3) and (1.4) to write $f(z)=\Psi (x)=x^{c}\psi (x)e^{\chi (x)}$
of equation (4.1) and use the expressions in (1.3) and (1.4) to write $f(z)=\Psi (x)=x^{c}\psi (x)e^{\chi (x)}$![]() , where $x=e^{z/h}$
, where $x=e^{z/h}$![]() , $h=1$
, $h=1$![]() or $h=2$
or $h=2$![]() . From the proof of [Reference Chiang and Yu11, theorem 1.2], we know that in the broken plane $\mathbb {C}^{-}$
. From the proof of [Reference Chiang and Yu11, theorem 1.2], we know that in the broken plane $\mathbb {C}^{-}$![]() equation (4.13) admits a solution of the form
equation (4.13) admits a solution of the form
where $\omega :=\chi '+\psi '/\psi +(2hc+1)/(2x)$![]() is rational function in the complex plane $\mathbb {C}$
is rational function in the complex plane $\mathbb {C}$![]() . By using Kovacic's algorithm in [Reference Kovacic22] and giving the same discussions as in the proof of [Reference Chiang and Yu11, theorem 3.1] to equation (4.13) for the two cases $b_3\not =1/4$
. By using Kovacic's algorithm in [Reference Kovacic22] and giving the same discussions as in the proof of [Reference Chiang and Yu11, theorem 3.1] to equation (4.13) for the two cases $b_3\not =1/4$![]() and $b_3=1/4$
and $b_3=1/4$![]() , respectively, we conclude that $l$
, respectively, we conclude that $l$![]() must be even. It follows that $f$
must be even. It follows that $f$![]() has the form in (1.4) and thus $p=1$
has the form in (1.4) and thus $p=1$![]() in (4.10) and $\alpha =1$
in (4.10) and $\alpha =1$![]() in (4.8). We write $f=\kappa e^{h}$
in (4.8). We write $f=\kappa e^{h}$![]() , where $\kappa$
, where $\kappa$![]() and $h'$
and $h'$![]() are both polynomials in $\zeta =e^z$
are both polynomials in $\zeta =e^z$![]() such that $\kappa (0)\not =0$
such that $\kappa (0)\not =0$![]() . We may also write $f=\kappa _ce^{h_c}$
. We may also write $f=\kappa _ce^{h_c}$![]() , where $\kappa _c=\kappa e^{cz}$
, where $\kappa _c=\kappa e^{cz}$![]() and $h_c'=h'-c$
and $h_c'=h'-c$![]() . Then, denoting $g_c=h_c'$
. Then, denoting $g_c=h_c'$![]() , we have from (4.1) that
, we have from (4.1) that
By lemma 4.2 and the expression in (1.4), we see that the constant $c$![]() in (1.4) satisfies $c^2=b_3$
in (1.4) satisfies $c^2=b_3$![]() .
.
Now, for the solution in (4.19), by lemma 4.3 we have $\rho _1+\rho _2=1$![]() and $\rho _1\rho _2=1/4-b_3$
and $\rho _1\rho _2=1/4-b_3$![]() , which yield $(\rho _1-\rho _2)^2=4b_3$
, which yield $(\rho _1-\rho _2)^2=4b_3$![]() . Then $\rho _1-\rho _2=-2c$
. Then $\rho _1-\rho _2=-2c$![]() and it follows that $\rho _1=(1-2c)/2$
and it follows that $\rho _1=(1-2c)/2$![]() and $\rho _2=(1+2c)/2$
and $\rho _2=(1+2c)/2$![]() . Thus the solutions in (4.19) can be written as
. Thus the solutions in (4.19) can be written as

when $\rho _1-\rho _2\not =0$![]() , or
, or

when $\rho _1-\rho _2=0$![]() . Note that $d=0$
. Note that $d=0$![]() in (4.22) when $\rho _1-\rho _2$
in (4.22) when $\rho _1-\rho _2$![]() is not an integer. On the other hand, for the solution $f=\kappa e^{h}$
is not an integer. On the other hand, for the solution $f=\kappa e^{h}$![]() , we may write the expression in (1.4) in the form $f=e^{cz}\sum _{j=0}^{\infty }d_je^{jz}$
, we may write the expression in (1.4) in the form $f=e^{cz}\sum _{j=0}^{\infty }d_je^{jz}$![]() . By comparing this series with the one in (4.22) or in (4.23), we conclude that the logarithmic term in $u_2$
. By comparing this series with the one in (4.22) or in (4.23), we conclude that the logarithmic term in $u_2$![]() does not occur. This implies that $d=0$
does not occur. This implies that $d=0$![]() or $E_2=0$
or $E_2=0$![]() in (4.22) and $E_2=0$
in (4.22) and $E_2=0$![]() in (4.23) when $f=\kappa e^{h}$
in (4.23) when $f=\kappa e^{h}$![]() .
.
With these preparations, we now suppose that $f_1$![]() and $f_2$
and $f_2$![]() are two linearly independent solutions of (4.1) such that $\max \{\lambda (f_1),\,\lambda (f_2)\}<\infty$
are two linearly independent solutions of (4.1) such that $\max \{\lambda (f_1),\,\lambda (f_2)\}<\infty$![]() . We write $l=2(m+1)$
. We write $l=2(m+1)$![]() for some integer $m\geq 0$
for some integer $m\geq 0$![]() and also write $s=2(m+1)-t$
and also write $s=2(m+1)-t$![]() for some integer $t\geq 1$
for some integer $t\geq 1$![]() .
.
Let $q$![]() be the smallest integer such that $s/l\leq [2(q+1)-1]/[2(q+1)]$
be the smallest integer such that $s/l\leq [2(q+1)-1]/[2(q+1)]$![]() . Since $l$
. Since $l$![]() and $s$
and $s$![]() are relatively prime, we see that the equality holds only when $q=m$
are relatively prime, we see that the equality holds only when $q=m$![]() . For each of $f_1$
. For each of $f_1$![]() and $f_2$
and $f_2$![]() , denoted by $f$
, denoted by $f$![]() , we may write $f=\kappa _ce^{h_c}$
, we may write $f=\kappa _ce^{h_c}$![]() , where $\kappa _c=\kappa e^{cz}$
, where $\kappa _c=\kappa e^{cz}$![]() . Then, denoting $g_c=h_c'$
. Then, denoting $g_c=h_c'$![]() , we have equation (4.21). By theorem 2.1, $g_c=h_c'=\sum _{j=0}^{q}c_je^{(m+1-jt)z}$
, we have equation (4.21). By theorem 2.1, $g_c=h_c'=\sum _{j=0}^{q}c_je^{(m+1-jt)z}$![]() , where $c_0,\,c_1,\,\cdots,\,c_q$
, where $c_0,\,c_1,\,\cdots,\,c_q$![]() are constants such that $c_0^2=1$
are constants such that $c_0^2=1$![]() and $c_1,\,\cdots,\,c_q$
and $c_1,\,\cdots,\,c_q$![]() satisfy certain relations. In both of the two cases where $q=1$
satisfy certain relations. In both of the two cases where $q=1$![]() and $q\geq 2$
and $q\geq 2$![]() , we have $2c_0c_1=b_2$
, we have $2c_0c_1=b_2$![]() and, by simple computations, that,
and, by simple computations, that,
where $t_j$![]() are positive integers such that $t_1<\cdots < t_q$
are positive integers such that $t_1<\cdots < t_q$![]() , and further that
, and further that

where $T_{q+j}$![]() are positive integers such that $T_{q+1}<\cdots < T_{2q}$
are positive integers such that $T_{q+1}<\cdots < T_{2q}$![]() . By substituting $g_c=\sum _{j=0}^{q}c_je^{(m+1-jt)z}$
. By substituting $g_c=\sum _{j=0}^{q}c_je^{(m+1-jt)z}$![]() into (4.21) together with theorem 2.1, we get
into (4.21) together with theorem 2.1, we get
when $q=0$![]() , and
, and

when $q\geq 1$![]() , where $C_{k_j}=C_{q+1+j}$
, where $C_{k_j}=C_{q+1+j}$![]() and $C_{2q+1}=0$
and $C_{2q+1}=0$![]() . By substituting equations (4.4) and (4.5) for $\kappa _{c}=e^{cz}(\sum _{i=1}^ka_ie^{iz})$
. By substituting equations (4.4) and (4.5) for $\kappa _{c}=e^{cz}(\sum _{i=1}^ka_ie^{iz})$![]() , $a_0a_k\not =0$
, $a_0a_k\not =0$![]() , into (4.26) or (4.27) and noting that $b_3=c^2$
, into (4.26) or (4.27) and noting that $b_3=c^2$![]() , we finally get
, we finally get

when $q=0$![]() , and
, and

when $q\geq 1$![]() . Note that the inequality $(2q-1)/(2q)< s/l\leq [2(q+1)-1]/[2(q+1)]$
. Note that the inequality $(2q-1)/(2q)< s/l\leq [2(q+1)-1]/[2(q+1)]$![]() implies $qt< m+1\leq (q+1)t$
implies $qt< m+1\leq (q+1)t$![]() , where the equality holds when $q=m$
, where the equality holds when $q=m$![]() . The left-hand side of equations (4.28) and (4.29) are polynomials in $e^{z}$
. The left-hand side of equations (4.28) and (4.29) are polynomials in $e^{z}$![]() of degree $k+m+1$
of degree $k+m+1$![]() and thus all coefficients of these two polynomials vanish. When $s=2(m+1)-t<2m+1$
and thus all coefficients of these two polynomials vanish. When $s=2(m+1)-t<2m+1$![]() , we have $q< m$
, we have $q< m$![]() and $t\geq 2$
and $t\geq 2$![]() . By looking at the highest-degree term in the resulting polynomial and noting that $a_k\not =0$
. By looking at the highest-degree term in the resulting polynomial and noting that $a_k\not =0$![]() , we find
, we find
Similarly, when $s=2m+1$![]() , we have $q=m$
, we have $q=m$![]() and $t=1$
and $t=1$![]() and find
and find
Let $c_+$![]() or $c_{-}$
or $c_{-}$![]() be any square root of $b_3$
be any square root of $b_3$![]() . We may write $f_1=\kappa _{1c}e^{h_{1c}}$
. We may write $f_1=\kappa _{1c}e^{h_{1c}}$![]() and $f_2=\kappa _{2c}e^{h_{2c}}$
and $f_2=\kappa _{2c}e^{h_{2c}}$![]() , where $\kappa _{1c}=\kappa _1e^{c_+z}$
, where $\kappa _{1c}=\kappa _1e^{c_+z}$![]() and $\kappa _{2c}=\kappa _2e^{c_{-}z}$
and $\kappa _{2c}=\kappa _2e^{c_{-}z}$![]() and $\kappa _{1}$
and $\kappa _{1}$![]() and $\kappa _{2}$
and $\kappa _{2}$![]() are two polynomials in $e^z$
are two polynomials in $e^z$![]() of degrees $k_1$
of degrees $k_1$![]() and $k_2$
and $k_2$![]() , respectively. Moreover, $h_{1c}$
, respectively. Moreover, $h_{1c}$![]() satisfies $h_{1c}'=\sum _{j=0}^{q}c_je^{(m+1-jt)z}$
satisfies $h_{1c}'=\sum _{j=0}^{q}c_je^{(m+1-jt)z}$![]() . Since $c_0^2=1$
. Since $c_0^2=1$![]() and since $2c_0c_1=b_2$
and since $2c_0c_1=b_2$![]() when $q\ge 1$
when $q\ge 1$![]() , we easily deduce from (4.24) that $h_{2c}=\pm h_{1c}$
, we easily deduce from (4.24) that $h_{2c}=\pm h_{1c}$![]() . Recall the elementary Wronskian determinant: $f_1'f_2-f_1f_2'=D$
. Recall the elementary Wronskian determinant: $f_1'f_2-f_1f_2'=D$![]() , where $D$
, where $D$![]() is a nonzero constant (see [Reference Laine23]). Then we have $(f_1/f_2)'=D/f_2^2$
is a nonzero constant (see [Reference Laine23]). Then we have $(f_1/f_2)'=D/f_2^2$![]() . If $h_{2c}=h_{1c}$
. If $h_{2c}=h_{1c}$![]() , then $f_1/f_2$
, then $f_1/f_2$![]() is of finite order while $f_1^2$
is of finite order while $f_1^2$![]() is of infinite order, a contradiction. Therefore, $h_{2c}=-h_{1c}$
is of infinite order, a contradiction. Therefore, $h_{2c}=-h_{1c}$![]() . We may suppose that $c_+=c$
. We may suppose that $c_+=c$![]() . When $s<2m+1$
. When $s<2m+1$![]() , from (4.30) we deduce that $c_+=c_{-}=c$
, from (4.30) we deduce that $c_+=c_{-}=c$![]() , which implies that $-2c=m+1+2k_1$
, which implies that $-2c=m+1+2k_1$![]() is a positive integer and hence $k_1=k_2$
is a positive integer and hence $k_1=k_2$![]() ; when $s=2m+1$
; when $s=2m+1$![]() , using (4.25) and the relation $2c_0c_1=b_2$
, using (4.25) and the relation $2c_0c_1=b_2$![]() we deduce from (4.31) that $c_++c_{-}+m+1+k_1+k_2=0$
we deduce from (4.31) that $c_++c_{-}+m+1+k_1+k_2=0$![]() , which implies that $c_+=c_{-}=c$
, which implies that $c_+=c_{-}=c$![]() and hence $-2c=m+1+k_1+k_2$
and hence $-2c=m+1+k_1+k_2$![]() is a positive integer. Now $\rho _1-\rho _2=-2c$
is a positive integer. Now $\rho _1-\rho _2=-2c$![]() is a positive integer. Together with (4.19) and previous preparations, we conclude that equation (4.13) admits in the broken plane $\mathbb {C}^{-}$
is a positive integer. Together with (4.19) and previous preparations, we conclude that equation (4.13) admits in the broken plane $\mathbb {C}^{-}$![]() two linearly independent solutions of the form $u_1=x^{\rho _1}v_1$
two linearly independent solutions of the form $u_1=x^{\rho _1}v_1$![]() and $u_2=x^{\rho _2}v_2$
and $u_2=x^{\rho _2}v_2$![]() , where $v_1$
, where $v_1$![]() and $v_2$
and $v_2$![]() are two entire functions such that $v_1(0)\not =0$
are two entire functions such that $v_1(0)\not =0$![]() and $v_2(0)\not =0$
and $v_2(0)\not =0$![]() , so that
, so that

where $D_j$![]() are constants, $h_{11}=\sum _{j=0}^{q}\frac {c_j}{m+1-jt}x^{m+1-jt}$
are constants, $h_{11}=\sum _{j=0}^{q}\frac {c_j}{m+1-jt}x^{m+1-jt}$![]() , and $\kappa _{11}$
, and $\kappa _{11}$![]() and $\kappa _{12}$
and $\kappa _{12}$![]() are two polynomials of degrees $k_1$
are two polynomials of degrees $k_1$![]() and $k_2$
and $k_2$![]() , respectively, such that $\kappa _{11}(0)\not =0$
, respectively, such that $\kappa _{11}(0)\not =0$![]() and $\kappa _{12}(0)\not =0$
and $\kappa _{12}(0)\not =0$![]() . Noting $\rho _1=(1-2c)/2$
. Noting $\rho _1=(1-2c)/2$![]() and $\rho _2=(1+2c)/2$
and $\rho _2=(1+2c)/2$![]() , we see from (4.22) that $D_2D_4\not =0$
, we see from (4.22) that $D_2D_4\not =0$![]() . Obviously, $E:=D_1D_4-D_2D_3\not =0$
. Obviously, $E:=D_1D_4-D_2D_3\not =0$![]() . From equation (4.32) we get
. From equation (4.32) we get
Since $v_1$![]() is an entire function with $v_1(0)\not =0$
is an entire function with $v_1(0)\not =0$![]() , we see from (4.33) that the function $w:=D_4\kappa _{11}e^{2h_{11}}-D_2\kappa _{12}$
, we see from (4.33) that the function $w:=D_4\kappa _{11}e^{2h_{11}}-D_2\kappa _{12}$![]() has a zero of order $-2c$
has a zero of order $-2c$![]() at the point $z=0$
at the point $z=0$![]() and so $w(0)=w'(0)=\cdots =w^{(-2c-1)}(0)=0$
and so $w(0)=w'(0)=\cdots =w^{(-2c-1)}(0)=0$![]() . Denote
. Denote

where $a_{1,0},\,a_{2,0},\,a_{1,k_1},\,a_{1,k_2}\not =0$![]() . $w(0)=0$
. $w(0)=0$![]() implies that $D_4a_{1,0}=D_2a_{2,0}$
implies that $D_4a_{1,0}=D_2a_{2,0}$![]() . Supposing that $a_{1,0}=a_{2,0}=1$
. Supposing that $a_{1,0}=a_{2,0}=1$![]() , we have $D_4=D_2$
, we have $D_4=D_2$![]() . Below we consider the case when $m\geq 1$
. Below we consider the case when $m\geq 1$![]() .
.
Consider first the case when $s/l<1/2$![]() . Since $m\geq 1$
. Since $m\geq 1$![]() , by theorem 1.1 and (4.30), we see that $k_1=k_2\geq 1$
, by theorem 1.1 and (4.30), we see that $k_1=k_2\geq 1$![]() . Now $w^{(m+1)}(0)=0$
. Now $w^{(m+1)}(0)=0$![]() implies that $a_{1,m+1}+2(m!)c_0=a_{2,m+1}$
implies that $a_{1,m+1}+2(m!)c_0=a_{2,m+1}$![]() . Here $a_{1,m+1}=0$
. Here $a_{1,m+1}=0$![]() if $m+1>k_1$
if $m+1>k_1$![]() and so is for $a_{2,m+1}$
and so is for $a_{2,m+1}$![]() . Obviously, $m+1\leq k_1$
. Obviously, $m+1\leq k_1$![]() . For each of $f_1$
. For each of $f_1$![]() and $f_2$
and $f_2$![]() , denoted by $f$
, denoted by $f$![]() , we may write $f=\kappa _ce^{h_c}$
, we may write $f=\kappa _ce^{h_c}$![]() . Then we have equation (4.28). Note that $1\leq s=2(m+1)-t\leq m$
. Then we have equation (4.28). Note that $1\leq s=2(m+1)-t\leq m$![]() . The left-hand side of equation (4.28) is a polynomial in $e^{z}$
. The left-hand side of equation (4.28) is a polynomial in $e^{z}$![]() of degree $m+1+k$
of degree $m+1+k$![]() and thus all coefficients of this polynomial vanish. Denoting $a_{-m-1}=\cdots =a_{-2}=a_{-1}=0$
and thus all coefficients of this polynomial vanish. Denoting $a_{-m-1}=\cdots =a_{-2}=a_{-1}=0$![]() and $a_{k+1}=\cdots =a_{k+m}=0$
and $a_{k+1}=\cdots =a_{k+m}=0$![]() , we obtain from equation (4.28) that $c_0(2c+2k+m+1)a_k=0$
, we obtain from equation (4.28) that $c_0(2c+2k+m+1)a_k=0$![]() , which yields (4.30), and
, which yields (4.30), and
By substituting $2c=-2k-m-1$![]() into the equations in (4.35) we get
into the equations in (4.35) we get
Since $1\leq s\leq m$![]() , by letting $i=1,\,2,\,\cdots,\,m$
, by letting $i=1,\,2,\,\cdots,\,m$![]() , we see that $a_1/a_0=K_1$
, we see that $a_1/a_0=K_1$![]() , $\cdots$
, $\cdots$![]() , $a_m/a_0=K_m$
, $a_m/a_0=K_m$![]() for some constants $K_1,\,\cdots,\,K_m$
for some constants $K_1,\,\cdots,\,K_m$![]() independent from $c_0$
independent from $c_0$![]() . Then by letting $i=m+1$
. Then by letting $i=m+1$![]() in (4.36) together with the relation $a_{1,m+1}+2(m!)c_0=a_{2,m+1}$
in (4.36) together with the relation $a_{1,m+1}+2(m!)c_0=a_{2,m+1}$![]() , we get $2k_1/(m+1)(2c+m+1)+2(m!)=-2k_2/(m+1)(2c+m+1)$
, we get $2k_1/(m+1)(2c+m+1)+2(m!)=-2k_2/(m+1)(2c+m+1)$![]() . Since $k_1=k_2$
. Since $k_1=k_2$![]() and $-2c=2k_1+m+1$
and $-2c=2k_1+m+1$![]() , we get $(m+1)!=1$
, we get $(m+1)!=1$![]() , which is impossible when $m\geq 1$
, which is impossible when $m\geq 1$![]() .
.
Consider next the case when $s/l>1/2$![]() and $s<2m+1$
and $s<2m+1$![]() . Now $qt< m+1< (q+1)t$
. Now $qt< m+1< (q+1)t$![]() for some integer $1\leq q< m$
for some integer $1\leq q< m$![]() . Recalling that $s=2(m+1)-t$
. Recalling that $s=2(m+1)-t$![]() and $l$
and $l$![]() and $s$
and $s$![]() are relatively prime, we see that $t\geq 3$
are relatively prime, we see that $t\geq 3$![]() is an odd integer. Denoting each of $f_1$
is an odd integer. Denoting each of $f_1$![]() and $f_2$
and $f_2$![]() by $f$
by $f$![]() , we may write $f=\kappa _ce^{h_c}$
, we may write $f=\kappa _ce^{h_c}$![]() . Then we have equation (4.29). Denote $M=m+1-qt$
. Then we have equation (4.29). Denote $M=m+1-qt$![]() for simplicity. Since $-2c=2k+m+1$
for simplicity. Since $-2c=2k+m+1$![]() and $C_{2q+1}=0$
and $C_{2q+1}=0$![]() and $C_{2q}=c_q^2$
and $C_{2q}=c_q^2$![]() , then by looking at the coefficient of the term $e^{Mz}$
, then by looking at the coefficient of the term $e^{Mz}$![]() on the left-hand side of equation (4.29), we find $M(2c+M)a_M+2ca_0c_q+Ma_0c_q=0$
on the left-hand side of equation (4.29), we find $M(2c+M)a_M+2ca_0c_q+Ma_0c_q=0$![]() , which gives $a_0c_q+Ma_M=0$
, which gives $a_0c_q+Ma_M=0$![]() . Recall that the function $w:=D_4\kappa _{11}e^{2h_{11}}-D_2\kappa _{12}$
. Recall that the function $w:=D_4\kappa _{11}e^{2h_{11}}-D_2\kappa _{12}$![]() has a zero of order $-2c$
has a zero of order $-2c$![]() at the point $z=0$
at the point $z=0$![]() . Then $w^{(M)}(0)=0$
. Then $w^{(M)}(0)=0$![]() implies that $a_{1,M}+2(M-1)!c_q=a_{2,M}$
implies that $a_{1,M}+2(M-1)!c_q=a_{2,M}$![]() . Using equation (4.24) together with $2c_0c_1=b_2$
. Using equation (4.24) together with $2c_0c_1=b_2$![]() and $a_0c_q+Ma_M=0$
and $a_0c_q+Ma_M=0$![]() , we get $M!=1$
, we get $M!=1$![]() , which implies that $M=1$
, which implies that $M=1$![]() . It follows that $m=qt$
. It follows that $m=qt$![]() . By looking at the coefficient of the term $e^{2z}$
. By looking at the coefficient of the term $e^{2z}$![]() on the left-hand side of equation (4.29), we find $2(2c+2)a_2+2(c+1)a_1c_q+a_0c_q^2+a_1c_q=0$
on the left-hand side of equation (4.29), we find $2(2c+2)a_2+2(c+1)a_1c_q+a_0c_q^2+a_1c_q=0$![]() , which together with $a_1=-a_0c_q$
, which together with $a_1=-a_0c_q$![]() yields $2a_2=a_0c_q^2$
yields $2a_2=a_0c_q^2$![]() . Then by looking at the coefficient of the term $e^{3z}$
. Then by looking at the coefficient of the term $e^{3z}$![]() on the left-hand side of equation (4.29), we find $3(2c+3)a_3+2(c+2)a_2c_q+a_2c_q+a_1c_q^2=0$
on the left-hand side of equation (4.29), we find $3(2c+3)a_3+2(c+2)a_2c_q+a_2c_q+a_1c_q^2=0$![]() , i.e., $(2c+3)(6a_3+c_q^3)=0$
, i.e., $(2c+3)(6a_3+c_q^3)=0$![]() and thus $6a_3+c_q^3=0$
and thus $6a_3+c_q^3=0$![]() . Now $w^{(3)}(0)=0$
. Now $w^{(3)}(0)=0$![]() implies that $a_{1,3}+6a_{1,2}c_q+12a_{1,1}c_q^2+8c_q^3=a_{2,3}$
implies that $a_{1,3}+6a_{1,2}c_q+12a_{1,1}c_q^2+8c_q^3=a_{2,3}$![]() , which together with the relation $a_1=-a_0c_q$
, which together with the relation $a_1=-a_0c_q$![]() and $2a_2=a_0c_q^2$
and $2a_2=a_0c_q^2$![]() gives $a_{1,3}-c_q^3=a_{2,3}$
gives $a_{1,3}-c_q^3=a_{2,3}$![]() . Then using equation (4.24) together with $2c_0c_1=b_2$
. Then using equation (4.24) together with $2c_0c_1=b_2$![]() and $c_q^3+6a_3=0$
and $c_q^3+6a_3=0$![]() , we get $c_q^3=0$
, we get $c_q^3=0$![]() , a contradiction to (4.24).
, a contradiction to (4.24).
Finally, we consider the case when $s=2m+1$![]() . Recall that $q=m$
. Recall that $q=m$![]() and $t=1$
and $t=1$![]() in (4.29). In this case, if $k_1=k_2$
in (4.29). In this case, if $k_1=k_2$![]() , then using (4.25) and the relation $2c_0c_1=b_2$
, then using (4.25) and the relation $2c_0c_1=b_2$![]() we get from (4.31) that $C_{m+1}=0$
we get from (4.31) that $C_{m+1}=0$![]() , a contradiction. Therefore, without loss of generality, we may suppose that $k_1>k_2\geq 0$
, a contradiction. Therefore, without loss of generality, we may suppose that $k_1>k_2\geq 0$![]() . If $k_2=0$
. If $k_2=0$![]() , then by theorem 1.1 have $2c+1=0$
, then by theorem 1.1 have $2c+1=0$![]() , which is impossible since $-2c=m+1+k_1+k_2$
, which is impossible since $-2c=m+1+k_1+k_2$![]() . Therefore, $k_2>0$
. Therefore, $k_2>0$![]() . Note that $C_{2m}=c_m^2$
. Note that $C_{2m}=c_m^2$![]() . Since $-2c=m+1+k_1+k_2$
. Since $-2c=m+1+k_1+k_2$![]() , then by looking at the coefficient of the terms $e^z$
, then by looking at the coefficient of the terms $e^z$![]() and $e^{2z}$
and $e^{2z}$![]() in equation (4.29), respectively, we find $a_{1}+a_{0}c_m=0$
in equation (4.29), respectively, we find $a_{1}+a_{0}c_m=0$![]() and $2(2c+2)a_2+(2c+3)c_ma_1+[c_m^2+(2c+2)c_{m-1}]a_0=0$
and $2(2c+2)a_2+(2c+3)c_ma_1+[c_m^2+(2c+2)c_{m-1}]a_0=0$![]() and so $2a_2-c_m^2a_0+c_{m-1}a_0=0$
and so $2a_2-c_m^2a_0+c_{m-1}a_0=0$![]() . Recall that the function $w:=D_4\kappa _{11}e^{2h_{11}}-D_2\kappa _{12}$
. Recall that the function $w:=D_4\kappa _{11}e^{2h_{11}}-D_2\kappa _{12}$![]() has a zero of order $-2c$
has a zero of order $-2c$![]() at the point $z=0$
at the point $z=0$![]() . Now $w''(0)=0$
. Now $w''(0)=0$![]() implies that $a_{1,2}+4a_{1,1}c_m+4c_{m-1}+4c_m^2=a_{2,2}$
implies that $a_{1,2}+4a_{1,1}c_m+4c_{m-1}+4c_m^2=a_{2,2}$![]() . Using equation (4.24) together with $2c_0c_1=b_2$
. Using equation (4.24) together with $2c_0c_1=b_2$![]() , we get $-c_{m-1}/2+4c_{m-1}=c_{m-1}/2$
, we get $-c_{m-1}/2+4c_{m-1}=c_{m-1}/2$![]() , which yields $c_{m-1}=0$
, which yields $c_{m-1}=0$![]() , a contradiction to (4.24).
, a contradiction to (4.24).
From the above reasoning, we conclude that $l=2$![]() . We complete the proof.
. We complete the proof.
In the rest of this section, we use theorem 2.1 to determine precisely all nontrivial solutions such that $\lambda (f)<\infty$![]() of equation (4.1) for the case $l=2$
of equation (4.1) for the case $l=2$![]() and $l=4$
and $l=4$![]() .
.
Theorem 4.4 Let $b_1$![]() , $b_2$
, $b_2$![]() and $b_3$
and $b_3$![]() be constants such that $b_1b_2\not =0$
be constants such that $b_1b_2\not =0$![]() and $s$
and $s$![]() and $l$
and $l$![]() be relatively prime integers such that $1\leq s< l\leq 4$
be relatively prime integers such that $1\leq s< l\leq 4$![]() . Suppose that (4.1) admits a nontrivial solution $f$
. Suppose that (4.1) admits a nontrivial solution $f$![]() such that $\lambda (f)<\infty$
such that $\lambda (f)<\infty$![]() . Then
. Then
(1) if $s=1$
 and $l=2,$
and $l=2,$ then $f=\kappa e^{h},$
then $f=\kappa e^{h},$ $\kappa =\sum _{i=-1}^ka_ie^{iz}$
$\kappa =\sum _{i=-1}^ka_ie^{iz}$ and $h=c_0e^{z}+cz,$
and $h=c_0e^{z}+cz,$ where $k\geq 0$
where $k\geq 0$ is an integer, $c_0$
is an integer, $c_0$ and $c$
and $c$ are constants such that $c_0^2=1,$
are constants such that $c_0^2=1,$ $2c_0(c+k)+c_0=b_2$
$2c_0(c+k)+c_0=b_2$ and $c^2=b_3,$
and $c^2=b_3,$ and $a_{-1},$
and $a_{-1},$ $a_0,$
$a_0,$ $\cdots,$
$\cdots,$ $a_k$
$a_k$ are constants such that $a_0a_k\not =0,$
are constants such that $a_0a_k\not =0,$ $a_{-1}=0$
$a_{-1}=0$ and
(4.37)\begin{equation} 2c_0(k+1-i)a_{i-1}=(2ic+i^2)a_i, \quad i=0,1,\cdots,k; \end{equation}
and
(4.37)\begin{equation} 2c_0(k+1-i)a_{i-1}=(2ic+i^2)a_i, \quad i=0,1,\cdots,k; \end{equation}
(2) if $s=1$
 and $l=4,$
and $l=4,$ then $f=\kappa e^{h},$
then $f=\kappa e^{h},$ $\kappa =\sum _{i=-2}^{k+1}a_ie^{iz}$
$\kappa =\sum _{i=-2}^{k+1}a_ie^{iz}$ and $h=(c_0/2)e^{2z}+cz,$
and $h=(c_0/2)e^{2z}+cz,$ where $k\geq 1$
where $k\geq 1$ is an integer, $c_0$
is an integer, $c_0$ and $c$
and $c$ are constants such that $c_0^2=1,$
are constants such that $c_0^2=1,$ $2c+2k+2=0$
$2c+2k+2=0$ and $c^2=b_3,$
and $c^2=b_3,$ and $a_{-2},$
and $a_{-2},$ $a_{-1},$
$a_{-1},$ $a_0,$
$a_0,$ $\cdots,$
$\cdots,$ $a_{k+1}$
$a_{k+1}$ are constants such that $a_0a_k\not =0,$
are constants such that $a_0a_k\not =0,$ $a_{-2}=a_{-1}=a_{k+1}=0$
$a_{-2}=a_{-1}=a_{k+1}=0$ and
(4.38)\begin{equation} 2c_0(k-i+2)a_{i-2}={-}b_2a_{i-1}+(2ic+i^2)a_i, \quad i=0,1,\cdots,k+1; \end{equation}
and
(4.38)\begin{equation} 2c_0(k-i+2)a_{i-2}={-}b_2a_{i-1}+(2ic+i^2)a_i, \quad i=0,1,\cdots,k+1; \end{equation}
(3) if $s=3$
 and $l=4,$
and $l=4,$ then $f=\kappa e^{h},$
then $f=\kappa e^{h},$ $\kappa =\sum _{i=-2}^{k+1}a_ie^{iz}$
$\kappa =\sum _{i=-2}^{k+1}a_ie^{iz}$ and $h=(c_0/2)e^{2z}+c_1e^{z}+cz,$
and $h=(c_0/2)e^{2z}+c_1e^{z}+cz,$ where $k\geq 0$
where $k\geq 0$ is an integer, $c_0$
is an integer, $c_0$ , $c_1$
, $c_1$ and $c$
and $c$ are constants such that $c_0^2=1,$
are constants such that $c_0^2=1,$ $2c_0c_1=b_2,$
$2c_0c_1=b_2,$ $c^2=b_3$
$c^2=b_3$ and $c_1^2+(2+2c+2k)c_0=0$
and $c_1^2+(2+2c+2k)c_0=0$ , and $a_{-2},$
, and $a_{-2},$ $a_{-1},$
$a_{-1},$ $a_0,$
$a_0,$ $\cdots,$
$\cdots,$ $a_{k+1}$
$a_{k+1}$ are constants such that $a_0a_k\not =0,$
are constants such that $a_0a_k\not =0,$ $a_{-2}=a_{-1}=a_{k+1}=0$
$a_{-2}=a_{-1}=a_{k+1}=0$ and
(4.39)\begin{equation} (2k-2i+4)c_0a_{i-2}=(2c+2i-1)c_1a_{i-1}+(2ic+i^2)a_{i}, \quad i=0,\cdots,k+1. \end{equation}
and
(4.39)\begin{equation} (2k-2i+4)c_0a_{i-2}=(2c+2i-1)c_1a_{i-1}+(2ic+i^2)a_{i}, \quad i=0,\cdots,k+1. \end{equation}
For the convenience to write the recursive formulas in (4.37)–(4.39), we have introduced some extra coefficients $a_{-2}$![]() , $a_{-1}$
, $a_{-1}$![]() , $a_{k+1}$
, $a_{k+1}$![]() , which are all equal to $0$
, which are all equal to $0$![]() .
.
When $s=1$![]() and $l=4$
and $l=4$![]() , since $a_0\not =0$
, since $a_0\not =0$![]() and $a_{k}\not =0$
and $a_{k}\not =0$![]() and $2c+2k+2=0$
and $2c+2k+2=0$![]() , the recursive formulas in (4.38) yield a polynomial equation $P(b_2)=0$
, the recursive formulas in (4.38) yield a polynomial equation $P(b_2)=0$![]() with respect to $b_2$
with respect to $b_2$![]() with coefficients formulated in terms of $c_0$
with coefficients formulated in terms of $c_0$![]() and $k$
and $k$![]() . For example, when $k=1$
. For example, when $k=1$![]() , we have $0=-b_2a_{0}+(2c+1)a_1$
, we have $0=-b_2a_{0}+(2c+1)a_1$![]() and $2c_0a_{0}=-b_2a_{1}$
and $2c_0a_{0}=-b_2a_{1}$![]() , which together with the equation $2c+4=0$
, which together with the equation $2c+4=0$![]() yield $b_2^2-6c_0=0$
yield $b_2^2-6c_0=0$![]() , etc.
, etc.
When $s=3$![]() and $l=4$
and $l=4$![]() , if $2c+1\not =0$
, if $2c+1\not =0$![]() , then we may solve from the first $k+1$
, then we may solve from the first $k+1$![]() equations in (4.39) that $a_{k-1}=P(c)a_k$
equations in (4.39) that $a_{k-1}=P(c)a_k$![]() for some polynomial $P(c)$
for some polynomial $P(c)$![]() with respect to $c$
with respect to $c$![]() with coefficients formulated in terms of $c_0$
with coefficients formulated in terms of $c_0$![]() and $c_1$
and $c_1$![]() . By combining this equation with the equation $2c_0a_{k-1}=(2c+k)c_1a_{k}$
. By combining this equation with the equation $2c_0a_{k-1}=(2c+k)c_1a_{k}$![]() together with the relation $c_1^2+(2+2c+2k) c_0=0$
together with the relation $c_1^2+(2+2c+2k) c_0=0$![]() we may obtain a polynomial equation $P(t)=0$
we may obtain a polynomial equation $P(t)=0$![]() with respect to $t=2c$
with respect to $t=2c$![]() with coefficients independent from $c_0$
with coefficients independent from $c_0$![]() and $c_1$
and $c_1$![]() . For example, when $k=1$
. For example, when $k=1$![]() , we have $0=(2c+1)(c_1a_{0}+a_{1})$
, we have $0=(2c+1)(c_1a_{0}+a_{1})$![]() and $2c_0a_{0}=(2c+3)c_1a_{1}$
and $2c_0a_{0}=(2c+3)c_1a_{1}$![]() , which yield $P(t)=(t+2)(t+5)=0$
, which yield $P(t)=(t+2)(t+5)=0$![]() and thus $2c=-2$
and thus $2c=-2$![]() or $2c=-5$
or $2c=-5$![]() , etc.
, etc.
Proof of theorem 4.4. Suppose that $f$![]() is a nontrivial solution such that $\lambda (f)<\infty$
is a nontrivial solution such that $\lambda (f)<\infty$![]() of equation (4.1). Following the proof of theorem 4.1, we may write $f=\kappa _c e^{h_c}$
of equation (4.1). Following the proof of theorem 4.1, we may write $f=\kappa _c e^{h_c}$![]() , where $\kappa _c=\kappa e^{cz}$
, where $\kappa _c=\kappa e^{cz}$![]() and $g_{c}=h_{c}'$
and $g_{c}=h_{c}'$![]() and then from (4.1) we get equation (4.21). Below we consider three cases: (1) $s=1$
and then from (4.1) we get equation (4.21). Below we consider three cases: (1) $s=1$![]() and $l=2$
and $l=2$![]() ; (2) $s=1$
; (2) $s=1$![]() and $l=4$
and $l=4$![]() ; (3) $s=3$
; (3) $s=3$![]() and $l=4$
and $l=4$![]() .
.
For the first two cases $s=1$![]() and $l=2$
and $l=2$![]() or $s=1$
or $s=1$![]() and $s=4$
and $s=4$![]() , we have $\kappa _c=e^{cz}(\sum _{i=0}^ka_ie^{iz})$
, we have $\kappa _c=e^{cz}(\sum _{i=0}^ka_ie^{iz})$![]() and $h_c=[c_0/(m+1)]e^{(m+1)z}$
and $h_c=[c_0/(m+1)]e^{(m+1)z}$![]() , where $m=0$
, where $m=0$![]() or $m=1$
or $m=1$![]() and $c_0$
and $c_0$![]() is a constant such that $c_0^2=1$
is a constant such that $c_0^2=1$![]() . Moreover, if $m=1$
. Moreover, if $m=1$![]() , then by theorem 1.1 we see $k\geq 1$
, then by theorem 1.1 we see $k\geq 1$![]() . From the proof of theorem 4.1, we have equations (4.26) and (4.28) with $s=1$
. From the proof of theorem 4.1, we have equations (4.26) and (4.28) with $s=1$![]() . When $l=2$
. When $l=2$![]() , since the left-hand side of equation (4.28) is a polynomial in $e^{z}$
, since the left-hand side of equation (4.28) is a polynomial in $e^{z}$![]() of degree $1+k$
of degree $1+k$![]() , all coefficients of this polynomial vanish. Therefore, denoting $a_{-1}=0$
, all coefficients of this polynomial vanish. Therefore, denoting $a_{-1}=0$![]() , we obtain from equation (4.28) that $[2c_0(c+k)+c_0-b_2]a_k=0$
, we obtain from equation (4.28) that $[2c_0(c+k)+c_0-b_2]a_k=0$![]() and
and
Since $a_k\not =0$![]() , we have $2c_0(c+k)+c_0-b_2=0$
, we have $2c_0(c+k)+c_0-b_2=0$![]() and then obtain the recursive formulas in (4.37) by substituting $2c_0c+c_0-b_2=-2c_0k$
and then obtain the recursive formulas in (4.37) by substituting $2c_0c+c_0-b_2=-2c_0k$![]() into the equations in (4.40). When $m=1$
into the equations in (4.40). When $m=1$![]() , we have the recursive formulas in (4.36) with $s=1$
, we have the recursive formulas in (4.36) with $s=1$![]() . Denoting $a_{-2}=a_{-1}=0$
. Denoting $a_{-2}=a_{-1}=0$![]() and $a_{k+1}=0$
and $a_{k+1}=0$![]() , we have the recursive formulas in (4.38).
, we have the recursive formulas in (4.38).
When $s=3$![]() and $l=4$
and $l=4$![]() , we have $\kappa _c=e^{cz}(\sum _{i=0}^ka_ie^{iz})$
, we have $\kappa _c=e^{cz}(\sum _{i=0}^ka_ie^{iz})$![]() and $h_c=(c_0/2)e^{2z}+c_1e^{z}$
and $h_c=(c_0/2)e^{2z}+c_1e^{z}$![]() , where $c_0$
, where $c_0$![]() , $c_1$
, $c_1$![]() are two constants such that $c_0^{2}=1$
are two constants such that $c_0^{2}=1$![]() , $2c_0c_1=b_2$
, $2c_0c_1=b_2$![]() . From the proof of theorem 4.1, we get equation (4.29) with $q=m=1$
. From the proof of theorem 4.1, we get equation (4.29) with $q=m=1$![]() . Similarly as in previous cases, denoting $a_{-2}=a_{-1}=a_{k+1}=0$
. Similarly as in previous cases, denoting $a_{-2}=a_{-1}=a_{k+1}=0$![]() , we finally get the recursive formulas in (4.39). We omit those details.
, we finally get the recursive formulas in (4.39). We omit those details.
By theorem 4.4, we may give a different formulation from the results in [Reference Chiang and Ismail10, theorem 1.6].
Corollary 4.5 Let $s=1$![]() and $l=2$
and $l=2$![]() . Then equation (4.1) admits two linearly independent solutions $f_1$
. Then equation (4.1) admits two linearly independent solutions $f_1$![]() and $f_2$
and $f_2$![]() such that $\max \{\lambda (f_1),\,\lambda (f_2)\}<\infty$
such that $\max \{\lambda (f_1),\,\lambda (f_2)\}<\infty$![]() if and only if there are two distinct nonnegative integers $k_1,\,k_2$
if and only if there are two distinct nonnegative integers $k_1,\,k_2$![]() such that $b_2=\pm (k_1-k_2)$
such that $b_2=\pm (k_1-k_2)$![]() and $4b_3=(k_1+k_2+1)^2$
and $4b_3=(k_1+k_2+1)^2$![]() . In particular, it is possible that $\min \{\lambda (f_1),\,\lambda (f_2)\}=0$
. In particular, it is possible that $\min \{\lambda (f_1),\,\lambda (f_2)\}=0$![]() .
.
Proof of corollary 4.5. Let $f_1$![]() and $f_2$
and $f_2$![]() be two linearly independent solutions of equation (4.1) such that $\max \{\lambda (f_1),\,\lambda (f_2)\}<\infty$
be two linearly independent solutions of equation (4.1) such that $\max \{\lambda (f_1),\,\lambda (f_2)\}<\infty$![]() . Let $c_+$
. Let $c_+$![]() or $c_{-}$
or $c_{-}$![]() be any square-root of $b_3$
be any square-root of $b_3$![]() . By theorem 4.4, we may write $f_1=\kappa _{1}e^{h_{1}}$
. By theorem 4.4, we may write $f_1=\kappa _{1}e^{h_{1}}$![]() and $f_2=\kappa _{2}e^{h_{2}}$
and $f_2=\kappa _{2}e^{h_{2}}$![]() , where $h_{1}=c_0e^{z}+c_+z$
, where $h_{1}=c_0e^{z}+c_+z$![]() and $c_0$
and $c_0$![]() is a constant such that $c_0^2=1$
is a constant such that $c_0^2=1$![]() , $h_{2}=\pm c_0e^{z}+c_{-}z$
, $h_{2}=\pm c_0e^{z}+c_{-}z$![]() , $\kappa _{1}$
, $\kappa _{1}$![]() and $\kappa _2$
and $\kappa _2$![]() are two polynomials in $e^z$
are two polynomials in $e^z$![]() of degrees $k_1$
of degrees $k_1$![]() and $k_2$
and $k_2$![]() , respectively. From the proof of theorem 4.1 we know that $h_{2}=-c_0e^{z}+c_{-}z$
, respectively. From the proof of theorem 4.1 we know that $h_{2}=-c_0e^{z}+c_{-}z$![]() . Since $2c_0(c_++k_1)+c_0=-2c_0(c_{-}+k_2)-c_0=b_2$
. Since $2c_0(c_++k_1)+c_0=-2c_0(c_{-}+k_2)-c_0=b_2$![]() , we see that $c_+=c_{-}$
, we see that $c_+=c_{-}$![]() for otherwise we have $1+k_1+k_2=0$
for otherwise we have $1+k_1+k_2=0$![]() , which is impossible. Letting $c_+=c_{-}=c$
, which is impossible. Letting $c_+=c_{-}=c$![]() , then we have $2c+k_{1}+k_{2}+1=0$
, then we have $2c+k_{1}+k_{2}+1=0$![]() and it follows that $b_2=c_0(k_1-k_2)$
and it follows that $b_2=c_0(k_1-k_2)$![]() . Since $b_2\not =0$
. Since $b_2\not =0$![]() and $b_3=c^2$
and $b_3=c^2$![]() , we have $k_1\not =k_2$
, we have $k_1\not =k_2$![]() and $4b_3=(k_1+k_2+1)^2$
and $4b_3=(k_1+k_2+1)^2$![]() .
.
Conversely, we let $k_1$![]() and $k_2$
and $k_2$![]() be two nonnegative integers such that $2c+k_{1}+k_{2}+1=0$
be two nonnegative integers such that $2c+k_{1}+k_{2}+1=0$![]() , where $c$
, where $c$![]() satisfies $c^2=b_3$
satisfies $c^2=b_3$![]() . We first define $f_1=\kappa _1e^{h_1}$
. We first define $f_1=\kappa _1e^{h_1}$![]() , where $\kappa _1=\sum _{i=-1}^{k_1}a_ie^{iz}$
, where $\kappa _1=\sum _{i=-1}^{k_1}a_ie^{iz}$![]() , $h_{1}=c_0e^{z}+cz$
, $h_{1}=c_0e^{z}+cz$![]() , $k_1\geq 0$
, $k_1\geq 0$![]() is an integer, $c_0$
is an integer, $c_0$![]() satisfies $c_0^2=1$
satisfies $c_0^2=1$![]() and $c_0[2(c+k_1)+1]=b_2$
and $c_0[2(c+k_1)+1]=b_2$![]() , and $a_{-1}$
, and $a_{-1}$![]() , $a_0$
, $a_0$![]() , $\cdots$
, $\cdots$![]() , $a_k$
, $a_k$![]() are constants such that $a_{-1}=0$
are constants such that $a_{-1}=0$![]() and
and
Also, we define $f_2=\kappa _2 e^{h_2}$![]() , where $\kappa _2=\sum _{i=-1}^{k_2}\hat {a}_ie^{iz}$
, where $\kappa _2=\sum _{i=-1}^{k_2}\hat {a}_ie^{iz}$![]() and $h_2=-c_0e^{z}+cz$
and $h_2=-c_0e^{z}+cz$![]() , $k_2\geq 0$
, $k_2\geq 0$![]() is an integer, $c_0$
is an integer, $c_0$![]() satisfies $c_0^2=1$
satisfies $c_0^2=1$![]() and $-c_0[2(c+k_2)+1]=b_2$
and $-c_0[2(c+k_2)+1]=b_2$![]() , and $\hat {a}_{-1}$
, and $\hat {a}_{-1}$![]() , $\hat {a}_0$
, $\hat {a}_0$![]() , $\cdots$
, $\cdots$![]() , $\hat {a}_k$
, $\hat {a}_k$![]() are constants such that $\hat {a}_{-1}=0$
are constants such that $\hat {a}_{-1}=0$![]() and
and
Then by theorem 4.4 we see that $f_1$![]() and $f_2$
and $f_2$![]() are two linearly independent solutions of (4.1) such that $\max \{\lambda (f_1),\,\lambda (f_2)\}<\infty$
are two linearly independent solutions of (4.1) such that $\max \{\lambda (f_1),\,\lambda (f_2)\}<\infty$![]() . Obviously, we may choose one of $k_1$
. Obviously, we may choose one of $k_1$![]() and $k_2$
and $k_2$![]() to be zero and thus $\min \{\lambda (f_1),\,\lambda (f_2)\}=0$
to be zero and thus $\min \{\lambda (f_1),\,\lambda (f_2)\}=0$![]() . We complete the proof.
. We complete the proof.
5. Concluding remarks
The oscillation of certain second-order linear differential equation (1.1) are investigated in this paper. If equation (1.1) with $A(z)$![]() being a linear combination of two exponential type functions admits a nontrivial solution such that $\lambda (f)<\infty$
being a linear combination of two exponential type functions admits a nontrivial solution such that $\lambda (f)<\infty$![]() , by Hadamard's factorization theorem we obtain a Tumura–Clunie type differential equation with coefficients being combinations of functions in $\mathcal {S}$
, by Hadamard's factorization theorem we obtain a Tumura–Clunie type differential equation with coefficients being combinations of functions in $\mathcal {S}$![]() . In § 2, we give the form of entire solutions of the Tumura–Clunie type differential equations. As an application, in § 3 we give a partial answer to an oscillation question concerning equation (3.1) proposed by Ishizaki [Reference Ishizaki19]. In § 4, we consider equation (1.1) for the case $A(z)=e^{lz}+b_2e^{sz}+b_3$
. In § 2, we give the form of entire solutions of the Tumura–Clunie type differential equations. As an application, in § 3 we give a partial answer to an oscillation question concerning equation (3.1) proposed by Ishizaki [Reference Ishizaki19]. In § 4, we consider equation (1.1) for the case $A(z)=e^{lz}+b_2e^{sz}+b_3$![]() , where $l$
, where $l$![]() and $s$
and $s$![]() are two relatively prime integers and $b_2,\,b_3$
are two relatively prime integers and $b_2,\,b_3$![]() are constants such that $b_2\not =0$
are constants such that $b_2\not =0$![]() . The general form of solutions such that $\lambda (f)<\infty$
. The general form of solutions such that $\lambda (f)<\infty$![]() are known. If there are two linearly independent such solutions, we prove that the only possible case is when $l=2$
are known. If there are two linearly independent such solutions, we prove that the only possible case is when $l=2$![]() .
.
By doing straightforward computations, we precisely characterize all solutions such that $\lambda (f)<\infty$![]() of equation (4.1) for the two cases $l=2$
of equation (4.1) for the two cases $l=2$![]() and $l=4$
and $l=4$![]() . Unfortunately, we are unable to include or exclude other possibilities. Although, by using theorems 3.1 and 4.1 together with lemma 4.2, when $l\not =2,\,4$
. Unfortunately, we are unable to include or exclude other possibilities. Although, by using theorems 3.1 and 4.1 together with lemma 4.2, when $l\not =2,\,4$![]() , we may also obtain some recursive formulas as in (4.37), (4.38) and (4.39) for the solutions such that $\lambda (f)<\infty$
, we may also obtain some recursive formulas as in (4.37), (4.38) and (4.39) for the solutions such that $\lambda (f)<\infty$![]() , it is difficult to verify the existence of $b_2$
, it is difficult to verify the existence of $b_2$![]() and $b_3$
and $b_3$![]() satisfying these recursive formulas. We conjecture that equation (4.1) can admit a nontrivial solution $f$
satisfying these recursive formulas. We conjecture that equation (4.1) can admit a nontrivial solution $f$![]() such that $\lambda (f)<\infty$
such that $\lambda (f)<\infty$![]() only when $l=2$
only when $l=2$![]() or $l=4$
or $l=4$![]() . We will study this conjecture further.
. We will study this conjecture further.
Acknowledgments
The author is supported by a Project funded by China Postdoctoral Science Foundation (2020M680334) and the Fundamental Research Funds for the Central Universities (FRF-TP-19-055A1). The author would like to thank professor Yik-man Chiang of the Hong Kong University of Science and Technology for sharing with the author the two references [Reference Chiang and Yu11] and [Reference Kovacic22]. This greatly simplifies the original proof of theorem 4.1. The author also would like to thank the referee for his/her very valuable suggestions and comments.