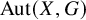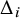Given a countable group G and a faithful G-flow X, we write
![]() $\mathrm {Aut}(X, G)$
for the group of homeomorphisms of X which commute with the G-action. When G is abelian,
$\mathrm {Aut}(X, G)$
for the group of homeomorphisms of X which commute with the G-action. When G is abelian,
![]() $\mathrm {Aut}(X, G)$
contains a natural copy of G resulting from the G-action, but in general this need not be the case. Much is unknown about how the properties of X restrict the complexity of
$\mathrm {Aut}(X, G)$
contains a natural copy of G resulting from the G-action, but in general this need not be the case. Much is unknown about how the properties of X restrict the complexity of
![]() $\mathrm {Aut}(X, G)$
; for instance, Cyr and Kra [Reference Cyr and Kra1] conjecture that when
$\mathrm {Aut}(X, G)$
; for instance, Cyr and Kra [Reference Cyr and Kra1] conjecture that when
![]() $G = \mathbb {Z}$
and
$G = \mathbb {Z}$
and
![]() $X\subseteq 2^{\mathbb {Z}}$
is a minimal,
$X\subseteq 2^{\mathbb {Z}}$
is a minimal,
![]() $0$
-entropy subshift, then
$0$
-entropy subshift, then
![]() $\mathrm {Aut}(X, \mathbb {Z})$
must be amenable. In fact, no counterexample is known even when restricting to any two of the three properties ‘minimal’, ‘
$\mathrm {Aut}(X, \mathbb {Z})$
must be amenable. In fact, no counterexample is known even when restricting to any two of the three properties ‘minimal’, ‘
![]() $0$
-entropy’ or ‘subshift’. In an effort to shed light on this question, Frisch and Tamuz [Reference Frisch and Tamuz3] define a probability measure
$0$
-entropy’ or ‘subshift’. In an effort to shed light on this question, Frisch and Tamuz [Reference Frisch and Tamuz3] define a probability measure
![]() $\mu $
on X to be characteristic if it is
$\mu $
on X to be characteristic if it is
![]() $\mathrm {Aut}(X, G)$
-invariant. They show that
$\mathrm {Aut}(X, G)$
-invariant. They show that
![]() $0$
-entropy subshifts always admit characteristic measures. More recently, Cyr and Kra [Reference Cyr and Kra2] provide several examples of flows which admit characteristic measures for nontrivial reasons, even in cases where
$0$
-entropy subshifts always admit characteristic measures. More recently, Cyr and Kra [Reference Cyr and Kra2] provide several examples of flows which admit characteristic measures for nontrivial reasons, even in cases where
![]() $\mathrm {Aut}(X, G)$
is nonamenable. Frisch and Tamuz asked (Question 1.5, [Reference Frisch and Tamuz3]) whether there exists, for any countable group G, some minimal G-flow without a characteristic measure. We give a strong affirmative answer.
$\mathrm {Aut}(X, G)$
is nonamenable. Frisch and Tamuz asked (Question 1.5, [Reference Frisch and Tamuz3]) whether there exists, for any countable group G, some minimal G-flow without a characteristic measure. We give a strong affirmative answer.
Theorem 0.1. For any countably infinite group G, there is a free minimal G-flow X so that X does not admit a characteristic measure. More precisely, there is a free
![]() $(G\times F_2)$
-flow X which is minimal as a G-flow and with no
$(G\times F_2)$
-flow X which is minimal as a G-flow and with no
![]() $F_2$
-invariant measure.
$F_2$
-invariant measure.
We remark that the X we construct will not in general be a subshift.
Over the course of proving Theorem 0.1, there are two main difficulties to overcome. The first difficulty is a collection of dynamical problems we refer to as minimal subdynamics. The general template of these questions is as follows.
Question 0.2. Given a countably infinite group
![]() $\Gamma $
and a collection
$\Gamma $
and a collection
![]() $\{\Delta _i: i\in I\}$
of infinite subgroups of
$\{\Delta _i: i\in I\}$
of infinite subgroups of
![]() $\Gamma $
, when is there a faithful (or essentially free, or free) minimal
$\Gamma $
, when is there a faithful (or essentially free, or free) minimal
![]() $\Gamma $
-flow for which the action of each
$\Gamma $
-flow for which the action of each
![]() $\Delta _i$
is also minimal? Is there a natural space of actions in which such flows are generic?
$\Delta _i$
is also minimal? Is there a natural space of actions in which such flows are generic?
In [Reference Zucker8], the author showed that this was possible in the case
![]() $\Gamma = G\times H$
and
$\Gamma = G\times H$
and
![]() $\Delta = G$
for any countably infinite groups G and H. We manage to strengthen this result considerably.
$\Delta = G$
for any countably infinite groups G and H. We manage to strengthen this result considerably.
Theorem 0.3. For any countably infinite group
![]() $\Gamma $
and any collection
$\Gamma $
and any collection
![]() $\{\Delta _n: n\in \mathbb {N}\}$
of infinite normal subgroups of
$\{\Delta _n: n\in \mathbb {N}\}$
of infinite normal subgroups of
![]() $\Gamma $
, there is a free
$\Gamma $
, there is a free
![]() $\Gamma $
-flow which is minimal as a
$\Gamma $
-flow which is minimal as a
![]() $\Delta _n$
-flow for every
$\Delta _n$
-flow for every
![]() $n\in \mathbb {N}$
.
$n\in \mathbb {N}$
.
In fact, what we show when proving Theorem 0.3 is considerably stronger. Recall that given a countably infinite group
![]() $\Gamma $
, a subshift
$\Gamma $
, a subshift
![]() $X\subseteq 2^\Gamma $
is strongly irreducible if there is some finite symmetric
$X\subseteq 2^\Gamma $
is strongly irreducible if there is some finite symmetric
![]() $D\subseteq \Gamma $
so that whenever
$D\subseteq \Gamma $
so that whenever
![]() $S_0, S_1\subseteq \Gamma $
satisfy
$S_0, S_1\subseteq \Gamma $
satisfy
![]() $DS_0\cap S_1 = \emptyset $
(i.e.,
$DS_0\cap S_1 = \emptyset $
(i.e.,
![]() $S_0$
and
$S_0$
and
![]() $S_1$
are D-apart), then for any
$S_1$
are D-apart), then for any
![]() $x_0, x_1\in X$
, there is
$x_0, x_1\in X$
, there is
![]() $y\in X$
with
$y\in X$
with
![]() $y|_{S_i} = x_i|_{S_i}$
for each
$y|_{S_i} = x_i|_{S_i}$
for each
![]() $i< 2$
. Write
$i< 2$
. Write
![]() $\mathcal {S}$
for the set of strongly irreducible subshifts, and write
$\mathcal {S}$
for the set of strongly irreducible subshifts, and write
![]() $\overline {\mathcal {S}}$
for its Vietoris closure. Frisch, Tamuz and Vahidi-Ferdowsi [Reference Frisch, Tamuz and Ferdowsi5] show that in
$\overline {\mathcal {S}}$
for its Vietoris closure. Frisch, Tamuz and Vahidi-Ferdowsi [Reference Frisch, Tamuz and Ferdowsi5] show that in
![]() $\overline {\mathcal {S}}$
, the minimal subshifts form a dense
$\overline {\mathcal {S}}$
, the minimal subshifts form a dense
![]() $G_\delta $
subset. In our proof of Theorem 0.3, we show that the shifts in
$G_\delta $
subset. In our proof of Theorem 0.3, we show that the shifts in
![]() $\overline {\mathcal {S}}$
which are
$\overline {\mathcal {S}}$
which are
![]() $\Delta _n$
-minimal for each
$\Delta _n$
-minimal for each
![]() $n\in \mathbb {N}$
also form a dense
$n\in \mathbb {N}$
also form a dense
![]() $G_\delta $
subset.
$G_\delta $
subset.
This brings us to the second main difficulty in the proof of Theorem 0.1. Using this stronger form of Theorem 0.3, one could easily prove Theorem 0.1 by finding a strongly irreducible
![]() $F_2$
-subshift which does not admit an invariant measure. This would imply the existence of a strongly irreducible
$F_2$
-subshift which does not admit an invariant measure. This would imply the existence of a strongly irreducible
![]() $(G\times F_2)$
-subshift without an
$(G\times F_2)$
-subshift without an
![]() $F_2$
-invariant measure. As not admitting an
$F_2$
-invariant measure. As not admitting an
![]() $F_2$
-invariant measure is a Vietoris-open condition, the genericity of G-minimal subshifts would then be enough to obtain the desired result. Unfortunately, whether such a strongly irreducible subshift can exist (for any nonamenable group) is an open question. To overcome this, we introduce a flexible weakening of the notion of a strongly irreducible shift.
$F_2$
-invariant measure is a Vietoris-open condition, the genericity of G-minimal subshifts would then be enough to obtain the desired result. Unfortunately, whether such a strongly irreducible subshift can exist (for any nonamenable group) is an open question. To overcome this, we introduce a flexible weakening of the notion of a strongly irreducible shift.
The paper is organized as follows. Section
![]() $1$
is a very brief background section on subsets of groups, subshifts and strong irreducibility. Section
$1$
is a very brief background section on subsets of groups, subshifts and strong irreducibility. Section
![]() $2$
introduces the notion of a UFO, a useful combinatorial gadget for constructing shifts where subgroups act minimally; Theorem 0.3 answers Question 3.6 from [Reference Zucker8]. Section
$2$
introduces the notion of a UFO, a useful combinatorial gadget for constructing shifts where subgroups act minimally; Theorem 0.3 answers Question 3.6 from [Reference Zucker8]. Section
![]() $3$
introduces the notion of
$3$
introduces the notion of
![]() $\mathcal {B}$
-irreduciblity for any group H, where
$\mathcal {B}$
-irreduciblity for any group H, where
![]() $\mathcal {B}\subseteq \mathcal {P}_f(H)$
is a right-invariant collection of finite subsets of H. When
$\mathcal {B}\subseteq \mathcal {P}_f(H)$
is a right-invariant collection of finite subsets of H. When
![]() $H = F_2$
, we will be interested in the case when
$H = F_2$
, we will be interested in the case when
![]() $\mathcal {B}$
is the collection of finite subsets of
$\mathcal {B}$
is the collection of finite subsets of
![]() $F_2$
which are connected in the standard left Cayley graph. Section 4 gives the proof of Theorem 0.1.
$F_2$
which are connected in the standard left Cayley graph. Section 4 gives the proof of Theorem 0.1.
1. Background
Let
![]() $\Gamma $
be a countably infinite group. Given
$\Gamma $
be a countably infinite group. Given
![]() $U, S\subseteq \Gamma $
with U finite, then we call S a (one-sided) U-spaced set if for every
$U, S\subseteq \Gamma $
with U finite, then we call S a (one-sided) U-spaced set if for every
![]() $g\neq h\in S$
we have
$g\neq h\in S$
we have
![]() $h\not \in Ug$
, and we call S a U-syndetic set if
$h\not \in Ug$
, and we call S a U-syndetic set if
![]() $US = \Gamma $
. A maximal U-spaced set is simply a U-spaced set which is maximal under inclusion. We remark that if S is a maximal U-spaced set, then S is
$US = \Gamma $
. A maximal U-spaced set is simply a U-spaced set which is maximal under inclusion. We remark that if S is a maximal U-spaced set, then S is
![]() $(U\cup U^{-1})$
-syndetic. We say that sets
$(U\cup U^{-1})$
-syndetic. We say that sets
![]() $S, T\subseteq \Gamma $
are (one-sided) U-apart if
$S, T\subseteq \Gamma $
are (one-sided) U-apart if
![]() $US\cap T = \emptyset $
and
$US\cap T = \emptyset $
and
![]() $S\cap UT = \emptyset $
. Notice that much of this discussion simplifies when U is symmetric, so we will often assume this. Also, notice that the properties of being U-spaced, maximal U-spaced, U-syndetic and U-apart are all right invariant.
$S\cap UT = \emptyset $
. Notice that much of this discussion simplifies when U is symmetric, so we will often assume this. Also, notice that the properties of being U-spaced, maximal U-spaced, U-syndetic and U-apart are all right invariant.
If A is a finite set or alphabet, then
![]() $\Gamma $
acts on
$\Gamma $
acts on
![]() $A^\Gamma $
by right shift, where given
$A^\Gamma $
by right shift, where given
![]() $x\in A^\Gamma $
and
$x\in A^\Gamma $
and
![]() $g, h\in \Gamma $
, we have
$g, h\in \Gamma $
, we have
![]() $(g{\cdot }x)(h) = x(hg)$
. A subshift of
$(g{\cdot }x)(h) = x(hg)$
. A subshift of
![]() $A^\Gamma $
is a nonempty, closed,
$A^\Gamma $
is a nonempty, closed,
![]() $\Gamma $
-invariant subset. Let
$\Gamma $
-invariant subset. Let
![]() $\mathrm {Sub}(A^\Gamma )$
denote the space of subshifts of
$\mathrm {Sub}(A^\Gamma )$
denote the space of subshifts of
![]() $A^\Gamma $
endowed with the Vietoris topology. This topology can be described as follows. Given
$A^\Gamma $
endowed with the Vietoris topology. This topology can be described as follows. Given
![]() $X\subseteq A^\Gamma $
and a finite
$X\subseteq A^\Gamma $
and a finite
![]() $U\subseteq \Gamma $
, the set of U-patterns of X is the set
$U\subseteq \Gamma $
, the set of U-patterns of X is the set
![]() $P_U(X) = \{x|_U: x\in X\}\subseteq A^U$
. Then the typical basic open neighborhood of
$P_U(X) = \{x|_U: x\in X\}\subseteq A^U$
. Then the typical basic open neighborhood of
![]() $X\in \mathrm {Sub}(A^\Gamma )$
is the set
$X\in \mathrm {Sub}(A^\Gamma )$
is the set
![]() $N_U(X):= \{Y\in \mathrm {Sub}(A^\Gamma ): P_U(Y) = P_U(X)\}$
, where U ranges over finite subsets of
$N_U(X):= \{Y\in \mathrm {Sub}(A^\Gamma ): P_U(Y) = P_U(X)\}$
, where U ranges over finite subsets of
![]() $\Gamma $
.
$\Gamma $
.
A subshift
![]() $X\subseteq A^\Gamma $
is U-irreducible if for any
$X\subseteq A^\Gamma $
is U-irreducible if for any
![]() $x_0, x_1\in X$
and any
$x_0, x_1\in X$
and any
![]() $S_0, S_1\subseteq \Gamma $
which are U-apart, there is
$S_0, S_1\subseteq \Gamma $
which are U-apart, there is
![]() $y\in X$
with
$y\in X$
with
![]() $y|_{S_i} = x_i|_{S_i}$
for each
$y|_{S_i} = x_i|_{S_i}$
for each
![]() $i< 2$
. If X is U-irreducible and
$i< 2$
. If X is U-irreducible and
![]() $V\supseteq U$
is finite, then X is also V-irreducible. We call X strongly irreducible if there is some finite
$V\supseteq U$
is finite, then X is also V-irreducible. We call X strongly irreducible if there is some finite
![]() $U\subseteq \Gamma $
with
$U\subseteq \Gamma $
with
![]() $X\ U$
-irreducible. By enlarging U if needed, we can always assume U is symmetric. Let
$X\ U$
-irreducible. By enlarging U if needed, we can always assume U is symmetric. Let
![]() $\mathcal {S}(A^\Gamma )\subseteq \mathrm {Sub}(A^\Gamma )$
denote the set of strongly irreducible subshifts of
$\mathcal {S}(A^\Gamma )\subseteq \mathrm {Sub}(A^\Gamma )$
denote the set of strongly irreducible subshifts of
![]() $A^\Gamma $
, and let
$A^\Gamma $
, and let
![]() $\overline {\mathcal {S}}(A^\Gamma )$
denote the closure of this set in the Vietoris topology.
$\overline {\mathcal {S}}(A^\Gamma )$
denote the closure of this set in the Vietoris topology.
More generally, if
![]() $2^{\mathbb {N}}$
denotes Cantor space, then
$2^{\mathbb {N}}$
denotes Cantor space, then
![]() $\Gamma $
acts on
$\Gamma $
acts on
![]() $(2^{\mathbb {N}})^\Gamma $
by right shift exactly as above. If
$(2^{\mathbb {N}})^\Gamma $
by right shift exactly as above. If
![]() $k< \omega $
, we let
$k< \omega $
, we let
![]() $\pi _k\colon 2^{\mathbb {N}}\to 2^k$
denote the restriction to the first k entries. This induces a factor map
$\pi _k\colon 2^{\mathbb {N}}\to 2^k$
denote the restriction to the first k entries. This induces a factor map
![]() $\tilde {\pi }_k\colon (2^{\mathbb {N}})^\Gamma \to (2^k)^\Gamma $
given by
$\tilde {\pi }_k\colon (2^{\mathbb {N}})^\Gamma \to (2^k)^\Gamma $
given by
![]() $\tilde {\pi }_k(x)(g) = \pi _k(x(g))$
; we also obtain a map
$\tilde {\pi }_k(x)(g) = \pi _k(x(g))$
; we also obtain a map
![]() $\overline {\pi }_k\colon \mathrm {Sub}((2^{\mathbb {N}})^\Gamma )\to \mathrm {Sub}((2^k)^\Gamma )$
(where
$\overline {\pi }_k\colon \mathrm {Sub}((2^{\mathbb {N}})^\Gamma )\to \mathrm {Sub}((2^k)^\Gamma )$
(where
![]() $2^k$
is viewed as a finite alphabet) given by
$2^k$
is viewed as a finite alphabet) given by
![]() $\overline {\pi }_k(X) = \tilde {\pi }_k[X]$
. The Vietoris topology on
$\overline {\pi }_k(X) = \tilde {\pi }_k[X]$
. The Vietoris topology on
![]() $\mathrm {Sub}((2^{\mathbb {N}})^\Gamma )$
is the coarsest topology making every such
$\mathrm {Sub}((2^{\mathbb {N}})^\Gamma )$
is the coarsest topology making every such
![]() $\overline {\pi }_k$
continuous. We call a subflow
$\overline {\pi }_k$
continuous. We call a subflow
![]() $X\subseteq (2^{\mathbb {N}})^\Gamma $
strongly irreducible if for every
$X\subseteq (2^{\mathbb {N}})^\Gamma $
strongly irreducible if for every
![]() $k< \omega $
, the subshift
$k< \omega $
, the subshift
![]() $\overline {\pi }_k(X)\subseteq (2^k)^\Gamma $
is strongly irreducible in the ordinary sense. We let
$\overline {\pi }_k(X)\subseteq (2^k)^\Gamma $
is strongly irreducible in the ordinary sense. We let
![]() $\mathcal {S}((2^{\mathbb {N}})^\Gamma )\subseteq \mathrm {Sub}((2^{\mathbb {N}})^\Gamma )$
denote the set of strongly irreducible subflows of
$\mathcal {S}((2^{\mathbb {N}})^\Gamma )\subseteq \mathrm {Sub}((2^{\mathbb {N}})^\Gamma )$
denote the set of strongly irreducible subflows of
![]() $(2^{\mathbb {N}})^\Gamma $
, and we let
$(2^{\mathbb {N}})^\Gamma $
, and we let
![]() $\overline {\mathcal {S}}((2^{\mathbb {N}})^\Gamma )$
denote its Vietoris closure.
$\overline {\mathcal {S}}((2^{\mathbb {N}})^\Gamma )$
denote its Vietoris closure.
The idea of considering the closure of the strongly irreducible shifts has it roots in [Reference Frisch and Tamuz4]. This is made more explicit in [Reference Frisch, Tamuz and Ferdowsi5], where it is shown that in
![]() $\overline {\mathcal {S}}(A^\Gamma )$
, the minimal subflows form a dense
$\overline {\mathcal {S}}(A^\Gamma )$
, the minimal subflows form a dense
![]() $G_\delta $
subset. More or less the same argument shows that the same holds in
$G_\delta $
subset. More or less the same argument shows that the same holds in
![]() $\overline {\mathcal {S}}((2^{\mathbb {N}})^\Gamma )$
(see [Reference Glasner, Tsankov, Weiss and Zucker6]). Recall that a
$\overline {\mathcal {S}}((2^{\mathbb {N}})^\Gamma )$
(see [Reference Glasner, Tsankov, Weiss and Zucker6]). Recall that a
![]() $\Gamma $
-flow X is free if for every
$\Gamma $
-flow X is free if for every
![]() $g\in \Gamma \setminus \{1_\Gamma \}$
and every
$g\in \Gamma \setminus \{1_\Gamma \}$
and every
![]() $x\in X$
, we have
$x\in X$
, we have
![]() $gx\neq x$
. The main reason for considering a Cantor space alphabet is the following result, which need not be true for finite alphabets.
$gx\neq x$
. The main reason for considering a Cantor space alphabet is the following result, which need not be true for finite alphabets.
Proposition 1.1. In
![]() $\overline {\mathcal {S}}((2^{\mathbb {N}})^\Gamma )$
, the free flows form a dense
$\overline {\mathcal {S}}((2^{\mathbb {N}})^\Gamma )$
, the free flows form a dense
![]() $G_\delta $
subset.
$G_\delta $
subset.
Proof. Fixing
![]() $g\in \Gamma $
, the set
$g\in \Gamma $
, the set
![]() $\{X\in \mathrm {Sub}((2^{\mathbb {N}})^\Gamma ): \forall x\in X\, (gx\neq x)\}$
is open; indeed, if
$\{X\in \mathrm {Sub}((2^{\mathbb {N}})^\Gamma ): \forall x\in X\, (gx\neq x)\}$
is open; indeed, if
![]() $X_n\to X$
is a convergent sequence in
$X_n\to X$
is a convergent sequence in
![]() $\mathrm {Sub}((2^{\mathbb {N}})^\Gamma )$
and
$\mathrm {Sub}((2^{\mathbb {N}})^\Gamma )$
and
![]() $x_n\in X_n$
is a point fixed by g, then passing to a subsequence, we may suppose
$x_n\in X_n$
is a point fixed by g, then passing to a subsequence, we may suppose
![]() $x_n\to x\in X$
, and we have
$x_n\to x\in X$
, and we have
![]() $gx = x$
. Intersecting over all
$gx = x$
. Intersecting over all
![]() $g\in \Gamma \setminus \{1_\Gamma \}$
, we see that freeness is a
$g\in \Gamma \setminus \{1_\Gamma \}$
, we see that freeness is a
![]() $G_\delta $
condition.
$G_\delta $
condition.
Thus, it remains to show that freeness is dense in
![]() $\overline {\mathcal {S}}((2^{\mathbb {N}})^\Gamma )$
. To that end, we fix
$\overline {\mathcal {S}}((2^{\mathbb {N}})^\Gamma )$
. To that end, we fix
![]() $g\in \Gamma \setminus \{1_\Gamma \}$
and show that the set of shifts in
$g\in \Gamma \setminus \{1_\Gamma \}$
and show that the set of shifts in
![]() $\mathcal {S}((2^{\mathbb {N}})^\Gamma )$
where g acts freely is dense. Fix
$\mathcal {S}((2^{\mathbb {N}})^\Gamma )$
where g acts freely is dense. Fix
![]() $X\in \mathcal {S}((2^{\mathbb {N}})^\Gamma )$
,
$X\in \mathcal {S}((2^{\mathbb {N}})^\Gamma )$
,
![]() $k< \omega $
and a finite
$k< \omega $
and a finite
![]() $U\subseteq \Gamma $
; so a typical open set in
$U\subseteq \Gamma $
; so a typical open set in
![]() $\mathcal {S}((2^{\mathbb {N}})^\Gamma )$
has the form
$\mathcal {S}((2^{\mathbb {N}})^\Gamma )$
has the form
![]() $\{X'\in \mathcal {S}((2^{\mathbb {N}})^\Gamma ): P_U(\overline {\pi }_k(X')) = P_U(\overline {\pi }_k(X))\}$
. We want to produce
$\{X'\in \mathcal {S}((2^{\mathbb {N}})^\Gamma ): P_U(\overline {\pi }_k(X')) = P_U(\overline {\pi }_k(X))\}$
. We want to produce
![]() $Y\in \mathrm {Sub}((2^{\mathbb {N}})^\Gamma )$
which is strongly irreducible, g-free and with
$Y\in \mathrm {Sub}((2^{\mathbb {N}})^\Gamma )$
which is strongly irreducible, g-free and with
![]() $P_U(\overline {\pi }_k(Y)) = P_U(\overline {\pi }_k(X))$
. In fact, we will produce such a Y with
$P_U(\overline {\pi }_k(Y)) = P_U(\overline {\pi }_k(X))$
. In fact, we will produce such a Y with
![]() $\overline {\pi }_k(Y) = \overline {\pi }_k(X)$
.
$\overline {\pi }_k(Y) = \overline {\pi }_k(X)$
.
Let
![]() $D\subseteq \Gamma $
be a finite symmetric set containing g and
$D\subseteq \Gamma $
be a finite symmetric set containing g and
![]() $1_\Gamma $
. Setting
$1_\Gamma $
. Setting
![]() $m = |D|$
, consider the subshift
$m = |D|$
, consider the subshift
![]() $\mathrm {Color}(D, m)\subseteq m^\Gamma $
defined by
$\mathrm {Color}(D, m)\subseteq m^\Gamma $
defined by
A greedy coloring argument shows that
![]() $\mathrm {Color}(D, m)$
is nonempty and D-irreducible. Moreover, g acts freely on
$\mathrm {Color}(D, m)$
is nonempty and D-irreducible. Moreover, g acts freely on
![]() $\mathrm {Color}(D, m)$
. Inject m into
$\mathrm {Color}(D, m)$
. Inject m into
![]() $2^{\{k,\ldots ,\ell -1\}}$
for some
$2^{\{k,\ldots ,\ell -1\}}$
for some
![]() $\ell> k$
and identify
$\ell> k$
and identify
![]() $\mathrm {Color}(D, m)$
as a subflow of
$\mathrm {Color}(D, m)$
as a subflow of
![]() $(2^{\{k,\ldots ,\ell -1\}})^\Gamma $
. Then
$(2^{\{k,\ldots ,\ell -1\}})^\Gamma $
. Then
![]() $Y:= \overline {\pi }_k(X)\times \mathrm {Color}(D, m)\subseteq (2^\ell )^\Gamma \subseteq (2^{\mathbb {N}})^\Gamma $
, where the last inclusion can be formed by adding strings of zeros to the end. Then Y is strongly irreducible, g-free and
$Y:= \overline {\pi }_k(X)\times \mathrm {Color}(D, m)\subseteq (2^\ell )^\Gamma \subseteq (2^{\mathbb {N}})^\Gamma $
, where the last inclusion can be formed by adding strings of zeros to the end. Then Y is strongly irreducible, g-free and
![]() $\overline {\pi }_k(Y) = \overline {\pi }_k(X)$
.
$\overline {\pi }_k(Y) = \overline {\pi }_k(X)$
.
2. UFOs and minimal subdynamics
Much of the construction will require us to reason about the product group
![]() $G\times F_2$
. So for the time being, fix countably infinite groups
$G\times F_2$
. So for the time being, fix countably infinite groups
![]() $\Delta \subseteq \Gamma $
. For our purposes,
$\Delta \subseteq \Gamma $
. For our purposes,
![]() $\Gamma $
will be
$\Gamma $
will be
![]() $G\times F_2$
, and
$G\times F_2$
, and
![]() $\Delta $
will be G, where we identify G with a subgroup of
$\Delta $
will be G, where we identify G with a subgroup of
![]() $G\times F_2$
in the obvious way. However, for this subsection, we will reason more generally.
$G\times F_2$
in the obvious way. However, for this subsection, we will reason more generally.
Definition 2.1. Let
![]() $\Delta \subseteq \Gamma $
be countably infinite groups. A finite subset
$\Delta \subseteq \Gamma $
be countably infinite groups. A finite subset
![]() $U\subseteq \Gamma $
is called a
$U\subseteq \Gamma $
is called a
![]() $(\Gamma , \Delta )$
-UFO if for any maximal U-spaced set
$(\Gamma , \Delta )$
-UFO if for any maximal U-spaced set
![]() $S\subseteq \Gamma $
, we have that S meets every right coset of
$S\subseteq \Gamma $
, we have that S meets every right coset of
![]() $\Delta $
in
$\Delta $
in
![]() $\Gamma $
.
$\Gamma $
.
We say that the inclusion of groups
![]() $\Delta \subseteq \Gamma $
admits UFOs if for every finite
$\Delta \subseteq \Gamma $
admits UFOs if for every finite
![]() $U\subseteq \Gamma $
, there is a finite
$U\subseteq \Gamma $
, there is a finite
![]() $V\subseteq \Gamma $
with
$V\subseteq \Gamma $
with
![]() $V\supseteq U$
which is a
$V\supseteq U$
which is a
![]() $(\Gamma , \Delta )$
-UFO.
$(\Gamma , \Delta )$
-UFO.
As a word of caution, we note that the property of being a
![]() $(\Gamma , \Delta )$
-UFO is not upwards closed.
$(\Gamma , \Delta )$
-UFO is not upwards closed.
The terminology comes from considering the case of a product group, that is,
![]() $\Gamma = \mathbb {Z}\times \mathbb {Z}$
and
$\Gamma = \mathbb {Z}\times \mathbb {Z}$
and
![]() $\Delta = \mathbb {Z}\times \{0\}$
. Figure 1 depicts a typical UFO subset of
$\Delta = \mathbb {Z}\times \{0\}$
. Figure 1 depicts a typical UFO subset of
![]() $\mathbb {Z}\times \mathbb {Z}$
.
$\mathbb {Z}\times \mathbb {Z}$
.

Figure 1 Sighting in Roswell; a
![]() $(\mathbb {Z}\times \mathbb {Z}, \mathbb {Z}\times \{0\})$
-UFO subset of
$(\mathbb {Z}\times \mathbb {Z}, \mathbb {Z}\times \{0\})$
-UFO subset of
![]() $\mathbb {Z}\times \mathbb {Z}$
.
$\mathbb {Z}\times \mathbb {Z}$
.
Proposition 2.2. Let
![]() $\Delta $
be a subgroup of
$\Delta $
be a subgroup of
![]() $\Gamma $
. If
$\Gamma $
. If
![]() $|\bigcap _{u \in U} u \Delta u^{-1}|$
is infinite for every finite set
$|\bigcap _{u \in U} u \Delta u^{-1}|$
is infinite for every finite set
![]() $U \subseteq \Gamma $
, then
$U \subseteq \Gamma $
, then
![]() $\Delta \subseteq \Gamma $
admits UFOs. In particular, if
$\Delta \subseteq \Gamma $
admits UFOs. In particular, if
![]() $\Delta $
contains an infinite subgroup that is normal in
$\Delta $
contains an infinite subgroup that is normal in
![]() $\Gamma $
, then
$\Gamma $
, then
![]() $\Delta \subseteq \Gamma $
admits UFOs.
$\Delta \subseteq \Gamma $
admits UFOs.
Proof. We prove the contrapositive. So assume that
![]() $\Delta \subseteq \Gamma $
does not admit UFOs. Let
$\Delta \subseteq \Gamma $
does not admit UFOs. Let
![]() $U \subseteq \Gamma $
be a finite symmetric set such that no finite
$U \subseteq \Gamma $
be a finite symmetric set such that no finite
![]() $V \subseteq \Gamma $
containing U is a
$V \subseteq \Gamma $
containing U is a
![]() $(\Gamma , \Delta )$
-UFO. Let
$(\Gamma , \Delta )$
-UFO. Let
![]() $D \subseteq \Delta $
be finite, symmetric and contain the identity. It will suffice to show that
$D \subseteq \Delta $
be finite, symmetric and contain the identity. It will suffice to show that
![]() $C = \bigcap _{u \in U} u D u^{-1}$
satisfies
$C = \bigcap _{u \in U} u D u^{-1}$
satisfies
![]() $|C| \leq |U|$
.
$|C| \leq |U|$
.
Set
![]() $V = U \cup D^2$
. Since V is not a
$V = U \cup D^2$
. Since V is not a
![]() $(\Gamma , \Delta )$
-UFO, there is a maximal V-spaced set
$(\Gamma , \Delta )$
-UFO, there is a maximal V-spaced set
![]() $S \subseteq \Gamma $
and
$S \subseteq \Gamma $
and
![]() $g \in \Gamma $
with
$g \in \Gamma $
with
![]() $S \cap \Delta g = \varnothing $
. Since S is V-spaced and
$S \cap \Delta g = \varnothing $
. Since S is V-spaced and
![]() $u^{-1} C^2 u \subseteq D^2 \subseteq V$
, the set
$u^{-1} C^2 u \subseteq D^2 \subseteq V$
, the set
![]() $C_u = (u S) \cap (C g)$
is
$C_u = (u S) \cap (C g)$
is
![]() $C^2$
-spaced for every
$C^2$
-spaced for every
![]() $u \in U$
. Of course, any
$u \in U$
. Of course, any
![]() $C^2$
-spaced subset of
$C^2$
-spaced subset of
![]() $C g$
is empty or a singleton, so
$C g$
is empty or a singleton, so
![]() $|C_u| \leq 1$
for each
$|C_u| \leq 1$
for each
![]() $u \in U$
. On the other hand, since S is maximal we have
$u \in U$
. On the other hand, since S is maximal we have
![]() $V S = \Gamma $
, and since
$V S = \Gamma $
, and since
![]() $S \cap \Delta g = \varnothing $
we must have
$S \cap \Delta g = \varnothing $
we must have
![]() $C g \subseteq U S$
. Therefore,
$C g \subseteq U S$
. Therefore,
![]() $|C| = |C g| = \sum _{u \in U} |C_u| \leq |U|$
.
$|C| = |C g| = \sum _{u \in U} |C_u| \leq |U|$
.
In the spaces
![]() $\overline {\mathcal {S}}(k^\Gamma )$
and
$\overline {\mathcal {S}}(k^\Gamma )$
and
![]() $\overline {\mathcal {S}}((2^{\mathbb {N}})^\Gamma )$
, the minimal flows form a dense
$\overline {\mathcal {S}}((2^{\mathbb {N}})^\Gamma )$
, the minimal flows form a dense
![]() $G_\delta $
. However, when
$G_\delta $
. However, when
![]() $\Delta \subseteq \Gamma $
is a subgroup, we can ask about the properties of members of
$\Delta \subseteq \Gamma $
is a subgroup, we can ask about the properties of members of
![]() $\overline {\mathcal {S}}(k^\Gamma )$
and
$\overline {\mathcal {S}}(k^\Gamma )$
and
![]() $\overline {\mathcal {S}}((2^{\mathbb {N}})^\Gamma )$
viewed as
$\overline {\mathcal {S}}((2^{\mathbb {N}})^\Gamma )$
viewed as
![]() $\Delta $
-flows.
$\Delta $
-flows.
Definition 2.3. Given a subshift
![]() $X\subseteq k^\Gamma $
and a finite
$X\subseteq k^\Gamma $
and a finite
![]() $E\subseteq \Gamma $
, we say that X is
$E\subseteq \Gamma $
, we say that X is
![]() $(\Delta , E)$
-minimal if for every
$(\Delta , E)$
-minimal if for every
![]() $x\in X$
and every
$x\in X$
and every
![]() $p\in P_E(X)$
, there is
$p\in P_E(X)$
, there is
![]() $g\in \Delta $
with
$g\in \Delta $
with
![]() $(gx)|_E = p$
. Given a subflow
$(gx)|_E = p$
. Given a subflow
![]() $X\subseteq (2^{\mathbb {N}})^\Gamma $
and
$X\subseteq (2^{\mathbb {N}})^\Gamma $
and
![]() $n\in \mathbb {N}$
, we say that X is
$n\in \mathbb {N}$
, we say that X is
![]() $(\Delta , E, n)$
-minimal if
$(\Delta , E, n)$
-minimal if
![]() $\overline {\pi }_n(X)\subseteq (2^n)^\Gamma $
is
$\overline {\pi }_n(X)\subseteq (2^n)^\Gamma $
is
![]() $(\Delta , E)$
-minimal. When
$(\Delta , E)$
-minimal. When
![]() $\Delta = \Gamma $
, we simply say that X is E-minimal or
$\Delta = \Gamma $
, we simply say that X is E-minimal or
![]() $(E, n)$
-minimal.
$(E, n)$
-minimal.
The set of
![]() $(\Delta , E)$
-minimal flows is open in
$(\Delta , E)$
-minimal flows is open in
![]() $\mathrm {Sub}(k^\Gamma )$
, and
$\mathrm {Sub}(k^\Gamma )$
, and
![]() $X\subseteq k^\Gamma $
is minimal as a
$X\subseteq k^\Gamma $
is minimal as a
![]() $\Delta $
-flow iff it is
$\Delta $
-flow iff it is
![]() $(\Delta , E)$
-minimal for every finite
$(\Delta , E)$
-minimal for every finite
![]() $E\subseteq \Gamma $
. Similarly, the set of
$E\subseteq \Gamma $
. Similarly, the set of
![]() $(\Delta , E, n)$
-minimal flows is open in
$(\Delta , E, n)$
-minimal flows is open in
![]() $\mathrm {Sub}((2^{\mathbb {N}})^\Gamma )$
, and
$\mathrm {Sub}((2^{\mathbb {N}})^\Gamma )$
, and
![]() $X\subseteq (2^{\mathbb {N}})^\Gamma $
is minimal as a
$X\subseteq (2^{\mathbb {N}})^\Gamma $
is minimal as a
![]() $\Delta $
-flow iff it is
$\Delta $
-flow iff it is
![]() $(\Delta , E, n)$
minimal for every finite
$(\Delta , E, n)$
minimal for every finite
![]() $E\subseteq \Gamma $
and every
$E\subseteq \Gamma $
and every
![]() $n\in \mathbb {N}$
.
$n\in \mathbb {N}$
.
In the proof of Proposition 2.4, it will be helpful to extend conventions about the shift action to subsets of
![]() $\Gamma $
. If
$\Gamma $
. If
![]() $U\subseteq \Gamma $
,
$U\subseteq \Gamma $
,
![]() $g\in G$
and
$g\in G$
and
![]() $p\in k^U$
, we write
$p\in k^U$
, we write
![]() $g{\cdot }p\in k^{Ug^{-1}}$
for the function where given
$g{\cdot }p\in k^{Ug^{-1}}$
for the function where given
![]() $h\in Ug^{-1}$
, we have
$h\in Ug^{-1}$
, we have
![]() $(g{\cdot }p)(h) = p(hg)$
.
$(g{\cdot }p)(h) = p(hg)$
.
Proposition 2.4. Suppose
![]() $\Delta \subseteq \Gamma $
are countably infinite groups and that
$\Delta \subseteq \Gamma $
are countably infinite groups and that
![]() $\Delta \subseteq \Gamma $
admits UFOs. Then
$\Delta \subseteq \Gamma $
admits UFOs. Then
![]() $\{X\in \overline {\mathcal {S}}(k^\Gamma ): X \text { is minimal as a}\ \Delta -\text {flow}\}$
is a dense
$\{X\in \overline {\mathcal {S}}(k^\Gamma ): X \text { is minimal as a}\ \Delta -\text {flow}\}$
is a dense
![]() $G_\delta $
subset. Similarly,
$G_\delta $
subset. Similarly,
![]() $\{X\in \overline {\mathcal {S}}(2^{\mathbb {N}})^\Gamma : X\text { is minimal as a}\ \Delta -\text {flow}\}$
is a dense
$\{X\in \overline {\mathcal {S}}(2^{\mathbb {N}})^\Gamma : X\text { is minimal as a}\ \Delta -\text {flow}\}$
is a dense
![]() $G_\delta $
subset.
$G_\delta $
subset.
Proof. We give the arguments for
![]() $k^\Gamma $
, as those for
$k^\Gamma $
, as those for
![]() $(2^{\mathbb {N}})^\Gamma $
are very similar.
$(2^{\mathbb {N}})^\Gamma $
are very similar.
It suffices to show for a given finite
![]() $E\subseteq \Gamma $
that the collection of
$E\subseteq \Gamma $
that the collection of
![]() $(\Delta , E)$
-minimal flows is dense in
$(\Delta , E)$
-minimal flows is dense in
![]() $\overline {\mathcal {S}}(k^\Gamma )$
. By enlarging E if needed, we can assume that E is symmetric.
$\overline {\mathcal {S}}(k^\Gamma )$
. By enlarging E if needed, we can assume that E is symmetric.
Consider a nonempty open
![]() $O\subseteq \overline {\mathcal {S}}(k^\Gamma )$
. By shrinking O and/or enlarging E if needed, we can assume that for some
$O\subseteq \overline {\mathcal {S}}(k^\Gamma )$
. By shrinking O and/or enlarging E if needed, we can assume that for some
![]() $X\in \mathcal {S}(k^\Gamma )$
, we have
$X\in \mathcal {S}(k^\Gamma )$
, we have
![]() $O = N_E(X)\cap \overline {\mathcal {S}}(k^\Gamma )$
. We will build a
$O = N_E(X)\cap \overline {\mathcal {S}}(k^\Gamma )$
. We will build a
![]() $(\Delta , E)$
-minimal shift Y with
$(\Delta , E)$
-minimal shift Y with
![]() $Y\in N_E(X)\cap \mathcal {S}(k^\Gamma )$
. Fix a finite symmetric
$Y\in N_E(X)\cap \mathcal {S}(k^\Gamma )$
. Fix a finite symmetric
![]() $D\subseteq \Gamma $
so that X is D-irreducible. Then fix a finite
$D\subseteq \Gamma $
so that X is D-irreducible. Then fix a finite
![]() $U\subseteq \Gamma $
which is large enough to contain an
$U\subseteq \Gamma $
which is large enough to contain an
![]() $EDE$
-spaced set
$EDE$
-spaced set
![]() $Q\subseteq U\cap \Delta $
of cardinality
$Q\subseteq U\cap \Delta $
of cardinality
![]() $|P_E(X)|$
, and enlarging U if needed, choose such a Q with
$|P_E(X)|$
, and enlarging U if needed, choose such a Q with
![]() $EQ\subseteq U$
. Fix a bijection
$EQ\subseteq U$
. Fix a bijection
![]() $Q\to P_E(X)$
by writing
$Q\to P_E(X)$
by writing
![]() $P_E(X) = \{p_g: g\in Q\}$
. Because X is D-irreducible, we can find
$P_E(X) = \{p_g: g\in Q\}$
. Because X is D-irreducible, we can find
![]() $\alpha \in P_U(X)$
so that
$\alpha \in P_U(X)$
so that
![]() $(gq)|_E = p_g$
for every
$(gq)|_E = p_g$
for every
![]() $g\in Q$
. By Proposition 2.2, fix a finite
$g\in Q$
. By Proposition 2.2, fix a finite
![]() $V\subseteq \Gamma $
with
$V\subseteq \Gamma $
with
![]() $V\supseteq UDU$
which is a
$V\supseteq UDU$
which is a
![]() $(\Gamma , \Delta )$
-UFO. We now form the shift
$(\Gamma , \Delta )$
-UFO. We now form the shift
Because
![]() $V = UDU$
and X is D-irreducible, we have that
$V = UDU$
and X is D-irreducible, we have that
![]() $Y\neq \emptyset $
. In particular, for any maximal V-spaced set
$Y\neq \emptyset $
. In particular, for any maximal V-spaced set
![]() $T\subseteq \Gamma $
, we can find
$T\subseteq \Gamma $
, we can find
![]() $y\in Y$
so that
$y\in Y$
so that
![]() $(gy)|_U = \alpha $
for every
$(gy)|_U = \alpha $
for every
![]() $g\in T$
. We also note that
$g\in T$
. We also note that
![]() $Y\in N_E(X)$
by our construction of
$Y\in N_E(X)$
by our construction of
![]() $\alpha $
.
$\alpha $
.
To see that Y is
![]() $(\Delta , E)$
-minimal, fix
$(\Delta , E)$
-minimal, fix
![]() $y\in Y$
and
$y\in Y$
and
![]() $p\in P_E(Y)$
. Suppose this is witnessed by the maximal V-spaced set
$p\in P_E(Y)$
. Suppose this is witnessed by the maximal V-spaced set
![]() $T\subseteq \Gamma $
. Because V is a
$T\subseteq \Gamma $
. Because V is a
![]() $(\Gamma , \Delta )$
-UFO, find
$(\Gamma , \Delta )$
-UFO, find
![]() $h\in \Delta \cap T$
. So
$h\in \Delta \cap T$
. So
![]() $(hy)|_U = \alpha $
. Now, suppose
$(hy)|_U = \alpha $
. Now, suppose
![]() $g\in Q$
is such that
$g\in Q$
is such that
![]() $p = p_g$
. We have
$p = p_g$
. We have
![]() $(ghy)|_E = (g\cdot ((hy)|_U)|_E = p_g$
.
$(ghy)|_E = (g\cdot ((hy)|_U)|_E = p_g$
.
To see that
![]() $Y\in \mathcal {S}(k^\Gamma )$
, we will show that Y is
$Y\in \mathcal {S}(k^\Gamma )$
, we will show that Y is
![]() $DUVUD$
-irreducible. Suppose
$DUVUD$
-irreducible. Suppose
![]() $y_0, y_1\in Y$
and
$y_0, y_1\in Y$
and
![]() $S_0, S_1\subseteq \Gamma $
are
$S_0, S_1\subseteq \Gamma $
are
![]() $DUVUD$
-apart. For each
$DUVUD$
-apart. For each
![]() $i< 2$
, fix
$i< 2$
, fix
![]() $T_i\subseteq \Gamma $
a maximal V-spaced set which witnesses that
$T_i\subseteq \Gamma $
a maximal V-spaced set which witnesses that
![]() $y_i$
is in Y. Set
$y_i$
is in Y. Set
![]() $B_i = \{g\in T_i: DUg\cap S_i\neq \emptyset \}$
. Notice that
$B_i = \{g\in T_i: DUg\cap S_i\neq \emptyset \}$
. Notice that
![]() $B_i\subseteq UDS_i$
. It follows that
$B_i\subseteq UDS_i$
. It follows that
![]() $B_0\cup B_1$
is V-spaced, so extend to a maximal V-spaced set B. It also follows that
$B_0\cup B_1$
is V-spaced, so extend to a maximal V-spaced set B. It also follows that
![]() $S_i\cup UB_i\subseteq U^2DS_i$
. Since
$S_i\cup UB_i\subseteq U^2DS_i$
. Since
![]() $V\supseteq UDU$
and by the definition of
$V\supseteq UDU$
and by the definition of
![]() $B_i$
, the collection of sets
$B_i$
, the collection of sets
![]() $\{S_i\cup UB_i: i< 2\}\cup \{Ug: g\in B\setminus (B_0\cup B_1)\}$
is pairwise D-apart. By the D-irreducibility of X, we can find
$\{S_i\cup UB_i: i< 2\}\cup \{Ug: g\in B\setminus (B_0\cup B_1)\}$
is pairwise D-apart. By the D-irreducibility of X, we can find
![]() $y\in X$
with
$y\in X$
with
![]() $y|_{S_i\cup UB_i} = y_i|_{S_i\cup UB_i}$
for each
$y|_{S_i\cup UB_i} = y_i|_{S_i\cup UB_i}$
for each
![]() $i< 2$
and with
$i< 2$
and with
![]() $(gy)|_U = \alpha $
for each
$(gy)|_U = \alpha $
for each
![]() $g\in B\setminus (B_0\cup B_1)$
. Since
$g\in B\setminus (B_0\cup B_1)$
. Since
![]() $B_i\subseteq T_i$
, we actually have
$B_i\subseteq T_i$
, we actually have
![]() $(gy)|_U = \alpha $
for each
$(gy)|_U = \alpha $
for each
![]() $g\in B$
. So
$g\in B$
. So
![]() $y\in Y$
and
$y\in Y$
and
![]() $y|_{S_i} = y_i|_{S_i}$
as desired.
$y|_{S_i} = y_i|_{S_i}$
as desired.
Proof of Theorem 0.3.
By Proposition 2.4, the generic member of
![]() $\overline {\mathcal {S}}((2^{\mathbb {N}})^\Gamma )$
is minimal as a
$\overline {\mathcal {S}}((2^{\mathbb {N}})^\Gamma )$
is minimal as a
![]() $\Delta _n$
-flow for each
$\Delta _n$
-flow for each
![]() $n\in \mathbb {N}$
, and by Proposition 1.1, the generic member of
$n\in \mathbb {N}$
, and by Proposition 1.1, the generic member of
![]() $\overline {\mathcal {S}}((2^{\mathbb {N}})^\Gamma $
is free.
$\overline {\mathcal {S}}((2^{\mathbb {N}})^\Gamma $
is free.
In contrast to Theorem 0.1, the next example shows that Question 0.2 is nontrivial to answer in full generality.
Theorem 2.5. Let
![]() $G=\sum _{\mathbb {N}} (\mathbb {Z}/2\mathbb {Z})$
, and let X be a G flow with infinite underlying space. Then there exists an infinite subgroup H such that X is not minimal as an H flow.
$G=\sum _{\mathbb {N}} (\mathbb {Z}/2\mathbb {Z})$
, and let X be a G flow with infinite underlying space. Then there exists an infinite subgroup H such that X is not minimal as an H flow.
Proof. We may assume that X is a minimal G-flow, as otherwise we may take
![]() $H = G$
. We construct a sequence
$H = G$
. We construct a sequence
![]() $X\supsetneq K_0\supseteq K_1\supseteq \cdots $
of proper, nonempty, closed subsets of X and a sequence of group elements
$X\supsetneq K_0\supseteq K_1\supseteq \cdots $
of proper, nonempty, closed subsets of X and a sequence of group elements
![]() $\{g_n: n\in \mathbb {N}\}$
so that by setting
$\{g_n: n\in \mathbb {N}\}$
so that by setting
![]() $K = \bigcap _{\mathbb {N}} K_n$
and
$K = \bigcap _{\mathbb {N}} K_n$
and
![]() $H = \langle g_n: n\in \mathbb {N}\rangle $
, then K will be a minimal H-flow. Start by fixing a closed, proper subset
$H = \langle g_n: n\in \mathbb {N}\rangle $
, then K will be a minimal H-flow. Start by fixing a closed, proper subset
![]() $K_0\subsetneq X$
with nonempty interior. Suppose
$K_0\subsetneq X$
with nonempty interior. Suppose
![]() $K_n$
has been created and is
$K_n$
has been created and is
![]() $\langle g_0,\ldots ,g_{n-1}\rangle $
-invariant. As X is a minimal G-flow, the set
$\langle g_0,\ldots ,g_{n-1}\rangle $
-invariant. As X is a minimal G-flow, the set
![]() $S_n:= \{g\in G: \mathrm {Int}(gK_n\cap K_n)\neq \emptyset \}$
is infinite. Pick any
$S_n:= \{g\in G: \mathrm {Int}(gK_n\cap K_n)\neq \emptyset \}$
is infinite. Pick any
![]() $g_n\in S_n\setminus \{1_G\}$
, and set
$g_n\in S_n\setminus \{1_G\}$
, and set
![]() $K_{n+1} = g_nK_n\cap K_n$
. As
$K_{n+1} = g_nK_n\cap K_n$
. As
![]() $g_n^2 = 1_G$
, we see that
$g_n^2 = 1_G$
, we see that
![]() $K_{n+1}$
is
$K_{n+1}$
is
![]() $g_n$
-invariant, and as G is abelian, we see that
$g_n$
-invariant, and as G is abelian, we see that
![]() $K_{n+1}$
is also
$K_{n+1}$
is also
![]() $g_i$
-invariant for each
$g_i$
-invariant for each
![]() $i< n$
. It follows that K will be H-invariant as desired.
$i< n$
. It follows that K will be H-invariant as desired.
Before moving on, we give a conditional proof of Theorem 0.1, which works as long as some nonamenable group admits a strongly irreducible shift without an invariant measure. It is the inspiration for our overall construction.
Proposition 2.6. Let G and H be countably infinite groups, and suppose that for some
![]() $k< \omega $
and some strongly irreducible flow
$k< \omega $
and some strongly irreducible flow
![]() $Y\subseteq k^H$
that Y does not admit an H-invariant measure. Then there is a minimal G-flow which does not admit a characteristic measure.
$Y\subseteq k^H$
that Y does not admit an H-invariant measure. Then there is a minimal G-flow which does not admit a characteristic measure.
Proof. Viewing
![]() $Z = k^G\times Y$
as a subshift of
$Z = k^G\times Y$
as a subshift of
![]() $k^{G\times H}$
, then Z is strongly irreducible and does not admit an H-invariant probability measure. The property of not possessing an H-invariant measure is an open condition in
$k^{G\times H}$
, then Z is strongly irreducible and does not admit an H-invariant probability measure. The property of not possessing an H-invariant measure is an open condition in
![]() $\mathrm {Sub}(k^{G\times H})$
; indeed, if
$\mathrm {Sub}(k^{G\times H})$
; indeed, if
![]() $X_n\to X$
is a convergent sequence in
$X_n\to X$
is a convergent sequence in
![]() $\mathrm {Sub}(k^{G\times H})$
and
$\mathrm {Sub}(k^{G\times H})$
and
![]() $\mu _n$
is an H-invariant probability measure supported on
$\mu _n$
is an H-invariant probability measure supported on
![]() $X_n$
, then by passing to a subsequence, we may suppose that the
$X_n$
, then by passing to a subsequence, we may suppose that the
![]() $\mu _n$
weak
$\mu _n$
weak
![]() $^*$
-converge to some H-invariant probability measure
$^*$
-converge to some H-invariant probability measure
![]() $\mu $
supported on X. By Proposition 2.4, we can therefore find
$\mu $
supported on X. By Proposition 2.4, we can therefore find
![]() $X\subseteq k^{G\times H}$
which is minimal as a G-flow and which does not admit an H-invariant measure. As H acts by G-flow automorphisms on X, we see that X does not admit a characteristic measure.
$X\subseteq k^{G\times H}$
which is minimal as a G-flow and which does not admit an H-invariant measure. As H acts by G-flow automorphisms on X, we see that X does not admit a characteristic measure.
Unfortunately, the question of if there exists any countable group H and a strongly irreducible H-subshift Y with no H-invariant measure is an open problem. Therefore, our construction proceeds by considering the free group
![]() $F_2$
and defining a suitable weakening of strongly irreducible subshift which is strong enough for G-minimality to be generic in
$F_2$
and defining a suitable weakening of strongly irreducible subshift which is strong enough for G-minimality to be generic in
![]() $(G\times F_2)$
-subshifts but weak enough for
$(G\times F_2)$
-subshifts but weak enough for
![]() $(G\times F_2)$
-subshifts without
$(G\times F_2)$
-subshifts without
![]() $F_2$
-invariant measures to exist.
$F_2$
-invariant measures to exist.
3. Variants of strong irreducibility
In this section, we investigate a weakening of strong irreducibility that one can define given any right-invariant collection
![]() $\mathcal {B}$
of finite subsets of a given countable group. For our overall construction, we will consider
$\mathcal {B}$
of finite subsets of a given countable group. For our overall construction, we will consider
![]() $F_2$
and
$F_2$
and
![]() $G\times F_2$
, but we give the definitions for any countably infinite group
$G\times F_2$
, but we give the definitions for any countably infinite group
![]() $\Gamma $
. Write
$\Gamma $
. Write
![]() $\mathcal {P}_f(\Gamma )$
for the collection of finite subsets of
$\mathcal {P}_f(\Gamma )$
for the collection of finite subsets of
![]() $\Gamma $
.
$\Gamma $
.
Definition 3.1. Fix a right-invariant subset
![]() $\mathcal {B}\subseteq \mathcal {P}_f(\Gamma )$
. Given
$\mathcal {B}\subseteq \mathcal {P}_f(\Gamma )$
. Given
![]() $k\in \mathbb {N}$
, we say that a subshift
$k\in \mathbb {N}$
, we say that a subshift
![]() $X\subseteq k^\Gamma $
is
$X\subseteq k^\Gamma $
is
![]() $\mathcal {B}$
-irreducible if there is a finite
$\mathcal {B}$
-irreducible if there is a finite
![]() $D\subseteq \Gamma $
so that for any
$D\subseteq \Gamma $
so that for any
![]() $m< \omega $
, any
$m< \omega $
, any
![]() $B_0,\ldots , B_{m-1}\in \mathcal {B}$
, and any
$B_0,\ldots , B_{m-1}\in \mathcal {B}$
, and any
![]() $x_0,\ldots ,x_{m-1}\in X$
, if the sets
$x_0,\ldots ,x_{m-1}\in X$
, if the sets
![]() $\{B_0,\ldots , B_{m-1}\}$
are pairwise D-apart, then there is
$\{B_0,\ldots , B_{m-1}\}$
are pairwise D-apart, then there is
![]() $y\in X$
with
$y\in X$
with
![]() $y|_{B_i} = x_i|_{B_i}$
for each
$y|_{B_i} = x_i|_{B_i}$
for each
![]() $i< m$
. We call D the witness to
$i< m$
. We call D the witness to
![]() $\mathcal {B}$
-irreducibility. If we have D in mind, we can say that X is
$\mathcal {B}$
-irreducibility. If we have D in mind, we can say that X is
![]() $\mathcal {B}$
-D-irreducible.
$\mathcal {B}$
-D-irreducible.
We say that a subflow
![]() $X\subseteq (2^{\mathbb {N}})^\Gamma $
is
$X\subseteq (2^{\mathbb {N}})^\Gamma $
is
![]() $\mathcal {B}$
-irreducible if for each
$\mathcal {B}$
-irreducible if for each
![]() $k\in \mathbb {N}$
, the subshift
$k\in \mathbb {N}$
, the subshift
![]() $\overline {\pi }_k(X)\subseteq (2^k)^\Gamma $
is
$\overline {\pi }_k(X)\subseteq (2^k)^\Gamma $
is
![]() $\mathcal {B}$
-irreducible.
$\mathcal {B}$
-irreducible.
We write
![]() $\mathcal {S}_{\mathcal {B}}(k^\Gamma )$
or
$\mathcal {S}_{\mathcal {B}}(k^\Gamma )$
or
![]() $\mathcal {S}_{\mathcal {B}}((2^{\mathbb {N}})^\Gamma )$
for the set of
$\mathcal {S}_{\mathcal {B}}((2^{\mathbb {N}})^\Gamma )$
for the set of
![]() $\mathcal {B}$
-irreducible subflows of
$\mathcal {B}$
-irreducible subflows of
![]() $k^\Gamma $
or
$k^\Gamma $
or
![]() $(2^{\mathbb {N}})^\Gamma $
, respectively, and we write
$(2^{\mathbb {N}})^\Gamma $
, respectively, and we write
![]() $\overline {\mathcal {S}}_{\mathcal {B}}(k^\Gamma )$
or
$\overline {\mathcal {S}}_{\mathcal {B}}(k^\Gamma )$
or
![]() $\overline {\mathcal {S}}_{\mathcal {B}}((2^{\mathbb {N}})^\Gamma )$
for the Vietoris closures.
$\overline {\mathcal {S}}_{\mathcal {B}}((2^{\mathbb {N}})^\Gamma )$
for the Vietoris closures.
Remark.
-
1. If
 $\mathcal {B}$
is closed under unions, it is enough to consider
$\mathcal {B}$
is closed under unions, it is enough to consider
 $m = 2$
. However, this will often not be the case.
$m = 2$
. However, this will often not be the case. -
2. By compactness, if
 $X\subseteq k^\Gamma $
is
$X\subseteq k^\Gamma $
is
 $\mathcal {B}$
-D-irreducible,
$\mathcal {B}$
-D-irreducible,
 $\{B_n: n< \omega \}\subseteq \mathcal {B}$
is pairwise D-apart, and
$\{B_n: n< \omega \}\subseteq \mathcal {B}$
is pairwise D-apart, and
 $\{x_n: n< \omega \}\subseteq X$
, then there is
$\{x_n: n< \omega \}\subseteq X$
, then there is
 $y\in X$
with
$y\in X$
with
 $y|_{B_i} = x_i|_{B_i}$
.
$y|_{B_i} = x_i|_{B_i}$
. -
3. If
 $\mathcal {B}\subseteq \mathcal {B}'$
, then
$\mathcal {B}\subseteq \mathcal {B}'$
, then
 $\mathcal {S}_{\mathcal {B}'}(k^\Gamma )\subseteq \mathcal {S}_{\mathcal {B}}(k^\Gamma )$
and
$\mathcal {S}_{\mathcal {B}'}(k^\Gamma )\subseteq \mathcal {S}_{\mathcal {B}}(k^\Gamma )$
and
 $\mathcal {S}_{\mathcal {B}'}((2^{\mathbb {N}})^\Gamma )\subseteq \mathcal {S}_{\mathcal {B}}((2^{\mathbb {N}})^\Gamma )$
$\mathcal {S}_{\mathcal {B}'}((2^{\mathbb {N}})^\Gamma )\subseteq \mathcal {S}_{\mathcal {B}}((2^{\mathbb {N}})^\Gamma )$
When
![]() $\mathcal {B}$
is the collection of all finite subsets of H, then we recover the notion of a strongly irreducible shift. Again, we consider Cantor space alphabets to obtain freeness.
$\mathcal {B}$
is the collection of all finite subsets of H, then we recover the notion of a strongly irreducible shift. Again, we consider Cantor space alphabets to obtain freeness.
Proposition 3.2. For any right-invariant collection
![]() $\mathcal {B}\subseteq \mathcal {P}_f(\Gamma )$
, the generic member of
$\mathcal {B}\subseteq \mathcal {P}_f(\Gamma )$
, the generic member of
![]() $\overline {\mathcal {S}}_{\mathcal {B}}((2^{\mathbb {N}})^\Gamma )$
is free.
$\overline {\mathcal {S}}_{\mathcal {B}}((2^{\mathbb {N}})^\Gamma )$
is free.
Proof. Analyzing the proof of Proposition 1.1, we see that the only properties that we need of the collections
![]() $\mathcal {S}_{\mathcal {B}}(k^\Gamma )$
and
$\mathcal {S}_{\mathcal {B}}(k^\Gamma )$
and
![]() $\mathcal {S}_{\mathcal {B}}((2^{\mathbb {N}})^\Gamma )$
for the proof to generalize are that they are closed under products and contain the flows
$\mathcal {S}_{\mathcal {B}}((2^{\mathbb {N}})^\Gamma )$
for the proof to generalize are that they are closed under products and contain the flows
![]() $\mathrm {Color}(D, m)$
. If
$\mathrm {Color}(D, m)$
. If
![]() $k, \ell \in \mathbb {N}$
an
$k, \ell \in \mathbb {N}$
an
![]() $X\subseteq k^\Gamma $
and
$X\subseteq k^\Gamma $
and
![]() $Y\subseteq \ell ^\Gamma $
are
$Y\subseteq \ell ^\Gamma $
are
![]() $\mathcal {B}$
-D-irreducible and
$\mathcal {B}$
-D-irreducible and
![]() $\mathcal {B}$
-E-irreducible for some finite
$\mathcal {B}$
-E-irreducible for some finite
![]() $D, E\subseteq \Gamma $
, then
$D, E\subseteq \Gamma $
, then
![]() $X\times Y\subseteq (k\times \ell )^\Gamma $
will be
$X\times Y\subseteq (k\times \ell )^\Gamma $
will be
![]() $\mathcal {B}$
-
$\mathcal {B}$
-
![]() $(D\cup E)$
-irreducible. And as
$(D\cup E)$
-irreducible. And as
![]() $\mathrm {Color}(D, m)$
is strongly irreducible, it is
$\mathrm {Color}(D, m)$
is strongly irreducible, it is
![]() $\mathcal {B}$
-irreducible.
$\mathcal {B}$
-irreducible.
Now, we consider the group
![]() $F_2$
. We consider the left Cayley graph of
$F_2$
. We consider the left Cayley graph of
![]() $F_2$
with respect to the standard generating set
$F_2$
with respect to the standard generating set
![]() $A:= \{a, b, a^{-1}, b^{-1}\}$
. We let
$A:= \{a, b, a^{-1}, b^{-1}\}$
. We let
![]() $d\colon F_2\times F_2\to \omega $
denote the graph metric. Write
$d\colon F_2\times F_2\to \omega $
denote the graph metric. Write
![]() $D_n = \{s\in F_2: d(s, 1_{F_2}) \leq n\}$
.
$D_n = \{s\in F_2: d(s, 1_{F_2}) \leq n\}$
.
Definition 3.3. Given n with
![]() $1\leq n< \omega $
, we set
$1\leq n< \omega $
, we set
Write
![]() $\mathcal {B}_\omega $
for the collection of finite, connected subsets of
$\mathcal {B}_\omega $
for the collection of finite, connected subsets of
![]() $F_2$
.
$F_2$
.
Proposition 3.4. Suppose
![]() $X\subseteq k^{F_2}$
is
$X\subseteq k^{F_2}$
is
![]() $\mathcal {B}_\omega $
-irreducible. Then there is some
$\mathcal {B}_\omega $
-irreducible. Then there is some
![]() $n< \omega $
for which X is
$n< \omega $
for which X is
![]() $\mathcal {B}_n$
-irreducible.
$\mathcal {B}_n$
-irreducible.
Proof. Suppose X is
![]() $\mathcal {B}_\omega $
-
$\mathcal {B}_\omega $
-
![]() $D_n$
-irreducible. We claim X is
$D_n$
-irreducible. We claim X is
![]() $\mathcal {B}_n$
-
$\mathcal {B}_n$
-
![]() $D_n$
-irreducible. Suppose
$D_n$
-irreducible. Suppose
![]() $m< \omega $
,
$m< \omega $
,
![]() $B_0,\ldots ,B_{m-1}\in \mathcal {B}_n$
are pairwise
$B_0,\ldots ,B_{m-1}\in \mathcal {B}_n$
are pairwise
![]() $D_n$
-apart, and
$D_n$
-apart, and
![]() $x_0,\ldots ,x_{m-1}\in X$
. For each
$x_0,\ldots ,x_{m-1}\in X$
. For each
![]() $i< m$
, we suppose
$i< m$
, we suppose
![]() $B_i$
has
$B_i$
has
![]() $n_i$
-many connected componenets, and we write
$n_i$
-many connected componenets, and we write
![]() $\{C_{i,j}: j< n_i\}$
for these components. Then the collection of connected sets
$\{C_{i,j}: j< n_i\}$
for these components. Then the collection of connected sets
![]() $\bigcup _{i< m} \{C_{i,j}: j< n_i\}$
is pairwise
$\bigcup _{i< m} \{C_{i,j}: j< n_i\}$
is pairwise
![]() $D_n$
-apart. As X is
$D_n$
-apart. As X is
![]() $\mathcal {B}_\omega $
-
$\mathcal {B}_\omega $
-
![]() $D_n$
-irreducible, we can find
$D_n$
-irreducible, we can find
![]() $y\in X$
so that for each
$y\in X$
so that for each
![]() $i< m$
and
$i< m$
and
![]() $j< n_i$
, we have
$j< n_i$
, we have
![]() $y|_{C_{i,j}} = x_i|_{C_{i,j}}$
. Hence,
$y|_{C_{i,j}} = x_i|_{C_{i,j}}$
. Hence,
![]() $y|_{B_i} = x_i|_{B_i}$
, showing that X is
$y|_{B_i} = x_i|_{B_i}$
, showing that X is
![]() $\mathcal {B}_n$
-
$\mathcal {B}_n$
-
![]() $D_n$
-irreducible.
$D_n$
-irreducible.
We now construct a
![]() $\mathcal {B}_\omega $
-irreducible subshift with no
$\mathcal {B}_\omega $
-irreducible subshift with no
![]() $F_2$
-invariant measure. We consider the alphabet
$F_2$
-invariant measure. We consider the alphabet
![]() $A^2$
and write
$A^2$
and write
![]() $\pi _0, \pi _1\colon A^2\to A$
for the projections. We set
$\pi _0, \pi _1\colon A^2\to A$
for the projections. We set
 $$ \begin{align*} X_{pdox} = \{x\in (A^2)^{F_2}:\, &\forall g, h\in F_2 \, \forall i, j< 2 \\ &(i, g)\neq (j, h)\Rightarrow \pi_i(x(g))\cdot g\neq \pi_j(x(h))\cdot h\}. \end{align*} $$
$$ \begin{align*} X_{pdox} = \{x\in (A^2)^{F_2}:\, &\forall g, h\in F_2 \, \forall i, j< 2 \\ &(i, g)\neq (j, h)\Rightarrow \pi_i(x(g))\cdot g\neq \pi_j(x(h))\cdot h\}. \end{align*} $$
More informally, the flow
![]() $X_{pdox}$
is the space of ‘
$X_{pdox}$
is the space of ‘
![]() $2$
-to-
$2$
-to-
![]() $1$
paradoxical decompositions’ of
$1$
paradoxical decompositions’ of
![]() $F_2$
using A. We remark that here, our decomposition need not be a partition of
$F_2$
using A. We remark that here, our decomposition need not be a partition of
![]() $F_2$
; we just ask for disjoint
$F_2$
; we just ask for disjoint
![]() $S_0, S_1\subseteq F_2$
such that for every
$S_0, S_1\subseteq F_2$
such that for every
![]() $g\in G$
and
$g\in G$
and
![]() $i< 2$
, we have
$i< 2$
, we have
![]() $Ag\cap S_i\neq \emptyset $
. This is in some sense the prototypical example of an
$Ag\cap S_i\neq \emptyset $
. This is in some sense the prototypical example of an
![]() $F_2$
-shift with no
$F_2$
-shift with no
![]() $F_2$
-invariant measure.
$F_2$
-invariant measure.
Lemma 3.5.
![]() $X_{pdox}$
has no
$X_{pdox}$
has no
![]() $F_2$
-invariant measure.
$F_2$
-invariant measure.
Proof. For
![]() $u \in A^2$
set
$u \in A^2$
set
![]() $Y_u = \{x \in X_{pdox} : x(1_G) = u\}$
. Notice that if
$Y_u = \{x \in X_{pdox} : x(1_G) = u\}$
. Notice that if
![]() $y \in Y_u$
,
$y \in Y_u$
,
![]() $i < 2$
and
$i < 2$
and
![]() $x = \pi _i(u) y$
, then
$x = \pi _i(u) y$
, then
![]() $x(\pi _i(u)^{-1}) = y(1_G) = u$
. Consequently, if
$x(\pi _i(u)^{-1}) = y(1_G) = u$
. Consequently, if
![]() $u, v\in A^2$
,
$u, v\in A^2$
,
![]() $x \in \pi _i(u) Y_u \cap \pi _j(v) Y_v$
then, since
$x \in \pi _i(u) Y_u \cap \pi _j(v) Y_v$
then, since
![]() $x \in X_{pdox}$
and
$x \in X_{pdox}$
and
we must have that
![]() $(i, \pi _i(u)) = (j, \pi _j(v))$
, and hence also
$(i, \pi _i(u)) = (j, \pi _j(v))$
, and hence also
Therefore,
![]() $\pi _i(u) Y_u \cap \pi _j(v) Y_v = \varnothing $
whenever
$\pi _i(u) Y_u \cap \pi _j(v) Y_v = \varnothing $
whenever
![]() $(i,u) \neq (j,v)$
.
$(i,u) \neq (j,v)$
.
If
![]() $\mu $
were an invariant Borel probability measure on
$\mu $
were an invariant Borel probability measure on
![]() $X_{pdox}$
, then we would have
$X_{pdox}$
, then we would have
which is a contradiction.
When proving that
![]() $X_{pdox}$
is
$X_{pdox}$
is
![]() $\mathcal {B}_\omega $
-irreducible, note that
$\mathcal {B}_\omega $
-irreducible, note that
![]() $D_1 = A\cup \{1_{F_2}\}$
.
$D_1 = A\cup \{1_{F_2}\}$
.
Proposition 3.6.
![]() $X_{pdox}$
is
$X_{pdox}$
is
![]() $\mathcal {B}_\omega $
-
$\mathcal {B}_\omega $
-
![]() $D_4$
-irreducible.
$D_4$
-irreducible.
Proof. The proof will use a
![]() $2$
-to-
$2$
-to-
![]() $1$
instance of Hall’s matching criterion [Reference Hall7] which we briefly describe. Fix a bipartite graph
$1$
instance of Hall’s matching criterion [Reference Hall7] which we briefly describe. Fix a bipartite graph
![]() $\mathbb {G} = (V, E)$
with partition
$\mathbb {G} = (V, E)$
with partition
![]() $V = V_0\sqcup V_1$
. Given
$V = V_0\sqcup V_1$
. Given
![]() $S\subseteq V_0$
, write
$S\subseteq V_0$
, write
![]() $N_{\mathbb {G}}(S) = \{v\in V_1: \exists u\in S (u, v)\in E\}$
. Then the matching condition we need states that if for every finite
$N_{\mathbb {G}}(S) = \{v\in V_1: \exists u\in S (u, v)\in E\}$
. Then the matching condition we need states that if for every finite
![]() $S\subseteq V_0$
, we have
$S\subseteq V_0$
, we have
![]() $|N_{\mathbb {G}}(S)|\geq 2S$
, then there is
$|N_{\mathbb {G}}(S)|\geq 2S$
, then there is
![]() $E'\subseteq E$
so that in the graph
$E'\subseteq E$
so that in the graph
![]() $\mathbb {G}':= (V, E')$
,
$\mathbb {G}':= (V, E')$
,
![]() $d_{\mathbb {G}'}(u) = 2$
for every
$d_{\mathbb {G}'}(u) = 2$
for every
![]() $u\in V_0$
.
$u\in V_0$
.
Let
![]() $B_0,\ldots ,B_{k-1}\in \mathcal {B}_\omega $
be pairwise
$B_0,\ldots ,B_{k-1}\in \mathcal {B}_\omega $
be pairwise
![]() $D_4$
-apart. Let
$D_4$
-apart. Let
![]() $x_0,\ldots ,x_{k-1}\in X_{pdox}$
. To construct
$x_0,\ldots ,x_{k-1}\in X_{pdox}$
. To construct
![]() $y\in X_{pdox}$
with
$y\in X_{pdox}$
with
![]() $y|_{B_i} = x_i|_{B_i}$
for each
$y|_{B_i} = x_i|_{B_i}$
for each
![]() $i< k$
, we need to verify a
$i< k$
, we need to verify a
![]() $2$
-to-
$2$
-to-
![]() $1$
Hall’s matching criterion on every finite subset of
$1$
Hall’s matching criterion on every finite subset of
![]() $F_2\setminus \bigcup _{i< k} B_i$
. Call
$F_2\setminus \bigcup _{i< k} B_i$
. Call
![]() $s\in F_2$
matched if for some
$s\in F_2$
matched if for some
![]() $i< k$
, some
$i< k$
, some
![]() $g\in B_i$
and some
$g\in B_i$
and some
![]() $j< 2$
, we have
$j< 2$
, we have
![]() $s = \pi _j(x_i(g))\cdot g$
. So we need for every finite
$s = \pi _j(x_i(g))\cdot g$
. So we need for every finite
![]() $E\in \mathcal {P}_f(F_2\setminus \bigcup _{i<k} B_i)$
that
$E\in \mathcal {P}_f(F_2\setminus \bigcup _{i<k} B_i)$
that
![]() $AE$
contains at least
$AE$
contains at least
![]() $2|E|$
-many unmatched elements. Towards a contradiction, let
$2|E|$
-many unmatched elements. Towards a contradiction, let
![]() $E\in \mathcal {P}_f(F_2\setminus \bigcup _{i<k} B_i)$
be a minimal failure of the Hall condition.
$E\in \mathcal {P}_f(F_2\setminus \bigcup _{i<k} B_i)$
be a minimal failure of the Hall condition.
In the left Cayley graph of
![]() $F_2$
, given a reduced word w in alphabet
$F_2$
, given a reduced word w in alphabet
![]() $A = \{a, b, a^{-1}, b^{-1}\}$
, write
$A = \{a, b, a^{-1}, b^{-1}\}$
, write
![]() $N_w$
for the set of reduced words which end with w. Now, find
$N_w$
for the set of reduced words which end with w. Now, find
![]() $t\in E$
(let us assume the leftmost character of t is a) so that all of
$t\in E$
(let us assume the leftmost character of t is a) so that all of
![]() $E\cap N_{at}$
,
$E\cap N_{at}$
,
![]() $E\cap N_{bt}$
and
$E\cap N_{bt}$
and
![]() $E\cap N_{b^{-1}t}$
are empty. If any two of
$E\cap N_{b^{-1}t}$
are empty. If any two of
![]() $at$
,
$at$
,
![]() $bt$
and
$bt$
and
![]() $b^{-1}t$
is an unmatched point in
$b^{-1}t$
is an unmatched point in
![]() $AE$
, then
$AE$
, then
![]() $E\setminus \{t\}$
is a smaller failure of Hall’s criterion. So there must be some
$E\setminus \{t\}$
is a smaller failure of Hall’s criterion. So there must be some
![]() $i< k$
, some
$i< k$
, some
![]() $g\in B_i$
and some
$g\in B_i$
and some
![]() $j< 2$
, we have
$j< 2$
, we have
![]() $\pi _j(x_i(g))\cdot g \in \{at, bt, b^{-1}t\}$
. Let us suppose
$\pi _j(x_i(g))\cdot g \in \{at, bt, b^{-1}t\}$
. Let us suppose
![]() $\pi _j(x_i(g))\cdot g = at$
. Note that since
$\pi _j(x_i(g))\cdot g = at$
. Note that since
![]() $g\not \in E$
, we must have
$g\not \in E$
, we must have
![]() $g\in \{bat, a^2t, b^{-1}at\}$
. But then since
$g\in \{bat, a^2t, b^{-1}at\}$
. But then since
![]() $B_i$
is connected, we have
$B_i$
is connected, we have
![]() $D_1B_i\cap \{bt, b^{-1}t\} = \emptyset $
, and since the other
$D_1B_i\cap \{bt, b^{-1}t\} = \emptyset $
, and since the other
![]() $B_q$
are at least distance
$B_q$
are at least distance
![]() $5$
from
$5$
from
![]() $B_i$
, we have
$B_i$
, we have
![]() $D_1B_q\cap \{bt, b^{-1}t\} = \emptyset $
for every
$D_1B_q\cap \{bt, b^{-1}t\} = \emptyset $
for every
![]() $q\in k\setminus \{i\}$
. In particular,
$q\in k\setminus \{i\}$
. In particular,
![]() $bt$
and
$bt$
and
![]() $b^{-1}t$
are unmatched points in
$b^{-1}t$
are unmatched points in
![]() $AE$
, a contradiction.
$AE$
, a contradiction.
We remark that
![]() $X_{pdox}$
is not
$X_{pdox}$
is not
![]() $D_n$
-irreducible for any
$D_n$
-irreducible for any
![]() $n\in \mathbb {N}$
. See Figure 2.
$n\in \mathbb {N}$
. See Figure 2.

Figure 2 A pair of outgoing edges, drawn in solid red, is chosen at each of
![]() $v_{00}$
,
$v_{00}$
,
![]() $v_{01}$
,
$v_{01}$
,
![]() $v_{10}$
and
$v_{10}$
and
![]() $v_{11}$
. Edges which must consequently be oriented in a particular direction are indicated with dashed red arrows. Most importantly,
$v_{11}$
. Edges which must consequently be oriented in a particular direction are indicated with dashed red arrows. Most importantly,
![]() $v_{\varnothing }$
is forced to direct an edge to
$v_{\varnothing }$
is forced to direct an edge to
![]() $u_\varnothing $
. By considering the generalization of this picture for any length of binary string, we see that
$u_\varnothing $
. By considering the generalization of this picture for any length of binary string, we see that
![]() $X_{pdox}$
cannot be
$X_{pdox}$
cannot be
![]() $D_n$
-irreducible for any
$D_n$
-irreducible for any
![]() $n\in \mathbb {N}$
.
$n\in \mathbb {N}$
.
4. The construction
Our goal for the rest of the paper is to use
![]() $X_{pdox}$
to build a subflow of
$X_{pdox}$
to build a subflow of
![]() $(2^{\mathbb {N}})^{G\times F_2}$
which is free, G-minimal and with no
$(2^{\mathbb {N}})^{G\times F_2}$
which is free, G-minimal and with no
![]() $F_2$
-invariant measure. In what follows, given an
$F_2$
-invariant measure. In what follows, given an
![]() $F_2$
-coset
$F_2$
-coset
![]() $\{g\}\times F_2$
, we endow this coset with the left Cayley graph for
$\{g\}\times F_2$
, we endow this coset with the left Cayley graph for
![]() $F_2$
using the generating set A exactly as above. We extend the definition of
$F_2$
using the generating set A exactly as above. We extend the definition of
![]() $\mathcal {B}_n$
to refer to finite subsets of any given
$\mathcal {B}_n$
to refer to finite subsets of any given
![]() $F_2$
-coset.
$F_2$
-coset.
Definition 4.1. Given n with
![]() $1\leq n\leq \omega $
, we set
$1\leq n\leq \omega $
, we set
Given
![]() $y\in k^{G\times F_2}$
and
$y\in k^{G\times F_2}$
and
![]() $g\in G$
, we define
$g\in G$
, we define
![]() $y_g\in k^{F_2}$
where given
$y_g\in k^{F_2}$
where given
![]() $s\in F_2$
, we set
$s\in F_2$
, we set
![]() $y_g(s) = y(g, s)$
. If
$y_g(s) = y(g, s)$
. If
![]() $X\subseteq k^{F_2}$
is
$X\subseteq k^{F_2}$
is
![]() $\mathcal {B}_n$
-irreducible, then the subshift
$\mathcal {B}_n$
-irreducible, then the subshift
![]() $X^G\subseteq k^{G\times F_2}$
is in
$X^G\subseteq k^{G\times F_2}$
is in
![]() $\mathcal {S}_{\mathcal {B}_n^*}$
, where we view
$\mathcal {S}_{\mathcal {B}_n^*}$
, where we view
![]() $X^G$
as the set
$X^G$
as the set
![]() $\{y\in k^{G\times F_2}: \forall g\in G\, (y_g\in X)\}$
. In particular,
$\{y\in k^{G\times F_2}: \forall g\in G\, (y_g\in X)\}$
. In particular,
![]() $(X_{pdox})^G$
is
$(X_{pdox})^G$
is
![]() $\mathcal {B}^*_4$
-irreducible. By encoding
$\mathcal {B}^*_4$
-irreducible. By encoding
![]() $(X_{pdox})^G$
as a subshift of
$(X_{pdox})^G$
as a subshift of
![]() $(2^m)^{G\times F_2}$
for some
$(2^m)^{G\times F_2}$
for some
![]() $m\in \mathbb {N}$
and considering
$m\in \mathbb {N}$
and considering
![]() $\tilde {\pi }_m^{-1}((X_{pdox})^G)\subseteq (2^{\mathbb {N}})^{G\times F_2}$
, we see that there is a
$\tilde {\pi }_m^{-1}((X_{pdox})^G)\subseteq (2^{\mathbb {N}})^{G\times F_2}$
, we see that there is a
![]() $\mathcal {B}_4^*$
-irreducible subflow of
$\mathcal {B}_4^*$
-irreducible subflow of
![]() $(2^{\mathbb {N}})^{G\times F_2}$
for which the
$(2^{\mathbb {N}})^{G\times F_2}$
for which the
![]() $F_2$
-action doesn’t fix a measure. It follows that such subflows constitute a nonempty open subset of
$F_2$
-action doesn’t fix a measure. It follows that such subflows constitute a nonempty open subset of
![]() $\Phi := \overline {\bigcup _n \mathcal {S}_{\mathcal {B}_n^*}((2^{\mathbb {N}})^{G\times F_2})}$
. Combining the next result with Proposition 3.2, we will complete the proof of Theorem 0.1.
$\Phi := \overline {\bigcup _n \mathcal {S}_{\mathcal {B}_n^*}((2^{\mathbb {N}})^{G\times F_2})}$
. Combining the next result with Proposition 3.2, we will complete the proof of Theorem 0.1.
Proposition 4.2. With
![]() $\Phi $
as above, the G-minimal flows are dense
$\Phi $
as above, the G-minimal flows are dense
![]() $G_\delta $
in
$G_\delta $
in
![]() $\Phi $
.
$\Phi $
.
Proof. We show the result for
![]() $\Phi _k:= \overline {\bigcup _n \mathcal {S}_{\mathcal {B}_n^*}(k^{G\times F_2})}$
to simplify notation; the proof in full generality is almost identical.
$\Phi _k:= \overline {\bigcup _n \mathcal {S}_{\mathcal {B}_n^*}(k^{G\times F_2})}$
to simplify notation; the proof in full generality is almost identical.
We only need to show density. To that end, fix a finite symmetric
![]() $E\subseteq G\times F_2$
which is connected in each
$E\subseteq G\times F_2$
which is connected in each
![]() $F_2$
-coset. It is enough to show that the
$F_2$
-coset. It is enough to show that the
![]() $(G, E)$
-minimal subshifts are dense in
$(G, E)$
-minimal subshifts are dense in
![]() $\Phi _k$
. Fix some nonempty open
$\Phi _k$
. Fix some nonempty open
![]() $O\subseteq \Phi _k$
. By enlarging E and/or shrinking O, we may assume that for some
$O\subseteq \Phi _k$
. By enlarging E and/or shrinking O, we may assume that for some
![]() $n< \omega $
and
$n< \omega $
and
![]() $X\in \mathcal {S}_{\mathcal {B}_n^*}(k^{G\times F_2})$
that
$X\in \mathcal {S}_{\mathcal {B}_n^*}(k^{G\times F_2})$
that
![]() $O = \{X'\in \Phi _k: P_E(X') = P_E(X)\}$
. We will build a
$O = \{X'\in \Phi _k: P_E(X') = P_E(X)\}$
. We will build a
![]() $(G, E)$
-minimal subshift
$(G, E)$
-minimal subshift
![]() $Y\subseteq k^{G\times F_2}$
so that
$Y\subseteq k^{G\times F_2}$
so that
![]() $P_E(Y) = P_E(X)$
and so that for some
$P_E(Y) = P_E(X)$
and so that for some
![]() $N< \omega $
, we have
$N< \omega $
, we have
![]() $Y\in \mathcal {S}_{\mathcal {B}_N^*}(k^{G\times F_2})$
.
$Y\in \mathcal {S}_{\mathcal {B}_N^*}(k^{G\times F_2})$
.
Recall that
![]() $D_n\subseteq F_2$
denotes the ball of radius n. Fix a finite, symmetric
$D_n\subseteq F_2$
denotes the ball of radius n. Fix a finite, symmetric
![]() $D\subseteq G\times F_2$
so that
$D\subseteq G\times F_2$
so that
![]() $\{1_G\}\times D_{2n}\subseteq D$
and X is
$\{1_G\}\times D_{2n}\subseteq D$
and X is
![]() $\mathcal {B}_n^*$
-D-irreducible. Find a finite symmetric
$\mathcal {B}_n^*$
-D-irreducible. Find a finite symmetric
![]() $U_0\subseteq G$
with
$U_0\subseteq G$
with
![]() $1_G\subseteq U_0$
and
$1_G\subseteq U_0$
and
![]() $r< \omega $
so that upon setting
$r< \omega $
so that upon setting
![]() $U = U_0\times D_r\subseteq G\times F_2$
, then U is large enough to contain an
$U = U_0\times D_r\subseteq G\times F_2$
, then U is large enough to contain an
![]() $EDE$
-spaced set
$EDE$
-spaced set
![]() $Q\subseteq G$
with
$Q\subseteq G$
with
![]() $EQ\subseteq U$
. As X is
$EQ\subseteq U$
. As X is
![]() $\mathcal {B}_n^*$
-D-irreducible, there is a pattern
$\mathcal {B}_n^*$
-D-irreducible, there is a pattern
![]() $\alpha \in P_U(X)$
so that
$\alpha \in P_U(X)$
so that
![]() $\{(g\alpha )|_E: g\in Q\} = P_E(X)$
.
$\{(g\alpha )|_E: g\in Q\} = P_E(X)$
.
Let
![]() $V\supseteq UD^2U$
be a
$V\supseteq UD^2U$
be a
![]() $(G\times F_2, G)$
-UFO. We remark that for most of the remainder of the proof, it would be enough to have
$(G\times F_2, G)$
-UFO. We remark that for most of the remainder of the proof, it would be enough to have
![]() $V\supseteq UDU$
; we only use the stronger assumption
$V\supseteq UDU$
; we only use the stronger assumption
![]() $V\supseteq UD^2U$
in the proof of the final claim. Consider the following subshift:
$V\supseteq UD^2U$
in the proof of the final claim. Consider the following subshift:
The proof that Y is nonempty and
![]() $(G, E)$
-minimal is exactly the same as the analogous proof from Proposition 2.4. Note that by construction, we have
$(G, E)$
-minimal is exactly the same as the analogous proof from Proposition 2.4. Note that by construction, we have
![]() $P_E(Y) = P_E(X)$
.
$P_E(Y) = P_E(X)$
.
We now show that
![]() $Y\in \mathcal {S}_{\mathcal {B}_N^*}(k^{G\times F_2})$
for
$Y\in \mathcal {S}_{\mathcal {B}_N^*}(k^{G\times F_2})$
for
![]() $N = 4r+3n$
. Set
$N = 4r+3n$
. Set
![]() $W = DUVUD$
. We show that Y is
$W = DUVUD$
. We show that Y is
![]() $\mathcal {B}_N^*$
-W-irreducible. Suppose
$\mathcal {B}_N^*$
-W-irreducible. Suppose
![]() $m< \omega $
,
$m< \omega $
,
![]() $y_0,\ldots ,y_{m-1}\in Y$
and
$y_0,\ldots ,y_{m-1}\in Y$
and
![]() $S_0,\ldots ,S_{m-1}\in \mathcal {B}_N^*$
are pairwise W-apart. Suppose for each
$S_0,\ldots ,S_{m-1}\in \mathcal {B}_N^*$
are pairwise W-apart. Suppose for each
![]() $i< m$
that
$i< m$
that
![]() $T_i\subseteq G\times F_2$
is a maximal V-spaced set which witness that
$T_i\subseteq G\times F_2$
is a maximal V-spaced set which witness that
![]() $y_i\in Y$
. Set
$y_i\in Y$
. Set
![]() $B_i = \{g\in T_i: DUg\cap S_i\neq \emptyset \}$
. Then
$B_i = \{g\in T_i: DUg\cap S_i\neq \emptyset \}$
. Then
![]() $\bigcup _{i< m} B_i$
is V-spaced, so enlarge to a maximal V-spaced set
$\bigcup _{i< m} B_i$
is V-spaced, so enlarge to a maximal V-spaced set
![]() $B\subseteq G\times F_2$
.
$B\subseteq G\times F_2$
.
For each
![]() $i< m$
, we enlarge
$i< m$
, we enlarge
![]() $S_i\cup UB_i$
to
$S_i\cup UB_i$
to
![]() $J_i\in \mathcal {B}_n^*$
as follows. Suppose
$J_i\in \mathcal {B}_n^*$
as follows. Suppose
![]() $C\subseteq G\times F_2$
is an
$C\subseteq G\times F_2$
is an
![]() $F_2$
-coset. Each set of the form
$F_2$
-coset. Each set of the form
![]() $C\cap Ug$
is connected. Since
$C\cap Ug$
is connected. Since
![]() $S_i\in \mathcal {B}_N^*$
, it follows that given
$S_i\in \mathcal {B}_N^*$
, it follows that given
![]() $g\in B_i$
, there is at most one connected component
$g\in B_i$
, there is at most one connected component
![]() $\Theta _{C, g}$
of
$\Theta _{C, g}$
of
![]() $S_i\cap C$
with
$S_i\cap C$
with
![]() $Ug\cap \Theta _{C, g} = \emptyset $
, but
$Ug\cap \Theta _{C, g} = \emptyset $
, but
![]() $Ug\cap D_n\Theta _{C, g}\neq \emptyset $
. We add the line segment in C connecting
$Ug\cap D_n\Theta _{C, g}\neq \emptyset $
. We add the line segment in C connecting
![]() $\Theta _{C, g}$
and
$\Theta _{C, g}$
and
![]() $Ug$
. Upon doing this for each
$Ug$
. Upon doing this for each
![]() $g\in B_i$
and each
$g\in B_i$
and each
![]() $F_2$
-coset C, this completes the construction of
$F_2$
-coset C, this completes the construction of
![]() $J_i$
. Observe that
$J_i$
. Observe that
![]() $J_i\subseteq D_{n-1}S_i\cap UB_i$
.
$J_i\subseteq D_{n-1}S_i\cap UB_i$
.
Claim. Let C be an
![]() $F_2$
-coset, and suppose
$F_2$
-coset, and suppose
![]() $Y_0$
is a connected component of
$Y_0$
is a connected component of
![]() $S_i\cap C$
. Let Y be the connected component of
$S_i\cap C$
. Let Y be the connected component of
![]() $J_i\cap C$
with
$J_i\cap C$
with
![]() $Y_0\subseteq Y$
. Then
$Y_0\subseteq Y$
. Then
![]() $Y\subseteq D_{2r+n}Y_0$
. In particular, if
$Y\subseteq D_{2r+n}Y_0$
. In particular, if
![]() $Y_0\neq Z_0$
are two connected components of
$Y_0\neq Z_0$
are two connected components of
![]() $S_i\cap C$
, then
$S_i\cap C$
, then
![]() $Y_0$
and
$Y_0$
and
![]() $Z_0$
do not belong to the same component of
$Z_0$
do not belong to the same component of
![]() $J_i\cap C$
.
$J_i\cap C$
.
Proof. Let
![]() $L = \{x_j: j< \omega \}\subseteq C$
be a ray with
$L = \{x_j: j< \omega \}\subseteq C$
be a ray with
![]() $x_0\in Y_0$
and
$x_0\in Y_0$
and
![]() $x_j\not \in Y_0$
for any
$x_j\not \in Y_0$
for any
![]() $j\geq 1$
. Then
$j\geq 1$
. Then
![]() $\{j< \omega : x_j\in J_i\cap C\}$
is some finite initial segment of
$\{j< \omega : x_j\in J_i\cap C\}$
is some finite initial segment of
![]() $\omega $
. We want to argue that for some
$\omega $
. We want to argue that for some
![]() $j\leq 2r+n+1$
, we have
$j\leq 2r+n+1$
, we have
![]() $x_j\not \in J_i\cap C$
. First, we argue that if
$x_j\not \in J_i\cap C$
. First, we argue that if
![]() $x_n\in J_i\cap C$
, then
$x_n\in J_i\cap C$
, then
![]() $x_n\in UB_i$
. Otherwise, we must have
$x_n\in UB_i$
. Otherwise, we must have
![]() $x_n\in D_{n-1}S_i$
. But since
$x_n\in D_{n-1}S_i$
. But since
![]() $x_n\not \in D_{n-1}Y_0$
, there must be another component
$x_n\not \in D_{n-1}Y_0$
, there must be another component
![]() $Y_1$
of
$Y_1$
of
![]() $S_i\cap C$
with
$S_i\cap C$
with
![]() $x_n\in D_nY_1$
. But this implies that
$x_n\in D_nY_1$
. But this implies that
![]() $Y_0$
and
$Y_0$
and
![]() $Y_1$
are not
$Y_1$
are not
![]() $D_{2n-1}$
-apart, a contradiction since
$D_{2n-1}$
-apart, a contradiction since
![]() $2n-1\leq 4r-3n = N$
.
$2n-1\leq 4r-3n = N$
.
Fix
![]() $g\in B_i$
with
$g\in B_i$
with
![]() $x_n\in Ug$
. Let
$x_n\in Ug$
. Let
![]() $q< \omega $
be least with
$q< \omega $
be least with
![]() $q> n$
and
$q> n$
and
![]() $x_q \not \in U_g$
. We must have
$x_q \not \in U_g$
. We must have
![]() $q\leq 2r+n+1$
. We claim that
$q\leq 2r+n+1$
. We claim that
![]() $x_q\not \in J_i\cap C$
. Towards a contradiction, suppose
$x_q\not \in J_i\cap C$
. Towards a contradiction, suppose
![]() $x_q\in J_i\cap C$
. We cannot have
$x_q\in J_i\cap C$
. We cannot have
![]() $x_q\in UB_i$
, so we must have
$x_q\in UB_i$
, so we must have
![]() $x_q\in D_{n-1}S_i$
. But now there must be some component
$x_q\in D_{n-1}S_i$
. But now there must be some component
![]() $Y_1$
of
$Y_1$
of
![]() $S_i\cap C$
with
$S_i\cap C$
with
![]() $x_q\in D_{n-1}Y_1$
. But then
$x_q\in D_{n-1}Y_1$
. But then
![]() $D_{2r+2n}Y_0\cap Y_1\neq \emptyset $
, a contradiction as
$D_{2r+2n}Y_0\cap Y_1\neq \emptyset $
, a contradiction as
![]() $Y_0$
and
$Y_0$
and
![]() $Y_1$
are
$Y_1$
are
![]() $D_N$
-apart. This concludes the proof that
$D_N$
-apart. This concludes the proof that
![]() $Y\subseteq D_{2r+n}Y_0$
.
$Y\subseteq D_{2r+n}Y_0$
.
Now, suppose
![]() $Y_0\neq Z_0$
are two connected components of
$Y_0\neq Z_0$
are two connected components of
![]() $S_i\cap C$
. Then
$S_i\cap C$
. Then
![]() $Y_0$
and
$Y_0$
and
![]() $Z_0$
are N-apart. In particular,
$Z_0$
are N-apart. In particular,
![]() $Z_0\not \subseteq D_{2r+n}Y_0$
, so cannot belong to the same connected component of
$Z_0\not \subseteq D_{2r+n}Y_0$
, so cannot belong to the same connected component of
![]() $J_i\cap C$
as
$J_i\cap C$
as
![]() $Y_0$
.
$Y_0$
.
Claim.
![]() $J_i\in \mathcal {B}_n^*$
.
$J_i\in \mathcal {B}_n^*$
.
Proof. Fix an
![]() $F_2$
-coset C and two connected components
$F_2$
-coset C and two connected components
![]() $Y\neq Z$
of
$Y\neq Z$
of
![]() $J_i\cap C$
. By the previous claim, each of Y and Z can only contain at most one nonempty component of
$J_i\cap C$
. By the previous claim, each of Y and Z can only contain at most one nonempty component of
![]() $S_i\cap C$
. The claim will be proven after considering three cases.
$S_i\cap C$
. The claim will be proven after considering three cases.
-
1. First, suppose each of Y and Z contain a nonempty component of
 $S_i\cap C$
, say
$S_i\cap C$
, say
 $Y_0\subseteq Y$
and
$Y_0\subseteq Y$
and
 $Z_0\subseteq Z$
. Then since
$Z_0\subseteq Z$
. Then since
 $Y_0$
and
$Y_0$
and
 $Z_0$
are
$Z_0$
are
 $D_{4r+3n}$
-apart, the previous claim implies that Y and Z are
$D_{4r+3n}$
-apart, the previous claim implies that Y and Z are
 $D_n$
-apart.
$D_n$
-apart. -
2. Now, suppose Y contains a nonempty component
 $Y_0$
of
$Y_0$
of
 $S_i\cap C$
and that Z does not. Then for some
$S_i\cap C$
and that Z does not. Then for some
 $g\in B_i$
, we have
$g\in B_i$
, we have
 $Z = Ug\cap C$
. Towards a contradiction, suppose
$Z = Ug\cap C$
. Towards a contradiction, suppose
 $D_nY\cap Ug \neq \emptyset $
. Let
$D_nY\cap Ug \neq \emptyset $
. Let
 $L = \{x_j: j\leq M\}$
be the line segment connecting Y and
$L = \{x_j: j\leq M\}$
be the line segment connecting Y and
 $Ug$
with
$Ug$
with
 $L\cap Y = \{x_0\}$
and
$L\cap Y = \{x_0\}$
and
 $L\cap Ug = \{x_M\}$
. We must have
$L\cap Ug = \{x_M\}$
. We must have
 $M\leq n$
. We cannot have
$M\leq n$
. We cannot have
 $x_0\in UB_i$
, so we must have
$x_0\in UB_i$
, so we must have
 $x_0\in D_{n-1}S_i$
. This implies that
$x_0\in D_{n-1}S_i$
. This implies that
 $x_0\in D_{n-1}Y_0$
. We cannot have
$x_0\in D_{n-1}Y_0$
. We cannot have
 $x_0\in Y_0$
, as otherwise, we would have connected
$x_0\in Y_0$
, as otherwise, we would have connected
 $Y_0$
and
$Y_0$
and
 $Ug\cap C$
when constructing
$Ug\cap C$
when constructing
 $J_i$
. It follows that for some
$J_i$
. It follows that for some
 $h\in B_i$
, we have that
$h\in B_i$
, we have that
 $x_0$
is on the line segment
$x_0$
is on the line segment
 $L' = \{x_j': j\leq M'\}$
connecting
$L' = \{x_j': j\leq M'\}$
connecting
 $Y_0$
and
$Y_0$
and
 $Uh\cap C$
, and we have
$Uh\cap C$
, and we have
 $M'\leq n$
. But this implies that
$M'\leq n$
. But this implies that
 $Ug\cap D_{2n}Uh\neq \emptyset $
, a contradiction since
$Ug\cap D_{2n}Uh\neq \emptyset $
, a contradiction since
 $V\supseteq UDU$
and
$V\supseteq UDU$
and
 $D\supseteq D_{2n}$
.
$D\supseteq D_{2n}$
. -
3. If neither Y nor Z contain a component of
 $S_i\cap C$
, then there are
$S_i\cap C$
, then there are
 $g\neq h\in B_i$
with
$g\neq h\in B_i$
with
 $Y = Uh\cap C$
and
$Y = Uh\cap C$
and
 $Z = Ug\cap C$
. It follows that Y and Z are
$Z = Ug\cap C$
. It follows that Y and Z are
 $D_n$
-apart.
$D_n$
-apart.
Claim. Suppose
![]() $i\neq j< m$
. Then
$i\neq j< m$
. Then
![]() $J_i$
and
$J_i$
and
![]() $J_j$
are D-apart.
$J_j$
are D-apart.
Proof. We have that
![]() $J_i\subseteq D_{n-1}S_i\cup UB_i$
, and likewise for j. As
$J_i\subseteq D_{n-1}S_i\cup UB_i$
, and likewise for j. As
![]() $UB_i\subseteq U^2DS_i$
and as
$UB_i\subseteq U^2DS_i$
and as
![]() $D\supseteq D_{2n}$
, we have
$D\supseteq D_{2n}$
, we have
![]() $J_i\subseteq U^2DS_i$
, and likewise for j. As
$J_i\subseteq U^2DS_i$
, and likewise for j. As
![]() $S_i$
and
$S_i$
and
![]() $S_j$
are W-apart and as
$S_j$
are W-apart and as
![]() $V\supseteq UDU$
, we see that
$V\supseteq UDU$
, we see that
![]() $J_i$
and
$J_i$
and
![]() $J_j$
are D-apart.
$J_j$
are D-apart.
Claim. Suppose
![]() $g\in B\setminus \bigcup _{i< m} B_i$
. Then
$g\in B\setminus \bigcup _{i< m} B_i$
. Then
![]() $Ug$
and
$Ug$
and
![]() $J_i$
are D-apart for any
$J_i$
are D-apart for any
![]() $i< m$
.
$i< m$
.
Proof. As
![]() $g\not \in B_i$
, we have
$g\not \in B_i$
, we have
![]() $U_g$
and
$U_g$
and
![]() $S_i$
are D-apart. Also, for any
$S_i$
are D-apart. Also, for any
![]() $h\in B$
with
$h\in B$
with
![]() $g\neq h$
, we have that
$g\neq h$
, we have that
![]() $Ug$
and
$Ug$
and
![]() $Uh$
are D-apart. Now, suppose
$Uh$
are D-apart. Now, suppose
![]() $DUg\cap J_i\neq \emptyset $
. If
$DUg\cap J_i\neq \emptyset $
. If
![]() $x\in DUg\cap J_i$
, then on the coset
$x\in DUg\cap J_i$
, then on the coset
![]() $C = F_2x$
, x must belong on the line between a component of
$C = F_2x$
, x must belong on the line between a component of
![]() $S_i\cap C$
and
$S_i\cap C$
and
![]() $Uh$
for some
$Uh$
for some
![]() $h\in B_i$
. Furthermore, we have
$h\in B_i$
. Furthermore, we have
![]() $x\in D_{n-1}Uh$
. But since
$x\in D_{n-1}Uh$
. But since
![]() $D_{2n}\subseteq D$
, this contradicts that
$D_{2n}\subseteq D$
, this contradicts that
![]() $Ug$
and
$Ug$
and
![]() $Uh$
are
$Uh$
are
![]() $D^2$
-apart (using the full assumption
$D^2$
-apart (using the full assumption
![]() $V\supseteq UD^2U$
).
$V\supseteq UD^2U$
).
We can now finish the proof of Proposition 4.2. The collection
![]() $\{J_i: i< m\}\cup \{Ug: g\in B\setminus (\bigcup _{i< m} B_i)\}$
is a pairwise D-apart collection of members of
$\{J_i: i< m\}\cup \{Ug: g\in B\setminus (\bigcup _{i< m} B_i)\}$
is a pairwise D-apart collection of members of
![]() $\mathcal {B}_n^*$
. As X is
$\mathcal {B}_n^*$
. As X is
![]() $\mathcal {B}_n^*$
-D-irreducible, we can find
$\mathcal {B}_n^*$
-D-irreducible, we can find
![]() $y\in X$
with
$y\in X$
with
![]() $y|_{J_i} = y_i|_{J_i}$
for each
$y|_{J_i} = y_i|_{J_i}$
for each
![]() $i< m$
and with
$i< m$
and with
![]() $(gy)|_U = \alpha $
for each
$(gy)|_U = \alpha $
for each
![]() $g\in B\setminus (\bigcup _{i< m} B_i)$
. As
$g\in B\setminus (\bigcup _{i< m} B_i)$
. As
![]() $J_i\supseteq UB_i$
and since
$J_i\supseteq UB_i$
and since
![]() $B_i\subseteq T_i$
, we actually have
$B_i\subseteq T_i$
, we actually have
![]() $(gy)|_U = \alpha $
for each
$(gy)|_U = \alpha $
for each
![]() $g\in B$
. As B is a maximal V-spaced set, it follows that
$g\in B$
. As B is a maximal V-spaced set, it follows that
![]() $y\in Y$
and
$y\in Y$
and
![]() $y|_{S_i} = y_i|_{S_i}$
as desired.
$y|_{S_i} = y_i|_{S_i}$
as desired.
Competing interest
The authors have no competing interest to declare.
Funding statement
J.F. was supported by NSF Grant DMS-2102838. B.S. was supported by NSF Grant DMS-1955090 and Sloan Grant FG-2021-16246. A.Z. was supported by NSF Grant DMS-2054302 and NSERC Grants RGPIN-2023-03269 and DGECR-2023-00412.