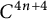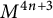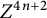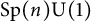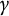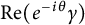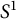1 Introduction
Hyperkähler manifolds C, equipped with a Riemannian metric
![]() $g_C$
, complex structures
$g_C$
, complex structures
![]() $(I_1, I_2, I_3)$
, and Kähler forms
$(I_1, I_2, I_3)$
, and Kähler forms
![]() $(\omega _1, \omega _2, \omega _3)$
, are a rich source of calibrated geometries. They feature not only familiar geometries arising from the Calabi–Yau structure – such as complex submanifolds and special Lagrangians – but also less-familiar ones specific to the hyperkähler setting. For example, a submanifold
$(\omega _1, \omega _2, \omega _3)$
, are a rich source of calibrated geometries. They feature not only familiar geometries arising from the Calabi–Yau structure – such as complex submanifolds and special Lagrangians – but also less-familiar ones specific to the hyperkähler setting. For example, a submanifold
![]() $N^{2k+2} \subset C^{4n+4}$
is complex isotropic with respect to
$N^{2k+2} \subset C^{4n+4}$
is complex isotropic with respect to
![]() $I_1$
if it is simultaneously
$I_1$
if it is simultaneously
Complex Lagrangians
![]() $N^{2n+2} \subset C^{4n+4}$
, those complex isotropic submanifolds of top dimension
$N^{2n+2} \subset C^{4n+4}$
, those complex isotropic submanifolds of top dimension
![]() $2n+2$
, are particularly remarkable, as they are at once complex submanifolds with respect to
$2n+2$
, are particularly remarkable, as they are at once complex submanifolds with respect to
![]() $I_1$
and special Lagrangian with respect to
$I_1$
and special Lagrangian with respect to
![]() $I_2$
and
$I_2$
and
![]() $I_3$
.
$I_3$
.
This paper seeks to systematically study the various calibrated cones of hyperkähler manifolds C, with a particular focus on complex isotropic cones. For this, it is of course necessary to assume that
![]() $(C^{4n+4}, g_C) = (\mathbb {R}^+ \times M^{4n+3}, dr^2 + r^2 g_M)$
is itself a Riemannian cone.
$(C^{4n+4}, g_C) = (\mathbb {R}^+ \times M^{4n+3}, dr^2 + r^2 g_M)$
is itself a Riemannian cone.
Hyperkähler cones
![]() $C^{4n+4}$
are themselves highly special objects: each induces three associated Einstein spaces, called M, Z, and Q, as we briefly recall. The first of these,
$C^{4n+4}$
are themselves highly special objects: each induces three associated Einstein spaces, called M, Z, and Q, as we briefly recall. The first of these,
![]() $M^{4n+3}$
, is just the link of C, which inherits a
$M^{4n+3}$
, is just the link of C, which inherits a
![]() $3$
-Sasakian structure. In view of the simple relationship between C and M,
$3$
-Sasakian structure. In view of the simple relationship between C and M,
![]() $3$
-Sasakian manifolds exhibit a wide array of semi-calibrated geometries. Indeed, each of the calibrated cones in C that we study has a semi-calibrated counterpart in M.
$3$
-Sasakian manifolds exhibit a wide array of semi-calibrated geometries. Indeed, each of the calibrated cones in C that we study has a semi-calibrated counterpart in M.

The entries of this table will be explained in Sections 2 and 3.
Now, since M is
![]() $3$
-Sasakian, it admits three linearly independent Reeb vector fields
$3$
-Sasakian, it admits three linearly independent Reeb vector fields
![]() $A_1, A_2, A_3$
. In fact, for each
$A_1, A_2, A_3$
. In fact, for each
![]() $v = (v_1, v_2, v_3) \in S^2$
, the Reeb field
$v = (v_1, v_2, v_3) \in S^2$
, the Reeb field
![]() $A_v = \sum v_i A_i$
yields a one-dimensional foliation
$A_v = \sum v_i A_i$
yields a one-dimensional foliation
![]() $\mathcal {F}_v$
on M, the projection
$\mathcal {F}_v$
on M, the projection
![]() $p_v \colon M \to M/\mathcal {F}_v$
is a principal
$p_v \colon M \to M/\mathcal {F}_v$
is a principal
![]() $S^1$
-orbibundle, and the quotient
$S^1$
-orbibundle, and the quotient
![]() $Z = M/\mathcal {F}_v$
is a
$Z = M/\mathcal {F}_v$
is a
![]() $(4n+2)$
-orbifold. It is well known that Z naturally admits both a Kähler–Einstein structure
$(4n+2)$
-orbifold. It is well known that Z naturally admits both a Kähler–Einstein structure
![]() $(g_{\mathrm {KE}}, J_{\mathrm {KE}}, \omega _{\mathrm {KE}})$
and a nearly Kähler structure
$(g_{\mathrm {KE}}, J_{\mathrm {KE}}, \omega _{\mathrm {KE}})$
and a nearly Kähler structure
![]() $(g_{\mathrm {NK}}, J_{\mathrm {NK}}, \omega _{\mathrm {NK}})$
. Indeed, Z is the twistor space of a quaternionic-Kähler
$(g_{\mathrm {NK}}, J_{\mathrm {NK}}, \omega _{\mathrm {NK}})$
. Indeed, Z is the twistor space of a quaternionic-Kähler
![]() $4n$
-orbifold Q of positive scalar curvature.
$4n$
-orbifold Q of positive scalar curvature.
The four Einstein spaces
![]() $C,M,Z,Q$
may be summarized in the following “diamond diagram” in which
$C,M,Z,Q$
may be summarized in the following “diamond diagram” in which
![]() $\tau \colon Z \to Q$
denotes the twistor
$\tau \colon Z \to Q$
denotes the twistor
![]() $S^2$
-bundle.
$S^2$
-bundle.

The flat model is
![]() $(C,M,Z,Q) = (\mathbb {H}^{n+1}, \mathbb {S}^{4n+3}, \mathbb {CP}^{2n+1}, \mathbb {HP}^n)$
, in which each
$(C,M,Z,Q) = (\mathbb {H}^{n+1}, \mathbb {S}^{4n+3}, \mathbb {CP}^{2n+1}, \mathbb {HP}^n)$
, in which each
![]() $p_v \colon \mathbb {S}^{4n+3} \to \mathbb {CP}^{2n+1}$
is a complex Hopf fibration, and
$p_v \colon \mathbb {S}^{4n+3} \to \mathbb {CP}^{2n+1}$
is a complex Hopf fibration, and
![]() $h \colon \mathbb {S}^{4n+3} \to \mathbb {HP}^n$
is a quaternionic Hopf fibration.
$h \colon \mathbb {S}^{4n+3} \to \mathbb {HP}^n$
is a quaternionic Hopf fibration.
In addition to all of the structure already discussed, we recover an observation of Alexandrov [Reference Alexandrov3] that twistor spaces Z admit a distinguished complex
![]() $3$
-form
$3$
-form
![]() $\gamma $
corresponding to an
$\gamma $
corresponding to an
![]() $\mathrm {Sp}(n)\mathrm {U}(1)$
-structure. In fact, we give two different proofs of this result, one in Section 4.2 via the
$\mathrm {Sp}(n)\mathrm {U}(1)$
-structure. In fact, we give two different proofs of this result, one in Section 4.2 via the
![]() $3$
-Sasakian geometry of M, and the other in Section 5.1 via the quaternionic-Kähler geometry of Q. Furthermore, we establish the new result that
$3$
-Sasakian geometry of M, and the other in Section 5.1 via the quaternionic-Kähler geometry of Q. Furthermore, we establish the new result that
![]() $\mathrm {Re}(\gamma )$
is a semi-calibration and we classify those
$\mathrm {Re}(\gamma )$
is a semi-calibration and we classify those
![]() $\mathrm {Re}(\gamma )$
-calibrated submanifolds that are
$\mathrm {Re}(\gamma )$
-calibrated submanifolds that are
![]() $\omega _{\mathrm {KE}}$
-isotropic. More precisely:
$\omega _{\mathrm {KE}}$
-isotropic. More precisely:
Theorem 1.1 Let Z be the
![]() $(4n+2)$
-dimensional twistor space of a positive quaternionic-Kähler
$(4n+2)$
-dimensional twistor space of a positive quaternionic-Kähler
![]() $4n$
-orbifold. Then Z admits an
$4n$
-orbifold. Then Z admits an
![]() $\mathrm {Sp}(n)\mathrm {U}(1)$
-structure
$\mathrm {Sp}(n)\mathrm {U}(1)$
-structure
![]() $\gamma \in \Omega ^3(Z; \mathbb {C})$
compatible with the Kähler–Einstein and nearly Kähler structures. Moreover:
$\gamma \in \Omega ^3(Z; \mathbb {C})$
compatible with the Kähler–Einstein and nearly Kähler structures. Moreover:
-
• The
 $3$
-form
$3$
-form
 $\mathrm {Re}(\gamma )$
is a semi-calibration (i.e., has comass one).
$\mathrm {Re}(\gamma )$
is a semi-calibration (i.e., has comass one). -
• If
 $\Sigma ^3$
is compact,
$\Sigma ^3$
is compact,
 $\mathrm {Re}(\gamma )$
-calibrated, and
$\mathrm {Re}(\gamma )$
-calibrated, and
 $\omega _{\mathrm {KE}}$
-isotropic, then with respect to the Kähler–Einstein metric,
$\omega _{\mathrm {KE}}$
-isotropic, then with respect to the Kähler–Einstein metric,
 $\Sigma $
is a geodesic circle bundle over a totally complex surface in Q. (See Definition 5.7.) Conversely, any such circle bundle is
$\Sigma $
is a geodesic circle bundle over a totally complex surface in Q. (See Definition 5.7.) Conversely, any such circle bundle is
 $\mathrm {Re}(\gamma )$
-calibrated and
$\mathrm {Re}(\gamma )$
-calibrated and
 $\omega _{\mathrm {KE}}$
-isotropic. (See Theorem 5.16.)
$\omega _{\mathrm {KE}}$
-isotropic. (See Theorem 5.16.)
We remark that there is a difference between the cases
![]() $n=1$
and
$n=1$
and
![]() $n \geq 2$
, so our proof handles them separately. In Section 4.3, we undertake a detailed study of
$n \geq 2$
, so our proof handles them separately. In Section 4.3, we undertake a detailed study of
![]() $\mathrm {Re}(\gamma )$
-calibrated
$\mathrm {Re}(\gamma )$
-calibrated
![]() $3$
-folds in
$3$
-folds in
![]() $Z^{4n+2}$
. In a certain precise sense, these are generalizations of special Lagrangian
$Z^{4n+2}$
. In a certain precise sense, these are generalizations of special Lagrangian
![]() $3$
-folds in nearly Kähler
$3$
-folds in nearly Kähler
![]() $6$
-manifolds.
$6$
-manifolds.
Geometric structures in place, we establish a series of relationships between the various classes of submanifolds in M, Z, and Q; see diagram (1.1). That is, given a submanifold
![]() $\Sigma \subset Z$
, we ask how various first-order conditions on
$\Sigma \subset Z$
, we ask how various first-order conditions on
![]() $\Sigma $
(e.g., complex and Lagrangian) influence the geometry of a local
$\Sigma $
(e.g., complex and Lagrangian) influence the geometry of a local
![]() $p_{(1,0,0)}$
-horizontal lift
$p_{(1,0,0)}$
-horizontal lift
![]() $\widehat {\Sigma } \subset M$
(provided one exists) and its
$\widehat {\Sigma } \subset M$
(provided one exists) and its
![]() $p_{(1,0,0)}$
-circle bundle
$p_{(1,0,0)}$
-circle bundle
![]() $p_{(1,0,0)}^{-1}(\Sigma ) \subset M$
, and vice versa. Similarly, starting with a totally complex
$p_{(1,0,0)}^{-1}(\Sigma ) \subset M$
, and vice versa. Similarly, starting with a totally complex
![]() $U \subset Q^{4n}$
, we study its
$U \subset Q^{4n}$
, we study its
![]() $\tau $
-horizontal lift
$\tau $
-horizontal lift
![]() $\widetilde {U} \subset Z$
and its geodesic circle bundle lift
$\widetilde {U} \subset Z$
and its geodesic circle bundle lift
![]() $\mathcal {L}(U) \subset Z$
:
$\mathcal {L}(U) \subset Z$
:
See Section 5.2 for a detailed discussion.
Altogether, the litany of propositions and theorems – proven in Sections 4.4, 5.2, and 6 – comprise a sort of “dictionary” of submanifold geometries. As an example, in Section 5.2, we obtain the following characterization of the compact submanifolds of Z that are Lagrangian with respect to both
![]() $\omega _{\mathrm {KE}}$
and
$\omega _{\mathrm {KE}}$
and
![]() $\omega _{\mathrm {NK}}$
, generalizing a result of Storm [Reference Storm30] to higher dimensions.
$\omega _{\mathrm {NK}}$
, generalizing a result of Storm [Reference Storm30] to higher dimensions.
Theorem 1.2 Recall diagram (1.1).
-
(1) If
 $\Sigma ^{2n+1} \subset Z^{4n+2}$
is a compact
$\Sigma ^{2n+1} \subset Z^{4n+2}$
is a compact
 $(2n+1)$
-dimensional submanifold that is both
$(2n+1)$
-dimensional submanifold that is both
 $\omega _{\mathrm {KE}}$
-Lagrangian and
$\omega _{\mathrm {KE}}$
-Lagrangian and
 $\omega _{\mathrm {NK}}$
-Lagrangian, then
$\omega _{\mathrm {NK}}$
-Lagrangian, then
 $\Sigma = \mathcal {L}(U)$
for some totally complex
$\Sigma = \mathcal {L}(U)$
for some totally complex
 $2n$
-fold
$2n$
-fold
 $U^{2n} \subset Q^{4n}$
(resp. superminimal surface if
$U^{2n} \subset Q^{4n}$
(resp. superminimal surface if
 $n = 1$
).
$n = 1$
). -
(2) Conversely, if
 $U^{2n} \subset Q^{4n}$
is totally complex and
$U^{2n} \subset Q^{4n}$
is totally complex and
 $n \geq 2$
, or if U is a superminimal surface and
$n \geq 2$
, or if U is a superminimal surface and
 $n = 1$
, then
$n = 1$
, then
 $\mathcal {L}(U) \subset Z$
is
$\mathcal {L}(U) \subset Z$
is
 $\omega _{\mathrm {KE}}$
-Lagrangian and
$\omega _{\mathrm {KE}}$
-Lagrangian and
 $\omega _{\mathrm {NK}}$
-Lagrangian.
$\omega _{\mathrm {NK}}$
-Lagrangian.
As another example, in Section 6, we provide several characterizations of complex isotropic cones in hyperkähler cones
![]() $C^{4n+4}$
in terms of submanifold geometries in M, Z, and Q. In particular, we prove the following theorem, generalizing a result of Ejiri and Tsukada [Reference Ejiri and Tsukada13] on complex isotropic cones of top dimension
$C^{4n+4}$
in terms of submanifold geometries in M, Z, and Q. In particular, we prove the following theorem, generalizing a result of Ejiri and Tsukada [Reference Ejiri and Tsukada13] on complex isotropic cones of top dimension
![]() $2n+2$
in
$2n+2$
in
![]() $C = \mathbb {H}^{n+1}$
.
$C = \mathbb {H}^{n+1}$
.
Theorem 1.3 Recall diagram (1.1). Let
![]() $L^{2k+1} \subset M^{4n+3}$
be a compact submanifold, where
$L^{2k+1} \subset M^{4n+3}$
be a compact submanifold, where
![]() $3 \leq 2k+1 \leq 2n+1$
. The following conditions are equivalent:
$3 \leq 2k+1 \leq 2n+1$
. The following conditions are equivalent:
-
(1) The cone
 $\mathrm {C}(L)$
is complex isotropic with respect to
$\mathrm {C}(L)$
is complex isotropic with respect to
 $\cos (\theta ) I_2 + \sin (\theta ) I_3$
for some
$\cos (\theta ) I_2 + \sin (\theta ) I_3$
for some
 $e^{i \theta } \in S^1$
.
$e^{i \theta } \in S^1$
. -
(2) The link L is locally of the form
 $p_{(0, \cos (\theta ), \sin (\theta ))}^{-1}(\widetilde {U})$
for some totally complex submanifold
$p_{(0, \cos (\theta ), \sin (\theta ))}^{-1}(\widetilde {U})$
for some totally complex submanifold
 $U^{2k} \subset Q$
(resp. superminimal surface if
$U^{2k} \subset Q$
(resp. superminimal surface if
 $n = 1$
) and some
$n = 1$
) and some
 $e^{i\theta } \in S^1$
.
$e^{i\theta } \in S^1$
. -
(3) The link L is locally a
 $p_{(1,0,0)}$
-horizontal lift of
$p_{(1,0,0)}$
-horizontal lift of
 $\mathcal {L}(U) \subset Z$
for some totally complex submanifold
$\mathcal {L}(U) \subset Z$
for some totally complex submanifold
 $U^{2k} \subset Q^{4n}$
(resp. superminimal surface
$U^{2k} \subset Q^{4n}$
(resp. superminimal surface
 $U^2 \subset Q^4$
if
$U^2 \subset Q^4$
if
 $n = 1$
).
$n = 1$
).
A more detailed statement appears as Theorem 6.1. Moreover, additional characterizations are available for complex isotropic cones
![]() $\mathrm {C}(L) \subset C$
of top dimension
$\mathrm {C}(L) \subset C$
of top dimension
![]() $2n+2$
and lowest dimension
$2n+2$
and lowest dimension
![]() $4$
: see Theorems 6.2 and 6.3, respectively.
$4$
: see Theorems 6.2 and 6.3, respectively.
Intuitively, Theorem 1.3 states that the link
![]() $L^{2k+1} \subset M$
of a complex isotropic cone in
$L^{2k+1} \subset M$
of a complex isotropic cone in
![]() $C^{4n+4}$
can be manufactured from a totally complex submanifold
$C^{4n+4}$
can be manufactured from a totally complex submanifold
![]() $U^{2k} \subset Q$
in two ways. By (2), one can first consider its
$U^{2k} \subset Q$
in two ways. By (2), one can first consider its
![]() $\tau $
-horizontal lift
$\tau $
-horizontal lift
![]() $\widetilde {U} \subset Z$
and then take the resulting
$\widetilde {U} \subset Z$
and then take the resulting
![]() $p_{(0, \cos (\theta ),\sin (\theta ))}$
-circle bundle. On the other hand, by (3), one could instead begin with the geodesic circle bundle lift
$p_{(0, \cos (\theta ),\sin (\theta ))}$
-circle bundle. On the other hand, by (3), one could instead begin with the geodesic circle bundle lift
![]() $\mathcal {L}(U) \subset Z$
and then take a
$\mathcal {L}(U) \subset Z$
and then take a
![]() $p_{(1,0,0)}$
-horizontal lift to M. Thus, in a sense, the operations of “circle bundle lift” and “horizontal lift” commute with one another.
$p_{(1,0,0)}$
-horizontal lift to M. Thus, in a sense, the operations of “circle bundle lift” and “horizontal lift” commute with one another.
Broadly speaking, Theorems 1.2 and 1.3 illustrate that a great variety of distinct classes of semi-calibrated submanifolds of a hyperkähler cone,
![]() $3$
-Sasakian manifold, or twistor space can only arise as particular constructions built from totally complex submanifolds, which is not at all evident from their definitions. Consequently, such submanifolds are essentially as plentiful as totally complex submanifolds. See Example 5.2 for some explicit totally complex submanifolds.
$3$
-Sasakian manifold, or twistor space can only arise as particular constructions built from totally complex submanifolds, which is not at all evident from their definitions. Consequently, such submanifolds are essentially as plentiful as totally complex submanifolds. See Example 5.2 for some explicit totally complex submanifolds.
1.1 Organization and conventions
In Section 2, we discuss several calibrated geometries in hyperkähler manifolds
![]() $C^{4n+4}$
, including the complex, special Lagrangian, complex isotropic, special isotropic, and Cayley submanifolds. Then, starting in Section 3, we assume that
$C^{4n+4}$
, including the complex, special Lagrangian, complex isotropic, special isotropic, and Cayley submanifolds. Then, starting in Section 3, we assume that
![]() $C = \mathrm {C}(M)$
is a hyperkähler cone over a
$C = \mathrm {C}(M)$
is a hyperkähler cone over a
![]() $3$
-Sasakian manifold
$3$
-Sasakian manifold
![]() $M^{4n+3}$
. We spend Section 3.1 reviewing
$M^{4n+3}$
. We spend Section 3.1 reviewing
![]() $3$
-Sasakian geometry, turning to the submanifold theory of M in Sections 3.2 and 3.3. In Section 3.4, we introduce a complex
$3$
-Sasakian geometry, turning to the submanifold theory of M in Sections 3.2 and 3.3. In Section 3.4, we introduce a complex
![]() $3$
-form
$3$
-form
![]() $\Gamma _1 \in \Omega ^3(M;\mathbb {C})$
and prove that it descends via
$\Gamma _1 \in \Omega ^3(M;\mathbb {C})$
and prove that it descends via
![]() $p_{(1,0,0)} \colon M \to Z$
to a
$p_{(1,0,0)} \colon M \to Z$
to a
![]() $3$
-form
$3$
-form
![]() $\gamma \in \Omega ^3(Z;\mathbb {C})$
on the twistor space.
$\gamma \in \Omega ^3(Z;\mathbb {C})$
on the twistor space.
Section 4 concerns submanifold theory in twistor spaces. After discussing
![]() $\mathrm {Sp}(n)\mathrm {U}(1)$
-structures on arbitrary
$\mathrm {Sp}(n)\mathrm {U}(1)$
-structures on arbitrary
![]() $(4n+2)$
-manifolds in Section 4.1, we show in Section 4.2 that the
$(4n+2)$
-manifolds in Section 4.1, we show in Section 4.2 that the
![]() $3$
-form
$3$
-form
![]() $\gamma \in \Omega ^3(Z;\mathbb {C})$
defines such a structure on the twistor space. Then, in Sections 4.3 and 4.4, we study various classes of submanifolds of Z, establishing a series of relationships between those in Z and those in M.
$\gamma \in \Omega ^3(Z;\mathbb {C})$
defines such a structure on the twistor space. Then, in Sections 4.3 and 4.4, we study various classes of submanifolds of Z, establishing a series of relationships between those in Z and those in M.
In Section 5.2, we consider totally complex submanifolds of quaternionic-Kähler manifolds Q and relate them to submanifold geometries in M and Z. Finally, in Section 6, we provide several characterizations of complex isotropic cones in C. This paper also includes two appendices: Appendix A.1 collects some results on the linear algebra of calibrations that we use, and Appendix A.2 gives a brief introduction to metric cones and their associated conical differential forms.
Notation and conventions.
-
• We often use
 $c_{\theta }, s_{\theta }$
to denote
$c_{\theta }, s_{\theta }$
to denote
 $\cos \theta , \sin \theta $
, respectively, for brevity.
$\cos \theta , \sin \theta $
, respectively, for brevity. -
• Repeated indices are summed over all of their allowed values unless explicitly stated otherwise. The symbol
 $\epsilon _{pqr}$
is the permutation symbol on three letters, so it vanishes if any two indices are equal, and it equals
$\epsilon _{pqr}$
is the permutation symbol on three letters, so it vanishes if any two indices are equal, and it equals
 $\mathrm {sgn}(\sigma )$
if
$\mathrm {sgn}(\sigma )$
if
 $p, q, r = \sigma (1), \sigma (2), \sigma (3)$
.
$p, q, r = \sigma (1), \sigma (2), \sigma (3)$
. -
• A superscript on a manifold always denotes its real dimension.
-
• For a manifold M, we use
 $\mathrm {C}(M) = \mathbb {R}^+ \times M$
with metric
$\mathrm {C}(M) = \mathbb {R}^+ \times M$
with metric
 $dr^2 + r^2 g_M$
to denote the metric cone over M, as discussed in Appendix A.2.
$dr^2 + r^2 g_M$
to denote the metric cone over M, as discussed in Appendix A.2. -
• If L is a submanifold of M, then
 $NL$
denotes its normal bundle. Submanifolds are assumed to be embedded. (Much of what we discuss works for immersed submanifolds, but not everything. See also Remark 5.15.) Unless stated otherwise, all submanifolds are assumed to be connected and orientable and thus have exactly two orientations.
$NL$
denotes its normal bundle. Submanifolds are assumed to be embedded. (Much of what we discuss works for immersed submanifolds, but not everything. See also Remark 5.15.) Unless stated otherwise, all submanifolds are assumed to be connected and orientable and thus have exactly two orientations. -
• We use interchangeably the terms semi-calibration and comass one. That is, a differential form
 $\alpha $
is a calibration if it is a semi-calibration that satisfies
$\alpha $
is a calibration if it is a semi-calibration that satisfies
 $d\alpha = 0$
.
$d\alpha = 0$
. -
• The twistor space
 $Z^{4n+2}$
and the quaternionic-Kähler
$Z^{4n+2}$
and the quaternionic-Kähler
 $Q^{4n}$
are in general orbifolds. However, we avoid technical complications and work only over the smooth parts of Z and Q. That is, all submanifolds are assumed to not pass through any orbifold points of Z or Q.
$Q^{4n}$
are in general orbifolds. However, we avoid technical complications and work only over the smooth parts of Z and Q. That is, all submanifolds are assumed to not pass through any orbifold points of Z or Q.
2 Calibrated geometry in hyperkähler manifolds
Let
![]() $C^{4n+4}$
be a hyperkähler manifold with
$C^{4n+4}$
be a hyperkähler manifold with
![]() $n \geq 1$
. The hyperkähler structure on C consists of the following data:
$n \geq 1$
. The hyperkähler structure on C consists of the following data:
-
• a Riemannian metric
 $g_C$
;
$g_C$
; -
• a triple of integrable almost-complex structures
 $(I_1, I_2, I_3) = (I,J,K)$
satisfying the quaternionic relations
$(I_1, I_2, I_3) = (I,J,K)$
satisfying the quaternionic relations
 $I_1 I_2 = I_3$
, etc., each of which is orthogonal with respect to
$I_1 I_2 = I_3$
, etc., each of which is orthogonal with respect to
 $g_C$
;
$g_C$
; -
• a triple of closed
 $2$
-forms
$2$
-forms
 $(\omega _1, \omega _2, \omega _3)$
given by
$(\omega _1, \omega _2, \omega _3)$
given by
 $\omega _p(X,Y) = g_C(I_p X, Y)$
.
$\omega _p(X,Y) = g_C(I_p X, Y)$
.
Note that
![]() $\omega _p$
is a Kähler form with respect to
$\omega _p$
is a Kähler form with respect to
![]() $I_p$
, so in particular it is of type
$I_p$
, so in particular it is of type
![]() $(1,1)$
with respect to
$(1,1)$
with respect to
![]() $I_p$
. This means that
$I_p$
. This means that
![]() $\omega _p (I_p X, I_p Y) = \omega (X, Y)$
and thus
$\omega _p (I_p X, I_p Y) = \omega (X, Y)$
and thus
![]() $g_C (X, Y) = \omega _p (X, I_p Y)$
. We also have
$g_C (X, Y) = \omega _p (X, I_p Y)$
. We also have
In fact, we have an
![]() $S^2$
-family of Kähler structures: for any
$S^2$
-family of Kähler structures: for any
![]() $v = (v_1, v_2, v_3) \in S^2$
, we can take
$v = (v_1, v_2, v_3) \in S^2$
, we can take
![]() $I_v = \sum _{p=1}^3 v_p I_p$
and
$I_v = \sum _{p=1}^3 v_p I_p$
and
![]() $\omega _v (X, Y) = g_C(I_v X, Y)$
.
$\omega _v (X, Y) = g_C(I_v X, Y)$
.
One can show that C inherits a triple of complex-symplectic forms
![]() $\sigma _1, \sigma _2, \sigma _3 \in \Omega ^2(C; \mathbb {C})$
via
$\sigma _1, \sigma _2, \sigma _3 \in \Omega ^2(C; \mathbb {C})$
via
A calculation shows that
![]() $\sigma _1$
is of
$\sigma _1$
is of
![]() $I_1$
-type
$I_1$
-type
![]() $(2,0)$
, and analogously for
$(2,0)$
, and analogously for
![]() $\sigma _2, \sigma _3$
. It follows that each
$\sigma _2, \sigma _3$
. It follows that each
![]() $\sigma _p$
is a holomorphic symplectic form with respect to
$\sigma _p$
is a holomorphic symplectic form with respect to
![]() $I_p$
.
$I_p$
.
Further, C inherits the following triple of
![]() $(2n+2)$
-forms
$(2n+2)$
-forms
![]() $\Upsilon _1, \Upsilon _2, \Upsilon _3$
:
$\Upsilon _1, \Upsilon _2, \Upsilon _3$
:
Each
![]() $\Upsilon _p$
is a holomorphic volume form with respect to
$\Upsilon _p$
is a holomorphic volume form with respect to
![]() $I_p$
, so that
$I_p$
, so that
![]() $(g_C, I_p, \omega _p, \Upsilon _p)$
is a Calabi–Yau structure on C. More generally, fixing
$(g_C, I_p, \omega _p, \Upsilon _p)$
is a Calabi–Yau structure on C. More generally, fixing
![]() $I_1$
as a reference, by considering the holomorphic volume form
$I_1$
as a reference, by considering the holomorphic volume form
![]() $e^{i (n+1)\theta } \Upsilon _1 = \frac {1}{(n+1)!} (e^{i \theta } \sigma _1)^{n+1}$
, we obtain an
$e^{i (n+1)\theta } \Upsilon _1 = \frac {1}{(n+1)!} (e^{i \theta } \sigma _1)^{n+1}$
, we obtain an
![]() $S^1$
-family of Calabi–Yau structures with respect to
$S^1$
-family of Calabi–Yau structures with respect to
![]() $I_1$
. Since
$I_1$
. Since
![]() $e^{i \theta } \sigma _1 = (c_\theta \omega _2 - s_\theta \omega _3) + i (s_\theta \omega _2 + c_\theta \omega _3)$
, this
$e^{i \theta } \sigma _1 = (c_\theta \omega _2 - s_\theta \omega _3) + i (s_\theta \omega _2 + c_\theta \omega _3)$
, this
![]() $S^1$
-family corresponds to rotating the orthogonal pair
$S^1$
-family corresponds to rotating the orthogonal pair
![]() $I_2, I_3$
by
$I_2, I_3$
by
![]() $\theta $
in the equator of
$\theta $
in the equator of
![]() $S^2$
determined by the poles
$S^2$
determined by the poles
![]() $\pm I_1$
.
$\pm I_1$
.
Finally, C also admits a quaternionic-Kähler structure via the real
![]() $4$
-form
$4$
-form
(See Definition 5.2 for our definition of quaternionic Kähler.)
In this section, we recall various classes of distinguished submanifolds of C. Some of these classes – e.g., the complex, Lagrangian, special Lagrangian, and quaternionic – arise from a Calabi–Yau or quaternionic-Kähler structure. Others arise from a complex-symplectic structure, or are otherwise special to the hyperkähler setting.
2.1 Submanifolds via the Calabi–Yau and QK structures
Recall that every hyperkähler manifold is a Kähler manifold in an
![]() $S^2$
-family of ways, and given such a choice, it is a Calabi–Yau manifold in an
$S^2$
-family of ways, and given such a choice, it is a Calabi–Yau manifold in an
![]() $S^1$
-family of ways. Due to these structures, we may consider the following classes of submanifolds.
$S^1$
-family of ways. Due to these structures, we may consider the following classes of submanifolds.
Definition 2.1 A submanifold
![]() $N^{2k} \subset C^{4n+4}$
is
$N^{2k} \subset C^{4n+4}$
is
![]() $I_1$
-complex if
$I_1$
-complex if
That is, if it is calibrated with respect to
![]() $\frac {1}{k!}\omega _1^k$
.
$\frac {1}{k!}\omega _1^k$
.
It is
![]() $I_1$
-anti-complex, or
$I_1$
-anti-complex, or
![]() $-I_1$
-complex, if it is calibrated with respect to
$-I_1$
-complex, if it is calibrated with respect to
![]() $-\frac {1}{k!}\omega _1^k$
. Equivalently, if it is
$-\frac {1}{k!}\omega _1^k$
. Equivalently, if it is
![]() $I_1$
-complex when equipped with the opposite orientation.
$I_1$
-complex when equipped with the opposite orientation.
A submanifold is
![]() $\pm I_1$
-complex if and only if its tangent spaces are
$\pm I_1$
-complex if and only if its tangent spaces are
![]() $I_1$
-invariant:
$I_1$
-invariant:
The definitions of
![]() $I_2$
-complex and
$I_2$
-complex and
![]() $I_3$
-complex are analogous.
$I_3$
-complex are analogous.
Definition 2.2 A submanifold
![]() $N \subset C^{4n+4}$
is
$N \subset C^{4n+4}$
is
![]() $\omega _1$
-isotropic if
$\omega _1$
-isotropic if
An
![]() $\omega _1$
-isotropic submanifold satisfies
$\omega _1$
-isotropic submanifold satisfies
![]() $\dim (N) \leq 2n+2$
. An
$\dim (N) \leq 2n+2$
. An
![]() $\omega _1$
-Lagrangian submanifold is an
$\omega _1$
-Lagrangian submanifold is an
![]() $\omega _1$
-isotropic submanifold of maximal dimension
$\omega _1$
-isotropic submanifold of maximal dimension
![]() $2n+2$
.
$2n+2$
.
Let
![]() $X, Y \in TL$
. Since
$X, Y \in TL$
. Since
![]() $\omega _1(X, Y) = g(I_1 X, Y)$
, we see that L is
$\omega _1(X, Y) = g(I_1 X, Y)$
, we see that L is
![]() $\omega _1$
-isotropic if and only if
$\omega _1$
-isotropic if and only if
![]() $I_1 (TL) \subseteq NL$
. If N has dimension
$I_1 (TL) \subseteq NL$
. If N has dimension
![]() $2n+2$
, then
$2n+2$
, then
![]() $I_1 (TL) = NL$
if and only if L is
$I_1 (TL) = NL$
if and only if L is
![]() $\omega _1$
-Lagrangian. We use these facts repeatedly.
$\omega _1$
-Lagrangian. We use these facts repeatedly.
Definition 2.3 Fix
![]() $\theta \in [0,2\pi )$
. A
$\theta \in [0,2\pi )$
. A
![]() $(2n+2)$
-dimensional submanifold
$(2n+2)$
-dimensional submanifold
![]() $N^{2n+2} \subset C^{4n+4}$
is called
$N^{2n+2} \subset C^{4n+4}$
is called
![]() $\Upsilon _1$
-special Lagrangian of phase
$\Upsilon _1$
-special Lagrangian of phase
![]() $e^{i \theta }$
if
$e^{i \theta }$
if
Equivalently [Reference Harvey and Blaine Lawson20, Corollary 1.11], there exists an orientation on
![]() $N^{2n+2}$
making it
$N^{2n+2}$
making it
![]() $\Upsilon _1$
-special Lagrangian of phase
$\Upsilon _1$
-special Lagrangian of phase
![]() $e^{i \theta }$
if and only if
$e^{i \theta }$
if and only if
When the phase is left unspecified, we assume it to be
![]() $e^{i \theta } = 1$
.
$e^{i \theta } = 1$
.
Remark 2.4 Every hyperkähler manifold is also quaternionic-Kähler, and such manifolds admit a distinguished class of quaternionic submanifolds. However, Gray [Reference Gray18] proved that such submanifolds are always totally geodesic. We will not consider quaternionic submanifolds in this paper.
2.2 Submanifolds via the hyperkähler structure
In addition to the submanifolds discussed above, hyperkähler manifolds also admit three more notable classes of submanifolds: the complex isotropic, special isotropic, and generalized Cayley submanifolds. We discuss each of these in turn.
2.2.1 Complex isotropic submanifolds
Definition 2.5 A
![]() $2k$
-dimensional submanifold
$2k$
-dimensional submanifold
![]() $L^{2k} \subset C^{4n+4}$
is called
$L^{2k} \subset C^{4n+4}$
is called
![]() $I_1$
-complex isotropic if it is both
$I_1$
-complex isotropic if it is both
![]() $I_1$
-complex and
$I_1$
-complex and
![]() $\sigma _1$
-isotropic. That is, if
$\sigma _1$
-isotropic. That is, if
Said another way, L is
![]() $I_1$
-complex,
$I_1$
-complex,
![]() $\omega _2$
-isotropic, and
$\omega _2$
-isotropic, and
![]() $\omega _3$
-isotropic:
$\omega _3$
-isotropic:
An
![]() $I_1$
-complex Lagrangian submanifold
$I_1$
-complex Lagrangian submanifold
![]() $L^{2n+2} \subset C^{4n+4}$
is an
$L^{2n+2} \subset C^{4n+4}$
is an
![]() $I_1$
-complex isotropic submanifold of maximal dimension
$I_1$
-complex isotropic submanifold of maximal dimension
![]() $2n+2$
. That is, an
$2n+2$
. That is, an
![]() $I_1$
-complex Lagrangian submanifold is simultaneously
$I_1$
-complex Lagrangian submanifold is simultaneously
![]() $I_1$
-complex,
$I_1$
-complex,
![]() $\omega _2$
-Lagrangian, and
$\omega _2$
-Lagrangian, and
![]() $\omega _3$
-Lagrangian. The definitions of
$\omega _3$
-Lagrangian. The definitions of
![]() $I_2$
- and
$I_2$
- and
![]() $I_3$
-complex isotropic (resp. complex Lagrangian) are analogous.
$I_3$
-complex isotropic (resp. complex Lagrangian) are analogous.
Complex isotropic submanifolds are interesting from several points of view. For example, in algebraic geometry, one often considers holomorphic symplectic manifolds that are fibered by complex Lagrangians, as in [Reference Sawon29]. As another example, Doan and Rezchikov [Reference Doan and Rezchikov11] use complex Lagrangians as part of a hyperkähler Floer theory. In the differential geometry literature, complex isotropic submanifolds have been studied by, for example, Bryant and Harvey [Reference Bryant and Harvey9], Hitchin [Reference Hitchin22], and Grantcharov and Verbitsky [Reference Grantcharov and Verbitsky17].
Proposition 2.6 Let
![]() $L^{2k} \subset C^{4n+4}$
be a
$L^{2k} \subset C^{4n+4}$
be a
![]() $2k$
-dimensional submanifold. The following are equivalent:
$2k$
-dimensional submanifold. The following are equivalent:
-
(1) L is
 $I_1$
-complex,
$I_1$
-complex,
 $\omega _2$
-isotropic, and
$\omega _2$
-isotropic, and
 $\omega _3$
-isotropic.
$\omega _3$
-isotropic. -
(2) L is
 $I_1$
-complex and
$I_1$
-complex and
 $\omega _2$
-isotropic.
$\omega _2$
-isotropic.
Proof One direction is immediate. For the converse, suppose L is
![]() $I_1$
-complex and
$I_1$
-complex and
![]() $\omega _2$
-isotropic. Let
$\omega _2$
-isotropic. Let
![]() $X \in TL$
, so that
$X \in TL$
, so that
![]() $I_1X \in TL$
, and thus
$I_1X \in TL$
, and thus
![]() $- I_3 X = I_2(I_1X) \in NL$
. Hence,
$- I_3 X = I_2(I_1X) \in NL$
. Hence,
![]() $I_3X \in NL$
. This shows that L is
$I_3X \in NL$
. This shows that L is
![]() $\omega _3$
-isotropic.
$\omega _3$
-isotropic.
In the complex Lagrangian case, we can say more:
Proposition 2.7 Let
![]() $L^{2n+2} \subset C^{4n+4}$
be a
$L^{2n+2} \subset C^{4n+4}$
be a
![]() $(2n+2)$
-dimensional submanifold. The following are equivalent:
$(2n+2)$
-dimensional submanifold. The following are equivalent:
-
(1) L is
 $I_1$
-complex,
$I_1$
-complex,
 $\omega _2$
-Lagrangian, and
$\omega _2$
-Lagrangian, and
 $\omega _3$
-Lagrangian.
$\omega _3$
-Lagrangian. -
(2) L is
 $I_1$
-complex and
$I_1$
-complex and
 $\omega _2$
-Lagrangian.
$\omega _2$
-Lagrangian. -
(3) L is
 $\omega _2$
-Lagrangian and
$\omega _2$
-Lagrangian and
 $\omega _3$
-Lagrangian.
$\omega _3$
-Lagrangian. -
(4) L is
 $I_1$
-complex,
$I_1$
-complex,
 $\Upsilon _2$
-special Lagrangian of phase
$\Upsilon _2$
-special Lagrangian of phase
 $i^{n+1}$
, and
$i^{n+1}$
, and
 $\Upsilon _3$
-special Lagrangian of phase
$\Upsilon _3$
-special Lagrangian of phase
 $1$
.
$1$
.
Proof The equivalence (i)
![]() $\iff $
(ii) was observed above. It is clear that (i)
$\iff $
(ii) was observed above. It is clear that (i)
![]() $\implies $
(iii). For (iii)
$\implies $
(iii). For (iii)
![]() $\implies $
(i), suppose that L is
$\implies $
(i), suppose that L is
![]() $\omega _2$
- and
$\omega _2$
- and
![]() $\omega _3$
-Lagrangian. Let
$\omega _3$
-Lagrangian. Let
![]() $X \in TL$
, so that
$X \in TL$
, so that
![]() $I_3X \in NL$
, and thus
$I_3X \in NL$
, and thus
![]() $I_1X = I_2(I_3X) \in TL$
. Hence, L is
$I_1X = I_2(I_3X) \in TL$
. Hence, L is
![]() $I_1$
-complex.
$I_1$
-complex.
It is clear that (iv)
![]() $\implies $
(i). For (i)
$\implies $
(i). For (i)
![]() $\implies $
(iv), suppose that L is
$\implies $
(iv), suppose that L is
![]() $I_1$
-complex,
$I_1$
-complex,
![]() $\omega _2$
-Lagrangian, and
$\omega _2$
-Lagrangian, and
![]() $\omega _3$
-Lagrangian. Then L satisfies
$\omega _3$
-Lagrangian. Then L satisfies
![]() $\left .\frac {1}{(n+1)!}\omega _1^{n+1}\right |_L = \mathrm {vol}_L$
and
$\left .\frac {1}{(n+1)!}\omega _1^{n+1}\right |_L = \mathrm {vol}_L$
and
![]() $\left .\omega _2\right |_L = 0$
and
$\left .\omega _2\right |_L = 0$
and
![]() $\left .\omega _3\right |_L = 0$
. Recalling that
$\left .\omega _3\right |_L = 0$
. Recalling that
we have
 $$ \begin{align*} \left.\text{Re}((-i)^{n+1} \Upsilon_2)\right|_L & = \left.\frac{1}{(n+1)!}\omega_1^{n+1}\right|_L = \mathrm{vol}_L, & \left.\text{Re}( \Upsilon_3)\right|_L = \left.\frac{1}{(n+1)!}\omega_1^{n+1}\right|_L = \mathrm{vol}_L. \end{align*} $$
$$ \begin{align*} \left.\text{Re}((-i)^{n+1} \Upsilon_2)\right|_L & = \left.\frac{1}{(n+1)!}\omega_1^{n+1}\right|_L = \mathrm{vol}_L, & \left.\text{Re}( \Upsilon_3)\right|_L = \left.\frac{1}{(n+1)!}\omega_1^{n+1}\right|_L = \mathrm{vol}_L. \end{align*} $$
2.2.2 Special isotropic submanifolds
The following definition is due to Bryant and Harvey [Reference Bryant and Harvey9]. We prove that these forms are calibrations in Theorem A.6 in the Appendix.
Definition 2.8 The special isotropic forms are the
![]() $2k$
-forms
$2k$
-forms
![]() $\Theta _{I,2k}, \Theta _{J,2k}, \Theta _{K,2k} \in \Omega ^{2k}(C)$
defined by
$\Theta _{I,2k}, \Theta _{J,2k}, \Theta _{K,2k} \in \Omega ^{2k}(C)$
defined by
A
![]() $2k$
-dimensional submanifold
$2k$
-dimensional submanifold
![]() $N^{2k} \subset C^{4n+4}$
is
$N^{2k} \subset C^{4n+4}$
is
![]() $\Theta _{I,2k}$
-special isotropic if it is calibrated by
$\Theta _{I,2k}$
-special isotropic if it is calibrated by
![]() $\Theta _{I,k}$
:
$\Theta _{I,k}$
:
The definitions of
![]() $\Theta _{J,2k}$
- and
$\Theta _{J,2k}$
- and
![]() $\Theta _{K,2k}$
-special isotropic
$\Theta _{K,2k}$
-special isotropic
![]() $2k$
-manifold are analogous.
$2k$
-manifold are analogous.
Let us highlight the cases
![]() $2k = 2, 4, 2n+2$
.
$2k = 2, 4, 2n+2$
.
Example 2.1
-
(1) For
 $2k = 2$
, the special isotropic
$2k = 2$
, the special isotropic
 $2$
-forms are In particular, a
$2$
-forms are In particular, a $$ \begin{align*} \Theta_{I,2} & = \omega_2, & \Theta_{J,2} & = \omega_3, & \Theta_{K,2} & = \omega_1. \end{align*} $$
$$ \begin{align*} \Theta_{I,2} & = \omega_2, & \Theta_{J,2} & = \omega_3, & \Theta_{K,2} & = \omega_1. \end{align*} $$
 $\Theta _{I,2}$
-special isotropic
$\Theta _{I,2}$
-special isotropic
 $2$
-fold is the same as an
$2$
-fold is the same as an
 $I_2$
-complex
$I_2$
-complex
 $2$
-fold.
$2$
-fold.
-
(2) For
 $2k = 4$
, the special isotropic
$2k = 4$
, the special isotropic
 $4$
-forms are In particular, if L is an
$4$
-forms are In particular, if L is an $$ \begin{align*} \Theta_{I,4} & = \frac{1}{2}(\omega_2^2 - \omega_3^2), & \Theta_{J,4} & = \frac{1}{2}(\omega_3^2 - \omega_1^2), & \Theta_{K,4} & = \frac{1}{2}(\omega_1^2 - \omega_2^2). \end{align*} $$
$$ \begin{align*} \Theta_{I,4} & = \frac{1}{2}(\omega_2^2 - \omega_3^2), & \Theta_{J,4} & = \frac{1}{2}(\omega_3^2 - \omega_1^2), & \Theta_{K,4} & = \frac{1}{2}(\omega_1^2 - \omega_2^2). \end{align*} $$
 $I_1$
-complex isotropic
$I_1$
-complex isotropic
 $4$
-fold, then L is both
$4$
-fold, then L is both
 $-\Theta _{J,4}$
-special isotropic and
$-\Theta _{J,4}$
-special isotropic and
 $\Theta _{K,4}$
-special isotropic.
$\Theta _{K,4}$
-special isotropic.
-
(3) For
 $2k = 2n+2$
, the special isotropic
$2k = 2n+2$
, the special isotropic
 $(2n+2)$
-forms are In particular, a
$(2n+2)$
-forms are In particular, a $$ \begin{align*} \Theta_{I,2n+2} & = \text{Re}(\Upsilon_1), & \Theta_{J, 2n+2} & = \text{Re}(\Upsilon_2), & \Theta_{K, 2n+2} & = \text{Re}(\Upsilon_3). \end{align*} $$
$$ \begin{align*} \Theta_{I,2n+2} & = \text{Re}(\Upsilon_1), & \Theta_{J, 2n+2} & = \text{Re}(\Upsilon_2), & \Theta_{K, 2n+2} & = \text{Re}(\Upsilon_3). \end{align*} $$
 $\Theta _{I, 2n+2}$
-special isotropic
$\Theta _{I, 2n+2}$
-special isotropic
 $(2n+2)$
-fold is the same as an
$(2n+2)$
-fold is the same as an
 $\Upsilon _1$
-special Lagrangian, which explains the name “special isotropic.”
$\Upsilon _1$
-special Lagrangian, which explains the name “special isotropic.”
At present, it appears that little is known about special isotropic
![]() $2k$
-folds in hyperkähler
$2k$
-folds in hyperkähler
![]() $(4n+4)$
-manifolds when
$(4n+4)$
-manifolds when
![]() $2 < 2k < 2n+2$
.
$2 < 2k < 2n+2$
.
2.2.3 Cayley
 $4$
-folds
$4$
-folds
The following definition is due to Bryant and Harvey [Reference Bryant and Harvey9], though our sign conventions are opposite to theirs.
Definition 2.9 The generalized Cayley
![]() $4$
-forms are the
$4$
-forms are the
![]() $4$
-forms
$4$
-forms
![]() $\Phi _1, \Phi _2, \Phi _3 \in \Omega ^4(C)$
defined by
$\Phi _1, \Phi _2, \Phi _3 \in \Omega ^4(C)$
defined by
Note that
and similarly for cyclic permutations. A four-dimensional submanifold
![]() $N^4 \subset C^{4n+4}$
is
$N^4 \subset C^{4n+4}$
is
![]() $\Phi _2$
-Cayley if it is calibrated by
$\Phi _2$
-Cayley if it is calibrated by
![]() $\Phi _2$
:
$\Phi _2$
:
The definitions of
![]() $\Phi _1$
-Cayley and
$\Phi _1$
-Cayley and
![]() $\Phi _3$
-Cayley are analogous.
$\Phi _3$
-Cayley are analogous.
Remark 2.10 Bryant and Harvey [Reference Bryant and Harvey9, Lemma 2.14] computed that the
![]() $\mathrm {SO}(4n+4)$
-stabilizer of the generalized Cayley
$\mathrm {SO}(4n+4)$
-stabilizer of the generalized Cayley
![]() $4$
-forms in
$4$
-forms in
![]() $\mathbb {R}^{4n+4}$
are
$\mathbb {R}^{4n+4}$
are
 $$ \begin{align*}\mathrm{Stab}(\Phi_1) = \begin{cases} \mathrm{Spin}(7), & \text{if } n = 1, \\ \mathrm{Sp}(n+1)\mathrm{O}(2), & \text{if } n \geq 2. \end{cases}\end{align*} $$
$$ \begin{align*}\mathrm{Stab}(\Phi_1) = \begin{cases} \mathrm{Spin}(7), & \text{if } n = 1, \\ \mathrm{Sp}(n+1)\mathrm{O}(2), & \text{if } n \geq 2. \end{cases}\end{align*} $$
This above definition was inspired by
![]() $\mathrm {Spin}(7)$
-geometry, as we now recall. If
$\mathrm {Spin}(7)$
-geometry, as we now recall. If
![]() $(X^8, (g, \omega , I, \Upsilon ))$
is a Calabi–Yau
$(X^8, (g, \omega , I, \Upsilon ))$
is a Calabi–Yau
![]() $8$
-manifold, where
$8$
-manifold, where
![]() $\omega \in \Omega ^2(X)$
is the Kähler form and
$\omega \in \Omega ^2(X)$
is the Kähler form and
![]() $\Upsilon \in \Omega ^4(X;\mathbb {C})$
is the holomorphic volume form, then X inherits a torsion-free
$\Upsilon \in \Omega ^4(X;\mathbb {C})$
is the holomorphic volume form, then X inherits a torsion-free
![]() $\mathrm {Spin}(7)$
-structure via the following formula:
$\mathrm {Spin}(7)$
-structure via the following formula:
The real
![]() $4$
-form
$4$
-form
![]() $\Phi \in \Omega ^4(X)$
is called the Cayley
$\Phi \in \Omega ^4(X)$
is called the Cayley
![]() $4$
-form, and a four-dimensional submanifold
$4$
-form, and a four-dimensional submanifold
![]() $N \subset X$
satisfying
$N \subset X$
satisfying
![]() $\Phi |_N = \mathrm {vol}_N$
is called Cayley. The following fact is well known, but we include a proof for completeness.
$\Phi |_N = \mathrm {vol}_N$
is called Cayley. The following fact is well known, but we include a proof for completeness.
Proposition 2.11 Let
![]() $(X^8, (g,\omega , I, \Upsilon ))$
be a Calabi–Yau
$(X^8, (g,\omega , I, \Upsilon ))$
be a Calabi–Yau
![]() $8$
-manifold, and equip X with its induced
$8$
-manifold, and equip X with its induced
![]() $\mathrm {Spin}(7)$
-structure. Let
$\mathrm {Spin}(7)$
-structure. Let
![]() $N^4 \subset X$
be a four-dimensional submanifold.
$N^4 \subset X$
be a four-dimensional submanifold.
-
(1) If N is complex, then N is Cayley.
-
(2) If N is special Lagrangian of phase
 $e^{i\pi } = -1$
, then N is Cayley.
$e^{i\pi } = -1$
, then N is Cayley.
Proof If N is complex, each tangent space
![]() $T_x N$
admits a basis of the form
$T_x N$
admits a basis of the form
![]() $\{ e_1, I e_1, e_2, I e_2 \}$
. Then
$\{ e_1, I e_1, e_2, I e_2 \}$
. Then
![]() $v_k = e_k - i I e_k$
is of type
$v_k = e_k - i I e_k$
is of type
![]() $(1,0)$
for
$(1,0)$
for
![]() $k = 1, 2$
, and
$k = 1, 2$
, and
![]() $T_x N = e_1 \wedge I e_1 \wedge e_2 \wedge I e_2$
is a multiple of
$T_x N = e_1 \wedge I e_1 \wedge e_2 \wedge I e_2$
is a multiple of
![]() $v_1 \wedge \overline {v_1} \wedge v_2 \wedge \overline {v_2}$
and thus of type
$v_1 \wedge \overline {v_1} \wedge v_2 \wedge \overline {v_2}$
and thus of type
![]() $(2,2)$
. Since
$(2,2)$
. Since
![]() $\text {Re}(\Upsilon )$
is type
$\text {Re}(\Upsilon )$
is type
![]() $(4,0) + (0,4)$
, it vanishes on
$(4,0) + (0,4)$
, it vanishes on
![]() $T_x N$
. But
$T_x N$
. But
![]() $\frac {1}{2} \omega ^2$
restricts to the volume form on
$\frac {1}{2} \omega ^2$
restricts to the volume form on
![]() $T_x N$
, so by (2.3), N is calibrated by
$T_x N$
, so by (2.3), N is calibrated by
![]() $\Phi $
.
$\Phi $
.
If N is special Lagrangian with phase
![]() $-1$
, it is calibrated by
$-1$
, it is calibrated by
![]() $- \text {Re}(\Upsilon )$
. Since it is also Lagrangian,
$- \text {Re}(\Upsilon )$
. Since it is also Lagrangian,
![]() $\frac {1}{2} \omega ^2$
vanishes on N, and thus, again by (2.3), N is calibrated by
$\frac {1}{2} \omega ^2$
vanishes on N, and thus, again by (2.3), N is calibrated by
![]() $\Phi $
.
$\Phi $
.
When the ambient space is hyperkähler, Bryant and Harvey showed that the above fact can be generalized to higher dimensions in the following sense.
Proposition 2.12 ([Reference Bryant and Harvey9, Theorem 8.20])
Let
![]() $C^{4n+4}$
be a hyperkähler
$C^{4n+4}$
be a hyperkähler
![]() $(4n+4)$
-manifold. Let
$(4n+4)$
-manifold. Let
![]() $L^4 \subset C^{4n+4}$
be a four-dimensional submanifold. Then:
$L^4 \subset C^{4n+4}$
be a four-dimensional submanifold. Then:
-
(1) If N is
 $I_1$
-complex or
$I_1$
-complex or
 $I_3$
-complex, then N is
$I_3$
-complex, then N is
 $\Phi _2$
-Cayley.
$\Phi _2$
-Cayley. -
(2) If N is
 $-\Theta _{I,4}$
-special isotropic or
$-\Theta _{I,4}$
-special isotropic or
 $\Theta _{K,4}$
-special isotropic, then N is
$\Theta _{K,4}$
-special isotropic, then N is
 $\Phi _2$
-Cayley.
$\Phi _2$
-Cayley. -
(3) If N is
 $I_1$
-complex isotropic, then N is simultaneously
$I_1$
-complex isotropic, then N is simultaneously
 $I_1$
-complex,
$I_1$
-complex,
 $-\Theta _{J,4}$
-special isotropic, and
$-\Theta _{J,4}$
-special isotropic, and
 $\Theta _{K,4}$
-special isotropic, and hence is
$\Theta _{K,4}$
-special isotropic, and hence is
 $\Phi _2$
-Cayley.
$\Phi _2$
-Cayley.
Proof Parts (a) and (b) are contained in [Reference Bryant and Harvey9, Theorem 8.20]. It is easy to see from (2.2) that (a) holds. For example, if N is
![]() $I_1$
-complex, then
$I_1$
-complex, then
![]() $\frac {1}{2} \omega _1^2$
restricts to the volume form, but
$\frac {1}{2} \omega _1^2$
restricts to the volume form, but
![]() $- \Theta _{I, 4} = - \mathrm {Re} (\frac {1}{2} \sigma _1^2)$
is of
$- \Theta _{I, 4} = - \mathrm {Re} (\frac {1}{2} \sigma _1^2)$
is of
![]() $I_1$
-type
$I_1$
-type
![]() $(4,0) + (0,4)$
, and thus vanishes on N since the tangent spaces of N are of
$(4,0) + (0,4)$
, and thus vanishes on N since the tangent spaces of N are of
![]() $I_1$
-type
$I_1$
-type
![]() $(2,2)$
. Part (b) is less obvious, and uses a normal form for the tangent spaces of N. Details are given in [Reference Bryant and Harvey9, Sections 2 and 3]. Part (c) is immediate from the first two.
$(2,2)$
. Part (b) is less obvious, and uses a normal form for the tangent spaces of N. Details are given in [Reference Bryant and Harvey9, Sections 2 and 3]. Part (c) is immediate from the first two.
Remark 2.13 Note that every calibration
![]() $\phi \in \Omega ^k(C)$
discussed in this section is stabilized by the Lie group
$\phi \in \Omega ^k(C)$
discussed in this section is stabilized by the Lie group
![]() $\mathrm {Sp}(n+1)$
, which acts transitively on the unit sphere in
$\mathrm {Sp}(n+1)$
, which acts transitively on the unit sphere in
![]() $T_xC \simeq \mathbb {R}^{4n+4}$
. Consequently, at any point
$T_xC \simeq \mathbb {R}^{4n+4}$
. Consequently, at any point
![]() $x \in C$
, every unit vector
$x \in C$
, every unit vector
![]() $v \in T_xC$
lies in some
$v \in T_xC$
lies in some
![]() $\phi $
-calibrated k-plane.
$\phi $
-calibrated k-plane.
2.3 Bookkeeping: summary of forms on C
Starting in the next section, we will assume that the hyperkähler manifold
![]() $C^{4n+4}$
is a metric cone, say
$C^{4n+4}$
is a metric cone, say
![]() $C = \mathrm {C}(M)$
for some Riemannian
$C = \mathrm {C}(M)$
for some Riemannian
![]() $(4n+3)$
-manifold M. Studying the geometry of M and its relationship with C will require the introduction of further tensors and differential forms. So, before continuing, we briefly summarize the tensors and forms already defined on C:
$(4n+3)$
-manifold M. Studying the geometry of M and its relationship with C will require the introduction of further tensors and differential forms. So, before continuing, we briefly summarize the tensors and forms already defined on C:
 $$ \begin{align*} & g_{\mathrm{C}} & \text{Riemannian metric} \\ & I_1, I_2, I_3 & \text{Complex structures} \\ & \omega_1, \omega_2, \omega_3 & \text{K\"{a}hler 2-forms} \\ & \Upsilon_1, \Upsilon_2, \Upsilon_3 & \text{Complex volume }(2n+2)\text{-forms} \\ & \sigma_1, \sigma_2, \sigma_3 & \text{Complex symplectic 2-forms} \\ & \Theta_{I,2k}, \Theta_{J,2k}, \Theta_{K,2k} & \text{Special isotropic } 2k\text{-forms} \\ & \Phi_1, \Phi_2, \Phi_3 & \text{Cayley 4-forms} \\ & \Lambda & \text{Quaternionic 4-form} \end{align*} $$
$$ \begin{align*} & g_{\mathrm{C}} & \text{Riemannian metric} \\ & I_1, I_2, I_3 & \text{Complex structures} \\ & \omega_1, \omega_2, \omega_3 & \text{K\"{a}hler 2-forms} \\ & \Upsilon_1, \Upsilon_2, \Upsilon_3 & \text{Complex volume }(2n+2)\text{-forms} \\ & \sigma_1, \sigma_2, \sigma_3 & \text{Complex symplectic 2-forms} \\ & \Theta_{I,2k}, \Theta_{J,2k}, \Theta_{K,2k} & \text{Special isotropic } 2k\text{-forms} \\ & \Phi_1, \Phi_2, \Phi_3 & \text{Cayley 4-forms} \\ & \Lambda & \text{Quaternionic 4-form} \end{align*} $$
3 Calibrated geometry in
 $3$
-Sasakian manifolds
$3$
-Sasakian manifolds
If
![]() $(C^{4n+4}, g_{\mathrm {C}}) = (M \times \mathbb {R}^+, dr^2 + r^2g_M)$
is a hyperkähler cone, then its link
$(C^{4n+4}, g_{\mathrm {C}}) = (M \times \mathbb {R}^+, dr^2 + r^2g_M)$
is a hyperkähler cone, then its link
![]() $M^{4n+3}$
inherits a
$M^{4n+3}$
inherits a
![]() $3$
-Sasakian structure, as we recall in Section 3.1. Then, in Sections 3.2 and 3.3, we explain how each of the calibrated geometries of C discussed previously has a semi-calibrated counterpart in the
$3$
-Sasakian structure, as we recall in Section 3.1. Then, in Sections 3.2 and 3.3, we explain how each of the calibrated geometries of C discussed previously has a semi-calibrated counterpart in the
![]() $3$
-Sasakian link M.
$3$
-Sasakian link M.
In Section 3.4, we recall that M is the total space of a natural
![]() $S^1$
-bundle
$S^1$
-bundle
![]() $p_1 \colon M \to Z$
. The base space,
$p_1 \colon M \to Z$
. The base space,
![]() $Z^{4n+2}$
, called a twistor space, admits both Kähler–Einstein and nearly Kähler structures. It is interesting to ask exactly how much geometric structure the map
$Z^{4n+2}$
, called a twistor space, admits both Kähler–Einstein and nearly Kähler structures. It is interesting to ask exactly how much geometric structure the map
![]() $p_1 \colon M \to Z$
preserves. In this regard, we discover that every
$p_1 \colon M \to Z$
preserves. In this regard, we discover that every
![]() $3$
-Sasakian manifold M admits a natural
$3$
-Sasakian manifold M admits a natural
![]() $\mathbb {C}$
-valued
$\mathbb {C}$
-valued
![]() $3$
-form
$3$
-form
![]() $\Gamma _1 \in \Omega ^3(M; \mathbb {C})$
that descends to a
$\Gamma _1 \in \Omega ^3(M; \mathbb {C})$
that descends to a
![]() $3$
-form on Z (Proposition 3.21). Later, in Section 4.2, we will prove that the descended
$3$
-form on Z (Proposition 3.21). Later, in Section 4.2, we will prove that the descended
![]() $3$
-form endows Z with a canonical
$3$
-form endows Z with a canonical
![]() $\mathrm {Sp}(n)\mathrm {U}(1)$
-structure.
$\mathrm {Sp}(n)\mathrm {U}(1)$
-structure.
Finally, in Theorem 3.20, we observe that
![]() $\mathrm {Re}(\Gamma _1) \in \Omega ^3(M)$
is a semi-calibration, and classify the
$\mathrm {Re}(\Gamma _1) \in \Omega ^3(M)$
is a semi-calibration, and classify the
![]() $\mathrm {Re}(\Gamma _1)$
-calibrated
$\mathrm {Re}(\Gamma _1)$
-calibrated
![]() $3$
-folds in terms of more familiar geometries.
$3$
-folds in terms of more familiar geometries.
3.1
 $3$
-Sasakian manifolds as links
$3$
-Sasakian manifolds as links
Definition 3.1 Let M be an odd-dimensional manifold. An almost contact metric structure on M is a triple
![]() $(g_M, \alpha , \mathsf {J})$
consisting of a Riemannian metric
$(g_M, \alpha , \mathsf {J})$
consisting of a Riemannian metric
![]() $g_M$
, a
$g_M$
, a
![]() $1$
-form
$1$
-form
![]() $\alpha \in \Omega ^1(M)$
, and an endomorphism
$\alpha \in \Omega ^1(M)$
, and an endomorphism
![]() $\mathsf {J} \in \Gamma (\mathrm {End}(TM))$
satisfying
$\mathsf {J} \in \Gamma (\mathrm {End}(TM))$
satisfying
where
![]() $A := \alpha ^\sharp \in \Gamma (TM)$
is the Reeb vector field. It follows that
$A := \alpha ^\sharp \in \Gamma (TM)$
is the Reeb vector field. It follows that
![]() $\alpha (A) = 1$
.
$\alpha (A) = 1$
.
Thus, if M is equipped with an almost contact metric structure, then each tangent space splits as
Further, restricting to the hyperplane
![]() $\mathrm {Ker}(\alpha |_x) \subset T_xM$
, the endomorphism
$\mathrm {Ker}(\alpha |_x) \subset T_xM$
, the endomorphism
![]() $\mathsf {J} \colon \mathrm {Ker}(\alpha |_x) \to \mathrm {Ker}(\alpha |_x)$
is a
$\mathsf {J} \colon \mathrm {Ker}(\alpha |_x) \to \mathrm {Ker}(\alpha |_x)$
is a
![]() $g_M$
-orthogonal complex structure. Thus, the hyperplane field
$g_M$
-orthogonal complex structure. Thus, the hyperplane field
![]() $\mathrm {Ker}(\alpha ) \subset TM$
is naturally endowed with the Hermitian structure
$\mathrm {Ker}(\alpha ) \subset TM$
is naturally endowed with the Hermitian structure
![]() $(g_M, \mathsf {J}, \Omega )$
, where
$(g_M, \mathsf {J}, \Omega )$
, where
![]() $\Omega := g_M(\mathsf {J} \cdot , \cdot )$
is the corresponding nondegenerate
$\Omega := g_M(\mathsf {J} \cdot , \cdot )$
is the corresponding nondegenerate
![]() $2$
-form.
$2$
-form.
Definition 3.2 Let M be a
![]() $(4n+3)$
-manifold. An
$(4n+3)$
-manifold. An
![]() $(\mathrm {Sp}(n) \times 3)$
-structure (or almost 3-contact metric structure) on M consists of data
$(\mathrm {Sp}(n) \times 3)$
-structure (or almost 3-contact metric structure) on M consists of data
![]() $(g_M, (\alpha _1, \alpha _2, \alpha _3), (\mathsf {J}_1, \mathsf {J}_2, \mathsf {J}_3))$
such that:
$(g_M, (\alpha _1, \alpha _2, \alpha _3), (\mathsf {J}_1, \mathsf {J}_2, \mathsf {J}_3))$
such that:
-
• each triple
 $(g_M, \alpha _p, \mathsf {J}_p)$
is an almost contact metric structure (
$(g_M, \alpha _p, \mathsf {J}_p)$
is an almost contact metric structure (
 $p = 1, 2, 3$
); and
$p = 1, 2, 3$
); and -
• letting
 $A_p := \alpha _p^\sharp \in \Gamma (TM)$
denote the corresponding Reeb fields, we require
$A_p := \alpha _p^\sharp \in \Gamma (TM)$
denote the corresponding Reeb fields, we require  $$ \begin{align*} \mathsf{J}_p \circ \mathsf{J}_q - \alpha_p \otimes A_q & = \epsilon_{pqr}\mathsf{J}_r - \delta_{pq}\,\mathrm{Id}, \\ \mathsf{J}_p(A_q) & = \epsilon_{pqr}A_r. \end{align*} $$
$$ \begin{align*} \mathsf{J}_p \circ \mathsf{J}_q - \alpha_p \otimes A_q & = \epsilon_{pqr}\mathsf{J}_r - \delta_{pq}\,\mathrm{Id}, \\ \mathsf{J}_p(A_q) & = \epsilon_{pqr}A_r. \end{align*} $$
Note that there is no sum over r in the above equations. For example, the above equations say
![]() $\mathsf {J}_1(A_1) = 0$
,
$\mathsf {J}_1(A_1) = 0$
,
![]() $\mathsf {J}_1(A_2) = A_3$
,
$\mathsf {J}_1(A_2) = A_3$
,
![]() $\mathsf {J}_1(A_3) = - A_2$
, that
$\mathsf {J}_1(A_3) = - A_2$
, that
![]() $\mathsf {J}_1^2 = - \mathrm {Id}$
on
$\mathsf {J}_1^2 = - \mathrm {Id}$
on
![]() $\mathrm {Ker}(\alpha _1)$
, and that
$\mathrm {Ker}(\alpha _1)$
, and that
![]() $\mathsf {J}_1 \mathsf {J}_2 = \mathsf {J}_3$
. Similarly for cyclic permutations of
$\mathsf {J}_1 \mathsf {J}_2 = \mathsf {J}_3$
. Similarly for cyclic permutations of
![]() $1, 2, 3$
.
$1, 2, 3$
.
Let
![]() $M^{4n+3}$
carry an
$M^{4n+3}$
carry an
![]() $(\mathrm {Sp}(n) \times 3)$
-structure. We make three remarks. First, for each
$(\mathrm {Sp}(n) \times 3)$
-structure. We make three remarks. First, for each
![]() $p = 1, 2, 3$
, the tangent bundle splits as
$p = 1, 2, 3$
, the tangent bundle splits as
and the hyperplane field
![]() $\mathrm {Ker}(\alpha _p) \subset TM$
carries a Hermitian structure
$\mathrm {Ker}(\alpha _p) \subset TM$
carries a Hermitian structure
![]() $(g_M, \mathsf {J}_p, \Omega _p)$
, where
$(g_M, \mathsf {J}_p, \Omega _p)$
, where
![]() $\Omega _p := g_M(\mathsf {J}_p \cdot , \cdot )$
. In fact, each
$\Omega _p := g_M(\mathsf {J}_p \cdot , \cdot )$
. In fact, each
![]() $\mathrm {Ker}(\alpha _p)$
is also endowed with the complex volume form
$\mathrm {Ker}(\alpha _p)$
is also endowed with the complex volume form
![]() $\Psi _p \in \Lambda ^{2n+1,0}(\mathrm {Ker}(\alpha _p))$
given by
$\Psi _p \in \Lambda ^{2n+1,0}(\mathrm {Ker}(\alpha _p))$
given by
 $$ \begin{align} \begin{aligned} \Psi_1 & = (\alpha_2 + i\alpha_3) \wedge \frac{1}{n!}(\Omega_2 + i\Omega_3)^n, \\ \Psi_2 & = (\alpha_3 + i\alpha_1) \wedge \frac{1}{n!}(\Omega_3 + i\Omega_1)^n, \\ \Psi_3 & = (\alpha_1 + i\alpha_2) \wedge \frac{1}{n!}(\Omega_1 + i\Omega_2)^n. \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} \Psi_1 & = (\alpha_2 + i\alpha_3) \wedge \frac{1}{n!}(\Omega_2 + i\Omega_3)^n, \\ \Psi_2 & = (\alpha_3 + i\alpha_1) \wedge \frac{1}{n!}(\Omega_3 + i\Omega_1)^n, \\ \Psi_3 & = (\alpha_1 + i\alpha_2) \wedge \frac{1}{n!}(\Omega_1 + i\Omega_2)^n. \end{aligned} \end{align} $$
Second, considering (3.1) for
![]() $p = 1, 2, 3$
simultaneously, we see that the tangent bundle splits further as
$p = 1, 2, 3$
simultaneously, we see that the tangent bundle splits further as
where
Note that the
![]() $4n$
-plane field
$4n$
-plane field
![]() $\widetilde {\mathsf {H}} \subset TM$
is preserved by the three endomorphisms
$\widetilde {\mathsf {H}} \subset TM$
is preserved by the three endomorphisms
![]() $\mathsf {J}_1, \mathsf {J}_2, \mathsf {J}_3$
. In fact, the restrictions of
$\mathsf {J}_1, \mathsf {J}_2, \mathsf {J}_3$
. In fact, the restrictions of
![]() $\mathsf {J}_1, \mathsf {J}_2, \mathsf {J}_3$
to
$\mathsf {J}_1, \mathsf {J}_2, \mathsf {J}_3$
to
![]() $\widetilde {\mathsf {H}}$
are
$\widetilde {\mathsf {H}}$
are
![]() $g_M$
-orthogonal complex structures that satisfy the quaternionic relations
$g_M$
-orthogonal complex structures that satisfy the quaternionic relations
![]() $\mathsf {J}_1 \mathsf {J}_2 = \mathsf {J}_3$
, etc.
$\mathsf {J}_1 \mathsf {J}_2 = \mathsf {J}_3$
, etc.
Third, we consider the relationship between the structure on a manifold
![]() $(M^{4n+3}, g_M)$
and that of its metric cone
$(M^{4n+3}, g_M)$
and that of its metric cone
In one direction, if
![]() $(M, g_M)$
is equipped with a compatible
$(M, g_M)$
is equipped with a compatible
![]() $(\mathrm {Sp}(n) \times 3)$
-structure
$(\mathrm {Sp}(n) \times 3)$
-structure
![]() $(g_M, (\alpha _p), (\mathsf {J}_p))$
, then the
$(g_M, (\alpha _p), (\mathsf {J}_p))$
, then the
![]() $(4n+4)$
-manifold C inherits a Riemannian metric
$(4n+4)$
-manifold C inherits a Riemannian metric
![]() $g_{\mathrm {C}}$
, a triple of
$g_{\mathrm {C}}$
, a triple of
![]() $g_{\mathrm {C}}$
-orthogonal almost-complex structures
$g_{\mathrm {C}}$
-orthogonal almost-complex structures
![]() $(I_1, I_2, I_3)$
satisfying
$(I_1, I_2, I_3)$
satisfying
![]() $I_1I_2 = I_3$
, etc., and a triple of nondegenerate
$I_1I_2 = I_3$
, etc., and a triple of nondegenerate
![]() $2$
-forms
$2$
-forms
![]() $\omega _p$
defined by
$\omega _p$
defined by
 $$ \begin{align*} g_{\mathrm{C}} & = dr^2 + r^2 g_M, & \omega_p(X,Y) & = g_{\mathrm{C}}(I_pX,Y), \\ I_p(X) & = \begin{cases} \mathsf{J}_pX - \alpha_p(X)r\partial_r, &\text{if } X \in TM, \\ A_p, & \text{if } X = r\partial_r, \end{cases} \end{align*} $$
$$ \begin{align*} g_{\mathrm{C}} & = dr^2 + r^2 g_M, & \omega_p(X,Y) & = g_{\mathrm{C}}(I_pX,Y), \\ I_p(X) & = \begin{cases} \mathsf{J}_pX - \alpha_p(X)r\partial_r, &\text{if } X \in TM, \\ A_p, & \text{if } X = r\partial_r, \end{cases} \end{align*} $$
where
![]() $X,Y \in TC$
. A computation shows that for each
$X,Y \in TC$
. A computation shows that for each
![]() $p = 1,2,3$
,
$p = 1,2,3$
,
Altogether, the data
![]() $(g_{\mathrm {C}}, (\omega _1, \omega _2, \omega _3), (I_1, I_2, I_3))$
are an almost hyper-Hermitian structure on C.
$(g_{\mathrm {C}}, (\omega _1, \omega _2, \omega _3), (I_1, I_2, I_3))$
are an almost hyper-Hermitian structure on C.
Conversely, if the metric cone
![]() $(C^{4n+4}, g_{\mathrm {C}} = dr^2 + r^2g_M)$
carries an almost hyper-Hermitian structure
$(C^{4n+4}, g_{\mathrm {C}} = dr^2 + r^2g_M)$
carries an almost hyper-Hermitian structure
![]() $(g_{\mathrm {C}}, (\omega _1, \omega _2, \omega _3), (I_1, I_2, I_3))$
that is conical in the sense of Definition A.9, namely that
$(g_{\mathrm {C}}, (\omega _1, \omega _2, \omega _3), (I_1, I_2, I_3))$
that is conical in the sense of Definition A.9, namely that
then its link
![]() $(M, g_M)$
inherits a compatible
$(M, g_M)$
inherits a compatible
![]() $(\mathrm {Sp}(n) \times 3)$
-structure
$(\mathrm {Sp}(n) \times 3)$
-structure
![]() $(g_M, (\alpha _p), (\mathsf {J}_p))$
via
$(g_M, (\alpha _p), (\mathsf {J}_p))$
via
 $$ \begin{align*} \alpha_p & = (r\partial_r\,\lrcorner\,\omega_p)|_M, & \mathsf{J}_p & = \begin{cases} I_p, & \text{on }\mathrm{Ker}(\alpha_p), \\ 0, & \text{on } \mathbb{R} A_p.\end{cases} \end{align*} $$
$$ \begin{align*} \alpha_p & = (r\partial_r\,\lrcorner\,\omega_p)|_M, & \mathsf{J}_p & = \begin{cases} I_p, & \text{on }\mathrm{Ker}(\alpha_p), \\ 0, & \text{on } \mathbb{R} A_p.\end{cases} \end{align*} $$
This relationship leads to the following definition:
Definition 3.3 Let M be a
![]() $(4n+3)$
-manifold. A
$(4n+3)$
-manifold. A
![]() $3$
-Sasakian structure on M is an
$3$
-Sasakian structure on M is an
![]() $(\mathrm {Sp}(n) \times 3)$
-structure
$(\mathrm {Sp}(n) \times 3)$
-structure
![]() $(g_M, (\alpha _p), (\mathsf {J}_p))$
for which the induced almost hyper-Hermitian structure
$(g_M, (\alpha _p), (\mathsf {J}_p))$
for which the induced almost hyper-Hermitian structure
![]() $(g_{\mathrm {C}}, (\omega _p), (I_p))$
on its metric cone
$(g_{\mathrm {C}}, (\omega _p), (I_p))$
on its metric cone
![]() $\mathrm {C}(M) = \mathbb {R}^+ \times M$
hyperkähler.
$\mathrm {C}(M) = \mathbb {R}^+ \times M$
hyperkähler.
Note that this is equivalent to requiring that the
![]() $2$
-forms
$2$
-forms
![]() $\omega _1, \omega _2, \omega _3$
are all closed. (See, for example, [Reference Hitchin21, Section 2].)
$\omega _1, \omega _2, \omega _3$
are all closed. (See, for example, [Reference Hitchin21, Section 2].)
3.1.1 Distinguished forms on
 $3$
-Sasakian manifolds
$3$
-Sasakian manifolds
For the remainder of this work,
![]() $M^{4n+3}$
will denote a
$M^{4n+3}$
will denote a
![]() $3$
-Sasakian
$3$
-Sasakian
![]() $(4n+3)$
-manifold with
$(4n+3)$
-manifold with
![]() $3$
-Sasakian structure
$3$
-Sasakian structure
![]() $(g_M, (\alpha _1, \alpha _2, \alpha _3), (\mathsf {J}_1, \mathsf {J}_2, \mathsf {J}_3))$
. The induced conical hyperkähler structure on
$(g_M, (\alpha _1, \alpha _2, \alpha _3), (\mathsf {J}_1, \mathsf {J}_2, \mathsf {J}_3))$
. The induced conical hyperkähler structure on
![]() $C^{4n+4} = \mathbb {R}^+ \times M$
will be denoted
$C^{4n+4} = \mathbb {R}^+ \times M$
will be denoted
![]() $(g_{\mathrm {C}}, (\omega _1, \omega _2, \omega _3), (I_1, I_2, I_3))$
. In this section, we record some of the distinguished differential forms on M and compute their exterior derivatives.
$(g_{\mathrm {C}}, (\omega _1, \omega _2, \omega _3), (I_1, I_2, I_3))$
. In this section, we record some of the distinguished differential forms on M and compute their exterior derivatives.
To begin, we consider the contact
![]() $1$
-forms
$1$
-forms
![]() $\alpha _1, \alpha _2, \alpha _3 \in \Omega ^1(M)$
and the transverse Kähler forms
$\alpha _1, \alpha _2, \alpha _3 \in \Omega ^1(M)$
and the transverse Kähler forms
![]() $\Omega _1, \Omega _2, \Omega _3 \in \Omega ^2(M)$
defined by
$\Omega _1, \Omega _2, \Omega _3 \in \Omega ^2(M)$
defined by
![]() $\Omega _p(X,Y) = g_M(\mathsf {J}_pX, Y)$
. By (3.4), we may compute
$\Omega _p(X,Y) = g_M(\mathsf {J}_pX, Y)$
. By (3.4), we may compute
which implies that
(The first equation in (3.5) shows that each
![]() $\alpha _p$
is indeed a contact form. That is, that
$\alpha _p$
is indeed a contact form. That is, that
![]() $\alpha _p \wedge (d\alpha _p)^{2n+1}$
is nowhere zero.)
$\alpha _p \wedge (d\alpha _p)^{2n+1}$
is nowhere zero.)
Next, we decompose the
![]() $2$
-forms
$2$
-forms
![]() $\Omega _1, \Omega _2, \Omega _3$
according to the splitting
$\Omega _1, \Omega _2, \Omega _3$
according to the splitting
One can show that each
![]() $\Omega _p$
has no component in
$\Omega _p$
has no component in
![]() $\widetilde {\mathsf {V}}^* \otimes \widetilde {\mathsf {H}}^*$
and that the
$\widetilde {\mathsf {V}}^* \otimes \widetilde {\mathsf {H}}^*$
and that the
![]() $\Lambda ^2(\widetilde {\mathsf {V}}^*)$
-component of
$\Lambda ^2(\widetilde {\mathsf {V}}^*)$
-component of
![]() $\Omega _1$
is
$\Omega _1$
is
![]() $\alpha _2 \wedge \alpha _3$
. Letting
$\alpha _2 \wedge \alpha _3$
. Letting
![]() $\kappa _1, \kappa _2, \kappa _3$
denote the
$\kappa _1, \kappa _2, \kappa _3$
denote the
![]() $\Lambda ^2(\widetilde {\mathsf {H}}^*)$
-component of
$\Lambda ^2(\widetilde {\mathsf {H}}^*)$
-component of
![]() $\Omega _p$
, we arrive at the formulas
$\Omega _p$
, we arrive at the formulas
Taking d of (3.6) and using (3.5) shows that
 $$ \begin{align} d\kappa_1 & = 2(\alpha_2 \wedge \Omega_3 - \alpha_3 \wedge \Omega_2) = 2(\alpha_2 \wedge \kappa_3 - \alpha_3 \wedge \kappa_2), \nonumber \\ d\kappa_2 & = 2(\alpha_3 \wedge \Omega_1 - \alpha_1 \wedge \Omega_3) = 2(\alpha_3 \wedge \kappa_1 - \alpha_1 \wedge \kappa_3), \\ d\kappa_3 & = 2(\alpha_1 \wedge \Omega_2 - \alpha_2 \wedge \Omega_1) = 2(\alpha_1 \wedge \kappa_2 - \alpha_2 \wedge \kappa_1). \nonumber \end{align} $$
$$ \begin{align} d\kappa_1 & = 2(\alpha_2 \wedge \Omega_3 - \alpha_3 \wedge \Omega_2) = 2(\alpha_2 \wedge \kappa_3 - \alpha_3 \wedge \kappa_2), \nonumber \\ d\kappa_2 & = 2(\alpha_3 \wedge \Omega_1 - \alpha_1 \wedge \Omega_3) = 2(\alpha_3 \wedge \kappa_1 - \alpha_1 \wedge \kappa_3), \\ d\kappa_3 & = 2(\alpha_1 \wedge \Omega_2 - \alpha_2 \wedge \Omega_1) = 2(\alpha_1 \wedge \kappa_2 - \alpha_2 \wedge \kappa_1). \nonumber \end{align} $$
Finally, recalling the transverse complex volume forms
![]() $\Psi _1, \Psi _2, \Psi _3 \in \Omega ^{2n+1}(M; \mathbb {C})$
of (3.2), we compute
$\Psi _1, \Psi _2, \Psi _3 \in \Omega ^{2n+1}(M; \mathbb {C})$
of (3.2), we compute
To conclude this section, we summarize the relationships between various forms on the hyperkähler cone
![]() $C^{4n+4}$
and those on its
$C^{4n+4}$
and those on its
![]() $3$
-Sasakian link
$3$
-Sasakian link
![]() $M^{4n+3}$
.
$M^{4n+3}$
.
Proposition 3.4 We have
Consequently,
 $$ \begin{align} \Upsilon_1 & = r^{2n+1}\,dr \wedge \Psi_1 + r^{2n+2}\,\frac{1}{(n+1)!} (\Omega_2 + i\Omega_3)^{n+1}, \\ \Theta_{I,4} & = r^3\,dr \wedge (\alpha_2 \wedge \Omega_2 - \alpha_3 \wedge \Omega_3) + r^4 \frac{1}{2}(\Omega_2^2 - \Omega_3^2), \nonumber \\ \Phi_1 & = r^3\,dr \wedge (-\alpha_1 \wedge \Omega_1 + \alpha_2 \wedge \Omega_2 + \alpha_3 \wedge \Omega_3) + r^4\, \frac{1}{2}(-\Omega_1^2 + \Omega_2^2 + \Omega_3^2), \nonumber \\ \Lambda & = r^3\,dr \wedge \frac{1}{3}(\alpha_1 \wedge \Omega_1 + \alpha_2 \wedge \Omega_2 + \alpha_3 \wedge \Omega_3) + r^4\, \frac{1}{6}(\Omega_1^2 + \Omega_2^2 + \Omega_3^2). \nonumber \end{align} $$
$$ \begin{align} \Upsilon_1 & = r^{2n+1}\,dr \wedge \Psi_1 + r^{2n+2}\,\frac{1}{(n+1)!} (\Omega_2 + i\Omega_3)^{n+1}, \\ \Theta_{I,4} & = r^3\,dr \wedge (\alpha_2 \wedge \Omega_2 - \alpha_3 \wedge \Omega_3) + r^4 \frac{1}{2}(\Omega_2^2 - \Omega_3^2), \nonumber \\ \Phi_1 & = r^3\,dr \wedge (-\alpha_1 \wedge \Omega_1 + \alpha_2 \wedge \Omega_2 + \alpha_3 \wedge \Omega_3) + r^4\, \frac{1}{2}(-\Omega_1^2 + \Omega_2^2 + \Omega_3^2), \nonumber \\ \Lambda & = r^3\,dr \wedge \frac{1}{3}(\alpha_1 \wedge \Omega_1 + \alpha_2 \wedge \Omega_2 + \alpha_3 \wedge \Omega_3) + r^4\, \frac{1}{6}(\Omega_1^2 + \Omega_2^2 + \Omega_3^2). \nonumber \end{align} $$
Proof Each of these follows from a straightforward calculation.
3.2 Submanifolds via the Sasaki–Einstein structure
By analogy with our discussion in Sections 2.1 and 2.2, we now consider the various classes of submanifolds of M. We begin with those defined in terms of a Sasaki–Einstein structure.
By Remark 2.13, we can apply Proposition A.1 to (3.11) with k replaced by
![]() $k+1$
. We deduce that for
$k+1$
. We deduce that for
![]() $p = 1,2,3$
, the
$p = 1,2,3$
, the
![]() $(2k+1)$
-forms
$(2k+1)$
-forms
are semi-calibrations. Their calibrated submanifolds are called
![]() $I_p$
-CR submanifolds. To be precise:
$I_p$
-CR submanifolds. To be precise:
Proposition 3.5 Let
![]() $L^{2k+1} \subset M^{4n+3}$
be a
$L^{2k+1} \subset M^{4n+3}$
be a
![]() $(2k+1)$
-dimensional submanifold. We say L is
$(2k+1)$
-dimensional submanifold. We say L is
![]() $I_1$
-CR if any of the following equivalent conditions holds:
$I_1$
-CR if any of the following equivalent conditions holds:
-
(1)
 $\mathrm {C}(L) \subset C$
is
$\mathrm {C}(L) \subset C$
is
 $I_1$
-complex. That is, each tangent space of
$I_1$
-complex. That is, each tangent space of
 $\mathrm {C}(L)$
is
$\mathrm {C}(L)$
is
 $I_1$
-invariant.
$I_1$
-invariant. -
(2)
 $\mathrm {C}(L)$
is (up to a change of orientation)
$\mathrm {C}(L)$
is (up to a change of orientation)
 $\frac {1}{(k+1)!}\omega _1^{k+1}$
-calibrated:
$\frac {1}{(k+1)!}\omega _1^{k+1}$
-calibrated:  $$ \begin{align*}\left.\frac{1}{(k+1)!}\,\omega_1^{k+1}\right|_{\mathrm{C}(L)} = \mathrm{vol}_{\mathrm{C}(L)}.\end{align*} $$
$$ \begin{align*}\left.\frac{1}{(k+1)!}\,\omega_1^{k+1}\right|_{\mathrm{C}(L)} = \mathrm{vol}_{\mathrm{C}(L)}.\end{align*} $$
-
(3) Each tangent space
 $T_xL$
is
$T_xL$
is
 $\mathsf {J}_1$
-invariant and contains the Reeb vector
$\mathsf {J}_1$
-invariant and contains the Reeb vector
 $A_1$
.
$A_1$
. -
(4) L satisfies (up to a change of orientation) that
 $$ \begin{align*}\left.\frac{1}{k!}(\alpha_1 \wedge \Omega_1^k)\right|_L = \mathrm{vol}_L.\end{align*} $$
$$ \begin{align*}\left.\frac{1}{k!}(\alpha_1 \wedge \Omega_1^k)\right|_L = \mathrm{vol}_L.\end{align*} $$
Proof The equivalences (i)
![]() $\iff $
(ii)
$\iff $
(ii)
![]() $\iff $
(iii) are well known. The equivalence (ii)
$\iff $
(iii) are well known. The equivalence (ii)
![]() $\iff $
(iv) follows from Proposition A.1.
$\iff $
(iv) follows from Proposition A.1.
Proposition 3.6 Let
![]() $L^k \subset M^{4n+3}$
be a submanifold. We say L is
$L^k \subset M^{4n+3}$
be a submanifold. We say L is
![]() $\alpha _1$
-isotropic (resp.
$\alpha _1$
-isotropic (resp.
![]() $\alpha _1$
-Legendrian if
$\alpha _1$
-Legendrian if
![]() $k = 2n+1$
) if any of the following equivalent conditions holds:
$k = 2n+1$
) if any of the following equivalent conditions holds:
-
(1)
 $\mathrm {C}(L)$
is
$\mathrm {C}(L)$
is
 $\omega _1$
-isotropic:
$\omega _1$
-isotropic:
 $\left .\omega _1\right |_{\mathrm {C}(L)} = 0.$
$\left .\omega _1\right |_{\mathrm {C}(L)} = 0.$
-
(2)
 $\left .\alpha _1\right |_L = 0.$
$\left .\alpha _1\right |_L = 0.$
-
(3)
 $\left .\alpha _1\right |_L = 0$
and
$\left .\alpha _1\right |_L = 0$
and
 $\left .\Omega _1\right |_L = 0.$
$\left .\Omega _1\right |_L = 0.$
In particular, an
![]() $\alpha _1$
-isotropic submanifold
$\alpha _1$
-isotropic submanifold
![]() $L \subset M$
satisfies
$L \subset M$
satisfies
![]() $\dim (L) \leq 2n+1$
.
$\dim (L) \leq 2n+1$
.
Proof The first equation in (3.5) shows the equivalence (ii)
![]() $\iff $
(iii). The equivalence (i)
$\iff $
(iii). The equivalence (i)
![]() $\iff $
(iii) follows from (3.9).
$\iff $
(iii) follows from (3.9).
Next, from formula (3.12) together with Proposition A.1 and Remark 2.13, we observe that for
![]() $p = 1,2,3$
and a constant
$p = 1,2,3$
and a constant
![]() $e^{i \theta } \in S^1$
, the
$e^{i \theta } \in S^1$
, the
![]() $(2n+1)$
-forms
$(2n+1)$
-forms
are semi-calibrations. Their calibrated submanifolds are called
![]() $\Psi _p$
-special Legendrian submanifolds of phase
$\Psi _p$
-special Legendrian submanifolds of phase
![]() $e^{i \theta }$
. We observe:
$e^{i \theta }$
. We observe:
Proposition 3.7 Let
![]() $L^{2n+1} \subset M^{4n+3}$
be a
$L^{2n+1} \subset M^{4n+3}$
be a
![]() $(2n+1)$
-dimensional submanifold. We say L is
$(2n+1)$
-dimensional submanifold. We say L is
![]() $\Psi _1$
-special Legendrian if any of the following equivalent conditions holds:
$\Psi _1$
-special Legendrian if any of the following equivalent conditions holds:
-
(1)
 $\mathrm {C}(L)$
is (up to a change of orientation)
$\mathrm {C}(L)$
is (up to a change of orientation)
 $\Upsilon _1$
-special Lagrangian:
$\Upsilon _1$
-special Lagrangian:
 $\left .\mathrm {Re}(\Upsilon _1)\right |_{\mathrm {C}(L)} = \mathrm {vol}_{\mathrm {C}(L)}$
.
$\left .\mathrm {Re}(\Upsilon _1)\right |_{\mathrm {C}(L)} = \mathrm {vol}_{\mathrm {C}(L)}$
. -
(2)
 $\mathrm {C}(L)$
satisfies
$\mathrm {C}(L)$
satisfies
 $\left .\omega _1\right |_{\mathrm {C}(L)} = 0$
and
$\left .\omega _1\right |_{\mathrm {C}(L)} = 0$
and
 $\left .\mathrm {Im}(\Upsilon _1)\right |_{\mathrm {C}(L)} = 0$
.
$\left .\mathrm {Im}(\Upsilon _1)\right |_{\mathrm {C}(L)} = 0$
. -
(3) L satisfies (up to a change of orientation) that
 $\left .\mathrm {Re}(\Psi _1)\right |_{L} = \mathrm {vol}_{L}$
.
$\left .\mathrm {Re}(\Psi _1)\right |_{L} = \mathrm {vol}_{L}$
. -
(4) L satisfies
 $\left .\alpha _1\right |_{L} = 0$
and
$\left .\alpha _1\right |_{L} = 0$
and
 $\left .\mathrm {Im}(\Psi _1)\right |_{L} = 0$
.
$\left .\mathrm {Im}(\Psi _1)\right |_{L} = 0$
.
3.3 Submanifolds via the
 $3$
-Sasakian structure
$3$
-Sasakian structure
We now turn to those submanifolds of M whose definition requires more than the Sasaki–Einstein structure. Here, we will discuss the CR isotropic, special isotropic, and associative submanifolds.
3.3.1 CR isotropic submanifolds
Proposition 3.8 Let
![]() $L^{2k+1} \subset M^{4n+3}$
be a
$L^{2k+1} \subset M^{4n+3}$
be a
![]() $(2k+1)$
-dimensional submanifold,
$(2k+1)$
-dimensional submanifold,
![]() ${1 \leq k \leq n}$
. We say L is
${1 \leq k \leq n}$
. We say L is
![]() $I_1$
-CR isotropic (resp.
$I_1$
-CR isotropic (resp.
![]() $I_1$
-CR Legendrian if
$I_1$
-CR Legendrian if
![]() $k = n$
) if any of the following equivalent conditions holds:
$k = n$
) if any of the following equivalent conditions holds:
-
(1)
 $\mathrm {C}(L) \subset C$
is
$\mathrm {C}(L) \subset C$
is
 $I_1$
-complex,
$I_1$
-complex,
 $\omega _2$
-isotropic, and
$\omega _2$
-isotropic, and
 $\omega _3$
-isotropic.
$\omega _3$
-isotropic. -
(2)
 $\mathrm {C}(L) \subset C$
is
$\mathrm {C}(L) \subset C$
is
 $I_1$
-complex and
$I_1$
-complex and
 $\omega _2$
-isotropic.
$\omega _2$
-isotropic. -
(3) L is
 $I_1$
-CR,
$I_1$
-CR,
 $\alpha _2$
-isotropic, and
$\alpha _2$
-isotropic, and
 $\alpha _3$
-isotropic.
$\alpha _3$
-isotropic. -
(4) L is
 $I_1$
-CR and
$I_1$
-CR and
 $\alpha _2$
-isotropic.
$\alpha _2$
-isotropic.
Proof The equivalence (i)
![]() $\iff $
(ii) was shown in Proposition 2.6. The equivalences (i)
$\iff $
(ii) was shown in Proposition 2.6. The equivalences (i)
![]() $\iff $
(iii) and (ii)
$\iff $
(iii) and (ii)
![]() $\iff $
(iv) both follow directly from Propositions 3.5 and 3.6.
$\iff $
(iv) both follow directly from Propositions 3.5 and 3.6.
In the CR Legendrian case, we can say more:
Corollary 3.9 Let
![]() $L^{2n+1} \subset M^{4n+3}$
be a
$L^{2n+1} \subset M^{4n+3}$
be a
![]() $(2n+1)$
-dimensional submanifold. The following are equivalent:
$(2n+1)$
-dimensional submanifold. The following are equivalent:
-
(1)
 $\mathrm {C}(L)$
is
$\mathrm {C}(L)$
is
 $I_1$
-complex,
$I_1$
-complex,
 $\omega _2$
-Lagrangian, and
$\omega _2$
-Lagrangian, and
 $\omega _3$
-Lagrangian (i.e.,
$\omega _3$
-Lagrangian (i.e.,
 $\mathrm {C}(L)$
is
$\mathrm {C}(L)$
is
 $I_1$
-complex Lagrangian).
$I_1$
-complex Lagrangian). -
(2)
 $\mathrm {C}(L)$
is
$\mathrm {C}(L)$
is
 $\omega _2$
-Lagrangian and
$\omega _2$
-Lagrangian and
 $\omega _3$
-Lagrangian.
$\omega _3$
-Lagrangian. -
(3)
 $\mathrm {C}(L)$
is
$\mathrm {C}(L)$
is
 $I_1$
-complex,
$I_1$
-complex,
 $\Upsilon _2$
-special Lagrangian of phase
$\Upsilon _2$
-special Lagrangian of phase
 $i^{n+1}$
, and
$i^{n+1}$
, and
 $\Upsilon _3$
-special Lagrangian of phase
$\Upsilon _3$
-special Lagrangian of phase
 $1$
.
$1$
. -
(4) L is
 $I_1$
-CR,
$I_1$
-CR,
 $\alpha _2$
-Legendrian, and
$\alpha _2$
-Legendrian, and
 $\alpha _3$
-Legendrian (i.e., L is
$\alpha _3$
-Legendrian (i.e., L is
 $I_1$
-CR Legendrian).
$I_1$
-CR Legendrian). -
(5) L is
 $\alpha _2$
-Legendrian and
$\alpha _2$
-Legendrian and
 $\alpha _3$
-Legendrian.
$\alpha _3$
-Legendrian. -
(6) L is
 $I_1$
-CR,
$I_1$
-CR,
 $\Psi _2$
-special Legendrian of phase
$\Psi _2$
-special Legendrian of phase
 $i^{n+1}$
, and
$i^{n+1}$
, and
 $\Psi _3$
-special Lagrangian of phase
$\Psi _3$
-special Lagrangian of phase
 $1$
.
$1$
.
Proof The equivalence (i)
![]() $\iff $
(ii)
$\iff $
(ii)
![]() $\iff $
(iii) was shown in Proposition 2.7. The equivalence (i)
$\iff $
(iii) was shown in Proposition 2.7. The equivalence (i)
![]() $\iff $
(iv) was shown in Proposition 3.8. Finally, (ii)
$\iff $
(iv) was shown in Proposition 3.8. Finally, (ii)
![]() $\iff $
(v) follows from Proposition 3.6, and (iii)
$\iff $
(v) follows from Proposition 3.6, and (iii)
![]() $\iff $
(vi) follows from Proposition 3.7.
$\iff $
(vi) follows from Proposition 3.7.
Examples of CR isotropic submanifolds can be constructed via Example 5.2 together with Corollary 5.12.
3.3.2 Special isotropic submanifolds
Definition 3.10 The special isotropic forms on M are the real
![]() $(2k-1)$
-forms
$(2k-1)$
-forms
![]() $\theta _{I,2k-1}, \theta _{J,2k-1}, \theta _{K,2k-1} \in \Omega ^{2k-1}(M)$
defined by
$\theta _{I,2k-1}, \theta _{J,2k-1}, \theta _{K,2k-1} \in \Omega ^{2k-1}(M)$
defined by
In particular, for
![]() $2k-1 = 1, 3, 2n+1$
, these are
$2k-1 = 1, 3, 2n+1$
, these are
 $$ \begin{align*} \theta_{I,1} & = \alpha_2, \\ \theta_{I,3} & = \alpha_2 \wedge \Omega_2 - \alpha_3 \wedge \Omega_3 = \alpha_2 \wedge \kappa_2 - \alpha_3 \wedge \kappa_3, \\ \theta_{I,2n+1} & = \text{Re}(\Psi_1). \end{align*} $$
$$ \begin{align*} \theta_{I,1} & = \alpha_2, \\ \theta_{I,3} & = \alpha_2 \wedge \Omega_2 - \alpha_3 \wedge \Omega_3 = \alpha_2 \wedge \kappa_2 - \alpha_3 \wedge \kappa_3, \\ \theta_{I,2n+1} & = \text{Re}(\Psi_1). \end{align*} $$
By Remark 2.13, Proposition A.1, and Theorem A.6, the special isotropic forms
![]() $\theta _{I, 2k-1}, \theta _{J, 2k-1}, \theta _{K,2k-1}$
are semi-calibrations.
$\theta _{I, 2k-1}, \theta _{J, 2k-1}, \theta _{K,2k-1}$
are semi-calibrations.
Proposition 3.11 Let
![]() $L^{2k-1} \subset M^{4n+3}$
be a
$L^{2k-1} \subset M^{4n+3}$
be a
![]() $(2k-1)$
-dimensional submanifold,
$(2k-1)$
-dimensional submanifold,
![]() $1 \leq k \leq n+1$
. We say L is
$1 \leq k \leq n+1$
. We say L is
![]() $\theta _{I,2k-1}$
-special isotropic if either of the following equivalent conditions holds:
$\theta _{I,2k-1}$
-special isotropic if either of the following equivalent conditions holds:
-
(1)
 $\mathrm {C}(L) \subset C$
is
$\mathrm {C}(L) \subset C$
is
 $\Theta _{I,2k}$
-special isotropic.
$\Theta _{I,2k}$
-special isotropic. -
(2) L is
 $\theta _{I,2k-1}$
-special isotropic.
$\theta _{I,2k-1}$
-special isotropic.
3.3.3 Associative
 $3$
-folds
$3$
-folds
The following definition is due to Bryant and Harvey [Reference Bryant and Harvey9].
Definition 3.12 The generalized associative
![]() $3$
-forms are the real
$3$
-forms are the real
![]() $3$
-forms
$3$
-forms
![]() $\phi _1, \phi _2, \phi _3 \in \Omega ^3(M)$
defined by
$\phi _1, \phi _2, \phi _3 \in \Omega ^3(M)$
defined by
 $$ \begin{align*} \phi_1 & = -\alpha_1 \wedge \Omega_1 + \alpha_2 \wedge \Omega_2 + \alpha_3 \wedge \Omega_3, \\ \phi_2 & = \alpha_1 \wedge \Omega_1 - \alpha_2 \wedge \Omega_2 + \alpha_3 \wedge \Omega_3, \\ \phi_3 & = \alpha_1 \wedge \Omega_1 + \alpha_2 \wedge \Omega_2 - \alpha_3 \wedge \Omega_3. \end{align*} $$
$$ \begin{align*} \phi_1 & = -\alpha_1 \wedge \Omega_1 + \alpha_2 \wedge \Omega_2 + \alpha_3 \wedge \Omega_3, \\ \phi_2 & = \alpha_1 \wedge \Omega_1 - \alpha_2 \wedge \Omega_2 + \alpha_3 \wedge \Omega_3, \\ \phi_3 & = \alpha_1 \wedge \Omega_1 + \alpha_2 \wedge \Omega_2 - \alpha_3 \wedge \Omega_3. \end{align*} $$
Equivalently,
 $$ \begin{align*} \phi_1 & = \alpha_1 \wedge \alpha_2 \wedge \alpha_3 - \alpha_1 \wedge \kappa_1 + \alpha_2 \wedge \kappa_2 + \alpha_3 \wedge \kappa_3, \\ \phi_2 & = \alpha_1 \wedge \alpha_2 \wedge \alpha_3 + \alpha_1 \wedge \kappa_1 - \alpha_2 \wedge \kappa_2 + \alpha_3 \wedge \kappa_3, \\ \phi_3 & = \alpha_1 \wedge \alpha_2 \wedge \alpha_3 + \alpha_1 \wedge \kappa_1 + \alpha_2 \wedge \kappa_2 - \alpha_3 \wedge \kappa_3, \end{align*} $$
$$ \begin{align*} \phi_1 & = \alpha_1 \wedge \alpha_2 \wedge \alpha_3 - \alpha_1 \wedge \kappa_1 + \alpha_2 \wedge \kappa_2 + \alpha_3 \wedge \kappa_3, \\ \phi_2 & = \alpha_1 \wedge \alpha_2 \wedge \alpha_3 + \alpha_1 \wedge \kappa_1 - \alpha_2 \wedge \kappa_2 + \alpha_3 \wedge \kappa_3, \\ \phi_3 & = \alpha_1 \wedge \alpha_2 \wedge \alpha_3 + \alpha_1 \wedge \kappa_1 + \alpha_2 \wedge \kappa_2 - \alpha_3 \wedge \kappa_3, \end{align*} $$
where the
![]() $\kappa _j$
were defined in (3.6). A three-dimensional submanifold
$\kappa _j$
were defined in (3.6). A three-dimensional submanifold
![]() $L^3 \subset M^{4n+3}$
is
$L^3 \subset M^{4n+3}$
is
![]() $\phi _1$
-associative if it is calibrated by
$\phi _1$
-associative if it is calibrated by
![]() $\phi _1$
:
$\phi _1$
:
The definitions of
![]() $\phi _2$
-associative and
$\phi _2$
-associative and
![]() $\phi _3$
-associative are analogous.
$\phi _3$
-associative are analogous.
Observing that
we obtain:
Proposition 3.13 Let
![]() $L^3 \subset M^{4n+3}$
be a three-dimensional submanifold. The following are equivalent:
$L^3 \subset M^{4n+3}$
be a three-dimensional submanifold. The following are equivalent:
-
(1)
 $\mathrm {C}(L) \subset C$
is
$\mathrm {C}(L) \subset C$
is
 $\Phi _1$
-Cayley.
$\Phi _1$
-Cayley. -
(2)
 $L \subset M$
is
$L \subset M$
is
 $\phi _1$
-associative.
$\phi _1$
-associative.
Finally, we remark on the relationships between the above submanifolds. Let us recall that a manifold is called Sasaki–Einstein if its cone is Calabi–Yau and that a
![]() $7$
-manifold is called nearly parallel
$7$
-manifold is called nearly parallel
![]() $\mathrm {G}_2$
if its cone is a
$\mathrm {G}_2$
if its cone is a
![]() $\mathrm {Spin}(7)$
-manifold. Suppose now that
$\mathrm {Spin}(7)$
-manifold. Suppose now that
![]() $(Y^7, (g, \alpha , \mathsf {J}, \Psi ))$
is a Sasaki–Einstein
$(Y^7, (g, \alpha , \mathsf {J}, \Psi ))$
is a Sasaki–Einstein
![]() $7$
-manifold. It is well known that Y inherits a nearly parallel
$7$
-manifold. It is well known that Y inherits a nearly parallel
![]() $\mathrm {G}_2$
-structure by the following formula:
$\mathrm {G}_2$
-structure by the following formula:
The real
![]() $3$
-form
$3$
-form
![]() $\phi \in \Omega ^3(M)$
is called the associative
$\phi \in \Omega ^3(M)$
is called the associative
![]() $3$
-form, and a three-dimensional submanifold
$3$
-form, and a three-dimensional submanifold
![]() $\Sigma ^3 \subset M$
satisfying
$\Sigma ^3 \subset M$
satisfying
![]() $\phi |_\Sigma = \mathrm {vol}_\Sigma $
is called associative. The following fact is well known, although we prove a more general result in Proposition 3.15.
$\phi |_\Sigma = \mathrm {vol}_\Sigma $
is called associative. The following fact is well known, although we prove a more general result in Proposition 3.15.
Proposition 3.14 Let
![]() $(Y^7, (g, \alpha , \mathsf {J}, \Psi ))$
be a Sasaki–Einstein
$(Y^7, (g, \alpha , \mathsf {J}, \Psi ))$
be a Sasaki–Einstein
![]() $7$
-manifold, and equip Y with its induced nearly parallel
$7$
-manifold, and equip Y with its induced nearly parallel
![]() $\mathrm {G}_2$
-structure
$\mathrm {G}_2$
-structure
![]() $\phi $
. Let
$\phi $
. Let
![]() $L^3 \subset Y$
be a three-dimensional submanifold. Then:
$L^3 \subset Y$
be a three-dimensional submanifold. Then:
-
(1) If L is CR, then L is associative.
-
(2) If L is special Legendrian of phase
 $e^{i\pi } = -1$
, then L is associative.
$e^{i\pi } = -1$
, then L is associative.
When the ambient space is
![]() $3$
-Sasakian, the above fact generalizes to higher dimensions in the following way.
$3$
-Sasakian, the above fact generalizes to higher dimensions in the following way.
Proposition 3.15 Let
![]() $M^{4n+3}$
be a
$M^{4n+3}$
be a
![]() $3$
-Sasakian
$3$
-Sasakian
![]() $(4n+3)$
-manifold. Let
$(4n+3)$
-manifold. Let
![]() $L^3 \subset M$
be a three-dimensional submanifold. Then:
$L^3 \subset M$
be a three-dimensional submanifold. Then:
-
(1) If L is
 $I_1$
-CR or
$I_1$
-CR or
 $I_3$
-CR, then L is
$I_3$
-CR, then L is
 $\phi _2$
-associative.
$\phi _2$
-associative. -
(2) If L is
 $-\theta _{I,3}$
-special isotropic or
$-\theta _{I,3}$
-special isotropic or
 $\theta _{K,3}$
-special isotropic, then L is
$\theta _{K,3}$
-special isotropic, then L is
 $\phi _2$
-associative.
$\phi _2$
-associative. -
(3) If L is
 $I_1$
-CR isotropic, then L is simultaneously
$I_1$
-CR isotropic, then L is simultaneously
 $I_1$
-CR,
$I_1$
-CR,
 $-\theta _{J,3}$
-special isotropic, and
$-\theta _{J,3}$
-special isotropic, and
 $\theta _{K,3}$
-special isotropic, and hence is
$\theta _{K,3}$
-special isotropic, and hence is
 $\phi _2$
-associative.
$\phi _2$
-associative.
Proof (a) If
![]() $L \subset M$
is
$L \subset M$
is
![]() $I_1$
-CR (resp.
$I_1$
-CR (resp.
![]() $I_3$
-CR), then Proposition 3.5 implies that its cone
$I_3$
-CR), then Proposition 3.5 implies that its cone
![]() $\mathrm {C}(L) \subset C$
is
$\mathrm {C}(L) \subset C$
is
![]() $I_1$
-complex (resp.
$I_1$
-complex (resp.
![]() $I_3$
-complex). By Proposition 2.12(a),
$I_3$
-complex). By Proposition 2.12(a),
![]() $\mathrm {C}(L)$
is
$\mathrm {C}(L)$
is
![]() $\Phi _2$
-Cayley, so by Proposition 3.13, L is
$\Phi _2$
-Cayley, so by Proposition 3.13, L is
![]() $\phi _2$
-associative.
$\phi _2$
-associative.
(b) If
![]() $L \subset M$
is
$L \subset M$
is
![]() $-\theta _{I,3}$
-special isotropic (resp.
$-\theta _{I,3}$
-special isotropic (resp.
![]() $\theta _{K,3}$
-special isotropic), then Proposition 3.11 implies that its cone
$\theta _{K,3}$
-special isotropic), then Proposition 3.11 implies that its cone
![]() $\mathrm {C}(L) \subset C$
is
$\mathrm {C}(L) \subset C$
is
![]() $-\Theta _{I,4}$
-special isotropic (resp.
$-\Theta _{I,4}$
-special isotropic (resp.
![]() $\Theta _{K,4}$
-special isotropic). By Proposition 2.12(b),
$\Theta _{K,4}$
-special isotropic). By Proposition 2.12(b),
![]() $\mathrm {C}(L)$
is
$\mathrm {C}(L)$
is
![]() $\Phi _2$
-Cayley, so by Proposition 3.13, L is
$\Phi _2$
-Cayley, so by Proposition 3.13, L is
![]() $\phi _2$
-associative.
$\phi _2$
-associative.
(c) If L is
![]() $I_1$
-CR isotropic, then Proposition 3.8 implies that
$I_1$
-CR isotropic, then Proposition 3.8 implies that
![]() $\mathrm {C}(L) \subset C$
is
$\mathrm {C}(L) \subset C$
is
![]() $I_1$
-complex isotropic, and the result follows from an argument analogous to those used in parts (a) and (b). Alternatively, if L is
$I_1$
-complex isotropic, and the result follows from an argument analogous to those used in parts (a) and (b). Alternatively, if L is
![]() $I_1$
-CR isotropic, then by definition, L is
$I_1$
-CR isotropic, then by definition, L is
![]() $I_1$
-CR,
$I_1$
-CR,
![]() $\alpha _2$
-isotropic, and
$\alpha _2$
-isotropic, and
![]() $\alpha _3$
-isotropic. Recalling that
$\alpha _3$
-isotropic. Recalling that
we observe that L is
![]() $-\theta _{J,3}$
- and
$-\theta _{J,3}$
- and
![]() $\theta _{K,3}$
-special isotropic.
$\theta _{K,3}$
-special isotropic.
Remark 3.16 Where associative
![]() $3$
-folds in
$3$
-folds in
![]() $3$
-Sasakian manifolds
$3$
-Sasakian manifolds
![]() $M^{4n+3}$
are concerned, the case
$M^{4n+3}$
are concerned, the case
![]() $n = 1$
has received the most attention in light of the connection to
$n = 1$
has received the most attention in light of the connection to
![]() $\mathrm {G}_2$
-geometry. Recently, several studies have considered the two one-parameter families of squashed associative
$\mathrm {G}_2$
-geometry. Recently, several studies have considered the two one-parameter families of squashed associative
![]() $3$
-forms on
$3$
-forms on
![]() $M^7$
given by
$M^7$
given by
 $$ \begin{align*} -\phi_{1,t}^- & = \alpha_1 \wedge \alpha_2 \wedge \alpha_3 + t^2(- \alpha_1 \wedge \kappa_1 + \alpha_2 \wedge \kappa_2 + \alpha_3 \wedge \kappa_3), \\ \phi_{1,t}^+ & = \alpha_1 \wedge \alpha_2 \wedge \alpha_3 - t^2(\alpha_1 \wedge \kappa_1 + \alpha_2 \wedge \kappa_2 + \alpha_3 \wedge \kappa_3). \end{align*} $$
$$ \begin{align*} -\phi_{1,t}^- & = \alpha_1 \wedge \alpha_2 \wedge \alpha_3 + t^2(- \alpha_1 \wedge \kappa_1 + \alpha_2 \wedge \kappa_2 + \alpha_3 \wedge \kappa_3), \\ \phi_{1,t}^+ & = \alpha_1 \wedge \alpha_2 \wedge \alpha_3 - t^2(\alpha_1 \wedge \kappa_1 + \alpha_2 \wedge \kappa_2 + \alpha_3 \wedge \kappa_3). \end{align*} $$
See, for example, [Reference Ball and Madnick6], [Reference Kennon and Lotay23], or [Reference Lotay and Oliveira24].
3.3.4 Summary
The following table summarizes the relationships discussed above.

With the exception of
![]() $\alpha _1$
-Legendrian and
$\alpha _1$
-Legendrian and
![]() $\alpha _1$
-isotropic submanifolds, all of the “link” submanifolds
$\alpha _1$
-isotropic submanifolds, all of the “link” submanifolds
![]() $L \subset M^{4n+3}$
that appear in the table are minimal (i.e., have zero mean curvature), because a calibrated cone is minimal, and the link of a minimal cone is minimal.
$L \subset M^{4n+3}$
that appear in the table are minimal (i.e., have zero mean curvature), because a calibrated cone is minimal, and the link of a minimal cone is minimal.
3.4
 $3$
-Sasakian manifolds as circle bundles
$3$
-Sasakian manifolds as circle bundles
From now on,
![]() $3$
-Sasakian
$3$
-Sasakian
![]() $(4n+3)$
-manifolds M are assumed to be compact. Above, we viewed M as the link of a hyperkähler cone C. In this section, we adopt a different perspective, viewing M as the total space of a circle bundle. The starting point is the following result.
$(4n+3)$
-manifolds M are assumed to be compact. Above, we viewed M as the link of a hyperkähler cone C. In this section, we adopt a different perspective, viewing M as the total space of a circle bundle. The starting point is the following result.
Theorem 3.17 (Boyer-Galicki [Reference Boyer and Galicki8], Theorems 7.5.1, 13.2.5, 13.3.1)
Let M be a compact
![]() $3$
-Sasakian
$3$
-Sasakian
![]() $(4n+3)$
-manifold. For
$(4n+3)$
-manifold. For
![]() $v = (v_1, v_2, v_3) \in S^2$
, let
$v = (v_1, v_2, v_3) \in S^2$
, let
![]() $A_v = v_1 A_1 + v_2 A_2 + v_3 A_3$
denote the corresponding Reeb field. Then:
$A_v = v_1 A_1 + v_2 A_2 + v_3 A_3$
denote the corresponding Reeb field. Then:
-
(1) Each
 $A_v$
defines a locally free
$A_v$
defines a locally free
 $S^1$
-action on M and quasi-regular foliation
$S^1$
-action on M and quasi-regular foliation
 $\mathcal {F}_v \subset M$
. Let
$\mathcal {F}_v \subset M$
. Let
 $Z_v := M/\mathcal {F}_v$
denote the corresponding leaf space, and let
$Z_v := M/\mathcal {F}_v$
denote the corresponding leaf space, and let
 $p_v \colon M \to Z_v$
denote the projection.
$p_v \colon M \to Z_v$
denote the projection. -
(2) The projection
 $p_v \colon M \to Z_v$
is a principal
$p_v \colon M \to Z_v$
is a principal
 $S^1$
-orbibundle with connection
$S^1$
-orbibundle with connection
 $1$
-form
$1$
-form
 ${\alpha _v = \sum v^i \alpha _i}$
, and it is an orbifold Riemannian submersion.
${\alpha _v = \sum v^i \alpha _i}$
, and it is an orbifold Riemannian submersion. -
(3) For
 $v, v' \in S^2$
, there is a diffeomorphism
$v, v' \in S^2$
, there is a diffeomorphism
 $Z_{v} \approx Z_{v'}$
. In fact, each
$Z_{v} \approx Z_{v'}$
. In fact, each
 $Z_v$
may be identified with the (orbifold) twistor space Z of the quaternionic-Kähler
$Z_v$
may be identified with the (orbifold) twistor space Z of the quaternionic-Kähler
 $4n$
-orbifold
$4n$
-orbifold
 ${Q = M/\mathcal {F}_A}$
, where
${Q = M/\mathcal {F}_A}$
, where
 $\mathcal {F}_A$
is the three-dimensional foliation determined by the vector fields
$\mathcal {F}_A$
is the three-dimensional foliation determined by the vector fields
 $A_1, A_2, A_3$
.
$A_1, A_2, A_3$
.
Thus, every compact
![]() $3$
-Sasakian
$3$
-Sasakian
![]() $(4n+3)$
-manifold M has a natural
$(4n+3)$
-manifold M has a natural
![]() $S^2$
-family of projections
$S^2$
-family of projections
![]() $p_v \colon M^{4n+3} \to Z^{4n+2}$
. For definiteness, we choose to work with
$p_v \colon M^{4n+3} \to Z^{4n+2}$
. For definiteness, we choose to work with
![]() $p_1 := p_{(1,0,0)} \colon M \to Z$
, with respect to which
$p_1 := p_{(1,0,0)} \colon M \to Z$
, with respect to which
![]() $\alpha _1 \in \Omega ^1(M)$
is a connection
$\alpha _1 \in \Omega ^1(M)$
is a connection
![]() $1$
-form. On M, the choice of
$1$
-form. On M, the choice of
![]() $p_1$
preferences the splitting
$p_1$
preferences the splitting
![]() $TM = \mathbb {R} A_1 \oplus \mathrm {Ker}(\alpha _1)$
. On the hyperkähler cone
$TM = \mathbb {R} A_1 \oplus \mathrm {Ker}(\alpha _1)$
. On the hyperkähler cone
![]() $C^{4n+4} = \mathrm {C}(M)$
, our choice distinguishes the Kähler structure
$C^{4n+4} = \mathrm {C}(M)$
, our choice distinguishes the Kähler structure
![]() $(g_{\mathrm {C}}, I_1, \omega _1)$
.
$(g_{\mathrm {C}}, I_1, \omega _1)$
.
3.4.1 The
 $3$
-forms
$3$
-forms
 $\Gamma _1, \Gamma _2, \Gamma _3$
and
$\Gamma _1, \Gamma _2, \Gamma _3$
and
 $4$
-forms
$4$
-forms
 $\Xi _1, \Xi _2, \Xi _3$
$\Xi _1, \Xi _2, \Xi _3$
We now introduce
![]() $\mathbb {C}$
-valued
$\mathbb {C}$
-valued
![]() $3$
-forms
$3$
-forms
![]() $\Gamma _1, \Gamma _2, \Gamma _3 \in \Omega ^3(M; \mathbb {C})$
and
$\Gamma _1, \Gamma _2, \Gamma _3 \in \Omega ^3(M; \mathbb {C})$
and
![]() $\mathbb {R}$
-valued
$\mathbb {R}$
-valued
![]() $4$
-forms
$4$
-forms
![]() $\Xi _1, \Xi _2, \Xi _3 \in \Omega ^4(M)$
that will play a key role in understanding the structure on the twistor space Z. These forms do not appear to have been studied before. Recalling the
$\Xi _1, \Xi _2, \Xi _3 \in \Omega ^4(M)$
that will play a key role in understanding the structure on the twistor space Z. These forms do not appear to have been studied before. Recalling the
![]() $2$
-forms
$2$
-forms
![]() $\kappa _j$
defined in (3.6), we define
$\kappa _j$
defined in (3.6), we define
 $$ \begin{align} \Gamma_1 & = (\alpha_2 - i\alpha_3) \wedge (\kappa_2 + i\kappa_3), \nonumber \\ \Gamma_2 & = (\alpha_3 - i\alpha_1) \wedge (\kappa_3 + i\kappa_1), \\ \Gamma_3 & = (\alpha_1 - i\alpha_2) \wedge (\kappa_1 + i\kappa_2),\nonumber \end{align} $$
$$ \begin{align} \Gamma_1 & = (\alpha_2 - i\alpha_3) \wedge (\kappa_2 + i\kappa_3), \nonumber \\ \Gamma_2 & = (\alpha_3 - i\alpha_1) \wedge (\kappa_3 + i\kappa_1), \\ \Gamma_3 & = (\alpha_1 - i\alpha_2) \wedge (\kappa_1 + i\kappa_2),\nonumber \end{align} $$
and
Note that the real and imaginary parts of
![]() $\Gamma _1$
are given by
$\Gamma _1$
are given by
 $$ \begin{align} \begin{aligned} \text{Re}(\Gamma_1) & = \alpha_2 \wedge \kappa_2 + \alpha_3 \wedge \kappa_3, \\ \text{Im}(\Gamma_1) & = \alpha_2 \wedge \kappa_3 - \alpha_3 \wedge \kappa_2. \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} \text{Re}(\Gamma_1) & = \alpha_2 \wedge \kappa_2 + \alpha_3 \wedge \kappa_3, \\ \text{Im}(\Gamma_1) & = \alpha_2 \wedge \kappa_3 - \alpha_3 \wedge \kappa_2. \end{aligned} \end{align} $$
Their exterior derivatives are given by:
Proposition 3.18 We have
 $$ \begin{align*} d\,\mathrm{Re}(\Gamma_1) & = 2\Xi_1 - 4 \alpha_2 \wedge \alpha_3 \wedge \kappa_1, \\ d\,\mathrm{Im}(\Gamma_1) & = 0, \\ d\Xi_1 & = -4\kappa_1 \wedge \mathrm{Im}(\Gamma_1). \end{align*} $$
$$ \begin{align*} d\,\mathrm{Re}(\Gamma_1) & = 2\Xi_1 - 4 \alpha_2 \wedge \alpha_3 \wedge \kappa_1, \\ d\,\mathrm{Im}(\Gamma_1) & = 0, \\ d\Xi_1 & = -4\kappa_1 \wedge \mathrm{Im}(\Gamma_1). \end{align*} $$
Proof This is a straightforward computation using the definitions (3.15) and (3.14) and the exterior derivative formulas (3.5) and (3.7).
Remark 3.19 We remark in passing that one can compute
showing that the natural
![]() $4$
-form
$4$
-form
![]() $\kappa _1^2 + \Xi _1 = \kappa _1^2 + \kappa _2^2 + \kappa _3^2$
is exact.
$\kappa _1^2 + \Xi _1 = \kappa _1^2 + \kappa _2^2 + \kappa _3^2$
is exact.
To clarify the geometric meaning of
![]() $\Gamma _1 \in \Omega ^3(M; \mathbb {C})$
, we consider the
$\Gamma _1 \in \Omega ^3(M; \mathbb {C})$
, we consider the
![]() $2$
-form
$2$
-form
Using equations (3.5)–(3.7), (3.15), and Proposition 3.18, we derive the identities
 $$ \begin{align*} d \widetilde{\Omega}_1 & = 3\,\mathrm{Im}(2\Gamma_1), \\ d\,\mathrm{Re}(2\Gamma_1) & = 2(2\Xi_1 - 4\alpha_2 \wedge \alpha_3 \wedge \kappa_1). \end{align*} $$
$$ \begin{align*} d \widetilde{\Omega}_1 & = 3\,\mathrm{Im}(2\Gamma_1), \\ d\,\mathrm{Re}(2\Gamma_1) & = 2(2\Xi_1 - 4\alpha_2 \wedge \alpha_3 \wedge \kappa_1). \end{align*} $$
When
![]() $n = 1$
, in which case
$n = 1$
, in which case
![]() $\dim (Z) = 6$
and
$\dim (Z) = 6$
and
![]() $\dim (M) = 7$
, there is a coincidence
$\dim (M) = 7$
, there is a coincidence
![]() ${\kappa _1^2 = \kappa _2^2 = \kappa _3^2}$
, which implies
${\kappa _1^2 = \kappa _2^2 = \kappa _3^2}$
, which implies
![]() $\Xi _1 = 2\kappa _1^2$
, and therefore
$\Xi _1 = 2\kappa _1^2$
, and therefore
 $$ \begin{align*} d \widetilde{\Omega}_1 & = 3\,\mathrm{Im}(2\Gamma_1), \\ d \,\mathrm{Re}(2\Gamma_1) & = 2\widetilde{\Omega}_1^2, \end{align*} $$
$$ \begin{align*} d \widetilde{\Omega}_1 & = 3\,\mathrm{Im}(2\Gamma_1), \\ d \,\mathrm{Re}(2\Gamma_1) & = 2\widetilde{\Omega}_1^2, \end{align*} $$
which is familiar from the geometry of nearly Kähler
![]() $6$
-manifolds [Reference Reyes Carrión and Salamon26]. So, when
$6$
-manifolds [Reference Reyes Carrión and Salamon26]. So, when
![]() $n = 1$
, the forms
$n = 1$
, the forms
![]() $\widetilde {\Omega }_1 \in \Omega ^2(M)$
and
$\widetilde {\Omega }_1 \in \Omega ^2(M)$
and
![]() $2\Gamma _1 \in \Omega ^3(M;\mathbb {C})$
are the pullbacks via
$2\Gamma _1 \in \Omega ^3(M;\mathbb {C})$
are the pullbacks via
![]() $p_1 \colon M^7 \to Z^6$
of the nearly Kähler
$p_1 \colon M^7 \to Z^6$
of the nearly Kähler
![]() $2$
-form and complex volume form on Z, respectively.
$2$
-form and complex volume form on Z, respectively.
In Sections 4.1 and 4.2, we will see that aspects of this picture persist in higher dimensions. That is, for any
![]() $n \geq 1$
, the
$n \geq 1$
, the
![]() $2$
-form
$2$
-form
![]() $\widetilde {\Omega }_1$
is the pullback of the nearly Kähler
$\widetilde {\Omega }_1$
is the pullback of the nearly Kähler
![]() $2$
-form, while
$2$
-form, while
![]() $2\Gamma _1$
is the pullback of a natural
$2\Gamma _1$
is the pullback of a natural
![]() $3$
-form that (together with other geometric data) defines an
$3$
-form that (together with other geometric data) defines an
![]() $\mathrm {Sp}(n)\mathrm {U}(1)$
-structure on Z. When
$\mathrm {Sp}(n)\mathrm {U}(1)$
-structure on Z. When
![]() $n = 1$
, the
$n = 1$
, the
![]() $\mathrm {Sp}(1)\mathrm {U}(1) \cong \mathrm {U}(2)$
-structure on Z induces the familiar
$\mathrm {Sp}(1)\mathrm {U}(1) \cong \mathrm {U}(2)$
-structure on Z induces the familiar
![]() $\mathrm {SU}(3)$
-structure, but when
$\mathrm {SU}(3)$
-structure, but when
![]() $n> 1$
the group
$n> 1$
the group
![]() $\mathrm {Sp}(n)\mathrm {U}(1)$
is not contained in
$\mathrm {Sp}(n)\mathrm {U}(1)$
is not contained in
![]() $\mathrm {SU}(2n+1)$
.
$\mathrm {SU}(2n+1)$
.
3.4.2
 $\mathrm {Re}(\Gamma _1)$
-calibrated
$\mathrm {Re}(\Gamma _1)$
-calibrated
 $3$
-folds
$3$
-folds
The real parts of the
![]() $3$
-forms
$3$
-forms
![]() $\Gamma _1, \Gamma _2, \Gamma _3 \in \Omega ^3(M;\mathbb {C})$
turn out to be semi-calibrations (Corollary 4.11), and thus give rise to a distinguished class of
$\Gamma _1, \Gamma _2, \Gamma _3 \in \Omega ^3(M;\mathbb {C})$
turn out to be semi-calibrations (Corollary 4.11), and thus give rise to a distinguished class of
![]() $3$
-folds of M. The following theorem characterizes these submanifolds; we defer the proof to Section 4.4, where the result is restated as Theorem 4.31.
$3$
-folds of M. The following theorem characterizes these submanifolds; we defer the proof to Section 4.4, where the result is restated as Theorem 4.31.
Theorem 3.20 Let
![]() $L^3 \subset M^{4n+3}$
be a three-dimensional submanifold. The following are equivalent:
$L^3 \subset M^{4n+3}$
be a three-dimensional submanifold. The following are equivalent:
-
(1)
 $\mathrm {C}(L)$
is a
$\mathrm {C}(L)$
is a
 $(c_\theta I_2 + s_\theta I_3)$
-complex isotropic
$(c_\theta I_2 + s_\theta I_3)$
-complex isotropic
 $4$
-fold for some constant
$4$
-fold for some constant
 $e^{i \theta } \in S^1$
.
$e^{i \theta } \in S^1$
. -
(2) L is a
 $(c_\theta I_2 + s_\theta I_3)$
-CR isotropic
$(c_\theta I_2 + s_\theta I_3)$
-CR isotropic
 $3$
-fold for some constant
$3$
-fold for some constant
 $e^{i \theta } \in S^1$
.
$e^{i \theta } \in S^1$
. -
(3) L is
 $\mathrm {Re}(\Gamma _1)$
-calibrated.
$\mathrm {Re}(\Gamma _1)$
-calibrated.
Examples of
![]() $\mathrm {Re}(\Gamma _1)$
-calibrated submanifolds can be constructed via Example 5.2 together with Theorem 6.3.
$\mathrm {Re}(\Gamma _1)$
-calibrated submanifolds can be constructed via Example 5.2 together with Theorem 6.3.
3.4.3 Descent to Z
To conclude this section, we observe that certain differential forms defined on M descend to the twistor space Z via the map
![]() $p_1 \colon M \to Z$
. For this, we recall that a k-form
$p_1 \colon M \to Z$
. For this, we recall that a k-form
![]() $\phi \in \Omega ^k(M)$
is called
$\phi \in \Omega ^k(M)$
is called
![]() $p_1$
-semibasic if
$p_1$
-semibasic if
![]() $\iota _X\phi = 0$
for all
$\iota _X\phi = 0$
for all
![]() $X \in \mathrm {Ker}( (p_1)_*)$
. Since the fibers of
$X \in \mathrm {Ker}( (p_1)_*)$
. Since the fibers of
![]() $p_1 \colon M \to Z$
are connected, it is a standard fact that a k-form
$p_1 \colon M \to Z$
are connected, it is a standard fact that a k-form
![]() $\phi \in \Omega ^k(M)$
descends to Z if and only if both
$\phi \in \Omega ^k(M)$
descends to Z if and only if both
![]() $\phi $
and
$\phi $
and
![]() $d\phi $
are
$d\phi $
are
![]() $p_1$
-semibasic.
$p_1$
-semibasic.
Proposition 3.21 Consider the projection
![]() $p := p_1 \colon M \to Z$
.
$p := p_1 \colon M \to Z$
.
-
(1) There exist
 $\mathbb {R}$
-valued differential
$\mathbb {R}$
-valued differential
 $2$
-forms
$2$
-forms
 $\omega _{\mathsf {V}}$
,
$\omega _{\mathsf {V}}$
,
 $\omega _{\mathsf {H}}$
,
$\omega _{\mathsf {H}}$
,
 $\omega _{\mathrm {KE}}, \omega _{\mathrm {NK}} \in \Omega ^2(Z)$
satisfying
$\omega _{\mathrm {KE}}, \omega _{\mathrm {NK}} \in \Omega ^2(Z)$
satisfying  $$ \begin{align*} \alpha_2 \wedge \alpha_3 & = p^*(\omega_{\mathsf{V}}), & \kappa_1 + \alpha_2 \wedge \alpha_3 = \Omega_1 & = p^*(\omega_{\mathrm{KE}}), \\ \kappa_1 & = p^*(\omega_{\mathsf{H}}), & 2\kappa_1 - \alpha_2 \wedge \alpha_3 = \widetilde{\Omega}_1 & = p^*(\omega_{\mathrm{NK}}). \end{align*} $$
$$ \begin{align*} \alpha_2 \wedge \alpha_3 & = p^*(\omega_{\mathsf{V}}), & \kappa_1 + \alpha_2 \wedge \alpha_3 = \Omega_1 & = p^*(\omega_{\mathrm{KE}}), \\ \kappa_1 & = p^*(\omega_{\mathsf{H}}), & 2\kappa_1 - \alpha_2 \wedge \alpha_3 = \widetilde{\Omega}_1 & = p^*(\omega_{\mathrm{NK}}). \end{align*} $$
-
(2) There exist a
 $\mathbb {C}$
-valued differential
$\mathbb {C}$
-valued differential
 $3$
-form
$3$
-form
 $\gamma \in \Omega ^3(Z; \mathbb {C})$
and an
$\gamma \in \Omega ^3(Z; \mathbb {C})$
and an
 $\mathbb {R}$
-valued differential
$\mathbb {R}$
-valued differential
 $4$
-form
$4$
-form
 $\xi \in \Omega ^4(Z)$
satisfying
$\xi \in \Omega ^4(Z)$
satisfying  $$ \begin{align*} \Gamma_1 & = p^*(\gamma), \\ \Xi_1 & = p^*(\xi). \end{align*} $$
$$ \begin{align*} \Gamma_1 & = p^*(\gamma), \\ \Xi_1 & = p^*(\xi). \end{align*} $$
Proof (a) By equations (3.5) and (3.7), we have
Therefore, both
![]() $\alpha _2 \wedge \alpha _3$
and
$\alpha _2 \wedge \alpha _3$
and
![]() $d(\alpha _2 \wedge \alpha _3)$
are
$d(\alpha _2 \wedge \alpha _3)$
are
![]() $p_1$
-semibasic, and similarly for
$p_1$
-semibasic, and similarly for
![]() $\kappa _1$
and
$\kappa _1$
and
![]() $d\kappa _1$
.
$d\kappa _1$
.
(b) By Proposition 3.18, we have
Therefore, both
![]() $\Gamma _1$
and
$\Gamma _1$
and
![]() $d\Gamma _1$
are
$d\Gamma _1$
are
![]() $p_1$
-semibasic, and similarly for
$p_1$
-semibasic, and similarly for
![]() $\Xi _1$
and
$\Xi _1$
and
![]() $d\Xi _1$
.
$d\Xi _1$
.
Remark 3.22 By contrast, one can check that the following forms on M do not descend via
![]() $p_1 \colon M \to Z$
to forms on Z:
$p_1 \colon M \to Z$
to forms on Z:
 $$ \begin{align*} & \kappa_2, \kappa_3, & & \Gamma_2, \Gamma_3, & & \alpha_1, \alpha_2, \alpha_3, & & \phi_1, \phi_2, \phi_3, \\ & \Omega_2, \Omega_3, & & \Xi_2, \Xi_3, & & \Psi_1, \Psi_2, \Psi_3. & & \end{align*} $$
$$ \begin{align*} & \kappa_2, \kappa_3, & & \Gamma_2, \Gamma_3, & & \alpha_1, \alpha_2, \alpha_3, & & \phi_1, \phi_2, \phi_3, \\ & \Omega_2, \Omega_3, & & \Xi_2, \Xi_3, & & \Psi_1, \Psi_2, \Psi_3. & & \end{align*} $$
Remark 3.23 One must be careful to distinguish the
![]() $3$
-form
$3$
-form
![]() $\Gamma _1 = (\alpha _2 - i\alpha _3) \wedge (\kappa _2 + i\kappa _3)$
from the special isotropic
$\Gamma _1 = (\alpha _2 - i\alpha _3) \wedge (\kappa _2 + i\kappa _3)$
from the special isotropic
![]() $3$
-form
$3$
-form
While
![]() $\Gamma _1$
descends to Z, the special isotropic
$\Gamma _1$
descends to Z, the special isotropic
![]() $3$
-form
$3$
-form
![]() $(r\partial _r\,\lrcorner \,\frac {1}{2}\sigma _1^2)|_M$
does not, because its exterior derivative has
$(r\partial _r\,\lrcorner \,\frac {1}{2}\sigma _1^2)|_M$
does not, because its exterior derivative has
![]() $\alpha _1$
terms. Note that for
$\alpha _1$
terms. Note that for
![]() $n = 1$
, the object
$n = 1$
, the object
![]() $(r\partial _r\,\lrcorner \,\frac {1}{2}\sigma _1^2)|_M = \Psi _1$
is a
$(r\partial _r\,\lrcorner \,\frac {1}{2}\sigma _1^2)|_M = \Psi _1$
is a
![]() $3$
-form on
$3$
-form on
![]() $M^7$
whose real part calibrates special Legendrian
$M^7$
whose real part calibrates special Legendrian
![]() $3$
-folds.
$3$
-folds.
4 Calibrated geometry in twistor spaces
We now turn to the submanifold theory of twistor spaces Z, organizing our discussion as follows. In Section 4.1, we briefly discuss
![]() $\mathrm {Sp}(n)\mathrm {U}(1)$
-geometry on arbitrary
$\mathrm {Sp}(n)\mathrm {U}(1)$
-geometry on arbitrary
![]() $(4n+2)$
-manifolds
$(4n+2)$
-manifolds
![]() $Y^{4n+2}$
. Then, in Section 4.2 (Theorem 4.7), we prove that every twistor space
$Y^{4n+2}$
. Then, in Section 4.2 (Theorem 4.7), we prove that every twistor space
![]() $Z^{4n+2}$
admits a canonical
$Z^{4n+2}$
admits a canonical
![]() $\mathrm {Sp}(n)\mathrm {U}(1)$
-structure, which (among other data) entails a distinguished
$\mathrm {Sp}(n)\mathrm {U}(1)$
-structure, which (among other data) entails a distinguished
![]() $3$
-form
$3$
-form
![]() $\gamma \in \Omega ^3(Z; \mathbb {C})$
. In Proposition 4.10, we prove that
$\gamma \in \Omega ^3(Z; \mathbb {C})$
. In Proposition 4.10, we prove that
![]() $\mathrm {Re}(\gamma ) \in \Omega ^3(Z)$
is a semi-calibration, and devote Section 4.3 to the study of
$\mathrm {Re}(\gamma ) \in \Omega ^3(Z)$
is a semi-calibration, and devote Section 4.3 to the study of
![]() $\mathrm {Re}(\gamma )$
-calibrated
$\mathrm {Re}(\gamma )$
-calibrated
![]() $3$
-folds. In a certain sense (Proposition 4.10(b)), these are higher-codimension generalizations of special Lagrangian
$3$
-folds. In a certain sense (Proposition 4.10(b)), these are higher-codimension generalizations of special Lagrangian
![]() $3$
-folds in six-dimensional nearly Kähler twistor spaces.
$3$
-folds in six-dimensional nearly Kähler twistor spaces.
Finally, in Section 4.4, we study the relationships between submanifolds of
![]() $M^{4n+3}$
and those in
$M^{4n+3}$
and those in
![]() $Z^{4n+2}$
. More specifically, distinguishing the map
$Z^{4n+2}$
. More specifically, distinguishing the map
![]() $p_1 \colon M \to Z$
, we consider how various submanifolds
$p_1 \colon M \to Z$
, we consider how various submanifolds
![]() $\Sigma ^k \subset Z$
behave under the operations of
$\Sigma ^k \subset Z$
behave under the operations of
![]() $p_1$
-circle bundle lift
$p_1$
-circle bundle lift
![]() $p_1^{-1}(\Sigma )^{k+1} \subset M$
and
$p_1^{-1}(\Sigma )^{k+1} \subset M$
and
![]() $p_1$
-horizontal lift
$p_1$
-horizontal lift
![]() $\widehat {\Sigma }^k \subset M$
.
$\widehat {\Sigma }^k \subset M$
.
We remind the reader that as mentioned in the introduction, we only consider submanifolds of Z that do not meet any orbifold points.
4.1
 $\mathrm {Sp}(n)\mathrm {U}(1)$
-structures
$\mathrm {Sp}(n)\mathrm {U}(1)$
-structures
Let
![]() $Y^{4n+2}$
be a smooth
$Y^{4n+2}$
be a smooth
![]() $(4n+2)$
-manifold with
$(4n+2)$
-manifold with
![]() $n \geq 1$
.
$n \geq 1$
.
Definition 4.1 A
![]() $(\mathrm {U}(2n) \times \mathrm {U}(1))$
-structure on
$(\mathrm {U}(2n) \times \mathrm {U}(1))$
-structure on
![]() $Y^{4n+2}$
is an almost-Hermitian structure
$Y^{4n+2}$
is an almost-Hermitian structure
![]() $(g, J_+, \omega _+)$
together with a distribution of
$(g, J_+, \omega _+)$
together with a distribution of
![]() $J_+$
-invariant
$J_+$
-invariant
![]() $4n$
-planes
$4n$
-planes
![]() $\mathsf {H} \subset TY$
. Equivalently, it is an almost-Hermitian structure
$\mathsf {H} \subset TY$
. Equivalently, it is an almost-Hermitian structure
![]() $(g, J_+, \omega _+)$
together with an orthogonal splitting
$(g, J_+, \omega _+)$
together with an orthogonal splitting
where
![]() $\mathsf {H} \subset TY$
and
$\mathsf {H} \subset TY$
and
![]() $\mathsf {V} \subset TY$
are
$\mathsf {V} \subset TY$
are
![]() $J_+$
-invariant subbundles with
$J_+$
-invariant subbundles with
![]() $\mathrm {rank}(\mathsf {H}) = 4n$
and
$\mathrm {rank}(\mathsf {H}) = 4n$
and
![]() $\mathrm {rank}(\mathsf {V}) = 2$
.
$\mathrm {rank}(\mathsf {V}) = 2$
.
Given a
![]() $(\mathrm {U}(2n) \times \mathrm {U}(1))$
-structure
$(\mathrm {U}(2n) \times \mathrm {U}(1))$
-structure
![]() $(g, J_+, \omega _+, \mathsf {H})$
, we split
$(g, J_+, \omega _+, \mathsf {H})$
, we split
![]() $(g, J_+, \omega _+)$
into horizontal and vertical parts as follows:
$(g, J_+, \omega _+)$
into horizontal and vertical parts as follows:
Further, we can extend it to a one-parameter family
![]() $(g(t), J_+, \omega _+(t), \mathsf {H})$
by defining
$(g(t), J_+, \omega _+(t), \mathsf {H})$
by defining
Moreover, by reversing the orientation of the vertical subbundle
![]() $\mathsf {V} \subset TY$
, we obtain a second one-parameter family
$\mathsf {V} \subset TY$
, we obtain a second one-parameter family
![]() $(g(t)$
,
$(g(t)$
,
![]() $J_-$
,
$J_-$
,
![]() $\omega _-(t)$
,
$\omega _-(t)$
,
![]() $\mathsf {H})$
by defining
$\mathsf {H})$
by defining
For calculations on Y, we will need local frames adapted to the geometry of the
![]() $(\mathrm {U}(2n) \times \mathrm {U}(1))$
-structure. To be precise:
$(\mathrm {U}(2n) \times \mathrm {U}(1))$
-structure. To be precise:
Definition 4.2 A
![]() $(\mathrm {U}(2n) \times \mathrm {U}(1))$
-coframe at
$(\mathrm {U}(2n) \times \mathrm {U}(1))$
-coframe at
![]() $y \in Y$
is a g-orthonormal coframe
$y \in Y$
is a g-orthonormal coframe
for which
 $$ \begin{align*} \left.\omega_{\mathsf{V}}\right|_y & = \mu_2 \wedge \mu_3, & \left.\omega_{\mathsf{H}}\right|_y & = \sum_{j=1}^n (\rho_{j0} \wedge \rho_{j1} + \rho_{j2} \wedge \rho_{j3}). \end{align*} $$
$$ \begin{align*} \left.\omega_{\mathsf{V}}\right|_y & = \mu_2 \wedge \mu_3, & \left.\omega_{\mathsf{H}}\right|_y & = \sum_{j=1}^n (\rho_{j0} \wedge \rho_{j1} + \rho_{j2} \wedge \rho_{j3}). \end{align*} $$
For example, we will soon recall (Theorem 4.6) that every twistor space
![]() $Z^{4n+2}$
admits a natural
$Z^{4n+2}$
admits a natural
![]() $(\mathrm {U}(2n) \times \mathrm {U}(1))$
-structure. In fact, we will show (Theorem 4.7) that twistor spaces admit an additional piece of data:
$(\mathrm {U}(2n) \times \mathrm {U}(1))$
-structure. In fact, we will show (Theorem 4.7) that twistor spaces admit an additional piece of data:
Definition 4.3 Let
![]() $Y^{4n+2}$
be a
$Y^{4n+2}$
be a
![]() $(4n+2)$
-manifold with a
$(4n+2)$
-manifold with a
![]() $(\mathrm {U}(2n) \times \mathrm {U}(1))$
-structure
$(\mathrm {U}(2n) \times \mathrm {U}(1))$
-structure
![]() $(g, J_+, \omega _+, \mathsf {H})$
. A compatible
$(g, J_+, \omega _+, \mathsf {H})$
. A compatible
![]() $\mathrm {Sp}(n)\mathrm {U}(1)$
-structure is a complex
$\mathrm {Sp}(n)\mathrm {U}(1)$
-structure is a complex
![]() $3$
-form
$3$
-form
![]() $\gamma \in \Omega ^3(Y;\mathbb {C})$
with the following property: At each
$\gamma \in \Omega ^3(Y;\mathbb {C})$
with the following property: At each
![]() $y \in Y$
, there exists a
$y \in Y$
, there exists a
![]() $(\mathrm {U}(2n) \times \mathrm {U}(1))$
-coframe
$(\mathrm {U}(2n) \times \mathrm {U}(1))$
-coframe
![]() $(\rho , \mu )$
such that
$(\rho , \mu )$
such that
 $$ \begin{align*}\left.\gamma\right|_y = (\mu_2 - i \mu_3) \wedge \sum_{j=1}^n (\rho_{j0} + i \rho_{j1}) \wedge (\rho_{j2} + i\rho_{j3}).\end{align*} $$
$$ \begin{align*}\left.\gamma\right|_y = (\mu_2 - i \mu_3) \wedge \sum_{j=1}^n (\rho_{j0} + i \rho_{j1}) \wedge (\rho_{j2} + i\rho_{j3}).\end{align*} $$
Note that if
![]() $\gamma $
is a compatible
$\gamma $
is a compatible
![]() $\mathrm {Sp}(n)\mathrm {U}(1)$
-structure, then
$\mathrm {Sp}(n)\mathrm {U}(1)$
-structure, then
![]() $\gamma $
has
$\gamma $
has
![]() $J_+$
-type
$J_+$
-type
![]() $(2,1)$
and
$(2,1)$
and
![]() $J_-$
-type
$J_-$
-type
![]() $(3,0)$
.
$(3,0)$
.
To justify this terminology, we make a digression into linear algebra. Consider the following
![]() $\mathrm {Sp}(n)\mathrm {U}(1)$
-representation on
$\mathrm {Sp}(n)\mathrm {U}(1)$
-representation on
![]() $\mathbb {R}^{4n+2}$
. For
$\mathbb {R}^{4n+2}$
. For
![]() $(A,\lambda ) \in \mathrm {Sp}(n) \times \mathrm {U}(1)$
and
$(A,\lambda ) \in \mathrm {Sp}(n) \times \mathrm {U}(1)$
and
![]() $(h,z) \in \mathbb {H}^n \oplus \mathbb {C}$
, define
$(h,z) \in \mathbb {H}^n \oplus \mathbb {C}$
, define
Identify
![]() $\mathbb {H}^n \simeq \mathbb {C}^{2n}$
by writing
$\mathbb {H}^n \simeq \mathbb {C}^{2n}$
by writing
![]() $h = h_1 + jh_2$
with
$h = h_1 + jh_2$
with
![]() $h_1, h_2 \in \mathbb {C}^n$
. This identification endows
$h_1, h_2 \in \mathbb {C}^n$
. This identification endows
![]() $\mathbb {H}^n$
with the complex structure given by right multiplication by i, which in turn yields an embedding
$\mathbb {H}^n$
with the complex structure given by right multiplication by i, which in turn yields an embedding
![]() $\iota \colon \mathrm {Sp}(n) \to \mathrm {U}(2n)$
. In this way, the representation (4.1) induces an embedding
$\iota \colon \mathrm {Sp}(n) \to \mathrm {U}(2n)$
. In this way, the representation (4.1) induces an embedding
 $$ \begin{align*} \mathrm{Sp}(n)\mathrm{U}(1) & \to \mathrm{U}(2n) \times \mathrm{U}(1) \\ (A,\lambda) & \mapsto (\iota(A)\lambda^{-1}, \, \lambda^{-2}). \end{align*} $$
$$ \begin{align*} \mathrm{Sp}(n)\mathrm{U}(1) & \to \mathrm{U}(2n) \times \mathrm{U}(1) \\ (A,\lambda) & \mapsto (\iota(A)\lambda^{-1}, \, \lambda^{-2}). \end{align*} $$
The image of this map is
Since
![]() $\mathrm {Sp}(n)$
contains the element
$\mathrm {Sp}(n)$
contains the element
![]() $-\text {Id}$
, the condition
$-\text {Id}$
, the condition
![]() $\nu ^{-1/2} B \in \mathrm {Sp}(n)$
does not depend on the choice of square root.
$\nu ^{-1/2} B \in \mathrm {Sp}(n)$
does not depend on the choice of square root.
Let
![]() $(e_{10}, e_{11}, e_{12}, e_{13}, \ldots , e_{n0}, e_{n1}, e_{n2}, e_{n3}, f_2, f_3)$
denote the standard basis of
$(e_{10}, e_{11}, e_{12}, e_{13}, \ldots , e_{n0}, e_{n1}, e_{n2}, e_{n3}, f_2, f_3)$
denote the standard basis of
![]() $\mathbb {R}^{4n+2}$
, and let
$\mathbb {R}^{4n+2}$
, and let
![]() $(e^{10}, e^{11}, e^{12}, e^{13}, \ldots , e^{n0}, e^{n1}, e^{n2}, e^{n3}, f^2, f^3)$
denote its dual basis. We identify
$(e^{10}, e^{11}, e^{12}, e^{13}, \ldots , e^{n0}, e^{n1}, e^{n2}, e^{n3}, f^2, f^3)$
denote its dual basis. We identify
![]() $\mathbb {R}^{4n+2} \simeq \mathbb {C}^{2n} \oplus \mathbb {C}$
via the complex structure
$\mathbb {R}^{4n+2} \simeq \mathbb {C}^{2n} \oplus \mathbb {C}$
via the complex structure
![]() $J_0$
whose Kähler form is
$J_0$
whose Kähler form is
Identifying
![]() $\mathbb {C}^{2n} \simeq \mathbb {H}^n$
, the standard hyperkähler triple on
$\mathbb {C}^{2n} \simeq \mathbb {H}^n$
, the standard hyperkähler triple on
![]() $\mathbb {H}^n$
is
$\mathbb {H}^n$
is
 $$ \begin{align} \begin{aligned} \beta_1 & = \sum (e^{j0} \wedge e^{j1} + e^{j2} \wedge e^{j3}), & \beta_2 & = \sum (e^{j0} \wedge e^{j2} - e^{j1} \wedge e^{j3}), \\ \beta_3 & = \sum (e^{j0} \wedge e^{j3} + e^{j1} \wedge e^{j2}). \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} \beta_1 & = \sum (e^{j0} \wedge e^{j1} + e^{j2} \wedge e^{j3}), & \beta_2 & = \sum (e^{j0} \wedge e^{j2} - e^{j1} \wedge e^{j3}), \\ \beta_3 & = \sum (e^{j0} \wedge e^{j3} + e^{j1} \wedge e^{j2}). \end{aligned} \end{align} $$
We consider the
![]() $3$
-form
$3$
-form
![]() $\gamma _0 \in \Lambda ^3( (\mathbb {R}^{4n+2})^*)$
given by
$\gamma _0 \in \Lambda ^3( (\mathbb {R}^{4n+2})^*)$
given by
Then:
Proposition 4.4 With respect to the standard
![]() $(\mathrm {U}(2n) \times \mathrm {U}(1))$
-action on
$(\mathrm {U}(2n) \times \mathrm {U}(1))$
-action on
![]() $\mathbb {R}^{4n+2}$
, the stabilizer of
$\mathbb {R}^{4n+2}$
, the stabilizer of
![]() $\gamma _0 \in \Lambda ^3( (\mathbb {R}^{4n+2})^*)$
is the subgroup
$\gamma _0 \in \Lambda ^3( (\mathbb {R}^{4n+2})^*)$
is the subgroup
![]() $\mathrm {Sp}(n)\mathrm {U}(1) \leq \mathrm {U}(2n) \times \mathrm {U}(1)$
given by (4.2).
$\mathrm {Sp}(n)\mathrm {U}(1) \leq \mathrm {U}(2n) \times \mathrm {U}(1)$
given by (4.2).
Proof Let
![]() $(B, \nu ) \in \mathrm {U}(2n) \times \mathrm {U}(1)$
, and set
$(B, \nu ) \in \mathrm {U}(2n) \times \mathrm {U}(1)$
, and set
![]() $\tau = f^2 - if^3$
and
$\tau = f^2 - if^3$
and
![]() $\beta = \beta _2 + i\beta _3$
. Since
$\beta = \beta _2 + i\beta _3$
. Since
![]() $\tau $
has
$\tau $
has
![]() $J_0$
-type
$J_0$
-type
![]() $(0,1)$
and
$(0,1)$
and
![]() $\beta $
has
$\beta $
has
![]() $J_0$
-type
$J_0$
-type
![]() $(2,0)$
, we have
$(2,0)$
, we have
and hence
If
![]() $(B,\nu ) \in \mathrm {Sp}(n)\mathrm {U}(1)$
, then
$(B,\nu ) \in \mathrm {Sp}(n)\mathrm {U}(1)$
, then
![]() $\nu ^{-1/2}B \in \mathrm {Sp}(n)$
by (4.2). Thus, since
$\nu ^{-1/2}B \in \mathrm {Sp}(n)$
by (4.2). Thus, since
![]() $\mathrm {Sp}(n)$
stabilizes
$\mathrm {Sp}(n)$
stabilizes
![]() $\beta _1, \beta _2, \beta _3$
, we get
$\beta _1, \beta _2, \beta _3$
, we get
Conversely, if
![]() $(B,\nu ) \in \mathrm {U}(2n) \times \mathrm {U}(1)$
stabilizes
$(B,\nu ) \in \mathrm {U}(2n) \times \mathrm {U}(1)$
stabilizes
![]() $\gamma _0$
, then
$\gamma _0$
, then
Contracting both sides with the vector
![]() $f_2 + if_3$
implies that
$f_2 + if_3$
implies that
![]() $\beta = (\nu ^{-1/2}B)^*\beta $
, so that
$\beta = (\nu ^{-1/2}B)^*\beta $
, so that
![]() $\nu ^{-1/2}B \in \mathrm {U}(2n)$
stabilizes
$\nu ^{-1/2}B \in \mathrm {U}(2n)$
stabilizes
![]() $\beta $
. Since the
$\beta $
. Since the
![]() $\mathrm {U}(2n)$
-stabilizer of
$\mathrm {U}(2n)$
-stabilizer of
![]() $\beta $
is
$\beta $
is
![]() $\mathrm {Sp}(n)$
, we deduce that
$\mathrm {Sp}(n)$
, we deduce that
![]() $\nu ^{-1/2}B \in \mathrm {Sp}(n)$
, and hence
$\nu ^{-1/2}B \in \mathrm {Sp}(n)$
, and hence
![]() $(B,\nu ) \in \mathrm {Sp}(n)\mathrm {U}(1)$
.
$(B,\nu ) \in \mathrm {Sp}(n)\mathrm {U}(1)$
.
Example 4.1 The case
![]() $n=1$
is particularly special. Let
$n=1$
is particularly special. Let
![]() $Y^6$
be a
$Y^6$
be a
![]() $6$
-manifold with a
$6$
-manifold with a
![]() $(\mathrm {U}(2) \times \mathrm {U}(1))$
-structure
$(\mathrm {U}(2) \times \mathrm {U}(1))$
-structure
![]() $(g, J_+, \omega _+, \mathsf {H})$
. By definition, a compatible
$(g, J_+, \omega _+, \mathsf {H})$
. By definition, a compatible
![]() $\mathrm {Sp}(1)\mathrm {U}(1)$
-structure is a complex
$\mathrm {Sp}(1)\mathrm {U}(1)$
-structure is a complex
![]() $3$
-form
$3$
-form
![]() $\gamma \in \Omega ^3(Y;\mathbb {C})$
such that at each
$\gamma \in \Omega ^3(Y;\mathbb {C})$
such that at each
![]() $y \in Y$
, there exists a
$y \in Y$
, there exists a
![]() $(\mathrm {U}(2) \times \mathrm {U}(1))$
-coframe
$(\mathrm {U}(2) \times \mathrm {U}(1))$
-coframe
![]() $(\rho _0, \rho _1, \rho _2, \rho _3, \mu _2, \mu _3) \colon T_yY \to \mathbb {R}^4 \times \mathbb {R}^2$
for which
$(\rho _0, \rho _1, \rho _2, \rho _3, \mu _2, \mu _3) \colon T_yY \to \mathbb {R}^4 \times \mathbb {R}^2$
for which
So,
![]() $\gamma $
is a nonvanishing
$\gamma $
is a nonvanishing
![]() $3$
-form of
$3$
-form of
![]() $J_-$
-type
$J_-$
-type
![]() $(3,0)$
satisfying
$(3,0)$
satisfying
As such,
![]() $\gamma \in \Omega ^3(Y;\mathbb {C})$
defines an
$\gamma \in \Omega ^3(Y;\mathbb {C})$
defines an
![]() $\mathrm {SU}(3)$
-structure on Y.
$\mathrm {SU}(3)$
-structure on Y.
Alternatively, the presence of a compatible
![]() $\mathrm {SU}(3)$
-structure on
$\mathrm {SU}(3)$
-structure on
![]() $Y^6$
follows abstractly from the following group isomorphism of
$Y^6$
follows abstractly from the following group isomorphism of
![]() $\mathrm {Sp}(1)\mathrm {U}(1) \cong \mathrm {U}(2)$
onto a subgroup of
$\mathrm {Sp}(1)\mathrm {U}(1) \cong \mathrm {U}(2)$
onto a subgroup of
![]() $\mathrm {SU}(3)$
. Using
$\mathrm {SU}(3)$
. Using
![]() $\mathrm {Sp}(1) \cong \mathrm {SU}(2)$
, we have
$\mathrm {Sp}(1) \cong \mathrm {SU}(2)$
, we have
 $$ \begin{align*} \mathrm{Sp}(1)\mathrm{U}(1) = \left\{ \begin{pmatrix} B & 0 \\ 0 & \nu \end{pmatrix} \colon \nu^{-1/2}B \in \mathrm{SU}(2) \right\} & \cong \left\{ \begin{pmatrix} T & 0 \\ 0 & (\det T)^{-1} \end{pmatrix} \colon T \in \mathrm{U}(2) \right\} \leq \mathrm{SU}(3), \\ \begin{pmatrix} B & 0 \\ 0 & \det B \end{pmatrix} & \mapsto \begin{pmatrix} B & 0 \\ 0 & (\det B)^{-1} \end{pmatrix}. \end{align*} $$
$$ \begin{align*} \mathrm{Sp}(1)\mathrm{U}(1) = \left\{ \begin{pmatrix} B & 0 \\ 0 & \nu \end{pmatrix} \colon \nu^{-1/2}B \in \mathrm{SU}(2) \right\} & \cong \left\{ \begin{pmatrix} T & 0 \\ 0 & (\det T)^{-1} \end{pmatrix} \colon T \in \mathrm{U}(2) \right\} \leq \mathrm{SU}(3), \\ \begin{pmatrix} B & 0 \\ 0 & \det B \end{pmatrix} & \mapsto \begin{pmatrix} B & 0 \\ 0 & (\det B)^{-1} \end{pmatrix}. \end{align*} $$
(This is a group homomorphism because
![]() $\mathrm {U}(1)$
is abelian.) The situation is described by the following diagram:
$\mathrm {U}(1)$
is abelian.) The situation is described by the following diagram:

Remark 4.5 The notation in this remark is that made standard in the monograph of Salamon [Reference Salamon28]. Let
![]() $T = \mathsf {H} \oplus \mathsf {V} \simeq \mathbb {R}^{4n+2}$
denote the (real)
$T = \mathsf {H} \oplus \mathsf {V} \simeq \mathbb {R}^{4n+2}$
denote the (real)
![]() $\mathrm {Sp}(n)\mathrm {U}(1)$
-representation of (4.1). Let
$\mathrm {Sp}(n)\mathrm {U}(1)$
-representation of (4.1). Let
![]() $E \simeq \mathbb {C}^{2n}$
denote the standard complex
$E \simeq \mathbb {C}^{2n}$
denote the standard complex
![]() $\mathrm {Sp}(n)$
-representation, and let
$\mathrm {Sp}(n)$
-representation, and let
![]() ${L \simeq \mathbb {C}}$
denote the standard complex
${L \simeq \mathbb {C}}$
denote the standard complex
![]() $\mathrm {U}(1)$
-representation. Then, by refining the splitting
$\mathrm {U}(1)$
-representation. Then, by refining the splitting
![]() $\Lambda ^2(T^*) = \Lambda ^2(\mathsf {H}^*) \otimes (\mathsf {H}^* \otimes \mathsf {V}^*) \otimes \Lambda ^2(\mathsf {V}^*)$
, one can decompose the space of real
$\Lambda ^2(T^*) = \Lambda ^2(\mathsf {H}^*) \otimes (\mathsf {H}^* \otimes \mathsf {V}^*) \otimes \Lambda ^2(\mathsf {V}^*)$
, one can decompose the space of real
![]() $2$
-forms into
$2$
-forms into
![]() $\mathrm {Sp}(n)\mathrm {U}(1)$
-irreducible representations as follows:
$\mathrm {Sp}(n)\mathrm {U}(1)$
-irreducible representations as follows:
 $$ \begin{align*} \Lambda^2(\mathsf{H}^*) & \cong \mathbb{R} \omega_{\mathsf{H}} \oplus [\mathrm{Sym}^2(E)] \oplus [\Lambda^2_0(E)] \oplus [\![ L^2 ]\!] \oplus [\![ \Lambda^2_0(E) \otimes L^2 ]\!] \\ \mathsf{H}^* \otimes \mathsf{V}^* & \cong [\![ E \otimes L^3 ]\!] \oplus [\![ E \otimes L ]\!] \\ \Lambda^2(\mathsf{V}^*) & \cong \mathbb{R} \omega_{\mathsf{V}}. \end{align*} $$
$$ \begin{align*} \Lambda^2(\mathsf{H}^*) & \cong \mathbb{R} \omega_{\mathsf{H}} \oplus [\mathrm{Sym}^2(E)] \oplus [\Lambda^2_0(E)] \oplus [\![ L^2 ]\!] \oplus [\![ \Lambda^2_0(E) \otimes L^2 ]\!] \\ \mathsf{H}^* \otimes \mathsf{V}^* & \cong [\![ E \otimes L^3 ]\!] \oplus [\![ E \otimes L ]\!] \\ \Lambda^2(\mathsf{V}^*) & \cong \mathbb{R} \omega_{\mathsf{V}}. \end{align*} $$
Alternatively, by refining the
![]() $J_+$
-type splitting
$J_+$
-type splitting
![]() $\Lambda ^2(T^*) = [\![\Lambda ^{2,0}]\!] \oplus [\Lambda ^{1,1}]$
, one obtains
$\Lambda ^2(T^*) = [\![\Lambda ^{2,0}]\!] \oplus [\Lambda ^{1,1}]$
, one obtains
 $$ \begin{align*} [\![ \Lambda^{2,0} ]\!] & \cong [\![ \Lambda^2_0(E) \otimes L^2 ]\!] \oplus [\![ L^2 ]\!] \oplus [\![ E \otimes L^3 ]\!] \\ [\Lambda^{1,1}] & \cong \mathbb{R}\omega_{\mathsf{V}} \oplus \mathbb{R} \omega_{\mathsf{H}} \oplus [\mathrm{Sym}^2_0(E)] \oplus [\Lambda^2_0(E)] \oplus [\![ E \otimes L ]\!]. \end{align*} $$
$$ \begin{align*} [\![ \Lambda^{2,0} ]\!] & \cong [\![ \Lambda^2_0(E) \otimes L^2 ]\!] \oplus [\![ L^2 ]\!] \oplus [\![ E \otimes L^3 ]\!] \\ [\Lambda^{1,1}] & \cong \mathbb{R}\omega_{\mathsf{V}} \oplus \mathbb{R} \omega_{\mathsf{H}} \oplus [\mathrm{Sym}^2_0(E)] \oplus [\Lambda^2_0(E)] \oplus [\![ E \otimes L ]\!]. \end{align*} $$
4.2 The geometry of twistor spaces
We now return to the study of twistor spaces Z. The following fact is well known:
Theorem 4.6 Let
![]() $M^{4n+3}$
be a
$M^{4n+3}$
be a
![]() $3$
-Sasakian manifold, and fix a projection
$3$
-Sasakian manifold, and fix a projection
![]() ${p = p_1 \colon M \to Z}$
. The quotient Z admits a
${p = p_1 \colon M \to Z}$
. The quotient Z admits a
![]() $(\mathrm {U}(2n) \times \mathrm {U}(1))$
-structure
$(\mathrm {U}(2n) \times \mathrm {U}(1))$
-structure
![]() $(g, J_+, \omega _+, \mathsf {H})$
for which:
$(g, J_+, \omega _+, \mathsf {H})$
for which:
-
•
 $\left (g(1),\, J_+,\, \omega _+(1)\right )$
is Kähler–Einstein with positive scalar curvature.
$\left (g(1),\, J_+,\, \omega _+(1)\right )$
is Kähler–Einstein with positive scalar curvature. -
•
 $\left (g(\sqrt {2}),\, J_-,\, \omega _-(\sqrt {2})\right )$
is nearly Kähler.
$\left (g(\sqrt {2}),\, J_-,\, \omega _-(\sqrt {2})\right )$
is nearly Kähler. -
•
 $p_*(\widetilde {\mathsf {H}}) = \mathsf {H}$
and
$p_*(\widetilde {\mathsf {H}}) = \mathsf {H}$
and
 $p_*(\mathrm {span}(A_2, A_3)) = \mathsf {V}$
.
$p_*(\mathrm {span}(A_2, A_3)) = \mathsf {V}$
.
Proof The Kähler–Einstein structure is very well known and has been extensively studied. The statement about the nearly Kähler structure is [Reference Boyer and Galicki8, Theorem 14.3.9]. Details can be found in [Reference Alexandrov, Grantcharov and Ivanov4] or [Reference Nagy25].
From now on, the twistor space Z will carry the
![]() $(\mathrm {U}(2n) \times \mathrm {U}(1))$
-structure
$(\mathrm {U}(2n) \times \mathrm {U}(1))$
-structure
![]() $(g, J_+, \omega _+, \mathsf {H})$
described in the previous proposition. We will write
$(g, J_+, \omega _+, \mathsf {H})$
described in the previous proposition. We will write
 $$ \begin{align*} (g_{\mathrm{KE}}, J_{\mathrm{KE}}, \omega_{\mathrm{KE}}) & := \left(g(1),\, J_+,\, \omega_+(1)\right), \\ (g_{\mathrm{NK}}, J_{\mathrm{NK}}, \omega_{\mathrm{NK}}) & := (g(\sqrt{2}),\, J_-,\, \omega_-(\sqrt{2})). \end{align*} $$
$$ \begin{align*} (g_{\mathrm{KE}}, J_{\mathrm{KE}}, \omega_{\mathrm{KE}}) & := \left(g(1),\, J_+,\, \omega_+(1)\right), \\ (g_{\mathrm{NK}}, J_{\mathrm{NK}}, \omega_{\mathrm{NK}}) & := (g(\sqrt{2}),\, J_-,\, \omega_-(\sqrt{2})). \end{align*} $$
In particular,
We now recover the important observation of Alexandrov [Reference Alexandrov3] that Z naturally admits even more structure:
Theorem 4.7 Let Z be a twistor space with its
![]() $(\mathrm {U}(2n) \times \mathrm {U}(1))$
-structure
$(\mathrm {U}(2n) \times \mathrm {U}(1))$
-structure
![]() $(g_{\mathrm {KE}}, J_{\mathrm {KE}}$
,
$(g_{\mathrm {KE}}, J_{\mathrm {KE}}$
,
![]() $\omega _{\mathrm {KE}}$
,
$\omega _{\mathrm {KE}}$
,
![]() $\mathsf {H})$
. Then Z naturally admits a compatible
$\mathsf {H})$
. Then Z naturally admits a compatible
![]() $\mathrm {Sp}(n)\mathrm {U}(1)$
-structure
$\mathrm {Sp}(n)\mathrm {U}(1)$
-structure
![]() $\gamma \in \Omega ^3(Z; \mathbb {C})$
.
$\gamma \in \Omega ^3(Z; \mathbb {C})$
.
Proof By Proposition 3.21(b), there exists a unique
![]() $3$
-form
$3$
-form
![]() $\gamma \in \Omega ^3(Z;\mathbb {C})$
satisfying
$\gamma \in \Omega ^3(Z;\mathbb {C})$
satisfying
This
![]() $3$
-form is an
$3$
-form is an
![]() $\mathrm {Sp}(n)\mathrm {U}(1)$
-structure.
$\mathrm {Sp}(n)\mathrm {U}(1)$
-structure.
In Section 5.1, we will give a second proof of Theorem 4.7 from the perspective of quaternionic-Kähler geometry. For now, using Proposition 3.21, we can compute the following exterior derivatives:
 $$ \begin{align*} d\omega_{\mathsf{V}} & = -\mathrm{Im}(2\gamma), & d\omega_{\mathrm{KE}} & = 0, & d\,\mathrm{Re}(\gamma) & = 2\xi - 4\omega_{\mathsf{H}} \wedge \omega_{\mathsf{V}}, \\ d\omega_{\mathsf{H}} & = \mathrm{Im}(2\gamma), & d\omega_{\mathrm{NK}} & = 3\,\mathrm{Im}(2\gamma), & d\,\mathrm{Im}(\gamma) & = 0, \\ & & & & d\xi & = -4\omega_{\mathsf{H}} \wedge \mathrm{Im}(\gamma). \end{align*} $$
$$ \begin{align*} d\omega_{\mathsf{V}} & = -\mathrm{Im}(2\gamma), & d\omega_{\mathrm{KE}} & = 0, & d\,\mathrm{Re}(\gamma) & = 2\xi - 4\omega_{\mathsf{H}} \wedge \omega_{\mathsf{V}}, \\ d\omega_{\mathsf{H}} & = \mathrm{Im}(2\gamma), & d\omega_{\mathrm{NK}} & = 3\,\mathrm{Im}(2\gamma), & d\,\mathrm{Im}(\gamma) & = 0, \\ & & & & d\xi & = -4\omega_{\mathsf{H}} \wedge \mathrm{Im}(\gamma). \end{align*} $$
Example 4.2 When
![]() $n = 1$
, there is a coincidence
$n = 1$
, there is a coincidence
![]() $\xi = 2\omega _{\mathsf {H}}^2$
. Therefore, in this case, using that
$\xi = 2\omega _{\mathsf {H}}^2$
. Therefore, in this case, using that
![]() $\omega _{\mathrm {NK}}^2 = (2\omega _{\mathsf {H}} - \omega _{\mathsf {V}})^2 = 4\omega _{\mathsf {H}}^2 - 4 \omega _{\mathsf {H}} \wedge \omega _{\mathsf {V}} = 2\xi - 4\omega _{\mathsf {H}} \wedge \omega _{\mathsf {V}}$
, we recover the equations
$\omega _{\mathrm {NK}}^2 = (2\omega _{\mathsf {H}} - \omega _{\mathsf {V}})^2 = 4\omega _{\mathsf {H}}^2 - 4 \omega _{\mathsf {H}} \wedge \omega _{\mathsf {V}} = 2\xi - 4\omega _{\mathsf {H}} \wedge \omega _{\mathsf {V}}$
, we recover the equations
 $$ \begin{align*} d\omega_{\mathrm{NK}} & = 3\,\mathrm{Im}(2\gamma), \\ d\,\mathrm{Re}(2\gamma) & = 2\, \omega_{\mathrm{NK}} \wedge \omega_{\mathrm{NK}}, \end{align*} $$
$$ \begin{align*} d\omega_{\mathrm{NK}} & = 3\,\mathrm{Im}(2\gamma), \\ d\,\mathrm{Re}(2\gamma) & = 2\, \omega_{\mathrm{NK}} \wedge \omega_{\mathrm{NK}}, \end{align*} $$
familiar from the theory of nearly Kähler
![]() $6$
-manifolds.
$6$
-manifolds.
4.3
 $\mathrm {Re}(\gamma )$
-calibrated
$\mathrm {Re}(\gamma )$
-calibrated
 $3$
-folds
$3$
-folds
Let
![]() $Z^{4n+2}$
be a twistor space equipped with the
$Z^{4n+2}$
be a twistor space equipped with the
![]() $(\mathrm {U}(2n) \times \mathrm {U}(1))$
-structure
$(\mathrm {U}(2n) \times \mathrm {U}(1))$
-structure
![]() $(g_{\mathrm {KE}}, J_{\mathrm {KE}}, \omega _{\mathrm {KE}}, \mathsf {H})$
. With respect to this structure, one can consider several classes of submanifolds of Z, such as:
$(g_{\mathrm {KE}}, J_{\mathrm {KE}}, \omega _{\mathrm {KE}}, \mathsf {H})$
. With respect to this structure, one can consider several classes of submanifolds of Z, such as:
-
•
 $J_{\mathrm {KE}}$
-complex (resp.
$J_{\mathrm {KE}}$
-complex (resp.
 $J_{\mathrm {NK}}$
-complex) submanifolds.
$J_{\mathrm {NK}}$
-complex) submanifolds. -
• Horizontal submanifolds (i.e. those tangent to
 $\mathsf {H}$
).
$\mathsf {H}$
). -
•
 $\omega _{\mathrm {KE}}$
-isotropic (resp.
$\omega _{\mathrm {KE}}$
-isotropic (resp.
 $\omega _{\mathrm {NK}}$
-isotropic) submanifolds.
$\omega _{\mathrm {NK}}$
-isotropic) submanifolds.
These submanifolds have been the subject of numerous studies, particularly when
![]() $\dim (Z) = 6$
. However, since we have now shown that Z admits a compatible
$\dim (Z) = 6$
. However, since we have now shown that Z admits a compatible
![]() $\mathrm {Sp}(n)\mathrm {U}(1)$
-structure
$\mathrm {Sp}(n)\mathrm {U}(1)$
-structure
![]() $\gamma \in \Omega ^3(Z; \mathbb {C})$
, twistor spaces also admit a distinguished class of
$\gamma \in \Omega ^3(Z; \mathbb {C})$
, twistor spaces also admit a distinguished class of
![]() $3$
-folds. In this section, we explore these.
$3$
-folds. In this section, we explore these.
We begin by showing that
![]() $\mathrm {Re}(\gamma ) \in \Omega ^3(Z)$
is a semi-calibration, for which we need a preliminary lemma.
$\mathrm {Re}(\gamma ) \in \Omega ^3(Z)$
is a semi-calibration, for which we need a preliminary lemma.
Lemma 4.8 For any horizontal unit vector
![]() $v \in \mathsf {H}$
, the
$v \in \mathsf {H}$
, the
![]() $2$
-form
$2$
-form
![]() $\iota _v(\mathrm {Re}(\gamma )) \in \Omega ^2(Z)$
is a semi-calibration. Moreover, its calibrated
$\iota _v(\mathrm {Re}(\gamma )) \in \Omega ^2(Z)$
is a semi-calibration. Moreover, its calibrated
![]() $2$
-planes lie in the
$2$
-planes lie in the
![]() $6$
-plane
$6$
-plane
![]() $L \oplus \mathsf {V}$
, where L is the quaternionic line spanned by v.
$L \oplus \mathsf {V}$
, where L is the quaternionic line spanned by v.
Proof It suffices to work at a fixed point
![]() $z \in Z$
. Let
$z \in Z$
. Let
![]() $(\rho ,\mu )$
be an
$(\rho ,\mu )$
be an
![]() $\mathrm {Sp}(n)\mathrm {U}(1)$
-coframe at z as in Definition 4.3. We may then write
$\mathrm {Sp}(n)\mathrm {U}(1)$
-coframe at z as in Definition 4.3. We may then write
![]() $\gamma |_z = \tau \wedge (\beta _2 + i\beta _3)$
, where
$\gamma |_z = \tau \wedge (\beta _2 + i\beta _3)$
, where
 $$ \begin{align*} \tau & = \mu_2 - i\mu_3, & \beta_2 & = \sum_{i=1}^n (\rho_{j0} \wedge \rho_{j2} - \rho_{j1} \wedge \rho_{j3}), & \beta_3 & = \sum_{i=1}^n (\rho_{j0} \wedge \rho_{j3} + \rho_{j1} \wedge \rho_{j2}). \end{align*} $$
$$ \begin{align*} \tau & = \mu_2 - i\mu_3, & \beta_2 & = \sum_{i=1}^n (\rho_{j0} \wedge \rho_{j2} - \rho_{j1} \wedge \rho_{j3}), & \beta_3 & = \sum_{i=1}^n (\rho_{j0} \wedge \rho_{j3} + \rho_{j1} \wedge \rho_{j2}). \end{align*} $$
Define complex structures
![]() $J_2$
and
$J_2$
and
![]() $J_3$
on
$J_3$
on
![]() $\mathsf {H}|_z$
by declaring
$\mathsf {H}|_z$
by declaring
 $$ \begin{align*} J_2(\rho_{j0}) & = \rho_{j2}, & J_3(\rho_{j0}) & = \rho_{j3}, \\ J_2(\rho_{j1}) & = -\rho_{j3}, & J_3(\rho_{j1}) & = \rho_{j2}, \end{align*} $$
$$ \begin{align*} J_2(\rho_{j0}) & = \rho_{j2}, & J_3(\rho_{j0}) & = \rho_{j3}, \\ J_2(\rho_{j1}) & = -\rho_{j3}, & J_3(\rho_{j1}) & = \rho_{j2}, \end{align*} $$
which implies
![]() $J_+J_2 = J_3$
and
$J_+J_2 = J_3$
and
![]() $g(J_2 \cdot , \cdot ) = \beta _2$
and
$g(J_2 \cdot , \cdot ) = \beta _2$
and
![]() $g(J_3 \cdot , \cdot ) = \beta _3$
. Note that
$g(J_3 \cdot , \cdot ) = \beta _3$
. Note that
![]() $\tau $
,
$\tau $
,
![]() $\beta _2, \beta _3$
, as well as
$\beta _2, \beta _3$
, as well as
![]() $J_2, J_3$
, depend on the choice of
$J_2, J_3$
, depend on the choice of
![]() $\mathrm {Sp}(n)\mathrm {U}(1)$
-frame.
$\mathrm {Sp}(n)\mathrm {U}(1)$
-frame.
Now, let
![]() $v \in \mathsf {H}$
be a horizontal unit vector. Let
$v \in \mathsf {H}$
be a horizontal unit vector. Let
![]() $w = J_2v$
, so that
$w = J_2v$
, so that
 $$ \begin{align*} \iota_v\gamma = \iota_v(\tau \wedge (\beta_2 + i\beta_3)) = \tau \wedge \iota_v(\beta_2 + i\beta_3) & = \tau \wedge (g(J_2v, \cdot) + ig(J_+J_2v, \cdot)) \\ & = \tau \wedge (w^\flat - iJ_+ w^\flat) \\ & = (\mu_2 - i \mu_3) \wedge (w^\flat - iJ_- w^\flat) \end{align*} $$
$$ \begin{align*} \iota_v\gamma = \iota_v(\tau \wedge (\beta_2 + i\beta_3)) = \tau \wedge \iota_v(\beta_2 + i\beta_3) & = \tau \wedge (g(J_2v, \cdot) + ig(J_+J_2v, \cdot)) \\ & = \tau \wedge (w^\flat - iJ_+ w^\flat) \\ & = (\mu_2 - i \mu_3) \wedge (w^\flat - iJ_- w^\flat) \end{align*} $$
since
![]() $J_+ = J_-$
on horizontal vectors. This
$J_+ = J_-$
on horizontal vectors. This
![]() $2$
-form is decomposable and has
$2$
-form is decomposable and has
![]() $J_-$
-type
$J_-$
-type
![]() $(2,0)$
. Moreover,
$(2,0)$
. Moreover,
![]() $\{\mu _2, \mu _3, w^\flat , J_- w^\flat \}$
is an orthonormal set. Thus, this
$\{\mu _2, \mu _3, w^\flat , J_- w^\flat \}$
is an orthonormal set. Thus, this
![]() $2$
-form is a standard complex volume form, and hence its real part is a semi-calibration.
$2$
-form is a standard complex volume form, and hence its real part is a semi-calibration.
Remark 4.9 The above proof shows slightly more, namely that the
![]() $\iota _v (\mathrm {Re}(\gamma ))$
-calibrated
$\iota _v (\mathrm {Re}(\gamma ))$
-calibrated
![]() $2$
-planes lie in the
$2$
-planes lie in the
![]() $4$
-plane
$4$
-plane
![]() $\text {span}(w, J_+w) \oplus \mathsf {V} = \text {span}(J_2 v, J_3 v) \oplus \mathsf {V}$
.
$\text {span}(w, J_+w) \oplus \mathsf {V} = \text {span}(J_2 v, J_3 v) \oplus \mathsf {V}$
.
Proposition 4.10 The
![]() $3$
-form
$3$
-form
![]() $\mathrm {Re}(\gamma ) \in \Omega ^3(Z)$
is a semi-calibration. Moreover, let
$\mathrm {Re}(\gamma ) \in \Omega ^3(Z)$
is a semi-calibration. Moreover, let
![]() ${E \in \mathrm {Gr}_3^+(TZ)}$
be an oriented
${E \in \mathrm {Gr}_3^+(TZ)}$
be an oriented
![]() $3$
-plane.
$3$
-plane.
-
(1) E is
 $\mathrm {Re}(\gamma )$
-calibrated if and only if
$\mathrm {Re}(\gamma )$
-calibrated if and only if
 $E = \mathbb {R} v \oplus E'$
for some
$E = \mathbb {R} v \oplus E'$
for some
 $v \in E \cap \mathsf {H}$
and some
$v \in E \cap \mathsf {H}$
and some
 $2$
-plane
$2$
-plane
 $E'$
that is
$E'$
that is
 $\iota _v(\mathrm {Re}(\gamma ))$
-calibrated.
$\iota _v(\mathrm {Re}(\gamma ))$
-calibrated. -
(2) If E is a
 $\mathrm {Re}(\gamma )$
-calibrated
$\mathrm {Re}(\gamma )$
-calibrated
 $3$
-plane, there is a quaternionic line
$3$
-plane, there is a quaternionic line
 $L \subset \mathsf {H}$
such that E is contained in
$L \subset \mathsf {H}$
such that E is contained in
 $L \oplus \mathsf {V}$
.
$L \oplus \mathsf {V}$
. -
(3) If E is
 $\mathrm {Re}(\gamma )$
-calibrated, then E is
$\mathrm {Re}(\gamma )$
-calibrated, then E is
 $\omega _{\mathrm {NK}}$
-isotropic.
$\omega _{\mathrm {NK}}$
-isotropic.
Proof If
![]() $E \in \mathrm {Gr}_3^+(T_zZ)$
is an oriented
$E \in \mathrm {Gr}_3^+(T_zZ)$
is an oriented
![]() $3$
-plane at
$3$
-plane at
![]() $z \in Z$
, then
$z \in Z$
, then
![]() $\dim (E \cap \mathsf {H}) \geq 1$
, so there exists a unit vector
$\dim (E \cap \mathsf {H}) \geq 1$
, so there exists a unit vector
![]() $v \in E \cap \mathsf {H}$
, and we may orthogonally split
$v \in E \cap \mathsf {H}$
, and we may orthogonally split
![]() $E = \mathbb {R} v \oplus E'$
. Then
$E = \mathbb {R} v \oplus E'$
. Then
by Lemma 4.8, so the comass of
![]() $\mathrm {Re} (\gamma )$
is at most
$\mathrm {Re} (\gamma )$
is at most
![]() $1$
. Now, let v be a horizontal unit vector and let
$1$
. Now, let v be a horizontal unit vector and let
![]() $E'$
be an
$E'$
be an
![]() $\iota _v (\mathrm {Re} (\gamma ))$
-calibrated
$\iota _v (\mathrm {Re} (\gamma ))$
-calibrated
![]() $2$
-plane, which exists by Lemma 4.8. Then
$2$
-plane, which exists by Lemma 4.8. Then
![]() $E = \mathbb {R} v \oplus E'$
is
$E = \mathbb {R} v \oplus E'$
is
![]() $\mathrm {Re}(\gamma )$
-calibrated, which shows that
$\mathrm {Re}(\gamma )$
-calibrated, which shows that
![]() $\mathrm {Re}(\gamma )$
has comass equal to one. Further, we have seen that an oriented
$\mathrm {Re}(\gamma )$
has comass equal to one. Further, we have seen that an oriented
![]() $3$
-plane E is
$3$
-plane E is
![]() $\mathrm {Re}(\gamma )$
-calibrated if and only if
$\mathrm {Re}(\gamma )$
-calibrated if and only if
![]() $E'$
is
$E'$
is
![]() $\iota _v(\mathrm {Re}(\gamma ))$
-calibrated, which proves (a).
$\iota _v(\mathrm {Re}(\gamma ))$
-calibrated, which proves (a).
Part (b) follows from Remark 4.9. Finally, since
![]() $\gamma $
is of
$\gamma $
is of
![]() $J_-$
-type
$J_-$
-type
![]() $(3,0)$
, part (c) follows from Proposition A.5.
$(3,0)$
, part (c) follows from Proposition A.5.
Returning to the
![]() $3$
-Sasakian manifold
$3$
-Sasakian manifold
![]() $M^{4n+3}$
, we can now establish the following:
$M^{4n+3}$
, we can now establish the following:
Corollary 4.11 The
![]() $3$
-form
$3$
-form
![]() $\mathrm {Re}(\Gamma _1) \in \Omega ^3(M)$
is a semi-calibration.
$\mathrm {Re}(\Gamma _1) \in \Omega ^3(M)$
is a semi-calibration.
Proof Recall that
![]() $p_1 \colon M \to Z$
is a Riemannian submersion, that
$p_1 \colon M \to Z$
is a Riemannian submersion, that
![]() $\mathrm {Re}(\Gamma _1) = p_1^*(\mathrm {Re}(\gamma ))$
, and that
$\mathrm {Re}(\Gamma _1) = p_1^*(\mathrm {Re}(\gamma ))$
, and that
![]() $\mathrm {Re}(\gamma ) \in \Omega ^3(Z)$
has comass one. The result now follows from Proposition A.4.
$\mathrm {Re}(\gamma ) \in \Omega ^3(Z)$
has comass one. The result now follows from Proposition A.4.
Remark 4.12 We pause to make two remarks. First, Proposition 4.10 shows that
![]() $\mathrm {Re}(\gamma )$
-calibrated
$\mathrm {Re}(\gamma )$
-calibrated
![]() $3$
-folds
$3$
-folds
![]() $L^3 \subset Z^{4n+2}$
are
$L^3 \subset Z^{4n+2}$
are
![]() $\omega _{\mathrm {NK}}$
-isotropic. However, we emphasize that such
$\omega _{\mathrm {NK}}$
-isotropic. However, we emphasize that such
![]() $3$
-folds need not be
$3$
-folds need not be
![]() $\omega _{\mathrm {KE}}$
-isotropic in general. Later (Theorem 5.16), we will characterize the
$\omega _{\mathrm {KE}}$
-isotropic in general. Later (Theorem 5.16), we will characterize the
![]() $\mathrm {Re}(\gamma )$
-calibrated
$\mathrm {Re}(\gamma )$
-calibrated
![]() $3$
-folds
$3$
-folds
![]() $L \subset Z$
satisfying
$L \subset Z$
satisfying
![]() $\left .\omega _{\mathrm {KE}}\right |_L = 0$
.
$\left .\omega _{\mathrm {KE}}\right |_L = 0$
.
Second, we clarify that Proposition 4.10 asserts
![]() $\mathrm {Re}(\gamma )$
is a semi-calibration with respect to the metric
$\mathrm {Re}(\gamma )$
is a semi-calibration with respect to the metric
![]() $g_{\mathrm {KE}}$
. Therefore, by Proposition A.3, the
$g_{\mathrm {KE}}$
. Therefore, by Proposition A.3, the
![]() $3$
-form
$3$
-form
![]() $\mathrm {Re}(t^2\gamma )$
is a semi-calibration with respect to the metric
$\mathrm {Re}(t^2\gamma )$
is a semi-calibration with respect to the metric
![]() $g(t) = t^2 g_{\mathsf {H}} + g_{\mathsf {V}}$
. In particular,
$g(t) = t^2 g_{\mathsf {H}} + g_{\mathsf {V}}$
. In particular,
![]() $\mathrm {Re}(2\gamma )$
is a semi-calibration with respect to
$\mathrm {Re}(2\gamma )$
is a semi-calibration with respect to
![]() $g_{\mathrm {NK}} = 2 g_{\mathsf {H}} + g_{\mathsf {V}}$
.
$g_{\mathrm {NK}} = 2 g_{\mathsf {H}} + g_{\mathsf {V}}$
.
4.3.1 A normal form for
 $\mathrm {Re}(\gamma )$
-calibrated
$\mathrm {Re}(\gamma )$
-calibrated
 $3$
-planes
$3$
-planes
We now aim to establish a normal form for
![]() $\mathrm {Re}(\gamma )$
-calibrated
$\mathrm {Re}(\gamma )$
-calibrated
![]() $3$
-planes in Z. Since the subsequent discussion is a matter of linear algebra, we work in
$3$
-planes in Z. Since the subsequent discussion is a matter of linear algebra, we work in
![]() $\mathbb {R}^{4n+2} \simeq \mathbb {H}^n \oplus \mathbb {C}$
. As we have done previously, we let
$\mathbb {R}^{4n+2} \simeq \mathbb {H}^n \oplus \mathbb {C}$
. As we have done previously, we let
denote the standard basis of
![]() $\mathbb {R}^{4n+2}$
, let
$\mathbb {R}^{4n+2}$
, let
![]() $(e^{10}, e^{11}, \ldots , f^2, f^3)$
denote its dual basis, let
$(e^{10}, e^{11}, \ldots , f^2, f^3)$
denote its dual basis, let
![]() $\beta _1, \beta _2, \beta _3$
be the standard hyperkähler triple on
$\beta _1, \beta _2, \beta _3$
be the standard hyperkähler triple on
![]() $\mathbb {H}^n$
as in (4.3), and consider the
$\mathbb {H}^n$
as in (4.3), and consider the
![]() $3$
-form
$3$
-form
![]() $\gamma _0 \in \Lambda ^3((\mathbb {R}^{4n+2})^*)$
given by
$\gamma _0 \in \Lambda ^3((\mathbb {R}^{4n+2})^*)$
given by
Now, for
![]() $e^{i \theta } \in S^1$
, define the
$e^{i \theta } \in S^1$
, define the
![]() $2$
-plane
$2$
-plane
In particular, we highlight
Proposition 4.13 Consider the
![]() $\mathrm {Sp}(n)\mathrm {U}(1)$
-action on
$\mathrm {Sp}(n)\mathrm {U}(1)$
-action on
![]() $\mathbb {H}^n \oplus \mathbb {C}$
given in (4.1). Let
$\mathbb {H}^n \oplus \mathbb {C}$
given in (4.1). Let
![]() ${E \subset \mathbb {H}^n \oplus \mathbb {C}}$
be a
${E \subset \mathbb {H}^n \oplus \mathbb {C}}$
be a
![]() $\mathrm {Re}(\gamma _0)$
-calibrated
$\mathrm {Re}(\gamma _0)$
-calibrated
![]() $3$
-plane. Then there exist
$3$
-plane. Then there exist
![]() $(A, \lambda ) \in \mathrm {Sp}(n)\mathrm {U}(1)$
and a unique
$(A, \lambda ) \in \mathrm {Sp}(n)\mathrm {U}(1)$
and a unique
![]() $\theta \in [0, \frac {\pi }{4}]$
such that
$\theta \in [0, \frac {\pi }{4}]$
such that
![]() $(A, \lambda ) \cdot E = \mathbb {R} e_{10} \oplus V_\theta $
. Moreover, the following are equivalent:
$(A, \lambda ) \cdot E = \mathbb {R} e_{10} \oplus V_\theta $
. Moreover, the following are equivalent:
-
(1)
 $\dim (E \cap \mathbb {H}^n) = 2$
.
$\dim (E \cap \mathbb {H}^n) = 2$
. -
(2)
 $E = (E \cap \mathbb {H}^n) \oplus (E \cap \mathbb {C})$
.
$E = (E \cap \mathbb {H}^n) \oplus (E \cap \mathbb {C})$
. -
(3) E is
 $\omega _{\mathrm {KE}}$
-isotropic.
$\omega _{\mathrm {KE}}$
-isotropic. -
(4)
 $\theta = \frac {\pi }{4}$
.
$\theta = \frac {\pi }{4}$
.
Proof Let
![]() $E \subset \mathbb {H}^n \oplus \mathbb {C}$
be a
$E \subset \mathbb {H}^n \oplus \mathbb {C}$
be a
![]() $\mathrm {Re}(\gamma _0)$
-calibrated
$\mathrm {Re}(\gamma _0)$
-calibrated
![]() $3$
-plane. By Proposition 4.10, there exists a quaternionic line
$3$
-plane. By Proposition 4.10, there exists a quaternionic line
![]() $L \subset \mathbb {H}^n$
for which
$L \subset \mathbb {H}^n$
for which
![]() $E \subset L \oplus \mathbb {C}$
. Since the subgroup
$E \subset L \oplus \mathbb {C}$
. Since the subgroup
![]() $\mathrm {Sp}(n) \leq \mathrm {Sp}(n) \mathrm {U}(1)$
acts transitively on the quaternionic lines of
$\mathrm {Sp}(n) \leq \mathrm {Sp}(n) \mathrm {U}(1)$
acts transitively on the quaternionic lines of
![]() $\mathbb {H}^n$
, there exists
$\mathbb {H}^n$
, there exists
![]() $A_0 \in \mathrm {Sp}(n)$
such that
$A_0 \in \mathrm {Sp}(n)$
such that
![]() $A_0 \cdot L = L_0$
, where
$A_0 \cdot L = L_0$
, where
![]() $L_0$
is the standard quaternionic line
$L_0$
is the standard quaternionic line
Thus,
![]() $(A_0, 1) \cdot E \subset L_0 \oplus \mathbb {C}$
, so we can without loss of generality suppose that
$(A_0, 1) \cdot E \subset L_0 \oplus \mathbb {C}$
, so we can without loss of generality suppose that
![]() ${E \subset L_0 \oplus \mathbb {C}}$
.
${E \subset L_0 \oplus \mathbb {C}}$
.
Now,
![]() $L_0 \oplus \mathbb {C}$
is a complex
$L_0 \oplus \mathbb {C}$
is a complex
![]() $3$
-plane, and the restriction of
$3$
-plane, and the restriction of
![]() $\gamma _0$
to
$\gamma _0$
to
![]() $L_0 \oplus \mathbb {C}$
is a complex volume form. Thus, the problem reduces to finding a normal form for special Lagrangian
$L_0 \oplus \mathbb {C}$
is a complex volume form. Thus, the problem reduces to finding a normal form for special Lagrangian
![]() $3$
-planes in a complex
$3$
-planes in a complex
![]() $3$
-space with respect to the action of
$3$
-space with respect to the action of
![]() $\mathrm {Sp}(1)\mathrm {U}(1) \cong \mathrm {U}(2)$
. Such a normal form was established in [Reference Aslan5, Proposition 3.2]. (Translating between notations, the
$\mathrm {Sp}(1)\mathrm {U}(1) \cong \mathrm {U}(2)$
. Such a normal form was established in [Reference Aslan5, Proposition 3.2]. (Translating between notations, the
![]() $b_1, i b_1, b_2, i b_2, b_3, i b_3$
of [Reference Aslan5] corresponds to our
$b_1, i b_1, b_2, i b_2, b_3, i b_3$
of [Reference Aslan5] corresponds to our
![]() $e_{10}, e_{11}, e_{12}, e_{13}, f_2, - f_3$
.)
$e_{10}, e_{11}, e_{12}, e_{13}, f_2, - f_3$
.)
For
![]() $\theta \in [0, \frac {\pi }{4}]$
, write
$\theta \in [0, \frac {\pi }{4}]$
, write
![]() $W_\theta = \mathbb {R} e_{10} \oplus V_\theta $
. We observe that the conditions (a), (b), and (c) above are invariant under the action of
$W_\theta = \mathbb {R} e_{10} \oplus V_\theta $
. We observe that the conditions (a), (b), and (c) above are invariant under the action of
![]() $\mathrm {Sp}(n) \mathrm {U}(1)$
, so it is enough to verify that for
$\mathrm {Sp}(n) \mathrm {U}(1)$
, so it is enough to verify that for
![]() $W_{\theta }$
they are equivalent to
$W_{\theta }$
they are equivalent to
![]() $\theta = \frac {\pi }{4}$
. If
$\theta = \frac {\pi }{4}$
. If
![]() $\theta = \frac {\pi }{4}$
, we have
$\theta = \frac {\pi }{4}$
, we have
so both (a) and (b) hold. If
![]() $\theta \neq \frac {\pi }{4}$
, then one can compute from (4.5) that
$\theta \neq \frac {\pi }{4}$
, then one can compute from (4.5) that
![]() $\dim (W_\theta \cap \mathbb {H}^n) = 1$
. Since a
$\dim (W_\theta \cap \mathbb {H}^n) = 1$
. Since a
![]() $\mathrm {Re}(\gamma _0)$
-calibrated
$\mathrm {Re}(\gamma _0)$
-calibrated
![]() $3$
-plane cannot contain any complex lines, we have
$3$
-plane cannot contain any complex lines, we have
![]() $\dim (W_\theta \cap \mathbb {C}) < 2$
, and hence
$\dim (W_\theta \cap \mathbb {C}) < 2$
, and hence
so both (a) and (b) do not hold.
With respect to the above basis, we have
![]() $\omega _{\mathrm {KE}} = \beta _1 + f^2 \wedge f^3$
. Letting
$\omega _{\mathrm {KE}} = \beta _1 + f^2 \wedge f^3$
. Letting
so
![]() $V_\theta = \mathrm {span}(v_2, v_3)$
and
$V_\theta = \mathrm {span}(v_2, v_3)$
and
![]() $W_{\theta } = \mathbb {R} e_{10} \oplus V_{\theta }$
, a computation shows that
$W_{\theta } = \mathbb {R} e_{10} \oplus V_{\theta }$
, a computation shows that
so
![]() $\left .\omega _{\mathrm {KE}}\right |_{W_{\theta }} = 0$
if and only if
$\left .\omega _{\mathrm {KE}}\right |_{W_{\theta }} = 0$
if and only if
![]() $\theta = \frac {\pi }{4}$
.
$\theta = \frac {\pi }{4}$
.
4.3.2 HV compatibility
Definition 4.14 A submanifold
![]() $\Sigma ^k \subset Z^{4n+2}$
is called HV-compatible if at each
$\Sigma ^k \subset Z^{4n+2}$
is called HV-compatible if at each
![]() $x \in \Sigma $
, we have
$x \in \Sigma $
, we have
HV compatibility is a rather stringent condition. Nevertheless, we now observe that certain natural classes of submanifolds of Z automatically satisfy it.
Proposition 4.15 Let
![]() $\Sigma ^k \subset Z^{4n+2}$
be a submanifold,
$\Sigma ^k \subset Z^{4n+2}$
be a submanifold,
![]() $1 \leq k \leq 2n+1$
.
$1 \leq k \leq 2n+1$
.
-
(1) If
 $\Sigma $
is HV-compatible, then
$\Sigma $
is HV-compatible, then
 $\Sigma $
is
$\Sigma $
is
 $\omega _{\mathrm {KE}}$
-isotropic if and only if
$\omega _{\mathrm {KE}}$
-isotropic if and only if
 $\Sigma $
is
$\Sigma $
is
 $\omega _{\mathrm {NK}}$
-isotropic.
$\omega _{\mathrm {NK}}$
-isotropic. -
(2) Suppose
 $\dim (\Sigma ) = 2n+1$
. If
$\dim (\Sigma ) = 2n+1$
. If
 $\Sigma $
is
$\Sigma $
is
 $\omega _{\mathrm {KE}}$
-Lagrangian and
$\omega _{\mathrm {KE}}$
-Lagrangian and
 $\omega _{\mathrm {NK}}$
-Lagrangian, then
$\omega _{\mathrm {NK}}$
-Lagrangian, then
 $\Sigma $
is HV-compatible. Moreover,
$\Sigma $
is HV-compatible. Moreover,
 $\dim (T_z\Sigma \cap \mathsf {H}) = 2n$
and
$\dim (T_z\Sigma \cap \mathsf {H}) = 2n$
and
 $\dim (T_z\Sigma \cap \mathsf {V}) = 1$
at each
$\dim (T_z\Sigma \cap \mathsf {V}) = 1$
at each
 $z \in \Sigma $
.
$z \in \Sigma $
. -
(3) Suppose
 $\dim (\Sigma ) = 3$
. If
$\dim (\Sigma ) = 3$
. If
 $\Sigma $
is
$\Sigma $
is
 $\mathrm {Re}(\gamma )$
-calibrated, then
$\mathrm {Re}(\gamma )$
-calibrated, then
 $\Sigma $
is HV-compatible if and only if
$\Sigma $
is HV-compatible if and only if
 $\Sigma $
is
$\Sigma $
is
 $\omega _{\mathrm {KE}}$
-isotropic. In this case,
$\omega _{\mathrm {KE}}$
-isotropic. In this case,
 $\dim (T_z\Sigma \cap \mathsf {H}) = 2$
and
$\dim (T_z\Sigma \cap \mathsf {H}) = 2$
and
 $\dim (T_z\Sigma \cap \mathsf {V}) = 1$
at each
$\dim (T_z\Sigma \cap \mathsf {V}) = 1$
at each
 $z \in \Sigma $
.
$z \in \Sigma $
.
Proof (a) Suppose
![]() $\Sigma $
is HV-compatible. If
$\Sigma $
is HV-compatible. If
![]() $\Sigma $
is
$\Sigma $
is
![]() $\omega _{\mathrm {KE}}$
-isotropic, then (4.4) says that
$\omega _{\mathrm {KE}}$
-isotropic, then (4.4) says that
We claim that
![]() $\omega _{\mathsf {H}}|_{\Sigma } = \omega _{\mathsf {V}}|_{\Sigma } = 0$
, which would imply again by (4.4) that
$\omega _{\mathsf {H}}|_{\Sigma } = \omega _{\mathsf {V}}|_{\Sigma } = 0$
, which would imply again by (4.4) that
![]() $\Sigma $
is also
$\Sigma $
is also
![]() $\omega _{\mathrm {NK}}$
-isotropic. Let
$\omega _{\mathrm {NK}}$
-isotropic. Let
![]() $u_1, u_2 \in T_x \Sigma $
, and decompose them orthogonally as
$u_1, u_2 \in T_x \Sigma $
, and decompose them orthogonally as
![]() $u_j = u_j^{\mathsf {H}} + u_j^{\mathsf {V}}$
, where
$u_j = u_j^{\mathsf {H}} + u_j^{\mathsf {V}}$
, where
![]() $u_j^{\mathsf {H}} \in \mathsf {H}$
and
$u_j^{\mathsf {H}} \in \mathsf {H}$
and
![]() $u_j^{\mathsf {V}} \in \mathsf {V}$
. Since
$u_j^{\mathsf {V}} \in \mathsf {V}$
. Since
![]() $\Sigma $
is HV-compatible, both
$\Sigma $
is HV-compatible, both
![]() $u_j^{\mathsf {H}}$
and
$u_j^{\mathsf {H}}$
and
![]() $u_j^{\mathsf {V}}$
are in
$u_j^{\mathsf {V}}$
are in
![]() $T_x \Sigma $
for
$T_x \Sigma $
for
![]() $j = 1, 2$
. Using (4.7) and the facts that
$j = 1, 2$
. Using (4.7) and the facts that
![]() $\omega _{\mathsf {H}} \in \Lambda ^2 (\mathsf {H}^*)$
and
$\omega _{\mathsf {H}} \in \Lambda ^2 (\mathsf {H}^*)$
and
![]() $\omega _{\mathsf {V}} \in \Lambda ^2 (\mathsf {V}^*)$
, we have
$\omega _{\mathsf {V}} \in \Lambda ^2 (\mathsf {V}^*)$
, we have
 $$ \begin{align*} \omega_{\mathsf{V}}(u_1, u_2) & = \omega_{\mathsf{V}}(u_1^{\mathsf{H}} + u_1^{\mathsf{V}}, u_2^{\mathsf{H}} + u_2^{\mathsf{V}}) = \omega_{\mathsf{V}}(u_1^{\mathsf{V}}, u_2^{\mathsf{V}}) \\ & = -\omega_{\mathsf{H}}(u_1^{\mathsf{V}}, u_2^{\mathsf{V}}) = 0. \end{align*} $$
$$ \begin{align*} \omega_{\mathsf{V}}(u_1, u_2) & = \omega_{\mathsf{V}}(u_1^{\mathsf{H}} + u_1^{\mathsf{V}}, u_2^{\mathsf{H}} + u_2^{\mathsf{V}}) = \omega_{\mathsf{V}}(u_1^{\mathsf{V}}, u_2^{\mathsf{V}}) \\ & = -\omega_{\mathsf{H}}(u_1^{\mathsf{V}}, u_2^{\mathsf{V}}) = 0. \end{align*} $$
The argument in the other direction is essentially the same, with (4.7) replaced by
![]() $\left .\omega _{\mathsf {V}}\right |_{\Sigma } = \left .2 \omega _{\mathsf {H}}\right |_{\Sigma }$
.
$\left .\omega _{\mathsf {V}}\right |_{\Sigma } = \left .2 \omega _{\mathsf {H}}\right |_{\Sigma }$
.
(b) Let
![]() $\Sigma ^{2n+1} \subset Z$
be
$\Sigma ^{2n+1} \subset Z$
be
![]() $\omega _{\mathrm {KE}}$
-Lagrangian and
$\omega _{\mathrm {KE}}$
-Lagrangian and
![]() $\omega _{\mathrm {NK}}$
-Lagrangian, so that
$\omega _{\mathrm {NK}}$
-Lagrangian, so that
![]() $\left .\omega _{\mathsf {V}}\right |_\Sigma = 0$
and
$\left .\omega _{\mathsf {V}}\right |_\Sigma = 0$
and
![]() $\left .\omega _{\mathsf {H}}\right |_\Sigma = 0$
. Fix
$\left .\omega _{\mathsf {H}}\right |_\Sigma = 0$
. Fix
![]() $z \in \Sigma $
, let
$z \in \Sigma $
, let
![]() $\pi _{\mathsf {H}} \colon T_zZ \to \mathsf {H}$
and
$\pi _{\mathsf {H}} \colon T_zZ \to \mathsf {H}$
and
![]() $\pi _{\mathsf {V}} \colon T_zZ \to \mathsf {V}$
denote the projection maps, so that
$\pi _{\mathsf {V}} \colon T_zZ \to \mathsf {V}$
denote the projection maps, so that
Let
![]() $(\rho , \mu ) \colon T_zZ \to \mathbb {R}^{4n + 2}$
be an
$(\rho , \mu ) \colon T_zZ \to \mathbb {R}^{4n + 2}$
be an
![]() $\mathrm {Sp}(n)\mathrm {U}(1)$
-coframe at z. Since
$\mathrm {Sp}(n)\mathrm {U}(1)$
-coframe at z. Since
![]() $\left .\mu ^2 \wedge \mu ^3\right |_\Sigma = \left .\omega _{\mathsf {V}}\right |_\Sigma = 0$
, we have
$\left .\mu ^2 \wedge \mu ^3\right |_\Sigma = \left .\omega _{\mathsf {V}}\right |_\Sigma = 0$
, we have
![]() $\left .\mu ^2 \wedge \mu ^3\right |_{\pi _{\mathsf {V}}(T_z\Sigma )} = 0$
, so that
$\left .\mu ^2 \wedge \mu ^3\right |_{\pi _{\mathsf {V}}(T_z\Sigma )} = 0$
, so that
![]() $\dim ( \pi _{\mathsf {V}}(T_z\Sigma )) \leq 1$
. Moreover, since
$\dim ( \pi _{\mathsf {V}}(T_z\Sigma )) \leq 1$
. Moreover, since
![]() $\omega _{\mathsf {H}}$
is a nondegenerate
$\omega _{\mathsf {H}}$
is a nondegenerate
![]() $2$
-form on the
$2$
-form on the
![]() $4n$
-plane
$4n$
-plane
![]() $\mathsf {H}$
, the condition
$\mathsf {H}$
, the condition
![]() $\omega _{\mathsf {H}}|_{ \pi _{\mathsf {H}}(T_z\Sigma ) } = 0$
implies that
$\omega _{\mathsf {H}}|_{ \pi _{\mathsf {H}}(T_z\Sigma ) } = 0$
implies that
![]() $\dim (\pi _{\mathsf {H}}(T_z\Sigma )) \leq 2n$
. Therefore, since
$\dim (\pi _{\mathsf {H}}(T_z\Sigma )) \leq 2n$
. Therefore, since
we deduce that
![]() $T_z\Sigma = \pi _{\mathsf {H}}(T_z\Sigma ) \oplus \pi _{\mathsf {V}}(T_z\Sigma )$
, which implies the result.
$T_z\Sigma = \pi _{\mathsf {H}}(T_z\Sigma ) \oplus \pi _{\mathsf {V}}(T_z\Sigma )$
, which implies the result.
(c) This is immediate from Proposition 4.13.
4.3.3 Other phases
Thus far, we have studied the real
![]() $3$
-form
$3$
-form
![]() $\mathrm {Re}(\gamma ) \in \Omega ^3(Z)$
. More generally, one can consider the
$\mathrm {Re}(\gamma ) \in \Omega ^3(Z)$
. More generally, one can consider the
![]() $S^1$
-family of real
$S^1$
-family of real
![]() $3$
-forms
$3$
-forms
![]() $\mathrm {Re}(e^{-i\theta }\gamma )$
for constant
$\mathrm {Re}(e^{-i\theta }\gamma )$
for constant
![]() $e^{i\theta } \in S^1$
. We now explore the corresponding submanifold theory, beginning with a familiar situation:
$e^{i\theta } \in S^1$
. We now explore the corresponding submanifold theory, beginning with a familiar situation:
Example 4.3 Suppose that
![]() $n = 1$
, so that the twistor space Z is six-dimensional, and
$n = 1$
, so that the twistor space Z is six-dimensional, and
![]() $\gamma \in \Omega ^3(Z;\mathbb {C})$
is an
$\gamma \in \Omega ^3(Z;\mathbb {C})$
is an
![]() $\mathrm {Sp}(1)\mathrm {U}(1) = \mathrm {U}(2)$
-structure. By the discussion in Examples 4.1 and 4.2, the
$\mathrm {Sp}(1)\mathrm {U}(1) = \mathrm {U}(2)$
-structure. By the discussion in Examples 4.1 and 4.2, the
![]() $3$
-form
$3$
-form
![]() $\gamma $
induces an
$\gamma $
induces an
![]() $\mathrm {SU}(3)$
-structure on
$\mathrm {SU}(3)$
-structure on
![]() $Z^6$
and satisfies
$Z^6$
and satisfies
 $$ \begin{align*} d\omega_{\mathrm{NK}} & = 3\,\mathrm{Im}(2\gamma), \\ d\,\mathrm{Re}(2\gamma) & = 2\, \omega_{\mathrm{NK}} \wedge \omega_{\mathrm{NK}}. \end{align*} $$
$$ \begin{align*} d\omega_{\mathrm{NK}} & = 3\,\mathrm{Im}(2\gamma), \\ d\,\mathrm{Re}(2\gamma) & = 2\, \omega_{\mathrm{NK}} \wedge \omega_{\mathrm{NK}}. \end{align*} $$
Now, let
![]() $L^3 \subset Z^6$
be an oriented three-dimensional submanifold. It is well known that L is
$L^3 \subset Z^6$
be an oriented three-dimensional submanifold. It is well known that L is
![]() $\omega _{\mathrm {NK}}$
-Lagrangian if and only if L is
$\omega _{\mathrm {NK}}$
-Lagrangian if and only if L is
![]() $\gamma $
-special Lagrangian of phase
$\gamma $
-special Lagrangian of phase
![]() $1$
. That is,
$1$
. That is,
More generally, one might wish to consider
![]() $\gamma $
-special Lagrangian
$\gamma $
-special Lagrangian
![]() $3$
-folds of other phases
$3$
-folds of other phases
![]() $e^{i\theta } \in S^1$
. However, it is well known that if
$e^{i\theta } \in S^1$
. However, it is well known that if
![]() $L^3 \subset Z^6$
satisfies
$L^3 \subset Z^6$
satisfies
![]() $\mathrm {Re}(e^{-i\theta }\gamma )|_L = \mathrm {vol}_L$
, then
$\mathrm {Re}(e^{-i\theta }\gamma )|_L = \mathrm {vol}_L$
, then
![]() $e^{-i\theta } = \pm 1$
.
$e^{-i\theta } = \pm 1$
.
Example 4.3 is the special case
![]() $n=1$
of the following more general statement, which is new:
$n=1$
of the following more general statement, which is new:
Proposition 4.16 Let
![]() $L^3 \subset Z^{4n+2}$
be a three-dimensional submanifold.
$L^3 \subset Z^{4n+2}$
be a three-dimensional submanifold.
-
(1) If L is
 $\mathrm {Re}(e^{-i\theta }\gamma )$
-calibrated, then
$\mathrm {Re}(e^{-i\theta }\gamma )$
-calibrated, then
 $e^{i\theta } = \pm 1$
.
$e^{i\theta } = \pm 1$
. -
(2) If L is
 $\mathrm {Re}(\gamma )$
-calibrated, then
$\mathrm {Re}(\gamma )$
-calibrated, then
 $\omega _{\mathrm {NK}}|_L = 0$
and
$\omega _{\mathrm {NK}}|_L = 0$
and
 $\mathrm {Im}(\gamma )|_L = 0$
. If
$\mathrm {Im}(\gamma )|_L = 0$
. If
 $n = 1$
, then the converse also holds.
$n = 1$
, then the converse also holds.
Proof Suppose that
![]() $L \subset Z^{4n+2}$
is
$L \subset Z^{4n+2}$
is
![]() $\mathrm {Re}(e^{-i\theta }\gamma )$
-calibrated. By the same argument as in Proposition 4.10, we have
$\mathrm {Re}(e^{-i\theta }\gamma )$
-calibrated. By the same argument as in Proposition 4.10, we have
![]() $\left .\omega _{\mathrm {NK}}\right |_L = 0$
. Since
$\left .\omega _{\mathrm {NK}}\right |_L = 0$
. Since
![]() $d\omega _{\mathrm {NK}} = 6\,\mathrm {Im}(\gamma )$
, it follows that
$d\omega _{\mathrm {NK}} = 6\,\mathrm {Im}(\gamma )$
, it follows that
![]() ${\left .\mathrm {Im}(\gamma )\right |_L = 0}$
. Therefore,
${\left .\mathrm {Im}(\gamma )\right |_L = 0}$
. Therefore,
Since
![]() $\mathrm {Re}(\gamma )$
has comass one, it follows that
$\mathrm {Re}(\gamma )$
has comass one, it follows that
![]() $\cos (\theta ) = \pm 1$
. (The converse of (b) when
$\cos (\theta ) = \pm 1$
. (The converse of (b) when
![]() $n=1$
is the well-known result discussed in Example 4.3.)
$n=1$
is the well-known result discussed in Example 4.3.)
4.4 Relations between submanifolds in M and Z
We now systematically discuss the relationships between the various classes of submanifolds in
![]() $Z^{4n+2}$
and those in
$Z^{4n+2}$
and those in
![]() $M^{4n+3}$
. Broadly speaking, given a submanifold
$M^{4n+3}$
. Broadly speaking, given a submanifold
![]() $\Sigma \subset Z$
, there are two natural ways to construct a corresponding submanifold of M. The first is to consider the circle bundle
$\Sigma \subset Z$
, there are two natural ways to construct a corresponding submanifold of M. The first is to consider the circle bundle
![]() $p_1^{-1}(\Sigma ) \subset M$
, and the second is to consider its
$p_1^{-1}(\Sigma ) \subset M$
, and the second is to consider its
![]() $p_1$
-horizontal lift
$p_1$
-horizontal lift
![]() $\widehat {\Sigma } \subset M$
(provided it exists). We will examine both constructions.
$\widehat {\Sigma } \subset M$
(provided it exists). We will examine both constructions.
4.4.1 Circle bundle constructions
We begin by considering submanifolds of the form
![]() $p_1^{-1}(\Sigma ) \subset M$
for some submanifold
$p_1^{-1}(\Sigma ) \subset M$
for some submanifold
![]() $\Sigma \subset Z$
. First, we consider those that are
$\Sigma \subset Z$
. First, we consider those that are
![]() $I_1$
-CR. In general, Proposition 3.15(a) shows that every
$I_1$
-CR. In general, Proposition 3.15(a) shows that every
![]() $I_1$
-CR
$I_1$
-CR
![]() $3$
-fold of M is
$3$
-fold of M is
![]() $\phi _2$
-associative. For circle bundles, the converse also holds:
$\phi _2$
-associative. For circle bundles, the converse also holds:
Proposition 4.17 Let
![]() $\Sigma ^{2k} \subset Z^{4n+2}$
be a submanifold,
$\Sigma ^{2k} \subset Z^{4n+2}$
be a submanifold,
![]() $2 \leq 2k \leq 4n$
. Then
$2 \leq 2k \leq 4n$
. Then
![]() $\Sigma $
is
$\Sigma $
is
![]() $J_+$
-complex if and only if
$J_+$
-complex if and only if
![]() $p_1^{-1}(\Sigma )$
is
$p_1^{-1}(\Sigma )$
is
![]() $I_1$
-CR. Moreover, in the case of
$I_1$
-CR. Moreover, in the case of
![]() $2k = 2$
, these conditions are also equivalent to:
$2k = 2$
, these conditions are also equivalent to:
![]() $p_1^{-1}(\Sigma )$
is
$p_1^{-1}(\Sigma )$
is
![]() $\phi _2$
-associative.
$\phi _2$
-associative.
Proof Let
![]() $\Sigma \subset Z$
be a submanifold, and set
$\Sigma \subset Z$
be a submanifold, and set
![]() $L = p_1^{-1}(\Sigma ) \subset M$
. Fix
$L = p_1^{-1}(\Sigma ) \subset M$
. Fix
![]() $x \in L$
and let
$x \in L$
and let
![]() ${z = p_1(x) \in \Sigma }$
. Note that
${z = p_1(x) \in \Sigma }$
. Note that
 $$ \begin{align*} \Sigma \text{ is }J_+\text{-complex} & \iff \left.(\omega_{\mathrm{KE}})^k\right|_\Sigma = k!\,\mathrm{vol}_\Sigma, \\ L \text{ is } I_1\text{-CR} & \iff \left.(\alpha_1 \wedge \Omega_1^k)\right|_L = k!\, \mathrm{vol}_L. \end{align*} $$
$$ \begin{align*} \Sigma \text{ is }J_+\text{-complex} & \iff \left.(\omega_{\mathrm{KE}})^k\right|_\Sigma = k!\,\mathrm{vol}_\Sigma, \\ L \text{ is } I_1\text{-CR} & \iff \left.(\alpha_1 \wedge \Omega_1^k)\right|_L = k!\, \mathrm{vol}_L. \end{align*} $$
Since
![]() $A_1 \in T_xL$
, we can write
$A_1 \in T_xL$
, we can write
![]() $T_xL = \mathbb {R} A_1 \oplus \widetilde {U}$
for some subspace
$T_xL = \mathbb {R} A_1 \oplus \widetilde {U}$
for some subspace
![]() $\widetilde {U} \subset \mathrm {Ker}(\alpha _1)$
. Let
$\widetilde {U} \subset \mathrm {Ker}(\alpha _1)$
. Let
![]() $\{\widetilde {u}_1, \ldots , \widetilde {u}_{2k-1}\}$
be an orthonormal basis of
$\{\widetilde {u}_1, \ldots , \widetilde {u}_{2k-1}\}$
be an orthonormal basis of
![]() $\widetilde {U}$
such that
$\widetilde {U}$
such that
![]() $\{A_1, \widetilde {u}_1, \ldots , \widetilde {u}_{2k-1}\}$
is an oriented orthonormal basis of
$\{A_1, \widetilde {u}_1, \ldots , \widetilde {u}_{2k-1}\}$
is an oriented orthonormal basis of
![]() $T_xL$
. Setting
$T_xL$
. Setting
![]() $u_j = (p_1)_*(\widetilde {u}_j)$
, and noting that
$u_j = (p_1)_*(\widetilde {u}_j)$
, and noting that
is an isometry, we see that
![]() $\{u_1, \ldots , u_{2k-1}\}$
is an orthonormal basis of
$\{u_1, \ldots , u_{2k-1}\}$
is an orthonormal basis of
![]() $T_z\Sigma $
. Therefore, recalling that
$T_z\Sigma $
. Therefore, recalling that
![]() $\Omega _1 = p_1^*(\omega _{\mathrm {KE}})$
, we have
$\Omega _1 = p_1^*(\omega _{\mathrm {KE}})$
, we have
 $$ \begin{align*} L \text{ is }I_1\text{-CR } \iff (\alpha_1 \wedge \Omega_1^k)(A_1, \widetilde{u}_1, \ldots, \widetilde{u}_{2k-1}) = k! & \iff \Omega_1^k(\widetilde{u}_1, \ldots, \widetilde{u}_{2k-1}) = k! \\ & \iff \omega_{\mathrm{KE}}^k(u_1, \ldots, u_{2k-1}) = k! \\ & \iff \Sigma \text{ is }J_+\text{-complex.} \end{align*} $$
$$ \begin{align*} L \text{ is }I_1\text{-CR } \iff (\alpha_1 \wedge \Omega_1^k)(A_1, \widetilde{u}_1, \ldots, \widetilde{u}_{2k-1}) = k! & \iff \Omega_1^k(\widetilde{u}_1, \ldots, \widetilde{u}_{2k-1}) = k! \\ & \iff \omega_{\mathrm{KE}}^k(u_1, \ldots, u_{2k-1}) = k! \\ & \iff \Sigma \text{ is }J_+\text{-complex.} \end{align*} $$
Now suppose
![]() $k = 1$
. Observe that
$k = 1$
. Observe that
 $$ \begin{align*} \phi_2 & = \alpha_1 \wedge \Omega_1 - \alpha_2 \wedge \Omega_2 + \alpha_3 \wedge \Omega_3 \\ & = \alpha_1 \wedge \Omega_1 - \alpha_2 \wedge \kappa_2 + \alpha_3 \wedge \kappa_3. \end{align*} $$
$$ \begin{align*} \phi_2 & = \alpha_1 \wedge \Omega_1 - \alpha_2 \wedge \Omega_2 + \alpha_3 \wedge \Omega_3 \\ & = \alpha_1 \wedge \Omega_1 - \alpha_2 \wedge \kappa_2 + \alpha_3 \wedge \kappa_3. \end{align*} $$
Since
![]() $\iota _{A_1}(-\alpha _2 \wedge \kappa _2 + \alpha _3 \wedge \kappa _3) = 0$
, we have
$\iota _{A_1}(-\alpha _2 \wedge \kappa _2 + \alpha _3 \wedge \kappa _3) = 0$
, we have
![]() $\left .(-\alpha _2 \wedge \kappa _2 + \alpha _3 \wedge \kappa _3)\right |_L = 0$
. Therefore, we see that
$\left .(-\alpha _2 \wedge \kappa _2 + \alpha _3 \wedge \kappa _3)\right |_L = 0$
. Therefore, we see that
![]() $\left .\phi _2\right |_L = \left .(\alpha _1 \wedge \Omega _1)\right |_L$
, which gives the result.
$\left .\phi _2\right |_L = \left .(\alpha _1 \wedge \Omega _1)\right |_L$
, which gives the result.
The previous proposition shows that a circle bundle
![]() $p_1^{-1}(\Sigma )$
is
$p_1^{-1}(\Sigma )$
is
![]() $I_1$
-CR if and only if
$I_1$
-CR if and only if
![]() $\Sigma $
is
$\Sigma $
is
![]() $J_+$
-complex. In fact, any
$J_+$
-complex. In fact, any
![]() $I_1$
-CR submanifold is locally a circle bundle:
$I_1$
-CR submanifold is locally a circle bundle:
Proposition 4.18 Let
![]() $L^{2k+1} \subset M^{4n+3}$
be a submanifold,
$L^{2k+1} \subset M^{4n+3}$
be a submanifold,
![]() $2 \leq 2k \leq 4n$
. Then L is
$2 \leq 2k \leq 4n$
. Then L is
![]() $I_1$
-CR if and only if L is locally of the form
$I_1$
-CR if and only if L is locally of the form
![]() $p_1^{-1}(\Sigma )$
for some
$p_1^{-1}(\Sigma )$
for some
![]() $J_+$
-complex submanifold
$J_+$
-complex submanifold
![]() $\Sigma ^{2k} \subset Z^{4n+2}$
.
$\Sigma ^{2k} \subset Z^{4n+2}$
.
Proof (
![]() $\Longleftarrow $
) This follows from Proposition 4.17.
$\Longleftarrow $
) This follows from Proposition 4.17.
(
![]() $\Longrightarrow $
) Let
$\Longrightarrow $
) Let
![]() $L \subset M$
be
$L \subset M$
be
![]() $I_1$
-CR, and abbreviate
$I_1$
-CR, and abbreviate
![]() $p := p_1$
. At each
$p := p_1$
. At each
![]() $x \in L$
, we have
$x \in L$
, we have
![]() ${\left .A_1\right |_x \in T_xL}$
, so (short-time) integral curves of
${\left .A_1\right |_x \in T_xL}$
, so (short-time) integral curves of
![]() $A_1$
lie in L. That is, at each
$A_1$
lie in L. That is, at each
![]() $x \in L$
, there exists an open set
$x \in L$
, there exists an open set
![]() $I_x \subset p^{-1}(p(x))$
such that
$I_x \subset p^{-1}(p(x))$
such that
![]() $x \in I_x$
and
$x \in I_x$
and
![]() $I_x \subset L$
.
$I_x \subset L$
.
We claim that
![]() $p(L) \subset Z$
is an embedded
$p(L) \subset Z$
is an embedded
![]() $2k$
-dimensional submanifold of Z. To see this, fix
$2k$
-dimensional submanifold of Z. To see this, fix
![]() $z \in p(L)$
, and let
$z \in p(L)$
, and let
![]() $x \in L$
have
$x \in L$
have
![]() $p(x) = z$
. Letting
$p(x) = z$
. Letting
![]() $\ell $
satisfy
$\ell $
satisfy
![]() $(2k+1) + \ell = 4n+3$
, we choose a neighborhood
$(2k+1) + \ell = 4n+3$
, we choose a neighborhood
![]() $W \subset M$
of x and a chart
$W \subset M$
of x and a chart
![]() $\widetilde {\phi } \colon W \to \mathbb {R}^{4n+3} = \mathbb {R}^{2k} \times \mathbb {R} \times \mathbb {R}^{\ell }$
with coordinate functions denoted
$\widetilde {\phi } \colon W \to \mathbb {R}^{4n+3} = \mathbb {R}^{2k} \times \mathbb {R} \times \mathbb {R}^{\ell }$
with coordinate functions denoted
![]() $\widetilde {\phi } = (t^1, \ldots , t^{2k}, u, v^1, \ldots , v^\ell )$
such that
$\widetilde {\phi } = (t^1, \ldots , t^{2k}, u, v^1, \ldots , v^\ell )$
such that
 $$ \begin{align*} \widetilde{\phi}(L \cap W) & \subset \mathbb{R}^{2k} \times \mathbb{R} \times 0, \\ \widetilde{\phi}_*(A_1) & = \frac{\partial}{\partial u} \ \ \ \ \text{on } L \cap W. \end{align*} $$
$$ \begin{align*} \widetilde{\phi}(L \cap W) & \subset \mathbb{R}^{2k} \times \mathbb{R} \times 0, \\ \widetilde{\phi}_*(A_1) & = \frac{\partial}{\partial u} \ \ \ \ \text{on } L \cap W. \end{align*} $$
Since
![]() $p \colon M \to Z$
is a submersion, it is an open map, and therefore
$p \colon M \to Z$
is a submersion, it is an open map, and therefore
![]() $p(W) \subset M$
is an open set. Letting
$p(W) \subset M$
is an open set. Letting
![]() $\pi \colon \mathbb {R}^{2k} \times \mathbb {R} \times \mathbb {R}^{\ell } \to \mathbb {R}^{2k} \times \mathbb {R}^{\ell }$
denote the natural projection map, we observe that
$\pi \colon \mathbb {R}^{2k} \times \mathbb {R} \times \mathbb {R}^{\ell } \to \mathbb {R}^{2k} \times \mathbb {R}^{\ell }$
denote the natural projection map, we observe that
![]() $\pi \circ \widetilde {\phi } \colon W \to \mathbb {R}^{4n+2} = \mathbb {R}^{2k} \times \mathbb {R}^{\ell }$
descends to a chart
$\pi \circ \widetilde {\phi } \colon W \to \mathbb {R}^{4n+2} = \mathbb {R}^{2k} \times \mathbb {R}^{\ell }$
descends to a chart
![]() $\phi \colon p(W) \to \mathbb {R}^{4n+2} = \mathbb {R}^{2k} \times \mathbb {R}^\ell $
such that
$\phi \colon p(W) \to \mathbb {R}^{4n+2} = \mathbb {R}^{2k} \times \mathbb {R}^\ell $
such that
This provides slice coordinates at
![]() $z \in p(L)$
, showing that
$z \in p(L)$
, showing that
![]() $p(L) \subset Z$
is an embedded
$p(L) \subset Z$
is an embedded
![]() $2k$
-fold.
$2k$
-fold.
It follows that
![]() $p^{-1}(p(L)) \subset M$
is an embedded
$p^{-1}(p(L)) \subset M$
is an embedded
![]() $(2k+1)$
-dimensional submanifold of M, so that
$(2k+1)$
-dimensional submanifold of M, so that
![]() $L \subset p^{-1}(p(L))$
is an open set for dimension reasons. That
$L \subset p^{-1}(p(L))$
is an open set for dimension reasons. That
![]() $\Sigma := p(L)$
is
$\Sigma := p(L)$
is
![]() $J_+$
-complex follows from Proposition 4.17.
$J_+$
-complex follows from Proposition 4.17.
Next, for any submanifold
![]() $\Sigma \subset Z$
, we note that its circle bundle
$\Sigma \subset Z$
, we note that its circle bundle
![]() $p_1^{-1}(\Sigma ) \subset M$
is never
$p_1^{-1}(\Sigma ) \subset M$
is never
![]() $\alpha _1$
-isotropic. However, in special situations, it can be
$\alpha _1$
-isotropic. However, in special situations, it can be
![]() $\alpha _2$
-isotropic. In this direction, we first observe:
$\alpha _2$
-isotropic. In this direction, we first observe:
Lemma 4.19 Let
![]() $\Sigma ^k \subset Z^{4n+2}$
be a submanifold with
$\Sigma ^k \subset Z^{4n+2}$
be a submanifold with
![]() $1 \leq k \leq 2n$
. The following are equivalent:
$1 \leq k \leq 2n$
. The following are equivalent:
-
(1)
 $p_1^{-1}(\Sigma )$
is
$p_1^{-1}(\Sigma )$
is
 $\alpha _2$
-isotropic.
$\alpha _2$
-isotropic. -
(2)
 $p_1^{-1}(\Sigma )$
is
$p_1^{-1}(\Sigma )$
is
 $\alpha _3$
-isotropic.
$\alpha _3$
-isotropic. -
(3)
 $\Sigma $
is horizontal.
$\Sigma $
is horizontal.
Proof Let
![]() $\Sigma \subset Z^{4n+2}$
be a submanifold with
$\Sigma \subset Z^{4n+2}$
be a submanifold with
![]() $\dim (\Sigma ) \leq 2n$
, and set
$\dim (\Sigma ) \leq 2n$
, and set
![]() $L = p_1^{-1}(\Sigma ) \subset M$
. Fix
$L = p_1^{-1}(\Sigma ) \subset M$
. Fix
![]() $x \in L$
and let
$x \in L$
and let
![]() $z = p_1(x) \in \Sigma $
.
$z = p_1(x) \in \Sigma $
.
(i)
![]() $\iff $
(ii). Suppose that L is
$\iff $
(ii). Suppose that L is
![]() $\alpha _2$
-isotropic at x. By Proposition 3.6, we have both
$\alpha _2$
-isotropic at x. By Proposition 3.6, we have both
![]() $T_xL \subset \mathrm {Ker}(\alpha _2)$
and
$T_xL \subset \mathrm {Ker}(\alpha _2)$
and
![]() $\Omega _2|_{T_xL} = 0$
. That is, the subspace
$\Omega _2|_{T_xL} = 0$
. That is, the subspace
![]() $T_xL \subset \mathrm {Ker}(\alpha _2)$
is
$T_xL \subset \mathrm {Ker}(\alpha _2)$
is
![]() $\Omega _2$
-isotropic. Therefore, since
$\Omega _2$
-isotropic. Therefore, since
![]() $A_1 \in T_xL$
, it follows that
$A_1 \in T_xL$
, it follows that
![]() $A_3 = -\mathsf {J}_2(A_1)$
is orthogonal to
$A_3 = -\mathsf {J}_2(A_1)$
is orthogonal to
![]() $T_xL$
, and hence
$T_xL$
, and hence
![]() $T_xL \subset \text {Ker}(\alpha _3)$
, showing that L is
$T_xL \subset \text {Ker}(\alpha _3)$
, showing that L is
![]() $\alpha _3$
-isotropic at x.
$\alpha _3$
-isotropic at x.
(ii)
![]() $\iff $
(iii). Since
$\iff $
(iii). Since
![]() $A_1 \in T_xL$
, we can write
$A_1 \in T_xL$
, we can write
![]() $T_xL = \mathbb {R} A_1 \oplus \widetilde {U}$
for some subspace
$T_xL = \mathbb {R} A_1 \oplus \widetilde {U}$
for some subspace
![]() $\widetilde {U} \subset \mathrm {Ker}(\alpha _1)$
. Since
$\widetilde {U} \subset \mathrm {Ker}(\alpha _1)$
. Since
![]() $p_1|_{\mathrm {Ker}(\alpha _1)} \colon \mathrm {Ker}(\alpha _1)|_x \to T_zZ$
is an isometry, it follows that
$p_1|_{\mathrm {Ker}(\alpha _1)} \colon \mathrm {Ker}(\alpha _1)|_x \to T_zZ$
is an isometry, it follows that
![]() ${(p_1)_*(\widetilde {U}) = T_z\Sigma }$
. Now, observe that
${(p_1)_*(\widetilde {U}) = T_z\Sigma }$
. Now, observe that
 $$ \begin{align*} T_z\Sigma \subset \mathsf{H} & \iff (p_1)_*(\widetilde{U}) \subset (p_1)_*(\widetilde{\mathsf{H}}) \iff \widetilde{U} \subset \mathrm{Ker}(\alpha_1, \alpha_2, \alpha_3) \\ & \iff T_xL \subset \mathrm{Ker}(\alpha_2, \alpha_3). \end{align*} $$
$$ \begin{align*} T_z\Sigma \subset \mathsf{H} & \iff (p_1)_*(\widetilde{U}) \subset (p_1)_*(\widetilde{\mathsf{H}}) \iff \widetilde{U} \subset \mathrm{Ker}(\alpha_1, \alpha_2, \alpha_3) \\ & \iff T_xL \subset \mathrm{Ker}(\alpha_2, \alpha_3). \end{align*} $$
Thus, if
![]() $\Sigma $
is horizontal at z, then
$\Sigma $
is horizontal at z, then
![]() $T_z\Sigma \subset \mathsf {H}$
, so that
$T_z\Sigma \subset \mathsf {H}$
, so that
![]() $T_xL \subset \mathrm {Ker}(\alpha _2, \alpha _3)$
, and hence L is both
$T_xL \subset \mathrm {Ker}(\alpha _2, \alpha _3)$
, and hence L is both
![]() $\alpha _2$
- and
$\alpha _2$
- and
![]() $\alpha _3$
-isotropic at x. Conversely, if L is
$\alpha _3$
-isotropic at x. Conversely, if L is
![]() $\alpha _2$
-isotropic at x, then by the previous paragraph, L is also
$\alpha _2$
-isotropic at x, then by the previous paragraph, L is also
![]() $\alpha _3$
-isotropic at x, so
$\alpha _3$
-isotropic at x, so
![]() $T_xL \subset \mathrm {Ker}(\alpha _2, \alpha _3)$
, and hence
$T_xL \subset \mathrm {Ker}(\alpha _2, \alpha _3)$
, and hence
![]() $\Sigma $
is horizontal at z.
$\Sigma $
is horizontal at z.
Corollary 4.20 Let
![]() $\Sigma ^{2k} \subset Z^{4n+2}$
be a submanifold,
$\Sigma ^{2k} \subset Z^{4n+2}$
be a submanifold,
![]() $2 \leq 2k \leq 2n$
. Then
$2 \leq 2k \leq 2n$
. Then
![]() $\Sigma $
is
$\Sigma $
is
![]() $J_+$
-complex and horizontal if and only if
$J_+$
-complex and horizontal if and only if
![]() $p_1^{-1}(\Sigma )$
is
$p_1^{-1}(\Sigma )$
is
![]() $I_1$
-CR isotropic (i.e.,
$I_1$
-CR isotropic (i.e.,
![]() $I_1$
-CR,
$I_1$
-CR,
![]() $\alpha _2$
-isotropic, and
$\alpha _2$
-isotropic, and
![]() $\alpha _3$
-isotropic).
$\alpha _3$
-isotropic).
Corollary 4.21 Let
![]() $L^{2k+1} \subset M^{4n+3}$
be a submanifold,
$L^{2k+1} \subset M^{4n+3}$
be a submanifold,
![]() $3 \leq 2k+1 \leq 2n+1$
. Then L is
$3 \leq 2k+1 \leq 2n+1$
. Then L is
![]() $I_1$
-CR isotropic if and only if L is locally of the form
$I_1$
-CR isotropic if and only if L is locally of the form
![]() $p_1^{-1}(\Sigma )$
for some horizontal
$p_1^{-1}(\Sigma )$
for some horizontal
![]() $J_+$
-complex submanifold
$J_+$
-complex submanifold
![]() $\Sigma ^{2k} \subset Z^{4n+2}$
.
$\Sigma ^{2k} \subset Z^{4n+2}$
.
When
![]() $\Sigma $
is
$\Sigma $
is
![]() $2n$
-dimensional, the situation is particularly special:
$2n$
-dimensional, the situation is particularly special:
Corollary 4.22 Let
![]() $\Sigma ^{2n} \subset Z^{4n+2}$
be
$\Sigma ^{2n} \subset Z^{4n+2}$
be
![]() $2n$
-dimensional. The following are equivalent:
$2n$
-dimensional. The following are equivalent:
-
(1)
 $\Sigma $
is
$\Sigma $
is
 $J_+$
-complex and horizontal.
$J_+$
-complex and horizontal. -
(2)
 $\Sigma $
is horizontal.
$\Sigma $
is horizontal. -
(3)
 $p_1^{-1}(\Sigma )$
is
$p_1^{-1}(\Sigma )$
is
 $\alpha _2$
-Legendrian.
$\alpha _2$
-Legendrian. -
(4)
 $p_1^{-1}(\Sigma )$
is
$p_1^{-1}(\Sigma )$
is
 $\alpha _3$
-Legendrian.
$\alpha _3$
-Legendrian. -
(5)
 $p_1^{-1}(\Sigma )$
is
$p_1^{-1}(\Sigma )$
is
 $I_1$
-CR Legendrian (i.e.,
$I_1$
-CR Legendrian (i.e.,
 $I_1$
-CR,
$I_1$
-CR,
 $\alpha _2$
-Legendrian, and
$\alpha _2$
-Legendrian, and
 $\alpha _3$
-Legendrian).
$\alpha _3$
-Legendrian). -
(6)
 $p_1^{-1}(\Sigma )$
is
$p_1^{-1}(\Sigma )$
is
 $\Psi _2$
-special Legendrian of phase
$\Psi _2$
-special Legendrian of phase
 $i^{n+1}$
and
$i^{n+1}$
and
 $\Psi _3$
-special Legendrian of phase
$\Psi _3$
-special Legendrian of phase
 $1$
.
$1$
.
Proof The equivalence (ii)
![]() $\iff $
(iii)
$\iff $
(iii)
![]() $\iff $
(iv) is Lemma 4.19. The equivalence (i)
$\iff $
(iv) is Lemma 4.19. The equivalence (i)
![]() $\iff $
(v) is Corollary 4.20.
$\iff $
(v) is Corollary 4.20.
It is clear that (v)
![]() $\implies $
(iv). Conversely, if (iv) holds, then
$\implies $
(iv). Conversely, if (iv) holds, then
![]() $L := p_1^{-1}(\Sigma )$
is both
$L := p_1^{-1}(\Sigma )$
is both
![]() $\alpha _3$
-Legendrian and
$\alpha _3$
-Legendrian and
![]() $\alpha _2$
-Legendrian, so that
$\alpha _2$
-Legendrian, so that
![]() $\mathrm {C}(L) \subset C$
is both
$\mathrm {C}(L) \subset C$
is both
![]() $\omega _2$
-Lagrangian and
$\omega _2$
-Lagrangian and
![]() $\omega _3$
-Lagrangian, and therefore
$\omega _3$
-Lagrangian, and therefore
![]() $\mathrm {C}(L)$
is
$\mathrm {C}(L)$
is
![]() $I_1$
-complex Lagrangian. This proves (v).
$I_1$
-complex Lagrangian. This proves (v).
It remains only to involve condition (vi). For this, note that (v)
![]() $\implies $
(vi) follows from Corollary 3.9, and (vi)
$\implies $
(vi) follows from Corollary 3.9, and (vi)
![]() $\implies $
(iii) follows from Proposition 3.7.
$\implies $
(iii) follows from Proposition 3.7.
The results of this subsection can be summarized in the following table.

4.4.2
 $p_1$
-horizontal lifts
$p_1$
-horizontal lifts
Let
![]() $L \subset M^{4n+3}$
be a submanifold, and recall that L is
$L \subset M^{4n+3}$
be a submanifold, and recall that L is
![]() $p_1$
-horizontal if and only if it is
$p_1$
-horizontal if and only if it is
![]() $\alpha _1$
-isotropic. In this case,
$\alpha _1$
-isotropic. In this case,
![]() $\dim (L) \leq 2n+1$
, and its projection
$\dim (L) \leq 2n+1$
, and its projection
![]() $p_1(L) \subset Z$
is
$p_1(L) \subset Z$
is
![]() $\omega _{\mathrm {KE}}$
-isotropic. Conversely:
$\omega _{\mathrm {KE}}$
-isotropic. Conversely:
Proposition 4.23 Let
![]() $\Sigma \subset Z^{4n+2}$
be a submanifold. Then
$\Sigma \subset Z^{4n+2}$
be a submanifold. Then
![]() $\Sigma $
locally lifts to a
$\Sigma $
locally lifts to a
![]() $p_1$
-horizontal submanifold of M if and only if
$p_1$
-horizontal submanifold of M if and only if
![]() $\Sigma $
is
$\Sigma $
is
![]() $\omega _{\mathrm {KE}}$
-isotropic. In this case,
$\omega _{\mathrm {KE}}$
-isotropic. In this case,
![]() $\dim (\Sigma ) \leq 2n+1$
.
$\dim (\Sigma ) \leq 2n+1$
.
Proof Suppose first that
![]() $\Sigma $
locally lifts to a
$\Sigma $
locally lifts to a
![]() $p_1$
-horizontal submanifold
$p_1$
-horizontal submanifold
![]() $\widehat {\Sigma } \subset M$
. Since
$\widehat {\Sigma } \subset M$
. Since
![]() $\widehat {\Sigma }$
is
$\widehat {\Sigma }$
is
![]() $p_1$
-horizontal, we have that
$p_1$
-horizontal, we have that
![]() $\left .\alpha _1\right |_{\widehat {\Sigma }} = 0$
. Therefore, Proposition 3.6 implies that
$\left .\alpha _1\right |_{\widehat {\Sigma }} = 0$
. Therefore, Proposition 3.6 implies that
![]() $\left .(p_1^*\omega _{\mathrm {KE}})\right |_{\widehat {\Sigma }} = \left .\Omega _1\right |_{\widehat {\Sigma }} = 0$
, and hence
$\left .(p_1^*\omega _{\mathrm {KE}})\right |_{\widehat {\Sigma }} = \left .\Omega _1\right |_{\widehat {\Sigma }} = 0$
, and hence
![]() $\left .\omega _{\mathrm {KE}}\right |_\Sigma = 0$
.
$\left .\omega _{\mathrm {KE}}\right |_\Sigma = 0$
.
Conversely, suppose that
![]() $\Sigma $
is
$\Sigma $
is
![]() $\omega _{\mathrm {KE}}$
-isotropic. Since
$\omega _{\mathrm {KE}}$
-isotropic. Since
![]() $p_1 \colon M \to Z$
is a Riemannian submersion, the restriction of the derivative
$p_1 \colon M \to Z$
is a Riemannian submersion, the restriction of the derivative
![]() $(p_1)_* \colon TM \to TZ$
to the
$(p_1)_* \colon TM \to TZ$
to the
![]() $p_1$
-horizontal subbundle
$p_1$
-horizontal subbundle
![]() $\mathrm {Ker}(\alpha _1) \subset TM$
is an isometric isomorphism. Consider the distribution on M defined by
$\mathrm {Ker}(\alpha _1) \subset TM$
is an isometric isomorphism. Consider the distribution on M defined by
![]() $D := (p_1)_*|_{\mathrm {Ker}(\alpha _1)}^{-1}(T\Sigma ) \subset TM$
. Since
$D := (p_1)_*|_{\mathrm {Ker}(\alpha _1)}^{-1}(T\Sigma ) \subset TM$
. Since
![]() $\Sigma $
is
$\Sigma $
is
![]() $\omega _{\mathrm {KE}}$
-isotropic, we have
$\omega _{\mathrm {KE}}$
-isotropic, we have
![]() $\omega _{\mathrm {KE}}|_{T\Sigma } = 0$
, and therefore
$\omega _{\mathrm {KE}}|_{T\Sigma } = 0$
, and therefore
![]() $2\Omega _1|_D = 2(p_1^*\omega _{\mathrm {KE}})|_{D} = 0$
. Since, by (3.5),
$2\Omega _1|_D = 2(p_1^*\omega _{\mathrm {KE}})|_{D} = 0$
. Since, by (3.5),
![]() $2\Omega _1$
is the curvature
$2\Omega _1$
is the curvature
![]() $2$
-form of the connection
$2$
-form of the connection
![]() $\alpha _1$
on the bundle
$\alpha _1$
on the bundle
![]() $p_1 \colon M \to Z$
, an application of the Frobenius theorem implies that D is locally integrable. By construction, the integral submanifolds of D are (local)
$p_1 \colon M \to Z$
, an application of the Frobenius theorem implies that D is locally integrable. By construction, the integral submanifolds of D are (local)
![]() $p_1$
-horizontal lifts of
$p_1$
-horizontal lifts of
![]() $\Sigma $
.
$\Sigma $
.
4.4.3
 $p_1$
-horizontality and CR isotropic submanifolds
$p_1$
-horizontality and CR isotropic submanifolds
Note that if
![]() $L \subset M$
is
$L \subset M$
is
![]() $p_1$
-horizontal, then L cannot be
$p_1$
-horizontal, then L cannot be
![]() $I_1$
-CR. Nevertheless, it is possible for L to be
$I_1$
-CR. Nevertheless, it is possible for L to be
![]() $I_2$
-CR or
$I_2$
-CR or
![]() $I_3$
-CR. Moreover, it is also possible for L to be both
$I_3$
-CR. Moreover, it is also possible for L to be both
![]() $p_1$
- and
$p_1$
- and
![]() $p_2$
-horizontal simultaneously. The following proposition elaborates on this.
$p_2$
-horizontal simultaneously. The following proposition elaborates on this.
Proposition 4.24 Let
![]() $L^{2k+1} \subset M$
be a
$L^{2k+1} \subset M$
be a
![]() $(2k+1)$
-dimensional submanifold,
$(2k+1)$
-dimensional submanifold,
![]() $3 \leq 2k+1 \leq 2n+1$
. Then:
$3 \leq 2k+1 \leq 2n+1$
. Then:
-
(1) L is
 $I_2$
-CR and
$I_2$
-CR and
 $p_1$
-horizontal if and only if L is
$p_1$
-horizontal if and only if L is
 $I_2$
-CR isotropic.
$I_2$
-CR isotropic. -
(2) Suppose
 $\dim (L) = 2n+1$
. Then L is
$\dim (L) = 2n+1$
. Then L is
 $I_2$
-CR and
$I_2$
-CR and
 $p_1$
-horizontal
$p_1$
-horizontal
 $\iff L$
is
$\iff L$
is
 $I_2$
-CR Legendrian
$I_2$
-CR Legendrian
 $\iff L$
is
$\iff L$
is
 $p_3$
-horizontal and
$p_3$
-horizontal and
 $p_1$
-horizontal.
$p_1$
-horizontal.
Proof (a) This follows from Proposition 3.8 (iii)
![]() $\iff $
(iv) with indices 1,2,3 replaced by
$\iff $
(iv) with indices 1,2,3 replaced by
![]() $2,1,-3$
.
$2,1,-3$
.
(b) This follows from Corollary 3.9 (iv)
![]() $\iff $
(v), again with 1,2,3 replaced by
$\iff $
(v), again with 1,2,3 replaced by
![]() $2,1,-3$
.
$2,1,-3$
.
Now, given a CR isotropic submanifold
![]() $L \subset M$
, we consider the geometric properties of its projection
$L \subset M$
, we consider the geometric properties of its projection
![]() $p_1(L) \subset Z$
. To state the result, we introduce the following notation. For a vertical unit vector
$p_1(L) \subset Z$
. To state the result, we introduce the following notation. For a vertical unit vector
![]() $V \in \mathsf {V}_z \subset T_zZ$
, we let
$V \in \mathsf {V}_z \subset T_zZ$
, we let
![]() $\beta _V := \iota _V(\mathrm {Re}\,\gamma )$
denote the induced nondegenerate
$\beta _V := \iota _V(\mathrm {Re}\,\gamma )$
denote the induced nondegenerate
![]() $2$
-form on
$2$
-form on
![]() $\mathsf {H}_z$
, and let
$\mathsf {H}_z$
, and let
![]() $J_V \in \mathrm {End}(\mathsf {H}_z)$
denote the corresponding complex structure on
$J_V \in \mathrm {End}(\mathsf {H}_z)$
denote the corresponding complex structure on
![]() $\mathsf {H}_z$
.
$\mathsf {H}_z$
.
Proposition 4.25 Let
![]() $L^{2k+1} \subset M$
be a
$L^{2k+1} \subset M$
be a
![]() $(2k+1)$
-dimensional submanifold,
$(2k+1)$
-dimensional submanifold,
![]() $3 \leq 2k+1 \leq 2n+1$
.
$3 \leq 2k+1 \leq 2n+1$
.
-
(1) If L is
 $\alpha _1$
-isotropic and
$\alpha _1$
-isotropic and
 $(-s_\theta \alpha _2 + c_\theta \alpha _3)$
-isotropic for some
$(-s_\theta \alpha _2 + c_\theta \alpha _3)$
-isotropic for some
 $e^{i\theta } \in S^1$
, then
$e^{i\theta } \in S^1$
, then
 $p_1(L) \subset Z$
is
$p_1(L) \subset Z$
is
 $\omega _{\mathrm {KE}}$
-isotropic and
$\omega _{\mathrm {KE}}$
-isotropic and
 $\omega _{\mathrm {NK}}$
-isotropic.
$\omega _{\mathrm {NK}}$
-isotropic. -
(2) If L is
 $(c_\theta I_2 + s_\theta I_3)$
-CR isotropic for some
$(c_\theta I_2 + s_\theta I_3)$
-CR isotropic for some
 $e^{i\theta } \in S^1$
, then
$e^{i\theta } \in S^1$
, then
 $\Sigma := p_1(L) \subset Z$
is
$\Sigma := p_1(L) \subset Z$
is
 $\omega _{\mathrm {KE}}$
-isotropic,
$\omega _{\mathrm {KE}}$
-isotropic,
 $\omega _{\mathrm {NK}}$
-isotropic, and HV-compatible. Moreover,
$\omega _{\mathrm {NK}}$
-isotropic, and HV-compatible. Moreover,
 $\dim (T_z\Sigma \cap \mathsf {V}) = 1$
for all
$\dim (T_z\Sigma \cap \mathsf {V}) = 1$
for all
 $z \in \Sigma $
, and the
$z \in \Sigma $
, and the
 $2k$
-plane
$2k$
-plane
 $T_z\Sigma \cap \mathsf {H}$
is
$T_z\Sigma \cap \mathsf {H}$
is
 $J_V$
-invariant for any vertical unit vector
$J_V$
-invariant for any vertical unit vector
 $V \in T_z\Sigma \cap \mathsf {V}$
.
$V \in T_z\Sigma \cap \mathsf {V}$
.
Proof (a) Suppose
![]() $L \subset M$
is
$L \subset M$
is
![]() $\alpha _1$
-isotropic and
$\alpha _1$
-isotropic and
![]() $(-s_\theta \alpha _2 + c_\theta \alpha _3)$
-isotropic for some constant
$(-s_\theta \alpha _2 + c_\theta \alpha _3)$
-isotropic for some constant
![]() $e^{i\theta } \in S^1$
. On L, we have
$e^{i\theta } \in S^1$
. On L, we have
![]() $\alpha _1 = 0$
and
$\alpha _1 = 0$
and
![]() $-s_\theta \alpha _2 + c_\theta \alpha _3 = 0$
. This second equation implies
$-s_\theta \alpha _2 + c_\theta \alpha _3 = 0$
. This second equation implies
and hence
![]() $\alpha _2 \wedge \alpha _3 = 0$
on L. Therefore,
$\alpha _2 \wedge \alpha _3 = 0$
on L. Therefore,
![]() $\alpha _1 = 0$
implies
$\alpha _1 = 0$
implies
![]() $0 = d\alpha _1 = 2 \Omega _1 = 2(\alpha _2 \wedge \alpha _3 + \kappa _1) = 2\kappa _1$
, so that
$0 = d\alpha _1 = 2 \Omega _1 = 2(\alpha _2 \wedge \alpha _3 + \kappa _1) = 2\kappa _1$
, so that
![]() $\kappa _1 = 0$
on L. We deduce that
$\kappa _1 = 0$
on L. We deduce that
![]() $\Omega _1|_L = 0$
and
$\Omega _1|_L = 0$
and
![]() $\widetilde {\Omega }_1|_L = 0$
. Therefore, on the projection
$\widetilde {\Omega }_1|_L = 0$
. Therefore, on the projection
![]() $p_1(L) \subset Z$
, we have both
$p_1(L) \subset Z$
, we have both
![]() $\left .\omega _{\mathrm {KE}}\right |_{p_1(L)} = 0$
and
$\left .\omega _{\mathrm {KE}}\right |_{p_1(L)} = 0$
and
![]() $\left .\omega _{\mathrm {NK}}\right |_{p_1(L)} = 0$
.
$\left .\omega _{\mathrm {NK}}\right |_{p_1(L)} = 0$
.
(b) Suppose
![]() $L \subset M$
is
$L \subset M$
is
![]() $(c_\theta I_2 + s_\theta I_3)$
-CR isotropic, so that L is
$(c_\theta I_2 + s_\theta I_3)$
-CR isotropic, so that L is
![]() $\alpha _1$
-isotropic and
$\alpha _1$
-isotropic and
![]() $(-s_\theta \alpha _2 + c_\theta \alpha _3)$
-isotropic, and
$(-s_\theta \alpha _2 + c_\theta \alpha _3)$
-isotropic, and
![]() $(c_\theta I_2 + s_\theta I_3)$
-CR. By part (a), the projection
$(c_\theta I_2 + s_\theta I_3)$
-CR. By part (a), the projection
![]() $\Sigma := p_1(L)$
is both
$\Sigma := p_1(L)$
is both
![]() $\omega _{\mathrm {KE}}$
-isotropic and
$\omega _{\mathrm {KE}}$
-isotropic and
![]() $\omega _{\mathrm {NK}}$
-isotropic.
$\omega _{\mathrm {NK}}$
-isotropic.
Fix
![]() $x \in L$
, let
$x \in L$
, let
![]() $z = p(x) \in \Sigma $
, set
$z = p(x) \in \Sigma $
, set
![]() $\widetilde {V} = c_\theta A_2 + s_\theta A_3 \in T_xM$
, and let
$\widetilde {V} = c_\theta A_2 + s_\theta A_3 \in T_xM$
, and let
![]() $\mathsf {J}_V = c_\theta \mathsf {J}_2 + s_\theta \mathsf {J}_3$
. By assumption, we can write
$\mathsf {J}_V = c_\theta \mathsf {J}_2 + s_\theta \mathsf {J}_3$
. By assumption, we can write
![]() $T_xL = H_L \oplus \mathbb {R} \widetilde {V}$
for some
$T_xL = H_L \oplus \mathbb {R} \widetilde {V}$
for some
![]() $\mathsf {J}_V$
-invariant
$\mathsf {J}_V$
-invariant
![]() $2k$
-plane
$2k$
-plane
![]() $H_L \subset \widetilde {\mathsf {H}}$
. It follows that
$H_L \subset \widetilde {\mathsf {H}}$
. It follows that
![]() $T_z\Sigma = H_\Sigma \oplus \mathbb {R} V,$
where
$T_z\Sigma = H_\Sigma \oplus \mathbb {R} V,$
where
![]() $H_\Sigma := p_*(H_L) \subset \mathsf {H}$
is a horizontal
$H_\Sigma := p_*(H_L) \subset \mathsf {H}$
is a horizontal
![]() $2k$
-plane, and
$2k$
-plane, and
![]() $V = p_*(\widetilde {V}) \in \mathsf {V}$
is a vertical unit vector. In particular, this shows that
$V = p_*(\widetilde {V}) \in \mathsf {V}$
is a vertical unit vector. In particular, this shows that
![]() $\Sigma $
is HV compatible, and that
$\Sigma $
is HV compatible, and that
![]() $\dim (T_z\Sigma \cap \mathsf {V}) = 1$
.
$\dim (T_z\Sigma \cap \mathsf {V}) = 1$
.
Now, since
![]() $\mathrm {Re}(\Gamma _1) = p^*(\mathrm {Re}(\gamma ))$
, we have that
$\mathrm {Re}(\Gamma _1) = p^*(\mathrm {Re}(\gamma ))$
, we have that
![]() $\iota _{\widetilde {V}}(\mathrm {Re}\,\Gamma _1) = p^*(\iota _{V}(\mathrm {Re}\,\gamma )) = p^*(\beta _V)$
on L. In particular, if
$\iota _{\widetilde {V}}(\mathrm {Re}\,\Gamma _1) = p^*(\iota _{V}(\mathrm {Re}\,\gamma )) = p^*(\beta _V)$
on L. In particular, if
![]() $Y \in H_L$
is a horizontal vector tangent to L, then
$Y \in H_L$
is a horizontal vector tangent to L, then
which shows that
Finally, if
![]() $X \in T_z\Sigma \cap \mathsf {H} = H_\Sigma $
, then
$X \in T_z\Sigma \cap \mathsf {H} = H_\Sigma $
, then
![]() $X = p_*(\widetilde {X})$
for some
$X = p_*(\widetilde {X})$
for some
![]() $\widetilde {X} \in H_L$
. Since
$\widetilde {X} \in H_L$
. Since
![]() $H_L$
is
$H_L$
is
![]() $\mathsf {J}_V$
-invariant, it follows that
$\mathsf {J}_V$
-invariant, it follows that
![]() $\mathsf {J}_V\widetilde {X} \in H_L$
. Therefore,
$\mathsf {J}_V\widetilde {X} \in H_L$
. Therefore,
![]() $J_VX = J_Vp_*(\widetilde {X}) = p_*(\mathsf {J}_V\widetilde {X}) \in p_*(H_L) = H_\Sigma $
, which shows that
$J_VX = J_Vp_*(\widetilde {X}) = p_*(\mathsf {J}_V\widetilde {X}) \in p_*(H_L) = H_\Sigma $
, which shows that
![]() $H_\Sigma $
is
$H_\Sigma $
is
![]() $J_V$
-invariant.
$J_V$
-invariant.
Conversely, we now ask which submanifolds
![]() $\Sigma \subset Z$
admit local
$\Sigma \subset Z$
admit local
![]() $p_1$
-horizontal lifts to CR isotropic submanifolds of M. As we now show, the necessary conditions given in Proposition 4.25(b) are in fact sufficient:
$p_1$
-horizontal lifts to CR isotropic submanifolds of M. As we now show, the necessary conditions given in Proposition 4.25(b) are in fact sufficient:
Proposition 4.26 Let
![]() $\Sigma ^k \subset Z^{4n+2}$
be a submanifold,
$\Sigma ^k \subset Z^{4n+2}$
be a submanifold,
![]() $3 \leq k \leq 2n+1$
, that is,
$3 \leq k \leq 2n+1$
, that is,
![]() $\omega _{\mathrm {KE}}$
-isotropic,
$\omega _{\mathrm {KE}}$
-isotropic,
![]() $\omega _{\mathrm {NK}}$
-isotropic, and HV-compatible.
$\omega _{\mathrm {NK}}$
-isotropic, and HV-compatible.
-
(1) If
 $\Sigma $
is nowhere tangent to
$\Sigma $
is nowhere tangent to
 $\mathsf {H}$
, then every local
$\mathsf {H}$
, then every local
 $p_1$
-horizontal lift of
$p_1$
-horizontal lift of
 $\Sigma $
is
$\Sigma $
is
 $\alpha _1$
-isotropic and
$\alpha _1$
-isotropic and
 $(-s_\theta \alpha _2 + c_\theta \alpha _3)$
-isotropic for some constant
$(-s_\theta \alpha _2 + c_\theta \alpha _3)$
-isotropic for some constant
 $e^{i\theta } \in S^1$
.
$e^{i\theta } \in S^1$
. -
(2) If
 $\dim (T_z\Sigma \cap \mathsf {V}) = 1$
for all
$\dim (T_z\Sigma \cap \mathsf {V}) = 1$
for all
 $z \in \Sigma $
, and if
$z \in \Sigma $
, and if
 $T_z\Sigma \cap \mathsf {H}$
is
$T_z\Sigma \cap \mathsf {H}$
is
 $J_V$
-invariant for any vertical unit vector
$J_V$
-invariant for any vertical unit vector
 $V \in T_z\Sigma \cap \mathsf {V}$
, then every local
$V \in T_z\Sigma \cap \mathsf {V}$
, then every local
 $p_1$
-horizontal lift of
$p_1$
-horizontal lift of
 $\Sigma $
is
$\Sigma $
is
 $(c_\theta I_2 + s_\theta I_3)$
-CR isotropic for some constant
$(c_\theta I_2 + s_\theta I_3)$
-CR isotropic for some constant
 $e^{i\theta } \in S^1$
.
$e^{i\theta } \in S^1$
.
Proof (a) Let
![]() $\Sigma \subset Z$
be as in the statement. Since
$\Sigma \subset Z$
be as in the statement. Since
![]() $\Sigma $
is
$\Sigma $
is
![]() $\omega _{\mathrm {KE}}$
-isotropic, Proposition 4.23 implies that
$\omega _{\mathrm {KE}}$
-isotropic, Proposition 4.23 implies that
![]() $\Sigma $
locally admits a
$\Sigma $
locally admits a
![]() $p_1$
-horizontal lift to a k-dimensional submanifold
$p_1$
-horizontal lift to a k-dimensional submanifold
![]() ${L \subset M}$
, which is automatically
${L \subset M}$
, which is automatically
![]() $\alpha _1$
-isotropic. Moreover, since
$\alpha _1$
-isotropic. Moreover, since
![]() $\Sigma $
is HV-compatible, and since
$\Sigma $
is HV-compatible, and since
![]() $(p_1)_*|_{\mathrm {Ker}(\alpha _1)} \colon \mathrm {Ker}(\alpha _1) \to TZ$
is an isomorphism that respects the horizontal-vertical splitting, it follows that
$(p_1)_*|_{\mathrm {Ker}(\alpha _1)} \colon \mathrm {Ker}(\alpha _1) \to TZ$
is an isomorphism that respects the horizontal-vertical splitting, it follows that
![]() $TL$
splits as
$TL$
splits as
Now, note that the system
![]() $\left .\omega _{\mathrm {KE}}\right |_\Sigma = \left .\omega _{\mathrm {NK}}\right |_\Sigma = 0$
is equivalent to
$\left .\omega _{\mathrm {KE}}\right |_\Sigma = \left .\omega _{\mathrm {NK}}\right |_\Sigma = 0$
is equivalent to
![]() $\left .\omega _{\mathsf {V}}\right |_\Sigma = \left .\omega _{\mathsf {H}}\right |_\Sigma = 0$
. Since
$\left .\omega _{\mathsf {V}}\right |_\Sigma = \left .\omega _{\mathsf {H}}\right |_\Sigma = 0$
. Since
![]() $p_1^*(\omega _{\mathsf {V}}) = \alpha _2 \wedge \alpha _3$
, it follows that
$p_1^*(\omega _{\mathsf {V}}) = \alpha _2 \wedge \alpha _3$
, it follows that
![]() $\{\alpha _2|_L, \alpha _3|_L\}$
is a linearly dependent set of
$\{\alpha _2|_L, \alpha _3|_L\}$
is a linearly dependent set of
![]() $1$
-forms on L. Moreover, since
$1$
-forms on L. Moreover, since
![]() $\Sigma $
is nowhere tangent to
$\Sigma $
is nowhere tangent to
![]() $\mathsf {H}$
, it follows that L is nowhere tangent to
$\mathsf {H}$
, it follows that L is nowhere tangent to
![]() $\widetilde {\mathsf {H}} = \mathrm {Ker}(\alpha _1, \alpha _2, \alpha _3)$
, and thus there is no point of L at which
$\widetilde {\mathsf {H}} = \mathrm {Ker}(\alpha _1, \alpha _2, \alpha _3)$
, and thus there is no point of L at which
![]() $\alpha _2|_L, \alpha _3|_L$
simultaneously vanish. Therefore, there is an
$\alpha _2|_L, \alpha _3|_L$
simultaneously vanish. Therefore, there is an
![]() $S^1$
-valued function
$S^1$
-valued function
![]() $e^{i\theta } \colon L \to S^1$
such that the
$e^{i\theta } \colon L \to S^1$
such that the
![]() $1$
-form
$1$
-form
vanishes on L. It remains to show that
![]() $e^{i\theta }$
is constant on L. For this, we compute on L that
$e^{i\theta }$
is constant on L. For this, we compute on L that
where we have used that
![]() $\alpha _1|_L = 0$
to compute
$\alpha _1|_L = 0$
to compute
![]() $d\alpha _2 = 2\kappa _2$
and
$d\alpha _2 = 2\kappa _2$
and
![]() $d\alpha _3 = 2\kappa _3$
. Now, the first term is in
$d\alpha _3 = 2\kappa _3$
. Now, the first term is in
![]() $(T^*L \otimes \widetilde {\mathsf {V}}^*)|_L$
, while the second is in
$(T^*L \otimes \widetilde {\mathsf {V}}^*)|_L$
, while the second is in
![]() $\Lambda ^2(\widetilde {\mathsf {H}}^*)|_L$
, so by equation (4.9), they vanish independently. In particular,
$\Lambda ^2(\widetilde {\mathsf {H}}^*)|_L$
, so by equation (4.9), they vanish independently. In particular,
![]() $d\theta \wedge (-s_\theta \alpha _2 + c_\theta \alpha _3) = 0$
. Together with the equation
$d\theta \wedge (-s_\theta \alpha _2 + c_\theta \alpha _3) = 0$
. Together with the equation
![]() $c_\theta \alpha _2 + s_\theta \alpha _3 = 0$
on L, this implies that
$c_\theta \alpha _2 + s_\theta \alpha _3 = 0$
on L, this implies that
![]() $d \theta \wedge \alpha _2 = 0 $
and
$d \theta \wedge \alpha _2 = 0 $
and
![]() $d \theta \wedge \alpha _3 = 0$
, which yields
$d \theta \wedge \alpha _3 = 0$
, which yields
![]() $d\theta = 0$
, so (since L is assumed connected)
$d\theta = 0$
, so (since L is assumed connected)
![]() $\theta $
is constant.
$\theta $
is constant.
(b) Let
![]() $\Sigma \subset Z$
be as in the statement. By part (a), every local
$\Sigma \subset Z$
be as in the statement. By part (a), every local
![]() $p_1$
-horizontal lift
$p_1$
-horizontal lift
![]() ${L \subset M}$
of the submanifold
${L \subset M}$
of the submanifold
![]() $\Sigma \subset Z$
is
$\Sigma \subset Z$
is
![]() $\alpha _1$
-isotropic and
$\alpha _1$
-isotropic and
![]() $(-s_\theta \alpha _2 + c_\theta \alpha _2)$
-isotropic for some
$(-s_\theta \alpha _2 + c_\theta \alpha _2)$
-isotropic for some
![]() ${e^{i\theta } \in S^1}$
. Thus, it remains only to show that L is
${e^{i\theta } \in S^1}$
. Thus, it remains only to show that L is
![]() $(c_\theta I_2 + s_\theta I_3)$
-CR.
$(c_\theta I_2 + s_\theta I_3)$
-CR.
Fix
![]() $x \in L$
, and let
$x \in L$
, and let
![]() $z = p_1(x) \in \Sigma $
. By assumption, we may split
$z = p_1(x) \in \Sigma $
. By assumption, we may split
![]() $T_z\Sigma = H_\Sigma \oplus \mathbb {R} V$
, where
$T_z\Sigma = H_\Sigma \oplus \mathbb {R} V$
, where
![]() $V \in \mathsf {V}$
is a unit vector, and
$V \in \mathsf {V}$
is a unit vector, and
![]() $H_\Sigma \subset \mathsf {H}$
is
$H_\Sigma \subset \mathsf {H}$
is
![]() $J_V$
-invariant. Therefore, since
$J_V$
-invariant. Therefore, since
![]() $(p_1)_*$
yields an isomorphism
$(p_1)_*$
yields an isomorphism
![]() $\mathrm {Ker}(\alpha _1)|_x \to T_zZ$
that respects the horizontal–vertical splittings, we may decompose
$\mathrm {Ker}(\alpha _1)|_x \to T_zZ$
that respects the horizontal–vertical splittings, we may decompose
![]() $TL = H_L \oplus \mathbb {R} \widetilde {V}$
, where
$TL = H_L \oplus \mathbb {R} \widetilde {V}$
, where
![]() $H_L \subset \widetilde {\mathsf {H}}$
satisfies
$H_L \subset \widetilde {\mathsf {H}}$
satisfies
![]() $p_*(H_L) = H_\Sigma $
and
$p_*(H_L) = H_\Sigma $
and
![]() $\widetilde {V} \in \widetilde {\mathsf {V}}$
satisfies
$\widetilde {V} \in \widetilde {\mathsf {V}}$
satisfies
![]() $p_*(\widetilde {V}) = V$
.
$p_*(\widetilde {V}) = V$
.
Now, since L is both
![]() $\alpha _1$
-isotropic and
$\alpha _1$
-isotropic and
![]() $(-s_\theta \alpha _2 + c_\theta \alpha _2)$
-isotropic, it follows that
$(-s_\theta \alpha _2 + c_\theta \alpha _2)$
-isotropic, it follows that
![]() $\widetilde {V} = c_\theta A_2 + s_\theta A_3$
. Let
$\widetilde {V} = c_\theta A_2 + s_\theta A_3$
. Let
![]() $\mathsf {J}_V = c_\theta \mathsf {J}_2 + s_\theta \mathsf {J}_3$
. If
$\mathsf {J}_V = c_\theta \mathsf {J}_2 + s_\theta \mathsf {J}_3$
. If
![]() $X \in H_L$
, then
$X \in H_L$
, then
![]() $p_*X \in H_\Sigma $
, so by (4.8) we have
$p_*X \in H_\Sigma $
, so by (4.8) we have
![]() $p_*(\mathsf {J}_VX) = J_V(p_*X) \in H_\Sigma = p_*(H_L)$
, and therefore
$p_*(\mathsf {J}_VX) = J_V(p_*X) \in H_\Sigma = p_*(H_L)$
, and therefore
![]() $\mathsf {J}_VX \in H_L$
. Thus,
$\mathsf {J}_VX \in H_L$
. Thus,
![]() $H_L$
is
$H_L$
is
![]() $\mathsf {J}_V$
-invariant, and so L is
$\mathsf {J}_V$
-invariant, and so L is
![]() $(c_\theta I_2 + s_\theta I_3)$
-CR.
$(c_\theta I_2 + s_\theta I_3)$
-CR.
In the highest and lowest dimensions, the relationship between CR isotropic submanifolds of M and their projections in Z becomes simpler. Indeed, in the top dimension:
-
(1) If
 $L^{2n+1} \subset M^{4n+3}$
is
$L^{2n+1} \subset M^{4n+3}$
is
 $(c_\theta I_2 + s_\theta I_3)$
-CR Legendrian for some
$(c_\theta I_2 + s_\theta I_3)$
-CR Legendrian for some
 $e^{i\theta } \in S^1$
, then
$e^{i\theta } \in S^1$
, then
 $p_1(L) \subset Z$
is
$p_1(L) \subset Z$
is
 $\omega _{\mathrm {KE}}$
-Lagrangian and
$\omega _{\mathrm {KE}}$
-Lagrangian and
 $\omega _{\mathrm {NK}}$
-Lagrangian.
$\omega _{\mathrm {NK}}$
-Lagrangian. -
(2) Conversely, if
 $\Sigma ^{2n+1} \subset Z^{4n+2}$
is
$\Sigma ^{2n+1} \subset Z^{4n+2}$
is
 $\omega _{\mathrm {KE}}$
-Lagrangian and
$\omega _{\mathrm {KE}}$
-Lagrangian and
 $\omega _{\mathrm {NK}}$
-Lagrangian, then every local
$\omega _{\mathrm {NK}}$
-Lagrangian, then every local
 $p_1$
-horizontal lift of
$p_1$
-horizontal lift of
 $\Sigma $
is
$\Sigma $
is
 $(c_\theta I_2 + s_\theta I_3)$
-CR Legendrian for some
$(c_\theta I_2 + s_\theta I_3)$
-CR Legendrian for some
 $e^{i\theta } \in S^1$
.
$e^{i\theta } \in S^1$
.
Proof (a) This follows from Proposition 4.25.
(b) Suppose
![]() $\Sigma \subset Z$
is
$\Sigma \subset Z$
is
![]() $\omega _{\mathrm {KE}}$
-Lagrangian and
$\omega _{\mathrm {KE}}$
-Lagrangian and
![]() $\omega _{\mathrm {NK}}$
-Lagrangian. By Proposition 4.15(b), it follows that
$\omega _{\mathrm {NK}}$
-Lagrangian. By Proposition 4.15(b), it follows that
![]() $\Sigma $
is HV compatible, and that
$\Sigma $
is HV compatible, and that
![]() $\dim (T_z\Sigma \cap \mathsf {V}) = 1$
at each
$\dim (T_z\Sigma \cap \mathsf {V}) = 1$
at each
![]() $z \in \Sigma $
. Therefore, by Proposition 4.26(a), every local
$z \in \Sigma $
. Therefore, by Proposition 4.26(a), every local
![]() $p_1$
-horizontal lift
$p_1$
-horizontal lift
![]() $L \subset M$
is
$L \subset M$
is
![]() $\alpha _1$
-Legendrian and
$\alpha _1$
-Legendrian and
![]() $(-s_\theta \alpha _2 + c_\theta \alpha _3)$
-Legendrian for some constant
$(-s_\theta \alpha _2 + c_\theta \alpha _3)$
-Legendrian for some constant
![]() $e^{i\theta } \in S^1$
. By Corollary 3.9(v)
$e^{i\theta } \in S^1$
. By Corollary 3.9(v)
![]() $\implies $
(iv), it follows that L is
$\implies $
(iv), it follows that L is
![]() $(c_\theta I_2 + s_\theta I_3)$
-CR Legendrian.
$(c_\theta I_2 + s_\theta I_3)$
-CR Legendrian.
-
(1) If
 $L^{3} \subset M^{4n+3}$
is
$L^{3} \subset M^{4n+3}$
is
 $(c_\theta I_2 + s_\theta I_3)$
-CR isotropic for some
$(c_\theta I_2 + s_\theta I_3)$
-CR isotropic for some
 $e^{i\theta } \in S^1$
, then
$e^{i\theta } \in S^1$
, then
 $p_1(L) \subset Z$
is (up to a change of orientation)
$p_1(L) \subset Z$
is (up to a change of orientation)
 $\mathrm {Re}(\gamma )$
-calibrated and
$\mathrm {Re}(\gamma )$
-calibrated and
 $\omega _{\mathrm {KE}}$
-isotropic.
$\omega _{\mathrm {KE}}$
-isotropic. -
(2) Conversely, if
 $\Sigma ^{3} \subset Z^{4n+2}$
is
$\Sigma ^{3} \subset Z^{4n+2}$
is
 $\mathrm {Re}(\gamma )$
-calibrated and
$\mathrm {Re}(\gamma )$
-calibrated and
 $\omega _{\mathrm {KE}}$
-isotropic, then every local
$\omega _{\mathrm {KE}}$
-isotropic, then every local
 $p_1$
-horizontal lift of
$p_1$
-horizontal lift of
 $\Sigma $
is
$\Sigma $
is
 $(c_\theta I_2 + s_\theta I_3)$
-CR isotropic for some
$(c_\theta I_2 + s_\theta I_3)$
-CR isotropic for some
 $e^{i \theta } \in S^1$
.
$e^{i \theta } \in S^1$
.
Proof (a) Let
![]() $L^{3} \subset M^{4n+3}$
be a
$L^{3} \subset M^{4n+3}$
be a
![]() $(c_\theta I_2 + s_\theta I_3)$
-CR isotropic
$(c_\theta I_2 + s_\theta I_3)$
-CR isotropic
![]() $3$
-fold. By Proposition 4.25(b),
$3$
-fold. By Proposition 4.25(b),
![]() $\Sigma := p_1(L) \subset Z$
is
$\Sigma := p_1(L) \subset Z$
is
![]() $\omega _{\mathrm {KE}}$
-isotropic, so it remains only to show that
$\omega _{\mathrm {KE}}$
-isotropic, so it remains only to show that
![]() $\Sigma $
is
$\Sigma $
is
![]() $\mathrm {Re}(\gamma )$
-calibrated.
$\mathrm {Re}(\gamma )$
-calibrated.
Fix
![]() $z \in \Sigma $
. Again, by Proposition 4.25(b), we may decompose
$z \in \Sigma $
. Again, by Proposition 4.25(b), we may decompose
![]() $T_z\Sigma = H_\Sigma \oplus \mathbb {R} V$
for some
$T_z\Sigma = H_\Sigma \oplus \mathbb {R} V$
for some
![]() $2$
-plane
$2$
-plane
![]() $H_\Sigma \subset \mathsf {H}$
and vertical unit vector
$H_\Sigma \subset \mathsf {H}$
and vertical unit vector
![]() $T \in \mathsf {V}_z$
. Let
$T \in \mathsf {V}_z$
. Let
![]() $N \in \mathsf {V}_z$
be the vertical unit vector such that
$N \in \mathsf {V}_z$
be the vertical unit vector such that
![]() $\{T, N\}$
is an oriented orthonormal basis of
$\{T, N\}$
is an oriented orthonormal basis of
![]() $\mathsf {V}_z$
, and let
$\mathsf {V}_z$
, and let
![]() $\beta _T, \beta _N \in \Lambda ^2(\mathsf {H}_z^*)$
be the induced nondegenerate
$\beta _T, \beta _N \in \Lambda ^2(\mathsf {H}_z^*)$
be the induced nondegenerate
![]() $2$
-forms from
$2$
-forms from
![]() $\gamma $
. Since
$\gamma $
. Since
![]() $H_\Sigma $
is
$H_\Sigma $
is
![]() $J_V$
-invariant, it follows that
$J_V$
-invariant, it follows that
![]() $\left .\beta _V\right |_{H_\Sigma } = \pm \mathrm {vol}_{H_\Sigma }$
. Therefore,
$\left .\beta _V\right |_{H_\Sigma } = \pm \mathrm {vol}_{H_\Sigma }$
. Therefore,
(b) Suppose
![]() $\Sigma ^{3} \subset Z^{4n+2}$
is
$\Sigma ^{3} \subset Z^{4n+2}$
is
![]() $\mathrm {Re}(\gamma )$
-calibrated and
$\mathrm {Re}(\gamma )$
-calibrated and
![]() $\omega _{\mathrm {KE}}$
-isotropic. By Proposition 4.15(c), it follows that
$\omega _{\mathrm {KE}}$
-isotropic. By Proposition 4.15(c), it follows that
![]() $\Sigma $
is HV compatible, so we may write
$\Sigma $
is HV compatible, so we may write
![]() $T_z\Sigma = H_\Sigma \oplus V_\Sigma $
, where
$T_z\Sigma = H_\Sigma \oplus V_\Sigma $
, where
![]() $H_\Sigma \subset \mathsf {H}$
and
$H_\Sigma \subset \mathsf {H}$
and
![]() $V_\Sigma \subset \mathsf {V}$
. The same proposition shows that
$V_\Sigma \subset \mathsf {V}$
. The same proposition shows that
![]() $\dim (V_\Sigma ) = 1$
. Now, let
$\dim (V_\Sigma ) = 1$
. Now, let
![]() $V \in V_\Sigma $
be a unit vector, let
$V \in V_\Sigma $
be a unit vector, let
![]() $\beta _V = \iota _V(\mathrm {Re}(\gamma ))$
denote the induced nondegenerate
$\beta _V = \iota _V(\mathrm {Re}(\gamma ))$
denote the induced nondegenerate
![]() $2$
-form on
$2$
-form on
![]() $\mathsf {H}_z$
, and let
$\mathsf {H}_z$
, and let
![]() $J_V$
be the corresponding complex structure on
$J_V$
be the corresponding complex structure on
![]() $\mathsf {H}_z$
. Since
$\mathsf {H}_z$
. Since
![]() $\left .\mathrm {Re}(\gamma )\right |_\Sigma = \mathrm {vol}_\Sigma = \mathrm {vol}_{V_\Sigma } \wedge \mathrm {vol}_{H_\Sigma }$
, it follows that
$\left .\mathrm {Re}(\gamma )\right |_\Sigma = \mathrm {vol}_\Sigma = \mathrm {vol}_{V_\Sigma } \wedge \mathrm {vol}_{H_\Sigma }$
, it follows that
![]() $\beta _V|_{H_\Sigma } = \pm \mathrm {vol}_{H_\Sigma }$
, which proves that
$\beta _V|_{H_\Sigma } = \pm \mathrm {vol}_{H_\Sigma }$
, which proves that
![]() $H_\Sigma $
is
$H_\Sigma $
is
![]() $J_V$
-invariant. Therefore, Proposition 4.26(b) gives the result.
$J_V$
-invariant. Therefore, Proposition 4.26(b) gives the result.
4.4.4
 $p_1$
-horizontality of special isotropic submanifolds
$p_1$
-horizontality of special isotropic submanifolds
By Proposition 3.15(b), every
![]() $-\theta _{I,3}$
-special isotropic
$-\theta _{I,3}$
-special isotropic
![]() $3$
-fold is
$3$
-fold is
![]() $\phi _2$
-associative. Moreover, since
$\phi _2$
-associative. Moreover, since
![]() $\iota _{A_1}(-\theta _{I,3}) = 0$
by Definition 3.10, Proposition A.2 implies that every
$\iota _{A_1}(-\theta _{I,3}) = 0$
by Definition 3.10, Proposition A.2 implies that every
![]() $-\theta _{I,3}$
-special isotropic
$-\theta _{I,3}$
-special isotropic
![]() $3$
-fold is
$3$
-fold is
![]() $p_1$
-horizontal. We now observe that these necessary conditions are sufficient:
$p_1$
-horizontal. We now observe that these necessary conditions are sufficient:
Proposition 4.29 Let
![]() $L^{2k+1} \subset M^{4n+3}$
be a
$L^{2k+1} \subset M^{4n+3}$
be a
![]() $(2k+1)$
-dimensional submanifold,
$(2k+1)$
-dimensional submanifold,
![]() $3 \leq 2k+1 \leq 2n+1$
.
$3 \leq 2k+1 \leq 2n+1$
.
-
(1) If L is
 $\theta _{I, 2k+1}$
-special isotropic, then L is
$\theta _{I, 2k+1}$
-special isotropic, then L is
 $p_1$
-horizontal.
$p_1$
-horizontal. -
(2) If L is
 $\Psi _1$
-special Legendrian, then L is
$\Psi _1$
-special Legendrian, then L is
 $p_1$
-horizontal.
$p_1$
-horizontal. -
(3) Suppose
 $\dim (L) = 3$
. Then L is
$\dim (L) = 3$
. Then L is
 $-\theta _{I,3}$
-special isotropic if and only if L is
$-\theta _{I,3}$
-special isotropic if and only if L is
 $\phi _2$
-associative and
$\phi _2$
-associative and
 $p_1$
-horizontal.
$p_1$
-horizontal.
Proof (a) Since
![]() $\iota _{A_1}(\theta _{I,2k+1}) = 0$
, Proposition A.2 gives the result.
$\iota _{A_1}(\theta _{I,2k+1}) = 0$
, Proposition A.2 gives the result.
(b) This is simply part (a) in the case of
![]() $\dim (L) = 2n+1$
.
$\dim (L) = 2n+1$
.
(c) Suppose
![]() $\dim (L) = 3$
. Then
$\dim (L) = 3$
. Then
 $$ \begin{align*} & L \text{ is }\phi_2\text{-associative and }p_1\text{-horizontal} \\ & \iff \left.\left( \alpha_1 \wedge \Omega_1 - \alpha_2 \wedge \Omega_2 + \alpha_3 \wedge \Omega_3 \right)\right|_L = \mathrm{vol}_L \, \text{ and } \, \alpha_1|_L = 0 \end{align*} $$
$$ \begin{align*} & L \text{ is }\phi_2\text{-associative and }p_1\text{-horizontal} \\ & \iff \left.\left( \alpha_1 \wedge \Omega_1 - \alpha_2 \wedge \Omega_2 + \alpha_3 \wedge \Omega_3 \right)\right|_L = \mathrm{vol}_L \, \text{ and } \, \alpha_1|_L = 0 \end{align*} $$
and
The result is now immediate.
Example 4.4 For
![]() $n = 1$
, Proposition 4.29(c) is the well-known fact that a
$n = 1$
, Proposition 4.29(c) is the well-known fact that a
![]() $3$
-fold
$3$
-fold
![]() ${L^3 \subset M^7}$
is
${L^3 \subset M^7}$
is
![]() $\phi _2$
-associative and
$\phi _2$
-associative and
![]() $p_1$
-horizontal if and only if it is
$p_1$
-horizontal if and only if it is
![]() $\Psi _1$
-special Legendrian of phase
$\Psi _1$
-special Legendrian of phase
![]() $-1$
.
$-1$
.
4.4.5
 $\mathrm {Re}(\Gamma _1)$
-calibrated
$\mathrm {Re}(\Gamma _1)$
-calibrated
 $3$
-folds of M
$3$
-folds of M
We now observe that
![]() $\mathrm {Re}(\Gamma _1)$
-calibrated
$\mathrm {Re}(\Gamma _1)$
-calibrated
![]() $3$
-folds
$3$
-folds
![]() $L^3 \subset M^{4n+3}$
are always
$L^3 \subset M^{4n+3}$
are always
![]() $p_1$
-horizontal, and describe their projections
$p_1$
-horizontal, and describe their projections
![]() $p_1(L) \subset Z$
. Namely:
$p_1(L) \subset Z$
. Namely:
Proposition 4.30 If
![]() $L^3 \subset M^{4n+3}$
is
$L^3 \subset M^{4n+3}$
is
![]() $\mathrm {Re}(\Gamma _1)$
-calibrated, then L is
$\mathrm {Re}(\Gamma _1)$
-calibrated, then L is
![]() $p_1$
-horizontal (equivalently,
$p_1$
-horizontal (equivalently,
![]() $\alpha _1$
-isotropic). Moreover:
$\alpha _1$
-isotropic). Moreover:
-
(1) If
 $L^3 \subset M^{4n+3}$
is
$L^3 \subset M^{4n+3}$
is
 $\mathrm {Re}(\Gamma _1)$
-calibrated, then L is locally a
$\mathrm {Re}(\Gamma _1)$
-calibrated, then L is locally a
 $p_1$
-horizontal lift of a
$p_1$
-horizontal lift of a
 $3$
-fold in Z that is both
$3$
-fold in Z that is both
 $\mathrm {Re}(\gamma )$
-calibrated and
$\mathrm {Re}(\gamma )$
-calibrated and
 $\omega _{\mathrm {KE}}$
-isotropic.
$\omega _{\mathrm {KE}}$
-isotropic. -
(2) Conversely, if
 $\Sigma ^3 \subset Z^{4n+2}$
is both
$\Sigma ^3 \subset Z^{4n+2}$
is both
 $\mathrm {Re}(\gamma )$
-calibrated and
$\mathrm {Re}(\gamma )$
-calibrated and
 $\omega _{\mathrm {KE}}$
-isotropic, then
$\omega _{\mathrm {KE}}$
-isotropic, then
 $\Sigma $
locally lifts to a
$\Sigma $
locally lifts to a
 $\mathrm {Re}(\Gamma _1)$
-calibrated
$\mathrm {Re}(\Gamma _1)$
-calibrated
 $3$
-fold in M.
$3$
-fold in M.
Proof Let
![]() $L \subset M$
be a
$L \subset M$
be a
![]() $\mathrm {Re}(\Gamma _1)$
-calibrated
$\mathrm {Re}(\Gamma _1)$
-calibrated
![]() $3$
-fold. Since
$3$
-fold. Since
![]() $\mathrm {Re}(\Gamma _1) = \alpha _2 \wedge \kappa _2 + \alpha _3 \wedge \kappa _3$
, we have
$\mathrm {Re}(\Gamma _1) = \alpha _2 \wedge \kappa _2 + \alpha _3 \wedge \kappa _3$
, we have
![]() $\iota _{A_1}(\mathrm {Re}(\Gamma _1)) = 0$
. In view of the splitting
$\iota _{A_1}(\mathrm {Re}(\Gamma _1)) = 0$
. In view of the splitting
![]() $TM = \mathbb {R} A_1 \oplus \mathrm {Ker}(\alpha _1)$
, Proposition A.2 implies that
$TM = \mathbb {R} A_1 \oplus \mathrm {Ker}(\alpha _1)$
, Proposition A.2 implies that
![]() $TL \subset \mathrm {Ker}(\alpha _1)$
, so that L is
$TL \subset \mathrm {Ker}(\alpha _1)$
, so that L is
![]() $p_1$
-horizontal (equivalently,
$p_1$
-horizontal (equivalently,
![]() $\alpha _1|_L = 0$
).
$\alpha _1|_L = 0$
).
Parts (a) and (b) now follow from Proposition 4.23 and the fact that
![]() $\Gamma _1 = p_1^*(\gamma )$
.
$\Gamma _1 = p_1^*(\gamma )$
.
We are now in a position to prove Theorem 3.20, which classifies the
![]() $\mathrm {Re}(\Gamma _1)$
-calibrated
$\mathrm {Re}(\Gamma _1)$
-calibrated
![]() $3$
-folds in terms of more familiar geometries.
$3$
-folds in terms of more familiar geometries.
Theorem 4.31 Let
![]() $L^3 \subset M^{4n+3}$
be a three-dimensional submanifold. The following are equivalent:
$L^3 \subset M^{4n+3}$
be a three-dimensional submanifold. The following are equivalent:
-
(1)
 $\mathrm {C}(L)$
is a
$\mathrm {C}(L)$
is a
 $(c_\theta I_2 + s_\theta I_3)$
-complex isotropic
$(c_\theta I_2 + s_\theta I_3)$
-complex isotropic
 $4$
-fold for some constant
$4$
-fold for some constant
 $e^{i \theta } \in S^1$
.
$e^{i \theta } \in S^1$
. -
(2) L is a
 $(c_\theta I_2 + s_\theta I_3)$
-CR isotropic
$(c_\theta I_2 + s_\theta I_3)$
-CR isotropic
 $3$
-fold for some constant
$3$
-fold for some constant
 $e^{i \theta } \in S^1$
.
$e^{i \theta } \in S^1$
. -
(3) L is locally of the form
 $p_v^{-1}(S)$
for some horizontal
$p_v^{-1}(S)$
for some horizontal
 $J_+$
-complex curve
$J_+$
-complex curve
 $S \subset Z$
and some
$S \subset Z$
and some
 $v = (0, c_\theta , s_\theta )$
.
$v = (0, c_\theta , s_\theta )$
. -
(4) L is locally a
 $p_1$
-horizontal lift of a
$p_1$
-horizontal lift of a
 $3$
-fold
$3$
-fold
 $\Sigma ^3 \subset Z$
that is
$\Sigma ^3 \subset Z$
that is
 $\mathrm {Re}(\gamma )$
-calibrated and
$\mathrm {Re}(\gamma )$
-calibrated and
 $\omega _{\mathrm {KE}}$
-isotropic.
$\omega _{\mathrm {KE}}$
-isotropic. -
(5) L is
 $\mathrm {Re}(\Gamma _1)$
-calibrated.
$\mathrm {Re}(\Gamma _1)$
-calibrated.
5 Submanifolds of quaternionic Kähler manifolds
Thus far, we have studied twistor spaces Z as
![]() $S^1$
-quotients of
$S^1$
-quotients of
![]() $3$
-Sasakian manifolds M. In Section 5.1, we adopt a different perspective, viewing Z as the total space of a canonical
$3$
-Sasakian manifolds M. In Section 5.1, we adopt a different perspective, viewing Z as the total space of a canonical
![]() $S^2$
-bundle
$S^2$
-bundle
![]() $\tau \colon Z \to Q$
over a quaternionic-Kähler manifold
$\tau \colon Z \to Q$
over a quaternionic-Kähler manifold
![]() $Q^{4n}$
. This leads to an alternative construction of the
$Q^{4n}$
. This leads to an alternative construction of the
![]() $\mathrm {Sp}(n)\mathrm {U}(1)$
-structure on Z, including the
$\mathrm {Sp}(n)\mathrm {U}(1)$
-structure on Z, including the
![]() $3$
-form
$3$
-form
![]() $\gamma \in \Omega ^3(Z;\mathbb {C})$
.
$\gamma \in \Omega ^3(Z;\mathbb {C})$
.
In Section 5.2, we turn our attention to totally complex submanifolds of
![]() $Q^{4n}$
, a class that is intimately related to the (semi-)calibrated geometries of previous sections. To explain these relations, we will recall that a totally complex submanifold
$Q^{4n}$
, a class that is intimately related to the (semi-)calibrated geometries of previous sections. To explain these relations, we will recall that a totally complex submanifold
![]() $U^{2k} \subset Q^{4n}$
admits two distinct lifts to Z, namely its
$U^{2k} \subset Q^{4n}$
admits two distinct lifts to Z, namely its
![]() $\tau $
-horizontal lift
$\tau $
-horizontal lift
![]() $\widetilde {U}^{2k} \subset Z$
, and its geodesic circle bundle lift
$\widetilde {U}^{2k} \subset Z$
, and its geodesic circle bundle lift
![]() $\mathcal {L}(U)^{2k+1} \subset Z$
.
$\mathcal {L}(U)^{2k+1} \subset Z$
.
Given such a circle bundle lift
![]() $\mathcal {L}(U) \subset Z$
, we will prove (Corollary 5.12) that its local
$\mathcal {L}(U) \subset Z$
, we will prove (Corollary 5.12) that its local
![]() $p_1$
-horizontal lifts to M are
$p_1$
-horizontal lifts to M are
![]() $(c_\theta I_2 + s_\theta I_3)$
-CR isotropic. The main result of this section (Theorem 5.14) is that the converse also holds: If
$(c_\theta I_2 + s_\theta I_3)$
-CR isotropic. The main result of this section (Theorem 5.14) is that the converse also holds: If
![]() $L \subset M$
is a compact
$L \subset M$
is a compact
![]() $(c_\theta I_2 + s_\theta I_3)$
-CR isotropic submanifold, then L is a
$(c_\theta I_2 + s_\theta I_3)$
-CR isotropic submanifold, then L is a
![]() $p_1$
-horizontal lift of some circle bundle
$p_1$
-horizontal lift of some circle bundle
![]() $\mathcal {L}(U)$
. As an application, we prove (Theorem 5.17) that every compact
$\mathcal {L}(U)$
. As an application, we prove (Theorem 5.17) that every compact
![]() $(2n+1)$
-fold
$(2n+1)$
-fold
![]() $\Sigma \subset Z$
that is Lagrangian with respect both
$\Sigma \subset Z$
that is Lagrangian with respect both
![]() $\omega _{\mathrm {KE}}$
and
$\omega _{\mathrm {KE}}$
and
![]() $\omega _{\mathrm {NK}}$
is of the form
$\omega _{\mathrm {NK}}$
is of the form
![]() $\mathcal {L}(U)$
, thereby generalizing a result of Storm [Reference Storm30] to higher dimensions.
$\mathcal {L}(U)$
, thereby generalizing a result of Storm [Reference Storm30] to higher dimensions.
We remind the reader that as mentioned in the introduction, we only consider submanifolds of Q that do not meet any orbifold points.
5.1 Quaternionic Kähler manifolds
Let
![]() $Q^{4n}$
be a smooth
$Q^{4n}$
be a smooth
![]() $4n$
-manifold,
$4n$
-manifold,
![]() $n \geq 1$
.
$n \geq 1$
.
Definition 5.1 An almost quaternionic-Hermitian structure (or
![]() $\mathrm {Sp}(n)\mathrm {Sp}(1)$
-structure) on Q is a pair
$\mathrm {Sp}(n)\mathrm {Sp}(1)$
-structure) on Q is a pair
![]() $(g_Q, E)$
consisting of an orientation and a Riemannian metric
$(g_Q, E)$
consisting of an orientation and a Riemannian metric
![]() $g_Q$
, and a rank
$g_Q$
, and a rank
![]() $3$
subbundle
$3$
subbundle
![]() $E \subset \mathrm {End}(TQ)$
such that:
$E \subset \mathrm {End}(TQ)$
such that:
-
(1) At each
 $q \in Q$
, there exists a local frame
$q \in Q$
, there exists a local frame
 $(j_1, j_2, j_3)$
of E, called an admissible frame, satisfying the quaternionic relations
$(j_1, j_2, j_3)$
of E, called an admissible frame, satisfying the quaternionic relations
 $j_1j_2 = j_3$
and
$j_1j_2 = j_3$
and
 $j_1^2 = j_2^2 = j_3^2 = -\mathrm {Id}$
.
$j_1^2 = j_2^2 = j_3^2 = -\mathrm {Id}$
. -
(2) Every
 $j \in E$
acts by isometries:
$j \in E$
acts by isometries:
 $g_Q(jX, jY) = g_Q(X,Y)$
, for all
$g_Q(jX, jY) = g_Q(X,Y)$
, for all
 $X,Y \in TQ$
.
$X,Y \in TQ$
.
Equivalently, an almost quaternionic-Hermitian structure may be defined as
![]() $4$
-form
$4$
-form
![]() $\Pi \in \Omega ^4(Q)$
such that at each
$\Pi \in \Omega ^4(Q)$
such that at each
![]() $q \in Q$
, there exists a coframe
$q \in Q$
, there exists a coframe
![]() $L \colon T_qQ \to \mathbb {R}^{4n}$
for which
$L \colon T_qQ \to \mathbb {R}^{4n}$
for which
![]() $\Pi |_q = \frac {1}{6}L^*(\beta _1^2 + \beta _2^2 + \beta _3^2)$
, where
$\Pi |_q = \frac {1}{6}L^*(\beta _1^2 + \beta _2^2 + \beta _3^2)$
, where
![]() $\{\beta _1, \beta _2, \beta _3\}$
is the standard hyperkähler triple on
$\{\beta _1, \beta _2, \beta _3\}$
is the standard hyperkähler triple on
![]() $\mathbb {R}^{4n} = \mathbb {H}^n$
. (See [Reference Salamon27] or [Reference Boyer and Galicki8] for details.)
$\mathbb {R}^{4n} = \mathbb {H}^n$
. (See [Reference Salamon27] or [Reference Boyer and Galicki8] for details.)
Definition 5.2 Let
![]() $n \geq 2$
. An almost quaternionic-Hermitian structure
$n \geq 2$
. An almost quaternionic-Hermitian structure
![]() $(g_Q, E)$
is quaternionic-Kähler (QK) if
$(g_Q, E)$
is quaternionic-Kähler (QK) if
![]() $E \subset \mathrm {End}(TQ)$
is a parallel subbundle (with respect to the connection
$E \subset \mathrm {End}(TQ)$
is a parallel subbundle (with respect to the connection
![]() $\nabla $
induced by
$\nabla $
induced by
![]() $g_Q$
). That is, if
$g_Q$
). That is, if
![]() $\sigma $
is a local section of E, then
$\sigma $
is a local section of E, then
![]() $\nabla \sigma $
is also a local section of E. An equivalent condition is that the
$\nabla \sigma $
is also a local section of E. An equivalent condition is that the
![]() $4$
-form
$4$
-form
![]() $\Pi \in \Omega ^4(Q)$
is
$\Pi \in \Omega ^4(Q)$
is
![]() $g_Q$
-parallel.
$g_Q$
-parallel.
For
![]() $n = 1$
, we say
$n = 1$
, we say
![]() $(Q^4, g_Q)$
is quaternionic-Kähler if the metric
$(Q^4, g_Q)$
is quaternionic-Kähler if the metric
![]() $g_Q$
is Einstein and anti-self-dual.
$g_Q$
is Einstein and anti-self-dual.
Remark 5.3 It is well known that if
![]() $(g_Q, E)$
is a QK structure, then
$(g_Q, E)$
is a QK structure, then
![]() $\mathrm {Hol}(g_Q) \leq \mathrm {Sp}(n)\mathrm {Sp}(1)$
. Conversely, for
$\mathrm {Hol}(g_Q) \leq \mathrm {Sp}(n)\mathrm {Sp}(1)$
. Conversely, for
![]() $n \geq 2$
, if g is a Riemannian metric on Q with
$n \geq 2$
, if g is a Riemannian metric on Q with
![]() $\mathrm {Hol}(g) \leq \mathrm {Sp}(n)\mathrm {Sp}(1)$
, then there exists a g-parallel rank
$\mathrm {Hol}(g) \leq \mathrm {Sp}(n)\mathrm {Sp}(1)$
, then there exists a g-parallel rank
![]() $3$
subbundle
$3$
subbundle
![]() $E \subset \mathrm {End}(TQ)$
such that
$E \subset \mathrm {End}(TQ)$
such that
![]() $(g,E)$
is a QK structure.
$(g,E)$
is a QK structure.
5.1.1 The twistor space
From now on,
![]() $(Q^{4n}, g_Q, E)$
denotes a quaternionic-Kähler
$(Q^{4n}, g_Q, E)$
denotes a quaternionic-Kähler
![]() $4n$
-manifold with positive scalar curvature. The twistor space of Q is the
$4n$
-manifold with positive scalar curvature. The twistor space of Q is the
![]() $(4n+2)$
-manifold
$(4n+2)$
-manifold
The obvious projection map
![]() $\tau \colon Z \to Q$
is then an
$\tau \colon Z \to Q$
is then an
![]() $S^2$
-bundle, and we let
$S^2$
-bundle, and we let
![]() $\mathsf {V} \subset TZ$
denote the (rank
$\mathsf {V} \subset TZ$
denote the (rank
![]() $2$
) vertical bundle. The Levi–Civita connection of
$2$
) vertical bundle. The Levi–Civita connection of
![]() $g_Q$
induces a connection on the vector bundle
$g_Q$
induces a connection on the vector bundle
![]() $E \subset \mathrm {End}(TZ)$
, and hence a connection on the
$E \subset \mathrm {End}(TZ)$
, and hence a connection on the
![]() $S^2$
-subbundle
$S^2$
-subbundle
![]() ${Z \subset E}$
, thereby yielding a
${Z \subset E}$
, thereby yielding a
![]() $4n$
-plane field
$4n$
-plane field
![]() $\mathsf {H} \subset TZ$
such that
$\mathsf {H} \subset TZ$
such that
We now recall the Kähler–Einstein structure
![]() $(g_{\mathrm {KE}}, \omega _{\mathrm {KE}}, J_{\mathrm {KE}})$
on Z. First, define a Riemannian metric
$(g_{\mathrm {KE}}, \omega _{\mathrm {KE}}, J_{\mathrm {KE}})$
on Z. First, define a Riemannian metric
![]() $g_{\mathrm {KE}}$
by requiring that
$g_{\mathrm {KE}}$
by requiring that
![]() $g_{\mathrm {KE}}(\mathsf {H}, \mathsf {V}) = 0$
and
$g_{\mathrm {KE}}(\mathsf {H}, \mathsf {V}) = 0$
and
-
(1) For
 $X,Y \in \mathsf {H}$
, we have
$X,Y \in \mathsf {H}$
, we have
 $g_{\mathrm {KE}}(X,Y) = g_Q(\tau _*X, \tau _*Y)$
.
$g_{\mathrm {KE}}(X,Y) = g_Q(\tau _*X, \tau _*Y)$
. -
(2) On
 $\mathsf {V}$
, the metric
$\mathsf {V}$
, the metric
 $g_{\mathrm {KE}}$
is induced by the fiber metric
$g_{\mathrm {KE}}$
is induced by the fiber metric
 $\langle \cdot , \cdot \rangle $
on
$\langle \cdot , \cdot \rangle $
on
 $E \subset \mathrm {End}(TZ)$
under the identifications
$E \subset \mathrm {End}(TZ)$
under the identifications
 $\mathsf {V}_z \simeq T_z(Z_{\tau (z)}) \subset T_z(E_{\tau (z)}) \simeq E_{\tau (z)}$
.
$\mathsf {V}_z \simeq T_z(Z_{\tau (z)}) \subset T_z(E_{\tau (z)}) \simeq E_{\tau (z)}$
.
Next, define an almost-complex structure
![]() $J_{\mathrm {KE}}$
on Z by requiring that both
$J_{\mathrm {KE}}$
on Z by requiring that both
![]() $\mathsf {H}$
and
$\mathsf {H}$
and
![]() $\mathsf {V}$
are
$\mathsf {V}$
are
![]() $J_{\mathrm {KE}}$
-invariant, and
$J_{\mathrm {KE}}$
-invariant, and
-
(1) On
 $\mathsf {H}_z$
, we set
$\mathsf {H}_z$
, we set
 $J_{\mathrm {KE}} = (\left .\tau _*\right |_{\mathsf {H}_z})^{-1} \circ z \circ \tau _*$
.
$J_{\mathrm {KE}} = (\left .\tau _*\right |_{\mathsf {H}_z})^{-1} \circ z \circ \tau _*$
. -
(2) On
 $\mathsf {V}_z$
, identifying vertical vectors
$\mathsf {V}_z$
, identifying vertical vectors
 $X \in \mathsf {V}_z \simeq T_z(Z_{\tau (z)})$
with endomorphisms
$X \in \mathsf {V}_z \simeq T_z(Z_{\tau (z)})$
with endomorphisms
 ${j_X \in z^\perp = \{j \in E_{\tau (z)} \colon \langle j,z \rangle = 0\}}$
, we set
${j_X \in z^\perp = \{j \in E_{\tau (z)} \colon \langle j,z \rangle = 0\}}$
, we set
 $J_{\mathrm {KE}}X = z \circ j_X$
.
$J_{\mathrm {KE}}X = z \circ j_X$
.
We let
![]() $\omega _{\mathrm {KE}}(X,Y) = g_{\mathrm {KE}}(J_{\mathrm {KE}}X, Y)$
. It is well known [Reference Salamon27] that the triple
$\omega _{\mathrm {KE}}(X,Y) = g_{\mathrm {KE}}(J_{\mathrm {KE}}X, Y)$
. It is well known [Reference Salamon27] that the triple
![]() $(g_{\mathrm {KE}}, \omega _{\mathrm {KE}}, J_{\mathrm {KE}})$
is a Kähler–Einstein structure.
$(g_{\mathrm {KE}}, \omega _{\mathrm {KE}}, J_{\mathrm {KE}})$
is a Kähler–Einstein structure.
Remark 5.4 The
![]() $(\mathrm {U}(2n) \times \mathrm {U}(1))$
-structure
$(\mathrm {U}(2n) \times \mathrm {U}(1))$
-structure
![]() $(g_{\mathrm {KE}}, \omega _{\mathrm {KE}}, J_{\mathrm {KE}}, \mathsf {H})$
just defined on Z coincides with the one described in Section 4.2. In brief, if
$(g_{\mathrm {KE}}, \omega _{\mathrm {KE}}, J_{\mathrm {KE}}, \mathsf {H})$
just defined on Z coincides with the one described in Section 4.2. In brief, if
![]() $Q^{4n}$
is a quaternionic-Kähler manifold of positive scalar curvature, then its Konishi bundle
$Q^{4n}$
is a quaternionic-Kähler manifold of positive scalar curvature, then its Konishi bundle
![]() $M^{4n+3} = F_{\mathrm {SO}(3)}(E)$
, which is the
$M^{4n+3} = F_{\mathrm {SO}(3)}(E)$
, which is the
![]() $\mathrm {SO}(3)$
-frame bundle of the rank
$\mathrm {SO}(3)$
-frame bundle of the rank
![]() $3$
vector bundle
$3$
vector bundle
![]() $E \to Q$
, admits a
$E \to Q$
, admits a
![]() $3$
-Sasakian structure, from which one can recover the
$3$
-Sasakian structure, from which one can recover the
![]() $(\mathrm {U}(2n) \times \mathrm {U}(1))$
-structure on Z. For details, see [Reference Boyer and Galicki8,
$(\mathrm {U}(2n) \times \mathrm {U}(1))$
-structure on Z. For details, see [Reference Boyer and Galicki8,
![]() $\mathrm{Sections}$
12.2 and 13.3.2].
$\mathrm{Sections}$
12.2 and 13.3.2].
Recall from Theorem 4.7 that there exists a canonical
![]() $\mathrm {Sp}(n)\mathrm {U}(1)$
-structure
$\mathrm {Sp}(n)\mathrm {U}(1)$
-structure
![]() ${\gamma \in \Omega ^3(Z; \mathbb {C})}$
on the twistor space
${\gamma \in \Omega ^3(Z; \mathbb {C})}$
on the twistor space
![]() $(Z, g_{\mathrm {KE}}, J_{\mathrm {KE}}, \mathsf {H})$
. We end this section by giving a different proof of the existence of this
$(Z, g_{\mathrm {KE}}, J_{\mathrm {KE}}, \mathsf {H})$
. We end this section by giving a different proof of the existence of this
![]() $\mathrm {Sp}(n)\mathrm {U}(1)$
-structure, working directly from the projection
$\mathrm {Sp}(n)\mathrm {U}(1)$
-structure, working directly from the projection
![]() $\tau \colon Z \to Q$
, without reference to M. At a point
$\tau \colon Z \to Q$
, without reference to M. At a point
![]() $z \in Z$
, choose an admissible frame
$z \in Z$
, choose an admissible frame
![]() $(z, j_2, j_3)$
at
$(z, j_2, j_3)$
at
![]() $\tau (z) \in Q$
. Via the isomorphism
$\tau (z) \in Q$
. Via the isomorphism
the points
![]() $j_2, j_3 \in E_{\tau (z)}$
define vertical vectors at z, and hence (via the metric)
$j_2, j_3 \in E_{\tau (z)}$
define vertical vectors at z, and hence (via the metric)
![]() $1$
-forms
$1$
-forms
![]() $\mu _2, \mu _3 \in \Lambda ^1(\mathsf {V}^*|_z)$
at z. On the other hand,
$\mu _2, \mu _3 \in \Lambda ^1(\mathsf {V}^*|_z)$
at z. On the other hand,
are
![]() $g_{\mathrm {KE}}$
-orthogonal complex structures on
$g_{\mathrm {KE}}$
-orthogonal complex structures on
![]() $\mathsf {H}_z$
, and hence yield
$\mathsf {H}_z$
, and hence yield
![]() $2$
-forms
$2$
-forms
![]() $\beta _2 := g_{\mathrm {KE}}(J_2 \cdot , \cdot )$
and
$\beta _2 := g_{\mathrm {KE}}(J_2 \cdot , \cdot )$
and
![]() $\beta _3 := g_{\mathrm {KE}}(J_3 \cdot , \cdot )$
on
$\beta _3 := g_{\mathrm {KE}}(J_3 \cdot , \cdot )$
on
![]() $\mathsf {H}_z$
. We can now define a
$\mathsf {H}_z$
. We can now define a
![]() $\mathbb {C}$
-valued
$\mathbb {C}$
-valued
![]() $3$
-form
$3$
-form
![]() $\gamma $
at
$\gamma $
at
![]() $z \in Z$
by
$z \in Z$
by
This
![]() $3$
-form is independent of the choice
$3$
-form is independent of the choice
![]() $(j_2, j_3)$
. That is, one can check that if
$(j_2, j_3)$
. That is, one can check that if
![]() $(z, \widetilde {j}_2, \widetilde {j}_3) = (z, c_\theta j_2 + s_\theta j_3, -s_\theta j_2 + c_\theta j_3)$
is another admissible frame at
$(z, \widetilde {j}_2, \widetilde {j}_3) = (z, c_\theta j_2 + s_\theta j_3, -s_\theta j_2 + c_\theta j_3)$
is another admissible frame at
![]() $\tau (z)$
, then the corresponding
$\tau (z)$
, then the corresponding
![]() $1$
-forms
$1$
-forms
![]() $\widetilde {\mu }_2, \widetilde {\mu }_3$
on
$\widetilde {\mu }_2, \widetilde {\mu }_3$
on
![]() $\mathsf {V}_z$
and
$\mathsf {V}_z$
and
![]() $2$
-forms
$2$
-forms
![]() $\widetilde {\beta }_2, \widetilde {\beta }_3$
on
$\widetilde {\beta }_2, \widetilde {\beta }_3$
on
![]() $\mathsf {H}_z$
satisfy
$\mathsf {H}_z$
satisfy
Remark 5.5 In fact, there is a natural one-parameter family of
![]() $3$
-forms on Z given by
$3$
-forms on Z given by
![]() $e^{i\theta }\gamma \in \Omega ^3(Z;\mathbb {C})$
for constants
$e^{i\theta }\gamma \in \Omega ^3(Z;\mathbb {C})$
for constants
![]() $e^{i\theta } \in S^1$
. In particular, the
$e^{i\theta } \in S^1$
. In particular, the
![]() $3$
-form defined by (5.2) agrees with that of Section 4.2 (viz., Theorem 4.7) up to a constant
$3$
-form defined by (5.2) agrees with that of Section 4.2 (viz., Theorem 4.7) up to a constant
![]() $\lambda \in S^1$
. The
$\lambda \in S^1$
. The
![]() $90^\circ $
rotation in formula (5.1) relating
$90^\circ $
rotation in formula (5.1) relating
![]() $(J_2, J_3)$
to
$(J_2, J_3)$
to
![]() $(j_2, j_3)$
was chosen to arrange for
$(j_2, j_3)$
was chosen to arrange for
![]() $\lambda = 1$
. (This follows from Theorem 6.3 and Proposition 4.16.)
$\lambda = 1$
. (This follows from Theorem 6.3 and Proposition 4.16.)
5.1.2 The diamond diagram
Altogether, the various spaces we have considered can be summarized by the diamond diagram:

-
• The flat model is
 $(C,M,Z,Q) = (\mathbb {H}^{n+1}, \mathbb {S}^{4n+3}, \mathbb {CP}^{2n+1}, \mathbb {HP}^n)$
, in which each
$(C,M,Z,Q) = (\mathbb {H}^{n+1}, \mathbb {S}^{4n+3}, \mathbb {CP}^{2n+1}, \mathbb {HP}^n)$
, in which each
 $p_v \colon \mathbb {S}^{4n+3} \to \mathbb {CP}^{2n+1}$
for
$p_v \colon \mathbb {S}^{4n+3} \to \mathbb {CP}^{2n+1}$
for
 $v \in S^2$
is a complex Hopf fibration,
$v \in S^2$
is a complex Hopf fibration,
 $h \colon \mathbb {S}^{4n+3} \to \mathbb {HP}^n$
is the quaternionic Hopf fibration, and
$h \colon \mathbb {S}^{4n+3} \to \mathbb {HP}^n$
is the quaternionic Hopf fibration, and
 $\tau \colon \mathbb {CP}^{2n+1} \to \mathbb {HP}^n$
is the classical twistor fibration.
$\tau \colon \mathbb {CP}^{2n+1} \to \mathbb {HP}^n$
is the classical twistor fibration. -
• Perhaps the second simplest family of examples is
where $$ \begin{align*}(M, Z, Q) = \left( \mathbb{S}(T^*\mathbb{CP}^{n+1}),\, \mathbb{P}(T^*\mathbb{CP}^{n+1}),\, \mathrm{Gr}_2(\mathbb{C}^{n+2}) \right)\!,\end{align*} $$
$$ \begin{align*}(M, Z, Q) = \left( \mathbb{S}(T^*\mathbb{CP}^{n+1}),\, \mathbb{P}(T^*\mathbb{CP}^{n+1}),\, \mathrm{Gr}_2(\mathbb{C}^{n+2}) \right)\!,\end{align*} $$
 $\mathbb {P}(T^*\mathbb {CP}^{n+1})$
and
$\mathbb {P}(T^*\mathbb {CP}^{n+1})$
and
 $\mathbb {S}(T^*\mathbb {CP}^{n+1})$
refer to the projectivized cotangent bundle and unit sphere subbundle of the cotangent bundle of
$\mathbb {S}(T^*\mathbb {CP}^{n+1})$
refer to the projectivized cotangent bundle and unit sphere subbundle of the cotangent bundle of
 $\mathbb {CP}^{n+1}$
, respectively [Reference Tsukada33]. In the case of
$\mathbb {CP}^{n+1}$
, respectively [Reference Tsukada33]. In the case of
 $n = 1$
, these spaces are
$n = 1$
, these spaces are
 $(M^7, Z^6, Q^4) = (N_{1,1},\, \frac {\mathrm {SU}(3)}{T^2},\, \mathbb {CP}^2)$
, where
$(M^7, Z^6, Q^4) = (N_{1,1},\, \frac {\mathrm {SU}(3)}{T^2},\, \mathbb {CP}^2)$
, where
 $N_{1,1} = \frac {\mathrm {SU}(3)}{\mathrm {U}(1)}$
is an exceptional Aloff–Wallach space.
$N_{1,1} = \frac {\mathrm {SU}(3)}{\mathrm {U}(1)}$
is an exceptional Aloff–Wallach space.
-
• An exceptional example is
 $\textstyle (M^{11}, Z^{10}, Q^8) = \left ( \frac {\mathrm {G}_2}{\mathrm {Sp}(1)_+}, \, \frac {\mathrm {G}_2}{\mathrm {U}(2)_+}, \, \frac {\mathrm {G}_2}{\mathrm {SO}(4)} \right )$
. Here,
$\textstyle (M^{11}, Z^{10}, Q^8) = \left ( \frac {\mathrm {G}_2}{\mathrm {Sp}(1)_+}, \, \frac {\mathrm {G}_2}{\mathrm {U}(2)_+}, \, \frac {\mathrm {G}_2}{\mathrm {SO}(4)} \right )$
. Here,
 $M^{11}$
and
$M^{11}$
and
 $Z^{10}$
should not be confused with
$Z^{10}$
should not be confused with
 $\frac {\mathrm {G}_2}{\mathrm {Sp}(1)_-} \cong V_2(\mathbb {R}^7)$
and
$\frac {\mathrm {G}_2}{\mathrm {Sp}(1)_-} \cong V_2(\mathbb {R}^7)$
and
 $\frac {\mathrm {G}_2}{\mathrm {U}(2)_-} \cong \mathrm {Gr}_2(\mathbb {R}^7)$
. See [Reference Boyer and Galicki8, Example 13.6.8].
$\frac {\mathrm {G}_2}{\mathrm {U}(2)_-} \cong \mathrm {Gr}_2(\mathbb {R}^7)$
. See [Reference Boyer and Galicki8, Example 13.6.8].
5.2 Totally complex submanifolds
We now turn to the various submanifolds of a quaternionic-Kähler manifold
![]() $(Q^{4n}, g_Q, E)$
, continuing to assume that
$(Q^{4n}, g_Q, E)$
, continuing to assume that
![]() $g_Q$
has positive scalar curvature.
$g_Q$
has positive scalar curvature.
Definition 5.6 A submanifold
![]() $U^{2k} \subset Q^{4n}$
is almost-complex if there exists a section
$U^{2k} \subset Q^{4n}$
is almost-complex if there exists a section
![]() $i \in \Gamma (Z|_U)$
such that
$i \in \Gamma (Z|_U)$
such that
![]() $i(T_uU) = T_uU$
for all
$i(T_uU) = T_uU$
for all
![]() $u \in U$
.
$u \in U$
.
We will be particularly interested in the following subclass of almost-complex submanifolds.
Definition 5.7 A submanifold
![]() $U^{2k} \subset Q^{4n}$
, for
$U^{2k} \subset Q^{4n}$
, for
![]() $1 \leq k \leq 2n$
, is called totally complex if there exists a section
$1 \leq k \leq 2n$
, is called totally complex if there exists a section
![]() $i \in \Gamma (Z|_U)$
such that at each
$i \in \Gamma (Z|_U)$
such that at each
![]() $u \in U$
:
$u \in U$
:
-
(1)
 $i(T_uU) = T_uU$
.
$i(T_uU) = T_uU$
. -
(2) For all
 $j \in Z_u$
with
$j \in Z_u$
with
 $\langle j,i \rangle = 0$
, we have
$\langle j,i \rangle = 0$
, we have
 $j(T_uU) \subset (T_uU)^\perp $
.
$j(T_uU) \subset (T_uU)^\perp $
.
A totally complex submanifold
![]() $U \subset Q^{4n}$
is called maximal if
$U \subset Q^{4n}$
is called maximal if
![]() $\dim (U) = 2n$
.
$\dim (U) = 2n$
.
Totally complex submanifolds were introduced by Funabashi [Reference Funabashi16], who proved that they are minimal (zero-mean curvature) provided
![]() $n \geq 2$
.
$n \geq 2$
.
-
• In
 $Q = \mathbb {HP}^n$
, the maximal totally complex submanifolds with parallel second fundamental form were classified by Tsukada [Reference Tsukada32]. The list consists of the two infinite families and four sporadic exceptions (in
$Q = \mathbb {HP}^n$
, the maximal totally complex submanifolds with parallel second fundamental form were classified by Tsukada [Reference Tsukada32]. The list consists of the two infinite families and four sporadic exceptions (in $$ \begin{align*} \mathbb{CP}^n & \to \mathbb{HP}^n & \mathbb{CP}^1 \times \frac{\mathrm{SO}(n+1)}{\mathrm{SO}(2) \times \mathrm{SO}(n-1)} & \to \mathbb{HP}^n \ \ \ \ (n \geq 2) \end{align*} $$
$$ \begin{align*} \mathbb{CP}^n & \to \mathbb{HP}^n & \mathbb{CP}^1 \times \frac{\mathrm{SO}(n+1)}{\mathrm{SO}(2) \times \mathrm{SO}(n-1)} & \to \mathbb{HP}^n \ \ \ \ (n \geq 2) \end{align*} $$
 $\mathbb {HP}^6, \mathbb {HP}^9, \mathbb {HP}^{15}$
, and
$\mathbb {HP}^6, \mathbb {HP}^9, \mathbb {HP}^{15}$
, and
 $\mathbb {HP}^{27}$
). Bedulli, Gori, and Podestà [Reference Bedulli, Gori and Podestà7] proved that a maximal totally complex submanifold of
$\mathbb {HP}^{27}$
). Bedulli, Gori, and Podestà [Reference Bedulli, Gori and Podestà7] proved that a maximal totally complex submanifold of
 $\mathbb {HP}^n$
is homogeneous if and only if it appears on Tsukada’s list.
$\mathbb {HP}^n$
is homogeneous if and only if it appears on Tsukada’s list.
-
• If
 $Q = \mathrm {Gr}_2(\mathbb {C}^{n+2})$
, the maximal totally complex submanifolds that are homogeneous have been recently classified by Tsukada [Reference Tsukada33].
$Q = \mathrm {Gr}_2(\mathbb {C}^{n+2})$
, the maximal totally complex submanifolds that are homogeneous have been recently classified by Tsukada [Reference Tsukada33]. -
• If Q is a quaternionic symmetric space, the maximal totally complex submanifolds that are totally geodesic have been classified by Takeuchi [Reference Takeuchi31].
Remark 5.8 Totally complex submanifolds are also studied by Alekseevsky and Marchiafava [Reference Alekseevsky and Marchiafava1, Reference Alekseevsky and Marchiafava2]. In particular, they prove the following results for almost-complex submanifolds
![]() $U^{2k} \subset Q^{4k}$
:
$U^{2k} \subset Q^{4k}$
:
-
• If
 $k \geq 2$
(so that
$k \geq 2$
(so that
 $n \geq 2$
), then For this reason, totally complex submanifolds U of real dimension
$n \geq 2$
), then For this reason, totally complex submanifolds U of real dimension $$ \begin{align*}\nabla_Xi = 0, \ \forall X \in TU \ \iff \ U \text{ is totally-complex} \ \iff \ \left(U, \left.g_Q\right|_{U}, \left.i\right|_{U}\right) \text{ is K\"{a}hler.}\end{align*} $$
$$ \begin{align*}\nabla_Xi = 0, \ \forall X \in TU \ \iff \ U \text{ is totally-complex} \ \iff \ \left(U, \left.g_Q\right|_{U}, \left.i\right|_{U}\right) \text{ is K\"{a}hler.}\end{align*} $$
 $\geq 4$
are sometimes called “Kähler submanifolds” in the literature.
$\geq 4$
are sometimes called “Kähler submanifolds” in the literature.
-
• If
 $k = 1$
and
$k = 1$
and
 $n \geq 2$
, then the equivalence continues to hold. By contrast, the condition that
$n \geq 2$
, then the equivalence continues to hold. By contrast, the condition that $$ \begin{align*}\nabla_Xi = 0, \ \forall X \in TU \ \ \iff \ \ U \text{ is totally complex}\end{align*} $$
$$ \begin{align*}\nabla_Xi = 0, \ \forall X \in TU \ \ \iff \ \ U \text{ is totally complex}\end{align*} $$
 $\left (U, \left .g_Q\right |_{U}, \left .i\right |_{U}\right )$
be Kähler is automatic.
$\left (U, \left .g_Q\right |_{U}, \left .i\right |_{U}\right )$
be Kähler is automatic.
-
• If
 $k = 1$
and
$k = 1$
and
 $n = 1$
, then every oriented surface
$n = 1$
, then every oriented surface
 $U^2 \subset Q^4$
is totally complex, and
$U^2 \subset Q^4$
is totally complex, and
 $\left (U, \left .g_Q\right |_{U}, \left .i\right |_{U}\right )$
is Kähler. By contrast,
$\left (U, \left .g_Q\right |_{U}, \left .i\right |_{U}\right )$
is Kähler. By contrast,
 $\nabla _X i = 0$
for all
$\nabla _X i = 0$
for all
 $X \in TU$
is equivalent to U being superminimal (or infinitesimally holomorphic), a condition on the second fundamental form (see, e.g., [Reference Bryant10, Reference Friedrich14, Reference Friedrich15]).
$X \in TU$
is equivalent to U being superminimal (or infinitesimally holomorphic), a condition on the second fundamental form (see, e.g., [Reference Bryant10, Reference Friedrich14, Reference Friedrich15]).
5.2.1 The horizontal lift
Given a totally complex submanifold
![]() $U^{2k} \subset Q^{4n}$
, there are two natural ways to lift U to a submanifold of the twistor space Z. The first of these is the horizontal lift
$U^{2k} \subset Q^{4n}$
, there are two natural ways to lift U to a submanifold of the twistor space Z. The first of these is the horizontal lift
![]() $\widetilde {U} \subset Z$
, defined as the union of
$\widetilde {U} \subset Z$
, defined as the union of
for
![]() $p \in U$
. The following results were proved in [Reference Takeuchi31, Theorem 4.1], and later generalized in [Reference Alekseevsky and Marchiafava2, Theorem 4.2 and Proposition 4.7].
$p \in U$
. The following results were proved in [Reference Takeuchi31, Theorem 4.1], and later generalized in [Reference Alekseevsky and Marchiafava2, Theorem 4.2 and Proposition 4.7].
Lemma 5.9 [Reference Alekseevsky and Marchiafava2]
Let
![]() $U \subset Q$
be a submanifold, let
$U \subset Q$
be a submanifold, let
![]() $i \in \Gamma (Z|_U)$
be a section over U, and let
$i \in \Gamma (Z|_U)$
be a section over U, and let
![]() $N = i(U) \subset Z$
be its image. Then
$N = i(U) \subset Z$
be its image. Then
![]() $N \subset Z$
is
$N \subset Z$
is
![]() $J_{\mathrm {KE}}$
-complex and horizontal if and only if
$J_{\mathrm {KE}}$
-complex and horizontal if and only if
![]() $(U,i)$
is almost-complex and
$(U,i)$
is almost-complex and
![]() $\nabla _V i = 0$
for all
$\nabla _V i = 0$
for all
![]() $V \in TU$
.
$V \in TU$
.
Proof (
![]() $\Longrightarrow )$
Suppose N is
$\Longrightarrow )$
Suppose N is
![]() $J_{\mathrm {KE}}$
-complex and horizontal. Fix
$J_{\mathrm {KE}}$
-complex and horizontal. Fix
![]() $u \in U$
, and let
$u \in U$
, and let
![]() ${z = i(u) \in N}$
. Let
${z = i(u) \in N}$
. Let
![]() $X \in T_uU$
, and write
$X \in T_uU$
, and write
![]() $X = \tau _*(\widetilde {X})$
for some
$X = \tau _*(\widetilde {X})$
for some
![]() $\widetilde {X} \in T_zN$
. Since
$\widetilde {X} \in T_zN$
. Since
![]() $T_zN \subset T_zZ$
is complex, we have
$T_zN \subset T_zZ$
is complex, we have
![]() $J_{\mathrm {KE}}\widetilde {X} \in T_zN$
. Since
$J_{\mathrm {KE}}\widetilde {X} \in T_zN$
. Since
![]() $\widetilde {X}$
is horizontal, we may calculate
$\widetilde {X}$
is horizontal, we may calculate
![]() $i(u)(X) = z(\tau _*\widetilde {X}) = \tau _*(J_{\mathrm {KE}}\widetilde {X}) \in \tau _*(T_zN) = T_uU$
. This shows that
$i(u)(X) = z(\tau _*\widetilde {X}) = \tau _*(J_{\mathrm {KE}}\widetilde {X}) \in \tau _*(T_zN) = T_uU$
. This shows that
![]() $(U,i)$
is almost-complex. Moreover, since
$(U,i)$
is almost-complex. Moreover, since
![]() $N = i(U)$
is horizontal, it follows that
$N = i(U)$
is horizontal, it follows that
![]() $\nabla _V i = 0$
for all
$\nabla _V i = 0$
for all
![]() $V \in TU$
.
$V \in TU$
.
![]() $(\Longleftarrow )$
Suppose
$(\Longleftarrow )$
Suppose
![]() $(U,i)$
is almost-complex and
$(U,i)$
is almost-complex and
![]() $\nabla _V i = 0$
for all
$\nabla _V i = 0$
for all
![]() $V \in TU$
. Since i is a parallel section, its image N is horizontal. Now, fix
$V \in TU$
. Since i is a parallel section, its image N is horizontal. Now, fix
![]() $z \in N$
, write
$z \in N$
, write
![]() $z = i(u)$
for
$z = i(u)$
for
![]() $u \in U$
, and let
$u \in U$
, and let
![]() $Y \in T_zN$
. Since
$Y \in T_zN$
. Since
![]() $(U,i)$
is almost-complex, we have
$(U,i)$
is almost-complex, we have
![]() $i(u)(\tau _*Y) \in T_uU$
. Therefore, since Y is horizontal, we have
$i(u)(\tau _*Y) \in T_uU$
. Therefore, since Y is horizontal, we have
![]() $\tau _*(J_{\mathrm {KE}}Y) = i(u)(\tau _*Y) \in T_uU = \tau _*(T_zN)$
. Since
$\tau _*(J_{\mathrm {KE}}Y) = i(u)(\tau _*Y) \in T_uU = \tau _*(T_zN)$
. Since
![]() $\tau _* \colon \mathsf {H}_z \to T_uQ$
is an isomorphism, it follows that
$\tau _* \colon \mathsf {H}_z \to T_uQ$
is an isomorphism, it follows that
![]() $J_{\mathrm {KE}}Y \in T_zN$
, which proves that N is
$J_{\mathrm {KE}}Y \in T_zN$
, which proves that N is
![]() $J_{\mathrm {KE}}$
-complex.
$J_{\mathrm {KE}}$
-complex.
Theorem 5.10 [Reference Alekseevsky and Marchiafava2, Reference Takeuchi31]
Let
![]() $\Sigma ^{2k} \subset Z^{4n+2}$
be a submanifold, where
$\Sigma ^{2k} \subset Z^{4n+2}$
be a submanifold, where
![]() $1 \leq k \leq n$
. Then
$1 \leq k \leq n$
. Then
![]() $\Sigma $
is
$\Sigma $
is
![]() $J_{\mathrm {KE}}$
-complex and horizontal if and only if
$J_{\mathrm {KE}}$
-complex and horizontal if and only if
![]() $\Sigma $
is locally of the form
$\Sigma $
is locally of the form
![]() $\widetilde {U}$
for some totally complex
$\widetilde {U}$
for some totally complex
![]() $U^{2k} \subset Q^{4n}$
(resp. a superminimal surface
$U^{2k} \subset Q^{4n}$
(resp. a superminimal surface
![]() $U^2 \subset Q^4$
if
$U^2 \subset Q^4$
if
![]() $n = 1$
).
$n = 1$
).
Proof
![]() $(\Longleftarrow )$
Suppose that
$(\Longleftarrow )$
Suppose that
![]() $\Sigma $
is locally of the form
$\Sigma $
is locally of the form
![]() $\widetilde {U}$
for some totally complex
$\widetilde {U}$
for some totally complex
![]() $U \subset Q$
(resp. superminimal surface if
$U \subset Q$
(resp. superminimal surface if
![]() $n = 1$
). By definition, U is almost-complex, so there exists a section
$n = 1$
). By definition, U is almost-complex, so there exists a section
![]() $i \in \Gamma (Z|_U)$
such that
$i \in \Gamma (Z|_U)$
such that
![]() $i(TU) = TU$
, and hence
$i(TU) = TU$
, and hence
![]() $\widetilde {U} = i(U) \cup -i(U)$
. Moreover, by Remark 5.8, we have
$\widetilde {U} = i(U) \cup -i(U)$
. Moreover, by Remark 5.8, we have
![]() $\nabla _Vi = 0$
for all
$\nabla _Vi = 0$
for all
![]() $V \in TU$
. Therefore, by Lemma 5.9, the submanifolds
$V \in TU$
. Therefore, by Lemma 5.9, the submanifolds
![]() $i(U)$
and
$i(U)$
and
![]() $-i(U)$
are
$-i(U)$
are
![]() $J_{\mathrm {KE}}$
-complex and horizontal, and hence
$J_{\mathrm {KE}}$
-complex and horizontal, and hence
![]() $\Sigma $
is, too.
$\Sigma $
is, too.
![]() $(\Longrightarrow )$
Suppose that
$(\Longrightarrow )$
Suppose that
![]() $\Sigma $
is
$\Sigma $
is
![]() $J_{\mathrm {KE}}$
-complex and horizontal. Since
$J_{\mathrm {KE}}$
-complex and horizontal. Since
![]() $\Sigma $
is horizontal, the Implicit Function Theorem implies that
$\Sigma $
is horizontal, the Implicit Function Theorem implies that
![]() $\Sigma $
is locally of the form
$\Sigma $
is locally of the form
![]() $i(U)$
for some horizontal section
$i(U)$
for some horizontal section
![]() $i \in \Gamma (Z|_U)$
over some submanifold
$i \in \Gamma (Z|_U)$
over some submanifold
![]() $U \subset Q$
. By Lemma 5.9,
$U \subset Q$
. By Lemma 5.9,
![]() $(U,i)$
is almost-complex and
$(U,i)$
is almost-complex and
![]() $\nabla _Vi = 0$
. Thus, by Remark 5.8, U is totally complex (and, in addition, superminimal if
$\nabla _Vi = 0$
. Thus, by Remark 5.8, U is totally complex (and, in addition, superminimal if
![]() $n = 1$
).
$n = 1$
).
5.2.2 The circle bundle lift
Let
![]() $U^{2k} \subset Q^{4n}$
be totally complex. The second natural lift of U is the circle bundle lift
$U^{2k} \subset Q^{4n}$
be totally complex. The second natural lift of U is the circle bundle lift
![]() $\mathcal {L}(U) \subset Z$
, defined as the union of
$\mathcal {L}(U) \subset Z$
, defined as the union of
for
![]() $p \in U$
. Each fiber
$p \in U$
. Each fiber
![]() $\mathcal {L}(U)|_p$
is a great circle in the
$\mathcal {L}(U)|_p$
is a great circle in the
![]() $2$
-sphere
$2$
-sphere
![]() $Z_p$
.
$Z_p$
.
The circle bundle lift was introduced by Ejiri and Tsukada [Reference Ejiri and Tsukada12], who proved that if
![]() $U^{2k} \subset Q^{4n}$
is totally complex and
$U^{2k} \subset Q^{4n}$
is totally complex and
![]() $k \geq 2$
, then
$k \geq 2$
, then
![]() $\mathcal {L}(U) \subset Z$
is a minimal submanifold that is both
$\mathcal {L}(U) \subset Z$
is a minimal submanifold that is both
![]() $\omega _{\mathrm {KE}}$
-isotropic and HV-compatible. In particular, if
$\omega _{\mathrm {KE}}$
-isotropic and HV-compatible. In particular, if
![]() $\dim (U) = 2n \geq 4$
, then
$\dim (U) = 2n \geq 4$
, then
![]() $\mathcal {L}(U) \subset Z$
is a minimal
$\mathcal {L}(U) \subset Z$
is a minimal
![]() $\omega _{\mathrm {KE}}$
-Lagrangian. In the case of
$\omega _{\mathrm {KE}}$
-Lagrangian. In the case of
![]() $k = n = 1$
, circle bundle lifts of superminimal surfaces
$k = n = 1$
, circle bundle lifts of superminimal surfaces
![]() $U^2 \subset Q^4$
were studied by Storm [Reference Storm30].
$U^2 \subset Q^4$
were studied by Storm [Reference Storm30].
We now explore these submanifolds further. Recall that if
![]() $V \in \mathsf {V}_z$
is a vertical unit vector, we let
$V \in \mathsf {V}_z$
is a vertical unit vector, we let
![]() $\beta _V := \iota _V(\mathrm {Re}(\gamma )) \in \Lambda ^2(\mathsf {H}_z^*)$
denote the induced nondegenerate
$\beta _V := \iota _V(\mathrm {Re}(\gamma )) \in \Lambda ^2(\mathsf {H}_z^*)$
denote the induced nondegenerate
![]() $2$
-form on
$2$
-form on
![]() $\mathsf {H}_z$
, and let
$\mathsf {H}_z$
, and let
![]() $J_V$
be the corresponding complex structure on
$J_V$
be the corresponding complex structure on
![]() $\mathsf {H}_z$
.
$\mathsf {H}_z$
.
Theorem 5.11 Let
![]() $U^{2k} \subset Q^{4n}$
be a submanifold with
$U^{2k} \subset Q^{4n}$
be a submanifold with
![]() $1 \leq k \leq n$
. If U is totally complex and
$1 \leq k \leq n$
. If U is totally complex and
![]() $n \geq 2$
, or if U is superminimal and
$n \geq 2$
, or if U is superminimal and
![]() $n = 1$
, then
$n = 1$
, then
![]() $\mathcal {L} := \mathcal {L}(U)$
satisfies the following:
$\mathcal {L} := \mathcal {L}(U)$
satisfies the following:
-
(1)
 $\mathcal {L} \subset Z$
is
$\mathcal {L} \subset Z$
is
 $\omega _{\mathrm {KE}}$
-isotropic,
$\omega _{\mathrm {KE}}$
-isotropic,
 $\omega _{\mathrm {NK}}$
-isotropic, HV-compatible, and satisfies
$\omega _{\mathrm {NK}}$
-isotropic, HV-compatible, and satisfies
 ${\dim (T_z\mathcal {L} \cap \mathsf {V}) = 1}$
at every
${\dim (T_z\mathcal {L} \cap \mathsf {V}) = 1}$
at every
 $z \in \mathcal {L}$
.
$z \in \mathcal {L}$
. -
(2) For any unit vector
 $V \in T_z\mathcal {L} \cap \mathsf {V}$
, the
$V \in T_z\mathcal {L} \cap \mathsf {V}$
, the
 $2k$
-plane
$2k$
-plane
 $T_z\mathcal {L} \cap \mathsf {H}$
is
$T_z\mathcal {L} \cap \mathsf {H}$
is
 $J_V$
-invariant.
$J_V$
-invariant.
Proof Suppose U is totally complex if
![]() $n \geq 2$
, or superminimal if
$n \geq 2$
, or superminimal if
![]() $n = 1$
, and set
$n = 1$
, and set
![]() ${\mathcal {L} := \mathcal {L}(U)}$
. In either case, there exists a section
${\mathcal {L} := \mathcal {L}(U)}$
. In either case, there exists a section
![]() $i \in \Gamma (Z|_U)$
such that
$i \in \Gamma (Z|_U)$
such that
![]() $i(TU) = TU$
and
$i(TU) = TU$
and
![]() $\nabla _Xi = 0$
for all
$\nabla _Xi = 0$
for all
![]() $X \in TU$
.
$X \in TU$
.
(a) Following [Reference Ejiri and Tsukada12, Proof of Lemma 2.1], we orthogonally decompose
![]() ${E|_U = \mathbb {R} i \oplus E'}$
. If
${E|_U = \mathbb {R} i \oplus E'}$
. If
![]() $\sigma \in \Gamma (E')$
is a local section, then
$\sigma \in \Gamma (E')$
is a local section, then
![]() $\langle \sigma , i \rangle = 0$
, so that
$\langle \sigma , i \rangle = 0$
, so that
![]() $\langle \nabla _X \sigma , i \rangle = 0$
, and thus
$\langle \nabla _X \sigma , i \rangle = 0$
, and thus
![]() $\nabla _X \sigma \in \Gamma (E')$
. Thus,
$\nabla _X \sigma \in \Gamma (E')$
. Thus,
![]() $E' \subset E|_U$
is a parallel subbundle. Since
$E' \subset E|_U$
is a parallel subbundle. Since
![]() $\mathcal {L} \subset E'$
is the unit sphere subbundle, it follows that
$\mathcal {L} \subset E'$
is the unit sphere subbundle, it follows that
![]() $\mathcal {L} \subset E'$
is a parallel fiber subbundle. This implies that
$\mathcal {L} \subset E'$
is a parallel fiber subbundle. This implies that
![]() $T\mathcal {L} = H_\Sigma \oplus V_\Sigma $
for subbundles
$T\mathcal {L} = H_\Sigma \oplus V_\Sigma $
for subbundles
![]() $H_\Sigma \subset \mathsf {H}$
and
$H_\Sigma \subset \mathsf {H}$
and
![]() $V_\Sigma \subset \mathsf {V}$
, meaning that
$V_\Sigma \subset \mathsf {V}$
, meaning that
![]() $\mathcal {L}$
is HV compatible.
$\mathcal {L}$
is HV compatible.
We now show that
![]() $\mathcal {L}$
is
$\mathcal {L}$
is
![]() $\omega _{\mathrm {KE}}$
-isotropic and
$\omega _{\mathrm {KE}}$
-isotropic and
![]() $\omega _{\mathrm {NK}}$
-isotropic. Fix
$\omega _{\mathrm {NK}}$
-isotropic. Fix
![]() $z \in \mathcal {L}$
, and recall that
$z \in \mathcal {L}$
, and recall that
Since
![]() $\mathcal {L}$
is HV compatible and
$\mathcal {L}$
is HV compatible and
![]() $\dim (T_z\mathcal {L} \cap \mathsf {V}) = 1$
, it follows that
$\dim (T_z\mathcal {L} \cap \mathsf {V}) = 1$
, it follows that
![]() $\left .\omega _{\mathsf {V}}\right |_{\mathcal {L}} = 0$
. Moreover, if
$\left .\omega _{\mathsf {V}}\right |_{\mathcal {L}} = 0$
. Moreover, if
![]() $X, Y \in T_z\mathcal {L} \cap \mathsf {H}$
, then
$X, Y \in T_z\mathcal {L} \cap \mathsf {H}$
, then
where in the last step we used that
![]() $z(T_{\tau (z)}U) \subset (T_{\tau (z)}U)^\perp $
. This shows that
$z(T_{\tau (z)}U) \subset (T_{\tau (z)}U)^\perp $
. This shows that
![]() $\left .\omega _{\mathsf {H}}\right |_{\mathcal {L}} = 0$
, and therefore
$\left .\omega _{\mathsf {H}}\right |_{\mathcal {L}} = 0$
, and therefore
![]() $\left .\omega _{\mathrm {KE}}\right |_{\mathcal {L}} = 0$
and
$\left .\omega _{\mathrm {KE}}\right |_{\mathcal {L}} = 0$
and
![]() $\left .\omega _{\mathrm {NK}}\right |_{\mathcal {L}} = 0$
.
$\left .\omega _{\mathrm {NK}}\right |_{\mathcal {L}} = 0$
.
(b) Fix
![]() $z \in \mathcal {L}$
, let
$z \in \mathcal {L}$
, let
![]() $u = \tau (z)$
, and let
$u = \tau (z)$
, and let
![]() $V \in T_z\mathcal {L} \cap \mathsf {V}$
be a vertical unit vector. Let
$V \in T_z\mathcal {L} \cap \mathsf {V}$
be a vertical unit vector. Let
![]() ${j \in \mathcal {L}|_{u} \cap z^\perp }$
denote the point on the great circle
${j \in \mathcal {L}|_{u} \cap z^\perp }$
denote the point on the great circle
![]() $\mathcal {L}|_u$
that corresponds to V under the natural isomorphism
$\mathcal {L}|_u$
that corresponds to V under the natural isomorphism
![]() $\mathsf {V}_z \simeq z^\perp $
. Set
$\mathsf {V}_z \simeq z^\perp $
. Set
![]() $i = z \circ j$
, so that
$i = z \circ j$
, so that
![]() $(z,j,i)$
is an admissible frame of
$(z,j,i)$
is an admissible frame of
![]() $E_u$
. By (5.1), we have
$E_u$
. By (5.1), we have
Since U is totally complex, the
![]() $2k$
-plane
$2k$
-plane
![]() $T_uU \subset T_uQ$
is i-invariant. Therefore, if
$T_uU \subset T_uQ$
is i-invariant. Therefore, if
![]() ${X \in T_z\mathcal {L} \cap \mathsf {H}}$
, then
${X \in T_z\mathcal {L} \cap \mathsf {H}}$
, then
![]() $i(\tau _*X) \in T_uU$
, so that
$i(\tau _*X) \in T_uU$
, so that
![]() $J_VX = (\left .\tau _*\right |_{\mathsf {H}_z})^{-1}( i(\tau _*X)) \in T_z\mathcal {L} \cap \mathsf {H}$
, proving that
$J_VX = (\left .\tau _*\right |_{\mathsf {H}_z})^{-1}( i(\tau _*X)) \in T_z\mathcal {L} \cap \mathsf {H}$
, proving that
![]() $T_z\mathcal {L} \cap \mathsf {H}$
is
$T_z\mathcal {L} \cap \mathsf {H}$
is
![]() $J_V$
-invariant.
$J_V$
-invariant.
5.2.3 Circle bundle lifts and CR isotropic submanifolds
We now prove that circle bundle lifts
![]() $\mathcal {L}(U) \subset Z$
are intimately related to CR isotropic submanifolds
$\mathcal {L}(U) \subset Z$
are intimately related to CR isotropic submanifolds
![]() $L \subset M$
. Indeed, the geometric properties of
$L \subset M$
. Indeed, the geometric properties of
![]() $\mathcal {L}(U)$
established in Theorem 5.11 are precisely those needed for its
$\mathcal {L}(U)$
established in Theorem 5.11 are precisely those needed for its
![]() $p_1$
-horizontal lift to be CR isotropic. That is:
$p_1$
-horizontal lift to be CR isotropic. That is:
Corollary 5.12 Let
![]() $U^{2k} \subset Q^{4n}$
be a submanifold with
$U^{2k} \subset Q^{4n}$
be a submanifold with
![]() $1 \leq k \leq n$
. If U is totally complex and
$1 \leq k \leq n$
. If U is totally complex and
![]() $n \geq 2$
, or if U is superminimal and
$n \geq 2$
, or if U is superminimal and
![]() $n = 1$
, then
$n = 1$
, then
![]() $\mathcal {L}(U) \subset Z$
admits local
$\mathcal {L}(U) \subset Z$
admits local
![]() $p_1$
-horizontal lifts to M, and every such lift is
$p_1$
-horizontal lifts to M, and every such lift is
![]() $(c_\theta I_2 + s_\theta I_3)$
-CR isotropic for some
$(c_\theta I_2 + s_\theta I_3)$
-CR isotropic for some
![]() $e^{i\theta } \in S^1$
.
$e^{i\theta } \in S^1$
.
We now aim to establish a converse in the case where L is compact. For this, we need a technical lemma.
Lemma 5.13 Let
![]() $\Sigma ^k \subset Z^{4n+2}$
be a compact submanifold. If
$\Sigma ^k \subset Z^{4n+2}$
be a compact submanifold. If
![]() $\Sigma $
is
$\Sigma $
is
![]() $\omega _{\mathrm {KE}}$
-isotropic, HV-compatible, and
$\omega _{\mathrm {KE}}$
-isotropic, HV-compatible, and
![]() $\dim (T_z\Sigma \cap \mathsf {V}) = 1$
for all
$\dim (T_z\Sigma \cap \mathsf {V}) = 1$
for all
![]() $z \in \Sigma $
, then
$z \in \Sigma $
, then
![]() $U := \tau (\Sigma ) \subset Q^{4n}$
is a
$U := \tau (\Sigma ) \subset Q^{4n}$
is a
![]() $(k-1)$
-dimensional submanifold, and
$(k-1)$
-dimensional submanifold, and
![]() $\left .\tau \right |_\Sigma \colon \Sigma \to U$
is an
$\left .\tau \right |_\Sigma \colon \Sigma \to U$
is an
![]() $S^1$
-bundle whose fibers are geodesics in Z with respect to the Kähler–Einstein metric.
$S^1$
-bundle whose fibers are geodesics in Z with respect to the Kähler–Einstein metric.
Proof Since
![]() $\Sigma $
is HV-compatible and
$\Sigma $
is HV-compatible and
![]() $\dim (T_z\Sigma \cap \mathsf {V}) = 1$
for all
$\dim (T_z\Sigma \cap \mathsf {V}) = 1$
for all
![]() $z \in \Sigma $
, it follows that
$z \in \Sigma $
, it follows that
![]() $\dim (T_z\Sigma \cap \mathsf {H}) = k-1$
. Therefore, the map
$\dim (T_z\Sigma \cap \mathsf {H}) = k-1$
. Therefore, the map
![]() $\left .\tau \right |_\Sigma \colon \Sigma \to Q$
has constant rank
$\left .\tau \right |_\Sigma \colon \Sigma \to Q$
has constant rank
![]() $k -1$
. By the Constant Rank Theorem, each fiber
$k -1$
. By the Constant Rank Theorem, each fiber
![]() $\left .\tau \right |_\Sigma ^{-1}(\tau (z)) \subset \Sigma $
is an embedded
$\left .\tau \right |_\Sigma ^{-1}(\tau (z)) \subset \Sigma $
is an embedded
![]() $1$
-manifold, and therefore (since
$1$
-manifold, and therefore (since
![]() $\Sigma $
is compact) is an at most countable union of disjoint circles.
$\Sigma $
is compact) is an at most countable union of disjoint circles.
We claim that each
![]() $S^1$
-fiber is a geodesic. For this, note that since
$S^1$
-fiber is a geodesic. For this, note that since
![]() $\Sigma $
is
$\Sigma $
is
![]() $\omega _{\mathrm {KE}}$
-isotropic, it admits local
$\omega _{\mathrm {KE}}$
-isotropic, it admits local
![]() $p_1$
-horizontal lifts to M. Let
$p_1$
-horizontal lifts to M. Let
![]() $L \subset M$
be such a lift. Since
$L \subset M$
be such a lift. Since
![]() $\Sigma $
is HV-compatible and
$\Sigma $
is HV-compatible and
![]() $p_1 \colon M \to Z$
respects the horizontal–vertical splitting, we may write
$p_1 \colon M \to Z$
respects the horizontal–vertical splitting, we may write
![]() $TL = H_L \oplus \mathbb {R} \widetilde {V}$
, where
$TL = H_L \oplus \mathbb {R} \widetilde {V}$
, where
![]() $H_L \subset \widetilde {\mathsf {H}}$
and
$H_L \subset \widetilde {\mathsf {H}}$
and
![]() $\widetilde {V} \in \widetilde {\mathsf {V}}$
. Moreover, Proposition 4.26(a) implies that L is
$\widetilde {V} \in \widetilde {\mathsf {V}}$
. Moreover, Proposition 4.26(a) implies that L is
![]() $\alpha _1$
-isotropic and
$\alpha _1$
-isotropic and
![]() $(-s_\theta \alpha _2 + c_\theta \alpha _3)$
-isotropic for some constant
$(-s_\theta \alpha _2 + c_\theta \alpha _3)$
-isotropic for some constant
![]() $e^{i\theta } \in S^1$
. Therefore,
$e^{i\theta } \in S^1$
. Therefore,
![]() $\widetilde {V} = c_\theta A_2 + s_\theta A_3$
is a Reeb vector field, so its integral curves are geodesics in M. Consequently, the integral curves of
$\widetilde {V} = c_\theta A_2 + s_\theta A_3$
is a Reeb vector field, so its integral curves are geodesics in M. Consequently, the integral curves of
![]() $(p_1)_*(\widetilde {V}) \in \mathsf {V} \subset TZ$
are geodesics in Z (and hence geodesics in L), and these are precisely the
$(p_1)_*(\widetilde {V}) \in \mathsf {V} \subset TZ$
are geodesics in Z (and hence geodesics in L), and these are precisely the
![]() $S^1$
-fibers
$S^1$
-fibers
![]() $\left .\tau \right |_\Sigma ^{-1}(\tau (z)) \subset \Sigma $
.
$\left .\tau \right |_\Sigma ^{-1}(\tau (z)) \subset \Sigma $
.
Consequently, since
![]() $\Sigma $
is compact, each
$\Sigma $
is compact, each
![]() $S^1$
-fiber
$S^1$
-fiber
![]() $\left .\tau \right |_\Sigma ^{-1}(\tau (z)) \subset \Sigma $
is an at most countable union of disjoint great circles in the twistor
$\left .\tau \right |_\Sigma ^{-1}(\tau (z)) \subset \Sigma $
is an at most countable union of disjoint great circles in the twistor
![]() $2$
-sphere. Since any two great circles in a round
$2$
-sphere. Since any two great circles in a round
![]() $2$
-sphere intersect, it follows that each
$2$
-sphere intersect, it follows that each
![]() $S^1$
-fiber consists of a single great circle.
$S^1$
-fiber consists of a single great circle.
It remains to show that
![]() $U := \tau (\Sigma )$
is a
$U := \tau (\Sigma )$
is a
![]() $(k-1)$
-dimensional submanifold of Q. For this, note that since
$(k-1)$
-dimensional submanifold of Q. For this, note that since
![]() $\Sigma $
is a union of great circles, each of which is the
$\Sigma $
is a union of great circles, each of which is the
![]() $p_1$
-image of a Reeb circle in M, it admits a free
$p_1$
-image of a Reeb circle in M, it admits a free
![]() $S^1$
-action. (The action is free because we are working on the regular part of M.) Therefore, the quotient
$S^1$
-action. (The action is free because we are working on the regular part of M.) Therefore, the quotient
![]() $\Sigma /S^1$
admits the structure of smooth
$\Sigma /S^1$
admits the structure of smooth
![]() $(k-1)$
-manifold, and the projection
$(k-1)$
-manifold, and the projection
![]() $\pi \colon \Sigma \to \Sigma /S^1$
is a smooth quotient map.
$\pi \colon \Sigma \to \Sigma /S^1$
is a smooth quotient map.
Now, let
![]() $\widehat {\tau } \colon \Sigma \to U$
denote the map
$\widehat {\tau } \colon \Sigma \to U$
denote the map
![]() $\tau |_\Sigma $
with restricted codomain, equip
$\tau |_\Sigma $
with restricted codomain, equip
![]() $U \subset Q$
with the subspace topology, and let
$U \subset Q$
with the subspace topology, and let
![]() $\iota \colon U \hookrightarrow Q$
be the inclusion map. If
$\iota \colon U \hookrightarrow Q$
be the inclusion map. If
![]() $V \subset U$
is open, then
$V \subset U$
is open, then
![]() $V = U \cap W$
for some open set
$V = U \cap W$
for some open set
![]() $W \subset Q$
, and hence
$W \subset Q$
, and hence
![]() $\widehat {\tau }^{-1}(V) = \Sigma \cap \tau ^{-1}(W)$
is open subset of
$\widehat {\tau }^{-1}(V) = \Sigma \cap \tau ^{-1}(W)$
is open subset of
![]() $\Sigma $
, which proves that
$\Sigma $
, which proves that
![]() $\widehat {\tau }$
is continuous. Since
$\widehat {\tau }$
is continuous. Since
![]() $\widehat {\tau }$
is a continuous surjection from a compact domain, it follows that
$\widehat {\tau }$
is a continuous surjection from a compact domain, it follows that
![]() $\widehat {\tau }$
is a quotient map. Since
$\widehat {\tau }$
is a quotient map. Since
![]() $\pi $
and
$\pi $
and
![]() $\widehat {\tau }$
are quotient maps that are constant on each other’s fibers, there exists a unique homeomorphism
$\widehat {\tau }$
are quotient maps that are constant on each other’s fibers, there exists a unique homeomorphism
![]() $F \colon \Sigma /S^1 \to U$
such that
$F \colon \Sigma /S^1 \to U$
such that
![]() $\widehat {\tau } = F \circ \pi $
. Choosing a smooth local section
$\widehat {\tau } = F \circ \pi $
. Choosing a smooth local section
![]() $\sigma \colon Y \to \Sigma $
of
$\sigma \colon Y \to \Sigma $
of
![]() $\pi $
, where
$\pi $
, where
![]() $Y \subset \Sigma /S^1$
is an open set, we observe that
$Y \subset \Sigma /S^1$
is an open set, we observe that
![]() $\tau |_\Sigma \circ \sigma \colon Y \to Q$
is a smooth map of rank
$\tau |_\Sigma \circ \sigma \colon Y \to Q$
is a smooth map of rank
![]() $k-1$
, which implies that
$k-1$
, which implies that
![]() $\iota \circ F \colon \Sigma /S^1 \to Q$
is also a smooth map of rank
$\iota \circ F \colon \Sigma /S^1 \to Q$
is also a smooth map of rank
![]() $k-1$
, and therefore a smooth embedding whose image is U.
$k-1$
, and therefore a smooth embedding whose image is U.
The converse to Corollary 5.12 is now given by the following.
Theorem 5.14 Let
![]() $L^{2k+1} \subset M^{4n+3}$
be a compact submanifold,
$L^{2k+1} \subset M^{4n+3}$
be a compact submanifold,
![]() $1 \leq k \leq n$
. If L is
$1 \leq k \leq n$
. If L is
![]() $(c_\theta I_2 + s_\theta I_3)$
-CR isotropic for some
$(c_\theta I_2 + s_\theta I_3)$
-CR isotropic for some
![]() $e^{i\theta } \in S^1$
, and if
$e^{i\theta } \in S^1$
, and if
![]() $p_1(L) \subset Z$
is embedded, then
$p_1(L) \subset Z$
is embedded, then
![]() $p_1(L) = \mathcal {L}(U)$
for some totally complex submanifold
$p_1(L) = \mathcal {L}(U)$
for some totally complex submanifold
![]() $U^{2k} \subset Q^{4n}$
(resp. a superminimal surface
$U^{2k} \subset Q^{4n}$
(resp. a superminimal surface
![]() $U^2 \subset Q^4$
if
$U^2 \subset Q^4$
if
![]() $n = 1$
).
$n = 1$
).
Proof Suppose that
![]() $L \subset M$
is a compact
$L \subset M$
is a compact
![]() $(c_\theta I_2 + s_\theta I_3)$
-CR isotropic
$(c_\theta I_2 + s_\theta I_3)$
-CR isotropic
![]() $(2k+1)$
-fold for some constant
$(2k+1)$
-fold for some constant
![]() $e^{i\theta } \in S^1$
and that
$e^{i\theta } \in S^1$
and that
![]() $\Sigma := p_1(L) \subset Z$
is embedded. By Proposition 4.25(b),
$\Sigma := p_1(L) \subset Z$
is embedded. By Proposition 4.25(b),
![]() $\Sigma $
is
$\Sigma $
is
![]() $\omega _{\mathrm {KE}}$
-isotropic,
$\omega _{\mathrm {KE}}$
-isotropic,
![]() $\omega _{\mathrm {NK}}$
-isotropic, HV-compatible, and
$\omega _{\mathrm {NK}}$
-isotropic, HV-compatible, and
![]() $\dim (T_z\Sigma \cap \mathsf {V}) = 1$
for all
$\dim (T_z\Sigma \cap \mathsf {V}) = 1$
for all
![]() $z \in \Sigma $
. Therefore, Lemma 5.13 implies that
$z \in \Sigma $
. Therefore, Lemma 5.13 implies that
![]() $U := \tau (\Sigma ) \subset Q$
is a
$U := \tau (\Sigma ) \subset Q$
is a
![]() $2k$
-dimensional submanifold, and
$2k$
-dimensional submanifold, and
![]() $\left .\tau \right |_\Sigma \colon \Sigma \to U$
is an
$\left .\tau \right |_\Sigma \colon \Sigma \to U$
is an
![]() $S^1$
-bundle with geodesic fibers.
$S^1$
-bundle with geodesic fibers.
Fix
![]() $z \in \Sigma $
and let
$z \in \Sigma $
and let
![]() $u = \tau (z)$
. Since
$u = \tau (z)$
. Since
![]() $\Sigma $
is HV compatible and
$\Sigma $
is HV compatible and
![]() $\dim (T_z\Sigma \cap \mathsf {V}) = 1$
, we can orthogonally split
$\dim (T_z\Sigma \cap \mathsf {V}) = 1$
, we can orthogonally split
where
![]() $V \in \mathsf {V}_z$
is a vertical unit vector, and
$V \in \mathsf {V}_z$
is a vertical unit vector, and
![]() $H_\Sigma \subset \mathsf {H}_z$
is
$H_\Sigma \subset \mathsf {H}_z$
is
![]() $2k$
-dimensional. On
$2k$
-dimensional. On
![]() $\mathsf {H}_z$
, let
$\mathsf {H}_z$
, let
![]() $\beta _V := \iota _{V}(\mathrm {Re}\,\gamma )$
denote the induced nondegenerate
$\beta _V := \iota _{V}(\mathrm {Re}\,\gamma )$
denote the induced nondegenerate
![]() $2$
-form, and let
$2$
-form, and let
![]() $J_V$
denote the corresponding complex structure. By Proposition 4.25(b), the
$J_V$
denote the corresponding complex structure. By Proposition 4.25(b), the
![]() $2k$
-plane
$2k$
-plane
![]() $H_\Sigma \subset \mathsf {H}_z$
is
$H_\Sigma \subset \mathsf {H}_z$
is
![]() $J_V$
-invariant.
$J_V$
-invariant.
Now, the
![]() $S^1$
-fiber
$S^1$
-fiber
![]() $\left .\tau \right |_\Sigma ^{-1}(u) \subset \Sigma $
is a great circle through z in the
$\left .\tau \right |_\Sigma ^{-1}(u) \subset \Sigma $
is a great circle through z in the
![]() $2$
-sphere
$2$
-sphere
![]() ${Z_u = \tau ^{-1} (u)}$
. Let
${Z_u = \tau ^{-1} (u)}$
. Let
![]() $j \in \left .\tau \right |_\Sigma ^{-1}(u) \cap z^\perp $
be the point on this circle that corresponds to V under the natural isomorphism
$j \in \left .\tau \right |_\Sigma ^{-1}(u) \cap z^\perp $
be the point on this circle that corresponds to V under the natural isomorphism
![]() $\mathsf {V}_z \simeq z^\perp $
. Setting
$\mathsf {V}_z \simeq z^\perp $
. Setting
![]() $i = z \circ j$
, we see that
$i = z \circ j$
, we see that
![]() $(z,j,i)$
is an admissible frame of
$(z,j,i)$
is an admissible frame of
![]() $E_u$
, which is the fiber over u of the bundle E from Definition 5.1. See Figure 1. We also have
$E_u$
, which is the fiber over u of the bundle E from Definition 5.1. See Figure 1. We also have
![]() $\left .\tau \right |_\Sigma ^{-1}(u) = \{k \in Z_u \colon \langle k,i\rangle = 0 \}$
, and
$\left .\tau \right |_\Sigma ^{-1}(u) = \{k \in Z_u \colon \langle k,i\rangle = 0 \}$
, and
In particular, the
![]() $J_V$
-invariance of the
$J_V$
-invariance of the
![]() $2k$
-plane
$2k$
-plane
![]() $H_\Sigma \subset \mathsf {H}_z$
implies that
$H_\Sigma \subset \mathsf {H}_z$
implies that
![]() $T_uU \subset T_uQ$
is i-invariant.
$T_uU \subset T_uQ$
is i-invariant.

Figure 1: The admissible frame
![]() $(z, j, i)$
of
$(z, j, i)$
of
![]() $E_u$
.
$E_u$
.
Now, let
![]() $X_1, X_2 \in T_{u}U$
, and let
$X_1, X_2 \in T_{u}U$
, and let
![]() $\widetilde {X}_j = (\left .\tau _*\right |_{H_\Sigma })^{-1}(X_j) \in H_\Sigma $
. Since
$\widetilde {X}_j = (\left .\tau _*\right |_{H_\Sigma })^{-1}(X_j) \in H_\Sigma $
. Since
![]() $\Sigma $
is
$\Sigma $
is
![]() $\omega _{\mathrm {KE}}$
-isotropic, and
$\omega _{\mathrm {KE}}$
-isotropic, and
![]() $\omega _{\mathrm {KE}} = f^2 \wedge f^3 + \beta _1$
, it follows that the
$\omega _{\mathrm {KE}} = f^2 \wedge f^3 + \beta _1$
, it follows that the
![]() $2k$
-plane
$2k$
-plane
![]() $H_\Sigma $
is
$H_\Sigma $
is
![]() $\beta _1$
-isotropic. Therefore,
$\beta _1$
-isotropic. Therefore,
which shows that
![]() $z(T_uU) \subset (T_uU)^\perp $
. Finally, if
$z(T_uU) \subset (T_uU)^\perp $
. Finally, if
![]() $X \in T_uU$
, then
$X \in T_uU$
, then
![]() $iX \in T_uU$
, so
$iX \in T_uU$
, so
![]() $jX = -z(iX) \in (T_uU)^\perp $
, demonstrating that
$jX = -z(iX) \in (T_uU)^\perp $
, demonstrating that
![]() $j(T_uU) \subset (T_uU)^\perp $
. This proves that U is totally complex and that
$j(T_uU) \subset (T_uU)^\perp $
. This proves that U is totally complex and that
Finally, suppose that
![]() $n = 1$
, so that
$n = 1$
, so that
![]() $k = 1$
. Then
$k = 1$
. Then
![]() $\Sigma ^3 = \mathcal {L}(U)$
is
$\Sigma ^3 = \mathcal {L}(U)$
is
![]() $\omega _{\mathrm {KE}}$
-Lagrangian and
$\omega _{\mathrm {KE}}$
-Lagrangian and
![]() $\omega _{\mathrm {NK}}$
-Lagrangian. By a result of Storm [Reference Storm30], the surface
$\omega _{\mathrm {NK}}$
-Lagrangian. By a result of Storm [Reference Storm30], the surface
![]() $U \subset Q^4$
is superminimal.
$U \subset Q^4$
is superminimal.
Remark 5.15 If U is an embedded submanifold of Q, then its geodesic circle bundle is embedded in Z. Therefore, in order to characterize those submanifolds
![]() $\Sigma $
of Z which are geodesic circle bundles in Z, we need to assume a priori that
$\Sigma $
of Z which are geodesic circle bundles in Z, we need to assume a priori that
![]() $\Sigma $
is embedded.
$\Sigma $
is embedded.
5.2.4 Applications
In previous sections, we considered
![]() $\mathrm {Re}(\gamma )$
-calibrated
$\mathrm {Re}(\gamma )$
-calibrated
![]() $3$
-folds
$3$
-folds
![]() $\Sigma ^3 \subset Z$
that are
$\Sigma ^3 \subset Z$
that are
![]() $\omega _{\mathrm {KE}}$
-isotropic, describing their
$\omega _{\mathrm {KE}}$
-isotropic, describing their
![]() $p_1$
-horizontal lifts
$p_1$
-horizontal lifts
![]() $L^3 \subset M^{4n+3}$
(Theorem 4.31). Now, we are in a position to classify such
$L^3 \subset M^{4n+3}$
(Theorem 4.31). Now, we are in a position to classify such
![]() $3$
-folds in Z as circle bundle lifts of totally complex surfaces in Q.
$3$
-folds in Z as circle bundle lifts of totally complex surfaces in Q.
-
(1) If
 $U^2 \subset Q^{4n}$
is totally complex and
$U^2 \subset Q^{4n}$
is totally complex and
 $n \geq 2$
, or if U is superminimal and
$n \geq 2$
, or if U is superminimal and
 $n = 1$
, then
$n = 1$
, then
 $\mathcal {L}(U) \subset Z$
is
$\mathcal {L}(U) \subset Z$
is
 $\mathrm {Re}(\gamma )$
-calibrated and
$\mathrm {Re}(\gamma )$
-calibrated and
 $\omega _{\mathrm {KE}}$
-isotropic.
$\omega _{\mathrm {KE}}$
-isotropic. -
(2) Conversely, if
 $\Sigma ^3 \subset Z^{4n+2}$
is a compact three-dimensional submanifold that is
$\Sigma ^3 \subset Z^{4n+2}$
is a compact three-dimensional submanifold that is
 $\mathrm {Re}(\gamma )$
-calibrated and
$\mathrm {Re}(\gamma )$
-calibrated and
 $\omega _{\mathrm {KE}}$
-isotropic, then
$\omega _{\mathrm {KE}}$
-isotropic, then
 $\Sigma = \mathcal {L}(U)$
for some totally complex surface
$\Sigma = \mathcal {L}(U)$
for some totally complex surface
 $U^2 \subset Q^{4n}$
. Moreover, if
$U^2 \subset Q^{4n}$
. Moreover, if
 $n = 1$
, then U is superminimal.
$n = 1$
, then U is superminimal.
Proof (a) Let
![]() $U^2 \subset Q^{4n}$
be totally complex if
$U^2 \subset Q^{4n}$
be totally complex if
![]() $n \geq 2$
, or superminimal if
$n \geq 2$
, or superminimal if
![]() $n = 1$
. By Theorem 5.11(a), the
$n = 1$
. By Theorem 5.11(a), the
![]() $3$
-fold
$3$
-fold
![]() $\mathcal {L}(U) \subset Z$
is
$\mathcal {L}(U) \subset Z$
is
![]() $\omega _{\mathrm {KE}}$
-isotropic. Fix
$\omega _{\mathrm {KE}}$
-isotropic. Fix
![]() $z \in L$
, and let
$z \in L$
, and let
![]() $L \subset M$
denote a
$L \subset M$
denote a
![]() $p_1$
-horizontal lift of a neighborhood of z. By Corollary 5.12, L is
$p_1$
-horizontal lift of a neighborhood of z. By Corollary 5.12, L is
![]() $(c_\theta I_2 + s_\theta I_3)$
-CR isotropic. Therefore, by Theorem 4.31((ii)
$(c_\theta I_2 + s_\theta I_3)$
-CR isotropic. Therefore, by Theorem 4.31((ii)
![]() $\implies $
(iv)),
$\implies $
(iv)),
![]() $p_1(L) \subset \mathcal {L}(U)$
is
$p_1(L) \subset \mathcal {L}(U)$
is
![]() $\mathrm {Re}(\gamma )$
-calibrated.
$\mathrm {Re}(\gamma )$
-calibrated.
(b) Suppose
![]() $\Sigma ^3 \subset Z$
is a compact three-dimensional submanifold that is
$\Sigma ^3 \subset Z$
is a compact three-dimensional submanifold that is
![]() $\mathrm {Re}(\gamma )$
-calibrated and
$\mathrm {Re}(\gamma )$
-calibrated and
![]() $\omega _{\mathrm {KE}}$
-isotropic. By Proposition 4.15(c),
$\omega _{\mathrm {KE}}$
-isotropic. By Proposition 4.15(c),
![]() $\Sigma $
is HV-compatible and
$\Sigma $
is HV-compatible and
![]() $\dim (T_z\Sigma \cap \mathsf {V}) = 1$
for all
$\dim (T_z\Sigma \cap \mathsf {V}) = 1$
for all
![]() $z \in \Sigma $
. Therefore, Lemma 5.13 implies that
$z \in \Sigma $
. Therefore, Lemma 5.13 implies that
![]() $U^2 = \tau (\Sigma ) \subset Q$
is a two-dimensional surface and that
$U^2 = \tau (\Sigma ) \subset Q$
is a two-dimensional surface and that
![]() $\left .\tau \right |_\Sigma \colon \Sigma \to U$
is an
$\left .\tau \right |_\Sigma \colon \Sigma \to U$
is an
![]() $S^1$
-bundle with geodesic fibers.
$S^1$
-bundle with geodesic fibers.
Fix
![]() $z \in \Sigma $
, and let
$z \in \Sigma $
, and let
![]() $u = \tau (z)$
. We may write
$u = \tau (z)$
. We may write
![]() $T_z\Sigma = H_\Sigma \oplus V_\Sigma $
for some
$T_z\Sigma = H_\Sigma \oplus V_\Sigma $
for some
![]() $2$
-plane
$2$
-plane
![]() $H_\Sigma \subset \mathsf {H}$
and line
$H_\Sigma \subset \mathsf {H}$
and line
![]() $V_\Sigma \subset \mathsf {V}$
. Let
$V_\Sigma \subset \mathsf {V}$
. Let
![]() $(e_{10}, \ldots , e_{n3}, f_2, f_3)$
be an
$(e_{10}, \ldots , e_{n3}, f_2, f_3)$
be an
![]() $\mathrm {Sp}(n)\mathrm {U}(1)$
-frame at z, with dual coframe
$\mathrm {Sp}(n)\mathrm {U}(1)$
-frame at z, with dual coframe
![]() $(\rho _{10}, \ldots , \rho _{n3}, \mu _2, \mu _3)$
, such that
$(\rho _{10}, \ldots , \rho _{n3}, \mu _2, \mu _3)$
, such that
Let
![]() $(\beta _1, \beta _2, \beta _3) = (\omega _{\mathsf {H}},\, \iota _{f_2}(\mathrm {Re}\,\gamma ), \, \iota _{f_3}(\mathrm {Re}\,\gamma ))$
denote the induced hyperkähler triple on
$(\beta _1, \beta _2, \beta _3) = (\omega _{\mathsf {H}},\, \iota _{f_2}(\mathrm {Re}\,\gamma ), \, \iota _{f_3}(\mathrm {Re}\,\gamma ))$
denote the induced hyperkähler triple on
![]() $\mathsf {H}_z$
, and let
$\mathsf {H}_z$
, and let
![]() $(J_1, J_2, J_3)$
be the corresponding complex structures on
$(J_1, J_2, J_3)$
be the corresponding complex structures on
![]() $\mathsf {H}_z$
.
$\mathsf {H}_z$
.
Now, the
![]() $S^1$
-fiber
$S^1$
-fiber
![]() $\left .\tau \right |_\Sigma ^{-1}(u) \subset \Sigma $
is a great circle through z in the twistor
$\left .\tau \right |_\Sigma ^{-1}(u) \subset \Sigma $
is a great circle through z in the twistor
![]() $2$
-sphere
$2$
-sphere
![]() $Z_u$
. Let
$Z_u$
. Let
![]() $j \in \left .\tau \right |_\Sigma ^{-1}(u) \cap z^\perp $
be the point on this circle that corresponds to V under the natural isomorphism
$j \in \left .\tau \right |_\Sigma ^{-1}(u) \cap z^\perp $
be the point on this circle that corresponds to V under the natural isomorphism
![]() $\mathsf {V}_z \simeq z^\perp $
. Setting
$\mathsf {V}_z \simeq z^\perp $
. Setting
![]() $i = z \circ j$
, we see that
$i = z \circ j$
, we see that
![]() $(z,j,i)$
is an admissible frame of
$(z,j,i)$
is an admissible frame of
![]() $E_u$
(see Figure 1), that
$E_u$
(see Figure 1), that
![]() $\left .\tau \right |_\Sigma ^{-1}(u) = \{k \in Z_u \colon \langle k,i\rangle = 0 \}$
, and moreover,
$\left .\tau \right |_\Sigma ^{-1}(u) = \{k \in Z_u \colon \langle k,i\rangle = 0 \}$
, and moreover,
Using (5.3), we compute
 $$ \begin{align*} \left.\mu_2\right|_{V_\Sigma} \wedge \mathrm{vol}_{H_\Sigma} = \mathrm{vol}_{T_z\Sigma} = \left.\mathrm{Re}(\gamma)\right|_{T_z\Sigma} & = \left.\left(\mu_2 \wedge \beta_2 + \mu_3 \wedge \beta_3\right)\right|_{T_z\Sigma} \\ & = \left.\mu_2\right|_{V_\Sigma} \wedge \left.\beta_2\right|_{H_\Sigma} + \left.\mu_3\right|_{V_\Sigma} \wedge \left.\beta_3\right|_{H_\Sigma} \\ & = \left.\mu_2\right|_{V_\Sigma} \wedge \left.\beta_2\right|_{H_\Sigma}. \end{align*} $$
$$ \begin{align*} \left.\mu_2\right|_{V_\Sigma} \wedge \mathrm{vol}_{H_\Sigma} = \mathrm{vol}_{T_z\Sigma} = \left.\mathrm{Re}(\gamma)\right|_{T_z\Sigma} & = \left.\left(\mu_2 \wedge \beta_2 + \mu_3 \wedge \beta_3\right)\right|_{T_z\Sigma} \\ & = \left.\mu_2\right|_{V_\Sigma} \wedge \left.\beta_2\right|_{H_\Sigma} + \left.\mu_3\right|_{V_\Sigma} \wedge \left.\beta_3\right|_{H_\Sigma} \\ & = \left.\mu_2\right|_{V_\Sigma} \wedge \left.\beta_2\right|_{H_\Sigma}. \end{align*} $$
Contracting with
![]() $f_2$
gives
$f_2$
gives
![]() $\beta _2|_{H_\Sigma } = \mathrm {vol}_{H_\Sigma }$
, which implies that the real
$\beta _2|_{H_\Sigma } = \mathrm {vol}_{H_\Sigma }$
, which implies that the real
![]() $2$
-plane
$2$
-plane
![]() $H_\Sigma \subset \mathsf {H}_z$
is
$H_\Sigma \subset \mathsf {H}_z$
is
![]() $J_2$
-invariant. Consequently,
$J_2$
-invariant. Consequently,
![]() $T_{u}U \subset T_{u}Q$
is i-invariant.
$T_{u}U \subset T_{u}Q$
is i-invariant.
Repeating the argument at the end of the proof of Theorem 5.14, we observe that
![]() $z(T_uU) \subset (T_uU)^\perp $
and
$z(T_uU) \subset (T_uU)^\perp $
and
![]() $j(T_uU) \subset (T_uU)^\perp $
. This proves that U is totally complex and that
$j(T_uU) \subset (T_uU)^\perp $
. This proves that U is totally complex and that
Finally, suppose that
![]() $n = 1$
. Since
$n = 1$
. Since
![]() $\Sigma ^3 = \mathcal {L}(U) \subset Z^6$
is
$\Sigma ^3 = \mathcal {L}(U) \subset Z^6$
is
![]() $\mathrm {Re}(\gamma )$
-calibrated, it follows from Proposition 4.16 that
$\mathrm {Re}(\gamma )$
-calibrated, it follows from Proposition 4.16 that
![]() $\Sigma $
is
$\Sigma $
is
![]() $\omega _{\mathrm {NK}}$
-Lagrangian. Thus,
$\omega _{\mathrm {NK}}$
-Lagrangian. Thus,
![]() $\mathcal {L}(U)$
is both
$\mathcal {L}(U)$
is both
![]() $\omega _{\mathrm {KE}}$
-Lagrangian and
$\omega _{\mathrm {KE}}$
-Lagrangian and
![]() $\omega _{\mathrm {NK}}$
-Lagrangian, so the superminimality of
$\omega _{\mathrm {NK}}$
-Lagrangian, so the superminimality of
![]() $U^2 \subset Q^4$
follows from Storm’s theorem [Reference Storm30].
$U^2 \subset Q^4$
follows from Storm’s theorem [Reference Storm30].
We can now classify the compact submanifolds of Z that are Lagrangian with respect to both
![]() $\omega _{\mathrm {KE}}$
and
$\omega _{\mathrm {KE}}$
and
![]() $\omega _{\mathrm {NK}}$
.
$\omega _{\mathrm {NK}}$
.
-
(1) If
 $U^{2n} \subset Q^{4n}$
is totally complex and
$U^{2n} \subset Q^{4n}$
is totally complex and
 $n \geq 2$
, or if U is superminimal and
$n \geq 2$
, or if U is superminimal and
 $n = 1$
, then
$n = 1$
, then
 $\mathcal {L}(U) \subset Z$
is
$\mathcal {L}(U) \subset Z$
is
 $\omega _{\mathrm {KE}}$
-Lagrangian and
$\omega _{\mathrm {KE}}$
-Lagrangian and
 $\omega _{\mathrm {NK}}$
-Lagrangian.
$\omega _{\mathrm {NK}}$
-Lagrangian. -
(2) Conversely, if
 $\Sigma ^{2n+1} \subset Z^{4n+2}$
is a compact
$\Sigma ^{2n+1} \subset Z^{4n+2}$
is a compact
 $(2n+1)$
-dimensional submanifold that is both
$(2n+1)$
-dimensional submanifold that is both
 $\omega _{\mathrm {KE}}$
-Lagrangian and
$\omega _{\mathrm {KE}}$
-Lagrangian and
 $\omega _{\mathrm {NK}}$
-Lagrangian, then
$\omega _{\mathrm {NK}}$
-Lagrangian, then
 $\Sigma = \mathcal {L}(U)$
for some (maximal) totally complex
$\Sigma = \mathcal {L}(U)$
for some (maximal) totally complex
 $2n$
-fold
$2n$
-fold
 $U^{2n} \subset Q^{4n}$
.
$U^{2n} \subset Q^{4n}$
.
Proof (a) This follows from Theorem 5.11(a).
(b) Suppose
![]() $\Sigma ^{2n+1} \subset Z$
is a compact submanifold that is both
$\Sigma ^{2n+1} \subset Z$
is a compact submanifold that is both
![]() $\omega _{\mathrm {KE}}$
-Lagrangian and
$\omega _{\mathrm {KE}}$
-Lagrangian and
![]() $\omega _{\mathrm {NK}}$
-Lagrangian. By Proposition 4.15(b),
$\omega _{\mathrm {NK}}$
-Lagrangian. By Proposition 4.15(b),
![]() $\Sigma $
is HV compatible,
$\Sigma $
is HV compatible,
![]() $\dim (T_z\Sigma \cap \mathsf {H}) = 2n$
, and
$\dim (T_z\Sigma \cap \mathsf {H}) = 2n$
, and
![]() $\dim (T_z\Sigma \cap \mathsf {V}) = 1$
for all
$\dim (T_z\Sigma \cap \mathsf {V}) = 1$
for all
![]() $z \in \Sigma $
. By Lemma 5.13,
$z \in \Sigma $
. By Lemma 5.13,
![]() $U := \tau (\Sigma ) \subset Q$
is a
$U := \tau (\Sigma ) \subset Q$
is a
![]() $2n$
-dimensional submanifold, and
$2n$
-dimensional submanifold, and
![]() $\left .\tau \right |_\Sigma \colon \Sigma \to U$
is an
$\left .\tau \right |_\Sigma \colon \Sigma \to U$
is an
![]() $S^1$
-bundle with geodesic fibers.
$S^1$
-bundle with geodesic fibers.
It remains to prove that U is totally complex and that
![]() $\tau |_\Sigma ^{-1}(u) = \left .\mathcal {L}(U)\right |_u$
. For this, note that Corollary 4.27(b) implies that every local
$\tau |_\Sigma ^{-1}(u) = \left .\mathcal {L}(U)\right |_u$
. For this, note that Corollary 4.27(b) implies that every local
![]() $p_1$
-horizontal lift of
$p_1$
-horizontal lift of
![]() $\Sigma $
is
$\Sigma $
is
![]() $(c_\theta I_2 + s_\theta I_3)$
-CR Legendrian for some
$(c_\theta I_2 + s_\theta I_3)$
-CR Legendrian for some
![]() $e^{i\theta } \in S^1$
. The proof now follows exactly as in Theorem 5.14.
$e^{i\theta } \in S^1$
. The proof now follows exactly as in Theorem 5.14.
6 Characterizations of complex Lagrangian cones
In a hyperkähler cone
![]() $C^{4n+4}$
, recall that a
$C^{4n+4}$
, recall that a
![]() $(2k+2)$
-dimensional cone
$(2k+2)$
-dimensional cone
![]() $\mathrm {C}(L)$
is
$\mathrm {C}(L)$
is
![]() $(c_\theta I_2 + s_\theta I_3)$
-complex isotropic provided that it satisfies the following three conditions:
$(c_\theta I_2 + s_\theta I_3)$
-complex isotropic provided that it satisfies the following three conditions:
As discussed in Section 3.3, this is equivalent to requiring that the
![]() $(2k+1)$
-dimensional link L be
$(2k+1)$
-dimensional link L be
![]() $(c_\theta I_2 + s_\theta I_3)$
-CR isotropic, meaning
$(c_\theta I_2 + s_\theta I_3)$
-CR isotropic, meaning
In this short section, we characterize complex isotropic cones
![]() $\mathrm {C}(L)^{2k+2} \subset C^{4n+4}$
,
$\mathrm {C}(L)^{2k+2} \subset C^{4n+4}$
,
![]() $1 \leq k \leq n$
, in terms of related geometries in
$1 \leq k \leq n$
, in terms of related geometries in
![]() $M^{4n+3}$
,
$M^{4n+3}$
,
![]() $Z^{4n+2}$
, and
$Z^{4n+2}$
, and
![]() $Q^{4n}$
.
$Q^{4n}$
.
To begin, we generalize a result of Ejiri and Tsukada [Reference Ejiri and Tsukada13] – originally established for complex Lagrangian cones (i.e.,
![]() $k = n$
) in the flat model
$k = n$
) in the flat model
![]() $C^{4n+4} = \mathbb {H}^{n+1}$
– to complex isotropic cones of any dimension
$C^{4n+4} = \mathbb {H}^{n+1}$
– to complex isotropic cones of any dimension
![]() $2k+2$
in arbitrary hyperkähler cones
$2k+2$
in arbitrary hyperkähler cones
![]() $C^{4n+4}$
.
$C^{4n+4}$
.
Theorem 6.1 Let
![]() $L^{2k+1} \subset M^{4n+3}$
, where
$L^{2k+1} \subset M^{4n+3}$
, where
![]() $3 \leq 2k+1 \leq 2n+1$
. The following conditions are equivalent:
$3 \leq 2k+1 \leq 2n+1$
. The following conditions are equivalent:
-
(1)
 $\mathrm {C}(L)$
is
$\mathrm {C}(L)$
is
 $(c_\theta I_2 + s_\theta I_3)$
-complex isotropic for some constant
$(c_\theta I_2 + s_\theta I_3)$
-complex isotropic for some constant
 $e^{i \theta } \in S^1$
.
$e^{i \theta } \in S^1$
. -
(2) L is
 $(c_\theta I_2 + s_\theta I_3)$
-CR isotropic for some constant
$(c_\theta I_2 + s_\theta I_3)$
-CR isotropic for some constant
 $e^{i \theta } \in S^1$
.
$e^{i \theta } \in S^1$
. -
(3) L is locally of the form
 $p_v^{-1}(V)$
for some horizontal
$p_v^{-1}(V)$
for some horizontal
 $J_{\mathrm {KE}}$
-complex submanifold
$J_{\mathrm {KE}}$
-complex submanifold
 ${V^{2k} \subset Z}$
and some
${V^{2k} \subset Z}$
and some
 $v = (0, c_\theta , s_\theta )$
.
$v = (0, c_\theta , s_\theta )$
. -
(4) L is locally of the form
 $p_v^{-1}(\widetilde {U})$
for some totally complex submanifold
$p_v^{-1}(\widetilde {U})$
for some totally complex submanifold
 $U^{2k} \subset Q$
(resp. superminimal surface if
$U^{2k} \subset Q$
(resp. superminimal surface if
 $n = 1$
) and some
$n = 1$
) and some
 $v = (0, c_\theta , s_\theta )$
.
$v = (0, c_\theta , s_\theta )$
.
If, in addition, L is compact and
![]() $p_1(L) \subset Z$
is embedded, then the above conditions are equivalent to:
$p_1(L) \subset Z$
is embedded, then the above conditions are equivalent to:
-
(1) L is a
 $p_1$
-horizontal lift of
$p_1$
-horizontal lift of
 $\mathcal {L}(U) \subset Z$
for some totally complex submanifold
$\mathcal {L}(U) \subset Z$
for some totally complex submanifold
 ${U^{2k} \subset Q^{4n}}$
(resp. superminimal surface
${U^{2k} \subset Q^{4n}}$
(resp. superminimal surface
 $U^2 \subset Q^4$
if
$U^2 \subset Q^4$
if
 $n = 1$
).
$n = 1$
).
Proof The equivalence (1)
![]() $\iff $
(2) is Proposition 3.8. The equivalence (2)
$\iff $
(2) is Proposition 3.8. The equivalence (2)
![]() $\iff $
(3) is Corollary 4.21. The equivalence (3)
$\iff $
(3) is Corollary 4.21. The equivalence (3)
![]() $\iff $
(4) follows from Theorem 5.10. (
$\iff $
(4) follows from Theorem 5.10. (
![]() $\star $
)
$\star $
)
![]() $\implies (2)$
. This is Corollary 5.12. (2)
$\implies (2)$
. This is Corollary 5.12. (2)
![]() $\implies $
(
$\implies $
(
![]() $\star $
). This is Theorem 5.14.
$\star $
). This is Theorem 5.14.
Therefore, given a
![]() $(c_\theta I_2 + s_\theta I_3)$
-complex isotropic cone
$(c_\theta I_2 + s_\theta I_3)$
-complex isotropic cone
![]() $\mathrm {C}(L) \subset C$
, its link
$\mathrm {C}(L) \subset C$
, its link
![]() $L \subset M$
can be viewed in two ways. On the one hand, L is a
$L \subset M$
can be viewed in two ways. On the one hand, L is a
![]() $p_{(1,0,0)}$
-horizontal lift of a circle bundle over a totally complex submanifold
$p_{(1,0,0)}$
-horizontal lift of a circle bundle over a totally complex submanifold
![]() $U \subset Q$
. On the other hand, L is also a
$U \subset Q$
. On the other hand, L is also a
![]() $p_{(0,c_\theta , s_\theta )}$
-circle bundle over a
$p_{(0,c_\theta , s_\theta )}$
-circle bundle over a
![]() $\tau $
-horizontal lift of a totally complex submanifold
$\tau $
-horizontal lift of a totally complex submanifold
![]() $U \subset Q$
. Thus, loosely speaking, the operations of “horizontal lift” and “circle bundle lift” form a commutative diagram of sorts:
$U \subset Q$
. Thus, loosely speaking, the operations of “horizontal lift” and “circle bundle lift” form a commutative diagram of sorts:

For complex Lagrangian cones in
![]() $C^{4n+4}$
, we are able to say more.
$C^{4n+4}$
, we are able to say more.
Theorem 6.2 Let
![]() $L^{2n+1} \subset M^{4n+3}$
be a
$L^{2n+1} \subset M^{4n+3}$
be a
![]() $(2n+1)$
-dimensional submanifold. The following five conditions are equivalent:
$(2n+1)$
-dimensional submanifold. The following five conditions are equivalent:
-
(1)
 $\mathrm {C}(L)$
is
$\mathrm {C}(L)$
is
 $(c_\theta I_2 + s_\theta I_3)$
-complex Lagrangian for some constant
$(c_\theta I_2 + s_\theta I_3)$
-complex Lagrangian for some constant
 $e^{i \theta } \in S^1$
.
$e^{i \theta } \in S^1$
. -
(2) L is
 $(c_\theta I_2 + s_\theta I_3)$
-CR Legendrian for some constant
$(c_\theta I_2 + s_\theta I_3)$
-CR Legendrian for some constant
 $e^{i \theta } \in S^1$
.
$e^{i \theta } \in S^1$
. -
(3) L is locally of the form
 $p_v^{-1}(V)$
for some horizontal
$p_v^{-1}(V)$
for some horizontal
 $J_{\mathrm {KE}}$
-complex submanifold
$J_{\mathrm {KE}}$
-complex submanifold
 ${V^{2n} \subset Z}$
and some
${V^{2n} \subset Z}$
and some
 $v = (0, c_\theta , s_\theta )$
.
$v = (0, c_\theta , s_\theta )$
. -
(4) L is locally of the form
 $p_v^{-1}(\widetilde {U})$
for some totally complex submanifold
$p_v^{-1}(\widetilde {U})$
for some totally complex submanifold
 $U^{2n} \subset Q$
(resp. superminimal surface if
$U^{2n} \subset Q$
(resp. superminimal surface if
 $n = 1$
) and some
$n = 1$
) and some
 $v = (0, c_\theta , s_\theta )$
.
$v = (0, c_\theta , s_\theta )$
. -
(5) L is locally a
 $p_1$
-horizontal lift of a
$p_1$
-horizontal lift of a
 $(2n+1)$
-fold
$(2n+1)$
-fold
 $\Sigma ^{2n+1} \subset Z$
that is
$\Sigma ^{2n+1} \subset Z$
that is
 $\omega _{\mathrm {KE}}$
-Lagrangian and
$\omega _{\mathrm {KE}}$
-Lagrangian and
 $\omega _{\mathrm {NK}}$
-Lagrangian.
$\omega _{\mathrm {NK}}$
-Lagrangian.
If, in addition, L is compact and
![]() $p_1(L) \subset Z$
is embedded, then the above conditions are equivalent to:
$p_1(L) \subset Z$
is embedded, then the above conditions are equivalent to:
-
(1) L is a
 $p_1$
-horizontal lift of
$p_1$
-horizontal lift of
 $\mathcal {L}(U) \subset Z$
for some totally complex submanifold
$\mathcal {L}(U) \subset Z$
for some totally complex submanifold
 ${U^{2n} \subset Q^{4n}}$
(resp. superminimal surface
${U^{2n} \subset Q^{4n}}$
(resp. superminimal surface
 $U^2 \subset Q^4$
if
$U^2 \subset Q^4$
if
 $n = 1$
).
$n = 1$
).
Proof The equivalence (1)
![]() $\iff $
(2)
$\iff $
(2)
![]() $\iff $
(3)
$\iff $
(3)
![]() $\iff $
(4)
$\iff $
(4)
![]() $\iff $
(
$\iff $
(
![]() $\star $
) was proven in Theorem 6.1. It remains only to involve condition (5). For this, note that (5)
$\star $
) was proven in Theorem 6.1. It remains only to involve condition (5). For this, note that (5)
![]() $\iff $
(2) is the content of Corollary 4.27. Alternatively, (5)
$\iff $
(2) is the content of Corollary 4.27. Alternatively, (5)
![]() $\iff $
(
$\iff $
(
![]() $\star $
) is Theorem 5.17.
$\star $
) is Theorem 5.17.
Finally, for four-dimensional complex isotropic cones in
![]() $C^{4n+4}$
, even more characterizations are available:
$C^{4n+4}$
, even more characterizations are available:
Theorem 6.3 Let
![]() $L^{3} \subset M^{4n+3}$
be a three-dimensional submanifold. The following six conditions are equivalent:
$L^{3} \subset M^{4n+3}$
be a three-dimensional submanifold. The following six conditions are equivalent:
-
(1)
 $\mathrm {C}(L)$
is
$\mathrm {C}(L)$
is
 $(c_\theta I_2 + s_\theta I_3)$
-complex isotropic for some constant
$(c_\theta I_2 + s_\theta I_3)$
-complex isotropic for some constant
 $e^{i \theta } \in S^1$
.
$e^{i \theta } \in S^1$
. -
(2) L is
 $(c_\theta I_2 + s_\theta I_3)$
-CR isotropic for some constant
$(c_\theta I_2 + s_\theta I_3)$
-CR isotropic for some constant
 $e^{i \theta } \in S^1$
.
$e^{i \theta } \in S^1$
. -
(3) L is locally of the form
 $p_v^{-1}(V)$
for some horizontal
$p_v^{-1}(V)$
for some horizontal
 $J_{\mathrm {KE}}$
-complex submanifold
$J_{\mathrm {KE}}$
-complex submanifold
 ${V^{2} \subset Z}$
and some
${V^{2} \subset Z}$
and some
 $v = (0, c_\theta , s_\theta )$
.
$v = (0, c_\theta , s_\theta )$
. -
(4) L is locally of the form
 $p_v^{-1}(\widetilde {U})$
for some totally complex submanifold
$p_v^{-1}(\widetilde {U})$
for some totally complex submanifold
 $U^{2} \subset Q$
(resp. superminimal surface if
$U^{2} \subset Q$
(resp. superminimal surface if
 $n = 1$
) and some
$n = 1$
) and some
 $v = (0, c_\theta , s_\theta )$
.
$v = (0, c_\theta , s_\theta )$
. -
(5) L is locally a
 $p_1$
-horizontal lift of a
$p_1$
-horizontal lift of a
 $\mathrm {Re}(\gamma )$
-calibrated
$\mathrm {Re}(\gamma )$
-calibrated
 $3$
-fold that is
$3$
-fold that is
 $\omega _{\mathrm {KE}}$
-isotropic.
$\omega _{\mathrm {KE}}$
-isotropic. -
(6) L is
 $\mathrm {Re}(\Gamma _1)$
-calibrated.
$\mathrm {Re}(\Gamma _1)$
-calibrated.
If, in addition, L is compact and
![]() $p_1(L) \subset Z$
is embedded, then the above conditions are equivalent to:
$p_1(L) \subset Z$
is embedded, then the above conditions are equivalent to:
-
(1) L is a
 $p_1$
-horizontal lift of
$p_1$
-horizontal lift of
 $\mathcal {L}(U) \subset Z$
for some totally complex submanifold
$\mathcal {L}(U) \subset Z$
for some totally complex submanifold
 $U^{2} \subset Q^{4n}$
(resp. superminimal surface
$U^{2} \subset Q^{4n}$
(resp. superminimal surface
 $U^2 \subset Q^4$
if
$U^2 \subset Q^4$
if
 $n = 1$
).
$n = 1$
).
A Appendix
A.1 Linear algebra of calibrations
Let
![]() $(V, g)$
be an n-dimensional oriented real inner product space. Recall that a k-form
$(V, g)$
be an n-dimensional oriented real inner product space. Recall that a k-form
![]() $\gamma $
on V is said to have comass one if
$\gamma $
on V is said to have comass one if
![]() $\gamma (P) \leq 1$
for any oriented orthonormal k-plane P in V, with equality on at least one such P. Equivalently, by writing
$\gamma (P) \leq 1$
for any oriented orthonormal k-plane P in V, with equality on at least one such P. Equivalently, by writing
![]() $P = e_1 \wedge \cdots \wedge e_k$
, this means that
$P = e_1 \wedge \cdots \wedge e_k$
, this means that
whenever
![]() $e_1, \ldots , e_k$
are orthonormal in V, with equality on at least one such set. Throughout this paper, a k-form with comass one will be called a semi-calibration. Let
$e_1, \ldots , e_k$
are orthonormal in V, with equality on at least one such set. Throughout this paper, a k-form with comass one will be called a semi-calibration. Let
![]() $\gamma \in \Lambda ^k (V^*)$
be a semi-calibration. An oriented k-plane P is called
$\gamma \in \Lambda ^k (V^*)$
be a semi-calibration. An oriented k-plane P is called
![]() $\gamma $
-calibrated if
$\gamma $
-calibrated if
![]() $\gamma (P) = 1$
.
$\gamma (P) = 1$
.
It is easy to see that
![]() $\gamma \in \Lambda ^k (V^*)$
is a semi-calibration if and only if
$\gamma \in \Lambda ^k (V^*)$
is a semi-calibration if and only if
![]() $\ast \gamma \in \Lambda ^{n-k} (V^*)$
is a semi-calibration, where
$\ast \gamma \in \Lambda ^{n-k} (V^*)$
is a semi-calibration, where
![]() $\ast $
is the Hodge star operator induced by the inner product and orientation on V. We collect here some results on semi-calibrations that we will need.
$\ast $
is the Hodge star operator induced by the inner product and orientation on V. We collect here some results on semi-calibrations that we will need.
Proposition A.1 Let
![]() $\gamma \in \Lambda ^k (V^*)$
, be a semi-calibration, and let
$\gamma \in \Lambda ^k (V^*)$
, be a semi-calibration, and let
![]() $L \subset V$
be an oriented one-dimensional subspace with oriented orthonormal basis
$L \subset V$
be an oriented one-dimensional subspace with oriented orthonormal basis
![]() $\{ e_1 \}$
. Write
$\{ e_1 \}$
. Write
![]() $V = L \oplus L^{\perp }$
, and
$V = L \oplus L^{\perp }$
, and
where
![]() $\alpha = \iota _{e_1} \gamma \in \Lambda ^{k-1} (L^{\perp })^*$
and
$\alpha = \iota _{e_1} \gamma \in \Lambda ^{k-1} (L^{\perp })^*$
and
![]() $\beta = \gamma - e_1^\flat \wedge \alpha \in \Lambda ^k (L^{\perp })^*$
.
$\beta = \gamma - e_1^\flat \wedge \alpha \in \Lambda ^k (L^{\perp })^*$
.
-
(1) If every oriented line in V lies in a
 $\gamma $
-calibrated k-plane, then
$\gamma $
-calibrated k-plane, then
 $\alpha $
is a semi-calibration.
$\alpha $
is a semi-calibration. -
(2) Suppose (a) holds. Then an oriented
 $(k-1)$
-plane W in
$(k-1)$
-plane W in
 $L^{\perp }$
is
$L^{\perp }$
is
 $\alpha $
-calibrated if and only if the oriented k-plane
$\alpha $
-calibrated if and only if the oriented k-plane
 $P = L \oplus W$
is
$P = L \oplus W$
is
 $\gamma $
-calibrated.
$\gamma $
-calibrated. -
(3) If every oriented line in V lies in a
 $(\ast \gamma )$
-calibrated
$(\ast \gamma )$
-calibrated
 $(n-k)$
-plane, then
$(n-k)$
-plane, then
 $\beta $
is a semi-calibration.
$\beta $
is a semi-calibration.
Proof Let W be an oriented
![]() $(k-1)$
-plane in
$(k-1)$
-plane in
![]() $L^{\perp }$
, where
$L^{\perp }$
, where
![]() $W = e_2 \wedge \cdots \wedge e_k$
for some oriented orthonormal bases
$W = e_2 \wedge \cdots \wedge e_k$
for some oriented orthonormal bases
![]() $e_2, \ldots , e_k$
of W. Then
$e_2, \ldots , e_k$
of W. Then
Since
![]() $\gamma (L \oplus W) \leq 1$
, the comass of
$\gamma (L \oplus W) \leq 1$
, the comass of
![]() $\alpha $
is at most
$\alpha $
is at most
![]() $1$
. By hypothesis, there exists a
$1$
. By hypothesis, there exists a
![]() $\gamma $
-calibrated k-plane P containing L. Let W be the unique oriented
$\gamma $
-calibrated k-plane P containing L. Let W be the unique oriented
![]() $(k-1)$
-plane in
$(k-1)$
-plane in
![]() $L^{\perp }$
that
$L^{\perp }$
that
![]() $P = L \oplus W$
. Then
$P = L \oplus W$
. Then
![]() $\alpha (W) = \gamma (L \oplus W) = \gamma (P) = 1$
, so
$\alpha (W) = \gamma (L \oplus W) = \gamma (P) = 1$
, so
![]() $\alpha $
is a semi-calibration. This proves (a), and then (b) is immediate from (A.1). For (c), observe that
$\alpha $
is a semi-calibration. This proves (a), and then (b) is immediate from (A.1). For (c), observe that
If every oriented line L lies in a
![]() $(\ast \gamma )$
-calibrated
$(\ast \gamma )$
-calibrated
![]() $(n-k)$
-plane, then (a) holds for
$(n-k)$
-plane, then (a) holds for
![]() $\ast \gamma $
, so
$\ast \gamma $
, so
![]() $ \iota _{e_1} (\ast \gamma ) = (-1)^k \ast _{L^{\perp }} \beta $
is a semi-calibration on
$ \iota _{e_1} (\ast \gamma ) = (-1)^k \ast _{L^{\perp }} \beta $
is a semi-calibration on
![]() $L^{\perp }$
, but then so is
$L^{\perp }$
, but then so is
![]() $\beta $
.
$\beta $
.
Proposition A.2 Let
![]() $\gamma $
be a semi-calibration on V, and suppose we have an orthogonal splitting
$\gamma $
be a semi-calibration on V, and suppose we have an orthogonal splitting
![]() $V = L \oplus L^{\perp }$
for some oriented line L, with oriented orthonormal basis
$V = L \oplus L^{\perp }$
for some oriented line L, with oriented orthonormal basis
![]() $\{ e_1 \}$
. If
$\{ e_1 \}$
. If
![]() $\iota _{e_1} \gamma = 0$
, then any
$\iota _{e_1} \gamma = 0$
, then any
![]() $\gamma $
-calibrated k-plane lies in
$\gamma $
-calibrated k-plane lies in
![]() $L^{\perp }$
.
$L^{\perp }$
.
Proof It is trivial that
![]() $\dim (P \cap L^{\perp }) \geq k-1$
. Therefore, we can find an oriented orthonormal basis
$\dim (P \cap L^{\perp }) \geq k-1$
. Therefore, we can find an oriented orthonormal basis
![]() $v_1, w_2, \ldots , w_k$
of P such that
$v_1, w_2, \ldots , w_k$
of P such that
![]() $v_1 = \cos (\theta ) e_1 + \sin (\theta ) w_1$
and
$v_1 = \cos (\theta ) e_1 + \sin (\theta ) w_1$
and
![]() $w_1, \ldots , w_k \in L^{\perp }$
orthonormal. Then since
$w_1, \ldots , w_k \in L^{\perp }$
orthonormal. Then since
![]() $\iota _{e_1} \gamma = 0$
, we have
$\iota _{e_1} \gamma = 0$
, we have
Thus,
![]() $\sin (\theta ) = 1$
, and
$\sin (\theta ) = 1$
, and
![]() $v_1 = w_1 \in P$
.
$v_1 = w_1 \in P$
.
Proposition A.3 Let
![]() $(W, g)$
be a finite-dimensional real inner product space, and suppose we have an orthogonal splitting
$(W, g)$
be a finite-dimensional real inner product space, and suppose we have an orthogonal splitting
![]() $W = H \oplus V$
, so that the inner product is given by
$W = H \oplus V$
, so that the inner product is given by
![]() $g = g_H + g_V$
. Define a new inner product
$g = g_H + g_V$
. Define a new inner product
![]() $\tilde g$
on V by
$\tilde g$
on V by
![]() $\tilde g = t^2 g_H + g_V$
. Let
$\tilde g = t^2 g_H + g_V$
. Let
![]() $\gamma $
be a semi-calibration on V such that
$\gamma $
be a semi-calibration on V such that
![]() $\gamma \in \Lambda ^m (H^*) \otimes \Lambda ^{k-m} (V^*)$
. Then
$\gamma \in \Lambda ^m (H^*) \otimes \Lambda ^{k-m} (V^*)$
. Then
![]() $t^m \gamma $
is a semi-calibration on
$t^m \gamma $
is a semi-calibration on
![]() $(W, \tilde g)$
.
$(W, \tilde g)$
.
Proof Let
![]() $\tilde e_1, \ldots , \tilde e_k$
be orthonormal for
$\tilde e_1, \ldots , \tilde e_k$
be orthonormal for
![]() $\tilde g$
. We can decompose
$\tilde g$
. We can decompose
![]() $\tilde e_j = h_j + v_j$
where
$\tilde e_j = h_j + v_j$
where
![]() $h_j \in H$
and
$h_j \in H$
and
![]() $v_j \in V$
, so
$v_j \in V$
, so
Thus, if we define
![]() $e_j = t h_j + v_j$
, then
$e_j = t h_j + v_j$
, then
![]() $e_1, \ldots , e_k$
are orthonormal for g. Using the fact that
$e_1, \ldots , e_k$
are orthonormal for g. Using the fact that
![]() $\gamma \in \Lambda ^m (H^*) \otimes \Lambda ^{k-m} (V^*)$
, we have
$\gamma \in \Lambda ^m (H^*) \otimes \Lambda ^{k-m} (V^*)$
, we have
is a sum of terms, each of which has exactly m of the
![]() $h_j$
’s and
$h_j$
’s and
![]() $k-m$
of the
$k-m$
of the
![]() $v_j$
’s in the argument of
$v_j$
’s in the argument of
![]() $t^m \gamma $
. By multilinearity, we can bring one factor of t in to each of the
$t^m \gamma $
. By multilinearity, we can bring one factor of t in to each of the
![]() $h_j$
arguments, to get
$h_j$
arguments, to get
Thus,
![]() $t^m \gamma $
has comass at most one with respect to
$t^m \gamma $
has comass at most one with respect to
![]() $\tilde g$
. But now it is clear that if
$\tilde g$
. But now it is clear that if
![]() ${P = e_1 \wedge \cdots \wedge e_k}$
is
${P = e_1 \wedge \cdots \wedge e_k}$
is
![]() $\gamma $
-calibrated with respect to g, then
$\gamma $
-calibrated with respect to g, then
![]() $\tilde P = \tilde e_1 \wedge \cdots \wedge \tilde e_k$
is
$\tilde P = \tilde e_1 \wedge \cdots \wedge \tilde e_k$
is
![]() $t^m \gamma $
-calibrated with respect to
$t^m \gamma $
-calibrated with respect to
![]() $\tilde g$
, where
$\tilde g$
, where
![]() $\tilde e_j = t^{-1} h_j + v_j$
if
$\tilde e_j = t^{-1} h_j + v_j$
if
![]() $e_j = h_j + v_j$
.
$e_j = h_j + v_j$
.
Proposition A.4 Let
![]() $(V, g)$
and
$(V, g)$
and
![]() $(W, h)$
be finite-dimensional real inner product spaces, and let
$(W, h)$
be finite-dimensional real inner product spaces, and let
![]() $p \colon V \to W$
be a Riemannian submersion. That is, p is a linear surjection that maps
$p \colon V \to W$
be a Riemannian submersion. That is, p is a linear surjection that maps
![]() $(\mathrm {Ker}\, p)^{\perp } \subset V$
isometrically onto W. If
$(\mathrm {Ker}\, p)^{\perp } \subset V$
isometrically onto W. If
![]() $\alpha \in \Lambda ^k (W^*)$
is a semi-calibration on
$\alpha \in \Lambda ^k (W^*)$
is a semi-calibration on
![]() $(W, h)$
, then
$(W, h)$
, then
![]() $p^* \alpha $
is a semi-calibration on
$p^* \alpha $
is a semi-calibration on
![]() $(V, g)$
.
$(V, g)$
.
Proof Let
![]() $v_1, \ldots , v_k$
be orthonormal vectors in V. We can orthogonally decompose
$v_1, \ldots , v_k$
be orthonormal vectors in V. We can orthogonally decompose
![]() $v_j = u_j + w_j$
where
$v_j = u_j + w_j$
where
![]() $u_j \in \mathrm {Ker}\, p$
and
$u_j \in \mathrm {Ker}\, p$
and
![]() $w_j \in (\mathrm {Ker}\, p)^{\perp }$
. Using that
$w_j \in (\mathrm {Ker}\, p)^{\perp }$
. Using that
![]() $\alpha $
is a semi-calibration,
$\alpha $
is a semi-calibration,
![]() $p \colon ((\mathrm {Ker}\, p)^{\perp }, g) \to (W, h)$
is an isometry, and Hadamard’s inequality, we have
$p \colon ((\mathrm {Ker}\, p)^{\perp }, g) \to (W, h)$
is an isometry, and Hadamard’s inequality, we have
 $$ \begin{align*} (p^* \alpha) (v_1, \ldots, v_k) & = (p^* \alpha)(u_1 + w_1, \ldots, u_k + w_k) = \alpha(p(w_1), \ldots, p(w_k)) \\ & \leq | p(w_1) \wedge \cdots \wedge p(w_k) | \leq | p(w_1) | \cdots | p(w_k) | = |w_1| \cdots |w_k| \leq 1. \end{align*} $$
$$ \begin{align*} (p^* \alpha) (v_1, \ldots, v_k) & = (p^* \alpha)(u_1 + w_1, \ldots, u_k + w_k) = \alpha(p(w_1), \ldots, p(w_k)) \\ & \leq | p(w_1) \wedge \cdots \wedge p(w_k) | \leq | p(w_1) | \cdots | p(w_k) | = |w_1| \cdots |w_k| \leq 1. \end{align*} $$
Thus, the comass of
![]() $p^* \alpha $
is at most one. Let
$p^* \alpha $
is at most one. Let
![]() $L \subset W$
be an oriented k-plane calibrated by
$L \subset W$
be an oriented k-plane calibrated by
![]() $\alpha $
, with oriented orthonormal basis
$\alpha $
, with oriented orthonormal basis
![]() $e_1, \ldots , e_k$
. For
$e_1, \ldots , e_k$
. For
![]() $1 \leq j \leq k$
, let
$1 \leq j \leq k$
, let
![]() $w_j$
be the unique vector in
$w_j$
be the unique vector in
![]() $(\mathrm {Ker}\, p)^{\perp }$
such that
$(\mathrm {Ker}\, p)^{\perp }$
such that
![]() $p(w_j) = e_j$
. Then it is clear that
$p(w_j) = e_j$
. Then it is clear that
![]() $w_1 \wedge \cdots \wedge w_k \subset V$
is calibrated by
$w_1 \wedge \cdots \wedge w_k \subset V$
is calibrated by
![]() $p^* \alpha $
.
$p^* \alpha $
.
Proposition A.5 Let
![]() $(V, g, \omega , I)$
be a Hermitian vector space of real dimension
$(V, g, \omega , I)$
be a Hermitian vector space of real dimension
![]() $2n$
, where I is the complex structure and
$2n$
, where I is the complex structure and
![]() $\omega = g(I \cdot , \cdot )$
is the associated real
$\omega = g(I \cdot , \cdot )$
is the associated real
![]() $(1,1)$
-form. Let
$(1,1)$
-form. Let
![]() $\gamma \in \Lambda ^k(V^*)$
be of type
$\gamma \in \Lambda ^k(V^*)$
be of type
![]() $(k,0) + (0,k)$
, where
$(k,0) + (0,k)$
, where
![]() $k \leq n$
. If
$k \leq n$
. If
![]() $P \subset V$
is an oriented k-plane on which
$P \subset V$
is an oriented k-plane on which
![]() $\gamma $
attains its maximum, then P is
$\gamma $
attains its maximum, then P is
![]() $\omega $
-isotropic. That is,
$\omega $
-isotropic. That is,
![]() $\omega |_P = 0$
.
$\omega |_P = 0$
.
Proof Let
![]() $P \subset V$
be an oriented k-plane, and write
$P \subset V$
be an oriented k-plane, and write
![]() $k = 2m+1$
if k is odd, and
$k = 2m+1$
if k is odd, and
![]() ${k = 2m}$
if k is even. By [Reference Harvey19, Lemma 7.18], which actually works for any k, there exists an orthonormal basis
${k = 2m}$
if k is even. By [Reference Harvey19, Lemma 7.18], which actually works for any k, there exists an orthonormal basis
![]() $(e_1, Ie_1, \ldots , e_n, Ie_n)$
of V and constants
$(e_1, Ie_1, \ldots , e_n, Ie_n)$
of V and constants
![]() $\theta _1, \ldots , \theta _m \in [0,2\pi )$
such that
$\theta _1, \ldots , \theta _m \in [0,2\pi )$
such that
 $$ \begin{align*} P & = e_1 \wedge (\sin(\theta_1) Ie_1 + \cos(\theta_1) e_2) \wedge \cdots \wedge ( \sin(\theta_m) I e_{2m-1} + \cos(\theta_m) e_{2m} ) \wedge e_{2m+1} \\ & \text{(for } k = 2m+1), \\ P & = e_1 \wedge (\sin(\theta_1) Ie_1 + \cos(\theta_1) e_2) \wedge \cdots \wedge ( \sin(\theta_m) I e_{2m-1} + \cos(\theta_m) e_{2m} ) \\ & \text{(for } k = 2m). \end{align*} $$
$$ \begin{align*} P & = e_1 \wedge (\sin(\theta_1) Ie_1 + \cos(\theta_1) e_2) \wedge \cdots \wedge ( \sin(\theta_m) I e_{2m-1} + \cos(\theta_m) e_{2m} ) \wedge e_{2m+1} \\ & \text{(for } k = 2m+1), \\ P & = e_1 \wedge (\sin(\theta_1) Ie_1 + \cos(\theta_1) e_2) \wedge \cdots \wedge ( \sin(\theta_m) I e_{2m-1} + \cos(\theta_m) e_{2m} ) \\ & \text{(for } k = 2m). \end{align*} $$
Since
![]() $\gamma $
is of type
$\gamma $
is of type
![]() $(k,0) + (0,k)$
, we have
$(k,0) + (0,k)$
, we have
![]() $\iota _{e_i}(\iota _{Ie_i}\gamma ) = 0$
. Therefore, we have
$\iota _{e_i}(\iota _{Ie_i}\gamma ) = 0$
. Therefore, we have
Since
![]() $\gamma $
attains its maximum at P, it follows that
$\gamma $
attains its maximum at P, it follows that
![]() $\theta _1 = \theta _2 = \cdots = \theta _m = 0$
. Therefore,
$\theta _1 = \theta _2 = \cdots = \theta _m = 0$
. Therefore,
![]() $P = e_1 \wedge \cdots \wedge e_k$
. In particular, if
$P = e_1 \wedge \cdots \wedge e_k$
. In particular, if
![]() $v \in P$
, then
$v \in P$
, then
![]() $I v \in P^{\perp }$
. Hence, P is
$I v \in P^{\perp }$
. Hence, P is
![]() $\omega $
-isotropic.
$\omega $
-isotropic.
Theorem A.6 Let
![]() $(V, g, \omega _1, \omega _2, \omega _3, I_1, I_2, I_3)$
be a quaternionic-Hermitian vector space of real dimension
$(V, g, \omega _1, \omega _2, \omega _3, I_1, I_2, I_3)$
be a quaternionic-Hermitian vector space of real dimension
![]() $4n$
, where
$4n$
, where
![]() $\omega _p = g(I_p \cdot , \cdot )$
is the associated real
$\omega _p = g(I_p \cdot , \cdot )$
is the associated real
![]() $2$
-form of
$2$
-form of
![]() $I_p$
-type
$I_p$
-type
![]() $(1,1)$
. Let
$(1,1)$
. Let
![]() $\sigma = \omega _2 + i \omega _3$
. It is easy to check that
$\sigma = \omega _2 + i \omega _3$
. It is easy to check that
![]() $\sigma $
is of
$\sigma $
is of
![]() $I_1$
-type
$I_1$
-type
![]() $(2,0)$
. Let
$(2,0)$
. Let
![]() $\Theta _{2k} = \mathrm {Re} (\frac {1}{k!} \sigma ^k) \in \Lambda ^{2k} (V^*)$
. Then
$\Theta _{2k} = \mathrm {Re} (\frac {1}{k!} \sigma ^k) \in \Lambda ^{2k} (V^*)$
. Then
![]() $\Theta _{2k}$
has comass one.
$\Theta _{2k}$
has comass one.
Proof We prove this by induction on k, for any n. The case
![]() $k=1$
is clear, because then
$k=1$
is clear, because then
![]() $\Theta _{2} = \omega _2$
. Note also that if
$\Theta _{2} = \omega _2$
. Note also that if
![]() $\Theta _{2k} = \mathrm {Re} (\frac {1}{k!} \sigma ^k)$
has comass one, then so does
$\Theta _{2k} = \mathrm {Re} (\frac {1}{k!} \sigma ^k)$
has comass one, then so does
![]() $\mathrm {Re} (e^{- i \theta } \frac {1}{k!} \sigma ^k)$
for any
$\mathrm {Re} (e^{- i \theta } \frac {1}{k!} \sigma ^k)$
for any
![]() $e^{i \theta } \in S^1$
, since this just corresponds to rotating the complex structures
$e^{i \theta } \in S^1$
, since this just corresponds to rotating the complex structures
![]() $I_2, I_3$
by
$I_2, I_3$
by
![]() $\theta $
, and thus again corresponds to a quaternionic-Hermitian structure. Thus, we can assume that
$\theta $
, and thus again corresponds to a quaternionic-Hermitian structure. Thus, we can assume that
![]() $k \geq 2$
and that both
$k \geq 2$
and that both
![]() $\mathrm {Re} (\frac {1}{(k-1)!} \sigma ^{k-1})$
and
$\mathrm {Re} (\frac {1}{(k-1)!} \sigma ^{k-1})$
and
![]() $\mathrm {Im} (\frac {1}{(k-1)!} \sigma ^{k-1})$
have comass one for any quaternionic dimension n.
$\mathrm {Im} (\frac {1}{(k-1)!} \sigma ^{k-1})$
have comass one for any quaternionic dimension n.
Let P be an oriented
![]() $2k$
-plane on which
$2k$
-plane on which
![]() $\Theta _{2k}$
attains its maximum. Since
$\Theta _{2k}$
attains its maximum. Since
![]() $\Theta _{2k}$
is of
$\Theta _{2k}$
is of
![]() $I_1$
-type
$I_1$
-type
![]() $(2k,0) + (0,2k)$
, we can apply Proposition A.5 to deduce that P is
$(2k,0) + (0,2k)$
, we can apply Proposition A.5 to deduce that P is
![]() $I_1$
-isotropic. In particular, P does not contain any
$I_1$
-isotropic. In particular, P does not contain any
![]() $I_1$
-complex lines. Let
$I_1$
-complex lines. Let
![]() $e_1$
be a unit vector in P. Complete
$e_1$
be a unit vector in P. Complete
![]() $e_1$
to a quaternionic orthonormal basis
$e_1$
to a quaternionic orthonormal basis
so that
 $$ \begin{align*}\omega_1 = \sum_{j=1}^n (e_j \wedge I_1 e_j + I_2 e_j \wedge I_3 e_j),\end{align*} $$
$$ \begin{align*}\omega_1 = \sum_{j=1}^n (e_j \wedge I_1 e_j + I_2 e_j \wedge I_3 e_j),\end{align*} $$
and similarly for
![]() $\omega _2, \omega _3$
by cyclically permuting
$\omega _2, \omega _3$
by cyclically permuting
![]() $1, 2, 3$
above. In particular, we have
$1, 2, 3$
above. In particular, we have
Write
![]() $P = e_1 \wedge Q$
for an oriented
$P = e_1 \wedge Q$
for an oriented
![]() $(2k-1)$
-plane, so
$(2k-1)$
-plane, so
Moreover, we have
where
and
is a quaternionic-Hermitian subspace of real dimension
![]() $4(n-1)$
. In particular, our induction hypothesis tells us that both
$4(n-1)$
. In particular, our induction hypothesis tells us that both
![]() $\mathrm {Re} (\frac {1}{(k-1)!} \sigma ^{k-1})$
and
$\mathrm {Re} (\frac {1}{(k-1)!} \sigma ^{k-1})$
and
![]() $\mathrm {Im} (\frac {1}{(k-1)!} \sigma ^{k-1})$
have comass one on
$\mathrm {Im} (\frac {1}{(k-1)!} \sigma ^{k-1})$
have comass one on
![]() $\widetilde V$
.
$\widetilde V$
.
We observe from
![]() $Q + \widetilde V \subset W \oplus \widetilde V$
that
$Q + \widetilde V \subset W \oplus \widetilde V$
that
 $$ \begin{align*} \dim(Q \cap \widetilde V) & = \dim Q + \dim \widetilde V - \dim (Q + \widetilde V) \\ & \geq (2k-1) + (4n-4) - (4n-2) = 2k-3, \end{align*} $$
$$ \begin{align*} \dim(Q \cap \widetilde V) & = \dim Q + \dim \widetilde V - \dim (Q + \widetilde V) \\ & \geq (2k-1) + (4n-4) - (4n-2) = 2k-3, \end{align*} $$
so we can write
![]() $Q = u_2 \wedge u_3 \wedge v_4 \wedge \cdots \wedge v_{2k}$
for an oriented orthonormal basis
$Q = u_2 \wedge u_3 \wedge v_4 \wedge \cdots \wedge v_{2k}$
for an oriented orthonormal basis
![]() $\{ u_2, u_3, v_4, \ldots , v_{2k} \}$
of Q, where
$\{ u_2, u_3, v_4, \ldots , v_{2k} \}$
of Q, where
![]() $v_4, \ldots , v_{2k} \in \widetilde V$
. We also have
$v_4, \ldots , v_{2k} \in \widetilde V$
. We also have
for some unit vectors
![]() $w_2, w_3 \in W$
and
$w_2, w_3 \in W$
and
![]() $v_2, v_3 \in \widetilde V$
. Abbreviating
$v_2, v_3 \in \widetilde V$
. Abbreviating
![]() $R = v_4 \wedge \cdots \wedge v_{2k}$
,
$R = v_4 \wedge \cdots \wedge v_{2k}$
,
![]() $\cos (\phi ) = c_{\phi }$
and similarly, we have
$\cos (\phi ) = c_{\phi }$
and similarly, we have
 $$ \begin{align*} Q & = u_2 \wedge u_3 \wedge R = (c_{\phi} w_2 + s_{\phi} v_2) \wedge (c_{\psi} w_3 + s_{\psi} v_3) \wedge R \\ & = c_{\phi} c_{\psi} w_2 \wedge w_3 \wedge R + c_{\phi} s_{\psi} w_2 \wedge v_3 \wedge R + s_{\phi} c_{\psi} v_2 \wedge w_3 \wedge R + s_{\phi} s_{\psi} v_2 \wedge v_3 \wedge R. \end{align*} $$
$$ \begin{align*} Q & = u_2 \wedge u_3 \wedge R = (c_{\phi} w_2 + s_{\phi} v_2) \wedge (c_{\psi} w_3 + s_{\psi} v_3) \wedge R \\ & = c_{\phi} c_{\psi} w_2 \wedge w_3 \wedge R + c_{\phi} s_{\psi} w_2 \wedge v_3 \wedge R + s_{\phi} c_{\psi} v_2 \wedge w_3 \wedge R + s_{\phi} s_{\psi} v_2 \wedge v_3 \wedge R. \end{align*} $$
From (A.3) and the above, we get
Since
![]() $\iota _{e_1} \Theta _{2k}$
is of
$\iota _{e_1} \Theta _{2k}$
is of
![]() $I_1$
-type
$I_1$
-type
![]() $(2k-1,0) + (0, 2k-1)$
, the first term in (A.4) must vanish because it contains the
$(2k-1,0) + (0, 2k-1)$
, the first term in (A.4) must vanish because it contains the
![]() $I_1$
-complex line
$I_1$
-complex line
![]() $w_2 \wedge w_3$
. Moreover, from (A.2), we have
$w_2 \wedge w_3$
. Moreover, from (A.2), we have
 $$ \begin{align*} \iota_{e_1} \Theta_{2k} & = \iota_{e_1} \mathrm{Re} \left( \frac{1}{k!} \sigma^k \right) = \mathrm{Re} \left( (\iota_{e_1} \sigma) \wedge \frac{1}{(k-1)!} \sigma^{k-1} \right) \\ & = I_2 e_1 \wedge \mathrm{Re} \left( \frac{1}{(k-1)!} \sigma^{k-1} \right) - I_3 e_1 \wedge \mathrm{Im} \left( \frac{1}{(k-1)!} \sigma^{k-1} \right). \end{align*} $$
$$ \begin{align*} \iota_{e_1} \Theta_{2k} & = \iota_{e_1} \mathrm{Re} \left( \frac{1}{k!} \sigma^k \right) = \mathrm{Re} \left( (\iota_{e_1} \sigma) \wedge \frac{1}{(k-1)!} \sigma^{k-1} \right) \\ & = I_2 e_1 \wedge \mathrm{Re} \left( \frac{1}{(k-1)!} \sigma^{k-1} \right) - I_3 e_1 \wedge \mathrm{Im} \left( \frac{1}{(k-1)!} \sigma^{k-1} \right). \end{align*} $$
Using the orthogonality of W and
![]() $\widetilde V$
and the above, the fourth term in (A.4) must also vanish, and we are left with
$\widetilde V$
and the above, the fourth term in (A.4) must also vanish, and we are left with
 $$ \begin{align*} \Theta_{2k}(P) & = c_{\phi} s_{\psi} \, g(I_2 e_1, w_2) \, \mathrm{Re} \left( \frac{1}{(k-1)!} \sigma^{k-1} \right) (v_3 \wedge R) \\ & \qquad {} + s_{\phi} c_{\psi} \, g(I_3 e_1, w_3) \, \mathrm{Im} \left( \frac{1}{(k-1)!} \sigma^{k-1} \right) (v_2 \wedge R). \end{align*} $$
$$ \begin{align*} \Theta_{2k}(P) & = c_{\phi} s_{\psi} \, g(I_2 e_1, w_2) \, \mathrm{Re} \left( \frac{1}{(k-1)!} \sigma^{k-1} \right) (v_3 \wedge R) \\ & \qquad {} + s_{\phi} c_{\psi} \, g(I_3 e_1, w_3) \, \mathrm{Im} \left( \frac{1}{(k-1)!} \sigma^{k-1} \right) (v_2 \wedge R). \end{align*} $$
Applying the induction hypothesis and Cauchy–Schwarz, we deduce that
so
![]() $\Theta _{2k}$
has comass at most one. But letting
$\Theta _{2k}$
has comass at most one. But letting
![]() $v_3 \wedge \cdots \wedge v_{2k}$
be a calibrated
$v_3 \wedge \cdots \wedge v_{2k}$
be a calibrated
![]() $(2k-2)$
-plane for
$(2k-2)$
-plane for
![]() $\mathrm {Re} (\frac {1}{(k-1)!} \sigma ^{k-1})$
and choosing
$\mathrm {Re} (\frac {1}{(k-1)!} \sigma ^{k-1})$
and choosing
 $$ \begin{align*} u_2 & = I_2 e_1 \in W, & & \text{so that} \cos(\phi) = 1, \sin(\phi) = 0, \text{and } g(I_2 e_1, w_2) = 1, \\ u_3 & = v_3 \in \widetilde V, & & \text{so that} \cos(\psi) = 0, \sin(\psi) = 1, \end{align*} $$
$$ \begin{align*} u_2 & = I_2 e_1 \in W, & & \text{so that} \cos(\phi) = 1, \sin(\phi) = 0, \text{and } g(I_2 e_1, w_2) = 1, \\ u_3 & = v_3 \in \widetilde V, & & \text{so that} \cos(\psi) = 0, \sin(\psi) = 1, \end{align*} $$
gives
![]() $\Theta _{2k}(P) = 1$
. Thus, the comass of
$\Theta _{2k}(P) = 1$
. Thus, the comass of
![]() $\Theta _{2k}$
is exactly one.
$\Theta _{2k}$
is exactly one.
Remark A.7 The case
![]() $k=2$
of Theorem A.6 is proved in [Reference Bryant and Harvey9, Theorem 2.38], where they also prove that a
$k=2$
of Theorem A.6 is proved in [Reference Bryant and Harvey9, Theorem 2.38], where they also prove that a
![]() $\Theta _{4}$
-calibrated
$\Theta _{4}$
-calibrated
![]() $4$
-plane is contained in a quaternionic
$4$
-plane is contained in a quaternionic
![]() $2$
-plane in V. It is likely that this fact remains true for general k. That is, a
$2$
-plane in V. It is likely that this fact remains true for general k. That is, a
![]() $\Theta _{2k}$
-calibrated
$\Theta _{2k}$
-calibrated
![]() $2k$
-plane in V is contained in a quaternionic k-plane. However, we do not have need for this fact.
$2k$
-plane in V is contained in a quaternionic k-plane. However, we do not have need for this fact.
A.2 Riemannian cones and homogeneous forms
Let
![]() $(M, g_M)$
be a Riemannian manifold. Let
$(M, g_M)$
be a Riemannian manifold. Let
![]() $C = \mathrm {C}(M) = (0, \infty ) \times M$
, and let r denote the standard coordinate on
$C = \mathrm {C}(M) = (0, \infty ) \times M$
, and let r denote the standard coordinate on
![]() $(0, \infty )$
. The cone metric
$(0, \infty )$
. The cone metric
![]() $g_C$
on C induced by
$g_C$
on C induced by
![]() $g_M$
is defined to be
$g_M$
is defined to be
The codimension one submanifold
![]() $\{ 1 \} \times M \cong M$
is called the link of the cone. We have a projection map
$\{ 1 \} \times M \cong M$
is called the link of the cone. We have a projection map
![]() $\pi \colon C \to M$
given by
$\pi \colon C \to M$
given by
![]() $\pi (r, x) = x$
. Given differential forms on the link M, we can regard them as forms on the cone C by pulling back by
$\pi (r, x) = x$
. Given differential forms on the link M, we can regard them as forms on the cone C by pulling back by
![]() $\pi \colon C \to M$
. We omit the explicit pullback notation.
$\pi \colon C \to M$
. We omit the explicit pullback notation.
Definition A.8 Consider the vector field
on the cone C. The flow
![]() $F_s$
of R is given by
$F_s$
of R is given by
![]() $(r,p) \mapsto (e^s r, p)$
. For this reason, R is called the dilation vector field on the cone.
$(r,p) \mapsto (e^s r, p)$
. For this reason, R is called the dilation vector field on the cone.
It follows that
![]() $\mathscr {L}_{R} g_C = 2 g_C$
. We say that
$\mathscr {L}_{R} g_C = 2 g_C$
. We say that
![]() $g_C$
is homogeneous of degree
$g_C$
is homogeneous of degree
![]() $2$
under dilations.
$2$
under dilations.
Definition A.9 Let
![]() $\gamma \in \Omega ^k (C)$
. We say that
$\gamma \in \Omega ^k (C)$
. We say that
![]() $\gamma $
is conical if
$\gamma $
is conical if
![]() $\gamma $
is homogeneous of degree k, or equivalently if
$\gamma $
is homogeneous of degree k, or equivalently if
![]() $\mathscr {L}_{R} \gamma = k \gamma $
.
$\mathscr {L}_{R} \gamma = k \gamma $
.
Proposition A.10 Let
![]() $\gamma \in \Omega ^k (C)$
be a closed form which is homogeneous of degree k. Then, in fact,
$\gamma \in \Omega ^k (C)$
be a closed form which is homogeneous of degree k. Then, in fact,
where
![]() $\alpha _0 = (\iota _{R} \gamma )|_M \in \Omega ^{k-1} (M)$
.
$\alpha _0 = (\iota _{R} \gamma )|_M \in \Omega ^{k-1} (M)$
.
Proof Write
![]() $\gamma = dr \wedge \alpha + \beta $
for some
$\gamma = dr \wedge \alpha + \beta $
for some
![]() $(k-1)$
-form
$(k-1)$
-form
![]() $\alpha $
and k-form
$\alpha $
and k-form
![]() $\beta $
on C such that
$\beta $
on C such that
![]() $\iota _{\frac {\partial }{\partial r}} \alpha = \iota _{\frac {\partial }{\partial r}} \beta = 0$
. That is,
$\iota _{\frac {\partial }{\partial r}} \alpha = \iota _{\frac {\partial }{\partial r}} \beta = 0$
. That is,
![]() $\alpha $
and
$\alpha $
and
![]() $\beta $
have no
$\beta $
have no
![]() $dr$
factor, so they can be considered as forms on M depending on a parameter r, pulled back to C by
$dr$
factor, so they can be considered as forms on M depending on a parameter r, pulled back to C by
![]() $\pi $
.
$\pi $
.
From
![]() $\gamma = dr \wedge \alpha + \beta $
, and denoting by
$\gamma = dr \wedge \alpha + \beta $
, and denoting by
![]() $\hat d$
the exterior derivative on M, we have
$\hat d$
the exterior derivative on M, we have
and thus
But from
![]() $\mathscr {L}_{R} \gamma = k \gamma $
, since
$\mathscr {L}_{R} \gamma = k \gamma $
, since
![]() $d \gamma = 0$
, we have
$d \gamma = 0$
, we have
![]() $k \gamma = d ( \iota _{R} \gamma )$
. Hence, since
$k \gamma = d ( \iota _{R} \gamma )$
. Hence, since
![]() $\iota _{R} \gamma = r \alpha $
, we obtain
$\iota _{R} \gamma = r \alpha $
, we obtain
Comparing the two sides above gives
The first equation in (A.8) gives
![]() $r \alpha ' = (k-1) \alpha $
, so
$r \alpha ' = (k-1) \alpha $
, so
![]() $\alpha = r^{k-1} \alpha _0$
where
$\alpha = r^{k-1} \alpha _0$
where
![]() $\alpha _0$
is independent of r. Then the second equation gives
$\alpha _0$
is independent of r. Then the second equation gives
![]() $k \beta = r \hat d (r^{k-1} \alpha _0) = r^k \hat d \alpha _0$
, so
$k \beta = r \hat d (r^{k-1} \alpha _0) = r^k \hat d \alpha _0$
, so
![]() $\beta = \frac {r^k}{k} \hat d \alpha _0$
. Note that the two equations in (A.7) are now automatically satisfied. Since
$\beta = \frac {r^k}{k} \hat d \alpha _0$
. Note that the two equations in (A.7) are now automatically satisfied. Since
![]() $\iota _{R} \gamma = r \alpha = r^k \alpha _0$
, we therefore conclude that
$\iota _{R} \gamma = r \alpha = r^k \alpha _0$
, we therefore conclude that
where
![]() $\alpha _0 = (r^k \alpha _0)|_M = (\iota _{R} \gamma )|_M$
.
$\alpha _0 = (r^k \alpha _0)|_M = (\iota _{R} \gamma )|_M$
.
Acknowledgements
The second author thanks Lucía Martín-Merchán for useful discussions. The third author thanks Laura Fredrickson, McKenzie Wang, and Micah Warren for conversations. All three authors are grateful to the referee for helpful suggestions that improved an earlier draft of this paper.