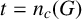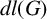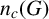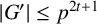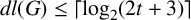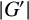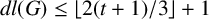1 Introduction
A finite group is said to be a Dedekind group if all its subgroups are normal. Such groups were precisely classified by Dedekind in [Reference Dedekind6]. Groups having only a few nonnormal subgroups can be considered close to Dedekind groups. There are many results about such groups that characterise the structure of finite groups with a small number of conjugacy classes of nonnormal subgroups (see [Reference Brandl3–Reference Chen and Chen5, Reference Gong, Cao and Chen7, Reference Mousavi9–Reference Mousavi11]). There are also explorations based on the number of orders of nonnormal subgroups.
Let G be a finite group. For convenience, we introduce the notation,
Obviously,
![]() $n_c(G)=0$
if and only if G is a Dedekind group. Passman in [Reference Passman12] classified finite p-groups, all of whose nonnormal subgroups are cyclic, including finite p-groups with
$n_c(G)=0$
if and only if G is a Dedekind group. Passman in [Reference Passman12] classified finite p-groups, all of whose nonnormal subgroups are cyclic, including finite p-groups with
![]() $n_c(G)=1$
. Later, Berkovich and Zhang in [Reference Berkovich2, Reference Zhang13] classified finite groups with
$n_c(G)=1$
. Later, Berkovich and Zhang in [Reference Berkovich2, Reference Zhang13] classified finite groups with
![]() $n_c(G)=1$
, and An in [Reference An1] classified finite p-groups with
$n_c(G)=1$
, and An in [Reference An1] classified finite p-groups with
![]() $n_c(G)=2$
. These results are mainly concerned with the structure of G. In particular, Passman in [Reference Passman12] gave several interesting properties of finite p-groups based on the orders of their nonnormal subgroups, which served as inspiration for this study.
$n_c(G)=2$
. These results are mainly concerned with the structure of G. In particular, Passman in [Reference Passman12] gave several interesting properties of finite p-groups based on the orders of their nonnormal subgroups, which served as inspiration for this study.
The aim of this paper is to estimate the derived length of a finite solvable group G in terms of
![]() $n_c(G)$
. We examine nilpotent groups (Section 2) and solvable nonnilpotent groups (Section 3). In fact, the derived length of a nilpotent group with
$n_c(G)$
. We examine nilpotent groups (Section 2) and solvable nonnilpotent groups (Section 3). In fact, the derived length of a nilpotent group with
![]() $n_c(G)=t$
is less than the derived length of p-groups with
$n_c(G)=t$
is less than the derived length of p-groups with
![]() $n_c(G)=t$
. Therefore, we consider finite p-groups instead of nilpotent groups.
$n_c(G)=t$
. Therefore, we consider finite p-groups instead of nilpotent groups.
In [Reference Passman12], Passman showed that, for a finite p-group G, if the maximal order of nonnormal subgroups of G is
![]() $p^m$
, then
$p^m$
, then
![]() $|G'|\leq p^m$
, and hence the nilpotent class
$|G'|\leq p^m$
, and hence the nilpotent class
![]() $c(G)\leq m+1$
. Also, it is trivial that
$c(G)\leq m+1$
. Also, it is trivial that
![]() $n_c(G)\leq m$
. We obtain the following result.
$n_c(G)\leq m$
. We obtain the following result.
Theorem 1.1. Let G be a p-group. If
![]() $n_c(G)=t $
, then
$n_c(G)=t $
, then
![]() $dl(G)\leq \lceil \log _2(2t+3)\rceil $
.
$dl(G)\leq \lceil \log _2(2t+3)\rceil $
.
Assume that G is a finite solvable nonnilpotent group. We establish an upper bound for the derived length
![]() $dl(G)$
in terms of
$dl(G)$
in terms of
![]() $n_c(G)$
.
$n_c(G)$
.
Theorem 1.2. Let G be a solvable nonnilpotent group. If
![]() $n_c(G)=t $
, then the derived length
$n_c(G)=t $
, then the derived length
![]() $dl(G)\leq \lfloor (2t+2)/3\rfloor +1 $
.
$dl(G)\leq \lfloor (2t+2)/3\rfloor +1 $
.
Let G be a finite solvable group with
![]() $|G|=\prod _{i=1}^kp_i^{\alpha _i}$
. For convenience, we define
$|G|=\prod _{i=1}^kp_i^{\alpha _i}$
. For convenience, we define
 $$ \begin{align*}s_p(G)=\sum_{i=1}^k\alpha_i.\end{align*} $$
$$ \begin{align*}s_p(G)=\sum_{i=1}^k\alpha_i.\end{align*} $$
For the remainder of this paper, all groups are finite and we refer to [Reference Kurzweil and Stellmacher8] for standard notation concerning the theory of finite groups.
2 The p-groups with
 $n_c(G)=t$
$n_c(G)=t$
In this section, we bound the order of
![]() $G'$
and the derived length
$G'$
and the derived length
![]() $dl(G)$
for a p-group G in terms of the number of orders of nonnormal subgroups
$dl(G)$
for a p-group G in terms of the number of orders of nonnormal subgroups
![]() $n_c(G)$
. We begin with four lemmas.
$n_c(G)$
. We begin with four lemmas.
Lemma 2.1 [Reference Berkovich2, Lemma 1.4].
Let G be a p-group and let
![]() $N\unlhd G$
. If N has no abelian normal subgroups of G of type
$N\unlhd G$
. If N has no abelian normal subgroups of G of type
![]() $(p,p)$
, then N is either cyclic or a
$(p,p)$
, then N is either cyclic or a
![]() $2$
-group of maximal class.
$2$
-group of maximal class.
Lemma 2.2 [Reference Passman12, Lemma 1.4].
Let N be a minimal nonnormal subgroup of a p-group P. Then N is cyclic.
Suppose that G is a group and
![]() $N\unlhd G$
. Note that
$N\unlhd G$
. Note that
![]() $n_c(G/N)$
is the number of orders of nonnormal subgroups of G containing N. The following lemma is easy but important, and it will frequently be used later in the paper.
$n_c(G/N)$
is the number of orders of nonnormal subgroups of G containing N. The following lemma is easy but important, and it will frequently be used later in the paper.
Lemma 2.3. Let G be a group. Assume that N is a normal subgroup of G. Then
![]() $n_c(G/N)\leq n_c(G)$
. Moreover, if
$n_c(G/N)\leq n_c(G)$
. Moreover, if
![]() $n_c(G/N)=n_c(G)$
, then the orders of all nonnormal subgroups of G are divisible by the order of N.
$n_c(G/N)=n_c(G)$
, then the orders of all nonnormal subgroups of G are divisible by the order of N.
Proof. Obviously, the projection of the nonnormal subgroups of
![]() $G/N$
onto G are still nonnormal, and hence
$G/N$
onto G are still nonnormal, and hence
![]() $n_c(G/N)\leq n_c(G)$
. If there exists a nonnormal subgroup of G whose order is not divisible by
$n_c(G/N)\leq n_c(G)$
. If there exists a nonnormal subgroup of G whose order is not divisible by
![]() $|N|$
, then
$|N|$
, then
![]() $n_c(G/N)<n_c(G)$
. This completes the proof.
$n_c(G/N)<n_c(G)$
. This completes the proof.
Let G be a p-group. We say that
![]() $H_1>H_2>\cdots >H_k$
is a chain of nonnormal subgroups of G if each
$H_1>H_2>\cdots >H_k$
is a chain of nonnormal subgroups of G if each
![]() $H_i\ntrianglelefteq G$
and if
$H_i\ntrianglelefteq G$
and if
![]() $|H_i:H_{i+1}|=p$
for
$|H_i:H_{i+1}|=p$
for
![]() $1\leq i\leq k-1$
. Passman in [Reference Passman12] used
$1\leq i\leq k-1$
. Passman in [Reference Passman12] used
![]() $\mathrm {chn}(G)$
to denote the maximum of the lengths of the chains of nonnormal subgroups of G, and proved that if
$\mathrm {chn}(G)$
to denote the maximum of the lengths of the chains of nonnormal subgroups of G, and proved that if
![]() $\mathrm {chn}(G)=t$
, then
$\mathrm {chn}(G)=t$
, then
![]() $s_p(G')\leq 2t+\lfloor 2/p\rfloor $
. It is trivial that
$s_p(G')\leq 2t+\lfloor 2/p\rfloor $
. It is trivial that
![]() $\mathrm {chn}(G)\leq n_c(G)$
. In the next lemma, we weaken the condition.
$\mathrm {chn}(G)\leq n_c(G)$
. In the next lemma, we weaken the condition.
Lemma 2.4. Let G be a p-group. If
![]() $n_c(G)=t$
, then
$n_c(G)=t$
, then
![]() $s_p(G')\leq 2t+1$
.
$s_p(G')\leq 2t+1$
.
Proof. Let G be a p-group and assume that
![]() $n_c(G)=t$
. If G has no elementary abelian normal subgroup of order
$n_c(G)=t$
. If G has no elementary abelian normal subgroup of order
![]() $p^2$
, then, by Lemma 2.1, G is either a cyclic group or a
$p^2$
, then, by Lemma 2.1, G is either a cyclic group or a
![]() $2$
-group of maximal class. It is easy to see that
$2$
-group of maximal class. It is easy to see that
![]() $s_p(G')\leq n_c(G)+1$
and the result follows.
$s_p(G')\leq n_c(G)+1$
and the result follows.
Now, suppose that there exists an elementary abelian normal subgroup N of order
![]() $p^2$
. In this case, we perform induction on t. If
$p^2$
. In this case, we perform induction on t. If
![]() $t=0$
, clearly, G is Dedekind and
$t=0$
, clearly, G is Dedekind and
![]() $s_p(G')\leq 1$
, as required. Next, suppose that
$s_p(G')\leq 1$
, as required. Next, suppose that
![]() $t\geq 1$
. We consider the factor group
$t\geq 1$
. We consider the factor group
![]() $G/N$
. Assume that M is a nonnormal subgroup of minimal order of G. Then M is cyclic by Lemma 2.2. Let
$G/N$
. Assume that M is a nonnormal subgroup of minimal order of G. Then M is cyclic by Lemma 2.2. Let
![]() $|M|=p^m$
. We claim that
$|M|=p^m$
. We claim that
![]() $n_c(G/N)\leq t-1$
. If
$n_c(G/N)\leq t-1$
. If
![]() $p^m\leq p^2$
, it follows from Lemma 2.3 that
$p^m\leq p^2$
, it follows from Lemma 2.3 that
![]() $n_c(G/N)\leq t-1$
. Conversely, if
$n_c(G/N)\leq t-1$
. Conversely, if
![]() $p^m>p^2$
, then
$p^m>p^2$
, then
![]() $G/N$
has no nonnormal subgroups of order
$G/N$
has no nonnormal subgroups of order
![]() $p^{m-2}$
. Otherwise, there exists a noncyclic nonnormal subgroup of order
$p^{m-2}$
. Otherwise, there exists a noncyclic nonnormal subgroup of order
![]() $p^m$
of G, which contradicts the minimality of M. Thus, according to Lemma 2.3, we have
$p^m$
of G, which contradicts the minimality of M. Thus, according to Lemma 2.3, we have
![]() $n_c(G/N)\leq t-1$
, as claimed. Here, by induction on t, it follows that
$n_c(G/N)\leq t-1$
, as claimed. Here, by induction on t, it follows that
![]() $s_p((G/N)')\leq 2(t-1)+1$
. Therefore,
$s_p((G/N)')\leq 2(t-1)+1$
. Therefore,
The proof is complete.
Corollary 2.5. Let G be a nilpotent group. If
![]() $n_c(G)=t$
, then
$n_c(G)=t$
, then
![]() $s_p(G')\leq 2t+1$
.
$s_p(G')\leq 2t+1$
.
Proof. Let
![]() $P_i\in \mathrm {Syl}_{p_i}(G)$
and assume that
$P_i\in \mathrm {Syl}_{p_i}(G)$
and assume that
![]() $G=P_1\times P_2\times \cdots \times P_k$
with
$G=P_1\times P_2\times \cdots \times P_k$
with
![]() $n_c(G)=t$
. If
$n_c(G)=t$
. If
![]() $k=1$
, the result is trivial by Lemma 2.4. Now, let
$k=1$
, the result is trivial by Lemma 2.4. Now, let
![]() $k\geq 1$
. We assume that
$k\geq 1$
. We assume that
![]() $G=H\times P_{k}$
. Since
$G=H\times P_{k}$
. Since
![]() $n_c(G)=t$
, we have
$n_c(G)=t$
, we have
![]() $n_c(H)< t/2$
and
$n_c(H)< t/2$
and
![]() $n_c(P_k)\leq t/2$
. By induction on k, it follows that
$n_c(P_k)\leq t/2$
. By induction on k, it follows that
![]() $s_p(H')<t+1$
and
$s_p(H')<t+1$
and
![]() $s_p({P_k}')<t+1$
. Therefore,
$s_p({P_k}')<t+1$
. Therefore,
![]() $s_p(G')\leq 2t+1$
.
$s_p(G')\leq 2t+1$
.
We denote by
![]() $c(G)$
the nilpotent class and use
$c(G)$
the nilpotent class and use
![]() $G_i$
and
$G_i$
and
![]() $G^{(i)}$
to denote the ith terms of the lower central series and the commutator series for a group G, respectively. We are now ready to prove Theorem 1.1
$G^{(i)}$
to denote the ith terms of the lower central series and the commutator series for a group G, respectively. We are now ready to prove Theorem 1.1
Proof of Theorem 1.1.
Let G be a p-group and assume that
![]() $n_c(G)=t$
. By Lemma 2.4, we see that
$n_c(G)=t$
. By Lemma 2.4, we see that
![]() $|G'|\leq p^{2t+1}$
and thus
$|G'|\leq p^{2t+1}$
and thus
![]() $c(G)\leq 2t+2$
. It suffices to show that
$c(G)\leq 2t+2$
. It suffices to show that
![]() $G^{(i)}\leq G_{2^i}$
for
$G^{(i)}\leq G_{2^i}$
for
![]() $ i\geq 1$
since, by induction on i,
$ i\geq 1$
since, by induction on i,
Note that
![]() $1=G_{2t+3}=G^{(dl(G))}\leq G_{2^{dl(G)}}$
. Consequently,
$1=G_{2t+3}=G^{(dl(G))}\leq G_{2^{dl(G)}}$
. Consequently,
![]() $2^{dl(G)}\leq 2t+3$
, that is,
$2^{dl(G)}\leq 2t+3$
, that is,
![]() $dl(G)\leq \lceil \log _2(2t+3)\rceil $
. This completes the proof.
$dl(G)\leq \lceil \log _2(2t+3)\rceil $
. This completes the proof.
3 The solvable nonnilpotent groups with
 $n_c(G)=t$
$n_c(G)=t$
In this section, we investigate the solvable nonnilpotent groups with
![]() $n_c(G)=t$
and prove the main result of this paper.
$n_c(G)=t$
and prove the main result of this paper.
First, we state the characterisation of finite groups with
![]() $n_c(G)=1$
and provide a basic fact about nilpotent groups.
$n_c(G)=1$
and provide a basic fact about nilpotent groups.
Lemma 3.1 [Reference Zhang13, Theorem 2.3].
Let G be a finite group. If all nonnormal subgroups of G possess the same order, then G is a finite p-group or
![]() $G=\langle a \rangle \rtimes \langle b \rangle $
, where
$G=\langle a \rangle \rtimes \langle b \rangle $
, where
![]() $o(a)=p_2$
,
$o(a)=p_2$
,
![]() $o(b)={p_1}^{n_{1}}$
,
$o(b)={p_1}^{n_{1}}$
,
![]() $p_1, p_2$
are primes with
$p_1, p_2$
are primes with
![]() $p_1< p_2$
and
$p_1< p_2$
and
![]() $[a, b^{p_1}]=1$
. Moreover, if
$[a, b^{p_1}]=1$
. Moreover, if
![]() $G=\langle a \rangle \rtimes \langle b \rangle $
, as stated, then all nonnormal subgroups of G are of order
$G=\langle a \rangle \rtimes \langle b \rangle $
, as stated, then all nonnormal subgroups of G are of order
![]() ${p_1}^{n_1} $
.
${p_1}^{n_1} $
.
Lemma 3.2 [Reference Kurzweil and Stellmacher8, Lemma 5.1.2].
Let G be a group and let
![]() $N \leq Z(G)$
. Then G is nilpotent if and only if
$N \leq Z(G)$
. Then G is nilpotent if and only if
![]() $G/N$
is nilpotent.
$G/N$
is nilpotent.
For solvable nonnilpotent groups, we have the following further conclusion based on Lemma 2.3.
Lemma 3.3. Let G be a solvable nonnilpotent group. Then there exists a minimal normal subgroup N such that
![]() $n_c(G/N)\leq n_c(G)-s_p(N)$
.
$n_c(G/N)\leq n_c(G)-s_p(N)$
.
Proof. By Lemma 2.3,
![]() $n_c(G/N)\leq n_c(G)$
. First, we claim that there exists a minimal normal subgroup N of G such that
$n_c(G/N)\leq n_c(G)$
. First, we claim that there exists a minimal normal subgroup N of G such that
![]() $n_c(G/N)<n_c(G)$
. Let
$n_c(G/N)<n_c(G)$
. Let
![]() $P_i\in \mathrm {Syl}_{p_i}(G)$
. Noting that G is nonnilpotent, we may assume that
$P_i\in \mathrm {Syl}_{p_i}(G)$
. Noting that G is nonnilpotent, we may assume that
![]() $P_1$
is a nonnormal Sylow subgroup of G. If, for
$P_1$
is a nonnormal Sylow subgroup of G. If, for
![]() $i\geq 2$
, there exists a Sylow subgroup
$i\geq 2$
, there exists a Sylow subgroup
![]() $P_i$
such that
$P_i$
such that
![]() $P_i$
is nonnormal, we may assume that
$P_i$
is nonnormal, we may assume that
![]() $P_2$
is nonnormal. Then
$P_2$
is nonnormal. Then
![]() $n_c(G/N)<n_c(G)$
is always true for any minimal normal subgroup
$n_c(G/N)<n_c(G)$
is always true for any minimal normal subgroup
![]() $N\neq 1$
. Otherwise, by Lemma 2.3, the orders of both
$N\neq 1$
. Otherwise, by Lemma 2.3, the orders of both
![]() $P_1$
and
$P_1$
and
![]() $P_2$
are divisible by the order of N, so that
$P_2$
are divisible by the order of N, so that
![]() $N=1$
, which is a contradiction. On the other hand, if
$N=1$
, which is a contradiction. On the other hand, if
![]() $P_i\unlhd G$
for all
$P_i\unlhd G$
for all
![]() $i\geq 2$
, we may take
$i\geq 2$
, we may take
![]() $N\leq P_2$
. According to Lemma 2.3 again,
$N\leq P_2$
. According to Lemma 2.3 again,
![]() $n_c(G/N)<n_c(G)$
since the order of
$n_c(G/N)<n_c(G)$
since the order of
![]() $P_1$
is not divisible by the order of N. This proves the claim.
$P_1$
is not divisible by the order of N. This proves the claim.
Since
![]() $ N $
is a minimal normal subgroup of G, it follows that N is an elementary abelian p-group and proper subgroups of N are nonnormal subgroups of G. There are
$ N $
is a minimal normal subgroup of G, it follows that N is an elementary abelian p-group and proper subgroups of N are nonnormal subgroups of G. There are
![]() $s_p(N)-1$
nonnormal subgroups of G contained by N. Thus,
$s_p(N)-1$
nonnormal subgroups of G contained by N. Thus,
Here, if
![]() $n_c(G/N)=n_c(G)-s_p(N)+1$
, then, similarly, both the orders of
$n_c(G/N)=n_c(G)-s_p(N)+1$
, then, similarly, both the orders of
![]() $P_1$
and
$P_1$
and
![]() $P_2$
are divisible by p, which is a contradiction. Hence,
$P_2$
are divisible by p, which is a contradiction. Hence,
![]() $n_c(G/N)\leq n_c(G)-s_p(N)$
and the proof is complete.
$n_c(G/N)\leq n_c(G)-s_p(N)$
and the proof is complete.
The next crucial lemma establishes an upper bound on the order of
![]() $G'$
in terms of
$G'$
in terms of
![]() $n_c(G)$
for a solvable nonnilpotent group G.
$n_c(G)$
for a solvable nonnilpotent group G.
Lemma 3.4. Let G be a solvable nonnilpotent group. If
![]() $n_c(G)=t$
, then
$n_c(G)=t$
, then
![]() $s_p(G')\leq t$
.
$s_p(G')\leq t$
.
Proof. Assume that
![]() $n_c(G)=t$
. The proof will be done by induction to t. If
$n_c(G)=t$
. The proof will be done by induction to t. If
![]() $t=1$
, then, by Lemma 3.1,
$t=1$
, then, by Lemma 3.1,
where
![]() $o(a)={p_2}$
,
$o(a)={p_2}$
,
![]() $o(b)={p_1}^{n_1}$
and
$o(b)={p_1}^{n_1}$
and
![]() $p_1, p_2$
are different primes. Since
$p_1, p_2$
are different primes. Since
![]() $G/\langle a\rangle $
is cyclic, we have
$G/\langle a\rangle $
is cyclic, we have
![]() $s_p(G')=1$
.
$s_p(G')=1$
.
Now, let
![]() $t\geq 2$
. According to the proof of Lemma 3.3, it suffices to show that there exists a minimal normal subgroup N such that
$t\geq 2$
. According to the proof of Lemma 3.3, it suffices to show that there exists a minimal normal subgroup N such that
![]() $n_c(G/N)<t$
.
$n_c(G/N)<t$
.
Case 1:
![]() $G/N$
is nonnilpotent.
$G/N$
is nonnilpotent.
In this case, since
![]() $n_c(G/N)<t$
, it follows that
$n_c(G/N)<t$
, it follows that
![]() $s_p((G/N)')\leq n_c(G/N)$
by induction on t. In addition,
$s_p((G/N)')\leq n_c(G/N)$
by induction on t. In addition,
![]() $|G'|=|G'\cap N||(G/N)'|$
because
$|G'|=|G'\cap N||(G/N)'|$
because
![]() $(G/N)'\cong G'/(G'\cap N)$
. Hence,
$(G/N)'\cong G'/(G'\cap N)$
. Hence,
![]() $|N||(G/N)'|$
is divisible by
$|N||(G/N)'|$
is divisible by
![]() $|G'|$
. Therefore,
$|G'|$
. Therefore,
By Lemma 3.3,
![]() $n_c(G/N)\leq n_c(G)-s_p(N)$
, and hence
$n_c(G/N)\leq n_c(G)-s_p(N)$
, and hence
This completes the proof in Case 1.
Case 2:
![]() $G/N$
is nilpotent. In this case, we consider the following two situations.
$G/N$
is nilpotent. In this case, we consider the following two situations.
Case 2a: there exists a minimal normal subgroup M such that
![]() $M\neq N$
.
$M\neq N$
.
Since G is a nonnilpotent group, it follows that
![]() $G/M$
is also nonnilpotent. Otherwise, since
$G/M$
is also nonnilpotent. Otherwise, since
![]() $G/(M\cap N) \lesssim G/M \times G/N$
, we see that
$G/(M\cap N) \lesssim G/M \times G/N$
, we see that
![]() $G/(M\cap N)$
is nilpotent. However,
$G/(M\cap N)$
is nilpotent. However,
![]() $G/(M\cap N)\cong G$
is nonnilpotent, which is a contradiction. Now, assume that
$G/(M\cap N)\cong G$
is nonnilpotent, which is a contradiction. Now, assume that
![]() $|M|=p^m$
and
$|M|=p^m$
and
![]() $|N|=q^n$
, where
$|N|=q^n$
, where
![]() $p,q$
are different primes. We consider two cases, namely,
$p,q$
are different primes. We consider two cases, namely,
![]() $m\geq 2$
and
$m\geq 2$
and
![]() $m=1$
. If
$m=1$
. If
![]() $m\geq 2$
, since
$m\geq 2$
, since
![]() $N_1M_1\ntrianglelefteq G$
for all
$N_1M_1\ntrianglelefteq G$
for all
![]() $1<M_1<M$
and
$1<M_1<M$
and
![]() $1\leq N_1\leq N$
, then
$1\leq N_1\leq N$
, then
Here, it follows easily by induction that
![]() $s_p((G/M)')\leq n_c(G/M)$
. This condition is similar to Case 1 and it follows that
$s_p((G/M)')\leq n_c(G/M)$
. This condition is similar to Case 1 and it follows that
Now suppose that
![]() $m=1$
, that is,
$m=1$
, that is,
![]() $|M|=p$
. If there exists a nonnormal subgroup H such that
$|M|=p$
. If there exists a nonnormal subgroup H such that
![]() $|H|$
is not divisible by p, then
$|H|$
is not divisible by p, then
![]() $n_c(G/M)\leq n_c(G)-1$
from Lemma 2.3, and so
$n_c(G/M)\leq n_c(G)-1$
from Lemma 2.3, and so
![]() $s_p((G/M)')\leq n_c(G/M)$
by induction. As before, the result holds. On the other hand, if, for every subgroup H of
$s_p((G/M)')\leq n_c(G/M)$
by induction. As before, the result holds. On the other hand, if, for every subgroup H of
![]() $G$
whose order is not divisible by p, H is always normal, then we may assume that
$G$
whose order is not divisible by p, H is always normal, then we may assume that
![]() $G=KP$
, where K is a Hall
$G=KP$
, where K is a Hall
![]() $p'$
-subgroup of G. Obviously, all subgroups of K are normal and P is nonnormal. We consider the following two cases.
$p'$
-subgroup of G. Obviously, all subgroups of K are normal and P is nonnormal. We consider the following two cases.
(i) If there exists a minimal normal subgroup T of G contained in K satisfying
![]() $T\neq N$
, then
$T\neq N$
, then
![]() $G/T$
is nonnilpotent. It suffices to show that
$G/T$
is nonnilpotent. It suffices to show that
![]() $n_c(G/T)\leq n_c(G)-1$
by Lemma 2.3, and thus
$n_c(G/T)\leq n_c(G)-1$
by Lemma 2.3, and thus
![]() $s_p((G/T)')\leq n_c(G/T)$
by induction. As before, the result holds.
$s_p((G/T)')\leq n_c(G/T)$
by induction. As before, the result holds.
(ii) If N is a unique minimal normal subgroup of G contained in K, then K is a group of prime power order. It follows from Lemma 2.1 that K is either a cyclic group or a
![]() $2$
-group of maximal class. In addition, since every subgroup of K is a normal subgroup of G, it follows that K is either a cyclic group or a quaternion group
$2$
-group of maximal class. In addition, since every subgroup of K is a normal subgroup of G, it follows that K is either a cyclic group or a quaternion group
![]() $Q_8$
. We claim that K is cyclic. Otherwise,
$Q_8$
. We claim that K is cyclic. Otherwise,
![]() $K\cong Q_8$
. Note that
$K\cong Q_8$
. Note that
![]() $N\leq Z(G)\cap Q_8$
and
$N\leq Z(G)\cap Q_8$
and
![]() $G/N$
is nilpotent. According to Lemma 3.2, G is nilpotent, which is a contradiction. Now, let K be a cyclic group of order
$G/N$
is nilpotent. According to Lemma 3.2, G is nilpotent, which is a contradiction. Now, let K be a cyclic group of order
![]() $q^r$
with
$q^r$
with
![]() $r\geq 2$
. For
$r\geq 2$
. For
![]() $1\leq K_1\leq K$
, it follows that
$1\leq K_1\leq K$
, it follows that
![]() $K_1P_1$
is nonnormal as
$K_1P_1$
is nonnormal as
![]() $P_1\leq P$
and
$P_1\leq P$
and
![]() $P_1\ntrianglelefteq G$
. Also, there exists a maximal subgroup M of P that is normal in P, but
$P_1\ntrianglelefteq G$
. Also, there exists a maximal subgroup M of P that is normal in P, but
![]() $MK_1$
is a nonnormal subgroup of G for
$MK_1$
is a nonnormal subgroup of G for
![]() $1\leq K_1<K$
. Hence,
$1\leq K_1<K$
. Hence,
By Lemma 2.4,
![]() $s_p((G/K)')\leq 2(t-r)/(r+1)+1$
. Note that
$s_p((G/K)')\leq 2(t-r)/(r+1)+1$
. Note that
![]() $n_c(G)=t\geq 2r+1$
and
$n_c(G)=t\geq 2r+1$
and
![]() $r\geq 2$
. Therefore,
$r\geq 2$
. Therefore,
 $$ \begin{align*} s_p(G')\leq s_p(K)+s_p((G/K)')&\leq r+\frac{2(t-r)}{r+1}+1 \\ &\leq \frac{r(r+1)+r(t-r)+(r+1)}{r+1} \leq \frac{r(t+1)+t-r}{r+1} =t. \notag \end{align*} $$
$$ \begin{align*} s_p(G')\leq s_p(K)+s_p((G/K)')&\leq r+\frac{2(t-r)}{r+1}+1 \\ &\leq \frac{r(r+1)+r(t-r)+(r+1)}{r+1} \leq \frac{r(t+1)+t-r}{r+1} =t. \notag \end{align*} $$
Case 2b: N is a unique minimal normal subgroup of G.
In this case,
![]() $G/H$
is nilpotent for
$G/H$
is nilpotent for
![]() $1\neq H\unlhd G$
. We can assume that
$1\neq H\unlhd G$
. We can assume that
![]() $G/N=P_1\rtimes P_2$
with
$G/N=P_1\rtimes P_2$
with
![]() $N\leq P_1$
. Let
$N\leq P_1$
. Let
![]() $|N|={p_1}^k$
. Then there are
$|N|={p_1}^k$
. Then there are
![]() $k-1$
nonnormal subgroups of G contained in N. Clearly, if
$k-1$
nonnormal subgroups of G contained in N. Clearly, if
![]() $NK$
is nonnormal in G for
$NK$
is nonnormal in G for
![]() $K\leq G$
, then
$K\leq G$
, then
![]() $K\ntrianglelefteq G$
. Note that
$K\ntrianglelefteq G$
. Note that
![]() $P_2N\unlhd G$
but
$P_2N\unlhd G$
but
![]() $P_2$
is a nonnormal subgroup of G. Moreover, we can always find
$P_2$
is a nonnormal subgroup of G. Moreover, we can always find
![]() $gN\in Z(G/N)$
such that
$gN\in Z(G/N)$
such that
![]() $g\in G-N$
and
$g\in G-N$
and
![]() $g^p\in N$
since
$g^p\in N$
since
![]() $G/N$
is nilpotent. Also,
$G/N$
is nilpotent. Also,
![]() $\langle g\rangle N\unlhd G$
but
$\langle g\rangle N\unlhd G$
but
![]() $\langle g\rangle $
is nonnormal in G. Therefore,
$\langle g\rangle $
is nonnormal in G. Therefore,
It follows that
![]() $n_c(G/N)\leq (t-k-1)/2$
and, by Lemma 2.5,
$n_c(G/N)\leq (t-k-1)/2$
and, by Lemma 2.5,
![]() $s_p((G/N)')\leq t-k$
. Hence,
$s_p((G/N)')\leq t-k$
. Hence,
The proof is complete.
Next, we will prove Theorem 1.2. To do this, we need the following lemma.
Lemma 3.5. Let G be a solvable group. If
![]() $s_p(G)=n$
, then
$s_p(G)=n$
, then
![]() $dl(G)\leq \lfloor (2n+2)/3\rfloor $
.
$dl(G)\leq \lfloor (2n+2)/3\rfloor $
.
Proof. We prove the result by induction on n. If
![]() $ n=1$
, the result is trivially true. Assume that
$ n=1$
, the result is trivially true. Assume that
![]() $n\geq 2$
. If
$n\geq 2$
. If
![]() $s_p(G/{G'})\geq 2$
, then
$s_p(G/{G'})\geq 2$
, then
![]() $s_p(G')\leq n-2$
. It follows that
$s_p(G')\leq n-2$
. It follows that
![]() $dl(G')\leq \lfloor (2n-2)/3\rfloor $
by the inductive hypothesis applied to
$dl(G')\leq \lfloor (2n-2)/3\rfloor $
by the inductive hypothesis applied to
![]() $G'$
. Hence,
$G'$
. Hence,
In this case, the proof is complete.
Now, let
![]() $s_p(G/{G'})=1$
, that is,
$s_p(G/{G'})=1$
, that is,
![]() $s_p(G')=n-1$
. We may assume that
$s_p(G')=n-1$
. We may assume that
![]() $dl(G)=k+1$
where
$dl(G)=k+1$
where
![]() $k\geq 2$
. Then
$k\geq 2$
. Then
![]() $G^{(k)}>1$
. Also, suppose that N is a maximal abelian normal subgroup of G containing
$G^{(k)}>1$
. Also, suppose that N is a maximal abelian normal subgroup of G containing
![]() $G^{(k)}$
. If
$G^{(k)}$
. If
![]() $s_p(N)\geq 2$
, we see that
$s_p(N)\geq 2$
, we see that
![]() $s_p(G/N)\leq n-2$
. Application of the inductive hypothesis to
$s_p(G/N)\leq n-2$
. Application of the inductive hypothesis to
![]() $G/N$
yields
$G/N$
yields
![]() $dl(G/N)\leq \lfloor (2n-2)/3\rfloor $
. Thus,
$dl(G/N)\leq \lfloor (2n-2)/3\rfloor $
. Thus,
and the result follows.
The remaining case is where
![]() $s_p(N)=1$
, which implies that
$s_p(N)=1$
, which implies that
![]() $N=G^{(k)}$
. Since
$N=G^{(k)}$
. Since
![]() $G/N=N_G(N)/C_G(N)\lesssim \mathrm {Aut}(N)$
is cyclic, it suffices to show that
$G/N=N_G(N)/C_G(N)\lesssim \mathrm {Aut}(N)$
is cyclic, it suffices to show that
![]() $N=G^{(k)}\leq Z(G')$
. Hence,
$N=G^{(k)}\leq Z(G')$
. Hence,
Now
![]() $G^{(k-1)}$
is nonabelian since
$G^{(k-1)}$
is nonabelian since
![]() $G^{(k)}\neq 1$
. We claim that
$G^{(k)}\neq 1$
. We claim that
![]() $s_p(G^{(k-1)})\geq 3$
. Otherwise,
$s_p(G^{(k-1)})\geq 3$
. Otherwise,
![]() $G^{(k-1)}$
is a nonabelian group of order
$G^{(k-1)}$
is a nonabelian group of order
![]() $pq$
with
$pq$
with
![]() $p\neq q$
. Since
$p\neq q$
. Since
![]() $G^{(k-1)}/{G^{(k)}}$
is cyclic, it suffices to show that
$G^{(k-1)}/{G^{(k)}}$
is cyclic, it suffices to show that
![]() $G^{(k-1)}$
is an abelian group, which is a contradiction. Hence,
$G^{(k-1)}$
is an abelian group, which is a contradiction. Hence,
![]() $s_p(G/G^{(k-1)})\leq n-3$
. Apply the inductive hypothesis to
$s_p(G/G^{(k-1)})\leq n-3$
. Apply the inductive hypothesis to
![]() $G/{G^{(k-1)}}$
. Then
$G/{G^{(k-1)}}$
. Then
![]() $dl(G/{G^{(k-1)}})\leq \lfloor (2n-4)/3\rfloor $
. Therefore,
$dl(G/{G^{(k-1)}})\leq \lfloor (2n-4)/3\rfloor $
. Therefore,
The proof is complete.
Finally, we are ready to prove Theorem 1.2.
Proof of Theorem 1.2.
Suppose that G is a solvable nonnilpotent group with
![]() $n_c(G)=t$
. From Lemma 3.4,
$n_c(G)=t$
. From Lemma 3.4,
![]() $s_p(G')\leq t$
, and hence, by Lemma 3.5,
$s_p(G')\leq t$
, and hence, by Lemma 3.5,
Hence,
![]() $dl(G)\leq \lfloor (2t+2)/3\rfloor +1$
. The proof is complete.
$dl(G)\leq \lfloor (2t+2)/3\rfloor +1$
. The proof is complete.
In addition, if G be a solvable nonnilpotent group, the number of prime divisors of
![]() $|G|$
can be bounded by
$|G|$
can be bounded by
![]() $n_c(G)$
. For convenience, we use
$n_c(G)$
. For convenience, we use
![]() $\pi (G)$
to denote the number of prime divisors of
$\pi (G)$
to denote the number of prime divisors of
![]() $|G|$
.
$|G|$
.
Corollary 3.6. Let G be a solvable nonnilpotent group. If
![]() $n_c(G)=t$
, then
$n_c(G)=t$
, then
![]() $\pi (G)\leq t+1$
.
$\pi (G)\leq t+1$
.
Proof. Assume that
![]() $\pi (G)\geq t+2$
. Since G is a solvable group, G possesses a Sylow system
$\pi (G)\geq t+2$
. Since G is a solvable group, G possesses a Sylow system
![]() $\mathcal {S}$
. Suppose that
$\mathcal {S}$
. Suppose that
![]() $\mathcal {S}=\{P_1,P_2,\ldots ,P_{t+2},\ldots \}$
. Note that G is nonnilpotent and we may assume that
$\mathcal {S}=\{P_1,P_2,\ldots ,P_{t+2},\ldots \}$
. Note that G is nonnilpotent and we may assume that
![]() $P_1$
is a nonnormal Sylow subgroup of G. Let
$P_1$
is a nonnormal Sylow subgroup of G. Let
Obviously, for
![]() $1\leq i\leq t+2$
,
$1\leq i\leq t+2$
,
![]() $P_1P_i$
is a subgroup of G. If, for the set
$P_1P_i$
is a subgroup of G. If, for the set
![]() $\mathcal {T}$
, there are two or more normal subgroups of G, then
$\mathcal {T}$
, there are two or more normal subgroups of G, then
![]() $P_1$
is a normal subgroup, which is a contradiction. Thus, at most one normal subgroup is contained in the set
$P_1$
is a normal subgroup, which is a contradiction. Thus, at most one normal subgroup is contained in the set
![]() $\mathcal {T}$
and it follows that
$\mathcal {T}$
and it follows that
![]() $n_c(G)\geq t+1$
. This contradicts the hypothesis and the proof is complete.
$n_c(G)\geq t+1$
. This contradicts the hypothesis and the proof is complete.