2.1 Geometry and governing equations

Our geometric configuration consists of a semi-infinite porous cylinder that is closed at the headwall while admitting a uniformly distributed sidewall injection. Considering any real function $\unicode[STIX]{x1D6FC}$ with zero mean, the cross-section is determined by the tangentially evolving radius, $r_{w}=a(1+\unicode[STIX]{x1D700}\unicode[STIX]{x1D6FC})$ , where $a$ is fixed and $\unicode[STIX]{x1D700}$ is a parameter. As shown in figure 1, the fluid is injected perpendicularly to the wavy surface at a constant speed $U_{w}$ . In view of this geometry, the steady incompressible Navier–Stokes equations are considered with all spatial coordinates, time, velocity and pressure variables made dimensionless using $a$ , $a/U_{w}$ , $U_{w}$ and $\unicode[STIX]{x1D70C}U_{w}^{2}$ , respectively. The corresponding cross-flow Reynolds number may be written as $Re=U_{w}a/\unicode[STIX]{x1D708}$ , where $\unicode[STIX]{x1D708}$ denotes the kinematic viscosity. Then using $\boldsymbol{u}=(u_{\bar{r}},u_{\bar{\unicode[STIX]{x1D703}}},u_{\bar{z}})$ and $p$ for the velocity and pressure, our system of equations reduces to

(2.1a,b ) $$\begin{eqnarray}\bar{\unicode[STIX]{x1D735}}\boldsymbol{\cdot }\boldsymbol{u}=0\quad \text{and}\quad \boldsymbol{u}\boldsymbol{\cdot }\bar{\unicode[STIX]{x1D735}}\boldsymbol{u}=-\bar{\unicode[STIX]{x1D735}}\boldsymbol{p}+{\displaystyle \frac{1}{Re}}\bar{\unicode[STIX]{x1D6FB}}^{2}\boldsymbol{u},\end{eqnarray}$$

where the overbar in $\bar{\unicode[STIX]{x1D6FB}}$ denotes differentiation with respect to the unmodified dimensionless variables $(\bar{r},\bar{\unicode[STIX]{x1D703}},\bar{z})$ .

2.2 Mapping to a circular cross-section

To simplify the application of the boundary conditions at the sidewall, and thus avoid the need for Taylor-series expansions about a fixed radius, it is helpful to map the dimensionless spatial coordinates $(\overline{r},\overline{\unicode[STIX]{x1D703}},\overline{z})$ in such a manner to relocate the wall boundary conditions to a spatially invariant point. This may be accomplished through the coordinate transformation:

(2.2) $$\begin{eqnarray}r={\displaystyle \frac{\overline{r}}{1+\unicode[STIX]{x1D700}\unicode[STIX]{x1D6FC}(\overline{\unicode[STIX]{x1D703}})}},\quad \unicode[STIX]{x1D703}=\overline{\unicode[STIX]{x1D703}},\quad z=\overline{z}.\end{eqnarray}$$

The vector basis $(\boldsymbol{e}_{r},\boldsymbol{e}_{\unicode[STIX]{x1D703}},\boldsymbol{e}_{z})$ defined in figure 1 remains unchanged. Although this substitution affects the form of the radial and tangential derivatives, the wall surface can now be specified using ${\mathcal{A}}(r)=r-1=0$ . The corresponding normal unit vector, $\boldsymbol{n}=n_{r}\boldsymbol{e}_{r}+n_{\unicode[STIX]{x1D703}}\boldsymbol{e}_{\unicode[STIX]{x1D703}}$ , becomes

(2.3) $$\begin{eqnarray}\boldsymbol{n}=\left.{\displaystyle \frac{\unicode[STIX]{x1D735}{\mathcal{A}}}{\Vert \unicode[STIX]{x1D735}{\mathcal{A}}\Vert }}\right|_{r=1}={\displaystyle \frac{(1+\unicode[STIX]{x1D700}\unicode[STIX]{x1D6FC})\boldsymbol{e}_{r}-\unicode[STIX]{x1D700}\unicode[STIX]{x1D6FC}p_{\prime }^{(2)\boldsymbol{e}_{\unicode[STIX]{x1D703}}}}{\sqrt{(1+\unicode[STIX]{x1D700}\unicode[STIX]{x1D6FC})^{2}+\unicode[STIX]{x1D700}\unicode[STIX]{x1D6FC}^{\prime 2}}}},\end{eqnarray}$$

and so the wall-normal injection condition simplifies to $\boldsymbol{u}=-\boldsymbol{n}$ at $r=1$ . Naturally, this substitution gives rise to a more complex form of the Navier–Stokes equations, which is detailed in appendix A.

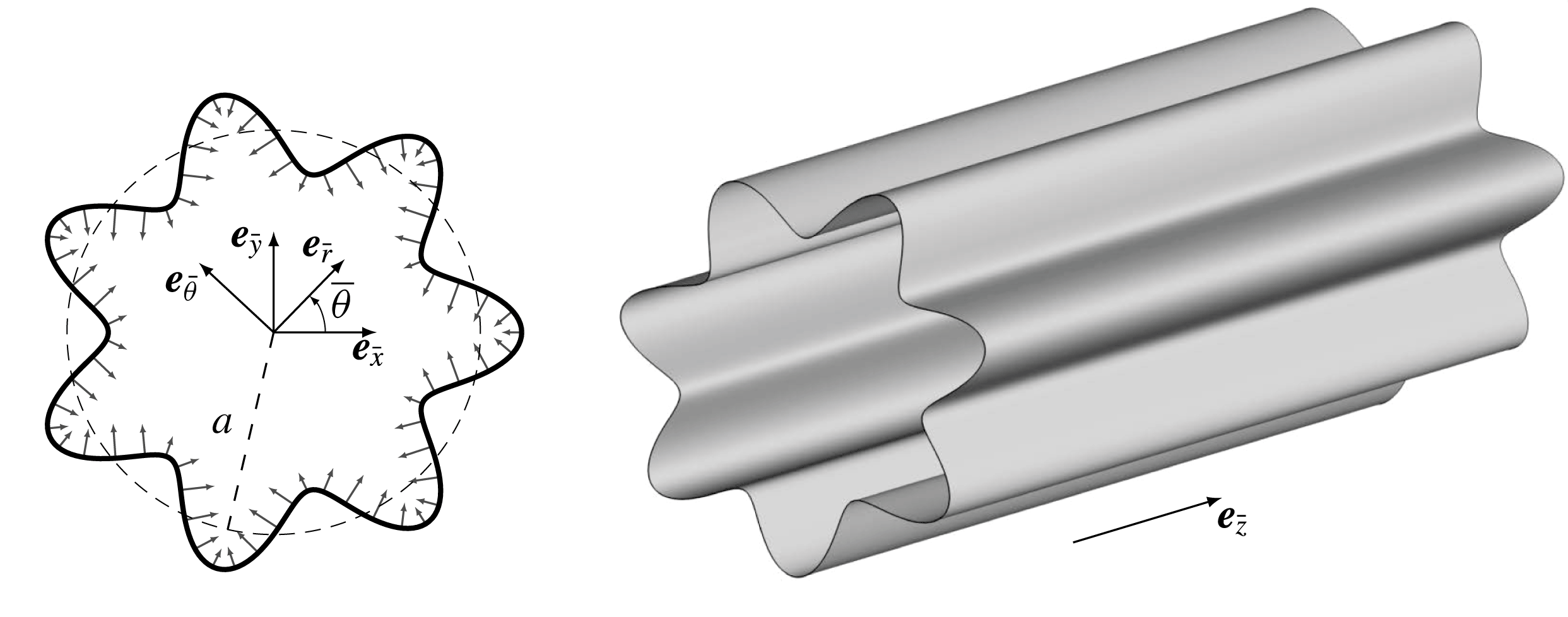
Figure 1.

Sketch of the geometric configuration and coordinate systems corresponding to a non-circular, wavy cross-section with $\unicode[STIX]{x1D6FC}=\cos (m\unicode[STIX]{x1D703})$ . The sketch corresponds to $m=7$ lobes and a 20 % radial deviation in  $\unicode[STIX]{x1D700}$ .

2.3 On the minimum perturbation order

In their elegant analysis of the axisymmetric flow in a porous tube, Balachandar et al. (Reference Balachandar, Buckmaster and Short2001) establish a framework in which small perturbations of the form $\unicode[STIX]{x1D700}\cos (m\unicode[STIX]{x1D703})$ may be imposed at the sidewall. By examining the asymptotic behaviour of the ensuing solution as $r\rightarrow 0$ , a viscous core is shown to be present near the centreline. Accordingly, viscous effects dominate on the scale of $r=O(1/\sqrt{Re})$ for wall perturbations of $O(\unicode[STIX]{x1D700})$ . Furthermore, as we enter the viscous core region, the axial vorticity, which accompanies the evolution of a finite tangential velocity, appears at $O(\unicode[STIX]{x1D700}Re)$ . Consequently, the linear perturbative analysis remains valid as long as $\unicode[STIX]{x1D700}Re\ll 1$ . To overcome this practical limitation, Balachandar et al. (Reference Balachandar, Buckmaster and Short2001) introduce a nonlinear patch on the scale of $r=O(\sqrt{\unicode[STIX]{x1D700}})$ . This viscous correction leads to a solution that extends the range of applicability to $\unicode[STIX]{x1D700}Re\gg 1$ , where the axial vorticity increases to $O(1)$ . A similar conclusion may be reached in our analysis, which requires second-order perturbations of $O(\unicode[STIX]{x1D700}^{2})$ to adequately capture the nonlinear interactions that evolve at previous orders. Moreover, a second-order approximation will be warranted to satisfy mass conservation requirements by virtue of the angular dependence being of the harmonic form, $\text{e}^{\text{i}m\unicode[STIX]{x1D703}}$ .

The approach that we follow is therefore compatible with Balachandar’s framework, as it seeks to derive a second-order viscous solution for a periodically distorted cross-section. In this process, however, an effort will be made to secure the no-slip condition in all three spatial directions, including the axial and tangential velocities at the sidewall, thus leading to a uniformly valid solution that extends from $r=0$ to 1 inclusively.

To justify the need to carry out a second-order approximation, it may be instructive to revisit the mass flow rate evaluation at the sidewall. We start by remarking that, for an identical mean radius, the circumference of the cross-section corresponding to a wavy wall, such as a star-shaped grain configuration, will always exceed that of its counterpart with a fixed circular radius. Then, recognizing that $\unicode[STIX]{x1D6FC}$ is a periodic function with a vanishing mean value, the mass surplus can be estimated using an asymptotic expansion of ${\dot{m}}_{w}(z)$ , namely,

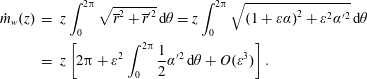(2.4) $$\begin{eqnarray}\displaystyle {\dot{m}}_{w}(z) & = & \displaystyle z\int _{0}^{2\unicode[STIX]{x03C0}}\sqrt{\overline{r}^{2}+\overline{r}^{\prime 2}}\,\text{d}\unicode[STIX]{x1D703}=z\int _{0}^{2\unicode[STIX]{x03C0}}\sqrt{\left(1+\unicode[STIX]{x1D700}\unicode[STIX]{x1D6FC}\right)^{2}+\unicode[STIX]{x1D700}^{2}\unicode[STIX]{x1D6FC}^{\prime 2}}\,\text{d}\unicode[STIX]{x1D703}\nonumber\\ \displaystyle & = & \displaystyle z\left[2\unicode[STIX]{x03C0}+\unicode[STIX]{x1D700}^{2}\int _{0}^{2\unicode[STIX]{x03C0}}{\displaystyle \frac{1}{2}}\unicode[STIX]{x1D6FC}^{\prime 2}\,\text{d}\unicode[STIX]{x1D703}+O(\unicode[STIX]{x1D700}^{3})\right].\end{eqnarray}$$

The resulting equality confirms that the first-order corrections have no bearing on the injected mass flow rate. In particular, the axial velocity, which contributes to the mass injection, cannot by itself secure the mass balance without taking into account its interactions at the second order. Moreover, a second-order representation will enable us to extend the validity of the model to larger deviation amplitudes with $\unicode[STIX]{x1D700}^{2}\ll 1$ , while simultaneously aiding in improving the permissible range of Reynolds numbers to $\unicode[STIX]{x1D700}Re\gg 1$ , as predicted by Balachandar et al. (Reference Balachandar, Buckmaster and Short2001).

2.4 Asymptotic expansion

Given the above considerations, the velocity and pressure fields, $(\boldsymbol{u},p)$ , may be decomposed using

(2.5) $$\begin{eqnarray}\left.\begin{array}{@{}c@{}}\boldsymbol{u}=\boldsymbol{u}^{(0)}+\unicode[STIX]{x1D700}\boldsymbol{u}^{(1)}+\unicode[STIX]{x1D700}^{2}\boldsymbol{u}^{(2)}+o(\unicode[STIX]{x1D700}^{2}),\\ p=p^{(0)}+\unicode[STIX]{x1D700}p^{(1)}+\unicode[STIX]{x1D700}^{2}p^{(2)}+o(\unicode[STIX]{x1D700}^{2}),\end{array}\right\}\end{eqnarray}$$

where superscripts denote successive asymptotic orders. This two-term approximation may be substituted back into the Navier–Stokes equations, expressed through (A 1), and then further linearized using binomial expansions of $(1+\unicode[STIX]{x1D700}\unicode[STIX]{x1D6FC})^{-1}$ terms. These operations enable us to identify and segregate three sets of equations that appear at $O(1)$ , $O(\unicode[STIX]{x1D700})$ and $O(\unicode[STIX]{x1D700}^{2})$ , consecutively. A similar expansion may be applied to the wall injection boundary condition (2.3), thus leading to

(2.6) $$\begin{eqnarray}\left.\begin{array}{@{}c@{}}u_{r}(\vphantom{u_{r}}\vphantom{1,\unicode[STIX]{x1D703},z}1,\unicode[STIX]{x1D703},z)=-{\displaystyle \frac{1+\unicode[STIX]{x1D700}\unicode[STIX]{x1D6FC}}{\sqrt{1+\unicode[STIX]{x1D700}\left[2\unicode[STIX]{x1D6FC}+\unicode[STIX]{x1D700}\left(\unicode[STIX]{x1D6FC}^{2}+\unicode[STIX]{x1D6FC}^{\prime 2}\right)\right]}}}=-1+{\displaystyle \frac{1}{2}}\unicode[STIX]{x1D6FC}^{\prime 2}\unicode[STIX]{x1D700}^{2}+o(\unicode[STIX]{x1D700}^{2}),\\ u_{\unicode[STIX]{x1D703}}(\vphantom{u_{\unicode[STIX]{x1D703}}}\vphantom{1,\unicode[STIX]{x1D703},z}1,\unicode[STIX]{x1D703},z)={\displaystyle \frac{\unicode[STIX]{x1D700}\unicode[STIX]{x1D6FC}^{\prime }}{\sqrt{1+\unicode[STIX]{x1D700}\left[2\unicode[STIX]{x1D6FC}+\unicode[STIX]{x1D700}\left(\unicode[STIX]{x1D6FC}^{2}+\unicode[STIX]{x1D6FC}^{\prime 2}\right)\right]}}}=\unicode[STIX]{x1D6FC}^{\prime }\unicode[STIX]{x1D700}-\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FC}^{\prime }\unicode[STIX]{x1D700}^{2}+o(\unicode[STIX]{x1D700}^{2}).\end{array}\right\}\end{eqnarray}$$

When translated to the asymptotic velocity corrections, these expressions give rise to an assortment of conditions that must be imposed at successively increasing orders, namely,

(2.7) $$\begin{eqnarray}\left.\begin{array}{@{}rclrclrcl@{}}u_{r}^{(0)}(1,\unicode[STIX]{x1D703},z)\ & =\ & -1, & \quad u_{\unicode[STIX]{x1D703}}^{(0)}(1,\unicode[STIX]{x1D703},z)\ & =\ & 0, & \quad u_{z}^{(0)}(1,\unicode[STIX]{x1D703},z)\ & =\ & 0,\\ u_{r}^{(1)}(1,\unicode[STIX]{x1D703},z)\ & =\ & 0, & \quad u_{\unicode[STIX]{x1D703}}^{(1)}(1,\unicode[STIX]{x1D703},z)\ & =\ & \unicode[STIX]{x1D6FC}^{\prime }, & \quad u_{z}^{(1)}(1,\unicode[STIX]{x1D703},z)\ & =\ & 0,\\ u_{r}^{(2)}(1,\unicode[STIX]{x1D703},z)\ & =\ & \unicode[STIX]{x1D6FC}^{\prime 2}/2, & \quad u_{\unicode[STIX]{x1D703}}^{(2)}(1,\unicode[STIX]{x1D703},z)\ & =\ & -\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FC}^{\prime }, & \quad u_{z}^{(2)}(1,\unicode[STIX]{x1D703},z)\ & =\ & 0.\end{array}\right\}\end{eqnarray}$$

The solution to the three sets of equations and their associated boundary conditions will be described in §§ 2.5–2.7.

Furthermore, to justify the use of the upcoming similarity transformation, it will be helpful to examine the mass conservation requirement. By equating the radial mass flow rate ${\dot{m}}_{w}(z)$ , which originates from the sidewall over a length of tubing that extends from the headwall to a point $z$ , to the axial mass flow rate ${\dot{m}}_{cross}(z)$ , crossing section $z$ , one arrives at the following equality:

(2.8) $$\begin{eqnarray}z\int _{0}^{2\unicode[STIX]{x03C0}}\sqrt{\overline{r}^{2}+\overline{r}^{\prime 2}}\,\text{d}\unicode[STIX]{x1D703}=\int _{0}^{2\unicode[STIX]{x03C0}}\!\int _{0}^{1}u_{z}\left(r,\unicode[STIX]{x1D703},z\right)r\,\text{d}r\,\text{d}\unicode[STIX]{x1D703}.\end{eqnarray}$$

A sufficient condition for $u_{z}$ to satisfy the previous relation (2.8) is to assume a linear variation with respect to $z$ , as foretold by Hiemenz (Reference Hiemenz1911). To make further headway, only separable product solutions are sought, thus turning the linear dependence on $z$ into a necessary condition. Procedurally, this enables us to specify the axial velocity corrections, $u_{z}^{(0)}$ , $u_{z}^{(1)}$ and $u_{z}^{(2)}$ , with a linear dependence on  $z$ .

2.5 Leading-order analysis

In the absence of angular wall deformation ( $\unicode[STIX]{x1D700}=0$ ), the classical problem of an injection-driven motion in a circular cylinder is restored. Being independent of $\unicode[STIX]{x1D703}$ , one recovers $u_{\unicode[STIX]{x1D703}}^{(0)}=0$ and $\unicode[STIX]{x2202}_{\unicode[STIX]{x1D703}}f=0$ for any scalar function $f$ . In this situation, Berman’s formulation may be employed with a streamfunction $\unicode[STIX]{x1D713}(r,z)=zF(r)$ , where $F(r)$ represents the characteristic mean flow function (Berman Reference Berman1953). The leading-order solution may be subsequently retrieved from Berman’s fourth-order nonlinear ordinary differential equation:

(2.9) $$\begin{eqnarray}\left.\begin{array}{@{}c@{}}\left[\left({\displaystyle \frac{F}{r}}\right)\left({\displaystyle \frac{F^{\prime }}{r}}\right)^{\prime }-\left({\displaystyle \frac{F^{\prime }}{r}}\right)^{2}\right]^{\prime }-{\displaystyle \frac{1}{Re}}\left[{\displaystyle \frac{1}{r}}\left(r\left({\displaystyle \frac{F^{\prime }}{r}}\right)^{\prime }\right)^{\prime }\right]^{\prime }=0,\\ \displaystyle \lim _{r\rightarrow 0}\left({\displaystyle \frac{F^{\prime }}{r}}\right)^{\prime }=\displaystyle \lim _{r\rightarrow 0}{\displaystyle \frac{F}{r}}=F^{\prime }(1)=0,\quad F(1)=1.\end{array}\right\}\end{eqnarray}$$

In the above, the boundary conditions may be ascribed to axisymmetry and wall-normal injection. In hindsight, the solutions obtained by Taylor (Reference Taylor1956) and Culick (Reference Culick1966) correspond to Berman’s formulation in the limit of $Re\rightarrow \infty$ . In fact, the Taylor–Culick profile begins to resemble Berman’s solution for $Re>100$ . Nonetheless, as we aim to extend the validity of the viscous model to a generic non-axisymmetric configuration, we continue to employ Berman’s model and retain its dependence on the cross-flow Reynolds number. Thus, for a given $Re$ , (2.9) may be solved numerically for $F(r)$ , and so the three velocity components and pressure at order $O(1)$ may be deduced directly from

(2.10a-d ) $$\begin{eqnarray}u_{r}^{(0)}=-{\displaystyle \frac{F(r)}{r}},\quad u_{\unicode[STIX]{x1D703}}^{(0)}=0,\quad u_{z}^{(0)}=z{\displaystyle \frac{F^{\prime }(r)}{r}},\quad p^{(0)}=P_{0}-{\displaystyle \frac{\unicode[STIX]{x1D705}_{0}}{2}}z^{2}-{\displaystyle \frac{F^{2}}{2r^{2}}},\end{eqnarray}$$

where both $P_{0}$ and $\unicode[STIX]{x1D705}_{0}$ represent undetermined integration constants that may be obtained from Berman’s expression in the modified coordinate system $(r,\unicode[STIX]{x1D703},z)$ .

2.6 First-order analysis

The system of linear equations (A 1) is written at the order $O(\unicode[STIX]{x1D700})$ and rearranged into (C 1). Guided by the wall-normal injection conditions requiring the appearance of $\unicode[STIX]{x1D6FC}$ and its derivative, a solution is sought using separation of variables. Note that no additional axial pressure gradient is required for product solutions, since the mass flow surplus (2.4) is of second order. The solution then simply reads

(2.11) $$\begin{eqnarray}\left.\begin{array}{@{}rcl@{}}u_{r}^{(1)}\ & =\ & v_{r}^{}(r)\unicode[STIX]{x1D6FC}(\unicode[STIX]{x1D703}),\\ u_{\unicode[STIX]{x1D703}}^{(1)}\ & =\ & v_{\unicode[STIX]{x1D703}}^{}(r)\unicode[STIX]{x1D6FC}^{\prime }(\unicode[STIX]{x1D703}),\\ u_{z}^{(1)}\ & =\ & zv_{z}^{}(r)\unicode[STIX]{x1D6FC}(\unicode[STIX]{x1D703}),\\ p^{(1)}\ & =\ & q^{}(r)\unicode[STIX]{x1D6FC}(\unicode[STIX]{x1D703}).\end{array}\right\}\end{eqnarray}$$

The substitution of these expressions into (C 1) gives rise to a $\unicode[STIX]{x1D703}$ -dependent system in which every equation can be collapsed into the form of $\unicode[STIX]{x1D719}(\vphantom{\unicode[STIX]{x1D719}}\vphantom{r}r)=-\unicode[STIX]{x1D6FC}^{\prime \prime }(\unicode[STIX]{x1D703})/\unicode[STIX]{x1D6FC}(\unicode[STIX]{x1D703})$ , where $\unicode[STIX]{x1D719}$ denotes an operator that may be constructed from the aforementioned functions and their derivatives. Naturally, without any loss of generality in the space of real functions, harmonic variations of the form $\unicode[STIX]{x1D6FC}(\unicode[STIX]{x1D703})=\cos (m\unicode[STIX]{x1D703})$ are retained, $m$ being a constant. Since $m$ represents the number of lobes along a fixed circular circumference, it will be referred to hereafter as the circular wavenumber. The underlying consequence of this choice for $\unicode[STIX]{x1D6FC}$ is that the mass flow conservation can be expressed at the third order using

(2.12) $$\begin{eqnarray}{\dot{m}}_{w}(z)=z\left[2\unicode[STIX]{x03C0}+{\textstyle \frac{1}{2}}\unicode[STIX]{x1D700}^{2}\unicode[STIX]{x03C0}m^{2}+o(\unicode[STIX]{x1D700}^{3})\right].\end{eqnarray}$$

For the reader’s convenience, the $\unicode[STIX]{x1D703}$ -dependent system of equations is provided in (C 2). The system consists of one first-order and three second-order ordinary differential equations. The corresponding injection conditions, which stem from (2.7), lead to $v_{\unicode[STIX]{x1D703}}^{}(1)=1$ and $v_{r}^{}(1)=v_{z}^{}(1)=0$ . In order to achieve closure, four additional constraints are still necessary, and these may be specified at $r=0$ by introducing Taylor-series expansions of the different functions with respect to $r$ in (C 3). After some effort, we arrive at $v_{r}^{\prime }(0)=-F^{\prime \prime }(0)/2$ and $v_{r}^{}(0)=v_{\unicode[STIX]{x1D703}}^{}(0)=v_{z}^{}(0)=0$ , with the additional realization that $m^{2}\neq (0,1)$ , to avoid a mathematically incongruent outcome. In practice, we are only interested in cross-sections with $m\geqslant 3$ .

With the advent of a sufficient number of boundary conditions, a collocation method, such as the one described by Canuto et al. (Reference Canuto, Hussaini, Quarteroni and Zang1988), may be used to discretize the system of equations and recover the first-order velocity and pressure corrections.

2.7 Second-order analysis

To make further headway, we proceed to decompose the second-order corrections using the following classical forms:

(2.13) $$\begin{eqnarray}\left.\begin{array}{@{}rcl@{}}u_{r}^{(2)}(r,\unicode[STIX]{x1D703},z)\ & =\ & u_{r,0}^{(2)}(r)+u_{r,2}^{(2)}(r)\cos (2m\unicode[STIX]{x1D703}),\\ u_{\unicode[STIX]{x1D703}}^{(2)}(r,\unicode[STIX]{x1D703},z)\ & =\ & -mu_{\unicode[STIX]{x1D703},2}^{(2)}(r)\sin (2m\unicode[STIX]{x1D703}),\\ u_{z}^{(2)}(r,\unicode[STIX]{x1D703},z)\ & =\ & z[u_{z,0}^{(2)}(r)+u_{z,2}^{(2)}(r)\cos (2m\unicode[STIX]{x1D703})],\\ p_{}^{(2)}(r,\unicode[STIX]{x1D703},z)\ & =\ & -{\textstyle \frac{1}{2}}\unicode[STIX]{x1D705}z^{2}+p_{0}^{(2)}(r)+p_{2}^{(2)}(r)\cos (2m\unicode[STIX]{x1D703}).\end{array}\right\}\end{eqnarray}$$

On the right-hand side of the resulting momentum equations at $O(\unicode[STIX]{x1D700}^{2})$ , terms that depend on the two previous orders, which are caused by nonlinear interactions, may be explicitly seen (appendix C). Computing this second-order correction will therefore enable us to capture the nonlinearities alluded to by Balachandar et al. (Reference Balachandar, Buckmaster and Short2001) when $\unicode[STIX]{x1D700}Re$ is no longer a small quantity. The resulting set of seven linear equations can be subsequently consolidated into two concise and independent systems: the first assortment consists of four linear equations that prescribe $(\boldsymbol{u}_{2}^{(2)},p_{2}^{(2)})$ , as given by (D 1), and the second entails three linear equations that control $(\boldsymbol{u}_{0}^{(2)},p_{0}^{(2)})$ , as given by (D 2). Being independent, these two systems may be solved separately. Moreover, since $u_{\unicode[STIX]{x1D703}}^{(2)}$ only appears in the first system, each set leads to a well-posed problem with the same number of equations and unknowns, except for the constant $\unicode[STIX]{x1D705}$ . Its determination will be described separately.

The boundary conditions associated with $\boldsymbol{u}_{2}^{(2)}$ may be readily obtained from (2.7), specifically at the wall and the centreline, using the $r\rightarrow 0$ Taylor-series expansions introduced previously. These produce

(2.14) $$\begin{eqnarray}\left.\begin{array}{@{}c@{}}u_{r,2}^{(2)}(1)=-m^{2}/4,\quad u_{\unicode[STIX]{x1D703},2}^{(2)}(1)=-1/2,\quad u_{z,2}^{(2)}(1)=0,\\ {u_{r,2}^{(2)}}^{\prime }(0)=u_{r,2}^{(2)}(0)=u_{\unicode[STIX]{x1D703},2}^{(2)}(0)={u_{z,2}^{(2)}}^{\prime }(0)=0.\end{array}\right\}\end{eqnarray}$$

With the boundary conditions in hand, the computation of $(\boldsymbol{u}_{2}^{(2)},p_{2}^{(2)})$ may be achieved easily using a discrete collocation, for instance.

Unlike $(\boldsymbol{u}_{2}^{(2)},p_{2}^{(2)})$ , the three linear equations for $(\boldsymbol{u}_{0}^{(2)},p_{0}^{(2)})$ may be carefully reduced into a single third-order ordinary differential equation that depends solely on $u_{r,0}^{(2)}$ . This equation is given by (D 3). The undetermined pressure constant $\unicode[STIX]{x1D705}$ , which appears on the right-hand side of (D 3), has a direct influence on $u_{z,0}^{(2)}(1)$ . Since $\unicode[STIX]{x1D705}$ appears as a forcing term in a linear relation, the connection between $u_{z,0}^{(2)}(1)$ and $\unicode[STIX]{x1D705}$ proves to be linear. At the outset, a unique value for $\unicode[STIX]{x1D705}$ may be retrieved for a given set of input parameters in order to secure $u_{z,0}^{(2)}(1)=0$ . For the reader’s convenience, its values for different ranges of $Re$ and $m$ are provided in table 1.

Table 1.

Calculated values of the pressure constant $\unicode[STIX]{x1D705}$ for different values of $m$ and $Re$ .

2.8 Characterization at successive orders and wavenumbers

In summary, the velocity and pressure fields may be expressed using

(2.15) $$\begin{eqnarray}\left.\begin{array}{@{}c@{}}u_{r}=-{\displaystyle \frac{F}{r}}+\unicode[STIX]{x1D700}v_{r}^{}\cos (m\unicode[STIX]{x1D703})+\unicode[STIX]{x1D700}^{2}\left[u_{r,0}^{(2)}+u_{r,2}^{(2)}\cos (2m\unicode[STIX]{x1D703})\right],\\ u_{\unicode[STIX]{x1D703}}=-m\unicode[STIX]{x1D700}v_{\unicode[STIX]{x1D703}}^{}\sin (m\unicode[STIX]{x1D703})-m\unicode[STIX]{x1D700}^{2}u_{\unicode[STIX]{x1D703},2}^{(2)}\sin (2m\unicode[STIX]{x1D703}),\\ u_{z}=z\left\{{\displaystyle \frac{F^{\prime }}{r}}+\unicode[STIX]{x1D700}v_{z}^{}\cos (m\unicode[STIX]{x1D703})+\unicode[STIX]{x1D700}^{2}\left[u_{z,0}^{(2)}+u_{z,2}^{(2)}\cos (2m\unicode[STIX]{x1D703})\right]\right\},\\ p=P_{0}-{\displaystyle \frac{\unicode[STIX]{x1D705}_{0}}{2}}z^{2}-{\displaystyle \frac{F^{2}}{2r^{2}}}-{\displaystyle \frac{F^{\prime }}{rRe}}+\unicode[STIX]{x1D700}q^{}\cos (m\unicode[STIX]{x1D703})+\unicode[STIX]{x1D700}^{2}\left[p_{0}^{(2)}+p_{2}^{(2)}\cos (2m\unicode[STIX]{x1D703})-{\displaystyle \frac{\unicode[STIX]{x1D705}}{2}}z^{2}\right].\end{array}\right\}\end{eqnarray}$$

To illustrate the behaviour of the solution, we confine our attention to a polar slice that extends between $\unicode[STIX]{x1D703}=0$ and $2\unicode[STIX]{x03C0}/m$ . In figure 2, we examine the sensitivity of the solution for $u_{r}$ and $u_{z}$ at increasing asymptotic orders using characteristic values of $\unicode[STIX]{x1D700}=0.1$ , $Re=100$ and $m=7$ . Only the radial variation is captured here, which may be accomplished by plotting the solution along a spoke at $\unicode[STIX]{x1D703}=0$ and a fixed value of $z$ . The radial velocity, which is featured on the left-hand side of the graph at three increasing orders of $\unicode[STIX]{x1D700}$ , confirms that even the first-order approximation, $u_{r}^{(1)}$ , is considerably dissimilar from the leading-order solution. This disparity implies that the radial displacement of the sidewall leads to a significant distortion of the mean flow field compared to the circular configuration. However, these results also suggest that the second-order correction, $u_{r}^{(2)}$ , only weakly affects the overall radial velocity. Although similar observations may be inferred for the tangential velocity, they are omitted here for the sake of brevity.

In contrast, by turning our attention to the axial velocity variation on the right-hand side, it may be seen that the second-order correction leads to a non-negligible shift in $u_{z}$ , especially as the centreline is approached, where the first-order contribution is nil by virtue of $u_{z}^{(1)}(0)=0$ . The need for a second-order correction is therefore pivotal. In fact, the discrepancy near the centreline between Berman’s leading-order solution and that at $O(\unicode[STIX]{x1D700}^{2})$ may be attributed to the mass flow rate increase reported in (2.4). Recalling that the mass flow rate entails an integration over $\unicode[STIX]{x1D703}$ , the contribution of the first-order correction $u_{z}^{(1)}$ multiplied by the periodic function $\cos (m\unicode[STIX]{x1D703})$ vanishes identically. However, the contribution of the second-order correction $u_{z}^{(2)}$ , which involves a $\unicode[STIX]{x1D703}$ -independent term ( $u_{z,0}^{(2)}$ ), leads to a finite contribution. Based on this simple comparison and mathematical verification, it may be concluded that the first-order correction affects all three velocity components, thus leading to marked differences from the circular configuration. As for the second-order correction, it proves to be essential to properly capture the behaviour of the axial velocity, especially near the centreline, and therefore helps to secure the principle of mass conservation.

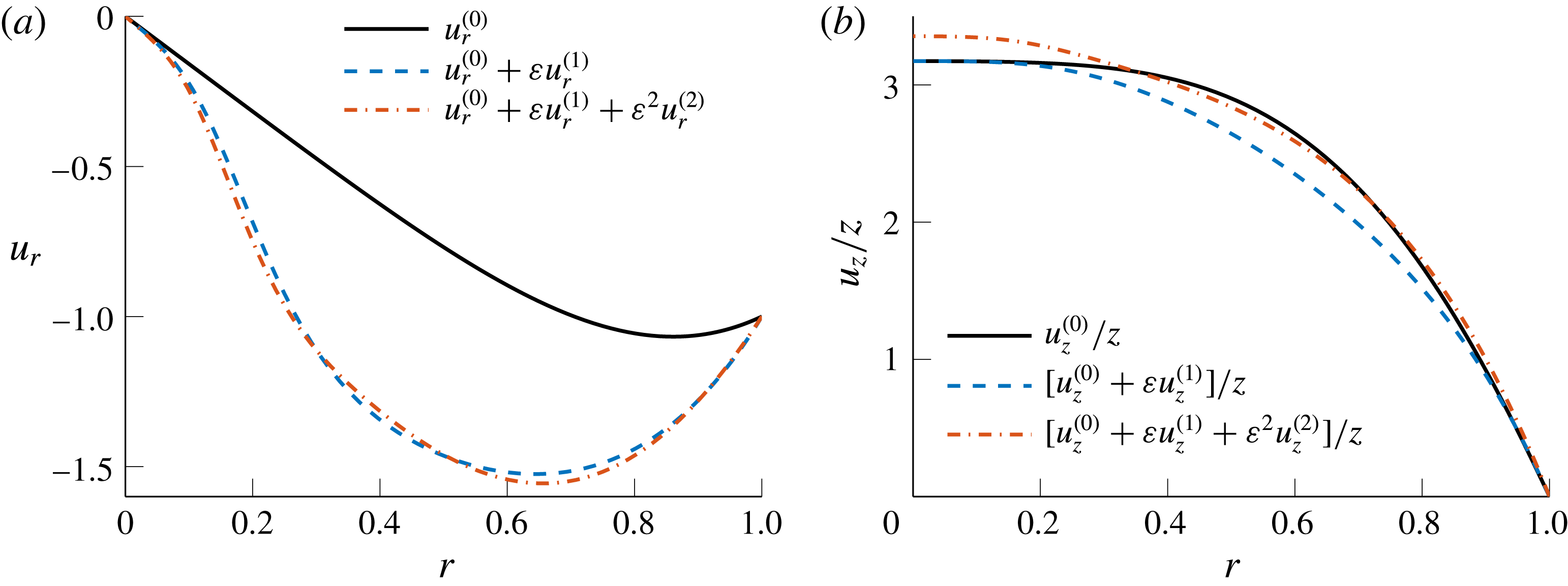
Figure 2.

Influence of the corrections of different orders on the asymptotic approximations for (a)  $u_{r}$ and (b)  $u_{z}/z$ at $\unicode[STIX]{x1D700}=0.1$ , $Re=100$ and $m=7$ .

Figure 3.

Influence of the circular wavenumber $m$ on (a)  $u_{\unicode[STIX]{x1D703}}$ along a spoke with $\unicode[STIX]{x1D703}=\unicode[STIX]{x03C0}/(4m)$ and (b)  $u_{z,0}^{(2)}$ at the centreline with $\unicode[STIX]{x1D703}=0$ . Here $\unicode[STIX]{x1D700}=0.1$ and $Re=100$ .

To better understand the effect of $m$ on the second-order approximation, both $u_{\unicode[STIX]{x1D703}}$ and the centreline value of $u_{z}$ are depicted in figure 3 at $\unicode[STIX]{x1D700}=0.1$ and $Re=100$ . The tangential velocity is featured in figure 3(a) along a spoke with $\unicode[STIX]{x1D703}=\unicode[STIX]{x03C0}/(4m)$ and $m=5$ , 6, 7, 8 and 9. Interestingly, the effect of the injection condition in (2.7) on the magnitude of $u_{\unicode[STIX]{x1D703}}$ may be captured at the sidewall, where $|u_{\unicode[STIX]{x1D703}}|$ increases incrementally with $m$ . The maximum values of $u_{\unicode[STIX]{x1D703}}$ also shift outwards towards the sidewall with successive increases in  $m$ .

It is also useful to explore the sensitivity of the centreline value of $u_{z}^{(2)}(0)$ to variations in $m\in [3,12]$ in figure 3(b). Since $u_{z,2}^{(2)}(0)=0$ , it is sufficient to illustrate the behaviour of $u_{z,0}^{(2)}(0)$ in order to infer the underlying trend. Although the relation between $u_{z,0}^{(2)}(0)$ and $m$ remains concealed in (D 2), the corresponding curve suggests the existence of a monotonically increasing quadratic polynomial of the form $u_{z,0}^{(2)}(0)=c_{0}+c_{1}m+c_{2}m^{2}$ , whose coefficients in figure 3(b) are $c_{0}=-1.242$ , $c_{1}=-0.1875$ and $c_{2}=0.817$ . Despite the appearance of $m^{2}$ in the equations explicitly, determining the quadratic solution analytically for any $Re$ and $\unicode[STIX]{x1D700}$ proves to be a daunting task. Nonetheless, based on this characteristic graph, it may be ascertained that the role of $u_{z,0}^{(2)}(0)$ can be significant, especially at increasing values of $m$ . Although not shown, we also find that the effect of increasing the Reynolds number on $u_{z,0}^{(2)}(0)$ is negligible in comparison to  $m$ .

As for flow rotationality, figure 4 displays isocontours of the tangential component of the steady-state vorticity $\unicode[STIX]{x1D6FA}_{z}$ in an arbitrary $\left(r,z\right)$ plane; also provided is a comparison of the streamlines for the present solution side by side with Berman’s. Based on this graph, it may be seen that the star-shaped configuration leads to deeper penetrating streamlines than the circular case. Specifically, the solid lines, which correspond to the present formulation, consistently approach the chamber axis more rapidly than the dashed lines of the non-wavy solution.

Figure 4.

Isocontours of the tangential component of the rotational vorticity in an $\left(r,z\right)$ plane along with the corresponding streamlines according to the present formulation (solid lines). Also shown are the streamlines obtained for Berman’s model in a circular cross-section (dashed lines). Here we use $\unicode[STIX]{x1D700}=0.1$ , $Re=100$ and $m=7$ .

3.1 Solver description

Our numerical simulations are performed using a compressible Navier–Stokes solver called CHARME, which belongs to the multi-solver suite CEDRE developed by the French Aerospace Laboratory (ONERA). A detailed overview of the code’s functionality is provided by Refloch et al. (Reference Refloch, Courbet, Murrone, Villedieu, Laurent, Gilbank, Troyes, Tessé, Chaineray and Dargaud2011), while examples of its computational capabilities, which include laminar flow simulations and verifications of linear stability analyses of rocket internal flow fields, are furnished by Chedevergne et al. (Reference Chedevergne, Casalis and Majdalani2012) and Boyer et al. (Reference Boyer, Casalis and Estivalèzes2013). In these studies, an excellent agreement is reported between theory and computations, thus showcasing the solver’s effectiveness in capturing the mean flow development as well as the unsteady hydrodynamic instabilities that evolve in a rocket chamber. As usual, the latter may be idealized as a porous tube with uniform wall injection, which is consistent with the geometric configuration used presently. As for the code, a second-order discretization stencil is implemented for spatial interpolation, while Euler’s fluxes are computed using a Roe scheme. Throughout these simulations, the length and mean radius of the porous tube are kept constant at $8a$ and $a=1$  cm, respectively. Although the value of $a$ may be modified, the aspect ratio is held constant. Furthermore, the wall injection speed $U_{w}$ is adjusted to calculate the targeted Reynolds numbers while ensuring that it remains sufficiently small to promote low compressibility levels. At the headwall, a slip condition that is compatible with our model is applied to avoid the development of an undesirable boundary layer. In the domain exit plane at $z=8a$ , a pressure outlet condition is imposed. The code is fully three-dimensional and the assumption of linear axial variation is not forced. Then, using a three-dimensional unstructured mesh with approximately four million total elements, 600 cells are selected to construct the axial grid along the sidewall, whereas 150 cells are distributed radially along the diameter. Although the mesh size can generally depend on $Re$ , $\unicode[STIX]{x1D700}$ and $m$ , the present discretization size is confidently chosen because of its demonstrated effectiveness in previous studies of analogous flow fields (Chedevergne et al. Reference Chedevergne, Casalis and Majdalani2012; Boyer et al. Reference Boyer, Casalis and Estivalèzes2013). In what follows, the term ‘model’ will be used to denote second-order asymptotic results obtained from the present framework, whereas ‘CFD’ will refer to numerical (computational fluid dynamics) simulations acquired from the nonlinear Navier–Stokes solver.

3.2 On the linearity of the axial velocity with respect to $z$

Inspired by Berman’s solution and the mass conservation relation (2.8), the axial velocity component can be assumed to be linear with respect to the axial coordinate $z$ . In order to verify that the CFD solution will indeed mimic this linear behaviour, figure 5 is used to compare our model to the computed solution for $\unicode[STIX]{x1D700}=0.1$ , $Re=100$ and $m=7$ . To magnify the possible departures from the expected linearity, the leading-order contribution of $O(1)$ , i.e. Berman’s solution, is subtracted from the axial velocity component $u_{z}$ , thus leaving only first- and second-order corrections. Based on this comparison, it is clear that the computed axial velocity remains linear with respect to $z$ up to approximately $z=7$ using $r=0.3$ . Beyond this location, it is possible for the outlet pressure condition to slightly influence the axial development of the flow field. Apart from this outlet effect, it may be argued that the Navier–Stokes solver in figure 5 helps to validate the assumption of a linear variation with respect to $z$ . Moreover, the visual agreement in the resulting slopes confirms that the simulation accurately reproduces the radial and tangential evolutions of the modelled flow. In fact, additional comparisons only reinforce this behaviour. In the interest of simplicity, subsequent results will be displayed halfway through the chamber at $z=4$ .

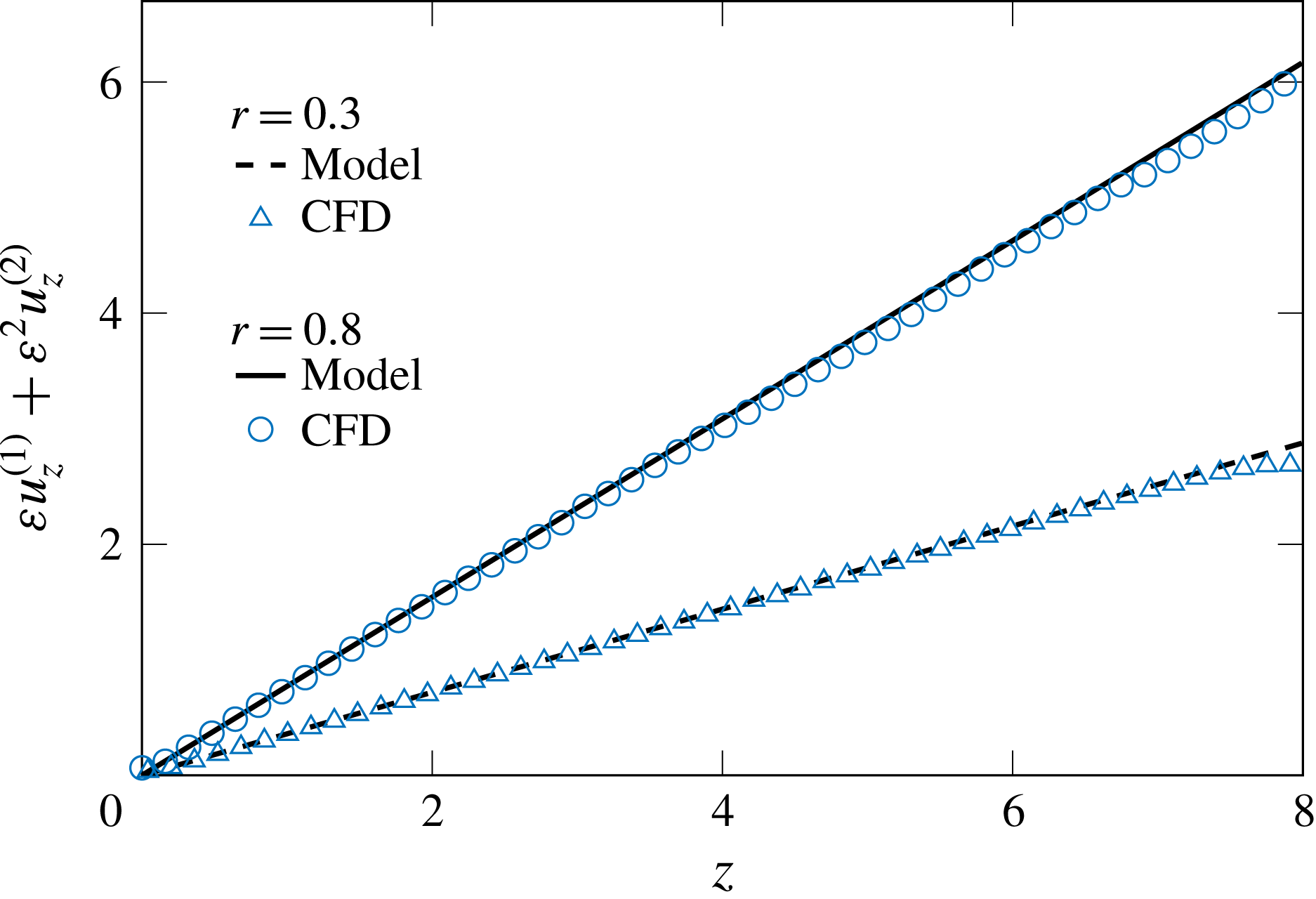
Figure 5.

Evolution along the domain of the axial velocity $\unicode[STIX]{x1D700}u_{z}^{(1)}+\unicode[STIX]{x1D700}^{2}u_{z}^{(2)}$ at two radial locations of $r=(0.3,0.8)$ in the $\unicode[STIX]{x1D703}=\unicode[STIX]{x03C0}/m$ plane for $\unicode[STIX]{x1D700}=0.1$ , $Re=100$ and $m=7$ .

Figure 6.

Isocontours of the radial, tangential and axial velocity components based on (a) nonlinear Navier–Stokes computations and (b) linear asymptotics at $O(\unicode[STIX]{x1D700}^{2})$ . Using $\unicode[STIX]{x1D700}=0.1$ , $Re=100$ , $z=4$ and $m=7$ , the spokes depicting extrema are identified with dashed lines at their corresponding angular locations.

3.3 Flow characterization based on both asymptotics and computations

To take advantage of the periodicity in the angular direction, flow field comparisons are reproduced in a polar slice that extends from $\unicode[STIX]{x1D703}=0$ to $2\unicode[STIX]{x03C0}/m$ . Note that the mesh used in conjunction with the Navier–Stokes simulations does not rely on periodic conditions; the tangential coordinate $\unicode[STIX]{x1D703}$ extends over the full range of $[0,2\unicode[STIX]{x03C0}]$ . We begin in figure 6 with the isocontours of the three velocity components using $\unicode[STIX]{x1D700}=0.1$ , $Re=100$ , $z=4$ and $m=7$ . Despite the linearization that affects the second-order asymptotic framework, an excellent agreement may be noted between the isocontours generated from the numerical simulations and those obtained from the asymptotic model for all three radial, tangential and axial velocity components.

By turning our attention first to the tangential velocity, it may be confirmed that its maximum absolute values occur at $\unicode[STIX]{x1D703}=\unicode[STIX]{x03C0}/(2m)$ and $3\unicode[STIX]{x03C0}/(2m)$ taken along the sidewall because of surface waviness; as for its sign, it depends on whether the flow is situated above or below the meridian line at $\unicode[STIX]{x1D703}=\unicode[STIX]{x03C0}/m$ , where the tangential velocity vanishes identically. The tangential velocity also vanishes at the domain delimiting lower and upper spoke lines located at $\unicode[STIX]{x1D703}=0$ and $2\unicode[STIX]{x03C0}/m$ , where the radial velocity $u_{r}$ matches the wall-normal velocity in both direction and magnitude. At those specific sites, both axial and tangential velocities vanish, thus leaving the flow to enter the chamber radially inwards towards the centreline (i.e. with no directional distortion). Naturally, $|u_{\unicode[STIX]{x1D703}}|$ diminishes while moving inwards away from the sidewall, or when moving tangentially towards the meridian lines as well as the upper and lower domain delimiting lines. In anticlockwise fashion, $u_{\unicode[STIX]{x1D703}}$ switches from negative to positive values as we cross from $0<\unicode[STIX]{x1D703}<\unicode[STIX]{x03C0}/m$ to $\unicode[STIX]{x03C0}/m<\unicode[STIX]{x1D703}<2\unicode[STIX]{x03C0}/m$ . Moreover, given that the tangential velocity is induced by small deviations from a circular cross-section, it remains smaller than its radial and axial counterparts, being asymptotically driven by $O(\unicode[STIX]{x1D700})$ surface displacements, unlike the radial and axial velocities, which are chiefly induced by the mass injection mechanism.

At this juncture, it may be helpful to recall that, in the absence of surface waviness, the isocontours of the axisymmetric axial velocity lead to concentric circles that exhibit a maximum value along the centreline. In the present configuration, the isocontours of $u_{z}$ stretch radially outwards along the meridian line of $\unicode[STIX]{x1D703}=\unicode[STIX]{x03C0}/m$ , where the chamber radius happens to be the shortest. Naturally, the area contraction in flow cross-section at this angular position induces a local increase in the axial velocity. Conversely, these isocontours shift radially inwards at the upper and lower boundaries where local wall expansions lead to an increase in the flow cross-section and, therefore, a corresponding reduction in  $u_{z}$ .

In fact, continuity may be used to partly explain the trends observed in the isocontours of the radial velocity. Upon close inspection of the corresponding graphs, it may be ascertained that $u_{r}$ vanishes along the centreline, where $u_{z}$ reaches its peak value, and that it increases in regions of axial velocity deficit. This behaviour may be attributed to the flow turning mechanism that affects the wall-injected stream, specifically as it negotiates a $90^{\circ }$ turn before merging axially with the core flow. At $\unicode[STIX]{x1D703}=\unicode[STIX]{x03C0}/m$ , owing to the stretched axial velocity isocontours, the radial velocity deceleration towards the centreline is more rapid than at the $\unicode[STIX]{x1D703}=0$ and $2\unicode[STIX]{x03C0}/m$ borderlines, where the flow may be seen to be radially expanded. Another characteristic of $u_{r}$ , which has been well documented in the literature, corresponds to its velocity overshoot compared to its wall value (Saad & Majdalani Reference Saad and Majdalani2010). Despite the unitary speed of $|u_{r}|=1$ at the sidewall, $|u_{r}|$ undergoes first an increase in absolute value due to the sudden radial pinching of the circumferential area that is normal to the injected flow, and which does not permit the flow to develop a sufficient $u_{z}$ component to adequately transport the mass axially. The resulting increase in $|u_{r}|$ may be noted in the peak contour points in figure 6, namely, those that materialize at some intermediate positions between the wall and the centreline. Naturally, when the flow is pinched, the locus of these extrema moves closer to the centreline.

As alluded to earlier, another byproduct of waviness and viscosity may be the production of axial vorticity, which is absent in the strictly axisymmetric Taylor–Culick model (Balachandar et al. Reference Balachandar, Buckmaster and Short2001). To illustrate the corresponding behaviour, isocontours of axial vorticity, namely, $\unicode[STIX]{x1D6FA}_{z}$ , are displayed in figure 7 for $\unicode[STIX]{x1D700}=0.1$ ,  $Re=100$ ,  $z=4$ and $m=7$ . Using the variable coordinate transformation at the wall, $\unicode[STIX]{x1D6FA}_{z}$ may be expressed as

(3.1) $$\begin{eqnarray}\unicode[STIX]{x1D6FA}_{z}={\displaystyle \frac{1}{1+\unicode[STIX]{x1D700}\cos (m\unicode[STIX]{x1D703})}}\left[\unicode[STIX]{x2202}_{r}u_{\unicode[STIX]{x1D703}}-{\displaystyle \frac{\unicode[STIX]{x1D700}m\sin (m\unicode[STIX]{x1D703})}{1+\unicode[STIX]{x1D700}\cos (m\unicode[STIX]{x1D703})}}\unicode[STIX]{x2202}_{r}u_{r}-{\displaystyle \frac{1}{r}}\unicode[STIX]{x2202}_{\unicode[STIX]{x1D703}}u_{r}+{\displaystyle \frac{u_{\unicode[STIX]{x1D703}}}{r}}\right].\end{eqnarray}$$

Note that this vorticity component vanishes for the axisymmetric case. In order to improve the velocity gradients and thus the vorticity, the spatial integration scheme within the Navier–Stokes solver is increased to the third order in figure 7. Graphically, one may infer that the Navier–Stokes computations tend to agree qualitatively with the second-order asymptotic solution, especially in the two bulk regions where the axial vorticity is largest. Nonetheless, discrepancies may also be seen at the sidewall near $\unicode[STIX]{x1D703}=\unicode[STIX]{x03C0}/(2m)$ and $3\unicode[STIX]{x03C0}/(2m)$ . The bulk vorticity regions that develop in this configuration are consistent with those detailed by Kurdyumov (Reference Kurdyumov2006). Furthermore, the dissimilarities observed near the sidewall may be attributed to the practical limitations associated with asymptotic expansions. They may also be ascribed to the compounded effects of numerical errors that accrue during the evaluation of velocity gradients within the Navier–Stokes solver.

Figure 7.

Isocontours of the axial vorticity based on (a) nonlinear Navier–Stokes computations and (b) linear asymptotics at $O(\unicode[STIX]{x1D700}^{2})$ . Here $\unicode[STIX]{x1D700}=0.1$ ,  $Re=100$ ,  $z=4$ and $m=7$ .

3.4 Sensitivity to various Reynolds numbers, radial deviations and wavenumbers

To further explore the effects of varying the Reynolds number, radial deviation amplitude and circular wavenumber on the flow development, the sensitivity of the three velocity components to these parameters may be quantified by comparing the second-order corrections to the individual computations taken along different polar angles. Guided by the isocontours of figure 6, both $u_{r}$ and $u_{z}$ seem to display interesting structures along angular cuts taken at $\unicode[STIX]{x1D703}=0$ and $\unicode[STIX]{x03C0}/m$ , whereas $u_{\unicode[STIX]{x1D703}}$ may be best featured at $\unicode[STIX]{x1D703}=\unicode[STIX]{x03C0}/(2m)$ . We therefore proceed to evaluate the three velocity components along their most representative inclination angles and showcase their outcomes in figures 8–10 using both asymptotics and computations.

As we seek to better understand the role of $\unicode[STIX]{x1D700}$ on the axial velocity, the second-order corrections obtained asymptotically are compared to those computed in figure 8(a) using $Re=100$ ,  $z=4$ ,  $m=7$ and two values of $\unicode[STIX]{x1D700}$ that correspond to $0.01$  and  $0.1$ . Results are deliberately displayed along a constant $\unicode[STIX]{x1D703}=\unicode[STIX]{x03C0}/m$ spoke where the largest deviations from the axisymmetric motion may be realized. To further magnify differences, the exact Berman solution that is recovered at leading order is subtracted from both solutions, and the outcome is divided by $\unicode[STIX]{x1D700}$ , thus leaving us with $[u_{z}^{(1)}+\unicode[STIX]{x1D700}u_{z}^{(2)}]/z$ . In view of the dual magnification levels that are implemented, it may be argued that the agreement between computations and asymptotics is satisfactory, especially in the ability of the model to capture both sidewall and centreline variations with $\unicode[STIX]{x1D700}$ rather consistently. The most noticeable discrepancies remain small and mostly confined to the annular region that extends approximately between $r\approx 0.4$ and 0.7.

In fact, because of the magnification effect, these discrepancies actually fall within the numerical uncertainty that accompanies our simulations. The reasons are these. Since the mesh is uniformly discretized along the $z$ direction, the accuracy of $u_{z}/z$ directly depends on the finite gap between two axial positions. Furthermore, the disparities can stem either from higher-order terms that are not accounted for in the asymptotic formulation, or from the diffusive nature of the second-order discretization scheme that is adopted in the Navier–Stokes solver.

Figure 8.

Comparison between (a) the axial velocity correction at $Re=100$ , $z=4$ and $\unicode[STIX]{x1D700}=(0.01,0.1)$ along a constant $\unicode[STIX]{x1D703}=\unicode[STIX]{x03C0}/m$ spoke, and (b) the radial velocity correction at $\unicode[STIX]{x1D700}=0.01$ , $z=4$ and $Re=(100,1000)$ along a constant $\unicode[STIX]{x1D703}=0$ spoke. Here we use both Navier–Stokes computations (symbols) and second-order asymptotics (lines) for $[u_{z}^{(1)}+\unicode[STIX]{x1D700}u_{z}^{(2)}]/z$ and $u_{r}^{(1)}+\unicode[STIX]{x1D700}u_{r}^{(2)}$ with $m=7$ crests.

As for the influence of the Reynolds number on the radial velocity, it is illustrated in figure 8(b) using $\unicode[STIX]{x1D700}=0.01$ , $m=7$ and two values of $Re$ that correspond to 100 and 1000, respectively. Choosing a relatively small value of $\unicode[STIX]{x1D700}$ enables us to compute the flow field with a large Reynolds number. Here, too, we display only the second-order correction in the radial velocity, $u_{r}^{(1)}+\unicode[STIX]{x1D700}u_{r}^{(2)}$ , by subtracting the leading-order contribution. The agreement that is achieved between the numerical simulations and the asymptotic formulation is gratifying to note, especially as the Reynolds number is set at 1000.

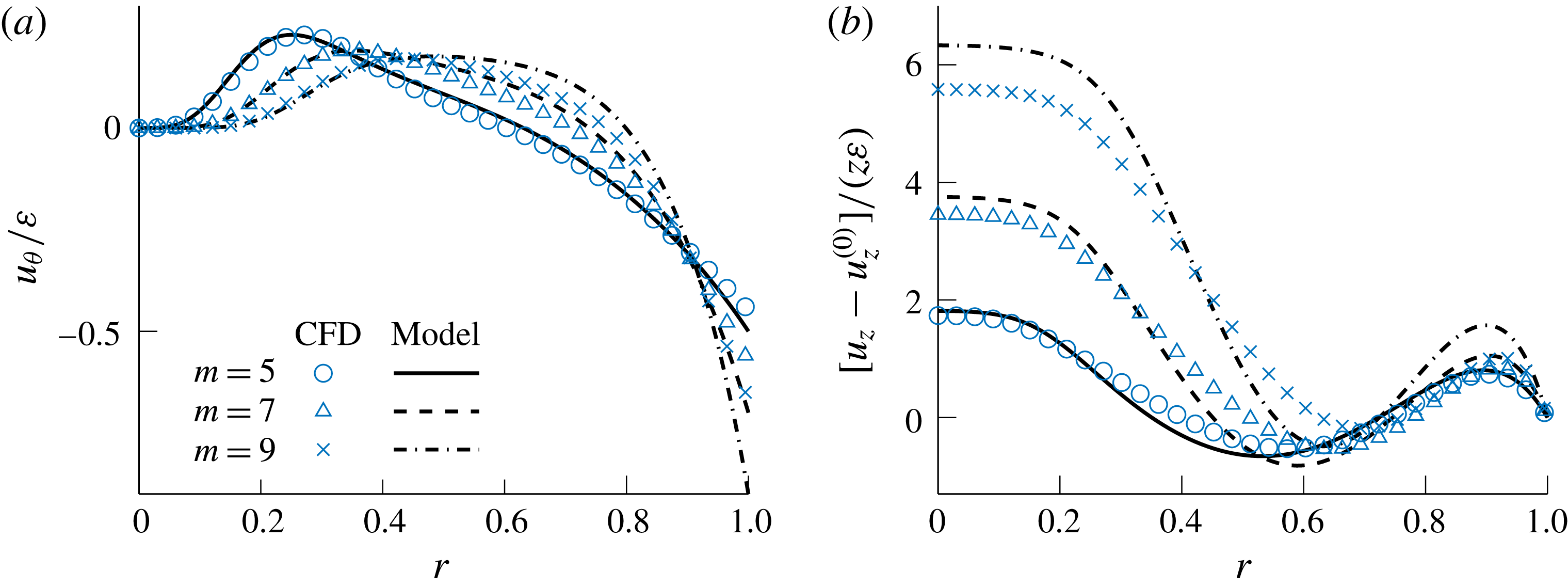
Figure 9.

Sensitivity of the tangential and axial velocities to variations in $m$ using both computations (symbols) and second-order asymptotics; here we take $\unicode[STIX]{x1D700}=0.1$ and $Re=100$ . Results are shown along constant angular spokes of (a)  $\unicode[STIX]{x1D703}=\unicode[STIX]{x03C0}/(2m)$ for the tangential velocity $u_{\unicode[STIX]{x1D703}}/\unicode[STIX]{x1D700}=u_{\unicode[STIX]{x1D703}}^{(1)}+\unicode[STIX]{x1D700}u_{\unicode[STIX]{x1D703}}^{(2)}$ and (b)  $\unicode[STIX]{x1D703}=0$ for the axial velocity $[u_{z}^{(1)}+\unicode[STIX]{x1D700}u_{z}^{(2)}]/z$ .

In figure 9(a), the sensitivity of the tangential velocity on the circular wavenumber is characterized by showcasing $u_{\unicode[STIX]{x1D703}}/\unicode[STIX]{x1D700}=u_{\unicode[STIX]{x1D703}}^{(1)}+\unicode[STIX]{x1D700}u_{\unicode[STIX]{x1D703}}^{(2)}$ along a polar angle of $\unicode[STIX]{x1D703}=\unicode[STIX]{x03C0}/(2m)$ using $\unicode[STIX]{x1D700}=0.1$ , $Re=100$ and $m=5$ , 7 and 9. The skipping of even values of $m$ reduces visual clutter by helping to distinguish between the remaining curves, especially since the use of $m=4$ , 6 and 8 leads to nearly identical trends. It is also guided by practical reasons, such as the preferred grain perforations in industry, which are invariably designed with an odd number of star points, crests or lobes, with the hope that such arrangements would help to mitigate the development of acoustic instabilities. Here, too, the agreement between computations and the modelled solution appears to be excellent in the core region. However, small differences begin to appear when the wavenumber is increased or when the sidewall is approached. We also remark that at $\unicode[STIX]{x1D703}=\unicode[STIX]{x03C0}/(2m)$ , the contribution of second-order terms to the tangential velocity become negligible because of the $\sin (2m\unicode[STIX]{x1D703})$ term that appears in the definition of $u_{\unicode[STIX]{x1D703}}^{(2)}$ . As one may surmise from (2.13), the minor disparities that are detected near the sidewall may be attributed to the omission of third-order terms in the asymptotic expansion of the injection velocity. Asymptotically, one must have

(3.2) $$\begin{eqnarray}u_{\unicode[STIX]{x1D703}}(1,\unicode[STIX]{x1D703},z)=\unicode[STIX]{x1D6FC}^{\prime }\unicode[STIX]{x1D700}+\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6FC}^{\prime }\unicode[STIX]{x1D700}^{2}+\unicode[STIX]{x1D6FC}^{\prime }\left(\unicode[STIX]{x1D6FC}^{2}-{\textstyle \frac{1}{2}}\unicode[STIX]{x1D6FC}^{\prime 2}\right)\unicode[STIX]{x1D700}^{3}+o(\unicode[STIX]{x1D700}^{3}),\end{eqnarray}$$

where the quantity $\unicode[STIX]{x1D6FC}^{\prime }(\unicode[STIX]{x1D6FC}^{2}-\frac{1}{2}\unicode[STIX]{x1D6FC}^{\prime 2})\unicode[STIX]{x1D700}^{3}$ reduces to $m^{3}\unicode[STIX]{x1D700}^{3}/2$ at $\unicode[STIX]{x1D703}=\unicode[STIX]{x03C0}/(2m)$ ; this third-order correction actually matches the gap between the computational and second-order asymptotic values at the wall, which widens with successive increases in $m$ and  $\unicode[STIX]{x1D700}$ .

Figure 10.

Isocontours of (a) the radial velocity $u_{r}$ for $m=5$ , (b) the radial velocity $u_{r}$ for $m=7$ , (c) the tangential velocity $u_{\unicode[STIX]{x1D703}}$ for $m=7$ and (d) the axial velocity $u_{z}$ for $m=7$ using $\unicode[STIX]{x1D700}=0.2$ and $Re=100$ .

The sensitivity of the axial velocity on the circular wavenumber is illustrated in figure 9(b) along a different polar angle, namely $\unicode[STIX]{x1D703}=0$ , at the same Reynolds number and deviation values. Here, Berman’s contribution $u_{z}^{(0)}$ is subtracted from the total axial velocity component in order to showcase the correction only, as done previously in figure 8. Consistently with the behaviour observed in the tangential velocity comparison, the agreement between computations and the modelled solution appears to be quite satisfactory for $m=5$ , although it slowly deteriorates as $m$ is increased. As before, the overshoot of the model near $r\approx 0.9$ may be attributed to the diffusivity of the Navier–Stokes solver; the accuracy of the simulation along the axis remains limited by the finite discretization in the axial direction. Since the absolute value of the axial velocity along the axis $|u_{z}^{(2)}(0)|$ increases with $m$ , so does the uncertainty associated with the axial mesh discretization, thus leading to a growing disparity between the simulations and the modelled solution. Furthermore, it may be helpful to note that the displayed velocity components are divided by $\unicode[STIX]{x1D700}$ to better differentiate among the curves. Nonetheless, the noted discrepancies remain small compared to the total velocity magnitude  $\boldsymbol{u}$ .

Before leaving this discussion, it may be instructive to note that, in the foregoing work, the product $\unicode[STIX]{x1D700}Re$ has been consistently smaller than 10. Nonetheless, comparisons could have been undertaken for values that reach $\unicode[STIX]{x1D700}Re\approx 30$ . Above this level, the Navier–Stokes solver will have difficulty converging onto a steady periodic solution. An example of the model’s validity for $\unicode[STIX]{x1D700}Re=20$ is provided in figure 10, where isocontours of the velocity are displayed at two different values of $m$ . By comparing the upper and lower sections of the graph, the ability of the model to mirror the computed solution seems gratifying, except in what concerns the negative peak magnitudes of $u_{r}$ in the model, which overshoot their computed values. The axial velocity in figure 10(d) also exhibits different lobe shapes when comparing the modelled solution to its simulation at the same contour levels.