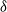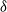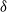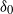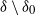1. Introduction
In this paper we are concerned with reciprocal random fields on undirected graphs. They contain the reciprocal chains as a special case, but have up to now received comparably little attention, and have suffered from a lingering ambiguity in their definition. We lay a solid foundation for the study of reciprocal random fields on undirected graphs by defining four properties, the factorizing, global, local, and pairwise reciprocal properties, in decreasing order of strength, with respect to a set of nodes
$\delta$
. The relations of the reciprocal properties to each other, and to the better-known Markov properties, are described in detail, as are the reciprocal properties of a reciprocal random field conditioned on the values at a set of nodes
$\delta_0$
. We first provide some background.
Continuous-time reciprocal processes, also called Bernstein processes, were introduced in [Reference Bernstein1] following an acclaimed paper by Schrödinger [Reference Schrödinger24] on the relation between certain problems in classical and quantum dynamics. A rigorous definition of a reciprocal process was provided in [Reference Jamison11, Reference Jamison12], with proofs of their basic properties. According to this definition, a real-valued process
$\{X_t;\;t\in[0,1]\}$
is reciprocal if
$\mathbb{P}(X_u\in\cdot \mid X_{s_1},\ldots,X_{s_m},X_{t_n},\ldots,X_{t_1}) =\mathbb{P}(X_u\in\cdot \mid X_{s_m},X_{t_n})$
for all
$0\leq s_1<\cdots <s_m<u<t_n<\cdots<t_1\leq 1$
. In particular, a Markov process is always a reciprocal process, but a reciprocal process is not always Markov. Reciprocal chains, i.e. discrete-time reciprocal processes, were introduced in [Reference Chay4] and studied in [Reference Levy, Frezza and Krener17], among others. A random sequence
$\{X_t;\;t=1,\ldots,n\}$
,
$n\geq3$
, is said to be a reciprocal chain if
$\mathbb{P}(X_k\in\cdot \mid X_1,\ldots,X_{j},X_{l},\ldots,X_n) =\mathbb{P}(X_k\in\cdot \mid X_j,X_l)$
for all
$0\leq j<k<l\leq n$
.
In much of the work on reciprocal processes, attention has been restricted to the stationary and/or Gaussian cases. In [Reference Carmichael, Masse and Theodorescu2, Reference Chay4, Reference Jamison11], characterizations of a stationary Gaussian reciprocal process in terms of its autocovariance function were given, and [Reference Chay4] gave conditions for stationary Gaussian reciprocal processes to be Markov. Later work has to a large extent dealt with the construction of representations of a reciprocal process by a second-order nearest-neigbour model driven by a locally correlated noise process; see [Reference Carravetta3, Reference Krener14, Reference Levy, Frezza and Krener17, Reference Sand23, Reference White and Carravetta29]. Such representations are then used to construct smoothing algorithms for hidden reciprocal processes. Examples of engineering applications of reciprocal chains include image simulation [Reference Picci and Carli21] and track extraction [Reference Stamatescu, White and Bruce-Doust27].
It should also be noted that in [Reference Carravetta3, Reference Stamatescu, White and Bruce-Doust27, Reference White and Carravetta29] and other papers, a different definition of a reciprocal chain was used: a random sequence
$\{X_t;\;t=1,\ldots,n\}$
,
$n\geq3$
, was said to be a reciprocal chain if
$\mathbb{P}(X_k\in\cdot \mid X_1,\ldots,X_{k-1},X_{k+1},\ldots,X_n) =\mathbb{P}(X_k\in\cdot \mid X_{k-1},X_{k+1})$
for all
$0<k<n$
. It was pointed out in [Reference Erhardsson, Saize and Yang9] that if the latter definition is used, some of the properties that a reciprocal chain is known to satisfy need not hold; for example that, conditionally on
$X_n$
, a reciprocal chain is a Markov chain.
In the present paper we take a different approach to reciprocal chains, assuming neither stationarity nor Gaussianity. Since any Markov chain is a reciprocal chain, and given the existence of a well-established theory for Markov random fields on undirected graphs, it is natural to attempt to define in a proper way a class of reciprocal random fields on undirected graphs, which should contain both Markov random fields and reciprocal chains as special cases. The theory of Markov random fields on undirected graphs was developed in [Reference Dobrushin7, Reference Dobrushin8, Reference Preston22, Reference Spitzer26], among others, originally as an attempt to extend the Ising model for ferromagnetic materials to a wider class of probabilistic models. Markov random fields have shown themselves useful in statistics (e.g. graphical models) and in probabilistic expert systems; see [Reference Darroch, Lauritzen and Speed6, Reference Lauritzen15, Reference Pearl20, Reference Whittaker30].
In the early literature, a random field
$\{X_t;\;t\in V\}$
is typically said to satisfy the Markov property if
$\mathbb{P}(\{X_t;\;t\in T\}\in\cdot \mid \{X_s;\;s\notin T\}) =\mathbb{P}(\{X_t;\;t\in T\}\in\cdot \mid \{X_s;\;s\in N_T\})$
for all
$T\subset V$
, where
$N_T$
is the set of nodes not in T that are neighbors of T in the graph. This property holds e.g. if the random field has a Gibbs distribution; see [Reference Kindermann and Snell13]. Later, it became standard to distinguish between four different Markov properties for random fields: the factorizing, global, local, and pairwise Markov properties, in order of decreasing strength. They are all satisfied if the random field has a Gibbs distribution. The relations between these properties have been studied by several authors [Reference Matúš18, Reference Speed25, Reference Studený28]. As for reciprocal properties of random fields, an early attempt to define such a property was the quasi-Markov, or L-Markov, property for random fields of the type
$\{X_t;\;t\in\mathbb{Z}^d\}$
, defined and investigated in [Reference Chay4].
The main contribution of the present paper is to define four so-called reciprocal properties for random fields on an undirected graph, all of them with respect to an arbitrary set of nodes
$\delta\subset V$
: the factorizing, global, local, and pairwise reciprocal properties, in order of decreasing strength. We find that these properties reduce to the corresponding Markov properties when
$\delta = \emptyset$
; in fact, the factorizing, global, and pairwise reciprocal properties reduce to the corresponding Markov properties whenever
$\delta$
is a complete set. Moreover, necessary and sufficient conditions on the graph for the global and local properties to be equivalent, as well as for the local and pairwise properties to be equivalent, and a sufficient condition for the pairwise property to imply the factorizing property, are given.
We also consider the conditional distributions of a random field on an undirected graph given the values at a subset of nodes
$\delta_0\subset V$
, and show that, for the subgraph induced by
$V\setminus\delta_0$
, under such a conditioning, all reciprocal properties are preserved with respect to the set of nodes
$\delta\setminus\delta_0$
. The converse statement is wrong: even if a random field does not satisfy any reciprocal property with respect to
$\delta$
, the subgraph induced by
$V\setminus\delta_0$
may still, conditionally on the values at
$\delta_0$
, satisfy any reciprocal property with respect to
$\delta\setminus\delta_0$
.
Specializing to reciprocal chains, we show that a random sequence is a reciprocal chain according to the definition in [Reference Chay4, Reference Levy, Frezza and Krener17] if and only if, when seen as a random field on an undirected graph, it has the global reciprocal property with respect to the node set
$\delta = \{0,n\}$
. Similarly, it is a ‘reciprocal chain’ according to the definition in [Reference Carravetta3] if and only if it has the (weaker) local reciprocal property with respect to
$\delta$
. More importantly, a random sequence has the factorizing reciprocal property with respect to
$\delta$
if and only if the joint distribution has a density
$f_X$
with respect to a product of
$\sigma$
-finite measures
$\mu$
of the form
$f_X(x) = \phi_n(x_0,x_n)\prod_{i=0}^{n-1}\phi_i(x_i,x_{i+1})$
$\mu$
-almost everywhere (a.e.) for some measurable functions
$\{\phi_i\colon\!\mathcal{X}_{\{i,i+1\}}\to\mathbb{R}_+;\;i = 0,1,\ldots,n-1\}$
,
$\phi_n\colon\!\mathcal{X}_{\{0,n\}}\to\mathbb{R}_+$
. The factorizing reciprocal property does not hold for reciprocal chains in general, but it does hold if the density
$f_X$
is positive; a result which, to the best of our knowledge, is new.
The rest of the paper is organised as follows. Section 2 contains some preliminary material on graphs, random fields, and conditional independence. In Section 3, definitions of the four reciprocal properties of a random field are given, and several results concerning the relations between these properties, and their relation to the Markov properties, are derived. In Section 4, conditional distributions of reciprocal random fields given the values at a set of nodes
$\delta_0$
are considered. Lastly, in Section 5, the results obtained are applied to the special case of reciprocal chains.
2. Preliminaries
This section contains some basic definitions and notation pertaining to undirected graphs and random fields on graphs, and some basic results on conditional independence. For more information, see [Reference Lauritzen15].
2.1. Undirected graphs
Let
$\mathcal{G} = (V,E)$
be a graph, where V is an ordered finite set of nodes, and E is a set of edges. The edges are always assumed to be undirected. An undirected edge between two nodes
$\alpha,\beta\in V$
is denoted by
$\langle\alpha,\beta\rangle$
, or equivalently
$\langle\beta,\alpha\rangle$
.
$\mathcal{G}$
is called simple if there is at most one edge between any pair of nodes, and if there are no edges of type
$\langle\alpha,\alpha\rangle$
for any
$\alpha\in V$
(these are called loops). In this paper we only consider simple graphs.
A graph
$\mathcal{G}_A = (A,E')$
is called a subgraph of
$\mathcal{G}$
if
$A\subset V$
and
$E'\subset E_A=\{\langle\alpha,\beta\rangle\in E; \alpha,\beta\in A\}$
. The particular subgraph
$\mathcal{G}_A = (A,E_A)$
is called the subgraph induced by A. A graph
$\mathcal{G}$
is said to be complete if
$E=\{\langle\alpha,\beta\rangle;\;\alpha\ne\beta,\, \alpha,\beta\in V\}$
. A subset
$A\subset V$
is said to be complete if the induced subgraph
$\mathcal{G}_A$
is complete. The collection of complete subsets of V is denoted
$\mathbb{K}$
. A complete subset which is maximal with respect to set inclusion is called a clique.
For any
$\alpha,\beta\in V$
, a sequence
$\{\alpha_0,\alpha_1,\ldots,\alpha_n\}$
of elements in V is called a path between
$\alpha$
and
$\beta$
of length n (
$n\geq 1$
) if
$\alpha_0 = \alpha$
,
$\alpha_n = \beta$
, and
$\langle\alpha_i,\alpha_{i+1}\rangle\in E$
for each
$i=0,1,\ldots,n-1$
.
$\alpha$
and
$\beta$
are said to be connected if either
$\alpha=\beta$
, or
$\alpha\ne\beta$
and there exists a path between
$\alpha$
and
$\beta$
. Two subsets
$A,B\subset V$
are said to be connected if either
$A\cap B\ne\emptyset$
, or
$A\cap B=\emptyset$
and there exists a path in
$\mathcal{G}$
between A and B, by which we mean a path between a node
$\alpha\in A$
and a node
$\beta\in B$
. Clearly, connectedness is an equivalence relation on V. The subgraphs of
$\mathcal{G}$
induced by the corresponding equivalence classes are called the connected components of
$\mathcal{G}$
.
For each triple (A, B, S) of disjoint subsets of V, S is said to separate A from B in
$\mathcal{G}$
if there is no path between A and B of length
$n = 1$
, and, for each path
$\{\alpha_0,\alpha_1,\ldots,\alpha_n\}$
between A and B of length
$n\geq 2$
, there is an
$i\in\{1,\ldots,n-1\}$
such that
$\alpha_i\in S$
.
For each
$\alpha\in V$
, the boundary of
$\alpha$
is defined by
$\rm{bd}(\alpha) = \{\beta\in V;\; \langle\alpha,\beta\rangle\in E\}$
, and the closure of
$\alpha$
is defined by
$\rm{cl}(\alpha) = \{\alpha\}\cup\rm{bd}(\alpha)$
.
2.2. Random fields
By a random field on an undirected graph
$\mathcal{G} = (V,E)$
, we mean a collection
$\{X_t;\; t\in V\}$
of random variables defined on the same probability space and indexed by the node set V. For each
$t\in V$
,
$X_t$
takes values in a measurable space
$(\mathcal{X}_t,\mathscr{B}_{\mathcal{X}_t})$
, which is assumed to be either
$(\mathbb{R}^d,\mathscr{R}^d)$
, i.e.
$\mathbb{R}^d$
equipped with its Borel
$\sigma$
-algebra, or a finite or countably infinite set equipped with its power
$\sigma$
-algebra (= the collection of all its subsets). For each
$A\subset V$
, we denote by
$X_A$
the random variable
$\{X_t;\; t\in A\}$
, taking values in the product space
$\mathcal{X}_A = \underset{i\in A}{\mathsf{X}}\mathcal{X}_i$
, equipped with the product
$\sigma$
-algebra
$\mathscr{B}_{\mathcal{X}_A}$
. The random variable
$X_V$
is denoted by X, the product space
$\mathcal{X}_V$
by
$\mathcal{X}$
, and the
$\sigma$
-algebra
$\mathscr{B}_{\mathcal{X}_V}$
by
$\mathscr{B}_{\mathcal{X}}$
. Also, for each
$x\in\mathcal{X}$
and each
$A\subset V$
, we denote by
$x_A$
the projection of x onto
$\mathcal{X}_A$
.
We denote by
$\mathscr{L}(\!\cdot\!)$
the probability distribution of a random variable. Throughout the paper we assume that
$\mathscr{L}(X)$
has a density
$f_X$
with respect to a product measure
$\mu = \underset{i\in V}{\mathsf{X}}\mathcal{\mu}_i$
on
$(\mathcal{X},\mathscr{B}_{\mathcal{X}})$
, where, for each
$i\in V$
,
$\mu_i$
is a
$\sigma$
-finite (non-negative) measure on
$(\mathcal{X}_i,\mathscr{B}_{\mathcal{X}_i})$
. For each
$A\subset V$
, we denote by
$\mu_A$
the product measure
$\mu_A = \underset{i\in A}{\mathsf{X}}\mathcal{\mu}_i$
on
$(\mathcal{X}_A,\mathscr{B}_{\mathcal{X}_A})$
, and by
$f_{X_A}$
the marginal density of
$\mathscr{L}(X_A)$
with respect to
$\mu_A$
, defined by
$f_{X_A}(x_A) = \int_{\mathcal{X}_{V\setminus A}}f_X(x_A,x_{V\setminus A})\,\textrm{d}\mu_{V\setminus A}(x_{V\setminus A})$
for all
$x_A\in\mathcal{X}_A$
.
We use the fact that, for each
$A\subset B\subset V$
, if
$N_A\in\mathscr{B}_{\mathcal{X}_A}$
is such that
$\mu_A(N_A)=0$
, then also
$\mu_B(N_A\times\mathcal{X}_{B\setminus A}) = 0$
, since
$\mu_{B\setminus A}$
is
$\sigma$
-finite. Furthermore, for each
$B\subset V$
,
\begin{equation} f_{X_A}(x_A) = 0 \ \Rightarrow\ f_{X_B}(x_A,x_{B\setminus A}) = 0\quad\textrm{for all}\ A\subset B\qquad \mu_B\rm{-}\textrm{a.e.}\end{equation}
To prove (2.1), define the sets
$\{N_{A}\in\mathscr{B}_{\mathcal{X}_A};\;A\subset V\}$
and
$\{N_{A,B}\in\mathscr{B}_{\mathcal{X}_B};\;A\subset B\subset V\}$
by
$N_{A} = \{x_A\in\mathcal{X}_A;\; f_{X_A}(x_A)=0\}$
and
$N_{A,B} = \{x_B\in\mathcal{X}_B;\; f_{X_A}(x_A)=0\} = N_A\times\mathcal{X}_{B\setminus A}$
. Then,
\begin{align*} 0 \leq \int_{N_{A,B}\cap N_{B}^c} f_{X_B}(x_B) \, \textrm{d}\mu_B(x_B) & = \int_{N_{A,B}\cap N_{B}^c}\int_{\mathcal{X}_{V\setminus B}} f_X(x_B,x_{V\setminus B}) \, \textrm{d}\mu_{V\setminus B}(x_{V\setminus B}) \, \textrm{d}\mu_B(x_B) \\[5pt] & = \int_{N_{A,V}\cap N_{B,V}^c}f_{X}(x) \, \textrm{d}\mu(x) \\[5pt] & \leq \int_{N_{A,V}} f_{X}(x) \, \textrm{d}\mu(x) \\[5pt] & = \int_{N_{A}}\int_{\mathcal{X}_{V\setminus A}}f_X(x_A,x_{V\setminus A}) \, \textrm{d}\mu_{V\setminus A}(x_{V\setminus A}) \, \textrm{d}\mu_A(x_A) \\[5pt] & = \int_{N_{A}}f_{X_A}(x_A) \, \textrm{d}\mu_A(x_A) = 0 \qquad \textrm{for all}\ A\subset B\subset V.\end{align*}
In order for the first integral to be 0, it is necessary that
$\mu_B(N_{A,B}\cap N_{B}^\textrm{c}) = 0$
. Since V has finitely many subsets, we obtain
$\mu_B\big(\bigcup_{A\subset B}(N_{A,B}\cap N_{B}^\textrm{c})\big) \leq\sum_{A\subset B}\mu(N_{A,B}\cap N_{B}^\textrm{c}) = 0$
for all
$B\subset V$
.
2.3. Conditional independence
For each pair (B, C) of disjoint subsets of V, there exists a regular conditional distribution of
$X_{B}$
given
$X_C$
that has a density
$f_{X_{B}\mid X_C}$
with respect to
$\mu_{B}$
. For each
$x_C\in\mathcal{X}_C$
such that
$f_{X_C}(x_C)>0$
,
$f_{X_{B}\mid X_C}(\cdot\!\mid x_C)$
can be (and is in this paper) chosen as
$f_{X_{B}\mid X_C}(x_{B}\mid x_C) = {f_{X_{B\cup C}}(x_B,x_C)}/{f_{X_C}(x_C)}$
for all
$x_{B}\in\mathcal{X}_{B}$
. For all
$x_C\in\mathcal{X}_C$
such that
$f_{X_C}(x_C)=0$
,
$f_{X_{B}\mid X_C}(\cdot\!\mid x_C)$
can be chosen as an arbitrary fixed density. Using (2.1), this gives
\begin{equation} f_{X_{B\cup C}}(x_B,x_C) = f_{X_{B}\mid X_C}(x_{B}\mid x_C)f_{X_C}(x_C) \qquad\rm{\mu_{B\cup C}-a.e.}\end{equation}
For each triple (A, B, C) of disjoint subsets of V, we say that
$X_A$
and
$X_B$
are conditionally independent given
$X_C$
, denoted
$X_A\perp X_B\mid X_C$
, if there exists a version of
$f_{X_{A\cup B\cup C}}$
such that, for each
$x_C\in\mathcal{X}_C$
such that
$f_{X_C}(x_C)>0$
,
\begin{equation} f_{X_{A\cup B\cup C}}(x_A,x_B,x_C) = \frac{f_{X_{A\cup C}}(x_A,x_C)}{f_{X_C}(x_C)}f_{X_{B\cup C}}(x_B,x_C) \quad \textrm{for all}\ (x_A,x_B)\in\mathcal{X}_{A\cup B}.\end{equation}
Using (2.1),
$X_A\perp X_B\mid X_C$
implies that
\begin{equation} f_{X_{A\cup B\cup C}}(x_A,x_B,x_C) = f_{X_A\mid X_C}(x_A\mid x_C)f_{X_{B\cup C}}(x_B,x_C) \qquad\rm{\mu_{A\cup B\cup C}-a.e.}\end{equation}
Note that (2.4) remains valid if
$f_{X_{B\cup C}}$
is replaced on the right-hand side by any
$\mu_{B\cup C}$
-version of
$f_{X_{B\cup C}}$
.
A sufficient condition for
$X_A\perp X_B\mid X_C$
to hold is that there exists a version of
$f_{X_{A\cup B\cup C}}$
and measurable functions
$h\colon\! \mathcal{X}_{A\cup C}\to\mathbb{R}_+$
and
$k\colon\! \mathcal{X}_{B\cup C}\to\mathbb{R}_+$
such that
\begin{equation} f_{X_{A\cup B\cup C}}(x_A,x_B,x_C) = h(x_A,x_C)k(x_B,x_C)\quad\textrm{for all}\ (x_A,x_B,x_C)\in\mathcal{X}_{A\cup B\cup C}.\end{equation}
To see this, note that the version of
$f_{X_{A\cup B\cup C}}$
given in (2.5) satisfies (2.3), since
\begin{align*} f_{X_C}(x_C) & = \int_{\mathcal{X}_A}h(x_A,x_C)d\mu_A(x_A)\int_{\mathcal{X}_B}k(x_B,x_C) \, \textrm{d}\mu_B(x_B) \quad & & \textrm{for all}\ x_C\in\mathcal{X}_C; \\[5pt] f_{X_{A\cup C}}(x_A,x_C) & = h(x_A,x_C)\int_{\mathcal{X}_B}k(x_B,x_C) \, \textrm{d}\mu_B(x_B) & & \textrm{for all}\ (x_A,x_C)\in\mathcal{X}_{A\cup C}; \\[5pt] f_{X_{B\cup C}}(x_B,x_C) & = k(x_B,x_C)\int_{\mathcal{X}_A}h(x_A,x_C) \, \textrm{d}\mu_A(x_A) & & \textrm{for all}\ (x_B,x_C)\in\mathcal{X}_{B\cup C}.\end{align*}
3. Reciprocal properties for random fields
Definition 3.1. A random field X on an undirected graph
$\mathcal{G} = (V,E)$
is said to satisfy the factorizing reciprocal property with respect to
$\delta\subset V$
, abbreviated
$F[\delta]$
, if
$\mathscr{L}(X)$
has a density
$f_X$
with respect to a product of
$\sigma$
-finite measures
$\mu$
of the form
\begin{equation} f_X(x) = \prod_{C\in\mathbb{K}^\delta}\phi_C(x) \qquad\rm{\mu-a.e.} \end{equation}
for some measurable functions
$\{\phi_C\colon\!\mathcal{X}_C\to\mathbb{R}_+;\;C\in\mathbb{K}^\delta\}$
, where
$\mathbb{K}^\delta$
is the collection of subsets of V defined as
$\mathbb{K}^\delta = \{C\subset V;\; (C\setminus\delta)\in\mathbb{K},\, (C\setminus\delta)\cup\{\alpha\}\in\mathbb{K}$
for all
$\alpha\in C\cap\delta\}$
.
Example 3.1. Consider an undirected graph
$\mathcal{G} = (V,E)$
for which the subgraph
$\mathcal{G}_A$
induced by
$A = \{1,2,3,4,5,6,7\}\subset V$
is
If
$\delta\cap A = \{1,2,6,7\}$
, then the sets
$\{1,3,4,6\}$
and
$\{2,4,5,7\}$
both belong to
$\mathbb{K}^\delta$
, even though neither of them belongs to
$\mathbb{K}$
. However, the set
$\{1,2,3,4\}$
, for example, does not belong to
$\mathbb{K}^\delta$
, since the edge
$\langle 2,3\rangle$
is not present.
Definition 3.2. A random field X on an undirected graph
$\mathcal{G} = (V,E)$
is said to satisfy the global reciprocal property with respect to
$\delta\subset V$
, abbreviated
$G[\delta]$
, if, for each triple (A, B, S) of disjoint subsets of V such that S separates A from
$B\cup(\delta\setminus S)$
,
$X_A\perp X_B \mid X_S$
.
Definition 3.3. A random field X on an undirected graph
$\mathcal{G} = (V,E)$
is said to satisfy the local reciprocal property with respect to
$\delta\subset V$
, abbreviated
$L[\delta]$
, if, for each
$\alpha\in V\setminus\delta$
,
$X_\alpha\perp X_{V\setminus\rm{cl}(\alpha)}\mid X_{\rm{bd}(\alpha)}$
.
Definition 3.4. A random field X on an undirected graph
$\mathcal{G} = (V,E)$
is said to satisfy the pairwise reciprocal property with respect to
$\delta\subset V$
, abbreviated
$P[\delta]$
, if, for each
$\alpha,\beta\in V$
such that
$\alpha\ne\beta$
,
$\alpha\in V\setminus\delta$
, and
$\langle\alpha,\beta\rangle\notin E$
,
$X_\alpha\perp X_\beta\mid X_{V\setminus\{\alpha,\beta\}}$
.
Remark 3.1. All four reciprocal properties reduce to the corresponding Markov properties in the case when
$\delta=\emptyset$
; cf. the definitions in [Reference Lauritzen15, Section 3.2].
Remark 3.2. It is easily seen that if
$\delta\subset\delta_1\subset V$
, then
$F[\delta] \Rightarrow F[\delta_1]$
,
$G[\delta] \Rightarrow G[\delta_1]$
,
$L[\delta] \Rightarrow L[\delta_1]$
, and
$P[\delta] \Rightarrow P[\delta_1]$
. In particular, each of the four Markov properties implies the corresponding reciprocal property with respect to any set
$\delta\subset V$
.
Theorem 3.1. Let X be a random field on an undirected graph
$\mathcal{G} = (V,E)$
, and let
$\delta\subset V$
. Then, X satisfies
$F[\delta]$
,
$G[\delta]$
,
$L[\delta]$
, or
$P[\delta]$
in
$\mathcal{G}$
if and only if X satisfies the same property in the undirected graph
$\mathcal{G}_\delta = (V,E^+_\delta)$
, where
$E^+_\delta = E\cup\{\langle\alpha,\beta\rangle;\;\alpha\ne\beta,\,\alpha,\beta\in\delta\}$
.
Proof. The claims for
$F[\delta]$
and
$L[\delta]$
follow from the easily checked facts that neither the collection
$\mathbb{K}^\delta$
nor, for any
$\alpha\in V\setminus\delta$
, the set
$\rm{bd}(\alpha)$
depends on which edges in
$\{\langle\alpha,\beta\rangle;\;\alpha\ne\beta,\,\alpha,\beta\in\delta\}$
belong to E. Similarly, the claim for
$P[\delta]$
follows since, for any
$\alpha,\beta\in V$
such that
$\alpha\ne\beta$
and
$\alpha\in V\setminus\delta$
,
$\langle\alpha,\beta\rangle\in E^+_\delta$
if and only if
$\langle\alpha,\beta\rangle\in E$
.
The claim for
$G[\delta]$
follows from the fact that, for any triple (A, B, S) of disjoint subsets of V, S separates A from
$B\cup(\delta\setminus S)$
in
$\mathcal{G}$
if and only if S separates A from
$B\cup(\delta\setminus S)$
in
$\mathcal{G}_\delta$
. To see this, we first observe that any path in
$\mathcal{G}$
between A and
$B\cup(\delta\setminus S)$
that does not intersect S must also be such a path in
$\mathcal{G}_\delta$
. Conversely, for
$n\geq 1$
, let
$\{\alpha_0,\alpha_1,\ldots,\alpha_n\}$
be a path in
$\mathcal{G}_\delta$
but not in
$\mathcal{G}$
between
$\alpha_0\in A$
and
$\alpha_n\in B\cup(\delta\setminus S)$
that does not intersect S. Then, there must exist
$0<k<n$
such that
$\alpha_k\in\delta\setminus S$
and
$\alpha_i\notin\delta$
for each
$i=1,\ldots,k-1$
. Hence,
$\{\alpha_0,\alpha_1,\ldots,\alpha_k\}$
is a path in
$\mathcal{G}$
between A and
$\delta\setminus S$
that does not intersect S.
Theorem 3.2. For a random field X on an undirected graph
$\mathcal{G} = (V,E)$
,
$F[\delta] \Rightarrow G[\delta] \Rightarrow L[\delta] \Rightarrow P[\delta]$
.
Proof. To prove
$F[\delta] \Rightarrow G[\delta]$
, let (A, B, S) be a triple of disjoint subsets of V such that S separates A from
$B\cup(\delta\setminus S)$
. Note that we implicitly assume that
$A\cap\delta = \emptyset$
. We also assume, without loss of generality, that
$A\cup B\cup S = V$
, and that
$\delta\subset B\cup S$
. That this can be done is seen as follows: let
$\widetilde A\subset V\setminus S$
be the set of nodes in
$V\setminus S$
that are connected to A in
$\mathcal{G}_{V\setminus S}$
. By construction,
$\widetilde A\cap(B\cup\delta) = \emptyset$
, and S separates
$\widetilde A$
from
$B\cup(\delta\setminus S)$
in
$\mathcal{G}$
. Define
$\widetilde B = V\setminus(\widetilde A\cup S)$
. Then,
$\widetilde A\cup\widetilde B\cup S = V$
, and S separates
$\widetilde A$
from
$\widetilde B$
.
Let
$C\in\mathbb{K}^\delta$
, and assume first that
$C\cap\delta = \emptyset$
, so that
$C\in\mathbb{K}$
. Then, we must have either
$C\subset A\cup S$
or
$C\subset B\cup S$
; both statements can hold only if
$C\subset S$
. Next, assume that
$C\cap\delta\ne\emptyset$
. By assumption,
$C\cap\delta\subset B\cup S$
. If
$C\cap\delta\subset S$
, then again we must have either
$C\subset A\cup S$
or
$C\subset B\cup S$
, or both if
$C\subset S$
. On the other hand, if there is a node
$\beta\in C\cap\delta$
such that
$\beta\in B$
, then, since
$(C\setminus\delta)\cup\{\beta\}\in\mathbb{K}$
, we must have
$C\setminus\delta\subset B\cup S$
, implying that
$C\subset B\cup S$
.
Define
$\mathbb{K}^\delta_A=\{C\in\mathbb{K}^\delta;\;C\subset A\cup S\}$
and
$\mathbb{K}^\delta_B=\{C\in\mathbb{K}^\delta;\;C\subset B\cup S\}$
; if
$C\subset S$
, we arbitrarily assign C to one of
$\mathbb{K}^\delta_A$
or
$\mathbb{K}^\delta_B$
. By (3.1), the joint probability distribution function
$f_X$
satisfies
\begin{align*} f_X(x) = \prod_{C\in\mathbb{K}^\delta}\phi_C(x_C) = \prod_{C\in\mathbb{K}^\delta_A}\phi_C(x_C)\prod_{C'\in\mathbb{K}^\delta_B}\phi_{C'}(x_{C'}) \qquad\rm{\mu-a.e.}, \end{align*}
where the first product depends only on
$(x_A,x_S)\in\mathcal{X}_{A\cup S}$
, and the second product depends only on
$(x_B,x_S)\in\mathcal{X}_{B\cup S}$
. It follows from (2.5) that
$X_A\perp X_B \mid X_S$
, which implies the claim.
To prove that
$G[\delta] \Rightarrow L[\delta]$
, for any
$\alpha\in V\setminus \delta$
let
$A=\{\alpha\}$
,
$B=V\setminus\rm{cl}(\alpha)$
, and
$S=\rm{bd}(\alpha)$
.
To prove that
$L[\delta] \Rightarrow P[\delta]$
, for any
$\alpha,\beta\in V$
such that
$\alpha\ne\beta$
,
$\alpha\in V\setminus\delta$
and
$\langle\alpha,\beta\rangle\notin E$
,
$X_\alpha\perp X_{V\setminus\rm{cl}(\alpha)}\mid X_{\rm{bd}(\alpha)}$
. Therefore,
$f_X(x) = f_{X_{\alpha}\mid X_{\rm{bd}(\alpha)}(x_{\alpha}\mid x_{\rm{bd}(\alpha)})} f_{X_{V\setminus\{\alpha\}}}(x_{V\setminus\{\alpha\}})$
$\mu$
-a.e. Since
$\langle\alpha,\beta\rangle\notin E$
we have
$\beta\notin\rm{cl}(\alpha)$
, so the first function in the product on the right-hand side depends only on
$x_{V\setminus\{\beta\}}\in\mathcal{X}_{V\setminus\{\beta\}}$
, while the second function in the product depends only on
$x_{V\setminus\{\alpha\}}\in\mathcal{X}_{V\setminus\{\alpha\}}$
. It follows from (2.5) that
$X_\alpha\perp X_\beta \mid X_{V\setminus\{\alpha,\beta\}}$
.
Theorem 3.3. For an undirected graph
$\mathcal{G} = (V,E)$
and a set
$\delta\subset V$
, the following conditions are equivalent:
-
(i) For any random field X on
$\mathcal{G}$
,
$L[\delta] \Rightarrow G[\delta]$
. -
(ii) No subset
$C\subset V$
exists of either of the following two types:
$C = \{\alpha_1,\alpha_2,\beta_1,\beta_2\}\subset V\setminus\delta$
, with induced subgraph
$\mathcal{G}_C = (C,\{\langle\alpha_1,\alpha_2\rangle,\langle\beta_1,\beta_2\rangle\})$
; or
$C = \{\alpha_1,\alpha_2,\beta\}\subset V$
, where
$\{\alpha_1,\alpha_2\}\subset V\setminus\delta$
and
$\beta\in\delta$
, with induced subgraph
$\mathcal{G}_C = (C,\{\langle\alpha_1,\alpha_2\rangle\})$
.
Proof. To prove that
$\textrm{(i)} \Rightarrow \textrm{(ii)}$
, assume, in order to derive a contradiction, that there exists a subset
$C = \{\alpha_1,\alpha_2,\beta_1,\beta_2\}\subset V\setminus\delta$
with induced subgraph
$\mathcal{G}_C = (C,\{\langle\alpha_1,\alpha_2\rangle,\langle\beta_1,\beta_2\rangle\})$
. Define a random field X on
$\mathcal{G}$
by
$X_{\alpha_1} = X_{\alpha_2} = X_{\beta_1} = X_{\beta_2} = Y$
, where Y is a non-degenerate random variable, and
$X_v = \gamma$
for each
$v\in V\setminus C$
, where
$\gamma\in\mathbb{R}$
is a constant. X trivially satisfies
$L[\delta]$
. It is also clear that
$S = V\setminus C$
separates
$\{\alpha_1\}$
from
$\{\beta_1\}\cup(\delta\setminus S)$
. However, since
$X_{\alpha_1}$
and
$X_{\beta_1}$
are not conditionally independent given
$X_S$
, X does not satisfy
$G[\delta]$
. The case when C is of the second type is handled similarly.
To prove that
$\textrm{(ii)}\Rightarrow \textrm{(i)}$
, assume that the random field X on
$\mathcal{G}$
satisfies
$L[\delta]$
. Let (A, B, S) be a triple of disjoint subsets of V such that S separates A from
$B\cup(\delta\setminus S)$
. As in the proof of Theorem 3.2, we assume without loss of generality that
$A\cup B\cup S = V$
, and that
$\delta\subset B\cup S$
. By (ii), one of two (possibly overlapping) cases must hold: in the first case, no nodes
$\alpha_1,\alpha_2\in A$
exist such that
$\langle\alpha_1,\alpha_2\rangle\in E$
; in the second case,
$B\cap\delta = \emptyset$
, and no nodes
$\beta_1,\beta_2\in B$
exist such that
$\langle\beta_1,\beta_2\rangle\in E$
. In the first case, we have
$\rm{bd}(\alpha)\subset S$
for each
$\alpha\in A$
. Let
$A = \{\alpha_i;\;i=1,\ldots,m\}$
. Using
$L[\delta]$
, we get
\begin{align*} f_X(x) & = f_{X_{\alpha_1}\mid X_{\rm{bd}(\alpha_1)}}(x_{\alpha_1}\mid x_{\rm{bd}(\alpha_1)}) f_{X_{V\setminus\{\alpha_1\}}}(x_{V\setminus\{\alpha_1\}}) \\[5pt] & = f_{X_{\alpha_1}\mid X_{\rm{bd}(\alpha_1)}}(x_{\alpha_1}\mid x_{\rm{bd}(\alpha_1)}) f_{X_{\alpha_2}\mid X_{\rm{bd}(\alpha_2)}}(x_{\alpha_2}\mid x_{\rm{bd}(\alpha_2)}) f_{X_{V\setminus\{\alpha_1,\alpha_2\}}}(x_{V\setminus\{\alpha_1,\alpha_2\}}) \\[5pt] & = \cdots = \prod_{i=1}^m f_{X_{\alpha_i}\mid X_{\rm{bd}(\alpha_i)}}(x_{\alpha_i}\mid x_{\rm{bd}(\alpha_i)}) f_{X_{V\setminus A}}(x_{V\setminus A}) \qquad\rm{\mu-a.e.} \end{align*}
By (2.5),
$X_A\perp X_B\mid X_S$
. The second case is handled analogously, with the roles of A and B interchanged. Hence, X satisfies
$G[\delta]$
.
Example 3.2. Consider an undirected graph
$\mathcal{G} = (V,E)$
for which the subgraph
$\mathcal{G}_C$
induced by
$C = \{1,2,3,4\}\subset V$
is
If
$\delta\cap C = \emptyset$
, then the implication
$L[\delta] \Rightarrow G[\delta]$
does not hold in
$\mathcal{G}$
. Suppose instead that the subgraph
$\mathcal{G}_D$
induced by
$D = \{1,2,3\}\subset V$
is
If
$\delta\cap D = \{3\}$
, then again the implication
$L[\delta] \Rightarrow G[\delta]$
does not hold in
$\mathcal{G}$
.
Theorem 3.4. For an undirected graph
$\mathcal{G} = (V,E)$
and a set
$\delta\subset V$
, the following conditions are equivalent:
-
(i) For any random field X on
$\mathcal{G}$
,
$P[\delta] \Rightarrow L[\delta]$
. -
(ii) No subset
$C\subset V$
exists of the type
$C = \{\alpha,\beta_1,\beta_2\}\subset V$
, where
$\alpha\in V\setminus\delta$
, with induced subgraph
$\mathcal{G}_C = (C,\{\langle\beta_1,\beta_2\rangle\})$
or
$\mathcal{G}_C = (C,\emptyset)$
.
Proof. To prove that
$\textrm{(i)}\Rightarrow \textrm{(ii)}$
, assume that there exists a subset
$C = \{\alpha,\beta_1,\beta_2\}\subset V$
, where
$\alpha\in V\setminus\delta$
, with induced subgraph
$\mathcal{G}_C = (C,\{\langle\beta_1,\beta_2\rangle\})$
or
$\mathcal{G}_C = (C,\emptyset)$
. Define a random field X on
$\mathcal{G}$
by
$X_{\alpha} = X_{\beta_1} = X_{\beta_2} = Y$
, where Y is a non-degenerate random variable, and
$X_v = \gamma$
for each
$v\in V\setminus C$
, where
$\gamma\in\mathbb{R}$
is a constant. X clearly satisfies
$P[\delta]$
. Since
$\rm{bd}(\alpha)\subset V\setminus\{\beta_1,\beta_2\}$
, but
$X_{\alpha}$
and
$X_{\beta_1}$
are not conditionally independent given
$X_{\rm{bd}(\alpha)}$
, X does not satisfy
$L[\delta]$
.
To prove that
$\textrm{(ii)}\Rightarrow \textrm{(i)}$
, assume that the random field X on
$\mathcal{G}$
satisfies
$P[\delta]$
. Let
$\alpha\in V\setminus\delta$
. By (ii),
$V\setminus\rm{cl}(\alpha)$
can contain at most one node. Assume that
$\beta\in V\setminus\rm{cl}(\alpha)$
. Using
$P[\delta]$
, we get
$f_X(x) = f_{X_{\alpha}\mid X_{\rm{bd}(\alpha)}}(x_{\alpha}\mid x_{\rm{bd}(\alpha)}) f_{X_{V\setminus\{\alpha\}}}(x_{V\setminus\{\alpha\}})$
$\mu$
-a.e. By (2.5),
$X_\alpha\perp X_\beta\mid X_{\rm{bd}(\alpha)}$
. Hence, X satisfies
$L[\delta]$
.
Example 3.3. Consider an undirected graph
$\mathcal{G} = (V,E)$
, for which the subgraph
$\mathcal{G}_D$
induced by
$D = \{1,2,3\}\subset V$
is either of
If
$\{3\}\subset V\setminus\delta$
, then the implication
$P[\delta] \Rightarrow P[\delta]$
does not hold in
$\mathcal{G}$
.
Theorem 3.5. Let X be a random field on an undirected graph
$\mathcal{G} = (V,E)$
. Assume that X satisfies the condition that, for any four disjoint subsets
$A,B,C,D\subset V$
such that either
$(A\cup C)\cap\delta = \emptyset$
or
$B\cap\delta = \emptyset$
,
\begin{equation} X_A\perp X_B\mid X_{C\cup D}\quad \rm{and}\quad X_C\perp X_B\mid X_{A\cup D} \quad \Rightarrow\quad X_{A\cup C}\perp X_B\mid X_D. \end{equation}
Then,
$G[\delta] \Leftrightarrow L[\delta] \Leftrightarrow P[\delta]$
.
Proof. By Theorem 3.2, we need only prove that
$P[\delta]\Rightarrow G[\delta]$
. Let (A, B, S) be a triple of disjoint subsets of V such that S separates A from
$B\cup(\delta\setminus S)$
. As in the proof of Theorem 3.2, we assume without loss of generality that
$A\cup B\cup S = V$
, and that
$\delta\subset B\cup S$
. We also assume, again without loss of generality, that both A and B are non-empty. The assertion is proved using backwards induction in the number of nodes of S.
Assume first that
$|S| = |V|- 2$
, so that A and B each contain one node. Since
$A\cap\delta = \emptyset$
,
$P[\delta]$
implies that
$X_A\perp X_B\mid X_S$
. Next, assume that the claim holds for
$|S| = n \leq |V|- 2$
, and consider the case when
$|S|=n-1$
. Since
$|S|<n$
, at least one of A or B contains more than one node. If A contains more than one node, choose any
$\alpha\in A$
. By the induction assumption, both
$X_{A\setminus\{\alpha\}}\perp X_B\mid X_{S\cup\{\alpha\}}$
and
$X_\alpha\perp X_B\mid X_{S\cup(A\setminus\{\alpha\})}$
hold, so, by (3.2),
$X_A\perp X_B\mid X_S$
. If B contains more than one node, choose any
$\beta\in B$
. As before, both
$X_A\perp X_{B\setminus\{\beta\}}\mid X_{S\cup\{\beta\}}$
and
$X_A\perp X_\beta\mid X_{S\cup(B\setminus\{\beta\})}$
hold, so again, by (3.2),
$X_A\perp X_B\mid X_S$
.
Theorem 3.6. Let X be a random field on an undirected graph
$\mathcal{G} = (V,E)$
such that
$\mathscr{L}(X)$
has a positive density
$f_X$
with respect to a product of
$\sigma$
-finite measures
$\mu$
. Then,
$F[\delta] \Leftrightarrow G[\delta] \Leftrightarrow L[\delta] \Leftrightarrow P[\delta]$
.
Proof. By Theorem 3.2, we need only prove that
$P[\delta] \Rightarrow F[\delta]$
. In the Markov case, Theorem 3.6 is known as the Clifford–Hammersley theorem, a version of which appears as [Reference Lauritzen15, Theorem 3.9]. We shall use the proof of the latter, with appropriate modifications. Fix
$x^*\in\mathcal{X}$
, and define, for all subsets
$C\subset V$
,
$H_C(x) = \ln f_X(x_C,x^*_{V\setminus C})$
and
$\psi_C(x) = \sum_{A\subset C}(\!-\!1)^{|C\setminus A|}H_A(x)$
for all
$x\in\mathcal{X}$
. By definition,
$H_C$
and
$\psi_C$
both depend on x through
$x_C\in\mathcal{X}_C$
. By Möbius inversion, cf. [Reference Lauritzen15, Lemma A.2],
$\ln f_X(x) = H_V(x) = \sum_{C\subset V}\psi_C(x)$
for all
$x\in\mathcal{X}$
, so we have proven the claim if we can show that
$\psi_C\equiv 0$
whenever
$C\notin\mathbb{K}^\delta$
; cf. Definition 3.1. If
$C\notin\mathbb{K}^\delta$
, then there exists
$\alpha\in C\setminus\delta$
and
$\beta\in C$
such that
$\alpha\ne\beta$
and
$\langle\alpha,\beta\rangle\notin E$
. Let
$C_0 = C\setminus\{\alpha,\beta\}$
and
$D = V\setminus\{\alpha,\beta\}$
. Then, as in the proof of [Reference Lauritzen15, Theorem 3.9],
\begin{equation*} \psi_C(x) = \sum_{B\subset C_0}(\!-\!1)^{|C_0\setminus B|} \bigl(H_B(x) - H_{B\cup\{\alpha\}}(x) - H_{B\cup\{\beta\}}(x) + H_{B\cup\{\alpha,\beta\}}(x)\bigr) \quad \text{for all } x\in\mathcal{X}, \end{equation*}
so, using property
$P[\delta]$
and (2.3), we get
\begin{align*} H_{B\cup\{\alpha,\beta\}}(x) - H_{B\cup\{\beta\}}(x) & = \ln\frac{f_X(x_\alpha,x_\beta,x_B,x^*_{D\setminus B})}{f_X(x^*_\alpha,x_\beta,x_B,x^*_{D\setminus B})} \\[5pt] & = \ln\frac{f_X(x_\alpha,x_B,x^*_{D\setminus B})f_X(x_\beta,x_B,x^*_{D\setminus B})}{f_X(x^*_\alpha,x_B,x^*_{D\setminus B})f_X(x_\beta,x_B,x^*_{D\setminus B})} \\[5pt] & = \ln\frac{f_X(x_\alpha,x_B,x^*_{D\setminus B})f_X(x^*_\beta,x_B,x^*_{D\setminus B})}{f_X(x^*_\alpha,x_B,x^*_{D\setminus B})f_X(x^*_\beta,x_B,x^*_{D\setminus B})} \\[5pt] & = H_{B\cup\{\alpha\}}(x) - H_{B}(x) \qquad \text{for all } x\in\mathcal{X}. \end{align*}
Theorem 3.7. Let X be a random field on an undirected graph
$\mathcal{G} = (V,E)$
, and let
$\delta\subset V$
. Then, X satisfies
$F[\delta]$
,
$G[\delta]$
, or
$P[\delta]$
if and only if X satisfies
$F[\emptyset]$
,
$G[\emptyset]$
, or
$P[\emptyset]$
in the undirected graph
$\mathcal{G}_\delta = (V,E^+_\delta)$
, where
$E^+_\delta = E\cup\{\langle\alpha,\beta\rangle;\;\alpha\ne\beta,\,\alpha,\beta\in\delta\}$
.
Proof. If X satisfies
$F[\emptyset]$
,
$G[\emptyset]$
, or
$P[\emptyset]$
in
$\mathcal{G}_\delta $
, then, by Remark 3.2, X satisfies
$F[\delta]$
,
$G[\delta]$
, or
$P[\delta]$
in
$\mathcal{G}_\delta$
, and, by Theorem 3.1, X also satisfies
$F[\delta]$
,
$G[\delta]$
, or
$P[\delta]$
in
$\mathcal{G}$
. It remains to prove the reverse implications.
We first prove that
$F[\delta]$
in
$\mathcal{G} \Rightarrow F[\emptyset]$
in
$\mathcal{G}_\delta$
. By Theorem 3.1, X satisfies
$F[\delta]$
in
$\mathcal{G}_\delta$
. Since
$\delta$
is a complete set in
$\mathcal{G}_\delta$
, it is easy to see that
$\mathbb{K}^\delta$
is equal to the collection of complete sets in
$\mathcal{G}_\delta$
. Hence, X satisfies
$F[\emptyset]$
in
$\mathcal{G}_\delta$
.
We then consider
$G[\delta]$
in
$\mathcal{G} \Rightarrow G[\emptyset]$
in
$\mathcal{G}_\delta$
. By Theorem 3.1, X satisfies
$G[\delta]$
in
$\mathcal{G}_\delta$
. Let (A, B, S) be a triple of disjoint subsets of V such that S separates A from B in
$\mathcal{G}_\delta$
. As in the proof of Theorem 3.2, we assume without loss of generality that
$A\cup B\cup S = V$
. Since
$\delta$
is a complete set in
$\mathcal{G}_\delta$
, either
$A\cap\delta =\emptyset$
, meaning that S separates A from
$B\cup(\delta\setminus S)$
in
$\mathcal{G}_\delta$
, or
$B\cap\delta = \emptyset$
, meaning that S separates B from
$A\cup(\delta\setminus S)$
in
$\mathcal{G}_\delta$
. Either way, it follows that
$X_A\perp X_B\mid X_S$
. Hence, X satisfies
$G[\emptyset]$
in
$\mathcal{G}_\delta$
.
Finally, we prove that
$P[\delta]$
in
$\mathcal{G} \Rightarrow P[\emptyset]$
in
$\mathcal{G}_\delta$
. By Theorem 3.1, X satisfies
$P[\delta]$
in
$\mathcal{G}_\delta$
. Since
$\delta$
is a complete set in
$\mathcal{G}_\delta$
, for any
$\alpha,\beta\in V$
such that
$\alpha\ne\beta$
and
$\langle\alpha,\beta\rangle\notin E^+_\delta$
, at least one of
$\alpha$
or
$\beta$
belongs to
$V\setminus\delta$
. It follows that
$X_\alpha\perp X_\beta\mid X_{V\setminus\{\alpha,\beta\}}$
. Hence, X satisfies
$P[\emptyset]$
in
$\mathcal{G}_\delta$
.
An immediate consequence of the preceding theorem is that if a random field X on an undirected graph
$\mathcal{G} = (V,E)$
satisfies
$F[\delta]$
,
$G[\delta]$
, or
$P[\delta]$
, where
$\delta\subset V$
is a complete set, then X also satisfies
$F[\emptyset]$
,
$G[\emptyset]$
, or
$P[\emptyset]$
in
$\mathcal{G}$
. However, the corresponding statement for
$L[\delta]$
is false, as the final example of this section shows.
Example 3.4. Consider
$\mathcal{G} = (V,E)$
, where
$V = \{0,1,2,3,4\}$
and
$E=\{\langle i,i+1\rangle;\; i=0,1,2,3\}$
, and let
$X_0=X$
,
$X_1=X$
,
$X_2=X+Y$
,
$X_3=Y$
, and
$X_4=X$
, where X and Y are two independent random variables having the common distribution
$P(X=0)=P(X=1) = \frac{1}{2}$
. It can be seen that this random field has the local reciprocal property with respect to
$\delta=\{4\}$
(which is a complete subset of V), but not the local Markov property.
4. Conditioned reciprocal random fields
Let X be a random field on an undirected graph
$\mathcal{G} = (V,E)$
such that
$\mathscr{L}(X)$
has a density
$f_X$
with respect to a product of
$\sigma$
-finite measures
$\mu$
. Recall that, for each
$\delta_0\subset V$
, there exists a regular conditional distribution of
$X_{V\setminus\delta_0}$
given
$X_{\delta_0}$
that has a density
$f_{X_{V\setminus\delta_0}\mid X_{\delta_0}}$
with respect to
$\mu_{V\setminus\delta_0}$
. For all
$x_{\delta_0}\in\mathcal{X}_{\delta_0}$
such that
$f_{X_{\delta_0}}(x_{\delta_0})>0$
,
$f_{X_{V\setminus\delta_0}\mid X_{\delta_0}}(\cdot\!\mid x_{\delta_0})$
can be chosen as
\begin{equation} f_{X_{V\setminus\delta_0}\mid X_{\delta_0}}(x_{V\setminus\delta_0}\mid x_{\delta_0}) = \frac{f_X(x_{V\setminus\delta_0},x_{\delta_0})}{f_{X_{\delta_0}}(x_{\delta_0})} \qquad \text{for all } x_{V\setminus\delta_0}\in\mathcal{X}_{V\setminus\delta_0}.\end{equation}
For all
$x_{\delta_0}\in\mathcal{X}_{\delta_0}$
such that
$f_{X_{\delta_0}}(x_{\delta_0}) = 0$
,
$f_{X_{V\setminus\delta_0}\mid X_{\delta_0}}(\cdot\!\mid x_{\delta_0})$
can be chosen as an arbitrary fixed density.
Theorem 4.1. Let X be a random field on an undirected graph
$\mathcal{G} = (V,E)$
such that
$\mathscr{L}(X)$
has a density
$f_X$
with respect to a product of
$\sigma$
-finite measures
$\mu$
. Assume that X satisfies
$F[\delta]$
,
$G[\delta]$
,
$L[\delta]$
, or
$P[\delta]$
. Then, for each
$\delta_0\subset V$
and each
$x_{\delta_0}\in\mathcal{X}_{\delta_0}$
such that
$f_{X_{\delta_0}}(x_{\delta_0})>0$
, under the conditional distribution of
$X_{V\setminus\delta_0}$
given
$X_{\delta_0}=x_{\delta_0}$
,
$X_{V\setminus\delta_0}$
satisfies
$F[\delta\setminus\delta_0]$
,
$G[\delta\setminus\delta_0]$
,
$L[\delta\setminus\delta_0]$
, or
$P[\delta\setminus\delta_0]$
, respectively.
Proof. We first show that
$F[\delta] \Rightarrow F[\delta\setminus\delta_0]$
. Since X satisfies
$F[\delta]$
,
$f_X$
has the form (3.1). Consider any function
$\phi_C\colon\! \mathcal{X}_C\to\mathbb{R}_+$
where
$C\in\mathbb{K}^\delta$
, and fix
$x^*_{\delta_0}\in\mathcal{X}_{\delta_0}$
such that
$f_{X_{\delta_0}}(x^*_{\delta_0})>0$
. Define
$\phi^*_{C\setminus\delta_0}\colon\! \mathcal{X}_{C\setminus\delta_0}\to\mathbb{R}_+$
by
$\phi^*_{C\setminus\delta_0}(x_{C\setminus\delta_0}) = \phi_C(x_{C\setminus\delta_0},x^*_{C\cap\delta_0})$
for all
$x_{C\setminus\delta_0}\in\mathcal{X}_{C\setminus\delta_0}$
. The conditional density (4.1) satisfies
\begin{align*} f_{X_{V\setminus\delta_0}\mid X_{\delta_0}}(x_{V\setminus\delta_0}\mid x^*_{\delta_0}) & = \frac{1}{f_{X_{\delta_0}}(x^*_{\delta_0})}\prod_{C\in\mathbb{K}^{\delta}} \phi_C(x_{C\setminus\delta_0},x^*_{C\cap\delta_0}) \\[5pt] & = \frac{1}{f_{X_{\delta_0}}(x^*_{\delta_0})}\prod_{C\in\mathbb{K}^{\delta}} \phi^*_{C\setminus\delta_0}(x_{C\setminus\delta_0}) \qquad \text{for all } x_{V\setminus\delta_0}\in\mathcal{X}_{V\setminus\delta_0}, \end{align*}
and it is easy to see that
$\{C\setminus\delta_0;\;C\in\mathbb{K}^{\delta}\} \subset\mathbb{K}^{\delta\setminus\delta_0}$
.
To prove that
$G[\delta] \Rightarrow G[\delta\setminus\delta_0]$
, let (A, B, S) be a triple of disjoint subsets of
$V\setminus\delta_0$
such that S separates A from
$B\cup((\delta\setminus\delta_0)\setminus S) = B\cup(\delta\setminus(S\cup\delta_0))$
in
$\mathcal{G}_{V\setminus\delta_0}$
. As in the proof of Theorem 3.2, we assume without loss of generality that
$A\cup B\cup S = V\setminus\delta_0$
, and that
$\delta\setminus\delta_0\subset B\cup S$
. This implies that
$S\cup\delta_0$
separates A from
$B\cup(\delta\setminus(S\cup\delta_0))$
in
$\mathcal{G}$
. By (2.4), a
$\mu$
-version of
$f_X$
is given by
$f_X(x) = f_{X_A\mid X_{S\cup\delta_0}}(x_A\mid x_S,x_{\delta_0})f_{X_{B\cup S\cup\delta_0}}(x_B,x_S,x_{\delta_0})$
for all
$x\in\mathcal{X}$
. Using this
$\mu$
-version of
$f_X$
, for each fixed
$x^*_{\delta_0}\in\mathcal{X}_{\delta_0}$
such that
$f_{X_{\delta_0}}(x^*_{\delta_0})>0$
, the conditional density (4.1) can be written, for all
$x_{V\setminus\delta_0}\in\mathcal{X}_{V\setminus\delta_0}$
as
\begin{equation*} f_{X_{V\setminus\delta_0}\mid X_{\delta_0}}(x_{V\setminus\delta_0}\mid x^*_{\delta_0}) = f_{X_A\mid X_{S\cup\delta_0}}(x_A\mid x_S,x^*_{\delta_0}) \frac{f_{X_{B\cup S\cup\delta_0}}(x_B,x_S,x^*_{\delta_0})}{f_{X_{\delta_0}}(x^*_{\delta_0})} . \end{equation*}
By (2.5), under the conditional distribution of
$X_{V\setminus\delta_0}$
given
$X_{\delta_0} = x^*_{\delta_0}$
we have
$X_A\perp X_B\mid X_S$
in
$\mathcal{G}_{V\setminus\delta_0}$
.
To prove that
$L[\delta] \Rightarrow L[\delta\setminus\delta_0]$
, let
$\alpha\in V\setminus(\delta\cup\delta_0)$
. Then,
$X_\alpha\perp X_{V\setminus\rm{cl}(\alpha)}\mid X_{\rm{bd}(\alpha)}$
in
$\mathcal{G}$
, so a
$\mu$
-version of
$f_X$
is given by
$f_X(x) = f_{X_\alpha\mid X_{\rm{bd}(\alpha)}}(x_\alpha\mid x_{\rm{bd}(\alpha)}) f_{X_{V\setminus\{\alpha\}}}(x_{V\setminus\{\alpha\}})$
for all
$x\in\mathcal{X}$
. Using this
$\mu$
-version of
$f_X$
, for each fixed
$x^*_{\delta_0}\in\mathcal{X}_{\delta_0}$
such that
$f_{X_{\delta_0}}(x^*_{\delta_0})>0$
, the conditional density (4.1) can be written, for all
$x_{V\setminus\delta_0}\in\mathcal{X}_{V\setminus\delta_0}$
, as
\begin{equation*} f_{X_{V\setminus\delta_0}\mid X_{\delta_0}}(x_{V\setminus\delta_0}\mid x^*_{\delta_0}) = f_{X_\alpha\mid X_{\rm{bd}(\alpha)}}(x_\alpha\mid x_{\rm{bd}(\alpha)\setminus\delta_0}, x^*_{\rm{bd}(\alpha)\cap\delta_0}) \frac{f_{X_{V\setminus\{\alpha\}}}(x_{V\setminus(\{\alpha\}\cup\delta_0)},x^*_{\delta_0})} {f_{X_{\delta_0}}(x^*_{\delta_0})}. \end{equation*}
By (2.5), under the conditional distribution of
$X_{V\setminus\delta_0}$
given
$X_{\delta_0} = x^*_{\delta_0}$
we have
$X_\alpha\perp X_{V\setminus(\rm{cl}(\alpha)\cup\delta_0)}\mid X_{\rm{bd}(\alpha)\setminus\delta_0}$
in
$\mathcal{G}_{V\setminus\delta_0}$
.
To show that
$P[\delta] \Rightarrow P[\delta\setminus\delta_0]$
, let
$\alpha\in V\setminus(\delta\cup\delta_0)$
and
$\beta\in V\setminus\delta_0$
be such that
$\alpha\ne\beta$
and
$\langle\alpha,\beta\rangle\notin E$
. Then,
$X_\alpha\perp X_\beta\mid X_{V\setminus\{\alpha,\beta\}}$
in
$\mathcal{G}$
, so a
$\mu$
-version of
$f_X$
is given by
$f_X(x) = f_{X_\alpha\mid X_{{V\setminus\{\alpha,\beta\}}}}(x_\alpha\mid x_{{V\setminus\{\alpha,\beta\}}}) f_{X_{V\setminus\{\alpha\}}}(x_{V\setminus\{\alpha\}})$
for all
$x\in\mathcal{X}$
. Using this
$\mu$
-version of
$f_X$
, for each fixed
$x^*_{\delta_0}\in\mathcal{X}_{\delta_0}$
such that
$f_{X_{\delta_0}}(x^*_{\delta_0})>0$
, the conditional density (4.1) can be written, for all
$x_{V\setminus\delta_0}\in\mathcal{X}_{V\setminus\delta_0}$
, as
\begin{equation*} f_{X_{V\setminus\delta_0}\mid X_{\delta_0}}(x_{V\setminus\delta_0}\mid x^*_{\delta_0}) = f_{X_\alpha\mid X_{V\setminus\{\alpha,\beta\}}}(x_\alpha\mid x_{V\setminus(\{\alpha,\beta\}\cup\delta_0)},x^*_{\delta_0}) \frac{f_{X_{V\setminus\{\alpha\}}}(x_{V\setminus(\{\alpha\}\cup\delta_0)},x^*_{\delta_0})} {f_{X_{\delta_0}}(x^*_{\delta_0})}. \end{equation*}
By (2.5), under the conditional distribution of
$X_{V\setminus\delta_0}$
given
$X_{\delta_0} = x^*_{\delta_0}$
we have
$X_\alpha\perp X_\beta\mid X_{V\setminus(\{\alpha,\beta\}\cup\delta_0)}$
in
$\mathcal{G}_{V\setminus\delta_0}$
.
The next example shows that the converse of Theorem 4.1 is false, in the sense that even if a random field X on an undirected graph
$\mathcal{G} = (V,E)$
does not satisfy
$P[\delta]$
, the subgraph induced by
$V\setminus\delta_0$
may still satisfy
$F[\delta\setminus\delta_0]$
conditionally on
$X_{\delta_0}$
.
Example 4.1. Consider the undirected graph
$\mathcal{G} = (V,E)$
where
$V = \{0,1,2,3,4\}$
and
$E=\{\langle i,i+1\rangle;\; i=0,1,2,3\}$
. Let
$\delta = \delta_0 = \{0,4\}$
, and let
$X_0=Y$
,
$X_1=Y + U$
,
$X_2=Y$
,
$X_3=Y + V$
, and
$X_4=Z$
, where Y, Z, U, and V are independent random variables having the common distribution
$P(Y=0) = P(Y=1) = \frac{1}{2}$
. Clearly, X does not satisfy
$P[\delta]$
, since
$X_0$
and
$X_2$
are not conditionally independent given
$X_{V\setminus\{0,2\}}$
. However, conditionally on
$X_{\delta_0} = (x^*_0,x^*_4)$
for any fixed
$(x^*_0,x^*_4)\in\{0,1\}^2$
,
$X_1$
and
$X_3$
are conditionally independent given
$X_2$
. For any fixed
$(x^*_0,x^*_4)\in\{0,1\}^2$
, writing
$f^*(x_1,x_2,x_3) = f_{X_1,X_2,X_3\mid X_0,X_4}(x_1,x_2,x_3\mid x^*_0,x^*_4)$
for all
$(x_1,x_2,x_3)\in\{0,1\}^3$
, we see that, by (2.4),
$f^*$
has the factorization
$f^*(x_1,x_2,x_3) = f^*_{X_1\mid X_2}(x_1\mid x_2)f^*_{X_2,X_3}(x_2,x_3)$
for all
$(x_1,x_2,x_3)\in\{0,1\}^3$
. Hence, conditionally on
$X_{\delta_0}$
,
$X_{V\setminus\delta_0}$
satisfies
$F[\emptyset]$
.
Theorem 4.2. Let X and Y be random fields on an undirected graph
$\mathcal{G}$
such that
$\mathscr{L}(X)$
and
$\mathscr{L}(Y)$
have densities
$f_X$
and
$f_Y$
with respect to a product of
$\sigma$
-finite measures
$\mu$
. Let
$\delta_0\subset V$
. Assume that, for each
$x\in\mathcal{X}$
such that
$f_{Y_{\delta_0}}(x_{\delta_0}) >0$
,
$f_{X_{\delta_0}}(x_{\delta_0}) >0$
and
\begin{align*} \frac{f_X(x_{V\setminus\delta_0},x_{\delta_0})}{f_{X_{\delta_0}}(x_{\delta_0})} = \frac{f_Y(x_{V\setminus\delta_0},x_{\delta_0})}{f_{Y_{\delta_0}}(x_{\delta_0})}.\end{align*}
If X satisfies
$F[\delta]$
,
$G[\delta]$
,
$L[\delta]$
, or
$P[\delta]$
, then Y satisfies
$F[\delta\cup\delta_0]$
,
$G[\delta\cup\delta_0]$
,
$L[\delta\cup\delta_0]$
, or
$P[\delta\cup\delta_0]$
. If, in addition, the function
$\phi_{\delta_0}\colon\!\mathcal{X}_{\delta_0}\to\mathbb{R}_+$
defined by
\begin{align*} \phi_{\delta_0}(x_{\delta_0}) = \begin{cases} {f_{Y_{\delta_0}}(x_{\delta_0})}/{f_{X_{\delta_0}}(x_{\delta_0})} & \rm{if f_{Y_{\delta_0}}(x_{\delta_0})>0,} \\[5pt] 0 & \rm{if f_{Y_{\delta_0}}(x_{\delta_0})=0} \end{cases}\end{align*}
has the form
\begin{equation} \phi_{\delta_0}(x_{\delta_0}) = \prod_{C\in\mathbb{K}^\delta}\psi_C(x_{C\cap\delta_0}) \qquad\rm{\mu_{\delta_0}-a.e.} \end{equation}
for some measurable functions
$\{\psi_C\colon\!\mathcal{X}_{C\cap\delta_0}\to\mathbb{R}_+;\;C\in\mathbb{K}^\delta\}$
, then Y satisfies
$F[\delta]$
,
$G[\delta]$
,
$L[\delta]$
, or
$P[\delta]$
.
Proof. By assumption, and using (2.2), we have
\begin{align} f_Y(x) & = f_{Y_{V\setminus\delta_0}\mid Y_{\delta_0}}(x_{V\setminus\delta_0}\mid x_{\delta_0})f_{Y_{\delta_0}}(x_{\delta_0}) \nonumber \\[5pt] & = f_{X_{V\setminus\delta_0}\mid X_{\delta_0}}(x_{V\setminus\delta_0}\mid x_{\delta_0})f_{Y_{\delta_0}}(x_{\delta_0}) = f_X(x)\phi_{\delta_0}(x_{\delta_0}) \qquad\rm{\mu-a.e.} \end{align}
We first assume that X satisfies
$F[\delta]$
. Since
$f_X$
has the form (3.1), we conclude that
$f_Y$
has the form (3.1) with
$\delta$
replaced by
$\delta\cup\delta_0$
, implying that Y satisfies
$F[\delta\cup\delta_0]$
. If
$\phi_{\delta_0}$
has the form (4.2), then
$f_Y$
has the form (3.1), implying that Y satisfies
$F[\delta]$
.
Assuming next that X satisfies
$G[\delta]$
, let (A, B, S) be a triple of disjoint subsets of V such that S separates A from
$B\cup((\delta\cup\delta_0)\setminus S)$
. As in the proof of Theorem 3.2, we assume without loss of generality that
$A\cup B\cup S = V$
, and that
$\delta\cup\delta_0\subset B\cup S$
. From (4.3) and (2.4),
\begin{equation} f_Y(x) = f_{X_A\mid X_S}(x_A\mid x_S)f_{X_{B\cup S}}(x_B,x_S)\phi_{\delta_0}(x_{\delta_0}) \qquad\rm{\mu-a.e.} \end{equation}
Since
$\delta\cup\delta_0\subset B\cup S$
, it follows from (2.5) that
$Y_A\perp Y_B\mid Y_S$
, implying that Y satisfies
$G[\delta\cup\delta_0]$
. If
$\phi_{\delta_0}$
has the form (4.2), then we let (A, B, S) be disjoint subsets of V such that S separates A from
$B\cup(\delta\setminus S)$
, and assume that
$A\cup B\cup S = V$
, and that
$\delta\subset B\cup S$
. It can be shown, as in the proof of Theorem 3.2, that, for each
$C\in\mathbb{K}^\delta$
, either
$C\in A\cup S$
or
$C\in B\cup S$
. Therefore, it follows from (4.4) and (2.5) that
$Y_A\perp Y_B\mid Y_S$
, implying that Y satisfies
$G[\delta]$
.
We then assume that X satisfies
$L[\delta]$
. For each
$\alpha\in V\setminus(\delta\cup\delta_0)$
, replace A, B, and S in (4.4) by
$\{\alpha\}$
,
$V\setminus\rm{cl}(\alpha)$
, and
$\rm{bd}(\alpha)$
, respectively, and conclude that Y satisfies
$L[\delta\cup\delta_0]$
. If
$\phi_{\delta_0}$
has the form (4.2), then, for each
$\alpha\in V\setminus\delta$
, replace A, B, and S in (4.4) by
$\{\alpha\}$
,
$V\setminus\rm{cl}(\alpha)$
, and
$\rm{bd}(\alpha)$
, and conclude that Y satisfies
$L[\delta]$
.
Finally, we assume that X satisfies
$P[\delta]$
. For each
$\alpha\in V\setminus(\delta\cup\delta_0)$
and
$\beta\in V$
such that
$\langle\alpha,\beta\rangle\notin E$
, replace A, B, and S in (4.4) by
$\{\alpha\}$
,
$\{\beta\}$
, and
$V\setminus\{\alpha,\beta\}$
, and conclude that Y satisfies
$P[\delta\cup\delta_0]$
. If
$\phi_{\delta_0}$
has the form (4.2), then, for each
$\alpha\in V\setminus\delta$
and
$\beta\in V$
such that
$\langle\alpha,\beta\rangle\notin E$
, replace A, B, and S in (4.4) by
$\{\alpha\}$
,
$\{\beta\}$
, and
$V\setminus\{\alpha,\beta\}$
, and conclude that Y satisfies
$P[\delta]$
.
Remark 4.1. (Schrödinger problems.) As an application of Theorem 4.2, we mention Schrödinger problems for random fields on undirected graphs; for more details, see [Reference Csiszár5], [Reference Föllmer10, Section 1.3], or [Reference Léonard, Rœlly and Zambrini16, Section 3]. Let X be a random field on an undirected graph
$\mathcal{G} = (V,E)$
, and let
$\pi_X = \mathscr{L}(X)$
.
$\pi_X$
is assumed to have a density
$f_X$
with respect to a product of
$\sigma$
-finite measures
$\mu$
. For each
$A\subset V$
, define
$\mathcal{P}_A$
as the set of all probability distributions on
$(\mathcal{X}_A,\mathscr{B}_{\mathcal{X}_A})$
, and let
$\mathcal{P} = \mathcal{P}_V$
. Let
$\delta_0\subset V$
, and let
$\mathcal{P}^\textrm{o}_{\delta_0}$
be a fixed convex subset of
$\mathcal{P}_{\delta_0}$
. Denote by
$D(\!\cdot\Vert\cdot\!)$
the relative entropy, also known as the Kullback–Leibler divergence. By the static and dynamic Schrödinger problems, we mean the following optimization problems:
\begin{align*} S_{\textrm{stat}}\colon\!\quad & \textrm{Minimize}\ D(\pi_{\delta_0}\Vert \pi_{X_{\delta_0}}) \text{ over all } \pi_{\delta_0}\in\mathcal{P}^\textrm{o}_{\delta_0}. \\[5pt] S_{\textrm{dyn}}\colon\!\quad & \textrm{Minimize}\ D(\pi_Y\Vert \pi_X) \text{ over all } \pi_Y\in\mathcal{P} \text{ such that } \pi_{Y_{\delta_0}}\in\mathcal{P}^\textrm{o}_{\delta_0}. \end{align*}
By the strict convexity of the relative entropy, both solutions are unique if they exist. If the solution
$\pi_{\delta_0}$
to
$S_{\rm{stat}}$
exists, it follows from the definition of relative entropy that
$\pi_{\delta_0}$
must have a density
$f_{\delta_0}$
with respect to
$\mu_{\delta_0}$
, which can be chosen so that
$f_{X_{\delta_0}}(x_{\delta_0}) = 0 \Rightarrow f_{\delta_0}(x_{\delta_0}) = 0$
. Moreover, from the chain rule of relative entropy, see [Reference Föllmer10, Section 1.3], a solution
$\pi_Y$
to
$S_{\rm{dyn}}$
exists that has a density
$f_Y$
with respect to
$\mu$
.
$f_Y$
can be chosen so that
$f_{Y_{\delta_0}} = f_{\delta_0}$
, and so that, for each
$x\in\mathcal{X}$
such that
$f_{Y_{\delta_0}}(x_{\delta_0}) > 0$
,
\begin{align*} \frac{f_X(x_{V\setminus\delta_0},x_{\delta_0})}{f_{X_{\delta_0}}(x_{\delta_0})} = \frac{f_Y(x_{V\setminus\delta_0},x_{\delta_0})}{f_{Y_{\delta_0}}(x_{\delta_0})}.\end{align*}
5. Reciprocal chains
In this section we apply the results of the previous sections to discrete-time reciprocal processes, better known as reciprocal chains.
Definition 5.1. A sequence of random variables
$\{X_t;\;t=0,1,\ldots,n\}$
, where
$n\geq2$
, is called a reciprocal chain if
\begin{equation} X_k\perp \{X_1,\ldots,X_{j-1},X_{l+1},\ldots,X_n\}\mid\{X_j,X_l\}\qquad\text{for all } 0\leq j<k<l\leq n. \end{equation}
As before, we assume that
$\mathscr{L}(X)$
has a density
$f_X$
with respect to a product of
$\sigma$
-finite measures
$\mu$
. We observe that any random sequence
$X = \{X_t;\;t=0,1,\ldots,n\}$
can be seen as a random field on the undirected graph
$\mathcal{G} = (V,E)$
, where
$V = \{0,1,\ldots,n\}$
and
$E=\{\langle i,i+1\rangle;\; i=0,1,\ldots,n-1\}$
. We identify X with this random field, since there is no risk of confusion.
Theorem 5.1. A random sequence
$X = \{X_t;\;t=0,1,\ldots,n\}$
is a reciprochal chain if and only if it satisfies
$G[\delta]$
with respect to
$\delta = \{0,n\}$
.
Proof. Assume that X satisfies
$G[\delta]$
with respect to
$\delta = \{0,n\}$
. For each fixed
$0\leq j<k<l\leq n$
, let
$A = \{k\}$
,
$S=\{j,l\}$
, and
$B = \{0,1,\ldots,j-1\}\cup\{l+1,\ldots,n\}$
. Then, S separates A from
$B\cup(\delta\setminus S)$
, so by property
$G[\delta]$
, X satisfies (5.1).
Assume instead that X satisfies (5.1). Let (A, B, S) be a triple of disjoint subsets of
$V = \{0,1,\ldots,n\}$
such that S separates A from
$B\cup(\delta\setminus S)$
. As in the proof of Theorem 3.2, we assume without loss of generality that
$A\cup B\cup S = V$
, and that
$\delta\subset B\cup S$
. We also assume without loss of generality that
$A\ne\emptyset$
. It must then hold that
$A = \cup_{i=1}^m A_i$
, where m is a positive integer, and
$A_i = \{\ell_i,\ell_i+1,\ldots, u_i\}$
for
$i=1,\ldots,m$
, where
$\{(\ell_i,u_i);\;i=1,\ldots,m\}$
are pairs of integers such that
$0<\ell_1\leq u_1<\ell_2-1<\ell_2\leq u_2<\ell_3-1<\cdots <\ell_m\leq u_m<n$
. Note also that, for each
$i=1,\ldots,m$
,
$\{\ell_i-1,u_i+1\}\subset S$
. Applying (5.1) and (2.4) to
$f_X$
for each
$k\in A_1$
in increasing order, we get
\begin{align*} f_X(x) & = f_{X_{\ell_1}\mid X_{\ell_1-1},X_{\ell_1+1}}(x_{\ell_1}\mid x_{\ell_1-1},x_{\ell_1+1}) \\[5pt] & \quad \times f_{X_0,\ldots,X_{\ell_1-1},X_{\ell_1+1},\ldots,X_n}(x_0,\ldots,x_{\ell_1-1},x_{\ell_1+1},\ldots,x_n) \\[5pt] & = f_{X_{\ell_1}\mid X_{\ell_1-1},X_{\ell_1+1}}(x_{\ell_1}\mid x_{\ell_1-1},x_{\ell_1+1}) f_{X_{\ell_1+1}\mid X_{\ell_1-1},X_{\ell_1+2}}(x_{\ell_1+1}\mid x_{\ell_1-1},x_{\ell_1+2}) \\[5pt] & \quad \times f_{X_0,\ldots,X_{\ell_1-1},X_{\ell_1+2},\ldots,X_n}(x_0,\ldots,x_{\ell_1-1},x_{\ell_1+2},\ldots,x_n) \\[5pt] & = \\[5pt] & \ \, \vdots \\[5pt] & = \prod_{r=0}^{u_1-\ell_1} f_{X_{\ell_1+r}\mid X_{\ell_1-1},X_{\ell_1+r+1}}(x_{\ell_1+r}\mid x_{\ell_1-1},x_{\ell_1+r+1}) \\[5pt] & \quad \times f_{X_0,\ldots,X_{\ell_1-1},X_{u_1+1},\ldots,X_n}(x_0,\ldots,x_{\ell_1-1},x_{u_1+1},\ldots,x_n) \qquad\rm{\mu-a.e.} \end{align*}
Proceeding in the same fashion for each
$k\in A\setminus A_1$
in increasing order, we end up with
\begin{equation*} f_X(x) = \prod_{i=1}^m\prod_{r=0}^{u_i-\ell_i} f_{X_{\ell_i+r}\mid X_{\ell_i-1},X_{\ell_i+r+1}}(x_{\ell_i+r}\mid x_{\ell_i-1},x_{\ell_i+r+1}) f_{X_{V\setminus A}}(x_{V\setminus A})\qquad\rm{\mu-a.e.} \end{equation*}
The expression on the right-hand side is a product of two functions, the first of which depends only on
$\mathcal{X}_{A\cup S}$
, while the second depends only on
$\mathcal{X}_{B\cup S}$
. By (2.5), this implies that
$X_A\perp X_B \mid X_S$
, so X satisfies
$G[\delta]$
.
Theorem 5.2. A random sequence
$X = \{X_t;\;t=0,1,\ldots,n\}$
satisfies
$F[\delta]$
with respect to
$\delta = \{0,n\}$
if and only if
$f_X$
has the form
$f_X(x) = \phi_n(x_0,x_n)\prod_{i=0}^{n-1}\phi_i(x_i,x_{i+1})$
$\mu$
-a.e. for some measurable functions
$\{\phi_i\colon\! \mathcal{X}_{\{i,i+1\}}\to\mathbb{R}_+;\ i = 0,1,\ldots,n-1\}$
,
$\phi_n\colon\! \mathcal{X}_{\{0,n\}}\to\mathbb{R}_+$
. In particular, if X is a reciprocal chain and
$f_X$
is positive, then X satisfies
$F[\delta]$
.
Proof. The first claim follows from Definition 3.1, and the second follows from Theorems 5.1 and 3.6.
Example 5.1. Let
$X = \{X_t;\;t=0,1,\ldots,n\}$
be a random sequence with a centered, non-singular Gaussian distribution. Then, by Theorem 5.2, X satisfies
$F[\delta]$
with respect to
$\delta=\{0,n\}$
if and only if the inverse covariance matrix
$C^{-1}$
has a cyclic tridiagonal structure, meaning that all its elements are 0 except possibly
$\{C^{-1}_{i,j};\;|i-j|\leq 1\}$
and
$C^{-1}_{0,n} = C^{-1}_{n,0}$
. This result was previously obtained in [Reference Levy, Frezza and Krener17, Theorem 3.2] by a completely different argument.
In the general case, a reciprocal chain need not satisfy
$F[\delta]$
with respect to
$\delta=\{0,n\}$
, as the following two examples show.
Example 5.2. Let
$X = \{X_0,X_1,X_2\}$
be a random sequence, where each of the random variables
$\{X_0,X_1,X_2\}$
takes values in
$\mathcal{X}_0 = \{0,1\}$
with a probability mass function
$f_X(x_0,x_1,x_2) = P\big(\bigcap_{i=0}^2\{X_i=x_i\}\big)$
for all
$x\in\{0,1\}^3$
such that
$f_X(0,0,0) = 0$
,
$f_X(0,0,1)>0$
,
$f_X(0,1,0)>0$
, and
$f_X(1,0,0)>0$
. Define
$V = \{0,1,2\}$
and
$\delta = \{0,2\}$
. X is (trivially) a reciprocal chain. Assume that X satisfies
$F[\delta]$
. Then, we must have
$f_X(x) = \phi_0(x_0,x_1)\phi_1(x_1,x_2)\phi_2(x_0,x_2)$
for all
$(x_0,x_1,x_2)\in\{0,1\}^3$
for some functions
$\{\phi_i\colon\!\{0,1\}^2\to\mathbb{R}_+;\;i = 0,1,2\}$
. However, the condition
$f_X(0,0,0) = 0$
implies that at least one of the factors
$\phi_0(0,0)$
,
$\phi_1(0,0)$
, and
$\phi_2(0,0)$
must be 0, while the conditions
$f_X(0,0,1)>0$
,
$f_X(0,1,0)>0$
, and
$f_X(1,0,0)>0$
imply that
$\phi_0(0,0)$
,
$\phi_1(0,0)$
, and
$\phi_2(0,0)$
must all be positive, which is a contradiction.
Example 5.3. Let
$X = \{X_0,X_1,X_2,X_3\}$
be a random sequence, where each of the random variables
$\{X_0,X_1,X_2,X_3\}$
takes values in
$\mathcal{X}_0 = \{0,1\}$
, with a probability mass function
$f_X(x_0,x_1,x_2,x_3) = P\big(\bigcap_{i=0}^3\{X_i=x_i\}\big)$
for all
$x\in\{0,1\}^4$
defined by
$f_X(0,0,0,0) = f_X(1,0,0,0) = f_X(1,1,0,0) = f_X(1,1,1,0) = f_X(0,0,0,1) = f_X(0,0,1,1) = f_X(0,1,1,1) = f_X(1,1,1,1) = \frac{1}{8}$
. Define
$V = \{0,1,2,3\}$
and
$\delta = \{0,3\}$
. X can be considered as a random field on
$\mathcal{G} = (V,E)$
, where
$E = \{\langle 0,1\rangle,\langle 1,2\rangle,\langle 2,3\rangle\}$
, but also as a random field on
$\mathcal{G}_\delta = (V,E^+_\delta)$
, where
$E^+_\delta = \{\langle 0,1\rangle,\langle 1,2\rangle,\langle 2,3\rangle,\langle 0,3\rangle\}$
. It was shown in [Reference Moussouris19] that X satisfies
$G[\emptyset]$
, but not
$F[\emptyset]$
, in
$\mathcal{G}_\delta$
. Therefore, by Theorem 3.7, X satisfies
$G[\delta]$
, but not
$F[\delta]$
, in
$\mathcal{G}$
.
Remark 5.1. As mentioned in Section 1, in a number of papers, starting with [Reference Carravetta3], a different definition of a reciprocal chain was used: a sequence of random variables
$\{X_t;\;t=0,1,\ldots,n\}$
, where
$n\geq2$
, is said to be a reciprocal chain if
\begin{equation*} X_k\perp \{X_1,\ldots,X_{k-2},X_{k+2},\ldots,X_n\}\mid\{X_{k-1},X_{k+1}\}\qquad\text{for all } 0<k<n. \end{equation*}
It follows from Definition 3.3 that
$X = \{X_t;\;t=0,1,\ldots,n\}$
satisfies this different definition if and only if it satisfies the local reciprocal property
$L[\delta]$
with respect to
$\delta = \{0,n\}$
. We propose to call such a process a local reciprocal chain.
Remark 5.2. (Markov chains.) Let
$X = \{X_t;\;t=0,1,\ldots,n\}$
be a random sequence such that
$\mathscr{L}(X)$
has a density
$f_X$
with respect to a product of
$\sigma$
-finite measures
$\mu$
. X is called a Markov chain if
$X_k\perp\{X_0,\ldots,X_{k-2}\}\mid X_{k-1}$
for all
$0<k\leq n$
. It is well known that
$f_X$
has the factorization
$f_X(x) = f_{X_0}(x_0)\prod_{i=0}^{n-1}f_{X_{i+1}\mid X_i}(x_{i+1}\mid x_i)$
$\mu$
-a.e. From this and Theorem 3.2, it follows that X is a Markov chain if and only if X has the factorizing Markov property,
$F[\emptyset]$
. As we have seen, this is not true for reciprocal chains in general.
Remark 5.3. Let
$X = \{X_t;\;t=0,1,\ldots,n\}$
, where
$n\geq 2$
, be a reciprocal chain, i.e. a random sequence satisfying
$G[\delta]$
, where
$\delta = \{0,n\}$
, and let
$\delta_0 = \{n\}$
. By Theorem 4.1, under the conditional distribution of
$X_{V\setminus\{n\}}$
given
$X_n=x_n$
for any
$x_n\in\mathcal{X}_n$
such that
$f_{X_n}(x_n) > 0$
,
$X_{V\setminus\{n\}}$
satisfies
$G[\{0\}]$
. Moreover, by Theorem 3.7 we have
$G[\{0\}] \Rightarrow G[\emptyset]$
, so, conditionally on
$X_n=x_n$
for any
$x_n\in\mathcal{X}_n$
such that
$f_{X_n}(x_n) > 0$
,
$X_{V\setminus\{n\}}$
is a Markov chain. In contrast, if X satisfies only
$L[\delta]$
, then, conditional on
$X_n=x_n$
, where
$x_n\in\mathcal{X}_n$
is such that
$f_{X_n}(x_n) > 0$
,
$X_{V\setminus\{n\}}$
need not satisfy
$L[\emptyset]$
; cf. Example 3.4.
Funding information
There are no funding bodies to thank relating to the creation of this article.
Competing interests
There were no competing interests to declare which arose during the preparation or publication process of this article.
