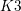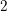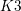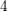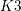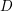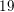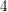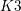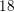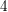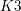Introduction
An important problem in algebraic geometry is to construct a geometric compactification for the moduli space of polarized degree-
![]() $d$
$d$
![]() $K3$
surfaces
$K3$
surfaces
![]() $\mathscr{K}_{d}$
. By global Torelli,
$\mathscr{K}_{d}$
. By global Torelli,
![]() $\mathscr{K}_{d}$
is isomorphic to a locally symmetric variety
$\mathscr{K}_{d}$
is isomorphic to a locally symmetric variety
![]() $\mathscr{F}_{d}$
and hence it has natural compactifications such as the Baily–Borel compactification
$\mathscr{F}_{d}$
and hence it has natural compactifications such as the Baily–Borel compactification
![]() $\mathscr{F}_{d}^{\ast }$
, Mumford’s toroidal compactifications, and more generally Looijenga’s semitoric compactifications. However, a priori, these compactifications are only birational to the ‘geometric’ compactifications, obtained, for example, by Geometric Invariant Theory (GIT). It is natural to compare the two kinds of compactifications. An understanding of the relationship between the Baily–Borel and GIT compactifications leads to deep results about the period map (e.g. see [Reference ShahSha80, Reference LooijengaLoo09]) and to results about the structure of the GIT quotient. The simplest instance of such comparison results is the isomorphism
$\mathscr{F}_{d}^{\ast }$
, Mumford’s toroidal compactifications, and more generally Looijenga’s semitoric compactifications. However, a priori, these compactifications are only birational to the ‘geometric’ compactifications, obtained, for example, by Geometric Invariant Theory (GIT). It is natural to compare the two kinds of compactifications. An understanding of the relationship between the Baily–Borel and GIT compactifications leads to deep results about the period map (e.g. see [Reference ShahSha80, Reference LooijengaLoo09]) and to results about the structure of the GIT quotient. The simplest instance of such comparison results is the isomorphism
between the compactified
![]() $j$
-line and the GIT moduli space of plane cubic curves. In a vast generalization of this fact, Looijenga [Reference LooijengaLoo03a, Reference LooijengaLoo03b] has devised a comparison framework that applies to locally symmetric varieties associated to type IV or
$j$
-line and the GIT moduli space of plane cubic curves. In a vast generalization of this fact, Looijenga [Reference LooijengaLoo03a, Reference LooijengaLoo03b] has devised a comparison framework that applies to locally symmetric varieties associated to type IV or
![]() $I_{1,n}$
Hermitian symmetric domains. This framework was successfully applied in the case of moduli of degree-
$I_{1,n}$
Hermitian symmetric domains. This framework was successfully applied in the case of moduli of degree-
![]() $2$
$2$
![]() $K3$
surfaces [Reference LooijengaLoo86, Reference ShahSha80], cubic fourfolds [Reference LooijengaLoo09, Reference LazaLaz10], and a few other related examples (e.g. cubic threefolds, del Pezzo surfaces, etc.). The nominal purpose of the present paper is to investigate the analogous cases of degree-
$K3$
surfaces [Reference LooijengaLoo86, Reference ShahSha80], cubic fourfolds [Reference LooijengaLoo09, Reference LazaLaz10], and a few other related examples (e.g. cubic threefolds, del Pezzo surfaces, etc.). The nominal purpose of the present paper is to investigate the analogous cases of degree-
![]() $4$
$4$
![]() $K3$
surfaces [Reference ShahSha81] and double Eisenbud–Popescu–Walter (EPW) sextics [Reference O’GradyO’Gr15, Reference O’GradyO’Gr16]. While studying these cases, we uncovered a rich and intriguing picture.
$K3$
surfaces [Reference ShahSha81] and double Eisenbud–Popescu–Walter (EPW) sextics [Reference O’GradyO’Gr15, Reference O’GradyO’Gr16]. While studying these cases, we uncovered a rich and intriguing picture.
The starting point of our investigation are two limitations in Looijenga’s construction. First of all, a certain technical assumption in Looijenga’s work does not hold for quartic
![]() $K3$
surfaces (nor for double EPW sextics), while it does hold for
$K3$
surfaces (nor for double EPW sextics), while it does hold for
![]() $K3$
surfaces of arbitrary degree
$K3$
surfaces of arbitrary degree
![]() $d\not =4$
(see Lemma 8.1 in [Reference LooijengaLoo03b]). Namely, for arithmetic reasons, the combinatorics of the hyperplane arrangement involved in Looijenga’s construction [Reference LooijengaLoo03b] is much richer for polarized
$d\not =4$
(see Lemma 8.1 in [Reference LooijengaLoo03b]). Namely, for arithmetic reasons, the combinatorics of the hyperplane arrangement involved in Looijenga’s construction [Reference LooijengaLoo03b] is much richer for polarized
![]() $K3$
surfaces of degree
$K3$
surfaces of degree
![]() $4$
than for polarized
$4$
than for polarized
![]() $K3$
surfaces of degree
$K3$
surfaces of degree
![]() $d\not =4$
(similarly, the hyperplane arrangement involved in the period map for double EPW sextics is much richer than the hyperplane arrangement relevant to cubic fourfolds). Secondly, and this is a consideration which applies to
$d\not =4$
(similarly, the hyperplane arrangement involved in the period map for double EPW sextics is much richer than the hyperplane arrangement relevant to cubic fourfolds). Secondly, and this is a consideration which applies to
![]() $K3$
surfaces of any degree, there exist a plethora of GIT models. In the low-degree cases considered here and in the literature, there might be a ‘natural’ choice for GIT, but this is misleading (see [Reference Casalaina-Martin, Jensen and LazaCMJL14] for a hint of what would happen already in degree
$K3$
surfaces of any degree, there exist a plethora of GIT models. In the low-degree cases considered here and in the literature, there might be a ‘natural’ choice for GIT, but this is misleading (see [Reference Casalaina-Martin, Jensen and LazaCMJL14] for a hint of what would happen already in degree
![]() $6$
). The solution that we propose in order to handle these two issues is to give flexibility to Looijenga’s construction by considering a continuous variation of models. More precisely, we recall that for a locally symmetric variety
$6$
). The solution that we propose in order to handle these two issues is to give flexibility to Looijenga’s construction by considering a continuous variation of models. More precisely, we recall that for a locally symmetric variety
![]() $\mathscr{F}=\mathscr{D}/\unicode[STIX]{x1D6E4}$
, Baily and Borel have shown that the homonymous compactification
$\mathscr{F}=\mathscr{D}/\unicode[STIX]{x1D6E4}$
, Baily and Borel have shown that the homonymous compactification
![]() $\mathscr{F}^{\ast }$
is the
$\mathscr{F}^{\ast }$
is the
![]() $\text{Proj}\,$
of the ring of automorphic functions, i.e.
$\text{Proj}\,$
of the ring of automorphic functions, i.e.
![]() $\mathscr{F}^{\ast }=\text{Proj}\,R(\mathscr{F},\unicode[STIX]{x1D706})$
, where
$\mathscr{F}^{\ast }=\text{Proj}\,R(\mathscr{F},\unicode[STIX]{x1D706})$
, where
![]() $\unicode[STIX]{x1D706}$
is the Hodge bundle. Looijenga’s deep insight was to observe that in certain situations of geometric interest, a certain GIT quotient
$\unicode[STIX]{x1D706}$
is the Hodge bundle. Looijenga’s deep insight was to observe that in certain situations of geometric interest, a certain GIT quotient
![]() $\mathfrak{M}$
is nothing but the
$\mathfrak{M}$
is nothing but the
![]() $\text{Proj}\,$
of the ring of meromorphic automorphic forms with poles on a (geometrically meaningful) Heegner (i.e. Noether–Lefschetz) divisor
$\text{Proj}\,$
of the ring of meromorphic automorphic forms with poles on a (geometrically meaningful) Heegner (i.e. Noether–Lefschetz) divisor
![]() $\unicode[STIX]{x1D6E5}$
, and thus
$\unicode[STIX]{x1D6E5}$
, and thus
![]() $\mathfrak{M}=\text{Proj}\,R(\mathscr{F},\unicode[STIX]{x1D706}+\unicode[STIX]{x1D6E5})$
. Furthermore, Looijenga has shown that under a certain assumption on
$\mathfrak{M}=\text{Proj}\,R(\mathscr{F},\unicode[STIX]{x1D706}+\unicode[STIX]{x1D6E5})$
. Furthermore, Looijenga has shown that under a certain assumption on
![]() $\unicode[STIX]{x1D6E5}$
(which fails for quartic
$\unicode[STIX]{x1D6E5}$
(which fails for quartic
![]() $K3$
surfaces and for double EPW sextics),
$K3$
surfaces and for double EPW sextics),
![]() $\text{Proj}\,R(\mathscr{F},\unicode[STIX]{x1D706}+\unicode[STIX]{x1D6E5})$
has an explicit combinatorial/arithmetic description. Our approach is to continuously interpolate between the two models by controlling the order of poles for the meromorphic automorphic function, i.e. to consider
$\text{Proj}\,R(\mathscr{F},\unicode[STIX]{x1D706}+\unicode[STIX]{x1D6E5})$
has an explicit combinatorial/arithmetic description. Our approach is to continuously interpolate between the two models by controlling the order of poles for the meromorphic automorphic function, i.e. to consider
![]() $\text{Proj}\,R(\mathscr{F},\unicode[STIX]{x1D706}+\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6E5})$
, where
$\text{Proj}\,R(\mathscr{F},\unicode[STIX]{x1D706}+\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6E5})$
, where
![]() $\unicode[STIX]{x1D6FD}\in [0,1]$
. This allows us to understand the case of quartics and, more importantly, to capture more GIT quotients.
$\unicode[STIX]{x1D6FD}\in [0,1]$
. This allows us to understand the case of quartics and, more importantly, to capture more GIT quotients.
While a variation of models
![]() $\text{Proj}\,R(\mathscr{F},\unicode[STIX]{x1D706}+\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6E5})$
makes sense for general Type IV locally symmetric varieties (and also ball quotients), we focus here on the so-called
$\text{Proj}\,R(\mathscr{F},\unicode[STIX]{x1D706}+\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6E5})$
makes sense for general Type IV locally symmetric varieties (and also ball quotients), we focus here on the so-called
![]() $D$
-tower of locally symmetric varieties, i.e. Type IV locally symmetric varieties associated to lattices
$D$
-tower of locally symmetric varieties, i.e. Type IV locally symmetric varieties associated to lattices
![]() $U^{2}\oplus D_{n}$
. More precisely, we let
$U^{2}\oplus D_{n}$
. More precisely, we let
![]() $\mathscr{F}(N)$
be the
$\mathscr{F}(N)$
be the
![]() $N$
-dimensional locally symmetric variety corresponding to the lattice
$N$
-dimensional locally symmetric variety corresponding to the lattice
![]() $\unicode[STIX]{x1D6EC}_{N}:=U^{2}\oplus D_{N-2}$
, and an arithmetic group
$\unicode[STIX]{x1D6EC}_{N}:=U^{2}\oplus D_{N-2}$
, and an arithmetic group
![]() $\unicode[STIX]{x1D6E4}_{N}$
, which is intermediate between the orthogonal group
$\unicode[STIX]{x1D6E4}_{N}$
, which is intermediate between the orthogonal group
![]() $O^{+}(\unicode[STIX]{x1D6EC}_{N})$
, and the stable orthogonal subgroup
$O^{+}(\unicode[STIX]{x1D6EC}_{N})$
, and the stable orthogonal subgroup
![]() $\widetilde{O}^{+}(\unicode[STIX]{x1D6EC}_{N})$
. With these definitions in place (see § 1 for details),
$\widetilde{O}^{+}(\unicode[STIX]{x1D6EC}_{N})$
. With these definitions in place (see § 1 for details),
![]() $\mathscr{F}(19)$
is the period space for quartic
$\mathscr{F}(19)$
is the period space for quartic
![]() $K3$
surfaces,
$K3$
surfaces,
![]() $\mathscr{F}(20)$
is the period space for double EPW sextics modulo the duality involution (or EPW cubes), and
$\mathscr{F}(20)$
is the period space for double EPW sextics modulo the duality involution (or EPW cubes), and
![]() $\mathscr{F}(18)$
is the period space for hyperelliptic quartic surfaces. Thus, we compare the Baily–Borel compactifications
$\mathscr{F}(18)$
is the period space for hyperelliptic quartic surfaces. Thus, we compare the Baily–Borel compactifications
![]() $\mathscr{F}(N)^{\ast }$
for
$\mathscr{F}(N)^{\ast }$
for
![]() $N\in \{18,19,20\}$
to the GIT moduli spaces
$N\in \{18,19,20\}$
to the GIT moduli spaces
![]() $\mathfrak{M}(N)$
, where
$\mathfrak{M}(N)$
, where
 $$\begin{eqnarray}\displaystyle \mathfrak{M}(18) & := & \displaystyle |\mathscr{O}_{\mathbb{P}^{1}}(4)\boxtimes \mathscr{O}_{\mathbb{P}^{1}}(4)|/\!\!/\text{Aut}(\mathbb{P}^{1}\times \mathbb{P}^{1}),\nonumber\\ \displaystyle \mathfrak{M}(19) & := & \displaystyle |\mathscr{O}_{\mathbb{P}^{3}}(4)|/\!\!/\text{PGL}(4),\nonumber\\ \displaystyle \mathfrak{M}(20) & := & \displaystyle \mathbb{LG}\Bigl(\bigwedge ^{3}\mathbb{C}^{6}\Bigr)/\!\!/\text{PGL}_{6}(\mathbb{C}).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \mathfrak{M}(18) & := & \displaystyle |\mathscr{O}_{\mathbb{P}^{1}}(4)\boxtimes \mathscr{O}_{\mathbb{P}^{1}}(4)|/\!\!/\text{Aut}(\mathbb{P}^{1}\times \mathbb{P}^{1}),\nonumber\\ \displaystyle \mathfrak{M}(19) & := & \displaystyle |\mathscr{O}_{\mathbb{P}^{3}}(4)|/\!\!/\text{PGL}(4),\nonumber\\ \displaystyle \mathfrak{M}(20) & := & \displaystyle \mathbb{LG}\Bigl(\bigwedge ^{3}\mathbb{C}^{6}\Bigr)/\!\!/\text{PGL}_{6}(\mathbb{C}).\nonumber\end{eqnarray}$$
(Actually, for
![]() $N=20$
, we should take the quotient of
$N=20$
, we should take the quotient of
![]() $\mathfrak{M}(20)$
modulo the duality involution; see (2.3.4).) We let
$\mathfrak{M}(20)$
modulo the duality involution; see (2.3.4).) We let
![]() $\unicode[STIX]{x1D706}(N)$
be the Hodge (or automorphic) orbiline bundle on
$\unicode[STIX]{x1D706}(N)$
be the Hodge (or automorphic) orbiline bundle on
![]() $\mathscr{F}(N)$
and we choose the boundary divisor
$\mathscr{F}(N)$
and we choose the boundary divisor
![]() $\unicode[STIX]{x1D6E5}(N)$
so that
$\unicode[STIX]{x1D6E5}(N)$
so that
![]() $\text{Proj}\,R(\mathscr{F}(N),\unicode[STIX]{x1D706}(N)+\unicode[STIX]{x1D6E5}(N))\cong \mathfrak{M}(N)$
. (We emphasize that
$\text{Proj}\,R(\mathscr{F}(N),\unicode[STIX]{x1D706}(N)+\unicode[STIX]{x1D6E5}(N))\cong \mathfrak{M}(N)$
. (We emphasize that
![]() $\unicode[STIX]{x1D6E5}(N)$
is a divisor inside the locally symmetric variety
$\unicode[STIX]{x1D6E5}(N)$
is a divisor inside the locally symmetric variety
![]() $\mathscr{F}(N)$
and in particular it has nothing to do with the boundary of the Baily–Borel compactification or toroidal compactifications. We use the word ‘boundary’ in accordance with standard terminology in minimal model program (MMP) and specifically variations of log canonical models.)
$\mathscr{F}(N)$
and in particular it has nothing to do with the boundary of the Baily–Borel compactification or toroidal compactifications. We use the word ‘boundary’ in accordance with standard terminology in minimal model program (MMP) and specifically variations of log canonical models.)
We will show that
![]() $\mathscr{F}(N)$
is isomorphic to a Heegner divisor
$\mathscr{F}(N)$
is isomorphic to a Heegner divisor
![]() $H_{h}(N+1)\subset \mathscr{F}(N+1)$
, which is the ‘main’ component of the boundary divisor
$H_{h}(N+1)\subset \mathscr{F}(N+1)$
, which is the ‘main’ component of the boundary divisor
![]() $\unicode[STIX]{x1D6E5}(N)$
. Hence, the varieties
$\unicode[STIX]{x1D6E5}(N)$
. Hence, the varieties
![]() $\mathscr{F}(N)$
fit into a tower joining periods of hyperelliptic quartics, quartic surfaces, and double EPW sextics (something which has a clear geometric counterpart). By a careful analysis of the
$\mathscr{F}(N)$
fit into a tower joining periods of hyperelliptic quartics, quartic surfaces, and double EPW sextics (something which has a clear geometric counterpart). By a careful analysis of the
![]() $D$
-tower, and an application of Borcherds’ results, we arrive at a conjecture predicting the behavior of the models
$D$
-tower, and an application of Borcherds’ results, we arrive at a conjecture predicting the behavior of the models
as
![]() $\unicode[STIX]{x1D6FD}$
varies between
$\unicode[STIX]{x1D6FD}$
varies between
![]() $0$
and
$0$
and
![]() $1$
. Below we summarize our predictions.
$1$
. Below we summarize our predictions.
Conjecture. Let
![]() $15\leqslant N\leqslant 23$
. The ring of sections
$15\leqslant N\leqslant 23$
. The ring of sections
![]() $R(\mathscr{F}(N),\unicode[STIX]{x1D706}(N)+\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6E5}(N))$
is finitely generated for
$R(\mathscr{F}(N),\unicode[STIX]{x1D706}(N)+\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6E5}(N))$
is finitely generated for
![]() $\unicode[STIX]{x1D6FD}\in [0,1]\cap \mathbb{Q}$
, and the walls of the Mori chamber decomposition of the cone
$\unicode[STIX]{x1D6FD}\in [0,1]\cap \mathbb{Q}$
, and the walls of the Mori chamber decomposition of the cone
are generated by
![]() $\unicode[STIX]{x1D706}(N)+(1/k)\unicode[STIX]{x1D6E5}(N)$
, where
$\unicode[STIX]{x1D706}(N)+(1/k)\unicode[STIX]{x1D6E5}(N)$
, where
![]() $k\in \{1,\ldots ,N-10\}$
and
$k\in \{1,\ldots ,N-10\}$
and
![]() $k\not =N-11$
. The behavior of
$k\not =N-11$
. The behavior of
![]() $\unicode[STIX]{x1D706}(N)+(1/k)\unicode[STIX]{x1D6E5}(N)$
, for
$\unicode[STIX]{x1D706}(N)+(1/k)\unicode[STIX]{x1D6E5}(N)$
, for
![]() $k$
as above, is described as follows. For
$k$
as above, is described as follows. For
![]() $k=1$
,
$k=1$
,
![]() $\mathscr{F}(N,1)$
is obtained from
$\mathscr{F}(N,1)$
is obtained from
![]() $\mathscr{F}(N,1-\unicode[STIX]{x1D716})$
by contracting the strict transform of
$\mathscr{F}(N,1-\unicode[STIX]{x1D716})$
by contracting the strict transform of
![]() $\operatorname{supp}\unicode[STIX]{x1D6E5}(N)$
. If
$\operatorname{supp}\unicode[STIX]{x1D6E5}(N)$
. If
![]() $2\leqslant k$
, then the birational map between
$2\leqslant k$
, then the birational map between
![]() $\mathscr{F}(N,1/k-\unicode[STIX]{x1D716})$
and
$\mathscr{F}(N,1/k-\unicode[STIX]{x1D716})$
and
![]() $\mathscr{F}(N,1/k+\unicode[STIX]{x1D716})$
is a flip whose center is described in Prediction 5.1.1.
$\mathscr{F}(N,1/k+\unicode[STIX]{x1D716})$
is a flip whose center is described in Prediction 5.1.1.
Specifically, let us spell out the conjecture for the case of quartic surfaces.
Prediction. The variation of models
![]() $\text{Proj}\,R(\mathscr{F}(19),\unicode[STIX]{x1D706}(19)+\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6E5}(19))$
interpolating between the Baily–Borel compactification
$\text{Proj}\,R(\mathscr{F}(19),\unicode[STIX]{x1D706}(19)+\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6E5}(19))$
interpolating between the Baily–Borel compactification
![]() $\mathscr{F}_{4}^{\ast }(\cong \mathscr{F}(19))$
for quartic
$\mathscr{F}_{4}^{\ast }(\cong \mathscr{F}(19))$
for quartic
![]() $K3$
surfaces (
$K3$
surfaces (
![]() $\unicode[STIX]{x1D6FD}=0$
) and the GIT quotient for quartic surfaces (
$\unicode[STIX]{x1D6FD}=0$
) and the GIT quotient for quartic surfaces (
![]() $\unicode[STIX]{x1D6FD}=1$
) undergoes birational transformations (flips, except for the two boundary cases) at the following critical values for
$\unicode[STIX]{x1D6FD}=1$
) undergoes birational transformations (flips, except for the two boundary cases) at the following critical values for
![]() $\unicode[STIX]{x1D6FD}$
:
$\unicode[STIX]{x1D6FD}$
:
Furthermore, the centers of the flips for
![]() $\unicode[STIX]{x1D6FD}<\frac{1}{5}$
correspond to
$\unicode[STIX]{x1D6FD}<\frac{1}{5}$
correspond to
![]() $T_{3,3,4}$
,
$T_{3,3,4}$
,
![]() $T_{2,4,5}$
, and
$T_{2,4,5}$
, and
![]() $T_{2,3,7}$
marked
$T_{2,3,7}$
marked
![]() $K3$
surfaces (loci inside the period space
$K3$
surfaces (loci inside the period space
![]() $\mathscr{F}(19)$
) and those loci are flipped to the loci in
$\mathscr{F}(19)$
) and those loci are flipped to the loci in
![]() $\mathfrak{M}(19)$
of quartics with
$\mathfrak{M}(19)$
of quartics with
![]() $E_{14}$
,
$E_{14}$
,
![]() $E_{13}$
, and
$E_{13}$
, and
![]() $E_{12}$
singularities, respectively (see Shah [Reference ShahSha80]).
$E_{12}$
singularities, respectively (see Shah [Reference ShahSha80]).
The birational modifications at the two ends of the interval were known by Shah and Looijenga, respectively. In [Reference Laza and O’GradyLO18b], we have given a complete geometric (partly conjectural, partly provable) matching between a slight refinement of Shah’s Type IV stratification [Reference ShahSha81, Theorem 2.4] (the indeterminacy locus of the period map) in the GIT quotient
![]() $\mathfrak{M}$
and the strata resulting from the flips predicted above (see [Reference Laza and O’GradyLO18b, §4.3]). Furthermore, the behavior at
$\mathfrak{M}$
and the strata resulting from the flips predicted above (see [Reference Laza and O’GradyLO18b, §4.3]). Furthermore, the behavior at
![]() $\unicode[STIX]{x1D6FD}=\frac{1}{9},\frac{1}{7},\frac{1}{6}$
and
$\unicode[STIX]{x1D6FD}=\frac{1}{9},\frac{1}{7},\frac{1}{6}$
and
![]() $\unicode[STIX]{x1D6FD}=\frac{1}{2}$
is understood (see [Reference Laza and O’GradyLO18b, §6] and [Reference Laza and O’GradyLO18b, §5.4], respectively).
$\unicode[STIX]{x1D6FD}=\frac{1}{2}$
is understood (see [Reference Laza and O’GradyLO18b, §6] and [Reference Laza and O’GradyLO18b, §5.4], respectively).
In [Reference Laza and O’GradyLO18a], we have proved that our conjecture holds for
![]() $N=18$
(hyperelliptic quartic
$N=18$
(hyperelliptic quartic
![]() $K3$
surfaces) by means of techniques similar to those employed in [Reference Casalaina-Martin, Jensen and LazaCMJL14]. Since our constructions are inductive, and since the geometric behavior (for hyperelliptic quartics) identified in [Reference Laza and O’GradyLO18a] matches what we predicted in [Reference Laza and O’GradyLO18b] (for quartics), we have no doubt of the validity of our conjecture for quartic
$K3$
surfaces) by means of techniques similar to those employed in [Reference Casalaina-Martin, Jensen and LazaCMJL14]. Since our constructions are inductive, and since the geometric behavior (for hyperelliptic quartics) identified in [Reference Laza and O’GradyLO18a] matches what we predicted in [Reference Laza and O’GradyLO18b] (for quartics), we have no doubt of the validity of our conjecture for quartic
![]() $K3$
surfaces. Similarly, earlier work on EPW sextics [Reference O’GradyO’Gr15, Reference O’GradyO’Gr16] seems compatible with our conjectures; presumably our predictions (for
$K3$
surfaces. Similarly, earlier work on EPW sextics [Reference O’GradyO’Gr15, Reference O’GradyO’Gr16] seems compatible with our conjectures; presumably our predictions (for
![]() $N=20$
) can be checked inductively.
$N=20$
) can be checked inductively.
Remark.
By decomposing the period map for quartic surfaces into elementary birational transformations, we open the door to wall-crossing arguments. For instance, starting from the cohomology of the GIT quotient for quartic surfaces (see Kirwan [Reference KirwanKir89]) and, following the flips discussed above, one can compute the cohomology of the Baily–Borel compactification
![]() $\mathscr{F}_{4}^{\ast }$
. For comparison’s sake, we recall that in the case of degree-
$\mathscr{F}_{4}^{\ast }$
. For comparison’s sake, we recall that in the case of degree-
![]() $2$
$2$
![]() $K3$
surfaces, there is no intermediate flip and thus the two extremal cases suffice to compare the GIT and the Baily–Borel compactifications (see [Reference ShahSha80] and [Reference LooijengaLoo86], and [Reference Kirwan and LeeKL89] for the computation of the cohomology).
$K3$
surfaces, there is no intermediate flip and thus the two extremal cases suffice to compare the GIT and the Baily–Borel compactifications (see [Reference ShahSha80] and [Reference LooijengaLoo86], and [Reference Kirwan and LeeKL89] for the computation of the cohomology).
The variational approach to the analysis of birational maps is the natural one from the perspective of contemporary MMP, and its power in the context of moduli has been in evidence since the appearance of Thaddeus’ work on Variation of Geometric Invariant Theory (VGIT) [Reference ThaddeusTha96]. An inspiration for our work is the so-called Hassett–Keel program (see [Reference Hassett and HyeonHH13]) for moduli of curves (which studies the variation of log canonical models
![]() $\text{Proj}\,R(\overline{M}_{g},K+\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6E5})$
of the Deligne–Mumford compactification
$\text{Proj}\,R(\overline{M}_{g},K+\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6E5})$
of the Deligne–Mumford compactification
![]() $\overline{M}_{g}$
). Experts in the field have speculated on the existence of an analogue of the Hassett–Keel program for (special) surfaces; our study can be viewed as a first example of a Hassett–Keel program for surfaces. Indeed, beyond the obvious analogy (
$\overline{M}_{g}$
). Experts in the field have speculated on the existence of an analogue of the Hassett–Keel program for (special) surfaces; our study can be viewed as a first example of a Hassett–Keel program for surfaces. Indeed, beyond the obvious analogy (
![]() $\unicode[STIX]{x1D706}+\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6E5}$
may easily be rewritten as
$\unicode[STIX]{x1D706}+\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6E5}$
may easily be rewritten as
![]() $K_{\mathscr{F}}+\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6E5}^{\prime }$
), the modular behavior is also similar: for instance, the first birational wall crossing for quartic
$K_{\mathscr{F}}+\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D6E5}^{\prime }$
), the modular behavior is also similar: for instance, the first birational wall crossing for quartic
![]() $K3$
surfaces is associated to Dolgachev singularities in a manner similar to the case of curves with cusp singularities.
$K3$
surfaces is associated to Dolgachev singularities in a manner similar to the case of curves with cusp singularities.
On the other hand, there is a richer structure compared to the Hassett–Keel program. Namely, the birational transformations that occur in our situation are controlled by the arithmetic and combinatorics of the hyperplane arrangement associated to
![]() $\unicode[STIX]{x1D6E5}$
. The emerging picture of periods of quartic
$\unicode[STIX]{x1D6E5}$
. The emerging picture of periods of quartic
![]() $K3$
surfaces is more complex and subtle than that of periods of degree-
$K3$
surfaces is more complex and subtle than that of periods of degree-
![]() $2$
$2$
![]() $K3$
surfaces, but nonetheless Looijenga’s insight that arithmetic controls the birational models of
$K3$
surfaces, but nonetheless Looijenga’s insight that arithmetic controls the birational models of
![]() $\mathscr{F}_{d}^{\ast }$
is still valid. We view our work as a quantitative and qualitative refinement of Looijenga’s seminal work [Reference LooijengaLoo03b].
$\mathscr{F}_{d}^{\ast }$
is still valid. We view our work as a quantitative and qualitative refinement of Looijenga’s seminal work [Reference LooijengaLoo03b].
The birational geometry of moduli spaces of
![]() $K3$
surfaces was previously studied from the perspective of the Kodaira dimension by Gritsenko et al. [Reference Gritsenko, Hulek and SankaranGHS07]. We share with them the main technical tool, namely Borcherds’ construction [Reference BorcherdsBor95] of automorphic forms for Type IV domains (and subsequent improvements due to Bruinier [Reference BruinierBru02] and Bergeron et al. [Reference Bergeron, Li, Millson and MoeglinBLMM17]).
$K3$
surfaces was previously studied from the perspective of the Kodaira dimension by Gritsenko et al. [Reference Gritsenko, Hulek and SankaranGHS07]. We share with them the main technical tool, namely Borcherds’ construction [Reference BorcherdsBor95] of automorphic forms for Type IV domains (and subsequent improvements due to Bruinier [Reference BruinierBru02] and Bergeron et al. [Reference Bergeron, Li, Millson and MoeglinBLMM17]).
Structure of the paper
In § 1, we introduce the
![]() $D$
-tower of period spaces
$D$
-tower of period spaces
![]() $\{\mathscr{F}(N)\}_{N\geqslant 3}$
. The focus here is on the arithmetic of
$\{\mathscr{F}(N)\}_{N\geqslant 3}$
. The focus here is on the arithmetic of
![]() $D$
-lattices. We define the main Heegner divisors, namely the nodal, hyperelliptic, and unigonal divisors in
$D$
-lattices. We define the main Heegner divisors, namely the nodal, hyperelliptic, and unigonal divisors in
![]() $\mathscr{F}(N)$
, denoted respectively
$\mathscr{F}(N)$
, denoted respectively
![]() $H_{n}(N)$
,
$H_{n}(N)$
,
![]() $H_{h}(N)$
, and
$H_{h}(N)$
, and
![]() $H_{u}(N)$
. If
$H_{u}(N)$
. If
![]() $N=19$
(the period space for quartic surfaces), they have a well-known geometric meaning and in other dimensions they are the arithmetic analogue of the divisors for
$N=19$
(the period space for quartic surfaces), they have a well-known geometric meaning and in other dimensions they are the arithmetic analogue of the divisors for
![]() $N=19$
. The salient point in the
$N=19$
. The salient point in the
![]() $D$
-tower is that
$D$
-tower is that
![]() $\mathscr{F}(N-1)$
is isomorphic to the hyperelliptic Heegner divisor
$\mathscr{F}(N-1)$
is isomorphic to the hyperelliptic Heegner divisor
![]() $H_{h}(N)$
of
$H_{h}(N)$
of
![]() $\mathscr{F}(N)$
. Our boundary divisor
$\mathscr{F}(N)$
. Our boundary divisor
![]() $\unicode[STIX]{x1D6E5}(N)$
is equal to
$\unicode[STIX]{x1D6E5}(N)$
is equal to
![]() $H_{h}(N)/2$
except when
$H_{h}(N)/2$
except when
![]() $N\equiv 3,4\hspace{0.6em}({\rm mod}\hspace{0.2em}8)$
, in which case
$N\equiv 3,4\hspace{0.6em}({\rm mod}\hspace{0.2em}8)$
, in which case
![]() $\unicode[STIX]{x1D6E5}(N)=(H_{h}(N)+H_{u}(N))/2$
. (Note that the factor
$\unicode[STIX]{x1D6E5}(N)=(H_{h}(N)+H_{u}(N))/2$
. (Note that the factor
![]() $\frac{1}{2}$
appears because the quotient map from the relevant Type IV domain to
$\frac{1}{2}$
appears because the quotient map from the relevant Type IV domain to
![]() $\mathscr{F}(N)$
is ramified over the hyperelliptic divisor, and also over the unigonal divisor, if
$\mathscr{F}(N)$
is ramified over the hyperelliptic divisor, and also over the unigonal divisor, if
![]() $N\equiv 3,4\hspace{0.6em}({\rm mod}\hspace{0.2em}8)$
.) This leads to an inductive behavior.
$N\equiv 3,4\hspace{0.6em}({\rm mod}\hspace{0.2em}8)$
.) This leads to an inductive behavior.
In the following § 2, we go through results which are (more or less) known, namely that
![]() $\mathscr{F}(19)$
is the period space of degree-
$\mathscr{F}(19)$
is the period space of degree-
![]() $4$
polarized
$4$
polarized
![]() $K3$
surfaces, that
$K3$
surfaces, that
![]() $\mathscr{F}(18)$
is the period space of hyperelliptic quartics, and that
$\mathscr{F}(18)$
is the period space of hyperelliptic quartics, and that
![]() $\mathscr{F}(20)$
is the period space of double EPW sextics up to the duality involution (alternatively, it is the period space of EPW cubes).
$\mathscr{F}(20)$
is the period space of double EPW sextics up to the duality involution (alternatively, it is the period space of EPW cubes).
In § 3, we study the quasi-pull-back of Borcherds’ celebrated automorphic form given by two embeddings of the lattice
![]() $\unicode[STIX]{x1D6EC}_{N}$
into
$\unicode[STIX]{x1D6EC}_{N}$
into
![]() $\text{II}_{2,26}$
. The resulting relations between the automorphic line bundle on
$\text{II}_{2,26}$
. The resulting relations between the automorphic line bundle on
![]() $\mathscr{F}(N)$
, and the Heegner divisors
$\mathscr{F}(N)$
, and the Heegner divisors
![]() $H_{n}(N)$
,
$H_{n}(N)$
,
![]() $H_{h}(N)$
, and
$H_{h}(N)$
, and
![]() $H_{u}(N)$
(see Theorems 3.1.1 and 3.1.2), are key results for our work.
$H_{u}(N)$
(see Theorems 3.1.1 and 3.1.2), are key results for our work.
Section 4 contains a proof that
![]() $\mathscr{F}(19,1)=\text{Proj}\,R(\mathscr{F}(19),\unicode[STIX]{x1D706}(19)+\unicode[STIX]{x1D6E5}(19))$
is isomorphic to the GIT moduli space
$\mathscr{F}(19,1)=\text{Proj}\,R(\mathscr{F}(19),\unicode[STIX]{x1D706}(19)+\unicode[STIX]{x1D6E5}(19))$
is isomorphic to the GIT moduli space
![]() $\mathfrak{M}(19)$
. An analogous proof shows that
$\mathfrak{M}(19)$
. An analogous proof shows that
![]() $\mathscr{F}(18,1)$
is isomorphic to the GIT moduli space
$\mathscr{F}(18,1)$
is isomorphic to the GIT moduli space
![]() $\mathfrak{M}(18)$
and we expect that a similar result holds for
$\mathfrak{M}(18)$
and we expect that a similar result holds for
![]() $N=20$
, i.e. that
$N=20$
, i.e. that
![]() $\mathscr{F}(20,1)$
is isomorphic to
$\mathscr{F}(20,1)$
is isomorphic to
![]() $\mathfrak{M}(20)$
modulo the duality involution. In other words, if
$\mathfrak{M}(20)$
modulo the duality involution. In other words, if
![]() $N\in \{18,19\}$
, then the schemes
$N\in \{18,19\}$
, then the schemes
![]() $\mathscr{F}(N,\unicode[STIX]{x1D6FD})$
, for
$\mathscr{F}(N,\unicode[STIX]{x1D6FD})$
, for
![]() $\unicode[STIX]{x1D6FD}\in (0,1)\cap \mathbb{Q}$
, interpolate between the Baily–Borel compactification
$\unicode[STIX]{x1D6FD}\in (0,1)\cap \mathbb{Q}$
, interpolate between the Baily–Borel compactification
![]() $\mathscr{F}(N)^{\ast }$
and the GIT compactification
$\mathscr{F}(N)^{\ast }$
and the GIT compactification
![]() $\mathfrak{M}(N)$
.
$\mathfrak{M}(N)$
.
In the last section (§ 5), we identify the critical values of
![]() $\unicode[STIX]{x1D6FD}$
and the corresponding centers. To describe our work, let us review the basic picture in Looijenga. The starting point for him is to note that frequently the GIT quotients
$\unicode[STIX]{x1D6FD}$
and the corresponding centers. To describe our work, let us review the basic picture in Looijenga. The starting point for him is to note that frequently the GIT quotients
![]() $\mathfrak{M}$
are obtained by contracting a certain Heegner divisor
$\mathfrak{M}$
are obtained by contracting a certain Heegner divisor
![]() $H$
in
$H$
in
![]() $\mathscr{F}$
. Since the divisor
$\mathscr{F}$
. Since the divisor
![]() $\unicode[STIX]{x1D706}+H$
restricts trivially to
$\unicode[STIX]{x1D706}+H$
restricts trivially to
![]() $H$
, one gets that the GIT quotient is the
$H$
, one gets that the GIT quotient is the
![]() $\text{Proj}\,$
of a ring of meromorphic automorphic forms with poles on
$\text{Proj}\,$
of a ring of meromorphic automorphic forms with poles on
![]() $H$
. The complication of recovering the GIT quotient, say
$H$
. The complication of recovering the GIT quotient, say
![]() $\mathfrak{M}\cong \text{Proj}\,R(\mathscr{F},\unicode[STIX]{x1D706}+H)$
, from
$\mathfrak{M}\cong \text{Proj}\,R(\mathscr{F},\unicode[STIX]{x1D706}+H)$
, from
![]() $\mathscr{F}^{\ast }=\text{Proj}\,R(\mathscr{F},\unicode[STIX]{x1D706})$
comes from the fact that the hyperplanes in the arrangement
$\mathscr{F}^{\ast }=\text{Proj}\,R(\mathscr{F},\unicode[STIX]{x1D706})$
comes from the fact that the hyperplanes in the arrangement
![]() $\mathscr{H}$
(defining the Heegner divisor
$\mathscr{H}$
(defining the Heegner divisor
![]() $H=\mathscr{H}/\unicode[STIX]{x1D6E4}$
) intersect and, according to [Reference LooijengaLoo03b], the intersection strata have to be flipped starting with the largest codimension. While this flipping behavior is easy to understand if the strata are not too deep (e.g. for degree-
$H=\mathscr{H}/\unicode[STIX]{x1D6E4}$
) intersect and, according to [Reference LooijengaLoo03b], the intersection strata have to be flipped starting with the largest codimension. While this flipping behavior is easy to understand if the strata are not too deep (e.g. for degree-
![]() $2$
$2$
![]() $K3$
surfaces or cubic fourfolds), it is clear that for the quartic examples, or other examples where lots of intersections occur, it is wise to consider a continuous variation of the parameter
$K3$
surfaces or cubic fourfolds), it is clear that for the quartic examples, or other examples where lots of intersections occur, it is wise to consider a continuous variation of the parameter
![]() $\unicode[STIX]{x1D706}+\unicode[STIX]{x1D6FD}H$
. Roughly,
$\unicode[STIX]{x1D706}+\unicode[STIX]{x1D6FD}H$
. Roughly,
![]() $\unicode[STIX]{x1D6FD}=0$
is the known case,
$\unicode[STIX]{x1D6FD}=0$
is the known case,
![]() $\unicode[STIX]{x1D6FD}=1$
is the target, and in between we understand the flipping behavior by wall crossings.
$\unicode[STIX]{x1D6FD}=1$
is the target, and in between we understand the flipping behavior by wall crossings.
By taking the variational point of view described above, we are able to give a quantitative refinement of the flipping behavior predicted by Looijenga. Specifically, our computations show that the critical value of
![]() $\unicode[STIX]{x1D6FD}$
for which a specified intersection stratum
$\unicode[STIX]{x1D6FD}$
for which a specified intersection stratum
![]() $Z$
should be flipped (in the variation of models given by
$Z$
should be flipped (in the variation of models given by
![]() $\unicode[STIX]{x1D706}+\unicode[STIX]{x1D6FD}H$
) is determined by the log canonical threshold of
$\unicode[STIX]{x1D706}+\unicode[STIX]{x1D6FD}H$
) is determined by the log canonical threshold of
![]() $Z\subset \mathbb{P}^{N}$
. The precise formulae (see § 5.1.1) are more complicated as one has to take into account the ramification behavior. While these arguments and computations are not explicitly contained in [Reference LooijengaLoo03b], it is natural to call the computations of the (potential) critical
$Z\subset \mathbb{P}^{N}$
. The precise formulae (see § 5.1.1) are more complicated as one has to take into account the ramification behavior. While these arguments and computations are not explicitly contained in [Reference LooijengaLoo03b], it is natural to call the computations of the (potential) critical
![]() $\unicode[STIX]{x1D6FD}$
the Looijenga predictions. The surprising aspect that we discovered in our study is that these are only first-order predictions. Namely, as explained below, some arithmetic corrections are needed. Our final results are discussed in § 5.1.2 (especially Prediction 5.1.1).
$\unicode[STIX]{x1D6FD}$
the Looijenga predictions. The surprising aspect that we discovered in our study is that these are only first-order predictions. Namely, as explained below, some arithmetic corrections are needed. Our final results are discussed in § 5.1.2 (especially Prediction 5.1.1).
By comparing the GIT quotient for quartic surfaces of Shah [Reference ShahSha81] with the predicted Looijenga [Reference LooijengaLoo03b] model, we have observed a puzzling thing: the flips associated to intersections of components of the hyperelliptic arrangement predicted by Looijenga do occur, but, roughly speaking, only up to half the dimension. The explanation for this is in the Borcherds–Gritsenko relations between the automorphic line bundle and the Heegner divisors that were established in § 3. In short, while, for large
![]() $N$
,
$N$
,
![]() $H_{h}(N)$
is birationally contractible in
$H_{h}(N)$
is birationally contractible in
![]() $\mathscr{F}(N)$
, this is far from true for
$\mathscr{F}(N)$
, this is far from true for
![]() $N$
small: in fact,
$N$
small: in fact,
![]() $H_{h}(N)$
is ample on
$H_{h}(N)$
is ample on
![]() $\mathscr{F}(N)$
(and proportional to
$\mathscr{F}(N)$
(and proportional to
![]() $\unicode[STIX]{x1D706}(N)$
) for
$\unicode[STIX]{x1D706}(N)$
) for
![]() $N\leqslant 10$
. (This last fact was previously observed by Gritsenko [Reference GritsenkoGri18] in a different context.) This leads to a different behavior for the flips associated to high-codimension intersection strata. Very roughly, all the sufficiently deep strata (in the
$N\leqslant 10$
. (This last fact was previously observed by Gritsenko [Reference GritsenkoGri18] in a different context.) This leads to a different behavior for the flips associated to high-codimension intersection strata. Very roughly, all the sufficiently deep strata (in the
![]() $D$
-tower example) will be flipped at once. In other words, the Looijenga predictions come from combinatorics of the hyperplane arrangement: this is the dominating factor for small codimension, while for high codimension there are arithmetic corrections that are dominating.
$D$
-tower example) will be flipped at once. In other words, the Looijenga predictions come from combinatorics of the hyperplane arrangement: this is the dominating factor for small codimension, while for high codimension there are arithmetic corrections that are dominating.
The essential ingredient that is missing for making our predictions/conjectures into theorems is to show that all the centers of the birational transformations that occur in a variation of models on
![]() $\mathscr{F}=\mathscr{D}/\unicode[STIX]{x1D6E4}$
associated to varying
$\mathscr{F}=\mathscr{D}/\unicode[STIX]{x1D6E4}$
associated to varying
![]() $\unicode[STIX]{x1D706}+\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6E5}$
are of Shimura type (i.e.
$\unicode[STIX]{x1D706}+\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6E5}$
are of Shimura type (i.e.
![]() $\mathscr{D}^{\prime }/\unicode[STIX]{x1D6E4}^{\prime }$
). This a Fulton-type arithmetic conjecture. As mentioned, we have checked this (in the
$\mathscr{D}^{\prime }/\unicode[STIX]{x1D6E4}^{\prime }$
). This a Fulton-type arithmetic conjecture. As mentioned, we have checked this (in the
![]() $D$
-tower case) for
$D$
-tower case) for
![]() $N=18$
[Reference Laza and O’GradyLO18a]; also, the case
$N=18$
[Reference Laza and O’GradyLO18a]; also, the case
![]() $N=19$
is essentially complete [Reference Laza and O’GradyLO18b].
$N=19$
is essentially complete [Reference Laza and O’GradyLO18b].
Notation and conventions
We follow established conventions on integral lattices following Nikulin [Reference NikulinNik80]. In particular, the lattice
![]() $\unicode[STIX]{x1D6EC}_{N}=D_{N-2}\oplus U^{2}$
plays an essential role in our paper.
$\unicode[STIX]{x1D6EC}_{N}=D_{N-2}\oplus U^{2}$
plays an essential role in our paper.
Throughout the paper,
![]() $\mathscr{F}=\mathscr{D}/\unicode[STIX]{x1D6E4}$
is a locally symmetric variety of Type IV, i.e. the quotient of a bounded symmetric domain of Type IV modulo an arithmetic group (see § 1.2 for a brief review). The notation
$\mathscr{F}=\mathscr{D}/\unicode[STIX]{x1D6E4}$
is a locally symmetric variety of Type IV, i.e. the quotient of a bounded symmetric domain of Type IV modulo an arithmetic group (see § 1.2 for a brief review). The notation
![]() $\mathscr{F}$
might come with various additional decorations, which help specify it, e.g.
$\mathscr{F}$
might come with various additional decorations, which help specify it, e.g.
![]() $\mathscr{F}_{\unicode[STIX]{x1D6EC}}(\unicode[STIX]{x1D6E4})$
indicates the underlying lattice
$\mathscr{F}_{\unicode[STIX]{x1D6EC}}(\unicode[STIX]{x1D6E4})$
indicates the underlying lattice
![]() $\unicode[STIX]{x1D6EC}$
of signature
$\unicode[STIX]{x1D6EC}$
of signature
![]() $(2,\ast )$
and arithmetic group
$(2,\ast )$
and arithmetic group
![]() $\unicode[STIX]{x1D6E4}\subset O(\unicode[STIX]{x1D6EC})$
. Starting with § 2,
$\unicode[STIX]{x1D6E4}\subset O(\unicode[STIX]{x1D6EC})$
. Starting with § 2,
![]() $\mathscr{F}(N)$
is a specific
$\mathscr{F}(N)$
is a specific
![]() $N$
-dimensional locally symmetric variety (see Proposition 1.2.3) associated to the lattice
$N$
-dimensional locally symmetric variety (see Proposition 1.2.3) associated to the lattice
![]() $\unicode[STIX]{x1D6EC}_{N}$
. There are natural inclusion maps
$\unicode[STIX]{x1D6EC}_{N}$
. There are natural inclusion maps
![]() $\mathscr{F}(N-1){\hookrightarrow}\mathscr{F}(N)$
(cf. (1.7.1)); our main focus is
$\mathscr{F}(N-1){\hookrightarrow}\mathscr{F}(N)$
(cf. (1.7.1)); our main focus is
![]() $\mathscr{F}(19)\cong \mathscr{F}_{4}$
, the moduli space of quartic
$\mathscr{F}(19)\cong \mathscr{F}_{4}$
, the moduli space of quartic
![]() $K3$
surfaces. The Baily–Borel compactifications are indicated by a superscript
$K3$
surfaces. The Baily–Borel compactifications are indicated by a superscript
![]() $^{\ast }$
, e.g.
$^{\ast }$
, e.g.
![]() $\mathscr{F}(N)^{\ast }$
. The GIT quotients are typically denoted by
$\mathscr{F}(N)^{\ast }$
. The GIT quotients are typically denoted by
![]() $\mathfrak{M}$
with various identifying decorations. We view the period map
$\mathfrak{M}$
with various identifying decorations. We view the period map
![]() $\mathfrak{p}$
as a birational map going from an appropriate GIT quotient
$\mathfrak{p}$
as a birational map going from an appropriate GIT quotient
![]() $\mathfrak{M}$
to a Baily–Borel compactification
$\mathfrak{M}$
to a Baily–Borel compactification
![]() $\mathscr{F}^{\ast }$
. The notation
$\mathscr{F}^{\ast }$
. The notation
![]() $\unicode[STIX]{x1D6FD}$
is used to denote a rational number in
$\unicode[STIX]{x1D6FD}$
is used to denote a rational number in
![]() $[0,1]$
, which should be understood as an interpolating parameter between a GIT quotient (
$[0,1]$
, which should be understood as an interpolating parameter between a GIT quotient (
![]() $\unicode[STIX]{x1D6FD}=1$
) and a Baily–Borel compactification (
$\unicode[STIX]{x1D6FD}=1$
) and a Baily–Borel compactification (
![]() $\unicode[STIX]{x1D6FD}=0$
). In the final § 5,
$\unicode[STIX]{x1D6FD}=0$
). In the final § 5,
![]() $\mathscr{F}(N,\unicode[STIX]{x1D6FD})$
denotes a birational modification of
$\mathscr{F}(N,\unicode[STIX]{x1D6FD})$
denotes a birational modification of
![]() $\mathscr{F}(N)^{\ast }$
.
$\mathscr{F}(N)^{\ast }$
.
We use repeatedly the Hodge bundle
![]() $\unicode[STIX]{x1D706}$
on
$\unicode[STIX]{x1D706}$
on
![]() $\mathscr{F}$
and the boundary divisor
$\mathscr{F}$
and the boundary divisor
![]() $\unicode[STIX]{x1D6E5}$
(Definition 1.3.6), which is a Heegner divisor on
$\unicode[STIX]{x1D6E5}$
(Definition 1.3.6), which is a Heegner divisor on
![]() $\mathscr{F}$
. We use various other Heegner divisors
$\mathscr{F}$
. We use various other Heegner divisors
![]() $H=\mathscr{H}/\unicode[STIX]{x1D6E4}\subset \mathscr{F}=\mathscr{D}/\unicode[STIX]{x1D6E4}$
(see § 1.3.1 for a quick review), especially the nodal
$H=\mathscr{H}/\unicode[STIX]{x1D6E4}\subset \mathscr{F}=\mathscr{D}/\unicode[STIX]{x1D6E4}$
(see § 1.3.1 for a quick review), especially the nodal
![]() $H_{n}$
, the hyperelliptic
$H_{n}$
, the hyperelliptic
![]() $H_{h}$
, and the unigonal
$H_{h}$
, and the unigonal
![]() $H_{u}$
divisors (see Definition 1.3.4). Typically, the divisors have the same decorations as the ambient locally symmetric variety (e.g.
$H_{u}$
divisors (see Definition 1.3.4). Typically, the divisors have the same decorations as the ambient locally symmetric variety (e.g.
![]() $H_{h}(N)$
is a divisor in
$H_{h}(N)$
is a divisor in
![]() $\mathscr{F}(N)$
). In general, Borcherds’ relations (e.g. (3.1.1)) refer to a linear equivalence between the Hodge bundle
$\mathscr{F}(N)$
). In general, Borcherds’ relations (e.g. (3.1.1)) refer to a linear equivalence between the Hodge bundle
![]() $\unicode[STIX]{x1D706}$
and some Heegner divisors on
$\unicode[STIX]{x1D706}$
and some Heegner divisors on
![]() $\mathscr{F}$
(viewed in
$\mathscr{F}$
(viewed in
![]() $\operatorname{Pic}(\mathscr{F})_{\mathbb{Q}}$
).
$\operatorname{Pic}(\mathscr{F})_{\mathbb{Q}}$
).
1
 $D$
-lattices and the associated locally symmetric varieties
$D$
-lattices and the associated locally symmetric varieties
We introduce
![]() $D$
locally symmetric varieties. There is one such variety (of dimension
$D$
locally symmetric varieties. There is one such variety (of dimension
![]() $N:=n+2$
) for each
$N:=n+2$
) for each
![]() $D_{n}$
-lattice. The period spaces of hyperelliptic quartic
$D_{n}$
-lattice. The period spaces of hyperelliptic quartic
![]() $K3$
surfaces, quartic
$K3$
surfaces, quartic
![]() $K3$
surfaces, and desingularized EPW sextics correspond to
$K3$
surfaces, and desingularized EPW sextics correspond to
![]() $D_{16}$
,
$D_{16}$
,
![]() $D_{17}$
, and
$D_{17}$
, and
![]() $D_{18}$
, respectively; see § 2. We will introduce the Heegner divisors on
$D_{18}$
, respectively; see § 2. We will introduce the Heegner divisors on
![]() $D$
locally symmetric varieties which are relevant for our work: the nodal, hyperelliptic, and unigonal divisors (Definition 1.3.4). These divisors are the generalization of the familiar divisors with the same name on the period space for quartic
$D$
locally symmetric varieties which are relevant for our work: the nodal, hyperelliptic, and unigonal divisors (Definition 1.3.4). These divisors are the generalization of the familiar divisors with the same name on the period space for quartic
![]() $K3$
surfaces. We will prove that the hyperelliptic Heegner divisor on a
$K3$
surfaces. We will prove that the hyperelliptic Heegner divisor on a
![]() $D$
period space of dimension
$D$
period space of dimension
![]() $N$
is isomorphic to the
$N$
is isomorphic to the
![]() $D$
locally symmetric variety of dimension
$D$
locally symmetric variety of dimension
![]() $N-1$
(Proposition 1.4.5); thus, we have an infinite tower of nested
$N-1$
(Proposition 1.4.5); thus, we have an infinite tower of nested
![]() $D$
locally symmetric varieties (§ 1.7). The introduction of this
$D$
locally symmetric varieties (§ 1.7). The introduction of this
![]() $D$
-tower allows us to make inductive arguments later on.
$D$
-tower allows us to make inductive arguments later on.
Remark 1.0.1.
![]() $D$
locally symmetric varieties of dimension up to
$D$
locally symmetric varieties of dimension up to
![]() $10$
have appeared in work of Gritsenko; see [Reference GritsenkoGri18, §3].
$10$
have appeared in work of Gritsenko; see [Reference GritsenkoGri18, §3].
1.1
 $D$
-lattices
$D$
-lattices
Let
![]() $\unicode[STIX]{x1D6EC}$
be a lattice, i.e. a finitely generated torsion-free abelian group equipped with an integral non-degenerate bilinear symmetric form
$\unicode[STIX]{x1D6EC}$
be a lattice, i.e. a finitely generated torsion-free abelian group equipped with an integral non-degenerate bilinear symmetric form
![]() $(\,,\,)$
. If
$(\,,\,)$
. If
![]() $v\in \unicode[STIX]{x1D6EC}$
, we let
$v\in \unicode[STIX]{x1D6EC}$
, we let
![]() $v^{2}=(v,v)$
. Given a ring
$v^{2}=(v,v)$
. Given a ring
![]() $R$
, we let
$R$
, we let
![]() $\unicode[STIX]{x1D6EC}_{R}:=\unicode[STIX]{x1D6EC}\otimes _{\mathbb{Z}}R$
and we extend by linearity the quadratic form to
$\unicode[STIX]{x1D6EC}_{R}:=\unicode[STIX]{x1D6EC}\otimes _{\mathbb{Z}}R$
and we extend by linearity the quadratic form to
![]() $\unicode[STIX]{x1D6EC}_{R}$
. We let
$\unicode[STIX]{x1D6EC}_{R}$
. We let
![]() $A_{\unicode[STIX]{x1D6EC}}:=\operatorname{Hom}(\unicode[STIX]{x1D6EC},\mathbb{Z})/\unicode[STIX]{x1D6EC}$
be the discriminant group of
$A_{\unicode[STIX]{x1D6EC}}:=\operatorname{Hom}(\unicode[STIX]{x1D6EC},\mathbb{Z})/\unicode[STIX]{x1D6EC}$
be the discriminant group of
![]() $\unicode[STIX]{x1D6EC}$
. The quadratic form defines an embedding
$\unicode[STIX]{x1D6EC}$
. The quadratic form defines an embedding
![]() $\operatorname{Hom}(\unicode[STIX]{x1D6EC},\mathbb{Z})\subset \unicode[STIX]{x1D6EC}_{\mathbb{Q}}$
. Let
$\operatorname{Hom}(\unicode[STIX]{x1D6EC},\mathbb{Z})\subset \unicode[STIX]{x1D6EC}_{\mathbb{Q}}$
. Let
![]() $v\in \unicode[STIX]{x1D6EC}$
. The divisibility of
$v\in \unicode[STIX]{x1D6EC}$
. The divisibility of
![]() $v$
is defined to be the positive generator of
$v$
is defined to be the positive generator of
![]() $(v,\unicode[STIX]{x1D6EC})$
and is denoted
$(v,\unicode[STIX]{x1D6EC})$
and is denoted
![]() $\operatorname{div}(v)$
. Thus,
$\operatorname{div}(v)$
. Thus,
![]() $v/\text{div}(v)$
is an element of
$v/\text{div}(v)$
is an element of
![]() $\unicode[STIX]{x1D6EC}_{\mathbb{Q}}$
which belongs to
$\unicode[STIX]{x1D6EC}_{\mathbb{Q}}$
which belongs to
![]() $\operatorname{Hom}(\unicode[STIX]{x1D6EC},\mathbb{Z})$
and hence it determines an element
$\operatorname{Hom}(\unicode[STIX]{x1D6EC},\mathbb{Z})$
and hence it determines an element
![]() $v^{\ast }\in A_{\unicode[STIX]{x1D6EC}}$
. Now suppose that
$v^{\ast }\in A_{\unicode[STIX]{x1D6EC}}$
. Now suppose that
![]() $\unicode[STIX]{x1D6EC}$
is an even lattice. The embedding
$\unicode[STIX]{x1D6EC}$
is an even lattice. The embedding
![]() $\operatorname{Hom}(\unicode[STIX]{x1D6EC},\mathbb{Z})\subset \unicode[STIX]{x1D6EC}_{\mathbb{Q}}$
induces a discriminant quadratic form
$\operatorname{Hom}(\unicode[STIX]{x1D6EC},\mathbb{Z})\subset \unicode[STIX]{x1D6EC}_{\mathbb{Q}}$
induces a discriminant quadratic form
![]() $q_{\unicode[STIX]{x1D6EC}}:A_{\unicode[STIX]{x1D6EC}}\rightarrow \mathbb{Q}/2\mathbb{Z}$
. We recommend the classical paper by Nikulin [Reference NikulinNik80] as a reference for definitions and results on lattices.
$q_{\unicode[STIX]{x1D6EC}}:A_{\unicode[STIX]{x1D6EC}}\rightarrow \mathbb{Q}/2\mathbb{Z}$
. We recommend the classical paper by Nikulin [Reference NikulinNik80] as a reference for definitions and results on lattices.
For us,
![]() $U$
is the standard hyperbolic plane and the standard
$U$
is the standard hyperbolic plane and the standard
![]() $ADE$
root lattices are negative definite. Thus,
$ADE$
root lattices are negative definite. Thus,
![]() $E_{8}$
is the unique even unimodular negative-definite lattice of rank
$E_{8}$
is the unique even unimodular negative-definite lattice of rank
![]() $8$
; in the literature, sometimes, it is denoted by
$8$
; in the literature, sometimes, it is denoted by
![]() $E_{8}(-1)$
or
$E_{8}(-1)$
or
![]() $-E_{8}$
. If
$-E_{8}$
. If
![]() $0<p\leqslant q$
and
$0<p\leqslant q$
and
![]() $p\equiv q\hspace{0.6em}({\rm mod}\hspace{0.2em}8)$
, then
$p\equiv q\hspace{0.6em}({\rm mod}\hspace{0.2em}8)$
, then
![]() $\text{II}_{p,q}$
stands for an even unimodular lattice of signature
$\text{II}_{p,q}$
stands for an even unimodular lattice of signature
![]() $(p,q)$
; such a lattice is unique up to isomorphism. For
$(p,q)$
; such a lattice is unique up to isomorphism. For
![]() $m\in \mathbb{Z}$
, we let
$m\in \mathbb{Z}$
, we let
![]() $(m)$
be the rank-
$(m)$
be the rank-
![]() $1$
lattice with quadratic form that takes the value
$1$
lattice with quadratic form that takes the value
![]() $m$
on a generator. We let
$m$
on a generator. We let
and we equip
![]() $D_{n}$
with the restriction of the negative of the standard Euclidean pairing on
$D_{n}$
with the restriction of the negative of the standard Euclidean pairing on
![]() $\mathbb{Z}^{n}$
. Thus,
$\mathbb{Z}^{n}$
. Thus,
![]() $D_{1}\cong (-4)$
,
$D_{1}\cong (-4)$
,
![]() $D_{2}\cong A_{1}\oplus A_{1}$
,
$D_{2}\cong A_{1}\oplus A_{1}$
,
![]() $D_{3}=A_{3}$
, and
$D_{3}=A_{3}$
, and
![]() $D_{n}$
is the negative-definite root lattice with Dynkin diagram
$D_{n}$
is the negative-definite root lattice with Dynkin diagram
![]() $D_{n}$
if
$D_{n}$
if
![]() $n\geqslant 4$
. Let
$n\geqslant 4$
. Let
![]() $\unicode[STIX]{x1D6FC}_{n},\unicode[STIX]{x1D6FD}_{n}\in A_{D_{n}}$
be the classes of
$\unicode[STIX]{x1D6FC}_{n},\unicode[STIX]{x1D6FD}_{n}\in A_{D_{n}}$
be the classes of
![]() $(1/2,1/2,\ldots ,1/2)$
and
$(1/2,1/2,\ldots ,1/2)$
and
![]() $(-1/2,1/2,\ldots ,1/2)$
, respectively. If
$(-1/2,1/2,\ldots ,1/2)$
, respectively. If
![]() $n$
is odd, then
$n$
is odd, then
![]() $4\unicode[STIX]{x1D6FC}_{n}=4\unicode[STIX]{x1D6FD}_{n}=0$
and
$4\unicode[STIX]{x1D6FC}_{n}=4\unicode[STIX]{x1D6FD}_{n}=0$
and
![]() $\unicode[STIX]{x1D6FC}_{n}+\unicode[STIX]{x1D6FD}_{n}=0$
. If
$\unicode[STIX]{x1D6FC}_{n}+\unicode[STIX]{x1D6FD}_{n}=0$
. If
![]() $n$
is even, then
$n$
is even, then
![]() $2\unicode[STIX]{x1D6FC}_{n}=2\unicode[STIX]{x1D6FD}_{n}=0$
. Moreover,
$2\unicode[STIX]{x1D6FC}_{n}=2\unicode[STIX]{x1D6FD}_{n}=0$
. Moreover,
The following result is an easy exercise.
Claim 1.1.1. If
![]() $n$
is odd, then
$n$
is odd, then
![]() $A_{D_{n}}$
is cyclic of order
$A_{D_{n}}$
is cyclic of order
![]() $4$
, generated by
$4$
, generated by
![]() $\unicode[STIX]{x1D6FC}_{n}$
. If
$\unicode[STIX]{x1D6FC}_{n}$
. If
![]() $n$
is even, then
$n$
is even, then
![]() $A_{D_{n}}$
is the Klein group, generated by
$A_{D_{n}}$
is the Klein group, generated by
![]() $\unicode[STIX]{x1D6FC}_{n}$
and
$\unicode[STIX]{x1D6FC}_{n}$
and
![]() $\unicode[STIX]{x1D6FD}_{n}$
.
$\unicode[STIX]{x1D6FD}_{n}$
.
For
![]() $N\geqslant 3$
, let
$N\geqslant 3$
, let
Notice that
Below is the key definition of the present subsection.
Definition 1.1.2. Let
![]() $N\geqslant 3$
. A lattice
$N\geqslant 3$
. A lattice
![]() $\unicode[STIX]{x1D6EC}$
is a dimension-
$\unicode[STIX]{x1D6EC}$
is a dimension-
![]() $N$
$N$
![]() $D$
-lattice if it is isomorphic to
$D$
-lattice if it is isomorphic to
![]() $\unicode[STIX]{x1D6EC}_{N}$
, and in that case a decoration of
$\unicode[STIX]{x1D6EC}_{N}$
, and in that case a decoration of
![]() $\unicode[STIX]{x1D6EC}$
is an element
$\unicode[STIX]{x1D6EC}$
is an element
![]() $\unicode[STIX]{x1D709}\in A_{\unicode[STIX]{x1D6EC}}$
of square
$\unicode[STIX]{x1D709}\in A_{\unicode[STIX]{x1D6EC}}$
of square
![]() $1$
(modulo
$1$
(modulo
![]() $2\mathbb{Z}$
). A dimension-
$2\mathbb{Z}$
). A dimension-
![]() $N$
decorated
$N$
decorated
![]() $D$
-lattice is a couple
$D$
-lattice is a couple
![]() $(\unicode[STIX]{x1D6EC},\unicode[STIX]{x1D709})$
, where
$(\unicode[STIX]{x1D6EC},\unicode[STIX]{x1D709})$
, where
![]() $\unicode[STIX]{x1D6EC}$
is a dimension-
$\unicode[STIX]{x1D6EC}$
is a dimension-
![]() $N$
$N$
![]() $D$
-lattice and
$D$
-lattice and
![]() $\unicode[STIX]{x1D709}\in A_{\unicode[STIX]{x1D6EC}}$
is a decoration.
$\unicode[STIX]{x1D709}\in A_{\unicode[STIX]{x1D6EC}}$
is a decoration.
Remark 1.1.3. Let
![]() $\unicode[STIX]{x1D6EC}$
be a dimension-
$\unicode[STIX]{x1D6EC}$
be a dimension-
![]() $N$
$N$
![]() $D$
-lattice. By (1.1.4) and (1.1.2), there exists a decoration of
$D$
-lattice. By (1.1.4) and (1.1.2), there exists a decoration of
![]() $\unicode[STIX]{x1D6EC}$
and it is unique unless
$\unicode[STIX]{x1D6EC}$
and it is unique unless
![]() $N\equiv 6\hspace{0.6em}({\rm mod}\hspace{0.2em}8)$
. Of course, when
$N\equiv 6\hspace{0.6em}({\rm mod}\hspace{0.2em}8)$
. Of course, when
![]() $\unicode[STIX]{x1D709}$
is unique, the decoration is irrelevant. However, including the decorations allows us to treat the exceptional cases (i.e.
$\unicode[STIX]{x1D709}$
is unique, the decoration is irrelevant. However, including the decorations allows us to treat the exceptional cases (i.e.
![]() $N\equiv 6\hspace{0.6em}({\rm mod}\hspace{0.2em}8)$
) uniformly and to make certain hidden structures more transparent. Note also that any two
$N\equiv 6\hspace{0.6em}({\rm mod}\hspace{0.2em}8)$
) uniformly and to make certain hidden structures more transparent. Note also that any two
![]() $N$
-dimensional decorated
$N$
-dimensional decorated
![]() $D$
-lattices are isomorphic.
$D$
-lattices are isomorphic.
Remark 1.1.4. If
![]() $N\geqslant 3$
, then
$N\geqslant 3$
, then
![]() $\unicode[STIX]{x1D6EC}_{N}\oplus E_{8}\cong \unicode[STIX]{x1D6EC}_{N+8}$
(both are even unimodular lattices, of signature
$\unicode[STIX]{x1D6EC}_{N}\oplus E_{8}\cong \unicode[STIX]{x1D6EC}_{N+8}$
(both are even unimodular lattices, of signature
![]() $(2,N+8)$
). More generally, writing
$(2,N+8)$
). More generally, writing
![]() $N-2=8k+a$
with
$N-2=8k+a$
with
![]() $0\leqslant k$
and
$0\leqslant k$
and
![]() $a\in \{0,\ldots ,7\}$
, we get
$a\in \{0,\ldots ,7\}$
, we get
1.2 Locally symmetric varieties of Type IV
Suppose that
![]() $\unicode[STIX]{x1D6EC}$
is a lattice of signature
$\unicode[STIX]{x1D6EC}$
is a lattice of signature
![]() $(2,m)$
. We let
$(2,m)$
. We let
Then
![]() $\mathscr{D}_{\unicode[STIX]{x1D6EC}}$
is a complex manifold of dimension
$\mathscr{D}_{\unicode[STIX]{x1D6EC}}$
is a complex manifold of dimension
![]() $m$
, with two connected components
$m$
, with two connected components
![]() $\mathscr{D}_{\unicode[STIX]{x1D6EC}}^{\pm }$
, interchanged by complex conjugation (the ‘real part’ projection
$\mathscr{D}_{\unicode[STIX]{x1D6EC}}^{\pm }$
, interchanged by complex conjugation (the ‘real part’ projection
![]() $\unicode[STIX]{x1D6EC}_{\mathbb{C}}\rightarrow \unicode[STIX]{x1D6EC}_{\mathbb{R}}$
identifies
$\unicode[STIX]{x1D6EC}_{\mathbb{C}}\rightarrow \unicode[STIX]{x1D6EC}_{\mathbb{R}}$
identifies
![]() $\mathscr{D}_{\unicode[STIX]{x1D6EC}}$
with the set of oriented positive-definite two-dimensional subspaces of
$\mathscr{D}_{\unicode[STIX]{x1D6EC}}$
with the set of oriented positive-definite two-dimensional subspaces of
![]() $\unicode[STIX]{x1D6EC}_{\mathbb{R}}$
). Each of
$\unicode[STIX]{x1D6EC}_{\mathbb{R}}$
). Each of
![]() $\mathscr{D}_{\unicode[STIX]{x1D6EC}}^{\pm }$
is a bounded symmetric domain of Type IV. The orthogonal group
$\mathscr{D}_{\unicode[STIX]{x1D6EC}}^{\pm }$
is a bounded symmetric domain of Type IV. The orthogonal group
![]() $O(\unicode[STIX]{x1D6EC})$
acts naturally on
$O(\unicode[STIX]{x1D6EC})$
acts naturally on
![]() $\mathscr{D}_{\unicode[STIX]{x1D6EC}}$
(left action). Let
$\mathscr{D}_{\unicode[STIX]{x1D6EC}}$
(left action). Let
![]() $O^{+}(\unicode[STIX]{x1D6EC})<O(\unicode[STIX]{x1D6EC})$
be the subgroup of elements fixing each of
$O^{+}(\unicode[STIX]{x1D6EC})<O(\unicode[STIX]{x1D6EC})$
be the subgroup of elements fixing each of
![]() $\mathscr{D}_{\unicode[STIX]{x1D6EC}}^{\pm }$
. By definition,
$\mathscr{D}_{\unicode[STIX]{x1D6EC}}^{\pm }$
. By definition,
![]() $O^{+}(\unicode[STIX]{x1D6EC})$
acts on
$O^{+}(\unicode[STIX]{x1D6EC})$
acts on
![]() $\mathscr{D}_{\unicode[STIX]{x1D6EC}}^{+}$
. For a finite-index subgroup
$\mathscr{D}_{\unicode[STIX]{x1D6EC}}^{+}$
. For a finite-index subgroup
![]() $\unicode[STIX]{x1D6E4}<O^{+}(\unicode[STIX]{x1D6EC})$
, we let
$\unicode[STIX]{x1D6E4}<O^{+}(\unicode[STIX]{x1D6EC})$
, we let
Then
![]() $\mathscr{F}_{\unicode[STIX]{x1D6EC}}(\unicode[STIX]{x1D6E4})$
is naturally a complex space of dimension
$\mathscr{F}_{\unicode[STIX]{x1D6EC}}(\unicode[STIX]{x1D6E4})$
is naturally a complex space of dimension
![]() $n$
. By a celebrated result of Baily and Borel, there exists a projective variety
$n$
. By a celebrated result of Baily and Borel, there exists a projective variety
![]() $\mathscr{F}_{\unicode[STIX]{x1D6EC}}(\unicode[STIX]{x1D6E4})^{\ast }$
(the Baily–Borel compactification of
$\mathscr{F}_{\unicode[STIX]{x1D6EC}}(\unicode[STIX]{x1D6E4})^{\ast }$
(the Baily–Borel compactification of
![]() $\mathscr{F}_{\unicode[STIX]{x1D6EC}}(\unicode[STIX]{x1D6E4})$
) containing an open dense subset isomorphic to
$\mathscr{F}_{\unicode[STIX]{x1D6EC}}(\unicode[STIX]{x1D6E4})$
) containing an open dense subset isomorphic to
![]() $\mathscr{F}_{\unicode[STIX]{x1D6EC}}(\unicode[STIX]{x1D6E4})$
as analytic space. In particular,
$\mathscr{F}_{\unicode[STIX]{x1D6EC}}(\unicode[STIX]{x1D6E4})$
as analytic space. In particular,
![]() $\mathscr{F}_{\unicode[STIX]{x1D6EC}}(\unicode[STIX]{x1D6E4})$
has a compatible structure of a quasi-projective variety.
$\mathscr{F}_{\unicode[STIX]{x1D6EC}}(\unicode[STIX]{x1D6E4})$
has a compatible structure of a quasi-projective variety.
Definition 1.2.1. Let
![]() $(\unicode[STIX]{x1D6EC},\unicode[STIX]{x1D709})$
be a dimension-
$(\unicode[STIX]{x1D6EC},\unicode[STIX]{x1D709})$
be a dimension-
![]() $N$
decorated
$N$
decorated
![]() $D$
-lattice. Then
$D$
-lattice. Then
![]() $O(\unicode[STIX]{x1D6EC})$
acts naturally on
$O(\unicode[STIX]{x1D6EC})$
acts naturally on
![]() $A_{\unicode[STIX]{x1D6EC}}$
and hence we may define
$A_{\unicode[STIX]{x1D6EC}}$
and hence we may define
We let
![]() $\mathscr{F}_{\unicode[STIX]{x1D6EC}}(\unicode[STIX]{x1D6E4}_{\unicode[STIX]{x1D709}})$
be the associated locally symmetric variety (of dimension
$\mathscr{F}_{\unicode[STIX]{x1D6EC}}(\unicode[STIX]{x1D6E4}_{\unicode[STIX]{x1D709}})$
be the associated locally symmetric variety (of dimension
![]() $N$
): this is a
$N$
): this is a
![]() $D$
locally symmetric variety. To simplify notation, we will write
$D$
locally symmetric variety. To simplify notation, we will write
![]() $\mathscr{F}(\unicode[STIX]{x1D6EC},\unicode[STIX]{x1D709})$
for
$\mathscr{F}(\unicode[STIX]{x1D6EC},\unicode[STIX]{x1D709})$
for
![]() $\mathscr{F}_{\unicode[STIX]{x1D6EC}}(\unicode[STIX]{x1D6E4}_{\unicode[STIX]{x1D709}})$
.
$\mathscr{F}_{\unicode[STIX]{x1D6EC}}(\unicode[STIX]{x1D6E4}_{\unicode[STIX]{x1D709}})$
.
We will compare
![]() $\unicode[STIX]{x1D6E4}_{\unicode[STIX]{x1D709}}$
to more familiar subgroups of
$\unicode[STIX]{x1D6E4}_{\unicode[STIX]{x1D709}}$
to more familiar subgroups of
![]() $O^{+}(\unicode[STIX]{x1D6EC})$
. First, we recall that if
$O^{+}(\unicode[STIX]{x1D6EC})$
. First, we recall that if
![]() $\unicode[STIX]{x1D6EC}$
is an even lattice, the stable orthogonal subgroup
$\unicode[STIX]{x1D6EC}$
is an even lattice, the stable orthogonal subgroup
![]() $\widetilde{O}(\unicode[STIX]{x1D6EC})<O(\unicode[STIX]{x1D6EC})$
is the kernel of the natural homomorphism
$\widetilde{O}(\unicode[STIX]{x1D6EC})<O(\unicode[STIX]{x1D6EC})$
is the kernel of the natural homomorphism
![]() $\widetilde{O}(\unicode[STIX]{x1D6EC})\rightarrow O(A_{\unicode[STIX]{x1D6EC}})$
. We let
$\widetilde{O}(\unicode[STIX]{x1D6EC})\rightarrow O(A_{\unicode[STIX]{x1D6EC}})$
. We let
![]() $\widetilde{O}^{+}(\unicode[STIX]{x1D6EC}):=O^{+}(\unicode[STIX]{x1D6EC})\cap \widetilde{O}(\unicode[STIX]{x1D6EC})$
. Notice that
$\widetilde{O}^{+}(\unicode[STIX]{x1D6EC}):=O^{+}(\unicode[STIX]{x1D6EC})\cap \widetilde{O}(\unicode[STIX]{x1D6EC})$
. Notice that
![]() $\widetilde{O}^{+}(\unicode[STIX]{x1D6EC})$
is of finite index in
$\widetilde{O}^{+}(\unicode[STIX]{x1D6EC})$
is of finite index in
![]() $O(\unicode[STIX]{x1D6EC})$
.
$O(\unicode[STIX]{x1D6EC})$
.
Example 1.2.2. Let
![]() $\unicode[STIX]{x1D6EC}$
be an even lattice and
$\unicode[STIX]{x1D6EC}$
be an even lattice and
![]() $r\in \unicode[STIX]{x1D6EC}$
non-isotropic. Let
$r\in \unicode[STIX]{x1D6EC}$
non-isotropic. Let
 $$\begin{eqnarray}\begin{array}{@{}ccc@{}}\unicode[STIX]{x1D6EC}_{\mathbb{Q}} & \overset{\unicode[STIX]{x1D70C}_{r}}{\longrightarrow } & \unicode[STIX]{x1D6EC}_{\mathbb{Q}}\\ x & \mapsto & x-{\displaystyle \frac{2(x,r)}{r^{2}}}r\end{array}\end{eqnarray}$$
$$\begin{eqnarray}\begin{array}{@{}ccc@{}}\unicode[STIX]{x1D6EC}_{\mathbb{Q}} & \overset{\unicode[STIX]{x1D70C}_{r}}{\longrightarrow } & \unicode[STIX]{x1D6EC}_{\mathbb{Q}}\\ x & \mapsto & x-{\displaystyle \frac{2(x,r)}{r^{2}}}r\end{array}\end{eqnarray}$$
be the reflection in the hyperplane
![]() $r^{\bot }$
. If
$r^{\bot }$
. If
![]() $r$
is primitive, then
$r$
is primitive, then
![]() $\unicode[STIX]{x1D70C}_{r}(\unicode[STIX]{x1D6EC})\subset \unicode[STIX]{x1D6EC}$
if and only if
$\unicode[STIX]{x1D70C}_{r}(\unicode[STIX]{x1D6EC})\subset \unicode[STIX]{x1D6EC}$
if and only if
![]() $r^{2}|2\operatorname{div}(r)$
; if this is the case we use the same symbol
$r^{2}|2\operatorname{div}(r)$
; if this is the case we use the same symbol
![]() $\unicode[STIX]{x1D70C}_{r}$
for the corresponding element of
$\unicode[STIX]{x1D70C}_{r}$
for the corresponding element of
![]() $O(\unicode[STIX]{x1D6EC})$
. One checks easily the following results:
$O(\unicode[STIX]{x1D6EC})$
. One checks easily the following results:
(1)
 $\unicode[STIX]{x1D70C}_{r}\in O^{+}(\unicode[STIX]{x1D6EC})$
if and only if
$\unicode[STIX]{x1D70C}_{r}\in O^{+}(\unicode[STIX]{x1D6EC})$
if and only if
 $r^{2}<0$
;
$r^{2}<0$
;(2) if
 $r^{2}=\pm 2$
, then
$r^{2}=\pm 2$
, then
 $\unicode[STIX]{x1D70C}_{r}\in \widetilde{O}(\unicode[STIX]{x1D6EC})$
.
$\unicode[STIX]{x1D70C}_{r}\in \widetilde{O}(\unicode[STIX]{x1D6EC})$
.
Let
![]() $(\unicode[STIX]{x1D6EC},\unicode[STIX]{x1D709})$
be a decorated
$(\unicode[STIX]{x1D6EC},\unicode[STIX]{x1D709})$
be a decorated
![]() $D$
-lattice; then
$D$
-lattice; then
Proposition 1.2.3. Let
![]() $(\unicode[STIX]{x1D6EC},\unicode[STIX]{x1D709})$
be a decorated
$(\unicode[STIX]{x1D6EC},\unicode[STIX]{x1D709})$
be a decorated
![]() $D$
-lattice of dimension
$D$
-lattice of dimension
![]() $N$
. Then:
$N$
. Then:
(1)
 $\widetilde{O}^{+}(\unicode[STIX]{x1D6EC})<\unicode[STIX]{x1D6E4}_{\unicode[STIX]{x1D709}}$
is of index
$\widetilde{O}^{+}(\unicode[STIX]{x1D6EC})<\unicode[STIX]{x1D6E4}_{\unicode[STIX]{x1D709}}$
is of index
 $2$
;
$2$
;(2)
 $\unicode[STIX]{x1D6E4}_{\unicode[STIX]{x1D709}}=O^{+}(\unicode[STIX]{x1D6EC})$
unless
$\unicode[STIX]{x1D6E4}_{\unicode[STIX]{x1D709}}=O^{+}(\unicode[STIX]{x1D6EC})$
unless
 $N\equiv 6\hspace{0.6em}({\rm mod}\hspace{0.2em}8)$
, in which case
$N\equiv 6\hspace{0.6em}({\rm mod}\hspace{0.2em}8)$
, in which case
 $\unicode[STIX]{x1D6E4}_{\unicode[STIX]{x1D709}}<O^{+}(\unicode[STIX]{x1D6EC})$
is of index
$\unicode[STIX]{x1D6E4}_{\unicode[STIX]{x1D709}}<O^{+}(\unicode[STIX]{x1D6EC})$
is of index
 $3$
;
$3$
;(3) if
 $N$
is odd,
$N$
is odd,
 $\mathscr{F}_{\unicode[STIX]{x1D6EC}}(O^{+}(\unicode[STIX]{x1D6EC}))=\mathscr{F}_{\unicode[STIX]{x1D6EC}}(\unicode[STIX]{x1D6E4}_{\unicode[STIX]{x1D709}})=\mathscr{F}_{\unicode[STIX]{x1D6EC}}(\widetilde{O}^{+}(\unicode[STIX]{x1D6EC}))$
;
$\mathscr{F}_{\unicode[STIX]{x1D6EC}}(O^{+}(\unicode[STIX]{x1D6EC}))=\mathscr{F}_{\unicode[STIX]{x1D6EC}}(\unicode[STIX]{x1D6E4}_{\unicode[STIX]{x1D709}})=\mathscr{F}_{\unicode[STIX]{x1D6EC}}(\widetilde{O}^{+}(\unicode[STIX]{x1D6EC}))$
;(4) if
 $N$
is even, the map
$N$
is even, the map
 $\mathscr{F}_{\unicode[STIX]{x1D6EC}}(\widetilde{O}^{+}(\unicode[STIX]{x1D6EC}))\rightarrow \mathscr{F}_{\unicode[STIX]{x1D6EC}}(\unicode[STIX]{x1D6E4}_{\unicode[STIX]{x1D709}})$
is a double cover.
$\mathscr{F}_{\unicode[STIX]{x1D6EC}}(\widetilde{O}^{+}(\unicode[STIX]{x1D6EC}))\rightarrow \mathscr{F}_{\unicode[STIX]{x1D6EC}}(\unicode[STIX]{x1D6E4}_{\unicode[STIX]{x1D709}})$
is a double cover.
Proof. The homomorphism
![]() $O(\unicode[STIX]{x1D6EC})\rightarrow O(q_{\unicode[STIX]{x1D6EC}})$
is surjective (see e.g. [Reference NikulinNik80, Theorem 1.14.2]). Since the reflection
$O(\unicode[STIX]{x1D6EC})\rightarrow O(q_{\unicode[STIX]{x1D6EC}})$
is surjective (see e.g. [Reference NikulinNik80, Theorem 1.14.2]). Since the reflection
![]() $\unicode[STIX]{x1D70C}_{r}$
, for
$\unicode[STIX]{x1D70C}_{r}$
, for
![]() $r\in \unicode[STIX]{x1D6EC}$
of square
$r\in \unicode[STIX]{x1D6EC}$
of square
![]() $2$
, acts trivially on
$2$
, acts trivially on
![]() $A_{\unicode[STIX]{x1D6EC}}$
and does not belong to the index-
$A_{\unicode[STIX]{x1D6EC}}$
and does not belong to the index-
![]() $2$
subgroup
$2$
subgroup
![]() $O^{+}(\unicode[STIX]{x1D6EC})$
, it follows that the homomorphism
$O^{+}(\unicode[STIX]{x1D6EC})$
, it follows that the homomorphism
![]() $O^{+}(\unicode[STIX]{x1D6EC})\rightarrow O(q_{\unicode[STIX]{x1D6EC}})$
is surjective as well. Since
$O^{+}(\unicode[STIX]{x1D6EC})\rightarrow O(q_{\unicode[STIX]{x1D6EC}})$
is surjective as well. Since
![]() $O(q_{\unicode[STIX]{x1D6EC}})\cong \mathbb{Z}/2$
for
$O(q_{\unicode[STIX]{x1D6EC}})\cong \mathbb{Z}/2$
for
![]() $N\not \equiv 6\hspace{0.6em}({\rm mod}\hspace{0.2em}8)$
, and
$N\not \equiv 6\hspace{0.6em}({\rm mod}\hspace{0.2em}8)$
, and
![]() $O(q_{\unicode[STIX]{x1D6EC}})\cong \unicode[STIX]{x1D6F4}_{3}$
otherwise, Items (1) and (2) follow. Notice that
$O(q_{\unicode[STIX]{x1D6EC}})\cong \unicode[STIX]{x1D6F4}_{3}$
otherwise, Items (1) and (2) follow. Notice that
![]() $-1(=-\text{id}_{\unicode[STIX]{x1D6EC}})\in \unicode[STIX]{x1D6E4}_{\unicode[STIX]{x1D709}}$
for all
$-1(=-\text{id}_{\unicode[STIX]{x1D6EC}})\in \unicode[STIX]{x1D6E4}_{\unicode[STIX]{x1D709}}$
for all
![]() $N$
, while
$N$
, while
![]() $-1\in \widetilde{O}(\unicode[STIX]{x1D6EC})$
if and only if
$-1\in \widetilde{O}(\unicode[STIX]{x1D6EC})$
if and only if
![]() $N$
is even. It follows that if
$N$
is even. It follows that if
![]() $N$
is odd, then
$N$
is odd, then
![]() $-1$
generates
$-1$
generates
![]() $\unicode[STIX]{x1D6E4}_{\unicode[STIX]{x1D709}}/\widetilde{O}^{+}(\unicode[STIX]{x1D6EC})\cong \mathbb{Z}/2$
. Since
$\unicode[STIX]{x1D6E4}_{\unicode[STIX]{x1D709}}/\widetilde{O}^{+}(\unicode[STIX]{x1D6EC})\cong \mathbb{Z}/2$
. Since
![]() $-1$
acts trivially on
$-1$
acts trivially on
![]() $\mathscr{D}_{\unicode[STIX]{x1D6EC}}$
, Item (3) follows. Item (4) holds because
$\mathscr{D}_{\unicode[STIX]{x1D6EC}}$
, Item (3) follows. Item (4) holds because
![]() $\widetilde{O}^{+}(\unicode[STIX]{x1D6EC})<\unicode[STIX]{x1D6E4}_{\unicode[STIX]{x1D709}}$
is of index
$\widetilde{O}^{+}(\unicode[STIX]{x1D6EC})<\unicode[STIX]{x1D6E4}_{\unicode[STIX]{x1D709}}$
is of index
![]() $2$
and
$2$
and
![]() $-1$
is the unique non-trivial element of
$-1$
is the unique non-trivial element of
![]() $O^{+}(\unicode[STIX]{x1D6EC})$
acting trivially on
$O^{+}(\unicode[STIX]{x1D6EC})$
acting trivially on
![]() $\mathscr{D}_{\unicode[STIX]{x1D6EC}}^{+}$
.◻
$\mathscr{D}_{\unicode[STIX]{x1D6EC}}^{+}$
.◻
1.3 Heegner divisors on
 $D$
locally symmetric varieties
$D$
locally symmetric varieties
1.3.1 Divisor classes on locally symmetric variety of Type IV
Let
![]() $X:=\mathscr{F}_{\unicode[STIX]{x1D6EC}}(\unicode[STIX]{x1D6E4})$
be a locally symmetric variety of Type IV. The Hodge bundle (or automorphic bundle), denoted by
$X:=\mathscr{F}_{\unicode[STIX]{x1D6EC}}(\unicode[STIX]{x1D6E4})$
be a locally symmetric variety of Type IV. The Hodge bundle (or automorphic bundle), denoted by
![]() $\mathscr{L}(\unicode[STIX]{x1D6EC},\unicode[STIX]{x1D6E4})$
, is a fundamental fractional (orbifold) line bundle on
$\mathscr{L}(\unicode[STIX]{x1D6EC},\unicode[STIX]{x1D6E4})$
, is a fundamental fractional (orbifold) line bundle on
![]() $\mathscr{F}_{\unicode[STIX]{x1D6EC}}(\unicode[STIX]{x1D6E4})$
; it is defined as the quotient of
$\mathscr{F}_{\unicode[STIX]{x1D6EC}}(\unicode[STIX]{x1D6E4})$
; it is defined as the quotient of
![]() $\mathscr{O}_{\mathscr{D}_{\unicode[STIX]{x1D6EC}}^{+}}(-1)$
by
$\mathscr{O}_{\mathscr{D}_{\unicode[STIX]{x1D6EC}}^{+}}(-1)$
by
![]() $\unicode[STIX]{x1D6E4}$
, where
$\unicode[STIX]{x1D6E4}$
, where
![]() $\mathscr{O}_{\mathscr{D}_{\unicode[STIX]{x1D6EC}}^{+}}(-1)$
is the restriction to
$\mathscr{O}_{\mathscr{D}_{\unicode[STIX]{x1D6EC}}^{+}}(-1)$
is the restriction to
![]() $\mathscr{D}_{\unicode[STIX]{x1D6EC}}^{+}$
of the tautological line bundle on
$\mathscr{D}_{\unicode[STIX]{x1D6EC}}^{+}$
of the tautological line bundle on
![]() $\mathbb{P}(\unicode[STIX]{x1D6EC}_{\mathbb{C}})$
. We recall that
$\mathbb{P}(\unicode[STIX]{x1D6EC}_{\mathbb{C}})$
. We recall that
![]() $\mathscr{L}(\unicode[STIX]{x1D6EC},\unicode[STIX]{x1D6E4})$
extends to an ample fractional line bundle
$\mathscr{L}(\unicode[STIX]{x1D6EC},\unicode[STIX]{x1D6E4})$
extends to an ample fractional line bundle
![]() $\mathscr{L}^{\ast }(\unicode[STIX]{x1D6EC},\unicode[STIX]{x1D6E4})$
on the Baily–Borel compactification
$\mathscr{L}^{\ast }(\unicode[STIX]{x1D6EC},\unicode[STIX]{x1D6E4})$
on the Baily–Borel compactification
![]() $\mathscr{F}_{\unicode[STIX]{x1D6EC}}(\unicode[STIX]{x1D6E4})^{\ast }$
, and that the sections of
$\mathscr{F}_{\unicode[STIX]{x1D6EC}}(\unicode[STIX]{x1D6E4})^{\ast }$
, and that the sections of
![]() $m\mathscr{L}^{\ast }(\unicode[STIX]{x1D6EC},\unicode[STIX]{x1D6E4})$
are precisely the weight-
$m\mathscr{L}^{\ast }(\unicode[STIX]{x1D6EC},\unicode[STIX]{x1D6E4})$
are precisely the weight-
![]() $m$
$m$
![]() $\unicode[STIX]{x1D6E4}$
-automorphic forms. We let
$\unicode[STIX]{x1D6E4}$
-automorphic forms. We let
![]() $\unicode[STIX]{x1D706}(\unicode[STIX]{x1D6EC},\unicode[STIX]{x1D6E4}):=c_{1}(\mathscr{L}(\unicode[STIX]{x1D6EC},\unicode[STIX]{x1D6E4}))$
; thus,
$\unicode[STIX]{x1D706}(\unicode[STIX]{x1D6EC},\unicode[STIX]{x1D6E4}):=c_{1}(\mathscr{L}(\unicode[STIX]{x1D6EC},\unicode[STIX]{x1D6E4}))$
; thus,
![]() $\unicode[STIX]{x1D706}(\unicode[STIX]{x1D6EC},\unicode[STIX]{x1D6E4})$
is a
$\unicode[STIX]{x1D706}(\unicode[STIX]{x1D6EC},\unicode[STIX]{x1D6E4})$
is a
![]() $\mathbb{Q}$
-Cartier divisor class.
$\mathbb{Q}$
-Cartier divisor class.
As is well known, any Weil divisor
![]() $D$
on the quasi-projective variety
$D$
on the quasi-projective variety
![]() $X$
is
$X$
is
![]() $\mathbb{Q}$
-Cartier. Thus, we may identify
$\mathbb{Q}$
-Cartier. Thus, we may identify
![]() $\operatorname{CH}^{1}(X)_{\mathbb{Q}}$
and
$\operatorname{CH}^{1}(X)_{\mathbb{Q}}$
and
![]() $\operatorname{Pic}(X)_{\mathbb{Q}}$
.
$\operatorname{Pic}(X)_{\mathbb{Q}}$
.
Heegner divisors on
![]() $\mathscr{F}_{\unicode[STIX]{x1D6EC}}(\unicode[STIX]{x1D6E4})$
are defined as follows. Let
$\mathscr{F}_{\unicode[STIX]{x1D6EC}}(\unicode[STIX]{x1D6E4})$
are defined as follows. Let
![]() $\unicode[STIX]{x1D70B}:\mathscr{D}_{\unicode[STIX]{x1D6EC}}^{+}\rightarrow \mathscr{F}_{\unicode[STIX]{x1D6EC}}(\unicode[STIX]{x1D6E4})$
be the quotient map. Given a non-zero
$\unicode[STIX]{x1D70B}:\mathscr{D}_{\unicode[STIX]{x1D6EC}}^{+}\rightarrow \mathscr{F}_{\unicode[STIX]{x1D6EC}}(\unicode[STIX]{x1D6E4})$
be the quotient map. Given a non-zero
![]() $v\in \unicode[STIX]{x1D6EC}$
, we let
$v\in \unicode[STIX]{x1D6EC}$
, we let
Notice that
![]() $g(v)^{\bot }\cap \mathscr{D}_{\unicode[STIX]{x1D6EC}}^{+}$
is empty if
$g(v)^{\bot }\cap \mathscr{D}_{\unicode[STIX]{x1D6EC}}^{+}$
is empty if
![]() $v^{2}\geqslant 0$
; hence, we will always assume that
$v^{2}\geqslant 0$
; hence, we will always assume that
![]() $v^{2}<0$
. Then
$v^{2}<0$
. Then
![]() $\mathscr{H}_{v,\unicode[STIX]{x1D6EC}}(\unicode[STIX]{x1D6E4})$
is a (particular) hyperplane arrangement (see [Reference LooijengaLoo03a, Reference LooijengaLoo03b]): we call it the pre-Heegner divisor associated to
$\mathscr{H}_{v,\unicode[STIX]{x1D6EC}}(\unicode[STIX]{x1D6E4})$
is a (particular) hyperplane arrangement (see [Reference LooijengaLoo03a, Reference LooijengaLoo03b]): we call it the pre-Heegner divisor associated to
![]() $v$
. One checks that
$v$
. One checks that
![]() $H_{v,\unicode[STIX]{x1D6EC}}(\unicode[STIX]{x1D6E4})$
is a prime divisor in the quasi-projective variety
$H_{v,\unicode[STIX]{x1D6EC}}(\unicode[STIX]{x1D6E4})$
is a prime divisor in the quasi-projective variety
![]() $\mathscr{F}_{\unicode[STIX]{x1D6EC}}(\unicode[STIX]{x1D6E4})$
. We say that
$\mathscr{F}_{\unicode[STIX]{x1D6EC}}(\unicode[STIX]{x1D6E4})$
. We say that
![]() $H_{v,\unicode[STIX]{x1D6EC}}(\unicode[STIX]{x1D6E4})$
is the Heegner divisor associated to
$H_{v,\unicode[STIX]{x1D6EC}}(\unicode[STIX]{x1D6E4})$
is the Heegner divisor associated to
![]() $v$
. Notice that
$v$
. Notice that
![]() $\mathscr{H}_{v,\unicode[STIX]{x1D6EC}}(\unicode[STIX]{x1D6E4})$
and
$\mathscr{H}_{v,\unicode[STIX]{x1D6EC}}(\unicode[STIX]{x1D6E4})$
and
![]() $H_{v,\unicode[STIX]{x1D6EC}}(\unicode[STIX]{x1D6E4})$
depend only on the
$H_{v,\unicode[STIX]{x1D6EC}}(\unicode[STIX]{x1D6E4})$
depend only on the
![]() $\unicode[STIX]{x1D6E4}$
-orbit of
$\unicode[STIX]{x1D6E4}$
-orbit of
![]() $v$
. We say that
$v$
. We say that
![]() $\mathscr{H}_{v,\unicode[STIX]{x1D6EC}}(\unicode[STIX]{x1D6E4})$
and
$\mathscr{H}_{v,\unicode[STIX]{x1D6EC}}(\unicode[STIX]{x1D6E4})$
and
![]() $H_{v,\unicode[STIX]{x1D6EC}}(\unicode[STIX]{x1D6E4})$
are reflective if the reflection
$H_{v,\unicode[STIX]{x1D6EC}}(\unicode[STIX]{x1D6E4})$
are reflective if the reflection
![]() $\unicode[STIX]{x1D70C}_{v}$
(see Example 1.2.1) belongs to
$\unicode[STIX]{x1D70C}_{v}$
(see Example 1.2.1) belongs to
![]() $\unicode[STIX]{x1D6E4}$
(in particular,
$\unicode[STIX]{x1D6E4}$
(in particular,
![]() $\unicode[STIX]{x1D70C}_{v}(\unicode[STIX]{x1D6EC})=\unicode[STIX]{x1D6EC}$
). If this is the case, we say that
$\unicode[STIX]{x1D70C}_{v}(\unicode[STIX]{x1D6EC})=\unicode[STIX]{x1D6EC}$
). If this is the case, we say that
![]() $v$
is a reflective vector of
$v$
is a reflective vector of
![]() $(\unicode[STIX]{x1D6EC},\unicode[STIX]{x1D6E4})$
. If
$(\unicode[STIX]{x1D6EC},\unicode[STIX]{x1D6E4})$
. If
![]() $(\unicode[STIX]{x1D6EC},\unicode[STIX]{x1D709})$
is a decorated
$(\unicode[STIX]{x1D6EC},\unicode[STIX]{x1D709})$
is a decorated
![]() $D$
-lattice, and
$D$
-lattice, and
![]() $\unicode[STIX]{x1D6E4}=\unicode[STIX]{x1D6E4}_{\unicode[STIX]{x1D709}}$
, then we say that
$\unicode[STIX]{x1D6E4}=\unicode[STIX]{x1D6E4}_{\unicode[STIX]{x1D709}}$
, then we say that
![]() $v$
is a reflective vector of
$v$
is a reflective vector of
![]() $(\unicode[STIX]{x1D6EC},\unicode[STIX]{x1D709})$
.
$(\unicode[STIX]{x1D6EC},\unicode[STIX]{x1D709})$
.
1.3.2 Relevant Heegner divisors for
 $D$
locally symmetric varieties
$D$
locally symmetric varieties
Let
![]() $(\unicode[STIX]{x1D6EC},\unicode[STIX]{x1D709})$
be a decorated
$(\unicode[STIX]{x1D6EC},\unicode[STIX]{x1D709})$
be a decorated
![]() $D$
-lattice. The Heegner divisors which are relevant for the present work are associated to vectors
$D$
-lattice. The Heegner divisors which are relevant for the present work are associated to vectors
![]() $v\in \unicode[STIX]{x1D6EC}$
(of negative square) which minimize
$v\in \unicode[STIX]{x1D6EC}$
(of negative square) which minimize
![]() $|v^{2}|$
among vectors such that
$|v^{2}|$
among vectors such that
![]() $v^{\ast }$
equals a given element of
$v^{\ast }$
equals a given element of
![]() $A_{\unicode[STIX]{x1D6EC}}$
. It will be convenient to write
$A_{\unicode[STIX]{x1D6EC}}$
. It will be convenient to write
Thus,
always, and
Remark 1.3.1. With notation as above, there exists
![]() $g\in \unicode[STIX]{x1D6E4}_{\unicode[STIX]{x1D709}}$
such that
$g\in \unicode[STIX]{x1D6E4}_{\unicode[STIX]{x1D709}}$
such that
![]() $g(\unicode[STIX]{x1D701})=\unicode[STIX]{x1D701}^{\prime }$
. In fact, it suffices to let
$g(\unicode[STIX]{x1D701})=\unicode[STIX]{x1D701}^{\prime }$
. In fact, it suffices to let
![]() $g=(\operatorname{Id}_{U^{2}},\unicode[STIX]{x1D70C})$
, where
$g=(\operatorname{Id}_{U^{2}},\unicode[STIX]{x1D70C})$
, where
![]() $\unicode[STIX]{x1D70C}\in O^{+}(D_{N-2})$
is the reflection in the vector
$\unicode[STIX]{x1D70C}\in O^{+}(D_{N-2})$
is the reflection in the vector
![]() $(2,0,\ldots ,0)$
, i.e.
$(2,0,\ldots ,0)$
, i.e.
![]() $\unicode[STIX]{x1D70C}(x_{1},\ldots ,x_{N-2})=(-x_{1},x_{2},\ldots ,x_{N-2})$
.
$\unicode[STIX]{x1D70C}(x_{1},\ldots ,x_{N-2})=(-x_{1},x_{2},\ldots ,x_{N-2})$
.
The result below will be used throughout the paper in order to classify
![]() $\unicode[STIX]{x1D6E4}_{\unicode[STIX]{x1D709}}$
-orbits of vectors of
$\unicode[STIX]{x1D6E4}_{\unicode[STIX]{x1D709}}$
-orbits of vectors of
![]() $\unicode[STIX]{x1D6EC}$
.
$\unicode[STIX]{x1D6EC}$
.
Proposition 1.3.2 (Eichler’s criterion, [Reference Gritsenko, Hulek and SankaranGHS09, Proposition 3.3]).
Let
![]() $\unicode[STIX]{x1D6EC}$
be an even lattice which contains
$\unicode[STIX]{x1D6EC}$
be an even lattice which contains
![]() $U\oplus U$
. Let
$U\oplus U$
. Let
![]() $v,w\in \unicode[STIX]{x1D6EC}$
be non-zero and primitive. There exists
$v,w\in \unicode[STIX]{x1D6EC}$
be non-zero and primitive. There exists
![]() $g\in \widetilde{O}^{+}(\unicode[STIX]{x1D6EC})$
such that
$g\in \widetilde{O}^{+}(\unicode[STIX]{x1D6EC})$
such that
![]() $g(v)=w$
if and only if
$g(v)=w$
if and only if
![]() $v^{2}=w^{2}$
and
$v^{2}=w^{2}$
and
![]() $v^{\ast }=w^{\ast }$
.
$v^{\ast }=w^{\ast }$
.
Proposition 1.3.3. Let
![]() $(\unicode[STIX]{x1D6EC},\unicode[STIX]{x1D709})$
be a decorated
$(\unicode[STIX]{x1D6EC},\unicode[STIX]{x1D709})$
be a decorated
![]() $D$
-lattice of dimension
$D$
-lattice of dimension
![]() $N$
. The following hold.
$N$
. The following hold.
(1) There exists
 $v\in \unicode[STIX]{x1D6EC}$
such that
$v\in \unicode[STIX]{x1D6EC}$
such that
 $v^{2}=-2$
and
$v^{2}=-2$
and
 $\operatorname{div}(v)=1$
, and it is unique up to
$\operatorname{div}(v)=1$
, and it is unique up to
 $\unicode[STIX]{x1D6E4}_{\unicode[STIX]{x1D709}}$
(notice that
$\unicode[STIX]{x1D6E4}_{\unicode[STIX]{x1D709}}$
(notice that
 $v^{\ast }=0$
).
$v^{\ast }=0$
).(2) There exists
 $v\in \unicode[STIX]{x1D6EC}$
such that
$v\in \unicode[STIX]{x1D6EC}$
such that
 $v^{2}=-4$
,
$v^{2}=-4$
,
 $\operatorname{div}(v)=2$
, and
$\operatorname{div}(v)=2$
, and
 $v^{\ast }=\unicode[STIX]{x1D709}$
. Such a
$v^{\ast }=\unicode[STIX]{x1D709}$
. Such a
 $v$
is unique up to
$v$
is unique up to
 $\unicode[STIX]{x1D6E4}_{\unicode[STIX]{x1D709}}$
.
$\unicode[STIX]{x1D6E4}_{\unicode[STIX]{x1D709}}$
.(3) Let
 $a\in \{0,\ldots ,7\}$
be the residue mod
$a\in \{0,\ldots ,7\}$
be the residue mod
 $8$
of
$8$
of
 $N-2$
. There exists
$N-2$
. There exists
 $v\in \unicode[STIX]{x1D6EC}$
such that:
$v\in \unicode[STIX]{x1D6EC}$
such that:(3a)
 $v^{2}=-4a$
,
$v^{2}=-4a$
,
 $\operatorname{div}(v)=4$
, and
$\operatorname{div}(v)=4$
, and
 $v^{\ast }=\unicode[STIX]{x1D701}$
(or
$v^{\ast }=\unicode[STIX]{x1D701}$
(or
 $v^{\ast }=\unicode[STIX]{x1D701}^{\prime }$
) if
$v^{\ast }=\unicode[STIX]{x1D701}^{\prime }$
) if
 $N$
is odd;
$N$
is odd;(3b)
 $v^{2}=-a$
,
$v^{2}=-a$
,
 $\operatorname{div}(v)=2$
, and
$\operatorname{div}(v)=2$
, and
 $v^{\ast }=\unicode[STIX]{x1D701}$
(or
$v^{\ast }=\unicode[STIX]{x1D701}$
(or
 $v^{\ast }=\unicode[STIX]{x1D701}^{\prime }$
) if
$v^{\ast }=\unicode[STIX]{x1D701}^{\prime }$
) if
 $N$
is even.
$N$
is even.
Such a
 $v$
is unique up to
$v$
is unique up to
 $\unicode[STIX]{x1D6E4}_{\unicode[STIX]{x1D709}}$
(recall that
$\unicode[STIX]{x1D6E4}_{\unicode[STIX]{x1D709}}$
(recall that
 $\unicode[STIX]{x1D6E4}_{\unicode[STIX]{x1D709}}$
exchanges
$\unicode[STIX]{x1D6E4}_{\unicode[STIX]{x1D709}}$
exchanges
 $\unicode[STIX]{x1D701}$
and
$\unicode[STIX]{x1D701}$
and
 $\unicode[STIX]{x1D701}^{\prime }$
).
$\unicode[STIX]{x1D701}^{\prime }$
).
Proof. (1) and (2): Existence is obvious. Such a
![]() $v$
is unique up to
$v$
is unique up to
![]() $\widetilde{O}^{+}(\unicode[STIX]{x1D6EC})$
by Eichler’s criterion, and hence also up to
$\widetilde{O}^{+}(\unicode[STIX]{x1D6EC})$
by Eichler’s criterion, and hence also up to
![]() $\unicode[STIX]{x1D6E4}_{\unicode[STIX]{x1D709}}$
, because
$\unicode[STIX]{x1D6E4}_{\unicode[STIX]{x1D709}}$
, because
![]() $\widetilde{O}^{+}(\unicode[STIX]{x1D6EC})<\unicode[STIX]{x1D6E4}_{\unicode[STIX]{x1D709}}$
. (3): Let us prove existence. Assume first that
$\widetilde{O}^{+}(\unicode[STIX]{x1D6EC})<\unicode[STIX]{x1D6E4}_{\unicode[STIX]{x1D709}}$
. (3): Let us prove existence. Assume first that
![]() $N-2\not \equiv 0\hspace{0.6em}({\rm mod}\hspace{0.2em}8)$
and hence
$N-2\not \equiv 0\hspace{0.6em}({\rm mod}\hspace{0.2em}8)$
and hence
![]() $a\in \{1,\ldots ,7\}$
. Let
$a\in \{1,\ldots ,7\}$
. Let
![]() $N-2=8k+a$
; by Remark 1.1.4, we may identify
$N-2=8k+a$
; by Remark 1.1.4, we may identify
![]() $\unicode[STIX]{x1D6EC}$
with
$\unicode[STIX]{x1D6EC}$
with
![]() $\text{II}_{2,2+8k}\oplus D_{a}$
. If
$\text{II}_{2,2+8k}\oplus D_{a}$
. If
![]() $N$
is odd, the vector
$N$
is odd, the vector
![]() $v:=(0_{4+8k},(2,\ldots ,2))\in \unicode[STIX]{x1D6EC}_{N}$
satisfies (3a) and, if
$v:=(0_{4+8k},(2,\ldots ,2))\in \unicode[STIX]{x1D6EC}_{N}$
satisfies (3a) and, if
![]() $N$
is even, the vector
$N$
is even, the vector
![]() $v:=(0_{4+8k},(1,\ldots ,1))\in \unicode[STIX]{x1D6EC}_{N}$
satisfies (3b). If
$v:=(0_{4+8k},(1,\ldots ,1))\in \unicode[STIX]{x1D6EC}_{N}$
satisfies (3b). If
![]() $N-2\equiv 0\hspace{0.6em}({\rm mod}\hspace{0.2em}8)$
, let
$N-2\equiv 0\hspace{0.6em}({\rm mod}\hspace{0.2em}8)$
, let
![]() $N=8k+2$
. Then
$N=8k+2$
. Then
![]() $\unicode[STIX]{x1D6EC}\cong \text{II}_{1,1+8k}\oplus U(2)$
by Theorem 1.13.2 of [Reference NikulinNik80]. With this identification understood, Item (3b) holds for
$\unicode[STIX]{x1D6EC}\cong \text{II}_{1,1+8k}\oplus U(2)$
by Theorem 1.13.2 of [Reference NikulinNik80]. With this identification understood, Item (3b) holds for
![]() $v:=(0_{2+8k},e)\in \unicode[STIX]{x1D6EC}$
, where
$v:=(0_{2+8k},e)\in \unicode[STIX]{x1D6EC}$
, where
![]() $e\in U(2)$
is a primitive isotropic vector. Lastly, we prove unicity of
$e\in U(2)$
is a primitive isotropic vector. Lastly, we prove unicity of
![]() $v$
up to
$v$
up to
![]() $\unicode[STIX]{x1D6E4}_{\unicode[STIX]{x1D709}}$
. Let
$\unicode[STIX]{x1D6E4}_{\unicode[STIX]{x1D709}}$
. Let
![]() $v_{1},v_{2}$
be two vectors such that (3a) holds for both, or (3b) holds for both. If
$v_{1},v_{2}$
be two vectors such that (3a) holds for both, or (3b) holds for both. If
![]() $v_{1}^{\ast }=v_{2}^{\ast }$
, then
$v_{1}^{\ast }=v_{2}^{\ast }$
, then
![]() $v_{1},v_{2}$
are
$v_{1},v_{2}$
are
![]() $\widetilde{O}^{+}(\unicode[STIX]{x1D6EC})$
-equivalent by Eichler’s criterion and hence they are
$\widetilde{O}^{+}(\unicode[STIX]{x1D6EC})$
-equivalent by Eichler’s criterion and hence they are
![]() $\unicode[STIX]{x1D6E4}_{\unicode[STIX]{x1D709}}$
-equivalent because
$\unicode[STIX]{x1D6E4}_{\unicode[STIX]{x1D709}}$
-equivalent because
![]() $\widetilde{O}^{+}(\unicode[STIX]{x1D6EC})<\unicode[STIX]{x1D6E4}_{\unicode[STIX]{x1D709}}$
. If
$\widetilde{O}^{+}(\unicode[STIX]{x1D6EC})<\unicode[STIX]{x1D6E4}_{\unicode[STIX]{x1D709}}$
. If
![]() $v_{1}^{\ast }\not =v_{2}^{\ast }$
, then
$v_{1}^{\ast }\not =v_{2}^{\ast }$
, then
![]() $\{v_{1}^{\ast },v_{2}^{\ast }\}=\{\unicode[STIX]{x1D701},\unicode[STIX]{x1D701}^{\prime }\}$
and hence by Remark 1.3.1 there exists
$\{v_{1}^{\ast },v_{2}^{\ast }\}=\{\unicode[STIX]{x1D701},\unicode[STIX]{x1D701}^{\prime }\}$
and hence by Remark 1.3.1 there exists
![]() $g\in \unicode[STIX]{x1D6E4}_{\unicode[STIX]{x1D709}}$
such that
$g\in \unicode[STIX]{x1D6E4}_{\unicode[STIX]{x1D709}}$
such that
![]() $g(v_{2})^{\ast }=v_{1}^{\ast }$
; thus,
$g(v_{2})^{\ast }=v_{1}^{\ast }$
; thus,
![]() $v_{1},v_{2}$
are
$v_{1},v_{2}$
are
![]() $\unicode[STIX]{x1D6E4}_{\unicode[STIX]{x1D709}}$
-equivalent by Eichler’s criterion.◻
$\unicode[STIX]{x1D6E4}_{\unicode[STIX]{x1D709}}$
-equivalent by Eichler’s criterion.◻
Below is a key definition for all that follows.
Definition 1.3.4. Let
![]() $(\unicode[STIX]{x1D6EC},\unicode[STIX]{x1D709})$
be a decorated
$(\unicode[STIX]{x1D6EC},\unicode[STIX]{x1D709})$
be a decorated
![]() $D$
-lattice.
$D$
-lattice.
(1) A vector
 $v\in \unicode[STIX]{x1D6EC}$
is nodal if Item (1) of Proposition 1.3.3 holds. The nodal pre-Heegner divisor and the nodal Heegner divisor are
$v\in \unicode[STIX]{x1D6EC}$
is nodal if Item (1) of Proposition 1.3.3 holds. The nodal pre-Heegner divisor and the nodal Heegner divisor are
 $\mathscr{H}_{v,\unicode[STIX]{x1D6EC}}(\unicode[STIX]{x1D6E4}_{\unicode[STIX]{x1D709}})$
and
$\mathscr{H}_{v,\unicode[STIX]{x1D6EC}}(\unicode[STIX]{x1D6E4}_{\unicode[STIX]{x1D709}})$
and
 $H_{v,\unicode[STIX]{x1D6EC}}(\unicode[STIX]{x1D6E4}_{\unicode[STIX]{x1D709}})$
, respectively, where
$H_{v,\unicode[STIX]{x1D6EC}}(\unicode[STIX]{x1D6E4}_{\unicode[STIX]{x1D709}})$
, respectively, where
 $v\in \unicode[STIX]{x1D6EC}$
is a nodal vector. We will denote them by
$v\in \unicode[STIX]{x1D6EC}$
is a nodal vector. We will denote them by
 $\mathscr{H}_{n}(\unicode[STIX]{x1D6EC},\unicode[STIX]{x1D709})$
and
$\mathscr{H}_{n}(\unicode[STIX]{x1D6EC},\unicode[STIX]{x1D709})$
and
 $H_{n}(\unicode[STIX]{x1D6EC},\unicode[STIX]{x1D709})$
, respectively.
$H_{n}(\unicode[STIX]{x1D6EC},\unicode[STIX]{x1D709})$
, respectively.(2) A vector
 $v\in \unicode[STIX]{x1D6EC}$
is hyperelliptic if Item (2) of Proposition 1.3.3 holds. The hyperelliptic pre-Heegner divisor and the hyperelliptic Heegner divisor are
$v\in \unicode[STIX]{x1D6EC}$
is hyperelliptic if Item (2) of Proposition 1.3.3 holds. The hyperelliptic pre-Heegner divisor and the hyperelliptic Heegner divisor are
 $\mathscr{H}_{v,\unicode[STIX]{x1D6EC}}(\unicode[STIX]{x1D6E4}_{\unicode[STIX]{x1D709}})$
and
$\mathscr{H}_{v,\unicode[STIX]{x1D6EC}}(\unicode[STIX]{x1D6E4}_{\unicode[STIX]{x1D709}})$
and
 $H_{v,\unicode[STIX]{x1D6EC}}(\unicode[STIX]{x1D6E4}_{\unicode[STIX]{x1D709}})$
, respectively, where
$H_{v,\unicode[STIX]{x1D6EC}}(\unicode[STIX]{x1D6E4}_{\unicode[STIX]{x1D709}})$
, respectively, where
 $v\in \unicode[STIX]{x1D6EC}$
is a hyperelliptic vector. We will denote them by
$v\in \unicode[STIX]{x1D6EC}$
is a hyperelliptic vector. We will denote them by
 $\mathscr{H}_{h}(\unicode[STIX]{x1D6EC},\unicode[STIX]{x1D709})$
and
$\mathscr{H}_{h}(\unicode[STIX]{x1D6EC},\unicode[STIX]{x1D709})$
and
 $H_{h}(\unicode[STIX]{x1D6EC},\unicode[STIX]{x1D709})$
, respectively.
$H_{h}(\unicode[STIX]{x1D6EC},\unicode[STIX]{x1D709})$
, respectively.(3) A vector
 $v\in \unicode[STIX]{x1D6EC}$
is unigonal if Item (3) of Proposition 1.3.3 holds. The unigonal pre-Heegner divisor and the unigonal Heegner divisor are
$v\in \unicode[STIX]{x1D6EC}$
is unigonal if Item (3) of Proposition 1.3.3 holds. The unigonal pre-Heegner divisor and the unigonal Heegner divisor are
 $\mathscr{H}_{v,\unicode[STIX]{x1D6EC}}(\unicode[STIX]{x1D6E4}_{\unicode[STIX]{x1D709}})$
and
$\mathscr{H}_{v,\unicode[STIX]{x1D6EC}}(\unicode[STIX]{x1D6E4}_{\unicode[STIX]{x1D709}})$
and
 $H_{v,\unicode[STIX]{x1D6EC}}(\unicode[STIX]{x1D6E4}_{\unicode[STIX]{x1D709}})$
, respectively, where
$H_{v,\unicode[STIX]{x1D6EC}}(\unicode[STIX]{x1D6E4}_{\unicode[STIX]{x1D709}})$
, respectively, where
 $v\in \unicode[STIX]{x1D6EC}$
is a unigonal vector. We will denote them by
$v\in \unicode[STIX]{x1D6EC}$
is a unigonal vector. We will denote them by
 $\mathscr{H}_{u}(\unicode[STIX]{x1D6EC},\unicode[STIX]{x1D709})$
and
$\mathscr{H}_{u}(\unicode[STIX]{x1D6EC},\unicode[STIX]{x1D709})$
and
 $H_{u}(\unicode[STIX]{x1D6EC},\unicode[STIX]{x1D709})$
, respectively. Notice that if
$H_{u}(\unicode[STIX]{x1D6EC},\unicode[STIX]{x1D709})$
, respectively. Notice that if
 $N\equiv 2\hspace{0.6em}({\rm mod}\hspace{0.2em}8)$
, then
$N\equiv 2\hspace{0.6em}({\rm mod}\hspace{0.2em}8)$
, then
 $\mathscr{H}_{u}(\unicode[STIX]{x1D6EC},\unicode[STIX]{x1D709})=0$
and
$\mathscr{H}_{u}(\unicode[STIX]{x1D6EC},\unicode[STIX]{x1D709})=0$
and
 $H_{u}(\unicode[STIX]{x1D6EC},\unicode[STIX]{x1D709})=0$
because
$H_{u}(\unicode[STIX]{x1D6EC},\unicode[STIX]{x1D709})=0$
because
 $v^{2}=0$
.
$v^{2}=0$
.
(The definition makes sense because by Proposition 1.3.3 there is a single
![]() $\unicode[STIX]{x1D6E4}_{\unicode[STIX]{x1D709}}$
-orbit of nodal, hyperelliptic, or unigonal vectors.)
$\unicode[STIX]{x1D6E4}_{\unicode[STIX]{x1D709}}$
-orbit of nodal, hyperelliptic, or unigonal vectors.)
1.3.3 Reflective Heegner divisors and the boundary of
 $D$
period spaces
$D$
period spaces
Proposition 1.3.5. Let
![]() $(\unicode[STIX]{x1D6EC},\unicode[STIX]{x1D709})$
be a dimension-
$(\unicode[STIX]{x1D6EC},\unicode[STIX]{x1D709})$
be a dimension-
![]() $N$
decorated
$N$
decorated
![]() $D$
-lattice. Let
$D$
-lattice. Let
![]() $v\in \unicode[STIX]{x1D6EC}$
be primitive, of negative square, i.e.
$v\in \unicode[STIX]{x1D6EC}$
be primitive, of negative square, i.e.
![]() $v^{2}<0$
. The reflection
$v^{2}<0$
. The reflection
![]() $\unicode[STIX]{x1D70C}_{v}$
(see (1.2.1)) belongs to
$\unicode[STIX]{x1D70C}_{v}$
(see (1.2.1)) belongs to
![]() $\unicode[STIX]{x1D6E4}_{\unicode[STIX]{x1D709}}$
(i.e.
$\unicode[STIX]{x1D6E4}_{\unicode[STIX]{x1D709}}$
(i.e.
![]() $v$
is a reflective vector of
$v$
is a reflective vector of
![]() $(\unicode[STIX]{x1D6EC},\unicode[STIX]{x1D709})$
) if and only if
$(\unicode[STIX]{x1D6EC},\unicode[STIX]{x1D709})$
) if and only if
![]() $v$
is either nodal or hyperelliptic, or
$v$
is either nodal or hyperelliptic, or
![]() $N\equiv 3,4\hspace{0.6em}({\rm mod}\hspace{0.2em}8)$
and
$N\equiv 3,4\hspace{0.6em}({\rm mod}\hspace{0.2em}8)$
and
![]() $v$
is unigonal.
$v$
is unigonal.
Proof. Assume that
![]() $\unicode[STIX]{x1D70C}_{v}$
belongs to
$\unicode[STIX]{x1D70C}_{v}$
belongs to
![]() $\unicode[STIX]{x1D6E4}_{\unicode[STIX]{x1D709}}$
. Since
$\unicode[STIX]{x1D6E4}_{\unicode[STIX]{x1D709}}$
. Since
![]() $\unicode[STIX]{x1D70C}_{v}(\unicode[STIX]{x1D6EC})=\unicode[STIX]{x1D6EC}$
, it follows that
$\unicode[STIX]{x1D70C}_{v}(\unicode[STIX]{x1D6EC})=\unicode[STIX]{x1D6EC}$
, it follows that
![]() $v^{2}|2\operatorname{div}(v)$
(see Example 1.2.1). On the other hand,
$v^{2}|2\operatorname{div}(v)$
(see Example 1.2.1). On the other hand,
![]() $A_{\unicode[STIX]{x1D6EC}}$
is isomorphic to
$A_{\unicode[STIX]{x1D6EC}}$
is isomorphic to
![]() $\mathbb{Z}/(4)$
if
$\mathbb{Z}/(4)$
if
![]() $N$
is odd and to the Klein group if
$N$
is odd and to the Klein group if
![]() $N$
is even. Thus, one of the following holds:
$N$
is even. Thus, one of the following holds:
(a)
 $v^{2}=-2$
and
$v^{2}=-2$
and
 $\operatorname{div}(v)\in \{1,2,4\}$
;
$\operatorname{div}(v)\in \{1,2,4\}$
;(b)
 $v^{2}=-4$
and
$v^{2}=-4$
and
 $\operatorname{div}(v)\in \{2,4\}$
;
$\operatorname{div}(v)\in \{2,4\}$
;(c)
 $v^{2}=-8$
and
$v^{2}=-8$
and
 $\operatorname{div}(v)=4$
.
$\operatorname{div}(v)=4$
.
Suppose that Item (a) holds. If
![]() $\operatorname{div}(v)=1$
, then
$\operatorname{div}(v)=1$
, then
![]() $v$
is nodal. Thus,
$v$
is nodal. Thus,
![]() $\unicode[STIX]{x1D70C}_{v}\in \widetilde{O}^{+}(\unicode[STIX]{x1D6EC})$
by Example 1.2.1 and hence
$\unicode[STIX]{x1D70C}_{v}\in \widetilde{O}^{+}(\unicode[STIX]{x1D6EC})$
by Example 1.2.1 and hence
![]() $\unicode[STIX]{x1D70C}_{v}\in \unicode[STIX]{x1D6E4}_{\unicode[STIX]{x1D709}}$
. If
$\unicode[STIX]{x1D70C}_{v}\in \unicode[STIX]{x1D6E4}_{\unicode[STIX]{x1D709}}$
. If
![]() $\operatorname{div}(v)=2$
, then
$\operatorname{div}(v)=2$
, then
![]() $q_{\unicode[STIX]{x1D6EC}}(v^{\ast })\equiv -1/2\hspace{0.6em}({\rm mod}\hspace{0.2em}2\mathbb{Z})$
. By (1.1.4), Claim 1.1.1, and (1.1.2), it follows that
$q_{\unicode[STIX]{x1D6EC}}(v^{\ast })\equiv -1/2\hspace{0.6em}({\rm mod}\hspace{0.2em}2\mathbb{Z})$
. By (1.1.4), Claim 1.1.1, and (1.1.2), it follows that
![]() $N\equiv 4\hspace{0.6em}({\rm mod}\hspace{0.2em}8)$
, and
$N\equiv 4\hspace{0.6em}({\rm mod}\hspace{0.2em}8)$
, and
![]() $v$
is unigonal. In particular,
$v$
is unigonal. In particular,
![]() $\unicode[STIX]{x1D6E4}_{\unicode[STIX]{x1D709}}=O^{+}(\unicode[STIX]{x1D6EC})$
by Proposition 1.2.3 and hence
$\unicode[STIX]{x1D6E4}_{\unicode[STIX]{x1D709}}=O^{+}(\unicode[STIX]{x1D6EC})$
by Proposition 1.2.3 and hence
![]() $\unicode[STIX]{x1D70C}_{v}\in \unicode[STIX]{x1D6E4}_{\unicode[STIX]{x1D709}}$
because
$\unicode[STIX]{x1D70C}_{v}\in \unicode[STIX]{x1D6E4}_{\unicode[STIX]{x1D709}}$
because
![]() $\unicode[STIX]{x1D70C}_{v}\in O^{+}(\unicode[STIX]{x1D6EC})$
. If
$\unicode[STIX]{x1D70C}_{v}\in O^{+}(\unicode[STIX]{x1D6EC})$
. If
![]() $\operatorname{div}(v)=4$
, then
$\operatorname{div}(v)=4$
, then
![]() $q_{\unicode[STIX]{x1D6EC}}(v^{\ast })\equiv -1/8\hspace{0.6em}({\rm mod}\hspace{0.2em}2\mathbb{Z})$
. On the other hand,
$q_{\unicode[STIX]{x1D6EC}}(v^{\ast })\equiv -1/8\hspace{0.6em}({\rm mod}\hspace{0.2em}2\mathbb{Z})$
. On the other hand,
![]() $N$
is odd because
$N$
is odd because
![]() $\operatorname{div}(v)=4$
and hence by (1.1.4), Claim 1.1.1, and (1.1.2), it follows that
$\operatorname{div}(v)=4$
and hence by (1.1.4), Claim 1.1.1, and (1.1.2), it follows that
![]() $-(N-2)/4\equiv -1/8\hspace{0.6em}({\rm mod}\hspace{0.2em}2\mathbb{Z})$
, which is absurd. Thus, the case
$-(N-2)/4\equiv -1/8\hspace{0.6em}({\rm mod}\hspace{0.2em}2\mathbb{Z})$
, which is absurd. Thus, the case
![]() $v^{2}=-2$
and
$v^{2}=-2$
and
![]() $\operatorname{div}(v)=4$
does not occur.
$\operatorname{div}(v)=4$
does not occur.
Now suppose that Item (b) holds. If
![]() $\operatorname{div}(v)=2$
, then either
$\operatorname{div}(v)=2$
, then either
![]() $v$
is hyperelliptic or
$v$
is hyperelliptic or
![]() $N\equiv 6\hspace{0.6em}({\rm mod}\hspace{0.2em}8)$
. If
$N\equiv 6\hspace{0.6em}({\rm mod}\hspace{0.2em}8)$
. If
![]() $v$
is hyperelliptic, then
$v$
is hyperelliptic, then
![]() $\unicode[STIX]{x1D70C}_{v}\in O^{+}(\unicode[STIX]{x1D6EC})$
by Example 1.2.1. Since
$\unicode[STIX]{x1D70C}_{v}\in O^{+}(\unicode[STIX]{x1D6EC})$
by Example 1.2.1. Since
![]() $\unicode[STIX]{x1D70C}_{v}(v)=-v$
and
$\unicode[STIX]{x1D70C}_{v}(v)=-v$
and
![]() $\unicode[STIX]{x1D709}=v^{\ast }$
, the reflection
$\unicode[STIX]{x1D709}=v^{\ast }$
, the reflection
![]() $\unicode[STIX]{x1D70C}_{v}$
fixes the
$\unicode[STIX]{x1D70C}_{v}$
fixes the
![]() $2$
-torsion element
$2$
-torsion element
![]() $\unicode[STIX]{x1D709}$
and hence belongs to
$\unicode[STIX]{x1D709}$
and hence belongs to
![]() $\unicode[STIX]{x1D6E4}_{\unicode[STIX]{x1D709}}$
. If, on the other hand,
$\unicode[STIX]{x1D6E4}_{\unicode[STIX]{x1D709}}$
. If, on the other hand,
![]() $N\equiv 6\hspace{0.6em}({\rm mod}\hspace{0.2em}8)$
and
$N\equiv 6\hspace{0.6em}({\rm mod}\hspace{0.2em}8)$
and
![]() $v$
is not hyperelliptic, we may assume that
$v$
is not hyperelliptic, we may assume that
![]() $v^{\ast }=\unicode[STIX]{x1D701}$
. Then
$v^{\ast }=\unicode[STIX]{x1D701}$
. Then
![]() $\unicode[STIX]{x1D70C}_{v}(\unicode[STIX]{x1D709})=\unicode[STIX]{x1D701}^{\prime }$
(let
$\unicode[STIX]{x1D70C}_{v}(\unicode[STIX]{x1D709})=\unicode[STIX]{x1D701}^{\prime }$
(let
![]() $N=8k+6$
, so that
$N=8k+6$
, so that
![]() $\unicode[STIX]{x1D6EC}\cong \text{II}_{2,2+8k}\oplus D_{4}$
, and compute) and hence
$\unicode[STIX]{x1D6EC}\cong \text{II}_{2,2+8k}\oplus D_{4}$
, and compute) and hence
![]() $\unicode[STIX]{x1D70C}_{v}\notin \unicode[STIX]{x1D6E4}_{\unicode[STIX]{x1D709}}$
. If
$\unicode[STIX]{x1D70C}_{v}\notin \unicode[STIX]{x1D6E4}_{\unicode[STIX]{x1D709}}$
. If
![]() $\operatorname{div}(v)=4$
, then
$\operatorname{div}(v)=4$
, then
![]() $q_{\unicode[STIX]{x1D6EC}}(v^{\ast })\equiv -1/4\hspace{0.6em}({\rm mod}\hspace{0.2em}2\mathbb{Z})$
. By (1.1.4), Claim 1.1.1, and (1.1.2), it follows that
$q_{\unicode[STIX]{x1D6EC}}(v^{\ast })\equiv -1/4\hspace{0.6em}({\rm mod}\hspace{0.2em}2\mathbb{Z})$
. By (1.1.4), Claim 1.1.1, and (1.1.2), it follows that
![]() $N\equiv 3\hspace{0.6em}({\rm mod}\hspace{0.2em}8)$
, and
$N\equiv 3\hspace{0.6em}({\rm mod}\hspace{0.2em}8)$
, and
![]() $v$
is unigonal. Then
$v$
is unigonal. Then
![]() $\unicode[STIX]{x1D6E4}_{\unicode[STIX]{x1D709}}=O^{+}(\unicode[STIX]{x1D6EC})$
by Proposition 1.2.3 and hence
$\unicode[STIX]{x1D6E4}_{\unicode[STIX]{x1D709}}=O^{+}(\unicode[STIX]{x1D6EC})$
by Proposition 1.2.3 and hence
![]() $\unicode[STIX]{x1D70C}_{v}\in \unicode[STIX]{x1D6E4}_{\unicode[STIX]{x1D709}}$
because
$\unicode[STIX]{x1D70C}_{v}\in \unicode[STIX]{x1D6E4}_{\unicode[STIX]{x1D709}}$
because
![]() $\unicode[STIX]{x1D70C}_{v}\in O^{+}(\unicode[STIX]{x1D6EC})$
.
$\unicode[STIX]{x1D70C}_{v}\in O^{+}(\unicode[STIX]{x1D6EC})$
.
Lastly, let us show that Item (c) cannot hold. In fact,
![]() $q_{\unicode[STIX]{x1D6EC}}(v^{\ast })\equiv -1/2\hspace{0.6em}({\rm mod}\hspace{0.2em}2\mathbb{Z})$
, and
$q_{\unicode[STIX]{x1D6EC}}(v^{\ast })\equiv -1/2\hspace{0.6em}({\rm mod}\hspace{0.2em}2\mathbb{Z})$
, and
![]() $N$
is odd because
$N$
is odd because
![]() $\operatorname{div}(v)=4$
; by (1.1.4), Claim 1.1.1, and (1.1.2), it follows that
$\operatorname{div}(v)=4$
; by (1.1.4), Claim 1.1.1, and (1.1.2), it follows that
![]() $-(N-2)/4\equiv -1/2\hspace{0.6em}({\rm mod}\hspace{0.2em}2\mathbb{Z})$
, which is absurd.◻
$-(N-2)/4\equiv -1/2\hspace{0.6em}({\rm mod}\hspace{0.2em}2\mathbb{Z})$
, which is absurd.◻
The following definition of the boundary divisor
![]() $\unicode[STIX]{x1D6E5}$
is motivated by the discussion of § 4.
$\unicode[STIX]{x1D6E5}$
is motivated by the discussion of § 4.
Definition 1.3.6. Let
![]() $(\unicode[STIX]{x1D6EC},\unicode[STIX]{x1D709})$
be a decorated
$(\unicode[STIX]{x1D6EC},\unicode[STIX]{x1D709})$
be a decorated
![]() $D$
-lattice of dimension
$D$
-lattice of dimension
![]() $N$
. Let
$N$
. Let
![]() $\unicode[STIX]{x1D6E5}(\unicode[STIX]{x1D6EC},\unicode[STIX]{x1D709})$
be the
$\unicode[STIX]{x1D6E5}(\unicode[STIX]{x1D6EC},\unicode[STIX]{x1D709})$
be the
![]() $\mathbb{Q}$
-Cartier divisor on
$\mathbb{Q}$
-Cartier divisor on
![]() $\mathscr{F}(\unicode[STIX]{x1D6EC},\unicode[STIX]{x1D709})$
defined as
$\mathscr{F}(\unicode[STIX]{x1D6EC},\unicode[STIX]{x1D709})$
defined as
1.3.4 Heegner divisors for the stable orthogonal group
Let
![]() $(\unicode[STIX]{x1D6EC},\unicode[STIX]{x1D709})$
be a dimension-
$(\unicode[STIX]{x1D6EC},\unicode[STIX]{x1D709})$
be a dimension-
![]() $N$
decorated
$N$
decorated
![]() $D$
-lattice. The main object of study in this paper is the geometry of the locally symmetric variety
$D$
-lattice. The main object of study in this paper is the geometry of the locally symmetric variety
![]() $\mathscr{F}_{\unicode[STIX]{x1D6EC}}(\unicode[STIX]{x1D6E4}_{\unicode[STIX]{x1D709}})$
. (The reason for this is the inductive behavior described in § 1.7.) It is more standard to discard the decoration
$\mathscr{F}_{\unicode[STIX]{x1D6EC}}(\unicode[STIX]{x1D6E4}_{\unicode[STIX]{x1D709}})$
. (The reason for this is the inductive behavior described in § 1.7.) It is more standard to discard the decoration
![]() $\unicode[STIX]{x1D709}$
and consider
$\unicode[STIX]{x1D709}$
and consider
![]() $\mathscr{F}_{\unicode[STIX]{x1D6EC}}(\widetilde{O}^{+}(\unicode[STIX]{x1D6EC}))$
, the variety associated to the stable orthogonal group. If
$\mathscr{F}_{\unicode[STIX]{x1D6EC}}(\widetilde{O}^{+}(\unicode[STIX]{x1D6EC}))$
, the variety associated to the stable orthogonal group. If
![]() $N$
is odd,
$N$
is odd,
![]() $\mathscr{F}_{\unicode[STIX]{x1D6EC}}(\widetilde{O}^{+}(\unicode[STIX]{x1D6EC}))\cong \mathscr{F}_{\unicode[STIX]{x1D6EC}}(\unicode[STIX]{x1D6E4}_{\unicode[STIX]{x1D709}})$
and there is nothing to be said. On the other hand, if
$\mathscr{F}_{\unicode[STIX]{x1D6EC}}(\widetilde{O}^{+}(\unicode[STIX]{x1D6EC}))\cong \mathscr{F}_{\unicode[STIX]{x1D6EC}}(\unicode[STIX]{x1D6E4}_{\unicode[STIX]{x1D709}})$
and there is nothing to be said. On the other hand, if
![]() $N$
is even, then
$N$
is even, then
![]() $\unicode[STIX]{x1D6E4}_{\unicode[STIX]{x1D709}}$
is an index-
$\unicode[STIX]{x1D6E4}_{\unicode[STIX]{x1D709}}$
is an index-
![]() $2$
subgroup of
$2$
subgroup of
![]() $\widetilde{O}^{+}(\unicode[STIX]{x1D6EC})$
(see Proposition 1.2.3) and hence we have a double cover map
$\widetilde{O}^{+}(\unicode[STIX]{x1D6EC})$
(see Proposition 1.2.3) and hence we have a double cover map
We will describe the inverse image by
![]() $\unicode[STIX]{x1D70C}$
of the Heegner divisors
$\unicode[STIX]{x1D70C}$
of the Heegner divisors
![]() $H_{n}$
,
$H_{n}$
,
![]() $H_{h}$
, and
$H_{h}$
, and
![]() $H_{u}$
.
$H_{u}$
.
Definition 1.3.7. Let
![]() $\unicode[STIX]{x1D6EC}$
be a dimension-
$\unicode[STIX]{x1D6EC}$
be a dimension-
![]() $N$
$N$
![]() $D$
-lattice. A minimal norm vector of
$D$
-lattice. A minimal norm vector of
![]() $\unicode[STIX]{x1D6EC}$
is a
$\unicode[STIX]{x1D6EC}$
is a
![]() $v\in \unicode[STIX]{x1D6EC}$
such that one of the following holds:
$v\in \unicode[STIX]{x1D6EC}$
such that one of the following holds:
(1)
 $v^{2}=-2$
and
$v^{2}=-2$
and
 $\operatorname{div}(v)=1$
; or
$\operatorname{div}(v)=1$
; or(2)
 $v^{2}=-4$
and
$v^{2}=-4$
and
 $\operatorname{div}(v)=2$
; or
$\operatorname{div}(v)=2$
; or(3)
 $(N-2)\not \equiv 0\hspace{0.6em}({\rm mod}\hspace{0.2em}8)$
and, letting
$(N-2)\not \equiv 0\hspace{0.6em}({\rm mod}\hspace{0.2em}8)$
and, letting
 $a$
be the residue of
$a$
be the residue of
 $(N-2)$
modulo
$(N-2)$
modulo
 $8$
:
$8$
:(3a)
 $v^{2}=-4a$
and
$v^{2}=-4a$
and
 $\operatorname{div}(v)=4$
if
$\operatorname{div}(v)=4$
if
 $N$
is odd; or else
$N$
is odd; or else(3b)
 $v^{2}=-a$
and
$v^{2}=-a$
and
 $\operatorname{div}(v)=2$
if
$\operatorname{div}(v)=2$
if
 $N$
is even.
$N$
is even.
Remark 1.3.8. Given
![]() $\unicode[STIX]{x1D702}\in A_{\unicode[STIX]{x1D6EC}}$
, there exists a minimal norm vector
$\unicode[STIX]{x1D702}\in A_{\unicode[STIX]{x1D6EC}}$
, there exists a minimal norm vector
![]() $v\in \unicode[STIX]{x1D6EC}$
such that
$v\in \unicode[STIX]{x1D6EC}$
such that
![]() $v^{\ast }=\unicode[STIX]{x1D702}$
and, by Eichler’s criterion (Proposition 1.3.2) the set of such minimal norm vectors is a single
$v^{\ast }=\unicode[STIX]{x1D702}$
and, by Eichler’s criterion (Proposition 1.3.2) the set of such minimal norm vectors is a single
![]() $\widetilde{O}^{+}(\unicode[STIX]{x1D6EC})$
-orbit. If
$\widetilde{O}^{+}(\unicode[STIX]{x1D6EC})$
-orbit. If
![]() $u\in \unicode[STIX]{x1D6EC}$
is another vector such that
$u\in \unicode[STIX]{x1D6EC}$
is another vector such that
![]() $u^{2}<0$
and
$u^{2}<0$
and
![]() $u^{\ast }=\unicode[STIX]{x1D702}$
, then
$u^{\ast }=\unicode[STIX]{x1D702}$
, then
![]() $u^{2}\leqslant v^{2}$
; this is the reason for our choice of terminology.
$u^{2}\leqslant v^{2}$
; this is the reason for our choice of terminology.
Definition 1.3.9. Let
![]() $\unicode[STIX]{x1D6EC}$
be a dimension-
$\unicode[STIX]{x1D6EC}$
be a dimension-
![]() $N$
$N$
![]() $D$
-lattice and
$D$
-lattice and
![]() $\unicode[STIX]{x1D702}\in A_{\unicode[STIX]{x1D6EC}}$
. We let
$\unicode[STIX]{x1D702}\in A_{\unicode[STIX]{x1D6EC}}$
. We let
where
![]() $v\in \unicode[STIX]{x1D6EC}$
is any minimal norm vector such that
$v\in \unicode[STIX]{x1D6EC}$
is any minimal norm vector such that
![]() $v^{\ast }=\unicode[STIX]{x1D702}$
. (The definition makes sense by Remark 1.3.8.)
$v^{\ast }=\unicode[STIX]{x1D702}$
. (The definition makes sense by Remark 1.3.8.)
Remark 1.3.10. Let
![]() $\unicode[STIX]{x1D6EC}$
be a dimension-
$\unicode[STIX]{x1D6EC}$
be a dimension-
![]() $N$
$N$
![]() $D$
-lattice with
$D$
-lattice with
![]() $N$
odd. Choose a decoration
$N$
odd. Choose a decoration
![]() $\unicode[STIX]{x1D709}$
of
$\unicode[STIX]{x1D709}$
of
![]() $\unicode[STIX]{x1D6EC}$
and let
$\unicode[STIX]{x1D6EC}$
and let
![]() $A_{\unicode[STIX]{x1D6EC}}=\{\unicode[STIX]{x1D709},\unicode[STIX]{x1D701},\unicode[STIX]{x1D701}^{\prime }\}$
, as usual. Then, under the identification
$A_{\unicode[STIX]{x1D6EC}}=\{\unicode[STIX]{x1D709},\unicode[STIX]{x1D701},\unicode[STIX]{x1D701}^{\prime }\}$
, as usual. Then, under the identification
![]() $\mathscr{F}_{\unicode[STIX]{x1D6EC}}(\widetilde{O}^{+}(\unicode[STIX]{x1D6EC}))\cong \mathscr{F}_{\unicode[STIX]{x1D6EC}}(\unicode[STIX]{x1D6E4}_{\unicode[STIX]{x1D709}})$
, we have
$\mathscr{F}_{\unicode[STIX]{x1D6EC}}(\widetilde{O}^{+}(\unicode[STIX]{x1D6EC}))\cong \mathscr{F}_{\unicode[STIX]{x1D6EC}}(\unicode[STIX]{x1D6E4}_{\unicode[STIX]{x1D709}})$
, we have
![]() $H_{0}(\unicode[STIX]{x1D6EC})=H_{n}(\unicode[STIX]{x1D6EC},\unicode[STIX]{x1D709})$
,
$H_{0}(\unicode[STIX]{x1D6EC})=H_{n}(\unicode[STIX]{x1D6EC},\unicode[STIX]{x1D709})$
,
![]() $H_{\unicode[STIX]{x1D709}}(\unicode[STIX]{x1D6EC})=H_{h}(\unicode[STIX]{x1D6EC},\unicode[STIX]{x1D709})$
, and
$H_{\unicode[STIX]{x1D709}}(\unicode[STIX]{x1D6EC})=H_{h}(\unicode[STIX]{x1D6EC},\unicode[STIX]{x1D709})$
, and
![]() $H_{\unicode[STIX]{x1D701}}(\unicode[STIX]{x1D6EC})=H_{\unicode[STIX]{x1D701}^{\prime }}(\unicode[STIX]{x1D6EC})=H_{u}(\unicode[STIX]{x1D6EC},\unicode[STIX]{x1D709})$
(notice that
$H_{\unicode[STIX]{x1D701}}(\unicode[STIX]{x1D6EC})=H_{\unicode[STIX]{x1D701}^{\prime }}(\unicode[STIX]{x1D6EC})=H_{u}(\unicode[STIX]{x1D6EC},\unicode[STIX]{x1D709})$
(notice that
![]() $\unicode[STIX]{x1D701}^{\prime }=-\unicode[STIX]{x1D701}$
because
$\unicode[STIX]{x1D701}^{\prime }=-\unicode[STIX]{x1D701}$
because
![]() $N$
is odd).
$N$
is odd).
Proposition 1.3.11. Let
![]() $(\unicode[STIX]{x1D6EC},\unicode[STIX]{x1D709})$
be a dimension-
$(\unicode[STIX]{x1D6EC},\unicode[STIX]{x1D709})$
be a dimension-
![]() $N$
decorated
$N$
decorated
![]() $D$
-lattice and assume that
$D$
-lattice and assume that
![]() $N$
is even. Let
$N$
is even. Let
![]() $\unicode[STIX]{x1D70C}$
be the double covering in (1.3.6). Then (notation as in Remark 1.3.10)
$\unicode[STIX]{x1D70C}$
be the double covering in (1.3.6). Then (notation as in Remark 1.3.10)
Proof. Let
![]() $v$
be a hyperelliptic vector of
$v$
be a hyperelliptic vector of
![]() $(\unicode[STIX]{x1D6EC},\unicode[STIX]{x1D709})$
and let
$(\unicode[STIX]{x1D6EC},\unicode[STIX]{x1D709})$
and let
![]() $\unicode[STIX]{x1D70C}_{v}$
be the associated reflection. Then
$\unicode[STIX]{x1D70C}_{v}$
be the associated reflection. Then
![]() $\unicode[STIX]{x1D70C}_{v}\in \unicode[STIX]{x1D6E4}_{\unicode[STIX]{x1D709}}$
, but
$\unicode[STIX]{x1D70C}_{v}\in \unicode[STIX]{x1D6E4}_{\unicode[STIX]{x1D709}}$
, but
![]() $\unicode[STIX]{x1D70C}_{v}\not \in \widetilde{O}^{+}(\unicode[STIX]{x1D6EC})$
(see Remark 1.3.1). Thus, the class of
$\unicode[STIX]{x1D70C}_{v}\not \in \widetilde{O}^{+}(\unicode[STIX]{x1D6EC})$
(see Remark 1.3.1). Thus, the class of
![]() $\unicode[STIX]{x1D70C}_{v}$
in
$\unicode[STIX]{x1D70C}_{v}$
in
![]() $\unicode[STIX]{x1D6E4}_{\unicode[STIX]{x1D709}}/\widetilde{O}^{+}(\unicode[STIX]{x1D6EC})$
is the covering involution of
$\unicode[STIX]{x1D6E4}_{\unicode[STIX]{x1D709}}/\widetilde{O}^{+}(\unicode[STIX]{x1D6EC})$
is the covering involution of
![]() $\unicode[STIX]{x1D70C}$
. One may choose a nodal vector
$\unicode[STIX]{x1D70C}$
. One may choose a nodal vector
![]() $w$
of
$w$
of
![]() $(\unicode[STIX]{x1D6EC},\unicode[STIX]{x1D709})$
which is orthogonal to
$(\unicode[STIX]{x1D6EC},\unicode[STIX]{x1D709})$
which is orthogonal to
![]() $v$
. Then
$v$
. Then
![]() $\unicode[STIX]{x1D70C}_{v}$
acts non-trivially on
$\unicode[STIX]{x1D70C}_{v}$
acts non-trivially on
![]() $w^{\bot }\cap \mathscr{D}_{\unicode[STIX]{x1D6EC}}^{+}$
; it follows that the covering involution of
$w^{\bot }\cap \mathscr{D}_{\unicode[STIX]{x1D6EC}}^{+}$
; it follows that the covering involution of
![]() $\unicode[STIX]{x1D70C}$
maps
$\unicode[STIX]{x1D70C}$
maps
![]() $H_{0}(\unicode[STIX]{x1D6EC})$
to itself and is not the identity. The first equality of (1.3.7) follows from this. On the other hand,
$H_{0}(\unicode[STIX]{x1D6EC})$
to itself and is not the identity. The first equality of (1.3.7) follows from this. On the other hand,
![]() $\unicode[STIX]{x1D70C}_{v}$
acts trivially on
$\unicode[STIX]{x1D70C}_{v}$
acts trivially on
![]() $v^{\bot }\cap \mathscr{D}_{\unicode[STIX]{x1D6EC}}^{+}$
and the second equality of (1.3.7) follows. Lastly,
$v^{\bot }\cap \mathscr{D}_{\unicode[STIX]{x1D6EC}}^{+}$
and the second equality of (1.3.7) follows. Lastly,
![]() $\unicode[STIX]{x1D70C}_{v}$
switches the vectors
$\unicode[STIX]{x1D70C}_{v}$
switches the vectors
![]() $\unicode[STIX]{x1D701}$
and
$\unicode[STIX]{x1D701}$
and
![]() $\unicode[STIX]{x1D701}^{\prime }$
in
$\unicode[STIX]{x1D701}^{\prime }$
in
![]() $A_{\unicode[STIX]{x1D6EC}}$
(cf. Remark 1.3.1) and this proves the third equality of (1.3.7).◻
$A_{\unicode[STIX]{x1D6EC}}$
(cf. Remark 1.3.1) and this proves the third equality of (1.3.7).◻
Applying
![]() $\unicode[STIX]{x1D70C}_{\ast }$
to the equalities in (1.3.7), we get the following result.
$\unicode[STIX]{x1D70C}_{\ast }$
to the equalities in (1.3.7), we get the following result.
Corollary 1.3.12. Keep assumptions as in Proposition 1.3.11. Then
Below is the last result of the present subsection.
Claim 1.3.13. Let
![]() $\unicode[STIX]{x1D6EC}$
be a
$\unicode[STIX]{x1D6EC}$
be a
![]() $D$
-lattice. Choose a decoration
$D$
-lattice. Choose a decoration
![]() $\unicode[STIX]{x1D709}$
of
$\unicode[STIX]{x1D709}$
of
![]() $\unicode[STIX]{x1D6EC}$
and let
$\unicode[STIX]{x1D6EC}$
and let
![]() $A_{\unicode[STIX]{x1D6EC}}=\{\unicode[STIX]{x1D709},\unicode[STIX]{x1D701},\unicode[STIX]{x1D701}^{\prime }\}$
, as usual. Then, with respect to the group
$A_{\unicode[STIX]{x1D6EC}}=\{\unicode[STIX]{x1D709},\unicode[STIX]{x1D701},\unicode[STIX]{x1D701}^{\prime }\}$
, as usual. Then, with respect to the group
![]() $\widetilde{O}^{+}(\unicode[STIX]{x1D6EC}_{N})$
, the following hold:
$\widetilde{O}^{+}(\unicode[STIX]{x1D6EC}_{N})$
, the following hold:
(1)
 $H_{0}(\unicode[STIX]{x1D6EC})$
is a reflective Heegner divisor;
$H_{0}(\unicode[STIX]{x1D6EC})$
is a reflective Heegner divisor;(2)
 $H_{\unicode[STIX]{x1D709}}(\unicode[STIX]{x1D6EC})$
is reflective if and only if
$H_{\unicode[STIX]{x1D709}}(\unicode[STIX]{x1D6EC})$
is reflective if and only if
 $N$
is odd;
$N$
is odd;(3)
 $H_{\unicode[STIX]{x1D701}}(\unicode[STIX]{x1D6EC})$
is reflective if and only if
$H_{\unicode[STIX]{x1D701}}(\unicode[STIX]{x1D6EC})$
is reflective if and only if
 $N\equiv 3,4\hspace{0.6em}({\rm mod}\hspace{0.2em}8)$
, and similarly for
$N\equiv 3,4\hspace{0.6em}({\rm mod}\hspace{0.2em}8)$
, and similarly for
 $H_{\unicode[STIX]{x1D701}^{\prime }}(\unicode[STIX]{x1D6EC})$
.
$H_{\unicode[STIX]{x1D701}^{\prime }}(\unicode[STIX]{x1D6EC})$
.
Proof. If
![]() $N$
is odd, the result follows from Proposition 1.3.5 because
$N$
is odd, the result follows from Proposition 1.3.5 because
![]() $\mathscr{F}_{\unicode[STIX]{x1D6EC}}(\widetilde{O}^{+}(\unicode[STIX]{x1D6EC}))=\mathscr{F}_{\unicode[STIX]{x1D6EC}}(\unicode[STIX]{x1D6E4}_{\unicode[STIX]{x1D709}})$
. Suppose that
$\mathscr{F}_{\unicode[STIX]{x1D6EC}}(\widetilde{O}^{+}(\unicode[STIX]{x1D6EC}))=\mathscr{F}_{\unicode[STIX]{x1D6EC}}(\unicode[STIX]{x1D6E4}_{\unicode[STIX]{x1D709}})$
. Suppose that
![]() $N$
is even. Item (1) holds because the reflection associated to
$N$
is even. Item (1) holds because the reflection associated to
![]() $v\in \unicode[STIX]{x1D6EC}$
with
$v\in \unicode[STIX]{x1D6EC}$
with
![]() $v^{2}=-2$
and
$v^{2}=-2$
and
![]() $\operatorname{div}(v)=1$
belongs to
$\operatorname{div}(v)=1$
belongs to
![]() $\widetilde{O}^{+}(\unicode[STIX]{x1D6EC})$
. On the other hand, as noted above, if
$\widetilde{O}^{+}(\unicode[STIX]{x1D6EC})$
. On the other hand, as noted above, if
![]() $v$
is a hyperelliptic vector of
$v$
is a hyperelliptic vector of
![]() $(\unicode[STIX]{x1D6EC},\unicode[STIX]{x1D709})$
, then
$(\unicode[STIX]{x1D6EC},\unicode[STIX]{x1D709})$
, then
![]() $\pm \unicode[STIX]{x1D70C}_{v}\not \in \widetilde{O}^{+}(\unicode[STIX]{x1D6EC})$
and Item (2) follows. In order to prove Item (3), let
$\pm \unicode[STIX]{x1D70C}_{v}\not \in \widetilde{O}^{+}(\unicode[STIX]{x1D6EC})$
and Item (2) follows. In order to prove Item (3), let
![]() $\unicode[STIX]{x1D70C}$
be the double covering in (1.3.6). If
$\unicode[STIX]{x1D70C}$
be the double covering in (1.3.6). If
![]() $H_{\unicode[STIX]{x1D701}}(\unicode[STIX]{x1D6EC})$
is reflective, then
$H_{\unicode[STIX]{x1D701}}(\unicode[STIX]{x1D6EC})$
is reflective, then
![]() $\unicode[STIX]{x1D70C}_{\ast }$
is reflective as well and hence
$\unicode[STIX]{x1D70C}_{\ast }$
is reflective as well and hence
![]() $N\equiv 3,4\hspace{0.6em}({\rm mod}\hspace{0.2em}8)$
by Proposition 1.3.5. On the other hand, one easily checks that if
$N\equiv 3,4\hspace{0.6em}({\rm mod}\hspace{0.2em}8)$
by Proposition 1.3.5. On the other hand, one easily checks that if
![]() $N\equiv 3,4\hspace{0.6em}({\rm mod}\hspace{0.2em}8)$
, the reflection associated to a unigonal vector is in
$N\equiv 3,4\hspace{0.6em}({\rm mod}\hspace{0.2em}8)$
, the reflection associated to a unigonal vector is in
![]() $\widetilde{O}^{+}(\unicode[STIX]{x1D6EC})$
.◻
$\widetilde{O}^{+}(\unicode[STIX]{x1D6EC})$
.◻
1.4 Hyperelliptic Heegner divisors
We will prove that the hyperelliptic Heegner divisor
![]() $H_{h}(\unicode[STIX]{x1D6EC}_{N},\unicode[STIX]{x1D709}_{N})$
is isomorphic to
$H_{h}(\unicode[STIX]{x1D6EC}_{N},\unicode[STIX]{x1D709}_{N})$
is isomorphic to
![]() $\mathscr{F}(\unicode[STIX]{x1D6EC}_{N-1},\unicode[STIX]{x1D709}_{N-1})$
.
$\mathscr{F}(\unicode[STIX]{x1D6EC}_{N-1},\unicode[STIX]{x1D709}_{N-1})$
.
Lemma 1.4.1. Let
![]() $N\geqslant 4$
, let
$N\geqslant 4$
, let
![]() $(\unicode[STIX]{x1D6EC},\unicode[STIX]{x1D709})$
be a dimension-
$(\unicode[STIX]{x1D6EC},\unicode[STIX]{x1D709})$
be a dimension-
![]() $N$
decorated
$N$
decorated
![]() $D$
-lattice, and let
$D$
-lattice, and let
![]() $v\in \unicode[STIX]{x1D6EC}$
be a hyperelliptic vector. Then
$v\in \unicode[STIX]{x1D6EC}$
be a hyperelliptic vector. Then
![]() $v^{\bot }$
is a dimension-
$v^{\bot }$
is a dimension-
![]() $(N-1)$
$(N-1)$
![]() $D$
-lattice.
$D$
-lattice.
Proof. We may assume that
![]() $\unicode[STIX]{x1D6EC}=\unicode[STIX]{x1D6EC}_{N}=U^{2}\oplus D_{N-2}$
. By Eichler’s criterion, i.e. Proposition 1.3.2, any two vectors of
$\unicode[STIX]{x1D6EC}=\unicode[STIX]{x1D6EC}_{N}=U^{2}\oplus D_{N-2}$
. By Eichler’s criterion, i.e. Proposition 1.3.2, any two vectors of
![]() $\unicode[STIX]{x1D6EC}_{N}$
of square
$\unicode[STIX]{x1D6EC}_{N}$
of square
![]() $-4$
and divisibility
$-4$
and divisibility
![]() $2$
are
$2$
are
![]() $O^{+}(\unicode[STIX]{x1D6EC}_{N})$
-equivalent. Thus, we may suppose that
$O^{+}(\unicode[STIX]{x1D6EC}_{N})$
-equivalent. Thus, we may suppose that
![]() $v=(\mathbf{0},(0,\ldots ,0,2))$
; it is obvious that
$v=(\mathbf{0},(0,\ldots ,0,2))$
; it is obvious that
![]() $v^{\bot }\cong \unicode[STIX]{x1D6EC}_{N-1}$
.◻
$v^{\bot }\cong \unicode[STIX]{x1D6EC}_{N-1}$
.◻
Remark 1.4.2. Let
![]() $N\geqslant 4$
, let
$N\geqslant 4$
, let
![]() $(\unicode[STIX]{x1D6EC},\unicode[STIX]{x1D709})$
be a dimension-
$(\unicode[STIX]{x1D6EC},\unicode[STIX]{x1D709})$
be a dimension-
![]() $N$
decorated
$N$
decorated
![]() $D$
-lattice, and let
$D$
-lattice, and let
![]() $v\in \unicode[STIX]{x1D6EC}$
be hyperelliptic. The
$v\in \unicode[STIX]{x1D6EC}$
be hyperelliptic. The
![]() $D$
-lattice
$D$
-lattice
![]() $v^{\bot }$
comes with a decoration. In fact, since
$v^{\bot }$
comes with a decoration. In fact, since
![]() $v^{2}=-4$
and
$v^{2}=-4$
and
![]() $\operatorname{div}(v)=2$
, the sublattice
$\operatorname{div}(v)=2$
, the sublattice
![]() $\langle v\rangle \oplus v^{\bot }$
has index
$\langle v\rangle \oplus v^{\bot }$
has index
![]() $2$
in
$2$
in
![]() $\unicode[STIX]{x1D6EC}$
. Thus, there exists
$\unicode[STIX]{x1D6EC}$
. Thus, there exists
![]() $w\in v^{\bot }$
, well determined modulo
$w\in v^{\bot }$
, well determined modulo
![]() $2v^{\bot }$
, such that
$2v^{\bot }$
, such that
![]() $(v+w)/2$
is contained in
$(v+w)/2$
is contained in
![]() $\unicode[STIX]{x1D6EC}$
. It follows that
$\unicode[STIX]{x1D6EC}$
. It follows that
![]() $(w/2,v^{\bot })\subset \mathbb{Z}$
and hence
$(w/2,v^{\bot })\subset \mathbb{Z}$
and hence
![]() $w/2$
represents an element
$w/2$
represents an element
![]() $\unicode[STIX]{x1D702}\in A_{v^{\bot }}$
, independent of the choice of
$\unicode[STIX]{x1D702}\in A_{v^{\bot }}$
, independent of the choice of
![]() $w$
. Moreover,
$w$
. Moreover,
![]() $q_{v^{\bot }}(\unicode[STIX]{x1D702})\equiv 1\hspace{0.6em}({\rm mod}\hspace{0.2em}2)$
because
$q_{v^{\bot }}(\unicode[STIX]{x1D702})\equiv 1\hspace{0.6em}({\rm mod}\hspace{0.2em}2)$
because
Thus,
![]() $(v^{\bot },\unicode[STIX]{x1D702})$
is a dimension-
$(v^{\bot },\unicode[STIX]{x1D702})$
is a dimension-
![]() $(N-1)$
decorated
$(N-1)$
decorated
![]() $D$
-lattice.
$D$
-lattice.
Proposition 1.4.3. Let
![]() $(\unicode[STIX]{x1D6EC},\unicode[STIX]{x1D709})$
be a dimension-
$(\unicode[STIX]{x1D6EC},\unicode[STIX]{x1D709})$
be a dimension-
![]() $N$
decorated
$N$
decorated
![]() $D$
-lattice and
$D$
-lattice and
![]() $v\in \unicode[STIX]{x1D6EC}$
be a hyperelliptic vector. Let
$v\in \unicode[STIX]{x1D6EC}$
be a hyperelliptic vector. Let
![]() $\unicode[STIX]{x1D702}$
be the decoration of the dimension-
$\unicode[STIX]{x1D702}$
be the decoration of the dimension-
![]() $(N-1)$
$(N-1)$
![]() $D$
-lattice
$D$
-lattice
![]() $v^{\bot }$
defined above. If
$v^{\bot }$
defined above. If
![]() $g\in \unicode[STIX]{x1D6E4}_{\unicode[STIX]{x1D702}}$
, then there exists a unique
$g\in \unicode[STIX]{x1D6E4}_{\unicode[STIX]{x1D702}}$
, then there exists a unique
![]() $\widetilde{g}\in \unicode[STIX]{x1D6E4}_{\unicode[STIX]{x1D709}}$
which fixes
$\widetilde{g}\in \unicode[STIX]{x1D6E4}_{\unicode[STIX]{x1D709}}$
which fixes
![]() $v$
and restricts to
$v$
and restricts to
![]() $g$
on
$g$
on
![]() $v^{\bot }$
.
$v^{\bot }$
.
Proof. Unicity of
![]() $\widetilde{g}$
is obvious; we must prove existence. Let
$\widetilde{g}$
is obvious; we must prove existence. Let
![]() $\widehat{g}\in O(\unicode[STIX]{x1D6EC}_{\mathbb{Q}})$
be the extension of
$\widehat{g}\in O(\unicode[STIX]{x1D6EC}_{\mathbb{Q}})$
be the extension of
![]() $g$
which maps
$g$
which maps
![]() $v$
to itself. There exists
$v$
to itself. There exists
![]() $u\in v^{\bot }$
such that
$u\in v^{\bot }$
such that
![]() $\widehat{g}(w/2)=w/2+u$
because
$\widehat{g}(w/2)=w/2+u$
because
![]() $g\in \unicode[STIX]{x1D6E4}_{\unicode[STIX]{x1D702}}$
(i.e.
$g\in \unicode[STIX]{x1D6E4}_{\unicode[STIX]{x1D702}}$
(i.e.
![]() $g[w/2]=[w/2]$
). Hence,
$g[w/2]=[w/2]$
). Hence,
![]() $\widehat{g}((v+w)/2)=(v+w)/2+u\in \unicode[STIX]{x1D6EC}$
and this proves that
$\widehat{g}((v+w)/2)=(v+w)/2+u\in \unicode[STIX]{x1D6EC}$
and this proves that
![]() $\widehat{g}(\unicode[STIX]{x1D6EC})\subset \unicode[STIX]{x1D6EC}$
. We set
$\widehat{g}(\unicode[STIX]{x1D6EC})\subset \unicode[STIX]{x1D6EC}$
. We set
![]() $\widetilde{g}:=\widehat{g}|_{\unicode[STIX]{x1D6EC}}$
. Then
$\widetilde{g}:=\widehat{g}|_{\unicode[STIX]{x1D6EC}}$
. Then
![]() $\widetilde{g}\in O(\unicode[STIX]{x1D6EC})$
,
$\widetilde{g}\in O(\unicode[STIX]{x1D6EC})$
,
![]() $\widetilde{g}(v)=v$
, and
$\widetilde{g}(v)=v$
, and
![]() $\widetilde{g}|_{v^{\bot }}=g$
. Since
$\widetilde{g}|_{v^{\bot }}=g$
. Since
![]() $\unicode[STIX]{x1D709}=[v/2]$
, the isometry
$\unicode[STIX]{x1D709}=[v/2]$
, the isometry
![]() $\widetilde{g}$
fixes
$\widetilde{g}$
fixes
![]() $\unicode[STIX]{x1D709}$
and moreover
$\unicode[STIX]{x1D709}$
and moreover
![]() $\widetilde{g}\in O^{+}(\unicode[STIX]{x1D6EC})$
because
$\widetilde{g}\in O^{+}(\unicode[STIX]{x1D6EC})$
because
![]() $g\in O^{+}(v^{\bot })$
; this proves that
$g\in O^{+}(v^{\bot })$
; this proves that
![]() $\widetilde{g}\in \unicode[STIX]{x1D6E4}_{\unicode[STIX]{x1D709}}$
.◻
$\widetilde{g}\in \unicode[STIX]{x1D6E4}_{\unicode[STIX]{x1D709}}$
.◻
By Proposition 1.4.3, we have an injection of groups
The following is immediate.
Claim 1.4.4. The injective homomorphism of (1.4.1) has image equal to the stabilizer
![]() $\text{Stab}(v)<\unicode[STIX]{x1D6E4}_{\unicode[STIX]{x1D709}}$
of
$\text{Stab}(v)<\unicode[STIX]{x1D6E4}_{\unicode[STIX]{x1D709}}$
of
![]() $v$
.
$v$
.
Let
![]() $(\unicode[STIX]{x1D6EC},\unicode[STIX]{x1D709})$
be a decorated
$(\unicode[STIX]{x1D6EC},\unicode[STIX]{x1D709})$
be a decorated
![]() $D$
-lattice and
$D$
-lattice and
![]() $v\in \unicode[STIX]{x1D6EC}$
be a hyperelliptic vector. Let
$v\in \unicode[STIX]{x1D6EC}$
be a hyperelliptic vector. Let
![]() $\unicode[STIX]{x1D6EC}^{\prime }:=v^{\bot }$
(a
$\unicode[STIX]{x1D6EC}^{\prime }:=v^{\bot }$
(a
![]() $D$
-lattice) and
$D$
-lattice) and
![]() $\unicode[STIX]{x1D709}^{\prime }$
be the associated decoration of
$\unicode[STIX]{x1D709}^{\prime }$
be the associated decoration of
![]() $\unicode[STIX]{x1D6EC}^{\prime }$
. We have defined an injection
$\unicode[STIX]{x1D6EC}^{\prime }$
. We have defined an injection
![]() $\unicode[STIX]{x1D6E4}_{\unicode[STIX]{x1D709}^{\prime }}{\hookrightarrow}\unicode[STIX]{x1D6E4}_{\unicode[STIX]{x1D709}}$
, see (1.4.1), and hence there is a well-defined regular map of quasi-projective varieties
$\unicode[STIX]{x1D6E4}_{\unicode[STIX]{x1D709}^{\prime }}{\hookrightarrow}\unicode[STIX]{x1D6E4}_{\unicode[STIX]{x1D709}}$
, see (1.4.1), and hence there is a well-defined regular map of quasi-projective varieties
Below is the main result of the present subsection.
Proposition 1.4.5. The map
![]() $f$
of (1.4.2) is an isomorphism onto the hyperelliptic Heegner divisor
$f$
of (1.4.2) is an isomorphism onto the hyperelliptic Heegner divisor
![]() $H_{h}(\unicode[STIX]{x1D6EC},\unicode[STIX]{x1D709})$
. Moreover, the intersection of
$H_{h}(\unicode[STIX]{x1D6EC},\unicode[STIX]{x1D709})$
. Moreover, the intersection of
![]() $H_{h}(\unicode[STIX]{x1D6EC},\unicode[STIX]{x1D709})$
and the singular locus of
$H_{h}(\unicode[STIX]{x1D6EC},\unicode[STIX]{x1D709})$
and the singular locus of
![]() $\mathscr{F}(\unicode[STIX]{x1D6EC},\unicode[STIX]{x1D709})$
has codimension at least two in
$\mathscr{F}(\unicode[STIX]{x1D6EC},\unicode[STIX]{x1D709})$
has codimension at least two in
![]() $H_{h}(\unicode[STIX]{x1D6EC},\unicode[STIX]{x1D709})$
.
$H_{h}(\unicode[STIX]{x1D6EC},\unicode[STIX]{x1D709})$
.
We will prove Proposition 1.4.5 at the end of the present subsubsection. First, we will go through a series of preliminary results.
Proposition 1.4.6. Let
![]() $(\unicode[STIX]{x1D6EC},\unicode[STIX]{x1D709})$
be a dimension-
$(\unicode[STIX]{x1D6EC},\unicode[STIX]{x1D709})$
be a dimension-
![]() $N$
decorated
$N$
decorated
![]() $D$
-lattice. Let
$D$
-lattice. Let
![]() $v\in \unicode[STIX]{x1D6EC}$
be a hyperelliptic vector and let
$v\in \unicode[STIX]{x1D6EC}$
be a hyperelliptic vector and let
![]() $\unicode[STIX]{x1D702}$
be the decoration of the dimension-
$\unicode[STIX]{x1D702}$
be the decoration of the dimension-
![]() $(N-1)$
$(N-1)$
![]() $D$
-lattice
$D$
-lattice
![]() $v^{\bot }$
defined above. Suppose that
$v^{\bot }$
defined above. Suppose that
![]() $w$
is a reflective vector of
$w$
is a reflective vector of
![]() $(v^{\bot },\unicode[STIX]{x1D702})$
. Then
$(v^{\bot },\unicode[STIX]{x1D702})$
. Then
![]() $w$
is a reflective vector of
$w$
is a reflective vector of
![]() $(\unicode[STIX]{x1D6EC},\unicode[STIX]{x1D709})$
as well. More precisely:
$(\unicode[STIX]{x1D6EC},\unicode[STIX]{x1D709})$
as well. More precisely:
(1) if
 $w$
is a nodal vector of
$w$
is a nodal vector of
 $(v^{\bot },\unicode[STIX]{x1D702})$
, then it is a nodal vector of
$(v^{\bot },\unicode[STIX]{x1D702})$
, then it is a nodal vector of
 $(\unicode[STIX]{x1D6EC},\unicode[STIX]{x1D709})$
;
$(\unicode[STIX]{x1D6EC},\unicode[STIX]{x1D709})$
;(2) if
 $w$
is a hyperelliptic vector of
$w$
is a hyperelliptic vector of
 $(v^{\bot },\unicode[STIX]{x1D702})$
, then it is a hyperelliptic vector of
$(v^{\bot },\unicode[STIX]{x1D702})$
, then it is a hyperelliptic vector of
 $(\unicode[STIX]{x1D6EC},\unicode[STIX]{x1D709})$
;
$(\unicode[STIX]{x1D6EC},\unicode[STIX]{x1D709})$
;(3) if
 $N\equiv 4\hspace{0.6em}({\rm mod}\hspace{0.2em}8)$
and
$N\equiv 4\hspace{0.6em}({\rm mod}\hspace{0.2em}8)$
and
 $w$
is a unigonal (reflective) vector of
$w$
is a unigonal (reflective) vector of
 $(v^{\bot },\unicode[STIX]{x1D702})$
, then it is a hyperelliptic vector of
$(v^{\bot },\unicode[STIX]{x1D702})$
, then it is a hyperelliptic vector of
 $(\unicode[STIX]{x1D6EC},\unicode[STIX]{x1D709})$
;
$(\unicode[STIX]{x1D6EC},\unicode[STIX]{x1D709})$
;(4) if
 $N\equiv 5\hspace{0.6em}({\rm mod}\hspace{0.2em}8)$
and
$N\equiv 5\hspace{0.6em}({\rm mod}\hspace{0.2em}8)$
and
 $w$
is a unigonal (reflective) vector of
$w$
is a unigonal (reflective) vector of
 $(v^{\bot },\unicode[STIX]{x1D702})$
, then it is a nodal vector of
$(v^{\bot },\unicode[STIX]{x1D702})$
, then it is a nodal vector of
 $(\unicode[STIX]{x1D6EC},\unicode[STIX]{x1D709})$
.
$(\unicode[STIX]{x1D6EC},\unicode[STIX]{x1D709})$
.
Proof. (1): Trivial. (2): We may assume that
![]() $\unicode[STIX]{x1D6EC}=U^{2}\oplus D_{N-2}$
and
$\unicode[STIX]{x1D6EC}=U^{2}\oplus D_{N-2}$
and
By Propositions 1.4.3 and 1.3.3, we may assume that
![]() $w=(0_{4},(0,\ldots ,0,2,0))$
, and (2) follows. (3): Let
$w=(0_{4},(0,\ldots ,0,2,0))$
, and (2) follows. (3): Let
![]() $N=4+8k$
, where
$N=4+8k$
, where
![]() $k\geqslant 0$
. We may assume that
$k\geqslant 0$
. We may assume that
![]() $\unicode[STIX]{x1D6EC}=\text{II}_{2,2+8k}\oplus D_{2}$
and
$\unicode[STIX]{x1D6EC}=\text{II}_{2,2+8k}\oplus D_{2}$
and
![]() $v=(0_{4+8k},(0,2))$
. By Propositions 1.4.3 and 1.3.3, we may assume that
$v=(0_{4+8k},(0,2))$
. By Propositions 1.4.3 and 1.3.3, we may assume that
![]() $w=(0_{4+8k},(2,0))$
, and (3) follows. (4): Let
$w=(0_{4+8k},(2,0))$
, and (3) follows. (4): Let
![]() $N=5+8k$
, where
$N=5+8k$
, where
![]() $k\geqslant 0$
. We may assume that
$k\geqslant 0$
. We may assume that
![]() $\unicode[STIX]{x1D6EC}=\text{II}_{2,2+8k}\oplus D_{3}$
and
$\unicode[STIX]{x1D6EC}=\text{II}_{2,2+8k}\oplus D_{3}$
and
![]() $v=(0_{4+8k},(0,0,2))$
. By Propositions 1.4.3 and 1.3.3, we may assume that
$v=(0_{4+8k},(0,0,2))$
. By Propositions 1.4.3 and 1.3.3, we may assume that
![]() $w=(0_{4+8k},(1,-1,0))$
, and (4) follows.◻
$w=(0_{4+8k},(1,-1,0))$
, and (4) follows.◻
Let
![]() $\unicode[STIX]{x1D6EC}$
be a lattice (any lattice, not necessarily a
$\unicode[STIX]{x1D6EC}$
be a lattice (any lattice, not necessarily a
![]() $D$
-lattice) and
$D$
-lattice) and
![]() $\unicode[STIX]{x1D6FA}\subset \unicode[STIX]{x1D6EC}$
a subgroup. We let
$\unicode[STIX]{x1D6FA}\subset \unicode[STIX]{x1D6EC}$
a subgroup. We let
![]() $\overline{\unicode[STIX]{x1D6FA}}\subset \unicode[STIX]{x1D6EC}$
be the saturation of
$\overline{\unicode[STIX]{x1D6FA}}\subset \unicode[STIX]{x1D6EC}$
be the saturation of
![]() $\unicode[STIX]{x1D6FA}$
, i.e. the subgroup of vectors
$\unicode[STIX]{x1D6FA}$
, i.e. the subgroup of vectors
![]() $v\in \unicode[STIX]{x1D6EC}$
such that
$v\in \unicode[STIX]{x1D6EC}$
such that
![]() $mv\in \unicode[STIX]{x1D6FA}$
for some
$mv\in \unicode[STIX]{x1D6FA}$
for some
![]() $0\not =m\in \mathbb{Z}$
.
$0\not =m\in \mathbb{Z}$
.
Lemma 1.4.7. Let
![]() $(\unicode[STIX]{x1D6EC},\unicode[STIX]{x1D709})$
be a decorated
$(\unicode[STIX]{x1D6EC},\unicode[STIX]{x1D709})$
be a decorated
![]() $D$
-lattice and
$D$
-lattice and
![]() $v_{1},\ldots ,v_{k}\in \unicode[STIX]{x1D6EC}$
. Suppose that the following hold:
$v_{1},\ldots ,v_{k}\in \unicode[STIX]{x1D6EC}$
. Suppose that the following hold:
(1)
 $v_{i}$
is a hyperelliptic vector for
$v_{i}$
is a hyperelliptic vector for
 $i\in \{1,\ldots ,k\}$
;
$i\in \{1,\ldots ,k\}$
;(2) if
 $i\not =j\in \{1,\ldots ,k\}$
, then
$i\not =j\in \{1,\ldots ,k\}$
, then
 $v_{i}\not =\pm v_{j}$
;
$v_{i}\not =\pm v_{j}$
;(3) the sublattice
 $\unicode[STIX]{x1D6FA}\subset \unicode[STIX]{x1D6EC}$
generated by
$\unicode[STIX]{x1D6FA}\subset \unicode[STIX]{x1D6EC}$
generated by
 $v_{1},\ldots ,v_{k}$
is negative definite.
$v_{1},\ldots ,v_{k}$
is negative definite.
Then the following hold.
(I) The formula
(1.4.3)defines an isomorphism of lattices $$\begin{eqnarray}F(x_{1},\ldots ,x_{k})=\frac{1}{2}\mathop{\sum }_{i=1}^{k}x_{i}v_{i}\end{eqnarray}$$
$$\begin{eqnarray}F(x_{1},\ldots ,x_{k})=\frac{1}{2}\mathop{\sum }_{i=1}^{k}x_{i}v_{i}\end{eqnarray}$$
 $F:D_{k}\overset{{\sim}}{\longrightarrow }\overline{\unicode[STIX]{x1D6FA}}$
. (In particular,
$F:D_{k}\overset{{\sim}}{\longrightarrow }\overline{\unicode[STIX]{x1D6FA}}$
. (In particular,
 $v_{1},\ldots ,v_{k}$
are pairwise orthogonal.)
$v_{1},\ldots ,v_{k}$
are pairwise orthogonal.)(II) A vector
 $v\in \overline{\unicode[STIX]{x1D6FA}}$
is hyperelliptic if and only if
$v\in \overline{\unicode[STIX]{x1D6FA}}$
is hyperelliptic if and only if
 $v=\pm v_{i}$
for some
$v=\pm v_{i}$
for some
 $i\in \{1,\ldots ,k\}$
.
$i\in \{1,\ldots ,k\}$
.
Proof. Let
![]() $u,w\in \overline{\unicode[STIX]{x1D6FA}}$
be hyperelliptic vectors such that
$u,w\in \overline{\unicode[STIX]{x1D6FA}}$
be hyperelliptic vectors such that
![]() $u\not =\pm w$
. Using the divisibility assumptions and that
$u\not =\pm w$
. Using the divisibility assumptions and that
![]() $\unicode[STIX]{x1D6FA}$
is negative definite, it is easy to see that
$\unicode[STIX]{x1D6FA}$
is negative definite, it is easy to see that
![]() $(u,w)=0$
. Thus,
$(u,w)=0$
. Thus,
![]() $(v_{i},v_{j})=0$
for
$(v_{i},v_{j})=0$
for
![]() $i,j\in \{1,\ldots ,k\}$
and hence
$i,j\in \{1,\ldots ,k\}$
and hence
![]() $\unicode[STIX]{x1D6FA}$
has rank
$\unicode[STIX]{x1D6FA}$
has rank
![]() $k$
. The vector
$k$
. The vector
![]() $(\sum _{i=1}^{k}x_{i}v_{i})/2$
belongs to
$(\sum _{i=1}^{k}x_{i}v_{i})/2$
belongs to
![]() $\overline{\unicode[STIX]{x1D6FA}}$
whenever
$\overline{\unicode[STIX]{x1D6FA}}$
whenever
![]() $\sum _{i=1}^{k}x_{i}$
is even because
$\sum _{i=1}^{k}x_{i}$
is even because
![]() $(v_{i}+v_{j})/2\in \overline{\unicode[STIX]{x1D6FA}}$
. It follows that (1.4.3) defines an isomorphism between
$(v_{i}+v_{j})/2\in \overline{\unicode[STIX]{x1D6FA}}$
. It follows that (1.4.3) defines an isomorphism between
![]() $D_{k}$
and the sublattice
$D_{k}$
and the sublattice
![]() $F(D_{k})\subset \overline{\unicode[STIX]{x1D6FA}}$
. Suppose that
$F(D_{k})\subset \overline{\unicode[STIX]{x1D6FA}}$
. Suppose that
![]() $F(D_{k})\not =\overline{\unicode[STIX]{x1D6FA}}$
; since
$F(D_{k})\not =\overline{\unicode[STIX]{x1D6FA}}$
; since
![]() $\det (D_{k})=(-1)^{k}4$
, it follows that
$\det (D_{k})=(-1)^{k}4$
, it follows that
![]() $\overline{\unicode[STIX]{x1D6FA}}$
is unimodular and that contradicts the hypothesis that each
$\overline{\unicode[STIX]{x1D6FA}}$
is unimodular and that contradicts the hypothesis that each
![]() $v_{i}$
has divisibility
$v_{i}$
has divisibility
![]() $2$
. Thus,
$2$
. Thus,
![]() $F(D_{k})=\overline{\unicode[STIX]{x1D6FA}}$
and this proves Item (I). Item (II) is similar.◻
$F(D_{k})=\overline{\unicode[STIX]{x1D6FA}}$
and this proves Item (I). Item (II) is similar.◻
Proposition 1.4.8. Let
![]() $(\unicode[STIX]{x1D6EC},\unicode[STIX]{x1D709})$
be a decorated
$(\unicode[STIX]{x1D6EC},\unicode[STIX]{x1D709})$
be a decorated
![]() $D$
-lattice. The hyperelliptic Heegner divisor
$D$
-lattice. The hyperelliptic Heegner divisor
![]() $H_{h}(\unicode[STIX]{x1D6EC},\unicode[STIX]{x1D709})$
is normal.
$H_{h}(\unicode[STIX]{x1D6EC},\unicode[STIX]{x1D709})$
is normal.
Proof. By definition,
![]() $H_{h}(\unicode[STIX]{x1D6EC},\unicode[STIX]{x1D709})=\unicode[STIX]{x1D6E4}_{\unicode[STIX]{x1D709}}\backslash \mathscr{H}_{h}(\unicode[STIX]{x1D6EC},\unicode[STIX]{x1D709})$
. Let
$H_{h}(\unicode[STIX]{x1D6EC},\unicode[STIX]{x1D709})=\unicode[STIX]{x1D6E4}_{\unicode[STIX]{x1D709}}\backslash \mathscr{H}_{h}(\unicode[STIX]{x1D6EC},\unicode[STIX]{x1D709})$
. Let
![]() $p\in H_{h}(\unicode[STIX]{x1D6EC},\unicode[STIX]{x1D709})$
and
$p\in H_{h}(\unicode[STIX]{x1D6EC},\unicode[STIX]{x1D709})$
and
![]() $[\unicode[STIX]{x1D70E}]\in \mathscr{H}_{h}(\unicode[STIX]{x1D6EC},\unicode[STIX]{x1D709})$
be a representative of
$[\unicode[STIX]{x1D70E}]\in \mathscr{H}_{h}(\unicode[STIX]{x1D6EC},\unicode[STIX]{x1D709})$
be a representative of
![]() $p$
. Let
$p$
. Let
![]() $\text{Stab}([\unicode[STIX]{x1D70E}])<\unicode[STIX]{x1D6E4}_{\unicode[STIX]{x1D709}}$
be the stabilizer of the line
$\text{Stab}([\unicode[STIX]{x1D70E}])<\unicode[STIX]{x1D6E4}_{\unicode[STIX]{x1D709}}$
be the stabilizer of the line
![]() $[\unicode[STIX]{x1D70E}]$
. By construction, we have the following isomorphisms of analytic germs:
$[\unicode[STIX]{x1D70E}]$
. By construction, we have the following isomorphisms of analytic germs:
Since
![]() $\unicode[STIX]{x1D70E}^{\bot }\cap \unicode[STIX]{x1D6EC}_{\mathbb{R}}$
is negative definite, the set of hyperelliptic vectors
$\unicode[STIX]{x1D70E}^{\bot }\cap \unicode[STIX]{x1D6EC}_{\mathbb{R}}$
is negative definite, the set of hyperelliptic vectors
![]() $v\in \unicode[STIX]{x1D70E}^{\bot }\cap \unicode[STIX]{x1D6EC}$
is finite (and non-empty). Let
$v\in \unicode[STIX]{x1D70E}^{\bot }\cap \unicode[STIX]{x1D6EC}$
is finite (and non-empty). Let
![]() $\{v_{1},\ldots ,v_{k}\}$
be a maximal collection of such vectors with the property that
$\{v_{1},\ldots ,v_{k}\}$
be a maximal collection of such vectors with the property that
![]() $v_{i}\not =\pm v_{j}$
for
$v_{i}\not =\pm v_{j}$
for
![]() $i\not =j$
. Let
$i\not =j$
. Let
![]() $\unicode[STIX]{x1D6FA}_{\unicode[STIX]{x1D70E}}\subset \unicode[STIX]{x1D6EC}$
be the subgroup generated by
$\unicode[STIX]{x1D6FA}_{\unicode[STIX]{x1D70E}}\subset \unicode[STIX]{x1D6EC}$
be the subgroup generated by
![]() $v_{1},\ldots ,v_{k}$
. As noticed above, the restriction of the quadratic form to
$v_{1},\ldots ,v_{k}$
. As noticed above, the restriction of the quadratic form to
![]() $\unicode[STIX]{x1D6FA}_{\unicode[STIX]{x1D70E}}$
is negative definite. Thus, the hypotheses of Lemma 1.4.7 are satisfied and hence the saturation
$\unicode[STIX]{x1D6FA}_{\unicode[STIX]{x1D70E}}$
is negative definite. Thus, the hypotheses of Lemma 1.4.7 are satisfied and hence the saturation
![]() $\overline{\unicode[STIX]{x1D6FA}}_{\unicode[STIX]{x1D70E}}$
is isomorphic (as a lattice) to
$\overline{\unicode[STIX]{x1D6FA}}_{\unicode[STIX]{x1D70E}}$
is isomorphic (as a lattice) to
![]() $D_{k}$
. (Notice that by Lemma 1.4.7,
$D_{k}$
. (Notice that by Lemma 1.4.7,
![]() $\unicode[STIX]{x1D6FA}_{\unicode[STIX]{x1D70E}}$
is independent of the choice of a maximal collection as above.) Let
$\unicode[STIX]{x1D6FA}_{\unicode[STIX]{x1D70E}}$
is independent of the choice of a maximal collection as above.) Let
![]() $R_{\unicode[STIX]{x1D70E}}^{\prime }$
be the set of
$R_{\unicode[STIX]{x1D70E}}^{\prime }$
be the set of
![]() $r\in \overline{\unicode[STIX]{x1D6FA}}_{\unicode[STIX]{x1D70E}}$
such that
$r\in \overline{\unicode[STIX]{x1D6FA}}_{\unicode[STIX]{x1D70E}}$
such that
![]() $r^{2}=-2$
and let
$r^{2}=-2$
and let
![]() $R_{\unicode[STIX]{x1D70E}}^{\prime \prime }$
be the set of hyperelliptic vectors of
$R_{\unicode[STIX]{x1D70E}}^{\prime \prime }$
be the set of hyperelliptic vectors of
![]() $\overline{\unicode[STIX]{x1D6FA}}_{\unicode[STIX]{x1D70E}}$
. Then
$\overline{\unicode[STIX]{x1D6FA}}_{\unicode[STIX]{x1D70E}}$
. Then
(The last equality holds by Lemma 1.4.7.) Let
![]() $R_{\unicode[STIX]{x1D70E}}:=R_{\unicode[STIX]{x1D70E}}^{\prime }\cup R_{\unicode[STIX]{x1D70E}}^{\prime \prime }$
. Notice that
$R_{\unicode[STIX]{x1D70E}}:=R_{\unicode[STIX]{x1D70E}}^{\prime }\cup R_{\unicode[STIX]{x1D70E}}^{\prime \prime }$
. Notice that
![]() $\unicode[STIX]{x1D70C}_{r}\in \unicode[STIX]{x1D6E4}_{\unicode[STIX]{x1D709}}$
for all
$\unicode[STIX]{x1D70C}_{r}\in \unicode[STIX]{x1D6E4}_{\unicode[STIX]{x1D709}}$
for all
![]() $r\in R_{\unicode[STIX]{x1D70E}}$
. Let
$r\in R_{\unicode[STIX]{x1D70E}}$
. Let
![]() $W_{\unicode[STIX]{x1D70E}},W_{\unicode[STIX]{x1D70E}}^{\prime },W_{\unicode[STIX]{x1D70E}}^{\prime \prime }<\text{Stab}([\unicode[STIX]{x1D70E}])$
be the subgroups generated by the reflections
$W_{\unicode[STIX]{x1D70E}},W_{\unicode[STIX]{x1D70E}}^{\prime },W_{\unicode[STIX]{x1D70E}}^{\prime \prime }<\text{Stab}([\unicode[STIX]{x1D70E}])$
be the subgroups generated by the reflections
![]() $\unicode[STIX]{x1D70C}_{r}$
for
$\unicode[STIX]{x1D70C}_{r}$
for
![]() $r\in R_{\unicode[STIX]{x1D70E}}$
,
$r\in R_{\unicode[STIX]{x1D70E}}$
,
![]() $r\in R_{\unicode[STIX]{x1D70E}}^{\prime }$
, and
$r\in R_{\unicode[STIX]{x1D70E}}^{\prime }$
, and
![]() $r\in R_{\unicode[STIX]{x1D70E}}^{\prime \prime }$
, respectively. Clearly,
$r\in R_{\unicode[STIX]{x1D70E}}^{\prime \prime }$
, respectively. Clearly,
![]() $W_{\unicode[STIX]{x1D70E}}$
is a normal subgroup of
$W_{\unicode[STIX]{x1D70E}}$
is a normal subgroup of
![]() $\text{Stab}([\unicode[STIX]{x1D70E}])$
; let
$\text{Stab}([\unicode[STIX]{x1D70E}])$
; let
![]() $G_{\unicode[STIX]{x1D70E}}:=\text{Stab}([\unicode[STIX]{x1D70E}])/W_{\unicode[STIX]{x1D70E}}$
. Then
$G_{\unicode[STIX]{x1D70E}}:=\text{Stab}([\unicode[STIX]{x1D70E}])/W_{\unicode[STIX]{x1D70E}}$
. Then
![]() $G_{\unicode[STIX]{x1D70E}}$
acts on
$G_{\unicode[STIX]{x1D70E}}$
acts on
![]() $W_{\unicode[STIX]{x1D70E}}\backslash \mathscr{D}_{\unicode[STIX]{x1D6EC}}^{+}$
and on
$W_{\unicode[STIX]{x1D70E}}\backslash \mathscr{D}_{\unicode[STIX]{x1D6EC}}^{+}$
and on
![]() $W_{\unicode[STIX]{x1D70E}}\backslash \mathscr{H}_{h}(\unicode[STIX]{x1D6EC},\unicode[STIX]{x1D709})$
. The analytic germ
$W_{\unicode[STIX]{x1D70E}}\backslash \mathscr{H}_{h}(\unicode[STIX]{x1D6EC},\unicode[STIX]{x1D709})$
. The analytic germ
![]() $(\text{Stab}([\unicode[STIX]{x1D70E}])\backslash \mathscr{H}_{h}(\unicode[STIX]{x1D6EC},\unicode[STIX]{x1D709}),\overline{[\unicode[STIX]{x1D70E}]})$
is isomorphic to the germ at
$(\text{Stab}([\unicode[STIX]{x1D70E}])\backslash \mathscr{H}_{h}(\unicode[STIX]{x1D6EC},\unicode[STIX]{x1D709}),\overline{[\unicode[STIX]{x1D70E}]})$
is isomorphic to the germ at
![]() $\overline{[\unicode[STIX]{x1D70E}]}$
of
$\overline{[\unicode[STIX]{x1D70E}]}$
of
![]() $W_{\unicode[STIX]{x1D70E}}\backslash \mathscr{H}_{h}(\unicode[STIX]{x1D6EC},\unicode[STIX]{x1D709})$
modulo the action of
$W_{\unicode[STIX]{x1D70E}}\backslash \mathscr{H}_{h}(\unicode[STIX]{x1D6EC},\unicode[STIX]{x1D709})$
modulo the action of
![]() $G_{\unicode[STIX]{x1D70E}}$
. Hence, it suffices to prove that
$G_{\unicode[STIX]{x1D70E}}$
. Hence, it suffices to prove that
![]() $W_{\unicode[STIX]{x1D70E}}\backslash \mathscr{H}_{h}(\unicode[STIX]{x1D6EC},\unicode[STIX]{x1D709})$
is smooth in a neighborhood of
$W_{\unicode[STIX]{x1D70E}}\backslash \mathscr{H}_{h}(\unicode[STIX]{x1D6EC},\unicode[STIX]{x1D709})$
is smooth in a neighborhood of
![]() $\overline{[\unicode[STIX]{x1D70E}]}$
.
$\overline{[\unicode[STIX]{x1D70E}]}$
.
We identify each
![]() $r\in R_{\unicode[STIX]{x1D70E}}$
with
$r\in R_{\unicode[STIX]{x1D70E}}$
with
![]() $F^{-1}(r)\in \mathbb{C}^{k}$
, where
$F^{-1}(r)\in \mathbb{C}^{k}$
, where
![]() $F$
is the isometry of (1.4.3), and we denote it by
$F$
is the isometry of (1.4.3), and we denote it by
![]() $r$
. Thus,
$r$
. Thus,
![]() $r\in R_{\unicode[STIX]{x1D70E}}^{\prime }$
,
$r\in R_{\unicode[STIX]{x1D70E}}^{\prime }$
,
![]() $r\in R_{\unicode[STIX]{x1D70E}}^{\prime \prime }$
are of the form
$r\in R_{\unicode[STIX]{x1D70E}}^{\prime \prime }$
are of the form
respectively. The action of
![]() $W_{\unicode[STIX]{x1D70E}}$
is trivial on
$W_{\unicode[STIX]{x1D70E}}$
is trivial on
![]() $\unicode[STIX]{x1D6FA}_{\unicode[STIX]{x1D70E}}^{\bot }$
. It follows that there exist local analytic coordinates
$\unicode[STIX]{x1D6FA}_{\unicode[STIX]{x1D70E}}^{\bot }$
. It follows that there exist local analytic coordinates
![]() $(\mathbf{x},\mathbf{t})=((x_{1},\ldots ,x_{k}),\mathbf{t})$
on
$(\mathbf{x},\mathbf{t})=((x_{1},\ldots ,x_{k}),\mathbf{t})$
on
![]() $\mathscr{D}_{\unicode[STIX]{x1D6EC}}^{+}$
, centered at
$\mathscr{D}_{\unicode[STIX]{x1D6EC}}^{+}$
, centered at
![]() $[\unicode[STIX]{x1D70E}]$
, such that
$[\unicode[STIX]{x1D70E}]$
, such that
![]() $x_{i}=0$
is a local equation of
$x_{i}=0$
is a local equation of
![]() $v_{i}^{\bot }\cap \mathscr{D}_{\unicode[STIX]{x1D6EC}}^{+}$
, and
$v_{i}^{\bot }\cap \mathscr{D}_{\unicode[STIX]{x1D6EC}}^{+}$
, and
where
![]() $(\mathbf{x},r)$
is the opposite of the standard Euclidean product of
$(\mathbf{x},r)$
is the opposite of the standard Euclidean product of
![]() $\mathbf{x}$
and
$\mathbf{x}$
and
![]() $r$
.
$r$
.
In order to describe
![]() $W_{\unicode[STIX]{x1D70E}}\backslash \mathscr{D}_{\unicode[STIX]{x1D6EC}}^{+}$
and
$W_{\unicode[STIX]{x1D70E}}\backslash \mathscr{D}_{\unicode[STIX]{x1D6EC}}^{+}$
and
![]() $W_{\unicode[STIX]{x1D70E}}\backslash \mathscr{H}_{h}(\unicode[STIX]{x1D6EC},\unicode[STIX]{x1D709})$
, we first take the quotient by the normal subgroup
$W_{\unicode[STIX]{x1D70E}}\backslash \mathscr{H}_{h}(\unicode[STIX]{x1D6EC},\unicode[STIX]{x1D709})$
, we first take the quotient by the normal subgroup
![]() $W_{\unicode[STIX]{x1D70E}}^{\prime \prime }$
and then we act by
$W_{\unicode[STIX]{x1D70E}}^{\prime \prime }$
and then we act by
![]() $W_{\unicode[STIX]{x1D70E}}^{\prime }/W_{\unicode[STIX]{x1D70E}}^{\prime \prime }$
on the quotient. Local analytic coordinates on
$W_{\unicode[STIX]{x1D70E}}^{\prime }/W_{\unicode[STIX]{x1D70E}}^{\prime \prime }$
on the quotient. Local analytic coordinates on
![]() $W_{\unicode[STIX]{x1D70E}}^{\prime \prime }\backslash \mathscr{D}_{\unicode[STIX]{x1D6EC}}^{+}$
are
$W_{\unicode[STIX]{x1D70E}}^{\prime \prime }\backslash \mathscr{D}_{\unicode[STIX]{x1D6EC}}^{+}$
are
![]() $(y_{1},\ldots ,y_{k},\mathbf{t})$
, where
$(y_{1},\ldots ,y_{k},\mathbf{t})$
, where
![]() $y_{i}=x_{i}^{2}$
. The action of
$y_{i}=x_{i}^{2}$
. The action of
![]() $W_{\unicode[STIX]{x1D70E}}^{\prime }/W_{\unicode[STIX]{x1D70E}}^{\prime \prime }$
on
$W_{\unicode[STIX]{x1D70E}}^{\prime }/W_{\unicode[STIX]{x1D70E}}^{\prime \prime }$
on
![]() $(y_{1},\ldots ,y_{k})$
is the standard representation of the symmetric group
$(y_{1},\ldots ,y_{k})$
is the standard representation of the symmetric group
![]() $\mathscr{S}_{k}$
. Thus, local analytic coordinates on
$\mathscr{S}_{k}$
. Thus, local analytic coordinates on
![]() $W_{\unicode[STIX]{x1D70E}}\backslash \mathscr{D}_{\unicode[STIX]{x1D6EC}}^{+}$
are
$W_{\unicode[STIX]{x1D70E}}\backslash \mathscr{D}_{\unicode[STIX]{x1D6EC}}^{+}$
are
![]() $(\unicode[STIX]{x1D70F}_{1},\ldots ,\unicode[STIX]{x1D70F}_{k},\mathbf{t})$
, where
$(\unicode[STIX]{x1D70F}_{1},\ldots ,\unicode[STIX]{x1D70F}_{k},\mathbf{t})$
, where
![]() $\unicode[STIX]{x1D70F}_{i}$
is the degree-
$\unicode[STIX]{x1D70F}_{i}$
is the degree-
![]() $i$
elementary symmetric function in
$i$
elementary symmetric function in
![]() $y_{1},\ldots ,y_{k}$
. In particular,
$y_{1},\ldots ,y_{k}$
. In particular,
![]() $W_{\unicode[STIX]{x1D70E}}\backslash \mathscr{D}_{\unicode[STIX]{x1D6EC}}^{+}$
is smooth in a neighborhood of
$W_{\unicode[STIX]{x1D70E}}\backslash \mathscr{D}_{\unicode[STIX]{x1D6EC}}^{+}$
is smooth in a neighborhood of
![]() $\overline{[\unicode[STIX]{x1D70E}]}$
. Since a local equation of
$\overline{[\unicode[STIX]{x1D70E}]}$
. Since a local equation of
![]() $\mathscr{H}_{h}(\unicode[STIX]{x1D6EC},\unicode[STIX]{x1D709})$
is given by
$\mathscr{H}_{h}(\unicode[STIX]{x1D6EC},\unicode[STIX]{x1D709})$
is given by
![]() $x_{1}\cdot \cdots \cdot x_{k}=0$
, a local equation of
$x_{1}\cdot \cdots \cdot x_{k}=0$
, a local equation of
![]() $W_{\unicode[STIX]{x1D70E}}\backslash \mathscr{H}_{h}(\unicode[STIX]{x1D6EC},\unicode[STIX]{x1D709})$
in
$W_{\unicode[STIX]{x1D70E}}\backslash \mathscr{H}_{h}(\unicode[STIX]{x1D6EC},\unicode[STIX]{x1D709})$
in
![]() $W_{\unicode[STIX]{x1D70E}}\backslash \mathscr{D}_{\unicode[STIX]{x1D6EC}}^{+}$
is
$W_{\unicode[STIX]{x1D70E}}\backslash \mathscr{D}_{\unicode[STIX]{x1D6EC}}^{+}$
is
![]() $\unicode[STIX]{x1D70F}_{k}=0$
. We have proved that
$\unicode[STIX]{x1D70F}_{k}=0$
. We have proved that
![]() $W_{\unicode[STIX]{x1D70E}}\backslash \mathscr{H}_{h}(\unicode[STIX]{x1D6EC},\unicode[STIX]{x1D709})$
is smooth in a neighborhood of
$W_{\unicode[STIX]{x1D70E}}\backslash \mathscr{H}_{h}(\unicode[STIX]{x1D6EC},\unicode[STIX]{x1D709})$
is smooth in a neighborhood of
![]() $\overline{[\unicode[STIX]{x1D70E}]}$
, as claimed.◻
$\overline{[\unicode[STIX]{x1D70E}]}$
, as claimed.◻
Proof of Proposition 1.4.5.
We adopt the notation introduced in the proof of Proposition 1.4.8. We start by noting that
![]() $f$
is surjective by definition. The composition of
$f$
is surjective by definition. The composition of
![]() $f$
and the inclusion
$f$
and the inclusion
![]() $H_{h}(\unicode[STIX]{x1D6EC},\unicode[STIX]{x1D709}){\hookrightarrow}\mathscr{F}^{\ast }(\unicode[STIX]{x1D6EC},\unicode[STIX]{x1D709})$
extends to a regular map
$H_{h}(\unicode[STIX]{x1D6EC},\unicode[STIX]{x1D709}){\hookrightarrow}\mathscr{F}^{\ast }(\unicode[STIX]{x1D6EC},\unicode[STIX]{x1D709})$
extends to a regular map
compatible with the Baily–Borel boundaries. Since the Baily–Borel compactifications are projective, it follows that
![]() $f$
is a projective map. By Claim 1.4.4, the fiber of
$f$
is a projective map. By Claim 1.4.4, the fiber of
![]() $f$
at the equivalence class represented by
$f$
at the equivalence class represented by
![]() $\unicode[STIX]{x1D70E}\in \mathscr{H}_{h}(\unicode[STIX]{x1D6EC},\unicode[STIX]{x1D709})$
is identified with the set of hyperelliptic vectors
$\unicode[STIX]{x1D70E}\in \mathscr{H}_{h}(\unicode[STIX]{x1D6EC},\unicode[STIX]{x1D709})$
is identified with the set of hyperelliptic vectors
![]() $v\in \unicode[STIX]{x1D6FA}_{\unicode[STIX]{x1D70E}}$
, modulo the action of
$v\in \unicode[STIX]{x1D6FA}_{\unicode[STIX]{x1D70E}}$
, modulo the action of
![]() $\text{Stab}([\unicode[STIX]{x1D70E}])$
(notice that
$\text{Stab}([\unicode[STIX]{x1D70E}])$
(notice that
![]() $-\text{Id}_{\unicode[STIX]{x1D6EC}}\in \text{Stab}([\unicode[STIX]{x1D70E}])$
). Hence, the proof of Proposition 1.4.8 shows that the fiber of
$-\text{Id}_{\unicode[STIX]{x1D6EC}}\in \text{Stab}([\unicode[STIX]{x1D70E}])$
). Hence, the proof of Proposition 1.4.8 shows that the fiber of
![]() $f$
is a singleton; in particular,
$f$
is a singleton; in particular,
![]() $f$
is birational. Now
$f$
is birational. Now
![]() $H_{h}(\unicode[STIX]{x1D6EC},\unicode[STIX]{x1D709})$
is normal by Proposition 1.4.8; since
$H_{h}(\unicode[STIX]{x1D6EC},\unicode[STIX]{x1D709})$
is normal by Proposition 1.4.8; since
![]() $f$
is birational and projective, it follows that it is an isomorphism.
$f$
is birational and projective, it follows that it is an isomorphism.
It remains to prove that the intersection of
![]() $H_{h}(\unicode[STIX]{x1D6EC},\unicode[STIX]{x1D709})$
and the singular locus of
$H_{h}(\unicode[STIX]{x1D6EC},\unicode[STIX]{x1D709})$
and the singular locus of
![]() $\mathscr{F}(\unicode[STIX]{x1D6EC},\unicode[STIX]{x1D709})$
has codimension at least
$\mathscr{F}(\unicode[STIX]{x1D6EC},\unicode[STIX]{x1D709})$
has codimension at least
![]() $2$
in
$2$
in
![]() $H_{h}(\unicode[STIX]{x1D6EC},\unicode[STIX]{x1D709})$
. Suppose the contrary: we will reach a contradiction. Since
$H_{h}(\unicode[STIX]{x1D6EC},\unicode[STIX]{x1D709})$
. Suppose the contrary: we will reach a contradiction. Since
![]() $\mathscr{F}(\unicode[STIX]{x1D6EC},\unicode[STIX]{x1D709})$
is normal, there is an irreducible component
$\mathscr{F}(\unicode[STIX]{x1D6EC},\unicode[STIX]{x1D709})$
is normal, there is an irreducible component
![]() $Z$
of
$Z$
of
![]() $H_{h}(\unicode[STIX]{x1D6EC},\unicode[STIX]{x1D709})\cap \operatorname{sing}\mathscr{F}(\unicode[STIX]{x1D6EC},\unicode[STIX]{x1D709})$
which has codimension
$H_{h}(\unicode[STIX]{x1D6EC},\unicode[STIX]{x1D709})\cap \operatorname{sing}\mathscr{F}(\unicode[STIX]{x1D6EC},\unicode[STIX]{x1D709})$
which has codimension
![]() $1$
in
$1$
in
![]() $H_{h}(\unicode[STIX]{x1D6EC},\unicode[STIX]{x1D709})$
. Let
$H_{h}(\unicode[STIX]{x1D6EC},\unicode[STIX]{x1D709})$
. Let
![]() $v\in \unicode[STIX]{x1D6EC}$
be a hyperelliptic vector and
$v\in \unicode[STIX]{x1D6EC}$
be a hyperelliptic vector and
![]() $\unicode[STIX]{x1D702}$
the decoration of the
$\unicode[STIX]{x1D702}$
the decoration of the
![]() $D$
-lattice
$D$
-lattice
![]() $v^{\bot }$
associated to
$v^{\bot }$
associated to
![]() $\unicode[STIX]{x1D709}$
. Let
$\unicode[STIX]{x1D709}$
. Let
![]() $\unicode[STIX]{x1D70B}:\mathscr{D}_{v^{\bot }}^{+}\longrightarrow H_{h}(\unicode[STIX]{x1D6EC},\unicode[STIX]{x1D709})$
be the natural map; we have proved that
$\unicode[STIX]{x1D70B}:\mathscr{D}_{v^{\bot }}^{+}\longrightarrow H_{h}(\unicode[STIX]{x1D6EC},\unicode[STIX]{x1D709})$
be the natural map; we have proved that
![]() $\unicode[STIX]{x1D70B}$
is the quotient map for the action of
$\unicode[STIX]{x1D70B}$
is the quotient map for the action of
![]() $\unicode[STIX]{x1D6E4}_{\unicode[STIX]{x1D702}}$
on
$\unicode[STIX]{x1D6E4}_{\unicode[STIX]{x1D702}}$
on
![]() $\mathscr{D}_{v^{\bot }}^{+}$
. Now let
$\mathscr{D}_{v^{\bot }}^{+}$
. Now let
![]() $\widetilde{Z}\subset \mathscr{D}_{v^{\bot }}^{+}$
be an irreducible component of
$\widetilde{Z}\subset \mathscr{D}_{v^{\bot }}^{+}$
be an irreducible component of
![]() $\unicode[STIX]{x1D70B}^{-1}Z$
. If
$\unicode[STIX]{x1D70B}^{-1}Z$
. If
![]() $[\unicode[STIX]{x1D70E}]\in \widetilde{Z}$
, then
$[\unicode[STIX]{x1D70E}]\in \widetilde{Z}$
, then
because
![]() $\unicode[STIX]{x1D70B}([\unicode[STIX]{x1D70E}])$
is a singular point of
$\unicode[STIX]{x1D70B}([\unicode[STIX]{x1D70E}])$
is a singular point of
![]() $\mathscr{F}(\unicode[STIX]{x1D6EC},\unicode[STIX]{x1D709})$
. We distinguish between the two cases.
$\mathscr{F}(\unicode[STIX]{x1D6EC},\unicode[STIX]{x1D709})$
. We distinguish between the two cases.
(1) For very general
 $[\unicode[STIX]{x1D70E}]\in \widetilde{Z}$
, the set of hyperelliptic vectors in
$[\unicode[STIX]{x1D70E}]\in \widetilde{Z}$
, the set of hyperelliptic vectors in
 $\unicode[STIX]{x1D70E}^{\bot }$
is
$\unicode[STIX]{x1D70E}^{\bot }$
is
 $\{v,-v\}$
.
$\{v,-v\}$
.(2) For very general
 $[\unicode[STIX]{x1D70E}]\in \widetilde{Z}$
, the set of hyperelliptic vectors in
$[\unicode[STIX]{x1D70E}]\in \widetilde{Z}$
, the set of hyperelliptic vectors in
 $\unicode[STIX]{x1D70E}^{\bot }$
has cardinality strictly greater than
$\unicode[STIX]{x1D70E}^{\bot }$
has cardinality strictly greater than
 $2$
.
$2$
.
Assume that (1) holds and let
![]() $[\unicode[STIX]{x1D70E}]\in \widetilde{Z}$
be very general. Let
$[\unicode[STIX]{x1D70E}]\in \widetilde{Z}$
be very general. Let
![]() $g\in (\text{Stab}([\unicode[STIX]{x1D70E}])\setminus \langle \unicode[STIX]{x1D70C}_{v},-1_{\unicode[STIX]{x1D6EC}}\rangle )$
. Then
$g\in (\text{Stab}([\unicode[STIX]{x1D70E}])\setminus \langle \unicode[STIX]{x1D70C}_{v},-1_{\unicode[STIX]{x1D6EC}}\rangle )$
. Then
![]() $g(v)=\pm v$
and hence, multiplying
$g(v)=\pm v$
and hence, multiplying
![]() $g$
by
$g$
by
![]() $\unicode[STIX]{x1D70C}_{v}$
if necessary, we may assume that
$\unicode[STIX]{x1D70C}_{v}$
if necessary, we may assume that
![]() $g(v)=v$
, i.e.
$g(v)=v$
, i.e.
![]() $g|_{v^{\bot }}\in \unicode[STIX]{x1D6E4}_{\unicode[STIX]{x1D702}}$
. Now
$g|_{v^{\bot }}\in \unicode[STIX]{x1D6E4}_{\unicode[STIX]{x1D702}}$
. Now
![]() $g|_{v^{\bot }}$
fixes every point of
$g|_{v^{\bot }}$
fixes every point of
![]() $\widetilde{Z}$
, which has codimension
$\widetilde{Z}$
, which has codimension
![]() $1$
in
$1$
in
![]() $\mathscr{D}_{v^{\bot }}^{+}$
. It follows that
$\mathscr{D}_{v^{\bot }}^{+}$
. It follows that
![]() $g|_{v^{\bot }}=\pm \unicode[STIX]{x1D70C}_{w}^{v^{\bot }}$
, where
$g|_{v^{\bot }}=\pm \unicode[STIX]{x1D70C}_{w}^{v^{\bot }}$
, where
![]() $w$
is a reflective vector of
$w$
is a reflective vector of
![]() $(v^{\bot },\unicode[STIX]{x1D702})$
and
$(v^{\bot },\unicode[STIX]{x1D702})$
and
![]() $\unicode[STIX]{x1D70C}_{w}^{v^{\bot }}$
denotes the associated reflection of
$\unicode[STIX]{x1D70C}_{w}^{v^{\bot }}$
denotes the associated reflection of
![]() $v^{\bot }$
. By Proposition 1.4.6, the vector
$v^{\bot }$
. By Proposition 1.4.6, the vector
![]() $w$
is a reflective vector of
$w$
is a reflective vector of
![]() $(\unicode[STIX]{x1D6EC},\unicode[STIX]{x1D709})$
as well; it follows that
$(\unicode[STIX]{x1D6EC},\unicode[STIX]{x1D709})$
as well; it follows that
![]() $g=\unicode[STIX]{x1D70C}_{w}$
. Thus,
$g=\unicode[STIX]{x1D70C}_{w}$
. Thus,
![]() $\widetilde{Z}=v^{\bot }\cap w^{\bot }\cap \mathscr{D}_{\unicode[STIX]{x1D6EC}}^{+}$
and hence
$\widetilde{Z}=v^{\bot }\cap w^{\bot }\cap \mathscr{D}_{\unicode[STIX]{x1D6EC}}^{+}$
and hence
![]() $\text{Stab}([\unicode[STIX]{x1D70E}])=\langle \unicode[STIX]{x1D70C}_{v},\unicode[STIX]{x1D70C}_{w},-1_{\unicode[STIX]{x1D6EC}}\rangle$
for a very general
$\text{Stab}([\unicode[STIX]{x1D70E}])=\langle \unicode[STIX]{x1D70C}_{v},\unicode[STIX]{x1D70C}_{w},-1_{\unicode[STIX]{x1D6EC}}\rangle$
for a very general
![]() $[\unicode[STIX]{x1D70E}]\in \widetilde{Z}$
. It follows that if
$[\unicode[STIX]{x1D70E}]\in \widetilde{Z}$
. It follows that if
![]() $[\unicode[STIX]{x1D70E}]\in \widetilde{Z}$
is very general, then
$[\unicode[STIX]{x1D70E}]\in \widetilde{Z}$
is very general, then
![]() $\mathscr{F}(\unicode[STIX]{x1D6EC},\unicode[STIX]{x1D709})$
is smooth at
$\mathscr{F}(\unicode[STIX]{x1D6EC},\unicode[STIX]{x1D709})$
is smooth at
![]() $\unicode[STIX]{x1D70B}([\unicode[STIX]{x1D70E}])$
, and that contradicts our assumption.
$\unicode[STIX]{x1D70B}([\unicode[STIX]{x1D70E}])$
, and that contradicts our assumption.
Lastly, assume that (2) holds. Let
![]() $[\unicode[STIX]{x1D70E}]\in \widetilde{Z}$
be very general. Since
$[\unicode[STIX]{x1D70E}]\in \widetilde{Z}$
be very general. Since
![]() $\widetilde{Z}$
has codimension
$\widetilde{Z}$
has codimension
![]() $2$
in
$2$
in
![]() $\mathscr{D}_{\unicode[STIX]{x1D6EC}}^{+}$
, the set of hyperelliptic vectors in
$\mathscr{D}_{\unicode[STIX]{x1D6EC}}^{+}$
, the set of hyperelliptic vectors in
![]() $\unicode[STIX]{x1D70E}^{\bot }$
is equal to
$\unicode[STIX]{x1D70E}^{\bot }$
is equal to
![]() $\{\pm v_{1},\pm v_{2}\}$
, where
$\{\pm v_{1},\pm v_{2}\}$
, where
![]() $v_{1},v_{2}$
are orthogonal hyperelliptic vectors, and moreover
$v_{1},v_{2}$
are orthogonal hyperelliptic vectors, and moreover
![]() $\text{Stab}([\unicode[STIX]{x1D70E}])=\langle \unicode[STIX]{x1D70C}_{v_{1}},\unicode[STIX]{x1D70C}_{v_{2}},-1_{\unicode[STIX]{x1D6EC}}\rangle$
. As shown in the proof of Proposition 1.4.8, it follows that
$\text{Stab}([\unicode[STIX]{x1D70E}])=\langle \unicode[STIX]{x1D70C}_{v_{1}},\unicode[STIX]{x1D70C}_{v_{2}},-1_{\unicode[STIX]{x1D6EC}}\rangle$
. As shown in the proof of Proposition 1.4.8, it follows that
![]() $\mathscr{F}(\unicode[STIX]{x1D6EC},\unicode[STIX]{x1D709})$
is smooth at
$\mathscr{F}(\unicode[STIX]{x1D6EC},\unicode[STIX]{x1D709})$
is smooth at
![]() $\unicode[STIX]{x1D70B}([\unicode[STIX]{x1D70E}])$
, and that contradicts our assumption.◻
$\unicode[STIX]{x1D70B}([\unicode[STIX]{x1D70E}])$
, and that contradicts our assumption.◻
1.5 Reflective unigonal divisors
1.5.1
 $N\equiv 3\hspace{0.6em}({\rm mod}\hspace{0.2em}8)$
$N\equiv 3\hspace{0.6em}({\rm mod}\hspace{0.2em}8)$
Let
![]() $(\unicode[STIX]{x1D6EC},\unicode[STIX]{x1D709})$
be a decorated
$(\unicode[STIX]{x1D6EC},\unicode[STIX]{x1D709})$
be a decorated
![]() $D$
-lattice of dimension
$D$
-lattice of dimension
![]() $N\equiv 3\hspace{0.6em}({\rm mod}\hspace{0.2em}8)$
. Let
$N\equiv 3\hspace{0.6em}({\rm mod}\hspace{0.2em}8)$
. Let
![]() $N=8k+3$
, where
$N=8k+3$
, where
![]() $k\geqslant 0$
. Let
$k\geqslant 0$
. Let
![]() $v\in \unicode[STIX]{x1D6EC}$
be a unigonal vector, i.e.
$v\in \unicode[STIX]{x1D6EC}$
be a unigonal vector, i.e.
![]() $v^{2}=-4$
and
$v^{2}=-4$
and
![]() $\operatorname{div}(v)=4$
. Then
$\operatorname{div}(v)=4$
. Then
![]() $\unicode[STIX]{x1D6EC}=\langle v\rangle \oplus v^{\bot }$
. Since
$\unicode[STIX]{x1D6EC}=\langle v\rangle \oplus v^{\bot }$
. Since
![]() $\det \unicode[STIX]{x1D6EC}=-4$
, it follows that
$\det \unicode[STIX]{x1D6EC}=-4$
, it follows that
![]() $v^{\bot }$
is unimodular. Thus,
$v^{\bot }$
is unimodular. Thus,
Given
![]() $g\in O^{+}(\text{II}_{2,2+8k})$
, let
$g\in O^{+}(\text{II}_{2,2+8k})$
, let
![]() $\widetilde{g}\in O(\unicode[STIX]{x1D6EC})$
be the isometry such that
$\widetilde{g}\in O(\unicode[STIX]{x1D6EC})$
be the isometry such that
Then
![]() $\widetilde{g}\in O^{+}(\unicode[STIX]{x1D6EC})$
because
$\widetilde{g}\in O^{+}(\unicode[STIX]{x1D6EC})$
because
![]() $g\in O^{+}(\text{II}_{2,2+8k})$
, and
$g\in O^{+}(\text{II}_{2,2+8k})$
, and
![]() $\widetilde{g}\in \widetilde{O}(\unicode[STIX]{x1D6EC})$
because
$\widetilde{g}\in \widetilde{O}(\unicode[STIX]{x1D6EC})$
because
![]() $A_{\unicode[STIX]{x1D6EC}}$
is generated by
$A_{\unicode[STIX]{x1D6EC}}$
is generated by
![]() $v^{\ast }$
. Thus, we have an injection of groups
$v^{\ast }$
. Thus, we have an injection of groups
It follows that the injection
![]() $\mathscr{D}_{v^{\bot }}^{+}{\hookrightarrow}\mathscr{D}_{\unicode[STIX]{x1D6EC}}^{+}$
descends to a regular map
$\mathscr{D}_{v^{\bot }}^{+}{\hookrightarrow}\mathscr{D}_{\unicode[STIX]{x1D6EC}}^{+}$
descends to a regular map
Proposition 1.5.1. Let
![]() $(\unicode[STIX]{x1D6EC},\unicode[STIX]{x1D709})$
be a decorated
$(\unicode[STIX]{x1D6EC},\unicode[STIX]{x1D709})$
be a decorated
![]() $D$
-lattice of dimension
$D$
-lattice of dimension
![]() $N\equiv 3\hspace{0.6em}({\rm mod}\hspace{0.2em}8)$
and let
$N\equiv 3\hspace{0.6em}({\rm mod}\hspace{0.2em}8)$
and let
![]() $N=8k+3$
, where
$N=8k+3$
, where
![]() $k\geqslant 0$
. The map
$k\geqslant 0$
. The map
![]() $l$
in (1.5.4) is an isomorphism onto the unigonal Heegner divisor
$l$
in (1.5.4) is an isomorphism onto the unigonal Heegner divisor
![]() $H_{u}(\unicode[STIX]{x1D6EC},\unicode[STIX]{x1D709})$
. Moreover, the intersection of
$H_{u}(\unicode[STIX]{x1D6EC},\unicode[STIX]{x1D709})$
. Moreover, the intersection of
![]() $H_{u}(\unicode[STIX]{x1D6EC},\unicode[STIX]{x1D709})$
and the singular locus of
$H_{u}(\unicode[STIX]{x1D6EC},\unicode[STIX]{x1D709})$
and the singular locus of
![]() $\mathscr{F}(\unicode[STIX]{x1D6EC},\unicode[STIX]{x1D709})$
has codimension at least
$\mathscr{F}(\unicode[STIX]{x1D6EC},\unicode[STIX]{x1D709})$
has codimension at least
![]() $2$
in
$2$
in
![]() $H_{u}(\unicode[STIX]{x1D6EC},\unicode[STIX]{x1D709})$
.
$H_{u}(\unicode[STIX]{x1D6EC},\unicode[STIX]{x1D709})$
.
Proof. The map
![]() $l$
is finite (see the proof of Proposition 1.4.5) and it has degree
$l$
is finite (see the proof of Proposition 1.4.5) and it has degree
![]() $1$
because
$1$
because
![]() $-\text{Id}_{\unicode[STIX]{x1D6EC}}\in \unicode[STIX]{x1D6E4}_{\unicode[STIX]{x1D709}}$
. Thus, in order to prove that
$-\text{Id}_{\unicode[STIX]{x1D6EC}}\in \unicode[STIX]{x1D6E4}_{\unicode[STIX]{x1D709}}$
. Thus, in order to prove that
![]() $l$
is an isomorphism, it suffices to prove that
$l$
is an isomorphism, it suffices to prove that
![]() $H_{u}(\unicode[STIX]{x1D6EC},\unicode[STIX]{x1D709})$
is normal. We claim that the pre-Heegner divisor
$H_{u}(\unicode[STIX]{x1D6EC},\unicode[STIX]{x1D709})$
is normal. We claim that the pre-Heegner divisor
![]() $\mathscr{H}_{u}(\unicode[STIX]{x1D6EC},\unicode[STIX]{x1D709})$
is smooth, i.e. that if
$\mathscr{H}_{u}(\unicode[STIX]{x1D6EC},\unicode[STIX]{x1D709})$
is smooth, i.e. that if
![]() $v_{1},v_{2}$
are non-proportional unigonal vectors, then
$v_{1},v_{2}$
are non-proportional unigonal vectors, then
![]() $v_{1}^{\bot }\cap v_{2}^{\bot }\cap \mathscr{D}_{\unicode[STIX]{x1D6EC}}^{+}=\varnothing$
. In fact, suppose the contrary. Then
$v_{1}^{\bot }\cap v_{2}^{\bot }\cap \mathscr{D}_{\unicode[STIX]{x1D6EC}}^{+}=\varnothing$
. In fact, suppose the contrary. Then
![]() $v_{1},v_{2}$
span a negative-definite rank-
$v_{1},v_{2}$
span a negative-definite rank-
![]() $2$
sublattice of
$2$
sublattice of
![]() $\unicode[STIX]{x1D6EC}$
; since
$\unicode[STIX]{x1D6EC}$
; since
![]() $v_{i}^{2}=-4$
and
$v_{i}^{2}=-4$
and
![]() $(v_{1},v_{2})\in 4\mathbb{Z}$
, it follows that
$(v_{1},v_{2})\in 4\mathbb{Z}$
, it follows that
![]() $v_{1}\bot v_{2}$
. On the other hand,
$v_{1}\bot v_{2}$
. On the other hand,
![]() $v_{1}^{\bot }\cong \text{II}_{2,2+8k}$
by (1.5.1) and hence
$v_{1}^{\bot }\cong \text{II}_{2,2+8k}$
by (1.5.1) and hence
![]() $v_{1}^{\bot }$
does not contain a primitive vector of divisibility greater than
$v_{1}^{\bot }$
does not contain a primitive vector of divisibility greater than
![]() $1$
. This proves that
$1$
. This proves that
![]() $\mathscr{H}_{u}(\unicode[STIX]{x1D6EC},\unicode[STIX]{x1D709})$
is smooth and hence
$\mathscr{H}_{u}(\unicode[STIX]{x1D6EC},\unicode[STIX]{x1D709})$
is smooth and hence
![]() $H_{u}(\unicode[STIX]{x1D6EC},\unicode[STIX]{x1D709})=\unicode[STIX]{x1D6E4}_{\unicode[STIX]{x1D709}}\backslash \mathscr{H}_{u}(\unicode[STIX]{x1D6EC},\unicode[STIX]{x1D709})$
is normal.
$H_{u}(\unicode[STIX]{x1D6EC},\unicode[STIX]{x1D709})=\unicode[STIX]{x1D6E4}_{\unicode[STIX]{x1D709}}\backslash \mathscr{H}_{u}(\unicode[STIX]{x1D6EC},\unicode[STIX]{x1D709})$
is normal.
The proof that
![]() $H_{u}(\unicode[STIX]{x1D6EC},\unicode[STIX]{x1D709})\cap \operatorname{sing}\mathscr{F}(\unicode[STIX]{x1D6EC},\unicode[STIX]{x1D709})$
has codimension at least
$H_{u}(\unicode[STIX]{x1D6EC},\unicode[STIX]{x1D709})\cap \operatorname{sing}\mathscr{F}(\unicode[STIX]{x1D6EC},\unicode[STIX]{x1D709})$
has codimension at least
![]() $2$
in
$2$
in
![]() $H_{u}(\unicode[STIX]{x1D6EC},\unicode[STIX]{x1D709})$
is similar to the analogous statement for
$H_{u}(\unicode[STIX]{x1D6EC},\unicode[STIX]{x1D709})$
is similar to the analogous statement for
![]() $H_{h}(\unicode[STIX]{x1D6EC},\unicode[STIX]{x1D709})$
; see Proposition 1.4.5. We leave details to the reader.◻
$H_{h}(\unicode[STIX]{x1D6EC},\unicode[STIX]{x1D709})$
; see Proposition 1.4.5. We leave details to the reader.◻
In order to simplify notation, from now on we let
A vector
![]() $v\in \text{II}_{2,2+8k}$
is nodal if it has square
$v\in \text{II}_{2,2+8k}$
is nodal if it has square
![]() $-2$
. By Eichler’s criterion, i.e. Proposition 1.3.2, any two nodal vectors of
$-2$
. By Eichler’s criterion, i.e. Proposition 1.3.2, any two nodal vectors of
![]() $\text{II}_{2,2+8k}$
are
$\text{II}_{2,2+8k}$
are
![]() $O^{+}(\text{II}_{2,2+8k})$
-equivalent. We let
$O^{+}(\text{II}_{2,2+8k})$
-equivalent. We let
![]() $H_{n}(\text{II}_{2,2+8k})$
be the Heegner divisor of
$H_{n}(\text{II}_{2,2+8k})$
be the Heegner divisor of
![]() $\mathscr{F}(\text{II}_{2,2+8k})$
corresponding to a nodal
$\mathscr{F}(\text{II}_{2,2+8k})$
corresponding to a nodal
![]() $v\in \text{II}_{2,2+8k}$
.
$v\in \text{II}_{2,2+8k}$
.
1.5.2
 $N\equiv 4\hspace{0.6em}({\rm mod}\hspace{0.2em}8)$
$N\equiv 4\hspace{0.6em}({\rm mod}\hspace{0.2em}8)$
Let
![]() $(\unicode[STIX]{x1D6EC},\unicode[STIX]{x1D709})$
be a decorated
$(\unicode[STIX]{x1D6EC},\unicode[STIX]{x1D709})$
be a decorated
![]() $D$
-lattice of dimension
$D$
-lattice of dimension
![]() $N\equiv 4\hspace{0.6em}({\rm mod}\hspace{0.2em}8)$
. Let
$N\equiv 4\hspace{0.6em}({\rm mod}\hspace{0.2em}8)$
. Let
![]() $N=8k+4$
, where
$N=8k+4$
, where
![]() $k\geqslant 0$
. Let
$k\geqslant 0$
. Let
![]() $v\in \unicode[STIX]{x1D6EC}$
be a unigonal vector, i.e.
$v\in \unicode[STIX]{x1D6EC}$
be a unigonal vector, i.e.
![]() $v^{2}=-2$
and
$v^{2}=-2$
and
![]() $\operatorname{div}(v)=2$
. Then
$\operatorname{div}(v)=2$
. Then
![]() $\unicode[STIX]{x1D6EC}=\langle v\rangle \oplus v^{\bot }$
. Moreover,
$\unicode[STIX]{x1D6EC}=\langle v\rangle \oplus v^{\bot }$
. Moreover,
In fact,
![]() $A_{\unicode[STIX]{x1D6EC}}=\mathbb{Z}/(2)\oplus A_{v^{\bot }}$
, where a generator of the first summand has square
$A_{\unicode[STIX]{x1D6EC}}=\mathbb{Z}/(2)\oplus A_{v^{\bot }}$
, where a generator of the first summand has square
![]() $-1/2$
modulo
$-1/2$
modulo
![]() $2\mathbb{Z}$
. It follows that the discriminant group of
$2\mathbb{Z}$
. It follows that the discriminant group of
![]() $v^{\bot }$
is
$v^{\bot }$
is
![]() $\mathbb{Z}/(2)$
and a generator has square
$\mathbb{Z}/(2)$
and a generator has square
![]() $-1/2$
modulo
$-1/2$
modulo
![]() $2\mathbb{Z}$
. Thus,
$2\mathbb{Z}$
. Thus,
![]() $v^{\bot }$
and
$v^{\bot }$
and
![]() $U^{2}\oplus E_{8}^{k}\oplus A_{1}$
have the same signature and isomorphic discriminant groups; thus, (1.5.6) follows from Theorem 1.13.2 of [Reference NikulinNik80]. Given
$U^{2}\oplus E_{8}^{k}\oplus A_{1}$
have the same signature and isomorphic discriminant groups; thus, (1.5.6) follows from Theorem 1.13.2 of [Reference NikulinNik80]. Given
![]() $g\in O^{+}(v^{\bot })$
, let
$g\in O^{+}(v^{\bot })$
, let
![]() $\widetilde{g}\in O(\unicode[STIX]{x1D6EC})$
be the isometry such that
$\widetilde{g}\in O(\unicode[STIX]{x1D6EC})$
be the isometry such that
Then
![]() $\widetilde{g}\in O^{+}(\unicode[STIX]{x1D6EC})$
because
$\widetilde{g}\in O^{+}(\unicode[STIX]{x1D6EC})$
because
![]() $g\in O^{+}(v^{\bot })$
, and
$g\in O^{+}(v^{\bot })$
, and
![]() $\widetilde{g}\in \widetilde{O}(\unicode[STIX]{x1D6EC})$
because
$\widetilde{g}\in \widetilde{O}(\unicode[STIX]{x1D6EC})$
because
![]() $O(v^{\bot })=\widetilde{O}(v^{\bot })$
, and
$O(v^{\bot })=\widetilde{O}(v^{\bot })$
, and
![]() $A_{\unicode[STIX]{x1D6EC}}=A_{v^{\bot }}\oplus \langle v^{\ast }\rangle$
. Thus, we have an injection of groups
$A_{\unicode[STIX]{x1D6EC}}=A_{v^{\bot }}\oplus \langle v^{\ast }\rangle$
. Thus, we have an injection of groups
It follows that the injection
![]() $\mathscr{D}_{v^{\bot }}^{+}{\hookrightarrow}\mathscr{D}_{\unicode[STIX]{x1D6EC}}^{+}$
descends to a regular map
$\mathscr{D}_{v^{\bot }}^{+}{\hookrightarrow}\mathscr{D}_{\unicode[STIX]{x1D6EC}}^{+}$
descends to a regular map
Proposition 1.5.2. Let
![]() $(\unicode[STIX]{x1D6EC},\unicode[STIX]{x1D709})$
be a decorated
$(\unicode[STIX]{x1D6EC},\unicode[STIX]{x1D709})$
be a decorated
![]() $D$
-lattice of dimension
$D$
-lattice of dimension
![]() $N\equiv 4\hspace{0.6em}({\rm mod}\hspace{0.2em}8)$
and let
$N\equiv 4\hspace{0.6em}({\rm mod}\hspace{0.2em}8)$
and let
![]() $N=8k+4$
, where
$N=8k+4$
, where
![]() $k\geqslant 0$
. The map
$k\geqslant 0$
. The map
![]() $m$
in (1.5.9) is an isomorphism onto the unigonal Heegner divisor
$m$
in (1.5.9) is an isomorphism onto the unigonal Heegner divisor
![]() $H_{u}(\unicode[STIX]{x1D6EC},\unicode[STIX]{x1D709})$
. Moreover, the intersection of
$H_{u}(\unicode[STIX]{x1D6EC},\unicode[STIX]{x1D709})$
. Moreover, the intersection of
![]() $H_{u}(\unicode[STIX]{x1D6EC},\unicode[STIX]{x1D709})$
and the singular locus of
$H_{u}(\unicode[STIX]{x1D6EC},\unicode[STIX]{x1D709})$
and the singular locus of
![]() $\mathscr{F}(\unicode[STIX]{x1D6EC},\unicode[STIX]{x1D709})$
has codimension at least
$\mathscr{F}(\unicode[STIX]{x1D6EC},\unicode[STIX]{x1D709})$
has codimension at least
![]() $2$
in
$2$
in
![]() $H_{u}(\unicode[STIX]{x1D6EC},\unicode[STIX]{x1D709})$
.
$H_{u}(\unicode[STIX]{x1D6EC},\unicode[STIX]{x1D709})$
.
Proof. The proof is similar to the proof of Proposition 1.5.1 (see also Proposition 1.4.5). We leave details to the reader. ◻
In order to simplify notation, from now on we let
A vector
![]() $v\in \text{II}_{2,2+8k}\oplus A_{1}$
is nodal if it has square
$v\in \text{II}_{2,2+8k}\oplus A_{1}$
is nodal if it has square
![]() $-2$
and divisibility
$-2$
and divisibility
![]() $1$
; it is unigonal if it has square
$1$
; it is unigonal if it has square
![]() $-2$
and divisibility
$-2$
and divisibility
![]() $2$
. By Eichler’s criterion, i.e. Proposition 1.3.2, any two nodal vectors of
$2$
. By Eichler’s criterion, i.e. Proposition 1.3.2, any two nodal vectors of
![]() $\text{II}_{2,2+8k}\oplus A_{1}$
are
$\text{II}_{2,2+8k}\oplus A_{1}$
are
![]() $O^{+}(\text{II}_{2,2+8k}\oplus A_{1})$
-equivalent, and similarly for any two unigonal vectors. We let
$O^{+}(\text{II}_{2,2+8k}\oplus A_{1})$
-equivalent, and similarly for any two unigonal vectors. We let
![]() $H_{n}(\text{II}_{2,2+8k}\oplus A_{1})$
and
$H_{n}(\text{II}_{2,2+8k}\oplus A_{1})$
and
![]() $H_{u}(\text{II}_{2,2+8k}\oplus A_{1})$
be the Heegner divisors of
$H_{u}(\text{II}_{2,2+8k}\oplus A_{1})$
be the Heegner divisors of
![]() $\mathscr{F}(\text{II}_{2,2+8k}\oplus A_{1})$
corresponding to a nodal or a unigonal
$\mathscr{F}(\text{II}_{2,2+8k}\oplus A_{1})$
corresponding to a nodal or a unigonal
![]() $v\in \text{II}_{2,2+8k}\oplus A_{1}$
, respectively.
$v\in \text{II}_{2,2+8k}\oplus A_{1}$
, respectively.
One describes the Heegner divisor
![]() $H_{u}(\text{II}_{2,2+8k}\oplus A_{1})$
proceeding as in § 1.5.1. In fact, let
$H_{u}(\text{II}_{2,2+8k}\oplus A_{1})$
proceeding as in § 1.5.1. In fact, let
![]() $v\in (\text{II}_{2,2+8k}\oplus A_{1})$
be a unigonal vector. Then
$v\in (\text{II}_{2,2+8k}\oplus A_{1})$
be a unigonal vector. Then
![]() $(\text{II}_{2,2+8k}\oplus A_{1})=\langle v\rangle \oplus v^{\bot }$
, and
$(\text{II}_{2,2+8k}\oplus A_{1})=\langle v\rangle \oplus v^{\bot }$
, and
![]() $v^{\bot }\cong \text{II}_{2,2+8k}$
is unimodular. It follows that the injection
$v^{\bot }\cong \text{II}_{2,2+8k}$
is unimodular. It follows that the injection
![]() $\mathscr{D}_{v^{\bot }}^{+}{\hookrightarrow}\mathscr{D}_{\unicode[STIX]{x1D6EC}}^{+}$
descends to a regular map
$\mathscr{D}_{v^{\bot }}^{+}{\hookrightarrow}\mathscr{D}_{\unicode[STIX]{x1D6EC}}^{+}$
descends to a regular map
which satisfies the following proposition.
Proposition 1.5.3. Let
![]() $k\geqslant 0$
. The map
$k\geqslant 0$
. The map
![]() $p$
of (1.5.11) is an isomorphism onto the unigonal Heegner divisor
$p$
of (1.5.11) is an isomorphism onto the unigonal Heegner divisor
![]() $H_{u}(\text{II}_{2,2+8k}\oplus A_{1})$
. Moreover, the intersection of
$H_{u}(\text{II}_{2,2+8k}\oplus A_{1})$
. Moreover, the intersection of
![]() $H_{u}(\text{II}_{2,2+8k}\oplus A_{1})$
and the singular locus of
$H_{u}(\text{II}_{2,2+8k}\oplus A_{1})$
and the singular locus of
![]() $\mathscr{F}(\text{II}_{2,2+8k}\oplus A_{1})$
has codimension at least
$\mathscr{F}(\text{II}_{2,2+8k}\oplus A_{1})$
has codimension at least
![]() $2$
in
$2$
in
![]() $H_{u}(\text{II}_{2,2+8k}\oplus A_{1})$
.
$H_{u}(\text{II}_{2,2+8k}\oplus A_{1})$
.
1.6 The (non-reflective) unigonal divisors for
 $N\equiv 5\hspace{0.6em}({\rm mod}\hspace{0.2em}8)$
$N\equiv 5\hspace{0.6em}({\rm mod}\hspace{0.2em}8)$
Let
![]() $(\unicode[STIX]{x1D6EC},\unicode[STIX]{x1D709})$
be a decorated
$(\unicode[STIX]{x1D6EC},\unicode[STIX]{x1D709})$
be a decorated
![]() $D$
-lattice of dimension
$D$
-lattice of dimension
![]() $N\equiv 5\hspace{0.6em}({\rm mod}\hspace{0.2em}8)$
. Let
$N\equiv 5\hspace{0.6em}({\rm mod}\hspace{0.2em}8)$
. Let
![]() $N=8k+5$
, where
$N=8k+5$
, where
![]() $k\geqslant 0$
; thus,
$k\geqslant 0$
; thus,
![]() $\unicode[STIX]{x1D6EC}\cong \text{II}_{2,2+8k}\oplus D_{3}$
. Let
$\unicode[STIX]{x1D6EC}\cong \text{II}_{2,2+8k}\oplus D_{3}$
. Let
![]() $v\in \unicode[STIX]{x1D6EC}$
be a unigonal vector, i.e.
$v\in \unicode[STIX]{x1D6EC}$
be a unigonal vector, i.e.
![]() $v^{2}=-12$
and
$v^{2}=-12$
and
![]() $\operatorname{div}(v)=4$
. Then
$\operatorname{div}(v)=4$
. Then
Given
![]() $g\in \widetilde{O}^{+}(v^{\bot })$
, let
$g\in \widetilde{O}^{+}(v^{\bot })$
, let
![]() $\widetilde{g}\in O(\unicode[STIX]{x1D6EC})$
be the isometry such that
$\widetilde{g}\in O(\unicode[STIX]{x1D6EC})$
be the isometry such that
![]() $\widetilde{g}(v)=v$
and
$\widetilde{g}(v)=v$
and
![]() $\widetilde{g}|_{v^{\bot }}=g$
. Then
$\widetilde{g}|_{v^{\bot }}=g$
. Then
![]() $\widetilde{g}\in O^{+}(\unicode[STIX]{x1D6EC})$
. Thus, we have an injection of groups
$\widetilde{g}\in O^{+}(\unicode[STIX]{x1D6EC})$
. Thus, we have an injection of groups
It follows that the injection
![]() $\mathscr{D}_{v^{\bot }}^{+}{\hookrightarrow}\mathscr{D}_{\unicode[STIX]{x1D6EC}}^{+}$
descends to a regular map
$\mathscr{D}_{v^{\bot }}^{+}{\hookrightarrow}\mathscr{D}_{\unicode[STIX]{x1D6EC}}^{+}$
descends to a regular map
The following proposition follows by similar arguments to those used above; we omit the proof.
Proposition 1.6.1. Let
![]() $(\unicode[STIX]{x1D6EC},\unicode[STIX]{x1D709})$
be a decorated
$(\unicode[STIX]{x1D6EC},\unicode[STIX]{x1D709})$
be a decorated
![]() $D$
-lattice of dimension
$D$
-lattice of dimension
![]() $N\equiv 5\hspace{0.6em}({\rm mod}\hspace{0.2em}8)$
and let
$N\equiv 5\hspace{0.6em}({\rm mod}\hspace{0.2em}8)$
and let
![]() $N=8k+5$
, where
$N=8k+5$
, where
![]() $k\geqslant 0$
. The map
$k\geqslant 0$
. The map
![]() $q$
in (1.6.3) is an isomorphism onto the unigonal Heegner divisor
$q$
in (1.6.3) is an isomorphism onto the unigonal Heegner divisor
![]() $H_{u}(\unicode[STIX]{x1D6EC},\unicode[STIX]{x1D709})$
. Moreover, the intersection of
$H_{u}(\unicode[STIX]{x1D6EC},\unicode[STIX]{x1D709})$
. Moreover, the intersection of
![]() $H_{u}(\unicode[STIX]{x1D6EC},\unicode[STIX]{x1D709})$
and the singular locus of
$H_{u}(\unicode[STIX]{x1D6EC},\unicode[STIX]{x1D709})$
and the singular locus of
![]() $\mathscr{F}(\unicode[STIX]{x1D6EC},\unicode[STIX]{x1D709})$
has codimension at least
$\mathscr{F}(\unicode[STIX]{x1D6EC},\unicode[STIX]{x1D709})$
has codimension at least
![]() $2$
in
$2$
in
![]() $H_{u}(\unicode[STIX]{x1D6EC},\unicode[STIX]{x1D709})$
.
$H_{u}(\unicode[STIX]{x1D6EC},\unicode[STIX]{x1D709})$
.
In order to simplify notation, from now on we let
A vector
![]() $v\in \text{II}_{2,2+8k}\oplus A_{2}$
is nodal if it has square
$v\in \text{II}_{2,2+8k}\oplus A_{2}$
is nodal if it has square
![]() $-2$
and divisibility
$-2$
and divisibility
![]() $1$
; it is unigonal if it has square
$1$
; it is unigonal if it has square
![]() $-12$
and divisibility
$-12$
and divisibility
![]() $3$
. Notice that the set of nodal vectors of
$3$
. Notice that the set of nodal vectors of
![]() $\text{II}_{2,2+8k}\oplus A_{2}$
is a single
$\text{II}_{2,2+8k}\oplus A_{2}$
is a single
![]() $\widetilde{O}^{+}(\text{II}_{2,2+8k}\oplus A_{2})$
-orbit, and similarly the set of unigonal vectors up to
$\widetilde{O}^{+}(\text{II}_{2,2+8k}\oplus A_{2})$
-orbit, and similarly the set of unigonal vectors up to
![]() $\pm 1$
is a single
$\pm 1$
is a single
![]() $\widetilde{O}^{+}(\text{II}_{2,2+8k}\oplus A_{2})$
-orbit. We let
$\widetilde{O}^{+}(\text{II}_{2,2+8k}\oplus A_{2})$
-orbit. We let
![]() $H_{n}(\text{II}_{2,2+8k}\oplus A_{2})$
and
$H_{n}(\text{II}_{2,2+8k}\oplus A_{2})$
and
![]() $H_{u}(\text{II}_{2,2+8k}\oplus A_{2})$
be the Heegner divisors of
$H_{u}(\text{II}_{2,2+8k}\oplus A_{2})$
be the Heegner divisors of
![]() $\mathscr{F}(\text{II}_{2,2+8k}\oplus A_{2})$
corresponding to a nodal or a unigonal
$\mathscr{F}(\text{II}_{2,2+8k}\oplus A_{2})$
corresponding to a nodal or a unigonal
![]() $v\in \text{II}_{2,2+8k}\oplus A_{2}$
, respectively (both are irreducible).
$v\in \text{II}_{2,2+8k}\oplus A_{2}$
, respectively (both are irreducible).
Let
![]() $v\in (\text{II}_{2,2+8k}\oplus A_{2})$
be a unigonal vector. Then
$v\in (\text{II}_{2,2+8k}\oplus A_{2})$
be a unigonal vector. Then
![]() $v^{\bot }\cong \text{II}_{2,2+8k}\oplus A_{1}$
. As in § 1.5.2, we get a regular map
$v^{\bot }\cong \text{II}_{2,2+8k}\oplus A_{1}$
. As in § 1.5.2, we get a regular map
Proposition 1.6.2. Let
![]() $k\geqslant 0$
. The map
$k\geqslant 0$
. The map
![]() $r$
of (1.6.5) is an isomorphism onto the unigonal Heegner divisor
$r$
of (1.6.5) is an isomorphism onto the unigonal Heegner divisor
![]() $H_{u}(\text{II}_{2,2+8k}\oplus A_{2})$
. Moreover, the intersection of
$H_{u}(\text{II}_{2,2+8k}\oplus A_{2})$
. Moreover, the intersection of
![]() $H_{u}(\text{II}_{2,2+8k}\oplus A_{2})$
and the singular locus of
$H_{u}(\text{II}_{2,2+8k}\oplus A_{2})$
and the singular locus of
![]() $\mathscr{F}(\text{II}_{2,2+8k}\oplus A_{2})$
has codimension at least
$\mathscr{F}(\text{II}_{2,2+8k}\oplus A_{2})$
has codimension at least
![]() $2$
in
$2$
in
![]() $H_{u}(\text{II}_{2,2+8k}\oplus A_{2})$
.
$H_{u}(\text{II}_{2,2+8k}\oplus A_{2})$
.
1.7 Nested locally symmetric varieties
1.7.1 The infinite tower of
 $D$
locally symmetric varieties
$D$
locally symmetric varieties
For
![]() $3\leqslant M$
, we let
$3\leqslant M$
, we let
![]() $\unicode[STIX]{x1D709}_{M}$
be a decoration of
$\unicode[STIX]{x1D709}_{M}$
be a decoration of
![]() $\unicode[STIX]{x1D6EC}_{M}$
. Choose
$\unicode[STIX]{x1D6EC}_{M}$
. Choose
![]() $N\geqslant 3$
. By Proposition 1.4.5, we have a sequence of inclusions of
$N\geqslant 3$
. By Proposition 1.4.5, we have a sequence of inclusions of
![]() $D$
period spaces:
$D$
period spaces:
Thus,
![]() $\operatorname{Im}f_{M}=H_{h}(\unicode[STIX]{x1D6EC}_{M},\unicode[STIX]{x1D709}_{M})$
for
$\operatorname{Im}f_{M}=H_{h}(\unicode[STIX]{x1D6EC}_{M},\unicode[STIX]{x1D709}_{M})$
for
![]() $4\leqslant M\leqslant N$
. There is a unique continuation of the above sequence. In fact, let
$4\leqslant M\leqslant N$
. There is a unique continuation of the above sequence. In fact, let
![]() $w\in \unicode[STIX]{x1D6EC}_{N}$
be a vector of divisibility
$w\in \unicode[STIX]{x1D6EC}_{N}$
be a vector of divisibility
![]() $2$
and such that
$2$
and such that
![]() $[v/2]=\unicode[STIX]{x1D709}_{N}$
(e.g. a hyperelliptic vector). Let
$[v/2]=\unicode[STIX]{x1D709}_{N}$
(e.g. a hyperelliptic vector). Let
![]() $L\subset (\unicode[STIX]{x1D6EC}_{N}\oplus (-4))_{\mathbb{Q}}$
be the sublattice generated by
$L\subset (\unicode[STIX]{x1D6EC}_{N}\oplus (-4))_{\mathbb{Q}}$
be the sublattice generated by
![]() $(\unicode[STIX]{x1D6EC}_{N}\oplus (-4))$
and
$(\unicode[STIX]{x1D6EC}_{N}\oplus (-4))$
and
![]() $(w/2,1/2)$
. Then
$(w/2,1/2)$
. Then
![]() $L$
and
$L$
and
![]() $\unicode[STIX]{x1D6EC}_{N+1}$
are even lattices of signature
$\unicode[STIX]{x1D6EC}_{N+1}$
are even lattices of signature
![]() $(2,N+1)$
and their discriminant groups (equipped with the discriminant quadratic forms) are isomorphic. By Theorem 1.13.2 of [Reference NikulinNik80], it follows that
$(2,N+1)$
and their discriminant groups (equipped with the discriminant quadratic forms) are isomorphic. By Theorem 1.13.2 of [Reference NikulinNik80], it follows that
![]() $L$
is isomorphic to
$L$
is isomorphic to
![]() $\unicode[STIX]{x1D6EC}_{N+1}$
; we choose an identification of
$\unicode[STIX]{x1D6EC}_{N+1}$
; we choose an identification of
![]() $L$
with
$L$
with
![]() $\unicode[STIX]{x1D6EC}_{N+1}$
. Let
$\unicode[STIX]{x1D6EC}_{N+1}$
. Let
![]() $\unicode[STIX]{x1D709}_{N+1}$
be the decoration of
$\unicode[STIX]{x1D709}_{N+1}$
be the decoration of
![]() $\unicode[STIX]{x1D6EC}_{N+1}$
(i.e.
$\unicode[STIX]{x1D6EC}_{N+1}$
(i.e.
![]() $L$
) defined by
$L$
) defined by
![]() $(0,1/2)$
. Then
$(0,1/2)$
. Then
![]() $v:=(0_{\unicode[STIX]{x1D6EC}_{N}},1)$
is a hyperelliptic vector of
$v:=(0_{\unicode[STIX]{x1D6EC}_{N}},1)$
is a hyperelliptic vector of
![]() $\unicode[STIX]{x1D6EC}_{N+1}$
, and
$\unicode[STIX]{x1D6EC}_{N+1}$
, and
![]() $v^{\bot }=\unicode[STIX]{x1D6EC}_{N}$
. Furthermore,
$v^{\bot }=\unicode[STIX]{x1D6EC}_{N}$
. Furthermore,
![]() $\unicode[STIX]{x1D709}_{N}$
is the decoration of
$\unicode[STIX]{x1D709}_{N}$
is the decoration of
![]() $v^{\bot }$
associated to
$v^{\bot }$
associated to
![]() $\unicode[STIX]{x1D709}_{N+1}$
. In conclusion, there is an infinite prolongation of (1.7.1), unique up to isomorphism:
$\unicode[STIX]{x1D709}_{N+1}$
. In conclusion, there is an infinite prolongation of (1.7.1), unique up to isomorphism:
For
![]() $3\leqslant M<N$
, we let
$3\leqslant M<N$
, we let
![]() $f_{M,N}:=f_{N}\circ f_{N-1}\circ \cdots \circ f_{M+1}$
. Thus,
$f_{M,N}:=f_{N}\circ f_{N-1}\circ \cdots \circ f_{M+1}$
. Thus,
1.7.2 Other building blocks of the
 $D$
tower
$D$
tower
Let
be the isomorphisms in (1.5.4), (1.5.9), (1.5.11), (1.6.3), and (1.6.5), respectively: the convention is that the subscript denotes the dimension of the period space containing the codomain as Heegner divisor (as for the maps
![]() $f_{N}$
).
$f_{N}$
).
Claim 1.7.1. Keeping notation as above,
![]() $f_{8k+4}\circ l_{8k+3}=m_{8k+4}\circ p_{8k+3}$
and
$f_{8k+4}\circ l_{8k+3}=m_{8k+4}\circ p_{8k+3}$
and
![]() $f_{8k+5}\circ m_{8k+4}=q_{8k+5}\circ r_{8k+4}$
.
$f_{8k+5}\circ m_{8k+4}=q_{8k+5}\circ r_{8k+4}$
.
Proof. Choose an isomorphism
![]() $\unicode[STIX]{x1D6EC}_{8k+4}\cong \text{II}_{2,2+8k}\oplus A_{1}^{2}$
and let
$\unicode[STIX]{x1D6EC}_{8k+4}\cong \text{II}_{2,2+8k}\oplus A_{1}^{2}$
and let
![]() $e_{1},e_{2}$
be generators of the addend
$e_{1},e_{2}$
be generators of the addend
![]() $A_{1}^{2}$
such that
$A_{1}^{2}$
such that
![]() $-2=e_{1}^{2}=e_{2}^{2}$
,
$-2=e_{1}^{2}=e_{2}^{2}$
,
![]() $(e_{1},e_{2})=0$
. Let
$(e_{1},e_{2})=0$
. Let
![]() $\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D6FF}$
be the obvious inclusions in the diagram
$\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D6FF}$
be the obvious inclusions in the diagram

The map
![]() $f_{8k+4}\circ l_{8k+3}$
is induced by the composition
$f_{8k+4}\circ l_{8k+3}$
is induced by the composition
![]() $\unicode[STIX]{x1D6FD}\circ \unicode[STIX]{x1D6FC}$
, and the map
$\unicode[STIX]{x1D6FD}\circ \unicode[STIX]{x1D6FC}$
, and the map
![]() $m_{8k+4}\circ p_{8k+3}$
is induced by the composition
$m_{8k+4}\circ p_{8k+3}$
is induced by the composition
![]() $\unicode[STIX]{x1D6FF}\circ \unicode[STIX]{x1D6FE}$
. Thus,
$\unicode[STIX]{x1D6FF}\circ \unicode[STIX]{x1D6FE}$
. Thus,
![]() $f_{8k+4}\circ l_{8k+3}=m_{8k+4}\circ p_{8k+3}$
because
$f_{8k+4}\circ l_{8k+3}=m_{8k+4}\circ p_{8k+3}$
because
![]() $\unicode[STIX]{x1D6FD}\circ \unicode[STIX]{x1D6FC}=\unicode[STIX]{x1D6FF}\circ \unicode[STIX]{x1D6FE}$
. A similar proof shows that
$\unicode[STIX]{x1D6FD}\circ \unicode[STIX]{x1D6FC}=\unicode[STIX]{x1D6FF}\circ \unicode[STIX]{x1D6FE}$
. A similar proof shows that
![]() $f_{8k+5}\circ m_{8k+4}=q_{8k+5}\circ r_{8k+4}$
.◻
$f_{8k+5}\circ m_{8k+4}=q_{8k+5}\circ r_{8k+4}$
.◻
The picture of the
![]() $D$
tower is periodic of period
$D$
tower is periodic of period
![]() $8$
:
$8$
:

1.7.3 Stratification of the support of the boundary divisor
Let
![]() $(\unicode[STIX]{x1D6EC},\unicode[STIX]{x1D709})$
be a decorated
$(\unicode[STIX]{x1D6EC},\unicode[STIX]{x1D709})$
be a decorated
![]() $D$
-lattice of dimension
$D$
-lattice of dimension
![]() $N$
. We let
$N$
. We let
![]() $\unicode[STIX]{x1D6E5}^{(1)}(\unicode[STIX]{x1D6EC},\unicode[STIX]{x1D709})\subset \mathscr{F}(\unicode[STIX]{x1D6EC},\unicode[STIX]{x1D709})$
be the support of the boundary divisor, i.e.
$\unicode[STIX]{x1D6E5}^{(1)}(\unicode[STIX]{x1D6EC},\unicode[STIX]{x1D709})\subset \mathscr{F}(\unicode[STIX]{x1D6EC},\unicode[STIX]{x1D709})$
be the support of the boundary divisor, i.e.
We let
![]() $\widetilde{\unicode[STIX]{x1D6E5}}^{(1)}(\unicode[STIX]{x1D6EC},\unicode[STIX]{x1D709})\subset \mathscr{D}_{\unicode[STIX]{x1D6EC}}^{+}$
be the inverse image of
$\widetilde{\unicode[STIX]{x1D6E5}}^{(1)}(\unicode[STIX]{x1D6EC},\unicode[STIX]{x1D709})\subset \mathscr{D}_{\unicode[STIX]{x1D6EC}}^{+}$
be the inverse image of
![]() $\unicode[STIX]{x1D6E5}^{(1)}(\unicode[STIX]{x1D6EC},\unicode[STIX]{x1D709})$
for the quotient map
$\unicode[STIX]{x1D6E5}^{(1)}(\unicode[STIX]{x1D6EC},\unicode[STIX]{x1D709})$
for the quotient map
Thus,
![]() $\widetilde{\unicode[STIX]{x1D6E5}}^{(1)}(\unicode[STIX]{x1D6EC},\unicode[STIX]{x1D709})$
is a linearized arrangement, in the terminology of Looijenga [Reference LooijengaLoo03a], and it is naturally stratified. The
$\widetilde{\unicode[STIX]{x1D6E5}}^{(1)}(\unicode[STIX]{x1D6EC},\unicode[STIX]{x1D709})$
is a linearized arrangement, in the terminology of Looijenga [Reference LooijengaLoo03a], and it is naturally stratified. The
![]() $k$
th stratum is defined to be
$k$
th stratum is defined to be
i.e. the set of points belonging to
![]() $k$
(at least) independent ‘hyperplanes’.Footnote
1
Let
$k$
(at least) independent ‘hyperplanes’.Footnote
1
Let
where
![]() $\unicode[STIX]{x1D70B}$
is the quotient map (1.7.12). The strata
$\unicode[STIX]{x1D70B}$
is the quotient map (1.7.12). The strata
![]() $\widetilde{\unicode[STIX]{x1D6E5}}^{(k)}(\unicode[STIX]{x1D6EC},\unicode[STIX]{x1D709})$
and
$\widetilde{\unicode[STIX]{x1D6E5}}^{(k)}(\unicode[STIX]{x1D6EC},\unicode[STIX]{x1D709})$
and
![]() $\unicode[STIX]{x1D6E5}^{(k)}(\unicode[STIX]{x1D6EC},\unicode[STIX]{x1D709})$
play a key rôle in Looijenga’s semitoric compactification of the complement of
$\unicode[STIX]{x1D6E5}^{(k)}(\unicode[STIX]{x1D6EC},\unicode[STIX]{x1D709})$
play a key rôle in Looijenga’s semitoric compactification of the complement of
![]() $\unicode[STIX]{x1D6E5}^{(1)}(\unicode[STIX]{x1D6EC},\unicode[STIX]{x1D709})$
in
$\unicode[STIX]{x1D6E5}^{(1)}(\unicode[STIX]{x1D6EC},\unicode[STIX]{x1D709})$
in
![]() $\mathscr{F}(\unicode[STIX]{x1D6EC},\unicode[STIX]{x1D709})$
. We will show that the subvarieties of
$\mathscr{F}(\unicode[STIX]{x1D6EC},\unicode[STIX]{x1D709})$
. We will show that the subvarieties of
![]() $\mathscr{F}(\unicode[STIX]{x1D6EC},\unicode[STIX]{x1D709})$
appearing in (1.7.10) are exactly the irreducible components of
$\mathscr{F}(\unicode[STIX]{x1D6EC},\unicode[STIX]{x1D709})$
appearing in (1.7.10) are exactly the irreducible components of
![]() $\unicode[STIX]{x1D6E5}^{(k)}(\unicode[STIX]{x1D6EC},\unicode[STIX]{x1D709})$
. In order to state our results, let
$\unicode[STIX]{x1D6E5}^{(k)}(\unicode[STIX]{x1D6EC},\unicode[STIX]{x1D709})$
. In order to state our results, let
We let
![]() $H_{h}^{(k)}(\unicode[STIX]{x1D6EC},\unicode[STIX]{x1D709})\subset \mathscr{F}(\unicode[STIX]{x1D6EC},\unicode[STIX]{x1D709})$
and
$H_{h}^{(k)}(\unicode[STIX]{x1D6EC},\unicode[STIX]{x1D709})\subset \mathscr{F}(\unicode[STIX]{x1D6EC},\unicode[STIX]{x1D709})$
and
![]() $H_{u}^{(k)}(\unicode[STIX]{x1D6EC},\unicode[STIX]{x1D709})\subset \mathscr{F}(\unicode[STIX]{x1D6EC},\unicode[STIX]{x1D709})$
be the images via
$H_{u}^{(k)}(\unicode[STIX]{x1D6EC},\unicode[STIX]{x1D709})\subset \mathscr{F}(\unicode[STIX]{x1D6EC},\unicode[STIX]{x1D709})$
be the images via
![]() $\unicode[STIX]{x1D70B}$
of
$\unicode[STIX]{x1D70B}$
of
![]() $\mathscr{H}_{h}^{(k)}(\unicode[STIX]{x1D6EC},\unicode[STIX]{x1D709})$
and
$\mathscr{H}_{h}^{(k)}(\unicode[STIX]{x1D6EC},\unicode[STIX]{x1D709})$
and
![]() $\mathscr{H}_{u}^{(k)}(\unicode[STIX]{x1D6EC},\unicode[STIX]{x1D709})$
, respectively. In order to simplify notation, we let
$\mathscr{H}_{u}^{(k)}(\unicode[STIX]{x1D6EC},\unicode[STIX]{x1D709})$
, respectively. In order to simplify notation, we let
where
![]() $\unicode[STIX]{x1D709}_{N}$
is a decoration of
$\unicode[STIX]{x1D709}_{N}$
is a decoration of
![]() $\unicode[STIX]{x1D6EC}_{N}$
. Below is the main result of the present subsubsection.
$\unicode[STIX]{x1D6EC}_{N}$
. Below is the main result of the present subsubsection.
Proposition 1.7.2. Let
![]() $N\geqslant 3$
and keep notation as above. Then
$N\geqslant 3$
and keep notation as above. Then
If, in addition,
![]() $N\geqslant 4$
and
$N\geqslant 4$
and
![]() $1\leqslant k\leqslant N-3$
, then
$1\leqslant k\leqslant N-3$
, then
We will prove Proposition 1.7.2 at the end of the present subsubsection.
Lemma 1.7.3. Let
![]() $(\unicode[STIX]{x1D6EC},\unicode[STIX]{x1D709})$
be a
$(\unicode[STIX]{x1D6EC},\unicode[STIX]{x1D709})$
be a
![]() $D$
-lattice of dimension
$D$
-lattice of dimension
![]() $N\equiv 3\hspace{0.6em}({\rm mod}\hspace{0.2em}8)$
. Then
$N\equiv 3\hspace{0.6em}({\rm mod}\hspace{0.2em}8)$
. Then
Proof. Suppose the contrary. Then there exists
![]() $[\unicode[STIX]{x1D70E}]\in \mathscr{D}_{\unicode[STIX]{x1D6EC}_{N}}^{+}$
such that
$[\unicode[STIX]{x1D70E}]\in \mathscr{D}_{\unicode[STIX]{x1D6EC}_{N}}^{+}$
such that
![]() $\unicode[STIX]{x1D70E}^{\bot }$
contains a unigonal vector
$\unicode[STIX]{x1D70E}^{\bot }$
contains a unigonal vector
![]() $w\in \unicode[STIX]{x1D6EC}_{N}$
(i.e.
$w\in \unicode[STIX]{x1D6EC}_{N}$
(i.e.
![]() $w^{2}=-4$
and
$w^{2}=-4$
and
![]() $\operatorname{div}(w)=4$
), and a vector
$\operatorname{div}(w)=4$
), and a vector
![]() $v$
which is either hyperelliptic or unigonal, and moreover
$v$
which is either hyperelliptic or unigonal, and moreover
![]() $v\not =\pm w$
. It follows that
$v\not =\pm w$
. It follows that
![]() $\langle v,w\rangle$
is a rank-
$\langle v,w\rangle$
is a rank-
![]() $2$
negative-definite lattice (
$2$
negative-definite lattice (
![]() $\unicode[STIX]{x1D70E}^{\bot }\cap \unicode[STIX]{x1D6EC}_{\mathbb{R}}$
is negative definite) and hence the determinant of
$\unicode[STIX]{x1D70E}^{\bot }\cap \unicode[STIX]{x1D6EC}_{\mathbb{R}}$
is negative definite) and hence the determinant of
![]() $\langle v,w\rangle$
is strictly positive. This in turn implies that
$\langle v,w\rangle$
is strictly positive. This in turn implies that
![]() $v\bot w$
(recall that
$v\bot w$
(recall that
![]() $(v,w)\in 4\mathbb{Z}$
). On the other hand,
$(v,w)\in 4\mathbb{Z}$
). On the other hand,
![]() $\unicode[STIX]{x1D6EC}=\mathbb{Z}w\oplus w^{\bot }$
because
$\unicode[STIX]{x1D6EC}=\mathbb{Z}w\oplus w^{\bot }$
because
![]() $w^{2}=-4$
and
$w^{2}=-4$
and
![]() $\operatorname{div}(w)=4$
. Since
$\operatorname{div}(w)=4$
. Since
![]() $\unicode[STIX]{x1D6EC}$
has determinant
$\unicode[STIX]{x1D6EC}$
has determinant
![]() $-4$
, it follows that the lattice
$-4$
, it follows that the lattice
![]() $w^{\bot }$
is unimodular. Now
$w^{\bot }$
is unimodular. Now
![]() $v$
belongs to the unimodular lattice
$v$
belongs to the unimodular lattice
![]() $w^{\bot }$
, and
$w^{\bot }$
, and
![]() $\operatorname{div}_{\unicode[STIX]{x1D6EC}}(v)\in \{2,4\}$
; that is a contradiction.◻
$\operatorname{div}_{\unicode[STIX]{x1D6EC}}(v)\in \{2,4\}$
; that is a contradiction.◻
By similar arguments, we obtain the following lemmas (we omit the proofs).
Lemma 1.7.4. Let
![]() $(\unicode[STIX]{x1D6EC},\unicode[STIX]{x1D709})$
be a
$(\unicode[STIX]{x1D6EC},\unicode[STIX]{x1D709})$
be a
![]() $D$
-lattice of dimension
$D$
-lattice of dimension
![]() $N\equiv 4\hspace{0.6em}({\rm mod}\hspace{0.2em}8)$
. If
$N\equiv 4\hspace{0.6em}({\rm mod}\hspace{0.2em}8)$
. If
![]() $w_{1},w_{2}$
are non-proportional unigonal vectors of
$w_{1},w_{2}$
are non-proportional unigonal vectors of
![]() $(\unicode[STIX]{x1D6EC},\unicode[STIX]{x1D709})$
, spanning a negative-definite sublattice, then
$(\unicode[STIX]{x1D6EC},\unicode[STIX]{x1D709})$
, spanning a negative-definite sublattice, then
![]() $\langle w_{1},w_{2}\rangle$
is isomorphic to
$\langle w_{1},w_{2}\rangle$
is isomorphic to
![]() $D_{2}$
, and
$D_{2}$
, and
In particular
![]() $\{w_{1}^{\ast },w_{2}^{\ast }\}=\{\unicode[STIX]{x1D701},\unicode[STIX]{x1D701}^{\prime }\}$
, where, as usual,
$\{w_{1}^{\ast },w_{2}^{\ast }\}=\{\unicode[STIX]{x1D701},\unicode[STIX]{x1D701}^{\prime }\}$
, where, as usual,
![]() $A_{\unicode[STIX]{x1D6EC}}=\{0,\unicode[STIX]{x1D709},\unicode[STIX]{x1D701},\unicode[STIX]{x1D701}^{\prime }\}$
.
$A_{\unicode[STIX]{x1D6EC}}=\{0,\unicode[STIX]{x1D709},\unicode[STIX]{x1D701},\unicode[STIX]{x1D701}^{\prime }\}$
.
Lemma 1.7.5. Let
![]() $(\unicode[STIX]{x1D6EC},\unicode[STIX]{x1D709})$
be a
$(\unicode[STIX]{x1D6EC},\unicode[STIX]{x1D709})$
be a
![]() $D$
-lattice of dimension
$D$
-lattice of dimension
![]() $N\equiv 4\hspace{0.6em}({\rm mod}\hspace{0.2em}8)$
. Let
$N\equiv 4\hspace{0.6em}({\rm mod}\hspace{0.2em}8)$
. Let
![]() $v,w$
be a hyperelliptic and a unigonal vector of
$v,w$
be a hyperelliptic and a unigonal vector of
![]() $(\unicode[STIX]{x1D6EC},\unicode[STIX]{x1D709})$
, respectively, spanning a negative-definite sublattice. Then
$(\unicode[STIX]{x1D6EC},\unicode[STIX]{x1D709})$
, respectively, spanning a negative-definite sublattice. Then
![]() $\langle v,w\rangle$
is isomorphic to
$\langle v,w\rangle$
is isomorphic to
![]() $D_{2}$
, and
$D_{2}$
, and
Lemma 1.7.6. Let
![]() $(\unicode[STIX]{x1D6EC},\unicode[STIX]{x1D709})$
be a decorated
$(\unicode[STIX]{x1D6EC},\unicode[STIX]{x1D709})$
be a decorated
![]() $D$
-lattice of dimension
$D$
-lattice of dimension
![]() $N\geqslant 4$
. Let
$N\geqslant 4$
. Let
![]() $v$
be a hyperelliptic vector of
$v$
be a hyperelliptic vector of
![]() $(\unicode[STIX]{x1D6EC},\unicode[STIX]{x1D709})$
and
$(\unicode[STIX]{x1D6EC},\unicode[STIX]{x1D709})$
and
![]() $\unicode[STIX]{x1D702}$
be the decoration of the
$\unicode[STIX]{x1D702}$
be the decoration of the
![]() $D$
-lattice
$D$
-lattice
![]() $v^{\bot }$
defined in Remark 1.4.2. Suppose that
$v^{\bot }$
defined in Remark 1.4.2. Suppose that
![]() $w$
is a hyperelliptic vector of
$w$
is a hyperelliptic vector of
![]() $(\unicode[STIX]{x1D6EC},\unicode[STIX]{x1D709})$
, orthogonal to
$(\unicode[STIX]{x1D6EC},\unicode[STIX]{x1D709})$
, orthogonal to
![]() $v$
. Then one of the following holds:
$v$
. Then one of the following holds:
(1)
 $w$
has divisibility
$w$
has divisibility
 $2$
in
$2$
in
 $v^{\bot }$
and it is a hyperelliptic vector of
$v^{\bot }$
and it is a hyperelliptic vector of
 $(v^{\bot },\unicode[STIX]{x1D702})$
;
$(v^{\bot },\unicode[STIX]{x1D702})$
;(2)
 $w$
has divisibility
$w$
has divisibility
 $4$
in
$4$
in
 $v^{\bot }$
,
$v^{\bot }$
,
 $\{v,w\}\text{}^{\bot }\cong \text{II}_{2,N-2}$
, and
$\{v,w\}\text{}^{\bot }\cong \text{II}_{2,N-2}$
, and
 $N\equiv 4\hspace{0.6em}({\rm mod}\hspace{0.2em}8)$
.
$N\equiv 4\hspace{0.6em}({\rm mod}\hspace{0.2em}8)$
.
Proposition 1.7.7. Let
![]() $N\geqslant 4$
and
$N\geqslant 4$
and
![]() $1\leqslant k\leqslant N-3$
. Let
$1\leqslant k\leqslant N-3$
. Let
![]() $(\unicode[STIX]{x1D6EC},\unicode[STIX]{x1D709})$
be a dimension-
$(\unicode[STIX]{x1D6EC},\unicode[STIX]{x1D709})$
be a dimension-
![]() $N$
$N$
![]() $D$
-lattice and
$D$
-lattice and
![]() $v_{1},\ldots ,v_{k}$
be pairwise-orthogonal hyperelliptic vectors of
$v_{1},\ldots ,v_{k}$
be pairwise-orthogonal hyperelliptic vectors of
![]() $(\unicode[STIX]{x1D6EC},\unicode[STIX]{x1D709})$
. Then, for any
$(\unicode[STIX]{x1D6EC},\unicode[STIX]{x1D709})$
. Then, for any
![]() $1\leqslant i\leqslant k-1$
,
$1\leqslant i\leqslant k-1$
,
![]() $\{v_{1},\ldots ,v_{i}\}\text{}^{\bot }$
carries a decoration
$\{v_{1},\ldots ,v_{i}\}\text{}^{\bot }$
carries a decoration
![]() $\unicode[STIX]{x1D709}(i)$
such that
$\unicode[STIX]{x1D709}(i)$
such that
![]() $(\{v_{1},\ldots ,v_{i-1}\}\text{}^{\bot },\unicode[STIX]{x1D709}(i-1))$
induces
$(\{v_{1},\ldots ,v_{i-1}\}\text{}^{\bot },\unicode[STIX]{x1D709}(i-1))$
induces
![]() $(\{v_{1},\ldots ,v_{i}\}\text{}^{\bot },\unicode[STIX]{x1D709}(i))$
as in Remark 1.4.2 (for
$(\{v_{1},\ldots ,v_{i}\}\text{}^{\bot },\unicode[STIX]{x1D709}(i))$
as in Remark 1.4.2 (for
![]() $i=1$
, this means that
$i=1$
, this means that
![]() $(\unicode[STIX]{x1D6EC},\unicode[STIX]{x1D709})$
induces
$(\unicode[STIX]{x1D6EC},\unicode[STIX]{x1D709})$
induces
![]() $(v_{1}^{\bot },\unicode[STIX]{x1D709}(1))$
) and
$(v_{1}^{\bot },\unicode[STIX]{x1D709}(1))$
) and
![]() $v_{i}$
is a hyperelliptic vector of
$v_{i}$
is a hyperelliptic vector of
![]() $(\{v_{1},\ldots ,v_{i}\}\text{}^{\bot },\unicode[STIX]{x1D709}(i))$
. Moreover, one of the following holds:
$(\{v_{1},\ldots ,v_{i}\}\text{}^{\bot },\unicode[STIX]{x1D709}(i))$
. Moreover, one of the following holds:
(1)
 $v_{k}$
is a hyperelliptic vector of
$v_{k}$
is a hyperelliptic vector of
 $(\{v_{1},\ldots ,v_{k-1}\}\text{}^{\bot },\unicode[STIX]{x1D709}(k-1))$
;
$(\{v_{1},\ldots ,v_{k-1}\}\text{}^{\bot },\unicode[STIX]{x1D709}(k-1))$
;(2)
 $k\geqslant 2$
,
$k\geqslant 2$
,
 $N\equiv k+2\hspace{0.6em}({\rm mod}\hspace{0.2em}8)$
,
$N\equiv k+2\hspace{0.6em}({\rm mod}\hspace{0.2em}8)$
,
 $v_{k}$
has divisibility
$v_{k}$
has divisibility
 $4$
in
$4$
in
 $\{v_{1},\ldots ,v_{k-1}\}\text{}^{\bot }$
, and
$\{v_{1},\ldots ,v_{k-1}\}\text{}^{\bot }$
, and
 $\{v_{1},\ldots ,v_{k}\}\text{}^{\bot }\cong \text{II}_{2,N-k}$
.
$\{v_{1},\ldots ,v_{k}\}\text{}^{\bot }\cong \text{II}_{2,N-k}$
.
Proof. By induction on
![]() $k$
. If
$k$
. If
![]() $k=1$
, the proposition holds by Lemma 1.4.1; if
$k=1$
, the proposition holds by Lemma 1.4.1; if
![]() $k=2$
, it holds by Lemma 1.7.6. Now let
$k=2$
, it holds by Lemma 1.7.6. Now let
![]() $k\geqslant 3$
. By the inductive hypothesis,
$k\geqslant 3$
. By the inductive hypothesis,
![]() $\{v_{1},\ldots ,v_{k-2}\}\text{}^{\bot }$
,
$\{v_{1},\ldots ,v_{k-2}\}\text{}^{\bot }$
,
![]() $\{v_{1},\ldots ,v_{k-1}\}\text{}^{\bot }$
, and
$\{v_{1},\ldots ,v_{k-1}\}\text{}^{\bot }$
, and
![]() $\{v_{1},\ldots ,v_{k-2},v_{k}\}\text{}^{\bot }$
are either
$\{v_{1},\ldots ,v_{k-2},v_{k}\}\text{}^{\bot }$
are either
![]() $D$
-lattices or unimodular. Since
$D$
-lattices or unimodular. Since
![]() $v_{k-1}$
and
$v_{k-1}$
and
![]() $v_{k}$
have divisibility
$v_{k}$
have divisibility
![]() $2$
in
$2$
in
![]() $\unicode[STIX]{x1D6EC}$
, it follows that
$\unicode[STIX]{x1D6EC}$
, it follows that
![]() $\{v_{1},\ldots ,v_{k-2}\}\text{}^{\bot }$
,
$\{v_{1},\ldots ,v_{k-2}\}\text{}^{\bot }$
,
![]() $\{v_{1},\ldots ,v_{k-1}\}\text{}^{\bot }$
, and
$\{v_{1},\ldots ,v_{k-1}\}\text{}^{\bot }$
, and
![]() $\{v_{1},\ldots ,v_{k-2},v_{k}\}\text{}^{\bot }$
are not unimodular and hence they are
$\{v_{1},\ldots ,v_{k-2},v_{k}\}\text{}^{\bot }$
are not unimodular and hence they are
![]() $D$
-lattices. In particular, by Lemma 1.7.6,
$D$
-lattices. In particular, by Lemma 1.7.6,
![]() $v_{k-1}$
and
$v_{k-1}$
and
![]() $v_{k}$
are hyperelliptic vectors of
$v_{k}$
are hyperelliptic vectors of
![]() $(\{v_{1},\ldots ,v_{k-2}\}\text{}^{\bot },\unicode[STIX]{x1D709}(k-2))$
. The proposition follows by applying Lemma 1.7.6 to the decorated
$(\{v_{1},\ldots ,v_{k-2}\}\text{}^{\bot },\unicode[STIX]{x1D709}(k-2))$
. The proposition follows by applying Lemma 1.7.6 to the decorated
![]() $D$
-lattice
$D$
-lattice
![]() $(\{v_{1},\ldots ,v_{k-2}\}\text{}^{\bot },\unicode[STIX]{x1D709}(k-2))$
and the vectors
$(\{v_{1},\ldots ,v_{k-2}\}\text{}^{\bot },\unicode[STIX]{x1D709}(k-2))$
and the vectors
![]() $v=v_{k-1}$
,
$v=v_{k-1}$
,
![]() $w=v_{k}$
.◻
$w=v_{k}$
.◻
Proof of Proposition 1.7.2.
Let us prove (1.7.18). It is obvious that
![]() $\unicode[STIX]{x1D6E5}^{(k)}(N)$
contains the set on the right-hand side. Next, we check that the left-hand side of (1.7.18) is contained in the right-hand side. If
$\unicode[STIX]{x1D6E5}^{(k)}(N)$
contains the set on the right-hand side. Next, we check that the left-hand side of (1.7.18) is contained in the right-hand side. If
![]() $N\not \equiv 3,4\hspace{0.6em}({\rm mod}\hspace{0.2em}8)$
, the containment is obvious because there are no reflective unigonal vectors. If
$N\not \equiv 3,4\hspace{0.6em}({\rm mod}\hspace{0.2em}8)$
, the containment is obvious because there are no reflective unigonal vectors. If
![]() $N\equiv 3\hspace{0.6em}({\rm mod}\hspace{0.2em}8)$
(and
$N\equiv 3\hspace{0.6em}({\rm mod}\hspace{0.2em}8)$
(and
![]() $k\geqslant 2$
), the containment follows from Lemma 1.7.3. It remains to prove that if
$k\geqslant 2$
), the containment follows from Lemma 1.7.3. It remains to prove that if
![]() $N\equiv 4\hspace{0.6em}({\rm mod}\hspace{0.2em}8)$
, then
$N\equiv 4\hspace{0.6em}({\rm mod}\hspace{0.2em}8)$
, then
![]() $\unicode[STIX]{x1D6E5}^{(2)}(N)\subset H_{h}^{(2)}(N)$
; this follows from Lemma 1.7.4.
$\unicode[STIX]{x1D6E5}^{(2)}(N)\subset H_{h}^{(2)}(N)$
; this follows from Lemma 1.7.4.
Lastly, we prove (1.7.19). Suppose that
![]() $\unicode[STIX]{x1D70B}([\unicode[STIX]{x1D70E}])\in H_{h}^{(k)}(N)$
, i.e. there exist linearly independent hyperelliptic vectors
$\unicode[STIX]{x1D70B}([\unicode[STIX]{x1D70E}])\in H_{h}^{(k)}(N)$
, i.e. there exist linearly independent hyperelliptic vectors
![]() $v_{1},\ldots ,v_{k}$
of
$v_{1},\ldots ,v_{k}$
of
![]() $(\unicode[STIX]{x1D6EC}_{N},\unicode[STIX]{x1D709}_{N})$
such that
$(\unicode[STIX]{x1D6EC}_{N},\unicode[STIX]{x1D709}_{N})$
such that
![]() $\unicode[STIX]{x1D70E}\in \{v_{1},\ldots ,v_{k}\}\text{}^{\bot }$
. The latter condition implies that the restriction of
$\unicode[STIX]{x1D70E}\in \{v_{1},\ldots ,v_{k}\}\text{}^{\bot }$
. The latter condition implies that the restriction of
![]() $(\,,\,)_{\unicode[STIX]{x1D6EC}}$
to the span of
$(\,,\,)_{\unicode[STIX]{x1D6EC}}$
to the span of
![]() $v_{1},\ldots ,v_{k}$
is negative definite and hence the vectors
$v_{1},\ldots ,v_{k}$
is negative definite and hence the vectors
![]() $v_{1},\ldots ,v_{k}$
are pairwise orthogonal by Lemma 1.4.7. Thus, we may apply Proposition 1.7.7; if Item (1) holds, then
$v_{1},\ldots ,v_{k}$
are pairwise orthogonal by Lemma 1.4.7. Thus, we may apply Proposition 1.7.7; if Item (1) holds, then
![]() $\unicode[STIX]{x1D70B}([\unicode[STIX]{x1D70E}])\in \operatorname{Im}f_{N-k,N}$
; if Item (2) holds, then
$\unicode[STIX]{x1D70B}([\unicode[STIX]{x1D70E}])\in \operatorname{Im}f_{N-k,N}$
; if Item (2) holds, then
![]() $N\equiv k+2\hspace{0.6em}({\rm mod}\hspace{0.2em}8)$
and
$N\equiv k+2\hspace{0.6em}({\rm mod}\hspace{0.2em}8)$
and
![]() $\unicode[STIX]{x1D70B}([\unicode[STIX]{x1D70E}])\in \operatorname{Im}(f_{N-k+1,N}\circ l_{N-k+1})$
. This proves that the left-hand side of (1.7.19) is contained in the right-hand side. The converse is obvious.◻
$\unicode[STIX]{x1D70B}([\unicode[STIX]{x1D70E}])\in \operatorname{Im}(f_{N-k+1,N}\circ l_{N-k+1})$
. This proves that the left-hand side of (1.7.19) is contained in the right-hand side. The converse is obvious.◻
Remark 1.7.8. Let
![]() $N=8s+4$
, where
$N=8s+4$
, where
![]() $s\geqslant 0$
. We have proved that
$s\geqslant 0$
. We have proved that
In particular, it follows from Lemma 1.7.3 that
![]() $\operatorname{Im}f_{N-2,N}\cap H_{u}^{(2)}(N)=\varnothing$
.
$\operatorname{Im}f_{N-2,N}\cap H_{u}^{(2)}(N)=\varnothing$
.
2 Locally symmetric spaces
 $\mathscr{F}(N)$
as period spaces for
$\mathscr{F}(N)$
as period spaces for
 $N\in \{18,19,20,21\}$
$N\in \{18,19,20,21\}$
We will denote by
![]() $\mathscr{F}(N)$
the locally symmetric variety
$\mathscr{F}(N)$
the locally symmetric variety
![]() $\mathscr{F}(\unicode[STIX]{x1D6EC}_{N},\unicode[STIX]{x1D709}_{N})$
, where
$\mathscr{F}(\unicode[STIX]{x1D6EC}_{N},\unicode[STIX]{x1D709}_{N})$
, where
![]() $(\unicode[STIX]{x1D6EC}_{N},\unicode[STIX]{x1D709}_{N})$
is a decorated dimension-
$(\unicode[STIX]{x1D6EC}_{N},\unicode[STIX]{x1D709}_{N})$
is a decorated dimension-
![]() $N$
$N$
![]() $D$
-lattice. As is well known, the period space for quartic
$D$
-lattice. As is well known, the period space for quartic
![]() $K3$
surfaces is
$K3$
surfaces is
![]() $\mathscr{F}_{\unicode[STIX]{x1D6EC}_{19}}(\widetilde{O}^{+}(\unicode[STIX]{x1D6EC}_{19}))$
, and the latter is equal to
$\mathscr{F}_{\unicode[STIX]{x1D6EC}_{19}}(\widetilde{O}^{+}(\unicode[STIX]{x1D6EC}_{19}))$
, and the latter is equal to
![]() $\mathscr{F}(19)$
by Proposition 1.2.3. We will prove that
$\mathscr{F}(19)$
by Proposition 1.2.3. We will prove that
![]() $\mathscr{F}(18)$
is the period space of hyperelliptic quartic
$\mathscr{F}(18)$
is the period space of hyperelliptic quartic
![]() $K3$
surfaces, see § 2.2, and that
$K3$
surfaces, see § 2.2, and that
![]() $\mathscr{F}(20)$
is the period space of desingularized EPW sextics (a quotient of the period space of double EPW sextics by the natural duality involution; see [Reference O’GradyO’Gr15]). Lastly, in § 2.3, we will establish a relation between
$\mathscr{F}(20)$
is the period space of desingularized EPW sextics (a quotient of the period space of double EPW sextics by the natural duality involution; see [Reference O’GradyO’Gr15]). Lastly, in § 2.3, we will establish a relation between
![]() $\mathscr{F}(21)$
and the period space of hyperkähler
$\mathscr{F}(21)$
and the period space of hyperkähler
![]() $10$
-folds of Type OG10.
$10$
-folds of Type OG10.
Notation 2.0.1. We will denote by
![]() $H_{h}(N),H_{u}(N)$
the hyperelliptic and unigonal divisors in
$H_{h}(N),H_{u}(N)$
the hyperelliptic and unigonal divisors in
![]() $\mathscr{F}(N)$
.
$\mathscr{F}(N)$
.
2.1 Quartic
 $K3$
surfaces and their periods
$K3$
surfaces and their periods
For us a
![]() $K3$
surface is a complex projective surface
$K3$
surface is a complex projective surface
![]() $X$
with DuVal singularities, trivial dualizing sheaf
$X$
with DuVal singularities, trivial dualizing sheaf
![]() $\unicode[STIX]{x1D714}_{X}$
, and
$\unicode[STIX]{x1D714}_{X}$
, and
![]() $H^{1}(\mathscr{O}_{X})=0$
. A polarization of degree
$H^{1}(\mathscr{O}_{X})=0$
. A polarization of degree
![]() $d$
on a
$d$
on a
![]() $K3$
surface
$K3$
surface
![]() $X$
is an ample line bundle
$X$
is an ample line bundle
![]() $L$
on
$L$
on
![]() $X$
such that
$X$
such that
![]() $c_{1}(L)$
is primitive and
$c_{1}(L)$
is primitive and
![]() $c_{1}(L)\cdot c_{1}(L)=d$
. The degree
$c_{1}(L)\cdot c_{1}(L)=d$
. The degree
![]() $d$
of a polarization is strictly positive and even and hence we may write
$d$
of a polarization is strictly positive and even and hence we may write
![]() $d=2g-2$
, with
$d=2g-2$
, with
![]() $g\geqslant 2$
; then
$g\geqslant 2$
; then
![]() $g$
is the arithmetic genus of curves in
$g$
is the arithmetic genus of curves in
![]() $|L|$
. A polarized
$|L|$
. A polarized
![]() $K3$
surface is a couple
$K3$
surface is a couple
![]() $(X,L)$
, where
$(X,L)$
, where
![]() $X$
is a
$X$
is a
![]() $K3$
surface and
$K3$
surface and
![]() $L$
is a polarization of
$L$
is a polarization of
![]() $X$
; the degree and genus of
$X$
; the degree and genus of
![]() $(X,L)$
are defined to be the degree and genus of
$(X,L)$
are defined to be the degree and genus of
![]() $L$
. We recall the following fundamental result.
$L$
. We recall the following fundamental result.
Theorem 2.1.1 (Mayer [Reference MayerMay72]).
Let
![]() $(X,L)$
be a polarized
$(X,L)$
be a polarized
![]() $K3$
of genus
$K3$
of genus
![]() $g$
. Then one of the following holds.
$g$
. Then one of the following holds.
(1) The map
 $\unicode[STIX]{x1D711}_{L}:S{\dashrightarrow}|L|^{\vee }\cong \mathbb{P}^{g}$
defined by
$\unicode[STIX]{x1D711}_{L}:S{\dashrightarrow}|L|^{\vee }\cong \mathbb{P}^{g}$
defined by
 $L$
is regular and is an isomorphism onto its image (a surface whose generic hyperplane section is a canonical curve of genus
$L$
is regular and is an isomorphism onto its image (a surface whose generic hyperplane section is a canonical curve of genus
 $g$
).
$g$
).(2) The map
 $\unicode[STIX]{x1D711}_{L}:S{\dashrightarrow}|L|^{\vee }\cong \mathbb{P}^{g}$
is regular and is a double cover of its image (a rational surface of degree
$\unicode[STIX]{x1D711}_{L}:S{\dashrightarrow}|L|^{\vee }\cong \mathbb{P}^{g}$
is regular and is a double cover of its image (a rational surface of degree
 $g-1$
).
$g-1$
).(3) The linear system
 $|L|$
has a fixed component, a smooth rational curve
$|L|$
has a fixed component, a smooth rational curve
 $R$
, and
$R$
, and
 $L(-R)\cong \mathscr{O}_{X}(gE)$
, where
$L(-R)\cong \mathscr{O}_{X}(gE)$
, where
 $E$
is an elliptic curve.
$E$
is an elliptic curve.
Actually Mayer considered big and nef divisors on a smooth
![]() $K3$
surface; one gets the result for a singular
$K3$
surface; one gets the result for a singular
![]() $K3$
surface
$K3$
surface
![]() $X$
upon replacing
$X$
upon replacing
![]() $X$
by its minimal desingularization
$X$
by its minimal desingularization
![]() $\widetilde{X}$
, and
$\widetilde{X}$
, and
![]() $L$
by the pull-back
$L$
by the pull-back
![]() $\widetilde{L}$
of
$\widetilde{L}$
of
![]() $L$
to
$L$
to
![]() $\widetilde{X}$
.
$\widetilde{X}$
.
Definition 2.1.2. A polarized K3 surface
![]() $(X,L)$
of degree
$(X,L)$
of degree
![]() $4$
is hyperelliptic if Item (2) of Theorem 2.1.1 holds, and it is unigonal if Item (3) of Theorem 2.1.1 holds.
$4$
is hyperelliptic if Item (2) of Theorem 2.1.1 holds, and it is unigonal if Item (3) of Theorem 2.1.1 holds.
Remark 2.1.3. Let
![]() $Q\subset \mathbb{P}^{3}$
be an irreducible quadric, i.e. either a smooth quadric or a quadric cone over a smooth conic. Let
$Q\subset \mathbb{P}^{3}$
be an irreducible quadric, i.e. either a smooth quadric or a quadric cone over a smooth conic. Let
![]() $B\in |\unicode[STIX]{x1D714}_{Q}^{-2}|$
and suppose that
$B\in |\unicode[STIX]{x1D714}_{Q}^{-2}|$
and suppose that
![]() $B$
has simple singularities. Let
$B$
has simple singularities. Let
![]() $\unicode[STIX]{x1D711}:X\rightarrow Q$
be the double cover ramified over
$\unicode[STIX]{x1D711}:X\rightarrow Q$
be the double cover ramified over
![]() $B$
and let
$B$
and let
![]() $L:=\unicode[STIX]{x1D711}^{\ast }\mathscr{O}_{Q}(1)$
. Then
$L:=\unicode[STIX]{x1D711}^{\ast }\mathscr{O}_{Q}(1)$
. Then
![]() $(X,L)$
is a hyperelliptic quartic
$(X,L)$
is a hyperelliptic quartic
![]() $K3$
surface and the image of
$K3$
surface and the image of
![]() $\unicode[STIX]{x1D711}_{L}:X\rightarrow |L|^{\vee }$
is identified with
$\unicode[STIX]{x1D711}_{L}:X\rightarrow |L|^{\vee }$
is identified with
![]() $Q$
. Conversely, every hyperelliptic quartic
$Q$
. Conversely, every hyperelliptic quartic
![]() $K3$
surface is obtained by this procedure.
$K3$
surface is obtained by this procedure.
Remark 2.1.4. Let
![]() $\mathbb{F}_{4}:=\mathbb{P}(\mathscr{O}_{\mathbb{P}^{1}}(4)\oplus \mathscr{O}_{\mathbb{P}^{1}})$
. Let
$\mathbb{F}_{4}:=\mathbb{P}(\mathscr{O}_{\mathbb{P}^{1}}(4)\oplus \mathscr{O}_{\mathbb{P}^{1}})$
. Let
![]() $\unicode[STIX]{x1D70C}:\mathbb{F}_{4}\rightarrow \mathbb{P}^{1}$
be the structure map, let
$\unicode[STIX]{x1D70C}:\mathbb{F}_{4}\rightarrow \mathbb{P}^{1}$
be the structure map, let
![]() $F$
be a fiber of
$F$
be a fiber of
![]() $\unicode[STIX]{x1D70C}$
, and let
$\unicode[STIX]{x1D70C}$
, and let
![]() $A:=\mathbb{P}(\mathscr{O}_{\mathbb{P}^{1}}(4))\subset \mathbb{F}_{4}$
be the negative section of
$A:=\mathbb{P}(\mathscr{O}_{\mathbb{P}^{1}}(4))\subset \mathbb{F}_{4}$
be the negative section of
![]() $\unicode[STIX]{x1D70C}$
. Let
$\unicode[STIX]{x1D70C}$
. Let
![]() $B\in |3A+12F|$
be reduced with simple singularities, and disjoint from
$B\in |3A+12F|$
be reduced with simple singularities, and disjoint from
![]() $A$
(the generic divisor in
$A$
(the generic divisor in
![]() $|3A+12F|$
has these properties because
$|3A+12F|$
has these properties because
![]() $B\cdot A=0$
). Let
$B\cdot A=0$
). Let
![]() $\unicode[STIX]{x1D70B}:X\rightarrow \mathbb{F}_{4}$
be the double cover branched over
$\unicode[STIX]{x1D70B}:X\rightarrow \mathbb{F}_{4}$
be the double cover branched over
![]() $A+B$
. Then
$A+B$
. Then
![]() $X$
is a
$X$
is a
![]() $K3$
surface because
$K3$
surface because
![]() $(A+B)\in |-2K_{\mathbb{F}_{4}}|$
. Since
$(A+B)\in |-2K_{\mathbb{F}_{4}}|$
. Since
![]() $\unicode[STIX]{x1D70B}$
is simply ramified over
$\unicode[STIX]{x1D70B}$
is simply ramified over
![]() $A$
, we have
$A$
, we have
![]() $\unicode[STIX]{x1D70B}^{\ast }A=2R$
, where
$\unicode[STIX]{x1D70B}^{\ast }A=2R$
, where
![]() $R$
is a smooth rational curve. Let
$R$
is a smooth rational curve. Let
![]() $E:=\unicode[STIX]{x1D70B}^{\ast }F$
; thus,
$E:=\unicode[STIX]{x1D70B}^{\ast }F$
; thus,
![]() $E$
is an elliptic curve, moving in the elliptic fibration
$E$
is an elliptic curve, moving in the elliptic fibration
![]() $\unicode[STIX]{x1D70C}\circ \unicode[STIX]{x1D70B}:X\rightarrow \mathbb{P}^{1}$
. Then
$\unicode[STIX]{x1D70C}\circ \unicode[STIX]{x1D70B}:X\rightarrow \mathbb{P}^{1}$
. Then
![]() $(X,\mathscr{O}_{X}(R+3E))$
is a unigonal quartic
$(X,\mathscr{O}_{X}(R+3E))$
is a unigonal quartic
![]() $K3$
surface and conversely every unigonal quartic is obtained by this procedure.
$K3$
surface and conversely every unigonal quartic is obtained by this procedure.
If
![]() $(X,L)$
is a quartic
$(X,L)$
is a quartic
![]() $K3$
surface, the period point
$K3$
surface, the period point
![]() $\unicode[STIX]{x1D6F1}(X,L)\in \mathscr{F}(19)$
is defined as follows. Let
$\unicode[STIX]{x1D6F1}(X,L)\in \mathscr{F}(19)$
is defined as follows. Let
![]() $\widetilde{X}$
be the minimal desingularization of
$\widetilde{X}$
be the minimal desingularization of
![]() $X$
and
$X$
and
![]() $\widetilde{L}$
be the pull-back of
$\widetilde{L}$
be the pull-back of
![]() $L$
to
$L$
to
![]() $\widetilde{X}$
. The lattices
$\widetilde{X}$
. The lattices
![]() $c_{1}(\widetilde{L})_{\mathbb{Z}}^{\bot }:=c_{1}(\widetilde{L})\text{}^{\bot }\cap H^{2}(\widetilde{X};\mathbb{Z})$
and
$c_{1}(\widetilde{L})_{\mathbb{Z}}^{\bot }:=c_{1}(\widetilde{L})\text{}^{\bot }\cap H^{2}(\widetilde{X};\mathbb{Z})$
and
![]() $\unicode[STIX]{x1D6EC}_{19}$
are isomorphic; let
$\unicode[STIX]{x1D6EC}_{19}$
are isomorphic; let
be an isomorphism, and
![]() $\unicode[STIX]{x1D713}_{\mathbb{C}}:c_{1}(\widetilde{L})\text{}^{\bot }\overset{{\sim}}{\longrightarrow }\unicode[STIX]{x1D6EC}_{19,\mathbb{C}}$
be the
$\unicode[STIX]{x1D713}_{\mathbb{C}}:c_{1}(\widetilde{L})\text{}^{\bot }\overset{{\sim}}{\longrightarrow }\unicode[STIX]{x1D6EC}_{19,\mathbb{C}}$
be the
![]() $\mathbb{C}$
-linear extension of
$\mathbb{C}$
-linear extension of
![]() $\unicode[STIX]{x1D713}$
. The line
$\unicode[STIX]{x1D713}$
. The line
![]() $\unicode[STIX]{x1D713}_{\mathbb{C}}(H^{2,0}(\widetilde{X}))$
belongs to
$\unicode[STIX]{x1D713}_{\mathbb{C}}(H^{2,0}(\widetilde{X}))$
belongs to
![]() $\mathscr{D}_{\unicode[STIX]{x1D6EC}_{19}}$
and, if necessary, we may precompose
$\mathscr{D}_{\unicode[STIX]{x1D6EC}_{19}}$
and, if necessary, we may precompose
![]() $\unicode[STIX]{x1D713}$
with an element of
$\unicode[STIX]{x1D713}$
with an element of
![]() $\widetilde{O}(c_{1}(\widetilde{L})\text{}^{\bot })$
so that
$\widetilde{O}(c_{1}(\widetilde{L})\text{}^{\bot })$
so that
![]() $\unicode[STIX]{x1D713}_{\mathbb{C}}(H^{2,0}(\widetilde{X}))$
belongs to
$\unicode[STIX]{x1D713}_{\mathbb{C}}(H^{2,0}(\widetilde{X}))$
belongs to
![]() $\mathscr{D}_{\unicode[STIX]{x1D6EC}_{19}}^{+}$
. Such a point is well determined up to
$\mathscr{D}_{\unicode[STIX]{x1D6EC}_{19}}^{+}$
. Such a point is well determined up to
![]() $\widetilde{O}^{+}(\unicode[STIX]{x1D6EC}_{19})$
and hence it determines
$\widetilde{O}^{+}(\unicode[STIX]{x1D6EC}_{19})$
and hence it determines
This is the period point of
![]() $(X,L)$
.
$(X,L)$
.
Now let
be the GIT moduli space of quartic surfaces in
![]() $\mathbb{P}^{3}$
(see [Reference ShahSha81] for many results about
$\mathbb{P}^{3}$
(see [Reference ShahSha81] for many results about
![]() $\mathfrak{M}(19)$
).
$\mathfrak{M}(19)$
).
Definition 2.1.5. Let
![]() $\mathscr{U}(19)\subset |\mathscr{O}_{\mathbb{P}^{3}}(4)|$
be the open subset parametrizing quartics with ADE singularities.
$\mathscr{U}(19)\subset |\mathscr{O}_{\mathbb{P}^{3}}(4)|$
be the open subset parametrizing quartics with ADE singularities.
Then
![]() $\mathscr{U}(19)$
is contained in the stable locus of
$\mathscr{U}(19)$
is contained in the stable locus of
![]() $|\mathscr{O}_{\mathbb{P}^{3}}(4)|$
for the natural action of
$|\mathscr{O}_{\mathbb{P}^{3}}(4)|$
for the natural action of
![]() $\text{PGL}(4)$
by [Reference ShahSha81]. By global Torelli for
$\text{PGL}(4)$
by [Reference ShahSha81]. By global Torelli for
![]() $K3$
surfaces, and Mayer’s theorem 2.1.1, the period map restricted to
$K3$
surfaces, and Mayer’s theorem 2.1.1, the period map restricted to
![]() $\mathscr{U}(19)/\!\!/\text{PGL}(4)$
defines an isomorphism
$\mathscr{U}(19)/\!\!/\text{PGL}(4)$
defines an isomorphism
Thus, we have a birational map
and one of the main goals of the present paper is to propose a conjectural decomposition of
![]() $\mathfrak{p}_{19}^{-1}$
as a composition of the
$\mathfrak{p}_{19}^{-1}$
as a composition of the
![]() $\mathbb{Q}$
-factorialization of
$\mathbb{Q}$
-factorialization of
![]() $\mathscr{F}(19)\text{}^{\ast }$
and a series of flips of subloci described by the
$\mathscr{F}(19)\text{}^{\ast }$
and a series of flips of subloci described by the
![]() $D$
tower of § 1.7. The geometric behavior of this decomposition is discussed in [Reference Laza and O’GradyLO18b].
$D$
tower of § 1.7. The geometric behavior of this decomposition is discussed in [Reference Laza and O’GradyLO18b].
2.2 Periods of hyperelliptic and unigonal quartics
The following is standard.
Proposition 2.2.1. Let
![]() $(X,L)$
be a quartic
$(X,L)$
be a quartic
![]() $K3$
surface. Then:
$K3$
surface. Then:
(1)
 $(X,L)$
is hyperelliptic if and only if
$(X,L)$
is hyperelliptic if and only if
 $\unicode[STIX]{x1D6F1}(X,L)\in H_{h}(19)$
; and
$\unicode[STIX]{x1D6F1}(X,L)\in H_{h}(19)$
; and(2)
 $(X,L)$
is unigonal if and only if
$(X,L)$
is unigonal if and only if
 $\unicode[STIX]{x1D6F1}(X,L)\in H_{u}(19)$
.
$\unicode[STIX]{x1D6F1}(X,L)\in H_{u}(19)$
.
Remark 2.2.2. By Proposition 1.4.5, there is a natural isomorphism between
![]() $\mathscr{F}(18)$
and the hyperelliptic divisor
$\mathscr{F}(18)$
and the hyperelliptic divisor
![]() $H_{h}(19)$
. By Proposition 2.2.1, it follows that we may identify
$H_{h}(19)$
. By Proposition 2.2.1, it follows that we may identify
![]() $\mathscr{F}(18)$
with the period space for hyperelliptic quartic
$\mathscr{F}(18)$
with the period space for hyperelliptic quartic
![]() $K3$
surfaces.
$K3$
surfaces.
There is a GIT moduli space which is in a relation to
![]() $\mathscr{F}(18)$
that is similar to the relation between
$\mathscr{F}(18)$
that is similar to the relation between
![]() $\mathfrak{M}(19)$
and
$\mathfrak{M}(19)$
and
![]() $\mathscr{F}(19)$
. In fact, let
$\mathscr{F}(19)$
. In fact, let
Definition 2.2.3. Let
![]() $\mathscr{U}(18)\subset |\mathscr{O}_{\mathbb{P}^{1}\times \mathbb{P}^{1}}(4,4)|$
be the open subset parametrizing curves with ADE singularities.
$\mathscr{U}(18)\subset |\mathscr{O}_{\mathbb{P}^{1}\times \mathbb{P}^{1}}(4,4)|$
be the open subset parametrizing curves with ADE singularities.
If
![]() $D\in \mathscr{U}(18)$
, the double cover
$D\in \mathscr{U}(18)$
, the double cover
![]() $\unicode[STIX]{x1D70B}:X\rightarrow \mathbb{P}^{1}\times \mathbb{P}^{1}$
branched over
$\unicode[STIX]{x1D70B}:X\rightarrow \mathbb{P}^{1}\times \mathbb{P}^{1}$
branched over
![]() $D$
is a
$D$
is a
![]() $K3$
surface, and
$K3$
surface, and
![]() $(X,\unicode[STIX]{x1D70B}^{\ast }(\mathscr{O}_{\mathbb{P}^{1}}(1)\boxtimes \mathscr{O}_{\mathbb{P}^{1}}(1)))$
is a hyperelliptic quartic
$(X,\unicode[STIX]{x1D70B}^{\ast }(\mathscr{O}_{\mathbb{P}^{1}}(1)\boxtimes \mathscr{O}_{\mathbb{P}^{1}}(1)))$
is a hyperelliptic quartic
![]() $K3$
surface. Now
$K3$
surface. Now
![]() $\mathscr{U}(18)$
is contained in the stable locus of
$\mathscr{U}(18)$
is contained in the stable locus of
![]() $|\mathscr{O}_{\mathbb{P}^{\times }\mathbb{P}^{1}}(4,4)|$
by [Reference ShahSha81, Theorem 4.8] and, by associating to the orbit of
$|\mathscr{O}_{\mathbb{P}^{\times }\mathbb{P}^{1}}(4,4)|$
by [Reference ShahSha81, Theorem 4.8] and, by associating to the orbit of
![]() $D\in \mathscr{U}(18)$
the period of
$D\in \mathscr{U}(18)$
the period of
![]() $(X,\unicode[STIX]{x1D70B}^{\ast }(\mathscr{O}_{\mathbb{P}^{1}}(1)\boxtimes \mathscr{O}_{\mathbb{P}^{1}}(1)))$
(notation as above), one gets an isomorphism
$(X,\unicode[STIX]{x1D70B}^{\ast }(\mathscr{O}_{\mathbb{P}^{1}}(1)\boxtimes \mathscr{O}_{\mathbb{P}^{1}}(1)))$
(notation as above), one gets an isomorphism
Thus, we have a birational period map
whose behavior is very similar to that of
![]() $\mathfrak{p}_{19}$
(see [Reference Laza and O’GradyLO18a] for a full discussion).
$\mathfrak{p}_{19}$
(see [Reference Laza and O’GradyLO18a] for a full discussion).
2.3 Periods of certain higher-dimensional hyperkähler varieties
2.3.1 Double EPW sextics
Let
![]() $(X,L)$
be a polarized hyperkähler (HK) variety of Type
$(X,L)$
be a polarized hyperkähler (HK) variety of Type
![]() $K3^{[2]}$
, where
$K3^{[2]}$
, where
![]() $q(c_{1}(L))=2$
(
$q(c_{1}(L))=2$
(
![]() $q$
is the Beauville–Bogomolov quadratic form on
$q$
is the Beauville–Bogomolov quadratic form on
![]() $H^{2}(X)$
). Then
$H^{2}(X)$
). Then
In the above equation, perpendicularity is with respect to the Beauville–Bogomolov quadratic form, and the first isomorphism is found in [Reference O’GradyO’Gr15]. The period space for degree-
![]() $2$
polarized HK varieties of Type
$2$
polarized HK varieties of Type
![]() $K3^{[2]}$
is
$K3^{[2]}$
is
![]() $\mathscr{F}_{\unicode[STIX]{x1D6EC}_{20}}(\widetilde{O}^{+}(\unicode[STIX]{x1D6EC}_{20}))$
; in fact, the moduli space of such (polarized) varieties is identified with an open dense subset of
$\mathscr{F}_{\unicode[STIX]{x1D6EC}_{20}}(\widetilde{O}^{+}(\unicode[STIX]{x1D6EC}_{20}))$
; in fact, the moduli space of such (polarized) varieties is identified with an open dense subset of
![]() $\mathscr{F}_{\unicode[STIX]{x1D6EC}_{20}}(\widetilde{O}^{+}(\unicode[STIX]{x1D6EC}_{20}))$
by Verbitsky’s global Torelli theorem. (One should introduce an analogue of DuVal singularities, in order to identify
$\mathscr{F}_{\unicode[STIX]{x1D6EC}_{20}}(\widetilde{O}^{+}(\unicode[STIX]{x1D6EC}_{20}))$
by Verbitsky’s global Torelli theorem. (One should introduce an analogue of DuVal singularities, in order to identify
![]() $\mathscr{F}_{\unicode[STIX]{x1D6EC}_{20}}(\widetilde{O}^{+}(\unicode[STIX]{x1D6EC}_{20}))$
with the moduli space of polarized varieties with mild singularities.) On the other hand, we have a natural degree-
$\mathscr{F}_{\unicode[STIX]{x1D6EC}_{20}}(\widetilde{O}^{+}(\unicode[STIX]{x1D6EC}_{20}))$
with the moduli space of polarized varieties with mild singularities.) On the other hand, we have a natural degree-
![]() $2$
covering map
$2$
covering map
because
![]() $\unicode[STIX]{x1D6E4}_{\unicode[STIX]{x1D709}_{20}}$
is an index-
$\unicode[STIX]{x1D6E4}_{\unicode[STIX]{x1D709}_{20}}$
is an index-
![]() $2$
subgroup of
$2$
subgroup of
![]() $\widetilde{O}^{+}(\unicode[STIX]{x1D6EC}_{20})$
. (See Item (4) of Proposition 1.2.3.)
$\widetilde{O}^{+}(\unicode[STIX]{x1D6EC}_{20})$
. (See Item (4) of Proposition 1.2.3.)
There is an analogue of the GIT moduli spaces
![]() $\mathfrak{M}(19)$
and
$\mathfrak{M}(19)$
and
![]() $\mathfrak{M}(18)$
in this case as well. In fact, let
$\mathfrak{M}(18)$
in this case as well. In fact, let
![]() $(X,L)$
be a generic degree-
$(X,L)$
be a generic degree-
![]() $2$
polarized HK variety of Type
$2$
polarized HK variety of Type
![]() $K3^{[2]}$
. Then the map
$K3^{[2]}$
. Then the map
![]() $\unicode[STIX]{x1D711}_{L}:X{\dashrightarrow}|L|^{\vee }\cong \mathbb{P}^{5}$
is regular, finite, of degree
$\unicode[STIX]{x1D711}_{L}:X{\dashrightarrow}|L|^{\vee }\cong \mathbb{P}^{5}$
is regular, finite, of degree
![]() $2$
onto a special sextic hypersurface: an EPW sextic. Conversely, given an EPW sextic
$2$
onto a special sextic hypersurface: an EPW sextic. Conversely, given an EPW sextic
![]() $Y\subset \mathbb{P}^{5}$
, there is a canonical double cover
$Y\subset \mathbb{P}^{5}$
, there is a canonical double cover
![]() $f:X\rightarrow Y$
and, if
$f:X\rightarrow Y$
and, if
![]() $Y$
is generic, then
$Y$
is generic, then
![]() $(X,f^{\ast }\mathscr{O}_{Y}(1))$
is a degree-
$(X,f^{\ast }\mathscr{O}_{Y}(1))$
is a degree-
![]() $2$
polarized HK variety of Type
$2$
polarized HK variety of Type
![]() $K3^{[2]}$
. (For the definition and properties of double EPW sextics, we refer to [Reference O’GradyO’Gr06] and [Reference O’GradyO’Gr16].) The parameter space for EPW sextics is (an open dense subset of)
$K3^{[2]}$
. (For the definition and properties of double EPW sextics, we refer to [Reference O’GradyO’Gr06] and [Reference O’GradyO’Gr16].) The parameter space for EPW sextics is (an open dense subset of)
![]() $\mathbb{LG}(\bigwedge ^{3}\mathbb{C}^{6})$
. Let
$\mathbb{LG}(\bigwedge ^{3}\mathbb{C}^{6})$
. Let
We have a birational period map
The dual of an EPW sextic is another EPW sextic, see [Reference O’GradyO’Gr08], and hence we have a (regular) duality involution
![]() $\unicode[STIX]{x1D6FF}:\mathfrak{M}(20)\rightarrow \mathfrak{M}(20)$
. This is the geometric version of the covering involution of the double cover
$\unicode[STIX]{x1D6FF}:\mathfrak{M}(20)\rightarrow \mathfrak{M}(20)$
. This is the geometric version of the covering involution of the double cover
![]() $\unicode[STIX]{x1D70C}$
in (2.3.1). The upshot is that we have a birational period map
$\unicode[STIX]{x1D70C}$
in (2.3.1). The upshot is that we have a birational period map
Thus, we may view
![]() $\mathscr{F}(20)$
as the period space for double EPW sextics up to duality. Alternatively,
$\mathscr{F}(20)$
as the period space for double EPW sextics up to duality. Alternatively,
![]() $\mathscr{F}(20)$
is the period space for the Calabi–Yau fourfolds obtained by blowing up a (generic) EPW sextic
$\mathscr{F}(20)$
is the period space for the Calabi–Yau fourfolds obtained by blowing up a (generic) EPW sextic
![]() $Y$
along its singular locus (a smooth surface).
$Y$
along its singular locus (a smooth surface).
The inverse images by
![]() $\unicode[STIX]{x1D70C}$
of the reflective Heegner divisors of
$\unicode[STIX]{x1D70C}$
of the reflective Heegner divisors of
![]() $\mathscr{F}(20)$
have appeared in [Reference O’GradyO’Gr15]. In fact,
$\mathscr{F}(20)$
have appeared in [Reference O’GradyO’Gr15]. In fact,
For a geometric interpretation of periods in
![]() $\mathbb{S}_{2}^{\star }$
,
$\mathbb{S}_{2}^{\star }$
,
![]() $\mathbb{S}_{4}$
,
$\mathbb{S}_{4}$
,
![]() $\mathbb{S}_{2}^{\prime }$
, and
$\mathbb{S}_{2}^{\prime }$
, and
![]() $\mathbb{S}_{2}^{\prime \prime }$
, see [Reference O’GradyO’Gr15, §5].
$\mathbb{S}_{2}^{\prime \prime }$
, see [Reference O’GradyO’Gr15, §5].
2.3.2 EPW cubes
Let
![]() $(X,L)$
be a polarized HK variety of Type
$(X,L)$
be a polarized HK variety of Type
![]() $K3^{[3]}$
, where
$K3^{[3]}$
, where
![]() $q(c_{1}(L))=4$
and
$q(c_{1}(L))=4$
and
![]() $\operatorname{div}(c_{1}(L))=2$
. Then
$\operatorname{div}(c_{1}(L))=2$
. Then
Moreover, one shows that the period space for polarized HK varieties of Type
![]() $K3^{[3]}$
of this kind is
$K3^{[3]}$
of this kind is
![]() $\mathscr{F}(20)$
. (We thank M. Kapustka and G. Mongardi for bringing this to our attention.) Iliev et al. [Reference Iliev, Kapustka, Kapustka and RanestadIKKR19] have proved that the generic such polarized HK variety is isomorphic to an EPW cube, a double cover of a codimension-
$\mathscr{F}(20)$
. (We thank M. Kapustka and G. Mongardi for bringing this to our attention.) Iliev et al. [Reference Iliev, Kapustka, Kapustka and RanestadIKKR19] have proved that the generic such polarized HK variety is isomorphic to an EPW cube, a double cover of a codimension-
![]() $3$
degeneracy locus in
$3$
degeneracy locus in
![]() $\text{Gr}(3,\mathbb{C}^{6})$
. The parameter space of EPW cubes is the same as that for double EPW sextics (but the EPW cubes parametrized by
$\text{Gr}(3,\mathbb{C}^{6})$
. The parameter space of EPW cubes is the same as that for double EPW sextics (but the EPW cubes parametrized by
![]() $A\in \mathbb{LG}(\bigwedge ^{3}\mathbb{C}^{6})$
and the dual Lagrangian
$A\in \mathbb{LG}(\bigwedge ^{3}\mathbb{C}^{6})$
and the dual Lagrangian
![]() $A^{\bot }\in \mathbb{LG}(\bigwedge ^{3}(\mathbb{C}^{6})^{\vee })$
are isomorphic).
$A^{\bot }\in \mathbb{LG}(\bigwedge ^{3}(\mathbb{C}^{6})^{\vee })$
are isomorphic).
2.3.3 Hyperkähler varieties of Type OG10
Let
![]() $X$
be a HK manifold of Type OG10. Then
$X$
be a HK manifold of Type OG10. Then
![]() $H^{2}(X;\mathbb{Z})$
equipped with the Beauville–Bogomolov quadratic form is isomorphic to
$H^{2}(X;\mathbb{Z})$
equipped with the Beauville–Bogomolov quadratic form is isomorphic to
![]() $\text{II}_{3,19}\oplus A_{2}$
; see [Reference RapagnettaRap08]. Let
$\text{II}_{3,19}\oplus A_{2}$
; see [Reference RapagnettaRap08]. Let
![]() $a,b\in A_{2}$
be standard generators (
$a,b\in A_{2}$
be standard generators (
![]() $a^{2}=b^{2}=(a+b)^{2}=-2$
) and
$a^{2}=b^{2}=(a+b)^{2}=-2$
) and
![]() $v\in \text{II}_{3,19}$
of square
$v\in \text{II}_{3,19}$
of square
![]() $2$
. Let
$2$
. Let
![]() $h:=(3v+a-b)$
; notice that
$h:=(3v+a-b)$
; notice that
![]() $h^{2}=12$
and
$h^{2}=12$
and
![]() $(h,H^{2}(X;\mathbb{Z}))=3\mathbb{Z}$
. The discriminant group and quadratic form of
$(h,H^{2}(X;\mathbb{Z}))=3\mathbb{Z}$
. The discriminant group and quadratic form of
![]() $h^{\bot }$
are isomorphic to the discriminant group and quadratic form of
$h^{\bot }$
are isomorphic to the discriminant group and quadratic form of
![]() $\unicode[STIX]{x1D6EC}_{21}$
, respectively, and hence
$\unicode[STIX]{x1D6EC}_{21}$
, respectively, and hence
![]() $h^{\bot }\cong \unicode[STIX]{x1D6EC}_{21}$
by Theorem 1.13.2 of [Reference NikulinNik80]. Thus,
$h^{\bot }\cong \unicode[STIX]{x1D6EC}_{21}$
by Theorem 1.13.2 of [Reference NikulinNik80]. Thus,
![]() $\mathscr{D}_{\unicode[STIX]{x1D6EC}_{21}}$
is the classifying space for the corresponding
$\mathscr{D}_{\unicode[STIX]{x1D6EC}_{21}}$
is the classifying space for the corresponding
![]() $10$
-dimensional polarized O’Grady HK manifolds. By Verbitsky’s global Torelli theorem [Reference VerbitskyVer13], the moduli space for such varieties is isomorphic to
$10$
-dimensional polarized O’Grady HK manifolds. By Verbitsky’s global Torelli theorem [Reference VerbitskyVer13], the moduli space for such varieties is isomorphic to
![]() $\mathscr{F}_{\unicode[STIX]{x1D6EC}_{21}}(\unicode[STIX]{x1D6E4})$
, where
$\mathscr{F}_{\unicode[STIX]{x1D6EC}_{21}}(\unicode[STIX]{x1D6E4})$
, where
![]() $\unicode[STIX]{x1D6E4}<O^{+}(\unicode[STIX]{x1D6EC}_{21})$
is the relevant monodromy group (a subgroup of finite index; see [Reference VerbitskyVer13]). See [Reference MongardiMon16] for a result regarding the monodromy group of O’Grady’s
$\unicode[STIX]{x1D6E4}<O^{+}(\unicode[STIX]{x1D6EC}_{21})$
is the relevant monodromy group (a subgroup of finite index; see [Reference VerbitskyVer13]). See [Reference MongardiMon16] for a result regarding the monodromy group of O’Grady’s
![]() $10$
-dimensional HK manifolds.
$10$
-dimensional HK manifolds.
3 Borcherds’ relations for
 $D$
locally symmetric varieties
$D$
locally symmetric varieties
3.1 Set-up and statement of the main results
Let
![]() $N\geqslant 3$
. We will derive relations among divisor classes on
$N\geqslant 3$
. We will derive relations among divisor classes on
![]() $\mathscr{F}(N)$
in the range
$\mathscr{F}(N)$
in the range
![]() $N\leqslant 25$
by considering suitable quasi-pull-backs of Borcherds’ celebrated reflective modular form for the orthogonal group
$N\leqslant 25$
by considering suitable quasi-pull-backs of Borcherds’ celebrated reflective modular form for the orthogonal group
![]() $O(\text{II}_{2,26})$
.
$O(\text{II}_{2,26})$
.
In order to state our results, we let
![]() $\unicode[STIX]{x1D707}(N)$
, for
$\unicode[STIX]{x1D707}(N)$
, for
![]() $3\leqslant N\leqslant 25$
, be defined by Table 1.
$3\leqslant N\leqslant 25$
, be defined by Table 1.
Table 1. Definition of
![]() $\unicode[STIX]{x1D707}(N)$
.
$\unicode[STIX]{x1D707}(N)$
.
Theorem 3.1.1 (First Borcherds’ relation).
Let
![]() $3\leqslant N\leqslant 25$
. Then
$3\leqslant N\leqslant 25$
. Then
where
![]() $\unicode[STIX]{x1D70F}(N)$
is equal to
$\unicode[STIX]{x1D70F}(N)$
is equal to
![]() $1$
if
$1$
if
![]() $N\equiv 3,4\hspace{0.6em}({\rm mod}\hspace{0.2em}8)$
and is equal to
$N\equiv 3,4\hspace{0.6em}({\rm mod}\hspace{0.2em}8)$
and is equal to
![]() $2$
otherwise.
$2$
otherwise.
Theorem 3.1.2 (Second Borcherds’ relation).
Let
![]() $3\leqslant N\leqslant 17$
. Then
$3\leqslant N\leqslant 17$
. Then
where
![]() $\unicode[STIX]{x1D70F}(N)$
is as in Theorem 3.1.1.
$\unicode[STIX]{x1D70F}(N)$
is as in Theorem 3.1.1.
Theorems 3.1.1 and 3.1.2 will be proved in § 3.2. Below we prove a corollary which is extremely important for our work.
Corollary 3.1.3 (Gritsenko’s relation, [Reference GritsenkoGri18, Theorem 3.2]).
Let
![]() $3\leqslant N\leqslant 17$
. Then
$3\leqslant N\leqslant 17$
. Then
Proof. Taking the difference between the identities (3.1.1) and (3.1.2), we see that the terms
![]() $H_{n}(N)$
cancel, giving the relationship above between
$H_{n}(N)$
cancel, giving the relationship above between
![]() $\unicode[STIX]{x1D706}(N)$
,
$\unicode[STIX]{x1D706}(N)$
,
![]() $H_{h}(N)$
, and
$H_{h}(N)$
, and
![]() $H_{u}(N)$
.◻
$H_{u}(N)$
.◻
Corollary 3.1.4. The following hold:
(1)
 $H_{h}(14)$
is linearly equivalent to
$H_{h}(14)$
is linearly equivalent to
 $H_{u}(14)$
;
$H_{u}(14)$
;(2) if
 $4\leqslant N<14$
, then
$4\leqslant N<14$
, then
 $H_{h}(N)$
is a big divisor;
$H_{h}(N)$
is a big divisor;(3) if
 $4\leqslant N\leqslant 10$
, then
$4\leqslant N\leqslant 10$
, then
 $H_{h}(N)$
is an ample divisor.
$H_{h}(N)$
is an ample divisor.
Proof. This is a direct consequence of (3.1.3). Insert
![]() $N=14$
into (3.1.3) to get Item (1). Next, for
$N=14$
into (3.1.3) to get Item (1). Next, for
![]() $N<14$
, we get
$N<14$
, we get
Since
![]() $(14-N)>0$
,
$(14-N)>0$
,
![]() $\unicode[STIX]{x1D706}(N)$
is ample, and
$\unicode[STIX]{x1D706}(N)$
is ample, and
![]() $\unicode[STIX]{x1D707}(N)\leqslant \unicode[STIX]{x1D707}(N+8)$
(for
$\unicode[STIX]{x1D707}(N)\leqslant \unicode[STIX]{x1D707}(N+8)$
(for
![]() $4\leqslant N<14$
), we get that
$4\leqslant N<14$
), we get that
![]() $H_{h}(N)$
is big. For
$H_{h}(N)$
is big. For
![]() $4\leqslant N\leqslant 10$
, the coefficient of
$4\leqslant N\leqslant 10$
, the coefficient of
![]() $H_{u}(N)$
is zero and hence
$H_{u}(N)$
is zero and hence
![]() $H_{h}(N)$
is ample.◻
$H_{h}(N)$
is ample.◻
3.2 Proof of Borcherds’ relations
3.2.1 Borcherds’ automorphic form
We recall that Borcherds [Reference BorcherdsBor95] constructed an automorphic form
![]() $\unicode[STIX]{x1D6F7}_{12}$
on
$\unicode[STIX]{x1D6F7}_{12}$
on
![]() $\mathscr{D}_{\text{II}_{2,26}}^{+}$
for the orthogonal group
$\mathscr{D}_{\text{II}_{2,26}}^{+}$
for the orthogonal group
![]() $O^{+}(\text{II}_{2,26})$
, of weight
$O^{+}(\text{II}_{2,26})$
, of weight
![]() $12$
, whose zero-locus is the union of the nodal hyperplanes (the intersections
$12$
, whose zero-locus is the union of the nodal hyperplanes (the intersections
![]() $\unicode[STIX]{x1D6FF}^{\bot }\cap \mathscr{D}_{\text{II}_{2,26}}^{+}$
, for
$\unicode[STIX]{x1D6FF}^{\bot }\cap \mathscr{D}_{\text{II}_{2,26}}^{+}$
, for
![]() $\unicode[STIX]{x1D6FF}$
a root of
$\unicode[STIX]{x1D6FF}$
a root of
![]() $\text{II}_{2,26}$
). Actually
$\text{II}_{2,26}$
). Actually
![]() $\unicode[STIX]{x1D6F7}_{12}$
vanishes with order one on each nodal hyperplane, i.e.
$\unicode[STIX]{x1D6F7}_{12}$
vanishes with order one on each nodal hyperplane, i.e.
where (as usual)
![]() $R(\text{II}_{2,26})$
is the set of roots of
$R(\text{II}_{2,26})$
is the set of roots of
![]() $\text{II}_{2,26}$
and
$\text{II}_{2,26}$
and
![]() $\unicode[STIX]{x1D6FF}_{0}$
is a chosen root of
$\unicode[STIX]{x1D6FF}_{0}$
is a chosen root of
![]() $\text{II}_{2,26}$
. In other words, the divisor of
$\text{II}_{2,26}$
. In other words, the divisor of
![]() $\unicode[STIX]{x1D6F7}_{12}$
is the pre-Heegner divisor associated to a root of
$\unicode[STIX]{x1D6F7}_{12}$
is the pre-Heegner divisor associated to a root of
![]() $\text{II}_{2,26}$
.
$\text{II}_{2,26}$
.
Remark 3.2.1. Let
![]() $\unicode[STIX]{x1D6EC}$
be a lattice of signature
$\unicode[STIX]{x1D6EC}$
be a lattice of signature
![]() $(2,m)$
, let
$(2,m)$
, let
![]() $\unicode[STIX]{x1D6E4}<O^{+}(\unicode[STIX]{x1D6EC})$
be a subgroup of finite index, and let
$\unicode[STIX]{x1D6E4}<O^{+}(\unicode[STIX]{x1D6EC})$
be a subgroup of finite index, and let
![]() $\unicode[STIX]{x1D6F7}$
be a
$\unicode[STIX]{x1D6F7}$
be a
![]() $\unicode[STIX]{x1D6E4}$
-automorphic form on
$\unicode[STIX]{x1D6E4}$
-automorphic form on
![]() $\mathscr{D}_{\unicode[STIX]{x1D6EC}}^{+}$
of weight
$\mathscr{D}_{\unicode[STIX]{x1D6EC}}^{+}$
of weight
![]() $w$
. Then
$w$
. Then
![]() $\unicode[STIX]{x1D6F7}$
descends to a regular section of
$\unicode[STIX]{x1D6F7}$
descends to a regular section of
![]() $\mathscr{L}(\unicode[STIX]{x1D6EC},\unicode[STIX]{x1D6E4})^{\otimes w}$
; see § 1.3.1. Thus, (3.2.1) gives that, on the locally symmetric variety
$\mathscr{L}(\unicode[STIX]{x1D6EC},\unicode[STIX]{x1D6E4})^{\otimes w}$
; see § 1.3.1. Thus, (3.2.1) gives that, on the locally symmetric variety
![]() $O^{+}(\text{II}_{2,26})\backslash \mathscr{D}_{\text{II}_{2,26}}^{+}$
, one has the relation
$O^{+}(\text{II}_{2,26})\backslash \mathscr{D}_{\text{II}_{2,26}}^{+}$
, one has the relation
![]() $12\unicode[STIX]{x1D706}(\text{II}_{2,26})=H_{n}(\text{II}_{2,26})$
, where
$12\unicode[STIX]{x1D706}(\text{II}_{2,26})=H_{n}(\text{II}_{2,26})$
, where
![]() $\unicode[STIX]{x1D706}(\text{II}_{2,26})$
is the first Chern class of the automorphic (or Hodge) line bundle and
$\unicode[STIX]{x1D706}(\text{II}_{2,26})$
is the first Chern class of the automorphic (or Hodge) line bundle and
![]() $H_{n}(\text{II}_{2,26})$
is the nodal Heegner divisor.
$H_{n}(\text{II}_{2,26})$
is the nodal Heegner divisor.
Now suppose that
![]() $\unicode[STIX]{x1D6EC}$
is a lattice of signature
$\unicode[STIX]{x1D6EC}$
is a lattice of signature
![]() $(2,n)$
and we are given a saturated embedding
$(2,n)$
and we are given a saturated embedding
![]() $\unicode[STIX]{x1D6EC}\subset \text{II}_{2,26}$
. The quasi-pull-back of
$\unicode[STIX]{x1D6EC}\subset \text{II}_{2,26}$
. The quasi-pull-back of
![]() $\unicode[STIX]{x1D6F7}_{12}$
is defined as
$\unicode[STIX]{x1D6F7}_{12}$
is defined as
 $$\begin{eqnarray}\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D6EC}}:=\frac{\unicode[STIX]{x1D6F7}_{12}}{\mathop{\prod }_{\pm \unicode[STIX]{x1D6FF}\in R(\unicode[STIX]{x1D6EC}^{\bot })}\ell _{\unicode[STIX]{x1D6FF}}}\Bigg|_{\mathscr{D}_{\unicode[STIX]{x1D6EC}}^{+}},\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D6EC}}:=\frac{\unicode[STIX]{x1D6F7}_{12}}{\mathop{\prod }_{\pm \unicode[STIX]{x1D6FF}\in R(\unicode[STIX]{x1D6EC}^{\bot })}\ell _{\unicode[STIX]{x1D6FF}}}\Bigg|_{\mathscr{D}_{\unicode[STIX]{x1D6EC}}^{+}},\end{eqnarray}$$
where
![]() $\ell _{\unicode[STIX]{x1D6FF}}$
is the restriction to
$\ell _{\unicode[STIX]{x1D6FF}}$
is the restriction to
![]() $\mathscr{D}_{\unicode[STIX]{x1D6EC}}^{+}$
of the linear form
$\mathscr{D}_{\unicode[STIX]{x1D6EC}}^{+}$
of the linear form
![]() $\unicode[STIX]{x1D70E}\mapsto (\unicode[STIX]{x1D6FF},\unicode[STIX]{x1D70E})$
. Then
$\unicode[STIX]{x1D70E}\mapsto (\unicode[STIX]{x1D6FF},\unicode[STIX]{x1D70E})$
. Then
![]() $\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D6EC}}$
is an automorphic form on
$\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D6EC}}$
is an automorphic form on
![]() $\mathscr{D}_{\unicode[STIX]{x1D6EC}}^{+}$
for the stable orthogonal group
$\mathscr{D}_{\unicode[STIX]{x1D6EC}}^{+}$
for the stable orthogonal group
![]() $\widetilde{O}^{+}(\unicode[STIX]{x1D6EC})$
; see [Reference Borcherds, Katzarkov, Pantev and Shepherd-BarronBKPSB98] and [Reference Gritsenko, Hulek and SankaranGHS07, §8]. Notice that our notation is somewhat imprecise: the automorphic form
$\widetilde{O}^{+}(\unicode[STIX]{x1D6EC})$
; see [Reference Borcherds, Katzarkov, Pantev and Shepherd-BarronBKPSB98] and [Reference Gritsenko, Hulek and SankaranGHS07, §8]. Notice that our notation is somewhat imprecise: the automorphic form
![]() $\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D6EC}}$
depends on the embedding of
$\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D6EC}}$
depends on the embedding of
![]() $\unicode[STIX]{x1D6EC}$
into
$\unicode[STIX]{x1D6EC}$
into
![]() $\text{II}_{2,26}$
and we will see instances of this later on. The weight and divisor of
$\text{II}_{2,26}$
and we will see instances of this later on. The weight and divisor of
![]() $\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D6EC}}$
are computed as follows.
$\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D6EC}}$
are computed as follows.
Recipe 3.2.2. The weight of
![]() $\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D6EC}}$
is equal to
$\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D6EC}}$
is equal to
![]() $12+w$
, where
$12+w$
, where
![]() $w=|R(\unicode[STIX]{x1D6EC}^{\bot })|/2$
is half the number of roots of
$w=|R(\unicode[STIX]{x1D6EC}^{\bot })|/2$
is half the number of roots of
![]() $\text{II}_{2,26}$
perpendicular to
$\text{II}_{2,26}$
perpendicular to
![]() $\unicode[STIX]{x1D6EC}$
. The divisor of
$\unicode[STIX]{x1D6EC}$
. The divisor of
![]() $\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D6EC}}$
is supported on the union of the intersections
$\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D6EC}}$
is supported on the union of the intersections
![]() $\unicode[STIX]{x1D6FF}^{\bot }\cap \mathscr{D}_{\unicode[STIX]{x1D6EC}}^{+}$
for
$\unicode[STIX]{x1D6FF}^{\bot }\cap \mathscr{D}_{\unicode[STIX]{x1D6EC}}^{+}$
for
![]() $\unicode[STIX]{x1D6FF}\in R(\text{II}_{2,26})\setminus R(\unicode[STIX]{x1D6EC}^{\bot })$
. More precisely,
$\unicode[STIX]{x1D6FF}\in R(\text{II}_{2,26})\setminus R(\unicode[STIX]{x1D6EC}^{\bot })$
. More precisely,
Remark 3.2.3. Let
![]() $\unicode[STIX]{x1D6FF}\in R(\text{II}_{2,26})\setminus R(\unicode[STIX]{x1D6EC}^{\bot })$
; then
$\unicode[STIX]{x1D6FF}\in R(\text{II}_{2,26})\setminus R(\unicode[STIX]{x1D6EC}^{\bot })$
; then
![]() $\unicode[STIX]{x1D6FF}^{\bot }\cap \mathscr{D}_{\unicode[STIX]{x1D6EC}}^{+}$
is non-empty if and only if
$\unicode[STIX]{x1D6FF}^{\bot }\cap \mathscr{D}_{\unicode[STIX]{x1D6EC}}^{+}$
is non-empty if and only if
![]() $\langle \unicode[STIX]{x1D6FF},\unicode[STIX]{x1D6EC}^{\bot }\rangle$
is negative definite. Given such a
$\langle \unicode[STIX]{x1D6FF},\unicode[STIX]{x1D6EC}^{\bot }\rangle$
is negative definite. Given such a
![]() $\unicode[STIX]{x1D6FF}$
, let
$\unicode[STIX]{x1D6FF}$
, let
![]() $\unicode[STIX]{x1D708}(\unicode[STIX]{x1D6FF})$
be a generator of
$\unicode[STIX]{x1D708}(\unicode[STIX]{x1D6FF})$
be a generator of
![]() $(\mathbb{Q}\unicode[STIX]{x1D6FF}\oplus \mathbb{Q}\unicode[STIX]{x1D6EC}^{\bot })\cap \unicode[STIX]{x1D6EC}$
(thus
$(\mathbb{Q}\unicode[STIX]{x1D6FF}\oplus \mathbb{Q}\unicode[STIX]{x1D6EC}^{\bot })\cap \unicode[STIX]{x1D6EC}$
(thus
![]() $\unicode[STIX]{x1D708}(\unicode[STIX]{x1D6FF})$
is determined up to multiplication by
$\unicode[STIX]{x1D708}(\unicode[STIX]{x1D6FF})$
is determined up to multiplication by
![]() $\pm 1$
). Then
$\pm 1$
). Then
Let
![]() $\text{Sat}\langle \unicode[STIX]{x1D6FF},\unicode[STIX]{x1D6EC}^{\bot }\rangle$
be the saturation of
$\text{Sat}\langle \unicode[STIX]{x1D6FF},\unicode[STIX]{x1D6EC}^{\bot }\rangle$
be the saturation of
![]() $\langle \unicode[STIX]{x1D6FF},\unicode[STIX]{x1D6EC}^{\bot }\rangle$
in
$\langle \unicode[STIX]{x1D6FF},\unicode[STIX]{x1D6EC}^{\bot }\rangle$
in
![]() $\text{II}_{2,26}$
. If
$\text{II}_{2,26}$
. If
![]() $\unicode[STIX]{x1D6FF}^{\prime }\in \text{Sat}\langle \unicode[STIX]{x1D6FF},\unicode[STIX]{x1D6EC}^{\bot }\rangle$
is another root which does not belong to
$\unicode[STIX]{x1D6FF}^{\prime }\in \text{Sat}\langle \unicode[STIX]{x1D6FF},\unicode[STIX]{x1D6EC}^{\bot }\rangle$
is another root which does not belong to
![]() $\unicode[STIX]{x1D6EC}^{\bot }$
, then
$\unicode[STIX]{x1D6EC}^{\bot }$
, then
![]() $\unicode[STIX]{x1D708}(\unicode[STIX]{x1D6FF}^{\prime })=\pm \unicode[STIX]{x1D708}(\unicode[STIX]{x1D6FF})$
. The upshot is that we may rewrite the right-hand side of (3.2.2) as a finite sum of pre-Heegner divisors
$\unicode[STIX]{x1D708}(\unicode[STIX]{x1D6FF}^{\prime })=\pm \unicode[STIX]{x1D708}(\unicode[STIX]{x1D6FF})$
. The upshot is that we may rewrite the right-hand side of (3.2.2) as a finite sum of pre-Heegner divisors
![]() $\mathscr{H}_{\unicode[STIX]{x1D708}(\unicode[STIX]{x1D6FF}_{i})}$
, where the coefficient of
$\mathscr{H}_{\unicode[STIX]{x1D708}(\unicode[STIX]{x1D6FF}_{i})}$
, where the coefficient of
![]() $\mathscr{H}_{\unicode[STIX]{x1D708}(\unicode[STIX]{x1D6FF}_{i})}$
is equal to half the number of the roots of
$\mathscr{H}_{\unicode[STIX]{x1D708}(\unicode[STIX]{x1D6FF}_{i})}$
is equal to half the number of the roots of
![]() $\text{Sat}\langle \unicode[STIX]{x1D6FF}_{i},\unicode[STIX]{x1D6EC}^{\bot }\rangle$
which do not belong to
$\text{Sat}\langle \unicode[STIX]{x1D6FF}_{i},\unicode[STIX]{x1D6EC}^{\bot }\rangle$
which do not belong to
![]() $\unicode[STIX]{x1D6EC}^{\bot }$
(call this number
$\unicode[STIX]{x1D6EC}^{\bot }$
(call this number
![]() $m(\unicode[STIX]{x1D6FF}_{i})$
):
$m(\unicode[STIX]{x1D6FF}_{i})$
):
Lastly, (3.2.3) descends to a relation between the Hodge bundle on
![]() $\widetilde{O}^{+}(\unicode[STIX]{x1D6EC})\backslash \mathscr{D}_{\unicode[STIX]{x1D6EC}}^{+}$
and the Heegner divisors corresponding to the vectors
$\widetilde{O}^{+}(\unicode[STIX]{x1D6EC})\backslash \mathscr{D}_{\unicode[STIX]{x1D6EC}}^{+}$
and the Heegner divisors corresponding to the vectors
![]() $\unicode[STIX]{x1D708}(\unicode[STIX]{x1D6FF}_{s})$
; see Remark 3.2.1.
$\unicode[STIX]{x1D708}(\unicode[STIX]{x1D6FF}_{s})$
; see Remark 3.2.1.
The plan is the following. We will choose embeddings of
![]() $\unicode[STIX]{x1D6EC}_{N}$
(for
$\unicode[STIX]{x1D6EC}_{N}$
(for
![]() $3\leqslant N\leqslant 25$
) into
$3\leqslant N\leqslant 25$
) into
![]() $\text{II}_{2,26}$
such that the pre-Heegner divisors appearing on the right-hand side of (3.2.3) are associated to minimal norm vectors (see Definition 1.3.7). For a given embedding, (3.2.3) descends to a relation between the Hodge bundle and the Heegner divisors of
$\text{II}_{2,26}$
such that the pre-Heegner divisors appearing on the right-hand side of (3.2.3) are associated to minimal norm vectors (see Definition 1.3.7). For a given embedding, (3.2.3) descends to a relation between the Hodge bundle and the Heegner divisors of
![]() $\mathscr{F}_{\unicode[STIX]{x1D6EC}_{N}}(\widetilde{O}^{+}(\unicode[STIX]{x1D6EC}_{N}))$
associated to minimal norm vectors. For
$\mathscr{F}_{\unicode[STIX]{x1D6EC}_{N}}(\widetilde{O}^{+}(\unicode[STIX]{x1D6EC}_{N}))$
associated to minimal norm vectors. For
![]() $N$
odd,
$N$
odd,
![]() $\mathscr{F}(N)=\mathscr{F}_{\unicode[STIX]{x1D6EC}_{N}}(\widetilde{O}^{+}(\unicode[STIX]{x1D6EC}_{N}))$
and the relations that we will get are those of Theorems 3.1.1 and 3.1.2. If
$\mathscr{F}(N)=\mathscr{F}_{\unicode[STIX]{x1D6EC}_{N}}(\widetilde{O}^{+}(\unicode[STIX]{x1D6EC}_{N}))$
and the relations that we will get are those of Theorems 3.1.1 and 3.1.2. If
![]() $N$
is even, we will get the relations in Theorems 3.1.1 and 3.1.2 by pushing forward via the double covering
$N$
is even, we will get the relations in Theorems 3.1.1 and 3.1.2 by pushing forward via the double covering
![]() $\mathscr{F}_{\unicode[STIX]{x1D6EC}_{N}}(\widetilde{O}^{+}(\unicode[STIX]{x1D6EC}_{N}))\rightarrow \mathscr{F}(N)$
.
$\mathscr{F}_{\unicode[STIX]{x1D6EC}_{N}}(\widetilde{O}^{+}(\unicode[STIX]{x1D6EC}_{N}))\rightarrow \mathscr{F}(N)$
.
3.2.2 Embeddings of
 $\unicode[STIX]{x1D6EC}_{N}$
into
$\unicode[STIX]{x1D6EC}_{N}$
into
 $\text{II}_{2,26}$
$\text{II}_{2,26}$
Lemma 3.2.4. If
![]() $3\leqslant N\leqslant 25$
, the lattice
$3\leqslant N\leqslant 25$
, the lattice
![]() $\unicode[STIX]{x1D6EC}_{N}$
has a saturated embedding into the unimodular lattice
$\unicode[STIX]{x1D6EC}_{N}$
has a saturated embedding into the unimodular lattice
![]() $\text{II}_{2,26}$
with orthogonal complement isomorphic to
$\text{II}_{2,26}$
with orthogonal complement isomorphic to
![]() $D_{26-N}$
and, if
$D_{26-N}$
and, if
![]() $3\leqslant N\leqslant 17$
, it also has a saturated embedding with orthogonal complement isomorphic to
$3\leqslant N\leqslant 17$
, it also has a saturated embedding with orthogonal complement isomorphic to
![]() $E_{8}\oplus D_{18-N}$
. Conversely, any saturated embedding of
$E_{8}\oplus D_{18-N}$
. Conversely, any saturated embedding of
![]() $D_{26-N}$
, or of
$D_{26-N}$
, or of
![]() $E_{8}\oplus D_{18-N}$
, into
$E_{8}\oplus D_{18-N}$
, into
![]() $\text{II}_{2,26}$
has orthogonal complement isomorphic to
$\text{II}_{2,26}$
has orthogonal complement isomorphic to
![]() $\unicode[STIX]{x1D6EC}_{N}$
.
$\unicode[STIX]{x1D6EC}_{N}$
.
Proof. If
![]() $3\leqslant N\leqslant 25$
, then by (1.1.2) and Claim 1.1.1 there exists an isomorphism of groups
$3\leqslant N\leqslant 25$
, then by (1.1.2) and Claim 1.1.1 there exists an isomorphism of groups
![]() $\unicode[STIX]{x1D711}:A_{\unicode[STIX]{x1D6EC}_{N}}\overset{{\sim}}{\longrightarrow }D_{26-N}$
which multiplies the discriminant quadratic form by
$\unicode[STIX]{x1D711}:A_{\unicode[STIX]{x1D6EC}_{N}}\overset{{\sim}}{\longrightarrow }D_{26-N}$
which multiplies the discriminant quadratic form by
![]() $-1$
, i.e.
$-1$
, i.e.
Let
![]() $L\subset (\unicode[STIX]{x1D6EC}_{N}\oplus D_{26-N})_{\mathbb{Q}}$
be the overlattice of
$L\subset (\unicode[STIX]{x1D6EC}_{N}\oplus D_{26-N})_{\mathbb{Q}}$
be the overlattice of
![]() $\unicode[STIX]{x1D6EC}_{N}\oplus D_{26-N}$
generated by vectors
$\unicode[STIX]{x1D6EC}_{N}\oplus D_{26-N}$
generated by vectors
![]() $(v,w)$
such that
$(v,w)$
such that
![]() $[v]\in A_{\unicode[STIX]{x1D6EC}_{N}}$
,
$[v]\in A_{\unicode[STIX]{x1D6EC}_{N}}$
,
![]() $[w]\in A_{D_{26-N}}$
, and
$[w]\in A_{D_{26-N}}$
, and
![]() $[w]=\unicode[STIX]{x1D711}([v])$
. Then, because of (3.2.4),
$[w]=\unicode[STIX]{x1D711}([v])$
. Then, because of (3.2.4),
![]() $L$
is even, unimodular, of signature
$L$
is even, unimodular, of signature
![]() $(2,26)$
, and hence is isomorphic to
$(2,26)$
, and hence is isomorphic to
![]() $\text{II}_{2,26}$
. By construction,
$\text{II}_{2,26}$
. By construction,
![]() $\unicode[STIX]{x1D6EC}_{N}$
is a saturated sublattice of
$\unicode[STIX]{x1D6EC}_{N}$
is a saturated sublattice of
![]() $L$
and its orthogonal complement is isomorphic to
$L$
and its orthogonal complement is isomorphic to
![]() $D_{26-N}$
. If
$D_{26-N}$
. If
![]() $3\leqslant N\leqslant 17$
, there exists an isomorphism of groups
$3\leqslant N\leqslant 17$
, there exists an isomorphism of groups
![]() $\unicode[STIX]{x1D713}:A_{\unicode[STIX]{x1D6EC}_{N}}\overset{{\sim}}{\longrightarrow }(E_{8}\oplus D_{18-N})$
which multiplies the discriminant quadratic forms by
$\unicode[STIX]{x1D713}:A_{\unicode[STIX]{x1D6EC}_{N}}\overset{{\sim}}{\longrightarrow }(E_{8}\oplus D_{18-N})$
which multiplies the discriminant quadratic forms by
![]() $-1$
, i.e.
$-1$
, i.e.
Proceeding as in the previous case, one constructs an overlattice of
![]() $\unicode[STIX]{x1D6EC}_{N}\oplus (E_{8}\oplus D_{18-N})$
which is isomorphic to
$\unicode[STIX]{x1D6EC}_{N}\oplus (E_{8}\oplus D_{18-N})$
which is isomorphic to
![]() $\text{II}_{2,26}$
, in which
$\text{II}_{2,26}$
, in which
![]() $\unicode[STIX]{x1D6EC}_{N}$
is saturated, with orthogonal complement isomorphic to
$\unicode[STIX]{x1D6EC}_{N}$
is saturated, with orthogonal complement isomorphic to
![]() $E_{8}\oplus D_{18-N}$
.
$E_{8}\oplus D_{18-N}$
.
Let us prove the last statement of the lemma. Suppose that
![]() $D_{26-N}\subset \text{II}_{2,26}$
, or
$D_{26-N}\subset \text{II}_{2,26}$
, or
![]() $(E_{8}\oplus D_{18-N})\subset \text{II}_{2,26}$
, is saturated. Let
$(E_{8}\oplus D_{18-N})\subset \text{II}_{2,26}$
, is saturated. Let
![]() $M:=D_{26-N}^{\bot }$
(respectively
$M:=D_{26-N}^{\bot }$
(respectively
![]() $M=(E_{8}\oplus D_{18-N})^{\bot }$
). The overlattice
$M=(E_{8}\oplus D_{18-N})^{\bot }$
). The overlattice
![]() $\text{II}_{2,26}\supset (D_{26-N}\oplus M)$
(respectively
$\text{II}_{2,26}\supset (D_{26-N}\oplus M)$
(respectively
![]() $\text{II}_{2,26}\supset (E_{8}\oplus D_{18-N})\oplus M$
) induces an isomorphism of groups
$\text{II}_{2,26}\supset (E_{8}\oplus D_{18-N})\oplus M$
) induces an isomorphism of groups
such that
![]() $q_{M}(g(\unicode[STIX]{x1D702}))=-q_{D_{26-N}}(\unicode[STIX]{x1D702})$
for all
$q_{M}(g(\unicode[STIX]{x1D702}))=-q_{D_{26-N}}(\unicode[STIX]{x1D702})$
for all
![]() $\unicode[STIX]{x1D702}\in A_{D_{26-N}}$
(respectively,
$\unicode[STIX]{x1D702}\in A_{D_{26-N}}$
(respectively,
![]() $q_{M}(g(\unicode[STIX]{x1D702}))=-q_{E_{8}\oplus D_{18-N}}(\unicode[STIX]{x1D702})$
for all
$q_{M}(g(\unicode[STIX]{x1D702}))=-q_{E_{8}\oplus D_{18-N}}(\unicode[STIX]{x1D702})$
for all
![]() $\unicode[STIX]{x1D702}\in A_{E_{8}\oplus D_{18-N}}$
). Thus,
$\unicode[STIX]{x1D702}\in A_{E_{8}\oplus D_{18-N}}$
). Thus,
![]() $M$
has the same signature, parity, and discriminant quadratic form as
$M$
has the same signature, parity, and discriminant quadratic form as
![]() $\unicode[STIX]{x1D6EC}_{N}$
and hence is isomorphic to
$\unicode[STIX]{x1D6EC}_{N}$
and hence is isomorphic to
![]() $\unicode[STIX]{x1D6EC}_{N}$
by Theorem 1.13.2 of [Reference NikulinNik80].◻
$\unicode[STIX]{x1D6EC}_{N}$
by Theorem 1.13.2 of [Reference NikulinNik80].◻
Remark 3.2.5. Let
![]() $3\leqslant N\leqslant 25$
. Suppose that
$3\leqslant N\leqslant 25$
. Suppose that
![]() $\unicode[STIX]{x1D6EC}_{N}\subset \text{II}_{2,26}$
is a saturated embedding and that
$\unicode[STIX]{x1D6EC}_{N}\subset \text{II}_{2,26}$
is a saturated embedding and that
![]() $\unicode[STIX]{x1D6EC}_{N}^{\bot }$
is isomorphic either to
$\unicode[STIX]{x1D6EC}_{N}^{\bot }$
is isomorphic either to
![]() $D_{26-N}$
or to
$D_{26-N}$
or to
![]() $E_{8}\oplus D_{18-N}$
(in this case
$E_{8}\oplus D_{18-N}$
(in this case
![]() $N\leqslant 17$
). Let
$N\leqslant 17$
). Let
![]() $(N-2)=8k+a$
, where
$(N-2)=8k+a$
, where
![]() $k\geqslant 0$
and
$k\geqslant 0$
and
![]() $a\in \{1,\ldots ,8\}$
. Then
$a\in \{1,\ldots ,8\}$
. Then
![]() $\unicode[STIX]{x1D6EC}_{N}\cong \text{II}_{2,2+8k}\oplus D_{a}$
and we identify the two lattices throughout.
$\unicode[STIX]{x1D6EC}_{N}\cong \text{II}_{2,2+8k}\oplus D_{a}$
and we identify the two lattices throughout.
(1) If
 $N\leqslant 25$
and
$N\leqslant 25$
and
 $\unicode[STIX]{x1D6EC}_{N}^{\bot }\cong D_{26-N}$
, then
$\unicode[STIX]{x1D6EC}_{N}^{\bot }\cong D_{26-N}$
, then
 $\text{II}_{2,26}$
is identified with the sublattice of generated by
$\text{II}_{2,26}$
is identified with the sublattice of generated by $$\begin{eqnarray}(\text{II}_{2,2+8k}\oplus D_{a}\oplus D_{26-N})_{\mathbb{Q}}\end{eqnarray}$$
$$\begin{eqnarray}(\text{II}_{2,2+8k}\oplus D_{a}\oplus D_{26-N})_{\mathbb{Q}}\end{eqnarray}$$
 $\text{II}_{2,2+8k}\oplus D_{a}\oplus D_{26-N}$
together with the following three vectors:
$\text{II}_{2,2+8k}\oplus D_{a}\oplus D_{26-N}$
together with the following three vectors:  $$\begin{eqnarray}\displaystyle & \displaystyle u_{1}:=(0_{4+8k},(\underbrace{{\textstyle \frac{1}{2}},\ldots ,{\textstyle \frac{1}{2}}}_{a}),(\underbrace{{\textstyle \frac{1}{2}},\ldots ,{\textstyle \frac{1}{2}}}_{26-N})),\quad u_{2}:=(0_{4+8k},(\underbrace{-{\textstyle \frac{1}{2}},{\textstyle \frac{1}{2}},\ldots ,{\textstyle \frac{1}{2}}}_{a}),(\underbrace{-{\textstyle \frac{1}{2}},{\textstyle \frac{1}{2}},\ldots ,{\textstyle \frac{1}{2}}}_{26-N})), & \displaystyle \nonumber\\ \displaystyle & \displaystyle u_{3}:=(0_{4+8k},(\underbrace{1,0,\ldots ,0}_{a}),(\underbrace{1,0,\ldots ,0}_{26-N})). & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle u_{1}:=(0_{4+8k},(\underbrace{{\textstyle \frac{1}{2}},\ldots ,{\textstyle \frac{1}{2}}}_{a}),(\underbrace{{\textstyle \frac{1}{2}},\ldots ,{\textstyle \frac{1}{2}}}_{26-N})),\quad u_{2}:=(0_{4+8k},(\underbrace{-{\textstyle \frac{1}{2}},{\textstyle \frac{1}{2}},\ldots ,{\textstyle \frac{1}{2}}}_{a}),(\underbrace{-{\textstyle \frac{1}{2}},{\textstyle \frac{1}{2}},\ldots ,{\textstyle \frac{1}{2}}}_{26-N})), & \displaystyle \nonumber\\ \displaystyle & \displaystyle u_{3}:=(0_{4+8k},(\underbrace{1,0,\ldots ,0}_{a}),(\underbrace{1,0,\ldots ,0}_{26-N})). & \displaystyle \nonumber\end{eqnarray}$$
(2) If
 $N\leqslant 17$
and
$N\leqslant 17$
and
 $\unicode[STIX]{x1D6EC}_{N}^{\bot }\cong E_{8}\oplus D_{18-N}$
, then
$\unicode[STIX]{x1D6EC}_{N}^{\bot }\cong E_{8}\oplus D_{18-N}$
, then
 $\text{II}_{2,26}$
is identified with the sublattice of generated by
$\text{II}_{2,26}$
is identified with the sublattice of generated by $$\begin{eqnarray}(\text{II}_{2,2+8k}\oplus D_{a}\oplus D_{18-N}\oplus E_{8})_{\mathbb{Q}}\end{eqnarray}$$
$$\begin{eqnarray}(\text{II}_{2,2+8k}\oplus D_{a}\oplus D_{18-N}\oplus E_{8})_{\mathbb{Q}}\end{eqnarray}$$
 $\text{II}_{2,2+8k}\oplus D_{a}\oplus D_{18-N}\oplus E_{8}$
together with the following three vectors:
$\text{II}_{2,2+8k}\oplus D_{a}\oplus D_{18-N}\oplus E_{8}$
together with the following three vectors: $$\begin{eqnarray}\displaystyle & \displaystyle u_{1}^{\prime }:=(0_{4+8k},(\underbrace{{\textstyle \frac{1}{2}},\ldots ,{\textstyle \frac{1}{2}}}_{a}),(\underbrace{{\textstyle \frac{1}{2}},\ldots ,{\textstyle \frac{1}{2}}}_{18-N}),0_{8}),\quad u_{2}^{\prime }:=(0_{4+8k},(\underbrace{-{\textstyle \frac{1}{2}},{\textstyle \frac{1}{2}},\ldots ,{\textstyle \frac{1}{2}}}_{a}),(\underbrace{-{\textstyle \frac{1}{2}},{\textstyle \frac{1}{2}},\ldots ,{\textstyle \frac{1}{2}}}_{18-N}),0_{8}), & \displaystyle \nonumber\\ \displaystyle & \displaystyle u_{3}^{\prime }:=(0_{4+8k},(\underbrace{1,0,\ldots ,0}_{a}),(\underbrace{1,0,\ldots ,0}_{18-N}),0_{8}). & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle u_{1}^{\prime }:=(0_{4+8k},(\underbrace{{\textstyle \frac{1}{2}},\ldots ,{\textstyle \frac{1}{2}}}_{a}),(\underbrace{{\textstyle \frac{1}{2}},\ldots ,{\textstyle \frac{1}{2}}}_{18-N}),0_{8}),\quad u_{2}^{\prime }:=(0_{4+8k},(\underbrace{-{\textstyle \frac{1}{2}},{\textstyle \frac{1}{2}},\ldots ,{\textstyle \frac{1}{2}}}_{a}),(\underbrace{-{\textstyle \frac{1}{2}},{\textstyle \frac{1}{2}},\ldots ,{\textstyle \frac{1}{2}}}_{18-N}),0_{8}), & \displaystyle \nonumber\\ \displaystyle & \displaystyle u_{3}^{\prime }:=(0_{4+8k},(\underbrace{1,0,\ldots ,0}_{a}),(\underbrace{1,0,\ldots ,0}_{18-N}),0_{8}). & \displaystyle \nonumber\end{eqnarray}$$
Remark 3.2.6. Suppose that
![]() $\unicode[STIX]{x1D6EC}_{N}\subset \text{II}_{2,26}$
is a saturated embedding. Then the orthogonal complement of
$\unicode[STIX]{x1D6EC}_{N}\subset \text{II}_{2,26}$
is a saturated embedding. Then the orthogonal complement of
![]() $\unicode[STIX]{x1D6EC}_{N}$
in
$\unicode[STIX]{x1D6EC}_{N}$
in
![]() $\text{II}_{2,26}$
is a lattice in the genus of
$\text{II}_{2,26}$
is a lattice in the genus of
![]() $D_{26-N}$
. We note the following:
$D_{26-N}$
. We note the following:
∙ if
 $1\leqslant k\leqslant 8$
, there is only one isometry class of lattices in the genus of
$1\leqslant k\leqslant 8$
, there is only one isometry class of lattices in the genus of
 $D_{k}$
, namely
$D_{k}$
, namely
 $D_{k}$
;
$D_{k}$
;∙ if
 $9\leqslant k\leqslant 16$
, there are at least two distinct classes, namely
$9\leqslant k\leqslant 16$
, there are at least two distinct classes, namely
 $D_{k}$
and
$D_{k}$
and
 $D_{k-8}\oplus E_{8}$
.
$D_{k-8}\oplus E_{8}$
.
In other words, there is one Borcherds relation for
![]() $N\geqslant 18$
and at least two such relations for
$N\geqslant 18$
and at least two such relations for
![]() $10\leqslant N\leqslant 17$
. For
$10\leqslant N\leqslant 17$
. For
![]() $N\leqslant 17$
, the relations relevant for us are those associated to
$N\leqslant 17$
, the relations relevant for us are those associated to
![]() $D_{k}$
and
$D_{k}$
and
![]() $D_{k-8}\oplus E_{8}$
as those involve only Heegner divisors associated to minimal norm vectors.
$D_{k-8}\oplus E_{8}$
as those involve only Heegner divisors associated to minimal norm vectors.
Remark 3.2.7. Let
![]() $m\geqslant 1$
. The non-zero elements of
$m\geqslant 1$
. The non-zero elements of
![]() $A_{D_{m}}$
are
$A_{D_{m}}$
are
![]() $\unicode[STIX]{x1D709},\unicode[STIX]{x1D701},\unicode[STIX]{x1D701}^{\prime }$
, where
$\unicode[STIX]{x1D709},\unicode[STIX]{x1D701},\unicode[STIX]{x1D701}^{\prime }$
, where
Let
![]() $v_{m}:=(2,0,\ldots ,0)\in D_{m}$
. Then the divisibility of
$v_{m}:=(2,0,\ldots ,0)\in D_{m}$
. Then the divisibility of
![]() $v_{m}$
is even (equal to
$v_{m}$
is even (equal to
![]() $2$
unless
$2$
unless
![]() $m=1$
) and
$m=1$
) and
![]() $[v_{m}/2]=\unicode[STIX]{x1D709}$
. Moreover, if
$[v_{m}/2]=\unicode[STIX]{x1D709}$
. Moreover, if
![]() $u\in D_{m}$
has even divisibility and
$u\in D_{m}$
has even divisibility and
![]() $[u/2]=\unicode[STIX]{x1D709}$
, then
$[u/2]=\unicode[STIX]{x1D709}$
, then
![]() $u^{2}\leqslant -4=v_{m}^{2}$
. Similarly, let
$u^{2}\leqslant -4=v_{m}^{2}$
. Similarly, let
Then
![]() $w_{m}^{\ast }=\unicode[STIX]{x1D701}$
and, if
$w_{m}^{\ast }=\unicode[STIX]{x1D701}$
and, if
![]() $u\in D_{m}$
is such that
$u\in D_{m}$
is such that
![]() $u^{\ast }=\unicode[STIX]{x1D701}$
, then
$u^{\ast }=\unicode[STIX]{x1D701}$
, then
Since the map
![]() $(x_{1},\ldots ,x_{m})\mapsto (-x_{1},x_{2},\ldots ,x_{m})$
defines an automorphism of
$(x_{1},\ldots ,x_{m})\mapsto (-x_{1},x_{2},\ldots ,x_{m})$
defines an automorphism of
![]() $D_{m}$
interchanging
$D_{m}$
interchanging
![]() $\unicode[STIX]{x1D701}$
with
$\unicode[STIX]{x1D701}$
with
![]() $\unicode[STIX]{x1D701}^{\prime }$
, an analogous result holds for the minimal absolute value of
$\unicode[STIX]{x1D701}^{\prime }$
, an analogous result holds for the minimal absolute value of
![]() $u^{2}$
for vectors
$u^{2}$
for vectors
![]() $u\in D_{m}$
such that
$u\in D_{m}$
such that
![]() $u^{\ast }=\unicode[STIX]{x1D701}^{\prime }$
. This fact has the following interesting consequence. Suppose that
$u^{\ast }=\unicode[STIX]{x1D701}^{\prime }$
. This fact has the following interesting consequence. Suppose that
![]() $\unicode[STIX]{x1D6EC}\subset \text{II}_{2,26}$
is a saturated sublattice and that one of the following holds:
$\unicode[STIX]{x1D6EC}\subset \text{II}_{2,26}$
is a saturated sublattice and that one of the following holds:
(1)
 $\unicode[STIX]{x1D6EC}^{\bot }\cong D_{26-N}$
and
$\unicode[STIX]{x1D6EC}^{\bot }\cong D_{26-N}$
and
 $N\in \{6,14\}$
; or
$N\in \{6,14\}$
; or(2)
 $\unicode[STIX]{x1D6EC}^{\bot }\cong (E_{8}\oplus D_{18-N})$
and
$\unicode[STIX]{x1D6EC}^{\bot }\cong (E_{8}\oplus D_{18-N})$
and
 $N=6$
.
$N=6$
.
Although there is no preferred decoration of the abstract dimension-
![]() $N$
$N$
![]() $D$
-lattice
$D$
-lattice
![]() $\unicode[STIX]{x1D6EC}$
(because
$\unicode[STIX]{x1D6EC}$
(because
![]() $q_{\unicode[STIX]{x1D6EC}}(\unicode[STIX]{x1D702})\equiv 1\hspace{0.6em}({\rm mod}\hspace{0.2em}2\mathbb{Z})$
for all non-zero
$q_{\unicode[STIX]{x1D6EC}}(\unicode[STIX]{x1D702})\equiv 1\hspace{0.6em}({\rm mod}\hspace{0.2em}2\mathbb{Z})$
for all non-zero
![]() $\unicode[STIX]{x1D701}\in A_{\unicode[STIX]{x1D6EC}}$
), there is a preferred decoration determined by the embedding
$\unicode[STIX]{x1D701}\in A_{\unicode[STIX]{x1D6EC}}$
), there is a preferred decoration determined by the embedding
![]() $\unicode[STIX]{x1D6EC}\subset \text{II}_{2,26}$
, namely
$\unicode[STIX]{x1D6EC}\subset \text{II}_{2,26}$
, namely
![]() $\unicode[STIX]{x1D702}:=g(\unicode[STIX]{x1D709})$
, where
$\unicode[STIX]{x1D702}:=g(\unicode[STIX]{x1D709})$
, where
![]() $g$
is the isomorphism in (3.2.5), and
$g$
is the isomorphism in (3.2.5), and
![]() $\unicode[STIX]{x1D709}\in A_{\unicode[STIX]{x1D6EC}^{\bot }}$
is the unique class for which there exists
$\unicode[STIX]{x1D709}\in A_{\unicode[STIX]{x1D6EC}^{\bot }}$
is the unique class for which there exists
![]() $v\in \unicode[STIX]{x1D6EC}^{\bot }$
of square
$v\in \unicode[STIX]{x1D6EC}^{\bot }$
of square
![]() $-4$
and even divisibility such that
$-4$
and even divisibility such that
![]() $[v/2]=\unicode[STIX]{x1D709}$
.
$[v/2]=\unicode[STIX]{x1D709}$
.
Definition 3.2.8. Let
![]() $\unicode[STIX]{x1D6EC}\subset \text{II}_{2,26}$
be a saturated sublattice such that
$\unicode[STIX]{x1D6EC}\subset \text{II}_{2,26}$
be a saturated sublattice such that
![]() $\unicode[STIX]{x1D6EC}^{\bot }$
is isomorphic to
$\unicode[STIX]{x1D6EC}^{\bot }$
is isomorphic to
![]() $D_{26-N}$
or to
$D_{26-N}$
or to
![]() $(E_{8}\oplus D_{18-N})$
(hence
$(E_{8}\oplus D_{18-N})$
(hence
![]() $\unicode[STIX]{x1D6EC}$
is a dimension-
$\unicode[STIX]{x1D6EC}$
is a dimension-
![]() $N$
$N$
![]() $D$
-lattice by Lemma 3.2.4). A decoration
$D$
-lattice by Lemma 3.2.4). A decoration
![]() $\unicode[STIX]{x1D702}$
of
$\unicode[STIX]{x1D702}$
of
![]() $\unicode[STIX]{x1D6EC}$
is admissible if
$\unicode[STIX]{x1D6EC}$
is admissible if
![]() $\unicode[STIX]{x1D702}=g(\unicode[STIX]{x1D709})$
, where
$\unicode[STIX]{x1D702}=g(\unicode[STIX]{x1D709})$
, where
![]() $g$
is the isomorphism in (3.2.5) and
$g$
is the isomorphism in (3.2.5) and
![]() $\unicode[STIX]{x1D709}\in A_{\unicode[STIX]{x1D6EC}^{\bot }}$
is a class for which there exists
$\unicode[STIX]{x1D709}\in A_{\unicode[STIX]{x1D6EC}^{\bot }}$
is a class for which there exists
![]() $v\in \unicode[STIX]{x1D6EC}^{\bot }$
of square
$v\in \unicode[STIX]{x1D6EC}^{\bot }$
of square
![]() $-4$
and even divisibility such that
$-4$
and even divisibility such that
![]() $[v/2]=\unicode[STIX]{x1D709}$
.
$[v/2]=\unicode[STIX]{x1D709}$
.
Remark 3.2.9. If
![]() $N\not \equiv 6\hspace{0.6em}({\rm mod}\hspace{0.2em}8)$
, the unique decoration of
$N\not \equiv 6\hspace{0.6em}({\rm mod}\hspace{0.2em}8)$
, the unique decoration of
![]() $\unicode[STIX]{x1D6EC}$
is admissible, if
$\unicode[STIX]{x1D6EC}$
is admissible, if
![]() $N=22$
, all three decorations of
$N=22$
, all three decorations of
![]() $\unicode[STIX]{x1D6EC}$
are admissible (any non-zero element of
$\unicode[STIX]{x1D6EC}$
are admissible (any non-zero element of
![]() $D_{4}$
is equal to
$D_{4}$
is equal to
![]() $[v/2]$
for a suitable
$[v/2]$
for a suitable
![]() $v\in \unicode[STIX]{x1D6EC}$
of square
$v\in \unicode[STIX]{x1D6EC}$
of square
![]() $-4$
and even divisibility), and if
$-4$
and even divisibility), and if
![]() $N\in \{6,14\}$
, then only one of the three decorations is admissible; see Remark 3.2.7.
$N\in \{6,14\}$
, then only one of the three decorations is admissible; see Remark 3.2.7.
3.2.3 The pre-Heegner divisors associated to the quasi-pull-backs of
 $\unicode[STIX]{x1D6F7}_{12}$
$\unicode[STIX]{x1D6F7}_{12}$
The following result will allow us to determine the vectors
![]() $\unicode[STIX]{x1D708}(\unicode[STIX]{x1D6FF})$
which appear in Remark 3.2.3 for the two embeddings of
$\unicode[STIX]{x1D708}(\unicode[STIX]{x1D6FF})$
which appear in Remark 3.2.3 for the two embeddings of
![]() $\unicode[STIX]{x1D6EC}_{N}$
into
$\unicode[STIX]{x1D6EC}_{N}$
into
![]() $\text{II}_{2,26}$
given by Lemma 3.2.4.
$\text{II}_{2,26}$
given by Lemma 3.2.4.
Proposition 3.2.10. Let
![]() $3\leqslant N\leqslant 25$
. Assume that
$3\leqslant N\leqslant 25$
. Assume that
![]() $\unicode[STIX]{x1D6EC}\subset \text{II}_{2,26}$
is a saturated sublattice and that
$\unicode[STIX]{x1D6EC}\subset \text{II}_{2,26}$
is a saturated sublattice and that
![]() $\unicode[STIX]{x1D6EC}^{\bot }$
is isomorphic to
$\unicode[STIX]{x1D6EC}^{\bot }$
is isomorphic to
![]() $D_{26-N}$
or to
$D_{26-N}$
or to
![]() $E_{8}\oplus D_{18-N}$
(in the latter case,
$E_{8}\oplus D_{18-N}$
(in the latter case,
![]() $N\leqslant 17$
) and hence
$N\leqslant 17$
) and hence
![]() $\unicode[STIX]{x1D6EC}$
is a dimension-
$\unicode[STIX]{x1D6EC}$
is a dimension-
![]() $N$
$N$
![]() $D$
-lattice by Lemma 3.2.4. Suppose that
$D$
-lattice by Lemma 3.2.4. Suppose that
![]() $\unicode[STIX]{x1D6FF}\in R(\text{II}_{2,26}\setminus \unicode[STIX]{x1D6EC}^{\bot })$
is such that
$\unicode[STIX]{x1D6FF}\in R(\text{II}_{2,26}\setminus \unicode[STIX]{x1D6EC}^{\bot })$
is such that
![]() $\langle \unicode[STIX]{x1D6EC}^{\bot },\unicode[STIX]{x1D6FF}\rangle$
is negative definite. Then
$\langle \unicode[STIX]{x1D6EC}^{\bot },\unicode[STIX]{x1D6FF}\rangle$
is negative definite. Then
![]() $\unicode[STIX]{x1D708}(\unicode[STIX]{x1D6FF})$
(notation as in Remark 3.2.3) is a minimal norm vector of
$\unicode[STIX]{x1D708}(\unicode[STIX]{x1D6FF})$
(notation as in Remark 3.2.3) is a minimal norm vector of
![]() $\unicode[STIX]{x1D6EC}$
(see Definition 1.3.7). Moreover, one of the following holds:
$\unicode[STIX]{x1D6EC}$
(see Definition 1.3.7). Moreover, one of the following holds:
(a)
 $\unicode[STIX]{x1D708}(\unicode[STIX]{x1D6FF})^{2}=-2$
;
$\unicode[STIX]{x1D708}(\unicode[STIX]{x1D6FF})^{2}=-2$
;(b)
 $\unicode[STIX]{x1D708}(\unicode[STIX]{x1D6FF})^{2}=-4$
,
$\unicode[STIX]{x1D708}(\unicode[STIX]{x1D6FF})^{2}=-4$
,
 $\operatorname{div}_{\unicode[STIX]{x1D6EC}}(\unicode[STIX]{x1D708}(\unicode[STIX]{x1D6FF}))=2$
, and
$\operatorname{div}_{\unicode[STIX]{x1D6EC}}(\unicode[STIX]{x1D708}(\unicode[STIX]{x1D6FF}))=2$
, and
 $\unicode[STIX]{x1D708}(\unicode[STIX]{x1D6FF})^{\ast }$
is an admissible decoration of
$\unicode[STIX]{x1D708}(\unicode[STIX]{x1D6FF})^{\ast }$
is an admissible decoration of
 $\unicode[STIX]{x1D6EC}$
;
$\unicode[STIX]{x1D6EC}$
;(c)
 $\unicode[STIX]{x1D708}(\unicode[STIX]{x1D6FF})^{2}=-4$
and
$\unicode[STIX]{x1D708}(\unicode[STIX]{x1D6FF})^{2}=-4$
and
 $\operatorname{div}_{\unicode[STIX]{x1D6EC}}(\unicode[STIX]{x1D708}(\unicode[STIX]{x1D6FF}))=4$
;
$\operatorname{div}_{\unicode[STIX]{x1D6EC}}(\unicode[STIX]{x1D708}(\unicode[STIX]{x1D6FF}))=4$
;(d)
 $\unicode[STIX]{x1D6EC}^{\bot }\cong D_{26-N}$
and
$\unicode[STIX]{x1D6EC}^{\bot }\cong D_{26-N}$
and
 $19\leqslant N$
;
$19\leqslant N$
;(e)
 $\unicode[STIX]{x1D6EC}^{\bot }\cong (E_{8}\oplus D_{18-N})$
and
$\unicode[STIX]{x1D6EC}^{\bot }\cong (E_{8}\oplus D_{18-N})$
and
 $11\leqslant N$
.
$11\leqslant N$
.
Proof. Let
![]() $m$
be the minimum strictly positive integer such that
$m$
be the minimum strictly positive integer such that
![]() $m\unicode[STIX]{x1D6FF}\in (\unicode[STIX]{x1D6EC}\oplus \unicode[STIX]{x1D6EC}^{\bot })$
. Thus,
$m\unicode[STIX]{x1D6FF}\in (\unicode[STIX]{x1D6EC}\oplus \unicode[STIX]{x1D6EC}^{\bot })$
. Thus,
and
![]() $m\in \{1,2,4\}$
; see Remark 3.2.5. Notice that
$m\in \{1,2,4\}$
; see Remark 3.2.5. Notice that
![]() $v\in \langle \unicode[STIX]{x1D708}(\unicode[STIX]{x1D6FF})\rangle$
and
$v\in \langle \unicode[STIX]{x1D708}(\unicode[STIX]{x1D6FF})\rangle$
and
![]() $\unicode[STIX]{x1D708}(\unicode[STIX]{x1D6FF})=\pm v$
if and only if
$\unicode[STIX]{x1D708}(\unicode[STIX]{x1D6FF})=\pm v$
if and only if
![]() $v$
is primitive. Let us prove that one of the following items holds:
$v$
is primitive. Let us prove that one of the following items holds:
(1)
 $m=1$
,
$m=1$
,
 $v^{2}=-2$
, and
$v^{2}=-2$
, and
 $\unicode[STIX]{x1D708}(\unicode[STIX]{x1D6FF})=\pm v$
;
$\unicode[STIX]{x1D708}(\unicode[STIX]{x1D6FF})=\pm v$
;(2)
 $m=2$
,
$m=2$
,
 $v^{2}\in \{-2,-6\}$
,
$v^{2}\in \{-2,-6\}$
,
 $\operatorname{div}_{\unicode[STIX]{x1D6EC}}(v)=2$
, and
$\operatorname{div}_{\unicode[STIX]{x1D6EC}}(v)=2$
, and
 $\unicode[STIX]{x1D708}(\unicode[STIX]{x1D6FF})=\pm v$
;
$\unicode[STIX]{x1D708}(\unicode[STIX]{x1D6FF})=\pm v$
;(3)
 $m=2$
,
$m=2$
,
 $v^{2}=-4$
,
$v^{2}=-4$
,
 $\operatorname{div}_{\unicode[STIX]{x1D6EC}}(v)=2$
,
$\operatorname{div}_{\unicode[STIX]{x1D6EC}}(v)=2$
,
 $\unicode[STIX]{x1D708}(\unicode[STIX]{x1D6FF})=\pm v$
, and
$\unicode[STIX]{x1D708}(\unicode[STIX]{x1D6FF})=\pm v$
, and
 $\unicode[STIX]{x1D708}(\unicode[STIX]{x1D6FF})^{\ast }$
is an admissible decoration of
$\unicode[STIX]{x1D708}(\unicode[STIX]{x1D6FF})^{\ast }$
is an admissible decoration of
 $\unicode[STIX]{x1D6EC}$
;
$\unicode[STIX]{x1D6EC}$
;(4)
 $m=2$
,
$m=2$
,
 $v^{2}=-4$
,
$v^{2}=-4$
,
 $\operatorname{div}_{\unicode[STIX]{x1D6EC}}(v)=4$
, and
$\operatorname{div}_{\unicode[STIX]{x1D6EC}}(v)=4$
, and
 $\unicode[STIX]{x1D708}(\unicode[STIX]{x1D6FF})=\pm v$
;
$\unicode[STIX]{x1D708}(\unicode[STIX]{x1D6FF})=\pm v$
;(5)
 $m=4$
,
$m=4$
,
 $N$
is odd,
$N$
is odd,
 $v^{2}=-4a$
, where
$v^{2}=-4a$
, where
 $a$
is the residue modulo
$a$
is the residue modulo
 $8$
of
$8$
of
 $(N-2)$
,
$(N-2)$
,
 $\operatorname{div}_{\unicode[STIX]{x1D6EC}}(v)=4$
, and
$\operatorname{div}_{\unicode[STIX]{x1D6EC}}(v)=4$
, and
 $\unicode[STIX]{x1D708}(\unicode[STIX]{x1D6FF})=\pm v$
.
$\unicode[STIX]{x1D708}(\unicode[STIX]{x1D6FF})=\pm v$
.
We have
![]() $\unicode[STIX]{x1D708}(\unicode[STIX]{x1D6FF})^{2}<0$
because
$\unicode[STIX]{x1D708}(\unicode[STIX]{x1D6FF})^{2}<0$
because
![]() $\langle \unicode[STIX]{x1D6EC}_{N}^{\bot },\unicode[STIX]{x1D6FF}\rangle$
is negative definite and hence
$\langle \unicode[STIX]{x1D6EC}_{N}^{\bot },\unicode[STIX]{x1D6FF}\rangle$
is negative definite and hence
![]() $v^{2}<0$
. Since
$v^{2}<0$
. Since
![]() $-2m^{2}=(m\unicode[STIX]{x1D6FF})^{2}=v^{2}+w^{2}$
, one of the following holds:
$-2m^{2}=(m\unicode[STIX]{x1D6FF})^{2}=v^{2}+w^{2}$
, one of the following holds:
(i)
 $m=1$
,
$m=1$
,
 $v^{2}=-2$
and
$v^{2}=-2$
and
 $\unicode[STIX]{x1D708}(\unicode[STIX]{x1D6FF})=\pm v$
;
$\unicode[STIX]{x1D708}(\unicode[STIX]{x1D6FF})=\pm v$
;(ii)
 $m=2$
,
$m=2$
,
 $v^{2}\in \{-2,-4,-6\}$
,
$v^{2}\in \{-2,-4,-6\}$
,
 $\unicode[STIX]{x1D708}(\unicode[STIX]{x1D6FF})=\pm v$
, and
$\unicode[STIX]{x1D708}(\unicode[STIX]{x1D6FF})=\pm v$
, and
 $\operatorname{div}_{\unicode[STIX]{x1D6EC}}(v)$
is either
$\operatorname{div}_{\unicode[STIX]{x1D6EC}}(v)$
is either
 $2$
or
$2$
or
 $4$
;
$4$
;(iii)
 $m=4$
,
$m=4$
,
 $v^{2}\in \{-2,-4,-6,-8,\ldots ,-30\}$
,
$v^{2}\in \{-2,-4,-6,-8,\ldots ,-30\}$
,
 $\unicode[STIX]{x1D708}(\unicode[STIX]{x1D6FF})=\pm v$
, and
$\unicode[STIX]{x1D708}(\unicode[STIX]{x1D6FF})=\pm v$
, and
 $\operatorname{div}_{\unicode[STIX]{x1D6EC}}(v)=4$
;
$\operatorname{div}_{\unicode[STIX]{x1D6EC}}(v)=4$
;(iv)
 $m=4$
,
$m=4$
,
 $v^{2}\in \{-8,-16,-18,-24\}$
, and
$v^{2}\in \{-8,-16,-18,-24\}$
, and
 $v$
is not primitive.
$v$
is not primitive.
If (i) holds, then Item (1) holds.
Suppose that (ii) holds. If
![]() $v^{2}=-2$
, then Item (2) holds. If
$v^{2}=-2$
, then Item (2) holds. If
![]() $v^{2}=-6$
, then by a discriminant quadratic form computation (see (1.1.2) and Claim 1.1.1) we get that
$v^{2}=-6$
, then by a discriminant quadratic form computation (see (1.1.2) and Claim 1.1.1) we get that
![]() $\operatorname{div}_{\unicode[STIX]{x1D6EC}_{N}}(v)=2$
and hence Item (2) holds. If
$\operatorname{div}_{\unicode[STIX]{x1D6EC}_{N}}(v)=2$
and hence Item (2) holds. If
![]() $v^{2}=-4$
and
$v^{2}=-4$
and
![]() $\operatorname{div}_{\unicode[STIX]{x1D6EC}_{N}}(v)=4$
, then Item (4) holds. Thus, we are left with the case
$\operatorname{div}_{\unicode[STIX]{x1D6EC}_{N}}(v)=4$
, then Item (4) holds. Thus, we are left with the case
![]() $v^{2}=-4$
and
$v^{2}=-4$
and
![]() $\operatorname{div}_{\unicode[STIX]{x1D6EC}_{N}}(v)=2$
. Since
$\operatorname{div}_{\unicode[STIX]{x1D6EC}_{N}}(v)=2$
. Since
![]() $m=2$
, the divisibility of
$m=2$
, the divisibility of
![]() $w$
in
$w$
in
![]() $\unicode[STIX]{x1D6EC}^{\bot }$
is even and hence
$\unicode[STIX]{x1D6EC}^{\bot }$
is even and hence
![]() $[w/2]\in A_{\unicode[STIX]{x1D6EC}^{\bot }}$
. Since
$[w/2]\in A_{\unicode[STIX]{x1D6EC}^{\bot }}$
. Since
![]() $g([w/2])=[v/2]$
, where
$g([w/2])=[v/2]$
, where
![]() $g$
is the isomorphism in (3.2.5) and
$g$
is the isomorphism in (3.2.5) and
![]() $w^{2}=-4$
, it follows that
$w^{2}=-4$
, it follows that
![]() $[v/2]=\unicode[STIX]{x1D708}(\unicode[STIX]{x1D6FF})^{\ast }$
is an admissible decoration. Thus, Item (3) holds. This finishes the proof that if (ii) holds, then one of Items (2), (3), and (4) holds.
$[v/2]=\unicode[STIX]{x1D708}(\unicode[STIX]{x1D6FF})^{\ast }$
is an admissible decoration. Thus, Item (3) holds. This finishes the proof that if (ii) holds, then one of Items (2), (3), and (4) holds.
If (iii) holds, then, by looking at the discriminant quadratic form of
![]() $\unicode[STIX]{x1D6EC}_{N}$
, we get that
$\unicode[STIX]{x1D6EC}_{N}$
, we get that
![]() $v^{2}=-4a$
, where
$v^{2}=-4a$
, where
![]() $a\in \{1,3,5,7\}$
and
$a\in \{1,3,5,7\}$
and
![]() $a\equiv (N-2)\hspace{0.6em}({\rm mod}\hspace{0.2em}8)$
. Thus, Item (5) holds.
$a\equiv (N-2)\hspace{0.6em}({\rm mod}\hspace{0.2em}8)$
. Thus, Item (5) holds.
Lastly, suppose that (iv) holds. We will arrive at a contradiction. First, let us show that
![]() $w$
is primitive. If
$w$
is primitive. If
![]() $v^{2}=-18$
, this is clear because
$v^{2}=-18$
, this is clear because
![]() $w^{2}=-14$
. If
$w^{2}=-14$
. If
![]() $v^{2}\in \{-8,-16,-24\}$
, then
$v^{2}\in \{-8,-16,-24\}$
, then
![]() $v=2u$
, where
$v=2u$
, where
![]() $u\in \unicode[STIX]{x1D6EC}^{\bot }$
(because by assumption
$u\in \unicode[STIX]{x1D6EC}^{\bot }$
(because by assumption
![]() $v$
is not primitive) and, if
$v$
is not primitive) and, if
![]() $w=rz$
with
$w=rz$
with
![]() $r\geqslant 2$
and
$r\geqslant 2$
and
![]() $z\in \unicode[STIX]{x1D6EC}^{\bot }$
, then
$z\in \unicode[STIX]{x1D6EC}^{\bot }$
, then
![]() $r=2$
because
$r=2$
because
![]() $w^{2}\in \{-24,-16,-8\}$
. Then
$w^{2}\in \{-24,-16,-8\}$
. Then
![]() $2\unicode[STIX]{x1D6FF}=u+z$
, contradicting our hypothesis. This proves that
$2\unicode[STIX]{x1D6FF}=u+z$
, contradicting our hypothesis. This proves that
![]() $w$
is primitive. Since the divisibility of
$w$
is primitive. Since the divisibility of
![]() $w$
in
$w$
in
![]() $\unicode[STIX]{x1D6EC}^{\bot }$
is a multiple of
$\unicode[STIX]{x1D6EC}^{\bot }$
is a multiple of
![]() $4$
, it follows that
$4$
, it follows that
![]() $\operatorname{div}_{\unicode[STIX]{x1D6EC}^{\bot }}(w)=4$
and hence
$\operatorname{div}_{\unicode[STIX]{x1D6EC}^{\bot }}(w)=4$
and hence
![]() $N$
is odd. Thus,
$N$
is odd. Thus,
![]() $w^{2}/16=q_{\unicode[STIX]{x1D6EC}^{\bot }}(w^{\ast })\equiv -(N-2)/4\hspace{0.6em}({\rm mod}\hspace{0.2em}2\mathbb{Z})$
and hence
$w^{2}/16=q_{\unicode[STIX]{x1D6EC}^{\bot }}(w^{\ast })\equiv -(N-2)/4\hspace{0.6em}({\rm mod}\hspace{0.2em}2\mathbb{Z})$
and hence
![]() $w^{2}=-4a$
, where
$w^{2}=-4a$
, where
![]() $a$
is odd. This is a contradiction because
$a$
is odd. This is a contradiction because
![]() $w^{2}\in \{-24,-16,-14,-8\}$
.
$w^{2}\in \{-24,-16,-14,-8\}$
.
Now we finish the proof of the proposition. First, if any one of Items (1)–(5) holds,
![]() $\unicode[STIX]{x1D708}(\unicode[STIX]{x1D6FF})$
is a minimal norm vector.
$\unicode[STIX]{x1D708}(\unicode[STIX]{x1D6FF})$
is a minimal norm vector.
It remains to prove that if Item (2) holds with
![]() $v^{2}=-6$
, or if Item (5) holds, then Item (d) or Item (e) of the proposition holds. We will assume that
$v^{2}=-6$
, or if Item (5) holds, then Item (d) or Item (e) of the proposition holds. We will assume that
![]() $\unicode[STIX]{x1D6EC}^{\bot }\cong D_{26-N}$
if
$\unicode[STIX]{x1D6EC}^{\bot }\cong D_{26-N}$
if
![]() $\unicode[STIX]{x1D6EC}^{\bot }\cong (E_{8}\oplus D_{18-N})$
is analogous.
$\unicode[STIX]{x1D6EC}^{\bot }\cong (E_{8}\oplus D_{18-N})$
is analogous.
Suppose that Item (2) holds with
![]() $v^{2}=-6$
. Since
$v^{2}=-6$
. Since
![]() $q_{\unicode[STIX]{x1D6EC}_{N}}(v^{\ast })\equiv -3/2\hspace{0.6em}({\rm mod}\hspace{0.2em}2\mathbb{Z})$
, we have
$q_{\unicode[STIX]{x1D6EC}_{N}}(v^{\ast })\equiv -3/2\hspace{0.6em}({\rm mod}\hspace{0.2em}2\mathbb{Z})$
, we have
![]() $N\equiv 0\hspace{0.6em}({\rm mod}\hspace{0.2em}8)$
; it follows that
$N\equiv 0\hspace{0.6em}({\rm mod}\hspace{0.2em}8)$
; it follows that
![]() $\unicode[STIX]{x1D6EC}^{\bot }\cong D_{26-N}=D_{2+8h}$
for
$\unicode[STIX]{x1D6EC}^{\bot }\cong D_{26-N}=D_{2+8h}$
for
![]() $h\in \{0,1,2\}$
. The divisibility of
$h\in \{0,1,2\}$
. The divisibility of
![]() $w$
as an element of
$w$
as an element of
![]() $\unicode[STIX]{x1D6EC}^{\bot }$
is even because
$\unicode[STIX]{x1D6EC}^{\bot }$
is even because
![]() $m=2$
and hence it is equal to
$m=2$
and hence it is equal to
![]() $2$
(e.g. because
$2$
(e.g. because
![]() $w^{2}=-2$
). Now
$w^{2}=-2$
). Now
![]() $q_{\unicode[STIX]{x1D6EC}_{N}^{\bot }}(w^{\ast })\equiv -1/2\hspace{0.6em}({\rm mod}\hspace{0.2em}2\mathbb{Z})$
and hence
$q_{\unicode[STIX]{x1D6EC}_{N}^{\bot }}(w^{\ast })\equiv -1/2\hspace{0.6em}({\rm mod}\hspace{0.2em}2\mathbb{Z})$
and hence
![]() $w^{\ast }\in \{\unicode[STIX]{x1D701},\unicode[STIX]{x1D701}^{\prime }\}$
, where notation is as in Remark 3.2.7. Since
$w^{\ast }\in \{\unicode[STIX]{x1D701},\unicode[STIX]{x1D701}^{\prime }\}$
, where notation is as in Remark 3.2.7. Since
![]() $w^{2}=-2$
, it follows from Remark 3.2.7 that
$w^{2}=-2$
, it follows from Remark 3.2.7 that
![]() $\unicode[STIX]{x1D6EC}^{\bot }\cong D_{2}$
, i.e.
$\unicode[STIX]{x1D6EC}^{\bot }\cong D_{2}$
, i.e.
![]() $N=24$
.
$N=24$
.
Lastly, suppose that Item (5) holds. Then
![]() $w^{2}=-4(8-a)$
and
$w^{2}=-4(8-a)$
and
![]() $\operatorname{div}_{\unicode[STIX]{x1D6EC}^{\bot }}(w)=4$
. Thus,
$\operatorname{div}_{\unicode[STIX]{x1D6EC}^{\bot }}(w)=4$
. Thus,
![]() $q_{\unicode[STIX]{x1D6EC}^{\bot }}(w^{\ast })\equiv -(8-a)/4\hspace{0.6em}({\rm mod}\hspace{0.2em}2\mathbb{Z})$
and hence
$q_{\unicode[STIX]{x1D6EC}^{\bot }}(w^{\ast })\equiv -(8-a)/4\hspace{0.6em}({\rm mod}\hspace{0.2em}2\mathbb{Z})$
and hence
![]() $w^{\ast }\in \{\unicode[STIX]{x1D701},\unicode[STIX]{x1D701}^{\prime }\}$
, with notation as in Remark 3.2.7. On the other hand,
$w^{\ast }\in \{\unicode[STIX]{x1D701},\unicode[STIX]{x1D701}^{\prime }\}$
, with notation as in Remark 3.2.7. On the other hand,
![]() $\unicode[STIX]{x1D6EC}^{\bot }\cong D_{8-a+h}$
, where
$\unicode[STIX]{x1D6EC}^{\bot }\cong D_{8-a+h}$
, where
![]() $h\geqslant 0$
. Since
$h\geqslant 0$
. Since
![]() $w^{2}=-(8-a)$
, it follows from Remark 3.2.7 that
$w^{2}=-(8-a)$
, it follows from Remark 3.2.7 that
![]() $h=0$
, i.e.
$h=0$
, i.e.
![]() $N\geqslant 19$
.◻
$N\geqslant 19$
.◻
3.2.4 Borcherds’ automorphic forms for
 $\widetilde{O}^{+}(\unicode[STIX]{x1D6EC}_{N})$
$\widetilde{O}^{+}(\unicode[STIX]{x1D6EC}_{N})$
Theorem 3.2.11. Let
![]() $3\leqslant N\leqslant 25$
. Let
$3\leqslant N\leqslant 25$
. Let
![]() $\unicode[STIX]{x1D6EC}_{N}\subset \text{II}_{2,26}$
be a saturated embedding with orthogonal complement isomorphic to
$\unicode[STIX]{x1D6EC}_{N}\subset \text{II}_{2,26}$
be a saturated embedding with orthogonal complement isomorphic to
![]() $D_{26-N}$
. Let
$D_{26-N}$
. Let
![]() $\unicode[STIX]{x1D709}\in A_{\unicode[STIX]{x1D6EC}_{N}}$
be an admissible decoration of
$\unicode[STIX]{x1D709}\in A_{\unicode[STIX]{x1D6EC}_{N}}$
be an admissible decoration of
![]() $\unicode[STIX]{x1D6EC}_{N}$
(see Definition 3.2.8) and let
$\unicode[STIX]{x1D6EC}_{N}$
(see Definition 3.2.8) and let
![]() $\unicode[STIX]{x1D701},\unicode[STIX]{x1D701}^{\prime }$
be the remaining non-zero elements of
$\unicode[STIX]{x1D701},\unicode[STIX]{x1D701}^{\prime }$
be the remaining non-zero elements of
![]() $A_{\unicode[STIX]{x1D6EC}_{N}}$
. Let
$A_{\unicode[STIX]{x1D6EC}_{N}}$
. Let
![]() $\unicode[STIX]{x1D6F9}_{N}$
be the quasi-pull-back of Borcherds’ automorphic form
$\unicode[STIX]{x1D6F9}_{N}$
be the quasi-pull-back of Borcherds’ automorphic form
![]() $\unicode[STIX]{x1D6F7}_{12}$
. Then
$\unicode[STIX]{x1D6F7}_{12}$
. Then
![]() $\unicode[STIX]{x1D6F9}_{N}$
has weight
$\unicode[STIX]{x1D6F9}_{N}$
has weight
![]() $(12+(26-N)(25-N))$
and
$(12+(26-N)(25-N))$
and
where
![]() $\unicode[STIX]{x1D707}(N)$
is as in Table 1.
$\unicode[STIX]{x1D707}(N)$
is as in Table 1.
Theorem 3.2.12. Let
![]() $3\leqslant N\leqslant 17$
. Let
$3\leqslant N\leqslant 17$
. Let
![]() $\unicode[STIX]{x1D6EC}_{N}\subset \text{II}_{2,26}$
be a saturated embedding with orthogonal complement isomorphic to
$\unicode[STIX]{x1D6EC}_{N}\subset \text{II}_{2,26}$
be a saturated embedding with orthogonal complement isomorphic to
![]() $E_{8}\oplus D_{18-N}$
. Let
$E_{8}\oplus D_{18-N}$
. Let
![]() $\unicode[STIX]{x1D709}\in A_{\unicode[STIX]{x1D6EC}_{N}}$
be an admissible decoration of
$\unicode[STIX]{x1D709}\in A_{\unicode[STIX]{x1D6EC}_{N}}$
be an admissible decoration of
![]() $\unicode[STIX]{x1D6EC}_{N}$
(see Definition 3.2.8) and let
$\unicode[STIX]{x1D6EC}_{N}$
(see Definition 3.2.8) and let
![]() $\unicode[STIX]{x1D701},\unicode[STIX]{x1D701}^{\prime }$
be the remaining non-zero elements of
$\unicode[STIX]{x1D701},\unicode[STIX]{x1D701}^{\prime }$
be the remaining non-zero elements of
![]() $A_{\unicode[STIX]{x1D6EC}_{N}}$
. Let
$A_{\unicode[STIX]{x1D6EC}_{N}}$
. Let
![]() $\unicode[STIX]{x1D6EF}_{N}$
be the quasi-pull-back of Borcherds’ automorphic form
$\unicode[STIX]{x1D6EF}_{N}$
be the quasi-pull-back of Borcherds’ automorphic form
![]() $\unicode[STIX]{x1D6F7}_{12}$
. Then
$\unicode[STIX]{x1D6F7}_{12}$
. Then
![]() $\unicode[STIX]{x1D6EF}_{N}$
has weight
$\unicode[STIX]{x1D6EF}_{N}$
has weight
![]() $(132+(18-N)(17-N))$
and
$(132+(18-N)(17-N))$
and
Before proving the above results, we introduce some notation.
Notation 3.2.13 (Extended exceptional series
 $E_{r}$
).
$E_{r}$
).
It is standard (e.g. in the context of del Pezzo surfaces; cf. [Reference Friedman and MorganFM02]) to extend the
![]() $E_{r}$
series for
$E_{r}$
series for
![]() $r<6$
as follows. Let
$r<6$
as follows. Let
![]() $(1)\oplus (-1)^{r}$
be
$(1)\oplus (-1)^{r}$
be
![]() $\mathbb{Z}^{r+1}$
with the quadratic form
$\mathbb{Z}^{r+1}$
with the quadratic form
![]() $q(x,y_{1},\ldots ,y_{r}):=x^{2}-\sum _{i=1}^{r}y_{i}^{2}$
. Then
$q(x,y_{1},\ldots ,y_{r}):=x^{2}-\sum _{i=1}^{r}y_{i}^{2}$
. Then
![]() $E_{r}$
is the sublattice of
$E_{r}$
is the sublattice of
![]() $(1)\oplus (-1)^{r}$
defined by
$(1)\oplus (-1)^{r}$
defined by
Of course, this is the usual
![]() $E_{r}$
for
$E_{r}$
for
![]() $r\in \{6,7,8\}$
, and
$r\in \{6,7,8\}$
, and
![]() $E_{5}=D_{5}$
,
$E_{5}=D_{5}$
,
![]() $E_{4}=A_{4}$
, and
$E_{4}=A_{4}$
, and
![]() $E_{3}=A_{2}\oplus A_{1}$
. The lattice
$E_{3}=A_{2}\oplus A_{1}$
. The lattice
![]() $E_{2}$
has Gram matrix
$E_{2}$
has Gram matrix
![]() $\big(\!\begin{smallmatrix}-4 & 1\\ 1 & -2\end{smallmatrix}\!\big)$
and is no longer a root lattice. We record for later use the cardinalities of the sets of roots of the
$\big(\!\begin{smallmatrix}-4 & 1\\ 1 & -2\end{smallmatrix}\!\big)$
and is no longer a root lattice. We record for later use the cardinalities of the sets of roots of the
![]() $E_{r}$
lattices:
$E_{r}$
lattices:
Proof of Theorem 3.2.11.
The weight is equal to
![]() $12+|R(\unicode[STIX]{x1D6EC}_{N}^{\bot })|/2=12+(26-N)(25-N)$
by Recipe 3.2.2 (recall that
$12+|R(\unicode[STIX]{x1D6EC}_{N}^{\bot })|/2=12+(26-N)(25-N)$
by Recipe 3.2.2 (recall that
![]() $|R(D_{m})|=2m(m-1)$
). Next, choose minimal norm vectors
$|R(D_{m})|=2m(m-1)$
). Next, choose minimal norm vectors
![]() $v_{0},v_{\unicode[STIX]{x1D709}},v_{\unicode[STIX]{x1D701}},v_{\unicode[STIX]{x1D701}^{\prime }}\in \unicode[STIX]{x1D6EC}_{N}$
representing
$v_{0},v_{\unicode[STIX]{x1D709}},v_{\unicode[STIX]{x1D701}},v_{\unicode[STIX]{x1D701}^{\prime }}\in \unicode[STIX]{x1D6EC}_{N}$
representing
![]() $0,\unicode[STIX]{x1D709},\unicode[STIX]{x1D701},\unicode[STIX]{x1D701}^{\prime }\in A_{\unicode[STIX]{x1D6EC}_{N}}$
, respectively (i.e.
$0,\unicode[STIX]{x1D709},\unicode[STIX]{x1D701},\unicode[STIX]{x1D701}^{\prime }\in A_{\unicode[STIX]{x1D6EC}_{N}}$
, respectively (i.e.
![]() $v_{0}^{\ast }=0$
,
$v_{0}^{\ast }=0$
,
![]() $v_{\unicode[STIX]{x1D709}}^{\ast }=\unicode[STIX]{x1D709}$
, etc.). For
$v_{\unicode[STIX]{x1D709}}^{\ast }=\unicode[STIX]{x1D709}$
, etc.). For
![]() $\unicode[STIX]{x1D702}\in A_{\unicode[STIX]{x1D6EC}_{N}}$
, let
$\unicode[STIX]{x1D702}\in A_{\unicode[STIX]{x1D6EC}_{N}}$
, let
By Recipe 3.2.2, (3.2.3), and Proposition 3.2.10,
(Of course, by Proposition 3.2.10,
![]() $0=a_{\unicode[STIX]{x1D701}}(N)=a_{\unicode[STIX]{x1D701}^{\prime }}(N)$
if
$0=a_{\unicode[STIX]{x1D701}}(N)=a_{\unicode[STIX]{x1D701}^{\prime }}(N)$
if
![]() $N\leqslant 18$
and
$N\leqslant 18$
and
![]() $N\not \in \{3,4,11,12\}$
.) It is clear that
$N\not \in \{3,4,11,12\}$
.) It is clear that
![]() $\text{Sat}\langle v_{0},\unicode[STIX]{x1D6EC}_{N}^{\bot }\rangle =\langle v_{0},\unicode[STIX]{x1D6EC}_{N}^{\bot }\rangle$
and hence
$\text{Sat}\langle v_{0},\unicode[STIX]{x1D6EC}_{N}^{\bot }\rangle =\langle v_{0},\unicode[STIX]{x1D6EC}_{N}^{\bot }\rangle$
and hence
![]() $a_{0}(N)=1$
. In order to compute
$a_{0}(N)=1$
. In order to compute
![]() $a_{\unicode[STIX]{x1D709}}(N)$
,
$a_{\unicode[STIX]{x1D709}}(N)$
,
![]() $a_{\unicode[STIX]{x1D701}}(N)$
, and
$a_{\unicode[STIX]{x1D701}}(N)$
, and
![]() $a_{\unicode[STIX]{x1D701}^{\prime }}(N)$
, we will refer to the embedding
$a_{\unicode[STIX]{x1D701}^{\prime }}(N)$
, we will refer to the embedding
![]() $\unicode[STIX]{x1D6EC}_{N}\subset \text{II}_{2,26}$
of Remark 3.2.5. Thus, we let
$\unicode[STIX]{x1D6EC}_{N}\subset \text{II}_{2,26}$
of Remark 3.2.5. Thus, we let
![]() $(N-2)=8k+a$
, where
$(N-2)=8k+a$
, where
![]() $k\geqslant 0$
,
$k\geqslant 0$
,
![]() $a\in \{1,\ldots ,8\}$
, and we identify
$a\in \{1,\ldots ,8\}$
, and we identify
![]() $\unicode[STIX]{x1D6EC}_{N}$
with
$\unicode[STIX]{x1D6EC}_{N}$
with
![]() $\text{II}_{2,2+8k}\oplus D_{a}$
. Notice that
$\text{II}_{2,2+8k}\oplus D_{a}$
. Notice that
is an admissible decoration of
![]() $\unicode[STIX]{x1D6EC}_{N}$
with respect to the embedding of Remark 3.2.5. We choose the minimal norm vector
$\unicode[STIX]{x1D6EC}_{N}$
with respect to the embedding of Remark 3.2.5. We choose the minimal norm vector
![]() $v_{\unicode[STIX]{x1D709}}:=(0_{4+8k},(2,0,\ldots ,0),0_{26-N})$
(if
$v_{\unicode[STIX]{x1D709}}:=(0_{4+8k},(2,0,\ldots ,0),0_{26-N})$
(if
![]() $N=3$
, we let
$N=3$
, we let
![]() $v_{\unicode[STIX]{x1D709}}:=(2e,(2,0,\ldots ,0),0_{26-N})$
, where
$v_{\unicode[STIX]{x1D709}}:=(2e,(2,0,\ldots ,0),0_{26-N})$
, where
![]() $e\in \text{II}_{2,2+8k}$
is primitive and isotropic). Then the saturation of
$e\in \text{II}_{2,2+8k}$
is primitive and isotropic). Then the saturation of
![]() $\langle v_{\unicode[STIX]{x1D709}},\unicode[STIX]{x1D6EC}_{N}^{\bot }\rangle$
is generated by
$\langle v_{\unicode[STIX]{x1D709}},\unicode[STIX]{x1D6EC}_{N}^{\bot }\rangle$
is generated by
![]() $\langle v_{\unicode[STIX]{x1D709}},\unicode[STIX]{x1D6EC}_{N}^{\bot }\rangle$
and the vector
$\langle v_{\unicode[STIX]{x1D709}},\unicode[STIX]{x1D6EC}_{N}^{\bot }\rangle$
and the vector
![]() $u_{3}$
of Remark 3.2.5 (if
$u_{3}$
of Remark 3.2.5 (if
![]() $N=3$
, we add
$N=3$
, we add
![]() $(e,(1,0,\ldots ,0),(1,0,\ldots ,0))$
). It follows that
$(e,(1,0,\ldots ,0),(1,0,\ldots ,0))$
). It follows that
![]() $\text{Sat}\langle v_{\unicode[STIX]{x1D709}},\unicode[STIX]{x1D6EC}_{N}^{\bot }\rangle$
is isomorphic to
$\text{Sat}\langle v_{\unicode[STIX]{x1D709}},\unicode[STIX]{x1D6EC}_{N}^{\bot }\rangle$
is isomorphic to
![]() $D_{27-N}$
and hence
$D_{27-N}$
and hence
![]() $a_{\unicode[STIX]{x1D709}}(N)=2(26-N)$
. We choose the minimal norm vector
$a_{\unicode[STIX]{x1D709}}(N)=2(26-N)$
. We choose the minimal norm vector
 $$\begin{eqnarray}v_{\unicode[STIX]{x1D701}}:=\left\{\begin{array}{@{}ll@{}}(0_{4+8k},(\underbrace{1,\ldots ,1}_{a}),0_{26-N})\quad & \text{if}~N~\text{is even,}\\ (0_{4+8k},(\underbrace{2,\ldots ,2}_{a}),0_{26-N})\quad & \text{if}~N~\text{is odd.}\end{array}\right.\end{eqnarray}$$
$$\begin{eqnarray}v_{\unicode[STIX]{x1D701}}:=\left\{\begin{array}{@{}ll@{}}(0_{4+8k},(\underbrace{1,\ldots ,1}_{a}),0_{26-N})\quad & \text{if}~N~\text{is even,}\\ (0_{4+8k},(\underbrace{2,\ldots ,2}_{a}),0_{26-N})\quad & \text{if}~N~\text{is odd.}\end{array}\right.\end{eqnarray}$$
By Proposition 3.2.10,
![]() $a_{\unicode[STIX]{x1D701}}(N)=0$
, unless
$a_{\unicode[STIX]{x1D701}}(N)=0$
, unless
![]() $19\leqslant N\leqslant 25$
, or
$19\leqslant N\leqslant 25$
, or
![]() $a\in \{1,2\}$
and
$a\in \{1,2\}$
and
![]() $N\in \{3,4,11,12\}$
. Assume first that
$N\in \{3,4,11,12\}$
. Assume first that
![]() $19\leqslant N\leqslant 25$
. Then
$19\leqslant N\leqslant 25$
. Then
![]() $a\in \{1,\ldots ,7\}$
and
$a\in \{1,\ldots ,7\}$
and
![]() $\unicode[STIX]{x1D6EC}_{N}^{\bot }=D_{26-N}=D_{8-a}$
. The saturation of
$\unicode[STIX]{x1D6EC}_{N}^{\bot }=D_{26-N}=D_{8-a}$
. The saturation of
![]() $\langle v_{\unicode[STIX]{x1D701}},D_{8-a}\rangle$
is generated by
$\langle v_{\unicode[STIX]{x1D701}},D_{8-a}\rangle$
is generated by
![]() $\langle v_{\unicode[STIX]{x1D701}},D_{8-a}\rangle$
together with the vector
$\langle v_{\unicode[STIX]{x1D701}},D_{8-a}\rangle$
together with the vector
![]() $u_{1}$
of Remark 3.2.5; it follows easily that
$u_{1}$
of Remark 3.2.5; it follows easily that
![]() $\text{Sat}\langle v_{\unicode[STIX]{x1D701}},D_{8-a}\rangle \cong E_{9-a}$
. Noting that
$\text{Sat}\langle v_{\unicode[STIX]{x1D701}},D_{8-a}\rangle \cong E_{9-a}$
. Noting that
![]() $a=N-18$
, we get that
$a=N-18$
, we get that
![]() $\text{Sat}\langle v_{\unicode[STIX]{x1D701}},\unicode[STIX]{x1D6EC}_{N}^{\bot }\rangle \cong E_{27-N}$
. Looking at (3.2.9), we get that
$\text{Sat}\langle v_{\unicode[STIX]{x1D701}},\unicode[STIX]{x1D6EC}_{N}^{\bot }\rangle \cong E_{27-N}$
. Looking at (3.2.9), we get that
![]() $a_{\unicode[STIX]{x1D701}}(N)=\unicode[STIX]{x1D707}(N)$
.
$a_{\unicode[STIX]{x1D701}}(N)=\unicode[STIX]{x1D707}(N)$
.
Next, suppose that
![]() $a=1$
and hence
$a=1$
and hence
![]() $N\in \{3,11\}$
. The saturation of
$N\in \{3,11\}$
. The saturation of
![]() $\langle v_{\unicode[STIX]{x1D701}},D_{23-8k}\rangle$
is the overlattice
$\langle v_{\unicode[STIX]{x1D701}},D_{23-8k}\rangle$
is the overlattice
![]() $D_{(3-k)8}^{+}$
of
$D_{(3-k)8}^{+}$
of
![]() $D_{(3-k)8}$
obtained by adjoining the vector
$D_{(3-k)8}$
obtained by adjoining the vector
![]() $(1/2,\ldots ,1/2)$
. Then
$(1/2,\ldots ,1/2)$
. Then
![]() $a_{\unicode[STIX]{x1D701}}(N)=\unicode[STIX]{x1D707}(N)$
follows from the equality
$a_{\unicode[STIX]{x1D701}}(N)=\unicode[STIX]{x1D707}(N)$
follows from the equality
![]() $|R(D_{(3-k)8})^{+}|=|R(D_{(3-k)8})|=2\cdot (24-8k)\cdot (23-8k)$
, valid for
$|R(D_{(3-k)8})^{+}|=|R(D_{(3-k)8})|=2\cdot (24-8k)\cdot (23-8k)$
, valid for
![]() $k\in \{0,1\}$
.
$k\in \{0,1\}$
.
Next, suppose that
![]() $a=2$
and hence
$a=2$
and hence
![]() $N\in \{4,12\}$
. The saturation of
$N\in \{4,12\}$
. The saturation of
![]() $\langle v_{\unicode[STIX]{x1D701}},D_{22-8k}\rangle$
is generated by
$\langle v_{\unicode[STIX]{x1D701}},D_{22-8k}\rangle$
is generated by
![]() $\langle v_{\unicode[STIX]{x1D701}},D_{22-8k}\rangle$
together with the vector
$\langle v_{\unicode[STIX]{x1D701}},D_{22-8k}\rangle$
together with the vector
![]() $u_{1}$
of Remark 3.2.5; one verifies easily that the roots of
$u_{1}$
of Remark 3.2.5; one verifies easily that the roots of
![]() $\text{Sat}\langle v_{\unicode[STIX]{x1D701}},D_{22-8k}\rangle$
are exactly
$\text{Sat}\langle v_{\unicode[STIX]{x1D701}},D_{22-8k}\rangle$
are exactly
![]() $\pm (0_{4+8k},(1,1),0_{26-N})$
and hence
$\pm (0_{4+8k},(1,1),0_{26-N})$
and hence
![]() $a_{\unicode[STIX]{x1D701}}(N)=1=\unicode[STIX]{x1D707}(N)$
.
$a_{\unicode[STIX]{x1D701}}(N)=1=\unicode[STIX]{x1D707}(N)$
.
Lastly,
![]() $a_{\unicode[STIX]{x1D701}^{\prime }}(N)=a_{\unicode[STIX]{x1D701}}(N)$
because there is an automorphism of
$a_{\unicode[STIX]{x1D701}^{\prime }}(N)=a_{\unicode[STIX]{x1D701}}(N)$
because there is an automorphism of
![]() $\text{II}_{2,26}$
mapping
$\text{II}_{2,26}$
mapping
![]() $\unicode[STIX]{x1D6EC}_{N}$
to itself and exchanging
$\unicode[STIX]{x1D6EC}_{N}$
to itself and exchanging
![]() $\unicode[STIX]{x1D701}$
and
$\unicode[STIX]{x1D701}$
and
![]() $\unicode[STIX]{x1D701}^{\prime }$
.◻
$\unicode[STIX]{x1D701}^{\prime }$
.◻
3.2.5 Borcherds’ relations for divisors on
 $\mathscr{F}_{\unicode[STIX]{x1D6EC}_{N}}(\widetilde{O}^{+}(\unicode[STIX]{x1D6EC}_{N}))$
and on
$\mathscr{F}_{\unicode[STIX]{x1D6EC}_{N}}(\widetilde{O}^{+}(\unicode[STIX]{x1D6EC}_{N}))$
and on
 $\mathscr{F}(N)$
$\mathscr{F}(N)$
We let
![]() $\unicode[STIX]{x1D706}(\widetilde{O}^{+}(\unicode[STIX]{x1D6EC}_{N}))$
be the Hodge orbifold line bundle on
$\unicode[STIX]{x1D706}(\widetilde{O}^{+}(\unicode[STIX]{x1D6EC}_{N}))$
be the Hodge orbifold line bundle on
![]() $\mathscr{F}_{\unicode[STIX]{x1D6EC}_{N}}(\widetilde{O}^{+}(\unicode[STIX]{x1D6EC}_{N}))$
.
$\mathscr{F}_{\unicode[STIX]{x1D6EC}_{N}}(\widetilde{O}^{+}(\unicode[STIX]{x1D6EC}_{N}))$
.
Lemma 3.2.14. Let
![]() $3\leqslant N\leqslant 25$
. Let
$3\leqslant N\leqslant 25$
. Let
![]() $\unicode[STIX]{x1D709}$
be a decoration of
$\unicode[STIX]{x1D709}$
be a decoration of
![]() $\unicode[STIX]{x1D6EC}_{N}$
and let
$\unicode[STIX]{x1D6EC}_{N}$
and let
![]() $\unicode[STIX]{x1D701},\unicode[STIX]{x1D701}^{\prime }\in A_{\unicode[STIX]{x1D6EC}_{N}}$
be the remaining non-zero elements. Then in
$\unicode[STIX]{x1D701},\unicode[STIX]{x1D701}^{\prime }\in A_{\unicode[STIX]{x1D6EC}_{N}}$
be the remaining non-zero elements. Then in
![]() $\operatorname{Pic}(\mathscr{F}_{\unicode[STIX]{x1D6EC}_{N}}(\widetilde{O}^{+}(\unicode[STIX]{x1D6EC}_{N})))_{\mathbb{Q}}$
we have the relation
$\operatorname{Pic}(\mathscr{F}_{\unicode[STIX]{x1D6EC}_{N}}(\widetilde{O}^{+}(\unicode[STIX]{x1D6EC}_{N})))_{\mathbb{Q}}$
we have the relation
where
![]() $\unicode[STIX]{x1D716}(N)$
is equal to
$\unicode[STIX]{x1D716}(N)$
is equal to
![]() $1$
if
$1$
if
![]() $N$
is odd and is equal to
$N$
is odd and is equal to
![]() $2$
if
$2$
if
![]() $N$
is even, while
$N$
is even, while
![]() $\unicode[STIX]{x1D70F}(N)$
is equal to
$\unicode[STIX]{x1D70F}(N)$
is equal to
![]() $1$
if
$1$
if
![]() $N\equiv 3,4\hspace{0.6em}({\rm mod}\hspace{0.2em}8)$
and is equal to
$N\equiv 3,4\hspace{0.6em}({\rm mod}\hspace{0.2em}8)$
and is equal to
![]() $2$
otherwise.
$2$
otherwise.
Proof. Let
![]() $\unicode[STIX]{x1D6EC}_{N}\subset \text{II}_{2,26}$
be a saturated embedding such that the decoration
$\unicode[STIX]{x1D6EC}_{N}\subset \text{II}_{2,26}$
be a saturated embedding such that the decoration
![]() $\unicode[STIX]{x1D709}$
is admissible (see Definition 3.2.8). Let
$\unicode[STIX]{x1D709}$
is admissible (see Definition 3.2.8). Let
![]() $\unicode[STIX]{x1D6F9}_{N}$
be the automorphic form in Theorem 3.2.11. If
$\unicode[STIX]{x1D6F9}_{N}$
be the automorphic form in Theorem 3.2.11. If
![]() $k\in \mathbb{N}_{+}$
is sufficiently divisible, then
$k\in \mathbb{N}_{+}$
is sufficiently divisible, then
![]() $\unicode[STIX]{x1D6F9}_{N}^{k}$
descends to a regular section
$\unicode[STIX]{x1D6F9}_{N}^{k}$
descends to a regular section
![]() $\unicode[STIX]{x1D70E}_{N}(k)$
of
$\unicode[STIX]{x1D70E}_{N}(k)$
of
![]() $\unicode[STIX]{x1D706}(\widetilde{O}^{+}(\unicode[STIX]{x1D6EC}_{N}))^{k(12+(26-N)(25-N))}$
, whose zero divisor pulls back to
$\unicode[STIX]{x1D706}(\widetilde{O}^{+}(\unicode[STIX]{x1D6EC}_{N}))^{k(12+(26-N)(25-N))}$
, whose zero divisor pulls back to
![]() $k$
times the right-hand side of (3.2.6). Taking into account Claim 1.3.13, one gets that
$k$
times the right-hand side of (3.2.6). Taking into account Claim 1.3.13, one gets that
![]() $\operatorname{div}(\unicode[STIX]{x1D70E}_{N}(k))$
is equal to
$\operatorname{div}(\unicode[STIX]{x1D70E}_{N}(k))$
is equal to
![]() $k$
times the right-hand side of (3.2.11). Dividing by
$k$
times the right-hand side of (3.2.11). Dividing by
![]() $k$
, we get (3.2.11).◻
$k$
, we get (3.2.11).◻
Proposition 3.2.15 (= Theorem 3.1.1).
Let
![]() $3\leqslant N\leqslant 25$
. Then in
$3\leqslant N\leqslant 25$
. Then in
![]() $\operatorname{Pic}(\mathscr{F}(N))_{\mathbb{Q}}$
we have the relation
$\operatorname{Pic}(\mathscr{F}(N))_{\mathbb{Q}}$
we have the relation
where
![]() $\unicode[STIX]{x1D70F}(N)$
is as in Lemma 3.2.14. If
$\unicode[STIX]{x1D70F}(N)$
is as in Lemma 3.2.14. If
![]() $N\in \{6,14\}$
, we also have the relation
$N\in \{6,14\}$
, we also have the relation
Proof. If
![]() $N$
is odd,
$N$
is odd,
![]() $\mathscr{F}_{\unicode[STIX]{x1D6EC}_{N}}(\widetilde{O}^{+}(\unicode[STIX]{x1D6EC}_{N}))=\mathscr{F}(N)$
, and (3.2.12) is simply a rewriting of (3.2.11).
$\mathscr{F}_{\unicode[STIX]{x1D6EC}_{N}}(\widetilde{O}^{+}(\unicode[STIX]{x1D6EC}_{N}))=\mathscr{F}(N)$
, and (3.2.12) is simply a rewriting of (3.2.11).
Let
![]() $N$
be even and let
$N$
be even and let
![]() $\unicode[STIX]{x1D70C}:\mathscr{F}_{\unicode[STIX]{x1D6EC}_{N}}(\widetilde{O}^{+}(\unicode[STIX]{x1D6EC}_{N}))\rightarrow \mathscr{F}(N)$
be the natural double covering map corresponding to the choice of decoration of
$\unicode[STIX]{x1D70C}:\mathscr{F}_{\unicode[STIX]{x1D6EC}_{N}}(\widetilde{O}^{+}(\unicode[STIX]{x1D6EC}_{N}))\rightarrow \mathscr{F}(N)$
be the natural double covering map corresponding to the choice of decoration of
![]() $\unicode[STIX]{x1D6EC}_{N}$
given by
$\unicode[STIX]{x1D6EC}_{N}$
given by
![]() $\unicode[STIX]{x1D709}$
(the only one if
$\unicode[STIX]{x1D709}$
(the only one if
![]() $N\not \equiv 6\hspace{0.6em}({\rm mod}\hspace{0.2em}8)$
). Then (3.2.12) is given by the push-forward by
$N\not \equiv 6\hspace{0.6em}({\rm mod}\hspace{0.2em}8)$
). Then (3.2.12) is given by the push-forward by
![]() $\unicode[STIX]{x1D70C}$
of (3.2.11). More precisely,
$\unicode[STIX]{x1D70C}$
of (3.2.11). More precisely,
![]() $\unicode[STIX]{x1D70C}_{\ast }\unicode[STIX]{x1D706}(\widetilde{O}^{+}(\unicode[STIX]{x1D6EC}_{N}))=2\unicode[STIX]{x1D706}(N)$
because
$\unicode[STIX]{x1D70C}_{\ast }\unicode[STIX]{x1D706}(\widetilde{O}^{+}(\unicode[STIX]{x1D6EC}_{N}))=2\unicode[STIX]{x1D706}(N)$
because
![]() $\unicode[STIX]{x1D70C}^{\ast }\unicode[STIX]{x1D706}(N)=\unicode[STIX]{x1D706}(\widetilde{O}^{+}(\unicode[STIX]{x1D6EC}_{N}))$
and Corollary 1.3.12 gives formulae for
$\unicode[STIX]{x1D70C}^{\ast }\unicode[STIX]{x1D706}(N)=\unicode[STIX]{x1D706}(\widetilde{O}^{+}(\unicode[STIX]{x1D6EC}_{N}))$
and Corollary 1.3.12 gives formulae for
![]() $\unicode[STIX]{x1D70C}_{\ast }$
of the Heegner divisors in the right-hand side of (3.2.11).
$\unicode[STIX]{x1D70C}_{\ast }$
of the Heegner divisors in the right-hand side of (3.2.11).
Now assume that
![]() $N\in \{6,14\}$
and choose the decoration of
$N\in \{6,14\}$
and choose the decoration of
![]() $\unicode[STIX]{x1D6EC}_{N}$
to be
$\unicode[STIX]{x1D6EC}_{N}$
to be
![]() $\unicode[STIX]{x1D701}$
; then (3.2.13) is given by the push-forward by
$\unicode[STIX]{x1D701}$
; then (3.2.13) is given by the push-forward by
![]() $\unicode[STIX]{x1D70C}$
of (3.2.11).◻
$\unicode[STIX]{x1D70C}$
of (3.2.11).◻
Corollary 3.2.16. If
![]() $N\in \{6,14\}$
, then in
$N\in \{6,14\}$
, then in
![]() $\operatorname{Pic}(\mathscr{F}(N))_{\mathbb{Q}}$
we have the relation
$\operatorname{Pic}(\mathscr{F}(N))_{\mathbb{Q}}$
we have the relation
![]() $H_{h}(N)=H_{u}(N)$
.
$H_{h}(N)=H_{u}(N)$
.
Starting from Theorem 3.2.12, and arguing as in the proof of Lemma 3.2.14 and Proposition 3.2.15, one gets the following results.
Lemma 3.2.17. Let
![]() $3\leqslant N\leqslant 17$
. Let
$3\leqslant N\leqslant 17$
. Let
![]() $\unicode[STIX]{x1D709}$
be a decoration of
$\unicode[STIX]{x1D709}$
be a decoration of
![]() $\unicode[STIX]{x1D6EC}_{N}$
and let
$\unicode[STIX]{x1D6EC}_{N}$
and let
![]() $\unicode[STIX]{x1D701},\unicode[STIX]{x1D701}^{\prime }\in A_{\unicode[STIX]{x1D6EC}_{N}}$
be the remaining non-zero elements. Then in
$\unicode[STIX]{x1D701},\unicode[STIX]{x1D701}^{\prime }\in A_{\unicode[STIX]{x1D6EC}_{N}}$
be the remaining non-zero elements. Then in
![]() $\operatorname{Pic}(\mathscr{F}_{\unicode[STIX]{x1D6EC}_{N}}(\widetilde{O}^{+}(\unicode[STIX]{x1D6EC}_{N})))_{\mathbb{Q}}$
we have the relation
$\operatorname{Pic}(\mathscr{F}_{\unicode[STIX]{x1D6EC}_{N}}(\widetilde{O}^{+}(\unicode[STIX]{x1D6EC}_{N})))_{\mathbb{Q}}$
we have the relation
where
![]() $\unicode[STIX]{x1D716}(N)$
and
$\unicode[STIX]{x1D716}(N)$
and
![]() $\unicode[STIX]{x1D70F}(N)$
are as in Lemma 3.2.14.
$\unicode[STIX]{x1D70F}(N)$
are as in Lemma 3.2.14.
Proposition 3.2.18 (= Theorem 3.1.2).
Let
![]() $3\leqslant N\leqslant 17$
. Then in
$3\leqslant N\leqslant 17$
. Then in
![]() $\operatorname{Pic}(\mathscr{F}(N))_{\mathbb{Q}}$
we have the relation
$\operatorname{Pic}(\mathscr{F}(N))_{\mathbb{Q}}$
we have the relation
where
![]() $\unicode[STIX]{x1D70F}(N)$
is as in Lemma 3.2.14.
$\unicode[STIX]{x1D70F}(N)$
is as in Lemma 3.2.14.
4 The boundary divisor
 $\unicode[STIX]{x1D6E5}(\unicode[STIX]{x1D6EC}_{N},\unicode[STIX]{x1D709}_{N})$
$\unicode[STIX]{x1D6E5}(\unicode[STIX]{x1D6EC}_{N},\unicode[STIX]{x1D709}_{N})$
4.1 Statement of results
In § 2, we have identified
![]() $\mathscr{F}(19)$
with the period space of quartic
$\mathscr{F}(19)$
with the period space of quartic
![]() $K3$
surfaces. Let
$K3$
surfaces. Let
![]() $\mathfrak{M}(19)$
be the GIT moduli space of quartic surfaces in
$\mathfrak{M}(19)$
be the GIT moduli space of quartic surfaces in
![]() $\mathbb{P}^{3}$
; then the natural period map
$\mathbb{P}^{3}$
; then the natural period map
is birational by the global Torelli theorem for
![]() $K3$
surfaces (by Piatetsky-Shapiro and Shafarevich). The projective variety
$K3$
surfaces (by Piatetsky-Shapiro and Shafarevich). The projective variety
![]() $\mathfrak{M}(19)=|\mathscr{O}_{\mathbb{P}^{3}}(4)|/\!\!/\text{PGL}(4)$
has Picard group (tensored with
$\mathfrak{M}(19)=|\mathscr{O}_{\mathbb{P}^{3}}(4)|/\!\!/\text{PGL}(4)$
has Picard group (tensored with
![]() $\mathbb{Q}$
) of rank
$\mathbb{Q}$
) of rank
![]() $1$
; let
$1$
; let
![]() $L(19)$
be the generator of
$L(19)$
be the generator of
![]() $\operatorname{Pic}(\mathfrak{M}(19))_{\mathbb{Q}}$
induced by the hyperplane line bundle on
$\operatorname{Pic}(\mathfrak{M}(19))_{\mathbb{Q}}$
induced by the hyperplane line bundle on
![]() $|\mathscr{O}_{\mathbb{P}^{3}}(4)|$
. In the present section, we will prove that
$|\mathscr{O}_{\mathbb{P}^{3}}(4)|$
. In the present section, we will prove that
Similar arguments also give that
These are the computations that motivate our choice of boundary divisor for
![]() $\mathscr{F}(N)$
(for any
$\mathscr{F}(N)$
(for any
![]() $N$
).
$N$
).
Remark 4.1.1. Let
![]() $\mathfrak{M}(20)$
be the GIT moduli space of double EPW sextics, let
$\mathfrak{M}(20)$
be the GIT moduli space of double EPW sextics, let
![]() $\unicode[STIX]{x1D6FF}$
be the duality involution of
$\unicode[STIX]{x1D6FF}$
be the duality involution of
![]() $\mathfrak{M}(20)$
, and let
$\mathfrak{M}(20)$
, and let
![]() $\mathfrak{p}_{20}:\mathfrak{M}(20)/\langle \unicode[STIX]{x1D6FF}\rangle {\dashrightarrow}\mathscr{F}(20)^{\ast }$
be the period map; see (2.3.4). Let
$\mathfrak{p}_{20}:\mathfrak{M}(20)/\langle \unicode[STIX]{x1D6FF}\rangle {\dashrightarrow}\mathscr{F}(20)^{\ast }$
be the period map; see (2.3.4). Let
![]() $L(20)$
be an ample generator of the Picard group of
$L(20)$
be an ample generator of the Picard group of
![]() $\mathfrak{M}(20)/\langle \unicode[STIX]{x1D6FF}\rangle$
. We expect that a result similar to (4.1.2) holds for
$\mathfrak{M}(20)/\langle \unicode[STIX]{x1D6FF}\rangle$
. We expect that a result similar to (4.1.2) holds for
![]() $(\mathfrak{p}_{20}^{-1})^{\ast }L(20)|_{\mathscr{F}(20)}$
, namely that it is a positive multiple of
$(\mathfrak{p}_{20}^{-1})^{\ast }L(20)|_{\mathscr{F}(20)}$
, namely that it is a positive multiple of
![]() $\unicode[STIX]{x1D706}(20)+\unicode[STIX]{x1D6E5}(20)$
.
$\unicode[STIX]{x1D706}(20)+\unicode[STIX]{x1D6E5}(20)$
.
An important result follows from (4.1.2). In order to state it, we introduce some notation. For
![]() $\unicode[STIX]{x1D6FD}\in [0,1]\cap \mathbb{Q}$
, let
$\unicode[STIX]{x1D6FD}\in [0,1]\cap \mathbb{Q}$
, let
(As usual,
![]() $H^{0}(\mathscr{F}(N),m(\unicode[STIX]{x1D706}(N)+\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6E5}(N)))=0$
unless
$H^{0}(\mathscr{F}(N),m(\unicode[STIX]{x1D706}(N)+\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6E5}(N)))=0$
unless
![]() $m(\unicode[STIX]{x1D706}(N)+\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6E5}(N))$
is an integral Cartier divisor.) Thus,
$m(\unicode[STIX]{x1D706}(N)+\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6E5}(N))$
is an integral Cartier divisor.) Thus,
![]() $\mathscr{R}(N,0)$
is the finitely generated algebra of automorphic forms and hence
$\mathscr{R}(N,0)$
is the finitely generated algebra of automorphic forms and hence
![]() $\mathscr{F}(N,0)$
is the Baily–Borel compactification
$\mathscr{F}(N,0)$
is the Baily–Borel compactification
![]() $\mathscr{F}(N)^{\ast }$
. If
$\mathscr{F}(N)^{\ast }$
. If
![]() $3\leqslant N\leqslant 10$
, then, by (3.1.3),
$3\leqslant N\leqslant 10$
, then, by (3.1.3),
![]() $\unicode[STIX]{x1D6E5}(N)$
is a positive multiple of
$\unicode[STIX]{x1D6E5}(N)$
is a positive multiple of
![]() $\unicode[STIX]{x1D706}(N)$
and hence in this range
$\unicode[STIX]{x1D706}(N)$
and hence in this range
![]() $\mathscr{F}(N,\unicode[STIX]{x1D6FD})=\mathscr{F}(N)^{\ast }$
for all
$\mathscr{F}(N,\unicode[STIX]{x1D6FD})=\mathscr{F}(N)^{\ast }$
for all
![]() $\unicode[STIX]{x1D6FD}\in [0,1]\cap \mathbb{Q}$
. On the other hand, we will see that if
$\unicode[STIX]{x1D6FD}\in [0,1]\cap \mathbb{Q}$
. On the other hand, we will see that if
![]() $N\geqslant 11$
, then
$N\geqslant 11$
, then
![]() $\mathscr{F}(N,\unicode[STIX]{x1D6FD})$
undergoes birational modifications as
$\mathscr{F}(N,\unicode[STIX]{x1D6FD})$
undergoes birational modifications as
![]() $\unicode[STIX]{x1D6FD}$
moves in
$\unicode[STIX]{x1D6FD}$
moves in
![]() $[0,1]\cap \mathbb{Q}$
.
$[0,1]\cap \mathbb{Q}$
.
Now let
![]() $N\in \{18,19\}$
and let
$N\in \{18,19\}$
and let
![]() $\unicode[STIX]{x1D70C}(N)$
be equal to
$\unicode[STIX]{x1D70C}(N)$
be equal to
![]() $1$
if
$1$
if
![]() $N=19$
, and equal to
$N=19$
, and equal to
![]() $2$
if
$2$
if
![]() $N=18$
. Let
$N=18$
. Let
![]() $m\geqslant 0$
and let
$m\geqslant 0$
and let
be the map induced by (4.1.2) if
![]() $N=19$
and by (4.1.3) if
$N=19$
and by (4.1.3) if
![]() $N=18$
. The following result should be compared to Theorem 8.6 of [Reference LooijengaLoo03b].
$N=18$
. The following result should be compared to Theorem 8.6 of [Reference LooijengaLoo03b].
Proposition 4.1.2. Let
![]() $N\in \{18,19\}$
. Then the map in (4.1.5) is an isomorphism for all
$N\in \{18,19\}$
. Then the map in (4.1.5) is an isomorphism for all
![]() $m\in \mathbb{Z}$
.
$m\in \mathbb{Z}$
.
Proof. The map is clearly injective. In order to prove surjectivity, it suffices to show that
![]() $\mathfrak{p}_{N}$
contracts no divisor. In order to prove this, let
$\mathfrak{p}_{N}$
contracts no divisor. In order to prove this, let
![]() $\mathscr{U}(19)\subset |\mathscr{O}_{\mathbb{P}^{3}}(4)|$
and
$\mathscr{U}(19)\subset |\mathscr{O}_{\mathbb{P}^{3}}(4)|$
and
![]() $\mathscr{U}(18)\subset |\mathscr{O}_{\mathbb{P}^{\times }\mathbb{P}^{1}}(4,4)|$
be the open subsets of Definition 2.1.5 and of Definition 2.2.3, respectively. The period maps
$\mathscr{U}(18)\subset |\mathscr{O}_{\mathbb{P}^{\times }\mathbb{P}^{1}}(4,4)|$
be the open subsets of Definition 2.1.5 and of Definition 2.2.3, respectively. The period maps
![]() $\mathfrak{p}_{N}$
, for
$\mathfrak{p}_{N}$
, for
![]() $N\in \{18,19\}$
, define isomorphisms between
$N\in \{18,19\}$
, define isomorphisms between
![]() $\mathscr{U}(N)/\!\!/G(N)$
(where
$\mathscr{U}(N)/\!\!/G(N)$
(where
![]() $G(19)=\text{PGL}(4)$
and
$G(19)=\text{PGL}(4)$
and
![]() $G(18)=\text{Aut}(\mathbb{P}^{1}\times \mathbb{P}^{1})$
) and the complement of the support of
$G(18)=\text{Aut}(\mathbb{P}^{1}\times \mathbb{P}^{1})$
) and the complement of the support of
![]() $\unicode[STIX]{x1D6E5}(N)$
; see (2.1.4) and (2.2.2). On the other hand, the complement of
$\unicode[STIX]{x1D6E5}(N)$
; see (2.1.4) and (2.2.2). On the other hand, the complement of
![]() $\mathscr{U}(N)/\!\!/G(N)$
in
$\mathscr{U}(N)/\!\!/G(N)$
in
![]() $\mathfrak{M}(N)$
has codimension greater than
$\mathfrak{M}(N)$
has codimension greater than
![]() $1$
. Thus,
$1$
. Thus,
![]() $\mathfrak{p}_{N}$
contracts no divisor, as claimed.◻
$\mathfrak{p}_{N}$
contracts no divisor, as claimed.◻
By Proposition 4.1.2, there is an isomorphism
Thus, for
![]() $N\in \{18,19\}$
, the schemes
$N\in \{18,19\}$
, the schemes
![]() $\mathscr{F}(N,\unicode[STIX]{x1D6FD})$
interpolate between the Baily–Borel compactification
$\mathscr{F}(N,\unicode[STIX]{x1D6FD})$
interpolate between the Baily–Borel compactification
![]() $\mathscr{F}(N)^{\ast }$
and the GIT moduli space
$\mathscr{F}(N)^{\ast }$
and the GIT moduli space
![]() $\mathfrak{M}(N)$
.
$\mathfrak{M}(N)$
.
4.2 Families of
 $K3$
surfaces
$K3$
surfaces
4.2.1 Hodge bundle on families of
 $K3$
surfaces
$K3$
surfaces
Let
![]() $f:\mathscr{X}\rightarrow B$
be a family of
$f:\mathscr{X}\rightarrow B$
be a family of
![]() $K3$
surfaces. We let
$K3$
surfaces. We let
![]() $\mathscr{L}_{B}:=f_{\ast }\unicode[STIX]{x1D714}_{\mathscr{X}/B}$
; this is the Hodge bundle on
$\mathscr{L}_{B}:=f_{\ast }\unicode[STIX]{x1D714}_{\mathscr{X}/B}$
; this is the Hodge bundle on
![]() $B$
(the notation is imprecise because the Hodge bundle is determined by
$B$
(the notation is imprecise because the Hodge bundle is determined by
![]() $f:\mathscr{X}\rightarrow B$
, not by
$f:\mathscr{X}\rightarrow B$
, not by
![]() $B$
alone). We let
$B$
alone). We let
![]() $\unicode[STIX]{x1D706}_{B}:=c_{1}(\mathscr{L}_{B})\in \operatorname{CH}^{1}(B)$
. Suppose that
$\unicode[STIX]{x1D706}_{B}:=c_{1}(\mathscr{L}_{B})\in \operatorname{CH}^{1}(B)$
. Suppose that
![]() $\mathscr{X}$
is a family of polarized quartic
$\mathscr{X}$
is a family of polarized quartic
![]() $K3$
surfaces and let
$K3$
surfaces and let
![]() $\unicode[STIX]{x1D707}:B\rightarrow \mathscr{F}(19)$
be the period map: then
$\unicode[STIX]{x1D707}:B\rightarrow \mathscr{F}(19)$
be the period map: then
Suppose that
![]() $\mathscr{X}$
and
$\mathscr{X}$
and
![]() $B$
are smooth. The exact sequence
$B$
are smooth. The exact sequence
and the isomorphism
![]() $f^{\ast }\mathscr{L}_{B}\cong \bigwedge ^{2}\unicode[STIX]{x1D6FA}_{\mathscr{X}/B}$
give the formula
$f^{\ast }\mathscr{L}_{B}\cong \bigwedge ^{2}\unicode[STIX]{x1D6FA}_{\mathscr{X}/B}$
give the formula
4.2.2 Families of quartic surfaces
Let
![]() $F,G\in \mathbb{C}[x_{0},\ldots ,x_{3}]_{4}$
be linearly independent and such that
$F,G\in \mathbb{C}[x_{0},\ldots ,x_{3}]_{4}$
be linearly independent and such that
![]() $\unicode[STIX]{x1D6E4}_{1}:=\langle \operatorname{Div}(F),\operatorname{Div}(G)\rangle$
is a Lefschetz pencil of quartic surfaces. Let
$\unicode[STIX]{x1D6E4}_{1}:=\langle \operatorname{Div}(F),\operatorname{Div}(G)\rangle$
is a Lefschetz pencil of quartic surfaces. Let
The projection onto the second factor is a family
![]() $f_{1}:\mathscr{X}_{1}\rightarrow \unicode[STIX]{x1D6E4}_{1}$
of polarized quartic surfaces.
$f_{1}:\mathscr{X}_{1}\rightarrow \unicode[STIX]{x1D6E4}_{1}$
of polarized quartic surfaces.
Now let us we define a one-parameter family of hyperelliptic
![]() $K3$
surfaces. Let
$K3$
surfaces. Let
![]() $\unicode[STIX]{x1D6E4}_{2}:=\mathbb{P}^{1}$
. Let
$\unicode[STIX]{x1D6E4}_{2}:=\mathbb{P}^{1}$
. Let
![]() $D\in |\mathscr{O}_{\unicode[STIX]{x1D6E4}_{2}}(2)\boxtimes \mathscr{O}_{\mathbb{P}^{1}\times \mathbb{P}^{1}}(4,4)|$
be generic and let
$D\in |\mathscr{O}_{\unicode[STIX]{x1D6E4}_{2}}(2)\boxtimes \mathscr{O}_{\mathbb{P}^{1}\times \mathbb{P}^{1}}(4,4)|$
be generic and let
![]() $\unicode[STIX]{x1D70C}:\mathscr{X}_{2}\rightarrow \unicode[STIX]{x1D6E4}_{2}\times (\mathbb{P}^{1})^{2}$
be the double cover branched over
$\unicode[STIX]{x1D70C}:\mathscr{X}_{2}\rightarrow \unicode[STIX]{x1D6E4}_{2}\times (\mathbb{P}^{1})^{2}$
be the double cover branched over
![]() $D$
. Let
$D$
. Let
![]() $f_{2}:\mathscr{X}_{2}\rightarrow \unicode[STIX]{x1D6E4}_{2}$
be the composition of the double cover map
$f_{2}:\mathscr{X}_{2}\rightarrow \unicode[STIX]{x1D6E4}_{2}$
be the composition of the double cover map
![]() $\unicode[STIX]{x1D70C}$
and the projection
$\unicode[STIX]{x1D70C}$
and the projection
![]() $\unicode[STIX]{x1D6E4}_{2}\times (\mathbb{P}^{1})^{2}\rightarrow \unicode[STIX]{x1D6E4}_{2}$
. Let
$\unicode[STIX]{x1D6E4}_{2}\times (\mathbb{P}^{1})^{2}\rightarrow \unicode[STIX]{x1D6E4}_{2}$
. Let
![]() $t\in \unicode[STIX]{x1D6E4}_{2}$
; then
$t\in \unicode[STIX]{x1D6E4}_{2}$
; then
![]() $X_{2,t}:=f_{2}^{-1}(t)$
is the double cover of
$X_{2,t}:=f_{2}^{-1}(t)$
is the double cover of
![]() $\mathbb{P}^{1}\times \mathbb{P}^{1}$
branched over the
$\mathbb{P}^{1}\times \mathbb{P}^{1}$
branched over the
![]() $(4,4)$
-curve
$(4,4)$
-curve
![]() $D_{t}:=D|_{\{t\}\times (\mathbb{P}^{1})^{2}}$
. Thus,
$D_{t}:=D|_{\{t\}\times (\mathbb{P}^{1})^{2}}$
. Thus,
![]() $X_{2,t}$
is a
$X_{2,t}$
is a
![]() $K3$
surface,
$K3$
surface,
![]() $\unicode[STIX]{x1D70C}^{\ast }(\mathscr{O}_{\mathbb{P}^{1}}(1)\boxtimes \mathscr{O}_{\mathbb{P}^{1}}(1))$
restricts to a polarization of
$\unicode[STIX]{x1D70C}^{\ast }(\mathscr{O}_{\mathbb{P}^{1}}(1)\boxtimes \mathscr{O}_{\mathbb{P}^{1}}(1))$
restricts to a polarization of
![]() $X_{2,t}$
, and with this polarization
$X_{2,t}$
, and with this polarization
![]() $X_{2,t}$
is a quartic hyperelliptic
$X_{2,t}$
is a quartic hyperelliptic
![]() $K3$
surface. From here on we assume that the pencil of branch curves
$K3$
surface. From here on we assume that the pencil of branch curves
![]() $D_{t}$
, for
$D_{t}$
, for
![]() $t\in \unicode[STIX]{x1D6E4}_{2}$
, is a Lefschetz pencil.
$t\in \unicode[STIX]{x1D6E4}_{2}$
, is a Lefschetz pencil.
Next, we define a one-parameter family of unigonal
![]() $K3$
surfaces. Let
$K3$
surfaces. Let
![]() $Y:=\mathbb{P}(\mathscr{O}_{\mathbb{P}^{2}}(4)\oplus \mathscr{O}_{\mathbb{P}^{2}})$
. Let
$Y:=\mathbb{P}(\mathscr{O}_{\mathbb{P}^{2}}(4)\oplus \mathscr{O}_{\mathbb{P}^{2}})$
. Let
![]() $\unicode[STIX]{x1D711}:Y\rightarrow \mathbb{P}^{2}$
be the structure map and
$\unicode[STIX]{x1D711}:Y\rightarrow \mathbb{P}^{2}$
be the structure map and
![]() $F:=\unicode[STIX]{x1D711}^{-1}(\text{line})$
. Let
$F:=\unicode[STIX]{x1D711}^{-1}(\text{line})$
. Let
![]() $A:=\mathbb{P}(\mathscr{O}_{\mathbb{P}^{2}}(4))\subset Y$
. Adjunction on
$A:=\mathbb{P}(\mathscr{O}_{\mathbb{P}^{2}}(4))\subset Y$
. Adjunction on
![]() $F\cong \mathbb{F}_{4}$
gives that
$F\cong \mathbb{F}_{4}$
gives that
Let
![]() $B\in |3A+12F|$
be generic; in particular, it is smooth and it does not intersect
$B\in |3A+12F|$
be generic; in particular, it is smooth and it does not intersect
![]() $A$
. Let
$A$
. Let
![]() $\unicode[STIX]{x1D70B}:Z\rightarrow Y$
be the double cover branched over
$\unicode[STIX]{x1D70B}:Z\rightarrow Y$
be the double cover branched over
![]() $A+B$
. If
$A+B$
. If
![]() $F$
is as above and generic, then
$F$
is as above and generic, then
![]() $\unicode[STIX]{x1D70B}^{-1}F$
is a smooth unigonal
$\unicode[STIX]{x1D70B}^{-1}F$
is a smooth unigonal
![]() $K3$
surface. We get a family of such
$K3$
surface. We get a family of such
![]() $K3$
surfaces by choosing a generic
$K3$
surfaces by choosing a generic
![]() $\mathscr{X}_{3}\in |\mathscr{O}_{Z}(\unicode[STIX]{x1D70B}^{\ast }F)\boxtimes \mathscr{O}_{\unicode[STIX]{x1D6E4}_{3}}(1)|$
, where
$\mathscr{X}_{3}\in |\mathscr{O}_{Z}(\unicode[STIX]{x1D70B}^{\ast }F)\boxtimes \mathscr{O}_{\unicode[STIX]{x1D6E4}_{3}}(1)|$
, where
![]() $\unicode[STIX]{x1D6E4}_{3}=\mathbb{P}^{1}$
. In fact, let
$\unicode[STIX]{x1D6E4}_{3}=\mathbb{P}^{1}$
. In fact, let
![]() $f_{3}:\mathscr{X}_{3}\rightarrow \unicode[STIX]{x1D6E4}_{3}$
be the restriction of projection and let
$f_{3}:\mathscr{X}_{3}\rightarrow \unicode[STIX]{x1D6E4}_{3}$
be the restriction of projection and let
![]() $t\in \unicode[STIX]{x1D6E4}_{3}$
. The surface
$t\in \unicode[STIX]{x1D6E4}_{3}$
. The surface
![]() $X_{3,t}:=f_{3}^{-1}(t)$
is equal to
$X_{3,t}:=f_{3}^{-1}(t)$
is equal to
![]() $\unicode[STIX]{x1D70B}^{-1}(\unicode[STIX]{x1D711}^{-1}(L_{t}))$
, where
$\unicode[STIX]{x1D70B}^{-1}(\unicode[STIX]{x1D711}^{-1}(L_{t}))$
, where
![]() $L_{t}\subset \mathbb{P}^{2}$
is a line (as
$L_{t}\subset \mathbb{P}^{2}$
is a line (as
![]() $t$
moves in
$t$
moves in
![]() $\unicode[STIX]{x1D6E4}_{3}$
, the line
$\unicode[STIX]{x1D6E4}_{3}$
, the line
![]() $L_{t}$
moves in a pencil) and
$L_{t}$
moves in a pencil) and
![]() $\unicode[STIX]{x1D711}^{-1}(L_{t})$
is isomorphic to
$\unicode[STIX]{x1D711}^{-1}(L_{t})$
is isomorphic to
![]() $\mathbb{F}_{4}$
. The restriction
$\mathbb{F}_{4}$
. The restriction
![]() $\unicode[STIX]{x1D70B}_{t}:X_{3,t}\rightarrow \unicode[STIX]{x1D711}^{-1}(L_{t})$
is a double cover and one checks easily that
$\unicode[STIX]{x1D70B}_{t}:X_{3,t}\rightarrow \unicode[STIX]{x1D711}^{-1}(L_{t})$
is a double cover and one checks easily that
![]() $X_{3,t}:=f_{3}^{-1}(t)$
is a
$X_{3,t}:=f_{3}^{-1}(t)$
is a
![]() $K3$
surface. Let
$K3$
surface. Let
![]() $A_{t}$
be the negative section of
$A_{t}$
be the negative section of
![]() $\unicode[STIX]{x1D711}^{-1}(L_{t})\cong \mathbb{F}_{4}$
; then
$\unicode[STIX]{x1D711}^{-1}(L_{t})\cong \mathbb{F}_{4}$
; then
![]() $\unicode[STIX]{x1D70B}_{t}^{\ast }A_{t}=2R_{t}$
, where
$\unicode[STIX]{x1D70B}_{t}^{\ast }A_{t}=2R_{t}$
, where
![]() $R_{t}$
is a (smooth) rational curve. Let
$R_{t}$
is a (smooth) rational curve. Let
![]() $E_{t}:=\unicode[STIX]{x1D70B}_{t}^{\ast }F_{t}$
, where
$E_{t}:=\unicode[STIX]{x1D70B}_{t}^{\ast }F_{t}$
, where
![]() $F_{t}$
is a fiber of the fibration
$F_{t}$
is a fiber of the fibration
![]() $\unicode[STIX]{x1D711}^{-1}(L_{t})\cong \mathbb{F}_{4}\rightarrow L_{t}$
. Then
$\unicode[STIX]{x1D711}^{-1}(L_{t})\cong \mathbb{F}_{4}\rightarrow L_{t}$
. Then
![]() $R_{t}+3E_{t}$
is a polarization of degree
$R_{t}+3E_{t}$
is a polarization of degree
![]() $4$
of
$4$
of
![]() $X_{3,t}$
and
$X_{3,t}$
and
![]() $(X_{3,t},R_{t}+3E_{t})$
is unigonal.
$(X_{3,t},R_{t}+3E_{t})$
is unigonal.
For
![]() $i\in \{1,2,3\}$
, we have period maps
$i\in \{1,2,3\}$
, we have period maps
Table 2. Intersection numbers of families of quartic
![]() $K3$
surfaces.
$K3$
surfaces.
Proposition 4.2.1. The intersection formulae of Table 2 hold.
Proof. First of all, notice that
Next, one computes
![]() $\deg \unicode[STIX]{x1D706}_{\unicode[STIX]{x1D6E4}_{i}}$
by applying (4.2.2). The intersection number
$\deg \unicode[STIX]{x1D706}_{\unicode[STIX]{x1D6E4}_{i}}$
by applying (4.2.2). The intersection number
![]() $\unicode[STIX]{x1D707}_{i,\ast }\unicode[STIX]{x1D6E4}_{i}\cdot H_{n}(19)$
is equal to the number, call it
$\unicode[STIX]{x1D707}_{i,\ast }\unicode[STIX]{x1D6E4}_{i}\cdot H_{n}(19)$
is equal to the number, call it
![]() $\unicode[STIX]{x1D6FF}(\unicode[STIX]{x1D6E4}_{i})$
, of singular fibers of
$\unicode[STIX]{x1D6FF}(\unicode[STIX]{x1D6E4}_{i})$
, of singular fibers of
![]() $f_{i}$
because
$f_{i}$
because
![]() $f_{i}$
is a Lefschetz fibration. The formula that gives
$f_{i}$
is a Lefschetz fibration. The formula that gives
![]() $\unicode[STIX]{x1D6FF}(\unicode[STIX]{x1D6E4}_{i})$
is the following:
$\unicode[STIX]{x1D6FF}(\unicode[STIX]{x1D6E4}_{i})$
is the following:
Thus, it suffices to compute the Euler characteristic of
![]() $\mathscr{X}_{i}$
; we leave details to the reader. The intersection numbers of the third and fourth columns are obtained as follows. First,
$\mathscr{X}_{i}$
; we leave details to the reader. The intersection numbers of the third and fourth columns are obtained as follows. First,
![]() $\varnothing =\unicode[STIX]{x1D707}_{1}(\unicode[STIX]{x1D6E4}_{1})\cap H_{h}(19)=\unicode[STIX]{x1D707}_{1}(\unicode[STIX]{x1D6E4}_{1})\cap H_{u}(19)$
by Proposition 2.2.1. Next,
$\varnothing =\unicode[STIX]{x1D707}_{1}(\unicode[STIX]{x1D6E4}_{1})\cap H_{h}(19)=\unicode[STIX]{x1D707}_{1}(\unicode[STIX]{x1D6E4}_{1})\cap H_{u}(19)$
by Proposition 2.2.1. Next,
![]() $\unicode[STIX]{x1D707}_{2}(\unicode[STIX]{x1D6E4}_{2})\cap H_{u}(19)=\varnothing$
and
$\unicode[STIX]{x1D707}_{2}(\unicode[STIX]{x1D6E4}_{2})\cap H_{u}(19)=\varnothing$
and
![]() $\unicode[STIX]{x1D707}_{3}(\unicode[STIX]{x1D6E4}_{3})\cap H_{h}(19)=\varnothing$
by Lemma 1.7.3. The remaining numbers are obtained by applying Borcherds’ relation for
$\unicode[STIX]{x1D707}_{3}(\unicode[STIX]{x1D6E4}_{3})\cap H_{h}(19)=\varnothing$
by Lemma 1.7.3. The remaining numbers are obtained by applying Borcherds’ relation for
![]() $N=19$
, which reads
$N=19$
, which reads
together with the computations that have already been proved. ◻
Proposition 4.2.2. A basis of
![]() $\operatorname{Pic}(\mathscr{F}(19))_{\mathbb{Q}}$
is provided by the choice of any three of the classes
$\operatorname{Pic}(\mathscr{F}(19))_{\mathbb{Q}}$
is provided by the choice of any three of the classes
![]() $\unicode[STIX]{x1D706}(19),H_{n}(19),H_{h}(19),H_{u}(19)$
. The space of linear relations among
$\unicode[STIX]{x1D706}(19),H_{n}(19),H_{h}(19),H_{u}(19)$
. The space of linear relations among
![]() $\unicode[STIX]{x1D706}(19),H_{n}(19),H_{h}(19),H_{u}(19)$
is generated by Borcherds’ relation (4.2.7).
$\unicode[STIX]{x1D706}(19),H_{n}(19),H_{h}(19),H_{u}(19)$
is generated by Borcherds’ relation (4.2.7).
Proof. Let
![]() $\mathscr{U}(19)\subset |\mathscr{O}_{\mathbb{P}^{3}}(4)|$
be the open subset of Definition 2.1.5. Then we have the isomorphism in (2.1.4). Now
$\mathscr{U}(19)\subset |\mathscr{O}_{\mathbb{P}^{3}}(4)|$
be the open subset of Definition 2.1.5. Then we have the isomorphism in (2.1.4). Now
![]() $\operatorname{CH}^{1}(\mathscr{U}(19)/\!\!/\text{PGL}(4))_{\mathbb{Q}}=\operatorname{Pic}(\mathscr{U}(19)/\!\!/\text{PGL}(4))_{\mathbb{Q}}$
(e.g. because
$\operatorname{CH}^{1}(\mathscr{U}(19)/\!\!/\text{PGL}(4))_{\mathbb{Q}}=\operatorname{Pic}(\mathscr{U}(19)/\!\!/\text{PGL}(4))_{\mathbb{Q}}$
(e.g. because
![]() $\mathscr{F}(19)$
is
$\mathscr{F}(19)$
is
![]() $\mathbb{Q}$
-factorial) and
$\mathbb{Q}$
-factorial) and
![]() $\operatorname{Pic}(\mathscr{U}(19)/\!\!/\text{PGL}(4))_{\mathbb{Q}}$
is isomorphic to the group of
$\operatorname{Pic}(\mathscr{U}(19)/\!\!/\text{PGL}(4))_{\mathbb{Q}}$
is isomorphic to the group of
![]() $\text{PGL}(4)$
-linearized line bundles on
$\text{PGL}(4)$
-linearized line bundles on
![]() $\mathscr{U}(19)$
(tensored with
$\mathscr{U}(19)$
(tensored with
![]() $\mathbb{Q}$
), which is a subgroup of
$\mathbb{Q}$
), which is a subgroup of
![]() $\operatorname{Pic}(\mathscr{U}(19))_{\mathbb{Q}}$
because
$\operatorname{Pic}(\mathscr{U}(19))_{\mathbb{Q}}$
because
![]() $\text{PGL}(4)$
has no non-trivial characters. On the other hand,
$\text{PGL}(4)$
has no non-trivial characters. On the other hand,
![]() $\operatorname{Pic}(\mathscr{U}(19))_{\mathbb{Q}}\cong \mathbb{Q}$
because
$\operatorname{Pic}(\mathscr{U}(19))_{\mathbb{Q}}\cong \mathbb{Q}$
because
![]() $|\mathscr{O}_{\mathbb{P}^{3}}(4)|\setminus \mathscr{U}(19)$
has codimension greater than
$|\mathscr{O}_{\mathbb{P}^{3}}(4)|\setminus \mathscr{U}(19)$
has codimension greater than
![]() $1$
in
$1$
in
![]() $|\mathscr{O}_{\mathbb{P}^{3}}(4)|$
. Thus,
$|\mathscr{O}_{\mathbb{P}^{3}}(4)|$
. Thus,
![]() $\operatorname{CH}^{1}(\mathscr{U}(19)/\!\!/\text{PGL}(4))_{\mathbb{Q}}\cong \mathbb{Q}$
and a generator is the class of the divisor parametrizing singular quartics. By (2.1.4), it follows that
$\operatorname{CH}^{1}(\mathscr{U}(19)/\!\!/\text{PGL}(4))_{\mathbb{Q}}\cong \mathbb{Q}$
and a generator is the class of the divisor parametrizing singular quartics. By (2.1.4), it follows that
and that the restriction of
![]() $H_{n}(19)$
is a generator. By the localization sequence associated to the inclusion of
$H_{n}(19)$
is a generator. By the localization sequence associated to the inclusion of
![]() $\mathscr{F}(19)\setminus (H_{h}(19)\cup H_{u}(19))$
into
$\mathscr{F}(19)\setminus (H_{h}(19)\cup H_{u}(19))$
into
![]() $\mathscr{F}(19)$
, it follows that
$\mathscr{F}(19)$
, it follows that
![]() $\operatorname{CH}^{1}(\mathscr{F}(19))_{\mathbb{Q}}$
is generated by
$\operatorname{CH}^{1}(\mathscr{F}(19))_{\mathbb{Q}}$
is generated by
![]() $H_{n}(19),H_{h}(19),H_{u}(19)$
. Table 2 shows that
$H_{n}(19),H_{h}(19),H_{u}(19)$
. Table 2 shows that
![]() $H_{n}(19),H_{h}(19),H_{u}(19)$
are linearly independent and also the remaining statements of the proposition.◻
$H_{n}(19),H_{h}(19),H_{u}(19)$
are linearly independent and also the remaining statements of the proposition.◻
Lastly, we define a family of quartic surfaces in
![]() $\mathbb{P}^{3}$
‘degenerating’ to a hyperelliptic
$\mathbb{P}^{3}$
‘degenerating’ to a hyperelliptic
![]() $K3$
surface. Let
$K3$
surface. Let
![]() $Q\in \mathbb{C}[x_{0},\ldots ,x_{3}]_{2}$
be a non-degenerate quadratic form and
$Q\in \mathbb{C}[x_{0},\ldots ,x_{3}]_{2}$
be a non-degenerate quadratic form and
![]() $G\in \mathbb{C}[x_{0},\ldots ,x_{3}]_{4}$
be such that
$G\in \mathbb{C}[x_{0},\ldots ,x_{3}]_{4}$
be such that
![]() $\operatorname{Div}(G)$
is transverse to
$\operatorname{Div}(G)$
is transverse to
![]() $\operatorname{Div}(Q)$
and such that the pencil of quartics
$\operatorname{Div}(Q)$
and such that the pencil of quartics
![]() $B:=\langle \operatorname{Div}(G),\operatorname{Div}(Q^{2})\rangle$
is a Lefschetz pencil away from
$B:=\langle \operatorname{Div}(G),\operatorname{Div}(Q^{2})\rangle$
is a Lefschetz pencil away from
![]() $\operatorname{Div}(Q^{2})$
. Let
$\operatorname{Div}(Q^{2})$
. Let
The family
![]() $\mathscr{Y}\rightarrow B$
is a family of quartics away from the inverse image of
$\mathscr{Y}\rightarrow B$
is a family of quartics away from the inverse image of
![]() $[1,0]$
. Let
$[1,0]$
. Let
![]() $\unicode[STIX]{x1D6E4}_{4}\rightarrow B$
be the double cover branched over
$\unicode[STIX]{x1D6E4}_{4}\rightarrow B$
be the double cover branched over
![]() $[1,0]$
and
$[1,0]$
and
![]() $[0,1]$
, and let
$[0,1]$
, and let
![]() $\mathscr{Y}_{4}\rightarrow \unicode[STIX]{x1D6E4}_{4}$
be the pull-back of
$\mathscr{Y}_{4}\rightarrow \unicode[STIX]{x1D6E4}_{4}$
be the pull-back of
![]() $\mathscr{Y}$
. Let
$\mathscr{Y}$
. Let
![]() $\mathscr{X}_{4}$
be the normalization of
$\mathscr{X}_{4}$
be the normalization of
![]() $\mathscr{Y}_{4}$
; the natural map
$\mathscr{Y}_{4}$
; the natural map
![]() $f_{4}:\mathscr{X}_{4}\rightarrow \unicode[STIX]{x1D6E4}_{4}$
is a family of polarized quartic
$f_{4}:\mathscr{X}_{4}\rightarrow \unicode[STIX]{x1D6E4}_{4}$
is a family of polarized quartic
![]() $K3$
surfaces. Let
$K3$
surfaces. Let
![]() $p\in \unicode[STIX]{x1D6E4}_{4}$
be the (unique) point mapping to
$p\in \unicode[STIX]{x1D6E4}_{4}$
be the (unique) point mapping to
![]() $[1,0]$
. The surface
$[1,0]$
. The surface
![]() $f_{4}^{-1}(p)$
is the double cover of the smooth quadric
$f_{4}^{-1}(p)$
is the double cover of the smooth quadric
![]() $\operatorname{Div}(Q)$
branched over
$\operatorname{Div}(Q)$
branched over
![]() $V(Q,G)$
, i.e. a hyperelliptic quartic
$V(Q,G)$
, i.e. a hyperelliptic quartic
![]() $K3$
. If
$K3$
. If
![]() $t\in (\unicode[STIX]{x1D6E4}_{4}\setminus \{p\})$
, then
$t\in (\unicode[STIX]{x1D6E4}_{4}\setminus \{p\})$
, then
![]() $f_{4}^{-1}(t)$
is a non-hyperelliptic (and non-unigonal) quartic
$f_{4}^{-1}(t)$
is a non-hyperelliptic (and non-unigonal) quartic
![]() $K3$
. We have the period map
$K3$
. We have the period map
Corollary 4.2.3. Keep notation as above. Then
Proof. Except for the second-to-last formula, these are obtained by arguments similar to those employed to obtain the formulae of Table 2. One gets the missing formula by applying Borcherds’ formula (4.2.7). ◻
Notice that the set-theoretic intersection
![]() $\unicode[STIX]{x1D707}_{4}(\unicode[STIX]{x1D6E4}_{3})\cap H_{h}(19)$
consists of a single point, namely
$\unicode[STIX]{x1D707}_{4}(\unicode[STIX]{x1D6E4}_{3})\cap H_{h}(19)$
consists of a single point, namely
![]() $\unicode[STIX]{x1D707}_{4}(p)$
, and it counts with multiplicity
$\unicode[STIX]{x1D707}_{4}(p)$
, and it counts with multiplicity
![]() $2a$
, for some
$2a$
, for some
![]() $a>1$
. In order to conclude that
$a>1$
. In order to conclude that
![]() $\unicode[STIX]{x1D707}_{4,\ast }(\unicode[STIX]{x1D6E4}_{3})\cdot H_{h}(19)=2$
, one needs a non-trivial computation; we avoid this thanks to Borcherds’ relation (4.2.7).
$\unicode[STIX]{x1D707}_{4,\ast }(\unicode[STIX]{x1D6E4}_{3})\cdot H_{h}(19)=2$
, one needs a non-trivial computation; we avoid this thanks to Borcherds’ relation (4.2.7).
Remark 4.2.4. In the present subsection, we have invoked Borcherds’ first relation in order to compute the degree of normal bundles. By employing the (elementary) results of § 5.3, one can avoid the use of Borcherds’ relations and in fact one can use the computations in this subsection in order to check the validity of Borcherds’ first relation for
![]() $N=19$
.
$N=19$
.
4.3 Proof of (4.1.2)
By Proposition 4.2.2, there exist
![]() $x,y,z\in \mathbb{Q}$
such that
$x,y,z\in \mathbb{Q}$
such that
We will compute
![]() $x,y$
by equating the intersection numbers of the two sides with complete curves in
$x,y$
by equating the intersection numbers of the two sides with complete curves in
![]() $\mathscr{F}(19)$
. For this to make sense, the complete curves must avoid the indeterminacy locus of
$\mathscr{F}(19)$
. For this to make sense, the complete curves must avoid the indeterminacy locus of
![]() $\mathfrak{p}_{19}^{-1}$
. Let
$\mathfrak{p}_{19}^{-1}$
. Let
![]() $I(19)^{\ast }\subset \mathscr{F}(19)^{\ast }$
be the indeterminacy locus of
$I(19)^{\ast }\subset \mathscr{F}(19)^{\ast }$
be the indeterminacy locus of
![]() $\mathfrak{p}_{19}^{-1}$
and
$\mathfrak{p}_{19}^{-1}$
and
![]() $I(19):=I(19)^{\ast }\cap \mathscr{F}(19)$
be the indeterminacy locus of
$I(19):=I(19)^{\ast }\cap \mathscr{F}(19)$
be the indeterminacy locus of
![]() $\mathfrak{p}_{19}^{-1}|_{\mathscr{F}(19)}$
. By (2.1.4),
$\mathfrak{p}_{19}^{-1}|_{\mathscr{F}(19)}$
. By (2.1.4),
![]() $I(19)$
is contained in
$I(19)$
is contained in
![]() $H_{h}(19)\cup H_{u}(19)$
. Since
$H_{h}(19)\cup H_{u}(19)$
. Since
![]() $\mathscr{F}(19)^{\ast }$
is normal,
$\mathscr{F}(19)^{\ast }$
is normal,
![]() $I(19)$
has codimension at least
$I(19)$
has codimension at least
![]() $2$
in
$2$
in
![]() $\mathscr{F}(19)$
and hence
$\mathscr{F}(19)$
and hence
![]() $I(19)=I_{h}(19)\sqcup I_{u}(19)$
, where
$I(19)=I_{h}(19)\sqcup I_{u}(19)$
, where
![]() $I_{h}(19)\subset H_{h}(19)$
and
$I_{h}(19)\subset H_{h}(19)$
and
![]() $I_{u}(19)\subset H_{u}(19)$
are proper closed subsets (recall that
$I_{u}(19)\subset H_{u}(19)$
are proper closed subsets (recall that
![]() $H_{h}(19)\cap H_{u}(19)=\varnothing$
). Now let
$H_{h}(19)\cap H_{u}(19)=\varnothing$
). Now let
![]() $\mathscr{X}_{1}\rightarrow \unicode[STIX]{x1D6E4}_{1}$
and
$\mathscr{X}_{1}\rightarrow \unicode[STIX]{x1D6E4}_{1}$
and
![]() $\mathscr{X}_{4}\rightarrow \unicode[STIX]{x1D6E4}_{4}$
be the complete families defined in § 4.2.2. Every surface
$\mathscr{X}_{4}\rightarrow \unicode[STIX]{x1D6E4}_{4}$
be the complete families defined in § 4.2.2. Every surface
![]() $f_{1}^{-1}(t)$
is a stable quartic and similarly for
$f_{1}^{-1}(t)$
is a stable quartic and similarly for
![]() $f_{4}^{-1}(t)$
if
$f_{4}^{-1}(t)$
if
![]() $t\not =p$
, while the semistable quartic surface in
$t\not =p$
, while the semistable quartic surface in
![]() $\mathbb{P}^{3}$
corresponding to
$\mathbb{P}^{3}$
corresponding to
![]() $p$
is to be understood as the double quadric
$p$
is to be understood as the double quadric
![]() $2V(Q)$
. Let
$2V(Q)$
. Let
![]() $\unicode[STIX]{x1D703}_{i}:\unicode[STIX]{x1D6E4}_{i}\rightarrow \mathfrak{M}(19)$
be the corresponding modular map for
$\unicode[STIX]{x1D703}_{i}:\unicode[STIX]{x1D6E4}_{i}\rightarrow \mathfrak{M}(19)$
be the corresponding modular map for
![]() $i\in \{1,4\}$
. The map
$i\in \{1,4\}$
. The map
![]() $\unicode[STIX]{x1D707}_{i}:\unicode[STIX]{x1D6E4}_{i}\rightarrow \mathscr{F}(19)$
considered in § 4.2.2 is equal to
$\unicode[STIX]{x1D707}_{i}:\unicode[STIX]{x1D6E4}_{i}\rightarrow \mathscr{F}(19)$
considered in § 4.2.2 is equal to
![]() $\mathfrak{p}_{19}\circ \unicode[STIX]{x1D703}_{i}$
. The curve
$\mathfrak{p}_{19}\circ \unicode[STIX]{x1D703}_{i}$
. The curve
![]() $\unicode[STIX]{x1D707}_{1}(\unicode[STIX]{x1D6E4}_{1})$
avoids the indeterminacy locus
$\unicode[STIX]{x1D707}_{1}(\unicode[STIX]{x1D6E4}_{1})$
avoids the indeterminacy locus
![]() $I(19)$
because it is disjoint from
$I(19)$
because it is disjoint from
![]() $H_{h}(19)\cup H_{u}(19)$
. On the other hand, the curve
$H_{h}(19)\cup H_{u}(19)$
. On the other hand, the curve
![]() $\unicode[STIX]{x1D707}_{4}(\unicode[STIX]{x1D6E4}_{4})$
intersects
$\unicode[STIX]{x1D707}_{4}(\unicode[STIX]{x1D6E4}_{4})$
intersects
![]() $H_{h}(19)\cup H_{u}(19)$
in a single point, namely
$H_{h}(19)\cup H_{u}(19)$
in a single point, namely
![]() $\unicode[STIX]{x1D707}_{4}(p)$
, which belongs to
$\unicode[STIX]{x1D707}_{4}(p)$
, which belongs to
![]() $H_{h}(19)$
. Since the double cover
$H_{h}(19)$
. Since the double cover
![]() $f_{4}^{-1}(p)\rightarrow V(Q)$
has an arbitrary branch curve (among those with ADE singularities), we may assume that
$f_{4}^{-1}(p)\rightarrow V(Q)$
has an arbitrary branch curve (among those with ADE singularities), we may assume that
![]() $\unicode[STIX]{x1D707}_{4}(p)\notin I_{h}(19)$
. Thus,
$\unicode[STIX]{x1D707}_{4}(p)\notin I_{h}(19)$
. Thus,
Equation (4.3.1), together with Table 2 and Corollary 4.2.3, gives
It follows that
![]() $x=1$
and
$x=1$
and
![]() $y=1/2$
. In order to prove that
$y=1/2$
. In order to prove that
![]() $z=1/2$
, we will show that
$z=1/2$
, we will show that
First,
![]() $\mathfrak{p}_{19}^{-1}$
is regular along the open dense
$\mathfrak{p}_{19}^{-1}$
is regular along the open dense
![]() $(H_{u}(19)\setminus I_{u}(19))\subset H_{u}(19)$
and
$(H_{u}(19)\setminus I_{u}(19))\subset H_{u}(19)$
and
where
![]() $q\in \mathfrak{M}(19)$
is the point parametrizing the
$q\in \mathfrak{M}(19)$
is the point parametrizing the
![]() $\text{PGL}(4)$
-orbit of the surface swept out by the tangents to a twisted cubic in
$\text{PGL}(4)$
-orbit of the surface swept out by the tangents to a twisted cubic in
![]() $\mathbb{P}^{3}$
(a closed orbit in
$\mathbb{P}^{3}$
(a closed orbit in
![]() $|\mathscr{O}_{\mathbb{P}^{3}}(4)|^{ss}$
); see [Reference ShahSha81, Theorem 3.17]. Let
$|\mathscr{O}_{\mathbb{P}^{3}}(4)|^{ss}$
); see [Reference ShahSha81, Theorem 3.17]. Let
![]() $Z^{\ast }\subset \mathscr{F}(19)^{\ast }\times \mathfrak{M}(19)$
be the closure of the graph of the restriction of
$Z^{\ast }\subset \mathscr{F}(19)^{\ast }\times \mathfrak{M}(19)$
be the closure of the graph of the restriction of
![]() $\mathfrak{p}_{19}^{-1}$
to its regular locus and
$\mathfrak{p}_{19}^{-1}$
to its regular locus and
![]() $Z:=Z^{\ast }\cap (\mathscr{F}(19)\times \mathfrak{M}(19))$
. Let
$Z:=Z^{\ast }\cap (\mathscr{F}(19)\times \mathfrak{M}(19))$
. Let
![]() $\unicode[STIX]{x1D70B}:Z\rightarrow \mathscr{F}(19)$
be the projection; note that
$\unicode[STIX]{x1D70B}:Z\rightarrow \mathscr{F}(19)$
be the projection; note that
![]() $\unicode[STIX]{x1D70B}$
is a projective map. We must prove that
$\unicode[STIX]{x1D70B}$
is a projective map. We must prove that
![]() $\unicode[STIX]{x1D70B}$
is an isomorphism over
$\unicode[STIX]{x1D70B}$
is an isomorphism over
![]() $H_{u}(19)$
. Assume the contrary, i.e. that
$H_{u}(19)$
. Assume the contrary, i.e. that
![]() $I_{u}(19)\not =\varnothing$
. Let
$I_{u}(19)\not =\varnothing$
. Let
![]() $\widetilde{H}_{u}(19)\subset Z$
be the closure of
$\widetilde{H}_{u}(19)\subset Z$
be the closure of
![]() $\unicode[STIX]{x1D70B}^{-1}(H_{u}(19)\setminus I_{u}(19))$
; thus,
$\unicode[STIX]{x1D70B}^{-1}(H_{u}(19)\setminus I_{u}(19))$
; thus,
![]() $\widetilde{H}_{u}(19)=H_{u}(19)\times q$
by (4.3.3). Let
$\widetilde{H}_{u}(19)=H_{u}(19)\times q$
by (4.3.3). Let
![]() $\operatorname{exc}(\unicode[STIX]{x1D70B})$
be the exceptional set of
$\operatorname{exc}(\unicode[STIX]{x1D70B})$
be the exceptional set of
![]() $\unicode[STIX]{x1D70B}$
; thus,
$\unicode[STIX]{x1D70B}$
; thus,
![]() $\unicode[STIX]{x1D70B}(\operatorname{exc}(\unicode[STIX]{x1D70B}))=I(19)$
. Since
$\unicode[STIX]{x1D70B}(\operatorname{exc}(\unicode[STIX]{x1D70B}))=I(19)$
. Since
![]() $\mathscr{F}(19)$
is
$\mathscr{F}(19)$
is
![]() $\mathbb{Q}$
-factorial,
$\mathbb{Q}$
-factorial,
![]() $\operatorname{exc}(\unicode[STIX]{x1D70B})$
has pure codimension
$\operatorname{exc}(\unicode[STIX]{x1D70B})$
has pure codimension
![]() $1$
in
$1$
in
![]() $Z$
. By Zariski’s main theorem, every fiber of
$Z$
. By Zariski’s main theorem, every fiber of
![]() $\unicode[STIX]{x1D70B}$
is connected; in particular, those over points of
$\unicode[STIX]{x1D70B}$
is connected; in particular, those over points of
![]() $I_{u}(19)$
. It follows that there exists one (at least) irreducible component of
$I_{u}(19)$
. It follows that there exists one (at least) irreducible component of
![]() $\operatorname{exc}(\unicode[STIX]{x1D70B})$
mapping to
$\operatorname{exc}(\unicode[STIX]{x1D70B})$
mapping to
![]() $I_{u}(19)$
and having non-empty intersection with
$I_{u}(19)$
and having non-empty intersection with
![]() $\widetilde{H}_{u}(19)$
; let
$\widetilde{H}_{u}(19)$
; let
![]() $D$
be such a component. Letting
$D$
be such a component. Letting
![]() $\unicode[STIX]{x1D719}:Z\rightarrow \mathfrak{M}(19)$
be the projection, the image
$\unicode[STIX]{x1D719}:Z\rightarrow \mathfrak{M}(19)$
be the projection, the image
![]() $\unicode[STIX]{x1D719}(D)$
contains
$\unicode[STIX]{x1D719}(D)$
contains
![]() $q$
and by hypothesis
$q$
and by hypothesis
![]() $\unicode[STIX]{x1D719}(D)\not =\{q\}$
. By Theorem 2.4 of [Reference ShahSha81],
$\unicode[STIX]{x1D719}(D)\not =\{q\}$
. By Theorem 2.4 of [Reference ShahSha81],
![]() $q$
is an isolated point of the indeterminacy locus of
$q$
is an isolated point of the indeterminacy locus of
![]() $\mathfrak{p}_{19}$
; it follows that there exists a subset
$\mathfrak{p}_{19}$
; it follows that there exists a subset
![]() $\unicode[STIX]{x1D719}(D)^{0}\subset \unicode[STIX]{x1D719}(D)$
which is a codimension-
$\unicode[STIX]{x1D719}(D)^{0}\subset \unicode[STIX]{x1D719}(D)$
which is a codimension-
![]() $1$
constructible subset of
$1$
constructible subset of
![]() $\mathfrak{M}(19)$
, contained in the regular locus of
$\mathfrak{M}(19)$
, contained in the regular locus of
![]() $\mathfrak{p}_{19}$
, which is contracted by
$\mathfrak{p}_{19}$
, which is contracted by
![]() $\mathfrak{p}_{19}$
(i.e.
$\mathfrak{p}_{19}$
(i.e.
![]() $\dim \mathfrak{p}_{19}(\unicode[STIX]{x1D719}(D)^{0})<18$
). This is absurd, e.g. by (2.1.4). This proves (4.3.2). By (4.3.3), it follows that the line bundle
$\dim \mathfrak{p}_{19}(\unicode[STIX]{x1D719}(D)^{0})<18$
). This is absurd, e.g. by (2.1.4). This proves (4.3.2). By (4.3.3), it follows that the line bundle
![]() $(\mathfrak{p}_{19}^{-1})^{\ast }L(19)$
is trivial on
$(\mathfrak{p}_{19}^{-1})^{\ast }L(19)$
is trivial on
![]() $H_{u}(19)$
and hence
$H_{u}(19)$
and hence
By Table 2, we get that
![]() $z=1/2$
.
$z=1/2$
.
Remark 4.3.1. Let
![]() $\unicode[STIX]{x1D6F1}:Z^{\ast }\rightarrow \mathscr{F}(19)^{\ast }$
be the projection and let
$\unicode[STIX]{x1D6F1}:Z^{\ast }\rightarrow \mathscr{F}(19)^{\ast }$
be the projection and let
![]() $H_{u}(19)^{\ast }\subset \mathscr{F}(19)^{\ast }$
be the closure of
$H_{u}(19)^{\ast }\subset \mathscr{F}(19)^{\ast }$
be the closure of
![]() $H_{u}(19)$
. The proof given above that
$H_{u}(19)$
. The proof given above that
![]() $\unicode[STIX]{x1D70B}$
is an isomorphism over
$\unicode[STIX]{x1D70B}$
is an isomorphism over
![]() $H_{u}(19)$
cannot be adapted to prove that
$H_{u}(19)$
cannot be adapted to prove that
![]() $\unicode[STIX]{x1D6F1}$
is an isomorphism over
$\unicode[STIX]{x1D6F1}$
is an isomorphism over
![]() $H_{u}(19)^{\ast }$
because
$H_{u}(19)^{\ast }$
because
![]() $\mathscr{F}(19)^{\ast }$
is not
$\mathscr{F}(19)^{\ast }$
is not
![]() $\mathbb{Q}$
-factorial at the boundary. In fact,
$\mathbb{Q}$
-factorial at the boundary. In fact,
![]() $\unicode[STIX]{x1D6F1}$
is not an isomorphism over
$\unicode[STIX]{x1D6F1}$
is not an isomorphism over
![]() $(H_{u}(19)^{\ast }\setminus H_{u}(19))$
.
$(H_{u}(19)^{\ast }\setminus H_{u}(19))$
.
5 Predictions for the variation of log canonical models
The goal of the present section is to predict the behavior of
for
![]() $N\geqslant 3$
and
$N\geqslant 3$
and
![]() $\unicode[STIX]{x1D6FD}\in [0,1]\cap \mathbb{Q}$
. Specifically, we will give a conjectural decomposition of
$\unicode[STIX]{x1D6FD}\in [0,1]\cap \mathbb{Q}$
. Specifically, we will give a conjectural decomposition of
![]() $\mathfrak{p}_{N}^{-1}$
as a product of flips and, as a last step, the contraction of the strict transform of the support of
$\mathfrak{p}_{N}^{-1}$
as a product of flips and, as a last step, the contraction of the strict transform of the support of
![]() $\unicode[STIX]{x1D6E5}(N)$
(denoted
$\unicode[STIX]{x1D6E5}(N)$
(denoted
![]() $\unicode[STIX]{x1D6E5}^{(1)}(N)$
; see § 1.7.3): here
$\unicode[STIX]{x1D6E5}^{(1)}(N)$
; see § 1.7.3): here
![]() $\mathfrak{p}_{N}$
is the period map considered in § 4.3 if
$\mathfrak{p}_{N}$
is the period map considered in § 4.3 if
![]() $N\in \{18,19\}$
and is to be understood as the inverse of the map
$N\in \{18,19\}$
and is to be understood as the inverse of the map
![]() $\mathscr{F}(N){\dashrightarrow}\text{Proj}\,R(\mathscr{F}(N),\unicode[STIX]{x1D706}(N)+\unicode[STIX]{x1D6E5}(N))$
otherwise. Each flip will correspond to a critical value
$\mathscr{F}(N){\dashrightarrow}\text{Proj}\,R(\mathscr{F}(N),\unicode[STIX]{x1D706}(N)+\unicode[STIX]{x1D6E5}(N))$
otherwise. Each flip will correspond to a critical value
![]() $\unicode[STIX]{x1D6FD}=\unicode[STIX]{x1D6FD}^{(k)}(N)\in (0,1)\cap \mathbb{Q}$
. The center of the flip corresponding to
$\unicode[STIX]{x1D6FD}=\unicode[STIX]{x1D6FD}^{(k)}(N)\in (0,1)\cap \mathbb{Q}$
. The center of the flip corresponding to
![]() $\unicode[STIX]{x1D6FD}^{(k)}(N)$
will be (the strict transform of) a building block of the
$\unicode[STIX]{x1D6FD}^{(k)}(N)$
will be (the strict transform of) a building block of the
![]() $D$
tower (see § 1.7) and it has codimension
$D$
tower (see § 1.7) and it has codimension
![]() $k$
. (Of course, the value
$k$
. (Of course, the value
![]() $\unicode[STIX]{x1D6FD}^{(1)}(N)=1$
corresponds to the contraction of
$\unicode[STIX]{x1D6FD}^{(1)}(N)=1$
corresponds to the contraction of
![]() $\unicode[STIX]{x1D6E5}^{(1)}(N)$
.) In the case of quartic surfaces (
$\unicode[STIX]{x1D6E5}^{(1)}(N)$
.) In the case of quartic surfaces (
![]() $N=19$
), it is possible to match our predicted flip centers with geometric loci in the GIT moduli space
$N=19$
), it is possible to match our predicted flip centers with geometric loci in the GIT moduli space
![]() $\mathfrak{M}(19)$
; this is discussed in the companion note [Reference Laza and O’GradyLO18b]. In the case of hyperelliptic quartics (
$\mathfrak{M}(19)$
; this is discussed in the companion note [Reference Laza and O’GradyLO18b]. In the case of hyperelliptic quartics (
![]() $N=18$
), using VGIT, we can go further and not only match the arithmetic predictions with the geometric ones (essentially the same matching as for quartics), but actually verify that both the arithmetic predictions and the geometric matching are correct. This is discussed in [Reference Laza and O’GradyLO18a].
$N=18$
), using VGIT, we can go further and not only match the arithmetic predictions with the geometric ones (essentially the same matching as for quartics), but actually verify that both the arithmetic predictions and the geometric matching are correct. This is discussed in [Reference Laza and O’GradyLO18a].
5.1 Main conjectures and results
Let
![]() $\unicode[STIX]{x1D6FD}\in (0,1]\cap \mathbb{Q}$
. Then the following hold.
$\unicode[STIX]{x1D6FD}\in (0,1]\cap \mathbb{Q}$
. Then the following hold.
∙
 $\unicode[STIX]{x1D706}(N)+\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6E5}(N)$
is a big line bundle with base locus contained in
$\unicode[STIX]{x1D706}(N)+\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6E5}(N)$
is a big line bundle with base locus contained in
 $\unicode[STIX]{x1D6E5}^{(1)}(N)$
because
$\unicode[STIX]{x1D6E5}^{(1)}(N)$
because
 $\unicode[STIX]{x1D706}(N)$
is ample and
$\unicode[STIX]{x1D706}(N)$
is ample and
 $\unicode[STIX]{x1D6E5}(N)$
is effective.
$\unicode[STIX]{x1D6E5}(N)$
is effective.∙ If
 $\unicode[STIX]{x1D6FD}<1$
, the restriction of
$\unicode[STIX]{x1D6FD}<1$
, the restriction of
 $\unicode[STIX]{x1D706}(N)+\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6E5}(N)$
to
$\unicode[STIX]{x1D706}(N)+\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6E5}(N)$
to
 $\unicode[STIX]{x1D6E5}^{(1)}(N)$
is big with base locus contained in
$\unicode[STIX]{x1D6E5}^{(1)}(N)$
is big with base locus contained in
 $\unicode[STIX]{x1D6E5}^{(2)}(N)$
; see Propositions 5.3.6, 5.3.7, and 5.3.8. In particular, assuming lifting of sections from
$\unicode[STIX]{x1D6E5}^{(2)}(N)$
; see Propositions 5.3.6, 5.3.7, and 5.3.8. In particular, assuming lifting of sections from
 $\unicode[STIX]{x1D6E5}^{(1)}(N)$
to
$\unicode[STIX]{x1D6E5}^{(1)}(N)$
to
 $\mathscr{F}(N)$
, the base locus of
$\mathscr{F}(N)$
, the base locus of
 $\unicode[STIX]{x1D706}(N)+\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6E5}(N)$
is contained in
$\unicode[STIX]{x1D706}(N)+\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6E5}(N)$
is contained in
 $\unicode[STIX]{x1D6E5}^{(2)}(N)$
.
$\unicode[STIX]{x1D6E5}^{(2)}(N)$
.∙ For
 $N\in \{18,19\}$
,
$N\in \{18,19\}$
,
 $\mathscr{F}(N)^{\ast }{\dashrightarrow}\mathscr{F}(N,1)\cong \mathfrak{M}(N)$
is a birational contraction of
$\mathscr{F}(N)^{\ast }{\dashrightarrow}\mathscr{F}(N,1)\cong \mathfrak{M}(N)$
is a birational contraction of
 $\unicode[STIX]{x1D6E5}^{(1)}(N)$
by Proposition 4.1.2. This is expected to hold for any
$\unicode[STIX]{x1D6E5}^{(1)}(N)$
by Proposition 4.1.2. This is expected to hold for any
 $N$
by the arguments of Looijenga.
$N$
by the arguments of Looijenga.
In order to understand what should be going on, it is convenient to let
![]() $\unicode[STIX]{x1D6FD}\in (0,1]\cap \mathbb{Q}$
decrease, starting from
$\unicode[STIX]{x1D6FD}\in (0,1]\cap \mathbb{Q}$
decrease, starting from
![]() $\unicode[STIX]{x1D6FD}=1$
. For anyone familiar with linearized arrangements, and in fact implicitly contained in Looijenga [Reference LooijengaLoo03b],
$\unicode[STIX]{x1D6FD}=1$
. For anyone familiar with linearized arrangements, and in fact implicitly contained in Looijenga [Reference LooijengaLoo03b],
![]() $\unicode[STIX]{x1D6E5}^{(1)}(N)$
should be contractible regularly away from
$\unicode[STIX]{x1D6E5}^{(1)}(N)$
should be contractible regularly away from
![]() $\unicode[STIX]{x1D6E5}^{(2)}(N)$
(with corresponding
$\unicode[STIX]{x1D6E5}^{(2)}(N)$
(with corresponding
![]() $\unicode[STIX]{x1D6FD}^{(1)}(N)=1$
), but, in order to contract it regularly, one must first flip
$\unicode[STIX]{x1D6FD}^{(1)}(N)=1$
), but, in order to contract it regularly, one must first flip
![]() $\unicode[STIX]{x1D6E5}^{(2)}(N)$
, at least away from
$\unicode[STIX]{x1D6E5}^{(2)}(N)$
, at least away from
![]() $\unicode[STIX]{x1D6E5}^{(3)}(N)$
, with corresponding
$\unicode[STIX]{x1D6E5}^{(3)}(N)$
, with corresponding
![]() $0<\unicode[STIX]{x1D6FD}^{(2)}(N)<1$
. The first-order predictions (§ 5.1.1) are obtained by iterating this procedure, i.e. following Looijenga [Reference LooijengaLoo03b]. These predictions are based on the combinatorics of the linearized arrangement
$0<\unicode[STIX]{x1D6FD}^{(2)}(N)<1$
. The first-order predictions (§ 5.1.1) are obtained by iterating this procedure, i.e. following Looijenga [Reference LooijengaLoo03b]. These predictions are based on the combinatorics of the linearized arrangement
![]() $\widetilde{\unicode[STIX]{x1D6E5}}^{(1)}(N)$
(see § 1.7.3); one essentially computes the log canonical threshold (at the generic point of
$\widetilde{\unicode[STIX]{x1D6E5}}^{(1)}(N)$
(see § 1.7.3); one essentially computes the log canonical threshold (at the generic point of
![]() $\unicode[STIX]{x1D6E5}^{(k)}(N)$
) as in [Reference MustaţăMus06], keeping track of the ramification.
$\unicode[STIX]{x1D6E5}^{(k)}(N)$
) as in [Reference MustaţăMus06], keeping track of the ramification.
5.1.1 First-order predictions
As we explained, the starting point of Looijenga is the observation that, in the embedding
![]() $\mathscr{D}_{N}^{+}\subset \check{\mathscr{D}}_{N}^{+}\subset \mathbb{P}^{N+1}$
(we let
$\mathscr{D}_{N}^{+}\subset \check{\mathscr{D}}_{N}^{+}\subset \mathbb{P}^{N+1}$
(we let
![]() $\mathscr{D}_{N}^{+}=\mathscr{D}_{\unicode[STIX]{x1D6EC}_{N}}^{+}$
), the automorphic bundle is the restriction of
$\mathscr{D}_{N}^{+}=\mathscr{D}_{\unicode[STIX]{x1D6EC}_{N}}^{+}$
), the automorphic bundle is the restriction of
![]() ${\mathcal{O}}_{\mathbb{P}^{N+1}}(-1)$
, while a Heegner divisor is a section of
${\mathcal{O}}_{\mathbb{P}^{N+1}}(-1)$
, while a Heegner divisor is a section of
![]() ${\mathcal{O}}_{\mathscr{D}_{N}^{+}}(1)$
. This fact suggests that
${\mathcal{O}}_{\mathscr{D}_{N}^{+}}(1)$
. This fact suggests that
![]() $\unicode[STIX]{x1D706}(N)+\unicode[STIX]{x1D6E5}(N)$
should contract
$\unicode[STIX]{x1D706}(N)+\unicode[STIX]{x1D6E5}(N)$
should contract
![]() $\unicode[STIX]{x1D6E5}^{(1)}(N)$
. As always, a linearized arrangement is stratified by linear strata of the intersections, and the first-order predictions (leading to candidates for the critical values
$\unicode[STIX]{x1D6E5}^{(1)}(N)$
. As always, a linearized arrangement is stratified by linear strata of the intersections, and the first-order predictions (leading to candidates for the critical values
![]() $\unicode[STIX]{x1D6FD}^{(k)}(N)$
) are a simple function of combinatorics, namely the number of hyperplanes intersecting in a stratum, versus the codimension of that stratum (compare [Reference MustaţăMus06]). Of course, in this situation, there is a slight complication due to the fact that these hyperplanes are reflection hyperplanes (note that our
$\unicode[STIX]{x1D6FD}^{(k)}(N)$
) are a simple function of combinatorics, namely the number of hyperplanes intersecting in a stratum, versus the codimension of that stratum (compare [Reference MustaţăMus06]). Of course, in this situation, there is a slight complication due to the fact that these hyperplanes are reflection hyperplanes (note that our
![]() $\unicode[STIX]{x1D6E5}$
involves a
$\unicode[STIX]{x1D6E5}$
involves a
![]() $\frac{1}{2}$
factor for this reason).
$\frac{1}{2}$
factor for this reason).
Concretely, for most values of
![]() $N$
and
$N$
and
![]() $k$
, we will prove (see Proposition 5.3.6 for a precise statement) that the following formula holds:
$k$
, we will prove (see Proposition 5.3.6 for a precise statement) that the following formula holds:
We recall (see Proposition 1.7.2) that for most choices of
![]() $N$
and
$N$
and
![]() $k$
,
$k$
,
![]() $\unicode[STIX]{x1D6E5}^{(k)}(N)=\operatorname{Im}f_{N-k,N}$
, and (5.1.1) should be read as
$\unicode[STIX]{x1D6E5}^{(k)}(N)=\operatorname{Im}f_{N-k,N}$
, and (5.1.1) should be read as
![]() $f_{N-k,N}^{\ast }(\unicode[STIX]{x1D706}(N)+\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6E5}(N))=(1-k\unicode[STIX]{x1D6FD})\unicode[STIX]{x1D706}(N-k)+\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6E5}(N-k)$
.
$f_{N-k,N}^{\ast }(\unicode[STIX]{x1D706}(N)+\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6E5}(N))=(1-k\unicode[STIX]{x1D6FD})\unicode[STIX]{x1D706}(N-k)+\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6E5}(N-k)$
.
If, following Looijenga, we assume that the stratum
![]() $\unicode[STIX]{x1D6E5}^{(k+1)}(N)$
is flipped before the stratum
$\unicode[STIX]{x1D6E5}^{(k+1)}(N)$
is flipped before the stratum
![]() $\unicode[STIX]{x1D6E5}^{(k)}(N)$
, we get the prediction
$\unicode[STIX]{x1D6E5}^{(k)}(N)$
, we get the prediction
In any case, note that
![]() $(\unicode[STIX]{x1D706}(N)+\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6E5}(N))_{\mid \unicode[STIX]{x1D6E5}^{(k)}}(N)$
is big for
$(\unicode[STIX]{x1D706}(N)+\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6E5}(N))_{\mid \unicode[STIX]{x1D6E5}^{(k)}}(N)$
is big for
![]() $\unicode[STIX]{x1D6FD}<1/k$
by (5.1.1). Thus, assuming a certain lifting of sections (a reasonable assumption, which we can prove in some cases), we get that the generic point of
$\unicode[STIX]{x1D6FD}<1/k$
by (5.1.1). Thus, assuming a certain lifting of sections (a reasonable assumption, which we can prove in some cases), we get that the generic point of
![]() $\unicode[STIX]{x1D6E5}^{(k)}(N)$
is not affected by the birational transformations occurring for
$\unicode[STIX]{x1D6E5}^{(k)}(N)$
is not affected by the birational transformations occurring for
![]() $\unicode[STIX]{x1D6FD}\in (0,1/k)$
.
$\unicode[STIX]{x1D6FD}\in (0,1/k)$
.
The two key ingredients that give (5.1.1) are the computation of intersections of distinct Heegner divisors (see § 5.2) and a normal bundle computation based on adjunction (see § 5.3). Of course, the actual computations depend on our particular lattices and Heegner divisors, but the method adopted here can be applied in many other instances. (Similar computations are implicitly or explicitly contained in [Reference Gritsenko, Hulek and SankaranGHS07] or [Reference LooijengaLoo03b].)
5.1.2 Refined predictions
The first-order predictions for quartic
![]() $K3$
surfaces are definitely wrong for
$K3$
surfaces are definitely wrong for
![]() $k>9$
; in fact, the indeterminacy locus of the period map
$k>9$
; in fact, the indeterminacy locus of the period map
![]() $\mathfrak{p}_{19}$
has dimension
$\mathfrak{p}_{19}$
has dimension
![]() $8$
, while the first-order predictions would give that it has higher dimension. This apparent contradiction has the following explanation. The key assumption in the first-order predictions is the contractibility of
$8$
, while the first-order predictions would give that it has higher dimension. This apparent contradiction has the following explanation. The key assumption in the first-order predictions is the contractibility of
![]() $\unicode[STIX]{x1D6E5}^{(k+1)}(N)$
inside
$\unicode[STIX]{x1D6E5}^{(k+1)}(N)$
inside
![]() $\unicode[STIX]{x1D6E5}^{(k)}(N)$
, but in the
$\unicode[STIX]{x1D6E5}^{(k)}(N)$
, but in the
![]() $D$
-tower we have the following trichotomy:
$D$
-tower we have the following trichotomy:
(1)
 $H_{h}(N)$
is birationally contractible in
$H_{h}(N)$
is birationally contractible in
 $\mathscr{F}(N)$
for
$\mathscr{F}(N)$
for
 $N>14$
;
$N>14$
;(2)
 $H_{h}(N)$
moves in a linear system of dimension at least
$H_{h}(N)$
moves in a linear system of dimension at least
 $1$
if
$1$
if
 $N\leqslant 14$
;
$N\leqslant 14$
;(3)
 $H_{h}(N)$
is ample on
$H_{h}(N)$
is ample on
 $\mathscr{F}(N)$
for
$\mathscr{F}(N)$
for
 $N\leqslant 10$
.
$N\leqslant 10$
.
Note: (2) and (3) are theorems, while (1) is conjectural in general, but known for
![]() $N=18,19$
; cf. § 4.3 (probably one can prove it also for
$N=18,19$
; cf. § 4.3 (probably one can prove it also for
![]() $N=20$
via double EPW sextics). The explanation for this comes from Borcherds’ relations discussed in § 3.
$N=20$
via double EPW sextics). The explanation for this comes from Borcherds’ relations discussed in § 3.
Taking into account the behavior of the hyperelliptic divisor described above, we correct our first-order predictions and arrive at the following result.
Prediction 5.1.1. Let
![]() $N\geqslant 15$
. The ring of sections
$N\geqslant 15$
. The ring of sections
![]() $R(\mathscr{F}(N),\unicode[STIX]{x1D706}(N)+\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6E5}(N))$
is finitely generated for
$R(\mathscr{F}(N),\unicode[STIX]{x1D706}(N)+\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6E5}(N))$
is finitely generated for
![]() $\unicode[STIX]{x1D6FD}\in [0,1]\cap \mathbb{Q}$
and the walls of the Mori chamber decomposition of the cone
$\unicode[STIX]{x1D6FD}\in [0,1]\cap \mathbb{Q}$
and the walls of the Mori chamber decomposition of the cone
are generated by
![]() $\unicode[STIX]{x1D706}(N)+(1/k)\unicode[STIX]{x1D6E5}(N)$
, where
$\unicode[STIX]{x1D706}(N)+(1/k)\unicode[STIX]{x1D6E5}(N)$
, where
![]() $k\in \{1,\ldots ,N-10\}$
and
$k\in \{1,\ldots ,N-10\}$
and
![]() $k\not =N-11$
. The behavior of
$k\not =N-11$
. The behavior of
![]() $\unicode[STIX]{x1D706}(N)+(1/k)\unicode[STIX]{x1D6E5}(N)$
, for
$\unicode[STIX]{x1D706}(N)+(1/k)\unicode[STIX]{x1D6E5}(N)$
, for
![]() $k$
as above, is described as follows. For
$k$
as above, is described as follows. For
![]() $k=1$
,
$k=1$
,
![]() $\mathscr{F}(N,1)$
is obtained from
$\mathscr{F}(N,1)$
is obtained from
![]() $\mathscr{F}(N,1-\unicode[STIX]{x1D716})$
by contracting the strict transform of
$\mathscr{F}(N,1-\unicode[STIX]{x1D716})$
by contracting the strict transform of
![]() $\unicode[STIX]{x1D6E5}^{(1)}(N)$
. If
$\unicode[STIX]{x1D6E5}^{(1)}(N)$
. If
![]() $2\leqslant k$
, then the birational map between
$2\leqslant k$
, then the birational map between
![]() $\mathscr{F}(N,1/k-\unicode[STIX]{x1D716})$
and
$\mathscr{F}(N,1/k-\unicode[STIX]{x1D716})$
and
![]() $\mathscr{F}(N,1/k+\unicode[STIX]{x1D716})$
is a flip whose center is:
$\mathscr{F}(N,1/k+\unicode[STIX]{x1D716})$
is a flip whose center is:
(1) the strict transform of
 $\operatorname{Im}f_{N-k,N}$
if
$\operatorname{Im}f_{N-k,N}$
if
 $2\leqslant k\leqslant N-14$
,
$2\leqslant k\leqslant N-14$
,
 $k\not \equiv N-2\hspace{0.6em}({\rm mod}\hspace{0.2em}8)$
, and either
$k\not \equiv N-2\hspace{0.6em}({\rm mod}\hspace{0.2em}8)$
, and either
 $k\not =4$
or
$k\not =4$
or
 $N\not \equiv 4\hspace{0.6em}({\rm mod}\hspace{0.2em}8)$
;
$N\not \equiv 4\hspace{0.6em}({\rm mod}\hspace{0.2em}8)$
;(2) the union of the strict transforms of
 $\operatorname{Im}f_{N-4,N}$
and
$\operatorname{Im}f_{N-4,N}$
and
 $\operatorname{Im}(f_{N-1,N}\circ l_{N-1})$
if
$\operatorname{Im}(f_{N-1,N}\circ l_{N-1})$
if
 $k=4$
and
$k=4$
and
 $N\equiv 4\hspace{0.6em}({\rm mod}\hspace{0.2em}8)$
;
$N\equiv 4\hspace{0.6em}({\rm mod}\hspace{0.2em}8)$
;(3) the union of the strict transforms of
 $\operatorname{Im}f_{N-k,N}$
and
$\operatorname{Im}f_{N-k,N}$
and
 $\operatorname{Im}(f_{N-(k-1),N}\circ l_{N-(k-1)})$
if
$\operatorname{Im}(f_{N-(k-1),N}\circ l_{N-(k-1)})$
if
 $3\leqslant k\leqslant N-10$
and
$3\leqslant k\leqslant N-10$
and
 $k\equiv N-2\hspace{0.6em}({\rm mod}\hspace{0.2em}8)$
(notice that this includes the case
$k\equiv N-2\hspace{0.6em}({\rm mod}\hspace{0.2em}8)$
(notice that this includes the case
 $k=N-10$
);
$k=N-10$
);(4) the strict transform of
 $\operatorname{Im}(f_{13,N}\circ q_{13})$
if
$\operatorname{Im}(f_{13,N}\circ q_{13})$
if
 $k=(N-13)$
;
$k=(N-13)$
;(5) the strict transform of
 $\operatorname{Im}(f_{12,N}\circ m_{12})$
if
$\operatorname{Im}(f_{12,N}\circ m_{12})$
if
 $k=(N-12)$
.
$k=(N-12)$
.
Remark 5.1.2 (Early termination).
The predictions in Prediction 5.1.1 differ from the first-order predictions for
![]() $k>N-14$
. In fact, the generic point of
$k>N-14$
. In fact, the generic point of
![]() $\unicode[STIX]{x1D6E5}^{(k)}(N)$
is unaffected by the birational transformations for
$\unicode[STIX]{x1D6E5}^{(k)}(N)$
is unaffected by the birational transformations for
![]() $\unicode[STIX]{x1D6FD}<1/(N-14)$
. More precisely,
$\unicode[STIX]{x1D6FD}<1/(N-14)$
. More precisely,
![]() $f_{13,N}(\mathscr{F}(13)\setminus H_{u}(13))$
(which is contained in
$f_{13,N}(\mathscr{F}(13)\setminus H_{u}(13))$
(which is contained in
![]() $\unicode[STIX]{x1D6E5}^{(N-13)}(N)$
) will be flipped when
$\unicode[STIX]{x1D6E5}^{(N-13)}(N)$
) will be flipped when
![]() $\unicode[STIX]{x1D6FD}=1/(N-14)$
(at once with
$\unicode[STIX]{x1D6FD}=1/(N-14)$
(at once with
![]() $\unicode[STIX]{x1D6E5}^{(N-14)}$
). Moreover,
$\unicode[STIX]{x1D6E5}^{(N-14)}$
). Moreover,
![]() $\unicode[STIX]{x1D6E5}^{(N-10)}(N)$
consists of two disjoint components
$\unicode[STIX]{x1D6E5}^{(N-10)}(N)$
consists of two disjoint components
![]() $f_{10,N}(\mathscr{F}(10))$
and
$f_{10,N}(\mathscr{F}(10))$
and
![]() $f_{11,N}(H_{u}(11))$
(see Proposition 1.7.2). The first component will be flipped at
$f_{11,N}(H_{u}(11))$
(see Proposition 1.7.2). The first component will be flipped at
![]() $\unicode[STIX]{x1D6FD}=1/(N-14)$
, while the second is the center of the flip for
$\unicode[STIX]{x1D6FD}=1/(N-14)$
, while the second is the center of the flip for
![]() $\unicode[STIX]{x1D6FD}=1/(N-10)$
(the smallest critical value).
$\unicode[STIX]{x1D6FD}=1/(N-10)$
(the smallest critical value).
5.2 Intersection of two distinct Heegner divisors
We proved (see Propositions 1.4.5, 1.5.1, and 1.5.2) that for
![]() $4\leqslant N$
there are isomorphisms
$4\leqslant N$
there are isomorphisms
We also proved that, for
![]() $k\geqslant 0$
, there are isomorphisms
$k\geqslant 0$
, there are isomorphisms
and
The key ingredient in the heuristics for our predictions is the computation of the restrictions of the line bundle
![]() $\unicode[STIX]{x1D706}(N)+\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6E5}(N)$
to the various strata
$\unicode[STIX]{x1D706}(N)+\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6E5}(N)$
to the various strata
![]() $\unicode[STIX]{x1D6E5}^{(k)}(N)$
. Via pull-back by
$\unicode[STIX]{x1D6E5}^{(k)}(N)$
. Via pull-back by
![]() $f_{N}$
(and
$f_{N}$
(and
![]() $l_{N}$
,
$l_{N}$
,
![]() $m_{N}$
, or
$m_{N}$
, or
![]() $q_{N}$
if applicable), this restriction is computed in an inductive manner. The result below is our starting point.
$q_{N}$
if applicable), this restriction is computed in an inductive manner. The result below is our starting point.
Proposition 5.2.1. With notation as above, the following formulae hold:
Remark 5.2.2. Let
![]() $N\equiv 3\hspace{0.6em}({\rm mod}\hspace{0.2em}8)$
. Then (5.2.5) reads
$N\equiv 3\hspace{0.6em}({\rm mod}\hspace{0.2em}8)$
. Then (5.2.5) reads
![]() $f_{N}^{\ast }H_{u}(N)=0$
because
$f_{N}^{\ast }H_{u}(N)=0$
because
![]() $H_{u}(N-1)=0$
; see Item (3) of Definition 1.3.4.
$H_{u}(N-1)=0$
; see Item (3) of Definition 1.3.4.
5.2.1 Set-up
Let
![]() $(\unicode[STIX]{x1D6EC}_{N},\unicode[STIX]{x1D709}_{N})$
be our standard decorated dimension-
$(\unicode[STIX]{x1D6EC}_{N},\unicode[STIX]{x1D709}_{N})$
be our standard decorated dimension-
![]() $N$
$N$
![]() $D$
-lattice. Let
$D$
-lattice. Let
![]() $v\in \unicode[STIX]{x1D6EC}_{N}$
and suppose that one of the following holds.
$v\in \unicode[STIX]{x1D6EC}_{N}$
and suppose that one of the following holds.
(1)
 $v$
is a hyperelliptic vector; thus,
$v$
is a hyperelliptic vector; thus,
 $v^{\bot }\cong \unicode[STIX]{x1D6EC}_{N-1}$
and it comes with a decoration
$v^{\bot }\cong \unicode[STIX]{x1D6EC}_{N-1}$
and it comes with a decoration
 $\unicode[STIX]{x1D709}_{N-1}$
; see § 1.4.
$\unicode[STIX]{x1D709}_{N-1}$
; see § 1.4.(2)
 $N=8k+3$
and
$N=8k+3$
and
 $v$
is unigonal; thus,
$v$
is unigonal; thus,
 $v^{\bot }\cong \text{II}_{2,2+8k}$
; see § 1.5.1.
$v^{\bot }\cong \text{II}_{2,2+8k}$
; see § 1.5.1.(3)
 $N=8k+4$
and
$N=8k+4$
and
 $v$
is unigonal; thus,
$v$
is unigonal; thus,
 $v^{\bot }\cong \text{II}_{2,2+8k}\oplus A_{1}$
; see § 1.5.2.
$v^{\bot }\cong \text{II}_{2,2+8k}\oplus A_{1}$
; see § 1.5.2.
Let
![]() $\unicode[STIX]{x1D6E4}_{v}<\unicode[STIX]{x1D6E4}_{\unicode[STIX]{x1D709}_{N}}$
be the stabilizer of
$\unicode[STIX]{x1D6E4}_{v}<\unicode[STIX]{x1D6E4}_{\unicode[STIX]{x1D709}_{N}}$
be the stabilizer of
![]() $v$
. Thus,
$v$
. Thus,
 $$\begin{eqnarray}\unicode[STIX]{x1D6E4}_{v}=\left\{\begin{array}{@{}ll@{}}\unicode[STIX]{x1D6E4}_{\unicode[STIX]{x1D709}_{N-1}}\quad & \text{if (1) holds,}\\ O^{+}(\text{II}_{2,2+8k})\quad & \text{if (2) holds,}\\ O^{+}(\text{II}_{2,2+8k}\oplus A_{1})\quad & \text{if (3) holds.}\\ \quad \end{array}\right.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6E4}_{v}=\left\{\begin{array}{@{}ll@{}}\unicode[STIX]{x1D6E4}_{\unicode[STIX]{x1D709}_{N-1}}\quad & \text{if (1) holds,}\\ O^{+}(\text{II}_{2,2+8k})\quad & \text{if (2) holds,}\\ O^{+}(\text{II}_{2,2+8k}\oplus A_{1})\quad & \text{if (3) holds.}\\ \quad \end{array}\right.\end{eqnarray}$$
Then we have a natural isomorphism
where
![]() $H_{v}(N):=H_{v,\unicode[STIX]{x1D6EC}_{N}}(\unicode[STIX]{x1D6E4}_{\unicode[STIX]{x1D709}_{N}})$
. In fact, if Item (1) holds then
$H_{v}(N):=H_{v,\unicode[STIX]{x1D6EC}_{N}}(\unicode[STIX]{x1D6E4}_{\unicode[STIX]{x1D709}_{N}})$
. In fact, if Item (1) holds then
![]() $\unicode[STIX]{x1D711}_{v}=f_{N}$
, if Item (2) holds then
$\unicode[STIX]{x1D711}_{v}=f_{N}$
, if Item (2) holds then
![]() $\unicode[STIX]{x1D711}_{v}=l_{N}$
, and if Item (3) holds then
$\unicode[STIX]{x1D711}_{v}=l_{N}$
, and if Item (3) holds then
![]() $\unicode[STIX]{x1D711}_{v}=m_{N}$
.
$\unicode[STIX]{x1D711}_{v}=m_{N}$
.
Definition 5.2.3. Let
![]() $v\in \unicode[STIX]{x1D6EC}_{N}$
be as above, i.e. we assume that one of Items (1), (2), or (3) holds. Given
$v\in \unicode[STIX]{x1D6EC}_{N}$
be as above, i.e. we assume that one of Items (1), (2), or (3) holds. Given
![]() $w\in \unicode[STIX]{x1D6EC}_{N}$
such that
$w\in \unicode[STIX]{x1D6EC}_{N}$
such that
![]() $\langle v,w\rangle$
is a rank-
$\langle v,w\rangle$
is a rank-
![]() $2$
subgroup of
$2$
subgroup of
![]() $\unicode[STIX]{x1D6EC}_{N}$
, we let
$\unicode[STIX]{x1D6EC}_{N}$
, we let
![]() $\unicode[STIX]{x1D70B}_{v^{\bot }}(w)$
be a generator of the intersection
$\unicode[STIX]{x1D70B}_{v^{\bot }}(w)$
be a generator of the intersection
![]() $(\mathbb{Q}v\oplus \mathbb{Q}w)\cap v_{\mathbb{Z}}^{\bot }$
(thus,
$(\mathbb{Q}v\oplus \mathbb{Q}w)\cap v_{\mathbb{Z}}^{\bot }$
(thus,
![]() $\unicode[STIX]{x1D70B}_{v^{\bot }}(w)$
is non-zero and determined up to
$\unicode[STIX]{x1D70B}_{v^{\bot }}(w)$
is non-zero and determined up to
![]() $\pm 1$
).
$\pm 1$
).
Proposition 5.2.4. Let
![]() $v\in \unicode[STIX]{x1D6EC}_{N}$
be as above, i.e. we assume that one of Items (1), (2), or (3) holds. Assume that
$v\in \unicode[STIX]{x1D6EC}_{N}$
be as above, i.e. we assume that one of Items (1), (2), or (3) holds. Assume that
![]() $w_{0}\in \unicode[STIX]{x1D6EC}_{N}$
is a primitive vector of negative square such that the associated Heegner divisor
$w_{0}\in \unicode[STIX]{x1D6EC}_{N}$
is a primitive vector of negative square such that the associated Heegner divisor
![]() $H_{w_{0}}(N)=H_{w_{0},\unicode[STIX]{x1D6EC}_{N}}(\unicode[STIX]{x1D6E4}_{\unicode[STIX]{x1D709}_{N}})$
is different from
$H_{w_{0}}(N)=H_{w_{0},\unicode[STIX]{x1D6EC}_{N}}(\unicode[STIX]{x1D6E4}_{\unicode[STIX]{x1D709}_{N}})$
is different from
![]() $H_{v}(N)$
. The following set-theoretic equality holds:
$H_{v}(N)$
. The following set-theoretic equality holds:
where
![]() $\langle v,w\rangle <0$
means that
$\langle v,w\rangle <0$
means that
![]() $\langle v,w\rangle$
is a negative-definite sublattice of
$\langle v,w\rangle$
is a negative-definite sublattice of
![]() $\unicode[STIX]{x1D6EC}_{N}$
. (And hence
$\unicode[STIX]{x1D6EC}_{N}$
. (And hence
![]() $\unicode[STIX]{x1D70B}_{v^{\bot }}(w)$
is a vector of negative square.)
$\unicode[STIX]{x1D70B}_{v^{\bot }}(w)$
is a vector of negative square.)
Proof. There is a single observation to be made, namely that if
![]() $[\unicode[STIX]{x1D70E}]\in v^{\bot }\cap w^{\bot }\cap \mathscr{D}_{\unicode[STIX]{x1D6EC}_{N}}^{+}$
, then
$[\unicode[STIX]{x1D70E}]\in v^{\bot }\cap w^{\bot }\cap \mathscr{D}_{\unicode[STIX]{x1D6EC}_{N}}^{+}$
, then
![]() $\langle v,w\rangle$
is a negative-definite sublattice of
$\langle v,w\rangle$
is a negative-definite sublattice of
![]() $\unicode[STIX]{x1D6EC}_{N}$
.◻
$\unicode[STIX]{x1D6EC}_{N}$
.◻
5.2.2 Intersection with the hyperelliptic Heegner divisor
Proposition 5.2.5.
and
Proof. We adopt the notation introduced in § 5.2.1; in particular,
![]() $v\in \unicode[STIX]{x1D6EC}$
is a fixed hyperelliptic vector. Let us prove that the right-hand side of (5.2.12) is contained in the left-hand side.
$v\in \unicode[STIX]{x1D6EC}$
is a fixed hyperelliptic vector. Let us prove that the right-hand side of (5.2.12) is contained in the left-hand side.
Let
![]() $w\in v^{\bot }$
be of square
$w\in v^{\bot }$
be of square
![]() $-2$
and divisibility
$-2$
and divisibility
![]() $1$
(as vector of
$1$
(as vector of
![]() $v^{\bot }$
). Then
$v^{\bot }$
). Then
![]() $w$
is a nodal vector of
$w$
is a nodal vector of
![]() $(\unicode[STIX]{x1D6EC}_{N},\unicode[STIX]{x1D709}_{N})$
and
$(\unicode[STIX]{x1D6EC}_{N},\unicode[STIX]{x1D709}_{N})$
and
![]() $\unicode[STIX]{x1D70B}_{v^{\bot }}(w)=w$
; thus,
$\unicode[STIX]{x1D70B}_{v^{\bot }}(w)=w$
; thus,
![]() $H_{n}(N-1)\subset f_{N}^{-1}H_{n}(N)$
by Proposition 5.2.4.
$H_{n}(N-1)\subset f_{N}^{-1}H_{n}(N)$
by Proposition 5.2.4.
Let us prove that
![]() $H_{h}(N-1)\subset f_{N}^{-1}H_{n}(N)$
. Let
$H_{h}(N-1)\subset f_{N}^{-1}H_{n}(N)$
. Let
![]() $u$
be a hyperelliptic vector of
$u$
be a hyperelliptic vector of
![]() $(v^{\bot },\unicode[STIX]{x1D709}_{N-1})$
. Let
$(v^{\bot },\unicode[STIX]{x1D709}_{N-1})$
. Let
![]() $w:=(v+u)/2$
; then
$w:=(v+u)/2$
; then
![]() $w\in \unicode[STIX]{x1D6EC}_{N}$
: see the definition of the decoration of
$w\in \unicode[STIX]{x1D6EC}_{N}$
: see the definition of the decoration of
![]() $v^{\bot }$
in § 1.4. We claim that
$v^{\bot }$
in § 1.4. We claim that
![]() $w$
is a nodal vector. In fact,
$w$
is a nodal vector. In fact,
![]() $w^{2}=-2$
and
$w^{2}=-2$
and
![]() $\operatorname{div}(w)=1$
because there exists
$\operatorname{div}(w)=1$
because there exists
![]() $z\in v^{\bot }$
such that
$z\in v^{\bot }$
such that
![]() $(u,z)=2$
(because
$(u,z)=2$
(because
![]() $\operatorname{div}_{v^{\bot }}(u)=2$
) and hence
$\operatorname{div}_{v^{\bot }}(u)=2$
) and hence
![]() $(w,z)=1$
. Since
$(w,z)=1$
. Since
![]() $\unicode[STIX]{x1D70B}_{v^{\bot }}(w)=u$
, it follows that
$\unicode[STIX]{x1D70B}_{v^{\bot }}(w)=u$
, it follows that
![]() $H_{h}(N-1)\subset f_{N}^{-1}H_{n}(N)$
by Proposition 5.2.4.
$H_{h}(N-1)\subset f_{N}^{-1}H_{n}(N)$
by Proposition 5.2.4.
Now assume that
![]() $N=8k+5$
. Then
$N=8k+5$
. Then
![]() $H_{u}(N-1)\subset f_{N}^{-1}H_{n}(N)$
by Item (4) of Proposition 1.4.6.
$H_{u}(N-1)\subset f_{N}^{-1}H_{n}(N)$
by Item (4) of Proposition 1.4.6.
Next, let us prove that the left-hand side of (5.2.12) is contained in the right-hand side. By Proposition 5.2.4, it suffices to prove that, if
![]() $w$
is a nodal vector of
$w$
is a nodal vector of
![]() $(\unicode[STIX]{x1D6EC},\unicode[STIX]{x1D709}_{N})$
such that
$(\unicode[STIX]{x1D6EC},\unicode[STIX]{x1D709}_{N})$
such that
![]() $\langle v,w\rangle$
is negative definite, then
$\langle v,w\rangle$
is negative definite, then
![]() $\unicode[STIX]{x1D70B}_{v^{\bot }}(w)$
is either a nodal or a hyperelliptic vector, or
$\unicode[STIX]{x1D70B}_{v^{\bot }}(w)$
is either a nodal or a hyperelliptic vector, or
![]() $N\equiv 5\hspace{0.6em}({\rm mod}\hspace{0.2em}8)$
and
$N\equiv 5\hspace{0.6em}({\rm mod}\hspace{0.2em}8)$
and
![]() $\unicode[STIX]{x1D70B}_{v^{\bot }}(w)$
is a unigonal vector. Computing the determinant of the restriction of the quadratic form to
$\unicode[STIX]{x1D70B}_{v^{\bot }}(w)$
is a unigonal vector. Computing the determinant of the restriction of the quadratic form to
![]() $\langle v,w\rangle$
(which is strictly positive), we conclude that
$\langle v,w\rangle$
(which is strictly positive), we conclude that
![]() $(v,w)\in \{0,\pm 2\}$
; multiplying
$(v,w)\in \{0,\pm 2\}$
; multiplying
![]() $w$
by
$w$
by
![]() $(-1)$
if necessary, we may assume that
$(-1)$
if necessary, we may assume that
![]() $(v,w)\in \{0,2\}$
.
$(v,w)\in \{0,2\}$
.
If
![]() $(v,w)=0$
, then
$(v,w)=0$
, then
![]() $\operatorname{div}_{v^{\bot }}(w)\in \{1,2\}$
. If
$\operatorname{div}_{v^{\bot }}(w)\in \{1,2\}$
. If
![]() $\operatorname{div}_{v^{\bot }}(w)=1$
, then
$\operatorname{div}_{v^{\bot }}(w)=1$
, then
![]() $w$
is a nodal class of
$w$
is a nodal class of
![]() $v^{\bot }$
. If
$v^{\bot }$
. If
![]() $\operatorname{div}_{v^{\bot }}(w)=2$
, then
$\operatorname{div}_{v^{\bot }}(w)=2$
, then
![]() $w$
is a unigonal class of
$w$
is a unigonal class of
![]() $v^{\bot }$
and then necessarily
$v^{\bot }$
and then necessarily
![]() $N\equiv 5\hspace{0.6em}({\rm mod}\hspace{0.2em}8)$
because the discriminant group
$N\equiv 5\hspace{0.6em}({\rm mod}\hspace{0.2em}8)$
because the discriminant group
![]() $A_{v^{\bot }}=A_{\unicode[STIX]{x1D6EC}_{N-1}}$
contains the class
$A_{v^{\bot }}=A_{\unicode[STIX]{x1D6EC}_{N-1}}$
contains the class
![]() $[w/2]$
of square
$[w/2]$
of square
![]() $-1/2$
modulo
$-1/2$
modulo
![]() $2\mathbb{Z}$
.
$2\mathbb{Z}$
.
If
![]() $(v,w)=2$
, let
$(v,w)=2$
, let
![]() $u:=v+2w$
. Then
$u:=v+2w$
. Then
![]() $\unicode[STIX]{x1D70B}_{v^{\bot }}(w)=u$
. We claim that
$\unicode[STIX]{x1D70B}_{v^{\bot }}(w)=u$
. We claim that
![]() $u$
is a hyperelliptic vector of
$u$
is a hyperelliptic vector of
![]() $(v^{\bot },\unicode[STIX]{x1D709}_{N-1})$
. First,
$(v^{\bot },\unicode[STIX]{x1D709}_{N-1})$
. First,
![]() $u^{2}=-4$
. It remains to check that
$u^{2}=-4$
. It remains to check that
![]() $\operatorname{div}_{v^{\bot }}(u)=2$
and
$\operatorname{div}_{v^{\bot }}(u)=2$
and
![]() $u^{\ast }$
is equal to the decoration that
$u^{\ast }$
is equal to the decoration that
![]() $v^{\bot }$
inherits from the decoration
$v^{\bot }$
inherits from the decoration
![]() $\unicode[STIX]{x1D709}_{N}$
of
$\unicode[STIX]{x1D709}_{N}$
of
![]() $\unicode[STIX]{x1D6EC}_{N}$
. Clearly,
$\unicode[STIX]{x1D6EC}_{N}$
. Clearly,
![]() $\operatorname{div}_{v^{\bot }}(u)$
is a multiple of
$\operatorname{div}_{v^{\bot }}(u)$
is a multiple of
![]() $2$
and hence we must show that
$2$
and hence we must show that
![]() $\operatorname{div}_{v^{\bot }}(u)\not =4$
. If
$\operatorname{div}_{v^{\bot }}(u)\not =4$
. If
![]() $\operatorname{div}_{v^{\bot }}(u)=4$
, then
$\operatorname{div}_{v^{\bot }}(u)=4$
, then
![]() $N=8k+4$
and hence
$N=8k+4$
and hence
![]() $\unicode[STIX]{x1D6EC}_{N}\cong \text{II}_{2,2+8k}\oplus A_{1}^{2}$
; let
$\unicode[STIX]{x1D6EC}_{N}\cong \text{II}_{2,2+8k}\oplus A_{1}^{2}$
; let
![]() $a,b$
be generators of the two
$a,b$
be generators of the two
![]() $A_{1}$
-summands. We may assume that
$A_{1}$
-summands. We may assume that
![]() $v=a+b$
because any two decorated dimension-
$v=a+b$
because any two decorated dimension-
![]() $N$
$N$
![]() $D$
-lattices are isomorphic. Then there exist
$D$
-lattices are isomorphic. Then there exist
![]() $r,m\in \mathbb{Z}$
, and a primitive
$r,m\in \mathbb{Z}$
, and a primitive
![]() $c\in \text{II}_{2,2+8k}$
, such that
$c\in \text{II}_{2,2+8k}$
, such that
In fact, write
![]() $w=ra+sb+tc$
, where
$w=ra+sb+tc$
, where
![]() $r,s,t\in \mathbb{Z}$
and
$r,s,t\in \mathbb{Z}$
and
![]() $c\in \text{II}_{2,2+8k}$
is primitive. Then
$c\in \text{II}_{2,2+8k}$
is primitive. Then
![]() $s=-(1+r)$
, because
$s=-(1+r)$
, because
![]() $(v,w)=2$
, and
$(v,w)=2$
, and
![]() $t$
is odd because the divisibility of
$t$
is odd because the divisibility of
![]() $w$
in
$w$
in
![]() $\unicode[STIX]{x1D6EC}_{N}$
is
$\unicode[STIX]{x1D6EC}_{N}$
is
![]() $1$
. Thus,
$1$
. Thus,
![]() $u=(1+2x)(a-b)+2(2m+1)c$
and, since
$u=(1+2x)(a-b)+2(2m+1)c$
and, since
![]() $\text{II}_{2,2+8k}$
is unimodular, it follows that
$\text{II}_{2,2+8k}$
is unimodular, it follows that
![]() $\operatorname{div}_{v^{\bot }}(u)\not =4$
. In order to prove that
$\operatorname{div}_{v^{\bot }}(u)\not =4$
. In order to prove that
![]() $u^{\ast }$
is the decoration of
$u^{\ast }$
is the decoration of
![]() $v^{\bot }$
, we recall that the latter is equal to
$v^{\bot }$
, we recall that the latter is equal to
![]() $[z/2]$
, where
$[z/2]$
, where
![]() $z\in v^{\bot }$
is such that
$z\in v^{\bot }$
is such that
![]() $(v+z)/2\in \unicode[STIX]{x1D6EC}$
; see § 1.4 (we have denoted by
$(v+z)/2\in \unicode[STIX]{x1D6EC}$
; see § 1.4 (we have denoted by
![]() $z$
the vector denoted
$z$
the vector denoted
![]() $w$
in § 1.4). Since
$w$
in § 1.4). Since
![]() $u=v+2w$
, it follows that
$u=v+2w$
, it follows that
![]() $[u/2]=-[z/2]=[z/2]$
in the discriminant group
$[u/2]=-[z/2]=[z/2]$
in the discriminant group
![]() $A_{v^{\bot }}$
. This proves that
$A_{v^{\bot }}$
. This proves that
![]() $\unicode[STIX]{x1D70B}_{v^{\bot }}(w)$
is hyperelliptic and finishes the proof of (5.2.12).
$\unicode[STIX]{x1D70B}_{v^{\bot }}(w)$
is hyperelliptic and finishes the proof of (5.2.12).
Now let us prove (5.2.13). Let
![]() $N-2=8k+a$
. If
$N-2=8k+a$
. If
![]() $a=0$
, then
$a=0$
, then
![]() $H_{u}(N)=0$
and hence (5.2.13) holds trivially. Thus, we may assume that
$H_{u}(N)=0$
and hence (5.2.13) holds trivially. Thus, we may assume that
![]() $a\in \{1,\ldots ,7\}$
. First, we will prove that the right-hand side is contained in the left-hand side. We may assume that
$a\in \{1,\ldots ,7\}$
. First, we will prove that the right-hand side is contained in the left-hand side. We may assume that
![]() $a\in \{2,\ldots ,7\}$
because if
$a\in \{2,\ldots ,7\}$
because if
![]() $a=1$
, then
$a=1$
, then
![]() $H_{h}(N-1)=0$
. By Remark 1.1.4, we may identify
$H_{h}(N-1)=0$
. By Remark 1.1.4, we may identify
![]() $\unicode[STIX]{x1D6EC}_{N}$
with
$\unicode[STIX]{x1D6EC}_{N}$
with
![]() $\text{II}_{2,2+8k}\oplus D_{a}$
. Let
$\text{II}_{2,2+8k}\oplus D_{a}$
. Let
![]() $v=(0_{4+8k},(0,\ldots ,0,2))$
; then
$v=(0_{4+8k},(0,\ldots ,0,2))$
; then
![]() $v^{2}=-4$
and
$v^{2}=-4$
and
![]() $\operatorname{div}(v)=2$
. We let
$\operatorname{div}(v)=2$
. We let
![]() $\unicode[STIX]{x1D709}_{N}=[v/2]$
and hence
$\unicode[STIX]{x1D709}_{N}=[v/2]$
and hence
![]() $v$
is hyperelliptic. Now suppose that
$v$
is hyperelliptic. Now suppose that
![]() $N$
is odd. Let
$N$
is odd. Let
![]() $w=(0_{4+8k},(2,\ldots ,2))$
; then
$w=(0_{4+8k},(2,\ldots ,2))$
; then
![]() $w$
is a unigonal vector of
$w$
is a unigonal vector of
![]() $(\unicode[STIX]{x1D6EC}_{N},\unicode[STIX]{x1D709}_{N})$
; see the proof of Proposition 1.3.3. Then
$(\unicode[STIX]{x1D6EC}_{N},\unicode[STIX]{x1D709}_{N})$
; see the proof of Proposition 1.3.3. Then
![]() $\unicode[STIX]{x1D70B}_{v^{\bot }}(w)=(0_{4+8k},(1,\ldots ,1))\in \text{II}_{2,2+8k}\oplus D_{a-1}$
. Since
$\unicode[STIX]{x1D70B}_{v^{\bot }}(w)=(0_{4+8k},(1,\ldots ,1))\in \text{II}_{2,2+8k}\oplus D_{a-1}$
. Since
![]() $\unicode[STIX]{x1D70B}_{v^{\bot }}(w)$
is a unigonal vector of
$\unicode[STIX]{x1D70B}_{v^{\bot }}(w)$
is a unigonal vector of
![]() $(\unicode[STIX]{x1D6EC}_{N-1},\unicode[STIX]{x1D709}_{N-1})$
(see the proof of Proposition 1.3.3), it follows that
$(\unicode[STIX]{x1D6EC}_{N-1},\unicode[STIX]{x1D709}_{N-1})$
(see the proof of Proposition 1.3.3), it follows that
![]() $f_{N}^{-1}H_{u}(N)\supset H_{u}(N-1)$
if
$f_{N}^{-1}H_{u}(N)\supset H_{u}(N-1)$
if
![]() $N$
is odd. The proof for
$N$
is odd. The proof for
![]() $N$
even is analogous.
$N$
even is analogous.
Lastly, we prove that the left-hand side of (5.2.13) is contained in the right-hand side. By Proposition 5.2.4, it suffices to prove that, if
![]() $w$
is a unigonal vector of
$w$
is a unigonal vector of
![]() $(\unicode[STIX]{x1D6EC},\unicode[STIX]{x1D709}_{N})$
such that
$(\unicode[STIX]{x1D6EC},\unicode[STIX]{x1D709}_{N})$
such that
![]() $\langle v,w\rangle$
is negative definite, then
$\langle v,w\rangle$
is negative definite, then
![]() $\unicode[STIX]{x1D70B}_{v^{\bot }}(w)$
is a unigonal vector. Let
$\unicode[STIX]{x1D70B}_{v^{\bot }}(w)$
is a unigonal vector. Let
![]() $a\in \{1,\ldots ,7\}$
be the residue of
$a\in \{1,\ldots ,7\}$
be the residue of
![]() $N-2$
modulo
$N-2$
modulo
![]() $8$
. Let us assume that
$8$
. Let us assume that
![]() $N$
is odd. Then
$N$
is odd. Then
![]() $w^{2}=-4a$
and
$w^{2}=-4a$
and
![]() $\operatorname{div}(w)=4.$
We claim that
$\operatorname{div}(w)=4.$
We claim that
In fact, we may assume that
![]() $w^{\ast }=\unicode[STIX]{x1D701}$
and
$w^{\ast }=\unicode[STIX]{x1D701}$
and
![]() $\unicode[STIX]{x1D709}=2\unicode[STIX]{x1D701}$
. Thus,
$\unicode[STIX]{x1D709}=2\unicode[STIX]{x1D701}$
. Thus,
and hence there exists
![]() $s\in \mathbb{Z}$
such that
$s\in \mathbb{Z}$
such that
![]() $(v,w)=-4a+8s$
. Since
$(v,w)=-4a+8s$
. Since
![]() $\langle v,w\rangle$
is negative definite, it follows that
$\langle v,w\rangle$
is negative definite, it follows that
![]() $a\in \{3,7\}$
(recall that
$a\in \{3,7\}$
(recall that
![]() $H_{h}(N-1)=0$
if
$H_{h}(N-1)=0$
if
![]() $a=1$
) and that
$a=1$
) and that
![]() $(v,w)=\pm 4$
. Moreover,
$(v,w)=\pm 4$
. Moreover,
![]() $(v+w)/2\in \unicode[STIX]{x1D6EC}$
because
$(v+w)/2\in \unicode[STIX]{x1D6EC}$
because
![]() $2[w/4]=[v/2]$
in the discriminant group. We have proved (5.2.14). Multiplying
$2[w/4]=[v/2]$
in the discriminant group. We have proved (5.2.14). Multiplying
![]() $w$
by
$w$
by
![]() $(-1)$
if necessary, we may assume that
$(-1)$
if necessary, we may assume that
![]() $(v,w)=4$
; it follows that
$(v,w)=4$
; it follows that
![]() $\unicode[STIX]{x1D70B}_{v^{\bot }}(w)=(v+w)/2$
. Now
$\unicode[STIX]{x1D70B}_{v^{\bot }}(w)=(v+w)/2$
. Now
![]() $(v+w)/2$
is a unigonal vector of
$(v+w)/2$
is a unigonal vector of
![]() $v^{\bot }$
, as required. Now assume that
$v^{\bot }$
, as required. Now assume that
![]() $N$
is even. Arguing as above, one shows that
$N$
is even. Arguing as above, one shows that
![]() $(v,w)=\pm 2$
and hence we may assume that
$(v,w)=\pm 2$
and hence we may assume that
![]() $(v,w)=2$
. Then
$(v,w)=2$
. Then
![]() $\unicode[STIX]{x1D70B}_{v^{\bot }}(w)=v+2w$
. Since
$\unicode[STIX]{x1D70B}_{v^{\bot }}(w)=v+2w$
. Since
![]() $v+2w$
is primitive,
$v+2w$
is primitive,
![]() $\operatorname{div}_{v^{\bot }}(v+2w)=4$
, and
$\operatorname{div}_{v^{\bot }}(v+2w)=4$
, and
![]() $(v+2w)^{2}=-4(a-1)$
, this proves that
$(v+2w)^{2}=-4(a-1)$
, this proves that
![]() $\unicode[STIX]{x1D70B}_{v^{\bot }}(w)$
is a unigonal vector of
$\unicode[STIX]{x1D70B}_{v^{\bot }}(w)$
is a unigonal vector of
![]() $v^{\bot }$
.◻
$v^{\bot }$
.◻
Let us prove (5.2.4) and (5.2.5). First, notice that
![]() $H_{n}(N-1)$
,
$H_{n}(N-1)$
,
![]() $H_{h}(N-1)$
, and
$H_{h}(N-1)$
, and
![]() $H_{u}(N-1)$
are irreducible. By Proposition 5.2.5, it remains to show that
$H_{u}(N-1)$
are irreducible. By Proposition 5.2.5, it remains to show that
In order to prove the above equalities, we fix a hyperelliptic vector
![]() $v$
of
$v$
of
![]() $(\unicode[STIX]{x1D6EC}_{N},\unicode[STIX]{x1D709}_{N})$
and we let
$(\unicode[STIX]{x1D6EC}_{N},\unicode[STIX]{x1D709}_{N})$
and we let
![]() $w\in v^{\bot }\cong \unicode[STIX]{x1D6EC}_{N-1}$
be a vector such that one of the following holds:
$w\in v^{\bot }\cong \unicode[STIX]{x1D6EC}_{N-1}$
be a vector such that one of the following holds:
(1)
 $w$
is a nodal vector of
$w$
is a nodal vector of
 $(\unicode[STIX]{x1D6EC}_{N-1},\unicode[STIX]{x1D709}_{N-1})$
;
$(\unicode[STIX]{x1D6EC}_{N-1},\unicode[STIX]{x1D709}_{N-1})$
;(2)
 $w$
is a hyperelliptic vector of
$w$
is a hyperelliptic vector of
 $(\unicode[STIX]{x1D6EC}_{N-1},\unicode[STIX]{x1D709}_{N-1})$
;
$(\unicode[STIX]{x1D6EC}_{N-1},\unicode[STIX]{x1D709}_{N-1})$
;(3)
 $w$
is a unigonal vector of
$w$
is a unigonal vector of
 $(\unicode[STIX]{x1D6EC}_{N-1},\unicode[STIX]{x1D709}_{N-1})$
.
$(\unicode[STIX]{x1D6EC}_{N-1},\unicode[STIX]{x1D709}_{N-1})$
.
Let
![]() $[\unicode[STIX]{x1D70E}]\in \{v,w\}\text{}^{\bot }\cap \mathscr{D}_{\unicode[STIX]{x1D6EC}_{N}}^{+}$
. Then
$[\unicode[STIX]{x1D70E}]\in \{v,w\}\text{}^{\bot }\cap \mathscr{D}_{\unicode[STIX]{x1D6EC}_{N}}^{+}$
. Then
![]() $[\unicode[STIX]{x1D70E}]\in f_{N}(H_{n}(N-1))$
if (1) holds,
$[\unicode[STIX]{x1D70E}]\in f_{N}(H_{n}(N-1))$
if (1) holds,
![]() $[\unicode[STIX]{x1D70E}]\in f_{N}(H_{h}(N-1))$
if (2) holds, and
$[\unicode[STIX]{x1D70E}]\in f_{N}(H_{h}(N-1))$
if (2) holds, and
![]() $[\unicode[STIX]{x1D70E}]\in f_{N}(H_{u}(N-1))$
if (3) holds. Since each of
$[\unicode[STIX]{x1D70E}]\in f_{N}(H_{u}(N-1))$
if (3) holds. Since each of
![]() $H_{n}(N-1)$
,
$H_{n}(N-1)$
,
![]() $H_{h}(N-1)$
, and
$H_{h}(N-1)$
, and
![]() $H_{u}(N-1)$
is irreducible, we may prove formulae (5.2.15)–(5.2.18) by analyzing the local structure of
$H_{u}(N-1)$
is irreducible, we may prove formulae (5.2.15)–(5.2.18) by analyzing the local structure of
![]() $\mathscr{F}(N)$
,
$\mathscr{F}(N)$
,
![]() $H_{h}(N)$
etc. at the
$H_{h}(N)$
etc. at the
![]() $\unicode[STIX]{x1D6E4}_{\unicode[STIX]{x1D709}_{N}}$
-orbit of
$\unicode[STIX]{x1D6E4}_{\unicode[STIX]{x1D709}_{N}}$
-orbit of
![]() $[\unicode[STIX]{x1D70E}]$
. We claim that the following hold.
$[\unicode[STIX]{x1D70E}]$
. We claim that the following hold.
(1′) If
 $w$
is a nodal vector of
$w$
is a nodal vector of
 $(\unicode[STIX]{x1D6EC}_{N-1},\unicode[STIX]{x1D709}_{N-1})$
, then and every non-trivial isometry of
$(\unicode[STIX]{x1D6EC}_{N-1},\unicode[STIX]{x1D709}_{N-1})$
, then and every non-trivial isometry of $$\begin{eqnarray}\unicode[STIX]{x1D6EC}_{N}\cap \langle v,w\rangle _{\mathbb{Q}}=\langle v,w\rangle _{\mathbb{Z}}:=\mathbb{Z}v+\mathbb{Z}w\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6EC}_{N}\cap \langle v,w\rangle _{\mathbb{Q}}=\langle v,w\rangle _{\mathbb{Z}}:=\mathbb{Z}v+\mathbb{Z}w\end{eqnarray}$$
 $\langle v,w\rangle _{\mathbb{Z}}$
is either the reflection in a reflective vector of
$\langle v,w\rangle _{\mathbb{Z}}$
is either the reflection in a reflective vector of
 $\langle v,w\rangle _{\mathbb{Z}}$
or multiplication by
$\langle v,w\rangle _{\mathbb{Z}}$
or multiplication by
 $-1$
.
$-1$
.(2′) If
 $w$
is a hyperelliptic vector of
$w$
is a hyperelliptic vector of
 $(\unicode[STIX]{x1D6EC}_{N-1},\unicode[STIX]{x1D709}_{N-1})$
, then and every non-trivial isometry of
$(\unicode[STIX]{x1D6EC}_{N-1},\unicode[STIX]{x1D709}_{N-1})$
, then and every non-trivial isometry of $$\begin{eqnarray}\unicode[STIX]{x1D6EC}_{N}\cap \langle v,w\rangle _{\mathbb{Q}}=\langle (v+w)/2,(v-w)/2\rangle _{\mathbb{Z}}\cong D_{2}\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6EC}_{N}\cap \langle v,w\rangle _{\mathbb{Q}}=\langle (v+w)/2,(v-w)/2\rangle _{\mathbb{Z}}\cong D_{2}\end{eqnarray}$$
 $\langle (v+w)/2,(v-w)/2\rangle _{\mathbb{Z}}$
is either the reflection in a reflective vector of
$\langle (v+w)/2,(v-w)/2\rangle _{\mathbb{Z}}$
is either the reflection in a reflective vector of
 $\langle (v+w)/2,(v-w)/2\rangle _{\mathbb{Z}}$
or multiplication by
$\langle (v+w)/2,(v-w)/2\rangle _{\mathbb{Z}}$
or multiplication by
 $-1$
.
$-1$
.
(3a′) If
 $w$
is a unigonal vector of
$w$
is a unigonal vector of
 $(\unicode[STIX]{x1D6EC}_{N-1},\unicode[STIX]{x1D709}_{N-1})$
and
$(\unicode[STIX]{x1D6EC}_{N-1},\unicode[STIX]{x1D709}_{N-1})$
and
 $N\equiv 4\hspace{0.6em}({\rm mod}\hspace{0.2em}8)$
, then
$N\equiv 4\hspace{0.6em}({\rm mod}\hspace{0.2em}8)$
, then
 $\unicode[STIX]{x1D6EC}_{N}\cap \langle v,w\rangle _{\mathbb{Q}}=\langle (v+w)/2,(v-w)/2\rangle _{\mathbb{Z}}\cong D_{2}$
and every non-trivial isometry of
$\unicode[STIX]{x1D6EC}_{N}\cap \langle v,w\rangle _{\mathbb{Q}}=\langle (v+w)/2,(v-w)/2\rangle _{\mathbb{Z}}\cong D_{2}$
and every non-trivial isometry of
 $\langle v,w\rangle _{\mathbb{Z}}$
is either the reflection in a reflective vector of
$\langle v,w\rangle _{\mathbb{Z}}$
is either the reflection in a reflective vector of
 $\langle (v+w)/2,(v-w)/2\rangle _{\mathbb{Z}}$
or multiplication by
$\langle (v+w)/2,(v-w)/2\rangle _{\mathbb{Z}}$
or multiplication by
 $-1$
.
$-1$
.(3b′) If
 $w$
is a unigonal vector of
$w$
is a unigonal vector of
 $(\unicode[STIX]{x1D6EC}_{N-1},\unicode[STIX]{x1D709}_{N-1})$
and
$(\unicode[STIX]{x1D6EC}_{N-1},\unicode[STIX]{x1D709}_{N-1})$
and
 $N\not \equiv 4\hspace{0.6em}({\rm mod}\hspace{0.2em}8)$
, then
$N\not \equiv 4\hspace{0.6em}({\rm mod}\hspace{0.2em}8)$
, then
 $\unicode[STIX]{x1D6EC}_{N}\cap \langle v,w\rangle _{\mathbb{Q}}=\langle v,w\rangle _{\mathbb{Z}}$
and every non-trivial isometry of
$\unicode[STIX]{x1D6EC}_{N}\cap \langle v,w\rangle _{\mathbb{Q}}=\langle v,w\rangle _{\mathbb{Z}}$
and every non-trivial isometry of
 $\langle v,w\rangle _{\mathbb{Z}}$
is either the reflection in a reflective vector of
$\langle v,w\rangle _{\mathbb{Z}}$
is either the reflection in a reflective vector of
 $\langle v,w\rangle _{\mathbb{Z}}$
or multiplication by
$\langle v,w\rangle _{\mathbb{Z}}$
or multiplication by
 $-1$
.
$-1$
.
In fact, in order to determine
![]() $\unicode[STIX]{x1D6EC}_{N}\cap \langle v,w\rangle _{\mathbb{Q}}$
, it suffices to recall that
$\unicode[STIX]{x1D6EC}_{N}\cap \langle v,w\rangle _{\mathbb{Q}}$
, it suffices to recall that
![]() $\unicode[STIX]{x1D6EC}_{N}$
is generated (over
$\unicode[STIX]{x1D6EC}_{N}$
is generated (over
![]() $\mathbb{Z}$
) by
$\mathbb{Z}$
) by
![]() $\mathbb{Z}v\oplus v^{\bot }$
, together with
$\mathbb{Z}v\oplus v^{\bot }$
, together with
![]() $(v+u)/2$
, where
$(v+u)/2$
, where
![]() $u\in v^{\bot }=\unicode[STIX]{x1D6EC}_{N-1}$
is a hyperelliptic vector of
$u\in v^{\bot }=\unicode[STIX]{x1D6EC}_{N-1}$
is a hyperelliptic vector of
![]() $(\unicode[STIX]{x1D6EC}_{N-1},\unicode[STIX]{x1D709}_{N-1})$
. Once
$(\unicode[STIX]{x1D6EC}_{N-1},\unicode[STIX]{x1D709}_{N-1})$
. Once
![]() $\unicode[STIX]{x1D6EC}_{N}\cap \langle v,w\rangle _{\mathbb{Q}}$
has been determined, the statements about non-trivial isometries are trivial. Now let
$\unicode[STIX]{x1D6EC}_{N}\cap \langle v,w\rangle _{\mathbb{Q}}$
has been determined, the statements about non-trivial isometries are trivial. Now let
![]() $[\unicode[STIX]{x1D70E}]$
be a very general point of
$[\unicode[STIX]{x1D70E}]$
be a very general point of
![]() $\{v,w\}\text{}^{\bot }\cap \mathscr{D}_{\unicode[STIX]{x1D6EC}_{N}}^{+}$
. Then
$\{v,w\}\text{}^{\bot }\cap \mathscr{D}_{\unicode[STIX]{x1D6EC}_{N}}^{+}$
. Then
and
![]() $-1_{\{v,w\}\text{}^{\bot }}$
is the only non-trivial element of
$-1_{\{v,w\}\text{}^{\bot }}$
is the only non-trivial element of
![]() $O(\unicode[STIX]{x1D6EC}_{N}\cap \{v,w\}\text{}_{\mathbb{Q}}^{\bot })$
stabilizing
$O(\unicode[STIX]{x1D6EC}_{N}\cap \{v,w\}\text{}_{\mathbb{Q}}^{\bot })$
stabilizing
![]() $[\unicode[STIX]{x1D70E}]$
. It follows that there is a natural embedding
$[\unicode[STIX]{x1D70E}]$
. It follows that there is a natural embedding
(Here
![]() $\text{Stab}([\unicode[STIX]{x1D70E}])<\unicode[STIX]{x1D6E4}_{\unicode[STIX]{x1D709}_{N}}$
is the stabilizer of
$\text{Stab}([\unicode[STIX]{x1D70E}])<\unicode[STIX]{x1D6E4}_{\unicode[STIX]{x1D709}_{N}}$
is the stabilizer of
![]() $[\unicode[STIX]{x1D70E}]$
.)
$[\unicode[STIX]{x1D70E}]$
.)
Claim 5.2.6. Let
![]() $[\unicode[STIX]{x1D70E}]$
be a very general point of
$[\unicode[STIX]{x1D70E}]$
be a very general point of
![]() $\{v,w\}\text{}^{\bot }\cap \mathscr{D}_{\unicode[STIX]{x1D6EC}_{N}}^{+}$
; hence, there is the natural embedding (5.2.19).
$\{v,w\}\text{}^{\bot }\cap \mathscr{D}_{\unicode[STIX]{x1D6EC}_{N}}^{+}$
; hence, there is the natural embedding (5.2.19).
(I) If
 $w$
is a reflective vector of
$w$
is a reflective vector of
 $(\unicode[STIX]{x1D6EC}_{N-1},\unicode[STIX]{x1D709}_{N-1})$
, i.e. Item (1) or Item (2) above holds, or
$(\unicode[STIX]{x1D6EC}_{N-1},\unicode[STIX]{x1D709}_{N-1})$
, i.e. Item (1) or Item (2) above holds, or
 $N\equiv 4,5\hspace{0.6em}({\rm mod}\hspace{0.2em}8)$
and Item (3) holds, then
$N\equiv 4,5\hspace{0.6em}({\rm mod}\hspace{0.2em}8)$
and Item (3) holds, then
 $T_{\unicode[STIX]{x1D70E}}$
is surjective.
$T_{\unicode[STIX]{x1D70E}}$
is surjective.(II) If
 $w$
is not a reflective vector of
$w$
is not a reflective vector of
 $(\unicode[STIX]{x1D6EC}_{N-1},\unicode[STIX]{x1D709}_{N-1})$
, i.e.
$(\unicode[STIX]{x1D6EC}_{N-1},\unicode[STIX]{x1D709}_{N-1})$
, i.e.
 $N\not \equiv 4,5\hspace{0.6em}({\rm mod}\hspace{0.2em}8)$
and Item (3) holds, then
$N\not \equiv 4,5\hspace{0.6em}({\rm mod}\hspace{0.2em}8)$
and Item (3) holds, then
 $\text{Stab}([\unicode[STIX]{x1D70E}])=\{\pm \unicode[STIX]{x1D70C}_{v}\}$
.
$\text{Stab}([\unicode[STIX]{x1D70E}])=\{\pm \unicode[STIX]{x1D70C}_{v}\}$
.
Let
![]() $w\in v^{\bot }$
be a vector such that (1), (2), or (3) above holds. Then Claim 5.2.6 allows us to describe explicitly a neighborhood in
$w\in v^{\bot }$
be a vector such that (1), (2), or (3) above holds. Then Claim 5.2.6 allows us to describe explicitly a neighborhood in
![]() $\mathscr{F}(N)$
of the
$\mathscr{F}(N)$
of the
![]() $\unicode[STIX]{x1D6E4}_{\unicode[STIX]{x1D709}}$
-orbit of a very general point
$\unicode[STIX]{x1D6E4}_{\unicode[STIX]{x1D709}}$
-orbit of a very general point
![]() $[\unicode[STIX]{x1D70E}]\in \{v,w\}\text{}^{\bot }\cap \mathscr{D}_{\unicode[STIX]{x1D6EC}_{N}}^{+}$
. First of all, since
$[\unicode[STIX]{x1D70E}]\in \{v,w\}\text{}^{\bot }\cap \mathscr{D}_{\unicode[STIX]{x1D6EC}_{N}}^{+}$
. First of all, since
![]() $-1_{\unicode[STIX]{x1D6EC}_{N}}$
acts trivially, we must deal only with the action of
$-1_{\unicode[STIX]{x1D6EC}_{N}}$
acts trivially, we must deal only with the action of
![]() $\text{Stab}^{0}([\unicode[STIX]{x1D70E}]):=\text{Stab}([\unicode[STIX]{x1D70E}])/\langle -1_{\unicode[STIX]{x1D6EC}_{N}}\rangle$
and, secondly, by Claim 5.2.6, the germ of
$\text{Stab}^{0}([\unicode[STIX]{x1D70E}]):=\text{Stab}([\unicode[STIX]{x1D70E}])/\langle -1_{\unicode[STIX]{x1D6EC}_{N}}\rangle$
and, secondly, by Claim 5.2.6, the germ of
![]() $\unicode[STIX]{x1D6E4}_{\unicode[STIX]{x1D709}}[\unicode[STIX]{x1D70E}]$
in
$\unicode[STIX]{x1D6E4}_{\unicode[STIX]{x1D709}}[\unicode[STIX]{x1D70E}]$
in
![]() $\mathscr{F}(N)$
is naturally isomorphic to the product of the smooth germ
$\mathscr{F}(N)$
is naturally isomorphic to the product of the smooth germ
![]() $(\{v,w\}\text{}^{\bot }\cap \mathscr{D}_{\unicode[STIX]{x1D6EC}_{N}}^{+},[\unicode[STIX]{x1D70E}])$
and the germ of
$(\{v,w\}\text{}^{\bot }\cap \mathscr{D}_{\unicode[STIX]{x1D6EC}_{N}}^{+},[\unicode[STIX]{x1D70E}])$
and the germ of
![]() $\text{Stab}^{0}([\unicode[STIX]{x1D70E}])\backslash \langle v,w\rangle _{\mathbb{C}}$
at the origin. Let
$\text{Stab}^{0}([\unicode[STIX]{x1D70E}])\backslash \langle v,w\rangle _{\mathbb{C}}$
at the origin. Let
![]() $(x_{1},x_{2})$
be coordinates on the vector space
$(x_{1},x_{2})$
be coordinates on the vector space
![]() $\langle v,w\rangle _{\mathbb{C}}$
corresponding to the basis
$\langle v,w\rangle _{\mathbb{C}}$
corresponding to the basis
![]() $\{v,w\}$
. Thus,
$\{v,w\}$
. Thus,
We claim that the following hold.
(1′′) If
 $w$
is a nodal vector of
$w$
is a nodal vector of
 $(\unicode[STIX]{x1D6EC}_{N-1},\unicode[STIX]{x1D709}_{N-1})$
, then
$(\unicode[STIX]{x1D6EC}_{N-1},\unicode[STIX]{x1D709}_{N-1})$
, then
 $\text{Stab}^{0}([\unicode[STIX]{x1D70E}])\backslash \langle v,w\rangle _{\mathbb{C}}\cong \mathbb{C}^{2}$
with coordinates
$\text{Stab}^{0}([\unicode[STIX]{x1D70E}])\backslash \langle v,w\rangle _{\mathbb{C}}\cong \mathbb{C}^{2}$
with coordinates
 $(y_{1},y_{2})$
given by
$(y_{1},y_{2})$
given by
 $y_{1}=x_{1}^{2}$
,
$y_{1}=x_{1}^{2}$
,
 $y_{2}=x_{2}^{2}$
.
$y_{2}=x_{2}^{2}$
.(2′′) If
 $w$
is a hyperelliptic vector of
$w$
is a hyperelliptic vector of
 $(\unicode[STIX]{x1D6EC}_{N-1},\unicode[STIX]{x1D709}_{N-1})$
, then
$(\unicode[STIX]{x1D6EC}_{N-1},\unicode[STIX]{x1D709}_{N-1})$
, then
 $\text{Stab}^{0}([\unicode[STIX]{x1D70E}])\backslash \langle v,w\rangle _{\mathbb{C}}\cong \mathbb{C}^{2}$
with coordinates
$\text{Stab}^{0}([\unicode[STIX]{x1D70E}])\backslash \langle v,w\rangle _{\mathbb{C}}\cong \mathbb{C}^{2}$
with coordinates
 $(y_{1},y_{2})$
given by
$(y_{1},y_{2})$
given by
 $y_{1}=x_{1}^{2}+x_{2}^{2}$
,
$y_{1}=x_{1}^{2}+x_{2}^{2}$
,
 $y_{2}=x_{1}^{2}x_{2}^{2}$
.
$y_{2}=x_{1}^{2}x_{2}^{2}$
.
(3′′a) If
 $w$
is a unigonal vector of
$w$
is a unigonal vector of
 $(\unicode[STIX]{x1D6EC}_{N-1},\unicode[STIX]{x1D709}_{N-1})$
, and
$(\unicode[STIX]{x1D6EC}_{N-1},\unicode[STIX]{x1D709}_{N-1})$
, and
 $N\equiv 4\hspace{0.6em}({\rm mod}\hspace{0.2em}8)$
, then
$N\equiv 4\hspace{0.6em}({\rm mod}\hspace{0.2em}8)$
, then
 $\text{Stab}^{0}([\unicode[STIX]{x1D70E}])\backslash \langle v,w\rangle _{\mathbb{C}}\cong \mathbb{C}^{2}$
with coordinates
$\text{Stab}^{0}([\unicode[STIX]{x1D70E}])\backslash \langle v,w\rangle _{\mathbb{C}}\cong \mathbb{C}^{2}$
with coordinates
 $(y_{1},y_{2})$
given by
$(y_{1},y_{2})$
given by
 $y_{1}=x_{1}^{2}+x_{2}^{2}$
,
$y_{1}=x_{1}^{2}+x_{2}^{2}$
,
 $y_{2}=x_{1}^{2}x_{2}^{2}$
.
$y_{2}=x_{1}^{2}x_{2}^{2}$
.
(3′′ba) If
 $w$
is a unigonal vector of
$w$
is a unigonal vector of
 $(\unicode[STIX]{x1D6EC}_{N-1},\unicode[STIX]{x1D709}_{N-1})$
, and
$(\unicode[STIX]{x1D6EC}_{N-1},\unicode[STIX]{x1D709}_{N-1})$
, and
 $N\equiv 5\hspace{0.6em}({\rm mod}\hspace{0.2em}8)$
, then
$N\equiv 5\hspace{0.6em}({\rm mod}\hspace{0.2em}8)$
, then
 $\text{Stab}^{0}([\unicode[STIX]{x1D70E}])\backslash \langle v,w\rangle _{\mathbb{C}}\cong \mathbb{C}^{2}$
with coordinates
$\text{Stab}^{0}([\unicode[STIX]{x1D70E}])\backslash \langle v,w\rangle _{\mathbb{C}}\cong \mathbb{C}^{2}$
with coordinates
 $(y_{1},y_{2})$
given by
$(y_{1},y_{2})$
given by
 $y_{1}=x_{1}^{2}$
,
$y_{1}=x_{1}^{2}$
,
 $y_{2}=x_{2}^{2}$
.
$y_{2}=x_{2}^{2}$
.(3′′bb) If
 $w$
is a unigonal vector of
$w$
is a unigonal vector of
 $(\unicode[STIX]{x1D6EC}_{N-1},\unicode[STIX]{x1D709}_{N-1})$
, and
$(\unicode[STIX]{x1D6EC}_{N-1},\unicode[STIX]{x1D709}_{N-1})$
, and
 $N\not \equiv 4,5\hspace{0.6em}({\rm mod}\hspace{0.2em}8)$
, then
$N\not \equiv 4,5\hspace{0.6em}({\rm mod}\hspace{0.2em}8)$
, then
 $\text{Stab}^{0}([\unicode[STIX]{x1D70E}])\backslash \langle v,w\rangle _{\mathbb{C}}\cong \mathbb{C}^{2}$
with coordinates
$\text{Stab}^{0}([\unicode[STIX]{x1D70E}])\backslash \langle v,w\rangle _{\mathbb{C}}\cong \mathbb{C}^{2}$
with coordinates
 $(y_{1},y_{2})$
given by
$(y_{1},y_{2})$
given by
 $y_{1}=x_{1}^{2}$
,
$y_{1}=x_{1}^{2}$
,
 $y_{2}=x_{2}$
.
$y_{2}=x_{2}$
.
In fact, the above statements follow from (
![]() $1^{\prime }$
), (
$1^{\prime }$
), (
![]() $2^{\prime }$
), (
$2^{\prime }$
), (
![]() $3^{\prime }$
), Claim 5.2.6, and Items (3) and (4) of Proposition 1.4.6. Now we are ready to prove the multiplicity formulae (5.2.15), (5.2.16), (5.2.17), and (5.2.18). Suppose that Item (1) holds. Since the relevant nodal vector of
$3^{\prime }$
), Claim 5.2.6, and Items (3) and (4) of Proposition 1.4.6. Now we are ready to prove the multiplicity formulae (5.2.15), (5.2.16), (5.2.17), and (5.2.18). Suppose that Item (1) holds. Since the relevant nodal vector of
![]() $(\unicode[STIX]{x1D6EC}_{N},\unicode[STIX]{x1D709}_{N})$
is
$(\unicode[STIX]{x1D6EC}_{N},\unicode[STIX]{x1D709}_{N})$
is
![]() $w$
itself, Item (
$w$
itself, Item (
![]() $1^{\prime \prime }$
) shows that the left-hand side of (5.2.15) is equal to the intersection number at
$1^{\prime \prime }$
) shows that the left-hand side of (5.2.15) is equal to the intersection number at
![]() $(0,0)$
of the coordinate axes of the plane
$(0,0)$
of the coordinate axes of the plane
![]() $\mathbb{C}^{2}$
(with coordinates
$\mathbb{C}^{2}$
(with coordinates
![]() $(y_{1},y_{2})$
) and hence
$(y_{1},y_{2})$
) and hence
![]() $1$
. Now suppose that Item (2) holds. Since the relevant nodal vector of
$1$
. Now suppose that Item (2) holds. Since the relevant nodal vector of
![]() $(\unicode[STIX]{x1D6EC}_{N},\unicode[STIX]{x1D709}_{N})$
is
$(\unicode[STIX]{x1D6EC}_{N},\unicode[STIX]{x1D709}_{N})$
is
![]() $(v\pm w)/2$
, Item (
$(v\pm w)/2$
, Item (
![]() $2^{\prime \prime }$
) shows that the left-hand side of (5.2.16) is equal to the intersection number at
$2^{\prime \prime }$
) shows that the left-hand side of (5.2.16) is equal to the intersection number at
![]() $(0,0)$
of
$(0,0)$
of
![]() $V(y_{1}^{2}-4y_{2}),V(y_{2})\subset \mathbb{C}^{2}$
and hence
$V(y_{1}^{2}-4y_{2}),V(y_{2})\subset \mathbb{C}^{2}$
and hence
![]() $2$
. Next, suppose that Item (3) holds and that
$2$
. Next, suppose that Item (3) holds and that
![]() $N\equiv 5\hspace{0.6em}({\rm mod}\hspace{0.2em}8)$
. Since the relevant nodal vector of
$N\equiv 5\hspace{0.6em}({\rm mod}\hspace{0.2em}8)$
. Since the relevant nodal vector of
![]() $(\unicode[STIX]{x1D6EC}_{N},\unicode[STIX]{x1D709}_{N})$
is
$(\unicode[STIX]{x1D6EC}_{N},\unicode[STIX]{x1D709}_{N})$
is
![]() $w$
itself, Item (
$w$
itself, Item (
![]() $3^{\prime \prime }\text{ba}$
) shows that the left-hand side of (5.2.17) is equal to
$3^{\prime \prime }\text{ba}$
) shows that the left-hand side of (5.2.17) is equal to
![]() $1$
. Lastly, suppose that Item (3) holds and that
$1$
. Lastly, suppose that Item (3) holds and that
![]() $N\not \equiv 5\hspace{0.6em}({\rm mod}\hspace{0.2em}8)$
. The relevant unigonal vector of
$N\not \equiv 5\hspace{0.6em}({\rm mod}\hspace{0.2em}8)$
. The relevant unigonal vector of
![]() $(\unicode[STIX]{x1D6EC}_{N},\unicode[STIX]{x1D709}_{N})$
is
$(\unicode[STIX]{x1D6EC}_{N},\unicode[STIX]{x1D709}_{N})$
is
![]() $(v\pm w)/2$
if
$(v\pm w)/2$
if
![]() $N$
is odd, and
$N$
is odd, and
![]() $(v\pm 2w)$
if
$(v\pm 2w)$
if
![]() $N$
is even (see the proof of Proposition 5.2.5); it follows by Items (
$N$
is even (see the proof of Proposition 5.2.5); it follows by Items (
![]() $3^{\prime \prime }\text{a}$
) and (
$3^{\prime \prime }\text{a}$
) and (
![]() $3^{\prime \prime }\text{bb}$
) that the left-hand side of (5.2.18) is equal to
$3^{\prime \prime }\text{bb}$
) that the left-hand side of (5.2.18) is equal to
![]() $1$
.
$1$
.
5.2.3 Intersections with the unigonal Heegner divisor
We will prove (5.2.6) and (5.2.7). Thus, we assume that
![]() $N\equiv 3\hspace{0.6em}({\rm mod}\hspace{0.2em}8)$
and write
$N\equiv 3\hspace{0.6em}({\rm mod}\hspace{0.2em}8)$
and write
![]() $N=8k+3$
. First, let us prove the set-theoretic equalities
$N=8k+3$
. First, let us prove the set-theoretic equalities
Let
![]() $v$
be a unigonal vector of
$v$
be a unigonal vector of
![]() $(\unicode[STIX]{x1D6EC}_{N},\unicode[STIX]{x1D709}_{N})$
. Thus,
$(\unicode[STIX]{x1D6EC}_{N},\unicode[STIX]{x1D709}_{N})$
. Thus,
![]() $v^{2}=-4$
,
$v^{2}=-4$
,
![]() $\operatorname{div}(v)=4$
, and
$\operatorname{div}(v)=4$
, and
![]() $v^{\bot }\cong \text{II}_{2,2+8k}$
.
$v^{\bot }\cong \text{II}_{2,2+8k}$
.
Let
![]() $w\in v^{\bot }$
be a nodal vector, i.e.
$w\in v^{\bot }$
be a nodal vector, i.e.
![]() $v^{2}=-2$
. Then
$v^{2}=-2$
. Then
![]() $w$
is a nodal vector of
$w$
is a nodal vector of
![]() $(\unicode[STIX]{x1D6EC}_{N},\unicode[STIX]{x1D709}_{N})$
and hence
$(\unicode[STIX]{x1D6EC}_{N},\unicode[STIX]{x1D709}_{N})$
and hence
![]() $l_{N}^{-1}H_{n}(N)\supset H_{n}(\text{II}_{2,2+8k})$
by Proposition 5.2.4. On the other hand, suppose that
$l_{N}^{-1}H_{n}(N)\supset H_{n}(\text{II}_{2,2+8k})$
by Proposition 5.2.4. On the other hand, suppose that
![]() $w\in \unicode[STIX]{x1D6EC}_{N}$
is a nodal vector such that
$w\in \unicode[STIX]{x1D6EC}_{N}$
is a nodal vector such that
![]() $\langle v,w\rangle$
is negative definite; then
$\langle v,w\rangle$
is negative definite; then
![]() $w\bot v$
because the determinant of the restriction of
$w\bot v$
because the determinant of the restriction of
![]() $(\,,\,)$
to
$(\,,\,)$
to
![]() $\langle v,w\rangle$
is positive and hence
$\langle v,w\rangle$
is positive and hence
![]() $w$
is a nodal vector of
$w$
is a nodal vector of
![]() $v^{\bot }$
. By Proposition 5.2.4, this proves the reverse inclusion, i.e.
$v^{\bot }$
. By Proposition 5.2.4, this proves the reverse inclusion, i.e.
![]() $l_{N}^{-1}H_{n}(N)\subset H_{n}(\text{II}_{2,2+8k})$
. This finishes the proof of the first equality of (5.2.20).
$l_{N}^{-1}H_{n}(N)\subset H_{n}(\text{II}_{2,2+8k})$
. This finishes the proof of the first equality of (5.2.20).
The second equality of (5.2.20) follows from (5.2.13) because
![]() $H_{u}(2)=0$
. It remains to prove that
$H_{u}(2)=0$
. It remains to prove that
![]() $\operatorname{mult}_{l_{N}(H_{n}(\text{II}_{2,2+8k}))}H_{u}(N)\cdot H_{n}(N)=1$
. The proof is analogous to the proof of (5.2.15); we leave details to the reader.
$\operatorname{mult}_{l_{N}(H_{n}(\text{II}_{2,2+8k}))}H_{u}(N)\cdot H_{n}(N)=1$
. The proof is analogous to the proof of (5.2.15); we leave details to the reader.
The cases of unigonal divisors for
![]() $N\equiv 4,5\hspace{0.6em}({\rm mod}\hspace{0.2em}8)$
(i.e. formulae (5.2.8), (5.2.9), (5.2.10), and (5.2.11)) are similar; we omit the details. (We refer the reader to §§ 1.5.2 and 1.6 for some arithmetic details specific to these cases.)
$N\equiv 4,5\hspace{0.6em}({\rm mod}\hspace{0.2em}8)$
(i.e. formulae (5.2.8), (5.2.9), (5.2.10), and (5.2.11)) are similar; we omit the details. (We refer the reader to §§ 1.5.2 and 1.6 for some arithmetic details specific to these cases.)
5.3 Normal bundle formulae
In the present subsection, we will prove the following result.
Proposition 5.3.1. Let
![]() $4\leqslant N$
and let
$4\leqslant N$
and let
![]() $f_{N}:\mathscr{F}(N-1)\overset{{\sim}}{\longrightarrow }H_{u}(N)$
be the isomorphism of Proposition 1.4.5. Then the following equalities hold:
$f_{N}:\mathscr{F}(N-1)\overset{{\sim}}{\longrightarrow }H_{u}(N)$
be the isomorphism of Proposition 1.4.5. Then the following equalities hold:
Similarly, let
![]() $l_{8k+3}:\mathscr{F}(\text{II}_{2,2+8k})\overset{{\sim}}{\longrightarrow }H_{u}(8k+3)$
,
$l_{8k+3}:\mathscr{F}(\text{II}_{2,2+8k})\overset{{\sim}}{\longrightarrow }H_{u}(8k+3)$
,
![]() $m_{8k+4}:\mathscr{F}(\text{II}_{2,2+8k}\oplus A_{1})\overset{{\sim}}{\longrightarrow }H_{h}(8k+4)$
, and
$m_{8k+4}:\mathscr{F}(\text{II}_{2,2+8k}\oplus A_{1})\overset{{\sim}}{\longrightarrow }H_{h}(8k+4)$
, and
![]() $q_{8k+5}:\mathscr{F}(\text{II}_{2,2+8k}\oplus A_{2})\overset{{\sim}}{\longrightarrow }H_{h}(8k+5)$
be the isomorphisms in (1.7.4), (1.7.5), and (1.7.7). Then
$q_{8k+5}:\mathscr{F}(\text{II}_{2,2+8k}\oplus A_{2})\overset{{\sim}}{\longrightarrow }H_{h}(8k+5)$
be the isomorphisms in (1.7.4), (1.7.5), and (1.7.7). Then
5.3.1 Adjunction
Let
![]() $\mathscr{F}=\mathscr{F}_{\unicode[STIX]{x1D6EC}}(\unicode[STIX]{x1D6E4})$
be a locally symmetric variety of Type IV, with notation as in § 1.2. We let
$\mathscr{F}=\mathscr{F}_{\unicode[STIX]{x1D6EC}}(\unicode[STIX]{x1D6E4})$
be a locally symmetric variety of Type IV, with notation as in § 1.2. We let
![]() $N:=\dim \mathscr{F}$
. Since
$N:=\dim \mathscr{F}$
. Since
![]() $\mathscr{F}$
has quotient singularities, the canonical bundle of
$\mathscr{F}$
has quotient singularities, the canonical bundle of
![]() $\mathscr{F}$
is a well-defined element
$\mathscr{F}$
is a well-defined element
![]() $K_{\mathscr{F}}\in \operatorname{Pic}(\mathscr{F}_{\unicode[STIX]{x1D6EC}}(\unicode[STIX]{x1D6E4}))_{\mathbb{Q}}$
. Let
$K_{\mathscr{F}}\in \operatorname{Pic}(\mathscr{F}_{\unicode[STIX]{x1D6EC}}(\unicode[STIX]{x1D6E4}))_{\mathbb{Q}}$
. Let
![]() $\unicode[STIX]{x1D706}_{\mathscr{F}}$
be the automorphic
$\unicode[STIX]{x1D706}_{\mathscr{F}}$
be the automorphic
![]() $\mathbb{Q}$
-line bundle on
$\mathbb{Q}$
-line bundle on
![]() $\mathscr{F}$
. Thus, sections of
$\mathscr{F}$
. Thus, sections of
![]() $\unicode[STIX]{x1D706}_{\mathscr{F}}^{\otimes d}$
are identified with weight-
$\unicode[STIX]{x1D706}_{\mathscr{F}}^{\otimes d}$
are identified with weight-
![]() $d$
automorphic forms on
$d$
automorphic forms on
![]() $\mathscr{D}_{\unicode[STIX]{x1D6EC}}^{+}$
and, letting
$\mathscr{D}_{\unicode[STIX]{x1D6EC}}^{+}$
and, letting
![]() $\unicode[STIX]{x1D70B}:\mathscr{D}_{\unicode[STIX]{x1D6EC}}^{+}\rightarrow \mathscr{F}$
be the quotient map,
$\unicode[STIX]{x1D70B}:\mathscr{D}_{\unicode[STIX]{x1D6EC}}^{+}\rightarrow \mathscr{F}$
be the quotient map,
![]() $\unicode[STIX]{x1D70B}^{\ast }\unicode[STIX]{x1D706}_{\mathscr{F}}\cong \mathscr{O}_{\mathscr{D}_{\unicode[STIX]{x1D6EC}}^{+}}(-1)$
.
$\unicode[STIX]{x1D70B}^{\ast }\unicode[STIX]{x1D706}_{\mathscr{F}}\cong \mathscr{O}_{\mathscr{D}_{\unicode[STIX]{x1D6EC}}^{+}}(-1)$
.
If
![]() $\unicode[STIX]{x1D6E4}$
acts freely on
$\unicode[STIX]{x1D6E4}$
acts freely on
![]() $\mathscr{D}_{\unicode[STIX]{x1D6EC}}^{+}$
(and hence
$\mathscr{D}_{\unicode[STIX]{x1D6EC}}^{+}$
(and hence
![]() $\mathscr{F}$
is smooth), then
$\mathscr{F}$
is smooth), then
In fact, the above formula follows by descent from the analogous formula
![]() $K_{\mathscr{D}_{\unicode[STIX]{x1D6EC}}^{+}}=N\mathscr{O}_{\mathscr{D}_{\unicode[STIX]{x1D6EC}}^{+}}(-1)$
(adjunction formula for a smooth quadric in
$K_{\mathscr{D}_{\unicode[STIX]{x1D6EC}}^{+}}=N\mathscr{O}_{\mathscr{D}_{\unicode[STIX]{x1D6EC}}^{+}}(-1)$
(adjunction formula for a smooth quadric in
![]() $\mathbb{P}^{N+1}$
). In general, there will be a correction term coming from the ramification of the map
$\mathbb{P}^{N+1}$
). In general, there will be a correction term coming from the ramification of the map
![]() $\unicode[STIX]{x1D70B}:\mathscr{D}_{\unicode[STIX]{x1D6EC}}^{+}\rightarrow \mathscr{F}$
.
$\unicode[STIX]{x1D70B}:\mathscr{D}_{\unicode[STIX]{x1D6EC}}^{+}\rightarrow \mathscr{F}$
.
Definition 5.3.2. Let
![]() $B(\mathscr{F})$
be the divisor on
$B(\mathscr{F})$
be the divisor on
![]() $\mathscr{F}$
which is the sum of all Heegner divisors
$\mathscr{F}$
which is the sum of all Heegner divisors
![]() $H_{v,\unicode[STIX]{x1D6EC}}(\unicode[STIX]{x1D6E4})$
, where
$H_{v,\unicode[STIX]{x1D6EC}}(\unicode[STIX]{x1D6E4})$
, where
![]() $v\in \unicode[STIX]{x1D6EC}$
is primitive,
$v\in \unicode[STIX]{x1D6EC}$
is primitive,
![]() $v^{2}<0$
,
$v^{2}<0$
,
![]() $\pm \unicode[STIX]{x1D70C}_{v}\in \unicode[STIX]{x1D6E4}$
, where only one hyperplane appears for each couple
$\pm \unicode[STIX]{x1D70C}_{v}\in \unicode[STIX]{x1D6E4}$
, where only one hyperplane appears for each couple
![]() $\{v,-v\}$
.
$\{v,-v\}$
.
Proposition 5.3.3. Keep notation as above. Then, in
![]() $\operatorname{Pic}(\mathscr{F})_{\mathbb{Q}}$
,
$\operatorname{Pic}(\mathscr{F})_{\mathbb{Q}}$
,
Proof. The ramification divisor of the quotient map
![]() $\unicode[STIX]{x1D70B}:\mathscr{D}_{\unicode[STIX]{x1D6EC}}^{+}\rightarrow \mathscr{F}$
is the sum of the pre-Heegner divisors
$\unicode[STIX]{x1D70B}:\mathscr{D}_{\unicode[STIX]{x1D6EC}}^{+}\rightarrow \mathscr{F}$
is the sum of the pre-Heegner divisors
![]() $\mathscr{H}_{v,\unicode[STIX]{x1D6EC}}(\unicode[STIX]{x1D6E4})$
, where
$\mathscr{H}_{v,\unicode[STIX]{x1D6EC}}(\unicode[STIX]{x1D6E4})$
, where
![]() $v\in \unicode[STIX]{x1D6EC}$
is primitive,
$v\in \unicode[STIX]{x1D6EC}$
is primitive,
![]() $v^{2}<0$
,
$v^{2}<0$
,
![]() $\pm \unicode[STIX]{x1D70C}_{v}\in \unicode[STIX]{x1D6E4}$
, where only one hyperplane appears for each couple
$\pm \unicode[STIX]{x1D70C}_{v}\in \unicode[STIX]{x1D6E4}$
, where only one hyperplane appears for each couple
![]() $\{v,-v\}$
. In fact, this is [Reference Gritsenko, Hulek and SankaranGHS07, Corollary 2.13]. Now let
$\{v,-v\}$
. In fact, this is [Reference Gritsenko, Hulek and SankaranGHS07, Corollary 2.13]. Now let
![]() $\unicode[STIX]{x1D6E4}_{0}\lhd \unicode[STIX]{x1D6E4}$
be a finite-index normal subgroup acting freely on
$\unicode[STIX]{x1D6E4}_{0}\lhd \unicode[STIX]{x1D6E4}$
be a finite-index normal subgroup acting freely on
![]() $\mathscr{D}_{\unicode[STIX]{x1D6EC}}^{+}$
, let
$\mathscr{D}_{\unicode[STIX]{x1D6EC}}^{+}$
, let
![]() $\mathscr{F}_{0}:=\unicode[STIX]{x1D6E4}_{0}\backslash \mathscr{D}_{\unicode[STIX]{x1D6EC}}^{+}$
, and let
$\mathscr{F}_{0}:=\unicode[STIX]{x1D6E4}_{0}\backslash \mathscr{D}_{\unicode[STIX]{x1D6EC}}^{+}$
, and let
![]() $\unicode[STIX]{x1D70B}_{0}:\mathscr{D}_{\unicode[STIX]{x1D6EC}}^{+}\rightarrow \mathscr{F}_{0}$
be the quotient map. The ramification divisor of the finite Galois cover
$\unicode[STIX]{x1D70B}_{0}:\mathscr{D}_{\unicode[STIX]{x1D6EC}}^{+}\rightarrow \mathscr{F}_{0}$
be the quotient map. The ramification divisor of the finite Galois cover
![]() $\mathscr{F}_{0}\rightarrow \mathscr{F}$
is identified with the image by
$\mathscr{F}_{0}\rightarrow \mathscr{F}$
is identified with the image by
![]() $\unicode[STIX]{x1D70B}_{0}:\mathscr{D}_{\unicode[STIX]{x1D6EC}}^{+}\rightarrow \mathscr{F}_{0}$
of the ramification divisor of
$\unicode[STIX]{x1D70B}_{0}:\mathscr{D}_{\unicode[STIX]{x1D6EC}}^{+}\rightarrow \mathscr{F}_{0}$
of the ramification divisor of
![]() $\unicode[STIX]{x1D70B}:\mathscr{D}_{\unicode[STIX]{x1D6EC}}^{+}\rightarrow \mathscr{F}$
. Equation (5.3.5) and Riemann–Hurwitz applied to
$\unicode[STIX]{x1D70B}:\mathscr{D}_{\unicode[STIX]{x1D6EC}}^{+}\rightarrow \mathscr{F}$
. Equation (5.3.5) and Riemann–Hurwitz applied to
![]() $\mathscr{F}_{0}\rightarrow \mathscr{F}$
give the proposition.◻
$\mathscr{F}_{0}\rightarrow \mathscr{F}$
give the proposition.◻
As before, let
![]() $B(N)$
be the Weil divisor on
$B(N)$
be the Weil divisor on
![]() $\mathscr{F}(N)$
defined by
$\mathscr{F}(N)$
defined by
By Proposition 1.3.5, we see that
![]() $B(N)$
is the branch divisor for
$B(N)$
is the branch divisor for
![]() $\mathscr{F}(N)$
(i.e.
$\mathscr{F}(N)$
(i.e.
![]() $B(N)=B(\mathscr{F}(\unicode[STIX]{x1D6EC},\unicode[STIX]{x1D709}))$
for
$B(N)=B(\mathscr{F}(\unicode[STIX]{x1D6EC},\unicode[STIX]{x1D709}))$
for
![]() $(\unicode[STIX]{x1D6EC},\unicode[STIX]{x1D709})$
a dimension-
$(\unicode[STIX]{x1D6EC},\unicode[STIX]{x1D709})$
a dimension-
![]() $N$
decorated
$N$
decorated
![]() $D$
-lattice). Thus, we have the following result.
$D$
-lattice). Thus, we have the following result.
Corollary 5.3.4. Keeping notation as above,
Let
![]() $\unicode[STIX]{x1D706}(\text{II}_{2,2+8k}):=\unicode[STIX]{x1D706}_{\mathscr{F}(\text{II}_{2,2+8k})}$
,
$\unicode[STIX]{x1D706}(\text{II}_{2,2+8k}):=\unicode[STIX]{x1D706}_{\mathscr{F}(\text{II}_{2,2+8k})}$
,
![]() $\unicode[STIX]{x1D706}(\text{II}_{2,2+8k}\oplus A_{1}):=\unicode[STIX]{x1D706}_{\mathscr{F}(\text{II}_{2,2+8k}\oplus A_{1})}$
, and
$\unicode[STIX]{x1D706}(\text{II}_{2,2+8k}\oplus A_{1}):=\unicode[STIX]{x1D706}_{\mathscr{F}(\text{II}_{2,2+8k}\oplus A_{1})}$
, and
![]() $\unicode[STIX]{x1D706}(\text{II}_{2,2+8k}\oplus A_{2}):=\unicode[STIX]{x1D706}_{\mathscr{F}(\text{II}_{2,2+8k}\oplus A_{2})}$
. The proof of the result below is omitted because it is analogous to the proof of Corollary 5.3.4.
$\unicode[STIX]{x1D706}(\text{II}_{2,2+8k}\oplus A_{2}):=\unicode[STIX]{x1D706}_{\mathscr{F}(\text{II}_{2,2+8k}\oplus A_{2})}$
. The proof of the result below is omitted because it is analogous to the proof of Corollary 5.3.4.
Corollary 5.3.5. Keep notation as above. The following equalities hold in
![]() $\operatorname{Pic}(\mathscr{F}(\text{II}_{2,2+8k}))_{\mathbb{Q}}$
,
$\operatorname{Pic}(\mathscr{F}(\text{II}_{2,2+8k}))_{\mathbb{Q}}$
,
![]() $\operatorname{Pic}(\mathscr{F}(\text{II}_{2,2+8k}\oplus A_{1}))_{\mathbb{Q}}$
, and
$\operatorname{Pic}(\mathscr{F}(\text{II}_{2,2+8k}\oplus A_{1}))_{\mathbb{Q}}$
, and
![]() $\operatorname{Pic}(\mathscr{F}(\text{II}_{2,2+8k}\oplus A_{2}))_{\mathbb{Q}}$
, respectively:
$\operatorname{Pic}(\mathscr{F}(\text{II}_{2,2+8k}\oplus A_{2}))_{\mathbb{Q}}$
, respectively:
 $$\begin{eqnarray}\displaystyle K_{\mathscr{F}(\text{II}_{2,2+8k})} & = & \displaystyle (8k+2)\unicode[STIX]{x1D706}(\text{II}_{2,2+8k})-{\textstyle \frac{1}{2}}H_{n}(\text{II}_{2,2+8k}),\nonumber\\ \displaystyle K_{\mathscr{F}(\text{II}_{2,2+8k}\oplus A_{1})} & = & \displaystyle (8k+3)\unicode[STIX]{x1D706}(\text{II}_{2,2+8k}\oplus A_{1})-{\textstyle \frac{1}{2}}H_{n}(\text{II}_{2,2+8k}\oplus A_{1})-{\textstyle \frac{1}{2}}H_{u}(\text{II}_{2,2+8k}\oplus A_{1}),\nonumber\\ \displaystyle K_{\mathscr{F}(\text{II}_{2,2+8k}\oplus A_{2})} & = & \displaystyle (8k+4)\unicode[STIX]{x1D706}(\text{II}_{2,2+8k}\oplus A_{2})-{\textstyle \frac{1}{2}}H_{n}(\text{II}_{2,2+8k}\oplus A_{2})-{\textstyle \frac{1}{2}}H_{u}(\text{II}_{2,2+8k}\oplus A_{2}).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle K_{\mathscr{F}(\text{II}_{2,2+8k})} & = & \displaystyle (8k+2)\unicode[STIX]{x1D706}(\text{II}_{2,2+8k})-{\textstyle \frac{1}{2}}H_{n}(\text{II}_{2,2+8k}),\nonumber\\ \displaystyle K_{\mathscr{F}(\text{II}_{2,2+8k}\oplus A_{1})} & = & \displaystyle (8k+3)\unicode[STIX]{x1D706}(\text{II}_{2,2+8k}\oplus A_{1})-{\textstyle \frac{1}{2}}H_{n}(\text{II}_{2,2+8k}\oplus A_{1})-{\textstyle \frac{1}{2}}H_{u}(\text{II}_{2,2+8k}\oplus A_{1}),\nonumber\\ \displaystyle K_{\mathscr{F}(\text{II}_{2,2+8k}\oplus A_{2})} & = & \displaystyle (8k+4)\unicode[STIX]{x1D706}(\text{II}_{2,2+8k}\oplus A_{2})-{\textstyle \frac{1}{2}}H_{n}(\text{II}_{2,2+8k}\oplus A_{2})-{\textstyle \frac{1}{2}}H_{u}(\text{II}_{2,2+8k}\oplus A_{2}).\nonumber\end{eqnarray}$$
5.3.2 Normal bundle formula for the hyperelliptic divisor
Proof of (5.3.1).
By Proposition 1.4.5, the intersection
![]() $H_{h}(N)\cap \operatorname{sing}\mathscr{F}(N)$
has codimension at least
$H_{h}(N)\cap \operatorname{sing}\mathscr{F}(N)$
has codimension at least
![]() $2$
in
$2$
in
![]() $H_{h}(N)$
and hence we may apply adjunction to compute the canonical class of
$H_{h}(N)$
and hence we may apply adjunction to compute the canonical class of
![]() $H_{h}(N)$
. Since
$H_{h}(N)$
. Since
![]() $f_{N}:\mathscr{F}(N-1)\rightarrow H_{h}(N)$
is an isomorphism, Corollary 5.3.4 gives
$f_{N}:\mathscr{F}(N-1)\rightarrow H_{h}(N)$
is an isomorphism, Corollary 5.3.4 gives
 $$\begin{eqnarray}\displaystyle K_{\mathscr{F}(N-1)} & = & \displaystyle f_{N}^{\ast }(K_{\mathscr{F}(N)}+H_{h}(N))\nonumber\\ \displaystyle & = & \displaystyle f_{N}^{\ast }(N\unicode[STIX]{x1D706}(N)-{\textstyle \frac{1}{2}}(B(N)-H_{h}(N))+{\textstyle \frac{1}{2}}H_{h}(N))\nonumber\\ \displaystyle & = & \displaystyle N\unicode[STIX]{x1D706}(N-1)-{\textstyle \frac{1}{2}}f_{N}^{\ast }(B(N)-H_{h}(N))+{\textstyle \frac{1}{2}}f_{N}^{\ast }H_{h}(N).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle K_{\mathscr{F}(N-1)} & = & \displaystyle f_{N}^{\ast }(K_{\mathscr{F}(N)}+H_{h}(N))\nonumber\\ \displaystyle & = & \displaystyle f_{N}^{\ast }(N\unicode[STIX]{x1D706}(N)-{\textstyle \frac{1}{2}}(B(N)-H_{h}(N))+{\textstyle \frac{1}{2}}H_{h}(N))\nonumber\\ \displaystyle & = & \displaystyle N\unicode[STIX]{x1D706}(N-1)-{\textstyle \frac{1}{2}}f_{N}^{\ast }(B(N)-H_{h}(N))+{\textstyle \frac{1}{2}}f_{N}^{\ast }H_{h}(N).\nonumber\end{eqnarray}$$
On the other hand, the canonical class of
![]() $\mathscr{F}(N-1)$
is given by (5.3.8); equating the two expressions for
$\mathscr{F}(N-1)$
is given by (5.3.8); equating the two expressions for
![]() $K_{\mathscr{F}(N-1)}$
, one gets
$K_{\mathscr{F}(N-1)}$
, one gets
◻
5.3.3 Normal bundle formula for the unigonal divisor
Proof of (5.3.2).
We let
![]() $N=8k+3$
. By Proposition 1.5.1, the intersection
$N=8k+3$
. By Proposition 1.5.1, the intersection
![]() $H_{u}(N)\cap \operatorname{sing}\mathscr{F}(N)$
has codimension at least
$H_{u}(N)\cap \operatorname{sing}\mathscr{F}(N)$
has codimension at least
![]() $2$
in
$2$
in
![]() $H_{u}(N)$
and hence we may apply adjunction to compute the canonical class of
$H_{u}(N)$
and hence we may apply adjunction to compute the canonical class of
![]() $H_{u}(N)$
. Since
$H_{u}(N)$
. Since
![]() $l_{N}:\mathscr{F}(\text{II}_{2,2+8k})\rightarrow H_{u}(N)$
is an isomorphism, Corollary 5.3.4 gives
$l_{N}:\mathscr{F}(\text{II}_{2,2+8k})\rightarrow H_{u}(N)$
is an isomorphism, Corollary 5.3.4 gives
 $$\begin{eqnarray}\displaystyle K_{\mathscr{F}(\text{II}_{2,2+8k})} & = & \displaystyle l_{N}^{\ast }(K_{\mathscr{F}(N)}+H_{u}(N))\nonumber\\ \displaystyle & = & \displaystyle l_{N}^{\ast }(N\unicode[STIX]{x1D706}(N)-{\textstyle \frac{1}{2}}(B(N)-H_{u}(N))+{\textstyle \frac{1}{2}}H_{u}(N))\nonumber\\ \displaystyle & = & \displaystyle N\unicode[STIX]{x1D706}(\text{II}_{2,2+8k})-{\textstyle \frac{1}{2}}l_{N}^{\ast }(B(N)-H_{u}(N))+{\textstyle \frac{1}{2}}l_{N}^{\ast }H_{u}(N).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle K_{\mathscr{F}(\text{II}_{2,2+8k})} & = & \displaystyle l_{N}^{\ast }(K_{\mathscr{F}(N)}+H_{u}(N))\nonumber\\ \displaystyle & = & \displaystyle l_{N}^{\ast }(N\unicode[STIX]{x1D706}(N)-{\textstyle \frac{1}{2}}(B(N)-H_{u}(N))+{\textstyle \frac{1}{2}}H_{u}(N))\nonumber\\ \displaystyle & = & \displaystyle N\unicode[STIX]{x1D706}(\text{II}_{2,2+8k})-{\textstyle \frac{1}{2}}l_{N}^{\ast }(B(N)-H_{u}(N))+{\textstyle \frac{1}{2}}l_{N}^{\ast }H_{u}(N).\nonumber\end{eqnarray}$$
On the other hand,
![]() $K_{\mathscr{F}(\text{II}_{2,2+8k})}=(2+8k)\unicode[STIX]{x1D706}(\text{II}_{2,2+8k})-\frac{1}{2}H_{n}(\text{II}_{2,2+8k})$
by Corollary 5.3.5. Comparing the two expressions for
$K_{\mathscr{F}(\text{II}_{2,2+8k})}=(2+8k)\unicode[STIX]{x1D706}(\text{II}_{2,2+8k})-\frac{1}{2}H_{n}(\text{II}_{2,2+8k})$
by Corollary 5.3.5. Comparing the two expressions for
![]() $K_{\mathscr{F}(\text{II}_{2,2+8k})}$
, and invoking (5.2.6) and (5.2.7), one gets (5.3.2).◻
$K_{\mathscr{F}(\text{II}_{2,2+8k})}$
, and invoking (5.2.6) and (5.2.7), one gets (5.3.2).◻
The computations of the normal bundle formulae for the unigonal divisor when
![]() $N\equiv 4,5\hspace{0.6em}({\rm mod}\hspace{0.2em}8)$
are similar; we omit the details.
$N\equiv 4,5\hspace{0.6em}({\rm mod}\hspace{0.2em}8)$
are similar; we omit the details.
5.3.4 Pull-back of
 $(\unicode[STIX]{x1D706}(N)+\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6E5}(N))$
$(\unicode[STIX]{x1D706}(N)+\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6E5}(N))$
Equations (5.3.1) and (5.2.5) give the following formula:
 $$\begin{eqnarray}f_{N}^{\ast }\unicode[STIX]{x1D6E5}(N)=\left\{\begin{array}{@{}ll@{}}-\unicode[STIX]{x1D706}(N-1)+\unicode[STIX]{x1D6E5}(N-1)\quad & \text{if }N\not \equiv 4,5\hspace{0.6em}({\rm mod}\hspace{0.2em}8),\\ -\unicode[STIX]{x1D706}(N-1)+\frac{1}{2}H_{h}(N-1)\quad & \text{if }N\equiv 5\hspace{0.6em}({\rm mod}\hspace{0.2em}8),\\ -\unicode[STIX]{x1D706}(N-1)+\unicode[STIX]{x1D6E5}(N-1)+H_{u}(N-1)\quad & \text{if }N\equiv 4\hspace{0.6em}({\rm mod}\hspace{0.2em}8).\end{array}\right.\end{eqnarray}$$
$$\begin{eqnarray}f_{N}^{\ast }\unicode[STIX]{x1D6E5}(N)=\left\{\begin{array}{@{}ll@{}}-\unicode[STIX]{x1D706}(N-1)+\unicode[STIX]{x1D6E5}(N-1)\quad & \text{if }N\not \equiv 4,5\hspace{0.6em}({\rm mod}\hspace{0.2em}8),\\ -\unicode[STIX]{x1D706}(N-1)+\frac{1}{2}H_{h}(N-1)\quad & \text{if }N\equiv 5\hspace{0.6em}({\rm mod}\hspace{0.2em}8),\\ -\unicode[STIX]{x1D706}(N-1)+\unicode[STIX]{x1D6E5}(N-1)+H_{u}(N-1)\quad & \text{if }N\equiv 4\hspace{0.6em}({\rm mod}\hspace{0.2em}8).\end{array}\right.\end{eqnarray}$$
(Recall that
![]() $H_{u}(M)=0$
if
$H_{u}(M)=0$
if
![]() $M\equiv 2\hspace{0.6em}({\rm mod}\hspace{0.2em}8)$
.) Repeated application of (5.3.10) gives the following result.
$M\equiv 2\hspace{0.6em}({\rm mod}\hspace{0.2em}8)$
.) Repeated application of (5.3.10) gives the following result.
Proposition 5.3.6. Let
![]() $N\geqslant 4$
and
$N\geqslant 4$
and
![]() $1\leqslant k\leqslant (N-3)$
. Then
$1\leqslant k\leqslant (N-3)$
. Then
 $$\begin{eqnarray}\displaystyle & & \displaystyle f_{N-k,N}^{\ast }(\unicode[STIX]{x1D706}(N)+\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6E5}(N))\nonumber\\ \displaystyle & & \displaystyle \qquad =\left\{\begin{array}{@{}ll@{}}(1-k\unicode[STIX]{x1D6FD})\unicode[STIX]{x1D706}(N-k)+\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6E5}(N-k)\quad & \text{if }N-k\not \equiv 4\hspace{0.6em}({\rm mod}\hspace{0.2em}8)\text{ and }k\geqslant 2,\\ \quad & \text{or }k=1\text{ and }N-1\not \equiv 3,4\hspace{0.6em}({\rm mod}\hspace{0.2em}8),\\ (1-k\unicode[STIX]{x1D6FD})\unicode[STIX]{x1D706}(N-k)+\frac{1}{2}\unicode[STIX]{x1D6FD}H_{h}(N-k)\quad & \text{if }N-k\equiv 4\hspace{0.6em}({\rm mod}\hspace{0.2em}8),\\ (1-k\unicode[STIX]{x1D6FD})\unicode[STIX]{x1D706}(N-k)+\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6E5}(N-k)+\unicode[STIX]{x1D6FD}H_{u}(N-k)\quad & \text{if }k=1\text{ and }N-1\equiv 3\hspace{0.6em}({\rm mod}\hspace{0.2em}8).\end{array}\right.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle f_{N-k,N}^{\ast }(\unicode[STIX]{x1D706}(N)+\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6E5}(N))\nonumber\\ \displaystyle & & \displaystyle \qquad =\left\{\begin{array}{@{}ll@{}}(1-k\unicode[STIX]{x1D6FD})\unicode[STIX]{x1D706}(N-k)+\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6E5}(N-k)\quad & \text{if }N-k\not \equiv 4\hspace{0.6em}({\rm mod}\hspace{0.2em}8)\text{ and }k\geqslant 2,\\ \quad & \text{or }k=1\text{ and }N-1\not \equiv 3,4\hspace{0.6em}({\rm mod}\hspace{0.2em}8),\\ (1-k\unicode[STIX]{x1D6FD})\unicode[STIX]{x1D706}(N-k)+\frac{1}{2}\unicode[STIX]{x1D6FD}H_{h}(N-k)\quad & \text{if }N-k\equiv 4\hspace{0.6em}({\rm mod}\hspace{0.2em}8),\\ (1-k\unicode[STIX]{x1D6FD})\unicode[STIX]{x1D706}(N-k)+\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6E5}(N-k)+\unicode[STIX]{x1D6FD}H_{u}(N-k)\quad & \text{if }k=1\text{ and }N-1\equiv 3\hspace{0.6em}({\rm mod}\hspace{0.2em}8).\end{array}\right.\nonumber\end{eqnarray}$$
It will be convenient to let
![]() $f_{N,N}:=\operatorname{Id}_{\mathscr{F}(N)}$
. The result below follows from Proposition 5.3.6, together with (5.2.7) and (5.3.2).
$f_{N,N}:=\operatorname{Id}_{\mathscr{F}(N)}$
. The result below follows from Proposition 5.3.6, together with (5.2.7) and (5.3.2).
Proposition 5.3.7. Suppose that
![]() $N\geqslant 3$
,
$N\geqslant 3$
,
![]() $0\leqslant k\leqslant (N-3)$
, and
$0\leqslant k\leqslant (N-3)$
, and
![]() $N-k\equiv 3\hspace{0.6em}({\rm mod}\hspace{0.2em}8)$
(hence
$N-k\equiv 3\hspace{0.6em}({\rm mod}\hspace{0.2em}8)$
(hence
![]() $l_{N-k}$
makes sense; see (1.7.4)). Then
$l_{N-k}$
makes sense; see (1.7.4)). Then
Proposition 5.3.8. Suppose that
![]() $N\geqslant 4$
,
$N\geqslant 4$
,
![]() $0\leqslant k\leqslant (N-4)$
, and
$0\leqslant k\leqslant (N-4)$
, and
![]() $N-k\equiv 4\hspace{0.6em}({\rm mod}\hspace{0.2em}8)$
(hence
$N-k\equiv 4\hspace{0.6em}({\rm mod}\hspace{0.2em}8)$
(hence
![]() $m_{N-k}$
and
$m_{N-k}$
and
![]() $p_{N-k-1}$
make sense; see (1.7.5) and (1.7.6))). Then
$p_{N-k-1}$
make sense; see (1.7.5) and (1.7.6))). Then
 $$\begin{eqnarray}\displaystyle & & \displaystyle (f_{N-k,N}\circ m_{N-k})^{\ast }(\unicode[STIX]{x1D706}(N)+\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6E5}(N))\nonumber\\ \displaystyle & & \displaystyle \qquad =\left\{\begin{array}{@{}ll@{}}(1-\unicode[STIX]{x1D6FD})\unicode[STIX]{x1D706}(\text{II}_{2,N-k-2}\oplus A_{1})+\frac{3}{2}\unicode[STIX]{x1D6FD}H_{u}(\text{II}_{2,N-k-2}\oplus A_{1})\quad & \text{if }k=0,\\ (1-k\unicode[STIX]{x1D6FD})\unicode[STIX]{x1D706}(\text{II}_{2,N-k-2}\oplus A_{1})+\unicode[STIX]{x1D6FD}H_{u}(\text{II}_{2,N-k-2}\oplus A_{1})\quad & \text{if }k\geqslant 1,\end{array}\right.\nonumber\\ \displaystyle & & \displaystyle (f_{N-k,N}\circ m_{N-k}\circ p_{N-k-1})^{\ast }(\unicode[STIX]{x1D706}(N)+\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6E5}(N))=\left\{\begin{array}{@{}ll@{}}(1-4\unicode[STIX]{x1D6FD})\unicode[STIX]{x1D706}(\text{II}_{2,N-k-2})\quad & \text{if }k=0,\\ (1-(k+2)\unicode[STIX]{x1D6FD})\unicode[STIX]{x1D706}(\text{II}_{2,N-k-2})\quad & \text{if }k\geqslant 1.\end{array}\right.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle (f_{N-k,N}\circ m_{N-k})^{\ast }(\unicode[STIX]{x1D706}(N)+\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6E5}(N))\nonumber\\ \displaystyle & & \displaystyle \qquad =\left\{\begin{array}{@{}ll@{}}(1-\unicode[STIX]{x1D6FD})\unicode[STIX]{x1D706}(\text{II}_{2,N-k-2}\oplus A_{1})+\frac{3}{2}\unicode[STIX]{x1D6FD}H_{u}(\text{II}_{2,N-k-2}\oplus A_{1})\quad & \text{if }k=0,\\ (1-k\unicode[STIX]{x1D6FD})\unicode[STIX]{x1D706}(\text{II}_{2,N-k-2}\oplus A_{1})+\unicode[STIX]{x1D6FD}H_{u}(\text{II}_{2,N-k-2}\oplus A_{1})\quad & \text{if }k\geqslant 1,\end{array}\right.\nonumber\\ \displaystyle & & \displaystyle (f_{N-k,N}\circ m_{N-k}\circ p_{N-k-1})^{\ast }(\unicode[STIX]{x1D706}(N)+\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6E5}(N))=\left\{\begin{array}{@{}ll@{}}(1-4\unicode[STIX]{x1D6FD})\unicode[STIX]{x1D706}(\text{II}_{2,N-k-2})\quad & \text{if }k=0,\\ (1-(k+2)\unicode[STIX]{x1D6FD})\unicode[STIX]{x1D706}(\text{II}_{2,N-k-2})\quad & \text{if }k\geqslant 1.\end{array}\right.\nonumber\end{eqnarray}$$
Proof. The first equation follows from Proposition 5.3.6, together with (5.2.9) and (5.3.3). Next, note that
![]() $f_{N-k,N}\circ m_{N-k}\circ p_{N-k-1}=f_{N-k,N}\circ f_{N-k}\circ l_{N-k-1}=f_{N-k-1,N}\circ l_{N-k-1}$
by Claim 1.7.1 and hence the second equation follows from Proposition 5.3.7.◻
$f_{N-k,N}\circ m_{N-k}\circ p_{N-k-1}=f_{N-k,N}\circ f_{N-k}\circ l_{N-k-1}=f_{N-k-1,N}\circ l_{N-k-1}$
by Claim 1.7.1 and hence the second equation follows from Proposition 5.3.7.◻
The proof of the result below is omitted because it is similar to the proof of Proposition 5.3.8.
Proposition 5.3.9. Suppose that
![]() $N\geqslant 5$
,
$N\geqslant 5$
,
![]() $0\leqslant k\leqslant (N-5)$
, and
$0\leqslant k\leqslant (N-5)$
, and
![]() $N-k\equiv 5\hspace{0.6em}({\rm mod}\hspace{0.2em}8)$
(hence
$N-k\equiv 5\hspace{0.6em}({\rm mod}\hspace{0.2em}8)$
(hence
![]() $q_{N-k}$
,
$q_{N-k}$
,
![]() $r_{N-k-1}$
and
$r_{N-k-1}$
and
![]() $p_{N-k-2}$
make sense; see (1.7.7), (1.7.8) and (1.7.6)). Then
$p_{N-k-2}$
make sense; see (1.7.7), (1.7.8) and (1.7.6)). Then
 $$\begin{eqnarray}\displaystyle & & \displaystyle (f_{N-k,N}\circ q_{N-k})^{\ast }(\unicode[STIX]{x1D706}(N)+\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6E5}(N))\nonumber\\ \displaystyle & & \displaystyle \qquad =(1-k\unicode[STIX]{x1D6FD})\unicode[STIX]{x1D706}(\text{II}_{2,N-k-3}\oplus A_{2})+\unicode[STIX]{x1D6FD}H_{u}(\text{II}_{2,N-k-3}\oplus A_{2}),\nonumber\\ \displaystyle & & \displaystyle (f_{N-k,N}\circ q_{N-k}\circ r_{N-k-1})^{\ast }(\unicode[STIX]{x1D706}(N)+\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6E5}(N))\nonumber\\ \displaystyle & & \displaystyle \qquad =(1-(k+1)\unicode[STIX]{x1D6FD})\unicode[STIX]{x1D706}(\text{II}_{2,N-k-3}\oplus A_{1})+\unicode[STIX]{x1D6FD}H_{u}(\text{II}_{2,N-k-3}\oplus A_{1}),\nonumber\\ \displaystyle & & \displaystyle (f_{N-k,N}\circ q_{N-k}\circ r_{N-k-1}\circ p_{N-k-2})^{\ast }(\unicode[STIX]{x1D706}(N)+\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6E5}(N))\nonumber\\ \displaystyle & & \displaystyle \qquad =(1-(k+3)\unicode[STIX]{x1D6FD})\unicode[STIX]{x1D706}(\text{II}_{2,N-k-3}).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle (f_{N-k,N}\circ q_{N-k})^{\ast }(\unicode[STIX]{x1D706}(N)+\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6E5}(N))\nonumber\\ \displaystyle & & \displaystyle \qquad =(1-k\unicode[STIX]{x1D6FD})\unicode[STIX]{x1D706}(\text{II}_{2,N-k-3}\oplus A_{2})+\unicode[STIX]{x1D6FD}H_{u}(\text{II}_{2,N-k-3}\oplus A_{2}),\nonumber\\ \displaystyle & & \displaystyle (f_{N-k,N}\circ q_{N-k}\circ r_{N-k-1})^{\ast }(\unicode[STIX]{x1D706}(N)+\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6E5}(N))\nonumber\\ \displaystyle & & \displaystyle \qquad =(1-(k+1)\unicode[STIX]{x1D6FD})\unicode[STIX]{x1D706}(\text{II}_{2,N-k-3}\oplus A_{1})+\unicode[STIX]{x1D6FD}H_{u}(\text{II}_{2,N-k-3}\oplus A_{1}),\nonumber\\ \displaystyle & & \displaystyle (f_{N-k,N}\circ q_{N-k}\circ r_{N-k-1}\circ p_{N-k-2})^{\ast }(\unicode[STIX]{x1D706}(N)+\unicode[STIX]{x1D6FD}\unicode[STIX]{x1D6E5}(N))\nonumber\\ \displaystyle & & \displaystyle \qquad =(1-(k+3)\unicode[STIX]{x1D6FD})\unicode[STIX]{x1D706}(\text{II}_{2,N-k-3}).\nonumber\end{eqnarray}$$
5.4 Heuristics for the predictions
Let
![]() $15\leqslant N$
. We define a collection
$15\leqslant N$
. We define a collection
![]() $\mathtt{Tower}(N)$
of closed subsets of
$\mathtt{Tower}(N)$
of closed subsets of
![]() $\mathscr{F}(N)$
as follows:
$\mathscr{F}(N)$
as follows:
![]() $X\subset \mathscr{F}(N)$
belongs to
$X\subset \mathscr{F}(N)$
belongs to
![]() $\mathtt{Tower}(N)$
if and only if one of the following holds:
$\mathtt{Tower}(N)$
if and only if one of the following holds:
(1)
 $X=\operatorname{Im}f_{M,N}$
for
$X=\operatorname{Im}f_{M,N}$
for
 $11\leqslant M\leqslant N$
;
$11\leqslant M\leqslant N$
;(2)
 $X=\operatorname{Im}(f_{M,N}\circ l_{M})$
for
$X=\operatorname{Im}(f_{M,N}\circ l_{M})$
for
 $11\leqslant M\leqslant N$
(recall that
$11\leqslant M\leqslant N$
(recall that
 $f_{N,N}=\text{id}_{\mathscr{F}(N)}$
) and
$f_{N,N}=\text{id}_{\mathscr{F}(N)}$
) and
 $M\equiv 3\hspace{0.6em}({\rm mod}\hspace{0.2em}8)$
;
$M\equiv 3\hspace{0.6em}({\rm mod}\hspace{0.2em}8)$
;(3)
 $X=\operatorname{Im}(f_{M,N}\circ m_{M})$
for
$X=\operatorname{Im}(f_{M,N}\circ m_{M})$
for
 $12\leqslant M\leqslant N$
and
$12\leqslant M\leqslant N$
and
 $M\equiv 4\hspace{0.6em}({\rm mod}\hspace{0.2em}8)$
;
$M\equiv 4\hspace{0.6em}({\rm mod}\hspace{0.2em}8)$
;(4)
 $X=\operatorname{Im}(f_{M,N}\circ q_{M})$
for
$X=\operatorname{Im}(f_{M,N}\circ q_{M})$
for
 $13\leqslant M\leqslant N$
and
$13\leqslant M\leqslant N$
and
 $M\equiv 5\hspace{0.6em}({\rm mod}\hspace{0.2em}8)$
.
$M\equiv 5\hspace{0.6em}({\rm mod}\hspace{0.2em}8)$
.
Every
![]() $X\in \mathtt{Tower}(N)$
is irreducible (and closed) because it is the image of a regular map, whose domain is a projective irreducible set.
$X\in \mathtt{Tower}(N)$
is irreducible (and closed) because it is the image of a regular map, whose domain is a projective irreducible set.
Definition 5.4.1. Let
![]() $N\geqslant 15$
. Given
$N\geqslant 15$
. Given
![]() $X\in \mathtt{Tower}(N)$
, we let:
$X\in \mathtt{Tower}(N)$
, we let:
(1)
 $t_{N}(X)=N-M$
if
$t_{N}(X)=N-M$
if(1a)
 $X=\operatorname{Im}f_{M,N}$
and
$X=\operatorname{Im}f_{M,N}$
and
 $14\leqslant M\leqslant N$
; or
$14\leqslant M\leqslant N$
; or(1b)
 $X=\operatorname{Im}(f_{M,N}\circ m_{M})$
, where
$X=\operatorname{Im}(f_{M,N}\circ m_{M})$
, where
 $12\leqslant M\leqslant N-1$
and
$12\leqslant M\leqslant N-1$
and
 $M\equiv 4\hspace{0.6em}({\rm mod}\hspace{0.2em}8)$
; or
$M\equiv 4\hspace{0.6em}({\rm mod}\hspace{0.2em}8)$
; or(1c)
 $X=\operatorname{Im}(f_{M,N}\circ q_{M})$
, where
$X=\operatorname{Im}(f_{M,N}\circ q_{M})$
, where
 $13\leqslant M\leqslant N$
and
$13\leqslant M\leqslant N$
and
 $M\equiv 5\hspace{0.6em}({\rm mod}\hspace{0.2em}8)$
;
$M\equiv 5\hspace{0.6em}({\rm mod}\hspace{0.2em}8)$
;
(2)
 $t_{N}(X)=N-M+1$
if
$t_{N}(X)=N-M+1$
if
 $X=\operatorname{Im}(f_{M,N}\circ l_{M})$
, where
$X=\operatorname{Im}(f_{M,N}\circ l_{M})$
, where
 $11\leqslant M\leqslant N$
, with
$11\leqslant M\leqslant N$
, with
 $M\not =N-1$
and
$M\not =N-1$
and
 $M\equiv 3\hspace{0.6em}({\rm mod}\hspace{0.2em}8)$
;
$M\equiv 3\hspace{0.6em}({\rm mod}\hspace{0.2em}8)$
;(3)
 $t_{N}(X)=N-14$
if
$t_{N}(X)=N-14$
if
 $X=\operatorname{Im}f_{M,N}$
and
$X=\operatorname{Im}f_{M,N}$
and
 $11\leqslant M\leqslant 13$
;
$11\leqslant M\leqslant 13$
;(4)
 $t_{N}(X)=1$
if
$t_{N}(X)=1$
if
 $X=\operatorname{Im}m_{N}$
, where
$X=\operatorname{Im}m_{N}$
, where
 $N\equiv 4\hspace{0.6em}({\rm mod}\hspace{0.2em}8)$
;
$N\equiv 4\hspace{0.6em}({\rm mod}\hspace{0.2em}8)$
;(5)
 $t_{N}(X)=4$
if
$t_{N}(X)=4$
if
 $X=\operatorname{Im}(f_{N-1,N}\circ l_{N-1})$
, where
$X=\operatorname{Im}(f_{N-1,N}\circ l_{N-1})$
, where
 $N\equiv 4\hspace{0.6em}({\rm mod}\hspace{0.2em}8)$
.
$N\equiv 4\hspace{0.6em}({\rm mod}\hspace{0.2em}8)$
.
Proposition 5.4.2. Let
![]() $15\leqslant N$
. Let
$15\leqslant N$
. Let
![]() $X\in \mathtt{Tower}(N)$
(and hence
$X\in \mathtt{Tower}(N)$
(and hence
![]() $X$
is
$X$
is
![]() $\mathbb{Q}$
-factorial). If
$\mathbb{Q}$
-factorial). If
![]() $\unicode[STIX]{x1D6FD}\in [0,1]\cap \mathbb{Q}$
, then we have an equality of
$\unicode[STIX]{x1D6FD}\in [0,1]\cap \mathbb{Q}$
, then we have an equality of
![]() $\mathbb{Q}$
-Cartier divisor classes:
$\mathbb{Q}$
-Cartier divisor classes:
where
![]() $D_{X}$
is an effective divisor whose support is a union of elements of
$D_{X}$
is an effective divisor whose support is a union of elements of
![]() $\mathtt{Tower}(N)$
.
$\mathtt{Tower}(N)$
.
Proof. First, we consider the case
![]() $X=\operatorname{Im}(f_{M,N})$
and
$X=\operatorname{Im}(f_{M,N})$
and
![]() $11\leqslant M\leqslant 13$
. There exists
$11\leqslant M\leqslant 13$
. There exists
![]() $c\geqslant 0$
such that
$c\geqslant 0$
such that
by Proposition 5.3.6. On the other hand, by (3.1.4) (with
![]() $N$
replaced by
$N$
replaced by
![]() $M$
), we have
$M$
), we have
Thus, (5.4.1) holds because
![]() $\unicode[STIX]{x1D707}(M)\leqslant \unicode[STIX]{x1D707}(M+8)$
for
$\unicode[STIX]{x1D707}(M)\leqslant \unicode[STIX]{x1D707}(M+8)$
for
![]() $4\leqslant M\leqslant 14$
and
$4\leqslant M\leqslant 14$
and
 $$\begin{eqnarray}H_{u}(M)=\left\{\begin{array}{@{}ll@{}}\operatorname{Im}l_{11}\quad & \text{if }M=11,\\ \operatorname{Im}m_{12}\quad & \text{if }M=12,\\ \operatorname{Im}q_{13}\quad & \text{if }M=13.\end{array}\right.\end{eqnarray}$$
$$\begin{eqnarray}H_{u}(M)=\left\{\begin{array}{@{}ll@{}}\operatorname{Im}l_{11}\quad & \text{if }M=11,\\ \operatorname{Im}m_{12}\quad & \text{if }M=12,\\ \operatorname{Im}q_{13}\quad & \text{if }M=13.\end{array}\right.\end{eqnarray}$$
This proves that (5.4.1) holds if
![]() $X=\operatorname{Im}(f_{M,N})$
and
$X=\operatorname{Im}(f_{M,N})$
and
![]() $11\leqslant M\leqslant 13$
. In all other cases, (5.4.1) is an immediate consequence of the results in § 5.3.4 and the isomorphisms in (1.7.4), (1.7.5), (1.7.6), (1.7.7), and (1.7.8).◻
$11\leqslant M\leqslant 13$
. In all other cases, (5.4.1) is an immediate consequence of the results in § 5.3.4 and the isomorphisms in (1.7.4), (1.7.5), (1.7.6), (1.7.7), and (1.7.8).◻
Because of (5.4.1), we expect that if
![]() $t_{N}(X)\not =0$
, then
$t_{N}(X)\not =0$
, then
![]() $(t_{N}(X)\unicode[STIX]{x1D706}(N)+\unicode[STIX]{x1D6E5}(N))$
generates a wall of the Mori chamber decomposition of the convex cone spanned by
$(t_{N}(X)\unicode[STIX]{x1D706}(N)+\unicode[STIX]{x1D6E5}(N))$
generates a wall of the Mori chamber decomposition of the convex cone spanned by
![]() $\unicode[STIX]{x1D706}(N)$
and
$\unicode[STIX]{x1D706}(N)$
and
![]() $\unicode[STIX]{x1D6E5}(N)$
, and that the center of the corresponding flip contains the strict transform of
$\unicode[STIX]{x1D6E5}(N)$
, and that the center of the corresponding flip contains the strict transform of
![]() $X$
. Now notice that if
$X$
. Now notice that if
![]() $X,Y\in \mathtt{Tower}(N)$
, and
$X,Y\in \mathtt{Tower}(N)$
, and
![]() $X\subset Y$
, then
$X\subset Y$
, then
![]() $t_{N}(X)\geqslant t_{N}(Y)$
. Thus, in order to list candidates for the centers of the flips, we give the definition below.
$t_{N}(X)\geqslant t_{N}(Y)$
. Thus, in order to list candidates for the centers of the flips, we give the definition below.
Definition 5.4.3. Let
![]() $15\leqslant N$
. We let
$15\leqslant N$
. We let
![]() $\mathtt{Center}(N)\subset \mathtt{Tower}(N)$
be the subset of
$\mathtt{Center}(N)\subset \mathtt{Tower}(N)$
be the subset of
![]() $X$
such that:
$X$
such that:
(1)
 $a_{N}(X)>0$
; and
$a_{N}(X)>0$
; and(2) if
 $Y\in \mathtt{Tower}(N)$
properly contains
$Y\in \mathtt{Tower}(N)$
properly contains
 $X$
, then
$X$
, then
 $a_{N}(X)>a_{N}(Y)$
.
$a_{N}(X)>a_{N}(Y)$
.
Let
![]() $X\in \mathtt{Tower}(N)$
, i.e. one of Items (1)–(5) of Definition 5.4.1 holds: then
$X\in \mathtt{Tower}(N)$
, i.e. one of Items (1)–(5) of Definition 5.4.1 holds: then
![]() $X$
does not belong to
$X$
does not belong to
![]() $\mathtt{Center}(N)$
if and only if Item (3) holds.
$\mathtt{Center}(N)$
if and only if Item (3) holds.
We can summarize Prediction 5.1.1 as follows: the walls of the Mori chamber decomposition of the convex cone spanned by
![]() $\unicode[STIX]{x1D706}(N)$
and
$\unicode[STIX]{x1D706}(N)$
and
![]() $\unicode[STIX]{x1D6E5}(N)$
are generated by the vectors
$\unicode[STIX]{x1D6E5}(N)$
are generated by the vectors
![]() $t_{N}(X)\unicode[STIX]{x1D706}(N)+\unicode[STIX]{x1D6E5}(N)$
, where
$t_{N}(X)\unicode[STIX]{x1D706}(N)+\unicode[STIX]{x1D6E5}(N)$
, where
![]() $X$
runs through the elements of
$X$
runs through the elements of
![]() $\mathtt{Center}(N)$
. If
$\mathtt{Center}(N)$
. If
![]() $t=t_{N}(X)$
for some
$t=t_{N}(X)$
for some
![]() $X\in \mathtt{Center}(N)$
, and
$X\in \mathtt{Center}(N)$
, and
![]() $t>1$
, then the center of the flip corresponding to
$t>1$
, then the center of the flip corresponding to
![]() $t_{N}(X)\unicode[STIX]{x1D706}(N)+\unicode[STIX]{x1D6E5}(N)$
is the union of the strict transforms of the elements
$t_{N}(X)\unicode[STIX]{x1D706}(N)+\unicode[STIX]{x1D6E5}(N)$
is the union of the strict transforms of the elements
![]() $Y\in \mathtt{Center}(N)$
such that
$Y\in \mathtt{Center}(N)$
such that
![]() $t_{N}(Y)=t$
. Lastly,
$t_{N}(Y)=t$
. Lastly,
![]() $\unicode[STIX]{x1D706}(N)+\unicode[STIX]{x1D6E5}(N)$
contracts the strict transforms of the elements
$\unicode[STIX]{x1D706}(N)+\unicode[STIX]{x1D6E5}(N)$
contracts the strict transforms of the elements
![]() $Y\in \mathtt{Center}(N)$
such that
$Y\in \mathtt{Center}(N)$
such that
![]() $t_{N}(Y)=1$
.
$t_{N}(Y)=1$
.
A more detailed description goes as follows. Consider the wall closest to the ray spanned by
![]() $\unicode[STIX]{x1D706}(N)$
, i.e. that spanned by
$\unicode[STIX]{x1D706}(N)$
, i.e. that spanned by
![]() $(\unicode[STIX]{x1D706}(N)+(N-10)^{-1}\unicode[STIX]{x1D6E5}(N))$
, with center
$(\unicode[STIX]{x1D706}(N)+(N-10)^{-1}\unicode[STIX]{x1D6E5}(N))$
, with center
![]() $X=\operatorname{Im}(f_{11,N}\circ l_{11})$
. Then
$X=\operatorname{Im}(f_{11,N}\circ l_{11})$
. Then
![]() $D_{X}=0$
by Proposition 5.3.7 and hence
$D_{X}=0$
by Proposition 5.3.7 and hence
![]() $(\unicode[STIX]{x1D706}(N)+(N-10)^{-1}\unicode[STIX]{x1D6E5}(N))|_{X}$
is the opposite of an ample class. What should we expect
$(\unicode[STIX]{x1D706}(N)+(N-10)^{-1}\unicode[STIX]{x1D6E5}(N))|_{X}$
is the opposite of an ample class. What should we expect
![]() $\mathscr{F}(N,(N-10)^{-1}+\unicode[STIX]{x1D716})$
to look like? In order to answer this, we recall Looijenga’s key observation: if
$\mathscr{F}(N,(N-10)^{-1}+\unicode[STIX]{x1D716})$
to look like? In order to answer this, we recall Looijenga’s key observation: if
![]() $X$
is an irreducible component of
$X$
is an irreducible component of
![]() $\unicode[STIX]{x1D6E5}^{(k)}(N)$
, then the exceptional divisor of
$\unicode[STIX]{x1D6E5}^{(k)}(N)$
, then the exceptional divisor of
![]() $Bl_{X}\mathscr{F}(N)$
(a weighted blow-up of
$Bl_{X}\mathscr{F}(N)$
(a weighted blow-up of
![]() $\mathscr{F}(N)$
with center
$\mathscr{F}(N)$
with center
![]() $X$
) is a trivial weighted projective bundle over
$X$
) is a trivial weighted projective bundle over
![]() $X$
, away from
$X$
, away from
![]() $\unicode[STIX]{x1D6E5}^{(k+1)}(N)$
(this is because
$\unicode[STIX]{x1D6E5}^{(k+1)}(N)$
(this is because
![]() $\unicode[STIX]{x1D6E5}^{(k)}(N)$
is the quotient by
$\unicode[STIX]{x1D6E5}^{(k)}(N)$
is the quotient by
![]() $\unicode[STIX]{x1D6E4}(N)$
of the points of intersection of
$\unicode[STIX]{x1D6E4}(N)$
of the points of intersection of
![]() $k$
hyperplane sections of
$k$
hyperplane sections of
![]() $\mathscr{D}_{\unicode[STIX]{x1D6EC}_{N}}^{+}$
). For our initial
$\mathscr{D}_{\unicode[STIX]{x1D6EC}_{N}}^{+}$
). For our initial
![]() $X$
, i.e.
$X$
, i.e.
![]() $\operatorname{Im}(f_{11,N}\circ l_{11})$
, this translates into the prediction that
$\operatorname{Im}(f_{11,N}\circ l_{11})$
, this translates into the prediction that
![]() $\mathscr{F}(N,(N-10)^{-1}+\unicode[STIX]{x1D716})$
is obtained from
$\mathscr{F}(N,(N-10)^{-1}+\unicode[STIX]{x1D716})$
is obtained from
![]() $\mathscr{F}(N,(N-10)^{-1}-\unicode[STIX]{x1D716})$
by replacing (the closure of)
$\mathscr{F}(N,(N-10)^{-1}-\unicode[STIX]{x1D716})$
by replacing (the closure of)
![]() $\operatorname{Im}(f_{11,N}\circ l_{11})$
with a
$\operatorname{Im}(f_{11,N}\circ l_{11})$
with a
![]() $w\mathbb{P}^{N-11}$
. What about the remaining flips, corresponding to
$w\mathbb{P}^{N-11}$
. What about the remaining flips, corresponding to
![]() $\unicode[STIX]{x1D706}(N)+k^{-1}\unicode[STIX]{x1D6E5}(N)$
for
$\unicode[STIX]{x1D706}(N)+k^{-1}\unicode[STIX]{x1D6E5}(N)$
for
![]() $k\in \{N-12,N-11,\ldots ,2\}$
? First, we note that if
$k\in \{N-12,N-11,\ldots ,2\}$
? First, we note that if
![]() $X\in \mathtt{Center}(N)$
, then (5.4.1) holds with
$X\in \mathtt{Center}(N)$
, then (5.4.1) holds with
![]() $D_{X}$
an effective divisor whose support is a union of elements of
$D_{X}$
an effective divisor whose support is a union of elements of
![]() $\mathtt{Tower}(N)$
, except if
$\mathtt{Tower}(N)$
, except if
![]() $X=\operatorname{Im}f_{14,N}$
. Suppose for the moment that
$X=\operatorname{Im}f_{14,N}$
. Suppose for the moment that
![]() $X\not =\operatorname{Im}f_{14,N}$
; then since
$X\not =\operatorname{Im}f_{14,N}$
; then since
![]() $t_{N}(Y)>t_{N}(X)$
for all prime divisors in the support of
$t_{N}(Y)>t_{N}(X)$
for all prime divisors in the support of
![]() $D_{X}$
(by definition of
$D_{X}$
(by definition of
![]() $\mathtt{Tower}(N)$
) and because
$\mathtt{Tower}(N)$
) and because
![]() $\mathscr{F}(N,k^{-1}+\unicode[STIX]{x1D716})$
is obtained from
$\mathscr{F}(N,k^{-1}+\unicode[STIX]{x1D716})$
is obtained from
![]() $\mathscr{F}(N,k^{-1}-\unicode[STIX]{x1D716})$
by replacing (the closure of) centers
$\mathscr{F}(N,k^{-1}-\unicode[STIX]{x1D716})$
by replacing (the closure of) centers
![]() $W$
such that
$W$
such that
![]() $t_{N}(W)=k$
with projective spaces of dimension
$t_{N}(W)=k$
with projective spaces of dimension
![]() $N-1-\operatorname{cod}(W,\mathscr{F}(N))$
, we see that the picture replicates itself. Lastly, let us look at the picture for
$N-1-\operatorname{cod}(W,\mathscr{F}(N))$
, we see that the picture replicates itself. Lastly, let us look at the picture for
![]() $X=\operatorname{Im}f_{14,N}$
. In this case Gritsenko’s relation, i.e. Corollary 3.1.3, reads
$X=\operatorname{Im}f_{14,N}$
. In this case Gritsenko’s relation, i.e. Corollary 3.1.3, reads
![]() $H_{h}(14)=H_{u}(14)$
. A geometric description of the rational equivalence
$H_{h}(14)=H_{u}(14)$
. A geometric description of the rational equivalence
![]() $H_{h}(14)=H_{u}(14)$
gives that
$H_{h}(14)=H_{u}(14)$
gives that
![]() $H_{h}(14)$
and
$H_{h}(14)$
and
![]() $H_{u}(14)$
are actually trivial outside
$H_{u}(14)$
are actually trivial outside
![]() $H_{h}(14)\cap H_{u}(14)$
and hence (5.4.1) for
$H_{h}(14)\cap H_{u}(14)$
and hence (5.4.1) for
![]() $X=\operatorname{Im}f_{14,N}$
holds with
$X=\operatorname{Im}f_{14,N}$
holds with
![]() $D_{X}=0$
. This then suggests that the usual description holds also for the flip corresponding to
$D_{X}=0$
. This then suggests that the usual description holds also for the flip corresponding to
![]() $\operatorname{Im}f_{14,N}$
.
$\operatorname{Im}f_{14,N}$
.
Remark 5.4.4. The set of values
![]() $t_{N}(X)$
for
$t_{N}(X)$
for
![]() $X\in \mathtt{Center}(N)$
is obtained by adding
$X\in \mathtt{Center}(N)$
is obtained by adding
![]() $1$
to each value
$1$
to each value
![]() $t_{N-1}(Y)$
for
$t_{N-1}(Y)$
for
![]() $Y\in \mathtt{Center}(N-1)$
and adjoining the value
$Y\in \mathtt{Center}(N-1)$
and adjoining the value
![]() $1=t_{N}(H_{h}(N))$
. This is explained by the formulae in Proposition 5.3.6. In fact, for simplicity suppose that
$1=t_{N}(H_{h}(N))$
. This is explained by the formulae in Proposition 5.3.6. In fact, for simplicity suppose that
![]() $N-1\not \equiv 3,4\hspace{0.6em}({\rm mod}\hspace{0.2em}8)$
. Then, for
$N-1\not \equiv 3,4\hspace{0.6em}({\rm mod}\hspace{0.2em}8)$
. Then, for
![]() $\unicode[STIX]{x1D6FD}\not =1$
, we have
$\unicode[STIX]{x1D6FD}\not =1$
, we have
This explains the behavior described above because, if
![]() $\unicode[STIX]{x1D6FD}/(1-\unicode[STIX]{x1D6FD})=1/k$
, then
$\unicode[STIX]{x1D6FD}/(1-\unicode[STIX]{x1D6FD})=1/k$
, then
![]() $\unicode[STIX]{x1D6FD}=1/(k+1)$
.
$\unicode[STIX]{x1D6FD}=1/(k+1)$
.
An induction on
![]() $N$
(see Remark 5.4.4) proves the following result.
$N$
(see Remark 5.4.4) proves the following result.
Proposition 5.4.5. Let
![]() $N\geqslant 11$
and let
$N\geqslant 11$
and let
be rational. If
![]() $C\subset \mathscr{F}(N)$
is a complete curve, then
$C\subset \mathscr{F}(N)$
is a complete curve, then
Remark 5.4.6. The locally symmetric varieties
![]() $\mathscr{F}(N)$
are not projective, but they are swept out by complete curves. In fact, the complement of
$\mathscr{F}(N)$
are not projective, but they are swept out by complete curves. In fact, the complement of
![]() $\mathscr{F}(N)$
in the Baily–Borel compactification
$\mathscr{F}(N)$
in the Baily–Borel compactification
![]() $\mathscr{F}(N)^{\ast }$
is of dimension
$\mathscr{F}(N)^{\ast }$
is of dimension
![]() $1$
, and the assertion follows because
$1$
, and the assertion follows because
![]() $\dim \mathscr{F}(N)=N\geqslant 3$
.
$\dim \mathscr{F}(N)=N\geqslant 3$
.
Acknowledgements
This project was started and first developed while both authors were visiting the IAS as participants in the special program on ‘Topology of Algebraic Varieties’. We are grateful to the IAS for hosting us and offering an ideal research environment. The IAS stay of the first author was partially supported by NSF institute grant DMS-1128155. The stay of the second author was partially supported by the Giorgio and Elena Petronio Fellowship Fund, the Giorgio and Elena Petronio Fellowship Fund II, and the Fund for Mathematics of the IAS.
We are indebted in more than one way to E. Looijenga. First, our work has been inspired by his ground-breaking papers [Reference LooijengaLoo03a, Reference LooijengaLoo03b] and secondly we had several discussions with him on the subject of this work. Lastly, Looijenga shared some unpublished notes with us (relevant to future investigation of the quartic case). Additionally, we have discussed with numerous people at various stages of the project. In particular, we thank V. Alexeev, S. Casalaina-Martin, G. Farkas, V. Gritsenko, K. Hulek, B. Hassett, S. Kondo, Z. Li, D. Oprea, R. Pandharipande, and L. Zhang.