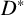1 Introduction
Let D be a division ring and
$D^*$
denote the multiplicative group of D. Recall that a subgroup N of
$D^*$
is subnormal in
$D^*$
if there is a finite sequence of subgroups
$$ \begin{align*}N=N_r\trianglelefteq N_{r-1}\trianglelefteq \cdots N_1 \trianglelefteq N_0=D^*.\end{align*} $$
The motivation of this paper is a result of Tits for linear groups. Tits showed that if N is a finitely generated subgroup of the general linear group
$\mathrm {GL}_n(F)$
over a field F, then N contains either a nonabelian free subgroup or a nilpotent normal subgroup H of finite index in N [Reference Tits13]. This famous result of Tits is now referred to as the Tits Alternative. For general linear groups over division rings, Lichtman [Reference Lichtman10] proved that there exists a division ring D such that
$D^*$
contains a finitely generated group which is not solvable-by-finite. Therefore, the Tits Alternative fails even for matrices of degree one over
$D^*$
. Also in [Reference Lichtman10], Lichtman remarked that it was not known whether the multiplicative group of a noncommutative division ring contains a nonabelian free subgroup. One year later, Lichtman showed in [Reference Lichtman11] that if N is a normal subgroup of
$D^*$
such that N contains a nonabelian nilpotent-by-finite subgroup, then N contains a nonabelian free subgroup. After that, Gonçalves and Mandel proposed the following conjecture.
Conjecture 1.1 [Reference Gonçalves and Mandel5, Conjecture 2].
For a division ring D with centre F and a subnormal subgroup N of
$D^*$
, if
$N\not \subseteq F$
, then N contains a nonabelian free subgroup.
We give an affirmative answer to this conjecture in the case when N contains a nonabelian solvable subgroup. This result can be seen as a generalisation of Lichtman’s result in [Reference Lichtman11].
Theorem 1.2 (Main Theorem).
Let D be a division ring and N a subnormal subgroup of the multiplicative group
$D^*$
. If N contains a nonabelian solvable subgroup, then N contains a nonabelian free subgroup.
We note that many special cases of the Main Theorem have been studied by many authors. For example, a subgroup N of
$D^*$
will contain nonabelian free subgroups if N satisfies any of the following assumptions:
-
• N is normal in
$D^*$
and N contains a nonabelian nilpotent-by-finite subgroup (Lichtman [Reference Lichtman11]); -
• N is normal in
$D^*$
and N contains a nonabelian locally solvable-by-locally-finite subgroup (Bell and Gonçalves [Reference Bell and Gonçalves1]); -
• N is subnormal in
$D^*$
, N contains a nonabelian locally solvable subgroup and the transcendence degree of the centre of D over its prime subfield is infinite (Bien and Hai [Reference Bien and Hai2]).
For convenience, throughout this paper, the phrase ‘free subgroup’ means ‘nonabelian free subgroup’. The idea of the proof of the Main Theorem comes from [Reference Bell and Gonçalves1]. We can sketch the proof as follows. Assume that N is a subnormal subgroup of
$D^*$
containing a nonabelian solvable subgroup. First, we will study the existence of free subgroups in subnormal subgroups of the division ring of fractions
$K(x,\sigma )$
of the skew polynomial ring
$K[x,\sigma ]$
in a single-variable x twisted by a nonidentity automorphism
$\sigma $
over a field K. Namely, we will prove that every subnormal subgroup of
$K(x,\sigma )^*$
containing x contains a free subgroup. After that, we shall build a subring of D which is isomorphic to
$K[x,\sigma ]$
, and based on the result on
$K(x,\sigma )$
, the Main Theorem will follow.
Some special cases for the existence of free subgroups have also been considered. For example, the following conjecture was proposed by Hai and Thin [Reference Hai and Thin8].
Conjecture 1.3 [Reference Hai and Thin8, Conjecture 1].
Every locally solvable subnormal subgroup of
$D^*$
is central.
In [Reference Hai and Thin7, Theorem 2.2], Hai and Thin proved that Conjecture 1.3 is true in the case of a locally nilpotent subnormal subgroup in an arbitrary division ring D and, in [Reference Hai and Thin7, Theorem 2.4], for the case of a division ring which is algebraic over its centre. After that, in [Reference Hai and Thin8], Conjecture 1.3 holds if D is a weakly locally finite division ring, that is, D satisfies the condition: for every finite subset S of D, the division subring
$P(S)$
generated by S and a prime subfield P of D is finite-dimensional over the centre
$\mathrm {Z}(P(S))$
. Recently, Conjecture 1.3 was fully confirmed in [Reference Danh and Khanh3, Theorem 1]. By applying the Main Theorem, we can also show that Conjecture 1.3 is true.
2 Proof of the main theorem
The fundamental result used in proving the Main Theorem is Theorem 2.6. Our approach to the proof of Theorem 2.6 comes from [Reference Bell and Gonçalves1]. However, thanks to insights from [Reference Bien and Hai2], our proof is more straightforward than that in [Reference Bell and Gonçalves1].
Let K be a field and
$\sigma $
be a field automorphism of K. Let us denote by
$K[x,\sigma ]$
the skew polynomial ring in an indeterminate x twisted by
$\sigma $
over K. Then
$K[x,\sigma ]$
is a principal left ideal domain and also a principal right ideal domain, that is, every one-sided ideal of
$K[x,\sigma ]$
can be generated by one element (see [Reference Goodearl and Warfield6, Theorem 2.8]). The division ring of fractions of
$K[x,\sigma ]$
is denoted by
$K(x,\sigma )$
. Every element of
$K(x,\sigma )$
is of the form
$f(x)\cdot g(x)^{-1}$
, where
$f(x)$
and
$g(x)$
are in
$K[x,\sigma ]$
. Additionally, we denote by
$K((x,\sigma ))$
the skew Laurent series ring in the indeterminate x twisted by
$\sigma $
over K. It is well known that
$K((x,\sigma ))$
is a division ring (see [Reference Lam9, Example 1.8]). Clearly,
$K[x,\sigma ]$
can be embedded into
$K((x,\sigma ))$
, and so
$K(x,\sigma )$
can be seen as a division subring of
$K((x,\sigma ))$
.
Let D be a division ring with the centre F. We can regard D as an F-algebra. If
$\mathrm {dim}_F(D)<\infty $
, then D is called centrally finite. From [Reference Lam9, Proposition 14.2],
$K((x,\sigma ))$
is centrally finite if and only if the order of
$\sigma $
is finite. As a corollary, if the order of
$\sigma $
is finite, then
$K(x,\sigma )$
is centrally finite. We give some results about the existence of free subgroups in
$K(x,\sigma )$
. We need the following property.
Lemma 2.1 [Reference Gonçalves4, Theorem 2.1].
Let D be a noncommutative centrally finite division ring and N a noncentral subnormal subgroup of
$D^*$
. Then N contains a free subgroup.
We immediately have the following result.
Corollary 2.2. Let
$K(x,\sigma )$
be the division ring of fractions of
$K[x,\sigma ]$
and N a noncentral subnormal subgroup of
$K(x,\sigma )^*$
. If
$\sigma $
has a finite order, then N contains a free subgroup.
For an arbitrary automorphism
$\sigma $
of K, whether a subnormal subgroup N of
$K(x,\sigma )^*$
contains a free subgroup is an open question. In this section, we shall answer the question in case
$\sigma $
is a nonidentity and
$x\in N$
.
Lemma 2.3 [Reference Bien and Hai2].
Let K be a field and
$\sigma $
a nonidentity automorphism of K with fixed subfield
$k=\{a\in K:\sigma (a)=a\}$
. Assume that there exists an element
$a\in K\setminus k$
such that
$k(a,\sigma (a),\sigma ^2(a),\ldots )$
is not a finitely generated extension of k. If N is a subnormal subgroup of
$K(x,\sigma )^*$
containing x, then N contains a free subgroup.
Proof. This is the assertion (i) of [Reference Bien and Hai2, Theorem 2.5].
With the notation as in Lemma 2.3, we shall now consider the remaining case, that is,
$k(a,\sigma (a),\sigma ^2(a),\ldots )$
is a finitely generated extension of k. The next lemma is the key lemma to resolve this case.
Lemma 2.4. Let K be a field and
$\sigma $
an automorphism of K with fixed subfield
$k=\{a\in K: \sigma (a)=a\}$
. Assume that there exists an element
$a\in K\setminus k$
such that
$E=k(a,\sigma (a), \sigma ^2(a),\ldots )$
is a finitely generated extension of k. Then, the following hold.
-
(i)
$E=k(\sigma ^{n_1}(a), \sigma ^{n_2}(a),\ldots , \sigma ^{n_r}(a))$
, where the
$n_i$
are integers with
$0\leq n_1<n_2<\cdots <n_r$
. -
(ii) The restriction of
$\sigma $
to the subfield E is an automorphism of E of finite order.
Proof. (i) Since
$E/k$
is a finitely generated extension,
$E=k(a_1,a_2,\ldots ,a_s)$
for some
$a_1, a_2, \ldots , a_s$
in E. For each
$i\in \overline {1,s}$
, there exist
$f_i$
and
$g_i$
in
$k[a,\sigma (a), \sigma ^2(a),\ldots ]$
such that
$a_i=f_ig_i^{-1}$
. We can select a finite number of elements
$\sigma ^{n_{i,1}}(a), \sigma ^{n_{i,2}}(a),\ldots ,\sigma ^{n_{i,\ell _i}}(a)$
such that
$f_i$
and
$g_i$
are in
$k[\sigma ^{n_{i,1}}(a), \sigma ^{n_{i,2}}(a),\ldots ,\sigma ^{n_{i,\ell _i}}(a)]$
. It follows that
$a_i\in k(\sigma ^{n_{i,1}}(a), \sigma ^{n_{i,2}}(a),\ldots ,\sigma ^{n_{i,\ell _i}}(a))$
. We have
$$ \begin{align*}E=k(a_i\mid 1\leq i\leq s)\subseteq k(\sigma^{n_{i,j}}(a)\mid 1\leq i\leq s, 1\leq j\leq \ell_i)\subseteq k(a,\sigma(a), \sigma^2(a),\ldots)=E.\end{align*} $$
This leads to
$E=k(\sigma ^{n_{i,j}}(a)\mid 1\leq i\leq s, 1\leq j\leq \ell _i)$
. Hence, we can write
$E=k(\sigma ^{n_1}(a), \sigma ^{n_2}(a),\ldots , \sigma ^{n_r}(a))$
for
$0\leq n_1<n_2<\cdots <n_r$
.
(ii) We have
$\sigma (E)\subseteq E$
because
$\sigma (\sigma ^{n}(a))=\sigma ^{n+1}(a)\in E$
. From assertion (i),
$E=k(\sigma ^{n_1}(a), \sigma ^{n_2}(a),\ldots , \sigma ^{n_r}(a))$
for
$0\leq n_1<n_2<\cdots <n_r$
. Put
$t_i=\sigma ^{n_i}(a)$
, and so
$E=k(t_1,t_2,\ldots ,t_r)$
. Remark that
$$ \begin{align*}\sigma^{n_i-n_j}(t_j)=\sigma^{n_i-n_j}(\sigma^{n_j}(a))=\sigma^{n_i}(a)=t_i \quad \text{for } 1\leq i,j\leq r.\end{align*} $$
Put
$n=(n_1-n_2)(n_2-n_3)\ldots (n_{r-1}-n_r)(n_r-n_1)$
. For each
$i=\overline {1,r}$
,
$$ \begin{align*}n=(n_i-n_{i+1})(n_{i+1}-n_{i+2})\ldots(n_{r-1}-n_r)(n_r-n_1)(n_1-n_2)\ldots(n_{i-1}-n_{i}),\end{align*} $$
and so
$$ \begin{align*} \sigma^n(t_i) & = \sigma^{(n_i-n_{i+1})(n_{i+1}-n_{i+2})\cdots(n_{r-1}-n_r)(n_r-n_1) (n_1-n_2)\cdots(n_{i-1}-n_{i})}(t_i)\\ & =\sigma^{n_i-n_{i+1}}(\sigma^{n_{i+1}-n_{i+2}}(\cdots(\sigma^{n_{r-1}-n_r}(\sigma^{n_r-n_1}(\sigma^{n_1-n_2}(\ldots(\sigma^{n_{i-1}-n_{i}}(t_i)))\cdots{\kern-2pt}) =t_i. \end{align*} $$
Thus, the restriction
$\sigma |_{E}$
has finite order. Suppose that the order of
$\sigma |_{E}$
is
$d>0$
. Since
$\sigma (E)\subseteq E$
, we have
$$ \begin{align*}E=\sigma^d(E)\subseteq \sigma^{d-1}(E)\subseteq \cdots \subseteq\sigma^{1}(E).\end{align*} $$
Hence,
$\sigma |_{E}$
is an automorphism of E.
Lemma 2.4 enables us to prove the next lemma.
Lemma 2.5. Let K be a field and
$\sigma $
a nonidentity automorphism of K with fixed subfield
$k=\{a\in K: \sigma (a)=a\}$
. Assume that there exists
$a\in K\setminus k$
such that
$E=k(a,\sigma (a), \sigma ^2(a),\ldots )$
is a finitely generated extension of k. If N is a subnormal subgroup of
$K(x,\sigma )^*$
containing x, then N contains a free subgroup.
Proof. By Lemma 2.4, the restriction
$\sigma |_{E}$
is an automorphism of E of finite order. Since
$\sigma |_{E}(a)=\sigma (a)\neq a$
, the automorphism
$\sigma |_{E}$
is a nonidentity. Thus,
$R=E(x,\sigma |_{E})$
is a noncommutative centrally finite division subring of
$K(x,\sigma )$
. Because N is subnormal in
$K(x,\sigma )^*$
, also
$H=N\cap R^*$
is subnormal in
$R^*$
. However, H is noncentral since
$x\in H$
. According to Lemma 2.2, H contains a nonabelian free subgroup. Hence, N contains a free subgroup.
Theorem 2.6. Let K be a field and
$\sigma $
a nonidentity automorphism of K. Assume that N is a subnormal subgroup of
$K(x,\sigma )^*$
. If
$x\in N$
, then N contains a free subgroup.
Proof. Let
$D=K(x,\sigma )$
, where K is a field and
$\sigma $
is a nonidentity automorphism of K with fixed subfield
$k=\{a\in K:\sigma (a)=a\}$
. Select
$a\in K\setminus k$
. Put
$E=k(a,\sigma (a), \sigma ^2(a),\ldots )$
,
$R=E(x,\sigma |_{E})$
and
$H=N\cap E^*$
. Then H is a subnormal subgroup of
$R^*$
containing x. It follows from Lemma 2.5 that if
$E/k$
is a finitely generated extension, then H contains a free subgroup. Otherwise, by Lemma 2.3, H also contains a free subgroup. Hence, in both cases, N contains a free subgroup. The proof is complete.
Proof of the Main Theorem.
Assume that N is a subnormal subgroup of
$D^*$
containing a nonabelian solvable subgroup G. Suppose that the derived length of G is
$r\geq 1$
with the derived series
$$ \begin{align*}\langle 1\rangle=G^{(r)} \trianglelefteq G^{(r-1)} \trianglelefteq \ldots\trianglelefteq G^{(1)} \trianglelefteq G^{(0)}=G.\end{align*} $$
Clearly,
$G^{(r-2)}$
is a nonabelian solvable subgroup. Replace G by
$G^{(r-2)}$
. Then
$G'$
is a nontrivial abelian subgroup of G. By Zorn’s lemma, the set
$$ \begin{align*}\mathcal{U}=\{A\leq G: A \text{ is abelian and } G'\subseteq A\}\end{align*} $$
has a maximal element M. Due to the maximality,
$M\not \subseteq \mathrm {Z}(G)$
. Additionally, since
$G'\subseteq M$
, M is normal in G. Select
$g\in G$
and
$u\in M$
such that
$ug\neq gu$
. The normality of M in G leads to
$u_n:=g^{n}ug^{-n}\in M$
for every
$n\in \mathbb {Z}$
, and so all these elements commute. Put
$F=\mathrm {Z}(D)$
. Then the division subring
$K=F(u_n\mid n\in \mathbb {Z})$
is a field and the map
$\sigma :K\to K$
,
$z\mapsto gzg^{-1}$
is a nonidentity automorphism of K.
Let
$R=K[g]$
be the subring of D generated by
$K\cup \{g\}$
and
$K[x,\sigma ]$
the ring of skew polynomials in an indeterminate x. We observe that the map
$\phi :K[x,\sigma ] \to R$
,
$\sum \nolimits _{i}a_ix^i\mapsto \sum \nolimits _{i}a_ig^i$
is a surjective F-algebra homomorphism. Put
$I=\mathrm {ker}\phi $
. We consider two cases.
Case 1:
$I=(0)$
. Then
$R\cong K[x,\sigma ]$
, and thus the division ring of fractions
$\overline {R}$
of R is isomorphic to
$K(x,\sigma )$
. The image of
$N\cap \overline {R}^*$
is a subnormal subgroup of
$K(x,\sigma )^*$
and contains x. By Theorem 2.6, this subgroup contains a free subgroup. Consequently,
$N\cap \overline {R}^*$
and also N contain a free subgroup.
Case 2:
$I\neq (0)$
. Then
$R\cong K[x,\sigma ]/I$
. This means
$K[x,\sigma ]/I$
is a domain and I is a prime ideal. Additionally,
$K[x,\sigma ]$
is a principal left ideal domain. This implies that
$I=(p)$
for some irreducible polynomial p in
$K[x,\sigma ]$
, that is, I is a maximal ideal of
$K[x,\sigma ]$
, and so
$K[x,\sigma ]/I$
is a division ring. However, by the divide algorithm for
$K[x,\sigma ]$
(see [Reference Ore12, The Euclidean algorithm]),
$K[x,\sigma ]/I$
is a finite dimensional K-vector space. Therefore, R is a centrally finite division subring. By Lemma 2.1,
$N\cap R^*$
contains a free subgroup. Hence, N also contains a free subgroup.
Finally, the Main Theorem gives the affirmation of Conjecture 1.3 as follows.
Corollary 2.7. Let D be a division ring. Then every locally solvable subnormal subgroup of
$D^*$
is central.
Proof. Let D be a division ring and N be a locally solvable subnormal subgroup of
$D^*$
. Assume that N is noncentral. Then N contains a finitely generated subgroup that is nonabelian and solvable. It follows from the Main Theorem that N contains a free subgroup. This is a contradiction to the local solvability of N. Hence, N is central.
