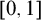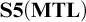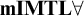1 Introduction
The reader is assumed to know basic facts on monadic fuzzy predicate logics and their Kripke semantics, including the most well-known fuzzy modal logic S5; on the other hand, he/she is also assumed to know t-norm based residuated fuzzy logic as presented in the most famous books [Reference Hájek26, Reference Noguera37]. Fuzzy logic is more suitable than classical logic to handle uncertain and fuzzy information, has become a subject of increasing interest as logics of vagueness [Reference Zadeh56]. Algebraic semantics underlying fuzzy logic involve various binary operations on the unit real interval
![]() $[0,1]$
, generalizing the classical Boolean truth functions on
$[0,1]$
, generalizing the classical Boolean truth functions on
![]() $\{0,1\}$
. For example, MV-algebras were introduced in [Reference Chang5] by Chang as algebraic semantics of the infinitely valued logic of Łukasiewicz
$\{0,1\}$
. For example, MV-algebras were introduced in [Reference Chang5] by Chang as algebraic semantics of the infinitely valued logic of Łukasiewicz ![]() , while BL-algebras were introduced in [Reference Hájek26] by Hájek as algebraic semantics of Basic fuzzy logic
, while BL-algebras were introduced in [Reference Hájek26] by Hájek as algebraic semantics of Basic fuzzy logic
![]() $\mathbf {BL}$
, a general framework in which tautologies of continuous t-norm and their residua can be captured [Reference Cignoli, Esteva, Godo and Torrens8]. Inspired by Hájek’s famous work, Esteva and Godo proposed in [Reference Esteva, Gispert, Godo and Montagan15] a new formal deductive system
$\mathbf {BL}$
, a general framework in which tautologies of continuous t-norm and their residua can be captured [Reference Cignoli, Esteva, Godo and Torrens8]. Inspired by Hájek’s famous work, Esteva and Godo proposed in [Reference Esteva, Gispert, Godo and Montagan15] a new formal deductive system
![]() $\mathbf {MTL}$
, called monoidal t-norm based logic, and intended to cope with left-continuous t-norms and their residua [Reference Jenei and Montagan33]. These logical systems have been called t-norm based residuated fuzzy logics and can be suitably placed in a hierarchy of logic depending on their characteristic axioms, all of them being extensions of the logic
$\mathbf {MTL}$
, called monoidal t-norm based logic, and intended to cope with left-continuous t-norms and their residua [Reference Jenei and Montagan33]. These logical systems have been called t-norm based residuated fuzzy logics and can be suitably placed in a hierarchy of logic depending on their characteristic axioms, all of them being extensions of the logic
![]() $\mathbf {MTL}$
, which also shows that the logic
$\mathbf {MTL}$
, which also shows that the logic
![]() $\mathbf {MTL}$
is the weakest t-norm based residuated fuzzy logic, and having classical logic as common extension [Reference Noguera37]. In the past two decades, studies in
$\mathbf {MTL}$
is the weakest t-norm based residuated fuzzy logic, and having classical logic as common extension [Reference Noguera37]. In the past two decades, studies in
![]() $\mathbf {MTL}$
and its formal extensions as well as on the algebraic semantics side draw attention to and establish strong connections between the fields [Reference Borzooei, Shoar and Ameri2, Reference Cignoli and Esteva7, Reference Cintula, Horčík and Noguera9, Reference Cintula and Noguera10, Reference Esteva, Gispert, Godo and Montagan15, Reference Esteva and Godo17, Reference Ghorbani20, Reference Gottwal and Jenei24, Reference Hájek27, Reference Pei39, Reference Zhang58].
$\mathbf {MTL}$
and its formal extensions as well as on the algebraic semantics side draw attention to and establish strong connections between the fields [Reference Borzooei, Shoar and Ameri2, Reference Cignoli and Esteva7, Reference Cintula, Horčík and Noguera9, Reference Cintula and Noguera10, Reference Esteva, Gispert, Godo and Montagan15, Reference Esteva and Godo17, Reference Ghorbani20, Reference Gottwal and Jenei24, Reference Hájek27, Reference Pei39, Reference Zhang58].
Monadic (Boolean) algebra
![]() $(L,\exists )$
, in the sense of Halmos [Reference Halmos32], is a Boolean algebra L equipped with a closure operator
$(L,\exists )$
, in the sense of Halmos [Reference Halmos32], is a Boolean algebra L equipped with a closure operator
![]() $\exists $
, which abstracts algebraic properties of the standard existential quantifier “for some” [Reference Tharp46]. The name “monadic” comes from the connection with predicate logics for languages having one placed predicates and just a single quantifier. Subsequently, monadic MV-algebras, the algebraic counterpart of monadic Łukasiewicz predicate logic, were introduced and studied in [Reference Di Nola and Grigolia11, Reference Di Nola, Grigolia and Lenzi12, Reference Hájek, Paris and Shepherdson31, Reference Rach ů nek and Šalounová42, Reference Rutledge45]. In order to algebraize the monadic basic fuzzy predicate logic
$\exists $
, which abstracts algebraic properties of the standard existential quantifier “for some” [Reference Tharp46]. The name “monadic” comes from the connection with predicate logics for languages having one placed predicates and just a single quantifier. Subsequently, monadic MV-algebras, the algebraic counterpart of monadic Łukasiewicz predicate logic, were introduced and studied in [Reference Di Nola and Grigolia11, Reference Di Nola, Grigolia and Lenzi12, Reference Hájek, Paris and Shepherdson31, Reference Rach ů nek and Šalounová42, Reference Rutledge45]. In order to algebraize the monadic basic fuzzy predicate logic
![]() $\mathbf {mBL\forall }$
, three kinds of monadic BL-algebras have been introduced and studied successively, one by Drăgulici [Reference Drŭgulici13], one by Grigolia [Reference Grigolia25] and another by Castaño [Reference Castaño, Cimadamore, Verela and Rueda4]. Along with the same line of the above works, monadic residuated
$\mathbf {mBL\forall }$
, three kinds of monadic BL-algebras have been introduced and studied successively, one by Drăgulici [Reference Drŭgulici13], one by Grigolia [Reference Grigolia25] and another by Castaño [Reference Castaño, Cimadamore, Verela and Rueda4]. Along with the same line of the above works, monadic residuated
![]() $\ell $
-monoids [Reference Rach ů nek and Švrček44], residuated lattices [Reference Rach ů nek and Šalounová43], bounded hoops [Reference Wang, He, Yang, Wang and He49], Heyting algebras [Reference Dzik and Wojtylak14, Reference Kurahashi34, Reference Olkhovikov and Badia38, Reference Poacik41] and other related monadic algebraic structures were introduced in [Reference Ghorbani21, Reference Wang, He and She48–Reference Wang, Xin and He54]. However, it should be pointed out here that some monadic algebras of t-norm based fuzzy residuated logic abandon the naturally containing relations between corresponding algebras. Indeed, readers please refer to Sections 2 and 3 for details,
$\ell $
-monoids [Reference Rach ů nek and Švrček44], residuated lattices [Reference Rach ů nek and Šalounová43], bounded hoops [Reference Wang, He, Yang, Wang and He49], Heyting algebras [Reference Dzik and Wojtylak14, Reference Kurahashi34, Reference Olkhovikov and Badia38, Reference Poacik41] and other related monadic algebraic structures were introduced in [Reference Ghorbani21, Reference Wang, He and She48–Reference Wang, Xin and He54]. However, it should be pointed out here that some monadic algebras of t-norm based fuzzy residuated logic abandon the naturally containing relations between corresponding algebras. Indeed, readers please refer to Sections 2 and 3 for details,
and
Thus the first aim of this paper is to make up this important drawback. In Section 2, we survey monadic algebras of t-norm based fuzzy residuated logic and revise some of their axiomatic systems, then showing that the relationships between monadic algebras of t-norm based fuzzy residuated logic completely conserve those between corresponding algebras of t-norm based fuzzy residuated logic.
In order to generalize fuzzy predicate logic
![]() $\mathbf {BL\forall }$
[Reference Hájek26, Reference Hájek28–Reference Hájek30], Esteva and Godo introduced a weaker fuzzy predicate logic
$\mathbf {BL\forall }$
[Reference Hájek26, Reference Hájek28–Reference Hájek30], Esteva and Godo introduced a weaker fuzzy predicate logic
![]() $\mathbf {MTL\forall }$
, which was built up from variables, predicate symbols, connectives
$\mathbf {MTL\forall }$
, which was built up from variables, predicate symbols, connectives
![]() $\sqcap $
(additive conjunction),
$\sqcap $
(additive conjunction),
![]() $ \& $
(multiplicative conjunction),
$ \& $
(multiplicative conjunction),
![]() $\sqcup $
(additive disjunction),
$\sqcup $
(additive disjunction),
![]() $\Rightarrow $
(multiplicative implication), the constant
$\Rightarrow $
(multiplicative implication), the constant
![]() $\bar{0} $
, and the quantifiers
$\bar{0} $
, and the quantifiers
![]() $\exists $
and
$\exists $
and
![]() $\forall $
[Reference Esteva and Godo16, Reference Esteva, Godo and Noguera18]. From the application point of view, fuzzy predicate logic is one of the most important techniques for the representation of knowledge. A familiarity with fuzzy predicate logic is important for the following reasons. First of all, logic is a formal method for reasoning. Many concepts that can be verbalized can also be translated into symbolic representations that closely approximate the meaning of these concepts. These symbolic structures can then be manipulated in programs to deduce various facts to carry out a form of automated reasoning. Second, logic offers the only formal approach to reasoning that has a sound theoretical foundation. This is especially important in order to mechanize or automate the reasoning process in that inferences should be correct and logically sound [Reference Torsun47].
$\forall $
[Reference Esteva and Godo16, Reference Esteva, Godo and Noguera18]. From the application point of view, fuzzy predicate logic is one of the most important techniques for the representation of knowledge. A familiarity with fuzzy predicate logic is important for the following reasons. First of all, logic is a formal method for reasoning. Many concepts that can be verbalized can also be translated into symbolic representations that closely approximate the meaning of these concepts. These symbolic structures can then be manipulated in programs to deduce various facts to carry out a form of automated reasoning. Second, logic offers the only formal approach to reasoning that has a sound theoretical foundation. This is especially important in order to mechanize or automate the reasoning process in that inferences should be correct and logically sound [Reference Torsun47].
Subsequently, Montagna and Ono introduced a Kripke semantics for
![]() $\mathbf {MTL\forall }$
, and proved a completeness theorem of
$\mathbf {MTL\forall }$
, and proved a completeness theorem of
![]() $\mathbf {MTL\forall }$
with respect to the above mentioned Kripke semantics [Reference Montagna and Ono36]. As an important monadic fragment of fuzzy predicate logic
$\mathbf {MTL\forall }$
with respect to the above mentioned Kripke semantics [Reference Montagna and Ono36]. As an important monadic fragment of fuzzy predicate logic
![]() $\mathbf {MTL\forall }$
, monadic fuzzy predicate logic
$\mathbf {MTL\forall }$
, monadic fuzzy predicate logic
![]() $\mathbf {mMTL\forall }$
, in which only a single individual variable occurs, has attracted an increasing amount of experts and scholars’ attention in recent years [Reference Hájek28, Reference Wang, He and She48–Reference Wang, Xin and He54]. Along with the same lines of Hájek’s equivalence between monadic fuzzy predicate logic
$\mathbf {mMTL\forall }$
, in which only a single individual variable occurs, has attracted an increasing amount of experts and scholars’ attention in recent years [Reference Hájek28, Reference Wang, He and She48–Reference Wang, Xin and He54]. Along with the same lines of Hájek’s equivalence between monadic fuzzy predicate logic
![]() $\mathbf {mBL\forall }$
and fuzzy modal logic
$\mathbf {mBL\forall }$
and fuzzy modal logic
![]() $\mathbf {S5(BL)}$
[Reference Hájek30], monadic fuzzy predicate logic
$\mathbf {S5(BL)}$
[Reference Hájek30], monadic fuzzy predicate logic
![]() $\mathbf {mMTL\forall }$
is actually equivalent to fuzzy modal logic
$\mathbf {mMTL\forall }$
is actually equivalent to fuzzy modal logic
![]() $\mathbf {S5(MTL)}$
because there is a natural correspondence between formulas of both logics, and between corresponding models and between the corresponding truth degrees. Thus in this paper we will work in the language of the fuzzy modal logic
$\mathbf {S5(MTL)}$
because there is a natural correspondence between formulas of both logics, and between corresponding models and between the corresponding truth degrees. Thus in this paper we will work in the language of the fuzzy modal logic
![]() $\mathbf {S5(MTL)}$
instead of in the monadic fuzzy predicate language of
$\mathbf {S5(MTL)}$
instead of in the monadic fuzzy predicate language of
![]() $\mathbf {mMTL{\forall }}$
. The logic
$\mathbf {mMTL{\forall }}$
. The logic
![]() $\mathbf {S5(MTL)}$
is defined semantically over the language of
$\mathbf {S5(MTL)}$
is defined semantically over the language of
![]() $\mathbf {MTL}$
augmented with the unary connectives
$\mathbf {MTL}$
augmented with the unary connectives ![]() and
and
![]() $\square $
, known as Kripke semantics, readers please refer to Section 4 for details. Several researchers initially were only interested in the tautologies of
$\square $
, known as Kripke semantics, readers please refer to Section 4 for details. Several researchers initially were only interested in the tautologies of
![]() $\mathbf {S5(MTL)}$
and its axiomatic extensions, but in [Reference Hájek30], a global consequence relation
$\mathbf {S5(MTL)}$
and its axiomatic extensions, but in [Reference Hájek30], a global consequence relation
![]() $\models _{\mathbf {S5(MTL)}}$
, which is finitary since
$\models _{\mathbf {S5(MTL)}}$
, which is finitary since
![]() $\mathbf {mMTL\forall }$
is a fragment of a finitary logic
$\mathbf {mMTL\forall }$
is a fragment of a finitary logic
![]() $\mathbf {MTL\forall }$
, is considered.
$\mathbf {MTL\forall }$
, is considered.
Latterly, Zahiri and Borumand Saeid [Reference Zahiri and Borumand Saeid57] have also introduced monadic monoidal t-norm based logic
![]() $\mathbf {MMTL}$
, which is a system of many valued logic capturing the tautologies of monadic MTL-algebras. The logic
$\mathbf {MMTL}$
, which is a system of many valued logic capturing the tautologies of monadic MTL-algebras. The logic
![]() $\mathbf {MMTL}$
is actually a Hilbert-style syntactic calculus in the language of
$\mathbf {MMTL}$
is actually a Hilbert-style syntactic calculus in the language of
![]() $\mathbf {S5(MTL)}$
, which is a logic
$\mathbf {S5(MTL)}$
, which is a logic
![]() $\mathbf {MTL}$
also together with the following axioms:
$\mathbf {MTL}$
also together with the following axioms:
-

 ,
, -
 $(\square 2)$
$(\square 2)$
 $\square (\nu \Rightarrow \varphi )\Rightarrow (\nu \Rightarrow \square \varphi )$
,
$\square (\nu \Rightarrow \varphi )\Rightarrow (\nu \Rightarrow \square \varphi )$
, -

 ,
, -
 $(\square 3)$
$(\square 3)$
 $\square (\nu \sqcup \varphi )\Rightarrow (\nu \sqcup \square \varphi )$
,
$\square (\nu \sqcup \varphi )\Rightarrow (\nu \sqcup \square \varphi )$
, -

 ,
,
where
![]() $\varphi $
is any formula and
$\varphi $
is any formula and
![]() $\nu $
is any propositional combination of formulas beginning with
$\nu $
is any propositional combination of formulas beginning with ![]() and
and
![]() $\square $
. The inference rules are Modus Ponens
$\square $
. The inference rules are Modus Ponens
![]() $\mathbf {MP}$
:
$\mathbf {MP}$
:
![]() $\varphi $
,
$\varphi $
,
![]() $\varphi \Rightarrow \phi \vdash \phi $
and Necessitation Rule
$\varphi \Rightarrow \phi \vdash \phi $
and Necessitation Rule
![]() $\mathbf {Nec}: \varphi /\square \varphi $
and the consequence relation is denoted by
$\mathbf {Nec}: \varphi /\square \varphi $
and the consequence relation is denoted by
![]() $\vdash _{\mathbf {S5(MTL)}}$
.
$\vdash _{\mathbf {S5(MTL)}}$
.
The second main goal of this paper is to investigate the consistency of the syntactic and the semantic for the logic
![]() $\mathbf {mMTL\forall }$
. This aim can be equivalently transformed into studying the corresponding consistency of
$\mathbf {mMTL\forall }$
. This aim can be equivalently transformed into studying the corresponding consistency of
![]() $\mathbf {S5(MTL)}$
by the equivalence of the logics
$\mathbf {S5(MTL)}$
by the equivalence of the logics
![]() $\mathbf {mMTL\forall }$
and
$\mathbf {mMTL\forall }$
and
![]() $\mathbf {S5(MTL)}$
. In order to achieve this goal, we have to prove
$\mathbf {S5(MTL)}$
. In order to achieve this goal, we have to prove
and thus prove the completeness theorem of the logic
![]() $\mathbf {S5(MTL)}$
. In Sections 3 and 4, we aim to prove this important result by using algebraic methods, and obtain some partial results towards this goal in Section 5.
$\mathbf {S5(MTL)}$
. In Sections 3 and 4, we aim to prove this important result by using algebraic methods, and obtain some partial results towards this goal in Section 5.
This paper is organized as follows: Section 2 summarizes some notions about t-norm based residuated fuzzy logics and their corresponding monadic fuzzy logics. Section 3 surveys the present state of knowledge on monadic algebras of t-norm based fuzzy residuated logic. Section 4 proves the completeness theorem for the logic
![]() $\mathbf {mMTL\forall }$
and its axiomatic extensions. Section 5 proves the strong completeness theorem for the logic
$\mathbf {mMTL\forall }$
and its axiomatic extensions. Section 5 proves the strong completeness theorem for the logic
![]() $\mathbf {mIMTL\forall }$
.
$\mathbf {mIMTL\forall }$
.
2 Preliminaries
In this section, we summarize some results about t-norm based residuated fuzzy logics and their corresponding monadic fuzzy predicate logics. In particular, all of t-norm based residuated fuzzy logics are extensions of the so-called monoidal logic (
![]() $\mathbf {ML}$
for short) [Reference Gottwal, García-Cerdaña and Bou23], which is the extension of Full Lambek calculus with exchange and weakening. In order to make the paper as self-contained as possible, we begin with
$\mathbf {ML}$
for short) [Reference Gottwal, García-Cerdaña and Bou23], which is the extension of Full Lambek calculus with exchange and weakening. In order to make the paper as self-contained as possible, we begin with
![]() $\mathbf {ML}$
and concentrate on its most notable extensions.
$\mathbf {ML}$
and concentrate on its most notable extensions.
Definition 2.1 [Reference Gottwal, García-Cerdaña and Bou23]
![]() $\mathbf {ML}$
is the logic given by the Hilbert-style calculus with
$\mathbf {ML}$
is the logic given by the Hilbert-style calculus with
![]() $\mathbf {MP}$
as its only inference rule and the following axioms:
$\mathbf {MP}$
as its only inference rule and the following axioms:
-
(1)
 $(\varphi \Rightarrow \phi )\Rightarrow ((\phi \Rightarrow \psi )\Rightarrow (\varphi \Rightarrow \psi ))$
,
$(\varphi \Rightarrow \phi )\Rightarrow ((\phi \Rightarrow \psi )\Rightarrow (\varphi \Rightarrow \psi ))$
, -
(2)
 $(\varphi \& \phi )\Rightarrow \varphi $
,
$(\varphi \& \phi )\Rightarrow \varphi $
, -
(3)
 $(\varphi \& \phi )\Rightarrow (\phi \& \varphi )$
,
$(\varphi \& \phi )\Rightarrow (\phi \& \varphi )$
, -
(4)
 $(\varphi \Rightarrow (\phi \Rightarrow \psi ))\Rightarrow (\varphi \& \phi \Rightarrow \psi )$
,
$(\varphi \Rightarrow (\phi \Rightarrow \psi ))\Rightarrow (\varphi \& \phi \Rightarrow \psi )$
, -
(5)
 $(\varphi \& \phi \Rightarrow \psi )\Rightarrow (\varphi \Rightarrow (\phi \Rightarrow \psi ))$
,
$(\varphi \& \phi \Rightarrow \psi )\Rightarrow (\varphi \Rightarrow (\phi \Rightarrow \psi ))$
, -
(6)
 $\varphi \sqcap \phi \Rightarrow \varphi $
,
$\varphi \sqcap \phi \Rightarrow \varphi $
, -
(7)
 $\varphi \sqcap \phi \Rightarrow \phi \& \varphi $
,
$\varphi \sqcap \phi \Rightarrow \phi \& \varphi $
, -
(8)
 $\bar{0}\Rightarrow \varphi $
,
$\bar{0}\Rightarrow \varphi $
, -
(9)
 $\varphi \Rightarrow \varphi \sqcup \phi $
,
$\varphi \Rightarrow \varphi \sqcup \phi $
, -
(10)
 $\phi \Rightarrow \varphi \sqcup \phi $
,
$\phi \Rightarrow \varphi \sqcup \phi $
, -
(11)
 $(\varphi \Rightarrow \psi )\Rightarrow ((\phi \Rightarrow \psi )\Rightarrow (\varphi \sqcup \phi \Rightarrow \psi ))$
,
$(\varphi \Rightarrow \psi )\Rightarrow ((\phi \Rightarrow \psi )\Rightarrow (\varphi \sqcup \phi \Rightarrow \psi ))$
, -
(12)
 $(\varphi \Rightarrow \phi )\Rightarrow ((\varphi \Rightarrow \psi )\Rightarrow (\varphi \Rightarrow \phi \sqcap \psi ))$
.
$(\varphi \Rightarrow \phi )\Rightarrow ((\varphi \Rightarrow \psi )\Rightarrow (\varphi \Rightarrow \phi \sqcap \psi ))$
.
The usual connectives in
![]() $\mathbf {ML}$
can be derived from
$\mathbf {ML}$
can be derived from
![]() $ \& ,\Rightarrow ,\sqcap $
are as follows:
$ \& ,\Rightarrow ,\sqcap $
are as follows:
Outstanding logics up in the hierarchy of extensions of
![]() $\mathbf {ML}$
are presented.
$\mathbf {ML}$
are presented.
Monoidal t-norm based logic
![]() $\mathbf {MTL}$
is
$\mathbf {MTL}$
is
![]() $\mathbf {ML}$
plus the axiom of pre-linearity:
$\mathbf {ML}$
plus the axiom of pre-linearity:
Divisible monoidal logic
![]() $\mathbf {ML_\ell }$
is
$\mathbf {ML_\ell }$
is
![]() $\mathbf {ML}$
plus the axiom of divisibility:
$\mathbf {ML}$
plus the axiom of divisibility:
Involutive monoidal logic
![]() $\mathbf {IML}$
is
$\mathbf {IML}$
is
![]() $\mathbf {ML}$
plus the axiom of involution:
$\mathbf {ML}$
plus the axiom of involution:
Intuitionistic logic
![]() $\mathbf {IL}$
is
$\mathbf {IL}$
is
![]() $\mathbf {ML}$
plus the axiom of idempotence:
$\mathbf {ML}$
plus the axiom of idempotence:
Basic fuzzy logic
![]() $\mathbf {BL}$
is
$\mathbf {BL}$
is
![]() $\mathbf {MTL}$
plus the axiom
$\mathbf {MTL}$
plus the axiom
![]() $\mathbf {(DIV)}$
.
$\mathbf {(DIV)}$
.
Gödel logic
![]() $\mathbf {G}$
is
$\mathbf {G}$
is
![]() $\mathbf {MTL}$
plus the axiom
$\mathbf {MTL}$
plus the axiom
![]() $\mathbf {(IDE)}$
.Footnote
1
$\mathbf {(IDE)}$
.Footnote
1
Łukasiewicz logic ![]() is
is
![]() $\mathbf {MTL}$
plus the following axiom:Footnote
2
$\mathbf {MTL}$
plus the following axiom:Footnote
2
Involutive monoidal t-norm based logic
![]() $\mathbf {IMTL}$
is
$\mathbf {IMTL}$
is
![]() $\mathbf {MTL}$
plus the axiom
$\mathbf {MTL}$
plus the axiom
![]() $\mathbf {(INV)}$
.
$\mathbf {(INV)}$
.
Nilpotent minimum logic
![]() $\mathbf {NM}$
is
$\mathbf {NM}$
is
![]() $\mathbf {IMTL}$
plus the axiom
$\mathbf {IMTL}$
plus the axiom
![]() $\mathbf {(WNM)}$
:Footnote
3
$\mathbf {(WNM)}$
:Footnote
3
Classical logic
![]() $\mathbf {CL}$
is
$\mathbf {CL}$
is
![]() $\mathbf {MTL}$
plus the axiom:
$\mathbf {MTL}$
plus the axiom:
As the author pointed out in [Reference Noguera37],
![]() $\mathbf {ML}$
is an implicative logic in the sense of Blok and Pigozzi [Reference Blok and Pigozzi1], and so it is an algebraic logic whose equivalent algebraic semantics Alg
$\mathbf {ML}$
is an implicative logic in the sense of Blok and Pigozzi [Reference Blok and Pigozzi1], and so it is an algebraic logic whose equivalent algebraic semantics Alg
![]() $^*\mathbf {ML}$
is the variety of residuated lattices that we usually denote by
$^*\mathbf {ML}$
is the variety of residuated lattices that we usually denote by
![]() $\mathbb {RL}$
.Footnote
4
$\mathbb {RL}$
.Footnote
4
Definition 2.2 [Reference Ward and Dilworth55]
An algebraic structure
![]() $(L,\wedge ,\vee ,\odot ,\rightarrow ,0,1)$
of type
$(L,\wedge ,\vee ,\odot ,\rightarrow ,0,1)$
of type
![]() $(2,2,2,2,0,0)$
is called a residuated lattice if it satisfies the following conditions:
$(2,2,2,2,0,0)$
is called a residuated lattice if it satisfies the following conditions:
-
(1)
 $(L,\wedge ,\vee ,0,1)$
is a bounded lattice.
$(L,\wedge ,\vee ,0,1)$
is a bounded lattice. -
(2)
 $(L,\odot ,1)$
is a commutative monoid.
$(L,\odot ,1)$
is a commutative monoid. -
(3)
 if and only if
if and only if  ,
,
for any
![]() $x,y,z\in L$
.
$x,y,z\in L$
.
In what follows, by L we denote the universe of a residuated lattice
![]() $(L,\wedge ,\vee ,\odot ,{\rightarrow,}0,1)$
. In any residuated lattice L, we define
$(L,\wedge ,\vee ,\odot ,{\rightarrow,}0,1)$
. In any residuated lattice L, we define
As a result of the general theory of algebraizability, every axiomatic extension of
![]() $\mathbf {ML}$
is algebraizable and its equivalent algebraic semantics is a subvariety of
$\mathbf {ML}$
is algebraizable and its equivalent algebraic semantics is a subvariety of
![]() $\mathbb {RL}$
. Namely, if
$\mathbb {RL}$
. Namely, if
![]() $\mathbf {C}$
is an axiomatic extension of
$\mathbf {C}$
is an axiomatic extension of
![]() $\mathbf {ML}$
, then the equivalent algebraic semantics Alg
$\mathbf {ML}$
, then the equivalent algebraic semantics Alg
![]() $^*\mathbf {C}$
is the subvariety of
$^*\mathbf {C}$
is the subvariety of
![]() $\mathbb {RL}$
determined by the equations of the form
$\mathbb {RL}$
determined by the equations of the form
![]() $\varphi \approx 1$
, where
$\varphi \approx 1$
, where
![]() $\varphi $
ranges over the axiom schemata of
$\varphi $
ranges over the axiom schemata of
![]() $\mathbf {C}$
[Reference Metcalfe and Montagna35]. As a consequence of the general theory of algebraizability and Figure 1, Figure 2 is naturally obtained.
$\mathbf {C}$
[Reference Metcalfe and Montagna35]. As a consequence of the general theory of algebraizability and Figure 1, Figure 2 is naturally obtained.

Figure 1 Relationships between t-norm based residuated fuzzy logics.

Figure 2 Relationships between algebras of t-norm based residuated fuzzy logic.
In particular:
-
• The equivalent algebraic semantics for
 $\mathbf {ML_\ell }$
is the variety
$\mathbf {ML_\ell }$
is the variety
 $\mathbb {RL_\ell }$
of residuated
$\mathbb {RL_\ell }$
of residuated
 $\ell $
-monoids, those residuated lattices satisfying (DIV)
$\ell $
-monoids, those residuated lattices satisfying (DIV)
 $x\wedge y=x\odot (x\rightarrow y)$
.
$x\wedge y=x\odot (x\rightarrow y)$
. -
• The equivalent algebraic semantics for
 $\mathbf {IML}$
is the variety
$\mathbf {IML}$
is the variety
 $\mathbb {IRL}$
of involutive residuated lattices, those residuated lattices satisfying (INV)
$\mathbb {IRL}$
of involutive residuated lattices, those residuated lattices satisfying (INV)
 $\neg \neg x=x$
.
$\neg \neg x=x$
. -
• The equivalent algebraic semantics for
 $\mathbf {MTL}$
is the variety
$\mathbf {MTL}$
is the variety
 $\mathbb {MTL}$
of MTL-algebras, those residuated lattices satisfying (PRL)
$\mathbb {MTL}$
of MTL-algebras, those residuated lattices satisfying (PRL)
 $(x\rightarrow y)\vee (y\rightarrow x)=1$
.
$(x\rightarrow y)\vee (y\rightarrow x)=1$
. -
• The equivalent algebraic semantics for
 $\mathbf {IL}$
is the variety
$\mathbf {IL}$
is the variety
 $\mathbb {HA}$
of Heyting algebras, those residuated lattices satisfying (IDE)
$\mathbb {HA}$
of Heyting algebras, those residuated lattices satisfying (IDE)
 $x\odot x=x$
.
$x\odot x=x$
. -
• The equivalent algebraic semantics for
 $\mathbf {IMTL}$
is the variety
$\mathbf {IMTL}$
is the variety
 $\mathbb {IMTL}$
of IMTL-algebras, those MTL-algebras satisfying the algebraic equation (INV).
$\mathbb {IMTL}$
of IMTL-algebras, those MTL-algebras satisfying the algebraic equation (INV). -
• The equivalent algebraic semantics for
 $\mathbf {BL}$
is the variety
$\mathbf {BL}$
is the variety
 $\mathbb {BL}$
of BL-algebras, those MTL-algebras satisfying the algebraic equation (PRL).
$\mathbb {BL}$
of BL-algebras, those MTL-algebras satisfying the algebraic equation (PRL). -
• The equivalent algebraic semantics for
 is the variety
is the variety
 $\mathbb {MV}$
of MV-algebras, those BL-algebras satisfying the algebraic equation (INV).
$\mathbb {MV}$
of MV-algebras, those BL-algebras satisfying the algebraic equation (INV). -
• The equivalent algebraic semantics for
 $\mathbf {G}$
is the variety
$\mathbf {G}$
is the variety
 $\mathbb {GA}$
of Gödel algebras, those MTL-algebras satisfying the algebraic equation (IDE).
$\mathbb {GA}$
of Gödel algebras, those MTL-algebras satisfying the algebraic equation (IDE). -
• The equivalent algebraic semantics for
 $\mathbf {NM}$
is the variety
$\mathbf {NM}$
is the variety
 $\mathbb {NM}$
of NM-algebras, those IMTL-algebras satisfying the algebraic equation (WNM)
$\mathbb {NM}$
of NM-algebras, those IMTL-algebras satisfying the algebraic equation (WNM)
 $\neg (x\odot y)\vee ((x\wedge y)\rightarrow (x\odot y))=1$
.
$\neg (x\odot y)\vee ((x\wedge y)\rightarrow (x\odot y))=1$
. -
• The equivalent algebraic semantics for
 $\mathbf {CL}$
is the variety
$\mathbf {CL}$
is the variety
 $\mathbb {BA}$
of Boolean algebras, those MTL-algebras satisfying the algebraic equation (EM)
$\mathbb {BA}$
of Boolean algebras, those MTL-algebras satisfying the algebraic equation (EM)
 $x\vee \neg x=1$
.
$x\vee \neg x=1$
.
Here we review some notions about monadic fuzzy predicate logic
![]() $\mathbf {mMTL\forall }$
[Reference Hájek30].
$\mathbf {mMTL\forall }$
[Reference Hájek30].
Definition 2.3 [Reference Esteva and Godo16]
![]() $\mathbf {MTL\forall }$
is a fuzzy predicate logic and has the following axioms:
$\mathbf {MTL\forall }$
is a fuzzy predicate logic and has the following axioms:
(P) the axioms resulting from the axioms of
![]() $\mathbf {MTL}$
by the substitution of the propositional variables by the
$\mathbf {MTL}$
by the substitution of the propositional variables by the
![]() $\mathbf {\Gamma }$
-formulas:Footnote
5
$\mathbf {\Gamma }$
-formulas:Footnote
5
-
 $(\forall 1)$
$(\forall 1)$
 $(\forall x)\varphi (x)\Rightarrow \varphi (t)$
, where t is substitutable for x in
$(\forall x)\varphi (x)\Rightarrow \varphi (t)$
, where t is substitutable for x in
 $\varphi $
,
$\varphi $
, -
 $(\exists 1)$
$(\exists 1)$
 $\varphi (t)\Rightarrow (\exists x)\varphi (x)$
, where t is substitutable for x in
$\varphi (t)\Rightarrow (\exists x)\varphi (x)$
, where t is substitutable for x in
 $\varphi $
,
$\varphi $
, -
 $(\forall 2)$
$(\forall 2)$
 $(\forall x)(\phi \Rightarrow \varphi )\Rightarrow (\phi \Rightarrow \forall (x)\varphi )$
, where x is not free in
$(\forall x)(\phi \Rightarrow \varphi )\Rightarrow (\phi \Rightarrow \forall (x)\varphi )$
, where x is not free in
 $\phi $
,
$\phi $
, -
 $(\exists 2)$
$(\exists 2)$
 $(\forall x)(\varphi \Rightarrow \phi )\Rightarrow ((\exists x)\varphi \Rightarrow \phi )$
, where x is not free in
$(\forall x)(\varphi \Rightarrow \phi )\Rightarrow ((\exists x)\varphi \Rightarrow \phi )$
, where x is not free in
 $\phi $
,
$\phi $
, -
 $(\forall 3)$
$(\forall 3)$
 $(\forall x)(\phi \sqcup \varphi )\Rightarrow \phi \sqcup \forall (x)\varphi )$
, where x is not free in
$(\forall x)(\phi \sqcup \varphi )\Rightarrow \phi \sqcup \forall (x)\varphi )$
, where x is not free in
 $\phi $
.
$\phi $
.
The deduction rules are those of
![]() $\mathbf {MTL}$
and generalization: from
$\mathbf {MTL}$
and generalization: from
![]() $\varphi $
infer
$\varphi $
infer
![]() $(\forall x)\varphi $
.
$(\forall x)\varphi $
.
Definition 2.4 [Reference Hájek28]
Monadic fuzzy predicate logic
![]() $\mathbf {mMTL\forall }$
is the monadic fragment of fuzzy predicate logic
$\mathbf {mMTL\forall }$
is the monadic fragment of fuzzy predicate logic
![]() $\mathbf {MTL\forall }$
, consisting of the formulas with unary predicates and just one object variable.
$\mathbf {MTL\forall }$
, consisting of the formulas with unary predicates and just one object variable.
3 Monadic algebras of t-norm based residuated fuzzy logic
In this section, we survey the present state of knowledge on monadic algebras of t-norm based residuated fuzzy logic, and show that the relationships between these monadic algebras completely inherit those between corresponding algebras. Considering the algebras of t-norm based residuated fuzzy logic are all particular case of residuated lattices, we review monadic residuated lattices in advance.
Definition 3.1 [Reference Rach ů nek and Šalounová43]
An algebraic structure
![]() $(L,\wedge ,\vee ,\odot ,\rightarrow ,\forall ,\exists ,0,1)$
is said to be a monadic residuated lattice if
$(L,\wedge ,\vee ,\odot ,\rightarrow ,\forall ,\exists ,0,1)$
is said to be a monadic residuated lattice if
![]() $(L,\wedge ,\vee ,\odot ,\rightarrow ,0,1)$
is a residuated lattice such that
$(L,\wedge ,\vee ,\odot ,\rightarrow ,0,1)$
is a residuated lattice such that
![]() $\forall $
and
$\forall $
and
![]() $\exists $
satisfy the following identities:
$\exists $
satisfy the following identities:
-
 $(\forall 1)$
$(\forall 1)$
 $\forall x\rightarrow x=1$
,
$\forall x\rightarrow x=1$
, -
 $(\exists 1)$
$(\exists 1)$
 $x\rightarrow \exists x=1$
,
$x\rightarrow \exists x=1$
, -
 $(\forall 2)$
$(\forall 2)$
 $\forall (x\rightarrow \exists y)=\exists x\rightarrow \exists y$
,
$\forall (x\rightarrow \exists y)=\exists x\rightarrow \exists y$
, -
 $(\forall 3)$
$(\forall 3)$
 $\forall (\exists x\rightarrow y)=\exists x\rightarrow \forall y$
,
$\forall (\exists x\rightarrow y)=\exists x\rightarrow \forall y$
, -
 $(\forall 4)$
$(\forall 4)$
 $\forall (x\vee \exists y)=\forall x\vee \exists y$
,
$\forall (x\vee \exists y)=\forall x\vee \exists y$
, -
 $(\forall 5)$
$(\forall 5)$
 $\forall \forall x=x$
,
$\forall \forall x=x$
, -
 $(\exists 2)$
$(\exists 2)$
 $\exists \forall x=\forall x$
,
$\exists \forall x=\forall x$
, -
 $(\exists 3)$
$(\exists 3)$
 $\exists (\exists x\odot \exists y)=\exists x\odot \exists y$
,
$\exists (\exists x\odot \exists y)=\exists x\odot \exists y$
, -
 $(\exists 4)$
$(\exists 4)$
 $\exists (x\odot x)=\exists x\odot \exists x$
,
$\exists (x\odot x)=\exists x\odot \exists x$
,
for any
![]() $x,y\in L$
.
$x,y\in L$
.
A monadic residuated lattice
![]() $(L,\wedge ,\vee ,\odot ,\rightarrow ,\forall ,\exists ,0,1)$
will be denoted simply by
$(L,\wedge ,\vee ,\odot ,\rightarrow ,\forall ,\exists ,0,1)$
will be denoted simply by
![]() $(L,\forall ,\exists )$
. The class of monadic residuated lattices will be denoted by
$(L,\forall ,\exists )$
. The class of monadic residuated lattices will be denoted by
![]() $\mathbb {MRL}$
. Clearly, in light of the above axiomatization,
$\mathbb {MRL}$
. Clearly, in light of the above axiomatization,
![]() $\mathbb {MRL}$
forms a variety.
$\mathbb {MRL}$
forms a variety.
Remark 3.2 [Reference Wang, She, He and Ma51]
![]() $(\exists 1)$
,
$(\exists 1)$
,
![]() $(\forall 5)$
, and
$(\forall 5)$
, and
![]() $(\exists 3)$
are redundant in Definition 3.1.
$(\exists 3)$
are redundant in Definition 3.1.
Zahiri and Borumand Saeid introduced the variety
![]() $\mathbb {MMTL}$
of monadic MTL-algebras and gave some important representations of monadic MTL-algebras in [Reference Zahiri and Borumand Saeid57].
$\mathbb {MMTL}$
of monadic MTL-algebras and gave some important representations of monadic MTL-algebras in [Reference Zahiri and Borumand Saeid57].
Definition 3.3 [Reference Zahiri and Borumand Saeid57]
An algebraic structure
![]() $(L,\wedge ,\vee ,\odot ,\rightarrow ,\forall ,\exists ,0,1)$
is said to be a monadic MTL-algebra if
$(L,\wedge ,\vee ,\odot ,\rightarrow ,\forall ,\exists ,0,1)$
is said to be a monadic MTL-algebra if
![]() $(L,\wedge ,\vee ,\odot ,\rightarrow ,0,1)$
is an MTL-algebra such that
$(L,\wedge ,\vee ,\odot ,\rightarrow ,0,1)$
is an MTL-algebra such that
![]() $\forall $
and
$\forall $
and
![]() $\exists $
satisfy the following identities:
$\exists $
satisfy the following identities:
![]() $(\forall 1)$
,
$(\forall 1)$
,
![]() $(\exists 4)$
, and
$(\exists 4)$
, and
 $$ \begin{align*} (\forall6) \ \forall(x\rightarrow\forall y)&=\exists x\rightarrow\forall y,\\ (\forall7) \ \forall(\forall x\rightarrow y)&=\forall x\rightarrow\forall y,\\ (\forall8) \ \forall(\exists x\vee y)&=\exists x\vee\forall y. \end{align*} $$
$$ \begin{align*} (\forall6) \ \forall(x\rightarrow\forall y)&=\exists x\rightarrow\forall y,\\ (\forall7) \ \forall(\forall x\rightarrow y)&=\forall x\rightarrow\forall y,\\ (\forall8) \ \forall(\exists x\vee y)&=\exists x\vee\forall y. \end{align*} $$
The variety of monadic MTL-algebras is denoted by
![]() $\mathbb {MMTL}$
.
$\mathbb {MMTL}$
.
The notion of monadic residuated lattices is a natural generalization of that with respect to monadic MTL-algebras.
Theorem 3.4. Let L be an MTL-algebra and
![]() $\forall :L\rightarrow L$
and
$\forall :L\rightarrow L$
and
![]() $\exists :L\rightarrow L$
be two unary operations on L. Then the sets
$\exists :L\rightarrow L$
be two unary operations on L. Then the sets
are equivalent.
Proof. G
![]() $\Rightarrow $
W:
$\Rightarrow $
W:
![]() $(\forall 6)$
By
$(\forall 6)$
By
![]() $(\exists 2)$
and
$(\exists 2)$
and
![]() $(\forall 3)$
, we have
$(\forall 3)$
, we have
![]() $(\forall 7)$
By
$(\forall 7)$
By
![]() $(\exists 2)$
and
$(\exists 2)$
and
![]() $(\forall 2)$
, we have
$(\forall 2)$
, we have
![]() $(\forall 8)$
By
$(\forall 8)$
By
![]() $(\forall 4)$
and
$(\forall 4)$
and
![]() $(\exists 2)$
, we have
$(\exists 2)$
, we have
and by the arbitrariness of
![]() $x,y$
, we also get
$x,y$
, we also get
Also, by
![]() $(\forall 4)$
and
$(\forall 4)$
and
![]() $(\exists 2)$
, we have
$(\exists 2)$
, we have
W
![]() $\Rightarrow $
G:
$\Rightarrow $
G:
The proofs of
![]() $(\forall 2), (\forall 3), (\forall 4)$
, and
$(\forall 2), (\forall 3), (\forall 4)$
, and
![]() $(\exists 2)$
can be directly obtained from Lemma 3.1 (5), (15), (18), and (6), respectively, in [Reference Zahiri and Borumand Saeid57].
$(\exists 2)$
can be directly obtained from Lemma 3.1 (5), (15), (18), and (6), respectively, in [Reference Zahiri and Borumand Saeid57].
Theorem 3.4 actually gives us an idea of introducing the notion of monadic MTL-algebra in a different way, which implies the following result immediately.
Theorem 3.5. The subvariety of
![]() $\mathbb {MRL}$
determined by the equation
$\mathbb {MRL}$
determined by the equation
is term-equivalent to the variety
![]() $\mathbb {MMTL}$
.
$\mathbb {MMTL}$
.
Several academics introduced three kinds of monadic BL-algebras and tried to provide a right algebraic semantics for Hájek’s monadic fuzzy logic
![]() $\mathbf {mBL\forall }$
[Reference Castaño, Cimadamore, Verela and Rueda4, Reference Drŭgulici13, Reference Grigolia25]. Here we will review Draŭgulici’s, Grigolia’s and Castaño’s axioms of monadic BL-algebras and discuss the relationship among them.
$\mathbf {mBL\forall }$
[Reference Castaño, Cimadamore, Verela and Rueda4, Reference Drŭgulici13, Reference Grigolia25]. Here we will review Draŭgulici’s, Grigolia’s and Castaño’s axioms of monadic BL-algebras and discuss the relationship among them.
Definition 3.6 ((Draŭgulici’s axioms) [Reference Drŭgulici13])
A monadic BL-algebra is a triple
![]() $(L,\forall ,\exists )$
, where L is a BL-algebra,
$(L,\forall ,\exists )$
, where L is a BL-algebra,
![]() $\forall :L\rightarrow L$
and
$\forall :L\rightarrow L$
and
![]() $\exists :L\rightarrow L$
are two unary operations on L satisfying the identities:
$\exists :L\rightarrow L$
are two unary operations on L satisfying the identities:
![]() $(\forall 1)$
,
$(\forall 1)$
,
![]() $(\exists 1)$
,
$(\exists 1)$
,
![]() $(\forall 4)$
,
$(\forall 4)$
,
![]() $(\forall 6)$
,
$(\forall 6)$
,
![]() $(\forall 7)$
and
$(\forall 7)$
and
Remark 3.7. (1)
![]() $(\forall 9)$
,
$(\forall 9)$
,
![]() $(\exists 1)$
and
$(\exists 1)$
and
![]() $(\forall 10)$
are redundant in Draŭgulici’s axioms.
$(\forall 10)$
are redundant in Draŭgulici’s axioms.
(2) The other one was introduced by Grigolia [Reference Grigolia25] as a triple
![]() $(L,\forall ,\exists )$
that satisfies the identities:
$(L,\forall ,\exists )$
that satisfies the identities:
![]() $(\forall 1)$
,
$(\forall 1)$
,
![]() $(\exists 1)$
,
$(\exists 1)$
,
![]() $(\forall 2)$
,
$(\forall 2)$
,
![]() $(\forall 3)$
and
$(\forall 3)$
and
![]() $(\forall 4)$
. It is also easily verified that
$(\forall 4)$
. It is also easily verified that
It is worth noticing in [Reference Hájek26] that the formula
is a theorem in
![]() $\mathbf {BL\forall }$
, and also belongs to
$\mathbf {BL\forall }$
, and also belongs to
![]() $\mathbf {mBL\forall }$
. However Example 3.8 shows that the last formula is independent of the axioms of Definition 3.6 and Remark 3.7(2).
$\mathbf {mBL\forall }$
. However Example 3.8 shows that the last formula is independent of the axioms of Definition 3.6 and Remark 3.7(2).
Example 3.8. Let
![]() $L=[0,1]$
. Define binary operations
$L=[0,1]$
. Define binary operations
![]() $\wedge ,\vee ,\odot ,\rightarrow $
by
$\wedge ,\vee ,\odot ,\rightarrow $
by

Then
![]() $(L,\wedge ,\vee ,\rightarrow ,\odot ,0,1)$
is a BL-algebra, and is called the standard MV-algebra. If we define two unary operations
$(L,\wedge ,\vee ,\rightarrow ,\odot ,0,1)$
is a BL-algebra, and is called the standard MV-algebra. If we define two unary operations
![]() $\forall :L\rightarrow L$
and
$\forall :L\rightarrow L$
and
![]() $\exists :L\rightarrow L$
by
$\exists :L\rightarrow L$
by
 $$ \begin{align*} \forall x= \begin{cases} 1, & x=1, \\ 0, & x\neq1, \end{cases}{\qquad} \exists x= \begin{cases} 0, & x=0, \\ 1, & x\neq0, \end{cases} \end{align*} $$
$$ \begin{align*} \forall x= \begin{cases} 1, & x=1, \\ 0, & x\neq1, \end{cases}{\qquad} \exists x= \begin{cases} 0, & x=0, \\ 1, & x\neq0, \end{cases} \end{align*} $$
then
![]() $\forall $
and
$\forall $
and
![]() $\exists $
satisfy the axioms of Definition 3.6 and Remark 3.7(2). However, the unary operation
$\exists $
satisfy the axioms of Definition 3.6 and Remark 3.7(2). However, the unary operation
![]() $\exists $
does not satisfy the above formula, since
$\exists $
does not satisfy the above formula, since
In order to solve the above drawback, Castaño et al. revised the variety
![]() $\mathbb {MBL}$
of monadic BL-algebras and proved that are the equivalent algebraic semantics of the monadic fuzzy logic
$\mathbb {MBL}$
of monadic BL-algebras and proved that are the equivalent algebraic semantics of the monadic fuzzy logic
![]() $\mathbf {mBL{\forall }}$
[Reference Castaño, Cimadamore, Verela and Rueda4].
$\mathbf {mBL{\forall }}$
[Reference Castaño, Cimadamore, Verela and Rueda4].
Definition 3.9 [Reference Castaño, Cimadamore, Verela and Rueda4]
A monadic BL-algebra is a triple
![]() $(L,\forall ,\exists )$
, where L is a BL-algebra,
$(L,\forall ,\exists )$
, where L is a BL-algebra,
![]() $\forall :L\rightarrow L$
and
$\forall :L\rightarrow L$
and
![]() $\exists :L\rightarrow L$
are two unary operations on L that satisfy
$\exists :L\rightarrow L$
are two unary operations on L that satisfy
![]() $(\forall 1), (\forall 6), (\forall 7), (\forall 8)$
and
$(\forall 1), (\forall 6), (\forall 7), (\forall 8)$
and
![]() $(\exists 4)$
.
$(\exists 4)$
.
Theorem 3.10. The subvariety of
![]() $\mathbb {MMTL}$
determined by the equation
$\mathbb {MMTL}$
determined by the equation
is term-equivalent to the variety
![]() $\mathbb {MBL}$
.
$\mathbb {MBL}$
.
Proof. Definitions 3.3 and 3.9 show that monadic BL-algebra and monadic MTL-algebra have the same axioms with respect to two quantifiers
![]() $\forall $
and
$\forall $
and
![]() $\exists $
.
$\exists $
.
Subsequently, in order to review the variety of monadic algebras of involutive monoidal t-norm based logic and their subvarieties, we study the variety
![]() $\mathbb {MIRL}$
of monadic involutive residuated lattices in advance.
$\mathbb {MIRL}$
of monadic involutive residuated lattices in advance.
Definition 3.11. A monadic involutive residuated lattice is a pair
![]() $(L,\forall )$
, where L is an involutive residuated lattice and
$(L,\forall )$
, where L is an involutive residuated lattice and
![]() $\forall :L\rightarrow L$
is an unary operation on L satisfying the following conditions:
$\forall :L\rightarrow L$
is an unary operation on L satisfying the following conditions:
![]() $(\forall 1),(\forall 7)$
and
$(\forall 1),(\forall 7)$
and
Theorem 3.12. The subvariety of
![]() $\mathbb {MRL}$
determined by the equation
$\mathbb {MRL}$
determined by the equation
is term-equivalent to the variety
![]() $\mathbb {MIRL}$
, where
$\mathbb {MIRL}$
, where
![]() $\exists =\neg \forall \neg $
.
$\exists =\neg \forall \neg $
.
Proof. Let
![]() $(L,\forall ,\exists )$
be a monadic residuated lattice that satisfies
$(L,\forall ,\exists )$
be a monadic residuated lattice that satisfies
![]() $\neg \neg x=x$
. Then L becomes an involutive residuated lattice. Here we will show that
$\neg \neg x=x$
. Then L becomes an involutive residuated lattice. Here we will show that
![]() $(L,\forall )$
is a monadic involutive residuated lattice.
$(L,\forall )$
is a monadic involutive residuated lattice.
-
 $(\forall 7)$
: The proof is similar to that of G
$(\forall 7)$
: The proof is similar to that of G
 $\Rightarrow $
W of Theorem 3.4.
$\Rightarrow $
W of Theorem 3.4. -
 $(\forall 11)$
: By
$(\forall 11)$
: By
 $(\exists 2)$
and
$(\exists 2)$
and
 $(\forall 4)$
, we have
$(\forall 4)$
, we have  $$ \begin{align*} \forall(\forall x\vee y)=\forall(\exists\forall x\vee y)=\exists\forall x\vee \forall y=\forall x\vee \forall y. \end{align*} $$
$$ \begin{align*} \forall(\forall x\vee y)=\forall(\exists\forall x\vee y)=\exists\forall x\vee \forall y=\forall x\vee \forall y. \end{align*} $$
-
 $(\forall 12)$
: By
$(\forall 12)$
: By
 $(\exists 4)$
and
$(\exists 4)$
and
 $\neg \exists \neg x=\forall x$
, we have
$\neg \exists \neg x=\forall x$
, we have  $$ \begin{align*} \forall(\neg x\rightarrow x)=\neg\exists\neg(\neg x\rightarrow x)\kern1.3pt{=}\kern1.3pt\neg\exists(\neg x\odot \neg x)\kern1.3pt{=}\kern1.3pt\neg(\exists \neg x\odot \exists\neg x)\kern1.3pt{=}\kern1.3pt\neg\forall x\kern1.3pt{\rightarrow}\kern1.3pt\forall x. \end{align*} $$
$$ \begin{align*} \forall(\neg x\rightarrow x)=\neg\exists\neg(\neg x\rightarrow x)\kern1.3pt{=}\kern1.3pt\neg\exists(\neg x\odot \neg x)\kern1.3pt{=}\kern1.3pt\neg(\exists \neg x\odot \exists\neg x)\kern1.3pt{=}\kern1.3pt\neg\forall x\kern1.3pt{\rightarrow}\kern1.3pt\forall x. \end{align*} $$
-
Conversely, let
 $(L,\forall )$
be a monadic involutive residuated lattice. Here we show that
$(L,\forall )$
be a monadic involutive residuated lattice. Here we show that
 $(L,\forall ,\exists )$
is a monadic residuated lattice, where for any
$(L,\forall ,\exists )$
is a monadic residuated lattice, where for any $$ \begin{align*} \exists x:=\neg\forall \neg x \end{align*} $$
$$ \begin{align*} \exists x:=\neg\forall \neg x \end{align*} $$
 $x\in L$
. Actually, we only need to show that
$x\in L$
. Actually, we only need to show that
 $(L,\forall ,\exists )$
satisfies the axioms of W by Theorem 3.4, which is indeed equivalent to the axioms of monadic residuated lattice defined in Definition 3.1.
$(L,\forall ,\exists )$
satisfies the axioms of W by Theorem 3.4, which is indeed equivalent to the axioms of monadic residuated lattice defined in Definition 3.1.
 $(\forall 6)$
: By Propositions 3.9(5), we have
$(\forall 6)$
: By Propositions 3.9(5), we have  $$ \begin{align*} \forall(x\rightarrow\forall y)=\forall(\neg\neg x\rightarrow \forall y)=\neg\forall \neg x\rightarrow\forall y=\exists x\rightarrow\forall y. \end{align*} $$
$$ \begin{align*} \forall(x\rightarrow\forall y)=\forall(\neg\neg x\rightarrow \forall y)=\neg\forall \neg x\rightarrow\forall y=\exists x\rightarrow\forall y. \end{align*} $$
-
 $(\forall 7)$
: By Propositions 3.9(5), we have
$(\forall 7)$
: By Propositions 3.9(5), we have  $$ \begin{align*} \forall(\forall x\rightarrow y)=\forall(\exists\forall x\rightarrow y)=\exists\forall x\rightarrow \forall y=\forall x\rightarrow\forall y. \end{align*} $$
$$ \begin{align*} \forall(\forall x\rightarrow y)=\forall(\exists\forall x\rightarrow y)=\exists\forall x\rightarrow \forall y=\forall x\rightarrow\forall y. \end{align*} $$
-
 $(\forall 8)$
: By (M11) and Proposition 3.7(6), we have
$(\forall 8)$
: By (M11) and Proposition 3.7(6), we have  $$ \begin{align*} \forall(\exists x\vee y)=\forall(\forall\exists x\vee y)=\forall\exists x\vee \forall y=\exists x\vee\forall y. \end{align*} $$
$$ \begin{align*} \forall(\exists x\vee y)=\forall(\forall\exists x\vee y)=\forall\exists x\vee \forall y=\exists x\vee\forall y. \end{align*} $$
-
 $(\exists 4)$
Applying
$(\exists 4)$
Applying
 $(\forall 12)$
and
$(\forall 12)$
and
 $\neg \forall \neg x=\exists x$
, we have Therefore,
$\neg \forall \neg x=\exists x$
, we have Therefore,
 $(L,\forall ,\exists )$
is a monadic residuated lattice.
$(L,\forall ,\exists )$
is a monadic residuated lattice.
Inspired by Theorem 3.12, we have the corresponding result of monadic IMTL-algebras and monadic MTL-algebras.
Theorem 3.13. The subvariety of
![]() $\mathbb {MMTL}$
determined by the equation
$\mathbb {MMTL}$
determined by the equation
is term-equivalent to the variety
![]() $\mathbb {MIMTL}$
, where
$\mathbb {MIMTL}$
, where
![]() $\exists =\neg \forall \neg $
.
$\exists =\neg \forall \neg $
.
Inspired by the above observation, we introduced the notion of monadic NM-algebras and proved that is the equivalent algebraic semantics of
![]() $\mathbf {mNM\forall }$
in [Reference Wang, He, Yang, Wang and He49].
$\mathbf {mNM\forall }$
in [Reference Wang, He, Yang, Wang and He49].
Definition 3.14 [Reference Wang, He, Yang, Wang and He49]
A monadic NM-algebra is a pair
![]() $(L,\forall )$
, where L is an NM-algebra and
$(L,\forall )$
, where L is an NM-algebra and
![]() $\forall :L\rightarrow L$
is an unary operation on L satisfying the following conditions:
$\forall :L\rightarrow L$
is an unary operation on L satisfying the following conditions:
![]() $(\forall 1),(\forall 7)$
,
$(\forall 1),(\forall 7)$
,
![]() $(\forall 11)$
and
$(\forall 11)$
and
![]() $(\forall 12)$
.
$(\forall 12)$
.
Theorem 3.15. The subvariety of
![]() $\mathbb {MIMTL}$
determined by the equation
$\mathbb {MIMTL}$
determined by the equation
is term-equivalent to the variety
![]() $\mathbb {MNM}$
.
$\mathbb {MNM}$
.
Proof. The proof is trivial and hence we omit them.
The variety
![]() $\mathbb {MMV}$
of monadic MV-algebras were introduced by Rutledge [Reference Rutledge45] as an algebra
$\mathbb {MMV}$
of monadic MV-algebras were introduced by Rutledge [Reference Rutledge45] as an algebra
![]() $(L,\oplus ,\odot ,^\ast ,\forall ,0,1)$
satisfies the following identities:
$(L,\oplus ,\odot ,^\ast ,\forall ,0,1)$
satisfies the following identities:
![]() $(\forall 1)$
,
$(\forall 1)$
,
![]() $(\forall 9)$
$(\forall 9)$
Remark 3.16. J. Rach ů nek and F. Švrček were first attempt to define unary operators with some properties of quantifiers for residuated
![]() $\ell $
-monoids using only the universal quantifier as the initial one, the resulting class of algebras called monadic residuated
$\ell $
-monoids using only the universal quantifier as the initial one, the resulting class of algebras called monadic residuated
![]() $\ell $
-monoids [Reference Rach ů nek and Švrček44]. The variety of monadic residuated
$\ell $
-monoids [Reference Rach ů nek and Švrček44]. The variety of monadic residuated
![]() $\ell $
-monoids is denoted by
$\ell $
-monoids is denoted by
![]() $\mathbb {MRL\ell }$
, which is analogously as for the variety
$\mathbb {MRL\ell }$
, which is analogously as for the variety
![]() $\mathbb {MMV}$
of monadic MV-algebras. But it seems to be more appropriate to introduce such monadic algebras similarly as the monadic residuated lattices, MTL-algebras and BL-algebras. The reason is that MV-algebras satisfy De Morgan and double negation laws, and thus in the definition of the corresponding monadic algebras, it is possible to use only one of the existential and universal quantifiers as primitive, the other being definable as the dual of the one defined, readers can refer to Proposition 4 in [Reference Rach ů nek and Šalounová42] for details. Namely, if
$\mathbb {MMV}$
of monadic MV-algebras. But it seems to be more appropriate to introduce such monadic algebras similarly as the monadic residuated lattices, MTL-algebras and BL-algebras. The reason is that MV-algebras satisfy De Morgan and double negation laws, and thus in the definition of the corresponding monadic algebras, it is possible to use only one of the existential and universal quantifiers as primitive, the other being definable as the dual of the one defined, readers can refer to Proposition 4 in [Reference Rach ů nek and Šalounová42] for details. Namely, if
![]() $\exists $
is an existential quantifier and
$\exists $
is an existential quantifier and
![]() $\forall $
is a universal one on an MV-algebra L, then
$\forall $
is a universal one on an MV-algebra L, then
![]() $\forall _\exists :L\rightarrow L$
and
$\forall _\exists :L\rightarrow L$
and
![]() $\exists _\forall :L\rightarrow L$
such that for any
$\exists _\forall :L\rightarrow L$
such that for any
![]() $x\in L$
,
$x\in L$
,
is a universal and an existential quantifier on L, respectively, and moreover
However, definitions of monadic BL-algebras, residuated lattices and residuated
![]() $\ell $
-monoids require the introduction of both kinds of quantifiers simultaneously, because these quantifiers are not mutually interdefinable. As a consequence of Theorems 3.4 and 3.10, monadic BL-algebra, MTL-algebra, residuated
$\ell $
-monoids require the introduction of both kinds of quantifiers simultaneously, because these quantifiers are not mutually interdefinable. As a consequence of Theorems 3.4 and 3.10, monadic BL-algebra, MTL-algebra, residuated
![]() $\ell $
-monoid and residuated lattice have the same axioms, that is, a monadic residuated
$\ell $
-monoid and residuated lattice have the same axioms, that is, a monadic residuated
![]() $\ell $
-monoid is indeed a triple
$\ell $
-monoid is indeed a triple
![]() $(L,\forall ,\exists )$
satisfying the identities:
$(L,\forall ,\exists )$
satisfying the identities:
![]() $(\forall 1),(\forall 6),(\forall 7),(\forall 8)$
and
$(\forall 1),(\forall 6),(\forall 7),(\forall 8)$
and
![]() $(\exists 4)$
.
$(\exists 4)$
.
Figallo Orellano also gave a characterization of monadic MV-algebras in [Reference Figallo Orellano19].
Theorem 3.17 [Reference Figallo Orellano19]
Let L be an MV-algebra and
![]() $\forall $
a unary operation on L. Then
$\forall $
a unary operation on L. Then
![]() $(L,\forall )$
is a monadic MV-algebra if and only if it satisfies
$(L,\forall )$
is a monadic MV-algebra if and only if it satisfies
![]() $(\forall 1),(\forall 7),(\forall 12)$
.
$(\forall 1),(\forall 7),(\forall 12)$
.
Theorem 3.18. The subvariety of
![]() $\mathbb {MMTL}$
determined by the equation
$\mathbb {MMTL}$
determined by the equation
is term-equivalent to the variety
![]() $\mathbb {MMV}$
.
$\mathbb {MMV}$
.
Proof. Let
![]() $(L,\forall ,\exists )$
be a monadic MTL-algebra satisfying the condition (MV). Then L becomes an MV-algebra, and by Definition 3.14 and Theorem 3.17,
$(L,\forall ,\exists )$
be a monadic MTL-algebra satisfying the condition (MV). Then L becomes an MV-algebra, and by Definition 3.14 and Theorem 3.17,
![]() $(L,\forall )$
is a monadic MV-algebra.
$(L,\forall )$
is a monadic MV-algebra.
Conversely, let
![]() $(L,\forall )$
be a monadic MV-algebra. Here we show that
$(L,\forall )$
be a monadic MV-algebra. Here we show that
![]() $(L,\forall ,\exists )$
is a monadic MTL-algebra, where
$(L,\forall ,\exists )$
is a monadic MTL-algebra, where
for any
![]() $x\in L$
. It is noted first that
$x\in L$
. It is noted first that
![]() $(\forall 11)$
hold. Indeed, for any
$(\forall 11)$
hold. Indeed, for any
![]() $x,y\in L$
, we have
$x,y\in L$
, we have
which implies ![]() . The reverse inequality holds trivially.
. The reverse inequality holds trivially.
The rest of proof can be deduced directly form Theorem 3.13.
As a consequence of Theorem 3.18, the following results are obtained.
Corollary 3.19. The subvariety of
![]() $\mathbb {MIMTL}$
determined by the equation
$\mathbb {MIMTL}$
determined by the equation
is term-equivalent to the variety
![]() $\mathbb {MMV}$
.
$\mathbb {MMV}$
.
Corollary 3.20. The subvariety of
![]() $\mathbb {MBL}$
determined by the equation
$\mathbb {MBL}$
determined by the equation
is term-equivalent to the variety
![]() $\mathbb {MMV}$
.
$\mathbb {MMV}$
.
Monadic Boolean algebras were introduced by Halmos [Reference Halmos32], as algebraic models for classical predicate logics for languages having one placed predicates and a single quantifier. More precisely, an algebra
![]() $(L,\wedge ,\vee ,\neg ,0,1,\exists )$
is said to be a monadic Boolean algebra if
$(L,\wedge ,\vee ,\neg ,0,1,\exists )$
is said to be a monadic Boolean algebra if
![]() $(L,\wedge ,\vee ,\neg ,0,1)$
is a Boolean algebra and in addition
$(L,\wedge ,\vee ,\neg ,0,1)$
is a Boolean algebra and in addition
![]() $\exists $
satisfies the identities:
$\exists $
satisfies the identities:
![]() $(\exists 1)$
,
$(\exists 1)$
,
The variety of monadic Boolean algebras is denoted by
![]() $\mathbb {MBA}$
.
$\mathbb {MBA}$
.
Theorem 3.21. The subvariety of
![]() $\mathbb {MRL}$
determined by adding the equation
$\mathbb {MRL}$
determined by adding the equation
is term-equivalent to the variety
![]() $\mathbb {MBA}$
.
$\mathbb {MBA}$
.

Figure 3 Relationships between monadic algebras of t-norm based residuated fuzzy logic.
Proof. Let
![]() $(L,\forall ,\exists )$
be a monadic residuated lattice satisfying the condition (EM). Then L becomes a Boolean algebra.
$(L,\forall ,\exists )$
be a monadic residuated lattice satisfying the condition (EM). Then L becomes a Boolean algebra.
-
 $(\exists 5)$
The proof is similar to that of Proposition 3.1(9) in [Reference Rach ů nek and Šalounová43].
$(\exists 5)$
The proof is similar to that of Proposition 3.1(9) in [Reference Rach ů nek and Šalounová43]. -
 $(\exists 6)$
Applying
$(\exists 6)$
Applying
 $(\forall 11)$
, for any
$(\forall 11)$
, for any
 $x,y\in L$
, we have and by the arbitrariness of
$x,y\in L$
, we have and by the arbitrariness of
 $x,y$
, we also get
$x,y$
, we also get
 $\exists (\exists x\wedge y)=\exists x\wedge \exists y$
.
$\exists (\exists x\wedge y)=\exists x\wedge \exists y$
.
4 Completeness for monadic fuzzy predicate logic
 $\mathbf {mMTL\forall }$
$\mathbf {mMTL\forall }$
In this section, the main aim of us to show that the variety of monadic MTL-algebras is the equivalent algebraic semantics of monadic fuzzy predicate logic
![]() $\mathbf {mMTL\forall }$
, and give an algebraic proof of completeness for this logic.
$\mathbf {mMTL\forall }$
, and give an algebraic proof of completeness for this logic.
Along with the same line of Hájek’s excellent work in [Reference Hájek30], similarly, we can prove that formulas of
![]() $\mathbf {S5(MTL)}$
are in the obvious one–one isomorphic correspondence with formulas of monadic fuzzy predicate calculus
$\mathbf {S5(MTL)}$
are in the obvious one–one isomorphic correspondence with formulas of monadic fuzzy predicate calculus
![]() $\mathbf {mMTL\forall }$
with unary predicates and just one object variable x, the atomic formula
$\mathbf {mMTL\forall }$
with unary predicates and just one object variable x, the atomic formula
![]() $P_i(x)$
corresponding to propositional variable
$P_i(x)$
corresponding to propositional variable
![]() $p_i$
and modalities
$p_i$
and modalities
![]() $\square $
and
$\square $
and ![]() correspond to the quantifiers
correspond to the quantifiers
![]() $(\forall x)$
and
$(\forall x)$
and
![]() $(\exists x)$
. Kripke semantics correspond in the obvious way to semantics for
$(\exists x)$
. Kripke semantics correspond in the obvious way to semantics for
![]() $\mathbf {mMTL\forall }$
, the correspondence maps tautologies of the fuzzy modal logic to tautologies of the monadic fuzzy predicate logic and the same for standard tautologies. Using the above equivalence, we continue the algebraic tradition of naming monadic the algebraic semantics of monadic fragments of several logics (Boolean, intuitionistic, Łukasiewicz, etc.), and opt to call the algebras corresponding to the fuzzy modal logic
$\mathbf {mMTL\forall }$
, the correspondence maps tautologies of the fuzzy modal logic to tautologies of the monadic fuzzy predicate logic and the same for standard tautologies. Using the above equivalence, we continue the algebraic tradition of naming monadic the algebraic semantics of monadic fragments of several logics (Boolean, intuitionistic, Łukasiewicz, etc.), and opt to call the algebras corresponding to the fuzzy modal logic
![]() $\mathbf {S5(MTL)}$
monadic MTL-algebras. However, in this section we will work in the language of the fuzzy modal logic
$\mathbf {S5(MTL)}$
monadic MTL-algebras. However, in this section we will work in the language of the fuzzy modal logic
![]() $\mathbf {S5(MTL)}$
instead of in the monadic fuzzy language of
$\mathbf {S5(MTL)}$
instead of in the monadic fuzzy language of
![]() $\mathbf {mMTL{\forall }}$
and prove that the variety of monadic MTL-algebras is the equivalent algebraic semantics of the logic
$\mathbf {mMTL{\forall }}$
and prove that the variety of monadic MTL-algebras is the equivalent algebraic semantics of the logic
![]() $\mathbf {S5(MTL)}$
in advance.
$\mathbf {S5(MTL)}$
in advance.
Here we first study m-relatively complete subalgebras with respect to monadic MTL-algebras. In particular, we characterize those subalgebras of a given MTL-algebra that may be the range of the quantifiers
![]() $\forall $
and
$\forall $
and
![]() $\exists $
. As a consequence of this characterization, we build the most important examples of monadic MTL-algebras, which will be called functional monadic MTL-algebras.
$\exists $
. As a consequence of this characterization, we build the most important examples of monadic MTL-algebras, which will be called functional monadic MTL-algebras.
Given an MTL-algebra L, we say that a subalgebra ![]() is m-relatively complete if the following conditions hold:
is m-relatively complete if the following conditions hold:
(S1) For every
![]() $a\in L$
, the subset
$a\in L$
, the subset ![]() has a greatest element and
has a greatest element and
![]() $\{s\in S\mid s\geq a\}$
has a least element.
$\{s\in S\mid s\geq a\}$
has a least element.
(S2) For every
![]() $a\in L$
and
$a\in L$
and
![]() $s_1,s_2\in S$
such that
$s_1,s_2\in S$
such that ![]() , there exists
, there exists
![]() $s_3\in S$
such that
$s_3\in S$
such that ![]() and
and ![]() .
.
(S3) For every
![]() $a\in L$
and
$a\in L$
and
![]() $s_1\in S$
such that
$s_1\in S$
such that ![]() , there exists
, there exists
![]() $s_2\in S$
such that
$s_2\in S$
such that ![]() and
and ![]() .
.
Theorem 4.1. Consider an MTL-algebra L and an m-relatively complete subalgebra S. If we define on L the operation
then
![]() $(L,\forall ,\exists )$
is a monadic MTL-algebra such that
$(L,\forall ,\exists )$
is a monadic MTL-algebra such that
![]() $\forall L=\exists L=S$
. Conversely, if
$\forall L=\exists L=S$
. Conversely, if
![]() $(L,\forall ,\exists )$
is a monadic MTL-algebra, then
$(L,\forall ,\exists )$
is a monadic MTL-algebra, then
![]() $\forall L=\exists L$
is an m-relatively complete subalgebra of L.
$\forall L=\exists L$
is an m-relatively complete subalgebra of L.
Proof. Clearly condition (S1) guarantees the existence of
![]() $\forall x$
and
$\forall x$
and
![]() $\exists x$
for any
$\exists x$
for any
![]() $x\in L$
. Then it remains to show that
$x\in L$
. Then it remains to show that
![]() $(L,\forall ,\exists )$
satisfies axioms
$(L,\forall ,\exists )$
satisfies axioms
![]() $(\forall 1),(\forall 6)$
–
$(\forall 1),(\forall 6)$
–
![]() $(\forall 8)$
and
$(\forall 8)$
and
![]() $(\exists 4)$
.
$(\exists 4)$
.
![]() $(\forall 1)$
From the definition of
$(\forall 1)$
From the definition of
![]() $\forall x$
, it is clear that
$\forall x$
, it is clear that ![]() . Thus
. Thus
![]() $\forall x\rightarrow x=1$
.
$\forall x\rightarrow x=1$
.
![]() $(\forall 6)$
From
$(\forall 6)$
From ![]() , we get
, we get ![]() . Then
. Then ![]() . Let us see that
. Let us see that ![]() . Indeed, if
. Indeed, if
![]() $s\in S$
, and
$s\in S$
, and ![]() , then
, then ![]() . Then, by definition of
. Then, by definition of
![]() $\exists x$
, we have
$\exists x$
, we have ![]() . Thus
. Thus ![]() , which implies that
, which implies that
![]() $\forall (x\rightarrow \forall y)=\exists x\rightarrow \forall y$
.
$\forall (x\rightarrow \forall y)=\exists x\rightarrow \forall y$
.
![]() $(\forall 7)$
From
$(\forall 7)$
From ![]() , we get
, we get ![]() , In addition, if
, In addition, if
![]() $s\in S$
and
$s\in S$
and ![]() , then
, then ![]() . Thus
. Thus ![]() and
and ![]() . Hence we have shown that
. Hence we have shown that
![]() $\forall (\forall x\rightarrow y)=\forall x\rightarrow \forall y$
.
$\forall (\forall x\rightarrow y)=\forall x\rightarrow \forall y$
.
![]() $(\forall 8)$
Since
$(\forall 8)$
Since ![]() . Now, if
. Now, if
![]() $s\in S$
and
$s\in S$
and ![]() , by condition (S2), there must be
, by condition (S2), there must be
![]() $s'\in S$
such that
$s'\in S$
such that ![]() and
and ![]() . Then
. Then ![]() and
and ![]() . Thus, we have shown that
. Thus, we have shown that
![]() $\forall (\exists x\vee y)=\exists x\vee \forall y$
.
$\forall (\exists x\vee y)=\exists x\vee \forall y$
.
![]() $(\exists 4)$
Clearly,
$(\exists 4)$
Clearly, ![]() . In addition, if
. In addition, if
![]() $s\in S$
and
$s\in S$
and ![]() , by condition (S3), there is
, by condition (S3), there is
![]() $s'\in S$
such that
$s'\in S$
such that ![]() and
and ![]() . Then
. Then ![]() and
and ![]() . Thus
. Thus
![]() $\exists (x\odot x)=\exists x\odot \exists x$
.
$\exists (x\odot x)=\exists x\odot \exists x$
.
Conversely, let
![]() $(L,\forall ,\exists )$
be a monadic MTL-algebra. Then we have that
$(L,\forall ,\exists )$
be a monadic MTL-algebra. Then we have that
![]() $\forall L$
is a subalgebra of L. Now, let us show that conditions (S1)–(S3) hold.
$\forall L$
is a subalgebra of L. Now, let us show that conditions (S1)–(S3) hold.
(S1) Using the basic properties of monadic MTL-algebra, we have that if ![]() for some
for some
![]() $s\in \forall L$
, then
$s\in \forall L$
, then ![]() . Thus
. Thus ![]() . Analogously
. Analogously
![]() $\exists x=\min \{s\in \forall L|s\geq x\}$
.
$\exists x=\min \{s\in \forall L|s\geq x\}$
.
(S2) Assume ![]() for some
for some
![]() $s_1,s_2\in \forall L$
,
$s_1,s_2\in \forall L$
,
![]() $x\in L$
. Then, using the basic properties of monadic MTL-algebras, we have
$x\in L$
. Then, using the basic properties of monadic MTL-algebras, we have ![]() and
and ![]() .
.
(S3) If ![]() for some
for some
![]() $s\in \forall L$
and
$s\in \forall L$
and
![]() $x\in L$
, then
$x\in L$
, then ![]() and
and ![]() ,
,
![]() $\exists x\in \forall L$
. This shows that
$\exists x\in \forall L$
. This shows that
![]() $\forall L$
is an m-relatively complete subalgebra of L.
$\forall L$
is an m-relatively complete subalgebra of L.
The following is the most important example of monadic MTL-algebras built according to the previous theorem.
Example 4.2. Considering a linearly ordered MTL-algebra L and a nonempty set X, we restrict our attention to those elements
![]() $f\in L^X$
such that
$f\in L^X$
such that
both exist in L. We denote by M the subset of
![]() $L^X$
of these safe elements. For every
$L^X$
of these safe elements. For every
![]() $f\in M$
, we define
$f\in M$
, we define
and
![]() $\forall _f$
and
$\forall _f$
and
![]() $\exists _f$
are both constant maps.
$\exists _f$
are both constant maps.
Remark 4.3. Let G be a subalgebra of
![]() $L^X$
contained in M such that for every f,
$L^X$
contained in M such that for every f,
![]() $\forall _f,\exists _f\in G$
. We will prove that G has a natural structure of monadic MTL-algebra. Let S be the subset of constant maps of
$\forall _f,\exists _f\in G$
. We will prove that G has a natural structure of monadic MTL-algebra. Let S be the subset of constant maps of
![]() $L^X$
. Then we prove that
$L^X$
. Then we prove that
![]() $G\cap S$
is an m-relatively complete subalgebra of G. Indeed, since G and S are subalgebra of
$G\cap S$
is an m-relatively complete subalgebra of G. Indeed, since G and S are subalgebra of
![]() $L^X$
, it is clear that
$L^X$
, it is clear that
![]() $G\cap S$
is a subalgebra of G.
$G\cap S$
is a subalgebra of G.
(S1) If
![]() $f\in G$
, then
$f\in G$
, then
![]() $\forall _f\in G$
, so
$\forall _f\in G$
, so ![]() . Analogously,
. Analogously,
![]() $\min \{s\in G\cap S|s\geq f\}=\exists _f\in G$
.
$\min \{s\in G\cap S|s\geq f\}=\exists _f\in G$
.
(S2) Since
![]() $G\cap S$
is totally ordered, we may check condition
$G\cap S$
is totally ordered, we may check condition
![]() $(s_2)$
. If
$(s_2)$
. If
![]() $1=s\vee f$
for some
$1=s\vee f$
for some
![]() $f\in G$
and
$f\in G$
and
![]() $s\in G\cap S$
. Putting
$s\in G\cap S$
. Putting
![]() $s(x)=s_0\in L,x\in X$
. Then
$s(x)=s_0\in L,x\in X$
. Then
![]() $s_0\vee f(x)=1$
for every
$s_0\vee f(x)=1$
for every
![]() $x\in X$
. As L is linearly ordered, either
$x\in X$
. As L is linearly ordered, either
![]() $s_0=1$
or
$s_0=1$
or
![]() $f(x)=1$
for every
$f(x)=1$
for every
![]() $x\in X$
.
$x\in X$
.
(S3) If ![]() for some
for some
![]() $f\in G$
and
$f\in G$
and
![]() $c\in G\cap S$
, then
$c\in G\cap S$
, then ![]() for any
for any
![]() $x\in X$
. Moreover,
$x\in X$
. Moreover, ![]() for any
for any
![]() $x,y\in X$
, since
$x,y\in X$
, since
Hence ![]() for a fixed
for a fixed
![]() $y\in X$
and any
$y\in X$
and any
![]() $x\in X$
. Thus
$x\in X$
. Thus ![]() , where
, where
![]() $\exists _f=\sup \{f(y)|y\in X\}$
. Now,
$\exists _f=\sup \{f(y)|y\in X\}$
. Now, ![]() for any
for any
![]() $y\in Y$
. Then
$y\in Y$
. Then ![]() and
and ![]() , which concludes the proof that
, which concludes the proof that
![]() $G\cap S$
is an m-relatively complete subalgebra of G.
$G\cap S$
is an m-relatively complete subalgebra of G.
Then it follows from Theorem 4.1 that
![]() $(G,\forall _f,\exists _f)$
is a monadic MTL-algebra. Monadic MTL-algebras of this form are called functional monadic MTL-algebras. Also, if L is
$(G,\forall _f,\exists _f)$
is a monadic MTL-algebra. Monadic MTL-algebras of this form are called functional monadic MTL-algebras. Also, if L is
![]() $|X|$
-complete, then
$|X|$
-complete, then
![]() $S=L^X$
and
$S=L^X$
and
![]() $(L^X,\forall _f,\exists _f)$
is a functional monadic MTL-algebra.
$(L^X,\forall _f,\exists _f)$
is a functional monadic MTL-algebra.
Here we show that the variety of monadic MTL-algebras is the equivalent algebraic semantics of monadic fuzzy predicate logic
![]() $\mathbf {mMTL\forall }$
, which will be used to prove the main result of this section.
$\mathbf {mMTL\forall }$
, which will be used to prove the main result of this section.
Definition 4.4. A Kripke model for
![]() $\mathbf {S5(MTL)}$
is a triple
$\mathbf {S5(MTL)}$
is a triple
![]() $K=(X,e,L)$
where X is a nonempty set of worlds, L is a linearly ordered MTL-algebra and
$K=(X,e,L)$
where X is a nonempty set of worlds, L is a linearly ordered MTL-algebra and
![]() $e:Prop\times X\rightarrow L$
is an evaluation map. The evaluation map extends to any formula:
$e:Prop\times X\rightarrow L$
is an evaluation map. The evaluation map extends to any formula:
-
 $(e_1)$
$(e_1)$
 $e(0,x)=0$
,
$e(0,x)=0$
,
 $e(1,x)=1$
,
$e(1,x)=1$
, -
 $(e_2)$
$(e_2)$
 $e(\varphi \sqcap \psi ,x)=e(\varphi ,x)\wedge e(\psi ,x)$
,
$e(\varphi \sqcap \psi ,x)=e(\varphi ,x)\wedge e(\psi ,x)$
, -
 $(e_3)$
$(e_3)$
 $e(\varphi \sqcup \psi ,x)=e(\varphi ,x)\vee e(\psi ,x)$
,
$e(\varphi \sqcup \psi ,x)=e(\varphi ,x)\vee e(\psi ,x)$
, -
 $(e_4)$
$(e_4)$
 $e(\varphi \& \psi ,x)=e(\varphi ,x)\odot e(\psi ,x)$
,
$e(\varphi \& \psi ,x)=e(\varphi ,x)\odot e(\psi ,x)$
, -
 $(e_5)$
$(e_5)$
 $e(\varphi \Rightarrow \psi ,x)=e(\varphi ,x)\rightarrow e(\psi ,x)$
,
$e(\varphi \Rightarrow \psi ,x)=e(\varphi ,x)\rightarrow e(\psi ,x)$
, -
 $(e_6)$
$(e_6)$
 $e(\square \varphi ,x)=\inf \{e(\varphi ,y):y\in X\}$
,
$e(\square \varphi ,x)=\inf \{e(\varphi ,y):y\in X\}$
, -
 $(e_7)$
$(e_7)$
 .
.
We can also define truth degree
![]() $\|\varphi \|_{K,\omega }$
of a formula
$\|\varphi \|_{K,\omega }$
of a formula
![]() $\varphi $
in K at the world
$\varphi $
in K at the world
![]() $\omega $
, which is due done recursively on the structure of
$\omega $
, which is due done recursively on the structure of
![]() $\varphi $
. For propositional variables
$\varphi $
. For propositional variables
![]() $p\in Prop$
, we have that
$p\in Prop$
, we have that
![]() $\|p\|_{K,\omega }=e(\omega ,p)$
. The definition of the truth value is then extended for the logical connectives of monoidal t-norm based logic in the usual way, and for the modal connectives by
$\|p\|_{K,\omega }=e(\omega ,p)$
. The definition of the truth value is then extended for the logical connectives of monoidal t-norm based logic in the usual way, and for the modal connectives by
the infima and suprema above may not exist in general; hence, we restrict our attention only to safe structures, that is, structure K for which
![]() $\|\varphi \|_{K,\omega }$
is defined for every formula
$\|\varphi \|_{K,\omega }$
is defined for every formula
![]() $\varphi $
at every world
$\varphi $
at every world
![]() $\omega $
. However, we are only interested in the tautologies of this logic, but here considered albeit implicitly, a global consequence relation
$\omega $
. However, we are only interested in the tautologies of this logic, but here considered albeit implicitly, a global consequence relation
![]() $\models _{\mathbf {S5(MTL)}}$
. Given a set of formulas
$\models _{\mathbf {S5(MTL)}}$
. Given a set of formulas
![]() $\Gamma $
we say that a safe structure
$\Gamma $
we say that a safe structure
![]() $K=(X,e,L)$
is a model of
$K=(X,e,L)$
is a model of
![]() $\Gamma $
if for every
$\Gamma $
if for every
![]() $\varphi \in \Gamma $
and every
$\varphi \in \Gamma $
and every
![]() $\omega \in W$
we have that
$\omega \in W$
we have that
![]() $\|\varphi \|_{K,\omega }=1$
. Thus, given a set of formulas
$\|\varphi \|_{K,\omega }=1$
. Thus, given a set of formulas
![]() $\Gamma $
and a formula
$\Gamma $
and a formula
![]() $\varphi $
we write
$\varphi $
we write
![]() $\Gamma \models _{\mathbf {S5(MTL)}}\varphi $
if and only if for every safe model
$\Gamma \models _{\mathbf {S5(MTL)}}\varphi $
if and only if for every safe model
![]() $K=(X,e,L)$
of
$K=(X,e,L)$
of
![]() $\Gamma $
we have that
$\Gamma $
we have that
![]() $\|\varphi \|_{K,\omega }=1$
for every
$\|\varphi \|_{K,\omega }=1$
for every
![]() $\omega \in W$
.
$\omega \in W$
.
We already noted that
![]() $\mathbf {S5(MTL)}$
is actually equivalent to
$\mathbf {S5(MTL)}$
is actually equivalent to
![]() $\mathbf {mMTL\forall }$
because there is a natural correspondence between formulas of both logics, between corresponding models and between the corresponding truth degrees. Thus, since the latter is finitary (being a fragment of a finitary logic), the consequence relation
$\mathbf {mMTL\forall }$
because there is a natural correspondence between formulas of both logics, between corresponding models and between the corresponding truth degrees. Thus, since the latter is finitary (being a fragment of a finitary logic), the consequence relation
![]() $\mathbf {S5(MTL)}$
is also finitary.
$\mathbf {S5(MTL)}$
is also finitary.
Theorem 4.5. The fuzzy modal logic
![]() $\mathbf {S5(MTL)}$
is strongly complete with respect to its general semantics, that is, the following statements are equivalent for every set of formulas
$\mathbf {S5(MTL)}$
is strongly complete with respect to its general semantics, that is, the following statements are equivalent for every set of formulas
![]() $\Gamma \cup \{\varphi \}$
:
$\Gamma \cup \{\varphi \}$
:
-
(1)
 $\Gamma \vdash \varphi $
,
$\Gamma \vdash \varphi $
, -
(2)
 $K\models \varphi $
for every safe model K of
$K\models \varphi $
for every safe model K of
 $\Gamma $
.
$\Gamma $
.
Proof. The proof is similar to that of Theorem 2 in [Reference Hájek30].
Considering a safe Kripke model
![]() $K=(X,e,L)$
, we can turn the map
$K=(X,e,L)$
, we can turn the map
![]() $e:Prop\times X\rightarrow L$
into a map
$e:Prop\times X\rightarrow L$
into a map
![]() $\overline {e}:Prop\rightarrow L^X$
given by the relation
$\overline {e}:Prop\rightarrow L^X$
given by the relation
![]() $\overline {e}(p)(x)=e(p,x)$
. Since K is safe,
$\overline {e}(p)(x)=e(p,x)$
. Since K is safe,
![]() $\overline {e}$
extends to formulas in the following way:
$\overline {e}$
extends to formulas in the following way:
-
 $(e_1)$
$(e_1)$
 $\overline {e}(x)=0$
,
$\overline {e}(x)=0$
,
 $\overline {e}(1)=1$
,
$\overline {e}(1)=1$
, -
 $(e_2)$
$(e_2)$
 $\overline {e}(\varphi \sqcap \psi )=\overline {e}(\varphi )\wedge \overline {e}(\psi )$
,
$\overline {e}(\varphi \sqcap \psi )=\overline {e}(\varphi )\wedge \overline {e}(\psi )$
, -
 $(e_3)$
$(e_3)$
 $\overline {e}(\varphi \sqcup \psi )=\overline {e}(\varphi )\vee \overline {e}(\psi )$
,
$\overline {e}(\varphi \sqcup \psi )=\overline {e}(\varphi )\vee \overline {e}(\psi )$
, -
 $(e_4)$
$(e_4)$
 $\overline {e}(\varphi \& \psi )=\overline {e}(\varphi )\odot \overline {e}(\psi )$
,
$\overline {e}(\varphi \& \psi )=\overline {e}(\varphi )\odot \overline {e}(\psi )$
, -
 $(e_5)$
$(e_5)$
 $\overline {e}(\varphi \Rightarrow \psi )=\overline {e}(\varphi )\rightarrow \overline {e}(\psi )$
,
$\overline {e}(\varphi \Rightarrow \psi )=\overline {e}(\varphi )\rightarrow \overline {e}(\psi )$
, -
 $(e_6)$
$(e_6)$
 $\overline {e}(\square \varphi )=\forall _f\overline {e}(\varphi )$
,
$\overline {e}(\square \varphi )=\forall _f\overline {e}(\varphi )$
, -
 $(e_7)$
$(e_7)$
 .
.
Thus it is clear that
![]() $\{\overline {e}(\varphi ):\varphi $
formula
$\{\overline {e}(\varphi ):\varphi $
formula
![]() $\}\subseteq L^X$
is the universe of a functional monadic MTL-algebra in Example 4.2.
$\}\subseteq L^X$
is the universe of a functional monadic MTL-algebra in Example 4.2.
Then we have the following result similar to Theorem 4.5.
Theorem 4.6. The following statements are equivalent for every set of formulas
![]() $\Gamma \cup \{\varphi \}$
:
$\Gamma \cup \{\varphi \}$
:
-
(1)
 $\Gamma \vdash \varphi $
,
$\Gamma \vdash \varphi $
, -
(2)
 $\overline {e}(\varphi )=1$
for every
$\overline {e}(\varphi )=1$
for every
 $\overline {e}:Prop\rightarrow G$
, where
$\overline {e}:Prop\rightarrow G$
, where
 $(G,\forall _f,\exists _f)$
is any functional monadic MTL-algebra and
$(G,\forall _f,\exists _f)$
is any functional monadic MTL-algebra and
 $\overline {e}(\gamma )=1$
for every
$\overline {e}(\gamma )=1$
for every
 $\gamma \in \Gamma $
.
$\gamma \in \Gamma $
.
Theorem 4.7. The variety
![]() $\mathbb {MMTL}$
is the equivalent algebraic semantics for the logic
$\mathbb {MMTL}$
is the equivalent algebraic semantics for the logic
![]() $\mathbf {S5(MTL)}$
.
$\mathbf {S5(MTL)}$
.
Proof. It is enough to show that the next two conditions hold for set for formulas
![]() $\Gamma \cup \{\varphi ,\phi \}$
:
$\Gamma \cup \{\varphi ,\phi \}$
:
-
(1)
 $\Gamma \vdash \varphi $
if and only if
$\Gamma \vdash \varphi $
if and only if
 $\{\psi \equiv 1|\psi \in \Gamma \}\vdash _{\mathbb {MMTL}}\varphi \equiv 1$
,
$\{\psi \equiv 1|\psi \in \Gamma \}\vdash _{\mathbb {MMTL}}\varphi \equiv 1$
, -
(2)
 $\varphi \equiv \phi \models _{\mathbb {MMTL}}(\varphi \Rightarrow \phi )\sqcap (\phi \Rightarrow \varphi )\equiv 1$
.
$\varphi \equiv \phi \models _{\mathbb {MMTL}}(\varphi \Rightarrow \phi )\sqcap (\phi \Rightarrow \varphi )\equiv 1$
.
Condition (2) is trivially verified. We only show the condition (1). For the forward implication, if
![]() $\Gamma \vdash \varphi $
, there exists a proof of
$\Gamma \vdash \varphi $
, there exists a proof of
![]() $\varphi $
from
$\varphi $
from
![]() $\Gamma $
and the axioms of
$\Gamma $
and the axioms of
![]() $\mathbf {S5(MTL)}$
by successive application of the reference rules
$\mathbf {S5(MTL)}$
by successive application of the reference rules
![]() $\mathbf {MP}$
and
$\mathbf {MP}$
and
![]() $\mathbf {Nec}$
. Thus, it is enough to show that the equation
$\mathbf {Nec}$
. Thus, it is enough to show that the equation
![]() $\varphi \equiv 1$
is valid in
$\varphi \equiv 1$
is valid in
![]() $\mathbb {MMTL}$
for every axiom
$\mathbb {MMTL}$
for every axiom
![]() $\varphi $
of
$\varphi $
of
![]() $\mathbf {S5(MTL)}$
and that the inference rules preserve validity. The former statement follows from the basic properties of monadic MTL-algebras. The preservation of
$\mathbf {S5(MTL)}$
and that the inference rules preserve validity. The former statement follows from the basic properties of monadic MTL-algebras. The preservation of
![]() $\mathbf {MP}$
and
$\mathbf {MP}$
and
![]() $\mathbf {Nec}$
are also easily verified. For the converse implication, simply observe that, since
$\mathbf {Nec}$
are also easily verified. For the converse implication, simply observe that, since
![]() $(G,\forall _f,\exists _f)$
is a monadic MTL-algebra, condition (2) of Theorem 4.6 holds.
$(G,\forall _f,\exists _f)$
is a monadic MTL-algebra, condition (2) of Theorem 4.6 holds.
Thus, from the general theory of Algebraic Logic, we get the next result.
Corollary 4.8. There is a one–one correspondence between axiomatic extensions of
![]() $\mathbf {S5(MTL})$
and subvarieties of
$\mathbf {S5(MTL})$
and subvarieties of
![]() $\mathbb {MMTL}$
.
$\mathbb {MMTL}$
.
Zahiri and Borumand Saeid give a Hilbert-style syntactic calculus in the language of
![]() $\mathbf {MMTL}$
, which is indeed equivalent to
$\mathbf {MMTL}$
, which is indeed equivalent to
![]() $\mathbf {S5(MTL)}$
whose consequence we denote by
$\mathbf {S5(MTL)}$
whose consequence we denote by
![]() $\vdash _{\mathbf {S5(MTL)}}$
. The axioms of this calculus are the instantiations of the axioms schemata
$\vdash _{\mathbf {S5(MTL)}}$
. The axioms of this calculus are the instantiations of the axioms schemata
![]() $\mathbf {MTL}$
for formulas in the language of
$\mathbf {MTL}$
for formulas in the language of
![]() $\mathbf {S5(MTL)}$
, plus the following axioms:
$\mathbf {S5(MTL)}$
, plus the following axioms:
-

 ,
, -
 $(\square 2)$
$(\square 2)$
 $\square (\nu \Rightarrow \varphi )\Rightarrow (\nu \Rightarrow \square \varphi )$
,
$\square (\nu \Rightarrow \varphi )\Rightarrow (\nu \Rightarrow \square \varphi )$
, -

 ,
, -
 $(\square 3)$
$(\square 3)$
 $\square (\nu \sqcup \varphi )\Rightarrow (\nu \sqcup \square \varphi )$
,
$\square (\nu \sqcup \varphi )\Rightarrow (\nu \sqcup \square \varphi )$
, -

 ,
,
where
![]() $\varphi $
is any formula and
$\varphi $
is any formula and
![]() $\nu $
is any propositional combination of formulas beginning with
$\nu $
is any propositional combination of formulas beginning with
![]() $\square $
or
$\square $
or ![]() . The inference rules are
. The inference rules are
![]() $\mathbf {MP}$
:
$\mathbf {MP}$
:
![]() $\varphi $
,
$\varphi $
,
![]() $\varphi \Rightarrow \phi \vdash \phi $
and
$\varphi \Rightarrow \phi \vdash \phi $
and
![]() $\mathbf {Nec}: \varphi /\square \varphi $
.
$\mathbf {Nec}: \varphi /\square \varphi $
.
Here we achieve the main aim of this section, namely, giving an algebraic proof of the completeness theorem for monadic fuzzy predicate logic
![]() $\mathbf {mMTL\forall }$
.
$\mathbf {mMTL\forall }$
.
Theorem 4.9. The following statements are equivalent for every set of formulas
![]() $\Gamma \cup \{\varphi \}$
:
$\Gamma \cup \{\varphi \}$
:
-
(1)
 $\mathbf {S5(MTL)}$
is complete, i.e., the following two statements are equivalent:
$\mathbf {S5(MTL)}$
is complete, i.e., the following two statements are equivalent:-
(i)
 $\Gamma \vdash _{\mathbf {S5(MTL)}}\varphi $
,
$\Gamma \vdash _{\mathbf {S5(MTL)}}\varphi $
, -
(ii)
 $\Gamma \models _{\mathbf {S5(MTL)}}\varphi $
.
$\Gamma \models _{\mathbf {S5(MTL)}}\varphi $
.
-
-
(2) The variety
 $\mathbb {MMTL}$
is generated by the functional monadic MTL-algebras.
$\mathbb {MMTL}$
is generated by the functional monadic MTL-algebras.
Proof. We prove first that (2) implies (1). The soundness and implication is straightforward and does not depend on the hypothesis. Assume
![]() $\Gamma \models _{\mathbf {S5(MTL)}}\varphi $
and since
$\Gamma \models _{\mathbf {S5(MTL)}}\varphi $
and since
![]() $\varphi \models _{\mathbf {S5(MTL)}}$
is finitary, we may also assume that
$\varphi \models _{\mathbf {S5(MTL)}}$
is finitary, we may also assume that
![]() $\Gamma $
is finite. By way of contradiction, suppose
$\Gamma $
is finite. By way of contradiction, suppose
![]() $\Gamma \nvdash _{\mathbf {S5(MTL)}}\varphi $
. Then
$\Gamma \nvdash _{\mathbf {S5(MTL)}}\varphi $
. Then
![]() $\Gamma \nvDash _{\mathbf {S5(MTL)}}\varphi $
(this is the consequence relation associated with the variety of
$\Gamma \nvDash _{\mathbf {S5(MTL)}}\varphi $
(this is the consequence relation associated with the variety of
![]() $\mathbb {MMTL}$
), which is equivalent to saying that
$\mathbb {MMTL}$
), which is equivalent to saying that
![]() $\mathbb {MMTL}$
does not satisfy the quasi-equation
$\mathbb {MMTL}$
does not satisfy the quasi-equation
where ![]() . By hypothesis, there is a functional algebra
. By hypothesis, there is a functional algebra
![]() $(M,\forall _f,\exists _f)\in \mathbb {MMTL}$
with
$(M,\forall _f,\exists _f)\in \mathbb {MMTL}$
with ![]() and L is an MTL-algebra, and a valuation h into
and L is an MTL-algebra, and a valuation h into
![]() $(M,\forall _f,\exists _f)$
such that
$(M,\forall _f,\exists _f)$
such that
![]() $h(\Gamma )\subseteq \{1\}$
but
$h(\Gamma )\subseteq \{1\}$
but
![]() $h(\varphi )\neq 1$
. Consider the structure
$h(\varphi )\neq 1$
. Consider the structure
![]() $K=(X,e,L)$
with
$K=(X,e,L)$
with
![]() $e(x,p)=h(p)(x)$
for
$e(x,p)=h(p)(x)$
for
![]() $x\in X$
and
$x\in X$
and
![]() $p\in Prop$
. For every
$p\in Prop$
. For every
![]() $\gamma \in \Gamma $
and
$\gamma \in \Gamma $
and
![]() $x\in X$
we have that
$x\in X$
we have that
![]() $\|\gamma \|_K,x=h(\gamma )(x)=1$
, but
$\|\gamma \|_K,x=h(\gamma )(x)=1$
, but
![]() $\|\gamma \|_K,x=h(\gamma )(x)\neq 1$
for some
$\|\gamma \|_K,x=h(\gamma )(x)\neq 1$
for some
![]() $x\in X$
, which is a contradiction.
$x\in X$
, which is a contradiction.
Conversely, we now prove that (1) implies (2). Assume
![]() $\mathbb {MMTL}$
is not generated by its functional members. Thus, there is an identity
$\mathbb {MMTL}$
is not generated by its functional members. Thus, there is an identity
that is on every functional monadic MTL-algebra, but is not true on the variety
![]() $\mathbb {MTL}$
. From the properties of algebraizable logics, we get that
$\mathbb {MTL}$
. From the properties of algebraizable logics, we get that ![]() . However, we claim that
. However, we claim that ![]() . Indeed, assume
. Indeed, assume
![]() $K=(X,e,L)$
is a model of
$K=(X,e,L)$
is a model of ![]() , where L is a linearly ordered MTL-algebra. Then
, where L is a linearly ordered MTL-algebra. Then
![]() $\|\gamma _i\|_K,x=h(\gamma _i)(x)=1$
for any
$\|\gamma _i\|_K,x=h(\gamma _i)(x)=1$
for any
![]() $x\in X$
and
$x\in X$
and ![]() . Let Fm be the set of propositional formulas in the language of
. Let Fm be the set of propositional formulas in the language of
![]() $\mathbf {S5(MTL)}$
. For each
$\mathbf {S5(MTL)}$
. For each
![]() $\psi \in Fm$
, we define
$\psi \in Fm$
, we define
![]() $f_\psi :X\rightarrow L$
such that
$f_\psi :X\rightarrow L$
such that
![]() $f_\psi (x)=\|\psi \|_K,x$
for every
$f_\psi (x)=\|\psi \|_K,x$
for every
![]() $x\in X$
. Consider
$x\in X$
. Consider
![]() $B=\{f_\psi |\psi \in Fm\}$
. Then
$B=\{f_\psi |\psi \in Fm\}$
. Then
![]() $B\subseteq L^X$
and, in addition, B is a subuniverse of the MTL-algebra
$B\subseteq L^X$
and, in addition, B is a subuniverse of the MTL-algebra
![]() $L^X$
. Moreover, it is straightforward to check that
$L^X$
. Moreover, it is straightforward to check that ![]() . Then
. Then
![]() $(L,\forall _f,\exists _f)$
is a functional monadic MTL-algebra. Consider now the interpretation
$(L,\forall _f,\exists _f)$
is a functional monadic MTL-algebra. Consider now the interpretation
![]() $e':Fm\rightarrow L$
given by
$e':Fm\rightarrow L$
given by
![]() $e'(\psi )=f_\psi $
for any
$e'(\psi )=f_\psi $
for any
![]() $\psi \in Fm$
. Then
$\psi \in Fm$
. Then
![]() $e'(\gamma _i)=1$
for
$e'(\gamma _i)=1$
for ![]() . By hypothesis,
. By hypothesis,
![]() $e'(\varphi )=1$
, that is,
$e'(\varphi )=1$
, that is,
![]() $f_\varphi =1$
, so
$f_\varphi =1$
, so
![]() $\|\varphi \|_K,x=1$
for any
$\|\varphi \|_K,x=1$
for any
![]() $x\in X$
. This completes the proof that
$x\in X$
. This completes the proof that ![]() .
.
5 Strong completeness for monadic fuzzy predicate logic
 $\mathbf {mIMTL\forall }$
$\mathbf {mIMTL\forall }$
In this section, we obtain the completeness theorem of some axiomatic extensions for monadic fuzzy predicate logic
![]() $\mathbf {mMTL\forall }$
, and then give a major application, proving the strong completeness theorem for monadic fuzzy predicate logic
$\mathbf {mMTL\forall }$
, and then give a major application, proving the strong completeness theorem for monadic fuzzy predicate logic
![]() $\mathbf {mIMTL\forall }$
.
$\mathbf {mIMTL\forall }$
.
Along with the same line of Section 4, we naturally extend some basic notions, including Kripke model and its related concepts, from the fuzzy modal logic
![]() $\mathbf {S5(MTL)}$
to a more general one,
$\mathbf {S5(MTL)}$
to a more general one,
![]() $\mathbf {S5(C)}$
which is indeed an S5-modal expansion of an axiomatic extension
$\mathbf {S5(C)}$
which is indeed an S5-modal expansion of an axiomatic extension
![]() $\mathbf {C}$
of the logic
$\mathbf {C}$
of the logic
![]() $\mathbf {MTL}$
, and denote a global consequence relation by
$\mathbf {MTL}$
, and denote a global consequence relation by
![]() $\models _{\mathbf {S5(C)}}$
.
$\models _{\mathbf {S5(C)}}$
.
Here we also introduce a Hilbert-style syntactic calculus in the language of
![]() $\mathbf {S5(C)}$
whose consequence relation is denoted by
$\mathbf {S5(C)}$
whose consequence relation is denoted by
![]() $\vdash _{\mathbf {S5(C)}}$
. The axiom of this calculus are the instantiations of the axiom schemata of
$\vdash _{\mathbf {S5(C)}}$
. The axiom of this calculus are the instantiations of the axiom schemata of
![]() $\mathbf {C}$
for formulas in the language of
$\mathbf {C}$
for formulas in the language of
![]() $\mathbf {S5(C)}$
, plusing the axioms:
$\mathbf {S5(C)}$
, plusing the axioms: ![]() ,
,
![]() $(\square 2)$
,
$(\square 2)$
, ![]() ,
,
![]() $(\square 3)$
and
$(\square 3)$
and ![]() . Moreover, Theorem 4.7 shows that the variety
. Moreover, Theorem 4.7 shows that the variety
![]() $\mathbb {MMTL}$
is the equivalent algebraic semantics of the logic
$\mathbb {MMTL}$
is the equivalent algebraic semantics of the logic
![]() $\mathbf {S5(MTL)}$
. As a consequence of the general theory of algebraizability all axiomatic extensions of
$\mathbf {S5(MTL)}$
. As a consequence of the general theory of algebraizability all axiomatic extensions of
![]() $\mathbf {S5(MTL)}$
are algebraizable logics and their equivalent algebraic semantics are precisely the subvarieties of
$\mathbf {S5(MTL)}$
are algebraizable logics and their equivalent algebraic semantics are precisely the subvarieties of
![]() $\mathbb {MMTL}$
, see Corollary 4.8. In particular, given any axiomatic extension
$\mathbb {MMTL}$
, see Corollary 4.8. In particular, given any axiomatic extension
![]() $\mathbf {C}$
of
$\mathbf {C}$
of
![]() $\mathbf {MTL}$
, the logic
$\mathbf {MTL}$
, the logic
![]() $\mathbf {S5(C)}$
is an axiomatic extension of
$\mathbf {S5(C)}$
is an axiomatic extension of
![]() $\mathbf {S5(MTL)}$
with an equivalent algebraic semantics Alg
$\mathbf {S5(MTL)}$
with an equivalent algebraic semantics Alg
![]() $^\ast \mathbf {S5(C)}$
, denote also by
$^\ast \mathbf {S5(C)}$
, denote also by
![]() $\mathbb {MMTL_C}$
. It is also worth noticing that
$\mathbb {MMTL_C}$
. It is also worth noticing that
![]() $\mathbf {S5(C)}$
is actually equivalent to the monadic fragment in one variable (without constants) of the first-order logic
$\mathbf {S5(C)}$
is actually equivalent to the monadic fragment in one variable (without constants) of the first-order logic
![]() $\mathbf {C\forall }$
because there is a natural correspondence between formulas of both logics, between corresponding models and between the corresponding truth degrees.
$\mathbf {C\forall }$
because there is a natural correspondence between formulas of both logics, between corresponding models and between the corresponding truth degrees.
Given an axiomatic extension
![]() $\mathbf {C}$
of
$\mathbf {C}$
of
![]() $\mathbf {MTL}$
, we say that a monadic MTL-algebra is
$\mathbf {MTL}$
, we say that a monadic MTL-algebra is
![]() $\mathbb {C}$
-functional if it is built in the previously defined way (Example 4.2 and Remark 4.3) from a linearly ordered MTL-algebra that belongs to Alg
$\mathbb {C}$
-functional if it is built in the previously defined way (Example 4.2 and Remark 4.3) from a linearly ordered MTL-algebra that belongs to Alg
![]() $\ast \mathbb {C}$
.
$\ast \mathbb {C}$
.
Along with the same line of Theorem 4.9, the following corollary naturally hold.
Corollary 5.1. Let
![]() $\mathbf {C}$
be an axiomatic extension of
$\mathbf {C}$
be an axiomatic extension of
![]() $\mathbf {MTL}$
. Then the following statements are equivalent:
$\mathbf {MTL}$
. Then the following statements are equivalent:
-
(1) For any formula
 $\varphi $
and any set of formulas
$\varphi $
and any set of formulas
 $\Gamma $
, we have
$\Gamma $
, we have  $$ \begin{align*} \Gamma\vdash_{\mathbf{S5(C)}}\varphi \text{ if and only if } \Gamma\models_{\mathbf{S5(C)}}\varphi. \end{align*} $$
$$ \begin{align*} \Gamma\vdash_{\mathbf{S5(C)}}\varphi \text{ if and only if } \Gamma\models_{\mathbf{S5(C)}}\varphi. \end{align*} $$
-
(2) The variety
 $\mathbb {MMTL_C}$
is generated, as a quasivariety, by its
$\mathbb {MMTL_C}$
is generated, as a quasivariety, by its
 $\mathbb {C}$
-functional algebras
$\mathbb {C}$
-functional algebras
Theorem 3.13 shows that a monadic IMTL-algebra is a monadic MTL-algebra that satisfies the identity
![]() $\neg \neg x=x$
. In other words, a monadic IMTL-algebra is a monadic MTL-algebra whose MTL-reduct is an IMTL-algebra. This monadic algebra was first introduced in [Reference Wang and Xin53] as an equivalent algebraic semantic for monadic fuzzy predicate logic based on involutive monoidal t-norm logic
$\neg \neg x=x$
. In other words, a monadic IMTL-algebra is a monadic MTL-algebra whose MTL-reduct is an IMTL-algebra. This monadic algebra was first introduced in [Reference Wang and Xin53] as an equivalent algebraic semantic for monadic fuzzy predicate logic based on involutive monoidal t-norm logic
![]() $\mathbf {mIMTL\forall }$
.
$\mathbf {mIMTL\forall }$
.
Here we prove a representation theorem of monadic IMTL-algebras, and use it to derive strong completeness of the calculus with respect to the chain-based models. In order to make this section as self-contained as possible, we recall that some results about model theory in advance, which is indeed a straightforward application of model theoretic techniques [Reference Chang and Keisler6].
Let A be a structure in the first-order language
![]() $\mathcal {L}$
, and let
$\mathcal {L}$
, and let
![]() $\{c_a:a\in A\}$
be a set of new constant symbols and put
$\{c_a:a\in A\}$
be a set of new constant symbols and put
![]() $\mathcal {L_A}=\mathcal {L}\cup \{c_a:a\in A\}$
. Given an
$\mathcal {L_A}=\mathcal {L}\cup \{c_a:a\in A\}$
. Given an
![]() $\mathcal {L}$
-structure B and a family
$\mathcal {L}$
-structure B and a family
![]() $\{b_a:a\in A\}$
of elements of B, we denote by
$\{b_a:a\in A\}$
of elements of B, we denote by
![]() $(B,\{b_a\}_{a\in A})$
the expansion of B to the language
$(B,\{b_a\}_{a\in A})$
the expansion of B to the language
![]() $\mathcal {L_A}$
that results by defining
$\mathcal {L_A}$
that results by defining
![]() $b_a$
as the interpretation of the constant
$b_a$
as the interpretation of the constant
![]() $c_a$
for any
$c_a$
for any
![]() $a\in A$
. The diagram of A, written diag(A), is the set of all atomic sentences and negations of atomic sentences in the language
$a\in A$
. The diagram of A, written diag(A), is the set of all atomic sentences and negations of atomic sentences in the language
![]() $\mathcal {L_A}$
which are true in
$\mathcal {L_A}$
which are true in
![]() $(A,\{b_a\}_{a\in A})$
.
$(A,\{b_a\}_{a\in A})$
.
Proposition 5.2 [Reference Chang and Keisler6]
Let
![]() $A,B$
be two
$A,B$
be two
![]() $\mathcal {L}$
-structures and let
$\mathcal {L}$
-structures and let
![]() $f:A\rightarrow B$
be a function. Then the following statements are equivalent:
$f:A\rightarrow B$
be a function. Then the following statements are equivalent:
-
(1) f is an embedding of A into B,
-
(2)
 $(B,\{f(a)\}_{a\in A})$
is a model of diag (A).
$(B,\{f(a)\}_{a\in A})$
is a model of diag (A).
Let
![]() $\mathbb {K}$
be a class of structures in a first-order language. A V-formation in
$\mathbb {K}$
be a class of structures in a first-order language. A V-formation in
![]() $\mathbb {K}$
is a 5-tuple
$\mathbb {K}$
is a 5-tuple
![]() $(A,A_1,A_2,\alpha _1,\alpha _2)$
consisting of three structures
$(A,A_1,A_2,\alpha _1,\alpha _2)$
consisting of three structures
![]() $A,A_1,A_2$
in
$A,A_1,A_2$
in
![]() $\mathbb {K}$
and two embeddings
$\mathbb {K}$
and two embeddings
![]() $\alpha _1:A\rightarrow A_1$
and
$\alpha _1:A\rightarrow A_1$
and
![]() $\alpha _2:A\rightarrow A_2$
. An amalgam in
$\alpha _2:A\rightarrow A_2$
. An amalgam in
![]() $\mathbb {K}$
of the V-formation is a triple
$\mathbb {K}$
of the V-formation is a triple
![]() $(B,\beta _1,\beta _2)$
consisting a structure B in
$(B,\beta _1,\beta _2)$
consisting a structure B in
![]() $\mathbb {K}$
and two embeddings
$\mathbb {K}$
and two embeddings
![]() $\beta _1:A_1\rightarrow B$
and
$\beta _1:A_1\rightarrow B$
and
![]() $\beta _2:A_2\rightarrow B$
satisfying
$\beta _2:A_2\rightarrow B$
satisfying
![]() $\beta _1\circ \alpha _1=\beta _2\circ \alpha _2$
.
$\beta _1\circ \alpha _1=\beta _2\circ \alpha _2$
.
The class
![]() $\mathbb {K}$
has the amalgamation property provided every V-formation in
$\mathbb {K}$
has the amalgamation property provided every V-formation in
![]() $\mathbb {K}$
has an amalgam in
$\mathbb {K}$
has an amalgam in
![]() $\mathbb {K}$
. Here (Figure 4) we define a generalization of the notion of V-formation and amalgam. Given a set I, an I-formation in
$\mathbb {K}$
. Here (Figure 4) we define a generalization of the notion of V-formation and amalgam. Given a set I, an I-formation in
![]() $\mathbb {K}$
is a triple
$\mathbb {K}$
is a triple
![]() $(A,(A_i)_{i\in I},\{a_i\}_{i\in I})$
where A and
$(A,(A_i)_{i\in I},\{a_i\}_{i\in I})$
where A and
![]() $A_i$
are a structure in
$A_i$
are a structure in
![]() $\mathbb {K}$
and each
$\mathbb {K}$
and each
![]() $\alpha _i:A\rightarrow A_i$
is an embedding. An amalgam in
$\alpha _i:A\rightarrow A_i$
is an embedding. An amalgam in
![]() $\mathbb {K}$
of the I-formation is a pair
$\mathbb {K}$
of the I-formation is a pair
![]() $(B,\{\beta _i\}_{i\in I})$
, where B is a structure in
$(B,\{\beta _i\}_{i\in I})$
, where B is a structure in
![]() $\mathbb {K}$
and
$\mathbb {K}$
and
![]() $\beta _i:A_i\rightarrow B$
are embeddings such that
$\beta _i:A_i\rightarrow B$
are embeddings such that
![]() $\beta _i\circ \alpha _i=\beta _j\circ \alpha _j$
for any
$\beta _i\circ \alpha _i=\beta _j\circ \alpha _j$
for any
![]() $i,j\in I$
. Here we have that
$i,j\in I$
. Here we have that
![]() $\mathbb {K}$
has the amalgamation property over I if any I-formation in
$\mathbb {K}$
has the amalgamation property over I if any I-formation in
![]() $\mathbb {K}$
has an amalgam in
$\mathbb {K}$
has an amalgam in
![]() $\mathbb {K}$
, readers refer to [Reference Chang and Keisler6, Reference Gil-Férez, Jipsen and Metcalfe22, Reference Pierce40] for more details about results and examples of amalgamation.
$\mathbb {K}$
, readers refer to [Reference Chang and Keisler6, Reference Gil-Férez, Jipsen and Metcalfe22, Reference Pierce40] for more details about results and examples of amalgamation.

Figure 4 An amalgamation diagram of
![]() $\mathbb {K}$
.
$\mathbb {K}$
.
In particular, Pierce studied amalgamations of lattice ordered groups in [Reference Pierce40].
Example 5.3 [Reference Pierce40]
The class of totally ordered Abelian
![]() $\ell $
-groups has the amalgamation property.
$\ell $
-groups has the amalgamation property.
Theorem 5.4 [Reference Chang and Keisler6]
Let
![]() $\mathbb {K}$
be a class of structures in a first-order language with the amalgamation property. Then
$\mathbb {K}$
be a class of structures in a first-order language with the amalgamation property. Then
![]() $\mathbb {K}$
has the amalgamation property over any finite set I. If
$\mathbb {K}$
has the amalgamation property over any finite set I. If
![]() $\mathbb {K}$
is an elementary class, then
$\mathbb {K}$
is an elementary class, then
![]() $\mathbb {K}$
has the amalgamation property over any set I.
$\mathbb {K}$
has the amalgamation property over any set I.
Theorem 5.4 can be applied to the class of totally ordered IMTL-algebras.
Corollary 5.5. The class of totally ordered IMTL-algebras has amalgamation property.
Proof. This result is a straightforward consequence of Example 5.3 by using Mundici’s well-known correspondence between totally ordered Abelian
![]() $\ell $
-groups and totally ordered IMTL-algebras in [Reference Esteva and Godo17].
$\ell $
-groups and totally ordered IMTL-algebras in [Reference Esteva and Godo17].
As a consequence of Theorem 5.4, we get the following stronger result.
Theorem 5.6. The class of totally ordered IMTL-algebras has amalgamation property over any set.
With the aid of the general amalgamation property we prove here that finitely subdirectly irreducible monadic IMTL-algebras are isomorphic to
![]() $\mathcal {L}$
-functional algebras. As a consequence we derive the strong completeness theorem of monadic involutive monoidal t-norm based predicate logic.
$\mathcal {L}$
-functional algebras. As a consequence we derive the strong completeness theorem of monadic involutive monoidal t-norm based predicate logic.
Proposition 5.7. Let
![]() $(L,\forall ,\exists )$
be a finitely subdirectly irreducible monadic IMTL-algebra. Then for any
$(L,\forall ,\exists )$
be a finitely subdirectly irreducible monadic IMTL-algebra. Then for any
![]() $x\in L$
, there is a prime filter F of the IMTL-algebra L such that
$x\in L$
, there is a prime filter F of the IMTL-algebra L such that
![]() $x/F=\exists x/F$
and
$x/F=\exists x/F$
and
![]() $F\cap \exists L=\{1\}$
.
$F\cap \exists L=\{1\}$
.
Proof. Denote
Here we now prove that there is a prime filter P in
![]() $\mathcal {F}$
.
$\mathcal {F}$
.
Obviously
![]() $\mathcal {F}$
is non-empty since
$\mathcal {F}$
is non-empty since ![]() . Indeed, if
. Indeed, if ![]() , then
, then
![]() $y\geq (\exists x\rightarrow x)^{2^n}$
for some positive integer. So
$y\geq (\exists x\rightarrow x)^{2^n}$
for some positive integer. So
The union of a chain of filters in
![]() $\mathcal {F}$
is also a filter in
$\mathcal {F}$
is also a filter in
![]() $\mathcal {F}$
, and hence by Zorn’s Lemma, there is a maximal filter M in
$\mathcal {F}$
, and hence by Zorn’s Lemma, there is a maximal filter M in
![]() $\mathcal {F}$
. Here we show that M is indeed a prime filter. If M is not prime, then there are
$\mathcal {F}$
. Here we show that M is indeed a prime filter. If M is not prime, then there are
![]() $x,y\in L$
such that
$x,y\in L$
such that
![]() $x\rightarrow y,y\rightarrow x \notin M$
. Thus M is properly contained in
$x\rightarrow y,y\rightarrow x \notin M$
. Thus M is properly contained in
By the maximality of M in
![]() $\mathcal {F}$
, we have that
$\mathcal {F}$
, we have that
If
then
Thus
![]() $z\vee w\in M\cap \exists L=\{1\}$
, that is,
$z\vee w\in M\cap \exists L=\{1\}$
, that is,
![]() $z\vee w=1$
. Also, since
$z\vee w=1$
. Also, since
![]() $\exists L$
is totally ordered,
$\exists L$
is totally ordered,
![]() $z=1$
or
$z=1$
or
![]() $w=1$
, which is a contradiction. This shows that M is a prime filter.
$w=1$
, which is a contradiction. This shows that M is a prime filter.
Proposition 5.8. Given a finite subdirectly irreducibleFootnote
6
monadic IMTL-algebra
![]() $(L,\forall ,\exists )$
, there exists a subdirect embedding
$(L,\forall ,\exists )$
, there exists a subdirect embedding
where each
![]() $L_i$
is a totally ordered IMTL-algebra and
$L_i$
is a totally ordered IMTL-algebra and
isFootnote
7
an embedding, where
![]() $\pi _i$
is the i-th projection map. Also, for any
$\pi _i$
is the i-th projection map. Also, for any
![]() $x\in L$
, there are
$x\in L$
, there are
![]() $i,j\in I$
such that
$i,j\in I$
such that
Proof. It suffices to consider the subdirect representation of an IMTL-algebra L given by
where
Along with the same line of Theorem 16 in [Reference Di Nola and Grigolia11] that
![]() $\bigcap \mathcal {P}=\{1\}$
, so the representation is subdirect. The condition
$\bigcap \mathcal {P}=\{1\}$
, so the representation is subdirect. The condition
![]() $P\cap \exists L=\{1\}$
guarantees that the projections on
$P\cap \exists L=\{1\}$
guarantees that the projections on
![]() $L/P$
are one–one correspondence on
$L/P$
are one–one correspondence on
![]() $\exists L$
. Now, given
$\exists L$
. Now, given
![]() $x\in L$
, there is
$x\in L$
, there is
![]() $P\in \mathcal {P}$
such that
$P\in \mathcal {P}$
such that
![]() $\exists x/P=x/P$
. Also, there is
$\exists x/P=x/P$
. Also, there is
![]() $P_1\in \mathcal {P}$
such that
$P_1\in \mathcal {P}$
such that
![]() $\exists \neg x/P_1=\neg x/P_1$
, so
$\exists \neg x/P_1=\neg x/P_1$
, so
![]() $\forall x/P_1=\neg \exists \neg x/P_1=\neg \neg x/P_1=x/P_1$
.
$\forall x/P_1=\neg \exists \neg x/P_1=\neg \neg x/P_1=x/P_1$
.
Theorem 5.9. Every finitely subdirectly irreducible monadic IMTL-algebra
![]() $(L,\forall ,\exists )$
is isomorphic to an
$(L,\forall ,\exists )$
is isomorphic to an
![]() $\mathcal {L}$
-functional monadic IMTL-algebra, that is, there exist a totally ordered IMTL-algebra B, an index set I and an embedding
$\mathcal {L}$
-functional monadic IMTL-algebra, that is, there exist a totally ordered IMTL-algebra B, an index set I and an embedding
![]() $\alpha :L\rightarrow B^I$
such that
$\alpha :L\rightarrow B^I$
such that
for any
![]() $x\in L$
and
$x\in L$
and
![]() $i\in I$
.
$i\in I$
.
Proof. Proposition 5.8 produces a family
![]() $\{L_i|i\in I\}$
of totally ordered IMTL-algebras and embedding
$\{L_i|i\in I\}$
of totally ordered IMTL-algebras and embedding
such that
is an embedding for any
![]() $i\in I$
. Consider the I-formation
$i\in I$
. Consider the I-formation
![]() $(\exists L,\{L_i|i\in I\},\pi _i\circ \alpha |\exists L|i\in I\}$
in the elementary class
$(\exists L,\{L_i|i\in I\},\pi _i\circ \alpha |\exists L|i\in I\}$
in the elementary class
![]() $\mathbb {K}$
of totally ordered IMTL-algebras. By Theorem 5.6, the I-information has an amalgam
$\mathbb {K}$
of totally ordered IMTL-algebras. By Theorem 5.6, the I-information has an amalgam
![]() $(B,\{\beta _i|i\in I\})$
in
$(B,\{\beta _i|i\in I\})$
in
![]() $\mathbb {K}$
. Let
$\mathbb {K}$
. Let
and note that
is an embedding. Here we prove that
for any
![]() $x\in L$
and
$x\in L$
and
![]() $i\in I$
.
$i\in I$
.
Indeed, because of the amalgamation of the I-formation, we have that
 $$ \begin{align*} (\beta\circ\alpha)(\exists x)(i)&= \beta(\alpha(\exists x))(i)\\ &= \beta_i(\alpha(\exists x))(i)\\ &= \beta_i(\pi_i(\alpha(\exists x)))\\ &= \beta_j(\pi_j(\alpha(\exists x)))\\ &= \beta_j(\alpha(\exists x))(j)\\ &= \beta(\alpha(\exists x))(j)\\ &= (\beta\circ\alpha)(\exists x)(j), \end{align*} $$
$$ \begin{align*} (\beta\circ\alpha)(\exists x)(i)&= \beta(\alpha(\exists x))(i)\\ &= \beta_i(\alpha(\exists x))(i)\\ &= \beta_i(\pi_i(\alpha(\exists x)))\\ &= \beta_j(\pi_j(\alpha(\exists x)))\\ &= \beta_j(\alpha(\exists x))(j)\\ &= \beta(\alpha(\exists x))(j)\\ &= (\beta\circ\alpha)(\exists x)(j), \end{align*} $$
for any
![]() $i,j\in I$
, and also know that there is
$i,j\in I$
, and also know that there is
![]() $i_0\in I$
such that
$i_0\in I$
such that
Then
 $$ \begin{align*} (\beta\circ\alpha)(x)(i_0)&= (\beta\circ\alpha)(\exists x)(j)\\ &\geq (\beta\circ\alpha)(\exists x)(j)\\ &\geq (\beta\circ\alpha)(x)(j), \end{align*} $$
$$ \begin{align*} (\beta\circ\alpha)(x)(i_0)&= (\beta\circ\alpha)(\exists x)(j)\\ &\geq (\beta\circ\alpha)(\exists x)(j)\\ &\geq (\beta\circ\alpha)(x)(j), \end{align*} $$
for any
![]() $j\in I$
, which shows that
$j\in I$
, which shows that
The proof of
![]() $\forall x$
is similar to that of
$\forall x$
is similar to that of
![]() $\exists x$
.
$\exists x$
.
Corollary 5.10. The variety of monadic IMTL-algebras is generated, as a quasivariety, by its
![]() $\mathcal {L}$
-functional members.
$\mathcal {L}$
-functional members.
The last result of this section is a strong completeness theorem with respect to chain-based models.
Theorem 5.11. For any formula
![]() $\varphi $
and any set of formulas
$\varphi $
and any set of formulas
![]() $\Gamma $
, we have
$\Gamma $
, we have
6 Concluding remarks and future work
The motivation of this paper is to give an algebraic proof of completeness for monadic fuzzy predicate logic
![]() $\mathbf {mMTL\forall }$
and some of its axiomatic extensions. In order to achieve our aim, we first survey the present state of knowledge on monadic algebras of t-norm based residuated fuzzy logic and show that the relationships for monadic algebras of t-norm based fuzzy residuated logic completely inherit that for corresponding algebras of t-norm based fuzzy residuated logic. The results of Section 4 proved that the variety of monadic MTL-algebras is the equivalent algebraic semantics of the logic
$\mathbf {mMTL\forall }$
and some of its axiomatic extensions. In order to achieve our aim, we first survey the present state of knowledge on monadic algebras of t-norm based residuated fuzzy logic and show that the relationships for monadic algebras of t-norm based fuzzy residuated logic completely inherit that for corresponding algebras of t-norm based fuzzy residuated logic. The results of Section 4 proved that the variety of monadic MTL-algebras is the equivalent algebraic semantics of the logic
![]() $\mathbf {mMTL\forall }$
and gave an algebraic proof of completeness for this logic. Along with the same line, we further obtained the completeness theorem of some axiomatic extensions of the logic
$\mathbf {mMTL\forall }$
and gave an algebraic proof of completeness for this logic. Along with the same line, we further obtained the completeness theorem of some axiomatic extensions of the logic
![]() $\mathbf {mMTL\forall }$
, and proved the strong completeness theorem of monadic fuzzy predicate logic
$\mathbf {mMTL\forall }$
, and proved the strong completeness theorem of monadic fuzzy predicate logic
![]() $\mathbf {mIMTL\forall }$
via functional representation of finitely subdirectly irreducible algebras in Section 5.
$\mathbf {mIMTL\forall }$
via functional representation of finitely subdirectly irreducible algebras in Section 5.
Hopefully this first step will allow us to prove a strong result, namely the strong standard completeness for monadic fuzzy predicate logic
![]() $\mathbf {mIMTL\forall }$
that is equivalent to fuzzy modal logic
$\mathbf {mIMTL\forall }$
that is equivalent to fuzzy modal logic
![]() $\mathbf {S5(IMTL)}$
, which is one of the topics in subsequent discussions.
$\mathbf {S5(IMTL)}$
, which is one of the topics in subsequent discussions.
Acknowledgments
The authors are extremely grateful to the editor and the referees for their valuable comments and suggestions which help to improve the presentation of this paper.
Funding
This work is supported by the National Natural Science Foundation of China (Grant Nos. 12331016, 12001423 and 61976244) and the Natural Science Basic Research Plan in Shaanxi Province of China (2023-JC-YB-027).