2.1. Classical approaches

It has been observed that some classical path planning approaches do not guarantee obtaining an obstacle-free path. These methods are considered least desirable for real-time implementation, since their main disadvantage is their high computational cost and inability to respond to environmental uncertainty [Reference Patle, Babu, Pandey, Parhi and Jagadeesh16]. In this paper, the classical approaches will be classified into grid-based techniques, sampling-based techniques, and artificial potential field techniques (APF).

2.1.1. Grid-based techniques

Grid-based approaches use multi-resolution grid data structures where object space is quantized into a finite number of cells. Necessary operations are then performed on the quantized space [Reference Pilevar and Sukumar17]. Fast processing time is a significant advantage of grid-based methods. However, the processing speed varies based on the number of cells in each dimension of quantified space [Reference Ilango and Mohan18]. A* and D* algorithms are two examples of grid-based path planning techniques [Reference Yakovlev, Baskin and Hramoin19].

A* algorithm is a well-known path search algorithm that was first introduced in 1963 [Reference Hart, Nilsson and Raphael20]. It is an extension of the Dijkstra technique with additional heuristic calculations to improve the performance [Reference Tang and Ma21]. Although the A* algorithm is successfully implemented on 2D robotic systems, its implementation on 3D robotic systems is still challenging [Reference Radmanesh, Kumar, Guentert and Sarim22]. The main drawback of this algorithm is that it requires a long computational time to find the shortest path [Reference Korkmaz and Durdu6]. Figure 2 illustrates an example of finding an obstacle-free path using A* algorithm. D* algorithm is another grid-based approach that was first proposed in 1994 as an improvement over the classical A* algorithm [Reference Stentz23]. The abbreviation D stands for “Dynamic” since it is similar to the A* algorithm except it is the dynamic variant of the A* algorithm. The algorithm can be used to solve path planning problems in unknown environments [Reference Stentz23]. On the other hand, the time it takes to do a simulation increases as the problem becomes more complex [Reference Reeves24]. Modified versions such as D*-Lite and Focussed D* have significantly replaced the conventional D* algorithm due to the fast execution capabilities [Reference Le, Bui, Le and Peter25, Reference Stentz26].

Figure 2.

Finding the obstacle-free path using the A* grid-based technique.

2.1.2. Sampling-based techniques

Sampling-based algorithms select sample points randomly from the entire space. Whenever the line separating two samples does not intersect with an obstacle, and the distance between these samples does not exceed the predetermined maximum distance, the samples will be interconnected. After that, the shortest path will be selected as the final path [Reference Kang, Kim, Lee, Oh, You and Choi27]. Rapidly exploring random trees (RRT) and probabilistic RoadMap (PRM) are two of the most well-known sampling-based techniques [Reference Karaman and Frazzoli28].

The PRM algorithm generates the probable path in a short amount of time, which enables it to be used in more reactive situations. However, it lacks smooth navigation since it wastes a lot of time preparing paths that will never be used. [Reference Santiago, De Ocampo, Ubando, Bandala and Dadios29]. Figure 3 shows an example of finding a feasible path using PRM technique. On the other hand, the RRT approaches are widely used to solve single-query path planning problems. However, producing paths on huge dynamic maps remains a challenge for these approaches [Reference Hidalgo-Paniagua, Bandera, Quintanilla and Bandera30]. The RRT*N algorithm is presented in ref. [Reference Mohammed, Romdhane and Jaradat31]. The objective of this modified algorithm is to improve the RRT algorithm’s processing speed. The RRT*N algorithm was successfully expanded to operate in a three-dimensional environment, demonstrating its ability to work with both dynamic and static obstacles. Additionally, in order to solve the problem of high computation cost, various modifications of RRT have been proposed such as RRT-Connect algorithm [Reference Kuffner and LaValle32], RRT* algorithm [Reference Karaman, Walter, Perez, Frazzoli and Teller33], and Bi-RRT algorithm [Reference Gul and Rahiman34].

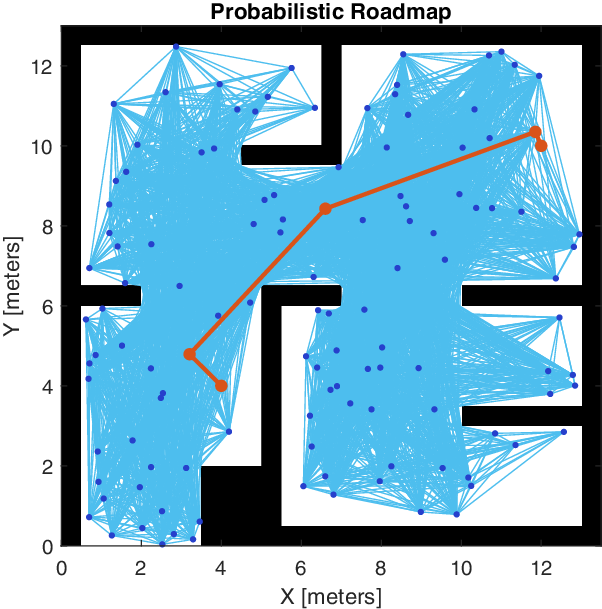
Figure 3.

Finding the obstacle-free path using a PRM planner.

2.1.3. Potential field techniques

The APF algorithm is used to reach the target point and avoid obstacles by modeling the robot as a charge point that is affected by the attractive force provided by the target point and repulsive forces caused by obstacles [Reference Zafar and Mohanta35]. The main advantage of this algorithm is its rapid convergence, as it may get the final path with fewer computations than grid-based and sampling-based approaches [Reference Montiel, Orozco-Rosas and Sepúlveda36]. Figure 4 illustrates an example of a path planning process using potential field method. However, since APF methods are based on optimization techniques, they suffer from the local minima problem. The authors in ref. [Reference Kovács, Szayer, Tajti, Burdelis and Korondi37] proposed a modified APF approach for multi-UAV systems. The suggested approach used a distance factor and jump methodology to address common challenges such as unreachable goals in a 3D multi-UAV environment.

Figure 4.

Finding the obstacle-free path using the potential field method.

2.2. AI-based techniques

AI is a field of computer science and engineering that aims to create machines and systems that can perform tasks that typically require human intelligence, such as visual perception, speech recognition, decision-making, and language understanding. AI is widely used in robotic path planning to enable robots to navigate through complex environments and complete tasks autonomously. AI is achieved through a combination of techniques such as machine learning, computer vision, natural language processing, and knowledge representation. Machine learning, in particular, is a method of teaching computers to learn from data, without being explicitly programed. In other words, learning is the process of automatically modifying an algorithm based on previous experiences without the need for human intervention [Reference Das and Behera38]. AI techniques including machine learning and computer vision are often used to help robots identify and avoid obstacles, as well as to make decisions about which path to take. For example, a robot equipped with AI might use machine learning algorithms to learn from previous experiences and optimize its path planning over time. Additionally, computer vision algorithms can be used to give the robot a sense of its environment, allowing it to detect and avoid obstacles in real time.

A well-known machine learning approach is the artificial neural networks (ANNs). A neural network is a type of machine learning model inspired by the structure and function of the human brain. It is composed of interconnected layers of artificial neurons that process and transmit information, allowing the network to learn and make decisions based on input data. AI is not explicit to mimicking human behavior. For example, the bio-inspired techniques are a set of methodologies that take inspiration from nature to design and develop new technologies and systems. These techniques aim to mimic the behavior, structure, and function of natural systems, such as the human body, animals, and plants, to solve problems in fields such as robotics, computer science, and engineering. In this paper, the AI-based approaches will be subdivided into ANN-based algorithms and the bio-inspired algorithms.

3.1. Leader–follower formation path planning

In the leader–follower approach, a single robot called the leader has full access to the navigation information. Therefore, this leader moves along the predefined trajectory and the followers (the other robot) follow the leader to the desired location. These followers don’t have any information about the path and the final destination [Reference Liu and Bucknall3]. The advantages of the leader–follower approach are that: it is easy to be designed and implemented, can be analyzed using standard control technique, efficient with respect to communication within the system (fewer communication channels), and energy-saving mechanism. The disadvantage of the leader–follower approach is that it is centralized control approach. Thus, it lacks robustness where leader’s fault can penalize the whole formation and feedback from followers to a leader is generally not applied in this approach [Reference Hou, Wang, Zhang and Han77, Reference Peng, Wen, Rahmani and Yu78].

Leader–follower formation has been applied for various robotic systems including USVs, UAVs, UGVs, and manipulators. Table II lists briefly various leader–follower techniques published recently in the literature. For USV systems, the works in refs. [Reference Liu and Bucknall44, Reference Liu and Bucknall45] have used fast marching (FM) as a path planning technique, while in ref. [Reference Kim, Kim, Kim, Shin, Myung and Kim46] Theta* technique has been used. In ref. [Reference Liu and Bucknall44], the FM proposed algorithm has achieved efficient computational time compared to competitive path planning systems. Another potential filed technique was proposed in ref. [Reference Wu, Xue and Wang47]. In ref. [Reference Kim, Kim, Kim, Shin, Myung and Kim46], the authors have utilized Theta* as a path planning technique for the proposed robotic system with the objective of extracting jellyfish from the sea. The authors have proposed a new mechanism named angular rate-constrained path planning system to solve the problem of minimum turning radius which is a known drawback of leader–follower approaches. The jellyfish removal process was successfully tested at Masan Bay in South Korea.

Table II.

Summary of the works done based on the formation type.

“Exp/Sim” column refers to “Experimental/Simulation.”

On the other hand, the works in refs. [Reference Alvarez, Gómez, Garrido and Moreno48, Reference Pan, Zhang, Xia, Xiong and Shao49] have implemented leader–follower UAV systems using potential field methods. UAV systems operate in a 3D environment which requires more processing time due to the huge amount of data to be processed. Therefore, the works in refs. [Reference Alvarez, Gómez, Garrido and Moreno48, Reference Pan, Zhang, Xia, Xiong and Shao49] have adopted potential field techniques which are known for fast execution. In ref. [Reference Alvarez, Gómez, Garrido and Moreno48], the authors have used the fast marching square ( $FM^2$ ) algorithm which is a potential field technique.

Finally, the literature has shown a larger number of papers proposing UGV leader–follower systems compared to USV and UAV systems. Variety path planning techniques were applied, including grid-based [Reference Lázaro, Urcola, Montano and Castellanos50], potential field [Reference Asl, Menhaj and Sajedin51–Reference Kowdiki, Barai and Bhattacharya53], optimization and machine learning [Reference Fan, Yang, Han and Ning54–Reference Yang, Fu, Li, Mao, Guo and Du58], and other techniques [Reference Barfoot, Clark, Rock and D’Eleuterio59–Reference Shapira and Agmon61]. Examining localization tasks in uncertain environments is the objective of the authors in ref. [Reference Lázaro, Urcola, Montano and Castellanos50]. They have used both simulations and experiments in order to check the performance of the proposed technique. On the other hand, the proposed leader–follower techniques in refs. [Reference Asl, Menhaj and Sajedin51–Reference Kowdiki, Barai and Bhattacharya53] have used the potential field method as a path planning technique. In addition to the potential field method, the asexual reproduction optimization method has been used in ref. [Reference Asl, Menhaj and Sajedin51] to enhance the performance of the proposed path planning system, while in ref. [Reference Garrido, Moreno, Gomez and Lima52], Voronoi FM method was proposed as a path planning technique. Another path planning category used in leader–follower UGV systems is the optimization and machine learning methods [Reference Fan, Yang, Han and Ning54–Reference Deng, Ma, Gu, Li, Xu and Wang57]. Q-Learning algorithm was utilized by the authors of [Reference Fan, Yang, Han and Ning54], while the Integer Programming method was used in ref. [Reference Otaki, Koide, Hayakawa, Okoso and Nishi55]. Moreover, the work in ref. [Reference Di Caro and Yousaf56] implemented the Bayesian optimization and Monte Carlo simulations to achieve the path planning tasks. Finally, artificial immune networks were used in ref. [Reference Deng, Ma, Gu, Li, Xu and Wang57] as a path planning technique. The literature has shown other path planning techniques adopted by leader–follower UGV systems such as Kmodynamic randomized motion planner (MP) algorithm [Reference Barfoot, Clark, Rock and D’Eleuterio59], Wifi-based positioning algorithm [Reference Srivastava and Manoj60], and adversarial formation algorithm [Reference Shapira and Agmon61]. Fig. 5 shows a leader–follower experiment. In ref. [Reference Muñoz, López, Quevedo, Barber, Garrido and Moreno62], the fingers of an end effector of a manipulator were treated as stand-alone robots. Therefore, a leader–follower approach based on $FM^2$ was implemented on UR3 robot to achieve grasping application.

Figure 5.

A leader–follower experiment conducted in ref. [Reference Cruz, McClintock, Perteet, Orqueda, Cao and Fierro145].

3.2. Virtual formation path planning

The formation design in the virtual structure approach considers all the N number of robots in the formation as a single rigid structure. Each robot in the formation is provided with the desired trajectories. Then a control scheme works on maintaining the formation by minimizing the error between the virtual structure and the current robot position. The advantage of this approach is that its structure depends on the feedback of the position of each robot. Thus, it is capable of identifying the faulty robots in the formation unlike the leader–follower approach. The disadvantage in this approach is that the obstacle avoidance mechanism is not easy to be implemented [Reference Peng, Wen, Rahmani and Yu78, Reference Soni and Hu79].

Virtual formation path planning has been used in UAV [Reference Chen, Yu, Su and Luo63] and UGV [Reference Tse, Wong, Tang, Duan, Leung and Shi64, Reference Roy, Chowdhury, Maitra and Bhattacharya65] systems. As shown in Table II, a limited number of works have focused on virtual formation techniques. In ref. [Reference Chen, Yu, Su and Luo63], the APF method integrated with the extra control force is proposed. In order to solve the multi-UAV formation path planning issue, the virtual target point and the virtual velocity rigid body were presented based on this approach. The simulation results proved the path planning method’s efficiency and the availability of realistic path following. On the other hand, virtual formation path planning has been used in [Reference Asama2, Reference Liu and Bucknall3] for UGV systems. In ref. [Reference Tse, Wong, Tang, Duan, Leung and Shi64], a graph-based approach for moving cooperative rectangular parcels in a warehouse utilizing unicycle robots is introduced. After the box has been securely fastened and moved, a virtual formation leader is created in the middle of the box, which eliminates the requirement for individual robot path planning. Experimental results have shown that the proposed approach is time-efficient and user-friendly. In ref. [Reference Roy, Chowdhury, Maitra and Bhattacharya65], an arbitrarily shaped control strategy is introduced for avoiding obstacles problem in a tough unknown environment. To avoid narrow paths and corners, a swarm-like architecture is established by creating an arbitrarily shaped virtual region followed by a series of packed circles. Simulation and experimental results have been presented to show the performance of the suggested controllers.

3.3. Behavior-based formation path planning

The behavior-based approach utilizes numerous behaviors for each robot. A final control action takes place based on the weighting of the relative importance of each behavior. The importance of each behavior is identified based on sensory inputs such as obstacle avoidance, goal-seeking, and formation keeping [Reference Soni and Hu79, Reference Issa and Rashid80]. The main advantages of this approach is that it is capable of dealing with multi-task missions. Furthermore, the approach is suitable to be used in an unknown or dynamic environment. The main disadvantages of the approach are related to the difficulty in mathematically expressing the system behavior. Moreover, it is difficult to prove and guarantee the system stability [Reference Liu and Bucknall3].

Behavior-based formation path planning is typically used to fulfill multi-task missions in unknown or dynamic environments. However, the main drawback is that it is difficult to prove and guarantee system stability. Therefore, the behavior-based formation has been mostly implemented within UGV systems [Reference Saez-Pons, Alboul, Penders and Nomdedeu66–Reference Wang, Zeng and Wang68]. Table II summarizes numerous behavior-based techniques that have been recently discussed in the literature. In ref. [Reference Saez-Pons, Alboul, Penders and Nomdedeu66], a group of autonomous assistant mobile robots has been developed to help firefighters in scouring the warehouse in the case of a fire. The robots assist firefighters on the scene by pointing out potential obstructions and preserving communication links. Therefore, robots must be able to fulfill particular behaviors such as remaining in a group. The potential field method is adopted here to control the generated model. On the other hand, the behavior-based technique proposed in ref. [Reference Panov and Yakovlev67] utilized a grid-based method to solve the smart relocation task for UGV systems. The authors used basic Theta* and limited angle algorithms as path planning techniques to produce smooth paths. Finally, a machine learning path planning method based on reinforcement learning is proposed in ref. [Reference Wang, Zeng and Wang68]. As part of the robot path planning process in an unknown environment, reinforcement learning is used to apply the robot’s behavioral decisions and to improve its predictive abilities. A visual simulation platform has been developed in order to enable researchers to test multi-robot motion control algorithms.

3.4. Dynamic formation

The dynamic formation refers to the robotic systems that modify its formation type during operation due to some special needs. The dynamic formation is used to improve the efficiency and reliability of the formation. The dynamic concept signifies the robustness of the formation. Although the dynamic formation is widely used in UGVs, it is also very useful for UAVs and heterogeneous robotic systems. Table II lists a number of dynamic formation techniques that have been recently addressed in the literature. For example, the work in ref. [Reference Alonso-Mora, Baker and Rus69] presented a team of UAVs and mobile manipulators that collaboratively carry an object. The performance of the proposed object transport approach was tested experimentally and through simulations. A sampling-based and nonlinear optimization technique have been applied in 2D and 3D environments to avoid static and moving obstacles. In addition, the authors in ref. [Reference Rizqi, Cahyadi and Adji76] proposed a dynamic formation path planning for UAV systems using the hybrid virtual and behavioral approach schema. The proposed formation control strategy was based on the potential field method to solve the local minima problem.

More works have been focused on UGV dynamic formation systems [Reference Liu, Sun and Zhu70–Reference Petrenko, Tebueva, Pavlov, Antonov and Kochanov75]. In order to achieve the intended formation goal, several path planning techniques have been applied. In ref. [Reference Liu, Sun and Zhu70], RRT algorithm was used as a path planning technique for mobile robots in order to operate autonomously in a cluttered environment. The proposed method has successfully addressed collision avoidance and formation forming problems through simulations and experiments. In addition, some works have applied a path planning technique in a dynamic environment containing static and moving obstacles using simulations and experiments such as A* algorithm [Reference Hao and Agrawal71] and FM square [Reference Gómez, Lumbier, Garrido and Moreno72]. Some dynamic formation systems have adopted meta-heuristic optimization techniques such as PSO [Reference Saska, Spurnỳ and Vonásek73] and artificial immune algorithm [Reference Deng, Ma, Gu and Li74]. Finally, the robotic system proposed in ref. [Reference Petrenko, Tebueva, Pavlov, Antonov and Kochanov75] had successfully implemented a dynamic formation system for a group of modular robots. Modular robots are self-reconfigurable robots with variable morphology. They are made up of distinct modules to form a kinematic structure. Their flexible design enables such robots to adjust their shape to be able to fulfill the task. The challenge is to form the required kinematic structure in real time. The work in ref. [Reference Petrenko, Tebueva, Pavlov, Antonov and Kochanov75] addressed the time problem and aimed to reduce the time required for the formation of the modular robot configuration using analytical geometry methods.

4.1. Centralized decision path planning

Centralized architectures contain a central control agent which can be a stand-alone computer or a robot. The control agent has global information about the environment as well as the information of every robot. This enables the central agent to communicate with all robots. The main advantage of the centralized architecture is that the central control agent has a global view of the world, whereby globally optimal plans can be produced. On the other hand, this architecture is typical for a small number of robots and ineffectual for large teams with a high number of robots. In addition, it is not robust in relation to dynamic environments or failures in communications and other uncertainties. In the case of a malfunction of the central control agent, a new agent must be available, or else the entire team will be disrupted [Reference Hou, Wang, Zhang and Han77].

Based on the aforementioned drawbacks, centralized decision-making has been applied to a limited number of works related to UGV systems [Reference Jose and Pratihar81–Reference Katsev, Yu and LaValle88]. In ref. [Reference Jose and Pratihar81], the task allocation was performed using a GA, and the path planning was performed using the A * algorithm. The authors in ref. [Reference Das, Behera, Das, Tripathy, Panigrahi and Pradhan82] proposed a hybrid algorithm to discover the optimal trajectory of the path for multi-mobile robots in a cluttered environment using improved particle swarm optimization (IPSO) and differentially perturbed velocity (DV) algorithm. According to the experimental and simulation findings, the suggested IPSO-DV outperforms IPSO and DE in terms of optimal trajectory path length and arrival time. However, the works in refs. [Reference Zhang and Xiong83, Reference Matoui, Boussaid, Metoui and Abdelkrim84] proposed a centralized architecture for trajectory planning in a dynamic environment based on the APF technique. An approach that relies on an external path planner for general configuration spaces was proposed in ref. [Reference van Den Berg, Snoeyink, Lin and Manocha85]. The approach decoupled the problem into a set of sub-problems whose solutions can be sequentially executed. The implementation showed that the algorithm is able to solve problems with many robots and a low degree of coupling. Finally, the literature has shown other path planning techniques adopted by centralized decision path planning for UGV systems such as centralized decoupled algorithm [Reference Oh, Park and Lim86], PUSH-AND-SWAP approach [Reference Luna and Bekris87], and two-level partition-based algorithm [Reference Katsev, Yu and LaValle88].

4.2. Decentralized decision path planning

In the decentralized control strategy, each robot makes its own decisions based on its measurements. Thus, several independent controllers are used to control the robots rather than a single centralized control scheme. Consequently, this strategy provides higher robustness than the centralized strategy to be used with large-scale systems. The disadvantages of this strategy are related to the coordination difficulty that might occur [Reference Hou, Wang, Zhang and Han77, Reference Tanner and Kumar141, Reference Yan, Jouandeau and Cherif142].

A large base of decentralized decision path planning research has been focused on UGVs rather than UAVs. For UAV systems, the authors in ref. [Reference Soltero, Schwager and Rus89] proposed a potential field path planning technique that constructs closed pathways for any coverage task such as environmental mapping or surveillance using gradient descent of a Voronoi-based cost function. However, in order to minimize the uncertainty of localization, the authors in ref. [Reference De Carli, Salaris and Giordano143] proposed an optimization path planning algorithm called the online optimization perceptual strategy. On the other hand, different decentralized decision path planning techniques have been applied to UGV systems, including optimization and machine learning [Reference Habib, Alam and Siddique90–Reference Wu92], potential field [Reference Sruthi, Rao and Jisha93–Reference Kloder and Hutchinson98], cellular automaton (CA) method [Reference Ioannidis, Sirakoulis and Andreadis99, Reference Oliveira, Silva, Ferreira, Couceiro, Amaral, Vargas and Martins100], hybrid algorithms [Reference Wee, Kim, An, Lee and Lee101, Reference Lin, Chen, Hsiao and Chuang102], sampling-based [Reference Desaraju and How103], and other techniques [Reference O’smiaıowski and Polkowski104–Reference Liu, Sun, Zhu and Shang106].

Several optimization and machine learning techniques were proposed such as GA [Reference Habib, Alam and Siddique90], convolutional neural network, graph neural network algorithm [Reference Li, Gama, Ribeiro and Prorok91], datagram congestion control protocol, and control barrier and Lyapunov function [Reference Wu92]. Potential field-based techniques were implemented to a number of works with different algorithms such as vector field algorithm [Reference Sruthi, Rao and Jisha93, Reference Kloder and Hutchinson98], switched local potentials [Reference Pathak and Agrawal96], and multi-stencils FM technique [Reference Elsheikh, El-Bardini and Fkirin97] to deal with the path planning task. The main objective in ref. [Reference Matoui, Boussaid, Metoui, Frej and Abdelkrim94] is to ensure the safety of robots while they interact with each other. The UGV formation system is considered as a network with a decentralized architecture. Each robot performs path planning based on a potential field approach. In addition, the work in ref. [Reference Metoui, Boussaid and Abdelkrim95] focused on combining a decentralized architecture with an APF technique to coordinate the motion of the robots. CA method was proposed in refs. [Reference Ioannidis, Sirakoulis and Andreadis99, Reference Oliveira, Silva, Ferreira, Couceiro, Amaral, Vargas and Martins100] to solve the path planning problem in a cooperative robotic team. The proposed method was implemented and tested in a real system using mobile robots.

Furthermore, the work in refs. [Reference Wee, Kim, An, Lee and Lee101, Reference Lin, Chen, Hsiao and Chuang102] utilized decentralized decision path planning using a hybrid technique. In ref. [Reference Wee, Kim, An, Lee and Lee101], a composite local path planning method was proposed using a repulsive function, A * algorithm, and unscented Kalman filter (UKF). The repulsive function in the potential field method was used to avoid collisions between robots and obstacles. On the other hand, the A * algorithm assisted the robots to find the optimal path. Moreover, an error estimator based on UKF was used to ensure that each robot’s path deviation during navigation is kept to a minimum. In addition, another hybrid technique for a UGV swarm system was proposed in ref. [Reference Lin, Chen, Hsiao and Chuang102] using a potential-based GA. The proposed algorithm consists of a global path planner (GPP) and a MP. The GPP searches for a path that the swarm robots should follow from the start to the goal within a Voronoi diagram of the workspace. The MP is developed using a GA algorithm based on artificial potential models. The potential functions are used to keep robots away from obstacles and to keep the robotic swarm within a certain distance from each other. In ref. [Reference Desaraju and How103], an algorithm based on a sampling-based method called decentralized multi-agent RRT algorithm was presented to handle the path planning for a multi-agent system in a complex environment. Finally, there are different path planning techniques adopted by decentralized decision strategy for UGV system such as rough mereological theory [Reference O’smiaıowski and Polkowski104], artificial moments method [Reference Xu, Chen, Zhao and Huang105], and dynamic priority strategy [Reference Liu, Sun, Zhu and Shang106].

4.3. Distributed decision path planning

The distributed control strategy is a modified version of the decentralized control strategy. The only difference is the communication channel between each robot in the formation. This structure overcomes the difficulty in coordination but requires a high amount of communication [Reference Hou, Wang, Zhang and Han77, Reference Tanner, Jadbabaie and Pappas144].

Several robotic systems have adopted the distributed decision path planning strategy ranging from UAVs [Reference Shao, Peng, He and Du107–Reference Zuo, Chu, Ding, Ma and Sun114], UGVs [Reference Matoui, Boussaid and Abdelkrim115–Reference Roy, Maitra and Bhattacharya129], and even heterogeneous (UAV-UGV) systems [Reference Mathew, Smith and Waslander130–Reference Williams, Browne and Carnegie134]. The PSO algorithm was commonly used as a path planning tool for several UAV applications for distributed decision systems such as military and civilian tasks [Reference Shao, Peng, He and Du107], surveillance, inspection, and rescue tasks [Reference Belkadi, Abaunza, Ciarletta, Castillo and Theilliol108], formation for reconnaissance and attack [Reference Shao, Yan, Zhou and Zhu109], and fleet formation control and target tracking [Reference Belkadi, Abaunza, Ciarletta, Castillo and Theilliol110]. Other optimization algorithms were also adopted such as Lin–Kernighan–Helsgaun heuristic algorithm [Reference Cho, Jang and Choi111] and hierarchical control structure [Reference Regula and Lantos112]. In ref. [Reference Huang, Sun, Zhou and Liu113], a grid-based algorithm named multi-robot coverage path planning-multiple land cover types method was proposed to develop a distributed decision path planning system.

On the other hand, the literature has shown that UGV systems have intensively focused on distributed systems [Reference Matoui, Boussaid and Abdelkrim115–Reference Roy, Maitra and Bhattacharya129]. In ref. [Reference Matoui, Boussaid and Abdelkrim115], the authors utilized the APF method to navigate through an environment with static and dynamic obstacles. The authors in ref. [Reference Dang and Horn116] have also used an APF-based technique named the rotational vector field method. Grid-based path planning algorithms were also adopted to create a distributed decision system, including A * algorithm [Reference Bennewitz, Burgard and Thrun117] and chessboard-shaped grid division algorithm [Reference Wang, Li and Yao118]. Graph-based algorithms were also adopted such as Bellman–Ford algorithm [Reference Habibi, Xie, Jellins and McLurkin119] and SplitAndGroup (SaG) algorithm [Reference Yu121]. However, most proposed systems have integrated some optimization and machine learning algorithms as part of the pathfinding process [Reference Chakraborty, Konar, Chakraborty and Jain123–Reference Roy, Maitra and Bhattacharya129]. The most successful optimization technique was the PSO algorithm [Reference Asma and Sadok126–Reference Roy, Maitra and Bhattacharya129]. The reason can be attributed to the fast execution speed of the algorithm, which is highly recommended for distributed systems. In refs. [Reference Asma and Sadok126, Reference Ayari and Bouamama128], a variation of the PSO algorithm named dynamic distributed PSO algorithm was utilized in a distributed system. Other optimization and machine learning techniques were also implemented within other works such as parallel differential evolution algorithms [Reference Chakraborty, Konar, Chakraborty and Jain123] and artificial bee colony algorithm [Reference Contreras-Cruz, Lopez-Perez and Ayala-Ramirez124, Reference Faridi, Sharma, Shukla, Tiwari and Dhar125]. Figure 6 shows a comparison between centralized, decentralized, and distributed robotic systems.

Figure 6.

A comparison between (a) centralized, (b) decentralized, and (c) distributed robotic systems.

4.4. Hybrid decision-making

Hybrid decision-making refers to the robotic systems that apply multiple decision-making approaches at once. Hybrid decision-making has been applied to a limited number of works. Some types of robots that have used hybrid decision systems are satellites [Reference Sarno, D’Errico, Guo and Gill135], UGVs [Reference Liu, Sun and Zhu136–Reference Otte and Correll139], and wireless sensor networks (WSNs) [Reference Aslam, Munir, Bilal, Asad, Ali, Shah and Bilal140]. The work in ref. [Reference Sarno, D’Errico, Guo and Gill135] compared centralized and decentralized approaches to spacecraft formations during reconfiguration. It was developed under the paradigms of cluster autonomy and safe maneuverability. The GA was used as a path planning approach. As a result, while decentralized architecture helps the algorithm to run faster, it also means that inter-satellite communication traffic is increased.

Regarding UGV systems, the authors in ref. [Reference Otte and Correll139] experimentally evaluated a distributed centralized multi-robot path planning algorithm called Dynamic Team Any-Com ISS. They aimed to develop solutions to a multi-robot path planning problem that are guaranteed to be complete, resilient to communication failure, and flexible enough to accommodate different team sizes. In ref. [Reference Liu, Sun and Zhu136], a path planning approach was presented to coordinate UGVs in an environment with static and dynamic obstacles. The pathfinding problem was modeled as a constrained optimization problem, and the motion plan to avoid dynamic obstacles was implemented through an online technique. In ref. [Reference Zagradjanin, Pamucar and Jovanovic137], the D * Lite algorithm was proposed to deal with complex and crowded environments. A new hybrid-based formation robotic system has been proposed in ref. [Reference Aslam, Munir, Bilal, Asad, Ali, Shah and Bilal140]. The new technique named hybrid advance distributed centralized clustering (HADCC) algorithm was proposed as an energy-efficient path planning technique for WSN networks in ref. [Reference Aslam, Munir, Bilal, Asad, Ali, Shah and Bilal140]. The proposed HADCC is based on hybrid cluster head selection algorithm. Moreover, an advance network topology is implemented to execute the proposed model.