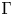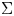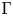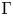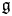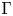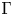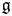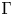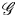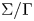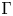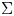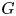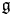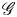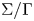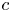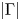1. Introduction
The Wess–Zumino–Witten model is a type of two-dimensional conformal field theory, which associates to an algebraic curve with marked points and integrable highest weight modules of an affine Kac–Moody Lie algebra associated to the points, a finite-dimensional vector space consisting of conformal blocks. The space of conformal blocks has many important properties including propagation of vacua and factorization. Deforming the pointed algebraic curves in a family, we get a sheaf of conformal blocks. This sheaf admits a flat projective connection when the family of pointed curves is a smooth family. The mathematical theory of conformal blocks was first established in a pioneering work by Tsuchiya, Ueno, and Yamada [Reference Tsuchiya, Ueno and YamadaTUY89] where all these properties were obtained. All the above properties are important ingredients in the proof of the celebrated Verlinde formula for the dimension of the space of conformal blocks (cf. [Reference BeauvilleBea96, Reference FaltingsFal94, Reference KumarKum22, Reference SorgerSor96, Reference VerlindeVer88]). This theory has a geometric counterpart in the theory of moduli spaces of principal bundles over algebraic curves and also the moduli of curves and its stable compactification.
In this paper, we study a twisted theory of conformal blocks on Galois covers of algebraic curves. More precisely, we consider an algebraic curve ![]() $\Sigma$ with an action of a finite group
$\Sigma$ with an action of a finite group ![]() $\Gamma$. Moreover, we take a group homomorphism
$\Gamma$. Moreover, we take a group homomorphism ![]() $\phi : \Gamma \to {\rm Aut}(\mathfrak {g})$ of
$\phi : \Gamma \to {\rm Aut}(\mathfrak {g})$ of ![]() $\Gamma$ acting on a simple Lie algebra
$\Gamma$ acting on a simple Lie algebra ![]() $\mathfrak {g}$. Given any smooth point
$\mathfrak {g}$. Given any smooth point ![]() $q\in \Sigma$, we attach an affine Lie algebra
$q\in \Sigma$, we attach an affine Lie algebra ![]() $\hat {L}(\mathfrak {g}, \Gamma _q)$ defined below Lemma 3.2 (in general, a twisted affine Lie algebra), where
$\hat {L}(\mathfrak {g}, \Gamma _q)$ defined below Lemma 3.2 (in general, a twisted affine Lie algebra), where ![]() $\Gamma _q$ is the stabilizer group of
$\Gamma _q$ is the stabilizer group of ![]() $\Gamma$ at
$\Gamma$ at ![]() $q$. The integrable highest weight representations of
$q$. The integrable highest weight representations of ![]() $\hat {L}(\mathfrak {g}, \Gamma _q)$ of level
$\hat {L}(\mathfrak {g}, \Gamma _q)$ of level ![]() $c$ (where
$c$ (where ![]() $c$ is a positive integer) are parametrized by certain finite set
$c$ is a positive integer) are parametrized by certain finite set ![]() $D_{c,q}$ of dominant weights of the reductive Lie algebra
$D_{c,q}$ of dominant weights of the reductive Lie algebra ![]() $\mathfrak {g}^{\Gamma _q}$, i.e. for any
$\mathfrak {g}^{\Gamma _q}$, i.e. for any ![]() $\lambda \in D_{c,q}$ we attach an integrable highest weight representation
$\lambda \in D_{c,q}$ we attach an integrable highest weight representation ![]() $\mathscr {H}(\lambda )$ of
$\mathscr {H}(\lambda )$ of ![]() $\hat {L}(\mathfrak {g}, \Gamma _q)$ of level
$\hat {L}(\mathfrak {g}, \Gamma _q)$ of level ![]() $c$ and conversely (cf. § 2). Given a collection
$c$ and conversely (cf. § 2). Given a collection ![]() $\vec {q}:=(q_1,\ldots, q_s)$ of smooth points in
$\vec {q}:=(q_1,\ldots, q_s)$ of smooth points in ![]() $\Sigma$ such that their
$\Sigma$ such that their ![]() $\Gamma$-orbits are disjoint and a collection of weights
$\Gamma$-orbits are disjoint and a collection of weights ![]() $\vec {\lambda } = (\lambda _1, \ldots, \lambda _s)$ with
$\vec {\lambda } = (\lambda _1, \ldots, \lambda _s)$ with ![]() $\lambda _i\in D_{c,q_i}$, we consider the representation
$\lambda _i\in D_{c,q_i}$, we consider the representation ![]() $\mathscr {H} (\vec {\lambda }):= \mathscr {H}(\lambda _1) \otimes \cdots \otimes \mathscr {H}(\lambda _s)$ (cf. Definition 3.5). Now, define the associated space of twisted covacua (or twisted dual conformal blocks) as follows:
$\mathscr {H} (\vec {\lambda }):= \mathscr {H}(\lambda _1) \otimes \cdots \otimes \mathscr {H}(\lambda _s)$ (cf. Definition 3.5). Now, define the associated space of twisted covacua (or twisted dual conformal blocks) as follows:
 \begin{align*} \mathscr{V}_{\Sigma, \Gamma, \phi}(\vec{q}, \vec{\lambda}):=\frac{\mathscr{H}(\vec{\lambda}) }{\mathfrak{g}[\Sigma\backslash \Gamma\cdot \vec{q} ]^\Gamma \cdot \mathscr{H}(\vec{\lambda}) }, \end{align*}
\begin{align*} \mathscr{V}_{\Sigma, \Gamma, \phi}(\vec{q}, \vec{\lambda}):=\frac{\mathscr{H}(\vec{\lambda}) }{\mathfrak{g}[\Sigma\backslash \Gamma\cdot \vec{q} ]^\Gamma \cdot \mathscr{H}(\vec{\lambda}) }, \end{align*}
where ![]() $\mathfrak {g}[\Sigma \backslash \Gamma \cdot \vec {q} ]^\Gamma$ is the Lie algebra of
$\mathfrak {g}[\Sigma \backslash \Gamma \cdot \vec {q} ]^\Gamma$ is the Lie algebra of ![]() $\Gamma$-equivariant regular functions from
$\Gamma$-equivariant regular functions from ![]() $\Sigma \backslash \Gamma \cdot \vec {q}$ to
$\Sigma \backslash \Gamma \cdot \vec {q}$ to ![]() $\mathfrak {g}$ acting on the
$\mathfrak {g}$ acting on the ![]() $i$th factor
$i$th factor ![]() $\mathscr {H}(\lambda _i)$ of
$\mathscr {H}(\lambda _i)$ of ![]() $\mathscr {H}(\vec {\lambda })$ via its Laurent series expansion at
$\mathscr {H}(\vec {\lambda })$ via its Laurent series expansion at ![]() $q_i$. In this paper, we often work with a more intrinsic but equivalent definition of the space of twisted covacua (see Definition 3.5), where we work with marked
$q_i$. In this paper, we often work with a more intrinsic but equivalent definition of the space of twisted covacua (see Definition 3.5), where we work with marked ![]() $\Gamma$-orbits.
$\Gamma$-orbits.
The following propagation of vacua is the first main result of the paper (cf. Corollary 4.5(a)).
Theorem A Assume that ![]() $\Gamma$ stabilizes a Borel subalgebra of
$\Gamma$ stabilizes a Borel subalgebra of ![]() $\mathfrak {g}$. Let
$\mathfrak {g}$. Let ![]() $q$ be a smooth point of
$q$ be a smooth point of ![]() $\Sigma$ such that
$\Sigma$ such that ![]() $q$ is not
$q$ is not ![]() $\Gamma$-conjugate to any point
$\Gamma$-conjugate to any point ![]() $\vec {q}$. Assume further that
$\vec {q}$. Assume further that ![]() $0\in D_{c, q}$ (cf. Corollary 2.2). Then, we have the following isomorphism of spaces of twisted covacua:
$0\in D_{c, q}$ (cf. Corollary 2.2). Then, we have the following isomorphism of spaces of twisted covacua:
In fact, a stronger version of Propagation Theorem is proved (cf. Theorem 4.3 and Corollary 4.5(b)). Even though we generally follow the argument given in [Reference BeauvilleBea96, Proposition 2.3], in our equivariant setting we need to generalize some important ingredients. For example, the fact that
in the proof of Proposition 2.3 of [Reference BeauvilleBea96], cannot easily be generalized to the twisted case. To prove an analogous result, we need to assume that ![]() $\Gamma$ stabilizes a Borel subalgebra of
$\Gamma$ stabilizes a Borel subalgebra of ![]() $\mathfrak {g}$, and use Lemma 2.5 crucially. It will be interesting to see whether this assumption can be removed.
$\mathfrak {g}$, and use Lemma 2.5 crucially. It will be interesting to see whether this assumption can be removed.
Let ![]() $q$ be a nodal point in
$q$ be a nodal point in ![]() $\Sigma$. Assume that the action of
$\Sigma$. Assume that the action of ![]() $\Gamma$ at
$\Gamma$ at ![]() $q$ is stable (see Definition 5.1) and the stabilizer group
$q$ is stable (see Definition 5.1) and the stabilizer group ![]() $\Gamma _q$ does not exchange the two formal branches around
$\Gamma _q$ does not exchange the two formal branches around ![]() $q$. Let
$q$. Let ![]() $\Sigma '$ be the normalization of
$\Sigma '$ be the normalization of ![]() $\Sigma$ at the points
$\Sigma$ at the points ![]() $\Gamma \cdot q$, and let
$\Gamma \cdot q$, and let ![]() $q',q''$ be the two smooth points in
$q',q''$ be the two smooth points in ![]() $\Sigma '$ over
$\Sigma '$ over ![]() $q$. The following factorization theorem is our second main result (cf. Theorem 5.4).
$q$. The following factorization theorem is our second main result (cf. Theorem 5.4).
Theorem B Assume that ![]() $\Gamma$ stabilizes a Borel subalgebra of
$\Gamma$ stabilizes a Borel subalgebra of ![]() $\mathfrak {g}$. Then, there exists a natural isomorphism:
$\mathfrak {g}$. Then, there exists a natural isomorphism:
where ![]() $\mu ^*$ is the dominant weight of
$\mu ^*$ is the dominant weight of ![]() $\mathfrak {g}^{\Gamma _{q'}}$ such that
$\mathfrak {g}^{\Gamma _{q'}}$ such that ![]() $V(\mu ^*)$ is the dual representation
$V(\mu ^*)$ is the dual representation ![]() $V(\mu )^*$ of
$V(\mu )^*$ of ![]() $\mathfrak {g}^{\Gamma _q}=\mathfrak {g}^{\Gamma _{q'}}=\mathfrak {g}^{\Gamma _{q''}}$.
$\mathfrak {g}^{\Gamma _q}=\mathfrak {g}^{\Gamma _{q'}}=\mathfrak {g}^{\Gamma _{q''}}$.
The formulation of the factorization theorem in the twisted case is a bit more delicate, since the parameter sets ![]() $D_{c, q'}$ and
$D_{c, q'}$ and ![]() $D_{c,q''}$ attached to the points
$D_{c,q''}$ attached to the points ![]() $q', q''$ are different in general; nevertheless they are related by the dual of representations under the assumption that the action of
$q', q''$ are different in general; nevertheless they are related by the dual of representations under the assumption that the action of ![]() $\Gamma$ at the simple node
$\Gamma$ at the simple node ![]() $q$ is stable and the stabilizer group
$q$ is stable and the stabilizer group ![]() $\Gamma _q$ does not exchange the branches (cf. Lemma 5.3). Its proof requires additional care (from that of the untwisted case) at several places. The assumption that
$\Gamma _q$ does not exchange the branches (cf. Lemma 5.3). Its proof requires additional care (from that of the untwisted case) at several places. The assumption that ![]() $\Gamma$ stabilizes a Borel subalgebra of
$\Gamma$ stabilizes a Borel subalgebra of ![]() $\mathfrak {g}$ also appears in this theorem as we use the propagation theorem in its proof.
$\mathfrak {g}$ also appears in this theorem as we use the propagation theorem in its proof.
As proved in Lemma 3.7, the space of twisted covacua is finite dimensional. We sheafify the notion of twisted covacua associated to a family of ![]() $s$-pointed
$s$-pointed ![]() $\Gamma$-curves as in Definition 7.7 and show that given a family
$\Gamma$-curves as in Definition 7.7 and show that given a family ![]() $(\Sigma _T, \vec {q})$ of
$(\Sigma _T, \vec {q})$ of ![]() $s$-pointed
$s$-pointed ![]() $\Gamma$-curves over an irreducible scheme
$\Gamma$-curves over an irreducible scheme ![]() $T$ and weights
$T$ and weights ![]() $\vec {\lambda }=(\lambda _1, \ldots, \lambda _s)$ with
$\vec {\lambda }=(\lambda _1, \ldots, \lambda _s)$ with ![]() $\lambda _i\in D_{c, q_i}$ as above, one can functorially attach a coherent sheaf
$\lambda _i\in D_{c, q_i}$ as above, one can functorially attach a coherent sheaf ![]() $\mathscr {V}_{\Sigma _T, \Gamma, \phi }(\vec {q}, \vec {\lambda })$ of twisted covacua over the base
$\mathscr {V}_{\Sigma _T, \Gamma, \phi }(\vec {q}, \vec {\lambda })$ of twisted covacua over the base ![]() $T$ (cf. Theorem 7.8). As explained below, we generalize the construction to define a coherent sheaf of twisted covacua over the Hurwitz stack
$T$ (cf. Theorem 7.8). As explained below, we generalize the construction to define a coherent sheaf of twisted covacua over the Hurwitz stack ![]() $\overline {\mathscr {H}M}_{g, \Gamma,\eta }$.
$\overline {\mathscr {H}M}_{g, \Gamma,\eta }$.
We prove the following stronger theorem (cf. Theorems 7.10 and 7.12).
Theorem C Assume that the family ![]() $\Sigma _T \to T$ is a smooth family over a smooth base
$\Sigma _T \to T$ is a smooth family over a smooth base ![]() $T$. Then, the sheaf
$T$. Then, the sheaf ![]() $\mathscr {V}_{\Sigma _T, \Gamma, \phi }(\vec {q}, \vec {\lambda })$ is locally free of finite rank over
$\mathscr {V}_{\Sigma _T, \Gamma, \phi }(\vec {q}, \vec {\lambda })$ is locally free of finite rank over ![]() $T$. In fact, there exists a flat projective connection on
$T$. In fact, there exists a flat projective connection on ![]() $\mathscr {V}_{\Sigma _T, \Gamma, \phi }(\vec {q}, \vec {\lambda })$.
$\mathscr {V}_{\Sigma _T, \Gamma, \phi }(\vec {q}, \vec {\lambda })$.
This theorem relies mainly on the Sugawara construction for the twisted affine Kac–Moody algebras. In the untwisted case, this construction is quite well-known (cf. [Reference KacKac90, § 12.8]). In the twisted case, the construction can be found in [Reference Kac and WakimotoKW88, Reference WakimotoWak86], where the formulae are written in terms of the abstract Kac–Moody presentation of ![]() $\hat {L}(\mathfrak {g}, \sigma )$, where
$\hat {L}(\mathfrak {g}, \sigma )$, where ![]() $\sigma$ is a finite-order automorphism of
$\sigma$ is a finite-order automorphism of ![]() $\mathfrak {g}$. For our application, we require the formulae in terms of the affine realization of
$\mathfrak {g}$. For our application, we require the formulae in terms of the affine realization of ![]() $\hat {L}(\mathfrak {g}, \sigma )$ as a central extension of the twisted loop algebra
$\hat {L}(\mathfrak {g}, \sigma )$ as a central extension of the twisted loop algebra ![]() $\mathfrak {g}((t))^{\sigma }$. We present such a formula in (79), (80) in § 6, which might be new (to our knowledge).
$\mathfrak {g}((t))^{\sigma }$. We present such a formula in (79), (80) in § 6, which might be new (to our knowledge).
Let ![]() $\overline {\mathscr {H}M}_{g, \Gamma,\eta }$ be the Hurwitz stack of stable
$\overline {\mathscr {H}M}_{g, \Gamma,\eta }$ be the Hurwitz stack of stable ![]() $s$-pointed
$s$-pointed ![]() $\Gamma$-curves of genus
$\Gamma$-curves of genus ![]() $g$ with marking data
$g$ with marking data ![]() $\eta$ at the marked points such that the set of
$\eta$ at the marked points such that the set of ![]() $\Gamma$-orbits of the marked points contains the full ramification divisor (cf. Definition 8.7). Then,
$\Gamma$-orbits of the marked points contains the full ramification divisor (cf. Definition 8.7). Then, ![]() $\overline {\mathscr {H}M}_{g, \Gamma,\eta }$ is a smooth and proper Deligne–Mumford stack of finite type (cf. Theorem 8.8). We can attach a collection
$\overline {\mathscr {H}M}_{g, \Gamma,\eta }$ is a smooth and proper Deligne–Mumford stack of finite type (cf. Theorem 8.8). We can attach a collection ![]() $\vec {\lambda }$ of dominant weights to the marking data
$\vec {\lambda }$ of dominant weights to the marking data ![]() $\eta$, and associate a coherent sheaf
$\eta$, and associate a coherent sheaf ![]() $\mathscr {V}_{g, \Gamma, \phi }(\eta, \vec {\lambda })$ of twisted covacua over the Hurwitz stack
$\mathscr {V}_{g, \Gamma, \phi }(\eta, \vec {\lambda })$ of twisted covacua over the Hurwitz stack ![]() $\overline {\mathscr {H}M}_{g, \Gamma,\eta }$. The presence of the Hurwitz stack is a new phenomenon in the twisted theory. We prove the following theorem (cf. Theorem 8.9).
$\overline {\mathscr {H}M}_{g, \Gamma,\eta }$. The presence of the Hurwitz stack is a new phenomenon in the twisted theory. We prove the following theorem (cf. Theorem 8.9).
Theorem D Assume that ![]() $\Gamma$ stabilizes a Borel subalgebra of
$\Gamma$ stabilizes a Borel subalgebra of ![]() $\mathfrak {g}$. Then, the sheaf
$\mathfrak {g}$. Then, the sheaf ![]() $\mathscr {V}_{g, \Gamma, \phi }(\eta, \vec {\lambda })$ is locally free over the stack
$\mathscr {V}_{g, \Gamma, \phi }(\eta, \vec {\lambda })$ is locally free over the stack ![]() $\overline {\mathscr {H}M}_{g, \Gamma,\eta }$.
$\overline {\mathscr {H}M}_{g, \Gamma,\eta }$.
Our proof of this theorem follows closely the work of Looijenga [Reference LooijengaLoo13] in the non-equivariant setting; in particular, we use the canonical smoothing deformation of nodal curves (Lemma 8.3) and gluing tensor elements (Lemma 8.5 and the construction before that). The factorization theorem also plays a crucial role in the proof. In the case ![]() $\Gamma$ is cyclic, Theorem A together with the factorization theorem allows us to reduce the computation of the dimension of the space of twisted covacua to the case of cyclic covers of projective line with three marked points (see Remark 8.11(1)).
$\Gamma$ is cyclic, Theorem A together with the factorization theorem allows us to reduce the computation of the dimension of the space of twisted covacua to the case of cyclic covers of projective line with three marked points (see Remark 8.11(1)).
When ![]() $\Gamma$ is of prime order and the marked points are unramified, the space
$\Gamma$ is of prime order and the marked points are unramified, the space ![]() $\mathscr {V}_{\Sigma, \Gamma, \phi }(\vec {q}, \vec {\lambda } )$ was studied earlier by Damiolini [Reference DamioliniDam20], where she proved the results described above in this case under some more constraints. Our work is a vast generalization of her work, since we do not need to put any restrictions on the
$\mathscr {V}_{\Sigma, \Gamma, \phi }(\vec {q}, \vec {\lambda } )$ was studied earlier by Damiolini [Reference DamioliniDam20], where she proved the results described above in this case under some more constraints. Our work is a vast generalization of her work, since we do not need to put any restrictions on the ![]() $\Gamma$-orbits, and the only restriction on
$\Gamma$-orbits, and the only restriction on ![]() $\Gamma$ is that
$\Gamma$ is that ![]() $\Gamma$ stabilizes a Borel subalgebra of
$\Gamma$ stabilizes a Borel subalgebra of ![]() $\mathfrak {g}$ (when
$\mathfrak {g}$ (when ![]() $\Gamma$ is a cyclic group it automatically holds). In particular, when
$\Gamma$ is a cyclic group it automatically holds). In particular, when ![]() $\Gamma$ has non-trivial stabilizers at the marked points, general twisted affine Kac–Moody Lie algebras and their representations occur naturally in this twisted theory of conformal blocks. Damiolini's work dealt with the untwisted affine Lie algebras since only the unramified points are marked in her setting. In our work, Kac's theory of twisted affine Lie algebras associated to finite order automorphisms and related Sugawara operators in the twisted setting are extensively employed. These new features bring considerably more Lie theoretic complexity for the results stated above, which enriches the twisted theory in a most natural way. Notably, the proof of Theorem A (or Theorem 4.3) is highly technical, where we have to introduce the technical condition that the finite group
$\Gamma$ has non-trivial stabilizers at the marked points, general twisted affine Kac–Moody Lie algebras and their representations occur naturally in this twisted theory of conformal blocks. Damiolini's work dealt with the untwisted affine Lie algebras since only the unramified points are marked in her setting. In our work, Kac's theory of twisted affine Lie algebras associated to finite order automorphisms and related Sugawara operators in the twisted setting are extensively employed. These new features bring considerably more Lie theoretic complexity for the results stated above, which enriches the twisted theory in a most natural way. Notably, the proof of Theorem A (or Theorem 4.3) is highly technical, where we have to introduce the technical condition that the finite group ![]() $\Gamma$ stabilizes a Borel subalgebra in
$\Gamma$ stabilizes a Borel subalgebra in ![]() $\mathfrak {g}$. Furthermore, the Hurwitz stack of
$\mathfrak {g}$. Furthermore, the Hurwitz stack of ![]() $\Gamma$-curves with only unramified points marked is not, in general, proper, i.e. such a pointed smooth
$\Gamma$-curves with only unramified points marked is not, in general, proper, i.e. such a pointed smooth ![]() $\Gamma$-curve may degenerate to a
$\Gamma$-curve may degenerate to a ![]() $\Gamma$-curve with non-free nodal
$\Gamma$-curve with non-free nodal ![]() $\Gamma$-orbits. Accordingly, it is desirable to have the factorization theorem (Theorem B) for the
$\Gamma$-orbits. Accordingly, it is desirable to have the factorization theorem (Theorem B) for the ![]() $\Gamma$-curves with general nodal
$\Gamma$-curves with general nodal ![]() $\Gamma$-orbits, which naturally involves the twisted conformal blocks with ramified points marked. Our more general theory of twisted conformal blocks fits perfectly with the compactification of Hurwitz stacks, and marking ramified points is very crucial towards a Verlinde-type formula for twisted conformal blocks of any kind.
$\Gamma$-orbits, which naturally involves the twisted conformal blocks with ramified points marked. Our more general theory of twisted conformal blocks fits perfectly with the compactification of Hurwitz stacks, and marking ramified points is very crucial towards a Verlinde-type formula for twisted conformal blocks of any kind.
There were also some earlier works related to the twisted theory of conformal blocks. For example Frenkel and Szczesny [Reference Frenkel and SzczesnyFS04] studied the twisted modules over Vertex algebras on algebraic curves, and Kuroki and Takebe [Reference Kuroki and TakebeKT97] studied a twisted Wess–Zumino–Witten model on elliptic curves. We also learnt from Mukhopadhyay that he obtained certain results (unpublished) in this direction in the setting of diagram automorphisms.
In the usual (untwisted) theory of conformal blocks, the space of conformal blocks has a beautiful geometric interpretation in that it can be identified with the space of generalized theta functions on the moduli space of parabolic ![]() $G$-bundles over the algebraic curve, where
$G$-bundles over the algebraic curve, where ![]() $G$ is the simply connected simple algebraic group associated to
$G$ is the simply connected simple algebraic group associated to ![]() $\mathfrak {g}$ (cf. Beauville and Laszlo [Reference Beauville and LaszloBL94], Faltings [Reference FaltingsFal94], Kumar, Narasimhan, and Ramanathan [Reference Kumar, Narasimhan and RamanathanKNR94], Laszlo and Sorger [Reference Laszlo and SorgerLS97], and Pauly [Reference PaulyPau96]).
$\mathfrak {g}$ (cf. Beauville and Laszlo [Reference Beauville and LaszloBL94], Faltings [Reference FaltingsFal94], Kumar, Narasimhan, and Ramanathan [Reference Kumar, Narasimhan and RamanathanKNR94], Laszlo and Sorger [Reference Laszlo and SorgerLS97], and Pauly [Reference PaulyPau96]).
From a ![]() $\Gamma$-curve
$\Gamma$-curve ![]() $\Sigma$ and an action of
$\Sigma$ and an action of ![]() $\Gamma$ on
$\Gamma$ on ![]() $G$, the
$G$, the ![]() $\Gamma$-invariants of Weil restriction produces a parahoric Bruhat–Tits group scheme
$\Gamma$-invariants of Weil restriction produces a parahoric Bruhat–Tits group scheme ![]() $\mathscr {G}$ on
$\mathscr {G}$ on ![]() $\bar {\Sigma } =\Sigma /\Gamma$. Recently, the geometry of the moduli stack
$\bar {\Sigma } =\Sigma /\Gamma$. Recently, the geometry of the moduli stack ![]() $\mathscr {B}un_{\mathscr {G}}$ of
$\mathscr {B}un_{\mathscr {G}}$ of ![]() $\mathscr {G}$-torsors over
$\mathscr {G}$-torsors over ![]() $\bar {\Sigma }$ has extensively been studied by Pappas and Rapoport [Reference Pappas and RapoportPR08, Reference Pappas and RapoportPR10], Heinloth [Reference HeinlothHei10], Zhu [Reference ZhuZhu14], and Balaji and Seshadri [Reference Balaji and SeshadriBS15]. A connection between generalized theta functions on
$\bar {\Sigma }$ has extensively been studied by Pappas and Rapoport [Reference Pappas and RapoportPR08, Reference Pappas and RapoportPR10], Heinloth [Reference HeinlothHei10], Zhu [Reference ZhuZhu14], and Balaji and Seshadri [Reference Balaji and SeshadriBS15]. A connection between generalized theta functions on ![]() $\mathscr {B}un_{\mathscr {G}}$ and twisted conformal blocks associated to the Lie algebra of
$\mathscr {B}un_{\mathscr {G}}$ and twisted conformal blocks associated to the Lie algebra of ![]() $\mathscr {G}$ was conjectured by Pappas and Rapoport [Reference Pappas and RapoportPR10]. Along this direction, some results have recently been obtained by Zelaci [Reference ZelaciZel19] when
$\mathscr {G}$ was conjectured by Pappas and Rapoport [Reference Pappas and RapoportPR10]. Along this direction, some results have recently been obtained by Zelaci [Reference ZelaciZel19] when ![]() $\Gamma$ is of order
$\Gamma$ is of order ![]() $2$ acting on
$2$ acting on ![]() $\mathfrak {g}=sl_{n}$ by certain involutions and very special weights.
$\mathfrak {g}=sl_{n}$ by certain involutions and very special weights.
We study this connection in full generality in the setting of ![]() $\Gamma$-curves
$\Gamma$-curves ![]() $\Sigma$. Let
$\Sigma$. Let ![]() $G$ be the simply connected simple algebraic group with the action of
$G$ be the simply connected simple algebraic group with the action of ![]() $\Gamma$ corresponding to
$\Gamma$ corresponding to ![]() $\phi :\Gamma \to {\rm Aut}(\mathfrak {g})$. We assume that
$\phi :\Gamma \to {\rm Aut}(\mathfrak {g})$. We assume that ![]() $\Sigma$ is a smooth irreducible projective curve with a collection
$\Sigma$ is a smooth irreducible projective curve with a collection ![]() $\vec {q}=(q_1,\ldots, q_s)$ of marked points such that their
$\vec {q}=(q_1,\ldots, q_s)$ of marked points such that their ![]() $\Gamma$-orbits are disjoint. To this, we attach a collection
$\Gamma$-orbits are disjoint. To this, we attach a collection ![]() $\vec {\lambda }=(\lambda _1,\ldots,\lambda _s)$ of weights with
$\vec {\lambda }=(\lambda _1,\ldots,\lambda _s)$ of weights with ![]() $\lambda _i\in D_{c,q_i}$ as before. Assume that
$\lambda _i\in D_{c,q_i}$ as before. Assume that ![]() $c$ is divisible by
$c$ is divisible by ![]() $|\Gamma |$. Then, the irreducible representation
$|\Gamma |$. Then, the irreducible representation ![]() $V(\lambda _i)$ of
$V(\lambda _i)$ of ![]() $\mathfrak {g}^{\Gamma _{q_i}}$ of highest weight
$\mathfrak {g}^{\Gamma _{q_i}}$ of highest weight ![]() $\lambda _i$ integrates to an algebraic representation of
$\lambda _i$ integrates to an algebraic representation of ![]() $G^{\Gamma _{q_i}}$ (cf. Proposition 10.9), where
$G^{\Gamma _{q_i}}$ (cf. Proposition 10.9), where ![]() $G^{\Gamma _{q_i}}$ is the fixed subgroup of
$G^{\Gamma _{q_i}}$ is the fixed subgroup of ![]() $\Gamma _{q_i}$ in
$\Gamma _{q_i}$ in ![]() $G$. Let
$G$. Let ![]() $P_i^{q_i}$ be the stabilizer in
$P_i^{q_i}$ be the stabilizer in ![]() $G^{\Gamma _{q_i}}$ of the highest weight line
$G^{\Gamma _{q_i}}$ of the highest weight line ![]() $\ell _{\lambda _i}\subset V(\lambda _i)$. Let
$\ell _{\lambda _i}\subset V(\lambda _i)$. Let ![]() $\mathscr {G}$ be the parahoric Bruhat–Tits group scheme over
$\mathscr {G}$ be the parahoric Bruhat–Tits group scheme over ![]() $\bar {\Sigma }:=\Sigma /\Gamma$ obtained from the
$\bar {\Sigma }:=\Sigma /\Gamma$ obtained from the ![]() $\Gamma$-invariants of the Weil restriction via
$\Gamma$-invariants of the Weil restriction via ![]() $\pi : \Sigma \to \bar {\Sigma }$ from the constant group scheme
$\pi : \Sigma \to \bar {\Sigma }$ from the constant group scheme ![]() $G\times \Sigma \to \Sigma$ over
$G\times \Sigma \to \Sigma$ over ![]() $\Sigma$ (cf. Definition 11.1). One can attach the moduli stack
$\Sigma$ (cf. Definition 11.1). One can attach the moduli stack ![]() $\mathscr {P}arbun_{\mathscr {G}}(\vec {P})$ of quasi-parabolic
$\mathscr {P}arbun_{\mathscr {G}}(\vec {P})$ of quasi-parabolic ![]() $\mathscr {G}$-torsors with parabolic subgroups
$\mathscr {G}$-torsors with parabolic subgroups ![]() $\vec {P}=(P_i^{q_i})$ attached to
$\vec {P}=(P_i^{q_i})$ attached to ![]() $q_i$ for each
$q_i$ for each ![]() $i$ (cf. Definition 11.2). With the assumption that
$i$ (cf. Definition 11.2). With the assumption that ![]() $c$ is divisible by
$c$ is divisible by ![]() $|\Gamma |$, we can define a line bundle
$|\Gamma |$, we can define a line bundle ![]() $\mathfrak {L}(c;\vec {\lambda })$ on
$\mathfrak {L}(c;\vec {\lambda })$ on ![]() $\mathscr {P}arbun_{\mathscr {G}}(\vec {P})$ (cf. Definition 11.6). The following is our last main theorem (cf. Theorem 12.1) confirming a conjecture of Pappas and Rapoport for
$\mathscr {P}arbun_{\mathscr {G}}(\vec {P})$ (cf. Definition 11.6). The following is our last main theorem (cf. Theorem 12.1) confirming a conjecture of Pappas and Rapoport for ![]() $\mathscr {G}$.
$\mathscr {G}$.
Theorem E Assume that ![]() $\Gamma$ stabilizes a Borel subalgebra of
$\Gamma$ stabilizes a Borel subalgebra of ![]() $\mathfrak {g}$ and that
$\mathfrak {g}$ and that ![]() $c$ is divisible by
$c$ is divisible by ![]() $|\Gamma |$. Then, there exists a canonical isomorphism:
$|\Gamma |$. Then, there exists a canonical isomorphism:
where ![]() $H^0( \mathscr {P}arbun_{\mathscr {G}}(\vec {P}), \mathfrak {L}(c, \vec {\lambda }) )$ denotes the space of global sections of the line bundle
$H^0( \mathscr {P}arbun_{\mathscr {G}}(\vec {P}), \mathfrak {L}(c, \vec {\lambda }) )$ denotes the space of global sections of the line bundle ![]() $\mathfrak {L}(c,\vec {\lambda })$ and
$\mathfrak {L}(c,\vec {\lambda })$ and ![]() $\mathscr {V}_{\Sigma, \Gamma, \phi }(\vec {q}, \vec {\lambda } )^{{{\dagger}} }$ denotes the space of twisted conformal blocks, i.e. the dual space of
$\mathscr {V}_{\Sigma, \Gamma, \phi }(\vec {q}, \vec {\lambda } )^{{{\dagger}} }$ denotes the space of twisted conformal blocks, i.e. the dual space of ![]() $\mathscr {V}_{\Sigma, \Gamma, \phi }(\vec {q}, \vec {\lambda })$.
$\mathscr {V}_{\Sigma, \Gamma, \phi }(\vec {q}, \vec {\lambda })$.
One of the main ingredients in the proof of this theorem is the connectedness of the ind-group ![]() ${\rm Mor}_{\Gamma }(\Sigma ^*, G)$ consisting of
${\rm Mor}_{\Gamma }(\Sigma ^*, G)$ consisting of ![]() $\Gamma$-equivariant morphisms from
$\Gamma$-equivariant morphisms from ![]() $\Sigma ^*$ to
$\Sigma ^*$ to ![]() $G$ (cf. Theorem 9.5), where
$G$ (cf. Theorem 9.5), where ![]() $\Sigma ^*$ is a
$\Sigma ^*$ is a ![]() $\Gamma$-stable affine open subset of
$\Gamma$-stable affine open subset of ![]() $\Sigma$. Another important ingredient is the uniformization theorem for the stack of
$\Sigma$. Another important ingredient is the uniformization theorem for the stack of ![]() $\mathscr {G}$-torsors on the parahoric Bruhat–Tits group scheme
$\mathscr {G}$-torsors on the parahoric Bruhat–Tits group scheme ![]() $\mathscr {G}$ due to Heinloth [Reference HeinlothHei10]; in fact, its parabolic analogue (cf. Theorem 11.3). Finally, yet another ingredient is the splitting of the central extension of the twisted loop group
$\mathscr {G}$ due to Heinloth [Reference HeinlothHei10]; in fact, its parabolic analogue (cf. Theorem 11.3). Finally, yet another ingredient is the splitting of the central extension of the twisted loop group ![]() $G(\mathbb {D}_q^\times )^{\Gamma _q}$ over
$G(\mathbb {D}_q^\times )^{\Gamma _q}$ over ![]() $\Xi = {\rm Mor}_{\Gamma }(\Sigma \backslash \Gamma \cdot q, G)$ and the reducedness and the irreducibility of
$\Xi = {\rm Mor}_{\Gamma }(\Sigma \backslash \Gamma \cdot q, G)$ and the reducedness and the irreducibility of ![]() $\Xi$ (cf. Theorem 10.7 and Corollary 11.5), where
$\Xi$ (cf. Theorem 10.7 and Corollary 11.5), where ![]() $q$ is a point in
$q$ is a point in ![]() $\Sigma$ and
$\Sigma$ and ![]() $\mathbb {D}_q^\times$ (respectively,
$\mathbb {D}_q^\times$ (respectively, ![]() $\mathbb {D}_q$) is the punctured formal disc (respectively, formal disc) around
$\mathbb {D}_q$) is the punctured formal disc (respectively, formal disc) around ![]() $q$ in
$q$ in ![]() $\Sigma$.
$\Sigma$.
In spite of the parallels with the classical case, there are some important essential differences in the twisted case. First of all the constant group scheme is to be replaced by the parahoric Bruhat–Tits group scheme ![]() $\mathscr {G}$. Further, the group
$\mathscr {G}$. Further, the group ![]() $\Xi$ could have non-trivial characters resulting in the splitting over
$\Xi$ could have non-trivial characters resulting in the splitting over ![]() $\Xi$ non-unique. (It might be mentioned that in the special case considered by Zelaci [Reference ZelaciZel19, Proposition 5.1] mentioned above,
$\Xi$ non-unique. (It might be mentioned that in the special case considered by Zelaci [Reference ZelaciZel19, Proposition 5.1] mentioned above, ![]() $\Xi$ has only trivial character.) To overcome this difficulty, we need to introduce a canonical splitting over
$\Xi$ has only trivial character.) To overcome this difficulty, we need to introduce a canonical splitting over ![]() $\Xi$ of the central extension of the twisted loop group
$\Xi$ of the central extension of the twisted loop group ![]() $G(\mathbb {D}^\times _q )^{\Gamma _q}$ (cf. Theorem 10.7). We are able to do it when
$G(\mathbb {D}^\times _q )^{\Gamma _q}$ (cf. Theorem 10.7). We are able to do it when ![]() $c$ is divisible by
$c$ is divisible by ![]() $|\Gamma |$ (cf. Remark 12.2(b)).
$|\Gamma |$ (cf. Remark 12.2(b)).
It is interesting to remark that Zhu [Reference ZhuZhu14] proved that for any line bundle on the moduli stack ![]() $\mathscr {B}un_{\mathscr {G}}$ for a ‘reasonably good’ parahoric Bruhat–Tits group scheme
$\mathscr {B}un_{\mathscr {G}}$ for a ‘reasonably good’ parahoric Bruhat–Tits group scheme ![]() $\mathscr {G}$ over a curve
$\mathscr {G}$ over a curve ![]() $\bar {\Sigma }$, the pull-back of the line bundle to the twisted affine Grassmannian at every point of
$\bar {\Sigma }$, the pull-back of the line bundle to the twisted affine Grassmannian at every point of ![]() $\bar {\Sigma }$ is of the same central charge. It matches the way we define the space of covacua, i.e. we attach integrable highest weight representations of twisted affine Lie algebras of the same central charge at every point.
$\bar {\Sigma }$ is of the same central charge. It matches the way we define the space of covacua, i.e. we attach integrable highest weight representations of twisted affine Lie algebras of the same central charge at every point.
Our work was initially motivated by a conjectural connection predicted by Fuchs and Schweigert [Reference Fuchs and SchweigertFS96] between the trace of diagram automorphism on the space of conformal blocks and certain conformal field theory related to twisted affine Lie algebras. A Verlinde-type formula for the trace of diagram automorphism on the space of conformal blocks has been proved recently by the first author [Reference HongHon18, Reference HongHon19], where the formula involves the twisted affine Kac–Moody algebras mysteriously.
Assuming a twisted analogue of Teleman's vanishing theorem of Lie algebra homology, in a recent paper [Reference Hong and KumarHK22], we derive an analogue of the Kac–Walton formula and the Verlinde formula for general ![]() $\Gamma$-curves (with mild restrictions on ramification types, but not requiring that
$\Gamma$-curves (with mild restrictions on ramification types, but not requiring that ![]() $\Gamma$ stabilizes a Borel subalgebra). In particular, if the Lie algebra
$\Gamma$ stabilizes a Borel subalgebra). In particular, if the Lie algebra ![]() $\mathfrak {g}$ is not of type
$\mathfrak {g}$ is not of type ![]() $D_4$, there are no restrictions on ramification types. Using the machinery of crossed modular categories, under the assumption that
$D_4$, there are no restrictions on ramification types. Using the machinery of crossed modular categories, under the assumption that ![]() $\Gamma$ stabilizes a Borel subalgebra of
$\Gamma$ stabilizes a Borel subalgebra of ![]() $\mathfrak {g}$, Deshpande and Mukhopadhyay [Reference Deshpande and MukhopadhyayDM23] deduced a Verlinde-type formula for the dimension of twisted conformal blocks, which is expressed in terms of S-matrices.
$\mathfrak {g}$, Deshpande and Mukhopadhyay [Reference Deshpande and MukhopadhyayDM23] deduced a Verlinde-type formula for the dimension of twisted conformal blocks, which is expressed in terms of S-matrices.
In the following we recall the structure of this paper.
In § 2, we introduce the twisted affine Lie algebra ![]() $\hat {L}(\mathfrak {g},\sigma )$ attached to a finite-order automorphism
$\hat {L}(\mathfrak {g},\sigma )$ attached to a finite-order automorphism ![]() $\sigma$ of
$\sigma$ of ![]() $\mathfrak {g}$ following [Reference KacKac90, Chap. 8]. We prove some preparatory lemmas which is used later in § 4.
$\mathfrak {g}$ following [Reference KacKac90, Chap. 8]. We prove some preparatory lemmas which is used later in § 4.
In § 3, we define the space of twisted covacua attached to a Galois cover of an algebraic curve. We prove that this space is finite dimensional under the assumption given in Definition 3.5.
Section 4 is devoted to proving the propagation theorem.
Section 5 is devoted to proving the factorization theorem.
In § 6, we prove the independence of parameters for integrable highest weight representations of twisted affine Kac–Moody algebras over a base. We also prove that the Sugawara operators acting on the integrable highest weight representations of twisted affine Kac–Moody algebras are independent of the parameters up to scalars. This section is preparatory for § 7.
In § 7, we define the sheaf of twisted covacua for a family ![]() $\Sigma _T$ of
$\Sigma _T$ of ![]() $s$-pointed
$s$-pointed ![]() $\Gamma$-curves. We further show that this sheaf is locally free of finite rank for a smooth family
$\Gamma$-curves. We further show that this sheaf is locally free of finite rank for a smooth family ![]() $\Sigma _T$ over a smooth base
$\Sigma _T$ over a smooth base ![]() $T$. In fact, it admits a flat projective connection.
$T$. In fact, it admits a flat projective connection.
In § 8, we consider stable families of ![]() $s$-pointed
$s$-pointed ![]() $\Gamma$-curves and we show that the sheaf of twisted covacua over the stable compactification of Hurwitz stack is locally free.
$\Gamma$-curves and we show that the sheaf of twisted covacua over the stable compactification of Hurwitz stack is locally free.
In § 9, we prove the connectedness of the ind-group ![]() ${\rm Mor}_{\Gamma }(\Sigma ^*, G)$, following an argument by Drinfeld in the non-equivariant case. In particular, we show that the twisted Grassmannian
${\rm Mor}_{\Gamma }(\Sigma ^*, G)$, following an argument by Drinfeld in the non-equivariant case. In particular, we show that the twisted Grassmannian ![]() $X^q= G(\mathbb {D}^*_q )^{\Gamma _q}/ G(\mathbb {D}_q )^{\Gamma _q}$ is irreducible.
$X^q= G(\mathbb {D}^*_q )^{\Gamma _q}/ G(\mathbb {D}_q )^{\Gamma _q}$ is irreducible.
In § 10, we construct the central extensions of the twisted loop group ![]() $G(\mathbb {D}^*_q )^{\Gamma _q}$ and prove the existence of its canonical splitting over
$G(\mathbb {D}^*_q )^{\Gamma _q}$ and prove the existence of its canonical splitting over ![]() $\Xi :={\rm Mor}_{\Gamma }(\Sigma \setminus \Gamma \cdot q, G)$.
$\Xi :={\rm Mor}_{\Gamma }(\Sigma \setminus \Gamma \cdot q, G)$.
In § 11, we introduce the moduli stack ![]() $\mathscr {P}arbun_{\mathscr {G}}$ of quasi-parabolic
$\mathscr {P}arbun_{\mathscr {G}}$ of quasi-parabolic ![]() $\mathscr {G}$-torsors over
$\mathscr {G}$-torsors over ![]() $\bar {\Sigma }$, where
$\bar {\Sigma }$, where ![]() $\mathscr {G}$ is the parahoric Bruhat–Tits group scheme. We further recall its uniformization theorem essentially due to Heinloth and construct the line bundles over
$\mathscr {G}$ is the parahoric Bruhat–Tits group scheme. We further recall its uniformization theorem essentially due to Heinloth and construct the line bundles over ![]() $\mathscr {P}arbun_{\mathscr {G}}$.
$\mathscr {P}arbun_{\mathscr {G}}$.
In § 12, we establish the identification of twisted conformal blocks and generalized theta functions on the moduli stack ![]() $\mathscr {P}arbun_{\mathscr {G}}$.
$\mathscr {P}arbun_{\mathscr {G}}$.
2. Twisted affine Kac–Moody algebras
This section is devoted to recalling the definition of twisted affine Kac–Moody Lie algebras and their basic properties (we need).
Let ![]() $\sigma$ be an operator of finite order
$\sigma$ be an operator of finite order ![]() $m$ acting on two vector spaces
$m$ acting on two vector spaces ![]() $V$ and
$V$ and ![]() $W$ over
$W$ over ![]() $\mathbb {C}$. Consider the diagonal action of
$\mathbb {C}$. Consider the diagonal action of ![]() $\sigma$ on
$\sigma$ on ![]() $V\otimes W$. We have the following decomposition of the
$V\otimes W$. We have the following decomposition of the ![]() $\sigma$-invariant subspace in
$\sigma$-invariant subspace in ![]() $V\otimes W$,
$V\otimes W$,
where the summation is over ![]() $m$th roots of unity and
$m$th roots of unity and ![]() $V_{\xi }$ (respectively,
$V_{\xi }$ (respectively, ![]() $W_{\xi ^{-1}}$) is the
$W_{\xi ^{-1}}$) is the ![]() $\xi$-eigenspace of
$\xi$-eigenspace of ![]() $V$ (respectively,
$V$ (respectively, ![]() $\xi ^{-1}$-eigenspace of
$\xi ^{-1}$-eigenspace of ![]() $W$). We say
$W$). We say ![]() $v\otimes w$ is pure or more precisely
$v\otimes w$ is pure or more precisely ![]() $\xi$-pure if
$\xi$-pure if ![]() $v\otimes w\in V_{\xi }\otimes W_{\xi ^{-1}}$. Throughout this paper, if we write
$v\otimes w\in V_{\xi }\otimes W_{\xi ^{-1}}$. Throughout this paper, if we write ![]() $v\otimes w\in (V\otimes W)^\sigma$, we mean
$v\otimes w\in (V\otimes W)^\sigma$, we mean ![]() $v\otimes w$ is pure.
$v\otimes w$ is pure.
Let ![]() $\mathfrak {l}$ be a Lie algebra over
$\mathfrak {l}$ be a Lie algebra over ![]() $\mathbb {C}$ and let
$\mathbb {C}$ and let ![]() $A$ be a commutative algebra over
$A$ be a commutative algebra over ![]() $\mathbb {C}$. Let
$\mathbb {C}$. Let ![]() $\sigma$ act on
$\sigma$ act on ![]() $\mathfrak {l}$ (respectively,
$\mathfrak {l}$ (respectively, ![]() $A$) as Lie algebra (respectively, algebra) automorphism of finite orders. For any
$A$) as Lie algebra (respectively, algebra) automorphism of finite orders. For any ![]() $x\otimes a\in \mathfrak {l}\otimes A$, we denote it by
$x\otimes a\in \mathfrak {l}\otimes A$, we denote it by ![]() $x[a]$ for brevity. There is a Lie algebra structure on
$x[a]$ for brevity. There is a Lie algebra structure on ![]() $\mathfrak {l}\otimes A$ with the Lie bracket given by
$\mathfrak {l}\otimes A$ with the Lie bracket given by
Then, ![]() $(\mathfrak {l}\otimes A)^\sigma$ is a Lie subalgebra.
$(\mathfrak {l}\otimes A)^\sigma$ is a Lie subalgebra.
Let ![]() $\mathfrak {g}$ be a simple Lie algebra over
$\mathfrak {g}$ be a simple Lie algebra over ![]() $\mathbb {C}$ with a Cartan subalgebra
$\mathbb {C}$ with a Cartan subalgebra ![]() $\mathfrak {h}$ and let
$\mathfrak {h}$ and let ![]() $\sigma$ be an automorphism of
$\sigma$ be an automorphism of ![]() $\mathfrak {g}$ such that
$\mathfrak {g}$ such that ![]() $\sigma ^m=1$ (
$\sigma ^m=1$ (![]() $\sigma$ is not necessarily of order
$\sigma$ is not necessarily of order ![]() $m$). Let
$m$). Let ![]() $\langle \cdot,\cdot \rangle$ be the invariant (symmetric, non-degenerate) bilinear form on
$\langle \cdot,\cdot \rangle$ be the invariant (symmetric, non-degenerate) bilinear form on ![]() $\mathfrak {g}$ normalized so that the induced form on the dual space
$\mathfrak {g}$ normalized so that the induced form on the dual space ![]() $\mathfrak {h}^*$ satisfies
$\mathfrak {h}^*$ satisfies ![]() $\langle \theta,\theta \rangle =2$ for the highest root
$\langle \theta,\theta \rangle =2$ for the highest root ![]() $\theta$ of
$\theta$ of ![]() $\mathfrak {g}$. The bilinear form
$\mathfrak {g}$. The bilinear form ![]() $\langle \cdot,\cdot \rangle$ is
$\langle \cdot,\cdot \rangle$ is ![]() $\sigma$-invariant since
$\sigma$-invariant since ![]() $\sigma$ is a Lie algebra automorphism of
$\sigma$ is a Lie algebra automorphism of ![]() $\mathfrak {g}$.
$\mathfrak {g}$.
Let ![]() $\mathcal {K} =\mathbb {C}((t)):= \mathbb {C} [[t]][t^{-1}]$ be the field of Laurent power series, and let
$\mathcal {K} =\mathbb {C}((t)):= \mathbb {C} [[t]][t^{-1}]$ be the field of Laurent power series, and let ![]() $\mathcal {O}$ be the ring of formal power series
$\mathcal {O}$ be the ring of formal power series ![]() $\mathbb {C}[[t]]$ with the maximal ideal
$\mathbb {C}[[t]]$ with the maximal ideal ![]() $\mathfrak {m}=t\mathcal {O}$. We fix a primitive
$\mathfrak {m}=t\mathcal {O}$. We fix a primitive ![]() $m$th root of unity
$m$th root of unity ![]() $\epsilon = \epsilon _m= e^{ {2\pi i}/{m}}$ throughout the paper. We define an action of
$\epsilon = \epsilon _m= e^{ {2\pi i}/{m}}$ throughout the paper. We define an action of ![]() $\sigma$ on
$\sigma$ on ![]() $\mathcal {K}$ as field automorphism by setting
$\mathcal {K}$ as field automorphism by setting
It gives rise to an action of ![]() $\sigma$ on the loop algebra
$\sigma$ on the loop algebra ![]() $L(\mathfrak {g}):=\mathfrak {g}\otimes _{\mathbb {C}}\mathcal {K}$. Under this action,
$L(\mathfrak {g}):=\mathfrak {g}\otimes _{\mathbb {C}}\mathcal {K}$. Under this action,
 \[ L(\mathfrak{g})^\sigma = \bigoplus_{j=0}^{m-1}\big(\mathfrak{g}_j\otimes \mathcal{K}_j\big), \]
\[ L(\mathfrak{g})^\sigma = \bigoplus_{j=0}^{m-1}\big(\mathfrak{g}_j\otimes \mathcal{K}_j\big), \]
where
We now define a central extension ![]() $\hat {L}(\mathfrak {g},\sigma ):=L(\mathfrak {g})^\sigma \oplus \mathbb {C}C$ of
$\hat {L}(\mathfrak {g},\sigma ):=L(\mathfrak {g})^\sigma \oplus \mathbb {C}C$ of ![]() $L(\mathfrak {g})^\sigma$ under the bracket
$L(\mathfrak {g})^\sigma$ under the bracket
for ![]() $x[P],x'[P']\in L(\mathfrak {g})^\sigma$,
$x[P],x'[P']\in L(\mathfrak {g})^\sigma$, ![]() $z, z'\in \mathbb {C}$; where
$z, z'\in \mathbb {C}$; where ![]() $\operatorname {\mathrm {Res}}_{t=0}$ denotes the coefficient of
$\operatorname {\mathrm {Res}}_{t=0}$ denotes the coefficient of ![]() $t^{-1}\,dt$. Let
$t^{-1}\,dt$. Let ![]() $\hat {L}(\mathfrak {g},\sigma )^{\geq 0}$ denote the subalgebra
$\hat {L}(\mathfrak {g},\sigma )^{\geq 0}$ denote the subalgebra
 \[ \hat{L}(\mathfrak{g},\sigma)^{\geq 0}:= \bigoplus_{j= 0}^{m-1} \mathfrak{g}_j\otimes \mathcal{O}_j \oplus \mathbb{C} C, \]
\[ \hat{L}(\mathfrak{g},\sigma)^{\geq 0}:= \bigoplus_{j= 0}^{m-1} \mathfrak{g}_j\otimes \mathcal{O}_j \oplus \mathbb{C} C, \]
where ![]() $\mathcal {O}_j=\mathcal {K}_j\cap \mathcal {O}$. We also denote
$\mathcal {O}_j=\mathcal {K}_j\cap \mathcal {O}$. We also denote
 \[ \hat{L}(\mathfrak{g},\sigma)^+:= \bigoplus_{j = 0}^{m-1} \mathfrak{g}_j\otimes \mathfrak{m}_{j} \quad \text{and}\quad \hat{L}(\mathfrak{g},\sigma)^-:= \bigoplus_{j< 0} \mathfrak{g}_j\otimes t^{j} , \]
\[ \hat{L}(\mathfrak{g},\sigma)^+:= \bigoplus_{j = 0}^{m-1} \mathfrak{g}_j\otimes \mathfrak{m}_{j} \quad \text{and}\quad \hat{L}(\mathfrak{g},\sigma)^-:= \bigoplus_{j< 0} \mathfrak{g}_j\otimes t^{j} , \]
where ![]() $\mathfrak {m}_j=\mathfrak {m}\cap \mathcal {O}_j$. Then,
$\mathfrak {m}_j=\mathfrak {m}\cap \mathcal {O}_j$. Then, ![]() $\hat {L}(\mathfrak {g},\sigma )^+$ is an ideal of
$\hat {L}(\mathfrak {g},\sigma )^+$ is an ideal of ![]() $\hat {L}(\mathfrak {g},\sigma )^{\geq 0}$ and the quotient
$\hat {L}(\mathfrak {g},\sigma )^{\geq 0}$ and the quotient ![]() $\hat {L}(\mathfrak {g},\sigma )^{\geq 0}/ \hat {L}(\mathfrak {g},\sigma )^+$ is isomorphic to
$\hat {L}(\mathfrak {g},\sigma )^{\geq 0}/ \hat {L}(\mathfrak {g},\sigma )^+$ is isomorphic to ![]() $\mathfrak {g}_0\oplus \mathbb {C}C$. Note that
$\mathfrak {g}_0\oplus \mathbb {C}C$. Note that ![]() $\mathfrak {g}_0$ is the Lie algebra
$\mathfrak {g}_0$ is the Lie algebra ![]() $\mathfrak {g}^\sigma$ of
$\mathfrak {g}^\sigma$ of ![]() $\sigma$-fixed points in
$\sigma$-fixed points in ![]() $\mathfrak {g}$. As vector spaces we have
$\mathfrak {g}$. As vector spaces we have
By the classification theorem of finite order automorphisms of simple Lie algebras (cf. [Reference KacKac90, Proposition 8.1, Theorems 8.5 and 8.6]), there exists a ‘compatible’ Cartan subalgebra ![]() $\mathfrak {h}$ and a ‘compatible’ Borel subalgebra
$\mathfrak {h}$ and a ‘compatible’ Borel subalgebra ![]() $\mathfrak {b} \supset \mathfrak {h}$ of
$\mathfrak {b} \supset \mathfrak {h}$ of ![]() $\mathfrak {g}$ both stable under the action of
$\mathfrak {g}$ both stable under the action of ![]() $\sigma$ such that
$\sigma$ such that
where ![]() $\tau$ is a diagram automorphism of
$\tau$ is a diagram automorphism of ![]() $\mathfrak {g}$ of order
$\mathfrak {g}$ of order ![]() $r$ preserving
$r$ preserving ![]() $\mathfrak {h}$ and
$\mathfrak {h}$ and ![]() $\mathfrak {b}$, and
$\mathfrak {b}$, and ![]() $\epsilon ^{{\rm ad}\, h}$ is the inner automorphism of
$\epsilon ^{{\rm ad}\, h}$ is the inner automorphism of ![]() $\mathfrak {g}$ such that for any root
$\mathfrak {g}$ such that for any root ![]() $\alpha$ of
$\alpha$ of ![]() $\mathfrak {g}$,
$\mathfrak {g}$, ![]() $\epsilon ^{{\rm ad}\, h}$ acts on the root space
$\epsilon ^{{\rm ad}\, h}$ acts on the root space ![]() $\mathfrak {g}_\alpha$ by the multiplication
$\mathfrak {g}_\alpha$ by the multiplication ![]() $\epsilon ^{\alpha (h)}$, and
$\epsilon ^{\alpha (h)}$, and ![]() $\epsilon ^{{\rm ad}\, h}$ acts on
$\epsilon ^{{\rm ad}\, h}$ acts on ![]() $\mathfrak {h}$ by the identity. We consider
$\mathfrak {h}$ by the identity. We consider ![]() $\tau = \operatorname {\mathrm {Id}}$ also as a diagram automorphism. Here
$\tau = \operatorname {\mathrm {Id}}$ also as a diagram automorphism. Here ![]() $h$ is an element in
$h$ is an element in ![]() $\mathfrak {h}^\tau$. In particular,
$\mathfrak {h}^\tau$. In particular, ![]() $\tau$ and
$\tau$ and ![]() $\epsilon ^{{\rm ad}\,h}$ commute. Moreover,
$\epsilon ^{{\rm ad}\,h}$ commute. Moreover, ![]() $\alpha (h) \in \mathbb {Z}^{\geq 0}$ for any simple root
$\alpha (h) \in \mathbb {Z}^{\geq 0}$ for any simple root ![]() $\alpha$ of
$\alpha$ of ![]() $\mathfrak {g}^\tau$,
$\mathfrak {g}^\tau$, ![]() $\beta (h) \in \mathbb {Z}$ for any simple root
$\beta (h) \in \mathbb {Z}$ for any simple root ![]() $\beta$ of
$\beta$ of ![]() $\mathfrak {g}$ and
$\mathfrak {g}$ and ![]() $\theta _0(h)\leq {m}/{r}$ where
$\theta _0(h)\leq {m}/{r}$ where ![]() $\theta _0\in (\mathfrak {h}^\tau )^*$ denotes the following weight of
$\theta _0\in (\mathfrak {h}^\tau )^*$ denotes the following weight of ![]() $\mathfrak {g}^\tau$:
$\mathfrak {g}^\tau$:
 \[ \theta_0=\begin{cases} \text{highest root of } \mathfrak{g}, & \text{if } r=1\\ \text{highest short root of } \mathfrak{g}^\tau, & \text{if } r>1 \text{ and }(\mathfrak{g}, r)\neq (A_{2n},2)\\ 2\cdot \text{highest short root} \text{ of } \mathfrak{g}^\tau, & \text{if } (\mathfrak{g},r)=(A_{2n},2). \end{cases} \]
\[ \theta_0=\begin{cases} \text{highest root of } \mathfrak{g}, & \text{if } r=1\\ \text{highest short root of } \mathfrak{g}^\tau, & \text{if } r>1 \text{ and }(\mathfrak{g}, r)\neq (A_{2n},2)\\ 2\cdot \text{highest short root} \text{ of } \mathfrak{g}^\tau, & \text{if } (\mathfrak{g},r)=(A_{2n},2). \end{cases} \]
Observe that ![]() $r$ divides
$r$ divides ![]() $m$, and
$m$, and ![]() $r$ can only be
$r$ can only be ![]() $1,2, 3$. Note that
$1,2, 3$. Note that ![]() $\mathfrak {g}^\sigma$ and
$\mathfrak {g}^\sigma$ and ![]() $\mathfrak {g}^{\tau }$ share the common Cartan subalgebra
$\mathfrak {g}^{\tau }$ share the common Cartan subalgebra ![]() $\mathfrak {h}^{\sigma }=\mathfrak {h}^{\tau }$.
$\mathfrak {h}^{\sigma }=\mathfrak {h}^{\tau }$.
Let ![]() $I(\mathfrak {g}^\tau )$ denote the set of vertices of the Dynkin diagram of
$I(\mathfrak {g}^\tau )$ denote the set of vertices of the Dynkin diagram of ![]() $\mathfrak {g}^\tau$. Let
$\mathfrak {g}^\tau$. Let ![]() $\alpha _i$ denote the simple root associated to
$\alpha _i$ denote the simple root associated to ![]() $i\in I(\mathfrak {g}^\tau )$. Let
$i\in I(\mathfrak {g}^\tau )$. Let ![]() $\hat {I}(\mathfrak {g},\sigma )$ denote the set
$\hat {I}(\mathfrak {g},\sigma )$ denote the set ![]() $I(\mathfrak {g}^\tau )\sqcup \{o\}$, where
$I(\mathfrak {g}^\tau )\sqcup \{o\}$, where ![]() $o$ is just a symbol. (Observe that
$o$ is just a symbol. (Observe that ![]() $\tau$ is determined from
$\tau$ is determined from ![]() $\sigma$.) Set
$\sigma$.) Set
 \[ s_i=\begin{cases} \alpha_i(h) &
\text{if } i\in I(\mathfrak{g}^\tau) \\
\dfrac{m}{r}-\theta_0(h) & \text{if } i=o . \end{cases}
\]
\[ s_i=\begin{cases} \alpha_i(h) &
\text{if } i\in I(\mathfrak{g}^\tau) \\
\dfrac{m}{r}-\theta_0(h) & \text{if } i=o . \end{cases}
\]
Then, ![]() $s=\{s_i \,|\, i\in \hat {I}(\mathfrak {g},\sigma ) \}$ is a tuple of non-negative integers. Let
$s=\{s_i \,|\, i\in \hat {I}(\mathfrak {g},\sigma ) \}$ is a tuple of non-negative integers. Let ![]() $\hat {L}(\mathfrak {g}, \tau )$ denote the Lie algebra with the construction similar to
$\hat {L}(\mathfrak {g}, \tau )$ denote the Lie algebra with the construction similar to ![]() $\hat {L}(\mathfrak {g}, \sigma )$ where
$\hat {L}(\mathfrak {g}, \sigma )$ where ![]() $\sigma$ is replaced by
$\sigma$ is replaced by ![]() $\tau$,
$\tau$, ![]() $m$ is replaced by
$m$ is replaced by ![]() $r$ and
$r$ and ![]() $\epsilon$ is replaced by
$\epsilon$ is replaced by ![]() $\epsilon ^{ {m}/{r}}$. There exists an isomorphism of Lie algebras (cf. [Reference KacKac90, Theorem 8.5]):
$\epsilon ^{ {m}/{r}}$. There exists an isomorphism of Lie algebras (cf. [Reference KacKac90, Theorem 8.5]):
given by ![]() $C\mapsto C$ and
$C\mapsto C$ and ![]() $x[t^j]\mapsto x[t^{( {m}/{r})j+k } ]$, for any
$x[t^j]\mapsto x[t^{( {m}/{r})j+k } ]$, for any ![]() $x$ an
$x$ an ![]() $\epsilon ^{ ({m}/{r})j}$-eigenvector of
$\epsilon ^{ ({m}/{r})j}$-eigenvector of ![]() $\tau$, and
$\tau$, and ![]() $x$ also a
$x$ also a ![]() $k$-eigenvector of
$k$-eigenvector of ![]() ${\rm ad}\,h$. We remark that in the case
${\rm ad}\,h$. We remark that in the case ![]() $(\mathfrak {g},r)=(A_{2n},2)$, our labelling for
$(\mathfrak {g},r)=(A_{2n},2)$, our labelling for ![]() $i=o$ is the same as
$i=o$ is the same as ![]() $i=n$ in [Reference KacKac90, Chapter 8]. It is well-known that
$i=n$ in [Reference KacKac90, Chapter 8]. It is well-known that ![]() $\hat {L}(\mathfrak {g},\tau )$ is an affine Lie algebra, more precisely
$\hat {L}(\mathfrak {g},\tau )$ is an affine Lie algebra, more precisely ![]() $\hat {L}(\mathfrak {g}, \tau )$ is untwisted if
$\hat {L}(\mathfrak {g}, \tau )$ is untwisted if ![]() $r=1$ and twisted if
$r=1$ and twisted if ![]() $r>1$.
$r>1$.
By Theorem 8.7 in [Reference KacKac90], there exists a ![]() $sl_2$-triple
$sl_2$-triple ![]() $x_i,y_i,h_i \in \mathfrak {g}$ for each
$x_i,y_i,h_i \in \mathfrak {g}$ for each ![]() $i\in \hat {I}(\mathfrak {g},\sigma )$ where:
$i\in \hat {I}(\mathfrak {g},\sigma )$ where:
•
 $x_i\in (\mathfrak {g}^\tau )_{\alpha _i}$,
$x_i\in (\mathfrak {g}^\tau )_{\alpha _i}$,  $y_i\in (\mathfrak {g}^\tau )_{-\alpha _i}$ when
$y_i\in (\mathfrak {g}^\tau )_{-\alpha _i}$ when  $i\in I(\mathfrak {g}^\tau )$;
$i\in I(\mathfrak {g}^\tau )$;•
 $x_{o}$ (respectively,
$x_{o}$ (respectively,  $y_{o}$) is a
$y_{o}$) is a  $(-\theta _0)$(respectively,
$(-\theta _0)$(respectively,  $\theta _0$)-weight vector with respect to the adjoint action of
$\theta _0$)-weight vector with respect to the adjoint action of  $\mathfrak {h}^\tau$ on
$\mathfrak {h}^\tau$ on  $\mathfrak {g}$, and is also an
$\mathfrak {g}$, and is also an  $\epsilon ^{ {m}/{r}}$ (respectively,
$\epsilon ^{ {m}/{r}}$ (respectively,  $\epsilon ^{- {m}/{r}}$)-eigenvector of
$\epsilon ^{- {m}/{r}}$)-eigenvector of  $\tau$;
$\tau$;•
 $x_i\in \mathfrak {n}$ for
$x_i\in \mathfrak {n}$ for  $i\in I(\mathfrak {g}^\tau )$ and
$i\in I(\mathfrak {g}^\tau )$ and  $x_o \in \mathfrak {n}^-$, where
$x_o \in \mathfrak {n}^-$, where  $\mathfrak {n}$ (respectively,
$\mathfrak {n}$ (respectively,  $\mathfrak {n}^-$) is the nilradical of
$\mathfrak {n}^-$) is the nilradical of  $\mathfrak {b}$ (respectively, the opposite Borel subalgebra
$\mathfrak {b}$ (respectively, the opposite Borel subalgebra  $\mathfrak {b}^-$); similarly,
$\mathfrak {b}^-$); similarly,  $y_i\in \mathfrak {n^-}$ for
$y_i\in \mathfrak {n^-}$ for  $i\in I(\mathfrak {g}^\tau )$ and
$i\in I(\mathfrak {g}^\tau )$ and  $y_o \in \mathfrak {n}$
$y_o \in \mathfrak {n}$
(see explicit construction of ![]() $x_i, y_i, i\in \hat {I}(\mathfrak {g},\sigma )$ in [Reference KacKac90, §§ 7.4, 8.3]), such that
$x_i, y_i, i\in \hat {I}(\mathfrak {g},\sigma )$ in [Reference KacKac90, §§ 7.4, 8.3]), such that
are Chevalley generators of ![]() $\hat {L}(\mathfrak {g},\sigma )$ and
$\hat {L}(\mathfrak {g},\sigma )$ and ![]() $\{x_i, y_i, [x_i, y_i]\}_{i\in \hat {I}(\mathfrak {g},\sigma ): s_i=0}$ are Chevalley generators of
$\{x_i, y_i, [x_i, y_i]\}_{i\in \hat {I}(\mathfrak {g},\sigma ): s_i=0}$ are Chevalley generators of ![]() $[\mathfrak {g}^\sigma, \mathfrak {g}^\sigma ]$. We set
$[\mathfrak {g}^\sigma, \mathfrak {g}^\sigma ]$. We set
Via the isomorphism ![]() $\phi _\sigma$, we have
$\phi _\sigma$, we have
and
Thus, ![]() $\deg \tilde {x}_i=s_i$ and
$\deg \tilde {x}_i=s_i$ and ![]() $\deg \tilde {y}_i=-s_i$. The Lie algebra
$\deg \tilde {y}_i=-s_i$. The Lie algebra ![]() $\hat {L}(\mathfrak {g},\sigma )$ is called an
$\hat {L}(\mathfrak {g},\sigma )$ is called an ![]() $(s,r)$-realization of the associated affine Lie algebra
$(s,r)$-realization of the associated affine Lie algebra ![]() $\hat {L}(\mathfrak {g},\tau )$.
$\hat {L}(\mathfrak {g},\tau )$.
From the above discussion, for any ![]() $i\in \hat {I}(\mathfrak {g}, \sigma )$, we have
$i\in \hat {I}(\mathfrak {g}, \sigma )$, we have
We fix a positive integer ![]() $c$ called the level or central charge. Let
$c$ called the level or central charge. Let ![]() $\operatorname {\mathrm {Rep}}_c$ be the set of isomorphism classes of integrable highest weight (in particular, irreducible)
$\operatorname {\mathrm {Rep}}_c$ be the set of isomorphism classes of integrable highest weight (in particular, irreducible) ![]() $\hat {L}(\mathfrak {g},\sigma )$-modules with central charge
$\hat {L}(\mathfrak {g},\sigma )$-modules with central charge ![]() $c$, where in our realization
$c$, where in our realization ![]() $C$ acts by
$C$ acts by ![]() $c$, the standard Borel subalgebra of
$c$, the standard Borel subalgebra of ![]() $\hat {L}(\mathfrak {g},\sigma )$ is generated by
$\hat {L}(\mathfrak {g},\sigma )$ is generated by ![]() $\{\tilde {x}_i, \tilde {h}_i\}_{i\in \hat {I}(\mathfrak {g}, \sigma )}$ and
$\{\tilde {x}_i, \tilde {h}_i\}_{i\in \hat {I}(\mathfrak {g}, \sigma )}$ and ![]() $\hat {L}(\mathfrak {g},\sigma )^-$ is generated by
$\hat {L}(\mathfrak {g},\sigma )^-$ is generated by
Thus, ![]() $\hat {L}(\mathfrak {g},\sigma )^{\geq 0}$ is a standard parabolic subalgebra of
$\hat {L}(\mathfrak {g},\sigma )^{\geq 0}$ is a standard parabolic subalgebra of ![]() $\hat {L}(\mathfrak {g},\sigma )$. For any
$\hat {L}(\mathfrak {g},\sigma )$. For any ![]() $\mathscr {H}\in \operatorname {\mathrm {Rep}}_c$, let
$\mathscr {H}\in \operatorname {\mathrm {Rep}}_c$, let ![]() $\mathscr {H}^0$ be the subspace of
$\mathscr {H}^0$ be the subspace of ![]() $\mathscr {H}$ annihilated by
$\mathscr {H}$ annihilated by ![]() $\hat {L}(\mathfrak {g},\sigma )^+$. Then,
$\hat {L}(\mathfrak {g},\sigma )^+$. Then, ![]() $\mathscr {H}^0$ is an irreducible finite-dimensional
$\mathscr {H}^0$ is an irreducible finite-dimensional ![]() $\mathfrak {g}^\sigma$-submodule of
$\mathfrak {g}^\sigma$-submodule of ![]() $\mathscr {H}$ with highest weight (say)
$\mathscr {H}$ with highest weight (say) ![]() $\lambda (\mathscr {H})\in (\mathfrak {h}^\sigma )^*=(\mathfrak {h}^\tau )^*$ for the choice of the Borel subalgebra of
$\lambda (\mathscr {H})\in (\mathfrak {h}^\sigma )^*=(\mathfrak {h}^\tau )^*$ for the choice of the Borel subalgebra of ![]() $\mathfrak {g}^\sigma$ generated by
$\mathfrak {g}^\sigma$ generated by ![]() $\mathfrak {h}^\sigma$ and
$\mathfrak {h}^\sigma$ and ![]() $\{x_i: s_i=0\}$. The correspondence
$\{x_i: s_i=0\}$. The correspondence ![]() $\mathscr {H}\mapsto \lambda (\mathscr {H})$ sets up an injective map
$\mathscr {H}\mapsto \lambda (\mathscr {H})$ sets up an injective map ![]() $\operatorname {\mathrm {Rep}}_c \to (\mathfrak {h}^\tau )^*$. Let
$\operatorname {\mathrm {Rep}}_c \to (\mathfrak {h}^\tau )^*$. Let ![]() $D_c$ be its image. For
$D_c$ be its image. For ![]() $\lambda \in D_c$, let
$\lambda \in D_c$, let ![]() $\mathscr {H}(\lambda )$ be the corresponding integrable highest weight
$\mathscr {H}(\lambda )$ be the corresponding integrable highest weight ![]() $\hat {L}(\mathfrak {g},\sigma )$-module with central charge
$\hat {L}(\mathfrak {g},\sigma )$-module with central charge ![]() $c$.
$c$.
For any ![]() $\lambda \in D_c$ and
$\lambda \in D_c$ and ![]() $i\in \hat {I}(\mathfrak {g},\sigma )=I(\mathfrak {g}^\tau )\sqcup \{o\}$, we associate an integer
$i\in \hat {I}(\mathfrak {g},\sigma )=I(\mathfrak {g}^\tau )\sqcup \{o\}$, we associate an integer ![]() $n_{\lambda, i}$ as follows. Set
$n_{\lambda, i}$ as follows. Set
For ![]() $\sigma = \tau$ a diagram automorphism of
$\sigma = \tau$ a diagram automorphism of ![]() $\mathfrak {g}$ (including
$\mathfrak {g}$ (including ![]() $\tau =\operatorname {\mathrm {Id}}$), by definition
$\tau =\operatorname {\mathrm {Id}}$), by definition ![]() $s_i= 0$ for
$s_i= 0$ for ![]() $i\in I(\mathfrak {g}^\tau )$ and
$i\in I(\mathfrak {g}^\tau )$ and ![]() $s_o = 1$.
$s_o = 1$.
For any diagram automorphism ![]() $\tau$ of order
$\tau$ of order ![]() $r$ (including
$r$ (including ![]() $r = 1$), we follow the concrete realization of
$r = 1$), we follow the concrete realization of ![]() $x_i, y_i,\ i\in {I}(\mathfrak {g}^\tau )\sqcup \{o\}$ in [Reference KacKac90, § 8.3]. We emphasize that in the case
$x_i, y_i,\ i\in {I}(\mathfrak {g}^\tau )\sqcup \{o\}$ in [Reference KacKac90, § 8.3]. We emphasize that in the case ![]() $(\mathfrak {g},r)=(A_{2n, 2})$, our labelling ‘
$(\mathfrak {g},r)=(A_{2n, 2})$, our labelling ‘![]() $o$’ corresponds to
$o$’ corresponds to ![]() $i=n$ in [Reference KacKac90, § 8.3]. When
$i=n$ in [Reference KacKac90, § 8.3]. When ![]() $(\mathfrak {g}, r)\not = (A_{2n}, 2)$, we have
$(\mathfrak {g}, r)\not = (A_{2n}, 2)$, we have
 \begin{equation} \langle x_i, y_i\rangle =\begin{cases} 1 & \text{if $\alpha_i$ is a long root for $i\in I(\mathfrak{g}^\tau)$,} \\ r & \text{if $i=o$, or $\alpha_i$ is a short root for $i\in I(\mathfrak{g}^\tau)$,} \end{cases} \end{equation}
\begin{equation} \langle x_i, y_i\rangle =\begin{cases} 1 & \text{if $\alpha_i$ is a long root for $i\in I(\mathfrak{g}^\tau)$,} \\ r & \text{if $i=o$, or $\alpha_i$ is a short root for $i\in I(\mathfrak{g}^\tau)$,} \end{cases} \end{equation}
and when ![]() $(\mathfrak {g}, r)= (A_{2n}, 2)$,
$(\mathfrak {g}, r)= (A_{2n}, 2)$,
 \begin{equation} \langle x_i, y_i\rangle =\begin{cases} 1 & \text{if $i=o$,} \\ 2 & \text{if $\alpha_i$ is a long root for $i\in I(\mathfrak{g}^\tau)$,}\\ 4 & \text{if $\alpha_i$ is a short root for $i\in I(\mathfrak{g}^\tau)$.} \end{cases} \end{equation}
\begin{equation} \langle x_i, y_i\rangle =\begin{cases} 1 & \text{if $i=o$,} \\ 2 & \text{if $\alpha_i$ is a long root for $i\in I(\mathfrak{g}^\tau)$,}\\ 4 & \text{if $\alpha_i$ is a short root for $i\in I(\mathfrak{g}^\tau)$.} \end{cases} \end{equation}Lemma 2.1 The set ![]() $D_c$ can be described as follows:
$D_c$ can be described as follows:
Proof. The lemma follows from the fact that the irreducible highest weight ![]() $\hat {L}(\mathfrak {g},\sigma )$-module
$\hat {L}(\mathfrak {g},\sigma )$-module ![]() $\mathscr {H}(\lambda )$ with highest weight
$\mathscr {H}(\lambda )$ with highest weight ![]() $\lambda$ is integrable if and only if the eigenvalues of
$\lambda$ is integrable if and only if the eigenvalues of ![]() $\tilde {h}_i$,
$\tilde {h}_i$, ![]() $i\in \hat {I}(\mathfrak {g}, \sigma )$ on the highest weight vector in
$i\in \hat {I}(\mathfrak {g}, \sigma )$ on the highest weight vector in ![]() $\mathscr {H}(\lambda )$ are non-negative integers.
$\mathscr {H}(\lambda )$ are non-negative integers.
Define
and let
As an immediate consequence of Lemma 2.1 and the identity (6), we get the following.
Corollary 2.2 For any integer ![]() $c\geq 1$,
$c\geq 1$, ![]() $0\in D_c$ if and only if
$0\in D_c$ if and only if ![]() $m$ divides
$m$ divides ![]() $\bar {s}c$.
$\bar {s}c$.
In particular, ![]() $0\in D_c$ if
$0\in D_c$ if ![]() $m$ divides
$m$ divides ![]() $c$.
$c$.
In addition, for a diagram automorphism ![]() $\sigma = \tau$,
$\sigma = \tau$, ![]() $0\in D_c$ for all
$0\in D_c$ for all ![]() $c$ if
$c$ if ![]() $(\mathfrak {g}, r) \neq (A_{2n}, 2)$. If
$(\mathfrak {g}, r) \neq (A_{2n}, 2)$. If ![]() $(\mathfrak {g}, r) = (A_{2n}, 2)$,
$(\mathfrak {g}, r) = (A_{2n}, 2)$, ![]() $0\in D_c$ if and only if
$0\in D_c$ if and only if ![]() $c$ is even.
$c$ is even.
We recall the following well-known result.
Lemma 2.3 For any automorphism ![]() $\sigma$ and any
$\sigma$ and any ![]() $c \geq 1$,
$c \geq 1$, ![]() $D_c \neq \emptyset$.
$D_c \neq \emptyset$.
Proof. By the isomorphism ![]() $\phi _\sigma$ (as in (4)), it suffices to prove the lemma for the diagram automorphisms
$\phi _\sigma$ (as in (4)), it suffices to prove the lemma for the diagram automorphisms ![]() $\tau$ (including
$\tau$ (including ![]() $\tau = \operatorname {\mathrm {Id}}$). By Corollary 2.2,
$\tau = \operatorname {\mathrm {Id}}$). By Corollary 2.2, ![]() $0\in D_c$ if
$0\in D_c$ if ![]() $(\mathfrak {g}, r) \neq (A_{2n}, 2)$. If
$(\mathfrak {g}, r) \neq (A_{2n}, 2)$. If ![]() $(\mathfrak {g}, r) = (A_{2n}, 2)$, take
$(\mathfrak {g}, r) = (A_{2n}, 2)$, take ![]() $\lambda = \omega _n$: the
$\lambda = \omega _n$: the ![]() $n$th fundamental weight of type
$n$th fundamental weight of type ![]() $B_n$ (following the Bourbaki convention of indexing as in [Reference BourbakiBou05, Planche II]). Then,
$B_n$ (following the Bourbaki convention of indexing as in [Reference BourbakiBou05, Planche II]). Then, ![]() $\omega _n \in D_c$ for odd values of
$\omega _n \in D_c$ for odd values of ![]() $c$ and
$c$ and ![]() $0\in D_c$ for even values of
$0\in D_c$ for even values of ![]() $c$.
$c$.
Let ![]() $V(\lambda )$ be the irreducible
$V(\lambda )$ be the irreducible ![]() $\mathfrak {g}^\sigma$-module with highest weight
$\mathfrak {g}^\sigma$-module with highest weight ![]() $\lambda$ and highest weight vector
$\lambda$ and highest weight vector ![]() $v_+$. Let
$v_+$. Let ![]() $\hat {M}(V(\lambda ),c)$ be the generalized Verma module
$\hat {M}(V(\lambda ),c)$ be the generalized Verma module ![]() $U( \hat {L}(\mathfrak {g},\sigma )) \otimes _{U( \hat {L}(\mathfrak {g},\sigma )^{\geq 0} ) } V(\lambda )$ with highest weight vector
$U( \hat {L}(\mathfrak {g},\sigma )) \otimes _{U( \hat {L}(\mathfrak {g},\sigma )^{\geq 0} ) } V(\lambda )$ with highest weight vector ![]() $v_+ =1\otimes v_+$, where the action of
$v_+ =1\otimes v_+$, where the action of ![]() $\hat {L}(\mathfrak {g},\sigma )^{\geq 0}$ on
$\hat {L}(\mathfrak {g},\sigma )^{\geq 0}$ on ![]() $V(\lambda )$ factors through the projection map
$V(\lambda )$ factors through the projection map ![]() $\hat {L}(\mathfrak {g},\sigma )^{\geq 0}\to \mathfrak {g}^\sigma \oplus \mathbb {C} C$ and the center
$\hat {L}(\mathfrak {g},\sigma )^{\geq 0}\to \mathfrak {g}^\sigma \oplus \mathbb {C} C$ and the center ![]() $C$ acts by
$C$ acts by ![]() $c$. If
$c$. If ![]() $\lambda \in D_c$, then the unique irreducible quotient of
$\lambda \in D_c$, then the unique irreducible quotient of ![]() $\hat {M}(V(\lambda ),c)$ is the integrable representation
$\hat {M}(V(\lambda ),c)$ is the integrable representation ![]() $\mathscr {H}(\lambda )$. Let
$\mathscr {H}(\lambda )$. Let ![]() $K_\lambda$ be the kernel of
$K_\lambda$ be the kernel of ![]() $\hat {M}(V(\lambda ),c)\to \mathscr {H}(\lambda )$. Set
$\hat {M}(V(\lambda ),c)\to \mathscr {H}(\lambda )$. Set
Then, as ![]() $U( \hat {L}(\mathfrak {g},\sigma ) )$-module,
$U( \hat {L}(\mathfrak {g},\sigma ) )$-module, ![]() $K_\lambda$ is generated by
$K_\lambda$ is generated by
Moreover, these elements are highest weight vectors.
Lemma 2.4 Fix ![]() $i\in \hat {I}(\mathfrak {g},\sigma )$. Let
$i\in \hat {I}(\mathfrak {g},\sigma )$. Let ![]() $f\in \mathcal {K}$ be such that
$f\in \mathcal {K}$ be such that ![]() $\sigma (f)=\epsilon ^{- s_i}f$ and
$\sigma (f)=\epsilon ^{- s_i}f$ and ![]() $f\equiv t^{s_i}\mod {t^{{s_i}+1}}$. Put
$f\equiv t^{s_i}\mod {t^{{s_i}+1}}$. Put ![]() $X=x_i[f]$ and
$X=x_i[f]$ and ![]() $Y=\tilde {y}_i=y_i[t^{-s_i}]$. For any
$Y=\tilde {y}_i=y_i[t^{-s_i}]$. For any ![]() $p> n_{\lambda,i}$ and
$p> n_{\lambda,i}$ and ![]() $q> 0$, there exists
$q> 0$, there exists ![]() $\alpha \neq 0$ such that
$\alpha \neq 0$ such that
in the generalized Verma module ![]() $\hat {M}(V(\lambda ),c)$.
$\hat {M}(V(\lambda ),c)$.
Proof. Let ![]() $H:=[X,Y]=h_i[t^{-s_i}f]+ ({\bar {s_i }}/{m}) C$. Then,
$H:=[X,Y]=h_i[t^{-s_i}f]+ ({\bar {s_i }}/{m}) C$. Then, ![]() $[H, Y]=-2y_i[t^{-2s_i}f]$ commutes with
$[H, Y]=-2y_i[t^{-2s_i}f]$ commutes with ![]() $Y$. Note that
$Y$. Note that ![]() $H\cdot v_+= n_{\lambda, i}v_+$. Then, one can check that, for
$H\cdot v_+= n_{\lambda, i}v_+$. Then, one can check that, for ![]() $d\geq 0$,
$d\geq 0$,
and, for ![]() $p\geq 0$,
$p\geq 0$,
By induction on ![]() $q$, the lemma follows.
$q$, the lemma follows.
Lemma 2.5 Let ![]() $\mathfrak {g}$ and
$\mathfrak {g}$ and ![]() $\sigma$ be as above and let
$\sigma$ be as above and let ![]() $\mathfrak {b}$ be a
$\mathfrak {b}$ be a ![]() $\sigma$-stable Borel subalgebra with
$\sigma$-stable Borel subalgebra with ![]() $\sigma$-stable Cartan subalgebra
$\sigma$-stable Cartan subalgebra ![]() $\mathfrak {h}\subset \mathfrak {b}$ of
$\mathfrak {h}\subset \mathfrak {b}$ of ![]() $\mathfrak {g}$. Then, any element
$\mathfrak {g}$. Then, any element ![]() $x$ of
$x$ of ![]() $\big (\mathfrak {n} \otimes \mathcal {K}\big )^\sigma$ acts locally nilpotently on any integrable highest weight
$\big (\mathfrak {n} \otimes \mathcal {K}\big )^\sigma$ acts locally nilpotently on any integrable highest weight ![]() $\hat {L}(\mathfrak {g}, \sigma )$-module
$\hat {L}(\mathfrak {g}, \sigma )$-module ![]() $\mathscr {H}(\lambda )$, where
$\mathscr {H}(\lambda )$, where ![]() $\mathfrak {n}$ is the nilradical of
$\mathfrak {n}$ is the nilradical of ![]() $\mathfrak {b}$.
$\mathfrak {b}$.
Replacing the Borel subalgebra ![]() $\mathfrak {b}$ by the opposite Borel subalgebra
$\mathfrak {b}$ by the opposite Borel subalgebra ![]() $\mathfrak {b}^-$, the lemma holds for any
$\mathfrak {b}^-$, the lemma holds for any ![]() $x\in \big (\mathfrak {n}^- \otimes \mathcal {K}\big )^\sigma$ as well, where
$x\in \big (\mathfrak {n}^- \otimes \mathcal {K}\big )^\sigma$ as well, where ![]() $\mathfrak {n}^-$ is the nilradical of
$\mathfrak {n}^-$ is the nilradical of ![]() $\mathfrak {b}^-$.
$\mathfrak {b}^-$.
Proof. Take a basis ![]() $\{y_\beta \}_\beta$ of
$\{y_\beta \}_\beta$ of ![]() $\mathfrak {n}$ consisting of common eigenvectors under the action of
$\mathfrak {n}$ consisting of common eigenvectors under the action of ![]() $\sigma$ as well as
$\sigma$ as well as ![]() $\mathfrak {h}^\sigma$ (which is possible since the adjoint action of
$\mathfrak {h}^\sigma$ (which is possible since the adjoint action of ![]() $\mathfrak {h}^\sigma$ on
$\mathfrak {h}^\sigma$ on ![]() $\mathfrak {g}$ commutes with the action of
$\mathfrak {g}$ commutes with the action of ![]() $\sigma$) and write
$\sigma$) and write ![]() $x=\sum _\beta y_\beta [P_\beta ]$ for some
$x=\sum _\beta y_\beta [P_\beta ]$ for some ![]() $P_\beta \in \mathcal {K}$. Since
$P_\beta \in \mathcal {K}$. Since ![]() $x$ is
$x$ is ![]() $\sigma$-invariant and each
$\sigma$-invariant and each ![]() $y_\beta$ is an eigenvector, each
$y_\beta$ is an eigenvector, each ![]() $y_\beta [P_\beta ]$ is
$y_\beta [P_\beta ]$ is ![]() $\sigma$-invariant. Let
$\sigma$-invariant. Let ![]() $\hat {L}(\mathfrak {g}, \sigma )_x$ be the Lie subalgebra of
$\hat {L}(\mathfrak {g}, \sigma )_x$ be the Lie subalgebra of ![]() $\hat {L}(\mathfrak {g}, \sigma )$ generated by the elements
$\hat {L}(\mathfrak {g}, \sigma )$ generated by the elements ![]() $\{ y_\beta [P_\beta ]\}_\beta$. Then, since
$\{ y_\beta [P_\beta ]\}_\beta$. Then, since ![]() $\mathfrak {n}$ is nilpotent (in particular,
$\mathfrak {n}$ is nilpotent (in particular, ![]() $N$-bracket of elements from
$N$-bracket of elements from ![]() $\mathfrak {n}$ is zero, for some large enough
$\mathfrak {n}$ is zero, for some large enough ![]() $N$),
$N$), ![]() $\hat {L}(\mathfrak {g}, \sigma )_x$ is a finite-dimensional nilpotent Lie algebra. (Observe that
$\hat {L}(\mathfrak {g}, \sigma )_x$ is a finite-dimensional nilpotent Lie algebra. (Observe that ![]() $\mathfrak {n}$ being nilpotent, for any two elements
$\mathfrak {n}$ being nilpotent, for any two elements ![]() $s_1, s_2 \in \mathfrak {n}, \langle s_1, s_2\rangle =0$.) Take any element
$s_1, s_2 \in \mathfrak {n}, \langle s_1, s_2\rangle =0$.) Take any element ![]() $v\in \mathscr {H}(\lambda )$ and let
$v\in \mathscr {H}(\lambda )$ and let ![]() $\mathscr {H}(x, v)$ be the
$\mathscr {H}(x, v)$ be the ![]() $\hat {L}(\mathfrak {g}, \sigma )_x$-submodule of
$\hat {L}(\mathfrak {g}, \sigma )_x$-submodule of ![]() $\mathscr {H}(\lambda )$ generated by
$\mathscr {H}(\lambda )$ generated by ![]() $v$. Since
$v$. Since ![]() $\sigma$ stabilizes the pair
$\sigma$ stabilizes the pair ![]() $(\mathfrak {b}, \mathfrak {h})$, the centralizer
$(\mathfrak {b}, \mathfrak {h})$, the centralizer ![]() $Z_{\mathfrak {g}}(\mathfrak {h}^\sigma )$ of
$Z_{\mathfrak {g}}(\mathfrak {h}^\sigma )$ of ![]() $\mathfrak {h}^\sigma$ in
$\mathfrak {h}^\sigma$ in ![]() $\mathfrak {g}$ equals
$\mathfrak {g}$ equals ![]() $\mathfrak {h}$. To prove this, we can write
$\mathfrak {h}$. To prove this, we can write ![]() $\sigma = \tau \circ \operatorname {\mathrm {Ad}}(t)$, for a diagram automorphism (possibly identity)
$\sigma = \tau \circ \operatorname {\mathrm {Ad}}(t)$, for a diagram automorphism (possibly identity) ![]() $\tau$ of
$\tau$ of ![]() $\mathfrak {g}$ associated to the pair
$\mathfrak {g}$ associated to the pair ![]() $(\mathfrak {b}, \mathfrak {h})$ and
$(\mathfrak {b}, \mathfrak {h})$ and ![]() $t\in T$ with Lie algebra
$t\in T$ with Lie algebra ![]() $\operatorname {\mathrm {Lie}} T =\mathfrak {h}$. Thus,
$\operatorname {\mathrm {Lie}} T =\mathfrak {h}$. Thus, ![]() $\mathfrak {h}^\sigma =\mathfrak {h}^\tau$ and, hence,
$\mathfrak {h}^\sigma =\mathfrak {h}^\tau$ and, hence, ![]() $Z_{\mathfrak {g}}(\mathfrak {h}^\sigma ) = Z_{\mathfrak {g}}(\mathfrak {h}^\tau ) = \mathfrak {h}$. Since
$Z_{\mathfrak {g}}(\mathfrak {h}^\sigma ) = Z_{\mathfrak {g}}(\mathfrak {h}^\tau ) = \mathfrak {h}$. Since ![]() $y_\beta$ is an eigenvector for the adjoint action of
$y_\beta$ is an eigenvector for the adjoint action of ![]() $\mathfrak {h}^\sigma$ with non-trivial action, any
$\mathfrak {h}^\sigma$ with non-trivial action, any ![]() $y_\beta [P_\beta ]$ can be written as a finite sum of commuting real root vectors for
$y_\beta [P_\beta ]$ can be written as a finite sum of commuting real root vectors for ![]() $\hat {L}(\mathfrak {g}, \sigma )$ and a
$\hat {L}(\mathfrak {g}, \sigma )$ and a ![]() $\sigma$-invariant element of the form
$\sigma$-invariant element of the form ![]() $y_\beta [P^+_\beta ]$ with
$y_\beta [P^+_\beta ]$ with ![]() $P^+_\beta \in t\mathbb {C}[[t]]$ (cf. [Reference KacKac90, Exercises 8.1 and 8.2, § 8.8]). Thus,
$P^+_\beta \in t\mathbb {C}[[t]]$ (cf. [Reference KacKac90, Exercises 8.1 and 8.2, § 8.8]). Thus, ![]() $y_\beta [P_\beta ]$ acts locally nilpotently on
$y_\beta [P_\beta ]$ acts locally nilpotently on ![]() $\mathscr {H}(\lambda )$ (in particular, on
$\mathscr {H}(\lambda )$ (in particular, on ![]() $\mathscr {H}(x, v)$). Now, using [Reference KumarKum02, Lemma 1.3.3(c
$\mathscr {H}(x, v)$). Now, using [Reference KumarKum02, Lemma 1.3.3(c![]() $_2$)], we get that
$_2$)], we get that ![]() $\mathscr {H}(x,v)$ is finite dimensional. Using Lie's theorem, the lemma follows.
$\mathscr {H}(x,v)$ is finite dimensional. Using Lie's theorem, the lemma follows.
3. Twisted analogue of conformal blocks
By a scheme we mean a quasi-compact and separated scheme over ![]() $\mathbb {C}$. By an algebraic curve, we mean a projective, reduced but not necessarily connected curve.
$\mathbb {C}$. By an algebraic curve, we mean a projective, reduced but not necessarily connected curve.
In this section we define the space of twisted covacua attached to a Galois cover of an algebraic curve. We prove that this space is finite dimensional.
For a smooth point ![]() $p$ in an algebraic curve
$p$ in an algebraic curve ![]() $\bar {\Sigma }$ over
$\bar {\Sigma }$ over ![]() $\mathbb {C}$, let
$\mathbb {C}$, let ![]() $\mathcal {K}_p$ denote the quotient field of the completed local ring
$\mathcal {K}_p$ denote the quotient field of the completed local ring ![]() $\hat {\mathscr {O}}_p$ of
$\hat {\mathscr {O}}_p$ of ![]() $\bar {\Sigma }$ at
$\bar {\Sigma }$ at ![]() $p$. We denote by
$p$. We denote by ![]() $\mathbb {D}_p$ (respectively,
$\mathbb {D}_p$ (respectively, ![]() $\mathbb {D}^\times _p$) the formal disc
$\mathbb {D}^\times _p$) the formal disc ![]() ${\rm Spec} \, \hat {\mathscr {O}}_p$ (respectively, the punctured formal disc
${\rm Spec} \, \hat {\mathscr {O}}_p$ (respectively, the punctured formal disc ![]() ${\rm Spec}\, \mathcal {K}_p$).
${\rm Spec}\, \mathcal {K}_p$).
Definition 3.1 A morphism ![]() $\pi : {\Sigma }\to \bar {\Sigma }$ of projective curves is said to be a Galois cover with finite Galois group
$\pi : {\Sigma }\to \bar {\Sigma }$ of projective curves is said to be a Galois cover with finite Galois group ![]() $\Gamma$ (for short
$\Gamma$ (for short ![]() $\Gamma$-cover) if the group
$\Gamma$-cover) if the group ![]() $\Gamma$ acts on
$\Gamma$ acts on ![]() ${\Sigma }$ as algebraic automorphisms and
${\Sigma }$ as algebraic automorphisms and ![]() ${\Sigma }/ \Gamma \simeq \bar {\Sigma }$ and no non-trivial element of
${\Sigma }/ \Gamma \simeq \bar {\Sigma }$ and no non-trivial element of ![]() $\Gamma$ fixes pointwise any irreducible component of
$\Gamma$ fixes pointwise any irreducible component of ![]() $\Sigma$.
$\Sigma$.
For any smooth point ![]() $q\in {\Sigma }$, the stabilizer group
$q\in {\Sigma }$, the stabilizer group ![]() $\Gamma _q$ of
$\Gamma _q$ of ![]() $\Gamma$ at
$\Gamma$ at ![]() $q$ is always cyclic. The order
$q$ is always cyclic. The order ![]() $e_q:=|\Gamma _q|$ is called the ramification index of
$e_q:=|\Gamma _q|$ is called the ramification index of ![]() $q$. Thus,
$q$. Thus, ![]() $q$ is unramified if and only if
$q$ is unramified if and only if ![]() $e_q=1$. Denote
$e_q=1$. Denote ![]() $p=\pi (q)$. We can also write
$p=\pi (q)$. We can also write ![]() $e_p=e_q$, since
$e_p=e_q$, since ![]() $e_{q}=e_{q'}$ for any
$e_{q}=e_{q'}$ for any ![]() $q,q'\in \pi ^{-1}(p)$. We also say that
$q,q'\in \pi ^{-1}(p)$. We also say that ![]() $e_p$ is the ramification index of
$e_p$ is the ramification index of ![]() $p$. Denote by
$p$. Denote by ![]() $d_p$ the cardinality of the fiber
$d_p$ the cardinality of the fiber ![]() $\pi ^{-1}(p)$. Then
$\pi ^{-1}(p)$. Then ![]() $|\Gamma |=e_p\cdot d_p$.
$|\Gamma |=e_p\cdot d_p$.
The action of ![]() $\Gamma _q$ on the tangent space
$\Gamma _q$ on the tangent space ![]() $T_q{\Sigma }$ induces a primitive character
$T_q{\Sigma }$ induces a primitive character ![]() $\chi _q: \Gamma _q\to \mathbb {C}^\times$, i.e.
$\chi _q: \Gamma _q\to \mathbb {C}^\times$, i.e. ![]() $\chi _q(\sigma _q)$ is a primitive
$\chi _q(\sigma _q)$ is a primitive ![]() $e_p$th root of unity for any generator
$e_p$th root of unity for any generator ![]() $\sigma _q$ in
$\sigma _q$ in ![]() $\Gamma _q$. From now on we shall fix
$\Gamma _q$. From now on we shall fix ![]() $\sigma _q\in \Gamma _q$ so that
$\sigma _q\in \Gamma _q$ so that
For any two smooth points ![]() $q, q'\in {\Sigma }$, if
$q, q'\in {\Sigma }$, if ![]() $\pi (q)=\pi (q')$, then
$\pi (q)=\pi (q')$, then
Moreover,
Given a smooth point ![]() $p\in \bar {\Sigma }$ such that
$p\in \bar {\Sigma }$ such that ![]() $\pi ^{-1}(p)$ consists of smooth points in
$\pi ^{-1}(p)$ consists of smooth points in ![]() ${\Sigma }$, let
${\Sigma }$, let ![]() $\pi ^{-1}(\mathbb {D}_p)$ (respectively,
$\pi ^{-1}(\mathbb {D}_p)$ (respectively, ![]() $\pi ^{-1}(\mathbb {D}^\times _p)$) denote the fiber product of
$\pi ^{-1}(\mathbb {D}^\times _p)$) denote the fiber product of ![]() ${\Sigma }$ and
${\Sigma }$ and ![]() $\mathbb {D}_p$ (respectively,
$\mathbb {D}_p$ (respectively, ![]() $\mathbb {D}_p^\times$) over
$\mathbb {D}_p^\times$) over ![]() $\bar {\Sigma }$. Then,
$\bar {\Sigma }$. Then,
where ![]() ${\mathbb {D}}_q$ (respectively,
${\mathbb {D}}_q$ (respectively, ![]() ${\mathbb {D}}_q^\times$) denotes the formal disc (respectively, formal punctured disc) in
${\mathbb {D}}_q^\times$) denotes the formal disc (respectively, formal punctured disc) in ![]() ${\Sigma }$ around
${\Sigma }$ around ![]() $q$.
$q$.
Let the finite group ![]() $\Gamma$ also act on
$\Gamma$ also act on ![]() $\mathfrak {g}$ as Lie algebra automorphisms.
$\mathfrak {g}$ as Lie algebra automorphisms.
Let ![]() $\mathfrak {g}[\pi ^{-1}(\mathbb {D}^\times _p) ]^\Gamma$ be the Lie algebra consisting of
$\mathfrak {g}[\pi ^{-1}(\mathbb {D}^\times _p) ]^\Gamma$ be the Lie algebra consisting of ![]() $\Gamma$-equivariant regular maps from
$\Gamma$-equivariant regular maps from ![]() $\pi ^{-1}(\mathbb {D}^\times _p )$ to
$\pi ^{-1}(\mathbb {D}^\times _p )$ to ![]() $\mathfrak {g}$. There is a natural isomorphism
$\mathfrak {g}$. There is a natural isomorphism ![]() $\mathfrak {g}[\pi ^{-1}(\mathbb {D}^\times _p) ]^\Gamma \simeq ( \mathfrak {g}\otimes \mathbb {C}[\pi ^{-1}(\mathbb {D}^\times _p)])^\Gamma$. Let
$\mathfrak {g}[\pi ^{-1}(\mathbb {D}^\times _p) ]^\Gamma \simeq ( \mathfrak {g}\otimes \mathbb {C}[\pi ^{-1}(\mathbb {D}^\times _p)])^\Gamma$. Let
be the central extension of ![]() $\mathfrak {g}[\pi ^{-1}(\mathbb {D}^\times _p) ]^\Gamma$ defined as follows:
$\mathfrak {g}[\pi ^{-1}(\mathbb {D}^\times _p) ]^\Gamma$ defined as follows:
 \begin{equation} [X, Y] =[X,Y]_0+ \frac{1}{|\Gamma|} \sum_{q\in \pi^{-1}(p) } {\rm Res}_{q} \langle d X, Y \rangle C, \end{equation}
\begin{equation} [X, Y] =[X,Y]_0+ \frac{1}{|\Gamma|} \sum_{q\in \pi^{-1}(p) } {\rm Res}_{q} \langle d X, Y \rangle C, \end{equation}
for any ![]() $X,Y \in \mathfrak {g}[\pi ^{-1}(\mathbb {D}^\times _p) ]^\Gamma$, where
$X,Y \in \mathfrak {g}[\pi ^{-1}(\mathbb {D}^\times _p) ]^\Gamma$, where ![]() $[,]_0$ denotes the point-wise Lie bracket induced from the bracket on
$[,]_0$ denotes the point-wise Lie bracket induced from the bracket on ![]() $\mathfrak {g}$. We set the subalgebra
$\mathfrak {g}$. We set the subalgebra
and
obtained by the restriction map ![]() $\mathbb {C}[\pi ^{-1}(\mathbb {D}_p)] \to \mathbb {C}[\pi ^{-1}(p)]$, where
$\mathbb {C}[\pi ^{-1}(\mathbb {D}_p)] \to \mathbb {C}[\pi ^{-1}(p)]$, where ![]() $\mathfrak {g}[\pi ^{-1}(p) ]^\Gamma$ denotes the Lie algebra consisting of
$\mathfrak {g}[\pi ^{-1}(p) ]^\Gamma$ denotes the Lie algebra consisting of ![]() $\Gamma$-equivariant maps
$\Gamma$-equivariant maps ![]() $x:\pi ^{-1}(p)\to \mathfrak {g}$. Let
$x:\pi ^{-1}(p)\to \mathfrak {g}$. Let ![]() $\mathfrak {g}_p$ denote
$\mathfrak {g}_p$ denote ![]() $\mathfrak {g}[ \pi ^{-1}(p) ]^\Gamma$. The following lemma is obvious.
$\mathfrak {g}[ \pi ^{-1}(p) ]^\Gamma$. The following lemma is obvious.
Lemma 3.2 The evaluation map ![]() ${\rm ev}_q: \mathfrak {g}_p\to \mathfrak {g}^{\Gamma _q}$ given by
${\rm ev}_q: \mathfrak {g}_p\to \mathfrak {g}^{\Gamma _q}$ given by
for any ![]() $x\in \mathfrak {g}_p$ and
$x\in \mathfrak {g}_p$ and ![]() $q\in \pi ^{-1}(p)$ is an isomorphism of Lie algebras.
$q\in \pi ^{-1}(p)$ is an isomorphism of Lie algebras.
Let ![]() $\sigma _q$ be the generator of
$\sigma _q$ be the generator of ![]() $\Gamma _q$ such that
$\Gamma _q$ such that ![]() $\chi _q(\sigma _q) = e^{ {2\pi i}/{e_p}}$. Let
$\chi _q(\sigma _q) = e^{ {2\pi i}/{e_p}}$. Let ![]() $\hat {L}(\mathfrak {g},\sigma _q)$ denote the affine Lie algebra associated to
$\hat {L}(\mathfrak {g},\sigma _q)$ denote the affine Lie algebra associated to ![]() $\mathfrak {g}$ and
$\mathfrak {g}$ and ![]() $\sigma _q$ as defined in § 2. We denote this algebra by
$\sigma _q$ as defined in § 2. We denote this algebra by ![]() $\hat {L}(\mathfrak {g}, \Gamma _q,\chi _q)$ or
$\hat {L}(\mathfrak {g}, \Gamma _q,\chi _q)$ or ![]() $\hat {L}(\mathfrak {g}, \Gamma _q )$ in short.
$\hat {L}(\mathfrak {g}, \Gamma _q )$ in short.
Lemma 3.3 The restriction map ![]() ${\rm res}_q: \hat {\mathfrak {g}}_p\to \hat {L}(\mathfrak {g}, \Gamma _q)$ given by
${\rm res}_q: \hat {\mathfrak {g}}_p\to \hat {L}(\mathfrak {g}, \Gamma _q)$ given by
is an isomorphism of Lie algebras, where ![]() $X\in \mathfrak {g}[\pi ^{-1}(\mathbb {D}^\times _p ) ]^\Gamma$ and
$X\in \mathfrak {g}[\pi ^{-1}(\mathbb {D}^\times _p ) ]^\Gamma$ and ![]() $X_q$ is the restriction of
$X_q$ is the restriction of ![]() $X$ to
$X$ to ![]() $\mathbb {D}_q^\times$. Moreover,
$\mathbb {D}_q^\times$. Moreover,
Proof. For any ![]() $X, Y\in \mathfrak {g}[\pi ^{-1}( \mathbb {D}^\times _p ) ]^\Gamma$, the restriction of
$X, Y\in \mathfrak {g}[\pi ^{-1}( \mathbb {D}^\times _p ) ]^\Gamma$, the restriction of ![]() $[X,Y]_0$ to
$[X,Y]_0$ to ![]() $\mathbb {D}_q^\times$ is equal to
$\mathbb {D}_q^\times$ is equal to ![]() $[X_q,Y_q]_0$. Note that for any
$[X_q,Y_q]_0$. Note that for any ![]() $\gamma \in \Gamma$ and
$\gamma \in \Gamma$ and ![]() $x,y\in \mathfrak {g}$, we have
$x,y\in \mathfrak {g}$, we have ![]() $\langle \gamma (x), \gamma (y) \rangle = \langle x,y \rangle$, which follows from the Killing form realization of
$\langle \gamma (x), \gamma (y) \rangle = \langle x,y \rangle$, which follows from the Killing form realization of ![]() $\langle,\rangle$ on
$\langle,\rangle$ on ![]() $\mathfrak {g}$. Since
$\mathfrak {g}$. Since ![]() $X, Y$ are
$X, Y$ are ![]() $\Gamma$-equivariant, for any
$\Gamma$-equivariant, for any ![]() $q, q'\in \pi ^{-1}(p)$ we have
$q, q'\in \pi ^{-1}(p)$ we have
It is now easy to see that ![]() ${\rm res}_q: \hat {\mathfrak {g}}_p\to \hat {L}(\mathfrak {g}, \Gamma _q)$ is an isomorphism of Lie algebras, and
${\rm res}_q: \hat {\mathfrak {g}}_p\to \hat {L}(\mathfrak {g}, \Gamma _q)$ is an isomorphism of Lie algebras, and
By the above lemma, we have a faithful functor ![]() ${\rm Rep}_c(\hat {\mathfrak {g}}_p)\to {\rm Rep}(\mathfrak {g}_p)$ from the category of integrable highest weight representations of
${\rm Rep}_c(\hat {\mathfrak {g}}_p)\to {\rm Rep}(\mathfrak {g}_p)$ from the category of integrable highest weight representations of ![]() $\hat {\mathfrak {g}}_p$ of level
$\hat {\mathfrak {g}}_p$ of level ![]() $c$ to the category of finite-dimensional representations of
$c$ to the category of finite-dimensional representations of ![]() $\mathfrak {g}_p$. We denote by
$\mathfrak {g}_p$. We denote by ![]() $D_{c,p}$ the parameter set of (irreducible) integrable highest weight representations of
$D_{c,p}$ the parameter set of (irreducible) integrable highest weight representations of ![]() $\hat {\mathfrak {g}}_p$ of level
$\hat {\mathfrak {g}}_p$ of level ![]() $c$ obtained as the subset of the set of dominant integral weights of
$c$ obtained as the subset of the set of dominant integral weights of ![]() $\mathfrak {g}_p$ under the above faithful functor. Let
$\mathfrak {g}_p$ under the above faithful functor. Let ![]() $D_{c,q}$ denote the parameter set of (irreducible) integrable highest weight representations of
$D_{c,q}$ denote the parameter set of (irreducible) integrable highest weight representations of ![]() $\hat {L}(\mathfrak {g}, \Gamma _q)$ as in § 2. Then, we can identify
$\hat {L}(\mathfrak {g}, \Gamma _q)$ as in § 2. Then, we can identify ![]() $D_{c,p}$ and
$D_{c,p}$ and ![]() $D_{c,q}$ via the restriction isomorphism
$D_{c,q}$ via the restriction isomorphism ![]() ${\rm res}_q: \hat {\mathfrak {g}}_p\to \hat {L}(\mathfrak {g}, \Gamma _q)$ as in Lemma 3.3.
${\rm res}_q: \hat {\mathfrak {g}}_p\to \hat {L}(\mathfrak {g}, \Gamma _q)$ as in Lemma 3.3.
Definition 3.4 For any ![]() $s\geq 1$, by an
$s\geq 1$, by an ![]() $s$-pointed curve, we mean the pair
$s$-pointed curve, we mean the pair ![]() $(\bar {\Sigma }, \vec {p}=(p_1, \ldots, p_s))$ consisting of distinct and smooth points
$(\bar {\Sigma }, \vec {p}=(p_1, \ldots, p_s))$ consisting of distinct and smooth points ![]() $\{p_1, \ldots, p_s\}$ of
$\{p_1, \ldots, p_s\}$ of ![]() $\bar {\Sigma }$, such that the following condition is satisfied.
$\bar {\Sigma }$, such that the following condition is satisfied.
![]() $(*)$ Each irreducible component of
$(*)$ Each irreducible component of ![]() $\bar {\Sigma }$ contains at least one point
$\bar {\Sigma }$ contains at least one point ![]() $p_i$.
$p_i$.
Similarly, by an ![]() $s$-pointed
$s$-pointed ![]() $\Gamma$-curve, we mean the pair
$\Gamma$-curve, we mean the pair ![]() $(\Sigma, \vec {q}=(q_1, \ldots, q_s))$ consisting of smooth points
$(\Sigma, \vec {q}=(q_1, \ldots, q_s))$ consisting of smooth points ![]() $\{q_1, \ldots, q_s\}$ of
$\{q_1, \ldots, q_s\}$ of ![]() $\Sigma$ such that
$\Sigma$ such that ![]() $(\bar {\Sigma }, \pi (\vec {q})=(\pi (q_1), \ldots, \pi (q_s)))$ is a
$(\bar {\Sigma }, \pi (\vec {q})=(\pi (q_1), \ldots, \pi (q_s)))$ is a ![]() $s$-pointed curve.
$s$-pointed curve.
From now on we fix an ![]() $s$-pointed curve
$s$-pointed curve ![]() $(\bar {\Sigma }, \vec {p})$ (for any
$(\bar {\Sigma }, \vec {p})$ (for any ![]() $s\geq 1$), where
$s\geq 1$), where ![]() $\vec {p}=(p_1, \ldots, p_s)$, and a Galois cover
$\vec {p}=(p_1, \ldots, p_s)$, and a Galois cover ![]() $\pi : {\Sigma } \to \bar {\Sigma }$ with the finite Galois group
$\pi : {\Sigma } \to \bar {\Sigma }$ with the finite Galois group ![]() $\Gamma$ such that the fiber
$\Gamma$ such that the fiber ![]() $\pi ^{-1}(p_i)$ consists of smooth points for any
$\pi ^{-1}(p_i)$ consists of smooth points for any ![]() $i=1,2,\ldots, s$. We also fix a simple Lie algebra
$i=1,2,\ldots, s$. We also fix a simple Lie algebra ![]() $\mathfrak {g}$ and a group homomorphism
$\mathfrak {g}$ and a group homomorphism ![]() $\phi : \Gamma \to {\rm Aut}(\mathfrak {g})$, where
$\phi : \Gamma \to {\rm Aut}(\mathfrak {g})$, where ![]() ${\rm Aut}(\mathfrak {g})$ is the group of automorphisms of
${\rm Aut}(\mathfrak {g})$ is the group of automorphisms of ![]() $\mathfrak {g}$.
$\mathfrak {g}$.
We now fix an ![]() $s$-tuple
$s$-tuple ![]() $\vec {\lambda }=(\lambda _{1},\ldots,\lambda _{s})$ of weights with
$\vec {\lambda }=(\lambda _{1},\ldots,\lambda _{s})$ of weights with ![]() $\lambda _{i}\in D_{c, p_i}$ ‘attached’ to the point
$\lambda _{i}\in D_{c, p_i}$ ‘attached’ to the point ![]() $p_i$. To this data, there is associated the space of (twisted) vacua
$p_i$. To this data, there is associated the space of (twisted) vacua ![]() $\mathscr {V}_{{\Sigma },\Gamma, \phi }(\vec {p},\vec {\lambda })^{{{\dagger}} }$ (or the space of (twisted) conformal blocks) and its dual space
$\mathscr {V}_{{\Sigma },\Gamma, \phi }(\vec {p},\vec {\lambda })^{{{\dagger}} }$ (or the space of (twisted) conformal blocks) and its dual space ![]() $\mathscr {V}_{{\Sigma },\Gamma,\phi }(\vec {p},\vec {\lambda })$ called the space of (twisted) covacua (or the space of (twisted) dual conformal blocks) defined as follows.
$\mathscr {V}_{{\Sigma },\Gamma,\phi }(\vec {p},\vec {\lambda })$ called the space of (twisted) covacua (or the space of (twisted) dual conformal blocks) defined as follows.
Definition 3.5 Let ![]() $\mathfrak {g}[{\Sigma }\backslash \pi ^{-1}( \vec {p}) ]^\Gamma$ denote the space of
$\mathfrak {g}[{\Sigma }\backslash \pi ^{-1}( \vec {p}) ]^\Gamma$ denote the space of ![]() $\Gamma$-equivariant regular maps
$\Gamma$-equivariant regular maps ![]() $f:{\Sigma }\backslash \pi ^{-1}(\vec {p}) \to \mathfrak {g}$. Then,
$f:{\Sigma }\backslash \pi ^{-1}(\vec {p}) \to \mathfrak {g}$. Then, ![]() $\mathfrak {g}[{\Sigma }\backslash \pi ^{-1}(\vec {p}) ]^\Gamma$ is a Lie algebra under the pointwise bracket.
$\mathfrak {g}[{\Sigma }\backslash \pi ^{-1}(\vec {p}) ]^\Gamma$ is a Lie algebra under the pointwise bracket.
Set
where ![]() $\mathscr {H}(\lambda _i)$ is the integrable highest weight representation of
$\mathscr {H}(\lambda _i)$ is the integrable highest weight representation of ![]() $\hat {\mathfrak {g}}_{p_i}$ of level
$\hat {\mathfrak {g}}_{p_i}$ of level ![]() $c$ with highest weight
$c$ with highest weight ![]() $\lambda _i\in D_{c, p_i}$.
$\lambda _i\in D_{c, p_i}$.
Define an action of the Lie algebra ![]() $\mathfrak {g}[{\Sigma }\backslash \pi ^{-1} ( \vec {p} ) ]^\Gamma$ on
$\mathfrak {g}[{\Sigma }\backslash \pi ^{-1} ( \vec {p} ) ]^\Gamma$ on ![]() $\mathscr {H}(\vec {\lambda })$ as follows:
$\mathscr {H}(\vec {\lambda })$ as follows:
 \begin{equation} X\cdot (v_{1}\otimes\cdots\otimes v_{s}) = \sum^{s}_{i=1}v_{1}\otimes\cdots\otimes X_{p_i}\cdot v_{i}\otimes \cdots\otimes v_{s}, \quad \text{for} \ X\in \mathfrak{g} [{\Sigma}\backslash \pi^{-1}(\vec{p}) ]^\Gamma, \ \text{and} \ v_{i}\in \mathscr{H}(\lambda_{i}), \end{equation}
\begin{equation} X\cdot (v_{1}\otimes\cdots\otimes v_{s}) = \sum^{s}_{i=1}v_{1}\otimes\cdots\otimes X_{p_i}\cdot v_{i}\otimes \cdots\otimes v_{s}, \quad \text{for} \ X\in \mathfrak{g} [{\Sigma}\backslash \pi^{-1}(\vec{p}) ]^\Gamma, \ \text{and} \ v_{i}\in \mathscr{H}(\lambda_{i}), \end{equation}
where ![]() $X_{p_{i}}$ denotes the restriction of
$X_{p_{i}}$ denotes the restriction of ![]() $X$ to
$X$ to ![]() $\pi ^{-1}(\mathbb {D}^\times _{p_i})$, hence
$\pi ^{-1}(\mathbb {D}^\times _{p_i})$, hence ![]() $X_{p_i}$ is an element in
$X_{p_i}$ is an element in ![]() $\hat {\mathfrak {g}}_{p_i}$.
$\hat {\mathfrak {g}}_{p_i}$.
By the residue theorem [Reference HartshorneHar77, Theorem 7.14.2, Chap. III],
Thus, the action (15) indeed is an action of the Lie algebra ![]() $\mathfrak {g}[{\Sigma }\backslash \pi ^{-1}( \vec {p}) ]^\Gamma$ on
$\mathfrak {g}[{\Sigma }\backslash \pi ^{-1}( \vec {p}) ]^\Gamma$ on ![]() $\mathscr {H}(\vec {\lambda })$.
$\mathscr {H}(\vec {\lambda })$.
Finally, we are ready to define the space of (twisted) vacua
and the space of (twisted) covacua
where ![]() $\mathbb {C}$ is considered as the trivial module under the action of
$\mathbb {C}$ is considered as the trivial module under the action of ![]() $\mathfrak {g}[{\Sigma }\backslash \pi ^{-1} (\vec {p})]^\Gamma$, and
$\mathfrak {g}[{\Sigma }\backslash \pi ^{-1} (\vec {p})]^\Gamma$, and ![]() $[\mathscr {H} (\vec {\lambda })]_{\mathfrak {g}[{\Sigma }\backslash \pi ^{-1} ( \vec {p} ) ]^\Gamma }$ denotes the space of covariants
$[\mathscr {H} (\vec {\lambda })]_{\mathfrak {g}[{\Sigma }\backslash \pi ^{-1} ( \vec {p} ) ]^\Gamma }$ denotes the space of covariants ![]() $\mathscr {H} (\vec {\lambda })/\bigl (\mathfrak {g}[{\Sigma }\backslash \pi ^{-1}( \vec {p} ) ]^\Gamma \cdot \mathscr {H} (\vec {\lambda })\bigr )$. Clearly,
$\mathscr {H} (\vec {\lambda })/\bigl (\mathfrak {g}[{\Sigma }\backslash \pi ^{-1}( \vec {p} ) ]^\Gamma \cdot \mathscr {H} (\vec {\lambda })\bigr )$. Clearly,
Remark 3.6 Fix any ![]() $q_i\in \pi ^{-1}(p_i)$. If we choose
$q_i\in \pi ^{-1}(p_i)$. If we choose ![]() $\vec {\lambda }=(\lambda _1,\ldots, \lambda _s)$ to be a set of weights, where for each
$\vec {\lambda }=(\lambda _1,\ldots, \lambda _s)$ to be a set of weights, where for each ![]() $i$,
$i$, ![]() $\lambda _i$ is a dominant weight of
$\lambda _i$ is a dominant weight of ![]() $\mathfrak {g}^{\Gamma _{q_i}}$ in
$\mathfrak {g}^{\Gamma _{q_i}}$ in ![]() $D_{c,q_i}$, we can transfer each
$D_{c,q_i}$, we can transfer each ![]() $\lambda _i$ to an element in
$\lambda _i$ to an element in ![]() $D_{c,p_i}$ through the restriction isomorphism
$D_{c,p_i}$ through the restriction isomorphism ![]() ${\mathfrak {g}}_{p_i}\simeq \mathfrak {g}^{\Gamma _{q_i}}$ via Lemma 3.2. Accordingly, we denote the associated space of covacua by
${\mathfrak {g}}_{p_i}\simeq \mathfrak {g}^{\Gamma _{q_i}}$ via Lemma 3.2. Accordingly, we denote the associated space of covacua by ![]() $\mathscr {V}_{{\Sigma },\Gamma,\phi }(\vec {q},\vec {\lambda })$. This terminology will often be used interchangeably.
$\mathscr {V}_{{\Sigma },\Gamma,\phi }(\vec {q},\vec {\lambda })$. This terminology will often be used interchangeably.
Lemma 3.7 With the notation and assumptions as in Definition 3.5, the space of covacua ![]() $\mathscr {V}_{{\Sigma },\Gamma, \phi }(\vec {p},\vec {\lambda })$ is finite dimensional and, hence, by (19), so is the space of vacua
$\mathscr {V}_{{\Sigma },\Gamma, \phi }(\vec {p},\vec {\lambda })$ is finite dimensional and, hence, by (19), so is the space of vacua ![]() $\mathscr {V}_{{\Sigma },\Gamma,\phi } (\vec {p},\vec {\lambda })^{{{\dagger}} }$.
$\mathscr {V}_{{\Sigma },\Gamma,\phi } (\vec {p},\vec {\lambda })^{{{\dagger}} }$.
Proof. Let ![]() $\mathfrak {g}[\pi ^{-1}(\mathbb {D}^\times _{\vec {p}} ) ]^\Gamma$ be the space of
$\mathfrak {g}[\pi ^{-1}(\mathbb {D}^\times _{\vec {p}} ) ]^\Gamma$ be the space of ![]() $\Gamma$-equivariant maps from the disjoint union of formal punctured discs
$\Gamma$-equivariant maps from the disjoint union of formal punctured discs ![]() $\sqcup _{q\in \pi ^{-1}(\vec {p}) } \mathbb {D}^\times _{q}$ to
$\sqcup _{q\in \pi ^{-1}(\vec {p}) } \mathbb {D}^\times _{q}$ to ![]() $\mathfrak {g}$. Define a Lie algebra bracket on
$\mathfrak {g}$. Define a Lie algebra bracket on
by declaring ![]() $C$ to be the central element and the Lie bracket is defined in the similar way as in (11).
$C$ to be the central element and the Lie bracket is defined in the similar way as in (11).
Now, define an embedding of Lie algebras:
where ![]() $X_{\vec {p}}$ is the restriction of
$X_{\vec {p}}$ is the restriction of ![]() $X$ to
$X$ to ![]() $\pi ^{-1}(\mathbb {D}^\times _{\vec {p}} )$ .
$\pi ^{-1}(\mathbb {D}^\times _{\vec {p}} )$ .
By the residue theorem, ![]() $\beta$ is indeed a Lie algebra homomorphism. Moreover, by Riemann–Roch theorem,
$\beta$ is indeed a Lie algebra homomorphism. Moreover, by Riemann–Roch theorem, ![]() $\operatorname {\mathrm {Im}} \beta + \mathfrak {g} [\pi ^{-1} (\mathbb {D}_{\vec {p}} )]^\Gamma$ has finite codimension in
$\operatorname {\mathrm {Im}} \beta + \mathfrak {g} [\pi ^{-1} (\mathbb {D}_{\vec {p}} )]^\Gamma$ has finite codimension in ![]() ${\hat {\mathfrak {g}}}_{\vec {p}}$, where
${\hat {\mathfrak {g}}}_{\vec {p}}$, where ![]() $\pi ^{-1}(\mathbb {D}_{\vec {p}} )$ is the disjoint union
$\pi ^{-1}(\mathbb {D}_{\vec {p}} )$ is the disjoint union ![]() $\sqcup _{q\in \pi ^{-1}(\vec {p})}\mathbb {D}_q$. Further, define the following surjective Lie algebra homomorphism from the direct sum Lie algebra
$\sqcup _{q\in \pi ^{-1}(\vec {p})}\mathbb {D}_q$. Further, define the following surjective Lie algebra homomorphism from the direct sum Lie algebra
 \[ \bigoplus^{s}_{i=1} \hat{\mathfrak{g}}_{p_i} \to {\hat{\mathfrak{g}}}_{\vec{p}} ,\quad \sum^{s}_{i=1} X_i \mapsto \sum^{s}_{i=1} \tilde{X}_i, \quad C_{i}\to C, \]
\[ \bigoplus^{s}_{i=1} \hat{\mathfrak{g}}_{p_i} \to {\hat{\mathfrak{g}}}_{\vec{p}} ,\quad \sum^{s}_{i=1} X_i \mapsto \sum^{s}_{i=1} \tilde{X}_i, \quad C_{i}\to C, \]
here ![]() $C_{i}$ is the center
$C_{i}$ is the center ![]() $C$ of
$C$ of ![]() $\hat {\mathfrak {g}}_{p_{i}}$, and the map
$\hat {\mathfrak {g}}_{p_{i}}$, and the map ![]() $X_i\in \mathfrak {g} [ \pi ^{-1} ( \mathbb {D}^\times _{p_i}) ]^\Gamma$ naturally extends to
$X_i\in \mathfrak {g} [ \pi ^{-1} ( \mathbb {D}^\times _{p_i}) ]^\Gamma$ naturally extends to ![]() $\tilde {X}_i \in \mathfrak {g}[ \pi ^{-1}(\mathbb {D}^\times _{\vec {p}} )]^\Gamma$ by taking
$\tilde {X}_i \in \mathfrak {g}[ \pi ^{-1}(\mathbb {D}^\times _{\vec {p}} )]^\Gamma$ by taking ![]() $\pi ^{-1}(\mathbb {D}^\times _{p_j} )$ to
$\pi ^{-1}(\mathbb {D}^\times _{p_j} )$ to ![]() $0$ if
$0$ if ![]() $j\neq i$.
$j\neq i$.
Now, the lemma follows from [Reference KumarKum02, Lemma 10.2.2].
4. Propagation of twisted vacua
We prove the propagation theorem in this section, which asserts that adding marked points and attaching weight 0 to those points does not alter the space of twisted vacua.
Let ![]() ${\Sigma }\to \bar {\Sigma }$ be a
${\Sigma }\to \bar {\Sigma }$ be a ![]() $\Gamma$-cover (cf. Definition 3.1). Moreover,
$\Gamma$-cover (cf. Definition 3.1). Moreover, ![]() $\phi :\Gamma \to {\rm Aut}(\mathfrak {g})$ is a group homomorphism.
$\phi :\Gamma \to {\rm Aut}(\mathfrak {g})$ is a group homomorphism.
Definition 4.1 Let ![]() $\vec {o}=(o_{1},\ldots,o_{s})$ and
$\vec {o}=(o_{1},\ldots,o_{s})$ and ![]() $\vec {p}=(p_{1},\ldots,p_{a})$ be two disjoint non-empty sets of smooth and distinct points in
$\vec {p}=(p_{1},\ldots,p_{a})$ be two disjoint non-empty sets of smooth and distinct points in ![]() $\bar {\Sigma }$ such that
$\bar {\Sigma }$ such that ![]() $(\bar {\Sigma }, \vec {o})$ is a
$(\bar {\Sigma }, \vec {o})$ is a ![]() $s$-pointed curve and let
$s$-pointed curve and let ![]() $\vec {\lambda }=(\lambda _{1},\ldots,\lambda _{s})$,
$\vec {\lambda }=(\lambda _{1},\ldots,\lambda _{s})$, ![]() $\vec {\mu }=(\mu _{1},\ldots,\mu _{a})$ be tuples of dominant weights such that
$\vec {\mu }=(\mu _{1},\ldots,\mu _{a})$ be tuples of dominant weights such that ![]() $\lambda _i\in D_{c, o_i}$ and
$\lambda _i\in D_{c, o_i}$ and ![]() $\mu _j\in D_{c,p_j}$ for each
$\mu _j\in D_{c,p_j}$ for each ![]() $1\leq i\leq s, 1\leq j\leq a$.
$1\leq i\leq s, 1\leq j\leq a$.
We assume that ![]() $\pi ^{-1}(o_i)$ and
$\pi ^{-1}(o_i)$ and ![]() $\pi ^{-1}(p_j)$ consist of smooth points.
$\pi ^{-1}(p_j)$ consist of smooth points.
Denote the tensor product
where ![]() $V(\mu _{k})$ is the irreducible
$V(\mu _{k})$ is the irreducible ![]() $\mathfrak {g}_{p_k}$-module with highest weight
$\mathfrak {g}_{p_k}$-module with highest weight ![]() $\mu _k$.
$\mu _k$.
Define a ![]() $\mathfrak {g}[{\Sigma }\backslash \pi ^{-1}( \vec {o}) ]^\Gamma$-module structure on
$\mathfrak {g}[{\Sigma }\backslash \pi ^{-1}( \vec {o}) ]^\Gamma$-module structure on ![]() $V(\vec {\mu })$ as follows:
$V(\vec {\mu })$ as follows:
 \begin{equation} X \cdot (v_{1}\otimes\cdots\otimes v_{a})=\sum^{a}_{k=1}v_{1}\otimes\cdots\otimes X|_{p_k}\cdot v_{k}\otimes\cdots\otimes v_{a}, \end{equation}
\begin{equation} X \cdot (v_{1}\otimes\cdots\otimes v_{a})=\sum^{a}_{k=1}v_{1}\otimes\cdots\otimes X|_{p_k}\cdot v_{k}\otimes\cdots\otimes v_{a}, \end{equation}
for ![]() $v_{k}\in V(\mu _{k}), X \in \mathfrak {g}[{\Sigma }\backslash \pi ^{-1}( \vec {o}) ]^\Gamma$, and
$v_{k}\in V(\mu _{k}), X \in \mathfrak {g}[{\Sigma }\backslash \pi ^{-1}( \vec {o}) ]^\Gamma$, and ![]() $X|_{p_k}$ denotes the restriction
$X|_{p_k}$ denotes the restriction ![]() $X|_{\pi ^{-1}(p_k)} \in \mathfrak {g}_{p_k}$. This gives rise to the tensor product
$X|_{\pi ^{-1}(p_k)} \in \mathfrak {g}_{p_k}$. This gives rise to the tensor product ![]() $\mathfrak {g}[\Sigma \backslash \pi ^{-1} ( \vec {o} ) ]^\Gamma$-module structure on
$\mathfrak {g}[\Sigma \backslash \pi ^{-1} ( \vec {o} ) ]^\Gamma$-module structure on ![]() $\mathscr {H} (\vec {\lambda })\otimes V(\vec {\mu })$.
$\mathscr {H} (\vec {\lambda })\otimes V(\vec {\mu })$.
The proof of the following lemma was communicated to us by Bernstein.
Lemma 4.2 Assume that ![]() $\Gamma$ stabilizes a Borel subalgebra
$\Gamma$ stabilizes a Borel subalgebra ![]() $\mathfrak {b}\subset \mathfrak {g}$. Then, there exist a Cartan subalgebra
$\mathfrak {b}\subset \mathfrak {g}$. Then, there exist a Cartan subalgebra ![]() $\mathfrak {h}\subset \mathfrak {b}$ such that
$\mathfrak {h}\subset \mathfrak {b}$ such that ![]() $\Gamma$ stabilizes
$\Gamma$ stabilizes ![]() $\mathfrak {h}$.
$\mathfrak {h}$.
Proof. Let ![]() $G$ be the simply connected simple algebraic group associated to
$G$ be the simply connected simple algebraic group associated to ![]() $\mathfrak {g}$, and let
$\mathfrak {g}$, and let ![]() $B$ be the Borel subgroup associated to
$B$ be the Borel subgroup associated to ![]() $\mathfrak {b}$. Let
$\mathfrak {b}$. Let ![]() $N$ be the unipotent radical of
$N$ be the unipotent radical of ![]() $B$. Then,
$B$. Then, ![]() $\Gamma$ acts on
$\Gamma$ acts on ![]() $N$. It is known that the space of all Cartan subalgebras in
$N$. It is known that the space of all Cartan subalgebras in ![]() $\mathfrak {b}$ is a
$\mathfrak {b}$ is a ![]() $N$-torsor (it follows easily from the conjugacy theorem of Cartan subalgebras). Let
$N$-torsor (it follows easily from the conjugacy theorem of Cartan subalgebras). Let ![]() $\mathfrak {h}_o$ be any fixed Cartan subalgebra in
$\mathfrak {h}_o$ be any fixed Cartan subalgebra in ![]() $\mathfrak {b}$. It defines a function
$\mathfrak {b}$. It defines a function ![]() $\psi : \Gamma \to N$ given by
$\psi : \Gamma \to N$ given by ![]() $\gamma \mapsto u_\gamma$, where
$\gamma \mapsto u_\gamma$, where ![]() $u_\gamma$ is the unique element in
$u_\gamma$ is the unique element in ![]() $N$ such that
$N$ such that ![]() ${\rm Ad}\,{ u_{\gamma }}(\mathfrak {h}_o)= \gamma (\mathfrak {h}_o)$. It is easy to check that
${\rm Ad}\,{ u_{\gamma }}(\mathfrak {h}_o)= \gamma (\mathfrak {h}_o)$. It is easy to check that ![]() $\psi$ is a 1-cocycle of
$\psi$ is a 1-cocycle of ![]() $\Gamma$ with values in
$\Gamma$ with values in ![]() $N$. Note that the group cohomology
$N$. Note that the group cohomology ![]() $H^1(\Gamma, N)=0$ since
$H^1(\Gamma, N)=0$ since ![]() $\Gamma$ is a finite group and
$\Gamma$ is a finite group and ![]() $N$ is unipotent. It follows that
$N$ is unipotent. It follows that ![]() $\psi$ is a
$\psi$ is a ![]() $1$-coboundary, i.e. there exists
$1$-coboundary, i.e. there exists ![]() $u_o\in N$ such that
$u_o\in N$ such that ![]() $\psi (\gamma )=\gamma ( u_o)^{-1}u_o$ for any
$\psi (\gamma )=\gamma ( u_o)^{-1}u_o$ for any ![]() $\gamma \in \Gamma$. Set
$\gamma \in \Gamma$. Set ![]() $\mathfrak {h}={\rm Ad}\,u_o(\mathfrak {h}_o)$. It is now easy to verify that
$\mathfrak {h}={\rm Ad}\,u_o(\mathfrak {h}_o)$. It is now easy to verify that ![]() $\mathfrak {h}$ is
$\mathfrak {h}$ is ![]() $\Gamma$-stable.
$\Gamma$-stable.
Theorem 4.3 With the notation and assumptions as in Definition 4.1, assume further that ![]() $\Gamma$ stabilizes a Borel subalgebra of
$\Gamma$ stabilizes a Borel subalgebra of ![]() $\mathfrak {g}$. Then, the canonical map
$\mathfrak {g}$. Then, the canonical map
is an isomorphism, where ![]() $\mathscr {V}_{\Sigma,\Gamma,\phi }$ is the space of covacua and the map
$\mathscr {V}_{\Sigma,\Gamma,\phi }$ is the space of covacua and the map ![]() $\theta$ is induced from the
$\theta$ is induced from the ![]() $\mathfrak {g}[{\Sigma }\backslash \pi ^{-1}( \vec {o})]^\Gamma$-module embedding
$\mathfrak {g}[{\Sigma }\backslash \pi ^{-1}( \vec {o})]^\Gamma$-module embedding
with ![]() $V(\mu _{j})$ identified as a
$V(\mu _{j})$ identified as a ![]() $\mathfrak {g}_{p_j}$-submodule of
$\mathfrak {g}_{p_j}$-submodule of ![]() $\mathscr {H} (\mu _{j})$ annihilated by
$\mathscr {H} (\mu _{j})$ annihilated by ![]() $\hat {\mathfrak {g}}_{p_j}^+$. (Observe that since the subspace
$\hat {\mathfrak {g}}_{p_j}^+$. (Observe that since the subspace ![]() $V(\mu _{j})\subset \mathscr {H} (\mu _{j})$ is annihilated by
$V(\mu _{j})\subset \mathscr {H} (\mu _{j})$ is annihilated by ![]() $\hat {\mathfrak {g}}_{p_j}^+$, the embedding
$\hat {\mathfrak {g}}_{p_j}^+$, the embedding ![]() $V(\mu _{j})\subset \mathscr {H} (\mu _{j})$ is indeed a
$V(\mu _{j})\subset \mathscr {H} (\mu _{j})$ is indeed a ![]() $\mathfrak {g}[{\Sigma }\backslash \pi ^{-1}( \vec {o} ) ]^\Gamma$-module embedding.)
$\mathfrak {g}[{\Sigma }\backslash \pi ^{-1}( \vec {o} ) ]^\Gamma$-module embedding.)
Proof. By Lemma 4.2, we may assume that ![]() $\Gamma$ stabilizes a Borel subalgebra
$\Gamma$ stabilizes a Borel subalgebra ![]() $\mathfrak {b}$ and a Cartan subalgebra
$\mathfrak {b}$ and a Cartan subalgebra ![]() $\mathfrak {h}$ contained in
$\mathfrak {h}$ contained in ![]() $\mathfrak {b}$. From now on we fix such a
$\mathfrak {b}$. From now on we fix such a ![]() $\mathfrak {b}$ and
$\mathfrak {b}$ and ![]() $\mathfrak {h}$.
$\mathfrak {h}$.
Let ![]() $\mathscr {H} :=\mathscr {H} (\vec {\lambda })\otimes V(\mu _{1})\otimes \cdots \otimes V(\mu _{a-1})$. By induction on
$\mathscr {H} :=\mathscr {H} (\vec {\lambda })\otimes V(\mu _{1})\otimes \cdots \otimes V(\mu _{a-1})$. By induction on ![]() $a$, it suffices to show that the inclusion
$a$, it suffices to show that the inclusion ![]() $V(\mu _{a})\hookrightarrow \mathscr {H} (\mu _{a})$ induces an isomorphism (abbreviating
$V(\mu _{a})\hookrightarrow \mathscr {H} (\mu _{a})$ induces an isomorphism (abbreviating ![]() $\mu _{a}$ by
$\mu _{a}$ by ![]() $\mu$ and
$\mu$ and ![]() $p_{a}$ by
$p_{a}$ by ![]() $p$)
$p$)
where ![]() ${\Sigma }^o := {\Sigma }\backslash \pi ^{-1} (\vec {o})$.
${\Sigma }^o := {\Sigma }\backslash \pi ^{-1} (\vec {o})$.
We first prove (23) replacing ![]() $\mathscr {H} (\mu )$ by the generalized Verma module
$\mathscr {H} (\mu )$ by the generalized Verma module ![]() $\hat {M}(V(\mu ),c)$ for
$\hat {M}(V(\mu ),c)$ for ![]() $\hat {\mathfrak {g}}_p$ and the parabolic subalgebra
$\hat {\mathfrak {g}}_p$ and the parabolic subalgebra ![]() $\hat {\mathfrak {p}}_p$, i.e.
$\hat {\mathfrak {p}}_p$, i.e.
Consider the Lie algebra
where ![]() $C$ is central in
$C$ is central in ![]() $\mathfrak {s}_p$ and
$\mathfrak {s}_p$ and
 \begin{equation} [X, Y]=[X,Y]_0+ \frac{1}{|\Gamma|} \sum_{q\in \pi^{-1}(p) } \operatorname{\mathrm{Res}}_{q} \langle dX,Y \rangle C,\quad\text{for}\ X, Y\in \mathfrak{g}[{\Sigma}^o \backslash \pi^{-1}(p) ]^\Gamma, \end{equation}
\begin{equation} [X, Y]=[X,Y]_0+ \frac{1}{|\Gamma|} \sum_{q\in \pi^{-1}(p) } \operatorname{\mathrm{Res}}_{q} \langle dX,Y \rangle C,\quad\text{for}\ X, Y\in \mathfrak{g}[{\Sigma}^o \backslash \pi^{-1}(p) ]^\Gamma, \end{equation}
where ![]() $[X,Y]_0$ is the point-wise Lie bracket.
$[X,Y]_0$ is the point-wise Lie bracket.
Let ![]() $\mathfrak {s}_p^{\geq 0}$ be the subalgebra of
$\mathfrak {s}_p^{\geq 0}$ be the subalgebra of ![]() $\mathfrak {s}_p$:
$\mathfrak {s}_p$:
Fix a point ![]() $q\in \pi ^{-1}(p)$ and a generator
$q\in \pi ^{-1}(p)$ and a generator ![]() $\sigma _q$ of
$\sigma _q$ of ![]() $\Gamma _q$ such that
$\Gamma _q$ such that ![]() $\sigma _q$ acts on
$\sigma _q$ acts on ![]() $T_q{\Sigma }$ by
$T_q{\Sigma }$ by ![]() $\epsilon _q :=e^{ {2\pi i}/{e_p}}$ (which is a primitive
$\epsilon _q :=e^{ {2\pi i}/{e_p}}$ (which is a primitive ![]() $e_p$th root of unity). By the Riemann–Roch theorem there exists a formal parameter
$e_p$th root of unity). By the Riemann–Roch theorem there exists a formal parameter ![]() $z_q$ around
$z_q$ around ![]() $q$ such that
$q$ such that ![]() $z_q^{-1}$ is a regular function on
$z_q^{-1}$ is a regular function on ![]() ${\Sigma }^o\backslash \{q\}$. Moreover, we require
${\Sigma }^o\backslash \{q\}$. Moreover, we require ![]() $z_q^{-1}$ to vanish at any other point
$z_q^{-1}$ to vanish at any other point ![]() $q'$ in
$q'$ in ![]() $\pi ^{-1}(p)$. Replacing
$\pi ^{-1}(p)$. Replacing ![]() $z_q^{-1}$ by
$z_q^{-1}$ by
 \[ \sum_{j=1}^{e_p} \epsilon_q^{-j}\sigma_q^j(z_q^{-1}), \]
\[ \sum_{j=1}^{e_p} \epsilon_q^{-j}\sigma_q^j(z_q^{-1}), \]
we can (and will) assume that
Recall the Lie algebras ![]() $\hat {L}(\mathfrak {g},\Gamma _q)$ and
$\hat {L}(\mathfrak {g},\Gamma _q)$ and ![]() $\hat {L}(\mathfrak {g},\Gamma _q)^-=(z_q^{-1}\mathfrak {g}[z_q^{-1}])^{\Gamma _q}$ from § 2. Since
$\hat {L}(\mathfrak {g},\Gamma _q)^-=(z_q^{-1}\mathfrak {g}[z_q^{-1}])^{\Gamma _q}$ from § 2. Since ![]() $z_q$ is a formal parameter at
$z_q$ is a formal parameter at ![]() $q$ with
$q$ with ![]() $\sigma _q\cdot z_q= \epsilon _q^{-1}z_q$, we have
$\sigma _q\cdot z_q= \epsilon _q^{-1}z_q$, we have
Define, for any ![]() $x\in \mathfrak {g}$ and
$x\in \mathfrak {g}$ and ![]() $k\geq 1$,
$k\geq 1$,
 \[ A(x[z_q^{-k}]) := \frac{1}{|\Gamma_q|} \sum_{\gamma\in \Gamma}\gamma\cdot (x[z_q^{-k}]) \in \mathfrak{s}_p, \]
\[ A(x[z_q^{-k}]) := \frac{1}{|\Gamma_q|} \sum_{\gamma\in \Gamma}\gamma\cdot (x[z_q^{-k}]) \in \mathfrak{s}_p, \]
and let ![]() $V\subset \mathfrak {s}_p$ be the span of
$V\subset \mathfrak {s}_p$ be the span of ![]() $\{A(x[z_q^{-k}])\}_{x\in \mathfrak {g}, k \geq 1}$. It is easy to check that
$\{A(x[z_q^{-k}])\}_{x\in \mathfrak {g}, k \geq 1}$. It is easy to check that
By Lemmas 3.2 and 3.3, we can view ![]() $\hat {M}(V(\mu ),c)$ as a generalized Verma module over
$\hat {M}(V(\mu ),c)$ as a generalized Verma module over ![]() $\hat {L}(\mathfrak {g},\Gamma _q)$ induced from
$\hat {L}(\mathfrak {g},\Gamma _q)$ induced from ![]() $V(\mu )$ as
$V(\mu )$ as ![]() $\hat {L}(\mathfrak {g}, \Gamma _q)^{\geq 0}$-module.
$\hat {L}(\mathfrak {g}, \Gamma _q)^{\geq 0}$-module.
Consider the embedding of the Lie algebra
by taking ![]() $C\mapsto C$ and any
$C\mapsto C$ and any ![]() $X\mapsto X_q$. We assert that the above embedding
$X\mapsto X_q$. We assert that the above embedding ![]() $\mathfrak {s}_p \hookrightarrow \hat {L}(\mathfrak {g}, \Gamma _q)$ induces a vector space isomorphism
$\mathfrak {s}_p \hookrightarrow \hat {L}(\mathfrak {g}, \Gamma _q)$ induces a vector space isomorphism
To prove the above isomorphism, observe first that ![]() $\gamma$ is injective: for
$\gamma$ is injective: for ![]() $\alpha \in \mathfrak {g}[{\Sigma }^o\setminus \pi ^{-1}(p)]^\Gamma$, if
$\alpha \in \mathfrak {g}[{\Sigma }^o\setminus \pi ^{-1}(p)]^\Gamma$, if ![]() $\gamma (\alpha )\in \hat {L}(\mathfrak {g}, \Gamma _q)^{\geq 0}$, then
$\gamma (\alpha )\in \hat {L}(\mathfrak {g}, \Gamma _q)^{\geq 0}$, then ![]() $\alpha \in \mathfrak {g}[({\Sigma }^o\setminus \pi ^{-1}(p))\cup \{q\}]$. The
$\alpha \in \mathfrak {g}[({\Sigma }^o\setminus \pi ^{-1}(p))\cup \{q\}]$. The ![]() $\Gamma$-invariance of
$\Gamma$-invariance of ![]() $\alpha$ forces
$\alpha$ forces ![]() $\alpha \in \mathfrak {g}[{\Sigma }^o]$, proving the injectivity of
$\alpha \in \mathfrak {g}[{\Sigma }^o]$, proving the injectivity of ![]() $\gamma$. To prove the surjectivity of
$\gamma$. To prove the surjectivity of ![]() $\gamma$, take a
$\gamma$, take a ![]() $\Gamma _q$-invariant
$\Gamma _q$-invariant ![]() $\alpha =x[z_q^{-k}]$ for
$\alpha =x[z_q^{-k}]$ for ![]() $k \geq 1$. Thus,
$k \geq 1$. Thus, ![]() $\sigma _q(x)= \epsilon _q^{-k}x$. By the definition, since
$\sigma _q(x)= \epsilon _q^{-k}x$. By the definition, since ![]() $z_q^{-1}$ vanishes at any point
$z_q^{-1}$ vanishes at any point ![]() $q'\in \pi ^{-1}(p)$ different from
$q'\in \pi ^{-1}(p)$ different from ![]() $q$,
$q$,
This proves the surjectivity of ![]() $\gamma$. Thus, by the Poincaré–Birkhoff–Witt theorem, as
$\gamma$. Thus, by the Poincaré–Birkhoff–Witt theorem, as ![]() $\mathfrak {s}_p$-modules
$\mathfrak {s}_p$-modules
Let ![]() $\mathfrak {g}[{\Sigma }^o\backslash \pi ^{-1}(p)]^\Gamma$ act on
$\mathfrak {g}[{\Sigma }^o\backslash \pi ^{-1}(p)]^\Gamma$ act on ![]() $\mathscr {H}$ as follows:
$\mathscr {H}$ as follows:
 \begin{align*} &X \cdot (v_1\otimes \cdots \otimes v_s\otimes w_1\otimes \cdots \otimes w_{a-1}) \\ &\quad= \sum_{i=1}^s v_1\otimes \cdots \otimes X_{o_i}\cdot v_i\otimes \cdots \otimes v_s\otimes w_1\otimes \cdots \otimes w_{a-1} \\ &\qquad + \sum_{j=1}^{a-1} v_1\otimes \cdots \otimes v_s\otimes w_1\otimes \cdots \otimes X|_{p_j}\cdot w_j\otimes \cdots \otimes w_{a-1} \end{align*}
\begin{align*} &X \cdot (v_1\otimes \cdots \otimes v_s\otimes w_1\otimes \cdots \otimes w_{a-1}) \\ &\quad= \sum_{i=1}^s v_1\otimes \cdots \otimes X_{o_i}\cdot v_i\otimes \cdots \otimes v_s\otimes w_1\otimes \cdots \otimes w_{a-1} \\ &\qquad + \sum_{j=1}^{a-1} v_1\otimes \cdots \otimes v_s\otimes w_1\otimes \cdots \otimes X|_{p_j}\cdot w_j\otimes \cdots \otimes w_{a-1} \end{align*}
for ![]() $X\in \mathfrak {g}[{\Sigma }^o\backslash \pi ^{-1}(p)]^\Gamma, v_i\in \mathscr {H}(\lambda _i)$ and
$X\in \mathfrak {g}[{\Sigma }^o\backslash \pi ^{-1}(p)]^\Gamma, v_i\in \mathscr {H}(\lambda _i)$ and ![]() $w_j \in V(\mu _j)$, and let
$w_j \in V(\mu _j)$, and let ![]() $C$ act on
$C$ act on ![]() $\mathscr {H}$ by the scalar
$\mathscr {H}$ by the scalar ![]() $-c$. By the residue theorem, these actions combine to make
$-c$. By the residue theorem, these actions combine to make ![]() $\mathscr {H}$ into an
$\mathscr {H}$ into an ![]() $\mathfrak {s}_p$-module. Thus, the action of
$\mathfrak {s}_p$-module. Thus, the action of ![]() $C$ on the tensor product
$C$ on the tensor product ![]() $\mathscr {H}\otimes \hat {M}(V(\mu ),c)$ is trivial.
$\mathscr {H}\otimes \hat {M}(V(\mu ),c)$ is trivial.
Now, by the isomorphism (31) (in the following, ![]() $\mathfrak {g}[{\Sigma }^o]^\Gamma$ acts on
$\mathfrak {g}[{\Sigma }^o]^\Gamma$ acts on ![]() $V(\mu )$ via its restriction on
$V(\mu )$ via its restriction on ![]() $\pi ^{-1}(p)$ and
$\pi ^{-1}(p)$ and ![]() $C$ acts via the scalar
$C$ acts via the scalar ![]() $c$)
$c$)
 \begin{align*} \big[ \mathscr{H}\otimes \hat{M}(V(\mu),c)\big]_{\mathfrak{g}[{\Sigma}^o\backslash \pi^{-1}(p)]^\Gamma} &= \big[\mathscr{H}\otimes \hat{M}(V(\mu),c)\big]_{\mathfrak{s}_p },\quad \text{since $C$ acts trivially}\\ &\simeq \mathscr{H}\otimes_{U(\mathfrak{s}_p )}\hat{M}(V(\mu),c)\\ &\simeq \mathscr{H}\otimes_{U(\mathfrak{s}_p )}\big(U(\mathfrak{s}_p )\otimes_{U(\mathfrak{g}[{\Sigma}^o]^\Gamma \oplus \mathbb{C}C)}V(\mu)\big)\\ &\simeq \mathscr{H}\otimes_{U(\mathfrak{g}[{\Sigma}^o]^\Gamma \oplus \mathbb{C}C)} V(\mu)\\ &= \mathscr{H}\otimes_{U(\mathfrak{g}[{\Sigma}^o]^\Gamma )}V(\mu)\\ &= [\mathscr{H}\otimes V(\mu)]_{\mathfrak{g}[{\Sigma}^o]^\Gamma}. \end{align*}
\begin{align*} \big[ \mathscr{H}\otimes \hat{M}(V(\mu),c)\big]_{\mathfrak{g}[{\Sigma}^o\backslash \pi^{-1}(p)]^\Gamma} &= \big[\mathscr{H}\otimes \hat{M}(V(\mu),c)\big]_{\mathfrak{s}_p },\quad \text{since $C$ acts trivially}\\ &\simeq \mathscr{H}\otimes_{U(\mathfrak{s}_p )}\hat{M}(V(\mu),c)\\ &\simeq \mathscr{H}\otimes_{U(\mathfrak{s}_p )}\big(U(\mathfrak{s}_p )\otimes_{U(\mathfrak{g}[{\Sigma}^o]^\Gamma \oplus \mathbb{C}C)}V(\mu)\big)\\ &\simeq \mathscr{H}\otimes_{U(\mathfrak{g}[{\Sigma}^o]^\Gamma \oplus \mathbb{C}C)} V(\mu)\\ &= \mathscr{H}\otimes_{U(\mathfrak{g}[{\Sigma}^o]^\Gamma )}V(\mu)\\ &= [\mathscr{H}\otimes V(\mu)]_{\mathfrak{g}[{\Sigma}^o]^\Gamma}. \end{align*}
This proves (24).
Now, we come to the proof of (23).
Let ![]() $K(\mu )$ be the kernel of the canonical projection
$K(\mu )$ be the kernel of the canonical projection ![]() $\hat {M}(V(\mu ),c)\twoheadrightarrow \mathscr {H} (\mu )$. In view of (24), to prove (23), it suffices to show that the image of
$\hat {M}(V(\mu ),c)\twoheadrightarrow \mathscr {H} (\mu )$. In view of (24), to prove (23), it suffices to show that the image of
is zero: from the isomorphism (30), we get
Moreover, write
and observe that any element of ![]() $\mathfrak {g}^{\Gamma _q}$ can be (uniquely) extended to an element of
$\mathfrak {g}^{\Gamma _q}$ can be (uniquely) extended to an element of ![]() $\mathfrak {g}_p:=\mathfrak {g}[\pi ^{-1}(p)]^\Gamma$ (cf. Lemma 3.2). Further,
$\mathfrak {g}_p:=\mathfrak {g}[\pi ^{-1}(p)]^\Gamma$ (cf. Lemma 3.2). Further, ![]() ${\Sigma }^o$ being affine, the restriction map
${\Sigma }^o$ being affine, the restriction map ![]() $\mathfrak {g}[{\Sigma }^o]^\Gamma \to \mathfrak {g}_p$ is surjective, and, of course,
$\mathfrak {g}[{\Sigma }^o]^\Gamma \to \mathfrak {g}_p$ is surjective, and, of course, ![]() $\mathfrak {g}[{\Sigma }^o]^\Gamma \subset \mathfrak {s}_p^{\geq 0}$. Thus, we get the decomposition:
$\mathfrak {g}[{\Sigma }^o]^\Gamma \subset \mathfrak {s}_p^{\geq 0}$. Thus, we get the decomposition:
and, hence, by the Poincaré–Birkhoff–Witt theorem, ![]() $U(\hat {L}(\mathfrak {g},\Gamma _q))$ is the span of elements of the form
$U(\hat {L}(\mathfrak {g},\Gamma _q))$ is the span of elements of the form
Consider the decomposition (3) for ![]() $\sigma _q$:
$\sigma _q$: ![]() $\sigma _q=\tau _q \epsilon _q^{{\rm ad}\, h}$, under a choice of
$\sigma _q=\tau _q \epsilon _q^{{\rm ad}\, h}$, under a choice of ![]() $\sigma _q$-stable Borel subalgebra
$\sigma _q$-stable Borel subalgebra ![]() $\mathfrak {b}_q$ containing the same Cartan subalgebra
$\mathfrak {b}_q$ containing the same Cartan subalgebra ![]() $\mathfrak {h}$ in the sense of § 2. (Since
$\mathfrak {h}$ in the sense of § 2. (Since ![]() $\Gamma$, in particular
$\Gamma$, in particular ![]() $\sigma _q$, stabilizes the pair
$\sigma _q$, stabilizes the pair ![]() $(\mathfrak {b}, \mathfrak {h})$, as in the proof of Lemma 2.5,
$(\mathfrak {b}, \mathfrak {h})$, as in the proof of Lemma 2.5, ![]() $\mathfrak {h}^{\sigma _q}=\mathfrak {h}^{\tau '_q}$ for some diagram automorphism
$\mathfrak {h}^{\sigma _q}=\mathfrak {h}^{\tau '_q}$ for some diagram automorphism ![]() $\tau '_q$ of
$\tau '_q$ of ![]() $\mathfrak {g}$ associated to the pair
$\mathfrak {g}$ associated to the pair ![]() $(\mathfrak {b}, \mathfrak {h})$. In particular, the centralizer
$(\mathfrak {b}, \mathfrak {h})$. In particular, the centralizer ![]() $Z_{\mathfrak {g}}(\mathfrak {h}^\sigma )$ of
$Z_{\mathfrak {g}}(\mathfrak {h}^\sigma )$ of ![]() $\mathfrak {h}^\sigma$ in
$\mathfrak {h}^\sigma$ in ![]() $\mathfrak {g}$ equals
$\mathfrak {g}$ equals ![]() $\mathfrak {h}$ and, hence, we can take
$\mathfrak {h}$ and, hence, we can take ![]() $\mathfrak {h}_q=\mathfrak {h}$.) Under such a choice, there exist
$\mathfrak {h}_q=\mathfrak {h}$.) Under such a choice, there exist ![]() $sl_2$-triples
$sl_2$-triples ![]() $x_i,y_i,h_i \in \mathfrak {g}$ for each
$x_i,y_i,h_i \in \mathfrak {g}$ for each ![]() $i\in \hat {I}(\mathfrak {g}, \sigma _q)$ such that
$i\in \hat {I}(\mathfrak {g}, \sigma _q)$ such that ![]() $\tilde {x}_i:=x_i[z_q^{s_i}], \tilde {y}_i:=y_{i}[z_q^{-s_i}], i\in \hat {I}(\mathfrak {g},\sigma _q)$ are Chevalley generators of
$\tilde {x}_i:=x_i[z_q^{s_i}], \tilde {y}_i:=y_{i}[z_q^{-s_i}], i\in \hat {I}(\mathfrak {g},\sigma _q)$ are Chevalley generators of ![]() $\hat {L}(\mathfrak {g}, \sigma _q)$. Moreover,
$\hat {L}(\mathfrak {g}, \sigma _q)$. Moreover, ![]() $x_i,y_i$ satisfy
$x_i,y_i$ satisfy
Let ![]() $v_+$ be the highest weight vector of
$v_+$ be the highest weight vector of ![]() $\hat {M}(V(\mu ),c)$. Recall (cf. (9)) that
$\hat {M}(V(\mu ),c)$. Recall (cf. (9)) that ![]() $K(\mu )$ is generated by
$K(\mu )$ is generated by ![]() $\tilde {y}^{n_{\mu,i}+1}_i\cdot v_+$, for
$\tilde {y}^{n_{\mu,i}+1}_i\cdot v_+$, for ![]() $i\in \hat {I}(\mathfrak {g},\sigma _q)^+$ consisting of
$i\in \hat {I}(\mathfrak {g},\sigma _q)^+$ consisting of ![]() $i\in \hat {I}(\mathfrak {g}, \sigma _q)$ such that
$i\in \hat {I}(\mathfrak {g}, \sigma _q)$ such that ![]() $s_i>0$.
$s_i>0$.
Thus, to prove the vanishing of the map ![]() $\iota$, it suffices to show that for any
$\iota$, it suffices to show that for any ![]() $i\in \hat {I}(\mathfrak {g},\sigma _q)^+$
$i\in \hat {I}(\mathfrak {g},\sigma _q)^+$
for ![]() $h\in \mathscr {H}$, any
$h\in \mathscr {H}$, any ![]() $n\geq 0$ and
$n\geq 0$ and ![]() $X_{j}\in \hat {L}(\mathfrak {g}, \Gamma _q)^+$. However,
$X_{j}\in \hat {L}(\mathfrak {g}, \Gamma _q)^+$. However, ![]() $\tilde {y}_i^{n_{\mu,i}+ 1}\cdot v_+$ being a highest weight vector,
$\tilde {y}_i^{n_{\mu,i}+ 1}\cdot v_+$ being a highest weight vector,
Thus, to prove (33), it suffices to show that for any ![]() $i\in \hat {I}(\mathfrak {g},\sigma _q)^+$
$i\in \hat {I}(\mathfrak {g},\sigma _q)^+$
Fix ![]() $i\in \hat {I}(\mathfrak {g}, \sigma _q)^+$. Take
$i\in \hat {I}(\mathfrak {g}, \sigma _q)^+$. Take ![]() $f\in \mathbb {C}[{\Sigma }^o]$ such that
$f\in \mathbb {C}[{\Sigma }^o]$ such that
and the order of vanishing of ![]() $f$ at any
$f$ at any ![]() $q'\neq q\in \pi ^{-1}(p)$ is at least
$q'\neq q\in \pi ^{-1}(p)$ is at least ![]() $(n_{\mu,i}+3)s_i$. Moreover, replacing
$(n_{\mu,i}+3)s_i$. Moreover, replacing ![]() $f$ by
$f$ by ![]() $ ({1}/{|\Gamma _q|})\sum _{j=1}^{|\Gamma _q|} \epsilon _q^{s_ij}\sigma _q^j\cdot f$, we can (and will) assume that
$ ({1}/{|\Gamma _q|})\sum _{j=1}^{|\Gamma _q|} \epsilon _q^{s_ij}\sigma _q^j\cdot f$, we can (and will) assume that
Now, take
Then, writing ![]() $Y=\tilde {y}_i$,
$Y=\tilde {y}_i$,
 \begin{align} Z^N Y^{n_{\mu,i}+ N+1}\cdot v_+&=\bigg(\sum_{\gamma \in \Gamma/\Gamma_q} \big( \gamma \cdot (x_i[f])\big)_q\bigg)^NY^{n_{\mu,i}+N+ 1}\cdot v_+ \nonumber\\ &=(x_i[f_q])^NY^{n_{\mu,i}+ N+1}\cdot v_+. \end{align}
\begin{align} Z^N Y^{n_{\mu,i}+ N+1}\cdot v_+&=\bigg(\sum_{\gamma \in \Gamma/\Gamma_q} \big( \gamma \cdot (x_i[f])\big)_q\bigg)^NY^{n_{\mu,i}+N+ 1}\cdot v_+ \nonumber\\ &=(x_i[f_q])^NY^{n_{\mu,i}+ N+1}\cdot v_+. \end{align}
To prove the last equality, observe that ![]() $\big (\gamma _1 \cdot (x_i[f])\big )_q \dots \big (\gamma _N \cdot (x_i[f])\big )_q$ has zero of order at least
$\big (\gamma _1 \cdot (x_i[f])\big )_q \dots \big (\gamma _N \cdot (x_i[f])\big )_q$ has zero of order at least ![]() $(n_{\mu,i}+3)s_i+(N-1)s_i$ unless each
$(n_{\mu,i}+3)s_i+(N-1)s_i$ unless each ![]() $\gamma _j\cdot \Gamma _q=\Gamma _q$. However,
$\gamma _j\cdot \Gamma _q=\Gamma _q$. However, ![]() $Y^{n_{\mu,i}+ N+1}$ has order of pole equal to
$Y^{n_{\mu,i}+ N+1}$ has order of pole equal to ![]() $(n_{\mu,i}+N+1)s_i$. Since
$(n_{\mu,i}+N+1)s_i$. Since ![]() $(n_{\mu,i}+3)s_i+(N-1)s_i >(n_{\mu,i}+N+1)s_i$, we get the last equality. Thus, by Lemma 2.4 for
$(n_{\mu,i}+3)s_i+(N-1)s_i >(n_{\mu,i}+N+1)s_i$, we get the last equality. Thus, by Lemma 2.4 for ![]() $X=x_i[f_q]$ and
$X=x_i[f_q]$ and ![]() $Y=\tilde {y}_i$, for any
$Y=\tilde {y}_i$, for any ![]() $N\geq 1$, there exists
$N\geq 1$, there exists ![]() $\alpha \neq 0$ such that
$\alpha \neq 0$ such that
 \begin{align*}
\iota\big(h\otimes (Y^{n_{\mu,i}+ 1}\cdot v_+)\big) &= \alpha \iota
\big(h\otimes X^{N}Y^{n_{\mu,i}+ N+1}\cdot v_+\big)\\
&=\alpha \iota \big(h\otimes Z^{N}Y^{n_{\mu,i}+ N+1}\cdot
v_+\big), \quad \text{by (35)}\\ &=
(-1)^{N}\alpha \iota\big(Z^{N}\cdot h\otimes Y^{n_{\mu,i} +
N+1}\cdot v_+\big)\\ &=
0,\quad\text{by Lemma 2.5 for large $N$ (see the
argument below).} \end{align*}
\begin{align*}
\iota\big(h\otimes (Y^{n_{\mu,i}+ 1}\cdot v_+)\big) &= \alpha \iota
\big(h\otimes X^{N}Y^{n_{\mu,i}+ N+1}\cdot v_+\big)\\
&=\alpha \iota \big(h\otimes Z^{N}Y^{n_{\mu,i}+ N+1}\cdot
v_+\big), \quad \text{by (35)}\\ &=
(-1)^{N}\alpha \iota\big(Z^{N}\cdot h\otimes Y^{n_{\mu,i} +
N+1}\cdot v_+\big)\\ &=
0,\quad\text{by Lemma 2.5 for large $N$ (see the
argument below).} \end{align*}
This proves (34) and, hence, completes the proof of the theorem.
We now explain more precisely how Lemma 2.5 implies ![]() $Z^N\cdot h=0$. With respect to the pair
$Z^N\cdot h=0$. With respect to the pair ![]() $(\mathfrak {b},\mathfrak {h})$ stable under
$(\mathfrak {b},\mathfrak {h})$ stable under ![]() $\Gamma$ (note that
$\Gamma$ (note that ![]() $\mathfrak {b}$ might not be the same as
$\mathfrak {b}$ might not be the same as ![]() $\mathfrak {b}_q$ given above (3) though
$\mathfrak {b}_q$ given above (3) though ![]() $\mathfrak {h}_q$ is taken to be
$\mathfrak {h}_q$ is taken to be ![]() $\mathfrak {h}$), since
$\mathfrak {h}$), since ![]() $\Gamma$ preserves the pair
$\Gamma$ preserves the pair ![]() $(\mathfrak {b},\mathfrak {h})$, the group
$(\mathfrak {b},\mathfrak {h})$, the group ![]() $\Gamma$ acts on the root system
$\Gamma$ acts on the root system ![]() $\Phi (\mathfrak {g},\mathfrak {h})$ of
$\Phi (\mathfrak {g},\mathfrak {h})$ of ![]() $\mathfrak {g}$ by factoring through the group of outer automorphisms with respect to the pair
$\mathfrak {g}$ by factoring through the group of outer automorphisms with respect to the pair ![]() $(\mathfrak {b}, \mathfrak {h})$. In particular,
$(\mathfrak {b}, \mathfrak {h})$. In particular, ![]() $\Gamma$ preserves the set of positive (respectively, negative) roots. From the construction of
$\Gamma$ preserves the set of positive (respectively, negative) roots. From the construction of ![]() $x_i$ in § 2,
$x_i$ in § 2, ![]() $x_i$ is either a linear combination of positive root vectors or a linear combination of negative root vectors with respect to
$x_i$ is either a linear combination of positive root vectors or a linear combination of negative root vectors with respect to ![]() $\mathfrak {b}_q$. Thus, either
$\mathfrak {b}_q$. Thus, either ![]() $\gamma \cdot x_i\in \mathfrak {n}$ for all
$\gamma \cdot x_i\in \mathfrak {n}$ for all ![]() $\gamma \in \Gamma$, or
$\gamma \in \Gamma$, or ![]() $\gamma \cdot x_i\in \mathfrak {n}^-$ for all
$\gamma \cdot x_i\in \mathfrak {n}^-$ for all ![]() $\gamma \in \Gamma$, where
$\gamma \in \Gamma$, where ![]() $\mathfrak {b}^-$ is the negative Borel of
$\mathfrak {b}^-$ is the negative Borel of ![]() $\mathfrak {b}$ and
$\mathfrak {b}$ and ![]() $\mathfrak {n}$ (respectively,
$\mathfrak {n}$ (respectively, ![]() $\mathfrak {n}^-$) is the nilradical of
$\mathfrak {n}^-$) is the nilradical of ![]() $\mathfrak {b}$ (respectively,
$\mathfrak {b}$ (respectively, ![]() $\mathfrak {b}^-$). Therefore, we may apply Lemma 2.5 to show
$\mathfrak {b}^-$). Therefore, we may apply Lemma 2.5 to show ![]() $Z^N\cdot h=0$.
$Z^N\cdot h=0$.
Remark 4.4 Observe that the condition that ![]() $\Gamma$ stabilizes a Borel subalgebra
$\Gamma$ stabilizes a Borel subalgebra ![]() $\mathfrak {b}$ and, hence, also a Cartan subalgebra
$\mathfrak {b}$ and, hence, also a Cartan subalgebra ![]() $\mathfrak {h}\subset \mathfrak {b}$ is equivalent to the condition that the image of
$\mathfrak {h}\subset \mathfrak {b}$ is equivalent to the condition that the image of ![]() $\Gamma$ in Aut
$\Gamma$ in Aut ![]() $\mathfrak {g}$ is contained in
$\mathfrak {g}$ is contained in ![]() $D\ltimes \text {Int} H$, where
$D\ltimes \text {Int} H$, where ![]() $D$ is the group of diagram automorphisms of
$D$ is the group of diagram automorphisms of ![]() $\mathfrak {g}$ and
$\mathfrak {g}$ and ![]() $H$ is the maximal torus of
$H$ is the maximal torus of ![]() $G$ with Lie algebra
$G$ with Lie algebra ![]() $\mathfrak {h}$ (
$\mathfrak {h}$ (![]() $G$ being the adjoint group with Lie algebra
$G$ being the adjoint group with Lie algebra ![]() $\mathfrak {g}$).
$\mathfrak {g}$).
The following result is the twisted analogue of ‘Propagation of Vacua’ due to Tsuchiya, Ueno, and Yamada [Reference Tsuchiya, Ueno and YamadaTUY89].
Corollary 4.5 With the notation and assumptions as in Theorem 4.3 (in particular, ![]() $(\bar {\Sigma } ,\vec {o})$ is a
$(\bar {\Sigma } ,\vec {o})$ is a ![]() $s$-pointed curve), for any smooth point
$s$-pointed curve), for any smooth point ![]() $q\in {\Sigma }^o := {\Sigma }\setminus \pi ^{-1}(\vec {o})$ (thus,
$q\in {\Sigma }^o := {\Sigma }\setminus \pi ^{-1}(\vec {o})$ (thus, ![]() $p=\pi (q)$ is a smooth point of
$p=\pi (q)$ is a smooth point of ![]() $\bar {\Sigma }$) with
$\bar {\Sigma }$) with ![]() $0\in D_{c, q}$ (cf. Corollary 2.2), there are canonical isomorphisms:
$0\in D_{c, q}$ (cf. Corollary 2.2), there are canonical isomorphisms:
(a)
 $\mathscr {V}_{\Sigma,\Gamma,\phi }(\vec {o},\vec {\lambda })\simeq \mathscr {V}_{\Sigma,\Gamma,\phi }((\vec {o},p),(\vec {\lambda },0))$; and
$\mathscr {V}_{\Sigma,\Gamma,\phi }(\vec {o},\vec {\lambda })\simeq \mathscr {V}_{\Sigma,\Gamma,\phi }((\vec {o},p),(\vec {\lambda },0))$; and(b) for
 $\bar {\Sigma }$ an irreducible curve,
$\bar {\Sigma }$ an irreducible curve,  $\mathscr {V}_{\Sigma,\Gamma,\phi }(\vec {o},\vec {\lambda })\simeq [\mathscr {H} (0)\otimes V(\vec {\lambda })]_{\mathfrak {g}[\Sigma \backslash \pi ^{-1}(p)]^\Gamma }$, where the point
$\mathscr {V}_{\Sigma,\Gamma,\phi }(\vec {o},\vec {\lambda })\simeq [\mathscr {H} (0)\otimes V(\vec {\lambda })]_{\mathfrak {g}[\Sigma \backslash \pi ^{-1}(p)]^\Gamma }$, where the point  $p$ is assigned weight
$p$ is assigned weight  $0$.
$0$.
Proof. (a) Apply Theorem 4.3 for the case ![]() $\vec {p}=(p)$ and
$\vec {p}=(p)$ and ![]() $\vec {\mu }=(0)$.
$\vec {\mu }=(0)$.
(b) It follows from Theorem 4.3 and part (a). (In Theorem 4.3 replace ![]() $\vec {o}$ by the singleton
$\vec {o}$ by the singleton ![]() $(p)$,
$(p)$, ![]() $\vec {\lambda }$ by
$\vec {\lambda }$ by ![]() $(0)$,
$(0)$, ![]() $\vec {p}$ by
$\vec {p}$ by ![]() $\vec {o}$ and
$\vec {o}$ and ![]() $\vec {\mu }$ by
$\vec {\mu }$ by ![]() $\vec {\lambda }$.)
$\vec {\lambda }$.)
Remark 4.6 (a) A much weaker form of part (a) of the above corollary (where ![]() $\Gamma$ is of order
$\Gamma$ is of order ![]() $2$ and
$2$ and ![]() $\vec {o}$ consists of all the ramification points) is proved in [Reference Frenkel and SzczesnyFS04, Lemma 7.1]. It should be mentioned that they use the more general setting of twisted vertex operator algebras.
$\vec {o}$ consists of all the ramification points) is proved in [Reference Frenkel and SzczesnyFS04, Lemma 7.1]. It should be mentioned that they use the more general setting of twisted vertex operator algebras.
(b) When all the marked points are unramified and ![]() $|\Gamma |$ is a prime, the propagation of vacua is proved in [Reference DamioliniDam20].
$|\Gamma |$ is a prime, the propagation of vacua is proved in [Reference DamioliniDam20].
5. Factorization theorem
The aim of this section is to prove the factorization theorem which identifies the space of covacua for a genus ![]() $g$ nodal curve
$g$ nodal curve ![]() $\bar {\Sigma }$ with a direct sum of the spaces of covacua for its normalization
$\bar {\Sigma }$ with a direct sum of the spaces of covacua for its normalization ![]() $\bar {\Sigma }'$ (which is a genus
$\bar {\Sigma }'$ (which is a genus ![]() $g-1$ curve).
$g-1$ curve).
Let ![]() $\pi : {\Sigma }\to \bar {\Sigma }$ be a
$\pi : {\Sigma }\to \bar {\Sigma }$ be a ![]() $\Gamma$-cover of a
$\Gamma$-cover of a ![]() $s$-pointed curve
$s$-pointed curve ![]() $(\bar {\Sigma }, \vec {o})$. We do not assume that
$(\bar {\Sigma }, \vec {o})$. We do not assume that ![]() $\bar {\Sigma }$ is irreducible. Moreover,
$\bar {\Sigma }$ is irreducible. Moreover, ![]() $\phi :\Gamma \to$ Aut
$\phi :\Gamma \to$ Aut![]() $(\mathfrak {g})$ is a group homomorphism.
$(\mathfrak {g})$ is a group homomorphism.
Definition 5.1 [Reference Bertin and RomagnyBR11, Définition 4.1.4]
Let ![]() ${\Sigma }$ be a reduced (but not necessarily connected) projective curve with at worst only simple nodal singularity. (Recall that a point
${\Sigma }$ be a reduced (but not necessarily connected) projective curve with at worst only simple nodal singularity. (Recall that a point ![]() $P\in {\Sigma }$ is called a simple node if analytically a neighborhood of
$P\in {\Sigma }$ is called a simple node if analytically a neighborhood of ![]() $P$ in
$P$ in ![]() ${\Sigma }$ is isomorphic with an analytic neighborhood of
${\Sigma }$ is isomorphic with an analytic neighborhood of ![]() $(0,0)$ in the curve
$(0,0)$ in the curve ![]() $xy=0$ in
$xy=0$ in ![]() $\mathbb {A}^2$.) Then, the action of
$\mathbb {A}^2$.) Then, the action of ![]() $\Gamma$ on
$\Gamma$ on ![]() $\Sigma$ at any simple node
$\Sigma$ at any simple node ![]() $q\in \Sigma$ is called stable if the derivative
$q\in \Sigma$ is called stable if the derivative ![]() $\dot {\sigma }$ of any element
$\dot {\sigma }$ of any element ![]() $\sigma \in \Gamma _q$ acting on the Zariski tangent space
$\sigma \in \Gamma _q$ acting on the Zariski tangent space ![]() $T_q(\Sigma )$ satisfies the following:
$T_q(\Sigma )$ satisfies the following:
We say that ![]() $\Gamma$ acts stably on
$\Gamma$ acts stably on ![]() $\Sigma$ if it acts stably on each of its nodes.
$\Sigma$ if it acts stably on each of its nodes.
From now on, by a node we will always mean a simple node.
Assume that ![]() $p\in \bar {\Sigma }$ is a node (possibly among other nodes) and also assume that the fiber
$p\in \bar {\Sigma }$ is a node (possibly among other nodes) and also assume that the fiber ![]() $\pi ^{-1}(p)$ consists of nodal points. Assume further that the action of
$\pi ^{-1}(p)$ consists of nodal points. Assume further that the action of ![]() $\Gamma$ at the points
$\Gamma$ at the points ![]() $q\in \pi ^{-1}(p)$ is stable. Observe that, in this case, since
$q\in \pi ^{-1}(p)$ is stable. Observe that, in this case, since ![]() $p$ is assumed to be a node, any
$p$ is assumed to be a node, any ![]() $\sigma \in \Gamma _q$ can not exchange the two branches at
$\sigma \in \Gamma _q$ can not exchange the two branches at ![]() $q$ for otherwise the point
$q$ for otherwise the point ![]() $p$ would be smooth.
$p$ would be smooth.
We fix a level ![]() $c\geq 1$.
$c\geq 1$.
Let ![]() $\bar {\Sigma }'$ be the curve obtained from
$\bar {\Sigma }'$ be the curve obtained from ![]() $\bar {\Sigma }$ by the normalization
$\bar {\Sigma }$ by the normalization ![]() $\bar {\nu }:\bar {\Sigma }'\to \bar {\Sigma }$ at only the point
$\bar {\nu }:\bar {\Sigma }'\to \bar {\Sigma }$ at only the point ![]() $p$. Thus,
$p$. Thus, ![]() $\bar {\nu }^{-1}(p)$ consists of two smooth points
$\bar {\nu }^{-1}(p)$ consists of two smooth points ![]() $p',p''$ in
$p',p''$ in ![]() $\bar {\Sigma }'$ and
$\bar {\Sigma }'$ and
is a biregular isomorphism. We denote the preimage of any point of ![]() $\bar {\Sigma }\backslash \{p\}$ in
$\bar {\Sigma }\backslash \{p\}$ in ![]() $\bar {\Sigma }'\backslash \{ p',p'' \}$ by the same symbol. Let
$\bar {\Sigma }'\backslash \{ p',p'' \}$ by the same symbol. Let ![]() $\pi ' : {\Sigma }' \to \bar {\Sigma }'$ be the pull-back of the Galois cover
$\pi ' : {\Sigma }' \to \bar {\Sigma }'$ be the pull-back of the Galois cover ![]() $\pi$ via
$\pi$ via ![]() $\bar {\nu }$. In particular,
$\bar {\nu }$. In particular, ![]() $\pi '$ is a Galois cover with Galois group
$\pi '$ is a Galois cover with Galois group ![]() $\Gamma$. Thus, we have the following fiber diagram.
$\Gamma$. Thus, we have the following fiber diagram.

Lemma 5.2 With the same notation and assumptions as in Definition 5.1:
(1) the map
 $\nu$ is a normalization of
$\nu$ is a normalization of  ${\Sigma }$ at every point
${\Sigma }$ at every point  $q\in \pi ^{-1}(p)$;
$q\in \pi ^{-1}(p)$;(2) there exists a natural
 $\Gamma$-equivariant bijection
$\Gamma$-equivariant bijection  $\kappa : \pi '^{-1}(p')\simeq \pi '^{-1}(p'')$;
$\kappa : \pi '^{-1}(p')\simeq \pi '^{-1}(p'')$;(3) for any
 $q\in \pi ^{-1}(p)$, we have
where
$q\in \pi ^{-1}(p)$, we have
where \[ \Gamma_{q}= \Gamma_{q'}= \Gamma_{q''} , \]
\[ \Gamma_{q}= \Gamma_{q'}= \Gamma_{q''} , \]
 $\nu ^{-1}(q)$ consists of two smooth points
$\nu ^{-1}(q)$ consists of two smooth points  $q',q''$, and
$q',q''$, and  $\Gamma _{q}$,
$\Gamma _{q}$,  $\Gamma _{q'}$, and
$\Gamma _{q'}$, and  $\Gamma _{q''}$ are stabilizer groups of
$\Gamma _{q''}$ are stabilizer groups of  $\Gamma$ at
$\Gamma$ at  $q$,
$q$,  $q'$, and
$q'$, and  $q''$, respectively. Moreover,
$q''$, respectively. Moreover,  $\Gamma _{q}= \Gamma _{q'}= \Gamma _{q''}$ is a cyclic group.
$\Gamma _{q}= \Gamma _{q'}= \Gamma _{q''}$ is a cyclic group.
Proof. Let ![]() $q$ be any point in
$q$ be any point in ![]() $\pi ^{-1}(p)$ of ramification index
$\pi ^{-1}(p)$ of ramification index ![]() $e_q$. Since
$e_q$. Since ![]() $\pi ^{-1}(p)$ consists of nodal points by assumption, there are two branches in the formal neighborhood of
$\pi ^{-1}(p)$ consists of nodal points by assumption, there are two branches in the formal neighborhood of ![]() $q$. If any
$q$. If any ![]() $\sigma \in \Gamma _q$ exchanges two branches, then the point
$\sigma \in \Gamma _q$ exchanges two branches, then the point ![]() $p=\pi (q)$ is smooth in
$p=\pi (q)$ is smooth in ![]() $\bar {\Sigma }$, which contradicts the assumption that
$\bar {\Sigma }$, which contradicts the assumption that ![]() $p$ is a nodal point. Thus,
$p$ is a nodal point. Thus, ![]() $\Gamma _q$ must preserve branches. In particular, since no non-trivial element of
$\Gamma _q$ must preserve branches. In particular, since no non-trivial element of ![]() $\Gamma$ fixes pointwise any irreducible component of
$\Gamma$ fixes pointwise any irreducible component of ![]() $\Sigma$,
$\Sigma$, ![]() $\Gamma _q$ is cyclic. Therefore, by the condition (36), we can choose a formal coordinate system
$\Gamma _q$ is cyclic. Therefore, by the condition (36), we can choose a formal coordinate system ![]() $z',z''$ around the nodal point
$z',z''$ around the nodal point ![]() $q$ such that
$q$ such that ![]() $\hat {\mathscr {O}}_{{\Sigma }, q }\simeq \mathbb {C}[[z',z'' ]]/(z'z'')$, and a generator
$\hat {\mathscr {O}}_{{\Sigma }, q }\simeq \mathbb {C}[[z',z'' ]]/(z'z'')$, and a generator ![]() $\sigma _q$ of
$\sigma _q$ of ![]() $\Gamma _q$ such that
$\Gamma _q$ such that
where ![]() $\epsilon := e^{ {2\pi i}/{e_q}}$ is the standard primitive
$\epsilon := e^{ {2\pi i}/{e_q}}$ is the standard primitive ![]() $e_q$th root of unity. (Observe that
$e_q$th root of unity. (Observe that ![]() $\epsilon$ must be a primitive
$\epsilon$ must be a primitive ![]() $e_q$th root of unity, since
$e_q$th root of unity, since ![]() $\Gamma _q$ acts faithfully on each of the two formal branches through
$\Gamma _q$ acts faithfully on each of the two formal branches through ![]() $q$.)
$q$.)
We can choose a formal coordinate system ![]() $x'$,
$x'$, ![]() $x''$ around
$x''$ around ![]() $p$ in
$p$ in ![]() $\bar {\Sigma }$ such that
$\bar {\Sigma }$ such that ![]() $\hat {\mathscr {O}}_{{\bar {\Sigma }}, p }\simeq \mathbb {C}[[ x',x'' ]]/(x'x'')$ and the embedding
$\hat {\mathscr {O}}_{{\bar {\Sigma }}, p }\simeq \mathbb {C}[[ x',x'' ]]/(x'x'')$ and the embedding ![]() $\hat {\mathscr {O}}_{{\bar {\Sigma }}, p } \hookrightarrow \hat {\mathscr {O}}_{{\Sigma }, q }$ is given by
$\hat {\mathscr {O}}_{{\bar {\Sigma }}, p } \hookrightarrow \hat {\mathscr {O}}_{{\Sigma }, q }$ is given by ![]() $x'\mapsto (z')^{e_q}, x''\mapsto (z'')^{e_q}$.
$x'\mapsto (z')^{e_q}, x''\mapsto (z'')^{e_q}$.
The node ![]() $p$ splits into two smooth points
$p$ splits into two smooth points ![]() $p',p''$ via
$p',p''$ via ![]() $\bar {\nu }$. Without loss of generality, we can assume
$\bar {\nu }$. Without loss of generality, we can assume ![]() $x'$ (respectively,
$x'$ (respectively, ![]() $x''$) is a formal coordinate around
$x''$) is a formal coordinate around ![]() $p'$ (respectively,
$p'$ (respectively, ![]() $p''$) in
$p''$) in ![]() $\bar {\Sigma }'$. Then,
$\bar {\Sigma }'$. Then, ![]() $q$ will also split into two smooth points
$q$ will also split into two smooth points ![]() $q',q''$ via the map
$q',q''$ via the map ![]() $\nu$, where
$\nu$, where ![]() $z'$ (respectively,
$z'$ (respectively, ![]() $z''$) is a formal coordinate around
$z''$) is a formal coordinate around ![]() $q'$ (respectively,
$q'$ (respectively, ![]() $q''$). It shows that the map
$q''$). It shows that the map ![]() $\nu$ is a normalization at every point
$\nu$ is a normalization at every point ![]() $q\in \pi ^{-1}(p)$.
$q\in \pi ^{-1}(p)$.
The pullback gives a decomposition
From the definition of the fiber product, there exist ![]() $\Gamma$-equivariant canonical bijections:
$\Gamma$-equivariant canonical bijections:
Hence, we get a ![]() $\Gamma$-equivariant canonical bijection
$\Gamma$-equivariant canonical bijection ![]() $\kappa : \pi '^{-1}(p')\simeq \pi '^{-1}(p'')$. For any
$\kappa : \pi '^{-1}(p')\simeq \pi '^{-1}(p'')$. For any ![]() $q\in \pi ^{-1}(p)$,
$q\in \pi ^{-1}(p)$, ![]() $\nu ^{-1}(q)=\{q',q''\}$. By the choice of
$\nu ^{-1}(q)=\{q',q''\}$. By the choice of ![]() $q',q''$ as above,
$q',q''$ as above, ![]() $\pi '(q')=p'$ and
$\pi '(q')=p'$ and ![]() $\pi '(q'')=p''$. Therefore,
$\pi '(q'')=p''$. Therefore, ![]() $\kappa$ maps
$\kappa$ maps ![]() $q'$ to
$q'$ to ![]() $q''$. Moreover, from (37), the stabilizer groups
$q''$. Moreover, from (37), the stabilizer groups ![]() $\Gamma _q$,
$\Gamma _q$, ![]() $\Gamma _{q'}$, and
$\Gamma _{q'}$, and ![]() $\Gamma _{q'}$ are all the same (and of order
$\Gamma _{q'}$ are all the same (and of order ![]() $e_q$). Since
$e_q$). Since ![]() $q'$ (respectively,
$q'$ (respectively, ![]() $q''$) is a smooth point of
$q''$) is a smooth point of ![]() $\Sigma '$,
$\Sigma '$, ![]() $\Gamma _{q'}$ (respectively,
$\Gamma _{q'}$ (respectively, ![]() $\Gamma _{q''}$) is cyclic.
$\Gamma _{q''}$) is cyclic.
Let ![]() $\mathfrak {g}_p$ denote the Lie algebra
$\mathfrak {g}_p$ denote the Lie algebra ![]() $\mathfrak {g}[\pi ^{-1}(p)]^\Gamma$ (observe that we can attach a Lie algebra
$\mathfrak {g}[\pi ^{-1}(p)]^\Gamma$ (observe that we can attach a Lie algebra ![]() $\mathfrak {g}_p$ regardless of the smoothness of
$\mathfrak {g}_p$ regardless of the smoothness of ![]() $p$). Then, the
$p$). Then, the ![]() $\Gamma$-equivariant bijections
$\Gamma$-equivariant bijections ![]() $\nu : \pi '^{-1}(p')\simeq \pi ^{-1}(p)$ and
$\nu : \pi '^{-1}(p')\simeq \pi ^{-1}(p)$ and ![]() $\nu : \pi '^{-1}(p'')\simeq \pi ^{-1}(p)$ (cf. (37)) induce isomorphisms of Lie algebras
$\nu : \pi '^{-1}(p'')\simeq \pi ^{-1}(p)$ (cf. (37)) induce isomorphisms of Lie algebras ![]() $\varkappa ': \mathfrak {g}_{p'}\simeq \mathfrak {g}_p$ and
$\varkappa ': \mathfrak {g}_{p'}\simeq \mathfrak {g}_p$ and ![]() $\varkappa '': \mathfrak {g}_{p''}\simeq \mathfrak {g}_{p}$, respectively. Recall that
$\varkappa '': \mathfrak {g}_{p''}\simeq \mathfrak {g}_{p}$, respectively. Recall that ![]() $p', p''$ are smooth points of
$p', p''$ are smooth points of ![]() $\bar {\Sigma }'$. Let
$\bar {\Sigma }'$. Let ![]() $D_{c,p'}$ (respectively,
$D_{c,p'}$ (respectively, ![]() $D_{c,p''}$) denote the finite set of highest weights of irreducible representations of
$D_{c,p''}$) denote the finite set of highest weights of irreducible representations of ![]() $\mathfrak {g}_p$ induced via the isomorphism
$\mathfrak {g}_p$ induced via the isomorphism ![]() $\varkappa '$ (respectively,
$\varkappa '$ (respectively, ![]() $\varkappa ''$) which give rise to integrable highest weight
$\varkappa ''$) which give rise to integrable highest weight ![]() $\hat {\mathfrak {g}}_{p'}$-modules (respectively,
$\hat {\mathfrak {g}}_{p'}$-modules (respectively, ![]() $\hat {\mathfrak {g}}_{p''}$-modules) with central charge
$\hat {\mathfrak {g}}_{p''}$-modules) with central charge ![]() $c$.
$c$.
Set
The map ![]() ${\nu }$ on restriction gives rise to an isomorphism
${\nu }$ on restriction gives rise to an isomorphism
which, in turn, gives rise to a Lie algebra homomorphism
Let ![]() $\vec {\lambda }=(\lambda _1, \ldots, \lambda _s)$ be an
$\vec {\lambda }=(\lambda _1, \ldots, \lambda _s)$ be an ![]() $s$-tuple of weights with
$s$-tuple of weights with ![]() $\lambda _i\in D_{c, o_i}$ ‘attached’ to
$\lambda _i\in D_{c, o_i}$ ‘attached’ to ![]() $o_i$. We denote the highest weight of the dual representation
$o_i$. We denote the highest weight of the dual representation ![]() $V(\mu )^*$ of
$V(\mu )^*$ of ![]() $\mathfrak {g}_p$ by
$\mathfrak {g}_p$ by ![]() $\mu ^*$, thus
$\mu ^*$, thus ![]() $V(\mu )^* \simeq V(\mu ^*)$.
$V(\mu )^* \simeq V(\mu ^*)$.
By Lemma 5.2, there exists a canonical bijection ![]() $\kappa : \pi '^{-1}(p')\simeq \pi '^{-1}(p'')$ compatible with the action of
$\kappa : \pi '^{-1}(p')\simeq \pi '^{-1}(p'')$ compatible with the action of ![]() $\Gamma$. Thus, it induces an isomorphism of Lie algebras
$\Gamma$. Thus, it induces an isomorphism of Lie algebras ![]() $\mathfrak {g}_{p'}\simeq \mathfrak {g}_{p''}$.
$\mathfrak {g}_{p'}\simeq \mathfrak {g}_{p''}$.
Lemma 5.3 In the same setting as in Lemma 5.2, we have:
(1) there exists an isomorphism
 $\hat {\mathfrak {g}}_{p'}\simeq \hat {\mathfrak {g}}_{p''}$ which restricts to the isomorphisms
(see the relevant notation in § 3);
$\hat {\mathfrak {g}}_{p'}\simeq \hat {\mathfrak {g}}_{p''}$ which restricts to the isomorphisms
(see the relevant notation in § 3); \[ \hat{\mathfrak{p}}_{p'}\simeq \hat{\mathfrak{p}}_{p''}, \quad \hat{\mathfrak{g}}^+_{p'}\simeq \hat{\mathfrak{g}}^+_{p''}, \quad \text{and} \quad \mathfrak{g}_{p'}\simeq \mathfrak{g}_{p''} \]
\[ \hat{\mathfrak{p}}_{p'}\simeq \hat{\mathfrak{p}}_{p''}, \quad \hat{\mathfrak{g}}^+_{p'}\simeq \hat{\mathfrak{g}}^+_{p''}, \quad \text{and} \quad \mathfrak{g}_{p'}\simeq \mathfrak{g}_{p''} \]
(2)
 $\mu \in D_{c,p'}$ if and only if
$\mu \in D_{c,p'}$ if and only if  $\mu ^* \in D_{c,p''}$.
$\mu ^* \in D_{c,p''}$.
Proof. For any ![]() $q\in \pi ^{-1}(p)$, in view of Lemma 3.3, the restriction gives isomorphisms
$q\in \pi ^{-1}(p)$, in view of Lemma 3.3, the restriction gives isomorphisms ![]() ${\rm res}_{q'}: \hat {\mathfrak {g}}_{p'}\simeq \hat {L}(\mathfrak {g}, \Gamma _{q'})$ and
${\rm res}_{q'}: \hat {\mathfrak {g}}_{p'}\simeq \hat {L}(\mathfrak {g}, \Gamma _{q'})$ and ![]() ${\rm res}_{q''}: \hat {\mathfrak {g}}_{p''}\simeq \hat {L}(\mathfrak {g}, \Gamma _{q''})$. By Lemma 5.2,
${\rm res}_{q''}: \hat {\mathfrak {g}}_{p''}\simeq \hat {L}(\mathfrak {g}, \Gamma _{q''})$. By Lemma 5.2, ![]() $\Gamma _{q'}=\Gamma _{q''}$. As in (3), let
$\Gamma _{q'}=\Gamma _{q''}$. As in (3), let ![]() $\mathfrak {b}'$ (respectively,
$\mathfrak {b}'$ (respectively, ![]() $\mathfrak {h}' \subset \mathfrak {b}'$) be a suitable Borel (respectively, Cartan) subalgebra of
$\mathfrak {h}' \subset \mathfrak {b}'$) be a suitable Borel (respectively, Cartan) subalgebra of ![]() $\mathfrak {g}$ stable under
$\mathfrak {g}$ stable under ![]() $\Gamma _{q'}$. This gives rise to Chevalley generators
$\Gamma _{q'}$. This gives rise to Chevalley generators ![]() $e_i \in \mathfrak {n}'$ and
$e_i \in \mathfrak {n}'$ and ![]() $f_i\in \mathfrak {n}'^-$, where
$f_i\in \mathfrak {n}'^-$, where ![]() $\mathfrak {n}'$ (respectively,
$\mathfrak {n}'$ (respectively, ![]() $\mathfrak {n}'^-$) is the nilradical of
$\mathfrak {n}'^-$) is the nilradical of ![]() $\mathfrak {b}'$ (respectively, the opposite Borel subalgebra
$\mathfrak {b}'$ (respectively, the opposite Borel subalgebra ![]() $\mathfrak {b}'^-$). Let
$\mathfrak {b}'^-$). Let ![]() $\omega :\mathfrak {g} \to \mathfrak {g}$ be the Cartan involution taking the Chevalley generators of
$\omega :\mathfrak {g} \to \mathfrak {g}$ be the Cartan involution taking the Chevalley generators of ![]() $\mathfrak {g}$:
$\mathfrak {g}$: ![]() $e_j\mapsto -f_j, f_j\mapsto -e_j$ and
$e_j\mapsto -f_j, f_j\mapsto -e_j$ and ![]() $h \mapsto -h$ for any
$h \mapsto -h$ for any ![]() $h\in \mathfrak {h}'$.
$h\in \mathfrak {h}'$.
Write as in § 2,
Thus,
However, by the definition of (any diagram automorphism) ![]() $\tau '$ and
$\tau '$ and ![]() $\omega$, it is easy to see that
$\omega$, it is easy to see that
We now need to consider two cases.
Case I: ![]() $\tau '$ is of order
$\tau '$ is of order ![]() $1$ or
$1$ or ![]() $2$. In this case,
$2$. In this case,
 \begin{align} \omega^{-1} \sigma_{q'}
\omega &= \tau'\epsilon^{-\mathrm{ad}\,h'},\quad \text{by
(38) and (39)}\nonumber\\ &=
\tau'^{-1}\epsilon^{-\mathrm{ad} \,h'},\quad \text{since
$\tau'$ is assumed to be of order $1$ or $2$} \nonumber\\
&=\sigma_{q'}^{-1}. \end{align}
\begin{align} \omega^{-1} \sigma_{q'}
\omega &= \tau'\epsilon^{-\mathrm{ad}\,h'},\quad \text{by
(38) and (39)}\nonumber\\ &=
\tau'^{-1}\epsilon^{-\mathrm{ad} \,h'},\quad \text{since
$\tau'$ is assumed to be of order $1$ or $2$} \nonumber\\
&=\sigma_{q'}^{-1}. \end{align}
Case II: ![]() $\tau '$ is of order
$\tau '$ is of order ![]() $3$. That is,
$3$. That is, ![]() $\mathfrak {g}$ is of type
$\mathfrak {g}$ is of type ![]() $D_4$ with labelled nodes
$D_4$ with labelled nodes

and ![]() $\tau '$ is the diagram automorphism induced from taking the nodes
$\tau '$ is the diagram automorphism induced from taking the nodes ![]() $1 \mapsto 3$,
$1 \mapsto 3$, ![]() $2\mapsto 2$,
$2\mapsto 2$, ![]() $3\mapsto 4$,
$3\mapsto 4$, ![]() $4 \mapsto 1$. Let
$4 \mapsto 1$. Let ![]() $\tau _1$ be the diagram automorphism induced from taking the nodes
$\tau _1$ be the diagram automorphism induced from taking the nodes ![]() $1 \mapsto 1$,
$1 \mapsto 1$, ![]() $2\mapsto 2$,
$2\mapsto 2$, ![]() $3\mapsto 4$,
$3\mapsto 4$, ![]() $4 \mapsto 3$. Then,
$4 \mapsto 3$. Then,
In this case, we have
 \begin{align}
(\omega\tau_1)^{-1} \sigma_{q'} \omega \tau_1&= \tau_1^{-1}\tau'\epsilon^{-\mathrm{ad} \,h'}\tau_1, \quad
\text{by (38) and (39)}\nonumber\\ &=
\tau'^{-1}\tau_1^{-1}\epsilon^{-\mathrm{ad}\,
h'}\tau_1,\quad \text{by (41)} \nonumber\\
&=\tau'^{-1}\epsilon^{-\mathrm{ad}\, h'},\quad \mbox{since}
(\tau_1)_{|\mathfrak{h}^{\tau'}}=\mbox{Id by Kac90, } \$ \mbox{8.3, Case 4}\nonumber\\ &=\sigma_{q'}^{-1}.
\end{align}
\begin{align}
(\omega\tau_1)^{-1} \sigma_{q'} \omega \tau_1&= \tau_1^{-1}\tau'\epsilon^{-\mathrm{ad} \,h'}\tau_1, \quad
\text{by (38) and (39)}\nonumber\\ &=
\tau'^{-1}\tau_1^{-1}\epsilon^{-\mathrm{ad}\,
h'}\tau_1,\quad \text{by (41)} \nonumber\\
&=\tau'^{-1}\epsilon^{-\mathrm{ad}\, h'},\quad \mbox{since}
(\tau_1)_{|\mathfrak{h}^{\tau'}}=\mbox{Id by Kac90, } \$ \mbox{8.3, Case 4}\nonumber\\ &=\sigma_{q'}^{-1}.
\end{align}
Let ![]() $\omega _o$ be the Cartan involution
$\omega _o$ be the Cartan involution ![]() $\omega$ in the first case and
$\omega$ in the first case and ![]() $\omega \tau _1$ in the second case. Extend
$\omega \tau _1$ in the second case. Extend ![]() $\omega _o$ to an isomorphism of twisted affine Lie algebras:
$\omega _o$ to an isomorphism of twisted affine Lie algebras:
for any ![]() $x\in \mathfrak {g}$ and
$x\in \mathfrak {g}$ and ![]() $P\in \mathcal {K}$, where
$P\in \mathcal {K}$, where ![]() $\sigma _{q'}$ and
$\sigma _{q'}$ and ![]() $\sigma _{q''}=\sigma _{q'}^{-1}$ are the preferred generators of
$\sigma _{q''}=\sigma _{q'}^{-1}$ are the preferred generators of ![]() $\Gamma _q=\Gamma _{q'}=\Gamma _{q''}$ acting on a formal coordinate
$\Gamma _q=\Gamma _{q'}=\Gamma _{q''}$ acting on a formal coordinate ![]() $z', z''$ around
$z', z''$ around ![]() $q', q''$, respectively, via
$q', q''$, respectively, via ![]() $\epsilon ^{-1}$ (see the proof of Lemma 5.2). Indeed,
$\epsilon ^{-1}$ (see the proof of Lemma 5.2). Indeed, ![]() $\hat {\omega }_o$ is an isomorphism by the identities (40) and (42). Observe that
$\hat {\omega }_o$ is an isomorphism by the identities (40) and (42). Observe that ![]() $\hat {\omega }_o$ restricted to
$\hat {\omega }_o$ restricted to ![]() $\mathfrak {h}^{\sigma _{q'}}=\mathfrak {h}^{\sigma _{q''}}$ is nothing but the Cartan involution. Clearly,
$\mathfrak {h}^{\sigma _{q'}}=\mathfrak {h}^{\sigma _{q''}}$ is nothing but the Cartan involution. Clearly, ![]() $\hat {\omega }_o$ restricts to an isomorphism
$\hat {\omega }_o$ restricts to an isomorphism ![]() $\hat {\mathfrak {p}}_{p'}\simeq \hat {\mathfrak {p}}_{p''}$,
$\hat {\mathfrak {p}}_{p'}\simeq \hat {\mathfrak {p}}_{p''}$, ![]() $\hat {\mathfrak {g}}^+_{p'}\simeq \hat {\mathfrak {g}}^+_{p''}$ and
$\hat {\mathfrak {g}}^+_{p'}\simeq \hat {\mathfrak {g}}^+_{p''}$ and ![]() $\mathfrak {g}_{p'}\simeq \mathfrak {g}_{p''}$ (see (12) and (13) for relevant notation). This proves the first part of the lemma.
$\mathfrak {g}_{p'}\simeq \mathfrak {g}_{p''}$ (see (12) and (13) for relevant notation). This proves the first part of the lemma.
From the isomorphism ![]() $\hat {\omega }_o$, the second part of the lemma follows immediately since
$\hat {\omega }_o$, the second part of the lemma follows immediately since ![]() $\mathfrak {n}'^{\sigma _{q'}}$ is a maximal nilpotent subalgebra of
$\mathfrak {n}'^{\sigma _{q'}}$ is a maximal nilpotent subalgebra of ![]() $\mathfrak {g}^{\sigma _{q'}}$.
$\mathfrak {g}^{\sigma _{q'}}$.
We also give another proof of the second part of the above lemma.
Another proof of Lemma 5.3, part (2). Let ![]() $\sigma _{q'}$ (respectively,
$\sigma _{q'}$ (respectively, ![]() $\sigma _{q''}$) be the canonical generator of
$\sigma _{q''}$) be the canonical generator of ![]() $\Gamma _{q'}$ (respectively,
$\Gamma _{q'}$ (respectively, ![]() $\Gamma _{q''}$). We can choose formal parameter
$\Gamma _{q''}$). We can choose formal parameter ![]() $z'$ (respectively,
$z'$ (respectively, ![]() $z''$) around
$z''$) around ![]() $q'$ (respectively,
$q'$ (respectively, ![]() $q''$) such that
$q''$) such that
where ![]() $\epsilon =e^{ {2\pi i}/{|\Gamma _q| } }$. As in § 2, we can write
$\epsilon =e^{ {2\pi i}/{|\Gamma _q| } }$. As in § 2, we can write ![]() $\sigma _{q'}=\tau '\cdot \epsilon ^{{\rm ad}\, h' }$. Let
$\sigma _{q'}=\tau '\cdot \epsilon ^{{\rm ad}\, h' }$. Let ![]() $x'_{i}, y'_i, h'_i=[x'_i,y'_i]$,
$x'_{i}, y'_i, h'_i=[x'_i,y'_i]$, ![]() $i\in \hat {I}(\mathfrak {g}, \sigma _{q'})$ be chosen as in § 2, where
$i\in \hat {I}(\mathfrak {g}, \sigma _{q'})$ be chosen as in § 2, where
where ![]() $\alpha '_i$ is the simple root of
$\alpha '_i$ is the simple root of ![]() $\mathfrak {g}^{\tau '}$ associated to
$\mathfrak {g}^{\tau '}$ associated to ![]() $i\in I(\mathfrak {g}^{\tau '})$, and
$i\in I(\mathfrak {g}^{\tau '})$, and
Let ![]() $s_i, i\in \hat {I}(\mathfrak {g}, \sigma _{q'})$ be the integers as in § 2. We have, by the identity (5),
$s_i, i\in \hat {I}(\mathfrak {g}, \sigma _{q'})$ be the integers as in § 2. We have, by the identity (5),
for any ![]() $i\in \hat {I}(\mathfrak {g}, \sigma _{q'})$. Moreover, as in § 2, the elements
$i\in \hat {I}(\mathfrak {g}, \sigma _{q'})$. Moreover, as in § 2, the elements ![]() $x_i'[z'^{s_i}], y'_i[z'^{-s_i}], h'_i+e_q^{-1}\langle x'_i, y'_i \rangle s_i C$ in
$x_i'[z'^{s_i}], y'_i[z'^{-s_i}], h'_i+e_q^{-1}\langle x'_i, y'_i \rangle s_i C$ in ![]() $\hat {L}(\mathfrak {g}, \sigma _{q'})$ are a set of Chevalley generators generating the non-completed Kac–Moody algebra
$\hat {L}(\mathfrak {g}, \sigma _{q'})$ are a set of Chevalley generators generating the non-completed Kac–Moody algebra ![]() $\tilde {L}(\mathfrak {g}, \sigma _{q'})\subset \hat {L}(\mathfrak {g}, \sigma _{q'})$, where
$\tilde {L}(\mathfrak {g}, \sigma _{q'})\subset \hat {L}(\mathfrak {g}, \sigma _{q'})$, where ![]() $e_q:=|\Gamma _{q'}|$. It is well-known that there is a natural bijection between the set of integrable highest weight representations of
$e_q:=|\Gamma _{q'}|$. It is well-known that there is a natural bijection between the set of integrable highest weight representations of ![]() $\hat {L}(\mathfrak {g}, \sigma _{q'})$ and
$\hat {L}(\mathfrak {g}, \sigma _{q'})$ and ![]() $\tilde {L}(\mathfrak {g}, \sigma _{q'})$.
$\tilde {L}(\mathfrak {g}, \sigma _{q'})$.
We now introduce the following notation:
for any ![]() $i\in \hat {I}(\mathfrak {g}, \sigma _{q'})$. Note that
$i\in \hat {I}(\mathfrak {g}, \sigma _{q'})$. Note that ![]() $\sigma _{q''}=(\sigma _{q'})^{-1}$. We can identify
$\sigma _{q''}=(\sigma _{q'})^{-1}$. We can identify ![]() $\hat {I}(\mathfrak {g}, \sigma _{q'})$ and
$\hat {I}(\mathfrak {g}, \sigma _{q'})$ and ![]() $\hat {I}(\mathfrak {g}, \sigma _{q''})$, since
$\hat {I}(\mathfrak {g}, \sigma _{q''})$, since ![]() $\mathfrak {g}^{\tau ''}=\mathfrak {g}^{\tau '}$ where
$\mathfrak {g}^{\tau ''}=\mathfrak {g}^{\tau '}$ where ![]() $\tau ''=\tau '^{-1}$ is the diagram automorphism part of
$\tau ''=\tau '^{-1}$ is the diagram automorphism part of ![]() $\sigma _{q''}$.
$\sigma _{q''}$.
Set ![]() $\alpha ''_i=-\alpha '_i$ for any
$\alpha ''_i=-\alpha '_i$ for any ![]() $i\in I(\mathfrak {g}^{\tau ''})$, and
$i\in I(\mathfrak {g}^{\tau ''})$, and ![]() $\theta ''_0=-\theta '_0$. We can choose
$\theta ''_0=-\theta '_0$. We can choose ![]() $\alpha ''_i, i\in I(\mathfrak {g}^{\tau ''})$ as a set of simple roots for
$\alpha ''_i, i\in I(\mathfrak {g}^{\tau ''})$ as a set of simple roots for ![]() $\mathfrak {g}^{\tau ''}$. Then,
$\mathfrak {g}^{\tau ''}$. Then, ![]() $\theta ''_0$ is the weight of
$\theta ''_0$ is the weight of ![]() $\mathfrak {g}^{\tau ''}$ as in § 2 with respect to this choice. Moreover,
$\mathfrak {g}^{\tau ''}$ as in § 2 with respect to this choice. Moreover, ![]() $x''_i, y''_i, i\in I(\mathfrak {g}^{\tau ''})$ is a set of Chevalley generators of
$x''_i, y''_i, i\in I(\mathfrak {g}^{\tau ''})$ is a set of Chevalley generators of ![]() $\mathfrak {g}^{\tau ''}$, and
$\mathfrak {g}^{\tau ''}$, and ![]() $x''_0\in (\mathfrak {g}^{\tau ''})_{-\theta ''_0}, y''_0\in (\mathfrak {g}^{\tau ''})_{\theta ''_0}$ also satisfies the choice as in [Reference KacKac90, § 8.3]. We also note that
$x''_0\in (\mathfrak {g}^{\tau ''})_{-\theta ''_0}, y''_0\in (\mathfrak {g}^{\tau ''})_{\theta ''_0}$ also satisfies the choice as in [Reference KacKac90, § 8.3]. We also note that
for any ![]() $i\in \hat {I}(\mathfrak {g}, \sigma _{q'})$. As above, we see that the elements
$i\in \hat {I}(\mathfrak {g}, \sigma _{q'})$. As above, we see that the elements ![]() $x''_i[ z''^{s_i}], y''_i[z''^{-s_i} ], h''_i + |\Gamma _{q''}|^{-1} \langle x''_i, y''_i \rangle s_i C$ as elements in
$x''_i[ z''^{s_i}], y''_i[z''^{-s_i} ], h''_i + |\Gamma _{q''}|^{-1} \langle x''_i, y''_i \rangle s_i C$ as elements in ![]() $\hat {L}(\mathfrak {g}, \sigma _{q''})$ are Chevalley generators generating the non-completed Kac–Moody algebra
$\hat {L}(\mathfrak {g}, \sigma _{q''})$ are Chevalley generators generating the non-completed Kac–Moody algebra ![]() $\tilde {L}(\mathfrak {g}, \sigma _{q''})\subset \hat {L}(\mathfrak {g}, \sigma _{q''})$. Again, there is a natural bijection between the set of integrable highest weight representations of
$\tilde {L}(\mathfrak {g}, \sigma _{q''})\subset \hat {L}(\mathfrak {g}, \sigma _{q''})$. Again, there is a natural bijection between the set of integrable highest weight representations of ![]() $\hat {L}(\mathfrak {g}, \sigma _{q''})$ and
$\hat {L}(\mathfrak {g}, \sigma _{q''})$ and ![]() $\tilde {L}(\mathfrak {g}, \sigma _{q''})$.
$\tilde {L}(\mathfrak {g}, \sigma _{q''})$.
We now get an isomorphism of Lie algebras:
given by
and
for any ![]() $i\in \hat {I}(\mathfrak {g}, \sigma _{q'})$. Note that
$i\in \hat {I}(\mathfrak {g}, \sigma _{q'})$. Note that ![]() $\langle x'_i, y'_i \rangle =\langle x''_i, y''_i\rangle$ for any
$\langle x'_i, y'_i \rangle =\langle x''_i, y''_i\rangle$ for any ![]() $i$. The map
$i$. The map ![]() $\hat {\omega }$ is indeed an isomorphism, since these Chevalley generators correspond to the same vertices of the affine Dynkin diagram.
$\hat {\omega }$ is indeed an isomorphism, since these Chevalley generators correspond to the same vertices of the affine Dynkin diagram.
Set
Similarly, we can introduce the Lie algebras ![]() $\tilde {L}(\mathfrak {g}, \sigma _{q''})^+$ and
$\tilde {L}(\mathfrak {g}, \sigma _{q''})^+$ and ![]() $\tilde {L}(\mathfrak {g}, \sigma _{q''})^{\geq 0}$. We can see easily that
$\tilde {L}(\mathfrak {g}, \sigma _{q''})^{\geq 0}$. We can see easily that
Recall that ![]() $\mathfrak {g}^{\Gamma _q} \oplus \mathbb {C} C$ is a Levi subalgebra of
$\mathfrak {g}^{\Gamma _q} \oplus \mathbb {C} C$ is a Levi subalgebra of ![]() $\tilde {L}(\mathfrak {g}, \sigma _{q'})$, which is generated by
$\tilde {L}(\mathfrak {g}, \sigma _{q'})$, which is generated by ![]() $x'_i, y'_i$ and
$x'_i, y'_i$ and ![]() $\mathfrak {h}^{\Gamma _q}\oplus \mathbb {C}C$ where
$\mathfrak {h}^{\Gamma _q}\oplus \mathbb {C}C$ where ![]() $i\in \hat {I}(\mathfrak {g}, \sigma _{q'})^0$ consisting of
$i\in \hat {I}(\mathfrak {g}, \sigma _{q'})^0$ consisting of ![]() $i\in \hat {I}(\mathfrak {g}, \sigma _{q'})$ such that
$i\in \hat {I}(\mathfrak {g}, \sigma _{q'})$ such that ![]() $s_i=0$. Therefore, the isomorphism
$s_i=0$. Therefore, the isomorphism ![]() $\hat {\omega }$ also induces a Cartan involution
$\hat {\omega }$ also induces a Cartan involution ![]() $\omega$ on
$\omega$ on ![]() $\mathfrak {g}^{\Gamma _q}$, given on the Chevalley generators by
$\mathfrak {g}^{\Gamma _q}$, given on the Chevalley generators by
for any ![]() $i\in \hat {I}(\mathfrak {g}, \sigma _{q'})^0$, and
$i\in \hat {I}(\mathfrak {g}, \sigma _{q'})^0$, and ![]() $h\in \mathfrak {h}^{\Gamma _q}$. It is now clear that the isomorphism
$h\in \mathfrak {h}^{\Gamma _q}$. It is now clear that the isomorphism ![]() $\hat {\omega }$ induces a bijection
$\hat {\omega }$ induces a bijection ![]() $\kappa : D_{c, q'}\simeq D_{c, q''}$ given by
$\kappa : D_{c, q'}\simeq D_{c, q''}$ given by ![]() $V\mapsto V^*$. This completes the other proof of Lemma 5.3, part (2).
$V\mapsto V^*$. This completes the other proof of Lemma 5.3, part (2).
Define the linear map
 \begin{equation} \hat{F}:\mathscr{H} (\vec{\lambda})\to \mathscr{H} (\vec{\lambda})\otimes \bigg(\bigoplus_{\mu\in D_{c,p''}} V (\mu^*) \otimes V(\mu)\bigg),\quad h\mapsto h\otimes \sum_{\mu\in D_{c,p''}} I_{\mu},\quad \text{for}\ h \in \mathscr{H}(\vec{\lambda}), \end{equation}
\begin{equation} \hat{F}:\mathscr{H} (\vec{\lambda})\to \mathscr{H} (\vec{\lambda})\otimes \bigg(\bigoplus_{\mu\in D_{c,p''}} V (\mu^*) \otimes V(\mu)\bigg),\quad h\mapsto h\otimes \sum_{\mu\in D_{c,p''}} I_{\mu},\quad \text{for}\ h \in \mathscr{H}(\vec{\lambda}), \end{equation}
where ![]() $I_{\mu }$ is the identity map thought of as an element of
$I_{\mu }$ is the identity map thought of as an element of ![]() $V(\mu ^*)\otimes V(\mu )\simeq \operatorname {\mathrm {End}}_{\mathbb {C}}(V(\mu ))$.
$V(\mu ^*)\otimes V(\mu )\simeq \operatorname {\mathrm {End}}_{\mathbb {C}}(V(\mu ))$.
We view ![]() $V(\mu ^*)$ (respectively,
$V(\mu ^*)$ (respectively, ![]() $V(\mu )$) as an irreducible representation of
$V(\mu )$) as an irreducible representation of ![]() $\mathfrak {g}_{p'}$ (respectively,
$\mathfrak {g}_{p'}$ (respectively, ![]() $\mathfrak {g}_{p''}$) via the isomorphism
$\mathfrak {g}_{p''}$) via the isomorphism ![]() $\varkappa '$ (respectively,
$\varkappa '$ (respectively, ![]() $\varkappa ''$) defined above Lemma 5.3. Let
$\varkappa ''$) defined above Lemma 5.3. Let ![]() $\mathscr {H}(\mu ^*)$ (respectively,
$\mathscr {H}(\mu ^*)$ (respectively, ![]() $\mathscr {H}(\mu )$) denote the highest weight integrable representation of
$\mathscr {H}(\mu )$) denote the highest weight integrable representation of ![]() $\hat {\mathfrak {g}}_{p'}$ (respectively,
$\hat {\mathfrak {g}}_{p'}$ (respectively, ![]() $\hat {\mathfrak {g}}_{p''}$) associated to
$\hat {\mathfrak {g}}_{p''}$) associated to ![]() $\mu ^*$ (respectively,
$\mu ^*$ (respectively, ![]() $\mu$) of level
$\mu$) of level ![]() $c$. Realize
$c$. Realize ![]() $\mathscr {H}(\vec {\lambda })\otimes \mathscr {H}(\mu ^*) \otimes \mathscr {H}(\mu )$ (which contains
$\mathscr {H}(\vec {\lambda })\otimes \mathscr {H}(\mu ^*) \otimes \mathscr {H}(\mu )$ (which contains ![]() $\mathscr {H} (\vec {\lambda })\otimes V (\mu ^*) \otimes V(\mu )$) as a
$\mathscr {H} (\vec {\lambda })\otimes V (\mu ^*) \otimes V(\mu )$) as a ![]() $\mathfrak {g}[ {\Sigma }^{\prime o} \backslash \pi '^{-1}\{ p',p'' \}]^\Gamma$-module at the points
$\mathfrak {g}[ {\Sigma }^{\prime o} \backslash \pi '^{-1}\{ p',p'' \}]^\Gamma$-module at the points ![]() $\vec {o}, p',p''$, respectively. Then,
$\vec {o}, p',p''$, respectively. Then, ![]() $I_\mu$ being a
$I_\mu$ being a ![]() $\mathfrak {g}_{p}$-invariant,
$\mathfrak {g}_{p}$-invariant, ![]() $\hat {F}$ is a
$\hat {F}$ is a ![]() $\mathfrak {g}[{\Sigma }^o]^\Gamma$-module map, where we realize the range as a
$\mathfrak {g}[{\Sigma }^o]^\Gamma$-module map, where we realize the range as a ![]() $\mathfrak {g}[{\Sigma }^o]^\Gamma$-module via the Lie algebra homomorphism
$\mathfrak {g}[{\Sigma }^o]^\Gamma$-module via the Lie algebra homomorphism ![]() ${\nu }^*$. Hence,
${\nu }^*$. Hence, ![]() $\hat {F}$ induces a linear map
$\hat {F}$ induces a linear map
The following theorem is the twisted analogue of the factorization theorem due to Tsuchiya, Ueno, and Yamada [Reference Tsuchiya, Ueno and YamadaTUY89].
Theorem 5.4 With the setting as in Lemma 5.2, we further assume that ![]() $\Gamma$ stabilizes a Borel subalgebra
$\Gamma$ stabilizes a Borel subalgebra ![]() $\mathfrak {b}$ and
$\mathfrak {b}$ and ![]() $\pi ^{-1}(\vec {o})$ consists of smooth points of
$\pi ^{-1}(\vec {o})$ consists of smooth points of ![]() $\Sigma$. Then, the map
$\Sigma$. Then, the map
is an isomorphism.
Dualizing the map ![]() $F$, we get an isomorphism
$F$, we get an isomorphism
Proof. As discussed above, the map ![]() $\hat {F}$ defined in (43) is
$\hat {F}$ defined in (43) is ![]() $\mathfrak {g}[ {\Sigma }^o ]^\Gamma$-equivariant. By the propagation theorem (Theorem 4.3) at points
$\mathfrak {g}[ {\Sigma }^o ]^\Gamma$-equivariant. By the propagation theorem (Theorem 4.3) at points ![]() $p'$ and
$p'$ and ![]() $p''$, taking covariants on both sides of
$p''$, taking covariants on both sides of ![]() $\hat {F}$ with respect to the action of
$\hat {F}$ with respect to the action of ![]() $\mathfrak {g}[ {\Sigma }^o]^\Gamma$ on the left side and with respect to the action of
$\mathfrak {g}[ {\Sigma }^o]^\Gamma$ on the left side and with respect to the action of ![]() $\mathfrak {g}[ {\Sigma }^{\prime o}]^\Gamma$ on the right side, we also obtain the map
$\mathfrak {g}[ {\Sigma }^{\prime o}]^\Gamma$ on the right side, we also obtain the map ![]() $F$.
$F$.
We first prove the surjectivity of ![]() $F$. Fix a point
$F$. Fix a point ![]() $q\in \pi ^{-1}(p)$, we may view
$q\in \pi ^{-1}(p)$, we may view ![]() $V(\mu ^*)$ and
$V(\mu ^*)$ and ![]() $V(\mu )$ as representations of the Lie algebra
$V(\mu )$ as representations of the Lie algebra ![]() $\mathfrak {g}^{\Gamma _q}$ via the evaluation map
$\mathfrak {g}^{\Gamma _q}$ via the evaluation map ![]() ${\rm ev}_{q}: \mathfrak {g}_{p}\simeq \mathfrak {g}^{\Gamma _q}$ (cf. Lemma 3.2). Correspondingly, we may view
${\rm ev}_{q}: \mathfrak {g}_{p}\simeq \mathfrak {g}^{\Gamma _q}$ (cf. Lemma 3.2). Correspondingly, we may view ![]() $D_{c,p''}$ as certain set of highest weights of
$D_{c,p''}$ as certain set of highest weights of ![]() $\mathfrak {g}^{\Gamma _q}$. Observe first that
$\mathfrak {g}^{\Gamma _q}$. Observe first that ![]() $\Gamma \cdot q'\cap \Gamma \cdot q'' = \emptyset$, since
$\Gamma \cdot q'\cap \Gamma \cdot q'' = \emptyset$, since ![]() $\pi '$ is
$\pi '$ is ![]() $\Gamma$-invariant and
$\Gamma$-invariant and ![]() $\pi '(\Gamma \cdot q') = p'$ and
$\pi '(\Gamma \cdot q') = p'$ and ![]() $\pi '(\Gamma \cdot q'' )=p''$. Choose a function
$\pi '(\Gamma \cdot q'' )=p''$. Choose a function ![]() $f\in \mathbb {C}[\Sigma '^o]$ such that
$f\in \mathbb {C}[\Sigma '^o]$ such that
For any ![]() $x\in \mathfrak {g}^{\Gamma _q}$, let
$x\in \mathfrak {g}^{\Gamma _q}$, let
 \begin{equation} A(x[f]):= \frac{1}{|\Gamma_q|}\sum_{\gamma \in \Gamma} \gamma\cdot (x[f])\in \mathfrak{g}[\Sigma^{\prime o}]^\Gamma. \end{equation}
\begin{equation} A(x[f]):= \frac{1}{|\Gamma_q|}\sum_{\gamma \in \Gamma} \gamma\cdot (x[f])\in \mathfrak{g}[\Sigma^{\prime o}]^\Gamma. \end{equation} For any ![]() $h\in \mathscr {H} (\vec {\lambda })$ and
$h\in \mathscr {H} (\vec {\lambda })$ and ![]() $v\in \bigoplus _{\mu \in D_{c, p''}}\bigl (V(\mu )^*\otimes V(\mu )\bigr )$, as elements of
$v\in \bigoplus _{\mu \in D_{c, p''}}\bigl (V(\mu )^*\otimes V(\mu )\bigr )$, as elements of
 \[ Q:= \mathscr{H} (\vec{\lambda})\otimes \biggl(\bigoplus_{\mu\in D_{c,p''}} V (\mu^*) \otimes V(\mu)\biggr), \]
\[ Q:= \mathscr{H} (\vec{\lambda})\otimes \biggl(\bigoplus_{\mu\in D_{c,p''}} V (\mu^*) \otimes V(\mu)\biggr), \]
we have the following equality (for any ![]() $x\in \mathfrak {g}^{\Gamma _q}$)
$x\in \mathfrak {g}^{\Gamma _q}$)
where the action ![]() $\odot$ of
$\odot$ of ![]() $\mathfrak {g}^{\Gamma _q}$ on
$\mathfrak {g}^{\Gamma _q}$ on ![]() $V(\mu ^{*})\otimes V(\mu )$ is via its action on the first factor only. In particular, as elements of
$V(\mu ^{*})\otimes V(\mu )$ is via its action on the first factor only. In particular, as elements of ![]() $Q$,
$Q$,
where ![]() $\beta$ is the map defined by
$\beta$ is the map defined by
Observe that ![]() $\operatorname {\mathrm {Im}}(\beta )$ is
$\operatorname {\mathrm {Im}}(\beta )$ is ![]() $\mathfrak {g}^{\Gamma _q} \oplus \mathfrak {g}^{\Gamma _q}$-stable under the component wise action of
$\mathfrak {g}^{\Gamma _q} \oplus \mathfrak {g}^{\Gamma _q}$-stable under the component wise action of ![]() $\mathfrak {g}^{\Gamma _q} \oplus \mathfrak {g}^{\Gamma _q}$ on
$\mathfrak {g}^{\Gamma _q} \oplus \mathfrak {g}^{\Gamma _q}$ on ![]() $V(\mu ^{*})\otimes V(\mu )$ since
$V(\mu ^{*})\otimes V(\mu )$ since ![]() $I_{\mu }$ is
$I_{\mu }$ is ![]() $\mathfrak {g}^{\Gamma _q}$-invariant under the diagonal action of
$\mathfrak {g}^{\Gamma _q}$-invariant under the diagonal action of ![]() $\mathfrak {g}^{\Gamma _q}$. Moreover,
$\mathfrak {g}^{\Gamma _q}$. Moreover, ![]() $V(\mu ^{*})\otimes V(\mu )$ is an irreducible
$V(\mu ^{*})\otimes V(\mu )$ is an irreducible ![]() $\mathfrak {g}^{\Gamma _q} \oplus \mathfrak {g}^{\Gamma _q}$-module with highest weight
$\mathfrak {g}^{\Gamma _q} \oplus \mathfrak {g}^{\Gamma _q}$-module with highest weight ![]() $(\mu ^{*},\mu )$; and
$(\mu ^{*},\mu )$; and ![]() $\operatorname {\mathrm {Im}}(\beta )$ has a non-zero component in each
$\operatorname {\mathrm {Im}}(\beta )$ has a non-zero component in each ![]() $V(\mu ^{*})\otimes V(\mu )$. Thus,
$V(\mu ^{*})\otimes V(\mu )$. Thus, ![]() $\beta$ is surjective.
$\beta$ is surjective.
From the surjectivity of ![]() $\beta$, we get that the map
$\beta$, we get that the map ![]() $F$ is surjective by combining the equation (47) and the propagation theorem (Theorem 4.3).
$F$ is surjective by combining the equation (47) and the propagation theorem (Theorem 4.3).
We next show that ![]() $F$ is injective. Equivalently, we show that the dual map
$F$ is injective. Equivalently, we show that the dual map
is surjective.
From the definition of ![]() $\mathscr {V}^{{{\dagger}} }_{{\Sigma },\Gamma,\phi }$ and identifying the domain of
$\mathscr {V}^{{{\dagger}} }_{{\Sigma },\Gamma,\phi }$ and identifying the domain of ![]() $F^{*}$ via Theorem 4.3, we think of
$F^{*}$ via Theorem 4.3, we think of ![]() $F^{*}$ as the map
$F^{*}$ as the map
 \[ F^{*}:\operatorname{\mathrm{Hom}}_{{\mathfrak{g}[{\Sigma}^{\prime o}]} ^\Gamma}\bigg(\mathscr{H} ( \vec{\lambda})\otimes \bigg(\bigoplus_{\mu\in D_{c, p'' }} V(\mu)^*\otimes V(\mu)\bigg),\mathbb{C} \bigg)\to \operatorname{\mathrm{Hom}}_{\mathfrak{g}[{\Sigma}^o]^\Gamma}(\mathscr{H} ( \vec{\lambda}),\mathbb{C}) \]
\[ F^{*}:\operatorname{\mathrm{Hom}}_{{\mathfrak{g}[{\Sigma}^{\prime o}]} ^\Gamma}\bigg(\mathscr{H} ( \vec{\lambda})\otimes \bigg(\bigoplus_{\mu\in D_{c, p'' }} V(\mu)^*\otimes V(\mu)\bigg),\mathbb{C} \bigg)\to \operatorname{\mathrm{Hom}}_{\mathfrak{g}[{\Sigma}^o]^\Gamma}(\mathscr{H} ( \vec{\lambda}),\mathbb{C}) \]
induced from the inclusion
 \[ \hat{F}:\quad \mathscr{H} ( \vec{\lambda})\to \mathscr{H} ( \vec{\lambda})\otimes \bigg(\bigoplus_{\mu\in D_{c, p'' }}V(\mu)^*\otimes V(\mu) \bigg),\quad h\mapsto h\otimes \sum_{\mu\in D_{c, p''}}I_{\mu},\quad\text{for}\ h\in \mathscr{H} ( \vec{\lambda}). \]
\[ \hat{F}:\quad \mathscr{H} ( \vec{\lambda})\to \mathscr{H} ( \vec{\lambda})\otimes \bigg(\bigoplus_{\mu\in D_{c, p'' }}V(\mu)^*\otimes V(\mu) \bigg),\quad h\mapsto h\otimes \sum_{\mu\in D_{c, p''}}I_{\mu},\quad\text{for}\ h\in \mathscr{H} ( \vec{\lambda}). \]
Let ![]() $\mathbb {C}_{p} [ {\Sigma }^o]\subset \mathbb {C}_{p''} [ {\Sigma }^{\prime o}]\subset \mathbb {C}[{\Sigma }^{\prime o}]$ be the ideals of
$\mathbb {C}_{p} [ {\Sigma }^o]\subset \mathbb {C}_{p''} [ {\Sigma }^{\prime o}]\subset \mathbb {C}[{\Sigma }^{\prime o}]$ be the ideals of ![]() $\mathbb {C}[{\Sigma }^{\prime o}]$:
$\mathbb {C}[{\Sigma }^{\prime o}]$:
and
(Observe that, under the canonical inclusion ![]() $\mathbb {C}[ {\Sigma }^o]\subset \mathbb {C}[{\Sigma }^{\prime o}]$,
$\mathbb {C}[ {\Sigma }^o]\subset \mathbb {C}[{\Sigma }^{\prime o}]$, ![]() $\mathbb {C}_{p} [ {\Sigma }^o]$ is an ideal of
$\mathbb {C}_{p} [ {\Sigma }^o]$ is an ideal of ![]() $\mathbb {C}[{\Sigma }^{\prime o}]$ consisting of those functions vanishing at
$\mathbb {C}[{\Sigma }^{\prime o}]$ consisting of those functions vanishing at ![]() $\pi '^{-1}\{p', p'' \}$.) Now, define the Lie ideals of
$\pi '^{-1}\{p', p'' \}$.) Now, define the Lie ideals of ![]() $\mathfrak {g}[ {\Sigma }^{\prime o}]^\Gamma$:
$\mathfrak {g}[ {\Sigma }^{\prime o}]^\Gamma$:
Define the linear map
where ![]() $x\in \mathfrak {g}^{\Gamma _q}$,
$x\in \mathfrak {g}^{\Gamma _q}$, ![]() $f\in \mathbb {C}_{p''} [ {\Sigma }^{\prime o}]$ is any function satisfying (44) and
$f\in \mathbb {C}_{p''} [ {\Sigma }^{\prime o}]$ is any function satisfying (44) and ![]() $A(x[f])$ is defined by (45).
$A(x[f])$ is defined by (45).
Clearly, the above map is independent of the choice of ![]() $f$ satisfying (44). Moreover, it is a Lie algebra homomorphism.
$f$ satisfying (44). Moreover, it is a Lie algebra homomorphism.
For ![]() $x,y\in \mathfrak {g}^{\Gamma _q}$,
$x,y\in \mathfrak {g}^{\Gamma _q}$,
 \begin{align*} \big[A(x[f]), A(y[f])\big]&=\frac{1}{|\Gamma_q|^2}\sum_{\gamma, \gamma'\in \Gamma} \big[\gamma\cdot (x[f]), \gamma'\cdot (y[f])\big]\\ &=\frac{1}{|\Gamma_q|^2}\sum_{\sigma\in \Gamma_q} \sum_{\gamma'\in \Gamma} \big[\gamma'\sigma\cdot (x[f]), \gamma'\cdot (y[f])\big]\\ &\quad +\frac{1}{|\Gamma_q|^2}\sum_{\gamma\notin \gamma'\Gamma_q}\sum_{\gamma'\in \Gamma} \big[\gamma\cdot (x[f]), \gamma'\cdot (y[f])\big]\\ &=\frac{1}{|\Gamma_q|}\sum_{ \gamma'\in \Gamma} \gamma'\cdot \big([x, y][f]\big)\ \text{mod}\ \mathfrak{g}_p[\Sigma^o]^\Gamma. \end{align*}
\begin{align*} \big[A(x[f]), A(y[f])\big]&=\frac{1}{|\Gamma_q|^2}\sum_{\gamma, \gamma'\in \Gamma} \big[\gamma\cdot (x[f]), \gamma'\cdot (y[f])\big]\\ &=\frac{1}{|\Gamma_q|^2}\sum_{\sigma\in \Gamma_q} \sum_{\gamma'\in \Gamma} \big[\gamma'\sigma\cdot (x[f]), \gamma'\cdot (y[f])\big]\\ &\quad +\frac{1}{|\Gamma_q|^2}\sum_{\gamma\notin \gamma'\Gamma_q}\sum_{\gamma'\in \Gamma} \big[\gamma\cdot (x[f]), \gamma'\cdot (y[f])\big]\\ &=\frac{1}{|\Gamma_q|}\sum_{ \gamma'\in \Gamma} \gamma'\cdot \big([x, y][f]\big)\ \text{mod}\ \mathfrak{g}_p[\Sigma^o]^\Gamma. \end{align*}
To prove the last equality, observe that, for ![]() $\gamma \notin \gamma '\Gamma _q$,
$\gamma \notin \gamma '\Gamma _q$, ![]() $(\gamma \cdot f)\cdot (\gamma ' \cdot f)\in \mathbb {C}_p[\Sigma ^o]$. In addition, for
$(\gamma \cdot f)\cdot (\gamma ' \cdot f)\in \mathbb {C}_p[\Sigma ^o]$. In addition, for ![]() $\sigma \in \Gamma _q$,
$\sigma \in \Gamma _q$, ![]() $\sigma \cdot f-f\in \mathbb {C}_p[\Sigma ^o]$ and
$\sigma \cdot f-f\in \mathbb {C}_p[\Sigma ^o]$ and ![]() $f^2-f\in \mathbb {C}_p[\Sigma ^o]$.
$f^2-f\in \mathbb {C}_p[\Sigma ^o]$.
Let
be the induced homomorphism of the enveloping algebras.
To prove the surjectivity of ![]() $F^{*}$, take
$F^{*}$, take ![]() $\Phi \in \operatorname {\mathrm {Hom}}_{\mathfrak {g}[{\Sigma }^o]^\Gamma }(\mathscr {H}( \vec {\lambda }),\mathbb {C})$ and define the linear map
$\Phi \in \operatorname {\mathrm {Hom}}_{\mathfrak {g}[{\Sigma }^o]^\Gamma }(\mathscr {H}( \vec {\lambda }),\mathbb {C})$ and define the linear map
 \[ \tilde{\Phi}:\mathscr{H}( \vec{\lambda})\otimes \bigg(\bigoplus_{\mu\in D_{c, p''}}V(\mu)^*\otimes V(\mu)\bigg)\to \mathbb{C} \]
\[ \tilde{\Phi}:\mathscr{H}( \vec{\lambda})\otimes \bigg(\bigoplus_{\mu\in D_{c, p''}}V(\mu)^*\otimes V(\mu)\bigg)\to \mathbb{C} \]
via
where ![]() $t:U(\mathfrak {g}^{\Gamma _q} )\to U(\mathfrak {g}^{\Gamma _q} )$ is the anti-automorphism taking
$t:U(\mathfrak {g}^{\Gamma _q} )\to U(\mathfrak {g}^{\Gamma _q} )$ is the anti-automorphism taking ![]() $x\mapsto -x$ for
$x\mapsto -x$ for ![]() $x\in \mathfrak {g}^{\Gamma _q}$,
$x\in \mathfrak {g}^{\Gamma _q}$, ![]() $\beta$ is the map defined by (48) and
$\beta$ is the map defined by (48) and ![]() $\varphi$ is defined above. (Observe that even though
$\varphi$ is defined above. (Observe that even though ![]() $\varphi (a)\cdot h$ is not well-defined, but
$\varphi (a)\cdot h$ is not well-defined, but ![]() $\Phi (\varphi (a)\cdot h)$ is well-defined, i.e. it does not depend upon the choice of the coset representatives in
$\Phi (\varphi (a)\cdot h)$ is well-defined, i.e. it does not depend upon the choice of the coset representatives in ![]() $\mathfrak {g}_{p''}[ {\Sigma }^{\prime o}]^\Gamma \big / \mathfrak {g}_{p}[ {\Sigma }^o]^\Gamma$.)
$\mathfrak {g}_{p''}[ {\Sigma }^{\prime o}]^\Gamma \big / \mathfrak {g}_{p}[ {\Sigma }^o]^\Gamma$.)
To show that ![]() $\tilde {\Phi }$ is well-defined, we need to show that for any
$\tilde {\Phi }$ is well-defined, we need to show that for any ![]() $a\in \operatorname {\mathrm {Ker}} \beta$ and
$a\in \operatorname {\mathrm {Ker}} \beta$ and ![]() $h\in \mathscr {H}( \vec {\lambda })$,
$h\in \mathscr {H}( \vec {\lambda })$,
This will be proved in the next Lemma 5.6.
We next show that ![]() $\tilde {\Phi }$ is a
$\tilde {\Phi }$ is a ![]() $\mathfrak {g}[{\Sigma }^{\prime o}]^\Gamma$-module map. For any element
$\mathfrak {g}[{\Sigma }^{\prime o}]^\Gamma$-module map. For any element ![]() $X=\sum x_i[g_i]\in \mathfrak {g}[{\Sigma }^{\prime o}]^\Gamma$ where
$X=\sum x_i[g_i]\in \mathfrak {g}[{\Sigma }^{\prime o}]^\Gamma$ where ![]() $x_i\in \mathfrak {g}$ and
$x_i\in \mathfrak {g}$ and ![]() $g_i\in \mathbb {C}[{\Sigma }^{\prime o}]$, we need to check that for any
$g_i\in \mathbb {C}[{\Sigma }^{\prime o}]$, we need to check that for any ![]() $h\in \mathscr {H}( \vec {\lambda })$ and
$h\in \mathscr {H}( \vec {\lambda })$ and ![]() $a\in U(\mathfrak {g}^{\Gamma _q} )$,
$a\in U(\mathfrak {g}^{\Gamma _q} )$,
Take any ![]() $\Gamma _q$-invariant
$\Gamma _q$-invariant ![]() $f'\in \mathbb {C}[{\Sigma }^{\prime o}]$ (respectively,
$f'\in \mathbb {C}[{\Sigma }^{\prime o}]$ (respectively, ![]() $f''\in \mathbb {C}[{\Sigma }^{\prime o}]$) satisfying (44) (respectively,
$f''\in \mathbb {C}[{\Sigma }^{\prime o}]$) satisfying (44) (respectively, ![]() $f''(q'')=1$ and
$f''(q'')=1$ and ![]() $f''_{|\Gamma \cdot q'\cup (\Gamma \cdot q''\setminus \{q''\})}=0$). Then,
$f''_{|\Gamma \cdot q'\cup (\Gamma \cdot q''\setminus \{q''\})}=0$). Then,
Thus,
It suffices to prove (51) in the following three cases of ![]() $X$.
$X$.
Case 1: ![]() $X\in \mathfrak {g}_p[{\Sigma }^o]^\Gamma$. In this case
$X\in \mathfrak {g}_p[{\Sigma }^o]^\Gamma$. In this case
 \begin{align*} \tilde{\Phi}\big(X\cdot (h\otimes \beta(a))\big) &= \tilde{\Phi} \big((X\cdot h)\otimes \beta(a)\big) +\tilde{\Phi}\big(h\otimes X\cdot\beta(a)\big) \\ &= \Phi \big(\varphi(a^{t})\cdot X\cdot h\big) ,\ \text{since} \ X\in \mathfrak{g}_p[{\Sigma}^o]^\Gamma \\ &= \Phi \big(X\cdot \varphi(a^{t})\cdot h\big)+\Phi \big([\varphi(a^{t}), X]\cdot h\big)\\ &= 0,\quad \text{since $\Phi$ is a $\mathfrak{g}[{\Sigma}^o]^\Gamma$-module map and $ [\varphi(a^{t}), X]\in \mathfrak{g}[{\Sigma}^o]^\Gamma$.} \end{align*}
\begin{align*} \tilde{\Phi}\big(X\cdot (h\otimes \beta(a))\big) &= \tilde{\Phi} \big((X\cdot h)\otimes \beta(a)\big) +\tilde{\Phi}\big(h\otimes X\cdot\beta(a)\big) \\ &= \Phi \big(\varphi(a^{t})\cdot X\cdot h\big) ,\ \text{since} \ X\in \mathfrak{g}_p[{\Sigma}^o]^\Gamma \\ &= \Phi \big(X\cdot \varphi(a^{t})\cdot h\big)+\Phi \big([\varphi(a^{t}), X]\cdot h\big)\\ &= 0,\quad \text{since $\Phi$ is a $\mathfrak{g}[{\Sigma}^o]^\Gamma$-module map and $ [\varphi(a^{t}), X]\in \mathfrak{g}[{\Sigma}^o]^\Gamma$.} \end{align*}
Case 2: ![]() $X\in \big (\mathfrak {g}\otimes S_{f'}\big )^\Gamma$. Write
$X\in \big (\mathfrak {g}\otimes S_{f'}\big )^\Gamma$. Write
Observe first that since ![]() $\{\gamma \cdot f'\}_{\gamma \in \Gamma /\Gamma _q}$ are linearly independent,
$\{\gamma \cdot f'\}_{\gamma \in \Gamma /\Gamma _q}$ are linearly independent, ![]() $x_1\in \mathfrak {g}^{\Gamma _q}$. Moreover, we claim that
$x_1\in \mathfrak {g}^{\Gamma _q}$. Moreover, we claim that
To prove (52), since ![]() $X$ and
$X$ and ![]() $\sum _{\gamma \in \Gamma /\Gamma _q}\gamma \cdot (x_1[ f'])$ both are
$\sum _{\gamma \in \Gamma /\Gamma _q}\gamma \cdot (x_1[ f'])$ both are ![]() $\Gamma$-invariant, it suffices to observe that their difference vanishes both at
$\Gamma$-invariant, it suffices to observe that their difference vanishes both at ![]() $q'$ and
$q'$ and ![]() $q''$. Now,
$q''$. Now,
 \begin{align*} \tilde{\Phi}\big(X\cdot (h\otimes \beta(a))\big) &= \tilde{\Phi} \big((X\cdot h)\otimes \beta(a)\big) +\tilde{\Phi}\big(h\otimes X\cdot\beta(a)\big) \\ &= \Phi \big(\varphi(a^{t})\cdot X\cdot h\big) - \Phi \big(\varphi(a^{t}x_1)\cdot h\big) \\ &= \Phi \big(\varphi(a^{t})(X-\varphi (x_1))\cdot h\big) \\ &= \Phi \big((X-\varphi (x_1))\varphi(a^{t}) \cdot h\big) + \Phi \big([\varphi(a^{t}), X-\varphi (x_1)]\cdot h\big)\\ &=0, \end{align*}
\begin{align*} \tilde{\Phi}\big(X\cdot (h\otimes \beta(a))\big) &= \tilde{\Phi} \big((X\cdot h)\otimes \beta(a)\big) +\tilde{\Phi}\big(h\otimes X\cdot\beta(a)\big) \\ &= \Phi \big(\varphi(a^{t})\cdot X\cdot h\big) - \Phi \big(\varphi(a^{t}x_1)\cdot h\big) \\ &= \Phi \big(\varphi(a^{t})(X-\varphi (x_1))\cdot h\big) \\ &= \Phi \big((X-\varphi (x_1))\varphi(a^{t}) \cdot h\big) + \Phi \big([\varphi(a^{t}), X-\varphi (x_1)]\cdot h\big)\\ &=0, \end{align*}
by (52) and since ![]() $\mathfrak {g}_p[{\Sigma }^o]^\Gamma$ is an ideal in
$\mathfrak {g}_p[{\Sigma }^o]^\Gamma$ is an ideal in ![]() $\mathfrak {g}[{\Sigma }^{\prime o}]^\Gamma$.
$\mathfrak {g}[{\Sigma }^{\prime o}]^\Gamma$.
Case 3: ![]() $X\in \big (\mathfrak {g}\otimes S_{f''}\big )^\Gamma$. Write
$X\in \big (\mathfrak {g}\otimes S_{f''}\big )^\Gamma$. Write
Same as in Case 2, we have ![]() $x_1\in \mathfrak {g}^{\Gamma _q}$. Moreover, we claim that
$x_1\in \mathfrak {g}^{\Gamma _q}$. Moreover, we claim that
To prove (53), it suffices to observe (from the ![]() $\Gamma$-invariance) that
$\Gamma$-invariance) that ![]() $X +\sum _{\gamma \in \Gamma /\Gamma _q}\gamma \cdot (x_1[ f'])$ takes the same value at both
$X +\sum _{\gamma \in \Gamma /\Gamma _q}\gamma \cdot (x_1[ f'])$ takes the same value at both ![]() $q'$ and
$q'$ and ![]() $q''$. Now,
$q''$. Now,
 \begin{align*} \tilde{\Phi}\big(X\cdot (h\otimes \beta(a))\big) &= \tilde{\Phi} \big((X\cdot h)\otimes \beta(a)\big) +\tilde{\Phi}\big(h\otimes X\cdot\beta(a)\big) \\ &= \tilde{\Phi} \big((X\cdot h)\otimes \beta(a)\big) +\tilde{\Phi}\big(h\otimes x_1\odot^r\beta(a)\big),\quad \text{where $\odot^r$ denotes the action}\\ & \quad \quad \quad \quad \quad \text{of $\mathfrak{g}^{\Gamma_q}$ on $V(\mu^*)\otimes V(\mu)$ on the second factor only} \\ &= \tilde{\Phi} \big((X\cdot h)\otimes \beta(a)\big) -\tilde{\Phi}\big(h\otimes \beta(ax_1)\big),\quad \text{since the actions $\odot$ and $\odot^r$ commute}\\ & \quad \quad \quad \quad \quad \text{and $I_\mu$ is a diagonal $\mathfrak{g}^{\Gamma_q}$-invariant} \\ &= \Phi \big(\varphi(a^{t})\cdot X\cdot h\big) + \Phi \big(\varphi(x_1)\varphi(a^{t})\cdot h\big) \\ &= \Phi \big([\varphi(a^{t}), X]\cdot h\big) + \Phi \big((X+\varphi(x_1))\varphi(a^{t})\cdot h\big) \\ &=0,\quad \text{since $[\varphi(a^{t}), X]\in \mathfrak{g}[{\Sigma}^o]^\Gamma$ and using (53)}. \end{align*}
\begin{align*} \tilde{\Phi}\big(X\cdot (h\otimes \beta(a))\big) &= \tilde{\Phi} \big((X\cdot h)\otimes \beta(a)\big) +\tilde{\Phi}\big(h\otimes X\cdot\beta(a)\big) \\ &= \tilde{\Phi} \big((X\cdot h)\otimes \beta(a)\big) +\tilde{\Phi}\big(h\otimes x_1\odot^r\beta(a)\big),\quad \text{where $\odot^r$ denotes the action}\\ & \quad \quad \quad \quad \quad \text{of $\mathfrak{g}^{\Gamma_q}$ on $V(\mu^*)\otimes V(\mu)$ on the second factor only} \\ &= \tilde{\Phi} \big((X\cdot h)\otimes \beta(a)\big) -\tilde{\Phi}\big(h\otimes \beta(ax_1)\big),\quad \text{since the actions $\odot$ and $\odot^r$ commute}\\ & \quad \quad \quad \quad \quad \text{and $I_\mu$ is a diagonal $\mathfrak{g}^{\Gamma_q}$-invariant} \\ &= \Phi \big(\varphi(a^{t})\cdot X\cdot h\big) + \Phi \big(\varphi(x_1)\varphi(a^{t})\cdot h\big) \\ &= \Phi \big([\varphi(a^{t}), X]\cdot h\big) + \Phi \big((X+\varphi(x_1))\varphi(a^{t})\cdot h\big) \\ &=0,\quad \text{since $[\varphi(a^{t}), X]\in \mathfrak{g}[{\Sigma}^o]^\Gamma$ and using (53)}. \end{align*}
This completes the proof of (51) and, hence, ![]() $\tilde {\Phi }$ is a
$\tilde {\Phi }$ is a ![]() $\mathfrak {g}[{\Sigma }^{\prime o}]^\Gamma$-module map.
$\mathfrak {g}[{\Sigma }^{\prime o}]^\Gamma$-module map.
From the definition of ![]() $\tilde {\Phi }$, it is clear that
$\tilde {\Phi }$, it is clear that ![]() $F^{*}(\tilde {\Phi })=\Phi$. This proves the surjectivity of
$F^{*}(\tilde {\Phi })=\Phi$. This proves the surjectivity of ![]() $F^{*}$ (and, hence, the injectivity of
$F^{*}$ (and, hence, the injectivity of ![]() $F$) modulo the next lemma. Thus, the theorem is proved (modulo the next lemma).
$F$) modulo the next lemma. Thus, the theorem is proved (modulo the next lemma).
Definition 5.5 For any ![]() $\mu \in D$ (where
$\mu \in D$ (where ![]() $D$ is the set of dominant integral weights of
$D$ is the set of dominant integral weights of ![]() $\mathfrak {g}^{\Gamma _q}$), consider the algebra homomorphism
$\mathfrak {g}^{\Gamma _q}$), consider the algebra homomorphism
defined by
Let ![]() $K_{\mu }$ be the kernel of
$K_{\mu }$ be the kernel of ![]() $\overline {\beta }_{\mu }$, which is a two-sided ideal of
$\overline {\beta }_{\mu }$, which is a two-sided ideal of ![]() $U(\mathfrak {g}^{\Gamma _q})$ (called a primitive ideal). From the definition of
$U(\mathfrak {g}^{\Gamma _q})$ (called a primitive ideal). From the definition of ![]() $\beta$ (cf. (48)), it is easy to see that, under the identification of
$\beta$ (cf. (48)), it is easy to see that, under the identification of ![]() $V(\mu ^*)\otimes V(\mu )$ with
$V(\mu ^*)\otimes V(\mu )$ with ![]() $\operatorname {\mathrm {End}}_{\mathbb {C}}(V(\mu ))$,
$\operatorname {\mathrm {End}}_{\mathbb {C}}(V(\mu ))$,
Thus,
From the definition of ![]() $\overline {\beta }_{\mu }$, it follows immediately that for any left ideal
$\overline {\beta }_{\mu }$, it follows immediately that for any left ideal ![]() $K\subset U(\mathfrak {g}^{\Gamma _q})$ such that
$K\subset U(\mathfrak {g}^{\Gamma _q})$ such that ![]() $U(\mathfrak {g}^{\Gamma _q})/K$ is an integrable
$U(\mathfrak {g}^{\Gamma _q})/K$ is an integrable ![]() $\mathfrak {g}^{\Gamma _q}$-module, if the
$\mathfrak {g}^{\Gamma _q}$-module, if the ![]() $\mathfrak {g}^{\Gamma _q}$-module
$\mathfrak {g}^{\Gamma _q}$-module ![]() $U(\mathfrak {g}^{\Gamma _q})/K$ has isotypic components of highest weights
$U(\mathfrak {g}^{\Gamma _q})/K$ has isotypic components of highest weights ![]() $\{\mu _{i}\}_{i\in \Lambda }\subset D$, then
$\{\mu _{i}\}_{i\in \Lambda }\subset D$, then
We are now ready to prove the following lemma.
Lemma 5.6 With the notation as in the proof of Theorem 5.4 (cf. identity (50)), for any ![]() $a\in \operatorname {\mathrm {Ker}} \beta$,
$a\in \operatorname {\mathrm {Ker}} \beta$, ![]() $\Phi \in \operatorname {\mathrm {Hom}}_{\mathfrak {g}[{\Sigma }^o ]^\Gamma }(\mathscr {H} ( \vec {\lambda }),\mathbb {C})$, and
$\Phi \in \operatorname {\mathrm {Hom}}_{\mathfrak {g}[{\Sigma }^o ]^\Gamma }(\mathscr {H} ( \vec {\lambda }),\mathbb {C})$, and ![]() $h\in \mathscr {H} ( \vec {\lambda })$,
$h\in \mathscr {H} ( \vec {\lambda })$,
Proof. Let ![]() $\mathfrak {s}_{p'}$ be the Lie algebra
$\mathfrak {s}_{p'}$ be the Lie algebra
where ![]() $\mathbb {C}_{p''} [{\Sigma }^{\prime o}\backslash \pi '^{-1}(p') ] \subset \mathbb {C}[{\Sigma }^{\prime o} \backslash \pi '^{-1}( p')]$ is the ideal consisting of functions vanishing at
$\mathbb {C}_{p''} [{\Sigma }^{\prime o}\backslash \pi '^{-1}(p') ] \subset \mathbb {C}[{\Sigma }^{\prime o} \backslash \pi '^{-1}( p')]$ is the ideal consisting of functions vanishing at ![]() $\pi '^{-1}(p'')$, with the Lie bracket defined as in formula (26) and
$\pi '^{-1}(p'')$, with the Lie bracket defined as in formula (26) and ![]() $C$ is central in
$C$ is central in ![]() $\mathfrak {s}_{p'}$. There is a Lie algebra embedding
$\mathfrak {s}_{p'}$. There is a Lie algebra embedding
Let ![]() $\mathscr {H} ( \vec {\lambda })^{*}$ be the full vector space dual of
$\mathscr {H} ( \vec {\lambda })^{*}$ be the full vector space dual of ![]() $\mathscr {H} ( \vec {\lambda })$. The Lie algebra
$\mathscr {H} ( \vec {\lambda })$. The Lie algebra ![]() $\mathfrak {s}_{p'}$ acts on
$\mathfrak {s}_{p'}$ acts on ![]() $\mathscr {H} ( \vec {\lambda })$ where
$\mathscr {H} ( \vec {\lambda })$ where ![]() $x[f]$ acts on
$x[f]$ acts on ![]() $\mathscr {H} ( \vec {\lambda })$ as in (15) and the center
$\mathscr {H} ( \vec {\lambda })$ as in (15) and the center ![]() $C$ acts by the scalar
$C$ acts by the scalar ![]() $-c$. By the residue theorem, it is indeed a Lie algebra action.
$-c$. By the residue theorem, it is indeed a Lie algebra action.
This gives rise to the (dual) action of ![]() $\mathfrak {s}_{p'}$ on
$\mathfrak {s}_{p'}$ on ![]() $\mathscr {H} ( \vec {\lambda })^{*}$. Let
$\mathscr {H} ( \vec {\lambda })^{*}$. Let ![]() $M\subset \mathscr {H} ( \vec {\lambda })^{*}$ be the
$M\subset \mathscr {H} ( \vec {\lambda })^{*}$ be the ![]() $\mathfrak {s}_{p'}$-submodule generated by
$\mathfrak {s}_{p'}$-submodule generated by ![]() $\Phi \in \mathscr {H}( \vec {\lambda })^{*}$. We claim that the action of
$\Phi \in \mathscr {H}( \vec {\lambda })^{*}$. We claim that the action of ![]() $\mathfrak {s}_{p'}$ on
$\mathfrak {s}_{p'}$ on ![]() $M$ extends to a
$M$ extends to a ![]() ${{\hat {\mathfrak {g}}}}_{p'}$-module structure on
${{\hat {\mathfrak {g}}}}_{p'}$-module structure on ![]() $M$ via the embedding (58). Let
$M$ via the embedding (58). Let ![]() $\mathfrak {s}_{p'}^+\subset \mathfrak {s}_{p'}$ be the subalgebra
$\mathfrak {s}_{p'}^+\subset \mathfrak {s}_{p'}$ be the subalgebra ![]() $\mathfrak {g}_{p }[{\Sigma }^o ]^\Gamma$ defined by (49) of Theorem 5.4. Then, by the definition of
$\mathfrak {g}_{p }[{\Sigma }^o ]^\Gamma$ defined by (49) of Theorem 5.4. Then, by the definition of ![]() $\Phi$,
$\Phi$,
For any element ![]() $X=\sum _ix_i[f_i]\in \mathfrak {s}_{p'}$ with a basis
$X=\sum _ix_i[f_i]\in \mathfrak {s}_{p'}$ with a basis ![]() $\{x_i\}$ of
$\{x_i\}$ of ![]() $\mathfrak {g}$ and
$\mathfrak {g}$ and ![]() $f_i\in \mathbb {C}_{p''} [{\Sigma }^{\prime o}\backslash \pi '^{-1}(p') ]$, we define
$f_i\in \mathbb {C}_{p''} [{\Sigma }^{\prime o}\backslash \pi '^{-1}(p') ]$, we define
where ![]() $o(f_{i})$ is the sum of orders of pole of
$o(f_{i})$ is the sum of orders of pole of ![]() $f_{i}$ at the points of
$f_{i}$ at the points of ![]() $\pi '^{-1}(p' )$. (If
$\pi '^{-1}(p' )$. (If ![]() $f_{i}$ is regular at a point in
$f_{i}$ is regular at a point in ![]() $\pi '^{-1}(p' )$, we say that the order of pole at that point is
$\pi '^{-1}(p' )$, we say that the order of pole at that point is ![]() $0$.)
$0$.)
Define an increasing filtration ![]() $\{\mathscr {F}_{d}(M)\}_{d\geq 0}$ of
$\{\mathscr {F}_{d}(M)\}_{d\geq 0}$ of ![]() $M$ by
$M$ by
 \[ \mathscr{F}_{d}(M)=\text{span of }\bigg\{\big(X_1\dots X_k\big)\cdot \Phi : X_i\in \mathfrak{s}_{p'} \ \text{and}\ \sum^{k}_{i=1}o(X_{i})\leq d\bigg\}. \]
\[ \mathscr{F}_{d}(M)=\text{span of }\bigg\{\big(X_1\dots X_k\big)\cdot \Phi : X_i\in \mathfrak{s}_{p'} \ \text{and}\ \sum^{k}_{i=1}o(X_{i})\leq d\bigg\}. \]
From (59), it is easy to see that for any ![]() $\Psi \in \mathscr {F}_{d}(M)$, and any
$\Psi \in \mathscr {F}_{d}(M)$, and any ![]() $Y=\sum x_i[g_i]\in \mathfrak {g}_{p}[\Sigma ^o]^\Gamma$ such that each
$Y=\sum x_i[g_i]\in \mathfrak {g}_{p}[\Sigma ^o]^\Gamma$ such that each ![]() $g_i$ vanishes at every point of
$g_i$ vanishes at every point of ![]() $\pi '^{-1}(p')$ of order at least
$\pi '^{-1}(p')$ of order at least ![]() $d+1$,
$d+1$,
Now, for any ![]() $y\in {\hat {\mathfrak {g}}}_{p'}$, pick
$y\in {\hat {\mathfrak {g}}}_{p'}$, pick ![]() $\hat {y} \in \mathfrak {s}_{p'}$ such that
$\hat {y} \in \mathfrak {s}_{p'}$ such that
where ![]() $\hat {y}_{p'}$ denotes the restriction of
$\hat {y}_{p'}$ denotes the restriction of ![]() $\hat {y}$ on
$\hat {y}$ on ![]() $\pi '^{ -1}(\mathbb {D}_{p'})$ and
$\pi '^{ -1}(\mathbb {D}_{p'})$ and ![]() $\hat {\mathfrak {g}}_{p'}^{ d+1}$ denotes elements of
$\hat {\mathfrak {g}}_{p'}^{ d+1}$ denotes elements of ![]() $\mathfrak {g}[\pi '^{ -1}(\mathbb {D}_{p'}) ]^\Gamma$ that vanish at each point of
$\mathfrak {g}[\pi '^{ -1}(\mathbb {D}_{p'}) ]^\Gamma$ that vanish at each point of ![]() $\pi '^{-1}(p')$ of order at least
$\pi '^{-1}(p')$ of order at least ![]() $d+1$ (note that
$d+1$ (note that ![]() $\hat {\mathfrak {g}}^1_{p'}=\hat {\mathfrak {g}}^+_{p'}$). In fact, if
$\hat {\mathfrak {g}}^1_{p'}=\hat {\mathfrak {g}}^+_{p'}$). In fact, if ![]() $y\in \mathfrak {t}[\pi '^{ -1}(\mathbb {D}_{p'})]^\Gamma$ for some
$y\in \mathfrak {t}[\pi '^{ -1}(\mathbb {D}_{p'})]^\Gamma$ for some ![]() $\Gamma$-stable subspace
$\Gamma$-stable subspace ![]() $\mathfrak {t}$ of
$\mathfrak {t}$ of ![]() $\mathfrak {g}$, then we can take
$\mathfrak {g}$, then we can take ![]() $\hat {y}\in \big (\mathfrak {t}\otimes \mathbb {C}_{p''} [{\Sigma }^{\prime o}\backslash \pi '^{-1}(p') ] \big )^\Gamma$. Define, for any
$\hat {y}\in \big (\mathfrak {t}\otimes \mathbb {C}_{p''} [{\Sigma }^{\prime o}\backslash \pi '^{-1}(p') ] \big )^\Gamma$. Define, for any ![]() $\Psi \in \mathscr {F}_{d}(M)$,
$\Psi \in \mathscr {F}_{d}(M)$,
From (60), it follows that (62) gives a well-defined action ![]() $y\cdot \Psi$ (i.e. it does not depend upon the choice of
$y\cdot \Psi$ (i.e. it does not depend upon the choice of ![]() $\hat {y}$ satisfying (61)). Observe that, taking
$\hat {y}$ satisfying (61)). Observe that, taking ![]() $\hat {y}=0$,
$\hat {y}=0$,
Of course, the action of ![]() ${{\hat {\mathfrak {g}}}}_{p'}$ on
${{\hat {\mathfrak {g}}}}_{p'}$ on ![]() $M$ defined by (62) extends the action of
$M$ defined by (62) extends the action of ![]() $\mathfrak {s}_{p'}$ on
$\mathfrak {s}_{p'}$ on ![]() $M$.
$M$.
We next show that this action indeed makes ![]() $M$ into a module for the Lie algebra
$M$ into a module for the Lie algebra ![]() ${{\hat {\mathfrak {g}}}}_{p'}$. To show this, it suffices to show that, for
${{\hat {\mathfrak {g}}}}_{p'}$. To show this, it suffices to show that, for ![]() $y_1, y_2\in \hat {\mathfrak {g}}_{p'}$ and
$y_1, y_2\in \hat {\mathfrak {g}}_{p'}$ and ![]() $\Psi \in \mathscr {F}_{d}(M)$,
$\Psi \in \mathscr {F}_{d}(M)$,
Take ![]() $\hat {y}_1, \hat {y}_2\in \mathfrak {s}_{p'}$ such that
$\hat {y}_1, \hat {y}_2\in \mathfrak {s}_{p'}$ such that
where, for ![]() $y=\sum _i x_i[f_i]\in \hat {\mathfrak {g}}_{p'}$,
$y=\sum _i x_i[f_i]\in \hat {\mathfrak {g}}_{p'}$, ![]() $o(y) :=\text {max}_i\{o(f_i)\}$,
$o(y) :=\text {max}_i\{o(f_i)\}$, ![]() $o(f_i)$ being the sum of the orders of poles at the points of
$o(f_i)$ being the sum of the orders of poles at the points of ![]() $\pi '^{-1}(p')$. Using the definition (62) and observing that
$\pi '^{-1}(p')$. Using the definition (62) and observing that ![]() $o(\hat {y}_j)= o(y_j)$, it is easy to see that (64) is equivalent to the same identity with
$o(\hat {y}_j)= o(y_j)$, it is easy to see that (64) is equivalent to the same identity with ![]() $y_1$ replaced by
$y_1$ replaced by ![]() $\hat {y}_1$ and
$\hat {y}_1$ and ![]() $y_2$ by
$y_2$ by ![]() $\hat {y}_2$. The latter of course follows since
$\hat {y}_2$. The latter of course follows since ![]() $M$ is a representation of
$M$ is a representation of ![]() $\mathfrak {s}_{p'}$. As a special case of (63), we get
$\mathfrak {s}_{p'}$. As a special case of (63), we get
We next show that ![]() $M$ is an integrable
$M$ is an integrable ![]() ${{\hat {\mathfrak {g}}}}_{p'}$-module. To prove this, it suffices to show that for any vector
${{\hat {\mathfrak {g}}}}_{p'}$-module. To prove this, it suffices to show that for any vector ![]() $y\in \big (\mathfrak {n}^\pm \otimes \mathbb {C}[\pi '^{-1}(\mathbb {D}^\times _{p'})]\big )^\Gamma$ (
$y\in \big (\mathfrak {n}^\pm \otimes \mathbb {C}[\pi '^{-1}(\mathbb {D}^\times _{p'})]\big )^\Gamma$ (![]() $\mathfrak {n}^+:=\mathfrak {n}$),
$\mathfrak {n}^+:=\mathfrak {n}$), ![]() $y$ acts locally nilpotently on
$y$ acts locally nilpotently on ![]() $M$, where
$M$, where ![]() $\mathfrak {n}$ (respectively,
$\mathfrak {n}$ (respectively, ![]() $\mathfrak {n}^-$) is the nilradical of the Borel subalgebra
$\mathfrak {n}^-$) is the nilradical of the Borel subalgebra ![]() $\mathfrak {b}$ (respectively, of the opposite Borel subalgebra
$\mathfrak {b}$ (respectively, of the opposite Borel subalgebra ![]() $\mathfrak {b}^-$) (cf. § 2). Since
$\mathfrak {b}^-$) (cf. § 2). Since ![]() $M$ is generated by
$M$ is generated by ![]() $\Phi$ as a
$\Phi$ as a ![]() ${{\hat {\mathfrak {g}}}}_{p'}$-module, by [Reference KumarKum02, Lemma 1.3.3 and Corollary 1.3.4], it suffices to show that
${{\hat {\mathfrak {g}}}}_{p'}$-module, by [Reference KumarKum02, Lemma 1.3.3 and Corollary 1.3.4], it suffices to show that ![]() $y$ acts nilpotently on
$y$ acts nilpotently on ![]() $\Phi$.
$\Phi$.
Choose ![]() $N_o >0$ such that
$N_o >0$ such that
For any ![]() $y\in \big (\mathfrak {n}^\pm \otimes \mathbb {C}[\pi '^{-1}(\mathbb {D}^\times _{p'})]\big )^\Gamma \subset \hat {\mathfrak {g}}_{p'}$, pick
$y\in \big (\mathfrak {n}^\pm \otimes \mathbb {C}[\pi '^{-1}(\mathbb {D}^\times _{p'})]\big )^\Gamma \subset \hat {\mathfrak {g}}_{p'}$, pick ![]() $\hat {y}\in \big (\mathfrak {n}^\pm \otimes \mathbb {C}_{p''} [{\Sigma }^{\prime o}\backslash \pi '^{-1}(p') ] \big )^\Gamma$ such that (cf. (61))
$\hat {y}\in \big (\mathfrak {n}^\pm \otimes \mathbb {C}_{p''} [{\Sigma }^{\prime o}\backslash \pi '^{-1}(p') ] \big )^\Gamma$ such that (cf. (61))
For any associative algebra ![]() $A$ and element
$A$ and element ![]() $y\in A$, define the operators
$y\in A$, define the operators ![]() $L_y (x)=yx$,
$L_y (x)=yx$, ![]() $R_{y}(x)=xy$, and
$R_{y}(x)=xy$, and ![]() $\mathrm {ad} (y)=L_{y}-R_{y}$. Considering the operator
$\mathrm {ad} (y)=L_{y}-R_{y}$. Considering the operator ![]() $R^{n}_{y}=(L_{y} - \mathrm {ad} (y))^{n}$ (for any
$R^{n}_{y}=(L_{y} - \mathrm {ad} (y))^{n}$ (for any ![]() $n\geq 1$) applied to
$n\geq 1$) applied to ![]() $\hat {y}_{p'}-y$ in the algebra
$\hat {y}_{p'}-y$ in the algebra ![]() $U(\hat {\mathfrak {g}}_{p'})$ and using the binomial theorem (since
$U(\hat {\mathfrak {g}}_{p'})$ and using the binomial theorem (since ![]() $L_y$ and
$L_y$ and ![]() $\mathrm {ad} (y)$ commute), we get
$\mathrm {ad} (y)$ commute), we get
 \begin{equation} (\hat{y}_{p'}-y)y^{n}=\sum^{k}_{j=0}\binom{n}{j}(-1)^j y^{n-j}\big((\mathrm{ad} (y))^{j}(\hat{y}_{p'}-y)\big), \end{equation}
\begin{equation} (\hat{y}_{p'}-y)y^{n}=\sum^{k}_{j=0}\binom{n}{j}(-1)^j y^{n-j}\big((\mathrm{ad} (y))^{j}(\hat{y}_{p'}-y)\big), \end{equation}
where the summation runs only up to ![]() $k=\text {min} \{n, N_o-1\}$ because of the choice of
$k=\text {min} \{n, N_o-1\}$ because of the choice of ![]() $N_o$ satisfying (66). Then, for any
$N_o$ satisfying (66). Then, for any ![]() $d\geq 1$, by induction on
$d\geq 1$, by induction on ![]() $d$ using (65) we get
$d$ using (65) we get
To prove the above, observe that ![]() $(\hat {y}-y)y^d \cdot \Phi =0$ by the choice of
$(\hat {y}-y)y^d \cdot \Phi =0$ by the choice of ![]() $\hat {y}$ satisfying (67) and the identities (68) and (65).
$\hat {y}$ satisfying (67) and the identities (68) and (65).
For any positive integer ![]() $N$, let
$N$, let ![]() $\mathbb {C}_{p}[{\Sigma }^o]^{ N} \subset \mathbb {C}[{\Sigma }^o]$ be the ideal consisting of those
$\mathbb {C}_{p}[{\Sigma }^o]^{ N} \subset \mathbb {C}[{\Sigma }^o]$ be the ideal consisting of those ![]() $g\in \mathbb {C}[{\Sigma }^o]$ such that its pull-back to
$g\in \mathbb {C}[{\Sigma }^o]$ such that its pull-back to ![]() $\Sigma '^o$ via
$\Sigma '^o$ via ![]() $\nu$ has a zero of order
$\nu$ has a zero of order ![]() $\geq N$ at any point of
$\geq N$ at any point of ![]() $\pi '^{-1}(p')$. Let
$\pi '^{-1}(p')$. Let ![]() $\mathfrak {g}_{p}[{\Sigma }^o ]^{\Gamma, N}\subset \mathfrak {g}[{\Sigma }^o ]^\Gamma$ be the Lie subalgebra defined as
$\mathfrak {g}_{p}[{\Sigma }^o ]^{\Gamma, N}\subset \mathfrak {g}[{\Sigma }^o ]^\Gamma$ be the Lie subalgebra defined as ![]() $\big [\mathfrak {g} \otimes \mathbb {C}_{p}[{\Sigma }^o]^{ N} \big ]^\Gamma$. By the same proof as that of Lemma 3.7,
$\big [\mathfrak {g} \otimes \mathbb {C}_{p}[{\Sigma }^o]^{ N} \big ]^\Gamma$. By the same proof as that of Lemma 3.7, ![]() $\mathfrak {g}_{p}[{\Sigma }^o ]^{\Gamma, N}\cdot \mathscr {H}( \vec {\lambda })$ is of finite codimension in
$\mathfrak {g}_{p}[{\Sigma }^o ]^{\Gamma, N}\cdot \mathscr {H}( \vec {\lambda })$ is of finite codimension in ![]() $\mathscr {H}( \vec {\lambda })$.
$\mathscr {H}( \vec {\lambda })$.
Let ![]() $V$ be a finite-dimensional complement of
$V$ be a finite-dimensional complement of ![]() $\mathfrak {g}_{p}[{\Sigma }^o ]^{\Gamma,o(y)(N_{o}-1)+1}\cdot \mathscr {H}( \vec {\lambda })$ in
$\mathfrak {g}_{p}[{\Sigma }^o ]^{\Gamma,o(y)(N_{o}-1)+1}\cdot \mathscr {H}( \vec {\lambda })$ in ![]() $\mathscr {H}( \vec {\lambda })$. Since
$\mathscr {H}( \vec {\lambda })$. Since ![]() $\hat {y}$ acts locally nilpotently on
$\hat {y}$ acts locally nilpotently on ![]() $\mathscr {H}( \vec {\lambda })$ (cf. Lemma 2.5) and
$\mathscr {H}( \vec {\lambda })$ (cf. Lemma 2.5) and ![]() $V$ is finite dimensional, there exists
$V$ is finite dimensional, there exists ![]() $N$ (which we take
$N$ (which we take ![]() $\geq N_{o}$) such that
$\geq N_{o}$) such that
Considering now the binomial theorem for the operator ![]() $L^{n}_{y}=(ad(y)+R_{y})^{n}$, we get (in any associative algebra)
$L^{n}_{y}=(ad(y)+R_{y})^{n}$, we get (in any associative algebra)
 \[ y^{n}x=\sum^{n}_{j=0}\binom{n}{j}\big((ad (y))^{j}x\big)y^{n-j}. \]
\[ y^{n}x=\sum^{n}_{j=0}\binom{n}{j}\big((ad (y))^{j}x\big)y^{n-j}. \]
Take any ![]() $\hat {z}\in \mathfrak {g}_{p}[{\Sigma }^o ]^{\Gamma,o(y)(N_{o}-1)+1}$. By the above identity in the enveloping algebra
$\hat {z}\in \mathfrak {g}_{p}[{\Sigma }^o ]^{\Gamma,o(y)(N_{o}-1)+1}$. By the above identity in the enveloping algebra ![]() $U\big ((\mathfrak {g}\otimes \mathbb {C}_{p''}[\Sigma '^o\setminus \pi '^{-1}(p')])^\Gamma\big)$, using the identity (66),
$U\big ((\mathfrak {g}\otimes \mathbb {C}_{p''}[\Sigma '^o\setminus \pi '^{-1}(p')])^\Gamma\big)$, using the identity (66),
 \[ \hat{y}^{N}\cdot \hat{z}=\sum^{N_{o}-1}_{j=0}\binom{N}{j}\big((\mathrm{ad}\, \hat{y})^{j}(\hat{z})\big)\hat{y}^{N-j}. \]
\[ \hat{y}^{N}\cdot \hat{z}=\sum^{N_{o}-1}_{j=0}\binom{N}{j}\big((\mathrm{ad}\, \hat{y})^{j}(\hat{z})\big)\hat{y}^{N-j}. \]
Thus,
Combining (69)–(71), we get that
This proves that ![]() $M\subset \mathscr {H}( \vec {\lambda })^{*}$ is an integrable
$M\subset \mathscr {H}( \vec {\lambda })^{*}$ is an integrable ![]() ${{\hat {\mathfrak {g}}}}_{p'}$-module (generated by
${{\hat {\mathfrak {g}}}}_{p'}$-module (generated by ![]() $\Phi$). Let
$\Phi$). Let ![]() $M_{o}\subset M$ be the
$M_{o}\subset M$ be the ![]() $\mathfrak {g}_{p'}$-submodule generated by
$\mathfrak {g}_{p'}$-submodule generated by ![]() $\Phi$. Decompose
$\Phi$. Decompose ![]() $M_{o}$ into irreducible components:
$M_{o}$ into irreducible components:
where ![]() $D$ is the set of dominant integral weights of
$D$ is the set of dominant integral weights of ![]() $\mathfrak {g}_{p'}$. Take any highest weight vector
$\mathfrak {g}_{p'}$. Take any highest weight vector ![]() $v_{o}$ in any irreducible
$v_{o}$ in any irreducible ![]() $\mathfrak {g}_{p'}$-submodule
$\mathfrak {g}_{p'}$-submodule ![]() $V(\mu )$ of
$V(\mu )$ of ![]() $M_{o}$. Since
$M_{o}$. Since ![]() ${\hat {\mathfrak {g}}}^+_{p'}$ annihilates
${\hat {\mathfrak {g}}}^+_{p'}$ annihilates ![]() $M_{o}$ (cf. (65)),
$M_{o}$ (cf. (65)), ![]() $v_{o}$ generates an integrable highest weight
$v_{o}$ generates an integrable highest weight ![]() ${{\hat {\mathfrak {g}}}}_{p'}$-submodule of
${{\hat {\mathfrak {g}}}}_{p'}$-submodule of ![]() $M$ of highest weight
$M$ of highest weight ![]() $\mu$ with central charge
$\mu$ with central charge ![]() $c$. In particular, any
$c$. In particular, any ![]() $V(\mu )$ appearing in
$V(\mu )$ appearing in ![]() $M_{o}$ satisfies
$M_{o}$ satisfies ![]() $\mu \in D_{c, p'}$ (by the definition of
$\mu \in D_{c, p'}$ (by the definition of ![]() $D_{c, p'}$), i.e.
$D_{c, p'}$), i.e. ![]() $\mu ^*\in D_{c, p''}$ by Lemma 5.3.
$\mu ^*\in D_{c, p''}$ by Lemma 5.3.
By the evaluation map ![]() ${\rm ev}_{q'}:\mathfrak {g}_{p'}\simeq \mathfrak {g}^{\Gamma _q}$, we may view
${\rm ev}_{q'}:\mathfrak {g}_{p'}\simeq \mathfrak {g}^{\Gamma _q}$, we may view ![]() $M_o$ as a module over
$M_o$ as a module over ![]() $\mathfrak {g}^{\Gamma _q}$ and each
$\mathfrak {g}^{\Gamma _q}$ and each ![]() $V(\mu )$ the irreducible representation of
$V(\mu )$ the irreducible representation of ![]() $\mathfrak {g}^{\Gamma _q}$. Thus, from (56) of Definition 5.5, applied to the map
$\mathfrak {g}^{\Gamma _q}$. Thus, from (56) of Definition 5.5, applied to the map
we get that for any ![]() $a\in \operatorname {\mathrm {Ker}} \beta$,
$a\in \operatorname {\mathrm {Ker}} \beta$, ![]() $a \cdot \Phi =0$, i.e.
$a \cdot \Phi =0$, i.e. ![]() $\Phi (\varphi (a^{t})\cdot h)=0$, for any
$\Phi (\varphi (a^{t})\cdot h)=0$, for any ![]() $h\in \mathscr {H}( \vec {\lambda })$. (Observe that
$h\in \mathscr {H}( \vec {\lambda })$. (Observe that ![]() $K_{\mu ^*}= K_\mu ^t$.) This proves the lemma and, hence, Theorem 5.4 is fully established.
$K_{\mu ^*}= K_\mu ^t$.) This proves the lemma and, hence, Theorem 5.4 is fully established.
6. Twisted Kac–Moody algebras and Sugawara construction over a base
We define twisted Kac–Moody Lie algebras, their Verma modules and integrable highest weight modules with parameters and prove the independence of parameters for the integrable highest weight modules. We also prove that the Sugawara operators acting on the integrable highest weight modules (of twisted affine Kac–Moody algebras) are independent of the parameters up to scalars.
Let ![]() $R$ be a commutative algebra over
$R$ be a commutative algebra over ![]() $\mathbb {C}$. In this section, all commutative algebras are over
$\mathbb {C}$. In this section, all commutative algebras are over ![]() $\mathbb {C}$, and we fix a root of unity
$\mathbb {C}$, and we fix a root of unity ![]() $\epsilon =e^{ {2\pi i}/{m}}$ of order
$\epsilon =e^{ {2\pi i}/{m}}$ of order ![]() $m$ and a central charge
$m$ and a central charge ![]() $c>0$. In addition, as earlier,
$c>0$. In addition, as earlier, ![]() $\mathfrak {g}$ is a simple Lie algebra over
$\mathfrak {g}$ is a simple Lie algebra over ![]() $\mathbb {C}$ and
$\mathbb {C}$ and ![]() $\sigma$ is a Lie algebra automorphism such that
$\sigma$ is a Lie algebra automorphism such that ![]() $\sigma ^m=\operatorname {\mathrm {Id}}$.
$\sigma ^m=\operatorname {\mathrm {Id}}$.
Definition 6.1 (a) We say that an ![]() $R$-algebra
$R$-algebra ![]() $\mathcal {O}_R$ is a complete local
$\mathcal {O}_R$ is a complete local ![]() $R$-algebra if there exists
$R$-algebra if there exists ![]() $t\in \mathcal {O}_R$ such that
$t\in \mathcal {O}_R$ such that ![]() $\mathcal {O}_R\simeq R[[t]]$ as an
$\mathcal {O}_R\simeq R[[t]]$ as an ![]() $R$-algebra, where
$R$-algebra, where ![]() $R[[t]]$ denotes the
$R[[t]]$ denotes the ![]() $R$-algebra of formal power series over
$R$-algebra of formal power series over ![]() $R$. We say such a
$R$. We say such a ![]() $t$ is an
$t$ is an ![]() $R$-parameter of
$R$-parameter of ![]() $\mathcal {O}_R$. Let
$\mathcal {O}_R$. Let ![]() $\mathcal {K}_R$ be the
$\mathcal {K}_R$ be the ![]() $R$-algebra containing
$R$-algebra containing ![]() $\mathcal {O}_R$ by inverting
$\mathcal {O}_R$ by inverting ![]() $t$. Thus,
$t$. Thus, ![]() $\mathcal {K}_R \simeq R((t))$. Note that
$\mathcal {K}_R \simeq R((t))$. Note that ![]() $\mathcal {K}_R$ does not depend on the choice of the
$\mathcal {K}_R$ does not depend on the choice of the ![]() $R$-parameters.
$R$-parameters.
(b) An ![]() $R$-rotation of
$R$-rotation of ![]() $\mathcal {O}_R$ of order
$\mathcal {O}_R$ of order ![]() $m$ is an
$m$ is an ![]() $R$-algebra automorphism
$R$-algebra automorphism ![]() $\sigma$ of
$\sigma$ of ![]() $\mathcal {O}_R$ (of order
$\mathcal {O}_R$ (of order ![]() $m$) such that
$m$) such that ![]() $\sigma (t)=\epsilon ^{-1}t$ for some
$\sigma (t)=\epsilon ^{-1}t$ for some ![]() $R$-parameter
$R$-parameter ![]() $t$. Such an
$t$. Such an ![]() $R$-parameter
$R$-parameter ![]() $t$ is called a
$t$ is called a ![]() $\sigma$-equivariant
$\sigma$-equivariant ![]() $R$-parameter. Observe that any
$R$-parameter. Observe that any ![]() $R$-algebra automorphism of
$R$-algebra automorphism of ![]() $\mathcal {O}_R$ of order
$\mathcal {O}_R$ of order ![]() $m$ may not be an
$m$ may not be an ![]() $R$-rotation. Clearly, an
$R$-rotation. Clearly, an ![]() $R$-algebra automorphism of
$R$-algebra automorphism of ![]() $\mathcal {O}_R$ extends uniquely as an automorphism of
$\mathcal {O}_R$ extends uniquely as an automorphism of ![]() $\mathcal {K}_R$, which we still denote by
$\mathcal {K}_R$, which we still denote by ![]() $\sigma$.
$\sigma$.
Given a pair ![]() $(\mathcal {O}_R, \sigma )$ of a complete local
$(\mathcal {O}_R, \sigma )$ of a complete local ![]() $R$-algebra
$R$-algebra ![]() $\mathcal {O}_R$ and an
$\mathcal {O}_R$ and an ![]() $R$-rotation of order
$R$-rotation of order ![]() $m$, we can attach an
$m$, we can attach an ![]() $R$-linear Kac–Moody algebra
$R$-linear Kac–Moody algebra ![]() $\hat {L}(\mathfrak {g}, \sigma )_R$,
$\hat {L}(\mathfrak {g}, \sigma )_R$,
where ![]() $C$ is a central element of
$C$ is a central element of ![]() $\hat {L}(\mathfrak {g}, \sigma )_R$, and for any
$\hat {L}(\mathfrak {g}, \sigma )_R$, and for any ![]() $x[g],y[h]\in (\mathfrak {g}\otimes _\mathbb {C} \mathcal {K}_R )^\sigma$,
$x[g],y[h]\in (\mathfrak {g}\otimes _\mathbb {C} \mathcal {K}_R )^\sigma$,
Here the residue ![]() ${\rm Res} (dg )h$ is well-defined and independent of the choice of
${\rm Res} (dg )h$ is well-defined and independent of the choice of ![]() $R$-parameters (cf. [Reference HartshorneHar77, Chap. III, Proof of Theorem 7.14.1]). We denote by
$R$-parameters (cf. [Reference HartshorneHar77, Chap. III, Proof of Theorem 7.14.1]). We denote by ![]() $\hat {L}(\mathfrak {g}, \sigma )_R^{\geq 0}$ the
$\hat {L}(\mathfrak {g}, \sigma )_R^{\geq 0}$ the ![]() $R$-Lie subalgebra
$R$-Lie subalgebra ![]() $(\mathfrak {g}\otimes _\mathbb {C} \mathcal {O}_R )^\sigma \oplus R \cdot C$.
$(\mathfrak {g}\otimes _\mathbb {C} \mathcal {O}_R )^\sigma \oplus R \cdot C$.
Given a complete local ![]() $R$-algebra
$R$-algebra ![]() $\mathcal {O}_R$, let
$\mathcal {O}_R$, let ![]() $\mathfrak {m}_R$ denote the ideal of
$\mathfrak {m}_R$ denote the ideal of ![]() $\mathcal {O}_R$ generated by a formal parameter
$\mathcal {O}_R$ generated by a formal parameter ![]() $t$. Note that
$t$. Note that ![]() $\mathfrak {m}_R$ does not depend on the choice of
$\mathfrak {m}_R$ does not depend on the choice of ![]() $t$. Then,
$t$. Then, ![]() $\mathcal {O}_R/\mathfrak {m}_R\simeq R$. This allows us to give a natural map for an
$\mathcal {O}_R/\mathfrak {m}_R\simeq R$. This allows us to give a natural map for an ![]() $R$-rotation
$R$-rotation ![]() $\sigma$ of
$\sigma$ of ![]() $\mathcal {O}_R$
$\mathcal {O}_R$
which is independent of the choice of the parameter ![]() $t$. Given any morphism of commutative
$t$. Given any morphism of commutative ![]() $\mathbb {C}$-algebras
$\mathbb {C}$-algebras ![]() $f:R\to R'$, we define
$f:R\to R'$, we define
Then, ![]() $\mathcal {O}_{R} \hat {\otimes }_R R'$ is a complete local
$\mathcal {O}_{R} \hat {\otimes }_R R'$ is a complete local ![]() $R'$-algebra. For any
$R'$-algebra. For any ![]() $R$-parameter
$R$-parameter ![]() $t\in \mathcal {O}_R$,
$t\in \mathcal {O}_R$, ![]() $t':=t\hat {\otimes } 1$ is an
$t':=t\hat {\otimes } 1$ is an ![]() $R'$-parameter of
$R'$-parameter of ![]() $\mathcal {O}_{R} \hat {\otimes }_R R'$. Let
$\mathcal {O}_{R} \hat {\otimes }_R R'$. Let ![]() $\sigma$ be any
$\sigma$ be any ![]() $R$-rotation of
$R$-rotation of ![]() $\mathcal {O}_R$ of order
$\mathcal {O}_R$ of order ![]() $m$. Then, it induces an
$m$. Then, it induces an ![]() $R'$-rotation of
$R'$-rotation of ![]() $\mathcal {O}_R\hat {\otimes }_R R'$. We still denote it by
$\mathcal {O}_R\hat {\otimes }_R R'$. We still denote it by ![]() $\sigma$.
$\sigma$.
Lemma 6.2 Let ![]() $\mathcal {O_R}$ be a complete local
$\mathcal {O_R}$ be a complete local ![]() $R$-algebra with an
$R$-algebra with an ![]() $R$-rotation
$R$-rotation ![]() $\sigma$ of order
$\sigma$ of order ![]() $m$. Given any finite morphism of commutative
$m$. Given any finite morphism of commutative ![]() $\mathbb {C}$-algebras
$\mathbb {C}$-algebras ![]() $f: R\to R'$, there exists a natural isomorphism of Lie algebras
$f: R\to R'$, there exists a natural isomorphism of Lie algebras ![]() $\hat {L}(\mathfrak {g}, \sigma )_R\otimes _R R' \simeq \hat {L}(\mathfrak {g}, \sigma )_{R'}$, where
$\hat {L}(\mathfrak {g}, \sigma )_R\otimes _R R' \simeq \hat {L}(\mathfrak {g}, \sigma )_{R'}$, where ![]() $\hat {L}(\mathfrak {g}, \sigma )_{R'}$ is the
$\hat {L}(\mathfrak {g}, \sigma )_{R'}$ is the ![]() $R'$-Kac–Moody algebra attached to
$R'$-Kac–Moody algebra attached to ![]() $\mathcal {O}_{R'}: =\mathcal {O}_R\hat {\otimes }_R R'$ and the induced rotation
$\mathcal {O}_{R'}: =\mathcal {O}_R\hat {\otimes }_R R'$ and the induced rotation ![]() $\sigma$.
$\sigma$.
Proof. It suffices to check that ![]() $\mathcal {K}_R\otimes _R R'\simeq \mathcal {K}_{R'}$, which is well-known (since
$\mathcal {K}_R\otimes _R R'\simeq \mathcal {K}_{R'}$, which is well-known (since ![]() $f$ is a finite morphism).
$f$ is a finite morphism).
Let ![]() $V$ be an irreducible representation of
$V$ be an irreducible representation of ![]() $\mathfrak {g}^\sigma$ with highest weight
$\mathfrak {g}^\sigma$ with highest weight ![]() $\lambda \in D_c$, where
$\lambda \in D_c$, where ![]() $D_{c}$ is defined in § 2. Then
$D_{c}$ is defined in § 2. Then ![]() $V_R:=V\otimes _{\mathbb {C}} R$ is naturally a representation of
$V_R:=V\otimes _{\mathbb {C}} R$ is naturally a representation of ![]() $\mathfrak {g}^\sigma \otimes _\mathbb {C} R$. Define the generalized Verma module
$\mathfrak {g}^\sigma \otimes _\mathbb {C} R$. Define the generalized Verma module
where ![]() $U_R(\cdot )$ denotes the universal enveloping algebra of
$U_R(\cdot )$ denotes the universal enveloping algebra of ![]() $R$-Lie algebra, and
$R$-Lie algebra, and ![]() $V_R$ is a module over
$V_R$ is a module over ![]() $U_R( \hat {L}(\mathfrak {g}, \sigma )_R^{\geq 0})$ via the projection map
$U_R( \hat {L}(\mathfrak {g}, \sigma )_R^{\geq 0})$ via the projection map ![]() $\hat {L}(\mathfrak {g}, \sigma )_R^{\geq 0}\to (\mathfrak {g}^\sigma \otimes _{\mathbb {C}} R)\oplus R \cdot C$ and such that
$\hat {L}(\mathfrak {g}, \sigma )_R^{\geq 0}\to (\mathfrak {g}^\sigma \otimes _{\mathbb {C}} R)\oplus R \cdot C$ and such that ![]() $C$ acts on
$C$ acts on ![]() $V_R$ by
$V_R$ by ![]() $c$.
$c$.
Lemma 6.3 The Verma module ![]() $\hat {M}(V, c)_{R}$ is a free
$\hat {M}(V, c)_{R}$ is a free ![]() $R$-module. Given any morphism
$R$-module. Given any morphism ![]() $R\to R'$ of
$R\to R'$ of ![]() $\mathbb {C}$-algebras, there exists a natural isomorphism
$\mathbb {C}$-algebras, there exists a natural isomorphism ![]() $\hat {M}(V, c)_R \otimes _R R' \simeq \hat {M}(V, c)_{R'}$ as
$\hat {M}(V, c)_R \otimes _R R' \simeq \hat {M}(V, c)_{R'}$ as ![]() $\hat {L}(\mathfrak {g},\sigma )_R \otimes R'$-modules, where
$\hat {L}(\mathfrak {g},\sigma )_R \otimes R'$-modules, where ![]() $\hat {M}(V, c)_{R'}$ is the generalized Verma module attached to
$\hat {M}(V, c)_{R'}$ is the generalized Verma module attached to ![]() $\mathcal {O}_{R'}:= \mathcal {O}_R\hat {\otimes }_R R'$ and the action of
$\mathcal {O}_{R'}:= \mathcal {O}_R\hat {\otimes }_R R'$ and the action of ![]() $\hat {L}(\mathfrak {g},\sigma )_R\otimes _R R'$ on
$\hat {L}(\mathfrak {g},\sigma )_R\otimes _R R'$ on ![]() $\hat {M}(V, c)_{R'}$ is via the canonical morphism
$\hat {M}(V, c)_{R'}$ is via the canonical morphism ![]() $\hat {L}(\mathfrak {g},\sigma )_R\otimes _R R' \to \hat {L}(\mathfrak {g},\sigma )_{R' }$.
$\hat {L}(\mathfrak {g},\sigma )_R\otimes _R R' \to \hat {L}(\mathfrak {g},\sigma )_{R' }$.
Proof. Let ![]() $t$ be a
$t$ be a ![]() $\sigma$-equivariant
$\sigma$-equivariant ![]() $R$-parameter. There exists a decomposition as
$R$-parameter. There exists a decomposition as ![]() $R$-module:
$R$-module:
Hence, ![]() $\hat {M}(V,c)_{R}\simeq {U}_R( ( \mathfrak {g}\otimes t^{-1} R[t^{-1}])^\sigma )\otimes _{\mathbb {C}}V$. Note that
$\hat {M}(V,c)_{R}\simeq {U}_R( ( \mathfrak {g}\otimes t^{-1} R[t^{-1}])^\sigma )\otimes _{\mathbb {C}}V$. Note that ![]() $( \mathfrak {g}\otimes t^{-1} R[t^{-1}])^\sigma$ is a Lie algebra which is a free module over
$( \mathfrak {g}\otimes t^{-1} R[t^{-1}])^\sigma$ is a Lie algebra which is a free module over ![]() $R$. By the Poincaré–Birkhoff–Witt theorem for any
$R$. By the Poincaré–Birkhoff–Witt theorem for any ![]() $R$-Lie algebra that is free as an
$R$-Lie algebra that is free as an ![]() $R$-module (cf. [Reference Cartan and EilenbergCE56, Theorem 3.1, Chapter XIII]),
$R$-module (cf. [Reference Cartan and EilenbergCE56, Theorem 3.1, Chapter XIII]), ![]() $\hat {M}(V,c)_{R}$ is a free
$\hat {M}(V,c)_{R}$ is a free ![]() $R$-module.
$R$-module.
Note that there is a natural morphism ![]() $\hat {L}(\mathfrak {g}, \sigma )_R\otimes _R R' \to \hat {L}(\mathfrak {g},\sigma )_{R'}$. It induces a natural morphism
$\hat {L}(\mathfrak {g}, \sigma )_R\otimes _R R' \to \hat {L}(\mathfrak {g},\sigma )_{R'}$. It induces a natural morphism ![]() $\kappa : \hat {M}(V,c)_R\otimes R' \to \hat {M}(V,c)_{R'}$. The map
$\kappa : \hat {M}(V,c)_R\otimes R' \to \hat {M}(V,c)_{R'}$. The map ![]() $\kappa$ is an isomorphism since it induces the following natural isomorphism
$\kappa$ is an isomorphism since it induces the following natural isomorphism
where ![]() $t'=t\hat {\otimes } 1$.
$t'=t\hat {\otimes } 1$.
We can choose a ![]() $\sigma$-stable Borel subalgebra
$\sigma$-stable Borel subalgebra ![]() $\mathfrak {b} \subset \mathfrak {g}$, a
$\mathfrak {b} \subset \mathfrak {g}$, a ![]() $\sigma$-stable Cartan subalgebra
$\sigma$-stable Cartan subalgebra ![]() $\mathfrak {h}\subset \mathfrak {b}$, the elements
$\mathfrak {h}\subset \mathfrak {b}$, the elements ![]() $\{x_i,y_i \}_{i\in \hat {I}(\mathfrak {g}, \sigma )}$, and the set of non-negative integers
$\{x_i,y_i \}_{i\in \hat {I}(\mathfrak {g}, \sigma )}$, and the set of non-negative integers ![]() $\{ s_i\,|\, i\in \hat {I}(\mathfrak {g}, \sigma ) \}$ as in § 2, such that
$\{ s_i\,|\, i\in \hat {I}(\mathfrak {g}, \sigma ) \}$ as in § 2, such that ![]() $\hat {L}(\mathfrak {g},\sigma )_R$ contains the elements
$\hat {L}(\mathfrak {g},\sigma )_R$ contains the elements ![]() $x_i[t^{s_i}], y_i[t^{-s_i}]$. Let
$x_i[t^{s_i}], y_i[t^{-s_i}]$. Let ![]() $V=V(\lambda )$ be the irreducible
$V=V(\lambda )$ be the irreducible ![]() $\mathfrak {g}^\sigma$-module with highest weight
$\mathfrak {g}^\sigma$-module with highest weight ![]() $\lambda \in D_c$ (cf. Lemma 2.1 for the description of
$\lambda \in D_c$ (cf. Lemma 2.1 for the description of ![]() $D_c$). Let
$D_c$). Let ![]() $\hat {N}(V,c)_R$ be the
$\hat {N}(V,c)_R$ be the ![]() $\hat {L}(\mathfrak {g},\sigma )_R$-submodule of
$\hat {L}(\mathfrak {g},\sigma )_R$-submodule of ![]() $\hat {M}(V, c)_R$ generated by
$\hat {M}(V, c)_R$ generated by ![]() $\{y_i[t^{-s_i}]^{n_{\lambda, i} +1 }\cdot v_\lambda \}_{i\in \hat {I}(\mathfrak {g}, \sigma )^+}$, where
$\{y_i[t^{-s_i}]^{n_{\lambda, i} +1 }\cdot v_\lambda \}_{i\in \hat {I}(\mathfrak {g}, \sigma )^+}$, where ![]() $v_\lambda$ is the highest weight vector of
$v_\lambda$ is the highest weight vector of ![]() $V (\lambda )$,
$V (\lambda )$, ![]() $n_{\lambda, i}$ is defined by the identity (6) and (as in § 2)
$n_{\lambda, i}$ is defined by the identity (6) and (as in § 2) ![]() $\hat {I}(\mathfrak {g}, \sigma )^+:= \{ i\in \hat {I}(\mathfrak {g}, \sigma ): s_i> 0\}$.
$\hat {I}(\mathfrak {g}, \sigma )^+:= \{ i\in \hat {I}(\mathfrak {g}, \sigma ): s_i> 0\}$.
Lemma 6.4 The module ![]() $\hat {N}(V,c)_R$ does not depend on the choice of the
$\hat {N}(V,c)_R$ does not depend on the choice of the ![]() $\sigma$-equivariant
$\sigma$-equivariant ![]() $R$-parameter
$R$-parameter ![]() $t$.
$t$.
Proof. Let ![]() $t'$ be another
$t'$ be another ![]() $\sigma$-equivariant
$\sigma$-equivariant ![]() $R$-parameter. It suffices to show that for each
$R$-parameter. It suffices to show that for each ![]() $i\in \hat {I}(\mathfrak {g},\sigma )^+$,
$i\in \hat {I}(\mathfrak {g},\sigma )^+$, ![]() $y_i[t'^{-s_i}]^{n_{\lambda, i} +1 }\cdot v_\lambda =c y_i[t^{-s_i}]^{n_{\lambda, i} +1 }\cdot v_\lambda$ for some constant
$y_i[t'^{-s_i}]^{n_{\lambda, i} +1 }\cdot v_\lambda =c y_i[t^{-s_i}]^{n_{\lambda, i} +1 }\cdot v_\lambda$ for some constant ![]() $c\in R^\times$ (where
$c\in R^\times$ (where ![]() $R^\times$ denotes the set of units in
$R^\times$ denotes the set of units in ![]() $R$). By the
$R$). By the ![]() $\sigma$-equivariance of
$\sigma$-equivariance of ![]() $t$ and
$t$ and ![]() $t'$, we can write
$t'$, we can write ![]() $t'^{-s_i}=c t^{-s_i}+ \sum _{k> -s_i, m|s_i+k} a_k t^{k}$, for some
$t'^{-s_i}=c t^{-s_i}+ \sum _{k> -s_i, m|s_i+k} a_k t^{k}$, for some ![]() $c\in R^\times$ and
$c\in R^\times$ and ![]() $a_k\in R$.
$a_k\in R$.
Case 1. If ![]() $i\in \hat {I}(\mathfrak {g}, \sigma )^+$ and
$i\in \hat {I}(\mathfrak {g}, \sigma )^+$ and ![]() $0< s_i < m$, then
$0< s_i < m$, then ![]() $t'^{-s_i}=c t^{-s_i}+ g$, where
$t'^{-s_i}=c t^{-s_i}+ g$, where ![]() $g=\sum _{k> 0} a_k t^{k}$ with
$g=\sum _{k> 0} a_k t^{k}$ with ![]() $a_k\in R$ (since
$a_k\in R$ (since ![]() $0< s_i< m$ and
$0< s_i< m$ and ![]() $m|(s_i+k)$). Since
$m|(s_i+k)$). Since ![]() $y_i[g]\cdot v_\lambda = 0$, it is clear that
$y_i[g]\cdot v_\lambda = 0$, it is clear that ![]() $y_i[t'^{-s_i}]^{n_{\lambda, i}+1} \cdot v_\lambda =\big (c y_i[t^{-s_i}]\big )^{n_{\lambda, i}+1} \cdot v_\lambda$.
$y_i[t'^{-s_i}]^{n_{\lambda, i}+1} \cdot v_\lambda =\big (c y_i[t^{-s_i}]\big )^{n_{\lambda, i}+1} \cdot v_\lambda$.
Case 2. If ![]() $s_o=m$, then
$s_o=m$, then ![]() $t'^{-m}=c t^{-m}+ g$, where
$t'^{-m}=c t^{-m}+ g$, where ![]() $g=\sum _{k\geq 0} a_k t^{k}$ with
$g=\sum _{k\geq 0} a_k t^{k}$ with ![]() $a_k\in R$. Since
$a_k\in R$. Since ![]() $s_o=m$, by [Reference KacKac90, Identity 8.5.6], each
$s_o=m$, by [Reference KacKac90, Identity 8.5.6], each ![]() $s_j= 0$ for
$s_j= 0$ for ![]() $j\neq o$ and
$j\neq o$ and ![]() $r=1$. Thus, the simple root vectors of
$r=1$. Thus, the simple root vectors of ![]() $\mathfrak {g}^\sigma$ are
$\mathfrak {g}^\sigma$ are ![]() $\{x_j\}_{j\neq o}$ with (simple) roots
$\{x_j\}_{j\neq o}$ with (simple) roots ![]() $\{\alpha _j\}_{j\neq o}$. Since
$\{\alpha _j\}_{j\neq o}$. Since ![]() $y_o$ is a root vector of the root
$y_o$ is a root vector of the root ![]() $\theta _0$ and
$\theta _0$ and ![]() $\theta _0$ is a positive linear combination
$\theta _0$ is a positive linear combination ![]() $\sum _{j \neq o} a_j\alpha _j$,
$\sum _{j \neq o} a_j\alpha _j$, ![]() $y_o$ is a positive root vector of
$y_o$ is a positive root vector of ![]() $\mathfrak {g}^\sigma$. Hence,
$\mathfrak {g}^\sigma$. Hence, ![]() $y_o\cdot v_\lambda =0$. Thus, it follows that
$y_o\cdot v_\lambda =0$. Thus, it follows that ![]() $y_o[g]\cdot v_\lambda =0$. Hence,
$y_o[g]\cdot v_\lambda =0$. Hence, ![]() $y_o[t'^{-m}]^{n_{\lambda, o}+1} \cdot v_\lambda =\big (c y_o[t^{-m}]\big )^{n_{\lambda, o}+1} \cdot v_\lambda$.
$y_o[t'^{-m}]^{n_{\lambda, o}+1} \cdot v_\lambda =\big (c y_o[t^{-m}]\big )^{n_{\lambda, o}+1} \cdot v_\lambda$.
Case 3. If ![]() $s_i=m$ for
$s_i=m$ for ![]() $i\neq o$, then again by [Reference KacKac90, Identity 8.5.6],
$i\neq o$, then again by [Reference KacKac90, Identity 8.5.6], ![]() $r=1$ and each
$r=1$ and each ![]() $s_j=0$ for
$s_j=0$ for ![]() $j\neq i$. Thus, the simple root vectors of
$j\neq i$. Thus, the simple root vectors of ![]() $\mathfrak {g}^\sigma$ are
$\mathfrak {g}^\sigma$ are ![]() $\{x_j\}_{j\neq i}$ with (simple) roots
$\{x_j\}_{j\neq i}$ with (simple) roots ![]() $\{\alpha _j\}_{j\notin \{i, o\}} \cup \{-\theta _0\}$. Hence,
$\{\alpha _j\}_{j\notin \{i, o\}} \cup \{-\theta _0\}$. Hence, ![]() $-a_i\alpha _i= -\theta _0+\sum _{j\notin \{i, o\}} a_j\alpha _j$ giving that
$-a_i\alpha _i= -\theta _0+\sum _{j\notin \{i, o\}} a_j\alpha _j$ giving that ![]() $-\alpha _i$ is a positive root of
$-\alpha _i$ is a positive root of ![]() $\mathfrak {g}^\sigma$ (since
$\mathfrak {g}^\sigma$ (since ![]() $a_i, a_j>0$ being coefficients of the highest root written as a sum of simple roots) and, hence,
$a_i, a_j>0$ being coefficients of the highest root written as a sum of simple roots) and, hence, ![]() $y_i \cdot v_\lambda = 0$. The rest of the argument is the same as in Case 2. This proves the lemma.
$y_i \cdot v_\lambda = 0$. The rest of the argument is the same as in Case 2. This proves the lemma.
We now define the following ![]() $R$-linear representation of
$R$-linear representation of ![]() $\hat {L}(\mathfrak {g}, \sigma )_R$:
$\hat {L}(\mathfrak {g}, \sigma )_R$:
Lemma 6.5 (1) The modules ![]() $\hat {N}(V,c)_R$ and
$\hat {N}(V,c)_R$ and ![]() $\mathscr {H}(V)_R$ are free over
$\mathscr {H}(V)_R$ are free over ![]() $R$. The module
$R$. The module ![]() $\hat {N}(V,c)_R$ is a
$\hat {N}(V,c)_R$ is a ![]() $R$-module direct summand of
$R$-module direct summand of ![]() $\hat {M}(V,c)_R$.
$\hat {M}(V,c)_R$.
(2) For any morphism ![]() $f: R\to R'$ of commutative
$f: R\to R'$ of commutative ![]() $\mathbb {C}$-algebras, there exists a natural isomorphism
$\mathbb {C}$-algebras, there exists a natural isomorphism ![]() $\hat {N}(V,c)_R\otimes _R R' \simeq \hat {N}(V,c)_{R'}$ and
$\hat {N}(V,c)_R\otimes _R R' \simeq \hat {N}(V,c)_{R'}$ and ![]() $\mathscr {H}(V)_R\otimes _R R'\simeq \mathscr {H}(V)_{R'}$ as modules over
$\mathscr {H}(V)_R\otimes _R R'\simeq \mathscr {H}(V)_{R'}$ as modules over ![]() $\hat {L}(\mathfrak {g},\sigma ) _R\otimes _R R'$, where the action of
$\hat {L}(\mathfrak {g},\sigma ) _R\otimes _R R'$, where the action of ![]() $\hat {L}(\mathfrak {g},\sigma ) _R\otimes _R R'$ on
$\hat {L}(\mathfrak {g},\sigma ) _R\otimes _R R'$ on ![]() $\hat {N}(V,c)_{R'}$ and
$\hat {N}(V,c)_{R'}$ and ![]() $\mathscr {H}(V)_{R'}$ is via the canonical morphism
$\mathscr {H}(V)_{R'}$ is via the canonical morphism ![]() $\hat {L}(\mathfrak {g},\sigma ) _R\otimes _R R' \to \hat {L}(\mathfrak {g},\sigma ) _{R'}$.
$\hat {L}(\mathfrak {g},\sigma ) _R\otimes _R R' \to \hat {L}(\mathfrak {g},\sigma ) _{R'}$.
(3) Choose any ![]() $\sigma$-equivariant
$\sigma$-equivariant ![]() $R$-parameter
$R$-parameter ![]() $t$. Then,
$t$. Then, ![]() $\hat {N}(V,c)_R\subset \hat {M}(V,c)_R^+$. Moreover, for any other
$\hat {N}(V,c)_R\subset \hat {M}(V,c)_R^+$. Moreover, for any other ![]() $\hat {L}(\mathfrak {g},\sigma ) _R$-graded submodule
$\hat {L}(\mathfrak {g},\sigma ) _R$-graded submodule ![]() $A$ of
$A$ of ![]() $\hat {M}(V,c)_R$ such that
$\hat {M}(V,c)_R$ such that ![]() $A\cap V_R =(0)$,
$A\cap V_R =(0)$, ![]() $A$ is contained in
$A$ is contained in ![]() $\hat {N}(V,c)_R$. Here
$\hat {N}(V,c)_R$. Here ![]() $\hat {M}(V,c)_R^+:= \bigoplus _{d\geq 1}\hat {M}(V,c)_R(d)$ and (for
$\hat {M}(V,c)_R^+:= \bigoplus _{d\geq 1}\hat {M}(V,c)_R(d)$ and (for ![]() $d \geq 0$)
$d \geq 0$)
Further, ![]() $A$ being graded means
$A$ being graded means ![]() $A= \bigoplus _{d\geq 0} A\cap (\hat {M}(V,c)_R(d))$.
$A= \bigoplus _{d\geq 0} A\cap (\hat {M}(V,c)_R(d))$.
Observe that ![]() $\hat {M}(V,c)_R (d)$ does depend upon the choice of the parameter
$\hat {M}(V,c)_R (d)$ does depend upon the choice of the parameter ![]() $t$.
$t$.
Hence, ![]() $\hat {N}(V,c)_R$ and
$\hat {N}(V,c)_R$ and ![]() $\mathscr {H}(V)_R$ do not depend on the choice of
$\mathscr {H}(V)_R$ do not depend on the choice of ![]() $\mathfrak {b},\mathfrak {h}$, and
$\mathfrak {b},\mathfrak {h}$, and ![]() $x_i,y_i, i\in \hat {I}(\mathfrak {g},\sigma )$.
$x_i,y_i, i\in \hat {I}(\mathfrak {g},\sigma )$.
Proof. Fix a ![]() $\sigma$-equivariant
$\sigma$-equivariant ![]() $R$-parameter
$R$-parameter ![]() $t$. For each
$t$. For each ![]() $i\in \hat {I}(\mathfrak {g},\sigma )^+$, the element
$i\in \hat {I}(\mathfrak {g},\sigma )^+$, the element ![]() $y_i[t^{-s_i}]^{n_{\lambda,i}+ 1} \cdot v_\lambda$ is a highest weight vector (cf. identity (9)). Hence,
$y_i[t^{-s_i}]^{n_{\lambda,i}+ 1} \cdot v_\lambda$ is a highest weight vector (cf. identity (9)). Hence,
Note that ![]() $U_R( ( \mathfrak {g}\otimes _{\mathbb {C}} R[t^{-1}] )^\sigma )\simeq U( ( \mathfrak {g}\otimes _{\mathbb {C}} \mathbb {C}[t^{-1}] )^\sigma ) \otimes _\mathbb {C}R$ as
$U_R( ( \mathfrak {g}\otimes _{\mathbb {C}} R[t^{-1}] )^\sigma )\simeq U( ( \mathfrak {g}\otimes _{\mathbb {C}} \mathbb {C}[t^{-1}] )^\sigma ) \otimes _\mathbb {C}R$ as ![]() $R$-algebras. Since
$R$-algebras. Since ![]() $R$ is flat over
$R$ is flat over ![]() $\mathbb {C}$, it is easy to see that (as a submodule of
$\mathbb {C}$, it is easy to see that (as a submodule of ![]() $\hat {M}(V,c)_R = \hat {M}(V,c)_\mathbb {C}\otimes _\mathbb {C} R$, where
$\hat {M}(V,c)_R = \hat {M}(V,c)_\mathbb {C}\otimes _\mathbb {C} R$, where ![]() $\hat {M}(V,c)_\mathbb {C} :=U( \hat {L}(\mathfrak {g}, \sigma )_\mathbb {C})\otimes _{U( \hat {L}(\mathfrak {g}, \sigma )_\mathbb {C}^{\geq 0})} V$ is a
$\hat {M}(V,c)_\mathbb {C} :=U( \hat {L}(\mathfrak {g}, \sigma )_\mathbb {C})\otimes _{U( \hat {L}(\mathfrak {g}, \sigma )_\mathbb {C}^{\geq 0})} V$ is a ![]() $\mathbb {C}$-lattice in
$\mathbb {C}$-lattice in ![]() $\hat {M}(V,c)_R$, which depends on the choice of
$\hat {M}(V,c)_R$, which depends on the choice of ![]() $t$, where
$t$, where ![]() $\hat {L}(\mathfrak {g}, \sigma )_\mathbb {C} := \big [\mathfrak {g}\otimes _\mathbb {C} \mathbb {C}((t))\big ]^\sigma \oplus \mathbb {C} C$ and
$\hat {L}(\mathfrak {g}, \sigma )_\mathbb {C} := \big [\mathfrak {g}\otimes _\mathbb {C} \mathbb {C}((t))\big ]^\sigma \oplus \mathbb {C} C$ and ![]() $\hat {L}(\mathfrak {g}, \sigma )_\mathbb {C}^{\geq 0} := \big [\mathfrak {g}\otimes _\mathbb {C} \mathbb {C}[[t]]\big ]^\sigma \oplus \mathbb {C} C$)
$\hat {L}(\mathfrak {g}, \sigma )_\mathbb {C}^{\geq 0} := \big [\mathfrak {g}\otimes _\mathbb {C} \mathbb {C}[[t]]\big ]^\sigma \oplus \mathbb {C} C$)
where ![]() $\hat {N}(V, c)_\mathbb {C}:= (\sum _{i\in \hat {I}(\mathfrak {g},\sigma )^+ } U( ( \mathfrak {g}\otimes _{\mathbb {C}} \mathbb {C}[t^{-1}] )^\sigma ) y_i[t^{-s_i}]^{n_{\lambda,i}+1} \cdot v_\lambda )$ is a
$\hat {N}(V, c)_\mathbb {C}:= (\sum _{i\in \hat {I}(\mathfrak {g},\sigma )^+ } U( ( \mathfrak {g}\otimes _{\mathbb {C}} \mathbb {C}[t^{-1}] )^\sigma ) y_i[t^{-s_i}]^{n_{\lambda,i}+1} \cdot v_\lambda )$ is a ![]() $\mathbb {C}$-lattice of
$\mathbb {C}$-lattice of ![]() $\hat {N}(V,c)_R$. Hence,
$\hat {N}(V,c)_R$. Hence, ![]() $\hat {N}(V,c)_R$ is free over
$\hat {N}(V,c)_R$ is free over ![]() $R$ and it is a direct summand (as an
$R$ and it is a direct summand (as an ![]() $R$-module) of
$R$-module) of ![]() $\hat {M}(V,c)_R$. From this we readily see that
$\hat {M}(V,c)_R$. From this we readily see that
where ![]() $\mathscr {H}(V)_\mathbb {C} :=\hat {M}(V,c)_\mathbb {C}/\hat {N}(V,c)_\mathbb {C}$ is a
$\mathscr {H}(V)_\mathbb {C} :=\hat {M}(V,c)_\mathbb {C}/\hat {N}(V,c)_\mathbb {C}$ is a ![]() $\mathbb {C}$-lattice in
$\mathbb {C}$-lattice in ![]() $\mathscr {H}(V)_R$ (depending on the choice of
$\mathscr {H}(V)_R$ (depending on the choice of ![]() $t$), and hence it is also free over
$t$), and hence it is also free over ![]() $R$. This finishes the proof of part (1) of the lemma.
$R$. This finishes the proof of part (1) of the lemma.
By the above equation (74) and the associativity of the tensor product: ![]() $(M\otimes _R S)\otimes _S T\simeq M\otimes _R T$, we also have
$(M\otimes _R S)\otimes _S T\simeq M\otimes _R T$, we also have ![]() $\hat {N}(V,c)_R\otimes _R R' \simeq \hat {N}(V,c)_{R'}$. Similarly, by the above equation (75),
$\hat {N}(V,c)_R\otimes _R R' \simeq \hat {N}(V,c)_{R'}$. Similarly, by the above equation (75), ![]() $\mathscr {H}(V)_R\otimes _R R' \simeq \mathscr {H}(V)_{R'}$. This concludes part (2) of the lemma.
$\mathscr {H}(V)_R\otimes _R R' \simeq \mathscr {H}(V)_{R'}$. This concludes part (2) of the lemma.
We now proceed to prove part (3) of the lemma. By (73), ![]() $\hat {N}(V,c)_R \subset \hat {M}(V,c)_R^+$. Observe first that
$\hat {N}(V,c)_R \subset \hat {M}(V,c)_R^+$. Observe first that
This is easy to see since ![]() $\mathscr {H}(V)_\mathbb {C}$ is an irreducible
$\mathscr {H}(V)_\mathbb {C}$ is an irreducible ![]() $\hat {L}(\mathfrak {g}, \sigma )_\mathbb {C}$-module. Choosing a basis of
$\hat {L}(\mathfrak {g}, \sigma )_\mathbb {C}$-module. Choosing a basis of ![]() $R$ over
$R$ over ![]() $\mathbb {C}$, from this we easily conclude that
$\mathbb {C}$, from this we easily conclude that
For any non-zero ![]() $v\in A':=A/(A\cap \hat {N}(V,c)_R)\hookrightarrow \mathscr {H}(V)_R$,
$v\in A':=A/(A\cap \hat {N}(V,c)_R)\hookrightarrow \mathscr {H}(V)_R$, ![]() $v=\sum v_d$ with
$v=\sum v_d$ with ![]() $v_d \in \mathscr {H}(V)_R (d)$, set
$v_d \in \mathscr {H}(V)_R (d)$, set ![]() $|v|=\sum d: v_d\neq 0$, where the gradation
$|v|=\sum d: v_d\neq 0$, where the gradation ![]() $\mathscr {H}(V)_R (d)$ is induced from that of
$\mathscr {H}(V)_R (d)$ is induced from that of ![]() $\hat {M}(V,c)_R$. Choose a non-zero
$\hat {M}(V,c)_R$. Choose a non-zero ![]() $v^o\in A'$ such that
$v^o\in A'$ such that ![]() $|v^o|\leq |v|$ for all non-zero
$|v^o|\leq |v|$ for all non-zero ![]() $v\in A'$. Then,
$v\in A'$. Then,
Otherwise, ![]() $|X[t^n]\cdot v^o|<|v^o|$, which contradicts the choice of
$|X[t^n]\cdot v^o|<|v^o|$, which contradicts the choice of ![]() $v^o$.
$v^o$.
By (77), we get that ![]() $v^o\in V_R$, which contradicts the choice of graded
$v^o\in V_R$, which contradicts the choice of graded ![]() $A$ since
$A$ since ![]() $A\cap V_R=(0)$. Thus,
$A\cap V_R=(0)$. Thus, ![]() $A'=0$, i.e.
$A'=0$, i.e. ![]() $A\subset \hat {N}(V,c)_R.$ This proves the third part of the lemma.
$A\subset \hat {N}(V,c)_R.$ This proves the third part of the lemma.
We now begin with the definition of Sugawara operators ![]() $\{\Xi _n\,|\, n\in \mathbb {Z}\}$ for the Kac–Moody algebra
$\{\Xi _n\,|\, n\in \mathbb {Z}\}$ for the Kac–Moody algebra ![]() $\hat {L}(\mathfrak {g}, \sigma )_R$ attached to a complete local
$\hat {L}(\mathfrak {g}, \sigma )_R$ attached to a complete local ![]() $R$-algebra
$R$-algebra ![]() $\mathcal {O}_R$ with an
$\mathcal {O}_R$ with an ![]() $R$-rotation of order
$R$-rotation of order ![]() $m$, and an automorphism
$m$, and an automorphism ![]() $\sigma$ of
$\sigma$ of ![]() $\mathfrak {g}$ such that
$\mathfrak {g}$ such that ![]() $\sigma ^m=\operatorname {\mathrm {Id}}$. We fix a
$\sigma ^m=\operatorname {\mathrm {Id}}$. We fix a ![]() $\sigma$-equivariant
$\sigma$-equivariant ![]() $R$-parameter
$R$-parameter ![]() $t$.
$t$.
Recall the eigenspace decomposition ![]() $\mathfrak {g}=\bigoplus _{\underline {n}\in \mathbb {Z}/m\mathbb {Z} } \mathfrak {g}_{\underline {n}}$ of
$\mathfrak {g}=\bigoplus _{\underline {n}\in \mathbb {Z}/m\mathbb {Z} } \mathfrak {g}_{\underline {n}}$ of ![]() $\sigma$, where
$\sigma$, where
Note that ![]() $\sigma$ preserves the normalized invariant form
$\sigma$ preserves the normalized invariant form ![]() $\langle \,{,}\,\rangle$ on
$\langle \,{,}\,\rangle$ on ![]() $\mathfrak {g}$, i.e. for any
$\mathfrak {g}$, i.e. for any ![]() $x,y\in \mathfrak {g}$ we have
$x,y\in \mathfrak {g}$ we have ![]() $\langle \sigma (x), \sigma (y)\rangle =\langle x,y\rangle$. For each
$\langle \sigma (x), \sigma (y)\rangle =\langle x,y\rangle$. For each ![]() $\underline {n}\in \mathbb {Z}/m\mathbb {Z}$ it induces a non-degenerate bilinear form
$\underline {n}\in \mathbb {Z}/m\mathbb {Z}$ it induces a non-degenerate bilinear form ![]() $\langle \,{,}\,\rangle :\mathfrak {g}_{\underline {n}} \times \mathfrak {g}_{-\underline {n}}\to \mathbb {C}$. We choose a basis
$\langle \,{,}\,\rangle :\mathfrak {g}_{\underline {n}} \times \mathfrak {g}_{-\underline {n}}\to \mathbb {C}$. We choose a basis ![]() $\{u_a \,|\, a \in A_{\underline {n}} \}$ of
$\{u_a \,|\, a \in A_{\underline {n}} \}$ of ![]() $\mathfrak {g}_{\underline {n}}$ indexed by a set
$\mathfrak {g}_{\underline {n}}$ indexed by a set ![]() $A_{\underline {n}}$. Let
$A_{\underline {n}}$. Let ![]() $\{u^a \,|\, a\in A_{\underline {n}} \}$ be the basis of
$\{u^a \,|\, a\in A_{\underline {n}} \}$ be the basis of ![]() $\mathfrak {g}_{-\underline {n}}$ dual to the basis
$\mathfrak {g}_{-\underline {n}}$ dual to the basis ![]() $\{u_a\,|\, a\in A_{\underline {n}} \}$ of
$\{u_a\,|\, a\in A_{\underline {n}} \}$ of ![]() $\mathfrak {g}_{\underline {n}}$.
$\mathfrak {g}_{\underline {n}}$.
The normalized invariant ![]() $R$-bilinear form on
$R$-bilinear form on ![]() $\hat {L}(\mathfrak {g}, \sigma )_R$ is given as follows (cf. [Reference KacKac90, Theorem 8.7]),
$\hat {L}(\mathfrak {g}, \sigma )_R$ is given as follows (cf. [Reference KacKac90, Theorem 8.7]),
where ![]() $x[f],y[g]\in \hat {L}(\mathfrak {g}, \sigma )_R$ and
$x[f],y[g]\in \hat {L}(\mathfrak {g}, \sigma )_R$ and ![]() $r$ is the order of the diagram automorphism associated to
$r$ is the order of the diagram automorphism associated to ![]() $\sigma$. Then, the following relation is satisfied:
$\sigma$. Then, the following relation is satisfied:
Definition 6.6 An ![]() $R$-linear
$R$-linear ![]() $\hat {L}(\mathfrak {g}, \sigma )_R$-module
$\hat {L}(\mathfrak {g}, \sigma )_R$-module ![]() $M_R$ is called smooth if for any
$M_R$ is called smooth if for any ![]() $v \in M_R$, there exists an integer
$v \in M_R$, there exists an integer ![]() $d$ (depending upon
$d$ (depending upon ![]() $v$) such that
$v$) such that
Observe that this definition does not depend upon the choice of the parameter ![]() $t$.
$t$.
The generalized Verma module ![]() $\hat {M}(V,c)_R$ (and, hence, the quotient module
$\hat {M}(V,c)_R$ (and, hence, the quotient module ![]() $\mathscr {H}(V)_R$) is clearly smooth.
$\mathscr {H}(V)_R$) is clearly smooth.
We construct the following ![]() $R$-linear Sugawara operators on any smooth representation
$R$-linear Sugawara operators on any smooth representation ![]() $M_R$ of
$M_R$ of ![]() $\hat {L}(\mathfrak {g}, \sigma )_R$ of level
$\hat {L}(\mathfrak {g}, \sigma )_R$ of level ![]() $c\neq -\check {h}$ (which depends on the choice of
$c\neq -\check {h}$ (which depends on the choice of ![]() $t$),
$t$),
 \begin{equation} L^t_0 := \frac{1}{2(c+\check{h})} \bigg(\sum_{a\in A_{\underline{0}}} u_{a}u^a + 2\sum_{ n>0 } \sum_{a\in A_{-\underline{n}}} u_{a}[t^{-n}] u^a[t^n] +\frac{1}{2m^2}\sum_{n=0}^{m-1} n(m-n)\dim \mathfrak{g}_{\underline{n}} \bigg), \end{equation}
\begin{equation} L^t_0 := \frac{1}{2(c+\check{h})} \bigg(\sum_{a\in A_{\underline{0}}} u_{a}u^a + 2\sum_{ n>0 } \sum_{a\in A_{-\underline{n}}} u_{a}[t^{-n}] u^a[t^n] +\frac{1}{2m^2}\sum_{n=0}^{m-1} n(m-n)\dim \mathfrak{g}_{\underline{n}} \bigg), \end{equation} \begin{align} L^t_k &:= \frac{1}{mk} [-t^{mk+1}\partial_t, L_0^t] \nonumber\\ &= \frac{1}{mk(c+\check{h})} \bigg(\sum_{ n>0 } n \sum_{a\in A_{-\underline{n}}} \big(u_{a}[t^{-n+mk}] u^a[t^n] -u_a[t^{-n}]u^a[t^{n+mk}]\big)\bigg), \quad \text{for $k\neq 0$}, \end{align}
\begin{align} L^t_k &:= \frac{1}{mk} [-t^{mk+1}\partial_t, L_0^t] \nonumber\\ &= \frac{1}{mk(c+\check{h})} \bigg(\sum_{ n>0 } n \sum_{a\in A_{-\underline{n}}} \big(u_{a}[t^{-n+mk}] u^a[t^n] -u_a[t^{-n}]u^a[t^{n+mk}]\big)\bigg), \quad \text{for $k\neq 0$}, \end{align}
where ![]() $\check {h}$ is the dual Coxeter number of
$\check {h}$ is the dual Coxeter number of ![]() $\mathfrak {g}$. Note that the smoothness ensures that
$\mathfrak {g}$. Note that the smoothness ensures that ![]() $L^t_k$ is a well-defined operator on
$L^t_k$ is a well-defined operator on ![]() $M_R$ for each
$M_R$ for each ![]() $k\in \mathbb {Z}$. Moreover, it is easy to see that
$k\in \mathbb {Z}$. Moreover, it is easy to see that ![]() $L^t_{k}$ does not depend upon the choice of the basis
$L^t_{k}$ does not depend upon the choice of the basis ![]() $\{u_{a}\}$ of
$\{u_{a}\}$ of ![]() $\mathfrak {g}$.
$\mathfrak {g}$.
The following result can be found in [Reference Kac and WakimotoKW88, § 3.4] and [Reference WakimotoWak86].
Proposition 6.7 For any ![]() $n, k\in \mathbb {Z}$ and
$n, k\in \mathbb {Z}$ and ![]() $x\in \mathfrak {g}_{\underline {n}}$, as operators on a smooth representation
$x\in \mathfrak {g}_{\underline {n}}$, as operators on a smooth representation ![]() $M_R$ of
$M_R$ of ![]() $\hat {L}(\mathfrak {g}, \sigma )_R$ of central charge
$\hat {L}(\mathfrak {g}, \sigma )_R$ of central charge ![]() $c\neq -\check {h}$.
$c\neq -\check {h}$.
(a) We have
In particular, ![]() $L_0^t$ commutes with
$L_0^t$ commutes with ![]() $\mathfrak {g}^\sigma$.
$\mathfrak {g}^\sigma$.
(b) We have
Let us recall the definition of the Virasoro algebra ![]() $\operatorname {\mathrm {Vir}}_R$ over
$\operatorname {\mathrm {Vir}}_R$ over ![]() $R$. It is the Lie algebra over
$R$. It is the Lie algebra over ![]() $R$ with
$R$ with ![]() $R$-basis
$R$-basis ![]() $\{d_{n};\bar {C}\}_{n\in \mathbb {Z}}$ and the commutation relation is given by
$\{d_{n};\bar {C}\}_{n\in \mathbb {Z}}$ and the commutation relation is given by
An ![]() $R$-derivation of
$R$-derivation of ![]() $\mathcal {K}_R$ is an
$\mathcal {K}_R$ is an ![]() $R$-linear map
$R$-linear map ![]() $\theta : \mathcal {K}_R\to \mathcal {K}_R$ such that
$\theta : \mathcal {K}_R\to \mathcal {K}_R$ such that ![]() $\theta (fg)=\theta (f)g+f\theta (g)$, for any
$\theta (fg)=\theta (f)g+f\theta (g)$, for any ![]() $f,g\in \mathcal {K}_R$. Let
$f,g\in \mathcal {K}_R$. Let ![]() $\Theta _{\mathcal {K}_R/R }$ denote the Lie algebra of all continuous
$\Theta _{\mathcal {K}_R/R }$ denote the Lie algebra of all continuous ![]() $R$-derivations of
$R$-derivations of ![]() $\mathcal {K}_R$, where we put the
$\mathcal {K}_R$, where we put the ![]() $\mathfrak {m}$-adic topology on
$\mathfrak {m}$-adic topology on ![]() $\mathcal {K}_R$, i.e.
$\mathcal {K}_R$, i.e. ![]() $\{f+\mathfrak {m}^N\}_{N\in \mathbb {Z}, f\in \mathcal {K}_R}$ is a basis of open subsets. (Here
$\{f+\mathfrak {m}^N\}_{N\in \mathbb {Z}, f\in \mathcal {K}_R}$ is a basis of open subsets. (Here ![]() $\mathfrak {m}^N$ denotes
$\mathfrak {m}^N$ denotes ![]() $t^N\mathcal {O}_R$, which does not depend upon the choice of
$t^N\mathcal {O}_R$, which does not depend upon the choice of ![]() $t$.) With the choice of the
$t$.) With the choice of the ![]() $R$-parameter
$R$-parameter ![]() $t$ in
$t$ in ![]() $\mathcal {O}_R$, we have the equality
$\mathcal {O}_R$, we have the equality ![]() $\Theta _{\mathcal {K}_R/R }=R((t))\partial _t$, where
$\Theta _{\mathcal {K}_R/R }=R((t))\partial _t$, where ![]() $\partial _t$ is the derivation on
$\partial _t$ is the derivation on ![]() $\mathcal {K}_R$ such that
$\mathcal {K}_R$ such that ![]() $\partial _t(R)=0$ and
$\partial _t(R)=0$ and ![]() $\partial _t(t)=1$. Let
$\partial _t(t)=1$. Let ![]() $\Theta _{\mathcal {K}_R,R }$ denote the
$\Theta _{\mathcal {K}_R,R }$ denote the ![]() $\mathbb {C}$-Lie algebra of all continuous
$\mathbb {C}$-Lie algebra of all continuous ![]() $\mathbb {C}$-linear derivations
$\mathbb {C}$-linear derivations ![]() $\theta$ of
$\theta$ of ![]() $\mathcal {K}_R$ that are liftable from
$\mathcal {K}_R$ that are liftable from ![]() $R$, i.e. the restriction
$R$, i.e. the restriction ![]() $\theta |_{R}$ is a
$\theta |_{R}$ is a ![]() $\mathbb {C}$-linear derivation of
$\mathbb {C}$-linear derivation of ![]() $R$. Let
$R$. Let ![]() $\Theta _R$ denote the Lie algebra of
$\Theta _R$ denote the Lie algebra of ![]() $\mathbb {C}$-linear derivations of
$\mathbb {C}$-linear derivations of ![]() $R$. There exists a short exact sequence:
$R$. There exists a short exact sequence:
where ![]() ${\rm Res}$ denotes the restriction map of derivations from
${\rm Res}$ denotes the restriction map of derivations from ![]() $\mathcal {K}_R$ to
$\mathcal {K}_R$ to ![]() $R$. See more details in [Reference LooijengaLoo13, § 2]. It induces the following short exact sequence:
$R$. See more details in [Reference LooijengaLoo13, § 2]. It induces the following short exact sequence:
where ![]() $\Theta _{\mathcal {K}_R/R}^\sigma$ (respectively,
$\Theta _{\mathcal {K}_R/R}^\sigma$ (respectively, ![]() $\Theta _{\mathcal {K}_R,R }^\sigma$) is the space of
$\Theta _{\mathcal {K}_R,R }^\sigma$) is the space of ![]() $\sigma$-equivariant derivations in
$\sigma$-equivariant derivations in ![]() $\Theta _{\mathcal {K}_R/R}$ (respectively,
$\Theta _{\mathcal {K}_R/R}$ (respectively, ![]() $\Theta _{\mathcal {K}_R,R }$). Then,
$\Theta _{\mathcal {K}_R,R }$). Then, ![]() $\Theta _{\mathcal {K}_R/R }^\sigma =R((t^m)) t\partial _t$. We define a central extension
$\Theta _{\mathcal {K}_R/R }^\sigma =R((t^m)) t\partial _t$. We define a central extension
of the ![]() $R$-Lie algebra
$R$-Lie algebra ![]() $\Theta _{\mathcal {K}_R/R}^\sigma$ by
$\Theta _{\mathcal {K}_R/R}^\sigma$ by
for ![]() $f\partial _{t}$,
$f\partial _{t}$, ![]() $g\partial _{t}\in R((t^m)) t \partial _{t}$, where
$g\partial _{t}\in R((t^m)) t \partial _{t}$, where ![]() $A$ is the operator
$A$ is the operator ![]() $t^{-m}(m+t\partial _t)$. Observe that this bracket corresponds to the bracket of the Virasoro algebra defined by the identity (81) if we take
$t^{-m}(m+t\partial _t)$. Observe that this bracket corresponds to the bracket of the Virasoro algebra defined by the identity (81) if we take ![]() $d_{k}=- ({1}/{m })t^{m k+1} \partial _{t }$ for any
$d_{k}=- ({1}/{m })t^{m k+1} \partial _{t }$ for any ![]() $k\in \mathbb {Z}$. In this case
$k\in \mathbb {Z}$. In this case ![]() $\bar {C}$ corresponds to
$\bar {C}$ corresponds to ![]() $\bar {C}$. Therefore,
$\bar {C}$. Therefore, ![]() $\widehat {\Theta _{\mathcal {K}_R/R}^\sigma }$ defines a completed version of the Virasoro algebra over
$\widehat {\Theta _{\mathcal {K}_R/R}^\sigma }$ defines a completed version of the Virasoro algebra over ![]() $R$.
$R$.
For any ![]() $\theta \in {\Theta _{\mathcal {K}_R/ R}^\sigma }$ with
$\theta \in {\Theta _{\mathcal {K}_R/ R}^\sigma }$ with ![]() $\theta =\sum _{k\geq -N} a_{mk+1} t^{mk+1}\partial _t$, we define a Sugawara operator associated to
$\theta =\sum _{k\geq -N} a_{mk+1} t^{mk+1}\partial _t$, we define a Sugawara operator associated to ![]() $\theta$
$\theta$
on smooth modules of ![]() $\hat {L}(\mathfrak {g},\sigma )_R$ of central charge
$\hat {L}(\mathfrak {g},\sigma )_R$ of central charge ![]() $c\neq - \check {h}$.
$c\neq - \check {h}$.
In the following lemma, the operator ![]() $L^t_{\theta }$ is described more explicitly on any smooth module.
$L^t_{\theta }$ is described more explicitly on any smooth module.
Lemma 6.8 For any ![]() $\theta \in R((t^m)) t\partial _t$, the operator
$\theta \in R((t^m)) t\partial _t$, the operator ![]() $L^t_{\theta }$ acts on any smooth module
$L^t_{\theta }$ acts on any smooth module ![]() $M_R$ with central charge
$M_R$ with central charge ![]() $c\neq -\check {h}$ as follows:
$c\neq -\check {h}$ as follows:
 \begin{equation} L^t_{\theta}(u_1[f_1]\cdots u_n[f_n] \cdot v )= u_1[f_1]\cdots u_n[f_n]\cdot L^t_\theta(v) + \sum_{i=1}^n \big(u_1[f_1]\cdots u_i[\theta(f_i)]\cdots u_n[f_n]\cdot v \big), \end{equation}
\begin{equation} L^t_{\theta}(u_1[f_1]\cdots u_n[f_n] \cdot v )= u_1[f_1]\cdots u_n[f_n]\cdot L^t_\theta(v) + \sum_{i=1}^n \big(u_1[f_1]\cdots u_i[\theta(f_i)]\cdots u_n[f_n]\cdot v \big), \end{equation}
where ![]() $u_1[f_1],\ldots, u_n[f_n]\in \hat {L}(\mathfrak {g},\sigma )_R$ and
$u_1[f_1],\ldots, u_n[f_n]\in \hat {L}(\mathfrak {g},\sigma )_R$ and ![]() $v\in M_R$.
$v\in M_R$.
Proof. It is enough to show that ![]() $[L^t_\theta, u_i[ f_i] ]=u_i[ \theta (f_i)]$ for each
$[L^t_\theta, u_i[ f_i] ]=u_i[ \theta (f_i)]$ for each ![]() $i=1,\ldots, n$:
$i=1,\ldots, n$:
 \begin{align} [L^t_\theta, u_i[ f_i] ] &=\sum_{k\geq -N} (-m a_{mk+1}) [L^t_k, u_i[ f_i] ]\nonumber\\ &=\sum_{k\geq -N} (- a_{mk+1}) u_i[- t^{mk+1}\partial_t (f_i) ] \nonumber\\ &=u_i[\theta(f_i)], \end{align}
\begin{align} [L^t_\theta, u_i[ f_i] ] &=\sum_{k\geq -N} (-m a_{mk+1}) [L^t_k, u_i[ f_i] ]\nonumber\\ &=\sum_{k\geq -N} (- a_{mk+1}) u_i[- t^{mk+1}\partial_t (f_i) ] \nonumber\\ &=u_i[\theta(f_i)], \end{align}where the first equality follows from the definition (85), and the second equality follows from part (a) of Proposition 6.7.
Note that the choice of a ![]() $\sigma$-equivariant
$\sigma$-equivariant ![]() $R$-parameter
$R$-parameter ![]() $t$ gives the
$t$ gives the ![]() $R$-module splitting
$R$-module splitting ![]() $\Theta _{\mathcal {K}_R,R }^\sigma = \Theta _{\mathcal {K}_R/R }^\sigma \oplus \iota _t(\Theta _R)$, where (for
$\Theta _{\mathcal {K}_R,R }^\sigma = \Theta _{\mathcal {K}_R/R }^\sigma \oplus \iota _t(\Theta _R)$, where (for ![]() $\delta \in \Theta _R$)
$\delta \in \Theta _R$) ![]() $\iota _t(\delta ) (f)=\sum _k \delta (a_k) t^k$ if
$\iota _t(\delta ) (f)=\sum _k \delta (a_k) t^k$ if ![]() $f=\sum _k a_k t^k$. For any
$f=\sum _k a_k t^k$. For any ![]() $f\partial _t\in \Theta _{\mathcal {K}_R/R }^\sigma$ and
$f\partial _t\in \Theta _{\mathcal {K}_R/R }^\sigma$ and ![]() $\delta \in \Theta _R$,
$\delta \in \Theta _R$,
and define
The ![]() $\mathbb {C}$-linear brackets (84) and (88) define a completed extended Virasoro algebra
$\mathbb {C}$-linear brackets (84) and (88) define a completed extended Virasoro algebra ![]() $\widehat {\Theta _{\mathcal {K}_R, R}^\sigma }$ over
$\widehat {\Theta _{\mathcal {K}_R, R}^\sigma }$ over ![]() $R$ (which is a
$R$ (which is a ![]() $\mathbb {C}$-Lie algebra), where
$\mathbb {C}$-Lie algebra), where
Take any smooth ![]() $\hat {L}(\mathfrak {g}, \sigma )_R$-module
$\hat {L}(\mathfrak {g}, \sigma )_R$-module ![]() $M_R$ with
$M_R$ with ![]() $\mathbb {C}$-lattice
$\mathbb {C}$-lattice ![]() $M_\mathbb {C}$ (i.e.
$M_\mathbb {C}$ (i.e. ![]() $M_\mathbb {C} \otimes R \simeq M_R$) stable under
$M_\mathbb {C} \otimes R \simeq M_R$) stable under ![]() $\hat {L}(\mathfrak {g}, \sigma )_\mathbb {C}$. (Observe that
$\hat {L}(\mathfrak {g}, \sigma )_\mathbb {C}$. (Observe that ![]() $\hat {L}(\mathfrak {g}, \sigma )_\mathbb {C}$ depends upon the choice of the parameter
$\hat {L}(\mathfrak {g}, \sigma )_\mathbb {C}$ depends upon the choice of the parameter ![]() $t$.) Let
$t$.) Let ![]() $\delta$ act
$\delta$ act ![]() $\mathbb {C}$-linearly on
$\mathbb {C}$-linearly on ![]() $M_R$ via its action only on the
$M_R$ via its action only on the ![]() $R$-factor under the decomposition
$R$-factor under the decomposition ![]() $M_R\simeq M_\mathbb {C}\otimes R$. We denote this action on
$M_R\simeq M_\mathbb {C}\otimes R$. We denote this action on ![]() $M_R$ by
$M_R$ by ![]() $L^t_\delta$. Observe that
$L^t_\delta$. Observe that ![]() $L^t_\delta$ depends upon the choice of the parameter
$L^t_\delta$ depends upon the choice of the parameter ![]() $t$ as well as the choice of the
$t$ as well as the choice of the ![]() $\mathbb {C}$-lattice
$\mathbb {C}$-lattice ![]() $M_\mathbb {C}$ in
$M_\mathbb {C}$ in ![]() $M_R$.
$M_R$.
For any ![]() $\theta \in \Theta _{\mathcal {K}_R, R}^\sigma$, write
$\theta \in \Theta _{\mathcal {K}_R, R}^\sigma$, write ![]() $\theta =\theta '+ \iota _t(\theta '')$ (uniquely), where
$\theta =\theta '+ \iota _t(\theta '')$ (uniquely), where ![]() $\theta '\in \Theta _{\mathcal {K}_R/ R}^\sigma$ and
$\theta '\in \Theta _{\mathcal {K}_R/ R}^\sigma$ and ![]() $\theta ''\in \Theta _R$. We define the extended Sugawara operator
$\theta ''\in \Theta _R$. We define the extended Sugawara operator ![]() $L^t_\theta$ associated to
$L^t_\theta$ associated to ![]() $\theta$ acting on any smooth
$\theta$ acting on any smooth ![]() $M_R := M_\mathbb {C}\otimes _\mathbb {C} R$ (with
$M_R := M_\mathbb {C}\otimes _\mathbb {C} R$ (with ![]() $\mathbb {C}$-lattice
$\mathbb {C}$-lattice ![]() $M_\mathbb {C}$ as above) by
$M_\mathbb {C}$ as above) by
Then,
 \begin{equation} L^t_{\theta''} ( u_1[f_1]\cdots u_n[f_n] \cdot v )= \sum_{i=1}^n u_1[f_1]\cdots u_i[ \iota_t(\theta'' )(f_i)]\cdots u_n[f_n]\cdot v , \end{equation}
\begin{equation} L^t_{\theta''} ( u_1[f_1]\cdots u_n[f_n] \cdot v )= \sum_{i=1}^n u_1[f_1]\cdots u_i[ \iota_t(\theta'' )(f_i)]\cdots u_n[f_n]\cdot v , \end{equation}
for ![]() $v\in M_\mathbb {C}$ and
$v\in M_\mathbb {C}$ and ![]() $u_i[f_i] \in \hat {L}(\mathfrak {g}, \sigma )_R.$ From this we can easily deduce the more general formula when
$u_i[f_i] \in \hat {L}(\mathfrak {g}, \sigma )_R.$ From this we can easily deduce the more general formula when ![]() $v\in M_R$.
$v\in M_R$.
The following proposition follows easily from Proposition 6.7 and the definition of the operator ![]() $L^t_\theta$.
$L^t_\theta$.
Proposition 6.9 (1) Let ![]() $M_R$ be a smooth module of
$M_R$ be a smooth module of ![]() $\hat {L}(\mathfrak {g}, \sigma )_R$ with
$\hat {L}(\mathfrak {g}, \sigma )_R$ with ![]() $\mathbb {C}$-lattice
$\mathbb {C}$-lattice ![]() $M_\mathbb {C}$ as above with respect to a
$M_\mathbb {C}$ as above with respect to a ![]() $\sigma$-equivariant
$\sigma$-equivariant ![]() $R$-parameter
$R$-parameter ![]() $t$ and central charge
$t$ and central charge ![]() $c\neq -\check {h}$. Then, we have a
$c\neq -\check {h}$. Then, we have a ![]() $\mathbb {C}$-Lie algebra homomorphism
$\mathbb {C}$-Lie algebra homomorphism
given by
Moreover, ![]() $\Psi$ is an
$\Psi$ is an ![]() $R$-module map under the
$R$-module map under the ![]() $R$-module structure on
$R$-module structure on ![]() $\operatorname {\mathrm {End}}_\mathbb {C}(M_R)$ given by
$\operatorname {\mathrm {End}}_\mathbb {C}(M_R)$ given by
Note that ![]() $\Theta _R$ is an
$\Theta _R$ is an ![]() $R$-module under
$R$-module under ![]() $(r\cdot \delta )(s)=r\cdot \delta (s)$, for
$(r\cdot \delta )(s)=r\cdot \delta (s)$, for ![]() $r,s\in R$ and
$r,s\in R$ and ![]() $\delta \in \Theta _R$.
$\delta \in \Theta _R$.
(2) Further, for any ![]() $\theta \in \Theta _{\mathcal {K}_R,R}^\sigma$,
$\theta \in \Theta _{\mathcal {K}_R,R}^\sigma$, ![]() $v\in M_R$ and
$v\in M_R$ and ![]() $a\in R$,
$a\in R$,
The following lemma shows that the representation of ![]() $\Theta _{\mathcal {K}_R,R}^\sigma$ on
$\Theta _{\mathcal {K}_R,R}^\sigma$ on ![]() $\hat {M}(V,c)_R$ (and, hence, on
$\hat {M}(V,c)_R$ (and, hence, on ![]() $\mathscr {H}(V)_R$) is independent of the choice of the
$\mathscr {H}(V)_R$) is independent of the choice of the ![]() $\sigma$-equivariant
$\sigma$-equivariant ![]() $R$-parameters up to a multiple of the identity operator.
$R$-parameters up to a multiple of the identity operator.
Lemma 6.10 Let ![]() $V=V(\lambda )$ be an irreducible
$V=V(\lambda )$ be an irreducible ![]() $\mathfrak {g}^\sigma$-module with highest weight
$\mathfrak {g}^\sigma$-module with highest weight ![]() $\lambda \in D_c$. Let
$\lambda \in D_c$. Let ![]() $t'$ be another
$t'$ be another ![]() $\sigma$-equivariant
$\sigma$-equivariant ![]() $R$-parameter in
$R$-parameter in ![]() $\mathcal {O}_R$. For any
$\mathcal {O}_R$. For any ![]() $\theta \in \Theta _{\mathcal {K}_R,R}^\sigma$ there exists
$\theta \in \Theta _{\mathcal {K}_R,R}^\sigma$ there exists ![]() $b(\theta, \lambda, t, t')\in \mathbb {C}$ such that
$b(\theta, \lambda, t, t')\in \mathbb {C}$ such that ![]() $L^t_{\theta }= L^{t'}_{\theta } + b(\theta, \lambda, t, t') \operatorname {\mathrm {Id}}$ on
$L^t_{\theta }= L^{t'}_{\theta } + b(\theta, \lambda, t, t') \operatorname {\mathrm {Id}}$ on ![]() $\hat {M}(V,c)_R$ and, hence, on
$\hat {M}(V,c)_R$ and, hence, on ![]() $\mathscr {H}(V)_R$.
$\mathscr {H}(V)_R$.
Here, with the choice of the parameter ![]() $t$, we have chosen the
$t$, we have chosen the ![]() $\mathbb {C}$-lattice
$\mathbb {C}$-lattice ![]() $\hat {M}(V,c)_\mathbb {C}$ of
$\hat {M}(V,c)_\mathbb {C}$ of ![]() $\hat {M}(V,c)_R$ to be
$\hat {M}(V,c)_R$ to be ![]() $U\big ((\mathfrak {g}\otimes \mathbb {C}((t)))^\sigma \oplus \mathbb {C} C\big )\cdot V$ and the
$U\big ((\mathfrak {g}\otimes \mathbb {C}((t)))^\sigma \oplus \mathbb {C} C\big )\cdot V$ and the ![]() $\mathbb {C}$-lattice of
$\mathbb {C}$-lattice of ![]() $\mathscr {H}(V)_R$ to be the image of
$\mathscr {H}(V)_R$ to be the image of ![]() $\hat {M}(V,c)_\mathbb {C}$.
$\hat {M}(V,c)_\mathbb {C}$.
Proof. Assume first that ![]() $\theta \in \Theta _{\mathcal {K}_R/R}^\sigma$. Let
$\theta \in \Theta _{\mathcal {K}_R/R}^\sigma$. Let ![]() $L^t_\theta$ and
$L^t_\theta$ and ![]() $L^{t'}_{\theta }$ denote the Sugawara operators associated to
$L^{t'}_{\theta }$ denote the Sugawara operators associated to ![]() $\theta$ with respect to the parameters
$\theta$ with respect to the parameters ![]() $t$ and
$t$ and ![]() $t'$, respectively. For any
$t'$, respectively. For any ![]() $u[f]\in \hat {L}(\mathfrak {g},\sigma )_R$, from the identity (87), we have the following formula:
$u[f]\in \hat {L}(\mathfrak {g},\sigma )_R$, from the identity (87), we have the following formula:
This gives
It follows that ![]() $L^t_\theta -L_\theta ^{t'}$ commutes with the action of
$L^t_\theta -L_\theta ^{t'}$ commutes with the action of ![]() $\hat {L}(\mathfrak {g}, \sigma )_R$ (and, hence, also with the action of
$\hat {L}(\mathfrak {g}, \sigma )_R$ (and, hence, also with the action of ![]() $L^t_0$ as in the identity (79)) on
$L^t_0$ as in the identity (79)) on ![]() $\hat {M}(V,c)_R$. In particular, using Proposition 6.7(a) for
$\hat {M}(V,c)_R$. In particular, using Proposition 6.7(a) for ![]() $k=0$,
$k=0$, ![]() $(L^t_\theta - L^{t'}_\theta )v_o = \lambda v_o$ for some
$(L^t_\theta - L^{t'}_\theta )v_o = \lambda v_o$ for some ![]() $\lambda \in \mathbb {C}$, where
$\lambda \in \mathbb {C}$, where ![]() $v_o$ is a highest weight vector of
$v_o$ is a highest weight vector of ![]() $V$. This shows that the
$V$. This shows that the ![]() $R$-linear map
$R$-linear map ![]() $L^t_\theta - L^{t'}_\theta = b(\theta, \lambda, t, t') \operatorname {\mathrm {Id}}$ on the whole of
$L^t_\theta - L^{t'}_\theta = b(\theta, \lambda, t, t') \operatorname {\mathrm {Id}}$ on the whole of ![]() $\hat {M}(V, c)_R$. This proves the lemma in the case
$\hat {M}(V, c)_R$. This proves the lemma in the case ![]() $\theta \in \Theta _{\mathcal {K}_R/R}^\sigma$.
$\theta \in \Theta _{\mathcal {K}_R/R}^\sigma$.
We now prove the general case. Different choices of ![]() $\sigma$-equivariant
$\sigma$-equivariant ![]() $R$-parameters
$R$-parameters ![]() $t,t'$ give different splittings
$t,t'$ give different splittings ![]() $\iota _t, \iota _{t'}$,
$\iota _t, \iota _{t'}$,
For any ![]() $\theta \in \Theta _{\mathcal {K}_R,R}^\sigma$, we may write uniquely
$\theta \in \Theta _{\mathcal {K}_R,R}^\sigma$, we may write uniquely
where ![]() $\theta '_t\in R((t^m))t \partial _t$,
$\theta '_t\in R((t^m))t \partial _t$, ![]() $\theta '_{t'}\in R((t'^m))t' \partial _{t'}$, and
$\theta '_{t'}\in R((t'^m))t' \partial _{t'}$, and ![]() $\theta ''_t, \theta ''_{t'} \in \Theta _R$. Observe that
$\theta ''_t, \theta ''_{t'} \in \Theta _R$. Observe that
Applying (95) to ![]() $t'$, we get
$t'$, we get
where ![]() $u=t'/t\in \mathcal {O}_R^\times$. Note that
$u=t'/t\in \mathcal {O}_R^\times$. Note that ![]() $ ({\iota _t(\theta ''_t)(u) }/({t\partial _t(u))) +u} t\partial _t \in R[[t^m]]t\partial _t$, and the constant coefficient of
$ ({\iota _t(\theta ''_t)(u) }/({t\partial _t(u))) +u} t\partial _t \in R[[t^m]]t\partial _t$, and the constant coefficient of ![]() $t\partial _t$ in
$t\partial _t$ in ![]() $ ({\iota _t(\theta ''_t)(u) }/({t\partial _t(u) +u})) t\partial _t$ is
$ ({\iota _t(\theta ''_t)(u) }/({t\partial _t(u) +u})) t\partial _t$ is ![]() $ {\theta _t''(u_0)}/{u_0}$ where
$ {\theta _t''(u_0)}/{u_0}$ where ![]() $u_0\in R^\times$ is the leading coefficient of
$u_0\in R^\times$ is the leading coefficient of ![]() $u=u_0+u_mt^m+\cdots \in R[[t^m]]$.
$u=u_0+u_mt^m+\cdots \in R[[t^m]]$.
As proved above, ![]() $L^t_{\theta '_{t'}}-L^{t'}_{\theta '_{t'}}$ is a scalar operator, as
$L^t_{\theta '_{t'}}-L^{t'}_{\theta '_{t'}}$ is a scalar operator, as ![]() $\theta '_{t'}\in \Theta _{\mathcal {K}_R/R}^\sigma$. Thus, to prove that
$\theta '_{t'}\in \Theta _{\mathcal {K}_R/R}^\sigma$. Thus, to prove that ![]() $L^t_\theta -L^{t'}_{\theta }$ is a scalar operator, it suffices to prove that
$L^t_\theta -L^{t'}_{\theta }$ is a scalar operator, it suffices to prove that ![]() $L^t_\beta +L^t_{\theta ^{\prime \prime }_t} - L^{t'}_{\theta ^{\prime \prime }_{t'}}$ is a scalar operator, since
$L^t_\beta +L^t_{\theta ^{\prime \prime }_t} - L^{t'}_{\theta ^{\prime \prime }_{t'}}$ is a scalar operator, since ![]() $L^t_\beta =L^t_{\theta '_t} - L^{t}_{\theta '_{t'}}$, where
$L^t_\beta =L^t_{\theta '_t} - L^{t}_{\theta '_{t'}}$, where ![]() $\beta := \theta '_t-\theta '_{t'}$. Now, for
$\beta := \theta '_t-\theta '_{t'}$. Now, for ![]() $u_1[f_1], \ldots, u_n[f_n]\in \hat {L}(\mathfrak {g}, \sigma )_R$ and
$u_1[f_1], \ldots, u_n[f_n]\in \hat {L}(\mathfrak {g}, \sigma )_R$ and ![]() $v\in V$, by the identities (86) and (90), we get
$v\in V$, by the identities (86) and (90), we get
 \begin{align*} &\big(L^t_\beta
+L^t_{\theta^{\prime\prime}_t} -
L^{t'}_{\theta^{\prime\prime}_{t'}}
\big) (u_1[f_1]\dots u_n[f_n]\cdot v)\\ &\quad=
u_1[f_1]\dots u_n[f_n]\cdot (L^t_\beta v) +\sum_{i=1}^n
u_1[f_1]\dots
u_i[\beta(f_i)+\iota_t(\theta^{\prime\prime}_t)f_i-\iota_{t'}(\theta^{\prime\prime}_{t'})f_i]\dots
u_n[f_n]\cdot v \\ &\quad=u_1[f_1]\dots u_n[f_n]\cdot
(L^t_\beta v) ,\quad \text{since $
\beta(f_i)+\iota_t(\theta^{\prime\prime}_t)f_i-\iota_{t'}(\theta^{\prime\prime}_{t'})f_i
=0$ by (95) }\\
&\quad=
\frac{m\theta^{\prime\prime}_t(u_0)}{u_0}
u_1[f_1]\dots u_n[f_n]\cdot (L^t_0 v), \quad \text{since
$L^t_k\cdot v=0$ for all $ k>0$ and $\beta \in
R[[t^m]]t\partial_t$}\\
&\quad=
\frac{m\theta^{\prime\prime}_t(u_0)}{u_0}
u_1[f_1]\dots u_n[f_n]\cdot dv, \quad \text{for some
constant $d\in \mathbb{C}$}, \end{align*}
\begin{align*} &\big(L^t_\beta
+L^t_{\theta^{\prime\prime}_t} -
L^{t'}_{\theta^{\prime\prime}_{t'}}
\big) (u_1[f_1]\dots u_n[f_n]\cdot v)\\ &\quad=
u_1[f_1]\dots u_n[f_n]\cdot (L^t_\beta v) +\sum_{i=1}^n
u_1[f_1]\dots
u_i[\beta(f_i)+\iota_t(\theta^{\prime\prime}_t)f_i-\iota_{t'}(\theta^{\prime\prime}_{t'})f_i]\dots
u_n[f_n]\cdot v \\ &\quad=u_1[f_1]\dots u_n[f_n]\cdot
(L^t_\beta v) ,\quad \text{since $
\beta(f_i)+\iota_t(\theta^{\prime\prime}_t)f_i-\iota_{t'}(\theta^{\prime\prime}_{t'})f_i
=0$ by (95) }\\
&\quad=
\frac{m\theta^{\prime\prime}_t(u_0)}{u_0}
u_1[f_1]\dots u_n[f_n]\cdot (L^t_0 v), \quad \text{since
$L^t_k\cdot v=0$ for all $ k>0$ and $\beta \in
R[[t^m]]t\partial_t$}\\
&\quad=
\frac{m\theta^{\prime\prime}_t(u_0)}{u_0}
u_1[f_1]\dots u_n[f_n]\cdot dv, \quad \text{for some
constant $d\in \mathbb{C}$}, \end{align*}
by the definition of ![]() $L^t_0$ since
$L^t_0$ since ![]() $\sum _{a\in A_{\underline {0}}}u_au^a$ is the Casimir operator of
$\sum _{a\in A_{\underline {0}}}u_au^a$ is the Casimir operator of ![]() $\mathfrak {g}^\sigma$. This proves the lemma.
$\mathfrak {g}^\sigma$. This proves the lemma.
7. Flat projective connection on sheaf of twisted covacua
We define the sheaf of twisted covacua for a family ![]() $\Sigma _T$ of
$\Sigma _T$ of ![]() $s$-pointed
$s$-pointed ![]() $\Gamma$-curves. We further show that this sheaf is locally free of finite rank for a smooth family
$\Gamma$-curves. We further show that this sheaf is locally free of finite rank for a smooth family ![]() $\Sigma _T$ over a smooth base
$\Sigma _T$ over a smooth base ![]() $T$. In fact, we prove that it admits a flat projective connection.
$T$. In fact, we prove that it admits a flat projective connection.
In this section, we take the parameter space ![]() $T$ to be an irreducible scheme over
$T$ to be an irreducible scheme over ![]() $\mathbb {C}$ and let
$\mathbb {C}$ and let ![]() $\Gamma$ be a finite group. We fix a group homomorphism
$\Gamma$ be a finite group. We fix a group homomorphism ![]() $\phi : \Gamma \to {\rm Aut}(\mathfrak {g})$.
$\phi : \Gamma \to {\rm Aut}(\mathfrak {g})$.
Definition 7.1 A family of curves over ![]() $T$ is a proper and flat morphism
$T$ is a proper and flat morphism ![]() $\xi : \Sigma _T\to T$ such that every geometric fiber is a connected reduced curve (but not necessary irreducible). For any
$\xi : \Sigma _T\to T$ such that every geometric fiber is a connected reduced curve (but not necessary irreducible). For any ![]() $b\in T$ the fiber
$b\in T$ the fiber ![]() $\xi ^{-1}(b)$ is denoted by
$\xi ^{-1}(b)$ is denoted by ![]() $\Sigma _b$.
$\Sigma _b$.
Let ![]() $\Gamma$ act faithfully on
$\Gamma$ act faithfully on ![]() $\Sigma _T$ and that
$\Sigma _T$ and that ![]() $\xi$ is
$\xi$ is ![]() $\Gamma$-invariant (where
$\Gamma$-invariant (where ![]() $\Gamma$ acts trivially on
$\Gamma$ acts trivially on ![]() $T$). Let
$T$). Let ![]() $\pi : \Sigma _T\to \Sigma _T/\Gamma = \bar {\Sigma }_T$ be the quotient map, and let
$\pi : \Sigma _T\to \Sigma _T/\Gamma = \bar {\Sigma }_T$ be the quotient map, and let ![]() $\bar {\xi }: \bar {\Sigma }_T \to T$ be the induced family of curves over
$\bar {\xi }: \bar {\Sigma }_T \to T$ be the induced family of curves over ![]() $T$. Observe that
$T$. Observe that ![]() $\bar {\xi }$ is also proper. For any section
$\bar {\xi }$ is also proper. For any section ![]() $p$ of
$p$ of ![]() $\bar {\xi }$, denote by
$\bar {\xi }$, denote by ![]() $\pi ^{-1}(p)$ the set of sections
$\pi ^{-1}(p)$ the set of sections ![]() $q$ of
$q$ of ![]() $\xi$ such that
$\xi$ such that ![]() $\pi \circ q=p$.
$\pi \circ q=p$.
Definition 7.2 A family of ![]() $s$-pointed
$s$-pointed ![]() $\Gamma$-curves over
$\Gamma$-curves over ![]() $T$ is a family of curves
$T$ is a family of curves ![]() $\xi : \Sigma _T\to T$ over
$\xi : \Sigma _T\to T$ over ![]() $T$ with an action of a finite group
$T$ with an action of a finite group ![]() $\Gamma$ as above, and a collection of sections
$\Gamma$ as above, and a collection of sections ![]() $\vec {q}:=(q_1,\ldots, q_s)$ of
$\vec {q}:=(q_1,\ldots, q_s)$ of ![]() $\xi$, such that:
$\xi$, such that:
(1)
 $p_1,\ldots,p_s$ are mutually non-intersecting to each other and, for each
$p_1,\ldots,p_s$ are mutually non-intersecting to each other and, for each  $i$,
$i$,  $\pi ^{-1}(p_i(T))$ is contained in the smooth locus of
$\pi ^{-1}(p_i(T))$ is contained in the smooth locus of  $\xi$ and
$\xi$ and  $\pi ^{-1}(p_i(T)) \to T$ is étale, where
$\pi ^{-1}(p_i(T)) \to T$ is étale, where  $p_i=\pi \circ q_i$ is the section of
$p_i=\pi \circ q_i$ is the section of  $\bar {\xi }$;
$\bar {\xi }$;(2) for any geometric point
 $b\in T$,
$b\in T$,  $\big (\bar {\Sigma }_b, p_1(b), \ldots, p_s(b)\big )$ is a
$\big (\bar {\Sigma }_b, p_1(b), \ldots, p_s(b)\big )$ is a  $s$-pointed curve in the sense of Definition 3.4; moreover,
$s$-pointed curve in the sense of Definition 3.4; moreover,  $\pi _b: \Sigma _b\to \bar {\Sigma }_b$ is a
$\pi _b: \Sigma _b\to \bar {\Sigma }_b$ is a  $\Gamma$-cover in the sense of Definition 3.1.
$\Gamma$-cover in the sense of Definition 3.1.
Let ![]() $\Sigma ^o_T$ denote the open subset
$\Sigma ^o_T$ denote the open subset ![]() $\Sigma _T\backslash \bigcup _i^s \pi ^{-1}(p_i(T))$ of
$\Sigma _T\backslash \bigcup _i^s \pi ^{-1}(p_i(T))$ of ![]() $\Sigma _T$. Let
$\Sigma _T$. Let ![]() $\xi ^o: \Sigma ^o_T\to T$ denote the restriction of
$\xi ^o: \Sigma ^o_T\to T$ denote the restriction of ![]() $\xi$.
$\xi$.
Lemma 7.3 The morphism ![]() $\xi ^o: \Sigma ^o_T\to T$ is affine.
$\xi ^o: \Sigma ^o_T\to T$ is affine.
Proof. See a proof by van Dobben de Bruyn on mathoverflow [Reference van Dobben de BruynvDdB].
Let ![]() $f:T'\to T$ be a morphism of schemes. Then, we can pull-back the triple
$f:T'\to T$ be a morphism of schemes. Then, we can pull-back the triple ![]() $({\Sigma }_{T},\Gamma, \vec {q} )$ to
$({\Sigma }_{T},\Gamma, \vec {q} )$ to ![]() $T'$ to get a family
$T'$ to get a family ![]() $(f^*(\Sigma _T), \Gamma, f^*(\vec {q}))$ of pointed
$(f^*(\Sigma _T), \Gamma, f^*(\vec {q}))$ of pointed ![]() $\Gamma$-curves over
$\Gamma$-curves over ![]() $T'$, where
$T'$, where ![]() $f^*(\Sigma _T)=T'\times _T \Sigma _T$,
$f^*(\Sigma _T)=T'\times _T \Sigma _T$, ![]() $f^*(\vec {q})=(f^*q_1,\ldots, f^*q_s)$.
$f^*(\vec {q})=(f^*q_1,\ldots, f^*q_s)$.
Lemma 7.4 Let ![]() $\Gamma$ act on each geometric fiber
$\Gamma$ act on each geometric fiber ![]() $\Sigma _b$ of
$\Sigma _b$ of ![]() $\Sigma _T$ stably (cf. Definition 5.1). Then, for any section
$\Sigma _T$ stably (cf. Definition 5.1). Then, for any section ![]() $p$ of
$p$ of ![]() $\bar {\xi }$ such that
$\bar {\xi }$ such that ![]() $\pi ^{-1}(p(T))$ is contained in the smooth locus of
$\pi ^{-1}(p(T))$ is contained in the smooth locus of ![]() $\xi$, if
$\xi$, if ![]() $\pi ^{-1}(p)$ is non-empty
$\pi ^{-1}(p)$ is non-empty ![]() $(\text{where }\pi ^{-1}(p) = \{\text {sections } q\ \text{of } \Sigma _T \to T\ \text{such that }\pi \circ q =p\})$, then:
$(\text{where }\pi ^{-1}(p) = \{\text {sections } q\ \text{of } \Sigma _T \to T\ \text{such that }\pi \circ q =p\})$, then:
(1) for any
 $q\neq q' \in \pi ^{-1}(p)$,
$q\neq q' \in \pi ^{-1}(p)$,  $q(T)$ and
$q(T)$ and  $q'(T)$ are disjoint;
$q'(T)$ are disjoint;(2)
 $\Gamma$ acts on
$\Gamma$ acts on  $\pi ^{-1}(p)$ transitively, and the stabilizer group
$\pi ^{-1}(p)$ transitively, and the stabilizer group  $\Gamma _q$ is equal to the stabilizer group
$\Gamma _q$ is equal to the stabilizer group  $\Gamma _{q(b)}$ at the point
$\Gamma _{q(b)}$ at the point  $q(b)\in \Sigma _b$ for any geometric point
$q(b)\in \Sigma _b$ for any geometric point  $b\in T$.
$b\in T$.
Proof. It is easy to see that ![]() $\pi ^{-1}(p)$ is finite (it also follows from (97)). Let
$\pi ^{-1}(p)$ is finite (it also follows from (97)). Let ![]() $\pi ^{-1}(p)=\{ q_1,q_2,\ldots, q_k \}$. For each
$\pi ^{-1}(p)=\{ q_1,q_2,\ldots, q_k \}$. For each ![]() $b\in T$,
$b\in T$, ![]() $\{ q_1(b), q_2(b),\ldots, q_k(b) \}$ is a
$\{ q_1(b), q_2(b),\ldots, q_k(b) \}$ is a ![]() $\Gamma$-stable set and it is contained in the fiber
$\Gamma$-stable set and it is contained in the fiber ![]() $\pi ^{-1}(p(b))$. Since
$\pi ^{-1}(p(b))$. Since ![]() $\Gamma$ acts on
$\Gamma$ acts on ![]() $\pi ^{-1}(p(b))$ transitively, it follows that
$\pi ^{-1}(p(b))$ transitively, it follows that
From this it is easy to see that ![]() $\Gamma$ acts transitively on
$\Gamma$ acts transitively on ![]() $\pi ^{-1}(p)$.
$\pi ^{-1}(p)$.
Set ![]() $Z:=\xi ( \bigcup _{i\neq j} q_i(T)\cap q_j(T) )$. Then,
$Z:=\xi ( \bigcup _{i\neq j} q_i(T)\cap q_j(T) )$. Then, ![]() $Z$ is a proper closed subset of
$Z$ is a proper closed subset of ![]() $T$. Let
$T$. Let ![]() $U$ be the open subset
$U$ be the open subset ![]() $T \backslash Z$ of
$T \backslash Z$ of ![]() $T$. Then,
$T$. Then, ![]() $\{ q_1(U),q_2(U), \ldots, q_k(U) \}$ are mutually disjoint to each other. In particular,
$\{ q_1(U),q_2(U), \ldots, q_k(U) \}$ are mutually disjoint to each other. In particular,
By [Reference Bertin and RomagnyBR11, Lemma 4.2.1], for each ![]() $1\leq i\leq k$, the order of the stabilizer group
$1\leq i\leq k$, the order of the stabilizer group ![]() $\Gamma _{q_i(b)}$ is constant along
$\Gamma _{q_i(b)}$ is constant along ![]() $T$. For any
$T$. For any ![]() $b' \in Z$, there exists
$b' \in Z$, there exists ![]() $i\neq j$ such that
$i\neq j$ such that ![]() $q_i(b')=q_j(b')$. It follows that
$q_i(b')=q_j(b')$. It follows that ![]() $ {|\Gamma | }/{|\Gamma _{q_i(b')}| } = |\pi ^{-1}(p(b'))|< k$, which is a contradiction. Therefore,
$ {|\Gamma | }/{|\Gamma _{q_i(b')}| } = |\pi ^{-1}(p(b'))|< k$, which is a contradiction. Therefore, ![]() $T=U$, i.e.
$T=U$, i.e. ![]() $\{q_1(T),q_2(T),\ldots, q_k(T) \}$ are disjoint to each other. This finishes the proof of part (1).
$\{q_1(T),q_2(T),\ldots, q_k(T) \}$ are disjoint to each other. This finishes the proof of part (1).
Let ![]() $\Gamma _q$ be the stabilizer group of
$\Gamma _q$ be the stabilizer group of ![]() $q\in \pi ^{-1}(p)$. It is clear that
$q\in \pi ^{-1}(p)$. It is clear that
We have
where the first equality follows from (97) (since ![]() $U=T$) and the second inequality follows from (98). The third inequality follows since
$U=T$) and the second inequality follows from (98). The third inequality follows since ![]() $k:=|\pi ^{-1}(p)|$. Thus, we get
$k:=|\pi ^{-1}(p)|$. Thus, we get ![]() $\Gamma _q=\Gamma _{q(b)}$ for any geometric point
$\Gamma _q=\Gamma _{q(b)}$ for any geometric point ![]() $b\in T$ by (98) and, moreover,
$b\in T$ by (98) and, moreover, ![]() $\Gamma$ acts transitively on
$\Gamma$ acts transitively on ![]() $\pi ^{-1}(p)$. This concludes part
$\pi ^{-1}(p)$. This concludes part ![]() $(2)$ of the lemma.
$(2)$ of the lemma.
Definition 7.5 (1) A formal disc over ![]() $T$ is a formal scheme
$T$ is a formal scheme ![]() $(T, \mathcal {O}_T )$ over
$(T, \mathcal {O}_T )$ over ![]() $T$ (in the sense of [Reference HartshorneHar77, Chap. II, § 9]), where
$T$ (in the sense of [Reference HartshorneHar77, Chap. II, § 9]), where ![]() $\mathcal {O}_T$ is an
$\mathcal {O}_T$ is an ![]() $\mathscr {O}_T$-algebra which has the following property: for any point
$\mathscr {O}_T$-algebra which has the following property: for any point ![]() $b\in T$ there exists an affine open subset
$b\in T$ there exists an affine open subset ![]() $U\subset T$ containing
$U\subset T$ containing ![]() $b$ such that
$b$ such that ![]() $\mathcal {O}_T(U )$ is a complete local
$\mathcal {O}_T(U )$ is a complete local ![]() $\mathscr {O}_T(U)$-algebra (see Definition 6.1(a)).
$\mathscr {O}_T(U)$-algebra (see Definition 6.1(a)).
Let ![]() $(T, \mathcal {K}_T )$ be the locally ringed space over
$(T, \mathcal {K}_T )$ be the locally ringed space over ![]() $T$ defined so that
$T$ defined so that ![]() $\mathcal {K}_T(U)$ is the
$\mathcal {K}_T(U)$ is the ![]() $\mathscr {O}_T(U)$-algebra containing
$\mathscr {O}_T(U)$-algebra containing ![]() $\mathcal {O}_T(U)$ obtained by inverting a (and, hence, any)
$\mathcal {O}_T(U)$ obtained by inverting a (and, hence, any) ![]() $\mathscr {O}_T(U)$-parameter
$\mathscr {O}_T(U)$-parameter ![]() $t_U$ of
$t_U$ of ![]() $\mathcal {O}_T(U)$. Then,
$\mathcal {O}_T(U)$. Then, ![]() $(T, \mathcal {K}_T )$ is called the associated formal punctured disc over
$(T, \mathcal {K}_T )$ is called the associated formal punctured disc over ![]() $T$.
$T$.
(2) A rotation of a formal disc ![]() $(T, \mathcal {O}_T )$ over
$(T, \mathcal {O}_T )$ over ![]() $T$ of order
$T$ of order ![]() $m$ is an
$m$ is an ![]() $\mathscr {O}_T$-module automorphism
$\mathscr {O}_T$-module automorphism ![]() $\sigma$ of
$\sigma$ of ![]() $(T, \mathcal {O}_T)$ of order
$(T, \mathcal {O}_T)$ of order ![]() $m$ such that, for any
$m$ such that, for any ![]() $b\in T$,
$b\in T$, ![]() $\sigma (t_U)=\epsilon ^{-1}t_U$ for some formal parameter
$\sigma (t_U)=\epsilon ^{-1}t_U$ for some formal parameter ![]() $t_U$ around
$t_U$ around ![]() $b$, where
$b$, where ![]() $\epsilon :=e^{ {2\pi i}/{m}}$.
$\epsilon :=e^{ {2\pi i}/{m}}$.
Lemma 7.6 With the assumption and notation as in Definition 7.1, let ![]() $q$ be a section of
$q$ be a section of ![]() $\xi : \Sigma _T\to T$ such that
$\xi : \Sigma _T\to T$ such that ![]() $q(T)$ is contained in the smooth locus of
$q(T)$ is contained in the smooth locus of ![]() $\xi$. Then:
$\xi$. Then:
(1) the formal scheme
 $(T, \xi _* \hat {\mathscr {O } }_{ \Sigma _T, q(T) } )$ is a formal disc over
$(T, \xi _* \hat {\mathscr {O } }_{ \Sigma _T, q(T) } )$ is a formal disc over  $T$, where
$T$, where  $\hat {\mathscr {O } }_{ \Sigma _T, q(T)}$ denotes the formal completion of
$\hat {\mathscr {O } }_{ \Sigma _T, q(T)}$ denotes the formal completion of  $\Sigma _T$ along
$\Sigma _T$ along  $q(T)$ (cf. [Reference HartshorneHar77, Chap. II, § 9]);
$q(T)$ (cf. [Reference HartshorneHar77, Chap. II, § 9]);(2) the stabilizer group
 $\Gamma _q$ is a cyclic group acting faithfully on the formal disc
$\Gamma _q$ is a cyclic group acting faithfully on the formal disc  $(T, \xi _*( \hat {\mathscr {O } }_{ \Sigma _T, q(T) } ))$; further,
$(T, \xi _*( \hat {\mathscr {O } }_{ \Sigma _T, q(T) } ))$; further,  $\Gamma _q$ has a generator
$\Gamma _q$ has a generator  $\tilde {\sigma }_q$ acting via rotation of
$\tilde {\sigma }_q$ acting via rotation of  $(T, \xi _*( \hat {\mathscr {O } }_{ \Sigma _T, q(T) } ))$; moreover, the action of
$(T, \xi _*( \hat {\mathscr {O } }_{ \Sigma _T, q(T) } ))$; moreover, the action of  $\Gamma _q$ on local
$\Gamma _q$ on local  $\tilde {\sigma }_q$-equivariant parameters is given by a primitive character
$\tilde {\sigma }_q$-equivariant parameters is given by a primitive character  $\chi$.
$\chi$.
Proof. Part (1) follows from [Reference GrothendieckGro97, Corollaire 16.9.9, Théorèm 17.12.1(c![]() $'$)]. For part (2), choose a formal parameter
$'$)]. For part (2), choose a formal parameter ![]() $t_U\in \big (\xi _* \hat {\mathscr {O } }_{ \Sigma _T, q(T) }\big ) (U)$. Let
$t_U\in \big (\xi _* \hat {\mathscr {O } }_{ \Sigma _T, q(T) }\big ) (U)$. Let ![]() $\sigma _q\in \Gamma _q$ be a generator. Set
$\sigma _q\in \Gamma _q$ be a generator. Set ![]() $\tilde {t}_U:= ({1}/{|\Gamma _q|})\sum _{i=0}^{|\Gamma _q|-1} \epsilon _q^{- ij} \sigma _q^i(t_U)$, where
$\tilde {t}_U:= ({1}/{|\Gamma _q|})\sum _{i=0}^{|\Gamma _q|-1} \epsilon _q^{- ij} \sigma _q^i(t_U)$, where ![]() $\epsilon _q :=e^{ {2\pi i}/{ |\Gamma _q| }}$ and
$\epsilon _q :=e^{ {2\pi i}/{ |\Gamma _q| }}$ and ![]() $\sigma _q(t_U)= \epsilon _q^jt_U+$ higher terms. Then,
$\sigma _q(t_U)= \epsilon _q^jt_U+$ higher terms. Then, ![]() $\tilde {t}_U$ is a formal parameter in
$\tilde {t}_U$ is a formal parameter in ![]() $\big (\xi _* \hat {\mathscr {O } }_{ \Sigma _T, q(T) }\big ) (U)$ such that
$\big (\xi _* \hat {\mathscr {O } }_{ \Sigma _T, q(T) }\big ) (U)$ such that
Since ![]() $\Gamma$ acts faithfully on
$\Gamma$ acts faithfully on ![]() $\Sigma _T$, the action of
$\Sigma _T$, the action of ![]() $\Gamma _q$ is faithful on the formal disc
$\Gamma _q$ is faithful on the formal disc ![]() $(T, \xi _* \hat {\mathscr {O } }_{ \Sigma _T, q(T) } )$. In particular, by (99),
$(T, \xi _* \hat {\mathscr {O } }_{ \Sigma _T, q(T) } )$. In particular, by (99), ![]() $\epsilon _q^j$ is a primitive
$\epsilon _q^j$ is a primitive ![]() $|\Gamma _q|$th root of unity. Thus, we can find a generator
$|\Gamma _q|$th root of unity. Thus, we can find a generator ![]() $\tilde {\sigma }_q(U)\in \Gamma _q$ such that
$\tilde {\sigma }_q(U)\in \Gamma _q$ such that
In fact, ![]() $\tilde {\sigma }_q(U)$ is the unique generator of
$\tilde {\sigma }_q(U)$ is the unique generator of ![]() $\Gamma _q$ satisfying the above equation (100) for any formal parameter
$\Gamma _q$ satisfying the above equation (100) for any formal parameter ![]() $\tilde {t}_U$. From this it is easy to see that the generator
$\tilde {t}_U$. From this it is easy to see that the generator ![]() $\tilde {\sigma }_q(U)$ does not depend upon
$\tilde {\sigma }_q(U)$ does not depend upon ![]() $U$. We denote it by
$U$. We denote it by ![]() $\tilde {\sigma }_q$. It determines the primitive character
$\tilde {\sigma }_q$. It determines the primitive character ![]() $\chi$ of
$\chi$ of ![]() $\Gamma _q$, which satisfies
$\Gamma _q$, which satisfies ![]() $\chi (\tilde {\sigma }_q)=\epsilon _q^{-1}$.
$\chi (\tilde {\sigma }_q)=\epsilon _q^{-1}$.
Denote by ![]() $\mathcal {O}_q$ the sheaf of
$\mathcal {O}_q$ the sheaf of ![]() $\mathscr {O}_T$-algebra
$\mathscr {O}_T$-algebra ![]() $\xi _* \hat {\mathscr {O } }_{ \Sigma _T, q(T) }$ over
$\xi _* \hat {\mathscr {O } }_{ \Sigma _T, q(T) }$ over ![]() $T$, and let
$T$, and let ![]() $(T,\mathcal {K}_q)$ be the associated formal punctured disc over
$(T,\mathcal {K}_q)$ be the associated formal punctured disc over ![]() $T$. For any section
$T$. For any section ![]() $q$ of
$q$ of ![]() $\xi$ contained in the smooth locus of
$\xi$ contained in the smooth locus of ![]() $\xi$, define the sheaf of Kac–Moody algebra
$\xi$, define the sheaf of Kac–Moody algebra ![]() $\hat {L}(\mathfrak {g}, \Gamma _q)_{T}$ over
$\hat {L}(\mathfrak {g}, \Gamma _q)_{T}$ over ![]() $T$ by
$T$ by
where the Lie bracket is defined as in (72). For any ![]() $\lambda \in D_{c,q}:=D_{c, \tilde {\sigma }_q}$ we define a sheaf of integrable representation
$\lambda \in D_{c,q}:=D_{c, \tilde {\sigma }_q}$ we define a sheaf of integrable representation ![]() $\mathscr {H}(\lambda )_T$ over
$\mathscr {H}(\lambda )_T$ over ![]() $T$ as follows: for any open affine subset
$T$ as follows: for any open affine subset ![]() $U\subset T$ such that
$U\subset T$ such that ![]() $\mathcal {O}_q(U)$ is a complete local
$\mathcal {O}_q(U)$ is a complete local ![]() $\mathscr {O}_T(U)$-algebra,
$\mathscr {O}_T(U)$-algebra,
By Lemma 6.5, this gives a well-defined sheaf over ![]() $T$. For each section
$T$. For each section ![]() $p$ of
$p$ of ![]() $\bar {\xi }$ such that
$\bar {\xi }$ such that ![]() $\pi ^{-1}(p)$ is non-empty and some (and, hence, any)
$\pi ^{-1}(p)$ is non-empty and some (and, hence, any) ![]() $q\in \pi ^{-1}(p)$ is contained in the smooth locus of
$q\in \pi ^{-1}(p)$ is contained in the smooth locus of ![]() $\xi$, we may define the following sheaf of Lie algebras over
$\xi$, we may define the following sheaf of Lie algebras over ![]() $\mathscr {O}_T$ (cf. Definition 3.1),
$\mathscr {O}_T$ (cf. Definition 3.1),
 \[ \hat{\mathfrak{g}}_p:=\bigg(\bigoplus_{q\in \pi^{-1}(p) } \mathfrak{g}\otimes_{\mathbb{C} } \mathcal{K}_q \bigg)^\Gamma\oplus \mathscr{O}_T \cdot C \quad \text{and}\quad \mathfrak{g}_p:= \bigg( \bigoplus _{q\in \pi^{-1}(p) } \mathfrak{g}\otimes_{\mathbb{C}} \xi_* \mathscr{O}_{q(T )} \bigg)^\Gamma. \]
\[ \hat{\mathfrak{g}}_p:=\bigg(\bigoplus_{q\in \pi^{-1}(p) } \mathfrak{g}\otimes_{\mathbb{C} } \mathcal{K}_q \bigg)^\Gamma\oplus \mathscr{O}_T \cdot C \quad \text{and}\quad \mathfrak{g}_p:= \bigg( \bigoplus _{q\in \pi^{-1}(p) } \mathfrak{g}\otimes_{\mathbb{C}} \xi_* \mathscr{O}_{q(T )} \bigg)^\Gamma. \]
The restriction gives an isomorphism ![]() $\hat {\mathfrak {g}}_p\simeq \hat {L}(\mathfrak {g}, \Gamma _q)_T$, and
$\hat {\mathfrak {g}}_p\simeq \hat {L}(\mathfrak {g}, \Gamma _q)_T$, and ![]() $\mathfrak {g}_p\simeq \mathfrak {g}^ {\Gamma _q}\otimes _\mathbb {C} \mathscr {O}_T$ as in Lemmas 3.2 and 3.3. For any
$\mathfrak {g}_p\simeq \mathfrak {g}^ {\Gamma _q}\otimes _\mathbb {C} \mathscr {O}_T$ as in Lemmas 3.2 and 3.3. For any ![]() $\lambda \in D_{c, q}$, we still denote by
$\lambda \in D_{c, q}$, we still denote by ![]() $\mathscr {H}(\lambda )_T$ the associated representation of
$\mathscr {H}(\lambda )_T$ the associated representation of ![]() $\hat {\mathfrak {g}}_p$ via the isomorphism
$\hat {\mathfrak {g}}_p$ via the isomorphism ![]() $\hat {\mathfrak {g}}_p\simeq \hat {L}(\mathfrak {g}, \Gamma _q)_T$.
$\hat {\mathfrak {g}}_p\simeq \hat {L}(\mathfrak {g}, \Gamma _q)_T$.
Definition 7.7 (Sheaf of twisted conformal blocks)
Let ![]() $({\Sigma }_{T},\Gamma, \vec {q})$ be a family of
$({\Sigma }_{T},\Gamma, \vec {q})$ be a family of ![]() $s$-pointed
$s$-pointed ![]() $\Gamma$-curves over an irreducible scheme
$\Gamma$-curves over an irreducible scheme ![]() $T$. Set
$T$. Set ![]() $\vec {p}=\pi \circ \vec {q}$. Let
$\vec {p}=\pi \circ \vec {q}$. Let ![]() $\vec {\lambda }=(\lambda _{1},\ldots, \lambda _{s})$ be a
$\vec {\lambda }=(\lambda _{1},\ldots, \lambda _{s})$ be a ![]() $s$-tuple of highest weights, where
$s$-tuple of highest weights, where ![]() $\lambda _i\in D_{c, q_i}$ for each
$\lambda _i\in D_{c, q_i}$ for each ![]() $i$.
$i$.
Now, let us consider the sheaf of ![]() $\mathscr {O}_{T}$-module:
$\mathscr {O}_{T}$-module:
and
 \begin{equation} \hat{\mathfrak{g}}_{\vec{p}}:= \bigg(\bigoplus_{i=1}^s \bigg(\bigoplus_{\bar{q}_i\in \pi^{-1}(p_i)} \mathfrak{g}\otimes_{\mathbb{C}}\mathcal{K}_{\bar{q}_i} \bigg)^\Gamma \bigg) \oplus \mathscr{O}_{T}C. \end{equation}
\begin{equation} \hat{\mathfrak{g}}_{\vec{p}}:= \bigg(\bigoplus_{i=1}^s \bigg(\bigoplus_{\bar{q}_i\in \pi^{-1}(p_i)} \mathfrak{g}\otimes_{\mathbb{C}}\mathcal{K}_{\bar{q}_i} \bigg)^\Gamma \bigg) \oplus \mathscr{O}_{T}C. \end{equation}
We can define a ![]() $\mathscr {O}_{T}$-linear bracket in
$\mathscr {O}_{T}$-linear bracket in ![]() $\hat {\mathfrak {g}}_{\vec {p}}$ as in (11); in particular,
$\hat {\mathfrak {g}}_{\vec {p}}$ as in (11); in particular, ![]() $C$ is a central element of
$C$ is a central element of ![]() $\hat {\mathfrak {g}}_{\vec {p}}$. Then,
$\hat {\mathfrak {g}}_{\vec {p}}$. Then, ![]() $\hat {\mathfrak {g}}_{\vec {p}}$ is a sheaf of
$\hat {\mathfrak {g}}_{\vec {p}}$ is a sheaf of ![]() $\mathscr {O}_{T}$-Lie algebra. There is a natural
$\mathscr {O}_{T}$-Lie algebra. There is a natural ![]() $\mathscr {O}_T$-linear Lie algebra homomorphism
$\mathscr {O}_T$-linear Lie algebra homomorphism
 \[ \bigoplus_{i=1}^s \hat{\mathfrak{g}}_{p_i} \to \hat{\mathfrak{g}}_{\vec{p}}, \quad\text{where $C_i\mapsto C$}. \]
\[ \bigoplus_{i=1}^s \hat{\mathfrak{g}}_{p_i} \to \hat{\mathfrak{g}}_{\vec{p}}, \quad\text{where $C_i\mapsto C$}. \]
The componentwise action of ![]() $\bigoplus _{i=1}^s \hat {\mathfrak {g}}_{p_i}$ on
$\bigoplus _{i=1}^s \hat {\mathfrak {g}}_{p_i}$ on ![]() $\mathscr {H}(\vec {\lambda })_T$ induces an action of
$\mathscr {H}(\vec {\lambda })_T$ induces an action of ![]() $\hat {\mathfrak {g}}_{\vec {p}}$ on
$\hat {\mathfrak {g}}_{\vec {p}}$ on ![]() $\mathscr {H}(\vec {\lambda })_T$. We also introduce the following
$\mathscr {H}(\vec {\lambda })_T$. We also introduce the following ![]() $\mathscr {O}_{T}$-Lie algebra under the pointwise bracket:
$\mathscr {O}_{T}$-Lie algebra under the pointwise bracket:
 \begin{equation} \mathfrak{g}( \Sigma_T^o )^\Gamma:=[\mathfrak{g}\otimes_{\mathbb{C}} \xi^o_{*} \mathscr{O}_{{\Sigma}^o_{T}} ]^\Gamma, \quad \text{where } \Sigma_T^o=\Sigma_T\backslash( \bigcup_{i=1}^s \pi^{-1}(p_i(T)) ) .\end{equation}
\begin{equation} \mathfrak{g}( \Sigma_T^o )^\Gamma:=[\mathfrak{g}\otimes_{\mathbb{C}} \xi^o_{*} \mathscr{O}_{{\Sigma}^o_{T}} ]^\Gamma, \quad \text{where } \Sigma_T^o=\Sigma_T\backslash( \bigcup_{i=1}^s \pi^{-1}(p_i(T)) ) .\end{equation}
There is an embedding of sheaves of ![]() $\mathscr {O}_{T}$-Lie algebras:
$\mathscr {O}_{T}$-Lie algebras:
for ![]() $x_k\in \mathfrak {g}$ and
$x_k\in \mathfrak {g}$ and ![]() $f_k\in \xi ^o_{*} \mathscr {O}_{{\Sigma }^o_{T}}$ such that
$f_k\in \xi ^o_{*} \mathscr {O}_{{\Sigma }^o_{T}}$ such that ![]() $\sum _kx_k[f_k]\in \mathfrak {g}[{\Sigma }^o_{T}]^\Gamma$, where
$\sum _kx_k[f_k]\in \mathfrak {g}[{\Sigma }^o_{T}]^\Gamma$, where ![]() $(f_k)_{q}$ denotes the image of
$(f_k)_{q}$ denotes the image of ![]() $f_k$ in
$f_k$ in ![]() $\mathcal {K}_q$ via the localization map
$\mathcal {K}_q$ via the localization map ![]() $\xi ^o_{*} \mathscr {O}_{{\Sigma }^o_{T}} \to \mathcal {K}_q$.
$\xi ^o_{*} \mathscr {O}_{{\Sigma }^o_{T}} \to \mathcal {K}_q$.
By the residue theorem, ![]() $\beta$ is indeed a Lie algebra embedding. (Observe that Lemma 7.3 has been used to show that
$\beta$ is indeed a Lie algebra embedding. (Observe that Lemma 7.3 has been used to show that ![]() $\beta$ is an embedding.)
$\beta$ is an embedding.)
Finally, define the sheaf of twisted covacua (also called the sheaf of twisted dual conformal blocks) ![]() $\mathscr {V}_{\Sigma _T, \Gamma, \phi }(\vec {q},\vec {\lambda })$ over
$\mathscr {V}_{\Sigma _T, \Gamma, \phi }(\vec {q},\vec {\lambda })$ over ![]() $T$ as the quotient sheaf of
$T$ as the quotient sheaf of ![]() $\mathscr {O}_{T}$-modules
$\mathscr {O}_{T}$-modules
where ![]() $\mathfrak {g}( \Sigma _T^o )^\Gamma$ acts on
$\mathfrak {g}( \Sigma _T^o )^\Gamma$ acts on ![]() $\mathscr {H}(\vec {\lambda })_{T}$ via the embedding
$\mathscr {H}(\vec {\lambda })_{T}$ via the embedding ![]() $\beta$ (given by (104)) and
$\beta$ (given by (104)) and ![]() $\mathfrak {g}( \Sigma _T^o )^\Gamma \cdot \mathscr {H}(\vec {\lambda })_{T}\subset \mathscr {H}(\vec {\lambda })_{T}$ denotes the image sheaf under the sheaf homomorphism
$\mathfrak {g}( \Sigma _T^o )^\Gamma \cdot \mathscr {H}(\vec {\lambda })_{T}\subset \mathscr {H}(\vec {\lambda })_{T}$ denotes the image sheaf under the sheaf homomorphism
induced from the action of ![]() $\mathfrak {g}( \Sigma _T^o )^\Gamma$ on
$\mathfrak {g}( \Sigma _T^o )^\Gamma$ on ![]() $\mathscr {H}(\vec {\lambda })_{T}$.
$\mathscr {H}(\vec {\lambda })_{T}$.
Here we use the notation ![]() $\mathscr {V}_{\Sigma _T, \Gamma, \phi }(\vec {q},\vec {\lambda })$ to denote the sheaf of twisted covacua (see Remark 3.6).
$\mathscr {V}_{\Sigma _T, \Gamma, \phi }(\vec {q},\vec {\lambda })$ to denote the sheaf of twisted covacua (see Remark 3.6).
Theorem 7.8 (1) The sheaf ![]() $\mathscr {V}_{\Sigma _T, \Gamma, \phi } (\vec {q}, \vec {\lambda } )$ is a coherent
$\mathscr {V}_{\Sigma _T, \Gamma, \phi } (\vec {q}, \vec {\lambda } )$ is a coherent ![]() $\mathscr {O}_T$-module.
$\mathscr {O}_T$-module.
(2) For any morphism ![]() $f: T'\to T$ between schemes, there exists a natural isomorphism
$f: T'\to T$ between schemes, there exists a natural isomorphism
In particular, for any point ![]() $b\in T$ the restriction
$b\in T$ the restriction ![]() $\mathscr {V}_{\Sigma _T, \Gamma, \phi } (\vec {q}, \vec {\lambda } )|_b$ is the space of twisted dual conformal blocks attached to
$\mathscr {V}_{\Sigma _T, \Gamma, \phi } (\vec {q}, \vec {\lambda } )|_b$ is the space of twisted dual conformal blocks attached to ![]() $(\Sigma _b, \Gamma, \phi, \vec {p}(b), \vec {\lambda })$.
$(\Sigma _b, \Gamma, \phi, \vec {p}(b), \vec {\lambda })$.
Proof. We first prove part (1). Recall the embedding ![]() $\beta : \mathfrak {g}( \Sigma _T^o )^\Gamma \hookrightarrow \hat {\mathfrak {g}}_{\vec {p}}$ of
$\beta : \mathfrak {g}( \Sigma _T^o )^\Gamma \hookrightarrow \hat {\mathfrak {g}}_{\vec {p}}$ of ![]() $\mathscr {O}_{T}$-Lie algebras from (104). In addition, consider the
$\mathscr {O}_{T}$-Lie algebras from (104). In addition, consider the ![]() $\mathscr {O}_T$-Lie subalgebra
$\mathscr {O}_T$-Lie subalgebra
 \[ {\hat{\mathfrak{p}}}_{\vec{p}}:= \bigg[\bigoplus_{q\in \pi^{-1} (\vec{p}) } \mathfrak{g}\otimes_{\mathbb{C}} \xi_* \hat{\mathscr{O } }_{ \Sigma_T, q(T) } \bigg]^\Gamma \oplus \mathscr{O}_{T}C \]
\[ {\hat{\mathfrak{p}}}_{\vec{p}}:= \bigg[\bigoplus_{q\in \pi^{-1} (\vec{p}) } \mathfrak{g}\otimes_{\mathbb{C}} \xi_* \hat{\mathscr{O } }_{ \Sigma_T, q(T) } \bigg]^\Gamma \oplus \mathscr{O}_{T}C \]
of ![]() $\hat {\mathfrak {g}}_{\vec {p}}$ and let
$\hat {\mathfrak {g}}_{\vec {p}}$ and let ![]() $\mathfrak {g}( \Sigma _T^o )^\Gamma +{\hat {\mathfrak {p}}}_{\vec {p}}$ be the
$\mathfrak {g}( \Sigma _T^o )^\Gamma +{\hat {\mathfrak {p}}}_{\vec {p}}$ be the ![]() $\mathscr {O}_T$-subsheaf of
$\mathscr {O}_T$-subsheaf of ![]() $\hat {\mathfrak {g}}_{\vec {p}}$ spanned by
$\hat {\mathfrak {g}}_{\vec {p}}$ spanned by ![]() $\text {Im}\beta$ and
$\text {Im}\beta$ and ![]() ${\hat {\mathfrak {p}}}_{\vec {p}}$. Then, as can be seen, the quotient sheaf
${\hat {\mathfrak {p}}}_{\vec {p}}$. Then, as can be seen, the quotient sheaf ![]() $\hat {\mathfrak {g}}_{\vec {p}} \big / \big ( \mathfrak {g}( \Sigma _T^o )^\Gamma +{\hat {\mathfrak {p}}}_{\vec {p}} \big )$ is a coherent
$\hat {\mathfrak {g}}_{\vec {p}} \big / \big ( \mathfrak {g}( \Sigma _T^o )^\Gamma +{\hat {\mathfrak {p}}}_{\vec {p}} \big )$ is a coherent ![]() $\mathscr {O}_{T}$-module (cf. [Reference LooijengaLoo13, Lemma 5.1]). Thus, locally we can find a finite set of elements
$\mathscr {O}_{T}$-module (cf. [Reference LooijengaLoo13, Lemma 5.1]). Thus, locally we can find a finite set of elements ![]() $\{x_{j}\}$ of
$\{x_{j}\}$ of ![]() $\hat {\mathfrak {g}}_{\vec {p}}$ such that each
$\hat {\mathfrak {g}}_{\vec {p}}$ such that each ![]() $x_{j}$ acts locally finitely on
$x_{j}$ acts locally finitely on ![]() $\mathscr {H}(\vec {\lambda })_T$ and
$\mathscr {H}(\vec {\lambda })_T$ and
(cf. [Reference KumarKum02, Proof of Lemma 10.2.2]). Now, following the proof of Lemma 3.7 and recalling that the Poincaré–Birkhoff–Witt theorem holds for any Lie algebra ![]() $\mathfrak {s}$ over a commutative ring
$\mathfrak {s}$ over a commutative ring ![]() $R$ such that
$R$ such that ![]() $\mathfrak {s}$ is free as an
$\mathfrak {s}$ is free as an ![]() $R$-module (cf. [Reference Cartan and EilenbergCE56, Theorem 3.1, Chapter XIII]), we get part (1) of the theorem.
$R$-module (cf. [Reference Cartan and EilenbergCE56, Theorem 3.1, Chapter XIII]), we get part (1) of the theorem.
We now prove part (2). By the definition of the sheaf of covacua, ![]() $\mathscr {V}_{\Sigma _T, \Gamma, \phi }(\vec {q},\vec {\lambda })$ is the cokernel of the
$\mathscr {V}_{\Sigma _T, \Gamma, \phi }(\vec {q},\vec {\lambda })$ is the cokernel of the ![]() $\mathscr {O}_T$-morphism
$\mathscr {O}_T$-morphism ![]() $\alpha _T: \mathfrak {g}(\Sigma _T^o )^\Gamma \otimes _{\mathscr {O}_{T}}\mathscr {H}(\vec {\lambda })_{T}\to \mathscr {H}(\vec {\lambda })_{T}$, which gives rise to the exact sequence (on tensoring with
$\alpha _T: \mathfrak {g}(\Sigma _T^o )^\Gamma \otimes _{\mathscr {O}_{T}}\mathscr {H}(\vec {\lambda })_{T}\to \mathscr {H}(\vec {\lambda })_{T}$, which gives rise to the exact sequence (on tensoring with ![]() $\mathscr {O}_{T'}$):
$\mathscr {O}_{T'}$):

where we have identified the bottom left term of the above under
 \[ \bigg(\mathscr{O}_{T'}\bigotimes_{\mathscr{O}_{T}}{\mathfrak{g}}(\Sigma^o_{T})^\Gamma\bigg)\bigotimes_{\mathscr{O}_{T'}} \bigg(\mathscr{O}_{T'}\bigotimes_{\mathscr{O}_{T}}\mathscr{H}(\vec{\lambda})_{T}\bigg)\simeq {\mathfrak{g}}(\Sigma^o_{T'})^\Gamma\bigotimes_{\mathscr{O}_{T'}}\mathscr{H}(\vec{\lambda})_{T'} \]
\[ \bigg(\mathscr{O}_{T'}\bigotimes_{\mathscr{O}_{T}}{\mathfrak{g}}(\Sigma^o_{T})^\Gamma\bigg)\bigotimes_{\mathscr{O}_{T'}} \bigg(\mathscr{O}_{T'}\bigotimes_{\mathscr{O}_{T}}\mathscr{H}(\vec{\lambda})_{T}\bigg)\simeq {\mathfrak{g}}(\Sigma^o_{T'})^\Gamma\bigotimes_{\mathscr{O}_{T'}}\mathscr{H}(\vec{\lambda})_{T'} \]
and the second vertical isomorphism is obtained by Lemma 6.5. The right-most vertical isomorphism follows from the five lemma, proving the second part of the lemma.
In the rest of this section we assume that the family ![]() $\xi :\Sigma _T\to T$ of
$\xi :\Sigma _T\to T$ of ![]() $s$-pointed
$s$-pointed ![]() $\Gamma$-curves is such that
$\Gamma$-curves is such that ![]() $T$ is a
$T$ is a ![]() ${smooth}$ and irreducible scheme over
${smooth}$ and irreducible scheme over ![]() $\mathbb {C}$ and
$\mathbb {C}$ and ![]() $\xi : \Sigma _T\to T$ is a smooth morphism. In particular,
$\xi : \Sigma _T\to T$ is a smooth morphism. In particular, ![]() $\Sigma _T$ is a smooth scheme.
$\Sigma _T$ is a smooth scheme.
Let ![]() $\Theta _T$ be the sheaf of vector fields on
$\Theta _T$ be the sheaf of vector fields on ![]() $T$. Let
$T$. Let ![]() $\Theta _{\Sigma ^o_T/T}$ denote the
$\Theta _{\Sigma ^o_T/T}$ denote the ![]() $\mathscr {O}_T$-module of vertical vector fields on
$\mathscr {O}_T$-module of vertical vector fields on ![]() $\Sigma ^o_T$ with respect to
$\Sigma ^o_T$ with respect to ![]() $\xi ^o$, and let
$\xi ^o$, and let ![]() $\Theta _{\Sigma ^o_T,T}$ denote the
$\Theta _{\Sigma ^o_T,T}$ denote the ![]() $\mathscr {O}_T$-module of vector fields
$\mathscr {O}_T$-module of vector fields ![]() $V$ on
$V$ on ![]() $\Sigma ^o_T$ that locally descend to vector fields on
$\Sigma ^o_T$ that locally descend to vector fields on ![]() $T$ (i.e. there exists an open cover
$T$ (i.e. there exists an open cover ![]() $U_i$ of
$U_i$ of ![]() $T$ such that
$T$ such that ![]() $(d\xi ^o) (V_{|{\xi ^o}^{-1}(U_i)})$ is a vector field on
$(d\xi ^o) (V_{|{\xi ^o}^{-1}(U_i)})$ is a vector field on ![]() $U_i$). Since
$U_i$). Since ![]() $\xi ^o: \Sigma ^o_T\to T$ is an affine and smooth morphism, there exists a short exact sequence of
$\xi ^o: \Sigma ^o_T\to T$ is an affine and smooth morphism, there exists a short exact sequence of ![]() $\mathscr {O}_T$-modules:
$\mathscr {O}_T$-modules:
This short exact sequence induces the following short exact sequence of ![]() $\mathscr {O}_T$-modules:
$\mathscr {O}_T$-modules:
where ![]() $\Theta _{\Sigma ^o_T/T}^\Gamma$ (respectively,
$\Theta _{\Sigma ^o_T/T}^\Gamma$ (respectively, ![]() $\Theta _{\Sigma ^o_T,T}^\Gamma$) denotes the
$\Theta _{\Sigma ^o_T,T}^\Gamma$) denotes the ![]() $\mathscr {O}_T$-submodule of
$\mathscr {O}_T$-submodule of ![]() $\Gamma$-invariant vector fields in
$\Gamma$-invariant vector fields in ![]() $\Theta _{{\Sigma }^o_{T}/T}$ (respectively,
$\Theta _{{\Sigma }^o_{T}/T}$ (respectively, ![]() $\Theta _{\Sigma ^o_T,T}$).
$\Theta _{\Sigma ^o_T,T}$).
For any ![]() $b\in T$, we can find an affine open subset
$b\in T$, we can find an affine open subset ![]() $b\in U\subset T$, and a
$b\in U\subset T$, and a ![]() $s$-tuple of formal parameters
$s$-tuple of formal parameters ![]() $\vec {t}:=(t_1,t_2,\ldots, t_s)$ where
$\vec {t}:=(t_1,t_2,\ldots, t_s)$ where ![]() $t_i$ is a formal
$t_i$ is a formal ![]() $\Gamma _{q_i}$-equivariant
$\Gamma _{q_i}$-equivariant ![]() $\mathscr {O}_T(U)$-parameter around
$\mathscr {O}_T(U)$-parameter around ![]() $q_i$ (cf. Lemma 7.6). For any
$q_i$ (cf. Lemma 7.6). For any ![]() $\theta \in \Theta _{\Sigma ^o_T, T}^\Gamma (U) :=\Theta _{\Sigma ^o_T, T}(U)^\Gamma$, we denote by
$\theta \in \Theta _{\Sigma ^o_T, T}^\Gamma (U) :=\Theta _{\Sigma ^o_T, T}(U)^\Gamma$, we denote by ![]() $\theta _i$ the image in
$\theta _i$ the image in ![]() $\Theta _{\mathcal {K}_{q_i}, T }(U) ^{\Gamma _{q_i}}$, where
$\Theta _{\mathcal {K}_{q_i}, T }(U) ^{\Gamma _{q_i}}$, where ![]() $\Theta _{\mathcal {K}_{q_i}, T }(U)$ is the space of continuous
$\Theta _{\mathcal {K}_{q_i}, T }(U)$ is the space of continuous ![]() $\mathbb {C}$-linear derivations of
$\mathbb {C}$-linear derivations of ![]() $\mathcal {K}_{q_i}$ under the
$\mathcal {K}_{q_i}$ under the ![]() $\mathfrak {m}$-adic topology (given below Proposition 6.7) that are liftable from the vector fields on
$\mathfrak {m}$-adic topology (given below Proposition 6.7) that are liftable from the vector fields on ![]() $U$. We define the operator
$U$. We define the operator ![]() $L^{\vec {t}}_{\theta }$ on
$L^{\vec {t}}_{\theta }$ on ![]() $\mathscr {H}(\vec {\lambda })_U$ by
$\mathscr {H}(\vec {\lambda })_U$ by
where, for ![]() $1\leq i \leq s$,
$1\leq i \leq s$, ![]() $L^{t_i}_{\theta _i}$ is the extended Sugawara operator associated to
$L^{t_i}_{\theta _i}$ is the extended Sugawara operator associated to ![]() $\theta _i$ with respect to the Kac–Moody algebra
$\theta _i$ with respect to the Kac–Moody algebra ![]() $\hat {L}(\mathfrak {g}, \Gamma _{q_i})_{U}$ defined by (89), where we choose the
$\hat {L}(\mathfrak {g}, \Gamma _{q_i})_{U}$ defined by (89), where we choose the ![]() $\mathbb {C}$-lattice in
$\mathbb {C}$-lattice in ![]() $\mathscr {H}(\lambda _i)_U$ as in Lemma 6.10.
$\mathscr {H}(\lambda _i)_U$ as in Lemma 6.10.
Lemma 7.9 For any ![]() $\theta \in \Theta _{\Sigma ^o_T,T} (U)^\Gamma$, the operator
$\theta \in \Theta _{\Sigma ^o_T,T} (U)^\Gamma$, the operator ![]() $L^{\vec {t}}_{ \theta }$ preserves
$L^{\vec {t}}_{ \theta }$ preserves ![]() $\mathfrak {g}(\Sigma ^o_U)^\Gamma \cdot \mathscr {H}(\vec {\lambda })_U$, where
$\mathfrak {g}(\Sigma ^o_U)^\Gamma \cdot \mathscr {H}(\vec {\lambda })_U$, where ![]() $\Sigma ^o_U:= {\xi ^o}^{-1}(U).$
$\Sigma ^o_U:= {\xi ^o}^{-1}(U).$
Proof. For any ![]() $x[f]\in \mathfrak {g}(\Sigma ^o_U)$, let
$x[f]\in \mathfrak {g}(\Sigma ^o_U)$, let ![]() $A(x[f])$ denote the average
$A(x[f])$ denote the average ![]() $\sum _{\sigma \in \Gamma } \sigma (x)[\sigma (f)]\in \mathfrak {g}(\Sigma ^o_U)^\Gamma$. For any
$\sum _{\sigma \in \Gamma } \sigma (x)[\sigma (f)]\in \mathfrak {g}(\Sigma ^o_U)^\Gamma$. For any ![]() $\vec {h} =h_1\otimes \cdots \otimes h_s\in \mathscr {H}(\vec {\lambda })_{U}$, and
$\vec {h} =h_1\otimes \cdots \otimes h_s\in \mathscr {H}(\vec {\lambda })_{U}$, and ![]() $\theta \in \Theta _{\Sigma ^o_T, T} (U)^\Gamma$, by the formulae (86) and (90), one can easily check that
$\theta \in \Theta _{\Sigma ^o_T, T} (U)^\Gamma$, by the formulae (86) and (90), one can easily check that
It thus follows that ![]() $L^{\vec {t}}_{ \theta }$ preserves
$L^{\vec {t}}_{ \theta }$ preserves ![]() $\mathfrak {g}(\Sigma ^o_U)^\Gamma \cdot \mathscr {H}(\vec {\lambda })_U$.
$\mathfrak {g}(\Sigma ^o_U)^\Gamma \cdot \mathscr {H}(\vec {\lambda })_U$.
From the above lemma, the operator ![]() $L^{\vec {t}}_{ \theta }$ induces an operator denoted
$L^{\vec {t}}_{ \theta }$ induces an operator denoted ![]() $\nabla ^{\vec {t}}_\theta$ on
$\nabla ^{\vec {t}}_\theta$ on ![]() $\mathscr {V}_{\Sigma _T, \Gamma,\phi }(\vec {q}, \vec {\lambda } )|_U$.
$\mathscr {V}_{\Sigma _T, \Gamma,\phi }(\vec {q}, \vec {\lambda } )|_U$.
Theorem 7.10 With the same notation and assumptions as in Theorem 7.8, assume, in addition, that ![]() $\xi :\Sigma _T\to T$ is a smooth morphism and
$\xi :\Sigma _T\to T$ is a smooth morphism and ![]() $T$ is smooth. Then,
$T$ is smooth. Then, ![]() $\mathscr {V}_{\Sigma _T, \Gamma, \phi }(\vec {q} ,\vec {\lambda })$ is a locally free
$\mathscr {V}_{\Sigma _T, \Gamma, \phi }(\vec {q} ,\vec {\lambda })$ is a locally free ![]() $\mathscr {O}_T$-module of finite rank.
$\mathscr {O}_T$-module of finite rank.
Proof. It is enough to show that the space of twisted covacua ![]() $\mathscr {V}_{\Sigma _T, \Gamma,\phi }(\vec {q}, \vec {\lambda } )|_U$ is locally free for any cover of affine open subsets
$\mathscr {V}_{\Sigma _T, \Gamma,\phi }(\vec {q}, \vec {\lambda } )|_U$ is locally free for any cover of affine open subsets ![]() $U\subset T$ with a
$U\subset T$ with a ![]() $s$-tuple of formal parameters
$s$-tuple of formal parameters ![]() $\vec {t}:=(t_1,\ldots, t_s)$ around
$\vec {t}:=(t_1,\ldots, t_s)$ around ![]() $\vec {q}:=(q_1,\ldots, q_s)$, where
$\vec {q}:=(q_1,\ldots, q_s)$, where ![]() $t_i$ is a
$t_i$ is a ![]() $\Gamma _{q_i}$-equivariant
$\Gamma _{q_i}$-equivariant ![]() $\mathscr {O}_T(U)$-parameter. From the short exact sequence (108), we may assume (by shrinking
$\mathscr {O}_T(U)$-parameter. From the short exact sequence (108), we may assume (by shrinking ![]() $U$ if necessary) that there exists a
$U$ if necessary) that there exists a ![]() $\mathscr {O}_T(U)$-linear section
$\mathscr {O}_T(U)$-linear section ![]() $a: \Theta _T(U)\to \Theta _{\Sigma ^o_T, T}(U)^\Gamma$ of
$a: \Theta _T(U)\to \Theta _{\Sigma ^o_T, T}(U)^\Gamma$ of ![]() $d\xi ^o|_U: \Theta _{\Sigma ^o_T, T}(U)^\Gamma \to \Theta _T(U)$. By part (2) of Proposition 6.9, the following map
$d\xi ^o|_U: \Theta _{\Sigma ^o_T, T}(U)^\Gamma \to \Theta _T(U)$. By part (2) of Proposition 6.9, the following map
defines a connection on ![]() $\mathscr {V}_{\Sigma _T, \Gamma,\phi }(\vec {q}, \vec {\lambda } )|_U$. Thus, by the same proof as in [Reference Hotta, Takeuchi and TanisakiHTT08, Theorem 1.4.10],
$\mathscr {V}_{\Sigma _T, \Gamma,\phi }(\vec {q}, \vec {\lambda } )|_U$. Thus, by the same proof as in [Reference Hotta, Takeuchi and TanisakiHTT08, Theorem 1.4.10], ![]() $\mathscr {V}_{\Sigma _T, \Gamma,\phi }(\vec {q}, \vec {\lambda } )|_U$ is locally free. By Theorem 7.8,
$\mathscr {V}_{\Sigma _T, \Gamma,\phi }(\vec {q}, \vec {\lambda } )|_U$ is locally free. By Theorem 7.8, ![]() $\mathscr {V}_{\Sigma _T, \Gamma,\phi }(\vec {q}, \vec {\lambda } )$ is a coherent
$\mathscr {V}_{\Sigma _T, \Gamma,\phi }(\vec {q}, \vec {\lambda } )$ is a coherent ![]() $\mathscr {O}_T$-module and, hence, it is of finite rank.
$\mathscr {O}_T$-module and, hence, it is of finite rank.
Let ![]() $\mathscr {V}$ be a locally free
$\mathscr {V}$ be a locally free ![]() $\mathscr {O}_T$-module of finite rank. Let
$\mathscr {O}_T$-module of finite rank. Let ![]() $\mathcal {D}_1(\mathscr {V})$ denote the
$\mathcal {D}_1(\mathscr {V})$ denote the ![]() $\mathscr {O}_T$-module of operators
$\mathscr {O}_T$-module of operators ![]() $P: \mathscr {V}\to \mathscr {V}$ such that for any
$P: \mathscr {V}\to \mathscr {V}$ such that for any ![]() $f\in \mathscr {O}_T$, the Lie bracket
$f\in \mathscr {O}_T$, the Lie bracket ![]() $[P, f]$ is an
$[P, f]$ is an ![]() $\mathscr {O}_T$-module morphism from
$\mathscr {O}_T$-module morphism from ![]() $\mathscr {V}$ to
$\mathscr {V}$ to ![]() $\mathscr {V}$. Clearly,
$\mathscr {V}$. Clearly, ![]() $\mathcal {D}_1(\mathscr {V})$ is a
$\mathcal {D}_1(\mathscr {V})$ is a ![]() $\mathbb {C}$-Lie algebra.
$\mathbb {C}$-Lie algebra.
Definition 7.11 [Reference LooijengaLoo13]
A flat projective connection over ![]() $\mathscr {V}$ is a sheaf of
$\mathscr {V}$ is a sheaf of ![]() $\mathscr {O}_T$-modules
$\mathscr {O}_T$-modules ![]() $\mathscr {L}\subset \mathcal {D}_1(\mathscr {V})$ containing
$\mathscr {L}\subset \mathcal {D}_1(\mathscr {V})$ containing ![]() $\mathscr {O}_T$ (where
$\mathscr {O}_T$ (where ![]() $\mathscr {O}_T$ acts on
$\mathscr {O}_T$ acts on ![]() $\mathscr {V}$ by multiplication) such that
$\mathscr {V}$ by multiplication) such that ![]() $\mathscr {L}$ is a
$\mathscr {L}$ is a ![]() $\mathbb {C}$-Lie subalgebra and
$\mathbb {C}$-Lie subalgebra and
is a short exact sequence, where ![]() ${\rm Symb}$ denotes the symbol map defined by
${\rm Symb}$ denotes the symbol map defined by
Observe that ![]() ${\rm Symb}$ is a Lie algebra homomorphism.
${\rm Symb}$ is a Lie algebra homomorphism.
Following this definition, choose a local section ![]() $\nabla : \Theta _U\to \mathscr {L}|_U$ of
$\nabla : \Theta _U\to \mathscr {L}|_U$ of ![]() ${\rm Symb}$ on some open subset
${\rm Symb}$ on some open subset ![]() $U\subset T$. Then,
$U\subset T$. Then, ![]() $\nabla$ defines a connection on
$\nabla$ defines a connection on ![]() $\mathscr {V}$ over
$\mathscr {V}$ over ![]() $U$, since for any
$U$, since for any ![]() $X\in \Theta _U, f\in \mathscr {O}_U$ and
$X\in \Theta _U, f\in \mathscr {O}_U$ and ![]() $v\in \mathscr {V}$,
$v\in \mathscr {V}$,
For any ![]() $X,Y\in \Theta _U$, the curvature
$X,Y\in \Theta _U$, the curvature ![]() $\mathscr {K}(X,Y):= [\nabla _{X},\nabla _Y]-\nabla _{[X,Y]}\in \mathscr {O}_U$.
$\mathscr {K}(X,Y):= [\nabla _{X},\nabla _Y]-\nabla _{[X,Y]}\in \mathscr {O}_U$.
We now construct a flat projective connection ![]() $\mathscr {L}_T$ on the sheaf of covacua
$\mathscr {L}_T$ on the sheaf of covacua ![]() $\mathscr {V}_{ \Sigma _T,\Gamma, \phi }(\vec {q}, \vec {\lambda } )$. Let
$\mathscr {V}_{ \Sigma _T,\Gamma, \phi }(\vec {q}, \vec {\lambda } )$. Let ![]() $U$ be any affine open subset of
$U$ be any affine open subset of ![]() $T$ with a
$T$ with a ![]() $s$-tuple of parameters
$s$-tuple of parameters ![]() $\vec {t}$ around
$\vec {t}$ around ![]() $\vec {q}$ as above. Define
$\vec {q}$ as above. Define ![]() $\mathscr {L}_T(U)$ to be the
$\mathscr {L}_T(U)$ to be the ![]() $\mathscr {O}_T(U)$-module spanned by
$\mathscr {O}_T(U)$-module spanned by ![]() $\{ \nabla ^{\vec {t}}_\theta \,|\, \theta \in \Theta _{\Sigma ^o_T,T}(U)^\Gamma \}$ and
$\{ \nabla ^{\vec {t}}_\theta \,|\, \theta \in \Theta _{\Sigma ^o_T,T}(U)^\Gamma \}$ and ![]() $\mathscr {O}_T(U)$. By Lemma 6.10,
$\mathscr {O}_T(U)$. By Lemma 6.10, ![]() $\mathscr {L}_T(U)$ does not depend on the choice of parameters
$\mathscr {L}_T(U)$ does not depend on the choice of parameters ![]() $\vec {t}$. Therefore, the assignment
$\vec {t}$. Therefore, the assignment ![]() $U\mapsto \mathscr {L}_T(U)$ glues to be a sheaf
$U\mapsto \mathscr {L}_T(U)$ glues to be a sheaf ![]() $\mathscr {L}_T$ over
$\mathscr {L}_T$ over ![]() $T$.
$T$.
Theorem 7.12 With the same notation and assumptions as in Theorem 7.10, assume further that the ramification locus in each geometric fiber ![]() $\Sigma _b$ of
$\Sigma _b$ of ![]() $\Sigma _T$ is contained in
$\Sigma _T$ is contained in ![]() $\Gamma \cdot \vec {q}(b)$. Then, the sheaf
$\Gamma \cdot \vec {q}(b)$. Then, the sheaf ![]() $\mathscr {L}_T$ of operators on
$\mathscr {L}_T$ of operators on ![]() $\mathscr {V}_{\Sigma _T, \Gamma, \phi }(\vec {q}, \vec {\lambda })$ is a flat projective connection on
$\mathscr {V}_{\Sigma _T, \Gamma, \phi }(\vec {q}, \vec {\lambda })$ is a flat projective connection on ![]() $\mathscr {V}_{\Sigma _T, \Gamma, \phi }(\vec {q}, \vec {\lambda })$.
$\mathscr {V}_{\Sigma _T, \Gamma, \phi }(\vec {q}, \vec {\lambda })$.
Proof. For any ![]() $b\in T$, choose an affine open subset
$b\in T$, choose an affine open subset ![]() $b\in U$ with an
$b\in U$ with an ![]() $s$-tuple of parameters
$s$-tuple of parameters ![]() $\vec {t}$ around
$\vec {t}$ around ![]() $\vec {q}$. Given
$\vec {q}$. Given ![]() $\theta _1,\theta _2 \in \Theta _{\Sigma ^o_T, T}(U)^\Gamma$, by Proposition 6.9 and formula (109), the difference
$\theta _1,\theta _2 \in \Theta _{\Sigma ^o_T, T}(U)^\Gamma$, by Proposition 6.9 and formula (109), the difference ![]() $\nabla ^{\vec {t}}_{[\theta _1,\theta _2]}-[\nabla ^{\vec {t}}_{\theta _1},\nabla ^{\vec {t}}_{\theta _2} ]$ is a
$\nabla ^{\vec {t}}_{[\theta _1,\theta _2]}-[\nabla ^{\vec {t}}_{\theta _1},\nabla ^{\vec {t}}_{\theta _2} ]$ is a ![]() $\mathscr {O}_T(U)$-scalar operator and so is
$\mathscr {O}_T(U)$-scalar operator and so is ![]() $[\nabla ^{\vec {t}}_\theta, f]$ for
$[\nabla ^{\vec {t}}_\theta, f]$ for ![]() $f\in \mathscr {O}_T(U)$. It follows that
$f\in \mathscr {O}_T(U)$. It follows that ![]() $\mathscr {L}_T$ is a sheaf of
$\mathscr {L}_T$ is a sheaf of ![]() $\mathbb {C}$-Lie algebra acting on
$\mathbb {C}$-Lie algebra acting on ![]() $\mathscr {V}_{\Sigma _T, \Gamma, \phi }(\vec {q}, \vec {\lambda })$.
$\mathscr {V}_{\Sigma _T, \Gamma, \phi }(\vec {q}, \vec {\lambda })$.
Note that ![]() $\Theta _{\Sigma ^o_T/T}^\Gamma |_b\simeq \Theta (\Sigma ^o_b)^\Gamma$, where
$\Theta _{\Sigma ^o_T/T}^\Gamma |_b\simeq \Theta (\Sigma ^o_b)^\Gamma$, where ![]() $\Sigma ^o_b$ is the affine curve
$\Sigma ^o_b$ is the affine curve ![]() $\Sigma _b\backslash \pi ^{-1}(\vec {p}(b))$,
$\Sigma _b\backslash \pi ^{-1}(\vec {p}(b))$, ![]() $\vec {p}=\pi \circ \vec {q}$ and
$\vec {p}=\pi \circ \vec {q}$ and ![]() $\Theta (\Sigma ^o_b)^\Gamma$ is the Lie algebra of
$\Theta (\Sigma ^o_b)^\Gamma$ is the Lie algebra of ![]() $\Gamma$-invariant vector fields on
$\Gamma$-invariant vector fields on ![]() $\Sigma ^o_b$. In view of part (2) of Theorem 7.8,
$\Sigma ^o_b$. In view of part (2) of Theorem 7.8, ![]() $\mathscr {V}_{\Sigma _T, \Gamma, \phi }(\vec {q}, \vec {\lambda })|_b\simeq \mathscr {V}_{\Sigma _b, \Gamma, \phi }(\vec {q}(b), \vec {\lambda })$. Therefore, the
$\mathscr {V}_{\Sigma _T, \Gamma, \phi }(\vec {q}, \vec {\lambda })|_b\simeq \mathscr {V}_{\Sigma _b, \Gamma, \phi }(\vec {q}(b), \vec {\lambda })$. Therefore, the ![]() $\mathscr {O}_T(U)$-linear map
$\mathscr {O}_T(U)$-linear map ![]() $\nabla ^{\vec {t}}: \Theta _{\Sigma ^o_T/T}(U)^\Gamma \to {\rm End}_{\mathscr {O}_T(U)} (\mathscr {V}_{\Sigma _T, \Gamma, \phi }(\vec {q}, \vec {\lambda })|_U)$ induces a projective representation of
$\nabla ^{\vec {t}}: \Theta _{\Sigma ^o_T/T}(U)^\Gamma \to {\rm End}_{\mathscr {O}_T(U)} (\mathscr {V}_{\Sigma _T, \Gamma, \phi }(\vec {q}, \vec {\lambda })|_U)$ induces a projective representation of ![]() $\Theta (\Sigma ^o_b)^\Gamma$ on the space of covacua
$\Theta (\Sigma ^o_b)^\Gamma$ on the space of covacua ![]() $\mathscr {V}_{\Sigma _b, \Gamma, \phi }(\vec {q}(b), \vec {\lambda })$ attached to the
$\mathscr {V}_{\Sigma _b, \Gamma, \phi }(\vec {q}(b), \vec {\lambda })$ attached to the ![]() $s$-pointed curve
$s$-pointed curve ![]() $(\Sigma _{b}, \vec {q}(b))$. By Lemma 6.10, the map
$(\Sigma _{b}, \vec {q}(b))$. By Lemma 6.10, the map ![]() $\nabla ^{\vec {t}}$ is independent of the choice of
$\nabla ^{\vec {t}}$ is independent of the choice of ![]() $\vec {t}$ if we consider it projectively as a map
$\vec {t}$ if we consider it projectively as a map
Note that ![]() $\Theta (\Sigma ^o_b)^\Gamma$ is isomorphic to the Lie algebra
$\Theta (\Sigma ^o_b)^\Gamma$ is isomorphic to the Lie algebra ![]() $\Theta (\bar {\Sigma }^o_{b})$ of vector fields on the affine curve
$\Theta (\bar {\Sigma }^o_{b})$ of vector fields on the affine curve ![]() $\bar {\Sigma }_b\backslash \vec {p}(b)$ (since
$\bar {\Sigma }_b\backslash \vec {p}(b)$ (since ![]() $\Gamma \cdot \vec {q}(b)$ contains the ramification locus). By [Reference Beilinson, Feigin and MazurBFM91, Lemma 2.5.1],
$\Gamma \cdot \vec {q}(b)$ contains the ramification locus). By [Reference Beilinson, Feigin and MazurBFM91, Lemma 2.5.1], ![]() $\Theta (\bar {\Sigma }^o_{b})$ and hence
$\Theta (\bar {\Sigma }^o_{b})$ and hence ![]() $\Theta (\Sigma ^o_b)^\Gamma$ is an infinite-dimensional simple Lie algebra. Since
$\Theta (\Sigma ^o_b)^\Gamma$ is an infinite-dimensional simple Lie algebra. Since ![]() $\mathscr {V}_{\Sigma _b, \Gamma, \phi }(\vec {q}(b), \vec {\lambda })$ is a finite-dimensional vector space,
$\mathscr {V}_{\Sigma _b, \Gamma, \phi }(\vec {q}(b), \vec {\lambda })$ is a finite-dimensional vector space, ![]() $\Theta (\Sigma ^o_b)^\Gamma$ can only act by scalars on
$\Theta (\Sigma ^o_b)^\Gamma$ can only act by scalars on ![]() $\mathscr {V}_{\Sigma _b, \Gamma, \phi }(\vec {q}(b), \vec {\lambda })$. Therefore, for any
$\mathscr {V}_{\Sigma _b, \Gamma, \phi }(\vec {q}(b), \vec {\lambda })$. Therefore, for any ![]() $\theta \in \Theta _{\Sigma ^o_T/ T}(U)^\Gamma$, the operator
$\theta \in \Theta _{\Sigma ^o_T/ T}(U)^\Gamma$, the operator ![]() $\nabla ^{\vec {t}}_{\theta }$ acts via multiplication by an element of
$\nabla ^{\vec {t}}_{\theta }$ acts via multiplication by an element of ![]() $\mathscr {O}_T(U)$ on
$\mathscr {O}_T(U)$ on ![]() $\mathscr {V}_{\Sigma _T, \Gamma, \phi }(\vec {q}, \vec {\lambda })|_U$. Thus, the sequence (110) for
$\mathscr {V}_{\Sigma _T, \Gamma, \phi }(\vec {q}, \vec {\lambda })|_U$. Thus, the sequence (110) for ![]() $\mathscr {L}=\mathscr {L}_T$ is exact. It follows that
$\mathscr {L}=\mathscr {L}_T$ is exact. It follows that ![]() $\mathscr {L}_T$ is indeed a flat projective connection on
$\mathscr {L}_T$ is indeed a flat projective connection on ![]() $\mathscr {V}_{\Sigma _T, \Gamma, \phi }(\vec {q}, \vec {\lambda })$.
$\mathscr {V}_{\Sigma _T, \Gamma, \phi }(\vec {q}, \vec {\lambda })$.
8. Local freeness of the sheaf of twisted conformal blocks on stable compactification of Hurwitz stacks
We consider families of stable ![]() $s$-pointed
$s$-pointed ![]() $\Gamma$-curves and we show that the sheaf of twisted covacua over the stable compactification of a Hurwitz stack is locally free.
$\Gamma$-curves and we show that the sheaf of twisted covacua over the stable compactification of a Hurwitz stack is locally free.
In this section, we fix a group homomorphism ![]() $\phi : \Gamma \to {\rm Aut\ }(\mathfrak {g})$ such that
$\phi : \Gamma \to {\rm Aut\ }(\mathfrak {g})$ such that ![]() $\Gamma$ stabilizes a Borel subalgebra
$\Gamma$ stabilizes a Borel subalgebra ![]() $\mathfrak {b}$ of
$\mathfrak {b}$ of ![]() $\mathfrak {g}$.
$\mathfrak {g}$.
Definition 8.1 [Reference Bertin and RomagnyBR11, Définition 4.3.4]
We say that a family of ![]() $s$-pointed
$s$-pointed ![]() $\Gamma$-curves
$\Gamma$-curves ![]() $(\Sigma _T, \vec {q})$ over a scheme
$(\Sigma _T, \vec {q})$ over a scheme ![]() $T$ (see Definition 7.2) is stable if:
$T$ (see Definition 7.2) is stable if:
(0) each geometric fiber
 $\Sigma _b$ of
$\Sigma _b$ of  $\Sigma _T$ is (connected) with only nodal singularity;
$\Sigma _T$ is (connected) with only nodal singularity;(1) the family of
 $s$-pointed curves
$s$-pointed curves  $( \bar {\Sigma }_T, \vec {p})$ is stable where
$( \bar {\Sigma }_T, \vec {p})$ is stable where  $\vec {p}:=\pi \circ \vec {q}$, i.e. for any geometric point
$\vec {p}:=\pi \circ \vec {q}$, i.e. for any geometric point  $b\in T$ the fiber
$b\in T$ the fiber  $\bar {\Sigma }_b$ is a connected reduced curve with at most nodal singularity and the automorphism group of the pointed curve
$\bar {\Sigma }_b$ is a connected reduced curve with at most nodal singularity and the automorphism group of the pointed curve  $(\bar {\Sigma }_b, \vec {p}(b))$ is finite;
$(\bar {\Sigma }_b, \vec {p}(b))$ is finite;(2) the action of
 $\Gamma$ on each geometric fiber
$\Gamma$ on each geometric fiber  $\Sigma _b$ is stable in the sense of Definition 5.1 (in particular,
$\Sigma _b$ is stable in the sense of Definition 5.1 (in particular,  $\Sigma _b$ has only nodal singularity); moreover,
$\Sigma _b$ has only nodal singularity); moreover,  $\Gamma \cdot \vec {q}(b)$ contains all the ramification points for any
$\Gamma \cdot \vec {q}(b)$ contains all the ramification points for any  $b\in T$.
$b\in T$.
A ![]() $s$-pointed
$s$-pointed ![]() $\Gamma$-curve is called stable if it is stable as a family over a point.
$\Gamma$-curve is called stable if it is stable as a family over a point.
Remark 8.2 For a family of ![]() $s$-pointed
$s$-pointed ![]() $\Gamma$-curves
$\Gamma$-curves ![]() $(\Sigma _T, \vec {q})$ over
$(\Sigma _T, \vec {q})$ over ![]() $T$ satisfying properties (0) and (2) as above, the stability of
$T$ satisfying properties (0) and (2) as above, the stability of ![]() $( \bar {\Sigma }_T, \vec {p})$ is equivalent to the stability of
$( \bar {\Sigma }_T, \vec {p})$ is equivalent to the stability of ![]() $(\Sigma _T, \Gamma \cdot \vec {q})$ (cf. [Reference Bertin and RomagnyBR11, Proposition 5.1.3]).
$(\Sigma _T, \Gamma \cdot \vec {q})$ (cf. [Reference Bertin and RomagnyBR11, Proposition 5.1.3]).
Moreover, under the assumption that ![]() $\Gamma \cdot \vec {q}$ contains all the ramification points in
$\Gamma \cdot \vec {q}$ contains all the ramification points in ![]() $\Sigma$, at any nodal point
$\Sigma$, at any nodal point ![]() $q\in \Sigma$,
$q\in \Sigma$, ![]() $q$ being unramified and stable,
$q$ being unramified and stable, ![]() ${\rm det}(\dot \sigma )=1$,
${\rm det}(\dot \sigma )=1$, ![]() $\sigma$ fixes the two branches for any
$\sigma$ fixes the two branches for any ![]() $\sigma \in \Gamma _q$ and
$\sigma \in \Gamma _q$ and ![]() $\Gamma _q$ is cyclic (cf. [Reference Bertin and RomagnyBR11, Corollaire 4.3.3 and the comment after Definition 6.2.3]). In this case, any stable
$\Gamma _q$ is cyclic (cf. [Reference Bertin and RomagnyBR11, Corollaire 4.3.3 and the comment after Definition 6.2.3]). In this case, any stable ![]() $s$-pointed
$s$-pointed ![]() $\Gamma$-curve
$\Gamma$-curve ![]() $(\Sigma, \vec {p})$ is exactly a
$(\Sigma, \vec {p})$ is exactly a ![]() $s$-pointed admissible
$s$-pointed admissible ![]() $\Gamma$-cover in the sense of Jarvis, Kaufmann, and Kimura [Reference Jarvis, Kaufmann and KimuraJKK05, Definitions 2.1 and 2.2]. The only difference is that, in our definition, stable
$\Gamma$-cover in the sense of Jarvis, Kaufmann, and Kimura [Reference Jarvis, Kaufmann and KimuraJKK05, Definitions 2.1 and 2.2]. The only difference is that, in our definition, stable ![]() $s$-pointed
$s$-pointed ![]() $\Gamma$-curves are connected, and admissible
$\Gamma$-curves are connected, and admissible ![]() $s$-pointed
$s$-pointed ![]() $\Gamma$-covers defined in [Reference Jarvis, Kaufmann and KimuraJKK05] can be disconnected.
$\Gamma$-covers defined in [Reference Jarvis, Kaufmann and KimuraJKK05] can be disconnected.
Let ![]() $(C_o, \vec {q}_o )$ be a
$(C_o, \vec {q}_o )$ be a ![]() $s$-pointed
$s$-pointed ![]() $\Gamma$-curve such that
$\Gamma$-curve such that ![]() $\Gamma$ acts stably on
$\Gamma$ acts stably on ![]() $C_o$ (cf. Definition 5.1). Let
$C_o$ (cf. Definition 5.1). Let ![]() $\tilde {C}_o$ be the normalization of
$\tilde {C}_o$ be the normalization of ![]() $C_o$ at the points
$C_o$ at the points ![]() $\Gamma \cdot r$, where
$\Gamma \cdot r$, where ![]() $r$ is a (stable) nodal point of
$r$ is a (stable) nodal point of ![]() $C_o$. The nodal point
$C_o$. The nodal point ![]() $r$ splits into two smooth points
$r$ splits into two smooth points ![]() $r',r''$ in
$r',r''$ in ![]() $\tilde {C}_o$. The following lemma shows that there exists a canonical smoothing deformation of
$\tilde {C}_o$. The following lemma shows that there exists a canonical smoothing deformation of ![]() $(C_o, \vec {q}_o )$ over a formal disc
$(C_o, \vec {q}_o )$ over a formal disc ![]() $\mathbb {D}_\tau :={\rm Spec}\, \mathbb {C}[[\tau ]]$. We denote by
$\mathbb {D}_\tau :={\rm Spec}\, \mathbb {C}[[\tau ]]$. We denote by ![]() $\mathbb {D}^\times _\tau$ the associated punctured formal disc
$\mathbb {D}^\times _\tau$ the associated punctured formal disc ![]() ${\rm Spec}\, \mathbb {C}((\tau ))$.
${\rm Spec}\, \mathbb {C}((\tau ))$.
Lemma 8.3 With the same notation as above, we assume that the stabilizer group ![]() $\Gamma _r$ at
$\Gamma _r$ at ![]() $r$ is cyclic and does not exchange the branches. Then, there exists a formal deformation
$r$ is cyclic and does not exchange the branches. Then, there exists a formal deformation ![]() $(C, \vec {q})$ of the
$(C, \vec {q})$ of the ![]() $s$-pointed
$s$-pointed ![]() $\Gamma$-curve
$\Gamma$-curve ![]() $(C_o, \vec {q}_o )$ over a formal disc
$(C_o, \vec {q}_o )$ over a formal disc ![]() $\mathbb {D}_\tau$ with the formal parameter
$\mathbb {D}_\tau$ with the formal parameter ![]() $\tau$, a family of
$\tau$, a family of ![]() $s$-pointed
$s$-pointed ![]() $\Gamma$-curves
$\Gamma$-curves ![]() $(\tilde {C}, \vec {\tilde {q}})$ over
$(\tilde {C}, \vec {\tilde {q}})$ over ![]() $\mathbb {D}_\tau$, and a morphism
$\mathbb {D}_\tau$, and a morphism ![]() $\zeta : \tilde {C}\to C$ of families of
$\zeta : \tilde {C}\to C$ of families of ![]() $s$-pointed
$s$-pointed ![]() $\Gamma$-curves over
$\Gamma$-curves over ![]() $\mathbb {D}_\tau$, such that the following properties hold:
$\mathbb {D}_\tau$, such that the following properties hold:
(1) over the closed point
 $o\in \mathbb {D}_\tau$,
$o\in \mathbb {D}_\tau$,  $\zeta |_o: \tilde {C}_o\to C_o$ is the normalization of
$\zeta |_o: \tilde {C}_o\to C_o$ is the normalization of  $C_o$ at the points
$C_o$ at the points  $\Gamma \cdot r$, and over the formal punctured disc
$\Gamma \cdot r$, and over the formal punctured disc  $\mathbb {D}^\times _\tau$, we have
$\mathbb {D}^\times _\tau$, we have  $\tilde {C}|_{\mathbb {D}^\times _\tau }\simeq \tilde {C}_o\times \mathbb {D}^\times _\tau$;
$\tilde {C}|_{\mathbb {D}^\times _\tau }\simeq \tilde {C}_o\times \mathbb {D}^\times _\tau$;(2) for each
 $i=1,\ldots, s$,
$i=1,\ldots, s$,  $\zeta \circ \tilde {q}_i=q_i$ and
$\zeta \circ \tilde {q}_i=q_i$ and  $\vec {q}(o)=\vec {q}_{o}$ (we also use
$\vec {q}(o)=\vec {q}_{o}$ (we also use  $\vec {q}$ to denote the sections
$\vec {q}$ to denote the sections  $\vec {\tilde {q}}$ in
$\vec {\tilde {q}}$ in  $\tilde {C}$ if there is no confusion);
$\tilde {C}$ if there is no confusion);(3) the completed local ring
 $\hat {\mathscr {O}}_{C, r}$ of
$\hat {\mathscr {O}}_{C, r}$ of  $\mathscr {O}_C$ at
$\mathscr {O}_C$ at  $r$ is isomorphic to
$r$ is isomorphic to  $\mathbb {C}[[z',z'', \tau ]]/\langle \tau - z'z''\rangle \simeq \mathbb {C}[[z',z'']]$, where
$\mathbb {C}[[z',z'', \tau ]]/\langle \tau - z'z''\rangle \simeq \mathbb {C}[[z',z'']]$, where  $\Gamma _r$ acts on
$\Gamma _r$ acts on  $z'$ (respectively,
$z'$ (respectively,  $z''$) via a primitive character
$z''$) via a primitive character  $\chi$ (respectively,
$\chi$ (respectively,  $\chi ^{-1}$); moreover,
$\chi ^{-1}$); moreover,  $(z', \tau /z')$ (respectively,
$(z', \tau /z')$ (respectively,  $(z'', \tau /z''$)) gives a formal coordinate around
$(z'', \tau /z''$)) gives a formal coordinate around  $r'$ (respectively,
$r'$ (respectively,  $r''$) in
$r''$) in  $\tilde {C}$, where we still denote by
$\tilde {C}$, where we still denote by  $z'$ (respectively,
$z'$ (respectively,  $z''$) the function around
$z''$) the function around  $r'$ (respectively,
$r'$ (respectively,  $r''$) by pulling back
$r''$) by pulling back  $z'$ (respectively,
$z'$ (respectively,  $z''$) via
$z''$) via  $\zeta$;
$\zeta$;(4) there exists a
 $\Gamma$-equivariant isomorphism of algebras
(111)where
$\Gamma$-equivariant isomorphism of algebras
(111)where \begin{equation} \kappa: \hat{\mathscr{O}}_{\tilde{C}\backslash \Gamma\cdot \{r', r''\}, \tilde{C}_o \backslash \Gamma \cdot \{r',r''\} }\simeq\mathscr{O}_{\tilde{C}_o\backslash \Gamma\cdot \{r',r''\}}[[\tau]], \end{equation}
\begin{equation} \kappa: \hat{\mathscr{O}}_{\tilde{C}\backslash \Gamma\cdot \{r', r''\}, \tilde{C}_o \backslash \Gamma \cdot \{r',r''\} }\simeq\mathscr{O}_{\tilde{C}_o\backslash \Gamma\cdot \{r',r''\}}[[\tau]], \end{equation} $\hat {\mathscr {O}}_{\tilde {C}\backslash \Gamma \cdot \{r', r''\}, \tilde {C}_o \backslash \Gamma \cdot \{r',r''\} }$ is the completion of
$\hat {\mathscr {O}}_{\tilde {C}\backslash \Gamma \cdot \{r', r''\}, \tilde {C}_o \backslash \Gamma \cdot \{r',r''\} }$ is the completion of  ${\mathscr {O}}_{\tilde {C}\backslash \Gamma \cdot \{r', r''\}}$ along
${\mathscr {O}}_{\tilde {C}\backslash \Gamma \cdot \{r', r''\}}$ along  $\tilde {C}_o \backslash \Gamma \cdot \{r',r''\}$; moreover,
$\tilde {C}_o \backslash \Gamma \cdot \{r',r''\}$; moreover,  $\vec {\tilde {q}}$ in
$\vec {\tilde {q}}$ in  $\tilde {C}$ and
$\tilde {C}$ and  $\vec {q}_{o}$ in
$\vec {q}_{o}$ in  $\tilde {C}_o$ are compatible under this isomorphism, i.e. the points
$\tilde {C}_o$ are compatible under this isomorphism, i.e. the points  $q_{o,i} \in \tilde {C}_o \backslash \Gamma \cdot \{r',r''\}$ (for
$q_{o,i} \in \tilde {C}_o \backslash \Gamma \cdot \{r',r''\}$ (for  $i= 1, \ldots, s$) identified with the algebra homomorphisms
$i= 1, \ldots, s$) identified with the algebra homomorphisms  $\beta _i: \mathscr {O}_{\tilde {C}_o\backslash \Gamma \cdot \{r',r''\}} \to \mathbb {C}$ extended to
under the identification
$\beta _i: \mathscr {O}_{\tilde {C}_o\backslash \Gamma \cdot \{r',r''\}} \to \mathbb {C}$ extended to
under the identification \begin{align*} \beta_i^\tau:\hat{\mathscr{O}}_{\tilde{C}\backslash \Gamma\cdot \{r', r''\}, \tilde{C}_o \backslash \Gamma \cdot \{r',r''\} }\to \mathbb{C}[[\tau]] \end{align*}
\begin{align*} \beta_i^\tau:\hat{\mathscr{O}}_{\tilde{C}\backslash \Gamma\cdot \{r', r''\}, \tilde{C}_o \backslash \Gamma \cdot \{r',r''\} }\to \mathbb{C}[[\tau]] \end{align*}
 $\kappa$ correspond to the section
$\kappa$ correspond to the section  $\tilde {q}_i$ of
$\tilde {q}_i$ of  $\tilde {C}\to \mathbb {D}_\tau$.
$\tilde {C}\to \mathbb {D}_\tau$.
Proof. In the non-equivariant case, this smoothing construction as formal deformation is sketched by Looijenga in [Reference LooijengaLoo13, § 6], and detailed argument from formal deformation to algebraic deformation can be found in [Reference DamioliniDam20, § 6.1]. These constructions/arguments can be easily generalized to the equivariant setting when ![]() $\Gamma _r$ acts on the node stably and does not exchange the branches.
$\Gamma _r$ acts on the node stably and does not exchange the branches.
Let ![]() $\hat {L}(\mathfrak {g}, \Gamma _{r'})$ (respectively,
$\hat {L}(\mathfrak {g}, \Gamma _{r'})$ (respectively, ![]() $\hat {L}(\mathfrak {g}, \Gamma _{r''})$) be the Kac–Moody algebra attached to the point
$\hat {L}(\mathfrak {g}, \Gamma _{r''})$) be the Kac–Moody algebra attached to the point ![]() $r'$ (respectively,
$r'$ (respectively, ![]() $r''$) in
$r''$) in ![]() $\tilde {C}_o$. Recall that (Lemma 5.3)
$\tilde {C}_o$. Recall that (Lemma 5.3) ![]() $\mu ^*\in D_{c, r'}$ if and only if
$\mu ^*\in D_{c, r'}$ if and only if ![]() $\mu \in D_{c, r''}$ where
$\mu \in D_{c, r''}$ where ![]() $V(\mu ^*)\simeq V(\mu )^*$. (By Lemma 5.2,
$V(\mu ^*)\simeq V(\mu )^*$. (By Lemma 5.2, ![]() $\Gamma _{r'}=\Gamma _{r''}$ and, hence,
$\Gamma _{r'}=\Gamma _{r''}$ and, hence, ![]() $\mathfrak {g}^{\Gamma _{r'}}=\mathfrak {g}^{\Gamma _{r''}}$.) Let
$\mathfrak {g}^{\Gamma _{r'}}=\mathfrak {g}^{\Gamma _{r''}}$.) Let ![]() $\mathscr {H}(\mu ^*)$ (respectively,
$\mathscr {H}(\mu ^*)$ (respectively, ![]() $\mathscr {H}(\mu )$) be the highest weight integrable representation of
$\mathscr {H}(\mu )$) be the highest weight integrable representation of ![]() $\hat {L}(\mathfrak {g}, \Gamma _{r'})$ (respectively,
$\hat {L}(\mathfrak {g}, \Gamma _{r'})$ (respectively, ![]() $\hat {L}(\mathfrak {g}, \Gamma _{r''})$) as usual.
$\hat {L}(\mathfrak {g}, \Gamma _{r''})$) as usual.
Lemma 8.4 There exists a non-degenerate pairing ![]() $b_\mu : \mathscr {H}(\mu ^*) \times \mathscr {H}(\mu )\to \mathbb {C}$ such that for any
$b_\mu : \mathscr {H}(\mu ^*) \times \mathscr {H}(\mu )\to \mathbb {C}$ such that for any ![]() $h_1\in \mathscr {H}(\mu ^*)$,
$h_1\in \mathscr {H}(\mu ^*)$, ![]() $h_2\in \mathscr {H}(\mu )$, and
$h_2\in \mathscr {H}(\mu )$, and ![]() $x[z'^n]\in \hat {L}(\mathfrak {g}, \Gamma _{r'})$,
$x[z'^n]\in \hat {L}(\mathfrak {g}, \Gamma _{r'})$,
Note that ![]() $x[z'^n]\in \hat {L}(\mathfrak {g}, \Gamma _{r'})$ if and only if
$x[z'^n]\in \hat {L}(\mathfrak {g}, \Gamma _{r'})$ if and only if ![]() $x[z''^{-n}]\in \hat {L}(\mathfrak {g}, \Gamma _{r''})$.
$x[z''^{-n}]\in \hat {L}(\mathfrak {g}, \Gamma _{r''})$.
Proof. From Lemma 5.3 (especially see ‘another proof of Lemma 5.3 Part (2)’), there exists an isomorphism ![]() $\hat {\omega }: \tilde {L}(\mathfrak {g}, \Gamma _{r'})\simeq \tilde {L}(\mathfrak {g}, \Gamma _{r''})$, such that the representation of
$\hat {\omega }: \tilde {L}(\mathfrak {g}, \Gamma _{r'})\simeq \tilde {L}(\mathfrak {g}, \Gamma _{r''})$, such that the representation of ![]() $\tilde {L}(\mathfrak {g}, \Gamma _{r''})$ on
$\tilde {L}(\mathfrak {g}, \Gamma _{r''})$ on ![]() $\mathscr {H}(\mu )$ via
$\mathscr {H}(\mu )$ via ![]() $\hat {\omega }^{-1}$ is isomorphic to
$\hat {\omega }^{-1}$ is isomorphic to ![]() $\mathscr {H}(\mu ^*)$, where
$\mathscr {H}(\mu ^*)$, where ![]() $\tilde {L}(\mathfrak {g}, \Gamma _{r'})$ is the non-completed Kac–Moody algebra. By [Reference KacKac90, § 9.4], there exists a contravariant form
$\tilde {L}(\mathfrak {g}, \Gamma _{r'})$ is the non-completed Kac–Moody algebra. By [Reference KacKac90, § 9.4], there exists a contravariant form ![]() $\bar {b}_\mu : \mathscr {H}(\mu ^*)\times \mathscr {H}(\mu ^*)\to \mathbb {C}$ such that
$\bar {b}_\mu : \mathscr {H}(\mu ^*)\times \mathscr {H}(\mu ^*)\to \mathbb {C}$ such that
where ![]() $\varpi$ is the Cartan involution of
$\varpi$ is the Cartan involution of ![]() $\tilde {L}(\mathfrak {g}, \Gamma _{r'})$ mapping
$\tilde {L}(\mathfrak {g}, \Gamma _{r'})$ mapping ![]() $x'_i[z'^{s_i}]$ (respectively,
$x'_i[z'^{s_i}]$ (respectively, ![]() $y'_i[z'^{-s_i}]$) to
$y'_i[z'^{-s_i}]$) to ![]() $-y'_i[z'^{-s_i}]$ (respectively,
$-y'_i[z'^{-s_i}]$ (respectively, ![]() $-x'_i[z'^{s_i}]$) for any
$-x'_i[z'^{s_i}]$) for any ![]() $i\in \hat {I}(\mathfrak {g},\Gamma _{r'})$, see these notation in the second proof of Lemma 5.3 part (2). Observe that the composition
$i\in \hat {I}(\mathfrak {g},\Gamma _{r'})$, see these notation in the second proof of Lemma 5.3 part (2). Observe that the composition ![]() $\hat {\omega }\circ \varpi : \tilde {L}(\mathfrak {g}, \Gamma _{r'})\to \tilde {L}(\mathfrak {g}, \Gamma _{r''})$ is an isomorphism of Lie algebras mapping
$\hat {\omega }\circ \varpi : \tilde {L}(\mathfrak {g}, \Gamma _{r'})\to \tilde {L}(\mathfrak {g}, \Gamma _{r''})$ is an isomorphism of Lie algebras mapping ![]() $x[z'^n]$ to
$x[z'^n]$ to ![]() $x[z''^{-n}]$. Hence, the lemma follows after we identify the second copy of
$x[z''^{-n}]$. Hence, the lemma follows after we identify the second copy of ![]() $\mathscr {H}(\mu ^*)$ in
$\mathscr {H}(\mu ^*)$ in ![]() $\bar {b}_\mu$ with
$\bar {b}_\mu$ with ![]() $\mathscr {H}(\mu )$ via
$\mathscr {H}(\mu )$ via ![]() $\hat {\omega }^{-1}$ mentioned above.
$\hat {\omega }^{-1}$ mentioned above.
There exist direct sum decompositions by ![]() $t$-degree (putting the
$t$-degree (putting the ![]() $t$-degree of the highest weight vectors at
$t$-degree of the highest weight vectors at ![]() $0$):
$0$):
 \begin{align*} \mathscr{H}(\mu^*)=\bigoplus_{d=0}^\infty \mathscr{H}(\mu^*)_{-d} ,\quad \mathscr{H}(\mu)=\bigoplus_{d=0}^\infty \mathscr{H}(\mu)_{-d}. \end{align*}
\begin{align*} \mathscr{H}(\mu^*)=\bigoplus_{d=0}^\infty \mathscr{H}(\mu^*)_{-d} ,\quad \mathscr{H}(\mu)=\bigoplus_{d=0}^\infty \mathscr{H}(\mu)_{-d}. \end{align*}
The non-degenerate pairing ![]() $b_\mu$ in Lemma 8.4 induces a non-degenerate pairing
$b_\mu$ in Lemma 8.4 induces a non-degenerate pairing ![]() $b_{\mu,d}: \mathscr {H}(\mu ^*)_{-d}\times \mathscr {H}(\mu )_{-d}\to \mathbb {C}$ for each
$b_{\mu,d}: \mathscr {H}(\mu ^*)_{-d}\times \mathscr {H}(\mu )_{-d}\to \mathbb {C}$ for each ![]() $d\geq 0$. Let
$d\geq 0$. Let ![]() $b^*_{\mu,d}\in (\mathscr {H}(\mu ^*)_{-d})^*\otimes (\mathscr {H}(\mu )_{-d})^*$ be the dual of
$b^*_{\mu,d}\in (\mathscr {H}(\mu ^*)_{-d})^*\otimes (\mathscr {H}(\mu )_{-d})^*$ be the dual of ![]() $b_{\mu, d}$. The contravariant form
$b_{\mu, d}$. The contravariant form ![]() $\bar {b}_\mu$ on
$\bar {b}_\mu$ on ![]() $\mathscr {H}(\mu ^*)$ with respect to
$\mathscr {H}(\mu ^*)$ with respect to ![]() $\tilde {L}(\mathfrak {g}, \Gamma _{r'})$ induces an isomorphism
$\tilde {L}(\mathfrak {g}, \Gamma _{r'})$ induces an isomorphism ![]() $c'_\mu : (\mathscr {H}(\mu ^*)_{-d})^*\simeq \mathscr {H}(\mu ^*)_{-d}$. Similarly, the contravariant form on
$c'_\mu : (\mathscr {H}(\mu ^*)_{-d})^*\simeq \mathscr {H}(\mu ^*)_{-d}$. Similarly, the contravariant form on ![]() $\mathscr {H}(\mu )$ with respect to
$\mathscr {H}(\mu )$ with respect to ![]() $\tilde {L}(\mathfrak {g}, \Gamma _{r''})$ induces an isomorphism
$\tilde {L}(\mathfrak {g}, \Gamma _{r''})$ induces an isomorphism ![]() $c''_\mu : (\mathscr {H}(\mu )_{-d})^*\simeq \mathscr {H}(\mu )_{-d}$ (the Cartan involution on
$c''_\mu : (\mathscr {H}(\mu )_{-d})^*\simeq \mathscr {H}(\mu )_{-d}$ (the Cartan involution on ![]() $\tilde {L}(\mathfrak {g}, \Gamma _{r''})$ taken here is obtained from
$\tilde {L}(\mathfrak {g}, \Gamma _{r''})$ taken here is obtained from ![]() $\varpi$ on
$\varpi$ on ![]() $\tilde {L}(\mathfrak {g}, \Gamma _{r'})$ via the isomorphism
$\tilde {L}(\mathfrak {g}, \Gamma _{r'})$ via the isomorphism ![]() $\hat {\omega }$). Set
$\hat {\omega }$). Set ![]() $\Delta _{\mu,d}: =(c'_\mu \otimes c''_\mu )(b^*_{\mu,d})\in \mathscr {H}(\mu ^*)_{-d}\otimes \mathscr {H}(\mu )_{-d}$ if
$\Delta _{\mu,d}: =(c'_\mu \otimes c''_\mu )(b^*_{\mu,d})\in \mathscr {H}(\mu ^*)_{-d}\otimes \mathscr {H}(\mu )_{-d}$ if ![]() $d\geq 0$ and
$d\geq 0$ and ![]() $0$ if
$0$ if ![]() $d<0$. Note that
$d<0$. Note that ![]() $\Delta _{\mu, 0}$ is exactly the element
$\Delta _{\mu, 0}$ is exactly the element ![]() $I_\mu$ induced from the identity map on
$I_\mu$ induced from the identity map on ![]() $V(\mu )$ (see the formula (43)). In view of Lemma 8.4,
$V(\mu )$ (see the formula (43)). In view of Lemma 8.4, ![]() $\Delta _{\mu, d}$ satisfies the following property (for any
$\Delta _{\mu, d}$ satisfies the following property (for any ![]() $d,n\in \mathbb {Z}$)
$d,n\in \mathbb {Z}$)
We now construct the following ‘gluing’ tensor element (following [Reference LooijengaLoo13, Lemma 6.5] in the non-equivariant setting),
Let ![]() $\theta ',\theta ''$ be the maps of pulling-back functions via the map
$\theta ',\theta ''$ be the maps of pulling-back functions via the map ![]() $\zeta : \tilde {C}\to C$
$\zeta : \tilde {C}\to C$
where ![]() $\hat {\mathscr {O}}_{C, r}$ is the completion of
$\hat {\mathscr {O}}_{C, r}$ is the completion of ![]() ${\mathscr {O}}_{C}$ along
${\mathscr {O}}_{C}$ along ![]() $r$, and
$r$, and ![]() $\hat { \mathscr {O}}_{\tilde {C}, r'}$ and
$\hat { \mathscr {O}}_{\tilde {C}, r'}$ and ![]() $\hat { \mathscr {O}}_{\tilde {C}, r''}$ are defined similarly. For any
$\hat { \mathscr {O}}_{\tilde {C}, r''}$ are defined similarly. For any ![]() $f(z',z'')=\sum _{i\geq 0,j\geq 0} a_{i,j}z'^i z''^j\in \hat {\mathscr {O}}_{C, r}$, we have
$f(z',z'')=\sum _{i\geq 0,j\geq 0} a_{i,j}z'^i z''^j\in \hat {\mathscr {O}}_{C, r}$, we have
 \[ \theta'(f)=f(z', \tau/z') =\sum_{j\geq 0} \bigg(\sum_{i\geq 0} a_{i,j} z'^{i-j} \bigg)\tau^j , \]
\[ \theta'(f)=f(z', \tau/z') =\sum_{j\geq 0} \bigg(\sum_{i\geq 0} a_{i,j} z'^{i-j} \bigg)\tau^j , \]
and
 \[ \theta''(f)=f(\tau/z'', z'') =\sum_{i\geq 0} \bigg(\sum_{j\geq 0} a_{i,j} z''^{j-i} \bigg) \tau^i . \]
\[ \theta''(f)=f(\tau/z'', z'') =\sum_{i\geq 0} \bigg(\sum_{j\geq 0} a_{i,j} z''^{j-i} \bigg) \tau^i . \]
The morphisms ![]() $\theta ',\theta ''$ induce a
$\theta ',\theta ''$ induce a ![]() $\mathbb {C}[[\tau ]]$-module morphism
$\mathbb {C}[[\tau ]]$-module morphism ![]() $\theta : (\mathfrak {g}\otimes \hat {\mathscr {O}}_{C, r} )^{\Gamma _{r}} \to ( \mathfrak {g}\otimes \mathbb {C}((z')) )^{\Gamma _{r'}}[[\tau ]] \oplus ( \mathfrak {g}\otimes \mathbb {C}((z'')) )^{\Gamma _{r''}} [[\tau ]]$, where
$\theta : (\mathfrak {g}\otimes \hat {\mathscr {O}}_{C, r} )^{\Gamma _{r}} \to ( \mathfrak {g}\otimes \mathbb {C}((z')) )^{\Gamma _{r'}}[[\tau ]] \oplus ( \mathfrak {g}\otimes \mathbb {C}((z'')) )^{\Gamma _{r''}} [[\tau ]]$, where ![]() $\tau$ acts on
$\tau$ acts on ![]() $\hat {\mathscr {O}}_{C, r}$ via
$\hat {\mathscr {O}}_{C, r}$ via
Thus, we get an injective map from ![]() $(\mathfrak {g}\otimes \hat {\mathscr {O}}_{C, r} )^{\Gamma _r}$ into
$(\mathfrak {g}\otimes \hat {\mathscr {O}}_{C, r} )^{\Gamma _r}$ into ![]() $\hat {L}(\mathfrak {g},\Gamma _{r'})[[\tau ]]\oplus \hat {L}(\mathfrak {g},\Gamma _{r''})[[\tau ]]$ (but not a Lie algebra homomorphism), which acts on
$\hat {L}(\mathfrak {g},\Gamma _{r'})[[\tau ]]\oplus \hat {L}(\mathfrak {g},\Gamma _{r''})[[\tau ]]$ (but not a Lie algebra homomorphism), which acts on ![]() $(\mathscr {H}(\mu ^*)\otimes \mathscr {H}(\mu ))[[\tau ]]$.
$(\mathscr {H}(\mu ^*)\otimes \mathscr {H}(\mu ))[[\tau ]]$.
Lemma 8.5 The element ![]() $\Delta _\mu \in \big (\mathscr {H}(\mu ^*)\otimes \mathscr {H}(\mu )\big )[[\tau ]]$ is annihilated by
$\Delta _\mu \in \big (\mathscr {H}(\mu ^*)\otimes \mathscr {H}(\mu )\big )[[\tau ]]$ is annihilated by ![]() $(\mathfrak {g}\otimes \hat { \mathscr {O}}_{C,r})^{\Gamma _r}$ via the morphism
$(\mathfrak {g}\otimes \hat { \mathscr {O}}_{C,r})^{\Gamma _r}$ via the morphism ![]() $\theta$ defined as above.
$\theta$ defined as above.
Proof. For any ![]() $x[z'^iz''^j]\in (\mathfrak {g}\otimes \hat {\mathscr {O}}_{C,r})^{\Gamma _r}$,
$x[z'^iz''^j]\in (\mathfrak {g}\otimes \hat {\mathscr {O}}_{C,r})^{\Gamma _r}$,
 \begin{align*} x[z'^iz''^j]\cdot \Delta_\mu &=\sum_{d\in \mathbb{Z}}(x[z'^{i-j}]\otimes 1) \Delta_{\mu, d}\tau^{d+j} + \sum_{d\in \mathbb{Z}} (1\otimes x[z''^{j-i}]) \Delta_{\mu, d}\tau^{d+i}\\ &= -\sum_{d\in \mathbb{Z}}(1\otimes x[z''^{j-i}]) \Delta_{\mu, d+j-i}\tau^{d+j}+ \sum_{d\in \mathbb{Z}} (1\otimes x[z''^{j-i}]) \Delta_{\mu, d}\tau^{d+i},\quad\text{by (112)}\\ &=0. \end{align*}
\begin{align*} x[z'^iz''^j]\cdot \Delta_\mu &=\sum_{d\in \mathbb{Z}}(x[z'^{i-j}]\otimes 1) \Delta_{\mu, d}\tau^{d+j} + \sum_{d\in \mathbb{Z}} (1\otimes x[z''^{j-i}]) \Delta_{\mu, d}\tau^{d+i}\\ &= -\sum_{d\in \mathbb{Z}}(1\otimes x[z''^{j-i}]) \Delta_{\mu, d+j-i}\tau^{d+j}+ \sum_{d\in \mathbb{Z}} (1\otimes x[z''^{j-i}]) \Delta_{\mu, d}\tau^{d+i},\quad\text{by (112)}\\ &=0. \end{align*}
From this it is easy to see that ![]() $x[f]\cdot \Delta _\mu =0$ for any
$x[f]\cdot \Delta _\mu =0$ for any ![]() $x[f]\in (\mathfrak {g}\otimes \hat {\mathscr {O}}_{C,r})^{\Gamma _r}$. This proves the lemma.
$x[f]\in (\mathfrak {g}\otimes \hat {\mathscr {O}}_{C,r})^{\Gamma _r}$. This proves the lemma.
For each ![]() $i=1,\dots, s$, let
$i=1,\dots, s$, let ![]() $\mathscr {H}(\lambda _i)_{\mathbb {D}_\tau }$ (respectively,
$\mathscr {H}(\lambda _i)_{\mathbb {D}_\tau }$ (respectively, ![]() $\mathscr {H}(\lambda _i)$) denote the integrable representation of
$\mathscr {H}(\lambda _i)$) denote the integrable representation of ![]() $\hat {L}(\mathfrak {g}, \Gamma _{q_i})_{\mathbb {D}_\tau }$ (respectively,
$\hat {L}(\mathfrak {g}, \Gamma _{q_i})_{\mathbb {D}_\tau }$ (respectively, ![]() $\hat {L}(\mathfrak {g}, \Gamma _{q_{i,o}})$) attached to
$\hat {L}(\mathfrak {g}, \Gamma _{q_{i,o}})$) attached to ![]() $\hat {\mathscr {O}}_{C, q_i}$ (respectively,
$\hat {\mathscr {O}}_{C, q_i}$ (respectively, ![]() $\hat {\mathscr {O}}_{C_o, q_{i,o}}$) as in § 6, and let
$\hat {\mathscr {O}}_{C_o, q_{i,o}}$) as in § 6, and let ![]() $\mathscr {H}(\vec {\lambda } )_{\mathbb {D}_\tau }$ (respectively,
$\mathscr {H}(\vec {\lambda } )_{\mathbb {D}_\tau }$ (respectively, ![]() $\mathscr {H}(\vec {\lambda } )$) denote their tensor product over
$\mathscr {H}(\vec {\lambda } )$) denote their tensor product over ![]() $\mathbb {C}[[\tau ]]$ (respectively,
$\mathbb {C}[[\tau ]]$ (respectively, ![]() $\mathbb {C}$). For each
$\mathbb {C}$). For each ![]() $i=1,\dots, s$, we choose a
$i=1,\dots, s$, we choose a ![]() $(\Gamma _{q_i},\chi _i)$-equivariant formal parameter
$(\Gamma _{q_i},\chi _i)$-equivariant formal parameter ![]() $z_i$ around
$z_i$ around ![]() $q_i$, i.e.
$q_i$, i.e. ![]() $\hat {\mathscr {O}}_{C,q_i}\simeq \mathbb {C}[[\tau ]][[z_i]]$, where
$\hat {\mathscr {O}}_{C,q_i}\simeq \mathbb {C}[[\tau ]][[z_i]]$, where ![]() $\chi _i$ is a primitive character of
$\chi _i$ is a primitive character of ![]() $\Gamma _{q_i}$. It gives rise to a trivialization (cf. formula (75))
$\Gamma _{q_i}$. It gives rise to a trivialization (cf. formula (75))
We now construct a morphism of ![]() $\mathbb {C}[[\tau ]]$-modules:
$\mathbb {C}[[\tau ]]$-modules:
given by
 \[ \sum_{i=0}^\infty h_i \tau^i \mapsto \sum_{i,d=0}^\infty (h_i\otimes \Delta_{\mu,d} )\tau^{i+d} , \]
\[ \sum_{i=0}^\infty h_i \tau^i \mapsto \sum_{i,d=0}^\infty (h_i\otimes \Delta_{\mu,d} )\tau^{i+d} , \]
where, for each ![]() $i$,
$i$, ![]() $h_i\in \mathscr {H}(\vec {\lambda } )$. Finally, we set
$h_i\in \mathscr {H}(\vec {\lambda } )$. Finally, we set
Consider the following canonical homomorphisms (obtained by pull-back and restrictions):
where the last isomorphism is obtained from the isomorphism ![]() $\kappa$ of Lemma 8.3 (see the isomorphism (111)). This gives rise to a Lie algebra homomorphism (depending upon the isomorphism
$\kappa$ of Lemma 8.3 (see the isomorphism (111)). This gives rise to a Lie algebra homomorphism (depending upon the isomorphism ![]() $\kappa$):
$\kappa$):
Hence, the Lie algebra ![]() $\mathfrak {g}[C\backslash \Gamma \cdot \vec {q}]^\Gamma$ acts on
$\mathfrak {g}[C\backslash \Gamma \cdot \vec {q}]^\Gamma$ acts on ![]() $\big ( \mathscr {H}(\vec {\lambda } )\otimes \mathscr {H}(\mu ^*)\otimes \mathscr {H}(\mu ) \big ) [[\tau ]]$ via the action of
$\big ( \mathscr {H}(\vec {\lambda } )\otimes \mathscr {H}(\mu ^*)\otimes \mathscr {H}(\mu ) \big ) [[\tau ]]$ via the action of ![]() $\big [\mathfrak {g}\otimes \mathscr {O}_{\tilde {C}_o\backslash \Gamma \cdot (\vec {q}_o\cup \{r',r''\}) }\big ]^\Gamma$ on
$\big [\mathfrak {g}\otimes \mathscr {O}_{\tilde {C}_o\backslash \Gamma \cdot (\vec {q}_o\cup \{r',r''\}) }\big ]^\Gamma$ on ![]() $\mathscr {H}(\vec {\lambda } )\otimes \mathscr {H}(\mu ^*)\otimes \mathscr {H}(\mu )$ at the points
$\mathscr {H}(\vec {\lambda } )\otimes \mathscr {H}(\mu ^*)\otimes \mathscr {H}(\mu )$ at the points ![]() $\{\vec {q}_o, r', r''\}$ as given just before Theorem 5.4 and extending it
$\{\vec {q}_o, r', r''\}$ as given just before Theorem 5.4 and extending it ![]() $\mathbb {C}[[\tau ]]$-linearly.
$\mathbb {C}[[\tau ]]$-linearly.
Recall from Definition 7.7 the action of ![]() $\mathfrak {g}[C\backslash \Gamma \cdot \vec {q} ]^\Gamma$ on
$\mathfrak {g}[C\backslash \Gamma \cdot \vec {q} ]^\Gamma$ on ![]() $\mathscr {H}(\vec {\lambda } )_{\mathbb {D}_\tau }$. Further,
$\mathscr {H}(\vec {\lambda } )_{\mathbb {D}_\tau }$. Further, ![]() $\mathfrak {g}[C\backslash \Gamma \cdot \vec {q} )^\Gamma$ acts on
$\mathfrak {g}[C\backslash \Gamma \cdot \vec {q} )^\Gamma$ acts on ![]() $(\mathscr {H}(\mu ^*)\otimes \mathscr {H}(\mu )) [[\tau ]]$ via the Lie algebra homomorphism (obtained by the restriction):
$(\mathscr {H}(\mu ^*)\otimes \mathscr {H}(\mu )) [[\tau ]]$ via the Lie algebra homomorphism (obtained by the restriction):
and the action of ![]() $(\mathfrak {g}\otimes \hat {\mathscr {O}}_{C, r})^{\Gamma _r}$ on
$(\mathfrak {g}\otimes \hat {\mathscr {O}}_{C, r})^{\Gamma _r}$ on ![]() $(\mathscr {H}(\mu ^*)\otimes \mathscr {H}(\mu )) [[\tau ]]$ (which is a Lie algebra action only projectively) is given just before Lemma 8.5.
$(\mathscr {H}(\mu ^*)\otimes \mathscr {H}(\mu )) [[\tau ]]$ (which is a Lie algebra action only projectively) is given just before Lemma 8.5.
Theorem 8.6 We have the following:
(1) the morphism
 $F_{\vec {\lambda }}$ is
$F_{\vec {\lambda }}$ is  $\mathfrak {g}[C\backslash \Gamma \cdot \vec {q}]^\Gamma$-equivariant;
$\mathfrak {g}[C\backslash \Gamma \cdot \vec {q}]^\Gamma$-equivariant;(2) the morphism
 $F_{\vec {\lambda }}$ induces an isomorphism of sheaf of covacua over
$F_{\vec {\lambda }}$ induces an isomorphism of sheaf of covacua over  $\mathbb {D}_\tau$,
(113)
$\mathbb {D}_\tau$,
(113) \begin{equation} \bar{F}_{\vec{\lambda}}: \mathscr{V}_{C, \Gamma, \phi}(\vec{q},\vec{\lambda} )\to \bigoplus_{\mu\in D_{c, r''}} \mathscr{V}_{ \tilde{C}_o, \Gamma,\phi }\big((\vec{q}_o, r', r'') , (\vec{\lambda}, \mu^*, \mu)\big) [[\tau]] . \end{equation}
\begin{equation} \bar{F}_{\vec{\lambda}}: \mathscr{V}_{C, \Gamma, \phi}(\vec{q},\vec{\lambda} )\to \bigoplus_{\mu\in D_{c, r''}} \mathscr{V}_{ \tilde{C}_o, \Gamma,\phi }\big((\vec{q}_o, r', r'') , (\vec{\lambda}, \mu^*, \mu)\big) [[\tau]] . \end{equation}
Note that here we take slightly different notation for the spaces/sheaves of covacua, see Remark 3.6.
Proof. By Lemma 8.5, the morphism
given by ![]() $h\mapsto \sum _{\mu \in D_{c,r''}} h\otimes \Delta _{\mu }$, is a morphism of
$h\mapsto \sum _{\mu \in D_{c,r''}} h\otimes \Delta _{\mu }$, is a morphism of ![]() $\mathfrak {g}[C\backslash \Gamma \cdot \vec {q} ]^\Gamma$-modules. Moreover, there exists an embedding obtained from the isomorphism
$\mathfrak {g}[C\backslash \Gamma \cdot \vec {q} ]^\Gamma$-modules. Moreover, there exists an embedding obtained from the isomorphism ![]() $t_{\vec {\lambda }}$:
$t_{\vec {\lambda }}$:
Observe that ![]() $F_{\vec {\lambda }}=i\circ F'_{\vec {\lambda }}$. This concludes part (1) of the theorem.
$F_{\vec {\lambda }}=i\circ F'_{\vec {\lambda }}$. This concludes part (1) of the theorem.
We now proceed to prove part (2) of the theorem. Using part (1) of the theorem and the morphism ![]() $\kappa _{\vec {q}}$, we get the
$\kappa _{\vec {q}}$, we get the ![]() $\mathbb {C}[[\tau ]]$-morphism (113). Taking quotient by
$\mathbb {C}[[\tau ]]$-morphism (113). Taking quotient by ![]() $\tau$, by the factorization theorem (Theorem 5.4) the morphism
$\tau$, by the factorization theorem (Theorem 5.4) the morphism ![]() $\bar {F}_{\vec {\lambda }}$ gives rise to an isomorphism
$\bar {F}_{\vec {\lambda }}$ gives rise to an isomorphism
As a consequence of the Nakayama lemma (cf. [Reference Atiyah and MacdonaldAM69, Exercise 10, Chap. 2]), ![]() $\bar {F}_{\vec {\lambda }}$ is surjective. (Observe that by Theorem 7.8, both the domain and the range of
$\bar {F}_{\vec {\lambda }}$ is surjective. (Observe that by Theorem 7.8, both the domain and the range of ![]() $\bar {F}_{\vec {\lambda }}$ are finitely generated
$\bar {F}_{\vec {\lambda }}$ are finitely generated ![]() $\mathbb {C}[[\tau ]]$-modules.) Now, since the range of
$\mathbb {C}[[\tau ]]$-modules.) Now, since the range of ![]() $\bar {F}_{\vec {\lambda }}$ is a free
$\bar {F}_{\vec {\lambda }}$ is a free ![]() $\mathbb {C}[[\tau ]]$-module, we get that
$\mathbb {C}[[\tau ]]$-module, we get that ![]() $\bar {F}_{\vec {\lambda }}$ splits over
$\bar {F}_{\vec {\lambda }}$ splits over ![]() $\mathbb {C}[[\tau ]]$. Thus, applying the Nakayama lemma (cf. [Reference Atiyah and MacdonaldAM69, Proposition 2.6]) again to the kernel
$\mathbb {C}[[\tau ]]$. Thus, applying the Nakayama lemma (cf. [Reference Atiyah and MacdonaldAM69, Proposition 2.6]) again to the kernel ![]() $K$ of
$K$ of ![]() $\bar {F}_{\vec {\lambda }}$, we get that
$\bar {F}_{\vec {\lambda }}$, we get that ![]() $K=0$. Thus,
$K=0$. Thus, ![]() $\bar {F}_{\vec {\lambda }}$ is an isomorphism, proving part (2).
$\bar {F}_{\vec {\lambda }}$ is an isomorphism, proving part (2).
Definition 8.7 We say that a stable ![]() $s$-pointed
$s$-pointed ![]() $\Gamma$-curve
$\Gamma$-curve ![]() $(\Sigma, q_1,\ldots, q_s)$ has marking data
$(\Sigma, q_1,\ldots, q_s)$ has marking data ![]() $\eta =\big ((\Gamma _1,\chi _1), (\Gamma _2,\chi _2),\ldots, (\Gamma _s, \chi _s)\big )$ if for each
$\eta =\big ((\Gamma _1,\chi _1), (\Gamma _2,\chi _2),\ldots, (\Gamma _s, \chi _s)\big )$ if for each ![]() $i$, the stabilizer group at
$i$, the stabilizer group at ![]() $q_i$ is a (cyclic) subgroup
$q_i$ is a (cyclic) subgroup ![]() $\Gamma _i \subset \Gamma$ and
$\Gamma _i \subset \Gamma$ and ![]() $\chi _i$ is the induced (automatically primitive) character of
$\chi _i$ is the induced (automatically primitive) character of ![]() $\Gamma _i$ on the tangent space
$\Gamma _i$ on the tangent space ![]() $T_{q_i} \Sigma$.
$T_{q_i} \Sigma$.
We now introduce the moduli stack ![]() $\overline {\mathscr {H}M}_{g, \Gamma, \eta }$, which associates to each
$\overline {\mathscr {H}M}_{g, \Gamma, \eta }$, which associates to each ![]() $\mathbb {C}$-scheme
$\mathbb {C}$-scheme ![]() $T$ the groupoid of stable family
$T$ the groupoid of stable family ![]() $\xi :\Sigma _T \to T$ of
$\xi :\Sigma _T \to T$ of ![]() $s$-pointed
$s$-pointed ![]() $\Gamma$-curves over
$\Gamma$-curves over ![]() $T$, such that each geometric fiber is of genus
$T$, such that each geometric fiber is of genus ![]() $g$ and is of marking data
$g$ and is of marking data ![]() $\eta$. In particular,
$\eta$. In particular, ![]() $\bigcup _{i=1}^s \Gamma \cdot q_i(T)$ contains the ramification divisor of
$\bigcup _{i=1}^s \Gamma \cdot q_i(T)$ contains the ramification divisor of ![]() $\pi : \Sigma _T \to \Sigma _T/\Gamma$ (cf. [Reference Bertin and RomagnyBR11, Definition 4.1.6]). Note that for any stable family of
$\pi : \Sigma _T \to \Sigma _T/\Gamma$ (cf. [Reference Bertin and RomagnyBR11, Definition 4.1.6]). Note that for any stable family of ![]() $s$-pointed
$s$-pointed ![]() $\Gamma$-curves in
$\Gamma$-curves in ![]() $\overline {\mathscr {H}{M}}_{g, \Gamma, \eta }$, its geometric fibers contain at worst only nodal singularity such that their stabilizer groups are cyclic which do not exchange the branches (cf. [Reference Bertin and RomagnyBR11, Corollaire 4.3.3], and the comment after [Reference Bertin and RomagnyBR11, Definition 6.2.3]).
$\overline {\mathscr {H}{M}}_{g, \Gamma, \eta }$, its geometric fibers contain at worst only nodal singularity such that their stabilizer groups are cyclic which do not exchange the branches (cf. [Reference Bertin and RomagnyBR11, Corollaire 4.3.3], and the comment after [Reference Bertin and RomagnyBR11, Definition 6.2.3]).
For any ![]() $\gamma _1, \ldots, \gamma _s\in \Gamma$,
$\gamma _1, \ldots, \gamma _s\in \Gamma$, ![]() $(\Sigma, \gamma _1q_1, \ldots, \gamma _sq_s)$ has the conjugate marking data
$(\Sigma, \gamma _1q_1, \ldots, \gamma _sq_s)$ has the conjugate marking data
where ![]() $(^{\gamma _i}\chi _i) (\gamma _ig_i\gamma _i^{-1}):= \chi _i(g_i)$, for
$(^{\gamma _i}\chi _i) (\gamma _ig_i\gamma _i^{-1}):= \chi _i(g_i)$, for ![]() $g_i\in \Gamma _i$. We denote by
$g_i\in \Gamma _i$. We denote by ![]() $[\eta ]$, the
$[\eta ]$, the ![]() $\Gamma ^s$-conjugacy class of
$\Gamma ^s$-conjugacy class of ![]() $\eta$.
$\eta$.
Theorem 8.8 The stack ![]() $\overline {\mathscr {H}{M}}_{g, \Gamma, \eta }$ is a proper and smooth Deligne–Mumford stack of finite type.
$\overline {\mathscr {H}{M}}_{g, \Gamma, \eta }$ is a proper and smooth Deligne–Mumford stack of finite type.
Proof. (Sketch) We can associate to ![]() $(\Sigma _T, \vec {q})$ (a stable family
$(\Sigma _T, \vec {q})$ (a stable family ![]() $\xi :\Sigma _T \to T$ of
$\xi :\Sigma _T \to T$ of ![]() $s$-pointed
$s$-pointed ![]() $\Gamma$-curves) the
$\Gamma$-curves) the ![]() $\Gamma$-stable relative Cartier divisor
$\Gamma$-stable relative Cartier divisor ![]() $\bigcup _{i}\Gamma \cdot (q_i(T))$ in
$\bigcup _{i}\Gamma \cdot (q_i(T))$ in ![]() $\Sigma _T$ which is étale over
$\Sigma _T$ which is étale over ![]() $T$. The
$T$. The ![]() $\Gamma ^{\times s}$-conjugacy classes
$\Gamma ^{\times s}$-conjugacy classes ![]() $[\eta ]$ of
$[\eta ]$ of ![]() $\eta$ is the marking type of
$\eta$ is the marking type of ![]() $\bigcup _{i} \Gamma \cdot (q_i(T))$. Let
$\bigcup _{i} \Gamma \cdot (q_i(T))$. Let ![]() $[\xi ]$ be the subclass of those conjugacy classes
$[\xi ]$ be the subclass of those conjugacy classes ![]() $[\Gamma _i,\chi _i]$ such that
$[\Gamma _i,\chi _i]$ such that ![]() $\Gamma _i$ is non-trivial. Then,
$\Gamma _i$ is non-trivial. Then, ![]() $[\xi ]$ is the associated ramification datum of stable
$[\xi ]$ is the associated ramification datum of stable ![]() $s$-pointed
$s$-pointed ![]() $\Gamma$-curves in
$\Gamma$-curves in ![]() $\overline {\mathscr {H}{M}}_{{g}, \Gamma, \eta }$. Let
$\overline {\mathscr {H}{M}}_{{g}, \Gamma, \eta }$. Let ![]() $\overline {\mathscr {H}M}_{g, \Gamma,[\xi ], [\eta ]}$ be the stable compactification of a Hurwitz stack defined in [Reference Bertin and RomagnyBR11, Definition 6.2.3]. The natural morphism
$\overline {\mathscr {H}M}_{g, \Gamma,[\xi ], [\eta ]}$ be the stable compactification of a Hurwitz stack defined in [Reference Bertin and RomagnyBR11, Definition 6.2.3]. The natural morphism ![]() $\overline {\mathscr {H}{M}}_{{g}, \Gamma, \eta }\to \overline {\mathscr {H}M}_{g, \Gamma,[\xi ], [\eta ]}$ is clearly representable, étale, and essentially surjective. By [Reference Bertin and RomagnyBR11, Théorèm 6.3.1],
$\overline {\mathscr {H}{M}}_{{g}, \Gamma, \eta }\to \overline {\mathscr {H}M}_{g, \Gamma,[\xi ], [\eta ]}$ is clearly representable, étale, and essentially surjective. By [Reference Bertin and RomagnyBR11, Théorèm 6.3.1], ![]() $\overline {\mathscr {H}M}_{g, \Gamma,[\xi ], [\eta ]}$ is a smooth proper Deligne–Mumford stack and, hence, so is
$\overline {\mathscr {H}M}_{g, \Gamma,[\xi ], [\eta ]}$ is a smooth proper Deligne–Mumford stack and, hence, so is ![]() $\overline {\mathscr {H}{M}}_{g, \Gamma, \eta }$.
$\overline {\mathscr {H}{M}}_{g, \Gamma, \eta }$.
Let ![]() $D_{c,i}$ be the set of dominant weights of
$D_{c,i}$ be the set of dominant weights of ![]() $\mathfrak {g}^{\Gamma _i}$ associated to the highest weight integrable (irreducible) representations of
$\mathfrak {g}^{\Gamma _i}$ associated to the highest weight integrable (irreducible) representations of ![]() $\hat {L}(\mathfrak {g}, \Gamma _i, \chi _i):= \hat {L}(\mathfrak {g}, \sigma _i)$, where
$\hat {L}(\mathfrak {g}, \Gamma _i, \chi _i):= \hat {L}(\mathfrak {g}, \sigma _i)$, where ![]() $\sigma _i\in \Gamma _i$ is the unique element such that
$\sigma _i\in \Gamma _i$ is the unique element such that ![]() $\chi _i(\sigma _i)= e^{ {2\pi i}/{|\Gamma _i|}}$. Choose a collection
$\chi _i(\sigma _i)= e^{ {2\pi i}/{|\Gamma _i|}}$. Choose a collection ![]() $\vec {\lambda }=(\lambda _1, \ldots, \lambda _s)$ of dominant weights, where
$\vec {\lambda }=(\lambda _1, \ldots, \lambda _s)$ of dominant weights, where ![]() $\lambda _i\in D_{c, i}$ for each
$\lambda _i\in D_{c, i}$ for each ![]() $i$. Recall that being a Deligne–Mumford stack,
$i$. Recall that being a Deligne–Mumford stack, ![]() $\overline {\mathscr {H}{M}}_{{g}, \Gamma, \eta }$ has an atlas
$\overline {\mathscr {H}{M}}_{{g}, \Gamma, \eta }$ has an atlas ![]() $\delta: X\to \overline {\mathscr {H}{M}}_{g, \Gamma, \eta }$ such that
$\delta: X\to \overline {\mathscr {H}{M}}_{g, \Gamma, \eta }$ such that ![]() $\delta$ is étale and surjective. By Theorem 8.8,
$\delta$ is étale and surjective. By Theorem 8.8, ![]() $X$ is a smooth (but not necessarily connected) scheme of finite type over
$X$ is a smooth (but not necessarily connected) scheme of finite type over ![]() $\mathbb {C}$.
$\mathbb {C}$.
We can attach to ![]() $\delta : X\to \overline {\mathscr {H}{M}}_{g, \Gamma, \eta }$ the coherent sheaf
$\delta : X\to \overline {\mathscr {H}{M}}_{g, \Gamma, \eta }$ the coherent sheaf ![]() $\mathscr {V}_{\Sigma _X, \Gamma,\phi }( \vec {q}_X , \vec {\lambda })$ of conformal blocks, where
$\mathscr {V}_{\Sigma _X, \Gamma,\phi }( \vec {q}_X , \vec {\lambda })$ of conformal blocks, where ![]() $(\Sigma _X, \vec {q}_X)$ is the associated stable family of
$(\Sigma _X, \vec {q}_X)$ is the associated stable family of ![]() $s$-pointed
$s$-pointed ![]() $\Gamma$-curves over
$\Gamma$-curves over ![]() $X$. This attachment can be done componentwise on
$X$. This attachment can be done componentwise on ![]() $X$ via Definition 7.7.
$X$ via Definition 7.7.
For any two atlases ![]() $X,Y$ of
$X,Y$ of ![]() $\overline {\mathscr {H}{M}}_{g, \Gamma, \eta }$ and a morphism
$\overline {\mathscr {H}{M}}_{g, \Gamma, \eta }$ and a morphism ![]() $f: Y\to X$ compatible with the atlas structures, by Theorem 7.8, there exists a canonical isomorphism
$f: Y\to X$ compatible with the atlas structures, by Theorem 7.8, there exists a canonical isomorphism
where ![]() $(\Sigma _X, \vec {q}_X)$ and
$(\Sigma _X, \vec {q}_X)$ and ![]() $(\Sigma _Y, \vec {q}_Y)$ are the families of stable
$(\Sigma _Y, \vec {q}_Y)$ are the families of stable ![]() $s$-pointed
$s$-pointed ![]() $\Gamma$-curves associated to these two atlases
$\Gamma$-curves associated to these two atlases ![]() $X,Y$. Given three atlases
$X,Y$. Given three atlases ![]() $X,Y,Z$ and morphisms
$X,Y,Z$ and morphisms ![]() $g:Z\to Y$ and
$g:Z\to Y$ and ![]() $f: Y\to X$, Theorem 7.8 ensures the obvious cocycle condition. Therefore, we get a coherent sheaf
$f: Y\to X$, Theorem 7.8 ensures the obvious cocycle condition. Therefore, we get a coherent sheaf ![]() $\mathscr {V}_{g, \Gamma, \phi }(\eta, \vec {\lambda })$ on
$\mathscr {V}_{g, \Gamma, \phi }(\eta, \vec {\lambda })$ on ![]() $\overline {\mathscr {H}{M}}_{g, \Gamma, \eta }$ such that
$\overline {\mathscr {H}{M}}_{g, \Gamma, \eta }$ such that ![]() $\delta ^* \mathscr {V}_{g, \Gamma, \phi }(\eta, \vec {\lambda }) \simeq \mathscr {V}_{\Sigma _X, \Gamma,\phi }( \vec {q}_X , \vec {\lambda })$ for any atlas
$\delta ^* \mathscr {V}_{g, \Gamma, \phi }(\eta, \vec {\lambda }) \simeq \mathscr {V}_{\Sigma _X, \Gamma,\phi }( \vec {q}_X , \vec {\lambda })$ for any atlas ![]() $\delta :X\to \overline {\mathscr {H}{M}}_{g, \Gamma, \eta }$. Some basics of coherent sheaves on Deligne–Mumford stacks can be found in [Reference KumarKum22, Definition C.20].
$\delta :X\to \overline {\mathscr {H}{M}}_{g, \Gamma, \eta }$. Some basics of coherent sheaves on Deligne–Mumford stacks can be found in [Reference KumarKum22, Definition C.20].
Theorem 8.9 For any genus ![]() $g\geq 0$, any marking data
$g\geq 0$, any marking data ![]() $\eta =\big ((\Gamma _1,\chi _1), (\Gamma _2,\chi _2),\ldots, (\Gamma _s, \chi _s)\big )$ and any set of dominant weights
$\eta =\big ((\Gamma _1,\chi _1), (\Gamma _2,\chi _2),\ldots, (\Gamma _s, \chi _s)\big )$ and any set of dominant weights ![]() $\vec {\lambda }=(\lambda _1, \ldots, \lambda _s)$ with
$\vec {\lambda }=(\lambda _1, \ldots, \lambda _s)$ with ![]() $\lambda _i\in D_{c,i}$, the sheaf of conformal blocks
$\lambda _i\in D_{c,i}$, the sheaf of conformal blocks ![]() $\mathscr {V}_{g, \Gamma, \phi }(\eta, \vec {\lambda })$ is locally free over
$\mathscr {V}_{g, \Gamma, \phi }(\eta, \vec {\lambda })$ is locally free over ![]() $\overline {\mathscr {H}{M}}_{g, \Gamma, \eta }$.
$\overline {\mathscr {H}{M}}_{g, \Gamma, \eta }$.
Proof. It suffices to show that the coherent sheaf ![]() $\mathscr {V}_{\Sigma _X, \Gamma,\phi }( \vec {q}_X , \vec {\lambda })$ is locally free, where
$\mathscr {V}_{\Sigma _X, \Gamma,\phi }( \vec {q}_X , \vec {\lambda })$ is locally free, where ![]() $X$ is an atlas of
$X$ is an atlas of ![]() $\overline {\mathscr {H}{M}}_{g, \Gamma, \eta }$. Since
$\overline {\mathscr {H}{M}}_{g, \Gamma, \eta }$. Since ![]() $X$ is a disjoint union of smooth irreducible schemes, we can work with a fixed component
$X$ is a disjoint union of smooth irreducible schemes, we can work with a fixed component ![]() $X_\alpha$ of
$X_\alpha$ of ![]() $X$, and show that the associated sheaf of conformal blocks restricted to
$X$, and show that the associated sheaf of conformal blocks restricted to ![]() $X_\alpha$ is locally free.
$X_\alpha$ is locally free.
We introduce a filtration on ![]() $\overline {\mathscr {H}{M}}_{g, \Gamma, \eta }$:
$\overline {\mathscr {H}{M}}_{g, \Gamma, \eta }$:
where ![]() $\overline {\mathscr {H}{M}}_{g, \Gamma, \eta }^i$ is the open substack of
$\overline {\mathscr {H}{M}}_{g, \Gamma, \eta }^i$ is the open substack of ![]() $\overline {\mathscr {H}{M}}_{g, \Gamma, \eta }$ with each geometric fiber consisting of at most
$\overline {\mathscr {H}{M}}_{g, \Gamma, \eta }$ with each geometric fiber consisting of at most ![]() $i$ many
$i$ many ![]() $\Gamma$-orbits of nodal points. Note that
$\Gamma$-orbits of nodal points. Note that ![]() $\overline {\mathscr {H}{M}}_{g, \Gamma, \eta }^0$ consists of stable smooth
$\overline {\mathscr {H}{M}}_{g, \Gamma, \eta }^0$ consists of stable smooth ![]() $s$-pointed
$s$-pointed ![]() $\Gamma$-curves. With the restriction on the genus to be fixed
$\Gamma$-curves. With the restriction on the genus to be fixed ![]() $g$, there exists
$g$, there exists ![]() $k\geq 0$ such that the number of orbits of nodal points is bounded by
$k\geq 0$ such that the number of orbits of nodal points is bounded by ![]() $k$. This filtration induces an open filtration on
$k$. This filtration induces an open filtration on ![]() $X_\alpha$ via
$X_\alpha$ via ![]() $\delta$,
$\delta$,
We now prove inductively that the coherent sheaf ![]() $\mathscr {V}_{\Sigma _{X_\alpha ^i}, \Gamma,\phi }( \vec {q}_{X_\alpha ^i} , \vec {\lambda })$ is locally free, where
$\mathscr {V}_{\Sigma _{X_\alpha ^i}, \Gamma,\phi }( \vec {q}_{X_\alpha ^i} , \vec {\lambda })$ is locally free, where ![]() $\vec {q}_{X_\alpha ^i}$ is the restriction of
$\vec {q}_{X_\alpha ^i}$ is the restriction of ![]() $\vec {q}$ to
$\vec {q}$ to ![]() $X_\alpha ^i$. When
$X_\alpha ^i$. When ![]() $i=0$, in view of Theorem 7.10,
$i=0$, in view of Theorem 7.10, ![]() $\mathscr {V}_{\Sigma _{X_\alpha ^0}, \Gamma,\phi }( \vec {q}_{X_\alpha ^0} , \vec {\lambda })$ is locally free. (Observe that by [Reference HartshorneHar77, Chap. III, Theorem 10.2],
$\mathscr {V}_{\Sigma _{X_\alpha ^0}, \Gamma,\phi }( \vec {q}_{X_\alpha ^0} , \vec {\lambda })$ is locally free. (Observe that by [Reference HartshorneHar77, Chap. III, Theorem 10.2], ![]() $\Sigma _{X_\alpha ^0}\to X_\alpha ^0$ is a smooth morphism.) Assume that
$\Sigma _{X_\alpha ^0}\to X_\alpha ^0$ is a smooth morphism.) Assume that ![]() $\mathscr {V}_{\Sigma _{X_\alpha ^{i-1}}, \Gamma,\phi }( \vec {q}_{X_\alpha ^{i-1}} , \vec {\lambda })$ is locally free where
$\mathscr {V}_{\Sigma _{X_\alpha ^{i-1}}, \Gamma,\phi }( \vec {q}_{X_\alpha ^{i-1}} , \vec {\lambda })$ is locally free where ![]() $i\geq 1$. By the smoothing construction in Lemma 8.3, for any
$i\geq 1$. By the smoothing construction in Lemma 8.3, for any ![]() $x\in X_\alpha ^i\backslash X_\alpha ^{i-1}$, there exists a morphism
$x\in X_\alpha ^i\backslash X_\alpha ^{i-1}$, there exists a morphism ![]() $\beta _x: \mathbb {D}_\tau \to \overline {\mathscr {H}{M}}_{g, \Gamma, \eta }^{i}$ such that
$\beta _x: \mathbb {D}_\tau \to \overline {\mathscr {H}{M}}_{g, \Gamma, \eta }^{i}$ such that ![]() $\beta _x(o)=\delta (x)$ and
$\beta _x(o)=\delta (x)$ and ![]() $\beta _x ( g_\tau )\in \overline {\mathscr {H}{M}}_{g, \Gamma, \eta }^{i-1}\backslash \overline {\mathscr {H}{M}}_{g, \Gamma, \eta }^{i-2}$, where
$\beta _x ( g_\tau )\in \overline {\mathscr {H}{M}}_{g, \Gamma, \eta }^{i-1}\backslash \overline {\mathscr {H}{M}}_{g, \Gamma, \eta }^{i-2}$, where ![]() $g_\tau$ is the generic point of
$g_\tau$ is the generic point of ![]() $\mathbb {D}_\tau$. Recall that
$\mathbb {D}_\tau$. Recall that ![]() $\delta : X\to \overline {\mathscr {H}{M}}_{g, \Gamma, \eta }$ is étale and surjective, hence
$\delta : X\to \overline {\mathscr {H}{M}}_{g, \Gamma, \eta }$ is étale and surjective, hence ![]() $\beta _x$ can be lifted to
$\beta _x$ can be lifted to ![]() $\beta _x': \mathbb {D}_\tau \to X_\alpha$ such that
$\beta _x': \mathbb {D}_\tau \to X_\alpha$ such that ![]() $\delta \circ \beta _x'=\beta _x$ and
$\delta \circ \beta _x'=\beta _x$ and ![]() $\beta _x'(o)=x$. It follows that
$\beta _x'(o)=x$. It follows that ![]() $\beta _x'(g_\tau )\in X_\alpha ^{i-1}\backslash X_\alpha ^{i-2}$. By Theorems 7.8 and 8.6, the rank of
$\beta _x'(g_\tau )\in X_\alpha ^{i-1}\backslash X_\alpha ^{i-2}$. By Theorems 7.8 and 8.6, the rank of ![]() $\mathscr {V}_{\Sigma _{X_\alpha ^{i-1}}, \Gamma,\phi }( \vec {q}_{X_\alpha ^{i-1}} , \vec {\lambda })$ (which is locally free by induction) is equal to the dimension of
$\mathscr {V}_{\Sigma _{X_\alpha ^{i-1}}, \Gamma,\phi }( \vec {q}_{X_\alpha ^{i-1}} , \vec {\lambda })$ (which is locally free by induction) is equal to the dimension of ![]() $\mathscr {V}_{\Sigma _x, \Gamma,\phi }( \vec {q}_x , \vec {\lambda })$. It follows that
$\mathscr {V}_{\Sigma _x, \Gamma,\phi }( \vec {q}_x , \vec {\lambda })$. It follows that ![]() $\mathscr {V}_{\Sigma _{X_\alpha ^{i}}, \Gamma,\phi }( \vec {q}_{X_\alpha ^{i}} , \vec {\lambda })$ is also locally free (cf. [Reference HartshorneHar77, Chap. II, Exercise 5.8(c)]). This concludes the proof of the theorem.
$\mathscr {V}_{\Sigma _{X_\alpha ^{i}}, \Gamma,\phi }( \vec {q}_{X_\alpha ^{i}} , \vec {\lambda })$ is also locally free (cf. [Reference HartshorneHar77, Chap. II, Exercise 5.8(c)]). This concludes the proof of the theorem.
The dimension of ![]() $\overline {\mathscr {H}{M}}_{g, \Gamma, \eta }$ is equal to
$\overline {\mathscr {H}{M}}_{g, \Gamma, \eta }$ is equal to ![]() $3\bar {g}-3+s$ (cf. [Reference Bertin and RomagnyBR11, Theorem 5.1.5]) if it is not empty, where by Riemann–Hurwitz formula the genus
$3\bar {g}-3+s$ (cf. [Reference Bertin and RomagnyBR11, Theorem 5.1.5]) if it is not empty, where by Riemann–Hurwitz formula the genus ![]() $\bar {g}$ of
$\bar {g}$ of ![]() $\Sigma /\Gamma$ for any
$\Sigma /\Gamma$ for any ![]() $\Sigma \in \overline {\mathscr {H}{M}}_{g, \Gamma, \eta }$, satisfies the following equation (cf. [Reference HartshorneHar77, Chap. IV, Corollary 2.4]):
$\Sigma \in \overline {\mathscr {H}{M}}_{g, \Gamma, \eta }$, satisfies the following equation (cf. [Reference HartshorneHar77, Chap. IV, Corollary 2.4]):
 \[ 2g-2= |\Gamma| (2\bar{g}-2) +\sum_{i=1}^s \frac{|\Gamma|}{|\Gamma_i|}( |\Gamma_i| -1) . \]
\[ 2g-2= |\Gamma| (2\bar{g}-2) +\sum_{i=1}^s \frac{|\Gamma|}{|\Gamma_i|}( |\Gamma_i| -1) . \]
If ![]() $\dim \overline {\mathscr {H}{M}}_{g, \Gamma, \eta }=0$, then we must have
$\dim \overline {\mathscr {H}{M}}_{g, \Gamma, \eta }=0$, then we must have ![]() $\bar {g}=0$ and
$\bar {g}=0$ and ![]() $s=3$.
$s=3$.
Lemma 8.10 If ![]() $\dim \overline {\mathscr {H}{M}}_{g, \Gamma, \eta }>0$, then any stable
$\dim \overline {\mathscr {H}{M}}_{g, \Gamma, \eta }>0$, then any stable ![]() $s$-pointed curve
$s$-pointed curve ![]() $(\bar {\Sigma },\vec {p})$ of genus
$(\bar {\Sigma },\vec {p})$ of genus ![]() $\bar {g}$ and consisting of only one node, admits a stable
$\bar {g}$ and consisting of only one node, admits a stable ![]() $s$-pointed
$s$-pointed ![]() $\Gamma$-cover
$\Gamma$-cover ![]() $(\Sigma, \vec {q})\in \overline {\mathscr {H}{M}}_{g, \Gamma, \eta }$.
$(\Sigma, \vec {q})\in \overline {\mathscr {H}{M}}_{g, \Gamma, \eta }$.
Proof. By assumption, ![]() $3\bar {g}-3 +s>0$. It follows that either
$3\bar {g}-3 +s>0$. It follows that either ![]() $\bar {g}\geq 1$ or
$\bar {g}\geq 1$ or ![]() $s\geq 4$. Hence, we can always find a stable
$s\geq 4$. Hence, we can always find a stable ![]() $s$-pointed curve
$s$-pointed curve ![]() $\bar {C}$ of genus
$\bar {C}$ of genus ![]() $\bar {g}$ over
$\bar {g}$ over ![]() $\mathbb {C}[[\tau ]]$ such that the special fiber
$\mathbb {C}[[\tau ]]$ such that the special fiber ![]() $\bar {C}_o$ has only one node, and the generic fiber
$\bar {C}_o$ has only one node, and the generic fiber ![]() $\bar {C}_{\mathcal {K}}$ is smooth, where
$\bar {C}_{\mathcal {K}}$ is smooth, where ![]() $\mathcal {K}=\mathbb {C}((\tau ))$. Let
$\mathcal {K}=\mathbb {C}((\tau ))$. Let ![]() $\overline {\mathscr {M}}_{\bar {g},s }$ be the moduli stack of stable
$\overline {\mathscr {M}}_{\bar {g},s }$ be the moduli stack of stable ![]() $s$-pointed curves of genus
$s$-pointed curves of genus ![]() $\bar {g}$. By [Reference Bertin and RomagnyBR11, Proposition 6.5.2(iii)], the morphism
$\bar {g}$. By [Reference Bertin and RomagnyBR11, Proposition 6.5.2(iii)], the morphism ![]() $\overline {\mathscr {H}{M}}_{g, \Gamma, \eta }\to \overline {\mathscr {M}}_{\bar {g},s }$ given by
$\overline {\mathscr {H}{M}}_{g, \Gamma, \eta }\to \overline {\mathscr {M}}_{\bar {g},s }$ given by ![]() $(\Sigma, \vec {q})\mapsto (\bar {\Sigma }, {\vec {\bar {q}}})$, where
$(\Sigma, \vec {q})\mapsto (\bar {\Sigma }, {\vec {\bar {q}}})$, where ![]() $\bar {\Sigma }=\Sigma /\Gamma$ and
$\bar {\Sigma }=\Sigma /\Gamma$ and ![]() ${\vec {\bar {q}}}$ is the image of
${\vec {\bar {q}}}$ is the image of ![]() $\vec {q}$ in
$\vec {q}$ in ![]() $\bar {\Sigma }$, is surjective. It follows that after a finite base change of
$\bar {\Sigma }$, is surjective. It follows that after a finite base change of ![]() $\mathcal {K}$,
$\mathcal {K}$, ![]() $\bar {C}_{\mathcal {K}}$ has a Galois cover
$\bar {C}_{\mathcal {K}}$ has a Galois cover ![]() ${C}_{\mathcal {K}}$ with Galois group
${C}_{\mathcal {K}}$ with Galois group ![]() $\Gamma$ and the prescribed marking data. By semi-stable reduction theorem (cf. [Reference Bertin and RomagnyBR11, Proposition 5.2.2]), after another finite base change of
$\Gamma$ and the prescribed marking data. By semi-stable reduction theorem (cf. [Reference Bertin and RomagnyBR11, Proposition 5.2.2]), after another finite base change of ![]() $\mathcal {K}$,
$\mathcal {K}$, ![]() ${C}_{\mathcal {K}}$ can be uniquely extended to a stable
${C}_{\mathcal {K}}$ can be uniquely extended to a stable ![]() $s$-pointed
$s$-pointed ![]() $\Gamma$-curve
$\Gamma$-curve ![]() ${C}$ over
${C}$ over ![]() $\mathbb {C}[[\tau ]]$ (cf. [Reference Bertin and RomagnyBR11, Proposition 5.1.2]). Hence, the special fiber
$\mathbb {C}[[\tau ]]$ (cf. [Reference Bertin and RomagnyBR11, Proposition 5.1.2]). Hence, the special fiber ![]() ${C}_o$ is a stable
${C}_o$ is a stable ![]() $s$-pointed
$s$-pointed ![]() $\Gamma$-curve, whose quotient
$\Gamma$-curve, whose quotient ![]() ${C}_o/\Gamma$ is exactly the given stable
${C}_o/\Gamma$ is exactly the given stable ![]() $s$-pointed curve
$s$-pointed curve ![]() $\bar {C}_o$. This concludes the proof of the lemma.
$\bar {C}_o$. This concludes the proof of the lemma.
Remark 8.11 (1) In the case ![]() $\Gamma$ is cyclic,
$\Gamma$ is cyclic, ![]() $\overline {\mathscr {H}{M}}_{g, \Gamma, \eta }$ is irreducible (which can be deduced from the irreducibility of
$\overline {\mathscr {H}{M}}_{g, \Gamma, \eta }$ is irreducible (which can be deduced from the irreducibility of ![]() $\overline {\mathscr {H}M}_{g, \Gamma,[\xi ], [\eta ]}$ proved in [Reference Bertin and RomagnyBR11, Corollary 6.4.3]). Then, by Lemma 8.10, Theorem 8.9 and the factorization theorem (Theorem 5.4), one can see that to compute the dimension of the space of conformal blocks on smooth stable
$\overline {\mathscr {H}M}_{g, \Gamma,[\xi ], [\eta ]}$ proved in [Reference Bertin and RomagnyBR11, Corollary 6.4.3]). Then, by Lemma 8.10, Theorem 8.9 and the factorization theorem (Theorem 5.4), one can see that to compute the dimension of the space of conformal blocks on smooth stable ![]() $s$-pointed
$s$-pointed ![]() $\Gamma$-curve, we are reduced to considering the case: cyclic covers over
$\Gamma$-curve, we are reduced to considering the case: cyclic covers over ![]() $\mathbb {P}^1$ with
$\mathbb {P}^1$ with ![]() $s=3$.
$s=3$.
(2) For any ![]() $s$-pointed smooth
$s$-pointed smooth ![]() $\Gamma$-curve
$\Gamma$-curve ![]() $(\Sigma, \vec {q})$ and weights
$(\Sigma, \vec {q})$ and weights ![]() $\vec {\lambda }=(\lambda _1, \ldots, \lambda _s)$ with
$\vec {\lambda }=(\lambda _1, \ldots, \lambda _s)$ with ![]() $\lambda _i\in D_{c, q_i}$, as in Definition 3.5, we can attach the space of conformal blocks. Here we do not need to assume that
$\lambda _i\in D_{c, q_i}$, as in Definition 3.5, we can attach the space of conformal blocks. Here we do not need to assume that ![]() $\bigcup _{i}\Gamma \cdot q_i$ contains all the ramified points of
$\bigcup _{i}\Gamma \cdot q_i$ contains all the ramified points of ![]() $\Sigma \to \bar {\Sigma }$. Thanks to the propagation theorem (Corollary 4.5(a)), the dimension of the space of conformal blocks in this case can be reduced to the case that all the ramified points are contained in
$\Sigma \to \bar {\Sigma }$. Thanks to the propagation theorem (Corollary 4.5(a)), the dimension of the space of conformal blocks in this case can be reduced to the case that all the ramified points are contained in ![]() $\bigcup _{i}\Gamma \cdot q_i$ when
$\bigcup _{i}\Gamma \cdot q_i$ when ![]() $0\in D_{c, q}$ for any ramified point
$0\in D_{c, q}$ for any ramified point ![]() $q$ in
$q$ in ![]() $\Sigma$.
$\Sigma$.
(3) The morphism ![]() $f: \overline {\mathscr {H}{M}}_{g, \Gamma, \eta } \to \overline {\mathscr {M}}_{g, s'}$ given by mapping the stable
$f: \overline {\mathscr {H}{M}}_{g, \Gamma, \eta } \to \overline {\mathscr {M}}_{g, s'}$ given by mapping the stable ![]() $s$-pointed
$s$-pointed ![]() $\Gamma$-curve
$\Gamma$-curve ![]() $(\Sigma, \vec {q})$ to the stable
$(\Sigma, \vec {q})$ to the stable ![]() $s'$-pointed curve
$s'$-pointed curve ![]() $(\Sigma, \bigcup _{i, \gamma \in \Gamma } \gamma \cdot q_i )$ (cf. Remark 8.2) (where
$(\Sigma, \bigcup _{i, \gamma \in \Gamma } \gamma \cdot q_i )$ (cf. Remark 8.2) (where ![]() $s'=\sum _{i=1}^s {|\Gamma |}/{|\Gamma _i|}$) is representable and finite (cf. [Reference Bertin and RomagnyBR11, Proposition 6.5.2] for the corresponding result for
$s'=\sum _{i=1}^s {|\Gamma |}/{|\Gamma _i|}$) is representable and finite (cf. [Reference Bertin and RomagnyBR11, Proposition 6.5.2] for the corresponding result for ![]() $\overline {\mathscr {H}M}_{g, \Gamma,[\xi ], [\eta ]}$; now composing this with the representable and finite morphism
$\overline {\mathscr {H}M}_{g, \Gamma,[\xi ], [\eta ]}$; now composing this with the representable and finite morphism ![]() $\overline {\mathscr {H}M}_{g, \Gamma, \eta } \to \overline {\mathscr {H}M}_{g, \Gamma,[\xi ], [\eta ]}$, the assertion about
$\overline {\mathscr {H}M}_{g, \Gamma, \eta } \to \overline {\mathscr {H}M}_{g, \Gamma,[\xi ], [\eta ]}$, the assertion about ![]() $f$ follows). By taking the pushforward, the locally free sheaf of conformal blocks on
$f$ follows). By taking the pushforward, the locally free sheaf of conformal blocks on ![]() $\overline {\mathscr {H}{M}}_{g, \Gamma, \eta }$ gives rise to many characteristic classes in the cohomology of
$\overline {\mathscr {H}{M}}_{g, \Gamma, \eta }$ gives rise to many characteristic classes in the cohomology of ![]() $\overline {\mathscr {M}}_{g, s'}$. It could give rise to interesting applications.
$\overline {\mathscr {M}}_{g, s'}$. It could give rise to interesting applications.
9. Connectedness of  $\operatorname {\mathrm {Mor}}_\Gamma (\Sigma ^{*},G)$
$\operatorname {\mathrm {Mor}}_\Gamma (\Sigma ^{*},G)$
In this section as well as in §§ 10–12, we consider a group homomorphism ![]() $\phi : \Gamma \to {\rm Aut\ }(\mathfrak {g})$ such that
$\phi : \Gamma \to {\rm Aut\ }(\mathfrak {g})$ such that ![]() $\Gamma$ stabilizes a Borel subalgebra
$\Gamma$ stabilizes a Borel subalgebra ![]() $\mathfrak {b}$ of
$\mathfrak {b}$ of ![]() $\mathfrak {g}$. Moreover,
$\mathfrak {g}$. Moreover, ![]() $\Sigma$ denotes a smooth irreducible projective curve with a faithful action of
$\Sigma$ denotes a smooth irreducible projective curve with a faithful action of ![]() $\Gamma$ with the projection
$\Gamma$ with the projection ![]() $\pi :\Sigma \to \bar \Sigma :=\Sigma /\Gamma$ and
$\pi :\Sigma \to \bar \Sigma :=\Sigma /\Gamma$ and ![]() $G$ the simply connected simple algebraic group over
$G$ the simply connected simple algebraic group over ![]() $\mathbb {C}$ with Lie algebra
$\mathbb {C}$ with Lie algebra ![]() $\mathfrak {g}$. Let
$\mathfrak {g}$. Let ![]() $B$ be the Borel subgroup of
$B$ be the Borel subgroup of ![]() $G$ with Lie algebra
$G$ with Lie algebra ![]() $\mathfrak {b}$. Observe that in earlier sections, we did not require
$\mathfrak {b}$. Observe that in earlier sections, we did not require ![]() $\Sigma$ to be smooth unless explicitly stated.
$\Sigma$ to be smooth unless explicitly stated.
We prove the connectedness of the ind-group ![]() ${\rm Mor}_{\Gamma }(\Sigma ^*, G)$. In particular, we show that the twisted Grassmannian
${\rm Mor}_{\Gamma }(\Sigma ^*, G)$. In particular, we show that the twisted Grassmannian ![]() $X^q= G(\mathbb {D}^*_q )^{\Gamma _q}/ G(\mathbb {D}_q )^{\Gamma _q}$ is irreducible.
$X^q= G(\mathbb {D}^*_q )^{\Gamma _q}/ G(\mathbb {D}_q )^{\Gamma _q}$ is irreducible.
Let ![]() $\operatorname {\mathscr {A}lg}$ be the category of commutative algebras with identity over
$\operatorname {\mathscr {A}lg}$ be the category of commutative algebras with identity over ![]() $\mathbb {C}$ (which are not necessarily finitely generated) and all
$\mathbb {C}$ (which are not necessarily finitely generated) and all ![]() $\mathbb {C}$-algebra homomorphisms between them.
$\mathbb {C}$-algebra homomorphisms between them.
Definition 9.1 A ![]() $\mathbb {C}$-space functor (respectively,
$\mathbb {C}$-space functor (respectively, ![]() $\mathbb {C}$-group functor) is a covariant functor
$\mathbb {C}$-group functor) is a covariant functor
which is a sheaf for the ![]() $\operatorname {\mathrm {fppf}}$ (faithfully flat of finite presentation—Fidèlement Plat de Présentation Finie) topology, i.e. for any
$\operatorname {\mathrm {fppf}}$ (faithfully flat of finite presentation—Fidèlement Plat de Présentation Finie) topology, i.e. for any ![]() $R\in \operatorname {\mathscr {A}lg}$ and any faithfully flat finitely presented
$R\in \operatorname {\mathscr {A}lg}$ and any faithfully flat finitely presented ![]() $R$-algebra
$R$-algebra ![]() $R'$, the diagram
$R'$, the diagram
in exact, where ![]() $\operatorname {\mathscr {S}et}$ (respectively,
$\operatorname {\mathscr {S}et}$ (respectively, ![]() $\mathscr {G}$roup) is the category of sets (respectively, groups). In particular,
$\mathscr {G}$roup) is the category of sets (respectively, groups). In particular, ![]() $\mathscr {F}(R)\to \mathscr {F}(R')$ is one-to-one.
$\mathscr {F}(R)\to \mathscr {F}(R')$ is one-to-one.
From now on we shall abbreviate faithfully flat finitely presented ![]() $R$-algebra by
$R$-algebra by ![]() $\operatorname {\mathrm {fppf}}$
$\operatorname {\mathrm {fppf}}$ ![]() $R$-algebra.
$R$-algebra.
By a ![]() $\mathbb {C}$-functor morphism
$\mathbb {C}$-functor morphism ![]() $\varphi : \mathscr {F}\to \mathscr {F}'$ between two
$\varphi : \mathscr {F}\to \mathscr {F}'$ between two ![]() $\mathbb {C}$-space functors, we mean a set map
$\mathbb {C}$-space functors, we mean a set map ![]() $\varphi _R: \mathscr {F}(R)\to \mathscr {F}' (R)$ for any
$\varphi _R: \mathscr {F}(R)\to \mathscr {F}' (R)$ for any ![]() $R\in \operatorname {\mathscr {A}lg}$ such that the following diagram is commutative for any algebra homomorphism
$R\in \operatorname {\mathscr {A}lg}$ such that the following diagram is commutative for any algebra homomorphism ![]() $R \to S$.
$R \to S$.

Direct limits exist in the category of ![]() $\mathbb {C}$-space (
$\mathbb {C}$-space (![]() $\mathbb {C}$-group) functors. For any ind-scheme
$\mathbb {C}$-group) functors. For any ind-scheme ![]() $X=(X_{n})_{n\geq 0}$ over
$X=(X_{n})_{n\geq 0}$ over ![]() $\mathbb {C}$, the functor
$\mathbb {C}$, the functor ![]() $\mathfrak {S}_{X}$ is a
$\mathfrak {S}_{X}$ is a ![]() $\mathbb {C}$-space functor by virtue of the faithfully flat descent (cf. [Reference GrothendieckGro71, VIII 5.1, 1.1 and 1.2]), where
$\mathbb {C}$-space functor by virtue of the faithfully flat descent (cf. [Reference GrothendieckGro71, VIII 5.1, 1.1 and 1.2]), where ![]() $\mathfrak {S}_{X} (R)$ is the set of all the morphisms
$\mathfrak {S}_{X} (R)$ is the set of all the morphisms ![]() $\operatorname {\mathrm {Mor}}(\operatorname {\mathrm {Spec}} R, X)$. This allows us to realize the category of ind-schemes over
$\operatorname {\mathrm {Mor}}(\operatorname {\mathrm {Spec}} R, X)$. This allows us to realize the category of ind-schemes over ![]() $\mathbb {C}$ as a full subcategory of the category of
$\mathbb {C}$ as a full subcategory of the category of ![]() $\mathbb {C}$-space functors.
$\mathbb {C}$-space functors.
We recall the following well-known lemma (cf. [Reference KumarKum22, Lemma B.2]).
Lemma 9.2 Let ![]() $\mathscr {F}^{o}:\operatorname {\mathscr {A}lg}\to \operatorname {\mathscr {S}et}$ be a covariant functor. Assume that
$\mathscr {F}^{o}:\operatorname {\mathscr {A}lg}\to \operatorname {\mathscr {S}et}$ be a covariant functor. Assume that
for any ![]() $R\in \operatorname {\mathscr {A}lg}$ and any
$R\in \operatorname {\mathscr {A}lg}$ and any ![]() $\operatorname {\mathrm {fppf}}$
$\operatorname {\mathrm {fppf}}$ ![]() $R$-algebra
$R$-algebra ![]() $R'$.
$R'$.
Then, there exists a ![]() $\mathbb {C}$-space functor
$\mathbb {C}$-space functor ![]() $\mathscr {F}$ containing
$\mathscr {F}$ containing ![]() $\mathscr {F}^{o}$ (i.e.
$\mathscr {F}^{o}$ (i.e. ![]() $\mathscr {F}^{o}(R)\subset \mathscr {F}(R)$ for any
$\mathscr {F}^{o}(R)\subset \mathscr {F}(R)$ for any ![]() $R$) such that for any
$R$) such that for any ![]() $\mathbb {C}$-space functor
$\mathbb {C}$-space functor ![]() $\mathscr {G}$ and a natural transformation
$\mathscr {G}$ and a natural transformation ![]() $\theta ^{o}:\mathscr {F}^{o}\to \mathscr {G}$, there exists a unique natural transformation
$\theta ^{o}:\mathscr {F}^{o}\to \mathscr {G}$, there exists a unique natural transformation ![]() $\theta :\mathscr {F}\to \mathscr {G}$ extending
$\theta :\mathscr {F}\to \mathscr {G}$ extending ![]() $\theta ^{o}$.
$\theta ^{o}$.
Moreover, such a ![]() $\mathscr {F}$ is unique up to a unique isomorphism extending the identity map of
$\mathscr {F}$ is unique up to a unique isomorphism extending the identity map of ![]() $\mathscr {F}^{o}$.
$\mathscr {F}^{o}$.
We call such a ![]() $\mathscr {F}$ the
$\mathscr {F}$ the ![]() $\operatorname {\mathrm {fppf}}$-sheafification of
$\operatorname {\mathrm {fppf}}$-sheafification of ![]() $\mathscr {F}^{o}$.
$\mathscr {F}^{o}$.
If ![]() $\mathscr {F}^{o}$ is a
$\mathscr {F}^{o}$ is a ![]() $\mathbb {C}$-group functor, then its
$\mathbb {C}$-group functor, then its ![]() $\operatorname {\mathrm {fppf}}$-sheafification
$\operatorname {\mathrm {fppf}}$-sheafification ![]() $\mathscr {F}$ is a
$\mathscr {F}$ is a ![]() $\mathbb {C}$-group functor.
$\mathbb {C}$-group functor.
We recall the following result communicated by Faltings. A detailed proof (due to B. Conrad) can be found in [Reference KumarKum22, Theorem 1.3.22].
Theorem 9.3 Let ![]() $\mathscr {G}=(\mathscr {G}_{n})_{n\geq 0}$ be an ind-affine group scheme filtered by (affine) finite type schemes over
$\mathscr {G}=(\mathscr {G}_{n})_{n\geq 0}$ be an ind-affine group scheme filtered by (affine) finite type schemes over ![]() $\mathbb {C}$ and let
$\mathbb {C}$ and let ![]() $\mathscr {G}^{\operatorname {\mathrm {red}}}=(\mathscr {G}^{\operatorname {\mathrm {red}}}_{n})_{n\geq 0}$ be the associated reduced ind-affine group scheme. Assume that the canonical ind-group morphism
$\mathscr {G}^{\operatorname {\mathrm {red}}}=(\mathscr {G}^{\operatorname {\mathrm {red}}}_{n})_{n\geq 0}$ be the associated reduced ind-affine group scheme. Assume that the canonical ind-group morphism ![]() $i:\mathscr {G}^{\operatorname {\mathrm {red}}}\to \mathscr {G}$ induces an isomorphism
$i:\mathscr {G}^{\operatorname {\mathrm {red}}}\to \mathscr {G}$ induces an isomorphism ![]() $(di)_{e}:\operatorname {\mathrm {Lie}} (\mathscr {G}^{\operatorname {\mathrm {red}}})\xrightarrow {\sim }\operatorname {\mathrm {Lie}} \mathscr {G}$ of the associated Lie algebras (cf. [Reference KumarKum22, Corollary B.21]). Then,
$(di)_{e}:\operatorname {\mathrm {Lie}} (\mathscr {G}^{\operatorname {\mathrm {red}}})\xrightarrow {\sim }\operatorname {\mathrm {Lie}} \mathscr {G}$ of the associated Lie algebras (cf. [Reference KumarKum22, Corollary B.21]). Then, ![]() $i$ is an isomorphism of ind-groups, i.e.
$i$ is an isomorphism of ind-groups, i.e. ![]() $\mathscr {G}$ is a reduced ind-scheme.
$\mathscr {G}$ is a reduced ind-scheme.
Definition 9.4 (Twisted affine Grassmannian)
Recall that for any affine scheme ![]() $Y=\operatorname {\mathrm {Spec}} S$ with the action of a group
$Y=\operatorname {\mathrm {Spec}} S$ with the action of a group ![]() $H$, the closed subset
$H$, the closed subset ![]() $Y^H$ acquires a closed subscheme structure by taking
$Y^H$ acquires a closed subscheme structure by taking
where ![]() $\langle g\cdot f-f\rangle$ denotes the ideal generated by the collection
$\langle g\cdot f-f\rangle$ denotes the ideal generated by the collection ![]() $g\cdot f-f$. With this scheme structure,
$g\cdot f-f$. With this scheme structure, ![]() $Y^H$ represents the functor
$Y^H$ represents the functor ![]() $R \rightsquigarrow \operatorname {\mathrm {Mor}}_H(\operatorname {\mathrm {Spec}} R, Y).$
$R \rightsquigarrow \operatorname {\mathrm {Mor}}_H(\operatorname {\mathrm {Spec}} R, Y).$
For any point ![]() $q\in \Sigma$, let
$q\in \Sigma$, let ![]() $\sigma _q$ be the generator of the stabilizer
$\sigma _q$ be the generator of the stabilizer ![]() $\Gamma _q$ such that
$\Gamma _q$ such that ![]() $\chi _q(\sigma _q) = \epsilon _q$, where
$\chi _q(\sigma _q) = \epsilon _q$, where ![]() $\epsilon _q:=e^{ {2\pi i}/{|\Gamma _q|}}$ (cf. Definition 3.1). Choose a formal parameter
$\epsilon _q:=e^{ {2\pi i}/{|\Gamma _q|}}$ (cf. Definition 3.1). Choose a formal parameter ![]() $z_q$ at
$z_q$ at ![]() $q$ in
$q$ in ![]() $\Sigma$ such that
$\Sigma$ such that
Consider the functor
Its fppf-sheafification is denoted by the functor ![]() $\mathscr {X}^q=\mathscr {X}(G,q, \Gamma )$.
$\mathscr {X}^q=\mathscr {X}(G,q, \Gamma )$.
Recall that there exists an open subset ![]() $\mathbb {V}\subset G((z_q))$ (where
$\mathbb {V}\subset G((z_q))$ (where ![]() $G((z_q)) :=G\big (\mathbb {C}((z_q))\big )$) such that the product map
$G((z_q)) :=G\big (\mathbb {C}((z_q))\big )$) such that the product map
where ![]() $G\big (R[z_q^{-1}]\big )^-$ is the kernel of
$G\big (R[z_q^{-1}]\big )^-$ is the kernel of ![]() $G\big (R[z_q^{-1}]\big )\to G(R), z_q^{-1}\mapsto 0$ (cf. [Reference FaltingsFal03, Corollary 3] or [Reference KumarKum22, Lemma 1.3.16]). Moreover, the functor
$G\big (R[z_q^{-1}]\big )\to G(R), z_q^{-1}\mapsto 0$ (cf. [Reference FaltingsFal03, Corollary 3] or [Reference KumarKum22, Lemma 1.3.16]). Moreover, the functor ![]() $G\big (R[z_q^{-1}]\big )^-$ is represented by an ind-group variety (in particular, reduced) structure on
$G\big (R[z_q^{-1}]\big )^-$ is represented by an ind-group variety (in particular, reduced) structure on ![]() $G[z_q^{-1}]^-$ (cf. [Reference FaltingsFal03, Corollary 3] and [Reference KumarKum22, Corollary 1.3.3 and Theorem 1.3.23]). This gives rise to a bijection
$G[z_q^{-1}]^-$ (cf. [Reference FaltingsFal03, Corollary 3] and [Reference KumarKum22, Corollary 1.3.3 and Theorem 1.3.23]). This gives rise to a bijection
Declare ![]() $\{g\mathbb {V}^{\Gamma _q}/G[[z_q]]^{\Gamma _q}\}_{g\in G((z_q))^{\Gamma _q}}$ as an open cover of
$\{g\mathbb {V}^{\Gamma _q}/G[[z_q]]^{\Gamma _q}\}_{g\in G((z_q))^{\Gamma _q}}$ as an open cover of
and put the ind-scheme structure on ![]() $g\mathbb {V}^{\Gamma _q}/G[[z_q]]^{\Gamma _q}$ via its bijection
$g\mathbb {V}^{\Gamma _q}/G[[z_q]]^{\Gamma _q}$ via its bijection
with the closed ind-subgroup scheme structure on ![]() $\big (G[z_q^{-1}]^-\big )^{\Gamma _q}$ coming from
$\big (G[z_q^{-1}]^-\big )^{\Gamma _q}$ coming from ![]() $G[z_q^{-1}]^-$. In particular,
$G[z_q^{-1}]^-$. In particular, ![]() $\big (G[z_q^{-1}]^-\big )^{\Gamma _q}$ represents the functor
$\big (G[z_q^{-1}]^-\big )^{\Gamma _q}$ represents the functor ![]() $\big (G(R[z_q^{-1}])^-\big )^{\Gamma _q}$. Thus, we get an ind-scheme structure on
$\big (G(R[z_q^{-1}])^-\big )^{\Gamma _q}$. Thus, we get an ind-scheme structure on ![]() $X^q$ such that the projection
$X^q$ such that the projection ![]() $G((z_q))^{\Gamma _q}\to X^q$ admits local sections in the Zariski topology. Moreover, the injection
$G((z_q))^{\Gamma _q}\to X^q$ admits local sections in the Zariski topology. Moreover, the injection ![]() $X^q\hookrightarrow G((z_q))/G[[z_q]]$ is a closed embedding. Further,
$X^q\hookrightarrow G((z_q))/G[[z_q]]$ is a closed embedding. Further, ![]() $X^q$ represents the functor
$X^q$ represents the functor ![]() $\mathscr {X}^q$ since the ind-projective variety
$\mathscr {X}^q$ since the ind-projective variety ![]() $G((z_q))/G[[z_q]]$ represents the fppf-sheafification of the functor
$G((z_q))/G[[z_q]]$ represents the fppf-sheafification of the functor ![]() $G\big (R((z_q))\big )/G\big (R[[z_q]]\big )$. In particular,
$G\big (R((z_q))\big )/G\big (R[[z_q]]\big )$. In particular,
Let ![]() $U$ (respectively,
$U$ (respectively, ![]() $U^-$) be the unipotent radical of
$U^-$) be the unipotent radical of ![]() $B$ (respectively, of the opposite Borel subgroup
$B$ (respectively, of the opposite Borel subgroup ![]() $B^-$). By considering the ind-subgroup schemes
$B^-$). By considering the ind-subgroup schemes ![]() $\big (U[z_q^{-1}]^-\big )^{\Gamma _q}$ and
$\big (U[z_q^{-1}]^-\big )^{\Gamma _q}$ and ![]() $\big (U^-[z_q^{-1}]^-\big )^{\Gamma _q}$ of
$\big (U^-[z_q^{-1}]^-\big )^{\Gamma _q}$ of ![]() $\big (G[z_q^{-1}]^-\big )^{\Gamma _q}$, it is easy to see that the Lie algebras
$\big (G[z_q^{-1}]^-\big )^{\Gamma _q}$, it is easy to see that the Lie algebras
since the Lie subalgebras ![]() $\big (\mathfrak {u}\otimes \mathbb {C}[z_q^{-1}]^-\big )^{\Gamma _q}$ and
$\big (\mathfrak {u}\otimes \mathbb {C}[z_q^{-1}]^-\big )^{\Gamma _q}$ and ![]() $\big (\mathfrak {u}^-\otimes \mathbb {C}[z_q^{-1}]^-\big )^{\Gamma _q}$ generate the Lie algebra
$\big (\mathfrak {u}^-\otimes \mathbb {C}[z_q^{-1}]^-\big )^{\Gamma _q}$ generate the Lie algebra ![]() $\big (\mathfrak {g}\otimes \mathbb {C}[z_q^{-1}]^-\big )^{\Gamma _q}$ (cf. § 2), where
$\big (\mathfrak {g}\otimes \mathbb {C}[z_q^{-1}]^-\big )^{\Gamma _q}$ (cf. § 2), where ![]() $Y_{\operatorname {\mathrm {red}}}$ denotes the corresponding reduced ind-subscheme. Thus,
$Y_{\operatorname {\mathrm {red}}}$ denotes the corresponding reduced ind-subscheme. Thus, ![]() $\big (G[z_q^{-1}]^-\big )^{\Gamma _q}$ is a (reduced) ind-group variety (cf. Theorem 9.3). Hence,
$\big (G[z_q^{-1}]^-\big )^{\Gamma _q}$ is a (reduced) ind-group variety (cf. Theorem 9.3). Hence, ![]() $X^q$ also is a (reduced) ind-projective variety.
$X^q$ also is a (reduced) ind-projective variety.
Observe that ![]() $X^q$ being reduced, it is the (twisted) affine Grassmannian considered in [Reference KumarKum02, § 7.1] based at
$X^q$ being reduced, it is the (twisted) affine Grassmannian considered in [Reference KumarKum02, § 7.1] based at ![]() $q$ corresponding to the twisted affine Lie algebra
$q$ corresponding to the twisted affine Lie algebra ![]() $\hat {\mathfrak {g}}_{\pi (q)}\simeq \hat {L}(\mathfrak {g}, \Gamma _q)$ (cf. § 2 and Lemma 3.3) and its parabolic subalgebra
$\hat {\mathfrak {g}}_{\pi (q)}\simeq \hat {L}(\mathfrak {g}, \Gamma _q)$ (cf. § 2 and Lemma 3.3) and its parabolic subalgebra ![]() $\hat {L}(\mathfrak {g}, \Gamma _q)^{\geq 0}$. To prove this, follow the same argument as in [Reference Laszlo and SorgerLS97, Proof of Proposition 4.7] and the construction of the projective representation of
$\hat {L}(\mathfrak {g}, \Gamma _q)^{\geq 0}$. To prove this, follow the same argument as in [Reference Laszlo and SorgerLS97, Proof of Proposition 4.7] and the construction of the projective representation of ![]() $G((z_q))^{\Gamma _q}$ given by (subsequent) Theorem 10.3.
$G((z_q))^{\Gamma _q}$ given by (subsequent) Theorem 10.3.
Let ![]() $\bar {q} =\{q_{1},\ldots,q_{s}\}$ be a set of points of
$\bar {q} =\{q_{1},\ldots,q_{s}\}$ be a set of points of ![]() $\Sigma$ (for
$\Sigma$ (for ![]() $s\geq 1$) with distinct
$s\geq 1$) with distinct ![]() $\Gamma$-orbits and let
$\Gamma$-orbits and let ![]() $\Sigma ^{*}:=\Sigma \backslash \Gamma \cdot \bar {q}$. Recall that
$\Sigma ^{*}:=\Sigma \backslash \Gamma \cdot \bar {q}$. Recall that ![]() $\Xi =\Xi _{\bar {q}}:=\operatorname {\mathrm {Mor}}_\Gamma (\Sigma ^{*},G)$ is an ind-affine group scheme, which is a closed ind-subgroup scheme of
$\Xi =\Xi _{\bar {q}}:=\operatorname {\mathrm {Mor}}_\Gamma (\Sigma ^{*},G)$ is an ind-affine group scheme, which is a closed ind-subgroup scheme of ![]() $\operatorname {\mathrm {Mor}}(\Sigma ^{*},G)$ as
$\operatorname {\mathrm {Mor}}(\Sigma ^{*},G)$ as ![]() $\Gamma$-fixed points. We abbreviate
$\Gamma$-fixed points. We abbreviate ![]() $\operatorname {\mathrm {Mor}}_\Gamma (\Sigma ^{*},G)= G(\mathbb {C}[\Sigma ^*])^\Gamma$ by
$\operatorname {\mathrm {Mor}}_\Gamma (\Sigma ^{*},G)= G(\mathbb {C}[\Sigma ^*])^\Gamma$ by ![]() $G(\Sigma ^*)^\Gamma$. Then,
$G(\Sigma ^*)^\Gamma$. Then, ![]() $\Xi$ represents the functor:
$\Xi$ represents the functor:
where ![]() $\Sigma ^{*}_{R}:=\Sigma ^{*}\times \operatorname {\mathrm {Spec}} R$, with the trivial action of
$\Sigma ^{*}_{R}:=\Sigma ^{*}\times \operatorname {\mathrm {Spec}} R$, with the trivial action of ![]() $\Gamma$ on
$\Gamma$ on ![]() $R$. This follows from the corresponding result for the functor
$R$. This follows from the corresponding result for the functor ![]() $R \rightsquigarrow \operatorname {\mathrm {Mor}}(\Sigma ^{*}_{R},G)$ (without the
$R \rightsquigarrow \operatorname {\mathrm {Mor}}(\Sigma ^{*}_{R},G)$ (without the ![]() $\Gamma$-action) which is represented by
$\Gamma$-action) which is represented by ![]() $G(\Sigma ^{*})$ (cf. [Reference KumarKum22, Lemma 5.2.10]).
$G(\Sigma ^{*})$ (cf. [Reference KumarKum22, Lemma 5.2.10]).
Let ![]() $\Xi ^{\text {an}}$ denote the group
$\Xi ^{\text {an}}$ denote the group ![]() $\Xi$ with the analytic topology. The following result in the non-equivariant case (i.e.
$\Xi$ with the analytic topology. The following result in the non-equivariant case (i.e. ![]() $\Gamma =(1)$) is due to Drinfeld. We adapt his arguments (cf. [Reference KumarKum22, Proof of Theorem 8.1.1]).
$\Gamma =(1)$) is due to Drinfeld. We adapt his arguments (cf. [Reference KumarKum22, Proof of Theorem 8.1.1]).
Theorem 9.5 The group ![]() $\Xi ^{\text {an}}$ is path-connected and, hence,
$\Xi ^{\text {an}}$ is path-connected and, hence, ![]() $\Xi$ is irreducible.
$\Xi$ is irreducible.
Proof. Take any points ![]() $q_{1}',\ldots, q'_n, q'_{n+1}\in \Sigma \setminus \Gamma \cdot \bar {q}$ with distinct
$q_{1}',\ldots, q'_n, q'_{n+1}\in \Sigma \setminus \Gamma \cdot \bar {q}$ with distinct ![]() $\Gamma$-orbits and set (for any
$\Gamma$-orbits and set (for any ![]() $0\leq i\leq n+1$)
$0\leq i\leq n+1$)
Consider the functor
It is easy to see that
Let ![]() $\widehat {\Xi _{n+1}/\Xi _{n}}$ be the fppf-sheafification of
$\widehat {\Xi _{n+1}/\Xi _{n}}$ be the fppf-sheafification of ![]() $\mathscr {F}^{\circ }$ (cf. Lemma 9.2).
$\mathscr {F}^{\circ }$ (cf. Lemma 9.2).
We claim that as the ![]() $\mathbb {C}$-space functors
$\mathbb {C}$-space functors
where ![]() $q=q'_{n+1}$. Define the morphism
$q=q'_{n+1}$. Define the morphism
where ![]() $\gamma _q$ is the power series expansion of
$\gamma _q$ is the power series expansion of ![]() $\gamma$ at
$\gamma$ at ![]() $q$ in the parameter
$q$ in the parameter ![]() $z_q$. The above morphism clearly factors through
$z_q$. The above morphism clearly factors through
and, hence, we get a morphism of ![]() $\mathbb {C}$-space functors
$\mathbb {C}$-space functors
Conversely, we define a map ![]() $\hat {\psi }:\mathscr {X}^q\to \widehat {\Xi _{n+1}/\Xi _{n}}$ as follows. Fix
$\hat {\psi }:\mathscr {X}^q\to \widehat {\Xi _{n+1}/\Xi _{n}}$ as follows. Fix ![]() $R\in \operatorname {\mathscr {A}lg}$. Take
$R\in \operatorname {\mathscr {A}lg}$. Take ![]() $\gamma _R\in G\big (R((z_q))\big )^{\Gamma _q}$. Let
$\gamma _R\in G\big (R((z_q))\big )^{\Gamma _q}$. Let ![]() $\mathscr {G}=\mathscr {G}(\Sigma, \Gamma, \phi )$ be the parahoric Bruhat–Tits group scheme (cf. Definition 11.1). Then, by [Reference HeinlothHei10, Proposition 4],
$\mathscr {G}=\mathscr {G}(\Sigma, \Gamma, \phi )$ be the parahoric Bruhat–Tits group scheme (cf. Definition 11.1). Then, by [Reference HeinlothHei10, Proposition 4], ![]() $\gamma _R$ corresponds to a
$\gamma _R$ corresponds to a ![]() $\mathscr {G}$-torsor over
$\mathscr {G}$-torsor over ![]() $\bar {\Sigma }\times \operatorname {\mathrm {Spec}} R$ together with a section
$\bar {\Sigma }\times \operatorname {\mathrm {Spec}} R$ together with a section ![]() $\sigma _{R}$ over
$\sigma _{R}$ over ![]() $(\bar {\Sigma }\backslash \pi (q))_{R}$ and a section
$(\bar {\Sigma }\backslash \pi (q))_{R}$ and a section ![]() $\mu _R$ over
$\mu _R$ over ![]() $(\mathbb {D}_{\pi (q)})_R$ such that
$(\mathbb {D}_{\pi (q)})_R$ such that
This is possible since ![]() $\gamma _R$ extends uniquely to an element of
$\gamma _R$ extends uniquely to an element of ![]() $\big (G(\pi ^{-1}\mathbb {D}^\times _{\pi (q)})^\Gamma \big )_R$ (cf. Definition 3.1). There exists an
$\big (G(\pi ^{-1}\mathbb {D}^\times _{\pi (q)})^\Gamma \big )_R$ (cf. Definition 3.1). There exists an ![]() $R$-algebra
$R$-algebra ![]() $R'$ with
$R'$ with ![]() $\operatorname {\mathrm {Spec}} R'\to \operatorname {\mathrm {Spec}} R$ an étale cover (in particular,
$\operatorname {\mathrm {Spec}} R'\to \operatorname {\mathrm {Spec}} R$ an étale cover (in particular, ![]() $R'$ is a fppf
$R'$ is a fppf ![]() $R$-algebra) such that the pull-back
$R$-algebra) such that the pull-back ![]() $\mathscr {G}$-torsor
$\mathscr {G}$-torsor ![]() $E_{\gamma _{R'}}$ over
$E_{\gamma _{R'}}$ over ![]() $\bar {\Sigma }_{R'}$ admits a section
$\bar {\Sigma }_{R'}$ admits a section ![]() $\theta _{R'}$ over
$\theta _{R'}$ over ![]() $(\pi (\Sigma ^*_n))_{R'}$ (cf. [Reference HeinlothHei10, Theorem 4]). (Observe that
$(\pi (\Sigma ^*_n))_{R'}$ (cf. [Reference HeinlothHei10, Theorem 4]). (Observe that ![]() $G$ being simply connected, generic
$G$ being simply connected, generic ![]() $\mathscr {G}_{\mathbb {C}(\Sigma )}$ is simply connected.) Define
$\mathscr {G}_{\mathbb {C}(\Sigma )}$ is simply connected.) Define
where ![]() $\sigma _{R'}$ is the pull-back of the section
$\sigma _{R'}$ is the pull-back of the section ![]() $\sigma _R$ to
$\sigma _R$ to ![]() $(\bar {\Sigma }\setminus \pi (q))_{R'}$ and
$(\bar {\Sigma }\setminus \pi (q))_{R'}$ and ![]() $\gamma _{R'}$ denotes the image of
$\gamma _{R'}$ denotes the image of ![]() $\gamma _R$ in
$\gamma _R$ in ![]() $G\big (R'((z_q))\big )^{\Gamma _q}$. Now, set
$G\big (R'((z_q))\big )^{\Gamma _q}$. Now, set ![]() $\hat {\psi }(\gamma _{R'})={\psi }_{\theta _{R'}}(\gamma _{R'})$ mod
$\hat {\psi }(\gamma _{R'})={\psi }_{\theta _{R'}}(\gamma _{R'})$ mod ![]() $\Xi _n(R')$. It is easy to see that
$\Xi _n(R')$. It is easy to see that ![]() $\hat {\psi }(\gamma _{R'})$ does not depend upon the choices of
$\hat {\psi }(\gamma _{R'})$ does not depend upon the choices of ![]() $\sigma _R$,
$\sigma _R$, ![]() $\mu _R$, and
$\mu _R$, and ![]() $\theta _{R'}$ satisfying (121). Moreover,
$\theta _{R'}$ satisfying (121). Moreover, ![]() $\hat {\psi }$ factors through
$\hat {\psi }$ factors through ![]() $G\big (R'[[z_q]]\big )^{\Gamma _q}$. Thus, we get a
$G\big (R'[[z_q]]\big )^{\Gamma _q}$. Thus, we get a ![]() $\mathbb {C}$-functor morphism (still denoted by)
$\mathbb {C}$-functor morphism (still denoted by) ![]() $\hat {\psi }: \mathscr {X}^{q} \to \widehat {\Xi _{n+1}/\Xi _{n}}$. Further, it is easy to see that
$\hat {\psi }: \mathscr {X}^{q} \to \widehat {\Xi _{n+1}/\Xi _{n}}$. Further, it is easy to see that ![]() $\hat {\theta }$ and
$\hat {\theta }$ and ![]() $\hat {\psi }$ are inverses of each other. This proves the assertion (120). In particular, the functor
$\hat {\psi }$ are inverses of each other. This proves the assertion (120). In particular, the functor ![]() $\widehat {\Xi _{n+1}/\Xi _{n}}$ is also representable represented by its
$\widehat {\Xi _{n+1}/\Xi _{n}}$ is also representable represented by its ![]() $\mathbb {C}$-points
$\mathbb {C}$-points ![]() $\widehat {\Xi _{n+1}/\Xi _{n}}(\mathbb {C})$. We abbreviate
$\widehat {\Xi _{n+1}/\Xi _{n}}(\mathbb {C})$. We abbreviate ![]() $\Xi _{i}(\mathbb {C})$ by
$\Xi _{i}(\mathbb {C})$ by ![]() $\Xi _{i}$. From (120), we see that
$\Xi _{i}$. From (120), we see that
Moreover, from the above definition of ![]() $\hat {\psi }$ and the identity (118),
$\hat {\psi }$ and the identity (118), ![]() $\hat {\psi }:\mathscr {X}^q(\mathbb {C})\xrightarrow {\sim }\widehat {\Xi _{n+1}/\Xi _{n}}(\mathbb {C})$ lands inside
$\hat {\psi }:\mathscr {X}^q(\mathbb {C})\xrightarrow {\sim }\widehat {\Xi _{n+1}/\Xi _{n}}(\mathbb {C})$ lands inside ![]() $\Xi _{n+1}/\Xi _{n}$. Thus, we get
$\Xi _{n+1}/\Xi _{n}$. Thus, we get
This identification gives rise to an ind-variety structure on ![]() $\Xi _{n+1}/\Xi _n$ transported from that of
$\Xi _{n+1}/\Xi _n$ transported from that of ![]() $X^q=\mathscr {X}^q(\mathbb {C})$. Moreover, with this ind-variety structure,
$X^q=\mathscr {X}^q(\mathbb {C})$. Moreover, with this ind-variety structure, ![]() $\Xi _{n+1}/\Xi _n$ represents the functor
$\Xi _{n+1}/\Xi _n$ represents the functor ![]() $\widehat {\Xi _{n+1}/\Xi _{n}}$. It is easy to see (by considering the corresponding map at
$\widehat {\Xi _{n+1}/\Xi _{n}}$. It is easy to see (by considering the corresponding map at ![]() $R$-points) that with this ind-variety structure on
$R$-points) that with this ind-variety structure on ![]() $\Xi _{n+1}/\Xi _n$, the action map:
$\Xi _{n+1}/\Xi _n$, the action map:
is a morphism of ind-schemes.
For any morphism ![]() $f: \operatorname {\mathrm {Spec}} R \to \Xi _{n+1}/\Xi _n$, there exists an étale cover
$f: \operatorname {\mathrm {Spec}} R \to \Xi _{n+1}/\Xi _n$, there exists an étale cover ![]() $\operatorname {\mathrm {Spec}} S \to \operatorname {\mathrm {Spec}} R$ such that the projection
$\operatorname {\mathrm {Spec}} S \to \operatorname {\mathrm {Spec}} R$ such that the projection ![]() $\Xi _{n+1} \to \Xi _{n+1}/\Xi _n$ splits over
$\Xi _{n+1} \to \Xi _{n+1}/\Xi _n$ splits over ![]() $\operatorname {\mathrm {Spec}} S$. From this it is easy to see that
$\operatorname {\mathrm {Spec}} S$. From this it is easy to see that ![]() $\big (\Xi _{n+1}/\Xi _{n}\big )^{\operatorname {\mathrm {an}}}$ has the quotient topology induced from
$\big (\Xi _{n+1}/\Xi _{n}\big )^{\operatorname {\mathrm {an}}}$ has the quotient topology induced from ![]() $\Xi _{n+1}^{\operatorname {\mathrm {an}}}$. Moreover, for any ind-variety
$\Xi _{n+1}^{\operatorname {\mathrm {an}}}$. Moreover, for any ind-variety ![]() $Y=(Y_n)_{n\geq 0}$, any compact subset of
$Y=(Y_n)_{n\geq 0}$, any compact subset of ![]() $Y^{\operatorname {\mathrm {an}}}$ lies in some
$Y^{\operatorname {\mathrm {an}}}$ lies in some ![]() $Y_N$ (which is easy to verify). Thus,
$Y_N$ (which is easy to verify). Thus, ![]() $\Xi _{n+1}^{\operatorname {\mathrm {an}}}\to \big (\Xi _{n+1}/\Xi _{n}\big )^{\operatorname {\mathrm {an}}}$ is a Serre fibration. This gives rise to an exact sequence (cf. [Reference SpanierSpa66, Chap. 7, § 2, Theorem 10])
$\Xi _{n+1}^{\operatorname {\mathrm {an}}}\to \big (\Xi _{n+1}/\Xi _{n}\big )^{\operatorname {\mathrm {an}}}$ is a Serre fibration. This gives rise to an exact sequence (cf. [Reference SpanierSpa66, Chap. 7, § 2, Theorem 10])
However,
from the Bruhat decomposition (cf. [Reference KumarKum02, Proposition 7.4.16]). Thus, we get
Now, we are ready to prove the theorem. Take
where ![]() $K$ is the quotient field of
$K$ is the quotient field of ![]() $\mathbb {C}[\Sigma ^{*}]$. Since
$\mathbb {C}[\Sigma ^{*}]$. Since ![]() $G$ is simply connected, by the following lemma,
$G$ is simply connected, by the following lemma, ![]() $G(K)^\Gamma$ is generated by subgroups
$G(K)^\Gamma$ is generated by subgroups ![]() $U(K)^\Gamma$ and
$U(K)^\Gamma$ and ![]() $U^-(K)^\Gamma$, where (as before)
$U^-(K)^\Gamma$, where (as before) ![]() $U$ (respectively,
$U$ (respectively, ![]() $U^-$) is the unipotent radical of
$U^-$) is the unipotent radical of ![]() $B$ (respectively, of the opposite Borel subgroup
$B$ (respectively, of the opposite Borel subgroup ![]() $B^-$). Moreover,
$B^-$). Moreover, ![]() $U$ and
$U$ and ![]() $U^-$ being unipotent groups and
$U^-$ being unipotent groups and ![]() $K\supset \mathbb {C}$,
$K\supset \mathbb {C}$, ![]() $U(K)^\Gamma \simeq \mathfrak {u}(K)^\Gamma$ under the exponential map (and similarly for
$U(K)^\Gamma \simeq \mathfrak {u}(K)^\Gamma$ under the exponential map (and similarly for ![]() $U^-$). Thus, we can write
$U^-$). Thus, we can write
Thus, there exists a finite set ![]() $\bar {q}'=\{q'_{1},\ldots,q'_{n+1}\}\subset \Sigma ^*$ with disjoint
$\bar {q}'=\{q'_{1},\ldots,q'_{n+1}\}\subset \Sigma ^*$ with disjoint ![]() $\Gamma$-orbits such that all the poles of any
$\Gamma$-orbits such that all the poles of any ![]() $x_{i}$ (which means the poles of
$x_{i}$ (which means the poles of ![]() $f_i^j$ writing
$f_i^j$ writing ![]() $x_i=\sum _j e^j\otimes f^j_i$ for a basis
$x_i=\sum _j e^j\otimes f^j_i$ for a basis ![]() $e^j$ of
$e^j$ of ![]() $\mathfrak {u}$ or
$\mathfrak {u}$ or ![]() $\mathfrak {u}^-$) are contained in
$\mathfrak {u}^-$) are contained in ![]() $\Gamma \cdot \bar {q}'$. Thus,
$\Gamma \cdot \bar {q}'$. Thus, ![]() $\sigma \in \Xi _{n+1}$. Consider the curve
$\sigma \in \Xi _{n+1}$. Consider the curve
Since
we get that ![]() $e$ and
$e$ and ![]() $\sigma$ lie in the same path component of
$\sigma$ lie in the same path component of ![]() $\Xi ^{\text {an}}$, thus
$\Xi ^{\text {an}}$, thus ![]() $\Xi ^{\text {an}}$ is path-connected. Using [Reference KumarKum02, Lemma 4.2.5] we get that
$\Xi ^{\text {an}}$ is path-connected. Using [Reference KumarKum02, Lemma 4.2.5] we get that ![]() $\Xi$ is irreducible.
$\Xi$ is irreducible.
Our original proof of the following lemma was more direct (and involved). We thank Philippe Gille for pointing out the following argument relying on results of Borel–Tits and Steinberg.
Lemma 9.6 Let ![]() $G, \Sigma, \Gamma$ be as in the beginning of this section and let
$G, \Sigma, \Gamma$ be as in the beginning of this section and let ![]() $K$ be the function field of
$K$ be the function field of ![]() $\Sigma$. Let
$\Sigma$. Let ![]() $U$ (respectively,
$U$ (respectively, ![]() $U^-$) be the unipotent radical of
$U^-$) be the unipotent radical of ![]() $B$ (respectively, of the opposite Borel subgroup
$B$ (respectively, of the opposite Borel subgroup ![]() $B^-$). Then,
$B^-$). Then, ![]() $G(K)^\Gamma$ is generated (as an abstract group) by
$G(K)^\Gamma$ is generated (as an abstract group) by ![]() $U(K)^\Gamma$ and
$U(K)^\Gamma$ and ![]() $U^-(K)^\Gamma$.
$U^-(K)^\Gamma$.
Proof. Denote ![]() $K_o=K^\Gamma$. Then,
$K_o=K^\Gamma$. Then, ![]() $G(K)^\Gamma$ can be considered as a group scheme over
$G(K)^\Gamma$ can be considered as a group scheme over ![]() $K_o$. Moreover, since
$K_o$. Moreover, since ![]() $\Gamma$ stabilizes the Borel subgroup
$\Gamma$ stabilizes the Borel subgroup ![]() $B$ of
$B$ of ![]() $G(\mathbb {C})$,
$G(\mathbb {C})$, ![]() $G(K)^\Gamma$ is a quasi-split group scheme (over
$G(K)^\Gamma$ is a quasi-split group scheme (over ![]() $K_o$). Moreover,
$K_o$). Moreover, ![]() $G(K\otimes _{K_o} \bar {K}_o)^\Gamma$ with the trivial action of
$G(K\otimes _{K_o} \bar {K}_o)^\Gamma$ with the trivial action of ![]() $\Gamma$ on
$\Gamma$ on ![]() $\bar {K}_o$ can be identified with
$\bar {K}_o$ can be identified with ![]() $G(\bar {K}_o)$ since
$G(\bar {K}_o)$ since ![]() $\Gamma$ acts faithfully on
$\Gamma$ acts faithfully on ![]() $K$, where
$K$, where ![]() $\bar {K}_o$ is the algebraic closure of
$\bar {K}_o$ is the algebraic closure of ![]() $K$. Now, the lemma follows from combining the results [Reference Borel and TitsBT73, Proposition 6.2 and Remark 6.6] and [Reference SteinbergSte16, Lemma 64].
$K$. Now, the lemma follows from combining the results [Reference Borel and TitsBT73, Proposition 6.2 and Remark 6.6] and [Reference SteinbergSte16, Lemma 64].
Remark 9.7 The above lemma is also true (by the same proof) for ![]() $K$ replaced by
$K$ replaced by ![]() $\mathbb {C}((z_q))$ and
$\mathbb {C}((z_q))$ and ![]() $\Gamma$ replaced by
$\Gamma$ replaced by ![]() $\Gamma _q$. In particular, this gives another proof of
$\Gamma _q$. In particular, this gives another proof of ![]() $\pi _0\big ((X^q)^{\text {an}}\big )=0$.
$\pi _0\big ((X^q)^{\text {an}}\big )=0$.
As a special case of Theorem 9.5, we get the following. The connectedness of ![]() $X^q$ in a more general setting is obtained by Pappas and Rapoport [Reference Pappas and RapoportPR08, Theorem 0.1].
$X^q$ in a more general setting is obtained by Pappas and Rapoport [Reference Pappas and RapoportPR08, Theorem 0.1].
Corollary 9.8 With the notation as in Definition 9.4, the (twisted) affine Grassmannian ![]() $X^q$ is an irreducible ind-projective (reduced) variety.
$X^q$ is an irreducible ind-projective (reduced) variety.
Proof. Let ![]() $\Sigma = \mathbb {P}^1, \bar {q}=\{\infty, 0\}$, and the action of
$\Sigma = \mathbb {P}^1, \bar {q}=\{\infty, 0\}$, and the action of ![]() $\Gamma = \Gamma _q$ given as follows: let
$\Gamma = \Gamma _q$ given as follows: let ![]() $\sigma _q$ be any generator of
$\sigma _q$ be any generator of ![]() $\Gamma _q$ (of order
$\Gamma _q$ (of order ![]() $e_q :=|\Gamma _q|$). Define the action of
$e_q :=|\Gamma _q|$). Define the action of ![]() $\Gamma _q$ on
$\Gamma _q$ on ![]() $\mathbb {P}^1$ by setting
$\mathbb {P}^1$ by setting
Consider the natural transformation between the functors
This gives rise to the morphism between the corresponding ind-schemes:
From the isomorphism (cf. (122) of Theorem 9.5):
applied to the above example of ![]() $\Sigma = \mathbb {P}^1, \bar {q}=\{\infty, 0\}$ and the action of
$\Sigma = \mathbb {P}^1, \bar {q}=\{\infty, 0\}$ and the action of ![]() $\Gamma$ as above, we get that
$\Gamma$ as above, we get that ![]() $\theta$ is surjective. Since
$\theta$ is surjective. Since ![]() $G\big (\mathbb {C}[z, z^{-1}]\big )^{\Gamma _q}$ is irreducible (by Theorem 9.5) and, hence, so is
$G\big (\mathbb {C}[z, z^{-1}]\big )^{\Gamma _q}$ is irreducible (by Theorem 9.5) and, hence, so is ![]() $X^q$. Observe that in the proof of Theorem 9.5 we used the connectedness and simply-connectedness of
$X^q$. Observe that in the proof of Theorem 9.5 we used the connectedness and simply-connectedness of ![]() $(X^q)^{\text {an}}$; in particular, this corollary builds upon the connectedness of
$(X^q)^{\text {an}}$; in particular, this corollary builds upon the connectedness of ![]() $(X^q)^{\text {an}}$ to prove the stronger result.
$(X^q)^{\text {an}}$ to prove the stronger result.
10. Central extension of twisted loop group and its splitting over  $\Xi$
$\Xi$
We construct the central extensions of the twisted loop group ![]() $G(\mathbb {D}^*_q )^{\Gamma _q}$. We introduce the notion of ‘canonical’ splitting and prove the existence of its canonical splitting over
$G(\mathbb {D}^*_q )^{\Gamma _q}$. We introduce the notion of ‘canonical’ splitting and prove the existence of its canonical splitting over ![]() $\Xi :={\rm Mor}_{\Gamma }(\Sigma \setminus \Gamma \cdot q, G)$ when
$\Xi :={\rm Mor}_{\Gamma }(\Sigma \setminus \Gamma \cdot q, G)$ when ![]() $c$ is divisible by
$c$ is divisible by ![]() $|\Gamma |$. The treatment in this section is parallel to that in [Reference KumarKum22, § 1.4], where the corresponding theory is explained in the untwisted case.
$|\Gamma |$. The treatment in this section is parallel to that in [Reference KumarKum22, § 1.4], where the corresponding theory is explained in the untwisted case.
We continue to have the same assumptions on ![]() $G, \Gamma$ and
$G, \Gamma$ and ![]() $\Sigma$ as in the beginning of § 9. Fix any base point
$\Sigma$ as in the beginning of § 9. Fix any base point ![]() $q\in \Sigma$ and let
$q\in \Sigma$ and let ![]() $\Sigma ^{*}:=\Sigma \backslash \Gamma \cdot q$ and
$\Sigma ^{*}:=\Sigma \backslash \Gamma \cdot q$ and ![]() $\Xi =\Xi _q:=\operatorname {\mathrm {Mor}}_\Gamma (\Sigma ^{*},G)$. Then,
$\Xi =\Xi _q:=\operatorname {\mathrm {Mor}}_\Gamma (\Sigma ^{*},G)$. Then, ![]() $\Xi$ is an irreducible ind-affine group scheme (cf. Theorem 9.5). Let
$\Xi$ is an irreducible ind-affine group scheme (cf. Theorem 9.5). Let ![]() $z_q$ be a formal parameter on
$z_q$ be a formal parameter on ![]() $\Sigma$ around
$\Sigma$ around ![]() $q$ satisfying the condition (116). This gives rise to a morphism
$q$ satisfying the condition (116). This gives rise to a morphism
obtained by taking the Laurent series expansion at ![]() $q$ (with respect to the parameter
$q$ (with respect to the parameter ![]() $z_q$ at
$z_q$ at ![]() $q$), where
$q$), where ![]() $\mathscr {L}^q_G:=G((z_q))^{\Gamma _q}$.
$\mathscr {L}^q_G:=G((z_q))^{\Gamma _q}$.
Definition 10.1 (Adjoint action of  $\mathscr {L}^q_G$)
$\mathscr {L}^q_G$)
Define the ![]() $R$-linear adjoint action of the group functor
$R$-linear adjoint action of the group functor ![]() $\mathscr {L}^q_G(R):=G\big (R((z_q))\big )^{\Gamma _q}$ on the Lie-algebra functor
$\mathscr {L}^q_G(R):=G\big (R((z_q))\big )^{\Gamma _q}$ on the Lie-algebra functor ![]() $\hat {L}(\mathfrak {g}, \Gamma _q)(R):=\big (\mathfrak {g}\otimes R((z_q))\big )^{\Gamma _q}\oplus R.C$ (extending
$\hat {L}(\mathfrak {g}, \Gamma _q)(R):=\big (\mathfrak {g}\otimes R((z_q))\big )^{\Gamma _q}\oplus R.C$ (extending ![]() $R$-linearly the bracket in
$R$-linearly the bracket in ![]() $\hat {L}(\mathfrak {g}, \Gamma _q)(R)$) by
$\hat {L}(\mathfrak {g}, \Gamma _q)(R)$) by
for ![]() $\gamma \in \mathscr {L}^q_G(R)$,
$\gamma \in \mathscr {L}^q_G(R)$, ![]() $x\in \big (\mathfrak {g}\otimes R((z_q))\big )^{\Gamma _q}$, and
$x\in \big (\mathfrak {g}\otimes R((z_q))\big )^{\Gamma _q}$, and ![]() $s\in R$, where
$s\in R$, where ![]() $\langle \,{,}\,\rangle$ is the
$\langle \,{,}\,\rangle$ is the ![]() $R((z_q))$-bilinear extension of the normalized invariant form on
$R((z_q))$-bilinear extension of the normalized invariant form on ![]() $\mathfrak {g}$ (normalized as in § 2) and taking an embedding
$\mathfrak {g}$ (normalized as in § 2) and taking an embedding ![]() $i:G\hookrightarrow \operatorname {SL}_{N}$ we view
$i:G\hookrightarrow \operatorname {SL}_{N}$ we view ![]() $G(R((z_q)))$ as a subgroup of
$G(R((z_q)))$ as a subgroup of ![]() $N\times N$ invertible matrices over the ring
$N\times N$ invertible matrices over the ring ![]() $R((z_q))$. From the functoriality of the conjugation,
$R((z_q))$. From the functoriality of the conjugation, ![]() $\gamma x\gamma ^{-1}\in \big (\mathfrak {g}\otimes R((z_q))\big )^{\Gamma _q}$ and it does not depend upon the choice of the embedding
$\gamma x\gamma ^{-1}\in \big (\mathfrak {g}\otimes R((z_q))\big )^{\Gamma _q}$ and it does not depend upon the choice of the embedding ![]() $i$. A similar remark applies to
$i$. A similar remark applies to ![]() $\gamma ^{-1}\,d\gamma$. Here
$\gamma ^{-1}\,d\gamma$. Here ![]() $d\gamma$ for
$d\gamma$ for ![]() $\gamma =(\gamma_{ij})\in M_{N}(R((z_q)))$ denotes
$\gamma =(\gamma_{ij})\in M_{N}(R((z_q)))$ denotes ![]() $d\gamma :=\big ( {\gamma_{ij}}/{dz_q}\big )$.
$d\gamma :=\big ( {\gamma_{ij}}/{dz_q}\big )$.
It is easy to check that for any ![]() $\gamma \in \mathscr {L}^q_G(R)$,
$\gamma \in \mathscr {L}^q_G(R)$, ![]() $\operatorname {{\mathscr {A}d}}\gamma :\hat {L}(\mathfrak {g}, \Gamma _q)(R)\to \hat {L}(\mathfrak {g}, \Gamma _q)(R)$ is a
$\operatorname {{\mathscr {A}d}}\gamma :\hat {L}(\mathfrak {g}, \Gamma _q)(R)\to \hat {L}(\mathfrak {g}, \Gamma _q)(R)$ is a ![]() $R$-linear Lie algebra homomorphism. Moreover, for
$R$-linear Lie algebra homomorphism. Moreover, for ![]() $\gamma _1, \gamma _2\in \mathscr {L}^q_G(R)$,
$\gamma _1, \gamma _2\in \mathscr {L}^q_G(R)$,
One easily sees that for any ![]() $\mathbb {C}$-algebra
$\mathbb {C}$-algebra ![]() $R$ and
$R$ and ![]() $x\in \big (\mathfrak {g}\otimes R((z_q))\big )^{\Gamma _q}$, the derivative
$x\in \big (\mathfrak {g}\otimes R((z_q))\big )^{\Gamma _q}$, the derivative
Let ![]() $\mathscr {H}(\lambda )$ be an integrable highest weight (irreducible) representation of
$\mathscr {H}(\lambda )$ be an integrable highest weight (irreducible) representation of ![]() $\hat {L}(\mathfrak {g}, \Gamma _q)$ (with central charge
$\hat {L}(\mathfrak {g}, \Gamma _q)$ (with central charge ![]() $c$). It clearly extends to a
$c$). It clearly extends to a ![]() $R$-linear representation
$R$-linear representation ![]() $\bar {\rho }_{R}$ of
$\bar {\rho }_{R}$ of ![]() $\hat {L}(\mathfrak {g}, \Gamma _q) (R)$ in
$\hat {L}(\mathfrak {g}, \Gamma _q) (R)$ in ![]() $\mathscr {H}(\lambda )_{R}:=\mathscr {H}(\lambda )\otimes _{\mathbb {C}} R$. A proof of the following result is parallel to the proof due to Faltings in the untwisted case (cf. [Reference Beauville and LaszloBL94, Lemma A.3]).
$\mathscr {H}(\lambda )_{R}:=\mathscr {H}(\lambda )\otimes _{\mathbb {C}} R$. A proof of the following result is parallel to the proof due to Faltings in the untwisted case (cf. [Reference Beauville and LaszloBL94, Lemma A.3]).
Proposition 10.2 For any ![]() $R\in \operatorname {\mathscr {A}lg}$ and
$R\in \operatorname {\mathscr {A}lg}$ and ![]() $\gamma \in G\big (R((z_q))\big )^{\Gamma _q}$, locally over
$\gamma \in G\big (R((z_q))\big )^{\Gamma _q}$, locally over ![]() $\operatorname {\mathrm {Spec}} R$, there exists an
$\operatorname {\mathrm {Spec}} R$, there exists an ![]() $R$-linear automorphism
$R$-linear automorphism ![]() $\hat {\rho }_R(\gamma )$ of
$\hat {\rho }_R(\gamma )$ of ![]() $\mathscr {H}(\lambda )_{R}$ uniquely determined up to an invertible element of
$\mathscr {H}(\lambda )_{R}$ uniquely determined up to an invertible element of ![]() $R$ satisfying
$R$ satisfying
As a corollary of the above proposition, we get the following.
Theorem 10.3 There exists a homomorphism ![]() $\rho _R:G\big (R((z_q))\big )^{\Gamma _q}\to \mathscr {P}GL_{\mathscr {H}(\lambda )}(R)$ of group functors such that
$\rho _R:G\big (R((z_q))\big )^{\Gamma _q}\to \mathscr {P}GL_{\mathscr {H}(\lambda )}(R)$ of group functors such that
coincides with the projective representation ![]() $\mathscr {H}(\lambda )$ of
$\mathscr {H}(\lambda )$ of ![]() $\big (\mathfrak {g}\otimes \mathbb {C}((z_q))\big )^{\Gamma _q}$.
$\big (\mathfrak {g}\otimes \mathbb {C}((z_q))\big )^{\Gamma _q}$.
Definition 10.4 (Central extension)
Let ![]() $0\in D_{c, q}$, where
$0\in D_{c, q}$, where ![]() $D_{c, q}$ denotes
$D_{c, q}$ denotes ![]() $D_c$ for the twisted affine Lie algebra
$D_c$ for the twisted affine Lie algebra ![]() $\hat {L}(\mathfrak {g}, \Gamma _q)$ (cf. Lemma 2.1 and Corollary 2.2). By the above theorem, we have a homomorphism of group functors:
$\hat {L}(\mathfrak {g}, \Gamma _q)$ (cf. Lemma 2.1 and Corollary 2.2). By the above theorem, we have a homomorphism of group functors:
where ![]() $\mathscr {H}_c:=\mathscr {H}(0)$ with central charge
$\mathscr {H}_c:=\mathscr {H}(0)$ with central charge ![]() $c$ for the twisted affine Lie algebra
$c$ for the twisted affine Lie algebra ![]() $\hat {L}(\mathfrak {g}, \Gamma _q)$. In addition, there is a canonical homomorphism of group functors
$\hat {L}(\mathfrak {g}, \Gamma _q)$. In addition, there is a canonical homomorphism of group functors
From this we get the fiber product group functor ![]() $\hat {\mathscr {G}}^q_c$:
$\hat {\mathscr {G}}^q_c$:
By definition, we get homomorphisms of group functors
making the following diagram commutative.

The following is the central extension we are seeking:
It is easy to see that the Lie algebra ![]() $\operatorname {\mathrm {Lie}} (\hat {\mathscr {G}}^q_c(R)):=T_{1}(\hat {\mathscr {G}}^q_c)_{R}$ is identified with the fiber product Lie algebra:
$\operatorname {\mathrm {Lie}} (\hat {\mathscr {G}}^q_c(R)):=T_{1}(\hat {\mathscr {G}}^q_c)_{R}$ is identified with the fiber product Lie algebra:
for any ![]() $\mathbb {C}$-algebra
$\mathbb {C}$-algebra ![]() $R$.
$R$.
Lemma 10.5 The Lie algebra ![]() $\hat {\mathfrak {g}}^q:=\operatorname {\mathrm {Lie}} \hat {\mathscr {G}}^q_c (\mathbb {C})$ can canonically be identified with the twisted affine Lie algebra
$\hat {\mathfrak {g}}^q:=\operatorname {\mathrm {Lie}} \hat {\mathscr {G}}^q_c (\mathbb {C})$ can canonically be identified with the twisted affine Lie algebra ![]() $\hat {L}(\mathfrak {g}, \Gamma _q)$.
$\hat {L}(\mathfrak {g}, \Gamma _q)$.
Proof. Define
From the definition of the bracket in ![]() $\hat {L}(\mathfrak {g}, \Gamma _q)$ and Theorem 10.3,
$\hat {L}(\mathfrak {g}, \Gamma _q)$ and Theorem 10.3, ![]() $\psi$ is an isomorphism of Lie algebras.
$\psi$ is an isomorphism of Lie algebras.
Combining Theorem 10.3, Definition 10.4, and Lemma 10.5, we get the following.
Corollary 10.6 We have a homomorphism of group functors,
such that its derivative at ![]() $R=\mathbb {C}$,
$R=\mathbb {C}$,
under the identification of Lemma 10.5 coincides with the Lie algebra representation
Moreover, for any ![]() $\hat {\gamma }\in \hat {\mathscr {G}}^q_c(R)$ and
$\hat {\gamma }\in \hat {\mathscr {G}}^q_c(R)$ and ![]() $x\in \hat {\mathfrak {g}}^q(R)$,
$x\in \hat {\mathfrak {g}}^q(R)$,
Theorem 10.7 (1) The central extension ![]() $p: \hat {\mathscr {G}}^q_c\to \mathscr {L}_G^q$ (as in Definition 10.4) splits over
$p: \hat {\mathscr {G}}^q_c\to \mathscr {L}_G^q$ (as in Definition 10.4) splits over ![]() $G[[z_q]]^{\Gamma _q}$ for any
$G[[z_q]]^{\Gamma _q}$ for any ![]() $c\geq 1$ such that
$c\geq 1$ such that ![]() $0\in D_c =D_{c, q}$. Moreover, we can choose the splitting so that the corresponding tangent map is the identity via Lemma 10.5.
$0\in D_c =D_{c, q}$. Moreover, we can choose the splitting so that the corresponding tangent map is the identity via Lemma 10.5.
(2) The above central extension splits over ![]() $\Xi$ if
$\Xi$ if ![]() $c$ is a multiple of
$c$ is a multiple of ![]() $|\Gamma |$. Moreover, we can choose the splitting so that the corresponding tangent map is the identity via Lemma 10.5.
$|\Gamma |$. Moreover, we can choose the splitting so that the corresponding tangent map is the identity via Lemma 10.5.
(By Corollary 2.2, if ![]() $|\Gamma |$ divides
$|\Gamma |$ divides ![]() $c$, then
$c$, then ![]() $0\in D_c$.)
$0\in D_c$.)
We call the unique splitting satisfying the above property canonical.
Proof. We first prove part (1) of the theorem. By Proposition 10.2 (using the fact, as in § 2, that the annihilator of ![]() $\mathfrak {g}[[z_q]]^{\Gamma _q}$ in
$\mathfrak {g}[[z_q]]^{\Gamma _q}$ in ![]() $\mathscr {H}_c$ is exactly
$\mathscr {H}_c$ is exactly ![]() $\mathbb {C}v_+$), the map
$\mathbb {C}v_+$), the map
restricted to ![]() $G[[z_q]]^{\Gamma _q}$ lands inside
$G[[z_q]]^{\Gamma _q}$ lands inside ![]() ${\rm PGL}^+_{\mathscr {H}_c}$ consisting of those (projective) automorphisms which take the highest weight vector
${\rm PGL}^+_{\mathscr {H}_c}$ consisting of those (projective) automorphisms which take the highest weight vector ![]() $v_+$ of
$v_+$ of ![]() $\mathscr {H}_c$ to
$\mathscr {H}_c$ to ![]() $\mathbb {C}^\times v_+$. Take the subgroup
$\mathbb {C}^\times v_+$. Take the subgroup ![]() ${\rm GL}^+_{\mathscr {H}_c}$ consisting of those automorphisms which take
${\rm GL}^+_{\mathscr {H}_c}$ consisting of those automorphisms which take ![]() $v_+\mapsto v_+$. Then, the map
$v_+\mapsto v_+$. Then, the map ![]() ${\rm GL}^+_{\mathscr {H}_c}\to {\rm PGL}^+_{\mathscr {H}_c}={\rm Im} ({\rm GL}^+_{\mathscr {H}_c})$ is an isomorphism providing the splitting of
${\rm GL}^+_{\mathscr {H}_c}\to {\rm PGL}^+_{\mathscr {H}_c}={\rm Im} ({\rm GL}^+_{\mathscr {H}_c})$ is an isomorphism providing the splitting of ![]() ${\rm GL}_{\mathscr {H}_c}\to {\rm PGL}_{\mathscr {H}_c}$ over
${\rm GL}_{\mathscr {H}_c}\to {\rm PGL}_{\mathscr {H}_c}$ over ![]() ${\rm PGL}^+_{\mathscr {H}_c}$. Thus, the central extension
${\rm PGL}^+_{\mathscr {H}_c}$. Thus, the central extension ![]() $p: \hat {\mathscr {G}}^q_c\to \mathscr {L}_G^q$ splits over
$p: \hat {\mathscr {G}}^q_c\to \mathscr {L}_G^q$ splits over ![]() $G[[z_a]]^{\Gamma _q}$. Denote this splitting by
$G[[z_a]]^{\Gamma _q}$. Denote this splitting by ![]() $\sigma$.
$\sigma$.
We next prove that ![]() $\dot {\sigma }$ (via Lemma 10.5) is the identity map: let
$\dot {\sigma }$ (via Lemma 10.5) is the identity map: let
where ![]() $\lambda : \mathfrak {g}[[z_q]]^{\Gamma _q}\to \mathbb {C}$ is a
$\lambda : \mathfrak {g}[[z_q]]^{\Gamma _q}\to \mathbb {C}$ is a ![]() $\mathbb {C}$-linear map. Thus, for any
$\mathbb {C}$-linear map. Thus, for any ![]() $x\in \mathfrak {g}[[z_q]]^{\Gamma _q}$,
$x\in \mathfrak {g}[[z_q]]^{\Gamma _q}$,
However, since ![]() $\hat {\rho }({\rm Im}(\sigma ))\subset {\rm GL}^+_{\mathscr {H} _c}$,
$\hat {\rho }({\rm Im}(\sigma ))\subset {\rm GL}^+_{\mathscr {H} _c}$,
Combining (132) and (133), we get ![]() $\lambda \equiv 0$. This proves that
$\lambda \equiv 0$. This proves that ![]() $\dot {\sigma }$ is the identity map.
$\dot {\sigma }$ is the identity map.
We now prove part (2) of the theorem. Consider the embedding obtained via the restriction:
In addition, consider the embedding
 \[ j_q=\prod j_q^\gamma: G(\mathbb{D}_q^*) \hookrightarrow \prod_{\gamma\in \widehat{ \Gamma/\Gamma_q}} G(\mathbb{D}_{\gamma\cdot q} ^*), \]
\[ j_q=\prod j_q^\gamma: G(\mathbb{D}_q^*) \hookrightarrow \prod_{\gamma\in \widehat{ \Gamma/\Gamma_q}} G(\mathbb{D}_{\gamma\cdot q} ^*), \]
where ![]() $j_q^\gamma : G(\mathbb {D}_q^*) \xrightarrow {\sim } G(\mathbb {D}_{\gamma \cdot q}^*)$ is defined by
$j_q^\gamma : G(\mathbb {D}_q^*) \xrightarrow {\sim } G(\mathbb {D}_{\gamma \cdot q}^*)$ is defined by
Here ![]() $\widehat { \Gamma /\Gamma _q}$ denotes a (fixed) set of coset representatives of the cosets
$\widehat { \Gamma /\Gamma _q}$ denotes a (fixed) set of coset representatives of the cosets ![]() $\Gamma /\Gamma _q$.
$\Gamma /\Gamma _q$.
Let ![]() $\bar {\mathscr {H}}_1$ denote the integrable highest weight module of highest weight 0 and central charge 1 of the untwisted affine Lie algebra
$\bar {\mathscr {H}}_1$ denote the integrable highest weight module of highest weight 0 and central charge 1 of the untwisted affine Lie algebra ![]() $\hat {L}(\mathfrak {g})$ based at
$\hat {L}(\mathfrak {g})$ based at ![]() $q$, i.e. the central extension of
$q$, i.e. the central extension of ![]() $\mathfrak {g}((z_q))$, where
$\mathfrak {g}((z_q))$, where ![]() $z_q$ is a formal parameter for
$z_q$ is a formal parameter for ![]() $\Sigma$ at
$\Sigma$ at ![]() $q$. Identifying
$q$. Identifying ![]() $G(\mathbb {D}_{\gamma \cdot q}^*)$ with
$G(\mathbb {D}_{\gamma \cdot q}^*)$ with ![]() $G(\mathbb {D}_q^*)$ via
$G(\mathbb {D}_q^*)$ via ![]() $j^\gamma _q$, we get a projective representation
$j^\gamma _q$, we get a projective representation ![]() $\rho$ and the commutative diagram
$\rho$ and the commutative diagram

where we take ![]() $|\Gamma /\Gamma _q|$ copies of
$|\Gamma /\Gamma _q|$ copies of ![]() $\bar {\mathscr {H}}_1$ and
$\bar {\mathscr {H}}_1$ and ![]() $\hat {\rho }$ (respectively,
$\hat {\rho }$ (respectively, ![]() $\hat {j}_q$) is the pull-back of
$\hat {j}_q$) is the pull-back of ![]() ${\rm GL}(\bar {\mathscr {H}_1 } \otimes \cdots \otimes \bar {\mathscr {H} }_1 )$ (respectively,
${\rm GL}(\bar {\mathscr {H}_1 } \otimes \cdots \otimes \bar {\mathscr {H} }_1 )$ (respectively, ![]() ${\hat {\mathscr {G}}}^{\Gamma \cdot q}$) induced from
${\hat {\mathscr {G}}}^{\Gamma \cdot q}$) induced from ![]() $\rho$ (respectively,
$\rho$ (respectively, ![]() $j_q$). Since
$j_q$). Since ![]() $\bar {\mathscr {H}}_1$ has central charge 1, it is easy to see that
$\bar {\mathscr {H}}_1$ has central charge 1, it is easy to see that ![]() $\tilde {\mathscr {G}}^q$ is the central extension of
$\tilde {\mathscr {G}}^q$ is the central extension of ![]() $G(\mathbb {D}_q^*)$ corresponding to the central charge
$G(\mathbb {D}_q^*)$ corresponding to the central charge ![]() $= |\Gamma /\Gamma _q|$.
$= |\Gamma /\Gamma _q|$.
Since the ![]() $\hat {L}(\mathfrak {g}, \Gamma _q)$-submodule of
$\hat {L}(\mathfrak {g}, \Gamma _q)$-submodule of ![]() $\bar {\mathscr {H}}_1$ generated by the highest weight vector is of central charge
$\bar {\mathscr {H}}_1$ generated by the highest weight vector is of central charge ![]() $|\Gamma _q|$ (cf. (2)), we get that the restriction
$|\Gamma _q|$ (cf. (2)), we get that the restriction ![]() $p_{\Gamma _q}$ of the central extension
$p_{\Gamma _q}$ of the central extension ![]() $p_q: \tilde {\mathscr {G}}^q \to G(\mathbb {D}_q^*)$ to
$p_q: \tilde {\mathscr {G}}^q \to G(\mathbb {D}_q^*)$ to ![]() $G(\mathbb {D}_q^*)^{\Gamma _q}$ is the central extension corresponding to the central charge
$G(\mathbb {D}_q^*)^{\Gamma _q}$ is the central extension corresponding to the central charge ![]() $|\Gamma |$. By the same proof as of [Reference SorgerSor99, Proposition 3.3] (see also [Reference KumarKum22, Theorem 8.2.1]), the central extension
$|\Gamma |$. By the same proof as of [Reference SorgerSor99, Proposition 3.3] (see also [Reference KumarKum22, Theorem 8.2.1]), the central extension ![]() $p_{\Gamma \cdot q}$ splits over
$p_{\Gamma \cdot q}$ splits over ![]() $G(\Sigma \backslash \Gamma \cdot q)$.
$G(\Sigma \backslash \Gamma \cdot q)$.
Now, any splitting ![]() $\sigma$ of
$\sigma$ of ![]() $p_{\Gamma \cdot q}$ over
$p_{\Gamma \cdot q}$ over ![]() $G(\Sigma \backslash \Gamma \cdot q)$ clearly induces a splitting
$G(\Sigma \backslash \Gamma \cdot q)$ clearly induces a splitting ![]() $\hat {\sigma }$ of the central extension
$\hat {\sigma }$ of the central extension ![]() $p_q: p_q^{-1}( G(\mathbb {D}_q^*)^{\Gamma _q} )\to G(\mathbb {D}_q^*) ^{\Gamma _q}$ over
$p_q: p_q^{-1}( G(\mathbb {D}_q^*)^{\Gamma _q} )\to G(\mathbb {D}_q^*) ^{\Gamma _q}$ over ![]() $G(\Sigma \backslash \Gamma \cdot q)^\Gamma$.
$G(\Sigma \backslash \Gamma \cdot q)^\Gamma$.
Observe next that any splitting ![]() $\sigma$ of
$\sigma$ of ![]() $p_{\Gamma \cdot q}: {\hat {\mathscr {G}}}^{\Gamma \cdot q} \to \prod _{\gamma \in \widehat { \Gamma /\Gamma _q}} G(\mathbb {D}_{\gamma \cdot q} ^*)$ over
$p_{\Gamma \cdot q}: {\hat {\mathscr {G}}}^{\Gamma \cdot q} \to \prod _{\gamma \in \widehat { \Gamma /\Gamma _q}} G(\mathbb {D}_{\gamma \cdot q} ^*)$ over ![]() $G(\Sigma \backslash \Gamma \cdot q)$ satisfies
$G(\Sigma \backslash \Gamma \cdot q)$ satisfies ![]() $\dot {\sigma } ={\rm Id}$. This follows trivially from the fact that
$\dot {\sigma } ={\rm Id}$. This follows trivially from the fact that
Now, the induced splitting ![]() $\hat {\sigma }$ of the central extension
$\hat {\sigma }$ of the central extension ![]() $p_q: p_q^{-1}( G(\mathbb {D}_q^*)^{\Gamma _q} )\to G(\mathbb {D}_q^*) ^{\Gamma _q}$ over
$p_q: p_q^{-1}( G(\mathbb {D}_q^*)^{\Gamma _q} )\to G(\mathbb {D}_q^*) ^{\Gamma _q}$ over ![]() $G(\Sigma \backslash \Gamma \cdot q)^\Gamma$ clearly satisfies
$G(\Sigma \backslash \Gamma \cdot q)^\Gamma$ clearly satisfies ![]() $\dot {\hat {\sigma }}={\rm Id}$. This proves the theorem.
$\dot {\hat {\sigma }}={\rm Id}$. This proves the theorem.
Remark 10.8 Because of the possible existence of non-trivial characters of ![]() $G^{\Gamma _q}$ (respectively,
$G^{\Gamma _q}$ (respectively, ![]() $G^{\Gamma _{q'}}$ for
$G^{\Gamma _{q'}}$ for ![]() $q'\in \Sigma \backslash \Gamma \cdot q$), the splittings of
$q'\in \Sigma \backslash \Gamma \cdot q$), the splittings of ![]() $\hat {\mathscr {G}}^q_c\to \mathscr {L}^q_G$ over
$\hat {\mathscr {G}}^q_c\to \mathscr {L}^q_G$ over ![]() $G[[z_q]]^{\Gamma _q}$ (respectively,
$G[[z_q]]^{\Gamma _q}$ (respectively, ![]() $G(\Sigma \backslash \Gamma \cdot q)^\Gamma$) may not be unique.
$G(\Sigma \backslash \Gamma \cdot q)^\Gamma$) may not be unique.
By a theorem of Steinberg (cf. [Reference SteinbergSte68]), the fixed subgroup ![]() $G^{\sigma }$ is connected for any finite order automorphism
$G^{\sigma }$ is connected for any finite order automorphism ![]() $\sigma$ of
$\sigma$ of ![]() $G$.
$G$.
Proposition 10.9 Let ![]() $\sigma$ be a finite order automorphism of
$\sigma$ be a finite order automorphism of ![]() $\mathfrak {g}$ of order
$\mathfrak {g}$ of order ![]() $m$ and let
$m$ and let ![]() $m$ divide
$m$ divide ![]() $\bar {s}c$, where
$\bar {s}c$, where ![]() $\bar {s}$ is defined above Corollary 2.2. For any
$\bar {s}$ is defined above Corollary 2.2. For any ![]() $\lambda \in D_c$, the irreducible
$\lambda \in D_c$, the irreducible ![]() $\mathfrak {g}^\sigma$-module
$\mathfrak {g}^\sigma$-module ![]() $V(\lambda )$ integrates to a representation of
$V(\lambda )$ integrates to a representation of ![]() $G^\sigma$.
$G^\sigma$.
Proof. Decompose ![]() $\sigma =\tau \epsilon ^{{\rm ad}\, h}$ as in (3). To prove that
$\sigma =\tau \epsilon ^{{\rm ad}\, h}$ as in (3). To prove that ![]() $V(\lambda )$ integrates to a
$V(\lambda )$ integrates to a ![]() $G^\sigma$-module, it suffices to show that the torus
$G^\sigma$-module, it suffices to show that the torus ![]() $H^\sigma =H^\tau$ acts on
$H^\sigma =H^\tau$ acts on ![]() $V(\lambda )$, where
$V(\lambda )$, where ![]() $H$ is the maximal torus of
$H$ is the maximal torus of ![]() $G$ with Lie algebra
$G$ with Lie algebra ![]() $\mathfrak {h}$ (
$\mathfrak {h}$ (![]() $\mathfrak {h}$ being a
$\mathfrak {h}$ being a ![]() $\sigma$-stable Cartan subalgebra). By Lemma 2.1, since
$\sigma$-stable Cartan subalgebra). By Lemma 2.1, since ![]() $m$ divides
$m$ divides ![]() $\bar {s} c$ (by assumption),
$\bar {s} c$ (by assumption), ![]() $\lambda (\alpha ^\vee _i)\in \mathbb {Z}$ for all the simple coroots
$\lambda (\alpha ^\vee _i)\in \mathbb {Z}$ for all the simple coroots ![]() $\alpha ^\vee _i$ of
$\alpha ^\vee _i$ of ![]() $\mathfrak {g}^\tau$, i.e.
$\mathfrak {g}^\tau$, i.e. ![]() $\lambda$ belongs to the weight lattice of
$\lambda$ belongs to the weight lattice of ![]() $\mathfrak {g}^\tau$. Thus, if
$\mathfrak {g}^\tau$. Thus, if ![]() $G^\tau$ is simply connected,
$G^\tau$ is simply connected, ![]() $\lambda$ gives rise to a character of
$\lambda$ gives rise to a character of ![]() $H^\tau$. Thus, in this case
$H^\tau$. Thus, in this case ![]() $H^\tau$ acts on
$H^\tau$ acts on ![]() $V(\lambda )$. Recall that for a diagram automorphism
$V(\lambda )$. Recall that for a diagram automorphism ![]() $\tau$,
$\tau$, ![]() $G^\tau$ is simply connected unless
$G^\tau$ is simply connected unless ![]() $(\mathfrak {g},r)=(A_{2n}, 2)$, where
$(\mathfrak {g},r)=(A_{2n}, 2)$, where ![]() $r$ is the order of
$r$ is the order of ![]() $\tau$. In this case
$\tau$. In this case ![]() $G^\tau =$ SO
$G^\tau =$ SO![]() $(2n+1)$ and following the notation of the identity (6),
$(2n+1)$ and following the notation of the identity (6),
with the Bourbaki convention [Reference BourbakiBou05, Planche II]. Since ![]() $n_{\lambda,i}$ is required to lie in
$n_{\lambda,i}$ is required to lie in ![]() $\mathbb {Z}_{\geq 0}$, for all
$\mathbb {Z}_{\geq 0}$, for all ![]() $i\in \hat {I}(\mathfrak {g}, \sigma )$, and
$i\in \hat {I}(\mathfrak {g}, \sigma )$, and ![]() $m$ divides
$m$ divides ![]() $\bar {s} c$, we get
$\bar {s} c$, we get
Thus, ![]() $\lambda$ belongs to the root lattice of
$\lambda$ belongs to the root lattice of ![]() $\mathfrak {g}^\tau$ and, hence,
$\mathfrak {g}^\tau$ and, hence, ![]() $\lambda$ gives rise to a character of
$\lambda$ gives rise to a character of ![]() $H^\tau$. This proves that
$H^\tau$. This proves that ![]() $H^\tau$ acts on
$H^\tau$ acts on ![]() $V(\lambda )$, proving the proposition.
$V(\lambda )$, proving the proposition.
11. Uniformization theorem (a review)
We continue to have the same assumptions on ![]() $G, \Gamma, \Sigma$ as in the beginning of § 9. We recall some results due to Heinloth [Reference HeinlothHei10] (conjectured by Pappas and Rapoport [Reference Pappas and RapoportPR08, Reference Pappas and RapoportPR10]) only in the generality we need and in the form suitable for our purposes. In particular, we recall the uniformization theorem due to Heinloth for the parahoric Bruhat–Tits group schemes
$G, \Gamma, \Sigma$ as in the beginning of § 9. We recall some results due to Heinloth [Reference HeinlothHei10] (conjectured by Pappas and Rapoport [Reference Pappas and RapoportPR08, Reference Pappas and RapoportPR10]) only in the generality we need and in the form suitable for our purposes. In particular, we recall the uniformization theorem due to Heinloth for the parahoric Bruhat–Tits group schemes ![]() $\mathscr {G}$ in our setting. We introduce the moduli stack
$\mathscr {G}$ in our setting. We introduce the moduli stack ![]() $\mathscr {P}arbun_{\mathscr {G}}$ of quasi-parabolic
$\mathscr {P}arbun_{\mathscr {G}}$ of quasi-parabolic ![]() $\mathscr {G}$-torsors over
$\mathscr {G}$-torsors over ![]() $\bar {\Sigma }$ and construct the line bundles over
$\bar {\Sigma }$ and construct the line bundles over ![]() $\mathscr {P}arbun_{\mathscr {G}}$.
$\mathscr {P}arbun_{\mathscr {G}}$.
Definition 11.1 (Parahoric Bruhat–Tits group scheme)
Consider the ![]() $\Gamma$-invariant Weil restriction
$\Gamma$-invariant Weil restriction ![]() $\mathscr {G}=\mathscr {G}(\Sigma, \Gamma, \phi )$ via
$\mathscr {G}=\mathscr {G}(\Sigma, \Gamma, \phi )$ via ![]() $\pi :\Sigma \to \bar {\Sigma }:=\Sigma /\Gamma$ of the constant group scheme
$\pi :\Sigma \to \bar {\Sigma }:=\Sigma /\Gamma$ of the constant group scheme ![]() $\Sigma \times G \to \Sigma$ over
$\Sigma \times G \to \Sigma$ over ![]() $\Sigma$. More precisely,
$\Sigma$. More precisely, ![]() $\mathscr {G}$ is given by the following group functor over
$\mathscr {G}$ is given by the following group functor over ![]() $\bar {\Sigma }$:
$\bar {\Sigma }$:
for any scheme ![]() $U$ over
$U$ over ![]() $\bar {\Sigma }$, where
$\bar {\Sigma }$, where ![]() $U\times _{\bar {\Sigma }} \Sigma$ is the fiber product of
$U\times _{\bar {\Sigma }} \Sigma$ is the fiber product of ![]() $U$ and
$U$ and ![]() $\Sigma$ over
$\Sigma$ over ![]() $\bar {\Sigma }$. Then,
$\bar {\Sigma }$. Then, ![]() $\mathscr {G}\to \bar {\Sigma }$ is a smooth affine group scheme over
$\mathscr {G}\to \bar {\Sigma }$ is a smooth affine group scheme over ![]() $\bar {\Sigma }$.
$\bar {\Sigma }$.
This provides a class of examples of parahoric Bruhat–Tits group schemes.
For any point ![]() $p\in \bar {\Sigma }$, the fiber
$p\in \bar {\Sigma }$, the fiber ![]() $\mathscr {G}_p\simeq G$ if
$\mathscr {G}_p\simeq G$ if ![]() $p$ is an unramified point. However, if
$p$ is an unramified point. However, if ![]() $p$ is a ramified point, the group
$p$ is a ramified point, the group ![]() $\mathscr {G}_p$ has unipotent radical
$\mathscr {G}_p$ has unipotent radical ![]() $U_p$ and
$U_p$ and
Take any point ![]() $q\in \pi ^{-1}(p)$ and let
$q\in \pi ^{-1}(p)$ and let ![]() $\mathbb {D}_p\subset \bar {\Sigma }$ (respectively,
$\mathbb {D}_p\subset \bar {\Sigma }$ (respectively, ![]() $\mathbb {D}_q\subset \Sigma$) be the formal disc around
$\mathbb {D}_q\subset \Sigma$) be the formal disc around ![]() $p$ in
$p$ in ![]() $\bar {\Sigma }$ (respectively, around
$\bar {\Sigma }$ (respectively, around ![]() $q$ in
$q$ in ![]() $\Sigma$). Then,
$\Sigma$). Then,
Similarly, for the punctured discs ![]() $\mathbb {D}^\times _p$ and
$\mathbb {D}^\times _p$ and ![]() $\mathbb {D}^\times _q$,
$\mathbb {D}^\times _q$,
Thus,
In particular, it is also an irreducible (reduced) ind-projective variety (cf. Corollary 9.8).
Definition 11.2 (Moduli stack of  $\mathscr {G}$-torsors)
$\mathscr {G}$-torsors)
Consider the stack ![]() $\mathscr {B}un_{\mathscr {G}}$ assigning to a commutative
$\mathscr {B}un_{\mathscr {G}}$ assigning to a commutative ![]() $\mathbb {C}$-algebra
$\mathbb {C}$-algebra ![]() $R$ the category of
$R$ the category of ![]() $\mathscr {G}_R$-torsors over
$\mathscr {G}_R$-torsors over ![]() $\bar {\Sigma }_R:=\bar {\Sigma }\times {\rm Spec} R$, where
$\bar {\Sigma }_R:=\bar {\Sigma }\times {\rm Spec} R$, where ![]() $\mathscr {G}_R$ is the pull-back of
$\mathscr {G}_R$ is the pull-back of ![]() $\mathscr {G}$ via the projection from
$\mathscr {G}$ via the projection from ![]() $\bar {\Sigma }_R$ to
$\bar {\Sigma }_R$ to ![]() $\bar {\Sigma }$. Then, as proved by Heinloth [Reference HeinlothHei10, Proposition 1],
$\bar {\Sigma }$. Then, as proved by Heinloth [Reference HeinlothHei10, Proposition 1], ![]() $\mathscr {B}un_{\mathscr {G}}$ is a smooth algebraic stack, which is locally of finite type.
$\mathscr {B}un_{\mathscr {G}}$ is a smooth algebraic stack, which is locally of finite type.
We need the following parabolic generalization of ![]() $\mathscr {B}un_{\mathscr {G}}$. Let
$\mathscr {B}un_{\mathscr {G}}$. Let ![]() $\vec {p}=(p_1,\ldots, p_s)$ (
$\vec {p}=(p_1,\ldots, p_s)$ (![]() $s\geq 1$) be a set of distinct points in
$s\geq 1$) be a set of distinct points in ![]() $\bar {\Sigma }$. Label the points
$\bar {\Sigma }$. Label the points ![]() $\vec {p}$ by parabolic subgroups
$\vec {p}$ by parabolic subgroups ![]() $\vec {P}=(P_1,\ldots, P_s)$, where
$\vec {P}=(P_1,\ldots, P_s)$, where ![]() $P_i$ is a parabolic subgroup of
$P_i$ is a parabolic subgroup of ![]() $\mathscr {G}_{p_i}$. Via the isomorphism (135), we can think of
$\mathscr {G}_{p_i}$. Via the isomorphism (135), we can think of ![]() $P_i$ as a parabolic subgroup
$P_i$ as a parabolic subgroup ![]() $P_i^{q_i}$ of
$P_i^{q_i}$ of ![]() $G^{\Gamma _{q_i}}$ for any
$G^{\Gamma _{q_i}}$ for any ![]() $q_i\in \pi ^{-1}(p_i)$.
$q_i\in \pi ^{-1}(p_i)$.
A quasi-parabolic ![]() $\mathscr {G}$-torsor of type
$\mathscr {G}$-torsor of type ![]() $\vec {P}$ over
$\vec {P}$ over ![]() $(\bar {\Sigma }, \vec {p})$ is, by definition, a
$(\bar {\Sigma }, \vec {p})$ is, by definition, a ![]() $\mathscr {G}$-torsor
$\mathscr {G}$-torsor ![]() $\mathscr {E}$ over
$\mathscr {E}$ over ![]() $\bar {\Sigma }$ together with points
$\bar {\Sigma }$ together with points ![]() $\sigma _i$ in
$\sigma _i$ in ![]() $\mathscr {E}_{p_i}/P_i$. This gives rise to the stack:
$\mathscr {E}_{p_i}/P_i$. This gives rise to the stack: ![]() $R\leadsto$ the category of
$R\leadsto$ the category of ![]() $\mathscr {G}_R$-torsors
$\mathscr {G}_R$-torsors ![]() $\mathscr {E}_R$ over
$\mathscr {E}_R$ over ![]() $\bar {\Sigma }_R$ together with sections
$\bar {\Sigma }_R$ together with sections ![]() $\sigma _i$ of
$\sigma _i$ of ![]() $({\mathscr {E}_R}_{|_{\{p_i\}\times {\rm Spec} R }})/P_i\to {\rm Spec} R$. We denote this stack by
$({\mathscr {E}_R}_{|_{\{p_i\}\times {\rm Spec} R }})/P_i\to {\rm Spec} R$. We denote this stack by ![]() $\mathscr {P}arbun_{\mathscr {G}}=\mathscr {P}arbun_{\mathscr {G}}(\vec {P})$.
$\mathscr {P}arbun_{\mathscr {G}}=\mathscr {P}arbun_{\mathscr {G}}(\vec {P})$.
We recall the following uniformization theorem. It was proved by Heinloth [Reference HeinlothHei10, Theorem 4, Proposition 4, and Theorem 5] (and conjectured by Pappas and Rapoport [Reference Pappas and RapoportPR10]) for ![]() $\mathscr {B}un_{\mathscr {G}}$ (in fact, he proved a more general result). Its extension to
$\mathscr {B}un_{\mathscr {G}}$ (in fact, he proved a more general result). Its extension to ![]() $\mathscr {P}arbun_{\mathscr {G}}$ follows by the same proof. (Since
$\mathscr {P}arbun_{\mathscr {G}}$ follows by the same proof. (Since ![]() $G$ is simply connected, it is easy to see that so is the generic
$G$ is simply connected, it is easy to see that so is the generic ![]() $\mathscr {G}_{\mathbb {C}(\Sigma )}$.)
$\mathscr {G}_{\mathbb {C}(\Sigma )}$.)
Theorem 11.3 Take any ![]() $q_i\in \pi ^{-1}(p_i)$,
$q_i\in \pi ^{-1}(p_i)$, ![]() $q\in \Sigma \backslash \pi ^{-1}\{p_1, \ldots, p_s\}$ and any parabolic type
$q\in \Sigma \backslash \pi ^{-1}\{p_1, \ldots, p_s\}$ and any parabolic type ![]() $\vec {P}$ at the points
$\vec {P}$ at the points ![]() $\vec {p}$. Then, as stacks,
$\vec {p}$. Then, as stacks,
 \begin{equation} \mathscr{P}arbun_{\mathscr{G}}(\vec{P})\simeq \bigg[ G(\Sigma\backslash \Gamma\cdot q)^\Gamma \bigg\backslash \bigg(X^q \times \prod_{i=1}^s (G^{\Gamma_{q_i}} /P_i^{q_i} ) \bigg) \bigg], \end{equation}
\begin{equation} \mathscr{P}arbun_{\mathscr{G}}(\vec{P})\simeq \bigg[ G(\Sigma\backslash \Gamma\cdot q)^\Gamma \bigg\backslash \bigg(X^q \times \prod_{i=1}^s (G^{\Gamma_{q_i}} /P_i^{q_i} ) \bigg) \bigg], \end{equation}
where ![]() $G(\Sigma \backslash \Gamma \cdot q)^\Gamma$ acts on
$G(\Sigma \backslash \Gamma \cdot q)^\Gamma$ acts on ![]() $X^q$ via its restriction to
$X^q$ via its restriction to ![]() $\mathbb {D}_q^*$ and it acts on
$\mathbb {D}_q^*$ and it acts on ![]() $G^{\Gamma _{q_i}} /P_i^{q_i}$ via its evaluation at
$G^{\Gamma _{q_i}} /P_i^{q_i}$ via its evaluation at ![]() $q_i$. Here
$q_i$. Here ![]() $[ G(\Sigma \backslash \Gamma \cdot q)^\Gamma \big \backslash \big (X^q\times \prod _{i=1}^s (G^{\Gamma _{q_i}} /P_i^{q_i} ) \big ) ]$ denotes the quotient stack (cf. [Reference KumarKum22, Example C.18(b)]) obtained by taking the quotient of the projective ind-variety
$[ G(\Sigma \backslash \Gamma \cdot q)^\Gamma \big \backslash \big (X^q\times \prod _{i=1}^s (G^{\Gamma _{q_i}} /P_i^{q_i} ) \big ) ]$ denotes the quotient stack (cf. [Reference KumarKum22, Example C.18(b)]) obtained by taking the quotient of the projective ind-variety ![]() $X^q\times \prod _{i=1}^s (G^{\Gamma _{q_i}} /P_i^{q_i} )$ by the ind-group
$X^q\times \prod _{i=1}^s (G^{\Gamma _{q_i}} /P_i^{q_i} )$ by the ind-group ![]() $G(\Sigma \backslash \Gamma \cdot q)^\Gamma$.
$G(\Sigma \backslash \Gamma \cdot q)^\Gamma$.
Moreover, the projection ![]() $X^q\times \prod _{i=1}^s (G^{\Gamma _{q_i}} /P_i^{q_i} )\to \mathscr {P}arbun_{\mathscr {G}}(\vec {P})$ is locally trivial in the smooth topology.
$X^q\times \prod _{i=1}^s (G^{\Gamma _{q_i}} /P_i^{q_i} )\to \mathscr {P}arbun_{\mathscr {G}}(\vec {P})$ is locally trivial in the smooth topology.
Remark 11.4 Even though we will not use it, there is also an isomorphism of stacks:
 \[ \mathscr{P}arbun_{\mathscr{G}}(\vec{P})\simeq \bigg[G(\Sigma\backslash \Gamma\cdot \vec{q})^\Gamma \bigg \backslash \bigg(\prod_{i=1}^s ( X^{q_i}(P_i^{q_i}) ) \bigg) \bigg], \]
\[ \mathscr{P}arbun_{\mathscr{G}}(\vec{P})\simeq \bigg[G(\Sigma\backslash \Gamma\cdot \vec{q})^\Gamma \bigg \backslash \bigg(\prod_{i=1}^s ( X^{q_i}(P_i^{q_i}) ) \bigg) \bigg], \]
where ![]() $\Gamma \cdot \vec {q}:= \bigcup _{i=1}^s \Gamma \cdot q_i$ and
$\Gamma \cdot \vec {q}:= \bigcup _{i=1}^s \Gamma \cdot q_i$ and ![]() $X^{q_i}(P_i^{q_i})$ is the partial twisted affine flag variety which is, by definition,
$X^{q_i}(P_i^{q_i})$ is the partial twisted affine flag variety which is, by definition, ![]() $G(\mathbb {D}^\times _{q_i} )^{\Gamma _{q_i}} /\mathscr {P}_i$ and
$G(\mathbb {D}^\times _{q_i} )^{\Gamma _{q_i}} /\mathscr {P}_i$ and ![]() $\mathscr {P}_i$ is the inverse image of
$\mathscr {P}_i$ is the inverse image of ![]() $P_i^{q_i}$ under the surjective evaluation map
$P_i^{q_i}$ under the surjective evaluation map ![]() $G(\mathbb {D}_{q_i} )^{\Gamma _{q_i}} \to G^{\Gamma _{q_i}}$.
$G(\mathbb {D}_{q_i} )^{\Gamma _{q_i}} \to G^{\Gamma _{q_i}}$.
Corollary 11.5 The ind-group scheme ![]() $G(\Sigma \backslash \Gamma \cdot q)^{\Gamma }$ is reduced. Moreover, it is irreducible by Theorem 9.5.
$G(\Sigma \backslash \Gamma \cdot q)^{\Gamma }$ is reduced. Moreover, it is irreducible by Theorem 9.5.
Proof. We follow the same argument as in [Reference Laszlo and SorgerLS97, § 5]. Consider the projection
 \[ \beta: X^q\times \prod_{i=1}^s (G^{\Gamma_{q_i}} /P_i^{q_i} )\to \mathscr{P}arbun_{\mathscr{G}}(\vec{P}) . \]
\[ \beta: X^q\times \prod_{i=1}^s (G^{\Gamma_{q_i}} /P_i^{q_i} )\to \mathscr{P}arbun_{\mathscr{G}}(\vec{P}) . \]
By Theorem 11.3, there exists a neighborhood ![]() $U\to \mathscr {P}arbun_{\mathscr {G}}(\vec {P})$ in the smooth topology such that
$U\to \mathscr {P}arbun_{\mathscr {G}}(\vec {P})$ in the smooth topology such that ![]() $\beta ^*(U)\simeq U\times G(\Sigma \backslash \Gamma \cdot q)^{\Gamma }$. Since
$\beta ^*(U)\simeq U\times G(\Sigma \backslash \Gamma \cdot q)^{\Gamma }$. Since ![]() $X^q$ is reduced by Corollary 9.8 and, of course,
$X^q$ is reduced by Corollary 9.8 and, of course, ![]() $G^{\Gamma _{q_i}} /P_i^{q_i}$ are reduced, we get that
$G^{\Gamma _{q_i}} /P_i^{q_i}$ are reduced, we get that ![]() $G(\Sigma \backslash \Gamma \cdot q)^{\Gamma }$ is reduced.
$G(\Sigma \backslash \Gamma \cdot q)^{\Gamma }$ is reduced.
Definition 11.6 (Line bundles on  $\mathscr {P}arbun_{\mathscr {G}}$)
$\mathscr {P}arbun_{\mathscr {G}}$)
Let ![]() $\Xi :=G(\Sigma \backslash \Gamma \cdot q)^{\Gamma }$ and assume that
$\Xi :=G(\Sigma \backslash \Gamma \cdot q)^{\Gamma }$ and assume that ![]() $0\in D_{c, q}$. Recall (cf., e.g., [Reference Beauville and LaszloBL94, § 7.1]) that, by virtue of Theorem 11.3,
$0\in D_{c, q}$. Recall (cf., e.g., [Reference Beauville and LaszloBL94, § 7.1]) that, by virtue of Theorem 11.3,
 \begin{equation} {\rm Pic} \big(\mathscr{P}arbun_{\mathscr{G}}(\vec{P}) \big) \simeq {\rm Pic}^{\Xi} \bigg(X^q\times \prod_{i=1}^s (G^{\Gamma_{q_i}} /P_i^{q_i} ) \bigg). \end{equation}
\begin{equation} {\rm Pic} \big(\mathscr{P}arbun_{\mathscr{G}}(\vec{P}) \big) \simeq {\rm Pic}^{\Xi} \bigg(X^q\times \prod_{i=1}^s (G^{\Gamma_{q_i}} /P_i^{q_i} ) \bigg). \end{equation}
Moreover, from the see-saw principle (also see [Reference HartshorneHar77, Chap. III, Exercise 12.6]), since ![]() $X^q$ is ind-projective and
$X^q$ is ind-projective and ![]() ${\rm Pic}$ of each factor is discrete,
${\rm Pic}$ of each factor is discrete,
 \[ {\rm Pic} \bigg( X^q \times \prod_{i=1}^s (G^{\Gamma_{q_i}} /P_i^{q_i} )\bigg) \simeq {\rm Pic} ( X^q) \times \prod_{i=1}^s {\rm Pic} (G^{\Gamma_{q_i}} /P_i^{q_i} ). \]
\[ {\rm Pic} \bigg( X^q \times \prod_{i=1}^s (G^{\Gamma_{q_i}} /P_i^{q_i} )\bigg) \simeq {\rm Pic} ( X^q) \times \prod_{i=1}^s {\rm Pic} (G^{\Gamma_{q_i}} /P_i^{q_i} ). \]
Let us consider the following canonical homomorphism:
 \[ {\rm Pic}^{\Xi}( X^q) \times \prod_{i=1}^s {\rm Pic}^{\Xi} (G^{\Gamma_{q_i}} /P_i^{q_i} ) \to {\rm Pic}^{\Xi} \bigg( X^q\times \prod_{i=1}^s (G^{\Gamma_{q_i}} /P_i^{q_i} ) \bigg). \]
\[ {\rm Pic}^{\Xi}( X^q) \times \prod_{i=1}^s {\rm Pic}^{\Xi} (G^{\Gamma_{q_i}} /P_i^{q_i} ) \to {\rm Pic}^{\Xi} \bigg( X^q\times \prod_{i=1}^s (G^{\Gamma_{q_i}} /P_i^{q_i} ) \bigg). \]
Consider the morphism
where ![]() $v_+$ is a highest weight vector of
$v_+$ is a highest weight vector of ![]() $\mathscr {H}_c$. This factors through a morphism (via Theorem 10.7(1)):
$\mathscr {H}_c$. This factors through a morphism (via Theorem 10.7(1)):
Pulling back the dual of the tautological line bundle on ![]() $\mathbb {P}(\mathscr {H}_c )$, we get a
$\mathbb {P}(\mathscr {H}_c )$, we get a ![]() $\hat {\mathscr {G} }^q_c$-equivariant line bundle
$\hat {\mathscr {G} }^q_c$-equivariant line bundle ![]() $\mathfrak {L}^q_c$ on
$\mathfrak {L}^q_c$ on ![]() $X^q$ given by the character
$X^q$ given by the character
Observe that the canonical splitting of ![]() $G(\mathbb {D}_q)^{\Gamma _q}$ is taken for the central extension
$G(\mathbb {D}_q)^{\Gamma _q}$ is taken for the central extension ![]() $\hat {\mathscr {G} }^q_c$ corresponding to the central charge
$\hat {\mathscr {G} }^q_c$ corresponding to the central charge ![]() $c$.
$c$.
Now, if ![]() $c$ is a multiple of
$c$ is a multiple of ![]() $|\Gamma |$, the central extension
$|\Gamma |$, the central extension ![]() $\hat {\mathscr {G} }^q_c\to G(\mathbb {D}_q^\times )^\Gamma$ splits over
$\hat {\mathscr {G} }^q_c\to G(\mathbb {D}_q^\times )^\Gamma$ splits over ![]() $\Xi$. As in Theorem 10.7(2), take the canonical splitting. This provides a
$\Xi$. As in Theorem 10.7(2), take the canonical splitting. This provides a ![]() $\Xi$-equivariant structure on the line bundle
$\Xi$-equivariant structure on the line bundle ![]() $\mathfrak {L}^q_c$ over
$\mathfrak {L}^q_c$ over ![]() $X^q$.
$X^q$.
Similarly, for any ![]() $\lambda _i\in D_{c,q_i}$, the
$\lambda _i\in D_{c,q_i}$, the ![]() $\mathfrak {g}^{\Gamma _{q_i}}$-module
$\mathfrak {g}^{\Gamma _{q_i}}$-module ![]() $V(\lambda _i)$ with highest weight
$V(\lambda _i)$ with highest weight ![]() $\lambda _i$ integrates to a
$\lambda _i$ integrates to a ![]() $G^{\Gamma _{q_i}}$-module
$G^{\Gamma _{q_i}}$-module ![]() $V(\lambda _i)$ if
$V(\lambda _i)$ if ![]() $|\Gamma |$ divides
$|\Gamma |$ divides ![]() $c$ (cf. Proposition 10.9). Take the highest weight vector
$c$ (cf. Proposition 10.9). Take the highest weight vector ![]() $v_+\in \mathscr {H}(\lambda _i)$ which is an (irreducible) integrable highest weight
$v_+\in \mathscr {H}(\lambda _i)$ which is an (irreducible) integrable highest weight ![]() $\hat {L}(\mathfrak {g}, \Gamma _{q_i})=\hat {\mathfrak {g}}_{q_i}$-module with highest weight
$\hat {L}(\mathfrak {g}, \Gamma _{q_i})=\hat {\mathfrak {g}}_{q_i}$-module with highest weight ![]() $\lambda _i$ and central charge
$\lambda _i$ and central charge ![]() $c$. Then,
$c$. Then, ![]() $V(\lambda _i)$ is the
$V(\lambda _i)$ is the ![]() $G^{\Gamma _{q_i}}$-submodule of
$G^{\Gamma _{q_i}}$-submodule of ![]() $\mathscr {H}(\lambda _i)$ generated by
$\mathscr {H}(\lambda _i)$ generated by ![]() $v_+$. Let
$v_+$. Let ![]() $P_i^{q_i}$ be the parabolic subgroup of
$P_i^{q_i}$ be the parabolic subgroup of ![]() $G^{\Gamma _{q_i}}$ which stabilizes the line
$G^{\Gamma _{q_i}}$ which stabilizes the line ![]() $\mathbb {C}v_+$. Define the
$\mathbb {C}v_+$. Define the ![]() $G^{\Gamma _{q_i}}$-equivariant ample line bundle
$G^{\Gamma _{q_i}}$-equivariant ample line bundle
Then, ![]() $\mathscr {L}^{q_i}(\lambda _i)$ is
$\mathscr {L}^{q_i}(\lambda _i)$ is ![]() $\Xi$-equivariant line bundle by virtue of the following evaluation map at
$\Xi$-equivariant line bundle by virtue of the following evaluation map at ![]() $q_i$:
$q_i$:
Thus, we obtain the ![]() $\Xi$-equivariant line bundle
$\Xi$-equivariant line bundle
over ![]() $X^q\times \prod _{i=1}^s (G^{\Gamma _{q_i}}/P_i^{q_i})$, for any
$X^q\times \prod _{i=1}^s (G^{\Gamma _{q_i}}/P_i^{q_i})$, for any ![]() $c$ divisible by
$c$ divisible by ![]() $|\Gamma |$ and
$|\Gamma |$ and ![]() $\lambda _i\in D_{c, q_i}$.
$\lambda _i\in D_{c, q_i}$.
Thus, under the isomorphism (139), we get the corresponding line bundle ![]() $\mathfrak {L}(c; \vec {\lambda })$ over the stack
$\mathfrak {L}(c; \vec {\lambda })$ over the stack ![]() $\mathscr {P}arbun_{\mathscr {G}}(\vec {P})$, where
$\mathscr {P}arbun_{\mathscr {G}}(\vec {P})$, where ![]() $\vec {P}=(P^{q_1}_1,\ldots, P^{q_i}_s)$ and
$\vec {P}=(P^{q_1}_1,\ldots, P^{q_i}_s)$ and ![]() $P_i^{q_i}$ is the stabilizer in
$P_i^{q_i}$ is the stabilizer in ![]() $G^{\Gamma _{q_i}}$ of the line
$G^{\Gamma _{q_i}}$ of the line ![]() $\mathbb {C}\cdot v_+\subset \mathscr {H}(\lambda _i)$.
$\mathbb {C}\cdot v_+\subset \mathscr {H}(\lambda _i)$.
12. Identification of twisted conformal blocks with the space of global sections of line bundles on moduli stack
In this final section, we establish the identification of twisted conformal blocks and generalized theta functions on the moduli stack ![]() $\mathscr {P}arbun_{\mathscr {G}}$.
$\mathscr {P}arbun_{\mathscr {G}}$.
We continue to have the same assumptions on ![]() $G$,
$G$, ![]() $\Gamma$,
$\Gamma$, ![]() $\Sigma$, and
$\Sigma$, and ![]() $\phi : \Gamma \to {\rm Aut}(\mathfrak {g})$ as in the beginning of § 9. Let
$\phi : \Gamma \to {\rm Aut}(\mathfrak {g})$ as in the beginning of § 9. Let ![]() $\vec {q}=(q_1,\ldots, q_s)$ (
$\vec {q}=(q_1,\ldots, q_s)$ (![]() $s \geq 1$) be marked points on
$s \geq 1$) be marked points on ![]() $\Sigma$ with distinct
$\Sigma$ with distinct ![]() $\Gamma$-orbits and let
$\Gamma$-orbits and let ![]() $\vec {\lambda }=(\lambda _1,\ldots, \lambda _s)$ be weights with
$\vec {\lambda }=(\lambda _1,\ldots, \lambda _s)$ be weights with ![]() $\lambda _i\in D_{c,q_i}$ attached to the points
$\lambda _i\in D_{c,q_i}$ attached to the points ![]() $q_i$. Let
$q_i$. Let ![]() $P^{q_i}_i$ be the stabilizer of the line
$P^{q_i}_i$ be the stabilizer of the line ![]() $\mathbb {C}v_+\subset \mathscr {H}(\lambda _i)$ in
$\mathbb {C}v_+\subset \mathscr {H}(\lambda _i)$ in ![]() $G^{\Gamma _{q_i}}$.
$G^{\Gamma _{q_i}}$.
Recall the definition of the moduli stack ![]() $\mathscr {P}arbun_{\mathscr {G}}(\vec {P})$ of quasi-parabolic
$\mathscr {P}arbun_{\mathscr {G}}(\vec {P})$ of quasi-parabolic ![]() $\mathscr {G}$-torsors over
$\mathscr {G}$-torsors over ![]() $(\bar {\Sigma }, \vec {p})$ of type
$(\bar {\Sigma }, \vec {p})$ of type ![]() $\vec {P}=(P_1^{q_1}, \ldots, P_s^{q_s})$ from Definition 11.2, where
$\vec {P}=(P_1^{q_1}, \ldots, P_s^{q_s})$ from Definition 11.2, where ![]() $\vec {p}=(\pi (q_1), \ldots, \pi (q_s))$. In addition, recall from Definition 11.6 the definition of the line bundle
$\vec {p}=(\pi (q_1), \ldots, \pi (q_s))$. In addition, recall from Definition 11.6 the definition of the line bundle ![]() $\mathfrak {L}^q_c$ over
$\mathfrak {L}^q_c$ over ![]() $X^q$ for any
$X^q$ for any ![]() $c$ such that
$c$ such that ![]() $0\in D_{c,q}$, and any
$0\in D_{c,q}$, and any ![]() $q\in \Sigma \backslash \bigcup _{i=1}^{s}\Gamma \cdot q_i$ and the definition of the ample homogeneous line bundle
$q\in \Sigma \backslash \bigcup _{i=1}^{s}\Gamma \cdot q_i$ and the definition of the ample homogeneous line bundle ![]() $\mathscr {L}^{q_i}(\lambda _i)$ over the flag variety
$\mathscr {L}^{q_i}(\lambda _i)$ over the flag variety ![]() $G^{\Gamma _{q_i}}/P_i^{q_i}$. When
$G^{\Gamma _{q_i}}/P_i^{q_i}$. When ![]() $|\Gamma |$ divides
$|\Gamma |$ divides ![]() $c$, these line bundles give rise to a line bundle
$c$, these line bundles give rise to a line bundle ![]() $\mathfrak {L}(c;\vec {\lambda })$ over the stack
$\mathfrak {L}(c;\vec {\lambda })$ over the stack ![]() $\mathscr {P}arbun_{\mathscr {G}}(\vec {P})$ (cf. Definition 11.6).
$\mathscr {P}arbun_{\mathscr {G}}(\vec {P})$ (cf. Definition 11.6).
The following result confirms a conjecture by Pappas and Rapoport [Reference Pappas and RapoportPR10, Conjecture 3.7] in the case of the parahoric Bruhat–Tits group schemes considered in our paper.
Theorem 12.1 Assume that ![]() $|\Gamma |$ divides
$|\Gamma |$ divides ![]() $c$ and
$c$ and ![]() $\Gamma$ stabilizes a Borel subgroup of
$\Gamma$ stabilizes a Borel subgroup of ![]() $G$. Then, there is a canonical isomorphism:
$G$. Then, there is a canonical isomorphism:
where ![]() $\mathscr {V}_{\Sigma, \Gamma, \phi }(\vec {p}, \vec {\lambda })^{{\dagger}}$ is the space of (twisted) vacua (cf. identity (17)).
$\mathscr {V}_{\Sigma, \Gamma, \phi }(\vec {p}, \vec {\lambda })^{{\dagger}}$ is the space of (twisted) vacua (cf. identity (17)).
Proof. From the uniformization theorem (Theorem 11.3), there is an isomorphism of stacks:
 \[ \mathscr{P}arbun_{\mathscr{G}}(\vec{P})\simeq \bigg[ G(\Sigma\backslash \Gamma\cdot q)^\Gamma \bigg \backslash \bigg(X^q \times \prod_{i=1}^s (G^{\Gamma_{q_i}} /P_i^{q_i} ) \bigg) \bigg] . \]
\[ \mathscr{P}arbun_{\mathscr{G}}(\vec{P})\simeq \bigg[ G(\Sigma\backslash \Gamma\cdot q)^\Gamma \bigg \backslash \bigg(X^q \times \prod_{i=1}^s (G^{\Gamma_{q_i}} /P_i^{q_i} ) \bigg) \bigg] . \]
Moreover, by definition, the line bundle ![]() $\mathfrak {L}(c,\vec {\lambda })$ over
$\mathfrak {L}(c,\vec {\lambda })$ over ![]() $\mathscr {P}arbun_{\mathscr {G}}(\vec {P})$ is the descent of the line bundle
$\mathscr {P}arbun_{\mathscr {G}}(\vec {P})$ is the descent of the line bundle
over ![]() $X^q\times \prod _{i=1}^s (G^{\Gamma _{q_i}} /P_i^{q_i} )$ (Definition 11.6). Thus, we have the following isomorphisms:
$X^q\times \prod _{i=1}^s (G^{\Gamma _{q_i}} /P_i^{q_i} )$ (Definition 11.6). Thus, we have the following isomorphisms:
 \begin{align*} H^0( \mathscr{P}arbun_{\mathscr{G}}(\vec{P}), \mathfrak{L}(c, \vec{\lambda}) ) &\simeq H^0 \bigg( X^q\times \prod_{i=1}^s (G^{\Gamma_{q_i}} /P_i^{q_i} ), \mathfrak{L}^q_c \boxtimes \mathscr{L}^{q_1}(\lambda_1) \boxtimes \cdots \boxtimes \mathscr{L}^{q_s}(\lambda_s) \bigg)^{G(\Sigma\backslash \Gamma\cdot q)^\Gamma}\\ &\simeq \big(\mathscr{H}_c^*\otimes V(\lambda_1)^*\otimes \cdots \otimes V(\lambda_s)^* \big)^{ G(\Sigma\backslash \Gamma\cdot q)^\Gamma }\\ &\simeq \big(\mathscr{H}_c^*\otimes V(\lambda_1)^*\otimes \cdots \otimes V(\lambda_s)^* \big)^{ \mathfrak{g}(\Sigma\backslash \Gamma\cdot q)^\Gamma }\\ &\simeq \mathscr{V}_{\Sigma, \Gamma, \phi}(\vec{p}, \vec{\lambda} )^{{{\dagger}}}, \end{align*}
\begin{align*} H^0( \mathscr{P}arbun_{\mathscr{G}}(\vec{P}), \mathfrak{L}(c, \vec{\lambda}) ) &\simeq H^0 \bigg( X^q\times \prod_{i=1}^s (G^{\Gamma_{q_i}} /P_i^{q_i} ), \mathfrak{L}^q_c \boxtimes \mathscr{L}^{q_1}(\lambda_1) \boxtimes \cdots \boxtimes \mathscr{L}^{q_s}(\lambda_s) \bigg)^{G(\Sigma\backslash \Gamma\cdot q)^\Gamma}\\ &\simeq \big(\mathscr{H}_c^*\otimes V(\lambda_1)^*\otimes \cdots \otimes V(\lambda_s)^* \big)^{ G(\Sigma\backslash \Gamma\cdot q)^\Gamma }\\ &\simeq \big(\mathscr{H}_c^*\otimes V(\lambda_1)^*\otimes \cdots \otimes V(\lambda_s)^* \big)^{ \mathfrak{g}(\Sigma\backslash \Gamma\cdot q)^\Gamma }\\ &\simeq \mathscr{V}_{\Sigma, \Gamma, \phi}(\vec{p}, \vec{\lambda} )^{{{\dagger}}}, \end{align*}
where the first isomorphism follows from [Reference Beauville and LaszloBL94, Lemma 7.2] (also see [Reference KumarKum22, Proposition C.23]); the second isomorphism follows from the standard Borel–Weil theorem and its generalization for the Kac–Moody case due to Kumar as well as Mathieu [Reference KumarKum02, Corollary 8.3.12]; the third isomorphism follows from [Reference Beauville and LaszloBL94, Proposition 7.4] since ![]() $G(\Sigma \backslash \Gamma \cdot q)^\Gamma$ is reduced and irreducible (Corollary 11.5) and
$G(\Sigma \backslash \Gamma \cdot q)^\Gamma$ is reduced and irreducible (Corollary 11.5) and ![]() $X^q$ is reduced and irreducible by Corollary 9.8; and the last isomorphism follows from propagation of vacua (Corollary 4.5(b)). This finishes the proof of the theorem.
$X^q$ is reduced and irreducible by Corollary 9.8; and the last isomorphism follows from propagation of vacua (Corollary 4.5(b)). This finishes the proof of the theorem.
Remark 12.2 (a) If we drop the assumption that
![]() $(*)$
$(*)$ ![]() $\Gamma$ stabilizes a Borel subgroup of
$\Gamma$ stabilizes a Borel subgroup of ![]() $G$,
$G$,
we still have the isomorphism:
since Theorem 11.3 remains valid without the assumption (![]() $*$). Since our Propagation Theorem (Corollary 4.5) requires the assumption (
$*$). Since our Propagation Theorem (Corollary 4.5) requires the assumption (![]() $*$), the space on the right side of (140) is not known to be isomorphic with
$*$), the space on the right side of (140) is not known to be isomorphic with ![]() $\mathscr {V}_{\Sigma, \Gamma, \phi }(\vec {p}, \vec {\lambda } )^{{{\dagger}} }$ in general.
$\mathscr {V}_{\Sigma, \Gamma, \phi }(\vec {p}, \vec {\lambda } )^{{{\dagger}} }$ in general.
(b) The condition ‘![]() $|\Gamma |$ divides
$|\Gamma |$ divides ![]() $c$’ cannot, in general, be dropped since for
$c$’ cannot, in general, be dropped since for ![]() $\lambda _i\in D_{c, q_i}$ to be a dominant integral weight of
$\lambda _i\in D_{c, q_i}$ to be a dominant integral weight of ![]() $\mathfrak {g}^{\Gamma _{q_i}}$ imposes some divisibility condition on
$\mathfrak {g}^{\Gamma _{q_i}}$ imposes some divisibility condition on ![]() $c$ with respect to
$c$ with respect to ![]() $\Gamma _{q_i}$ (cf. Lemma 2.1 and Proposition 10.9).
$\Gamma _{q_i}$ (cf. Lemma 2.1 and Proposition 10.9).
In addition, Heinloth's example [Reference HeinlothHei10, Remark 19(4)] shows that the line bundle
does not, in general, descend to the moduli stack ![]() $\mathscr {P}arbun_{\mathscr {G}}(\vec {P})$ for an arbitrary
$\mathscr {P}arbun_{\mathscr {G}}(\vec {P})$ for an arbitrary ![]() $c$.
$c$.
Acknowledgements
We would like to thank Prakash Belkale, Joseph Bernstein, Chiara Damiolini, Zhiwei Yun and Xinwen Zhu for some helpful conversations. We also would like to thank Matthieu Romagny for answering some questions on stable compactification of Hurwitz stacks. We thank the referee for carefully reading the manuscript and providing various suggestions for improvement. J. Hong is partially supported by the Simons Foundation Collaboration Grant 524406 and NSF grant DMS-2001365; S. Kumar is partially supported by the NSF grant DMS-1501094.
Conflicts of Interest
None.