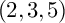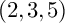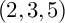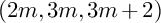1 Introduction
We work in the holomorphic setting. All manifolds and maps are holomorphic, unless stated otherwise. Open subsets refer to Euclidean topology. A Zariski-open subset of a complex manifold is the complement of a closed analytic subset. We use the following terminology on distributions.
Definition 1.1. A distribution on a complex manifold M is a vector subbundle
![]() $D \subset TM$
of the tangent bundle of M.
$D \subset TM$
of the tangent bundle of M.
-
(i) Lie brackets of local sections of D give a homomorphism
 $$ \begin{align*} \mathrm{Levi}^D: \wedge^2 D \to TM/D, \end{align*} $$
$$ \begin{align*} \mathrm{Levi}^D: \wedge^2 D \to TM/D, \end{align*} $$
called the Levi tensor of D.
-
(ii) There is a sequence of vector bundles, called the weak derived system of D,
 $$ \begin{align*}D = \partial^{(0)}D \subset \partial D = \partial^{(1)}D \subset \partial^{(2)} D \subset \cdots \subset \partial^{(d)} D = \partial^{(d+1)} D\end{align*} $$
$$ \begin{align*}D = \partial^{(0)}D \subset \partial D = \partial^{(1)}D \subset \partial^{(2)} D \subset \cdots \subset \partial^{(d)} D = \partial^{(d+1)} D\end{align*} $$
defined on a Zariski-open subset of M such that their associated sheaves satisfy
 $$ \begin{align*}{\mathcal O}(\partial^{(i+1)}D) = [ {\mathcal O}(\partial^{(i)}D), {\mathcal O}(D)] + {\mathcal O}(\partial^{(i)} D) \end{align*} $$
$$ \begin{align*}{\mathcal O}(\partial^{(i+1)}D) = [ {\mathcal O}(\partial^{(i)}D), {\mathcal O}(D)] + {\mathcal O}(\partial^{(i)} D) \end{align*} $$
for each
 $0 \leq i \leq d+1.$
We say that D is regular at
$0 \leq i \leq d+1.$
We say that D is regular at
 $x \in M$
, if the weak derived system of D is a sequence of vector bundles in a neighborhood of x.
$x \in M$
, if the weak derived system of D is a sequence of vector bundles in a neighborhood of x. -
(iii) The sequence of integers
 $$ \begin{align*}(\mathrm{rank}(D), \mathrm{rank}(\partial D), \mathrm{ rank}(\partial^{(2)}D), \ldots, \mathrm{rank}(\partial^{(d)}D))\end{align*} $$
$$ \begin{align*}(\mathrm{rank}(D), \mathrm{rank}(\partial D), \mathrm{ rank}(\partial^{(2)}D), \ldots, \mathrm{rank}(\partial^{(d)}D))\end{align*} $$
is called the small growth vector of D.
-
(iv) When D is regular at
 $x \in M$
, the graded vector space
$x \in M$
, the graded vector space  $$ \begin{align*}\mathrm{symb}_x(D) := \oplus_{i=1}^d (\partial^{(i)}D)_x / (\partial^{(i-1)}D)_x\end{align*} $$
$$ \begin{align*}\mathrm{symb}_x(D) := \oplus_{i=1}^d (\partial^{(i)}D)_x / (\partial^{(i-1)}D)_x\end{align*} $$
has a natural structure of a nilpotent graded Lie algebra induced by Lie brackets of local sections. It is called the symbol algebra of D at x.
In the celebrated paper [Reference CartanC], Cartan studied distributions on five-dimensional manifolds with the small growth vector
![]() $(2,3,5)$
, commonly called
$(2,3,5)$
, commonly called
![]() $(2,3,5)$
-distributions. Cartan investigated the local equivalence problem for
$(2,3,5)$
-distributions. Cartan investigated the local equivalence problem for
![]() $(2,3,5)$
-distributions and many mathematicians have developed this study further (see the references in [Reference Ishikawa, Kitagawa, Tsuchida and YukunoIKTY]). A remarkable development in 1990s was the theory of abnormal extremals of
$(2,3,5)$
-distributions and many mathematicians have developed this study further (see the references in [Reference Ishikawa, Kitagawa, Tsuchida and YukunoIKTY]). A remarkable development in 1990s was the theory of abnormal extremals of
![]() $(2,3,5)$
-distributions, originated from geometric control theory (see [Reference Bryant and HsuBH] and [Reference ZelenkoZ] and the references therein). It associates a certain contact manifold of dimension 5 to each
$(2,3,5)$
-distributions, originated from geometric control theory (see [Reference Bryant and HsuBH] and [Reference ZelenkoZ] and the references therein). It associates a certain contact manifold of dimension 5 to each
![]() $(2,3,5)$
-distribution. By reinterpreting this result from the viewpoint of complex geometry, the following one-to-one correspondence has been discovered in Theorems 5.10 and 5.12 of [Reference Hwang and LiHL], where small growth vector is abbreviated to s.g.v.:
$(2,3,5)$
-distribution. By reinterpreting this result from the viewpoint of complex geometry, the following one-to-one correspondence has been discovered in Theorems 5.10 and 5.12 of [Reference Hwang and LiHL], where small growth vector is abbreviated to s.g.v.:
 $$ \begin{align*} \left\{ \begin{array}{cc} \mbox{distributions of} \\ \mbox{s.g.v.} (2,3,5) \end{array} \right\} \stackrel{(\textsf{Corr.}1)}{\Longleftrightarrow} \left\{ \begin{array}{cc} \mbox{nondegenerate lines on contact} \\ \mbox{manifolds of dimension 5} \end{array} \right\}. \end{align*} $$
$$ \begin{align*} \left\{ \begin{array}{cc} \mbox{distributions of} \\ \mbox{s.g.v.} (2,3,5) \end{array} \right\} \stackrel{(\textsf{Corr.}1)}{\Longleftrightarrow} \left\{ \begin{array}{cc} \mbox{nondegenerate lines on contact} \\ \mbox{manifolds of dimension 5} \end{array} \right\}. \end{align*} $$
See Definition 3.8 for the precise meaning of the right-hand side. Note that nondegenerate lines are called “contact unbendable rational curves of Cartan type” in Definition 5.8 of [Reference Hwang and LiHL]. A local version of this correspondence, where the right-hand side is replaced by Lagrangian cone structures on contact manifolds of dimension 5 satisfying certain conditions, is given in Theorem 3.1 of [Reference Ishikawa, Kitagawa, Tsuchida and YukunoIKTY]. From the viewpoint of [Reference Hwang and LiHL], the Lagrangian cone structure is a local description of the VMRT of the nondegenerate lines (see Lemma 3.3).
In the current paper, we generalize this correspondence to higher dimensions as the following one-to-one correspondence:
 $$ \begin{align*} \left\{ \begin{array}{cc} \mbox{some distributions of} \\ \mbox{s.g.v.} (2m, 3m, 3m+2) \end{array} \right\} \stackrel{(\textsf{Corr.}m)}{\Longleftrightarrow} \left\{ \begin{array}{cc} \mbox{nondegenerate lines on contact} \\ \mbox{manifolds of dimension } 2m+3 \end{array} \right\}. \end{align*} $$
$$ \begin{align*} \left\{ \begin{array}{cc} \mbox{some distributions of} \\ \mbox{s.g.v.} (2m, 3m, 3m+2) \end{array} \right\} \stackrel{(\textsf{Corr.}m)}{\Longleftrightarrow} \left\{ \begin{array}{cc} \mbox{nondegenerate lines on contact} \\ \mbox{manifolds of dimension } 2m+3 \end{array} \right\}. \end{align*} $$
The major difference from the case
![]() $m=1$
is that the distributions on the left-hand side are not determined by the small growth vector alone: their symbol algebras must be of the form
$m=1$
is that the distributions on the left-hand side are not determined by the small growth vector alone: their symbol algebras must be of the form
![]() ${\mathfrak g}_+(F)$
described in Definition 3.14, where F is a nondegenerate cubic form on a vector space of dimension m. For simplicity, we call distributions on the left-hand side
${\mathfrak g}_+(F)$
described in Definition 3.14, where F is a nondegenerate cubic form on a vector space of dimension m. For simplicity, we call distributions on the left-hand side
![]() ${\mathfrak g}_+$
-distributions. Our main results are Theorems 3.15 and 4.4, which give a precise statement of the correspondence (Corr. m). When
${\mathfrak g}_+$
-distributions. Our main results are Theorems 3.15 and 4.4, which give a precise statement of the correspondence (Corr. m). When
![]() $m=1$
, the Lie algebra
$m=1$
, the Lie algebra
![]() ${\mathfrak g}_+(F)$
is determined by the small growth vector because all nondegenerate cubic forms on a vector space of dimension 1 are isomorphic. Thus,
${\mathfrak g}_+(F)$
is determined by the small growth vector because all nondegenerate cubic forms on a vector space of dimension 1 are isomorphic. Thus,
![]() ${\mathfrak g}_+$
-distributions in dimension
${\mathfrak g}_+$
-distributions in dimension
![]() $5$
are just
$5$
are just
![]() $(2,3,5)$
-distributions. There is more than one isomorphism type of nondegenerate cubic forms when
$(2,3,5)$
-distributions. There is more than one isomorphism type of nondegenerate cubic forms when
![]() $m \geq 2.$
So when
$m \geq 2.$
So when
![]() $m \geq 2$
, the small growth vector alone cannot determine the type of our distributions. As a matter of fact, when
$m \geq 2$
, the small growth vector alone cannot determine the type of our distributions. As a matter of fact, when
![]() $m \geq 3$
, there are nontrivial moduli of nondegenerate cubic forms and the isomorphism types of symbol algebras of a
$m \geq 3$
, there are nontrivial moduli of nondegenerate cubic forms and the isomorphism types of symbol algebras of a
![]() ${\mathfrak g}_+$
-distribution may vary from point to point. A classical example of (Corr. m) is the following.
${\mathfrak g}_+$
-distribution may vary from point to point. A classical example of (Corr. m) is the following.
Example 1.2. Let
![]() ${\mathfrak g}$
be a simple Lie algebra, and let G be a complex Lie group with Lie algebra
${\mathfrak g}$
be a simple Lie algebra, and let G be a complex Lie group with Lie algebra
![]() ${\mathfrak g}$
. Let
${\mathfrak g}$
. Let
![]() $X^{{\mathfrak g}}$
be the adjoint variety of
$X^{{\mathfrak g}}$
be the adjoint variety of
![]() ${\mathfrak g}$
, namely, the highest weight orbit of the coadjoint representation on
${\mathfrak g}$
, namely, the highest weight orbit of the coadjoint representation on
![]() ${\mathbb P} {\mathfrak g}^{\vee }$
, and let
${\mathbb P} {\mathfrak g}^{\vee }$
, and let
![]() $2m+3$
be the dimension of
$2m+3$
be the dimension of
![]() $X^{{\mathfrak g}}$
. The variety
$X^{{\mathfrak g}}$
. The variety
![]() $X^{{\mathfrak g}}$
has a natural G-invariant contact structure and is covered by nondegenerate lines. The space of lines on
$X^{{\mathfrak g}}$
has a natural G-invariant contact structure and is covered by nondegenerate lines. The space of lines on
![]() $X^{{\mathfrak g}} \subset {\mathbb P} {\mathfrak g}^{\vee }$
is a rational homogeneous space
$X^{{\mathfrak g}} \subset {\mathbb P} {\mathfrak g}^{\vee }$
is a rational homogeneous space
![]() $Y^{{\mathfrak g}}= G/P$
for some parabolic subgroup
$Y^{{\mathfrak g}}= G/P$
for some parabolic subgroup
![]() $P \subset G$
. If
$P \subset G$
. If
![]() ${\mathfrak g}$
is not of type A or C, there exists a G-invariant distribution
${\mathfrak g}$
is not of type A or C, there exists a G-invariant distribution
![]() $D^{{\mathfrak g}} \subset TY^{{\mathfrak g}}$
of rank
$D^{{\mathfrak g}} \subset TY^{{\mathfrak g}}$
of rank
![]() $2m$
whose symbol algebras are isomorphic to
$2m$
whose symbol algebras are isomorphic to
![]() ${\mathfrak g}_+(F)$
for a homaloidal EKP cubic F (using the terminology in Theorem 3 of [Reference DolgachevD]), which is the cubic form whose associated cubic hypersurface is either
${\mathfrak g}_+(F)$
for a homaloidal EKP cubic F (using the terminology in Theorem 3 of [Reference DolgachevD]), which is the cubic form whose associated cubic hypersurface is either
-
(i) the union of a hyperplane and a quadratic cone with one isolated singular point outside the hyperplane, or
-
(ii) the secant variety of one of the four Severi varieties.
The correspondence (Corr. m) in this case is
 $$ \begin{align*} \begin{array}{cc} \mbox{distribution } D^{{\mathfrak g}} \text{ on } Y^{{\mathfrak g}} \text{ of } \\ \mbox{s.g.v.} (2m, 3m, 3m+2) \end{array} \Longleftrightarrow \begin{array}{cc} \mbox{ lines on the contact manifold } \\ X^{{\mathfrak g}} \mbox{ of dimension } 2m+3.\end{array} \end{align*} $$
$$ \begin{align*} \begin{array}{cc} \mbox{distribution } D^{{\mathfrak g}} \text{ on } Y^{{\mathfrak g}} \text{ of } \\ \mbox{s.g.v.} (2m, 3m, 3m+2) \end{array} \Longleftrightarrow \begin{array}{cc} \mbox{ lines on the contact manifold } \\ X^{{\mathfrak g}} \mbox{ of dimension } 2m+3.\end{array} \end{align*} $$
One interesting consequence of (Corr.
m) is that there are many examples of holomorphic contact manifolds covered by nondegenerate lines, which is already nontrivial when
![]() $m=1$
. Another interesting aspect of (Corr.
m) is its potential application in Riemannian geometry. A well-known conjecture in complex geometry, which is equivalent to the LeBrun–Salamon conjecture (page 110 of [Reference LeBrun and SalaomonLS]) on quaternionic-Kähler manifolds, is that a Fano contact manifold whose automorphism group is reductive is biholomorphic to an adjoint variety in Example 1.2. There is an approach to this conjecture using lines on Fano contact manifolds of Picard number 1 (see, e.g., [Reference Buczynski, Kapustka and KapustkaBKK], [Reference KebekusK1], [Reference KebekusK2]). The lines in this case are expected to be nondegenerate (see Remark 3.9) and we have the associated
$m=1$
. Another interesting aspect of (Corr.
m) is its potential application in Riemannian geometry. A well-known conjecture in complex geometry, which is equivalent to the LeBrun–Salamon conjecture (page 110 of [Reference LeBrun and SalaomonLS]) on quaternionic-Kähler manifolds, is that a Fano contact manifold whose automorphism group is reductive is biholomorphic to an adjoint variety in Example 1.2. There is an approach to this conjecture using lines on Fano contact manifolds of Picard number 1 (see, e.g., [Reference Buczynski, Kapustka and KapustkaBKK], [Reference KebekusK1], [Reference KebekusK2]). The lines in this case are expected to be nondegenerate (see Remark 3.9) and we have the associated
![]() ${\mathfrak g}_+$
-distributions via (Corr.
m). We believe that it is important to understand the geometry of these distributions for this approach to the LeBrun–Salamon conjecture. Note that, if the cubic forms are homaloidal EKP cubics, it is already proved that the Fano contact manifold is an adjoint variety (by Main Theorem in §2 of [Reference MokM]).
${\mathfrak g}_+$
-distributions via (Corr.
m). We believe that it is important to understand the geometry of these distributions for this approach to the LeBrun–Salamon conjecture. Note that, if the cubic forms are homaloidal EKP cubics, it is already proved that the Fano contact manifold is an adjoint variety (by Main Theorem in §2 of [Reference MokM]).
Let us discuss briefly the content of the paper and the methods employed. The key ingredients in establishing (Corr.
m) come from deformation theory of rational curves, in particular, the theory of VMRT, some standard results of which are recalled in §2. Section 3 discusses how to go from the right-hand side to the left-hand side of (Corr.
m). The proof of the main result, Theorem 3.15, is much more involved than the proof in the case of
![]() $m=1$
, because the structure of the symbol algebras of the distributions is more intricate in higher dimensions. Its proof uses some special features of deformation theory of rational curves on contact manifolds. Section 4 discusses how to go from the left-hand side to the right-hand side of (Corr.
m). The proof of the main result, Theorem 4.4, is a generalization of that of Theorem 5.10 in [Reference Hwang and LiHL] to higher dimensions and the idea has originated from [Reference ZelenkoZ].
$m=1$
, because the structure of the symbol algebras of the distributions is more intricate in higher dimensions. Its proof uses some special features of deformation theory of rational curves on contact manifolds. Section 4 discusses how to go from the left-hand side to the right-hand side of (Corr.
m). The proof of the main result, Theorem 4.4, is a generalization of that of Theorem 5.10 in [Reference Hwang and LiHL] to higher dimensions and the idea has originated from [Reference ZelenkoZ].
2 Unbendable rational curves and VMRT
Definition 2.1. Let X be a complex manifold of dimension n, and let
![]() $\mathrm {Douady}(X)$
be its Douady space parameterizing all compact analytic subspaces of X.
$\mathrm {Douady}(X)$
be its Douady space parameterizing all compact analytic subspaces of X.
-
(i) A smooth rational curve
 ${\mathbb P}^1 \cong C \subset X$
is unbendable if its normal bundle
${\mathbb P}^1 \cong C \subset X$
is unbendable if its normal bundle
 $N_C$
is isomorphic to
$N_C$
is isomorphic to
 ${\mathcal O}(1)^{\oplus p} \oplus {\mathcal O}^{\oplus (n-1-p)}$
for some nonnegative integer
${\mathcal O}(1)^{\oplus p} \oplus {\mathcal O}^{\oplus (n-1-p)}$
for some nonnegative integer
 $p \leq n-1$
. Consequently,
$p \leq n-1$
. Consequently,  $$ \begin{align*}TX|_C \cong {\mathcal O}(2) \oplus {\mathcal O}(1)^{\oplus p} \oplus {\mathcal O}^{\oplus(n-1-p)}\end{align*} $$
$$ \begin{align*}TX|_C \cong {\mathcal O}(2) \oplus {\mathcal O}(1)^{\oplus p} \oplus {\mathcal O}^{\oplus(n-1-p)}\end{align*} $$
with
 $TC \subset TX|_C$
corresponding to
$TC \subset TX|_C$
corresponding to
 ${\mathcal O}(2)$
. In this case, we denote by
${\mathcal O}(2)$
. In this case, we denote by
 $N_C^+$
(resp.
$N_C^+$
(resp.
 $TX|_C^+$
) the subbundle of
$TX|_C^+$
) the subbundle of
 $N_C$
(resp.
$N_C$
(resp.
 $TX|_C$
) corresponding to
$TX|_C$
) corresponding to
 ${\mathcal O}(1)^{\oplus p}$
(resp.
${\mathcal O}(1)^{\oplus p}$
(resp.
 ${\mathcal O}(2) \oplus {\mathcal O}(1)^{\oplus p}$
).
${\mathcal O}(2) \oplus {\mathcal O}(1)^{\oplus p}$
). -
(ii) Let
 $\mathrm {URC}(X)$
be the subset of
$\mathrm {URC}(X)$
be the subset of
 $\mathrm {Douady}(X)$
parameterizing all unbendable rational curves on X. It is an open subset of
$\mathrm {Douady}(X)$
parameterizing all unbendable rational curves on X. It is an open subset of
 $\mathrm {Douady}(X)$
because the vector bundle
$\mathrm {Douady}(X)$
because the vector bundle
 $N_C \cong {\mathcal O}(1)^{\oplus p} \oplus {\mathcal O}^{\oplus (n-1-p)}$
on
$N_C \cong {\mathcal O}(1)^{\oplus p} \oplus {\mathcal O}^{\oplus (n-1-p)}$
on
 $C \cong {\mathbb P}^1$
has no nontrivial deformation. Using the basic deformation theory of rational curves (e.g., Main Theorem of [Reference KodairaK3]) and
$C \cong {\mathbb P}^1$
has no nontrivial deformation. Using the basic deformation theory of rational curves (e.g., Main Theorem of [Reference KodairaK3]) and
 $H^1(C, N_C) =0$
, we see that
$H^1(C, N_C) =0$
, we see that
 $\mathrm {URC}(X)$
is an open subset in the smooth locus of
$\mathrm {URC}(X)$
is an open subset in the smooth locus of
 $\mathrm {Douady}(X)$
.
$\mathrm {Douady}(X)$
.
It is convenient to use the following notion.
Definition 2.2. Let C be a complex manifold, and let
![]() ${\mathcal E}$
be a vector bundle on C. For a point
${\mathcal E}$
be a vector bundle on C. For a point
![]() $x \in C$
, denote by
$x \in C$
, denote by
![]() $H^0(C, {\mathcal E} \otimes \mathbf {m}_x)$
the vector space of sections of
$H^0(C, {\mathcal E} \otimes \mathbf {m}_x)$
the vector space of sections of
![]() ${\mathcal E}$
vanishing at x. The homomorphism
${\mathcal E}$
vanishing at x. The homomorphism
is defined by taking the derivative at x of sections vanishing at x.
The following is well known (see, e.g., page 58 of [Reference Hwang and MokHM] and Lemma 3.3 of [Reference Hwang and LiHL]).
Proposition 2.3. In Definition 2.1, let Y be a connected open subset of
![]() $\mathrm {URC}(X).$
Let
$\mathrm {URC}(X).$
Let
![]() $Y \stackrel {\rho }{\leftarrow } Z \stackrel {\mu }{\rightarrow } X$
be the associated universal family morphisms. Define the following distributions on Z:
$Y \stackrel {\rho }{\leftarrow } Z \stackrel {\mu }{\rightarrow } X$
be the associated universal family morphisms. Define the following distributions on Z:
 $$ \begin{align*} {\mathcal V} &:= \mathrm{Ker} (\mathrm{d} \mu), \\ {\mathcal F} &:= \mathrm{Ker} (\mathrm{d} \rho), \\ {\mathcal T}^0 &= {\mathcal V} \oplus {\mathcal F}. \end{align*} $$
$$ \begin{align*} {\mathcal V} &:= \mathrm{Ker} (\mathrm{d} \mu), \\ {\mathcal F} &:= \mathrm{Ker} (\mathrm{d} \rho), \\ {\mathcal T}^0 &= {\mathcal V} \oplus {\mathcal F}. \end{align*} $$
For the point
![]() $y =[C] \in Y$
corresponding to an unbendable rational curve
$y =[C] \in Y$
corresponding to an unbendable rational curve
![]() $C \subset X$
and a point
$C \subset X$
and a point
![]() $z \in \rho ^{-1}(y) \subset Z$
, set
$z \in \rho ^{-1}(y) \subset Z$
, set
![]() $\mu (z) = x \in C.$
$\mu (z) = x \in C.$
-
(i) We have the following natural identifications:
 $$ \begin{align*} T_y Y & = H^0(C, N_C), \\ T_z Z & = H^0(C, TX|_C)/H^0(C, TC \otimes \mathbf{m}_x), \\ {\mathcal V}_z & = H^0(C, N_C^+\otimes \mathbf{m}_x), \\ {\mathcal F}_z & = H^0(C, TC)/H^0(C, TC \otimes \mathbf{m}_x) = T_x C, \end{align*} $$
$$ \begin{align*} T_y Y & = H^0(C, N_C), \\ T_z Z & = H^0(C, TX|_C)/H^0(C, TC \otimes \mathbf{m}_x), \\ {\mathcal V}_z & = H^0(C, N_C^+\otimes \mathbf{m}_x), \\ {\mathcal F}_z & = H^0(C, TC)/H^0(C, TC \otimes \mathbf{m}_x) = T_x C, \end{align*} $$
where the third (resp. fourth) identification is induced by the differential
 $\mathrm {d}_z \rho : T_z Z \to T_y Y$
(resp.
$\mathrm {d}_z \rho : T_z Z \to T_y Y$
(resp.
 $\mathrm {d}_z \mu : T_z Z \to T_x X$
).
$\mathrm {d}_z \mu : T_z Z \to T_x X$
). -
(ii) Define
 ${\mathcal T}^1:= \partial {\mathcal T}^0.$
It is a vector subbundle of
${\mathcal T}^1:= \partial {\mathcal T}^0.$
It is a vector subbundle of
 $TZ$
and the Lie brackets of sections induce a natural isomorphism of vector bundles
$TZ$
and the Lie brackets of sections induce a natural isomorphism of vector bundles
 $\psi : {\mathcal F} \otimes {\mathcal V} \to {\mathcal T}^1/{\mathcal T}^0$
.
$\psi : {\mathcal F} \otimes {\mathcal V} \to {\mathcal T}^1/{\mathcal T}^0$
. -
(iii) The differential
 $\mathrm {d}_z \mu $
sends
$\mathrm {d}_z \mu $
sends
 ${\mathcal T}_z^1/{\mathcal T}_z^0$
to
${\mathcal T}_z^1/{\mathcal T}_z^0$
to
 $N_{C,x}^+ \subset T_x X/T_xC$
such that in combination with (i) and (ii), we have the commutative diagram
$N_{C,x}^+ \subset T_x X/T_xC$
such that in combination with (i) and (ii), we have the commutative diagram  $$ \begin{align*}\begin{array}{ccc} {\mathcal F}_z \otimes {\mathcal V}_z & = & T_x C \otimes H^0(C, N_C^+ \otimes \mathbf{m}_x) \\ \psi \downarrow & & \downarrow \mathbf{j}_x \\ {\mathcal T}_z^1/{\mathcal T}_z^0 & \stackrel{\mathrm{d}_z \mu}{\longrightarrow} & N_{C,x}^+, \end{array}\end{align*} $$
$$ \begin{align*}\begin{array}{ccc} {\mathcal F}_z \otimes {\mathcal V}_z & = & T_x C \otimes H^0(C, N_C^+ \otimes \mathbf{m}_x) \\ \psi \downarrow & & \downarrow \mathbf{j}_x \\ {\mathcal T}_z^1/{\mathcal T}_z^0 & \stackrel{\mathrm{d}_z \mu}{\longrightarrow} & N_{C,x}^+, \end{array}\end{align*} $$
where
 $\mathbf {j}_x$
is the contraction of vectors in
$\mathbf {j}_x$
is the contraction of vectors in
 $T_x C$
with the image of
$T_x C$
with the image of  $$ \begin{align*}\mathrm{ jet}^{N_C^+}_x : H^0(C, N_C^+ \otimes \mathbf{m}_x) \to T^{\vee}_x C \otimes N^+_{C,x}.\end{align*} $$
$$ \begin{align*}\mathrm{ jet}^{N_C^+}_x : H^0(C, N_C^+ \otimes \mathbf{m}_x) \to T^{\vee}_x C \otimes N^+_{C,x}.\end{align*} $$
-
(iv) We have isomorphisms
 ${\mathcal F}|_{\rho ^{-1}(y)} = TC \cong {\mathcal O}(2) $
and
${\mathcal F}|_{\rho ^{-1}(y)} = TC \cong {\mathcal O}(2) $
and  $$ \begin{align*} {\mathcal V}|_{\rho^{-1}(y)} = \mathop{\mathrm{Hom}}\nolimits(TC, N_C^+) \cong {\mathcal O}(-1)^{\oplus m} .\end{align*} $$
$$ \begin{align*} {\mathcal V}|_{\rho^{-1}(y)} = \mathop{\mathrm{Hom}}\nolimits(TC, N_C^+) \cong {\mathcal O}(-1)^{\oplus m} .\end{align*} $$
Definition 2.4. In Proposition 2.3, the tangent map
![]() $\tau : Z \to {\mathbb P} TX$
sending
$\tau : Z \to {\mathbb P} TX$
sending
![]() $z \in Z$
to
$z \in Z$
to
![]() $[\mathrm {d} \mu ({\mathcal F}_z)] \in {\mathbb P} T_x X$
is an immersion whose image
$[\mathrm {d} \mu ({\mathcal F}_z)] \in {\mathbb P} T_x X$
is an immersion whose image
![]() ${\mathcal C} \subset {\mathbb P} TX$
is called the variety of minimal rational tangents (to be abbreviated as VMRT) of the family Y. The fiber
${\mathcal C} \subset {\mathbb P} TX$
is called the variety of minimal rational tangents (to be abbreviated as VMRT) of the family Y. The fiber
![]() ${\mathcal C}_x \subset {\mathbb P} T_x X$
at
${\mathcal C}_x \subset {\mathbb P} T_x X$
at
![]() $x \in \mu (Z)$
is called the VMRT at x. Often, we replace Y by a suitable connected open subset to assume that
$x \in \mu (Z)$
is called the VMRT at x. Often, we replace Y by a suitable connected open subset to assume that
![]() ${\mathcal C} \subset {\mathbb P} TX$
and
${\mathcal C} \subset {\mathbb P} TX$
and
![]() ${\mathcal C}_x$
are submanifolds in
${\mathcal C}_x$
are submanifolds in
![]() ${\mathbb P} TX$
.
${\mathbb P} TX$
.
Notation 2.5. Let W be a vector space, and let
![]() $S \subset {\mathbb P} W$
be a (not necessarily closed) submanifold. For a point
$S \subset {\mathbb P} W$
be a (not necessarily closed) submanifold. For a point
![]() $s\in S$
, we denote by
$s\in S$
, we denote by
![]() $\widehat {s} \subset \widehat {S}$
the corresponding affine cones in W. Let
$\widehat {s} \subset \widehat {S}$
the corresponding affine cones in W. Let
![]() $N_S $
be the normal bundle of S in
$N_S $
be the normal bundle of S in
![]() ${\mathbb P} W$
. The second fundamental form
${\mathbb P} W$
. The second fundamental form
![]() $\mathrm {II}_{S}: \mathop {\mathrm {Sym}}\nolimits ^2 TS \to N_{S}$
is a homomorphism of vector bundles. Let
$\mathrm {II}_{S}: \mathop {\mathrm {Sym}}\nolimits ^2 TS \to N_{S}$
is a homomorphism of vector bundles. Let
![]() $\mathrm { Dom}(\mathrm {III}_S) \subset S$
be the Zariski-open subset where the image of
$\mathrm { Dom}(\mathrm {III}_S) \subset S$
be the Zariski-open subset where the image of
![]() $\mathrm {II}_S$
is a vector subbundle
$\mathrm {II}_S$
is a vector subbundle
![]() $N^{(2)}_{S}$
of
$N^{(2)}_{S}$
of
![]() $N_S$
. Then we have the third fundamental form
$N_S$
. Then we have the third fundamental form
for each
![]() $s \in \mathrm {Dom}(\mathrm {III}_S).$
Denoting by
$s \in \mathrm {Dom}(\mathrm {III}_S).$
Denoting by
![]() $\widehat {T}_s S \subset W$
the affine tangent space of S at s, we write
$\widehat {T}_s S \subset W$
the affine tangent space of S at s, we write
![]() $\widehat {N}_{S,s}$
for
$\widehat {N}_{S,s}$
for
![]() $W/\widehat {T}_s S$
and
$W/\widehat {T}_s S$
and
![]() $\widehat {N}^{(2)}_{S,s}$
for the vector subspace of
$\widehat {N}^{(2)}_{S,s}$
for the vector subspace of
![]() $\widehat {N}_{S,s}$
such that we have natural identifications
$\widehat {N}_{S,s}$
such that we have natural identifications
The following is well known (see, e.g., the proof of Proposition 1.4 in [Reference HwangH1] and Corollary 3.14 and Proposition 3.16 in [Reference Hwang and LiHL])
Proposition 2.6. In Definitions 2.1 and 2.4, replace Y by a neighborhood of y to assume that
![]() ${\mathcal C}$
and
${\mathcal C}$
and
![]() ${\mathcal C}_x$
are submanifolds of
${\mathcal C}_x$
are submanifolds of
![]() ${\mathbb P} TX$
and the immersion
${\mathbb P} TX$
and the immersion
![]() $\tau $
in Definition 2.4 is an embedding. Let us identify Z with
$\tau $
in Definition 2.4 is an embedding. Let us identify Z with
![]() ${\mathcal C} \subset {\mathbb P} TX$
by the embedding
${\mathcal C} \subset {\mathbb P} TX$
by the embedding
![]() $\tau $
.
$\tau $
.
-
(i) The affine tangent space
 $\widehat {T}_z {\mathcal C}_x \subset T_x X$
satisfies
$\widehat {T}_z {\mathcal C}_x \subset T_x X$
satisfies  $$ \begin{align*} \widehat{T}_z {\mathcal C}_x & = \mathrm{d}_z \mu ({\mathcal T}^1_z), \\ \widehat{T}_z {\mathcal C}_x / T_x C & = N^+_{C,x}. \end{align*} $$
$$ \begin{align*} \widehat{T}_z {\mathcal C}_x & = \mathrm{d}_z \mu ({\mathcal T}^1_z), \\ \widehat{T}_z {\mathcal C}_x / T_x C & = N^+_{C,x}. \end{align*} $$
-
(ii) The natural isomorphism
 $$ \begin{align*}\mathrm{d}_z (\tau|_{\mu^{-1}(x)}): {\mathcal V}_z = H^0(C, N^+_C \otimes \mathbf{m}_x) \ \to \ T_z {\mathcal C}_x = T^{\vee}_x C \otimes N^+_{C,x} \end{align*} $$
$$ \begin{align*}\mathrm{d}_z (\tau|_{\mu^{-1}(x)}): {\mathcal V}_z = H^0(C, N^+_C \otimes \mathbf{m}_x) \ \to \ T_z {\mathcal C}_x = T^{\vee}_x C \otimes N^+_{C,x} \end{align*} $$
coincides with
 $\mathrm {jet}^{N_C^+}_x$
.
$\mathrm {jet}^{N_C^+}_x$
. -
(iii) For a local section
 $\vec {f}$
of
$\vec {f}$
of
 ${\mathcal F}$
and local sections
${\mathcal F}$
and local sections
 $\vec {v}_1, \vec {v}_2$
of
$\vec {v}_1, \vec {v}_2$
of
 ${\mathcal V}$
near
${\mathcal V}$
near
 $z \in {\mathcal C}$
with values
$z \in {\mathcal C}$
with values
 $v_1, v_2 \in {\mathcal V}_z$
at z,
$v_1, v_2 \in {\mathcal V}_z$
at z,  $$ \begin{align*} ([\vec{v}_2, [\vec{v}_1, \vec{f}]]_z\quad \mod {\mathcal T}^1_z) \ = \ \vec{f}_z \otimes \mathrm{II}_{{\mathcal C}_x, z}(v_1, v_2), \ \end{align*} $$
$$ \begin{align*} ([\vec{v}_2, [\vec{v}_1, \vec{f}]]_z\quad \mod {\mathcal T}^1_z) \ = \ \vec{f}_z \otimes \mathrm{II}_{{\mathcal C}_x, z}(v_1, v_2), \ \end{align*} $$
where the left-hand side is regarded as an element of
 $\widehat {N}_{{\mathcal C}_x, z} = N_{C,x}/N_{C,x}^+$
by (i) and Proposition 2.3(iii), and
$\widehat {N}_{{\mathcal C}_x, z} = N_{C,x}/N_{C,x}^+$
by (i) and Proposition 2.3(iii), and
 $\vec {f}_z \otimes $
stands for the contraction of
$\vec {f}_z \otimes $
stands for the contraction of
 $\vec {f}_z \in {\mathcal F}_z = T_x C$
with
$\vec {f}_z \in {\mathcal F}_z = T_x C$
with  $$ \begin{align*} \mathrm{II}_{{\mathcal C}_x, z}(v_1, v_2) \in T^{\vee}_x C \otimes \widehat{N}^{(2)}_{{\mathcal C}_x, z} \subset T^{\vee}_x C \otimes \widehat{N}_{{\mathcal C}_x,z}. \end{align*} $$
$$ \begin{align*} \mathrm{II}_{{\mathcal C}_x, z}(v_1, v_2) \in T^{\vee}_x C \otimes \widehat{N}^{(2)}_{{\mathcal C}_x, z} \subset T^{\vee}_x C \otimes \widehat{N}_{{\mathcal C}_x,z}. \end{align*} $$
-
(iv) Assume that
 $z \in {\mathcal C}_x$
is in
$z \in {\mathcal C}_x$
is in
 $\mathrm {Dom}(\mathrm {III}_{{\mathcal C}_x})$
. Then
$\mathrm {Dom}(\mathrm {III}_{{\mathcal C}_x})$
. Then
 ${\mathcal T}^2 = \partial {\mathcal T}^1 = \partial ^{(2)}{\mathcal T}^0$
is a vector subbundle of
${\mathcal T}^2 = \partial {\mathcal T}^1 = \partial ^{(2)}{\mathcal T}^0$
is a vector subbundle of
 $TZ$
in a neighborhood of
$TZ$
in a neighborhood of
 $\rho ^{-1}(y)$
in Z and
$\rho ^{-1}(y)$
in Z and  $$ \begin{align*} \widehat{N}^{(2)}_{{\mathcal C}_x, z} = ( \mathrm{d}_z \mu ({\mathcal T}^2_z)\quad \mod \widehat{T}_z {\mathcal C}_x) \end{align*} $$
$$ \begin{align*} \widehat{N}^{(2)}_{{\mathcal C}_x, z} = ( \mathrm{d}_z \mu ({\mathcal T}^2_z)\quad \mod \widehat{T}_z {\mathcal C}_x) \end{align*} $$
as subspaces of
 $\widehat {N}_{{\mathcal C}_x, z} = N_{C,x}/N^+_{C,x}.$
$\widehat {N}_{{\mathcal C}_x, z} = N_{C,x}/N^+_{C,x}.$
-
(v) In (iv), for a local section
 $\vec {f}$
of
$\vec {f}$
of
 ${\mathcal F}$
and local sections
${\mathcal F}$
and local sections
 $\vec {v}_1, \vec {v}_2, \vec {v}_3$
of
$\vec {v}_1, \vec {v}_2, \vec {v}_3$
of
 ${\mathcal V}$
near
${\mathcal V}$
near
 $z \in {\mathcal C}$
with values
$z \in {\mathcal C}$
with values
 $v_1, v_2, v_3 \in {\mathcal V}_z$
at z,
$v_1, v_2, v_3 \in {\mathcal V}_z$
at z,  $$ \begin{align*}([\vec{v}_3, [\vec{v}_2, [\vec{v}_1, \vec{f}]]]_z\quad \mod {\mathcal T}^2_z) = \vec{f}_z \otimes \mathrm{III}_{{\mathcal C}_x, z}(v_1, v_2, v_3) ,\end{align*} $$
$$ \begin{align*}([\vec{v}_3, [\vec{v}_2, [\vec{v}_1, \vec{f}]]]_z\quad \mod {\mathcal T}^2_z) = \vec{f}_z \otimes \mathrm{III}_{{\mathcal C}_x, z}(v_1, v_2, v_3) ,\end{align*} $$
where the left hand-side is regarded as an element of
 $\widehat {N}_{{\mathcal C}_x,z}/\widehat {N}^{(2)}_{{\mathcal C}_x,z}$
by (iv), and
$\widehat {N}_{{\mathcal C}_x,z}/\widehat {N}^{(2)}_{{\mathcal C}_x,z}$
by (iv), and
 $\vec {f}_z \otimes $
stands for the contraction of
$\vec {f}_z \otimes $
stands for the contraction of
 $\vec {f}_z \in {\mathcal F}_z = T_x C$
with
$\vec {f}_z \in {\mathcal F}_z = T_x C$
with  $$ \begin{align*}\mathrm{III}_{{\mathcal C}_x, z}(v_1, v_2, v_3) \in T^{\vee}_x C \otimes \widehat{N}_{{\mathcal C}_x,z}/\widehat{N}^{(2)}_{{\mathcal C}_x, z}.\end{align*} $$
$$ \begin{align*}\mathrm{III}_{{\mathcal C}_x, z}(v_1, v_2, v_3) \in T^{\vee}_x C \otimes \widehat{N}_{{\mathcal C}_x,z}/\widehat{N}^{(2)}_{{\mathcal C}_x, z}.\end{align*} $$
Definition 2.7. In Proposition 2.3, define
![]() ${\mathcal D}_y := H^0(C, N_C^+) \subset T_y Y$
. This determines a distribution
${\mathcal D}_y := H^0(C, N_C^+) \subset T_y Y$
. This determines a distribution
![]() ${\mathcal D} \subset TY$
of rank
${\mathcal D} \subset TY$
of rank
![]() $2m.$
For each
$2m.$
For each
![]() $x \in C,$
define
$x \in C,$
define
the two-dimensional vector space of rational functions on C with at most one pole at x and define
such that we have a canonical tensor decomposition
![]() ${\mathcal D}_y = U_x \otimes V_x$
.
${\mathcal D}_y = U_x \otimes V_x$
.
Proposition 2.8. In Definition 2.7, let
![]() $\mathbf {1}_x \in U_x$
be the constant function on C with value 1. The differential
$\mathbf {1}_x \in U_x$
be the constant function on C with value 1. The differential
![]() $\mathrm {d}_z \rho : T_z Z \to T_y Y$
induces an identification
$\mathrm {d}_z \rho : T_z Z \to T_y Y$
induces an identification
![]() ${\mathcal T}^1_z/{\mathcal F}_z = {\mathcal D}_y$
such that
${\mathcal T}^1_z/{\mathcal F}_z = {\mathcal D}_y$
such that
Moreover, when
![]() $ z\in \mathrm {Dom}(\mathrm {III}_{{\mathcal C}_x}),$
it induces an identification
$ z\in \mathrm {Dom}(\mathrm {III}_{{\mathcal C}_x}),$
it induces an identification
![]() ${\mathcal T}^2_z/{\mathcal F}_z = (\partial {\mathcal D})_y.$
${\mathcal T}^2_z/{\mathcal F}_z = (\partial {\mathcal D})_y.$
Proof. The identification
![]() ${\mathcal T}^1_z/{\mathcal F}_z = {\mathcal D}_y$
follows from Propositions 1 and 8 of [Reference Hwang and MokHM] (see Proposition 3.7 of [Reference Hwang and LiHL]). Then
${\mathcal T}^1_z/{\mathcal F}_z = {\mathcal D}_y$
follows from Propositions 1 and 8 of [Reference Hwang and MokHM] (see Proposition 3.7 of [Reference Hwang and LiHL]). Then
![]() ${\mathcal V}_z = \mathbf {1}_x \otimes V_x$
follows from Proposition 2.3(i) and the identification
${\mathcal V}_z = \mathbf {1}_x \otimes V_x$
follows from Proposition 2.3(i) and the identification
![]() ${\mathcal T}^2_z/{\mathcal F}_z = (\partial {\mathcal D})_y$
comes from
${\mathcal T}^2_z/{\mathcal F}_z = (\partial {\mathcal D})_y$
comes from
![]() ${\mathcal T}^2 = \partial {\mathcal T}^1$
in Proposition 2.6(iv).
${\mathcal T}^2 = \partial {\mathcal T}^1$
in Proposition 2.6(iv).
We skip the proof of the following two elementary lemmata.
Lemma 2.9. In Proposition 2.8, let
![]() $f \in U_x$
be a nonconstant rational function on C.
$f \in U_x$
be a nonconstant rational function on C.
-
(i) The homomorphism
 $$ \begin{align*}\mathbf{res}_x: \wedge^2 H^0(C, {\mathcal O}(x)) \to T_x C\end{align*} $$
$$ \begin{align*}\mathbf{res}_x: \wedge^2 H^0(C, {\mathcal O}(x)) \to T_x C\end{align*} $$
that sends
 $\mathbf {1}_x \wedge f$
to
$\mathbf {1}_x \wedge f$
to  $$ \begin{align*}\mathrm{Res}_x ( f \ \mathrm{d}t ) \frac{\partial}{\partial t},\end{align*} $$
$$ \begin{align*}\mathrm{Res}_x ( f \ \mathrm{d}t ) \frac{\partial}{\partial t},\end{align*} $$
where t is a local holomorphic coordinate on C centered at x and
 $\mathrm {Res}_x( f \ \mathrm {d} t)$
is the residue of the logarithmic form
$\mathrm {Res}_x( f \ \mathrm {d} t)$
is the residue of the logarithmic form
 $f \ \mathrm {d}t$
at x, is independent of the choice of the coordinate t and gives a canonical identification of
$f \ \mathrm {d}t$
at x, is independent of the choice of the coordinate t and gives a canonical identification of
 $\wedge ^2 U_x$
with
$\wedge ^2 U_x$
with
 $T_x C$
.
$T_x C$
. -
(ii) Write
 $\vec {f}_x := \mathbf {res}_x (\mathbf {1}_x \wedge f) \in T_x C$
. For any vector bundle
$\vec {f}_x := \mathbf {res}_x (\mathbf {1}_x \wedge f) \in T_x C$
. For any vector bundle
 ${\mathcal E}$
on C and a section
${\mathcal E}$
on C and a section
 $v \in H^0(C, {\mathcal E} \otimes \mathbf {m}_x)$
, let
$v \in H^0(C, {\mathcal E} \otimes \mathbf {m}_x)$
, let
 $ \vec {f}_x (v) \in {\mathcal E}_x$
be the contraction of
$ \vec {f}_x (v) \in {\mathcal E}_x$
be the contraction of
 $\vec {f}_x$
with
$\vec {f}_x$
with
 $ \mathrm {jet}^{{\mathcal E}}_x(v) \in T_x^{\vee } C \otimes {\mathcal E}_x.$
Then
$ \mathrm {jet}^{{\mathcal E}}_x(v) \in T_x^{\vee } C \otimes {\mathcal E}_x.$
Then  $$ \begin{align*}\vec{f}_x (v) = (f \otimes v) (x) \ \in {\mathcal E}_x,\end{align*} $$
$$ \begin{align*}\vec{f}_x (v) = (f \otimes v) (x) \ \in {\mathcal E}_x,\end{align*} $$
where
 $f \otimes v $
stands for the section of
$f \otimes v $
stands for the section of
 $H^0(C, {\mathcal E})$
under the natural homomorphism
$H^0(C, {\mathcal E})$
under the natural homomorphism  $$ \begin{align*}U_x \otimes H^0(C, {\mathcal E} \otimes \mathbf{m}_x) \to H^0(C, {\mathcal E}).\end{align*} $$
$$ \begin{align*}U_x \otimes H^0(C, {\mathcal E} \otimes \mathbf{m}_x) \to H^0(C, {\mathcal E}).\end{align*} $$
Lemma 2.10. In Lemma 2.9, for any point
![]() $x' \in C$
different from x, define
$x' \in C$
different from x, define
Then we have canonical isomorphisms
coming from multiplication by rational functions. Moreover, for any
![]() $f \in A_x^{x'}$
and
$f \in A_x^{x'}$
and
![]() $v \in V_x$
, we have
$v \in V_x$
, we have
![]() $f \otimes v = \mathbf {1}_{x'} \otimes f v$
under the two tensor decompositions
$f \otimes v = \mathbf {1}_{x'} \otimes f v$
under the two tensor decompositions
![]() ${\mathcal D}_y = U_x \otimes V_x = U_{x'} \otimes V_{x'}.$
${\mathcal D}_y = U_x \otimes V_x = U_{x'} \otimes V_{x'}.$
Proposition 2.11. In Definition 2.7, for a local section
![]() $\vec {f}$
of
$\vec {f}$
of
![]() ${\mathcal F}$
and
${\mathcal F}$
and
![]() $\vec {v}$
of
$\vec {v}$
of
![]() ${\mathcal V}$
near
${\mathcal V}$
near
![]() $z \in {\mathcal C}$
, denote by
$z \in {\mathcal C}$
, denote by
![]() $f \in U_x$
a rational function satisfying
$f \in U_x$
a rational function satisfying
![]() $\mathrm {d}_z \mu (\vec {f}_z) = \mathbf { res}_x (\mathbf {1}_x \wedge f)$
in Lemma 2.9 and by
$\mathrm {d}_z \mu (\vec {f}_z) = \mathbf { res}_x (\mathbf {1}_x \wedge f)$
in Lemma 2.9 and by
![]() $v \in {\mathcal V}_z = V_x$
the value of
$v \in {\mathcal V}_z = V_x$
the value of
![]() $\vec {v}$
at z. Then
$\vec {v}$
at z. Then
Proof. The vector
![]() $[\vec {v}, \vec {f}]_z \in T_z Z$
is represented by a section
$[\vec {v}, \vec {f}]_z \in T_z Z$
is represented by a section
![]() $w \in H^0(C, TX)$
by Proposition 2.3(i). Regarding v as an element of
$w \in H^0(C, TX)$
by Proposition 2.3(i). Regarding v as an element of
![]() $H^0(C, N^+_C \otimes \mathbf {m}_x)$
, Proposition 2.3(iii) says that
$H^0(C, N^+_C \otimes \mathbf {m}_x)$
, Proposition 2.3(iii) says that
This implies that the value
![]() $w_x$
at x of the section w of
$w_x$
at x of the section w of
![]() $TX|_C$
satisfies
$TX|_C$
satisfies
Since
![]() $\mathrm {d}_z \rho ([\vec {v}, \vec {f}]_z)$
in
$\mathrm {d}_z \rho ([\vec {v}, \vec {f}]_z)$
in
![]() $T_y Y = H^0(C, N_C)$
is represented by w modulo
$T_y Y = H^0(C, N_C)$
is represented by w modulo
![]() $H^0(C, TC)$
, its value modulo
$H^0(C, TC)$
, its value modulo
![]() $\mathbf {1}_x \otimes V_x = H^0(C, N_C \otimes \mathbf {m}_x)$
is just
$\mathbf {1}_x \otimes V_x = H^0(C, N_C \otimes \mathbf {m}_x)$
is just
So the left-hand side of (2.1) is just
![]() $\vec {f}_z(v)$
in Lemma 2.9(ii). Then Lemma 2.9(ii) says that this is equal to
$\vec {f}_z(v)$
in Lemma 2.9(ii). Then Lemma 2.9(ii) says that this is equal to
![]() $(f\otimes v) (x)$
, the right-hand side of (2.1).
$(f\otimes v) (x)$
, the right-hand side of (2.1).
Proposition 2.12. In Proposition 2.11, for
![]() $u_1, u_2 \in U_x$
and
$u_1, u_2 \in U_x$
and
![]() $v_1, v_2 \in V_x$
, let
$v_1, v_2 \in V_x$
, let
![]() $u_1 \otimes v_1, u_2 \otimes v_2$
be elements of
$u_1 \otimes v_1, u_2 \otimes v_2$
be elements of
![]() ${\mathcal D}_y = U_x \otimes V_x$
. Then we have
${\mathcal D}_y = U_x \otimes V_x$
. Then we have
where the second fundamental form
![]() $\mathrm {II}_{{\mathcal C}_x,z}: \mathop {\mathrm {Sym}}\nolimits ^2 V_x \to T^{\vee }_x C \otimes (N_{C,x}/N^+_{C,x})$
is interpreted as a homomorphism
$\mathrm {II}_{{\mathcal C}_x,z}: \mathop {\mathrm {Sym}}\nolimits ^2 V_x \to T^{\vee }_x C \otimes (N_{C,x}/N^+_{C,x})$
is interpreted as a homomorphism
via the isomorphism
![]() $\mathbf {res}_x: T_x C \cong \wedge ^2 U_x$
in Lemma 2.9(i) and the natural isomorphism
$\mathbf {res}_x: T_x C \cong \wedge ^2 U_x$
in Lemma 2.9(i) and the natural isomorphism
![]() $ H^0(C, N_C/N_C^+) = N_{C,x}/N_{C,x}^+$
coming from
$ H^0(C, N_C/N_C^+) = N_{C,x}/N_{C,x}^+$
coming from
![]() $N_C/N_C^+ \cong {\mathcal O}^{\oplus (n-m-1)}$
.
$N_C/N_C^+ \cong {\mathcal O}^{\oplus (n-m-1)}$
.
Proof. We may check (2.2) assuming
![]() $u_1 = f$
and
$u_1 = f$
and
![]() $u_2= \mathbf {1}_x$
. It is a direct consequence of
$u_2= \mathbf {1}_x$
. It is a direct consequence of
from Proposition 2.6(iii). In fact, the vector
![]() $v_2 \in {\mathcal V}_z$
is sent by
$v_2 \in {\mathcal V}_z$
is sent by
![]() $\mathrm {d}_z \rho $
to the corresponding element
$\mathrm {d}_z \rho $
to the corresponding element
![]() $v_2 \in V_x = H^0(C, N_C^+ \otimes \mathbf {m}_x)$
, which is just
$v_2 \in V_x = H^0(C, N_C^+ \otimes \mathbf {m}_x)$
, which is just
![]() $\mathbf {1}_x \otimes v_2$
in
$\mathbf {1}_x \otimes v_2$
in
![]() $U_x \otimes V_x = {\mathcal D}_y$
. The vector
$U_x \otimes V_x = {\mathcal D}_y$
. The vector
![]() $ [\vec {v}_1, \vec {f}]_z $
is sent to
$ [\vec {v}_1, \vec {f}]_z $
is sent to
![]() $f \otimes v_1$
modulo
$f \otimes v_1$
modulo
![]() $\mathbf {1}_x \otimes V_x$
by Proposition 2.11. Then the left-hand side of (2.3) is equal to
$\mathbf {1}_x \otimes V_x$
by Proposition 2.11. Then the left-hand side of (2.3) is equal to
![]() $\mathrm {Levi}^{{\mathcal D}}(u_2 \otimes v_2, u_1 \otimes v_1)$
. By Lemma 2.9, the isomorphism
$\mathrm {Levi}^{{\mathcal D}}(u_2 \otimes v_2, u_1 \otimes v_1)$
. By Lemma 2.9, the isomorphism
![]() $\mathbf {res}_x$
identifies
$\mathbf {res}_x$
identifies
![]() $\vec {f}_z$
with
$\vec {f}_z$
with
![]() $-\mathbf {1}_x \wedge f = - u_1 \wedge u_2$
. Thus, the right-hand side of (2.3) is
$-\mathbf {1}_x \wedge f = - u_1 \wedge u_2$
. Thus, the right-hand side of (2.3) is
This proves (2.2).
Proposition 2.13. In Proposition 2.11, assume that
![]() ${\mathcal D}$
is regular at
${\mathcal D}$
is regular at
![]() $y \in Y$
. Then for any
$y \in Y$
. Then for any
![]() $f \in U_x, v_1, v_2, v_3 \in V_x$
, the Lie bracket in
$f \in U_x, v_1, v_2, v_3 \in V_x$
, the Lie bracket in
![]() $\mathrm {symb}_y ({\mathcal D})$
satisfies
$\mathrm {symb}_y ({\mathcal D})$
satisfies
where
![]() $\mathrm {III}_{{\mathcal C}_x, z}: \mathop {\mathrm {Sym}}\nolimits ^3 V_x \to T^{\vee }_x C \otimes (\widehat {N}_{{\mathcal C}_x,z}/\widehat {N}^{(2)}_{{\mathcal C}_x,z})$
is interpreted as a homomorphism
$\mathrm {III}_{{\mathcal C}_x, z}: \mathop {\mathrm {Sym}}\nolimits ^3 V_x \to T^{\vee }_x C \otimes (\widehat {N}_{{\mathcal C}_x,z}/\widehat {N}^{(2)}_{{\mathcal C}_x,z})$
is interpreted as a homomorphism
via the isomorphism
![]() $\mathbf {res}_x: T_x C \cong \wedge ^2 U_x$
and the isomorphisms
$\mathbf {res}_x: T_x C \cong \wedge ^2 U_x$
and the isomorphisms
3 From nondegenerate lines on contact manifolds to distributions with symbols
 ${\mathfrak g}_+(F)$
${\mathfrak g}_+(F)$
Definition 3.1. Let X be a complex manifold of dimension
![]() $2m +3, m \geq 1,$
and let
$2m +3, m \geq 1,$
and let
![]() ${\mathcal H} \subset TX$
be a contact distribution, namely, a distribution of rank
${\mathcal H} \subset TX$
be a contact distribution, namely, a distribution of rank
![]() $2m+2$
such that the Levi tensor
$2m+2$
such that the Levi tensor
![]() $\mathrm {Levi}^{{\mathcal H}}: \wedge ^2 {\mathcal H} \to TX/{\mathcal H}$
gives a symplectic form, that is, a nondegenerate anti-symmetric form, on each fiber of
$\mathrm {Levi}^{{\mathcal H}}: \wedge ^2 {\mathcal H} \to TX/{\mathcal H}$
gives a symplectic form, that is, a nondegenerate anti-symmetric form, on each fiber of
![]() ${\mathcal H}_x$
. The pair
${\mathcal H}_x$
. The pair
![]() $(X, {\mathcal H})$
is called a contact manifold. The quotient line bundle
$(X, {\mathcal H})$
is called a contact manifold. The quotient line bundle
![]() ${\mathcal L}:= TX/{\mathcal H}$
is called the contact line bundle on X. An unbendable smooth rational curve
${\mathcal L}:= TX/{\mathcal H}$
is called the contact line bundle on X. An unbendable smooth rational curve
![]() $C \subset X$
satisfying
$C \subset X$
satisfying
![]() ${\mathcal L}|_C \cong {\mathcal O}(1)$
is called a line. Denote by
${\mathcal L}|_C \cong {\mathcal O}(1)$
is called a line. Denote by
![]() $\mathrm {Lines}(X, {\mathcal H})$
, the open subset of
$\mathrm {Lines}(X, {\mathcal H})$
, the open subset of
![]() $\mathrm {URC}(X) \subset \mathrm {Douady}(X)$
parameterizing lines.
$\mathrm {URC}(X) \subset \mathrm {Douady}(X)$
parameterizing lines.
Definition 3.2. Fix a one-dimensional vector space
![]() $\mathbf {L}$
, and let
$\mathbf {L}$
, and let
![]() $\omega : \wedge ^2 W \to \mathbf {L}$
be a symplectic form on a vector space W of dimension
$\omega : \wedge ^2 W \to \mathbf {L}$
be a symplectic form on a vector space W of dimension
![]() $2m+2$
.
$2m+2$
.
-
(i) For a subspace
 $B \subset W$
, define
$B \subset W$
, define
 $B^{\perp } := \{ w \in W \mid \omega (w, B) =0\}.$
$B^{\perp } := \{ w \in W \mid \omega (w, B) =0\}.$
-
(ii) A subspace
 $B \subset W$
is Lagrangian if
$B \subset W$
is Lagrangian if
 $B^{\perp } = B$
. In this case, the dimension of B is
$B^{\perp } = B$
. In this case, the dimension of B is
 $m+1$
.
$m+1$
. -
(iii) A submanifold
 $S \subset {\mathbb P} W$
is Legendrian if its affine tangent space
$S \subset {\mathbb P} W$
is Legendrian if its affine tangent space
 $\widehat {T}_s S \subset W$
at every point
$\widehat {T}_s S \subset W$
at every point
 $s \in S$
is a Lagrangian subspace of W.
$s \in S$
is a Lagrangian subspace of W.
Lemma 3.3. In Definition 3.1, choose a connected open subset
![]() $Y \subset \mathrm {Lines}(X, {\mathcal H})$
such that
$Y \subset \mathrm {Lines}(X, {\mathcal H})$
such that
![]() ${\mathcal C} \subset {\mathbb P} TX$
in Definition 2.4 is a submanifold.
${\mathcal C} \subset {\mathbb P} TX$
in Definition 2.4 is a submanifold.
-
(i) For each line
 $C \subset X$
, the normal bundle
$C \subset X$
, the normal bundle
 $N_C$
is isomorphic to
$N_C$
is isomorphic to
 ${\mathcal O}(1)^{\oplus m} \oplus {\mathcal O}^{\oplus (m+2)}$
and
${\mathcal O}(1)^{\oplus m} \oplus {\mathcal O}^{\oplus (m+2)}$
and
 ${\mathcal H}|_C$
is isomorphic to
${\mathcal H}|_C$
is isomorphic to
 ${\mathcal O}(2) \oplus {\mathcal O}(1)^{\oplus m} \oplus {\mathcal O}^{\oplus m} \oplus {\mathcal O}(-1)$
. In other words, the integer p in Definition 2.1 is exactly
${\mathcal O}(2) \oplus {\mathcal O}(1)^{\oplus m} \oplus {\mathcal O}^{\oplus m} \oplus {\mathcal O}(-1)$
. In other words, the integer p in Definition 2.1 is exactly
 $m = \frac {1}{2}(\dim X-3)$
.
$m = \frac {1}{2}(\dim X-3)$
. -
(ii) For each
 $x \in C$
, the VMRT
$x \in C$
, the VMRT
 ${\mathcal C}_x \subset {\mathbb P} T_x X$
is contained in
${\mathcal C}_x \subset {\mathbb P} T_x X$
is contained in
 ${\mathbb P} {\mathcal H}_x$
and is Legendrian with respect to the symplectic form
${\mathbb P} {\mathcal H}_x$
and is Legendrian with respect to the symplectic form
 $\mathrm {Levi}^{{\mathcal H}}_x$
on
$\mathrm {Levi}^{{\mathcal H}}_x$
on
 ${\mathcal H}_x$
.
${\mathcal H}_x$
.
Proof. From the well-known relation
![]() $\det TX = {\mathcal L}^{\otimes (m+2)}$
(e.g., from (2.2) of [Reference LeBrunLB]), we have the isomorphism
$\det TX = {\mathcal L}^{\otimes (m+2)}$
(e.g., from (2.2) of [Reference LeBrunLB]), we have the isomorphism
![]() $N_C \cong {\mathcal O}(1)^{\oplus m} \oplus {\mathcal O}^{\oplus (m+2)}.$
Consequently,
$N_C \cong {\mathcal O}(1)^{\oplus m} \oplus {\mathcal O}^{\oplus (m+2)}.$
Consequently,
Since
![]() $TC \cong {\mathcal O}(2)$
, it must belong to the kernel of the projection
$TC \cong {\mathcal O}(2)$
, it must belong to the kernel of the projection
![]() $TX|_C \to ({\mathcal L} = TX/{\mathcal H})|_C \cong {\mathcal O}(1).$
Since this holds for all lines represented by elements in the parameter space Y, we have
$TX|_C \to ({\mathcal L} = TX/{\mathcal H})|_C \cong {\mathcal O}(1).$
Since this holds for all lines represented by elements in the parameter space Y, we have
![]() ${\mathcal C}\subset {\mathbb P}{\mathcal H}$
. By Proposition 2.6(i),
${\mathcal C}\subset {\mathbb P}{\mathcal H}$
. By Proposition 2.6(i),
![]() $\widehat {T}_z\mathcal {C}_x/T_xC=N^+_{C, x}$
, where
$\widehat {T}_z\mathcal {C}_x/T_xC=N^+_{C, x}$
, where
![]() $x\in C$
and
$x\in C$
and
![]() $z=\mathbb {P}T_xC\in \mathcal {C}_x$
. It follows that
$z=\mathbb {P}T_xC\in \mathcal {C}_x$
. It follows that
![]() ${\mathcal O}(2) \oplus {\mathcal O}(1)^{\oplus m}$
is contained in
${\mathcal O}(2) \oplus {\mathcal O}(1)^{\oplus m}$
is contained in
![]() ${\mathcal H}|_C$
. This gives
${\mathcal H}|_C$
. This gives
![]() ${\mathcal H}|_C \cong {\mathcal O}(2) \oplus {\mathcal O}(1)^{\oplus m} \oplus {\mathcal O}^{\oplus m} \oplus {\mathcal O}(-1)$
, completing the proof of (i). By (i), any line is tangent to
${\mathcal H}|_C \cong {\mathcal O}(2) \oplus {\mathcal O}(1)^{\oplus m} \oplus {\mathcal O}^{\oplus m} \oplus {\mathcal O}(-1)$
, completing the proof of (i). By (i), any line is tangent to
![]() ${\mathcal H}$
, and
${\mathcal H}$
, and
![]() ${\mathcal C}_x \subset {\mathbb P} {\mathcal H}_x$
. Moreover, the Levi tensor gives a family of nondegenerate antisymmetric forms on the bundle
${\mathcal C}_x \subset {\mathbb P} {\mathcal H}_x$
. Moreover, the Levi tensor gives a family of nondegenerate antisymmetric forms on the bundle
![]() ${\mathcal H}$
, that is, a homomorphism
${\mathcal H}$
, that is, a homomorphism
The subspace
![]() $({\mathcal O}(2) \oplus {\mathcal O}(1)^{\oplus m})_x$
is a Lagrangian subspace of
$({\mathcal O}(2) \oplus {\mathcal O}(1)^{\oplus m})_x$
is a Lagrangian subspace of
![]() ${\mathcal H}_x$
with respect to this antisymmetric form. As this subspace corresponds to the affine tangent space of
${\mathcal H}_x$
with respect to this antisymmetric form. As this subspace corresponds to the affine tangent space of
![]() ${\mathcal C}_x$
at
${\mathcal C}_x$
at
![]() ${\mathbb P} T_x C$
by Proposition 2.6(i), the VMRT must be Legendrian, proving (ii).
${\mathbb P} T_x C$
by Proposition 2.6(i), the VMRT must be Legendrian, proving (ii).
Definition 3.4. In Definition 3.1, let
![]() $Y \subset \mathrm {Lines}(X, {\mathcal H})$
be a connected open subset, and let
$Y \subset \mathrm {Lines}(X, {\mathcal H})$
be a connected open subset, and let
![]() $Y \stackrel {\rho }{\leftarrow } Z \stackrel {\mu }{\rightarrow } X$
be the universal family. Given
$Y \stackrel {\rho }{\leftarrow } Z \stackrel {\mu }{\rightarrow } X$
be the universal family. Given
![]() $z \in Z$
, write
$z \in Z$
, write
![]() $x= \mu (z), y = \rho (z)$
and
$x= \mu (z), y = \rho (z)$
and
![]() $ C = \mu (\rho ^{-1}(y)) \subset X$
. Using the symplectic form
$ C = \mu (\rho ^{-1}(y)) \subset X$
. Using the symplectic form
![]() $\mathrm {Levi}_x^{{\mathcal H}}$
on
$\mathrm {Levi}_x^{{\mathcal H}}$
on
![]() ${\mathcal H}_x$
, define
${\mathcal H}_x$
, define
Then
![]() ${\mathcal R}^+ \subset {\mathcal R} $
are vector subbundles of the vector bundle
${\mathcal R}^+ \subset {\mathcal R} $
are vector subbundles of the vector bundle
![]() ${\mathcal H}$
on Z, of rank
${\mathcal H}$
on Z, of rank
![]() $m+1$
and
$m+1$
and
![]() $2m+1$
, respectively. Denote by
$2m+1$
, respectively. Denote by
![]() ${\mathcal R}^+_C \subset {\mathcal R}_C \subset {\mathcal H}|_C$
the corresponding vector subbundles on C.
${\mathcal R}^+_C \subset {\mathcal R}_C \subset {\mathcal H}|_C$
the corresponding vector subbundles on C.
Lemma 3.5. In Definition 3.4, we have the following.
-
(i) The vector bundle
 ${\mathcal R}_C$
(resp.
${\mathcal R}_C$
(resp.
 ${\mathcal R}^+_C$
) is isomorphic to the subbundle
${\mathcal R}^+_C$
) is isomorphic to the subbundle  $$ \begin{align*}{\mathcal O}(2) \oplus {\mathcal O}(1)^{\oplus m} \oplus {\mathcal O}^{\oplus m} \ (\mbox{ resp. } {\mathcal O}(2) \oplus {\mathcal O}(1)^{\oplus m})\end{align*} $$
$$ \begin{align*}{\mathcal O}(2) \oplus {\mathcal O}(1)^{\oplus m} \oplus {\mathcal O}^{\oplus m} \ (\mbox{ resp. } {\mathcal O}(2) \oplus {\mathcal O}(1)^{\oplus m})\end{align*} $$
of
 ${\mathcal H}|_C$
from Lemma 3.3(i).
${\mathcal H}|_C$
from Lemma 3.3(i). -
(ii) If
 $s \in H^0(C, TX|_C)$
satisfies
$s \in H^0(C, TX|_C)$
satisfies
 $s_x \in {\mathcal R}_{C,x}$
for a point
$s_x \in {\mathcal R}_{C,x}$
for a point
 $x \in C$
, then
$x \in C$
, then
 $s \in H^0(C, {\mathcal H}|_C).$
$s \in H^0(C, {\mathcal H}|_C).$
-
(iii)
 $\mathrm {Levi}^{{\mathcal H}}$
induces a perfect pairing of vector bundles on C
$\mathrm {Levi}^{{\mathcal H}}$
induces a perfect pairing of vector bundles on C  $$ \begin{align*}N_C^+ \otimes {\mathcal R}_C/(TX|_C)^+ \to {\mathcal L}|_C.\end{align*} $$
$$ \begin{align*}N_C^+ \otimes {\mathcal R}_C/(TX|_C)^+ \to {\mathcal L}|_C.\end{align*} $$
Proof. Note that
![]() $\mathrm {Levi}^{{\mathcal H}}$
gives a perfect paring
$\mathrm {Levi}^{{\mathcal H}}$
gives a perfect paring
This implies (i). From (i), the quotient bundle
![]() $TX|_C/{\mathcal R}_C$
is isomorphic to
$TX|_C/{\mathcal R}_C$
is isomorphic to
![]() ${\mathcal O}^{\oplus 2}$
. The assumption
${\mathcal O}^{\oplus 2}$
. The assumption
![]() $s_x \in {\mathcal R}_{C,x}$
implies that s modulo
$s_x \in {\mathcal R}_{C,x}$
implies that s modulo
![]() ${\mathcal R}_C$
defines a section of
${\mathcal R}_C$
defines a section of
![]() ${\mathcal O}^{\oplus 2}$
vanishing at x. Hence, it vanishes identically. This shows that
${\mathcal O}^{\oplus 2}$
vanishing at x. Hence, it vanishes identically. This shows that
![]() $s \in H^0(C, {\mathcal H}) = H^0(C, {\mathcal R})$
, proving (ii). (iii) is immediate from (i).
$s \in H^0(C, {\mathcal H}) = H^0(C, {\mathcal R})$
, proving (ii). (iii) is immediate from (i).
Definition 3.6. A cubic form
![]() $F \in \mathop {\mathrm {Sym}}\nolimits ^3 V^{\vee }$
on a vector space V is nondegenerate if
$F \in \mathop {\mathrm {Sym}}\nolimits ^3 V^{\vee }$
on a vector space V is nondegenerate if
Definition 3.7. In Definition 3.2, let
![]() $S \subset {\mathbb P} W$
be a Legendrian submanifold. We say that S has nondegenerate fundamental forms at
$S \subset {\mathbb P} W$
be a Legendrian submanifold. We say that S has nondegenerate fundamental forms at
![]() $s \in S$
if the following are satisfied.
$s \in S$
if the following are satisfied.
-
(i) The point s is contained in
 $ \mathrm {Dom}(\mathrm {III}_S)$
.
$ \mathrm {Dom}(\mathrm {III}_S)$
. -
(ii) The image of the second fundamental form
 $\widehat {N}^{(2)}_{S,s}$
is equal to
$\widehat {N}^{(2)}_{S,s}$
is equal to
 $\widehat {s}^{\perp }/\widehat {T}_s S$
.
$\widehat {s}^{\perp }/\widehat {T}_s S$
. -
(iii) The third fundamental form
 $\mathrm {III}_{S,s}: \mathop {\mathrm {Sym}}\nolimits ^3 T_s S \to \widehat {s}^{\vee } \otimes W/\widehat {s}^{\perp }$
is a nondegenerate cubic form on
$\mathrm {III}_{S,s}: \mathop {\mathrm {Sym}}\nolimits ^3 T_s S \to \widehat {s}^{\vee } \otimes W/\widehat {s}^{\perp }$
is a nondegenerate cubic form on
 $T_s S$
in the sense of Definition 3.6.
$T_s S$
in the sense of Definition 3.6. -
(iv) For any
 $v_1, v_2 \in T_s S$
, the element
$v_1, v_2 \in T_s S$
, the element  $$ \begin{align*}\mathrm{III}_{S,s}(v_1, v_2, \cdot) \in T^{\vee}_sS \otimes \widehat{s}^{\vee} \otimes W/\widehat{s}^{\perp}\end{align*} $$
$$ \begin{align*}\mathrm{III}_{S,s}(v_1, v_2, \cdot) \in T^{\vee}_sS \otimes \widehat{s}^{\vee} \otimes W/\widehat{s}^{\perp}\end{align*} $$
coincides with
 $$ \begin{align*}\mathrm{II}_{S,s}(v_1, v_2) \in \widehat{s}^{\vee} \otimes \widehat{N}^{(2)}_{S,s} = \widehat{s}^{\vee}\otimes \widehat{s}^{\perp}/\widehat{T}_s S\end{align*} $$
$$ \begin{align*}\mathrm{II}_{S,s}(v_1, v_2) \in \widehat{s}^{\vee} \otimes \widehat{N}^{(2)}_{S,s} = \widehat{s}^{\vee}\otimes \widehat{s}^{\perp}/\widehat{T}_s S\end{align*} $$
via the natural isomorphisms
 $$ \begin{align*}\widehat{s}^{\perp}/\widehat{T}_s S = (\widehat{T}_s S/\widehat{s})^{\vee} \otimes \mathbf{L} \mbox{ and } W/\widehat{s}^{\perp} = \widehat{s}^{\vee} \otimes \mathbf{L}\end{align*} $$
$$ \begin{align*}\widehat{s}^{\perp}/\widehat{T}_s S = (\widehat{T}_s S/\widehat{s})^{\vee} \otimes \mathbf{L} \mbox{ and } W/\widehat{s}^{\perp} = \widehat{s}^{\vee} \otimes \mathbf{L}\end{align*} $$
induced by
 $\omega $
.
$\omega $
.
Definition 3.8. A line C on a contact manifold
![]() $(X, {\mathcal H})$
is a nondegenerate line, if for some point
$(X, {\mathcal H})$
is a nondegenerate line, if for some point
![]() $x\in C$
, the VMRT
$x\in C$
, the VMRT
![]() ${\mathcal C}_x$
at x has nondegenerate fundamental forms at the point
${\mathcal C}_x$
at x has nondegenerate fundamental forms at the point
![]() ${\mathbb P} T_x C \in {\mathcal C}_x$
. Let
${\mathbb P} T_x C \in {\mathcal C}_x$
. Let
![]() $\mathrm {NDL}(X, {\mathcal H})$
be the subset of
$\mathrm {NDL}(X, {\mathcal H})$
be the subset of
![]() $\mathrm {Lines}(X, {\mathcal H})$
parameterizing nondegenerate lines. It is a Zariski-open subset in
$\mathrm {Lines}(X, {\mathcal H})$
parameterizing nondegenerate lines. It is a Zariski-open subset in
![]() $\mathrm {Lines}(X, {\mathcal H})$
.
$\mathrm {Lines}(X, {\mathcal H})$
.
Remark 3.9. The conditions in Definition 3.7 may look technical, but actually they hold at general points of a general Legendrian submanifold. For example, §3 of [Reference Landsberg and ManivelLM] shows that if the Legendrian submanifold
![]() $S \subset {\mathbb P} W$
is a smooth projective variety different from a linear subspace, then S has nondegenerate fundamental forms at a general point
$S \subset {\mathbb P} W$
is a smooth projective variety different from a linear subspace, then S has nondegenerate fundamental forms at a general point
![]() $s \in S$
. When
$s \in S$
. When
![]() $(X, {\mathcal H})$
is a Fano contact manifold of Picard number 1, Theorem 1.1 of [Reference KebekusK2] implies that the VMRT at a general point is a smooth projective variety. Thus a general line is nondegenerate in the sense of Definition 3.8, unless the VMRT’s are linear. It is expected that the latter situation does not occur and [Reference Buczynski, Kapustka and KapustkaBKK] proposes an approach to exclude this possibility.
$(X, {\mathcal H})$
is a Fano contact manifold of Picard number 1, Theorem 1.1 of [Reference KebekusK2] implies that the VMRT at a general point is a smooth projective variety. Thus a general line is nondegenerate in the sense of Definition 3.8, unless the VMRT’s are linear. It is expected that the latter situation does not occur and [Reference Buczynski, Kapustka and KapustkaBKK] proposes an approach to exclude this possibility.
Proposition 3.10. In Definitions 3.8, assume that
![]() $Y \subset \mathrm {NDL}(X, {\mathcal H}).$
Then the second fundamental forms of the VMRT determine a surjective homomorphism
$Y \subset \mathrm {NDL}(X, {\mathcal H}).$
Then the second fundamental forms of the VMRT determine a surjective homomorphism
![]() $\mathrm {II}: \mathop {\mathrm { Sym}}\nolimits ^2 {\mathcal V} \to {\mathcal F}^{\vee } \otimes {\mathcal R}/{\mathcal R}^+$
and the third fundamental forms of the VMRT determine a surjective homomorphism
$\mathrm {II}: \mathop {\mathrm { Sym}}\nolimits ^2 {\mathcal V} \to {\mathcal F}^{\vee } \otimes {\mathcal R}/{\mathcal R}^+$
and the third fundamental forms of the VMRT determine a surjective homomorphism
![]() $\mathrm {III}: \mathop {\mathrm {Sym}}\nolimits ^3 {\mathcal V} \to {\mathcal F}^{\vee } \otimes ({\mathcal H}/{\mathcal R}).$
In particular, we have
$\mathrm {III}: \mathop {\mathrm {Sym}}\nolimits ^3 {\mathcal V} \to {\mathcal F}^{\vee } \otimes ({\mathcal H}/{\mathcal R}).$
In particular, we have
for any
![]() $z \in Z$
.
$z \in Z$
.
Proof. It is immediate from the definition of a nondegenerate line that the second and the third fundamental forms of VMRT determine homomorphisms
![]() $\mathrm {II}$
and
$\mathrm {II}$
and
![]() $\mathrm {III},$
which are surjective at general points of Z. By Proposition 2.3(iv) and
$\mathrm {III},$
which are surjective at general points of Z. By Proposition 2.3(iv) and
![]() $ ({\mathcal H}|_C/{\mathcal R}_C) \cong {\mathcal O}(-1)$
from Lemma 3.5(i), the two homomorphisms are surjective at every point of Z. Then
$ ({\mathcal H}|_C/{\mathcal R}_C) \cong {\mathcal O}(-1)$
from Lemma 3.5(i), the two homomorphisms are surjective at every point of Z. Then
![]() ${\mathcal T}^2_z = (\mathrm {d}_z \mu )^{-1} ({\mathcal R}_z)$
follows from Proposition 2.6(iv).
${\mathcal T}^2_z = (\mathrm {d}_z \mu )^{-1} ({\mathcal R}_z)$
follows from Proposition 2.6(iv).
Proposition 3.11. Under the hypotheses of Proposition 3.10, the two subspaces
![]() $(\partial {\mathcal D})_y$
and
$(\partial {\mathcal D})_y$
and
![]() $H^0(C, {\mathcal H}|_C/TC)$
of
$H^0(C, {\mathcal H}|_C/TC)$
of
![]() $T_y Y = H^0(C, N_C)$
coincide. Consequently, the two quotient spaces
$T_y Y = H^0(C, N_C)$
coincide. Consequently, the two quotient spaces
![]() $T_y Y /(\partial {\mathcal D})_y$
and
$T_y Y /(\partial {\mathcal D})_y$
and
can be identified in a natural way.
Proof. By Lemma 3.5(ii), the subspace
![]() ${\mathcal T}_z^2 = (\mathrm {d}_z \mu )^{-1} {\mathcal R}_z \subset T_z Z$
in Proposition 3.10 can be identified with
${\mathcal T}_z^2 = (\mathrm {d}_z \mu )^{-1} {\mathcal R}_z \subset T_z Z$
in Proposition 3.10 can be identified with
under the identification in Proposition 2.3(i). Since
![]() $\mathrm {d}_z \rho : T_z Z \to T_y Y$
is the quotient map
$\mathrm {d}_z \rho : T_z Z \to T_y Y$
is the quotient map
the subspace
![]() $(\mathrm {d}_z \mu )^{-1} {\mathcal R}$
is sent to
$(\mathrm {d}_z \mu )^{-1} {\mathcal R}$
is sent to
![]() $H^0(C, {\mathcal H}|_C/TC) \subset T_y Y$
. This agrees with
$H^0(C, {\mathcal H}|_C/TC) \subset T_y Y$
. This agrees with
![]() $(\partial {\mathcal D})_y$
because
$(\partial {\mathcal D})_y$
because
![]() $\mathrm {d}_z \rho ({\mathcal T}^2_z) = \partial {\mathcal D}$
by Proposition 2.8.
$\mathrm {d}_z \rho ({\mathcal T}^2_z) = \partial {\mathcal D}$
by Proposition 2.8.
Lemma 3.12. In Proposition 3.11, define
and write
![]() $\mathbf {F}_x: \mathop {\mathrm { Sym}}\nolimits ^3 V_x \to I_x$
for
$\mathbf {F}_x: \mathop {\mathrm { Sym}}\nolimits ^3 V_x \to I_x$
for
![]() $\mathrm {III}_{{\mathcal C}_x, z}$
. For each pair
$\mathrm {III}_{{\mathcal C}_x, z}$
. For each pair
![]() $x \neq x' \in C$
, recall from Lemma 2.10 the one-dimensional vector space
$x \neq x' \in C$
, recall from Lemma 2.10 the one-dimensional vector space
![]() $A_x^{x'}$
of rational functions on C with pole at x and zero at
$A_x^{x'}$
of rational functions on C with pole at x and zero at
![]() $x'$
.
$x'$
.
-
(i) There is a canonical isomorphism between
 $(A^{x'}_x)^{\otimes 3} \otimes I_x$
and
$(A^{x'}_x)^{\otimes 3} \otimes I_x$
and
 $I_{x'}$
. For
$I_{x'}$
. For
 $f \in A^{x'}_x$
and
$f \in A^{x'}_x$
and
 $j \in I_x$
, denote by
$j \in I_x$
, denote by
 $f^3 \cdot j$
the element of
$f^3 \cdot j$
the element of
 $I_{x'}$
corresponding to
$I_{x'}$
corresponding to
 $ f^3 \otimes j \in (A^{x'}_x)^{\otimes 3} \otimes I_x$
.
$ f^3 \otimes j \in (A^{x'}_x)^{\otimes 3} \otimes I_x$
. -
(ii) For any
 $v_1, v_2, v_3 \in V_{x}$
and
$v_1, v_2, v_3 \in V_{x}$
and
 $f \in A^{x'}_x$
,
$f \in A^{x'}_x$
,  $$ \begin{align*}f^3 \cdot \mathbf{F}_x(v_1, v_2, v_3) = \mathbf{F}_{x'}(f \cdot v_1, f \cdot v_2, f \cdot v_3).\end{align*} $$
$$ \begin{align*}f^3 \cdot \mathbf{F}_x(v_1, v_2, v_3) = \mathbf{F}_{x'}(f \cdot v_1, f \cdot v_2, f \cdot v_3).\end{align*} $$
Proof. Fix a base point
![]() $x_0 \in C$
and define a line bundle
$x_0 \in C$
and define a line bundle
![]() ${\mathcal A}$
on C whose fiber at x is
${\mathcal A}$
on C whose fiber at x is
![]() $A_x^{x_0}$
. Then
$A_x^{x_0}$
. Then
![]() ${\mathcal A}$
is isomorphic to
${\mathcal A}$
is isomorphic to
![]() ${\mathcal O}(1)$
. Let
${\mathcal O}(1)$
. Let
![]() ${\mathcal I}$
be the line bundle on C whose fiber at
${\mathcal I}$
be the line bundle on C whose fiber at
![]() $x \in C$
is
$x \in C$
is
![]() $I_x$
. Then
$I_x$
. Then
![]() ${\mathcal I}$
is isomorphic to
${\mathcal I}$
is isomorphic to
![]() ${\mathcal O}(-3)$
. Thus we have a canonical trivialization of the line bundle
${\mathcal O}(-3)$
. Thus we have a canonical trivialization of the line bundle
![]() ${\mathcal A}^{\otimes 3} \otimes {\mathcal I} = I_{x_0} \times C,$
which shows (i).
${\mathcal A}^{\otimes 3} \otimes {\mathcal I} = I_{x_0} \times C,$
which shows (i).
Note that
![]() ${\mathcal V}|_{\rho ^{-1}(y)} \cong {\mathcal O}(-1)^{\oplus m}$
from Proposition 2.3(iv). Thus the collection of the homomorphisms
${\mathcal V}|_{\rho ^{-1}(y)} \cong {\mathcal O}(-1)^{\oplus m}$
from Proposition 2.3(iv). Thus the collection of the homomorphisms
![]() $\mathbf {F}_x$
for all
$\mathbf {F}_x$
for all
![]() $x\in C$
gives rise to a surjective homomorphism between trivial vector bundles
$x\in C$
gives rise to a surjective homomorphism between trivial vector bundles
![]() $ \mathop {\mathrm {Sym}}\nolimits ^3 ({\mathcal V} \otimes {\mathcal A}) \to {\mathcal A}^{\otimes 3} \otimes {\mathcal I},$
which corresponds to
$ \mathop {\mathrm {Sym}}\nolimits ^3 ({\mathcal V} \otimes {\mathcal A}) \to {\mathcal A}^{\otimes 3} \otimes {\mathcal I},$
which corresponds to
![]() $\mathbf {F}_{x_0}: \mathop {\mathrm {Sym}}\nolimits ^3 V_{x_0} \to I_{x_0}$
under the canonical trivialization
$\mathbf {F}_{x_0}: \mathop {\mathrm {Sym}}\nolimits ^3 V_{x_0} \to I_{x_0}$
under the canonical trivialization
![]() ${\mathcal A}^{\otimes 3} \otimes {\mathcal I}$
. This shows (ii).
${\mathcal A}^{\otimes 3} \otimes {\mathcal I}$
. This shows (ii).
Proposition 3.13. In Proposition 3.11, there are natural identifications:
-
(i)
 ${\mathcal D}_y = U_x \otimes V_x, $
${\mathcal D}_y = U_x \otimes V_x, $
-
(ii)
 $(\partial {\mathcal D})_y/{\mathcal D}_y = \wedge ^2 U_x \otimes I_x \otimes V^{\vee }_x,$
and
$(\partial {\mathcal D})_y/{\mathcal D}_y = \wedge ^2 U_x \otimes I_x \otimes V^{\vee }_x,$
and -
(iii)
 $T_y Y/ (\partial {\mathcal D})_y = \wedge ^2 U_x \otimes I_x \otimes U_x.$
$T_y Y/ (\partial {\mathcal D})_y = \wedge ^2 U_x \otimes I_x \otimes U_x.$
In particular, for any pair
![]() $x \neq x' \in C$
, there is a natural identification of
$x \neq x' \in C$
, there is a natural identification of
![]() $ \wedge ^2 U_x \otimes I_x \otimes U_x$
and
$ \wedge ^2 U_x \otimes I_x \otimes U_x$
and
![]() $\wedge ^2 U_{x'} \otimes I_{x'} \otimes U_{x'}$
compatible with the identification
$\wedge ^2 U_{x'} \otimes I_{x'} \otimes U_{x'}$
compatible with the identification
![]() $({\mathcal A}_{x}^{x'})^{\otimes 3} \otimes I_x = I_{x'}$
in Lemma 3.12 and the identification
$({\mathcal A}_{x}^{x'})^{\otimes 3} \otimes I_x = I_{x'}$
in Lemma 3.12 and the identification
![]() ${\mathcal A}_{x'}^x \otimes U_{x'} = U_x$
in Lemma 2.10.
${\mathcal A}_{x'}^x \otimes U_{x'} = U_x$
in Lemma 2.10.
Proof. We have already seen (i) in Definition 2.7. (ii) is from
![]() $(\partial {\mathcal D})_y/{\mathcal D}_y = {\mathcal T}_z^2/{\mathcal T}_z^1$
in Proposition 2.8, the identification
$(\partial {\mathcal D})_y/{\mathcal D}_y = {\mathcal T}_z^2/{\mathcal T}_z^1$
in Proposition 2.8, the identification
![]() $\wedge ^2 U_x = T_x C$
from Lemma 2.9, and
$\wedge ^2 U_x = T_x C$
from Lemma 2.9, and
from Lemma 3.5(iii). (iii) follows from
where the first equality is by Proposition 3.11.
Definition 3.14. Let
![]() ${\mathbb U}$
be a vector space of dimension 2, and let
${\mathbb U}$
be a vector space of dimension 2, and let
![]() ${\mathbb V}$
be a vector space of dimension
${\mathbb V}$
be a vector space of dimension
![]() $m \geq 1.$
Fix a one-dimensional vector space
$m \geq 1.$
Fix a one-dimensional vector space
![]() ${\mathbb I}$
. Let
${\mathbb I}$
. Let
![]() ${\mathfrak g}_+ = {\mathfrak g}_1 \oplus {\mathfrak g}_2 \oplus {\mathfrak g}_3$
be the vector space defined by
${\mathfrak g}_+ = {\mathfrak g}_1 \oplus {\mathfrak g}_2 \oplus {\mathfrak g}_3$
be the vector space defined by
Fix a cubic form
![]() $F: \mathop {\mathrm {Sym}}\nolimits ^3 {\mathbb V} \to {\mathbb I}$
on
$F: \mathop {\mathrm {Sym}}\nolimits ^3 {\mathbb V} \to {\mathbb I}$
on
![]() ${\mathbb V}$
which is nondegenerate in the sense of Definition 3.6. For
${\mathbb V}$
which is nondegenerate in the sense of Definition 3.6. For
![]() $v_1, v_2 \in {\mathbb V}$
, define
$v_1, v_2 \in {\mathbb V}$
, define
![]() $F_{v_1 v_2} \in {\mathbb I} \otimes {\mathbb V}^{\vee }$
by
$F_{v_1 v_2} \in {\mathbb I} \otimes {\mathbb V}^{\vee }$
by
We define a graded Lie algebra structure on
![]() ${\mathfrak g}_+ := {\mathfrak g}_1 \oplus {\mathfrak g}_2 \oplus {\mathfrak g}_3$
by
${\mathfrak g}_+ := {\mathfrak g}_1 \oplus {\mathfrak g}_2 \oplus {\mathfrak g}_3$
by
By the nondegeneracy of F, (3.1) implies
![]() $[{\mathfrak g}_1, {\mathfrak g}_1] = {\mathfrak g}_2$
. Thus (3.2) is sufficient to determine the Lie bracket
$[{\mathfrak g}_1, {\mathfrak g}_1] = {\mathfrak g}_2$
. Thus (3.2) is sufficient to determine the Lie bracket
![]() $[{\mathfrak g}_1, {\mathfrak g}_2]$
. It is easy to check that this gives a graded Lie algebra structure on
$[{\mathfrak g}_1, {\mathfrak g}_2]$
. It is easy to check that this gives a graded Lie algebra structure on
![]() ${\mathfrak g}_+$
. Note that the Lie bracket
${\mathfrak g}_+$
. Note that the Lie bracket
![]() $[{\mathfrak g}_1, {\mathfrak g}_2] \to {\mathfrak g}_3$
is independent of F and satisfies
$[{\mathfrak g}_1, {\mathfrak g}_2] \to {\mathfrak g}_3$
is independent of F and satisfies
for any
![]() $u_1, u_2, u_3 \in {\mathbb U}, v_3 \in {\mathbb V}$
and
$u_1, u_2, u_3 \in {\mathbb U}, v_3 \in {\mathbb V}$
and
![]() $v^* \in {\mathbb I} \otimes V^{\vee }$
. Sometimes, we write
$v^* \in {\mathbb I} \otimes V^{\vee }$
. Sometimes, we write
![]() ${\mathfrak g}_+ = {\mathfrak g}_+(F)$
to indicate that the Lie algebra structure depends on the cubic form F.
${\mathfrak g}_+ = {\mathfrak g}_+(F)$
to indicate that the Lie algebra structure depends on the cubic form F.
The following is the precise formulation of going from the right-hand side to the left-hand side of (Corr. m) in §1.
Theorem 3.15. Let
![]() $(X, {\mathcal H})$
be a contact manifold of dimension
$(X, {\mathcal H})$
be a contact manifold of dimension
![]() $2m+3$
. Let
$2m+3$
. Let
![]() $C \subset (X, {\mathcal H})$
be a nondegenerate line, and let
$C \subset (X, {\mathcal H})$
be a nondegenerate line, and let
![]() $y \in \mathrm {NDL}(X, {\mathcal H})$
be the corresponding point. Then the symbol algebra
$y \in \mathrm {NDL}(X, {\mathcal H})$
be the corresponding point. Then the symbol algebra
![]() $\mathrm {symb}_y ({\mathcal D})$
of the natural distribution
$\mathrm {symb}_y ({\mathcal D})$
of the natural distribution
![]() ${\mathcal D}$
on
${\mathcal D}$
on
![]() $\mathrm {NDL}(X, {\mathcal H})$
is isomorphic to
$\mathrm {NDL}(X, {\mathcal H})$
is isomorphic to
![]() ${\mathfrak g}_+(F_y)$
in Definition 3.14 for some nondegenerate cubic form
${\mathfrak g}_+(F_y)$
in Definition 3.14 for some nondegenerate cubic form
![]() $F_y$
on an m-dimensional vector space
$F_y$
on an m-dimensional vector space
![]() ${\mathbb V}$
.
${\mathbb V}$
.
Proof. Let
![]() $\mathbf {F}_x: \mathop {\mathrm {Sym}}\nolimits ^3 V_x \to I_x$
be the cubic form given by
$\mathbf {F}_x: \mathop {\mathrm {Sym}}\nolimits ^3 V_x \to I_x$
be the cubic form given by
via the natural isomorphism
![]() $V_x \cong {\mathcal V}_x$
for a point
$V_x \cong {\mathcal V}_x$
for a point
![]() $x \in C$
. Using Proposition 3.13, let us identify
$x \in C$
. Using Proposition 3.13, let us identify
![]() $\mathrm {symb}_y({\mathcal D})$
with
$\mathrm {symb}_y({\mathcal D})$
with
![]() ${\mathfrak g}_+$
as graded vector spaces by setting
${\mathfrak g}_+$
as graded vector spaces by setting
![]() ${\mathbb U} = U_{x}, {\mathbb V} = V_{x}$
and
${\mathbb U} = U_{x}, {\mathbb V} = V_{x}$
and
![]() ${\mathbb I} = I_{x}$
. It suffices to show that the Lie algebra structure of
${\mathbb I} = I_{x}$
. It suffices to show that the Lie algebra structure of
![]() $\mathrm {symb}_y({\mathcal D})$
agrees with that of
$\mathrm {symb}_y({\mathcal D})$
agrees with that of
![]() ${\mathfrak g}_+(\mathbf {F}_{x}),$
namely, it satisfies (3.1) and (3.2).
${\mathfrak g}_+(\mathbf {F}_{x}),$
namely, it satisfies (3.1) and (3.2).
For any
![]() $x \in C$
and
$x \in C$
and
![]() $v_1, v_2 \in V_x$
, let
$v_1, v_2 \in V_x$
, let
![]() $F_{v_1 v_2} \in I_x \otimes V_x^{\vee }$
be the contraction of
$F_{v_1 v_2} \in I_x \otimes V_x^{\vee }$
be the contraction of
![]() $F= \mathbf {F}_{x}$
with
$F= \mathbf {F}_{x}$
with
![]() $v_1, v_2$
. Fix a nonconstant rational function
$v_1, v_2$
. Fix a nonconstant rational function
![]() $f \in U_x$
. For
$f \in U_x$
. For
![]() $v_1, v_2 \in V_{x},$
Proposition 2.12, combined with Definition 3.7(iv), says that in
$v_1, v_2 \in V_{x},$
Proposition 2.12, combined with Definition 3.7(iv), says that in
![]() $\mathrm {symb}_y({\mathcal D})$
,
$\mathrm {symb}_y({\mathcal D})$
,
Thus the Lie algebra
![]() $\mathrm {symb}_y({\mathcal D})$
satisfies (3.1) with
$\mathrm {symb}_y({\mathcal D})$
satisfies (3.1) with
![]() $F= \mathbf {F}_{x}$
.
$F= \mathbf {F}_{x}$
.
For
![]() $v_1, v_2, v_3 \in V_x,$
Proposition 2.13 says
$v_1, v_2, v_3 \in V_x,$
Proposition 2.13 says
as elements in
![]() $ (\wedge ^2 U_x) \otimes I_x \otimes U_x. $
Thus, the Lie algebra
$ (\wedge ^2 U_x) \otimes I_x \otimes U_x. $
Thus, the Lie algebra
![]() $\mathrm {symb}_y({\mathcal D})$
satisfies (3.2) with
$\mathrm {symb}_y({\mathcal D})$
satisfies (3.2) with
![]() $F= \mathbf {F}_{x}$
when
$F= \mathbf {F}_{x}$
when
![]() $ u_3 = \mathbf {1}_{x}$
. It remains to check (3.2) when
$ u_3 = \mathbf {1}_{x}$
. It remains to check (3.2) when
![]() $u_3 $
is a nonconstant function in
$u_3 $
is a nonconstant function in
![]() $ U_{x}.$
$ U_{x}.$
For a given nonconstant function
![]() $f \in U_{x}$
, let
$f \in U_{x}$
, let
![]() $x' \in C$
be the zero of f such that
$x' \in C$
be the zero of f such that
![]() $f \in {\mathcal A}^{x'}_x$
in the notation of Lemma 3.12. For
$f \in {\mathcal A}^{x'}_x$
in the notation of Lemma 3.12. For
![]() $v_1, v_2, v_3 \in V_{x}$
, we have
$v_1, v_2, v_3 \in V_{x}$
, we have
![]() $ w_1, w_2, w_3 \in V_{x'}$
such that
$ w_1, w_2, w_3 \in V_{x'}$
such that
![]() $w_i = f \cdot v_i$
for
$w_i = f \cdot v_i$
for
![]() $i=1,2,3$
. Let
$i=1,2,3$
. Let
![]() $h \in {\mathcal A}^x_{x'}$
be the rational function
$h \in {\mathcal A}^x_{x'}$
be the rational function
![]() $\frac {1}{f}$
. Then
$\frac {1}{f}$
. Then
for
![]() $i=1,2,3,$
under the tensor decomposition
$i=1,2,3,$
under the tensor decomposition
![]() $H^0(C, N_C^+) = U_x \otimes V_x = U_{x'} \otimes V_{x'}$
. From (3.4) applied to the point
$H^0(C, N_C^+) = U_x \otimes V_x = U_{x'} \otimes V_{x'}$
. From (3.4) applied to the point
![]() $x' \in C$
,
$x' \in C$
,
as elements of
![]() $T_y Y/(\partial {\mathcal D})_y = (\wedge ^2 U_{x'}) \otimes I_{x'} \otimes U_{x'}.$
By (3.5), the left-hand side of (3.6) is equal to
$T_y Y/(\partial {\mathcal D})_y = (\wedge ^2 U_{x'}) \otimes I_{x'} \otimes U_{x'}.$
By (3.5), the left-hand side of (3.6) is equal to
![]() $ [f \otimes v_3, [f \otimes v_2, \mathbf {1}_x \otimes v_1] ].$
On the other hand, the right-hand side of (3.6) is
$ [f \otimes v_3, [f \otimes v_2, \mathbf {1}_x \otimes v_1] ].$
On the other hand, the right-hand side of (3.6) is
by Lemma 3.12. Using the compatibility of the tensor multiplication by
![]() ${\mathcal A}_x^{x'}$
in the identification (iii) of Proposition 3.13, this is equal to
${\mathcal A}_x^{x'}$
in the identification (iii) of Proposition 3.13, this is equal to
 $$ \begin{align*}&f^2 \cdot (\mathbf{1}_{x'} \wedge h) \otimes \mathbf{F}_x(v_1, v_2, v_3) \otimes (f \cdot \mathbf{1}_{x'})\\&\quad = (f \wedge \mathbf{1}_x) \otimes \mathbf{F}_x(v_1, v_2, v_3) \otimes f.\end{align*} $$
$$ \begin{align*}&f^2 \cdot (\mathbf{1}_{x'} \wedge h) \otimes \mathbf{F}_x(v_1, v_2, v_3) \otimes (f \cdot \mathbf{1}_{x'})\\&\quad = (f \wedge \mathbf{1}_x) \otimes \mathbf{F}_x(v_1, v_2, v_3) \otimes f.\end{align*} $$
Thus, (3.6) gives
This proves (3.2) when
![]() $u_3$
is a nonconstant function
$u_3$
is a nonconstant function
![]() $f \in U_{x}$
.
$f \in U_{x}$
.
4 From distributions with symbols
 ${\mathfrak g}_+(F)$
to nondegenerate lines on contact manifolds
${\mathfrak g}_+(F)$
to nondegenerate lines on contact manifolds
Definition 4.1. Let
![]() $D \subset TM$
be a distribution on a complex manifold M, and let
$D \subset TM$
be a distribution on a complex manifold M, and let
![]() $D^{\perp } \subset T^{\vee } M$
be its annihilator.
$D^{\perp } \subset T^{\vee } M$
be its annihilator.
-
(i) Consider the null space of the Levi tensor at
 $y \in M$
,
$y \in M$
,  $$ \begin{align*}\mathrm{Null}(\mathrm{Levi}_y^D):= \{ v \in D_y \mid \mathrm{Levi}^D_y (v, u) =0 \mbox{ for all } u \in D_y \}.\end{align*} $$
$$ \begin{align*}\mathrm{Null}(\mathrm{Levi}_y^D):= \{ v \in D_y \mid \mathrm{Levi}^D_y (v, u) =0 \mbox{ for all } u \in D_y \}.\end{align*} $$
As y varies over M, the null spaces define a distribution
 $\mathrm {Ch}(D) $
on a Zariski-open subset of M, called the Cauchy characteristic of D. It is easy to see that this is an integrable distribution, defining a holomorphic foliation on the Zariski-open subset of M.
$\mathrm {Ch}(D) $
on a Zariski-open subset of M, called the Cauchy characteristic of D. It is easy to see that this is an integrable distribution, defining a holomorphic foliation on the Zariski-open subset of M. -
(ii) For each
 $y \in M$
and
$y \in M$
and
 $\alpha \in D_y^{\perp } \subset T^{\vee }_y M,$
define the anti-symmetric form on
$\alpha \in D_y^{\perp } \subset T^{\vee }_y M,$
define the anti-symmetric form on
 $D_y$
,
$D_y$
,  $$ \begin{align*} \alpha \circ \mathrm{Levi}_y^D: \wedge^2 D_y \to {\mathbb C} \end{align*} $$
$$ \begin{align*} \alpha \circ \mathrm{Levi}_y^D: \wedge^2 D_y \to {\mathbb C} \end{align*} $$
and its null-space by
 $$ \begin{align*} \mathrm{Null}(\alpha \circ \mathrm{Levi}_y^D) = \{ v \in D_y \mid \alpha \circ \mathrm{Levi}_y^D (v, u) = 0 \mbox{ for all } u \in D_y\}. \end{align*} $$
$$ \begin{align*} \mathrm{Null}(\alpha \circ \mathrm{Levi}_y^D) = \{ v \in D_y \mid \alpha \circ \mathrm{Levi}_y^D (v, u) = 0 \mbox{ for all } u \in D_y\}. \end{align*} $$
Notation 4.2. The projectivization
![]() ${\mathbb P} T^{\vee } M$
of the cotangent bundle of a complex manifold M has a natural
${\mathbb P} T^{\vee } M$
of the cotangent bundle of a complex manifold M has a natural
![]() ${\mathcal O}_{{\mathbb P} T^{\vee }M} (1)$
-valued 1-form
${\mathcal O}_{{\mathbb P} T^{\vee }M} (1)$
-valued 1-form
![]() $\vartheta ^M$
such that
$\vartheta ^M$
such that
![]() $\mathrm {Ker}(\vartheta ^M)$
is a contact structure on
$\mathrm {Ker}(\vartheta ^M)$
is a contact structure on
![]() ${\mathbb P} T^{\vee }M$
(see Notation 2.4 of [Reference HwangH2] for more details).
${\mathbb P} T^{\vee }M$
(see Notation 2.4 of [Reference HwangH2] for more details).
The following is Proposition 3.6 of [Reference HwangH2] (note that
![]() $\mathrm {Levi}^{\widetilde {H}}_{\alpha }$
is written as
$\mathrm {Levi}^{\widetilde {H}}_{\alpha }$
is written as
![]() $\check {\mathrm {d}}_{\alpha } (\vartheta ^M|_{{\mathbb P} D^{\perp }})$
in [Reference HwangH2]).
$\check {\mathrm {d}}_{\alpha } (\vartheta ^M|_{{\mathbb P} D^{\perp }})$
in [Reference HwangH2]).
Proposition 4.3. In the setting of Definition 4.1, the restriction
![]() $\vartheta ^M|_{{\mathbb P} D^{\perp }}$
defines a distribution
$\vartheta ^M|_{{\mathbb P} D^{\perp }}$
defines a distribution
![]() $\widetilde {{\mathcal H}}$
of corank 1 on the manifold
$\widetilde {{\mathcal H}}$
of corank 1 on the manifold
![]() ${\mathbb P} D^{\perp }$
. For any
${\mathbb P} D^{\perp }$
. For any
![]() $y \in M$
and any nonzero
$y \in M$
and any nonzero
![]() $a \in D^{\perp }_y$
with the corresponding point
$a \in D^{\perp }_y$
with the corresponding point
![]() $\alpha \in {\mathbb P} D^{\perp }_y$
, we have an isomorphism
$\alpha \in {\mathbb P} D^{\perp }_y$
, we have an isomorphism
induced by the natural projection
![]() ${\mathbb P} D^{\perp } \to M$
.
${\mathbb P} D^{\perp } \to M$
.
The following is the precise formulation of going from the left-hand side to the right-hand side of (Corr. m) in §1.
Theorem 4.4. Let
![]() ${\mathcal D} \subset TY$
be a distribution regular at every point of
${\mathcal D} \subset TY$
be a distribution regular at every point of
![]() $ Y$
such that the symbol algebra
$ Y$
such that the symbol algebra
![]() $\mathrm {symb}_y({\mathcal D})$
is isomorphic to
$\mathrm {symb}_y({\mathcal D})$
is isomorphic to
![]() ${\mathfrak g}_+(F_y)$
in Definition 3.14 for a nondegenerate cubic form
${\mathfrak g}_+(F_y)$
in Definition 3.14 for a nondegenerate cubic form
![]() $F_y$
for each
$F_y$
for each
![]() $y \in Y$
. Let
$y \in Y$
. Let
![]() ${\mathcal W} \subset T^{\vee } Y$
be the annihilator of
${\mathcal W} \subset T^{\vee } Y$
be the annihilator of
![]() $\partial {\mathcal D}$
. Denote by
$\partial {\mathcal D}$
. Denote by
![]() $\varrho : {\mathbb P} {\mathcal W} \to Y$
the
$\varrho : {\mathbb P} {\mathcal W} \to Y$
the
![]() ${\mathbb P}^1$
-bundle obtained by the projectivization of
${\mathbb P}^1$
-bundle obtained by the projectivization of
![]() ${\mathcal W}$
. Then, for each
${\mathcal W}$
. Then, for each
![]() $y \in Y$
, there exists an open neighborhood
$y \in Y$
, there exists an open neighborhood
![]() $O^y \subset Y$
of y and a submersion
$O^y \subset Y$
of y and a submersion
![]() $\mu _y: \varrho ^{-1}(O^y) \to X^y$
of relative dimension m onto a complex manifold
$\mu _y: \varrho ^{-1}(O^y) \to X^y$
of relative dimension m onto a complex manifold
![]() $X^y$
equipped with a contact structure
$X^y$
equipped with a contact structure
![]() ${\mathcal H}^y \subset TX^y$
with the following properties.
${\mathcal H}^y \subset TX^y$
with the following properties.
-
(i) The distribution of corank 1 on
 $\varrho ^{-1} (O^y)$
given by the restriction of
$\varrho ^{-1} (O^y)$
given by the restriction of
 $\vartheta ^Y$
to the submanifold
$\vartheta ^Y$
to the submanifold
 ${\mathbb P} {\mathcal W} \subset {\mathbb P} T^{\vee }$
has the fiber at
${\mathbb P} {\mathcal W} \subset {\mathbb P} T^{\vee }$
has the fiber at
 $\alpha \in \varrho ^{-1} (O^y) \subset {\mathbb P} {\mathcal W}$
equal to
$\alpha \in \varrho ^{-1} (O^y) \subset {\mathbb P} {\mathcal W}$
equal to
 $(\mathrm { d}_{\alpha } \mu _y)^{-1} ({\mathcal H}^y_{\mu _y(\alpha )})$
.
$(\mathrm { d}_{\alpha } \mu _y)^{-1} ({\mathcal H}^y_{\mu _y(\alpha )})$
. -
(ii) For two distinct points
 $\alpha _1 \neq \alpha _2 \in {\mathbb P} {\mathcal W}_y$
, the two vector spaces
$\alpha _1 \neq \alpha _2 \in {\mathbb P} {\mathcal W}_y$
, the two vector spaces
 $\mathrm {Ker}(\mathrm {d}_{\alpha _1} \mu _y) \subset T_{\alpha _1} {\mathbb P} {\mathcal W}$
and
$\mathrm {Ker}(\mathrm {d}_{\alpha _1} \mu _y) \subset T_{\alpha _1} {\mathbb P} {\mathcal W}$
and
 $\mathrm { Ker}(\mathrm {d}_{\alpha _2} \mu _y) \subset T_{\alpha _2} {\mathbb P} {\mathcal W}$
satisfy
$\mathrm { Ker}(\mathrm {d}_{\alpha _2} \mu _y) \subset T_{\alpha _2} {\mathbb P} {\mathcal W}$
satisfy  $$ \begin{align*}\mathrm{d}_{\alpha_1} \varrho (\mathrm{Ker}(\mathrm{d}_{\alpha_1} \mu_y)) \ \cap \ \mathrm{ d}_{\alpha_2} \varrho (\mathrm{Ker}(\mathrm{d}_{\alpha_2} \mu_y)) \ = \ 0. \end{align*} $$
$$ \begin{align*}\mathrm{d}_{\alpha_1} \varrho (\mathrm{Ker}(\mathrm{d}_{\alpha_1} \mu_y)) \ \cap \ \mathrm{ d}_{\alpha_2} \varrho (\mathrm{Ker}(\mathrm{d}_{\alpha_2} \mu_y)) \ = \ 0. \end{align*} $$
-
(iii) The submersion
 $\mu _y$
sends the fibers of
$\mu _y$
sends the fibers of
 $\varrho $
to lines on
$\varrho $
to lines on
 $(X^y, {\mathcal H}^y)$
.
$(X^y, {\mathcal H}^y)$
. -
(iv) The lines on
 $(X^y, {\mathcal H}^y)$
in (iii) form a
$(X^y, {\mathcal H}^y)$
in (iii) form a
 $(3m+2)$
-dimensional family, that is, all of their small deformations on
$(3m+2)$
-dimensional family, that is, all of their small deformations on
 $X^y$
come from the
$X^y$
come from the
 $\mu _y$
-images of the fibers of
$\mu _y$
-images of the fibers of
 $\varrho $
.
$\varrho $
. -
(v) The lines in (iii) are nondegenerate.
We need the following two lemmata. We skip the proof of the first one, which is straightforward. The second is well known (e.g., Lemma 3.5 of [Reference KebekusK1]), but we reproduce the proof for the reader’s convenience.
Lemma 4.5. In Definition 3.14, denote by
![]() $\varsigma : \wedge ^2 ({\mathfrak g}_1 + {\mathfrak g}_2) \to {\mathfrak g}_3$
be the homomorphism defined by the Lie bracket of
$\varsigma : \wedge ^2 ({\mathfrak g}_1 + {\mathfrak g}_2) \to {\mathfrak g}_3$
be the homomorphism defined by the Lie bracket of
![]() ${\mathfrak g}$
modulo
${\mathfrak g}$
modulo
![]() ${\mathfrak g}_1 + {\mathfrak g}_2$
. It is independent of F and for any
${\mathfrak g}_1 + {\mathfrak g}_2$
. It is independent of F and for any
![]() $a \in {\mathfrak g}_3^{\vee }$
the anti-symmetric form
$a \in {\mathfrak g}_3^{\vee }$
the anti-symmetric form
![]() $a \circ \varsigma $
on
$a \circ \varsigma $
on
![]() ${\mathfrak g}_1 + {\mathfrak g}_2$
satisfies
${\mathfrak g}_1 + {\mathfrak g}_2$
satisfies
where
![]() $a^{\perp } = \{ u \in {\mathbb U} \mid a (u) =0\}.$
$a^{\perp } = \{ u \in {\mathbb U} \mid a (u) =0\}.$
Lemma 4.6. For a contact manifold
![]() $(X, {\mathcal H})$
of dimension
$(X, {\mathcal H})$
of dimension
![]() $2m+3$
with the contact line bundle
$2m+3$
with the contact line bundle
![]() ${\mathcal L} = TX/{\mathcal H}$
, let
${\mathcal L} = TX/{\mathcal H}$
, let
![]() $C \subset X$
be a smooth rational curve such that
$C \subset X$
be a smooth rational curve such that
![]() ${\mathcal L}|_C\cong {\mathcal O}(1)$
and
${\mathcal L}|_C\cong {\mathcal O}(1)$
and
![]() $TX|_C$
is semipositive, that is,
$TX|_C$
is semipositive, that is,
for some nonnegative integers
![]() $ l_1 \geq \cdots \geq l_{2m+3} \geq 0.$
Then C is a line on
$ l_1 \geq \cdots \geq l_{2m+3} \geq 0.$
Then C is a line on
![]() $(X, {\mathcal H})$
.
$(X, {\mathcal H})$
.
Proof. It suffices to show that C is unbendable. Let
![]() $\lambda : TX \to {\mathcal L}$
be the quotient homomorphism. Since
$\lambda : TX \to {\mathcal L}$
be the quotient homomorphism. Since
![]() $TC \cong {\mathcal O}(2)$
and
$TC \cong {\mathcal O}(2)$
and
![]() ${\mathcal L}|_C \cong {\mathcal O}(1)$
, we have
${\mathcal L}|_C \cong {\mathcal O}(1)$
, we have
![]() $\lambda (T C) =0, $
which implies that C is tangent to
$\lambda (T C) =0, $
which implies that C is tangent to
![]() ${\mathcal H} = \mathrm {Ker}(\lambda )$
. Since
${\mathcal H} = \mathrm {Ker}(\lambda )$
. Since
![]() $\det TX = \mathcal{L}^{\otimes (m+2)}$
, we have
$\det TX = \mathcal{L}^{\otimes (m+2)}$
, we have
Let
for
![]() $k_1 \geq \cdots \geq k_{2m+2}$
. Since
$k_1 \geq \cdots \geq k_{2m+2}$
. Since
![]() $\mathrm {Levi}^{{\mathcal H}}$
gives symplectic forms on fibers of
$\mathrm {Levi}^{{\mathcal H}}$
gives symplectic forms on fibers of
![]() ${\mathcal H}$
with values in
${\mathcal H}$
with values in
![]() ${\mathcal L}$
, we have
${\mathcal L}$
, we have
Thus
![]() $k_1 \geq \cdots \geq k_{m+1} \geq 1$
and
$k_1 \geq \cdots \geq k_{m+1} \geq 1$
and
![]() $0 \geq k_{m+2} \geq \cdots \geq k_{2m+2}$
. Combining
$0 \geq k_{m+2} \geq \cdots \geq k_{2m+2}$
. Combining
![]() $2 \leq k_1 \leq l_1$
and
$2 \leq k_1 \leq l_1$
and
![]() $k_i \leq l_i$
for
$k_i \leq l_i$
for
![]() $1 \leq i \leq 2m+2$
with (4.1), we conclude
$1 \leq i \leq 2m+2$
with (4.1), we conclude
 $$ \begin{align*} l_1 &=k_1= 2, \ l_2 = \cdots = l_{m+1} = k_2 = \cdots = k_{m+1} = 1,\\l_{m+2} &= \cdots = l_{2m+3} = k_{m+1} = \cdots k_{2m+1} =0, \ k_{2m+2} = -1. \end{align*} $$
$$ \begin{align*} l_1 &=k_1= 2, \ l_2 = \cdots = l_{m+1} = k_2 = \cdots = k_{m+1} = 1,\\l_{m+2} &= \cdots = l_{2m+3} = k_{m+1} = \cdots k_{2m+1} =0, \ k_{2m+2} = -1. \end{align*} $$
Thus, C is unbendable.
Proof of Theorem 4.4
By Lemma 4.5, for any
![]() $y \in Y$
, any
$y \in Y$
, any
![]() $\alpha _1 \neq \alpha _2 \in {\mathbb P} {\mathcal W}_y$
and corresponding nonzero vectors
$\alpha _1 \neq \alpha _2 \in {\mathbb P} {\mathcal W}_y$
and corresponding nonzero vectors
![]() $a_1 \neq a_2 \in {\mathcal W}_y$
, we have
$a_1 \neq a_2 \in {\mathcal W}_y$
, we have
and
Applying Proposition 4.3 with
![]() $M=Y, D = \partial {\mathcal D}, D^{\perp } = {\mathcal W}$
, (4.2) shows that the Cauchy characteristic of
$M=Y, D = \partial {\mathcal D}, D^{\perp } = {\mathcal W}$
, (4.2) shows that the Cauchy characteristic of
![]() $\widetilde {{\mathcal H}}$
is a distribution defined on the whole
$\widetilde {{\mathcal H}}$
is a distribution defined on the whole
![]() ${\mathbb P} (\partial {\mathcal D})^{\perp }$
. For each
${\mathbb P} (\partial {\mathcal D})^{\perp }$
. For each
![]() $y \in Y$
, we can choose a neighborhood
$y \in Y$
, we can choose a neighborhood
![]() $O^y$
such that the space of leaves of the foliation
$O^y$
such that the space of leaves of the foliation
![]() $\mathrm {Ch}(\widetilde {{\mathcal H}})$
in
$\mathrm {Ch}(\widetilde {{\mathcal H}})$
in
![]() $\varrho ^{-1} (O^y)$
becomes a complex manifold
$\varrho ^{-1} (O^y)$
becomes a complex manifold
![]() $X^y$
(e.g., by Lemma 5.6 of [Reference Hwang and LiHL]) and the quotient map becomes a submersion
$X^y$
(e.g., by Lemma 5.6 of [Reference Hwang and LiHL]) and the quotient map becomes a submersion
![]() $\mu _y: \varrho ^{-1}(O^y) \to X^y$
. Then
$\mu _y: \varrho ^{-1}(O^y) \to X^y$
. Then
![]() $\widetilde {{\mathcal H}}$
descends to a contact structure
$\widetilde {{\mathcal H}}$
descends to a contact structure
![]() ${\mathcal H}^y \subset T X^y$
on
${\mathcal H}^y \subset T X^y$
on
![]() $X^y$
, satisfying (i). (ii) follows from (4.3).
$X^y$
, satisfying (i). (ii) follows from (4.3).
To check (iii), let
![]() $C \subset X^y$
be the image of
$C \subset X^y$
be the image of
![]() $\varrho ^{-1}(y)$
under
$\varrho ^{-1}(y)$
under
![]() $\mu _y$
. Then
$\mu _y$
. Then
![]() ${\mathcal L}^y|_C \cong {\mathcal O}(1)$
for the contact line bundle
${\mathcal L}^y|_C \cong {\mathcal O}(1)$
for the contact line bundle
![]() ${\mathcal L}^y= T X^y/{\mathcal H}^y$
by (i) together with the fact that
${\mathcal L}^y= T X^y/{\mathcal H}^y$
by (i) together with the fact that
![]() $\vartheta ^M|_{{\mathbb P} W}$
is
$\vartheta ^M|_{{\mathbb P} W}$
is
![]() ${\mathcal O}_{{\mathbb P} {\mathcal W}}(1)$
-valued 1-form. Since
${\mathcal O}_{{\mathbb P} {\mathcal W}}(1)$
-valued 1-form. Since
![]() $\mu _y$
is a submersion, the vector bundle
$\mu _y$
is a submersion, the vector bundle
![]() $T X^y|_C$
is semipositive. This shows that C is a line by Lemma 4.6.
$T X^y|_C$
is semipositive. This shows that C is a line by Lemma 4.6.
To prove (iv), we need to check that there exists no arc
![]() $\Delta \subset Y$
with
$\Delta \subset Y$
with
![]() $y \in \Delta $
such that the surface
$y \in \Delta $
such that the surface
![]() $\varrho ^{-1}(\Delta )$
is sent to a single curve in
$\varrho ^{-1}(\Delta )$
is sent to a single curve in
![]() $X^y$
by
$X^y$
by
![]() $\mu _y$
. But if such an arc
$\mu _y$
. But if such an arc
![]() $\Delta $
exists, for two distinct point
$\Delta $
exists, for two distinct point
![]() $\alpha _1 \neq \alpha _2 \in {\mathbb P} {\mathcal W}_y$
, we have
$\alpha _1 \neq \alpha _2 \in {\mathbb P} {\mathcal W}_y$
, we have
a contradiction to (ii).
By (iv), after shrinking
![]() $O^y$
if necessary, we may regard
$O^y$
if necessary, we may regard
![]() $O^y$
as an open subset of
$O^y$
as an open subset of
![]() $\mathrm {Lines}(X^y, {\mathcal H}^y)$
and identify
$\mathrm {Lines}(X^y, {\mathcal H}^y)$
and identify
![]() $\varrho ^{-1}(O^y)$
with the open subset
$\varrho ^{-1}(O^y)$
with the open subset
![]() $Z:= \rho ^{-1}(O^y)$
in the universal family. By Proposition 4.3 and Lemma 4.5, the distribution
$Z:= \rho ^{-1}(O^y)$
in the universal family. By Proposition 4.3 and Lemma 4.5, the distribution
![]() ${\mathcal D}$
is spanned by the images of
${\mathcal D}$
is spanned by the images of
![]() $\mathrm {d}\varrho (\mathrm {Ker}(\mathrm {d}_{\alpha } \mu _y))$
for
$\mathrm {d}\varrho (\mathrm {Ker}(\mathrm {d}_{\alpha } \mu _y))$
for
![]() $\alpha \in \varrho ^{-1}(y)$
. Thus
$\alpha \in \varrho ^{-1}(y)$
. Thus
![]() ${\mathcal D}|_{O^y}$
agrees with the distribution
${\mathcal D}|_{O^y}$
agrees with the distribution
![]() ${\mathcal D}$
of Definition 2.7 under the identification of
${\mathcal D}$
of Definition 2.7 under the identification of
![]() $O^y$
as an open subset of
$O^y$
as an open subset of
![]() $\mathrm {URC}(X^y)$
. Let
$\mathrm {URC}(X^y)$
. Let
![]() $C := \mu _y(\varrho ^{-1}(y))$
be the line in
$C := \mu _y(\varrho ^{-1}(y))$
be the line in
![]() $(X^y, {\mathcal H}^y)$
corresponding to y. By Proposition 2.12, we see that
$(X^y, {\mathcal H}^y)$
corresponding to y. By Proposition 2.12, we see that
![]() $\mathrm {II}_{{\mathcal C}_x,z}$
for a point
$\mathrm {II}_{{\mathcal C}_x,z}$
for a point
![]() $z \in \varrho ^{-1}(y)$
satisfies (i) and (ii) of Definition 3.7. By Proposition 2.13, we see that
$z \in \varrho ^{-1}(y)$
satisfies (i) and (ii) of Definition 3.7. By Proposition 2.13, we see that
![]() $\mathrm {III}_{{\mathcal C}_x, z}$
satisfies (iii) and (iv) of Definition 3.7. It follows that C is a nondegenerate line.
$\mathrm {III}_{{\mathcal C}_x, z}$
satisfies (iii) and (iv) of Definition 3.7. It follows that C is a nondegenerate line.
The arguments in the proof of Theorem 4.4 show that the constructions in Theorems 3.15 and 4.4 are the inverse of each other.
Competing Interests
The authors declare none.