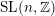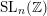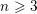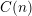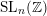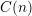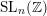1 Introduction
A word is an element in a free group. Given a word
![]() $w=w(x_{1},\ldots ,x_{d})\in F_{d}$
and a group
$w=w(x_{1},\ldots ,x_{d})\in F_{d}$
and a group
![]() $\unicode[STIX]{x1D6E4}$
, we have the word map
$\unicode[STIX]{x1D6E4}$
, we have the word map
![]() $w:\unicode[STIX]{x1D6E4}^{d}\rightarrow \unicode[STIX]{x1D6E4}$
defined by substitution. The set of
$w:\unicode[STIX]{x1D6E4}^{d}\rightarrow \unicode[STIX]{x1D6E4}$
defined by substitution. The set of
![]() $w$
-values is the set
$w$
-values is the set
Sets of word values in many families of groups have been extensively studied. See the book [Reference SegalSeg09] and the references therein for results on free and hyperbolic groups, nilpotent groups,
![]() $p$
-adic analytic groups, and general finite groups (the last part is the main ingredient in the proof by Nikolov and Segal of Serre’s conjecture that any finite-index subgroup in a finitely generated pro-finite group is open). We briefly describe some of the results that are relevant to this work.
$p$
-adic analytic groups, and general finite groups (the last part is the main ingredient in the proof by Nikolov and Segal of Serre’s conjecture that any finite-index subgroup in a finitely generated pro-finite group is open). We briefly describe some of the results that are relevant to this work.
Sets of word values in algebraic groups are large. Borel proved in [Reference BorelBor83] that if
![]() $w$
is a non-trivial word and
$w$
is a non-trivial word and
![]() $G$
is a connected simple algebraic group defined over an algebraically closed field
$G$
is a connected simple algebraic group defined over an algebraically closed field
![]() $k$
, then
$k$
, then
![]() $w(G(k))$
contains a Zariski open dense set. For Lie groups, the situation is more complicated. For example, Thom [Reference ThomTho13, Corollary 1.2] and Lindenstrauss (unpublished) proved that sets of word values in the unitary group
$w(G(k))$
contains a Zariski open dense set. For Lie groups, the situation is more complicated. For example, Thom [Reference ThomTho13, Corollary 1.2] and Lindenstrauss (unpublished) proved that sets of word values in the unitary group
![]() $U_{n}$
can have arbitrarily small radii. Nevertheless, Borel’s theorem implies that, for any semisimple Lie group
$U_{n}$
can have arbitrarily small radii. Nevertheless, Borel’s theorem implies that, for any semisimple Lie group
![]() $\mathbf{G}$
and any non-trivial word
$\mathbf{G}$
and any non-trivial word
![]() $w$
, the set of word values
$w$
, the set of word values
![]() $w(\mathbf{G})$
contains an open ball. It follows that, if
$w(\mathbf{G})$
contains an open ball. It follows that, if
![]() $\mathbf{G}$
is compact, there is a constant
$\mathbf{G}$
is compact, there is a constant
![]() $C$
(depending on
$C$
(depending on
![]() $\mathbf{G}$
and
$\mathbf{G}$
and
![]() $w$
) such that any element of
$w$
) such that any element of
![]() $\mathbf{G}$
is a product of at most
$\mathbf{G}$
is a product of at most
![]() $C$
word values. For arithmetic groups, sets of word values are very mysterious, even for simple words. For example, for every
$C$
word values. For arithmetic groups, sets of word values are very mysterious, even for simple words. For example, for every
![]() $n\geqslant 3$
, the question whether every element of
$n\geqslant 3$
, the question whether every element of
![]() $\operatorname{SL}_{n}(\mathbb{Z})$
is a commutator is wide open. We do, however, know that the set of commutators in
$\operatorname{SL}_{n}(\mathbb{Z})$
is a commutator is wide open. We do, however, know that the set of commutators in
![]() $\operatorname{SL}_{n}(\mathbb{Z})$
is quite large: Dennis and Vasserstein proved in [Reference Dennis and VasersteinDV88] that every element in
$\operatorname{SL}_{n}(\mathbb{Z})$
is quite large: Dennis and Vasserstein proved in [Reference Dennis and VasersteinDV88] that every element in
![]() $\operatorname{SL}_{n}(\mathbb{Z})$
is a product of at most six commutators if
$\operatorname{SL}_{n}(\mathbb{Z})$
is a product of at most six commutators if
![]() $n$
is large enough.
$n$
is large enough.
A remarkable theorem of Larsen and Shalev [Reference Larsen and ShalevLS09] says that a stronger statement holds for finite simple groups: for every non-trivial word
![]() $w$
, if
$w$
, if
![]() $\unicode[STIX]{x1D6E4}$
is a large enough finite simple group, then every element of
$\unicode[STIX]{x1D6E4}$
is a large enough finite simple group, then every element of
![]() $\unicode[STIX]{x1D6E4}$
is a product of two word values.
$\unicode[STIX]{x1D6E4}$
is a product of two word values.
Our first result generalizes the theorem of Dennis and Vasserstein in a form similar to the theorem of Larsen and Shalev.
Theorem 1.1. There is a constant
![]() $C$
with the following property: for any word
$C$
with the following property: for any word
![]() $w$
, there is
$w$
, there is
![]() $n_{w}$
such that, for all
$n_{w}$
such that, for all
![]() $n>n_{w}$
, every element of
$n>n_{w}$
, every element of
![]() $\operatorname{SL}_{n}(\mathbb{Z})$
is a product of at most
$\operatorname{SL}_{n}(\mathbb{Z})$
is a product of at most
![]() $C$
elements of
$C$
elements of
![]() $w(\operatorname{SL}_{n}(\mathbb{Z}))$
. In fact,
$w(\operatorname{SL}_{n}(\mathbb{Z}))$
. In fact,
![]() $C$
can be taken to be equal to
$C$
can be taken to be equal to
![]() $87$
.
$87$
.
In general, we cannot expect the subgroup generated by
![]() $w(\operatorname{SL}_{n}(\mathbb{Z}))$
to be equal to
$w(\operatorname{SL}_{n}(\mathbb{Z}))$
to be equal to
![]() $\operatorname{SL}_{n}(\mathbb{Z})$
. We define the width of
$\operatorname{SL}_{n}(\mathbb{Z})$
. We define the width of
![]() $w$
in
$w$
in
![]() $\operatorname{SL}_{n}(\mathbb{Z})$
to be the minimum of the numbers
$\operatorname{SL}_{n}(\mathbb{Z})$
to be the minimum of the numbers
![]() $C$
such that any element of
$C$
such that any element of
![]() $\langle w(\operatorname{SL}_{n}(\mathbb{Z}))\rangle$
is a product of at most
$\langle w(\operatorname{SL}_{n}(\mathbb{Z}))\rangle$
is a product of at most
![]() $C$
elements of
$C$
elements of
![]() $w(\operatorname{SL}_{n}(\mathbb{Z}))$
. If no such number exists, we say that the width of
$w(\operatorname{SL}_{n}(\mathbb{Z}))$
. If no such number exists, we say that the width of
![]() $w$
is infinite.
$w$
is infinite.
Our next theorem provides uniform bounds for width, for a fixed
![]() $n$
.
$n$
.
Theorem 1.2. For any
![]() $n\geqslant 3$
there is an integer
$n\geqslant 3$
there is an integer
![]() $C=C(n)$
such that, for any word
$C=C(n)$
such that, for any word
![]() $w$
, the width of
$w$
, the width of
![]() $w$
in
$w$
in
![]() $\operatorname{SL}_{n}(\mathbb{Z})$
is less than
$\operatorname{SL}_{n}(\mathbb{Z})$
is less than
![]() $C$
.
$C$
.
Remark 1.3. Theorems 1.1 and 1.2 are optimal in the following sense: for every
![]() $C$
there are infinitely many pairs
$C$
there are infinitely many pairs
![]() $(n,w)$
such that the width of
$(n,w)$
such that the width of
![]() $w$
in
$w$
in
![]() $\operatorname{SL}_{n}(\mathbb{Z})$
is greater than
$\operatorname{SL}_{n}(\mathbb{Z})$
is greater than
![]() $C$
. This easily follows from [Reference LubotzkyLub14, Theorem 1].
$C$
. This easily follows from [Reference LubotzkyLub14, Theorem 1].
We do, however, have the following result which is uniform in
![]() $n$
and
$n$
and
![]() $w$
.
$w$
.
Theorem 1.4. There is a constant
![]() $C$
such that, for every any non-trivial word
$C$
such that, for every any non-trivial word
![]() $w$
, there is
$w$
, there is
![]() $d=d(w)\in \mathbb{Z}$
such that for every
$d=d(w)\in \mathbb{Z}$
such that for every
![]() $n\geqslant 3$
, every element of the
$n\geqslant 3$
, every element of the
![]() $d$
-congruence subgroup
$d$
-congruence subgroup
![]() $\operatorname{SL}_{n}(\mathbb{Z};d)$
is a product of at most
$\operatorname{SL}_{n}(\mathbb{Z};d)$
is a product of at most
![]() $C$
elements of
$C$
elements of
![]() $w(\operatorname{SL}_{n}(\mathbb{Z}))$
. If
$w(\operatorname{SL}_{n}(\mathbb{Z}))$
. If
![]() $n$
is large enough,
$n$
is large enough,
![]() $C$
can be taken to be equal to
$C$
can be taken to be equal to
![]() $80$
.
$80$
.
Remark 1.5. Let
![]() $O$
be the ring of integers in a number field, let
$O$
be the ring of integers in a number field, let
![]() $S$
be a finite set of primes of
$S$
be a finite set of primes of
![]() $O$
, and let
$O$
, and let
![]() $O_{S}$
denote the localization of
$O_{S}$
denote the localization of
![]() $O$
by
$O$
by
![]() $S$
. The proofs below also show similar bounds for
$S$
. The proofs below also show similar bounds for
![]() $\operatorname{SL}_{n}(O_{S})$
, but the bounds obtained by these proofs depend on
$\operatorname{SL}_{n}(O_{S})$
, but the bounds obtained by these proofs depend on
![]() $O_{S}$
. While we do not know whether widths of words in
$O_{S}$
. While we do not know whether widths of words in
![]() $\operatorname{SL}_{n}(O_{S})$
are bounded uniformly in
$\operatorname{SL}_{n}(O_{S})$
are bounded uniformly in
![]() $O_{S}$
, [Reference Morgan, Rapinchuk and SuryMRS18, Corollary 4.6] gives some indication that this is indeed the case. In another direction, we do not even know whether words in other higher-rank non-uniform lattices (especially non-split) have finite width. We exclude lattices of rank
$O_{S}$
, [Reference Morgan, Rapinchuk and SuryMRS18, Corollary 4.6] gives some indication that this is indeed the case. In another direction, we do not even know whether words in other higher-rank non-uniform lattices (especially non-split) have finite width. We exclude lattices of rank
![]() $1$
from the discussion since these include free groups and hyperbolic groups for which the the width of every non-trivial word is infinite; see [Reference Myasnikov and NikolaevMN14].
$1$
from the discussion since these include free groups and hyperbolic groups for which the the width of every non-trivial word is infinite; see [Reference Myasnikov and NikolaevMN14].
Remark 1.6. Let
![]() $\unicode[STIX]{x1D6E4}$
be an irreducible arithmetic lattice in a higher-rank semisimple group
$\unicode[STIX]{x1D6E4}$
be an irreducible arithmetic lattice in a higher-rank semisimple group
![]() $G$
, and assume that there exist a compact semisimple Lie group
$G$
, and assume that there exist a compact semisimple Lie group
![]() $K$
and a dense embedding
$K$
and a dense embedding
![]() $\unicode[STIX]{x1D70B}:\unicode[STIX]{x1D6E4}{\hookrightarrow}K$
(this implies that
$\unicode[STIX]{x1D70B}:\unicode[STIX]{x1D6E4}{\hookrightarrow}K$
(this implies that
![]() $\unicode[STIX]{x1D6E4}$
is cocompcat in
$\unicode[STIX]{x1D6E4}$
is cocompcat in
![]() $G$
). By the result of Thomas and Lindenstrauss mentioned above, there are words
$G$
). By the result of Thomas and Lindenstrauss mentioned above, there are words
![]() $w\in F_{2}$
such that
$w\in F_{2}$
such that
![]() $\unicode[STIX]{x1D70B}(w(\unicode[STIX]{x1D6E4}))$
is contained in an arbitrarily small neighborhood of the identity. It follows that the width of
$\unicode[STIX]{x1D70B}(w(\unicode[STIX]{x1D6E4}))$
is contained in an arbitrarily small neighborhood of the identity. It follows that the width of
![]() $w$
can be arbitrarily large. This means that the analog of Theorem 1.2 fails for
$w$
can be arbitrarily large. This means that the analog of Theorem 1.2 fails for
![]() $\unicode[STIX]{x1D6E4}$
. Noting that the image under
$\unicode[STIX]{x1D6E4}$
. Noting that the image under
![]() $\unicode[STIX]{x1D70B}$
of any finite-index subgroup of
$\unicode[STIX]{x1D70B}$
of any finite-index subgroup of
![]() $\unicode[STIX]{x1D6E4}$
is dense, we get that Theorem 1.4 also fails. We do not know whether every word has finite width in higher-rank cocompact lattices, nor whether the analog of Theorems 1.1 holds for the class of cocompact lattices.
$\unicode[STIX]{x1D6E4}$
is dense, we get that Theorem 1.4 also fails. We do not know whether every word has finite width in higher-rank cocompact lattices, nor whether the analog of Theorems 1.1 holds for the class of cocompact lattices.
We briefly sketch the proofs of the main theorems. For
![]() $n\geqslant 2$
and
$n\geqslant 2$
and
![]() $q\in \mathbb{Z}$
, denote by
$q\in \mathbb{Z}$
, denote by
![]() $U_{n}(\mathbb{Z};q)$
the subgroup of all unipotent upper triangular matrices in
$U_{n}(\mathbb{Z};q)$
the subgroup of all unipotent upper triangular matrices in
![]() $\operatorname{SL}_{n}(\mathbb{Z})$
whose off-diagonal entries are divisible by
$\operatorname{SL}_{n}(\mathbb{Z})$
whose off-diagonal entries are divisible by
![]() $q$
. Denote similarly
$q$
. Denote similarly
![]() $L_{n}(\mathbb{Z};q)$
, replacing upper triangular by lower triangular. Finally, for a group
$L_{n}(\mathbb{Z};q)$
, replacing upper triangular by lower triangular. Finally, for a group
![]() $G$
, a subset
$G$
, a subset
![]() $X\subset G$
, and a natural number
$X\subset G$
, and a natural number
![]() $n$
, we denote
$n$
, we denote
![]() $X^{n}=\{x_{1}\cdots x_{n}\mid x_{i}\in X\cup \{1\}\}$
.
$X^{n}=\{x_{1}\cdots x_{n}\mid x_{i}\in X\cup \{1\}\}$
.
The main step is to prove the following theorem.
Theorem 1.7. There is a constant
![]() $C$
such that, for any
$C$
such that, for any
![]() $n\geqslant 3$
and any
$n\geqslant 3$
and any
![]() $q\in \mathbb{Z}$
,
$q\in \mathbb{Z}$
,
![]() $(U_{n}(\mathbb{Z};q)L_{n}(\mathbb{Z};q))^{C}$
is a finite-index subgroup of
$(U_{n}(\mathbb{Z};q)L_{n}(\mathbb{Z};q))^{C}$
is a finite-index subgroup of
![]() $\operatorname{SL}_{n}(\mathbb{Z})$
.
$\operatorname{SL}_{n}(\mathbb{Z})$
.
Theorem 1.7 is proved by induction on
![]() $n$
in §2. The case
$n$
in §2. The case
![]() $n=3$
is essentially due to Carter, Keller, and Paige (see [Reference Witte MorrisWit07] for an exposition of the proof). The argument for the induction step follows Dennis and Vaserstein [Reference Dennis and VasersteinDV88].
$n=3$
is essentially due to Carter, Keller, and Paige (see [Reference Witte MorrisWit07] for an exposition of the proof). The argument for the induction step follows Dennis and Vaserstein [Reference Dennis and VasersteinDV88].
Given Theorem 1.7, we deduce Theorem 1.4 without the explicit bound on
![]() $C$
in §3. A short argument implies that
$C$
in §3. A short argument implies that
![]() $w(\operatorname{SL}_{3}(\mathbb{Z}))^{2}$
contains an elementary matrix. Using various embeddings of
$w(\operatorname{SL}_{3}(\mathbb{Z}))^{2}$
contains an elementary matrix. Using various embeddings of
![]() $\operatorname{SL}_{3}(\mathbb{Z})$
into
$\operatorname{SL}_{3}(\mathbb{Z})$
into
![]() $\operatorname{SL}_{n}(\mathbb{Z})$
, we show that
$\operatorname{SL}_{n}(\mathbb{Z})$
, we show that
![]() $w(\operatorname{SL}_{n}(\mathbb{Z}))^{C^{\prime }}$
contains
$w(\operatorname{SL}_{n}(\mathbb{Z}))^{C^{\prime }}$
contains
![]() $U_{n}(\mathbb{Z};q)$
and
$U_{n}(\mathbb{Z};q)$
and
![]() $L_{n}(\mathbb{Z};q)$
for some
$L_{n}(\mathbb{Z};q)$
for some
![]() $C$
and
$C$
and
![]() $q$
. Theorems 1.1 and 1.2 follow from Theorem 1.4, a
$q$
. Theorems 1.1 and 1.2 follow from Theorem 1.4, a
![]() $p$
-adic open mapping theorem, and the Larsen–Shalev theorem [Reference Larsen and ShalevLS09].
$p$
-adic open mapping theorem, and the Larsen–Shalev theorem [Reference Larsen and ShalevLS09].
2 Proof of Theorem 1.7
In this section, we prove Theorem 1.7. We start by setting up the notation and recalling some facts.
Definition 2.1. Let
![]() $A$
be a commutative ring with unit, let
$A$
be a commutative ring with unit, let
![]() $I$
be an ideal in
$I$
be an ideal in
![]() $A$
, and let
$A$
, and let
![]() $n\geqslant 2$
be an integer.
$n\geqslant 2$
be an integer.
(1)
 $\operatorname{SL}_{n}(A;I)$
is the subgroup of
$\operatorname{SL}_{n}(A;I)$
is the subgroup of
 $\operatorname{SL}_{n}(A)$
consisting of the matrices which are congruent to the identity matrix modulo the ideal
$\operatorname{SL}_{n}(A)$
consisting of the matrices which are congruent to the identity matrix modulo the ideal
 $I$
. The subgroup
$I$
. The subgroup
 $\operatorname{SL}_{n}(A;I)$
is called the
$\operatorname{SL}_{n}(A;I)$
is called the
 $I$
-congruence subgroup of
$I$
-congruence subgroup of
 $\operatorname{SL}_{n}(A)$
.
$\operatorname{SL}_{n}(A)$
.(2)
 $U_{n}(A;I)$
is the subgroup of
$U_{n}(A;I)$
is the subgroup of
 $\operatorname{SL}_{n}(A;I)$
consisting of unipotent upper triangular matrices.
$\operatorname{SL}_{n}(A;I)$
consisting of unipotent upper triangular matrices.(3)
 $L_{n}(A;I)$
is the subgroup of
$L_{n}(A;I)$
is the subgroup of
 $\operatorname{SL}_{n}(A;I)$
consisting of unipotent lower triangular matrices.
$\operatorname{SL}_{n}(A;I)$
consisting of unipotent lower triangular matrices.(4) In the case where
 $A=\mathbb{Z}$
and
$A=\mathbb{Z}$
and
 $I=q\mathbb{Z}$
we sometimes write
$I=q\mathbb{Z}$
we sometimes write
 $\operatorname{SL}_{n}(\mathbb{Z};q)$
,
$\operatorname{SL}_{n}(\mathbb{Z};q)$
,
 $U_{n}(\mathbb{Z};q)$
and
$U_{n}(\mathbb{Z};q)$
and
 $L_{n}(\mathbb{Z};q)$
instead of
$L_{n}(\mathbb{Z};q)$
instead of
 $\operatorname{SL}_{n}(\mathbb{Z};I)$
,
$\operatorname{SL}_{n}(\mathbb{Z};I)$
,
 $U_{n}(\mathbb{Z};I)$
and
$U_{n}(\mathbb{Z};I)$
and
 $L_{n}(\mathbb{Z};I)$
.
$L_{n}(\mathbb{Z};I)$
.
Definition 2.2. Let
![]() $A$
be a commutative ring with a unit, let
$A$
be a commutative ring with a unit, let
![]() $I$
be an ideal in
$I$
be an ideal in
![]() $A$
, and let
$A$
, and let
![]() $n\geqslant 2$
be an integer.
$n\geqslant 2$
be an integer.
(1) For
 $x\in A$
and
$x\in A$
and
 $1\leqslant i\neq j\leqslant n$
, let
$1\leqslant i\neq j\leqslant n$
, let
 $e_{i,j}(x)$
denote the
$e_{i,j}(x)$
denote the
 $n\times n$
matrix with ones along the diagonal,
$n\times n$
matrix with ones along the diagonal,
 $x$
as
$x$
as
 $(i,j)$
th entry, and zero in all other entries.
$(i,j)$
th entry, and zero in all other entries.(2) Denote by
 $E(n,A;I)$
the subgroup generated by the elementary matrices
$E(n,A;I)$
the subgroup generated by the elementary matrices
 $e_{i,j}(x)$
, for
$e_{i,j}(x)$
, for
 $x\in I$
. We will write
$x\in I$
. We will write
 $E(n,A)$
instead of
$E(n,A)$
instead of
 $E(n,A;A)$
.
$E(n,A;A)$
.(3) Denote by
 $E^{\lhd }(n,A;I)$
the normal subgroup of
$E^{\lhd }(n,A;I)$
the normal subgroup of
 $E(n,A)$
generated by
$E(n,A)$
generated by
 $E(n,A;I)$
.
$E(n,A;I)$
.(4) In the case where
 $A=\mathbb{Z}$
and
$A=\mathbb{Z}$
and
 $I=q\mathbb{Z}$
we sometimes write
$I=q\mathbb{Z}$
we sometimes write
 $E(n,\mathbb{Z};q)$
and
$E(n,\mathbb{Z};q)$
and
 $E^{\lhd }(n,\mathbb{Z};q)$
instead of
$E^{\lhd }(n,\mathbb{Z};q)$
instead of
 $E(n,\mathbb{Z};I)$
and
$E(n,\mathbb{Z};I)$
and
 $E^{\lhd }(n,\mathbb{Z};I)$
.
$E^{\lhd }(n,\mathbb{Z};I)$
.
The following result is [Reference TitsTit76, Proposition 2].
Proposition 2.3 (Tits).
If
![]() $A$
is a commutative ring,
$A$
is a commutative ring,
![]() $I$
is an ideal of
$I$
is an ideal of
![]() $A$
, and
$A$
, and
![]() $n\geqslant 3$
, then
$n\geqslant 3$
, then
![]() $E^{\lhd }(n,A;I^{2})\subseteq \langle U_{n}(A;I)\cup L_{n}(A;I)\rangle$
.
$E^{\lhd }(n,A;I^{2})\subseteq \langle U_{n}(A;I)\cup L_{n}(A;I)\rangle$
.
The following theorem is proved in [Reference Witte MorrisWit07].
Theorem 2.4 (Carter, Keller, and Paige).
There is a first-order statement
![]() $\unicode[STIX]{x1D711}$
in the language of rings with the following properties:
$\unicode[STIX]{x1D711}$
in the language of rings with the following properties:
(1)
 $\unicode[STIX]{x1D711}$
holds in
$\unicode[STIX]{x1D711}$
holds in
 $\mathbb{Z}$
;
$\mathbb{Z}$
;(2) if
 $A$
is a ring satisfying
$A$
is a ring satisfying
 $\unicode[STIX]{x1D711}$
and
$\unicode[STIX]{x1D711}$
and
 $I$
is an ideal of
$I$
is an ideal of
 $A$
, then
$A$
, then
 $[\operatorname{SL}_{n}(A;I):E^{\lhd }(n,A;I)]\leqslant 2\cdot 8!$
.
$[\operatorname{SL}_{n}(A;I):E^{\lhd }(n,A;I)]\leqslant 2\cdot 8!$
.
Remark 2.5. Theorem 2.4 is proved in [Reference Witte MorrisWit07]. More precisely, if we take
![]() $\unicode[STIX]{x1D711}$
to be the conjunction of the conditions
$\unicode[STIX]{x1D711}$
to be the conjunction of the conditions
![]() $SR_{1\frac{1}{2}}$
,
$SR_{1\frac{1}{2}}$
,
![]() $\text{Gen}(2\cdot 8!,1)$
,
$\text{Gen}(2\cdot 8!,1)$
,
![]() $\text{Exp}(2\cdot 8!,2)$
(see [Reference Witte MorrisWit07, Definitions 2.10, 3.2, 3.6]), then [Reference Witte MorrisWit07, Lemma 2.13, Corollary 3.5, Theorem 3.9] imply that
$\text{Exp}(2\cdot 8!,2)$
(see [Reference Witte MorrisWit07, Definitions 2.10, 3.2, 3.6]), then [Reference Witte MorrisWit07, Lemma 2.13, Corollary 3.5, Theorem 3.9] imply that
![]() $\mathbb{Z}$
satisfies
$\mathbb{Z}$
satisfies
![]() $\unicode[STIX]{x1D711}$
and (2) is [Reference Witte MorrisWit07, Theorem 3.12].
$\unicode[STIX]{x1D711}$
and (2) is [Reference Witte MorrisWit07, Theorem 3.12].
Corollary 2.6. There is a constant
![]() $C=C(n)$
such that the following holds: for any
$C=C(n)$
such that the following holds: for any
![]() $q\in \mathbb{N}^{+}$
, there are
$q\in \mathbb{N}^{+}$
, there are
![]() $g_{1},\ldots ,g_{2\cdot 8!}\in \operatorname{SL}_{n}(\mathbb{Z};q^{2})$
such that
$g_{1},\ldots ,g_{2\cdot 8!}\in \operatorname{SL}_{n}(\mathbb{Z};q^{2})$
such that
![]() $\operatorname{SL}_{n}(A;q^{2})$
is contained in the union of the translations by
$\operatorname{SL}_{n}(A;q^{2})$
is contained in the union of the translations by
![]() $g_{1},\ldots ,g_{2\cdot 8!}$
of the set
$g_{1},\ldots ,g_{2\cdot 8!}$
of the set
![]() $(U_{n}(\mathbb{Z};q)L_{n}(\mathbb{Z};q))^{C}$
.
$(U_{n}(\mathbb{Z};q)L_{n}(\mathbb{Z};q))^{C}$
.
Proof. Let
![]() $A$
is a ring which is elementarily equivalent to
$A$
is a ring which is elementarily equivalent to
![]() $\mathbb{Z}$
(i.e. satisfies the same first-order sentences as
$\mathbb{Z}$
(i.e. satisfies the same first-order sentences as
![]() $\mathbb{Z}$
) and let
$\mathbb{Z}$
) and let
![]() $I$
be an ideal of
$I$
be an ideal of
![]() $A$
. Proposition 2.3 and Theorem 2.4 imply that
$A$
. Proposition 2.3 and Theorem 2.4 imply that
Assume the corollary is false. Then, for every
![]() $k\in \mathbb{N}$
, there are
$k\in \mathbb{N}$
, there are
![]() $q_{k}\in \mathbb{N}^{+}$
and matrices
$q_{k}\in \mathbb{N}^{+}$
and matrices
![]() $g_{k,1},\ldots ,g_{k,2\cdot 8!+1}\in \operatorname{SL}_{n}(\mathbb{Z};q_{k}^{2})$
such that
$g_{k,1},\ldots ,g_{k,2\cdot 8!+1}\in \operatorname{SL}_{n}(\mathbb{Z};q_{k}^{2})$
such that
![]() $(g_{k,i})^{-1}g_{k,j}\notin (U_{n}(\mathbb{Z};q_{k})L_{n}(\mathbb{Z};q_{k}))^{k}$
if
$(g_{k,i})^{-1}g_{k,j}\notin (U_{n}(\mathbb{Z};q_{k})L_{n}(\mathbb{Z};q_{k}))^{k}$
if
![]() $i\neq j$
.
$i\neq j$
.
Choose a non-principal ultrafilter
![]() ${\mathcal{U}}$
on
${\mathcal{U}}$
on
![]() $\mathbb{N}$
, and let
$\mathbb{N}$
, and let
![]() $A$
be the ultrapower of
$A$
be the ultrapower of
![]() $\mathbb{Z}$
over
$\mathbb{Z}$
over
![]() ${\mathcal{U}}$
. Then
${\mathcal{U}}$
. Then
![]() $A$
is elementarily equivalent to
$A$
is elementarily equivalent to
![]() $\mathbb{Z}$
and
$\mathbb{Z}$
and
![]() $\operatorname{SL}_{n}(A)$
is isomorphic to the ultrapower of
$\operatorname{SL}_{n}(A)$
is isomorphic to the ultrapower of
![]() $\operatorname{SL}_{n}(\mathbb{Z})$
over
$\operatorname{SL}_{n}(\mathbb{Z})$
over
![]() ${\mathcal{U}}$
. Let
${\mathcal{U}}$
. Let
![]() $I$
be the ideal of
$I$
be the ideal of
![]() $A$
represented by
$A$
represented by
![]() $\prod _{k}q_{k}\mathbb{Z}$
, and for every
$\prod _{k}q_{k}\mathbb{Z}$
, and for every
![]() $1\leqslant i\leqslant k$
, let
$1\leqslant i\leqslant k$
, let
![]() $g_{i}\in \operatorname{SL}_{n}(A;I^{2})$
be the element represented by
$g_{i}\in \operatorname{SL}_{n}(A;I^{2})$
be the element represented by
![]() $(g_{k,i})_{k}$
. Then
$(g_{k,i})_{k}$
. Then
![]() $g_{1},\ldots ,g_{2\cdot 8!+1}$
belong to different cosets of
$g_{1},\ldots ,g_{2\cdot 8!+1}$
belong to different cosets of
![]() $\langle U_{n}(A;I)L_{n}(A;I)\rangle$
, contradicting (1).◻
$\langle U_{n}(A;I)L_{n}(A;I)\rangle$
, contradicting (1).◻
The following two technical lemmas will be needed in the proof of Proposition 2.9 below.
Lemma 2.7. Let
![]() $G$
be a group, and let
$G$
be a group, and let
![]() $X\subset G$
be a symmetric set such that there are
$X\subset G$
be a symmetric set such that there are
![]() $d$
translates of
$d$
translates of
![]() $X$
that cover
$X$
that cover
![]() $G$
. Then
$G$
. Then
![]() $X^{4d+2}$
is a group.
$X^{4d+2}$
is a group.
Proof. Denote
![]() $Y=X^{2}$
. Then
$Y=X^{2}$
. Then
![]() $1\in Y$
and there are
$1\in Y$
and there are
![]() $d$
translates of
$d$
translates of
![]() $Y$
that cover
$Y$
that cover
![]() $G$
. Since
$G$
. Since
![]() $1\in Y$
,
$1\in Y$
,
![]() $Y^{k}\subseteq Y^{k+1}$
for every
$Y^{k}\subseteq Y^{k+1}$
for every
![]() $k$
. It is enough to show that
$k$
. It is enough to show that
![]() $Y^{k}=Y^{k+1}$
for some
$Y^{k}=Y^{k+1}$
for some
![]() $k\leqslant 2d+1$
. Suppose that
$k\leqslant 2d+1$
. Suppose that
![]() $G=\bigcup _{i=1}^{d}g_{i}Y$
for some
$G=\bigcup _{i=1}^{d}g_{i}Y$
for some
![]() $g_{1},\ldots ,g_{d}\in G$
. We can assume that
$g_{1},\ldots ,g_{d}\in G$
. We can assume that
![]() $g_{1}=1$
. For every
$g_{1}=1$
. For every
![]() $k$
, if
$k$
, if
![]() $Y^{k}\neq Y^{k+1}$
, choose
$Y^{k}\neq Y^{k+1}$
, choose
![]() $h\in Y^{k+1}\smallsetminus Y^{k}$
. By assumption, there is
$h\in Y^{k+1}\smallsetminus Y^{k}$
. By assumption, there is
![]() $i$
such that
$i$
such that
![]() $h\in g_{i}Y$
. Then
$h\in g_{i}Y$
. Then
![]() $g_{i}\in Y^{k+2}$
but
$g_{i}\in Y^{k+2}$
but
![]() $g_{i}\notin Y^{k}$
. By induction we see that if
$g_{i}\notin Y^{k}$
. By induction we see that if
![]() $Y^{2k-1}\neq Y^{2k}$
for some
$Y^{2k-1}\neq Y^{2k}$
for some
![]() $1\leqslant k$
, then
$1\leqslant k$
, then
![]() $Y^{2k+1}$
contains at least
$Y^{2k+1}$
contains at least
![]() $k$
distinct
$k$
distinct
![]() $g_{i}$
. This implies that
$g_{i}$
. This implies that
![]() $Y^{2d+1}=Y^{2d+2}$
.◻
$Y^{2d+1}=Y^{2d+2}$
.◻
Lemma 2.8. Let
![]() $K\subseteq H\subseteq G$
be groups such that
$K\subseteq H\subseteq G$
be groups such that
![]() $[H:K]<\infty$
. Let
$[H:K]<\infty$
. Let
![]() $X\subseteq G$
be a symmetric subset. Assume that
$X\subseteq G$
be a symmetric subset. Assume that
![]() $HX=G$
and that
$HX=G$
and that
![]() $K\subseteq X$
. Then
$K\subseteq X$
. Then
![]() $X^{4[H:K]}$
is a subgroup.
$X^{4[H:K]}$
is a subgroup.
Proof. Since
![]() $1\in K\subseteq X$
, the sets
$1\in K\subseteq X$
, the sets
![]() $(X^{n}K\cap H)\subseteq H$
are non-decreasing. Hence, there is
$(X^{n}K\cap H)\subseteq H$
are non-decreasing. Hence, there is
![]() $n\leqslant 4[H:K]-3$
such that
$n\leqslant 4[H:K]-3$
such that
Since
![]() $HX=G$
, we have
$HX=G$
, we have
![]() $X^{n+3}\subseteq (X^{n+4}\cap H)X$
. Thus,
$X^{n+3}\subseteq (X^{n+4}\cap H)X$
. Thus,
so
![]() $X^{n+2}$
is a group.◻
$X^{n+2}$
is a group.◻
Proposition 2.9. There is a constant
![]() $D=D(n)$
such that, for any
$D=D(n)$
such that, for any
![]() $q\in \mathbb{N}^{+}$
, the set
$q\in \mathbb{N}^{+}$
, the set
![]() $(U_{n}(\mathbb{Z};q)L_{n}(\mathbb{Z};q))^{D}$
is a group, and, therefore, equal to
$(U_{n}(\mathbb{Z};q)L_{n}(\mathbb{Z};q))^{D}$
is a group, and, therefore, equal to
![]() $\langle U_{n}(\mathbb{Z};q)L_{n}(\mathbb{Z};q)\rangle$
.
$\langle U_{n}(\mathbb{Z};q)L_{n}(\mathbb{Z};q)\rangle$
.
Proof. For any
![]() $k$
, the set
$k$
, the set
![]() $(L_{n}(\mathbb{Z};q)U_{n}(\mathbb{Z};q))^{k+1}$
contains the symmetric subset
$(L_{n}(\mathbb{Z};q)U_{n}(\mathbb{Z};q))^{k+1}$
contains the symmetric subset
![]() $(L_{n}(\mathbb{Z};q)U_{n}(\mathbb{Z};q))^{k}\cup (U_{n}(\mathbb{Z};q)L_{n}(\mathbb{Z};q))^{k}$
. Corollary 2.6 and Lemma 2.7 imply that there is a constant
$(L_{n}(\mathbb{Z};q)U_{n}(\mathbb{Z};q))^{k}\cup (U_{n}(\mathbb{Z};q)L_{n}(\mathbb{Z};q))^{k}$
. Corollary 2.6 and Lemma 2.7 imply that there is a constant
![]() $D^{\prime }$
such that
$D^{\prime }$
such that
![]() $(L_{n}(\mathbb{Z};q)U_{n}(\mathbb{Z};q))^{D^{\prime }}$
contains a subgroup
$(L_{n}(\mathbb{Z};q)U_{n}(\mathbb{Z};q))^{D^{\prime }}$
contains a subgroup
![]() $S(I)$
of
$S(I)$
of
![]() $\operatorname{SL}_{n}(\mathbb{Z};q^{2})$
of index at most
$\operatorname{SL}_{n}(\mathbb{Z};q^{2})$
of index at most
![]() $2\cdot 8!$
.
$2\cdot 8!$
.
Note that
![]() $\operatorname{SL}_{n}(\mathbb{Z},q)/\text{SL}_{n}(\mathbb{Z},q^{2})$
is abelian so
$\operatorname{SL}_{n}(\mathbb{Z},q)/\text{SL}_{n}(\mathbb{Z},q^{2})$
is abelian so
![]() $\operatorname{SL}_{n}(\mathbb{Z},q^{2})L_{n}(\mathbb{Z};q)U_{n}(\mathbb{Z};q)$
is a subgroup of
$\operatorname{SL}_{n}(\mathbb{Z},q^{2})L_{n}(\mathbb{Z};q)U_{n}(\mathbb{Z};q)$
is a subgroup of
![]() $\operatorname{SL}_{n}(\mathbb{Z})$
. The desired result follows by applying Lemma 2.8 to
$\operatorname{SL}_{n}(\mathbb{Z})$
. The desired result follows by applying Lemma 2.8 to
![]() $K=S(I)$
,
$K=S(I)$
,
![]() $H=\operatorname{SL}_{n}(\mathbb{Z};q^{2})$
,
$H=\operatorname{SL}_{n}(\mathbb{Z};q^{2})$
,
![]() $G=\operatorname{SL}_{n}(\mathbb{Z},q^{2})L_{n}(\mathbb{Z};q)U_{n}(\mathbb{Z};q)$
, and
$G=\operatorname{SL}_{n}(\mathbb{Z},q^{2})L_{n}(\mathbb{Z};q)U_{n}(\mathbb{Z};q)$
, and
![]() $X=(L_{n}(\mathbb{Z};q)U_{n}(\mathbb{Z};q))^{D^{\prime }}\cup (U_{n}(\mathbb{Z};q)L_{n}(\mathbb{Z}:q))^{D^{\prime }}\subseteq (L_{n}(\mathbb{Z};q)U_{n}(\mathbb{Z};q))^{D^{\prime }+1}$
.◻
$X=(L_{n}(\mathbb{Z};q)U_{n}(\mathbb{Z};q))^{D^{\prime }}\cup (U_{n}(\mathbb{Z};q)L_{n}(\mathbb{Z}:q))^{D^{\prime }}\subseteq (L_{n}(\mathbb{Z};q)U_{n}(\mathbb{Z};q))^{D^{\prime }+1}$
.◻
In order to prove Theorem 1.7 we have to show that the constant
![]() $D(n)$
in Proposition 2.9 can be made independent of
$D(n)$
in Proposition 2.9 can be made independent of
![]() $n$
. The following technical generalization of Proposition 2.3 is needed.
$n$
. The following technical generalization of Proposition 2.3 is needed.
Lemma 2.10. Let
![]() $n\geqslant 3$
and let
$n\geqslant 3$
and let
![]() $I$
be an ideal in a commutative ring
$I$
be an ideal in a commutative ring
![]() $A$
. Then
$A$
. Then
![]() $E^{\lhd }(n+1;A,I^{2})$
is contained in the subgroup
$E^{\lhd }(n+1;A,I^{2})$
is contained in the subgroup
Proof. We follow the proof of [Reference TitsTit76, Proposition 2.3].
Let
![]() $1\leqslant i\neq j\leqslant n+1$
,
$1\leqslant i\neq j\leqslant n+1$
,
![]() $1\leqslant r\neq s\leqslant n+1$
, and
$1\leqslant r\neq s\leqslant n+1$
, and
![]() $a,b\in A$
. Recall the following relations:
$a,b\in A$
. Recall the following relations:
 $$\begin{eqnarray}\left\{\begin{array}{@{}ll@{}}e_{r,s}(b)e_{i,j}(a)e_{r,s}(b)^{-1}=e_{i,j}(a)e_{i,s}(-ab)\quad & \text{if }j=r\text{ and }i\neq s,\\ e_{r,s}(b)e_{i,j}(a)e_{r,s}(b)^{-1}=e_{i,j}(a)e_{r,j}(ab)\quad & \text{if }j\neq r\text{ and }i=s,\\ e_{r,s}(b)e_{i,j}(a)e_{r,s}(b)^{-1}=e_{i,j}(a)\quad & \text{if }j\neq r\text{ and }i\neq s.\end{array}\right.\end{eqnarray}$$
$$\begin{eqnarray}\left\{\begin{array}{@{}ll@{}}e_{r,s}(b)e_{i,j}(a)e_{r,s}(b)^{-1}=e_{i,j}(a)e_{i,s}(-ab)\quad & \text{if }j=r\text{ and }i\neq s,\\ e_{r,s}(b)e_{i,j}(a)e_{r,s}(b)^{-1}=e_{i,j}(a)e_{r,j}(ab)\quad & \text{if }j\neq r\text{ and }i=s,\\ e_{r,s}(b)e_{i,j}(a)e_{r,s}(b)^{-1}=e_{i,j}(a)\quad & \text{if }j\neq r\text{ and }i\neq s.\end{array}\right.\end{eqnarray}$$
For every
![]() $1\leqslant i\neq j\leqslant n+1$
, denote
$1\leqslant i\neq j\leqslant n+1$
, denote
![]() $F_{i,j}(I^{2}):=\langle e_{i,j}(a),e_{j,i}(a)\mid a\in I^{2}\rangle$
. Let
$F_{i,j}(I^{2}):=\langle e_{i,j}(a),e_{j,i}(a)\mid a\in I^{2}\rangle$
. Let
![]() $F_{i,j}^{\lhd }(I^{2})$
be the minimal normal subgroup of
$F_{i,j}^{\lhd }(I^{2})$
be the minimal normal subgroup of
![]() $F_{i,j}:=F_{i,j}(A)$
which contains
$F_{i,j}:=F_{i,j}(A)$
which contains
![]() $F_{i,j}(I^{2})$
. Define
$F_{i,j}(I^{2})$
. Define
![]() $F^{\lhd }(I^{2}):=\langle F_{i,j}^{\lhd }(I^{2})\mid 1\leqslant i\neq j\leqslant n+1\rangle$
. Equation (2) implies that for every
$F^{\lhd }(I^{2}):=\langle F_{i,j}^{\lhd }(I^{2})\mid 1\leqslant i\neq j\leqslant n+1\rangle$
. Equation (2) implies that for every
![]() $1\leqslant i\neq j\leqslant n+1$
and every
$1\leqslant i\neq j\leqslant n+1$
and every
![]() $a\in A$
,
$a\in A$
,
![]() $e_{i,j}(a)F^{\lhd }(I^{2})e_{i,j}(a)^{-1}=F^{\lhd }(I^{2})$
. Thus
$e_{i,j}(a)F^{\lhd }(I^{2})e_{i,j}(a)^{-1}=F^{\lhd }(I^{2})$
. Thus
![]() $F^{\lhd }(I^{2})$
is a normal subgroup of
$F^{\lhd }(I^{2})$
is a normal subgroup of
![]() $E(n+1,A)$
containing all
$E(n+1,A)$
containing all
![]() $e_{i,j}(a)$
,
$e_{i,j}(a)$
,
![]() $a\in I^{2}$
, so it must be equal to
$a\in I^{2}$
, so it must be equal to
![]() $E^{\lhd }(n+1,A,I^{2})$
. Thus, in order to finish the proof it is enough to show that for every
$E^{\lhd }(n+1,A,I^{2})$
. Thus, in order to finish the proof it is enough to show that for every
![]() $1\leqslant i<j\leqslant n+1$
,
$1\leqslant i<j\leqslant n+1$
,
![]() $F_{i,j}^{\lhd }(I^{2})\subseteq K(I)$
.
$F_{i,j}^{\lhd }(I^{2})\subseteq K(I)$
.
Let
![]() $E^{+}(n,A;I)$
and
$E^{+}(n,A;I)$
and
![]() $E^{-}(n,A;I)$
be the images of
$E^{-}(n,A;I)$
be the images of
![]() $E(n,A,I)$
in
$E(n,A,I)$
in
![]() $\operatorname{SL}_{n+1}(A)$
under the embeddings
$\operatorname{SL}_{n+1}(A)$
under the embeddings
![]() $M\mapsto (\!\begin{smallmatrix}M & 0\\ 0 & 1\end{smallmatrix}\!)$
and
$M\mapsto (\!\begin{smallmatrix}M & 0\\ 0 & 1\end{smallmatrix}\!)$
and
![]() $M\mapsto (\!\begin{smallmatrix}1 & 0\\ 0 & M\end{smallmatrix}\!)$
. By applying Proposition 2.3 with respect to
$M\mapsto (\!\begin{smallmatrix}1 & 0\\ 0 & M\end{smallmatrix}\!)$
. By applying Proposition 2.3 with respect to
![]() $E^{+}(n,A;I)$
and
$E^{+}(n,A;I)$
and
![]() $E^{-}(n,A;I)$
, we see that
$E^{-}(n,A;I)$
, we see that
![]() $K(I)$
contains
$K(I)$
contains
![]() $F_{i,j}^{\lhd }(I^{2})$
for every
$F_{i,j}^{\lhd }(I^{2})$
for every
![]() $1\leqslant i<j\leqslant n+1$
such that
$1\leqslant i<j\leqslant n+1$
such that
![]() $(i,j)\neq (1,n+1)$
.
$(i,j)\neq (1,n+1)$
.
Equation (2) implies that
![]() $K(I)$
in normalized by
$K(I)$
in normalized by
![]() $e_{1,n+1}(a)$
and
$e_{1,n+1}(a)$
and
![]() $e_{n+1,1}(a)$
for every
$e_{n+1,1}(a)$
for every
![]() $a\in R$
. For every
$a\in R$
. For every
![]() $a,b\in I$
,
$a,b\in I$
,
![]() $e_{1,n+1}(ab)=[e_{1,2}(a),e_{2,n+1}(-b)]\in K(I)$
and
$e_{1,n+1}(ab)=[e_{1,2}(a),e_{2,n+1}(-b)]\in K(I)$
and
![]() $e_{n+1,1}(ab)=[e_{n+1,2}(a),e_{2,1}(-b)]\in K(I)$
. Thus,
$e_{n+1,1}(ab)=[e_{n+1,2}(a),e_{2,1}(-b)]\in K(I)$
. Thus,
![]() $F_{1,n+1}^{\lhd }(I^{2})\leqslant K(I)$
.◻
$F_{1,n+1}^{\lhd }(I^{2})\leqslant K(I)$
.◻
The next lemma is the key ingredient in the proof of Theorem 1.7.
Lemma 2.11. Let
![]() $n\geqslant 3$
and
$n\geqslant 3$
and
![]() $q\in \mathbb{N}^{+}$
and assume that
$q\in \mathbb{N}^{+}$
and assume that
![]() $(U_{n}(\mathbb{Z};q)L_{n}(\mathbb{Z};q))^{D}=\langle U_{n}(\mathbb{Z};q)L_{n}(\mathbb{Z};q)\rangle$
. Then for every
$(U_{n}(\mathbb{Z};q)L_{n}(\mathbb{Z};q))^{D}=\langle U_{n}(\mathbb{Z};q)L_{n}(\mathbb{Z};q)\rangle$
. Then for every
![]() $m\geqslant n$
,
$m\geqslant n$
,
![]() $(U_{m}(\mathbb{Z};q)L_{m}(\mathbb{Z};q))^{D}=\langle U_{m}(\mathbb{Z};q)L_{m}(\mathbb{Z};q)\rangle$
.
$(U_{m}(\mathbb{Z};q)L_{m}(\mathbb{Z};q))^{D}=\langle U_{m}(\mathbb{Z};q)L_{m}(\mathbb{Z};q)\rangle$
.
Proof. The proof follows [Reference Dennis and VasersteinDV88, proof of Lemma 7] and is by induction on
![]() $m$
. The base case
$m$
. The base case
![]() $m=n$
is clear. It remains to show that if the claim is true for some
$m=n$
is clear. It remains to show that if the claim is true for some
![]() $m\geqslant 3$
then it is also true for
$m\geqslant 3$
then it is also true for
![]() $m+1$
.
$m+1$
.
Let
![]() $T:=(U_{m+1}(\mathbb{Z};q)L_{m+1}(\mathbb{Z};q))^{D}$
and
$T:=(U_{m+1}(\mathbb{Z};q)L_{m+1}(\mathbb{Z};q))^{D}$
and
![]() $H=\{g\in \operatorname{SL}_{m+1}(\mathbb{Z})\mid gT=T\}$
. Since
$H=\{g\in \operatorname{SL}_{m+1}(\mathbb{Z})\mid gT=T\}$
. Since
![]() $H$
is a group, it is enough to prove that
$H$
is a group, it is enough to prove that
![]() $H$
contains both
$H$
contains both
![]() $U_{m+1}(\mathbb{Z};q)$
(which is clear) and
$U_{m+1}(\mathbb{Z};q)$
(which is clear) and
![]() $L_{m+1}(\mathbb{Z};q)$
.
$L_{m+1}(\mathbb{Z};q)$
.
We embed
![]() $L_{m}(\mathbb{Z};q)$
and
$L_{m}(\mathbb{Z};q)$
and
![]() $U_{m}(\mathbb{Z};q)$
in
$U_{m}(\mathbb{Z};q)$
in
![]() $\operatorname{SL}_{m+1}(\mathbb{Z};q)$
by the embedding
$\operatorname{SL}_{m+1}(\mathbb{Z};q)$
by the embedding
![]() $M\mapsto (\!\begin{smallmatrix}M & 0\\ 0 & 1\end{smallmatrix}\!)$
. We denote the abelian group
$M\mapsto (\!\begin{smallmatrix}M & 0\\ 0 & 1\end{smallmatrix}\!)$
. We denote the abelian group
![]() $\langle e_{i,m+1}(a)\mid 1\leqslant i\leqslant m,~a\in q\mathbb{Z}\rangle$
by
$\langle e_{i,m+1}(a)\mid 1\leqslant i\leqslant m,~a\in q\mathbb{Z}\rangle$
by
![]() $C_{m+1}(\mathbb{Z};q)$
and the abelian group
$C_{m+1}(\mathbb{Z};q)$
and the abelian group
![]() $\langle e_{m+1,i}(q)\mid 1\leqslant i\leqslant m,~a\in q\mathbb{Z}\rangle$
by
$\langle e_{m+1,i}(q)\mid 1\leqslant i\leqslant m,~a\in q\mathbb{Z}\rangle$
by
![]() $R_{m+1}(\mathbb{Z};q)$
. We have that
$R_{m+1}(\mathbb{Z};q)$
. We have that
![]() $U_{m+1}(\mathbb{Z};q)=U_{m}(\mathbb{Z};q)\ltimes C_{m}(\mathbb{Z};q)$
, that
$U_{m+1}(\mathbb{Z};q)=U_{m}(\mathbb{Z};q)\ltimes C_{m}(\mathbb{Z};q)$
, that
![]() $L_{m+1}(\mathbb{Z};q)=L_{m}(\mathbb{Z};q)\ltimes R_{m}(\mathbb{Z};q)$
, and that
$L_{m+1}(\mathbb{Z};q)=L_{m}(\mathbb{Z};q)\ltimes R_{m}(\mathbb{Z};q)$
, and that
![]() $U_{m}(\mathbb{Z};q)$
and
$U_{m}(\mathbb{Z};q)$
and
![]() $L_{m}(\mathbb{Z};q)$
each normalize both
$L_{m}(\mathbb{Z};q)$
each normalize both
![]() $C_{m}(\mathbb{Z};q)$
and
$C_{m}(\mathbb{Z};q)$
and
![]() $R_{m}(\mathbb{Z};q)$
. The induction hypothesis implies that
$R_{m}(\mathbb{Z};q)$
. The induction hypothesis implies that
 $$\begin{eqnarray}\displaystyle & & \displaystyle L_{m}(\mathbb{Z}:q)(U_{m+1}(\mathbb{Z}:q)L_{m+1}(\mathbb{Z};q))^{D}\nonumber\\ \displaystyle & & \displaystyle \quad =L_{m}(\mathbb{Z}:q)(U_{m}(\mathbb{Z}:q)C_{m}(\mathbb{Z}:q)L_{m}(\mathbb{Z}:q)R_{m}(\mathbb{Z}:q))^{D}\nonumber\\ \displaystyle & & \displaystyle \quad =L_{m}(\mathbb{Z}:q)(U_{m}(\mathbb{Z}:q)L_{m}(\mathbb{Z}:q))^{D}\cdot (C_{m}(\mathbb{Z}:q)R_{m}(\mathbb{Z}:q))^{D}\nonumber\\ \displaystyle & & \displaystyle \quad =(U_{m}(\mathbb{Z}:q)L_{m}(\mathbb{Z}:q))^{D}\cdot (C_{m}(\mathbb{Z}:q)R_{m}(\mathbb{Z}:q))^{D}\nonumber\\ \displaystyle & & \displaystyle \quad =(U_{m}(\mathbb{Z}:q)C_{m}(\mathbb{Z}:q)L_{m}(\mathbb{Z}:q)R_{m}(\mathbb{Z}:q))^{D}\nonumber\\ \displaystyle & & \displaystyle \quad =(U_{m+1}(\mathbb{Z}:q)L_{m+1}(\mathbb{Z}:q))^{D}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle L_{m}(\mathbb{Z}:q)(U_{m+1}(\mathbb{Z}:q)L_{m+1}(\mathbb{Z};q))^{D}\nonumber\\ \displaystyle & & \displaystyle \quad =L_{m}(\mathbb{Z}:q)(U_{m}(\mathbb{Z}:q)C_{m}(\mathbb{Z}:q)L_{m}(\mathbb{Z}:q)R_{m}(\mathbb{Z}:q))^{D}\nonumber\\ \displaystyle & & \displaystyle \quad =L_{m}(\mathbb{Z}:q)(U_{m}(\mathbb{Z}:q)L_{m}(\mathbb{Z}:q))^{D}\cdot (C_{m}(\mathbb{Z}:q)R_{m}(\mathbb{Z}:q))^{D}\nonumber\\ \displaystyle & & \displaystyle \quad =(U_{m}(\mathbb{Z}:q)L_{m}(\mathbb{Z}:q))^{D}\cdot (C_{m}(\mathbb{Z}:q)R_{m}(\mathbb{Z}:q))^{D}\nonumber\\ \displaystyle & & \displaystyle \quad =(U_{m}(\mathbb{Z}:q)C_{m}(\mathbb{Z}:q)L_{m}(\mathbb{Z}:q)R_{m}(\mathbb{Z}:q))^{D}\nonumber\\ \displaystyle & & \displaystyle \quad =(U_{m+1}(\mathbb{Z}:q)L_{m+1}(\mathbb{Z}:q))^{D}.\nonumber\end{eqnarray}$$
Hence,
![]() $L_{m}(\mathbb{Z}:q)\subseteq H$
, that is, for every
$L_{m}(\mathbb{Z}:q)\subseteq H$
, that is, for every
![]() $1\leqslant i<j\leqslant m$
and
$1\leqslant i<j\leqslant m$
and
![]() $a\in I$
, we have
$a\in I$
, we have
![]() $e_{j,i}(a)\in H$
. Arguing similarly using the embedding
$e_{j,i}(a)\in H$
. Arguing similarly using the embedding
![]() $M\mapsto (\!\begin{smallmatrix}1 & 0\\ 0 & M\end{smallmatrix}\!)$
, we get that
$M\mapsto (\!\begin{smallmatrix}1 & 0\\ 0 & M\end{smallmatrix}\!)$
, we get that
![]() $e_{j,i}(a)\in H$
, for every
$e_{j,i}(a)\in H$
, for every
![]() $2\leqslant i<j\leqslant m+1$
and
$2\leqslant i<j\leqslant m+1$
and
![]() $a\in I$
. It remains to show that for every
$a\in I$
. It remains to show that for every
![]() $a\in I$
,
$a\in I$
,
![]() $e_{m+1,1}(a)\in H$
.
$e_{m+1,1}(a)\in H$
.
The main theorem of [Reference MennickeMen65] says that
![]() $E^{\lhd }(n,\mathbb{Z},k)=\operatorname{SL}_{n}(\mathbb{Z},k)$
for every
$E^{\lhd }(n,\mathbb{Z},k)=\operatorname{SL}_{n}(\mathbb{Z},k)$
for every
![]() $k\in \mathbb{N}^{+}$
. Thus, Lemma 2.10 implies that
$k\in \mathbb{N}^{+}$
. Thus, Lemma 2.10 implies that
![]() $\operatorname{SL}_{m+1}(\mathbb{Z};q^{2})=E^{\lhd }(m+1,\mathbb{Z};q^{2})\subseteq H$
. Since
$\operatorname{SL}_{m+1}(\mathbb{Z};q^{2})=E^{\lhd }(m+1,\mathbb{Z};q^{2})\subseteq H$
. Since
![]() $\operatorname{SL}_{m+1}(\mathbb{Z};q)/\text{SL}_{m+1}(\mathbb{Z};q^{2})$
is abelian,
$\operatorname{SL}_{m+1}(\mathbb{Z};q)/\text{SL}_{m+1}(\mathbb{Z};q^{2})$
is abelian,
![]() $e_{m+1,1}(a)U_{m+1}(\mathbb{Z}:q)e_{m+1,1}(a)^{-1}\subseteq \operatorname{SL}_{m+1}(\mathbb{Z};q^{2})\cdot U_{m+1}(\mathbb{Z}:q)$
, for every
$e_{m+1,1}(a)U_{m+1}(\mathbb{Z}:q)e_{m+1,1}(a)^{-1}\subseteq \operatorname{SL}_{m+1}(\mathbb{Z};q^{2})\cdot U_{m+1}(\mathbb{Z}:q)$
, for every
![]() $a\in I$
. It follows that, for every
$a\in I$
. It follows that, for every
![]() $a\in I$
,
$a\in I$
,
 $$\begin{eqnarray}\displaystyle & & \displaystyle e_{m+1,1}(a)(U_{m+1}(\mathbb{Z}:q)L_{m+1}(\mathbb{Z}:q))^{D}\nonumber\\ \displaystyle & & \displaystyle \quad =e_{m+1,1}(a)U_{m+1}(\mathbb{Z}:q)e_{m+1,1}(a)^{-1}e_{m+1,1}(a)L_{m+1}(\mathbb{Z}:q)(U_{m+1}(\mathbb{Z}:q)L_{m+1}(\mathbb{Z}:q))^{D-1}\nonumber\\ \displaystyle & & \displaystyle \quad \subseteq \operatorname{SL}_{m+1}(\mathbb{Z};q^{2})\cdot U_{m+1}(\mathbb{Z}:q)L_{m+1}(\mathbb{Z}:q)(U_{m+1}(\mathbb{Z}:q)L_{m+1}(\mathbb{Z}:q))^{D-1}\nonumber\\ \displaystyle & & \displaystyle \quad =(U_{m+1}(\mathbb{Z}:q)L_{m+1}(\mathbb{Z}:q))^{D}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle e_{m+1,1}(a)(U_{m+1}(\mathbb{Z}:q)L_{m+1}(\mathbb{Z}:q))^{D}\nonumber\\ \displaystyle & & \displaystyle \quad =e_{m+1,1}(a)U_{m+1}(\mathbb{Z}:q)e_{m+1,1}(a)^{-1}e_{m+1,1}(a)L_{m+1}(\mathbb{Z}:q)(U_{m+1}(\mathbb{Z}:q)L_{m+1}(\mathbb{Z}:q))^{D-1}\nonumber\\ \displaystyle & & \displaystyle \quad \subseteq \operatorname{SL}_{m+1}(\mathbb{Z};q^{2})\cdot U_{m+1}(\mathbb{Z}:q)L_{m+1}(\mathbb{Z}:q)(U_{m+1}(\mathbb{Z}:q)L_{m+1}(\mathbb{Z}:q))^{D-1}\nonumber\\ \displaystyle & & \displaystyle \quad =(U_{m+1}(\mathbb{Z}:q)L_{m+1}(\mathbb{Z}:q))^{D}.\nonumber\end{eqnarray}$$
In particular, for every
![]() $a\in I$
,
$a\in I$
,
![]() $e_{m+1,1}(a)\in H$
. Hence,
$e_{m+1,1}(a)\in H$
. Hence,
![]() $L_{m+1}(\mathbb{Z}:q)\subseteq H$
as desired.◻
$L_{m+1}(\mathbb{Z}:q)\subseteq H$
as desired.◻
Proof of Theorem 1.7.
Proposition 2.9 implies that there is a constant
![]() $C=D(3)$
such that
$C=D(3)$
such that
![]() $(U_{3}(\mathbb{Z};q)L_{3}(\mathbb{Z};q))^{C}=\langle U_{3}(\mathbb{Z};q)L_{3}(\mathbb{Z};q)\rangle$
. Lemma 2.11 implies that
$(U_{3}(\mathbb{Z};q)L_{3}(\mathbb{Z};q))^{C}=\langle U_{3}(\mathbb{Z};q)L_{3}(\mathbb{Z};q)\rangle$
. Lemma 2.11 implies that
![]() $(U_{n}(\mathbb{Z};q)L_{n}(\mathbb{Z};q))^{C}=\langle U_{n}(\mathbb{Z};q)L_{n}(\mathbb{Z};q)\rangle$
for every
$(U_{n}(\mathbb{Z};q)L_{n}(\mathbb{Z};q))^{C}=\langle U_{n}(\mathbb{Z};q)L_{n}(\mathbb{Z};q)\rangle$
for every
![]() $n\geqslant 3$
. Proposition 2.3 implies that
$n\geqslant 3$
. Proposition 2.3 implies that
![]() $(U_{n}(\mathbb{Z};q)L_{n}(\mathbb{Z};q))^{C}$
contains the congruence subgroup
$(U_{n}(\mathbb{Z};q)L_{n}(\mathbb{Z};q))^{C}$
contains the congruence subgroup
![]() $\operatorname{SL}_{n}(\mathbb{Z};q^{2})$
and this subgroup has a finite index in
$\operatorname{SL}_{n}(\mathbb{Z};q^{2})$
and this subgroup has a finite index in
![]() $\operatorname{SL}(n,\mathbb{Z})$
. ◻
$\operatorname{SL}(n,\mathbb{Z})$
. ◻
3 Proof of Theorem 1.4 without an explicit bound
We will need the following lemma, which we state without a proof.
Lemma 3.1. All upper-triangular matrices
![]() $g\in U_{n}(\mathbb{Z};q)$
such that
$g\in U_{n}(\mathbb{Z};q)$
such that
![]() $g_{i,i+1}=q$
, for all
$g_{i,i+1}=q$
, for all
![]() $i$
, are conjugate.
$i$
, are conjugate.
Proof of Theorem 1.4 without an explicit bound.
Identify
![]() $\operatorname{SL}_{2}(\mathbb{Z})$
with its image in
$\operatorname{SL}_{2}(\mathbb{Z})$
with its image in
![]() $\operatorname{SL}_{3}(\mathbb{Z})$
under the embedding
$\operatorname{SL}_{3}(\mathbb{Z})$
under the embedding
![]() $M\mapsto (\!\begin{smallmatrix}M & 0\\ 0 & 1\end{smallmatrix}\!)$
. Since
$M\mapsto (\!\begin{smallmatrix}M & 0\\ 0 & 1\end{smallmatrix}\!)$
. Since
![]() $\operatorname{SL}_{2}(\mathbb{Z})$
contains a non-abelian free group there exists
$\operatorname{SL}_{2}(\mathbb{Z})$
contains a non-abelian free group there exists
![]() $\pm I_{2}\neq g\in w(\operatorname{SL}_{2}(\mathbb{Z}))$
. There exists
$\pm I_{2}\neq g\in w(\operatorname{SL}_{2}(\mathbb{Z}))$
. There exists
![]() $h\in \langle e_{1,3}(1),e_{2,3}(1)\rangle$
such that
$h\in \langle e_{1,3}(1),e_{2,3}(1)\rangle$
such that
![]() $[g,h]=g^{-1}h^{-1}gh$
is a non-trivial element and this element is conjugate to
$[g,h]=g^{-1}h^{-1}gh$
is a non-trivial element and this element is conjugate to
![]() $e_{1,3}(q)$
for some positive
$e_{1,3}(q)$
for some positive
![]() $q\in \mathbb{N}$
. For the chosen
$q\in \mathbb{N}$
. For the chosen
![]() $g$
and
$g$
and
![]() $h$
, we have
$h$
, we have
![]() $[g,h]^{n}=[g,h^{n}]\in w(\operatorname{SL}_{3}(\mathbb{Z}))^{2}$
. Since
$[g,h]^{n}=[g,h^{n}]\in w(\operatorname{SL}_{3}(\mathbb{Z}))^{2}$
. Since
![]() $w(\operatorname{SL}_{3}(\mathbb{Z}))^{2}$
is a normal subset,
$w(\operatorname{SL}_{3}(\mathbb{Z}))^{2}$
is a normal subset,
![]() $\langle e_{1,3}(q)\rangle \subseteq w(\operatorname{SL}_{3}(\mathbb{Z}))^{2}$
. We will show that the statement of Theorem 1.4 holds with respect to
$\langle e_{1,3}(q)\rangle \subseteq w(\operatorname{SL}_{3}(\mathbb{Z}))^{2}$
. We will show that the statement of Theorem 1.4 holds with respect to
![]() $d=q^{2}$
.
$d=q^{2}$
.
We claim that for any integers
![]() $a_{1},\ldots ,a_{n-1}$
, there is
$a_{1},\ldots ,a_{n-1}$
, there is
![]() $g\in w(\operatorname{SL}_{n}(\mathbb{Z}))^{8}\cap U_{n}(\mathbb{Z};q)$
such that for every
$g\in w(\operatorname{SL}_{n}(\mathbb{Z}))^{8}\cap U_{n}(\mathbb{Z};q)$
such that for every
![]() $i$
,
$i$
,
![]() $g_{i,i+1}=qa_{i}$
. Using two different embeddings of the group
$g_{i,i+1}=qa_{i}$
. Using two different embeddings of the group
![]() $\operatorname{SL}_{3}(\mathbb{Z})\times \cdots \times \operatorname{SL}_{3}(\mathbb{Z})$
(
$\operatorname{SL}_{3}(\mathbb{Z})\times \cdots \times \operatorname{SL}_{3}(\mathbb{Z})$
(
![]() $\lfloor n/3\rfloor$
times) into
$\lfloor n/3\rfloor$
times) into
![]() $\operatorname{SL}_{n}(\mathbb{Z})$
as block-diagonal matrices, we get that there is a matrix
$\operatorname{SL}_{n}(\mathbb{Z})$
as block-diagonal matrices, we get that there is a matrix
![]() $g^{1}\in w(\operatorname{SL}_{n}(\mathbb{Z}))^{4}\cap U_{n}(\mathbb{Z};q)$
such that
$g^{1}\in w(\operatorname{SL}_{n}(\mathbb{Z}))^{4}\cap U_{n}(\mathbb{Z};q)$
such that
![]() $g_{i,i+1}^{1}=qa_{i}$
if
$g_{i,i+1}^{1}=qa_{i}$
if
![]() $i\equiv 1\text{ (mod 3)}$
and
$i\equiv 1\text{ (mod 3)}$
and
![]() $g_{i,i+1}^{1}=0$
otherwise. Using one embedding of the group
$g_{i,i+1}^{1}=0$
otherwise. Using one embedding of the group
![]() $\operatorname{SL}_{3}(\mathbb{Z})\times \cdots \times \operatorname{SL}_{3}(\mathbb{Z})$
(
$\operatorname{SL}_{3}(\mathbb{Z})\times \cdots \times \operatorname{SL}_{3}(\mathbb{Z})$
(
![]() $\lfloor n/3\rfloor$
times) into
$\lfloor n/3\rfloor$
times) into
![]() $\operatorname{SL}_{n}(\mathbb{Z})$
as block-diagonal matrices, we get that there is a matrix
$\operatorname{SL}_{n}(\mathbb{Z})$
as block-diagonal matrices, we get that there is a matrix
![]() $g^{2}\in w(\operatorname{SL}_{n}(\mathbb{Z}))^{2}\cap U_{n}(\mathbb{Z};q)$
such that
$g^{2}\in w(\operatorname{SL}_{n}(\mathbb{Z}))^{2}\cap U_{n}(\mathbb{Z};q)$
such that
![]() $g_{i,i+1}^{2}=qa_{i}$
if
$g_{i,i+1}^{2}=qa_{i}$
if
![]() $i\equiv 2\text{ (mod 3)}$
and
$i\equiv 2\text{ (mod 3)}$
and
![]() $g_{i,i+1}^{2}=0$
otherwise. Similarly, there is
$g_{i,i+1}^{2}=0$
otherwise. Similarly, there is
![]() $g^{3}\in w(\operatorname{SL}_{n}(\mathbb{Z}))^{2}\cap U_{n}(\mathbb{Z};q)$
such that
$g^{3}\in w(\operatorname{SL}_{n}(\mathbb{Z}))^{2}\cap U_{n}(\mathbb{Z};q)$
such that
![]() $g_{i,i+1}^{3}=qa_{i}$
if
$g_{i,i+1}^{3}=qa_{i}$
if
![]() $i\equiv 3\text{ (mod 3)}$
and
$i\equiv 3\text{ (mod 3)}$
and
![]() $g_{i,i+1}^{3}=0$
otherwise. The matrix
$g_{i,i+1}^{3}=0$
otherwise. The matrix
![]() $g=g^{0}g^{1}g^{2}\in w(\operatorname{SL}_{n}(\mathbb{Z}))^{8}\cap U_{n}(\mathbb{Z};q)$
satisfies
$g=g^{0}g^{1}g^{2}\in w(\operatorname{SL}_{n}(\mathbb{Z}))^{8}\cap U_{n}(\mathbb{Z};q)$
satisfies
![]() $g_{i,i+1}=qa_{i}$
. The proof of the claim in now complete.
$g_{i,i+1}=qa_{i}$
. The proof of the claim in now complete.
It follows from Lemma 3.1 that
![]() $w(\operatorname{SL}_{n}(\mathbb{Z}))^{8}$
contains all elements
$w(\operatorname{SL}_{n}(\mathbb{Z}))^{8}$
contains all elements
![]() $g\in U_{n}(\mathbb{Z};q)$
such that
$g\in U_{n}(\mathbb{Z};q)$
such that
![]() $g_{i,i+1}=q$
for every
$g_{i,i+1}=q$
for every
![]() $i$
.
$i$
.
Next, we claim that
![]() $U_{n}(\mathbb{Z};q)\subseteq w(\operatorname{SL}_{n}(\mathbb{Z}))^{16}$
. Indeed, let
$U_{n}(\mathbb{Z};q)\subseteq w(\operatorname{SL}_{n}(\mathbb{Z}))^{16}$
. Indeed, let
![]() $h\in U_{n}(\mathbb{Z};q)$
. There is an element
$h\in U_{n}(\mathbb{Z};q)$
. There is an element
![]() $f\in w(\operatorname{SL}_{n}(\mathbb{Z}))^{8}\cap U_{n}(\mathbb{Z};q)$
such that for every
$f\in w(\operatorname{SL}_{n}(\mathbb{Z}))^{8}\cap U_{n}(\mathbb{Z};q)$
such that for every
![]() $i$
,
$i$
,
![]() $f_{i,i+1}=q-h_{i,i+1}$
. Then
$f_{i,i+1}=q-h_{i,i+1}$
. Then
![]() $hf\in U_{n}(\mathbb{Z};q)$
and, for every
$hf\in U_{n}(\mathbb{Z};q)$
and, for every
![]() $i$
,
$i$
,
![]() $(fh)_{i,i+1}=q$
, so
$(fh)_{i,i+1}=q$
, so
![]() $fh\in w(\operatorname{SL}_{n}(\mathbb{Z}))^{8}$
. Since
$fh\in w(\operatorname{SL}_{n}(\mathbb{Z}))^{8}$
. Since
![]() $w(\operatorname{SL}_{n}(\mathbb{Z}))^{8}$
is symmetric, it follows that
$w(\operatorname{SL}_{n}(\mathbb{Z}))^{8}$
is symmetric, it follows that
![]() $h\in w(\operatorname{SL}_{n}(\mathbb{Z}))^{16}$
. Similarly,
$h\in w(\operatorname{SL}_{n}(\mathbb{Z}))^{16}$
. Similarly,
![]() $L_{n}(\mathbb{Z};q)\subseteq w(\operatorname{SL}_{n}(\mathbb{Z}))^{16}$
.
$L_{n}(\mathbb{Z};q)\subseteq w(\operatorname{SL}_{n}(\mathbb{Z}))^{16}$
.
By Theorem 1.7, there is a constant
![]() $C$
(independent of
$C$
(independent of
![]() $q$
) such that
$q$
) such that
Propositon 2.3 implies that
![]() $\operatorname{SL}_{n}(\mathbb{Z},q^{2})\leqslant \langle U_{n}(\mathbb{Z};q)U_{n}(\mathbb{Z};q)\rangle$
.◻
$\operatorname{SL}_{n}(\mathbb{Z},q^{2})\leqslant \langle U_{n}(\mathbb{Z};q)U_{n}(\mathbb{Z};q)\rangle$
.◻
4 Proof of Theorems 1.2 and 1.1
In order to deduce Theorems 1.1 and 1.2 from Theorem 1.4, we need to study word values in
![]() $\operatorname{SL}_{n}(\mathbb{Z}/q\mathbb{Z})$
uniformly in
$\operatorname{SL}_{n}(\mathbb{Z}/q\mathbb{Z})$
uniformly in
![]() $q$
. Equivalently, we need to study word values in
$q$
. Equivalently, we need to study word values in
![]() $\operatorname{SL}_{n}(\widehat{\mathbb{Z}})$
where
$\operatorname{SL}_{n}(\widehat{\mathbb{Z}})$
where
![]() $\widehat{\mathbb{Z}}$
is the pro-finite completion of
$\widehat{\mathbb{Z}}$
is the pro-finite completion of
![]() $\mathbb{Z}$
. We will use a version of the open mapping theorem which is well known, but for which we were unable to find a reference.
$\mathbb{Z}$
. We will use a version of the open mapping theorem which is well known, but for which we were unable to find a reference.
For
![]() $a\in \mathbb{Z}_{p}^{n}$
, denote
$a\in \mathbb{Z}_{p}^{n}$
, denote
![]() $\Vert a\Vert =\max \{|a_{i}|_{p}\}$
, where
$\Vert a\Vert =\max \{|a_{i}|_{p}\}$
, where
![]() $|a|_{p}$
is the
$|a|_{p}$
is the
![]() $p$
-adic valuation of
$p$
-adic valuation of
![]() $a$
. The function
$a$
. The function
![]() $d(a,b)=\Vert a-b\Vert$
is a metric on
$d(a,b)=\Vert a-b\Vert$
is a metric on
![]() $\mathbb{Z}_{p}^{n}$
. Let
$\mathbb{Z}_{p}^{n}$
. Let
![]() $X\subset \mathbb{A}_{\mathbb{Z}_{p}}^{n}$
be an affine
$X\subset \mathbb{A}_{\mathbb{Z}_{p}}^{n}$
be an affine
![]() $\mathbb{Z}_{p}$
-scheme, that is, the zero locus of a collection of polynomials in
$\mathbb{Z}_{p}$
-scheme, that is, the zero locus of a collection of polynomials in
![]() $\mathbb{Z}_{p}[x_{1},\ldots ,x_{n}]$
. We denote the set of solutions of
$\mathbb{Z}_{p}[x_{1},\ldots ,x_{n}]$
. We denote the set of solutions of
![]() $X$
with coordinates in
$X$
with coordinates in
![]() $\mathbb{Z}_{p}$
by
$\mathbb{Z}_{p}$
by
![]() $X(\mathbb{Z}_{p})$
. The restriction of
$X(\mathbb{Z}_{p})$
. The restriction of
![]() $d$
to
$d$
to
![]() $X(\mathbb{Z}_{p})$
is a metric on
$X(\mathbb{Z}_{p})$
is a metric on
![]() $X(\mathbb{Z}_{p})$
.Footnote
1
Let
$X(\mathbb{Z}_{p})$
.Footnote
1
Let
![]() $\mathbb{Z}_{p}[X]$
be the ring of regular functions on
$\mathbb{Z}_{p}[X]$
be the ring of regular functions on
![]() $X$
(the restrictions of polynomials with
$X$
(the restrictions of polynomials with
![]() $\mathbb{Z}_{p}$
coefficients to
$\mathbb{Z}_{p}$
coefficients to
![]() $X$
). For
$X$
). For
![]() $f\in \mathbb{Z}_{p}[X]$
, we define
$f\in \mathbb{Z}_{p}[X]$
, we define
![]() $\operatorname{val}_{p}(f)=\max \{k\mid f\in p^{k}\mathbb{Z}_{p}[X]\}$
. More generally, if
$\operatorname{val}_{p}(f)=\max \{k\mid f\in p^{k}\mathbb{Z}_{p}[X]\}$
. More generally, if
![]() $f:X\rightarrow Y$
is a map of affine
$f:X\rightarrow Y$
is a map of affine
![]() $\mathbb{Z}_{p}$
-schemes, we define
$\mathbb{Z}_{p}$
-schemes, we define
![]() $\operatorname{val}_{p}(f)$
as the minimum of the valuations of its coordinates. Note that if
$\operatorname{val}_{p}(f)$
as the minimum of the valuations of its coordinates. Note that if
![]() $\operatorname{val}(f)\geqslant k$
, then
$\operatorname{val}(f)\geqslant k$
, then
![]() $d(f(a),f(b))\leqslant p^{-k}d(a,b)$
, for every
$d(f(a),f(b))\leqslant p^{-k}d(a,b)$
, for every
![]() $a,b\in X(\mathbb{Z}_{p})$
.
$a,b\in X(\mathbb{Z}_{p})$
.
Recall that
![]() $X$
is called smooth at
$X$
is called smooth at
![]() $a\in X(\mathbb{Z}_{p})$
if there are
$a\in X(\mathbb{Z}_{p})$
if there are
![]() $\unicode[STIX]{x1D713}_{1},\ldots ,\unicode[STIX]{x1D713}_{c}\in \mathbb{Z}_{p}[x_{1},\ldots ,x_{n}]$
such that
$\unicode[STIX]{x1D713}_{1},\ldots ,\unicode[STIX]{x1D713}_{c}\in \mathbb{Z}_{p}[x_{1},\ldots ,x_{n}]$
such that
![]() $X$
is the common zero locus of
$X$
is the common zero locus of
![]() $\unicode[STIX]{x1D713}_{i}$
and the reductions of
$\unicode[STIX]{x1D713}_{i}$
and the reductions of
![]() $\unicode[STIX]{x1D6FB}\unicode[STIX]{x1D713}_{i}(a)$
modulo
$\unicode[STIX]{x1D6FB}\unicode[STIX]{x1D713}_{i}(a)$
modulo
![]() $p$
are linearly independent. In this case
$p$
are linearly independent. In this case
![]() $n-c$
is called the dimension of
$n-c$
is called the dimension of
![]() $X$
at
$X$
at
![]() $a$
.
$a$
.
Lemma 4.1. Let
![]() $X\subseteq \mathbb{A}_{\mathbb{Z}_{p}}^{n}$
be a
$X\subseteq \mathbb{A}_{\mathbb{Z}_{p}}^{n}$
be a
![]() $\mathbb{Z}_{p}$
-scheme and
$\mathbb{Z}_{p}$
-scheme and
![]() $a\in X(\mathbb{Z}_{p})$
. Assume that
$a\in X(\mathbb{Z}_{p})$
. Assume that
![]() $X$
is smooth in
$X$
is smooth in
![]() $a$
. Then there is a subset
$a$
. Then there is a subset
![]() $S\subset \{1,\ldots ,n\}$
such that the coordinate projection
$S\subset \{1,\ldots ,n\}$
such that the coordinate projection
![]() $\unicode[STIX]{x1D70B}:\mathbb{Z}_{p}^{n}\rightarrow \mathbb{Z}_{p}^{S}$
satisfies the following statements:
$\unicode[STIX]{x1D70B}:\mathbb{Z}_{p}^{n}\rightarrow \mathbb{Z}_{p}^{S}$
satisfies the following statements:
(1) the restriction of
 $\unicode[STIX]{x1D70B}$
to
$\unicode[STIX]{x1D70B}$
to
 $X(\mathbb{Z}_{p})\cap B(a,p^{-1})$
is one-to-one, where
$X(\mathbb{Z}_{p})\cap B(a,p^{-1})$
is one-to-one, where
 $B(a,p^{-1})$
is the closed ball of radius
$B(a,p^{-1})$
is the closed ball of radius
 $p^{-1}$
around
$p^{-1}$
around
 $a$
;
$a$
;(2)
 $\unicode[STIX]{x1D70B}(T_{a}X(\mathbb{Z}_{p}))=\mathbb{Z}_{p}^{S}$
.
$\unicode[STIX]{x1D70B}(T_{a}X(\mathbb{Z}_{p}))=\mathbb{Z}_{p}^{S}$
.
Proof. Let
![]() $\unicode[STIX]{x1D713}_{i}$
be as in the definition of smoothness. After permutation of the indices, we can assume that the
$\unicode[STIX]{x1D713}_{i}$
be as in the definition of smoothness. After permutation of the indices, we can assume that the
![]() $c\times c$
matrix
$c\times c$
matrix
![]() $(\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D713}_{i}}{\unicode[STIX]{x2202}x_{j}}(a))$
is invertible over
$(\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D713}_{i}}{\unicode[STIX]{x2202}x_{j}}(a))$
is invertible over
![]() $\mathbb{Z}_{p}$
. For any
$\mathbb{Z}_{p}$
. For any
![]() $f\in \mathbb{Z}_{p}[x_{1},\ldots ,x_{n}]$
and any
$f\in \mathbb{Z}_{p}[x_{1},\ldots ,x_{n}]$
and any
![]() $a,b\in \mathbb{Z}_{p}^{n}$
with
$a,b\in \mathbb{Z}_{p}^{n}$
with
![]() $0<d(a,b)<1$
, we have
$0<d(a,b)<1$
, we have
![]() $|f(a)-f(b)-\langle \unicode[STIX]{x1D6FB}f(a),a-b\rangle |\leqslant \Vert a-b\Vert ^{2}<\Vert a-b\Vert$
. If
$|f(a)-f(b)-\langle \unicode[STIX]{x1D6FB}f(a),a-b\rangle |\leqslant \Vert a-b\Vert ^{2}<\Vert a-b\Vert$
. If
![]() $a,b\in X(\mathbb{Z}_{p})$
and
$a,b\in X(\mathbb{Z}_{p})$
and
![]() $d(a,b)<1$
, we have
$d(a,b)<1$
, we have
![]() $\unicode[STIX]{x1D713}_{i}(a)=\unicode[STIX]{x1D713}_{i}(b)=0$
, so
$\unicode[STIX]{x1D713}_{i}(a)=\unicode[STIX]{x1D713}_{i}(b)=0$
, so
![]() $|\langle \unicode[STIX]{x1D6FB}\unicode[STIX]{x1D713}_{i}(a),a-b\rangle |<\Vert a-b\Vert$
. If, in addition,
$|\langle \unicode[STIX]{x1D6FB}\unicode[STIX]{x1D713}_{i}(a),a-b\rangle |<\Vert a-b\Vert$
. If, in addition,
![]() $\unicode[STIX]{x1D70B}(a)=\unicode[STIX]{x1D70B}(b)$
, write
$\unicode[STIX]{x1D70B}(a)=\unicode[STIX]{x1D70B}(b)$
, write
![]() $a-b=(v,0)$
, where
$a-b=(v,0)$
, where
![]() $v\in p\mathbb{Z}_{p}^{c}$
and then
$v\in p\mathbb{Z}_{p}^{c}$
and then
Since invertible matrices do not decrease norm, this is a contradiction. This completes the proof of statement (1). Denoting
![]() $S:=\{c+1,\ldots ,n\}$
, statement (2) readily follows form the assumption that
$S:=\{c+1,\ldots ,n\}$
, statement (2) readily follows form the assumption that
![]() $(\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D713}_{i}}{\unicode[STIX]{x2202}x_{j}}(a))$
is invertible.◻
$(\frac{\unicode[STIX]{x2202}\unicode[STIX]{x1D713}_{i}}{\unicode[STIX]{x2202}x_{j}}(a))$
is invertible.◻
Lemma 4.2. Let
![]() $X,Y$
be affine
$X,Y$
be affine
![]() $\mathbb{Z}_{p}$
-schemes. Let
$\mathbb{Z}_{p}$
-schemes. Let
![]() $f:X\rightarrow Y$
be a morphism, let
$f:X\rightarrow Y$
be a morphism, let
![]() $a\in X(\mathbb{Z}_{p})$
, and let
$a\in X(\mathbb{Z}_{p})$
, and let
![]() $k\geqslant 0$
be an integer. Suppose that the following statements hold:
$k\geqslant 0$
be an integer. Suppose that the following statements hold:
(1)
 $\operatorname{val}_{p}(f)\geqslant k$
;
$\operatorname{val}_{p}(f)\geqslant k$
;(2)
 $df(a)(T_{a}X(\mathbb{Z}_{p}))\supseteq p^{k}T_{f(a)}Y(\mathbb{Z}_{p})$
;
$df(a)(T_{a}X(\mathbb{Z}_{p}))\supseteq p^{k}T_{f(a)}Y(\mathbb{Z}_{p})$
;(3)
 $X$
is smooth at
$X$
is smooth at
 $a$
and
$a$
and
 $Y$
is smooth at
$Y$
is smooth at
 $f(a)$
.
$f(a)$
.
Then
![]() $f(X(\mathbb{Z}_{p}))$
contains the closed ball of radius
$f(X(\mathbb{Z}_{p}))$
contains the closed ball of radius
![]() $p^{-k-1}$
around
$p^{-k-1}$
around
![]() $f(a)$
.
$f(a)$
.
Proof. We first reduce the claim to the case where
![]() $X$
is an affine space. Suppose that
$X$
is an affine space. Suppose that
![]() $X\subset \mathbb{A}^{n}$
is
$X\subset \mathbb{A}^{n}$
is
![]() $d$
-dimensional. By smoothness, it is given as the zero locus of
$d$
-dimensional. By smoothness, it is given as the zero locus of
![]() $\unicode[STIX]{x1D711}_{1},\ldots ,\unicode[STIX]{x1D711}_{n-d}\in \mathbb{Z}_{p}[x_{1},\ldots ,x_{n}]$
such that the reductions modulo
$\unicode[STIX]{x1D711}_{1},\ldots ,\unicode[STIX]{x1D711}_{n-d}\in \mathbb{Z}_{p}[x_{1},\ldots ,x_{n}]$
such that the reductions modulo
![]() $p$
of
$p$
of
![]() $\unicode[STIX]{x1D6FB}\unicode[STIX]{x1D711}_{i}(a)$
are linearly independent. Consider the map
$\unicode[STIX]{x1D6FB}\unicode[STIX]{x1D711}_{i}(a)$
are linearly independent. Consider the map
![]() $F:\mathbb{A}^{n}\rightarrow Y\times \mathbb{A}^{n-d}$
given by
$F:\mathbb{A}^{n}\rightarrow Y\times \mathbb{A}^{n-d}$
given by
![]() $x\mapsto (f(x),p^{k}\unicode[STIX]{x1D711}_{1}(x),\ldots ,p^{k}\unicode[STIX]{x1D711}_{n-d}(x))$
. Then
$x\mapsto (f(x),p^{k}\unicode[STIX]{x1D711}_{1}(x),\ldots ,p^{k}\unicode[STIX]{x1D711}_{n-d}(x))$
. Then
![]() $F$
satisfies the conditions of the lemma. If the claim holds for
$F$
satisfies the conditions of the lemma. If the claim holds for
![]() $F$
, then it holds for
$F$
, then it holds for
![]() $f$
.
$f$
.
Next, we reduce the claim to the case where
![]() $X$
and
$X$
and
![]() $Y$
are affine spaces. Indeed, let
$Y$
are affine spaces. Indeed, let
![]() $e$
be the dimension of
$e$
be the dimension of
![]() $Y$
at
$Y$
at
![]() $f(a)$
. Item (1) of Lemma 4.1 allows us to assume that the coordinate projection
$f(a)$
. Item (1) of Lemma 4.1 allows us to assume that the coordinate projection
![]() $\unicode[STIX]{x1D70B}:Y\rightarrow \mathbb{A}^{e}$
is one-to-one on
$\unicode[STIX]{x1D70B}:Y\rightarrow \mathbb{A}^{e}$
is one-to-one on
![]() $B(f(a),p^{-1})$
. Item (2) of Lemma 4.1 implies that the function
$B(f(a),p^{-1})$
. Item (2) of Lemma 4.1 implies that the function
![]() $\unicode[STIX]{x1D70B}\circ f$
satisfies the conditions of the lemma, and the claim for
$\unicode[STIX]{x1D70B}\circ f$
satisfies the conditions of the lemma, and the claim for
![]() $\unicode[STIX]{x1D70B}\circ f$
implies the claim for
$\unicode[STIX]{x1D70B}\circ f$
implies the claim for
![]() $f$
.
$f$
.
Finally, we prove the claim in the case
![]() $X=\mathbb{A}^{n}$
and
$X=\mathbb{A}^{n}$
and
![]() $Y=\mathbb{A}^{m}$
. We can assume that
$Y=\mathbb{A}^{m}$
. We can assume that
![]() $a=0$
and
$a=0$
and
![]() $f(a)=0$
. Since the coefficients of
$f(a)=0$
. Since the coefficients of
![]() $f$
are in
$f$
are in
![]() $\mathbb{Z}_{p}$
, we have that
$\mathbb{Z}_{p}$
, we have that
![]() $df(a^{\prime })(\mathbb{Z}_{p}^{n})\supseteq p^{k}\mathbb{Z}_{p}^{m}$
, for any
$df(a^{\prime })(\mathbb{Z}_{p}^{n})\supseteq p^{k}\mathbb{Z}_{p}^{m}$
, for any
![]() $a^{\prime }\in p\mathbb{Z}_{p}^{n}$
. Let
$a^{\prime }\in p\mathbb{Z}_{p}^{n}$
. Let
![]() $b\in p^{k+1}\mathbb{Z}_{p}^{m}$
. We will construct a sequence
$b\in p^{k+1}\mathbb{Z}_{p}^{m}$
. We will construct a sequence
![]() $a_{\ell }\in p\mathbb{Z}_{p}^{n}$
such that
$a_{\ell }\in p\mathbb{Z}_{p}^{n}$
such that
![]() $\Vert f(a_{\ell })-b\Vert <p^{-k-\ell }$
. Taking a limit point of the
$\Vert f(a_{\ell })-b\Vert <p^{-k-\ell }$
. Taking a limit point of the
![]() $a_{\ell }$
, we get that
$a_{\ell }$
, we get that
![]() $b\in f(\mathbb{Z}_{p}^{n})$
.
$b\in f(\mathbb{Z}_{p}^{n})$
.
The sequence
![]() $a_{\ell }$
is defined by recursion starting from
$a_{\ell }$
is defined by recursion starting from
![]() $a_{0}=0$
. Given
$a_{0}=0$
. Given
![]() $a_{\ell }$
, the assumptions imply that there is
$a_{\ell }$
, the assumptions imply that there is
![]() $\unicode[STIX]{x1D716}\in p^{\ell +1}\mathbb{Z}_{p}^{n}$
such that
$\unicode[STIX]{x1D716}\in p^{\ell +1}\mathbb{Z}_{p}^{n}$
such that
![]() $df(a_{\ell })(\unicode[STIX]{x1D716})=b-f(a_{\ell })$
. We have
$df(a_{\ell })(\unicode[STIX]{x1D716})=b-f(a_{\ell })$
. We have
since the function
![]() $x\mapsto f(a_{\ell }+x)-f(a_{\ell })-df(a_{\ell })(x)$
is a polynomial without constant or linear term and its coefficients are divisible by
$x\mapsto f(a_{\ell }+x)-f(a_{\ell })-df(a_{\ell })(x)$
is a polynomial without constant or linear term and its coefficients are divisible by
![]() $p^{k}$
.◻
$p^{k}$
.◻
Definition 4.3. For elements
![]() $g,h\in \operatorname{SL}_{n}$
, let
$g,h\in \operatorname{SL}_{n}$
, let
![]() $\unicode[STIX]{x1D6F7}_{g,h}:\operatorname{SL}_{n}\times \operatorname{SL}_{n}\rightarrow \operatorname{SL}_{n}$
be the map
$\unicode[STIX]{x1D6F7}_{g,h}:\operatorname{SL}_{n}\times \operatorname{SL}_{n}\rightarrow \operatorname{SL}_{n}$
be the map
![]() $\unicode[STIX]{x1D6F7}_{g,h}^{R}(x,y)=g^{x}h^{y}$
.
$\unicode[STIX]{x1D6F7}_{g,h}^{R}(x,y)=g^{x}h^{y}$
.
Lemma 4.4. Let
![]() $n\geqslant 3$
and assume that
$n\geqslant 3$
and assume that
![]() $a,b\in \operatorname{SL}_{n}(\mathbb{F}_{q})$
generate
$a,b\in \operatorname{SL}_{n}(\mathbb{F}_{q})$
generate
![]() $\operatorname{SL}_{n}(\mathbb{F}_{p})$
where
$\operatorname{SL}_{n}(\mathbb{F}_{p})$
where
![]() $\mathbb{F}_{q}$
is a finite field of order
$\mathbb{F}_{q}$
is a finite field of order
![]() $q$
. Then the differential of
$q$
. Then the differential of
![]() $\unicode[STIX]{x1D6F7}_{a,b}$
at
$\unicode[STIX]{x1D6F7}_{a,b}$
at
![]() $(1,1)$
is onto.
$(1,1)$
is onto.
Proof. After identifying
![]() $T_{ab}\operatorname{SL}_{n}=ab+ab\mathfrak{sl}_{n}$
and
$T_{ab}\operatorname{SL}_{n}=ab+ab\mathfrak{sl}_{n}$
and
![]() $\mathfrak{sl}_{n}$
, the differential of
$\mathfrak{sl}_{n}$
, the differential of
![]() $\unicode[STIX]{x1D6F7}_{a,b}$
is
$\unicode[STIX]{x1D6F7}_{a,b}$
is
![]() $(X,Y)\mapsto (X-X^{a})^{b}+(Y-Y^{b})$
. Let
$(X,Y)\mapsto (X-X^{a})^{b}+(Y-Y^{b})$
. Let
![]() $\unicode[STIX]{x1D711}\in \operatorname{M}_{n}(\mathbb{F}_{q})^{\ast }$
and assume it vanishes on the image of
$\unicode[STIX]{x1D711}\in \operatorname{M}_{n}(\mathbb{F}_{q})^{\ast }$
and assume it vanishes on the image of
![]() $d\unicode[STIX]{x1D6F7}_{a,b}$
. Then there is
$d\unicode[STIX]{x1D6F7}_{a,b}$
. Then there is
![]() $A\in \operatorname{M}_{n}(\mathbb{F}_{q})$
such that
$A\in \operatorname{M}_{n}(\mathbb{F}_{q})$
such that
![]() $\unicode[STIX]{x1D711}(X)=\operatorname{tr}(AX)$
. For every
$\unicode[STIX]{x1D711}(X)=\operatorname{tr}(AX)$
. For every
![]() $Y\in \mathfrak{sl}_{n}(\mathbb{F}_{p})$
,
$Y\in \mathfrak{sl}_{n}(\mathbb{F}_{p})$
,
![]() $\unicode[STIX]{x1D711}(Y-Y^{b})=0$
, so
$\unicode[STIX]{x1D711}(Y-Y^{b})=0$
, so
![]() $\operatorname{tr}(Y\cdot (A^{b^{-1}}-A))=\operatorname{tr}(A(Y-Y^{b}))=0$
. Thus,
$\operatorname{tr}(Y\cdot (A^{b^{-1}}-A))=\operatorname{tr}(A(Y-Y^{b}))=0$
. Thus,
![]() $A^{b^{-1}}-A$
is a scalar. Similarly, using the assumption that
$A^{b^{-1}}-A$
is a scalar. Similarly, using the assumption that
![]() $\unicode[STIX]{x1D711}((X-X^{a})^{b})=0$
, we get that
$\unicode[STIX]{x1D711}((X-X^{a})^{b})=0$
, we get that
![]() $(A^{b^{-1}})^{a^{-1}}-A^{b^{-1}}$
is a scalar. Using the fact that
$(A^{b^{-1}})^{a^{-1}}-A^{b^{-1}}$
is a scalar. Using the fact that
![]() $A^{b^{-1}}-A$
is a scalar, we get that
$A^{b^{-1}}-A$
is a scalar, we get that
![]() $A^{a^{-1}}-A$
is also a scalar. The set
$A^{a^{-1}}-A$
is also a scalar. The set
![]() $X=\{g\in \operatorname{SL}_{n}(\mathbb{F}_{q})\mid A^{g}-A\text{ is a scalar}\}$
is closed under multiplication. Since
$X=\{g\in \operatorname{SL}_{n}(\mathbb{F}_{q})\mid A^{g}-A\text{ is a scalar}\}$
is closed under multiplication. Since
![]() $a^{-1},b^{-1}\in X$
, we get
$a^{-1},b^{-1}\in X$
, we get
![]() $X=\operatorname{SL}_{n}(\mathbb{F}_{q})$
. Since
$X=\operatorname{SL}_{n}(\mathbb{F}_{q})$
. Since
![]() $\operatorname{SL}_{n}(\mathbb{F}_{p})$
is perfect and the function
$\operatorname{SL}_{n}(\mathbb{F}_{p})$
is perfect and the function
![]() $g\mapsto A^{g}-A$
is a homomorphism between
$g\mapsto A^{g}-A$
is a homomorphism between
![]() $\operatorname{SL}_{n}(\mathbb{F}_{q})$
and
$\operatorname{SL}_{n}(\mathbb{F}_{q})$
and
![]() $\mathbb{F}_{q}\operatorname{Id}$
, we get that this homomorphism must be trivial. Hence,
$\mathbb{F}_{q}\operatorname{Id}$
, we get that this homomorphism must be trivial. Hence,
![]() $A$
commutes with
$A$
commutes with
![]() $\operatorname{SL}_{n}(\mathbb{F}_{q})$
, so it must be scalar. It follows that the restriction of
$\operatorname{SL}_{n}(\mathbb{F}_{q})$
, so it must be scalar. It follows that the restriction of
![]() $\unicode[STIX]{x1D711}$
to
$\unicode[STIX]{x1D711}$
to
![]() $\mathfrak{sl}_{n}(\mathbb{F}_{q})$
is zero.◻
$\mathfrak{sl}_{n}(\mathbb{F}_{q})$
is zero.◻
Lemma 4.5. For every non-trivial word
![]() $w$
, there is
$w$
, there is
![]() $n_{0}$
such that, for any integer
$n_{0}$
such that, for any integer
![]() $n\geqslant n_{0}$
, we have
$n\geqslant n_{0}$
, we have
![]() $w(\operatorname{SL}_{n}(\widehat{\mathbb{Z}}))^{7}=\operatorname{SL}_{n}(\widehat{\mathbb{Z}})$
.
$w(\operatorname{SL}_{n}(\widehat{\mathbb{Z}}))^{7}=\operatorname{SL}_{n}(\widehat{\mathbb{Z}})$
.
Proof. By [Reference Larsen and ShalevLS09], there is
![]() $n_{0}$
such that, if
$n_{0}$
such that, if
![]() $n\geqslant n_{0}$
and
$n\geqslant n_{0}$
and
![]() $p$
is any prime, then
$p$
is any prime, then
![]() $w(\operatorname{SL}_{n}(\mathbb{F}_{p}))^{2}$
contains all non-scalar matrices. In particular,
$w(\operatorname{SL}_{n}(\mathbb{F}_{p}))^{2}$
contains all non-scalar matrices. In particular,
![]() $w(\operatorname{SL}_{n}(\mathbb{F}_{p}))^{3}=\operatorname{SL}_{n}(\mathbb{F}_{p})$
. Fix a prime
$w(\operatorname{SL}_{n}(\mathbb{F}_{p}))^{3}=\operatorname{SL}_{n}(\mathbb{F}_{p})$
. Fix a prime
![]() $p$
. Choosing generators
$p$
. Choosing generators
![]() $a,b\in \operatorname{SL}_{n}(\mathbb{F}_{p})$
(which are not scalars), there are
$a,b\in \operatorname{SL}_{n}(\mathbb{F}_{p})$
(which are not scalars), there are
![]() $g,h\in w(\operatorname{SL}_{n}(\mathbb{Z}_{p}))^{2}$
such that the reductions of
$g,h\in w(\operatorname{SL}_{n}(\mathbb{Z}_{p}))^{2}$
such that the reductions of
![]() $g,h$
modulo
$g,h$
modulo
![]() $p$
are
$p$
are
![]() $a,b$
respectively. We get that
$a,b$
respectively. We get that
![]() $w(\operatorname{SL}_{n}(\mathbb{Z}_{p}))^{4}\supset \unicode[STIX]{x1D6F7}_{g,h}(\operatorname{SL}_{n}(\mathbb{Z}_{p})\times \operatorname{SL}_{n}(\mathbb{Z}_{p}))$
. It is well known that
$w(\operatorname{SL}_{n}(\mathbb{Z}_{p}))^{4}\supset \unicode[STIX]{x1D6F7}_{g,h}(\operatorname{SL}_{n}(\mathbb{Z}_{p})\times \operatorname{SL}_{n}(\mathbb{Z}_{p}))$
. It is well known that
![]() $\operatorname{SL}_{n}$
and thus also
$\operatorname{SL}_{n}$
and thus also
![]() $\operatorname{SL}_{n}\times \operatorname{SL}_{n}$
are smooth at every point. Lemmas 4.4 and 4.2 imply that
$\operatorname{SL}_{n}\times \operatorname{SL}_{n}$
are smooth at every point. Lemmas 4.4 and 4.2 imply that
![]() $w(\operatorname{SL}_{n}(\mathbb{Z}_{p}))^{4}$
contains the coset
$w(\operatorname{SL}_{n}(\mathbb{Z}_{p}))^{4}$
contains the coset
![]() $gh\operatorname{SL}_{n}(\mathbb{Z}_{p};p)$
. Hence,
$gh\operatorname{SL}_{n}(\mathbb{Z}_{p};p)$
. Hence,
![]() $w(\operatorname{SL}_{n}(\mathbb{Z}_{p}))^{7}=\operatorname{SL}_{n}(\mathbb{Z}_{p})$
.
$w(\operatorname{SL}_{n}(\mathbb{Z}_{p}))^{7}=\operatorname{SL}_{n}(\mathbb{Z}_{p})$
.
Since
![]() $w(\operatorname{SL}_{n}(\widehat{\mathbb{Z}}))=\prod _{p}w(\operatorname{SL}_{n}(\mathbb{Z}_{p}))$
, the claim follows.◻
$w(\operatorname{SL}_{n}(\widehat{\mathbb{Z}}))=\prod _{p}w(\operatorname{SL}_{n}(\mathbb{Z}_{p}))$
, the claim follows.◻
We move on to the proof of Theorem 1.2.
Lemma 4.6. For every
![]() $n\geqslant 2$
there is a constant
$n\geqslant 2$
there is a constant
![]() $C$
such that the following holds: if
$C$
such that the following holds: if
![]() $p$
is a prime and
$p$
is a prime and
![]() $A\in \mathfrak{sl}_{n}(\mathbb{F}_{p})$
is non-central, then every element of
$A\in \mathfrak{sl}_{n}(\mathbb{F}_{p})$
is non-central, then every element of
![]() $\mathfrak{sl}_{n}(\mathbb{F}_{p})$
is equal to the sum of at most
$\mathfrak{sl}_{n}(\mathbb{F}_{p})$
is equal to the sum of at most
![]() $C$
elements of
$C$
elements of
![]() $\{x^{-1}Ax\mid x\in \operatorname{SL}_{n}(\mathbb{F}_{p})\}$
.
$\{x^{-1}Ax\mid x\in \operatorname{SL}_{n}(\mathbb{F}_{p})\}$
.
Proof. It is well known that the only non-trivial
![]() $\operatorname{SL}_{n}(\mathbb{F}_{p})$
-invariant subspace of
$\operatorname{SL}_{n}(\mathbb{F}_{p})$
-invariant subspace of
![]() $\mathfrak{sl}_{n}(\mathbb{F}_{p})$
is the subset consisting of scalar matrices. Hence, for every
$\mathfrak{sl}_{n}(\mathbb{F}_{p})$
is the subset consisting of scalar matrices. Hence, for every
![]() $p$
, there is a constant
$p$
, there is a constant
![]() $C_{p}$
such that every element of
$C_{p}$
such that every element of
![]() $\mathfrak{sl}_{n}(\mathbb{F}_{p})$
is equal to the sum of at most
$\mathfrak{sl}_{n}(\mathbb{F}_{p})$
is equal to the sum of at most
![]() $C_{p}$
elements of
$C_{p}$
elements of
![]() $\{x^{-1}Ax\mid x\in \operatorname{SL}_{n}(\mathbb{F}_{p})\}$
. Therefore, in order to find a uniform
$\{x^{-1}Ax\mid x\in \operatorname{SL}_{n}(\mathbb{F}_{p})\}$
. Therefore, in order to find a uniform
![]() $C$
, we can and will assume that
$C$
, we can and will assume that
![]() $p$
is large. In particular, we assume that
$p$
is large. In particular, we assume that
![]() $p\neq 2$
.
$p\neq 2$
.
For
![]() $1\leqslant i\neq j\leqslant n$
, let
$1\leqslant i\neq j\leqslant n$
, let
![]() $E_{i,j}(a)$
be the matrix whose
$E_{i,j}(a)$
be the matrix whose
![]() $(i,j)$
th entry is
$(i,j)$
th entry is
![]() $a$
and with all other entries zero. Note that
$a$
and with all other entries zero. Note that
![]() $E_{1,2}(a)$
is conjugate to
$E_{1,2}(a)$
is conjugate to
![]() $E_{1,2}(ab^{2})$
, for every
$E_{1,2}(ab^{2})$
, for every
![]() $b\in \mathbb{F}_{p}$
. Since every element in
$b\in \mathbb{F}_{p}$
. Since every element in
![]() $\mathbb{F}_{p}$
is a sum of two squares, we get that, for any
$\mathbb{F}_{p}$
is a sum of two squares, we get that, for any
![]() $a\in \mathbb{F}_{p}^{\times }$
, any element of the form
$a\in \mathbb{F}_{p}^{\times }$
, any element of the form
![]() $E_{1,2}(b)$
is the sum of at most two conjugates of
$E_{1,2}(b)$
is the sum of at most two conjugates of
![]() $E_{1,2}(a)$
. In particular, there exists a one-dimensional linear subspace of
$E_{1,2}(a)$
. In particular, there exists a one-dimensional linear subspace of
![]() $\mathfrak{sl}_{n}(\mathbb{F}_{p})$
such that all its elements are sums of two conjugates of
$\mathfrak{sl}_{n}(\mathbb{F}_{p})$
such that all its elements are sums of two conjugates of
![]() $E_{1,2}(a)$
. Using the fact that the only
$E_{1,2}(a)$
. Using the fact that the only
![]() $\operatorname{SL}_{n}(\mathbb{F}_{p})$
-invariant subspace of
$\operatorname{SL}_{n}(\mathbb{F}_{p})$
-invariant subspace of
![]() $\mathfrak{sl}_{n}(\mathbb{F}_{p})$
is the subset consisting of scalar matrices once again, we see that if
$\mathfrak{sl}_{n}(\mathbb{F}_{p})$
is the subset consisting of scalar matrices once again, we see that if
![]() $a\neq 0$
, then every matrix in
$a\neq 0$
, then every matrix in
![]() $\mathfrak{sl}_{n}(\mathbb{F}_{p})$
is the sum of at most
$\mathfrak{sl}_{n}(\mathbb{F}_{p})$
is the sum of at most
![]() $2(n^{2}-1)$
conjugates of
$2(n^{2}-1)$
conjugates of
![]() $E_{1,2}(a)$
. Therefore, it is enough to prove that there is a constant
$E_{1,2}(a)$
. Therefore, it is enough to prove that there is a constant
![]() $C$
such that, for some
$C$
such that, for some
![]() $a\in \mathbb{F}_{p}$
, the matrix
$a\in \mathbb{F}_{p}$
, the matrix
![]() $E_{1,2}(a)$
is a sum of
$E_{1,2}(a)$
is a sum of
![]() $C$
conjugates of
$C$
conjugates of
![]() $A$
. We divide the proof into several steps.
$A$
. We divide the proof into several steps.
Step A. Assume that
![]() $A$
is nilpotent. By using Jordan’s normal form we see that
$A$
is nilpotent. By using Jordan’s normal form we see that
![]() $A$
is conjugate to a block-diagonal matrix and each block-diagonal matrix has the from
$A$
is conjugate to a block-diagonal matrix and each block-diagonal matrix has the from
 $$\begin{eqnarray}\left(\begin{array}{@{}ccccc@{}}0 & a & & & \\ & 0 & 1 & & \\ & & \ddots & \ddots & \\ & & & 0 & 1\\ & & & & 0\end{array}\right),\end{eqnarray}$$
$$\begin{eqnarray}\left(\begin{array}{@{}ccccc@{}}0 & a & & & \\ & 0 & 1 & & \\ & & \ddots & \ddots & \\ & & & 0 & 1\\ & & & & 0\end{array}\right),\end{eqnarray}$$
where
![]() $0\neq a\in \mathbb{F}_{p}$
(we cannot assume that
$0\neq a\in \mathbb{F}_{p}$
(we cannot assume that
![]() $a=1$
since we are conjugating with a matrix in
$a=1$
since we are conjugating with a matrix in
![]() $\operatorname{SL}_{n}(\mathbb{F}_{p})$
and not
$\operatorname{SL}_{n}(\mathbb{F}_{p})$
and not
![]() $\operatorname{GL}_{n}(\mathbb{F}_{p})$
). A straightforward argument implies that it is enough to deal with the case where there is just one block. Clearly, we can assume that the dimension of this block is at least 3. Then there exists
$\operatorname{GL}_{n}(\mathbb{F}_{p})$
). A straightforward argument implies that it is enough to deal with the case where there is just one block. Clearly, we can assume that the dimension of this block is at least 3. Then there exists
![]() $\unicode[STIX]{x1D700}\in \{-1,1\}$
such that the diagonal matrix
$\unicode[STIX]{x1D700}\in \{-1,1\}$
such that the diagonal matrix
![]() $\operatorname{diag}(\unicode[STIX]{x1D700},1,-1,\ldots ,(-1)^{n})$
belongs to
$\operatorname{diag}(\unicode[STIX]{x1D700},1,-1,\ldots ,(-1)^{n})$
belongs to
![]() $\operatorname{SL}_{n}(\mathbb{F}_{p})$
. Denote
$\operatorname{SL}_{n}(\mathbb{F}_{p})$
. Denote
![]() $B:=\operatorname{diag}(\unicode[STIX]{x1D700},1,-1,\ldots ,(-1)^{n})+E_{2,n}(1)$
. Then the
$B:=\operatorname{diag}(\unicode[STIX]{x1D700},1,-1,\ldots ,(-1)^{n})+E_{2,n}(1)$
. Then the
![]() $n$
th coordinate of the first row of
$n$
th coordinate of the first row of
![]() $A+B^{-1}AB$
is non-zero while all the other rows equal zero. Thus,
$A+B^{-1}AB$
is non-zero while all the other rows equal zero. Thus,
![]() $A+B^{-1}AB$
is conjugate to
$A+B^{-1}AB$
is conjugate to
![]() $E_{1,2}(a)$
for some non-zero
$E_{1,2}(a)$
for some non-zero
![]() $a$
.
$a$
.
Step B. Assume that
![]() $n=2$
. If
$n=2$
. If
![]() $A$
is nilpotent, it is conjugate to
$A$
is nilpotent, it is conjugate to
![]() $E_{1,2}(a)$
, for some
$E_{1,2}(a)$
, for some
![]() $a$
, and the claim holds. In general, since
$a$
, and the claim holds. In general, since
![]() $A$
is not scalar, it is conjugate to
$A$
is not scalar, it is conjugate to
![]() $(\!\begin{smallmatrix}0 & a\\ b & 0\end{smallmatrix}\!)$
. We claim that, if
$(\!\begin{smallmatrix}0 & a\\ b & 0\end{smallmatrix}\!)$
. We claim that, if
![]() $p\geqslant 11$
, there are
$p\geqslant 11$
, there are
![]() $x,y,z\in \mathbb{F}_{p}^{\times }$
such that
$x,y,z\in \mathbb{F}_{p}^{\times }$
such that
![]() $x^{2}+y^{2}+z^{2}=0$
and
$x^{2}+y^{2}+z^{2}=0$
and
![]() $x^{-2}+y^{-2}+z^{-2}\neq 0$
. If this claim holds, then
$x^{-2}+y^{-2}+z^{-2}\neq 0$
. If this claim holds, then
 $$\begin{eqnarray}\displaystyle & & \displaystyle \left(\begin{array}{@{}cc@{}}x & \\ & x^{-1}\end{array}\right)A\left(\begin{array}{@{}cc@{}}x^{-1} & \\ & x\end{array}\right)+\left(\begin{array}{@{}cc@{}}y & \\ & y^{-1}\end{array}\right)A\left(\begin{array}{@{}cc@{}}y^{-1} & \\ & y\end{array}\right)+\left(\begin{array}{@{}cc@{}}z & \\ & z^{-1}\end{array}\right)A\left(\begin{array}{@{}cc@{}}z^{-1} & \\ & z\end{array}\right)\nonumber\\ \displaystyle & & \displaystyle \quad =\left(\begin{array}{@{}cc@{}}0 & 0\\ b(x^{-2}+y^{-2}+z^{-2}) & 0\end{array}\right),\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \left(\begin{array}{@{}cc@{}}x & \\ & x^{-1}\end{array}\right)A\left(\begin{array}{@{}cc@{}}x^{-1} & \\ & x\end{array}\right)+\left(\begin{array}{@{}cc@{}}y & \\ & y^{-1}\end{array}\right)A\left(\begin{array}{@{}cc@{}}y^{-1} & \\ & y\end{array}\right)+\left(\begin{array}{@{}cc@{}}z & \\ & z^{-1}\end{array}\right)A\left(\begin{array}{@{}cc@{}}z^{-1} & \\ & z\end{array}\right)\nonumber\\ \displaystyle & & \displaystyle \quad =\left(\begin{array}{@{}cc@{}}0 & 0\\ b(x^{-2}+y^{-2}+z^{-2}) & 0\end{array}\right),\nonumber\end{eqnarray}$$
which is nilpotent.
To prove the claim, let
![]() $X$
be the projective curve defined by
$X$
be the projective curve defined by
![]() $x^{2}+y^{2}+z^{2}=0$
. Then
$x^{2}+y^{2}+z^{2}=0$
. Then
![]() $X$
has
$X$
has
![]() $p+1$
points over
$p+1$
points over
![]() $\mathbb{F}_{p}$
, and at most six of them have a zero in some coordinate. At most four of the points of
$\mathbb{F}_{p}$
, and at most six of them have a zero in some coordinate. At most four of the points of
![]() $X$
satisfy the equation
$X$
satisfy the equation
![]() $x^{-2}+y^{-2}+z^{-2}=0$
(because these points satisfy
$x^{-2}+y^{-2}+z^{-2}=0$
(because these points satisfy
![]() $1=(y^{2}+z^{2})(y^{-2}+z^{-2})$
). In particular, if
$1=(y^{2}+z^{2})(y^{-2}+z^{-2})$
). In particular, if
![]() $p\geqslant 11$
, the claim is true.
$p\geqslant 11$
, the claim is true.
Step C. Assume
![]() $n>2$
and the claim is true for all numbers smaller than
$n>2$
and the claim is true for all numbers smaller than
![]() $n$
. We consider the following cases.
$n$
. We consider the following cases.
Case C1. Assume that
![]() $\det A=0$
. By conjugating
$\det A=0$
. By conjugating
![]() $A$
we can assume that it is of the form
$A$
we can assume that it is of the form
where
![]() $B\in \mathfrak{sl}_{n-1}(\mathbb{F}_{p})$
. If
$B\in \mathfrak{sl}_{n-1}(\mathbb{F}_{p})$
. If
![]() $B=0$
then
$B=0$
then
![]() $A$
is a nilpotent matrix and we are done by step 1. Otherwise, we can assume that
$A$
is a nilpotent matrix and we are done by step 1. Otherwise, we can assume that
![]() $p>n-1$
so
$p>n-1$
so
![]() $B$
is a non-scalar matrix since its trace is equal to zero. Then by the induction hypothesis the sum of a bounded number of conjugates of
$B$
is a non-scalar matrix since its trace is equal to zero. Then by the induction hypothesis the sum of a bounded number of conjugates of
![]() $A$
is a non-zero nilpotent matrix and we are done by step 1.
$A$
is a non-zero nilpotent matrix and we are done by step 1.
Case C2. Assume now that
![]() $\det A\neq 0$
. By using the rational canonical normal form we see that there exist non-zero
$\det A\neq 0$
. By using the rational canonical normal form we see that there exist non-zero
![]() $a,b\in \mathbb{F}_{p}$
such that
$a,b\in \mathbb{F}_{p}$
such that
![]() $A$
is conjugate to a block-diagonal matrix and one of the blocks of
$A$
is conjugate to a block-diagonal matrix and one of the blocks of
![]() $A$
(for notational ease, assume it is the first) is of the form
$A$
(for notational ease, assume it is the first) is of the form
 $$\begin{eqnarray}\left(\begin{array}{@{}ccccc@{}}0 & a & & & \\ & 0 & 1 & & \\ & & \ddots & \ddots & \\ & & & 0 & 1\\ b & \ast & \cdots \, & \ast & \ast \end{array}\right).\end{eqnarray}$$
$$\begin{eqnarray}\left(\begin{array}{@{}ccccc@{}}0 & a & & & \\ & 0 & 1 & & \\ & & \ddots & \ddots & \\ & & & 0 & 1\\ b & \ast & \cdots \, & \ast & \ast \end{array}\right).\end{eqnarray}$$
Denote
![]() $B:=\operatorname{diag}(-1,-1,1,\ldots ,1)$
. Then
$B:=\operatorname{diag}(-1,-1,1,\ldots ,1)$
. Then
![]() $A+B^{-1}AB$
is a non-zero singular matrix and we are done by case C1.◻
$A+B^{-1}AB$
is a non-zero singular matrix and we are done by case C1.◻
Remark 4.7. The proof of Lemma 4.6 can be adapted to work over all finite fields of characteristic different than 2. For fields of characteristic 2, the argument of step B should be replaced.
Lemma 4.8. For any
![]() $n\geqslant 3$
there is
$n\geqslant 3$
there is
![]() $C$
such that the following statements hold.
$C$
such that the following statements hold.
(1) For any
 $p$
, if
$p$
, if
 $X\subseteq \operatorname{SL}_{n}(\mathbb{Z}_{p})$
is symmetric and invariant to conjugation, then
$X\subseteq \operatorname{SL}_{n}(\mathbb{Z}_{p})$
is symmetric and invariant to conjugation, then
 $X^{C}=\langle X\rangle$
.
$X^{C}=\langle X\rangle$
.(2) For any non-trivial word
 $w$
, the width of
$w$
, the width of
 $w$
in
$w$
in
 $\operatorname{SL}_{n}(\widehat{\mathbb{Z}})$
is less than
$\operatorname{SL}_{n}(\widehat{\mathbb{Z}})$
is less than
 $C$
.
$C$
.
Proof. (1) Let
![]() $k=\min \{i\mid (\exists g\in X)g\text{ is not central modulo }p^{k+1}\}$
. Clearly,
$k=\min \{i\mid (\exists g\in X)g\text{ is not central modulo }p^{k+1}\}$
. Clearly,
![]() $\langle X\rangle \subseteq Z(\operatorname{SL}_{n}(\mathbb{Z}_{p}))\cdot \operatorname{SL}_{n}(\mathbb{Z}_{p};p^{k})$
. We will show that there is
$\langle X\rangle \subseteq Z(\operatorname{SL}_{n}(\mathbb{Z}_{p}))\cdot \operatorname{SL}_{n}(\mathbb{Z}_{p};p^{k})$
. We will show that there is
![]() $C$
such that
$C$
such that
![]() $\operatorname{SL}_{n}(\mathbb{Z}_{p};p^{k})\subseteq X^{C}$
, and it will follow that
$\operatorname{SL}_{n}(\mathbb{Z}_{p};p^{k})\subseteq X^{C}$
, and it will follow that
![]() $X^{C+|Z(\operatorname{SL}_{n}(\mathbb{Z}_{p}))|}=\langle X\rangle$
, which proves the claim since
$X^{C+|Z(\operatorname{SL}_{n}(\mathbb{Z}_{p}))|}=\langle X\rangle$
, which proves the claim since
![]() $|Z(\operatorname{SL}_{n}(\mathbb{Z}_{p}))|\leqslant n$
.
$|Z(\operatorname{SL}_{n}(\mathbb{Z}_{p}))|\leqslant n$
.
Case 1:
![]() $k=0$
. Let
$k=0$
. Let
![]() $\overline{X}\subseteq \operatorname{SL}_{n}(\mathbb{F}_{p})$
be the reduction of
$\overline{X}\subseteq \operatorname{SL}_{n}(\mathbb{F}_{p})$
be the reduction of
![]() $X$
modulo
$X$
modulo
![]() $p$
. By assumption,
$p$
. By assumption,
![]() $\overline{X}$
is non-central, so [Reference Liebeck and ShalevLS01, Corollary 1.9] implies that there is
$\overline{X}$
is non-central, so [Reference Liebeck and ShalevLS01, Corollary 1.9] implies that there is
![]() $C_{1}$
, depending only on
$C_{1}$
, depending only on
![]() $n$
, such that
$n$
, such that
![]() $\overline{X}^{C_{1}}=\operatorname{SL}_{n}(\mathbb{F}_{p})$
. Let
$\overline{X}^{C_{1}}=\operatorname{SL}_{n}(\mathbb{F}_{p})$
. Let
![]() $a,b\in X^{C_{1}}$
such that their reductions modulo
$a,b\in X^{C_{1}}$
such that their reductions modulo
![]() $p$
generate
$p$
generate
![]() $\operatorname{SL}_{n}(\mathbb{F}_{p})$
. By Lemma 4.4, the differential of the map
$\operatorname{SL}_{n}(\mathbb{F}_{p})$
. By Lemma 4.4, the differential of the map
![]() $\unicode[STIX]{x1D6F7}_{\overline{a},\overline{b}}$
at
$\unicode[STIX]{x1D6F7}_{\overline{a},\overline{b}}$
at
![]() $(1,1)$
is onto, which implies that
$(1,1)$
is onto, which implies that
![]() $d\unicode[STIX]{x1D6F7}_{a,b}(\mathfrak{sl}_{n}^{2}(\mathbb{Z}_{p}))=\mathfrak{sl}_{n}(\mathbb{Z}_{p})$
, since
$d\unicode[STIX]{x1D6F7}_{a,b}(\mathfrak{sl}_{n}^{2}(\mathbb{Z}_{p}))=\mathfrak{sl}_{n}(\mathbb{Z}_{p})$
, since
![]() $d\unicode[STIX]{x1D6F7}_{a,b}$
is
$d\unicode[STIX]{x1D6F7}_{a,b}$
is
![]() $\mathbb{Z}_{p}$
-linear. By Lemma 4.2,
$\mathbb{Z}_{p}$
-linear. By Lemma 4.2,
![]() $ab\operatorname{SL}_{n}(\mathbb{Z}_{p};p)\subseteq \unicode[STIX]{x1D6F7}_{a,b}(\operatorname{SL}_{n}(\mathbb{Z}_{p})\times \operatorname{SL}_{n}(\mathbb{Z}_{p}))\subseteq X^{2C_{1}}$
. It follows that
$ab\operatorname{SL}_{n}(\mathbb{Z}_{p};p)\subseteq \unicode[STIX]{x1D6F7}_{a,b}(\operatorname{SL}_{n}(\mathbb{Z}_{p})\times \operatorname{SL}_{n}(\mathbb{Z}_{p}))\subseteq X^{2C_{1}}$
. It follows that
![]() $X^{3C_{1}}=\operatorname{SL}_{n}(\mathbb{Z}_{p})$
.
$X^{3C_{1}}=\operatorname{SL}_{n}(\mathbb{Z}_{p})$
.
Case 2:
![]() $k>0$
. Let
$k>0$
. Let
![]() $g\in X$
be such that
$g\in X$
be such that
![]() $g$
is not a scalar modulo
$g$
is not a scalar modulo
![]() $p^{k+1}$
. Since
$p^{k+1}$
. Since
![]() $g$
is a scalar modulo
$g$
is a scalar modulo
![]() $p^{k}$
, there exists
$p^{k}$
, there exists
![]() $h\in \operatorname{SL}_{n}(\mathbb{Z}_{p})$
such that
$h\in \operatorname{SL}_{n}(\mathbb{Z}_{p})$
such that
![]() $g^{|Z(\operatorname{SL}_{n}(\mathbb{Z}_{p}))|-1}h^{-1}gh\in X^{|Z(\operatorname{SL}_{n}(\mathbb{Z}_{p}))|}$
belongs to
$g^{|Z(\operatorname{SL}_{n}(\mathbb{Z}_{p}))|-1}h^{-1}gh\in X^{|Z(\operatorname{SL}_{n}(\mathbb{Z}_{p}))|}$
belongs to
![]() $\operatorname{SL}_{n}(\mathbb{Z}_{p};p^{k})$
and is not a scalar modulo
$\operatorname{SL}_{n}(\mathbb{Z}_{p};p^{k})$
and is not a scalar modulo
![]() $p^{k+1}$
. Since
$p^{k+1}$
. Since
![]() $\operatorname{SL}_{n}(\mathbb{Z}_{p};p^{k})/\text{SL}_{n}(\mathbb{Z}_{p};p^{k+1})=\mathfrak{sl}_{n}(\mathbb{F}_{p})$
as
$\operatorname{SL}_{n}(\mathbb{Z}_{p};p^{k})/\text{SL}_{n}(\mathbb{Z}_{p};p^{k+1})=\mathfrak{sl}_{n}(\mathbb{F}_{p})$
as
![]() $\operatorname{SL}_{n}(\mathbb{Z}_{p})$
-modules, Lemma 4.6 implies that there is a constant
$\operatorname{SL}_{n}(\mathbb{Z}_{p})$
-modules, Lemma 4.6 implies that there is a constant
![]() $C$
, independent of
$C$
, independent of
![]() $X$
, such that
$X$
, such that
![]() $X^{C}\cdot \operatorname{SL}_{n}(\mathbb{Z}_{p};p^{k+1})\supseteq \operatorname{SL}_{n}(\mathbb{Z}_{p};p^{k})$
. Let
$X^{C}\cdot \operatorname{SL}_{n}(\mathbb{Z}_{p};p^{k+1})\supseteq \operatorname{SL}_{n}(\mathbb{Z}_{p};p^{k})$
. Let
![]() $\overline{a}$
be a maximal nilpotent Jordan block and let
$\overline{a}$
be a maximal nilpotent Jordan block and let
![]() $\overline{b}=\overline{a}^{T}$
. Note that the intersection of the centralizers of
$\overline{b}=\overline{a}^{T}$
. Note that the intersection of the centralizers of
![]() $\overline{a},\overline{b}$
in
$\overline{a},\overline{b}$
in
![]() $\operatorname{M}_{n}$
is the collection of scalar matrices. Choose
$\operatorname{M}_{n}$
is the collection of scalar matrices. Choose
![]() $a,b\in X^{C}\cap \operatorname{SL}_{n}(\mathbb{Z}_{p};p^{k})$
whose images in
$a,b\in X^{C}\cap \operatorname{SL}_{n}(\mathbb{Z}_{p};p^{k})$
whose images in
![]() $\operatorname{SL}_{n}(\mathbb{Z}_{p};p^{k})/\text{SL}_{n}(\mathbb{Z}_{p};p^{k+1})=\mathfrak{sl}_{n}(\mathbb{F}_{p})$
are
$\operatorname{SL}_{n}(\mathbb{Z}_{p};p^{k})/\text{SL}_{n}(\mathbb{Z}_{p};p^{k+1})=\mathfrak{sl}_{n}(\mathbb{F}_{p})$
are
![]() $\overline{a}$
and
$\overline{a}$
and
![]() $\overline{b}$
. We will show that
$\overline{b}$
. We will show that
![]() $\unicode[STIX]{x1D6F7}_{a,b}:\operatorname{SL}_{n}\times \operatorname{SL}_{n}\rightarrow \operatorname{SL}_{n}$
satisfies the conditions of Lemma 4.2.
$\unicode[STIX]{x1D6F7}_{a,b}:\operatorname{SL}_{n}\times \operatorname{SL}_{n}\rightarrow \operatorname{SL}_{n}$
satisfies the conditions of Lemma 4.2.
Since
![]() $a-1$
is divisible by
$a-1$
is divisible by
![]() $p^{k}$
, we have
$p^{k}$
, we have
![]() $\operatorname{val}_{p}(x\mapsto x^{-1}ax-a)\geqslant k$
. It follows that the derivative of this map also has
$\operatorname{val}_{p}(x\mapsto x^{-1}ax-a)\geqslant k$
. It follows that the derivative of this map also has
![]() $p$
-valuation at least
$p$
-valuation at least
![]() $k$
. Similarly,
$k$
. Similarly,
![]() $\unicode[STIX]{x1D6F7}_{a,b}$
satisfies the first condition of Lemma 4.2.
$\unicode[STIX]{x1D6F7}_{a,b}$
satisfies the first condition of Lemma 4.2.
Note that
![]() $d\unicode[STIX]{x1D6F7}_{a,b}(\mathfrak{sl}(\mathbb{Z}_{p})^{2})\subset p^{k}\mathfrak{sl}(\mathbb{Z}_{p})$
. In order to show the reverse containment, it is enough to show that the composition of
$d\unicode[STIX]{x1D6F7}_{a,b}(\mathfrak{sl}(\mathbb{Z}_{p})^{2})\subset p^{k}\mathfrak{sl}(\mathbb{Z}_{p})$
. In order to show the reverse containment, it is enough to show that the composition of
![]() $d\unicode[STIX]{x1D6F7}_{a,b}$
and the reduction map
$d\unicode[STIX]{x1D6F7}_{a,b}$
and the reduction map
![]() $p^{k}\mathfrak{sl}_{n}(\mathbb{Z}_{p})\rightarrow p^{k}\mathfrak{sl}_{n}(\mathbb{Z}_{p})/p^{k+1}\mathfrak{sl}_{n}(\mathbb{Z}_{p})$
is onto. This composition is the map
$p^{k}\mathfrak{sl}_{n}(\mathbb{Z}_{p})\rightarrow p^{k}\mathfrak{sl}_{n}(\mathbb{Z}_{p})/p^{k+1}\mathfrak{sl}_{n}(\mathbb{Z}_{p})$
is onto. This composition is the map
![]() $(X,Y)\mapsto [\overline{X},\overline{a}]+[\overline{Y},\overline{b}]$
(where
$(X,Y)\mapsto [\overline{X},\overline{a}]+[\overline{Y},\overline{b}]$
(where
![]() $[x,y]$
is the Lie bracket), so we need to show that there is no non-zero linear functional that vanishes on all elements of the form
$[x,y]$
is the Lie bracket), so we need to show that there is no non-zero linear functional that vanishes on all elements of the form
![]() $[\overline{X},\overline{a}]$
and
$[\overline{X},\overline{a}]$
and
![]() $[\overline{X},\overline{b}]$
, for
$[\overline{X},\overline{b}]$
, for
![]() $\overline{X}\in \mathfrak{sl}_{n}(\mathbb{F}_{p})$
. Any such functional has the form
$\overline{X}\in \mathfrak{sl}_{n}(\mathbb{F}_{p})$
. Any such functional has the form
![]() $\operatorname{tr}(A\cdot )$
for some
$\operatorname{tr}(A\cdot )$
for some
![]() $A\in \mathfrak{sl}_{n}(\mathbb{F}_{p})$
. Since
$A\in \mathfrak{sl}_{n}(\mathbb{F}_{p})$
. Since
![]() $\operatorname{tr}(A[B,C])=\operatorname{tr}([A,B]C)$
for every three matrices
$\operatorname{tr}(A[B,C])=\operatorname{tr}([A,B]C)$
for every three matrices
![]() $A$
,
$A$
,
![]() $B$
and
$B$
and
![]() $C$
, the assumption that
$C$
, the assumption that
![]() $\operatorname{tr}(A[\overline{a},\overline{X}])=0$
for all
$\operatorname{tr}(A[\overline{a},\overline{X}])=0$
for all
![]() $\overline{X}\in \mathfrak{sl}_{n}(\mathbb{F}_{p})$
implies that
$\overline{X}\in \mathfrak{sl}_{n}(\mathbb{F}_{p})$
implies that
![]() $[A,\overline{a}]=\unicode[STIX]{x1D6FC}I$
, for some
$[A,\overline{a}]=\unicode[STIX]{x1D6FC}I$
, for some
![]() $\unicode[STIX]{x1D6FC}$
. Similarly,
$\unicode[STIX]{x1D6FC}$
. Similarly,
![]() $[A,\overline{b}]=\unicode[STIX]{x1D6FD}I$
, for some
$[A,\overline{b}]=\unicode[STIX]{x1D6FD}I$
, for some
![]() $\unicode[STIX]{x1D6FD}$
. From
$\unicode[STIX]{x1D6FD}$
. From
![]() $[A,\overline{a}]=\unicode[STIX]{x1D6FC}I$
we get (by induction) that
$[A,\overline{a}]=\unicode[STIX]{x1D6FC}I$
we get (by induction) that
![]() $A_{i+1,i}=-i\unicode[STIX]{x1D6FC}$
, whereas from
$A_{i+1,i}=-i\unicode[STIX]{x1D6FC}$
, whereas from
![]() $[A,\overline{b}]=\unicode[STIX]{x1D6FD}I$
we get that
$[A,\overline{b}]=\unicode[STIX]{x1D6FD}I$
we get that
![]() $A_{i+1,i}=A_{i+2,i+1}$
. Since
$A_{i+1,i}=A_{i+2,i+1}$
. Since
![]() $n\geqslant 3$
, we get
$n\geqslant 3$
, we get
![]() $\unicode[STIX]{x1D6FC}=0$
. Similarly,
$\unicode[STIX]{x1D6FC}=0$
. Similarly,
![]() $\unicode[STIX]{x1D6FD}=0$
. Consequently,
$\unicode[STIX]{x1D6FD}=0$
. Consequently,
![]() $A$
commutes with
$A$
commutes with
![]() $\overline{a}$
and
$\overline{a}$
and
![]() $\overline{b}$
, so
$\overline{b}$
, so
![]() $A=0$
, a contradiction.
$A=0$
, a contradiction.
Applying Lemma 4.2 to
![]() $\unicode[STIX]{x1D6F7}_{a,b}$
, we get that any element in
$\unicode[STIX]{x1D6F7}_{a,b}$
, we get that any element in
![]() $ab\operatorname{SL}_{n}(\mathbb{Z}_{p};p^{k+1})$
is in
$ab\operatorname{SL}_{n}(\mathbb{Z}_{p};p^{k+1})$
is in
![]() $\unicode[STIX]{x1D6F7}_{a,b}(\operatorname{SL}_{n}(\mathbb{Z}_{p})^{2})$
, so, in particular,
$\unicode[STIX]{x1D6F7}_{a,b}(\operatorname{SL}_{n}(\mathbb{Z}_{p})^{2})$
, so, in particular,
![]() $ab\operatorname{SL}_{n}(\mathbb{Z}_{p};p^{k+1})\subset X^{2C}$
and
$ab\operatorname{SL}_{n}(\mathbb{Z}_{p};p^{k+1})\subset X^{2C}$
and
![]() $\operatorname{SL}_{n}(\mathbb{Z}_{p};p^{k+1})\subset X^{4C}$
. Since
$\operatorname{SL}_{n}(\mathbb{Z}_{p};p^{k+1})\subset X^{4C}$
. Since
![]() $X^{C}\operatorname{SL}_{n}(\mathbb{Z}_{p};p^{k+1})\supseteq \operatorname{SL}_{n}(\mathbb{Z}_{p};p^{k})$
, we get that
$X^{C}\operatorname{SL}_{n}(\mathbb{Z}_{p};p^{k+1})\supseteq \operatorname{SL}_{n}(\mathbb{Z}_{p};p^{k})$
, we get that
![]() $X^{5C}\supseteq \operatorname{SL}_{n}(\mathbb{Z}_{p};p^{k})$
, proving the claim in this case.
$X^{5C}\supseteq \operatorname{SL}_{n}(\mathbb{Z}_{p};p^{k})$
, proving the claim in this case.
(2) Since
![]() $w(\operatorname{SL}_{n}(\widehat{\mathbb{Z}}))=\prod w(\operatorname{SL}_{n}(\mathbb{Z}_{p}))$
, the claim follows from the first claim.◻
$w(\operatorname{SL}_{n}(\widehat{\mathbb{Z}}))=\prod w(\operatorname{SL}_{n}(\mathbb{Z}_{p}))$
, the claim follows from the first claim.◻
5 Proof of Theorems 1.1 and 1.4 with explicit bounds
The goal of this section is to prove the explicit bound of Theorem 1.1. The proof follows the arguments in [Reference Dennis and VasersteinDV88].
Lemma 5.1. Let
![]() $q,m\in \mathbb{N}^{+}$
and denote
$q,m\in \mathbb{N}^{+}$
and denote
![]() $n:=3m$
. Assume that
$n:=3m$
. Assume that
![]() $g_{1},\ldots ,g_{m}\in \operatorname{SL}_{3}(\mathbb{Z};q)$
and
$g_{1},\ldots ,g_{m}\in \operatorname{SL}_{3}(\mathbb{Z};q)$
and
![]() $g_{1}\cdots g_{m}=e$
. Then
$g_{1}\cdots g_{m}=e$
. Then
![]() $g:=\operatorname{diag}(g_{1},\ldots ,g_{m})\in L_{n}(\mathbb{Z};q)\tilde{U} _{n}(\mathbb{Z};q)U_{n}(\mathbb{Z};q)$
where
$g:=\operatorname{diag}(g_{1},\ldots ,g_{m})\in L_{n}(\mathbb{Z};q)\tilde{U} _{n}(\mathbb{Z};q)U_{n}(\mathbb{Z};q)$
where
![]() $\tilde{U} _{n}(\mathbb{Z};q):=\{hkh^{-1}\mid k\in U_{n}(\mathbb{Z};q)\wedge h\in \operatorname{SL}_{n}(\mathbb{Z})\}$
.
$\tilde{U} _{n}(\mathbb{Z};q):=\{hkh^{-1}\mid k\in U_{n}(\mathbb{Z};q)\wedge h\in \operatorname{SL}_{n}(\mathbb{Z})\}$
.
Proof. Let
![]() $I_{3}$
be the identity matrix of
$I_{3}$
be the identity matrix of
![]() $\operatorname{SL}_{3}(\mathbb{Z})$
and identify
$\operatorname{SL}_{3}(\mathbb{Z})$
and identify
![]() $M_{n}(\mathbb{Z})$
with
$M_{n}(\mathbb{Z})$
with
![]() $M_{m}(M_{3}(\mathbb{Z}))$
, where
$M_{m}(M_{3}(\mathbb{Z}))$
, where
![]() $M_{k}(R)$
is the ring of
$M_{k}(R)$
is the ring of
![]() $k\times k$
matrices over the ring
$k\times k$
matrices over the ring
![]() $R$
. Let
$R$
. Let
![]() $l_{1}$
be the matrix of
$l_{1}$
be the matrix of
![]() $M_{m}(M_{3}(\mathbb{Z}))$
with
$M_{m}(M_{3}(\mathbb{Z}))$
with
![]() $I_{3}$
on the diagonal,
$I_{3}$
on the diagonal,
![]() $g_{i}^{-1}$
on the
$g_{i}^{-1}$
on the
![]() $(i+1,i)$
th entry for every
$(i+1,i)$
th entry for every
![]() $1\leqslant i\leqslant m-1$
, and zero elsewhere. Let
$1\leqslant i\leqslant m-1$
, and zero elsewhere. Let
![]() $l_{2}$
be the matrix of
$l_{2}$
be the matrix of
![]() $M_{m}(M_{3}(\mathbb{Z}))$
with
$M_{m}(M_{3}(\mathbb{Z}))$
with
![]() $I_{3}$
on the diagonal,
$I_{3}$
on the diagonal,
![]() $I_{3}$
on the
$I_{3}$
on the
![]() $(i+1,i)$
th entry for every
$(i+1,i)$
th entry for every
![]() $1\leqslant i\leqslant m-1$
, and zero elsewhere. Let
$1\leqslant i\leqslant m-1$
, and zero elsewhere. Let
![]() $u_{1}$
be the matrix of
$u_{1}$
be the matrix of
![]() $M_{m}(M_{3}(\mathbb{Z}))$
with
$M_{m}(M_{3}(\mathbb{Z}))$
with
![]() $I_{3}$
on the diagonal,
$I_{3}$
on the diagonal,
![]() $1-g_{1}\cdots g_{i}$
on the
$1-g_{1}\cdots g_{i}$
on the
![]() $(i,i+1)$
th entry for every
$(i,i+1)$
th entry for every
![]() $1\leqslant i\leqslant m-1$
, and zero elsewhere. Let
$1\leqslant i\leqslant m-1$
, and zero elsewhere. Let
![]() $u_{2}$
be the matrix of
$u_{2}$
be the matrix of
![]() $M_{m}(M_{3}(\mathbb{Z}))$
with
$M_{m}(M_{3}(\mathbb{Z}))$
with
![]() $I_{3}$
on the diagonal,
$I_{3}$
on the diagonal,
![]() $(1-g_{1}\cdots g_{i})g_{i+1}$
on the
$(1-g_{1}\cdots g_{i})g_{i+1}$
on the
![]() $(i,i+1)$
th entry for every
$(i,i+1)$
th entry for every
![]() $1\leqslant i\leqslant m-1$
, and zero elsewhere. Then
$1\leqslant i\leqslant m-1$
, and zero elsewhere. Then
![]() $g=l_{1}^{-1}u_{1}^{-1}l_{2}u_{2}=(l_{1}^{-1}l_{2})(l_{2}^{-1}u_{1}^{-1}l_{2})u_{2}\in L_{n}(\mathbb{Z};q)\tilde{U} _{n}(\mathbb{Z};q)U_{n}(\mathbb{Z};q)$
.◻
$g=l_{1}^{-1}u_{1}^{-1}l_{2}u_{2}=(l_{1}^{-1}l_{2})(l_{2}^{-1}u_{1}^{-1}l_{2})u_{2}\in L_{n}(\mathbb{Z};q)\tilde{U} _{n}(\mathbb{Z};q)U_{n}(\mathbb{Z};q)$
.◻
Lemma 5.2. Let
![]() $q,m\in \mathbb{N}^{+}$
and denote
$q,m\in \mathbb{N}^{+}$
and denote
![]() $n:=3m$
. Assume that
$n:=3m$
. Assume that
![]() $g_{1},\ldots ,g_{m}\in U_{3}(\mathbb{Z};q)L_{3}(\mathbb{Z};q)$
. Denote
$g_{1},\ldots ,g_{m}\in U_{3}(\mathbb{Z};q)L_{3}(\mathbb{Z};q)$
. Denote
![]() $g:=\operatorname{diag}(g_{1}\cdots g_{m},I_{3},\ldots ,I_{3})\in \operatorname{SL}_{n}(\mathbb{Z};q)$
and
$g:=\operatorname{diag}(g_{1}\cdots g_{m},I_{3},\ldots ,I_{3})\in \operatorname{SL}_{n}(\mathbb{Z};q)$
and
![]() $\tilde{U} _{n}(\mathbb{Z};q):=\{hkh^{-1}\mid k\in U_{n}(\mathbb{Z};q)\wedge h\in \operatorname{SL}_{n}(\mathbb{Z})\}$
. Then
$\tilde{U} _{n}(\mathbb{Z};q):=\{hkh^{-1}\mid k\in U_{n}(\mathbb{Z};q)\wedge h\in \operatorname{SL}_{n}(\mathbb{Z})\}$
. Then
![]() $g\in L_{n}(\mathbb{Z};q)\tilde{U} _{n}(\mathbb{Z};q)U_{n}(\mathbb{Z};q)L_{n}(\mathbb{Z};q)$
.
$g\in L_{n}(\mathbb{Z};q)\tilde{U} _{n}(\mathbb{Z};q)U_{n}(\mathbb{Z};q)L_{n}(\mathbb{Z};q)$
.
Proof. Define
![]() $h:=\operatorname{diag}(g_{m},g_{m-1},\ldots ,g_{1})\in U_{n}(\mathbb{Z};q)L_{n}(\mathbb{Z};q)$
. Lemma 5.1 implies that
$h:=\operatorname{diag}(g_{m},g_{m-1},\ldots ,g_{1})\in U_{n}(\mathbb{Z};q)L_{n}(\mathbb{Z};q)$
. Lemma 5.1 implies that
![]() $gh^{-1}\in L_{n}(\mathbb{Z};q)\tilde{U} _{n}(\mathbb{Z};q)U_{n}(\mathbb{Z};q)$
. Thus,
$gh^{-1}\in L_{n}(\mathbb{Z};q)\tilde{U} _{n}(\mathbb{Z};q)U_{n}(\mathbb{Z};q)$
. Thus,
Lemma 5.3. Let
![]() $n\geqslant m\geqslant 3$
and
$n\geqslant m\geqslant 3$
and
![]() $q\geqslant 1$
. Denote
$q\geqslant 1$
. Denote
![]() $E^{\ast }(m,\mathbb{Z};q):=\{\operatorname{diag}(1,\ldots ,1,g)\in \operatorname{SL}_{n}(\mathbb{Z})\mid g\in E(m,\mathbb{Z};q)\}$
. Then
$E^{\ast }(m,\mathbb{Z};q):=\{\operatorname{diag}(1,\ldots ,1,g)\in \operatorname{SL}_{n}(\mathbb{Z})\mid g\in E(m,\mathbb{Z};q)\}$
. Then
![]() $E(n,\mathbb{Z};q)=L_{n}(\mathbb{Z};q)U_{n}(\mathbb{Z};q)L_{n}(\mathbb{Z};q)E^{\ast }(m,\mathbb{Z};q)U_{n}(\mathbb{Z};q)$
.
$E(n,\mathbb{Z};q)=L_{n}(\mathbb{Z};q)U_{n}(\mathbb{Z};q)L_{n}(\mathbb{Z};q)E^{\ast }(m,\mathbb{Z};q)U_{n}(\mathbb{Z};q)$
.
Proof. Let
![]() $q\geqslant 1$
. The proof is by induction on
$q\geqslant 1$
. The proof is by induction on
![]() $n$
. The base case
$n$
. The base case
![]() $n=m$
is clear. Assume that the statement is true for some
$n=m$
is clear. Assume that the statement is true for some
![]() $n\geqslant m$
. We have to show that the statement is true also for
$n\geqslant m$
. We have to show that the statement is true also for
![]() $n+1$
. Let
$n+1$
. Let
![]() $U_{n}^{-}(\mathbb{Z};q)$
and
$U_{n}^{-}(\mathbb{Z};q)$
and
![]() $L_{n}^{-}(\mathbb{Z};q)$
be the images in
$L_{n}^{-}(\mathbb{Z};q)$
be the images in
![]() $\operatorname{SL}_{n+1}(\mathbb{Z})$
of
$\operatorname{SL}_{n+1}(\mathbb{Z})$
of
![]() $U_{n}(\mathbb{Z};q)$
and
$U_{n}(\mathbb{Z};q)$
and
![]() $L_{n}(\mathbb{Z};q)$
under the map
$L_{n}(\mathbb{Z};q)$
under the map
![]() $M\mapsto \operatorname{diag}(1,M)$
. Denote
$M\mapsto \operatorname{diag}(1,M)$
. Denote
![]() $C_{n}^{-}(q):=\langle e_{j,1}(q)\mid 2\leqslant j\leqslant n+1\rangle$
and
$C_{n}^{-}(q):=\langle e_{j,1}(q)\mid 2\leqslant j\leqslant n+1\rangle$
and
![]() $R_{n}^{-}(q):=\langle e_{1,j}(q)\mid 2\leqslant j\leqslant n+1\rangle$
. Finally, recall that the main theorem of [Reference MennickeMen65] implies that for every
$R_{n}^{-}(q):=\langle e_{1,j}(q)\mid 2\leqslant j\leqslant n+1\rangle$
. Finally, recall that the main theorem of [Reference MennickeMen65] implies that for every
![]() $k\geqslant 3$
,
$k\geqslant 3$
,
Let
![]() $g\in E(n+1,\mathbb{Z};q)$
. Then
$g\in E(n+1,\mathbb{Z};q)$
. Then
![]() $\gcd (g_{1,1},g_{2,1},\ldots ,g_{n,1})=1$
and
$\gcd (g_{1,1},g_{2,1},\ldots ,g_{n,1})=1$
and
![]() $\gcd (qg_{1,1},g_{2,1},\ldots ,g_{n,1})=q$
. Recall that
$\gcd (qg_{1,1},g_{2,1},\ldots ,g_{n,1})=q$
. Recall that
![]() $\mathbb{Z}$
satisfies the following stable range condition: if
$\mathbb{Z}$
satisfies the following stable range condition: if
![]() $m\geqslant 3$
and
$m\geqslant 3$
and
![]() $a_{1},\ldots ,a_{m}\in \mathbb{Z}$
then there exist
$a_{1},\ldots ,a_{m}\in \mathbb{Z}$
then there exist
![]() $t_{2},\ldots ,t_{m}\in \mathbb{Z}$
such that
$t_{2},\ldots ,t_{m}\in \mathbb{Z}$
such that
![]() $\gcd (a_{1},\ldots ,a_{m})=\gcd (a_{2}-t_{2}a_{1},\ldots ,a_{n}-t_{n}a_{1})$
. Thus, there exists
$\gcd (a_{1},\ldots ,a_{m})=\gcd (a_{2}-t_{2}a_{1},\ldots ,a_{n}-t_{n}a_{1})$
. Thus, there exists
![]() $h\in C_{n}^{-}(\mathbb{Z};q)g$
such that
$h\in C_{n}^{-}(\mathbb{Z};q)g$
such that
![]() $\gcd (h_{2,1},\ldots ,h_{n,1})=q$
. Since
$\gcd (h_{2,1},\ldots ,h_{n,1})=q$
. Since
![]() $h\in E(n,\mathbb{Z};q)$
, we have
$h\in E(n,\mathbb{Z};q)$
, we have
![]() $h_{1,1}=1$
modulo
$h_{1,1}=1$
modulo
![]() $q^{2}$
so there exists
$q^{2}$
so there exists
![]() $h^{\prime }\in R_{n}^{-}(\mathbb{Z};q)h$
such that
$h^{\prime }\in R_{n}^{-}(\mathbb{Z};q)h$
such that
![]() $h_{1,1}^{\prime }=1$
. Finally, there exists
$h_{1,1}^{\prime }=1$
. Finally, there exists
![]() $h^{\prime \prime }\in C_{n}^{-}(q)h^{\prime }R_{n}^{-}(q)$
such that
$h^{\prime \prime }\in C_{n}^{-}(q)h^{\prime }R_{n}^{-}(q)$
such that
![]() $h^{\prime \prime }=\operatorname{diag}(1,g^{\prime })$
for some
$h^{\prime \prime }=\operatorname{diag}(1,g^{\prime })$
for some
![]() $g^{\prime }\in \operatorname{SL}_{n}(\mathbb{Z};q)$
. Note that
$g^{\prime }\in \operatorname{SL}_{n}(\mathbb{Z};q)$
. Note that
![]() $g^{\prime }\in E(n,\mathbb{Z};q)$
since its diagonal entries are equal to 1 modulo
$g^{\prime }\in E(n,\mathbb{Z};q)$
since its diagonal entries are equal to 1 modulo
![]() $q^{2}$
. Thus, the induction hypothesis implies that
$q^{2}$
. Thus, the induction hypothesis implies that
![]() $h^{\prime \prime }\in L_{n}^{-}(\mathbb{Z};q)U_{n}^{-}(\mathbb{Z};q)L_{n}^{-}(\mathbb{Z};q)E^{\ast }(m,\mathbb{Z};q)U_{n}^{-}(\mathbb{Z};q)$
. It follows that
$h^{\prime \prime }\in L_{n}^{-}(\mathbb{Z};q)U_{n}^{-}(\mathbb{Z};q)L_{n}^{-}(\mathbb{Z};q)E^{\ast }(m,\mathbb{Z};q)U_{n}^{-}(\mathbb{Z};q)$
. It follows that
![]() $g$
belongs to
$g$
belongs to
Since both
![]() $U_{n}^{-}(\mathbb{Z};q)$
and
$U_{n}^{-}(\mathbb{Z};q)$
and
![]() $L_{n}^{-}(\mathbb{Z};q)$
normalize
$L_{n}^{-}(\mathbb{Z};q)$
normalize
![]() $C_{n}^{-}(\mathbb{Z};q)$
and
$C_{n}^{-}(\mathbb{Z};q)$
and
![]() $R_{n}^{-}(\mathbb{Z};q)$
, we have
$R_{n}^{-}(\mathbb{Z};q)$
, we have
 $$\begin{eqnarray}\displaystyle & & \displaystyle C_{n}^{-}(\mathbb{Z};q)R_{n}^{-}(\mathbb{Z};q)C_{n}^{-}(\mathbb{Z};q)L_{n}^{-}(\mathbb{Z};q)U_{n}^{-}(\mathbb{Z};q)L_{n}^{-}(\mathbb{Z};q)E^{\ast }(m,\mathbb{Z};q)U_{n}^{-}(\mathbb{Z};q)R_{n}^{-}(\mathbb{Z};q)\nonumber\\ \displaystyle & & \displaystyle \quad =C_{n}^{-}(\mathbb{Z};q)L_{n}^{-}(\mathbb{Z};q)R_{n}^{-}(\mathbb{Z};q)U_{n}^{-}(\mathbb{Z};q)C_{n}^{-}(\mathbb{Z};q)L_{n}^{-}(\mathbb{Z};q)E^{\ast }(m,\mathbb{Z};q)U_{n}^{-}(\mathbb{Z};q)R_{n}^{-}(\mathbb{Z};q)\nonumber\\ \displaystyle & & \displaystyle \quad =L_{n+1}(\mathbb{Z};q)U_{n+1}(\mathbb{Z};q)L_{n+1}(\mathbb{Z};q)E^{\ast }(m,\mathbb{Z};q)U_{n+1}(\mathbb{Z};q).\square\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle C_{n}^{-}(\mathbb{Z};q)R_{n}^{-}(\mathbb{Z};q)C_{n}^{-}(\mathbb{Z};q)L_{n}^{-}(\mathbb{Z};q)U_{n}^{-}(\mathbb{Z};q)L_{n}^{-}(\mathbb{Z};q)E^{\ast }(m,\mathbb{Z};q)U_{n}^{-}(\mathbb{Z};q)R_{n}^{-}(\mathbb{Z};q)\nonumber\\ \displaystyle & & \displaystyle \quad =C_{n}^{-}(\mathbb{Z};q)L_{n}^{-}(\mathbb{Z};q)R_{n}^{-}(\mathbb{Z};q)U_{n}^{-}(\mathbb{Z};q)C_{n}^{-}(\mathbb{Z};q)L_{n}^{-}(\mathbb{Z};q)E^{\ast }(m,\mathbb{Z};q)U_{n}^{-}(\mathbb{Z};q)R_{n}^{-}(\mathbb{Z};q)\nonumber\\ \displaystyle & & \displaystyle \quad =L_{n+1}(\mathbb{Z};q)U_{n+1}(\mathbb{Z};q)L_{n+1}(\mathbb{Z};q)E^{\ast }(m,\mathbb{Z};q)U_{n+1}(\mathbb{Z};q).\square\nonumber\end{eqnarray}$$
Corollary 5.4. For every
![]() $n\geqslant 3$
denote
$n\geqslant 3$
denote
![]() $\tilde{U} _{n}(\mathbb{Z};q):=\{hkh^{-1}\mid k\in U_{n}(\mathbb{Z};q)\wedge h\in \operatorname{SL}_{n}(\mathbb{Z})\}=\{hkh^{-1}\mid k\in L_{n}(\mathbb{Z};q)\wedge h\in \operatorname{SL}_{n}(\mathbb{Z})\}$
. There exists an integer
$\tilde{U} _{n}(\mathbb{Z};q):=\{hkh^{-1}\mid k\in U_{n}(\mathbb{Z};q)\wedge h\in \operatorname{SL}_{n}(\mathbb{Z})\}=\{hkh^{-1}\mid k\in L_{n}(\mathbb{Z};q)\wedge h\in \operatorname{SL}_{n}(\mathbb{Z})\}$
. There exists an integer
![]() $N$
such that, for every
$N$
such that, for every
![]() $n\geqslant N$
and every
$n\geqslant N$
and every
![]() $q\in \mathbb{Z}$
,
$q\in \mathbb{Z}$
,
Proof. Proposition 2.9 implies that there exists a constant
![]() $D$
such that for every
$D$
such that for every
![]() $q\in \mathbb{Z}$
,
$q\in \mathbb{Z}$
,
![]() $(U_{3}(\mathbb{Z};q)L_{3}(\mathbb{Z};q))^{D}=\langle U_{3}(\mathbb{Z};q)L_{3}(\mathbb{Z};q)\rangle$
. Denote
$(U_{3}(\mathbb{Z};q)L_{3}(\mathbb{Z};q))^{D}=\langle U_{3}(\mathbb{Z};q)L_{3}(\mathbb{Z};q)\rangle$
. Denote
![]() $E^{\ast }(3,\mathbb{Z};q):=\{\operatorname{diag}(1,\ldots ,1,g)\in \operatorname{SL}_{3D}(\mathbb{Z})\mid g\in E(3,\mathbb{Z};q)\}$
. Lemma 5.2 shows that, for any
$E^{\ast }(3,\mathbb{Z};q):=\{\operatorname{diag}(1,\ldots ,1,g)\in \operatorname{SL}_{3D}(\mathbb{Z})\mid g\in E(3,\mathbb{Z};q)\}$
. Lemma 5.2 shows that, for any
![]() $q$
,
$q$
,
![]() $E^{\ast }(3,\mathbb{Z};q)\subseteq L_{3D}(\mathbb{Z};q)\widetilde{U}_{3D}(\mathbb{Z};q)U_{3D}(\mathbb{Z};q)L_{3D}(\mathbb{Z};q)$
. Lemma 5.3 implies that
$E^{\ast }(3,\mathbb{Z};q)\subseteq L_{3D}(\mathbb{Z};q)\widetilde{U}_{3D}(\mathbb{Z};q)U_{3D}(\mathbb{Z};q)L_{3D}(\mathbb{Z};q)$
. Lemma 5.3 implies that
Since
![]() $L_{n}(\mathbb{Z};q)U_{n}(\mathbb{Z};q)L_{n}(\mathbb{Z};q)\subset L_{n}(\mathbb{Z};q)\tilde{U} _{n}(\mathbb{Z};q)$
and
$L_{n}(\mathbb{Z};q)U_{n}(\mathbb{Z};q)L_{n}(\mathbb{Z};q)\subset L_{n}(\mathbb{Z};q)\tilde{U} _{n}(\mathbb{Z};q)$
and
![]() $U_{n}(\mathbb{Z};q)L_{n}(\mathbb{Z};q)U_{n}(\mathbb{Z};q)\subset \tilde{U} _{n}(\mathbb{Z};q)U_{n}(\mathbb{Z};q)$
, we get the result.◻
$U_{n}(\mathbb{Z};q)L_{n}(\mathbb{Z};q)U_{n}(\mathbb{Z};q)\subset \tilde{U} _{n}(\mathbb{Z};q)U_{n}(\mathbb{Z};q)$
, we get the result.◻
Proof of Theorems 1.1 and 1.4 (with explicit bounds).
Let
![]() $n\geqslant 3$
. The proof of Theorem 1.4 shows that there is a non-zero
$n\geqslant 3$
. The proof of Theorem 1.4 shows that there is a non-zero
![]() $q\in \mathbb{Z}$
such that
$q\in \mathbb{Z}$
such that
![]() $U_{n}(\mathbb{Z};q)$
and
$U_{n}(\mathbb{Z};q)$
and
![]() $L_{n}(\mathbb{Z};q)$
are contained in
$L_{n}(\mathbb{Z};q)$
are contained in
![]() $w(\operatorname{SL}_{n}(\mathbb{Z}))^{16}$
. Since
$w(\operatorname{SL}_{n}(\mathbb{Z}))^{16}$
. Since
![]() $w(\operatorname{SL}_{n}(\mathbb{Z}))$
is a normal subset, the set
$w(\operatorname{SL}_{n}(\mathbb{Z}))$
is a normal subset, the set
![]() $\tilde{U} _{n}(\mathbb{Z};q):=\{hkh^{-1}\mid k\in U_{n}(\mathbb{Z};q)\wedge h\in \operatorname{SL}_{n}(\mathbb{Z})\}$
is contained in
$\tilde{U} _{n}(\mathbb{Z};q):=\{hkh^{-1}\mid k\in U_{n}(\mathbb{Z};q)\wedge h\in \operatorname{SL}_{n}(\mathbb{Z})\}$
is contained in
![]() $w(\operatorname{SL}_{n}(\mathbb{Z}))^{16}$
. Corollary 5.4 implies that if
$w(\operatorname{SL}_{n}(\mathbb{Z}))^{16}$
. Corollary 5.4 implies that if
![]() $n$
is large enough then
$n$
is large enough then
![]() $E(n,\mathbb{Z};q)\subseteq w(\operatorname{SL}_{n}(\mathbb{Z}))^{16\cdot 5}$
. Since
$E(n,\mathbb{Z};q)\subseteq w(\operatorname{SL}_{n}(\mathbb{Z}))^{16\cdot 5}$
. Since
![]() $E(n,\mathbb{Z};q)$
contains a congruence subgroup, we have proved the bound in Theorem 1.4. Finally, Lemma 4.5 implies that if
$E(n,\mathbb{Z};q)$
contains a congruence subgroup, we have proved the bound in Theorem 1.4. Finally, Lemma 4.5 implies that if
![]() $n$
is large enough then
$n$
is large enough then
![]() $\operatorname{SL}_{n}(\mathbb{Z})\subseteq w(\operatorname{SL}_{n}(\mathbb{Z}))^{16\cdot 5+7}$
.◻
$\operatorname{SL}_{n}(\mathbb{Z})\subseteq w(\operatorname{SL}_{n}(\mathbb{Z}))^{16\cdot 5+7}$
.◻
Acknowledgements
The authors thank Andrei Rapinchuk and Ariel Karelin for helpful conversations. They are also grateful to the anonymous referee for improving the bounds of Theorems 1.1 and 1.4 and for simplifying the proof of Lemma 4.6. N.A. was partially supported by NSF grant DMS-1303205 and BSF grant 2012247. C.M. was partially supported by BSF grant 2014099 and ISF grant 662/15.