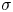1. Introduction
This paper develops a theory of footing in Harmonic Serialism (HS; Prince & Smolensky Reference Prince and Smolensky1993/2004; McCarthy Reference McCarthy2000, Reference McCarthy2016) where Con contains only directionally evaluated constraints (Eisner Reference Eisner2000, Reference Eisner2002; Lamont Reference Lamont2019, Reference Lamont2022a, Reference Lamont2022b). Directional constraints harmonically order candidates by the location of violations, rather than by the total number of violations. A central result of adopting directional evaluation is that the constraint Parse(
$\sigma$) not only motivates iterative footing but also determines where feet surface. This obviates the need for alignment constraints (McCarthy & Prince Reference McCarthy and Prince1993; McCarthy Reference McCarthy2003; Hyde Reference Hyde2012a, Reference Hyde2016), which determine where feet are parsed in HS with constraints that count loci (Pruitt Reference Pruitt2010, Reference Pruitt2012). The theory uses fewer constraints, is empirically adequate, and makes more restrictive predictions than HS with counting constraints and parallel Optimality Theory (OT; Prince & Smolensky Reference Prince and Smolensky1993/2004) with directional constraints.
Standard OT constraints evaluate candidates by counting their total number of loci, mapping candidates or input/candidate pairs onto violation counts, which are concatenated into violation vectors according to the constraint ranking. Whichever candidates’ violation vectors are lexicographically minimal are optimal. Instead of counting loci, directional constraints record where they occur, relative to the input (Eisner Reference Eisner2000, Reference Eisner2002). This is realised by mapping input/candidate pairs onto violation vectors, with as many positions as there are segments in the input.Footnote 1 A violation is recorded in the vector if the candidate has a locus at the corresponding location. Violation vectors are concatenated according to the constraint ranking and ordered lexicographically.
Under directional evaluation, candidates with distinct loci are not harmonically equivalent, even if they have the same total number of loci. Consequently, directional constraints eliminate problematic ties (see Lamont Reference Lamont2022a for discussion) and empower HS to model iterative processes such as feature spreading with locally defined constraints (Lamont Reference Lamont2019, Reference Lamont2021), obviating mechanisms such as Share constraints (McCarthy Reference McCarthy2010; Mullin Reference Mullin2011).
As a concrete example, consider the constraint Agree(nasal), which penalises adjacent segments with different specifications of the feature [nasal]. This constraint cannot motivate iterative nasal spreading in HS if it counts loci (Pater et al. Reference Pater, Bhatt and Potts2007), as the tableau in (1) illustrates. Nasalisation replaces the faithful locus [ma] with the unfaithful locus [ãw] and does not improve on Agree(nasal) (1b). *Link(nasal) disprefers the unfaithful candidate, and the derivation converges on [mawa] (1a).
(1)
Under directional evaluation, Agree(nasal) does distinguish between the loci [ma] and [ãw], because they appear at different positions relative to the input, as in the tableau in (2), which illustrates the hypothetical derivation mapping /mawa/ onto 
$[mw]$. The arrows along the left side of the tableau indicate that the output of one step is the input to the next. In this example, the input to each step contains four segments, and the constraints Agree(nasal) and *Link(nasal) map candidates onto violation vectors of length 4. These vectors range from 
${0_1}{1}{0}{2}{0}{3}{0}{4}$ with no violations to 
${1}{1}{1}{2}{1}{3}{1}{4}$ with a violation at every position. The superscript right arrows 
$^\Rightarrow$ indicate that both constraints are evaluated left-to-right, meaning that loci are strictly worse than their successors. Accordingly, moving the locus of Agree(nasal) one position to the right in each step of the derivation is harmonically improving. For example, in the first step Agree(nasal) assigns the violation vector 0100 to the faithful candidate (2a), which is lexicographically larger than the violation vector 
${0}{1}{0}{2}{1}{3}{0}{4}$ assigned to the unfaithful candidate (2b). As discussed below, violations are assigned to the rightmost segment of loci under left-to-right evaluation. By the end of the derivation, the entire string is nasalised (2f).
(2)
Under right-to-left evaluation, pushing loci rightward is not harmonically improving, as the tableau in (3) illustrates. The faithful candidate (3a) is assigned the violation vector 
${0}{4}{0}{3}{0}{2}{1}{1}$, which is smaller than the vector 
${0}{4}{0}{3}{1}{2}{0}{1}$ assigned to the unfaithful candidate (3b). Under right-to-left evaluation, violations are assigned to the leftmost segment of loci.
(3)
Violations are assigned to the opposite edge of loci, (i.e. the rightmost/leftmost segment of loci under left-to-right/right-to-left evaluation) to prevent non-convergent derivations such as (4). In this tableau, Agree(nasal) assigns a violation to every position that a locus occupies, not just to its rightmost segment. Consequently, folding loci into fewer positions is harmonically improving, and derivations may insert an infinite number of segments.
(4)
Assigning violations to the opposite edge of loci solves the problem, because epenthesis is not harmonically improving unless it removes a locus or shifts the entire locus further to the right. This is illustrated in the tableau in (5) (see Lamont Reference Lamont2022b for discussion).
(5)
Whether constraints are evaluated directionally is independent of whether Gen is restricted, as in HS, or unrestricted, as in parallel OT (see Finley Reference Finley2008 for a theory of vowel harmony in parallel OT with directional constraints). By restricting Gen, HS with constraints that count has been shown to avoid global effects produced by parallel OT (McCarthy Reference McCarthy2006, Reference McCarthy2008a), and these benefits extend to HS with directional constraints. For example, Wilson (Reference Wilson2003: 64–65) demonstrates that parallel OT with directional constraints produces unattested non-local blocking effects, or sour grapes, as the tableaux in (6) illustrate. As in (3), Agree(nasal) is evaluated right-to-left. Consequently, progressive nasalisation is harmonically improving only when it removes a locus, such as when nasalisation spreads to the end of the word as in (6a.iv). Partial progressive nasalisation is impossible, because the unfaithful locus is strictly worse than the faithful locus. Thus, when total nasalisation is blocked, for example by the presence of a fricative (6b.v), no nasalisation occurs (6b.i). An HS grammar with these constraints predicts that nasalisation should spread up to the fricative /mawas/ 
$\to$ 
$m\w\s$, which is attested (see Walker Reference Walker2011 for examples).
(6)
Within the domain of footing, global effects manifest as non-local parity effects, whereby some property of footing systematically depends on whether strings contain an even or odd number of syllables. For example, Pruitt (Reference Pruitt2010, Reference Pruitt2012) identifies a pattern of non-local trochaic shortening whereby final heavy syllables (H) are shortened to light syllables (L) only if they are preceded by an odd number of light syllables, as in (7); Alber (Reference Alber2005) discusses additional parity effects in parallel OT. Light-syllable strings are parsed into trochees from right-to-left, leaving word-initial unfooted syllables in odd-parity strings (7b). Heavy syllables are either parsed as monosyllabic feet (
${H}$) or shortened and parsed into disyllabic feet /LH/ 
$\to$ [(ĹL)], avoiding unbalanced trochees *[(ĹH)]. In /L
$^n$H/ strings, this is decided in favour of exhaustive footing: if 
$n$ is even, then a monosyllabic foot is parsed (7c), and if 
$n$ is odd, shortening occurs (7d), avoiding an initial stray syllable *[L(ĹL)(
$H$)]. A grammar for non-local trochaic shortening is discussed in §4.
(7)
As Pruitt demonstrates, this unattested pattern is not replicated in HS. To parse from right to left, the derivation must begin by parsing the rightmost syllable(s) into a foot. With locally defined constraints, there is insufficient information to parse a final heavy syllable correctly into a monosyllabic foot (
$H$) or into an unbalanced trochee (
$H$) which would be shortened later in the derivation.
In a more dramatic illustration of parity effects, Koser & Jardine (Reference Koser and Jardine2020) identify a pattern they dub sour grapes stress, wherein strings are exhaustively footed only if they are of even parity (8). Exhaustive parsing is motivated in even-parity strings to satisfy a constraint that penalises unfooted syllables that follow feet. In odd-parity strings, this is impossible without parsing monosyllabic feet, which are banned. As in (6), non-exhaustive footing *[
$(\acute \sigma \sigma )(\acute \sigma \sigma )\sigma$] fails to satisfy a markedness constraint and unnecessarily violates constraints on foot form. A grammar for sour grapes stress is discussed in §4.
(8)
As with non-local trochaic shortening, HS cannot model sour grapes stress with locally defined constraints. After parsing the initial foot, there is insufficient information to decide whether to continue parsing. These two cases illustrate that HS correctly avoids making unattested predictions made by parallel OT.
This paper investigates quantity-insensitive footing in HS with directional constraints, and systematically compares it to footing in parallel OT with directional constraints and HS with counting constraints. I show that directional HS accounts for the same range of empirical phenomena as recent work by Martínez-Paricio & Kager (Reference Martínez-Paricio and Kager2015). I demonstrate further that directional HS is typologically restrictive, producing a strict subset of the languages produced by HS with counting constraints and avoiding parity effects produced in parallel OT with counting and directional constraints. Further, it is a more parsimonious theory in that it requires fewer constraints, notably obviating alignment constraints (McCarthy & Prince Reference McCarthy and Prince1993; McCarthy Reference McCarthy2003; Hyde Reference Hyde2012a, Reference Hyde2016). The results reported in this paper are supported computationally by software developed to calculate factorial typologies in directional HS. That software and the factorial typologies of directional HS, directional OT and HS with counting constraints are provided in the supplementary materials.
The theory of footing in directional HS is presented in §2 and applied in a case study of exhaustive bidirectional footing in Waorani in §3. Section 4 presents the factorial typology, and §5 concludes.
2. Footing in directional Harmonic Serialism
This section presents the theory of footing in Harmonic Serialism with directional constraints. Operations and constraints are defined in sections 2.1 and 2.2, respectively.
2.1. Operations
Assuming the operation set proposed by Pruitt (Reference Pruitt2010, Reference Pruitt2012), Gen can parse one foot at a time, and cannot apply any other operation simultaneously (see also McCarthy Reference McCarthy2008b; Torres-Tamarit & Jurgec Reference Torres-Tamarit and Jurgec2015; McCarthy et al. Reference McCarthy, Pater and Pruitt2016; Moore-Cantwell Reference Moore-Cantwell2016; Topintzi Reference Topintzi2016; Breteler Reference Breteler2018; Pruitt Reference Pruitt2019). Specifically, Gen can parse a single unfooted syllable into a monosyllabic foot, and it can parse two adjacent unfooted syllables into a trochee or iamb. (Throughout this paper, trochee and iamb denote only disyllabic feet, not monosyllabic feet.) (9) lists the eleven candidates generated from a four-syllable string. As a simplification, analyses in this paper do not distinguish between primary and secondary stress; see Pruitt (Reference Pruitt2012, Reference Pruitt2019) for discussion of primary stress in HS.
(9)
Following Pruitt (Reference Pruitt2010), feet cannot be altered or removed. From an input with a trochee 
$(\acute \sigma \sigma )\sigma \sigma$, Gen cannot remove the trochee 
$(\acute \sigma \sigma )\sigma \sigma \not \to \sigma \sigma \sigma \sigma$, cannot shorten it 
$(\acute \sigma \sigma )\sigma \sigma \not \to (\acute \sigma )\sigma \sigma \sigma$, and cannot change its headedness 
$(\acute \sigma \sigma )\sigma \sigma \not \to (\sigma \acute \sigma )\sigma \sigma$.
2.2. Constraints
Following Pruitt (Reference Pruitt2010, Reference Pruitt2012), parsing syllables into feet does not violate any faithfulness constraints. Therefore, footing is controlled exclusively by markedness constraints. This section introduces the constraint set, which overlaps significantly with that used by Pruitt (Reference Pruitt2010, Reference Pruitt2012), the differences being the omission of alignment constraints and FtBin and the inclusion of a constraint on adjacent feet to model ternary rhythm. Because the focus is on quantity-insensitive parsing, underlying representations are taken to be strings of syllables rather than segments. This streamlines the discussion by omitting the question of syllabification and reduces the size of tableaux by defining positions in violation vectors in terms of syllables rather than segments.
The constraint Parse(
$\sigma$) motivates iterative footing by penalising unfooted syllables (10). While footing does not violate any faithfulness constraints, it does compete with the faithful candidate in any given step and must be harmonically improving to be optimal. Because loci of Parse(
$\sigma$) are single syllables, their positions correspond exactly to the positions of their violations.
(10)
Under directional evaluation, Parse(
$\sigma$) not only motivates footing but also decides which syllables to foot by harmonically ordering candidates in terms of their unfooted syllables, as in (11)–(12). Under both directions of evaluation, the worst candidate 
$\sigma \sigma \sigma \sigma$ has no feet, and the second-worst candidate has a monosyllabic foot at the wrong edge of the word: 
$\sigma \sigma \sigma (\acute \sigma$) under left-to-right evaluation and 
$(\acute \sigma )\sigma \sigma \sigma$ under right-to-left. The remaining candidates form three groups, increasing in harmony with the leftmost/rightmost footed syllable. Within each group, disyllabic feet are preferred to monosyllabic feet, and trochees and iambs are not distinguished. Note that the preference for disyllabic feet is made only locally within these groups. Because directional evaluation cares only about where violations occur and not their total number, there are monosyllabic footing candidates that are strictly better than disyllabic footing candidates, such as 
$\sigma \sigma (\acute \sigma \sigma )\prec (\acute \sigma )\sigma \sigma \sigma$ under left-to-right evaluation.
(11)
(12)
Parse(
$\sigma$) imposes a total harmonic order on candidates with a given foot type, as in (13)–(14). As these harmonic orders illustrate, Parse
$(\sigma )$ replicates the directional effects of alignment constraints, obviating their use.
(13)
(14)
Whether disyllabic feet are left- or right-headed is determined by the relative ranking of Trochee (shown in (15)–(17)) and Iamb (shown in (18)–(20)). Trochee penalises right-headed feet *
$\{(\sigma \acute \sigma ),\ (\acute \sigma )\}$ and Iamb penalises left-headed feet *
$\{(\acute \sigma \sigma ),\ (\acute \sigma )\}$. Under the ranking Trochee 
$\gg$ Iamb, disyllabic feet are left-headed, and under the opposite ranking, they are right-headed. As the harmonic orderings below illustrate, Trochee/Iamb prefer unfooted candidates and candidates with trochees/iambs to candidates with monosyllabic feet and iambs/trochees. Dispreferred candidates are ordered according to the location of their penalised feet. As discussed in the introduction, loci are right/left-aligned under left-to-right/right-to-left evaluation. Thus, 
${\sigma }{\tiny 1}{\tiny 2}){\sigma }{\tiny 3}{\sigma}{\tiny 4}$ and 
$({\sigma }{\tiny 1}{\acute \sigma }{\tiny 2}){\sigma}{\tiny 3}{\sigma}{\tiny 4}$ are harmonically equivalent for Trochee
$^\Rightarrow$.
(15)
(16)
(17)
(18)
(19)
(20)
The definitions above differ from how Trochee and Iamb are often defined, in that both constraints penalise monosyllabic feet. For Pruitt (Reference Pruitt2010, Reference Pruitt2012), these constraints are satisfied by monosyllabic feet, predicting grammars that parse every syllable into its own foot. To avoid that prediction, it is sufficient for either Trochee or Iamb to penalise monosyllabic feet (Martínez-Paricio & Kager Reference Martínez-Paricio and Kager2015: 473–474). However, having both constraints penalise monosyllabic feet obviates the constraint FtBin, yielding a more parsimonious theory.
To see why FtBin is redundant, consider the stress systems of Murinbata (21)Footnote 2 and Pintupi (22). Both languages parse trochees from left to right but differ in whether they allow monosyllabic feet. Odd-parity words surface in Murinbata with final monosyllabic feet (21a,c,e) and with final unfooted syllables in Pintupi (22b,d,f). This difference derives from the relative ranking of Parse
$(\sigma )$ and Trochee; the former is dominant in Murinbata, whereas the latter is dominant in Pintupi. As the analyses below illustrate, FtBin is unnecessary.
(21)
(22)
In even-parity words, ranking Parse
$(\sigma )$ and Trochee above Iamb derives the surface pattern, as the tableaux in (23) illustrate. It is necessary to evaluate Parse
$(\sigma )$ left-to-right to model odd-parity words, but, as discussed below, the directionalities of Trochee and Iamb are irrelevant, and are evaluated left-to-right by default. For the first step of the derivation, the entire candidate set is shown in (23a–k); all following tableaux show only relevant candidates to save space. The faithful candidate (23a) is ruled out by Parse
$(\sigma )$, and loses to candidate (23i) with a trochee at its left edge, which violates Iamb. Candidates with monosyllabic feet (23b–e) are harmonically bounded: they violate both Trochee and Iamb, and, because it is possible to parse a disyllabic foot in this step, are dispreferred by Parse
$(\sigma )$. Trochee rules out candidates (23f–h) with iambs, leaving candidates (23i–k) with trochees as possible optima. Because none of these candidates violate Trochee, the choice among them is made by Parse
$(\sigma )$, which prefers to foot the leftmost syllables (23i). In the next step, the remaining two syllables are footed, satisfying Parse
$(\sigma )$ at the additional expense of Iamb (23m). As this derivation illustrates, Parse
$(\sigma )$, Trochee, and Iamb adequately prevent monosyllabic feet from surfacing in even-parity words, and there is no need for FtBin.
(23)
In odd-parity words, the relative ranking of Parse
$(\sigma )$ and Trochee determines whether parsing is exhaustive and is relevant only for the final step of the derivation. Up to that point, candidates with monosyllabic feet have been harmonically bounded. They are contenders only when they compete with unfooted syllables and are preferred by Parse
$(\sigma )$. Monosyllabic feet surface when Parse
$(\sigma )$ dominates Trochee (24) and fail to surface otherwise (25). Thus, the relative ranking of Parse
$(\sigma )$ and Trochee control whether monosyllabic feet surface, and there is no need for FtBin.
(24)
(25)
In general, there is no need to posit a constraint on monosyllabic feet with these definitions of Trochee and Iamb, which reduces the set of relevant constraints. The relative ranking of Parse
$(\sigma )$ and the dominant foot form constraint adequately determines whether monosyllabic feet surface. This result was verified computationally by calculating factorial typologies with and without FtBin and confirming that the typologies contained identical sets of languages.
In iterative footing languages, the directionality of Parse
$(\sigma )$ determines where feet surface. The directionalities of Trochee and Iamb do not affect the outcome and are assumed to be left-to-right by default. As in (23), when it is possible to parse a trochee, the relative ranking of Parse(
$\sigma$) and Trochee is irrelevant: Trochee does not penalise trochees and thus has no influence on where they surface. This implies that the directionality of Trochee plays no role in iterative footing; its effect is only to prevent iambs from surfacing. Similarly, because Parse(
$\sigma$) must dominate Iamb for trochees to surface, the directionality of Iamb is irrelevant. Of the candidates that parse trochees (23i–k), Parse(
$\sigma$) prefers the candidate with the leftmost trochee (23i), whereas Iamb prefers the candidate with the rightmost trochee (23k). Because Parse(
$\sigma$) is dominant, its preference determines the outcome. Thus, like Trochee, the directionality of Iamb can be freely set without affecting the outcome of iterative footing.
The directionalities of Trochee and Iamb are relevant only in non-iterative footing languages where stress assignment is motivated by Hd(
$\omega$), as defined in (26). This constraint requires prosodic words to dominate some foot, but does not specify its location; constraints along those lines are discussed below. It is active only when Trochee and Iamb both dominate Parse
$(\sigma )$ and all other constraints that motivate footing. If Hd(
$\omega$) and Trochee dominate Iamb, then a trochee will be parsed at a location determined by Iamb. Neither Hd(
$\omega$) nor Trochee penalises candidates with trochees, and so neither constraint can choose among them. The decision falls to Iamb, which prefers that the trochee surface towards the right/left edge under left-to-right/right-to-left evaluation, respectively. Because Iamb dominates Parse
$(\sigma )$ in these languages, its preference determines the outcome. In these cases, the directionalities of Parse
$(\sigma )$, Hd(
$\omega$), and Trochee are irrelevant.
(26)
The analysis of Macedonian, which assigns stress to the antepenultimate syllable in words that are at least trisyllabic, as in (27), illustrates this effect. Following Franks (Reference Franks1987), Macedonian disallows word-final syllables from being parsed into feet, satisfying the constraint NonFinality, stated in (28) (see Beasley & Crosswhite Reference Beasley and Crosswhite2003; Hyde Reference Hyde2012a, Reference Hyde2016 for alternative analyses). Like Hd(
$\omega$), NonFinality assigns violations to prosodic words. Tableaux with these constraints assume that, like syllables, prosodic words are already present (see McCarthy et al. Reference McCarthy, Pater and Pruitt2016 for discussion of non-monotonic structure building in HS). This is straightforward to implement, and the additional steps and constraints are omitted for space and relevance. In candidates with exactly one prosodic word, the directionalities of Hd(
$\omega$) and NonFinality determine only where violations are assigned and are irrelevant.
(27)
(28)
The derivation of antepenultimate stress is illustrated by the tableau in (29). Hd(
$\omega$) requires the presence of some foot, ruling out the faithful candidate (29a). Because it is possible to parse disyllabic feet, monosyllabic feet are harmonically bounded and excluded from consideration. Trochee rules out iambic candidates (29b–d), leaving trochaic candidates (29e–g) as possible optima. These candidates all violate Iamb, which, because it is evaluated left-to-right, prefers that trochees surface as far to the right as possible. However, because parsing a trochee at the right edge fatally violates NonFinality (29g), it is optimal to parse a trochee one syllable to the left (29f). Thus the antepenultimate syllable is stressed, and because Trochee and Iamb dominate Parse
$(\sigma )$, no other feet surface. This tableau further emphasises the point that alignment constraints are unnecessary: when Parse
$(\sigma )$ is inactive, directionality effects are replicated by Trochee and Iamb.
(29)
Similar effects occur in non-iterative footing languages with initial extrametricality, where the constraint NonInitiality is active (Buckley Reference Buckley1994; Weber Reference Weber2016). For example, evaluating Trochee left-to-right derives postpeninitial stress in an iambic language. In general, when Hd
$(\omega )$ is active, primary stress falls within a three-syllable window at one end of the word.
The final constraints used to motivate footing are FootLeft and FootRight, as defined in (30) and (31), which require prosodic word edges to be coextensive with foot edges. Like Hd
$(\omega )$ and NonFinality, because these constraints' loci are prosodic words, their directionalities are irrelevant to candidates with only one prosodic word.
(30)
(31)
FootLeft and FootRight are necessary to model bidirectional stress systems wherein a foot surfaces at one edge of the word and feet are parsed iteratively from the opposite edge. These languages typically exhibit word-internal lapse in odd-parity words, as in Garawa (32), but may also exhibit word-internal clashes, as in Waorani, which is discussed in §3. Garawa words surface with initial primary stress and with secondary stresses on the penultimate syllable and alternating syllables to its left in words of at least four syllables. In odd-parity words, secondary stress does not surface on the third syllable (32b,d,f,h), implying a ban on monosyllabic feet.
(32)
Bidirectional stress is derived by first parsing a foot at one edge of the word and then iteratively parsing from the opposite edge. This occurs when FootLeft dominates Parse
$(\sigma )^\Leftarrow$ or FootRight dominates Parse
$(\sigma )^\Rightarrow$. The former is illustrated in the tableaux in (33). In the first step of the derivation, a trochee is parsed at the left edge of the word, satisfying FootLeft (33b). Trochees are then parsed from the right edge in the next two steps, and the derivation converges in the fourth step on [
$(\acute \sigma \sigma )\sigma (\acute \sigma \sigma )(\acute \sigma \sigma )$]. The third syllable is left unfooted because Trochee dominates Parse
$(\sigma )$, preferring the faithful (33j) over the fully footed (33k) as an output (33i).
(33)
The constraint *FootFoot, stated in (34), penalises contiguous feet, producing ternary rhythm when ranked above Parse
$(\sigma )$ (Kager Reference Kager1994; Elenbaas & Kager Reference Elenbaas and Kager1999; Torres-Tamarit & Jurgec Reference Torres-Tamarit and Jurgec2015). Iterative languages otherwise parse contiguous strings of feet, because Parse
$(\sigma )$ prefers the leftmost/rightmost syllables to be footed in any given step. *FootFoot models ternary rhythm as underparsing, leaving unfooted syllables between feet, and contrasts with structural accounts such as internally layered feet (Martínez-Paricio & Kager Reference Martínez-Paricio and Kager2015, Reference Martínez-Paricio and Kager2021). While a thorough comparison of these structures is beyond the scope of this paper, their typological predictions are discussed later.
(34)
The prototypical example of a language with ternary rhythm is Cayuvava, which parses words into non-contiguous trochees from right to left, as in (35). Primary stress is antepenultimate in words of at least three syllables, with secondary stresses surfacing every three syllables to its left. Words that cannot be evenly divided into dactyls surface with one or two unfooted syllables at their left edge.
(35)
Cayuvava is modelled by ranking NonFinality and *FootFoot above Parse(
$\sigma )^\Leftarrow$, as the tableaux in (36) illustrate. As discussed below, the directionality of *FootFoot is irrelevant. At each step of the derivation, trochees are parsed as far to the right as possible, leaving an unfooted syllable word-finally and an unfooted syllable between feet. Those stray syllables cannot be footed without violating NonFinality or *FootFoot, and the derivation converges in the fourth step on [
$(\acute \sigma \sigma )\sigma (\acute \sigma \sigma )\sigma (\acute \sigma \sigma )\sigma$].
(36)
Like many other constraints, the directionality of *FootFoot is irrelevant. As in the tableau above, it rules out candidates with contiguous feet (36o,r) but cannot distinguish between candidates that satisfy it. Thus, when it dominates a footing-imperative constraint, its directionality can be set arbitrarily. When it is dominated by a footing-imperative constraint, its preferences are overridden, exactly like Iamb in an iterative trochaic language.
2.3. Summary
In directional Harmonic Serialism, Con contains only directional constraints, which are evaluated either left-to-right (
$\Rightarrow$) or right-to-left (
$\Leftarrow$). As this section demonstrated, the directionalities of most constraints relevant to quantity-insensitive footing can be set arbitrarily. The only exceptions are Parse
$(\sigma )$, which determines the direction of iterative footing, and the foot form constraints Trochee and Iamb, which determine where a foot surfaces, but only when Hd
$(\omega )$ is active. By adequately deciding where to parse feet, these constraints fill the role standardly filled by alignment constraints, making them redundant.
Further reduction of Con derives from the definitions of Trochee and Iamb. Both constraints penalise monosyllabic feet, and their ranking relative to footing-imperative constraints determines whether monosyllabic feet surface. This obviates the need for the constraint FtBin. However, this result holds only in directional HS. The next section analyses bidirectional footing in Waorani using the constraints defined in this section. It further argues that without FtBin, parallel Optimality Theory is unable to model the language. In this respect, HS is able to do more than parallel OT using fewer constraints.
3. Bidirectional footing in Waorani
Waorani (Saint & Pike Reference Saint and Pike1962; Pike Reference Pike1964; Lester Reference Lester1994; see Halle & Kenstowicz Reference Halle and Kenstowicz1991; Hayes Reference Hayes1995; Fitzgerald Reference Fitzgerald2000 for previous analyses) is a language isolate spoken in Ecuador. Words are organised into stems, which comprise one or more root morphemes and an optional string of suffixes. Waorani exhibits a bidirectional stress system with trochaic feet. The head foot surfaces at the right edge of words, with a string of secondary feet built from the left edge. It is unique cross-linguistically in that all other known bidirectional languages are non-exhaustive (Hyde Reference Hyde2008, Reference Hyde2012a,Reference Hydeb, Reference Hyde2016; see also Pater Reference Pater2000; Pruitt Reference Pruitt2012: 211–213 for a discussion of English along these lines). I single Waorani out for a case study because it is typologically unique and because the apparent lack of exhaustive bidirectional languages has been used as evidence against serial footing and other theories (Hyde Reference Hyde2012a,Reference Hydeb). As the analysis argues, iterative footing occurs in two phases, parsing first the suffix string and then the stem. The analysis not only provides a case study for directional Harmonic Serialism but also highlights its parsimony. Whereas directional HS models Waorani stress with the constraints defined in §2, deriving the pattern in parallel Optimality Theory requires a FtBin constraint and additional prosodic structure.
The basic stress pattern of Waorani is illustrated by the words in (37)–(39). These words are composed of stems with up to six syllables that surface without suffixes (37), with suffix strings of one syllable (38), and with suffix strings of two syllables (39). To my knowledge, there are no examples of larger stems in the descriptive literature.Footnote 3 In the cited examples, hyphens indicate the boundary between the stem and the suffix string; for full morpheme-by-morpheme glosses, see Lester (Reference Lester1994). These words exhibit exhaustive bidirectional footing, surfacing with a trochee at their right edge and feet parsed from their left edge.
(37)
(38)
(39)
As in the words above, suffix strings up to two syllables long are parsed entirely into the head foot. Longer suffix strings are parsed into the head foot and a second foot, which may dominate one stem syllable. This is illustrated by the words in (40)–(42), with suffix strings of up to five syllables. To my knowledge, longer suffix strings are unattested. All feet that dominate suffixes are disyllabic. Consequently, in words with trisyllabic suffix strings (40), one foot crosses into the stem, avoiding strings such as *[(dà.dõ)-(tà)(bó.pa)]. Tetrasyllabic suffix strings are parsed evenly into two trochees, as in (41), and pentasyllabic suffix strings are non-exhaustively footed, as in (42), preventing a monosyllabic foot dominating a suffix 
$[(d)-(t)(b.pa)]$ from surfacing. The treatment of monosyllabic feet is not the only morphophonological difference between stems and suffixes; Lester (Reference Lester1994: 13) notes that closed syllables occur only in stems, and that complex onsets occur only in suffixes.
(40)
(41)
(42)
Pentasyllabic suffix strings indicate that suffixes are parsed from left to right and before stems; otherwise, they would be exhaustively footed. Footing right-to-left incorrectly predicts a foot should cross into the stem, just like words with trisyllabic suffix strings (40), e.g. 
$/p-..m.na.pa/$ 
$\to$ 
$p-k.d.m.(n.pa)$ 
$\to$ 
$p-k.(d.m)(n.pa)$ 
$\to$ 
$[(p-k)(d.m)(n.pa)$, as does footing the stem first, e.g. 
$/p-k.d.m.na.pa$ 
$\to$ 
$p-k.d.m.(n.pa)$ 
$\to$ 
$(p{o}-k).d.m.(n.pa)$ 
$\to$ 
$[(p-k)(d.m)(n.pa)]$.
The analysis derives Waorani footing in three stages: first, the head foot is parsed at the right edge of the word, then suffixes are footed, and finally the stem is footed. Lexically indexed constraints (Pater Reference Pater2007, Reference Pater2010) are used to distinguish stem and suffix morphemes: suffixes are subject to the constraints Trochee
$_{\rm suffix}$ and Parse
$(\sigma )$
$_{\rm suffix}$, and stem morphemes are handled by their unindexed copies. Under the rankings Trochee
$_{\rm suffix}$ 
$\gg$ Parse
$(\sigma )$
$_{\rm suffix}$ and Parse
$(\sigma )$ 
$\gg$ Trochee, monosyllabic feet surface only in the stem. Ranking Parse
$(\sigma )$
$_{\rm suffix}$ above Parse
$(\sigma )$ motivates footing the suffix string before the stem.
The tableaux in (43) illustrate the derivation of an unsuffixed stem. In the first step, a trochee is parsed at the right edge of the word, satisfying FootRight (43c). Parsing an iamb fatally violates Trochee (43d) and, because it is possible to parse a disyllabic foot in this step, parsing a monosyllabic foot is harmonically bounded (43e). The derivation continues by parsing a trochee at the left edge of the word (43g), and then, because Parse
$(\sigma )$ dominates Trochee, a monosyllabic foot word-medially (43j), converging on [
$(\grave \sigma \sigma )(\grave {\sigma })(\acute {\sigma }\sigma )$].
(43)
Words with monosyllabic and disyllabic suffix strings undergo exactly the same derivation as unsuffixed stems. Because the head foot dominates all of the suffix syllables, their derivations do not pass through the additional phase of parsing the suffix string.
Longer suffix strings motivate an intermediate phase of parsing, as in (44). As above, the first step parses a trochee at the right edge of the word (44d). A trochee is then parsed at the left edge of the suffix string, improving on the lexically indexed 
$\textsc{Parse}(\sigma)_{\rm suffix}$ (44h). In the remaining three steps, (44j–t), the stem is exhaustively footed from left to right. Footing the remaining suffix syllable fatally violates Trochee
$_{\rm suffix}$ (44o).
(44)
The derivations of words with tri- and tetrasyllabic suffix strings are identical, as summarised in (45). After the head foot is parsed (step i), the leftmost syllable(s) of the suffix string are footed (step ii). With a trisyllabic suffix string, this foot crosses into the stem as in (45a.ii), satisfying both Trochee constraints and improving on the general Parse
$(\sigma )$. Crossing into the stem is unmotivated with a tetrasyllabic suffix string, because it leaves suffix syllables unfooted. The derivations continue by parsing the stem (steps iii–v), converging on exhaustively footed outputs.
(45)
Setting aside the morphophonological differences between stems and suffixes, the analysis of Waorani differs minimally from the analysis of Garawa in §2. In both languages, a foot is first parsed at one edge of the word, and then feet are parsed iteratively from the other. Whether monosyllabic feet surface word-medially depends on the relative ranking of Parse
$(\sigma )$ and Trochee. Between Waorani and Garawa, both rankings are attested.
The HS analysis of Waorani straightforwardly derives two aspects of its stress system that pose problems in parallel OT: head feet dominate two syllables in odd-parity words, and pentasyllabic suffix strings are underparsed, even in even-parity words. These aspects reflect the relative timing of parsing in the HS analysis. An adequate monostratal analysis in parallel OT must draw on additional constraints and posit additional prosodic structure.
The parallel OT analysis requires a FtBin constraint to derive odd-parity words. FootRight requires prosodic words to end with feet but does not distinguish between final monosyllabic or disyllabic feet. As discussed above, monosyllabic feet cannot compete with disyllabic feet in HS and are not parsed until late in a derivation. Thus, the first foot to be parsed is always disyllabic, and the structure of odd-parity words follows automatically. FootRight does not have the same effect in parallel OT, because all feet are parsed simultaneously, as the tableau in (46) illustrates. The exhaustive footing candidates (46e–g) all satisfy FootRight and Parse
$(\sigma )$ and are not distinguished by them. Trochee pushes the monosyllabic foot to the right edge of the word (46g), dispreferring the desired output (46f). With the constraint set defined in §2, parallel OT cannot model Waorani.
(46)
In order to select the attested surface form [
$(\grave \sigma \sigma )(\grave \sigma )(\acute \sigma \sigma )$], some constraint must prefer it to candidate (46g). Assuming a high-ranking constraint that maintains primary stress on the rightmost foot, an obvious choice is HdFtBin, which penalises monosyllabic feet with primary stress (Itô & Mester Reference Itô and Mester2007). The general FtBin would not be useful under directional evaluation. Like Trochee, it would prefer that monosyllabic feet surface at one edge of the word, minimising their violation.
The parallel OT analysis requires additional prosodic structure to derive pentasyllabic suffix strings. Suffix strings are footed before stems in the HS analysis. Accordingly, the foot structure of suffix strings is unaffected by the shape of the stem, and pentasyllabic suffix strings always surface with an unfooted syllable. This does not hold in parallel OT, which predicts that pentasyllabic suffixes should be exhaustively parsed with odd-parity stems as in (47). The attested surface form (47b) is dispreferred by Trochee and both Parse
$(\sigma )$ constraints to a candidate that parses the word evenly into five trochees (47c).
(47)
While it is clear that the constraints introduced so far are inadequate to derive words with pentasyllabic suffix strings in parallel OT, the most economical analysis is not obvious. It is possible to derive underparsing in pentasyllabic suffix strings with three recursive prosodic words: one dominating the entire word, one dominating the stem, and one dominating the suffix string. The first two can be derived with Match constraints (Selkirk Reference Selkirk2011) that require the morphosyntactic word and the stem to be coextensive with prosodic words. The suffix prosodic word can be motivated by requiring both children of the morphosyntactic prosodic word to be prosodic words (Myrberg Reference Myrberg2013). With this structure in place, pentasyllabic stems can be modelled by indexing FootLeft to the suffix prosodic word and ranking it above Parse
$(\sigma )$. That approach suffices for pentasyllabic suffix strings but has the disadvantage of motivating footing in the suffix string with two separate constraints. Parse
$(\sigma )$
$_{\rm suffix}$ is necessary to prefer the surface form of words such as 
$(m.n)(m)(k-d)(n.pa)]$ ‘they make ear holes (pierced)’ to an underparsing candidate that satisfies Trochee: 
$(m.n)(m.ka)-d.(n.pa)]$.
Waorani exhibits exhaustive bidirectional footing, a pattern that is otherwise unattested cross-linguistically. Directional HS predicts the existence of this pattern, and captures it using ordinary footing constraints. By contrast, while it is possible to model Waorani in parallel OT, doing so requires additional constraints and may require additional prosodic structure. This case study highlights the relative economy of directional HS; the next section argues that its typological predictions are empirically adequate and restrictive.
4. Factorial typology
The previous two sections provide a coarse overview of the footing patterns predicted by directional Harmonic Serialism. To calculate an exact typology, Python scripts were written to implement the theory, and the scripts and typologies they produced are available as an online supplement to this article. The inputs to the calculation were strings of two to nine syllables, with Con comprising left-to-right and right-to-left copies of Parse
$(\sigma )$, Trochee, Iamb, FootLeft, FootRight, NonFinality, *FootFoot, and Hd(
$\omega )$. Copies of each constraint were used so that their directionalities could be set via constraint ranking, obviating the need for a parameter-setting component. The typology is empirically adequate and restrictive relative to other theories. Before presenting the results, this section first explains how they were calculated.
The typology calculator follows roughly the same steps as OT-Help (Staubs et al. Reference Staubs, Becker, Potts, Pratt, McCarthy and Pater2010). It iterates over the set of inputs, finding the set of all possible derivations that start from each input. As it does this, it compares the ranking conditions on each derivation against those calculated for previous inputs, keeping only those combinations with satisfiable ranking conditions. The fusional reduction algorithm (Brasoveanu & Prince Reference Brasoveanu and Prince2011) is used to determine ranking conditions and (un)satisfiability. The output of the calculation is a set of languages that contain derivations for each input and a constraint ranking, organised by the set of surface forms.
Figure 1 illustrates how derivations are generated from a given input. Each node in the tree represents an intermediate form, and its child nodes represent the output of Gen with it passed in as input. Nodes in grey do not have satisfiable ranking conditions, either because they are harmonically bounded in the step they were generated or because their ranking conditions are inconsistent with their mothers’. The root of the tree /
$\sigma \sigma \sigma \sigma$/ is recursively expanded in a breadth-first manner until all of its branches converge or become inconsistent. Every path through the tree that starts at the root and terminates in a convergent form in square brackets represents a derivation with a satisfiable ranking condition. For example, the path that follows the top branches represents a derivation that parses trochees from left to right.
Possible derivations from /
$\sigma \sigma \sigma \sigma$/; candidates in grey are not possible optima, and are not passed back into Gen
Once the calculator has derivations for multiple inputs, it iterates through all possible pairs of derivations, keeping only those with satisfiable ranking conditions. Figure 2 illustrates this process for the derivations from a four-syllable input (left) and a two-syllable input (right). Of the 76 combinations (
$19\times 4$), only the 27 represented with thick lines have satisfiable ranking conditions. These 27 combinations would then be combined with another input's derivations, iterating pairwise through all derivation sets.
Combining the derivations generated from four- and two-syllable strings; combinations with thick black lines have satisfiable ranking conditions, and those with thin grey lines require inconsistent rankings
The 179 optimal combinations generate the 154 languages reported in the supplemental materials. Twenty-four derivations do not generate a unique set of surface strings.
Each grammar's ranking was simplified by determining whether constraints’ directionalities were relevant to the outcome. A constraint’s directionality is irrelevant if its two copies are not ranked relative to each other. For example, the Hasse diagram in Fig. 3a gives the full constraint ranking for antepenultimate stress, and the one in Fig. 3b gives the simplified version. Because Iamb
$^\Rightarrow$ dominates Iamb
$^\Leftarrow$, Iamb must be evaluated left-to-right to derive the correct surface forms. No other constraint's directionality must be set to a specific value, and they are left unspecified in the simplified Hasse diagram.
Full (a) and simplified (b) Hasse diagrams of the constraint ranking for antepenultimate stress
Of the 179 grammars in the calculated typology, there are 144 grammars where the direction of Parse
$(\sigma )$ matters, 12 grammars where the direction of Trochee matters, and 11 grammars where the direction of Iamb matters. No other constraint's directionality is ever relevant, supporting the arguments in §2.
4.1. Empirical adequacy
To assess the empirical adequacy of the typology, its predictions were compared primarily against those reported by Martínez-Paricio & Kager (Reference Martínez-Paricio and Kager2015, Reference Martínez-Paricio and Kager2021). Surveys of footing by Gordon (Reference Gordon2002), van der Hulst et al. (Reference van der Hulst, Goedemans and van Zanten2010) and Hyde (Reference Hyde2016) were also consulted. The directional HS typology models all of the languages modelled by Martínez-Paricio & Kager (Reference Martínez-Paricio and Kager2015, Reference Martínez-Paricio and Kager2021), except for the seven exceptions discussed below. These patterns can all be derived with additional constraints or have been questioned in the descriptive literature. Therefore, directional HS appears to be empirically adequate as a model of quantity-insensitive footing.
The directional HS typology omits the languages Choguita Rarámuri (Caballero Reference Caballero2008), Hoc
$a$k (Miner Reference Miner1979), and Kashaya (Buckley Reference Buckley1994), which can all place primary stress on postpeninitial syllables. As mentioned in §2, these patterns can be derived with a constraint that penalises word-initial syllables that are dominated by a foot, à la NonFinality.
Another language that requires additional constraints in directional HS is Sentani (Elenbaas Reference Elenbaas1999). Sentani exhibits bidirectional inexhaustive footing, as the words in (48) illustrate. Other than the trochaic head foot, feet are iambic. Because the head foot surfaces at the right edge of words, its headedness reflects a ban on stressed final syllables, which requires a variant of NonFinality (see Hyde Reference Hyde2011 for other examples of rhythmic reversal). The other aspect of Sentani that requires an additional constraint is underparsing in six-syllable words (48e). This can be derived with the constraint *Clash-Head, which penalises stress clash involving the primary stress (Pater Reference Pater2000: 246). Under the ranking FootLeft 
$\gg$ *Clash-Head 
$\gg$ Parse
$(\sigma )$, only the foot parsed at the left edge of the word may surface adjacent to the head foot. Hence, tetrasyllabic words surface with stress clash (48c), but longer even-parity words do not (48e). With these two additional constraints, directional HS derives the pattern.
(48)
Martínez-Paricio & Kager (Reference Martínez-Paricio and Kager2015: 486) cite Baxoje-Jiwere (also called Ioway-Oto; Whitman Reference Whitman1947) as a potential example of a language with non-iterative secondary stress. Whitman (Reference Whitman1947, 238) describes Baxoje-Jiwere as placing primary stress on one of the two initial syllables, with secondary stress surfacing three syllables later, implying no other secondary stresses. The placement of primary stress is lexicalised, reflecting a weight distinction that was neutralised diachronically (Miner Reference Miner1979; Rice Reference Rice2011; Greer Reference Greer2016). However, because Whitman (Reference Whitman1947) does not provide examples, Martínez-Paricio & Kager (Reference Martínez-Paricio and Kager2015: 486) state that they are hesitant to include it in their typology. If the language does in fact exhibit non-iterative secondary stress, it is not obvious how it would be derived in directional HS, and it thus challenges the theory.
The descriptions of the remaining two languages, Indonesian and Estonian, have been questioned in recent literature. Martínez-Paricio & Kager (Reference Martínez-Paricio and Kager2015) appear to include Cohn's (Reference Cohn1989) description of Indonesian stress in their typology (see p. 6 of the supplemental materials to Martínez-Paricio & Kager Reference Martínez-Paricio and Kager2015). However, in instrumental studies, Maskikit-Essed & Gussenhoven (Reference Maskikit-Essed and Gussenhoven2016) argue that the language does not exhibit any word-level prominence. Directional HS does derive the pattern Cohn (Reference Cohn1989) attributes to Indonesian, but I do not mark it as attested in the typology in the supplemental materials. Martínez-Paricio & Kager (Reference Martínez-Paricio and Kager2015: 483) attribute an exhaustive footing strategy to Estonian that parses as many ternary feet as possible, as well as one or two binary feet. This results in heptasyllabic words being parsed as [
$(\acute \sigma \sigma \sigma )(\grave \sigma \sigma )(\grave \sigma \sigma )$], with two binary feet surfacing to avoid a monosyllabic foot *[
$(\acute \sigma \sigma \sigma )(\grave \sigma \sigma \sigma )(\grave \sigma )$] or an unfooted syllable *[
$(\acute \sigma \sigma \sigma )(\grave \sigma \sigma \sigma )\sigma$]. Deriving these patterns would instantiate a lookahead effect in HS, making it impossible to model. Parsing left-to-right, the choice between leaving an unparsed syllable between feet [
$\dots (\grave \sigma \sigma )\sigma (\grave \sigma \sigma )\dots$] or not [
$\dots (\grave \sigma \sigma )(\grave \sigma \sigma )\sigma \dots$] would depend on whether a binary foot could be parsed in the next step. However, it is not clear exactly what the Estonian pattern is. Secondary literature citing Hint (Reference Hint1973) reports that secondary stress varies freely between binary and ternary rhythm (Prince Reference Prince1980; Hayes Reference Hayes1995), and more recent work describes it as primarily trochaic (Viitso Reference Viitso2007: 16–17). Furthermore, a phonetic study by Asu & Lippus (Reference Asu and Lippus2018) does not find any acoustic evidence of secondary stress, and they question its existence (see Golston Reference Golston2021 for further discussion). Thus, like Baxoje-Jiwere, Estonian presents an interesting challenge to directional HS but one that demands further descriptive work.
Overall, the theory of footing presented in this article appears to be empirically adequate. The languages excluded from the factorial typology are modelled straightforwardly by including additional constraints. This parallels the discussion of Waorani footing in §3, in that both HS and parallel OT can model the language, but parallel OT requires additional constraints. However, to model Waorani, the parallel OT analysis may also require inferred prosodic structure, which is not the case with the languages discussed above. Baxoje-Jiwere and Estonian present the most compelling challenges to the theory, but it is difficult at present to evaluate themcarefully.
4.2. Comparison to other theories
To compare the typological predictions of directional HS against other theories, two additional factorial typologies were calculated. These are also reported in the supplemental materials. One used exactly the same set of constraints but lifted the restrictions on Gen, yielding a typology of parallel OT with directional constraints. In the other, constraints were evaluated by counting loci, yielding a typology of HS with counting constraints. The counting typology also included the constraints AllFt-L (49) and AllFt-R (50) (McCarthy & Prince Reference McCarthy and Prince1993; McCarthy Reference McCarthy2003; Hyde Reference Hyde2012a, Reference Hyde2016) to regulate where feet are parsed (see Pruitt Reference Pruitt2012: ch. 5 for arguments against other approaches in HS with counting constraints). These comparisons independently test Gen, whether mappings are serial or parallel, as well as Con, whether constraints are directional or not. While Martínez-Paricio & Kager (Reference Martínez-Paricio and Kager2015) assume different prosodic structures and a different constraint set, a less systematic comparison to their reported factorial typology is also discussed below.
(49)
(50)
Overall, all four theories offer equivalent empirical coverage. The parallel theories require additional constraints to model Waorani, and the three calculated typologies require additional constraints to model the languages discussed in §4.1. The parallel OT typology with directional constraints models 120 of the 154 languages in the directional HS typology, plus five patterns that are not attested. The HS typology with counting constraints models all of the languages in the directional HS typology plus 76 unattested patterns. The main division between typologies reflects differences in Con: while many of the pathologies reported by Martínez-Paricio & Kager (Reference Martínez-Paricio and Kager2015) occur in the HS typology with counting constraints, none occur in the directionaltypologies.
4.2.1. Parallel Optimality Theory
The parallel OT typology with directional constraints largely overlaps with the directional HS typology. It models 120 of the 154 languages in the directional HS typology. The 34 languages it does not model comprise 10 exhaustive bidirectional languages, 22 languages with long lapse (although it does not categorically avoid long lapse languages) and two dual-stress languages that surface with a monosyllabic foot in tetrasyllabic words to avoid adjacent feet. Of these 34 languages, the only one that is attested corresponds to Waorani footing, which can be modelled using additional constraints as in §3.
The five languages that are produced only by parallel OT all exhibit ternary rhythm and surface with one or two monosyllabic feet at one end of the word. One example is given in (51). All the words in this language satisfy FootRight and *FootFoot. Words with 3
$n$ syllables surface with two monosyllabic feet towards their right edge (51b,e,h). Final dactyls *[
$\ldots (\acute \sigma \sigma )\sigma$] are dispreferred by FootRight, and a final right-aligned trochee *[
$\ldots \sigma (\acute \sigma \sigma )$] is dispreferred by Parse
$(\sigma )^\Rightarrow$.
(51)
As in the discussion of Estonian in the previous subsection, deriving these patterns in HS would require lookahead. Parsing left-to-right, whether a trochee or a monosyllabic foot should be parsed would depend on the next step. A trochee is parsed if it would leave at least two unfooted syllables and a monosyllabic foot would be parsed otherwise.
Overall, parallel OT and HS produce comparable typologies with directional constraints. However, as discussed in the introduction, parallel OT with directional constraints is still capable of producing unattested global effects. The tableaux in (52) illustrate the derivation of non-local trochaic shortening, following Pruitt (Reference Pruitt2010, Reference Pruitt2012). Odd-parity words of all light syllables L are parsed into right-aligned trochees, leaving an unfooted syllable at the left edge of the word (52a). Final heavy syllables preceded by strings of light syllables are either parsed into monosyllabic feet (
$H$) or shortened and parsed into trochees (ĹL), depending on the parity of the string of light syllables. With an even number of light syllables, as in (52b), the string can be exhaustively parsed without shortening (52b.ii).Footnote 4 Parsing the heavy syllable into a trochee fatally violates the constraint on unbalanced trochee *(ĹH) (52b.iv), and shortening it needlessly violates Parse
$(\sigma )$ and Max
$(\mu )$ (52b.v). However, when there is an odd number of light syllables, it is optimal to shorten final heavy syllables (52c). Otherwise, an unbalanced trochee would be parsed (52c.ii) or a syllable would be left unfooted (52c.iv). Thus, the surface form of final heavy syllables depends on the parity of the preceding string.
(52)
The same is true of the model Martínez-Paricio & Kager (Reference Martínez-Paricio and Kager2015, Reference Martínez-Paricio and Kager2021) propose, which is also couched in parallel OT. Because they are not modelling dual-stress systems (Martínez-Paricio & Kager Reference Martínez-Paricio and Kager2015: 487), their factorial typology does not include the constraints FootLeft and FootRight. When these constraints are included, their system models sour grapes stress, an unattested pattern where multiple feet surface only in even-parity words, as in (8) (Koser & Jardine Reference Koser and Jardine2020). The derivation is illustrated in the tableaux in (54). These tableaux include the constraint Chain-R (53), which penalises unfooted syllables that are followed by feet (Martínez-Paricio & Kager Reference Martínez-Paricio and Kager2015: 470). FootLeft causes all words to surface with initial iambs, and additional feet surface only when this would satisfy FootRight. Parsing feet only at the word edges is ruled out by Chain-R, as in (54a.iv) and (54b.iv), and monosyllabic feet fatally violate Iamb (54b.vi). Consequently, FootRight can be optimally satisfied only by a string of iambs that spans the entire word, which is only possible in even-parity words (54a.v). In odd-parity words, FootRight cannot be satisfied without violating higher-ranked constraints, inexhaustive parsing fatally violates Trochee (54b.v), and only one iamb surfaces (54b.iii).
(53)
(54)
The pattern holds whether these constraints are evaluated by counting loci as in (54) or directionally. Just as in the tableaux in (6), violations of Trochee are tolerated only for candidates that satisfy FootRight.
In summary, HS and parallel OT produce comparable typologies of quantity-insensitive footing with directional constraints. However, because parallel OT predicts unattested global interactions, HS is more restrictive. This echoes similar arguments that favour HS with counting constraints (McCarthy Reference McCarthy2006, Reference McCarthy2008a).
4.2.2. Harmonic Serialism with counting constraints
The HS typology with counting constraints produces a strict superset of the directional HS typology. It models all of the 154 languages in the directional HS typology as well as 76 additional languages. These include 30 languages with ternary rhythm and 14 bidirectional languages. More notable are the 30 languages that exhibit a novel pathology and the two languages that exhibit a variant of a pathology identified by Martínez-Paricio & Kager (Reference Martínez-Paricio and Kager2015). This section focuses on the 32 pathological languages, demonstrating why they are not reproduced in directional HS.
The novel pathologies delay parsing certain syllables into feet until late in the derivation. This results in some languages consistently surfacing with word-final monosyllabic feet or multiple word-internal stress clashes. I will refer to these pathologies as pseudo-nonfinality and pseudo-ternary rhythm, respectively.
Pseudo-nonfinality is illustrated in (55). All words with at least three syllables surface with a final monosyllabic foot (55b–h), and even-parity words with at least four syllables surface with an initial monosyllabic foot as well (55c,e,g).
(55)
Pseudo-nonfinality is derived in two stages: non-final syllables are exhaustively footed from right to left, and then the final syllable is parsed into a monosyllabic foot. The tableaux in (56) illustrate the derivation of a six-syllable word. In the first two steps, trochees are parsed as far to the right as possible. NonFinality prevents a foot from being parsed at the right edge in the first step (56f), and monosyllabic feet are not contenders when disyllabic feet are available. Because Parse
$(\sigma )$ dominates Trochee, a monosyllabic foot is parsed in the third step (56k). Finally, because Parse
$(\sigma )$ also dominates NonFinality, the final syllable is footed (56n). The derivation converges on an output with monosyllabic feet at both edges [
$(\acute \sigma )(\acute \sigma \sigma )(\acute \sigma \sigma )(\acute \sigma )$].
(56)
HS with counting constraints models pseudo-nonfinality, because Parse
$(\sigma )$ and AllFt-R are separate constraints, and it is possible to rank NonFinality between them. Under the ranking NonFinality 
$\gg$ AllFt-R, it is not optimal to parse the final syllable when another disyllabic foot is available. Under the ranking Parse
$(\sigma )$ 
$\gg$ NonFinality, it is not optimal to leave the final syllable unparsed, and it surfaces in a monosyllabic foot by the end of the derivation. In directional HS, Parse
$(\sigma )$ subsumes AllFt-R, and NonFinality cannot be ranked between the footing imperative and the constraint that regulates where feet surface. It either dominates Parse
$(\sigma )$, and the final syllable surfaces unparsed, or is dominated by Parse
$(\sigma )$, the final syllable surfacing in a foot.
Similarly, ranking *FootFoot between Parse
$(\sigma )$ and the dominant alignment constraint produces pseudo-ternary rhythm, as illustrated in (57). In this pathology, strings are parsed into alternating strings of trochees and monosyllabic feet.
(57)
Pseudo-ternary rhythm is derived by first parsing non-adjacent feet and then returning to fill the gaps. The tableaux in (58) illustrate the derivation of a six-syllable word. In the first two steps, non-adjacent trochees are parsed from left to right, deriving a dactylic rhythm. Because Parse
$(\sigma )$ dominates Trochee, the stray syllables are then parsed into monosyllabic feet in the last two steps. The derivation converges on an output with monosyllabic feet word-medially and finally [
$(\acute \sigma \sigma )(\acute \sigma )(\acute \sigma \sigma )(\acute \sigma$)].
(58)
Pseudo-ternary rhythm results from the same mechanism as pseudo-nonfinality: *FootFoot is ranked between Parse
$(\sigma )$ and AllFt-L, and is able to keep feet separated for only part of the derivation. Because these constraints are unified in directional HS, it does not reproduce the pathology.
In the third pathology produced by HS with counting constraints, only disyllabic words are parsed into feet. Longer words do not contain feet; therefore, they do not bear stress. This resembles trisyllabic exceptionality, a pattern identified by Martínez-Paricio & Kager (Reference Martínez-Paricio and Kager2015: 489), wherein ternary feet surface only in trisyllabic words; longer words exhibit strictly binary rhythm. The tableaux in (59) illustrate the short-word pathology. With both alignment constraints ranked above Parse
$(\sigma )$, feet can surface only when they would coincide with both word edges (59a). In words longer than two syllables, feet do not surface (59b).
(59)
The short-word pathology requires constraints that penalise feet which surface away from a word edge. There is no such constraint in the proposed directional HS theory of footing, and the pathology is correctly avoided.
In summary, HS produces a strictly smaller typology with directional constraints than with counting constraints. HS with counting constraints was shown to generate three pathological patterns that result from the footing imperative constraint being different from the constraints that regulate where feet surface. Directional HS correctly avoids these pathologies by unifying these constraints.
4.3. Summary
The factorial typology of directional HS footing is empirically adequate insofar as it adequately replicates the empirical coverage of the typology reported by Martínez-Paricio & Kager (Reference Martínez-Paricio and Kager2015, Reference Martínez-Paricio and Kager2021). The languages not captured by the set of constraints used in the reported calculation can be modelled straightforwardly with additional constraints.
The directional HS typology compares favourably against typologies for HS with counting constraints and parallel OT with directional constraints. Like Martínez-Paricio & Kager's parallel OT model, parallel OT with directional constraints produces unattested global interactions, which are not generated in HS. HS generates strictly more languages with counting constraints than directional constraints, including pathologies wherein certain syllables are not parsed until late in the derivation.
Comparing the factorial typologies of these theories is useful because it reveals what patterns each theory is able to represent. This approach is only one perspective on evaluating the overgeneration of a model. None of the theories here take into account the fact that trochaic languages are more robustly attested than iambic languages or that unidirectional footing is more common than bidirectional footing (Goedemans Reference Goedemans2010). Nor do they consider computational results correlating ease of learning with how robustly attested a stress pattern is (Heinz Reference Heinz2007, Reference Heinz2009; Bane & Riggle Reference Bane and Riggle2008; Staubs Reference Staubs2014a,Reference Staubsb; Stanton Reference Stanton2016). Incorporating these pressures into formal models is an obvious direction to take this research in. Furthermore, evaluating any theory empirically requires caveats about sampling bias (McCollum et al. Reference McCollum, Baković, Mai and Meinhardt2020) and the evidentiary strength of descriptions (de Lacy Reference de Lacy2014).
5. Conclusion
Directional Harmonic Serialism is a constraint-based framework where Gen can only make one change at a time and Con contains only directional constraints. As the introduction highlights, directional constraints empower Harmonic Serialism to model iterative processes with locally defined constraints. This eliminates the need for more complex mechanisms, and formally unifies diverse empirical phenomena (see Lamont Reference Lamont2019, Reference Lamont2021 for preliminary work on feature-spreading). One goal of this project is to develop an empirically adequate theory of phonology that assumes as few formal mechanisms as possible, along the lines of iterative rule-based models (Brown Reference Brown1972; Howard Reference Howard1972; Johnson Reference Johnson1972; Jensen & Stong-Jensen Reference Jensen and Stong-Jensen1973; Cearley Reference Cearley1974; Vago & Battistella Reference Vago and Battistella1982; Archangeli & Pulleyblank Reference Archangeli and Pulleyblank1994). This paper is the first step towards that goal, applying directional Harmonic Serialism to the domain of quantity-insensitive footing.
This paper proposes and demonstrates a theory of footing in directional Harmonic Serialism, building on work by Pruitt (Reference Pruitt2010, Reference Pruitt2012). The theory uses fewer constraints than Pruitt's theory, notably omitting alignment constraints and FtBin. The directionalities of Parse
$(\sigma )$, Trochee, and Iamb replicate the effects of alignment constraints in determining where feet surface. For all other constraints, directionality is irrelevant to the grammar and does not contribute additional languages to the typology. How widely this holds in other empirical domains is not known; however, the directions of faithfulness constraints generally appear irrelevant (Lamont Reference Lamont2022a). Thus, while directional constraints are uncommon in the literature, working with the theory is not significantly different from others that may be more familiar to practicing phonologists.
I have also presented software to calculate typologies in directional HS to test its typological predictions. In doing so, I have shown that directional HS has desirable typological properties. For the range of phenomena considered, directional HS has comparable empirical coverage to work by Martínez-Paricio & Kager (Reference Martínez-Paricio and Kager2015, Reference Martínez-Paricio and Kager2021) and avoids pathological predictions associated with other theories of footing. Furthermore, because the software is modular and freely available, it empowers other phonologists to work with the theory and test it.
Competing interests
The author declares that there are no conflicts of interest regarding the publication of this paper.
Acknowledgments
This work has greatly benefited from thoughtful comments by three anonymous reviewers for Phonology and the associate editor, discussions with Michael Becker, Brett Hyde, Gaja Jarosz, John McCarthy, Joe Pater, Kathryn Pruitt, and Kristine Yu, and participants in the UMass Sound Workshop and audiences at PhoNE 2019 and AMP 2020. All remaining errors are of course my own.
Supplementary material
Files used for analyses in the current paper are available as supplementary materials at https://doi.org/10.1017/S0952675722000082.
The supplemental materials present three factorial typologies of footing: Harmonic Serialism with directional constraints; Harmonic Serialism with counting constraints; and parallel Optimality Theory with directional constraints. The Python scripts used to calculate them are also included.
Open access
