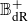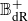1. Introduction
Let X be a proper smooth rigid analytic variety over a complete algebraically closed non-archimedean field
![]() $\mathbb{C}$
of mixed characteristic p. It is well known that there is a Hodge–Tate spectral sequence
$\mathbb{C}$
of mixed characteristic p. It is well known that there is a Hodge–Tate spectral sequence
from Hodge cohomology groups converging to the p-adic étale cohomology. The Hodge–Tate spectral sequences play an important role in some of the recent breakthroughs in arithmetic geometry, namely it is used to define Hodge–Tate period maps as in [ Reference ScholzeSch15 ], [ Reference Caraiani and ScholzeCS17 ] and [ Reference Caraiani and ScholzeCS19 ], which is applied to prove the modularity theorem, and many other important results in [ Reference Allen, Calegari, Caraiani, Gee, Helm, Le Hung, Newton, Scholze, Taylor and ThorneACC+18 ].
The spectral sequence is constructed from the truncated filtration
![]() $\tau_{\leq q} R\nu_{*} \hat{\mathcal{O}}_X$
on
$\tau_{\leq q} R\nu_{*} \hat{\mathcal{O}}_X$
on
![]() $R\nu_{*} \hat{\mathcal{O}}_X$
, where
$R\nu_{*} \hat{\mathcal{O}}_X$
, where
is the structure map from the proétale site to the étale site of X, and
![]() $\hat{\mathcal{O}}_X$
is the p-adic completion of the structure sheaf
$\hat{\mathcal{O}}_X$
is the p-adic completion of the structure sheaf
![]() $\nu^* \mathcal{O}_{X_{\acute{\text{e}}\text{t}}}$
. In other words, it is the Grothendieck spectral sequence associated to the composite derived functor
$\nu^* \mathcal{O}_{X_{\acute{\text{e}}\text{t}}}$
. In other words, it is the Grothendieck spectral sequence associated to the composite derived functor
![]() $R\Gamma(X_{\acute{\text{e}}\text{t}}, - ) \circ R\nu_{*}$
evaluated on
$R\Gamma(X_{\acute{\text{e}}\text{t}}, - ) \circ R\nu_{*}$
evaluated on
![]() $\hat{\mathcal{O}}_X$
. The crucial ingredients in the construction are that we have canonical isomorphisms
$\hat{\mathcal{O}}_X$
. The crucial ingredients in the construction are that we have canonical isomorphisms
![]() $ H^i(X_{\text{pro}\acute{\text{e}}\text{t}}, \hat{\mathcal{O}}_X) \cong H^i(X_{\acute{\text{e}}\text{t}}, \mathbb{Q}_p) \otimes_{\mathbb{Q}_p} \mathbb{C}$
, and
$ H^i(X_{\text{pro}\acute{\text{e}}\text{t}}, \hat{\mathcal{O}}_X) \cong H^i(X_{\acute{\text{e}}\text{t}}, \mathbb{Q}_p) \otimes_{\mathbb{Q}_p} \mathbb{C}$
, and
![]() $R^q\nu_{*} \hat{\mathcal{O}}_X \cong \Omega^q_{X_{\acute{\text{e}}\text{t}}}({-}\;\!q)$
, see [
Reference ScholzeSch12
, section 3·3].
$R^q\nu_{*} \hat{\mathcal{O}}_X \cong \Omega^q_{X_{\acute{\text{e}}\text{t}}}({-}\;\!q)$
, see [
Reference ScholzeSch12
, section 3·3].
On the other hand, we know from [
Reference Bhatt, Morrow and ScholzeBMS18
, section 13] (see also [
Reference GuoGuo21a
] for a site theoretic construction of it) that there is a
![]() $\mathbb{B}^+_{\text{dR}}$
-cohomology theory
$\mathbb{B}^+_{\text{dR}}$
-cohomology theory
associated to X, where
![]() $\mathbb{B}^+_{\text{dR}}$
is the
$\mathbb{B}^+_{\text{dR}}$
is the
![]() $\xi$
-adic completion of
$\xi$
-adic completion of
![]() $W(\mathcal{O}_{\mathbb{C}^{\flat}})[{1}/{p}]$
, with
$W(\mathcal{O}_{\mathbb{C}^{\flat}})[{1}/{p}]$
, with
![]() $\mathbb{C}^{\flat}$
the tilt of
$\mathbb{C}^{\flat}$
the tilt of
![]() $\mathbb{C}$
and
$\mathbb{C}$
and
![]() $\xi$
a generator of the kernel of the canonical morphism
$\xi$
a generator of the kernel of the canonical morphism
![]() $W(\mathcal{O}_{\mathbb{C}^{\flat}}) \rightarrow \mathcal{O}_{\mathbb{C}}$
. They are finite free
$W(\mathcal{O}_{\mathbb{C}^{\flat}}) \rightarrow \mathcal{O}_{\mathbb{C}}$
. They are finite free
![]() $\mathbb{B}^+_{\text{dR}}$
-modules equipped with canonical morphisms
$\mathbb{B}^+_{\text{dR}}$
-modules equipped with canonical morphisms
which induces identifications
where
![]() $\mathbb{B}_{\text{dR}} := \mathbb{B}_{\text{dR}}^+[{1}/{\xi}]$
.
$\mathbb{B}_{\text{dR}} := \mathbb{B}_{\text{dR}}^+[{1}/{\xi}]$
.
We view the above identification as providing a
![]() $\mathbb{B}_{\text{dR}}^+$
-lattice
$\mathbb{B}_{\text{dR}}^+$
-lattice
![]() $ H^i_{\text{crys}}(X/\mathbb{B}^+_{\text{dR}})$
in the
$ H^i_{\text{crys}}(X/\mathbb{B}^+_{\text{dR}})$
in the
![]() $\mathbb{B}_{\text{dR}}$
-vector space
$\mathbb{B}_{\text{dR}}$
-vector space
![]() $ H^{i}_{\acute{\text{e}}\text{t}}(X,\mathbb{Q}_p) \otimes_{\mathbb{Q}_p} \mathbb{B}_{\text{dR}}$
. Note that there is another natural
$ H^{i}_{\acute{\text{e}}\text{t}}(X,\mathbb{Q}_p) \otimes_{\mathbb{Q}_p} \mathbb{B}_{\text{dR}}$
. Note that there is another natural
![]() $\mathbb{B}_{\text{dR}}^+$
-lattice
$\mathbb{B}_{\text{dR}}^+$
-lattice
![]() $ H^{i}_{\acute{\text{e}}\text{t}}(X,\mathbb{Q}_p) \otimes_{\mathbb{Q}_p} \mathbb{B}_{\text{dR}}^+$
inside it, and the relative position of the two lattices is measured by
$ H^{i}_{\acute{\text{e}}\text{t}}(X,\mathbb{Q}_p) \otimes_{\mathbb{Q}_p} \mathbb{B}_{\text{dR}}^+$
inside it, and the relative position of the two lattices is measured by
viewed as subspaces
![]() $\text{Fil}_m $
of
$\text{Fil}_m $
of
The main result of this paper confirms that this is the same filtration induced by Hodge–Tate spectral sequence on
![]() $ H^{i}_{\acute{\text{e}}\text{t}}(X,\mathbb{Q}_p) \otimes_{\mathbb{Q}_p} \mathbb{C}$
.
$ H^{i}_{\acute{\text{e}}\text{t}}(X,\mathbb{Q}_p) \otimes_{\mathbb{Q}_p} \mathbb{C}$
.
Theorem 1·1. The filtration
![]() $\textrm{Fil}_m ({-}\;\!m)$
is the same as the filtration induced by Hodge–Tate spectral sequence on
$\textrm{Fil}_m ({-}\;\!m)$
is the same as the filtration induced by Hodge–Tate spectral sequence on
![]() $ H^{i}_{\acute{\text{e}}\text{t}}(X,\mathbb{Q}_p) \otimes_{\mathbb{Q}_p} \mathbb{C}$
. More precisely,
$ H^{i}_{\acute{\text{e}}\text{t}}(X,\mathbb{Q}_p) \otimes_{\mathbb{Q}_p} \mathbb{C}$
. More precisely,
![]() $\textrm{Fil}_m({-}\;\!m)$
is equal to the image of
$\textrm{Fil}_m({-}\;\!m)$
is equal to the image of
where
![]() $\tau_{\leq m}$
is the canonical truncation up to cohomological degree m, and we have a canonical identification
$\tau_{\leq m}$
is the canonical truncation up to cohomological degree m, and we have a canonical identification
The result is well known among experts. For example, the interpretation in terms of the Bialynicki–Birula map and the theory in [
Reference ScholzeSch13
] (to be explained in the following remarks) is used in one of the constructions of Hodge–Tate period maps as in [
Reference Caraiani and ScholzeCS17
] and [
Reference HansenHan16
]. However, to the best of the author’s knowledge, the formulation as in the theorem in terms of
![]() $ H^i_{\text{crys}}(X/\mathbb{B}^+_{\text{dR}})$
is not explicit in the literature. It gives a new construction of the Hodge–Tate filtration in terms of the
$ H^i_{\text{crys}}(X/\mathbb{B}^+_{\text{dR}})$
is not explicit in the literature. It gives a new construction of the Hodge–Tate filtration in terms of the
![]() $\mathbb{B}^+_{\text{dR}}$
-cohomology
$\mathbb{B}^+_{\text{dR}}$
-cohomology
![]() $ H^i_{\text{crys}}(X/\mathbb{B}^+_{\text{dR}})$
.Footnote 1
$ H^i_{\text{crys}}(X/\mathbb{B}^+_{\text{dR}})$
.Footnote 1
The proof is to study a refinement of the decalage functor
![]() $L\eta$
introduced in [
Reference Bhatt, Morrow and ScholzeBMS18
]. It is a functor
$L\eta$
introduced in [
Reference Bhatt, Morrow and ScholzeBMS18
]. It is a functor
from the derived category of a ringed topos T to its filtered derived category. Its graded pieces can be identified, so does its reduction mod
![]() $\mathcal{I}$
. As for the functor
$\mathcal{I}$
. As for the functor
![]() $L\eta$
in [
Reference Bhatt, Morrow and ScholzeBMS18
],
$L\eta$
in [
Reference Bhatt, Morrow and ScholzeBMS18
],
![]() $L\eta_{\mathcal{I},\bullet}$
is also a special case of the functors considered in [
Reference Berthelot and OgusBO78
, definition 8·6] with p replaced by
$L\eta_{\mathcal{I},\bullet}$
is also a special case of the functors considered in [
Reference Berthelot and OgusBO78
, definition 8·6] with p replaced by
![]() $\mathcal{I}$
.Footnote 2
$\mathcal{I}$
.Footnote 2
As a byproduct of our treatment of the Hodge–Tate filtration, we give a new proof of the torsion-freeness of
![]() $ H^i_{\text{crys}}(X/\mathbb{B}^+_{\text{dR}})$
that is independent of Conrad–Gabber. It is complementary to the proofs found in the literature (see [
Reference Bhatt, Morrow and ScholzeBMS18
, 13·19] and [
Reference GuoGuo21a
, theorem 7·3·5]), which to the best of the author’s knowledge all make use of Conrad–Gabber.
$ H^i_{\text{crys}}(X/\mathbb{B}^+_{\text{dR}})$
that is independent of Conrad–Gabber. It is complementary to the proofs found in the literature (see [
Reference Bhatt, Morrow and ScholzeBMS18
, 13·19] and [
Reference GuoGuo21a
, theorem 7·3·5]), which to the best of the author’s knowledge all make use of Conrad–Gabber.
Moreover, we provide a conceptual explanation of the equivalence between degeneration of Hodge–de Rham and Hodge–Tate spectral sequence, which is implicit in the proof of [ Reference Bhatt, Morrow and ScholzeBMS18 , theorem 13·3].
Remark 1·2. The statement of the theorem includes that the Hodge–Tate spectral sequence degenerates at
![]() $E_2$
. This is actually used as an input in the proof. More precisely, we use the degeneration of both Hodge–de Rham and Hodge–Tate spectral sequencesFootnote
3
, which is proved in [
Reference Bhatt, Morrow and ScholzeBMS18
, theorem 13·3], see also [
Reference GuoGuo21a
, theorem 7·3·5], and [
Reference GuoGuo22
, theorem 1·1·3]. Both approaches depend on Conrad–Gabber spreading theorem. It would be interesting if we can find a direct proof of the degeneration.
$E_2$
. This is actually used as an input in the proof. More precisely, we use the degeneration of both Hodge–de Rham and Hodge–Tate spectral sequencesFootnote
3
, which is proved in [
Reference Bhatt, Morrow and ScholzeBMS18
, theorem 13·3], see also [
Reference GuoGuo21a
, theorem 7·3·5], and [
Reference GuoGuo22
, theorem 1·1·3]. Both approaches depend on Conrad–Gabber spreading theorem. It would be interesting if we can find a direct proof of the degeneration.
Remark 1·3. The
![]() $\mathbb{B}_{\text{dR}}^+$
-lattices in
$\mathbb{B}_{\text{dR}}^+$
-lattices in
![]() $ H^{i}_{\acute{\text{e}}\text{t}}(X,\mathbb{Q}_p) \otimes_{\mathbb{Q}_p} \mathbb{B}_{\text{dR}}$
are parameterised by the
$ H^{i}_{\acute{\text{e}}\text{t}}(X,\mathbb{Q}_p) \otimes_{\mathbb{Q}_p} \mathbb{B}_{\text{dR}}$
are parameterised by the
![]() $\mathbb{C}$
-points of
$\mathbb{C}$
-points of
![]() $\mathbb{B}_{\text{dR}}^+$
-affine Grassmannian
$\mathbb{B}_{\text{dR}}^+$
-affine Grassmannian
![]() $Gr_{GL_n}^{\mathbb{B}_{\text{dR}}^+}$
as defined in [
Reference Caraiani and ScholzeCS17
, definition 3·4·1], see [
Reference Scholze and WeinsteinSW20
, lecture 19] as well, where n is the dimension of
$Gr_{GL_n}^{\mathbb{B}_{\text{dR}}^+}$
as defined in [
Reference Caraiani and ScholzeCS17
, definition 3·4·1], see [
Reference Scholze and WeinsteinSW20
, lecture 19] as well, where n is the dimension of
![]() $ H^{i}_{\acute{\text{e}}\text{t}}(X,\mathbb{Q}_p)$
. The subspaces
$ H^{i}_{\acute{\text{e}}\text{t}}(X,\mathbb{Q}_p)$
. The subspaces
![]() $\textrm{Fil}_m({-}\;\!m)$
are parameterised by the (
$\textrm{Fil}_m({-}\;\!m)$
are parameterised by the (
![]() $\mathbb{C}$
-points of) flag variety with respect to the vector space
$\mathbb{C}$
-points of) flag variety with respect to the vector space
![]() $ H^{i}_{\acute{\text{e}}\text{t}}(X,\mathbb{Q}_p) \otimes_{\mathbb{Q}_p} \mathbb{C}$
, and
$ H^{i}_{\acute{\text{e}}\text{t}}(X,\mathbb{Q}_p) \otimes_{\mathbb{Q}_p} \mathbb{C}$
, and
![]() $\textrm{Fil}_m({-}\;\!m)$
associated to the lattice
$\textrm{Fil}_m({-}\;\!m)$
associated to the lattice
![]() $ H^i_{\text{crys}}(X/\mathbb{B}^+_{\text{dR}})$
is exactly its image under the Bialynicki–Birula map as defined in [
Reference Caraiani and ScholzeCS17
, proposition 3·4·3] from the affine Grassmannian to the flag variety.Footnote
4
$ H^i_{\text{crys}}(X/\mathbb{B}^+_{\text{dR}})$
is exactly its image under the Bialynicki–Birula map as defined in [
Reference Caraiani and ScholzeCS17
, proposition 3·4·3] from the affine Grassmannian to the flag variety.Footnote
4
Remark 1·4. When X is defined over a discretely valued field, we know from the results in [
Reference Bhatt, Morrow and ScholzeBMS18
, section 13] that
![]() $ H^i_{\text{crys}}(X_{\mathbb{C}}/\mathbb{B}^+_{\text{dR}})$
can be computed as the de Rham cohomology of X base changed to
$ H^i_{\text{crys}}(X_{\mathbb{C}}/\mathbb{B}^+_{\text{dR}})$
can be computed as the de Rham cohomology of X base changed to
![]() $\mathbb{B}^+_{\text{dR}}$
. Then the theorem follows from [
Reference ScholzeSch13
, theorem 8·4].
$\mathbb{B}^+_{\text{dR}}$
. Then the theorem follows from [
Reference ScholzeSch13
, theorem 8·4].
Moreover, using the spreading theorem of Conrad–Gabber (see [
Reference Bhatt, Morrow and ScholzeBMS18
, corollary 13·16]), we can deduce the theorem from [
Reference ScholzeSch13
, theorem 8·8, and proposition 7·9]. Note that the condition of theorem 8·8. in
![]() $loc.cit.$
is proved in [
Reference Scholze and WeinsteinSW20
, theorem 10·5·1] and the paragraph following it. We believe that it is more natural to prove the theorem directly from the very construction of
$loc.cit.$
is proved in [
Reference Scholze and WeinsteinSW20
, theorem 10·5·1] and the paragraph following it. We believe that it is more natural to prove the theorem directly from the very construction of
![]() $ H^i_{\text{crys}}(X/\mathbb{B}^+_{\text{dR}})$
, thereby avoiding the use of theory of
$ H^i_{\text{crys}}(X/\mathbb{B}^+_{\text{dR}})$
, thereby avoiding the use of theory of
![]() $\mathcal{O}\mathbb{B}^+_{\text{dR}}$
-modules in [
Reference ScholzeSch13
]. However, we still cannot avoid Conrad–Gabber in our treatment, see Remark 1·2.
$\mathcal{O}\mathbb{B}^+_{\text{dR}}$
-modules in [
Reference ScholzeSch13
]. However, we still cannot avoid Conrad–Gabber in our treatment, see Remark 1·2.
2. Recollections
Let us first recall the construction of
![]() $ H^i_{\text{crys}}(X/\mathbb{B}^+_{\text{dR}})$
. The original construction in [
Reference Bhatt, Morrow and ScholzeBMS18
] is to construct an explicit complex for each small affinoid X, and then glue. In [
Reference GuoGuo21a
], Guo defined an infinitesimal site and reconstruct
$ H^i_{\text{crys}}(X/\mathbb{B}^+_{\text{dR}})$
. The original construction in [
Reference Bhatt, Morrow and ScholzeBMS18
] is to construct an explicit complex for each small affinoid X, and then glue. In [
Reference GuoGuo21a
], Guo defined an infinitesimal site and reconstruct
![]() $ H^i_{\text{crys}}(X/\mathbb{B}^+_{\text{dR}})$
as the cohomology of the structure sheaf on this site. Further, the
$ H^i_{\text{crys}}(X/\mathbb{B}^+_{\text{dR}})$
as the cohomology of the structure sheaf on this site. Further, the
![]() $\mathbb{B}^+_{\text{dR}}$
-prismatic site is introduced in [
Reference GuoGuo21b
], which unifies the previous constructions. We will use the formulation of
$\mathbb{B}^+_{\text{dR}}$
-prismatic site is introduced in [
Reference GuoGuo21b
], which unifies the previous constructions. We will use the formulation of
![]() $\mathbb{B}^+_{\text{dR}}$
-prismatic site for convenience, but the original construction of [
Reference Bhatt, Morrow and ScholzeBMS18
] can also be invoked here.
$\mathbb{B}^+_{\text{dR}}$
-prismatic site for convenience, but the original construction of [
Reference Bhatt, Morrow and ScholzeBMS18
] can also be invoked here.
For our purpose, we only need to know that
![]() $ H^i_{\text{crys}}(X/\mathbb{B}^+_{\text{dR}})$
can be computed as the cohomology of a sheaf of complexes
$ H^i_{\text{crys}}(X/\mathbb{B}^+_{\text{dR}})$
can be computed as the cohomology of a sheaf of complexes
on the étale site
![]() $X_{\acute{\text{e}}\text{t}}$
of X, where
$X_{\acute{\text{e}}\text{t}}$
of X, where
![]() $L\eta_{\xi}$
is the decalage functor with respect to
$L\eta_{\xi}$
is the decalage functor with respect to
![]() $\xi$
as defined in [
Reference Bhatt, Morrow and ScholzeBMS18
, section 6], and
$\xi$
as defined in [
Reference Bhatt, Morrow and ScholzeBMS18
, section 6], and
![]() $\Delta_{X/\mathbb{B}^+_{\text{dR}}}$
is the sheaf of complexesFootnote 5 of
$\Delta_{X/\mathbb{B}^+_{\text{dR}}}$
is the sheaf of complexesFootnote 5 of
![]() $\mathbb{B}^+_{\text{dR}}$
-modules on
$\mathbb{B}^+_{\text{dR}}$
-modules on
![]() $X_{\acute{\text{e}}\text{t}}$
which sends every affinoid to its derived
$X_{\acute{\text{e}}\text{t}}$
which sends every affinoid to its derived
![]() $\mathbb{B}^+_{\text{dR}}$
-prismatic cohomology (with respect to the structure sheaf) as defined in [
Reference GuoGuo21b
, section 2]. In other words, we have
$\mathbb{B}^+_{\text{dR}}$
-prismatic cohomology (with respect to the structure sheaf) as defined in [
Reference GuoGuo21b
, section 2]. In other words, we have
which is [ Reference GuoGuo21b , theorem 6·0·1].
It is proved in [ Reference GuoGuo21b , theorem 5·1·1] and the discussion before it that we have a canonical quasi-isomorphism
where the first isomorphism is [
Reference Bhatt, Morrow and ScholzeBMS18
, proposition 6·12], and
![]() $\Omega_X^{\bullet}$
is the de Rham complex of X.
$\Omega_X^{\bullet}$
is the de Rham complex of X.
Moreover, there is a natural quasi-isomorphism
where
![]() $\mathbb{B}^+_{\text{dR}}$
is, by abuse of notation, the
$\mathbb{B}^+_{\text{dR}}$
is, by abuse of notation, the
![]() $\mathbb{B}^+_{\text{dR}}$
-period sheaf on
$\mathbb{B}^+_{\text{dR}}$
-period sheaf on
![]() $X_{\text{pro}\acute{\text{e}}\text{t}}$
as defined in [
Reference ScholzeSch13
, definition 6·1]. The first isomorphism is [
Reference GuoGuo21b
, theorem 7·2·1], the second is in the proof of [
Reference ScholzeSch13
, theorem 8·4]. The canonical comparison morphism
$X_{\text{pro}\acute{\text{e}}\text{t}}$
as defined in [
Reference ScholzeSch13
, definition 6·1]. The first isomorphism is [
Reference GuoGuo21b
, theorem 7·2·1], the second is in the proof of [
Reference ScholzeSch13
, theorem 8·4]. The canonical comparison morphism
is induced from the canonical map
together with the identification. Note that
![]() $\iota$
exists because
$\iota$
exists because
![]() $\Delta_{X/\mathbb{B}^+_{\text{dR}}} \in D_{\geq 0}$
and
$\Delta_{X/\mathbb{B}^+_{\text{dR}}} \in D_{\geq 0}$
and
![]() $ H^0(\Delta_{X/\mathbb{B}^+_{\text{dR}}} )$
is
$ H^0(\Delta_{X/\mathbb{B}^+_{\text{dR}}} )$
is
![]() $\xi$
-torsion-free.
$\xi$
-torsion-free.
Lastly, it follows from the proof of [ Reference GuoGuo21b , theorem 7·2·1] that we have a natural quasi-isomorphism
where
![]() $\nu: X_{\text{pro}\acute{\text{e}}\text{t}} \rightarrow X_{\acute{\text{e}}\text{t}}$
and
$\nu: X_{\text{pro}\acute{\text{e}}\text{t}} \rightarrow X_{\acute{\text{e}}\text{t}}$
and
![]() $\hat{\mathcal{O}}_X$
are as in the introduction.
$\hat{\mathcal{O}}_X$
are as in the introduction.
3. A refinement of
 $L\eta$
-functor
$L\eta$
-functor
In this section, we construct a refinement of the decalage functor
![]() $L\eta$
introduced in [
Reference Bhatt, Morrow and ScholzeBMS18
], which is a special case of the construction in [
Reference Berthelot and OgusBO78
, definition 8·6] with p replaced by
$L\eta$
introduced in [
Reference Bhatt, Morrow and ScholzeBMS18
], which is a special case of the construction in [
Reference Berthelot and OgusBO78
, definition 8·6] with p replaced by
![]() $\mathcal{I}$
. We work in the same setting as [
Reference Bhatt, Morrow and ScholzeBMS18
].
$\mathcal{I}$
. We work in the same setting as [
Reference Bhatt, Morrow and ScholzeBMS18
].
Let
![]() $(T, \mathcal{O}_T)$
be a ringed topos, and
$(T, \mathcal{O}_T)$
be a ringed topos, and
![]() $D(\mathcal{O}_T)$
the derived category of
$D(\mathcal{O}_T)$
the derived category of
![]() $\mathcal{O}_T$
-modules. Let
$\mathcal{O}_T$
-modules. Let
![]() $\mathcal{I} \subset \mathcal{O}_T$
be an invertible ideal sheaf.
$\mathcal{I} \subset \mathcal{O}_T$
be an invertible ideal sheaf.
Recall that a complex
![]() $K^{\bullet}$
of
$K^{\bullet}$
of
![]() $\mathcal{O}_T$
-modules is said to be
$\mathcal{O}_T$
-modules is said to be
![]() $\mathcal{I}$
-torsion-free if the canonical map
$\mathcal{I}$
-torsion-free if the canonical map
![]() $\mathcal{I}\otimes K^i \rightarrow K^i$
is injective for every i, and we can define a complex
$\mathcal{I}\otimes K^i \rightarrow K^i$
is injective for every i, and we can define a complex
![]() $(\eta_{\mathcal{I}} K)^{\bullet}$
with terms
$(\eta_{\mathcal{I}} K)^{\bullet}$
with terms
where
![]() $K^{\bullet}$
is a
$K^{\bullet}$
is a
![]() $\mathcal{I}$
-torsion-free complex, and there is a natural differential map making
$\mathcal{I}$
-torsion-free complex, and there is a natural differential map making
![]() $\eta_{\mathcal{I}} K^{\bullet} $
a complex. By [
Reference Bhatt, Morrow and ScholzeBMS18
, lemma 6·4], we have
$\eta_{\mathcal{I}} K^{\bullet} $
a complex. By [
Reference Bhatt, Morrow and ScholzeBMS18
, lemma 6·4], we have
so we can derive the construction to obtain a functor
Definition 3·1. Let
![]() $m \in \mathbb{Z}$
, and
$m \in \mathbb{Z}$
, and
![]() $K^{\bullet }$
an
$K^{\bullet }$
an
![]() $\mathcal{I}$
-torsion-free complex of
$\mathcal{I}$
-torsion-free complex of
![]() $\mathcal{O}_T$
-modules. Define a new complex
$\mathcal{O}_T$
-modules. Define a new complex
![]() $(\eta_{\mathcal{I},m} K)^{\bullet}$
with terms
$(\eta_{\mathcal{I},m} K)^{\bullet}$
with terms
 \begin{equation*}(\eta_{\mathcal{I},m} K)^i =\begin{cases} (\eta_{\mathcal{I}}K)^i & i \geq m \\ K^i \otimes_{\mathcal{O}_T} \mathcal{I}^{\otimes m} & i < m. \end{cases}\end{equation*}
\begin{equation*}(\eta_{\mathcal{I},m} K)^i =\begin{cases} (\eta_{\mathcal{I}}K)^i & i \geq m \\ K^i \otimes_{\mathcal{O}_T} \mathcal{I}^{\otimes m} & i < m. \end{cases}\end{equation*}
The differential is inherited from that of
![]() $\eta_{\mathcal{I}}K$
(resp.
$\eta_{\mathcal{I}}K$
(resp.
![]() $K^{\bullet}$
(
$K^{\bullet}$
(
![]() $\otimes \text{Id}_{\mathcal{I}^{\otimes m}}$
)) for
$\otimes \text{Id}_{\mathcal{I}^{\otimes m}}$
)) for
![]() $i \geq m$
(resp.
$i \geq m$
(resp.
![]() $i< m-1$
). For
$i< m-1$
). For
![]() $i=m-1$
, the differential
$i=m-1$
, the differential
is defined to be
![]() $d \otimes \text{Id}_{\mathcal{I}^{\otimes m}}$
.
$d \otimes \text{Id}_{\mathcal{I}^{\otimes m}}$
.
We first compute the cohomology of
![]() $\eta_{\mathcal{I},m} K^{\bullet}$
.
$\eta_{\mathcal{I},m} K^{\bullet}$
.
Lemma 3·2. Let
![]() $K^{\bullet}$
be an
$K^{\bullet}$
be an
![]() $\mathcal{I}$
-torsion-free complex, then we have a natural isomorphism
$\mathcal{I}$
-torsion-free complex, then we have a natural isomorphism
 \begin{equation*} H^i(\eta_{\mathcal{I},m} K^{\bullet}) \cong\begin{cases} H^i(\eta_{\mathcal{I}} K^{\bullet}) & i > m \\ H^i( K^{\bullet}) \otimes_{\mathcal{O}_T} \mathcal{I}^{\otimes m} & i \leq m. \end{cases}\end{equation*}
\begin{equation*} H^i(\eta_{\mathcal{I},m} K^{\bullet}) \cong\begin{cases} H^i(\eta_{\mathcal{I}} K^{\bullet}) & i > m \\ H^i( K^{\bullet}) \otimes_{\mathcal{O}_T} \mathcal{I}^{\otimes m} & i \leq m. \end{cases}\end{equation*}
Proof. This is obvious except for
![]() $i=m,m-1$
. For
$i=m,m-1$
. For
![]() $i=m-1$
, we simply note that
$i=m-1$
, we simply note that
![]() $(\eta_{\mathcal{I}}K)^m$
is a subspace of
$(\eta_{\mathcal{I}}K)^m$
is a subspace of
![]() $K^m \otimes_{\mathcal{O}_T} \mathcal{I}^{\otimes m}$
, so the kernel of d at
$K^m \otimes_{\mathcal{O}_T} \mathcal{I}^{\otimes m}$
, so the kernel of d at
![]() $m-1$
is the same as
$m-1$
is the same as
![]() $Z^{m-1}(K^{\bullet}) \otimes_{\mathcal{O}_T} \mathcal{I}^{\otimes m} $
, the cocycles of
$Z^{m-1}(K^{\bullet}) \otimes_{\mathcal{O}_T} \mathcal{I}^{\otimes m} $
, the cocycles of
![]() $K^{\bullet}$
twisted by
$K^{\bullet}$
twisted by
![]() $\mathcal{I}^{\otimes m} $
.
$\mathcal{I}^{\otimes m} $
.
For
![]() $i=m$
, we observe that the cocycle space is
$i=m$
, we observe that the cocycle space is
![]() $Z^m(K^{\bullet}) \otimes_{\mathcal{O}_T} \mathcal{I}^{\otimes m} $
, and the coboundary is exactly
$Z^m(K^{\bullet}) \otimes_{\mathcal{O}_T} \mathcal{I}^{\otimes m} $
, and the coboundary is exactly
![]() $B^m(K^{\bullet}) \otimes_{\mathcal{O}_T} \mathcal{I}^{\otimes m}$
.
$B^m(K^{\bullet}) \otimes_{\mathcal{O}_T} \mathcal{I}^{\otimes m}$
.
We can now dervie the
![]() $\eta_{\mathcal{I},m}$
-construction to obtain a functor
$\eta_{\mathcal{I},m}$
-construction to obtain a functor
The most important property of
![]() $L\eta_{\mathcal{I},m}$
is that it forms a filtration. In other words, for every
$L\eta_{\mathcal{I},m}$
is that it forms a filtration. In other words, for every
![]() $\mathcal{I}$
-torsion-free complex
$\mathcal{I}$
-torsion-free complex
![]() $K^{\bullet}$
, we have a canonical filtration
$K^{\bullet}$
, we have a canonical filtration
The inclusion
![]() $\eta_{\mathcal{I},m+1} K^{\bullet} \subset \eta_{\mathcal{I},m} K^{\bullet} $
at degrees
$\eta_{\mathcal{I},m+1} K^{\bullet} \subset \eta_{\mathcal{I},m} K^{\bullet} $
at degrees
![]() $i\geq m+1$
(resp.
$i\geq m+1$
(resp.
![]() $i\leq m-1$
) is the identity of
$i\leq m-1$
) is the identity of
![]() $(\eta_{\mathcal{I}} K^{\bullet})^i$
(resp.
$(\eta_{\mathcal{I}} K^{\bullet})^i$
(resp.
![]() $\text{id}_{K^i \otimes_{\mathcal{O}_T} \mathcal{I}^{\otimes m}} \otimes (\mathcal{I} \hookrightarrow \mathcal{O}_T) $
). For degree m, it is given by the canonical inclusion
$\text{id}_{K^i \otimes_{\mathcal{O}_T} \mathcal{I}^{\otimes m}} \otimes (\mathcal{I} \hookrightarrow \mathcal{O}_T) $
). For degree m, it is given by the canonical inclusion
induced by
![]() $(\mathcal{I} \hookrightarrow \mathcal{O}_T )\otimes \text{id}_{\mathcal{I}^{\otimes m}}$
. We can summarise the information as in the diagram
$(\mathcal{I} \hookrightarrow \mathcal{O}_T )\otimes \text{id}_{\mathcal{I}^{\otimes m}}$
. We can summarise the information as in the diagram

We can compute the graded pieces of the filtration.
Lemma 3·3. Let
![]() $K^{\bullet}$
be an
$K^{\bullet}$
be an
![]() $\mathcal{I}$
-torsion-free complex, we have a canonical isomorphism
$\mathcal{I}$
-torsion-free complex, we have a canonical isomorphism
Proof. This is obvious except for degree m. We compute that
but this is exactly the degree m part of
![]() $\tau_{\leq m} (K^{\bullet} \otimes_{\mathcal{O}_T} \mathcal{O}_T/\mathcal{I}) \otimes_{\mathcal{O}_T} \mathcal{I}^{\otimes m}$
by definition of
$\tau_{\leq m} (K^{\bullet} \otimes_{\mathcal{O}_T} \mathcal{O}_T/\mathcal{I}) \otimes_{\mathcal{O}_T} \mathcal{I}^{\otimes m}$
by definition of
![]() $\tau_{\leq m} $
.
$\tau_{\leq m} $
.
A good way to package the information of
![]() $\eta_{\mathcal{I},m}$
-construction is to view
$\eta_{\mathcal{I},m}$
-construction is to view
![]() $\{ L \eta_{\mathcal{I},m} \}_{m \in \mathbb{Z}}$
as a functor
$\{ L \eta_{\mathcal{I},m} \}_{m \in \mathbb{Z}}$
as a functor
from the derived category
![]() $D(\mathcal{O}_T)$
to the filtered derived category of
$D(\mathcal{O}_T)$
to the filtered derived category of
![]() $\mathcal{O}_T$
. Moreover, the graded quotient functor can be identified as
$\mathcal{O}_T$
. Moreover, the graded quotient functor can be identified as
The next result we want to establish is the behaviour of
![]() $L \eta_{\mathcal{I},\bullet}$
under the quotient by
$L \eta_{\mathcal{I},\bullet}$
under the quotient by
![]() $\mathcal{I}$
. Recall as in [
Reference Bhatt, Morrow and ScholzeBMS18
, proposition 6·12] we have a canonical quasi-isomorphism
$\mathcal{I}$
. Recall as in [
Reference Bhatt, Morrow and ScholzeBMS18
, proposition 6·12] we have a canonical quasi-isomorphism
where
![]() $ H^{\bullet}( K/\mathcal{I})$
is the complex whose degree i th term is
$ H^{\bullet}( K/\mathcal{I})$
is the complex whose degree i th term is
![]() $ H^i(K \otimes^L_{\mathcal{O}_T} \mathcal{O}_T/\mathcal{I}) \otimes_{\mathcal{O}_T} \mathcal{I}^{\otimes i}$
and the differential is given by the Bockstein map with respect to
$ H^i(K \otimes^L_{\mathcal{O}_T} \mathcal{O}_T/\mathcal{I}) \otimes_{\mathcal{O}_T} \mathcal{I}^{\otimes i}$
and the differential is given by the Bockstein map with respect to
We will prove a slight refinement of the result for
![]() $L \eta_{\mathcal{I},\bullet}$
.
$L \eta_{\mathcal{I},\bullet}$
.
Let
![]() $K^{\bullet}$
be a
$K^{\bullet}$
be a
![]() $\mathcal{I}$
-torsion-free complex, we first observe that there is a canonical filtration
$\mathcal{I}$
-torsion-free complex, we first observe that there is a canonical filtration
which in particular explains why
![]() $\eta_{\mathcal{I},m} K^{\bullet}/\eta_{\mathcal{I},m+1} K^{\bullet}$
is an
$\eta_{\mathcal{I},m} K^{\bullet}/\eta_{\mathcal{I},m+1} K^{\bullet}$
is an
![]() $\mathcal{O}_T / \mathcal{I}$
-complex. We have identified the second graded piece, and the first graded piece can also be computed as follows.
$\mathcal{O}_T / \mathcal{I}$
-complex. We have identified the second graded piece, and the first graded piece can also be computed as follows.
Proposition 3·4. Let
![]() $K^{\bullet}$
be an
$K^{\bullet}$
be an
![]() $\mathcal{I}$
-torsion-free complex, then we have a canonical quasi-isomorphism
$\mathcal{I}$
-torsion-free complex, then we have a canonical quasi-isomorphism
where
![]() $ F_{m+1}$
is the stupid filtration of complexes, i.e.
$ F_{m+1}$
is the stupid filtration of complexes, i.e.
 \begin{equation*}( F_{m+1} C^{\bullet})^i =\begin{cases} C^i & i \geq m+1 \\ 0 & i \leq m. \end{cases}\end{equation*}
\begin{equation*}( F_{m+1} C^{\bullet})^i =\begin{cases} C^i & i \geq m+1 \\ 0 & i \leq m. \end{cases}\end{equation*}
Proof. We see immediately from the definition that the degree
![]() $\geq m+1$
(resp.
$\geq m+1$
(resp.
![]() $\leq m-1$
) part of the left-hand side is
$\leq m-1$
) part of the left-hand side is
![]() $(\eta_{\mathcal{I}} K^{\bullet})^i \otimes_{\mathcal{O}_T} \mathcal{O}_T/\mathcal{I}$
(resp. 0). It remains to identify the degree m-part of the LHS.
$(\eta_{\mathcal{I}} K^{\bullet})^i \otimes_{\mathcal{O}_T} \mathcal{O}_T/\mathcal{I}$
(resp. 0). It remains to identify the degree m-part of the LHS.
By definition
which is identified through the differential with
where
![]() $B^{m+1}(K^{\bullet} \otimes_{\mathcal{O}_T} \mathcal{O}_T / \mathcal{I})$
is the image of
$B^{m+1}(K^{\bullet} \otimes_{\mathcal{O}_T} \mathcal{O}_T / \mathcal{I})$
is the image of
![]() $(K^{\bullet} \otimes_{\mathcal{O}_T} \mathcal{O}_T / \mathcal{I})^m$
inside
$(K^{\bullet} \otimes_{\mathcal{O}_T} \mathcal{O}_T / \mathcal{I})^m$
inside
![]() $(K^{\bullet} \otimes_{\mathcal{O}_T} \mathcal{O}_T / \mathcal{I})^{m+1}$
.
$(K^{\bullet} \otimes_{\mathcal{O}_T} \mathcal{O}_T / \mathcal{I})^{m+1}$
.
We first prove that the m th cohomology of the LHS is trivial. This is equivalent to the differential map
being injective. But this is clear, if
![]() $x \in K^m$
is mapped to
$x \in K^m$
is mapped to
![]() $\mathcal{I} \{ y \in K^{m+1} | dy \in \mathcal{I} K^{m+2} \} $
, namely
$\mathcal{I} \{ y \in K^{m+1} | dy \in \mathcal{I} K^{m+2} \} $
, namely
![]() $dx \in \mathcal{I} \{ y \in K^{m+1} | dy \in \mathcal{I} K^{m+2} \} \subset \mathcal{I} K^{m+1}$
, proving that
$dx \in \mathcal{I} \{ y \in K^{m+1} | dy \in \mathcal{I} K^{m+2} \} \subset \mathcal{I} K^{m+1}$
, proving that
![]() $\bar{x}$
is zero in the left-hand side.
$\bar{x}$
is zero in the left-hand side.
We can now proceed exactly as in the proof of [ Reference Bhatt, Morrow and ScholzeBMS18 , proposition 6·12]. We have canonical maps
which induces the quasi-isomorphism
We have a commutative diagram

where the differential on the right-hand side is induced from the Bockstein map, except the second to the lowest one, which is the canonical inclusion.
It induces a quasi-isomorphism in degrees
![]() $\geq m+2$
by [
Reference Bhatt, Morrow and ScholzeBMS18
, proposition 6·12], and we have seen that the degree m cohomology of both sides are trivial. Thus it remains to show that it induces a quasi-isomorphism in degree
$\geq m+2$
by [
Reference Bhatt, Morrow and ScholzeBMS18
, proposition 6·12], and we have seen that the degree m cohomology of both sides are trivial. Thus it remains to show that it induces a quasi-isomorphism in degree
![]() $m+1$
, this is the same as the proof of
$m+1$
, this is the same as the proof of
![]() $loc.cit.$
.
$loc.cit.$
.
We first prove that the map on
![]() $m+1$
th cohomology is surjective. Let
$m+1$
th cohomology is surjective. Let
![]() $\bar{x}\in Z^{m+1}(K^{\bullet} \otimes_{\mathcal{O}_T} \mathcal{O}_T/\mathcal{I})$
be a cocycle under Bockstein map, then by definition there exists a lift
$\bar{x}\in Z^{m+1}(K^{\bullet} \otimes_{\mathcal{O}_T} \mathcal{O}_T/\mathcal{I})$
be a cocycle under Bockstein map, then by definition there exists a lift
![]() $x \in K^{m+1}$
of
$x \in K^{m+1}$
of
![]() $\bar{x}$
together with
$\bar{x}$
together with
![]() $y \in \mathcal{I} K^{m+1}$
such that
$y \in \mathcal{I} K^{m+1}$
such that
![]() $dx \equiv dy \ \text{mod} \ \mathcal{I}^2 K^{m+2}$
. This implies that
$dx \equiv dy \ \text{mod} \ \mathcal{I}^2 K^{m+2}$
. This implies that
![]() $x \in \{ x \in K^{m+1} | dx \in \mathcal{I} K^{m+2} \} $
. Moreover, it tells us that
$x \in \{ x \in K^{m+1} | dx \in \mathcal{I} K^{m+2} \} $
. Moreover, it tells us that
![]() $dx \in \mathcal{I} \{ x \in K^{m+2} | dx \in \mathcal{I} K^{m+3} \} $
, which means x defines a cocycle on the LHS that maps to
$dx \in \mathcal{I} \{ x \in K^{m+2} | dx \in \mathcal{I} K^{m+3} \} $
, which means x defines a cocycle on the LHS that maps to
![]() $\bar{x}$
.
$\bar{x}$
.
Now we show that the map on cohomology is injective. Let
![]() $x \in \{ x \in K^{m+1} | dx \in \mathcal{I} K^{m+2} \} $
whose reduction in
$x \in \{ x \in K^{m+1} | dx \in \mathcal{I} K^{m+2} \} $
whose reduction in
![]() $\{ x \in K^{m+1} | dx \in \mathcal{I} K^{m+2} \}/ \mathcal{I} \{ x \in K^{m+1} | dx \in \mathcal{I} K^{m+2} \}$
is a cocycle on the LHS. Moreover, we assume that its reduction
$\{ x \in K^{m+1} | dx \in \mathcal{I} K^{m+2} \}/ \mathcal{I} \{ x \in K^{m+1} | dx \in \mathcal{I} K^{m+2} \}$
is a cocycle on the LHS. Moreover, we assume that its reduction
![]() $\bar{x} \in K^{m+1}/\mathcal{I}$
lies in
$\bar{x} \in K^{m+1}/\mathcal{I}$
lies in
![]() $B^{m+1}(K^{\bullet} \otimes_{\mathcal{O}_T} \mathcal{O}_T / \mathcal{I})$
. By the isomorphism of the lower horizontal map, there exists
$B^{m+1}(K^{\bullet} \otimes_{\mathcal{O}_T} \mathcal{O}_T / \mathcal{I})$
. By the isomorphism of the lower horizontal map, there exists
![]() $y \in K^m$
such that
$y \in K^m$
such that
![]() $dy \equiv x \ \text{mod} \ \mathcal{I} K^{m+1}$
. The cocycle condition implies that
$dy \equiv x \ \text{mod} \ \mathcal{I} K^{m+1}$
. The cocycle condition implies that
![]() $dx \in \mathcal{I}^2 \{ x \in K^{m+2} | dx \in \mathcal{I} K^{m+3} \}$
, but this implies that
$dx \in \mathcal{I}^2 \{ x \in K^{m+2} | dx \in \mathcal{I} K^{m+3} \}$
, but this implies that
![]() $dy \equiv x \ \text{mod} \ \mathcal{I} \{ x \in K^{m+1} | dx \in \mathcal{I} K^{m+2} \}$
, i.e. x defines a trivial cohomological class on the LHS.
$dy \equiv x \ \text{mod} \ \mathcal{I} \{ x \in K^{m+1} | dx \in \mathcal{I} K^{m+2} \}$
, i.e. x defines a trivial cohomological class on the LHS.
Corollary 3·5. Let
![]() $K^{\bullet}$
be a
$K^{\bullet}$
be a
![]() $\mathcal{I}$
-torsion-free complex, then
$\mathcal{I}$
-torsion-free complex, then
 \begin{equation*} H^i(\eta_{\mathcal{I},m} K^{\bullet} \otimes_{\mathcal{O}_T} \mathcal{O}_T /\mathcal{I} )\cong\begin{cases} H^i( H^{\bullet}(K/\mathcal{I})) & i \geq m+1 \\ Z^m( H^{\bullet}(K/\mathcal{I})) & i=m \\ H^i(K^{\bullet} \otimes_{\mathcal{O}_T} \mathcal{O}_T/\mathcal{I}) \otimes_{\mathcal{O}_T} \mathcal{I}^{\otimes m} & i \leq m-1. \end{cases}\end{equation*}
\begin{equation*} H^i(\eta_{\mathcal{I},m} K^{\bullet} \otimes_{\mathcal{O}_T} \mathcal{O}_T /\mathcal{I} )\cong\begin{cases} H^i( H^{\bullet}(K/\mathcal{I})) & i \geq m+1 \\ Z^m( H^{\bullet}(K/\mathcal{I})) & i=m \\ H^i(K^{\bullet} \otimes_{\mathcal{O}_T} \mathcal{O}_T/\mathcal{I}) \otimes_{\mathcal{O}_T} \mathcal{I}^{\otimes m} & i \leq m-1. \end{cases}\end{equation*}
Moreover, the connecting morphism
of the distinguished triangle
factorises as

where
![]() $\beta$
is the differential of the complex
$\beta$
is the differential of the complex
![]() $ H^{\bullet}(K/\mathcal{I})$
, namely the Bockstein map.
$ H^{\bullet}(K/\mathcal{I})$
, namely the Bockstein map.
Lastly, the long exact sequence associated to the distinguished triangle gives
which is identified with
Proof. The statement follows immediately from the long exact sequence associated to the distinguished triangle together with Proposition 3·4 and Lemma 3·3, once we have identified the connecting morphism.
The factorisation of the connecting morphism follows from an easy t-structure argument, by noting that the source (resp. target) lies in
![]() $D_{\leq m}(\mathcal{O}_T)$
(resp.
$D_{\leq m}(\mathcal{O}_T)$
(resp.
![]() $D_{\geq m}(\mathcal{O}_T)$
). We now prove that the factorisation
$D_{\geq m}(\mathcal{O}_T)$
). We now prove that the factorisation
![]() $\beta$
is the Bockstein differential map. This follows easily from a diagram chasing. We write down the diagram of the distinguished triangle
$\beta$
is the Bockstein differential map. This follows easily from a diagram chasing. We write down the diagram of the distinguished triangle

Given
![]() $\bar{x} \in Z^m(K^{\bullet}/\mathcal{I}K^{\bullet})$
representing an element of
$\bar{x} \in Z^m(K^{\bullet}/\mathcal{I}K^{\bullet})$
representing an element of
![]() $ H^{\bullet}(K/\mathcal{I})^m$
, we choose a lift
$ H^{\bullet}(K/\mathcal{I})^m$
, we choose a lift
![]() $x \in \{ x \in K^m | dx \in \mathcal{I} K^{m+1} \}$
of it. Then
$x \in \{ x \in K^m | dx \in \mathcal{I} K^{m+1} \}$
of it. Then
![]() $\beta(\bar{x})$
is represented by dx viewed as an element of
$\beta(\bar{x})$
is represented by dx viewed as an element of
![]() $ \mathcal{I} K^{m+1} / \mathcal{I} \{ x \in K^{m+1} | dx \in \mathcal{I} K^{m+2} \}$
, but this clearly also represents the Bockstein map of
$ \mathcal{I} K^{m+1} / \mathcal{I} \{ x \in K^{m+1} | dx \in \mathcal{I} K^{m+2} \}$
, but this clearly also represents the Bockstein map of
![]() $\bar{x}$
.
$\bar{x}$
.
We have another natural inclusion
giving rise to the distinguished triangle
with connecting morphism
which has to be zero since the source and target sit in different cohomological degrees. Thus we have a splitting
Then Proposition 3·4 and Lemma 3·3 identify the direct summand.
Corollary 3·6. Let
![]() $K^{\bullet}$
be a
$K^{\bullet}$
be a
![]() $\mathcal{I}$
-torsion-free complex, we have an identification
$\mathcal{I}$
-torsion-free complex, we have an identification
which splits the distinguished triangle
Moreover, the distinguished triangle
is compatible with the splitting in the sense that we have a commutative diagram

where the the arrows a and b are the canonical map corresponding to the Hodge filtration and standard truncated filtration respectively, while c and d are graded quotient maps corresponding to them.
4. Proof
We now start the proof of the theorem. We first observe that the Bialynicki–Birula type construction of Fil
![]() $_m$
is fundamentally on cohomology groups, whereas the Hodge–Tate filtration, in the classical construction, originates from a filtration on complexes. Thus a natural way to proceed is to upgrade
$_m$
is fundamentally on cohomology groups, whereas the Hodge–Tate filtration, in the classical construction, originates from a filtration on complexes. Thus a natural way to proceed is to upgrade
![]() $\text{Fil}_m$
to a filtration on complexes and then compare the two filtration on the derived category level. This is achieved by the
$\text{Fil}_m$
to a filtration on complexes and then compare the two filtration on the derived category level. This is achieved by the
![]() $L\eta_{\xi,\bullet}$
-operation introduced in the previous section. In some sense, we need to have a suitably derived Bialynicki–Birula construction.
$L\eta_{\xi,\bullet}$
-operation introduced in the previous section. In some sense, we need to have a suitably derived Bialynicki–Birula construction.
Let
![]() $m \in \mathbb{Z}_{\geq 0}$
, and we consider
$m \in \mathbb{Z}_{\geq 0}$
, and we consider
which is naturally a subcomplex of
![]() $L\eta_{\xi}\Delta_{X/\mathbb{B}^+_{\text{dR}}}$
. By Lemma 3·3, we have
$L\eta_{\xi}\Delta_{X/\mathbb{B}^+_{\text{dR}}}$
. By Lemma 3·3, we have
which implies that under the canonical map
Footnote 6 the image of
![]() $ H^i(X, L\eta_{\xi,m} \Delta_{X/\mathbb{B}^+_{\text{dR}}})$
inside
$ H^i(X, L\eta_{\xi,m} \Delta_{X/\mathbb{B}^+_{\text{dR}}})$
inside
is exactly (m th Tate twist of) the m th Hodge–Tate filtration.
We observe that there is a natural map
and we want to prove that it induces an identification of
![]() $ H^i(X, L\eta_{\xi,m} \Delta_{X/\mathbb{B}^+_{\text{dR}}})$
with
$ H^i(X, L\eta_{\xi,m} \Delta_{X/\mathbb{B}^+_{\text{dR}}})$
with
which completes the proof.
Proposition 4·1.
![]() $ H^i(X, L\eta_{\xi,m} \Delta_{X/\mathbb{B}^+_{\text{dR}}})$
is
$ H^i(X, L\eta_{\xi,m} \Delta_{X/\mathbb{B}^+_{\text{dR}}})$
is
![]() $\xi$
-torsion-free for all
$\xi$
-torsion-free for all
![]() $i, m \in \mathbb{Z}_{\geq 0}$
.
$i, m \in \mathbb{Z}_{\geq 0}$
.
First proof. We prove that
![]() $ H^i(X, L\eta_{\xi,m} \Delta_{X/\mathbb{B}^+_{\text{dR}}})$
is
$ H^i(X, L\eta_{\xi,m} \Delta_{X/\mathbb{B}^+_{\text{dR}}})$
is
![]() $\xi$
-torsion-free by descending induction on m. The base case is when m is big enough so we have
$\xi$
-torsion-free by descending induction on m. The base case is when m is big enough so we have
![]() $L\eta_{\xi,m} \Delta_{X/\mathbb{B}^+_{\text{dR}}} = \Delta_{X/\mathbb{B}^+_{\text{dR}}}(m)$
, in which case the torsion-freeness follows from the primitive comparison theorem
$L\eta_{\xi,m} \Delta_{X/\mathbb{B}^+_{\text{dR}}} = \Delta_{X/\mathbb{B}^+_{\text{dR}}}(m)$
, in which case the torsion-freeness follows from the primitive comparison theorem
Now assume that
![]() $ H^i(X, L\eta_{\xi,m+1} \Delta_{X/\mathbb{B}^+_{\text{dR}}})$
is
$ H^i(X, L\eta_{\xi,m+1} \Delta_{X/\mathbb{B}^+_{\text{dR}}})$
is
![]() $\xi$
-torsion-free, we want to prove that the same is true for
$\xi$
-torsion-free, we want to prove that the same is true for
![]() $ H^i(X, L\eta_{\xi,m} \Delta_{X/\mathbb{B}^+_{\text{dR}}})$
. Using the long exact sequence associated to
$ H^i(X, L\eta_{\xi,m} \Delta_{X/\mathbb{B}^+_{\text{dR}}})$
. Using the long exact sequence associated to
it is enough to prove that the natural map
is surjective.
We have the commutative diagram

corresponding to the map of distinguished triangles

We note that the map a is surjective by our induction hypothesis. Namely, the connecting map
is 0 since the right-hand side is torsion free by induction hypothesis.
We have that h is surjective as well. This is again because of our inductive hypothesis that
![]() $ H^{i+1}(X, L\eta_{\xi,m+1} \Delta_{X/\mathbb{B}^+_{\text{dR}}})$
is torsion-free, so the natural map
$ H^{i+1}(X, L\eta_{\xi,m+1} \Delta_{X/\mathbb{B}^+_{\text{dR}}})$
is torsion-free, so the natural map
is surjective, but Corollary 3·6 implies that
composing the projection to second factor with p implies that h is surjective.
Now we prove that f is surjective, which completes the proof. Given
![]() $x \in H^i(X, L\eta_{\xi,m} \Delta_{X/\mathbb{B}^+_{\text{dR}}}/\xi L\eta_{\xi,m} \Delta_{X/\mathbb{B}^+_{\text{dR}}})$
, we can find
$x \in H^i(X, L\eta_{\xi,m} \Delta_{X/\mathbb{B}^+_{\text{dR}}}/\xi L\eta_{\xi,m} \Delta_{X/\mathbb{B}^+_{\text{dR}}})$
, we can find
![]() $y \in H^i(X, L\eta_{\xi,m} \Delta_{X/\mathbb{B}^+_{\text{dR}}})$
such that
$y \in H^i(X, L\eta_{\xi,m} \Delta_{X/\mathbb{B}^+_{\text{dR}}})$
such that
![]() $d(f(y)) = a(y) = d(x)$
by surjectivity of a. Thus
$d(f(y)) = a(y) = d(x)$
by surjectivity of a. Thus
![]() $x-f(y) \in \text{Ker}(d)=\text{Im}(b)$
, so there exists
$x-f(y) \in \text{Ker}(d)=\text{Im}(b)$
, so there exists
![]() $w \in H^i(X,L\eta_{\xi,m+1} \Delta_{X/\mathbb{B}^+_{\text{dR}}}/\xi L\eta_{\xi,m} \Delta_{X/\mathbb{B}^+_{\text{dR}}})$
such that
$w \in H^i(X,L\eta_{\xi,m+1} \Delta_{X/\mathbb{B}^+_{\text{dR}}}/\xi L\eta_{\xi,m} \Delta_{X/\mathbb{B}^+_{\text{dR}}})$
such that
![]() $b(w) =x-f(y)$
, the surjectivity of h tells us that
$b(w) =x-f(y)$
, the surjectivity of h tells us that
![]() $w= h(z)$
for
$w= h(z)$
for
![]() $z \in H^i(X,L\eta_{\xi,m+1} \Delta_{X/\mathbb{B}^+_{\text{dR}}})$
, which implies that
$z \in H^i(X,L\eta_{\xi,m+1} \Delta_{X/\mathbb{B}^+_{\text{dR}}})$
, which implies that
proving the surjectivity of f.
Second proof. We prove that
![]() $ H^i(X, L\eta_{\xi,m} \Delta_{X/\mathbb{B}^+_{\text{dR}}})$
is
$ H^i(X, L\eta_{\xi,m} \Delta_{X/\mathbb{B}^+_{\text{dR}}})$
is
![]() $\xi$
-torsion-free by ascending induction on m. The base case
$\xi$
-torsion-free by ascending induction on m. The base case
![]() $m=0$
is [
Reference Bhatt, Morrow and ScholzeBMS18
, theorem 13·19] since
$m=0$
is [
Reference Bhatt, Morrow and ScholzeBMS18
, theorem 13·19] since
which follows from
![]() $\Delta_{X/\mathbb{B}^+_{\text{dR}}} \in D_{\geq 0}$
and
$\Delta_{X/\mathbb{B}^+_{\text{dR}}} \in D_{\geq 0}$
and
![]() $\xi$
-torsion-freeness of
$\xi$
-torsion-freeness of
![]() $ H^0(\Delta_{X/\mathbb{B}^+_{\text{dR}}})$
.
$ H^0(\Delta_{X/\mathbb{B}^+_{\text{dR}}})$
.
Now assume that
![]() $ H^i(X, L\eta_{\xi,m} \Delta_{X/\mathbb{B}^+_{\text{dR}}})$
is
$ H^i(X, L\eta_{\xi,m} \Delta_{X/\mathbb{B}^+_{\text{dR}}})$
is
![]() $\xi$
-torsion-free, we want to prove that the same is true for
$\xi$
-torsion-free, we want to prove that the same is true for
![]() $ H^i(X, L\eta_{\xi,m+1} \Delta_{X/\mathbb{B}^+_{\text{dR}}})$
. It is enough to prove that the natural map
$ H^i(X, L\eta_{\xi,m+1} \Delta_{X/\mathbb{B}^+_{\text{dR}}})$
. It is enough to prove that the natural map
is injective. Using the long exact sequence associated to the distinguished triangle
it is enough to show that
is 0. Note that the
![]() $i=0$
case is trivial, as the left–hand side cohomology group is 0.
$i=0$
case is trivial, as the left–hand side cohomology group is 0.
We have the commutative diagram

where the middle row and column are exact, being part of the long exact sequence associated to distinguished triangles. The first row is the connecting morphism as specified in Corollary 3·5, and the square is commutative since it is induced by the morphism of distinguished triangles

The arrow b is injective by our inductive hypothesis, so a is injective as well.
We know from (2) and Corollary 3·5 that
![]() $\beta$
factorises as
$\beta$
factorises as

where
![]() $Z^{m+1}\Omega_X^{\bullet}$
is the sheaf of closed
$Z^{m+1}\Omega_X^{\bullet}$
is the sheaf of closed
![]() $m+1$
-forms, and d is the usual differential of de Rham complexes. By the degeneration of Hodge–de Rham spectral sequence proved in [
Reference Bhatt, Morrow and ScholzeBMS18
, theorem 13·3], we know that
$m+1$
-forms, and d is the usual differential of de Rham complexes. By the degeneration of Hodge–de Rham spectral sequence proved in [
Reference Bhatt, Morrow and ScholzeBMS18
, theorem 13·3], we know that
is 0, and we claim that this implies that the composition
is 0, so
![]() $\beta$
is 0 as well.
$\beta$
is 0 as well.
Indeed, filtering both
![]() $ \Omega_X^m[-m]$
and
$ \Omega_X^m[-m]$
and
![]() $ F_{m+1} \Omega_X^{\bullet}[1]$
by the Hodge filtration, we see that the map on the first graded piece is
$ F_{m+1} \Omega_X^{\bullet}[1]$
by the Hodge filtration, we see that the map on the first graded piece is
![]() $ H^{i-1}(X, \Omega_X^m[-m]) \overset{d}{\longrightarrow } H^{i-1}(X, \Omega_X^{m+1}[-m])$
which we have seen to be 0. The map on other graded pieces are also 0, since
$ H^{i-1}(X, \Omega_X^m[-m]) \overset{d}{\longrightarrow } H^{i-1}(X, \Omega_X^{m+1}[-m])$
which we have seen to be 0. The map on other graded pieces are also 0, since
![]() $\Omega_X^m[-m]$
has only one non-zero graded piece, proving the claim.
$\Omega_X^m[-m]$
has only one non-zero graded piece, proving the claim.
Now let
![]() $x \in H^{i-1} (X, Gr^m \Delta_{X/\mathbb{B}^+_{\text{dR}}})$
, then
$x \in H^{i-1} (X, Gr^m \Delta_{X/\mathbb{B}^+_{\text{dR}}})$
, then
![]() $f(x) \in \text{Ker}(h)$
since
$f(x) \in \text{Ker}(h)$
since
![]() $\beta =0$
, so we have
$\beta =0$
, so we have
![]() $f(x) = a(y)$
for some
$f(x) = a(y)$
for some
![]() $y \in H^i(X, \xi L\eta_{\xi,m} \Delta_{X/\mathbb{B}^+_{\text{dR}}})$
. Then
$y \in H^i(X, \xi L\eta_{\xi,m} \Delta_{X/\mathbb{B}^+_{\text{dR}}})$
. Then
![]() $b(y)=g(a(y))=g(f(x))=0$
, which implies that
$b(y)=g(a(y))=g(f(x))=0$
, which implies that
![]() $y=0$
by injectivity of b, so
$y=0$
by injectivity of b, so
![]() $f(x)=a(y)=0$
. Hence we have
$f(x)=a(y)=0$
. Hence we have
![]() $f=0$
, finishing the induction.
$f=0$
, finishing the induction.
Remark 4·2. The first proof has the advantage that it is independent of the Conrad–Gabber spreading theorem. In particular, we give a Conrad–Gabber independent proof the
![]() $\xi$
-torsion-freeness of
$\xi$
-torsion-freeness of
![]() $ H^i_{crys}(X,\mathbb{B}^+_{\text{dR}})$
. See [
Reference Bhatt, Morrow and ScholzeBMS18
, 13·19], and [
Reference GuoGuo21a
, theorem 7·3·5] for proofs that involves the spreading theorem.
$ H^i_{crys}(X,\mathbb{B}^+_{\text{dR}})$
. See [
Reference Bhatt, Morrow and ScholzeBMS18
, 13·19], and [
Reference GuoGuo21a
, theorem 7·3·5] for proofs that involves the spreading theorem.
The proposition tells us that long exact sequence assoicated to the distinguished triangle (5) splits into short exact sequences
indeed,
![]() $ H^i(X, \tau_{\leq m}\overline{ \Delta}_{X/\mathbb{B}^+_{\text{dR}}}) (m)$
is
$ H^i(X, \tau_{\leq m}\overline{ \Delta}_{X/\mathbb{B}^+_{\text{dR}}}) (m)$
is
![]() $\xi$
-torsion which admits no non-zero connecting morphism to the
$\xi$
-torsion which admits no non-zero connecting morphism to the
![]() $\xi$
-torsion-free module
$\xi$
-torsion-free module
![]() $ H^{i+1}(X, L\eta_{\xi,m+1} \Delta_{X/\mathbb{B}^+_{\text{dR}}}) $
. In particular,
$ H^{i+1}(X, L\eta_{\xi,m+1} \Delta_{X/\mathbb{B}^+_{\text{dR}}}) $
. In particular,
so the canonical map
is injective. We now prove that it is also surjective.
We proceed by induction on m. The base case
![]() $m=0$
is clear, as both sides are
$m=0$
is clear, as both sides are
![]() $ H^i(X, L\eta_{\xi} \Delta_{X/\mathbb{B}^+_{\text{dR}}})$
. Assume that the map is surjective for m, we prove it is also surjective for
$ H^i(X, L\eta_{\xi} \Delta_{X/\mathbb{B}^+_{\text{dR}}})$
. Assume that the map is surjective for m, we prove it is also surjective for
![]() $m+1$
. We consider the commutative diagram
$m+1$
. We consider the commutative diagram

where the two vertical sequences are exact, the middle horizontal arrow is an isomorphism by our inductive hypothesis, and the bottom horizontal arrow is injective by the degeneration of Hodge–Tate spectral sequence ([ Reference Bhatt, Morrow and ScholzeBMS18 , theorem 13·3]). Now an easy diagram chasing proves that the first horizontal arrow is surjective, finishing the induction.
5. Miscellany
We document an interesting byproduct in our treatment of Hodge–Tate filtration, namely we can give a conceptual explanation why the degeneration of Hodge–Tate spectral sequences is equivalent to that of Hodge–de Rham spectral sequences. The claim is clear in the proof of [
Reference Bhatt, Morrow and ScholzeBMS18
, theorem 13·3], which is by dimension counting. Note that the torsion-freeness of
![]() $ H^i_{\text{crys}}(X/\mathbb{B}^+_{\text{dR}})$
is used in
$ H^i_{\text{crys}}(X/\mathbb{B}^+_{\text{dR}})$
is used in
![]() $loc.cit.$
as a bridge between the dimension of the de Rham cohomology and étale cohomology.
$loc.cit.$
as a bridge between the dimension of the de Rham cohomology and étale cohomology.
Proposition 5·1. Let X be a proper smooth rigid analytic variety over a complete algebraically closed non-archimedean field
![]() $\mathbb{C}$
of mixed characteristic p, the degeneration of the Hodge–Tate spectral sequence
$\mathbb{C}$
of mixed characteristic p, the degeneration of the Hodge–Tate spectral sequence
is equivalent to the degeneration of Hodge–de Rham spectral sequence
More precisely, in the natural diagram

where f and g are the canonical maps corresponding to the truncation filtration and Hodge filtration respectively, we have that
as subspaces of
![]() $ H^{i}(X,\Omega_{X}^m[-m])$
.
$ H^{i}(X,\Omega_{X}^m[-m])$
.
Proof. We know that the Hodge–Tate spectral sequence is induced from the filtration
![]() $ H^i(X, \tau_{\leq m}\overline{\Delta}_{X/\mathbb{B}^+_{\text{dR}}})$
corresponding to standard truncation, and the Hodge–de Rham spectral sequence is induced from the Hodge filtration
$ H^i(X, \tau_{\leq m}\overline{\Delta}_{X/\mathbb{B}^+_{\text{dR}}})$
corresponding to standard truncation, and the Hodge–de Rham spectral sequence is induced from the Hodge filtration
![]() $ H^{i}(X,F_m\Omega_{X}^{\bullet})$
. It is then clear that the equivalence of degeneration is implied by the claim on f and g.
$ H^{i}(X,F_m\Omega_{X}^{\bullet})$
. It is then clear that the equivalence of degeneration is implied by the claim on f and g.
We now prove the claim. We have a commutative diagram

where the vertical and horizontal sequences are both short exact sequences, which follows from Proposition 4·1. The factorisation h is induced by the canonical map
and h is surjective because it is a factorisation of a surjective map.
Now Corollary 3·6 gives us a commutative diagram

and the claim in the proposition follows immediately.
Acknowledgement
I would like to thank Yu Min and Yupeng Wang for discussions related to this work. I would like to thank Peter Scholze for corrections on the draft.