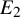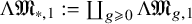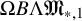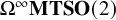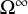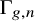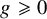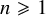1 Introduction
The Madsen–Weiss theorem [Reference Madsen and Weiss14] can be formulated as follows: let
![]() $\mathfrak {M}_{g,1}$
denote the moduli space of Riemann surfaces of genus
$\mathfrak {M}_{g,1}$
denote the moduli space of Riemann surfaces of genus
![]() $g\geqslant 0$
with one parametrised boundary curve. By [Reference Miller19] and [Reference Bödigheimer4], the collection
$g\geqslant 0$
with one parametrised boundary curve. By [Reference Miller19] and [Reference Bödigheimer4], the collection
 $$\begin{align*}\mathfrak{M}_{*,1}:=\coprod_{g\geqslant0}\mathfrak{M}_{g,1}\end{align*}$$
$$\begin{align*}\mathfrak{M}_{*,1}:=\coprod_{g\geqslant0}\mathfrak{M}_{g,1}\end{align*}$$
admits the structure of an
![]() $E_2$
-algebra, more precisely an algebra over the little
$E_2$
-algebra, more precisely an algebra over the little
![]() $2$
-discs operad
$2$
-discs operad
![]() ${\mathscr {D}}_2$
. Madsen and Weiss identify the group completion
${\mathscr {D}}_2$
. Madsen and Weiss identify the group completion
![]() $\Omega B\mathfrak {M}_{*,1}$
with the infinite loop space
$\Omega B\mathfrak {M}_{*,1}$
with the infinite loop space
![]() $\Omega ^{\infty }\mathbf {MTSO}(2)$
, where
$\Omega ^{\infty }\mathbf {MTSO}(2)$
, where
![]() $\mathbf {MTSO}(2)$
is the two-dimensional oriented tangential Thom spectrum [Reference Galatius, Madsen, Tillmann and Weiss8].
$\mathbf {MTSO}(2)$
is the two-dimensional oriented tangential Thom spectrum [Reference Galatius, Madsen, Tillmann and Weiss8].
One can consider the analogous problem with
![]() $\mathfrak {M}_{*,1}$
replaced by the mapping space
$\mathfrak {M}_{*,1}$
replaced by the mapping space
![]() ${\mathrm {map}}(X,\mathfrak {M}_{*,1})$
. This space is again a
${\mathrm {map}}(X,\mathfrak {M}_{*,1})$
. This space is again a
![]() ${\mathscr {D}}_2$
-algebra by pointwise composition, and it is our goal to understand its group completion
${\mathscr {D}}_2$
-algebra by pointwise composition, and it is our goal to understand its group completion
![]() $\Omega B\,{\mathrm {map}}(X,\mathfrak {M}_{*,1})$
. Note that the
$\Omega B\,{\mathrm {map}}(X,\mathfrak {M}_{*,1})$
. Note that the
![]() ${\mathscr {D}}_2$
-algebra structure extends to an algebra structure over Tillmann’s surface operad built out of
${\mathscr {D}}_2$
-algebra structure extends to an algebra structure over Tillmann’s surface operad built out of
![]() $\mathfrak {M}_{*,1}$
, so the main theorem of [Reference Tillmann26] implies the homotopy type we wish to understand is an infinite loop space.
$\mathfrak {M}_{*,1}$
, so the main theorem of [Reference Tillmann26] implies the homotopy type we wish to understand is an infinite loop space.
In this article, we will focus on the simplest non-trivial case
![]() $X=S^1$
: i.e., we consider the free loop space
$X=S^1$
: i.e., we consider the free loop space
![]() $\Lambda \mathfrak {M}_{*,1}:={\mathrm {map}}(S^1,\mathfrak {M}_{*,1})$
; we will briefly discuss in the appendix the general case, which is very similar.
$\Lambda \mathfrak {M}_{*,1}:={\mathrm {map}}(S^1,\mathfrak {M}_{*,1})$
; we will briefly discuss in the appendix the general case, which is very similar.
For any discrete group
![]() $\Gamma $
, one can identify
$\Gamma $
, one can identify
![]() $\Lambda B\Gamma \simeq \coprod _{[\gamma ] \in {\mathrm {Conj}}(\Gamma )} BZ(\gamma ,\Gamma )$
, where
$\Lambda B\Gamma \simeq \coprod _{[\gamma ] \in {\mathrm {Conj}}(\Gamma )} BZ(\gamma ,\Gamma )$
, where
![]() ${\mathrm {Conj}}(\Gamma )$
denotes the set of conjugacy classes of
${\mathrm {Conj}}(\Gamma )$
denotes the set of conjugacy classes of
![]() $\Gamma $
, and
$\Gamma $
, and
![]() $Z(\gamma ,\Gamma )$
is the centraliser of
$Z(\gamma ,\Gamma )$
is the centraliser of
![]() $\gamma \in \Gamma $
. Note also that the isomorphism type of the group
$\gamma \in \Gamma $
. Note also that the isomorphism type of the group
![]() $Z(\gamma ,\Gamma )$
only depends on the conjugacy class of
$Z(\gamma ,\Gamma )$
only depends on the conjugacy class of
![]() $\gamma \in \Gamma $
.
$\gamma \in \Gamma $
.
The problem we address in this paper is strongly related to analysing the structure of centralisers of elements of mapping class groups: indeed, recall that
![]() $\mathfrak {M}_{g,1}$
is a classifying space for the mapping class group
$\mathfrak {M}_{g,1}$
is a classifying space for the mapping class group
![]() $\Gamma _{g,1}$
of a smooth oriented surface of genus g with one parametrised boundary curve; we then have a homotopy equivalence
$\Gamma _{g,1}$
of a smooth oriented surface of genus g with one parametrised boundary curve; we then have a homotopy equivalence
 $$\begin{align*}\Lambda\mathfrak{M}_{*,1}\simeq \coprod_{g\geqslant 0}\Lambda B\Gamma_{g,1} \simeq \coprod_{g\geqslant 0}\coprod_{[\varphi]\in{\mathrm{Conj}}(\Gamma_{g,1})} BZ(\varphi,\Gamma_{g,1}).\end{align*}$$
$$\begin{align*}\Lambda\mathfrak{M}_{*,1}\simeq \coprod_{g\geqslant 0}\Lambda B\Gamma_{g,1} \simeq \coprod_{g\geqslant 0}\coprod_{[\varphi]\in{\mathrm{Conj}}(\Gamma_{g,1})} BZ(\varphi,\Gamma_{g,1}).\end{align*}$$
Results
The free loop space of the moduli space of surfaces of genus g with n parametrised boundary circles,
![]() $\Lambda \mathfrak {M}_{g,n}$
, admits an action by the isometry group of the disjoint union of n oriented circles: that is, by
$\Lambda \mathfrak {M}_{g,n}$
, admits an action by the isometry group of the disjoint union of n oriented circles: that is, by
![]() $T^n \rtimes \mathfrak {S}_n=(S^1)^n\rtimes \mathfrak {S}_n$
.
$T^n \rtimes \mathfrak {S}_n=(S^1)^n\rtimes \mathfrak {S}_n$
.
We introduce an irreducibility criterion for mapping classes that is invariant under conjugation. We then consider, for any
![]() $n\geqslant 1$
and
$n\geqslant 1$
and
![]() $g \geqslant 0$
, the subspace
$g \geqslant 0$
, the subspace
![]() $\mathfrak C_{g,n} \subseteq \Lambda \mathfrak {M}_{g,n}$
of free loops whose corresponding conjugacy classes of elements in
$\mathfrak C_{g,n} \subseteq \Lambda \mathfrak {M}_{g,n}$
of free loops whose corresponding conjugacy classes of elements in
![]() $\pi _0 (\mathfrak {M}_{g,n}) \cong \Gamma _{g,n}$
are irreducible. The pointwise action of
$\pi _0 (\mathfrak {M}_{g,n}) \cong \Gamma _{g,n}$
are irreducible. The pointwise action of
![]() $T^n \rtimes \mathfrak {S}_n$
on
$T^n \rtimes \mathfrak {S}_n$
on
![]() $\Lambda \mathfrak {M}_{g,n}$
restricts to an action on
$\Lambda \mathfrak {M}_{g,n}$
restricts to an action on
![]() $\mathfrak C_{g,n}$
, and the main result of this work is the following identification, where
$\mathfrak C_{g,n}$
, and the main result of this work is the following identification, where
![]() stands for homotopy quotient.
stands for homotopy quotient.
Theorem 1.1. There is a weak homotopy equivalence

The key to proving this theorem is a good understanding of mapping class groups of surfaces (also with more than one boundary component) as well as an extension of classical operadic techniques to a coloured setting. As a first step, we prove a structure result for centralisers of mapping classes in
![]() $\Gamma _{g,n}$
, which might be of independent interest: see Proposition 3.8.
$\Gamma _{g,n}$
, which might be of independent interest: see Proposition 3.8.
Second, we develop a machinery for N-coloured operads with homological stability
![]() ${\mathscr {O}}$
containing a suboperad
${\mathscr {O}}$
containing a suboperad
![]() ${\mathscr {P}}$
, such as a family of topological groups: the group completion of the derived relatively free algebra
${\mathscr {P}}$
, such as a family of topological groups: the group completion of the derived relatively free algebra
![]() $\tilde {F}_{{\mathscr {P}}}^{{\mathscr {O}}}(\boldsymbol {X})$
over a
$\tilde {F}_{{\mathscr {P}}}^{{\mathscr {O}}}(\boldsymbol {X})$
over a
![]() ${\mathscr {P}}$
-algebra
${\mathscr {P}}$
-algebra
![]() $\boldsymbol {X}$
is computed colourwise as an infinite loop space, under suitable assumptions on
$\boldsymbol {X}$
is computed colourwise as an infinite loop space, under suitable assumptions on
![]() ${\mathscr {O}}$
and
${\mathscr {O}}$
and
![]() ${\mathscr {P}}$
; see Theorem 5.9. This part of the work is a generalisation of [Reference Tillmann26] and [Reference Basterra, Bobkova, Ponto, Tillmann and Yeakel1] to the coloured and relative setting.
${\mathscr {P}}$
; see Theorem 5.9. This part of the work is a generalisation of [Reference Tillmann26] and [Reference Basterra, Bobkova, Ponto, Tillmann and Yeakel1] to the coloured and relative setting.
The two ingredients are put together by proving that
![]() $\Lambda \mathfrak {M}_{*,1}$
is the colour-
$\Lambda \mathfrak {M}_{*,1}$
is the colour-
![]() $1$
part of a relatively free algebra over a coloured version
$1$
part of a relatively free algebra over a coloured version
![]() ${\mathscr {M}}$
of Tillmann’s surface operad, relative to a sub-operad built out of
${\mathscr {M}}$
of Tillmann’s surface operad, relative to a sub-operad built out of
![]() $T^n \rtimes \mathfrak {S}_n$
; the ‘relative generators’ are precisely the spaces
$T^n \rtimes \mathfrak {S}_n$
; the ‘relative generators’ are precisely the spaces
![]() $\mathfrak C_{g,n}$
mentioned above: see Theorem 6.5.
$\mathfrak C_{g,n}$
mentioned above: see Theorem 6.5.
Related work
One approach to studying classifying spaces of diffeomorphism groups pertains to the notion of cobordism categories. It was pioneered with the breakthrough theorem by Madsen and Weiss and refined by Galatius, Madsen, Tillmann and Weiss [Reference Galatius, Madsen, Tillmann and Weiss8].
Recall that, in the orientable setting, the cobordism category
![]() $\mathrm {Cob}_d$
is a topological category, with object space given by the union of all moduli spaces of closed, oriented
$\mathrm {Cob}_d$
is a topological category, with object space given by the union of all moduli spaces of closed, oriented
![]() $(d-1)$
-manifolds, and morphism space given by the union of all moduli spaces of compact, oriented d-manifolds with incoming and outgoing boundary. It is natural to study two related generalisations of
$(d-1)$
-manifolds, and morphism space given by the union of all moduli spaces of compact, oriented d-manifolds with incoming and outgoing boundary. It is natural to study two related generalisations of
![]() $\mathrm {Cob}_d$
, in an equivariant and a parametrised direction:
$\mathrm {Cob}_d$
, in an equivariant and a parametrised direction:
-
1. for a (topological) group G, we can consider the G-equivariant cobordism category
 $\mathrm {Cob}_d^G$
: objects and morphisms are, respectively,
$\mathrm {Cob}_d^G$
: objects and morphisms are, respectively,
 $(d-1)$
- and d-manifolds endowed with an (continuous) action of G by orientation-preserving diffeomorphisms;
$(d-1)$
- and d-manifolds endowed with an (continuous) action of G by orientation-preserving diffeomorphisms; -
2. for a topological space Y, we can consider the Y-parametrised cobordism category
 $\mathrm {Cob}_d(Y)$
: objects and morphisms are, respectively, orientable
$\mathrm {Cob}_d(Y)$
: objects and morphisms are, respectively, orientable
 $(d-1)$
- and d-manifold bundles over Y.
$(d-1)$
- and d-manifold bundles over Y.
In the case
![]() $G=\mathbb {Z}$
and
$G=\mathbb {Z}$
and
![]() $Y=S^1$
, there is a continuous functor
$Y=S^1$
, there is a continuous functor
![]() $\mathrm {Cob}_d^{\mathbb {Z}}\to \mathrm {Cob}_d(S^1)$
, given by taking mapping tori: using that every smooth bundle over
$\mathrm {Cob}_d^{\mathbb {Z}}\to \mathrm {Cob}_d(S^1)$
, given by taking mapping tori: using that every smooth bundle over
![]() $S^1$
is induced from a diffeomorphism, this functor is in fact a levelwise equivalence. For more general groups G and
$S^1$
is induced from a diffeomorphism, this functor is in fact a levelwise equivalence. For more general groups G and
![]() $Y = BG$
, the analogous argument pertaining to G-actions and bundles over
$Y = BG$
, the analogous argument pertaining to G-actions and bundles over
![]() $BG$
can fail: see [Reference Reinhold22] for a discussion of this phenomenon and counterexamples in case
$BG$
can fail: see [Reference Reinhold22] for a discussion of this phenomenon and counterexamples in case
![]() $G = \text {SU}(2)$
.
$G = \text {SU}(2)$
.
Our work can be seen as a contribution toward understanding the homotopy type of
![]() ${\mathrm {Cob}_d^{\mathbb {Z}}\simeq \mathrm {Cob}_d(S^1)}$
: gluing a pair of pants gives a map of monoids
${\mathrm {Cob}_d^{\mathbb {Z}}\simeq \mathrm {Cob}_d(S^1)}$
: gluing a pair of pants gives a map of monoids
![]() $\Lambda \mathfrak {M}_{*,1}\to \mathrm {Cob}_2(S^1)|_{S^1}$
, where
$\Lambda \mathfrak {M}_{*,1}\to \mathrm {Cob}_2(S^1)|_{S^1}$
, where
![]() $\mathrm {Cob}_2(S^1)|_{S^1}$
denotes the full subcategory of
$\mathrm {Cob}_2(S^1)|_{S^1}$
denotes the full subcategory of
![]() $\mathrm {Cob}_2(S^1)$
on a single object represented by a trivial
$\mathrm {Cob}_2(S^1)$
on a single object represented by a trivial
![]() $S^1$
-bundle over
$S^1$
-bundle over
![]() $S^1$
.
$S^1$
.
In the non-parametrised setting, the composition
![]() $\mathfrak {M}_{*,1}\to \mathrm {Cob}_2|_{S^1}\to \mathrm {Cob}_2$
is known to induce an equivalence after taking classifying spaces; we hope that in a similar way, the understanding of
$\mathfrak {M}_{*,1}\to \mathrm {Cob}_2|_{S^1}\to \mathrm {Cob}_2$
is known to induce an equivalence after taking classifying spaces; we hope that in a similar way, the understanding of
![]() $B\Lambda \mathfrak {M}_{*,1}$
can shed some light on the homotopy type of
$B\Lambda \mathfrak {M}_{*,1}$
can shed some light on the homotopy type of
![]() $B\mathrm {Cob}_2^{\mathbb {Z}} \simeq B\mathrm {Cob}_2(S^1)$
in future work.
$B\mathrm {Cob}_2^{\mathbb {Z}} \simeq B\mathrm {Cob}_2(S^1)$
in future work.
In the case of a finite group G, the homotopy type of
![]() $\mathrm {Cob}_d^{G}$
was recently determined by Szűcs and Galatius [Reference Galatius and Szűcs9]. In work by Raptis and Steimle [Reference Raptis and Steimle20], parametrised cobordism categories
$\mathrm {Cob}_d^{G}$
was recently determined by Szűcs and Galatius [Reference Galatius and Szűcs9]. In work by Raptis and Steimle [Reference Raptis and Steimle20], parametrised cobordism categories
![]() $\mathrm {Cob}_d(Y)$
featured as a tool to prove index theorems; however, it was not necessary for the scopes of that work to describe the homotopy type of the classifying spaces of these categories. The much older work of Kreck on bordisms of diffeomorphisms [Reference Kreck13] can be seen as a description of
$\mathrm {Cob}_d(Y)$
featured as a tool to prove index theorems; however, it was not necessary for the scopes of that work to describe the homotopy type of the classifying spaces of these categories. The much older work of Kreck on bordisms of diffeomorphisms [Reference Kreck13] can be seen as a description of
![]() $\pi _0\left (\mathrm {Cob}_d(S^1)\right )$
.
$\pi _0\left (\mathrm {Cob}_d(S^1)\right )$
.
Outline
In Section 2, we recall Alexander’s method concerning arc systems. We apply these concepts to associate with a mapping class
![]() $\varphi \in \Gamma _{g,n}$
a canonical decomposition of
$\varphi \in \Gamma _{g,n}$
a canonical decomposition of
![]() $\Sigma _{g,n}$
along a system of simple closed curves, called the cut locus of
$\Sigma _{g,n}$
along a system of simple closed curves, called the cut locus of
![]() $\varphi $
. The goal of Section 3 is a detailed understanding of centralisers of mapping classes: this uses the canonical decomposition described in the previous section in a crucial way.
$\varphi $
. The goal of Section 3 is a detailed understanding of centralisers of mapping classes: this uses the canonical decomposition described in the previous section in a crucial way.
In Section 4, we recall some basic definitions and constructions related to coloured operads and introduce the coloured surface operad
![]() ${\mathscr {M}}$
. In Section 5, we introduce the notion of a coloured operad with homological stability and prove a levelwise splitting result in the spirit of [Reference Basterra, Bobkova, Ponto, Tillmann and Yeakel1], which applies in particular to
${\mathscr {M}}$
. In Section 5, we introduce the notion of a coloured operad with homological stability and prove a levelwise splitting result in the spirit of [Reference Basterra, Bobkova, Ponto, Tillmann and Yeakel1], which applies in particular to
![]() ${\mathscr {M}}$
. Finally, in Section 6, we show that
${\mathscr {M}}$
. Finally, in Section 6, we show that
![]() $\Lambda \mathfrak {M}_{*,1}$
is the colour-
$\Lambda \mathfrak {M}_{*,1}$
is the colour-
![]() $1$
part of a relatively free
$1$
part of a relatively free
![]() ${\mathscr {M}}$
-algebra, which in combination with the splitting result concludes the proof of Theorem 1.1.
${\mathscr {M}}$
-algebra, which in combination with the splitting result concludes the proof of Theorem 1.1.
We briefly discuss in Appendix A the analogue of Theorem 1.1 for a general parametrising space X (see Theorem A.2) as well as a weak form of naturality in X of the equivalence (see Theorem A.7); in Appendix B, we address two similar problems concerning group completion of free loop spaces, related to braid groups and symmetric groups, respectively.
2 Arc systems and the cut locus
The aim of this and the next section is to study centralisers in mapping class groups of surfaces. This interest is motivated by the following observation: for
![]() $g\geqslant 1$
, the space
$g\geqslant 1$
, the space
![]() $\Lambda \mathfrak {M}_{g,1}\simeq \Lambda B\Gamma _{g,1}$
has one connected component for each conjugacy class
$\Lambda \mathfrak {M}_{g,1}\simeq \Lambda B\Gamma _{g,1}$
has one connected component for each conjugacy class
![]() $[\varphi ]\in {\mathrm {Conj}}(\Gamma _{g,1})$
; this component is homotopy equivalent to
$[\varphi ]\in {\mathrm {Conj}}(\Gamma _{g,1})$
; this component is homotopy equivalent to
![]() $B Z(\varphi ,\Gamma _{g,1})$
, where we denote by
$B Z(\varphi ,\Gamma _{g,1})$
, where we denote by
![]() $Z(\varphi ,\Gamma _{g,1})\subset \Gamma _{g,1}$
the centraliser of
$Z(\varphi ,\Gamma _{g,1})\subset \Gamma _{g,1}$
the centraliser of
![]() $\varphi $
in
$\varphi $
in
![]() $\Gamma _{g,1}$
: that is, the subgroup of all mapping classes
$\Gamma _{g,1}$
: that is, the subgroup of all mapping classes
![]() $\psi \in \Gamma _{g,1}$
commuting with
$\psi \in \Gamma _{g,1}$
commuting with
![]() $\varphi $
.
$\varphi $
.
In this section, we will first introduce some notation for surfaces and mapping class groups and then define the cut locus of a mapping class.
2.1 Surfaces and mapping class groups
We work in the entire article with smooth, oriented surfaces and orientation-preserving diffeomorphisms of surfaces.
Notation 2.1. We usually denote by
![]() $\mathcal {S}$
a smooth, compact, oriented, possibly disconnected surface, such that each component of
$\mathcal {S}$
a smooth, compact, oriented, possibly disconnected surface, such that each component of
![]() $\mathcal {S}$
has non-empty boundary; we denote the boundary of
$\mathcal {S}$
has non-empty boundary; we denote the boundary of
![]() $\mathcal {S}$
by
$\mathcal {S}$
by
![]() $\partial \mathcal {S}\subset \mathcal {S}$
.
$\partial \mathcal {S}\subset \mathcal {S}$
.
The boundary
![]() $\partial \mathcal {S}$
is equipped with a decomposition
$\partial \mathcal {S}$
is equipped with a decomposition
![]() $\partial \mathcal {S}=\partial ^{\text {in}}\mathcal {S}\sqcup \partial ^{\text {out}}\mathcal {S}$
, into unions of connected components: the incoming boundary
$\partial \mathcal {S}=\partial ^{\text {in}}\mathcal {S}\sqcup \partial ^{\text {out}}\mathcal {S}$
, into unions of connected components: the incoming boundary
![]() $\partial ^{\text {in}}\mathcal {S}$
is allowed to be empty, whereas each component of
$\partial ^{\text {in}}\mathcal {S}$
is allowed to be empty, whereas each component of
![]() $\mathcal {S}$
is required to intersect the outgoing boundary in at least one curve; see Figure 1 for an example.
$\mathcal {S}$
is required to intersect the outgoing boundary in at least one curve; see Figure 1 for an example.

Figure 1 A surface
![]() $\mathcal {S}$
with
$\mathcal {S}$
with
![]() $5$
incoming and
$5$
incoming and
![]() $4$
outgoing boundary curves.
$4$
outgoing boundary curves.
Both parts of the boundary are equipped with an ordering and a parametrisation: that is, there are preferred diffeomorphisms
![]() $\vartheta ^{\text {in}}\colon \{1,\dotsc ,n\}\times S^1\to \partial ^{\text {in}} \mathcal {S}$
and
$\vartheta ^{\text {in}}\colon \{1,\dotsc ,n\}\times S^1\to \partial ^{\text {in}} \mathcal {S}$
and
![]() $\vartheta ^{\text {out}}\colon \{1,\dotsc ,n'\}\times S^1\to \partial ^{\text {out}} \mathcal {S}$
, where
$\vartheta ^{\text {out}}\colon \{1,\dotsc ,n'\}\times S^1\to \partial ^{\text {out}} \mathcal {S}$
, where
![]() $n=\#\pi _0(\partial ^{\text {in}}\mathcal {S})$
and
$n=\#\pi _0(\partial ^{\text {in}}\mathcal {S})$
and
![]() $n'=\#\pi _0(\partial ^{\text {out}}\mathcal {S})$
.
$n'=\#\pi _0(\partial ^{\text {out}}\mathcal {S})$
.
Note that each boundary component
![]() $c\subset \partial \mathcal {S}$
is endowed with two natural orientations: the first is induced from the orientation of
$c\subset \partial \mathcal {S}$
is endowed with two natural orientations: the first is induced from the orientation of
![]() $\mathcal {S}$
, that is, it is the unique orientation of c that, concatenated with a vector field along c pointing out of
$\mathcal {S}$
, that is, it is the unique orientation of c that, concatenated with a vector field along c pointing out of
![]() $\mathcal {S}$
, returns the orientation of
$\mathcal {S}$
, returns the orientation of
![]() $\mathcal {S}$
; the second orientation comes from the parametrisation of c. For an incoming boundary component
$\mathcal {S}$
; the second orientation comes from the parametrisation of c. For an incoming boundary component
![]() $c\subset \partial ^{\text {in}}\mathcal {S}$
, we require that these two orientations coincide, whereas for an outgoing boundary component
$c\subset \partial ^{\text {in}}\mathcal {S}$
, we require that these two orientations coincide, whereas for an outgoing boundary component
![]() $c\subset \partial ^{\text {out}}\mathcal {S}$
, we require that these two orientations differ.
$c\subset \partial ^{\text {out}}\mathcal {S}$
, we require that these two orientations differ.
We usually denote a surface by
![]() $(\mathcal {S},\vartheta )$
, or shortly by
$(\mathcal {S},\vartheta )$
, or shortly by
![]() $\mathcal {S}$
when it is not necessary to mention the parametrisation of the boundary; here
$\mathcal {S}$
when it is not necessary to mention the parametrisation of the boundary; here
![]() $\vartheta $
is the map
$\vartheta $
is the map
![]() $\left \{1,\dots ,n+n'\right \}\times S^1\to \partial \mathcal {S}$
obtained by concatenation of
$\left \{1,\dots ,n+n'\right \}\times S^1\to \partial \mathcal {S}$
obtained by concatenation of
![]() $\vartheta ^{\text {in}}$
and
$\vartheta ^{\text {in}}$
and
![]() $\vartheta ^{\text {out}}$
.
$\vartheta ^{\text {out}}$
.
Definition 2.2. Let
![]() $\Phi \colon (\mathcal {S},\vartheta )\to (\mathcal {S}',\vartheta ')$
be an orientation-preserving diffeomorphism of surfaces. We say that
$\Phi \colon (\mathcal {S},\vartheta )\to (\mathcal {S}',\vartheta ')$
be an orientation-preserving diffeomorphism of surfaces. We say that
![]() $\Phi $
preserves the boundary parametrisation if the following conditions hold:
$\Phi $
preserves the boundary parametrisation if the following conditions hold:
-
○
 $\Phi $
restricts to diffeomorphisms
$\Phi $
restricts to diffeomorphisms
 $\Phi \colon \partial ^{\text {in}}\mathcal {S}\overset {\cong }{\to }\partial ^{\text {in}}\mathcal {S}'$
and
$\Phi \colon \partial ^{\text {in}}\mathcal {S}\overset {\cong }{\to }\partial ^{\text {in}}\mathcal {S}'$
and
 $\Phi \colon \partial ^{\text {out}}\mathcal {S}\overset {\cong }{\to }\partial ^{\text {out}}\mathcal {S}'$
.
$\Phi \colon \partial ^{\text {out}}\mathcal {S}\overset {\cong }{\to }\partial ^{\text {out}}\mathcal {S}'$
. -
○ If
 $n:= \#\pi _0(\partial ^{\text {in}}\mathcal {S})=\#\pi _0(\partial ^{\text {in}}\mathcal {S}')$
and
$n:= \#\pi _0(\partial ^{\text {in}}\mathcal {S})=\#\pi _0(\partial ^{\text {in}}\mathcal {S}')$
and
 $n':=\#\pi _0(\partial ^{\text {out}}\mathcal {S})=\#\pi _0(\partial ^{\text {out}}\mathcal {S}')$
, then there exist permutations
$n':=\#\pi _0(\partial ^{\text {out}}\mathcal {S})=\#\pi _0(\partial ^{\text {out}}\mathcal {S}')$
, then there exist permutations
 $\sigma ^{\text {in}}\in \mathfrak {S}_n$
and
$\sigma ^{\text {in}}\in \mathfrak {S}_n$
and
 $\sigma ^{\text {out}}\in \mathfrak {S}_{n'}$
such that
$\sigma ^{\text {out}}\in \mathfrak {S}_{n'}$
such that-
–
 $(\Phi \circ \vartheta ^{\text {in}})(j,\zeta ) =(\vartheta ')^{\text {in}}(\sigma ^{\text {in}}(j),\zeta )$
for each
$(\Phi \circ \vartheta ^{\text {in}})(j,\zeta ) =(\vartheta ')^{\text {in}}(\sigma ^{\text {in}}(j),\zeta )$
for each
 $1\leqslant j\leqslant n$
and
$1\leqslant j\leqslant n$
and
 $\zeta \in S^1$
;
$\zeta \in S^1$
; -
–
 $(\Phi \circ \vartheta ^{\text {out}})(j,\zeta ) =(\vartheta ')^{\text {out}}(\sigma ^{\text {out}}(j),\zeta )$
for each
$(\Phi \circ \vartheta ^{\text {out}})(j,\zeta ) =(\vartheta ')^{\text {out}}(\sigma ^{\text {out}}(j),\zeta )$
for each
 $1\leqslant j\leqslant n'$
and
$1\leqslant j\leqslant n'$
and
 $\zeta \in S^1$
.
$\zeta \in S^1$
.
-
Note that in the previous definition, we do not require that
![]() $\Phi $
also preserves the orderings of the incoming and outgoing components of
$\Phi $
also preserves the orderings of the incoming and outgoing components of
![]() $\partial \mathcal {S}$
and
$\partial \mathcal {S}$
and
![]() $\partial \mathcal {S}'$
: that is, the permutations
$\partial \mathcal {S}'$
: that is, the permutations
![]() $\sigma ^{\text {in}}\in \mathfrak {S}_n$
and
$\sigma ^{\text {in}}\in \mathfrak {S}_n$
and
![]() $\sigma ^{\text {out}}\in \mathfrak {S}_{n'}$
may be non-trivial. To emphasise this, we distinguish between the words ‘ordering’ and ‘parametrisation’. In Section 4, when introducing the coloured operad
$\sigma ^{\text {out}}\in \mathfrak {S}_{n'}$
may be non-trivial. To emphasise this, we distinguish between the words ‘ordering’ and ‘parametrisation’. In Section 4, when introducing the coloured operad
![]() ${\mathscr {M}}$
, we will also consider surfaces equipped with a parametrisation of collar neighbourhoods of the incoming and the outgoing boundary.
${\mathscr {M}}$
, we will also consider surfaces equipped with a parametrisation of collar neighbourhoods of the incoming and the outgoing boundary.
Notation 2.3. For all
![]() $g\geqslant 0$
and
$g\geqslant 0$
and
![]() $n\geqslant 1$
, we fix a model surface
$n\geqslant 1$
, we fix a model surface
![]() $\Sigma _{g,n}$
: it is a connected surface of genus g with n outgoing and no incoming boundary components. We say that
$\Sigma _{g,n}$
: it is a connected surface of genus g with n outgoing and no incoming boundary components. We say that
![]() $\mathcal {S}$
is of type
$\mathcal {S}$
is of type
![]() $\Sigma _{g,n}$
if there exists a diffeomorphism
$\Sigma _{g,n}$
if there exists a diffeomorphism
![]() $\mathcal {S}\to \Sigma _{g,n}$
preserving the boundary parametrisation.
$\mathcal {S}\to \Sigma _{g,n}$
preserving the boundary parametrisation.
Definition 2.4. The mapping class group
![]() $\Gamma (\mathcal {S},\partial \mathcal {S})$
is the group of isotopy classes of diffeomorphisms
$\Gamma (\mathcal {S},\partial \mathcal {S})$
is the group of isotopy classes of diffeomorphisms
![]() $\Phi \colon \mathcal {S}\to \mathcal {S}$
that fix the boundary pointwise: that is,
$\Phi \colon \mathcal {S}\to \mathcal {S}$
that fix the boundary pointwise: that is,
![]() $\Phi \circ \vartheta =\vartheta $
. Such a
$\Phi \circ \vartheta =\vartheta $
. Such a
![]() $\Phi $
is called a diffeomorphism of
$\Phi $
is called a diffeomorphism of
![]() $(\mathcal {S},\partial \mathcal {S})$
. For
$(\mathcal {S},\partial \mathcal {S})$
. For
![]() $\mathcal {S}=\Sigma _{g,n}$
, we also write
$\mathcal {S}=\Sigma _{g,n}$
, we also write
![]() $\Gamma _{g,n}$
for
$\Gamma _{g,n}$
for
![]() $\Gamma (\mathcal {S},\partial \mathcal {S})$
. We usually denote isotopy classes by small Greek letters
$\Gamma (\mathcal {S},\partial \mathcal {S})$
. We usually denote isotopy classes by small Greek letters
![]() $\varphi $
and use capital Greek letters for diffeomorphisms.
$\varphi $
and use capital Greek letters for diffeomorphisms.
Remark 2.5. Note that any diffeomorphism
![]() $\Xi \colon \mathcal {S}\to \mathcal {S}'$
induces an identification of the groups
$\Xi \colon \mathcal {S}\to \mathcal {S}'$
induces an identification of the groups
![]() $\Gamma (\mathcal {S},\partial \mathcal {S})\cong \Gamma (\mathcal {S}',\partial \mathcal {S}')$
by conjugation with
$\Gamma (\mathcal {S},\partial \mathcal {S})\cong \Gamma (\mathcal {S}',\partial \mathcal {S}')$
by conjugation with
![]() $\Xi $
: the mapping class
$\Xi $
: the mapping class
![]() $\varphi \in \Gamma (\mathcal {S},\partial \mathcal {S})$
, represented by the diffeomorphism
$\varphi \in \Gamma (\mathcal {S},\partial \mathcal {S})$
, represented by the diffeomorphism
![]() $\Phi $
, corresponds to the mapping class
$\Phi $
, corresponds to the mapping class
![]() $\varphi ^\Xi \in \Gamma (\mathcal {S}',\partial \mathcal {S}')$
, represented by
$\varphi ^\Xi \in \Gamma (\mathcal {S}',\partial \mathcal {S}')$
, represented by
![]() $\Xi \circ \Phi \circ \Xi ^{-1}$
.
$\Xi \circ \Phi \circ \Xi ^{-1}$
.
Definition 2.6. Let
![]() $\mathfrak {H}\subset \mathfrak {S}_{\pi _0(\partial ^{\text {out}}\mathcal {S})}\times \mathfrak {S}_{\pi _0(\partial ^{\text {in}}\mathcal {S})}$
be a subgroup, where ‘
$\mathfrak {H}\subset \mathfrak {S}_{\pi _0(\partial ^{\text {out}}\mathcal {S})}\times \mathfrak {S}_{\pi _0(\partial ^{\text {in}}\mathcal {S})}$
be a subgroup, where ‘
![]() $\mathfrak {S}$
’ denotes the symmetric group on the finite set given as index. We define the extended mapping class group
$\mathfrak {S}$
’ denotes the symmetric group on the finite set given as index. We define the extended mapping class group
![]() $\Gamma ^{\mathfrak {H}}(\mathcal {S})$
as the group of isotopy classes of diffeomorphisms
$\Gamma ^{\mathfrak {H}}(\mathcal {S})$
as the group of isotopy classes of diffeomorphisms
![]() $\Phi \colon \mathcal {S}\to \mathcal {S}$
that preserve the orientation of
$\Phi \colon \mathcal {S}\to \mathcal {S}$
that preserve the orientation of
![]() $\mathcal {S}$
and the boundary parametrisation, and permute the boundary components of
$\mathcal {S}$
and the boundary parametrisation, and permute the boundary components of
![]() $\partial ^{\text {out}}\mathcal {S}$
and
$\partial ^{\text {out}}\mathcal {S}$
and
![]() $\partial ^{\text {in}}\mathcal {S}$
according to a pair of permutations in
$\partial ^{\text {in}}\mathcal {S}$
according to a pair of permutations in
![]() $\mathfrak {H}$
.
$\mathfrak {H}$
.
If we take
![]() $\mathfrak {H}=\mathfrak {S}_{\pi _0(\partial ^{\text {out}}\mathcal {S})}\times \mathfrak {S}_{\pi _0(\partial ^{\text {in}}\mathcal {S})}$
, we also write
$\mathfrak {H}=\mathfrak {S}_{\pi _0(\partial ^{\text {out}}\mathcal {S})}\times \mathfrak {S}_{\pi _0(\partial ^{\text {in}}\mathcal {S})}$
, we also write
![]() $\Gamma (\mathcal {S})$
for the extended mapping class group. If
$\Gamma (\mathcal {S})$
for the extended mapping class group. If
![]() $\mathcal {S}=\Sigma _{g,n}$
, we also write
$\mathcal {S}=\Sigma _{g,n}$
, we also write
![]() $\Gamma _{g,n}^{\mathfrak {H}}=\Gamma ^{\mathfrak {H}}(\mathcal {S})$
and
$\Gamma _{g,n}^{\mathfrak {H}}=\Gamma ^{\mathfrak {H}}(\mathcal {S})$
and
![]() $\Gamma _{g,(n)}=\Gamma (\mathcal {S})$
for the extended mapping class groups.
$\Gamma _{g,(n)}=\Gamma (\mathcal {S})$
for the extended mapping class groups.
Note that we have an extension
![]() $1\to \Gamma (\mathcal {S},\partial \mathcal {S})\to \Gamma ^{\mathfrak {H}}(\mathcal {S})\to \mathfrak {H}\to 1$
.
$1\to \Gamma (\mathcal {S},\partial \mathcal {S})\to \Gamma ^{\mathfrak {H}}(\mathcal {S})\to \mathfrak {H}\to 1$
.
Definition 2.7. If G is a group, we denote by
![]() ${\mathrm {Conj}}(G)$
the set of conjugacy classes of G. For a group element
${\mathrm {Conj}}(G)$
the set of conjugacy classes of G. For a group element
![]() $\gamma \in G$
, we denote by
$\gamma \in G$
, we denote by
![]() $Z(\gamma ,G)\subseteq G$
the centraliser of
$Z(\gamma ,G)\subseteq G$
the centraliser of
![]() $\gamma $
: that is, the subgroup of all elements
$\gamma $
: that is, the subgroup of all elements
![]() $\gamma '\in G$
that commute with
$\gamma '\in G$
that commute with
![]() $\gamma $
.
$\gamma $
.
Notation 2.8. We fix, once and for all, for all conjugacy classes in
![]() ${\mathrm {Conj}}(\Gamma _{g,n})$
, a representative of the class. We denote by
${\mathrm {Conj}}(\Gamma _{g,n})$
, a representative of the class. We denote by
![]() $\mathfrak {g}\colon \Gamma _{g,n}\to \Gamma _{g,n}$
the function of sets assigning to each element of
$\mathfrak {g}\colon \Gamma _{g,n}\to \Gamma _{g,n}$
the function of sets assigning to each element of
![]() $\Gamma _{g,n}$
the representative of its class.
$\Gamma _{g,n}$
the representative of its class.
Definition 2.9. Let
![]() $\mathcal {S}$
be a surface. We denote by
$\mathcal {S}$
be a surface. We denote by
![]() $\mathfrak {M}(\mathcal {S})$
the moduli space of Riemann structures on
$\mathfrak {M}(\mathcal {S})$
the moduli space of Riemann structures on
![]() $\mathcal {S}$
; two Riemann structures on
$\mathcal {S}$
; two Riemann structures on
![]() $\mathcal {S}$
are considered equivalent if there is a diffeomorphism
$\mathcal {S}$
are considered equivalent if there is a diffeomorphism
![]() $\Psi \colon \mathcal {S}\to \mathcal {S}$
fixing
$\Psi \colon \mathcal {S}\to \mathcal {S}$
fixing
![]() $\partial \mathcal {S}$
pointwise and pulling back one Riemann structure to the other. If
$\partial \mathcal {S}$
pointwise and pulling back one Riemann structure to the other. If
![]() $\mathcal {S}=\Sigma _{g,n}$
, we also write
$\mathcal {S}=\Sigma _{g,n}$
, we also write
![]() $\mathfrak {M}_{g,n}$
for the moduli space
$\mathfrak {M}_{g,n}$
for the moduli space
![]() $\mathfrak {M}(\Sigma _{g,n})$
.
$\mathfrak {M}(\Sigma _{g,n})$
.
The hypothesis that every connected component of
![]() $\mathcal {S}$
has non-empty boundary implies that
$\mathcal {S}$
has non-empty boundary implies that
![]() $\mathfrak {M}(\mathcal {S})$
is a classifying space for the group
$\mathfrak {M}(\mathcal {S})$
is a classifying space for the group
![]() $\Gamma (\mathcal {S},\partial \mathcal {S})$
.
$\Gamma (\mathcal {S},\partial \mathcal {S})$
.
2.2 Arcs and the Alexander method
For the rest of this section, we fix a connected surface
![]() $\mathcal {S}$
of type
$\mathcal {S}$
of type
![]() $\Sigma _{g,n}$
, with
$\Sigma _{g,n}$
, with
![]() $g\geqslant 0$
and
$g\geqslant 0$
and
![]() $n\geqslant 1$
, and focus on the mapping class group
$n\geqslant 1$
, and focus on the mapping class group
![]() $\Gamma (\mathcal {S},\partial \mathcal {S})$
. Given a mapping class
$\Gamma (\mathcal {S},\partial \mathcal {S})$
. Given a mapping class
![]() $\varphi \in \Gamma (\mathcal {S},\partial \mathcal {S})$
, we construct a system of simple closed curves on
$\varphi \in \Gamma (\mathcal {S},\partial \mathcal {S})$
, we construct a system of simple closed curves on
![]() $\mathcal {S}$
cutting
$\mathcal {S}$
cutting
![]() $\mathcal {S}$
into two subsurfaces W and Y: the subsurface
$\mathcal {S}$
into two subsurfaces W and Y: the subsurface
![]() $W\subset \mathcal {S}$
is the white subsurface and is, up to isotopy, the maximal subsurface of
$W\subset \mathcal {S}$
is the white subsurface and is, up to isotopy, the maximal subsurface of
![]() $\mathcal {S}$
satisfying the following conditions:
$\mathcal {S}$
satisfying the following conditions:
-
○ all connected components of W touch
 $\partial \mathcal {S}$
;
$\partial \mathcal {S}$
; -
○
 $\varphi $
can be represented by a diffeomorphism of
$\varphi $
can be represented by a diffeomorphism of
 $\mathcal {S}$
fixing W pointwise.
$\mathcal {S}$
fixing W pointwise.
We start by recalling some standard facts about embedded arcs in surfaces. The material of this subsection is taken, up to minor changes, from [Reference Farb and Margalit7]. For the following definition see [Reference Farb and Margalit7, § 1.2.7].
Definition 2.10. An arc in
![]() $\mathcal {S}$
is a smooth embedding
$\mathcal {S}$
is a smooth embedding
![]() $\alpha \colon [0;1]\hookrightarrow \mathcal {S}$
such that
$\alpha \colon [0;1]\hookrightarrow \mathcal {S}$
such that
![]() $\alpha ^{-1}(\partial \mathcal {S})=\{0,1\}$
and
$\alpha ^{-1}(\partial \mathcal {S})=\{0,1\}$
and
![]() $\alpha $
is transverse to
$\alpha $
is transverse to
![]() $\partial \mathcal {S}$
. Two arcs are disjoint if their images are disjoint (also at the endpoints). An arc is essential if it does not cut
$\partial \mathcal {S}$
. Two arcs are disjoint if their images are disjoint (also at the endpoints). An arc is essential if it does not cut
![]() $\mathcal {S}$
in two parts, one of which is a disc.
$\mathcal {S}$
in two parts, one of which is a disc.
Two arcs
![]() $\alpha $
and
$\alpha $
and
![]() $\alpha '$
are directly isotopic if
$\alpha '$
are directly isotopic if
![]() $\alpha (0)=\alpha '(0)$
,
$\alpha (0)=\alpha '(0)$
,
![]() $\alpha (1)=\alpha '(1)$
, and there is an isotopy of embeddings
$\alpha (1)=\alpha '(1)$
, and there is an isotopy of embeddings
![]() $[0;1]\to \mathcal {S}$
that is stationary on
$[0;1]\to \mathcal {S}$
that is stationary on
![]() $\left \{0,1\right \}$
and connects
$\left \{0,1\right \}$
and connects
![]() $\alpha $
to
$\alpha $
to
![]() $\alpha '$
. Two arcs are inversely isotopic if the previous holds after reparametrising one of the two arcs in the opposite direction. Two arcs are isotopic if they are directly or inversely isotopic; we write
$\alpha '$
. Two arcs are inversely isotopic if the previous holds after reparametrising one of the two arcs in the opposite direction. Two arcs are isotopic if they are directly or inversely isotopic; we write
![]() $\alpha \sim \alpha '$
if
$\alpha \sim \alpha '$
if
![]() $\alpha $
and
$\alpha $
and
![]() $\alpha '$
are isotopic.
$\alpha '$
are isotopic.
Two arcs
![]() $\alpha $
and
$\alpha $
and
![]() $\beta $
are in minimal position if they are disjoint at their endpoints, they intersect transversely, and the number of intersection points in
$\beta $
are in minimal position if they are disjoint at their endpoints, they intersect transversely, and the number of intersection points in
![]() $\alpha \cup \beta $
is minimal among all choices of
$\alpha \cup \beta $
is minimal among all choices of
![]() $\alpha '\sim \alpha $
and
$\alpha '\sim \alpha $
and
![]() $\beta '\sim \beta $
with
$\beta '\sim \beta $
with
![]() $\alpha '$
and
$\alpha '$
and
![]() $\beta '$
transverse.
$\beta '$
transverse.
Note that we only consider isotopy classes of arcs relative to their endpoints; two arcs sharing one endpoint are never considered in minimal position (and, by convention, cannot be isotoped to be in minimal position). In particular, unless
![]() $\mathcal {S}$
is a disc, there are more than countably many isotopy classes of essential arcs in
$\mathcal {S}$
is a disc, there are more than countably many isotopy classes of essential arcs in
![]() $\mathcal {S}$
.
$\mathcal {S}$
.
If
![]() $\chi (\mathcal {S})=2-2g-n\leqslant 0$
, then according to [Reference Farb and Margalit7, § 1.2.7], the following statement holds: given a collection of essential arcs
$\chi (\mathcal {S})=2-2g-n\leqslant 0$
, then according to [Reference Farb and Margalit7, § 1.2.7], the following statement holds: given a collection of essential arcs
![]() $\alpha _1,\dots ,\alpha _k$
in
$\alpha _1,\dots ,\alpha _k$
in
![]() $\mathcal {S}$
, which have all distinct endpoints and are pairwise non-isotopic, one can replace each
$\mathcal {S}$
, which have all distinct endpoints and are pairwise non-isotopic, one can replace each
![]() $\alpha _i$
with an arc
$\alpha _i$
with an arc
![]() $\alpha ^{\prime }_i\sim \alpha _i$
so that
$\alpha ^{\prime }_i\sim \alpha _i$
so that
![]() $\alpha ^{\prime }_1,\dots ,\alpha ^{\prime }_k$
are pairwise in minimal position. In fact, it suffices to choose a Riemannian metric of constant curvature on
$\alpha ^{\prime }_1,\dots ,\alpha ^{\prime }_k$
are pairwise in minimal position. In fact, it suffices to choose a Riemannian metric of constant curvature on
![]() $\mathcal {S}$
such that
$\mathcal {S}$
such that
![]() $\partial \mathcal {S}$
is geodesic, and replace each
$\partial \mathcal {S}$
is geodesic, and replace each
![]() $\alpha _i$
with its geodesic representative relative to the endpoints: the hypothesis on
$\alpha _i$
with its geodesic representative relative to the endpoints: the hypothesis on
![]() $\chi (\mathcal {S})$
ensures that we get a non-positively curved metric, so that geodesic representatives are unique; moreover, geodesic representatives are automatically pairwise in minimal position.
$\chi (\mathcal {S})$
ensures that we get a non-positively curved metric, so that geodesic representatives are unique; moreover, geodesic representatives are automatically pairwise in minimal position.
Among all connected surfaces with non-empty boundary, the only one with positive Euler characteristic is
![]() $\Sigma _{0,1}$
, that is, the disc: note that the statement holds vacuously also for the disc, which contains no essential arc. The following is a special case of the Alexander method [Reference Farb and Margalit7, Prop. 2.8].
$\Sigma _{0,1}$
, that is, the disc: note that the statement holds vacuously also for the disc, which contains no essential arc. The following is a special case of the Alexander method [Reference Farb and Margalit7, Prop. 2.8].
Proposition 2.11. Let
![]() $\alpha _0,\dots ,\alpha _k$
and
$\alpha _0,\dots ,\alpha _k$
and
![]() $\beta $
be a collection of essential arcs in
$\beta $
be a collection of essential arcs in
![]() $\mathcal {S}$
, and assume the following:
$\mathcal {S}$
, and assume the following:
-
○ all arcs are pairwise in minimal position;
-
○ the arcs
 $\alpha _0,\dots ,\alpha _k$
are pairwise disjoint.
$\alpha _0,\dots ,\alpha _k$
are pairwise disjoint.
Let
![]() $\Phi $
be a diffeomorphism of
$\Phi $
be a diffeomorphism of
![]() $(\mathcal {S},\partial \mathcal {S})$
, and suppose that
$(\mathcal {S},\partial \mathcal {S})$
, and suppose that
![]() $\Phi $
fixes each of
$\Phi $
fixes each of
![]() $\alpha _0,\dots ,\alpha _k$
and
$\alpha _0,\dots ,\alpha _k$
and
![]() $\beta $
up to isotopy relative to the endpoints. Then
$\beta $
up to isotopy relative to the endpoints. Then
![]() $\Phi $
can be isotoped to a diffeomorphism
$\Phi $
can be isotoped to a diffeomorphism
![]() $\Phi '$
of
$\Phi '$
of
![]() $\mathcal {S}$
that fixes
$\mathcal {S}$
that fixes
![]() $\alpha _0\cup \dotsb \cup \alpha _k\cup \beta $
pointwise.
$\alpha _0\cup \dotsb \cup \alpha _k\cup \beta $
pointwise.
In Proposition 2.11, one can enhance the requirement on
![]() $\Phi '$
to be the following: the map
$\Phi '$
to be the following: the map
![]() $\Phi '$
fixes pointwise a small neighbourhood
$\Phi '$
fixes pointwise a small neighbourhood
![]() $U\subset \mathcal {S}$
of the union
$U\subset \mathcal {S}$
of the union
![]() $\alpha _0\cup \dotsb \cup \alpha _k\cup \beta \cup \partial \mathcal {S}$
. Here and in the following, a small neighbourhood is required to deformation retract onto
$\alpha _0\cup \dotsb \cup \alpha _k\cup \beta \cup \partial \mathcal {S}$
. Here and in the following, a small neighbourhood is required to deformation retract onto
![]() $\alpha _0\cup \dotsb \cup \alpha _k\cup \beta \cup \partial \mathcal {S}$
by restriction of an ambient homotopy, defined on
$\alpha _0\cup \dotsb \cup \alpha _k\cup \beta \cup \partial \mathcal {S}$
by restriction of an ambient homotopy, defined on
![]() $\mathcal {S}$
and stationary on
$\mathcal {S}$
and stationary on
![]() $\alpha _0\cup \dotsb \cup \alpha _k\cup \beta \cup \partial \mathcal {S}$
.
$\alpha _0\cup \dotsb \cup \alpha _k\cup \beta \cup \partial \mathcal {S}$
.
Remark 2.12. The Alexander method, as stated in [Reference Farb and Margalit7], only applies under the additional hypothesis that the arcs
![]() $\alpha _0,\dots ,\alpha _k$
and
$\alpha _0,\dots ,\alpha _k$
and
![]() $\beta $
are pairwise non-isotopic. We remark, however, that this hypothesis is not essential.
$\beta $
are pairwise non-isotopic. We remark, however, that this hypothesis is not essential.
To see this, suppose that
![]() $\alpha _0,\dots ,\alpha _k$
and
$\alpha _0,\dots ,\alpha _k$
and
![]() $\beta $
is a collection of arcs as in Proposition 2.11: up to reordering the arcs
$\beta $
is a collection of arcs as in Proposition 2.11: up to reordering the arcs
![]() $\alpha _i$
, we can assume that there is
$\alpha _i$
, we can assume that there is
![]() $0\leqslant k'\leqslant k$
such that the arcs
$0\leqslant k'\leqslant k$
such that the arcs
![]() $\alpha _0,\dots ,\alpha _{k'}$
and
$\alpha _0,\dots ,\alpha _{k'}$
and
![]() $\beta $
are pairwise non-isotopic, and, moreover, each
$\beta $
are pairwise non-isotopic, and, moreover, each
![]() $\alpha _i$
with
$\alpha _i$
with
![]() $i\geqslant k'+1$
is isotopic to some
$i\geqslant k'+1$
is isotopic to some
![]() $\alpha _j$
with
$\alpha _j$
with
![]() $j\leqslant k'$
.
$j\leqslant k'$
.
We can then apply the Alexander method to the collection
![]() $\alpha _0,\dots ,\alpha _{k'}$
and
$\alpha _0,\dots ,\alpha _{k'}$
and
![]() $\beta $
, obtaining a diffeomorphism
$\beta $
, obtaining a diffeomorphism
![]() $\Phi '$
that fixes a small neighbourhood U of
$\Phi '$
that fixes a small neighbourhood U of
![]() $\alpha _0\cup \dotsb \cup \alpha _{k'}\cup \beta $
pointwise. We then argue as follows: for each index
$\alpha _0\cup \dotsb \cup \alpha _{k'}\cup \beta $
pointwise. We then argue as follows: for each index
![]() $i\geqslant k'+1$
, there is an index
$i\geqslant k'+1$
, there is an index
![]() $j\leqslant k'$
such that
$j\leqslant k'$
such that
![]() $\alpha _i$
and
$\alpha _i$
and
![]() $\alpha _j$
are isotopic and in minimal position: this implies that they cobound (together with two segments in
$\alpha _j$
are isotopic and in minimal position: this implies that they cobound (together with two segments in
![]() $\partial \mathcal {S}$
) a rectangle in
$\partial \mathcal {S}$
) a rectangle in
![]() $\mathcal {S}$
, and, up to shrinking, we can assume that this rectangle lies already inside U: that is, we can assume that
$\mathcal {S}$
, and, up to shrinking, we can assume that this rectangle lies already inside U: that is, we can assume that
![]() $\alpha _i$
is fixed pointwise by
$\alpha _i$
is fixed pointwise by
![]() $\Phi '$
as well.
$\Phi '$
as well.
2.3 The cut locus of a mapping class
In this subsection, we fix a class
![]() $\varphi \in \Gamma (\mathcal {S},\partial \mathcal {S})$
, represented by a diffeomorphism
$\varphi \in \Gamma (\mathcal {S},\partial \mathcal {S})$
, represented by a diffeomorphism
![]() $\Phi $
, and study the isotopy classes of arcs and curves that it fixes.
$\Phi $
, and study the isotopy classes of arcs and curves that it fixes.
Definition 2.13. Two arcs
![]() $\alpha $
and
$\alpha $
and
![]() $\alpha '$
in
$\alpha '$
in
![]() $\mathcal {S}$
are directly parallel if they are disjoint and there is an embedding
$\mathcal {S}$
are directly parallel if they are disjoint and there is an embedding
![]() $[0;1]\times [0;1]\hookrightarrow \mathcal {S}$
restricting to
$[0;1]\times [0;1]\hookrightarrow \mathcal {S}$
restricting to
![]() $\alpha $
on
$\alpha $
on
![]() $[0;1]\times \left \{0\right \}$
and to
$[0;1]\times \left \{0\right \}$
and to
![]() $\alpha '$
on
$\alpha '$
on
![]() $[0;1]\times \left \{1\right \}$
, and restricting to an embedding
$[0;1]\times \left \{1\right \}$
, and restricting to an embedding
![]() $\left \{0,1\right \}\times [0;1]\hookrightarrow \partial \mathcal {S}$
.
$\left \{0,1\right \}\times [0;1]\hookrightarrow \partial \mathcal {S}$
.
Two arcs
![]() $\alpha $
and
$\alpha $
and
![]() $\alpha '$
are inversely parallel if the previous holds after reparametrising one of the two arcs in the opposite direction. Two arcs
$\alpha '$
are inversely parallel if the previous holds after reparametrising one of the two arcs in the opposite direction. Two arcs
![]() $\alpha $
and
$\alpha $
and
![]() $\alpha '$
are parallel if they are directly or inversely parallel.
$\alpha '$
are parallel if they are directly or inversely parallel.
Note that in the previous definition, we do not insist that the embedding
![]() $[0;1]\times [0;1]\hookrightarrow \mathcal {S}$
is orientation-preserving; see Figure 2.
$[0;1]\times [0;1]\hookrightarrow \mathcal {S}$
is orientation-preserving; see Figure 2.

Figure 2 A maximal collection of six pairwise non-parallel arcs
![]() $\alpha _0,\dotsc ,\alpha _5$
on a surface of type
$\alpha _0,\dotsc ,\alpha _5$
on a surface of type
![]() $\Sigma _{1,2}$
.
$\Sigma _{1,2}$
.
Definition 2.14. The fixed-arc complex of
![]() $\varphi $
is an abstract simplicial complex whose vertices are all isotopy classes of essential arcs
$\varphi $
is an abstract simplicial complex whose vertices are all isotopy classes of essential arcs
![]() $\alpha $
in
$\alpha $
in
![]() $\mathcal {S}$
fixed by
$\mathcal {S}$
fixed by
![]() $\varphi $
. A collection of isotopy classes of arcs
$\varphi $
. A collection of isotopy classes of arcs
![]() $\alpha _0,\dotsc ,\alpha _k$
spans a k-simplex if the arcs
$\alpha _0,\dotsc ,\alpha _k$
spans a k-simplex if the arcs
![]() $\alpha _0,\dotsc ,\alpha _k$
can be isotoped to disjoint, pairwise non-parallel arcs
$\alpha _0,\dotsc ,\alpha _k$
can be isotoped to disjoint, pairwise non-parallel arcs
![]() $\alpha ^{\prime }_0,\dotsc ,\alpha ^{\prime }_k$
.
$\alpha ^{\prime }_0,\dotsc ,\alpha ^{\prime }_k$
.
The mapping class
![]() $\varphi $
is called
$\varphi $
is called
![]() $\partial $
-irreducible if its fixed-arc complex is empty and if
$\partial $
-irreducible if its fixed-arc complex is empty and if
![]() $\mathcal {S}$
is not of type
$\mathcal {S}$
is not of type
![]() $\Sigma _{0,1}$
.
$\Sigma _{0,1}$
.
Example 2.15. Every isotopy class of essential arcs in
![]() $\mathcal {S}$
is fixed (up to isotopy) by the identity
$\mathcal {S}$
is fixed (up to isotopy) by the identity
![]() . Therefore
. Therefore
![]() is not
is not
![]() $\partial $
-irreducible, provided that
$\partial $
-irreducible, provided that
![]() $\mathcal {S}$
admits some essential arc; if
$\mathcal {S}$
admits some essential arc; if
![]() $\mathcal {S}$
does not admit essential arcs, then
$\mathcal {S}$
does not admit essential arcs, then
![]() $\mathcal {S}$
is a disc
$\mathcal {S}$
is a disc
![]() $\Sigma _{0,1}$
and we have prescribed, also in this case, that
$\Sigma _{0,1}$
and we have prescribed, also in this case, that
![]() is not
is not
![]() $\partial $
-irreducible. The reason to regard
$\partial $
-irreducible. The reason to regard
![]() as not being
as not being
![]() $\partial $
-irreducible will become clear later; for the moment we make a simple comparison and say that, in a similar way,
$\partial $
-irreducible will become clear later; for the moment we make a simple comparison and say that, in a similar way,
![]() $1\in \mathbb {Z}$
is not considered a prime number.
$1\in \mathbb {Z}$
is not considered a prime number.
Example 2.16. The fixed-arc complex of
![]() $\varphi \in \Gamma _{0,2}\cong \mathbb {Z}$
is empty if
$\varphi \in \Gamma _{0,2}\cong \mathbb {Z}$
is empty if
![]() and consists of uncountably many vertices, joined by no higher simplex if
and consists of uncountably many vertices, joined by no higher simplex if
![]() . Therefore every non-trivial element in
. Therefore every non-trivial element in
![]() $\Gamma _{0,2}$
is
$\Gamma _{0,2}$
is
![]() $\partial $
-irreducible.
$\partial $
-irreducible.
Example 2.17. For
![]() $g\geqslant 1$
the boundary Dehn twist
$g\geqslant 1$
the boundary Dehn twist
![]() $T_{\partial }\in \Gamma _{g,1}$
is
$T_{\partial }\in \Gamma _{g,1}$
is
![]() $\partial $
-irreducible, though there are plenty of isotopy classes of simple closed curves in
$\partial $
-irreducible, though there are plenty of isotopy classes of simple closed curves in
![]() $\Sigma _{g,1}$
that are fixed by
$\Sigma _{g,1}$
that are fixed by
![]() $T_{\partial }$
: in fact, all simple closed curves are fixed, up to isotopy, by
$T_{\partial }$
: in fact, all simple closed curves are fixed, up to isotopy, by
![]() $T_{\partial }$
. Nevertheless, no isotopy class of essential arcs is fixed by
$T_{\partial }$
. Nevertheless, no isotopy class of essential arcs is fixed by
![]() $\varphi $
; here it is crucial to consider isotopy classes of arcs relative to the endpoints.
$\varphi $
; here it is crucial to consider isotopy classes of arcs relative to the endpoints.
Note that a simplex in the fixed-arc complex of a class
![]() $\varphi \in \Gamma (\mathcal {S},\partial \mathcal {S})$
has dimension at most
$\varphi \in \Gamma (\mathcal {S},\partial \mathcal {S})$
has dimension at most
![]() $-3\chi (\mathcal {S})-1$
if
$-3\chi (\mathcal {S})-1$
if
![]() $\chi (\mathcal {S})<0$
, and at most
$\chi (\mathcal {S})<0$
, and at most
![]() $0$
if
$0$
if
![]() $\mathcal {S}$
is of type
$\mathcal {S}$
is of type
![]() $\Sigma _{0,2}$
. In the second case, just note that each two disjoint essential arcs in
$\Sigma _{0,2}$
. In the second case, just note that each two disjoint essential arcs in
![]() $\Sigma _{0,2}$
are parallel. In the first case, let
$\Sigma _{0,2}$
are parallel. In the first case, let
![]() $\alpha _0,\dots ,\alpha _k$
be disjoint, pairwise non-parallel and essential arcs in
$\alpha _0,\dots ,\alpha _k$
be disjoint, pairwise non-parallel and essential arcs in
![]() $\mathcal {S}$
; then cutting
$\mathcal {S}$
; then cutting
![]() $\mathcal {S}$
along the arcs
$\mathcal {S}$
along the arcs
![]() $\alpha _i$
yields a surface whose connected components are either hexagons or connected surfaces of negative Euler characteristic. Up to adjoining more arcs (and thus increase k), we can assume to have only hexagons. Each hexagon has 3 sides coming from
$\alpha _i$
yields a surface whose connected components are either hexagons or connected surfaces of negative Euler characteristic. Up to adjoining more arcs (and thus increase k), we can assume to have only hexagons. Each hexagon has 3 sides coming from
![]() $\partial \mathcal {S}$
and 3 sides coming from the cuts. If
$\partial \mathcal {S}$
and 3 sides coming from the cuts. If
![]() $\ell \geqslant 1$
denotes the number of hexagons, we have
$\ell \geqslant 1$
denotes the number of hexagons, we have
![]() $3\ell =2(k+1)$
, as each arc contributes to 2 hexagons; moreover
$3\ell =2(k+1)$
, as each arc contributes to 2 hexagons; moreover
![]() $\chi (\mathcal {S})=\ell -(k+1)$
, implying
$\chi (\mathcal {S})=\ell -(k+1)$
, implying
![]() $3\chi (\mathcal {S})=3\ell -3(k+1)=-k-1$
.
$3\chi (\mathcal {S})=3\ell -3(k+1)=-k-1$
.
Construction 2.18. Let
![]() $\mathcal {S}$
be not of type
$\mathcal {S}$
be not of type
![]() $\Sigma _{0,1}$
, let
$\Sigma _{0,1}$
, let
![]() $\varphi \in \Gamma (\mathcal {S},\partial \mathcal {S})$
, and let
$\varphi \in \Gamma (\mathcal {S},\partial \mathcal {S})$
, and let
![]() $\alpha _0,\dots, \alpha _k$
be disjoint, essential, pairwise non-parallel arcs in
$\alpha _0,\dots, \alpha _k$
be disjoint, essential, pairwise non-parallel arcs in
![]() $\mathcal {S}$
, representing a maximal simplex in the fixed-arc complex of
$\mathcal {S}$
, representing a maximal simplex in the fixed-arc complex of
![]() $\varphi $
. Let U be a closed, small neighbourhood of the union
$\varphi $
. Let U be a closed, small neighbourhood of the union
![]() $\alpha _0\cup \dotsb \cup \alpha _k\cup \partial \mathcal {S}$
. The complement
$\alpha _0\cup \dotsb \cup \alpha _k\cup \partial \mathcal {S}$
. The complement
![]() $\mathcal {S}\smallsetminus U$
consists of many regions, some of which may be discs: let
$\mathcal {S}\smallsetminus U$
consists of many regions, some of which may be discs: let
![]() $W\subset \mathcal {S}$
denote the union of U and all discs in
$W\subset \mathcal {S}$
denote the union of U and all discs in
![]() $\mathcal {S}\smallsetminus U$
. Then W is a closed, possibly disconnected subsurface of
$\mathcal {S}\smallsetminus U$
. Then W is a closed, possibly disconnected subsurface of
![]() $\mathcal {S}$
; we denote by Y the closure of
$\mathcal {S}$
; we denote by Y the closure of
![]() $\mathcal {S}\smallsetminus W$
. If
$\mathcal {S}\smallsetminus W$
. If
![]() $\partial W$
denotes the union of all boundary components of W, and
$\partial W$
denotes the union of all boundary components of W, and
![]() $\partial Y$
denotes the union of all boundary components of Y, then
$\partial Y$
denotes the union of all boundary components of Y, then
![]() $\partial W$
takes the form
$\partial W$
takes the form
![]() $\partial \mathcal {S}\cup c_1\cup \dotsb \cup c_h$
, for some
$\partial \mathcal {S}\cup c_1\cup \dotsb \cup c_h$
, for some
![]() $h\geqslant 0$
and some curves
$h\geqslant 0$
and some curves
![]() $c_1,\dots ,c_h\subset \mathcal {S}$
; similarly
$c_1,\dots ,c_h\subset \mathcal {S}$
; similarly
![]() $\partial Y=c_1\cup \dotsb \cup c_h$
. The curves
$\partial Y=c_1\cup \dotsb \cup c_h$
. The curves
![]() $c_1,\dots ,c_h$
inherit a canonical boundary orientation from Y, which is oriented as subsurface of
$c_1,\dots ,c_h$
inherit a canonical boundary orientation from Y, which is oriented as subsurface of
![]() $\mathcal {S}$
.
$\mathcal {S}$
.
Definition 2.19. For
![]() $\varphi $
and
$\varphi $
and
![]() $\alpha _0,\dots, \alpha _k$
as above, we define the cut locus of
$\alpha _0,\dots, \alpha _k$
as above, we define the cut locus of
![]() $\varphi $
, relative to the simplex
$\varphi $
, relative to the simplex
![]() $\alpha _0,\dots ,\alpha _k$
, as the isotopy class of the multicurve
$\alpha _0,\dots ,\alpha _k$
, as the isotopy class of the multicurve
![]() $c_1,\dots ,c_h$
, denoted
$c_1,\dots ,c_h$
, denoted
![]() $[c_1,\dots ,c_h]$
. Here and in the following, a multicurve is an unordered collection of disjoint and oriented simple closed curves, and two multicurves are considered isotopic if there is an ambient isotopy bringing the first to the second.
$[c_1,\dots ,c_h]$
. Here and in the following, a multicurve is an unordered collection of disjoint and oriented simple closed curves, and two multicurves are considered isotopic if there is an ambient isotopy bringing the first to the second.
The two regions W and Y are called the associated white and yellow regions or subsurfaces of
![]() $\mathcal {S}$
, and they depend, as subsets of
$\mathcal {S}$
, and they depend, as subsets of
![]() $\mathcal {S}$
, on a choice of a multicurve representing the cut locus. If
$\mathcal {S}$
, on a choice of a multicurve representing the cut locus. If
![]() , we declare the cut locus to be empty and W to be the entire surface
, we declare the cut locus to be empty and W to be the entire surface
![]() $\Sigma _{0,1}$
.
$\Sigma _{0,1}$
.
See Figure 3 for an example of the cut locus of a mapping class obtained as a simple product of Dehn twists. Note that it is possible that two curves
![]() $c_i$
and
$c_i$
and
![]() $c_j$
cobound a cylinder in Y: in this case, the two curves are isotopic as non-oriented simple closed curves, but the isotopy bringing
$c_j$
cobound a cylinder in Y: in this case, the two curves are isotopic as non-oriented simple closed curves, but the isotopy bringing
![]() $c_i$
to
$c_i$
to
![]() $c_j$
, spanned by the cylinder of Y, ends with an orientation-reversing diffeomorphism
$c_j$
, spanned by the cylinder of Y, ends with an orientation-reversing diffeomorphism
![]() $c_i\cong c_j$
, as the two curves inherit their orientation from Y while being on opposite sides of the cylinder contained in Y. Hence the isotopy classes of the curves
$c_i\cong c_j$
, as the two curves inherit their orientation from Y while being on opposite sides of the cylinder contained in Y. Hence the isotopy classes of the curves
![]() $c_1,\dots ,c_h$
, considered as oriented curves, are all distinct.
$c_1,\dots ,c_h$
, considered as oriented curves, are all distinct.

Figure 3 Two examples of a decomposition into the ‘yellow’ and the ‘white’ region according to a fixed mapping class
![]() $\varphi $
. In the first case,
$\varphi $
. In the first case,
![]() $\varphi $
is given by the product of the Dehn twists along the curves
$\varphi $
is given by the product of the Dehn twists along the curves
![]() $d_1,\dotsc ,d_7$
, and in the second case, it is just the Dehn twist along the single green curve d. In the second case, the mapping class
$d_1,\dotsc ,d_7$
, and in the second case, it is just the Dehn twist along the single green curve d. In the second case, the mapping class
![]() $\varphi $
is
$\varphi $
is
![]() $\partial $
-irreducible, the cut locus consists of the only isotopy class of d, oriented as a boundary of the yellow region, and the white region is just a collar neighbourhood of
$\partial $
-irreducible, the cut locus consists of the only isotopy class of d, oriented as a boundary of the yellow region, and the white region is just a collar neighbourhood of
![]() $\partial \mathcal {S}$
.
$\partial \mathcal {S}$
.
Note that the cut locus of the identity
![]() is empty, and the white and yellow decomposition consists of a white region
is empty, and the white and yellow decomposition consists of a white region
![]() $W=\mathcal {S}$
and an empty yellow region. Vice versa, the cut locus of a non-trivial mapping class
$W=\mathcal {S}$
and an empty yellow region. Vice versa, the cut locus of a non-trivial mapping class
![]() $\varphi \in \Gamma (\mathcal {S},\partial \mathcal {S})$
is always non-empty.
$\varphi \in \Gamma (\mathcal {S},\partial \mathcal {S})$
is always non-empty.
Definition 2.19 depends a priori on a choice of a maximal simplex in the fixed-arc complex of
![]() $\varphi $
; there is, moreover, a subtle detail that we should check to guarantee that Definition 2.19 is well-posed: suppose that the disjoint arcs
$\varphi $
; there is, moreover, a subtle detail that we should check to guarantee that Definition 2.19 is well-posed: suppose that the disjoint arcs
![]() $\alpha ^{\prime }_0,\dotsc ,\alpha ^{\prime }_k$
are isotopic to the disjoint arcs
$\alpha ^{\prime }_0,\dotsc ,\alpha ^{\prime }_k$
are isotopic to the disjoint arcs
![]() $\alpha _0,\dotsc ,\alpha _k$
(that is,
$\alpha _0,\dotsc ,\alpha _k$
(that is,
![]() $\alpha ^{\prime }_i\sim \alpha _i$
for all
$\alpha ^{\prime }_i\sim \alpha _i$
for all
![]() $0\leqslant i\leqslant k$
), so that the two collections of arcs represent the same maximal simplex in the fixed-arc complex of
$0\leqslant i\leqslant k$
), so that the two collections of arcs represent the same maximal simplex in the fixed-arc complex of
![]() $\varphi $
; then we need to check that the two collections of arcs give rise to the same collection of isotopy classes of oriented, disjoint simple closed curves
$\varphi $
; then we need to check that the two collections of arcs give rise to the same collection of isotopy classes of oriented, disjoint simple closed curves
![]() $c_1,\dots , c_h$
.
$c_1,\dots , c_h$
.
We will prove directly that the cut locus only depends on
![]() $\varphi $
, and not on the chosen maximal simplex (and its representative) in the fixed-arc complex of
$\varphi $
, and not on the chosen maximal simplex (and its representative) in the fixed-arc complex of
![]() $\varphi $
.
$\varphi $
.
Lemma 2.20. Let
![]() $\varphi $
and
$\varphi $
and
![]() $\alpha _0,\dots ,\alpha _k$
be as in Definition 2.19, and let
$\alpha _0,\dots ,\alpha _k$
be as in Definition 2.19, and let
![]() $\beta $
be an arc whose endpoints are disjoint from the endpoints of
$\beta $
be an arc whose endpoints are disjoint from the endpoints of
![]() $\alpha _0,\dots ,\alpha _k$
. Suppose that the isotopy class of
$\alpha _0,\dots ,\alpha _k$
. Suppose that the isotopy class of
![]() $\beta $
is fixed by
$\beta $
is fixed by
![]() $\varphi $
; then
$\varphi $
; then
![]() $\beta $
can be isotoped, relative to its endpoints, to an arc
$\beta $
can be isotoped, relative to its endpoints, to an arc
![]() $\hat \beta $
lying in a small neighbourhood U of
$\hat \beta $
lying in a small neighbourhood U of
![]() $\alpha _0\cup \dotsb \cup \alpha _k\cup \partial \mathcal {S}$
.
$\alpha _0\cup \dotsb \cup \alpha _k\cup \partial \mathcal {S}$
.
Proof. Up to isotoping
![]() $\beta $
to another arc, we can assume that
$\beta $
to another arc, we can assume that
![]() $\beta $
is in minimal position with respect to the arcs
$\beta $
is in minimal position with respect to the arcs
![]() $\alpha _0,\dots ,\alpha _k$
. By Proposition 2.11, we can represent
$\alpha _0,\dots ,\alpha _k$
. By Proposition 2.11, we can represent
![]() $\varphi $
by a diffeomorphism
$\varphi $
by a diffeomorphism
![]() $\Phi $
that fixes a closed neighbourhood
$\Phi $
that fixes a closed neighbourhood
![]() $U'$
of the union
$U'$
of the union
![]() $\alpha _0\cup \dotsb \cup \alpha _k\cup \beta \cup \partial \mathcal {S}$
. Let
$\alpha _0\cup \dotsb \cup \alpha _k\cup \beta \cup \partial \mathcal {S}$
. Let
![]() $U\subset U'$
be a small neighbourhood of
$U\subset U'$
be a small neighbourhood of
![]() $\alpha _0\cup \dotsb \cup \alpha _k\cup \partial \mathcal {S}$
.
$\alpha _0\cup \dotsb \cup \alpha _k\cup \partial \mathcal {S}$
.
If
![]() $\beta $
is disjoint from the arcs
$\beta $
is disjoint from the arcs
![]() $\alpha _i$
, by maximality of the simplex
$\alpha _i$
, by maximality of the simplex
![]() $\alpha _0,\dots ,\alpha _k$
in the fixed-arc complex of
$\alpha _0,\dots ,\alpha _k$
in the fixed-arc complex of
![]() $\varphi $
, we obtain that either
$\varphi $
, we obtain that either
![]() $\beta $
is not essential (and can then be isotoped inside a small neighbourhood of
$\beta $
is not essential (and can then be isotoped inside a small neighbourhood of
![]() $\partial \mathcal {S}$
, hence inside U) or
$\partial \mathcal {S}$
, hence inside U) or
![]() $\beta $
is parallel to one of the arcs
$\beta $
is parallel to one of the arcs
![]() $\alpha _i$
(and can then be isotoped to a small neighbourhood of
$\alpha _i$
(and can then be isotoped to a small neighbourhood of
![]() $\partial \mathcal {S}\cup \alpha _i$
, hence inside U).
$\partial \mathcal {S}\cup \alpha _i$
, hence inside U).
If
![]() $\beta $
is not disjoint from the arcs
$\beta $
is not disjoint from the arcs
![]() $\alpha _i$
, let
$\alpha _i$
, let
![]() $\ell \geqslant 1$
be the number of transverse intersections of
$\ell \geqslant 1$
be the number of transverse intersections of
![]() $\beta $
with
$\beta $
with
![]() $\alpha _0\cup \dotsb \cup \alpha _k$
: by induction, let us suppose that the statement of the lemma holds whenever
$\alpha _0\cup \dotsb \cup \alpha _k$
: by induction, let us suppose that the statement of the lemma holds whenever
![]() $\beta $
is replaced by an arc that can be isotoped so as to have at most
$\beta $
is replaced by an arc that can be isotoped so as to have at most
![]() $\ell -1$
intersection points with the arcs
$\ell -1$
intersection points with the arcs
![]() $\alpha _i$
. Suppose that p is one intersection point of
$\alpha _i$
. Suppose that p is one intersection point of
![]() $\beta $
with one arc
$\beta $
with one arc
![]() $\alpha _i$
: suppose further that the segment
$\alpha _i$
: suppose further that the segment
![]() $[\alpha _i(0);p]\subset \alpha _i$
contains no other point of
$[\alpha _i(0);p]\subset \alpha _i$
contains no other point of
![]() $\alpha _i\cap \beta $
in its interior (this means that p is an outermost point of
$\alpha _i\cap \beta $
in its interior (this means that p is an outermost point of
![]() $\alpha _i\cap \beta $
along
$\alpha _i\cap \beta $
along
![]() $\alpha _i$
).
$\alpha _i$
).
We can operate a surgery on
![]() $\beta $
and produce two arcs
$\beta $
and produce two arcs
![]() $\beta '$
and
$\beta '$
and
![]() $\beta ''$
also contained in
$\beta ''$
also contained in
![]() $U'$
and transverse to
$U'$
and transverse to
![]() $\alpha _0\cup \dotsb \cup \alpha _k$
; see Figure 4: the arc
$\alpha _0\cup \dotsb \cup \alpha _k$
; see Figure 4: the arc
![]() $\beta '$
is obtained by smoothing the concatenation of the segments
$\beta '$
is obtained by smoothing the concatenation of the segments
![]() $[\beta (0);p]\subset \beta $
and
$[\beta (0);p]\subset \beta $
and
![]() $[p;\alpha _i(0)]\subset \alpha _i$
, whereas the arc
$[p;\alpha _i(0)]\subset \alpha _i$
, whereas the arc
![]() $\beta ''$
is obtained by smoothing the concatenation of the segments
$\beta ''$
is obtained by smoothing the concatenation of the segments
![]() $[\alpha _i(0);p]\subset \alpha _i$
and
$[\alpha _i(0);p]\subset \alpha _i$
and
![]() $[p;\beta (1)]\subset \beta $
. We assume that
$[p;\beta (1)]\subset \beta $
. We assume that
![]() $\beta '$
and
$\beta '$
and
![]() $\beta ''$
are disjoint and have an endpoint on a small interval of
$\beta ''$
are disjoint and have an endpoint on a small interval of
![]() $\partial \mathcal {S}$
centred at
$\partial \mathcal {S}$
centred at
![]() $\alpha _i(0)$
, on opposite sides with respect to
$\alpha _i(0)$
, on opposite sides with respect to
![]() $\alpha _i(0)$
.
$\alpha _i(0)$
.

Figure 4 If
![]() $\varphi $
is the Dehn twist along the curve d, then the blue arcs
$\varphi $
is the Dehn twist along the curve d, then the blue arcs
![]() $\alpha _0,\dotsc ,\alpha _3$
constitute a maximal simplex in the fixed-arc complex of
$\alpha _0,\dotsc ,\alpha _3$
constitute a maximal simplex in the fixed-arc complex of
![]() $\varphi $
; the subset U is a small neighbourhood of the union of the blue arcs and the black boundary curve. The red arc
$\varphi $
; the subset U is a small neighbourhood of the union of the blue arcs and the black boundary curve. The red arc
![]() $\beta $
intersects
$\beta $
intersects
![]() $\alpha _2$
transversally, and the surgery produces the yellow and violet arcs
$\alpha _2$
transversally, and the surgery produces the yellow and violet arcs
![]() $\beta '$
and
$\beta '$
and
![]() $\beta ''$
.
$\beta ''$
.
Both
![]() $\beta '$
and
$\beta '$
and
![]() $\beta ''$
are contained in
$\beta ''$
are contained in
![]() $U'$
, hence they are fixed pointwise by
$U'$
, hence they are fixed pointwise by
![]() $\Phi $
: in particular the isotopy classes of
$\Phi $
: in particular the isotopy classes of
![]() $\beta '$
and
$\beta '$
and
![]() $\beta ''$
are fixed by
$\beta ''$
are fixed by
![]() $\Phi $
. Moreover, each of
$\Phi $
. Moreover, each of
![]() $\beta '$
and
$\beta '$
and
![]() $\beta ''$
has strictly less than
$\beta ''$
has strictly less than
![]() $\ell $
intersections with
$\ell $
intersections with
![]() $\alpha _0\cup \dotsb \cup \alpha _k$
, and hence, by inductive hypothesis, each of
$\alpha _0\cup \dotsb \cup \alpha _k$
, and hence, by inductive hypothesis, each of
![]() $\beta '$
and
$\beta '$
and
![]() $\beta ''$
can be isotoped to lie in U, relative to its endpoints.
$\beta ''$
can be isotoped to lie in U, relative to its endpoints.
Let
![]() $\hat \beta '$
and
$\hat \beta '$
and
![]() $\hat \beta ''$
be the two arcs obtained in this way, and assume that
$\hat \beta ''$
be the two arcs obtained in this way, and assume that
![]() $\hat \beta '$
and
$\hat \beta '$
and
![]() $\hat \beta ''$
are transverse. If
$\hat \beta ''$
are transverse. If
![]() $\hat \beta '$
and
$\hat \beta '$
and
![]() $\hat \beta ''$
are not in minimal position, they must form some bigon in
$\hat \beta ''$
are not in minimal position, they must form some bigon in
![]() $\mathcal {S}$
; the possibility of half-bigons in the sense of [Reference Farb and Margalit7, § 1.2.7] is irrelevant, since we consider arcs up to isotopy relative to the endpoints. Clearly, we can simplify all bigons formed by
$\mathcal {S}$
; the possibility of half-bigons in the sense of [Reference Farb and Margalit7, § 1.2.7] is irrelevant, since we consider arcs up to isotopy relative to the endpoints. Clearly, we can simplify all bigons formed by
![]() $\hat \beta '$
and
$\hat \beta '$
and
![]() $\hat \beta ''$
without losing that these two arcs are contained in U.
$\hat \beta ''$
without losing that these two arcs are contained in U.
Suppose therefore that
![]() $\hat \beta '$
and
$\hat \beta '$
and
![]() $\hat \beta ''$
are in minimal position: then they are disjoint because
$\hat \beta ''$
are in minimal position: then they are disjoint because
![]() $\beta '$
and
$\beta '$
and
![]() $\beta ''$
were disjoint (in particular, it is automatic that
$\beta ''$
were disjoint (in particular, it is automatic that
![]() $\hat \beta '$
and
$\hat \beta '$
and
![]() $\hat \beta ''$
do not form half-bigons). The arc
$\hat \beta ''$
do not form half-bigons). The arc
![]() $\beta $
is homotopic, relative to its endpoints, to the concatenation of the arcs
$\beta $
is homotopic, relative to its endpoints, to the concatenation of the arcs
![]() $\hat \beta '$
and
$\hat \beta '$
and
![]() $\hat \beta ''$
, which can be connected using a small segment near
$\hat \beta ''$
, which can be connected using a small segment near
![]() $\alpha _i(0)$
. Note that this concatenation gives an embedded arc
$\alpha _i(0)$
. Note that this concatenation gives an embedded arc
![]() $\hat \beta $
with the same endpoints as
$\hat \beta $
with the same endpoints as
![]() $\beta $
; since homotopic arcs relative to their endpoints are also isotopic relative to their endpoints, we have that
$\beta $
; since homotopic arcs relative to their endpoints are also isotopic relative to their endpoints, we have that
![]() $\beta $
is isotopic to
$\beta $
is isotopic to
![]() $\hat \beta $
; moreover,
$\hat \beta $
; moreover,
![]() $\hat \beta $
lies in U.
$\hat \beta $
lies in U.
Proposition 2.21. Let
![]() $\varphi \in \Gamma (\mathcal {S},\partial \mathcal {S})$
, and let
$\varphi \in \Gamma (\mathcal {S},\partial \mathcal {S})$
, and let
![]() $\alpha _0,\dots ,\alpha _k$
and
$\alpha _0,\dots ,\alpha _k$
and
![]() $\beta _0,\dots ,\beta _{k'}$
be two sequences of arcs representing two different maximal simplices in the fixed-arc complex of
$\beta _0,\dots ,\beta _{k'}$
be two sequences of arcs representing two different maximal simplices in the fixed-arc complex of
![]() $\varphi $
; we assume that all arcs
$\varphi $
; we assume that all arcs
![]() $\alpha _0,\dots ,\alpha _k,\beta _0,\dots ,\beta _{k'}$
are in minimal position. Then the associated cut loci constitute the same isotopy class of an oriented multicurve in
$\alpha _0,\dots ,\alpha _k,\beta _0,\dots ,\beta _{k'}$
are in minimal position. Then the associated cut loci constitute the same isotopy class of an oriented multicurve in
![]() $\mathcal {S}$
.
$\mathcal {S}$
.
Proof. Let
![]() $U_{\alpha }$
be a closed small neighbourhood of
$U_{\alpha }$
be a closed small neighbourhood of
![]() $\alpha _0\cup \dotsb \cup \alpha _k\cup \partial \mathcal {S}$
and
$\alpha _0\cup \dotsb \cup \alpha _k\cup \partial \mathcal {S}$
and
![]() $U_{\beta }$
be a closed small neighbourhood of
$U_{\beta }$
be a closed small neighbourhood of
![]() $\beta _0\cup \dotsb \cup \beta _{k'}\cup \partial \mathcal {S}$
; let
$\beta _0\cup \dotsb \cup \beta _{k'}\cup \partial \mathcal {S}$
; let
![]() $W_{\alpha }$
and
$W_{\alpha }$
and
![]() $W_{\beta }$
be obtained from
$W_{\beta }$
be obtained from
![]() $U_{\alpha }$
and
$U_{\alpha }$
and
![]() $U_{\beta }$
by adjoining the disc components of
$U_{\beta }$
by adjoining the disc components of
![]() $\mathcal {S}\smallsetminus U_{\alpha }$
and
$\mathcal {S}\smallsetminus U_{\alpha }$
and
![]() $\mathcal {S}\smallsetminus U_{\beta }$
, respectively (see Definition 2.19).
$\mathcal {S}\smallsetminus U_{\beta }$
, respectively (see Definition 2.19).
By Lemma 2.20, we can find an isotopy of the identity of
![]() $(\mathcal {S},\partial \mathcal {S})$
bringing
$(\mathcal {S},\partial \mathcal {S})$
bringing
![]() $U_{\alpha }$
in the interior of
$U_{\alpha }$
in the interior of
![]() $U_{\beta }$
, and hence in the interior of
$U_{\beta }$
, and hence in the interior of
![]() $W_{\beta }$
: without loss of generality, in the following assume
$W_{\beta }$
: without loss of generality, in the following assume
![]() $U_{\alpha }\subseteq U_{\beta }\subseteq W_{\beta }$
. If D is a disc component of
$U_{\alpha }\subseteq U_{\beta }\subseteq W_{\beta }$
. If D is a disc component of
![]() $\mathcal {S}\smallsetminus U_{\alpha }$
, then
$\mathcal {S}\smallsetminus U_{\alpha }$
, then
![]() $D\smallsetminus U_{\beta }$
is a union of discs contained in
$D\smallsetminus U_{\beta }$
is a union of discs contained in
![]() $\mathcal {S}\smallsetminus U_{\beta }$
, and therefore
$\mathcal {S}\smallsetminus U_{\beta }$
, and therefore
![]() $D\subset W_{\beta }$
. It follows that
$D\subset W_{\beta }$
. It follows that
![]() $W_{\alpha }\subseteq W_{\beta }$
. Since every component of
$W_{\alpha }\subseteq W_{\beta }$
. Since every component of
![]() $W_{\beta }$
touches
$W_{\beta }$
touches
![]() $\partial \mathcal {S}$
, the map
$\partial \mathcal {S}$
, the map
![]() $\pi _0(\partial \mathcal {S})\to \pi _0(W_\beta )$
is surjective. This map factors through the canonical map
$\pi _0(\partial \mathcal {S})\to \pi _0(W_\beta )$
is surjective. This map factors through the canonical map
![]() $\pi _0(W_{\alpha })\to \pi _0(W_{\beta })$
, as
$\pi _0(W_{\alpha })\to \pi _0(W_{\beta })$
, as
![]() $\partial \mathcal {S}\subset W_\alpha $
. We conclude that
$\partial \mathcal {S}\subset W_\alpha $
. We conclude that
![]() $\pi _0(W_{\alpha })\to \pi _0(W_{\beta })$
is surjective.
$\pi _0(W_{\alpha })\to \pi _0(W_{\beta })$
is surjective.
By the same argument we can find an isotopy of the identity of
![]() $\mathcal {S}$
bringing
$\mathcal {S}$
bringing
![]() $U_{\beta }$
in the interior of
$U_{\beta }$
in the interior of
![]() $U_{\alpha }$
, and hence
$U_{\alpha }$
, and hence
![]() $W_{\beta }$
in the interior of
$W_{\beta }$
in the interior of
![]() $W_{\alpha }$
: as a consequence we can obtain a surjection
$W_{\alpha }$
: as a consequence we can obtain a surjection
![]() $\pi _0(W_{\beta })\to \pi _0(W_{\alpha })$
, showing that
$\pi _0(W_{\beta })\to \pi _0(W_{\alpha })$
, showing that
![]() $\#\pi _0(W_{\beta })=\#\pi _0(W_{\alpha })$
and that the map
$\#\pi _0(W_{\beta })=\#\pi _0(W_{\alpha })$
and that the map
![]() $\pi _0(W_{\alpha })\to \pi _0(W_{\beta })$
induced by the inclusion is in fact a bijection.
$\pi _0(W_{\alpha })\to \pi _0(W_{\beta })$
induced by the inclusion is in fact a bijection.
We next prove that each component V of
![]() $W_{\beta }\smallsetminus W_{\alpha }$
is a cylinder with one boundary curve equal to some
$W_{\beta }\smallsetminus W_{\alpha }$
is a cylinder with one boundary curve equal to some
![]() $c_i$
and one boundary curve equal to some
$c_i$
and one boundary curve equal to some
![]() $\smash {c^{\prime }_j}$
. Fix a component
$\smash {c^{\prime }_j}$
. Fix a component
![]() $\smash {\bar W_{\beta }\subset W_{\beta }}$
, and let
$\smash {\bar W_{\beta }\subset W_{\beta }}$
, and let
![]() $\bar W_{\alpha }\subset W_{\alpha }$
be the unique component of
$\bar W_{\alpha }\subset W_{\alpha }$
be the unique component of
![]() $W_{\alpha }$
contained in
$W_{\alpha }$
contained in
![]() $\bar W_{\beta }$
. We know that, conversely,
$\bar W_{\beta }$
. We know that, conversely,
![]() $\bar W_{\beta }$
can be embedded in
$\bar W_{\beta }$
can be embedded in
![]() $\bar W_{\alpha }$
: since the genus is weakly increasing along embeddings of orientable surfaces with boundary, the surfaces
$\bar W_{\alpha }$
: since the genus is weakly increasing along embeddings of orientable surfaces with boundary, the surfaces
![]() $\bar W_{\alpha }$
and
$\bar W_{\alpha }$
and
![]() $\bar W_{\beta }$
must have the same genus; this implies in particular every component V of
$\bar W_{\beta }$
must have the same genus; this implies in particular every component V of
![]() $\bar W_{\beta }\smallsetminus \bar W_{\alpha }$
has genus
$\bar W_{\beta }\smallsetminus \bar W_{\alpha }$
has genus
![]() $0$
and touches at most one curve
$0$
and touches at most one curve
![]() $c_i\in \partial \bar W_{\alpha }$
.
$c_i\in \partial \bar W_{\alpha }$
.
Since
![]() $\bar W_{\alpha }$
and
$\bar W_{\alpha }$
and
![]() $\bar W_{\beta }$
are connected, we have that a component V of
$\bar W_{\beta }$
are connected, we have that a component V of
![]() $\bar W_{\beta }\smallsetminus \bar W_{\alpha }$
touches exactly one curve
$\bar W_{\beta }\smallsetminus \bar W_{\alpha }$
touches exactly one curve
![]() $c_i\subset \partial \bar W_{\alpha }$
, and since V cannot be a disc, we obtain that V is a surface of genus
$c_i\subset \partial \bar W_{\alpha }$
, and since V cannot be a disc, we obtain that V is a surface of genus
![]() $0$
with at least two boundary components; more precisely, one boundary component of V is a curve
$0$
with at least two boundary components; more precisely, one boundary component of V is a curve
![]() $c_i\subset \partial \bar W_{\alpha }$
, and all other boundary components are curves
$c_i\subset \partial \bar W_{\alpha }$
, and all other boundary components are curves
![]() $c^{\prime }_j\subset \partial \bar W_{\beta }$
.
$c^{\prime }_j\subset \partial \bar W_{\beta }$
.
This proves in particular that the number of boundary components of
![]() $\bar W_{\beta }$
is greater or equal to the number of boundary components of
$\bar W_{\beta }$
is greater or equal to the number of boundary components of
![]() $\bar W_{\alpha }$
; we can again reverse the rôles of
$\bar W_{\alpha }$
; we can again reverse the rôles of
![]() $\alpha $
and
$\alpha $
and
![]() $\beta $
and conclude that
$\beta $
and conclude that
![]() $\bar W_{\alpha }$
and
$\bar W_{\alpha }$
and
![]() $\bar W_{\beta }$
have the same number of boundary component; this in turn implies that every connected component V of
$\bar W_{\beta }$
have the same number of boundary component; this in turn implies that every connected component V of
![]() $\bar W_{\beta }\smallsetminus \bar W_{\alpha }$
is a cylinder with one boundary curve equal to some
$\bar W_{\beta }\smallsetminus \bar W_{\alpha }$
is a cylinder with one boundary curve equal to some
![]() $c_i$
and one boundary curve equal to some
$c_i$
and one boundary curve equal to some
![]() $c^{\prime }_j$
.
$c^{\prime }_j$
.
Thus, we obtain a bijection between the curves
![]() $c_1,\dots ,c_h$
and the curves
$c_1,\dots ,c_h$
and the curves
![]() $c^{\prime }_1,\dots ,c^{\prime }_{h'}$
, showing in particular that
$c^{\prime }_1,\dots ,c^{\prime }_{h'}$
, showing in particular that
![]() $h=h'$
; note also that the bijection associates with each curve
$h=h'$
; note also that the bijection associates with each curve
![]() $c_i$
a curve
$c_i$
a curve
![]() $c^{\prime }_j$
in the same isotopy class of oriented curves.
$c^{\prime }_j$
in the same isotopy class of oriented curves.
When referring to the cut locus of a mapping class
![]() $\varphi \in \Gamma (\mathcal {S},\partial \mathcal {S})$
, we will henceforth mean the cut locus of
$\varphi \in \Gamma (\mathcal {S},\partial \mathcal {S})$
, we will henceforth mean the cut locus of
![]() $\varphi $
with respect to any maximal simplex in the fixed-arc complex of
$\varphi $
with respect to any maximal simplex in the fixed-arc complex of
![]() $\varphi $
.
$\varphi $
.
The cut locus of a mapping class behaves well under conjugation of the mapping class, as explained in the following Lemma.
Lemma 2.22. Let
![]() $\varphi ,\psi \in \Gamma (\mathcal {S},\partial \mathcal {S})$
be mapping classes, let
$\varphi ,\psi \in \Gamma (\mathcal {S},\partial \mathcal {S})$
be mapping classes, let
![]() $\Psi $
be a diffeomorphism representing
$\Psi $
be a diffeomorphism representing
![]() $\psi $
, and let
$\psi $
, and let
![]() $[c_1,\dots ,c_h]$
be the cut locus of
$[c_1,\dots ,c_h]$
be the cut locus of
![]() $\varphi $
; then
$\varphi $
; then
![]() $[\Psi (c_1),\dots ,\Psi (c_h)]$
is the cut locus of
$[\Psi (c_1),\dots ,\Psi (c_h)]$
is the cut locus of
![]() $\psi \varphi \psi ^{-1}$
. In particular, if
$\psi \varphi \psi ^{-1}$
. In particular, if
![]() $\varphi $
and
$\varphi $
and
![]() $\psi $
commute, then
$\psi $
commute, then
![]() $\psi $
preserves the cut locus of
$\psi $
preserves the cut locus of
![]() $\varphi $
as an unordered collection of isotopy classes of oriented simple closed curves.
$\varphi $
as an unordered collection of isotopy classes of oriented simple closed curves.
Proof. Let
![]() $\alpha _0,\dots ,\alpha _k$
be disjoint arcs representing a maximal simplex in the fixed-arc complex of
$\alpha _0,\dots ,\alpha _k$
be disjoint arcs representing a maximal simplex in the fixed-arc complex of
![]() $\varphi $
, and represent
$\varphi $
, and represent
![]() $\varphi $
by a diffeomorphism
$\varphi $
by a diffeomorphism
![]() $\Phi $
fixing pointwise a small neighbourhood U of
$\Phi $
fixing pointwise a small neighbourhood U of
![]() $\alpha _0\cup \dots \cup \alpha _k\cup \partial \mathcal {S}$
; finally, represent the cut locus of
$\alpha _0\cup \dots \cup \alpha _k\cup \partial \mathcal {S}$
; finally, represent the cut locus of
![]() $\varphi $
by curves
$\varphi $
by curves
![]() $c_1,\dots ,c_h$
contained in U. Then
$c_1,\dots ,c_h$
contained in U. Then
![]() $\Psi $
induces an isomorphism from the fixed-arc complex of
$\Psi $
induces an isomorphism from the fixed-arc complex of
![]() $\varphi $
to the fixed arc complex of
$\varphi $
to the fixed arc complex of
![]() $\psi \varphi \psi ^{-1}$
; in particular
$\psi \varphi \psi ^{-1}$
; in particular
![]() $\Psi (\alpha _0),\dots ,\Psi (\alpha _k)$
are disjoint arcs representing a maximal simplex in the fixed-arc complex of
$\Psi (\alpha _0),\dots ,\Psi (\alpha _k)$
are disjoint arcs representing a maximal simplex in the fixed-arc complex of
![]() $\psi \varphi \psi ^{-1}$
. Moreover,
$\psi \varphi \psi ^{-1}$
. Moreover,
![]() $\Psi (U)$
is a small neighbourhood of
$\Psi (U)$
is a small neighbourhood of
![]() $\Psi (\alpha _0)\cup \dots \cup \Psi (\alpha _k)\cup \partial \mathcal {S}$
, which is fixed pointwise by the representative
$\Psi (\alpha _0)\cup \dots \cup \Psi (\alpha _k)\cup \partial \mathcal {S}$
, which is fixed pointwise by the representative
![]() $\Psi \Phi \Psi ^{-1}$
of
$\Psi \Phi \Psi ^{-1}$
of
![]() $\psi \varphi \psi ^{-1}$
. We can represent the cut locus of
$\psi \varphi \psi ^{-1}$
. We can represent the cut locus of
![]() $\varphi $
by curves
$\varphi $
by curves
![]() $c_1,\dots ,c_h\subset \partial U$
; then
$c_1,\dots ,c_h\subset \partial U$
; then
are automatically curves representing the cut locus of
![]() $\psi \varphi \psi ^{-1}$
, according to Construction 2.18.
$\psi \varphi \psi ^{-1}$
, according to Construction 2.18.
3 Centralisers of mapping classes
We fix a surface
![]() $\mathcal {S}\cong \Sigma _{g,n}$
and a mapping class
$\mathcal {S}\cong \Sigma _{g,n}$
and a mapping class
![]() $\varphi \in \Gamma (\mathcal {S},\partial \mathcal {S})\cong \Gamma _{g,n}$
as in the previous section. In this section, we prove a structural result for the centraliser
$\varphi \in \Gamma (\mathcal {S},\partial \mathcal {S})\cong \Gamma _{g,n}$
as in the previous section. In this section, we prove a structural result for the centraliser
![]() $Z(\varphi ,\Gamma (\mathcal {S},\partial \mathcal {S}))$
of
$Z(\varphi ,\Gamma (\mathcal {S},\partial \mathcal {S}))$
of
![]() $\varphi $
in
$\varphi $
in
![]() $\Gamma (\mathcal {S},\partial \mathcal {S})$
; see Proposition 3.8.
$\Gamma (\mathcal {S},\partial \mathcal {S})$
; see Proposition 3.8.
3.1 Yellow components, similarity and irreducibility
We fix oriented simple closed curves
![]() $c_1,\dots ,c_h\subset \mathcal {S}$
representing the cut locus of
$c_1,\dots ,c_h\subset \mathcal {S}$
representing the cut locus of
![]() $\varphi $
, and we let
$\varphi $
, and we let
![]() $W\cup Y$
be the associated decomposition of
$W\cup Y$
be the associated decomposition of
![]() $\mathcal {S}$
into its white and yellow regions.
$\mathcal {S}$
into its white and yellow regions.
Recall from Construction 2.18 that the curves
![]() $c_1,\dots ,c_h$
inherit an orientation from Y: we fix an orientation-compatible parametrisation of each curve
$c_1,\dots ,c_h$
inherit an orientation from Y: we fix an orientation-compatible parametrisation of each curve
![]() $c_i$
: that is, an identification with
$c_i$
: that is, an identification with
![]() $S^1$
. Note that in this way
$S^1$
. Note that in this way
![]() $c_1,\dots ,c_h$
are incoming curves for W and outgoing for Y. In fact, we have
$c_1,\dots ,c_h$
are incoming curves for W and outgoing for Y. In fact, we have
![]() $\partial Y=\partial ^{\text {out}}Y=c_1\cup \dotsb \cup c_h =\partial ^{\text {in}}W$
, whereas
$\partial Y=\partial ^{\text {out}}Y=c_1\cup \dotsb \cup c_h =\partial ^{\text {in}}W$
, whereas
![]() $\partial ^{\text {out}}W=\partial ^{\text {out}}\mathcal {S}=\partial \mathcal {S}$
.
$\partial ^{\text {out}}W=\partial ^{\text {out}}\mathcal {S}=\partial \mathcal {S}$
.
We fix a representative
![]() $\Phi \colon \mathcal {S}\to \mathcal {S}$
of
$\Phi \colon \mathcal {S}\to \mathcal {S}$
of
![]() $\varphi $
, which fixes the white region W pointwise: to see that this is possible, choose arcs
$\varphi $
, which fixes the white region W pointwise: to see that this is possible, choose arcs
![]() $\alpha _0,\dots ,\alpha _k$
in a maximal simplex of the fixed-arc complex of
$\alpha _0,\dots ,\alpha _k$
in a maximal simplex of the fixed-arc complex of
![]() $\varphi $
, choose a first representative
$\varphi $
, choose a first representative
![]() $\Phi '$
of
$\Phi '$
of
![]() $\varphi $
fixing pointwise a small neighbourhood U of
$\varphi $
fixing pointwise a small neighbourhood U of
![]() $\alpha _0\cup \dots \cup \alpha _k\cup \partial \mathcal {S}$
, construct W and Y starting from U, and use that the group
$\alpha _0\cup \dots \cup \alpha _k\cup \partial \mathcal {S}$
, construct W and Y starting from U, and use that the group
![]() $\operatorname {\mathrm {Diff}}(D^2,\partial D^2)$
of diffeomorphisms of a disc relative to its boundary is contractible, and in particular connected, in order to isotope
$\operatorname {\mathrm {Diff}}(D^2,\partial D^2)$
of diffeomorphisms of a disc relative to its boundary is contractible, and in particular connected, in order to isotope
![]() $\Phi '$
relative to U to a diffeomorphism
$\Phi '$
relative to U to a diffeomorphism
![]() $\Phi $
fixing W pointwise.
$\Phi $
fixing W pointwise.
We note that this representative
![]() $\Phi $
is unique up to an isotopy that is stationary on W: to see this, first note that there is a fibration
$\Phi $
is unique up to an isotopy that is stationary on W: to see this, first note that there is a fibration
where
![]() $\mathrm {Emb}_{\partial ^{\text {out}}}(W,\mathcal {S})$
denotes the space of embeddings of W into
$\mathrm {Emb}_{\partial ^{\text {out}}}(W,\mathcal {S})$
denotes the space of embeddings of W into
![]() $\mathcal {S}$
restricting to the identity on the boundary
$\mathcal {S}$
restricting to the identity on the boundary
![]() $\partial ^{\text {out}}W=\partial \mathcal {S}$
. A result of Earle–Schatz [Reference Earle and Schatz5] ensures that
$\partial ^{\text {out}}W=\partial \mathcal {S}$
. A result of Earle–Schatz [Reference Earle and Schatz5] ensures that
![]() $\operatorname {\mathrm {Diff}}(\mathcal {S},\partial \mathcal {S})$
has contractible components for every compact orientable surface
$\operatorname {\mathrm {Diff}}(\mathcal {S},\partial \mathcal {S})$
has contractible components for every compact orientable surface
![]() $\mathcal {S}$
such that every connected component of
$\mathcal {S}$
such that every connected component of
![]() $\mathcal {S}$
is connected; in particular,
$\mathcal {S}$
is connected; in particular,
![]() $\operatorname {\mathrm {Diff}}(Y,\partial Y)$
also has contractible components. A result of Gramain [Reference Gramain10, Thm. 5] ensures that for disjoint, properly embedded arcs
$\operatorname {\mathrm {Diff}}(Y,\partial Y)$
also has contractible components. A result of Gramain [Reference Gramain10, Thm. 5] ensures that for disjoint, properly embedded arcs
![]() $\alpha _0,\dots ,\alpha _k\subset \mathcal {S}$
, the space
$\alpha _0,\dots ,\alpha _k\subset \mathcal {S}$
, the space
![]() $\mathrm {Emb}_{\coprod \partial \alpha _i}(\coprod \alpha _i,\mathcal {S})$
has also contractible components; this, together with contractibility of
$\mathrm {Emb}_{\coprod \partial \alpha _i}(\coprod \alpha _i,\mathcal {S})$
has also contractible components; this, together with contractibility of
![]() $\operatorname {\mathrm {Diff}}(D^2,\partial D^2)$
, implies that also
$\operatorname {\mathrm {Diff}}(D^2,\partial D^2)$
, implies that also
![]() $\mathrm {Emb}_{\partial ^{\text {out}}}(W,\mathcal {S})$
has contractible connected components. Thus, all spaces involved in the above fibration have contractible connected components; in particular the component
$\mathrm {Emb}_{\partial ^{\text {out}}}(W,\mathcal {S})$
has contractible connected components. Thus, all spaces involved in the above fibration have contractible connected components; in particular the component
![]() $\operatorname {\mathrm {Diff}}(\mathcal {S},\partial \mathcal {S})_{\varphi }$
intersects the fibre
$\operatorname {\mathrm {Diff}}(\mathcal {S},\partial \mathcal {S})_{\varphi }$
intersects the fibre
![]() $\mathfrak {p}^{-1}(W\subset \mathcal {S})\cong \operatorname {\mathrm {Diff}}(Y,\partial Y)$
in a connected or empty subspace, and the representative
$\mathfrak {p}^{-1}(W\subset \mathcal {S})\cong \operatorname {\mathrm {Diff}}(Y,\partial Y)$
in a connected or empty subspace, and the representative
![]() $\Phi $
of
$\Phi $
of
![]() $\varphi $
witnesses that this intersection is non-empty, hence contractible, in particular connected.
$\varphi $
witnesses that this intersection is non-empty, hence contractible, in particular connected.
For each path component
![]() $P\subseteq Y$
, the diffeomorphism
$P\subseteq Y$
, the diffeomorphism
![]() $\Phi $
restricts to
$\Phi $
restricts to
![]() $\Phi |_P\colon P\to P$
, giving an element
$\Phi |_P\colon P\to P$
, giving an element
![]() $\varphi _P\in \Gamma (P,\partial P)$
.
$\varphi _P\in \Gamma (P,\partial P)$
.
Definition 3.1. Two path components P and
![]() $P'$
of Y are similar if there is a diffeomorphism
$P'$
of Y are similar if there is a diffeomorphism
![]() $\Xi \colon P\to P'$
preserving the boundary parametrisation and such that
$\Xi \colon P\to P'$
preserving the boundary parametrisation and such that
![]() $\smash {\varphi _P=(\varphi _{P'})^\Xi }$
. Note that the path components of
$\smash {\varphi _P=(\varphi _{P'})^\Xi }$
. Note that the path components of
![]() $\partial P$
are not equipped with a preferred order, as well as the path components of
$\partial P$
are not equipped with a preferred order, as well as the path components of
![]() $\partial P'$
; yet Definition 2.2 is meaningful here. See also Remark 2.5.
$\partial P'$
; yet Definition 2.2 is meaningful here. See also Remark 2.5.
Notation 3.2. We write
![]() $Y=\coprod _{i=1}^r\coprod _{j=1}^{s_i}Y_{i,j}$
, where
$Y=\coprod _{i=1}^r\coprod _{j=1}^{s_i}Y_{i,j}$
, where
![]() $Y_{1,1},\dotsc ,Y_{r,s_r}\subseteq Y$
are the connected components of Y and
$Y_{1,1},\dotsc ,Y_{r,s_r}\subseteq Y$
are the connected components of Y and
![]() $Y_{i,j}$
is similar to
$Y_{i,j}$
is similar to
![]() $Y_{i',j'}$
if and only if
$Y_{i',j'}$
if and only if
![]() $i=i'$
. We also let
$i=i'$
. We also let
![]() $Y_i:= \coprod _{j=1}^{s_i}Y_{i,j}$
. Here
$Y_i:= \coprod _{j=1}^{s_i}Y_{i,j}$
. Here
![]() $r\geqslant 0$
is the number of similarity classes of components of Y (it can be
$r\geqslant 0$
is the number of similarity classes of components of Y (it can be
![]() $0$
if Y is empty, i.e., if
$0$
if Y is empty, i.e., if
![]() $\varphi $
is the identity mapping class), whereas
$\varphi $
is the identity mapping class), whereas
![]() $s_i\geqslant 1$
is the number of components of Y belonging to the i
th similarity class.
$s_i\geqslant 1$
is the number of components of Y belonging to the i
th similarity class.
For each
![]() $1\leqslant i\leqslant r$
, there are unique
$1\leqslant i\leqslant r$
, there are unique
![]() $g_i\geqslant 0$
and
$g_i\geqslant 0$
and
![]() $n_i\geqslant 1$
such that
$n_i\geqslant 1$
such that
![]() $Y_{i,j}$
is of type
$Y_{i,j}$
is of type
![]() $\Sigma _{g_i,n_i}$
. We denote by
$\Sigma _{g_i,n_i}$
. We denote by
![]() $\varphi _{i,j}\in \Gamma (Y_{i,j},\partial Y_{i,j})$
the class represented by the restriction
$\varphi _{i,j}\in \Gamma (Y_{i,j},\partial Y_{i,j})$
the class represented by the restriction
![]() $\Phi |_{Y_{i,j}}$
, Moreover, we fix diffeomorphisms
$\Phi |_{Y_{i,j}}$
, Moreover, we fix diffeomorphisms
![]() $\Xi _{i,j}\colon Y_{i,j}\to \Sigma _{g_i,n_i}$
and assume that
$\Xi _{i,j}\colon Y_{i,j}\to \Sigma _{g_i,n_i}$
and assume that
![]() $\Xi _{i,j}$
preserves the boundary parametrisation.
$\Xi _{i,j}$
preserves the boundary parametrisation.
The conjugation by
![]() $\Xi _{i,j}$
induces an identification
$\Xi _{i,j}$
induces an identification
![]() $\Gamma (Y_{i,j},\partial Y_{i,j})\to \Gamma _{g_i,n_i}$
, under which
$\Gamma (Y_{i,j},\partial Y_{i,j})\to \Gamma _{g_i,n_i}$
, under which
![]() $\varphi _{i,j}$
corresponds to some element
$\varphi _{i,j}$
corresponds to some element
![]() $\smash {\bar \varphi _{i,j}:=\smash {(\varphi _{i,j})}^{\smash {\Xi _{i,j}}}}\in \Gamma _{g_i,n_i}$
. Up to replacing
$\smash {\bar \varphi _{i,j}:=\smash {(\varphi _{i,j})}^{\smash {\Xi _{i,j}}}}\in \Gamma _{g_i,n_i}$
. Up to replacing
![]() $\Xi _{i,j}$
by another diffeomorphism
$\Xi _{i,j}$
by another diffeomorphism
![]() $Y_{i,j}\to \Sigma _{g_i,n_i}$
, we can assume that
$Y_{i,j}\to \Sigma _{g_i,n_i}$
, we can assume that
![]() $\bar \varphi _{i,j}\in \Gamma _{g,n}$
coincides with
$\bar \varphi _{i,j}\in \Gamma _{g,n}$
coincides with
![]() $\mathfrak {g}(\bar \varphi _{i,j})$
: that is, it is the representative of its own conjugacy class (see Notation 2.8). Note that the diffeomorphism replacing
$\mathfrak {g}(\bar \varphi _{i,j})$
: that is, it is the representative of its own conjugacy class (see Notation 2.8). Note that the diffeomorphism replacing
![]() $\Xi _{i,j}$
is not required to induce the same bijection of sets of boundary components as
$\Xi _{i,j}$
is not required to induce the same bijection of sets of boundary components as
![]() $\Xi _{i,j}$
. It can be helpful to remark that
$\Xi _{i,j}$
. It can be helpful to remark that
![]() $\pi _0(\partial Y_{i,j})$
is not equipped a priori with a preferred order, and only after choosing
$\pi _0(\partial Y_{i,j})$
is not equipped a priori with a preferred order, and only after choosing
![]() $\Xi _{i,j}$
, we obtain an order on
$\Xi _{i,j}$
, we obtain an order on
![]() $\pi _0(\partial Y_{i,j})$
by pulling back the canonical order on
$\pi _0(\partial Y_{i,j})$
by pulling back the canonical order on
![]() $\pi _0(\partial \Sigma _{g_i,n_i})$
. Under the assumption that the diffeomorphisms
$\pi _0(\partial \Sigma _{g_i,n_i})$
. Under the assumption that the diffeomorphisms
![]() $\Xi _{i,j}$
are well-chosen, we also have
$\Xi _{i,j}$
are well-chosen, we also have
![]() $\bar \varphi _{i,j}=\bar \varphi _{i,j'}$
for all
$\bar \varphi _{i,j}=\bar \varphi _{i,j'}$
for all
![]() $1\leqslant i\leqslant r$
and
$1\leqslant i\leqslant r$
and
![]() $1\leqslant j,j'\leqslant s_i$
. We therefore write
$1\leqslant j,j'\leqslant s_i$
. We therefore write
![]() $\bar \varphi _i:=\bar \varphi _{i,j}$
.
$\bar \varphi _i:=\bar \varphi _{i,j}$
.
Note that, counting the components of
![]() $\partial Y$
, we obtain
$\partial Y$
, we obtain
![]() $h=\sum _{i=1}^r n_i\cdot s_i$
.
$h=\sum _{i=1}^r n_i\cdot s_i$
.
Lemma 3.3. In the situation above, for each
![]() $1\leqslant i\leqslant r$
and
$1\leqslant i\leqslant r$
and
![]() $1\leqslant j\leqslant s_i$
, we have that
$1\leqslant j\leqslant s_i$
, we have that
![]() $\varphi _{i,j} \in \Gamma (Y_{i,j},\partial Y_{i,j})$
is
$\varphi _{i,j} \in \Gamma (Y_{i,j},\partial Y_{i,j})$
is
![]() $\partial $
-irreducible.
$\partial $
-irreducible.
Proof. Suppose that there is an essential arc
![]() $\beta \subset Y_{i,j}$
(that is, the endpoints of
$\beta \subset Y_{i,j}$
(that is, the endpoints of
![]() $\beta $
are on
$\beta $
are on
![]() $\partial Y_{i,j}$
) that is fixed up to isotopy by
$\partial Y_{i,j}$
) that is fixed up to isotopy by
![]() $\varphi _{i,j}$
. Then we can isotope
$\varphi _{i,j}$
. Then we can isotope
![]() $\Phi $
relative to
$\Phi $
relative to
![]() $\mathcal {S}\smallsetminus \smash {\mathring {Y}_{i,j}}$
so that
$\mathcal {S}\smallsetminus \smash {\mathring {Y}_{i,j}}$
so that
![]() $\Phi $
fixes
$\Phi $
fixes
![]() $\beta $
pointwise; without loss of generality, we assume that
$\beta $
pointwise; without loss of generality, we assume that
![]() $\Phi $
already fixes
$\Phi $
already fixes
![]() $\beta $
pointwise.
$\beta $
pointwise.
We can extend
![]() $\beta $
to an arc
$\beta $
to an arc
![]() $\alpha \subset \mathcal {S}$
with endpoints on
$\alpha \subset \mathcal {S}$
with endpoints on
![]() $\partial \mathcal {S}$
by joining the endpoints of
$\partial \mathcal {S}$
by joining the endpoints of
![]() $\beta $
inside W with
$\beta $
inside W with
![]() $\partial \mathcal {S}$
. Then
$\partial \mathcal {S}$
. Then
![]() $\Phi $
fixes
$\Phi $
fixes
![]() $\alpha $
pointwise. By Lemma 2.20, we can isotope
$\alpha $
pointwise. By Lemma 2.20, we can isotope
![]() $\alpha $
into the region W. This implies that
$\alpha $
into the region W. This implies that
![]() $\alpha $
is not in minimal position with respect to
$\alpha $
is not in minimal position with respect to
![]() $\partial Y_{i,j}$
, and therefore
$\partial Y_{i,j}$
, and therefore
![]() $\alpha $
must form a bigon with the multicurve
$\alpha $
must form a bigon with the multicurve
![]() $\partial Y_{i,j}$
. Since
$\partial Y_{i,j}$
. Since
![]() $\alpha $
intersects
$\alpha $
intersects
![]() $\partial Y_{i,j}$
in exactly two points, namely the endpoints of
$\partial Y_{i,j}$
in exactly two points, namely the endpoints of
![]() $\beta $
, there must be a bigon with one side equal to
$\beta $
, there must be a bigon with one side equal to
![]() $\beta $
and the other contained in
$\beta $
and the other contained in
![]() $\partial Y_{i,j}$
. This bigon is contained in
$\partial Y_{i,j}$
. This bigon is contained in
![]() $Y_{i,j}$
, contradicting the assumption that
$Y_{i,j}$
, contradicting the assumption that
![]() $\beta $
is essential in
$\beta $
is essential in
![]() $Y_{i,j}$
.
$Y_{i,j}$
.
3.2 The group
 $\tilde Z(\varphi )$
and its relation to
$\tilde Z(\varphi )$
and its relation to
 $Z(\varphi ,\Gamma (\mathcal {S},\partial \mathcal {S}\,))$
$Z(\varphi ,\Gamma (\mathcal {S},\partial \mathcal {S}\,))$
In this subsection, we introduce a certain group
![]() $\tilde Z(\varphi )$
built out of small mapping class groups and symmetric groups. The peculiarity of
$\tilde Z(\varphi )$
built out of small mapping class groups and symmetric groups. The peculiarity of
![]() $\tilde Z(\varphi )$
is that it admits a natural map
$\tilde Z(\varphi )$
is that it admits a natural map
![]() $\varepsilon \colon \tilde Z(\varphi )\to Z(\varphi ,\Gamma (\mathcal {S},\partial \mathcal {S}))\subset \Gamma (\mathcal {S},\partial \mathcal {S})$
. In the next subsection, we will identify the kernel of
$\varepsilon \colon \tilde Z(\varphi )\to Z(\varphi ,\Gamma (\mathcal {S},\partial \mathcal {S}))\subset \Gamma (\mathcal {S},\partial \mathcal {S})$
. In the next subsection, we will identify the kernel of
![]() $\varepsilon $
, and we will prove in the final subsection that
$\varepsilon $
, and we will prove in the final subsection that
![]() $\varepsilon $
is surjective.
$\varepsilon $
is surjective.
Recall that
![]() $\varphi _Y\in \Gamma (Y,\partial Y)$
denotes the mapping class represented by
$\varphi _Y\in \Gamma (Y,\partial Y)$
denotes the mapping class represented by
![]() $\Phi |_Y$
. We consider the centraliser
$\Phi |_Y$
. We consider the centraliser
![]() $Z(\varphi _Y)\subset \Gamma (Y)$
of
$Z(\varphi _Y)\subset \Gamma (Y)$
of
![]() $\varphi _Y$
in the extended mapping class group
$\varphi _Y$
in the extended mapping class group
![]() $\Gamma (Y)$
using the natural inclusion
$\Gamma (Y)$
using the natural inclusion
![]() $\Gamma (Y,\partial Y)\subset \Gamma (Y)$
. Note that
$\Gamma (Y,\partial Y)\subset \Gamma (Y)$
. Note that
![]() $\Gamma (Y)$
admits a natural map to
$\Gamma (Y)$
admits a natural map to
![]() $\mathfrak {S}_h\cong \mathfrak {S}_{\smash {\pi _0(\partial Y)}}$
given by the action of mapping classes on boundary components. This map restricts to a map
$\mathfrak {S}_h\cong \mathfrak {S}_{\smash {\pi _0(\partial Y)}}$
given by the action of mapping classes on boundary components. This map restricts to a map
![]() $Z(\varphi _Y)\to \mathfrak {S}_h$
.
$Z(\varphi _Y)\to \mathfrak {S}_h$
.
Similarly, we can consider the extended mapping class group
![]() $\Gamma ^{\mathfrak {S}_h}(W)$
that contains mapping classes of W that fix
$\Gamma ^{\mathfrak {S}_h}(W)$
that contains mapping classes of W that fix
![]() $\partial ^{\text {out}}W=\partial \mathcal {S}$
pointwise but may permute the h incoming boundary components of W: here we identify
$\partial ^{\text {out}}W=\partial \mathcal {S}$
pointwise but may permute the h incoming boundary components of W: here we identify
![]() $\mathfrak {S}_h\cong \mathfrak {S}_{\pi _0(\partial ^{\text {in}} W)}\subset \mathfrak {S}_{\pi _0(\partial ^{\text {out}} W)}\times \mathfrak {S}_{\pi _0(\partial ^{\text {in}} W)}$
.
$\mathfrak {S}_h\cong \mathfrak {S}_{\pi _0(\partial ^{\text {in}} W)}\subset \mathfrak {S}_{\pi _0(\partial ^{\text {out}} W)}\times \mathfrak {S}_{\pi _0(\partial ^{\text {in}} W)}$
.
Definition 3.4. We define
![]() $\tilde Z(\varphi )$
as the fibre product
$\tilde Z(\varphi )$
as the fibre product
Gluing Y and W along
![]() $\partial Y=\partial ^{\text {in}} W$
yields a map of groups
$\partial Y=\partial ^{\text {in}} W$
yields a map of groups
Explicitly, for a couple of mapping classes
![]() $(\psi _W,\psi _Y)$
, we choose representatives
$(\psi _W,\psi _Y)$
, we choose representatives
![]() $\Psi _W\colon W\to W$
and
$\Psi _W\colon W\to W$
and
![]() $\Psi _Y\colon Y\to Y$
. The fact that
$\Psi _Y\colon Y\to Y$
. The fact that
![]() $\psi _W$
and
$\psi _W$
and
![]() $\psi _Y$
project to the same permutation of
$\psi _Y$
project to the same permutation of
![]() $\pi _0(\partial ^{\text {in}}W)=\pi _0(\partial Y)\cong \left \{1,\dots ,h\right \}$
, together with the fact that both
$\pi _0(\partial ^{\text {in}}W)=\pi _0(\partial Y)\cong \left \{1,\dots ,h\right \}$
, together with the fact that both
![]() $\Psi _W$
and
$\Psi _W$
and
![]() $\Psi _Y$
preserve the boundary parametrisation, implies that
$\Psi _Y$
preserve the boundary parametrisation, implies that
![]() $\Psi _Y|_{\partial Y}=\Psi _W|_{\partial ^{\text {in}}W}$
, and hence we can glue the two diffeomorphisms to a diffeomorphism of
$\Psi _Y|_{\partial Y}=\Psi _W|_{\partial ^{\text {in}}W}$
, and hence we can glue the two diffeomorphisms to a diffeomorphism of
![]() $\mathcal {S}$
(we skip all details about smoothing the output homeomorphism near the gluing curves).
$\mathcal {S}$
(we skip all details about smoothing the output homeomorphism near the gluing curves).
Lemma 3.5. The restriction
![]() $\varepsilon =\hat \varepsilon |_{\tilde Z(\varphi )}$
has image inside
$\varepsilon =\hat \varepsilon |_{\tilde Z(\varphi )}$
has image inside
![]() $Z(\varphi ,\Gamma (\mathcal {S},\partial \mathcal {S}))\subset \Gamma (\mathcal {S},\partial \mathcal {S})$
.
$Z(\varphi ,\Gamma (\mathcal {S},\partial \mathcal {S}))\subset \Gamma (\mathcal {S},\partial \mathcal {S})$
.
Proof. Note that
![]() is a central element of
is a central element of
![]() $\tilde Z(\varphi )$
: indeed, given a pair
$\tilde Z(\varphi )$
: indeed, given a pair
![]() $(\psi _W,\psi _Y)\in \tilde Z(\varphi )$
, we have that
$(\psi _W,\psi _Y)\in \tilde Z(\varphi )$
, we have that
![]() $\psi _Y\in Z(\varphi _Y)$
, so
$\psi _Y\in Z(\varphi _Y)$
, so
![]() $\psi _Y$
commutes with
$\psi _Y$
commutes with
![]() $\varphi _Y$
, and clearly
$\varphi _Y$
, and clearly
![]() commutes with
commutes with
![]() $\psi _W$
in
$\psi _W$
in
![]() $\Gamma ^{\mathfrak {S}_h}(W)$
. Applying
$\Gamma ^{\mathfrak {S}_h}(W)$
. Applying
![]() $\varepsilon $
, we obtain that
$\varepsilon $
, we obtain that
![]() $\varepsilon (\psi _W,\psi _Y)$
commutes with
$\varepsilon (\psi _W,\psi _Y)$
commutes with
![]() .
.
In the following lemma, we decompose
![]() $Z(\varphi _Y)$
, which is the second factor appearing in the formula for
$Z(\varphi _Y)$
, which is the second factor appearing in the formula for
![]() $\tilde Z(\varphi )$
.
$\tilde Z(\varphi )$
.
Lemma 3.6. There is an isomorphism of groups
 $$\begin{align*}Z(\varphi_Y)\cong\prod_{i=1}^r Z(\bar\varphi_i)\wr \mathfrak{S}_{s_i},\end{align*}$$
$$\begin{align*}Z(\varphi_Y)\cong\prod_{i=1}^r Z(\bar\varphi_i)\wr \mathfrak{S}_{s_i},\end{align*}$$
where
![]() $Z(\bar \varphi _i)\subset \Gamma _{g_i,(n_i)}$
is the centraliser in the extended mapping class group, and where
$Z(\bar \varphi _i)\subset \Gamma _{g_i,(n_i)}$
is the centraliser in the extended mapping class group, and where
![]() $\smash {Z(\bar \varphi _i)\wr \mathfrak {S}_{s_i}=\big (Z(\bar \varphi _i)\big )^{s_i}\rtimes \mathfrak {S}_{s_i}}$
denotes the wreath product.
$\smash {Z(\bar \varphi _i)\wr \mathfrak {S}_{s_i}=\big (Z(\bar \varphi _i)\big )^{s_i}\rtimes \mathfrak {S}_{s_i}}$
denotes the wreath product.
Proof. Let
![]() $\psi _Y\in Z(\varphi _Y)$
be a centralising mapping class, and represent
$\psi _Y\in Z(\varphi _Y)$
be a centralising mapping class, and represent
![]() $\psi _Y$
by a diffeomorphism
$\psi _Y$
by a diffeomorphism
![]() $\Psi _Y$
preserving the boundary parametrisation. Furthermore, let
$\Psi _Y$
preserving the boundary parametrisation. Furthermore, let
![]() $P,P'\subset Y$
be two connected components with
$P,P'\subset Y$
be two connected components with
![]() $\Psi _Y(P)=P'$
; then restricting the commutativity of
$\Psi _Y(P)=P'$
; then restricting the commutativity of
![]() $\psi _Y$
and
$\psi _Y$
and
![]() $\varphi _Y$
to these two components, we obtain the equality
$\varphi _Y$
to these two components, we obtain the equality
![]() $\smash {\smash {\varphi _Y|}_{P}^{\smash {\Psi _Y}}=\varphi _Y|_{P'}}$
in
$\smash {\smash {\varphi _Y|}_{P}^{\smash {\Psi _Y}}=\varphi _Y|_{P'}}$
in
![]() $\Gamma (P',\partial P')$
. This implies that P and
$\Gamma (P',\partial P')$
. This implies that P and
![]() $P'$
are similar, and using Notation 3.2, we have that each
$P'$
are similar, and using Notation 3.2, we have that each
![]() $Y_i$
is
$Y_i$
is
![]() $\Psi _Y$
-invariant and therefore
$\Psi _Y$
-invariant and therefore
 $$\begin{align*}Z(\varphi_Y)=\prod_{i=1}^r Z(\varphi|_{Y_i}),\end{align*}$$
$$\begin{align*}Z(\varphi_Y)=\prod_{i=1}^r Z(\varphi|_{Y_i}),\end{align*}$$
where
![]() $\varphi |_{Y_i}$
is defined using that
$\varphi |_{Y_i}$
is defined using that
![]() $Y_i$
is a
$Y_i$
is a
![]() $\varphi $
-invariant union of connected components of Y. Now fix
$\varphi $
-invariant union of connected components of Y. Now fix
![]() $1\leqslant i\leqslant r$
; using the diffeomorphisms
$1\leqslant i\leqslant r$
; using the diffeomorphisms
![]() $\Xi _{i,j}$
for varying
$\Xi _{i,j}$
for varying
![]() $1\leqslant j\leqslant s_i$
, we can identify the surface
$1\leqslant j\leqslant s_i$
, we can identify the surface
![]() $Y_i$
with
$Y_i$
with
![]() $\coprod _{1\leqslant j\leqslant s_i} \Sigma _{g_i,n_i}$
and thus identify
$\coprod _{1\leqslant j\leqslant s_i} \Sigma _{g_i,n_i}$
and thus identify
![]() $\Gamma (Y_i)$
with
$\Gamma (Y_i)$
with
![]() $\Gamma _{g_i,(n_i)}\wr \mathfrak {S}_{s_i}$
. Thus,
$\Gamma _{g_i,(n_i)}\wr \mathfrak {S}_{s_i}$
. Thus,
![]() $\varphi |_{Y_i}$
corresponds to the element
$\varphi |_{Y_i}$
corresponds to the element
It follows that
![]() $Z(\varphi |_{Y_i})$
is isomorphic to
$Z(\varphi |_{Y_i})$
is isomorphic to
![]() $Z(\bar \varphi _i)\wr \mathfrak {S}_{s_i}$
.
$Z(\bar \varphi _i)\wr \mathfrak {S}_{s_i}$
.
We conclude the subsection by analysing the actual subgroup of
![]() $\mathfrak {S}_h$
over which the fibre product
$\mathfrak {S}_h$
over which the fibre product
![]() $\tilde Z(\varphi )$
lives. Now we will focus on the case in which W is connected because the exposition is a bit easier: indeed, the natural map
$\tilde Z(\varphi )$
lives. Now we will focus on the case in which W is connected because the exposition is a bit easier: indeed, the natural map
![]() $\Gamma ^{\mathfrak {S}_h}(W)\to \mathfrak {S}_h$
is surjective under this hypothesis on W, so we just have to describe the image of the map
$\Gamma ^{\mathfrak {S}_h}(W)\to \mathfrak {S}_h$
is surjective under this hypothesis on W, so we just have to describe the image of the map
![]() $Z(\varphi _Y)\to \mathfrak {S}_h$
.
$Z(\varphi _Y)\to \mathfrak {S}_h$
.
Notation 3.7. We denote by
![]() $\mathfrak {H}_i\subset \mathfrak {S}_{n_i}$
the image of
$\mathfrak {H}_i\subset \mathfrak {S}_{n_i}$
the image of
![]() $Z(\bar \varphi _i)$
under the natural map
$Z(\bar \varphi _i)$
under the natural map
![]() $\Gamma _{g_i,(n_i)}\to \mathfrak {S}_{n_i}$
.
$\Gamma _{g_i,(n_i)}\to \mathfrak {S}_{n_i}$
.
The proof of Lemma 3.6 shows that the image of
![]() $Z(\varphi _Y)\to \mathfrak {S}_h\cong \mathfrak {S}_{\pi _0(\partial Y)}$
is the subgroup
$Z(\varphi _Y)\to \mathfrak {S}_h\cong \mathfrak {S}_{\pi _0(\partial Y)}$
is the subgroup
![]() $\prod _i\mathfrak {H}_i\wr \mathfrak {S}_{s_i}$
consisting of those permutations of the set
$\prod _i\mathfrak {H}_i\wr \mathfrak {S}_{s_i}$
consisting of those permutations of the set
![]() $\pi _0(\partial Y)$
that preserve each subset
$\pi _0(\partial Y)$
that preserve each subset
![]() $\pi _0(\partial Y_i)$
for each
$\pi _0(\partial Y_i)$
for each
![]() $1\leqslant i\leqslant r$
, and send each subset
$1\leqslant i\leqslant r$
, and send each subset
![]() $\pi _0(\partial Y_{i,j})$
to some subset
$\pi _0(\partial Y_{i,j})$
to some subset
![]() $\pi _0(\partial Y_{i,j'})$
in a way that, under the identifications
$\pi _0(\partial Y_{i,j'})$
in a way that, under the identifications
![]() $\pi _0(\partial Y_{i,j})\cong \{1,\dots ,n_i\}\cong \pi _0(\partial Y_{i,j'})$
, gives a permutation in
$\pi _0(\partial Y_{i,j})\cong \{1,\dots ,n_i\}\cong \pi _0(\partial Y_{i,j'})$
, gives a permutation in
![]() $\mathfrak {S}_{n_i}$
, which can also be attained by projecting an element
$\mathfrak {S}_{n_i}$
, which can also be attained by projecting an element
![]() $\bar \psi _i\in Z(\bar \varphi _i)$
.
$\bar \psi _i\in Z(\bar \varphi _i)$
.
3.3 The kernel of
 $\varepsilon $
$\varepsilon $
Recall the gluing homomorphism
![]() $\hat \varepsilon \colon \Gamma ^{\mathfrak {S}_h}(W)\times ^{\mathfrak {S}_h}\Gamma (Y)\to \Gamma (\mathcal {S},\partial \mathcal {S})$
from the previous subsection. We proceed by identifying the kernel of
$\hat \varepsilon \colon \Gamma ^{\mathfrak {S}_h}(W)\times ^{\mathfrak {S}_h}\Gamma (Y)\to \Gamma (\mathcal {S},\partial \mathcal {S})$
from the previous subsection. We proceed by identifying the kernel of
![]() $\hat \varepsilon $
. Note that
$\hat \varepsilon $
. Note that
![]() $\hat \varepsilon $
has its image in the subgroup
$\hat \varepsilon $
has its image in the subgroup
![]() $\smash {\Gamma (\mathcal {S},\partial \mathcal {S})_{[c_1,\dots ,c_h]}}$
of
$\smash {\Gamma (\mathcal {S},\partial \mathcal {S})_{[c_1,\dots ,c_h]}}$
of
![]() $\Gamma (\mathcal {S},\partial \mathcal {S})$
containing all mapping classes
$\Gamma (\mathcal {S},\partial \mathcal {S})$
containing all mapping classes
![]() $\psi $
that preserve the cut locus
$\psi $
that preserve the cut locus
![]() $[c_1,\dots ,c_h]$
of
$[c_1,\dots ,c_h]$
of
![]() $\varphi $
: that is, send each oriented homotopy class of a curve
$\varphi $
: that is, send each oriented homotopy class of a curve
![]() $c_i$
to the oriented homotopy class of some (possibly different) curve
$c_i$
to the oriented homotopy class of some (possibly different) curve
![]() $c_j$
. If
$c_j$
. If
![]() $(\psi _W,\psi _Y)\in \Gamma ^{\mathfrak {S}_h}(W)\times ^{\mathfrak {S}_h}\Gamma (Y)$
belongs to the kernel of
$(\psi _W,\psi _Y)\in \Gamma ^{\mathfrak {S}_h}(W)\times ^{\mathfrak {S}_h}\Gamma (Y)$
belongs to the kernel of
![]() $\hat \varepsilon $
, then in particular
$\hat \varepsilon $
, then in particular
![]() $\hat \varepsilon (\psi _W,\psi _Y)$
acts trivially on the components of the cut locus. It follows that both
$\hat \varepsilon (\psi _W,\psi _Y)$
acts trivially on the components of the cut locus. It follows that both
![]() $\psi _W$
and
$\psi _W$
and
![]() $\psi _Y$
project to the identity element in
$\psi _Y$
project to the identity element in
![]() $\mathfrak {S}_h$
: that is,
$\mathfrak {S}_h$
: that is,
![]() $(\psi _W,\psi _Y)$
is in fact contained in the subgroup
$(\psi _W,\psi _Y)$
is in fact contained in the subgroup
![]() $\Gamma (W,\partial W)\times \Gamma (Y,\partial Y)$
of
$\Gamma (W,\partial W)\times \Gamma (Y,\partial Y)$
of
![]() $\Gamma ^{\mathfrak {S}_h}(W)\times ^{\mathfrak {S}_h}\Gamma (Y)$
. Hence the kernel of
$\Gamma ^{\mathfrak {S}_h}(W)\times ^{\mathfrak {S}_h}\Gamma (Y)$
. Hence the kernel of
![]() $\hat \varepsilon $
coincides with the kernel of the restriction of
$\hat \varepsilon $
coincides with the kernel of the restriction of
![]() $\hat \varepsilon $
to
$\hat \varepsilon $
to
![]() $\Gamma (W,\partial W)\times \Gamma (Y,\partial Y)$
.
$\Gamma (W,\partial W)\times \Gamma (Y,\partial Y)$
.
We can now use [Reference Farb and Margalit7, Thm. 3.18], in the version for disconnected surfaces: since no component of W or Y is a disc, the kernel of
is generated by the couples
![]() $(D_{c_i},D_{c_i}^{-1})$
, where
$(D_{c_i},D_{c_i}^{-1})$
, where
![]() $D_{c_i}$
denotes the Dehn twist about the curve
$D_{c_i}$
denotes the Dehn twist about the curve
![]() $c_i$
.
$c_i$
.
Since each component of W has at least one outgoing boundary, whereas the curves
![]() $c_i$
are incoming for W, we can apply [Reference Farb and Margalit7, Lem. 3.17] to the first coordinates of the elements
$c_i$
are incoming for W, we can apply [Reference Farb and Margalit7, Lem. 3.17] to the first coordinates of the elements
![]() $(D_{c_i},D_{c_i}^{-1})$
and conclude that they generate a subgroup of
$(D_{c_i},D_{c_i}^{-1})$
and conclude that they generate a subgroup of
![]() $\Gamma (W,\partial W)\times \Gamma (Y,\partial Y)$
isomorphic to
$\Gamma (W,\partial W)\times \Gamma (Y,\partial Y)$
isomorphic to
![]() $\mathbb {Z}^h$
. Finally, we note that the elements
$\mathbb {Z}^h$
. Finally, we note that the elements
![]() $(D_{c_i},D_{c_i}^{-1})$
belong to the subgroup
$(D_{c_i},D_{c_i}^{-1})$
belong to the subgroup
![]() $\tilde Z(\varphi )$
, as
$\tilde Z(\varphi )$
, as
![]() $D_{c_i}^{-1}\in \Gamma (Y,\partial Y)$
, being the inverse of a boundary twist, is a central element and in particular it commutes with
$D_{c_i}^{-1}\in \Gamma (Y,\partial Y)$
, being the inverse of a boundary twist, is a central element and in particular it commutes with
![]() $\varphi _Y$
. It follows that the kernel of
$\varphi _Y$
. It follows that the kernel of
![]() $\varepsilon $
is the free abelian group of rank h generated by the elements
$\varepsilon $
is the free abelian group of rank h generated by the elements
![]() $(D_{c_i},D_{c_i}^{-1})$
.
$(D_{c_i},D_{c_i}^{-1})$
.
3.4 Surjectivity of
 $\varepsilon $
$\varepsilon $
We now prove that the map
![]() $\varepsilon \colon \tilde Z(\varphi )\to Z(\varphi ,\Gamma (\mathcal {S},\partial \mathcal {S}))$
is surjective. In order to do so, let
$\varepsilon \colon \tilde Z(\varphi )\to Z(\varphi ,\Gamma (\mathcal {S},\partial \mathcal {S}))$
is surjective. In order to do so, let
![]() $\psi \in Z(\varphi ,\Gamma (\mathcal {S},\partial \mathcal {S})) \subset \Gamma (\mathcal {S},\partial \mathcal {S})$
be a centralising mapping class (see Definition 2.7). Then, by Lemma 2.22,
$\psi \in Z(\varphi ,\Gamma (\mathcal {S},\partial \mathcal {S})) \subset \Gamma (\mathcal {S},\partial \mathcal {S})$
be a centralising mapping class (see Definition 2.7). Then, by Lemma 2.22,
![]() $\psi $
preserves the cut locus of
$\psi $
preserves the cut locus of
![]() $\varphi $
.
$\varphi $
.
We can fix a representative
![]() $\Psi \colon \mathcal {S}\to \mathcal {S}$
of
$\Psi \colon \mathcal {S}\to \mathcal {S}$
of
![]() $\psi $
that permutes the curves
$\psi $
that permutes the curves
![]() $c_1,\dots ,c_h$
preserving their parametrisation. In particular,
$c_1,\dots ,c_h$
preserving their parametrisation. In particular,
![]() $\Psi $
restricts to a diffeomorphism of W and of Y, respectively. Moreover,
$\Psi $
restricts to a diffeomorphism of W and of Y, respectively. Moreover,
![]() $\Psi $
fixes pointwise
$\Psi $
fixes pointwise
![]() $\partial \mathcal {S}=\partial ^{\text {out}}W$
, and both
$\partial \mathcal {S}=\partial ^{\text {out}}W$
, and both
![]() $\Psi |_W$
and
$\Psi |_W$
and
![]() $\Psi |_Y$
are diffeomorphisms preserving the boundary parametrisation of W and Y, respectively. Consider now the mapping class
$\Psi |_Y$
are diffeomorphisms preserving the boundary parametrisation of W and Y, respectively. Consider now the mapping class
![]() $\varphi _Y\in \Gamma (Y,\partial Y)$
represented by
$\varphi _Y\in \Gamma (Y,\partial Y)$
represented by
![]() $\Phi |_Y$
, and note that also
$\Phi |_Y$
, and note that also
![]() $(\Psi |_Y)\circ (\Phi |_Y)\circ (\Psi ^{-1}|_Y)$
represents a mapping class in
$(\Psi |_Y)\circ (\Phi |_Y)\circ (\Psi ^{-1}|_Y)$
represents a mapping class in
![]() $\Gamma (Y,\partial Y)$
, which we denote by
$\Gamma (Y,\partial Y)$
, which we denote by
![]() $\smash {\varphi _Y^{\smash {\Psi |_Y}}}$
.
$\smash {\varphi _Y^{\smash {\Psi |_Y}}}$
.
We claim that
![]() $\varphi _Y=\varphi _Y^{\smash {\Psi |_Y}}$
holds in
$\varphi _Y=\varphi _Y^{\smash {\Psi |_Y}}$
holds in
![]() $\Gamma (Y,\partial Y)$
. To see this, note that gluing with the identity in
$\Gamma (Y,\partial Y)$
. To see this, note that gluing with the identity in
![]() $\Gamma (W,\partial W)$
gives a map
$\Gamma (W,\partial W)$
gives a map
![]() $\smash {\lambda _Y^{\mathcal {S}}\colon \Gamma (Y,\partial Y)\to \Gamma (\mathcal {S},\partial \mathcal {S})}$
, which is injective by [Reference Farb and Margalit7, Thm. 3.18]; the claim follows from the observation that
$\smash {\lambda _Y^{\mathcal {S}}\colon \Gamma (Y,\partial Y)\to \Gamma (\mathcal {S},\partial \mathcal {S})}$
, which is injective by [Reference Farb and Margalit7, Thm. 3.18]; the claim follows from the observation that
![]() $\smash {\lambda _Y^{\mathcal {S}}(\varphi _Y^{\smash {\Psi |_Y}})=\varphi ^\Psi }$
, which by the hypothesis on
$\smash {\lambda _Y^{\mathcal {S}}(\varphi _Y^{\smash {\Psi |_Y}})=\varphi ^\Psi }$
, which by the hypothesis on
![]() $\Psi $
is equal to
$\Psi $
is equal to
![]() $\varphi =\lambda _Y^{\mathcal {S}}(\varphi _Y)$
.
$\varphi =\lambda _Y^{\mathcal {S}}(\varphi _Y)$
.
It follows that
![]() $\Psi |_Y$
represents a mapping class
$\Psi |_Y$
represents a mapping class
![]() $\psi _Y\in \Gamma (Y)$
that belongs to
$\psi _Y\in \Gamma (Y)$
that belongs to
![]() $Z(\varphi _Y)$
. Similarly,
$Z(\varphi _Y)$
. Similarly,
![]() $\Psi |_W$
represents a class in
$\Psi |_W$
represents a class in
![]() $\Gamma ^{\mathfrak {S}_h}(W)$
, and it is clear that
$\Gamma ^{\mathfrak {S}_h}(W)$
, and it is clear that
![]() $\psi _W$
and
$\psi _W$
and
![]() $\psi _Y$
project to the same element of
$\psi _Y$
project to the same element of
![]() $\mathfrak {S}_h$
: that is, the couple
$\mathfrak {S}_h$
: that is, the couple
![]() $(\psi _W,\psi _Y)$
gives an element of
$(\psi _W,\psi _Y)$
gives an element of
![]() $\tilde Z(\varphi )$
. It is also evident that
$\tilde Z(\varphi )$
. It is also evident that
![]() $\varepsilon (\psi _W,\psi _Y)=\psi $
. This implies that
$\varepsilon (\psi _W,\psi _Y)=\psi $
. This implies that
![]() $\varepsilon $
is surjective. Putting together the discussion of this and the previous subsections, we conclude the following.
$\varepsilon $
is surjective. Putting together the discussion of this and the previous subsections, we conclude the following.
Proposition 3.8. Let
![]() $g\geqslant 0, n\geqslant 1$
, let
$g\geqslant 0, n\geqslant 1$
, let
![]() $\mathcal {S}$
be a surface of type
$\mathcal {S}$
be a surface of type
![]() $\Sigma _{g,n}$
, let
$\Sigma _{g,n}$
, let
![]() $\varphi \in \Gamma (\mathcal {S},\partial \mathcal {S})$
, let
$\varphi \in \Gamma (\mathcal {S},\partial \mathcal {S})$
, let
![]() $c_1,\dots ,c_h$
be a system of oriented curves representing the cut locus of
$c_1,\dots ,c_h$
be a system of oriented curves representing the cut locus of
![]() $\varphi $
, and let W and Y be the corresponding white and yellow regions of
$\varphi $
, and let W and Y be the corresponding white and yellow regions of
![]() $\mathcal {S}$
, using Notation 3.2. Then there is an isomorphism of groups induced by
$\mathcal {S}$
, using Notation 3.2. Then there is an isomorphism of groups induced by
![]() $\varepsilon $
$\varepsilon $
where
![]() $\mathbb {Z}^h$
is the free abelian group generated by the elements
$\mathbb {Z}^h$
is the free abelian group generated by the elements
![]() $(D_{c_i},D_{c_i}^{-1})$
. If, moreover, W is connected, we can use Notation 3.7 and rewrite the isomorphism as
$(D_{c_i},D_{c_i}^{-1})$
. If, moreover, W is connected, we can use Notation 3.7 and rewrite the isomorphism as

4 Generalities on coloured operads
In this section, we establish the operadic framework that we will use in the rest of the article. The reader who is well-acquainted with the language of coloured operads may skip this interlude and go directly to Section 5.
4.1 Notation and diagram categories
By ‘space’, we mean a topological space that is compactly generated and has the weak Hausdorff property. Let
![]() $\mathbf {Top}$
be the category of spaces; it is Cartesian closed, complete, and cocomplete.
$\mathbf {Top}$
be the category of spaces; it is Cartesian closed, complete, and cocomplete.
For a topologically enriched category
![]() $\mathbf {I}$
and two objects
$\mathbf {I}$
and two objects
![]() $k,n\in {\mathrm {ob}}(\mathbf {I})$
, we denote by
$k,n\in {\mathrm {ob}}(\mathbf {I})$
, we denote by
![]() $\mathbf {I}\tbinom {k}{n}$
the space of morphisms from k to n, and we denote the identity of n by
$\mathbf {I}\tbinom {k}{n}$
the space of morphisms from k to n, and we denote the identity of n by
![]() .
.
Notation 4.1. Let
![]() $\mathbf {Inj}$
be the small category with objects
$\mathbf {Inj}$
be the small category with objects
![]() $\underline {r}=\left \{1,\dots ,r\right \}$
for all non-negative integers
$\underline {r}=\left \{1,\dots ,r\right \}$
for all non-negative integers
![]() $r\in \{0,1,2,\dotsc \}$
, and with morphisms
$r\in \{0,1,2,\dotsc \}$
, and with morphisms
![]() $\underline {r}\to \underline {r}'$
being all injective maps of finite sets. Moreover, let
$\underline {r}\to \underline {r}'$
being all injective maps of finite sets. Moreover, let
![]() $\mathbf {\Sigma }\subseteq \mathbf {Inj}$
be the subcategory of all bijective maps.
$\mathbf {\Sigma }\subseteq \mathbf {Inj}$
be the subcategory of all bijective maps.
The category
![]() $\mathbf {Inj}$
is spanned by two sorts of maps: on the one hand, permutations
$\mathbf {Inj}$
is spanned by two sorts of maps: on the one hand, permutations
![]() $\tau \in \mathfrak {S}_r$
, which constitute the category
$\tau \in \mathfrak {S}_r$
, which constitute the category
![]() $\mathbf {\Sigma }$
, and on the other hand, the top cofaces
$\mathbf {\Sigma }$
, and on the other hand, the top cofaces
![]() $d^r\colon \underline {\smash {r-1}}\to \underline {r}$
, where for each
$d^r\colon \underline {\smash {r-1}}\to \underline {r}$
, where for each
![]() $1\leqslant i\leqslant r$
, we denote by
$1\leqslant i\leqslant r$
, we denote by
![]() $d^i$
the unique strictly monotone function whose image does not contain the element
$d^i$
the unique strictly monotone function whose image does not contain the element
![]() $i\in \underline {r}$
. Whenever we apply a contravariant functor to
$i\in \underline {r}$
. Whenever we apply a contravariant functor to
![]() $\mathbf {Inj}$
, we write
$\mathbf {Inj}$
, we write
![]() $d_i:= (d^i)^*$
.
$d_i:= (d^i)^*$
.
Notation 4.2. Let N be a fixed set,
![]() $r\geqslant 0$
, and let
$r\geqslant 0$
, and let
![]() $K=(k_1,\dotsc ,k_r)$
be a tuple of elements of N. We write
$K=(k_1,\dotsc ,k_r)$
be a tuple of elements of N. We write
![]() $\# K:= r$
for the length of K. If
$\# K:= r$
for the length of K. If
![]() $u\colon \underline {s}\hookrightarrow \underline {r}$
is a map in
$u\colon \underline {s}\hookrightarrow \underline {r}$
is a map in
![]() $\mathbf {Inj}$
, we write
$\mathbf {Inj}$
, we write
![]() $u^*K := \big (k_{u(1)},\dotsc ,k_{u(s)}\big )$
. If
$u^*K := \big (k_{u(1)},\dotsc ,k_{u(s)}\big )$
. If
![]() $\boldsymbol {X}:= (X_n)_{n\in N}$
is a family of objects in a category with finite products, we write
$\boldsymbol {X}:= (X_n)_{n\in N}$
is a family of objects in a category with finite products, we write
![]() $\boldsymbol {X}(K) := X_{\smash {k_1}} \times \dotsb \times X_{\smash {k_r}}$
;
$\boldsymbol {X}(K) := X_{\smash {k_1}} \times \dotsb \times X_{\smash {k_r}}$
;
For tuples
![]() $K=(k_1,\dotsc ,k_r)$
and
$K=(k_1,\dotsc ,k_r)$
and
![]() $K'=(k^{\prime }_1,\dotsc ,k^{\prime }_{r'})$
of elements of N, we denote by
$K'=(k^{\prime }_1,\dotsc ,k^{\prime }_{r'})$
of elements of N, we denote by
![]() $\smash {\mathbf {Inj} \tbinom {\smash {K\,}}{K'}\subset \mathbf {Inj}\tbinom {\underline {r}\,}{\underline {r}'}}$
the subset of all
$\smash {\mathbf {Inj} \tbinom {\smash {K\,}}{K'}\subset \mathbf {Inj}\tbinom {\underline {r}\,}{\underline {r}'}}$
the subset of all
![]() $u\colon \underline {r}\hookrightarrow \underline {r}'$
with
$u\colon \underline {r}\hookrightarrow \underline {r}'$
with
![]() $u^*K'=K$
, and we write
$u^*K'=K$
, and we write
![]() $\smash {\mathbf {\Sigma }\tbinom {K\,}{K'}}:=\smash {\mathbf {Inj}\tbinom {K\,}{K'}\cap \mathbf {\Sigma }\tbinom {\underline {r}\,}{\underline {r}'}}$
.
$\smash {\mathbf {\Sigma }\tbinom {K\,}{K'}}:=\smash {\mathbf {Inj}\tbinom {K\,}{K'}\cap \mathbf {\Sigma }\tbinom {\underline {r}\,}{\underline {r}'}}$
.
Definition 4.3. Let N be an index set and let
![]() $\boldsymbol {G}:= (G_n)_{n\in N}$
be a family of topological groups. We define the wreath product
$\boldsymbol {G}:= (G_n)_{n\in N}$
be a family of topological groups. We define the wreath product
![]() $\boldsymbol {G}\wr \mathbf {Inj}$
as the following topologically enriched category:
$\boldsymbol {G}\wr \mathbf {Inj}$
as the following topologically enriched category:
-
1. the objects of
 $\boldsymbol {G}\wr \mathbf {Inj}$
are all tuples
$\boldsymbol {G}\wr \mathbf {Inj}$
are all tuples
 $K=(k_1,\dotsc ,k_r)$
with
$K=(k_1,\dotsc ,k_r)$
with
 $r\geqslant 0$
and
$r\geqslant 0$
and
 $k_i\in N$
;
$k_i\in N$
; -
2. for two tuples K and
 $K'$
, we define
$K'$
, we define
 $(\boldsymbol {G}\wr \mathbf {Inj})\smash {\tbinom {K}{K'}} = \boldsymbol {G}(K)\times \mathbf {Inj}\smash {\tbinom {K\,}{K'}}$
: that is, a morphism
$(\boldsymbol {G}\wr \mathbf {Inj})\smash {\tbinom {K}{K'}} = \boldsymbol {G}(K)\times \mathbf {Inj}\smash {\tbinom {K\,}{K'}}$
: that is, a morphism
 $K\to K'$
in
$K\to K'$
in
 $\boldsymbol {G}\wr \mathbf {Inj}$
is a pair
$\boldsymbol {G}\wr \mathbf {Inj}$
is a pair
 $(\boldsymbol {\gamma },u)$
consisting of a tuple
$(\boldsymbol {\gamma },u)$
consisting of a tuple
 $\boldsymbol {\gamma }\in {\boldsymbol {G}}(K)$
and an injection
$\boldsymbol {\gamma }\in {\boldsymbol {G}}(K)$
and an injection
 $u\colon \underline {r}\hookrightarrow \underline {r}'$
satisfying
$u\colon \underline {r}\hookrightarrow \underline {r}'$
satisfying
 $K=u^*K'$
;
$K=u^*K'$
; -
3. we let
 $(\boldsymbol {\gamma }',u')\circ (\boldsymbol {\gamma },u) := (u^*\boldsymbol {\gamma }'\cdot \boldsymbol {\gamma },u'\circ u)$
, where
$(\boldsymbol {\gamma }',u')\circ (\boldsymbol {\gamma },u) := (u^*\boldsymbol {\gamma }'\cdot \boldsymbol {\gamma },u'\circ u)$
, where
 $u^*\boldsymbol {\gamma }' =(\gamma ^{\prime }_{u(1)},\dotsc ,\gamma ^{\prime }_{u(r)})$
, and ‘
$u^*\boldsymbol {\gamma }' =(\gamma ^{\prime }_{u(1)},\dotsc ,\gamma ^{\prime }_{u(r)})$
, and ‘
 $\cdot $
’ denotes component-wise multiplication.
$\cdot $
’ denotes component-wise multiplication.
For each tuple K, we define
![]() $\boldsymbol {G}[K]\subseteq \boldsymbol {G}\wr \mathbf {Inj}$
as the full subcategory spanned by objects of the form
$\boldsymbol {G}[K]\subseteq \boldsymbol {G}\wr \mathbf {Inj}$
as the full subcategory spanned by objects of the form
![]() $\tau ^*K$
for
$\tau ^*K$
for
![]() $\tau \in \mathfrak {S}_r$
. Moreover, we let
$\tau \in \mathfrak {S}_r$
. Moreover, we let
![]() $\boldsymbol {G}\wr \mathbf {\Sigma }$
be the subgroupoid with morphism spaces given by
$\boldsymbol {G}\wr \mathbf {\Sigma }$
be the subgroupoid with morphism spaces given by
![]() ${\boldsymbol {G}}(K)\times \mathbf {\Sigma }\tbinom {K\,}{K'}$
.
${\boldsymbol {G}}(K)\times \mathbf {\Sigma }\tbinom {K\,}{K'}$
.
If
![]() $(G_n)_{n\in N}$
is the trivial sequence
$(G_n)_{n\in N}$
is the trivial sequence
![]() $G_n=1$
of groups, then we write
$G_n=1$
of groups, then we write
![]() $N\wr \mathbf {Inj}$
for the wreath product, and we also write
$N\wr \mathbf {Inj}$
for the wreath product, and we also write
![]() $N\wr \mathbf {\Sigma }$
, respectively
$N\wr \mathbf {\Sigma }$
, respectively
![]() $N[K]$
for the corresponding subgroupoids.
$N[K]$
for the corresponding subgroupoids.
Example 4.4. If
![]() $\boldsymbol {X}=(X_n)_{n\in N}$
is a sequence of spaces, then we obtain a functor
$\boldsymbol {X}=(X_n)_{n\in N}$
is a sequence of spaces, then we obtain a functor
Construction 4.5. Let
![]() $\boldsymbol {X}:= (X_n)_{n\in N}$
be a family of based spaces, together with based left actions of
$\boldsymbol {X}:= (X_n)_{n\in N}$
be a family of based spaces, together with based left actions of
![]() $G_n$
on
$G_n$
on
![]() $X_n$
for each
$X_n$
for each
![]() $n\in N$
. Then the functor from Example 4.4 can be extended to a functor
$n\in N$
. Then the functor from Example 4.4 can be extended to a functor
![]() $\boldsymbol {G}\wr \mathbf {Inj}\to \mathbf {Top}$
as follows. For each injective map
$\boldsymbol {G}\wr \mathbf {Inj}\to \mathbf {Top}$
as follows. For each injective map
![]() $u\colon \underline {r}\hookrightarrow \underline {r}'$
, each fibre has at most one element; therefore we obtain an extension
$u\colon \underline {r}\hookrightarrow \underline {r}'$
, each fibre has at most one element; therefore we obtain an extension
![]() $N\wr \mathbf {Inj}\to \mathbf {Top}$
by
$N\wr \mathbf {Inj}\to \mathbf {Top}$
by
where we define
![]() $x_\varnothing $
to be the basepoint.
$x_\varnothing $
to be the basepoint.
Moreover,
![]() $\boldsymbol {G}(K)$
acts on
$\boldsymbol {G}(K)$
acts on
![]() $\boldsymbol {X}(K)$
component-wise, so for a morphism
$\boldsymbol {X}(K)$
component-wise, so for a morphism
![]() $(\boldsymbol {\gamma },u)$
in
$(\boldsymbol {\gamma },u)$
in
![]() $\boldsymbol {G}\wr \mathbf {Inj}$
, we can define
$\boldsymbol {G}\wr \mathbf {Inj}$
, we can define
![]() $(\boldsymbol {\gamma },u)_*(x) := u_*(\boldsymbol {\gamma }\cdot x)$
.
$(\boldsymbol {\gamma },u)_*(x) := u_*(\boldsymbol {\gamma }\cdot x)$
.
Definition 4.6. Let
![]() $\mathbf {I}$
be a small and topologically enriched category and let
$\mathbf {I}$
be a small and topologically enriched category and let
![]() $H\colon \mathbf {I}^{\operatorname {op}}\times \mathbf {I}\to {\large \mathbf {Top}}$
be a functor. Then we define the coend to be the coequaliser
$H\colon \mathbf {I}^{\operatorname {op}}\times \mathbf {I}\to {\large \mathbf {Top}}$
be a functor. Then we define the coend to be the coequaliser

4.2 Coloured operads
We assume that the reader is familiar with the classical notion of an operad, as it is for example presented in [Reference Markl, Shnider and Stasheff15]; in particular, the visualisation of operations by trees is taken for granted.
We will give a brief introduction to the notion of a coloured operad mostly for the purpose of fixing the notation we will use later. For a detailed introduction to coloured operads, we refer the reader to [Reference Yau28].
Definition 4.7. Let N be a fixed set. An N-coloured operad is a family of functors
![]() ${\mathscr {O}}\tbinom {-}{n}\colon (N\wr \mathbf {\Sigma })^{\operatorname {op}}\to \mathbf {Top}$
for each
${\mathscr {O}}\tbinom {-}{n}\colon (N\wr \mathbf {\Sigma })^{\operatorname {op}}\to \mathbf {Top}$
for each
![]() $n\in N$
, together with:
$n\in N$
, together with:
-
1. choices of identities
 ;
; -
2. composition maps for each
 $n,k_i,l_{ij}\in N$
, which are of the form
$n,k_i,l_{ij}\in N$
, which are of the form  $$\begin{align*}{\mathscr{O}}\tbinom{k_1,\dotsc,k_r}{n}\times\prod_{i=1}^r {\mathscr{O}}\tbinom{l_{i1},\dotsc,l_{is_i}}{k_i}\to {\mathscr{O}}\tbinom{l_{11},\dotsc,l_{rs_r}}{n},\quad\! (\mu;\mu^{\prime}_1,\dotsc,\mu^{\prime}_r)\mapsto \mu\circ (\mu^{\prime}_1,\dotsc,\mu^{\prime}_r);\end{align*}$$
$$\begin{align*}{\mathscr{O}}\tbinom{k_1,\dotsc,k_r}{n}\times\prod_{i=1}^r {\mathscr{O}}\tbinom{l_{i1},\dotsc,l_{is_i}}{k_i}\to {\mathscr{O}}\tbinom{l_{11},\dotsc,l_{rs_r}}{n},\quad\! (\mu;\mu^{\prime}_1,\dotsc,\mu^{\prime}_r)\mapsto \mu\circ (\mu^{\prime}_1,\dotsc,\mu^{\prime}_r);\end{align*}$$
such that the usual coherence axioms from [Reference Yau28, § 11.2] are satisfied. For
![]() $\mu \in {\mathscr {O}}\tbinom {k_1,\dotsc ,k_r}{n}$
, we will call n the output,
$\mu \in {\mathscr {O}}\tbinom {k_1,\dotsc ,k_r}{n}$
, we will call n the output,
![]() $(k_1,\dotsc ,k_r)$
the input profile, and
$(k_1,\dotsc ,k_r)$
the input profile, and
![]() $\# \mu := r$
the arity of
$\# \mu := r$
the arity of
![]() $\mu $
. For the first few values of r, we call
$\mu $
. For the first few values of r, we call
![]() $\mu $
nullary, unary, respectively binary if
$\mu $
nullary, unary, respectively binary if
![]() $\mu $
has arity
$\mu $
has arity
![]() $0$
,
$0$
,
![]() $1$
, respectively
$1$
, respectively
![]() $2$
. For the empty tuple, we will write
$2$
. For the empty tuple, we will write
![]() ${\mathscr {O}}\tbinom {}{n}$
for the space of nullaries. We say that
${\mathscr {O}}\tbinom {}{n}$
for the space of nullaries. We say that
![]() ${\mathscr {O}}$
is
${\mathscr {O}}$
is
![]() $\mathfrak {S}$
-free if for each
$\mathfrak {S}$
-free if for each
![]() $K=(k_1,\dotsc ,k_r)$
, the subgroup
$K=(k_1,\dotsc ,k_r)$
, the subgroup
![]() $\mathfrak {S}_K\subseteq \mathfrak {S}_r$
, which fixes the tuple K acts freely on
$\mathfrak {S}_K\subseteq \mathfrak {S}_r$
, which fixes the tuple K acts freely on
![]() ${\mathscr {O}}\tbinom {K}{n}$
.
${\mathscr {O}}\tbinom {K}{n}$
.
We call
![]() ${\mathscr {O}}$
monochromatic if
${\mathscr {O}}$
monochromatic if
![]() $N=*$
is just a singleton. In this case, we also write
$N=*$
is just a singleton. In this case, we also write
![]() ${\mathscr {O}}(r):= {\mathscr {O}}\tbinom {*,\dotsc ,*}{*}$
for the space of r-ary operations. For an N-coloured operad
${\mathscr {O}}(r):= {\mathscr {O}}\tbinom {*,\dotsc ,*}{*}$
for the space of r-ary operations. For an N-coloured operad
![]() ${\mathscr {O}}$
and a fixed colour
${\mathscr {O}}$
and a fixed colour
![]() $n\in N$
, we also consider the monochromatic operad
$n\in N$
, we also consider the monochromatic operad
![]() ${\mathscr {O}}|_n$
with operation spaces
${\mathscr {O}}|_n$
with operation spaces
![]() $({\mathscr {O}}|_n)(r) := {\mathscr {O}}\tbinom {n,\dotsc ,n}{n}$
.
$({\mathscr {O}}|_n)(r) := {\mathscr {O}}\tbinom {n,\dotsc ,n}{n}$
.
Additionally, we will use the short notation for ‘partial’ composition: for
![]() $\mu \in {\mathscr {O}}\tbinom {k_1,\dotsc ,k_r}{n}$
and
$\mu \in {\mathscr {O}}\tbinom {k_1,\dotsc ,k_r}{n}$
and
![]() $\mu '\in {\mathscr {O}}\tbinom {l_1,\dotsc ,l_s}{k_i}$
, we will write
$\mu '\in {\mathscr {O}}\tbinom {l_1,\dotsc ,l_s}{k_i}$
, we will write
Example 4.8.
-
1. The little d-discs operads
 ${\mathscr {D}}_d$
for
${\mathscr {D}}_d$
for
 $1\leqslant d\leqslant \infty $
are examples of monochromatic operads. In our setting, we put
$1\leqslant d\leqslant \infty $
are examples of monochromatic operads. In our setting, we put
 ${\mathscr {D}}_d(0)=\{\mathfrak {v}\}$
, the single nullary operation given by an empty configuration of discs (thus,
${\mathscr {D}}_d(0)=\{\mathfrak {v}\}$
, the single nullary operation given by an empty configuration of discs (thus,
 $\mathfrak {v}$
stands for ‘void’).
$\mathfrak {v}$
stands for ‘void’). -
2. Each small topologically enriched category
 $\mathbf {I}$
is a coloured operad with colour set
$\mathbf {I}$
is a coloured operad with colour set
 ${\mathrm {ob}}(\mathbf {I})$
and only unaries.
${\mathrm {ob}}(\mathbf {I})$
and only unaries.
Definition 4.9. Let
![]() ${\mathscr {O}}$
be an N-coloured operad. An
${\mathscr {O}}$
be an N-coloured operad. An
![]() ${\mathscr {O}}$
-algebra is an N-indexed family
${\mathscr {O}}$
-algebra is an N-indexed family
![]() $\boldsymbol {X}:= (X_n)_{n\in N}$
of spaces, together with maps
$\boldsymbol {X}:= (X_n)_{n\in N}$
of spaces, together with maps
such that the usual coherence axioms from [Reference Yau28, § 13] are satisfied.
A morphism
![]() $f\colon \boldsymbol {X}\to \boldsymbol {X}'$
of
$f\colon \boldsymbol {X}\to \boldsymbol {X}'$
of
![]() ${\mathscr {O}}$
-algebras is a family
${\mathscr {O}}$
-algebras is a family
![]() $(f_n\colon X_n\to X^{\prime }_n)_{n\in N}$
of maps satisfying
$(f_n\colon X_n\to X^{\prime }_n)_{n\in N}$
of maps satisfying
![]() $f_n(\mu (x_1,\dotsc ,x_r)) = \mu (f_{k_1}(x_1),\dotsc ,f_{k_r}(x_r))$
for all operations
$f_n(\mu (x_1,\dotsc ,x_r)) = \mu (f_{k_1}(x_1),\dotsc ,f_{k_r}(x_r))$
for all operations
![]() $\mu $
and all elements
$\mu $
and all elements
![]() $x_i$
. This gives rise to the category
$x_i$
. This gives rise to the category
![]() ${\mathscr {O}}\text {-}\mathbf {Alg}$
.
${\mathscr {O}}\text {-}\mathbf {Alg}$
.
Example 4.10. For each N-coloured operad
![]() ${\mathscr {O}}$
, we have an
${\mathscr {O}}$
, we have an
![]() ${\mathscr {O}}$
-algebra by the family
${\mathscr {O}}$
-algebra by the family
![]() $({\mathscr {O}}\tbinom {}{n})_{n\in N}$
. This algebra is initial in
$({\mathscr {O}}\tbinom {}{n})_{n\in N}$
. This algebra is initial in
![]() ${\mathscr {O}}\text {-}\mathbf {Alg}$
by construction, so we call it the initial
${\mathscr {O}}\text {-}\mathbf {Alg}$
by construction, so we call it the initial
![]() ${\mathscr {O}}$
-algebra. For
${\mathscr {O}}$
-algebra. For
![]() $1\leqslant d\leqslant \infty $
, the initial
$1\leqslant d\leqslant \infty $
, the initial
![]() ${\mathscr {D}}_d$
-algebra is just a single point.
${\mathscr {D}}_d$
-algebra is just a single point.
Definition 4.11. For a fixed colour set N, a morphism
![]() $\rho \colon {\mathscr {P}}\to {\mathscr {O}}$
of N-coloured operads is a family
$\rho \colon {\mathscr {P}}\to {\mathscr {O}}$
of N-coloured operads is a family
![]() $\rho ^-_n\colon {\mathscr {P}}\tbinom {-}{n}\Rightarrow {\mathscr {O}}\tbinom {-}{n}$
of transformations such that we have, abbreviating
$\rho ^-_n\colon {\mathscr {P}}\tbinom {-}{n}\Rightarrow {\mathscr {O}}\tbinom {-}{n}$
of transformations such that we have, abbreviating
![]() $\rho :=\rho ^K_n$
for all K and n,
$\rho :=\rho ^K_n$
for all K and n,
-
1.
 for each
for each
 $n\in N$
;
$n\in N$
; -
2.
 $\rho (\mu )\circ (\rho (\mu ^{\prime }_1),\dotsc ,\rho (\mu ^{\prime }_r)) = \rho (\mu \circ (\mu ^{\prime }_1,\dotsc ,\mu ^{\prime }_r))$
.
$\rho (\mu )\circ (\rho (\mu ^{\prime }_1),\dotsc ,\rho (\mu ^{\prime }_r)) = \rho (\mu \circ (\mu ^{\prime }_1,\dotsc ,\mu ^{\prime }_r))$
.
Each operad morphism
![]() $\rho \colon {\mathscr {P}}\to {\mathscr {O}}$
gives rise to a base-change adjunction
$\rho \colon {\mathscr {P}}\to {\mathscr {O}}$
gives rise to a base-change adjunction
as follows: each
![]() ${\mathscr {O}}$
-algebra is a
${\mathscr {O}}$
-algebra is a
![]() ${\mathscr {P}}$
-algebra by restriction. For the converse, we consider the absolute adjunction
${\mathscr {P}}$
-algebra by restriction. For the converse, we consider the absolute adjunction
, where
![]() $U^{{\mathscr {O}}}$
just forgets the action, and where for each N-indexed family
$U^{{\mathscr {O}}}$
just forgets the action, and where for each N-indexed family
![]() ${\boldsymbol {X}}$
of spaces, we define
${\boldsymbol {X}}$
of spaces, we define
![]() $F^{{\mathscr {O}}}({\boldsymbol {X}})_n := \smash {\int ^{K\in N\wr \mathbf {\Sigma }}{\mathscr {O}}\tbinom {K}{n}\times \boldsymbol {X}(K)}$
. Then each
$F^{{\mathscr {O}}}({\boldsymbol {X}})_n := \smash {\int ^{K\in N\wr \mathbf {\Sigma }}{\mathscr {O}}\tbinom {K}{n}\times \boldsymbol {X}(K)}$
. Then each
![]() ${\mathscr {P}}$
-algebra
${\mathscr {P}}$
-algebra
![]() ${\boldsymbol {X}}$
can be presented as the reflexive coequaliser of
${\boldsymbol {X}}$
can be presented as the reflexive coequaliser of
![]() $F^{\mathscr {P}} U^{\mathscr {P}} F^{\mathscr {P}} U^{\mathscr {P}} {\boldsymbol {X}} \rightrightarrows F^{\mathscr {P}} U^{\mathscr {P}}{\boldsymbol {X}}$
, whence the induced
$F^{\mathscr {P}} U^{\mathscr {P}} F^{\mathscr {P}} U^{\mathscr {P}} {\boldsymbol {X}} \rightrightarrows F^{\mathscr {P}} U^{\mathscr {P}}{\boldsymbol {X}}$
, whence the induced
![]() ${\mathscr {O}}$
-algebra
${\mathscr {O}}$
-algebra
![]() $\rho _!{\boldsymbol {X}}$
is the reflexive coequaliser of
$\rho _!{\boldsymbol {X}}$
is the reflexive coequaliser of
![]() $F^{\mathscr {O}} U^{\mathscr {P}} F^{\mathscr {P}} U^{\mathscr {P}} {\boldsymbol {X}} \rightrightarrows F^{\mathscr {O}} U^{\mathscr {P}}{\boldsymbol {X}}$
, compare [Reference Berger and Moerdijk2, § 4].
$F^{\mathscr {O}} U^{\mathscr {P}} F^{\mathscr {P}} U^{\mathscr {P}} {\boldsymbol {X}} \rightrightarrows F^{\mathscr {O}} U^{\mathscr {P}}{\boldsymbol {X}}$
, compare [Reference Berger and Moerdijk2, § 4].
Intuitively,
![]() $\rho _!{\boldsymbol {X}}$
is a quotient of the free
$\rho _!{\boldsymbol {X}}$
is a quotient of the free
![]() ${\mathscr {O}}$
-algebra over
${\mathscr {O}}$
-algebra over
![]() ${\boldsymbol {X}}$
by the existing
${\boldsymbol {X}}$
by the existing
![]() ${\mathscr {P}}$
-action on
${\mathscr {P}}$
-action on
![]() ${\boldsymbol {X}}$
. This adjunction clearly respects compositions: if
${\boldsymbol {X}}$
. This adjunction clearly respects compositions: if
![]() $\rho \colon {\mathscr {Q}}\to {\mathscr {P}}$
and
$\rho \colon {\mathscr {Q}}\to {\mathscr {P}}$
and
![]() $\rho '\colon {\mathscr {P}}\to {\mathscr {O}}$
are two morphisms of N-coloured operads, then we clearly have
$\rho '\colon {\mathscr {P}}\to {\mathscr {O}}$
are two morphisms of N-coloured operads, then we clearly have
![]() $(\rho '\circ \rho )^* = \rho ^*\circ \rho '{}^*$
, so by the uniqueness of left adjoints, we also have
$(\rho '\circ \rho )^* = \rho ^*\circ \rho '{}^*$
, so by the uniqueness of left adjoints, we also have
![]() $(\rho '\circ \rho )_! \cong \rho ^{\prime }_!\circ \rho _!$
. When
$(\rho '\circ \rho )_! \cong \rho ^{\prime }_!\circ \rho _!$
. When
![]() $\rho $
is clear from the context, we also write
$\rho $
is clear from the context, we also write
![]() for the base-change adjunction.
for the base-change adjunction.
4.3 The coloured surface operad
We define an
![]() $\mathbb {N}_{\geqslant 1}$
-coloured operad
$\mathbb {N}_{\geqslant 1}$
-coloured operad
![]() ${\mathscr {M}}$
, which is a ‘coloured’ version of Tillmann’s surface operad [Reference Tillmann26]; see Figure 5.
${\mathscr {M}}$
, which is a ‘coloured’ version of Tillmann’s surface operad [Reference Tillmann26]; see Figure 5.

Figure 5 An element in
![]() . Note that the colours green, yellow and red only indicate which inputs belong together, while the actual ‘colours’ of the inputs are
. Note that the colours green, yellow and red only indicate which inputs belong together, while the actual ‘colours’ of the inputs are
![]() $2$
,
$2$
,
![]() $1$
and
$1$
and
![]() $2$
, respectively.
$2$
, respectively.
We first recall Segal’s cobordism category
![]() $\mathbf {M}$
[Reference Segal25], which is a topologically enriched category: objects of
$\mathbf {M}$
[Reference Segal25], which is a topologically enriched category: objects of
![]() $\mathbf {M}$
are non-negative integers
$\mathbf {M}$
are non-negative integers
![]() $n\geqslant 0$
; a morphism from n to
$n\geqslant 0$
; a morphism from n to
![]() $n'$
is represented by a (possibly disconnected) Riemann surface W with n incoming and
$n'$
is represented by a (possibly disconnected) Riemann surface W with n incoming and
![]() $n'$
outgoing boundary components; the surface W is equipped with a choice of collar neighbourhoods
$n'$
outgoing boundary components; the surface W is equipped with a choice of collar neighbourhoods
![]() $U^{\text {in}}_{\partial W}$
and
$U^{\text {in}}_{\partial W}$
and
![]() $U^{\text {in}}_{\partial W}$
of
$U^{\text {in}}_{\partial W}$
of
![]() $\partial ^{\text {in}}W$
and
$\partial ^{\text {in}}W$
and
![]() $\partial ^{\text {out}}W$
, respectively; these neighbourhoods are equipped with:
$\partial ^{\text {out}}W$
, respectively; these neighbourhoods are equipped with:
-
1. a holomorphic parametrisation
 $\tilde \vartheta ^{\text {in}}\colon \left \{1,\dots ,n\right \} \times S^1\times [0;1)\to U^{\text {in}}_{\partial W}$
; and
$\tilde \vartheta ^{\text {in}}\colon \left \{1,\dots ,n\right \} \times S^1\times [0;1)\to U^{\text {in}}_{\partial W}$
; and -
2. an antiholomorphic parametrisation
 $\tilde \vartheta ^{\text {out}}\colon \left \{1,\dots ,n'\right \} \times S^1\times [0;1)\to U^{\text {out}}_{\partial W}$
.
$\tilde \vartheta ^{\text {out}}\colon \left \{1,\dots ,n'\right \} \times S^1\times [0;1)\to U^{\text {out}}_{\partial W}$
.
Note that restricting
![]() $\tilde \vartheta ^{\text {in}}$
and
$\tilde \vartheta ^{\text {in}}$
and
![]() $\tilde \vartheta ^{\text {out}}$
to
$\tilde \vartheta ^{\text {out}}$
to
![]() $\left \{1,\dots ,n\right \}\times S^1\times 0$
and
$\left \{1,\dots ,n\right \}\times S^1\times 0$
and
![]() $\left \{1,\dots ,n'\right \}\times S^1\times 0$
, respectively, we obtain parametrisations of
$\left \{1,\dots ,n'\right \}\times S^1\times 0$
, respectively, we obtain parametrisations of
![]() $\partial ^{\text {in}}W$
and
$\partial ^{\text {in}}W$
and
![]() $\partial ^{\text {out}}W$
, respectively, as in Notation 2.1.
$\partial ^{\text {out}}W$
, respectively, as in Notation 2.1.
The space of morphisms
![]() $\mathbf {M}\tbinom {n\,}{n'}$
is the moduli space of conformal classes of such Riemann surfaces W, considered up to biholomorphism compatible with the choice of parametrised collar neighbourhoods of the incoming and outgoing boundary. We usually denote by
$\mathbf {M}\tbinom {n\,}{n'}$
is the moduli space of conformal classes of such Riemann surfaces W, considered up to biholomorphism compatible with the choice of parametrised collar neighbourhoods of the incoming and outgoing boundary. We usually denote by
![]() $(W,\tilde \vartheta )$
a morphism, or shortly by W when it is not necessary to mention the parametrisation of the collar neighbourhood of the boundary; here
$(W,\tilde \vartheta )$
a morphism, or shortly by W when it is not necessary to mention the parametrisation of the collar neighbourhood of the boundary; here
![]() $\smash {\tilde \vartheta \colon \left \{1,\dots ,n+n'\right \} \times S^1\times [0;1)\to W}$
is obtained by concatenation of
$\smash {\tilde \vartheta \colon \left \{1,\dots ,n+n'\right \} \times S^1\times [0;1)\to W}$
is obtained by concatenation of
![]() $\tilde \vartheta ^{\text {in}}$
and
$\tilde \vartheta ^{\text {in}}$
and
![]() $\tilde \vartheta ^{\text {out}}$
.
$\tilde \vartheta ^{\text {out}}$
.
The composition of two morphisms
![]() $(W,\tilde \vartheta )\colon n\to n'$
and
$(W,\tilde \vartheta )\colon n\to n'$
and
![]() $(W',\tilde \vartheta ')\colon n'\to n''$
is given by gluing the Riemann surfaces
$(W',\tilde \vartheta ')\colon n'\to n''$
is given by gluing the Riemann surfaces
![]() $W\smallsetminus \partial ^{\text {out}}W$
and
$W\smallsetminus \partial ^{\text {out}}W$
and
![]() $W'\smallsetminus \partial ^{\text {in}}W'$
, using the identification
$W'\smallsetminus \partial ^{\text {in}}W'$
, using the identification
![]() $U^{\text {out}}_{\partial W}\smallsetminus \partial ^{\text {out}}W \cong U^{\text {in}}_{\partial W'}\smallsetminus \partial ^{\text {in}}W'$
given by
$U^{\text {out}}_{\partial W}\smallsetminus \partial ^{\text {out}}W \cong U^{\text {in}}_{\partial W'}\smallsetminus \partial ^{\text {in}}W'$
given by
for all
![]() $1\leqslant j\leqslant n'$
,
$1\leqslant j\leqslant n'$
,
![]() $\zeta \in S^1$
and
$\zeta \in S^1$
and
![]() $0<t<1$
. The resulting surface
$0<t<1$
. The resulting surface
![]() $W''$
is also endowed with collar neighbourhoods of the incoming and outgoing boundaries whose parametrisations are given by
$W''$
is also endowed with collar neighbourhoods of the incoming and outgoing boundaries whose parametrisations are given by
![]() $\tilde \vartheta ^{\text {in}}$
and
$\tilde \vartheta ^{\text {in}}$
and
![]() $(\tilde \vartheta ')^{\text {out}}$
, respectively. The identity of
$(\tilde \vartheta ')^{\text {out}}$
, respectively. The identity of
![]() $n\in \mathbf {M}$
is described in Construction 4.13.
$n\in \mathbf {M}$
is described in Construction 4.13.
Definition 4.12. For each
![]() $n\geqslant 1$
, the Lie group
$n\geqslant 1$
, the Lie group
![]() $T^n\rtimes \mathfrak {S}_n=(S^1)^n\rtimes \mathfrak {S}_n$
will be denoted by
$T^n\rtimes \mathfrak {S}_n=(S^1)^n\rtimes \mathfrak {S}_n$
will be denoted by
![]() $R_n$
.
$R_n$
.
We can regard
![]() $R_n$
as a kind of twisted torus; it is the isometry group of
$R_n$
as a kind of twisted torus; it is the isometry group of
![]() $\coprod _n S^1$
.
$\coprod _n S^1$
.
Construction 4.13. We can embed
![]() $R_n$
in the endomorphism space
$R_n$
in the endomorphism space
![]() $\mathbf {M}\tbinom {n}{n}$
; see Figure 6: given an element
$\mathbf {M}\tbinom {n}{n}$
; see Figure 6: given an element
![]() $(z_1,\dotsc ,z_n,\sigma )\in R_n$
, we consider the morphism
$(z_1,\dotsc ,z_n,\sigma )\in R_n$
, we consider the morphism
![]() $(W,\tilde \vartheta )\colon n\to n$
given by the following:
$(W,\tilde \vartheta )\colon n\to n$
given by the following:
-
1. as a Riemann surface, W is
 $\left \{1,\dots ,n\right \}\times S^1\times [0;1]$
, with the canonical Riemann structure;
$\left \{1,\dots ,n\right \}\times S^1\times [0;1]$
, with the canonical Riemann structure; -
2. we let
 $U_{\partial W}^{\text {in}}=W\smallsetminus \partial ^{\text {out}}W$
, and
$U_{\partial W}^{\text {in}}=W\smallsetminus \partial ^{\text {out}}W$
, and
 $\tilde \vartheta ^{\text {in}}\colon \left \{1,\dots ,n\right \}\times S^1\times [0;1)\hookrightarrow W$
is the canonical inclusion;
$\tilde \vartheta ^{\text {in}}\colon \left \{1,\dots ,n\right \}\times S^1\times [0;1)\hookrightarrow W$
is the canonical inclusion; -
3. we let
 $U_{\partial W}^{\text {out}}=W\smallsetminus \partial ^{\text {in}}W$
, and let
$U_{\partial W}^{\text {out}}=W\smallsetminus \partial ^{\text {in}}W$
, and let
 $\tilde \vartheta ^{\text {out}}\colon \left \{1,\dots ,n\right \}\times S^1\times [0;1)\hookrightarrow W$
be
$\tilde \vartheta ^{\text {out}}\colon \left \{1,\dots ,n\right \}\times S^1\times [0;1)\hookrightarrow W$
be  $$\begin{align*}\tilde\vartheta^{\text{out}}(j,\zeta,t)=\left(\sigma^{-1}(j),z_j\cdot \zeta,1-t\right).\end{align*}$$
$$\begin{align*}\tilde\vartheta^{\text{out}}(j,\zeta,t)=\left(\sigma^{-1}(j),z_j\cdot \zeta,1-t\right).\end{align*}$$

Figure 6 An instance of
![]() $R_n\hookrightarrow \mathbf {M}\tbinom {n}{n}$
.
$R_n\hookrightarrow \mathbf {M}\tbinom {n}{n}$
.
This assignment embeds in fact
![]() $R_n$
as a group into the automorphisms of
$R_n$
as a group into the automorphisms of
![]() $n\in \mathbf {M}$
; in particular, the identity of n can be described as the image of the unit of
$n\in \mathbf {M}$
; in particular, the identity of n can be described as the image of the unit of
![]() $R_n$
along the embedding; see Figure 6.
$R_n$
along the embedding; see Figure 6.
Consider now the subcategory
![]() $\mathbf {M}_\partial \subseteq \mathbf {M}$
containing all objects and those cobordisms W whose components have non-empty outgoing boundary. In detail, for fixed
$\mathbf {M}_\partial \subseteq \mathbf {M}$
containing all objects and those cobordisms W whose components have non-empty outgoing boundary. In detail, for fixed
![]() $k,n\geqslant 0$
, the morphism space
$k,n\geqslant 0$
, the morphism space
![]() $\mathbf {M}_\partial (k,n)$
looks as follows:
$\mathbf {M}_\partial (k,n)$
looks as follows:
![]() $\pi _0\left (\mathbf {M}_\partial (k,n)\right )$
is indexed by the number
$\pi _0\left (\mathbf {M}_\partial (k,n)\right )$
is indexed by the number
![]() $1\leqslant l\leqslant n$
of path components, an unordered partition
$1\leqslant l\leqslant n$
of path components, an unordered partition
![]() $\{1,\dotsc ,n\}=\boldsymbol {n}_1\sqcup \dotsb \sqcup \boldsymbol {n}_l$
into non-empty subsets with
$\{1,\dotsc ,n\}=\boldsymbol {n}_1\sqcup \dotsb \sqcup \boldsymbol {n}_l$
into non-empty subsets with
![]() $\min (\boldsymbol {n}_j)<\min (\boldsymbol {n}_{j+1})$
, an ordered partition
$\min (\boldsymbol {n}_j)<\min (\boldsymbol {n}_{j+1})$
, an ordered partition
![]() $\{1,\dotsc ,k\} = \boldsymbol {k}_1\sqcup \dotsb \sqcup \boldsymbol {k}_l$
into possibly empty sets, and genera
$\{1,\dotsc ,k\} = \boldsymbol {k}_1\sqcup \dotsb \sqcup \boldsymbol {k}_l$
into possibly empty sets, and genera
![]() $g_1,\dotsc ,g_l\geqslant 0$
. If we let
$g_1,\dotsc ,g_l\geqslant 0$
. If we let
![]() $n_j:=\#\boldsymbol {n}_j$
and
$n_j:=\#\boldsymbol {n}_j$
and
![]() $k_j:= \# \boldsymbol {k}_j$
, then the corresponding path component is homotopy equivalent to
$k_j:= \# \boldsymbol {k}_j$
, then the corresponding path component is homotopy equivalent to
![]() $\mathfrak {M}_{g_1,k_1+n_1}\times \dotsb \times \mathfrak {M}_{g_l,k_l+n_l}$
, by restricting collar parametrisations to boundary parametrisations.
$\mathfrak {M}_{g_1,k_1+n_1}\times \dotsb \times \mathfrak {M}_{g_l,k_l+n_l}$
, by restricting collar parametrisations to boundary parametrisations.
Let
![]() $n,n'\in \mathbf {M}_\partial $
, and note that the embedding
$n,n'\in \mathbf {M}_\partial $
, and note that the embedding
![]() $R_n\subset \mathbf {M}\tbinom {n}{n}$
has image inside
$R_n\subset \mathbf {M}\tbinom {n}{n}$
has image inside
![]() $\mathbf {M}_\partial \tbinom {n}{n}$
. In the following lemma, we consider the right action of
$\mathbf {M}_\partial \tbinom {n}{n}$
. In the following lemma, we consider the right action of
![]() $R_n$
on
$R_n$
on
![]() $\mathbf {M}_\partial \tbinom {n}{n'}$
by precomposition.
$\mathbf {M}_\partial \tbinom {n}{n'}$
by precomposition.
Lemma 4.14. The group
![]() $R_n$
acts freely on the space
$R_n$
acts freely on the space
![]() $\mathbf {M}_\partial \tbinom {n\,}{n'}$
.
$\mathbf {M}_\partial \tbinom {n\,}{n'}$
.
Proof. Let
![]() $(W,\tilde \vartheta )\colon n\to n'$
be a morphism in
$(W,\tilde \vartheta )\colon n\to n'$
be a morphism in
![]() $\mathbf {M}\tbinom {n\,}{n'}$
, let
$\mathbf {M}\tbinom {n\,}{n'}$
, let
![]() $(z_1,\dotsc ,z_n,\sigma )\in R_n$
, and suppose that
$(z_1,\dotsc ,z_n,\sigma )\in R_n$
, and suppose that
![]() $(W,\tilde \vartheta )=(W,\tilde \vartheta ) \circ (z_1,\dotsc ,z_n,\sigma )$
. Note that the morphism
$(W,\tilde \vartheta )=(W,\tilde \vartheta ) \circ (z_1,\dotsc ,z_n,\sigma )$
. Note that the morphism
![]() $(W,\tilde \vartheta ) \cdot (z_1,\dotsc ,z_n,\sigma )$
is represented by the pair
$(W,\tilde \vartheta ) \cdot (z_1,\dotsc ,z_n,\sigma )$
is represented by the pair
![]() $(W',\tilde \vartheta ')$
, where:
$(W',\tilde \vartheta ')$
, where:
-
1.
 $W'=W$
and
$W'=W$
and
 $(\tilde \vartheta ')^{\text {out}}=\tilde \vartheta ^{\text {out}}$
;
$(\tilde \vartheta ')^{\text {out}}=\tilde \vartheta ^{\text {out}}$
; -
2.
 $(\tilde \vartheta ')^{\text {in}}$
is the postcomposition of
$(\tilde \vartheta ')^{\text {in}}$
is the postcomposition of
 $\tilde \vartheta ^{\text {in}}\colon \left \{1,\dots ,n\right \}\times S^1\times [0;1)\to W$
with the automorphism of
$\tilde \vartheta ^{\text {in}}\colon \left \{1,\dots ,n\right \}\times S^1\times [0;1)\to W$
with the automorphism of
 $\left \{1,\dots ,n\right \}\times S^1\times [0;1)$
given by
$\left \{1,\dots ,n\right \}\times S^1\times [0;1)$
given by
 $(j,\zeta ,t)\mapsto (\sigma ^{-1}(j),z_j\cdot \zeta ,t)$
.
$(j,\zeta ,t)\mapsto (\sigma ^{-1}(j),z_j\cdot \zeta ,t)$
.
If
![]() $\psi \colon W\to W'$
is a diffeomorphism exhibiting the equivalence of
$\psi \colon W\to W'$
is a diffeomorphism exhibiting the equivalence of
![]() $(W,\tilde \vartheta )$
and
$(W,\tilde \vartheta )$
and
![]() $(W',\tilde \vartheta ')$
in
$(W',\tilde \vartheta ')$
in
![]() $\mathbf {M}_\partial \tbinom {n\,}{n'}$
, then the first two conditions imply that
$\mathbf {M}_\partial \tbinom {n\,}{n'}$
, then the first two conditions imply that
![]() $\psi $
restricts to the identity of
$\psi $
restricts to the identity of
![]() $U_{\partial W}^{\text {out}}$
: that is, on the image of
$U_{\partial W}^{\text {out}}$
: that is, on the image of
![]() $\tilde \vartheta ^{\text {out}}$
. Since
$\tilde \vartheta ^{\text {out}}$
. Since
![]() $\psi $
is a holomorphic map, it must be the identity on a closed and open subset of W; since each connected component of W has non-empty outgoing boundary, and thus intersects
$\psi $
is a holomorphic map, it must be the identity on a closed and open subset of W; since each connected component of W has non-empty outgoing boundary, and thus intersects
![]() $U_{\partial W}^{\text {out}}$
, we conclude that
$U_{\partial W}^{\text {out}}$
, we conclude that
![]() $\psi $
must be the identity of W.
$\psi $
must be the identity of W.
It then follows that the automorphism of
![]() $\left \{1,\dots ,n\right \}\times S^1\times [0;1)$
given by
$\left \{1,\dots ,n\right \}\times S^1\times [0;1)$
given by
![]() $(j,\zeta ,t)\mapsto (\sigma ^{-1}(j),z_j\cdot \zeta ,t)$
is in fact the identity of
$(j,\zeta ,t)\mapsto (\sigma ^{-1}(j),z_j\cdot \zeta ,t)$
is in fact the identity of
![]() $\left \{1,\dots ,n\right \}\times S^1\times [0;1)$
, and this implies that
$\left \{1,\dots ,n\right \}\times S^1\times [0;1)$
, and this implies that
![]() $(z_1,\dots ,z_n,\sigma )$
is the identity of
$(z_1,\dots ,z_n,\sigma )$
is the identity of
![]() $R_n$
, as desired.
$R_n$
, as desired.
Definition 4.15. We consider
![]() $\mathbf {M}_\partial $
as a symmetric monoidal category with monoidal sum being the disjoint union; since the monoidal sum behaves as the usual sum of natural numbers on objects, we have an associated coloured operad
$\mathbf {M}_\partial $
as a symmetric monoidal category with monoidal sum being the disjoint union; since the monoidal sum behaves as the usual sum of natural numbers on objects, we have an associated coloured operad
![]() ${\mathscr {M}}$
with colours
${\mathscr {M}}$
with colours
![]() $\mathbb {N}_{\geqslant 1}=\{1,2,\dotsc \}$
and
$\mathbb {N}_{\geqslant 1}=\{1,2,\dotsc \}$
and
Note that the restriction
![]() ${\mathscr {M}}|_1$
to the colour
${\mathscr {M}}|_1$
to the colour
![]() $1$
is exactly Tillmann’s surface operad [Reference Tillmann26]. For each
$1$
is exactly Tillmann’s surface operad [Reference Tillmann26]. For each
![]() ${\mathscr {M}}$
-algebra
${\mathscr {M}}$
-algebra
![]() $\boldsymbol {X}=(X_n)_{n\geqslant 1}$
, the space
$\boldsymbol {X}=(X_n)_{n\geqslant 1}$
, the space
![]() $X_1$
is an algebra over the classical surface operad
$X_1$
is an algebra over the classical surface operad
![]() ${\mathscr {M}}|_1$
.
${\mathscr {M}}|_1$
.
Example 4.16. In contrast to the little disc operads, the initial
![]() ${\mathscr {M}}$
-algebra is non-trivial: for instance, its colour-
${\mathscr {M}}$
-algebra is non-trivial: for instance, its colour-
![]() $1$
part
$1$
part
![]() ${\mathscr {M}}\tbinom {}{1}$
homotopy equivalent to the familiar collection of moduli spaces
${\mathscr {M}}\tbinom {}{1}$
homotopy equivalent to the familiar collection of moduli spaces
 $$\begin{align*}{\mathscr{M}}\tbinom{}{1} = \mathbf{M}_\partial\tbinom{0}{1} \simeq \coprod_{g\geqslant 0}\mathfrak{M}_{g,1}.\end{align*}$$
$$\begin{align*}{\mathscr{M}}\tbinom{}{1} = \mathbf{M}_\partial\tbinom{0}{1} \simeq \coprod_{g\geqslant 0}\mathfrak{M}_{g,1}.\end{align*}$$
4.4 Tensor products and based operads
Definition 4.17. In [Reference Boardman and Vogt3, § II.3], Boardman and Vogt constructed a tensor product for operads. We are only interested in the following special case: let
![]() $\mathscr {A}$
be a monochromatic operad and
$\mathscr {A}$
be a monochromatic operad and
![]() $\mathbf {I}$
be a small, topologically enriched category with object set N. Then
$\mathbf {I}$
be a small, topologically enriched category with object set N. Then
![]() $\mathscr {A}\otimes \mathbf {I}$
is an N-coloured operad with operation spaces
$\mathscr {A}\otimes \mathbf {I}$
is an N-coloured operad with operation spaces
 $$\begin{align*}(\mathscr{A}\otimes\mathbf{I})\tbinom{k_1,\dotsc,k_r}{n} = \mathscr{A}(r)\times \prod_{i=1}^r \mathbf{I}\tbinom{k_i}{n},\end{align*}$$
$$\begin{align*}(\mathscr{A}\otimes\mathbf{I})\tbinom{k_1,\dotsc,k_r}{n} = \mathscr{A}(r)\times \prod_{i=1}^r \mathbf{I}\tbinom{k_i}{n},\end{align*}$$
together with the following structure, where we denote operations in
![]() $\mathscr {A}\otimes \mathbf {I}$
by
$\mathscr {A}\otimes \mathbf {I}$
by
![]() $\mu \otimes (\nu _1,\dotsc ,\nu _r)$
with
$\mu \otimes (\nu _1,\dotsc ,\nu _r)$
with
![]() $\mu \in \mathscr {A}(r)$
and
$\mu \in \mathscr {A}(r)$
and
![]() $\nu _i\in \mathbf {I}\tbinom {k_i}{n}$
:
$\nu _i\in \mathbf {I}\tbinom {k_i}{n}$
:
-
1. symmetric actions
 $\tau ^*(\mu \otimes (\nu _1,\dotsc ,\nu _r)) = (\tau ^*\mu )\otimes (\nu _{\tau (1)},\dotsc ,\nu _{\tau (r)})$
;
$\tau ^*(\mu \otimes (\nu _1,\dotsc ,\nu _r)) = (\tau ^*\mu )\otimes (\nu _{\tau (1)},\dotsc ,\nu _{\tau (r)})$
; -
2. identities
 ;
; -
3. compositions
 $$ \begin{align*} & \left(\mu\otimes (\nu_1,\dotsc,\nu_r)\right)\circ \left(\mu_1\otimes (\nu_{1,1},\dotsc,\nu_{1,s_1}),\dotsc,\mu_r\otimes (\nu_{r,1},\dotsc,\nu_{r,s_r})\right) \\ &:= \left(\mu\circ (\mu_1,\dotsc,\mu_r)\right)\otimes \left(\nu_1\circ\nu_{1,1},\dotsc,\nu_1\circ\nu_{1,s_1},\dotsc, \nu_r\circ\nu_{r,1},\dotsc,\nu_r\circ\nu_{r,s_r}\right). \end{align*} $$
$$ \begin{align*} & \left(\mu\otimes (\nu_1,\dotsc,\nu_r)\right)\circ \left(\mu_1\otimes (\nu_{1,1},\dotsc,\nu_{1,s_1}),\dotsc,\mu_r\otimes (\nu_{r,1},\dotsc,\nu_{r,s_r})\right) \\ &:= \left(\mu\circ (\mu_1,\dotsc,\mu_r)\right)\otimes \left(\nu_1\circ\nu_{1,1},\dotsc,\nu_1\circ\nu_{1,s_1},\dotsc, \nu_r\circ\nu_{r,1},\dotsc,\nu_r\circ\nu_{r,s_r}\right). \end{align*} $$
For
![]() $n\in N$
, we also abbreviate
$n\in N$
, we also abbreviate
![]() . Note that
. Note that
![]() $(\mathscr {A}\otimes \mathbf {I})$
-algebras are the same as enriched functors
$(\mathscr {A}\otimes \mathbf {I})$
-algebras are the same as enriched functors
![]() $\mathbf {I}\to \mathscr {A}\text {-}\mathbf {Alg}$
.
$\mathbf {I}\to \mathscr {A}\text {-}\mathbf {Alg}$
.
This construction is bifunctorial: if
![]() $\rho _1\colon \mathscr {A}\to \mathscr {A}'$
is a morphism of operads and
$\rho _1\colon \mathscr {A}\to \mathscr {A}'$
is a morphism of operads and
![]() $\rho _2\colon \mathbf {I}\to \mathbf {I}'$
is a functor that is the identity on objects, then we get a morphism
$\rho _2\colon \mathbf {I}\to \mathbf {I}'$
is a functor that is the identity on objects, then we get a morphism
![]() $\rho _1\otimes \rho _2\colon \mathscr {A}\otimes \mathbf {I}\to {\mathscr {A}'}\otimes {\mathbf {I}'}$
.
$\rho _1\otimes \rho _2\colon \mathscr {A}\otimes \mathbf {I}\to {\mathscr {A}'}\otimes {\mathbf {I}'}$
.
Example 4.18. Regard N as the discrete category with objects N. Then we get
 $$\begin{align*}(\mathscr{A}\otimes N)\tbinom{k_1,\dotsc,k_r}{n} = \begin{cases}\mathscr{A}(r) & \text{for}\ k_1=\dotsb=k_r=n\\\varnothing & \text{else,}\end{cases}\end{align*}$$
$$\begin{align*}(\mathscr{A}\otimes N)\tbinom{k_1,\dotsc,k_r}{n} = \begin{cases}\mathscr{A}(r) & \text{for}\ k_1=\dotsb=k_r=n\\\varnothing & \text{else,}\end{cases}\end{align*}$$
and
![]() $(\mathscr {A}\otimes N)$
-algebras are just N-indexed families of
$(\mathscr {A}\otimes N)$
-algebras are just N-indexed families of
![]() $\mathscr {A}$
-algebras. One example that will be of particular importance for us later is the operad
$\mathscr {A}$
-algebras. One example that will be of particular importance for us later is the operad
![]() ${\mathscr {D}}_1\otimes N$
, which has a copy of the little
${\mathscr {D}}_1\otimes N$
, which has a copy of the little
![]() $1$
-discs operad
$1$
-discs operad
![]() ${\mathscr {D}}_1$
in each colour
${\mathscr {D}}_1$
in each colour
![]() $n\in N$
.
$n\in N$
.
Definition 4.19. Consider the monochromatic operad
![]() ${\mathscr {B}}$
with only two operations, namely the identity
${\mathscr {B}}$
with only two operations, namely the identity
![]() and a single nullary
and a single nullary
![]() ${\mathscr {B}}(0)=\{\mathfrak {v}\}$
. Then
${\mathscr {B}}(0)=\{\mathfrak {v}\}$
. Then
![]() $({\mathscr {B}}\otimes N)$
-algebras are the same as families
$({\mathscr {B}}\otimes N)$
-algebras are the same as families
![]() $\boldsymbol {X}=(X_n)_{n\in N}$
of based spaces.
$\boldsymbol {X}=(X_n)_{n\in N}$
of based spaces.
A based N-coloured operad is an N-coloured operad
![]() ${\mathscr {O}}$
, together with an operad morphism
${\mathscr {O}}$
, together with an operad morphism
![]() ${\mathscr {B}}\otimes N\to {\mathscr {O}}$
. A morphism of based N-coloured operads is an operad map
${\mathscr {B}}\otimes N\to {\mathscr {O}}$
. A morphism of based N-coloured operads is an operad map
![]() $\rho \colon {\mathscr {O}}\to {\mathscr {P}}$
commuting with the two maps from
$\rho \colon {\mathscr {O}}\to {\mathscr {P}}$
commuting with the two maps from
![]() ${\mathscr {B}}\otimes N$
.
${\mathscr {B}}\otimes N$
.
Remark 4.20.
-
1. A based N-coloured operad is the same as an N-coloured operad
 ${\mathscr {O}}$
, together with a choice of nullary operation
${\mathscr {O}}$
, together with a choice of nullary operation
 $\mathfrak {v}_n\in {\mathscr {O}}\tbinom {}{n}$
for each colour
$\mathfrak {v}_n\in {\mathscr {O}}\tbinom {}{n}$
for each colour
 $n\in N$
, and a morphism
$n\in N$
, and a morphism
 $\rho \colon {\mathscr {O}}\to {\mathscr {P}}$
of based operads has to additionally satisfy
$\rho \colon {\mathscr {O}}\to {\mathscr {P}}$
of based operads has to additionally satisfy
 $\rho (\mathfrak {v}^{\mathscr {O}}_n)=\rho (\mathfrak {v}^{\mathscr {P}}_n)$
.
$\rho (\mathfrak {v}^{\mathscr {O}}_n)=\rho (\mathfrak {v}^{\mathscr {P}}_n)$
. -
2. The nullaries
 $\mathfrak {v}_n$
of a based operad can be used to ‘block’ inputs by precomposition with them. More precisely, for each input profile
$\mathfrak {v}_n$
of a based operad can be used to ‘block’ inputs by precomposition with them. More precisely, for each input profile
 $K=(k_1,\dotsc ,k_r)$
and
$K=(k_1,\dotsc ,k_r)$
and
 $1\leqslant i\leqslant r$
, we have a map In this way the functors
$1\leqslant i\leqslant r$
, we have a map In this way the functors $$\begin{align*}d_i\colon {\mathscr{O}}\tbinom{K}{n}\to {\mathscr{O}}\tbinom{d_iK}{n},\quad \mu\mapsto \mu\circ_i \mathfrak{v}_{k_i}.\end{align*}$$
$$\begin{align*}d_i\colon {\mathscr{O}}\tbinom{K}{n}\to {\mathscr{O}}\tbinom{d_iK}{n},\quad \mu\mapsto \mu\circ_i \mathfrak{v}_{k_i}.\end{align*}$$
 ${\mathscr {O}}\tbinom {-}{n}\colon (N\wr \mathbf {\Sigma })^{\operatorname {op}}\to \mathbf {Top}$
can be extended to
${\mathscr {O}}\tbinom {-}{n}\colon (N\wr \mathbf {\Sigma })^{\operatorname {op}}\to \mathbf {Top}$
can be extended to
 ${\mathscr {O}}\tbinom {-}{n}\colon (N\wr \mathbf {Inj})^{\operatorname {op}}\to \mathbf {Top}$
. Using these functors, one can give a concise description of the free
${\mathscr {O}}\tbinom {-}{n}\colon (N\wr \mathbf {Inj})^{\operatorname {op}}\to \mathbf {Top}$
. Using these functors, one can give a concise description of the free
 ${\mathscr {O}}$
-algebra over a family
${\mathscr {O}}$
-algebra over a family
 ${\boldsymbol {X}}:= (X_n)_{n\in N}$
of based spaces: for each
${\boldsymbol {X}}:= (X_n)_{n\in N}$
of based spaces: for each
 $n\in N$
, we have
$n\in N$
, we have  $$\begin{align*}F^{\mathscr{O}}_{{\mathscr{B}}\otimes N}({\boldsymbol{X}})_n \cong \int^{K\in N\wr\mathbf{Inj}}{\mathscr{O}}\tbinom{K}{n}\times {\boldsymbol{X}}(K).\end{align*}$$
$$\begin{align*}F^{\mathscr{O}}_{{\mathscr{B}}\otimes N}({\boldsymbol{X}})_n \cong \int^{K\in N\wr\mathbf{Inj}}{\mathscr{O}}\tbinom{K}{n}\times {\boldsymbol{X}}(K).\end{align*}$$
Example 4.21.
-
1. The little discs operads
 ${\mathscr {D}}_d$
have precisely one nullary operation and are thus canonically based. The same applies to
${\mathscr {D}}_d$
have precisely one nullary operation and are thus canonically based. The same applies to
 ${\mathscr {D}}_d\otimes N$
for each colour set N.
${\mathscr {D}}_d\otimes N$
for each colour set N. -
2. For each small and topologically enriched category
 $\mathbf {I}$
, the tensor product
$\mathbf {I}$
, the tensor product
 ${\mathscr {B}}\otimes \mathbf {I}$
differs from
${\mathscr {B}}\otimes \mathbf {I}$
differs from
 $\mathbf {I}$
only by the single nullary operation
$\mathbf {I}$
only by the single nullary operation
 $\mathfrak {v}_n\in ({\mathscr {B}}\otimes \mathbf {I})\tbinom {}{n}$
for each colour n. Note that
$\mathfrak {v}_n\in ({\mathscr {B}}\otimes \mathbf {I})\tbinom {}{n}$
for each colour n. Note that
 $({\mathscr {B}}\otimes \mathbf {I})$
-algebras are precisely functors
$({\mathscr {B}}\otimes \mathbf {I})$
-algebras are precisely functors
 $\mathbf {I}\to \mathbf {Top}_*$
to the category of based topological spaces.
$\mathbf {I}\to \mathbf {Top}_*$
to the category of based topological spaces. -
3. As a particular case of the previous example, let
 $\boldsymbol {G}=(G_n)_{n\in N}$
be a sequence of groups, and consider
$\boldsymbol {G}=(G_n)_{n\in N}$
be a sequence of groups, and consider
 $\boldsymbol {G}$
as a groupoid. Then a
$\boldsymbol {G}$
as a groupoid. Then a
 $({\mathscr {B}}\otimes \boldsymbol {G})$
-algebra is a sequence of based spaces
$({\mathscr {B}}\otimes \boldsymbol {G})$
-algebra is a sequence of based spaces
 $(X_n)_{n\in N}$
with a basepoint-preserving left action of
$(X_n)_{n\in N}$
with a basepoint-preserving left action of
 $G_n$
on
$G_n$
on
 $X_n$
for all
$X_n$
for all
 $n\in N$
.
$n\in N$
.
5 Infinite loop spaces from coloured operads with homological stability
In this section, we address the following problem: if
![]() ${\mathscr {O}}$
is an N-coloured operad with homological stability (which will be made precise soon),
${\mathscr {O}}$
is an N-coloured operad with homological stability (which will be made precise soon),
![]() $\mathbf {I}$
is a topological category together with a map
$\mathbf {I}$
is a topological category together with a map
![]() ${\mathscr {B}}\otimes \mathbf {I}\to {\mathscr {O}}$
, and if
${\mathscr {B}}\otimes \mathbf {I}\to {\mathscr {O}}$
, and if
![]() $\boldsymbol {X}=(X_n)_{n\in N}$
an
$\boldsymbol {X}=(X_n)_{n\in N}$
an
![]() $({\mathscr {B}}\otimes \mathbf {I})$
-algebra, what can we say about the homotopy type of
$({\mathscr {B}}\otimes \mathbf {I})$
-algebra, what can we say about the homotopy type of
![]() $F^{\mathscr {O}}_{\mathscr {G}}(\boldsymbol {X})$
? By answering this question, we extend the methods from [Reference Basterra, Bobkova, Ponto, Tillmann and Yeakel1, § 5], where the monochromatic and non-relative case was treated: that is,
$F^{\mathscr {O}}_{\mathscr {G}}(\boldsymbol {X})$
? By answering this question, we extend the methods from [Reference Basterra, Bobkova, Ponto, Tillmann and Yeakel1, § 5], where the monochromatic and non-relative case was treated: that is,
![]() $\mathbf {I}=N=*$
, so
$\mathbf {I}=N=*$
, so
![]() ${\mathscr {B}}\otimes \mathbf {I}={\mathscr {B}}$
.
${\mathscr {B}}\otimes \mathbf {I}={\mathscr {B}}$
.
We briefly summarise the strategy of [Reference Basterra, Bobkova, Ponto, Tillmann and Yeakel1, § 5]: in a first step, a notion of (monochromatic) ‘operad with homological stability’ is introduced: such an operad
![]() ${\mathscr {O}}$
comes in particular with a morphism of operads
${\mathscr {O}}$
comes in particular with a morphism of operads
![]() $\imath \colon {\mathscr {D}}_1\to {\mathscr {O}}$
, satisfying the weak homotopy commutativity condition, which demands that
$\imath \colon {\mathscr {D}}_1\to {\mathscr {O}}$
, satisfying the weak homotopy commutativity condition, which demands that
![]() $\imath ({{\mathscr {D}}_1(2)})\subseteq {\mathscr {O}}(2)$
lies in a single path componentFootnote
1
; hence it makes sense to consider group completions of
$\imath ({{\mathscr {D}}_1(2)})\subseteq {\mathscr {O}}(2)$
lies in a single path componentFootnote
1
; hence it makes sense to consider group completions of
![]() ${\mathscr {O}}$
-algebras.
${\mathscr {O}}$
-algebras.
In a second step, the authors of [Reference Basterra, Bobkova, Ponto, Tillmann and Yeakel1] focus on operads with homological stability
![]() ${\mathscr {O}}$
, which come with a map
${\mathscr {O}}$
, which come with a map
![]() $\pi \colon {\mathscr {O}}\to {\mathscr {D}}_\infty $
of operads under
$\pi \colon {\mathscr {O}}\to {\mathscr {D}}_\infty $
of operads under
![]() ${\mathscr {D}}_1$
. Thus, we have for each based space X two maps of
${\mathscr {D}}_1$
. Thus, we have for each based space X two maps of
![]() ${\mathscr {O}}$
-algebras:
${\mathscr {O}}$
-algebras:
-
1.
 $F^{\mathscr {O}}_{\mathscr {B}}(X) \to F^{\mathscr {O}}_{\mathscr {B}}(*)={\mathscr {O}}(0)$
induced by
$F^{\mathscr {O}}_{\mathscr {B}}(X) \to F^{\mathscr {O}}_{\mathscr {B}}(*)={\mathscr {O}}(0)$
induced by
 $X\to *$
;
$X\to *$
; -
2.
 $F^{\mathscr {O}}_{\mathscr {B}}(X)\to \pi ^*F^{{\mathscr {D}}_\infty }_{\mathscr {B}}(X)$
, the unit of the base-change adjunction.
$F^{\mathscr {O}}_{\mathscr {B}}(X)\to \pi ^*F^{{\mathscr {D}}_\infty }_{\mathscr {B}}(X)$
, the unit of the base-change adjunction.
Intuitively, the first map forgets the space X, while the second map forgets the operad
![]() ${\mathscr {O}}$
. In [Reference Basterra, Bobkova, Ponto, Tillmann and Yeakel1, Thm. 5.4], it is shown that the product map induces a weak equivalence
${\mathscr {O}}$
. In [Reference Basterra, Bobkova, Ponto, Tillmann and Yeakel1, Thm. 5.4], it is shown that the product map induces a weak equivalence
![]() $\Omega BF^{\mathscr {O}}_{\mathscr {B}}(X)\to \Omega B{\mathscr {O}}(0)\times \Omega ^\infty \Sigma ^\infty X$
on group completions, after identifying the group completion of
$\Omega BF^{\mathscr {O}}_{\mathscr {B}}(X)\to \Omega B{\mathscr {O}}(0)\times \Omega ^\infty \Sigma ^\infty X$
on group completions, after identifying the group completion of
![]() $F^{{\mathscr {D}}^\infty }_{{\mathscr {B}}}(X)$
with
$F^{{\mathscr {D}}^\infty }_{{\mathscr {B}}}(X)$
with
![]() $\Omega ^\infty \Sigma ^\infty X$
.
$\Omega ^\infty \Sigma ^\infty X$
.
Finally, an operad with homological stability
![]() ${\mathscr {O}}$
admits a replacement by another operad with homological stability
${\mathscr {O}}$
admits a replacement by another operad with homological stability
![]() ${\mathscr {O}}':= {\mathscr {O}}\times {\mathscr {D}}_\infty $
, which has a comparison map
${\mathscr {O}}':= {\mathscr {O}}\times {\mathscr {D}}_\infty $
, which has a comparison map
![]() $\pi \colon {\mathscr {O}}'\to {\mathscr {D}}_\infty $
, and under mild extra assumptions, the free algebras
$\pi \colon {\mathscr {O}}'\to {\mathscr {D}}_\infty $
, and under mild extra assumptions, the free algebras
![]() $F^{\mathscr {O}}_{\mathscr {B}}(X)$
and
$F^{\mathscr {O}}_{\mathscr {B}}(X)$
and
![]() $F^{{\mathscr {O}}'}_{\mathscr {B}}(X)$
are equivalent as
$F^{{\mathscr {O}}'}_{\mathscr {B}}(X)$
are equivalent as
![]() $A_\infty $
-algebras and thus have equivalent group completions.
$A_\infty $
-algebras and thus have equivalent group completions.
5.1 Coloured operads with homological stability
Definition 5.1. An operad under
![]() ${\mathscr {D}}_1$
is an N-coloured operad
${\mathscr {D}}_1$
is an N-coloured operad
![]() ${\mathscr {O}}$
together with an operad morphism
${\mathscr {O}}$
together with an operad morphism
![]() $\imath \colon {\mathscr {D}}_1\otimes N\to {\mathscr {O}}$
satisfying the weak homotopy commutativity condition levelwise, meaning that
$\imath \colon {\mathscr {D}}_1\otimes N\to {\mathscr {O}}$
satisfying the weak homotopy commutativity condition levelwise, meaning that
![]() $\imath (({\mathscr {D}}_1\otimes N)\tbinom {n,n}{n})\subseteq {\mathscr {O}}\tbinom {n,n}{n}$
is contained in a single path component.
$\imath (({\mathscr {D}}_1\otimes N)\tbinom {n,n}{n})\subseteq {\mathscr {O}}\tbinom {n,n}{n}$
is contained in a single path component.
-
1. If
 ${\mathscr {O}}$
is an operad under
${\mathscr {O}}$
is an operad under
 ${\mathscr {D}}_1$
, then
${\mathscr {D}}_1$
, then
 ${\mathscr {O}}$
is based by
${\mathscr {O}}$
is based by
 $\mathfrak {v}_n := \imath (\mathfrak {v}\otimes n)\in {\mathscr {O}}\tbinom {}{n}$
. This gives rise to the input blocking maps
$\mathfrak {v}_n := \imath (\mathfrak {v}\otimes n)\in {\mathscr {O}}\tbinom {}{n}$
. This gives rise to the input blocking maps  $$\begin{align*}\beta\colon {\mathscr{O}}\tbinom{k_1,\dotsc,k_r}{n}\to {\mathscr{O}}\tbinom{}{n},\quad \mu\mapsto \mu(\mathfrak{v}_{k_1},\dotsc,\mathfrak{v}_{k_r}).\end{align*}$$
$$\begin{align*}\beta\colon {\mathscr{O}}\tbinom{k_1,\dotsc,k_r}{n}\to {\mathscr{O}}\tbinom{}{n},\quad \mu\mapsto \mu(\mathfrak{v}_{k_1},\dotsc,\mathfrak{v}_{k_r}).\end{align*}$$
-
2. If
 ${\mathscr {O}}$
is an operad under
${\mathscr {O}}$
is an operad under
 ${\mathscr {D}}_1$
, then each
${\mathscr {D}}_1$
, then each
 ${\mathscr {O}}$
-algebra
${\mathscr {O}}$
-algebra
 $\boldsymbol {M}$
is levelwise an H-commutative
$\boldsymbol {M}$
is levelwise an H-commutative
 ${\mathscr {D}}_1$
-algebra, so for each
${\mathscr {D}}_1$
-algebra, so for each
 $n\in N$
, the set
$n\in N$
, the set
 $\pi _0(M_n)$
is an abelian monoid whose (unique) binary operation we denote by ‘
$\pi _0(M_n)$
is an abelian monoid whose (unique) binary operation we denote by ‘
 ’; there is a bar construction of
’; there is a bar construction of
 $M_n$
, and by the group completion theorem [Reference McDuff and Segal18], we have an isomorphism
$M_n$
, and by the group completion theorem [Reference McDuff and Segal18], we have an isomorphism
 $H_\bullet (\Omega BM_n)\cong H_\bullet (M_n)[\pi _0(M_n)^{-1}]$
.
$H_\bullet (\Omega BM_n)\cong H_\bullet (M_n)[\pi _0(M_n)^{-1}]$
.
A morphism
![]() $\rho \colon {\mathscr {O}}\to {\mathscr {O}}'$
of operads
$\rho \colon {\mathscr {O}}\to {\mathscr {O}}'$
of operads
![]() $\imath \colon {\mathscr {D}}_1\otimes N\to {\mathscr {O}}$
and
$\imath \colon {\mathscr {D}}_1\otimes N\to {\mathscr {O}}$
and
![]() $\imath '\colon {\mathscr {D}}_1\otimes N\to {\mathscr {O}}'$
under
$\imath '\colon {\mathscr {D}}_1\otimes N\to {\mathscr {O}}'$
under
![]() ${\mathscr {D}}_1$
is a morphism of operads such that
${\mathscr {D}}_1$
is a morphism of operads such that
![]() $\rho \circ \imath =\imath '$
holds. In that case, for each
$\rho \circ \imath =\imath '$
holds. In that case, for each
![]() ${\mathscr {O}}'$
-algebra
${\mathscr {O}}'$
-algebra
![]() $\boldsymbol {X}$
, the levelwise group completions of the
$\boldsymbol {X}$
, the levelwise group completions of the
![]() ${\mathscr {O}}'$
-algebra
${\mathscr {O}}'$
-algebra
![]() $\boldsymbol {X}$
and of the
$\boldsymbol {X}$
and of the
![]() ${\mathscr {O}}$
-algebra
${\mathscr {O}}$
-algebra
![]() $\rho ^*(\boldsymbol {X})$
coincide, as they only depend on the
$\rho ^*(\boldsymbol {X})$
coincide, as they only depend on the
![]() ${\mathscr {D}}_1\otimes N$
-structure.
${\mathscr {D}}_1\otimes N$
-structure.
Notation 5.2. Let
![]() $\imath \colon {\mathscr {D}}_1\otimes N\to {\mathscr {O}}$
be an operad under
$\imath \colon {\mathscr {D}}_1\otimes N\to {\mathscr {O}}$
be an operad under
![]() ${\mathscr {D}}_1$
. We fix an operation
${\mathscr {D}}_1$
. We fix an operation
![]() $\mathfrak {p}\in {\mathscr {D}}_1(2)$
, and we abbreviate
$\mathfrak {p}\in {\mathscr {D}}_1(2)$
, and we abbreviate
![]() for operations
for operations
![]() $\mu \in {\mathscr {O}}\tbinom {K}{n}$
and
$\mu \in {\mathscr {O}}\tbinom {K}{n}$
and
![]() $\mu '\in {\mathscr {O}}\tbinom {K'}{n}$
If
$\mu '\in {\mathscr {O}}\tbinom {K'}{n}$
If
![]() $(M_n)_{n\in N}$
is an
$(M_n)_{n\in N}$
is an
![]() ${\mathscr {O}}$
-algebra and
${\mathscr {O}}$
-algebra and
![]() $x,x'\in M_n$
, then we also write
$x,x'\in M_n$
, then we also write
![]() .
.
The notation ‘
![]() ’ is pictorially inspired by the following example:
’ is pictorially inspired by the following example:
Example 5.3. Recall Definition 4.15 and Example 4.18. We have a map of operads
![]() $\imath _{\mathscr {M}}\colon {\mathscr {D}}_2\otimes \mathbb {N}_{\geqslant 1}\to {\mathscr {M}}$
given by applying the classical inclusion of
$\imath _{\mathscr {M}}\colon {\mathscr {D}}_2\otimes \mathbb {N}_{\geqslant 1}\to {\mathscr {M}}$
given by applying the classical inclusion of
![]() ${\mathscr {D}}_2$
into Tillmann’s surface operad level-wise; see Figure 7. This morphism restricts to a map
${\mathscr {D}}_2$
into Tillmann’s surface operad level-wise; see Figure 7. This morphism restricts to a map
![]() ${\mathscr {D}}_1\otimes \mathbb {N}_{\geqslant 1}\to {\mathscr {M}}$
of operads satisfying the weak homotopy commutativity condition and thus turns
${\mathscr {D}}_1\otimes \mathbb {N}_{\geqslant 1}\to {\mathscr {M}}$
of operads satisfying the weak homotopy commutativity condition and thus turns
![]() ${\mathscr {M}}$
into an operad under
${\mathscr {M}}$
into an operad under
![]() ${\mathscr {D}}_1$
.
${\mathscr {D}}_1$
.

Figure 7 An instance of
![]() .
.
The input blocking maps
![]() $\beta \colon {\mathscr {M}}\tbinom {K}{n}\to {\mathscr {M}}\tbinom {}{n}$
are induced by capping each ingoing boundary curve with a disc, and the abelian monoid
$\beta \colon {\mathscr {M}}\tbinom {K}{n}\to {\mathscr {M}}\tbinom {}{n}$
are induced by capping each ingoing boundary curve with a disc, and the abelian monoid
![]() $\pi _0({\mathscr {M}}\tbinom {}{n})$
contains all isomorphism types of surfaces
$\pi _0({\mathscr {M}}\tbinom {}{n})$
contains all isomorphism types of surfaces
![]() $\mathcal {S}$
with n ordered outgoing boundary curves and no incoming boundary curve with
$\mathcal {S}$
with n ordered outgoing boundary curves and no incoming boundary curve with
![]() $\mathcal {S}$
possibly disconnected, such that each path component of
$\mathcal {S}$
possibly disconnected, such that each path component of
![]() $\mathcal {S}$
has non-empty boundary. The addition on
$\mathcal {S}$
has non-empty boundary. The addition on
![]() $\pi _0({\mathscr {M}}\tbinom {}{n})$
is given by gluing n pairs of pants; the neutral element is given by an ordered collection of n discs. The abelian monoid
$\pi _0({\mathscr {M}}\tbinom {}{n})$
is given by gluing n pairs of pants; the neutral element is given by an ordered collection of n discs. The abelian monoid
![]() $\pi _0({\mathscr {M}}\tbinom {}{n})$
is finitely generated: for instance, it can be generated by the following elements
$\pi _0({\mathscr {M}}\tbinom {}{n})$
is finitely generated: for instance, it can be generated by the following elements
![]() $e_n^i$
and
$e_n^i$
and
![]() $\smash {e_n^{\smash {i,j}}}$
; see Figure 8:
$\smash {e_n^{\smash {i,j}}}$
; see Figure 8:
-
1. For
 $1\leqslant i\leqslant n$
, we let
$1\leqslant i\leqslant n$
, we let
 $e_n^i$
be the isomorphism type of surfaces with n path components, such that the component carrying the i
th boundary curve has genus
$e_n^i$
be the isomorphism type of surfaces with n path components, such that the component carrying the i
th boundary curve has genus
 $1$
, whereas all others components are discs.
$1$
, whereas all others components are discs. -
2. For each
 $1\leqslant i<j\leqslant n$
, we let
$1\leqslant i<j\leqslant n$
, we let
 $e_n^{\smash {i,j}}$
be the isomorphism type of surfaces with
$e_n^{\smash {i,j}}$
be the isomorphism type of surfaces with
 $n-1$
path components, all of genus
$n-1$
path components, all of genus
 $0$
, such that one component is a cylinder carrying the i
th and the j
th boundary curve.
$0$
, such that one component is a cylinder carrying the i
th and the j
th boundary curve.

Figure 8 The three generators
![]() $e_2^1$
,
$e_2^1$
,
![]() $e_2^2$
and
$e_2^2$
and
![]() $e_2^{1,2}$
of
$e_2^{1,2}$
of
![]() $\pi _0({\mathscr {M}}\tbinom {}{2})$
.
$\pi _0({\mathscr {M}}\tbinom {}{2})$
.
Construction 5.4 Stable operation space
We call an N-coloured operad
![]() ${\mathscr {O}}$
under
${\mathscr {O}}$
under
![]() ${\mathscr {D}}_1$
admissibly graded if for each
${\mathscr {D}}_1$
admissibly graded if for each
![]() $n\in N$
, the abelian monoid
$n\in N$
, the abelian monoid
![]() $\pi _0({\mathscr {O}}\tbinom {}{n})$
is finitely generated and, for each source profile
$\pi _0({\mathscr {O}}\tbinom {}{n})$
is finitely generated and, for each source profile
![]() $(k_1,\dotsc ,k_r)$
, the degree map
$(k_1,\dotsc ,k_r)$
, the degree map
is surjective.Footnote
2
In this case we write for each
![]() $\delta \in \pi _0({\mathscr {O}}\tbinom {}{n})$
$\delta \in \pi _0({\mathscr {O}}\tbinom {}{n})$
We choose for each
![]() $n\in N$
a finite generating set
$n\in N$
a finite generating set
![]() $E_n\subseteq \pi _0({\mathscr {O}}\tbinom {}{n})$
and let
$E_n\subseteq \pi _0({\mathscr {O}}\tbinom {}{n})$
and let
![]() $e_n$
be the sum of all elements from
$e_n$
be the sum of all elements from
![]() $E_n$
. If we fix a nullary operation
$E_n$
. If we fix a nullary operation
![]() $\tilde {e}_n\in {\mathscr {O}}\tbinom {}{n}$
with
$\tilde {e}_n\in {\mathscr {O}}\tbinom {}{n}$
with
![]() $\lvert \tilde {e}_n\rvert =e_n$
, called propagator, then we obtain for each component
$\lvert \tilde {e}_n\rvert =e_n$
, called propagator, then we obtain for each component
![]() $\delta \in \pi _0({\mathscr {O}}\tbinom {}{n})$
and each input profile
$\delta \in \pi _0({\mathscr {O}}\tbinom {}{n})$
and each input profile
![]() $ K$
a stabilising map
$ K$
a stabilising map
From this, we can form the space of stable operations from K to n,

Definition 5.5. Let
![]() ${\mathscr {O}}$
be an N-coloured operad under
${\mathscr {O}}$
be an N-coloured operad under
![]() ${\mathscr {D}}_1$
, which is admissibly graded. By the associativity of the operadic composition, input blocking and stabilisation commute: that is, for each
${\mathscr {D}}_1$
, which is admissibly graded. By the associativity of the operadic composition, input blocking and stabilisation commute: that is, for each
![]() $\delta $
, the square
$\delta $
, the square

commutes. Hence we obtain a stable input blocking
![]() $\beta ^K_n\colon {\mathscr {O}}\tbinom {K}{n}^\infty \to {\mathscr {O}}\tbinom {}{n}^\infty $
for each input profile K, which depends, up to homotopy, only on the path component from which the propagator is chosen: that is, on the choice of generating set
$\beta ^K_n\colon {\mathscr {O}}\tbinom {K}{n}^\infty \to {\mathscr {O}}\tbinom {}{n}^\infty $
for each input profile K, which depends, up to homotopy, only on the path component from which the propagator is chosen: that is, on the choice of generating set
![]() $E_n$
.
$E_n$
.
We call
![]() ${\mathscr {O}}$
an operad with homological stability if there is a choice of generating sets such that all stable input blockings
${\mathscr {O}}$
an operad with homological stability if there is a choice of generating sets such that all stable input blockings
![]() $\beta ^K_n$
induce isomorphisms in integral homology.
$\beta ^K_n$
induce isomorphisms in integral homology.
Example 5.6. The coloured surface operad
![]() ${\mathscr {M}}$
is admissibly graded, and we may use the generating sets from Example 5.3.
${\mathscr {M}}$
is admissibly graded, and we may use the generating sets from Example 5.3.
It is even an operad with homological stability: here we use that multiplying with the propagator automatically yields a connected cobordism and increases the genus by at least one; see Figure 9, so the stable input blocking is the capping map
![]() $\mathfrak {M}_{\infty ,n+k_1+\dotsb +k_r}\to \mathfrak {M}_{\infty ,n}$
between stable moduli spaces of Riemann surfaces: this is a homology equivalence by Harer’s stability theorem [Reference Harer11].
$\mathfrak {M}_{\infty ,n+k_1+\dotsb +k_r}\to \mathfrak {M}_{\infty ,n}$
between stable moduli spaces of Riemann surfaces: this is a homology equivalence by Harer’s stability theorem [Reference Harer11].

Figure 9 A single stabilisation step on
![]() . Note that
. Note that
![]() is the isomorphism class of surfaces of type
is the isomorphism class of surfaces of type
![]() $\Sigma _{2,2}$
.
$\Sigma _{2,2}$
.
5.2 Derived base-change and a splitting result
Recall that we want to establish an analogue of [Reference Basterra, Bobkova, Ponto, Tillmann and Yeakel1, Thm. 5.4] for the coloured case and relative case: that is, we want to consider relatively free algebras, relative to a map
![]() ${\mathscr {P}}\to {\mathscr {O}}$
of based operads, where we will soon restrict to the case
${\mathscr {P}}\to {\mathscr {O}}$
of based operads, where we will soon restrict to the case
![]() ${\mathscr {P}}={\mathscr {B}}\otimes \mathbf {I}$
for an enriched category
${\mathscr {P}}={\mathscr {B}}\otimes \mathbf {I}$
for an enriched category
![]() $\mathbf {I}$
.
$\mathbf {I}$
.
The most convenient setting for such a discussion does not use the strict functor
![]() $F^{\mathscr {O}}_{\mathscr {P}}$
, but a homotopically better behaved one, which we denote by
$F^{\mathscr {O}}_{\mathscr {P}}$
, but a homotopically better behaved one, which we denote by
![]() $\tilde F^{\mathscr {O}}_{\mathscr {P}}$
. This simplifies many point-set issues, and with regard to our original problem, it will turn out to be equivalent to the space we want to understand.
$\tilde F^{\mathscr {O}}_{\mathscr {P}}$
. This simplifies many point-set issues, and with regard to our original problem, it will turn out to be equivalent to the space we want to understand.
The functor
![]() $\tilde F^{\mathscr {O}}_{\mathscr {P}}$
can be constructed by considering the model structure on the categories of
$\tilde F^{\mathscr {O}}_{\mathscr {P}}$
can be constructed by considering the model structure on the categories of
![]() ${\mathscr {O}}$
- and
${\mathscr {O}}$
- and
![]() ${\mathscr {P}}$
-algebras as in [Reference Berger and Moerdijk2], but we decided to give an explicit description. Here we assume that the reader is familiar with monads and their two-sided bar constructions, as introduced in [Reference May17].
${\mathscr {P}}$
-algebras as in [Reference Berger and Moerdijk2], but we decided to give an explicit description. Here we assume that the reader is familiar with monads and their two-sided bar constructions, as introduced in [Reference May17].
Construction 5.7. Let
![]() ${\mathscr {P}}\to {\mathscr {O}}$
be a morphism of based N-coloured operads. Then we obtain monads
${\mathscr {P}}\to {\mathscr {O}}$
be a morphism of based N-coloured operads. Then we obtain monads
![]() $\mathbb {O}:= U^{\mathscr {O}}_{\smash {{\mathscr {B}}\otimes N}} F^{\mathscr {O}}_{\smash {{\mathscr {B}}\otimes N}}$
and
$\mathbb {O}:= U^{\mathscr {O}}_{\smash {{\mathscr {B}}\otimes N}} F^{\mathscr {O}}_{\smash {{\mathscr {B}}\otimes N}}$
and
![]() $\mathbb {P}:= U^{\mathscr {P}}_{\smash {{\mathscr {B}}\otimes N}} F^{\mathscr {P}}_{\smash {{\mathscr {B}}\otimes N}}$
on
$\mathbb {P}:= U^{\mathscr {P}}_{\smash {{\mathscr {B}}\otimes N}} F^{\mathscr {P}}_{\smash {{\mathscr {B}}\otimes N}}$
on
![]() $\mathbf {Top}_*^N$
, and
$\mathbf {Top}_*^N$
, and
![]() $\mathbb {O}$
is a left
$\mathbb {O}$
is a left
![]() $\mathbb {P}$
-functor by the transformation
$\mathbb {P}$
-functor by the transformation
![]() $\mathbb {O}\mathbb {P}\Rightarrow \mathbb {O}^2\Rightarrow \mathbb {O}$
. For each
$\mathbb {O}\mathbb {P}\Rightarrow \mathbb {O}^2\Rightarrow \mathbb {O}$
. For each
![]() ${\mathscr {P}}$
-algebra
${\mathscr {P}}$
-algebra
![]() ${\boldsymbol {X}}$
, we consider the two-sided bar construction
${\boldsymbol {X}}$
, we consider the two-sided bar construction
![]() $B_\bullet (\mathbb {O},\mathbb {P},{\boldsymbol {X}})$
with p-simplices
$B_\bullet (\mathbb {O},\mathbb {P},{\boldsymbol {X}})$
with p-simplices
![]() $B_p(\mathbb {O},\mathbb {P},{\boldsymbol {X}})=\mathbb {O}\mathbb {P}^p U^{\mathscr {P}}_{\smash {{\mathscr {B}}\otimes N}}{\boldsymbol {X}}$
, which is an N-coloured simplicial space, and define the derived free algebra
$B_p(\mathbb {O},\mathbb {P},{\boldsymbol {X}})=\mathbb {O}\mathbb {P}^p U^{\mathscr {P}}_{\smash {{\mathscr {B}}\otimes N}}{\boldsymbol {X}}$
, which is an N-coloured simplicial space, and define the derived free algebra
![]() $\tilde F^{\mathscr {O}}_{\smash {\mathscr {P}}}({\boldsymbol {X}}):= |B_\bullet (\mathbb {O},\mathbb {P},{\boldsymbol {X}})|$
to be its levelwise geometric realisation. Then
$\tilde F^{\mathscr {O}}_{\smash {\mathscr {P}}}({\boldsymbol {X}}):= |B_\bullet (\mathbb {O},\mathbb {P},{\boldsymbol {X}})|$
to be its levelwise geometric realisation. Then
![]() $\tilde F^{\mathscr {O}}_{\smash {\mathscr {P}}}({\boldsymbol {X}})$
is itself an
$\tilde F^{\mathscr {O}}_{\smash {\mathscr {P}}}({\boldsymbol {X}})$
is itself an
![]() ${\mathscr {O}}$
-algebra with multiplication
${\mathscr {O}}$
-algebra with multiplication
where the first identification is due to [Reference May17, Lem. 9.7] and the last map is given by
![]() $|B_\bullet (\kappa ,\mathbb {P},{\boldsymbol {X}})|$
for the operadic composition
$|B_\bullet (\kappa ,\mathbb {P},{\boldsymbol {X}})|$
for the operadic composition
![]() $\kappa \colon \mathbb {O}^2\Rightarrow \mathbb {O}$
. Second, we have a morphism
$\kappa \colon \mathbb {O}^2\Rightarrow \mathbb {O}$
. Second, we have a morphism
![]() $\tilde F^{\mathscr {O}}_{\smash {\mathscr {P}}}({\boldsymbol {X}})\to F^{\mathscr {O}}_{\smash {\mathscr {P}}}({\boldsymbol {X}})$
of
$\tilde F^{\mathscr {O}}_{\smash {\mathscr {P}}}({\boldsymbol {X}})\to F^{\mathscr {O}}_{\smash {\mathscr {P}}}({\boldsymbol {X}})$
of
![]() ${\mathscr {O}}$
-algebras, by noticing that
${\mathscr {O}}$
-algebras, by noticing that
![]() $F^{\mathscr {O}}_{\smash {\mathscr {P}}}({\boldsymbol {X}})$
is the reflexive coequaliser of
$F^{\mathscr {O}}_{\smash {\mathscr {P}}}({\boldsymbol {X}})$
is the reflexive coequaliser of
![]() $B_1(\mathbb {O},\mathbb {P},{\boldsymbol {X}})\rightrightarrows B_0(\mathbb {O},\mathbb {P},{\boldsymbol {X}})$
; see Definition 4.11.
$B_1(\mathbb {O},\mathbb {P},{\boldsymbol {X}})\rightrightarrows B_0(\mathbb {O},\mathbb {P},{\boldsymbol {X}})$
; see Definition 4.11.
Before stating our main theorem, let us fix once and for all the point-set requirements we want to assume:
Setting 5.8. Throughout this section, we consider the following:
-
1. Let
 ${\mathscr {O}}$
be an N-coloured
${\mathscr {O}}$
be an N-coloured
 $\mathfrak {S}$
-free operad with homological stability such that, additionally, the inclusions
$\mathfrak {S}$
-free operad with homological stability such that, additionally, the inclusions
 are cofibrations.
are cofibrations. -
2. Let
 $\mathbf {I}$
be a topologically enriched category with object set N such that the inclusions
$\mathbf {I}$
be a topologically enriched category with object set N such that the inclusions
 are cofibrations. We assume that there is a map
are cofibrations. We assume that there is a map
 ${\mathscr {B}}\otimes \mathbf {I}\to {\mathscr {O}}$
of based N-coloured operads.
${\mathscr {B}}\otimes \mathbf {I}\to {\mathscr {O}}$
of based N-coloured operads. -
3. Let
 ${\boldsymbol {X}}=(X_n)_{n\in N}$
be an
${\boldsymbol {X}}=(X_n)_{n\in N}$
be an
 $({\mathscr {B}}\otimes \mathbf {I})$
-algebra, or in other words, an enriched functor
$({\mathscr {B}}\otimes \mathbf {I})$
-algebra, or in other words, an enriched functor
 $X_\bullet \colon \mathbf {I}\to \mathbf {Top}_*$
, and we assume that each
$X_\bullet \colon \mathbf {I}\to \mathbf {Top}_*$
, and we assume that each
 $X_n$
is well-based.
$X_n$
is well-based.
Moreover, we assume that all involved spaces are Hausdorff.
Of course, the example we have in mind is
![]() ${\mathscr {O}}$
being the surface operad
${\mathscr {O}}$
being the surface operad
![]() ${\mathscr {M}}$
and
${\mathscr {M}}$
and
![]() $\mathbf {I}$
being the family
$\mathbf {I}$
being the family
![]() $\boldsymbol {R}=(R_n)_{n\geqslant 1}$
of twisted tori. We want to show the following theorem:
$\boldsymbol {R}=(R_n)_{n\geqslant 1}$
of twisted tori. We want to show the following theorem:
Theorem 5.9 Splitting theorem
In the above Setting 5.8, we have, for each
![]() $n\in N$
, a weak equivalence of loop spaces
$n\in N$
, a weak equivalence of loop spaces
The proof of Theorem 5.9 will occupy the rest of this section. Let us start by establishing a map that compares the two sides. To do so, we start by constructing an N-coloured version of the
![]() $E_\infty $
-operad
$E_\infty $
-operad
![]() ${\mathscr {D}}_\infty $
and show that we can, without loss of generality, assume that there is a comparison map from
${\mathscr {D}}_\infty $
and show that we can, without loss of generality, assume that there is a comparison map from
![]() ${\mathscr {O}}$
to it:
${\mathscr {O}}$
to it:
Construction 5.10. For each colour set N, we consider the chaotic category
![]() $EN$
with object set N and morphism spaces
$EN$
with object set N and morphism spaces
![]() $(EN)\tbinom {k}{n}=*$
for all
$(EN)\tbinom {k}{n}=*$
for all
![]() $k,n\in N$
. We consider the category
$k,n\in N$
. We consider the category
![]() ${\mathscr {D}}_\infty \otimes EN$
.
${\mathscr {D}}_\infty \otimes EN$
.
Lemma 5.11. For the proof of Theorem 5.9, we can without loss of generality assume a map
![]() $\pi \colon {\mathscr {O}}\to {\mathscr {D}}_\infty \otimes EN$
such that the diagram
$\pi \colon {\mathscr {O}}\to {\mathscr {D}}_\infty \otimes EN$
such that the diagram

commutes, where all arrows apart from
![]() $\pi $
are either given or induced by the canonical maps
$\pi $
are either given or induced by the canonical maps
![]() ${\mathscr {B}}\to {\mathscr {D}}_1\to {\mathscr {D}}_\infty $
and
${\mathscr {B}}\to {\mathscr {D}}_1\to {\mathscr {D}}_\infty $
and
![]() $N\to \mathbf {I}\to EN$
.
$N\to \mathbf {I}\to EN$
.
Proof. The commutativity of the square is part of the general setting: recall that we assumed that
![]() ${\mathscr {B}}\otimes \mathbf {I}\to {\mathscr {O}}$
is a map of based operads, and
${\mathscr {B}}\otimes \mathbf {I}\to {\mathscr {O}}$
is a map of based operads, and
![]() ${\mathscr {O}}$
is canonically based as an operad under
${\mathscr {O}}$
is canonically based as an operad under
![]() ${\mathscr {D}}_1$
. To establish the map
${\mathscr {D}}_1$
. To establish the map
![]() $\pi $
, we replace
$\pi $
, we replace
![]() ${\mathscr {O}}$
by a slightly larger operad: if we consider the product operad
${\mathscr {O}}$
by a slightly larger operad: if we consider the product operad
![]() ${\mathscr {O}}':= {\mathscr {O}}\times ({\mathscr {D}}_\infty \otimes EN)$
, together with:
${\mathscr {O}}':= {\mathscr {O}}\times ({\mathscr {D}}_\infty \otimes EN)$
, together with:
-
○ the diagonal inclusion
 ${\mathscr {D}}_1\otimes N \to {\mathscr {O}}'$
,
${\mathscr {D}}_1\otimes N \to {\mathscr {O}}'$
, -
○ the diagonal inclusion
 ${\mathscr {B}}\otimes \mathbf {I}\to {\mathscr {O}}'$
,
${\mathscr {B}}\otimes \mathbf {I}\to {\mathscr {O}}'$
, -
○ the second projection
 ${\mathscr {O}}'\to {\mathscr {D}}_\infty \otimes EN$
,
${\mathscr {O}}'\to {\mathscr {D}}_\infty \otimes EN$
,
then the above diagram clearly commutes with
![]() ${\mathscr {O}}$
instead of
${\mathscr {O}}$
instead of
![]() ${\mathscr {O}}'$
. Moreover, note that each operation space of
${\mathscr {O}}'$
. Moreover, note that each operation space of
![]() ${\mathscr {D}}_\infty \otimes EN$
is contractible: hence
${\mathscr {D}}_\infty \otimes EN$
is contractible: hence
![]() ${\mathscr {O}}'$
is again admissibly graded with
${\mathscr {O}}'$
is again admissibly graded with
![]() $\pi _0({\mathscr {O}}'\tbinom {}{n})=\pi _0({\mathscr {O}}\tbinom {}{n})$
and
$\pi _0({\mathscr {O}}'\tbinom {}{n})=\pi _0({\mathscr {O}}\tbinom {}{n})$
and
![]() ${\mathscr {O}}'$
is again an operad with homological stability, satisfying
${\mathscr {O}}'$
is again an operad with homological stability, satisfying
![]() ${\mathscr {O}}'\tbinom {}{n}={\mathscr {O}}\tbinom {}{n}$
.
${\mathscr {O}}'\tbinom {}{n}={\mathscr {O}}\tbinom {}{n}$
.
Finally, the first projection
![]() ${\mathscr {O}}'\to {\mathscr {O}}$
induces a morphism of monads
${\mathscr {O}}'\to {\mathscr {O}}$
induces a morphism of monads
![]() $\mathbb {O}'\Rightarrow \mathbb {O}$
and hence a map
$\mathbb {O}'\Rightarrow \mathbb {O}$
and hence a map
![]() $\smash {\tilde F^{{\mathscr {O}}'}_{\smash {{\mathscr {B}}\otimes \mathbf {I}}}({\boldsymbol {X}})\to U^{\mathscr {O}}_{\smash {{\mathscr {O}}'}}\tilde F^{{\mathscr {O}}}_{\smash {{\mathscr {B}}\otimes \mathbf {I}}}({\boldsymbol {X}})}$
of
$\smash {\tilde F^{{\mathscr {O}}'}_{\smash {{\mathscr {B}}\otimes \mathbf {I}}}({\boldsymbol {X}})\to U^{\mathscr {O}}_{\smash {{\mathscr {O}}'}}\tilde F^{{\mathscr {O}}}_{\smash {{\mathscr {B}}\otimes \mathbf {I}}}({\boldsymbol {X}})}$
of
![]() ${\mathscr {O}}'$
-algebras, which is in particular a map of
${\mathscr {O}}'$
-algebras, which is in particular a map of
![]() $A_\infty $
-algebras. If we denote by
$A_\infty $
-algebras. If we denote by
![]() $\mathbb {I}$
the monad for
$\mathbb {I}$
the monad for
![]() ${\mathscr {B}}\otimes \mathbf {I}$
, then we can easily see that, since
${\mathscr {B}}\otimes \mathbf {I}$
, then we can easily see that, since
![]() ${\mathscr {O}}$
is
${\mathscr {O}}$
is
![]() $\mathfrak {S}$
-free, each
$\mathfrak {S}$
-free, each
![]() $X_n$
is well-based, and every space is Hausdorff, the simplicial map
$X_n$
is well-based, and every space is Hausdorff, the simplicial map
![]() $B_\bullet (\mathbb {O}',\mathbb {I},{\boldsymbol {X}})\to B_\bullet (\mathbb {O},\mathbb {I},{\boldsymbol {X}})$
is levelwise an equivalence. Second, both simplicial spaces are proper in the sense of [Reference May17, § 11], by using that the inclusions of the identities are cofibrations. Therefore, by [Reference May16, Thm. A.4], the induced map on the geometric realisations
$B_\bullet (\mathbb {O}',\mathbb {I},{\boldsymbol {X}})\to B_\bullet (\mathbb {O},\mathbb {I},{\boldsymbol {X}})$
is levelwise an equivalence. Second, both simplicial spaces are proper in the sense of [Reference May17, § 11], by using that the inclusions of the identities are cofibrations. Therefore, by [Reference May16, Thm. A.4], the induced map on the geometric realisations
![]() $\smash {\tilde F^{{\mathscr {O}}'}_{\smash {{\mathscr {B}}\otimes \mathbf {I}}}({\boldsymbol {X}})}$
and
$\smash {\tilde F^{{\mathscr {O}}'}_{\smash {{\mathscr {B}}\otimes \mathbf {I}}}({\boldsymbol {X}})}$
and
![]() $\smash {\tilde F^{\mathscr {O}}_{\smash {{\mathscr {B}}\otimes \mathbf {I}}}({\boldsymbol {X}})}$
is again an equivalence, whence their group completions are equivalent as loop spaces.
$\smash {\tilde F^{\mathscr {O}}_{\smash {{\mathscr {B}}\otimes \mathbf {I}}}({\boldsymbol {X}})}$
is again an equivalence, whence their group completions are equivalent as loop spaces.
Using the lemma, we obtain, as in the monochromatic case, two maps:
-
1. The map
 ${\boldsymbol {X}}\to *$
to
${\boldsymbol {X}}\to *$
to
 $* = (*)_{n\in N}$
induces a map
$* = (*)_{n\in N}$
induces a map
 $\tilde F^{\mathscr {O}}_{\smash {{\mathscr {B}}\otimes \mathbf {I}}}({\boldsymbol {X}})\to \tilde F^{\mathscr {O}}_{\smash {{\mathscr {B}}\otimes \mathbf {I}}}(*)$
of
$\tilde F^{\mathscr {O}}_{\smash {{\mathscr {B}}\otimes \mathbf {I}}}({\boldsymbol {X}})\to \tilde F^{\mathscr {O}}_{\smash {{\mathscr {B}}\otimes \mathbf {I}}}(*)$
of
 ${\mathscr {O}}$
-algebras, which is in particular a map of levelwise
${\mathscr {O}}$
-algebras, which is in particular a map of levelwise
 $A_\infty $
-algebras.
$A_\infty $
-algebras. -
2. The morphism
 ${\mathscr {O}}\to {\mathscr {D}}_\infty \otimes EN$
induces a map
${\mathscr {O}}\to {\mathscr {D}}_\infty \otimes EN$
induces a map
 $\tilde F^{\mathscr {O}}_{\smash {{\mathscr {B}}\otimes \mathbf {I}}}({\boldsymbol {X}})\to \tilde F^{{\mathscr {D}}_\infty \otimes EN}_{\smash {{\mathscr {B}}\otimes \mathbf {I}}}({\boldsymbol {X}})$
of levelwise
$\tilde F^{\mathscr {O}}_{\smash {{\mathscr {B}}\otimes \mathbf {I}}}({\boldsymbol {X}})\to \tilde F^{{\mathscr {D}}_\infty \otimes EN}_{\smash {{\mathscr {B}}\otimes \mathbf {I}}}({\boldsymbol {X}})$
of levelwise
 $A_\infty $
-algebras.
$A_\infty $
-algebras.
The two targets can be identified with the following spaces:
Lemma 5.12. For each
![]() $n\in N$
, we have equivalences of
$n\in N$
, we have equivalences of
![]() $A_\infty $
-algebras
$A_\infty $
-algebras
 $$ \begin{align*} \tilde F^{\mathscr{O}}_{\smash{{\mathscr{B}}\otimes \mathbf{I}}}(*)_n &\simeq {\mathscr{O}}\tbinom{}{n},\\[2px] \tilde F^{{\mathscr{D}}_\infty\otimes EN}_{\smash{{\mathscr{B}}\otimes \mathbf{I}}}({\boldsymbol{X}})_n &\simeq F^{{\mathscr{D}}_\infty}_{\smash{{\mathscr{B}}}}({\mathrm{hocolim}}_{\mathbf{I}} (X_\bullet)). \end{align*} $$
$$ \begin{align*} \tilde F^{\mathscr{O}}_{\smash{{\mathscr{B}}\otimes \mathbf{I}}}(*)_n &\simeq {\mathscr{O}}\tbinom{}{n},\\[2px] \tilde F^{{\mathscr{D}}_\infty\otimes EN}_{\smash{{\mathscr{B}}\otimes \mathbf{I}}}({\boldsymbol{X}})_n &\simeq F^{{\mathscr{D}}_\infty}_{\smash{{\mathscr{B}}}}({\mathrm{hocolim}}_{\mathbf{I}} (X_\bullet)). \end{align*} $$
Proof. For the first equivalence, we note that since
![]() $({\mathscr {B}}\otimes \mathbf {I})\tbinom {}{n}=*$
, we have
$({\mathscr {B}}\otimes \mathbf {I})\tbinom {}{n}=*$
, we have
![]() $F^{{\mathscr {B}}\otimes \mathbf {I}}_{\smash {{\mathscr {B}}\otimes N}}(*)_n=*$
. Now consider the natural map
$F^{{\mathscr {B}}\otimes \mathbf {I}}_{\smash {{\mathscr {B}}\otimes N}}(*)_n=*$
. Now consider the natural map
This map arises from the augmentation
![]() $B_\bullet := B_\bullet (\mathbb {O},\mathbb {I},\mathbb {I}(*))\to B_{-1}:= \mathbb {O}(*)$
, which has a (colour-wise) extra degeneracy
$B_\bullet := B_\bullet (\mathbb {O},\mathbb {I},\mathbb {I}(*))\to B_{-1}:= \mathbb {O}(*)$
, which has a (colour-wise) extra degeneracy
![]() $s_{-1}\colon B_{p}\to B_{p+1}$
from the unit of
$s_{-1}\colon B_{p}\to B_{p+1}$
from the unit of
![]() $\mathbb {I}$
and hence is an equivalence by [Reference Riehl23, Cor. 4.5.2].
$\mathbb {I}$
and hence is an equivalence by [Reference Riehl23, Cor. 4.5.2].
For the second equivalence, we start with the general observation that for a sequence
![]() ${\mathscr {Q}}\to {\mathscr {P}}\to {\mathscr {O}}$
of N-coloured operads, we have a levelwise equivalence of
${\mathscr {Q}}\to {\mathscr {P}}\to {\mathscr {O}}$
of N-coloured operads, we have a levelwise equivalence of
![]() ${\mathscr {O}}$
-algebras among the derived algebras
${\mathscr {O}}$
-algebras among the derived algebras
![]() $\smash {\tilde F^{\mathscr {O}}_{\smash {\mathscr {Q}}}({\boldsymbol {X}})\simeq \tilde F^{\mathscr {O}}_{\smash {\mathscr {P}}}(\tilde F^{\mathscr {P}}_{\smash {\mathscr {Q}}}({\boldsymbol {X}}))}$
: by construction, the left side is the geometric realisation of the bisimplicial space with
$\smash {\tilde F^{\mathscr {O}}_{\smash {\mathscr {Q}}}({\boldsymbol {X}})\simeq \tilde F^{\mathscr {O}}_{\smash {\mathscr {P}}}(\tilde F^{\mathscr {P}}_{\smash {\mathscr {Q}}}({\boldsymbol {X}}))}$
: by construction, the left side is the geometric realisation of the bisimplicial space with
![]() $B_{p,q}=\mathbb {O}\mathbb {P}^{p+1}\mathbb {Q}^q{\boldsymbol {X}}$
. If we first realise each
$B_{p,q}=\mathbb {O}\mathbb {P}^{p+1}\mathbb {Q}^q{\boldsymbol {X}}$
. If we first realise each
![]() $B_{p,\bullet }$
, then we obtain a simplicial space
$B_{p,\bullet }$
, then we obtain a simplicial space
![]() $\tilde B_\bullet $
with
$\tilde B_\bullet $
with
![]() $\tilde B_p = |B_\bullet (\mathbb {O}\mathbb {P}^{p+1},\mathbb {Q},{\boldsymbol {X}})|$
. Again, we have an augmentation map
$\tilde B_p = |B_\bullet (\mathbb {O}\mathbb {P}^{p+1},\mathbb {Q},{\boldsymbol {X}})|$
. Again, we have an augmentation map
![]() $\tilde B_\bullet \to \tilde B_{-1}:= |B_\bullet (\mathbb {O},\mathbb {Q},{\boldsymbol {X}})|$
, which admits an extra degeneracy by the unit of
$\tilde B_\bullet \to \tilde B_{-1}:= |B_\bullet (\mathbb {O},\mathbb {Q},{\boldsymbol {X}})|$
, which admits an extra degeneracy by the unit of
![]() $\mathbb {P}$
, whence the induced map
$\mathbb {P}$
, whence the induced map
![]() $|B_{\bullet ,\bullet }|\simeq |\tilde B_\bullet |\to \tilde B_{-1}$
is an equivalence, as desired. In our case, we obtain for each
$|B_{\bullet ,\bullet }|\simeq |\tilde B_\bullet |\to \tilde B_{-1}$
is an equivalence, as desired. In our case, we obtain for each
![]() $n\in N$
an equivalence of
$n\in N$
an equivalence of
![]() ${\mathscr {D}}_\infty $
-algebras
${\mathscr {D}}_\infty $
-algebras
where for the last equivalence, we use that
![]() $\tilde F^{{\mathscr {B}}\otimes EN}_{\smash {{\mathscr {B}}\otimes \mathbf {I}}}({\boldsymbol {X}})$
is, when regarded as a functor
$\tilde F^{{\mathscr {B}}\otimes EN}_{\smash {{\mathscr {B}}\otimes \mathbf {I}}}({\boldsymbol {X}})$
is, when regarded as a functor
![]() $EN\to \mathbf {Top}_*$
, the constant diagram with value
$EN\to \mathbf {Top}_*$
, the constant diagram with value
![]() ${\mathrm {hocolim}}_{\mathbf {I}}({\boldsymbol {X}})$
, and
${\mathrm {hocolim}}_{\mathbf {I}}({\boldsymbol {X}})$
, and
![]() $\smash {\tilde F^{\smash {{\mathscr {D}}_\infty \otimes EN}}_{\smash {{\mathscr {B}}\otimes EN}}}$
is equivalent to the postcomposition with
$\smash {\tilde F^{\smash {{\mathscr {D}}_\infty \otimes EN}}_{\smash {{\mathscr {B}}\otimes EN}}}$
is equivalent to the postcomposition with
![]() $F^{{\mathscr {D}}_\infty }_{\smash {\mathscr {B}}}$
, using that the natural map
$F^{{\mathscr {D}}_\infty }_{\smash {\mathscr {B}}}$
, using that the natural map
![]() $\smash {\tilde F^{{\mathscr {D}}_\infty }_{\smash {\mathscr {B}}}(X)\to F^{{\mathscr {D}}_\infty }_{\smash {\mathscr {B}}}(X)}$
is an equivalence for each based space X, as the underlying simplicial space is constant.
$\smash {\tilde F^{{\mathscr {D}}_\infty }_{\smash {\mathscr {B}}}(X)\to F^{{\mathscr {D}}_\infty }_{\smash {\mathscr {B}}}(X)}$
is an equivalence for each based space X, as the underlying simplicial space is constant.
Putting everything together, we get, for each
![]() $n\in N$
, a map of
$n\in N$
, a map of
![]() $A_\infty $
-algebras
$A_\infty $
-algebras
which, after group completion, gives us the map from Theorem 5.9. In the next subsection, we will show that it is an equivalence and, by doing so, prove the theorem.
5.3 Proof of the splitting theorem
For the proof of Theorem 5.9, we denote the monads associated with
![]() ${\mathscr {O}}$
, respectively
${\mathscr {O}}$
, respectively
![]() ${\mathscr {D}}_\infty \otimes EN$
by
${\mathscr {D}}_\infty \otimes EN$
by
![]() $\mathbb {O}$
, respectively
$\mathbb {O}$
, respectively
![]() $\mathbb {D}$
, and we also write
$\mathbb {D}$
, and we also write
![]() $\mathbb {O}({\boldsymbol {X}})_n$
, respectively
$\mathbb {O}({\boldsymbol {X}})_n$
, respectively
![]() $\mathbb {D}({\boldsymbol {X}})_n$
for the n
th level.
$\mathbb {D}({\boldsymbol {X}})_n$
for the n
th level.
Since permuting and blocking inputs preserve the degree of the operations, we get, for each colour
![]() $n\in N$
and each degree
$n\in N$
and each degree
![]() $\delta \in \pi _0({\mathscr {O}}\tbinom {}{n})$
, a functor
$\delta \in \pi _0({\mathscr {O}}\tbinom {}{n})$
, a functor
![]() $\smash {{\mathscr {O}}\tbinom {-}{n}^\delta \colon (N\wr \mathbf {Inj})^{\operatorname {op}}\to \mathbf {Top}}$
. This gives rise to a decomposition
$\smash {{\mathscr {O}}\tbinom {-}{n}^\delta \colon (N\wr \mathbf {Inj})^{\operatorname {op}}\to \mathbf {Top}}$
. This gives rise to a decomposition
 $$\begin{align*}\mathbb{O}(\boldsymbol{X})_n=\coprod_{\delta}\mathbb{O}(\boldsymbol{X})^\delta_n\quad\text{with}\quad \mathbb{O}(\boldsymbol{X})^\delta_n:= \int^{K\in N\wr\kern.5px\mathbf{Inj}}{\mathscr{O}}\tbinom{K}{n}^\delta\times \boldsymbol{X}(K).\end{align*}$$
$$\begin{align*}\mathbb{O}(\boldsymbol{X})_n=\coprod_{\delta}\mathbb{O}(\boldsymbol{X})^\delta_n\quad\text{with}\quad \mathbb{O}(\boldsymbol{X})^\delta_n:= \int^{K\in N\wr\kern.5px\mathbf{Inj}}{\mathscr{O}}\tbinom{K}{n}^\delta\times \boldsymbol{X}(K).\end{align*}$$
We denote by
![]() $\tilde {x}_n=[\tilde {e}_n;()]\in \mathbb {O}(\boldsymbol {X})^{e_n}_n$
the image of the propagator and define, in analogy with Construction 5.4,
$\tilde {x}_n=[\tilde {e}_n;()]\in \mathbb {O}(\boldsymbol {X})^{e_n}_n$
the image of the propagator and define, in analogy with Construction 5.4,

Again, we have two relevant maps:
-
1. The map
 $f\colon \mathbb {O}(\boldsymbol {X})\to \mathbb {O}(*)$
decomposes into maps
$f\colon \mathbb {O}(\boldsymbol {X})\to \mathbb {O}(*)$
decomposes into maps
 $f^\delta _n\colon \mathbb {O}(\boldsymbol {X})^\delta _n\to \mathbb {O}(*)^\delta _n$
, which are compatible with stabilisations. Thus, we get a map between the mapping telescopes
$f^\delta _n\colon \mathbb {O}(\boldsymbol {X})^\delta _n\to \mathbb {O}(*)^\delta _n$
, which are compatible with stabilisations. Thus, we get a map between the mapping telescopes
 $f_n^\infty \colon \mathbb {O}(\boldsymbol {X})^\infty _n \to \mathbb {O}(*)_n^\infty $
.
$f_n^\infty \colon \mathbb {O}(\boldsymbol {X})^\infty _n \to \mathbb {O}(*)_n^\infty $
. -
2. The map of
 ${\mathscr {O}}$
-algebras
${\mathscr {O}}$
-algebras
 $\eta \colon \mathbb {O}(\boldsymbol {X})\to \mathbb {D}(\boldsymbol {X})$
restricts to maps of spaces
$\eta \colon \mathbb {O}(\boldsymbol {X})\to \mathbb {D}(\boldsymbol {X})$
restricts to maps of spaces
 $\eta ^\delta _n\colon \mathbb {O}(\boldsymbol {X})^\delta _n\to \mathbb {D}(\boldsymbol {X})_n$
, and the triangle is H-commutative, whence we obtain a map from the mapping telescope
$\eta ^\delta _n\colon \mathbb {O}(\boldsymbol {X})^\delta _n\to \mathbb {D}(\boldsymbol {X})_n$
, and the triangle is H-commutative, whence we obtain a map from the mapping telescope
 $\eta _n^\infty \colon \mathbb {O}(\boldsymbol {X})^\infty _n\to \mathbb {D}(\boldsymbol {X})_n$
.
$\eta _n^\infty \colon \mathbb {O}(\boldsymbol {X})^\infty _n\to \mathbb {D}(\boldsymbol {X})_n$
.
Lemma 5.13 Key Lemma
For each colour
![]() $n\in N$
, the product map
$n\in N$
, the product map
is a homology equivalence.
Let us first prove Theorem 5.9 using the Key Lemma 5.13.
Proof of Theorem 5.9
Let us abbreviate
![]() $\tilde {\mathbb {O}}:= \tilde {F}^{\mathscr {O}}_{\smash {{\mathscr {B}}\otimes \mathbf {I}}}$
and
$\tilde {\mathbb {O}}:= \tilde {F}^{\mathscr {O}}_{\smash {{\mathscr {B}}\otimes \mathbf {I}}}$
and
![]() $\tilde {\mathbb {D}}:= \tilde {F}^{{\mathscr {D}}_\infty \otimes EN}_{\smash {{\mathscr {B}}\otimes \mathbf {I}}}$
. Then we have to show that the map
$\tilde {\mathbb {D}}:= \tilde {F}^{{\mathscr {D}}_\infty \otimes EN}_{\smash {{\mathscr {B}}\otimes \mathbf {I}}}$
. Then we have to show that the map
![]() $(f,\eta )\colon \tilde {\mathbb {O}}({\boldsymbol {X}})\to \tilde {\mathbb {O}}(*)\times \tilde {\mathbb {D}}({\boldsymbol {X}})$
from the previous section is levelwise an equivalence.
$(f,\eta )\colon \tilde {\mathbb {O}}({\boldsymbol {X}})\to \tilde {\mathbb {O}}(*)\times \tilde {\mathbb {D}}({\boldsymbol {X}})$
from the previous section is levelwise an equivalence.
To this aim, we study the stabilisations for
![]() $\tilde {\mathbb {O}}$
: as before, restricting the operation spaces of
$\tilde {\mathbb {O}}$
: as before, restricting the operation spaces of
![]() ${\mathscr {O}}$
gives rise to a grading of each level
${\mathscr {O}}$
gives rise to a grading of each level
![]() $B_\bullet (\mathbb {O},\mathbb {I},{\boldsymbol {X}})_n$
, and we denote the components by
$B_\bullet (\mathbb {O},\mathbb {I},{\boldsymbol {X}})_n$
, and we denote the components by
![]() $B_\bullet (\mathbb {O},\mathbb {I},{\boldsymbol {X}})^\delta _n$
and their realisation by
$B_\bullet (\mathbb {O},\mathbb {I},{\boldsymbol {X}})^\delta _n$
and their realisation by
![]() $\tilde {\mathbb {O}}({\boldsymbol {X}})_n^\delta $
. Adding the propagator gives rise to maps
$\tilde {\mathbb {O}}({\boldsymbol {X}})_n^\delta $
. Adding the propagator gives rise to maps
![]() of simplicial spaces and thus also to maps
of simplicial spaces and thus also to maps
![]() . We denote the colimits by
. We denote the colimits by
![]() $B_\bullet (\mathbb {O},\mathbb {I},{\boldsymbol {X}})^\infty _n$
and
$B_\bullet (\mathbb {O},\mathbb {I},{\boldsymbol {X}})^\infty _n$
and
![]() $\tilde {\mathbb {O}}({\boldsymbol {X}})_n^\infty $
; then clearly
$\tilde {\mathbb {O}}({\boldsymbol {X}})_n^\infty $
; then clearly
![]() $\tilde {\mathbb {O}}({\boldsymbol {X}})_n^\infty \simeq |B_\bullet (\mathbb {O},\mathbb {I},{\boldsymbol {X}})^\infty _n|$
.
$\tilde {\mathbb {O}}({\boldsymbol {X}})_n^\infty \simeq |B_\bullet (\mathbb {O},\mathbb {I},{\boldsymbol {X}})^\infty _n|$
.
Again, we obtain a product map
![]() $(f_n^\infty ,\eta ^\infty _n)\colon \tilde {\mathbb {O}}({\boldsymbol {X}})^\infty _n\to \tilde {\mathbb {O}}(*)^\infty _n\times \tilde {\mathbb {D}}({\boldsymbol {X}})_n$
, and we claim that it is a homology equivalence: since we have seen already that the simplicial spaces are proper, we can invoke the spectral sequence for the geometric realisation from [Reference Segal24, Prop. A1], whence it is enough to see that, for each dimension
$(f_n^\infty ,\eta ^\infty _n)\colon \tilde {\mathbb {O}}({\boldsymbol {X}})^\infty _n\to \tilde {\mathbb {O}}(*)^\infty _n\times \tilde {\mathbb {D}}({\boldsymbol {X}})_n$
, and we claim that it is a homology equivalence: since we have seen already that the simplicial spaces are proper, we can invoke the spectral sequence for the geometric realisation from [Reference Segal24, Prop. A1], whence it is enough to see that, for each dimension
![]() $p\geqslant 0$
and each
$p\geqslant 0$
and each
![]() $n\in N$
, the map
$n\in N$
, the map
![]() $B_p(\mathbb {O},\mathbb {I},{\boldsymbol {X}})^\infty _n\to B_p(\mathbb {O},\mathbb {I},*)^\infty _n\times B_p(\mathbb {D},\mathbb {I},{\boldsymbol {X}})_n$
is a homology equivalence. As we have
$B_p(\mathbb {O},\mathbb {I},{\boldsymbol {X}})^\infty _n\to B_p(\mathbb {O},\mathbb {I},*)^\infty _n\times B_p(\mathbb {D},\mathbb {I},{\boldsymbol {X}})_n$
is a homology equivalence. As we have
![]() $B_p(\mathbb {O},\mathbb {I},*)^\infty _n=\mathbb {O}(*)^\infty _n$
, the map in question is exactly the map from the Key Lemma 5.13 for the sequence
$B_p(\mathbb {O},\mathbb {I},*)^\infty _n=\mathbb {O}(*)^\infty _n$
, the map in question is exactly the map from the Key Lemma 5.13 for the sequence
![]() $\mathbb {I}^p{\boldsymbol {X}}$
. This shows the subclaim.
$\mathbb {I}^p{\boldsymbol {X}}$
. This shows the subclaim.
The rest of the proof is a combinatorially enhanced variation of the first part of the proof of [Reference Basterra, Bobkova, Ponto, Tillmann and Yeakel1, Thm. 5.4] that uses the classical group completion theorem: let us denote by
![]() $\boldsymbol {e}_n\in \pi _0(\tilde {\mathbb {O}}(*)_n\times \tilde {\mathbb {D}}({\boldsymbol {X}})_n)$
the component of the
$\boldsymbol {e}_n\in \pi _0(\tilde {\mathbb {O}}(*)_n\times \tilde {\mathbb {D}}({\boldsymbol {X}})_n)$
the component of the
![]() $0$
-simplex
$0$
-simplex
![]() $(\tilde {e}_n,[{\mathfrak {v}};\varnothing ])$
: that is, the propagator and the unit, and by
$(\tilde {e}_n,[{\mathfrak {v}};\varnothing ])$
: that is, the propagator and the unit, and by
![]() $\boldsymbol {x}_n\in \pi _0(\tilde {\mathbb {O}}({\boldsymbol {X}})_n)$
the component of the
$\boldsymbol {x}_n\in \pi _0(\tilde {\mathbb {O}}({\boldsymbol {X}})_n)$
the component of the
![]() $0$
-simplex
$0$
-simplex
![]() $\tilde {x}_n$
. By a classical telescope argument, the subclaim implies that the map
$\tilde {x}_n$
. By a classical telescope argument, the subclaim implies that the map
that is induced by the map of Pontrjagin rings is an isomorphism.
Now recall that all input blocking maps
![]() $\smash {\beta ^K_n\colon {\mathscr {O}}\tbinom {K}{n}\to \pi _0({\mathscr {O}}\tbinom {}{n})}$
are assumed to be surjective. Then
$\smash {\beta ^K_n\colon {\mathscr {O}}\tbinom {K}{n}\to \pi _0({\mathscr {O}}\tbinom {}{n})}$
are assumed to be surjective. Then
![]() $(f_n,\eta _n)_*\colon \pi _0(\tilde {\mathbb {O}}({\boldsymbol {X}})_n)\to \pi _0(\tilde {\mathbb {O}}(*)_n\times \tilde {\mathbb {D}}({\boldsymbol {X}})_n)$
is surjective as well, so under the above map, the multiplicative submonoid
$(f_n,\eta _n)_*\colon \pi _0(\tilde {\mathbb {O}}({\boldsymbol {X}})_n)\to \pi _0(\tilde {\mathbb {O}}(*)_n\times \tilde {\mathbb {D}}({\boldsymbol {X}})_n)$
is surjective as well, so under the above map, the multiplicative submonoid
![]() $\pi _0(\tilde {\mathbb {O}}({\boldsymbol {X}})_n)$
is sent surjectively onto the the submonoid
$\pi _0(\tilde {\mathbb {O}}({\boldsymbol {X}})_n)$
is sent surjectively onto the the submonoid
![]() $\pi _0(\tilde {\mathbb {O}}(*)_n\times \tilde {\mathbb {D}}({\boldsymbol {X}})_n)$
. Therefore, we can localise further, with respect to the multiplicative submonoids of all path components on both sides, still obtaining an isomorphism. We get a diagram
$\pi _0(\tilde {\mathbb {O}}(*)_n\times \tilde {\mathbb {D}}({\boldsymbol {X}})_n)$
. Therefore, we can localise further, with respect to the multiplicative submonoids of all path components on both sides, still obtaining an isomorphism. We get a diagram

where the vertical isomorphisms between the second and the third row follow from the group completion theorem [Reference McDuff and Segal18] for
![]() ${\mathscr {D}}_1$
-algebras. This shows that
${\mathscr {D}}_1$
-algebras. This shows that
![]() $\Omega B(f_n,\eta _n)$
is a homology equivalence of loop spaces and thus a weak equivalence.
$\Omega B(f_n,\eta _n)$
is a homology equivalence of loop spaces and thus a weak equivalence.
The pending proof of Key Lemma 5.13 requires some further preparation. Recall from Definition 4.3 that for each tuple K, we denote by
![]() $N[K]\subseteq N\wr \mathbf {Inj}$
the full subgroupoid spanned by all objects of the form
$N[K]\subseteq N\wr \mathbf {Inj}$
the full subgroupoid spanned by all objects of the form
![]() $\tau ^*K$
. For an input profile K and an output
$\tau ^*K$
. For an input profile K and an output
![]() $n\in N$
, recall the stable operation spaces
$n\in N$
, recall the stable operation spaces
![]() ${\mathscr {O}}\tbinom {K}{n}^\infty $
. Since input permutation and precomposition commutes with stabilisation, these spaces assemble, for each
${\mathscr {O}}\tbinom {K}{n}^\infty $
. Since input permutation and precomposition commutes with stabilisation, these spaces assemble, for each
![]() $n\in N$
and each tuple K, into a functor
$n\in N$
and each tuple K, into a functor
![]() ${\mathscr {O}}\tbinom {-}{n}^\infty \colon N[K]^{\operatorname {op}}\to \mathbf {Top}$
.
${\mathscr {O}}\tbinom {-}{n}^\infty \colon N[K]^{\operatorname {op}}\to \mathbf {Top}$
.
Now let
![]() $\boldsymbol {Q}\colon N[K]\to \mathbf {Top}$
be any functor. Again, we have two maps: first, for each tuple
$\boldsymbol {Q}\colon N[K]\to \mathbf {Top}$
be any functor. Again, we have two maps: first, for each tuple
![]() $L=\tau ^*K$
and each
$L=\tau ^*K$
and each
![]() $n\in N$
, we have the stable input block map
$n\in N$
, we have the stable input block map
![]() ${\mathscr {O}}\tbinom {L}{n}^\infty \times {\boldsymbol {Q}}(L)\to {\mathscr {O}}\tbinom {}{n}^\infty $
, which ignores the factor
${\mathscr {O}}\tbinom {L}{n}^\infty \times {\boldsymbol {Q}}(L)\to {\mathscr {O}}\tbinom {}{n}^\infty $
, which ignores the factor
![]() ${\boldsymbol {Q}}(L)$
. These maps define a natural transformation of functors from
${\boldsymbol {Q}}(L)$
. These maps define a natural transformation of functors from
![]() ${\mathscr {O}}\tbinom {-}{n}^\infty \times \boldsymbol {Q}(-)$
to the constant functor
${\mathscr {O}}\tbinom {-}{n}^\infty \times \boldsymbol {Q}(-)$
to the constant functor
![]() $N[K]^{\operatorname {op}}\times N[K]\to \mathbf {Top}$
with value
$N[K]^{\operatorname {op}}\times N[K]\to \mathbf {Top}$
with value
![]() ${\mathscr {O}}\tbinom {}{n}^\infty $
, so we get
${\mathscr {O}}\tbinom {}{n}^\infty $
, so we get
 $$\begin{align*}\alpha_1\colon \int^{L}{\mathscr{O}}\tbinom{L}{n}^\infty\times{\boldsymbol{Q}}(L) \to {\mathscr{O}}\tbinom{}{n}^\infty.\end{align*}$$
$$\begin{align*}\alpha_1\colon \int^{L}{\mathscr{O}}\tbinom{L}{n}^\infty\times{\boldsymbol{Q}}(L) \to {\mathscr{O}}\tbinom{}{n}^\infty.\end{align*}$$
Second, the morphism
![]() $\pi \colon {\mathscr {O}}\to {\mathscr {D}}_\infty \otimes EN$
gives, for each
$\pi \colon {\mathscr {O}}\to {\mathscr {D}}_\infty \otimes EN$
gives, for each
![]() $n\in N$
, rise to a natural transformation
$n\in N$
, rise to a natural transformation
![]() ${\mathscr {O}}^\infty \tbinom {-}{n}\Rightarrow ({\mathscr {D}}_\infty \otimes EN)\tbinom {}{n}$
of functors
${\mathscr {O}}^\infty \tbinom {-}{n}\Rightarrow ({\mathscr {D}}_\infty \otimes EN)\tbinom {}{n}$
of functors
![]() $N[K]^{\operatorname {op}}\to \mathbf {Top}$
, so we obtain a map, where L ranges in
$N[K]^{\operatorname {op}}\to \mathbf {Top}$
, so we obtain a map, where L ranges in
![]() $N[K]$
,
$N[K]$
,
 $$\begin{align*}\alpha_2\colon \int^{L}{\mathscr{O}}\tbinom{L}{n}^\infty\times{\boldsymbol{Q}}(L) \to \int^{L}({\mathscr{D}}_\infty\otimes EN)\tbinom{L}{n}\times{\boldsymbol{Q}}(L) \cong {\mathscr{D}}_\infty\times_{\mathfrak{S}_r}\coprod_{L=\tau^* K}\boldsymbol{Q}(L).\end{align*}$$
$$\begin{align*}\alpha_2\colon \int^{L}{\mathscr{O}}\tbinom{L}{n}^\infty\times{\boldsymbol{Q}}(L) \to \int^{L}({\mathscr{D}}_\infty\otimes EN)\tbinom{L}{n}\times{\boldsymbol{Q}}(L) \cong {\mathscr{D}}_\infty\times_{\mathfrak{S}_r}\coprod_{L=\tau^* K}\boldsymbol{Q}(L).\end{align*}$$
The following lemma is a coloured version of [Reference Basterra, Bobkova, Ponto, Tillmann and Yeakel1, Lem. 5.2]:
Lemma 5.14. The product map
![]() $\alpha _{\boldsymbol {Q}}:= (\alpha _1,\alpha _2)$
is a homology equivalence:
$\alpha _{\boldsymbol {Q}}:= (\alpha _1,\alpha _2)$
is a homology equivalence:
 $$\begin{align*}\alpha_{\boldsymbol{Q}}\colon \int^{L\in N[K]}{\mathscr{O}}\tbinom{L}{n}^\infty\times {\boldsymbol{Q}}(L) \to {\mathscr{O}}\tbinom{}{n}^\infty\times {\mathscr{D}}_\infty(r)\times_{\mathfrak{S}_r}\coprod_{L\in N[K]} {\boldsymbol{Q}}(L).\end{align*}$$
$$\begin{align*}\alpha_{\boldsymbol{Q}}\colon \int^{L\in N[K]}{\mathscr{O}}\tbinom{L}{n}^\infty\times {\boldsymbol{Q}}(L) \to {\mathscr{O}}\tbinom{}{n}^\infty\times {\mathscr{D}}_\infty(r)\times_{\mathfrak{S}_r}\coprod_{L\in N[K]} {\boldsymbol{Q}}(L).\end{align*}$$
Proof. Since
![]() ${\mathscr {D}}_\infty (r)$
is contractible, the sequence
${\mathscr {D}}_\infty (r)$
is contractible, the sequence
induces a split long exact sequence of homotopy groups for each
![]() $L=\tau ^*K$
and each choice of basepoint. If we take for the total space and the base space the disjoint union over all such L, the common fibre for each component is
$L=\tau ^*K$
and each choice of basepoint. If we take for the total space and the base space the disjoint union over all such L, the common fibre for each component is
![]() ${\mathscr {O}}\tbinom {L}{n}^\infty \cong {\mathscr {O}}\tbinom {K}{n}^\infty $
. If we moreover quotient by the free and compatible
${\mathscr {O}}\tbinom {L}{n}^\infty \cong {\mathscr {O}}\tbinom {K}{n}^\infty $
. If we moreover quotient by the free and compatible
![]() $\mathfrak {S}_r$
-actions on total space and base space, we finally obtain a long exact sequence of homotopy groups that is induced by
$\mathfrak {S}_r$
-actions on total space and base space, we finally obtain a long exact sequence of homotopy groups that is induced by
 $$\begin{align*}{\mathscr{O}}\tbinom{K}{n}^\infty \to \int^{L}{\mathscr{O}}\tbinom{L}{n}^\infty\times{\boldsymbol{Q}}(L) \to {\mathscr{D}}_\infty(r)\times_{\mathfrak{S}_r}\coprod_{L=\tau^*K}{\boldsymbol{Q}}(L).\end{align*}$$
$$\begin{align*}{\mathscr{O}}\tbinom{K}{n}^\infty \to \int^{L}{\mathscr{O}}\tbinom{L}{n}^\infty\times{\boldsymbol{Q}}(L) \to {\mathscr{D}}_\infty(r)\times_{\mathfrak{S}_r}\coprod_{L=\tau^*K}{\boldsymbol{Q}}(L).\end{align*}$$
Now the product map
![]() $\alpha _{\boldsymbol {Q}}$
is the composition of the two middle vertical maps in the following
$\alpha _{\boldsymbol {Q}}$
is the composition of the two middle vertical maps in the following
![]() $(3\times 3)$
-diagram, where we abbreviate
$(3\times 3)$
-diagram, where we abbreviate
![]() $\mathfrak {S}:=\mathfrak {S}_r$
,
$\mathfrak {S}:=\mathfrak {S}_r$
,

Here the top-left square commutes up to homotopy, and all other squares commute strictly. We have already seen that the top row induces a long exact sequence on homotopy groups, and the second row is clearly a fibration. By the 5-lemma, the first middle vertical map is a weak equivalence. Similarly, we know that both the second and third rows are fibrations, so we obtain a morphism between the associated Serre spectral sequences in homology. Since
![]() ${\mathscr {O}}$
is an operad with homological stability, the map
${\mathscr {O}}$
is an operad with homological stability, the map
![]() $\beta ^K_n$
between the fibres is a homology equivalence, so by a standard comparison argument [Reference Weibel27, 5.2.12], the second middle vertical map is also a homology equivalence.
$\beta ^K_n$
between the fibres is a homology equivalence, so by a standard comparison argument [Reference Weibel27, 5.2.12], the second middle vertical map is also a homology equivalence.
Now we have everything together to prove the Key Lemma 5.13.
Proof of the Key Lemma 5.13
Recall that, after identifying the stable spaces
![]() ${\mathbb {O}(*)^\infty _n}$
with
${\mathbb {O}(*)^\infty _n}$
with
![]() ${\mathscr {O}}\tbinom {}{n}^\infty $
, our aim is to show that the map
${\mathscr {O}}\tbinom {}{n}^\infty $
, our aim is to show that the map
induces isomorphisms on homology. If we denote by
![]() $(N\wr \mathbf {Inj})_{\leqslant r}$
the full subcategory of
$(N\wr \mathbf {Inj})_{\leqslant r}$
the full subcategory of
![]() $N\wr \mathbf {Inj}$
with objects tuples of length at most r, then the two sides of q are exhaustively filtered by
$N\wr \mathbf {Inj}$
with objects tuples of length at most r, then the two sides of q are exhaustively filtered by
![]() $F_{-1}=F^{\prime }_{-1}=\varnothing $
and
$F_{-1}=F^{\prime }_{-1}=\varnothing $
and
 $$ \begin{align*} F_r &:= \int^{K\in (N\kern-.2px\wr\kern.5px\mathbf{Inj})_{\leqslant r}}{\mathscr{O}}\tbinom{K}{n}^\infty\times{\boldsymbol{X}}(K)\\ \text{respectively}\quad F^{\prime}_r&:= {\mathscr{O}}\tbinom{}{n}^\infty\times \int^{K\in (N\kern-.2px\wr\kern.5px\mathbf{Inj})_{\leqslant r}}({\mathscr{D}}_\infty\otimes EN)\tbinom{K}{n}\times \boldsymbol{X}(K), \end{align*} $$
$$ \begin{align*} F_r &:= \int^{K\in (N\kern-.2px\wr\kern.5px\mathbf{Inj})_{\leqslant r}}{\mathscr{O}}\tbinom{K}{n}^\infty\times{\boldsymbol{X}}(K)\\ \text{respectively}\quad F^{\prime}_r&:= {\mathscr{O}}\tbinom{}{n}^\infty\times \int^{K\in (N\kern-.2px\wr\kern.5px\mathbf{Inj})_{\leqslant r}}({\mathscr{D}}_\infty\otimes EN)\tbinom{K}{n}\times \boldsymbol{X}(K), \end{align*} $$
and the map q is filtration-preserving. Let us fix a system
![]() $S_r\subseteq N^r$
of representatives for unordered tuples and set
$S_r\subseteq N^r$
of representatives for unordered tuples and set
![]() ${\boldsymbol {Q}}(K) := X_{k_1}\wedge \dotsb \wedge X_{k_r}$
. Then the filtration quotients are of the form
${\boldsymbol {Q}}(K) := X_{k_1}\wedge \dotsb \wedge X_{k_r}$
. Then the filtration quotients are of the form
 $$ \begin{align*} F_r/F_{r-1} &\cong\bigvee_{K\in S_r}\int^{L\in N[K]}{\mathscr{O}}\tbinom{L}{n}^\infty_+\wedge {\boldsymbol{Q}}(L)\\ F^{\prime}_r/F^{\prime}_{r-1} &\cong \bigvee_{K\in S_r}{\mathscr{O}}\tbinom{}{n}^\infty_+\wedge {\mathscr{D}}_\infty(r)_+\wedge_{\mathfrak{S}_r}\bigvee_{L=\tau^*K}{\boldsymbol{Q}}(L), \end{align*} $$
$$ \begin{align*} F_r/F_{r-1} &\cong\bigvee_{K\in S_r}\int^{L\in N[K]}{\mathscr{O}}\tbinom{L}{n}^\infty_+\wedge {\boldsymbol{Q}}(L)\\ F^{\prime}_r/F^{\prime}_{r-1} &\cong \bigvee_{K\in S_r}{\mathscr{O}}\tbinom{}{n}^\infty_+\wedge {\mathscr{D}}_\infty(r)_+\wedge_{\mathfrak{S}_r}\bigvee_{L=\tau^*K}{\boldsymbol{Q}}(L), \end{align*} $$
and the map
![]() $q_r\colon F_r/F_{r-1}\to F^{\prime }_r/F^{\prime }_{r-1}$
between the filtration quotients splits as a bouquet
$q_r\colon F_r/F_{r-1}\to F^{\prime }_r/F^{\prime }_{r-1}$
between the filtration quotients splits as a bouquet
![]() $q_r=\bigvee _{K\!\in S_r}q_K$
. We show that each
$q_r=\bigvee _{K\!\in S_r}q_K$
. We show that each
![]() $q_K$
is a homology equivalence; then it follows that also the map
$q_K$
is a homology equivalence; then it follows that also the map
![]() $q_r$
between the filtration quotients is a homology equivalence, so by applying a comparison argument [Reference Weibel27, 5.2.12] to the morphism of spectral sequences assigned to the filtration-preserving map q, we get that q itself is a homology equivalence.
$q_r$
between the filtration quotients is a homology equivalence, so by applying a comparison argument [Reference Weibel27, 5.2.12] to the morphism of spectral sequences assigned to the filtration-preserving map q, we get that q itself is a homology equivalence.
In order to see that each
![]() $q_K$
is indeed a homology equivalence, we use that
$q_K$
is indeed a homology equivalence, we use that
![]() ${\boldsymbol {X}}$
is well-based and obtain that the induced maps
${\boldsymbol {X}}$
is well-based and obtain that the induced maps
 $$ \begin{align*} \int^{L\in N[K]}{\mathscr{O}}\tbinom{L}{n}^\infty &\to \int^{L\in N[K]}{\mathscr{O}}\tbinom{L}{n}^\infty\times{\boldsymbol{Q}}(L)\\[3px] \text{and}\quad{\mathscr{D}}_\infty(r)\times_{\mathfrak{S}_r}[K] &\to {\mathscr{D}}_\infty(r)\times_{\mathfrak{S}_r}\coprod_{L=\tau^*K}{\boldsymbol{Q}}(L) \end{align*} $$
$$ \begin{align*} \int^{L\in N[K]}{\mathscr{O}}\tbinom{L}{n}^\infty &\to \int^{L\in N[K]}{\mathscr{O}}\tbinom{L}{n}^\infty\times{\boldsymbol{Q}}(L)\\[3px] \text{and}\quad{\mathscr{D}}_\infty(r)\times_{\mathfrak{S}_r}[K] &\to {\mathscr{D}}_\infty(r)\times_{\mathfrak{S}_r}\coprod_{L=\tau^*K}{\boldsymbol{Q}}(L) \end{align*} $$
are cofibrations, where we write
![]() $[K]:= \{\tau ^*K;\,\tau \in \mathfrak {S}_r\}$
. If we write
$[K]:= \{\tau ^*K;\,\tau \in \mathfrak {S}_r\}$
. If we write
![]() $\alpha _{\boldsymbol {Q}}$
for the product map from Lemma 5.14 and
$\alpha _{\boldsymbol {Q}}$
for the product map from Lemma 5.14 and
![]() $\alpha _0$
for the analogous one for the trivial family
$\alpha _0$
for the analogous one for the trivial family
![]() $*=(*)_{n\in N}$
, then we obtain a morphism of cofibre sequences (written vertically for space reasons)
$*=(*)_{n\in N}$
, then we obtain a morphism of cofibre sequences (written vertically for space reasons)

where L ranges in
![]() $N[K]$
. By Lemma 5.14,
$N[K]$
. By Lemma 5.14,
![]() $\alpha _0$
and
$\alpha _0$
and
![]() $\alpha _{\boldsymbol {Q}}$
induce isomorphisms in homology, so by the 5-lemma applied to the long exact sequence associated to the cofibre sequence, we obtain that also
$\alpha _{\boldsymbol {Q}}$
induce isomorphisms in homology, so by the 5-lemma applied to the long exact sequence associated to the cofibre sequence, we obtain that also
![]() $q_K$
is a homology equivalence.
$q_K$
is a homology equivalence.
6
 $\Lambda \mathfrak {M}_{*,1}$
as a relatively free algebra
$\Lambda \mathfrak {M}_{*,1}$
as a relatively free algebra
In this section, we combine the insights from the previous sections: we translate the results of Section 2 and Section 3, which are expressed in terms of groups, into the analogous results in terms of classifying spaces.
This will lead to Theorem 6.5, expressing
![]() $\Lambda \mathfrak {M}_{*,1}$
as the colour-
$\Lambda \mathfrak {M}_{*,1}$
as the colour-
![]() $1$
part of a relatively free
$1$
part of a relatively free
![]() ${\mathscr {M}}$
-algebra, with generators an algebra over the family of twisted tori, which depends on
${\mathscr {M}}$
-algebra, with generators an algebra over the family of twisted tori, which depends on
![]() $\partial $
-irreducible mapping classes. Using the results of Section 4 and Section 5, we deduce the identification from Theorem 1.1.
$\partial $
-irreducible mapping classes. Using the results of Section 4 and Section 5, we deduce the identification from Theorem 1.1.
6.1 Recollections from Section 2 and Section 4
Recall Definition 2.14 and Definition 2.19, let
![]() $\mathcal {S}$
be a surface of type
$\mathcal {S}$
be a surface of type
![]() $\Sigma _{g,n}$
for some
$\Sigma _{g,n}$
for some
![]() $g\geqslant 0$
and
$g\geqslant 0$
and
![]() $n\geqslant 1$
, and note that a mapping class
$n\geqslant 1$
, and note that a mapping class
![]() $\varphi \in \Gamma (\mathcal {S},\partial \mathcal {S})$
is
$\varphi \in \Gamma (\mathcal {S},\partial \mathcal {S})$
is
![]() $\partial $
-irreducible if and only if the cut locus of
$\partial $
-irreducible if and only if the cut locus of
![]() $\varphi $
is equal to
$\varphi $
is equal to
![]() $[\partial \mathcal {S}]$
: that is, it is the collection of oriented isotopy classes of all boundary curves of
$[\partial \mathcal {S}]$
: that is, it is the collection of oriented isotopy classes of all boundary curves of
![]() $\mathcal {S}$
. Note in particular the following special cases:
$\mathcal {S}$
. Note in particular the following special cases:
-
○ if
 $\mathcal {S}$
is a cylinder,
$\mathcal {S}$
is a cylinder,
 $[\partial \mathcal {S}]$
contains two isotopy classes, as the two curves of
$[\partial \mathcal {S}]$
contains two isotopy classes, as the two curves of
 $\partial \mathcal {S}$
are not isotopic as oriented curves; the mapping class
$\partial \mathcal {S}$
are not isotopic as oriented curves; the mapping class
 has empty cut locus, and every other mapping class is
has empty cut locus, and every other mapping class is
 $\partial $
-irreducible and has cut locus equal to
$\partial $
-irreducible and has cut locus equal to
 $[\partial \mathcal {S}]$
;
$[\partial \mathcal {S}]$
; -
○ if
 $\mathcal {S}$
is a disc,
$\mathcal {S}$
is a disc,
 $[\partial \mathcal {S}]$
contains one isotopy class (of a null-homotopic curve); the unique mapping class
$[\partial \mathcal {S}]$
contains one isotopy class (of a null-homotopic curve); the unique mapping class
 has empty cut locus and was declared not to be
has empty cut locus and was declared not to be
 $\partial $
-irreducible.
$\partial $
-irreducible.
Alternatively, we saw that
![]() $\varphi $
is
$\varphi $
is
![]() $\partial $
-irreducible if and only if the white part
$\partial $
-irreducible if and only if the white part
![]() $W\subset \mathcal {S}$
deformation retracts onto
$W\subset \mathcal {S}$
deformation retracts onto
![]() $\partial ^{\text {out}}W=\partial \mathcal {S}$
. Being
$\partial ^{\text {out}}W=\partial \mathcal {S}$
. Being
![]() $\partial $
-irreducible is an invariant of conjugacy classes in
$\partial $
-irreducible is an invariant of conjugacy classes in
![]() $\Gamma (\mathcal {S},\partial \mathcal {S})$
, and in fact even of conjugacy classes of
$\Gamma (\mathcal {S},\partial \mathcal {S})$
, and in fact even of conjugacy classes of
![]() $\Gamma (\mathcal {S})$
that are contained in the normal subgroup
$\Gamma (\mathcal {S})$
that are contained in the normal subgroup
![]() $\Gamma (\mathcal {S},\partial \mathcal {S})$
.
$\Gamma (\mathcal {S},\partial \mathcal {S})$
.
Recall Construction 4.13. We have a similar action of
![]() $R_n=T^n\rtimes \mathfrak {S}_n$
on the space
$R_n=T^n\rtimes \mathfrak {S}_n$
on the space
![]() ${\mathscr {M}}\tbinom {}{n}=\mathbf {M}_\partial \tbinom {0}{n}$
by postcomposition, regarding
${\mathscr {M}}\tbinom {}{n}=\mathbf {M}_\partial \tbinom {0}{n}$
by postcomposition, regarding
![]() $R_n\subset \mathbf {M}_\partial \tbinom {n}{n}$
. By taking this action pointwise over
$R_n\subset \mathbf {M}_\partial \tbinom {n}{n}$
. By taking this action pointwise over
![]() $S^1$
, we obtain an action of
$S^1$
, we obtain an action of
![]() $R_n$
on
$R_n$
on
![]() $\Lambda {\mathscr {M}}\tbinom {}{n}$
.
$\Lambda {\mathscr {M}}\tbinom {}{n}$
.
Notation 6.1. For
![]() $g\geqslant 0$
and
$g\geqslant 0$
and
![]() $n\geqslant 1$
, we denote by
$n\geqslant 1$
, we denote by
![]() ${\mathscr {M}}_{g,n}\subset {\mathscr {M}}\tbinom {}{n}=\mathbf {M}_\partial \tbinom {0}{n}$
the subspace corresponding to conformal classes
${\mathscr {M}}_{g,n}\subset {\mathscr {M}}\tbinom {}{n}=\mathbf {M}_\partial \tbinom {0}{n}$
the subspace corresponding to conformal classes
![]() $(W,\tilde \vartheta )$
with W of type
$(W,\tilde \vartheta )$
with W of type
![]() $\Sigma _{g,n}$
$\Sigma _{g,n}$
We have a homotopy equivalence
![]() ${\mathscr {M}}_{g,n}\to \mathfrak {M}_{g,n}$
given by sending
${\mathscr {M}}_{g,n}\to \mathfrak {M}_{g,n}$
given by sending
![]() $(W,\tilde \vartheta )$
to
$(W,\tilde \vartheta )$
to
![]() $(W,\vartheta )$
, where
$(W,\vartheta )$
, where
![]() $\vartheta $
is obtained by restricting
$\vartheta $
is obtained by restricting
![]() $\tilde \vartheta $
to (the preimage of)
$\tilde \vartheta $
to (the preimage of)
![]() $\partial W$
. We have therefore a homotopy equivalence
$\partial W$
. We have therefore a homotopy equivalence
 $$\begin{align*}\Lambda{\mathscr{M}}_{g,n}\simeq \Lambda\mathfrak{M}_{g,n}\simeq \coprod_{[\varphi]\in {\mathrm{Conj}}(\Gamma_{g,n})}BZ(\varphi,\Gamma_{g,n}).\end{align*}$$
$$\begin{align*}\Lambda{\mathscr{M}}_{g,n}\simeq \Lambda\mathfrak{M}_{g,n}\simeq \coprod_{[\varphi]\in {\mathrm{Conj}}(\Gamma_{g,n})}BZ(\varphi,\Gamma_{g,n}).\end{align*}$$
In the following, we will mostly replace the spaces
![]() $\Lambda \mathfrak {M}_{g,n}$
by the spaces
$\Lambda \mathfrak {M}_{g,n}$
by the spaces
![]() $\Lambda {\mathscr {M}}_{g,n}$
. In particular, we denote
$\Lambda {\mathscr {M}}_{g,n}$
. In particular, we denote
 $$\begin{align*}\Lambda{\mathscr{M}}_{*,1}:=\coprod_{g\geqslant0}\Lambda{\mathscr{M}}_{g,1}\simeq\Lambda\mathfrak{M}_{*,1},\end{align*}$$
$$\begin{align*}\Lambda{\mathscr{M}}_{*,1}:=\coprod_{g\geqslant0}\Lambda{\mathscr{M}}_{g,1}\simeq\Lambda\mathfrak{M}_{*,1},\end{align*}$$
where the last equivalence is an equivalence of
![]() ${\mathscr {D}}_2$
-algebras.
${\mathscr {D}}_2$
-algebras.
6.2 Action of
 $\mathfrak {S}_n$
on
$\mathfrak {S}_n$
on
 $\Lambda {\mathscr {M}}_{g,n}$
$\Lambda {\mathscr {M}}_{g,n}$
In this subsection, we analyse the action of
![]() $\mathfrak {S}_n$
on the set of components of
$\mathfrak {S}_n$
on the set of components of
![]() $\Lambda {\mathscr {M}}_{g,n}$
and classify the orbits of this action.
$\Lambda {\mathscr {M}}_{g,n}$
and classify the orbits of this action.
Notation 6.2. For a mapping class
![]() $\varphi \in \Gamma _{g,n}$
, we denote by
$\varphi \in \Gamma _{g,n}$
, we denote by
![]() $\Lambda \mathfrak {M}_{g,n}(\varphi )$
the connected component of
$\Lambda \mathfrak {M}_{g,n}(\varphi )$
the connected component of
![]() $\Lambda \mathfrak {M}_{g,n}$
corresponding to
$\Lambda \mathfrak {M}_{g,n}$
corresponding to
![]() $BZ(\varphi ,\Gamma _{g,n})$
. It contains all free loops
$BZ(\varphi ,\Gamma _{g,n})$
. It contains all free loops
![]() $\lambda \colon S^1\to \mathfrak {M}_{g,n}$
with the following property: if
$\lambda \colon S^1\to \mathfrak {M}_{g,n}$
with the following property: if
![]() $\mathcal {S}$
is a Riemann surface of type
$\mathcal {S}$
is a Riemann surface of type
![]() $\Sigma _{g,n}$
representing
$\Sigma _{g,n}$
representing
![]() $\lambda (1)$
and if
$\lambda (1)$
and if
![]() $\varphi '\in \Gamma (\mathcal {S},\partial \mathcal {S})$
is the monodromy of
$\varphi '\in \Gamma (\mathcal {S},\partial \mathcal {S})$
is the monodromy of
![]() $\lambda $
, then there is a diffeomorphism
$\lambda $
, then there is a diffeomorphism
![]() $\Xi \colon \mathcal {S}\to \Sigma _{g,n}$
preserving the parametrisation and the ordering of the boundary components, with
$\Xi \colon \mathcal {S}\to \Sigma _{g,n}$
preserving the parametrisation and the ordering of the boundary components, with
![]() $(\varphi ')^\Xi =\varphi \in \Gamma _{g,n}$
. We denote by
$(\varphi ')^\Xi =\varphi \in \Gamma _{g,n}$
. We denote by
![]() $\Lambda {\mathscr {M}}_{g,n}(\varphi )$
the corresponding component of
$\Lambda {\mathscr {M}}_{g,n}(\varphi )$
the corresponding component of
![]() $\Lambda {\mathscr {M}}_{g,n}$
.
$\Lambda {\mathscr {M}}_{g,n}$
.
Note that
![]() $\Lambda {\mathscr {M}}_{g,n}(\varphi )\subset \Lambda {\mathscr {M}}_{g,n}$
is invariant under the action of
$\Lambda {\mathscr {M}}_{g,n}(\varphi )\subset \Lambda {\mathscr {M}}_{g,n}$
is invariant under the action of
![]() $T^n\subset R_n$
but not necessarily under the action of
$T^n\subset R_n$
but not necessarily under the action of
![]() $\mathfrak {S}_n$
. We denote by
$\mathfrak {S}_n$
. We denote by
![]() $\mathfrak {S}_n\cdot \Lambda {\mathscr {M}}_{g,n}(\varphi )\subset \Lambda {\mathscr {M}}_{g,n}$
the orbit of
$\mathfrak {S}_n\cdot \Lambda {\mathscr {M}}_{g,n}(\varphi )\subset \Lambda {\mathscr {M}}_{g,n}$
the orbit of
![]() ${\mathscr {M}}_{g,n}(\varphi )$
under the action of
${\mathscr {M}}_{g,n}(\varphi )$
under the action of
![]() $\mathfrak {S}_n$
or, equivalently, under the action of
$\mathfrak {S}_n$
or, equivalently, under the action of
![]() $R_n$
. We have
$R_n$
. We have
where
![]() $\varphi '$
ranges over all conjugates of
$\varphi '$
ranges over all conjugates of
![]() $\varphi $
in the extended mapping class group
$\varphi $
in the extended mapping class group
![]() $\Gamma _{g,(n)}$
. Note that these conjugates still lie in the subgroup
$\Gamma _{g,(n)}$
. Note that these conjugates still lie in the subgroup
![]() $\Gamma _{g,n}\subset \Gamma _{g,(n)}$
, which is normal. Note also that
$\Gamma _{g,n}\subset \Gamma _{g,(n)}$
, which is normal. Note also that
![]() $\Lambda {\mathscr {M}}_{g,n}(\varphi ')=\Lambda {\mathscr {M}}_{g,n}(\varphi )$
if and only if
$\Lambda {\mathscr {M}}_{g,n}(\varphi ')=\Lambda {\mathscr {M}}_{g,n}(\varphi )$
if and only if
![]() $\varphi $
and
$\varphi $
and
![]() $\varphi '$
are conjugate not only in
$\varphi '$
are conjugate not only in
![]() $\Gamma _{g,(n)}$
, but also in
$\Gamma _{g,(n)}$
, but also in
![]() $\Gamma _{g,n}$
: see Figure 10 for an example that shows the difference.
$\Gamma _{g,n}$
: see Figure 10 for an example that shows the difference.

Figure 10 If we denote by
![]() $D_i:= D_{d_i}$
the Dehn twist along
$D_i:= D_{d_i}$
the Dehn twist along
![]() $d_i$
, then the mapping classes
$d_i$
, then the mapping classes
![]() $D_1D_2D_4$
and
$D_1D_2D_4$
and
![]() $D_1D_3D_4$
are both
$D_1D_3D_4$
are both
![]() $\partial $
-irreducible in
$\partial $
-irreducible in
![]() $\Gamma _{3,2}$
and not conjugate to each other, but they are conjugate in the extended mapping class group
$\Gamma _{3,2}$
and not conjugate to each other, but they are conjugate in the extended mapping class group
![]() $\Gamma _{3,(2)}$
.
$\Gamma _{3,(2)}$
.
The subspace of
![]() $\mathfrak {M}_{g,n}$
corresponding to
$\mathfrak {M}_{g,n}$
corresponding to
![]() $\mathfrak {S}_n\cdot \Lambda \mathfrak {M}_{g,n}(\varphi )\subset \Lambda \mathfrak {M}_{g,n}$
can be described as follows: it contains all free loops
$\mathfrak {S}_n\cdot \Lambda \mathfrak {M}_{g,n}(\varphi )\subset \Lambda \mathfrak {M}_{g,n}$
can be described as follows: it contains all free loops
![]() $\lambda \colon S^1\to \mathfrak {M}_{g,n}$
with the same property as in Notation 6.2, but where
$\lambda \colon S^1\to \mathfrak {M}_{g,n}$
with the same property as in Notation 6.2, but where
![]() $\Xi $
is only required to preserve the parametrisation, and not necessarily the order, of the boundary components.
$\Xi $
is only required to preserve the parametrisation, and not necessarily the order, of the boundary components.
Lemma 6.3. Let
![]() $\varphi \in \Gamma _{g,n}$
, and let
$\varphi \in \Gamma _{g,n}$
, and let
![]() $\mathfrak {H}\subset \mathfrak {S}_n$
be the image of
$\mathfrak {H}\subset \mathfrak {S}_n$
be the image of
![]() $Z(\varphi ,\Gamma _{g,(n)})$
under the natural map
$Z(\varphi ,\Gamma _{g,(n)})$
under the natural map
![]() $\Gamma _{g,(n)}\to \mathfrak {S}_n$
. Then there is a bijection of
$\Gamma _{g,(n)}\to \mathfrak {S}_n$
. Then there is a bijection of
![]() $\mathfrak {S}_n$
-sets
$\mathfrak {S}_n$
-sets
Proof. The action of
![]() $\mathfrak {S}_n$
on
$\mathfrak {S}_n$
on
![]() $\pi _0(\Lambda {\mathscr {M}}_{g,n})$
can be described as follows: given
$\pi _0(\Lambda {\mathscr {M}}_{g,n})$
can be described as follows: given
![]() $\sigma \in \mathfrak {S}_n$
, we choose a mapping class
$\sigma \in \mathfrak {S}_n$
, we choose a mapping class
![]() $\xi \in \Gamma _{g,(n)}$
, which is sent to
$\xi \in \Gamma _{g,(n)}$
, which is sent to
![]() $\sigma $
under the natural map
$\sigma $
under the natural map
![]() $\Gamma _{g,(n)}\to \mathfrak {S}_n$
, and a representative
$\Gamma _{g,(n)}\to \mathfrak {S}_n$
, and a representative
![]() $\Xi $
of
$\Xi $
of
![]() $\xi $
; then the component
$\xi $
; then the component
![]() $\pi _0(\Lambda {\mathscr {M}}_{g,n}(\varphi '))$
is sent by
$\pi _0(\Lambda {\mathscr {M}}_{g,n}(\varphi '))$
is sent by
![]() $\sigma $
to the component
$\sigma $
to the component
![]() $\pi _0(\Lambda {\mathscr {M}}_{g,n}((\varphi ')^\Xi ))$
.
$\pi _0(\Lambda {\mathscr {M}}_{g,n}((\varphi ')^\Xi ))$
.
The action of
![]() $\mathfrak {S}_n$
on
$\mathfrak {S}_n$
on
![]() $\pi _0(\mathfrak {S}_n\cdot \Lambda {\mathscr {M}}_{g,n}(\varphi ))$
is transitive, so it suffices to check that the stabiliser of the component
$\pi _0(\mathfrak {S}_n\cdot \Lambda {\mathscr {M}}_{g,n}(\varphi ))$
is transitive, so it suffices to check that the stabiliser of the component
![]() $\Lambda {\mathscr {M}}_{g,n}(\varphi )$
is the subgroup
$\Lambda {\mathscr {M}}_{g,n}(\varphi )$
is the subgroup
![]() $\mathfrak {H}$
. First, note that an element
$\mathfrak {H}$
. First, note that an element
![]() $\sigma \in \mathfrak {H}$
can be lifted to a class
$\sigma \in \mathfrak {H}$
can be lifted to a class
![]() $\xi \in \Gamma _{g,(n)}$
that commutes with
$\xi \in \Gamma _{g,(n)}$
that commutes with
![]() $\varphi $
; this implies that
$\varphi $
; this implies that
![]() $\mathfrak {H}$
is contained in the stabiliser of
$\mathfrak {H}$
is contained in the stabiliser of
![]() $\Lambda {\mathscr {M}}_{g,n}(\varphi )$
. Vice versa, if
$\Lambda {\mathscr {M}}_{g,n}(\varphi )$
. Vice versa, if
![]() $\sigma \in \mathfrak {S}_n$
belongs to the stabiliser of
$\sigma \in \mathfrak {S}_n$
belongs to the stabiliser of
![]() $\Lambda {\mathscr {M}}_{g,n}(\varphi )$
, then we can choose a lift
$\Lambda {\mathscr {M}}_{g,n}(\varphi )$
, then we can choose a lift
![]() $\xi \in \Gamma _{g,(n)}$
of
$\xi \in \Gamma _{g,(n)}$
of
![]() $\sigma $
and a representative
$\sigma $
and a representative
![]() $\Xi $
such that
$\Xi $
such that
![]() $\Lambda {\mathscr {M}}_{g,n}(\varphi ^\Xi )$
is equal to
$\Lambda {\mathscr {M}}_{g,n}(\varphi ^\Xi )$
is equal to
![]() $\Lambda {\mathscr {M}}_{g,n}(\varphi ))$
; this implies that
$\Lambda {\mathscr {M}}_{g,n}(\varphi ))$
; this implies that
![]() $\varphi ^\Xi $
is conjugate to
$\varphi ^\Xi $
is conjugate to
![]() $\varphi $
in
$\varphi $
in
![]() $\Gamma _{g,n}$
: that is, there is a mapping class
$\Gamma _{g,n}$
: that is, there is a mapping class
![]() $\bar \xi \in \Gamma _{g,n}$
and a representative
$\bar \xi \in \Gamma _{g,n}$
and a representative
![]() $\bar \Xi $
with
$\bar \Xi $
with
![]() $\varphi ^{\Xi }=\varphi ^{\bar \Xi }$
. As a consequence
$\varphi ^{\Xi }=\varphi ^{\bar \Xi }$
. As a consequence
![]() $\xi ^{-1}\bar \xi \in \Gamma _{g,(n)}$
commutes with
$\xi ^{-1}\bar \xi \in \Gamma _{g,(n)}$
commutes with
![]() $\varphi $
, and since
$\varphi $
, and since
![]() $\xi ^{-1}\bar \xi $
also projects to
$\xi ^{-1}\bar \xi $
also projects to
![]() $\sigma $
along the natural map
$\sigma $
along the natural map
![]() $\Gamma _{g,(n)}\to \mathfrak {S}_n$
, we conclude that
$\Gamma _{g,(n)}\to \mathfrak {S}_n$
, we conclude that
![]() $\sigma \in \mathfrak {H}$
.
$\sigma \in \mathfrak {H}$
.
6.3 Relative generators for the
 ${\mathscr {M}}|_1$
-algebra
${\mathscr {M}}|_1$
-algebra
 $\Lambda {\mathscr {M}}_{*,1}$
$\Lambda {\mathscr {M}}_{*,1}$
Definition 6.4. For all
![]() $n\geqslant 1$
and
$n\geqslant 1$
and
![]() $g\geqslant 0$
, we define the space
$g\geqslant 0$
, we define the space
 $$\begin{align*}\mathfrak{C}_{g,n} := \coprod_{\substack{[\varphi]\in{\mathrm{Conj}}(\Gamma_{g,n})\\\partial\text{-irreducible}}} \Lambda{\mathscr{M}}_{g,n}(\varphi).\end{align*}$$
$$\begin{align*}\mathfrak{C}_{g,n} := \coprod_{\substack{[\varphi]\in{\mathrm{Conj}}(\Gamma_{g,n})\\\partial\text{-irreducible}}} \Lambda{\mathscr{M}}_{g,n}(\varphi).\end{align*}$$
The action of
![]() $R_n$
on
$R_n$
on
![]() $\Lambda {\mathscr {M}}_{g,n}$
restricts to an action on those path components that constitute
$\Lambda {\mathscr {M}}_{g,n}$
restricts to an action on those path components that constitute
![]() $\mathfrak {C}_{g,n}$
. We furthermore set, for all
$\mathfrak {C}_{g,n}$
. We furthermore set, for all
![]() $n\geqslant 1$
,
$n\geqslant 1$
,
 $$\begin{align*}\mathfrak{C}_n:= \coprod_{g\geqslant 0} \mathfrak{C}_{g,n}\end{align*}$$
$$\begin{align*}\mathfrak{C}_n:= \coprod_{g\geqslant 0} \mathfrak{C}_{g,n}\end{align*}$$
and obtain a
![]() $\boldsymbol {R}$
-algebra
$\boldsymbol {R}$
-algebra
![]() $\boldsymbol {\mathfrak {C}}:=(\mathfrak {C}_n)_{n\geqslant 1}$
, where
$\boldsymbol {\mathfrak {C}}:=(\mathfrak {C}_n)_{n\geqslant 1}$
, where
![]() $\boldsymbol {R}=(R_n)_{n\geqslant 1}$
.
$\boldsymbol {R}=(R_n)_{n\geqslant 1}$
.
To see that the action of
![]() $R_n$
on
$R_n$
on
![]() $\Lambda \mathfrak {M}_{g,n}$
indeed restricts to an action on
$\Lambda \mathfrak {M}_{g,n}$
indeed restricts to an action on
![]() $\mathfrak {C}_{g,n}$
, we note that, for every
$\mathfrak {C}_{g,n}$
, we note that, for every
![]() $\partial $
-irreducible mapping class
$\partial $
-irreducible mapping class
![]() $\varphi \in \Gamma _{g,n}$
, the entire orbit
$\varphi \in \Gamma _{g,n}$
, the entire orbit
![]() $\mathfrak {S}_n\cdot \Lambda {\mathscr {M}}_{g,n}(\varphi )$
is contained in
$\mathfrak {S}_n\cdot \Lambda {\mathscr {M}}_{g,n}(\varphi )$
is contained in
![]() $\mathfrak {C}_{g,n}$
. Note also that, though
$\mathfrak {C}_{g,n}$
. Note also that, though
![]() $\mathfrak {S}_n\cdot \Lambda {\mathscr {M}}_{g,n}(\varphi )$
may be disconnected, by Lemma 6.3 the action of
$\mathfrak {S}_n\cdot \Lambda {\mathscr {M}}_{g,n}(\varphi )$
may be disconnected, by Lemma 6.3 the action of
![]() $R_n$
is transitive on the connected components of
$R_n$
is transitive on the connected components of
![]() $\mathfrak {S}_n\cdot \Lambda {\mathscr {M}}_{g,n}(\varphi )$
.
$\mathfrak {S}_n\cdot \Lambda {\mathscr {M}}_{g,n}(\varphi )$
.
We now want to look at the relatively free
![]() ${\mathscr {M}}$
-algebra
${\mathscr {M}}$
-algebra
![]() $F^{\mathscr {M}}_{\boldsymbol {R}}(\boldsymbol {\mathfrak {C}})$
. Here we see, levelwise, that for each
$F^{\mathscr {M}}_{\boldsymbol {R}}(\boldsymbol {\mathfrak {C}})$
. Here we see, levelwise, that for each
![]() $n\geqslant 1$
, we have
$n\geqslant 1$
, we have
 $$\begin{align*}F^{\mathscr{M}}_{\boldsymbol{R}}(\boldsymbol{\mathfrak{C}})_n \cong \int^{(k_1,\dotsc,k_r)\in \mathbb{N}_{\geqslant 1}\wr\kern.5px\mathbf{\Sigma}} {\mathscr{M}}\tbinom{k_1,\dotsc,k_r}{n}\times_{R_{k_1}\times\dotsb\times R_{k_r}} \big(\mathfrak{C}_{k_1}\times\dotsb\times\mathfrak{C}_{k_r}\big).\end{align*}$$
$$\begin{align*}F^{\mathscr{M}}_{\boldsymbol{R}}(\boldsymbol{\mathfrak{C}})_n \cong \int^{(k_1,\dotsc,k_r)\in \mathbb{N}_{\geqslant 1}\wr\kern.5px\mathbf{\Sigma}} {\mathscr{M}}\tbinom{k_1,\dotsc,k_r}{n}\times_{R_{k_1}\times\dotsb\times R_{k_r}} \big(\mathfrak{C}_{k_1}\times\dotsb\times\mathfrak{C}_{k_r}\big).\end{align*}$$
Theorem 6.5. There is an equivalence of
![]() ${\mathscr {M}}|_1$
-algebras
${\mathscr {M}}|_1$
-algebras
The proof of Theorem 6.5 occupies the remainder of this section.
Recall the initial
![]() ${\mathscr {M}}$
-algebra
${\mathscr {M}}$
-algebra
![]() $({\mathscr {M}}\tbinom {}{n})_{n\geqslant 1}$
. Note that
$({\mathscr {M}}\tbinom {}{n})_{n\geqslant 1}$
. Note that
![]() $\Lambda {\mathscr {M}}\tbinom {}{n}$
has several connected components, and the ones corresponding to connected surfaces form precisely the subspace
$\Lambda {\mathscr {M}}\tbinom {}{n}$
has several connected components, and the ones corresponding to connected surfaces form precisely the subspace
![]() $\Lambda {\mathscr {M}}_{*,n}:=\coprod _{g\geqslant 0}\Lambda {\mathscr {M}}_{g,n}$
. We therefore have an inclusion of
$\Lambda {\mathscr {M}}_{*,n}:=\coprod _{g\geqslant 0}\Lambda {\mathscr {M}}_{g,n}$
. We therefore have an inclusion of
![]() $\boldsymbol {R}$
-algebras
$\boldsymbol {R}$
-algebras
![]() $\boldsymbol {\mathfrak {C}}\subset (\Lambda {\mathscr {M}}\tbinom {}{n})_{n\geqslant 1}$
. This inclusion is adjoint to a morphism of
$\boldsymbol {\mathfrak {C}}\subset (\Lambda {\mathscr {M}}\tbinom {}{n})_{n\geqslant 1}$
. This inclusion is adjoint to a morphism of
![]() ${\mathscr {M}}$
-algebras
${\mathscr {M}}$
-algebras
![]() $F^{{\mathscr {M}}}_{\boldsymbol {R}}(\boldsymbol {\mathfrak {C}})\to (\Lambda {\mathscr {M}}\tbinom {}{n})_{n\geqslant 1}$
, which can be restricted to a morphism of
$F^{{\mathscr {M}}}_{\boldsymbol {R}}(\boldsymbol {\mathfrak {C}})\to (\Lambda {\mathscr {M}}\tbinom {}{n})_{n\geqslant 1}$
, which can be restricted to a morphism of
![]() ${\mathscr {M}}|_1$
-algebras
${\mathscr {M}}|_1$
-algebras
![]() $\kappa \colon F^{{\mathscr {M}}}_{\boldsymbol {R}}(\boldsymbol {\mathfrak {C}})_1 \to \Lambda {\mathscr {M}}\tbinom {}{1} = \Lambda {\mathscr {M}}_{*,1}$
. It suffices to prove that
$\kappa \colon F^{{\mathscr {M}}}_{\boldsymbol {R}}(\boldsymbol {\mathfrak {C}})_1 \to \Lambda {\mathscr {M}}\tbinom {}{1} = \Lambda {\mathscr {M}}_{*,1}$
. It suffices to prove that
![]() $\kappa $
is a weak equivalence at the level of spaces. The right-hand side can be decomposed into its connected components as
$\kappa $
is a weak equivalence at the level of spaces. The right-hand side can be decomposed into its connected components as
 $$\begin{align*}\Lambda{\mathscr{M}}_{*,1}=\coprod_{\substack{g\geqslant 0\\{[\varphi]}\in{\mathrm{Conj}}(\Gamma_{g,1})}} \Lambda{\mathscr{M}}_{g,1}(\varphi).\end{align*}$$
$$\begin{align*}\Lambda{\mathscr{M}}_{*,1}=\coprod_{\substack{g\geqslant 0\\{[\varphi]}\in{\mathrm{Conj}}(\Gamma_{g,1})}} \Lambda{\mathscr{M}}_{g,1}(\varphi).\end{align*}$$
Fix
![]() $g\geqslant 0$
and a mapping class
$g\geqslant 0$
and a mapping class
![]() $\varphi \in \Gamma _{g,1}$
. Decompose
$\varphi \in \Gamma _{g,1}$
. Decompose
![]() $\Sigma _{g,1}$
along a system of curves
$\Sigma _{g,1}$
along a system of curves
![]() $c_1,\dots ,c_h$
representing the cut locus of
$c_1,\dots ,c_h$
representing the cut locus of
![]() $\varphi $
, and let W and Y denote the white and the yellow regions. We use Notation 3.2 and write
$\varphi $
, and let W and Y denote the white and the yellow regions. We use Notation 3.2 and write
![]() $Y=\coprod _{i=1}^r\coprod _{j=1}^{s_i}Y_{i,j}$
. Each component
$Y=\coprod _{i=1}^r\coprod _{j=1}^{s_i}Y_{i,j}$
. Each component
![]() $Y_{i,j}$
of Y is of type
$Y_{i,j}$
of Y is of type
![]() $\Sigma _{g_i,n_i}$
, and the restriction
$\Sigma _{g_i,n_i}$
, and the restriction
![]() $\varphi _{i,j}\in \Gamma (Y_{i,j},\partial Y_{i,j})$
of
$\varphi _{i,j}\in \Gamma (Y_{i,j},\partial Y_{i,j})$
of
![]() $\varphi $
is conjugated by a suitable diffeomorphism
$\varphi $
is conjugated by a suitable diffeomorphism
![]() $\Xi _{i,j}\colon Y_{i,j}\to \Sigma _{g_i,n_i}$
to
$\Xi _{i,j}\colon Y_{i,j}\to \Sigma _{g_i,n_i}$
to
![]() $\bar \varphi _i\in \Gamma _{g_i,n_i}$
.
$\bar \varphi _i\in \Gamma _{g_i,n_i}$
.
Note that W is a connected surface: each component of W touches some component of
![]() $\partial ^{\text {out}}W$
, and there is precisely one outgoing boundary component, since
$\partial ^{\text {out}}W$
, and there is precisely one outgoing boundary component, since
![]() $\partial ^{\text {out}}W=\partial \Sigma _{g,1}\cong S^1$
. We denote by
$\partial ^{\text {out}}W=\partial \Sigma _{g,1}\cong S^1$
. We denote by
![]() ${\mathscr {M}}(W)\subset {\mathscr {M}}\tbinom {s_1\times n_1,\dotsc , s_r\times n_r}{1}$
the component of the surface type of W, with one outgoing boundary component and
${\mathscr {M}}(W)\subset {\mathscr {M}}\tbinom {s_1\times n_1,\dotsc , s_r\times n_r}{1}$
the component of the surface type of W, with one outgoing boundary component and
![]() $h=\sum _{i}s_i\cdot n_i$
incoming boundary curves partitioned as follows: for
$h=\sum _{i}s_i\cdot n_i$
incoming boundary curves partitioned as follows: for
![]() $1\leqslant i\leqslant r$
and
$1\leqslant i\leqslant r$
and
![]() $1\leqslant j\leqslant s_i$
the curves
$1\leqslant j\leqslant s_i$
the curves
![]() $\partial Y_{i,j}\subset \partial ^{\text {in}}W$
form a piece of the partition, corresponding to an input of colour
$\partial Y_{i,j}\subset \partial ^{\text {in}}W$
form a piece of the partition, corresponding to an input of colour
![]() $n_i$
. The total number of inputs is thus
$n_i$
. The total number of inputs is thus
![]() $s_1+\dotsb +s_r$
. Consider now the following subspace, which a priori is a union of connected components of
$s_1+\dotsb +s_r$
. Consider now the following subspace, which a priori is a union of connected components of
![]() $F^{{\mathscr {M}}}_{\boldsymbol {R}}(\boldsymbol {\mathfrak {C}})_1$
$F^{{\mathscr {M}}}_{\boldsymbol {R}}(\boldsymbol {\mathfrak {C}})_1$
 $$ \begin{align*} F^{{\mathscr{M}}}_{\boldsymbol{R}}(\boldsymbol{\mathfrak{C}})_\varphi &:= {\mathscr{M}}(W) \times_{\prod_i R_{n_i}^{s_i}\rtimes \mathfrak{S}_{s_i}} \prod_{i=1}^r\left(\mathfrak{S}_{n_i}\cdot\Lambda{\mathscr{M}}_{g_i,n_i}(\bar\varphi_i)\right)^{s_i}\\ &\>= {\mathscr{M}}(W) \times_{T^{h} \rtimes \prod_i (\mathfrak{S}_{n_i}^{s_i}\rtimes\mathfrak{S}_{s_i})} \prod_{i=1}^r\left(\mathfrak{S}_{n_i}\cdot\Lambda{\mathscr{M}}_{g_i,n_i}(\bar\varphi_i)\right)^{s_i} \subset F^{{\mathscr{M}}}_{\boldsymbol{R}}(\boldsymbol{\mathfrak{C}})_1. \end{align*} $$
$$ \begin{align*} F^{{\mathscr{M}}}_{\boldsymbol{R}}(\boldsymbol{\mathfrak{C}})_\varphi &:= {\mathscr{M}}(W) \times_{\prod_i R_{n_i}^{s_i}\rtimes \mathfrak{S}_{s_i}} \prod_{i=1}^r\left(\mathfrak{S}_{n_i}\cdot\Lambda{\mathscr{M}}_{g_i,n_i}(\bar\varphi_i)\right)^{s_i}\\ &\>= {\mathscr{M}}(W) \times_{T^{h} \rtimes \prod_i (\mathfrak{S}_{n_i}^{s_i}\rtimes\mathfrak{S}_{s_i})} \prod_{i=1}^r\left(\mathfrak{S}_{n_i}\cdot\Lambda{\mathscr{M}}_{g_i,n_i}(\bar\varphi_i)\right)^{s_i} \subset F^{{\mathscr{M}}}_{\boldsymbol{R}}(\boldsymbol{\mathfrak{C}})_1. \end{align*} $$
Lemma 6.6. The space
![]() $F^{{\mathscr {M}}}_{\boldsymbol {R}}(\boldsymbol {\mathfrak {C}})_\varphi $
is connected.
$F^{{\mathscr {M}}}_{\boldsymbol {R}}(\boldsymbol {\mathfrak {C}})_\varphi $
is connected.
Proof. We observe that
![]() ${\mathscr {M}}(W)$
is connected; therefore, in order to prove that
${\mathscr {M}}(W)$
is connected; therefore, in order to prove that
![]() $F^{{\mathscr {M}}}_{\boldsymbol {R}}(\boldsymbol {\mathfrak {C}})_\varphi $
is connected, it suffices to check that
$F^{{\mathscr {M}}}_{\boldsymbol {R}}(\boldsymbol {\mathfrak {C}})_\varphi $
is connected, it suffices to check that
![]() $T^{h} \rtimes \prod _{i=1}^r (\mathfrak {S}_{n_i}^{s_i}\rtimes \mathfrak {S}_{s_i})$
acts transitively on the connected components of
$T^{h} \rtimes \prod _{i=1}^r (\mathfrak {S}_{n_i}^{s_i}\rtimes \mathfrak {S}_{s_i})$
acts transitively on the connected components of
![]() $\prod _{i=1}^r\left (\mathfrak {S}_{n_i}\cdot \Lambda {\mathscr {M}}_{g_i,n_i}(\bar \varphi _i)\right )^{s_i}$
.
$\prod _{i=1}^r\left (\mathfrak {S}_{n_i}\cdot \Lambda {\mathscr {M}}_{g_i,n_i}(\bar \varphi _i)\right )^{s_i}$
.
This reduces to checking that for all
![]() $1\leqslant i\leqslant r$
, the group
$1\leqslant i\leqslant r$
, the group
![]() $(\mathfrak {S}_{n_i}^{s_i}\rtimes \mathfrak {S}_{s_i})$
acts transitively on the components of
$(\mathfrak {S}_{n_i}^{s_i}\rtimes \mathfrak {S}_{s_i})$
acts transitively on the components of
![]() $\left (\mathfrak {S}_{n_i}\cdot \Lambda {\mathscr {M}}_{g_i,n_i}(\bar \varphi _i)\right )^{s_i}$
, and to this aim it suffices to check that
$\left (\mathfrak {S}_{n_i}\cdot \Lambda {\mathscr {M}}_{g_i,n_i}(\bar \varphi _i)\right )^{s_i}$
, and to this aim it suffices to check that
![]() $\mathfrak {S}_{n_i}$
acts transitively on the components of
$\mathfrak {S}_{n_i}$
acts transitively on the components of
![]() $\mathfrak {S}_{n_i}\cdot \Lambda {\mathscr {M}}_{g_i,n_i}(\bar \varphi _i)$
, which is clear by definition.
$\mathfrak {S}_{n_i}\cdot \Lambda {\mathscr {M}}_{g_i,n_i}(\bar \varphi _i)$
, which is clear by definition.
Using Notation 3.7, the proof of Lemma 6.6 shows in fact that there is a homeomorphism
 $$\begin{align*}F^{{\mathscr{M}}}_{\boldsymbol{R}}(\boldsymbol{\mathfrak{C}})_\varphi\cong {\mathscr{M}}(W) \times_{T^h \rtimes \prod_i (\mathfrak{H}_i^{s_i}\rtimes\mathfrak{S}_{s_i})} \prod_{i=1}^r\left(\Lambda{\mathscr{M}}_{g_i,n_i}(\bar\varphi_i)\right)^{s_i},\end{align*}$$
$$\begin{align*}F^{{\mathscr{M}}}_{\boldsymbol{R}}(\boldsymbol{\mathfrak{C}})_\varphi\cong {\mathscr{M}}(W) \times_{T^h \rtimes \prod_i (\mathfrak{H}_i^{s_i}\rtimes\mathfrak{S}_{s_i})} \prod_{i=1}^r\left(\Lambda{\mathscr{M}}_{g_i,n_i}(\bar\varphi_i)\right)^{s_i},\end{align*}$$
using that
![]() $\mathfrak {H}_i\subseteq \mathfrak {S}_{n_i}$
is the stabiliser of the path component
$\mathfrak {H}_i\subseteq \mathfrak {S}_{n_i}$
is the stabiliser of the path component
![]() $\Lambda {\mathscr {M}}_{g,n}(\bar \varphi _i)\subseteq \mathfrak {C}_{g_i,n_i}$
. The following proposition directly implies Theorem 6.5, since
$\Lambda {\mathscr {M}}_{g,n}(\bar \varphi _i)\subseteq \mathfrak {C}_{g_i,n_i}$
. The following proposition directly implies Theorem 6.5, since
![]() $F^{{\mathscr {M}}}_{\boldsymbol {R}}(\boldsymbol {\mathfrak {C}})_\varphi $
and
$F^{{\mathscr {M}}}_{\boldsymbol {R}}(\boldsymbol {\mathfrak {C}})_\varphi $
and
![]() $\Lambda {\mathscr {M}}_{g,1}(\varphi )$
are the connected components of
$\Lambda {\mathscr {M}}_{g,1}(\varphi )$
are the connected components of
![]() $F^{{\mathscr {M}}}_{\boldsymbol {R}}(\boldsymbol {\mathfrak {C}})_1$
and
$F^{{\mathscr {M}}}_{\boldsymbol {R}}(\boldsymbol {\mathfrak {C}})_1$
and
![]() $\Lambda {\mathscr {M}}_{*,1}$
.
$\Lambda {\mathscr {M}}_{*,1}$
.
Proposition 6.7. The map
![]() $\kappa $
restricts to a homotopy equivalence
$\kappa $
restricts to a homotopy equivalence
Proof. The space
![]() ${\mathscr {M}}(W)$
classifies the group
${\mathscr {M}}(W)$
classifies the group
![]() $\Gamma (W,\partial W)$
, whereas the product
$\Gamma (W,\partial W)$
, whereas the product
![]() $\prod _{i}\left (\Lambda {\mathscr {M}}_{g_i,n_i}(\bar \varphi _i)\right )^{s_i}$
is a classifying space for the group
$\prod _{i}\left (\Lambda {\mathscr {M}}_{g_i,n_i}(\bar \varphi _i)\right )^{s_i}$
is a classifying space for the group
![]() $\prod _{i} (Z(\bar \varphi _i,\Gamma _{g_i,n_i}))^{s_i}$
. This implies that there is a homotopy equivalence
$\prod _{i} (Z(\bar \varphi _i,\Gamma _{g_i,n_i}))^{s_i}$
. This implies that there is a homotopy equivalence
 $$\begin{align*}{\mathscr{M}}(W) \times \prod_{i=1}^r\left(\Lambda{\mathscr{M}}_{g_i,n_i}(\bar\varphi_i)\right)^{s_i} \simeq B\left(\Gamma(W,\partial W)\times \prod_{i=1}^r (Z(\bar\varphi_i,\Gamma_{g_i,n_i}))^{s_i}\right).\end{align*}$$
$$\begin{align*}{\mathscr{M}}(W) \times \prod_{i=1}^r\left(\Lambda{\mathscr{M}}_{g_i,n_i}(\bar\varphi_i)\right)^{s_i} \simeq B\left(\Gamma(W,\partial W)\times \prod_{i=1}^r (Z(\bar\varphi_i,\Gamma_{g_i,n_i}))^{s_i}\right).\end{align*}$$
For
![]() $\mathfrak {H}:= \prod _i(\mathfrak {H}^{s_i}_i\rtimes \mathfrak {S}_{s_i})\subseteq \mathfrak {S}_h$
, the compact Lie group
$\mathfrak {H}:= \prod _i(\mathfrak {H}^{s_i}_i\rtimes \mathfrak {S}_{s_i})\subseteq \mathfrak {S}_h$
, the compact Lie group
![]() $T^{h} \rtimes \mathfrak {H} \subseteq R_n$
acts freely on
$T^{h} \rtimes \mathfrak {H} \subseteq R_n$
acts freely on
![]() ${\mathscr {M}}(W)$
by Lemma 4.14. Since
${\mathscr {M}}(W)$
by Lemma 4.14. Since
![]() ${\mathscr {M}}(W)\times \prod _i (\Lambda {\mathscr {M}}_{g_i,n_i}(\bar \varphi _i))^{s_i}$
is a Tychonoff space, [Reference Körschgen12, Thm. A8viii] ensures that we obtain a principal fibre bundle
${\mathscr {M}}(W)\times \prod _i (\Lambda {\mathscr {M}}_{g_i,n_i}(\bar \varphi _i))^{s_i}$
is a Tychonoff space, [Reference Körschgen12, Thm. A8viii] ensures that we obtain a principal fibre bundle
 $$\begin{align*}T^{h} \!\rtimes \mathfrak{H} \to {\mathscr{M}}(W) \times \prod_{i=1}^r\left(\Lambda{\mathscr{M}}_{g_i,n_i}(\bar\varphi_i)\right)^{s_i} \to {\mathscr{M}}(W) \times\!_{T^{h} \rtimes \mathfrak{H}} \prod_{i=1}^r\left(\Lambda{\mathscr{M}}_{g_i,n_i}(\bar\varphi_i)\right)^{s_i}.\end{align*}$$
$$\begin{align*}T^{h} \!\rtimes \mathfrak{H} \to {\mathscr{M}}(W) \times \prod_{i=1}^r\left(\Lambda{\mathscr{M}}_{g_i,n_i}(\bar\varphi_i)\right)^{s_i} \to {\mathscr{M}}(W) \times\!_{T^{h} \rtimes \mathfrak{H}} \prod_{i=1}^r\left(\Lambda{\mathscr{M}}_{g_i,n_i}(\bar\varphi_i)\right)^{s_i}.\end{align*}$$
We will split the fibre bundle in two stages, involving separately the factors
![]() $\mathfrak {H}$
and
$\mathfrak {H}$
and
![]() $T^{h}$
of the fibre. First, consider the principal fibre bundle
$T^{h}$
of the fibre. First, consider the principal fibre bundle
from which we conclude that
![]() $\smash {{\mathscr {M}}(W) \times _{\mathfrak {H}} \prod _{i} \left (\Lambda {\mathscr {M}}_{g_i,n_i}(\bar \varphi _i)\right )^{s_i}}$
is connected and aspherical.
$\smash {{\mathscr {M}}(W) \times _{\mathfrak {H}} \prod _{i} \left (\Lambda {\mathscr {M}}_{g_i,n_i}(\bar \varphi _i)\right )^{s_i}}$
is connected and aspherical.
In fact,
![]() $\smash {{\mathscr {M}}(W) \times _{\mathfrak {H}} \prod _{i}\left (\Lambda {\mathscr {M}}_{g_i,n_i}(\bar \varphi _i)\right )^{s_i}}$
is a classifying space for the group
$\smash {{\mathscr {M}}(W) \times _{\mathfrak {H}} \prod _{i}\left (\Lambda {\mathscr {M}}_{g_i,n_i}(\bar \varphi _i)\right )^{s_i}}$
is a classifying space for the group
![]() $\smash {\tilde Z(\varphi )}$
introduced in Definition 3.4: the space
$\smash {\tilde Z(\varphi )}$
introduced in Definition 3.4: the space
![]() ${\mathscr {M}}(W)\simeq B\Gamma (W,\partial W)$
admits a free action of the finite group
${\mathscr {M}}(W)\simeq B\Gamma (W,\partial W)$
admits a free action of the finite group
![]() $\mathfrak {H}$
, and the quotient
$\mathfrak {H}$
, and the quotient
![]() ${\mathscr {M}}(W)/\mathfrak {H}$
is a classifying space for the extended mapping class group
${\mathscr {M}}(W)/\mathfrak {H}$
is a classifying space for the extended mapping class group
![]() $\Gamma ^{\mathfrak {H}}(W)$
(see Definition 2.6). Similarly, the homotopy quotient
$\Gamma ^{\mathfrak {H}}(W)$
(see Definition 2.6). Similarly, the homotopy quotient

is a classifying space for
![]() $Z(\varphi _Y,\Gamma (Y))$
, which by Lemma 3.6 is isomorphic to
$Z(\varphi _Y,\Gamma (Y))$
, which by Lemma 3.6 is isomorphic to
![]() $\prod _{i}(Z(\bar \varphi _i,\Gamma _{g_i,(n_i)})^{s_i}\rtimes \mathfrak {S}_{s_i})$
. The balanced product
$\prod _{i}(Z(\bar \varphi _i,\Gamma _{g_i,(n_i)})^{s_i}\rtimes \mathfrak {S}_{s_i})$
. The balanced product
![]() ${\mathscr {M}}(W) \times _{\mathfrak {H}}\prod _{i}\left (\Lambda {\mathscr {M}}_{g_i,n_i}(\bar \varphi _i)\right )^{s_i}$
is then homotopy equivalent to
${\mathscr {M}}(W) \times _{\mathfrak {H}}\prod _{i}\left (\Lambda {\mathscr {M}}_{g_i,n_i}(\bar \varphi _i)\right )^{s_i}$
is then homotopy equivalent to
 $$\begin{align*}{\mathscr{M}}(W)\times_{\mathfrak{H}} \left(\prod_{i=1}^r\left(\Lambda{\mathscr{M}}_{g_i,n_i}(\bar\varphi_i)\right)^{s_i}\times E\mathfrak{H}\right),\end{align*}$$
$$\begin{align*}{\mathscr{M}}(W)\times_{\mathfrak{H}} \left(\prod_{i=1}^r\left(\Lambda{\mathscr{M}}_{g_i,n_i}(\bar\varphi_i)\right)^{s_i}\times E\mathfrak{H}\right),\end{align*}$$
which is a classifying space for
![]() $\tilde Z(\varphi )$
. The last step is to consider the fibre bundle (which is no longer a principal bundle)
$\tilde Z(\varphi )$
. The last step is to consider the fibre bundle (which is no longer a principal bundle)
 $$\begin{align*}T^{h} \to {\mathscr{M}}(W) \times\!_{\mathfrak{H}}\prod_{i=1}^r\left(\Lambda{\mathscr{M}}_{g_i,n_i}(\bar\varphi_i)\right)^{s_i} \to {\mathscr{M}}(W) \times_{T^{h} \rtimes \mathfrak{H}}\prod_{i=1}^r\left(\Lambda{\mathscr{M}}_{g_i,n_i}(\bar\varphi_i)\right)^{s_i}.\end{align*}$$
$$\begin{align*}T^{h} \to {\mathscr{M}}(W) \times\!_{\mathfrak{H}}\prod_{i=1}^r\left(\Lambda{\mathscr{M}}_{g_i,n_i}(\bar\varphi_i)\right)^{s_i} \to {\mathscr{M}}(W) \times_{T^{h} \rtimes \mathfrak{H}}\prod_{i=1}^r\left(\Lambda{\mathscr{M}}_{g_i,n_i}(\bar\varphi_i)\right)^{s_i}.\end{align*}$$
Since the fibre and the total space are aspherical, the base space is also aspherical: note that the base is precisely
![]() $F^{{\mathscr {M}}}_{\boldsymbol {R}}(\boldsymbol {\mathfrak {C}})_\varphi $
. The above fibre bundle shows that the fundamental group of
$F^{{\mathscr {M}}}_{\boldsymbol {R}}(\boldsymbol {\mathfrak {C}})_\varphi $
. The above fibre bundle shows that the fundamental group of
![]() $F^{{\mathscr {M}}}_{\boldsymbol {R}}(\boldsymbol {\mathfrak {C}})_\varphi $
is a quotient of
$F^{{\mathscr {M}}}_{\boldsymbol {R}}(\boldsymbol {\mathfrak {C}})_\varphi $
is a quotient of
![]() $\tilde Z(\varphi )$
by a normal subgroup
$\tilde Z(\varphi )$
by a normal subgroup
![]() $\mathbb {Z}^h$
. Consider the gluing map
$\mathbb {Z}^h$
. Consider the gluing map
 $$\begin{align*}\tilde\kappa\colon{\mathscr{M}}(W) \times_{\mathfrak{H}}\prod_{i=1}^r \left(\Lambda{\mathscr{M}}_{g_i,n_i}(\bar\varphi_i)\right)^{s_i} \to \Lambda{\mathscr{M}}_{g,1}(\varphi).\end{align*}$$
$$\begin{align*}\tilde\kappa\colon{\mathscr{M}}(W) \times_{\mathfrak{H}}\prod_{i=1}^r \left(\Lambda{\mathscr{M}}_{g_i,n_i}(\bar\varphi_i)\right)^{s_i} \to \Lambda{\mathscr{M}}_{g,1}(\varphi).\end{align*}$$
The map induced by
![]() $\tilde \kappa $
on fundamental groups is
$\tilde \kappa $
on fundamental groups is
![]() $\varepsilon \colon \tilde Z_\partial (\varphi )\to Z_\partial (\varphi )$
, so by Proposition 3.8, we just have to identify the kernel of
$\varepsilon \colon \tilde Z_\partial (\varphi )\to Z_\partial (\varphi )$
, so by Proposition 3.8, we just have to identify the kernel of
![]() $\varepsilon $
and the subgroup
$\varepsilon $
and the subgroup
 $$\begin{align*}\pi_1(T^h)\subset\pi_1\left( {\mathscr{M}}(W) \times\!_{\mathfrak{H}} \prod_{i=1}^r\left(\Lambda{\mathscr{M}}_{g_i,n_i}(\bar\varphi_i)\right)^{s_i}\right).\end{align*}$$
$$\begin{align*}\pi_1(T^h)\subset\pi_1\left( {\mathscr{M}}(W) \times\!_{\mathfrak{H}} \prod_{i=1}^r\left(\Lambda{\mathscr{M}}_{g_i,n_i}(\bar\varphi_i)\right)^{s_i}\right).\end{align*}$$
The inclusion of the fibre
![]() $T^{h} \hookrightarrow {\mathscr {M}}(W) \times _{\mathfrak {H}}\prod _i\left (\Lambda {\mathscr {M}}_{g_i,n_i}(\bar \varphi _i)\right )^{s_i}$
lifts to the covering space
$T^{h} \hookrightarrow {\mathscr {M}}(W) \times _{\mathfrak {H}}\prod _i\left (\Lambda {\mathscr {M}}_{g_i,n_i}(\bar \varphi _i)\right )^{s_i}$
lifts to the covering space
![]() ${\mathscr {M}}(W) \times \prod _{i}\left (\Lambda {\mathscr {M}}_{g_i,n_i}(\bar \varphi _i)\right )^{s_i}$
of the right-hand side and becomes part of the inclusion of the fibre
${\mathscr {M}}(W) \times \prod _{i}\left (\Lambda {\mathscr {M}}_{g_i,n_i}(\bar \varphi _i)\right )^{s_i}$
of the right-hand side and becomes part of the inclusion of the fibre
![]() $T^{h}\rtimes \mathfrak {H}\hookrightarrow {\mathscr {M}}(W)\times \prod _{i}\left (\Lambda {\mathscr {M}}_{g_i,n_i}(\bar \varphi _i)\right )^{s_i}$
of the first principal bundle that we considered above. In particular, the inclusion
$T^{h}\rtimes \mathfrak {H}\hookrightarrow {\mathscr {M}}(W)\times \prod _{i}\left (\Lambda {\mathscr {M}}_{g_i,n_i}(\bar \varphi _i)\right )^{s_i}$
of the first principal bundle that we considered above. In particular, the inclusion
![]() $\pi _1(T^h)\hookrightarrow \tilde Z(\varphi ) =\pi _1\left ({\mathscr {M}}(W) \times _{\mathfrak {H}}\prod _{i} \left (\Lambda {\mathscr {M}}_{g_i,n_i}(\bar \varphi _i)\right )^{s_i}\right )$
has its image inside
$\pi _1(T^h)\hookrightarrow \tilde Z(\varphi ) =\pi _1\left ({\mathscr {M}}(W) \times _{\mathfrak {H}}\prod _{i} \left (\Lambda {\mathscr {M}}_{g_i,n_i}(\bar \varphi _i)\right )^{s_i}\right )$
has its image inside
 $$\begin{align*}\Gamma(W,\partial W)\times Z(\varphi_Y,\Gamma(Y,\partial Y)) =\pi_1\left({\mathscr{M}}(W) \times \prod_{i=1}^r \left(\Lambda{\mathscr{M}}_{g_i,n_i}(\bar\varphi_i)\right)^{s_i}\right).\end{align*}$$
$$\begin{align*}\Gamma(W,\partial W)\times Z(\varphi_Y,\Gamma(Y,\partial Y)) =\pi_1\left({\mathscr{M}}(W) \times \prod_{i=1}^r \left(\Lambda{\mathscr{M}}_{g_i,n_i}(\bar\varphi_i)\right)^{s_i}\right).\end{align*}$$
Recall
![]() $T^h$
is included into
$T^h$
is included into
![]() ${\mathscr {M}}(W) \times \prod _{i}\left (\Lambda {\mathscr {M}}_{g_i,n_i}(\bar \varphi _i)\right )^{s_i}$
as an orbit of the balanced diagonal
${\mathscr {M}}(W) \times \prod _{i}\left (\Lambda {\mathscr {M}}_{g_i,n_i}(\bar \varphi _i)\right )^{s_i}$
as an orbit of the balanced diagonal
![]() $T^h$
-action on the two main factors of the latter space. The action of
$T^h$
-action on the two main factors of the latter space. The action of
![]() $(z_1,\dots ,z_h)\in T^h$
is on right on the first factor, by precomposition with
$(z_1,\dots ,z_h)\in T^h$
is on right on the first factor, by precomposition with
![]() $(z_1,\dots ,z_h)\in R_n\subset \mathbf {M}_\partial \tbinom {h}{h}$
, and is on left on the second factor, by postcomposition with the inverse of
$(z_1,\dots ,z_h)\in R_n\subset \mathbf {M}_\partial \tbinom {h}{h}$
, and is on left on the second factor, by postcomposition with the inverse of
![]() $(z_1,\dots ,z_h)\in R_n\subset \mathbf {M}_\partial \tbinom {h}{h}$
.
$(z_1,\dots ,z_h)\in R_n\subset \mathbf {M}_\partial \tbinom {h}{h}$
.
At the level of fundamental groups, the i
th generator of
![]() $\pi _1(T^h)\cong \mathbb {Z}^h$
is mapped to
$\pi _1(T^h)\cong \mathbb {Z}^h$
is mapped to
![]() $(D_{c_i},D_{c_i}^{-1})\in \Gamma (W,\partial W)\times Z(\varphi _Y,\Gamma (Y,\partial Y))$
. We saw that these h couples generate the kernel of
$(D_{c_i},D_{c_i}^{-1})\in \Gamma (W,\partial W)\times Z(\varphi _Y,\Gamma (Y,\partial Y))$
. We saw that these h couples generate the kernel of
![]() $\varepsilon $
as a free abelian group of rank h.
$\varepsilon $
as a free abelian group of rank h.
Putting together Theorem 6.5 and Theorem 5.9, we obtain Theorem 1.1:
Proof of Theorem 1.1
The point-set requirements for our Setting 5.8 are clearly satisfied in the case
![]() ${\mathscr {O}}={\mathscr {M}}$
,
${\mathscr {O}}={\mathscr {M}}$
,
![]() $\mathbf {C}=\boldsymbol {R}$
, and
$\mathbf {C}=\boldsymbol {R}$
, and
![]() ${\boldsymbol {X}}=\boldsymbol {\mathfrak {C}}_+$
. Hence, we can apply Theorem 5.9 and obtain
${\boldsymbol {X}}=\boldsymbol {\mathfrak {C}}_+$
. Hence, we can apply Theorem 5.9 and obtain
Consider the left side first: we claim that
![]() $\varphi \colon \tilde F^{\mathscr {M}}_{{\mathscr {B}}\otimes \boldsymbol {R}}(\boldsymbol {\mathfrak {C}}_+) \to F^{\mathscr {M}}_{{\mathscr {B}}\otimes \boldsymbol {R}}(\boldsymbol {\mathfrak {C}}_+)$
, the map of
$\varphi \colon \tilde F^{\mathscr {M}}_{{\mathscr {B}}\otimes \boldsymbol {R}}(\boldsymbol {\mathfrak {C}}_+) \to F^{\mathscr {M}}_{{\mathscr {B}}\otimes \boldsymbol {R}}(\boldsymbol {\mathfrak {C}}_+)$
, the map of
![]() ${\mathscr {M}}$
-algebras from the derived relatively free algebra to the actual one is an equivalence: here we use that the basepoints are isolated, whence the map splits into
${\mathscr {M}}$
-algebras from the derived relatively free algebra to the actual one is an equivalence: here we use that the basepoints are isolated, whence the map splits into
![]() $\coprod _{K\in S}\varphi _K$
for a system
$\coprod _{K\in S}\varphi _K$
for a system
![]() $S\subseteq \coprod _r \mathbb {N}_{\geqslant 1}^r$
of representatives of tuples with respect to coordinate permutation. If we denote again by
$S\subseteq \coprod _r \mathbb {N}_{\geqslant 1}^r$
of representatives of tuples with respect to coordinate permutation. If we denote again by
![]() $r(k)\geqslant 0$
the number of occurrences of k in the sequence K, then the compact Lie group
$r(k)\geqslant 0$
the number of occurrences of k in the sequence K, then the compact Lie group
![]() $G:= \prod _{k\geqslant 0}R_{k}\wr \mathfrak {S}_{r_k}$
acts on
$G:= \prod _{k\geqslant 0}R_{k}\wr \mathfrak {S}_{r_k}$
acts on
![]() $Y:= {\mathscr {M}}\tbinom {K}{n}\times \prod _i\mathfrak {C}_{k_i}$
, and
$Y:= {\mathscr {M}}\tbinom {K}{n}\times \prod _i\mathfrak {C}_{k_i}$
, and
![]() $\varphi _K$
is exactly the map that compares the homotopy quotient of this action with the actual quotient. However, Y is a Hausdorff space and G acts freely on Y, since
$\varphi _K$
is exactly the map that compares the homotopy quotient of this action with the actual quotient. However, Y is a Hausdorff space and G acts freely on Y, since
![]() ${\mathscr {M}}$
is
${\mathscr {M}}$
is
![]() $\mathfrak {S}$
-free and
$\mathfrak {S}$
-free and
![]() $R_k$
acts freely on
$R_k$
acts freely on
![]() ${\mathscr {M}}$
by precomposition; see Lemma 4.14. In this situation, [Reference Körschgen12, Thm. A.7] tells us that the map comparing the homotopy quotient with the actual quotient is an equivalence. In particular, for
${\mathscr {M}}$
by precomposition; see Lemma 4.14. In this situation, [Reference Körschgen12, Thm. A.7] tells us that the map comparing the homotopy quotient with the actual quotient is an equivalence. In particular, for
![]() $n=1$
, the left side is equivalent, as a loop space, to the group completion
$n=1$
, the left side is equivalent, as a loop space, to the group completion
![]() $\Omega B\Lambda \mathfrak {M}_{*,1}$
by Theorem 6.5. Let us now look at the right side: here we see that
$\Omega B\Lambda \mathfrak {M}_{*,1}$
by Theorem 6.5. Let us now look at the right side: here we see that
where
denotes the homotopy quotient. If we focus again on the case
![]() $n=1$
, then we saw in Example 4.16 that the first level of the initial
$n=1$
, then we saw in Example 4.16 that the first level of the initial
![]() ${\mathscr {M}}$
-algebra,
${\mathscr {M}}$
-algebra,
![]() ${\mathscr {M}}\tbinom {}{1}$
, coincides with the old
${\mathscr {M}}\tbinom {}{1}$
, coincides with the old
![]() ${\mathscr {M}}|_1$
-algebra
${\mathscr {M}}|_1$
-algebra
![]() $\coprod _{g}\mathfrak {M}_{g,1}$
whose group completion is accessible by the Madsen–Weiss theorem. Hence, we can replace the factor
$\coprod _{g}\mathfrak {M}_{g,1}$
whose group completion is accessible by the Madsen–Weiss theorem. Hence, we can replace the factor
![]() $\Omega B{\mathscr {M}}\tbinom {}{1}$
by
$\Omega B{\mathscr {M}}\tbinom {}{1}$
by
![]() $\Omega ^\infty \mathbf {MTSO}(2)$
. This proves the claim.
$\Omega ^\infty \mathbf {MTSO}(2)$
. This proves the claim.
A General mapping spaces into
 $\mathfrak {M}_{*,1}$
$\mathfrak {M}_{*,1}$
In this first appendix, we briefly discuss a variation of Theorem 1.1 for a generic parametrising topological space X, highlighting the main enhancements that the proof requires.
We chose to restrict ourselves to the case
![]() $X=S^1$
throughout the main part of the article because this special context already presents all the relevant complexity of the problem, and we believe that it is more instructive to consider the special case first.
$X=S^1$
throughout the main part of the article because this special context already presents all the relevant complexity of the problem, and we believe that it is more instructive to consider the special case first.
A.1 General parametrising spaces X
Our goal is to give a description of
![]() $\Omega B({\mathrm {map}}(X,\mathfrak {M}_{*,1}))$
as an infinite loop space. We assume for simplicity that X has the homotopy type of a connected CW complex.
$\Omega B({\mathrm {map}}(X,\mathfrak {M}_{*,1}))$
as an infinite loop space. We assume for simplicity that X has the homotopy type of a connected CW complex.
Let
![]() $G:= \pi _1(X)$
. For all
$G:= \pi _1(X)$
. For all
![]() $g\geqslant 0$
and
$g\geqslant 0$
and
![]() $n\geqslant 1$
, we replace the space
$n\geqslant 1$
, we replace the space
![]() $\mathfrak {M}_{g,n}$
with the homotopy equivalent space
$\mathfrak {M}_{g,n}$
with the homotopy equivalent space
![]() ${\mathscr {M}}_{g,n}$
, which admits an action of the group
${\mathscr {M}}_{g,n}$
, which admits an action of the group
![]() $R_n$
. Since
$R_n$
. Since
![]() ${\mathscr {M}}_{g,n}$
is aspherical, the space
${\mathscr {M}}_{g,n}$
is aspherical, the space
![]() ${\mathrm {map}}(X,{\mathscr {M}}_{g,n})$
is homotopy equivalent to
${\mathrm {map}}(X,{\mathscr {M}}_{g,n})$
is homotopy equivalent to
![]() ${\mathrm {map}}(BG,{\mathscr {M}}_{g,n})$
.
${\mathrm {map}}(BG,{\mathscr {M}}_{g,n})$
.
More precisely, let
![]() ${\mathrm {Conj}}(G\to \Gamma _{g,n})$
be the set of conjugacy classes of homomorphisms
${\mathrm {Conj}}(G\to \Gamma _{g,n})$
be the set of conjugacy classes of homomorphisms
![]() $G \to \Gamma _{g,n}$
, where two such homomorphisms
$G \to \Gamma _{g,n}$
, where two such homomorphisms
![]() $\varphi ,\varphi '$
are conjugate if there exists
$\varphi ,\varphi '$
are conjugate if there exists
![]() $\xi \in \Gamma _{g,n}$
, represented by
$\xi \in \Gamma _{g,n}$
, represented by
![]() $\Xi $
, with
$\Xi $
, with
![]() $\varphi '=\varphi ^\Xi $
: then we can identify
$\varphi '=\varphi ^\Xi $
: then we can identify
 $$\begin{align*}{\mathrm{map}}(X,{\mathscr{M}}_{g,n})= \coprod_{[\varphi]\in{\mathrm{Conj}}(G\to\Gamma_{g,n})}{\mathrm{map}}(X,{\mathscr{M}}_{g,n})(\varphi) \simeq \coprod_{[\varphi]\in{\mathrm{Conj}}(G\to\Gamma_{g,n})} BZ(\varphi,\Gamma_{g,n}),\end{align*}$$
$$\begin{align*}{\mathrm{map}}(X,{\mathscr{M}}_{g,n})= \coprod_{[\varphi]\in{\mathrm{Conj}}(G\to\Gamma_{g,n})}{\mathrm{map}}(X,{\mathscr{M}}_{g,n})(\varphi) \simeq \coprod_{[\varphi]\in{\mathrm{Conj}}(G\to\Gamma_{g,n})} BZ(\varphi,\Gamma_{g,n}),\end{align*}$$
where
![]() $Z(\varphi ,\Gamma _{g,n})$
denotes the centraliser of the image of
$Z(\varphi ,\Gamma _{g,n})$
denotes the centraliser of the image of
![]() $\varphi $
in
$\varphi $
in
![]() $\Gamma _{g,n}$
.
$\Gamma _{g,n}$
.
Definition A.1. A homomorphism
![]() $\varphi \colon G\to \Gamma _{g,n}$
is called
$\varphi \colon G\to \Gamma _{g,n}$
is called
![]() $\partial $
-irreducible if it is not the trivial representation in
$\partial $
-irreducible if it is not the trivial representation in
![]() $\Gamma _{0,1}$
and there is no isotopy class of an essential arc
$\Gamma _{0,1}$
and there is no isotopy class of an essential arc
![]() $\alpha \subset \Sigma _{g,n}$
, which is fixed by the entire image of
$\alpha \subset \Sigma _{g,n}$
, which is fixed by the entire image of
![]() $\varphi $
. Being
$\varphi $
. Being
![]() $\partial $
-irreducible is a conjugacy-invariant property of representations. We denote by
$\partial $
-irreducible is a conjugacy-invariant property of representations. We denote by
 $$\begin{align*}\mathfrak{C}_{g,n}(X) := \coprod_{\substack{[\varphi]\in{\mathrm{Conj}}(G\to\Gamma_{g,n})\\\partial\text{-irreducible}}} {\mathrm{map}}(X,{\mathscr{M}}_{g,n})(\varphi).\end{align*}$$
$$\begin{align*}\mathfrak{C}_{g,n}(X) := \coprod_{\substack{[\varphi]\in{\mathrm{Conj}}(G\to\Gamma_{g,n})\\\partial\text{-irreducible}}} {\mathrm{map}}(X,{\mathscr{M}}_{g,n})(\varphi).\end{align*}$$
For all
![]() $n\geqslant 1$
, there is a natural action of the group
$n\geqslant 1$
, there is a natural action of the group
![]() $R_n$
on
$R_n$
on
![]() $\mathfrak {C}_{g,n}(X)$
, and the analogue of Theorem 1.1 is the following:
$\mathfrak {C}_{g,n}(X)$
, and the analogue of Theorem 1.1 is the following:
Theorem A.2. In the above setting and with the above definitions, there is an equivalence of loop spaces

In order to prove Theorem A.2, the main obstacle is, at the very beginning, to generalise Proposition 2.11 from the context of a single diffeomorphism
![]() $\Phi $
, representing a single mapping class
$\Phi $
, representing a single mapping class
![]() $\varphi \in \Gamma (\mathcal {S},\partial \mathcal {S})$
, to the context of a representation
$\varphi \in \Gamma (\mathcal {S},\partial \mathcal {S})$
, to the context of a representation
![]() $\varphi \colon G\to \Gamma (\mathcal {S},\partial \mathcal {S})$
. This is done as follows:
$\varphi \colon G\to \Gamma (\mathcal {S},\partial \mathcal {S})$
. This is done as follows:
Proposition A.3. Let
![]() $\alpha _0,\dots ,\alpha _k,\beta $
be a collection of essential arcs in a connected surface with non-empty boundary
$\alpha _0,\dots ,\alpha _k,\beta $
be a collection of essential arcs in a connected surface with non-empty boundary
![]() $\mathcal {S}$
satisfying the two properties listed in Proposition 2.11. Let U be a small neighbourhood of
$\mathcal {S}$
satisfying the two properties listed in Proposition 2.11. Let U be a small neighbourhood of
![]() $\alpha _0\cup \dots \cup \alpha _k\cup \beta \cup \partial \mathcal {S}\subset \mathcal {S}$
in
$\alpha _0\cup \dots \cup \alpha _k\cup \beta \cup \partial \mathcal {S}\subset \mathcal {S}$
in
![]() $\mathcal {S}$
, let
$\mathcal {S}$
, let
![]() $\operatorname {\mathrm {Diff}}(\mathcal {S},U)\subset \operatorname {\mathrm {Diff}}(\mathcal {S},\partial \mathcal {S})$
be the group of diffeomorphisms of
$\operatorname {\mathrm {Diff}}(\mathcal {S},U)\subset \operatorname {\mathrm {Diff}}(\mathcal {S},\partial \mathcal {S})$
be the group of diffeomorphisms of
![]() $\mathcal {S}$
fixing U pointwise, and let
$\mathcal {S}$
fixing U pointwise, and let
![]() $\Gamma (\mathcal {S},U)$
be the associated mapping class group.
$\Gamma (\mathcal {S},U)$
be the associated mapping class group.
Then the canonical homomorphism of groups
![]() $\Gamma (\mathcal {S},U)\to \Gamma (\mathcal {S},\partial \mathcal {S})$
, induced by the inclusion
$\Gamma (\mathcal {S},U)\to \Gamma (\mathcal {S},\partial \mathcal {S})$
, induced by the inclusion
![]() $\operatorname {\mathrm {Diff}}(\mathcal {S},U)\subset \operatorname {\mathrm {Diff}}(\mathcal {S},\partial \mathcal {S})$
, is injective. Moreover, a homomorphism
$\operatorname {\mathrm {Diff}}(\mathcal {S},U)\subset \operatorname {\mathrm {Diff}}(\mathcal {S},\partial \mathcal {S})$
, is injective. Moreover, a homomorphism
![]() $\varphi \colon G\to \Gamma (\mathcal {S},\partial \mathcal {S})$
lifts to
$\varphi \colon G\to \Gamma (\mathcal {S},\partial \mathcal {S})$
lifts to
![]() $\Gamma (\mathcal {S},U)$
if and only if for all
$\Gamma (\mathcal {S},U)$
if and only if for all
![]() $\gamma \in G$
the mapping class
$\gamma \in G$
the mapping class
![]() $\varphi (\gamma )\in \Gamma (\mathcal {S},\partial \mathcal {S})$
fixes up to isotopy each of the arcs
$\varphi (\gamma )\in \Gamma (\mathcal {S},\partial \mathcal {S})$
fixes up to isotopy each of the arcs
![]() $\alpha _0,\dots ,\alpha _k$
and
$\alpha _0,\dots ,\alpha _k$
and
![]() $\beta $
.
$\beta $
.
Proof. Note that U is a connected surface with at least three boundary components, and in particular U is neither a disc nor an annulus. We can then apply [Reference Farb and Margalit7, Thm. 3.18] (see also the remark after the cited Theorem) and conclude that the homomorphism of mapping class groups
![]() $\Gamma (\mathcal {S}\smallsetminus U,\partial (\mathcal {S}\smallsetminus U))\to \Gamma (\mathcal {S},\partial \mathcal {S})$
is injective. Composing with the natural isomorphism
$\Gamma (\mathcal {S}\smallsetminus U,\partial (\mathcal {S}\smallsetminus U))\to \Gamma (\mathcal {S},\partial \mathcal {S})$
is injective. Composing with the natural isomorphism
![]() $\Gamma (\mathcal {S}\smallsetminus U,\partial (\mathcal {S}\smallsetminus U))\cong \Gamma (\mathcal {S},U)$
, we obtain precisely the canonical homomorphism of groups
$\Gamma (\mathcal {S}\smallsetminus U,\partial (\mathcal {S}\smallsetminus U))\cong \Gamma (\mathcal {S},U)$
, we obtain precisely the canonical homomorphism of groups
![]() $\Gamma (\mathcal {S},U)\to \Gamma (\mathcal {S},\partial \mathcal {S})$
, which hence is injective.
$\Gamma (\mathcal {S},U)\to \Gamma (\mathcal {S},\partial \mathcal {S})$
, which hence is injective.
For the second claim, the injectivity of
![]() $\Gamma (\mathcal {S}\smallsetminus U,\partial (\mathcal {S}\smallsetminus U))\to \Gamma (\mathcal {S},U)$
implies that
$\Gamma (\mathcal {S}\smallsetminus U,\partial (\mathcal {S}\smallsetminus U))\to \Gamma (\mathcal {S},U)$
implies that
![]() $\varphi \colon G\to \Gamma (\mathcal {S},\partial \mathcal {S})$
lifts to
$\varphi \colon G\to \Gamma (\mathcal {S},\partial \mathcal {S})$
lifts to
![]() $\Gamma (\mathcal {S},U)$
if and only if, for all
$\Gamma (\mathcal {S},U)$
if and only if, for all
![]() $\gamma \in G$
, the mapping class
$\gamma \in G$
, the mapping class
![]() $\varphi (\gamma )\in \Gamma (\mathcal {S},\partial \mathcal {S})$
lies in the image of the canonical homomorphism, and Proposition 2.11 ensures that this is equivalent to requiring, for all
$\varphi (\gamma )\in \Gamma (\mathcal {S},\partial \mathcal {S})$
lies in the image of the canonical homomorphism, and Proposition 2.11 ensures that this is equivalent to requiring, for all
![]() $\gamma \in G$
, that the mapping class
$\gamma \in G$
, that the mapping class
![]() $\varphi (\gamma )$
fixes up to isotopy each of the arcs
$\varphi (\gamma )$
fixes up to isotopy each of the arcs
![]() $\alpha _0,\dots ,\alpha _k$
, and
$\alpha _0,\dots ,\alpha _k$
, and
![]() $\beta $
.
$\beta $
.
For a homomorphism
![]() $\varphi \colon G\to \Gamma (\mathcal {S},\partial \mathcal {S})$
, we define the fixed arc complex of
$\varphi \colon G\to \Gamma (\mathcal {S},\partial \mathcal {S})$
, we define the fixed arc complex of
![]() $\varphi $
as in Definition 2.14, but we require vertices to be isotopy classes of arcs fixed by every mapping class in the image of
$\varphi $
as in Definition 2.14, but we require vertices to be isotopy classes of arcs fixed by every mapping class in the image of
![]() $\varphi $
: in fact the fixed arc complex of
$\varphi $
: in fact the fixed arc complex of
![]() $\varphi $
is the intersection of the arc complexes of
$\varphi $
is the intersection of the arc complexes of
![]() $\varphi (\gamma )$
for
$\varphi (\gamma )$
for
![]() $\gamma $
ranging in G, where we consider all arc complexes as simplicial subcomplexes of the arc complex of
$\gamma $
ranging in G, where we consider all arc complexes as simplicial subcomplexes of the arc complex of
![]() .
.
The bound on the dimension of the fixed arc complex of
![]() $\varphi $
in terms of
$\varphi $
in terms of
![]() $\chi (\mathcal {S})$
is proved in the same way. The white-yellow decomposition of
$\chi (\mathcal {S})$
is proved in the same way. The white-yellow decomposition of
![]() $\mathcal {S}$
along the cut locus is defined in the same way as in Construction 2.18: by choosing a maximal simplex in the fixed-arc complex of the homomorphism
$\mathcal {S}$
along the cut locus is defined in the same way as in Construction 2.18: by choosing a maximal simplex in the fixed-arc complex of the homomorphism
![]() $\varphi $
. The proof of Lemma 2.20 can be extended to this generalised context as follows:
$\varphi $
. The proof of Lemma 2.20 can be extended to this generalised context as follows:
Lemma A.4. Let
![]() $\varphi \colon G\to \Gamma (\mathcal {S},\partial \mathcal {S})$
, let
$\varphi \colon G\to \Gamma (\mathcal {S},\partial \mathcal {S})$
, let
![]() $\alpha _0,\dots ,\alpha _k$
be arcs representing a maximal simplex in the cut locus of
$\alpha _0,\dots ,\alpha _k$
be arcs representing a maximal simplex in the cut locus of
![]() $\varphi $
, and let
$\varphi $
, and let
![]() $\beta $
be another arc fixed up to isotopy by
$\beta $
be another arc fixed up to isotopy by
![]() $\varphi $
; then
$\varphi $
; then
![]() $\beta $
can be isotoped relative to endpoints to an arc lying in a small neighbourhood U of
$\beta $
can be isotoped relative to endpoints to an arc lying in a small neighbourhood U of
![]() $\alpha _0\cup \dots \cup \alpha _k\cup \partial \mathcal {S}$
.
$\alpha _0\cup \dots \cup \alpha _k\cup \partial \mathcal {S}$
.
Proof. We assume without loss of generality that
![]() $\beta $
is in minimal position with respect to
$\beta $
is in minimal position with respect to
![]() $\alpha _0,\dots ,\alpha _k$
. By Proposition A.3, we can lift
$\alpha _0,\dots ,\alpha _k$
. By Proposition A.3, we can lift
![]() $\varphi $
to a homomorphism
$\varphi $
to a homomorphism
![]() $\tilde \varphi \colon G\to \Gamma (\mathcal {S},U')$
, where
$\tilde \varphi \colon G\to \Gamma (\mathcal {S},U')$
, where
![]() $U'$
is a small neighbourhood of
$U'$
is a small neighbourhood of
![]() $\alpha _0\cup \dotsb \cup \alpha _k\cup \beta \cup \partial \mathcal {S}$
. For each
$\alpha _0\cup \dotsb \cup \alpha _k\cup \beta \cup \partial \mathcal {S}$
. For each
![]() $\gamma \in G$
, we can thus represent
$\gamma \in G$
, we can thus represent
![]() $\tilde \varphi (\gamma )$
by a diffeomorphism
$\tilde \varphi (\gamma )$
by a diffeomorphism
![]() $\Phi _{\gamma }\colon \mathcal {S}\to \mathcal {S}$
fixing U pointwise.
$\Phi _{\gamma }\colon \mathcal {S}\to \mathcal {S}$
fixing U pointwise.
The rest of the proof is the same as for Lemma 2.20: in particular, we use the representatives
![]() $\Phi _{\gamma }$
to check that
$\Phi _{\gamma }$
to check that
![]() $\beta '$
and
$\beta '$
and
![]() $\beta ''$
are fixed up to isotopy by
$\beta ''$
are fixed up to isotopy by
![]() $\varphi (\gamma )$
for all
$\varphi (\gamma )$
for all
![]() $\gamma \in G$
.
$\gamma \in G$
.
The proof of Proposition 2.21 can be repeated word by word in the generalised context, and the analogue of Lemma 2.22 is the following:
Lemma A.5. Let
![]() $\psi \in \Gamma (\mathcal {S},\partial \mathcal {S})$
be a mapping class, and let
$\psi \in \Gamma (\mathcal {S},\partial \mathcal {S})$
be a mapping class, and let
![]() $\Psi $
be a diffeomorphism representing
$\Psi $
be a diffeomorphism representing
![]() $\psi $
. Moreover, let
$\psi $
. Moreover, let
![]() $\varphi \colon G\to \Gamma (\mathcal {S},\partial \mathcal {S})$
be a group homomorphism and let
$\varphi \colon G\to \Gamma (\mathcal {S},\partial \mathcal {S})$
be a group homomorphism and let
![]() $[c_1,\dots ,c_h]$
be the cut locus of
$[c_1,\dots ,c_h]$
be the cut locus of
![]() $\varphi $
.
$\varphi $
.
Then
![]() $[\Psi (c_1),\dots ,\Psi (c_h)]$
is the cut locus of the conjugate
$[\Psi (c_1),\dots ,\Psi (c_h)]$
is the cut locus of the conjugate
![]() $\psi \varphi \psi ^{-1}$
, which is defined by
$\psi \varphi \psi ^{-1}$
, which is defined by
![]() $(\psi \varphi \psi ^{-1})(\gamma ) := \psi \cdot \varphi (\gamma )\cdot \psi ^{-1}$
. In particular, if the image of
$(\psi \varphi \psi ^{-1})(\gamma ) := \psi \cdot \varphi (\gamma )\cdot \psi ^{-1}$
. In particular, if the image of
![]() $\varphi $
commutes with
$\varphi $
commutes with
![]() $\psi $
, then
$\psi $
, then
![]() $\psi $
preserves the cut locus of
$\psi $
preserves the cut locus of
![]() $\varphi $
as an unordered collection of isotopy classes of oriented simple closed curves.
$\varphi $
as an unordered collection of isotopy classes of oriented simple closed curves.
Proof. The proof is the same as for Lemma 2.22, with the exception that we first lift
![]() $\varphi $
to a homomorphism
$\varphi $
to a homomorphism
![]() $\tilde \varphi \colon G\to \Gamma (\mathcal {S},U)$
, where U is a small neighbourhood of
$\tilde \varphi \colon G\to \Gamma (\mathcal {S},U)$
, where U is a small neighbourhood of
![]() $\alpha _0\cup \dots \cup \alpha _k\cup \partial \mathcal {S}$
, and then we compare this morphism with the conjugate
$\alpha _0\cup \dots \cup \alpha _k\cup \partial \mathcal {S}$
, and then we compare this morphism with the conjugate
![]() $\psi \tilde \varphi \psi ^{-1}\colon G\to \Gamma (\mathcal {S},\Psi (U))$
.
$\psi \tilde \varphi \psi ^{-1}\colon G\to \Gamma (\mathcal {S},\Psi (U))$
.
This shows that, given a homomorphism
![]() $\varphi \colon G\to \Gamma (\mathcal {S},\partial \mathcal {S})$
, we can associate with it a cut locus
$\varphi \colon G\to \Gamma (\mathcal {S},\partial \mathcal {S})$
, we can associate with it a cut locus
![]() $c_1,\dots ,c_h$
separating
$c_1,\dots ,c_h$
separating
![]() $\mathcal {S}$
into a white region W and a yellow region Y. We fix a parametrisation by
$\mathcal {S}$
into a white region W and a yellow region Y. We fix a parametrisation by
![]() $S^1$
of each curve in the cut locus as in Subsection 3.1.
$S^1$
of each curve in the cut locus as in Subsection 3.1.
We can also lift uniquely
![]() $\varphi $
to a morphism
$\varphi $
to a morphism
![]() $\tilde \varphi \colon G\to \Gamma (\mathcal {S},W)$
. For each component
$\tilde \varphi \colon G\to \Gamma (\mathcal {S},W)$
. For each component
![]() $P\subset Y$
, we then have a morphism
$P\subset Y$
, we then have a morphism
![]() $\varphi _P\colon G\to \Gamma (P,\partial P)$
obtained by composing
$\varphi _P\colon G\to \Gamma (P,\partial P)$
obtained by composing
![]() $\tilde \varphi $
with the restriction
$\tilde \varphi $
with the restriction
![]() $\Gamma (\mathcal {S},W)\to \Gamma (P,\partial P)$
. Mimicking Definition 3.1, we say that two path components P and
$\Gamma (\mathcal {S},W)\to \Gamma (P,\partial P)$
. Mimicking Definition 3.1, we say that two path components P and
![]() $P'$
of Y are similar for
$P'$
of Y are similar for
![]() $\varphi $
if there is a a diffeomorphism
$\varphi $
if there is a a diffeomorphism
![]() $\Xi \colon P\to P'$
preserving the boundary parametrisations and conjugating the homomorphism
$\Xi \colon P\to P'$
preserving the boundary parametrisations and conjugating the homomorphism
![]() $\varphi _P$
to
$\varphi _P$
to
![]() $\varphi _{P'}$
. We write
$\varphi _{P'}$
. We write
![]() $Y=\coprod _{i=1}^r\coprod _{j=1}^{s_i}Y_{i,j}$
as in Notation 3.2, and introduce morphisms
$Y=\coprod _{i=1}^r\coprod _{j=1}^{s_i}Y_{i,j}$
as in Notation 3.2, and introduce morphisms
![]() $\bar \varphi _{i,j}\colon G\to \Gamma _{g_i,n_i}$
conjugate to
$\bar \varphi _{i,j}\colon G\to \Gamma _{g_i,n_i}$
conjugate to
![]() $\varphi _{Y_{i,j}}$
in an analogue way.
$\varphi _{Y_{i,j}}$
in an analogue way.
We denote by
![]() $\varphi _Y\colon G\to \Gamma (Y,\partial Y)$
the composition of
$\varphi _Y\colon G\to \Gamma (Y,\partial Y)$
the composition of
![]() $\tilde \varphi $
and the restriction map
$\tilde \varphi $
and the restriction map
![]() $\Gamma (\mathcal {S},W)\to \Gamma (Y,\partial Y)$
, and denote by
$\Gamma (\mathcal {S},W)\to \Gamma (Y,\partial Y)$
, and denote by
![]() $Z(\varphi _Y)\subset \Gamma (Y)$
the subgroup of elements that commute with the entire image of
$Z(\varphi _Y)\subset \Gamma (Y)$
the subgroup of elements that commute with the entire image of
![]() $\varphi _Y$
. Definition 3.4 and Lemma 3.5 then carry over to the generalised context.
$\varphi _Y$
. Definition 3.4 and Lemma 3.5 then carry over to the generalised context.
In Section 3, one only has to replace ‘
![]() $\varphi \in \Gamma (\mathcal {S},\partial \mathcal {S})$
’ by ‘homomorphism
$\varphi \in \Gamma (\mathcal {S},\partial \mathcal {S})$
’ by ‘homomorphism
![]() $\varphi \colon G\to \Gamma (\mathcal {S},\partial \mathcal {S})$
’, as well as ‘representative
$\varphi \colon G\to \Gamma (\mathcal {S},\partial \mathcal {S})$
’, as well as ‘representative
![]() $\Phi $
of
$\Phi $
of
![]() $\varphi $
fixing U’ by ‘the unique lift of
$\varphi $
fixing U’ by ‘the unique lift of
![]() $\varphi $
to a homomorphism
$\varphi $
to a homomorphism
![]() $\tilde \varphi \colon G\to \Gamma (\mathcal {S},U)$
’.
$\tilde \varphi \colon G\to \Gamma (\mathcal {S},U)$
’.
Finally, the discussion of Section 6 generalises straightforwardly to the context of a generic parametrising space X, leading to Theorem A.2.
A.2 Functoriality in X
Both sides of the equivalence in Theorem A.2 depend on a space X, and the left-hand side can be regarded as an enriched, contravariant functor from the category of (connected) topological spaces to the category of loop spaces. In fact, each space
![]() $\Omega B({\mathrm {map}}(X,\mathfrak {M}_{*,1}))$
admits a natural infinite loop space structure, and for a map of spaces
$\Omega B({\mathrm {map}}(X,\mathfrak {M}_{*,1}))$
admits a natural infinite loop space structure, and for a map of spaces
![]() $f\colon X\to X'$
, the corresponding map
$f\colon X\to X'$
, the corresponding map
is defined as the group completion of a map of
![]() ${\mathscr {M}}|_1$
-algebras, and hence a map of infinite loop spaces. We can thus consider
${\mathscr {M}}|_1$
-algebras, and hence a map of infinite loop spaces. We can thus consider
![]() $\Omega B({\mathrm {map}}(-,\mathfrak {M}_{*,1}))$
as a functor from connected topological spaces to infinite loop spaces. Now it would be interesting to describe this functor solely in terms of the right-hand side: that is, to upgrade the assignment
$\Omega B({\mathrm {map}}(-,\mathfrak {M}_{*,1}))$
as a functor from connected topological spaces to infinite loop spaces. Now it would be interesting to describe this functor solely in terms of the right-hand side: that is, to upgrade the assignment
![]() to an enriched functor from topological spaces to infinite loop spaces, such that the equivalences given by Theorem A.2, for varying X, assemble into a natural equivalence of functors. We will content ourselves with a weaker but explicit result about functoriality.
to an enriched functor from topological spaces to infinite loop spaces, such that the equivalences given by Theorem A.2, for varying X, assemble into a natural equivalence of functors. We will content ourselves with a weaker but explicit result about functoriality.
Definition A.6. A map of connected topological spaces
![]() $f\colon X\to X'$
induces a map of fundamental groups
$f\colon X\to X'$
induces a map of fundamental groups
![]() $f_*\colon \pi _1(X)\to \pi _1(X')$
, which is defined up to conjugation and which, in turn, allows us to transform any homomorphism
$f_*\colon \pi _1(X)\to \pi _1(X')$
, which is defined up to conjugation and which, in turn, allows us to transform any homomorphism
![]() $\varphi \colon \pi _1(X')\to \Gamma _{g,n}$
into a homomorphism
$\varphi \colon \pi _1(X')\to \Gamma _{g,n}$
into a homomorphism
![]() $f^*\varphi =\varphi \circ f_*\colon \pi _1(X)\to \Gamma _{g,n}$
, for all
$f^*\varphi =\varphi \circ f_*\colon \pi _1(X)\to \Gamma _{g,n}$
, for all
![]() $g\geqslant 0$
and
$g\geqslant 0$
and
![]() $n\geqslant 1$
.
$n\geqslant 1$
.
We say that f is
![]() $\partial $
-faithful if
$\partial $
-faithful if
![]() $f^*\varphi $
is
$f^*\varphi $
is
![]() $\partial $
-irreducible whenever
$\partial $
-irreducible whenever
![]() $\varphi $
is
$\varphi $
is
![]() $\partial $
-irreducible, for all
$\partial $
-irreducible, for all
![]() $g\geqslant 0$
and
$g\geqslant 0$
and
![]() $n\geqslant 1$
. We denote by
$n\geqslant 1$
. We denote by
![]() $\mathbf {Top}^\partial $
the (topologically enriched) category of connected topological spaces that are homotopy equivalent to a CW complex, with morphisms being
$\mathbf {Top}^\partial $
the (topologically enriched) category of connected topological spaces that are homotopy equivalent to a CW complex, with morphisms being
![]() $\partial $
-faithful continuous maps.
$\partial $
-faithful continuous maps.
Note that being
![]() $\partial $
-faithful is a homotopy-invariant property of continuous maps: that is, morphism spaces in
$\partial $
-faithful is a homotopy-invariant property of continuous maps: that is, morphism spaces in
![]() $\mathbf {Top}^\partial $
are obtained by selecting unions of connected components from the morphism spaces in
$\mathbf {Top}^\partial $
are obtained by selecting unions of connected components from the morphism spaces in
![]() $\mathbf {Top}$
. Recall Definition A.1: if
$\mathbf {Top}$
. Recall Definition A.1: if
![]() $f\colon X\to X'$
is a
$f\colon X\to X'$
is a
![]() $\partial $
-faithful map, then we obtain for each
$\partial $
-faithful map, then we obtain for each
![]() $g\geqslant 0$
and
$g\geqslant 0$
and
![]() $n\geqslant 1$
a map
$n\geqslant 1$
a map
Thus, we can consider
![]() $\mathfrak {C}_{g,n}$
as a contravariant functor from
$\mathfrak {C}_{g,n}$
as a contravariant functor from
![]() $\mathbf {Top}^\partial $
to
$\mathbf {Top}^\partial $
to
![]() $\mathbf {Top}$
, for all
$\mathbf {Top}$
, for all
![]() $g\geqslant 0$
and
$g\geqslant 0$
and
![]() $n\geqslant 1$
. Putting together all values of g and n, and taking the actions of the groups
$n\geqslant 1$
. Putting together all values of g and n, and taking the actions of the groups
![]() $R_n$
into account, we can consider
$R_n$
into account, we can consider
![]() $\mathfrak {C}$
as a contravariant functor from
$\mathfrak {C}$
as a contravariant functor from
![]() $\mathbf {Top}^\partial $
to
$\mathbf {Top}^\partial $
to
![]() $\boldsymbol {R}\text {-}\mathbf {Alg}$
. We can then repeat the proof of Theorem 6.5 and obtain an equivalence of (contravariant, enriched) functors
$\boldsymbol {R}\text {-}\mathbf {Alg}$
. We can then repeat the proof of Theorem 6.5 and obtain an equivalence of (contravariant, enriched) functors
Composing with the group completion functor, we then obtain the following enriched version of Theorem A.2.
Theorem A.7. Let
![]() $\Omega \text {-}\mathbf {Top}$
and
$\Omega \text {-}\mathbf {Top}$
and
![]() $\Omega ^\infty \text {-}\mathbf {Top}$
denote the (enriched) categories of loop spaces and infinite loop spaces, respectively. Then there is is a weak equivalence between the following two enriched contravariant functors from
$\Omega ^\infty \text {-}\mathbf {Top}$
denote the (enriched) categories of loop spaces and infinite loop spaces, respectively. Then there is is a weak equivalence between the following two enriched contravariant functors from
![]() $\mathbf {Top}^\partial $
to
$\mathbf {Top}^\partial $
to
![]() $\Omega \text {-}\mathbf {Top}$
:
$\Omega \text {-}\mathbf {Top}$
:
-
○ the functor
 $\Omega B({\mathrm {map}}(-,\mathfrak {M}_{*,1}))$
;
$\Omega B({\mathrm {map}}(-,\mathfrak {M}_{*,1}))$
; -
○ the composition of the contravariant functor
from
 $\mathbf {Top}^\partial $
to
$\mathbf {Top}^\partial $
to
 $\Omega ^\infty \text {-}\mathbf {Top}$
and the covariant, forgetful functor from
$\Omega ^\infty \text {-}\mathbf {Top}$
and the covariant, forgetful functor from
 $\Omega ^\infty \text {-}\mathbf {Top}$
to
$\Omega ^\infty \text {-}\mathbf {Top}$
to
 $\Omega \text {-}\mathbf {Top}$
.
$\Omega \text {-}\mathbf {Top}$
.
The weak equivalence of functors assigns to
![]() $X\in \mathbf {Top}^\partial $
the weak equivalence of loop spaces given by Theorem A.2.
$X\in \mathbf {Top}^\partial $
the weak equivalence of loop spaces given by Theorem A.2.
Example A.8. We briefly discuss an example showing why Theorem A.7 cannot be generalised to an analogue statement concerning the entire category
![]() $\mathbf {Top}$
of connected topological spaces with the homotopy type of a CW complex, together with all continuous maps: let X be a connected CW complex and let
$\mathbf {Top}$
of connected topological spaces with the homotopy type of a CW complex, together with all continuous maps: let X be a connected CW complex and let
![]() $f\colon *\to X$
be the inclusion of a point. We note that
$f\colon *\to X$
be the inclusion of a point. We note that
![]() $\coprod _{n\geqslant 1}\coprod _{g\geqslant 0} \mathfrak {C}_{g,n}(*)$
is the empty space, whence
$\coprod _{n\geqslant 1}\coprod _{g\geqslant 0} \mathfrak {C}_{g,n}(*)$
is the empty space, whence
is just a point A straightforward generalisation of Theorem A.7 would predict that the following square commutes up to homotopy, where the horizontal isomorphisms are given by Theorem A.2:

However, we can apply the functor
![]() $\pi _0(-)$
, taking values in groups, as all terms in the previous diagram are loop spaces. Applying
$\pi _0(-)$
, taking values in groups, as all terms in the previous diagram are loop spaces. Applying
![]() $\pi _0$
to the top row, we obtain the group
$\pi _0$
to the top row, we obtain the group
![]() $\mathbb {Z}\oplus (\bigoplus _{n\geqslant 1}\bigoplus _{g\geqslant 0}\mathbb {Z}^{\oplus \pi _0(\mathfrak {C}_{g,n}(X))})$
, whereas applying
$\mathbb {Z}\oplus (\bigoplus _{n\geqslant 1}\bigoplus _{g\geqslant 0}\mathbb {Z}^{\oplus \pi _0(\mathfrak {C}_{g,n}(X))})$
, whereas applying
![]() $\pi _0$
to the bottom row, we obtain the group
$\pi _0$
to the bottom row, we obtain the group
![]() $\mathbb {Z}$
.
$\mathbb {Z}$
.
After applying
![]() $\pi _0$
, of the left vertical map sends the first summand
$\pi _0$
, of the left vertical map sends the first summand
![]() $\mathbb {Z}$
isomorphically onto
$\mathbb {Z}$
isomorphically onto
![]() $\mathbb {Z}$
, and the standard generator of each further summand
$\mathbb {Z}$
, and the standard generator of each further summand
![]() $\mathbb {Z}^{\oplus \pi _0(\mathfrak {C}_{g,n}(X))}$
to
$\mathbb {Z}^{\oplus \pi _0(\mathfrak {C}_{g,n}(X))}$
to
![]() $g+n-1\in \mathbb {Z}$
, while the right vertical map sends the first summand
$g+n-1\in \mathbb {Z}$
, while the right vertical map sends the first summand
![]() $\mathbb {Z}$
isomorphically onto
$\mathbb {Z}$
isomorphically onto
![]() $\mathbb {Z}$
, and each further summand
$\mathbb {Z}$
, and each further summand
![]() $\mathbb {Z}^{\oplus \pi _0(\mathfrak {C}_{g,n}(X))}$
constantly to
$\mathbb {Z}^{\oplus \pi _0(\mathfrak {C}_{g,n}(X))}$
constantly to
![]() $0$
.
$0$
.
Note that it suffices to take
![]() $X=S^1$
to have
$X=S^1$
to have
![]() $\pi _0(\mathfrak {C}_{g,n}(X))\neq \varnothing $
for some choice of g and n and thus to ensure that the previous example is not void: see Example 2.17.
$\pi _0(\mathfrak {C}_{g,n}(X))\neq \varnothing $
for some choice of g and n and thus to ensure that the previous example is not void: see Example 2.17.
As an application of Theorem A.7, let
![]() $k\in \mathbb {Z}\smallsetminus \left \{0\right \}$
, and consider the power map
$k\in \mathbb {Z}\smallsetminus \left \{0\right \}$
, and consider the power map
![]() $(-)^k\colon S^1\to S^1$
, which induces multiplication by k on the fundamental group
$(-)^k\colon S^1\to S^1$
, which induces multiplication by k on the fundamental group
![]() $\pi _1(S^1)\cong \mathbb {Z}$
. The following lemma proves that
$\pi _1(S^1)\cong \mathbb {Z}$
. The following lemma proves that
![]() $(-)^k$
is
$(-)^k$
is
![]() $\partial $
-faithful; hence it induces a self map of the infinite loop space
$\partial $
-faithful; hence it induces a self map of the infinite loop space
![]() that can be described using Theorem A.7.
that can be described using Theorem A.7.
Lemma A.9. Let
![]() $\mathcal {S}$
be a surface of type
$\mathcal {S}$
be a surface of type
![]() $\Sigma _{g,n}$
for some
$\Sigma _{g,n}$
for some
![]() $g\geqslant 0$
and
$g\geqslant 0$
and
![]() $n\geqslant 1$
. Let
$n\geqslant 1$
. Let
![]() $\varphi \in \Gamma (\mathcal {S},\partial \mathcal {S})$
be a mapping class, let
$\varphi \in \Gamma (\mathcal {S},\partial \mathcal {S})$
be a mapping class, let
![]() $k\in \mathbb {Z}\smallsetminus \left \{0\right \}$
, and let
$k\in \mathbb {Z}\smallsetminus \left \{0\right \}$
, and let
![]() $\bar \alpha $
be an essential arc in
$\bar \alpha $
be an essential arc in
![]() $\mathcal {S}$
. Suppose that the isotopy class
$\mathcal {S}$
. Suppose that the isotopy class
![]() $[\bar \alpha ]$
of
$[\bar \alpha ]$
of
![]() $\bar \alpha $
relative to its endpoints is in the fixed-arc complex of
$\bar \alpha $
relative to its endpoints is in the fixed-arc complex of
![]() $\varphi ^k$
. Then
$\varphi ^k$
. Then
![]() $[\bar \alpha ]$
is in the fixed-arc complex of
$[\bar \alpha ]$
is in the fixed-arc complex of
![]() $\varphi $
.
$\varphi $
.
Proof. Since the fixed-arc complexes of
![]() $\varphi $
and
$\varphi $
and
![]() $\varphi ^{-1}$
are equal, we can assume without loss of generality that
$\varphi ^{-1}$
are equal, we can assume without loss of generality that
![]() $k\geqslant 1$
. The case
$k\geqslant 1$
. The case
![]() $k=1$
is tautological, so we henceforth assume
$k=1$
is tautological, so we henceforth assume
![]() $k\geqslant 2$
.
$k\geqslant 2$
.
Let
![]() $p,q\in \partial \mathcal {S}$
be the endpoints of
$p,q\in \partial \mathcal {S}$
be the endpoints of
![]() $\bar \alpha $
, and consider the set
$\bar \alpha $
, and consider the set
![]() $\mathrm {Arc}(p,q)$
of isotopy classes
$\mathrm {Arc}(p,q)$
of isotopy classes
![]() $[\alpha ]$
of essential arcs
$[\alpha ]$
of essential arcs
![]() $\alpha $
in
$\alpha $
in
![]() $\mathcal {S}$
from p to q. An essential arc
$\mathcal {S}$
from p to q. An essential arc
![]() $\alpha $
is a map
$\alpha $
is a map
![]() $\alpha \colon [0,1]\to \mathcal {S}$
, but we will abuse notation and denote by
$\alpha \colon [0,1]\to \mathcal {S}$
, but we will abuse notation and denote by
![]() $\alpha $
also the image of this map, which is a subset of
$\alpha $
also the image of this map, which is a subset of
![]() $\mathcal {S}$
.
$\mathcal {S}$
.
Let
![]() $\alpha $
and
$\alpha $
and
![]() $\beta $
be two essential arcs from p to q. We say that
$\beta $
be two essential arcs from p to q. We say that
![]() $\alpha $
and
$\alpha $
and
![]() $\alpha '$
are transverse if they have linearly independent velocities at each intersection point, including the endpoints p and q. Moreover, we say that
$\alpha '$
are transverse if they have linearly independent velocities at each intersection point, including the endpoints p and q. Moreover, we say that
![]() $\alpha $
and
$\alpha $
and
![]() $\alpha '$
are in minimal position away from the endpoints if the number of intersection points of
$\alpha '$
are in minimal position away from the endpoints if the number of intersection points of
![]() $\alpha $
and
$\alpha $
and
![]() $\alpha '$
, excluding p and q, is minimal among all pairs of transverse arcs
$\alpha '$
, excluding p and q, is minimal among all pairs of transverse arcs
![]() $\alpha '$
and
$\alpha '$
and
![]() $\beta '$
with
$\beta '$
with
![]() $\alpha \sim \alpha '$
and
$\alpha \sim \alpha '$
and
![]() $\beta \sim \beta '$
. The bigon criterion applies:
$\beta \sim \beta '$
. The bigon criterion applies:
![]() $\alpha $
and
$\alpha $
and
![]() $\beta $
are in minimal position if and only if they do not form bigons.
$\beta $
are in minimal position if and only if they do not form bigons.
In particular, if
![]() $\alpha $
and
$\alpha $
and
![]() $\beta $
are non-isotopic arcs from p to q in minimal position away from the endpoints, then we can compare the velocities of
$\beta $
are non-isotopic arcs from p to q in minimal position away from the endpoints, then we can compare the velocities of
![]() $\alpha $
and
$\alpha $
and
![]() $\beta $
at p: these are linearly independent vectors in
$\beta $
at p: these are linearly independent vectors in
![]() $T_p\mathcal {S}$
pointing inside
$T_p\mathcal {S}$
pointing inside
![]() $\mathcal {S}$
: we say that
$\mathcal {S}$
: we say that
![]() $\alpha $
is on right of
$\alpha $
is on right of
![]() $\beta $
if the sequence
$\beta $
if the sequence
![]() $(\frac {d}{dt}\alpha (0),\frac {d}{dt}\beta (0))$
is a positive basis of
$(\frac {d}{dt}\alpha (0),\frac {d}{dt}\beta (0))$
is a positive basis of
![]() $T_p\mathcal {S}$
.
$T_p\mathcal {S}$
.
The Alexander method guarantees the following: let
![]() $\alpha ,\alpha ',\beta ,\beta '$
be four essential arcs in
$\alpha ,\alpha ',\beta ,\beta '$
be four essential arcs in
![]() $\mathcal {S}$
from p to q, with
$\mathcal {S}$
from p to q, with
![]() $\alpha \sim \alpha '\not \sim \beta \sim \beta '$
, and suppose that
$\alpha \sim \alpha '\not \sim \beta \sim \beta '$
, and suppose that
![]() $\alpha $
and
$\alpha $
and
![]() $\beta $
, as well as
$\beta $
, as well as
![]() $\alpha '$
and
$\alpha '$
and
![]() $\beta '$
, are in minimal position away from their endpoints. Then there is an isotopy of
$\beta '$
, are in minimal position away from their endpoints. Then there is an isotopy of
![]() $\mathcal {S}$
bringing
$\mathcal {S}$
bringing
![]() $\alpha \cup \beta $
to
$\alpha \cup \beta $
to
![]() $\alpha '\cup \beta '$
. In particular,
$\alpha '\cup \beta '$
. In particular,
![]() $\alpha $
is on right of
$\alpha $
is on right of
![]() $\beta $
if and only if
$\beta $
if and only if
![]() $\alpha '$
is on right of
$\alpha '$
is on right of
![]() $\beta '$
. We can now put a total order on
$\beta '$
. We can now put a total order on
![]() $\mathrm {Arc}(p,q)$
: for two distinct isotopy classes
$\mathrm {Arc}(p,q)$
: for two distinct isotopy classes
![]() $[\alpha ]$
and
$[\alpha ]$
and
![]() $[\beta ]$
, we say that
$[\beta ]$
, we say that
![]() $[\alpha ]\prec [\beta ]$
if, for any two representatives
$[\alpha ]\prec [\beta ]$
if, for any two representatives
![]() $\alpha $
and
$\alpha $
and
![]() $\beta $
, which are in minimal position away from the endpoints,
$\beta $
, which are in minimal position away from the endpoints,
![]() $\alpha $
is on right of
$\alpha $
is on right of
![]() $\beta $
.
$\beta $
.
The action of
![]() $\Gamma (\mathcal {S},\partial \mathcal {S})$
on
$\Gamma (\mathcal {S},\partial \mathcal {S})$
on
![]() $\mathrm {Arc}(p,q)$
preserves the total order
$\mathrm {Arc}(p,q)$
preserves the total order
![]() $\prec $
: for this, let
$\prec $
: for this, let
![]() $\Phi $
be a diffeomorphism representing
$\Phi $
be a diffeomorphism representing
![]() $\varphi \in \Gamma (\mathcal {S},\partial \mathcal {S})$
and assume that
$\varphi \in \Gamma (\mathcal {S},\partial \mathcal {S})$
and assume that
![]() $\Phi $
fixes a neighbourhood of
$\Phi $
fixes a neighbourhood of
![]() $p\in \partial \mathcal {S}$
pointwise. Moreover, let
$p\in \partial \mathcal {S}$
pointwise. Moreover, let
![]() $\alpha $
and
$\alpha $
and
![]() $\beta $
represent classes
$\beta $
represent classes
![]() $[\alpha ],[\beta ]\in \mathrm {Arc}(p,q)$
, and assume that
$[\alpha ],[\beta ]\in \mathrm {Arc}(p,q)$
, and assume that
![]() $\alpha $
and
$\alpha $
and
![]() $\beta $
are in minimal position away from the endpoints and that
$\beta $
are in minimal position away from the endpoints and that
![]() $\alpha $
is on right of
$\alpha $
is on right of
![]() $\beta $
, thus witnessing
$\beta $
, thus witnessing
![]() $[\alpha ]\prec [\beta ]$
: then
$[\alpha ]\prec [\beta ]$
: then
![]() $\Phi (\alpha )$
and
$\Phi (\alpha )$
and
![]() $\Phi (\beta )$
are also in minimal position away from the endpoints, and
$\Phi (\beta )$
are also in minimal position away from the endpoints, and
![]() $\Phi (\alpha )$
is on right of
$\Phi (\alpha )$
is on right of
![]() $\Phi (\beta )$
, witnessing that
$\Phi (\beta )$
, witnessing that
![]() $\varphi ([\alpha ])=[\Phi (\alpha )]\prec [\Phi (\beta )]=\varphi ([\beta ])$
.
$\varphi ([\alpha ])=[\Phi (\alpha )]\prec [\Phi (\beta )]=\varphi ([\beta ])$
.
Let now
![]() $[\bar \alpha ]$
be as in the hypothesis of the theorem, and assume for the sake of contradiction that
$[\bar \alpha ]$
be as in the hypothesis of the theorem, and assume for the sake of contradiction that
![]() $[\bar \alpha ]\neq \varphi ([\bar \alpha ])\in \mathrm {Arc}(p,q)$
: then without loss of generality, we can assume
$[\bar \alpha ]\neq \varphi ([\bar \alpha ])\in \mathrm {Arc}(p,q)$
: then without loss of generality, we can assume
![]() $[\bar \alpha ]\prec \varphi ([\bar \alpha ])$
. We then have a chain of inequalities
$[\bar \alpha ]\prec \varphi ([\bar \alpha ])$
. We then have a chain of inequalities
hence
![]() $[\bar \alpha ]\prec \varphi ^k([\bar \alpha ])$
, contradicting the hypothesis
$[\bar \alpha ]\prec \varphi ^k([\bar \alpha ])$
, contradicting the hypothesis
![]() $[\bar \alpha ]=\varphi ^k([\bar \alpha ])$
.
$[\bar \alpha ]=\varphi ^k([\bar \alpha ])$
.
B Braid groups, symmetric groups and free loops
In this second appendix, we sketch two results that are parallel to the identification in Theorem 1.1.
The first pertains to automorphisms of surfaces that have no genus but instead punctures; we thus replace mapping class groups by braid groups. A particular model of the corresponding classifying space is given by the collection of unordered configuration spaces of the
![]() $2$
-dimensional disc.
$2$
-dimensional disc.
In analogy to that, the collection of configuration spaces of the
![]() $\infty $
-dimensional disc is a model for the classifying space of symmetric groups. We outline the corresponding result for that setting.
$\infty $
-dimensional disc is a model for the classifying space of symmetric groups. We outline the corresponding result for that setting.
B.1 Braid groups
First recall that the r
th braid group
![]() $\operatorname {\mathrm {Br}}_r$
can be defined as the fundamental group of the unordered configuration space
$\operatorname {\mathrm {Br}}_r$
can be defined as the fundamental group of the unordered configuration space
![]() $C_r(\mathring {D}^2) := \tilde {C}_r(\mathring {D}^2)/\mathfrak {S}_r$
of the
$C_r(\mathring {D}^2) := \tilde {C}_r(\mathring {D}^2)/\mathfrak {S}_r$
of the
![]() $2$
-dimensional disc, where
$2$
-dimensional disc, where
The contractible topological group
![]() $\operatorname {\mathrm {Diff}}_{\partial }(D^2)$
of diffeomorphisms of
$\operatorname {\mathrm {Diff}}_{\partial }(D^2)$
of diffeomorphisms of
![]() $D^2$
that are the identity in a neighbourhood of the boundary acts on
$D^2$
that are the identity in a neighbourhood of the boundary acts on
![]() $C_r(\mathring {D}^2)$
; the stabiliser of a point
$C_r(\mathring {D}^2)$
; the stabiliser of a point
![]() $P := \{p_1, \dots , p_r\} \in \operatorname {\mathrm {C}}_r(D^2)$
with respect to this this action is the subgroup
$P := \{p_1, \dots , p_r\} \in \operatorname {\mathrm {C}}_r(D^2)$
with respect to this this action is the subgroup
![]() $\operatorname {\mathrm {Diff}}_{\partial }(D^2,P)$
of diffeomorphisms that preserve P as a set. The induced long exact sequence on homotopy groups of the resulting fibration
$\operatorname {\mathrm {Diff}}_{\partial }(D^2,P)$
of diffeomorphisms that preserve P as a set. The induced long exact sequence on homotopy groups of the resulting fibration
thus implies that
![]() $\operatorname {\mathrm {Br}}_r \cong \pi _0 \operatorname {\mathrm {Diff}}_{\partial }(D^2,P)$
, the mapping class group of a genus
$\operatorname {\mathrm {Br}}_r \cong \pi _0 \operatorname {\mathrm {Diff}}_{\partial }(D^2,P)$
, the mapping class group of a genus
![]() $0$
surface with r (unordered) punctures. A classical argument by Fadell and Neuwirth [Reference Fadell and Neuwirth6] shows that the configuration spaces
$0$
surface with r (unordered) punctures. A classical argument by Fadell and Neuwirth [Reference Fadell and Neuwirth6] shows that the configuration spaces
![]() $\tilde {C}_r(\mathring {D}^2)$
and
$\tilde {C}_r(\mathring {D}^2)$
and
![]() $C_r(\mathring {D}^2)$
are aspherical, which implies the well-known result
$C_r(\mathring {D}^2)$
are aspherical, which implies the well-known result
![]() $C_r(\mathring {D}^2)\simeq B\operatorname {\mathrm {Br}}_r$
.
$C_r(\mathring {D}^2)\simeq B\operatorname {\mathrm {Br}}_r$
.
We remark that Alexander’s theory of arc systems developed in detail for surfaces in Section 2, Definitions 2.10, 2.14, 2.19, Propositions 2.11 and 2.21, Construction 2.18 and Lemma 2.20 has a canonical analogue if the surfaces with boundary considered before are replaced by a punctured disc: now the arcs are required to start and end in
![]() $\partial D^2 = S^1$
and their interior must lie in
$\partial D^2 = S^1$
and their interior must lie in
![]() $\mathring {D}^2\smallsetminus \{p_1,\dotsc ,p_r\}$
. Most importantly, we can also define the notion of irreducibility of elements of braid groups as follows.
$\mathring {D}^2\smallsetminus \{p_1,\dotsc ,p_r\}$
. Most importantly, we can also define the notion of irreducibility of elements of braid groups as follows.
Definition B.1.
-
1. A braid
 $\gamma \in \operatorname {\mathrm {Br}}_r$
is reducible if there exists an essential arc in
$\gamma \in \operatorname {\mathrm {Br}}_r$
is reducible if there exists an essential arc in
 $\mathring {D}^2 \smallsetminus \{p_1, \dots , p_r\}$
that is fixed by
$\mathring {D}^2 \smallsetminus \{p_1, \dots , p_r\}$
that is fixed by
 $\gamma $
; otherwise it is called irreducible. In other words, a braid
$\gamma $
; otherwise it is called irreducible. In other words, a braid
 $\gamma $
is reducible if it is conjugate to a block sum of braids; see Figure 11.
$\gamma $
is reducible if it is conjugate to a block sum of braids; see Figure 11.
Figure 11 The left braid is reducible as it is conjugate to a block sum of two braids, whereas the second one is not.
-
2. Let
 $\mathfrak I_r \subseteq \Lambda C_r(\mathring {D}^2)=\Lambda B\mathrm {Br}_r$
denote the subspace of free loops whose corresponding conjugacy classes in
$\mathfrak I_r \subseteq \Lambda C_r(\mathring {D}^2)=\Lambda B\mathrm {Br}_r$
denote the subspace of free loops whose corresponding conjugacy classes in
 $\operatorname {\mathrm {Br}}_r$
consist of irreducible elements.
$\operatorname {\mathrm {Br}}_r$
consist of irreducible elements.
The genus-
![]() $0$
and colour-
$0$
and colour-
![]() $1$
part of
$1$
part of
![]() ${\mathscr {M}}$
, which coincides with the framed little
${\mathscr {M}}$
, which coincides with the framed little
![]() $2$
-disc operad
$2$
-disc operad
![]() $\smash {{\mathscr {D}}_2^{\text {fr}}}$
, acts on the union
$\smash {{\mathscr {D}}_2^{\text {fr}}}$
, acts on the union
![]() $\Lambda \coprod _{r\geqslant 0}C_r(\mathring {D}^2)$
; the Lie group
$\Lambda \coprod _{r\geqslant 0}C_r(\mathring {D}^2)$
; the Lie group
![]() $R_1\cong S^1$
acts on
$R_1\cong S^1$
acts on
![]() $\mathfrak {I}:= \coprod _{r\geqslant 1} \mathfrak {I}_r$
, and analogous to Theorem 6.5 one obtains that
$\mathfrak {I}:= \coprod _{r\geqslant 1} \mathfrak {I}_r$
, and analogous to Theorem 6.5 one obtains that
The free
![]() $\smash {{\mathscr {D}}_2^{\mathrm {fr}}}$
-algebra over a given
$\smash {{\mathscr {D}}_2^{\mathrm {fr}}}$
-algebra over a given
![]() $S^1$
-space is, as a
$S^1$
-space is, as a
![]() ${\mathscr {D}}_2$
-algebra, equivalent to the free
${\mathscr {D}}_2$
-algebra, equivalent to the free
![]() ${\mathscr {D}}_2$
-algebra over the underlying space without the
${\mathscr {D}}_2$
-algebra over the underlying space without the
![]() $S^1$
-action as the operation spaces
$S^1$
-action as the operation spaces
![]() ${\mathscr {D}}^{\mathrm {fr}}_2(r)$
and
${\mathscr {D}}^{\mathrm {fr}}_2(r)$
and
![]() ${\mathscr {D}}_2(r)\times (S^1)^r$
are equivalent as free right
${\mathscr {D}}_2(r)\times (S^1)^r$
are equivalent as free right
![]() $(S^1)^r$
-spaces, whence the coend construction just cancels the toric factor. We therefore obtain, after group completion, the following identification.
$(S^1)^r$
-spaces, whence the coend construction just cancels the toric factor. We therefore obtain, after group completion, the following identification.
Theorem B.2. There is a homotopy equivalence
 $$\begin{align*}\Omega B\Lambda \coprod_{n \geqslant 1} B \operatorname{\mathrm{Br}}_r \simeq \Omega^2 \Sigma_+^2 \coprod_{r\geqslant 1} \coprod_{\substack{[\gamma] \in {\mathrm{Conj}}(\operatorname{\mathrm{Br}}_r)\\ \text{irreducible}}} B Z(\gamma,\operatorname{\mathrm{Br}}_r).\end{align*}$$
$$\begin{align*}\Omega B\Lambda \coprod_{n \geqslant 1} B \operatorname{\mathrm{Br}}_r \simeq \Omega^2 \Sigma_+^2 \coprod_{r\geqslant 1} \coprod_{\substack{[\gamma] \in {\mathrm{Conj}}(\operatorname{\mathrm{Br}}_r)\\ \text{irreducible}}} B Z(\gamma,\operatorname{\mathrm{Br}}_r).\end{align*}$$
B.2 Symmetric groups
We conclude by considering free loop spaces of configuration spaces of an infinite-dimensional disc
![]() $\mathring {D}^{\infty }$
. These are classifying spaces of symmetric groups: that is,
$\mathring {D}^{\infty }$
. These are classifying spaces of symmetric groups: that is,
![]() $\smash {C_r(\mathring {D}^{\infty }) \simeq B\mathfrak {S}_r}$
. The analogous notion of irreducibility is even simpler: an element of
$\smash {C_r(\mathring {D}^{\infty }) \simeq B\mathfrak {S}_r}$
. The analogous notion of irreducibility is even simpler: an element of
![]() $\mathfrak {S}_r$
(that is, a permutation) is irreducible if and only if it comprises a single cycle. In this case, its centraliser is cyclic of order r, and as above, one obtains that
$\mathfrak {S}_r$
(that is, a permutation) is irreducible if and only if it comprises a single cycle. In this case, its centraliser is cyclic of order r, and as above, one obtains that
After group completion, we obtain the analogue of Theorem B.2 for symmetric groups [Reference Reinhold21, Cor. 4.32].
Theorem B.3. There is a homotopy equivalence
Acknowledgments
We are indebted to Søren Galatius for suggesting the problem treated in this paper to the third named author, who would also like to thank Rachael Boyd and Adva Wolf for helpful discussions that were part of a first attempt to solve it. Moreover, we are grateful to Carl-Friedrich Bödigheimer, Søren Galatius and Oscar Randal-Williams for fruitful conversations.
We would also like to thank Manuel Krannich, Ulrike Tillmann and Nathalie Wahl for useful comments they made on a first draft. Finally, we are deeply grateful to the anonymous referee for a detailed list of corrections on the first version and for suggesting a way to sensibly simplify and at the same time generalise the discussion in Section 5.
Funding statement
Andrea Bianchi was partially supported by the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) under Germany’s Excellence Strategy (EXC-2047/1, 390685813), by the European Research Council under the European Union’s Seventh Framework Programme (ERC StG 716424 – CASe, PI Karim Adiprasito) and by the Danish National Research Foundation through the Copenhagen Centre for Geometry and Topology (DNRF151).
Florian Kranhold was supported by the Max Planck Institute for Mathematics in Bonn, by the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) under Germany’s Excellence Strategy (EXC-2047/1, 390685813) and by the Promotionsförderung of the Studienstiftung des Deutschen Volkes.
Jens Reinhold was supported by the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) – SFB 1442 427320536, Geometry: Deformations and Rigidity, as well as under Germany’s Excellence Strategy EXC-2044, Mathematics Münster: Dynamics – Geometry – Structure.
Competing interests
None.