1. Introduction

Ice streams are zones of fast-moving ice within ice sheets (Reference BentleyBentley, 1987). Of particular interest are the ice streams that discharge from the interior of the West Antarctic ice sheet across the Siple Coast into the Ross Ice Shelf and ultimately the Ross Sea (Reference Alley and WhillansAlley and Whillans, 1991). The high speed (100–1000 m a⁻¹) of these ice streams is achieved with a very low driving stress (∼10 kPa). Deformation through the thickness of the ice (∼1 km) is expected to contribute < 1% of the speed at the upper surface. Almost all of the total velocity is produced by motion at the base (Reference Engelhardt and KambEngelhardt and Kamb, 1998). Discovery of a weak layer of dilated till beneath parts of Ice Stream B (Reference Blankenship, Bentley, Rooney and AlleyBlankenship and others, 1987; Reference Engelhardt, Humphrey and KambEngelhardt and others, 1990) has led to the notion that lubrication by soft till is responsible for the fast motion at the low driving stress.

The high speed could be achieved by some combination of distributed deformation within the till layer, or slip on discrete interfaces, such as the ice–till interface, within the till or at the till base (Reference AlleyAlley, 1989; Reference Engelhardt and KambEngelhardt and Kamb, 1998; Reference Truffer, Motyka, Harrison, Echelmeyer, Fisk and TulaczykTruffer and others, 1999). Pervasive deformation of the till and slip at the ice–till interface have been the focus of most previous investigations relevant to the West Antarctic ice streams. There is observational evidence for both of these processes, but no conclusive evidence regarding which process is most important (Reference Engelhardt and KambEngelhardt and Kamb, 1997). This open question represents a major gap in fundamental understanding of fast ice-stream motion and related geomorphic issues concerning till transport, erosion required to replace till carried away and till discharge to deltas deposited at the grounding line of ice streams.

This paper addresses the partitioning of the basal motion between till deformation and slip at the ice base. The primary assumption is that the till–ice boundary is a sharp, well-lubricated interface which may be expected under conditions in which there is net heat flow to the base of the ice (Reference Engelhardt, Humphrey and KambEngelhardt and others, 1990), melting of the ice and lack of adhesion of till components to it. In this circumstance, stress is transmitted between the ice and till by roughness elements of the ice–till interface. The resulting mean shear stress can cause deformation through the thickness of the till. Slip in the presence of the roughness elements can occur by local deformations in the till, which we analyze using the classic theory of ice sliding (Reference NyeNye, 1969) with the primary modification that the ice is assumed to be rigid and the till to deform like an incompressible viscous fluid, thus reversing the role of ice and bed. In this regard, both the shearing through the till thickness and the slip at the ice–till interface are mediated by deformation in the till. Both mean till deformation and slip increase with increasing softness of the till. The primary control variables affecting the relative amount of sliding and till deformation are the interface roughness and the vertical thickness of the till that can deform. We explore how the ratio of sliding to till deformation depends on these two variables, and examine some implications concerning motions in the till imposed by the sliding.

2. Physical description of the problem

Figure 1 illustrates the configuration of ice, till and bedrock. The interaction between these elements is complex. For practical analysis we introduce assumptions and simplifications about the mechanical behavior of the ice, ice–till contact zone and till that are not generally realistic for a comprehensive treatment of soft-bed mechanics. We argue that they are adequate to make useful conclusions concerning the relative amount of till deformation and sliding where there is net heat flow to a well-defined interface between clean ice and weak, fine-grained till at very high mean pore pressure. These conditions are generally thought to hold at many locations at the base of the West Antarctic ice streams (Reference Engelhardt, Humphrey and KambEngelhardt and others, 1990; Reference Engelhardt and KambEngelhardt and Kamb, 1997).

Fig. 1. The geometry of the problem. The velocity of the ice is U = U _s + U _d , where s stands for sliding and d for till deformation (shearing).

Assumption 1 is that the ice–till contact is well lubricated and does not support shear stress locally. This is the primary and most crucial assumption of the analysis. We expect that it will be reasonable for the conditions defined above. Continuous generation of meltwater at the interface would form a layer of negligible shear strength composed of water or super-fluidized till that is much weaker than the bulk material beneath. This layer is assumed to be thin compared to the amplitude of roughness on the interface.

Certainly some circumstances would cause this assumption to break down. Debris load in the basal ice would be exposed by melting, and partially exhumed particles would have to plow through the till beneath before they were released. If there were basal freezing or low pore pressure in the till, ice would invade the pore space of the till. If the till were strong and/or contained clasts with size comparable to the till thickness, then clasts might be driven into the ice base. All of these would tend to diffuse the interface and suppress lubrication (Reference IversonIverson, 1999). Less clear is the small-scale geometry of the ice sole as shaped by thermodynamic interaction with the surfaces of the finegrained till particles. One point of view is that the high pore pressure responsible for weakening the till and the continual regression of the ice interface by net melting prevents invasion of the ice into the till and maintains a locally smooth interface. If this were not true, then the slip process envisioned as a velocity discontinuity between the ice and till would not be applicable, but it could still occur by concentrated shearing in a thin boundary layer of till slurry.

Assumption 2 is that the till is a single bulk continuum. In reality, the till is a water-saturated, granular medium. For this assumption to be valid the thickness of the lubricating layer, the roughness height, the horizontal scale of the roughness and the thickness of the till must all be significantly larger than the typical grain-size. Reference Tulaczyk, Kamb, Scherer and EngelhardtTulaczyk and others (1998) found that particles ∼10⁻¹ mm and smaller accounted for 75% of the mass in the till beneath Ice Stream B, so this is not a serious limitation for that environment. Furthermore, the assumption requires the pore water and rock matrix to move together without diffusion of pore water and/or its pressure through the matrix. To make an initial assessment, we compare the time τ _d for diffusion of water pressure to the time τ ₁ to change the loading. Each is related to the horizontal distance δ between the protruding and re-entrant interface roughness components moving over the till (e.g. δ = λ/2 in Fig. 1). These are estimated, following Reference IversonIverson (1999), as: τ _d ≈ δ ² αη _w/k with till matrix elastic compressibility α, till permeability k and pore-water viscosity η _w; τ ₁ = U/δ where U is the slip velocity. The condition τ _d = τ ₁ defines a transition scale δ _t = (k/αη _w U). For δ ≤ δ _t, there will be time for pore pressure to diffuse before the stress is changed by displacement of the roughness. For reasonable values expected for the till beneath Ice Stream B (Reference IversonIverson, 1999, p. 51) (α =10⁻⁶ Pa⁻¹, k = 2 × 10⁻¹⁶ m⁻², η _w = 1.8 × 10⁻³ Pa s⁻¹ and U > 10² m a⁻¹), δ _t < 0.03 m. Horizontal scales λ need to be significantly larger than this for the single continuum assumption to hold.

Assumption 3 is that the till continuum is viscously incompressible. Incompressibility will hold only as long as assumption 2 is valid, since the pore water then resists compression of the pore space. From the discussion of assumption 2, this third assumption can fail at horizontal scales below about 1 m where the sideways displacement of material is in part pore water without horizontal displacement of the matrix, which would instead contract and extend vertically. The resulting accommodation of the moving roughness is an additional process and will speed the sliding by an amount limited by pore-water diffusion. This added deformation process should enhance sliding more than bulk shearing. Thus, neglecting the compressibility of the till should cause an underestimate of slip vs bulk till shearing in the basal motion.

Assumption 4 is that shearing in the till is like a linearly viscous fluid. To allow for change of effective till viscosity with distance from the interface z (Fig. 1), it is described by

(1)

where h = ξ ⁻¹ is a scale height for the viscosity increase. For example, an increase of till viscosity with distance from the source of water by melting at the ice–till interface can be accommodated. The assumption of linear viscous behavior is made for practical convenience as others have done (e.g. Reference Alley, Blankenship, Rooney and BentleyAlley and others, 1987; Reference HindmarshHindmarsh, 1998a). Actually the till is expected to be nearly frictional-plastic (Reference KambKamb, 1991; Reference Iverson, Hooyer and BakerIverson and others; 1998; Reference Tulaczyk, Kamb and EngelhardtTulaczyk and others, 2000). The lubricated roughness of the rigid ice base causes stress concentrations and associated local motions just beneath them. Introducing more realistic non-linear strain-rate softening behavior would concentrate deformation in a narrower zone below the ice–till interface. Excess pore pressure effects (Reference IversonIverson, 1999) might also soften the till near the interface. These can be simulated by using a stronger increase in effective viscosity below the ice–till contact. Thus, neglecting non-linearity in the shearing should also cause an underestimate of slip vs bulk till shearing in the basal motion.

Assumption 5 is that the ice is rigid. It is justified by the huge effective viscosity contrast between the ice and till that is implied by the large fraction of total motion produced at the base by shearing and/or slip over a layer (H _t) that is much thinner than the ice thickness (H _i). The ratio of effective viscosity of the ice (η _i) and the till (η _t) can be approximated by

with H _i ∼ 10³ m, H _t ∼ 10⁰ to 10¹ m, U _t/U _i ∼ 10² to 10⁵. This ratio is about 10⁴ to 10⁸. In other instances the viscosity contrast may not be so extreme, and deformation of the ice would also have to be considered (Reference HindmarshHindmarsh, 1998a, Reference Hindmarshb).

We also make the simplifying geometrical assumption about the ice-till contact (Fig. 1) that the roughness is two-dimensional with low slopes (A/λ ≪ 1).

3. Till deformation and sliding

The basal velocity of an ice stream, U (∼ surface velocity), is the sum of slip velocity U _s at the interface and the velocity U _d due to mean shearing through the till thickness. U _s is examined following Reference NyeNye (1969). This analysis relates U _s to motions in the till introduced by roughness of the ice–till interface and to the resulting drag. The drag is then used to calculate mean shearing in the till and U _d. The separation of the analysis into slip-induced motion of till around roughness elements and mean shearing is justified by the assumption of linearly viscous till properties and is consistent with the perturbation solution of the full problem assuming low roughness of the ice base.

Till deformation only occurs over a limited thickness, ultimately limited by the thickness of the till H (∼10⁰ m to 10¹ m; Reference Blankenship, Bentley, Rooney and AlleyBlankenship and others, 1986, Reference Blankenship, Bentley, Rooney and Alley1987) or possibly by a progressive increase of effective viscosity with distance away from the ice–till interface (ξ > 0 in Equation (1)). The solution for ξ ≠ 0 will be referred to as the “variable viscosity” solution. We also calculate the deformation assuming that the viscosity is constant within a till layer of fixed thickness H. This will be referred to as the “constant viscosity” solution. Both end-member cases are solved, but the development of solutions focuses on the variable viscosity solution. We will use when the same formula applies equivalently to the scale height or till layer thickness.

3.1. Field equations for till deformation

Let point downward and be parallel to the mean ice sole (Fig. 1). Let the velocity components in the till be given by [U _d(z)+u ₁ (x, z), 0, w ₁(x, z)], where u ₁ and w ₁ are the velocities associated with the motion of till around roughness elements. Using the governing equations for incompressible viscous flow we derive a general solution for the velocities in the till. Then we apply the boundary conditions, assuming that the roughness of the ice sole is small. This allows us to derive analytical solutions through perturbation analysis.

The governing equations for slow, steady-state flow of an incompressible, viscous fluid with vertical variation of viscosity, in two dimensions, without body forces and inertia terms, are

(2)

(3)

where p is the pressure. Here, and in the following, ∂_xp = ∂p/∂x and so forth.

The Fourier transforms of Equations (2) and (3) with respect to the x space variable gives

(4)

(5)

(6)

Elimination of in Equation (5) by substitution from Equation (4) gives

(7)

Differentiating Equation (7) with respect to z and substituting for the lefthand side of Equation (6) gives

(8)

The four roots of the characteristic Equation (8) are given as

Where

(9)

Thus, the general solution for may be expressed as

(10)

Substitution of Equation (10) into Equation (4) gives

(11)

A, B, C and D are constants to be determined from boundary conditions.

3.2. Boundary conditions and till motion induced by sliding

The ice–till interface is assumed to have a low-amplitude, two-dimensional waviness described by

(12)

where f(x) is O(1). The development below requires small slopes (∊f′(x) ≪ 1) and also small amplitude compared to the layer thickness . The mean square amplitude of the bed relief is

(13)

where l is the length of the perturbed part of the bed.

The following boundary conditions apply on z ₁(x). Till velocity normal to the interface is zero (no flux of till in or out of the ice), which leads to w = ∊(U – u)f′(x), or using tan α = dz ₁/dx = ∊f′(x) and U – u = U _s

(14)

There is no shear stress on the interface (no adhesion), which gives

(15)

where τ_xx = −τ_zz are the deviatoric normal stresses.

Since τ_xz = η(∂_zu + ∂_xw) and τ_xx = 2η∂_xu, this gives

(16)

where ∂_zu, ∂_xw, ∂_xu and tan α are all of O(∊).

Following Reference NyeNye (1969), Equations (14) and (15) when expressed to O(∊) on z = 0 become

(17)

The corresponding expressions in wavenumber domain are

(18)

(19)

The formulation of the boundary conditions on z = 0 rather than z ₁ (x) also requires that .

The boundary conditions at the base of the till are different for the cases of variable and constant viscosity. The variable viscosity solution corresponds to a half-space with an exponential depth variation of viscosity. In this case, the boundary condition is zero deformation as z → ∞ and requires C = D = 0. Equations (10), (11), (18) and (19) require

(20)

These values for A, B, C and D plugged into Equations (10) and (11) complete the solution for and .

The constant viscosity solution corresponds to a layer of constant viscosity of specified thickness H. The boundary conditions at z = H are u ₁(x, H) = w ₁(x, H) = 0, assuming no sliding of the till. Manipulation of Equations (10), (11), (18) and (19) leads to

(21)

where

(22)

The two alternative solutions transformed back to the space domain look very similar when scale height h = 1/ξ and till thickness H are the same.

3.3. Drag and mean shearing of the till

The drag transmitted between the ice and till is found by integration of the normal stress on the wavy interface given by Equation (5) as

(23)

The solution for normal stress (Equation (23)) with the variable viscosity gives

(24)

where is

(25)

The corresponding force in the x direction on the bed (z = 0) per unit width in the y direction is

(26)

where the asterisk denotes the complex conjugate. This is a general formula for the force, into which we may substitute the expression for given by the complex conjugate of Equation (24).

Drag is the force per unit area, 〈τ_xz 〉 = F/l which leads to

(27)

using Equations (24) and (26).

For we find

(28)

where depends on the scale height and wavenumber. In the limit ξ → 0 (h → ∞) we get and thus , which is the solution found by Reference NyeNye (1969). The constant viscosity solution for the drag is solved in an analogous manner.

The drag induces a shear stress τ_xz that is nearly constant through the till thickness. The corresponding shear rate results in velocity

(29)

Hereafter we will write .

The spatial form of u ₁ and w ₁ for the single wavelength interface is

(30)

and

(31)

which we obtain by inverse Fourier transform.

The total velocity associated with motions around roughness elements and the mean shearing is [u ₁(x, z) + U _d(z), w ₁ (x, z)]. Figures 2 and 3 show this total velocity field, using the sinusoidal perturbation of the ice–till interface, for wavelengths of 30 and 0.3 m, respectively.

Fig. 2. The instantaneous velocity field in the till. Here the wavelength is 30 m, the scale height h = 5 m, U _s = 458 m a⁻¹ and the amplitude (the roughness ). Maximum vertical velocity is 46 m a⁻¹ and maximum horizontal velocity is 42 m a⁻¹ The rigid ice moves at U = 500 m a⁻¹ (the arrow for the ice movement only indicates the direction).

Fig. 3. The instantaneous velocity field in the till, for λ = 30 cm, h = 5 m, U _s = 240 m a⁻¹ and amplitude mm (the roughness ). Maximum vertical velocity is 24 m a⁻¹ and maximum horizontal velocity is 260 m a⁻¹. The rigid ice moves at U = 500 m a⁻¹ (the arrow for the ice movement only indicates the direction).

4. Comparison of sliding and shearing

We use the ratio U _d/U _s to describe the relative contribution of shearing in the till and of sliding at the ice–till interface to the total basal motion. For the variable viscosity solution, Equations (28) and (29) give

(32)

Re-writing, using a = 2α/ξ and b = 2β/ξ,

(33)

where

(34)

For the constant viscosity solution, the ratio between sliding and till deformation is

(35)

Figure 4 shows the velocity ratio U _s/U _d (reciprocal of Equations (33) and (35)) for the variable and constant viscosity solutions, for comparison. Note that a rather large roughness is used. The two solutions converge for large values (short wavelengths or large scale height). For small (long wavelengths or short scale height) the fixed bottom of the deformable till layer in the constant viscosity case limits the contribution to the surface velocity from deformation compared to the variable viscosity case.

Fig. 4. The ratio of sliding velocity to deformational velocity for the variable viscosity and constant viscosity solution as a function of The roughtness is . The requirement means that results for are suspect.

Figure 5 shows sliding as a percentage of total speed (100 × U _s/(U _s + U _d)) for the variable viscosity solution (Equation (33)) for a range of roughness , scale height (h) and wavelength (λ = 2π/k) for sinusoidal ice–till interface , with and . Note that we have plotted the ratio as the percentage contribution of sliding and till deformation to the total ice velocity. The contribution from sliding increases as the roughness decreases. The contribution from till deformation increases as the thickness of the till layer increases. This is the qualitative behavior that one would expect.

Fig. 5. The contribution of sliding and deformational velocity to the total ice velocity for the variable viscosity case. For all of these cases the requirement is met.

The wavelength at which sliding contributes more to the ice motion (U _s/U _d > 1) depends on roughness , and till thickness h. Examples are: h = 5 m, , then λ must be >0.3 m; h = 5 m, , λ > 75 mm; h = 5 m, , λ > 3 mm (Fig. 5).

Our conclusion is that sliding dominates till shearing when the thickness of till is order 10 m or less, unless there is substantial roughness on the ice–till interface at scale of order 10⁻¹ m or less.

5. Discussion

The motion in the till induced by sliding has possible implications for mixing of till components, which can be important with regard to the distribution in the till of distinctive components relevant to the history of deposition (e.g. Reference Scherer, Aldahan, Tulaczyk, Possnert, Engelhardt and KambScherer and others, 1998). The energy generation caused by the distribution of strain in the till may influence changes in the ice–till interface by differential melting. The details of the spatial pattern of till deformation will be influenced by the specific mechanical behavior of the till (assumptions 2–4). However, the general pattern of the deformation and associated generation of heat follow from continuity.

5.1. Motion pattern in the till

Unless all of the shearing is beneath the deepest roughness elements, vertical motion is forced in the till when a rough ice base moves over it. When the motion is predominantly by sliding U _s, a vertical motion scale is ΔV = U _s α (Equation (14)), where α is the amplitude of the slope fluctuations of the roughness. The corresponding vertical strain scale is U _s α/l, where is the thickness of roughness-induced deformation in the till. The vertical motion and corresponding strain rate are maximum under locations of maximum slope deviation of the ice–till interface.

When the till is incompressible, the vertical straining forces a similar horizontal straining and a variation of horizontal velocity ΔU = U _s αδ/l, where δ is the horizontal scale distance between the protrusions and re-entrants (assumption 3 for δ ≥ 1 m). The fluctuations ΔU will be maximum in between the locations of maximum slope deviation and under the protrusions and re-entrants. ΔU will interact with the mean motion U _d introduced by mean shearing in the till; it will become larger than U _d when (U _s/U _d)(αδ/l) > 1, which is expected for long horizontal scales.

The combination of vertical and horizontal motions induces a circulation that migrates through the till. Figures 2 and 3 show realizations of this motion for our assumption of viscous fluid. Figure 6 shows corresponding particle tracks for four single-wavelength ice–till interfaces λ = 1 m, 5 m, 10 m and 100 m, with h = 5 m and . Note that since we fix the roughness , the amplitude of the ice–till interface varies with wavelength λ. For short wavelengths (e.g. λ = 1 m, Fig. 6a) the particles move at an almost constant rate horizontally, induced by mean shearing, with comparatively little vertical movement. Compressibility of the till, which can be more important at this and shorter scales, would result in even smaller horizontal speed variations. As the wavelength gets longer (λ = 5 m, Fig. 6b) the relative vertical motion increases, and the horizontal motion becomes variable, but still unidirectional. For yet longer wavelength (λ = 10 m, Fig. 6c) the vertical motions become more pronounced and the horizontal motion is now both along and against the ice-flow direction. Thus, the particles start tracing out loops within the till. For very long wavelengths (λ = 100 m, Fig. 6d) the particles trace an elongated ellipse that is very slowly being advected downstream by the mean shearing in the till. If the ice base has roughness at different scales, then the interaction between these kinds of patterns is likely to produce substantial vertical mixing of the till.

Fig. 6. Tracks for particles starting at x = 0 and a depth beneath the ice of λ/10 for λ = 1 m (a), 5 m (b), 10 m (c), 100 m (d). In all cases h = 5 m and . Notice how the motion changes from mostly horizontal left to right to circular motion as the wavelength increases.

The progression in Figure 6 illustrates the kind of behavior expected from the simple scale analysis above. Compressibility of the till matrix in the case of high permeability would reduce the circulating motion of the rock particles, but that would have to be taken up by a similar circulation of the pore water. The circulating motion at long horizontal scale can only be avoided by bonding the ice–till interface (no sliding) and forcing all of the motion to be from shearing beneath the deepest roughness elements. If that shearing is on discrete surfaces (e.g. Reference Truffer, Motyka, Harrison, Echelmeyer, Fisk and TulaczykTruffer and others, 1999), then the roughness of those surfaces becomes an issue.

5.2. Evolution of the ice–till interface

A crucial question is what determines the roughness of the ice–till interface. Reference HindmarshHindmarsh (1998a, b) considers the deformation of both the ice and the till and the resulting stability of the ice–till boundary. This difficult analysis could predict the interface roughness. Hindmarsh assumes adhesion between the ice and the till, which is quite different from our assumed boundary condition. With a condition of extreme contrast in effective viscosity between the ice and deformable till and a slippery interface, we suspect that the evolution of the ice base will be controlled by differential melting rather than deformation of the ice.

The general features of strain heat generation can be seen from the foregoing scale analysis. The resulting heating will be located where strain rate is maximum. For the sliding-induced motion, this maximum is beneath the locations of maximum slope deviation of the interface. The heating induced by the mean shearing will be maximum under the deepest protrusions of the ice, where the differential shearing motion is accommodated over a shorter vertical distance. Examples of the instantaneous total heat production rate per unit volume for the total motions (sliding-induced and mean shearing) are shown in Figure 7 for the incompressible fluid assumption with a short and long wavelength. The patterns illustrate the above general expectations.

Fig. 7. The heat generation within the till, for (a) λ = 0.3 m and (b) λ = 30 m. In both cases h = 5 m, U = 500 m a⁻¹, η₀ = 5 × 10⁹ Pa s and . The maximum heat generation is 0.89 W m⁻¹ at z = 0.05 m for λ = 0.3 m and 1.4 mW m⁻¹ at z = 3 m for λ = 30 m.

These patterns are being moved through the till at the slip velocity. The question is whether the till is differentially heated to a sufficient degree to cause differential melting on the ice sole. In order to assess whether the ice sole sees the average field of the heat generation within the till or individual peaks, we estimate the relative time-scales for vertical diffusion and horizontal movement. The time-scale for the motion of the ice over the spatial pattern of heat generation in the till is t _v = λ/(2U _s), the time it takes the ice to move half a wavelength. The time-scale for vertical diffusion is approximately t _d = d ²/κ, where d is the distance to the heat maximum from the ice–till interface and κ is thermal diffusivity of the till (on the order of 10⁻⁶ m² s⁻¹). The ice sole sees the average of the heat generated if the ratio t _d/t _v is large. t _d will be large if the source is deep and t _v will be small if U _s is large. For λ ≃ 30 m, U _s = 458 m a⁻¹ and d = 3 m (Fig. 7b) this leads to t _d/t _v ≃ 10. The ice should thus see the average of the heat generated. For short wavelength, λ = 0.3 m, U _s = 240 m a⁻¹, d = 0.05 m and (Fig. 7a) we find that t _d/t _v ≃ 0.25. Therefore we expect that melting of the ice base will reflect to some extent the spatial pattern of heat generation beneath.

Another relevant time-scale is how long it takes to flatten out the waviness of the sole. The sole of the ice is an isotherm (at pressure-melting point). The roughness of the sole distorts isotherms below, which causes focusing of the upwelling heat flux and thus differential melting. There is also an effect from the strain heating, due to the spatial distribution of heat generation depending on the sliding velocity and horizontal roughness scale as discussed above. The differential melting rate is given roughly by

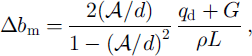
where is the heat flux due to the mean heat production in a layer of thickness l _d, the product ρL ≃ 303.5 MJ m⁻³, G is the geothermal heat flux, assumed to be G = 75 mW m⁻², and d is the depth to the top of the heat-producing layer. Here we have assumed that the scale for the focusing of the geothermal heat flux is roughly λ/(2π), which is also roughly the depth to the maximum in strain heating. For λ = 30 m, h = 5 m and , we find that q _d = 2.4 mW m⁻², using , l _d = 2 m and d = 2 m (Fig. 7b). The differential melting rate is then about 4 mm a⁻¹. It would thus take ∼100 years to completely flatten the roughness For ice speed of 500 m a⁻¹, this means a distance of ∼10–100 km. Since we use the maximum value here, this is an upper limit for the differential melting. Differential melting is therefore ineffective in removing large-scale roughness. In contrast, for λ = 0.3 m and h = 5 m and , we find that q _d = 56 mW m, using , l _d = 0.08 m and d = 0.02 m (Fig. 7a). The differential melting rate is then 7 mm a⁻¹, whereas the amplitude in this case is only 4.8 mm. This kind of a short-scale roughness would thus be smoothed out very quickly (∼1 year).

6. Conclusions

Given our assumptions (1–4) about the till and the ice–till interface, sliding at the ice–till interface must be the dominant mechanism of basal motion. Accounting for strain-rate softening and compressibility of the till (relaxing assumptions 3 and 4) will not alter the conclusion. If, in fact, till shearing is dominant, then either there is adhesion of till to the ice base (assumption 1 inapplicable), a mechanism for continuous generation of short-scale roughness on the interface, or a weak interface in the till (failure of assumption 2). One question we have not addressed is the origin of waviness at the ice–till interface, but we have shown that the roughness at which till deformation contributes significantly to the velocity is smoothed out very quickly by melting. Even without mean till deformation, sliding over a rough ice base will tend to induce coupled vertical and horizontal motion in the till that may mix the till.